y=ax2+bx+c的图像和性质练习题(含答案)(可编辑修改word版)

合集下载

二次函数y=ax2+bx+c的图象和性质(七大类型)(题型专练)(原卷版)

专题06 二次函数y=ax2+bx+c的图象和性质（七大类型）【题型1：二次函数的y=ax2+bx+c顶点、对称轴与最值问题】【题型2: 二次函数y=ax2+bx+c图像变换问题】【题型3：二次函数y=ax2+bx+c的性质】【题型4:二次函数y=ax2+bx+c的y值大小比较】【题型5:二次函数y=ax2+bx+c的最值问题探究】【题型6: 二次函数y=ax2+bx+c的图像问题】【题型7: 二次函数y=ax2+bx+c中a,b,c系数间的关系】【题型1：二次函数的y=ax2+bx+c顶点、对称轴问题】1．（2023•高阳县校级模拟）抛物线y＝x2﹣2x﹣3的顶点为（）A．（1，﹣4）B．（1，4）C．（0，﹣3）D．（2，﹣3）2．（2022秋•合川区期末）抛物线y＝﹣x2﹣6x的顶点坐标是（）A．（﹣3，9）B．（﹣3，﹣9）C．（3，﹣9）D．（3，9）3.（2023春•宁波月考）已知抛物线y＝ax2+bx+2经过A（4，9），B（12，9）两点，则它的对称轴是（）A．直线x＝7B．直线x＝8C．直线x＝9D．无法确定4．（2022秋•连平县校级期末）二次函数y＝ax2+bx+c图象上部分点的坐标满足下表，则该函数图象的顶点坐标为（）x…﹣3﹣2﹣101…y…﹣3﹣2﹣3﹣6﹣11…A．（﹣3，﹣3）B．（﹣2，﹣2）C．（﹣1，﹣3）D．（0，﹣6）5．（2022秋•南充期末）若二次函数y＝x2+2x+c﹣1图象的顶点在x轴上，则常数c的值为（）A．c＝2B．c＝1C．c＝﹣2D．c＝06．（2022秋•新会区期末）二次函数y＝﹣x2+2x+m图象的顶点坐标是（1，3），则m＝（）A．1B．2C．3D．57．（2022秋•兰山区校级期末）已知抛物线的解析式为y＝﹣x2﹣6x﹣7，则这条抛物线的顶点坐标是（）A．（2，3）B．（﹣3，2）C．（﹣3，﹣2）D．（3，﹣2）8．（2023•亳州模拟）下列抛物线中，与抛物线y＝x2﹣2x+8具有相同对称轴的是（）A．y＝4x2+2x+4B．y＝x2﹣4x C．y＝2x2﹣x+4D．y＝﹣2x2+4x 9．（2023春•宁波月考）已知抛物线y＝ax2+bx+2经过A（4，9），B（12，9）两点，则它的对称轴是（）A．直线x＝7B．直线x＝8C．直线x＝9D．无法确定【题型2: 二次函数y=ax2+bx+c图像变换问题】10．（2021秋•门头沟区期末）如果将抛物线y＝2x2先向左平移2个单位，再向上平移3个单位后得到一条新的抛物线，这条新的抛物线的表达式是（）A．y＝2（x﹣2）2+3B．y＝2（x+2）2﹣3C．y＝2（x﹣2）2﹣3D．y＝2（x+2）2+311.（2023•温州二模）将二次函数y＝x2﹣8x+2的图象向左平移m（m＞0）个单位后过点（5，2），则m的值为（）A．2B．3C．4D．512.（2023•双流区模拟）在平面直角坐标系中，如果抛物线y＝﹣x2+2x﹣1经过平移可以与抛物线y＝﹣x2互相重合，那么这个平移是（）A．向上平移1个单位B．向下平移1个单位C．向左平移1个单位D．向右平移1个单位13．（2023•神木市一模）把抛物线y＝x2+bx+c向右平移4个单位，再向下平移3个单位，得到抛物线y＝x2﹣4x+3，则b、c的值分别为（）A．b＝﹣12，c＝32B．b＝4，c＝﹣3C．b＝0，c＝6D．b＝4，c＝614．（2023•阳泉二模）某抛物线向右平移1个单位，再向上平移4个单位后得到的表达式为y＝x2﹣6x+14，则原抛物线的表达式为（）A．y＝x2﹣4x+1B．y＝x2﹣4x+5C．y＝x2﹣8x+25D．y＝x2﹣8x+17 15．（2023•宁波模拟）将抛物线y＝x2+4x+3向右平移n（n＞0）个单位得到一条新抛物线，若点A（2，y1），B（4，y2）在新抛物线上，且y1＞y2，则n 的值可以是（）A．3B．4C．5D．6 16．（2023•涡阳县模拟）将二次函数y＝x2﹣2x+2的图象向上平移2个单位长度，再向左平移2个单位长度，得到的抛物线的表达式为（）A．y＝x2﹣2x+3B．y＝x2﹣2x+4C．y＝x2+2x+4D．y＝x2+2x+3 17．（2023•宛城区校级模拟）将抛物线y＝x2﹣2x+1向上平移2个单位长度，再向左平移3个单位长度，得到抛物线y＝x2+bx+c，则b，c的值为（）A．b＝﹣8，c＝18B．b＝8，c＝14C．b＝﹣4，c＝6D．b＝4，c＝6 18．（2023•坪山区一模）把二次函数y＝x2+2x+1先向右平移2个单位长度，再向上平移1个单位长度，新二次函数表达式变为（）A．y＝（x+3）2+2B．y＝（x﹣1）2+2C．y＝（x﹣1）2+1 D．y＝（x+3）2﹣1【题型3：二次函数y=ax2+bx+c的性质】19.（2022秋•巩义市期末）已知抛物线y＝x2﹣2x+3，下列结论错误的是（）A．抛物线开口向上B．抛物线的对称轴为直线x＝1C．抛物线的顶点坐标为（1，2）D．当x＞1时，y随x的增大而减小20.（2022秋•西湖区期末）已知二次函数y＝ax2+bx+c，函数值y与自变量x的部分对应值如表：x…﹣10123…y…188202…则当y＞8时，x的取值范围是（）A．0＜x＜4B．0＜x＜5C．x＜0或x＞4D．x＜0或x＞5 21．（2023•碑林区校级模拟）已知二次函数y＝x2﹣2x﹣2，当y＞1时，则x的取值范围为（）A．﹣1＜x＜3B．﹣3＜x＜1C．x＜﹣1或x＞3D．x＜﹣3或x＞1 22．（2023•成都模拟）下列关于抛物线y＝x2+4x﹣5的说法正确的是（）①开口方向向上；②对称轴是直线x＝﹣4；③当x＜﹣2时，y随x的增大而减小；④当x＜﹣5或x＞1时，y＞0．A．①③B．①④C．①③④D．①②③④23．（2022秋•绵阳期末）抛物线y＝ax2+bx+c（a≠0）中，y与x的部分对应值如表：x…1346…y…8182018…下列结论中，正确的是（）A．抛物线开口向上B．对称轴是直线x＝4C．当x＞4时，y随x的增大而减小D．当x＜4.5时，y随x的增大而增大24．（2022秋•巩义市期末）已知抛物线y＝x2﹣2x+3，下列结论错误的是（）A．抛物线开口向上B．抛物线的对称轴为直线x＝1C．抛物线的顶点坐标为（1，2）D．当x＞1时，y随x的增大而减小25．（2022秋•苏州期末）若抛物线y＝x2+ax+2的对称轴是y轴，则a的值是（）A．﹣2B．﹣1C．0D．2 26．（2023•会昌县模拟）已知抛物线y＝ax2+bx+c上部分点的横坐标x与纵坐标y的对应值如下表：x…﹣10123…y…30﹣1m3…则以下结论错误的是（）A．抛物线开口向上B．抛物线的对称轴为直线x＝﹣1C．m的值为0D．抛物线不经过第三象限27．（2022秋•槐荫区期末）下列关于抛物线y＝x2+2x﹣3的说法正确的是①开口方向向上；②对称轴是直线x＝﹣2；③当x＜﹣1时，y随x的增大而减小；④当x＜﹣1或x＞3时，y＞0．（）A．①③B．①④C．①③④D．①②③④28．（2023•青白江区模拟）已知二次函数y＝﹣2x2+8x﹣7，下列结论正确的是（）A．对称轴为直线x＝﹣2B．顶点坐标为（2，﹣1）C．当x＜0时，y随x的增大而增大D．与x轴只有一个交点【题型4:二次函数y=ax2+bx+c的y值大小比较】29．（2023•天宁区模拟）已知点A（m，y1）B（m+2，y2）、C（x0，y0）在二次函数y＝ax2+2ax+c（a≠0）的图象上，且C为抛物线的顶点．若y0≥y2＞y1，则m的取值范围是（）A．m＜﹣3B．m＞﹣3C．m＜﹣2D．m＞﹣2 30．（2023•碑林区校级模拟）已知抛物线：y＝mx2﹣2mx+8（m≠0），若点A （x1，y1），B（x2，y2），C（4，0）均在该抛物线上，且x1＜﹣2＜x2＜4，则下列结论正确的是（）A．y1＞y2＞0B．0＞y2＞y1C．0＞y1＞y2D．y2＞0＞y1 31．（2022秋•盐湖区期末）抛物线y＝a（x﹣2）2+k的开口向上，点A（﹣1，y1），B（3，y2）是抛物线上两点，则y1，y2的大小关系是（）A．y1＞y2B．y1＜y2C．y1＝y2D．无法比较32．（2023•碑林区校级模拟）已知二次函数y＝﹣x2+2x﹣3，点A（x1，y1）、B （x2，y2）在该函数图象上，若x1+x2＞2，x1＞x2，则y1与y2的大小关系是（）A．y1＜y2B．y1＞y2C．y1＝y2D．无法判断33．（2023•灞桥区校级模拟）已知点A（n，y1）、B（n+2，y2）、C（x，y0）在二次函数y＝ax2+4ax+c（a≠0）的图象上，且C为抛物线的顶点，若y0≥y1＞y2，则n的取值范围是（）A．n＞﹣3B．n＜﹣3C．n＜﹣2D．n＞﹣2 34．（2023•莲池区二模）已知点A（n﹣2，y1），B（n，y2）在二次函数的y＝﹣x2+2x+3图象上，若y1＜y2，则n的取值范围为（）A．n≤1B．n＜2C．1＜n＜2D．n＞2【题型5:二次函数y=ax2+bx+c的最值问题探究】35．（2023•山丹县模拟）二次函数y＝2x2﹣8x﹣2的最小值是（）A．﹣2B．﹣10C．﹣6D．6 36．（2022秋•汝阳县期末）二次函数y＝ax2+bx的图象如图所示，当﹣1＜x＜m时，y随x的增大而增大，则m的取值范围是（）A．m＞1B．﹣1＜m≤1C．m＞0D．﹣1＜m＜2 37.（2022秋•蔡甸区校级月考）已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣638.（2023•碑林区校级模拟）已知二次函数y＝mx2﹣2mx+2（m≠0）在﹣2≤x＜2时有最小值﹣2，则m＝（）A．﹣4或﹣B．4或﹣C．﹣4或D．4或39．（2022秋•沈河区校级期末）二次函数y＝﹣x2﹣4x+c的最大值为0，则c 的值等于（）A．4B．﹣4C．﹣16D．1640．（2022秋•桥西区校级期末）已知二次函数y＝mx2+2mx+1（m≠0）在﹣2≤x≤2时有最小值﹣4，则m等于（）A．5B．﹣5或C．5或D．﹣5或41．（2022秋•长安区期末）若二次函数y＝﹣x2+bx+c的图象的最高点是（﹣1，﹣3），则b、c的值分别是（）A．b＝2，c＝4B．b＝﹣2，c＝﹣4C．b＝2，c＝﹣4D．b＝﹣2，c＝4 42．（2022秋•宜阳县期末）当x＝﹣时，二次函数y＝2x2+3x﹣1的函数值最小．43．（2022秋•东丽区期末）当m≤x≤m+1，函数y＝x2﹣2x+1的最小值为1，则m的值为．44．（2022秋•天河区校级期末）当a﹣2≤x≤a+1时，函数，y＝﹣x2+2x+3的最大值为3，则a的值为．【题型6: 二次函数y=ax2+bx+c的图像问题】45．（2023•大观区校级二模）二次函数y＝ax2+bx+c的图象如图所示，则一次函数的图象可能是（）A．B．C．D．46．（2023•老河口市模拟）二次函数y＝mx2+2x+n（m≠0）与一次函数y＝mx+mn 在同一平面直角坐标系中的图象可能是（）A．B．C．D．47.（2023•全椒县一模）如图，在同一平面直角坐标系中，二次函数y＝ax2+bx+c（a≠0）与一次函数y＝acx+b的图象可能是（）A．B．C．D．48.（2023•莱芜区模拟）一次函数y＝ax+bc与二次函数y＝ax2+bx+c在同一平面直角坐标系中的图象可能是（）A．B．C．D．49．（2023•莱芜区模拟）一次函数y＝ax+bc与二次函数y＝ax2+bx+c在同一平面直角坐标系中的图象可能是（）A．B．C．D．【题型7: 二次函数y=ax2+bx+c中a,b,c系数间的关系】50．（2023•顺庆区校级三模）如图，二次函数y＝ax2+bx+c（a≠0）的图象经过点（1，2）且与x轴交点的横坐标分别为x1，x2，其中﹣1＜x1＜0，1＜x2＜2，下列结论：①abc＞0．②2a+b＜0．③4a+2b+c＜0．④4ac﹣b2＞8a．⑤a≤﹣1．其中，结论正确的个数有（）A．2个B．3个C．4个D．5个51．（2023•兴庆区模拟）在平面直角坐标系中，已知二次函数y＝ax2+bx+c（a ≠0）的图象如图所示，个结论：①abc＞0；②2a+b＝0；③9a+3b+c＞0；④b2＞4ac；⑤当x＝1数有最大值；⑥当0＜x＜1时，函数y的值随x的增大而减小；其中正确的序号有（）A．①②④B．②③⑤C．④⑤⑥D．②④⑤52．（2023•潮南区模拟）如图，二次函数y＝ax2+bx+c（a，b，c为常数，a≠0）的图象经过点A（1，0），其对称轴为直线x＝﹣1，有下列结论：①abc＞0：②2a+c＞0；③函数的最大值为﹣4a；④当﹣3≤x≤0时，0≤y≤c．其中正确结论的个数是（）A．4B．1C．2D．3。

九年级数学二次函数y=ax2bxc(a≠0)的图像与性质(知识讲解2)Word版含解析

专题2.13 二次函数y=ax2+bx+c(a≠0)的图像与性质（知识讲解2）-2021-2022学年九年级数学下册基础知识专项讲练（北师大版）专题2．13 二次函数y=ax²+bx+c(a≠0)的图像与性质（知识讲解2）类型六、两个二次函数图像的综合判断1．已知二次函数y ＝ax 2与y ＝﹣2x 2+c ．（1）随着系数a 和c 的变化，分别说出这两个二次函数图象的变与不变；（2）若这两个函数图象的形状相同，则a ＝；若抛物线y ＝ax 2沿y 轴向下平移2个单位就能与y ＝﹣2x 2+c 的图象完全重合，则c ＝；（3）二次函数y ＝﹣2x 2+c 中x 、y 的几组对应值如表：表中m 、n 、p 的大小关系为（用“＜”连接）．2．如图，抛物线F ：2y ax bx c =++的顶点为P ，抛物线：与y 轴交于点A ，与直线OP 交于点B ．过点P 作PD ⊥x 轴于点D ，平移抛物线F 使其经过点A 、D 得到抛物线F ′：2y a x b x c '''=++，抛物线F ′与x 轴的另一个交点为C ．（1）当a = 1，b =－2，c = 3时，求点C 的坐标(直接写出答案)；（2）若a 、b 、c 满足了22b ac =，⊥求b ：b ′的值；⊥探究四边形OABC 的形状，并说明理由．类型七、根据二次函数图象判断式的符号3．如图，二次函数2y ax bx c =++的图象开口向上，图象经过点()1,2-和()1,0，且与y 轴相交于负半轴．第()1问：给出四个结论：①0a >；②0b >；③0c >；④0a b c ++=．写出其中正确结论的序号（答对得3分，少选、错选均不得分）第 ()2问：给出四个结论：⊥abc ＜0；⊥2a +b ＞0；⊥a +c =1；⊥a ＞1．写出其中正确结论的序号．4．抛物线()20y ax bx c a =++≠的图象如图所示：（1）判断a ，b ，c ，24b ac -的符号；（2）当OA OB =时，求a ，b ，c 满足的关系．5．已知抛物线2y ax bx c =++，如图所示，直线1x =-是其对称轴，()1确定a ，b ，c ，24b ac =-的符号；()2求证：0a b c -+>；()3当x 取何值时，0y >，当x 取何值时0y <．类型八、根据抛物线上的对称点求对称轴6．已知二次函数y=ax2+bx 的图象过点（6，0），（﹣2，8）．（1）求二次函数的关系式；（2）写出它的对称轴和顶点坐标．7．已知二次函数2y x bx c =-++，函数值y 与自变量x 之间的部分对应值如表：（1）写出二次函数图象的对称轴．（2）求二次函数的表达式．（3）当41x -<<-时，写出函数值y 的取值范围．8．已知二次函数y ＝ax 2﹣2ax ．（1）二次函数图象的对称轴是直线x ＝；（2）当0≤x ≤3时，y 的最大值与最小值的差为4，求该二次函数的表达式；（3）若a ＜0，对于二次函数图象上的两点P （x 1，y 1），Q （x 2，y 2），当t ≤x 1≤t +1，x 2≥3时，均满足y 1≥y 2，请结合函数图象，直接写出t 的取值范围．9．如图，已知抛物线2142y x x =--+与x 轴交于点A 、B （点A 在点B 的左侧），与y 轴交于C.（1）求点A 、B 、C 的坐标；（2）若点E 与点C 关于抛物线的对称轴对称，求梯形AOCE 的面积.类型九、二次函数y=ax2 +bx+c (a≠0)的最值10．如图在平面直角坐标系中，一次函数y kx b =+的图像经过点()0,4A -、()2,0B 交反比例函数m y x=()0x >的图像于点()3,C a ，点P 在反比例函数的图像上，横坐标为n ()03n <<，//PQ y 轴交直线AB 于点Q ，D 是y 轴上任意一点，连接PD 、QD ．（1）求一次函数和反比例函数的表达式；（2）求DPQ 面积的最大值．11．已知二次函数y ＝ax 2+bx ﹣3的图象经过点（1，﹣4）和（﹣1，0）．（1）求这个二次函数的表达式；（2）x 在什么范围内，y 随x 增大而减小？该函数有最大值还是有最小值？求出这个最值．12．已知二次函数的图象经过三点（1,0)()3,0-，30,2⎛⎫- ⎪⎝⎭ (1)求二次函数的解析式；(2)求抛物线的顶点坐标，对称轴以及抛物线与坐标轴的交点；(3)当x 为何值时，函数有最大值或最小值？最大值或最小值是多少？类型十、二次函数y=ax2 +bx+c (a≠0)图象中的将军饮马问题13．如图，抛物线y ＝﹣x 2+bx+c （a≠0）与x 轴交于A （1，0），B （﹣4，0）两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴于C 点，在该抛物线的对称轴上求出Q 点的坐标使得⊥QAC 的周长最小．14．如图，抛物线y ＝﹣x 2+bx+c （a≠0）与x 轴交于A （1，0），B （﹣4，0）两点．（1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴于C 点，在该抛物线的对称轴上求出Q 点的坐标使得⊥QAC 的周长最小．15．如图，在平面直角坐标系中，抛物线l 1：y ＝x 2+bx+c 过点C(0，﹣3)，且与抛物线l 2：y ＝﹣12x 2﹣32x+2的一个交点为A ，已知点A 的横坐标为2．点P 、Q 分别是抛物线l 1、抛物线l 2上的动点．（1）求抛物线l 1对应的函数表达式；（2）若点P 在点Q 下方，且PQ⊥y 轴，求PQ 长度的最大值；（3）若以点A 、C 、P 、Q 为顶点的四边形为平行四边形，直接写出点P 的坐标．16．如图，抛物线212y x bx c =++与直线132y x =+分别相交于A 、B 两点，其中点A 在y 轴上，且此抛物线与x 轴的一个交点为()3,0C -．（1）求抛物线的解析式（2）在抛物线对称轴l 上找一点M ，使MBC ∆的周长最小，请求出这个周长的最小值．类型十一、二次函数图象的平移17．已知：抛物线y ＝﹣x 2+bx +c 经过点B （﹣1，0）和点C （2，3）．（1）求此抛物线的表达式；（2）如果此抛物线沿y 轴平移一次后过点（﹣2，1），试确定这次平移的方向和距离．18．已知抛物线212y x bx c =-++经过点（1，0），（0，32）．（1）求该抛物线的函数表达式；（2）抛物线212y x bx c =-++可以由抛物线212y x =-怎样平移得到？请写出一种平移的方法．19．已知二次函数y ＝x 2－4x ＋3．（1）直接写出函数图象的顶点坐标、与x 轴交点的坐标；（2）将图象先向左平移2个单位，再向下平移2个单位，得到新的函数图象，直接写出平移后的图象与y 轴交点的坐标．类型十二、二次函数综合20．如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点0(1)A ，,(50)B ，,4(0)C ，．（1）求抛物线的解析式和对称轴；（2）P 是抛物线对称轴上的一点，求满足PA PC +的值为最小的点P 坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点E ，使四边形OEBF 是以OB 为对角线且面积为12的平行四边形？若存在，请求出点E 坐标，若不存在请说明理由.（请在图2中探索） 21．已知抛物线23y ax bx =++过()30A -,，()10B ,两点，交y 轴于点C ．（1）求该抛物线的表达式．（2）设P 是该抛物线上的动点，当PAB 的面积等于ABC 的面积时，求P 点的坐标．22．已知m,n是方程x2－6x+5=0的两个实数根，且m<n，抛物线y=－x2+bx+c的图象经过点A(m,0)、B(0,n)．(1)求这个抛物线的解析式；(2)设（1）中抛物线与x轴的另一交点为C,抛物线的顶点为D，试求出点C、D的坐标和⊥BCD的面积；(3)P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把⊥PCH 分成面积之比为2：3的两部分，请求出P点的坐标．23．如图，抛物线y＝x2﹣2x﹣3与x轴交于A，B两点，与y轴交于点D，抛物线的顶点为C．（1）求A，B，C，D的坐标；（2）求四边形ABCD的面积．参考答案：1．（1）二次函数y＝ax2的图象随着a的变化，开口大小和开口方向都会变化，但是对称轴、顶点坐标不会改变；二次函数y＝﹣2x2+c的图象随着c的变化，开口大小和开口方向都没有改变，对称轴也没有改变，但是，顶点坐标会发生改变；（2）±2，﹣2；（3）p＜m＜n 【分析】(1)根据二次函数的性质即可得到结论；(2)由函数图象的形状相同得到a=±2，根据上加下减的平移规律即可求得函数y =ax2-2，根据完全重合，得到c =-2．(3)由二次函数的解析式得到开口方向和对称轴，然后根据点到对称轴的距离即可判断．【详解】解：（1）二次函数y＝ax2的图象随着a的变化，开口大小和开口方向都会变化，但是对称轴、顶点坐标不会改变；二次函数y＝﹣2x2+c的图象随着c的变化，开口大小和开口方向都没有改变，对称轴也没有改变，但是，顶点坐标会发生改变；（2）⊥函数y＝ax2与函数y＝﹣2x2+c的形状相同，⊥a＝±2，⊥抛物线y＝ax2沿y轴向下平移2个单位得到y＝ax2﹣2，与y＝﹣2x2+c的图象完全重合，⊥c＝﹣2，故答案为：±2，﹣2．（3）由函数y＝﹣2x2+c可知，抛物线开口向下，对称轴为y轴，⊥1﹣0＜0﹣（﹣2）＜5﹣0，⊥p＜m＜n，故答案为：p＜m＜n．【点睛】本题考查了二次函数的性质，二次函数图象与几何变换，二次函数图象上点的坐标特征，熟知图形平移不变性的性质是解答此题的关键．2．（1）C（3，0）；（2）⊥2：3；⊥矩形，理由见解析【分析】（1）由于抛物线F′由抛物线F平移所得，开口方向和开口大小都无变化，因此a＝a′＝1；由于两条抛物线都与y轴交于A点，那么c＝c′＝3．然后可根据抛物线F的坐标求出其顶点坐标，即可得出D点的坐标，然后将D的坐标代入抛物线F′中，即可求出抛物线F′的解析式，进而可求出C点的坐标．（2）⊥与（1）的方法类似，在求出D的坐标后，将D的坐标代入抛物线F′中，即可得出关于b，b′的关系式即可得出b，b′的比例关系．⊥探究四边形OABC的形状，无非是平行四边形，菱形，矩形这几种．那么首先要证的是四边形OABC 是个平行四边形，已知了OA //BC ，只需看A ，B 的纵坐标是否相等，即OA 是否与BC 的长相等．根据抛物线F 的解析式可求出P 点的坐标，然后用待定系数法可求出OP 所在直线的解析式．进而可求出抛物线F 与直线OP 的交点B 的坐标，然后判断B 的纵坐标是否与A 点相同，如果相同，则四边形OABC 是矩形（⊥AOC ＝90°），如果B ，A 点的纵坐标不相等，那么四边形AOCB 是个直角梯形．【详解】解：（1） ⊥a = 1，b =－2，c = 3⊥223y x x =-+=()212x -+⊥P （1，2）⊥过点P 作PD ⊥x 轴于点D ，⊥D （1，0）由于抛物线F ′由抛物线F 平移所得，开口方向和开口大小都无变化，因此a ＝a ′＝1；由于两条抛物线都与y 轴交于A 点，那么c ＝c ′＝3．⊥抛物线F ′：23y x b x '=++，代入D （1，0）得0=1+b ’+3解得b ’=-4⊥243y x x =-+=()()13x x --⊥点C 的坐标为（3，0）；（2）⊥抛物线2y ax bx c =++，令x =0，则y =c ，⊥A 点坐标（0，c ）．⊥22b ac =， ⊥244224442ac b ac ac ac c a a a --===， ⊥点P 的坐标为（2b a -，2c ）． ⊥PD ⊥x 轴于D ，⊥点D 的坐标为（2b a -，0）．根据题意，得a =a ′，c = c ′，⊥抛物线F ′的解析式为2'y ax b x c =++．又⊥抛物线F ′经过点D （2b a-，0），⊥220()42b b a b c a a'=⨯+-+． ⊥2024b bb ac '=-+．又⊥22b ac =，⊥2032b bb '=-．⊥b :b ′=23．⊥由⊥得，抛物线F ′为232y ax bx c =++．令y =0，则2302ax bx c ++=． ⊥12,2b b x x a a=-=-． ⊥点D 的横坐标为2b a- ⊥点C 的坐标为（ba -，0）．设直线OP 的解析式为y kx =．⊥点P 的坐标为（,22b c a -）， ⊥22c b k a =-， ⊥22222ac ac b b k b b b =-=-=-=-， ⊥2b y x =-． ⊥点B 是抛物线F 与直线OP 的交点， ⊥22b ax bxc x ++=-． ⊥12,2b b x x a a=-=-． ⊥点P 的横坐标为2b a-， ⊥点B 的横坐标为ba -．把b x a =-代入2b y x =-，得22()222b b b ac y c a a a=--===． ⊥点B 的坐标为(,)b c a-． ⊥BC //OA ，AB //OC ．（或BC //OA ，BC =OA ），⊥四边形OABC 是平行四边形．又⊥⊥AOC =90°，⊥四边形OABC 是矩形．【点睛】本题着重考查了待定系数法求二次函数的性质、函数的平移变换、探究矩形的构成情况等重要知识点．3．（1）正确的序号为⊥⊥；（2）正确的序号为⊥⊥⊥．【分析】（1）根据抛物线开口向上对⊥进行判断；根据抛物线对称轴x=-2b a在y 轴右侧对⊥进行判断；根据抛物线与y 轴的交点在x 轴下方对⊥进行判断；根据x=1时，y=0对⊥进行判断；（2）有（1）得到a>0，b<0，c<0，则可对⊥进行判断；根据0<-2b a<1可对⊥进行判断；把点(-1,2)和(1,0)代入解析式得a ﹣b +c =2，a +b +c =0,整理有a+c=1，则可对⊥进行判断；根据a=1-c ，c<0可对⊥进行判断．【详解】（1）⊥由抛物线的开口方向向上可推出a ＞0，正确；⊥因为对称轴在y 轴右侧，对称轴为x =2b a-＞0．又⊥a ＞0，⊥b ＜0，错误；⊥由抛物线与y 轴的交点在y 轴的负半轴上，⊥c ＜0，错误；⊥由图象可知：当x =1时y =0，⊥a +b +c =0，正确．故（1）中，正确结论的序号是⊥⊥．（2）⊥⊥a ＞0，b ＜0，c ＜0，⊥abc ＞0，错误；⊥由图象可知：对称轴x =2b a -＞0且对称轴x =2b a -＜1，⊥2a +b ＞0，正确； ⊥由图象可知：当x =﹣1时y =2，⊥a ﹣b +c =2，当x =1时y =0，⊥a +b +c =0；a ﹣b +c =2与a +b +c =0相加得2a +2c =2，解得：a +c =1，正确；⊥⊥a +c =1，移项得：a =1﹣c ．又⊥c ＜0，⊥a ＞1，正确．故（2）中，正确结论的序号是⊥⊥⊥．【点睛】二次函数y =ax 2+bx +c 系数符号的确定：（1）a 由抛物线开口方向确定：开口方向向上，则a ＞0；否则a ＜0．（2）b 由对称轴和a 的符号确定：由对称轴公式x =2b a-判断符号．（3）c 由抛物线与y 轴的交点确定：交点在y 轴正半轴，则c ＞0；否则c ＜0．（4）b 2﹣4ac 由抛物线与x 轴交点的个数确定：2个交点，b 2﹣4ac ＞0；1个交点，b 2﹣4ac =0；没有交点，b 2﹣4ac ＜0．4．（1）240b ac ->；（2）10ac b -+=．【分析】（1）根据图形，开口向下得a ＜0，x =0时可得c ＞0，由对称轴可得b ＞0，与x 轴有两个不同交点可得b 2﹣4ac ＞0；（2）由于B 点坐标可以表示为：（0，c ），|OA |=|OB |，可知A （﹣c ，0）即可进行求解．【详解】（1）由图象可知，抛物线开口向下，可得：a ＜0；x =0时，y =c ＞0；⊥对称轴x =02b a->，a ＜0，⊥b ＞0；图象与x 轴有两个不同交点可得b 2﹣4ac ＞0；（2）当|OA |=|OB |时，即A 点坐标为（﹣c ，0），代入抛物线方程得y =ac 2﹣bc +c 两边同时除以c 得：ac ﹣b +1=0．【点睛】本题考查了二次函数图象与系数的关系，难度一般，关键在已知条件下表示出A 点的坐标代入抛物线方程．5．（1）0a <，0b <，0c >，240b ac =->；（2）详见解析；（3）当31x -<<时，0y >；当3x <-或1x >时，0y <．【分析】（1）根据开口方向确定a 的符号，根据对称轴的位置确定b 的符号，根据抛物线与y 轴的交点确定c 的符号，根据抛物线与x 轴交点的个数确定b 2-4ac 的符号；（2）根据图象和x=-1的函数值确定a -b+c 与0的关系；（3）抛物线在x 轴上方时y ＞0；抛物线在x 轴下方时y ＜0．【详解】()1∵抛物线开口向下，∴0a <，∵对称轴12b x a=-=-， ∴0b <，∵抛物线与y 轴的交点在x 轴的上方，∴0c >，∵抛物线与x 轴有两个交点，∴240b ac =->；()2证明：∵抛物线的顶点在x 轴上方，对称轴为1x =-，∴当1x =-时，0y a b c =-+>；()3根据图象可知，当31x -<<时，0y >；当3x <-或1x >时，0y <．【点睛】本题考查了二次函数图象与系数的关系，解题的关键是熟练的掌握二次函数图象与系数的关系.6．（1）y=12x2﹣3x ；（2）对称轴为直线x=3、顶点坐标为（3，﹣92）．【分析】（1）根据图像过点（6，0），（﹣2，8）列方程组求出a 、b 的值即可，（2）把解析式配方后即可确定对称轴和顶点坐标．【详解】（1）⊥y=ax 2+bx 的图象过点（6，0），（﹣2，8）．⊥3660428a b a b +=⎧⎨-=⎩，解得：123a b ⎧=⎪⎨⎪=-⎩ ， ⊥二次函数解析式为y=12x 2﹣3x ；（2）⊥y=12x 2﹣3x=12（x ﹣3）2﹣92， ⊥抛物线的对称轴为直线x=3、顶点坐标为（3，﹣92）．【点睛】本题考查了待定系数法求二次函数的解析式、二次函数的三种形式．将二次函数的一般解析式转化为顶点式时，可采用了“配方法”．灵活运用二次函数的三种形式是解题关键. 7．（1）x=2；（2）242y x x =---；（3）22y -<≤【分析】（1）二次函数是轴对称图形，而（-4，-2），（0，-2）关于对称轴对此，利用中点坐标公式可求，（2）求二次函数解析式2y x bx c =-++，可知b,c 待定，但（-4，-2），（0，-2）只能取一点，取两点坐标（-1，1），（0，-2）代入解之即可，（3）由于对称轴与x 轴交点横坐标，在41x -<<-，说明x=-4与x=-1取值不是最大值，为此x=-4与x=-1对应的函数值的最小值与x=-2时函数值即可．【详解】解：（1）⊥二次函数是轴对称图形，4x =-、0x =时的函数值相等，都是2-，对称轴是（-4，-2），（0，-2）两点连结的中垂线，⊥此函数图象的对称轴为直线4022x -+==-；（2）由点（-1，1），（0，-2）在抛物线上将()1,1-，()0,2-代入2y x bx c =-++，得：112b c c --+=⎧⎨=-⎩，解得：42b c =-⎧⎨=-⎩， ⊥二次函数的表达式为：242y x x =---；（3）⊥()224222y x x x =---=-++，⊥当2x =-时，y 取得最大值2，由表可知当4x =-时=2y -，当=1x -时1y =，⊥当41x -<<-时，22y -<≤．【点睛】本题考查利用列表求对称轴表示式，二次函数解析式，函数值范围，关键利用数形结合思想，掌握二次函数的性质，函数值的求法，抛物线最值．8．（1）1；（2）y ＝x 2﹣2x 或y ＝﹣x 2+2x ；（3）﹣1≤t ≤2【分析】（1）由对称轴是直线x ＝2b a -，可求解；（2）分a ＞0或a ＜0两种情况讨论，求出y 的最大值和最小值，即可求解；（3）利用函数图象的性质可求解．【详解】解：（1）由题意可得：对称轴是直线x ＝22a a--＝1，故答案为：1；（2）当a ＞0时，⊥对称轴为x ＝1，当x ＝1时，y 有最小值为﹣a ，当x ＝3时，y 有最大值为3a ，⊥3a ﹣（﹣a ）＝4．⊥a ＝1，⊥二次函数的表达式为：y ＝x 2﹣2x ；当a ＜0时，同理可得y 有最大值为﹣a ； y 有最小值为3a ，⊥﹣a ﹣3a ＝4，⊥a ＝﹣1，⊥二次函数的表达式为：y ＝﹣x 2+2x ；综上所述，二次函数的表达式为y ＝x 2﹣2x 或y ＝﹣x 2+2x ；（3）⊥a ＜0，对称轴为x ＝1，⊥x ≤1时，y 随x 的增大而增大，x ＞1时，y 随x 的增大而减小，x ＝﹣1和x ＝3时的函数值相等，⊥t ≤x 1≤t +1，x 2≥3时，均满足y 1≥y 2，⊥t ≥﹣1，t +1≤3，⊥﹣1≤t ≤2．【点睛】本题考查了二次函数的性质，二次函数图象上点的坐标特征等知识点的综合应用，能利用分类思想解决问题是本题的关键．9．（1）A （-4,0），B （2,0），C,0,4）；（2）12【分析】（1）在抛物线的解析式中，令x=0可以求出点C 的坐标，令y=0可以求出A 、B 点的坐标；（2）先求出E 点坐标，然后求出OA ，OC ，CE 的长计算面积即可.【详解】解：（1）当y=0时，212x --x+4=0，解得x 1=－4，x 2=2， ⊥A （－4，0），B （2，0），当x=0时，y=4，⊥C （0，4）；（2）y=212x -﹣x+4=12-（x+1）2+92， ⊥抛物线y=212x -﹣x+4的对称轴是直线x=－1， ⊥E 的坐标为（－2，4），则OA=4，OC=4，CE=2，S 梯形AOCE =(24)4122+⨯= 【点睛】本题是对二次函数的基础考查，熟练掌握二次函数与x 轴，y 轴交点坐标的求解及梯形面积知识是解决本题的关键.10．（1）624,y x y x=-=；（2）4. 【分析】（1）利用点()0,4A -、()2,0B 求解一次函数的解析式，再求C 的坐标，再求反比例函数解析式；（2）设6,,P n n ⎛⎫ ⎪⎝⎭则(),24,Q n n -再表示PQ 的长度，列出三角形面积与n 的函数关系式，利用函数的性质可得答案．【详解】解：（1）设直线AB 为,y kx b =+把点()0,4A -、()2,0B 代入解析式得：420b k b =-⎧⎨+=⎩解得：24k b =⎧⎨=-⎩∴ 直线AB 为24,y x =-把()3,C a 代入得：2342,a =⨯-=()3,2,C ∴把()3,2C 代入：,m y x= 236m ∴=⨯=，6,y x∴= （2）设6,,P n n ⎛⎫ ⎪⎝⎭//PQ y 轴，则(),24,Q n n - 由0＜n ＜3，()666242424,PQ n n n n n n∴=--=-+=-+ 16242DPQ S n n n ⎛⎫∴=-+ ⎪⎝⎭()222314,n n n =-++=--+即当1n =时， 4.DPQ S ∴=最大【点睛】本题考查的是利用待定系数法求解一次函数与反比例函数的解析式，以及利用二次函数的性质求解面积的最值，掌握以上知识是解题的关键．11．（1）y ＝x 2﹣2x ﹣3；（2）当x ＜1时，y 随x 增大而减小，该函数有最小值，最小值为﹣4．【分析】（1）将（1，﹣4）和（﹣1，0）代入解析式中，即可求出结论；（2）将二次函数的表达式转化为顶点式，然后根据二次函数的图象及性质即可求出结论．【详解】（1）根据题意得3430a b a b +-=-⎧⎨--=⎩，解得12a b =⎧⎨=-⎩，所以抛物线解析式为y ＝x 2﹣2x ﹣3；（2）∵y ＝（x ﹣1）2﹣4，∴抛物线的对称轴为直线x ＝1，顶点坐标为（1，﹣4），∵a ＞0，∴当x ＜1时，y 随x 增大而减小，该函数有最小值，最小值为﹣4．【点睛】此题考查的是二次函数的综合大题，掌握利用待定系数法求二次函数解析式、二次函数的图象及性质是解决此题的关键．12．(1)21322y x x =+-；(2)顶点()1,2--，对称轴=1x -，交点：()()31,0,3,0,0,2⎛⎫-- ⎪⎝⎭；(3)=1x -时函数有最小值为2-．【分析】（1）抛物线的点过（1,0)3,0，可以设抛物线的解析式为y=a(x -1)(x+3)，把点30,2⎛⎫- ⎪⎝⎭代入解得a 即可；（2）由配方法，得出抛物线解析式的顶点式，可得顶点坐标，对称轴以及抛物线与坐标轴的交点；（3）由抛物线的开口向上，可得函数有最小值，顶点坐标的纵坐标是函数的最小值．【详解】(1)设抛物线解析式为y=a(x -1)(x+3)，将30,2⎛⎫- ⎪⎝⎭代入，解得12a =，所以抛物线解析式为21322y x x =+-，故答案为：21322y x x =+-；（2）抛物线解析式为21322y x x =+-，配方可得，()221123=1222y x x x =+-+-（）， ⊥顶点()1,2-- ，对称轴=1x -，由（1）知，交点：()()31,0,3,0,0,2⎛⎫-- ⎪⎝⎭，故答案为：顶点()1,2--，对称轴=1x -，交点：()()31,0,3,0,0,2⎛⎫-- ⎪⎝⎭； (3)由（2）可知，函数解析式为()21122y x =+-，开口向上，函数有最小值，当=1x - 时函数有最小值为2-，故答案为：=1x -时函数有最小值为2-．【点睛】本题考查了二次函数的解析式求法，二次函数的性质，熟练掌握二次函数的性质是解题的关键．13．（1）y ＝﹣x 2﹣3x+4（2）Q （﹣32，52）【分析】（1）函数的表达式为：y ＝﹣（x ﹣1）（x+4），即可求解；（2）点B 为点A 关于函数对称轴的对称点，连接BC 交函数对称轴与点Q ，则点Q 为所求，即可求解．【详解】解：（1）函数的表达式为：y ＝﹣（x ﹣1）（x+4）＝﹣x 2﹣3x+4；（2）抛物线的对称轴为：x ＝﹣32，点B 为点A 关于函数对称轴的对称点，连接BC 交函数对称轴与点Q ，则点Q 为所求，点C（0，4），将点B、C坐标代入一次函数表达式：y＝kx+m得：404k mm-+=⎧⎨=⎩，解得：14km=⎧⎨=⎩，故直线BC的表达式为：y＝x+4，当x＝﹣32时，y＝52，则点Q（﹣32，52）．【点睛】本题考查了利用待定系数法求二次函数解析式，周长最小本质上考查抛物线的对称轴上求出Q点的坐标使得QA+QC最短，点B为点A关于函数对称轴的对称点，连接BC 交函数对称轴与点Q，原理是是两点之间线段最短14．（1）y＝﹣x2﹣3x+4（2）Q（﹣32，52）【分析】（1）函数的表达式为：y＝﹣（x﹣1）（x+4），即可求解；（2）点B为点A关于函数对称轴的对称点，连接BC交函数对称轴与点Q，则点Q为所求，即可求解．【详解】解：（1）函数的表达式为：y＝﹣（x﹣1）（x+4）＝﹣x2﹣3x+4；（2）抛物线的对称轴为：x＝﹣32，点B为点A关于函数对称轴的对称点，连接BC交函数对称轴与点Q，则点Q为所求，点C（0，4），将点B、C坐标代入一次函数表达式：y＝kx+m得：404k mm-+=⎧⎨=⎩，解得：14km=⎧⎨=⎩，故直线BC的表达式为：y＝x+4，当x＝﹣32时，y＝52，则点Q（﹣32，52）．【点睛】本题考查了利用待定系数法求二次函数解析式，周长最小本质上考查抛物线的对称轴上求出Q点的坐标使得QA+QC最短，点B为点A关于函数对称轴的对称点，连接BC 交函数对称轴与点Q，原理是是两点之间线段最短15．（1）y＝x2﹣2x﹣3；（2）12124；（3）(﹣1，0)或(3，0)或(43-，139)或(﹣3，12)【分析】（1）将x＝2代入y＝﹣12x2﹣32x+2，从而得出点A的坐标，再将A（2，﹣3），C（0，﹣3）代入y＝x2+bx+c，解得b与c的值，即可求得抛物线l1对应的函数表达式；（2）设点P的坐标为（m，m2﹣2m﹣3），则可得点Q的坐标为（m，﹣12m2﹣32m+2），从而PQ等于点Q的纵坐标减去点P的纵坐标，利用二次函数的性质求解即可；（3）设点P的坐标为（n，n2﹣2n﹣3），分两类情况：第一种情况：AC为平行四边形的一条边；第二种情况：AC为平行四边形的一条对角线．分别根据平行四边形的性质及点在抛物线上，得出关于n的方程，解得n的值，则点P的坐标可得．【详解】解：（1）将x＝2代入y＝﹣12x2﹣32x+2，得y＝﹣3，⊥点A的坐标为（2，﹣3）．将A（2，﹣3），C（0，﹣3）代入y＝x2+bx+c，得23=2+23b cc⎧-+⎨-=⎩，解得23bc=-⎧⎨=-⎩，⊥抛物线l1对应的函数表达式为y＝x2﹣2x﹣3；（2）⊥点P、Q分别是抛物线l1、抛物线l2上的动点．⊥设点P的坐标为（m，m2﹣2m﹣3），⊥点P在点Q下方，PQ⊥y轴，⊥点Q的坐标为（m，﹣12m2﹣32m+2），⊥PQ＝﹣12m2﹣32m+2﹣（m2﹣2m﹣3），＝﹣32m2+12m+5，⊥当m＝﹣112=3622⎛⎫⨯-⎪⎝⎭时，PQ长度有最大值，最大值为：﹣23126⎛⎫⨯ ⎪⎝⎭+1126⨯+5＝12124；⊥PQ长度的最大值为121 24；（3）设点P的坐标为（n，n2﹣2n﹣3），第一种情况：AC为平行四边形的一条边．AC=2⊥当点Q在点P右侧时，点Q的坐标为（n+2，﹣12（n+2）2﹣32（n+2）+2），将Q的坐标代入y＝﹣12x2﹣32x+2，，得n2﹣2n﹣3＝﹣12（n+2）2﹣32（n+2）+2，解得，n＝0或n＝﹣1．⊥n＝0时，点P与点C重合，不符合题意，舍去，⊥n＝﹣1，⊥点P的坐标为（﹣1，0）；⊥当点Q在点P左侧时，点Q的坐标为（n﹣2，﹣12（n﹣2）2﹣32（n﹣2）+2），将Q的坐标代入y＝﹣12x2﹣32x+2，得n2﹣2n﹣3＝﹣12（n﹣2）2﹣32（n﹣2）+2，解得n＝3或n＝﹣43．⊥此时点P的坐标为（3，0）或（﹣43，139）；第二种情况：AC为平行四边形的一条对角线．Q点的纵坐标y Q，n2-2n-3-(-3)=-3-y Q，y Q=-n2+2n-3，点Q的坐标为（2﹣n，﹣n2+2n﹣3），将Q的坐标代入y＝﹣12x2﹣32x+2，得﹣n2+2n﹣3＝﹣12（2﹣n）2﹣32（2﹣n）+2，解得，n＝0或n＝﹣3．⊥n＝0时，点P与点C重合，不符合题意，舍去，⊥n＝﹣3，⊥点P的坐标为（﹣3，12）．综上所述，点P的坐标为(﹣1，0)或(3，0)或(43，139)或(﹣3，12)．【点睛】本题考查抛物线解析式，平行y轴线段的最值，平行四边形的性质，掌握抛物线解析式，平行y轴线段的最值，平行四边形的性质，利用平形四边形的性质构造方程是解题关键．16．（1）215322y x x =++；（2【分析】（1）利用132y x =+的解析式求解A 的坐标，把()0,3A ，()3,0C -代入212y x bx c =++，利用待定系数法列方程组，解方程组可得答案；（2）联立两个函数解析式，求解B 的坐标，线段BC 的长度，如图，要使MBC 的周长最小，则MB MC +最小，设二次函数215322y x x =++与x 轴的另一交点为D ，抛物线的对称轴为：552,1222x =-=-⨯ 点()2,0D -，连接,BD 交对称轴于,M MD MC =，此时，MB MC MB MD BD +=+=最小，再利用勾股定理求解BD =【详解】.解：（1）抛物线212y x bx c =++与直线132y x =+交于y 轴上一点A ，令0,x = 则3,y =∴ 点()0,3A 把()0,3A ，()3,0C -代入212y x bx c =++得： 39302c b c =⎧⎪⎨-+=⎪⎩，解得：523b c ⎧=⎪⎨⎪=⎩， ∴抛物线的解析式是215322y x x =++；（2）将直线132y x =+与二次函数215322y x x =++联立得方程组： 213215322y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ 215133,222x x x ∴++=+ 240,x x ∴-=解得：0x =或4x =-，04,,31x x y y ==-⎧⎧∴⎨⎨==⎩⎩()0,3A ，()4,1B ∴-BC ∴=如图，要使MBC 的周长最小，则MB MC +最小，设二次函数215322y x x=++与x 轴的另一交点为D ，抛物线的对称轴为：552,1222x =-=-⨯ ()3,0C - ∴ 点()2,0D -，连接,BD 交对称轴于,MMD MC ∴=，此时，MB MC MB MD BD +=+=最小，此时：BD ==MBC ∴【点睛】本题考查的是利用待定系数法求解二次函数的解析式，二次函数的性质，利用轴对称的性质求解三角形的周长的最小值，掌握以上知识是解题的关键．17．（1）y =﹣x 2+2x +3；（2）需将抛物线向上平移4个单位【分析】（1）把点B 和点C 的坐标代入函数解析式解方程组即可；（2）求出原抛物线上x ＝－2时，y 的值为－5，则抛物线上点（－2，－5）平移后的对应点为（－2，－1），根据纵坐标的变化可得平移的方向和平移的距离．【详解】解：（1）把B （﹣1，0）和点C （2，3）代入y ＝﹣x 2＋bx ＋c得10423b c b c --+=⎧⎨-++=⎩，解得23b c =⎧⎨=⎩，所以抛物线解析式为y ＝﹣x 2＋2x +3；（2）把x ＝﹣2代入y ＝﹣x 2＋2x +3得y ＝﹣4﹣4＋3＝﹣5，点（﹣2，﹣5）向上平移4个单位得到点（﹣2，﹣1），所以需将抛物线向上平移4个单位．【点睛】本题主要考查待定系数法求二次函数的解析式及抛物线的平移，熟练掌握待定系数法求二次函数的解析式是解题的关键．18．（1）213y 22x x =--+；（2）先向左平移1单位，再向上平移2个单位【分析】（1）把已知点的坐标代入抛物线解析式求出b 与c 的值即可；（2）先将抛物线的一般式转化为顶点式，然后指出满足题意的平移方法即可．【详解】解：（1）把()1,0，30,2⎛⎫ ⎪⎝⎭代入抛物线解析式得： 10232b c c ⎧-++=⎪⎪⎨⎪=⎪⎩，解得：132b c =-⎧⎪⎨=⎪⎩，则抛物线解析式为213y 22x x =--+；（2）抛物线解析式为22131y (1)2222x x x =--+=-++，抛物线213y 22x x =--+可以由抛物线212y x =-先向左平移1单位，再向上平移2个单位．【点睛】本题考查了二次函数图象与几何变换，二次函数的性质，二次函数图象上点的坐标特征，以及待定系数法求二次函数解析式，熟练掌握二次函数性质是解本题的关键． 19．（1）顶点坐标为()2,1-，与x 轴的交点坐标为()1,0，()3,0；（2）()0,3-．【分析】（1）根据配方法，可得顶点式解析式，根据函数值为零，可得相应自变量的值；（2）根据图象向左平移加，向右平移减，向上平移加，向下平移减，可得平移后的解析式，根据自变量与函数值的关系，可得答案．【详解】解：（1）()22x 4321y x x =--＝－＋，顶点坐标为()2,1-，当0y =时，2430x x -+=，解得1x =或3x =，即图象与x 轴的交点坐标为()1,0，()3,0；（2）图象先向左平移2个单位，再向下平移2个单位，得()2,2212y x =-+--，化简得23y x =-，当0x =时，3y =-，即平移后的图象与y 轴交点的坐标()0,3-．【点睛】本题考查了二次函数的性质，利用配方法得出顶点坐标，利用图象向左平移加，向右平移减，向上平移加，向下平移减得出平移后的解析式是解题关键．20．（1）2545442y x x -+＝，函数的对称轴为：3x ＝；（2）点8(3)5P ，；（3）存在，点E 的坐标为12(2,)5-或12,)5(4-．【分析】1（）根据点AB 、的坐标可设二次函数表达式为：()()()21565y a x x a x x +--＝﹣＝，由C 点坐标即可求解；2（）连接B C 、交对称轴于点P ，此时PA PC +的值为最小，即可求解； 3（）512E E OEBF S OB y y ⨯⨯四边形＝＝＝，则125E y ＝，将该坐标代入二次函数表达式即可求解．【详解】解：1（）根据点0(1)A ，,(50)B ，的坐标设二次函数表达式为：()()()21565y a x x a x x +--＝﹣＝，⊥抛物线经过点4(0)C ，，则54a ＝，解得：45a ＝，抛物线的表达式为：()()2224416465345555245y x x x x x --+--+＝=＝，函数的对称轴为：3x ＝； 2（）连接B C 、交对称轴于点P ，此时PA PC +的值为最小，设BC 的解析式为：y kx b +＝，将点B C 、的坐标代入一次函数表达式：y kx b +＝得：05,4k b b =+⎧⎨=⎩解得：4,54k b ⎧=-⎪⎨⎪=⎩ 直线BC 的表达式为：4y x 45=-+，当3x ＝时，85y ＝，故点835P （，）； 3（）存在，理由：四边形OEBF 是以OB 为对角线且面积为12的平行四边形，则512E E OEBF S OB y y ⨯⨯四边形＝＝＝，点E 在第四象限，故：则125E y ＝-，将该坐标代入二次函数表达式得：()24126555y x x -+＝＝-，解得：2x ＝或4，故点E 的坐标为122,5（-）或12,5（4-）．【点睛】本题考查二次函数综合运用，涉及到一次函数、平行四边形性质、图形的面积计算等，其中2（），求线段和的最小值，采取用的是点的对称性求解，这也是此类题目的一般解法．21．（1）y=-x 2-2x +3；（2）P 坐标为（-，-3）或（-1-3）．【分析】（1）把A与B坐标代入求出a与b的值，即可确定出表达式；（2）根据已知三角形面积相等求出P的坐标即可．【详解】解：（1）把A与B坐标代入得：9330a ba b c-+=⎧⎨++=⎩，解得：12ab=-⎧⎨=-⎩，则该抛物线的表达式为y=-x2-2x+3；（2）由抛物线解析式得：C（0，3），⊥⊥ABC面积为12×3×4=6，⊥⊥P AB面积为6，即12×|Py|×4=6，即Py=3或-3，当P y=3时，可得3=-x2-2x+3，解得：x=-2或x=0（舍去），此时P坐标为（-2，3）；当y P=-3时，可得-3=-x2-2x+3，解得：x=-此时P坐标为（-，-3）或（-1-3）．【点睛】本题考查了待定系数法求二次函数解析式，以及二次函数图象上点的坐标特征，熟练掌握待定系数法是解本题的关键．22．(1)、y=－x2－4x+5；(2)、15；(3)、(－,0)或(－,0).【详解】试题分析：(1)、首先求出方程的解得出点A和点B的坐标，然后利用待定系数法求出函数解析式；(2)、根据二次函数的解析式得出点C的坐标和顶点坐标，过D作x轴的垂线交x轴于M，从而求出⊥DMC、梯形MDBO和⊥BOC的面积，然后得出面积；(3)、设P点的坐标为（a,0），得出直线BC的方程，则PH与直线BC的交点坐标为(a，a+5)，PH与抛物线的交点坐标为H(a,－a2－4a+5)，然后根据EH=EP和EH=EP两种情况分别求出点P的坐标.试题解析：(1)、解方程x2－6x+5=0，得x1=5,x2=1.由m<n，m=1,n=5,。

二次函数的图象和性质3(含答案)

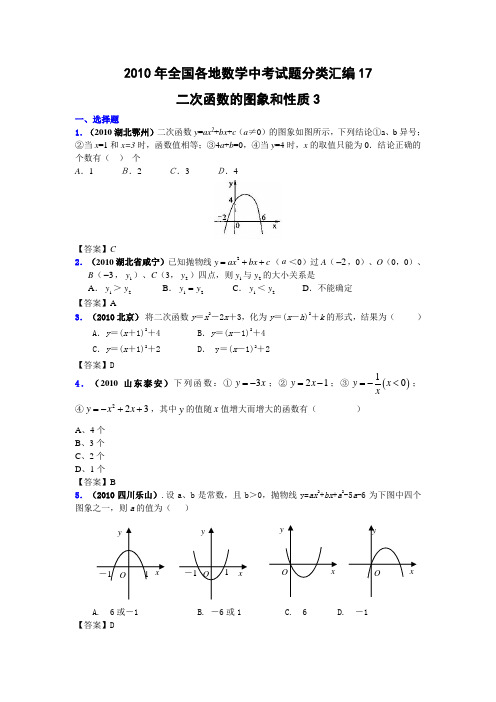
2010年全国各地数学中考试题分类汇编17二次函数的图象和性质3一、选择题 1．（2010湖北鄂州）二次函数y =ax 2+bx +c （a ≠0）的图象如图所示，下列结论①a 、b 异号；②当x =1和x=3时，函数值相等；③4a +b =0，④当y =4时，x 的取值只能为0．结论正确的个数有（）个A ．1 Ｂ．2 Ｃ．3 Ｄ．4【答案】C2．（2010湖北省咸宁）已知抛物线2y ax bx c =++（a ＜0）过A （2-，0）、O （0，0）、 B （3-，1y ）、C （3，2y ）四点，则1y 与2y 的大小关系是 A ．1y ＞2y B ．1y 2y = C ．1y ＜2y D ．不能确定【答案】A3．（2010北京）将二次函数y ＝x 2－2x ＋3，化为y ＝(x －h )2＋k 的形式，结果为（）A ．y ＝(x ＋1)2＋4 B ．y ＝(x －1)2＋4 C ．y ＝(x ＋1)2＋2D ． y ＝(x －1)2＋2【答案】D4．（2010山东泰安）下列函数：①3y x =-；②21y x =-；③()10y x x=-<；④223y x x =-++，其中y 的值随x 值增大而增大的函数有（）A 、4个B 、3个C 、2个D 、1个【答案】B5．（2010四川乐山）.设a 、b 是常数，且b ＞0，抛物线y=ax 2+bx +a 2-5a -6为下图中四个图象之一，则a 的值为（）A. 6或－1B. －6或1C. 6D. －1【答案】DyxO yx Oyx O1 －1 yxO1 －16．（2010黑龙江哈尔滨）在抛物线42-=x y 上的一个点是（）（A ）（4，4）（B ）（1，－4）（C ）（2，0）（D ）．（0，4）【答案】C7．（2010江苏徐州）平面直角坐标系中，若平移二次函数y=(x-2009)(x-2010)+4的图象，使其与x 轴交于两点，且此两点的距离为1个单位，则平移方式为 A ．向上平移4个单位 B ．向下平移4个单位 C ．向左平移4个单位 D ．向右平移4个单位【答案】B8．（2010陕西西安）已知抛物线103:2-==x x y C ，将抛物线C 平移得到抛物线C '若两条抛物线C 、C ' 关于直线1=x 对称，则下列平移方法中，正确的是A ．将抛物线C 向右平移25个单位 B ．将抛物线C 向右平移3个单位 C ．将抛物线C 向右平移5个单位 D ．将抛物线C 向右平移6个单位【答案】C9．（2010 福建三明）抛物线772--=x kx y 的图象和x 轴有交点，则k 的取值范围是（）A ．47-≥k B ．47-≥k 且0≠k C ．47->k D ．47->k 且0≠k 【答案】B10．（2010 山东东营）二次函数2y ax bx c =++的图象如图所示，则一次函数ac bx y -=与反比例函数xcb a y +-=在同一坐标系内的图象大致为（）【答案】B二、填空题1．（2010江苏扬州）y ＝2x 2－bx ＋3的对称轴是直线x ＝1，则b 的值为__________．x(B)x(A)x(C)(D)【答案】42．（2010山东泰安）将y=2x 2-12x-12变为y=a （x-m ）2+n 的形式，则m·n=. 【答案】-903．（2010湖北襄樊）将抛物线212y x =-向上平移2个单位，再向右平移1个单位后，得到的抛物线的解析式为____________．．【答案】21(1)22x --+或21322x x -++ 4．（2010江苏镇江）已知实数y x y x x y x +=-++则满足,033,2的最大值为 .【答案】45．6．7．8．9．10．11．12．13．14．15．16．17．18．19．20 三、解答题1．（2010湖北鄂州）如图，在直角坐标系中，A （-1，0），B （0，2），一动点P 沿过B 点且垂直于AB 的射线BM 运动，P 点的运动速度为每秒1个单位长度，射线BM 与x 轴交与点C ．（1）求点C 的坐标．（2）求过点A 、B 、C 三点的抛物线的解析式．（3）若P 点开始运动时，Q 点也同时从C 出发，以P 点相同的速度沿x 轴负方向向点A 运动，t 秒后，以P 、Q 、C 为顶点的三角形为等腰三角形．（点P 到点C 时停止运动，点Q 也同时停止运动）求t 的值．（4）在（2）（3）的条件下，当CQ =CP 时，求直线OP 与抛物线的交点坐标．【答案】（1）点C 的坐标是（4，0）；（2）设过点A 、B 、C 三点的抛物线的解析式为y =ax 2+bx +c （a ≠0），将点A 、B 、C 三点的坐标代入得：020164a b c c a b c =-+⎧⎪=⎨⎪=++⎩解得12322a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩，∴抛物线的解析式是：y = 12-x 2+32x +2．（3）设P 、Q 的运动时间为t 秒，则BP =t ，CQ =t ．以P 、Q 、C 为顶点的三角形为等腰三角形，可分三种情况讨论．①若CQ =PC ，如图所示，则PC = CQ =BP =t ．∴有2t =BC =5t 5②若PQ =QC ，如图所示，过点Q 作DQ ⊥BC 交CB 于点D ，则有CD =PD ．由△ABC ∽△QDC ，可得出PD =CD =255t ，∴555t =，解得t =40511-． ③若PQ =PC ，如图所示，过点P 作PE ⊥AC 交AC 于点E ，则EC =QE =255PC ，∴12t =255（5t ），解得t 32540-（4）当CQ =PC 时，由（3）知t 5P 的坐标是（2，1），∴直线OP 的解析式是：y =12x ，因而有12x =12-x 2+32x +2，即x 2-2x -4=0，解得x =15OP 与抛物线的交点坐标为（5152）和（5，152）． 2．（2010湖北省咸宁）已知二次函数2y x bx c =+-的图象与x 轴两交点的坐标分别为（m ，0），（3m -，0）（0m ≠）．（1）证明243c b =；（2）若该函数图象的对称轴为直线1x =，试求二次函数的最小值．【答案】（1）证明：依题意，m ，3m -是一元二次方程20x bx c +-=的两根．根据一元二次方程根与系数的关系，得(3)m m b +-=-，(3)m m c ⨯-=-． ∴2b m =，23c m =． ∴224312c b m ==．（2）解：依题意，12b-=，∴2b =-．由（1）得2233(2)344c b ==⨯-=．∴2223(1)4y x x x =--=--． ∴二次函数的最小值为4-．3．（2010湖北恩施自治州）如图，在平面直角坐标系中，二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），与y 轴交于C （0，-3）点，点P 是直线BC 下方的抛物线上一动点. （1）求这个二次函数的表达式．（2）连结PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP /C ，那么是否存在点P ，使四边形POP /C 为菱形？若存在，请求出此时点P 的坐标；若不存在，请说明理由．（3）当点P 运动到什么位置时，四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.【答案】解：（1）将B 、C 两点的坐标代入得⎩⎨⎧-==+33c c b解得：⎩⎨⎧-=-=32c b所以二次函数的表达式为：322--=x x y（2）存在点P ，使四边形POP /C 为菱形．设P 点坐标为（x ，322--x x ）， PP /交CO 于E若四边形POP /C 是菱形，则有PC ＝PO ．连结PP / 则PE ⊥CO 于E ，∴OE=EC =23∴y =23-．∴322--x x =23-解得1x =2102+，2x =2102-（不合题意，舍去） ∴P 点的坐标为（2102+，23-）…………………………8分（3）过点P 作y 轴的平行线与BC 交于点Q ，与OB 交于点F ，设P （x ，322--x x ），易得，直线BC 的解析式为3-=x y 则Q 点的坐标为（x ，x －3）.EB QP OE QP OC AB S S S S CPQ BPQ ABC ABPC ⋅+⋅+⋅=++=∆∆∆212121四边形 3)3(2134212⨯+-+⨯⨯=x x =87523232+⎪⎭⎫ ⎝⎛--x当23=x 时，四边形ABPC 的面积最大此时P 点的坐标为⎪⎭⎫⎝⎛-415,23，四边形ABPC 的面积875的最大值为． 4．（2010北京）在平面直角坐标系xOy 中，抛物线23454122+-++--=m x x mx m y 与x 轴的交点分别为原点O 和点A ，点B （2，n ）在这条抛物线上．（1）求B 点的坐标；（2）点P 在线段OA 上，从O 点出发向A 点运动，过P 点作x 轴的垂线，与直线OB 交与点E ，延长PE 到点D ，使得ED =PE ，以PD 为斜边，在PD 右侧做等等腰直角三角形PCD （当P 点运动时，C 点、D 点也随之运动）．① 当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求OP 的长；② 若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位（当Q 点到达O 点时停止运动，P 点也同时停止运动）．过Q 点做x 轴的垂线，与直线AB 交与点F ，延长QF 到点M ，使得FM =QF ，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN （当Q点运动时，M 点、N 点也随之运动）．若P 点运动到t分别有一条边恰好落在同一条直线上，求此刻t 的值．【答案】解：（1）∵抛物线23454122+-++--=m m x mx m y 经过原点， ∴m 2—3m +2=0. 解的m 1=1，m 2=2. 由题意知m ≠1. ∴m =2，∴抛物线的解析式为x x y 25412+-= ∵点B （2，n ）在抛物线x x y 25412+-=，n=4.∴B 点的坐标为（2，4）（2）①设直线OB 的解析式为y =k 1x 求得直线OB 的解析式y =2x ∵A 点是抛物线与x 轴的一个交点，可求得A 点的坐标为（10，0），设P 点的坐标为（a ，0），则E 点的坐标为（a ，2a ）．根据题意做等腰直角三角形PCD ，如图1.（第24题）可求得点C 的坐标为（3a ，2a ），有C 点在抛物线上，得2a =－41x （3a ）2+25x 3a . 即49a 2— 211a =0解得 a 1=922，a 2=0（舍去）∴OP =922②依题意作等腰直角三角形QMN . 设直线AB 的解析式y =k 2x +b由点A (10 ，0)，点B （2，4），求得直线AB 的解析式为y =－21x +5 当P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，有以下三种情况：第一种情况：CD 与NQ 在同一条直线上，如图2所示，可证△DPQ 为等腰直角三角形．此时QP 、OP 、AQ 的长可依次表示为t 、4t 、 2t 个单位． ∴PQ = DP = 4t ∴t +4t +2t =10 ∴t=710第二种情况：PC 与MN 在同一条直线上，如图3所示．可证△PQM 为等腰直角三角形．此时OP 、AQ 的长依次表示为t 、2t 个单位， ∴OQ = 10 － 2t ∵F 点在直线AB 上 ∴FQ =t ∵MQ =2t ∴PQ =MQ =CQ =2t ∴t +2t +2t =10 ∴t =2.第三种情况：点P 、Q 重合时，PD 、QM 在同一条直线上，如图4所示，此时OP 、AQ 的长依次表示为t 、2t 个单位．∴t +2t=10 ∴t =310 综上，符合题意的值分别为710，2，310． 5．（2010云南红河哈尼族彝族自治州）二次函数2x y =的图像如图8所示，请将此图像向右平移1个单位，再向下平移2个单位.（1）画出经过两次平移后所得到的图像，并写出函数的解析式.（2）求经过两次平移后的图像与x 轴的交点坐标，指出当x 满足什么条件时，函数值大于0？【答案】解：画图如图所示：依题意得：2)1(2--=x y=2122-+-x x =122--x x∴平移后图像的解析式为：122--x x （2）当y=0时，122--x x =0 2)1(2=-x 21±=-x 212121+=-=x x ，∴平移后的图像与x 轴交与两点，坐标分别为（21-，0）和（21+，0）由图可知，当x<21-或x>21+时，二次函数2)1(2--=x y 的函数值大于0. 6．（2010云南楚雄）已知：如图，抛物线2y ax bx c =++与x 轴相交于两点A (1，0)，B (3，0).与y 轴相较于点C （0，3）．（1）求抛物线的函数关系式；（2）若点D （7,2m ）是抛物线2y ax bx c =++上一点，请求出m 的值，并求处此时△ABD 的面积．【答案】解：（1）由题意可知09303a b c a b c c ++=⎧⎪++=⎨⎪=⎩ 解得143a b c =⎧⎪=-⎨⎪=⎩所以抛物线的函数关系式为243y x x =-+．（2）把D （7,2m ）代人函数解析式243y x x =-+中，得2775()43224m =-⨯+=．所以155(31)244ABD S ∆=⨯-⨯=． 7．（2010湖北随州）已知抛物线2(0)y ax bx c a =++≠顶点为C （1，1）且过原点O.过抛物线上一点P （x ，y ）向直线54y =作垂线，垂足为M ，连FM （如图）. （1）求字母a ，b ，c 的值；（2）在直线x ＝1上有一点3(1,)4F ，求以PM 为底边的等腰三角形PFM 的P 点的坐标，并证明此时△PFM 为正三角形；（3）对抛物线上任意一点P ，是否总存在一点N （1，t ），使PM ＝PN 恒成立，若存在请求出t 值，若不存在请说明理由.【答案】（1）a ＝－1，b ＝2，c ＝0（2）过P 作直线x=1的垂线，可求P 的纵坐标为14，横坐标为1132.此时，MP ＝MF ＝PF ＝1，故△MPF 为正三角形. （3）不存在.因为当t ＜54，x ＜1时，PM 与PN 不可能相等，同理，当t ＞54，x ＞1时，PM 与PN 不可能相等.8．（2010河南）在平面直角坐标系中，已知抛物线经过A(4，0)，B(0，一4)，C(2，0)三点.(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S.求S 关于m 的函数关系式，并求出S 的最大值；(3)若点P 是抛物线上的动点，点Q 是直线y=－x 上的动点，判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标.【答案】（1）设抛物线的解析式为y =ax 2+bx +c (a ≠0)，则有1640,4,420.a b c c a b c -+=⎧⎪=-⎨⎪++=⎩解得1,21,4.a b c ⎧=⎪⎪=⎨⎪=-⎪⎩∴抛物线的解析式y =12x 2+x ﹣4（2）过点M 作MD ⊥x 轴于点D .设M 点的坐标为（m ，n ）. 则AD =m +4，MD =﹣n ，n =12m 2＋m －4 . ∴S = S △AMD +S 梯形DMBO －S △ABO =12( m +4) (﹣n )＋12(﹣n ＋4) (﹣m ) －12×4×4 = ﹣2n -2m -8 = ﹣2(12m 2＋m －4) -2m -8 = ﹣m 2-4m (－4< m < 0)∴S 最大值 = 4（3）满足题意的Q 点的坐标有四个，分别是：（-4 ，4 ），（4 ，-4），（-2+52－25-2－52＋59．（2010四川乐山）如图(13.1)，抛物线y ＝x2+bx+c 与x 轴交于A ，B 两点，与y 轴交于点C(0，2)，连接AC ，若tan ∠OAC ＝2． (1)求抛物线对应的二次函数的解析式；(2)在抛物线的对称轴l 上是否存在点P ，使∠APC ＝90°，若存在，求出点P 的坐标；若不存在，请说明理由；(3)如图(13.2)所示，连接BC ，M 是线段BC 上(不与B 、C 重合)的一个动点，过点M 作直线l ′∥l ，交抛物线于点N ，连接CN 、BN ，设点M 的横坐标为t ．当t 为何值时，△BCN 的面积最大？最大面积为多少？【答案】解：（1）∵抛物线y=x2＋bx＋c过点C(0,2). ∴x=2又∵tan∠OAC=OCOA=2, ∴OA=1,即A(1,0).又∵点A在抛物线y=x2＋bx＋2上. ∴0=12＋b×1＋2,b=－3 ∴抛物线对应的二次函数的解析式为y=x2－3x＋2（2）存在过点C作对称轴l的垂线,垂足为D,如图所示,∴x=－332212ba-=-=⨯.∴AE=OE-OA=32-1=12,∵∠APC=90°,∴tan∠PAE= tan∠CPD∴PE CDEA DP=,即12PE322PE=-，解得PE=12或PE=32，∴点P的坐标为（32，12）或（32，32）。

17【基础】二次函数y=ax^2+bx+c(a≠0)的图象与性质(基础课程讲义例题练习含答案)

二次函数y=ax 2+bx+c(a ≠0)的图象与性质—知识讲解（提高）【学习目标】1. 会用描点法画二次函数2(0)y ax bx c a =++≠的图象；会用配方法将二次函数2y ax bx c =++的解析式写成2()y a x h k =-+的形式；2.通过图象能熟练地掌握二次函数2y ax bx c =++的性质；3.经历探索2y ax bx c =++与2()y a x h k =-+的图象及性质紧密联系的过程，能运用二次函数的图象和性质解决简单的实际问题，深刻理解数学建模思想以及数形结合的思想．【要点梳理】要点一、二次函数2(0)y ax bx c a =++≠与=-+≠2()(0)y a x h k a 之间的相互关系 1.顶点式化成一般式从函数解析式2()y a x h k =-+我们可以直接得到抛物线的顶点(h ，k)，所以我们称2()y a x h k =-+为顶点式，将顶点式2()y a x h k =-+去括号，合并同类项就可化成一般式2y ax bx c =++．2.一般式化成顶点式2222222b b b b y ax bx c a x x c a x x c a a a a ⎡⎤⎛⎫⎛⎫⎛⎫=++=++=++-+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦22424b ac b a x a a -⎛⎫=++⎪⎝⎭．对照2()y a x h k =-+，可知2bh a=-，244ac b k a -=．∴ 抛物线2y ax bx c =++的对称轴是直线2bx a =-，顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭．要点诠释：1．抛物线2y ax bx c =++的对称轴是直线2bx a =-，顶点坐标是24,24b ac b aa ⎛⎫-- ⎪⎝⎭，可以当作公式加以记忆和运用．2．求抛物线2y ax bx c =++的对称轴和顶点坐标通常用三种方法：配方法、公式法、代入法，这三种方法都有各自的优缺点，应根据实际灵活选择和运用．要点二、二次函数2(0)y ax bx c a =++≠的图象的画法1.一般方法：列表、描点、连线；2.简易画法：五点定形法. 其步骤为：(1)先根据函数解析式，求出顶点坐标和对称轴，在直角坐标系中描出顶点M ，并用虚线画出对称轴． (2)求抛物线2y ax bx c =++与坐标轴的交点，当抛物线与x 轴有两个交点时，描出这两个交点A 、B 及抛物线与y 轴的交点C ，再找到点C 关于对称轴的对称点D ，将A 、B 、C 、D 及M 这五个点按从左到右的顺序用平滑曲线连结起来．要点诠释：当抛物线与x 轴只有一个交点或无交点时，描出抛物线与y 轴的交点C 及对称点D ，由C 、M 、D 三点可粗略地画出二次函数图象的草图；如果需要画出比较精确的图象，可再描出一对对称点A 、B ，然后顺次用平滑曲线连结五点，画出二次函数的图象，要点三、二次函数2(0)y ax bx c a =++≠的图象与性质 1.二次函数20()y ax bx c a =++≠图象与性质函数二次函数2y ax bx c =++（a 、b 、c 为常数，a ≠0）图象0a >0a <开口方向向上向下对称轴直线2b x a=-直线2b x a=-顶点坐标24,24b ac b a a ⎛⎫-- ⎪⎝⎭24,24b ac b a a ⎛⎫-- ⎪⎝⎭增减性在对称轴的左侧，即当2b x a <-时，y 随x 的增大而减小；在对称轴的右侧，即当2b x a>-时，y 随x 的增大而增大．简记：左减右增在对称轴的左侧，即当2bx a<-时，y 随x 的增大而增大；在对称轴的右侧，即当2b x a>-时，y 随x 的增大而减小．简记：左增右减最大(小)值抛物线有最低点，当2b x a =-时，y 有最小值，抛物线有最高点，当2bx a=-时，y 有2.二次函数20()y ax bx c a =++≠图象的特征与a 、b 、c 及b 2-4ac 的符号之间的关系要点四、求二次函数2(0)y ax bx c a =++≠的最大（小）值的方法如果自变量的取值范围是全体实数，那么函数在顶点处取得最大（或最小）值，即当2bx a=-时，244ac b y a-=最值．要点诠释：如果自变量的取值范围是x 1≤x ≤x 2，那么首先要看2ba-是否在自变量的取值范围x 1≤x ≤x 2内，若在此范围内，则当2bx a=-时，244ac b y a -=最值，若不在此范围内，则需要考虑函数在x 1≤x ≤x 2范围内的增减性，如果在此范围内，y 随x 的增大而增大，则当x ＝x 2时，222y ax bx c =++最大值；当x ＝x 1时，211y ax bx c =++最小值，如果在此范围内，y 随x 的增大而减小，则当x ＝x 1时，211=ax +bx +y c 最大值；当x ＝x 2时，222=ax +bx +y c 最小值，如果在此范围内，y 值有增有减，则需考察x ＝x 1，x ＝x 2，2b x a=-时y 值的情况．【典型例题】类型一、二次函数2(0)y ax bx c a =++≠的图象与性质1. 抛物线2(1)y x m x m =-+-+与y 轴交于(0，3)点： (1)求出m 的值并画出这条抛物线；(2)求它与x 轴的交点和抛物线顶点的坐标； (3)x 取什么值时，抛物线在x 轴上方？(4)x 取什么值时，y 的值随x 值的增大而减小？【答案与解析】(1)由抛物线2(1)y x m x m =-+-+与y 轴交于(0，3)可得m ＝3．∴ 抛物线解析式为223y x x =-++，如图所示．(2)由2230x x -++=得11x =-，23x =．∴ 抛物线与x 轴的交点为(-1，0)、(3，0)． ∵ 2223(1)4y x x x =-++=--+，∴ 抛物线的顶点坐标为(1，4)．(3)由图象可知：当-1＜x ＜3时，抛物线在x 轴上方． (4)由图象可知：当x ≥1时，y 的值随x 值的增大而减小．【总结升华】研究函数问题一般都应与图象结合起来，借助于图象的直观性求解更形象与简洁．(1)将点(0，3)代入解析式中便可求出m 的值，然后用描点法或五点作图法画抛物线； (2)令y ＝0可求抛物线与x 轴的交点，利用配方法或公式法可求抛物线顶点的坐标； (3)、(4)均可利用图象回答，注意形数结合的思想，举一反三：【变式】（•泰安）某同学在用描点法画二次函数y=ax 2+bx+c 的图象时，列出了下面的表格：x … ﹣2 ﹣1 0 1 2 … y … ﹣11 ﹣2 1 ﹣2 ﹣5… 由于粗心，他算错了其中一个y 值，则这个错误的数值是（） A. -11 B. -2 C. 1 D. -5 【答案】D.提示：由函数图象关于对称轴对称，得（﹣1，﹣2），（0，1），（1，2）在函数图象上，把（﹣1，﹣2），（0，1），（1，﹣2）代入函数解析式，得，解得，函数解析式为y=﹣3x 2+1 x=2时y=﹣11，故选：D ．类型二、二次函数2(0)y ax bx c a =++≠的最值2. 分别在下列范围内求函数223y x x =--的最大值或最小值． (1)0＜x ＜2； (2)2≤x ≤3．【答案与解析】∵ 2223(1)4y x x x =--=--，∴ 顶点坐标为(1，-4)．(1)∵ x ＝1在0＜x ＜2范围内，且a ＝1＞0， ∴ 当x ＝1时y 有最小值，4y =-最小值．∵ x ＝1是0＜x ＜2范围的中点，在x ＝1两侧图象左右对称，端点处取不到，不存在最大值．(2)∵ x ＝1不在2≤x ≤3范围内(如图所示)，又因为函数223y x x =--(2≤x ≤3)的图象是抛物线223y x x =--的一部分，且当2≤x ≤3时，y 随x 的增大而增大，∴ 当x ＝3时，232330y =-⨯-=最大值；当x ＝2时，222233y =-⨯-=-最小值．【总结升华】先求出抛物线223y x x =--的顶点坐标，然后看顶点的横坐标是否在所规定的自变量的取值范围内，根据不同情况求解，也可画出图象，借助于图象的直观性求解，如图所示，2≤x≤3为图中实线部分，易看出x ＝3时，0y =最大值；x ＝2时，3y =-最小值．类型三、二次函数2(0)y ax bx c a =++≠性质的综合应用3.（•梅州）对于二次函数y=﹣x 2+2x ．有下列四个结论：①它的对称轴是直线x=1；②设y 1=﹣x 12+2x 1，y 2=﹣x 22+2x 2，则当x 2＞x 1时，有y 2＞y 1；③它的图象与x 轴的两个交点是（0，0）和（2，0）；④当0＜x ＜2时，y ＞0．其中正确的结论的个数为（） A.1 B. 2 C. 3 D. 4 【答案】C. 【解析】解：y=﹣x 2+2x=﹣（x ﹣1）2+1，故①它的对称轴是直线x=1，①正确；②∵直线x=1两旁部分增减性不一样，∴设y 1=﹣x 12+2x 1，y 2=﹣x 22+2x 2，则当x 2＞x 1时，有y 2＞y 1，②错误；③当y=0，则x （﹣x+2）=0，解得：x 1=0，x 2=2，故它的图象与x 轴的两个交点是（0，0）和（2，0），③正确； ④∵a=﹣1＜0，∴抛物线开口向下，∵它的图象与x 轴的两个交点是（0，0）和（2，0）， ∴当0＜x ＜2时，y ＞0，④正确．故选：C ．【总结升华】此题主要考查了二次函数的性质以及一元二次方程的解法，得出抛物线的对称轴和其交点坐标是解题关键．4. 一条抛物线2y ax bx c =++经过A （2，0）和B （6，0），最高点C 的纵坐标是1．（1）求这条抛物线的解析式，并用描点法画出抛物线；x y（2）设抛物线的对称轴与轴的交点为D ，抛物线与y 轴的交点为E ，请你在抛物线上另找一点P(除点A 、B 、C 、E 外)，先求点C 、A 、E 、P 分别到点D 的距离，再求这些点分别到直线2y =的距离；(3)观察(2)的计算结果，你发现这条抛物线上的点具有何种规律?请用文字写出这个规律．【答案与解析】(1)由已知可得抛物线的对称轴是4x =． ∴ 最高点C 的坐标为(4，1)．则420,3660,164 1.a b c b c a b c ++=⎧⎪++=⎨⎪++=⎩ 解得1,42,3.a b c ⎧=-⎪⎪=⎨⎪=-⎪⎩∴ 所求抛物线的解析式为21234y x x =-+-． x -2 0 2 4 6 8 10 y-8-31-3-8描点、连线，如图所示：（2）取点（-2，-8）为所要找的点P ，如图所示，运用勾股定理求得ED ＝5，PD ＝10，观察图象知AD ＝2，CD ＝1，点E 、P 、A 、C 到直线y ＝2的距离分别是5、10、2、1．（3）抛物线上任一点到点D 的距离等于该点到直线y ＝2的距离．【总结升华】(1)描点画图时，应先确定抛物线的对称轴，然后以对称轴为参照，左右对称取点．(2)计算两点之间的距离应构造两直角边分别平行于两坐标轴的直角三角形，然后运用勾股定理求得．举一反三：【变式】已知二次函数2y ax bx c =++（其中a >0，b >0，c <0），关于这个二次函数的图象有如下说法：①图象的开口一定向上；②图象的顶点一定在第四象限；③图象与x 轴的交点至少有一个在y 轴的右侧．以上说法正确的个数为（）A ．0B ．1C ．2D ．3 【答案】C.二次函数y=ax 2+bx+c(a ≠0)的图象与性质—巩固练习（提高）【巩固练习】一、选择题1. （•南昌）已知抛物线y=ax 2+bx+c （a ＞0）过（﹣2，0），（2，3）两点，那么抛物线的对称轴（）.A ．只能是x=﹣1B ．可能是y 轴C ．在y 轴右侧且在直线x=2的左侧D ．在y 轴左侧且在直线x=﹣2的右侧2．已知抛物线2(0)y ax bx c a =++<过点(2,0)A -，(0,0)O ，1(3,)B y -，2(3,)C y 四点，则1y 与2y 的大小关系是（）．A ．12y y >B ．12y y =C ．12y y <D ．不能确定3．小强从如图所示的二次函数2y ax bx c =++的图象中，观察得出了下面五条信息：①0a <；②1c >；③0b >；④0a b c ++>；⑤0a b c -+>．你认为其中信息正确的有（）．A ．2个B ．3个C ．4个D ．5个4．已知二次函数2y ax bx c =++中，其函数y 与自变量x 之间的部分对应值如下表所示：x …… 0 1 2 3 4 …… y……4114……点A(x 1，y 1)，B(x 2，y 2)在函数的图象上，则当1＜x 1＜2，3＜x 2＜4时，y 1与y 2的大小关系正确的是( )A ．y 1＞y 2B ．y 1＜y 2C ．y 1≥y 2D ．y 1≤y 25．如图所示，平面直角坐标系中，两条抛物线有相同的对称轴，则下列关系正确的是( ) A ．m ＝n ，k ＞h B ．m ＝n ，k ＜h C ．m ＞n ，k ＝h D ．m ＜n ，k ＝h第5题第6题6．已知二次函数的图象(0≤x ≤3)如图所示，关于该函数在自变量取值范围内，下列说法正确的是( ) A ．有最小值0，有最大值3 B ．有最小值-1，有最大值0 C ．有最小值-1，有最大值3 D ．有最小值-1，无最大值二、填空题7．把抛物线2y ax bx c =++的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是235y x x =-+，则a+b+c ＝________．8．如图所示，是二次函数2(0)y ax bx c a =++≠在平面直角坐标系中的图象．根据图形判断①c ＞0； ②a+b+c ＜0；③2a-b ＜0；④284b a ac +>中正确的是________（填写序号）．9．（•长春）如图，在平面直角坐标系中，点A在抛物线y=x2﹣2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为．10．抛物线y=x2+bx+c与x轴的正半轴交于A，B两点，与y轴交于C点，且线段AB的长为1，△ABC的面积为1，则b的值是_____.11．抛物线y=x2+kx-2k通过一个定点，这个定点的坐标是_ ____.12．已知抛物线y=x2+x+b2经过点，则y1的值是___ __.三、解答题13．（•北京）在平面直角坐标系xOy中，过点（0，2）且平行于x轴的直线，与直线y=x﹣1交于点A，点A关于直线x=1的对称点为B，抛物线C1：y=x2+bx+c经过点A，B．（1）求点A，B的坐标；（2）求抛物线C1的表达式及顶点坐标；（3）若抛物线C2：y=ax2（a≠0）与线段AB恰有一个公共点，结合函数的图象，求a的取值范围．14．如图，已知抛物线的图象与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴与x轴交于点D. 点M从O点出发，以每秒1个单位长度的速度向B运动，过M作x轴的垂线，交抛物线于点P，交BC于Q.(1)求点B和点C的坐标；(2)设当点M运动了x(秒)时，四边形OBPC的面积为S，求S与x的函数关系式，并指出自变量x取值范围.(3)在线段BC上是否存在点Q，使得△DBQ成为以BQ为一腰的等腰三角形？若存在，求出点Q的坐标，若不存在，说明理由.15.如图，抛物线经过直线与坐标轴的两个交点，此抛物线与轴的另一个交点为，抛物线的顶点为.(1)求此抛物线的解析式；(2)点为抛物线上的一个动点，求使的点的坐标.【答案与解析】一、选择题1.【答案】D ；【解析】∵抛物线y=ax 2+bx+c （a ＞0）过（﹣2，0），（2，3）两点，∴点（﹣2，0）关于对称轴的对称点横坐标x 2满足：﹣2＜x 2＜2，∴﹣2＜＜0，∴抛物线的对称轴在y 轴左侧且在直线x=﹣2的右侧．故选D ．2.【答案】A ；【解析】由于抛物线2y ax bx c =++经过点A(-2，0)，O(0，0)，所以其对称轴为1x =-，根据抛物线对称性知当3x =-和1x =时，其函数值相等，∵ 0a <，开口向下，当2x >-时，y 随x 增大而减小，又213-<<，∴ 12y y >．3.【答案】C ；【解析】由图象知0a <，1c >，02b a->，∴ 0b >，当1x =时，0a b c ++>，当1x =-时，0a b c -+<，∴ ①②③④正确．4.【答案】B ；【解析】由表可知1＜x 1＜2，∴ 0＜y 1＜1，3＜x 2＜4，∴ 1＜y 2＜4，故y 1＜y 2.5.【答案】A ；【解析】由顶点(n ，k)在(m ，h)的上方，且对称轴相同，∴ m ＝n ，k ＞h.6.【答案】C ；【解析】观察图象在0≤x ≤3时的最低点为(1，-1)，最高点为(3，3)，故有最小值-1，有最大值3.二、填空题7．【答案】11 ；【解析】将235y x x =-+向左平移3个单位，再向上平移2个单位，得237y x x =++．∴ a ＝1，b ＝3，c ＝7.8．【答案】②④；【解析】观察图象知抛物线与y 轴交于负半轴，则0c <，故①是错误的；当1x =时，0y <，即0a b c ++<，故②是正确的；由于抛物线对称轴在y 轴右侧，则02b a ->， ∵ 0a >，∴ 0b <，故20a b ->，故③是错误的；∵ 0a >，240b ac ->，∴ 284b a ac +>，故④是正确的．9．【答案】1；【解析】∵y=x 2﹣2x+2=（x ﹣1）2+1，∴抛物线的顶点坐标为（1，1），∵四边形ABCD 为矩形，∴BD=AC ，而AC ⊥x 轴，∴AC 的长等于点A 的纵坐标，当点A 在抛物线的顶点时，点A 到x 轴的距离最小，最小值为1，∴对角线BD 的最小值为1．10．【答案】-3；【解析】设抛物线y=x 2+bx+c 与x 轴交点的坐标是x 1、x 2，则x 2- x 1=1，△ABC 的面积为1得c=2,由根与系数关系化为123x x +=±，即=3b a -±，由20b a -＞得=3b a-，3b =-. 11．【答案】(2，4)；【解析】若抛物线y=x 2+kx-2k 通过一个定点，则与k 值无关，即整理y=x 2+kx-2k 得y=x 2+k （x-2），x-2=0，解得x=2,代入y=x 2+k （x-2），y=4,所以过点(2，4).12．【答案】 34；【解析】又因为函数图象经过，所以，代入即可求得. 三、解答题13.【答案与解析】解：（1）当y=2时，则2=x ﹣1，解得：x=3，∴A （3，2），∵点A 关于直线x=1的对称点为B ，∴B （﹣1，2）．（2）把（3，2），（﹣2，2）代入抛物线C 1：y=x 2+bx+c 得：解得：∴y=x 2﹣2x ﹣1．顶点坐标为（1，﹣2）．（3）如图，当C 2过A 点，B 点时为临界，代入A（3，2）则9a=2，解得：a=，代入B（﹣1，2），则a（﹣1）2=2，解得：a=2，∴14.【答案与解析】(1)把x=0代入得点C的坐标为C(0，2)把y=0代入得点B的坐标为B(3，0)；(2)连结OP，设点P的坐标为P(x，y)==∵点M运动到B点上停止，∴，∴()；(3)存在. BC==①若BQ=DQ ∵ BQ=DQ，BD=2∴ BM=1 ∴OM=3-1=2∴∴QM=所以Q的坐标为Q(2，)；②若BQ=BD=2∵△BQM∽△BCO，∴==∴=∴ QM=∵=∴=∴BM=∴ OM=所以Q的坐标为Q(，).15.【答案与解析】(1)直线与坐标轴的交点，.则解得此抛物线的解析式.(2)抛物线的顶点，与轴的另一个交点.设，则.化简得.当，得或. 或当时，即，此方程无解.综上所述，满足条件的点的坐标为或.。

y=ax2+bx+c的图像和性质练习题(含答案)

2二次函数的图像和性质=++y ax bx c一、填空题：1、二次函数在上有最小值，则的值为___________.2、将抛物线y＝x2＋1先向左平移2个单位，再向下平移3个单位，那么所得抛物线的函数关系式是3、直线y = 2x＋b右移3个单位长度后过抛物线y = 2x2－2x＋4的顶点，则b = 。

4、已知二次函数x+2的图象与x轴分别交于A、B两点（如图所示），与y轴交于点C，点P 是其对称轴上一动点，当PB+PC取得最小值时，点P的坐标为．5、如图，抛物线y=ax2+bx+c(与x轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则a的取值范围是。

6、如图，菱形ABCD的三个顶点在二次函数y=ax2－2ax+（a＜0）的图象上，点A、B分别是该抛物线的顶点和抛物线与y轴的交点，则点D的坐标为．7、如图，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=（x＞0）上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A 的坐标是.二、选择题：8、抛物线y=x2的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为（）。

A.y=x2+4x+3B. y=x2+4x+5C. y=x2－4x+3D.y=x2－4x－59、无论m为任何实数，抛物线y＝＋（2－m）x＋m总过的点是（）A（1，3）B（1，0）C（－1，3）D（－1，0）10、在平面直角坐标系中，如果抛物线y＝2x2不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是( ) A．y＝2(x + 2)2－2 B．y＝2(x－2)2 + 2 C．y＝2(x －2)2－2 D．y＝2(x + 2)2 + 211、已知一元二次方程的一根为-3，在二次函数的图像上有三点、、，、、的大小关系是（）A. B. C. D.12、抛物线2=++的图象向左平移2个单位,再向下平移1个单位,所得抛物线为y ax bx c2=-+，原抛物线为（）y2x4x32C.y2x4x2D.y2x12x20=-+=++2=-+2=++2A.y2x4x4B.y2x12x1813、如果抛物线的顶点到轴的距离是3，那么的值等于（）A、8B、14C、8或14D、-8或-1414、若二次函数y=x2-2mx+1+m2．当≤3时，随的增大而减小，则的取值范围是（）A．=3 B．>3 C．≥3 D．≤315、二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（）．16、已知二次函数的图象（﹣0.7≤x≤2）如图所示、关于该函数在所给自变量x的取值范围内，下列说法正确的是（）A.有最小值1,最大值2 B.有最小值-1,最大值1 C.有最小值-1,最大值2 D.有最小值-1,无最大值17、二次函数（a，b，c是常数，a≠0）图象的对称轴是直线，其图象一部分如图所示，对于下列说法：①；②；③；④当时，．其中正确的是（）A．①②B．①④C．②③D．②③④18、已知抛物线的图象如图所示，则下列结论：①＞0；②；③＜；④＞1.其中正确的结论是（）A. ①②B. ②③C. ③④D. ②④19、抛物线的部分图象如图所示，若，则的取值范围是（）A．B．C．或D．或20、已知二次函数的图象如图所示对称轴为．下列结论中，正确的是（）A．B．C．D．21、如图6，抛物线与交于点，过点作轴的平行线，分别交两条抛物线于点．则以下结论：①无论取何值，的值总是正数．②．③当时，．④．其中正确结论是（）A．①②Ｂ．②③Ｃ．③④Ｄ．①④三、简答题：22、已知二次函数的图象如图所示，它与x轴的一个交点坐标为（－1，0），与y轴的交点坐标为（0，3）。

二次函数的图像和性质的练习题

论是【
】
A ．①④
B ．①③
C ．②④
D ．①②
15.抛物线 y 3x2 x 4 与坐标轴的交点个数
是【
】
A ． 3 B ．2 C． 1 D ．0
16.如图，二次函数的图象经过（－
是【
】
2，－ 1），（ 1，1）两点，则下列关于此二次函数的说法正确的
A ． y 的最大值小于 0
B．当 x=0 时， y 的值大于 1
④ 2AB=3AC ；其中正确结论是【
】
A ．①②
B ．②③
C ．③④
D ．①④
24.二次函数 y ax2 bx c 的图象如图所示，则函数值 y 0 时 x 的取值范围是【
】
A． x 1
B．x＞3
C．－ 1＜ x＜ 3
D． x 1或 x
25.抛物线 y＝－ 2x 2＋ 1 的对称轴是【
】
1 A ．直线 x=
y1＜ y 2，此时 M=0 ．下列判断：
①当 x＞ 0 时， y 1＞ y2； ②当 x＜ 0 时， x 值越大， M 值越小；
③使得 M 大于 2 的 x 值不存在； ④使得 M=1 的 x 值是或．
其中正确的是【
】
A ．①②
B ．①④
C．②③
D ．③④
2
4. 已知二次函数 y=a x 2 +c a > 0 ，当自变量 x 分别取 2 ， 3 ， 0 时，对应的值分别为
C． 15
D ． 15
23.如图，抛物线 y 1=a（ x ＋ 2）2－ 3 与 y2= 1 （ x － 3） 2＋1 交于点 A （ 1，3），过点 A 作 x 轴的平 2
行线，分别交两条抛物线于点 B， C．则以下结论：

人教版九年级数学专题《二次函数图像和性质》(含答案及解析)

专题22.1 二次函数的图像和性质知识点解读 1.定义一般地，如果c b a c bx ax y ,,(2++=是常数，)0≠a ，那么y 叫做x 的二次函数。

其中x 是自变量，a 、b 、c 分别是函数解析式的二次项系数、一次项系数、常数项。

2.抛物线的三要素：开口方向、对称轴、顶点。

①a 的符号决定抛物线的开口方向：当0>a 时，开口向上；当0<a 时，开口向下；a 相等，抛物线的开口大小、形状相同。

②平行于y 轴（或重合）的直线记作h x =.特别地，y 轴记作直线0=x 。

3.几种特殊的二次函数的图像特征如下4.求抛物线的顶点、对称轴的方法①公式法：a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=， ∴顶点是），（ab ac a b 4422--，对称轴是直线abx 2-=。

②配方法：运用配方的方法，将抛物线的解析式化为()k h x a y +-=2的形式，得到顶点为(h ,k )，对称轴是直线h x =。

③运用抛物线的对称性：由于抛物线是以对称轴为轴的轴对称图形，对称轴与抛物线的交点是顶点。

若已知抛物线上两点12(,)(,)、x y x y （及y 值相同），则对称轴方程可以表示为：122x x x +=5.抛物线c bx ax y ++=2中， a 、b 、c 的作用①a 决定开口方向及开口大小，这与2ax y =中的a 完全一样。

②b 和a 共同决定抛物线对称轴的位置.由于抛物线c bx ax y ++=2的对称轴是直线abx 2-=，故：①0=b 时，对称轴为y 轴；②0>a b （即a 、b 同号）时，对称轴在y 轴左侧；③0<ab（即a 、b 异号）时，对称轴在y 轴右侧。

③c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置。

当0=x 时，c y =，∴抛物线c bx ax y ++=2与y 轴有且只有一个交点（0，c ）： ①0=c ，抛物线经过原点; ②0>c ,与y 轴交于正半轴； ③0<c ,与y 轴交于负半轴.以上三点中，当结论和条件互换时，仍成立.如抛物线的对称轴在y 轴右侧，则 0<ab6.用待定系数法求二次函数的解析式一般情况下设二次函数的解析式为y=ax 2+bx+c ，结合题中条件解出a 、b 、c 就可以求出二次函数的解析式。

21.3二次函数y=ax2+bx+c的图像及性质同步基础练习题（含答案）

21.3⼆次函数y=ax2+bx+c的图像及性质同步基础练习题（含答案）22.3 ⼆次函数的图像及性质在同⼀直⾓坐标系下，做下列函数的图形⼀、的图像及性质（1）（2）性质：三、（）的图像及性质（1）（2）四、（）的图像及性质：性质：⽅向配⽅：= == ==此时：；；性质：⼀、选择题(本⼤题共22⼩题)1.将抛物线y=2x2向右平移3个单位，再向下平移5个单位，得到的抛物线的表达式为（）C.y=2（x-3）2+5D.y=2（x+3）2-52.已知⼆次函数y=a（x-1）2+b（a≠0）有最⼤值，则a，b的⼤⼩⽐较为（）A.a＞bB.a＜bC.a=bD.不能确定3.⼆次函数y=x2+4x+a的最⼩值是2，则a的值是（）A.4B.5C.6D.74.⼆次函数y=-2（x-3）2+1的图象的对称轴是（）A.直线x=-2B.直线x=-3C.直线x=3D.直线x=15.抛物线y=-x2+3的顶点坐标是（）A.（-1，3）B.（0，3）C.（1，3）D.（3，0）6.下列表格是⼆次函数y=ax2+bx+c的⾃变量x与函数值y的对应值，判断⽅程ax2+bx+c=0（a≠0，a，b，c为常xA.-2.14＜x＜2.13B.-2.13＜x＜-2.12C.-2.12＜x＜-2.11D.-2.11＜x＜-2.107.抛物线y=2x2，y=-2x2，y=2x2+1共有的性质是（）A.开⼝向上B.对称轴都是y轴C.都有最⾼点A.（2，0）B.（-2，0）C.（0，2）D.（0，-2）9.抛物线y=x2-1的顶点坐标是（）A.（0，-1）B.（0，1）C.（-1，0）D.（1，0）10.⼆次函数y=-（x+1）2-2的最⼤值是（）A.-2B.-1C.1D.211.不在抛物线y=x2-2x-3上的⼀个点是（）A.（-1，0）B.（3，0）C.（0，-3）D.（1，4）12.将函数y=-3x2+1的图象向右平移个单位得到的新图象的函数解析式为（）A. B. C.y=-3x2+ D.y=-3x2-13.设A（-2，y1），B（1，y2），C（2，y3）是抛物线y=-（x+1）2+m上的三点，则（）A.y1＞y2＞y3B.y1＞y3＞y2C.y3＞y2＞y1D.y2＞y1＞y314.⼆次函数y=-2（x-1）2-3的图象顶点坐标是（）A.（-1，3）B.（-1，-3）C.（1，3）D.（1，-3）15.若将函数y=2x2的图象向左平移1个单位，再向上平移3个单位，可得到的抛物线是（）A.y=2（x-1）2-3B.y=2（x-1）2+316.抛物线y=2（x-3）2-1的顶点坐标为（）A.（-3，1）B.（-3，-1）C.（3，1）D.（3，-1）17.⼆次函数的图象的开⼝⽅向、对称轴、顶点坐标分别是（）A.向上，直线x=3，（3，4）B.向上，直线x=-3，（-3，4）C.向上，直线x=3，（3，-4）D.向下，直线x=3，（3，4）18.将抛物线y=3x2向左平移2个单位，再向下平移1个单位，所得抛物线为（）A.y=3（x+2）2-1B.y=3（x-2）2+1C.y=3（x-2）2-1D.y=3（x+2）2+119.将抛物线=-2x2向右平移⼀个位，再上移个单位后，抛物线的表式（）A.y=-2（x-1）2+2B.y=-2（x-1）2-2C.y=-2（x+1）2+2D.y=-2（x+1）2-220.对抛物线y=-x2+2x-3⽽⾔，下列结论正确的是（）A.与x轴有两个公共点；B.与y轴的交点坐标是（0，3）；C.当x＜1时，y随x的增⼤⽽增⼤；当x＞1时，y随x的增⼤⽽减⼩；D.开⼝向上．21.下列抛物线中，顶点坐标是（-2，0）的是（）A.y=x2+2B.y=x2-2C.y=（x+2）2D.y=（x-2）222.对称轴平⾏于y轴的抛物线的顶点为点（2，3）且抛物线经过点（3，1），那么抛物线解析式是（）A.y=-2x2+8x+3B.y=-2x?2-8x+3⼆、填空题(本⼤题共8⼩题)23.将抛物线y=x2+bx+c向右平⾏移动2个单位，再向下平⾏移动1个单位长度得抛物线的解析式为y=（x-1）2+1，则⽐抛物线的解析式为______ ．24.⼆次函数y=x2-bx+c的图象上有两点A（3，-8），B（-5，-8），则此抛物线的对称轴是直线x= ______ ．25.已知A（1，y1）、B（-，y2）、C（-2，y3）都在y=-2（x+1）2-的图象上，则y1、y2、y3的⼤⼩关系是______ ．（请⽤“＜”连接）26.已知函数y=3x2-6x+k（k为常数）的图象经过点A（1，y1），B（2，y2），C（-3，y3），则y1，y2，y3从⼩到⼤排列顺序为______ ．27.已知，⼆次函数y=ax2+bx+c（a≠0）的图象如图所⽰，当x=2时，y的值为______ ．28.若抛物线y=a（x-3）2+2经过点（1，-2），则a= ______ ．29.⼆次函数y=-3(x-2)2+5，在对称轴的左侧，y随x的增⼤⽽____________．2①抛物线与x轴的交点坐标是____________和____________；②抛物线经过点(-3，____________)；③在对称轴右侧，y随x增⼤⽽____________；(2)试确定抛物线y=ax2+bx+c的解析式．三、解答题(本⼤题共16⼩题)31.已知抛物线y=2x2+2x-3经过点A（-3，a），求a的值．32.已知抛物线y=ax2+x+b上的⼀点为（-1，-7），与y轴交点为（0，-5）（1）求抛物线的解析式．（2）求抛物线的对称轴和顶点坐标．33.⼆次函数的图象经过A（4，0），B（0，-4），C（2，-4）三点：（1）求这个函数的解析式；34.⼰知⼆次函数y=x2-2x-1．（1）写出其顶点坐标为______ ，对称轴为______ ；（2）在右边平⾯直⾓坐标系内画出该函数图象；（3）根据图象写出满⾜y＞2的x的取值范围______ ．35.抛物线y=-2x2+8x-6．（1）⽤配⽅法求顶点坐标，对称轴；（2）x取何值时，y随x的增⼤⽽减⼩？36.如图，已知抛物线y=x2+bx+c经过A（-1，0）、B（3，0）两点．（1）求抛物线的解析式和顶点坐标；（2）当0＜x＜3时，求y的取值范围；（3）点P为抛物线上⼀点，若S△PAB=10，求出此时点P的坐标．37.已知⼆次函数图象的顶点是(-1，2)，且过点．(1)求⼆次函数的表达式，并在图中画出它的图象；(2)求证：对任意实数m，点M(m，-m2)都不在这个⼆次函数的图象上．38.已知⼆次函数y=x2+bx+c的图象经过点（2，0）和（-3，0），求b、c的值．39.已知⼆次函数y=x2-2mx+m-1（1）当⼆次函数的图象经过坐标原点O（0，0）时，求⼆次函数的解析式；（2）如图，当m=2时，该抛物线与y轴交于点C，顶点为D，求C、D两点的坐标．2（1）求该函数的表达式；（2）当y＜5时，x的取值范围是______ ．41.如图，⼆次函数y=（x-2）2+m的图象与y轴交于点C，点A的坐标为（1，0），点B是点C关于该函数图象对称轴对称的点．（1）求⼆次函数的解析式；（2）求点B的坐标．42.⼰知⼆次函数y=--2x+6．（1）求函数图象的顶点坐标和对称轴．（2）⾃变量x在什么范围内时，函数值y＞0？y随x的增⼤⽽减⼩？43.已知抛物线y=x2+bx+c经过点（1，-4）和（-1，2），求这个抛物线的顶点坐标．44.⼆次函数y=ax2-2x+3的图象经过点（3，6）．（1）求该⼆次函数的关系式；（2）证明：⽆论x取何值，函数值y总不等于1；（3）将该抛物线先向______ （填“左”或“右”）平移______ 个单位，再向______ （填“上”或“下”）平移______ 个单位，使得该抛物线的顶点为原点．45.如图，已知⼆次函数y=ax2-4x+c的图象与坐标轴交于点A（-1，0）和点B（0，-5）．（1）求该⼆次函数的解析式；（2）求该⼆次函数图象的顶点坐标，并指出x在哪个范围内y随着x的增⼤⽽增⼤．（1）求关于的⼆次函数解析式；（2）求m的值．【答案】3.C4.C5.B6.B7.B8.A9.A 10.A 11.D 12.A 13.A 14.D 15.D 16.D 17.A 18.A 19.A 20.C 21.C 22.C23.y=x2+2x+324.-125.y1＜y3＜y226.y1＜y2＜y327.228.-129.增⼤30.(-2，0);(1，0);8;增⼤31.解：∵抛物线y=2x2+2x-3经过点A（-3，a），∴a=2×（-3）2+2×（-3）-3，=2×9-6-3，=9．32.解：（1）将点（-1，-7）、（0，-5）代⼊y=ax2+x+b，，解得：，∴抛物线的解析式为y=-x2+x-5．（2）∵y=-x2+x-5=--，∴抛物线的对称轴为x=，顶点坐标为（，-）．33.解：（1）设抛物线的解析式为y=a（x-h）2+k∵B、C的纵坐标都是-4，∴B、C关于抛物线的对称轴对称，∴抛物线的对称轴为：x=1，即h=1，∴y=a（x-1）2+k，将A（4，0）和B（0，-4）代⼊上式，解得：∴抛物线的解析式为：y=（x-1）2-∴抛物线与x轴的交点坐标为：（4，0）或（-2，0）∵抛物线与y轴的交点坐标为：（0，-4）∴抛物线与坐标轴的交点围成的三⾓形的⾯积为：×6×4=1234.（1，-2）；x=1；x＜-1或x＞335.解：（1）∵y=-2x2+8x-6=-2（x2-4x）-6=-2（x2-4x+4）+8-6=-2（x-2）2+2，（2）∵a=-2＜0，∴当x≥2时，y随x的增⼤⽽减⼩．36.解：（1）把A（-1，0）、B（3，0）分别代⼊y=x2+bx+c中，得：，解得：，∴抛物线的解析式为y=x2-2x-3．∵y=x2-2x-3=（x-1）2-4，∴顶点坐标为（1，-4）．（2）由图可得当0＜x＜3时，-4≤y＜0．（3）∵A（-1，0）、B（3，0），∴AB=4．设P（x，y），则S△PAB=AB?|y|=2|y|=10，∴|y|=5，∴y=±5．①当y=5时，x2-2x-3=5，解得：x1=-2，x2=4，此时P点坐标为（-2，5）或（4，5）；②当y=-5时，x2-2x-3=-5，⽅程⽆解；综上所述，P点坐标为（-2，5）或（4，5）．37.解：(1)依题意可设此⼆次函数的表达式为y=a(x+1)2+2，⼜点(0，)在它的图象上，所以=a+2，解得，，所求为y=-(x+1)2+2，或y=-x2-x+．令y=0，得x1=1，x2=-3，画出其图象；(2)证明：若点M在此⼆次函数的图象上，则-m2=-(m+1)2+2，得m2-2m+3=0，⽅程的判别式：4-12=-8＜0，该⽅程⽆实根，所以，对任意实数m，点M(m，-m2)都不在这个⼆次函数的图象上．38.解：把（2，0）与（-3，0）代⼊得：，解得：b=1，c=-6．39.解：（1）∵⼆次函数的图象经过坐标原点O（0，0），∴代⼊⼆次函数y=x2-2mx+m-1，得出：m-1=0，解得：m=1，∴⼆次函数的解析式为：y=x2-2x；（2）∵m=2，∴⼆次函数y=x2-2mx+m-1得：y=x2-4x+1=（x-4）2-7，∴抛物线的顶点为：D（4，-7），当x=0时，y=1，∴C点坐标为：（0，1），∴C（0，1）、D（4，-7）．40.1＜x＜441.解：（1）把A（1，0）代⼊y=（x-2）2+m得1+m=0，解得m=-1，所以⼆次函数的解析式为y=（x-2）2-1；（2）抛物线的对称轴为直线x=2，当x=0时，y=（x-2）2-1=3，则C（0，3），因为点B是点C关于该函数图象对称轴对称的点，所以B点坐标为（4，3）．42.解：（1）∵y=--2x+6=-（x2+4x）+6=-[（x+2）2-4]+6=-（x+2）2+8，∴顶点坐标为（-2，8），对称轴为x=-2．（2）令y=0得到--2x+6=0，解得x=-6或2，∴观察图象可知，-6＜x＜2时，y＞0，当x＞-2时，y随x的增⼤⽽减⼩．43.解：（1）把点（1，-4）和（-1，2）代⼊y=x2+bx+c，得，解得，所以抛物线的解析式为y=x2-3x-2．y=x2-3x-2=（x-）2+，所以抛物线的顶点坐标为（，）．44.左；1；下；245.解：（1）根据题意，得，解得，∴⼆次函数的表达式为y=x2-4x-5；（2）将⼆次函数的表达式y=x2-4x-5化为顶点式y=（x-2）2-9，∴顶点坐标为（2，-9）；对称轴为x=2，∴当x＞2时，y随x的增⼤⽽增⼤．46.解：（1）设此⼆次函数解析式为y=ax2+bx+c，由题意列出⽅程组，解得a=1，b=-1，c=-2，所以⼆次函数解析式为y=x2-x-2．（2）将x=4代⼊解析式得m=10．。

人教版九年级上册数学二次函数y=ax2+bx+c的图象和性质同步训练(含答案)

人教版九年级上册数学22.1.4 二次函数y=ax ²＋bx ＋c 的图象和性质同步训练一、单选题1．二次函数245y x x =-+的最小值是（）A ．1B ．3C ．4D ．52．点1P （－1，1y ），2P （3，2y ），3P （5，3y ）均在二次函数22y x x c =-++的图象上，则1y ，2y ，3y 的大小关系是（）A ．123y y y =>B ．312y y y >=C ．123y y y >>D ．23y y y << 3．已知二次函数24y x x c =++的图象与x 轴的一个交点为（-1，0），则它与x 轴的另一个交点的坐标是（）A ．（-3，0）B ．（3，0）C ．（1，0）D ．（-2，0） 4．关于抛物线y ＝x 2﹣2x ，下列说法错误的是（）A ．该抛物线经过原点B ．该抛物线的对称轴是直线x ＝1C ．该二次函数的最小值是0D ．当x ＜0时，y 随x 增大而减小5．已知二次函数y =2x 2−4x −1在0≤x ≤a 时，y 取得的最大值为15，则a 的值为（） A ．1 B ．2 C ．3 D ．4 6．若二次函数y ＝x 2+2x +k 的图象经过点（1，y 1），（﹣2，y 2），则y 1，y 2与的大小关系为（）A ．y 1＞y 2B ．y 1＝y 2C ．y 1＜y 2D ．不能确定 7．如图，抛物线2(0)y ax bx c a =++≠的对称轴为2x =-，下列结论正确的是（）A ．0a <B ．0c >C ．当2x <-时，y 随x 的增大而减小D ．当2x >-时，y 随x 的增大而减小 8．已知二次函数2(0)y ax bx c a =++≠的图象如图所示，有下列结论：①0abc >；①420a b c ++>；①b a c ->；①3a c >-；①()a b m am b +>+（1m ≠，m 为实数），其中正确的结论有（）个．A ．2个B ．3个C ．4个D ．5个二、填空题9．已知两条抛物线223y x x =+-和223y x x =+-，请至少写出两条它们的共同特点： ________________．10．已知点（－1，y 1），（2，y 2）在抛物线y ＝x 2－2x ＋c 上，则y 1，y 2的大小关系是y 1_______y 2（填“>”，“<”或“＝”）．11．已知y ＝x 2+2kx +k ﹣1，当﹣1＜x ＜2时，有最小值﹣1，则k 的值为___． 12．将抛物线()213y x =--+向左平移1个单位长度，再向下平移2个单位长度，则平移后的抛物线解析式为_______．13．二次函数2246y x x =-+-图像的对称轴是直线___________．14．若2230x x y ---=，且03x <<，则y 的取值范围为______．15．将函数24y x =的图象向左平移2个单位再向上平移3个单位后的图象所表示的解析式是______．16．在平面直角坐标系中，二次函数23y x mx =-++过点（4，3），若当0≤x ≤a 时，y 有最大值 7，最小值 3，则 a 的取值范围是_____．三、解答题17．在平面直角坐标系内，二次函数2y x bx c =++的图象经过点()3,0A 和()2,3B -．(1)求这个二次函数的表达式；(2)求出二次函数的顶点坐标；(3)将该二次函数的图象向右平移几个单位，可使平移后所得的图象经过坐标原点，请在图中直接画出平移后的二次函数的大致图象，并写出平移后的图象与x轴的另一个交点D的坐标．18．已知抛物线y=ax2+bx﹣3（a≠0）经过点（﹣1，0），（3，0），求a，b的值．19．已知抛物线2y x bx c=-++经过点A（3，0），B（﹣1，0）．（1）求抛物线的解析式；（2）求抛物线的顶点坐标．20．如图，在平面直角坐标系中，抛物线y＝ax2+bx+2经过A（12-，0），B（3，72）两点，与y轴交于点C．(1)求抛物线的解析式；(2)点P在抛物线上，过P作PD①x轴，交直线BC于点D，若以P、D、O、C为顶点的四边形是平行四边形，求点P的横坐标；(3)抛物线上是否存在点Q，使①QCB＝45°？若存在，请直接写出点Q的坐标；若不存在，请说明理由．参考答案：1．A2．A3．A4．C5．D6．A7．C8．B9．①开口都向上，①与y轴的交点都是（0，-3）10．＞11．012．21y x=-13．1x=14．40y-≤<15．()2423y x=++16．2≤a≤4．17．(1)223y x x=--(2)()1,4-(3)()4,018．a的值是1，b的值是﹣2．19．（1）2y x2x3=-++（2）（1，4）20．(1)272 2y x x =-++(2)点P的横坐标为1或2(3)存在，点Q的坐标为2313(,)618或17(,)22。

二次函数图像和性质习题精选(含答案)_百度文库

2
洛杉矶自由行，先看点评更安心
TripAdvisor猫途鹰,为您提供全球旅行者的,旅游点评。
下载
23．（2012•北辰区一模）在﹣ 3≤x≤0 范围内，二次函数结论： ①y1 有最大值 1、没有最小值； ②y1 有最大值 1、最小值﹣3； y1 随 x 的增大而增大； ③函数值 2 ④方程 ax +bx+c=2 无解； ⑤若 y2=2x+4，则 y1≤y2．其中正确的个数是（） A． 2 B． 3 C． 4 D． 5
下一篇

搜索推荐
上海大闸蟹专卖店生理学试题及答案大闸蟹是发物吗大闸蟹礼券北京阳澄湖大闸蟹螃蟹的做法二次函数的解析式阳澄湖大闸蟹礼券上海阳澄湖大闸蟹求二次函数最大值小学生经典阅读上海大闸蟹价格习题及答案二次函数的应用 qq头像带字的女生二次函数知识点小学阅读题及答案根与系数的关系
人走茶蛋凉
新闻
网页
贴吧
知道
音乐
图片
视频地图百科加入VIP | 个人中心区
分类初中教育数学教育精品机构合作VIP个人中心高考题库
二次函数图像和性质习题精选(含答案) kongziaaa 上传于 2016-07-22 | 暂无评价 |30 32人阅读 | 1次下载 | 暂无简介 | 举报文档在手机打开一．选择题（共小题） 2 1．（2014•宁夏）已知 a≠0，在同一直角坐标系中，函数 y=ax 与 y=ax 的图象有可能是（ A． B． C． D．
2
D．无法可求
29．已知直线经过点 A（0，2），B（2，0），点 C 在抛物线 y=x 的图象上，则使得 S△ ABC=2 的点有（
A．4
B．3

2 2 4 二次函数y=ax2+bx+c的图象与性质北师大版九年级数学下册课时作业(含答案)

2.2 二次函数的图象与性质第4课时二次函数y=ax2+bx+c的图象与性质一、选择题1.用配方法将二次函数y=x2-8x-9化为y=a(x-h)2+k的形式为()A.y=(x-4)2+7B.y=(x-4)2-25C.y=(x+4)2+7D.y=(x+4)2-252.抛物线y=-3x2+6x+2的对称轴是()A.直线x=2B.直线x=-2C.直线x=1D.直线x=-13.关于二次函数y=2x2+4x-1,下列说法正确的是()A.图象与y轴的交点坐标为(0,1)B.图象的对称轴在y轴的右侧C.当x<0时,y的值随x值的增大而减小D.y的最小值为-34.如果二次函数y=ax2+bx+c的图象全部在x轴的下方,那么下列判断正确的是()A.a<0,b<0B.a>0,b<0C.a<0,c>0D.a<0,c<05.若点(-1,y1),(1,y2),(4,y3)都在抛物线y=-x2+4x+m上,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y3<y2<y1C.y3<y1<y2D.y1<y3<y26.已知抛物线y=-x2+bx+4经过(-2,n)和(4,n)两点,则n的值为()A.-2B.-4C.2D.47.一次函数y=ax+b和反比例函数y=c在同一平面直角坐标系中的图象如图1所示,则二次函x数y=ax2+bx+c的图象大致为()图1图28.二次函数y=ax2+bx+c的图象如图3所示,有如下结论:①abc>0;①2a+b=0;①3b-2c<0;①am2+bm≥a+b(m为实数).其中正确结论的个数是()图3A.1B.2C.3D.4二、填空题9.当二次函数y=x2+4x+9取最小值时,x的值为.10.某市政府大楼前的广场上有一喷水池,水从地面喷出,喷出水的路径是一条抛物线.若以水平地面为x轴,建立如图4所示的平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x的一部分,则水喷出的最大高度是米.图411.将抛物线y=x2-2x向下平移3个单位长度,再向右平移4个单位长度得到的抛物线的表达式是.12.如图5,在平面直角坐标系xOy中,A,B为x轴上的点,C,D为抛物线y=-x2+2x+3上的两点(点C在点D的右侧),且四边形ABCD是正方形,则正方形ABCD的面积是.图5三、解答题13.已知二次函数y=-2x2+4x+6.(1)求出该函数图象的顶点坐标、对称轴及图象与x轴、y轴的交点坐标,并在如图6所示的网格中画出这个函数的大致图象.(2)利用函数图象回答:①当x在什么范围内时,y随x的增大而增大?当x在什么范围内时,y随x的增大而减小?①当x在什么范围内时,y>0?图614.已知抛物线y=x(x-2)+2.(1)用配方法把这个抛物线的表达式化成y=a(x-h)2+k的形式,并写出它的顶点坐标;(2)将抛物线y=x(x-2)+2上下平移,使顶点移到x轴上,求新抛物线的表达式.15.如图7,一位篮球运动员在离篮圈水平距离4 m处跳起投篮,球运行的高度y(m)与运行的水平距离x(m)满足关系式y=ax2+x+2.25.球在空中达到最大高度后,准确落入篮圈内.已知篮圈中心离地面的距离为3.05 m.(1)当球运行的水平距离为多少时达到最大高度?最大高度为多少?(2)若该运动员身高1.8 m,这次跳投时,球在他头顶上方0.25 m处出手,则球出手时,他跳离地面多高?图7参考答案1.B2.C3.D4.D5.D6.B7.C8.D9.-2.10.411.y=x2-10x+2112.24-8√513.解:(1)①a=-2,b=4,c=6,①-b2a =-42×(-2)=1,4ac-b2 4a =4×(-2)×6−164×(−2)=8,①该函数图象的顶点坐标为(1,8),对称轴为直线x=1.当y=0时,-2x2+4x+6=0,解得x1=3,x2=-1;当x=0时,y=6,①函数图象与x轴的交点坐标为(-1,0),(3,0),与y轴的交点坐标为(0,6).画图略.(2)①当x<1时,y随x的增大而增大;当x>1时,y随x的增大而减小.①当-1<x<3时,y>0.14.解:(1)y=x(x-2)+2=x2-2x+2=(x-1)2+1,则它的顶点坐标为(1,1).(2)由(1)知抛物线y=x(x-2)+2的顶点坐标为(1,1),将抛物线向下平移1个单位长度,所得抛物线的顶点坐标为(1,0),在x轴上,此时新抛物线的表达式为y=(x-1)2.15.解:(1)依题意,知抛物线y=ax2+x+2.25经过点(4,3.05),①16a+4+2.25=3.05,解得a=-0.2.①y=-0.2x2+x+2.25=-0.2(x-2.5)2+3.5.①当球运行的水平距离为2.5 m时达到最大高度,最大高度为3.5 m.(2)①当x=0时,y=2.25,①2.25-0.25-1.8=0.2(m),即球出手时,他跳离地面0.2 m.。

部编数学九年级上册二次函数y=ax2+bx+c的图象和性质2(重点突围)重难点专题提优含答案

专题07 二次函数y =ax ²+bx +c 的图象和性质（2）考点一二次函数图象判断各项系数与式子的符号考点二一次函数、反比例函数与二次函数图象综合判断考点三利用二次函数的对称性求最短路径考点四二次函数与几何图形的综合应用考点一二次函数图象判断各项系数与式子的符号例题：（2022·贵州毕节·中考真题）在平面直角坐标系中，已知二次函数2(0)y ax bx c a =++¹的图象如图所示，有下列5个结论：①0abc >；②20a b -=；③930a b c ++>；④24b ac >；⑤a c b +<．其中正确的有（）A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【详解】解：①∵抛物线的开口方向向下，∴a ＜0，∵对称轴在y 轴右侧，∴对称轴为x ＝2b a-＞0，∵a ＜0，∴b ＞0，∵抛物线与y 轴的交点在y 轴的正半轴上，∴c ＞0，∴abc ＜0，故①错误；②∵对称轴为x ＝2b a-＝1，∴b ＝﹣2a ，∴2a +b ＝0，故②错误；③由图象的对称性可知：当x ＝3时，y ＜0，∴9a ＋3b +c ＜0，故③错误；④由图象可知，该抛物线与x 轴有两个不同的交点，∴b 2﹣4ac ＞0，即b 2＞4ac ；故④正确；⑤由图象可知当x ＝﹣1时，y ＜0，∴a ﹣b +c ＜0，∴a c b +<，故⑤正确．综上所述，正确的结论是：④⑤．故选：B ．【点睛】本题考查了图象与二次函数系数之间的关系，利用对称轴的范围求a 与b 的关系、熟练掌握二次函数与方程之间的转换是基础，数形结合的方法是解题的关键．【变式训练】1．（2022·内蒙古·包头市第三十五中学三模）已知二次函数2(0)y ax bx c a =++¹的图象如图所示，有下列结论：①0abc >；②420a b c ++>；③b a c ->；④3a c >-；⑤()a b m am b +>+（1m ¹，m 为实数），其中正确的结论有（）个．A ．2个B ．3个C ．4个D ．5个【答案】B【解析】【分析】直接根据二次函数的图像与系数的关系及性质进行求解即可．【详解】解：由图像可知：对称轴为直线1,x =即200,0,0a b a b c +=，＜＞＞，∴①0,abc ＜，故错误．②由二次函数的图像可知与x 轴的一个交点在0和1-之间，根据二次函数的对称性可知抛物线与x 轴的另外一个交点在2和3之间，∴当2x =时，即420y a b c =++＞，故正确．③1x =-Q 时0,y <即0,a b c -+<,b ac \->故正确．④ 1x =-Q 时，0,y <即0y a b c =-+＜，又∵对称轴1,x =1,2b a\-=20,a b \+=30,a c \+<3,a c \<-故错误．⑤由图像可得当1x =时，函数取得最大值，即y a b c =++，当x m =时，2()1y am bm c m =++¹，2a b am bm \++＞，(),a b m ma b \+>+故正确．所以正确的有：②③⑤．故选：B ．【点睛】本题主要考查二次函数的图像跟性质，熟练掌握二次函数的图像与系数的关系及性质是解题的关键．2．（2022·辽宁抚顺·模拟预测）二次函数2y ax bx c =++的图象如图所示，对称轴为x =12，且经过点（2，0）．下列结论：①abc <0；②-2b +c =0；③6a +c >0；④若（12-，y 1），（52，y 2）是抛物线上的两点，则y 1<y 2；⑤14b >m （am +b ）（其中m ≠12）．正确的个数是（）A ．2个B ．3个C ．4个D ．5个【答案】B【解析】【分析】抛物线开口向下，且交y 轴于正半轴及对称轴为x =12，推导出a ＜0，b ＞0、c ＞0以及a 与b 之间的关系：b =-a ；根据二次函数图象经过点（2，0），可得出0=4a +2b +c ；再由二次函数的对称性，当a ＜0时，距离对称轴越远x 所对应的y 越小；由抛物线开口向下，对称轴是直线x =12，可知当x =12时，y 有最大值．【详解】解：∵抛物线开口向下，且交y 轴于正半轴，∴a ＜0，c ＞0，∵对称轴x =-2b a =12，即b =-a ，∴b ＞0，∴abc ＜0，故①正确；又可知b =-a ，∴0=-4b +2b +c ，即-2b +c =0，故②正确；∵二次函数y =ax 2+bx +c （a ≠0）的图象过点（2，0），∴根据对称性可得，二次函数y =ax 2+bx +c （a ≠0）的图象过点（-1，0），∴当x =-2时，420y a b c =-+<∵=-b a ，∴424(2)60y a b c a a c a c =-+=--+=+<，故③不正确；∵抛物线开口向下，对称轴是直线x =12，且12−(−12)=1，52-12=2，∴y 1＞y 2，故④不正确；∵抛物线开口向下，对称轴是直线x =12，∴当x =12时，抛物线y 取得最大值ymax =（12）2a +12b +c =14b +c ，当x =m 时，ym =am 2+bm +c =m （am +b ）+c ，且m ≠12，∴14b +c ＞m (am +b )+c （其中m ≠12）．故⑤正确，综上，结论①②⑤正确，共3个故选：B ．【点睛】本题考查二次函数图象与系数的关系及二次函数图象上点的坐标特征，需要充分掌握二次函数各系数的意义，以及它们跟二次函数图象之间的联系．考点二一次函数、反比例函数与二次函数图象综合判断例题：（2022·全国·九年级课时练习）已知函数()()y x m x n =--（其中m n <）的图象如图所示，则函数y nx m =+的图象可能正确的是（）A ．B ．C ．D ．=【答案】D【解析】【分析】根据题意可得二次函数与x 轴的交点为（m ，0），（n ，0），从而得到1,01m n <-<<，进而得到函数y nx m=+经过第一三四象限，且与y 轴的交点位于点（0，-1）的下方，即可求解．【详解】解：令y =0，则()()0x m x n --=，解得：12,x m x n ==，∴二次函数与x 轴的交点为（m ，0），（n ，0），∵m n <，∴1,01m n <-<<，∴函数y nx m =+经过第一、三、四象限，且与y 轴的交点位于点（0，-1）的下方．故选：D【点睛】本题主要考查了二次函数和一次函数的图象和性质，熟练掌握二次函数和一次函数的图象和性质是解题的关键．【变式训练】1．（2022·全国·九年级课时练习）函数y ＝ax 2＋bx ＋c 的图象如图所示，则选项中函数y ＝a （x ﹣b ）2＋c 的图象正确的是（）A ．B ．C ．D ．【答案】B【解析】【分析】先根据y ＝ax 2+bx +c 的图象得到a 、b 、c 的正负情况，从而得到函数y ＝a （x ﹣b ）2+c 的图象的开口方向和顶点坐标所在的位置，分析判断即可得到正确的函数图象．【详解】解：由y ＝ax 2+bx +c 的图象可得a ＜0，b ＞0，c ＞0，∵函数y ＝a （x ﹣b ）2+c ，∴该函数的图象开口向下，顶点坐标为（b ，c ），且该函数图象的顶点在第一象限，故选：B【点睛】本题考查由二次函数图象判断各项系数的符号，牢记相关知识点是解题关键．2．（2021·全国·九年级专题练习）二次函数2y ax bx c =++的图象如下左图，则一次函数24y ax b ac =+-与反比例函数b c y x+=．在同一坐标系内的图象大致为（）A ．B ．C ．D ．【答案】C【解析】【分析】根据二次函数图像，确定二次函数系数的符号，再确定一次函数与反比例函数的系数，即可求得．【详解】解：二次函数图像开口向上，得到0a >二次函数图像与x 轴有两个交点，得到240b ac ->二次函数的与y 轴交点在x 轴的下方，得到0c <二次函数的对称轴b x 02a =->，得到0b <∴0b c +<∴一次函数24y ax b ac =+-图像经过一、二、三象限反比例函数b c y x +=的图像经过二、四象限故选：C ．【点睛】此题主要考查了一次函数、反比例函数与二次函数图像与系数的关系，熟练掌握相关知识是解题的关键．考点三利用二次函数的对称性求最短路径例题:（2022·全国·九年级课时练习）已知：二次函数y ＝x 2＋bx ＋c 的图象与x 轴交于A ，B 两点，其中A 点坐标为（﹣3，0），与y 轴交于点C ，点D （﹣2，﹣3）在抛物线上．(1)求抛物线的解析式；(2)抛物线的对称轴上有一动点P ，求△PAD 周长的最小值．【答案】(1)223y x x =+-(2+【解析】【分析】（1）根据,A D 的坐标，待定系数法求解析式即可；（2）先求得点B 的坐标，根据抛物线的对称性可得，当△PAD 周长确定最小值时，,,D P B 三点共线，进而根据勾股定理求两点坐标距离即可求得最小值．(1)()()3,0,2,3A D ---Q 在二次函数y ＝x 2＋bx ＋c 的图象上，930423b c b c -+=ì\í-+=-î解得23b c =ìí=-î\抛物线的解析式为223y x x =+-(2)Q 223y x x =+-()214x =+-\对称轴为1x =-如图，连接DB ，,A B Q 关于1x =-轴对称PA PB\=APD △的周长等于AD PA PD AD PB PD AD DP ++=++³+，当,,D P B 三点共线时，APD △的周长取得最小值，最小值为AD DP+由抛物线解析式223y x x =+-，令0y =，即2230x x +-=解得123,1x x =-=()1,0B \()()()3,0,2,3,1,0A D B ---QAD ==Q ，DB ==\APD △【点睛】本题考查了待定系数法求二次函数解析式，根据抛物线的对称性求线段和的最小值，掌握二次函数图象的性质是解题的关键．【变式训练】1．（2022·山东临沂·一模）如图，抛物线214y x bx c =-++与x 轴交于A 、B 两点，与y 轴交于点C ，直线114y x =-+过B 、C 两点，连接AC ．(1)求抛物线的解析式．(2)点M (3，1)是抛物线上的一点，点D 为抛物线上位于直线BC 上方的一点，过点D 作DE ⊥x 轴交直线BC 于点E ，点P 为抛物线对称轴上一动点，当线段DE 的长度最大时，求PD +PM 的最小值．【答案】(1)213144y x x =-++(2【解析】【分析】（1）根据一次函数解析式可求出点B ，C 的坐标，再代入抛物线解析式进而求解即可；（2）设点D 的坐标为（x ，213144x x -++），则点E 的坐标为（x ，114x -+），由坐标得DE ＝213144x x -++－（114x -+）=21(2)14x --+，当x ＝2时，线段DE 的长度最大，此时，点D 的坐标为（2，32），点C 和点M 关于对称轴对称，连接CD 交对称轴于点P ，此时PD ＋PM 最小，连接CM 交直线DE 于点F ，则∠DFC ＝90°，由勾股定理得CD，根据PD ＋PM ＝PC ＋PD ＝CD ，即可求解．(1)解：∵直线114y x =-+过B 、C 两点，且B ，C 分别在x 轴和y 轴上当x =0时，y =1当y =0时，x =4∴点B （4，0），点C （0，1）∵抛物线214y x bx c =-++与x 轴交于点B ，与y 轴交于点C ，∴4401b c c -++=ìí=î，解得341b c ì=ïíï=î，∴抛物线的解析式为：213144y x x =-++．(2)解：设点D 的坐标为（x ，213144x x -++），则点E 的坐标为（x ，114x -+），∵点D 为抛物线上位于直线BC 上方的一点，∴DE ＝213144x x -++－（114x -+）=21(2)14x --+，∵14-＜0，∴当x ＝2时，线段DE 的长度最大，此时，点D 的坐标为（2，32），∵C （0，1），M （3，1），∴点C 和点M 关于对称轴对称，连接CD 交对称轴于点P ，此时PD ＋PM 最小，连接CM 交直线DE 于点F ，则∠DFC ＝90°，点F 的坐标为（2，1），∴CD ，∵PD ＋PM ＝PC ＋PD∴PD ＋PM ．【点睛】本题考查二次函数的图象与性质，解决本题的关键是数形结合思想，熟练掌握二次函数的性质、二次函数的对称性．2．（2022·天津滨海新·二模）已知：抛物线213y x bx c =-++（b ，c 为常数），经过点A （－2，0），C （0，4），点B 为抛物线与x 轴的另一个交点．(1)求抛物线的解析式；(2)点P 为直线BC 上方抛物线上的一个动点，当△PBC 的面积最大时，求点P 的坐标；(3)设点M ，N 是该抛物线对称轴上的两个动点，且2MN =，点M 在点N 下方，求四边形AMNC 周长的最小值．【答案】(1)214433y x x =-++(2)（3，5）(3)2【解析】【分析】(1)利用待定系数法即可求出抛物线的函数表达式；(2)首先点B 的坐标，再求出直线BC 的解析式，过点P 作PF ⊥x 轴于F ，交BC 于点Q ，设点214433P m m m -++（，），243Q m m -+（，）,当3m =时，PBC S D 有最大值,即可求出点P 的坐标；（3）由四边形AMNC 的周长AM MN CN AC =+++，得到当AM +CN 最小时，四边形AMNC 的周长最小，得出AM +CN=AM +DM ，求出AM DM +的最小值即可得到结论.(1)解：∵抛物线213y x bx c =-++经过点A （-2，0），C （0，4），∴42034b c c ì--+=ïíï=î解得434b c ì=ïíï=î∴该抛物线的解析式： 214433y x x =-++(2)解：∵点B 是抛物线214433y x x =-++与x 轴的交点，∴ 2144033x x -++=，∴1226x x =-=，，∴点B 的坐标为（6，0），设直线BC 的解析式为y=kx+n ，∵点B （6，0），C (0，4)∴604k n n +=ìí=î解得234k n ì=-ïíï=î ，∴直线BC 解析式为：243y x =-+，如图，过点P 作PF ⊥x 轴于F ，交BC 于点Q ，设点214433P m m m -++（，），243Q m m -+（，） ∴2214214423333PQ m m m m m æöæö=-++--+=-+ç÷ç÷èøèø，∴()221116239223PBC S OB PQ m m m æö=××=´´-+=--+ç÷èøV ∴当3m =时，PBC S D 有最大值，∴点P 的坐标为（3，5）．(3)解：∵A （-2，0），C （0，4），∴AC ==，∵四边形AMNC 的周长AM MN CN AC =+++，2MN =，∴当AM +CN 最小时，四边形AMNC 的周长最小.将CN 向下平移2个单位长度，得到对应线段DM，∴点C 的对应点D 的坐标为（0，2），∴AM +CN=AM +DM ，可知抛物线213y x bx c =-++的对称轴为直线2x =，如图，作点D 关于对称轴2x =的对称点D ¢，可求得D ¢（4，2），连接AD ¢，则AD AM MD AM DM ¢¢=+=+，过点D ¢作D E ¢⊥x 轴于点E ，2D E ¢=，6AE =，∴AM DM +的最小值为AD ==¢∴四边形AMNC 周长的最小值为2AC MN AD ++=¢．【点睛】本题为二次函数中考压轴题，考查了二次函数的图象与性质、待定系数法、最短路线问题等知识点，正确作出辅助线是解题的关键．考点四二次函数与几何图形的综合应用例题：（2022·吉林·长春市绿园区教师进修学校二模）如图，在平面直角坐标系中，抛物线232y ax x =--与x 轴正半轴交于点()3,0A ．以OA 为边在x 轴上方作正方形OABC ，延长CB 交抛物线于点D ，再以BD 为边向上作正方形BDEF ．则点E 的坐标是______．【答案】(1，1【解析】【分析】先将点A （3，0）代入求出关系式，由正方形的性质可知点D 的纵坐标是3，即可求出点D 的横坐标，可得答案．【详解】将点A （3，0）代入232y ax x =--，得39302a --=，解得12a =，∴抛物线的关系式为21322y x x =--．∵四边形OABC 是正方形，∴CO=AO=3，∴点D 的纵坐标是3．当y=3时，213322x x --=，解得=1x +1x =-（舍），∴点D 的横坐标是1∵四边形EFBD 是正方形，∴1C D A F ==+，∴点E 的坐标是(1++．故答案为：(1．【点睛】这是一道二次函数和正方形的综合问题，考查了正方形的性质，求二次函数关系式等．【变式训练】1．（2022·山东烟台·中考真题）如图，已知直线y ＝43x +4与x 轴交于点A ，与y 轴交于点C ，抛物线y ＝ax 2+bx +c 经过A ，C 两点，且与x 轴的另一个交点为B ，对称轴为直线x ＝﹣1．(1)求抛物线的表达式；(2)D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；(3)若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．【答案】(1)y＝﹣43x2﹣83x+4(2)S最大＝334，D（﹣32，5）(3)存在，Q（﹣2，198）【解析】【分析】（1）先求得A，C，B三点的坐标，将抛物线设为交点式，进一步求得结果；（2）作DF⊥AB于F，交AC于E，根据点D和点E坐标可表示出DE的长，进而表示出三角形ADC的面积，进而表示出S的函数关系式，进一步求得结果；（3）根据菱形性质可得PA＝PC，进而求得点P的坐标，根据菱形性质，进一步求得点Q坐标．(1)解：当x＝0时，y＝4，∴C（0，4），当y＝0时，43x+4＝0，∴x＝﹣3，∴A（﹣3，0），∵对称轴为直线x＝﹣1，∴B（1，0），∴设抛物线的表达式：y ＝a （x ﹣1）•（x +3），∴4＝﹣3a ，∴a ＝﹣43，∴抛物线的表达式为：y ＝﹣43（x ﹣1）•（x +3）＝﹣43x 2﹣83x +4；(2)如图1，作DF ⊥AB 于F ，交AC 于E ，∴D （m ，﹣243m ﹣83m +4），E （m ，﹣43m +4），∴DE ＝﹣243m ﹣83m +4﹣（43m +4）＝﹣43m 2﹣4m ，∴S △ADC ＝12DE ×OA ＝32•（﹣43m 2﹣4m ）＝﹣2m 2﹣6m ，∵S △ABC ＝12AB OC ×＝1432´´＝6，∴S ＝﹣2m 2﹣6m +6＝﹣2（m +32）2+334，∴当m ＝﹣32时，S 最大＝334，当m ＝﹣32时，y ＝﹣433(1)(3)322´--´-+＝5，∴D （﹣32，5）；(3)设P （﹣1，n ），∵以A ，C ，P ，Q 为顶点的四边形是以AC 为对角线的菱形，∴PA ＝PC ，即：PA 2＝PC 2，∴（﹣1+3）2+n 2＝1+（n ﹣4）2，∴n ＝138，∴P （﹣1，138），∵xP +xQ ＝xA +xC ，yP +yQ ＝yA +yC∴xQ ＝﹣3﹣（﹣1）＝﹣2，yQ ＝4﹣138＝198，∴Q （﹣2，198）．【点睛】本题考查了二次函数及其图象性质，勾股定理，菱形性质等知识，解决问题的关键是熟练掌握相关二次函数和菱形性质2．（2022·内蒙古·包头市第三十五中学三模）如图，抛物线23y ax bx =++交x 轴于(3,0)(1,0)A B -,两点，交y 轴于点C ．(1)求抛物线的解析式和对称轴．(2)若R 为抛物线上一点，满足45BCR Ð=°，求R 的坐标．(3)若点P 在抛物线的对称轴上，点Q 是平面直角坐标系内的任意一点，是否存在点P 使得A 、C 、P 、Q 为顶点的四边形是矩形，若存在，请直接写出所有符合条件的点Q 的坐标，若不存在，请说明理由．【答案】(1)2y x 2x 3=-++，对称轴为直线1x =(2)（4，-5）(3)存在，（4，1）或（-2，1）或æççè或æççè【解析】【分析】（1）利用待定系数解答，即可求解；（2）过点B 作BM ⊥BC 交CR 于点M ，过点M 作ME ⊥x 轴于点E ，证明△BOC ≌△MBE ，可得点E （2，-1），然后求出直线CR 的解析式，再与抛物线解析式联立，即可求解；（3）设(1,)P t ，点Q （m ，n ），分两种情况讨论：然后分两种情况讨论：当AC 为边时，当AC 为对角线时，即可求解．(1)解：∵抛物线23y ax bx =++交x 轴于()3,0A ，()1,0B -两点，∴933030a b a b ++=ìí-+=î，解得：12a b =-ìí=î，∴该抛物线的解析式为()222314y x x x =-++=--+，∴对称轴为直线1x =；(2)解：当x =0时，3y =，∴OC =3，∵点B （-1，0），∴OB =1，如图，过点B 作BM ⊥BC 交CR 于点M ，过点M 作ME ⊥x 轴于点E ，∵∠BCR =45°，∴△BCM 为等腰直角三角形，∠CBO +∠EBM =90°，∴BM =BC ，∵∠EBM +∠BME =90°，∴∠CBO =∠BME ，∵∠BEM =∠BOC =90°，∴△BOC ≌△MBE ，∴EM =BO =1，BE =OC =3，∴OE =2，∴点E （2，-1），设直线CR 的解析式为()10y kx b k =+¹把点C （0，3），M （2，-1）代入得：11321b k b =ìí+=-î，解得：123k b =-ìí=î，∴直线CR 的解析式为23y x =-+，联立得：22323y x x y x ì=-++í=-+î，解得： 045x y =ìí=-î 或03x y =ìí=î（舍去），∴点R （4，-5）；(3)解：存在．设(1,)P t ，点Q （m ，n ），当以AC 为边时，点C 向点P （或点Q ）平移的方向和距离与点A 向点Q （或点P ）平移的方向和距离相同，且AP =CQ （或AQ =CP ），∴()()222201330133m t n t m n ì-=-ïï-=-íï-+=+-ïî或()()222203130133m n t t m n ì-=-ïï-=-íï+-=-+ïî，解得：441t m n =ìï=íï=î或221t m n =-ìï=-íï=î，∴此时点Q 的坐标为（4，1）或（-2，1）如图，当AC 为对角线时，AC =PQ ，且PQ 与AC 的中点重合，如图，PQ =AC ==∴()()(22213223221m n t m n t +ì=ïï+ï=íïï-+-=ïî，解得：n m t ì=ïïïíïï=ïî或n m t ìïïïíïï=ïî，∴此时点Q的坐标为æççè或æççè；综上所述，点Q 的坐标为（4，1）或（-2，1）或æççè或æççè【点睛】本题主要考查了二次函数的综合题，一次函数的图像和性质，矩形的性质，熟练掌握二次函数的综合题，一次函数的图像和性质，矩形的性质，利用数形结合思想解答是解题的关键，是中考的压轴题．一、选择题1．（2022·湖南株洲·中考真题）已知二次函数()20y ax bx c a =+-¹，其中0b >、0c >，则该函数的图象可能为（）A ．B ．C ．D ．【答案】C【解析】【分析】利用排除法，由0c -<得出抛物线与y 轴的交点应该在y 轴的负半轴上，排除A 选项和D 选项，根据B 选项和C 选项中对称轴02b x a-=>，得出0a <，抛物线开口向下，排除B 选项，即可得出C 为正确答案．【详解】解：对于二次函数()20y ax bx c a =+-¹，令0x =，则y c =-，∴抛物线与y 轴的交点坐标为()0,c -∵0c >，∴0c -<，∴抛物线与y 轴的交点应该在y 轴的负半轴上，∴可以排除A 选项和D 选项；B 选项和C 选项中，抛物线的对称轴02b x a-=>，∵ 0b >，∴0a <，∴抛物线开口向下，可以排除B 选项，故选C ．【点睛】本题考查二次函数的图象的性质，熟练掌握二次函数图象与三个系数之间的关系是解题的关键．2．（2022·湖北鄂州·中考真题）如图，已知二次函数y ＝ax 2+bx +c （a 、b 、c 为常数，且a ≠0）的图像顶点为P （1，m ），经过点A （2，1）；有以下结论：①a <0；②abc ＞0；③4a +2b +c ＝1；④x >1时，y 随x 的增大而减小；⑤对于任意实数t ，总有at 2+bt ≤a +b ，其中正确的有（）A ．2个B ．3个C ．4个D ．5个【答案】C【解析】【分析】①根据抛物线的开口方向向下即可判定；②先运用二次函数图像的性质确定a 、b 、c 的正负即可解答；③将点A 的坐标代入即可解答；④根据函数图像即可解答；⑤运用作差法判定即可．【详解】解：①由抛物线的开口方向向下，则a ＜0，故①正确；②∵抛物线的顶点为P （1，m ）∴12b a-=，b =-2a ∵a ＜0∴b ＞0∵抛物线与y 轴的交点在正半轴∴c ＞0∴abc ＜0，故②错误；③∵抛物线经过点A （2，1）∴1＝a ·22+2b +c ，即4a +2b +c ＝1，故③正确；④∵抛物线的顶点为P （1，m ），且开口方向向下∴x >1时，y 随x 的增大而减小，即④正确；⑤∵a ＜0∴at2+bt-（a+b）= at2-2at-a+2a= at2-2at+a=a（t2-2t+1）= a（t-1）2≤0∴at2+bt≤a+b，则⑤正确综上，正确的共有4个．故答案为C．【点睛】本题主要考查了二次函数图像的性质，灵活运用二次函数图像的性质以及掌握数形结合思想成为解答本题的关键．3．（2022·全国·九年级课时练习）在同一平面直角坐标系中，函数2=+与y＝ax＋b的图象不可能是y ax bx()A．B．C．D．【答案】D【解析】【分析】根据二次函数与一次函数的图象与性质进行判断即可．【详解】解：当a >0，b >0时，y =ax 2+bx 的开口上，与x 轴的一个交点在x 轴的负半轴，y =ax +b 经过第一、二、三象限，且两函数图象交于x 的负半轴，无选项符合；当a >0，b <0时，y =ax 2+bx 的开口向上，与x 轴的一个交点在x 轴的正半轴，y =ax +b 经过第一、三、四象限，且两函数图象交于x 的正半轴，故选项A 正确，不符合题意题意；当a <0，b >0时，y =ax 2+bx 的开口向下，与x 轴的一个交点在x 轴的正半轴，y =ax +b 经过第一、二、四象限，且两函数图象交于x 的正半轴，C 选项正确，不符合题意；当a <0，b <0时，y =ax 2+bx 的开口向下，与x 轴的一个交点在x 轴的负半轴，y =ax +b 经过第二、三、四象限，B 选项正确，不符合题意；只有选项D 的两图象的交点不经过x 轴，故选D .【点睛】本题考查二次函数与一次函数图象的性质，解题的关键是根据a 、b 与0的大小关系进行分类讨论．4．（2022·天津和平·三模）二次函数2y ax bx c =++（a ，b ，c 为常数，0a ¹）的图像开口向下，与x 轴交于()1,0和()0m ,，且21m -<<-．有下列结论：①0abc >；②20a c +<；③若方程()()110a x m x ---=有两个不相等的实数根，则244ac b a -<；④当32m =-时，若方程21ax bx c ++=有四个根，则这四个根的和为-1．其中，正确结论的个数是（）A ．1B ．2C ．3D ．4【答案】C【解析】【分析】根据图像得到a <0，对称轴在y 轴左侧，图像与x 轴有两个交点，即为b <0，c >0，由此判断①正确；根据图像与x 轴交点可知a+b+c = 0，-2<m <-1，且抛物线开口向下，得到当x =-2时，y=4a-2b+c <0，当x =-1时，y=a-b+c >0，联立a+ b+c = 0和y= 4a- 2b+c < 0可得2a+c < 0，故结论②正确；若a (x- m )(x - 1) - 1 = 0有两个不相等的实数根，则a (x - m )(x - 1) = 1有两个不相等的实数根，则原抛物线的顶点纵坐标大于1，即2414ac b a->，由此判断③错误；当32m =-时，利用公式求出抛物线的对称轴，再根据抛物线的对称性得到四个根的和为1122144æöæö-´+-´=-ç÷ç÷èøèø，由此判断④正确．【详解】解：∵二次函数2y ax bx c =++（a ，b ，c 为常数，0a ¹）的图像开口向下，与x 轴交于()1,0和()0m ,，且21m -<<-．∴a <0，对称轴在y 轴左侧，图像与x 轴有两个交点，∴b <0，c >0，∴0abc >，故①正确；根据交点(1，0)，可知a+b+c = 0，根据交点(m ，0)，可知am 2 + bm +c = 0，∵-2<m <-1，且抛物线开口向下，∴当x =-2时，y=4a-2b+c <0，当x =-1时，y=a-b+c >0，联立a+ b+c = 0和y= 4a- 2b+c < 0可得 4a - 2(-a-c )+c < 0，化简得 2a+c < 0，故结论②正确；若a (x- m )(x - 1) - 1 = 0有两个不相等的实数根，∴a (x - m )(x - 1) = 1有两个不相等的实数根，则原抛物线的顶点纵坐标大于1，即2414ac b a->，∴244ac b a ->，故③错误；当32m =-时，抛物线的对称轴为31112224m -++==-，若方程21ax bx c ++=有四个根，则这四个根中有两个在x 轴上方，且关于对称轴对称；有两个在x 轴下方，且关于对称轴对称，故四个根的和为1122144æöæö-´+-´=-ç÷ç÷èøèø，故④正确；故选：C ．【点睛】此题考查了抛物线的性质，利用抛物线的图像判断式子的正负，正确理解抛物线的图像得到相关信息是解题的关键．二、填空题5．（2022·云南·红河县教育科学研究室九年级期末）已知二次函数2y ax bx c =++的图象如图所示，对称轴为直线1x =-，经过点（0，1）．有以下结论：①0a b c ++<；②0a b c -+<；③0abc >；④240b ac ->．其中所有正确结论的序号是________．【答案】①③④【解析】【分析】根据抛物线开口方向判断a 的符号，根据对称轴及与y 轴交点坐标判断b 和c 的符号，据此可判断③的正误；根据函数在x =1和x =－1时的函数值判断①②的正误；根据抛物线与x 轴交点的个数判断④的正误．【详解】解：∵抛物线开口朝下，∴a <0，∵抛物线对称轴为x =-1，过（0，1），∴b <0，c >0，∴abc >0，③正确；由函数图象知，x =1时，y =a +b +c <0，故①正确；当x =－1时，y =a －b +c >0，故②错误；∵抛物线与x 轴有两个交点，∴240b ac ->，故④正确；综上所述，正确答案的序号为：①③④．故答案为：①③④．【点睛】本题考查了二次函数的图象与系数间的关系，掌握抛物线对称轴与a 、b 的关系及函数与方程间的转换是解题关键．6．（2022·全国·九年级课时练习）平面直角坐标系中，将抛物线2y x =-平移得到抛物线C ，如图所示，且抛物线C 经过点()1,0A -和()0,3B ，点P 是抛物线C 上第一象限内一动点，过点P 作x 轴的垂线，垂足为Q ，则OQ PQ +的最大值为______．【答案】214【解析】【分析】求得抛物线C 的解析式，设Q （x ，0），则P （x ，-x 2+2x +3），即可得出OQ +PQ ，根据二次函数的性质即可求得．【详解】解：设平移后的解析式为y =-x 2+bx +c ，∵抛物线C 经过点A （-1，0）和B （0，3），∴103b c c --+=ìí=î，解得23b c =ìí=î，∴抛物线C 的解析式为y =-x 2+2x +3，设Q （x ，0），则P （x ，-x 2+2x +3），∵点P 是抛物线C 上第一象限内一动点，∴OQ +PQ =x +（-x 2+2x +3）=-x 2+3x +32321(24x =--+∴OQ +PQ 的最大值为214故答案为：214【点睛】本题考查了二次函数的性质，平移，二次函数图象与几何变换，根据题意得出OQ +PQ =-x 2+3x +3是解题的关键．7．（2022·安徽合肥·模拟预测）如图，在平面直角坐标系中，正方形OABC 的顶点A 在x 轴正半轴上，顶点C 在y 轴正半轴上，抛物线22y ax ax c =-+经过点B 、C ．（1）点B 的坐标为______．（2）若抛物线22y ax ax c =-+的顶点在正方形OABC 的内部，则a 的取值范围是______．【答案】 B （2，2） 0<a <2【解析】【分析】（1）观察图象即可得到0a >，求得对称轴为直线1x =，即可求得2BC =，即可求出点B 的坐标；（2）易求得2c =，得到抛物线为222y ax ax =-+，根据题意得到()422024a a a ´--<<，即可求解．【详解】解：（1）∵抛物线22y ax ax c =-+开口向上，∴0a >．∵对称轴为直线12b x a=-=，且经过点B 、C ，∴2BC =，∴正方形的边长为2，∴22B （，），故答案为：B （2，2）；（2）可求得点C 坐标为（0，2），∴2c =．∴抛物线为222y ax ax =-+．∵抛物线22y ax ax c =-+的顶点在正方形OABC 的内部，∴()2422024a a a ´--<<，解得2a <，∴02a <<．故答案为：02a <<.【点睛】本题考查了二次函数图象与系数的关系，坐标与图形、二次函数图象上点的坐标特征，正方形的性质、解一元一次不等式组，根据题意得到关于a 的不等式组是解题的关键．8．（2022·四川·隆昌市蓝天育才学校一模）已知二次函数2(0)y ax bx c a =++¹的图象如图所示，有下列5个结论：①0abc <；②0a b c -+>；③420a b c ++>；④23c b <；⑤()(1a b m am b m +<+¹的实数），其中正确结论的序号有____．【答案】①③④【解析】【分析】根据图象开口方向，与y 轴交点及对称轴判断①；由x =-1时，y <0判断②；由图象与x 轴的另一个交点在2与3之间，由此判断③；由对称轴得到2b a =-，代入a -b +c <0，得到02b b c --+<，由此判断④；由x =1时，函数有最大值判断⑤．【详解】解：由图象得a <0，c >0，∵对称轴在y 轴右侧，a <0，∴b >0，∴abc <0，故①正确；由图象知，当x =-1时，y <0，即a -b +c <0，故②错误；∵抛物线的对称轴为直线x =1，图象与x 轴的一个交点在-1与0之间，∴图象与x 轴另一个交点在2与3之间，∴当x =2时y >0，即420a b c ++>，故③正确；∵抛物线的对称轴为直线x =1，即12b a-=，∴2b a =-，∵a -b +c <0，∴02b bc --+<，∴23c b <，故④正确；∵抛物线的对称轴为直线x =1，∴当x =1时，函数有最大值，即最大值为y =a +b +c ，∴当x =m （1m ¹）时，a +b +c >am 2+bm +c ，∴a +b >m （am +b ），故⑤错误，故答案为：①③④．【点睛】此题考查了二次函数的性质，二次函数的图象，二次函数的最值，二次函数的对称轴，熟记二次函数的综合知识是解题的关键．三、解答题9．（2022·重庆市涪陵第十八中学校九年级阶段练习）如图，已知抛物线与x 轴交于A (﹣2，0)，B (6，0)两点，与y 轴交于点C (0，﹣2)，点P 是抛物线上位于直线BC 下方的一点．(1)求抛物线的解析式；(2)如图1，连接AC ，过点P 作PG ∥AC 交BC 于点G ，求PG 长度的最大值及此时点P 的坐标；(3)如图2，将抛物线沿射线CB 的方向平移，使得新抛物线y '经过点（2，﹣），并记新抛物线y '的顶点为D ，若点M 为新抛物线y ′对称轴上的一动点，点N 为坐标平面内的任意一点，直接写出所有使得以A ，D ，M ，N 为顶点的四边形是菱形的点N 的坐标，并把求其中一个点N 的坐标的过程写出来．【答案】(1)126y =-(2)PG P 的坐标为5(3,)2-(3)当点N 的坐标为（10，0）或（-2，-10）或(2,-或(2--，时，以A 、D 、M 、N 为顶点的四边形是菱形【解析】【分析】（1）根据抛物线与x 轴交于A (﹣2，0)，B (6，0)两点，可设两点式，再把点C (0，﹣2)代入，即可得；（2）先求出直线BC 的解析式，过点P 作直线l BC ∥，只有当直线l 与抛物线相切，PG 有最大值，此时P 、G 的位置分别为1P ，1G ，抛物线与直线联立，令=0D ，可求出直线的解析式，从而求得点P 的坐标，在求出AC 的解析式，由直线PG 与AC 平行，可求得直线PG 的解析式，与直线BC 联立，可求得点G 的坐标，从而求得PG 的长度；（3）过点C 作直线CE x ∥轴，过点B 作CE 的垂线，垂足为E ，求出BE 1CE 3=，设抛物线沿射线CB 的方向平移，使点C 平移到点G ，过点G 作GH CE ^，可证CHG CEB △∽△，则可以设抛物线沿着射线CB 方向向右平移t 个单位长度，向上平移13t 个单位长度，即可求出平移后的抛物线的解析式，可求得D 点的坐标，然后根据菱形的性质分别讨论：当DM ，AN 以A 、D 、M 、N 为顶点的菱形的对角线时，当DM ，MA 以A 、D 、M 、N 为顶点的菱形的邻边时，当AD ，MD 以A 、D 、M 、N 为顶点的菱形的邻边时，进行求解即可得．(1)解：∵抛物线与x 轴交于A (﹣2，0)，B (6，0)两点，∴设抛物线解析式为：(2)(6)y a x x =+-，把点C (0，﹣2)代入(2)(6)y a x x =+-，得2(6)2a -=-g 122a -=-解得，16a =，则抛物线的解析式为：2112(2)(6)2663y x x x x =+-=--．(2)解：设直线BC 的解析式为：y kx b =+，把B (6，0)，点C (0，﹣2)代入y kx b =+中，得602k b b +=ìí=-î，解得，132k b ì=ïíï=-î，即直线BC 的解析式为：123y x =-，如图所示，过点P 作直线l BC ∥，只有当直线l 与抛物线相切，PG 有最大值，此时P 、G 的位置分别为1P ，1G ，设此时直线l 的解析式为：13y x b =+，联立21312263y x b y x x ì=+ïïíï=--ïî，得21206x x b ---=，2142(1)4(2)1063b b +=--´´--=+=Δ，解得，72b =-，即2172062x x --+=，2690x x -+=解得，3x =，即1P 的横坐标为3，代入直线l 解析式得，其纵坐标为1753322´-=-，故1P 的坐标为：5(3,)2-，即PG 长度最大时点P 的坐标为5(3,2-，。

二次函数y=ax2+bx+c的图象和性质测试卷(含答案)

二次函数y ＝ax ²＋bx ＋c 的图象和性质测试卷一、选择题（每题3分）1．对于二次函数y=x 2-4x+7的图象，下列说法正确的是（）A ．开口向下B ．对称轴是x=-2C ．顶点坐标是（2，3）D ．与x 轴有两个交点2．抛物线223y x x =-++的顶点坐标是()A ．(-1，4)B ．(1，3)C ．(-1，3)D ．(1，4)3．已知抛物线y ＝ax 2＋bx ＋c 的开口向上，顶点坐标为(3，-2)，那么该抛物线有()A ．最小值-2B ．最大值-2C ．最小值3D ．最大值34．已知二次函数y=ax 2+bx+c （a ＜0）的图象如图所示，当-5≤x≤0时，下列说法正确的是（）A ．有最小值-5、最大值0B ．有最小值-3、最大值6C ．有最小值0、最大值6D ．有最小值2、最大值65．已知开口向下的抛物线的顶点坐标为（2，0），则函数y 随x 的增大而增大的取值范围为（）．A ．x ＞0B ．x ＜0C ．x ＞2D ．x ＜26．函数y=-2x 2-8x+m 的图象上有两点A （x 1，y 1），B （x 2，y 2），若-2＜x 1＜x 2，则A ．21y y <B ．21y y >C ．21y y =D ．1y 、2y 的大小不确定7．把二次函数y ＝－x 2－x ＋3用配方法化成y ＝a （x －h ）2＋k 的形式（）A ．y ＝－（x －2）2＋2B ．y ＝（x －2）2＋4C ．y ＝－（x ＋2）2＋4D ．y ＝2＋38．若b ＜0，则二次函数y=x 2-bx-1的图象的顶点在：A ．第一象限B ．第二象限C ．第三象限D ．第四象限9．抛物线222y x x =-＋-经过平移得到2y x =-，平移方法是（）A ．向右平移1个单位，再向下平移1个单位B ．向右平移1个单位，再向上平移1个单位C ．向左平移1个单位，再向下平移1个单位D ．向左平移1个单位，再向上平移1个单位10．函数y=x 2+3x －4的图象与y 轴的交点坐标是A ．（2，0）B ．（－2，0）C ．（0，4）D ．（0，－4）二、填空题（每题3分）11．抛物线y ＝2x 2-bx ＋3的对称轴是直线x ＝1，则b 的值为___12．已知二次函数222y x mx =++，当x ＞2时，y 的值随x 值的增大而增大，则实数m 的取值范围是__．13．二次函数226y x x =-+的最小值是____．14．抛物线y=x 2﹣4x+3的顶点坐标是．15．抛物线332-+-=x x y 与y 轴的交点坐标为___________．16．二次函数y=x 2+2x 的顶点坐标为，对称轴是直线．17．将抛物线22y x x =-向上平移3个单位，再向右平移4个单位得到的抛物线是_______．18．若二次函数24y ax x a -+＝的最小值是－3，则a ＝_________．19．将二次函数y ＝2x －2x －3化为y ＝（x －h ）2＋k 的形式，则__________________．20．已知A （﹣2，y 1）、B （0，y 2）、C （1，y 3）三点都在抛物线y=kx 2+2kx+k 2+k （k ＜0）的图象上，则y 1、y 2、y 3的大小关系是．三、计算题（每题10分）21.画出二次函数y=﹣x 2+2x+3的图像，并根据图像解答下列问题：（1）x 取何值时，函数值y 随x 的增大而减小；（2）x 取何值时，y≤3．22.已知二次函数y=﹣x 2+x+4．（1）求抛物线的顶点坐标和对称轴；（2）当x 取何值时，y 随x 的增大而增大？当x 取何值时，y 随x 的增大而减小？当x 取何值时，y 有最大值还是最小值？是多少？23.如图，已知二次函数21232y x x =-+的图象的顶点为A ，且与y 轴交于点C ．（1）求点A 与点C 的坐标；（2）若将此函数的图象沿z 轴向右平移1个单位，再沿y 轴向下平移3个单位，请直接写出平移后图象所对应的函数关系式及点C 的对应点的坐标；（3）若A （m ，1y ），B （m ＋1，2y ）两点都在此函数的图象上，试比较1y 与2y 的大小．1．把函数2241y x x =-++的图象先向左平移2个单位，再向上平移3个单位，所得的抛物线解析式是（）A ．22(1)6y x =--+B ．22(1)6y x =---C ．22(1)6y x =-++D ．22(1)6y x =-+-2．已知抛物线y=x 2﹣ax+a+3对称轴在y 轴的右侧，顶点在x 轴上，则a 的值是（）A ．6B ．﹣2C ．6或﹣2D ．43．已知函数4212--=x x y ，当函数值y 随x 的增大而减小时，x 的取值范围是（）A ．x ＜1B ．x ＞1C ．x ＞－2D ．－2＜x ＜44．二次函数y=a 2x +bx ﹣1（a≠0）的图象经过点（1，1），则a+b+1的值是（）A ．﹣3B ．﹣1C ．2D ．35．二次函数522-+=x x y 取最小值时，自变量x 的值是（）A ．2B ．-2C ．1D ．-16．抛物线y=x 2﹣2x+3的顶点坐标是（）A ．（1，﹣2）B ．（1，2）C ．（﹣1，2）D ．（﹣1，﹣2）7．已知抛物线y=-2x 2+12x-13，则下列关于此抛物线说法正确的是（）A ．开口向下，对称轴为直线x=-3B ．顶点坐标为（-3，5）C ．最小值为5D ．当x ＞3时，y 随x 的增大而减小8．用配方法将二次函数y=3x 2-4x-2写成形如y=a （x+m ）2+n 的形式，则m 、n 的值分别是（）A ．m=32，n=310B ．m=-32，n=-310C ．m=2，n=6D ．m=2，n=-29．二次函数y=x 2﹣4x+5的最小值是()A ．﹣1B ．1C ．3D ．510．若点A （2，y 1），B （﹣3，y 2），C （﹣1，y 3）三点在抛物线y=x 2﹣4x ﹣m 的图象上，则y 1、y 2、y 3的大小关系是（）A.y 1＞y 2＞y 3B.y 2＞y 1＞y 3C.y 2＞y 3＞y 1D.y 3＞y 1＞y 211．抛物线2256y x x =-+的对称轴是（）A 、54x =B 、52x =C 、54x =-D 、52x =-12.二次函数243y x x =--的顶点坐标是（，）．13．函数y=x 2+2x+1，当y=0时，x=_______________；当1＜x ＜2时，y 随x 的增大而_____________（填写“增大”或“减小”）14．将抛物线的解析式y=向上平移3个单位长度，在向右平移1个单位长度后，得到的抛物线的解析式是．15．函数y=x 2+4ax+2在x≤6时，y 随着x 的增大而减小，则a 的取值范围是．16．二次函数1232+-=x x y 的图象的开口方向________，顶点是________，对称轴是________．17．二次函数622+-=x x y 的最小值是．18．已知二次函数2y ax bx c =++中，函数y 与自变量x 的部分对应值如下表：x…－2－1012…y…－3－4－35…则此二次函数的对称轴为．19．函数342++-=x x y 有值（填“最大”或“最小”），所求最值是.20．小颖在二次函数y=2x 2+4x+5的图象上找到三点（－1，y 1），（21，y 2），（－321，y 3），则你认为y 1，y 2，y 3的大小关系应为．三、计算题（每题10分）21.已知二次函数y=x 2+2x-1．（1）写出它的顶点坐标；（2）当x 取何值时，y 随x 的增大而增大；22.已知抛物线4212+--=x x y ，（1）用配方法确定它的顶点坐标、对称轴；（2）x 取何值时，y 随x 增大而减小？23.如图，在平面直角坐标系中，抛物线224233y x x =--+与x 轴交于B 、C 两点（点B 在点C 的左侧），与y 轴交于点A ，抛物线的顶点为D ．（1）填空：点A 的坐标为（，），点B 的坐标为（，），点C 的坐标为（，），点D 的坐标为（，）；（2）点P 是线段BC 上的动点（点P 不与点B 、C 重合），过点P 作x 轴的垂线交抛物线于点E ，若PE=PC ，求点E 的坐标；二次函数y ＝ax ²＋bx ＋c 的图象和性质练习答案一、选择题（每题3分）1．对于二次函数y=x 2-4x+7的图象，下列说法正确的是（）A ．开口向下B ．对称轴是x=-2C ．顶点坐标是（2，3）D ．与x 轴有两个交点【答案】C ．【解析】试题解析：∵y=x 2-4x+7=（x-2）2+3，∴对称轴为x=2，顶点坐标为（2，3），故B 错误，C 正确，故选C ．考点：二次函数的性质．2．抛物线223y x x =-++的顶点坐标是()A ．(-1，4)B ．(1，3)C ．(-1，3)D ．(1，4)【答案】D 【解析】试题分析：将二次函数配成顶点式为：y=－(2x －2x)+3=－(2x －2x+1－1)+3=－2(1)x -+4，则顶点坐标为(1,4)；本题也可以直接利用二次函数的顶点坐标(－2ba，244ac b a -)进行求解.考点：二次函数的顶点坐标3．已知抛物线y ＝ax 2＋bx ＋c 的开口向上，顶点坐标为(3，-2)，那么该抛物线有()A ．最小值-2B ．最大值-2C ．最小值3D ．最大值3【答案】A ．【解析】试题解析：由抛物线y=ax2+bx+c 的开口向上，顶点坐标为（3，-2），可知该抛物线有最小值-2，故选A ．考点：二次函数的最值．4．已知二次函数y=ax 2+bx+c （a ＜0）的图象如图所示，当-5≤x≤0时，下列说法正确的是（）A ．有最小值-5、最大值0B ．有最小值-3、最大值6C ．有最小值0、最大值6D ．有最小值2、最大值6【答案】B ．【解析】试题解析：由二次函数的图象可知，∵-5≤x≤0，∴当x=-2时函数有最大值，y 最大=6；当x=-5时函数值最小，y 最小=-3．故选B ．考点：二次函数的最值．5．已知开口向下的抛物线的顶点坐标为（2，0），则函数y 随x 的增大而增大的取值范围为（）．A ．x ＞0B ．x ＜0C ．x ＞2D ．x ＜2【答案】D ．【解析】试题分析：因为顶点坐标是（2，0），所以对称轴是直线x=2，又因为抛物线开口向下，所以在对称轴左侧，函数y 随x 的增大而增大，故自变量的取值范围是x ＜2，故选D ．考点：函数的增减性．6．函数y=-2x 2-8x+m 的图象上有两点A （x 1，y 1），B （x 2，y 2），若-2＜x 1＜x 2，则A ．21y y <B ．21y y >C ．21y y =D ．1y 、2y 的大小不确定【答案】B ．【解析】试题解析：∵y=-2x 2-8x+m=-2（x+2）2+m+8，∴对称轴是x=-2，开口向下，距离对称轴越近，函数值越大，∵-2＜x 1＜x 2，∴y 1＞y 2．故选B ．考点：1．二次函数图象上点的坐标特征；2．二次函数的性质．7．把二次函数y ＝－x 2－x ＋3用配方法化成y ＝a （x －h ）2＋k 的形式（）A ．y ＝－（x －2）2＋2B ．y ＝（x －2）2＋4C ．y ＝－（x ＋2）2＋4D ．y ＝2＋3【答案】C ．【解析】试题分析：y=-x 2-x+3=-（x 2+4x+4）+1+3=-（x+2）2+4,故答案选C ．考点：二次函数的解析式的三种形式．8．若b ＜0，则二次函数y=x 2-bx-1的图象的顶点在：A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C ．【解析】试题解析：二次函数y=x 2-bx-1的图象的顶点为（-21b -⨯，()()241141b ⨯⨯---⨯），即（2b ，244b --），∵b ＜0，∴2b＜0，244b --＜0，∴（2b ，244b --）在第三象限．故选C ．考点：二次函数图象与系数的关系．9．抛物线222y x x =-＋-经过平移得到2y x =-，平移方法是（）A ．向右平移1个单位，再向下平移1个单位B ．向右平移1个单位，再向上平移1个单位C ．向左平移1个单位，再向下平移1个单位D ．向左平移1个单位，再向上平移1个单位【答案】D 【解析】试题分析：因为2222(1)3y x x x ==----＋-，所以抛物线222y x x =-＋-向左平移1个单位，再向上平移1个单位可以得到2y x =-，故选：D ．考点：抛物线的平移．10．函数y=x 2+3x －4的图象与y 轴的交点坐标是A ．（2，0）B ．（－2，0）C ．（0，4）D ．（0，－4）【答案】D ．【解析】试题解析：把x=0代入y=x 2+3x-4得y=-4，所以函数y=x 2+3x-4的图象与y 轴的交点坐标为（0，-4）．考点：二次函数图象上点的坐标特征．二、填空题（每题3分）11．抛物线y ＝2x 2-bx ＋3的对称轴是直线x ＝1，则b 的值为___【答案】-4.【解析】试题解析：∵-22b-⨯=-1，∴b=-4考点：二次函数的性质．12．已知二次函数222y x mx =++，当x ＞2时，y 的值随x 值的增大而增大，则实数m 的取值范围是__．【答案】2m ≥-．【解析】试题分析：抛物线的对称轴为直线x=221m-⨯=﹣m ，∵当x ＞2时，y 的值随x 值的增大而增大，∴﹣m≤2，解得m≥﹣2．故答案为：m≥﹣2．考点：二次函数的性质．13．二次函数226y x x =-+的最小值是____．【答案】5．【解析】试题分析：226y x x =-+=2(1)5x -+，可见，二次函数的最小值为5．故答案为：5．考点：二次函数的最值．14．抛物线y=x 2﹣4x+3的顶点坐标是．【答案】（2，-1）【解析】试题分析：因为二次函数2()y a x h k =-+的顶点坐标是（h ，k ），所以函数y=x 2﹣4x+3=（x-2）2-1的图象的顶点坐标是（2，－1）．考点：二次函数的顶点坐标15．抛物线332-+-=x x y 与y 轴的交点坐标为___________．【答案】（0，-3）．【解析】试题分析：因为抛物线与y 轴交点的横坐标是0，所以将x=0代入解析式，得y=-3，所以抛物线332-+-=x x y 与y 轴的交点坐标为（0，-3）．考点：抛物线与坐标轴交点坐标的规律．16．二次函数y=x 2+2x 的顶点坐标为，对称轴是直线．【答案】（-1，-1），x=-1．【解析】试题分析：二次函数y=ax 2+bx+c 中，顶点坐标是（-a b 2，aac 4-4b 2），对称轴是直线x=-a b2，所给二次函数中，a=1，b=2，c=0，代入公式中，对称轴是直线x=-a b 2=-22=-1；顶点横坐标是-1，顶点纵坐标是aac 4-4b 2=4-22=-1．所以顶点坐标为（-1，-1），对称轴是直线x=-1．考点：二次函数的对称轴与顶点坐标公式．17．将抛物线22y x x =-向上平移3个单位，再向右平移4个单位得到的抛物线是_______．【答案】2(5)2y x =-+或21027y x x =-+．【解析】试题分析：22y x x =-=2(1)1x --，根据平移规律，向上平移3个单位，再向右平移4个单位得到的抛物线是：2(5)2y x =-+，将顶点式展开得，21027y x x =-+．故答案为：2(5)2y x =-+或21027y x x =-+．考点：1．二次函数图象与几何变换；2．压轴题；3．几何变换．18．若二次函数24y ax x a -+＝的最小值是－3，则a ＝_________．【答案】1【解析】试题分析：因为二次函数24y ax x a -+＝的最小值是－3，所以241634a y a-==-，解得a=1或-4，又二次函数有最小值，所以a ＞0，所以a=1．考点：二次函数的最值19．将二次函数y ＝2x －2x －3化为y ＝（x －h ）2＋k 的形式，则__________________．【答案】y ＝（x －1）2－4【解析】试题分析：y ＝2x －2x －3=2x －2x+1-4=（x －1）2－4．考点：配方法．20．已知A （﹣2，y 1）、B （0，y 2）、C （1，y 3）三点都在抛物线y=kx 2+2kx+k 2+k （k ＜0）的图象上，则y 1、y 2、y 3的大小关系是．【答案】y1=y2＞y3【解析】试题分析：对称轴为直线x=﹣22kk=﹣1，∵A（﹣2，y1）、B（0，y2），∴A、B是对称点，∴y1=y2，∵k＜0，∴x＞﹣1时，y的值随x的增大而减小，∴y2＞y3，∴y1=y2＞y3．故答案为：y1=y2＞y3．考点：二次函数图象上点的坐标特征.三、计算题（每题10分）21.画出二次函数y=﹣x2+2x+3的图像，并根据图像解答下列问题：（1）x取何值时，函数值y随x的增大而减小；（2）x取何值时，y≤3．【答案】正确画出图像；（1）x≥1；（2）x≤0或x≥2【解析】试题分析：（1）确定出二次函数的对称轴即可解答；（2）利用图象直接解答即可．试题解析：（1）原式可化为：y=﹣x2+2x+3=-（x-1）2+4，则函数图象的对称轴为x=1，∵函数图象开口向下，所以自变量x≥1时，y随x的增大而减小；（2）由图可知当0＜x＜2时，y＞3，所以当x≤0或x≥2时，y≤3．考点：二次函数的图像及性质．22.已知二次函数y=﹣x 2+x+4．（1）求抛物线的顶点坐标和对称轴；（2）当x 取何值时，y 随x 的增大而增大？当x 取何值时，y 随x 的增大而减小？当x 取何值时，y 有最大值还是最小值？是多少？【答案】（1）顶点坐标为（1，29），对称轴为x=1；（2）当x ＜1时，y 随x 的增大而增大；当x ＞1时y 随x 的增大而减小；函数有最大值为29．【解析】试题分析：（1）根据函数解析式可求出顶点坐标，对称轴及与坐标轴的交点；（2）根据确定的对称轴及顶点坐标确定其增减性即可．试题解析：（1）∵y=﹣21x 2+x+4=﹣21（x 2﹣2x+1﹣1）+4=﹣21（x ﹣1）2+29，∴顶点坐标为（1，29），对称轴为x=1；（2）∵开口向下且对称轴为x=1，∴当x ＜1时，y 随x 的增大而增大；当x ＞1时y 随x 的增大而减小；函数有最大值为29．考点：1.二次函数的性质；2.二次函数的最值．23.如图，已知二次函数21232y x x =-+的图象的顶点为A ，且与y 轴交于点C ．（1）求点A 与点C 的坐标；（2）若将此函数的图象沿z 轴向右平移1个单位，再沿y 轴向下平移3个单位，请直接写出平移后图象所对应的函数关系式及点C 的对应点的坐标；（3）若A （m ，1y ），B （m ＋1，2y ）两点都在此函数的图象上，试比较1y 与2y 的大小．【答案】（1）A(2，1)，C （0，3）；(2)21(3)22y x =--，C′（1，0）；（3）当32m <时，12y y >，当32m =时，12y y =，当32m >时，12y y <．【解析】试题分析：（1）把抛物线的解析式配方即可得到顶点A 的坐标，令抛物线解析式的x=0，算出y ，即可得到抛物线y 轴交于点C 的坐标；（2）根据平移规律即可得到平移后的解析式和点C 对应点的坐标；（3）把m 和m+1代入抛物线解析式，算出2132y y m -=-，进行讨论即可．试题解析：（1）21232y x x =-+=21(2)12x -+，∴顶点A 的坐标为(2，1)，在21232y x x =-+中，令x=0，得y=3，∴C （0，3）；（2）平移后的抛物线方程为：21(3)22y x =--，点C 的对应点的坐标为（1，0）；（3）211232y m m =-+，221(1)2(1)32y m m =+-++，2132y y m -=-，∴当32m <时，12y y >，当32m =时，12y y =，当32m >时，12y y <．考点：1．二次函数的图象；2．二次函数的性质；3．二次函数与几何变换．（时间：60分钟，满分90分）班级：___________姓名：___________得分：___________一、选择题（每题3分）1．把函数2241y x x =-++的图象先向左平移2个单位，再向上平移3个单位，所得的抛物线解析式是（）A ．22(1)6y x =--+B ．22(1)6y x =---C ．22(1)6y x =-++D ．22(1)6y x =-+-【答案】C ．【解析】试题分析：原抛物线的顶点坐标为（1，3），向左平移2个单位，再向上平移3个单位得到新抛物线的顶点坐标为（﹣1，6）．可设新抛物线的解析式为：22()y x h k =--+，代入得：22(1)6y x =-++．故选C ．考点：二次函数图象与几何变换．2．已知抛物线y=x 2﹣ax+a+3对称轴在y 轴的右侧，顶点在x 轴上，则a 的值是（）A ．6B ．﹣2C ．6或﹣2D ．4【答案】A ．【解析】试题解析：y=x 2-ax+a+3对称轴在y 轴的右侧，顶点在x 轴上，x=2a＞0，241(3)()41a a ⨯⨯+--⨯=0解得a=6，a=-2（不符合题意的要舍去）．故选：A ．考点：二次函数的性质．3．已知函数4212--=x x y ，当函数值y 随x 的增大而减小时，x 的取值范围是（）A ．x ＜1B ．x ＞1C ．x ＞－2D ．－2＜x ＜4【答案】A 【解析】试题分析：因为1121b x a -=-=-=，且12a =＞0，所以当x ＜1时，函数值y 随x 的增大而减小，故选：A ．考点：二次函数的性质．4．二次函数y=a 2x +bx ﹣1（a≠0）的图象经过点（1，1），则a+b+1的值是（）A ．﹣3B ．﹣1C ．2D ．3【答案】D 【解析】试题分析：将点（1，1）代入可得：a+b －1=1，即a+b=2，则a+b+1=3．考点：函数上的点，整体思想5．二次函数522-+=x x y 取最小值时，自变量x 的值是（）A ．2B ．-2C ．1D ．-1【答案】D 【解析】试题分析：对于二次函数，当a ＞0时，x=－2b a 时，y 有最小值，最小值为244ac b a -．根据题意可得：－2ba=－1．考点：二次函数的顶点6．抛物线y=x 2﹣2x+3的顶点坐标是（）A ．（1，﹣2）B ．（1，2）C ．（﹣1，2）D ．（﹣1，﹣2）【答案】B ．【解析】试题解析：∵y=x 2﹣2x+3=x 2﹣2x+1﹣1+3=（x ﹣1）2+2，∴抛物线y=x 2﹣2x+3的顶点坐标是（1，2）．故选B ．考点：二次函数的性质．7．已知抛物线y=-2x 2+12x-13，则下列关于此抛物线说法正确的是（）A ．开口向下，对称轴为直线x=-3B ．顶点坐标为（-3，5）C ．最小值为5D ．当x ＞3时，y 随x 的增大而减小【答案】D 【解析】试题分析：函数的顶上坐标为（3,5），则对称轴为直线x=3，最大值为5，当x ＞3时，y 随想的增大而减小．考点：二次函数的性质8．用配方法将二次函数y=3x 2-4x-2写成形如y=a （x+m ）2+n 的形式，则m 、n 的值分别是（）A ．m=32，n=310B ．m=-32，n=-310C ．m=2，n=6D ．m=2，n=-2【答案】B 【解析】试题分析：y=32x －4x －2=324()3x x -－2=32444()399x x -+-－2=32210(33x --，则m=－23，n=－103．考点：二次函数的顶点式．9．二次函数y=x 2﹣4x+5的最小值是()A ．﹣1B ．1C ．3D ．5【答案】B.【解析】试题分析：化为顶点式得：y=x 2﹣4x+5=x 2﹣4x+22+1=（x ﹣2）2+1，当x=2时，二次函数y=x 2﹣4x+5取得最小值为1．故选B ．考点：二次函数的最值．10．若点A （2，y 1），B （﹣3，y 2），C （﹣1，y 3）三点在抛物线y=x 2﹣4x ﹣m 的图象上，则y 1、y 2、y 3的大小关系是（）A.y 1＞y 2＞y 3B.y 2＞y 1＞y 3C.y 2＞y 3＞y 1D.y 3＞y 1＞y 2【答案】C 【解析】试题分析：根据函数的解析式可知a=1＞0，所以开口向上，再求出二次函数y=x 2﹣4x ﹣m 的图象的对称轴x=﹣2ba=2，然后判断出A （2，y 1）中x=2，因此y 1最小，B （﹣3，y 2），C （﹣1，y 3）在抛物线上的都在对称轴的左侧，再根据二次函数的增减性，在对称轴的左侧，y 随x 得增大而减小，故y 2＞y 3．即y 2＞y 3＞y 1.故选C ．考点：二次函数的性质；二次函数的图象11．抛物线2256y x x =-+的对称轴是（）A 、54x =B 、52x =C 、54x =-D 、52x =-【答案】A 【解析】试题分析：根据对称轴公式2b x a =-,可得54x =.考点：二次函数二、填空题（每题3分）12.二次函数243y x x =--的顶点坐标是（，）．【答案】（2，﹣7）．【解析】试题分析：∵243y x x =--=2(2)7x --，∴二次函数243y x x =--的顶点坐标为（2，﹣7）．故答案为：（2，﹣7）．考点：二次函数的性质．13．函数y=x 2+2x+1，当y=0时，x=_______________；当1＜x ＜2时，y 随x 的增大而_____________（填写“增大”或“减小”）【答案】－1；增大．【解析】试题分析：将y=0代入函数，求出一元二次方程的解；对于开口向上的函数，当x ＞对称轴时，y 随x 的增大而增大，当x ＜对称轴时，y 随x 的增大而减小．当y=0时，即2x +2x+1=0，解得：x=－1；根据函数解析式可得函数的对称轴为直线x=－1，则当1＜x ＜2时，y 随x 的增大而增大．考点：二次函数的性质．14．将抛物线的解析式y=向上平移3个单位长度，在向右平移1个单位长度后，得到的抛物线的解析式是．【答案】y=【解析】试题分析：因为2265(3)4y x x x =-+=--，所以根据抛物线的平移规律可知：将抛物线的解析式y=向上平移3个单位长度，在向右平移1个单位长度后，得到的抛物线的解析式是22(4)1815y x x x =--=-+．考点：抛物线的平移．15．函数y=x 2+4ax+2在x≤6时，y 随着x 的增大而减小，则a 的取值范围是．【答案】a≤-3．【解析】试题分析：先利用二次函数的性质求出抛物线的对称轴为直线x=-2a ，则当x ＜-2a 时，y 的值随x 值的增大而减小，由于x≤6时，y 的值随x 值的增大而减小，于是得到-2a≤1．从而求出a 的取值范围．试题解析：抛物线的对称轴为直线x=-2a 由于抛物线开口向上，当x ＜-2a 时，y 的值随x 值的增大而减小，而x≤6时，y 的值随x 值的增大而减小，所以-2a≥6解得：a≤-3．考点：二次函数的性质．16．二次函数1232+-=x x y 的图象的开口方向________，顶点是________，对称轴是________．【答案】向上，⎪⎭⎫⎝⎛32,31，直线31=x 【解析】试题分析：因为a=3＞0，所以图象的开口方向上，又1232+-=x x y =223()13x x -+=22113()1393x x -++-2123(33x =-+，所以顶点是⎪⎭⎫⎝⎛32,31，对称轴是直线31=x ．考点：二次函数的性质．17．二次函数622+-=x x y 的最小值是．【答案】5【解析】试题分析：：∵二次函数y=x 2-2x+6可化为y=（x-1）2+5的形式，∴二次函数y=x 2-2x+6的最小值是5．故答案为：5考点：二次函数的最值18．已知二次函数2y ax bx c =++中，函数y 与自变量x 的部分对应值如下表：x…－2－1012…y …－3－4－305…则此二次函数的对称轴为．【答案】直线1x =-．【解析】试题分析：观察表格发现函数的图象经过点（﹣2，﹣3）和（0，﹣3），∵两点的纵坐标相同，∴两点关于对称轴对称，∴对称轴为：2012x -+==-，故答案为：直线1x =-．考点：二次函数的性质．19．函数342++-=x x y 有值（填“最大”或“最小”），所求最值是.【答案】最大,7.【解析】试题分析：由于a=-1＜0，知二次函数有最大值，代入顶点坐标公式即可求出最大值.试题解析：y=-x 2+4x+3=-(x-2)2+7∵a=-1＜0，∴二次函数y=-x 2+4x+3有最大值，最大值为7.考点：二次函数的最大值.20．小颖在二次函数y=2x 2+4x+5的图象上找到三点（－1，y 1），（21，y 2），（－321，y 3），则你认为y 1，y 2，y 3的大小关系应为．【答案】321y y y 【解析】试题分析：对于开口向上的二次函数，到对称轴距离越远的点所对应的函数值就越大．本题中的对称轴为直线x=1．考点：二次函数的函数值大小比较．三、计算题（每题10分）21.已知二次函数y=x 2+2x-1．（1）写出它的顶点坐标；（2）当x 取何值时，y 随x 的增大而增大；【答案】（1）（-1，-2）；（2）当x ＞-1时，y 随x 的增大而增大；【解析】试题分析：（1）配方后直接写出顶点坐标即可；（2）确定对称轴后根据其开口方向确定其增减性即可；试题解析：（1）y=x 2+2x-1=（x+1）2-2，∴顶点坐标为：（-1，-2）；（2）∵y=x 2+2x-1=（x+1）2-2的对称轴为：x=-1，开口向上，∴当x ＞-1时，y 随x 的增大而增大；考点：二次函数的性质22.已知抛物线4212+--=x x y ，（1）用配方法确定它的顶点坐标、对称轴；（2）x 取何值时，y 随x 增大而减小？【答案】（1）y 29)1(212++-x ，它的顶点坐标为（-1，29），对称轴为直线1-=x 。

人教版数学九年级上册第22章 22.1.3二次函数y=ax2+bx+c的图像和性质同步练习(含答案

人教版数学九年级上册第22章22.1.3二次函数y=ax2+bx+c的图像和性质同步练习一、单选题（共12题；共24分）1.抛物线（m是常数）的顶点在（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.a≠0，函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是（）A. B. C. D.3.抛物线y=﹣（x+ ）2﹣3的顶点坐标是（）A. （，﹣3）B. （﹣，﹣3）C. （，3）D. （﹣，3）4.矩形ABCD的两条对称轴为坐标轴，点A的坐标为（2,1）.一张透明纸上画有一个点和一条抛物线，平移透明纸，这个点与点A重合，此时抛物线的函数表达式为y=x2，再次平移透明纸，使这个点与点C重合，则该抛物线的函数表达式变为（）A. y=x2+8x+14B. y=x2-8x+14C. y=x2+4x+3D. y=x2-4x+35.函数y=﹣21（x﹣2）2+5的顶点坐标为（）A. （2，5）B. （﹣2，5）C. （2，﹣5）D. （﹣2，-5）6.对于二次函数y=x2﹣2mx﹣3，下列结论错误的是（）A. 它的图象与x轴有两个交点B. 方程x2﹣2mx=3的两根之积为﹣3C. 它的图象的对称轴在y轴的右侧D. x＜m时，y随x的增大而减小7.抛物线y=2（x﹣3）2+4顶点坐标是（）A. （3，4）B. （﹣3，4）C. （3，﹣4）D. （2，4）8.对于函数y=﹣2（x﹣m）2的图象，下列说法不正确的是（）A. 开口向下B. 对称轴是x=mC. 最大值为0D. 与y轴不相交9.抛物线y=x2﹣2x+3 的对称轴为（）A. 直线x=﹣1B. 直线x=﹣2C. 直线x=1D. 直线x=210.二次函数y=x2+2x﹣3的顶点坐标是（）A. （﹣1，﹣3）B. （1，﹣4）C. （﹣1，﹣2）D. （﹣1，﹣4）11.抛物线y=3（x﹣5）2的顶点坐标是（）A. （5，0）B. （3，5）C. （-3，5）D. （﹣5，0）12.由于被墨水污染，一道数学题仅能见到如下文字：已知二次函数y=ax2+bx+c的图象过点（1，0）…求证：这个二次函数的图象关于直线x=2对称，根据现有信息，题中的二次函数具有的性质：（1 ）过点（3，0）（2 ）顶点是（1，﹣2）（3 ）在x轴上截得的线段的长度是2（4 ）c=3a正确的个数（）A. 4个B. 3个C. 2个D. 1个二、填空题（共5题；共8分）13.当x=________时，二次函数y=x2﹣2x+6有最小值________．14.经过A（4，0），B（﹣2，0），C（0，3）三点的抛物线解析式是________．15.已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是________．（只需写一个）16.对于实数p，q，我们用符号min{p，q}表示p，q两数中较小的数，如min{1，2}=1，因此，min{﹣，﹣}=________；若min{（x﹣1）2，x2}=1，则x=________．17.如图，在边长为6cm的正方形ABCD中，点E、F、G、H分别从点A、B、C、D同时出发，均以1cm/s 的速度向点B、C、D、A匀速运动，当点E到达点B时，四个点同时停止运动，在运动过程中，当运动时间为________ s时，四边形EFGH的面积最小，其最小值是________ cm2．三、解答题（共2题；共10分）18.已知抛物线的顶点为（﹣1，2），且过点（2，1），求该抛物线的函数解析式．19.已知当x=2时，二次函数有最大值8，且图象过点（0，4），求此函数的关系式．四、综合题（共2题；共30分）20.在平面直角坐标系xOy中，抛物线y=ax2+bx+2过点A（﹣2，0），B（2，2），与y轴交于点C．（1）求抛物线y=ax2+bx+2的函数表达式；（2）若点D在抛物线y=ax2+bx+2的对称轴上，求△ACD的周长的最小值；（3）在抛物线y=ax2+bx+2的对称轴上是否存在点P，使△ACP是直角三角形？若存在直接写出点P的坐标，若不存在，请说明理由．21.如图1，抛物线y=ax2+bx+2与x轴交于A，B两点，与y轴交于点C，AB=4，矩形OBDC的边CD=1，延长DC交抛物线于点E．（1）求抛物线的解析式；（2）如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO于点G，作PH⊥EO，垂足为H．设PH的长为l，点P的横坐标为m，求l与m的函数关系式（不必写出m的取值范围），并求出l的最大值；（3）如果点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M，A，C，N为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M的坐标；若不存在，请说明理由．答案解析部分一、单选题1.【答案】A【解析】【解答】解：∵y=x2-2x+m2+2.∴y=（x-1）2+m2+1.∴顶点坐标（1，m2+1）.∴顶点坐标在第一象限.故答案为A.【分析】根据配方法得出顶点坐标，从而判断出象限.2.【答案】D【解析】【解答】解：当a＞0时，函数y= 的图象位于一、三象限，y=﹣ax2+a的开口向下，交y轴的正半轴，没有符合的选项，当a＜0时，函数y= 的图象位于二、四象限，y=﹣ax2+a的开口向上，交y轴的负半轴，D选项符合；故选D．【分析】分a＞0和a＜0两种情况分类讨论即可确定正确的选项．3.【答案】B【解析】【解答】解：y=﹣（x+ ）2﹣3是抛物线的顶点式，根据顶点式的坐标特点可知，顶点坐标为（﹣，﹣3）．故选B．【分析】已知抛物线解析式为顶点式，可直接写出顶点坐标．4.【答案】A【解析】【解答】解：如图，A（2,1），则可得C（-2，-1）.由A（2,1）到C（-2，-1），需要向左平移4个单位，向下平移2个单位，则抛物线的函数表达式为y=x2，经过平移变为y=（x+4）2-2= x2+8x+14，故选A.【分析】题中的意思就是将抛物线y=x2平移后，点A平移到了点C，由A的坐标不难得出C的坐标，由平移的性质可得点A怎样平移到点C，那么抛物线y=x2，就怎样平移到新的抛物线.5.【答案】A【解析】【解答】解：因为y=﹣21（x﹣2）2+5是抛物线的顶点式，根据顶点式的坐标特点可知，顶点坐标为（2，5）；故选A．【分析】根据二次函数的顶点式直接求解．6.【答案】C【解析】【解答】解：A、∵b2﹣4ac=（2m）2+12=4m2+12＞0，∴二次函数的图象与x轴有两个交点，故此选项正确，不合题意；B、方程x2﹣2mx=3的两根之积为：=﹣3，故此选项正确，不合题意；C、m的值不能确定，故它的图象的对称轴位置无法确定，故此选项错误，符合题意；D、∵a=1＞0，对称轴x=m，∴x＜m时，y随x的增大而减小，故此选项正确，不合题意；故选：C．【分析】直接利用二次函数与x轴交点个数、二次函数的性质以及二次函数与方程之间关系分别分析得出答案．7.【答案】A【解析】【解答】解：y=2（x﹣3）2+4是抛物线的顶点式，根据顶点式的坐标特点可知，顶点坐标为（3，4）．故选A．【分析】已知解析式为顶点式，可直接根据顶点式的坐标特点，求顶点坐标．8.【答案】D【解析】【解答】解：对于函数y=﹣2（x﹣m）2的图象，∵a=﹣2＜0，∴开口向下，对称轴x=m，顶点坐标为（m，0），函数有最大值0，故A、B、C正确，故选D．【分析】根据二次函数的性质即可一一判断．9.【答案】C【解析】【解答】解：∵y=x2﹣2x+3=（x﹣1）2+2，∴对称轴为x=1，故选C．【分析】把抛物线化为顶点式可求得答案．10.【答案】D【解析】【解答】解：∵y=x2+2x﹣3=（x+1）2﹣4，∴抛物线顶点坐标为（﹣1，﹣4），故选D．【分析】把二次函数化为顶点式可求得答案．11.【答案】A【解析】【解答】解：抛物线y=3（x﹣5）2的顶点坐标是（5，0）．故选A．【分析】根据顶点式解析式写出顶点坐标即可．12.【答案】B【解析】【解答】解：（1）因为图象过点（1，0），且对称轴是直线x=2，另一个对称点为（3，0），正确；（2）顶点的横坐标应为对称轴，本题的顶点坐标与已知对称轴矛盾，错误；（3）抛物线与x轴两交点为（1，0），（3，0），故在x轴上截得的线段长是2，正确；（4）图象过点（1，0），且对称轴是直线x=﹣=2时，则b=﹣4a，即a﹣4a+c=0，即可得出c=3a，正确．正确个数为3．故选B．【分析】分别利用二次函数的对称性以及二次函数图象上点的坐标性质进而得出答案．二、填空题13.【答案】1；5【解析】【解答】解：∵y=x2﹣2x+6=（x﹣1）2+5，∴当x=1时，二次函数y=x2﹣2x+6有最小值5．故答案为：1、5．【分析】把x2﹣2x+6化成（x﹣1）2+5，即可求出二次函数y=x2﹣2x+6的最小值是多少．14.【答案】y=﹣x2+ x+3【解析】【解答】解：根据题意设抛物线解析式为y=a（x+2）（x﹣4），把C（0，3）代入得：﹣8a=3，即a=﹣，则抛物线解析式为y=﹣（x+2）（x﹣4）=﹣x2+ x+3，故答案为y=﹣x2+ x+3．【分析】根据A与B坐标特点设出抛物线解析式为y=a（x﹣2）（x﹣4），把C坐标代入求出a的值，即可确定出解析式．15.【答案】y=2x2﹣1【解析】【解答】解：∵抛物线的顶点坐标为（0，﹣1），∴该抛武线的解析式为y=ax2﹣1，又∵二次函数的图象开口向上，∴a＞0，∴这个二次函数的解析式可以是y=2x2﹣1，故答案为：y=2x2﹣1．【分析】根据顶点坐标知其解析式满足y=ax2﹣1，由开口向上知a＞0，据此写出一个即可．16.【答案】；2或﹣1【解析】【解答】解：min{﹣，﹣}=﹣，∵min{（x﹣1）2，x2}=1，∴当x＞0.5时，（x﹣1）2=1，x﹣1=±1，x﹣1=1，x﹣1=﹣1，解得：x1=2，x2=0（不合题意，舍去），当x≤0.5时，x2=1，解得：x1=1（不合题意，舍去），x2=﹣1，故答案为：；2或﹣1．【分析】首先理解题意，进而可得min{﹣，﹣}=﹣，min{（x﹣1）2，x2}=1时再分情况讨论，当x＞0.5时和x≤0.5时，进而可得答案．17.【答案】3；18【解析】【解答】解：设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t，根据题意得：S四边形EFGH=S正方形ABCD﹣4S△AEH=6×6﹣4× t（6﹣t）=2t2﹣12t+36=2（t﹣3）2+18，∴当t=3时，四边形EFGH的面积取最小值，最小值为18．故答案为：3；18【分析】设运动时间为t（0≤t≤6），则AE=t，AH=6﹣t，由四边形EFGH的面积=正方形ABCD的面积﹣4个△AEH的面积，即可得出S四边形EFGH关于t的函数关系式，配方后即可得出结论．三、解答题18.【答案】解：∵抛物线的顶点为（﹣1，2），∴设抛物线的解析式为y=a（x+1）2+2，∵经过点（2，1），∴代入得：1=a（2+1）2+2，解得：a=﹣，即y=﹣（x+1）2+2【解析】【分析】设抛物线的解析式为y=a（x+1）2+2，把点（1，4）代入得出1=a（1+2）2+2，求出a即可．19.【答案】解：∵当x=2时，二次函数有最大值8，∴顶点坐标为（2，8）；设二次函数的解析式为y=a（x﹣2）2+8；将点（0，4）代入得，a=﹣1，∴二次函数的解析式为：y=﹣（x﹣2）2+8【解析】【分析】根据二次函数的对称轴为x=2，函数的最小值为8，可知其顶点坐标为（2，8）；因此本题可用顶点式设所求的二次函数解析式，然后将点（0，4）的坐标代入抛物线中即可求得函数的解析式．四、综合题20.【答案】（1）解：把点A（﹣2，0），B（2，2）代入抛物线y=ax2+bx+2中，，解得：，∴抛物线函数表达式为：y=﹣x2+ x+2（2）解：y=﹣x2+ x+2=﹣（x﹣1）2+ ；∴对称轴是：直线x=1，如图1，过B作BE⊥x轴于E，∵C（0，2），B（2，2），对称轴是：x=1，∴C与B关于x=1对称，∴CD=BD，连接AB交对称轴于点D，此时△ACD的周长最小，∵BE=2，AE=2+2=4，OC=2，OA=2，∴AB= =2 ，AC= =2 ，∴△ACD的周长=AC+CD+AD=AC+BD+AD=AC+AB=2 +2 ；答：△ACD的周长的最小值是2 +2（3）解：存在，分两种情况：①当∠ACP=90°时，△ACP是直角三角形，如图2，过P作PD⊥y轴于D，设P（1，y），则△CGP∽△AOC，∴，∴，∴CG=1，∴OG=2﹣1=1，∴P（1，1）；②当∠CAP=90°时，△ACP是直角三角形，如图3，设P（1，y），则△PEA∽△AOC，∴，∴= ，∴PE=3，∴P（1，﹣3）；综上所述，△ACP是直角三角形时，点P的坐标为（1，1）或（1，﹣3）．【解析】【分析】（1）利用待定系数法求抛物线的函数表达式；（2）由轴对称的最短路径得：因为B与C关于对称轴对称，所以连接AB交对称轴于点D，此时△ACD的周长最小，利用勾股定理求其三边相加即可；（3）存在，当A和C分别为直角顶点时，画出直角三角形，设P（1，y），根据三角形相似列比例式可得P的坐标．21.【答案】（1）解：∵矩形OBDC的边CD=1，∴OB=1，∵AB=4，∴OA=3，∴A（﹣3，0），B（1，0），把A、B两点坐标代入抛物线解析式可得，解得，∴抛物线解析式为y=﹣x2﹣x+2；（2）解：在y=﹣x2﹣x+2中，令y=2可得2=﹣x2﹣x+2，解得x=0或x=﹣2，∴E（﹣2，2），∴直线OE解析式为y=﹣x，由题意可得P（m，﹣m2﹣m+2），∵PG∥y轴，∴G（m，﹣m），∵P在直线OE的上方，∴PG=﹣m2﹣m+2﹣（﹣m）=﹣m2﹣m+2=﹣（m+ ）2+ ，∵直线OE解析式为y=﹣x，∴∠PGH=∠COE=45°，∴l= PG= [﹣（m+ ）2+ ]=﹣（m+ ）2+ ，∴当m=﹣时，l有最大值，最大值为；（3）解：①当AC为平行四边形的边时，则有MN∥AC，且MN=AC，如图，过M作对称轴的垂线，垂足为F，设AC交对称轴于点L，则∠ALF=∠ACO=∠FNM，在△MFN和△AOC中∴△MFN≌△AOC（AAS），∴MF=AO=3，∴点M到对称轴的距离为3，又y=﹣x2﹣x+2，∴抛物线对称轴为x=﹣1，设M点坐标为（x，y），则|x+1|=3，解得x=2或x=﹣4，当x=2时，y=﹣，当x=﹣4时，y= ，∴M点坐标为（2，﹣）或（﹣4，﹣）；②当AC为对角线时，设AC的中点为K，∵A（﹣3，0），C（0，2），∴K（﹣，1），∵点N在对称轴上，∴点N的横坐标为﹣1，设M点横坐标为x，∴x+（﹣1）=2×（﹣）=﹣3，解得x=﹣2，此时y=2，∴M（﹣2，2）；综上可知点M的坐标为（2，﹣）或（﹣4，﹣）或（﹣2，2）．【解析】【分析】（1）由条件可求得A、B的坐标，利用待定系数法可求得抛物线解析式；（2）可先求得E点坐标，从而可求得直线OE解析式，可知∠PGH=45°，用m可表示出PG的长，从而可表示出l的长，再利用二次函数的性质可求得其最大值；（3）分AC为边和AC为对角线，当AC为边时，过M作对称轴的垂线，垂足为F，则可证得△MFN≌△AOC，可求得M到对称轴的距离，从而可求得M点的横坐标，可求得M点的坐标；当AC为对角线时，设AC的中点为K，可求得K的横坐标，从而可求得M的横坐标，代入抛物线解析式可求得M点坐标．。

2020—2021年最新华东师大版九年级数学下册二次函数y=ax2+bx+c的图像与性质(含答案).doc

（新课标）华东师大版九年级下册26.2.2二次函数y=ax2+bx+c的图像与性质一．选择题（共8小题）1．已知二次函数y=ax2﹣2x+2（a＞0），那么它的图象一定不经过（）A．第一象限B．第二象限C．第三象限D．第四象限2．抛物线y=2x2，y=﹣2x2，y=x2共有的性质是（）A．开口向下B．对称轴是y轴 C．都有最低点D．y的值随x的增大而减小3．抛物线y=2x2+1的顶点坐标是（）A．（2，1） B．（0，1） C．（1，0） D．（1，2）4．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（）A．开口向下B．对称轴是x=﹣1 C．顶点坐标是（1，2）D．与x轴有两个交点5．二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（）A．函数有最小值B．对称轴是直线x= C．当x＜，y随x的增大而减小D．当﹣1＜x＜2时，y＞06．如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M是抛物线y=x2+bx+c的顶点，则方程x2+bx+c=1的解的个数是（）A．0或2 B．0或1 C．1或2 D．0，1或27．已知二次函数y=a（x﹣h）2+k（a＞0），其图象过点A（0，2），B（8，3），则h的值可以是（）A．6 B．5 C．4 D．38．抛物线y=（x﹣1）2﹣3的对称轴是（）A．y轴B．直线x=﹣1 C．直线x=1 D．直线x=﹣3二．填空题（共6小题）9．如果抛物线y=x2+（m﹣1）x﹣m+2的对称轴是y轴，那么m的值是_________ ．10．抛物线y=2x2﹣1在y轴右侧的部分是_________ （填“上升”或“下降”）．11．已知抛物线y=x2+bx+c经过点A（0，5）、B（4，5），那么此抛物线的对称轴是_________ ．12．二次函数y=x2﹣4x﹣5的图象的对称轴是直线_________ ．13．如果抛物线y=（a+3）x2﹣5不经过第一象限，那么a的取值范围是_________ ．14．若抛物线y=2x2﹣mx﹣m的对称轴是直线x=2，则m= _________ ．三．解答题（共6小题）15．在同一平面内画出函数y=2x2与y=2x2+1的图象．16．如图，已知二次函数y=a（x﹣h）2+的图象经过原点O（0，0），A（2，0）．（1）写出该函数图象的对称轴；（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？17．已知抛物线y=x2﹣x﹣1．（1）求抛物线y=x2﹣x﹣1的顶点坐标、对称轴；（2）抛物线y=x2﹣x﹣1与x轴的交点为（m，0），求代数式m2+的值．18．如图，已知抛物线y=x2﹣x﹣6，与x轴交于点A和B，点A在点B的左边，与y轴的交点为C．（1）用配方法求该抛物线的顶点坐标；（2）求sin∠OCB的值；（3）若点P（m，m）在该抛物线上，求m的值．19．若二次函数y=a1x2+b1x+c1的图象记为C1，其顶点为A，二次函数y=a2x2+b2x+c2的图象记为C2，其顶点为B，且满足点A在C2上，点B在C1上，则称这两个二次函数互为“伴侣二次函数”．（1）一个二次函数的“伴侣二次函数”有_________ 个；（2）①求二次函数y=x2+3x+2与x轴的交点；②求以上述交点为顶点的二次函数y=x2+3x+2的“伴侣二次函数”．（3）试探究a1与a2满足的数量关系．20．已知二次函数y=﹣x2+2x+3图象的对称轴为直线．（1）请求出该函数图象的对称轴；（2）在坐标系内作出该函数的图象；（3）有一条直线过点P（1，5），若该直线与二次函数y=﹣x2+2x+3只有一个交点，请求出所有满足条件的直线的关系式．26.2.2二次函数y=ax2+bx+c的图像与性质参考答案与试题解析一．选择题（共8小题）1．知二次函数y=ax2﹣2x+2（a＞0），那么它的图象一定不经过（）A．第一象限B．第二象限 C．第三象限 D．第四象限考点：二次函数的性质．分析：先根据题意判断出二次函数的对称轴方程，再令x=0求出y的值，进而可得出结论．解答：解：∵二次函数y=ax2﹣2x+2（a＞0）的对称轴为直线x=﹣=﹣=＞0，∴其顶点坐标在第一或四象限，∵当x=0时，y=2，∴抛物线一定经过第二象限，∴此函数的图象一定不经过第三象限．故选C．点评：本题考查的是二次函数的性质，熟知二次函数的对称轴方程是解答此题的关键．2抛物线y=2x2，y=﹣2x2，y=x2共有的性质是（）A．开口向下B．对称轴是y轴 C．都有最低点 D．y的值随x的增大而减小考点：二次函数的性质．分析：结合抛物线的解析式和二次函数的性质，逐项判断即可．解答：解：∵y=2x2，y=x2开口向上，∴A不正确，∵y=﹣2x2，开口向下，∴有最高点，∴C不正确，∵在对称轴两侧的增减性不同，∴D不正确，∵三个抛物线中都不含有一次项，∴其对称轴为y轴，∴B正确，故选B．点评：本题主要考查二次函数的性质，掌握二次函数的开口方向、对称轴、最值、增减性等基础知识是解题的关键．3．抛物线y=2x2+1的顶点坐标是（）A．（2，1）B．（0，1）C．（1，0）D．（1，2）考点：二次函数的性质．分析：根据二次函数的顶点式可求得其顶点坐标．解答：解：∵y=2x2+1=2（x﹣0）2+1，∴抛物线的顶点坐标为（0，1），故选B．点评：本题主要考查抛物线的顶点坐标，掌握顶点式方程y=a（x﹣h）2+k的顶点坐标为（h，k）是解题的关键．4．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（）A．开口向下B．对称轴是x=﹣1 C．顶点坐标是（1，2） D．与x 轴有两个交点考点：二次函数的性质．专题：常规题型．分析：根据抛物线的性质由a=1得到图象开口向上，根据顶点式得到顶点坐标为（1，2），对称轴为直线x=1，从而可判断抛物线与x轴没有公共点．解答：解：二次函数y=（x﹣1）2+2的图象开口向上，顶点坐标为（1，2），对称轴为直线x=1，抛物线与x轴没有公共点．故选：C．点评：本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点式为y=a（x﹣）2+，的顶点坐标是（﹣，），对称轴直线x=﹣b2a，当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，当a＜0时，抛物线y=ax2+bx+c （a≠0）的开口向下．5．二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（）A．函数有最小值 B．对称轴是直线x= C．当x＜，y随x的增大而减小D．当﹣1＜x＜2时，y＞0考点：二次函数的性质．专题：压轴题；数形结合．分析：根据抛物线的开口方向，利用二次函数的性质判断A；根据图形直接判断B；根据对称轴结合开口方向得出函数的增减性，进而判断C；根据图象，当﹣1＜x＜2时，抛物线落在x轴的下方，则y＜0，从而判断D．解答：解：A、由抛物线的开口向上，可知a＞0，函数有最小值，正确，故A 选项不符合题意；B、由图象可知，对称轴为x=，正确，故B选项不符合题意；C、因为a＞0，所以，当x＜时，y随x的增大而减小，正确，故C选项不符合题意；D、由图象可知，当﹣1＜x＜2时，y＜0，错误，故D选项符合题意．故选：D．点评：本题考查了二次函数的图象和性质，解题的关键是利用数形结合思想解题．6．如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M 是抛物线y=x2+bx+c的顶点，则方程x2+bx+c=1的解的个数是（）A．0或2 B．0或1 C．1或2 D．0，1或2考点：二次函数的性质．专题：数形结合；分类讨论；方程思想．分析：分三种情况：点M的纵坐标小于1；点M的纵坐标等于1；点M的纵坐标大于1；进行讨论即可得到方程x2+bx+c=1的解的个数．解答：解：分三种情况：点M的纵坐标小于1，方程x2+bx+c=1的解是2个不相等的实数根；点M的纵坐标等于1，方程x2+bx+c=1的解是2个相等的实数根；点M的纵坐标大于1，方程x2+bx+c=1的解的个数是0．故方程x2+bx+c=1的解的个数是0，1或2．故选：D．点评：考查了二次函数的性质，本题涉及分类思想和方程思想的应用．7．已知二次函数y=a（x﹣h）2+k（a＞0），其图象过点A（0，2），B（8，3），则h的值可以是（）A．6 B．5 C．4 D． 3考点：二次函数的性质．专题：计算题．分析：根据抛物线的顶点式得到抛物线的对称轴为直线x=h，由于所给数据都是正数，所以当对称轴在y轴的右侧时，比较点A和点B到对称轴的距离可得到h＜4．解答：解：∵抛物线的对称轴为直线x=h，∴当对称轴在y轴的右侧时，A（0，2）到对称轴的距离比B（8，3）到对称轴的距离小，∴x=h＜4．故选：D．点评：本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点坐标为（﹣，），对称轴直线x=﹣，二次函数y=ax2+bx+c（a≠0）的图象具有如下性质：①当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x=﹣时，y取得最小值，即顶点是抛物线的最低点．②当a＜0时，抛物线y=ax2+bx+c （a≠0）的开口向下，x＜﹣时，y随x的增大而增大；x＞﹣时，y随x的增大而减小；x=﹣时，y取得最大值，即顶点是抛物线的最高点．8．抛物线y=（x﹣1）2﹣3的对称轴是（）A．y轴B．直线x=﹣1 C．直线x=1 D．直线x=﹣3考点：二次函数的性质．分析：根据二次函数的顶点式y=（x﹣h）2+k，对称轴为直线x=h，得出即可．解答：解：抛物线y=（x﹣1）2﹣3的对称轴是直线x=1．故选：C．点评：本题考查了二次函数的性质，解答此题时要注意抛物线的对称轴是直线，这是此题易忽略的地方．二．填空题（共6小题）9．如果抛物线y=x2+（m﹣1）x﹣m+2的对称轴是y轴，那么m的值是 1 ．考点：二次函数的性质．分析：由对称轴是y轴可知一次项系数为0，可求得m的值．解答：解：∵y=x2+（m﹣1）x﹣m+2的对称轴是y轴，∴m﹣1=0，解得m=1，故答案为：1．点评：本题主要考查抛物线的对称轴，掌握抛物线的对称轴为y轴其一次项系数为0是解题的关键．10．抛物线y=2x2﹣1在y轴右侧的部分是上升（填“上升”或“下降”）．考点：二次函数的性质．分析：根据抛物线解析式可求得其对称轴，结合抛物线的增减性可得到答案．解答：解：∵y=2x2﹣1，∴其对称轴为y轴，且开口向上，∴在y轴右侧，y随x增大而增大，∴其图象在y轴右侧部分是上升，故答案为：上升．点评：本题主要考查二次函数的增减性，掌握开口向上的二次函数在对称轴右侧y随x的增大而增大是解题的关键．11．已知抛物线y=x2+bx+c经过点A（0，5）、B（4，5），那么此抛物线的对称轴是直线x=2 ．考点：二次函数的性质．分析：根据点A、B的纵坐标相等判断出A、B关于对称轴对称，然后列式计算即可得解．解答：解：∵点A（0，5）、B（4，5）的纵坐标都是5相同，∴抛物线的对称轴为直线x==2．故答案为：直线x=2．点评：本题考查了二次函数的性质，观察出A、B是对称点是解题的关键．12．二次函数y=x2﹣4x﹣5的图象的对称轴是直线x=2 ．考点：二次函数的性质．分析：根据二次函数的对称轴公式列式计算即可得解．解答：解：对称轴为直线x=﹣=﹣=2，即直线x=2．故答案为：x=2．点评：本题考查了二次函数的性质，主要利用了对称轴公式，需熟记．13．如果抛物线y=（a+3）x2﹣5不经过第一象限，那么a的取值范围是a＜﹣3 ．考点：二次函数的性质．分析：根据抛物线y=（a+3）x2﹣5不经过第一象限可以确定不等式的开口方向，从而确定a的取值范围．解答：解：∵抛物线y=（a+3）x2﹣5不经过第一象限，∴a+3＜0，解得：a＜﹣3，故答案为：a＜﹣3．点评：考查了二次函数的性质，根据抛物线的开口方向，与y轴的交点，对称轴判断抛物线经过的象限．14．若抛物线y=2x2﹣mx﹣m的对称轴是直线x=2，则m= 8 ．考点：二次函数的性质．分析：根据二次函数的对称轴公式列方程求解即可．解答：解：由题意得，﹣=2，解得m=8．故答案为：8．点评：本题考查了二次函数的性质，熟记对称轴的求法是解题的关键．三．解答题（共6小题）15．在同一平面内画出函数y=2x2与y=2x2+1的图象．考点：二次函数的图象．分析：首先利用描点法作出y=2x2的图象，然后向上移动1个单位得到y=2x2+1的图象即可；解答：解：列表得：﹣2 ﹣1 0 1 2y=2x28 2 0 2 8y=2x2+1 9 3 1 3 9点评：本题考查了二次函数的图象，解题的关键是正确的列表、描点．16．如图，已知二次函数y=a（x﹣h）2+的图象经过原点O（0，0），A（2，0）．（1）写出该函数图象的对称轴；（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？考点：二次函数的性质；坐标与图形变化-旋转．分析：（1）由于抛物线过点O（0，0），A（2，0），根据抛物线的对称性得到抛物线的对称轴为直线x=1；（2）作A′B⊥x轴与B，先根据旋转的性质得OA′=OA=2，∠A′OA=60°，再根据含30度的直角三角形三边的关系得OB=OA′=1，A′B=OB=，则A′点的坐标为（1，），根据抛物线的顶点式可判断点A′为抛物线y=﹣（x﹣1）2+的顶点．解答：解：（1）∵二次函数y=a（x﹣h）2+的图象经过原点O（0，0），A（2，0）．解得：h=1，a=﹣，∴抛物线的对称轴为直线x=1；（2）点A′是该函数图象的顶点．理由如下：如图，作A′B⊥x轴于点B，∵线段OA绕点O逆时针旋转60°到OA′，∴OA′=OA=2，∠A′OA=60°，在Rt△A′OB中，∠OA′B=30°，∴OB=OA′=1，∴A′B=OB=，∴A′点的坐标为（1，），∴点A′为抛物线y=﹣（x﹣1）2+的顶点．点评：本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点坐标为（﹣，），对称轴直线x=﹣，二次函数y=ax2+bx+c（a≠0）的图象具有如下性质：①当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x=﹣时，y取得最小值，即顶点是抛物线的最低点．②当a＜0时，抛物线y=ax2+bx+c （a≠0）的开口向下，x＜﹣时，y随x的增大而增大；x＞﹣时，y随x的增大而减小；x=﹣时，y取得最大值，即顶点是抛物线的最高点．也考查了旋转的性质．17．已知抛物线y=x2﹣x﹣1．（1）求抛物线y=x2﹣x﹣1的顶点坐标、对称轴；（2）抛物线y=x2﹣x﹣1与x轴的交点为（m，0），求代数式m2+的值．考点：二次函数的性质；抛物线与x轴的交点．分析：（1）根据配方法，可得顶点式解析式，根据顶点式解析式，可得答案；（2）根据函数值为0，可得一元二次方程，根据解一元二次方程，可得m的值，根据m的值，可得代数式的值．解答：解：A、y=x2﹣x﹣1=x2﹣x+﹣1﹣=（x﹣）2﹣，顶点坐标是（，﹣），对称轴是x=；（2）当y=0时x2﹣x﹣1=0，解得x=，x=，当m=时，m2+=（）2+===3，当m=时，m2+=（）2===3，m2+=3．点评：本题考查了二次函数的性质，配方法的顶点式解析式，函数值为0时得一元二次方程，注意把符合条件的分别代入求值．18．如图，已知抛物线y=x2﹣x﹣6，与x轴交于点A和B，点A在点B的左边，与y轴的交点为C．（1）用配方法求该抛物线的顶点坐标；（2）求sin∠OCB的值；（3）若点P（m，m）在该抛物线上，求m的值．考点：二次函数的性质；二次函数图象上点的坐标特征；勾股定理．分析：（1）根据配方法，可得顶点式解析式，根据顶点式解析式，可得抛物线的顶点；（2）根据函数值为0，可得B点坐标，根据自变量为0，可得C点坐标，根据勾股定理，可得BC的长，根据正弦的意义，可得答案；（3）根据图象上的点的坐标满足函数解析式，可得一元二次方程，根据解一元二次方程，可得答案．解答：解：（1）∵，∴抛物线的顶点坐标为（，）；（2）令x2﹣x﹣6=0，解得x1=﹣2，x2=3，∴点B的坐标为（3，0），又点C的坐标为（0，﹣6），∴，∴；（3）∵点P（m，m）在这个二次函数的图象上，∴m2﹣m﹣6=m，即m2﹣2m﹣6=0，解得，．点评：本题考查了二次函数的性质，配方法可把一般式转化成顶点式，图象上点的坐标满足函数解析式．19．若二次函数y=a1x2+b1x+c1的图象记为C1，其顶点为A，二次函数y=a2x2+b2x+c2的图象记为C2，其顶点为B，且满足点A在C2上，点B在C1上，则称这两个二次函数互为“伴侣二次函数”．（1）一个二次函数的“伴侣二次函数”有无数个；（2）①求二次函数y=x2+3x+2与x轴的交点；②求以上述交点为顶点的二次函数y=x2+3x+2的“伴侣二次函数”．（3）试探究a1与a2满足的数量关系．考点：二次函数的性质．专题：新定义．分析：（1）根据伴侣二次函数的定义，可得答案；（2）①根据函数值为0，可得函数与x轴的交点的横坐标就是，可得答案；②根据伴侣二次函数的定义，顶点坐标，可得伴侣二次函数；（3）根据伴侣二次函数的顶点在对方的图象上，二元一次方程组，根据解方程组，可得答案．解答：解：（1）无数；（2）①令y=0，即x2+3x+2=0．解得：x1=﹣1，x2=﹣2．∴二次函数y=x2+3x+2与x轴的交点坐标为（﹣2，0），（﹣1，0）．（3分）②∵y=x2+3x+2=（x+）2﹣∴顶点坐标为（﹣，﹣）．设以（﹣2，0）为顶点且经过（﹣，﹣）的抛物线的函数关系式为y=a（x+2）2，将x=﹣，y=﹣代入y=a（x+2）2得 a=﹣1．∴二次函数y=x2+3x+2的一个“伴侣二次函数”为y=﹣（x+2）2=﹣x2﹣4x﹣4，同理可求以（﹣1，0）为顶点且经过（﹣，﹣）的抛物线的函数关系式．即二次函数y=x2+3x+2的另一个“伴侣二次函数”为y=﹣（x+1）2=﹣x2﹣2x﹣1；（3）设y=a1（x+m）2+n，其顶点为（﹣m，n）；y=a2（x+h）2+k，其顶点为（﹣h，k）．根据“伴侣二次函数”定义可得∴a1（﹣h+m）2=﹣a2（﹣m+h）2．当﹣h≠m时，a1=﹣a2当﹣h=m时，a1、a2为任意不为零的实数．点评：本题考查了二次函数的性质，伴侣二次函数的顶点在对方的图象上是解题关键．20．已知二次函数y=﹣x2+2x+3图象的对称轴为直线．（1）请求出该函数图象的对称轴；（2）在坐标系内作出该函数的图象；（3）有一条直线过点P（1，5），若该直线与二次函数y=﹣x2+2x+3只有一个交点，请求出所有满足条件的直线的关系式．考点：二次函数的性质；二次函数的图象．分析：（1）根据对称轴的公式，可得答案；（2）根据画函数图象的方法，可得抛物线的图象；（3）根据直线与抛物线相切，可得交点是一个，可得答案．解答：解：（1）；（2）图象（3）因为抛物线的对称轴是x=1，点p（1，5）当过点p且与y轴平行的直线满足与抛物线只有一个交点所以直线x=1为所求直线当过点p的直线不与y轴平行时，设直线的解析式为y=kx+b，令﹣x2+2x+3=kx+b整理得﹣x2+（2﹣k）x+3﹣b=0由题意得△=（2﹣k）2+4（3﹣b）=0即：k2﹣4k+16﹣4b=0又因为y=kx+b，过点p（1，5）所以5=k+b所以k2﹣4=0解得k=±2，当k=2时，b=3；当k=﹣2时，b=7所以解析式为y1=2x+3，y2=﹣2x+7，所以满足条件的直线有三条：直线x=1；y1=2x+3，y2=﹣2x+7．点评：本题考查了二次函数的性质，a＜0时，图象开口向下，对称轴是x=﹣．。

二次函数的图像和性质练习(含答案)

二次函数的图像和性质一、选择题（每题3分）1．下列四个函数中，一定是二次函数的是（）A ．21y x x=+ B ．y=ax 2+bx+c C ．y=x 2﹣（x+7）2 D ．y=（x+1）（2x ﹣1）【答案】D【解析】试题分析：因为形如y=ax 2+bx+c （0a ≠）的函数叫二次函数，所以选项A 、B 、C 错误，D 正确，故选：D ．考点：二次函数的概念.2．若函数y=-2(x-1)2+(a-1)x 2为二次函数，则a 的取值范围为（） A.a≠0 B.a≠1 C.a≠2 D.a≠3【答案】D ．【解析】试题分析：根据二次函数的定义化成一般式为()2342y a x x =-+-，则30a -≠3a ≠故选D ．考点：二次函数的定义．3.下列函数中，不是二次函数的是（）A ．y ＝1－x 2B ．y ＝2（x －1）2＋4C ．y ＝（x －1）（x ＋4）D ．y ＝（x －2）2－x 2【答案】D ．【解析】试题分析：选项A ，y=1-x 2=-x 2+1，是二次函数，选项A 正确；选项B ，y=2（x-1）2+4=2x 2-4x+6，是二次函数，选项B 正确；选项C ，y=（x-1）（x+4）=x 2+x-2，是二次函数，选项C 正确；选项 D ，y=（x-2）2-x 2=-4x+4，是一次函数，选项D 错误．故答案选D ．考点：二次函数的定义．二、填空题（每题3分）4.若函数y ＝（m －3）是二次函数，则m ＝______．【答案】5．【解析】试题分析：已知函数y ＝（m －3）是二次函数，可得且m －3≠0，解得m=-5．考点：二次函数的定义．5.．一个圆柱的高等于底面半径，写出它的表面积S 与底面半径r 的函数关系式为_________．【答案】S=4π2r【解析】试题分析：根据题意可得h=2r ，则S=2πrh=4π2r ．考点：二次函数的实际应用（时间：15分钟，满分25分）班级：___________姓名：___________得分：___________一、选择题（每题3分）1.下列函数中，不属于二次函数的是（）A ．y=（x ﹣2）2B ．y=﹣2（x+1）（x ﹣1）C ．y=1﹣x ﹣x 2D ．y=211x 【答案】D【解析】试题分析：整理一般形式后根据二次函数的定义判定即可：A 、整理为y=x 2﹣4x+4，是二次函数，不合题意；B 、整理为y=﹣2x 2+2，是二次函数，不合题意；C 、整理为y=﹣x 2﹣x+1，是二次函数，不合题意；D 、不是整式方程，符合题意．故选：D ．考点：二次函数的定义2．下列函数中属于二次函数的是（）A ．12-=x yB ．12-=ax yC ．222)1(2x x y --=D ．)2)(1(π+-=x x y【答案】D ．【解析】试题分析：A ．12-=x y 是一次函数，故本选项错误；B ．当0a =时，12-=ax y 不是二次函数，故本选项错误；C ．222)1(2x x y --==42x -+是一次函数，故本选项错误；D )2)(1(π+-=x x y 是二次函数，故本选项正确．故选D ．考点：二次函数的定义．3．若函数222(1)(1)y x a x =--+-为二次函数，则a 的取值范围为（）A ．0a ≠B ．1a ≠C ．2a ≠D ．3a ≠【答案】D ．【解析】试题分析：由原函数解析式得到：222(1)(1)y x a x =--+-=2(3)42a x x -+-．∵函数 222(1)(1)y x a x =--+-为二次函数，∴30a -≠，解得3a ≠．故选D ．考点：二次函数的定义．二、填空题（每题3分）4.在边长为16cm 的正方形铁皮上剪去一个圆，则剩下的铁皮的面积S （cm 2）与圆的半径r （cm ）之间的函数表达式为（不要求写自变量的取值范围）．【答案】2256r S π-=【解析】试题分析：剩下的面积为：正方形的面积-圆的面积=162-πr 2=256-πr 2故答案为：2256r S π-=考点：函数的表达式.5.．用长为8米的铝合金制成如图所示的窗框，若设窗框的宽为x 米，窗户的透光面积为S 平方米，则S 关于x 的函数关系式．【答案】S=x x 4232+-【解析】试题分析：设窗框的宽为x 米，则长为238x -米 ∴S=x x x x 4232382+-=⨯- 考点：实际问题抽象二次函数三、计算题（每题10分）6.已知，若函数2(1)3m y m x =-+是关于x 的一次函数．（1）求m 的值，并写出解析式；（2）若函数是关于x 的二次函数，求m 的值，．【答案】（1）1m =-；（2）m =．【解析】试题分析：（1）先根据一次函数的定义求出m 的值；（2）由22m =可得出m =试题解析：（1）∵函数2(1)3m y m x =-+是一次函数，∴21m =，解得1m =或1m =-，又∵10m -≠，∴1m ≠，∴1m =-，∴函数为：23y x =-+；m=可得出m=（2）由22考点：1．一次函数的定义；2．二次函数的定义．。

初中数学二次函数的图象与性质能力达标测试题1(附答案详解)

初中数学二次函数的图象与性质能力达标测试题1（附答案详解）1．已知二次函数y=ax 2+bx+c （a≠0）的图象如图，在下列代数式中（1）a+b+c ＞0；（2）﹣4a ＜b ＜﹣2a （3）abc ＞0；（4）5a ﹣b+2c ＜0；其中正确的个数为（）A ．1个B ．2个C ．3个D ．4个2．已知二次函数的图像y=ax²+bx+c(a≠0)如右图所示，下列结论⑴a+b+c=0 ⑵a -b+c ﹥0 ⑶abc ﹥0 ⑷b=-2a 其中正确的结论个数有（）A ．1个B ．2个C ．3个D ．4个3．已知点A （﹣2，a ），B （12，b ），C （52，c ）都在二次函数y=﹣x 2+2x+3的图象上，那么a 、b 、c 的大小是（）A ．a ＜b ＜cB ．b ＜c ＜aC ．a ＜c ＜bD ．c ＜b ＜a4．若抛物线y ＝(x －m)2＋(1－m)的顶点在第一象限，则m 的取值范围为（）A ．m>0B ．m>1C ．－1<m<0D ．0<m<1 5．如图，抛物线()20y ax bx c a =++≠与x 轴交于A （－1，0），B （3，0）两点，与y 轴交于点C ，顶点为D ，下列结论正确的是（）A ．abc ＜0B ．3a+c=0C ．4a-2b+c ＜0D ．方程ax 2+bx+c=-2（a≠0）有两个不相等的实数根6．如图是二次函数y=ax 2+bx+c 的图象的一部分，对称轴是直线x=1．①b 2＞4ac ；②b ＜0；③y 随x 的增大而减小； ④若（﹣2，y 1），（5，y 2）是抛物线上的两点，则y 1＜y 2．上述4个判断中，正确的是（）A ．①②④B ．①④C ．①③④D ．②③④ 7．抛物线的图象一定经过（） A ．第一、二象限B ．第三、四象限C ．第一、三象限D ．第二、四象限 8．二次函数()20y ax bx c a =++≠的图象如图所示，下列四个结论：①0ac <；②0a b c ++>；③420a b c -+<；④240ac b ->．其中正确的结论有（）A ．1B ．2C ．3D ．49．如图，抛物线的表达式是（）A ．y ＝x 2－x ＋2B ．y ＝x 2＋x ＋2C ．y ＝－x 2－x ＋2D ．y ＝－x 2＋x ＋2 10．如图，在平面直角坐标系中，点A 是抛物线y=a （x+32）2+k 与y 轴的交点，点B 是这条抛物线上的另一点，且AB ∥x 轴，则以AB 为边的正方形ABCD 的周长为_____．11．函数242y x x =++的最小值是________.12．已知二次函数()20y ax bx c a =++≠的图象如图所示，有下列5个结论： ①20a b +=；②b a c <+；③2124b a ac +=；④()a b m am b +>+，（1m ≠的实数）； ⑤240b ac ->，其中正确的结论有________．13．若二次函数232y x x m =-+的最小值是2，则m =________．14．如果一条抛物线的形状与y=﹣2x 2+2的形状相同，且顶点坐标是（4，﹣2），则它的解析式是________．15．已知二次函数2y ax bx c =++中，函数y 与自变量x 的部分对应值如下表：则此二次函数的对称轴为____．16．二次函数y =x （x ﹣6）的图象的对称轴是______．17．二次函数y=﹣x 2+bx+c 的图象如图所示：若点A （x 1，y 1），B （x 2，y 2）在此函数图象上，x 1＜x 2＜1，y 1与y 2的大小关系是y 1_____y 2（填“＞”、“＜”、“=”）18．把抛物线y=2x 2向右平移3个单位，再向下平移2个单位，得到的新的抛物线的表达式是_____．19．已知抛物线y=ax 2经过点A （﹣2，﹣8）．（1）求此抛物线的函数解析式；（2）写出这个二次函数图象的顶点坐标、对称轴；（3）判断点B （﹣1，﹣4）是否在此抛物线上；（4）求出此抛物线上纵坐标为﹣6的点的坐标．20．已知抛物线y=ax 2﹣4x+c 经过点A （0，﹣6）和B （3，﹣9）．（1）求出抛物线的解析式；（2）通过配方，写出抛物线的对称轴方程及顶点坐标．21．二次函数2y ax =与直线21y x =-的图象交于点()1,P m()1求a ，m 的值；()2写出二次函数的表达式，并指出x 取何值时该表达式y 随x 的增大而增大？()3写出该抛物线的顶点坐标和对称轴．22．某商场经营一种海产品，进价是20元/kg ，根据市场调查发现，每日的销售量y （kg ）与售价x （元/kg ）是一次函数关系，如图所示.（1）求y 与x 的函数关系式.（不求自变量的取值范围）（2）某日该商场销售这种海产品获得了21000元的利润，问：该海产品的售价是多少？（3）若某日该商场销售这种海产品的销量不少于650kg ，问：该商场销售这种海产品获得的最大利润是多少？23．如图，抛物线y=ax 2+bx+c 与x 轴交于A ，B （1，0）两点，与y 轴交于点C ，直线y=x ﹣2经过A ，C 两点，抛物线的顶点为D ．（1）求抛物线的解析式；（2）求抛物线的顶点D 的坐标；（3）在y 轴上是否存在一点G ，使得GD +GB 的值最小？若存在，求出点G 的坐标；若不存在，请说明理由；（4）在直线AC 的上方抛物线上是否存在点P ，使△PAC 的面积最大？若存在，直接写出P 点坐标及△PAC 面积的最大值．24．如图，抛物线y=﹣x 2+bx+c 经过直线y=﹣x+3与坐标轴的两个交点A 、B ．（1）求抛物线的解析式；（2）画出抛物线的图象．25．如图1，在平面直角坐标系xOy 中，已知点A 和点B 的坐标分别为()2,0A -，()0,6B -，将Rt AOB ∆绕点O 按顺时针分别旋转90，180得到1Rt AOC ∆，Rt EOF ∆，抛物线1C 经过点C ，A ，B ；抛物线2C 经过点C ，E ，F .（1）点C 的坐标为________，点E 的坐标为________；抛物线1C 的解析式为________，抛物线2C 的解析式为________；（2）如果点(),P x y 是直线BC 上方抛物线1C 上的一个动点.①若PCA ABO ∠=∠，求P 点的坐标；②如图2，过点P 作x 轴的垂线交直线BC 于点M ，交抛物线2C 于点N ，记2h PM NM BM =++，求h 与x 的函数关系式.当52x -≤≤-时，求h 的取值范围. 26．如图，已知抛物线y=ax 2+32x+4的对称轴是直线x=3，且与轴相交于A 、B 两点（B 点在A 点的右侧），与轴交于C 点．（1）A 点的坐标是；B 点坐标是；（2）直线BC 的解析式是：；（3）点P 是直线BC 上方的抛物线上的一动点（不与B 、C 重合），是否存在点P ，使△PBC 的面积最大．若存在，请求出△PBC 的最大面积，若不存在，试说明理由；（4）若点M 在x 轴上，点N 在抛物线上，以A 、C 、M 、N 为顶点的四边形是平行四边形时，请直接写出点M 点坐标．参考答案1．A【解析】【分析】由抛物线开口向上得到a 大于0，再由对称轴在y 轴右侧得到a 与b 异号，即b 小于0，由抛物线与y 轴交于正半轴，得到c 大于0，可得出abc 的符合，对于（3）作出判断；由x=1时对应的函数值小于0，将x=1代入二次函数解析式得到a+b+c 小于0，（1）错误；根据对称轴在1和2之间，利用对称轴公式列出不等式，由a 大于0，得到-2a 小于0，在不等式两边同时乘以-2a ，不等号方向改变，可得出不等式，对（2）作出判断；由x=-1时对应的函数值大于0，将x=-1代入二次函数解析式得到a-b+c 大于0，又4a 大于0，c 大于0，可得出a-b+c+4a+c 大于0，合并后得到（4）正确，综上，即可得到正确的个数．【详解】解：由图形可知：抛物线开口向上，与y 轴交点在正半轴，∴a >0，b <0，c >0，即abc <0，故(3)错误；又x =1时，对应的函数值小于0，故将x =1代入得：a +b +c <0，故(1)错误；∵对称轴在1和2之间， ∴122b a<-<，又a >0， ∴在不等式左右两边都乘以−2a 得：−2a >b >−4a ，故(2)正确；又x =−1时，对应的函数值大于0，故将x =1代入得：a −b +c >0，又a >0，即4a >0，c >0，∴5a −b +2c =(a −b +c )+4a +c >0，故(4)错误，综上，正确的有1个，为选项(2).故选:A.【点睛】考查二次函数图象与系数的关系，掌握二次函数系数对图象的影响是解题的关键. 2．C【解析】【分析】解答本题，根据图象可知f(1)＜0和f(-1)＞0，结合函数解析式即可判断a+b+c 和a-b+c 是否大于0；由图可知，对称轴x=b2a-=-1，a＜0，故可知b=2a＜0；结合图像和函数解析式可知f(0)=c＞0，据此即可判断abc是否大于0. 【详解】求f(1)和f(-1)得a+b+c=0，a-b+c＞0；对称轴x=b2a-=-1，a＜0，得b=2a＜0，f(0)=c＞0得abc＞0.【点睛】本题考查对二次函数的理解，解题的关键是合理利用图像的坐标.3．C【解析】【分析】先计算对称轴为直线x=1，抛物线开口向下，再根据A、B、C三点与对称轴的远近，比较纵坐标的大小．【详解】比较A、B、C三点横坐标与坐标轴的距离，可知距离差分别为A ：3 B：0.5 C：1.5 ∴b＞c＞a，选C.【点睛】本题考查了二次函数图像上点的坐标特征，解题的关键是掌握二次函数图像的性质.4．D【解析】分析:根据二次函数的解析式可得顶点坐标是(m,1-m),因为二次函数顶点坐标在第一象限,根据点在第一象限的符号特征可得:10mm>⎧⎨->⎩,解不等式组即可求解.详解:因为抛物线y＝(x－m)2＋(1－m)的顶点在第一象限,所以10mm>⎧⎨->⎩,解得0<m<1,故选D.点睛:本题主要考查二次函数的顶点坐标和平面直角坐标系内点的符号特征,解决本题的关键是要熟练根据二次函数解析式求二次函数的顶点坐标.5．B【解析】【分析】由抛物线的对称轴的位置判断ab的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．【详解】由图象可得，a＞0，b＜0，c＜0，∴abc＞0，故选项A错误，∵抛物线y=ax2+bx+c（a≠0）与x轴交于A（-1，0）、B（3，0）两点，∴-13=22ba-+=1，得b=-2a，当x=-1时，y=a-b+c=a+2a+c=3a+c=0，故选项B正确，当x=-2时，y=4a-2b+c＞0，故选项C错误，由函数图象可知，如果函数y=ax2+bx+c（a≠0）顶点的纵坐标大于-2，则方程ax2+bx+c=-2（a≠0）没有实数根，故选项D错误，故选B．【点睛】本题主要考查了图象与二次函数系数之间的关系，二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定．6．A【解析】【分析】根据图象与x轴有2个交点，确定b2-4ac>0，即可判断①；根据开口向上可判断a>0，-b2a=1，可得b=-2a<0，可判断②；根据二次函数的增减性可判断③；④．【详解】解：∵图象与x轴有2个交点，∴b2−4ac>0,b2>4ac，故①正确；∵−b2a=1，又a>0，∴b<0，故②正确；当x>1时，y随x的增大而增大，故③错误；由对称轴为x=1，当x=−2时和x=4时，函数值相等，根据函数性质，x=5的函数值大于x=4的函数值，∴y1<y2，故④正确.所以正确的是①②④，故选A.【点睛】本题考查了二次函数的知识点，解题的关键是熟练的掌握二次函数图象与系数的关系. 7．B【解析】【分析】根据抛物线的开口方向以及顶点即可判断其图像所经过的象限.【详解】∵a＜0，∴抛物线y＝ax2的图像开口向下，由抛物线的解析式易知其顶点为（0,0），∴y＝ax2的图像一定经过第三、四象限.故选B.【点睛】本题主要考查二次函数的图像与性质，熟练掌握相关知识点是解答此类问题的关键.8．B【解析】【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．【详解】∵抛物线开口向下，交y轴于正半轴，∴a<0，c>0，∴ac<0，故①正确；∵x=1时，y<0，∴a+b+c<0，故②错误；由图象可知：当x=−2时，y<0，∴4a−2b+c<0，故③正确；由抛物线交x轴于两点，∴b2−4ac>0，∴4ac−b2<0，故④错误；故选：B.【点睛】考查二次函数与系数的关系.二次项系数a决定抛物线的开口方向，,a b共同决定了对称轴的位置，常数项c决定了抛物线与y轴的交点位置.9．D【解析】【分析】根据题意，把抛物线经过的三点代入函数的表达式，列出方程组，解出各系数则可．【详解】解：根据题意，设二次函数的表达式为y=ax2+bx+c，抛物线过（-1，0），（0，2），（2，0），所以2420 a b cca b c-+=⎧⎪=⎨⎪++=⎩，解得a=-1，b=1，c=2，这个二次函数的表达式为y=-x2+x+2．故选A．【点睛】本题考查了用待定系数法求函数表达式的方法，同时还考查了方程组的解法等知识，是比较常见的题目．10．12【解析】【分析】根据题意和二次函数的性质可以求得线段AB的长度，从而可以求得正方形ABCD的周长．【详解】∵在平面直角坐标系中，点A是抛物线y=a（x+32）2+k与y轴的交点，∴点A的横坐标是0，该抛物线的对称轴为直线x=﹣32，∵点B是这条抛物线上的另一点，且AB∥x轴，∴点B 的横坐标是﹣3，∴AB=|0﹣（﹣3）|=3，∴正方形ABCD 的周长为：3×4=12，故答案为：12．【点睛】本题考查了二次函数图象上点的坐标特征、正方形的性质，解题的关键是找出所求问题需要的条件．11．-2【解析】【分析】将函数解析式写成顶点式便可得出最小值.【详解】解：242y x x =++=2442x x ++-=()22x +-2∴顶点坐标为（-2,2），且开口向上；∴函数242y x x =++的最小值是-2.故答案为：-2.【点睛】本题考查了二次函数的最值，关键将解析式写成顶点式.12．①③④⑤【解析】【分析】根据抛物线的对称轴可判断①；代入x=-1，结合图像可判断②；根据顶点坐标公式及图像中的顶点坐标可判断③；利用抛物线的最大值可判断④；根据抛物线与x 轴交点的个数可判断⑤.【详解】由图像知2b a-=1，则20a b +=，①正确；当x=-1时，y=a-b+c ，由图像可知此时y ＜0，即a-b+c ＜0，则b ＞a+c ，②错误；由图可知顶点坐标为（1,3），则2434b ac a-=，即2124b a ac +=，③正确；当x=1时，y=a+b+c 为最大值，当x=m 时，y=am 2+bm+c ，由于m≠1，故a+b+c ＞am 2+bm+c ，即a+b ＞am 2+bm=m(am+b)，④正确；由图可知，抛物线与x 轴有两个交点，则b 2-4ac ＞0，⑤正确；故答案为：①③④⑤.【点睛】本题综合考察了二次函数的解析式和图像的性质特点，一定要深入理解二次函数解析式各项参数与图像的对应关系，同时对一些特殊值要有敏感度.13．178【解析】【分析】可以由函数解析式得出对称轴的表达式，运用该函数在对称轴处可以得到最小值即可得出答案.【详解】对称轴33x==212⨯，所以带入可得m= 178，故填 178. 【点睛】本题考查了由二次函数图像得出最值，熟悉理解二次函数最值的取得是解决本题的关键. 14．y=﹣2（x ﹣4）2﹣2或y=2（x ﹣4）2﹣2【解析】试题解析：∵一条抛物线的形状与222y x =-+的形状相同，∴a =±2，设抛物线的顶点式为22()y x h k =±-+，∵顶点坐标是(4,−2)，∴抛物线的顶点式为22(4)2y x =---或22(4) 2.y x =--故答案为：22(4)2y x =---或22(4) 2.y x =--15．1x =-【解析】观察、分析表格中的数据可得，当20x x =-=，时，二次函数2y ax bx c =++的函数值相等，都是3-，∴此二次函数的对称轴为直线：2012x -+==-，即1x =-. 故答案为：1x =-.16．x =3．【解析】解：令y =0，得：x （x ﹣6）=0，解得：x =0或x =6，∴对称轴为直线x =062+ =3．故答案为x =3．17．<【解析】【分析】利用二次函数的性质解决问题．【详解】∵抛物线的对称轴为直线x=1，∴当x 1＜x 2＜1，∴y 1＜y 2．故答案为＜．【点睛】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．18．y=2（x ﹣3）2﹣2．【解析】【分析】抛物线的平移，实际上就是顶点的平移，先求出原抛物线的顶点坐标，再根据平移规律，推出新抛物线的顶点坐标，根据顶点式可求新抛物线的解析式．【详解】∵y =2x 2的顶点坐标为（0，0），∴把抛物线右平移3个单位，再向下平移2个单位，得新抛物线顶点坐标为（3，﹣2），∵平移不改变抛物线的二次项系数，∴平移后的抛物线的解析式是y=2（x﹣3）2﹣2．故答案为y=2（x﹣3）2﹣2．【点睛】本题考查了二次函数图象的平移，其规律是是：将二次函数解析式转化成顶点式y=a(x-h)2+k（a，b，c为常数，a≠0），确定其顶点坐标(h，k)，在原有函数的基础上“h 值正右移，负左移；k值正上移，负下移”．19．（1）y=﹣2x2；（2）顶点坐标为（0，0），对称轴为y轴；（3）不在；（4）（3，﹣6）或（﹣3，﹣6）．【解析】分析：(1)根据二次函数图象上点的坐标满足其解析式,把A点坐标代入解析式得到关于a的方程,然后解方程即可.(2)根据图象和性质直接写出顶点坐标、对称轴即可.(3)把点B(-1,-4)代入解析式,即可判断;(4)把y=-6代入解析式,即可求得;详解：（1）∵抛物线y=ax2经过点A（﹣2，﹣8），∴a•（﹣2）2=﹣8，∴a=﹣2，∴此抛物线对应的函数解析式为y=﹣2x2．（2）由题可得，抛物线的顶点坐标为（0，0），对称轴为y轴；（3）把x=﹣1代入得，y=﹣2×（﹣1）2=﹣2≠﹣4，∴点B（﹣1，﹣4）不在此抛物线上；（4）把y=﹣6代入y=﹣2x2得，﹣6=﹣2x2，解得x=±，∴抛物线上纵坐标为﹣6的点的坐标为（，﹣6）或（﹣，﹣6）．点睛：本题主要考查了待定系数法求解析式,二次函数的性质以及二次函数图象上点的坐标特征,函数解析式与图象上的点之间的关系,点在图象上,则满足解析式;反之,满足解析式则在函数图象上.20．（1）抛物线的解析式为：y=x 2﹣4x ﹣6；（2）对称轴方程为x=2；顶点坐标（2，﹣10）．【解析】【分析】把A （0，﹣6）和B （3，﹣9）代入y =ax 2﹣4x +c ，用待定系数法即可求出抛物线的解析式；（2）根据配方法把y =x 2﹣4x ﹣6化为y =（x ﹣2）2﹣10解答即可.【详解】（1）依题意有，即，∴； ∴抛物线的解析式为：y=x 2﹣4x ﹣6．（2）把y=x 2﹣4x ﹣6配方得，y=（x ﹣2）2﹣10，∴对称轴方程为x=2；顶点坐标（2，﹣10）．【点睛】本题考查了待定系数法求二次函数解析式及配方法的应用，熟练掌握待定系数法是解答（1）的关键；熟练掌握配方法是解答（2）的关键.21．（1）a=1；m=1;（2）2y x =, 当0x >时，y 随x 的增大而增大；（3）顶点坐标为()0,0，对称轴为y 轴．【解析】【分析】（1）把点P （1，m ）分别代入二次函数y=ax 2与直线y=2x-1即可求出未知数的值；（2）把a 代入二次函数y=ax 2与即可求出二次函数表达式；根据二次函数的对称轴及增减性判断出x 的取值．（3）根据二次函数的性质直接写出即可．【详解】()1点()1,P m 在21y x =-的图象上∴2111m =⨯-=代入2y ax =（2）二次函数表达式：2y x =因为函数2y x =的开口向上，对称轴为y 轴，当0x >时，y 随x 的增大而增大；（3）2y x =的顶点坐标为()0,0，对称轴为y 轴．【点睛】本题考查了用待定系数法求函数解析式的方法，及二次函数的增减性．22．（1）y=-10x+1200；（2）该海产品的售价是50元或90元．（3）22750.【解析】【分析】（1），设y 与x 之间的函数关系式为y=kx+b ，将图形上已知的两点代入解方程组，即可求出k 与b 的值，进而确定y 与x 之间的函数关系式；（2）根据题目信息可得(-10x+1200)(x-20)=21000，接下来解方程即可使问题得解；(3) 设所获利润为W ，根据题目信息可得W=(-10x+1200)(x-20)，然后对其进行配方，结合x 的取值范围与二次函数的性质进行解答即可．【详解】（1）设y 与x 的函数关系式为：y=kx+b ，将（25，950），（40，800）代入得：2595040800k b k b +⎧⎨+⎩＝＝，解得：101200k b -⎧⎨⎩＝＝，故y 与x 的函数关系式为：y=-10x+1200；（2）由（1）得：（-10x+1200）（x-20）=21000，解得：x 1=50，x 2=90，答：该海产品的售价是50元或90元．(3) 设所获利润为W ，则根据题目信息可得W=(-10x+1200)(x-20)=-10(x-70)2+25000.∵-10x+1200≥650，当x=55时，W有最大值.故W的最大值为：-10(55-70)2+25000=22750.【点睛】此题主要考查了一元二次方程的应用以及一次函数的应用，正确求出函数解析式是解题关键．23．（1）y=﹣x2+x﹣2；（2）顶点D（，）；（3）存在点G（0，）使得GD+GB的值最小．理由见解析；（4）在直线AC的上方抛物线上存在点P（2，1），使△PAC的面积最大，最大值为4．理由见解析.【解析】【分析】（1）利用一次函数是性质求得点A、C的坐标，然后把点A、B、C的坐标分别代入二次函数解析式，利用待定系数法求得二次函数解析式即可；（2）将二次函数解析式转化为顶点式方程，可以直接得到答案；（3）利用轴对称﹣最短路径方法证得点G，结合一次函数图象上点的坐标特征求得点G的坐标；（4）利用分割法求得△PAC的面积为二次函数的形式，利用二次函数最值的求法进行解答．【详解】（1）把x=0代入y=x﹣2中得：y=﹣2，把y=0代入y=x﹣2中得：x=4，∴A（4，0），C（0，﹣2），把A（4，0），B（1，0），C（0，﹣2）分别代入y=ax2+bx+c，得，解得，则该抛物线的解析式为：y=﹣x2+x﹣2；（2）由（1）知，该抛物线的解析式为y=﹣x2+x﹣2，∴y=﹣x2+x﹣2=﹣（x﹣）2+，∴顶点D（，）；（3）存在点G（0，）使得GD+GB的值最小．理由如下：如图1，作点B关于y轴的对称点B′，连接B′D交y轴于点G，则B′（﹣1，0）．设直线B′D的解析式为y=kx+b．则，解得：，∴直线B′D的解析式为y=x+，把x=0代入，得y=，∴存在点G（0，）使得GD+GB的值最小；（4）在直线AC的上方抛物线上存在点P（2，1），使△PAC的面积最大，最大值为4．理由如下：如图2，过点P作PQ∥y轴交AC于Q，连接PC，PA．设P（x，﹣x2+x﹣2），则Q（x，x﹣2）．∴PQ=﹣x2+x﹣2﹣（x﹣2）=﹣x2+2x=﹣（x﹣2）2+2．又∵S△PAC=S△PQC+S△PQA=x•PQ+（4﹣x）•PQ=2PQ，∴S△PAC=﹣（x﹣2）2+4，∴当x=2时，S△PAC最大值为4，此时﹣x2+x﹣2=1，∴在直线AC的上方抛物线上存在点P（2，1），使△PAC的面积最大，最大值为4．【点睛】本题考查的是二次函数综合题，涉及了轴对称的性质、一次函数的应用、待定系数法等知识，学会利用参数构建方程解决问题，学会用数形结合的思想思考问题是解题的关键. 24．(1) y=﹣x2+2x+3 ;(2)见解析.【解析】【分析】（1）先求得点A和点B的坐标，然后将点A和点B的坐标代入抛物线的解析式求得b，c 的值即可；（2）依据抛物线解析式为y=﹣x2+bx+c，列表，描点，连线即可．【详解】解：（1）将x=0代入AB的解析式y=﹣x+3得：y=3，∴B（0，3）．将y=0代入AB的解析式y=﹣x+3得：﹣x+3=0，解得x=3，即A（3，0）．将点A和点B的坐标代入y=﹣x2+bx+c，解得：b=2，c=3．∴抛物线的解析式为y=﹣x2+2x+3．（2）列表：抛物线的图象如下：【点睛】本题考查的是二次函数的综合应用，熟练掌握二次函数的性质是解题的关键.25．（1）(6,0)C -，(2,0)E ，1C ：21462y x x =---，2C ：21262y x x =--+.（2）①符合条件的点P 的坐标为810(,39P -）或414(,39P --）.②1721h ≤≤. 【解析】分析：（1）根据旋转的性质，可得C ，E ，F 的坐标，根据待定系数法求解析式；（2）①根据P 点关于直线CA 或关于x 轴对称直线与抛物线交点坐标，求出解析式，联立方程组求解；②根据图象上的点满足函数解析式，可得P 、N 、M 纵坐标，根据平行于y 轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据x 取值范围讨论h 范围．详解：（1）由旋转可知，OC=6，OE=2，则点C 坐标为（-6，0），E 点坐标为（2，0），分别利用待定系数法求C 1解析式为：y=-12x 2−4x −6，C 2解析式为：y=-12x 2−2x +6 （2）①若点P 在x 轴上方，∠PCA=∠ABO 时，则CA 1与抛物线C 1的交点即为点P ，如图，设直线CA 1的解析式为：y=k 1x+b 1∴111062k b b -+⎧⎨⎩＝＝解得11132k b ⎧⎪⎨⎪⎩＝＝∴直线CA 1的解析式为：y=13x+2 联立：21462123y x x y x ⎧---⎪⎪⎨⎪+⎪⎩＝＝，解得1183109x y ⎧-⎪⎪⎨⎪⎪⎩＝＝或2260x y =-⎧⎨=⎩（舍去）， ∴P(810,39-) 若点P 在x 轴下方，∠PCA=∠ABO 时，则CH 与抛物线C 1的交点即为点P ，如图，易知OH=OA，∴H（0，-2）设直线CH的解析式为：y=k2x+b2∴222062k bb-+⎧⎨-⎩＝＝解得11132kb⎧-⎪⎨⎪-⎩＝＝∴直线CH的解析式为：y=13-x-2联立：21462123y x xy x⎧---⎪⎪⎨⎪--⎪⎩＝＝，解得1143149xy⎧-⎪⎪⎨⎪-⎪⎩＝＝或226xy=-⎧⎨=⎩（舍去），∴414(,39P--）；∴符合条件的点P的坐标为810(,39P-）或414(,39P--）.②设直线BC的解析式为：y kx b=+，∴066k bb=-+⎧⎨-=⎩，解得16kb=-⎧⎨=-⎩，∴直线BC的解析式为：6y x=--，过点B作BD MN⊥于点D，则2BM BD=，设P(x ，-12x 2−4x −6) ∴222BM BD x ==，2h PM NM BM =++()()2P M N M y y y y x =-+-+ 22P N M y y y x =+--()2211462626222x x x x x x =-----+---- 2612x x =--+，2612h x x =--+，()2321h x =-++，当3x =-时，h 的最大值为21.∵52x -≤≤-，当5x =-时，()2532117h =--++=；当2x =-时，()2232120h =--++=；当52x -≤≤-时，h 的取值范围是1721h ≤≤.点睛：本题考查二次函数综合题，解（1）的关键是利用旋转的性质得出C ，E 的坐标，又利用了待定系数法；解（2）①的关键是利用解方程组，要分类讨论，以防遗漏；解（2）②的关键是利用平行于y 轴直线上两点间的距离是较大的纵坐标减较小的纵坐标得出二次函数，又利用了二次函数的性质．26．（1）A （2-，0） B （8，0）；（2）142y x =-+ ；（3）存在点P ，使△PBC 的面积最大，最大面积是16 ；（4）（8-，0），（4，0），（541+，0），（541-，0）.【解析】【分析】可得a 的值，求出解析式.由解析式可得出C 和B 的坐标，从而得出直线的解析式.运用假设法，连接辅助线可以设出P,D 的坐标，表达出相应△PBC 的面积解析式，分析可得出结果.由平行四边形的定义可求出答案.【详解】（1）A （2-，0） B （8，0）；（2）142y x =-+ ；（3）假设存在点P ，连结PB 、PC ，过点P 作PD ∥y 轴交直线BC 于点D ，设点P （m ，213442m m -++）则点D （m ，142m -+）所以PD =213442m m -++- 142m ⎛⎫-+ ⎪⎝⎭ =2124m m -+ ∴211128224PBC S PD OB m m ⎛⎫=⨯⨯=⨯-+⨯ ⎪⎝⎭()228416m m m =-+=--+∵点P 是直线BC 上方的抛物线上的一动点（不与B 、C 重合）∴08m <<∴当4m =时，△PBC 的面积最大，最大面积是16∴存在点P ，使△PBC 的面积最大，最大面积是16（4）（8-，0），（4， 0），（5+0），（5，0） .【点睛】本题考查了一元二次方程的解析式的结构，和直线解析式的求解，以及品行四边形的定义，熟练掌握这些是解决本题的关键.。

2019年初升高数学衔接辅导之二次函数y=ax2+bx+c的图像和性质(含答案)

04二次函数y ＝ax 2＋bx ＋c 的图像和性质高中必备知识点1：二次函数图像的伸缩变换问题函数y ＝ax 2与y ＝x 2的图象之间存在怎样的关系？为了研究这一问题，我们可以先画出y ＝2x 2，y ＝12x 2，y ＝－2x 2的图象，通过这些函数图象与函数y ＝x 2的图象之间的关系，推导出函数y ＝ax 2与y ＝x 2的图象之间所存在的关系．先画出函数y ＝x 2，y ＝2x 2的图象．先列表：再描点、连线，就分别得到了函数y ＝x 2，y ＝2x 2的图象（如图2－1所示），从图2－1我们可以得到这两个函数图象之间的关系：函数y ＝2x 2的图象可以由函数y ＝x 2的图象各点的纵坐标变为原来的两倍得到．同学们也可以用类似于上面的方法画出函数y ＝12x 2，y ＝－2x 2的图象，并研究这两个函数图象与函数y ＝x 2的图象之间的关系．通过上面的研究，我们可以得到以下结论：二次函数y ＝ax 2(a ≠0)的图象可以由y ＝x 2的图象各点的纵坐标变为原来的a 倍得到．在二次函数y ＝ax 2(a ≠0)中，二次项系数a 决定了图象的开口方向和在同一个坐标系中的开口的大小．典型考题【典型例题】二次函数的图象如图所示，有下列结论：①；②；③；④，其中正确的结论个数是A．1个B．2 个C．3 个D．4 个【变式训练】下列说法错误的是( )A．二次函数y=－2x2中，当x=0时，y有最大值是0B．二次函数y=4x2中，当x>0时，y随x的增大而增大C．在三条抛物线y=2x2，y=－0.5x2，y=－x2中，y=2x2的图象开口最大，y=－x2的图象开口最小D．不论a是正数还是负数，抛物线y=ax2(a≠0)的顶点一定是坐标原点【能力提升】抛物线y=x2，y=﹣3x2，y=﹣x2，y=2x2的图象开口最大的是（）A．y=x2B．y=﹣3x2C．y=﹣x2D．y=2x2高中必备知识点2：二次函数图像的平移变换函数y ＝a (x ＋h )2＋k 与y ＝ax 2的图象之间存在怎样的关系？同样地，我们可以利用几个特殊的函数图象之间的关系来研究它们之间的关系．同学们可以作出函数y ＝2(x ＋1)2＋1与y ＝2x 2的图象（如图2－2所示），从函数的同学我们不难发现，只要把函数y ＝2x 2的图象向左平移一个单位，再向上平移一个单位，就可以得到函数y ＝2(x ＋1)2＋1的图象．这两个函数图象之间具有“形状相同，位置不同”的特点．类似地，还可以通过画函数y ＝－3x 2，y ＝－3(x －1)2＋1的图象，研究它们图象之间的相互关系．通过上面的研究，我们可以得到以下结论：二次函数y ＝a (x ＋h )2＋k (a ≠0)中，a 决定了二次函数图象的开口大小及方向；h 决定了二次函数图象的左右平移，而且“h 正左移，h 负右移”；k 决定了二次函数图象的上下平移，而且“k 正上移，k 负下移”．由上面的结论，我们可以得到研究二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象的方法：由于y ＝ax 2＋bx ＋c ＝a (x 2＋b x a )＋c ＝a (x 2＋b x a＋224b a )＋c －24b a224()24b b aca x a a-=++，所以，y ＝ax 2＋bx ＋c (a ≠0)的图象可以看作是将函数y ＝ax 2的图象作左右平移、上下平移得到的，于是，二次函数y ＝ax 2＋bx ＋c (a ≠0)具有下列性质：（1）当a ＞0时，函数y ＝ax 2＋bx ＋c 图象开口向上；顶点坐标为24(,)24b ac b a a--，对称轴为直线x ＝－2ba；当x ＜2b a -时，y 随着x 的增大而减小；当x ＞2b a -时，y 随着x 的增大而增大；当x ＝2ba-时，函数取最小值y ＝244ac b a -．（2）当a ＜0时，函数y ＝ax 2＋bx ＋c 图象开口向下；顶点坐标为24(,)24b ac b a a--，对称轴为直线x ＝－2ba；当x ＜2b a -时，y 随着x 的增大而增大；当x ＞2b a -时，y 随着x 的增大而减小；当x ＝2ba-时，函数取最大值y ＝244ac b a -．典型考题【典型例题】如图，已知抛物线C 1：y ＝﹣x 2+4，将抛物线C 1沿x 轴翻折，得到抛物线C 2（1）求出抛物线C 2的函数表达式；（2）现将抛物线C 1向左平移m 个单位长度，平移后得到的新抛物线的顶点为M ，与x 轴的交点从左到右依次为A ，B ；将抛物线C 2向右也平移m 个单位长度，平移后得到的新抛物线的顶点为N ，与x 轴交点从左到右依次为D ，E ．在平移过程中，是否存在以点A ，N ，E ，M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由．【变式训练】如图，抛物线轴的负半轴相交于点，将抛物线平移得到抛物线相交于点，直线于点，且.(1)求点的坐标；(2)写出一种将抛物线平移到抛物线的方法；(3)在轴上找点，使得的值最小，求点的坐标.【能力提升】已知抛物线y＝﹣x2+bx+c经过点B（﹣1，0）和点C（2，3）．（1）求此抛物线的函数表达式；（2）如果此抛物线上下平移后过点（﹣2，﹣1），试确定平移的方向和平移的距离．专题验收测试题1．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：从上表可知，下列说法正确的有多少个①抛物线与x轴的一个交点为（﹣2，0）；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是直线x=；④抛物线与x轴的另一个交点为（3，0）；⑤在对称轴左侧，y随x增大而减少．A．2 B．3 C．4 D．52．如图，一条抛物线与x轴相交于A（x1，0）、B（x2，0）两点（点B在点A的右侧），其顶点P在线段MN上移动，M、N的坐标分别为（﹣1，2）、（1，2），x1的最小值为﹣4，则x2的最大值为（）A．6 B．4 C．2 D．﹣23．如图，已知抛物线y＝x2+bx+c与直线y＝x交于（1，1）和（3，3）两点，现有以下结论：①b2﹣4c＞0；②3b+c+6＝0；③当x2+bx+c＞2x时，x＞2；④当1＜x＜3时，x2+（b﹣1）x+c＜0，其中正确的序号是（）A．①②④B．②③④C．②④D．③④4．定义运算“※”为：a※b=，如：1※（﹣2）=﹣1×（﹣2）2=﹣4．则函数y=2※x 的图象大致是（）A．B．C．D．5．若抛物线y＝ax2+2ax+4a(a＞0)上有A(32，y1)、B(2，y2)、C(32，y3)三点，则y1、y2、y 3的大小关系为( ). A ．y 1＜y 2＜y 3B ．y 1＜y 3＜y 2C ．y 3＜y 1＜y 2D ．y 2＜y 3＜y 16．下列函数是二次函数的是( ). A ．y ＝2x B ．y =1x+x C ．y ＝x +5D ．y ＝(x +1)(x ﹣3)7．下列对二次函数2y x x =-的图象的描述，正确的是（） A ．经过原点 B ．对称轴是y 轴 C ．开口向下D ．在对称右侧部分是向下的8．已知函数y ＝（x ﹣a ）（x ﹣b ）（其中a ＞b ）的图象如图所示，则函数y ＝ax +b 的图象大致是（）A ．B ．C ．D ．9．如图，已知抛物线y ＝ax 2+bx +c 经过点(﹣1，0)，以下结论：①2a +b ＞0；②a +c ＜0；③4a +2b +c ＞0；④b 2﹣5a 2＞2a c ．其中正确的是( )A ．①②B ．③④C ．②③④D ．①②③④10．二次函数y ＝ax 2+bx +c (a ≠0)的大致图象如图所示，顶点坐标为(﹣2，﹣9a )，下列结论：①abc ＞0；②4a +2b +c ＞0；③5a ﹣b +c ＝0；④若方程a (x +5)(x ﹣1)＝﹣1有两个根x 1和x 2，且x 1＜x 2，则﹣5＜x 1＜x 2＜1；⑤若方程|ax 2+bx +c |＝2有四个根，则这四个根的和为﹣4．其中正确的结论有( )A ．2个B ．3个C ．4个D ．5个11．如图，与抛物线y ＝x 2﹣2x ﹣3关于直线x ＝2成轴对称的函数表达式为______．12．已知关于x 的一元二次方程ax 2+bx +c ＝5的一个根是2，且二次函数y ＝ax 2+bx +c 的对称轴是直线x ＝2，则抛物线y ＝ax 2+bx +c 的顶点坐标为_____．13．二次函数21212y x x =-+ 中，二次项系数为____，一次项是____，常数项是___ 14．如图，二次函数y ＝ax 2+bx +c （a ≠0）．图象的顶点为D ，其图象与x 轴的交点A 、B 的横坐标分别为﹣1、3，与y 轴负半轴交于点C ．下面三个结论：①2a +b ＝0；②a +b +c ＞0；③只有当12a =时，△ABD 是等腰直角三角形；那么，其中正确的结论是_____．（只填你认为正确结论的序号）15．把二次函数y=x2+2x+3的图象向左平移1个单位长度，再向下平移1个单位长度，就得到二次函数____的图象．16．已知当2≤x≤3时，关于x的多项式x2﹣2kx+k2﹣k﹣1（k为大于2的常数）有最小值﹣2，则常数k的值为___．17．已知二次函数y=a（x-m）2-a（x-m）（a，m为常数，且a≠0）．（1）求证：不论a与m为何值，该函数的图象与x轴总有两个公共点；（2）设该函数的图象与x轴的两个交点为A（x1，0），B（x2，0），且x12+x22=25，求m的值；（3）设该函数的图象的顶点为C，与x轴交于A，B两点，且△ABC的面积为1，求a的值．18．如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线对称轴DE交x轴于点E，连接B D．（1）求经过A，B，C三点的抛物线的函数表达式；（2）点P是线段BD上一点，当PE＝PC时，求点P的坐标．19．如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣2，0），B（4，0），与直线y＝32x﹣3交于点C（0，﹣3），直线y＝32x﹣3与x轴交于点D．（1）求该抛物线的解析式（2）点P是抛物线上第四象限上的一个动点连接PC，PD，当△PCD的面积最大时，求点P的坐标；（3）将抛物线的对称轴向左平移3个长度单位得到直线l，点E是直线l上一点，连接OE，BE，若直线l上存在使sin∠BEO最大的点E，请直接写出满足条件的点E的坐标；若不存在，请说明理由．20．已知抛物线y＝ax2+bx+2经过A（﹣1，0），B（2，0），C三点．直线y＝mx+12交抛物线于A，Q两点，点P是抛物线上直线AQ上方的一个动点，作PF⊥x轴，垂足为F，交AQ于点N．（1）求抛物线的解析式；（2）如图①，当点P运动到什么位置时，线段PN＝2NF，求出此时点P的坐标；（3）如图②，线段AC的垂直平分线交x轴于点E，垂足为D，点M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，请求出点G的坐标；若不存在，请说明理由．21．现有一次函数y＝mx+n和二次函数y＝mx2+nx+1，其中m≠0，（1）若二次函数y＝mx2+nx+1经过点（2，0），（3，1），试分别求出两个函数的解析式．（2）若一次函数y＝mx+n经过点（2，0），且图象经过第一、三象限．二次函数y＝mx2+nx+1经过点（a，y1）和（a+1，y2），且y1＞y2，请求出a的取值范围．（3）若二次函数y＝mx2+nx+1的顶点坐标为A（h，k）（h≠0），同时二次函数y＝x2+x+1也经过A点，已知﹣1＜h＜1，请求出m的取值范围．22．如图，在直角坐标系中，直线y＝13x+1与x轴、y轴的交点分别为A、B，以x＝﹣1为对称轴的抛物线y＝﹣x2+bx+c与x轴分别交于点A、C．（1）求抛物线的解析式；（2）若点P是第二象限内抛物线上的动点，设抛物线的对称轴l与x轴交于一点D，连接PD，交AB于E，求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标；（3）若点Q在第二象限内，且tan∠AQD＝2，线段CQ是否存在最小值？如果存在直接写出最小值，如果不存在，请说明理由．专题04二次函数y＝ax2＋bx＋c的图像和性质高中必备知识点1：二次函数图像的伸缩变换问题函数y＝ax2与y＝x2的图象之间存在怎样的关系？为了研究这一问题，我们可以先画出y ＝2x 2，y ＝12x 2，y ＝－2x 2的图象，通过这些函数图象与函数y ＝x 2的图象之间的关系，推导出函数y ＝ax 2与y ＝x 2的图象之间所存在的关系．先画出函数y ＝x 2，y ＝2x 2的图象．先列表：再描点、连线，就分别得到了函数y ＝x 2，y ＝2x 2的图象（如图2－1所示），从图2－1我们可以得到这两个函数图象之间的关系：函数y ＝2x 2的图象可以由函数y ＝x 2的图象各点的纵坐标变为原来的两倍得到．同学们也可以用类似于上面的方法画出函数y ＝12x 2，y ＝－2x 2的图象，并研究这两个函数图象与函数y ＝x 2的图象之间的关系．通过上面的研究，我们可以得到以下结论：二次函数y ＝ax 2(a ≠0)的图象可以由y ＝x 2的图象各点的纵坐标变为原来的a 倍得到．在二次函数y ＝ax 2(a ≠0)中，二次项系数a 决定了图象的开口方向和在同一个坐标系中的开口的大小．典型考题【典型例题】二次函数的图象如图所示，有下列结论：①；②；③；④，其中正确的结论个数是A．1个B．2 个C．3 个D．4 个【答案】C【解析】由图象可得，，，故错误，当时，，故正确，当时，，由得，，则，得，故正确，，得，故正确，故选：C．【变式训练】下列说法错误的是( )A．二次函数y=－2x2中，当x=0时，y有最大值是0B．二次函数y=4x2中，当x>0时，y随x的增大而增大C．在三条抛物线y=2x2，y=－0.5x2，y=－x2中，y=2x2的图象开口最大，y=－x2的图象开口最小D．不论a是正数还是负数，抛物线y=ax2(a≠0)的顶点一定是坐标原点【答案】C【解析】A、a=-2＜0，抛物线开口向下，当x=0时，y有最大值是0，故该选项正确；B、二次函数y=4x2中，当x＞0时，y随x的增大而增大，故该选正确；C、因为|2|＞|-1|＞|-0.5|，所以，y=2x2的图象开口最小，y=-0.5x2的图象开口最大，故该选错误；D、不论a是正数还是负数，抛物线y=ax2（a≠0）的顶点一定是坐标原点，故该选正确．故选C．【能力提升】抛物线y=x2，y=﹣3x2，y=﹣x2，y=2x2的图象开口最大的是（）A．y=x2B．y=﹣3x2C．y=﹣x2D．y=2x2【答案】A【解析】∵二次函数中|a|的值越小，则函数图象的开口也越大，又∵，∴抛物线y=x2，y=﹣3x2，y=﹣x2，y=2x2的图象开口最大的是y=x2，故选A．高中必备知识点2：二次函数图像的平移变换函数y＝a(x＋h)2＋k与y＝ax2的图象之间存在怎样的关系？同样地，我们可以利用几个特殊的函数图象之间的关系来研究它们之间的关系．同学们可以作出函数y＝2(x＋1)2＋1与y＝2x2的图象（如图2－2所示），从函数的同学我们不难发现，只要把函数y＝2x2的图象向左平移一个单位，再向上平移一个单位，就可以得到函数y＝2(x ＋1)2＋1的图象．这两个函数图象之间具有“形状相同，位置不同”的特点．类似地，还可以通过画函数y ＝－3x 2，y ＝－3(x －1)2＋1的图象，研究它们图象之间的相互关系．通过上面的研究，我们可以得到以下结论：二次函数y ＝a (x ＋h )2＋k (a ≠0)中，a 决定了二次函数图象的开口大小及方向；h 决定了二次函数图象的左右平移，而且“h 正左移，h 负右移”；k 决定了二次函数图象的上下平移，而且“k 正上移，k 负下移”．由上面的结论，我们可以得到研究二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象的方法：由于y ＝ax 2＋bx ＋c ＝a (x 2＋b x a )＋c ＝a (x 2＋b x a＋224b a )＋c －24b a224()24b b aca x a a-=++，所以，y ＝ax 2＋bx ＋c (a ≠0)的图象可以看作是将函数y ＝ax 2的图象作左右平移、上下平移得到的，于是，二次函数y ＝ax 2＋bx ＋c (a ≠0)具有下列性质：（1）当a ＞0时，函数y ＝ax 2＋bx ＋c 图象开口向上；顶点坐标为24(,)24b ac b a a--，对称轴为直线x ＝－2ba；当x ＜2b a -时，y 随着x 的增大而减小；当x ＞2b a -时，y 随着x 的增大而增大；当x ＝2ba-时，函数取最小值y ＝244ac b a -．（2）当a ＜0时，函数y ＝ax 2＋bx ＋c 图象开口向下；顶点坐标为24(,)24b ac b a a--，对称轴为直线x ＝－2ba；当x ＜2b a -时，y 随着x 的增大而增大；当x ＞2b a -时，y 随着x 的增大而减小；当x ＝2ba-时，函数取最大值y ＝244ac b a -．典型考题【典型例题】如图，已知抛物线C 1：y ＝﹣x 2+4，将抛物线C 1沿x 轴翻折，得到抛物线C 2（1）求出抛物线C 2的函数表达式；（2）现将抛物线C 1向左平移m 个单位长度，平移后得到的新抛物线的顶点为M ，与x 轴的交点从左到右依次为A ，B ；将抛物线C 2向右也平移m 个单位长度，平移后得到的新抛物线的顶点为N ，与x 轴交点从左到右依次为D ，E ．在平移过程中，是否存在以点A ，N ，E ，M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由．【答案】（1）y ＝x 2﹣4（2）当m ＝3时，以点A ，N ，E ，M 为顶点的四边形是矩形【解析】（1）∵抛物线C 1的顶点为（0，4）， ∴沿x 轴翻折后顶点的坐标为（0．﹣4），∴抛物线C 2的函数表达式为y ＝x 2﹣4；（2）存在连接AN ，NE ，EM ，MA ，依题意可得：M （﹣m ，4），N （m ，﹣4），∴M，N关于原点O对称OM＝ON，原C1、C2抛物线与x轴的两个交点分别（﹣2，0），（2，0），∴A（﹣2﹣m，0），E（2+m，0），∴A，E关于原点O对称，∴OA＝OE∴四边形ANEM为平行四边形，∴AM2＝22+42＝20，ME2＝（2+m+m）2+42＝4m2+8m+20，AE2＝（2+m+2+m）2＝4m2+16m+16，若AM2+ME2＝AE2，∴20+4m2+8m+20＝4m2+16m+16，解得m＝3，此时△AME是直角三角形，且∠AME＝90，∴当m＝3时，以点A，N，E，M为顶点的四边形是矩形．【变式训练】如图，抛物线轴的负半轴相交于点，将抛物线平移得到抛物线相交于点，直线于点，且.(1)求点的坐标；(2)写出一种将抛物线平移到抛物线的方法；(3)在轴上找点，使得的值最小，求点的坐标.【答案】(1)A(-2，0)，B(3，5)，C(8，10)；(2)先将向右平移5个单位，再向上平移5个单位得到；(3)P(0，).【解析】（1）M1：y=x2-4与x轴的负半轴相交于点A，∴A（-2，0），∵AB=BC，C（8，m），∴，设AB直线解析式为y=kx+b，∵y=x2-4与相交于点A和B，∴m=10，∴B（3，5），C（8，10）；（2）∵抛物线M1平移得到抛物线M2，∴a=1，∵B（3，5），C（8，10）在抛物线y=x2+bx+c上，∴y=x2-10+26=（x-5）2+1，由M1平移得到抛物线M2先向右平移5个单位长度，再向上平移5个单位长度；（3）作点B关于y轴的对称点B'，连接CB'与y轴的交点即为P，∴B'（-3，5），设直线B'C的直线解析式为y=mx+n，.【能力提升】已知抛物线y＝﹣x2+bx+c经过点B（﹣1，0）和点C（2，3）．（1）求此抛物线的函数表达式；（2）如果此抛物线上下平移后过点（﹣2，﹣1），试确定平移的方向和平移的距离．【答案】（1）y＝﹣x2+2x+3；（2）将抛物线向上平移4个单位．【解析】（1）把B（﹣1，0）和点C（2，3）代入y＝﹣x2+bx+c得，解得，所以抛物线解析式为y＝﹣x2+2x+3；（2）把x＝﹣2代入y＝﹣x2+2x+3得y＝﹣4﹣4+3＝﹣5，点（﹣2，﹣5）向上平移4个单位得到点（﹣2，﹣1），所以需将抛物线向上平移4个单位．专题验收测试题1．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：从上表可知，下列说法正确的有多少个①抛物线与x轴的一个交点为（﹣2，0）；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是直线x=；④抛物线与x轴的另一个交点为（3，0）；⑤在对称轴左侧，y随x增大而减少．A．2 B．3 C．4 D．5【答案】C【解析】的对称性，逐一判断．【详解】根据图表，抛物线与x轴的一个交点为（﹣2，0），∴①正确；根据图表，抛物线与y轴交与（0，6），②正确；∵抛物线经过点（0，6）和（1，6），∴对称轴为x=，∴③正确；设抛物线经过点（x，0），∴x=解得：x=3∴抛物线一定经过（3，0），④正确；在对称轴左侧，y随x增大而增大，∴⑤错误，故选C.2．如图，一条抛物线与x轴相交于A（x1，0）、B（x2，0）两点（点B在点A的右侧），其顶点P在线段MN上移动，M、N的坐标分别为（﹣1，2）、（1，2），x1的最小值为﹣4，则x2的最大值为（）A．6 B．4 C．2 D．﹣2【答案】B【解析】由题意可知，当P在M点时，x1有最小值﹣4，∵M的坐标分别为（﹣1，2），∴x2＝2；∴x2与对称轴的距离是3；当P在N点时，x2有最大值，∵N的坐标分别为（1，2），∴x2的最大值为4.故选B．3．如图，已知抛物线y＝x2+bx+c与直线y＝x交于（1，1）和（3，3）两点，现有以下结论：①b2﹣4c＞0；②3b+c+6＝0；③当x2+bx+c＞2x时，x＞2；④当1＜x＜3时，x2+（b﹣1）x+c＜0，其中正确的序号是（）A．①②④B．②③④C．②④D．③④【答案】C【解析】∵函数y＝x2+bx+c与x轴无交点，∴b2﹣4ac＜0；∴b2﹣4c＜0故①不正确；当x＝3时，y＝9+3b+c＝3，即3b+c+6＝0；故②正确；把（1，1）（3，3）代入y＝x2+bx+c，得抛物线的解析式为y＝x2﹣3x+3，当x＝2时，y＝x2﹣3x+3＝1，y＝2x＝1，抛物线和双曲线的交点坐标为（2，1）第一象限内，当x＞2时，x2+bx+c＞2x；或第三象限内，当x＜0时，x2+bx+c＞2x；故③错误；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确；故选：C．4．定义运算“※”为：a※b=，如：1※（﹣2）=﹣1×（﹣2）2=﹣4．则函数y=2※x 的图象大致是（）A．B．C．D．【答案】C【解析】解:y=2※x=，当x>0时,图象是y=对称轴右侧的部分;当x＜0时,图象是y=对称轴左侧的部分，所以C选项是正确的.5．若抛物线y＝ax2+2ax+4a(a＞0)上有A(32，y1)、B(2，y2)、C(32，y3)三点，则y1、y2、y3的大小关系为( ).A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y1＜y2D．y2＜y3＜y1【答案】B【解析】解：抛物线的对称轴是x＝﹣1，开口向上，且与x轴无交点，∴与对称轴距离越近的点对应的纵坐标越小．A、B、C三点与对称轴距离按从小到大顺序是A、C、B，∴y1＜y3＜y2，故选：B．6．下列函数是二次函数的是( ).A ．y ＝2xB ．y =1x +xC ．y ＝x +5D ．y ＝(x +1)(x ﹣3)【答案】D【解析】解：A 、y ＝2x ，是一次函数，故此选项错误；B 、y ＝1x +x ，不是整式，故此选项错误；C 、y ＝x +5，是一次函数，故此选项错误；D 、y ＝(x +1)(x ﹣3)，是二次函数，故此选项正确．故选：D ．7．下列对二次函数2y x x =-的图象的描述，正确的是（）A ．经过原点B ．对称轴是y 轴C ．开口向下D ．在对称右侧部分是向下的【答案】A【解析】解：A 、当x ＝0时，y ＝x 2﹣x ＝0，∴抛物线经过原点，选项A 正确；B 、∵122ba -=, ∴抛物线的对称轴为直线12x =，选项B 不正确；C 、∵a ＝1＞0，∴抛物线开口向上，选项C 不正确；D 、∵a ＞0，抛物线的对称轴为直线12x =， ∴当12x >时，y 随x 值的增大而增大，选项D 不正确．故选：A ．8．已知函数y＝（x﹣a）（x﹣b）（其中a＞b）的图象如图所示，则函数y＝ax+b的图象大致是（）A．B．C．D．【答案】C【解析】解：∵y＝（x﹣a）（x﹣b）＝x2﹣（a+b）x+ab，∵抛物线的开口向上知二次项系数＞0，与y轴的交点为在y轴负半轴上，∴ab＜0，∵对称轴在y轴的右侧，二次项系数大于0，∴﹣（a+b）＞0．∴a+b＜0，∵a＞b，∴a＞0，b＜0，∴y＝ax+b的图象是C选项，故选：C．9．如图，已知抛物线y＝ax2+bx+c经过点(﹣1，0)，以下结论：①2a+b＞0；②a+c＜0；③4a+2b+c ＞0；④b2﹣5a2＞2a c．其中正确的是( )A ．①②B ．③④C ．②③④D ．①②③④【答案】B【解析】解：由图象可知a ＜0，0＜﹣2b a ＜1， ∴b ＜﹣2a ，∴2a +b ＜0，所以①错误； ∵﹣2b a＞0，a ＜0， ∴b ＞0，当x ＝﹣1时，y 1＝a ﹣b +c ＝0，∴a +c ＝b ＞0，所以②错误；∵当x ＝2时，y ＞0，∴4a +2b +c ＞0﹣﹣﹣﹣②，所以③正确；∵过(﹣1，0)，代入得a ﹣b +c ＝0，∴b 2﹣2ac ﹣5a 2＝(a +c )2﹣2ac ﹣5a 2＝c 2﹣4a 2＝(c +2a )(c ﹣2a )又∵4a +2b +c ＞04a +2(a +c )+c ＞0即2a +c ＞0①∵a ＜0，∴c ＞0则c ﹣2a ＞0②由①②知(c +2a )(c ﹣2a )＞0，所以b 2﹣2ac ﹣5a 2＞0，即b 2﹣5a 2＞2ac ，所以④正确．故选：B ．10．二次函数y ＝ax 2+bx +c (a ≠0)的大致图象如图所示，顶点坐标为(﹣2，﹣9a )，下列结论：①abc ＞0；②4a +2b +c ＞0；③5a ﹣b +c ＝0；④若方程a (x +5)(x ﹣1)＝﹣1有两个根x 1和x 2，且x 1＜x 2，则﹣5＜x 1＜x 2＜1；⑤若方程|ax 2+bx +c |＝2有四个根，则这四个根的和为﹣4．其中正确的结论有( )A ．2个B ．3个C ．4个D ．5个【答案】A【解析】解：∵抛物线的开口向上，则a ＞0，对称轴在y 轴的左侧，则b ＞0，交y 轴的负半轴，则c ＜0，∴abc ＜0，所以①结论错误；∵抛物线的顶点坐标(﹣2，﹣9a )， ∴﹣b 2a -＝﹣2，244ac b a-＝﹣9a ， ∴b ＝4a ，c ＝﹣5a ，∴抛物线的解析式为y ＝ax 2+4ax ﹣5a ，∴4a +2b +c ＝4a +8a ﹣5a ＝7a ＞0，所以②结论正确，5a ﹣b +c ＝5a ﹣4a ﹣5a ＝﹣4a ＜0，故③结论错误，∵抛物线y ＝ax 2+4ax ﹣5a 交x 轴于(﹣5，0)，(1，0)，∴若方程a (x +5)(x ﹣1)＝﹣1有两个根x 1和x 2，且x 1＜x 2，则﹣5＜x 1＜x 2＜1，正确，故结论④正确，若方程|ax 2+bx +c |＝1有四个根，设方程ax 2+bx +c ＝1的两根分别为x 1，x 2，则122x x +＝﹣2，可得x 1+x 2＝﹣4，设方程ax 2+bx +c ＝1的两根分别为x 3，x 4，则342x x +＝﹣2，可得x 3+x 4＝﹣4，所以这四个根的和为﹣8，故结论⑤错误，故选：A ．11．如图，与抛物线y ＝x 2﹣2x ﹣3关于直线x ＝2成轴对称的函数表达式为______．【答案】y ＝(x ﹣3)2﹣4【解析】解：y ＝x 2﹣2x ﹣3的顶点是（1，﹣4），（1，﹣4）关于x ＝2的对称点是（3，﹣4），y ＝x 2﹣2x ﹣3关于直线x ＝2成轴对称的函数表达式为y ＝（x ﹣3）2﹣4，故答案为：y ＝（x ﹣3）2﹣4．12．已知关于x 的一元二次方程ax 2+bx +c ＝5的一个根是2，且二次函数y ＝ax 2+bx +c 的对称轴是直线x ＝2，则抛物线y ＝ax 2+bx +c 的顶点坐标为_____．【答案】（2，5）【解析】解：∵二次函数y ＝ax 2+bx +c 的对称轴是直线x ＝2，方程ax 2+bx +c ＝5的一个根是2，∴当x ＝2时，y ＝ax 2+bx +c ＝5，∴抛物线的顶点坐标是（2，5）．故答案为：（2，5）．13．二次函数21212y x x =-+ 中，二次项系数为____，一次项是____，常数项是___ 【答案】12 -2x , 1 【解析】∵y =ax 2+bx +c （a ，b ，c 是常数且a ≠0）．在一般形式中ax 2叫二次项，bx 叫一次项，c 是常数项．其中a ，b ，c 分别叫二次项系数，一次项系数，常数项∴21212y x x =-+ 中，二次项系数为12，一次项是-2x ，常数项是1. 故答案是：12; -2x;1. 14．如图，二次函数y ＝ax 2+bx +c （a ≠0）．图象的顶点为D ，其图象与x 轴的交点A 、B 的横坐标分别为﹣1、3，与y 轴负半轴交于点C ．下面三个结论：①2a +b ＝0；②a +b +c ＞0；③只有当12a =时，△ABD 是等腰直角三角形；那么，其中正确的结论是_____．（只填你认为正确结论的序号）【答案】①③【解析】解：①∵图象与x 轴的交点A ，B 的横坐标分别为﹣1，3，∴AB ＝4，∴对称轴x ＝﹣b 2a ＝1，即2a +b ＝0．故选项正确；②由抛物线的开口方向向上可推出a ＞0，而﹣b 2a＝1， ∴b ＜0，∵对称轴x ＝1，∴当x ＝1时，y ＜0，∴a +b +c ＜0．故选项错误；③要使△ABD 为等腰直角三角形，必须保证D 到x 轴的距离等于AB 长的一半； D 到x 轴的距离就是当x ＝1时y 的值的绝对值．当x ＝1时，y ＝a +b +c ，即|a +b +c |＝2，∵当x＝1时y＜0，∴a+b+c＝﹣2，又∵图象与x轴的交点A，B的横坐标分别为﹣1，3，∴当x＝﹣1时y＝0，即a﹣b+c＝0，x＝3时y＝0，即9a+3b+c＝0，解这三个方程可得：b＝﹣1，a＝12，c＝﹣32，故选项正确．故答案为：①③．15．把二次函数y=x2+2x+3的图象向左平移1个单位长度，再向下平移1个单位长度，就得到二次函数____的图象．【答案】y=（x+2）2+1或y=x2+2x+5．【解析】∵y=x2+2x+3=（x+1）2+2，∴抛物线y=x2+2x+3先向左平移1个单位，再向下平移1个单位，平移后的函数关系式是：y=（x+2）2+1或y=x2+2x+5．故答案为：y=（x+2）2+1或y=x2+2x+5．16．已知当2≤x≤3时，关于x的多项式x2﹣2kx+k2﹣k﹣1（k为大于2的常数）有最小值﹣2，则常数k的值为___．【答案】4．【解析】解：x2﹣2kx+k2﹣k﹣1＝（x﹣k）2﹣k﹣1（k＞2），①当2＜k≤3时，当x＝k时取最小值，∴﹣k﹣1＝﹣2，∴k＝2，不合题意；②当k＞3时，当x＝3时取最小值，∴9﹣6k+k2﹣k﹣1＝﹣2，∴k＝4或2.5，∵k＞3，∴k＝4；综上，k＝4；故答案为：4．17．已知二次函数y=a（x-m）2-a（x-m）（a，m为常数，且a≠0）．（1）求证：不论a与m为何值，该函数的图象与x轴总有两个公共点；（2）设该函数的图象与x轴的两个交点为A（x1，0），B（x2，0），且x12+x22=25，求m的值；（3）设该函数的图象的顶点为C，与x轴交于A，B两点，且△ABC的面积为1，求a的值．【答案】（1）证明见解析；（2）m的值为-4或3；（3）a的值是±8．【解析】（1）证明：令y=0，a（x-m）2-a（x-m）=0，△=（-a）2-4a×0=a2，∵a≠0，∴a2＞0，∴不论a与m为何值，该函数的图象与x轴总有两个公共点；（2）解：y=0，则a（x-m）2-a（x-m）=a（x-m）（x-m-1）=0，解得x1=m，x2=m+1，∵x12+x22=25，∴m2+（m+1）2=25，解得m1=-4，m2=3．故m的值为-4或3；（3）解：∵x1=m，x2=m+1，∴AB=（m+1）-m=1，y=a（x-m）2-a（x-m）=a（x-m-12）2-4a，△ABC的面积=12×1×|-4a|=1，解得a=±8．故a的值是±8．18．如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线对称轴DE交x轴于点E，连接B D．（1）求经过A，B，C三点的抛物线的函数表达式；（2）点P是线段BD上一点，当PE＝PC时，求点P的坐标．【答案】（1）y＝﹣x2+2x+3；（2）点P的坐标为（2，2）．【解析】解：（1）∵抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，∴10930b cb c--+=⎧⎨-++=⎩，解得23bc=⎧⎨=⎩，∴所求的抛物线的函数表达式为y＝﹣x2+2x+3；（2）如图，连接PC，PE．抛物线的对称轴为x＝222(1)ba-=-⨯-＝1．当x＝1时，y＝4，∴点D的坐标为（1，4）．设直线BD的解析式为y＝kx+b，则4 30 k bk b+=⎧⎨+=⎩，解得26kb=-⎧⎨=⎩．∴直线BD的解析式为：y＝2x+6，设点P的坐标为（x，﹣2x+6），又C（0，3），E（1，0），则PC2＝x2+（3+2x﹣6）2，PE2＝（x﹣1）2+（﹣2x+6）2，∵PC＝PE，∴x2+（3+2x﹣6）2＝（x﹣1）2+（﹣2x+6）2，解得，x＝2，则y ＝﹣2×2+6＝2， ∴点P 的坐标为（2，2）．19．如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +c （a ≠0）与x 轴交于点A （﹣2，0），B （4，0），与直线y ＝32x ﹣3交于点C （0，﹣3），直线y ＝32x ﹣3与x 轴交于点D ．（1）求该抛物线的解析式（2）点P 是抛物线上第四象限上的一个动点连接PC ，PD ，当△PCD 的面积最大时，求点P 的坐标；（3）将抛物线的对称轴向左平移3个长度单位得到直线l ，点E 是直线l 上一点，连接OE ，BE ，若直线l 上存在使sin ∠BEO 最大的点E ，请直接写出满足条件的点E 的坐标；若不存在，请说明理由．【答案】（1）233384y x x =--；（2）P （3，﹣815）；（3）点E 的坐标为（﹣2，）或（﹣2，﹣. 【解析】解：（1）用交点式函数表达式得：y ＝a （x +2）（x ﹣4）＝a （x 2﹣2x ﹣8），即﹣8a ＝﹣3，解得：a ＝38，则函数的表达式为：233384y x x =--；（2）y ＝32x ﹣3，令y ＝0，则x ＝2，即点D （2，0），连接OP ，设点P （x ，233384x x --）， S △PCD ＝S △PDO +S △PCO ﹣S △OCD ＝22133113272(3)323(3)2842288x x x x ⨯-+++⨯⨯-⨯⨯=--+， ∵﹣38＜0，∴S △PCD 有最大值，此时点P （3，﹣815）；（3）如图，经过点O 、B 的圆F 与直线l 相切于点E ，此时，sin ∠BEO 最大，过圆心F 作HF ⊥x 轴于点H ，则OH ＝12OB ＝2＝OA ，OF ＝EF ＝4，∴HF ＝，过点E 的坐标为（﹣2，﹣；同样当点E 在x 轴的上方时，其坐标为（﹣2，；故点E 的坐标为（﹣2，2，﹣）．20．已知抛物线y ＝ax 2+bx +2经过A （﹣1，0），B （2，0），C 三点．直线y ＝mx +12交抛物线于A ，Q 两点，点P 是抛物线上直线AQ 上方的一个动点，作PF ⊥x 轴，垂足为F ，交AQ 于点N ．（1）求抛物线的解析式；（2）如图①，当点P运动到什么位置时，线段PN＝2NF，求出此时点P的坐标；（3）如图②，线段AC的垂直平分线交x轴于点E，垂足为D，点M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，请求出点G的坐标；若不存在，请说明理由．【答案】（1）y＝﹣x2+x+2；（2）点P的坐标为（12，94）；（3）在直线DE上存在一点G，使△CMG的周长最小，此时G（﹣38，1516）．【解析】（1）∵抛物线y＝ax2+bx+2经过A（﹣1，0），B（2，0），∴将点A和点B的坐标代入得：204220a ba b-+=⎧⎨++=⎩，解得a＝﹣1，b＝1，∴抛物线的解析式为y＝﹣x2+x+2．（2）直线y＝mx+12交抛物线与A、Q两点，把A（﹣1，0）代入解析式得：m＝12，∴直线AQ的解析式为y＝12x+12．设点P的横坐标为n，则P（n，﹣n2+n+2），N（n，12n+12），F（n，0），∴PN＝﹣n2+n+2﹣（12n+12）＝﹣n2+12n+32，NF＝12n+12．∵PN＝2NF，即﹣n2+12n+32＝2×（12n+12），解得：n＝﹣1或12．当n＝﹣1时，点P与点A重合，不符合题意舍去．∴点P的坐标为（12，94）．（3）∵y＝﹣x2+x+2，＝﹣（x﹣12）2+94，∴M（12，94）．如图所示，连结AM交直线DE与点G，连结CG、CM此时，△CMG的周长最小．设直线AM的函数解析式为y＝kx+b，且过A（﹣1，0），M（12，94）．根据题意得：1924k bk b-+=⎧⎪⎨+=⎪⎩，解得3232kb⎧=⎪⎪⎨⎪=⎪⎩．∴直线AM的函数解析式为y＝32x+32．∵D为AC的中点，∴D（﹣12，1）．设直线AC的解析式为y＝kx+2，将点A的坐标代入得：﹣k+2＝0，解得k＝2，∴AC的解析式为y＝2x+2．设直线DE的解析式为y＝﹣12x+c，将点D的坐标代入得：14+c＝1，解得c＝34，∴直线DE的解析式为y＝﹣12x+34．将y＝﹣12x+34与y＝32x+32联立，解得：x＝﹣38，y＝1516．∴在直线DE上存在一点G，使△CMG的周长最小，此时G（﹣38，1516）．21．现有一次函数y＝mx+n和二次函数y＝mx2+nx+1，其中m≠0，（1）若二次函数y＝mx2+nx+1经过点（2，0），（3，1），试分别求出两个函数的解析式．（2）若一次函数y＝mx+n经过点（2，0），且图象经过第一、三象限．二次函数y＝mx2+nx+1经过点（a，y1）和（a+1，y2），且y1＞y2，请求出a的取值范围．（3）若二次函数y＝mx2+nx+1的顶点坐标为A（h，k）（h≠0），同时二次函数y＝x2+x+1也经过A 点，已知﹣1＜h ＜1，请求出m 的取值范围．【答案】（1）y ＝x ﹣2，y =12-x 2+32+1；（2）a ＜12；（3）m ＜﹣2或m ＞0．【解析】（1）将点（2，0），（3，1），代入一次函数y ＝mx +n 中，0213m nm n =+⎧⎨=+⎩，解得12m n =⎧⎨=-⎩，∴一次函数的解析式是y ＝x ﹣2，再将点（2，0），（3，1），代入二次函数y ＝mx 2+nx +1，04211931m n m n =++⎧⎨=++⎩，解得1232m n ⎧=-⎪⎪⎨⎪=⎪⎩，∴二次函数的解析式是213122y x =-++．（2）∵一次函数y ＝mx +n 经过点（2，0）， ∴n ＝﹣2m ，∵二次函数y ＝mx 2+nx +1的对称轴是x ＝n 2m-， ∴对称轴为x ＝1，又∵一次函数y ＝mx +n 图象经过第一、三象限， ∴m ＞0， ∵y 1＞y 2， ∴1﹣a ＞1+a ﹣1， ∴a ＜12．（3）∵y ＝mx 2+nx +1的顶点坐标为A （h ，k ）， ∴k ＝mh 2+nh +1，且h ＝n 2m-，又∵二次函数y＝x2+x+1也经过A点，∴k＝h2+h+1，∴mh2+nh+1＝h2+h+1，∴11 hm=-+，又∵﹣1＜h＜1，∴m＜﹣2或m＞0．22．如图，在直角坐标系中，直线y＝13x+1与x轴、y轴的交点分别为A、B，以x＝﹣1为对称轴的抛物线y＝﹣x2+bx+c与x轴分别交于点A、C．（1）求抛物线的解析式；（2）若点P是第二象限内抛物线上的动点，设抛物线的对称轴l与x轴交于一点D，连接PD，交AB于E，求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标；（3）若点Q在第二象限内，且tan∠AQD＝2，线段CQ是否存在最小值？如果存在直接写出最小值，如果不存在，请说明理由．【答案】（1）y＝﹣x2﹣2x+3；（2）点P的坐标是（﹣1，4）或（﹣2，3）；（3）存在，CQ【解析】解：（1）∵直线y＝13x+1与x轴交点为A，∴点A的坐标为（﹣3，0），∵抛物线的对称轴为x＝﹣1，∴点C的坐标为（1，0），∵抛物线y＝﹣x2+bx+c与x轴分别交于点A、C，。

二次函数系数abc与图像的关系精选练习题

二次函数系数a、b、c与图像的关系知识要点二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2-4ac的符号由抛物线与x轴交点的个数确定：2个交点，b2-4ac＞0；1个交点，b2-4ac=0；没有交点，b2-4ac＜0．（5）当x=1时，可确定a+b+c的符号，当x=-1时，可确定a-b+c的符号．（6）由对称轴公式x=，可确定2a+b的符号．一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．42．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．45．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜37．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个10、（2011?重庆）已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞011、（2011?雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤12、（2011?孝感）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（12，1），下列结论：①ac＜0；②a+b=0；③4ac-b2=4a；④a+b+c＜0．其中正确结论的个数是（）A、1B、2C、3D、4答案一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a，又∵c=0，∴y=3a，（故③错误）；x=m对应的函数值为y=am2+bm+c，x=﹣1对应的函数值为y=a﹣b+c，又∵x=﹣1时函数取得最小值，∴a﹣b+c＜am2+bm+c，即a﹣b＜am2+bm，∵b=2a，∴am2+bm+a＞0（m≠﹣1）．（故④正确）．故选：C．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．2．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c ＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x轴交点负半轴明显大于﹣1，∴y=a﹣b+c＜0，故②正确；③由抛物线的开口向下知a＜0，∵对称轴为0＜x=﹣＜1，∴2a+b＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵图象开口向下，∴a＜0；故本选项正确；②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点评：本题主要考查了二次函数的图象和性质，解答本题关键是掌握二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解答：解：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；③正确；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确．故选C．点评：主要考查图象与二次函数系数之间的关系．此题难度适中，注意掌握数形结合思想的应用．5．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④考点：二次函数图象与系数的关系．分析：根据抛物线开口方向得到a＞0，根据抛物线的对称轴得b=2a＞0，则2a﹣b=0，则可对②进行判断；根据抛物线与y轴的交点在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x=﹣2时，y＜0，则得到4a﹣2b+c ＜0，则可对③进行判断；通过点（﹣5，y1）和点（2，y2）离对称轴的远近对④进行判断．解答：解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；∵点（﹣5，y1）离对称轴要比点（2，y2）离对称轴要远，∴y1＞y2，所以④正确．故选D．点评：本题考查了二次函数图象与系数的关系：二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小，当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）．抛物线与y轴交于（0，c）．抛物线与x轴交点个数：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜3考点：二次函数图象与系数的关系．分析：由于二次函数的对称轴在y轴右侧，根据对称轴的公式即可得到关于m的不等式，由图象交y轴于负半轴也可得到关于m的不等式，再求两个不等式的公共部分即可得解．解答：解：∵二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，∴m﹣3＜0，解得m＜3，∵对称轴在y轴的右侧，∴x=，解得m＞2，∴2＜m＜3．故选：D．点评：此题主要考查了二次函数的性质，解题的关键是利用对称轴的公式以及图象与y轴的交点解决问题．7．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：∵抛物线的开口方向向下，∴a＜0；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，①正确；由图象可知：对称轴x==﹣1，∴2a=b，2a+b=4a，∵a≠0，∴2a+b≠0，②错误；∵图象过点A（﹣3，0），∴9a﹣3b+c=0，2a=b，所以9a﹣6a+c=0，c=﹣3a，③正确；∵抛物线与y轴的交点在y轴的正半轴上，∴c＞0由图象可知：当x=1时y=0，∴a+b+c=0，④正确．故选C．点评：考查了二次函数图象与系数的关系，解答本题关键是掌握二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④考点：二次函数图象与系数的关系．分析：①由抛物线的对称轴为直线x=1，一个交点A（﹣1，0），得到另一个交点坐标，利用图象即可对于选项①作出判断；②根据抛物线开口方向判定a的符号，由对称轴方程求得b与a的关系是b=﹣2a，将其代入（3a+b），并判定其符号；③根据两根之积=﹣3，得到a=，然后根据c的取值范围利用不等式的性质来求a的取值范围；④把顶点坐标代入函数解析式得到n=a+b+c=c，利用c的取值范围可以求得n的取值范围．解答：解：①∵抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），对称轴直线是x=1，∴该抛物线与x轴的另一个交点的坐标是（3，0），∴根据图示知，当x＞3时，y＜0．故①正确；②根据图示知，抛物线开口方向向下，则a＜0．∵对称轴x==1，∴b=﹣2a，∴3a+b=3a﹣2a=a＜0，即3a+b＜0．故②错误；③∵抛物线与x轴的两个交点坐标分别是（﹣1，0），（3，0），∴﹣1×3=﹣3，=﹣3，则a=．∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3，∴﹣1≤≤，即﹣1≤a≤．故③正确；④根据题意知，a=，=1，∴b=﹣2a=，∴n=a+b+c=c．∵2≤c≤3，≤≤4，≤n≤4．故④正确．综上所述，正确的说法有①③④．故选D．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定．9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，∴对称轴在y轴的右侧，即：﹣＞0，∵a＞0∴b＜0，故①正确；②显然函数图象与y轴交于负半轴，∴c＜0正确；③∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），∴a﹣b+c=0，即a+c=b，∵b＜0，∴a+c＜0正确；④∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），且a＞0，∴当x=﹣2时，y=4a﹣2b+c＞0，故④正确，故选D．点评：主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．。

《二次函数y = ax^2+bx+c的图象与性质》典型例题

《二次函数y=ax 2+bx+c 的图象与性质》典型例题例 1 函数a ax y +=2与)0(≠=a xa y 在同一坐标系中的图像可能是如图中的（）例2 如果以y 轴为对称轴的抛物线y=ax 2+bx+c 的图象如图13-25所示，那么代数式b+c-a 与零的关系是（）+c-a=0； +c-a ＞0； +c-a ＜0； D.不能确定。

例3 二次函数y=ax 2+bx+c 与一次函数y=ax+c 在同一坐标系中的图象大致是（）例4 已知函数23212++-=x x y . （1）求函数图像的顶点坐标和对称轴；（2）求函数图像与坐标轴的交点坐标；（3）作出函数的图像.参考答案例1 解法一：直接法0≠a ，∴a 的取值只有两种可能：0>a 或0<a .当0>a 时，有xa y =的图像在第一、三象限；a ax y +=2的图像开口向上，顶点),0(a 在x 轴的上方，四个选择支无一适合.所以，没有符合条件的图像. 当0<a 时，有xa y =的图像在第二、四象限；a ax y +=2的图像开口向下，顶点),0(a 在x 轴的下方，符合条件的图像有D.故应选D.解法二：排除法0≠a ，函数a ax y +=2的图像顶点在y 轴上，故排除A ；对于B ，由反比例函数x a y =的图像可知：0>a ，但由a ax y +=2的图像得0<a ，产生矛盾，故B 排除；对于C ，由反比例函数xa y =的图像可知：0>a ，但由a ax y +=2的图像与y 轴交于负半轴得0<a ，产生矛盾，故C 排除.故答案应选D.例2 解：从图13-25上看出抛物线开口向下，所以a ＜0.当x=0时，y 的值为正，所以c ＞0.又因为抛物线以y 轴为对称轴，所以b=0。

综上分析知b+c-a ＞0，应选B 。

注意：这个题考察了二次函数中三个系数a 、b 、c 的含义，二次项系数a 决定抛物线开口方向，c 为抛物线在y 轴上的截距即抛物线与y 轴交点的纵坐标，抛物线的对称轴方程为2b x a=-，要根据图象具体分析才能得出正确结论。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

是其对称轴上一动点，当PB+PC 取得最小值时，点P 的坐标为．二次函数y =ax2+bx +c的图像和性质一、填空题：1、二次函数在上有最小值，则的值为.2、将抛物线y＝x2＋1 先向左平移2 个单位，再向下平移3 个单位，那么所得抛物线的函数关系式是3、直线y = 2x＋b 右移3 个单位长度后过抛物线y = 2x2－2x＋4 的顶点，则b =。

4、已知二次函数x+2 的图象与x 轴分别交于A、B 两点（如图所示），与y 轴交于点C，点P5、如图，抛物线y=ax2+bx+c(与x 轴的一个交点A 在点（-2，0）和（-1，0）之间（包括这两点），顶点C 是矩形DEFG 上（包括边界和内部）的一个动点，则a 的取值范围是。

6、如图，菱形ABCD 的三个顶点在二次函数y=ax2－2ax+（a＜0）的图象上，点A、B 分别是该抛物线的顶点和抛物线与y 轴的交点，则点D 的坐标为．7、如图，在第一象限内作射线O C，与x 轴的夹角为30°，在射线OC 上取一点A，过点A 作AH⊥x轴于点H．在抛物线y= （x＞0）上取点P，在y 轴上取点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A 的坐标是.二、选择题：8、抛物线y=x2的图象向左平移2 个单位，再向下平移1 个单位，则所得抛物线的解析式为（）。

A.y=x2+4x+3B. y=x2+4x+5C. y=x2－4x+3D.y=x2－4x－59、无论m 为任何实数，抛物线y＝＋（2－m）x＋m总过的点是（）A（1，3）B（1，0）C（－1，3）D（－1，0）10、在平面直角坐标系中，如果抛物线y＝2x2不动，而把x 轴、y 轴分别向上、向右平移2 个单位，那么在新坐标系下抛物线的解析式是( ) A．y＝2(x+ 2)2－2 B．y＝2(x－2)2+ 2 C．y＝2(x－2)2－2 D．y＝2(x + 2)2 + 211、已知一元二次方程的一根为-3，在二次函数的图像上有三点、、，、、的大小关系是（）A. B. C. D.12、抛物线y = ax2+ bx + c 的图象向左平移2 个单位,再向下平移1 个单位,所得抛物线为y = 2x2- 4x + 3 ，原抛物线为（）A.y = 2x2+ 4x + 4B.y = 2x2-12x +18C.y = 2x2+ 4x + 2D.y = 2x2-12x + 2013、如果抛物线的顶点到轴的距离是3，那么的值等于（）A、8B、14C、8 或14D、-8 或-1414、若二次函数y=x2-2mx+1+m2．当≤3时，随的增大而减小，则的取值范围是（）A．=3 B．>3 C．≥3D．≤315、二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（）．16、已知二次函数的图象（﹣0.7≤x≤2）如图所示、关于该函数在所给自变量x 的取值范围内，下列说法正确的是（）A.有最小值1,最大值2 B.有最小值-1,最大值1 C.有最小值-1,最大值2 D.有最小值-1,无最大值17、二次函数（a，b，c 是常数，a≠0）图象的对称轴是直线，其图象一部分如图所示，对于下列说法：①；②；③；④当时，．其中正确的是（）A．①②B．①④C．②③D．②③④C ．或时，．18、已知抛物线的图象如图所示，则下列结论：① ＞0；② ； ③ ＜；④ ＞1.其中正确的结论是（）A. ①②B. ②③C. ③④D. ②④19、抛物线的部分图象如图所示，若，则的取值范围是（）A ．B ． D ．20、已知二次函数的图象如图所示对称轴为．下列结论中，正确的是（）A ．B ．C ．D ．21、如图6，抛物线与交于点，过点作轴的平行线，分别交两条抛物线于点．则以下结论：①无论取何值，的值总是正数．② ．③当④ ．其中正确结论是（） A ．①②Ｂ．②③Ｃ．③④Ｄ．①④三、简答题： 22、已知二次函数的图象如图所示，它与 x 轴的一个交点坐标为（－1，0），与y 轴的交点坐标为（0，3）。

（1）求出b ，c 的值，并写出此二次函数的解析式；（2）根据图象，写出函数值y 为正数时，自变量x 的取值范围。

23、已知：二次函数的图象与X 轴交于A （1，0）、B （5，0），抛物线的顶点为P ，且PB=，求：（1）二次函数的解析式。

（2）求出这个二次函数的图象；（3）根据图象回答：当x 取什么值时，y 的值不小于0。

24、已知：二次函数的表达式为．（1）写出这个函数图象的对称轴和顶点坐标；并画出图像。

（2）求图象与轴的交点坐标；（3）观察图象，指出使函数值y ＞时自变量 x 的取值范围或．25、足球比赛中，某运动员将在地面上的足球对着球门踢出，图中的抛物线是足球的飞行高度y （m ）关于飞行时间x （s ）的函数图象（不考虑空气的阻力），已知足球飞出1s 时，足球的飞行高度是2.44m ，足球从飞出到落地共用3s ．（1）求y 关于x 的函数关系式；（2）足球的飞行高度能否达到4.88 米？请说明理由；（3）假设没有拦挡，足球将擦着球门左上角射入球门，球门的高为2.44m （如图所示，足球的大小忽略不计）．如果为了能及时将足球扑出，那么足球被踢出时，离球门左边框12m 处的守门员至少要以多大的平均速度到球门的左边框？26、如图，在平面直角坐标系中，直线y=-2x+42 交x 轴与点A,交直线y=x 于点B,抛物线分别交线段AB 、OB 于点C 、D ，点C 和点D 的横坐标分别为16 和4，点P 在这条抛物线上．（1）求点C 、D 的纵坐标．（2）求a 、c 的值．（3）若Q 为线段OB 上一点，且P 、Q 两点的纵坐标都为5，求线段PQ 的长．（4）若Q 为线段OB 或线段AB 上的一点，PQ⊥x 轴，设P 、Q 两点之间的距离为d （d ＞0），点Q 的横坐标为m ，直接写出d 随m 的增大而减小时m 的取值范围．（参考公式：二次函数图像的顶点坐标为27、如图，已知二次函数y ＝－ x 2＋bx ＋c 的图象经过A (2,0)，B (0，－6)两点 (1) 求这个二次函数的解析式；(2) 设该二次函数的对称轴与x 轴交于点C ，连接BA 、BC ，求△ABC 的面积．28、已知二次函数y =x 2＋bx ＋c 与x 轴交于A （－1，0）、B （1，0）两点.（1）求这个二次函数的关系式；（2）若有一半径为r 的⊙P ，且圆心P 在抛物线上运动，当⊙P 与两坐标轴都相切时，求半径r 的值.（3）半径为1 的⊙P 在抛物线上，当点P 的纵坐标在什么范围内取值时，⊙P 与y 轴相离、相交？29、如图，抛物线经过两点，此抛物线的对称轴为直线，顶点为，且与直线交于点．（1）求此抛物线的解析式；（2）直接写出此抛物线的对称轴和顶点坐标；（3）连接，求证：；30、已知抛物线：（1）求抛物线的顶点坐标.（2）将抛物线向右平移 2 个单位，再向上平移 1 个单位，得到抛物线，求抛物线的解析式.（3）如下图，抛物线的顶点为P，轴上有一动点M，在、这两条抛物线上是否存在点N，使O（原点）、P、M、N 四点构成以OP 为一边的平行四边形，若存在，求出N 点的坐标；若不存在，请说明理由.【提示：抛物线（≠0）的对称轴是顶点坐标是】参考答案一、填空题1、2、3、17/2 4、(-1, )5、6、（2，）7、（3，√3）二、选择题8、A 9、A 10、A 11、C 12、D, 13、D 14、C 15、答案：D16、考点：二次函数的最值．.分析：直接根据函数的图象顶点坐标及最低点求出该函数在所给自变量的取值范围内的最大及最小值即可．解答：解：由函数图象可知，此函数的顶点坐标为（1，2），∵此抛物线开口向下，∴此函数有最大值，最大值为 2；∵﹣0.7≤x≤2，∴当 x=﹣0.7 时，函数最小值为﹣1．故选 C．点评：本题考查的是二次函数的最值及二次函数的图象，解答此题时要注意应用数形结合的思想求解．17、答案：C 18、D 19、B； 20、考点：二次函数图象与系数的关系。

解答：解：A、∵开口向上，∴a＞0，∵与y 轴交与负半轴，∴c＜0，∵对称轴在y 轴左侧，∴﹣＜0，∴b＞0，∴abc＜0，故本选项错误；B、∵对称轴：x=﹣=﹣，∴a=b，故本选项错误；C、当x=1 时，a+b+c=2b+c＜0，故本选项错误；D、∵对称轴为x=﹣，与x 轴的一个交点的取值范围为x1＞1，∴与x 轴的另一个交点的取值范围为x2＜﹣2，∴当x=﹣2时，4a﹣2b+c＜0，即4a+c＜2b，故本选项正确．故选D．21、D三、简答题22、（1）（2）23、解（1）由题意，设二次函数的解析式为 y=a(x-1)(x-5),即 y=ax2-6ax+5a对称轴为 x=3，设对称轴与 x 轴的交点为 C(3,0)∴OC=3∵OB=5∴BC=2∵P是顶点，BP= ∴PC=4P（3，-4）∴∴∴二次函数的解析式为（2）略（3）当 1<x<5 时，y<024、解（1）y=- (x-1)2+2 (2)3 或-1 图像略（3）0＜x ＜2． 25、解：（1）设 y 关于 x 的函数关系式为 y=ax 2+bx ．（1 分）依题可知：当 x=1 时，y=2.44；当 x=3 时，y=0．∴，（3 分）∴ ，∴y=-1.22x 2+3.66x ．（5 分）（2）不能．理由：∵y=4.88，∴4.88=-1.22x 2+3.66x ，（6 分）∴x 2-3x+4=0．∵(-3)2-4×4＜0，∴方程 4.88=-1.22x2+3.66x 无解．∴足球的飞行高度不能达到 4.88m ．（7 分）（3）∵y=2.44，∴2.44=-1.22x 2+3.66x ，（8 分）∴x 2-3x+2=0，∴x 1=1（不合题意，舍去），x 2=2．∴平均速度至少为 =6（m/s ）．（9 分） 26、解析：（1）把 x=16 代入 y=-2x+42 得 y=10，把 x=,4 代入 y=x 得 y=4.点 C 的纵坐标为 10，点,D 的纵坐标为 4.（2）把 C(16,10)D(4,4)代入得0=256a-32+c ，4=16a-8+c解之得：a= c=10（3）把 y=5 代入 y=x 得 x=4 把 y=5 代入 y= 得 y= ，PQ=5- = （4）7<m<11考查知识：待定系数法求二次函数解析式、坐标系上两点间距离、求点的坐标。

27、解：(1)把A(2,0)，B(0，－6)代入y＝－x2＋bx＋c，得，解得.∴这个二次函数的解析式为y＝－x2＋4x－6.(2)∵该抛物线对称轴为直线x＝－＝4，∴点C 的坐标为(4,0)，∴AC＝OC－OA＝4－2＝2，∴S△ABC＝×AC×OB＝×2×6＝6.28、解：（1）由题意，得解得………………………4分∴二次函数的关系式是y=x2－1．（2）设点 P 坐标为（x，y），则当⊙P与两坐标轴都相切时，有y=±x．由y=x，得x2－1=x，即x2－x－1=0，解得x= ．由y=－x，得x2－1=－x，即x2＋x－1=0，解得x= ．∴⊙P 的半径为r=|x|= ．…分（3）设点 P 坐标为（x，y），∵⊙P 的半径为 1，∴当y＝0 时，x2－1=0，即x＝±1，即⊙P 与y 轴相切，又当x＝0 时，y＝－1，∴当y＞0 时，⊙P 与y 相离；当－1≤y＜0 时，⊙P 与y 相交. ……………………四、实验,探究29、解：（1）抛物线解此抛物线的解析式为：．（2）由（1）可得此抛物线的对称轴为，顶点的坐标为．（3）证明：过两点的直线解析式为，当时，．点的纵坐标为，．作于点，则．，由勾股定理得，五、综合题30、解：（1）依题意………………………………………………1分∴，…………………………3分∴顶点坐标是（2，2）解析式中的二次项系数为……………………………………………………（2）根据题意可知y25 分的顶点坐标是（4，3）…....................................................................................6 分且y2∴y2＝－，即：y2＝……………………………（3）符合条件的N 点存在… .......................................................................................9 分如图：若四边形OPMN 为符合条件的平行四边形，则∥，且∴，作轴于点A，轴于点B∴，则有（AAS）∴∵点P 的坐标为（4,3）∴……10分∵点N 在抛物线、上，且P 点为、的最高点∴符合条件的N 点只能在轴下方①点N 在抛物线上，则有：解得：或……②点N 在抛物线上，则有：解得：或……………∴符合条件的N 点有四个：……………………………………………14 分。