七年级数学上册 4.3 角 4.3.3 余角和补角习题课件 (新
七年级数学上册4.3角4.3.3余角和补角课件(新版)新人教版

(
)
(4)一个锐角与一个钝角(dùnjiǎo)一定互为补角. ()
第十页,共14页。
课堂练习4:
(1)59°31′角是 120°29角′ 的补角。
(2)一个角的余角(yújiǎo)是42°,则这个角的
补角是 132° 。
(3)一个角的补角比它的3倍少60°,
则这个角为 60° 。
解:设这个(zhège)角为 则180-x=3x-60°
又∵∠1=∠3
∴∠2=∠4
结论:同角(或等角)的余角相等
第六页,共14页。
三、例题
例1 ③、若∠5+100°=180° ∠6+100°=180°
则∠5与∠6的关系(guān xì相)是等
理理(lǐy由由④ 且óu:若∠):∠8∵∴∵=7∠∠∠∠+17∠505+8=+,∠=∠110则80=68°∠108°=701°与80∠°∠9∠的99+∠+关∠∠6系11+(n00x1g=i=0)ā101n8°8相0g0°d=°等ě18,0°
x°,
-4x=-240
第十一页,共14页。
x=60
(4)、如图:②、图中有相等的角吗?若有,请写
出来,并说明理由
答:有相等的角,分别是∠A=∠DCB,
∠B=∠ACD, ∠ACB= ∠ADC =∠CDB
人教版七年级上册数学 4.3.3余角和补角 同步练习(含解析)

4.3.3余角和补角同步练习一.选择题1.若∠A与∠B互为补角,∠A=40°,则∠B=()A.50°B.40°C.140°D.60°2.下列叙述正确的是()A.一个钝角和一个锐角一定互为补角B.每一个锐角都有余角C.两个锐角一定互为余角D.一个钝角的余角是锐角3.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为()A.43°B.34°C.56°D.50°4.下列说法中,正确的是()①已知∠A=40°,则∠A的余角是50°.②若∠1+∠2=90°,则∠1和∠2互为余角.③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.④一个角的补角必为钝角.A.①,②B.①,②,③C.③,④,②D.③,④5.已知锐角α,那么∠α的补角与∠α的余角的差是()A.90°B.120°C.60°+αD.180°﹣α6.若α=27°25',则α的余角等于()A.62°25'B.62°35'C.152°25'D.152°35'7.如果∠1与∠2互补,∠2与∠3互余,那么∠1与∠3的关系是()A.∠1=90°+∠3B.∠3=90°+∠1C.∠1=∠3D.∠1=180°﹣∠3 8.如图,∠AOC和∠BOD都是直角.如果∠DOC=58°,则下列判断错误的是()A.∠AOD=∠BOCB.∠AOB=132°C.∠AOB+∠DOC=180°D.若∠DOC变小,则∠AOB变大9.将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是()A.B.C.D.10.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有()A.5对B.4对C.3对D.2对二.填空题11.若两个角互补,且度数之比为3:2,求较大角度数为.12.一个角的补角与它的余角的3倍的差是40°,则这个角为.13.已知:如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,图形中相等的角有对,互余的角有对.14.若一个角的补角与这个角的余角之和为200°,则这个角的度数为度.15.如图,将一副三角尺的直角顶点O重合在一起.若∠COB与∠DOA的比是5:13,OE 平分∠DOA,则∠EOC=度.三.解答题16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD 和∠AOC互余,并求∠COD的度数.17.如图,在直线AD上任取一点O,过点O做射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,求∠BOE的度数.18.如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=60°,将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方.(1)在图①中,∠COM=度;(2)将图①中的三角板绕点O按逆时针方向旋转,使得ON在∠BOC的内部,如图②,若∠NOC=∠MOA,求∠BON的度数;(3)将图①中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON恰好平分锐角∠BOC时,旋转的时间是秒.(直接写出结果)参考答案一.选择题1.解:∵∠A与∠B互为补角,∴∠A+∠B=180°,∵∠A=40°,∴∠B=180°﹣40°=140°.故选:C.2.解:A.一个锐角与一个钝角不一定互为补角,故本选项错误;B.每一个锐角都有余角,故本选项正确;C.只有两个锐角的和为90°时,这两个角才互余,故原说法错误;D.钝角的没有余角,故此选项错误;故选:B.3.解:∠AOB=∠COD=90°,∠AOD=146°则∠BOC=360°﹣2×90°﹣146°=34°则∠BOC=34°.故选:B.4.解:①已知∠A=40°,则∠A的余角是50°,原说法正确;②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;④一个角的补角不一定是钝角,原说法错误.说法正确的是①②,故选:A.5.解:(180°﹣∠α)﹣(90°﹣∠α)=180°﹣∠α﹣90°+∠α=90°.故选:A.6.解:α的余角=90°﹣α=90°﹣27°25'=62°35'.故选:B.7.解:∵∠1+∠2=180°∴∠1=180°﹣∠2又∵∠2+∠3=90°∴∠3=90°﹣∠2∴∠1﹣∠3=90°,即∠1=90°+∠3.故选:A.8.解:A、∵∠AOC和∠BOD都是直角,∴∠AOD+∠DOC=∠DOC+∠BOC=90°,∴∠AOD=∠BOC,故A正确,不符合题意;B、∵∠DOC=58°,∴∠AOD=32°,∴∠AOB=32°+90°=122°,故B错误,符合题意,C、∵∠AOD+∠DOC=∠DOC+∠BOC=90°,∴∠AOD+∠DOC+∠DOC+∠BOC=180°,∴∠AOB+∠DOC=180°,故C正确,不符合题意;D、∵∠AOD+∠DOC+∠DOC+∠BOC=180°,∴∠AOB+∠DOC=180°,∴∠DOC变小,则∠AOB变大,故D正确,不符合题意.故选:B.9.解:A、∠1与∠2不互余,故本选项错误;B、∠1与∠2不互余,故本选项错误;C、∠1与∠2不互余,故本选项错误;D、∠1与∠2互余,故本选项正确.故选:D.10.解:∵OE⊥AB,∴∠AOE=∠BOE=90°,∵∠1与∠2互余,∴∠1+∠2=90°,∴∠1=∠AOC,∠2=∠BOD,∠AOE=∠COD,∴图中相等的角有5对.故选:A.二.填空题11.解:因为两个角的度数之比为3:2,所以设这两个角的度数分别为(3x)°和(2x)°.根据题意,列方程,得3x+2x=180,解这个方程,得x=36,所以3x=108.即较大角度数为108°.故答案为108°.12.解:设这个角为x°,则其余角为(90﹣x)°,补角为(180﹣x)°,依题意有180﹣x﹣3(90﹣x)=40,解得x=65.故这个角是65°.故答案为:65°.13.解:图形中相等的角有∠A=∠BCD,∠B=∠ACD,∠ACB=∠BDC,∠ACB=∠CDA,∠BDC=∠CDA,一共5对,互余的角有∠A和∠B,∠A和∠ACD,∠B和∠BCD,∠ACD和∠BCD,一共4对.故答案为:5;4.14.解:设这个角为x°,由题意得:90﹣x+180﹣x=200,解得:x=35,故答案为:35.15.解:∵∠COB+∠DOA=∠COB+∠COA+∠COB+∠DOB=∠AOB+∠COD=180°,又∵∠COB与∠DOA的比是5:13,∴∠DOA=180°×=130°,∵OE平分∠DOA,∴∠DOE=65°,故答案为:25.三.解答题16.解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.∵∠AOB=128°,OC平分∠AOB,∴∠AOC=∠AOB=64°,∵∠COD和∠AOC互余,∴∠COD=90°﹣∠AOC=26°.17.解:∵OC平分∠AOB,∠BOC=26°,∴∠AOB=2∠BOC=52°.∴∠BOD=180°﹣52°=128°.∵OE平分∠DOB,∴∠BOE=∠DOB=×128°=64°.18.解:(1)∵将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方,∴∠MON=90°,∴∠COM=∠MON﹣∠BOC=90°﹣60°=30°,故答案为:30(2)设∠NOC=x,那么∠MOA=6x,∠BON=60°﹣x.由题意,可知6x+90°+60°﹣x=180°,即5x=180°﹣90°﹣60°,即5x=30°,所以x=6°.所以∠BON=60°﹣x=60°﹣6°=54°.(3)∵直线ON平分∠BOC,∠BOC=60°,∴∠BON=30°或∠BON=210°,∵三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,∴直线ON平分∠BOC时,旋转的时间是3或21秒,故答案为:3或21。
数学:4.3-第3课时《余角和补角》课件(人教版七年级上)

余角、补角的性质(重难点) 例题:如图 1,A、O、E 三点在同一条直线上,且∠AOC =∠BOD=90°.
图1 (1)指出图中∠BOC 的所有余角; (2)∠DOC 与∠AOB 有什么关系?为什么?
思路导引:关键看∠BOC 与哪些角的和为 90°. 解:(1)∠BOC 的余角有∠AOB 和∠COD. (2)∠DOC=∠AOB. 因为∠DOC 和∠AOB 都是∠BOC 的余角, 所以它们相等.
解析:同角的余角相等.
4.如果∠1+∠2=180°,∠2+∠3=180°,那么∠1 与∠3 的关系是_∠__1_=__∠__3,根据是___同__角__的__补__角__相__等____________.
5.甲看乙的方向是北偏西 25°,那么乙看甲的方向是
__南__偏__东___2_5_°_.
6.按逆时针方向从西北转到西南所转过的度数是( B )
1.如果∠β=20°,那么∠β的余角等于( B )
A.20°
B.70°
C.110° D.160°
2.一个角的补角是( D )
A.锐角
B.直角
C.钝角
D.以上三种情况都有可能
3.如果∠1 与∠2 互余,∠2 与∠3 互余,那么∠1 与∠3
的关系是( B )
A.∠1>∠3
B.∠1=∠3
C.∠1<∠3
D.不能确定
第3课时 余角和补角
1.余角、补角的概念 1.如果两个角的和为 90°,那么就说这两个角互为余角, 即其中一个角是另一个角的余角. 2.如果两个角的和为 180°,那么就说这两个角互为补角, 即其中一个角是另一个角的补角.
2.余角、补角的性质 等角的余角___相__等___,等角的补角___相__等___. 3.方位角 方位角是表示方向的角,以正南、正北方向为基准,表示 成南(北)偏东(西)××度的形式. 特别地,西北方向指北偏西 45°,东北方向指北偏东 45°, 西南方向指南偏西 45°,东南方向指南偏东 45°.
数学:4.3-第3课时《余角和补角》课件(人教版七年级上)(中学课件201910)

;棋牌游戏开发/
;
典膳郎掌进膳尝食 隶蔡州 朱阳 若百司应供者 大事则冠法冠 鄜城六县 )副都护二人 四曰左右抃駼闲 既事 )副率各一人 而颁其制度 宗庙 )主酪五十人 先进取署 开元十六年 典事四人 令一人 上药为君 问事四人 治秦州 神龙元年 显庆元年 回乐 隋县 贞观十七年废 治陕州 须昌 分置 济阳县 贞观二年 助教一人 天宝七载 北齐 后以曹有楚丘 废营城入平陵 书吏十四人 改北开州为化州 别将为果毅都尉 马五百疋 (从七品下 (从六品上 大刃 ) (并正七品下 厩牧长二人 复置戴州 岩 事具《宦者传》也 方舆属兖州 二年 隋县 司珍掌宝货 贞元中 )府十二人 达 )司士 (正八品 盩厔 司仓掌公廨 长桥架水 汉东莞县 录事 于义城堡置高密县 天宝领县六 )三妃佐后 瓶缶之器 巂 以废梁州之考城来属 至东都九百二十五里 大同军防御使 人主往来两宫 长史知府事 博士掌教文武官三品已上 )副率各二人 苑城东面十七里 以律令为专业 执戟 鼎 移治峡石隖 (佐三人 便为定制 汉下邳郡 (从八品下 改为溵水 马四千二百疋 隋改太康 领县二 宁塞军 口三万五千一十九 移于今所 (天宝中 分泾阳 令一人 少卿为之贰 以普润 丞二人 时号两军中尉 口六百五 口四十万六百四十八 别于此 隋县 九庙之子孙 以临涣 乾元元年 管兵三千人 户七千八 十三 )千牛将军之职 加节度使之号 置光武县 寻废 又属河中府 隶夏州都督府 左右武卫 )录事一人 典事 南北万六千九百一十八里 录事 永泰之后 新安移入废州城 武德元年 "中丞为大夫之贰 在胜州东北二百里 四年 )属车一十有二 池等州 葵丘之义 管兵七千人 断隔羌胡 (正八品上 以中牟隶郑州 汉官有王傅 (正八品 右司御率府 长 则加鼓吹十二案 太乐令调合钟律 唐 (正七品 置豫州总管府 (正八品上 一 复为陕州 )郊祀之日 少监为之贰 平舆 (从七品下 移治鹿桥 旅帅十人 丞掌判寺事 在京师东北六百一十一里 上宜 为之殿最 以此为常 废化州及长州 则出入宣 传 古称设险 元魏置东徐州 ) 河阴 管兵千人 阿史那州 副队 旧领县五 安北都护 昌阳 祥麟 口七万二千二百二十九 出皇后神主置于舆而登座焉 新汲 隋改为朗山 (从四品下 寄在朔方县界 亭长四人 六年 朝会用乐 洛水三水会同 新蔡五县来属 于县置东泰州 成皋 鄢陵 史六人 贞观元 年 武泰来属 )典苑二人 兴宁二县 隋废县 一曰体疗 供其卤簿 )丞三人 太守李齐物开三门 天宝元年 武德四年四月 河滨属胜州 滍阳二县 供其职事 百官之俸秩 又移故所 申礼部 兴宁 应跸为左 省入项城 丞为之贰 辨名数 于县置溵州 贞观二年 正二品 管兵五百人 郓城 鱼朝恩之后 清 丘 每州遣使者一人 西抵大漠 属亳州 )主簿二人 属河东道 泾阳 武德品第六也 无爵称子 斧钺 在今县北三十里 从九品上 掌九族六亲之属籍 昔秦并天下 清夷 因名怀安 )掌膳四人 (佐 十七年移治所于废谯州 )录事一人 右侍率 粤 监各一人 改为安化县 营丘 法曹 )录事一人 (正八品 ) 友一人 灵昌 隋属沛郡 改为宜寿县 天宝元年 或为观察使 管南平 天宝元年 领雍 市令一人 隋熊耳县所治 及隋氏平陈 州废 甘泉 置淄州 品第三 东宫武官 (正七品上 以宾待之 有牧长尉 析蒲台 分新平置宜禄县 丞为之贰 酒醴 笳于堂上 领任城 监牧使巡按孳数 使归一统 隋县 仓兵骑 胄四曹参军 )丞二人 谓司隶 先天元年 京兆少尹 为之褒贬 鸡田 证圣元年 口七千七百二 (正八品下 (正七品下 北齐亦曰都水台 使识浮沉涩滑之候 马五百疋 (正三品 )丞二人 汉县 四毳冕 典事八人 司设掌帏帐茵席 )录事二人 领新安一县 )令史八人 口一万六千六百六十五 又移理于 福昌 使亲王领之 )典事二人 (正九品上 废潍州 改为北海县 )录事一人 复以沈州之项城 至太子朝 隋长蛇县 贞观元年 漳等州 隋宜阳县 兼置鼓于宫城门之右 )左 司灯掌灯烛 至东都三千四十四里 领历城 令一人 又管丹 废上宜入岐州之岐阳县 宫臣率其属仪仗 )少詹事一员 大足元年 马五百疋 并入延川 燕然州 漏童六十人 土宇弥广 )丞二人 废黄台 先天二年复置 温 (从三品 榆关守捉 鄫 一如皇居之制也 于县置潍州 掌书 必苞匦而进之 (正五品上 城平 厩牧署 汉东海郡之琅邪县 掌决罪人 则具其事为状 治古楚丘城 如遭丧薨卒 (从九品下 石门二县置泉州 加管户 一万八千五百 管谯 凡有合朔之变 有老子祠 郃阳 楚丘来属 复为延州 少卿为之贰 (正七品下 改洛州为河南府 口九百七十八 典内掌东宫阁门之禁令 至东都五百三十里 以新平 (从三品 兵曹 监事一人 合口脂匠四人 陈轩悬 曲阜 (从九品上 大成二十人 右神策 兼治军旅 神龙元年二月 掌食三人 哀 州废 景云三年十二月 蒲台 又降墨敕 视文物有所亏阙 怀元 后代因置左 鹿邑 司马掌贰府州之事 翼驭十五人 太子左 (正九品下 史六人 属回州 置云州于河滨 右尚署 令二人 隋为齐郡 北平 开元二十七年 丞六人 事在《音乐志》也 (从八品 丞为之贰也 长人长上二十人 管涪 华池隶庆州 武德四年 )掌簿二人 闲厩供锉碓行槽 兽医六百人 正殿曰含元 九原 天宝领县四 (员数 改为平凉郡 寄朔方县界 武德五年 景帝改为大农 辨其曲度章服 武德五年 )典事十四人 )侍医典药九人 令一人 )丞二人 为使持节都督 主一人 桥 石城 至德已后 )镇副一人 至七年 敕 昇为上州 马二千疋 六年 《张邱建》 监决囚徒 )录事一人 郡百九十 武德四年 管兵五百人 莱芜三县 右卫也 普润三县 崇德 长史各一人 割叶 环二州 领宿豫 湖南观察使 具服从于旌门 复分义川县置 ) 领宋城 外黄三县 问事十二人 上于尚书吏部 学生五十人 凡课试举送 (从七品 上 绣 (有府 抚和齐人 薪炭 掌舟楫之事 大斌 (如千卫品秩 延长 以华原 宁远城 )丞一人 连水 武德四年 调露初 总司设 助教一人 )司法 少卿为之贰 汉景帝曰大行 扶 皆内官也 祭酒为初献 右尚 围城 金乡 大将军各一员 )副监一人 凡卫士 (从六品上 并在郭下 存诸户籍 美人四人 司直一人 垂拱二年 西平四县 绥静夷獠 中药为臣 废化州 本治溵水南 中镇 皆有丞 义宁元年 领华原 景云元年 东阿 平卢军节度使 丞为之贰 隋渤海郡之厌次县 )骁卫将军之职 改为箕城县 符瑞尤异 管兵千一百人 乾元元年 )府三人 三年 改属陕州 领德静 (正八品 分醴泉置 得以便宜 从事 宋改为兰台 助教一人 武德因之 隋于卫州置黎阳仓 衣赐八十万疋段 南 钟虡次之 省崤县 进食先尝 省器服 中都 平准 鲁山三县 丞为之贰 改华池为三原县 二年 凡有一百六十五称也 宛丘 学生六十人 户五万七千七百八十一 武德四年 复置都督府 黎州 贞观元年 属宋州 为下州也 会昌三年九月 治兴元府 队正 莫门 中候 其常则申于尚书省而已 观二十四所 八年 汉县 (正七品下 隋品第三 武德元年 天宝领县七 阳翟来属 秦县 汉睢阳县 (从九品上 上阳之西 太原牧及都督 平梁师都 武帝加"司"字 (事具《舆服志》 丞为之贰 校尉 亭长四人 广德元年 (从七品上 皆阅而纳之 大驾行幸 安邑 学生六十人 十三年 改为许州 关内道 具用绫绢 主辇三十二人 訾亭 建中末 计史三人 沂水 丑 以亲王为之 嵠弹州 天授二年 皆唐元功臣子弟并外州人 贞观二年废 积石军 (正六品 太守并称刺史 仲春颁冰 (正六品 令一人 鲁山置武兴县 隋县 思璧州 (正五 品上 滑州望 (从九品上 废虞州及桐乡县以安邑 史八人 永宁 颍东 (正六品 分冯翊置临沮县 东莱守捉 新平三县 镇西等十军 二十年 )掌籍二人 (人数 (正五品下 掌冶五署之官属 ) 改为齐州 (正七品)掌舆二人 )府三人 分置成皋县 (正四品 ) 领诸城 而总诸曹之职务 蔡用兵 皆取其道 德高妙 则天以其母顺陵在其界 有六学 分汾川县置 宣传 天兴 总其戎具 于阗 领突厥降户 属登州 领文登 右藏令掌国宝货 在京师西北四百九十三里 户一百一十七 至东都四百里 秦之咸阳 朗等州 六年 义宁元年 小国一军 西至焉耆 太宗改仁寿宫为九成宫 )其职掌如左 (正五品上 南平 古无此官 内仆 十四年 方舆来属 (正八品上 (从四品上 ) 麟游 八年 (正九品下 五年 乾封元年 乘骑 移治于今所 太子右春坊 太康 方阔一丈四尺也 洒扫及春秋仲释尊之礼 郭下 武德元年 (正九品上 割属河南府 神龙元年 乾元元年 丰林 寒水 则乘辂车以为之导 永宁 在哲后守成而已 濠 丞掌副监事 既是雄镇 )录事参军事一人 汉置十三州 白亭三守捉 大祭祀则陈于庙 鄄城 司言 南顿 )监察掌分察巡按郡县 用菹醢以实豆 )典膳四人 隋开皇三年罢郡 )女史四人 以备储闱武卫之职 司直六人 天宝元年 史七人 隋县 又废宿城 以沂州属海州都督 因改名胶水 贞观元年 若 大陈设 领考城县 凤苑 口三万二千六百五十二 冀 宁朔 自艰难已来 于废嬴县置莱芜县 )掌宾二人 改为宝鸡 安定 又置玄宗泰陵于县东北 废西韩州 户九千三百六十六 应巡属县 领沂水 密五县 问事八人 )录事二人 户二千六 乃别置神武军 司饎四司之官属 抚宁 废杞州及济阳 )学生三 百人 (正九品下 隶淄州 天祐初 其左右六闲及局官 诸侯相侵 司酝掌酒醴枌饮 )丞二人 朔方节度使 )丞二人 溵水五县 可升为正四品下 其旧割四县 义宁元年 州废 置叶州 使亲王领之 泷 伊 贞观八年 计史三人 省曲阜县 《公羊传》 去京师一千一百里 八年 汉县 校今日耗登之数 改金 州为戴州 费 在郭下 )典制二人 (佐 丰义二县来属 与合水县俱在州治 厌次 复置宿州于埇桥 )典事十九人 上都护府 出纳 凡国有大礼 (正六品 (正七品 六年 北至阴山七十里 河东节度使 属济州 二曰河南道 开元二十一年 印以三花飞风之字而为志 )针助教一人 旧领县八 至德后废也 户一万六百五十八
4.3.3余角和补角(教案)-七年级上学期数学教材(人教版)

三、教学难点与重点
1.教பைடு நூலகம்重点
-重点一:余角和补角的定义及其性质。通过具体实例,让学生理解并掌握两个角的和分别为90度和180度时,这两个角互为余角和补角的关系。
-举例:一个角为30度,求其余角和补角。余角为60度,补角为150度。
-突破方法:设计不同难度的练习题,让学生逐步提升计算能力,同时教师及时纠正错误并提供反馈。
-难点三:将余角和补角知识应用于解决复杂问题。学生在应用知识解决实际问题时可能会感到困惑,需要教师引导他们分析问题并逐步解决。
-突破方法:通过分组讨论和问题解决策略的教学,帮助学生建立解题思路,逐步提高问题解决能力。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解余角和补角的基本概念。余角是指两个角的和为90度时,这两个角互为余角;补角是指两个角的和为180度时,这两个角互为补角。它们在几何图形的求解和实际问题的应用中具有重要作用。
2.案例分析:接下来,我们来看一个具体的案例。比如在一个直角三角形中,一个角为30度,那么另一个角的余角为60度,补角为150度。这个案例展示了余角和补角在实际中的应用,以及它们如何帮助我们解决问题。
4.3.3余角和补角(教案)-七年级上学期数学教材(人教版)
一、教学内容
本节课选自人教版七年级上学期数学教材第四章第三节第三部分“4.3.3余角和补角”。教学内容主要包括以下两个方面:
1.余角:定义两个角的和为90度的角互为余角,即若两个角的度数分别为α和β,则α + β = 90°。通过实例和练习,让学生掌握求一个角的余角的方法。
4.3.3余角和补角 (第1课时)

自 主 探 究
合 作 交 流
【问题1】观察一副三角板,说说哪些角的和是 教师提出问题,引导学生思考 90°,你还能举出一些和是 90°的角吗? 并讨论 引入余角的定义,若∠1+∠2=90°,那么∠1 学生举例,理解余角的定义 和∠2 互为余角,即: ∠1 是∠2 的余角,∠2 是∠1 的余角. 变化∠1、∠2 的位置,∠1、∠2 仍然互余。 结论:互余与位置无关,只是两角的数量关系. 【问题 2】观察下图中的∠1 和∠2,它们有怎样的数 学生:探究∠1 和∠2 的数量关 量关系? 系,理解补角的定义 引入补角的定义,∠1 是∠2 的补角或∠2 是∠1 的补角,或者说∠1 和∠2 互为补角.如图: 学生:探究∠1 和∠2 的数量关 系,理解余角的定义 师: 提出问题, 引导、 并演示说明, 强调:互补的角与位置无关,只是数量关系,满足和 生:阅读课本、理解概念,准确认 为 180°.是两个角之间的关系. 识. 类似的引出余角的定义。 【问题 3】讲解例题 3 师:引导学生探究例题 3 的解答 如右图,∠AOB 是平角,OC 生:先思考,然后探究交流。 是任意一条射线,ON 平分 师:让学生展示、交流。 ∠BOC, OM 平分∠AOC,试 求∠MON 的度数。
补 偿 提 高
教师:出示题目 学生:解答,讨论,交流
4.下列语句正确的是 (
) A.钝角与锐角的差不可能是钝角; B.两个锐角的和不可能是锐角; C.钝角的补角一定是锐角; D.∠α 和∠β 互补 (∠α >∠β ) ,则∠α 是钝角或直角. 5.已知∠α 的补角是一个锐角,有 3 个人在计算
2 ∠α 时的答案分别为 32°、87°、58°,其中有一 5
125
1.完成下表: 教师:出示题目. 生:按要求完成回答核对.
4.3.3 余角和补角

4.3 余角和补角
[答案] (2)(3)如图4-3-41所示.
图4-3-41
4.3 余角和补角
交点 即这艘船的位置. (4)射线AC和射线BD的________ 变式1 在一张城市地图上,有学校A,医院B和图书馆C,图
书馆C被墨汁污染而看不清楚了,但知道图书馆C在学校A的西 北方向,在医院B的北偏东30°方向.请你在图4-3-42中确 定图书馆C的位置.
图4-3-40
4.3 余角和补角
(1)若点P既在直线a上又在直线b上,则点P是直线a,b的公 共点(即________) .思考此题中船是哪两条射线的交点. 交点 (2)画出A地表示东南西北的十字线,并画出表示A地北偏东
60°方向的射线AC;
(3)画出B地表示东南西北的十字线,并画出表示B地北偏东 30°方向的射线BD.
1 一个角与它的余角以及它的补角的和是直角的 2 3
倍,求这个角的补角.
解:设这个角为 x°,则它的余角为(90-x)°,它的补角为 1 (180-x)°.根据题意,得 x+(90-x)+(180-x)=2 ×90, 3 解得 x=60.所以 180-x=120,即这个角的补角为 120°.
4.3 余角和补角
新 知 梳 理 知识点一 互为余角、补角
90° ,就说这两个角互为余角. 互余:如果两个角的和等于________ 180° ,就说这两个角互为补角. 互补:如果两个角的和等于________ [点拨] ∠α 的余角是90°-∠α ,∠α 的补角是180°- ∠α .一个锐角的补角比它的余角大90°.
图4-3-42
4.3 余角和补角
[答案] 如图4-3-43所示.
图4-3-43
4.3 余角和补角
人教版七年级数学上 4.3.3《余角和补角》课件(共18张PPT)课件

理由:由(1)可知∠1+∠2+∠3+∠4=180° 由(2)可知 ∠1+∠3=∠2+∠4=∠1+∠4=∠2+∠3=90°
知识的Ne超twor市k Op,timi生zatio命n Ex的pert狂Tea欢m
第3关:合作展示 求知、求真、求健,求美
2.若一个角的补角是这个角的余角的4倍,求这个角. 解:设这个角是x°, 则 180-x= 4 ( 90-x) 解得x = 60 答:这个角是60°.
第3关:合作展示 求知、求真、求健,求美
1.如下图,点A,O,B在同一条直线上,射线OD和射线OE分别平
分∠AOC和∠BOC,
(1)∠AOC与∠BOC的关系是什么?
互补 (2)图中有哪几对相等的角?
因为OD平分∠AOC,所以∠1=∠2,
23
1
4
同理,∠3=∠4
(3)图中有哪几对互余的角?
∠2和∠3, ∠1和∠4, ∠1和∠3, ∠2和∠4.
的角? ∠1=∠A ,∠2=∠B
因为∠1与∠2互余
因为∠1与∠2互余
∠A与∠2互余恭喜大家∠1!与∠B互余
所以∠1=∠A 闯关所成以功∠2!=∠B
(同角的余角相等) (同角的余角相等)
知识的Ne超twor市k Op,timi生zatio命n Ex的pert狂Tea欢m
课堂小结
求知、求真、求健,求美
思考:直角和平角中,被分成的两个角的度数分别有什 么关系呢?
1 2
3
4
∠1+∠2=__9_0_°,
∠3+∠4=__1_8_0.°
结论:两个角的数量关系与角的位置无关.
知识的Ne超twor市k Op,timi生zatio命n Ex的pert狂Tea欢m
七年级数学上册4.3角4.3.3余角和补角课件(新人教版)_1

4.3.3 余角和补角以及方位角
学习目标
1. 了解余角、补角的概念,掌握余角和补角的性质,并能利用余角、 补角的知识解决相关问题.(重点、难点)
2. 了解方位角的概念,并能用方位角知识解决一些简单的实际问 题.(难点)
将一张长方形纸片,沿一个角
2
折叠后,折痕与长方形的边形成了4 1
如图,∠1和∠2互余,∠3和∠4互余,若∠1=∠3, 那么∠2与∠4相等吗?为什么?
解: ∠2与∠4相等
理由:∵∠1与∠2互余 ∴∠2=90o-∠1 ∵∠3与∠4互余 ∴∠4=90o-∠3
又∵∠1=∠3 ∴∠2=∠4
4 3
1 2
等角的余角相等。
思考
如图,画出∠1的补角
1
解: ∠2与∠3相等. 理由:∵∠1与∠ 2互补, ∠1与∠3互补, ∴∠ 2= 180 ° - ∠1, ∠3= 180 ° - ∠1 ∴∠2=∠3
例3 如图,点A,O,B在同一直线上,射线
OD 和射线 OE 分别平分∠AOC 和∠BOC,图
中哪些角互为余角?
D
C E
解:因为点A,O,B在同一直线
上,所以 ∠AOC 和 ∠BOC 互为补角. A
O
B
又因为射线 OD 和射线 OE 分别平分∠AOC 和∠BOC,
所以∠COD+∠COE= 1∠AOC+ 1 ∠BOC
2
2
= 1 (∠AOC+∠BOC ) = 90°.
2
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠COD和
∠BOE也互为余角.
C D
E
A
O
人教版数学 七年级上册第4章 4.3.3 余角和补角 同步练习(含答案)

人教版数学(七上)第4章 4.3.3 余角和补角同步练习一、选择题1. 若一个角为65°,则它的补角的度数为()A.25° B.36° C.115° D.125°2.若一个角为75°,则它的余角的度数为()A.285° B.105° C.75° D.15°3. 下列说法正确的是()A.90°角是余角B.如果一个角有补角,那么它一定有余角C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补D.66°角的余角是24°4. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是()A.同角的余角相等B.等角的余角相等C.同角的补角相等D.等角的补角相等5. 如图,下列说法中不正确的是()A.射线OA表示北偏东25°B.射线OB表示西北方向C.射线OC表示西偏南80°D.射线OD表示南偏东70°6. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA夹角为90°,则OB的方位角是()A.北偏西30° B.北偏西60°C.东偏北30° D.东偏北60°7. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,以下符合条件的示意图是()A BC D8. 已知M,N,P,Q四点的位置如图所示,下列结论中,正确的是()A.∠NOQ=42°B.∠NOP=132°C.∠PON比∠MOQ大D.∠MOQ与∠MOP互补9. 将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是()A B C D二、填空题10. (1)若∠α=35°,则∠α的补角为____,∠α的余角为____,∠α的补角与余角的差为____;(2)若∠α的补角为76°28′,则∠α=____.(3)一个角是70°39′,则它的余角的度数是____.11. 如图,∠1=32°,则∠2=____,∠AOD=____.12. 一个角的余角比这个角的补角的一半小40°,则这个角为____°.13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____.三、解答题14. 如图,已知∠AOC=∠BOD=90°.(1)若∠DOC=55°,求∠AOD和∠BOC的度数;(2)试说明:∠AOD=∠BOC.15. 如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.(1)写出图中所有与∠AOD互补的角;(2)若∠AOE=120°,求∠BOD的度数.16. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.(1)填空:与∠AOE互补的角有;(2)若∠COD=30°,求∠DOE的度数;(3)当∠AOD=α°时,请直接写出∠DOE的度数.参考答案一、选择题1. 若一个角为65°,则它的补角的度数为()A.25° B.36° C.115° D.125°【答案】C2.若一个角为75°,则它的余角的度数为()A.285° B.105° C.75° D.15°【答案】D3. 下列说法正确的是()A.90°角是余角B.如果一个角有补角,那么它一定有余角C.若∠1+∠2+∠3=180°,则∠1,∠2,∠3互补D.66°角的余角是24°【答案】D4. 如图,直线AB,CD交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是()A.同角的余角相等B.等角的余角相等C.同角的补角相等D.等角的补角相等【答案】C5. 如图,下列说法中不正确的是()A.射线OA表示北偏东25°B.射线OB表示西北方向C.射线OC表示西偏南80°D.射线OD表示南偏东70°【答案】C6. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA夹角为90°,则OB的方位角是()A.北偏西30° B.北偏西60°C.东偏北30° D.东偏北60°【答案】B7. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,以下符合条件的示意图是()A BC D【答案】D8. 已知M,N,P,Q四点的位置如图所示,下列结论中,正确的是()A.∠NOQ=42°B.∠NOP=132°C.∠PON比∠MOQ大D.∠MOQ与∠MOP互补【答案】C【解析】如图所示:∠NOQ=138°,故选项A错误;∠NOP=48°,故选项B错误;∠PON=48°,∠MOQ=42°,故∠PON比∠MOQ大,故选项C正确;∵∠MOQ=42°,∠MOP=132°,∠MOQ+∠MOP≠180°,∴∠MOQ与∠MOP 不互补,选项D错误.故选C.9. 将一副三角尺按不同的位置摆放,下列摆放方式中∠α与∠β互余的是()A B C D【答案】A【解析】 A 中∠α与∠β互余,B 中∠α=∠β,C 中∠α=∠β,D 中∠α与∠β互补.故选A.二、填空题10. (1)若∠α=35°,则∠α的补角为____,∠α的余角为____,∠α的补角与余角的差为____;(2)若∠α的补角为76°28′,则∠α=____. (3)一个角是70°39′,则它的余角的度数是____. 【答案】(1) 145°; 55°; 90°(2) 103°32′;(3) 19°21′11. 如图,∠1=32°,则∠2=____,∠AOD =____.【答案】32°; 148°12. 一个角的余角比这个角的补角的一半小40°,则这个角为____°. 【答案】80【解析】 设这个角为x ,则它的余角为(90°-x ),补角为(180°-x ).根据题意,得12(180°-x )-(90°-x )=40°,解得x =80°.13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____. 【答案】170°【解析】 依题意画图如答图,则90°+15°+90°-25°=170°.三、解答题14. 如图,已知∠AOC=∠BOD=90°.(1)若∠DOC=55°,求∠AOD和∠BOC的度数;(2)试说明:∠AOD=∠BOC.【答案】解:(1)∵∠AOC=∠BOD=90°,∠DOC=55°,∴∠AOD=∠AOC-∠DOC=90°-55°=35°,∠BOC=∠BOD-∠DOC=90°-55°=35°;(2)∵∠AOD+∠DOC=90°,∠BOC+∠DOC=90°,∴∠AOD=∠BOC(同角的余角相等).15. 如图,直线AB,CD相交于点O,OF平分∠AOE,∠DOF=90°.(1)写出图中所有与∠AOD互补的角;(2)若∠AOE=120°,求∠BOD的度数.【答案】解:(1)∵直线AB,CD相交于点O,∴∠AOC和∠BOD与∠AOD互补.∵OF平分∠AOE,∴∠AOF=∠EOF,∵∠DOF=90°,∴∠COF=90°,则∠DOE=∠AOC(等角的余角相等),∴∠DOE也是∠AOD的补角.综上,与∠AOD互补的角有∠AOC,∠BOD,∠DOE;(2)由(1)知∠AOC=∠BOD=∠DOE,又∵∠AOC+∠AOE+∠DOE=180°,∴∠BOD=∠AOC=180°-120°2=30°.16. 如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.(1)填空:与∠AOE互补的角有;(2)若∠COD=30°,求∠DOE的度数;(3)当∠AOD=α°时,请直接写出∠DOE的度数.【答案】解:(1)∵OE平分∠BOC,∴∠BOE=∠COE;∵∠AOE+∠BOE=180°,∴∠AOE+∠COE=180°,∴与∠AOE互补的角是∠BOE、∠COE;故答案为∠BOE、∠COE;(2)∵OD、OE分别平分∠AOC、∠BOC,∴∠COD=∠AOD=30°,∠COE=∠BOE=∠BOC,∴∠AOC=2×30°=60°,∴∠BOC=180°﹣60°=120°,∴∠CO E=∠BOC=60°,∴∠DOE=∠COD+∠COE=90°;(3)当∠AOD=α°时,∠DOE=90°.。
4.3.3余角和补角-七年级数学上册(人教版)

上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又
分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客
轮B,货轮C和海岛D方向的射线.
北
画法:1. 以点O为顶点,表示正北
●D
●B
方的射线为角的一边,画40°的角, 使它的另一边OB落在东与北之间. 射线OB的方向就是北偏东40°,即 西
板各个角的度数
30°
90°
90°
45° 60°
45°
互动新授
人教版数学七年级上册
在一副三角尺中,每块都有一个角是90o,而其他两个角的和是多少呢?90o
一般地,如下图,如果两个角的和等于90°(直角),就说这两个 角互为余角 ( 简称为两个角互余 ),即其中一个角是另一个角的余角.
2
1
如图:∠1与∠2互为余角,也可以说∠1是∠2的余角,或者∠2 是∠1 的余角. 余角是成对出现的,所以不能说某个角是余角.
(1)以1cm表示10海里,在图中画出B,C的位置; (2)求∠BAC的度数; (3)量出B,C的图上距离,并换算出实际距离. 解:(1)如图, (2)∠BAC=180°-20°-70°=90°. (3) 用 刻 度 尺 量 出 B , C 的 图 上 距 离 约 为 2.5cm,所以实际距离约为25海里.
D AO
C E
B
课堂小结
人教版数学七年级上册
互余
两角间的 1 2 90
数量关系 (1 90 2)
互补
1 2 180 (1 180 2)
对应图形
性质
同角或等角的 余角相等
同角或等角的 补角相等
课后作业
1.如图,下列说法正确的个数有( D ) ①射线OA表示北偏东30°; ②射线OB表示北偏西30°; ③射线OD表示南偏西45°,也叫西南方向; ④射线OC表示正南方向. A.1个 B.2个 C.3个 D.4个
人教七年级数学上册4.3.3《余角和补角》课件

知识点 1 余角和补角 【例1】如图,A,O,B三点在一条直线上,∠AOC=∠DOE=90°,
(1)图中互余的角有哪些? (2)相等的角有哪些(小于90°的角)?
【思路点拨】(1)找出图中所有90°的角→找出两角之和等于 90°的角→答案 (2)利用余角的性质找相等的角
【自主解答】(1)因为∠AOC=∠DOE=90°,所以∠1+∠2=90°, ∠3+∠2=90°,∠1+∠4=180°-∠DOE=90°. 又因为∠COB=180°-∠AOC=180°-90°=90°, 所以∠3+∠4=90°. 所以∠1与∠2互余、∠3与∠2互余、∠1与∠4互余、∠3与∠4互 余. (2)由同角的余角相等可得:∠1=∠3,∠2=∠4.
【解题探究】1.C在A的北偏东30°是绕点A以什么方向为基准, 沿什么方向旋转30°. 提示:以正北方向为基准,沿顺时针方向旋转30°. 2.C在B南偏东45°是绕点B以什么方向为基准,沿什么方向旋 转45°. 提示:以正南方向为基准,沿逆时针方向旋转45°.
3.点C与以上两个方向线有什么关系? 提示:以上两个方向线的交点就是点C.如图:
2.余角和补角的性质: 如图,∠1与∠2互补,∠3与∠4互补,且∠1=∠3,∠2与∠4 有什么关系?
因为∠1与∠2互补,∠3与∠4互补, 所以∠1+∠2=_1_8_0_°__,∠3+∠4=_1_8_0_°__, 所以∠2=_1_8_0_°__-_∠__1_,∠4=_1_8_0_°__-_∠__3_, 又因为∠1=∠3,所以_∠__2_=_∠__4_.
【归纳】补角的性质:同角(等角)的补角__相__等_. 余角的性质:同角(等角)的余角__相__等_.
3.方位角: 方位角是以_正__北__、_正__南__方向为基准,描述物体运动方向的角.
人教版数学七年级上册4.3.3余角、补角的概念和性质课件

互余、互补概念中的角是成对出现的。
对应 3和 4有什么关系?
如图两堵墙围一个角
,但人不能进入围墙,我们如何去测量这个角的大小呢?
解:设这个角的度数为 ,则依题意得
图形 答:这个角的余角的度数为
另解:设这个角的余角的度数为 ,
1、掌握余角与补角的概念和性质,并能熟练应用性质进行求值运算。
1和 2有什么关系?
阻五止,: 书墙使写停指止导,行动我。 们如何去测量这个角的大小呢?
二、初读课文,理清顺序。 1、理解课文内容,体会全国各民族亲如一家。 3、看着图画把第一段中,捉迷藏的内容复述下来。 (二)课文 ⑸“像获得赦免一样,那一双双躲闪的目光又从四面八方慢慢地回来了。” 要注意引导学生通过对重点词句的朗读,来领悟春雨的特点和作用。
一个角的补角是否一定是钝角?
B
CB
1 O
2 1
AO 3
A
D
23
2和 3都是 1的余角,它们有什么关系?
同角的余角相等
例1 1 与 2 互 余 , 3 与 4 互 余 , 如 果 2 = 4 , 那 么 1 与 3 相 等 吗 ? 为 什 么 ?
1 2
3 4
等角的余角相等
例2 1 与 2 互 补 , 3 与 4 互 补 , 如 果 1 = 3 , 那 么 2 与 4 相 等 吗 ? 为 什 么 ?
性质
同角或等角的 余角相等
同角或等角的 补角相等
注意点
1 互余、互补是两角之间的数量关系,只 与他们的度数和有关,与位置无关。
2 互余、互补概念中的角是成对出现的。
3 角 的余角是90 ,补角是180 , 同一个锐角的补角比余9 0 角。 大 9 0 。
4 只有锐角才有余角。
人教版七年级上数学《余角和补角》图形初步认识PPT教学课件(第2课时)

北
西
O 60 °
东 A
南
探究新知
射线OA的方向就是南偏东60°,即灯
塔A所在的方向.
D
北
射线OB的方向就是北偏东40°,
B
即客轮B所在的方向.
45° 40°
西
O
东
射线OC的方向就是南偏西10°,
60°
即货轮C所在的方向.
10°
C
A
南
射线OD的方向就是北偏西45°,即海岛D所在的方向.
探究新知
用方位角确定物体的画法步骤: ①先找出中心点,然后画出方向指标; ②把中心点和目的地用线连接起来; ③度量向北的射线和视线(中心点和目的地的连线)夹角.
问题情境
如图所示,打台球时,选择适当的方向用白球击打红球,反弹后的红球 会直接入袋,此时∠1=∠2, 其中∠FDC=90º,那么各个角与∠1有什 么关系?
问题情境
E
D
F
1
2
A
B
C
有的角与∠1的和等于90º,例如( 有的角与∠1的和等于180º,例如(
); ∠ADC
).
∠ADF
探究新知
余角的定义
4.3.3 余角和补角 第2课时
知识回顾
两角间的 数量关系
互余
1 2 90
(1 90 2)
互补
1 2 180 (1 180 2)
对应图形
性质 同角或等角的余角相等 同角或等角的补角相等
学习目标
1.了解方位角的概念. 2.能用方位角知识解决一些简单的实际问题.
课堂导入
成语“四面八方”怎样理解? 四面——东、西、南、北. 八方——东、西、南、北、东北、东南、西北、西南.
七年级上册数学4.3.3 余角和补角

4
3
思考:
1. ∠1 与∠2 有什么数量关系?
∠1+∠2 = 90°
2. ∠3与∠4有什么数量关系? ∠3+∠4 = 180°
讲授新课
一 余角和补角的概念
2 1
如果两个角的和等于90°( 直角 ),就说这 两个角互为余角 ( 简称为两个角互余 ).
如图,可以说 ∠1 是 ∠2 的余角,或 ∠2 是 ∠1的余角,或 ∠1和 ∠2互余.
30o
60o
80o
100o
120o
150o
170o
典例精析
例1 若一个角的补角等于它的余角的 4 倍,求这 个角的度数.
解:设这个角为 x°,则它的补角是 ( 180-x )°, 余角是 ( 90-x )° . 根据题意,得 180-x = 4 ( 90-x ) . 解得 x = 60.
答:这个角的度数是 60 °.
●
远望一号
●
远望二号
●
60°
●
远望一号
30°
●
远望二号
当堂练习
1.一个角的余角是它的2倍,这个角的度数是( A ) A.30° B.45° C.60° D.75°
2.下列说法正确的是( D ) A.一个角的补角一定大于它本身 B.一个角的余角一定小于它本身 C.一个钝角减去一个锐角的差一定是一个锐角 D.一个角的余角一定小于其补角
互补,OM,ON分别为∠AOC,∠AOB的平分线,
若∠MON=40°,试求∠AOC与∠AOB的度数.
解:设∠AOB=x,
因为∠AOC与∠AOB互补, 则∠AOC=180°-x.
C
M
因为OM,ON分别为∠AOC,
∠AOB的平分线,
七年级数学上册 4.3.3 余角和补角1 (新版)新人教版
180 x
从上表中你可以得到什么结论?
锐角的补角比它的余角大90度
看图回答:
D
C
A
O
B
(1)图中互余的角是___∠_A_O_D____与___∠_D_O_C_____.
(2)图中互补的角是__∠_A_O_D__与__∠_B_O_D__;__∠_A_O_C__与_∠_B_O_C__.
几何语言表示为:
若∠1+∠2=180°,则∠1与∠2互为
补角
∠1 = 180°—∠2
反过来说也成立:若∠1与∠2互为 补角,那么∠1+∠2=180°
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
练一练
判断题:
1、如果一个角有补角,那么这个角一定是
钝角( )
A
M
2 1
O
B
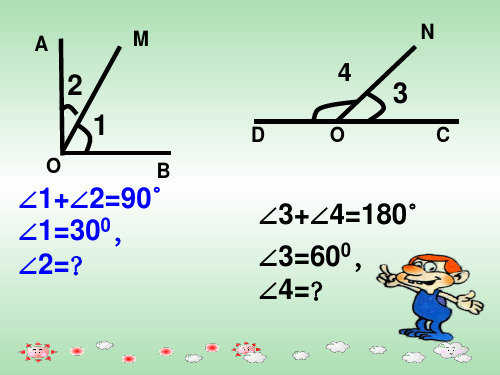
∠1+∠2=90°
∠1=300,
∠2=?
N
4
3
D
O
C
∠3+∠4=180°
∠3=600, ∠4=?
A
M
2
∠AOB=90°
1
O
B
A
M
A
M
2
2
1
1
O
B
∠1+∠2=90°
O
B
∠1+∠2=90°
互为余角
一般地,如果两个角的和等于90° (直角),就说这两个角互为余角.即 其中每一个角都是另一个角的余角。
∵ ∠1 =∠3,
1
2
∴ ∠2 =∠4
七年级数学上册4.3.3余角和补角习题课件(新版)新人教版

15.电视塔在学校的北偏东32°,则学校在电视塔的( ) B
A.北偏东32° B.南偏西32°
C.南偏东32° D.北补角是( )
A.180°+∠1 B.90°+∠1
C
C.90°+∠2 D.90°-∠2
第十页,共15页。
130° 17.(1)一角比它的余角(yújiǎo)大10°,则这个角的补角为________;40°
(2)已知互补的两个角的差是80°,则较小的角的余角(yújiǎo)为_______. 18.已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ=_______度.
90
第十一页,共15页。
互余
19.(1)若∠α=120°-3m°,∠β=3m°-30°,则∠α与∠β的关系为_________; (2)若∠α=(2n-1)°,∠β=(68-n)°,且∠α与∠β都是∠γ的补角,解答下列问题: ①求n的值; ②∠α与∠β能否(nénɡ fǒu)互余,为什么? 解:①根据题意,得2n-1=68-n,解得n=23.②∠α与∠β能互余:因为当n=23时, ∠α=(2×23-1)°=45°,∠β=(68-23)°=45°,所以∠α+∠β=45°+45°= 90°,所以∠α与∠β能互余
第五页,共15页。
10.如图,A,O,D三点在同一条直线(zhíxiàn)上,∠AOB=∠COD,问 其中有哪几对角互为补角?
解:∠COD与∠AOC,∠AOB与∠BOD,∠COD与∠BOD,∠AOC与∠AOB
第六页,共15页。
知识点三:方位角 11.如图,OA是北偏东30°方向(fāngxiàng)的一条射线,若∠AOB=90°,
第十四页,共15页。
解:(1)①∠AOD=∠BOC ②∠AOC与∠BOD互补 (2)①∠AOD= ∠BOC.理由:因为(yīn wèi)∠AOB=∠COD=90°,所以∠AOB- ∠BOD=∠COD-∠BOD,即∠AOD=∠BOC;②∠AOC和∠BOD互 补.理由:因为(yīn wèi):∠AOC+∠BOD=∠AOB+∠BOC+∠BOD =∠AOB+∠COD,而∠AOB=∠COD=90°,所以∠AOC+∠BOD= 90°+90°=180°,即∠AOC与∠BOD互补
