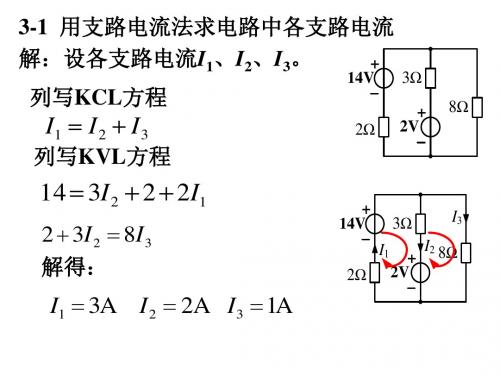
[工学]电路分析 大学教材 第三章NEW

基本关系式:
电场能量
t
du iC dt
t
1 2 uidt Cudu Cu 0 0 2 结论： 储能元件
§3.2 换路定则与电压和电流初始值的确定
一“稳态”与 “暂态”的概念:
K
+
_
R
+
R E _ C 电路处于新稳态
E
uC
uC
电路处于旧稳态
暂态过程 : 旧稳态 新稳态
uC
E
暂态
稳态
t
（二）产生暂态过程的电路及原因 电阻电路
第三章
电路的暂态分析
第三章 电路的暂态分析
§3.1 电阻元件、电感元件、电容元件
§3.2 换路定则与电压和电流初始值的确定
§3.3 RC电路的响应 §3.4 一阶线性电路暂态分析的三要素法
§3.5 微分电路和积分电路
§3.6 RL电路的响应
§3.1 电阻元件、电感元件、电容元件
电阻元件
电压与电流的关系 u
（电压、电流随时间变化的关系）
终点
f ( )
0.632 [ f () f (0 )]


起点
f (0 )

t
“三要素”的计算（之一)
初始值
f (0 )

的计算:
步骤: (1)求换路前的
uC (0 )、iL (0 )
u C ( 0 ) uC ( 0 ) iL (0 ) iL (0 )
说明：
学习重点：直流电路、交流电路都存在暂态过程。 我们学习的重点是直流电路的暂态过程。
研究暂态过程的意义：暂态过程是一种自然现象，
对它的研究很重要。暂态过程的存在有利有弊。有
利的方面，如电子技术中常用它来产生各种波形；
不利的方面，如在暂态过程发生的瞬间，可能出现
过压或过流，致使设备损坏，必须采取防范措施。
iL 0 A
U i(0 ) R uL (0 )
uL (0 ) 20 0 20V


uL 发生了突跳
iL (0 ), u L (0 )

例2
K . U V R 解: 换路前
已知:
L
U 20V , R 1K, L 1h
iL
电压表内阻 RV 500K, 设开关K在 t = 0 时打开。



i1
E 1.5mA

R1 2K
_
+
R2 1K 3V
uL
E uC (0 ) i2 (0 ) R2 3m A


iL (0 )
u（ C 0 ）

i (0 ) i1 (0 ) i2 (0 ) 4.5m A




uL (0 ) E i1 (0 ) R1 3V
其中:
A为积分常数 p为特征方程式的根
u"C 随时间变化，故通常称为自由分量或
暂态分量。
求P值:
将
u"C Ae
pt
代入齐次方程:
du C RC uC 0 dt RCP 1 0
得特征方程：
故：
1 P RC
t RC
求A:
uC (t ) u 'C u"C uc() Ae
由数学分析知此种微分方程的解由两部分组成：
u'C 方程的特解 u"C 对应齐次方程的通解（补函数）
即：
uC (t ) u'C u"C
1. 求特解 ----
u' C
u'C K （常数）。代入方程
K E
u ' C 和外加激励信号具有相同的形式。在该
电路中，令 得：
dK RC K E dt
初始值 ---稳态值 ---时间常数----
其中三要素为:
f (0 )
f ( )

利用求三要素的方法求解暂态过程，称为三要素 法。只要是一阶电路，就可以用三要素法。
三要素法求解暂态过程要点：
. 分别求初始值、稳态值、时间常数； . 将以上结果代入暂态过程通用表达式； . 画出暂态过程曲线（由初始值稳态值）。
3 3


I S V 2010 50010 10000 V
I S iL (0 ) 20mA
注意:实际使用中要加保护措施
例3
+
2 K R
i K
1
E
2K
_ 6V
uC
已知: K 在“1”处停留已久，在t=0时合向 “2” 求: i、i1、i2、uC、uL 的初始值，即 t=(0+)时刻的值。
uC (t ) E Ee
RC
1 定义： RC P
称为时间常数
单位
R: 欧姆 C：法拉
：秒
§3.4 一阶线性电路暂态分析的三要素法
K 根据经典法推导的结果： + _E R C
i
uC
uC (t ) u 'C u"C t uc () [uc (0 ) uc ()] e RC
可得一阶电路微分方程解的通用表达式：
f (t ) f () [ f (0 ) f ()] e
式中

t

f (t ) 代表一阶电路中任一电压、电流函数。
f (t ) f () [ f (0 ) f ()]e
式中


t

f (t ) 代表一阶电路中任一电压、电流函数。
电感电路
K
R iL
储能元件
暂态
E
+ t=0 _
iL
稳态
t
电感为储能元件，它储存的能量为磁场能量， 其大小为：
1 2 WL uidt Li 0 2
t
因为能量的存储和释放需要一个过程，所以有电 感的电路存在暂态过程。
结论
有储能元件（L、C）的电路在电路状态发生 变化时（如：电路接入电源、从电源断开、电路 参数改变等）存在暂态过程； 没有储能作用的电阻（R）电路，不存在暂态 过程。 电路中的 u、i在暂态过程期间，从“旧稳态”进 入“新稳态”，此时u、i 都处于暂时的不稳定状态， 所以暂态过程又称为电路的过渡过程。
(三） 换路定理及初始值的确定
电感中的电流不能突变。
设：t=0 时换路

1 换路定理：在换路瞬间，电容上的电压、
0
--- 换路前瞬间
0


--- 换路后瞬间

则：
uC (0 ) uC (0 )
iL (0 ) iL (0 )

换路瞬间，电容上的电压、电感中的电流不能突 变的原因解释如下：



(2) 根据电路的基本定律和换路后的等效
电路，确定其它电量的初始值。
例1
U
K t=0
uR
解:
根据换路定理

iL
uL
iL (0 ) iL (0 ) 0 ( A)
i L 不能突变
换路时电压方程 :
已知: R=1KΩ, L=1H , U=20 V、
开关闭合前
设t 求:
0 时开关闭合
在电路中，通常取换路后的新稳态值作特解，即
u 'C (t ) uC ()
，故此特解也称为稳态分量或强
制分量。所以该电路的特解为：
u'C (t ) uc() E
2. 求齐次方程的通解 ----
u" C
的解。
pt
du C 通解即： RC uC 0 dt
其形式为指数。设：
u"C Ae
求稳态值举例
t=0
+
4k 10v 3k
t=0 4k
2
3
iL
3 L
-
C
uc
4mA
3 uC () 10 3 4 // 4 6v
3 iL () 4 33 2 mA
“三要素”的计算（之三)
的物理意义: 决定电路暂态过程变化的快慢。
K R
时间常数
i
+ _E

iL (0 ) I0 0 电感相当于恒流源， ，电感相当于断路。 其值等于 I ； i ( 0 ) 0 L 0
§3.3 RC电路的响应
一阶电路的概念:
根据电路规律列写电压、电流的微分方程，若 微分方程是一阶的，则该电路为一阶电路（一阶电 路中一般仅含一个储能元件。）如： K R i + _E 电压方程 C
i
R
u iR
功率
欧姆定律
t t

0
uidt Ri dt
2 0
结论：
耗能元件
电感元件
i
d eL N dt
基本关系式： 磁场能量
N L i
u
L
di uL dt
1 2 0 uidt 0 Lidi 2 Li
t t
结论：
储能元件
电容元件
i
u
C
dq i dt
q c u
该电路中： u
C (t ) E Ae t RC
uC (t ) u'C u"C uc() Ae
代入初始条件
t
RC
uC (0 ) uc() Ae


0
得：A uC (0 ) uc()
该电路的起始条件为： C C 所以
u (0 ) u (0 ) 0
* 自然界物体所具有的能量不能突变，能量的积累或