_重庆实验外国语学校2018-2019学年八年级(上)期末数学试题
重庆实验外国语学校2024-2025学年九年级上学期入学考试数学试题+答案

初2025届九上开学数学定时作业(全卷共三个大题,满分150分,考试时间120分钟)参考公式:抛物线()20y ax bx c a ++≠的顶点坐标为24,24b ac b a a −− ,对称轴为2b x a =−. 一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡...上题号右侧正确答案所对应的方框涂黑.1.下列四个实数中,是无理数的是( )A .1.010010001B .237C .πD .2.下列四种图案是2024年巴黎奥运会中部分运动项目的示意图,其中是轴对称图形的是( )A .B .C .D .3.如果单项式42a x y −与单项式533b x y −−的和仍是一个单项式,则点(),a b −在( )A .第一象限B .第二象限C .第三象限D .第四象限4.估计 ) A .2到3之间B .3到4之间C .4到5之间D .5到6之间 5.一组图形按下列规律排序,其中第①个图形有5个圆球,第②个图形有8个圆球,第③个图形有13个圆球,…,按此规律排列下去,则第⑧个图形的圆球的个数是( )A .53B .55C .68D .696.如图,AB CD ,50EFB ∠=°,FM 平分BFG ∠,过点G 作GH FM ⊥于点H ,则HGM ∠的度数是( )A .25°B .30°C .40°D .20°7.为了让大家都能用上实惠药,医保局与药商多次谈判,将一种原价每盒100元的药品,经过两次降价后每盒64元,两次降价的百分率相同,则每次降价的百分率为( )A .20%B .22%C .25%D .80%8.如图,A 、B 、C 是O 的圆周上三点,DE 与O 相切于点C ,连接AB 、BC 、AC ,若AB AC =,40BCD ∠=°,则ACE ∠的度数为( )A .40°B .60°C .70°D .80°9.如图,在正方形ABCD 中,点E 在边BC 上,点F 在边CD 上,连接AE 、AF 、EF ,有EF BE DF =+,BAE EFC ∠=∠,若2DF =,求AB 的长为( )A .8B .4+C .4D .12−10.在多项式a b c d e −+−−(其中0a b c d e >>>>>)中,任选两个字母,在两侧加绝对值后再去掉绝对值化简可能得到的式子,称为第一轮“绝对操作”.例如,选择d ,e 进行“绝对操作”,得到a b c d e a b c d e −+−−=−+−+,…在第一轮“绝对操作”后的式子进行同样的操作,称为第二轮“绝对操作”,如:a b c d e a b c d e −+−+=−−+−,…按此方法,进行第()1n n ≥轮“绝对操作”.以下说法:①存在某种第一轮“绝对操作”的结果与原多项式相等;②对原多项式进行第一轮“绝对操作”后,共有8种不同结果;③存在第()1k k ≥轮“绝对操作”,使得结果与原多项式的和为0. 其中正确的个数为( )A .0个B .1个C .2个D .3个二、填空题:(本大题8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡...中对应的横线上.11.计算:22024112− −−=______________. 12.如果一个多边形的每一个外角都是30°,那么这个多边形的边数为______________.13x 的取值范围是______________. 14.2024年暑假重庆各旅游景区持续火热,小明和小亮相约来到重庆旅游,两人分别从洪崖洞,磁器口,解放碑,李子坝四个景点中随机选择一个景点游览,小明和小亮选择不同景点的概率为______________.15.如图,ABC △的面积为4,将ABC △沿AD 方向平移,使A 的对应点A ′满足14AA AD ′=,则平移前后两三角形重叠部分的面积是______________. 16.若关于x 的一元一次不等式组113232x x x a− +> +≥ 恰有2个偶数解,且关于y 的分式方程23122a y y y −−=+−−的解为非负整数,则所有满足条件的整数a 的值之和是______________.17.如图,AB 是O 的直径,BC 是O 的切线,连接AC 交O 于点D ,点E 为O 上一点,满足 DEDB =,连接BE 交AC 于点F ,若1CD=,BC =,则BF=______________,EF =______________.18.若一个四位自然数M 的千位数字、百位数字与十位数字的和恰好等于个位数字的平方,则称这个四位数M 为“方和数”.若“方和数”M abcd =且(19a b c d ≤≤、、、),将“方和数”M 的千位数字与十位数字对调、百位数字与个位数字对调得到新数N ,规定()()()2129d b c d a G M +−++−=,若()G M 为整数,M N +除以13余7,则b c +的值为______________,满足条件的M 的值为______________.三、解答题:(本大题8个小题,第19题8分,其余每题各10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线)请将解答过程书写在答题卡...中对应的位置上. 19.计算:(1)()()222x y x x y −−+; (2)()22214424m m m m m m +−+−−−÷−. 20.为了解学生的暑期每日学习时间情况,学校开学进行了问卷调查.现从高二、高三的学生中各随机抽取20名学生的问卷调查进行收集、整理、描述、分析.所有学生的学习时长均高于2小时(时间用x 表示,共分成四组:A.25x <≤;B.58x <≤;C.811x <≤;D.11x <),下面给出了部分信息:高二年级20名学生的学习时长为:2.1,2.2,3,3,,5.2,7,8,8,8,8,8.5,9,10,12,12,12.5,13,13,14. 高三年级20名学生的学习时长在C 组的数据是:8.2,8.6,9,9.4,9.6,10. 高二、高三所抽取学生的学习时长统计表年级高二年级 高三年级 平均数 8.15 8.15 中位数8 b 众数 a7.5 高三所抽取学生的学习时长统计图根据以上信息,解答下列问题:(1)上述图表中a =_____________,b =_____________,m =_____________;(2)根据以上数据分析,你认为该校高二、高三年级中哪个年级学生的学习时长较好?请说明理由(写出一条理由即可)(3)该校高二年级有2000名学生、高三年级有1800名学生参加了此次问卷调查,估计该校高二、高三年级参加此次问卷调查学习时长8x >的学生人数是多少?21.在学习了矩形与菱形的相关知识后,重外数学兴趣小组进行了更深入的研究,他们发现,过菱形的一条对角线的两个端点分别作一组对边的垂线,与菱形两边相交的两点和这条对角线的两个端点构成的四边形是矩形,可先证得到的图形是平行四边形继而得到此结论.根据他们的想法与思路,完成以下作图..和填空..: (1)如图,在菱形ABCD 中,DE AB ⊥于点E .用尺规过点B 作CD 的垂线交于点F (不写作法,保留作图痕迹).(2)已知:菱形ABCD 中,DE AB ⊥于点E ,BF CD ⊥于点F .求证:四边形DEBF 是矩形.证明: 四边形ABCD 是菱形,AD BC ∴=,AB CD =,___①_____又180BCF BCD DAE DAB ∠+∠=∠+∠=°BCF DAE ∴∠=∠.DE AB ⊥ ,___②_____90BFC DEA ∴∠=∠=°,()CFB AED AAS ∴≌△△∴____③____DF BE ∴=,又AB CD ,∴四边形DEBF 是平行四边形.DE AB ⊥ ,∴四边形DEBF 是矩形.进一步思考,如果“菱形ABCD ”改为“平行四边形ABCD ”还有相同的结论么?请你写出你猜想的结论: ______________________________④__________________________________22.经重庆市发改委统筹考虑重庆电力供需状况、电网负荷特性、居民用电习惯等,在保持价格总水平基本稳定的前提下,现制定分时电价标准,分成三个时段计费,即高峰时段、低谷时段和平段.1.高峰时段:11:00一17:00、20:00一22:00,在平段电价基础上提高0.10元/千瓦时.2.低谷时段:00:00一08:00,在平段电价基础上降低0.18元/千瓦时.3.平段:08:00一11:00、17:00-20:00、22:00一24:00,平段电价为国家规定的销售电价.(1)某家庭8月份总电量400千瓦时,其中平段电量为总电量30%.低谷电量占总电量14,根据相关政策,使用新方案计算电费与原来全部按照平段电价费用一样,则平段电价为多少元/千瓦时?(2)电力公司采用新能源节约成本,9月份将所有时段电费单价在(1)中的费用的情况下均降低相同费用,若该家庭9月份高峰时段费用与低谷时段费用一样,而低谷时段电量为高峰时段电量的2倍,则降价后高峰时段电价为多少元/千瓦时?23.如图1,在菱形ABCD 中,对角线AC 与BD 交于点O ,点P 沿着A B O A →→→的方向每秒1个单位运动,点Q 沿着A D O C →→→的方向每秒1个单位运动,连接PQ ,点P ,Q 的距离为y ,两动点同时出发,设运动时间为x 秒,当两动点到达终点时即12x =时,8y =.(1)请直接写出y 关于x 的函数表达式,并注明自变量x 的取值范围;(2)在给定的平面直角坐标系中,画出函数y 的图象,并写出函数y 的一条性质;(3)结合函数图象,请直接写出23y k =+有3个解时k 的取值范围.24.小明和小玲游览一处景点,如图,两人同时从景区大门A 出发,小明沿正东方向步行60米到一处小山B 处,再沿着BC 前往寺庙C 处,在B 处测得亭台D 在北偏东15°方向上,而寺庙C 在B 的北偏东30°方向上,小玲沿着A 的东北方向上步行一段时间到达亭台D 处,再步行至正东方向的寺庙C 处.(1)求小山B 与亭台D 之间的距离;(结果保留根号)(2)若两人步行速度一样,则谁先到达寺庙C 处.(结果精确到个位, 1.41≈ 1.73≈,2.45≈)25.如图1,已知抛物线2142y x x =+−的图象与x 轴交于A ,B 两点(A 在B 左侧),与y 轴交于点C . (1)抛物线顶点为D ,连接AD 、AC 、CD ,求点D 到AC 的距离;(2)如图2,在y 轴正半轴有一点E 满足2OC OE =,点P 为直线AC 下方抛物线上的一个动点,连接PA 、AE ,过点E 作EF AP 交x 轴于点F ,M 为y 轴上一个动点,N 为x 轴上一个动点,平面内有一点75,28G −−,连接PM 、MN 、NG ,当APF S △最大时,求PM MN NG ++的最小值;(3)如图3,连接AC 、BC ,将抛物线沿着射线BC 平移y ′,y ′上是否存在一点R ,使得45RAC BCO ∠+∠=°?若存在,直接写出点R 的坐标,若不存在,请说明理由.26.如图,在ABC △中,90BAC ∠=°,D 在AB 边上,E 在AC 边上,连接EB 、CD ,点G 为BE 上一点且满足GA GB =.(1)如图1,若BE 平分ABC ∠,10BC =,AG =,5CE =,求ABC △的面积;(2)如图2,若BD CE =,取CD 中点为F ,连接FG ,求证:CE =;(3)如图3,在(1)的条件下,点F 为直线AC 上一点,连接BF ,若2CF BD =,则12CD BF +最小时,直接写出ADG S △的值.重庆实验外国语学校2024-2025学年度(上)初2025届九上开学定时作业参考答案(全卷共三个大题,满分150分,考试时间120分钟)参考公式:抛物线()20y ax bx c a ++≠的顶点坐标为24,24b ac b a a −− ,对称轴为直线2b x a =−. 一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答卷上对应的方框涂黑.1.C 2.D 3.B 4.B 5.C 6.A 7.A 8.C 9.C 10.D10答案:①对ab “绝对操作”后结果与原多项式一样,所以①对;②依次取ab ,ac ,ad …结果有8种;③先对ac “绝对操作”后得到a b c d e a b c d e −+−−=−+−−−,再对刚刚式子进行ce “绝对操作”后得到a b c d e a b c d e −+−−−=−+−++,所以③对. 二、填空题:(本大题共8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上.11.5 12.十二 13.1x > 14.3415.94 16.4− 17 18.10 655416.不等式解得243a x −≤<解得42a −<≤,解得302a y +=≥且2≠,解得3a =−,1−,整数a 的值之和4−.17.导角得BFC C ∠=∠,BF BC ∴==,连接AE ,则AEF BDF △△∽,3AF =,EF =18.解:由题意可得:2a b c d ++=, ()()()()2212121222999d b c d a b c d d d b c a G M +−++−−+++−−−−∴===,15b ≤≤ ,16c ≤≤,()G M 为整数,10b c ∴+=;210d a b c a =++=+ ,故4d =,6a =;设100010010M a b c d =+++,100010010N c d a b =+++,()71010101010111710110107M N a c b d a c b d ∴+−=+++−=+++−, ()()()()10110107101749710172919590957151313131313a c b d c c c M N +++−+−++++−∴====+,故5c =,5b =,6a ∴=,5b =,5c =,4d =;故答案为:10;6554.三、解答题:(本大题8个小题,19小题8分,20-26题每小题10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡...中对应的位置上. 19.(1)222442x xy y x xy −+−−264xy y =−+ 4分(2)21m m− 8分 20.(1)8,8.8,30;(2)高三年级学生学习时长较好,高三年级的中位数8.8高于高二年级的中位数8,整体上看高三年级学生学习时长较好;(3)96200030%180019802020 ×++×=(人), 答:该校高二、高三年级参加此次问卷调查学习时长8x >的学生人数是1980人. 10分21.(1)如图所示,即为所求作; 6分(2)①BCD DAB ∠=∠;②BF CD ⊥;③CF AE =;④过平行四边形的一条对角线的两端点分别作一组对边的垂线,与平行四边形两边相交的两点和这条对角线的两个端点构成的四边形是矩形. 10分22.(1)设平段电价为x 元/千瓦时,则高峰电价为()0.1x +元/千瓦时,低谷电价为()0.18x −元/千瓦时,则()()()114000.18400130%0.1400130%44x x x ×⋅−+×−−⋅+=×−解得0.5x = 答:平段电价为0.5元/千瓦时. 4分(2)高峰电价()0.10.6x +=元/千瓦时,低谷电价为()0.180.32x −=元/千瓦时, 设降价a 元/千瓦时,9月份高峰时段费用,费用为y 万元 则20.60.32y y a a×=−− 7分 解得0.04a = 经检验0.04a =是原方程的解 9分降价后高峰电价0.60.60.040.56a −=−=元/千瓦时,答:降价后高峰电价0.60.60.040.56a −=−=元/千瓦时, 10分23.解:(1)6,055162,58216,812x x y x x x x ≤≤ =−<< −≤≤;(y 解析式及范围均正确给1分) 3分 2.如图所示,即为所求: 6分 性质:05x <<时,y 随x 58x <<时,y 随x 增大而减小,812x <<时,y 随x 增大而增大;(y 的图象3分,性质2分,有1处错扣1分,全错0分) 8分 3. 1.5 1.5k −<<. 10分24.解:(1)作BE AD ⊥于点E ,60AB =,45A ∠=°,9015105ABD ∠=°+°=°,9030120CBA ∠=°+°=°,1801054530ADB ∠=°−°−°=°在Rt ABE △中,BE AE ==在Rt BDE △中,ED =DF =米 ∴小山B 与亭台D之间的距离米 4分(2)延长AB ,作DF BA ⊥于点F ,作CG BA ⊥于点G ,则18060CBG CBA ∠=°−∠=°, 则在Rt AFD △中,30DF AF ==+,30CG DF ==+米,在Rt BCG △中,30BG =+,260BC BG ==60CD FG AB BG AF ∴==+−=−60141.2S AD CD ∴+++−≈玲米,6060154.6S AB BC =+=++≈明米,141.2154.6< 且两人速度一致,∴小玲先到.答:小玲先到达寺庙C 处. 10分25.(1)当0x =时,4y =−,故()0,4C −,当0y =时,4x =−或2x =,故()4,0A −,()2,0B , 对称轴1x =−,当1x =−时,92y =−,故91,2D −−,易求得3ACD S =△,AC =, 132BCD S AC h ==⋅⋅△,得h =D ∴到AC2分 (2)设AE 解析式为y kx m =+,代入()0,2E ,()4,0A −,得042k m m =−+ = ,解得122k m = = , AE ∴的解析式为122y x =+; 连接PE ,作PQ y 轴交AE 于QEF AP12APF APE E A S S PQ x x ∴==⋅⋅−△△设21,42P m m m+− ,则1,22Q m m + ,即211622PQ m m =−−+, 21122APF APE E A S S PQ x x m m ==⋅⋅−=−−+△△ 当12m =−时,max 494APF S =△,此时P 的坐标为135,28 −− 6分 将P 的关于y 轴对称得到P ′坐标为135,28 − ,将G 的关于x 轴对称得到G ′坐标为75,28 − 连接P G ′′交于y 轴于点M ,交于x 轴于点N,则PM MN NG P M MN NG P G ′′′′++=++≥=(3)平移后的新抛物线21342y x x ′=+−,在y 轴上找点S 满足OS OB =,则OSA OBC ≌△△, 1122AS y x =−−,联立21221342y x y x x =−− =+−,解得x y = =x y = = (舍) 228AS y x =−−,联立2281342y x y x x =−− =+−,解得52x y =− =−或52x y =− =+ (舍)所以R(22R −− 26.(1)GA GB =12∴∠=∠90BAC ∠=°142390∴∠+∠=∠+∠=°43∴∠=∠GA GB GE ∴=== 设AB x =,AE y =在Rt ABE △中,222BE AB AE =+,(222x y ∴=+ 在Rt ABC △中,222BC AB AC =+,()()222105x y ∴=++3x ∴=,6y =即8AC AE EC =+=,6AB =11862422ABC S AC AB ∴=⋅=××=△ 3分 法二:过E 作EF BC ⊥于点F ,则ABC FEC △△∽,故设2AB a =,AE EF a ==在Rt ABE △中,222BE AB AE =+,(()2222a a ∴=+,3a ∴=下同(2)CE =简证如下: 倍长CG 至点Q ,连接DQ ,由(1)得GB GE =, BQG ECG ∴≌△△QB EC ∴=,ECG BQG ∠=∠ EC QB ∴90QBD BAC ∴∠=∠=°, BD CE =BD BQ ∴=BQD ∴△为等腰直角三角形QD ∴==CD 中点为F ,GB GE =2QD FF ∴=2FF =CE ∴(3)1211ADG S =△ 10分。
2019重庆中考数学第24题专题训练---- 平行四边形(含大部分题目答案)
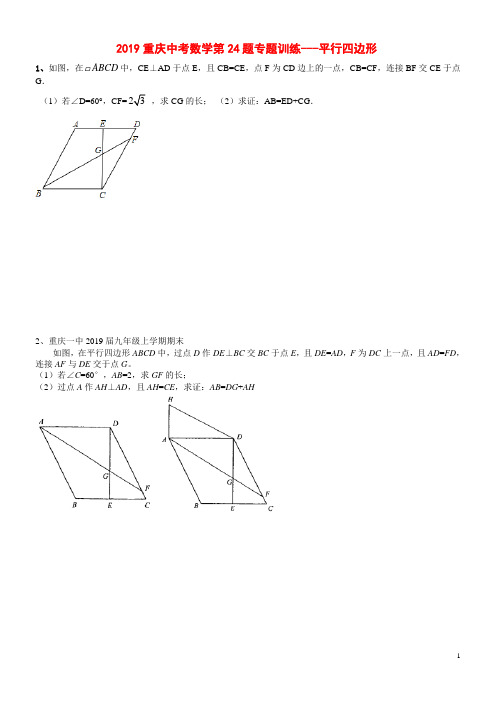
6、重庆市沙坪坝区 2019 届九年级上学期期末
A E
D
G
F
A
D
G
E
F
B
C
第 24 题图 1
B
C
第 24 题图 2
3
7、已知,在平行四边形 ABCD 中,AE⊥BC,且 E 为 BC 的中点,AE=2BE,P 为 BC 上一点,连接 DP,作 EF⊥DP 于点 F,连接 AF. (1)若 AD=4,求 AE 的长; (2)求证: 2 AF+EF=DF.
G.点 H 在 BC 的延长线上,且 CH=AG, 连接 EH.
(1)若 BC 12 2 ,AB=13,求 AF 的长; (2)求证:EB=EH.
9
19、重庆市 2018 年初中学业水平暨高中招生考试数学( A 卷)
A
F
D
O
H
G
B
E
C
10
2019 重庆中考数学第 24 题专题训练---平行四边形答案
连接 AF 与 DE 交于点 G。 (1)若∠C=60°,AB=2,求 GF 的长; (2)过点 A 作 AH⊥AD,且 AH=CE,求证:AB=DG+AH
1
3、如图,已知 ABCD 中,DE⊥BC 于点 E,DH⊥AB 于点 H,AF 平分∠BAD,分别交 DC、DE、DH 于点 F、G、M,
(1)若∠F=60°,∠C=45°,BC= 2 6 ,请求出 AB 的长;(2)求证:CD=BF+DF.
F
E
D
A
B
G
C
6
13、重庆一中初 2019 级 17-18 学年度下期期末
已知在平行四边形 ABCD 中,过点 D 作 DE BC 于点 E ,且 AD DE .连接 AC 交 DE 于点 F ,作 DG AC 于点 G . (1)如图 1,若 EF 1 , AF 13 ,求 DG 的长;
2018-2019学年重庆实验外国语学校七年级(上)第一次月考数学试卷(含解析)

2018-2019学年重庆实验外国语学校七年级(上)第一次月考数学试卷(考试时间:120分钟满分:150分)一、选择题(每小题4分,共40分)1.﹣5的倒数是()A.B.5 C.﹣D.﹣52.一种巧克力的质量标识为“23±0.25千克”,则下列哪种巧克力的质量是合格的()A.23.30千克B.22.70千克C.23.55千克D.22.80千克3.计算﹣12018的值为()A.1 B.﹣1 C.2018 D.﹣20184.在﹣(﹣2)、|﹣1|、﹣|﹣3|、(﹣3)2、﹣(﹣4)2中,正数有()A.1个B.2个C.3个D.4个5.已知点A、B、C是数轴上的三个点,点A表示的数是﹣5,点B表示的数是1,且A、B两点间的距离是B、C两点间距离的2倍,则点C表示的数是()A.4 B.﹣1 C.﹣1或3 D.﹣2或46.若a3+b3=0,那么有理数a,b的关系是()A.a=b=0 B.a,b至少一个是0C.a+b=0 D.a,b不都是07.下列说法正确的有()个①0是绝对值最小的有理数;②相反数大于本身的数是负数;③数轴上原点两侧的数互为相反数;④|a|=|b|,则a=b.A.1 B.2 C.3 D.48.墨尔本与北京的时差是+3小时(即同一时刻墨尔本时间比北京时间早3小时).班机从墨尔本飞到北京需用12小时,若乘坐从题尔本10:00(当地时间)起飞的航班,到达北京机场时,北京时间是()A.22:00 B.19:00 C.18:00 D.15:009.若|a|=1,|b|=4,且|a﹣b|=a﹣b,则a﹣b等于()A.5 B.3 C.﹣5或5 D.5或310.有一列数a1,a2,a3,…,a n,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a1=2,则a2018为()A.2017 B.C.2 D.﹣1二、填空题(每小题4分,共40分)11.用“>”“<”或“=”填空:(1)0 2018;(2)0.33;(3)﹣(+5)﹣|﹣5|12.﹣9的绝对值是,的相反数是,﹣1的倒数是.13.用四舍五入法,将100.009精确到十分位为.14.已知|x+3|+(y﹣2)2=0,则x+y=.15.设a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,则a﹣b+c=.16.大于﹣2且不大于3的所有非负整数的和是.17.当x=时,式子﹣|x﹣3|+5有值.18.已知a,b互为相反数,c,d互为倒数,x的绝对值等于2,则式子x2+cd+a+b的值为.19.如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,若取最左端3个格子中的后两个数记作m、n,那么|m﹣n|是.9 m n ﹣6 2 …20.我校每年12月30日晚上各班的元旦晚会是同学们施展才艺的舞台.在某班晚会上,主持人为同学们准备了一个游戏:从100个外形相同的气球中找到唯一的里面装有奖品的气球.主持人将这些气球按1至100的顺序编号排成一列,第一次先请一位同学从中取出所有序号为单数的球,均没发现装有奖品.接着主持人将剩下的球又按1﹣50重新编号排成一列(即原来的2号变为1号,原来的4号变为2号,…,原来的100号变为50号),又请一位同学从中取出所有新序号为单数的球,也没有发现奖品,…如此下去,直到最后一个气球才是装有奖品的,那么这个装有奖品的气球最初的序号是.三、解答题(共70分)21.(6分)在规定直线上画出数轴,将数字0,﹣3,2,﹣1,0.5表示在数轴上,并用“<”符号将这些数连接起来.22.(24分)计算:(1)(+4.3)﹣(﹣4)+(﹣2.3)﹣(+4)(2)﹣49÷×(﹣)÷(﹣10)(3)﹣32×(﹣2)+(﹣4)2﹣(﹣2)+(4)3﹣36×(﹣+)(5)|﹣1.2+3|﹣3﹣|4.5﹣5.2| (6)19×(﹣8)+19.5×6﹣1.5×6 (10分)某自行车厂规定每天要生产200辆自行车,由于各种原因实际每天生产量与规定量相比有出入.下23.表是某一周的实际生产情况(超产为正、减产为负):星期一二三四五六日与规定量的差值+6 ﹣3 ﹣4 +12 ﹣9 +17 ﹣11(1)根据记录可知前三天共生产辆;(2)产量最多的一天比产量最少的一天多生产辆;(3)该厂实行每天计件工资制,每生产一辆车可得50元,若超额完成任务,则超过部分每辆另奖25元;少生产一辆则扣10元,那么该厂工人这一周的工资总额是多少?24.(8分)已知,|a|=5、|b|=3、c2=81,又知,|a+b|=a+b且|a+c|=a+c,求2a﹣3b+c的值.25.(10分)我们知道,|x|表示x在数轴上对应的点到原点的距离我们可以把|x|看作|x﹣0|,所以,|x ﹣3|就表示x在数轴上对应的点到3的距离,|x+1|=|x﹣(﹣1)|就表示x在数轴上对应的点到﹣1的距离,由上面绝对值的几何意义,解答下列问题:(1)求|x﹣4|+|x+2|的最小值,并写出此时x的取值情况;(2)求|x﹣3|+|x+2|+|x+6|的最小值,并写出此时x的取值情况;(3)已知|x﹣1|+|x+2|+|y﹣3|+|y+4|=10,求2x+y的最大值和最小值.26.(12分)如图,数轴上有两个长方形ABCD和FFGH,这两个长方形的宽都是1个单位长度,长方形ABCD 的长AD是2个单位长度,长方形EFGH的长EH是4个单位长度,点E在数轴上表示的数是5,且E、D两点之间的距离为12.(1)填空:点H在数轴上表示的数是,点A在数轴上表示的数是;(2)若长方形ABCD以每秒2个单位的速度向右匀速运动,当点D运动到E时,两个长方形开始有重叠部分,此时长方形ABCD运动了秒;若长方形ABCD继续向右运动,再经过秒后,两个长方形不再有重叠部分.经过6.5秒时,两个长方形重叠部分的面积是个平方单位;(3)设AD的中点为M,若两个长方形ABCD和EFGH同时从图中位置出发,长方形EFGH以每秒2个单位的速度向左匀速运动,长方形ABCD仍以每秒2个单位的速度向右匀速运动,运动多少秒时,点M与线段EH 端点E的距离为1个单位长度.1.【解答】解:﹣5的倒数是.故选:C.2.【解答】解:∵23+0.25=23.25,23﹣0.25=22.75,∴巧克力的重量在23.25与22.75kg之间.故选:D.3.【解答】解:﹣12018=﹣1.故选:B.4.【解答】解:﹣(﹣2)=2、|﹣1|=1、﹣|﹣3|=﹣2、(﹣3)2=9、﹣(﹣4)2=﹣16,则正数有3个,故选:C.5.【解答】解:设点C表示的数是x,由题意得|1﹣(﹣5)|=2|1﹣x|,解得:x=﹣2或8.故选:D.6.【解答】解:∵a3+b3=0,∴a3与b3互为相反数,∴a与b互为相反数.故选:C.7.【解答】解:①0是绝对值最小的有理数是正确的;②相反数大于本身的数是负数是正确的;③数轴上原点两侧的数并且与原点的距离相等的数互为相反数,故错误;④|a|=|b|,则a=b或a=﹣b,故错误.故选:B.8.【解答】解:10+12﹣3=19,即乘坐从墨尔本10:00(当地时间)起飞的航班,到达北京机场时,北京时间是19:00.故选:B.9.【解答】解:∵|a|=1,|b|=4,且|a﹣b|=a﹣b,∴a=1或﹣1,b=﹣8,∴a﹣b等于5或3.故选:D.10.【解答】解:依题意得:a1=2,a2=1﹣=,a3=1﹣2=﹣6,a4=1+1=3;周期为3;所以a2018=a2=.故选:B.11.【解答】解:(1)0<2018;(2)<0.33;(3)﹣(+5)=﹣|﹣5|,故答案为:<;<;=.12.【解答】解:﹣9的绝对值是 9,的相反数是﹣,﹣1的倒数是﹣,故答案为:9,﹣,﹣.13.【解答】解:将100.009精确到十分位为100.0,故答案为:100.0.14.【解答】解:∵|x+3|+(y﹣2)2=3,∴x=﹣3,y=2,故答案为:﹣1.15.【解答】解:根据题意,最小的正整数是1,最大的负整数﹣1,绝对值最小的有理数是0,∴a=1,b=﹣1,c=0,故应填2.16.【解答】解:大于﹣2且不大于3的所有非负整数为:0,1,2,80+1+2+3=5,故答案为:617.【解答】解:∵﹣|x﹣3|≤0,∴﹣|x﹣3|+5≤8,故答案为:3,最大.18.【解答】解:∵a,b互为相反数,c,d互为倒数,x的绝对值等于2,∴a+b=0,cd=1,x=±2,∴x2+cd+a+b=4+6+0故答案为:5.19.【解答】解:设第四个数为x,∵任意三个相邻格子中所填整数之和都相等,解得x=9,∴m=﹣6,第9个数与第三个数相同,即n=2,故答案为:8.20.【解答】解:第一次取出的是单号的气球,剩下的气球的序号是2的倍数,因为原来是100只,所以还剩50只;第二次取出后,剩下的气球的序号是4的倍数,所以还剩25只;第四次取出后,剩下的气球的序号是16的倍数,所以还剩6只;第六次取出后,剩下的气球的序号是64的倍数,所以还剩1只;故答案为:64.21.【解答】解:所画数轴和数轴上表示数如图所示:由数轴的特点可知,﹣3<﹣1<7<0.5<2.22.【解答】解:(1)(+4.3)﹣(﹣4)+(﹣2.4)﹣(+4)=4.3+4+(﹣2.3)+(﹣4)(2)﹣49÷×(﹣)÷(﹣10)=﹣;=﹣9×(﹣2)+16+4+=36;=5﹣8+27﹣3(5)|﹣1.2+3|﹣3﹣|4.5﹣6.2|=﹣1.9;=(19+)×(﹣8)+(19.5﹣1.5)×8=﹣152﹣7.5+108=﹣51.5.23.【解答】解:(1)3×200+6﹣3﹣7=599(辆);(2)17﹣(﹣11)=28(辆);=1408×50+35×25﹣27×10=70400+875﹣270=71005(元).答:该厂工人这一周的工资总额是71005元.24.【解答】解:∵|a|=5、|b|=3、c2=81,|a+b|=a+b且|a+c|=a+c,∴a=±7,b=±3,c=±9,a+b≥0,a+c≥0,当a=4,b=﹣3,c=9时,原式=10+9+9=28.25.【解答】解:(1)|x﹣4|+|x+2|的最小值为4﹣(﹣2)=3,此时x的取值情况是﹣2≤x≤4;(2)|x﹣3|+|x+2|+|x+6|的最小值为(﹣2+6)+0+(3+5)=9,此时x的取值情况是x=﹣2;∴﹣2≤x≤1,﹣7≤y≤3,故2x+y的最大值为5,最小值为﹣8.26.【解答】解:(1)∵点E在数轴上表示的数是5,EH是4个单位长度,∴H点表示9,∴D点表示﹣7,∴A点表示﹣9,(2)∵E、D之间的距离是12,长方形ABCD以每秒2个单位的速度向右匀速运动,∵当A点运动到H时,两个长方形没有重叠,∴A运动到H,运动了9秒;此时D点在数轴上表示的点是2,故答案为6,9,1;此时t=12÷4=7秒;②当E在D的左侧,距离为2时,此时t=14÷4=3.5秒;综上所述:当E、D运动3秒,4.5秒时,点M与线段EH端点E的距离为1个单位长度。
重庆市实验外国语学校2024-2025学年高三上学期第三次考试数学试题

重庆市实验外国语学校2024-2025学年高三上学期第三次考试数学试题一、单选题1.设全集{}1,2,3,4,5U =,集合{}{}1,4,2,5M N ==,则U N M =ð( )A .{}2,3,5B .{}1,3,4C .{}1,2,4,5D .{}2,3,4,52.22π7πsin sin 1212−=( ).A B .12C .12−D .3.函数()3log (0)2x af x a x +=>−是奇函数,则a =( ) A .1B .2C .3D .44.设θ∈R ,则“sin tan 0θθ<”是“θ为第二象限角”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件5.已知7sin cos 5θθ−=,则πtan 4θ⎛⎫+= ⎪⎝⎭( )A .17或7B .17或17−C .7或-7D .-7或17−6.已知函数()2log ,13,1a x x f x x ax x ≥⎧=⎨−+−<⎩在R 上单调递增,则a 的取值范围是( )A .[]2,3B .[2,4]C .(]1,4D .[)2,+∞7.为迎接中秋佳节,某公司开展抽奖活动,规则如下:在不透明的容器中有除颜色外完全相同的2个红球和3个白球,每位员工从中摸出2个小球.若摸到一红球一白球,可获得价值a 百元代金券;摸到两白球,可获得价值b 百元代金券;摸到两红球,可获得价值ab 百元代金券(,a b 均为整数).已知每位员工平均可得5.4百元代金券,则运气最好者获得至多( )百元代金券 A .5.4B .9C .12D .188.函数()sin f x x =与()()()lg 1,0,lg 1,0x x g x x x ⎧+≥⎪=⎨−−+<⎪⎩的图象有( )个交点A .5B .6C .7D .8二、多选题9.下列关于函数sin 3y x π⎛⎫=+ ⎪⎝⎭的说法正确的是( )A .在区间5,66ππ⎡⎤−⎢⎥⎣⎦上单调递增B .最小正周期是πC .图象关于点,06π⎛⎫⎪⎝⎭中心对称 D .图象关于直线65x π=−轴对称10.已知二项式32nx ⎛⎫ ⎪⎝⎭的展开式中各项系数之和是164,则下列说法正确的是( )A .展开式共有6项B .二项式系数最大的项是第4项C .展开式的常数项为540D .展开式含有2x11.关于函数()2ln 2x f x a x bx =++,下列说法正确的是( )A .若()f x 存在极值点,则240b a −<B .若0<a ,则()f x 有且只有一个极值点C .若()f x 有两个极值点,则0ab <D .若1是()f x 的极大值点,则1a >三、填空题12.计算:tan 2025︒= .13.若某人打算将5个数字1,1,2,3,5进行排列得到密码,则可设置的不同密码有 种.14.如图,圆O 与x 轴的正半轴的交点为A ,点C ,B 在圆O 上,且点C 位于第一象限,点B 的坐标为43,55⎛⎫− ⎪⎝⎭,AOC α∠=.若1BC =2sincos2222ααα−−的值为 .四、解答题15.已知函数()()()33log log 52f x x a x =+−−,且()21f =. (1)求a 的值及()f x 的定义域; (2)求不等式()1f x >的解集.16.某校机器人社团为了解市民对历年"数博会"科技成果的关注情况,在市内随机抽取了1000名市民进行问卷调查,问卷调查的成绩ξ近似服从正态分布()277,N σ,且()77800.3P ξ≤≤=.(1)估计抽取市民中问卷成绩在80分以上的市民人数;(2)若本次问卷调查得分超过80分,则认为该市民对“数博会”的关注度较高,现从市内随机抽取3名市民,记对“数博会”关注度较高的市民人数为随机变量X ,求X 的分布列和数学期望.17.已知,αβ为锐角,且()()()()11πsin 2πcos cos π23πsin sin 3πcos 2αααααα⎛⎫++− ⎪⎝⎭=⎛⎫−−− ⎪⎝⎭. (1)求2sin cos αα+的值;(2)若()1cos 3αβ+=,求sin β的值.18.已知函数()2ln f x x x =.(1)求函数()f x 的极值;(2)证明:对任意的()0,x ∈+∞,有()1f x x ≥−; (3)若()12,0,1x x ∈,证明:()()1212f x f x x x −≤−.19.已知函数()sin cos n nf x x x =+,其中x ∈R ,整数3n ≥.(1)当4n =时,求函数()f x 的值域;(2)已知对任意的()0,1x ∈,有(1)1m m x x +−<,求实数m 的取值范围; (3)求函数()f x 的最大值和最小值.。
2021-2022学年八年级数学上学期期中期末精选50题压轴版原卷

期末精选50题(压轴版)一、单选题1.(2020·全国·苏州市吴江区同里中学期末)如图,在△ABC中,AD是BC边上的高,∠BAF=∠CAG=90°,AB=AF,AC=AG,连接FG,交DA的延长线于点E,连接BG,CF,则下列结论:①BG=CF;②BG⊥CF;③∠EAF=∠ABC;④EF=EG,其中正确的有()A.①②③B.①②④C.①③④D.①②③④⨯的网格中,每一个小正方形的边长都是2.(2021·河南浉河·八年级期末)如图,在331,点A,B,C,D都在格点上,连接AC,BD相交于P,那么APB∠的大小是()A.80︒B.60︒C.45︒D.303.(2020·福建宁德·七年级期末)如图,点P 在∠MAN的角平分线上,点B ,C 分别在AM,AN上,作PR⊥AM,PS⊥AN,垂足分别是R,S.若∠ABP +∠ACP = 180︒,则下面三个结论:① AS =AR;②PC∥AB;③△BRP≌△CSP .其中正确的是()A.①②B.②③C.①③D.①②③4.(2021·山西阳城·八年级期末)程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.有以下结论:①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ其中所有正确结论的序号是( )A .②③B .③④C .②③④D .①②③④5.(2020·浙江浙江·八年级期末)如图,ABC 中,60BAC BAC ∠=︒∠,的平分线AD 与边BC 的垂直平分线MD 相交于D ,DE AB ⊥交AB 的延长线于E ,DF AC ⊥于F ,现有下列结论:①DE DF =;②DE DF AD +=;③DM 平分EDF ∠;④2AB AC AE +=,其中正确的有( )A .1个B .2个C .3个D .4个6.(2020·浙江浙江·八年级期末)如图在ABC 中,ABC ∠和ACB ∠的平分线交于点G ,过点G 作//EF BC 交AB 于E ,交AC 于F ,过点G 作GD AC ⊥于D ,下列四个结论:其中正确的结论有( )个.①EF BE CF =+;②90BGC A ∠=︒+∠;③点G 到ABC 各边的距离相等;④设GD m =,AE AF n +=,则AEF S mn =△;⑤AEF 的周长等于+AB AC 的和.A .1B .2C .3D .47.(2020·浙江浙江·八年级期末)如图,在ABC 中,45,ABC AD BE ∠=︒,分别为,BC AC 边上的高,,AD BE 相交于点F ,连接CF ,则下列结论:①BF AC =;②FCD DAC ∠=∠;③CF AB ⊥;④若2BF EC =,则FDC △周长等于AB 的长.其中正确的有( )A .①②B .①③④C .①③D .②③④8.(2020·重庆·七年级期末)已知关于x ,y 的方程组35225x y a x y a -=⎧⎨-=-⎩,则下列结论中正确的是( )①当a =5时,方程组的解是1020x y =⎧⎨=⎩;②当x ,y 的值互为相反数时,a =20;③当2216x y =时,a =18;④不存在一个实数a 使得x =y .A .①②④B .②③④C .②③D .②④9.(2021·山东泗水·八年级期末)在矩形ABCD 内将两张边长分别为a 和()b a b >的正方形纸片按图1和图2两种方式放置(图1和图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为1S ,图2中阴影部分的面积为2S .当4AD AB -=时,21S S -的值为( )A .4aB .4bC .44a b -D .5b10.(2021·河南省淮滨县第一中学八年级期末)若220x x +-=,则3222016x x x +-+等于( )A .2020B .2019C .2018D .-202011.(2021·重庆万州·八年级期末)已知x y 、、z 满足12x z -=,236xz y +=-,则2x y z ++的值为( )A .4B .1C .0D .-812.(2020·湖北江岸·八年级期末)某种产品的原料提价,因而厂家决定对产品进行提价,现有3种方案:①第一次提价%m ,第二次提价%n ;②第一次提价%n ,第二次提价%m ;③第一次、第二次提价均为%2m n +.其中m 和n 是不相等的正数.下列说法正确的是( ) A .方案①提价最多B .方案②提价最多C .方案③提价最多D .三种方案提价一样多13.(2020·福建厦门·八年级期末)下列四个多项式,可能是2x 2+mx -3 (m 是整数)的因式的是A .x -2B .2x +3C .x +4D .2x 2-114.(2021·湖北江岸·八年级期末)当x 分别取2020、2018、2016、…、2、0、12、14、…、12016、12018、12020时,计算分式11x x -+的值,再将所得结果相加,其和等于( )A .1-B .1C .0D .202015.(2021·重庆云阳·八年级期末)若关于x 的不等式组()3222x x a x x ⎧-->-⎪⎨+<⎪⎩有解,关于y 的分式方程13244ay y y -+=---有整数解,则符合条件的所有整数a 的和为( ) A .0 B .1 C .2 D .5二、填空题16.(2020·黑龙江香坊·七年级期末)如图,直线AB ∥CD ,点E 、M 分别为直线AB 、CD 上的点,点N 为两平行线间的点,连接NE 、NM ,过点N 作NG 平分∠ENM ,交直线CD 于点G ,过点N 作NF ⊥NG ,交直线CD 于点F ,若∠BEN =160°,则∠NGD ﹣∠MNF =__度.17.(2021·山东城阳·七年级期末)如图,在△ABC 中,∠ACB =90°,CE ⊥AB 于点E ,AD=AC ,AF 平分∠CAB 交CE 于点F ,DF 的延长线交AC 于点G ,以下结论:①DF //BC ;②FG =FE;③∠ACF =∠B ;④EF +CG >CF .其中正确的有_________(填正确结论的序号)18.(2021·江苏·景山中学七年级期末)如图,在△ABC 中,∠ACB =90°,∠A <∠B ,点D 为AB 边上一点且不与A 、B 重合,将△ACD 沿CD 翻折得到△ECD ,直线CE 与直线AB 相交于点F .若∠A =40°,当△DEF 为等腰三角形时,∠ACD =__________________.19.(2021·湖北襄州·八年级期末)将一副三角板按如图所示的方式摆放,其中ABC 为含有45°角的三角板,直线AD 是等腰直角三角板的对称轴,且斜边上的点D 为另一块三角板DMN 的直角顶点,DM 、DN 分别交AB 、AC 于点E 、F .则下列四个结论:①BD AD CD ==;②AED CFD △△≌;③BE CF AB +=;④218AEDF S BC =四边形.其中正确结论是______.(把你认为正确结论的序号都填上).20.(2019·广东湛江·八年级期末)现在生活人们已经离不开密码,如取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式44x y -,因式分解的结果是()22()()x y x y x y -++,若取9x =,9y =时则各个因式的值是:0x y -=,18x y +=,22162x y +=,把这些值从小到大排列得到018162,于是就可以把“018162”作为一个六位数的密码.对于多项式324x xy -,取10x =,10y =时,请你写出用上述方法产生的密码_________.21.(2020·江苏锡山·七年级期末)如果三角形的两个内角α与β满足3α+β=90°,那么我们称这样的三角形为“准直角三角形”.如图,B 、C 为直线l 上两点,点A 在直线l 外,且∠ABC =45°.若P 是l 上一点,且△ABP 是“准直角三角形”,则∠APB 的所有可能的度数为__.22.(2020·江苏姜堰·七年级期末)如图,在△ABC 中,∠ACB =60°,∠ABC =α(20°<α<120°),AE 平分△ABC 的外角∠BAD ,CF 将∠ACB 分成1:2两部分.若AE 、CF 交于点G ,则∠AGC 的度数为_________(用含α的代数式表示).23.(2020·福建福州·七年级期末)如图,已知//AB CD ,点E 在两平行线之间,连接BE ,CE ,ABE ∠的平分线与BEC ∠的平分线的反向延长线交于点F ,若50BFE ∠=︒,则C ∠的度数是_________.24.(2021·陕西凤翔·七年级期末)如图,在锐角ABC 中,AC =10,25ABC S =,∠BAC 的平分线交BC 于点D ,点M ,N 分别是AD 和AB 上的动点,则BM +MN 的最小值是_______________25.(2020·山东东平·七年级期末)如图所示,ABC 的外角ACD ∠的平分线CP 与ABC ∠的平分线相交于点P ,若36BPC ∠=︒,则CAP ∠=_______.26.(2020·浙江杭州·八年级期末)已知在ABC 中,16C ∠=︒且为最小的内角,过顶点B 的一条直线把这个三角形分割成两个等腰三角形,则B ∠=_______︒27.(2021·天津滨海新·八年级期末)如图,AB =AC ,BD ⊥AC 于点D ,点E ,F 分别为AB ,BD 上的动点,且AE =BF ,∠DBA =34°.(1)CE 与BD 的大小关系______(填“≥”或“≤”);(2)当CE +AF 取得最小值时,∠BEC 的度数是__________.28.(2020·浙江浙江·八年级期末)如图,已知点P 是射线BM 上一动点(点P 不与点B 重合),45AOB ∠=︒,60ABM ∠=︒,则当OAP ∠=______时,以A ,O ,B 三点中的任意两点和P 点为顶点的三角形是等腰三角形.29.(2021·新疆喀什·八年级期末)已知2a b -=,则222a ab b -+=________.30.(2020·山东青岛·八年级期末)观察等式:232222+=-;23422222++=-;2345222222已知按一定规律排列的一组数:502、512、522、⋯、992、1002.若502a =,用含a 的式子表示这组数的和是____.31.(2019·山东山东·八年级期末)通过计算几何图形的面积,可表示一些代数恒等式,如图所示,我们可以得到恒等式:2232a ab b ++=______.32.(2021·福建省福州第一中学八年级期末)若关于x 的分式方程1243x a x -=-无解,则a =________.33.(2021·河南鹿邑·八年级期末)如果关于x 的分式方程1311a x x x --=++有负整数解,且关于x 的不等式组2()43412a x x x x ---⎧⎪⎨+<+⎪⎩的解集为2x <-,那么符合条件的所有整数a 的和为________________.34.(2021·四川开江·八年级期末)若240x y z -+=,4320x y z +-=.则222xy yz zx x y z ++++的值为______35.(2021·重庆南开中学七年级期末)如图,在锐角△ABC 中,点D 在线段CA 的延长线上,BC 边的垂直平分线分别交AB 边于点E ,交∠BAC 的平分线于点M ,交BAD 的平分线于点N ,过点C 作AM 的垂线分别交AM 于点F ,交MN 于点O ,过点O 作OG ⊥AB 于点G ,点G 恰为AB 边的中点,过点A 作AI ⊥BC 于点I ,交OC 于点H ,连接OA 、OB ,则下列结论中,(1)∠MAN =90°;(2)∠AOB =2∠ACB ;(3)OH =2OG ;(4)△AFO ≌△AFH ;(5)AE +AC =2AG .正确的是________.(填序号)三、解答题36.(2021·山东平阴·七年级期末)如图,在ABC 中,ACB ∠为锐角,点D 为直线BC 上一动点,以AD 为直角边且在AD 的右侧作等腰直角三角形ADE ,90DAE ∠=︒,AD AE =.(1)如果AB AC =,90BAC ∠=︒:①当点D 在线段BC 上时,如图1,线段CE 、BD 的位置关系为_____________,数量关系为_____________.②当点D 在线段BC 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.(2)如图3,如果AB AC ≠,90BAC ∠≠︒,点D 在线段BC 上运动、探究:当ACB ∠等于多少度时,CE BD ⊥?请说明理由.37.(2021·浙江东阳·七年级期末)如图1,在△ABC 中,∠B =65°,∠BAC =75°,D 为AC 边上一点,分别过点A 、D 作BC 、AB 的平行线交于点E .(1)求∠E的度数.(2)点P为直线AC上的一个动点,过点P作PF∥AE,且PF=AE,连DF.①如图2,当点P在点C的右侧,且∠PFD=25°时,判断DE与DF的位置关系,并说明理由.②在整个运动中,是否存在点P,使得∠PFD=2∠EDF?若存在,请求出∠PFD的度数,若不存在,请说明理由.38.(2021·广东湘桥·七年级期末)如图1,在平面直角坐标系中,点A(a,0)在x轴正半轴上,点B是第四象限内一点,BC⊥y轴于点C(0.c c+3|=0,S四边形ABCO=9.(1)求点B的坐标;(2)如图2,D点是线段OC上一动点,DE∥AB交BC于点E,∠ODE的角平分线与∠BAF的角平分线交于第四象限的一点G,AB与DG交于点H,求∠AGD的度数;(3)如图3,将点C向左平移4个单位得到点H,连接AH,AH与y轴交于点D.①求点D的坐标;②y轴上是否存在点M,使三角形AHM和三角形AHB的面积相等?若存在,求出点M的坐标;若不存在,请说明理由.39.(2021·广东番禺·七年级期末)(1)如图,点D在射线BC上,求证:ACD A B∠=∠+∠.(2)如图,在直角坐标系xOy中,点A在y轴上,点C在x轴上,点F是线段AC上一点,满足FOC FCO∠=∠,点E是线段OA上一动点(不与A,O重合),连接CE交OF于点H.当点E在线段OA上运动的过程中,OHC ACEOEC∠+∠∠的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.40.(2021·湖南岳阳·七年级期末)(1)如图1,在三角形ABC 中,CD 平分ACB ∠,点E 在边AC 上,12∠=∠,试说明DE 与BC 的位置关系,并予以证明;(2)如图2,在(1)的条件下,若CBD CDB ∠=∠,CDE ∠的平分线交AC 于点F ,连接BF .求证:90DBF DFB ∠+∠=︒;(3)如图3,在前面的条件下,若ACD ∠的平分线与AB 、DF 分别交于G 、H 两点,且54BGC ∠=︒,求ACB ∠的度数.41.(2021·四川成都·期末)如图,ABC中,过点A,B分别作直线AM,BN,且AM//BN,过点C作直线DE交直线AM于D,交直线BN于E,设AD=a,BE=b.(3)如图2,若AC=AB,且∠DEB=∠BAC=60°,求DC的长.(用含a,b的式子表示)42.(2021·辽宁建昌·八年级期末)如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.(1)如图1,若点D在边BC上,直接写出CE,CF与CD之间的数量关系;(2)如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由;(3)如图3,若点D在边CB的延长线上,请直接写出CE,CF与CD之间的数量关系.43.(2021·四川绵阳·七年级期末)如图1,在平面直角坐标系xOy 中,(,0)A a ,(,)B b c ,且2(8)|3|0a b -+-,连接AB ,222()AB a b c =-+.(1)求点A 和点B 的坐标和线段AB 的长度;(2)如图2,点P 是射线AO 上一动点,连接BP ,将ABP ∆沿着直线BP 翻折至QBP △,当//PQ AB 时,求点P 和点Q 的坐标;(3)在(2)的情况下,如图3,点F 是线段AP 延长线上一动点,连接BF ,将ABF 沿着MQ QMF ∠QBF ∠MQB ∠44.(2021·山东肥城·八年级期末)实数a,b,c,d满足222519a b c d+++=+d的值.45.(2021·陕西金台·八年级期末)阅读下列材料:材料1:将一个形如x²+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n则可以把x²+px+q因式分解成(x+m)(x+n),如:(1)x2+4x+3=(x+1)(x+3);(2)x2﹣4x﹣12=(x﹣6)(x+2).材料2:因式分解:(x+y)2+2(x+y)+1,解:将“x+y看成一个整体,令xy=A,则原式=A²+2A+1=(A+1)²,再将“A”还原得:原式=(x+y+1)²上述解题用到“整体思想”整体思想是数学解题中常见的一种思想方法,请你解答下列问题:(1)根据材料1,把x2+2x﹣24分解因式;46.(2021·重庆市育才中学八年级期末)已知一个三位自然数,若满足百位数字等于十位数字与个位数字之和,则称这个数为“好数”,若满足百位数字等于十位数字与个位数字的平方差,则称这个数为“友数”.如果一个数既是“好数”,又是“友数”,则称这个数为“好友数”.例如321,∵3=2+1,∴321是“好数”,∵3=22﹣12,∴321是“友数”,∴321是“好友数”.(1)最小的好友数是 ,最大的好友数是 ;(2)证明:任意“好友数”的十位数字比个位数字大1;(3)已知m =10b +3c +817(0≤b ≤5,1≤c ≤9,且b ,c 均为整数)是一个“好数”,请求出所有符合条件的m 的值.47.(2021·重庆实验外国语学校八年级期末)对任意一个四位自然数n ,如果各个数位上的数字均不为0,且千位与个位上的数字之积减去百位与十位上的数字之积等于8,则称n 为“8阶乘差数”.例如:四位自然数5434,5×4﹣4×3=8,所以5434是一个“8阶乘差数”.(1)请任意写出两个千位和百位的数字均为2的“8阶乘差数”;(2)如果四位数abcd 是“8阶乘差数”, ()()42b a d c -+ 也为“8阶乘差数”,且b >d ,求所有满足以上条件的“8阶乘差数”abcd .48.(2021·全国·八年级期末)已知点A在x轴正半轴上,以OA为边作等边OAB,A(x,0),其中x是方程312223162x x-=--的解.(1)求点A的坐标;(2)如图1,点C在y轴正半轴上,以AC为边在第一象限内作等边ACD,连DB并延长交y轴于点E,求BEO∠的度数;(3)如图2,点F为x轴正半轴上一动点,点F在点A的右边,连接FB,以FB为边在第一象限内作等边FBG,连GA并延长交y轴于点H,当点F运动时,GH AF-的值是否发生变化?若不变,求其值;若变化,求出其变化的范围.49.(2021·福建永春·八年级期末)某商店决定购进A、B两种纪念品.已知每件A种纪念品的价格比每件B种纪念品的价格多5元,用800元购进A种纪念品的数量与用400元购进B种纪念品的数量相同.(1)求购进A、B两种纪念品每件各需多少元?(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于800元,且不超过850元,那么该商店共有几种进货方案?(3)已知商家出售一件A种纪念品可获利m元,出售一件B种纪念品可获利(6﹣m)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)50.(2021·河北唐山·八年级期末)某校利用暑假进行田径场的改造维修,项目承包单位派遣一号施工队进场施工,计划用30天时间完成整个工程.当一号施工队工作10天后,承包单位接到通知,有一大型活动要在该田径场举行,要求比原计划提前8天完成整个工程,于是承包单位派遣二号与一号施工队共同完成剩余工程,结果按通知要求如期完成整个工程.(1)若二号施工队单独施工,完成整个工程需要多少天?(2)若此项工程一号、二号施工队同时进场施工,完成整个工程需要多少天?。
八年级(上)开学数学试卷(含答案)新人教版

成都市外国语学校2018-2019学年八年级上学期开学考试数学试题(考试时间:120分钟 满分:150分)A 卷(共100分)一、选择题(每小题3分,共30分)1、下列四个图案中,不是轴对称图案的是( )A B C D 2、 下列各式中,计算正确的是( ) A. b a a b an n 1110)2()5(++=-⋅- B. c b a c b b a b a 643222221)()4(=⋅-⋅-C. z y x xy z x xy 332236)()3(=⋅-⋅- D. 1311331)61)(2(-+-=-n n n n b a ab b a 3、若25)3(22+--x a x 是完全平方式,那么a 的值是( )A . -2,8 B. 2 C. 8 D. ±24、在一个不透明的盒子中,装有4个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球40次,其中10次摸到黑球,则估计盒子中大约有白球( )A 、12个B 、16个C 、20个D 、30个 5、下列说法:①已知734=-y x ,若用x 的代数式表示y ,则437yx +=;②数轴上的点与有理数对一一对应;③由两个二元一次方程组成的方程组一定是二元一次方程组;④等腰三角形是对称图形,顶角的角平分线是它的对称轴;其中正确的说法个数是( )A 、1B 、2C 、3D 、06、解方程组2,78ax by cx y +=⎧⎨-=⎩时,一学生把c 看错而得到⎩⎨⎧=-=22y x ,而正解是⎩⎨⎧-==23y x ,则c b a 、、的值是( )A 、不能确定B 、254-===c b a ,,C 、b a 、不能确定,2-=cD 、274===c b a ,,7、小李骑车沿直线旅行,先前进了a 千米,休息了一段时间,又原路返回b 千米(b <a ),再前进c 千米,则他离起点的距离s 与时间t 的关系示意图是( )8、已知,如图AE =CF ,∠AFD =∠CEB ,那么添加下列一个条件后,仍无法判定CBE ADF ∆≅∆的是( )A. ∠A =∠CB. AD =CBC. BE =DFD. AD //BC9、如图,AD 是△ABC 中∠BAC 的角平分线,DE ⊥AB 于点E ,S △ABC =18,DE =3,AB =8,则AC 长是( )A .3B .4C .6D .510、已知:如图在△ABC ,△ADE 中,∠BAC =∠DAE =90°,AB =AC ,AD =AE ,点C ,D ,E 三点在同一条直线上,连接BD ,BE .以下四个结论:①BD =CE ;②BD ⊥CE ; ③∠ACE +∠DBC =45°;④BE =AC +AD 。
重庆实验外国语学校2018-2019学年上学期月考初二英语试题(解析版)

重庆实验外国语学校2018-2019学年上学期月考初二英语试题第一卷I听力测试(共30分)略II单項选择(每小题1分,共15分)从A、B、C、D四个选项中选出可以填入空白处的最佳答案,并把答题卡上对应题目的答案标号标黑。
21.Jimmy often plays piano and she wants to be musician when she grows up.A. a; theB. the; theC. the;aD. a ; a【答案】C【难度】易【解析】冠词的使用play the piano 乐器前要加定冠词一个音乐家要加不定冠词a【易错点】冠词的使用错误22.【答案】D【难度】【解析】【易错点】23.My birthday is on the day of the lunar month.A. ninth; twelvethB. nineth; twelfthC.ninth; twelfthD. nineth; twelveth【答案】C【难度】易【解析】序数词的书写第九ninth 第十二twelfth【易错点】拼写错误24.-My computer!It doesn’t work!-Let me have a look. And you can use if you have something important to do.A. mineB.meC.myD. myself【答案】A【难度】中【解析】名词性物主代词的语法名词型物主代词后不接名词形容词性物主代词后要接名词【易错点】名词性物主代词和形容词性物主代词的混用25.- is the nearest hospital from here?-Er, it’s about ten minutes’ walk.A. How farB. How longC. How oftenD. How soon【答案】A【难度】难【解析】How 的提问;答句的回答20分钟的路程,说明提问的是距离所以用how far【易错点】how far和how long的混淆how long 提问的时间26.If you like the shoes, you can .A. try on itB. try it onC. try on themD. try them on【答案】D【难度】中【解析】代词的位置;try on尝试shoes但是复数代词用them 放在中间【易错点】代词的选择错误和位置错误27.-I got a message saying my phone number won ﹩3000!-Too good to be true! Don’t it.A.doB. haveC. makeD. believe【答案】D【难度】中【解析】词义辨析,根据句意,不要相信他【易错点】词意的混淆28.Both of her two daughter are teacher. One teaches English, and teaches Chinese.A. anotherB. the otherC. otherD. others【难度】难【解析】固定搭配;两者中的一者,另一者用“one。
重庆市九龙坡区重庆实验外国语学校2023-2024学年九年级上学期第十次自主练习数学试题

重庆市九龙坡区重庆实验外国语学校2023-2024学年九年级上学期第十次自主练习数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.利用圆内接正多边形,可以设计出非常有趣的图案.下列图案中,是中心对称图形,但不是轴对称图形的是( )A .B .C .D . 2.下列说法正确的个数有( )①相等的弦所对的圆心角相等;②平分弦的直径垂直于这条弦;③直径所对的弧是半圆;④圆是轴对称图形,其对称轴有无数条,对称轴是圆的直径.A .1个B .2个C .3个D .4个 3.如图,某一时刻两个建筑物AB 和CD 在太阳光照射下影子的端点刚好重合在地面的点E 处,若8CD =米,15DE =米,30BD =米(点B 、D 、E 在同一水平线上,A 、B 、C 、D 、E 在同一平面内),则建筑物AB 的高度为( )A .8米B .16米C .24米D .32米 4.如图,正五边形ABCDE 内接于O e ,点F 为O e 上一点,则∠EFC 的度数为( )A .36°B .45°C .60°D .72° 5.如图,在△ABC 中,AB =5,AC =3,BC =4,将△ABC 绕点A 逆时针旋转30°后得到△ADE ,点B 经过的路径为弧BD ,则图中阴影部分的面积为( )A .2512πB .43πC .34πD .512π 6.如图,ABC V 是等腰三角形,AB 过原点O ,底边BC x ∥轴,双曲线k y x =过,A B 两点,过点C 作CD y ∥轴交双曲线于点D ,若12BCD S =V ,则k 的值是( )A .6-B .12-C .92- D .9-7.如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积( )A .π4-B .2π4-C .4π-D .42π-8.二次函数2y ax bx c =++(a ≠0)的图象如图所示,则下列命题中正确的是( )A .a >b >cB .一次函数y =ax +c 的图象不经第四象限C .m (am +b )+b <a (m 是任意实数)D .3b +2c >09.如图,在正方形ABCD 中,O 为对角线AC 的中点,E 为正方形内一点,连接BE ,BE BA =,连接CE 并延长,与ABE ∠的平分线交于点F ,连接OF ,若2AB =,则OF 的长度为( )A.2 B C .1 D 10.有两个整数,,x y 把整数对(),x y 进行操作后可得到()()(),,,,,x y y x y y y x +-中的某一个整数对,将得到的新整数对继续按照上述规则操作下去,每得到一个新的整数对称为一次操作.若将整数对()2,32按照上述规则进行操作,则以下结论正确的个数是( ) ①若m 次操作后得到的整数对仍然为()2,32,则m 的最小值为2;②三次操作后得到的整数对可能为()2,30-;③不管经过多少次操作,得到的整数对都不会是()3,18-.A .3个B .2个C .1个D .0个二、填空题11.计算:221tan 602-⎛⎫-︒= ⎪⎝⎭.12.为了解本地区人均淡水消耗量,需要从四名同学(两名男生,两名女生)中随机抽取两人,组成调查小组进行社会调查,恰好抽到一名男生和一名女生的概率是. 13.如图,在ABC V 中,90C ∠=︒,3AC =,4BC =,则ABC V 的内切圆半径r =.14.如图,P 为正比例函数32y x =图象上的一个动点,P e 的半径为3,当P e 与直线2x =相切时,则点P 的坐标为.15.如图,在四边形ABCD 中,AB CD P ,AD AB ⊥,以D 为圆心,AD 为半径的弧恰好与BC 相切,切点为E ,若13AB CD =,则sin C 的值是.16.若关于x 的一元一次不等式组2123,325x x x a x -⎧+<-⎪⎨⎪+≤+⎩的解集为2x >,且关于y 的分式方程531222y a y y y -+=-+--的解为非负整数,则所有满足条件的a 的值之积为. 17.如图,正方形ABCD 中,E 为BC 上一点,过B 作BG AE ⊥于G ,延长BG 至点F 使45CFB ∠=︒,延长FC AE 、交于点M ,连接DF BM 、,若C 为FM 中点,10BM =,则FD =.18.一个四位正整数m ,如果m 满足各个数位上的数字均不为0,千位数字与个位数字相等,百位数字与十位数字相等,则称m 为“对称数”,将m的千位数字与百位数字对调,十位数字与个位数字对调得到一个新数m ',记()81m m F m '-=.例如:对称数7337m =时,3373m '=,则()7337377373374481F -==.已知s 、t 都是“对称数”,记s 的千位数字与百位数字分别为a ,b ,t 的千位数字与百位数字分别为x ,y ,其中19b a ≤<≤,1x ≤,9y ≤,a ,b ,x ,y 均为整数.若()F s 能被8整除,则a b -=;同时,若()F s 、()F t 还满足()()64138F s F t a b x y xy +=++-+,则()F t 所有可能值的和为.三、解答题19.计算:(1)()()23x y x x y --- (2)2222132193a a a a a a a ⎛⎫++++÷+- ⎪-+⎝⎭ 20.如图,在ABC V 中,AB AC =,过点A 作AD BC ⊥交BC 于点D .点E 是线段AD 上一点,连接BE ,请完成下面的作图和填空.(1)用尺规完成以下基本作图:以点C 为顶点,在BC 的右侧作BCF EBD ∠=∠,射线CF 交AD 的延长线于点F ,连接BF ,CE .(保留作图痕迹,不写作法,不下结论)(2)求证:四边形BECF 是菱形.证明:AB AC =Q ,AD BC ⊥∴______BE CE ∴=在BED V 和CFD △中,_____BDE CDF BD DC∠=∠⎧⎪=⎨⎪⎩BED CFD ∴≌△△BE CF ∴=EBD BCF ∠=∠Q∴______∴四边形BECF 是平行四边形Q ______∴四边形BECF 是菱形21.北京时间8月24日中午12点,日本福岛第一核电站启动核污染水排海,预估排放时间将长达30年.某学校为了解该校学生对此事件的关注与了解程度,对全校学生进行问卷测试,得分采用百分制,得分越高,则对事件的关注与了解程度就越高.现从七、八年级学生中随机抽取20名学生的测试得分进行整理和分析(得分用x 表示,且得分为整数,共分为5组,A 组:060x ≤<,B 组:6070x ≤<,C 组:7080x ≤<,D 组:8090x ≤<,E 组:90100x ≤≤),下面给出了部分信息:七年级被抽取的学生测试得分的所有数据为:48,62,79,95,88,70,88,55,74,87,88,93,66,90,74,86,63,68,84,82;八年级被抽取的学生测试得分中C 等级包含的所有数据为:72,77,78,79,75; 七年级、八年级被抽取的学生测试得分统计表八年级被抽取的学生测试得分扇形统计图根据以上信息,解答下列问题:(1)上述图表中:=a ______,b =______,c =______;(2)根据以上数据,你认为该校七年级、八年级学生在关注与了解日本核污染水排海事件上,哪个年级的学生对事件的关注与了解程度更高?请说明理由(一条理由即可);(3)若该校七年级有学生900人,八年级有学生800人,估计该校这两个年级的学生测试得分在C 组的人数一共有多少人?22.备受瞩目的2023成都世界科幻大会将于10月18日启幕.这是世界科幻大会第一次走进中国,成都也将成为亚洲第二个、中国首个举办世界最高规格科幻盛会的城市.某书店正在销售A 、B 两种科幻书,它们的进价和售价如表,若老板进A 种科幻书200本和B 种科幻书300本,则需资金18000元;若老板进A 种科幻书300套和B 种科幻书400本,则需要资金25000元.(1)求A 、B 两种科幻书的进价;(2)该书店打算在今年10月把科幻书A 进行降价促销,若按原价销售则平均每天卖出6本,经调查发现每降价1元,平均每天可多售3本,将销售价定为每本多少元时,才能使科幻书A 平均每天的销售利润为225元?23.如图1,在平行四边形ABCD 中,30A ∠=︒,8AB =,4=AD ,点E 为AD 中点,动点P 以每秒2个单位长度的速度从点A 出发,沿折线A B A →→方向运动,当动点P 返回到A 点时停止运动.动点Q 以每秒1个单位长度的速度从点C 出发,沿C B →方向运动,到达点B 时停止运动.P 、Q 两点同时出发,设运动时间为x 秒,PAE △的面积为1y ,BDQ △的面积为2y .(1)请直接写出1y 、2y 关于x 的函数关系式,并注明自变量x 的取值范围;(2)如图2,在给定的平面直角坐标系中,画出1y ,2y 的函数图象,并写出函数1y 的一条性质;(3)根据图象直接写出当12y y ≥时,x 的取值范围为______.24.五一节日到来,重庆又一次成为全国火热城市,小明和小亮两人相约去观赏洪崖洞夜景,小明从A 地出发,小亮从B 地出发,相约到C 地观景.在A 处测得C 在A 的北偏东45︒方向上,在B 处测得C 在B 的正北方向上,且B 在A 的北偏东75︒方向上.小明小亮同时分别从A 、B 两地出发,他们约定先在AC 上的D 处汇合,小明沿着AC 方向慢跑,小亮沿着北偏西60︒以150m /min 的速度跑了2分钟到达D 1.73≈,1.412.45≈).(1)求AB 的长度(结果保留根号);(2)他们在D 处汇合的时间恰好为18:58,若他们汇合之后立即沿DC 方向同行的速度为200m /min (汇合时间忽略不计)则他们能在19:00之前到达C 地吗? 25.如图,在平面直角坐标系中,抛物线2y x bx c =++经过()1,0A -,()3,0B ,与y 轴交与点C .(1)求抛物线的函数解析式;(2)点P 是直线BC 下方抛物线上的一动点,PD y ∥轴交直线BC 于点D ,DE AC ∥交y轴于点E ,试判断PD 是否有最大值.若有,请求出最大值及此时点P 的坐标;若无,请说明理由;(3)已知点()2,0M ,过点M 作MF x ⊥轴交直线BC 于点F .将BMF V 沿直线BC 方向平移到B M F '''△,在平面内确定一点N ,使得以点A ,C ,M ',N 为顶点的四边形是矩形,直接写出所有符合条件的点N 的坐标.26.在ABC V 中,90ACB ∠=︒,AC BC =,点D 为平面内一点.(1)如图1,若点D 在线段AC 上,且ABD CBD ∠=∠,求tan CBD ∠;(2)如图2,若点D 为ABC V 内部一点,且135CDB ∠=︒,连接AD ,点E 为AD 的中点,连接CE CD +=; (3)如图3,若点D 为直线BC 上一动点,连接AD ,点E 为AD 中点,连接CE ,将EC 绕点E 顺时针旋转90︒得到EF ,连接AF ,点G 为BC 边上另一动点,始终满足AF CG =,连接FG .当2ABC S =△FG 的最小值.。
重庆市九龙坡区重庆实验外国语学校2022-2023学年七年级下学期第三次月考数学试题

重庆市九龙坡区重庆实验外国语学校2022-2023学年七年级下学期第三次月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题A.垂线段最短C.两点之间,线段最短3.现有两根长度分别则应选取的第三根木棒长不可能为(A.5cm4.如图,直线AB数为()A.55︒5.下列说法正确的是(A.若a b>,则a-C.若a b>,则ac和6.如图,在ABC需再添加一个条件即可,这个条件不可以是(A .B D ∠=∠B .7.估算214+的值在(A .4到5之间B .8.下列命题是真命题的是(A .相等的角是对顶角C .等角的余角相等9.甲、乙两人在相距30而行,且甲比乙先出发2度.设甲的速度为x 千米A .4044-B .4050-二、填空题11.五边形的内角和是度.12.若2320a a b -++=,那么a b -=13.已知AB x ⊥轴,A 点的坐标为()2,1-,且14.如图,在ABC 中,90C ∠=︒,BD 平分∠于E ,若9AC =,12BC =,15AB =,则ADE V15.如图,在Rt ABC △中,B Ð若12EF =,4GE =,2BG =,则阴影部分的面积为16.如图,在ABC 中,AB AC =一点,连接AE 、CE ,且满足∠为.17.已知关于x 、y 的方程组16213346x x m x⎧+≤+⎪⎨⎪-->⎩有且仅有四个整数解,则满足条件的整数18.如图,在EFG 至点B ,使GD BF =于点C ,交EF 于点的是.(请填写序号)①GB AF =;②当FEB ∠⑤若125EG =,BE三、解答题根据图中提供的信息,解答下列问题:(1)本次调查的样本容量为______,并补全条形统计图;(2)在扇形统计图中,m =______;喜欢“A 外语电影配音比赛”人数对应的圆心角α=______度;(3)我校共有学生6000名,请根据上述调查结果,估计学校共有多少学生喜欢“B 外语话剧比赛”?23.如图,在平面直角坐标系中,已知()2,2A --,()3,1B ,()0,2C .(1)若把ABC 向左平移2个单位长度再向上平移3个单位长度,得到A B C ''' ,直接写出点A '的坐标:(______,______),B '的坐标:(______,______),C '的坐标:(______,______);(2)在图中画出平移后的A B C ''' ;(3)请求出A B C ''' 的面积.24.如图1,在四边形ABCD 中,AB CD ∥,AB BC =,AB BC ⊥,过点A 作AH BD ⊥于点H ,过点C 作CE BD ⊥于点E .(1)若3CE =,求BH 的长;(2)如图2,连接AC ,F 为AC 上一点,连接EF 并延长,交AH 于点G ,若HE HG =,(1)当点P 在AB 上运动,且Q 由B C →运动时,若2BQ AP =,求t 的值;(2)在运动过程中,连接DP DQ MQ 、、,记D 、P 、M 、Q 围成的图形面积为出S 与t 的关系式,并写出t 的取值范围;(3)在运动过程中,是否存在某个时刻,使点B 、D 、P 围成的三角形与点B 、的三角形全等,若存在请直接写出t 的值,若不存在请说明理由.。
重庆市九龙坡区重庆实验外国语学校2023-2024学年八年级上学期开学考试数学试题

重庆市九龙坡区重庆实验外国语学校2023-2024学年八年级
上学期开学考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
....
A .(1,0)-
B .(1,1)--9.如图,在四边形ABCD 中,BD 平分∠A .3αB .902α︒+10.已知在213x +=和3312x y -++=-下列说法:
二、填空题
14.从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时骑行走小时骑40km,下坡每小时骑行走50km
16.如图,在五边形ABCDE
AE=,则五边形ABCDE
6
(1)尺规作图:作AC的垂直平分线交AC 痕迹,不写作法,不用下结论);
根据统计图中的信息,解答下列问题:
(1)在本次抽样调查中,样本容量为______,在扇形统计图中,表示“劳动体验圆心角度数为_____;
(2)将条形统计图补充完整;
(1)先将ABC 向下平5个单位长度后得到△222A B C △,请画出111A B C △与222A B C △;
(2)请求出将ABC 向下平移5个单位长度得到(3)若ABC 边上有一点(,)M a b ,将ABC 经过(
(1)若40ACE ∠=︒,20EFB ∠=︒,求AFE ∠(2)若1
2
AD EF =
,求证:AB AE ⊥.26.如图,在平面直角坐标系xoy 中,已知点()
5,53A ,动点P 从点O 出发,以每秒2。
重庆市九龙坡区重庆实验外国语学校2022-2023学年八年级下学期第三次月考数学试题

y1 y2 ,那么 m 的取值范围是( )
A. m 1 2
B. m 1 2
C. m 1
5.若 13 1 在两个相邻整数之间,则这两个整数是( )
A.1 和 2
B.2 和 3
C.3 和 4
6.下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
3
试卷第 2 页,共 7 页
③若多项式 mA x nB 的取值与 x 无关,则 m 2 , n 1 ;
5
5
④代数式| 2A B 2 | | 2A B | | 2A B 2 | 化简后总共有 6 种不同表达式;
⑤多项式 2A2 9B2 6A B 8A 2039 的最小值为 2023.
位数的十位,N 的百位与个位数字分别为作为 2 个两位数的个位,把按照这种方式组成
的所有两位数的和记为 F(N) .①当 N 3163 ,则 F(N) ;②当 F(N) 能被 7 整除时,
则满足条件的 N 的最小值为.
三、解答题 19.计算
(1) 5x(x 2y) (x y)2
(2)
3a a
乙相遇后,甲再经过 1 分钟与乙相距 20 米,其中正确的有( )
A.①②
B.①②③
C.②③④
D.①②③④
10.已知两个多项式 A x2 2x 1, B 2x2 x 1,x 为实数,将 A、B 进行加减乘除
运算:
①当 x= 1时,则 A B 8 ; ②若 A B 10 ,则 x 2或 5 ;
2 1
1
a
9 4a2 2 2a
1
20.解方程
(1) 4x2 3x 1 0
(2) 2(3x 1)2 9x2 1 21.在开展“童心向党”系列活动中,某校举办了一场“党史知识你我知”的知识竞赛,现 分别从七年级、八年级各随机抽取了10 名学生的竞赛成绩(单位:分,满分:100 分) 进行整理、描述和分析(成绩得分用 x 表示,共分为四组:A :80 x 85 ,B :85 x 90 , C : 90 x 95 , D : 95 x 100 ),下面给出部分信息: 七年级抽取的10 名学生的竞赛成绩在 C 组的是: 92 , 94 , 92 , 90 八年级抽取的10 名学生的竞赛成绩是: 80 ,100 , 81, 83 , 89 ,88 , 88 , 97 , 96 , 98 七、八年级抽取的学生竞赛成绩统计表
四川省成都实验外国语学校西区2018-2019学年八年级(上)月考数学试卷(10月份) 含解析

外国语学校西区2018-2019学年八年级(上)月考数学试卷A卷一、选择题(每小题3分,共30分)1.如图,阴影部分是一个长方形,它的面积是()A.3cm2B.4cm2C.5cm2D.6cm22.三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是()A.等边三角形B.钝角三角形C.直角三角形D.锐角三角形3.△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是()A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3C.a2=c2﹣b2D.a:b:c=3:4:64.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是()A.B.C.9 D.65.下列说法错误的有()①无限小数是无理数;②无理数都是带根号的数;③只有正数才有平方根;④3的平方根是;⑤﹣2是(﹣2)2的平方根.A.1个B.2个C.3个D.4个6.下列各组数中互为相反数的是()A.﹣2 与B.﹣2 与C.﹣2 与﹣D.2与|﹣2|7.估计+1的值是()A.在2和3之间B.在3和4之间C.在4和5之间D.在5和6之间8.下列各组二次根式中,同类二次根式的是()A.B.C.D.9.比较2,,的大小,正确的是()A.B.C.D.10.小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,则旗杆的高是()A.8米B.10米C.12米D.14米二、填空题(每小题4分,共16分)11.2﹣的绝对值是;的算术平方根是12.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为.13.六个数:0.123,,3.1416,﹣2π,(﹣1.5)3,0.1020020002(相邻两个2之间0的个数逐次加1),若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z =三、解答题(共54分)15.计算:(1)﹣3×+﹣(π+1)0×()﹣1(2)()×(﹣2)2﹣+(3)(3x﹣1)2=(﹣5)2(4)(x+3)3=416.计算:(1)已知x﹣2的平方根是±4,2x﹣y+12的立方根是4,求(x﹣y)x+y的值;(2)在Rt△ABC中,∠C=90°,若c=10cm,a:b=3:4,求△ABC的周长;(3)已知a=,b=,试求a2+b2、a2+3ab+b2的值.17.如图,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点S处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点F处有食物,求蚂蚁要吃到食物所走的最短路线长度.(画出侧面展开图并计算)18.如图,已知长方形ABCD中,AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求EF的长.19.已知,点P是正方形ABCD内的一点,连接PA、PB、PC(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1)①设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域的面积;②若PA=2,PB=4,∠APB=135°,求PC的长;(2)如图2,在(1)的条件下,若PA2+PC2=2PB2,请说明点P必在对角线AC上.B卷一、填空(每题4分,共20分)B卷(满分20分)20.一个正数m的平方根是2a+5和a﹣2,则m=.21.若a,b为实数,且b=,则a+b=.22.若实数x,y,z满足条件(x+y+z+9),则xyz的值=.23.已知a、b为有理数,m、n分别表示5﹣的整数部分和小数部分,且am+bn=9,则a+b=.24.如图,在△ABC中,AB=AC=1,BC边上有2013个不同的点P1,P2,…P2013,记m i=AP i2+BP i •P i C(i=1,2,…,2013),则m1+m2+…+m2013=.二、解答题(共30分)25.已知△ABC中,AB=AC.(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长26.阅读下面问题:==﹣1,==﹣,==﹣2…试求:(1)根据你发现的规律,请计算(+++…++)×(1+)的值;(2)求+++…+的值;(3)如果有理数a,b满足ab﹣2=+,试求:+++…+.27.已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图①,若点P在线段AB上,且AC=1+,PA=,则:①线段PB=,PC=;②猜想:PA2,PB2,PQ2三者之间的数量关系为;(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)若动点P满足=,求的值.(提示:请利用备用图进行探求)参考答案与试题解析A卷一.选择题(共10小题)1.如图,阴影部分是一个长方形,它的面积是()A.3cm2B.4cm2C.5cm2D.6cm2【分析】由勾股定理求出直角三角形的斜边长,再由长方形的面积公式即可得出结果.【解答】解:由勾股定理得:=5(cm),∴阴影部分的面积=5×1=5(cm2);故选:C.2.三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是()A.等边三角形B.钝角三角形C.直角三角形D.锐角三角形【分析】对等式进行整理,再判断其形状.【解答】解:化简(a+b)2=c2+2ab,得,a2+b2=c2所以三角形是直角三角形,故选:C.3.△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是()A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3C.a2=c2﹣b2D.a:b:c=3:4:6【分析】由三角形内角和定理及勾股定理的逆定理进行判断即可.【解答】解:A、∠A+∠B=∠C,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;B、∠A:∠B:∠C=1:2:3,又∠A+∠B+∠C=180°,则∠C=90°,是直角三角形;C、由a2=c2﹣b2,得a2+b2=c2,符合勾股定理的逆定理,是直角三角形;D、32+42≠62,不符合勾股定理的逆定理,不是直角三角形.故选:D.4.在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是()A.B.C.9 D.6【分析】设点C到斜边AB的距离是h,根据勾股定理求出AB的长,再根据三角形的面积公式即可得出结论.【解答】解:设点C到斜边AB的距离是h,∵在Rt△ABC中,∠C=90°,AC=9,BC=12,∴AB==15,∴h==.故选:A.5.下列说法错误的有()①无限小数是无理数;②无理数都是带根号的数;③只有正数才有平方根;④3的平方根是;⑤﹣2是(﹣2)2的平方根.A.1个B.2个C.3个D.4个【分析】根据无理数是无限不循环小数,可得无理数,可判断①②;根据平方根,可判断③④⑤.【解答】解:①无限循环小数是有理数,故①错误;②无限不循环小数是无理数,故②错误;③0的平方根是0,故③错误;④3的平方根是±,故④错误;⑤±,故⑤正确,故选:D.6.下列各组数中互为相反数的是()A.﹣2 与B.﹣2 与C.﹣2 与﹣D.2与|﹣2|【分析】根据相反数的意义求解即可.【解答】解:A、只有符号不同的数互为相反数,故A符合题意;B、都是﹣2,故B不符合题意;C、互为倒数,故C不符合题意;D、都是2,故D不符合题意;故选:A.7.估计+1的值是()A.在2和3之间B.在3和4之间C.在4和5之间D.在5和6之间【分析】应先找到所求的无理数在哪两个和它接近的整数之间,然后判断出所求的无理数的范围.【解答】解:∵32=9,42=16,∴,∴+1在4到5之间.故选:C.8.下列各组二次根式中,同类二次根式的是()A.B.C.D.【分析】将选项中的二次根式化为最简,然后根据同类二次根式的被开方数相同即可得出答案.【解答】解:A、与3的被开方数不同,不是同类二次根式,故本选项错误;B、3与的被开方数不同,不是同类二次根式,故本选项错误;C、=,=,被开方数相同,是同类二次根式,故本选项正确;D、=2,=,被开方数不同,不是同类二次根式,故本选项错误;故选:C.9.比较2,,的大小,正确的是()A.B.C.D.【分析】首先把各数同时立方,然后比较被开方数的大小,即可解决问题.【解答】解:∵23=8,()3=5≈11.2,()3=7∴<2<.故选:C.10.小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,则旗杆的高是()A.8米B.10米C.12米D.14米【分析】根据题意设旗杆的高AB为x米,则绳子AC的长为(x+1)米,再利用勾股定理即可求得AB的长,即旗杆的高.【解答】解:画出示意图如下所示:设旗杆的高AB为xm,则绳子AC的长为(x+1)m,在Rt△ABC中,AB2+BC2=AC2,∴x2+52=(x+1)2,解得:x=12,∴AB=12m,即旗杆的高是12m.故选:C.二.填空题(共3小题)11.2﹣的绝对值是﹣2 ;的算术平方根是 2【分析】由绝对值的性质求解即可;先求得=4,然后再求得4的算术平方根即可.【解答】解:|2﹣|=﹣2;∵=4,∴的算术平方根是2.故答案为:﹣2,2.12.等腰三角形的腰长为10,底边长为12,则这个等腰三角形的面积为48 .【分析】作出图形,过顶点A作AD⊥BC于D,根据等腰三角形三线合一的性质可得BD=BC,然后利用勾股定理列式求出AD,再根据三角形的面积公式列式计算即可得解.【解答】解:如图,过顶点A作AD⊥BC于D,则BD=BC=×12=6,由勾股定理得,AD===8,这个等腰三角形的面积=×12×8=48.故答案为:48.13.六个数:0.123,,3.1416,﹣2π,(﹣1.5)3,0.1020020002(相邻两个2之间0的个数逐次加1),若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z = 6【分析】由于无理数就是无限不循环小数.初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及0.1010010001…,等有这样规律的数,由此即可判定无理数x的值,根据整数的定义非负数的定义即可判定y、z的值,然后即可求解.【解答】解:无理数有:﹣2π,0.1020020002(相邻两个2之间0的个数逐次加1),则x=2;没有整数:则y=0;非负数有:0.123,,3.1416,0.1020020002(相邻两个2之间0的个数逐次加1),共4个;则z=4.则x+y+z=6.故答案为:6.三.解答题(共5小题)15.计算:(1)﹣3×+﹣(π+1)0×()﹣1(2)()×(﹣2)2﹣+(3)(3x﹣1)2=(﹣5)2(4)(x+3)3=4【分析】(1)本题涉及零指数幂、负整数指数幂、二次根式化简、三次根式化简4个知识点.在计算时,需要针对每个知识点分别进行计算,然后根据实数的运算法则求得计算结果.(2)本题涉及平方、二次根式化简、三次根式化简3个知识点.在计算时,需要针对每个知识点分别进行计算,然后根据实数的运算法则求得计算结果.(3)直接开平方即可求解;(4)先系数化为1,再直接开立方即可求解.【解答】解:(1)﹣3×+﹣(π+1)0×()﹣1=2﹣﹣2﹣1×=2﹣﹣2﹣=﹣2;(2)()×(﹣2)2﹣+=×4++=2++=3;(3)(3x﹣1)2=(﹣5)2,3x﹣1=±5,解得x1=﹣,x2=2;(4)(x+3)3=4,(x+3)3=8,x+3=2,x=﹣1.16.计算:(1)已知x﹣2的平方根是±4,2x﹣y+12的立方根是4,求(x﹣y)x+y的值;(2)在Rt△ABC中,∠C=90°,若c=10cm,a:b=3:4,求△ABC的周长;(3)已知a=,b=,试求a2+b2、a2+3ab+b2的值.【分析】(1)根据平方根的性质和立方根的性质得出x﹣2=16,2x﹣y+12=64,求出x 和y的值,再代入计算即可;(2)设a=3xcm,b=4xcm,由勾股定理得出方程,解方程求出x,得出a和b,即可得出结果;(3)首先化简a==2﹣,b==2+,进一步代入分别求得答案即可.【解答】解:(1)∵x﹣2的平方根是±4,2x﹣y+12的立方根是4,∴x﹣2=16,2x﹣y+12=64,∴x=18,y=﹣16,∴(x﹣y)x+y=342=1156;(2)设a=3xcm,b=4xcm,∵∠C=90°,∴(3x)2+(4x)2=102,解得:x=2,∴a=6,b=8,∴△ABC的周长=a+b+c=6+8+10=24(cm);(3)∵a==2﹣,b==2+,∴a2+b2=7﹣4+7+4=14;a2+3ab+b2=7﹣4+7+4+3×1=17.17.如图,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点S处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点F处有食物,求蚂蚁要吃到食物所走的最短路线长度.(画出侧面展开图并计算)【分析】先将圆柱的侧面展开,再根据勾股定理求解即可.【解答】解:如图所示,∵圆柱形玻璃容器,高8cm,底面周长为30cm,∴SD=15cm,∴SF===17(cm).答:蚂蚁要吃到食物所走的最短路线长度是17cm.18.如图,已知长方形ABCD中,AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求EF的长.【分析】先根据折叠求出AF=10,进而用勾股定理求出BF,即可求出CF,最后用勾股定理即可得出结论.【解答】解:∵四边形ABCD是矩形,∴AD=BC=10cm,CD=AB=8cm,根据题意得:Rt△ADE≌Rt△AFE,∴∠AFE=90°,AF=10cm,EF=DE,设EF=xcm,则DE=EF=xcm,CE=CD﹣CE=(8﹣x)cm,在Rt△ABF中,由勾股定理得:AB2+BF2=AF2,即82+BF2=102,∴BF=6cm,∴CF=BC﹣BF=10﹣6=4(cm),在Rt△ECF中,由勾股定理可得:EF2=CE2+CF2,即x2=(8﹣x)2+42,∴x=5即:EF的长为5cm.19.已知,点P是正方形ABCD内的一点,连接PA、PB、PC(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1)①设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域的面积;②若PA=2,PB=4,∠APB=135°,求PC的长;(2)如图2,在(1)的条件下,若PA2+PC2=2PB2,请说明点P必在对角线AC上.【分析】(1)①△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积实际是大扇形BAC与小扇形BPP′的面积差,且这两个扇形的圆心角同为90度;②连接PP′,证△PBP′为等腰直角三角形,从而可在Rt△PP′C中,用勾股定理求得PC=6;(2)将△PAB绕点B顺时针旋转90°到△P′CB的位置,由勾股定理的逆定理证出∠P′CP=90°,再证∠BPC+∠APB=180°,即点P在对角线AC上.【解答】(1)解:①∵△PAB绕点B顺时针旋转90°到△P′CB,如图1所示:∴S△ABP=S△BP′C,∴S阴影=S扇形ABC+S△BP′C﹣S扇形PBP′﹣S△ABP=S扇形ABC﹣S扇形PBP′==(a2﹣b2);②连接PP′,如图2所示:根据旋转的性质可知:BP=BP′,∠PBP′=90°,即:△PBP′为等腰直角三角形,∴∠BPP′=45°,∵∠BPA=∠BP′C=135°,∠BP′P=45°,∴∠BPA+∠BPP′=180°,即A、P、P′共线,∴∠PP′C=135°﹣45°=90°;在Rt△PP′C中,PP′=4,P′C=PA=2,根据勾股定理可得PC==6;(2)证明:连接PP′,如图3所示:∵△PAB绕点B顺时针旋转90°到△P′CB,∴PA=P′C,由(1)①可知:△BPP′是等腰直角三角形,即PP′2=2PB2,∵PA2+PC2=2PB2=PP′2,∴PC2+P′C2=PP′2,∴∠P′CP=90°;∵∠PBP′=∠PCP′=90°,∴在四边形BPCP′中,∠BP′C+∠BPC=180°;∵∠BPA=∠BP′C,∴∠BPC+∠APB=180°,即点P在对角线AC上.B卷一.填空题(共5小题)20.一个正数m的平方根是2a+5和a﹣2,则m=9 .【分析】由于一个正数的平方根有两个,它们互为相反数,由此即可得到关于a方程,解方程即可解决问题.【解答】解:∵正数m的平方根是2a+5和a﹣2,∴它们是相反数,则有:2a+5+a﹣2=0,∴a=﹣1,a﹣2=﹣3,∴m=(﹣3)2=9.故答案为:9.21.若a,b为实数,且b=,则a+b=.【分析】根据二次根式有意义的条件、分式有意义的条件列出不等式,解不等式即可.【解答】解:由题意得,a2﹣1=0,1﹣a2=0,a+1≠0,解得,a=1,则b=,则a+b=,故答案为:.22.若实数x,y,z满足条件(x+y+z+9),则xyz的值=120 .【分析】分析题中条件不难发现等号左边含有未知数的项都有根号,而等号右边的则都没有.由此可以想到将等式移项,并配方成三个完全平方数之和等于0的形式,从而可以分别求出x、y、z的值.【解答】解:将题中等式移项并将等号两边同乘以4得x﹣4+y﹣4+z﹣4+9=0,∴(x﹣4+4)+(y﹣1﹣4+4)+(z﹣2﹣4+4)=0∴(﹣2)2+(﹣2)2+(﹣2)2=0∴﹣2=0且﹣2=0且﹣2=0∴=2 =2 =2∴x=4 y﹣1=4 z﹣2=4,∴x=4 y=5 z=6∴xyz=120.故答案为:120.23.已知a、b为有理数,m、n分别表示5﹣的整数部分和小数部分,且am+bn=9,则a+b= 4.5 .【分析】估算出5﹣的整数与小数部分得出m与n,代入已知等式求出a与b的值,即可求出a+b的值.【解答】解:∵4<7<9,∴2<<3,即m=2,n=5﹣﹣2=3﹣,∴am+bn=2a+(3﹣)b=9,即2a+3b﹣b=9,可得2a+3b=9,b=0,解得:a=4.5,b=0,则a+b=4.5,故答案为:4.524.如图,在△ABC中,AB=AC=1,BC边上有2013个不同的点P1,P2,…P2013,记m i=AP i2+BP i •P i C(i=1,2,…,2013),则m1+m2+…+m2013=2013 .【分析】利用勾股定理求出APi2=AD2+PiD2,进一步推出APi2+BPi•PiC=1,解答即可.【解答】解:∵APi2=AD2+PiD2=AD2+(BD﹣BPi)2=AD2+BD2﹣2BD•BPi+BPi2=1+BPi(BPi﹣BC)=1﹣BPi•PiC,∴APi2+BPi•PiC=1,∴m1+m2+…+m2013=2013,故答案为2013.二.解答题(共3小题)25.已知△ABC中,AB=AC.(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=6,CD=8,求BD的长【分析】(1)由∠DAE=∠BAC,得出∠BAE=∠CAD,由SAS证得△BAE≌△CAD,即可得出结论;(2)连接BE,由AD=AE,∠DAE=60°,得出△ADE是等边三角形,由CD垂直平分AE,得出∠CDA=∠ADE=30°,由△BAE≌△CAD,得出BE=CD=8,∠BEA=∠CDA=30°,得出BE⊥DE,DE=AD=6,由勾股定理即可得出结果.【解答】(1)证明:∵∠DAE=∠BAC,∴∠BAE=∠CAD,在△BAE和△CAD中,,∴△BAE≌△CAD(SAS),∴CD=BE;(2)解:连接BE,如图2所示:∵AD=AE,∠DAE=60°,∴△ADE是等边三角形,∵CD垂直平分AE,∴∠CDA=∠ADE=×60°=30°,∵△BAE≌△CAD,∴BE=CD=8,∠BEA=∠CDA=30°,∴BE⊥DE,DE=AD=6,∴BD===10.26.阅读下面问题:==﹣1,==﹣,==﹣2…试求:(1)根据你发现的规律,请计算(+++…++)×(1+)的值;(2)求+++…+的值;(3)如果有理数a,b满足ab﹣2=+,试求:+++…+.【分析】(1)根据材料的值分别代入,再利用平方差公式进行计算;(2)分别分母有理化,找规律,并化简可得结论;(3)先根据二次根式的非负性计算a和b的值,代入,由(2)同理可得结论.【解答】解:(1)(+++…++)×(1+),=(﹣1+﹣+﹣+…+﹣+﹣)×(1+),=(﹣1+)(1+),=2017﹣1,=2016;(2)+++…+,=+++…+,=+++…+,=1﹣+﹣+﹣+…+﹣,=1﹣,=1﹣,=;(3)∵ab﹣2=+,∴b﹣1=0,ab﹣2=0,∴a=2,b=1,∴+++…+,=+++…+,=1﹣+﹣+﹣+…+﹣,=1﹣,=.27.已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:(1)如图①,若点P在线段AB上,且AC=1+,PA=,则:①线段PB=,PC= 2 ;②猜想:PA2,PB2,PQ2三者之间的数量关系为PA2+PB2=PQ2;(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)若动点P满足=,求的值.(提示:请利用备用图进行探求)【分析】(1)①在Rt△ABC中,可求得AB,由PB=AB﹣PA可求得PB,过C作CD⊥AB于点D,则可求得CD=AD=DB,可求得PD的长,在Rt△PCD中可求得PC的长;②把AP2和PB2都用PC和CD表示出来,结合Rt△PCD中,可找到PC和PD和CD的关系,从而可找到PA2,PB2,PQ2三者之间的数量关系;(2)过C作CD⊥AB于点D,由(1)中②的方法,可证得结论;(3)分点P在线段AB上和线段BA的延长线上,分别利用=可找到PA和CD的关系,从而可找到PD和CD的关系,在Rt△CPD和Rt△ACD中,利用勾股定理可分别找到PC、AC 和CD的关系,从而可求得的值.【解答】解:(1)①∵△ABC是等腰直角三角形,AC=1+,∴AB===+,∵PA=,∴PB=AB﹣PA=,如图1,过C作CD⊥AB于点D,则AD=CD=AB=,∴PD=AD﹣PA=,在Rt△PCD中,PC==2,故答案为:;2;证明如下:如图1,∵△ACB为等腰直角三角形,CD⊥AB,∴CD=AD=DB,∵PA2=(AD﹣PD)2=(CD﹣PD)2=CD2﹣2CD•PD+PD2,PB2=(BD+PD)2=(CD+PD)2=CD2﹣2CD•PD+PD2,∴PA2+PB2=2CD2+2PD2=2(CD2+PD2),在Rt△PCD中,由勾股定理可得PC2=CD2+PD2,∴PA2+PB2=2PC2,∵△CPQ为等腰直角三角形,且∠PCQ=90°,∴2PC2=PQ2,∴PA2+PB2=PQ2,故答案为:PA2+PB2=PQ2;(2)证明:如图2,过C作CD⊥AB于点D,∵△ACB为等腰直角三角形,CD⊥AB,∴CD=AD=DB,∵PA2=(AD+PD)2=(CD+PD)2=CD2﹣2CD•PD+PD2,PB2=(DP﹣BD)2=(PD﹣CD)2=CD2﹣2CD•PD+PD2,∴PA2+PB2=2CD2+2PD2=2(CD2+PD2),在Rt△PCD中,由勾股定理可得PC2=CD2+PD2,∴PA2+PB2=2PC2,∵△CPQ为等腰直角三角形,且∠PCQ=90°,∴PA2+PB2=PQ2;(3)过点C作CD⊥AB于点D,∵=,∴点P只能在线段AB上或在线段BA的延长线上,①如图3,当点P在线段AB上时,∵=,∴PA=AB=CD=PD,在Rt△CPD中,由勾股定理可得CP===CD,在Rt△ACD中,由勾股定理可得AC===CD,∴==;②如图4,当点P在线段BA的延长上时,∵=,∴PA=AB=CD,在Rt△CPD中,由勾股定理可得CP===CD,在Rt△ACD中,由勾股定理可得AC===CD,∴==;综上可知的值为或.。
重庆实验外国语学校2024-2025学年八年级上学期第一次月考数学试题

重庆实验外国语学校2024-2025学年八年级上学期第一次月考数学试题一、单选题1.下列各数是无理数的是( )A B .3.1415 C .2.18&& D .π2.下列运算正确的是( )A .235a a a +=B .()32626a a =C .()()233262a a a -+=D .4416a a a ⨯=3.下列从左到右的变形,属于因式分解的是( )A .()22442xy xy x x y ++=+B .()()22224x y x y x y +-=-C .()()234223x x x x x +-=+-+D .211x x x x ⎛⎫+=+ ⎪⎝⎭ 4.下列命题正确的是( )A .内错角相等B .垂直于同一直线的两直线平行C .三角形的一个外角大于任意一个内角D .连接直线外一点与直线上各点的所有线段中,垂线段最短5.若a ,b ,c 是ABC V 的三边长,则()22a b c --的结果( )A .大于零B .等于零C .小于零D .不确定 6.若22925x mxy y ++是完全平方式,则m 的值为( )A .15B .30C .15±D .30±7.若32x =,35y =,则123x y +-的值为( )A .20-B .19-C .625D .358.如图,下列图形是由同样大小的棋子按照一定规律排列而成的,其中,图①中有5颗棋子,图②中有8颗棋子,图③中有13颗棋子,图④中有20颗棋子,按照此规律排列下去,第图⑧的棋子颗数为( )A .55B .68C .72D .859.如图,在ADB V 中,60D ∠=︒,5AD =,ABC V 为等边三角形,过点C 作CE DB ⊥的延长线于点E ,若 1.5BE =,则BD 的长为( )A .6.5B .6.8C .7D .7.210.定义一种新运算:()0(0)a b ab a b a b ab ⎧-≥=⎨+<⎩> ①若23x =>,则1x =或5x =;②若123x -≥>,则6x ≥;③若()()130x x --<,则()()43248x x x --++>的最小值为14;④若关于m n ,的二元一次方程组4423m n a m n b -=⎧⎨-=⎩的解为32m n =⎧⎨=⎩,则关于x y ,的方程组 ()()()()()()()2222222221274454123639x x x x y y y a x x x y y y b ⎧⎡⎤⎡⎤++-++-+--=⎪⎣⎦⎣⎦⎨⎡⎤⎡⎤-++---+=⎪⎣⎦⎣⎦⎩>>>>的解x y 、满足:x y x y =+>. 以上说法正确的有( )A .1个B .2个C .3个D .4个二、填空题11.分解因式:226x x -=12.一个正多边形的每一个外角都是72︒,则这个正多边形的边数为.13.若2210m m --=,则代数式2632024m m -+值为.14.如图,在ABC V 中,AD 平分CAB ∠交BC 于点D ,且AB AC BD =+,若CDA α∠=︒,则B ∠的度数为.15.若()()32x a x -+的结果中不含x 的一次项,则a 的值为.16.计算222500251249=-. 17.已知直角三角形两直角边的长度分别为,a b ,若8a b +=,2248a b +=,则该三角形的面积是.18.如图,在ABC V 中,已知BD 为ABC V 的中线,过点A 作AE BD ⊥分别交BD BC 、于点F E 、,连接CF ,若1DF =,3AF =,:3:1BE EC =,则ABC S =V .三、单选题19.若关于x 的不等式组()2213124x x x a x ⎧+≥+⎪⎨-++<⎪⎩有解且最多有3个奇数解,关于y 的方程()222a y +-=的解为整数,则所有满足条件的整数a 的个数为.四、填空题20.如图,在等腰Rt ABC △中,AB AC =,在AC 边上取一点D ,连接BD ,点E 为线段BD 上一点,以BE 为斜边作等腰Rt BEF △.连接AE AF 、、CE ,AF 交BD 于G ,M 为CE 上一点,连接AM ;在下列结论中:①EAD ABD ∠=∠;②若AE 垂直平分GD ,则45AFE ABD ∠+∠=︒;③若AE 垂直平分GD ,则AD GF AB +=;④若45FAM ∠=︒,则2EC EM =;其中正确的结论有.(填写正确结论的序号)五、解答题21.(1()2013π 3.143-⎛⎫-+-+- ⎪⎝⎭; (2)解不等式组:3225132x x x x -≥⎧⎪+⎨->⎪⎩. 22.先化简,再求值:()()()()232x y x y y x x ⎡⎤+-+-÷-⎣⎦,其中x ,y 满足24410x x y +++-=. 23.如图,点D 是ABC V 的边AB 的延长线上一点,过点A 作AE BC ∥且AE AC =,点F 是线段AC 上一点,连接EF ,此时EFC CBD ∠=∠.(1)求证:ABC EFA V V ≌;(2)若2BC =,6AE =,求FC 的长度.24.巴黎奥运会举办期间,全球范围内掀起了一股体育健身的热潮.小颖随机抽取部分学生,对“周末的体育锻炼时长”进行了问卷调查,并将调查结果绘制成如下几幅不完整的图表.请根据图中信息,解答下列问题:(1)请你补全条形统计图;(2)m =______,选项B 对应扇形的圆心角的度数为______;(3)若该校有3200名学生,请你估计周末的体育锻炼时长至少三小时的学生共有多少名? 25.如图,在边长为1个单位长度的小正方形网格中建立平面直角坐标系.已知ABC V 的顶点A 的坐标为()1,4-,顶点B 的坐标为()4,3-,顶点C 的坐标为()3,1-.(1)请在下图中画出与ABC V 关于y 轴对称的111A B C △;(2)求ABC V 的面积;(3)连接1AC ,在y 轴是否存在点P ,使得12AC P ABC S S =△△.若存在,请直接写出点P 的坐标,若不存在,请说明理由.26.某水果批发商八月份销售了苹果270箱、梨子250箱.已知苹果每箱售价是梨子每箱售价的23,且这两种水果八月份的销售额共为7740元. (1)求该水果商八月份苹果和梨子的每箱售价分别为多少元;(2)随着市场的变化,该水果批发商九月份对苹果和梨子的售价进行了调整.每箱苹果的售价在八月份的基础上下调了5%6a ,每箱梨子的售价在八月份的基础上上涨了3%5a ,九月份这两种水果的销量在八月份的基础上都上涨了%a ,要使得这两种水果九月份的总销售额不低于八月份的总销售额的32,求a 的最小值. 27.如图,点D 为ABC V 所在平面内的一点,连接AD CD 、,30ABC ∠=︒.(1)如图1,点D 为ABC V 外一点,点E 在边AC 的延长线上,连接BE .若B E A D =,AB AC =,440DAC CBE ∠=∠=︒,求D ∠的度数:(2)如图2,点D 为ABC V 内一点,若ABD ACD ∠=∠,DCB ABC ∠=∠,求证:BD AC AD =+; (3)如图3,在(2)的条件下,延长AD 交BC 于点F ,当ABF △为等腰三角形时,请直接写出AD BC的值.。
重庆实验外国语学校2024-2025学年高二上学期期中考试数学试题

重庆实验外国语学校2024-2025学年高二上学期期中考试数学试题一、单选题1.圆22210x y x ++-=的圆心坐标和半径分别是()A .(1,0)-和2B .(1,0)和2C .(1,0)-D .()1,02.若2AB a b =+ ,56BC a b =-+,72CD a b =- 且向量a ,b 不共线,则一定共线的三点是()A .A 、B 、DB .A 、B 、CC .B 、C 、DD .A 、C 、D3.若直线1:210l ax y ++=和直线()23:3102l x a y +--=平行,则1l 与2l 之间的距离为()A B .13C .13D 4.“02t <<”是“曲线2212x y t t+=-表示椭圆”的()A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件5.如图,空间四边形OABC 中,点M 、N 分别是OA 、BC 的中点,设MN xOA yOB zOC =++,则2x y z -+=()A .1-B .0C .12D .16.如图,该几何体由半圆柱体与直三棱柱构成,半圆柱体底面直径4BC =,AB AC =,90BAC ∠= ,D 为半圆弧的中点,若异面直线BD 和1AB 所成角的余弦值为23,则该几何体的体积为()A .168+πB .1616π+C .328π+D .1632π+7.已知圆()22:216C x y +-=的圆心为点C ,直线:40l x my --=与圆C 交于M ,N 两点,点A 在圆C 上,且//CA MN ,若MN =,则AN AM ⋅=()A .6B .8C .D .8.对于平面上点P 和曲线C ,任取C 上一点Q ,若线段PQ 的长度存在最小值,则称该值为点P 到曲线C 的距离,记作(),d P C .下列结论中正确的个数为()①若曲线C 是一个点,则点集(){},2D P d P C =≤所表示的图形的面积为4π;②若曲线C 是一个半径为2的圆,则点集(){},1D P d P C =≤所表示的图形的面积为9π;③若曲线C 是一个长度为2的线段,则点集(){},1D P d P C =≤所表示的图形的面积为π4+;④若曲线C 是边长为9的等边三角形,则点集(){},1D P d P C =≤所表示的图形的面积为54π+-.A .1B .2C .3D .4二、多选题9.下列四个结论不正确...的是()A .任意向量a ,b ,若0a b ⋅=,则0a =或0b = B .若空间中任意四点O ,A ,B ,C 满足1233OC OA OB =+,则A ,B ,C 三点共线C .空间中任意向量a ,b ,c都满足()()a b c a b c⋅⋅=⋅⋅ D .已知向量()1,1,a x = ,()2,,4b x =- ,若25x <,则,a b 为钝角三、单选题10.直线():sin 30R l x y θθ-+=∈的倾斜角可以为()A .56πB .34πC .3πD .6π四、多选题11.已知正方体1111ABCD A B C D -棱长为1,动点M 满足()1,,AM xAB y AD z AA x y z =++∈R,则下列选项正确的是()A .当12x y z ===时,直线AM ⊥平面1A BD B .当1x =,3y =,2z =时,点M 到直线BD C .当x y =,1z =,[]0,1x ∈时,AM MB +的值可能为3D .当1x y z ++=且0x y z ≥、、,当AM =M 五、填空题12.已知()3,2,1a =- ,()2,1,2b =r,当()()2ka b a b +⊥- 时,实数k 的值为.13.已知椭圆的对称轴为坐标轴,一个焦点坐标为()1,0,且椭圆的两个焦点和短轴的一个端点构成一个等腰直角三角形,则此椭圆的标准方程为.14.已知圆22:4O x y +=上有一动点P ,记点P 到直线:40l x y --=的距离为0d ,平面上有一定点(A -,则012PA d +的最小值为.六、解答题15.已知()0,0A ,()1,1B ,()2,3C .(1)求点A 到直线BC 的距离;(2)求ABC V 的外接圆的方程.16.如图,在四棱锥P ABCD -中,AD BC ∥,224PA BC AD AB ====,AD ⊥平面PAB ,PA AB ⊥,E ,F 分别是棱PB ,PC 的中点.(1)证明://DF 平面ACE .(2)求二面角P AD E --的余弦值.17.已知圆()22:00C x y ax by a ++-=>关于直线2y x =-对称,且过点()0,4P .(1)求证:圆C 与直线280x y +-=相切;(2)若直线l 过点()3,4-与圆C 交于A 、B 两点,且2AB =,求此时直线l 的方程.18.如图,在四棱锥P ABCD -中,已知底面ABCD 为矩形,PA BC ⊥,平面PAD ⊥平面ABCD.(1)求证:PA ⊥平面ABCD ;(2)若2,PA AD AB ===点M 在棱PD 上,且二面角M AC B --的大小为120 .设Q 是棱BC 上的动点,求直线MQ 与平面MAC 所成角的正弦值的最大值.19.行列式是解决复杂代数运算的算法,二阶行列式其运算法则如下:11122122a b a b a b a b =-.若111111111222222222ij k y z x z x y a b x y z i j k y z x z x y x y z ⨯==-+ ,则称a b ⨯ 为空间向量a 与b 的向量积,其中()111111,,a x i y j z k x y z =++∈R,()222222,,b x i y j z k x y z =++∈R ,{},,i j k 为单位正交基底.以O 为坐标原点,分别以,,i j k的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系,已知,A B 是空间直角坐标系中异于O 的不同两点,且,,O A B 三点不共线.(1)①若()1,2,1A ,()0,1,1B -,求OA OB ⨯;②求证:OA OB ⨯是平面OAB 的一个法向量;且0OA OB OB OA ⨯+⨯= .(2)①记AOB V 的面积为AOB S ,证明:12AOB S OA OB =⨯.②三棱锥O ABC -,其中OA a = ,OB b = ,OC c = ,求三棱锥的体积O ABC V -.(用a,b ,c表示)(3)如图,,P Q 两点分别是三角形ABC 的两条边,AB AC 上的动点(不含端点),其中BQ 的中点为M ,其中CP 的中点为N .求证:三角形AMN 面积是四边形BCQP 面积的四分之一.。
重庆市九龙坡区重庆实验外国语学校2022-2023学年八年级下学期6月月考数学试题

重庆市九龙坡区重庆实验外国语学校2022-2023学年八年级
下学期6月月考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
....
A .(0,0)
B .9.从-3,-2,-1,1,2,2
6122-=--a x x x x
有整数解,且使关于条件的a 的个数是()A .0
B .10.如图,AOB 为等边三角形,点
二、填空题
三、解答题
(1)请直接写出12,y y与x之间的函数关系式以及对应x的取值范围;
(2)在给定的平面直角坐标系中画出函数12,y y的图象,并结合图象完成下列问题:
(1)求直线AB 的函数表达式;
(2)P ,Q 分别为y 轴和直线BC 上的动点,使APQ △的周长最小,求周长的最小值;(3)直线AB 与y 轴交于点H .将OBH △沿AB 翻折得到HBG ,M 为直线AB 上一动点,N 为平面内一点,是否存在这样的点M 、N ,使得以H 、M 、N 、G 为顶点的四边形是菱形,若存在,直接写出点M 的坐标,若不存在,说明理由.。
重庆市九龙坡区重庆实验外国语学校2023-2024学年八年级下学期期中数学试题

重庆市九龙坡区重庆实验外国语学校2023-2024学年八年级下学期期中数学试题一、单选题1.下列图形中是轴对称图形的是( )A .B .C .D .2.下列调查中,适合采用抽样调查的是( ) A .调查一批电池的使用寿命B .调查重庆实验外国语学校初三1班同学的视力C .为保证“神州十八号”的成功发射,对其零部件进行调查D .对乘坐某班次客车的乘客进行安检3.下列各式中不.是多项式39a b ab −的因式的是( ) A .ab B .3a + C .3a − D .9a −4.下列说法正确的是( )A .对角线互相垂直的平行四边形是矩形B .有一个角是直角的平行四边形是矩形C .有一组邻边相等的平行四边形是矩形D .对角线互相垂直且相等的四边形是矩形5的值应在( ) A .8和9之间B .9和10之间C .10和11之间D .11和12之间6.某商场四月份的营业额为400万元,六月份的营业额为625万元,设该商场五、六两个月营业额的月平均增长率为x ,则可列方程为( )A .()24001625x +=B .24003400625x ⨯+=C .4004003625x +⨯=D .()24001625x +=7.已知点()11,A y −, ()22,B y , ()35,C y 都在二次函数()223y x a =−−+的图象上,则1y ,2y ,3y 的大小关系为( )A .123y y y >>B .213y y y >>C .231y y y >>D .321y y y >>8.如图,在ABC 中,90ABC ∠=︒,点E 为AC 的中点,在AFC △中,90AFC ∠=︒,连接BE ,BF ,EF ,若50∠=°ACB ,24ECF ∠=︒,则EFB ∠的度数为( )A .14︒B .16︒C .18︒D .20︒9.如图,点E 为正方形ABCD 外一点,连接,BE BE BA =,连接EC 并延长,与ABE ∠的角平分线交于点F ,若72AB CE ==,则CF 的长度为( )A .B .C .5D .5.510.对于实数a ,b ,定义新运算()&()ab a a b a b ab b a b ⎧−≥=⎨−−<⎩,下列结论:①2&34=;②若&&a b b a =,则0a b ==;③若12x x 、为关于x 的一元二次方程.2230x mx m −+−=的两根,且满足(1203x x <−<),则()()1221&3&36x x x x −+−=−;④若函数()()12&2y x x =−−的图象与直线y m =有三个不同的交点,则102m −<≤.其中正确的有( )个;A .1B .2C .3D .4二、填空题11.计算:()101π 3.143−⎛⎫+−= ⎪⎝⎭.12.若235a b −=,则代数式346a b −+的值为 .13.若关于x 的一元二次方程²320x x m −++=有两个不相等的实数根,则m 的取值范围是 .14.如图,五边形ABCDE 是正五边形,过点A 作PQ CD ∥,则∠PAB 的度数为 .15.如图,四边形OABC 是平行四边形,()00O ,,()50A ,,()14C ,,若直线3y kx =−平分四边形OABC 的面积,则k = .16.若关于x 的方程2422x m m x x ++=−−的解为整数,且关于y 的不等式组()5131136222y y y y m ⎧−>−⎪⎨≤−+⎪⎩有解且最多有四个奇数解,则所有满足条件的整数m 的值之和为 .17.如图,矩形ABCD 中,点E 在CD 边上,4,1AD DE ==,将ADE V 沿AE 翻折得到AFE △,连接CF ,若CF AE ∥,则点F 到CD 的距离为 .18.一个四位正整数abcd ,若满足()3a b d c +=−,则称这个四位正整数为“三思而行数”.例如,四位正整数5113,()51331+=⨯−,5113∴是“三思而行数”;又如,四位正整数7215,()72351+≠⨯−,7215∴不是“三思而行数”.若m 是“三思而行数”,则m 的最小值为 ;若abcd 是“三思而行数”,且11abcd d +能被13整除,则abcd 的最大值为 .三、解答题 19.解方程: (1)2480x x −−=; (2)()3260y y y −+−=.20.先化简,再求值∶2222111112x x x x x x x −−⎛⎫÷−−− ⎪−++⎝⎭,其中²10x x +−=. 21.如图,四边形ABCD 是平行四边形.(1)尺规作图∶ 作出ABC ∠的角平分线BE ,交AD 于点E ;在线段BC 上截取.BF BA =,连接EF ;(不写作法,保留作图痕迹)(2)在(2)所作图中,证明四边形ABFE 是菱形.请完成下面的填空,补全证明过程. 证明:∵四边形ABCD 是平行四边形, ∴ ①∴CBE AEB ∠=∠, ∵BE 平分ABC ∠, ∴CBE ABE ∠=∠ ∴AEB ∠= ② ∴AB = ③ AB BF =, AE BF ∴=,又∵AE BF ∥,∴四边形ABFE 是 ④ , ∵BA BF =,∴四边形ABFE 是菱形.22.为丰富学生的课余生活,锻炼学生的体能体魄,我校体育教研组新编了体能操《霍元甲》,并组织了七、八年级全体学生进行学习.为了解七、八年级学生的学习情况,现从七、八年级中各随机抽取10名学生进行汇报展示,并由体育老师评分.将被抽取学生的汇报展示成绩(百分制)进行整理、描述和分析(成绩得分用x 表示,共分成四组:A .85x ≤;B .8590x <≤;C .9095x <≤;D .95100x <≤),下面给出了部分信息:七年级10名学生成绩是:70,91,78,93,87,81,84,93,94,96 八年级10名学生的成绩在B 组中的数据是:86,87,86. 七、八年级被抽取学生的成绩统计表八年级被抽取学生的成绩扇形统计图根据以上信息,解答下列问题: (1)=a _____;b =_____;m =______;(2)根据以上数据,你认为我校七、八年级中哪个年级学生学习自编操情况更好?请说明理由(一条即可);(3)我校七年级有1950人,八年级有 1800人,请估计七、八年级学生自编操汇报展示成绩达到优秀(90x >)等级的学生共有多少名?23.如图,四边形ABCD 中,AD BC ∥,4590B ADC ∠=︒∠=︒,,E 为AB 中点,4AD DC ==.动点P 从点B 出发,沿着折线B C D →→运动,到达点D 停止运动,连接DE EP PD ,,.设点P 的运动路程为x ,EPD △的面积记为1y ,请解答下列问题:(1)直接写出1y 关于x 的函数关系式,并写出x 的取值范围;(2)在给定的平面直角坐标系中画出1y 的函数图象,并写出该函数的一条性质; (3)函数212833y x =−+,直接写出当y y ≥₁₂时,x 的取值范围.24.清明至,青团香,清明节吃青团的传统习俗承载着深厚的文化内涵和象征意义.王老板4月份购进豆沙和蛋黄肉松两种口味的青团进行销售.4月份第一周,王老板卖出两种口味的青团共900盒,豆沙青团的售价为每盒10元,蛋黄肉松青团的售价为每盒18元,蛋黄肉松青团的销售额比豆沙青团的销售额多5000元. (1)4月份第一周王老板卖出两种口味的青团各多少盒?(2)4月份第二周,王老板将两种口味的青团售价进行了调整.豆沙青团每盒的售价在第一周的基础上降低2%a ,蛋黄肉松青团每盒的售价在第一周的基础上降低5%6a ,结果第二周豆沙青团卖出750盒,蛋黄肉松青团比第一周多卖出3%a ,最终4月份第二周两种口味的青团的总销售额为16500元, 求a 的值.25.如图,抛物线2y ax bx c =++与x 轴交于点()2,0A −和点()4,0B ,与y 轴交于点()0,4C ,作直线BC .(1)求该抛物线的解析式;(2)如图1,已知直线BC 上方抛物线上有一点P ,过点P 作PEy 轴与BC 交于点E ,过点P 作PF x ∥轴与y 轴交于点F ,求PE PF +的最大值和此时点P 的坐标;(3)如图2,将原抛物线向下平移1个单位长度得到新抛物线,新抛物线与y 轴交于点D ,已知点M 为新抛物线上的一点,且290ODB MDB ∠+∠=︒,请直接写出所有符合条件的点M 的横坐标.26.在ABC 中,AB AC =.(1)如图1,若120,4BAC AB ∠=︒=, 以AC 为边在AC 下方作等边,ACD ,AD 与BC 交于点O ,连接BD ,求四边形ABDC 的面积;(2)如图2,若120BAC ∠>︒,以AC 为边在AC 下方作等边ACD ,连接BD ,过点A 作AE BC ⊥于点E ,求证∶AE BD +=;(3)如图3,若135BAC ∠=︒,在AB 下方作等腰Rt ,90,BAF BAF AB AF ∠=︒=△,过点F 作FG BA P 交BC 延长线于点G ,T 为FG 中点,M 为BA 延长线上一点,将FA 绕点F 顺时针旋转至FA ',旋转角为9(0)0αα︒<<︒,连接MA ',TA ',GA ',1AF =,6AM =,当MA TA ''+最小时,直接写出TGA 'V 的面积.。
重庆市九龙坡区重庆实验外国语学校2022-2023学年七年级下学期期中数学试题

C.过一点有且只有一条直线与已知直线平行
D.两点之间,线段最短 5.若 x y ,则下列不等式一定成立的是( )
试卷第 1 页,共 7 页
D. 58
A. ax ay
B. x2 y2
6.估计 47 2 的值在( )
C. x y 33
D. x 3 y 3
A.6 到 7 之间
B.5 到 6 之间
的中点.若 DE 9,则 AB 的长为( )
A.48
B.52
C.60
D.66
12.若关于
x
的方程
x
2
3(x
1)
a
的解为正整数,且关于
y
的不等式组yΒιβλιοθήκη y4a 3 1 33
2
y
的解集为 y 2,则所有满足条件的整数 a 的值之和为( )
A.3
B.4
C.8
D.9
二、填空题 13.已知 a 36,则 a 的补角的度数是__________. 14.(﹣5)2 的平方根是_____.
试卷第 3 页,共 7 页
18.材料:对于一个四位正整数 abcd ,若 a c b d 11,则称这个数为“尚美数”,
并记 f (abcd) b d , G abcd ab cd .例如:对于四位正整数 3586,∵ 3 8 11, ac 5 6 11,∴3586 是“尚美数”,且 f (3586) 5 6 1 ,G(M ) 35 86 51.若一个“尚
2y 3y
13 8
;
(2)解不等式组:
5
y 3
2
1
3
y 2
5
.
2( y 3) 0
21.先化简,再求值: a3b a2b3 1 4ab 6a2b3 1 2 ab a2b3 ,其中 a , b 满足 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页,总9页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………姓名:____________班级:____________学号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………重庆实验外国语学校2018-2019学年八年级(上)期末数学试题考试时间:**分钟 满分:**分姓名:____________班级:____________学号:___________题号 一 二 三 总分 核分人 得分注意事项:1、填写答题卡的内容用2B铅笔填写2、提前 15 分钟收取答题卡第Ⅰ卷 客观题第Ⅰ卷的注释评卷人 得分一、单选题(共12题)1. 下列不能判定一个四边形是平行四边形的是( )A .两组对边分别平行的四边形是平行四边形B .两组对边分别相等的四边形是平行四边形C .一组对边平行另一组对边相等的四边形是平行四边形D .对角线互相平分的四边形是平行四边形2. 如图,图形中是中心对称图形的是( )A .B .C .D .3. 下列各式中正确的是( ) A .B .C .D .4. 下列不等式的变形不正确的是( )A .若,则B .若则:C .若,则D .若,则5. 为鼓励同学们阅读经典,了解同学们课外阅读经典名著的情况,在某年级随机抽查了20名同学每期的课外阅读名著的情况,调查结果如表:课外名著阅读量(本) 8 9 10 11 12 学生数33464则关于这20名周学课外阅读经典名著的情况,下列说法正确的是( )A .中位数是10B .平均数是10.25C .众数是12D .以上说法均不正确答案第2页,总9页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………6. 以下各组数为三角形的三边长,其中能够构成直角三角形的是( )A .,,B .7,24,25C .8,13,17D .10,15,20 7. 《九章算术》中有这样一个问题:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十 .问甲、乙持钱各几何?”题意为:今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?设甲的钱数为x ,乙的钱数为y ,则列方程组为( )A .B .C .D .8. 观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第8个图形中,十字星与五角星的个数和为( )A .25B .27C .28D .319. 已知,将点A 1(4,2)向左平移3个单位到达点A 2的位置,再向上平移4个单位到达点A 3的位置,△A 1A 2A 3绕点A 2逆时针方向旋转90°,则旋转后A 3的坐标为( )A .B .C .D .10. 若直线y=2x -1与y=x -k 的交点在第四象限,则k 的取值范围是( )A .B .C .或D .11. 如图,将长16cm ,宽8cm 的矩形纸片ABCD 折叠,使点A 与点C 重合,则折痕EF 的长为( )cm .第3页,总9页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………姓名:____________班级:____________学号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………A .6B .4C .10D .212. 已知关于x 的方程9x -3=kx+14有整数解,且关于x 的不等式组有且只有4个整数解,则满足条件的整数k 有( )个.A .1B .2C .3D .0第Ⅱ卷 主观题第Ⅱ卷的注释评卷人 得分一、填空题(共6题)1. 若关于x 、y 的二元一次方程组的解也是二元一次方程的解,则k 的值为______.2. 一个多边形的内角和是它的外角和的4倍,这个多边形是______边形.3. 一次函数y=(k -1)x -k 的图象不经过第三象限,则k 的取值范围是______.4. 如图,在△ABC 中,△C=90°,AD 平分△CAB ,DE△AB 于E ,且DE=15cm ,BE=8cm ,则BC=______cm .5. 小明和父亲在一直线公路AB 上进行(A→B→A )往返跑训练,两人同时从A 点出发,父亲以较快的速度匀速跑到点B 休息2分钟后立即原速跑回A 点,小明先匀速慢跑了3分钟后,把速度提高到原来的倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B 点看到休息的父亲,然后立即以出发时的速度跑回A 点,若两人之间的距离记为y (米),小明的跑步时间记为x (分),y 和x 的部分函数关系如图所示,则当父亲回到A 点时小明距A 点______米.6. 初202l 届数学组的老师们为了拍摄《燃烧我的数学》的MTV ,从全年级选了m 人(m >200)进行队列变换,现把m 人排成一个10排的矩形队列,每排人数相等,然后把这个矩形队列平均分成A 、B 两个答案第4页,总9页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………队列,如果从A 队列中抽调36人到B 队列,这样A 、B 队列都可以形成一个正方形队列,则m 的值为______. 评卷人 得分二、解答题(共8题)7. (1)计算:+×-|-2|;(2)解不等式组:8. 先化简,再求值:(x -3y )2-(3y+2x )(3y -2x )+4x (-x+y ),其中x 、y 满足|x -2y|+(x+2)2=09. 如图,在△ABC 中,AB=BC ,△ABC=45°,点D 是AC 的中点,连接BD ,作AE△BC 于E ,交BD 于点F ,点G 是BC 的中点,连接FG ,过点B 作BH△AB 交FG 的延长线于H . (1)若AB=3,求AF的长;(2)求证;BH+2CE=AB .10. 已知:如图,平行四边形ABCD 中,AC ,BD 交于点O ,AE △BD 于点E ,CF △BD 于点F .求证:OE =OF .11. 榴莲是热带著名水果之一,榴莲营养极为丰富,含有蛋白质、糖类、多种维生素、膳食纤维、脂肪、叶酸,氨基酸和矿物质,有强身健体、滋阴补阳之功效.它的气味浓烈、爱之者赞其香,厌之者怨其臭,喜欢榴莲的人也喜欢榴莲干,榴莲千层,榴莲披萨、榴莲酥等榴莲加工制品,某校数学兴趣小组为了了解本校学生喜爱榴莲的情况,随机抽取了200名学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:每一位同学在任何一种分类统计中只有一种选择)第5页,总9页…………○…………外…………○…………装…………○…………订…………○…………线…………○…………姓名:____________班级:____________学号:___________…………○…………内…………○…………装…………○…………订…………○…………线…………○…………请根据统计图完成下列问题: (1)扇形统计图中,“很喜欢”所对应的圆心角度数为______度;喜欢榴莲千层的人数为______人;请补全条形统计图. (2)若该校学生人数为8000人,请根据上述调查结果,估计该校学生中最爱吃榴莲干和榴莲酥的人数之和.12. 如图,直线AB :y=3x+3交x 轴于点A ;直线y=-x 平移后经过点B ,交x 轴于点C (7,0),另一直线y=kx -k 交x 轴于点D ,交直线BC 于点E ,连接DB ,BD△x 轴. (1)求直线BC 的解析式和点B 的坐标;(2)若直线DE 将△BDC 的面积分为1:2的两部分,求k 的值.13. 小明爸爸销售A 、B 两种品牌的保暖衣服,10月份第一周售出A 品牌保暖衣服3件和B 品牌保暖衣服4件,销售额为1000元,第二周售出A 品牌保暖衣服17件和B 品牌保暖衣服8件,销售额为4200元. (1)求A 、B 两种品牌保暖衣服的售价各是多少元? (2)已知10月份A 品牌保暖衣服和B 品牌保暖衣服的销售量分别为1000件、500件,11月份是保暖衣服销售的旺季,为拓展市场、薄利多销,小明爸爸决定11月份将A 品牌保暖衣服和B 品牌保暖衣服的销售价格在10月份的础上分别降低m%,%,11月份的销售量比10月份的销售量分别增长30%、20%.若11月份的销售额不低于233000元,求m 的最大值. 14. 如图1,在平面直角坐标系中,直线y=-x -与x 轴交于点A ,与y 轴交于点B ,点C 在x 轴正半轴上,且OC=3AO ,过点A作BC的平行线l .答案第6页,总9页………○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※………○…………内…………○…………装…………○…………订…………○…………线…………○…………(1)求直线BC 的解析式; (2)作点A 关于BC 的对称点D ,一动点P 从C 点出发按某一路径运动到直线l 上的点M ,再沿垂直BC 的方向运动到直线BC 上的点N ,再沿某一路径运动到D 点,求点P 运动的最短路径的长以及此时点N 的坐标; (3)如图2,将△AOB 绕点B 旋转,使得A′O′△BC ,得到△A′O′B ,将△A′O′B 沿直线BC 平移得到△A″O″B′,连接A″、B″、C ,是否存在点A″,使得△A″B′C 为等腰三角形?若存在,请直接写出点A″的坐标;若不存在,请说明理由.参数答案1.【答案】:mx_answer_6077227.png 【解释】:mx_parse_6077227.png 2.【答案】:mx_answer_7888518.png 【解释】:mx_parse_7888518.png 3.【答案】:mx_answer_7888519.png 【解释】:mx_parse_7888519.png 4.【答案】:mx_answer_7888520.png 【解释】:mx_parse_7888520.png第7页,总9页5.【答案】:mx_answer_7847834.png 【解释】:mx_parse_7847834.png 6.【答案】:mx_answer_7888521.png 【解释】:mx_parse_7888521.png 7.【答案】:mx_answer_7888522.png 【解释】:mx_parse_7888522.png 8.【答案】:mx_answer_7888523.png 【解释】:mx_parse_7888523.png 9.【答案】:mx_answer_7888524.png 【解释】:mx_parse_7888524.png 10.【答案】:mx_answer_7888525.png 【解释】:mx_parse_7888525.png 11.【答案】:mx_answer_7829538.png 【解释】:mx_parse_7829538.png 12.【答案】:mx_answer_7888526.png 【解释】:mx_parse_7888526.png 【答案】:mx_answer_1102785.png 【解释】:mx_parse_1102785.png 【答案】:mx_answer_7888527.png 【解释】:mx_parse_7888527.png 【答案】:答案第8页,总9页mx_answer_7888528.png 【解释】:mx_parse_7888528.png 【答案】:mx_answer_7888529.png 【解释】:mx_parse_7888529.png 【答案】:mx_answer_7888530.png 【解释】:mx_parse_7888530.png 【答案】:mx_answer_7888531.png 【解释】:mx_parse_7888531.png 【答案】:mx_answer_7888532.png 【解释】:mx_parse_7888532.png 【答案】:mx_answer_7888533.png 【解释】:mx_parse_7888533.png 【答案】:mx_answer_7888534.png 【解释】:mx_parse_7888534.png 【答案】:mx_answer_7888535.png 【解释】:mx_parse_7888535.png 【答案】:mx_answer_7888536.png第9页,总9页【解释】:mx_parse_7888536.png 【答案】:mx_answer_7888537.png 【解释】:mx_parse_7888537.png 【答案】:mx_answer_7888538.png 【解释】:mx_parse_7888538.png 【答案】:mx_answer_7888539.png 【解释】:mx_parse_7888539.png。
