2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (206)
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (381)

21.(2 分)在 Rt△ABC 中,∠C=Rt∠,∠A=3∠B+10°,则∠B= . 22.(2 分)在△ABC 中,若 AC2+AB2=BC2,则∠B+∠C= 度. 23.(2 分)如图,在 Rt △ABC 中,∠ACB=90°,CD⊥AB 于点 D,点 M 平分 AB,已知
CD=5 cm,CM 6cm,则△ACB 的面积是
6.(2 分)已知等腰腰上的高线等于腰长的一半,那么这个等腰三角形的一个底角等于 ()
A.15°
B.75°
C.15°或 75° D.150°或 30°
7.(2 分)如图 AB=AC,DE⊥AB,DF⊥AC,AD⊥BC,则图中的全等三角形有( )
A.1 对
B.2 对
C.3 对
D.4 对
8.(2 分)在△ABC 中,分析下列条件:①有一个角等于 60°的等腰三角形;②有两个角等
评卷人 得分
一、选择题
1.B
2.B 3.D 4.A 5.B 6.C 7.C 8.C 9.A
10.C 11.A 12.C 13.C 14.B 15.B 16.D 17.D 18.C
评卷人 得分
二、填空题
19.8.4 20.60, 25 3
4 21.20° 22.90 23.30 C.2
D.8 或 5
18.(2 分)已知等腰三角形的顶角为 l00°,则该三角形两腰的垂直平分线的交点位于
()
A.三角形内部
B.三角形的边上 C.三角形外部 D.无法确定
评卷人 得分
二、填空题
19.(2 分) Rt△ARC 中,∠C=90°,若 CD 是 AB 边的中线,且 CD=4cm,则 AB= cm, AD= BD= cm. 20.(2 分)如图,在 Rt△ABC 中,CD 是斜边上的中线,CE 是高.已知 AB=10cm, DE=2.5 cm,则∠BDC= 度,S△BCD= cm2
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (336)

A.50°
B.40°
如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点 0,过点 O 作 EF∥BC,
交 AB 于点 E,交 AC 于点 F,△ABC 的周长是 24cm ,BC=10cm,则△AEF 的周长是
()
A.10 cm
B.12cm
C.14 cm
D.34 cm
7.(2 分)下列判断中,正确的是( ) A.顶角相等的两个等腰三角形全等 B.腰相等的两个等腰三角形全等 C.有一边及锐角相等的两个直角三角形全等 D.顶角和底边分别相等的两个等腰三角形全等 8.(2 分)设 M 表示直角三角形,N 表示等腰三角形,P 表示等边三角形,Q 表示等腰直角 三角形,下图中能表示它们之间关系的是 ( )
26.(2 分)如果一个三角形一边上的中线恰好与该边上的高重合,那么这个三角形 (填
“一定”或“不一定”)是等腰三角形.
评卷人 得分
三、解答题
27.(7 分)如图,AB=AC,BD=BC. 若∠A = 38°,求∠DBC 的度数.
28.(7 分)如图,在△ABC 中,AB =AC,D 为 BC 边上的一点,∠BAD = ∠CAD,BD = 6cm,求 BC 的长.
评卷人 得分
一、选择题
1.C 2.D 3.C 4.A 5.D 6.C 7.D 8.A 9.D 10.C 11.B 12.B 13.D 14.D
评卷人
得分
二、填空题
15.答案: 5
16.40°或 70°
17. 2
2 18.6
19.30
20.勾股数(1)5(2)(2)10(3)13(4)17
21.24
29.(7 分)如图所示,△ABC 和△ABD 是有公共斜边的两个直角三角形,且 AC=2, BC=1.5,AD=2.4,求 AB 和 BD 的长.
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (810)

浙教版初中数学试卷2019-2020年八年级数学上册《特殊三角形》测试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.(2分)如图 ,在 Rt △ABC 中,∠B = 90°,ED 垂直平分AC ,交AC 边于点D ,交BC 边于E. ∠C= 35°,则∠BAE 为( )A . 10°B .15°C .20°D .25°2.(2分)若直角三角形的一条直角边长为 5,斜边上的中线长为 6.5,则另一条直角边长等于( )A . 3B .12C . 7D . 43.(2分)如图,△ABC 中,AB=AC ,过AC 上一点作DE ⊥AC ,EF ⊥BC ,若∠BDE=140°,则∠DEF= ( )A .55°B .60C .65°D .70°4.(2分)如图,ABC △是等腰直角三角形,BC 是斜边,将ABP △绕点A 逆时针旋转后,能与ACP '△重合,如果3AP =,那么PP '的长等于( )A .B .C .D .5.(2分)如图,在等边ABC △中,9AC =,点O 在AC 上,且3AO =,点P 是AB 上一动点,连结OP ,将线段OP 绕点O 逆时针旋转60得到线段OD .要使点D 恰好落在BC 上,则AP 的长是( )A .4B .5C .6D .86.(2分)满足下列条件的△ABC ,不是直角三角形的是( )A .222b a c =-B .∠C=∠A 一∠BC .∠A :∠B :∠C=3:4:5D .a :b: c=12:13:5 7.(2分)如图,在下列三角形中,若AB=AC ,则不能被一条直线分成两个小等腰三角形的是( )A .B .C .D . 8.(2分)如果△ABC 是等腰三角形,那么∠A ,∠B 的度数可以是( )A .∠A=60°,∠B=50°B .∠A=70°,∠B=40°C .∠A=80°,∠B=60°D .∠A=90°,∠B=30°9.(2分)等腰三角形是轴对称图形,它的对称轴是( )A .过顶点的直线B .底边上的高所在的直线C .顶角平分线所在的直线D .腰上的高所在的直线二、填空题10.(2分) Rt △ARC 中,∠C=90°,若CD 是AB 边的中线,且CD=4cm ,则AB= cm ,AD= BD= cm.11.(2分)如图,在△ABC 中,∠C=∠ABC=2∠A ,BD 是AC 边上的高,则∠DBC= .12.(2分)如图所示,在等腰三角形ABC 中,12cm AB AC ==,30ABC =∠,那么底边上的高AD = cm .13.(2分)如图,B 、C 是河岸两点,A 是对岸一点,测得∠ABC=45°,BC=60m ,∠ACB=45°,则点A 到岸边BC 的距离是 m .14.(2分)有一个角等于70°的等腰三角形的另外两个角的度数是 .15.(2分) 和 对应相等的两个直角三角形全等,简写成“斜边直角边”或“ ”.16.(2分)如图,是一长方形公园,如果要从景点A 走到景点C ,那么至少要走 m .17.(2分)在△ABC 中,∠A :∠B :∠C=1:2:3,BC=4,那么AB= .18.(2分)正三角形是轴对称图形,对称轴有 条.19.(2分)如图,在△ABC 中,若 ,∠BAD=∠CAD ,则BD=CD.20.(2分)在方格纸上有一个△ABC,它的顶点位置如图,则这个三角形是三角形.三、解答题21.(7分)如图,在△ABC中,AB =AC,D 为 BC边上的一点,∠BAD = ∠CAD,BD = 6cm,求BC的长.22.(7分)已知:如图,在Rt△ABC中,∠C=90°,AC=BC,AD是∠A的平分线.试说明AC+CD=AB成立的理由.23.(7分)如图,∠A=36°,∠DBC=36°,∠C=72°,找出图中的一个等腰三角形,并给予证明.我找的等腰三角形是: .证明:24.(7分).有一块菜地,地形如图,试求它的面积s(单位:m).25.(7分)如图,在△ABC中,AB=AC=41 cm,D是AC上的点,DC= 1cm,BD=9 cm,求△ABC的面积.26.(7分)如图所示,Rt△ABC中,∠C=90,分别以AC、BC、AB为直径向外画半圆,这三个半圆的面积之间有什么关系?为什么?27.(7分)一个寻宝探险小队,从A处出发探寻宝藏,他们向东行走4 km到达C点,然后又向正北行走2.5 km到达D点,接着他们又向正东继续行走2 km到达E点,最后他们又向正北前进了5.5 km,才找到了宝藏,你能准确地求出宝藏藏匿点到出发点的距离吗?28.(7分)如图,在四边形ABCD中,∠BAD=90°,∠DBC=90°,AD=3,AB=4,CD =13,求BC的长.29.(7分)如图,已知等腰直角三角形ABC中,∠BAC=90°,∠ABC的平分线交AC于D,过C作BD的垂线交BD的延长线于E,交BA的延长线于F,请说明:(1)△BCF是等腰三角形;(2)△ABD≌△ACF;(3)BD=2CE.30.(7分)如图,在△ABC 中,AB=AC,∠A= 50°,AB 的垂直平分线 ED 交AC于 D,交 AB 于 E,求∠DBC 的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.C2.B3.C4.A5.C6.C7.B8.B9.C二、填空题10.8.411.18°12.613.3014.55°,55°或70°,40°15.斜边,直角边,HL16.50017.818.319.AB=AC或∠B=∠C20.等腰三、解答题21.∵∠BAD=∠CAD,∴AD是∠BAC的平分线.∵AB=AC,∴△ABC是等腰三角形.∴AD是△ABC的BC边上的中线,∴BD=CD=12 BC.∵BD=6cm,∴BC=12(cm)22.略23.我所找的等腰三角形是:△ABC(或△BDC或△DAB).证明:在△ABC中,∵∠A=36°,∠C=72°,∴∠ABC=180°-(72°+36°)=72°.∵∠C=∠ABC,∴AB=AC,∴△ABC是等腰三角形.24.24m225.184.5 cm226.设以AC、AB、BC为直径的半圆面积分别为S1、S2、S3:.则有S1+S3=S2;理由略27.10 km28.1229.(1)利用△CBE≌△FBE来说明;(2)利用ASA说明;(3)利用CF=2CE而CF=BD来说明30.15°。
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (105)

A.线段
B.角
C.直角三角形 D.等腰三角形
6.(2 分)已知 △ABC 的三边长分别为 5,13,12,则△ABC 的面积为( )
A.30
B.60
C.78
D.不能确定
7.(2 分)如图,在△ABC 中,AB=AC=5,BC=6,点 M 为 BC 中点,MN⊥AC 于点 N,则
MN 等于( )
A. 6
A.8
B.5
C.2
D.8 或 5
14.(2 分)已知等腰三角形的顶角为 l00°,则该三角形两腰的垂直平分线的交点位于
()
A.三角形内部 评卷人 得分
B.三角形的边上 C.三角形外部 D.无法确定 二、填空题
15.(2 分) 如图,将等腰直角三角形 ABC 沿 DE 对折后,直角顶点 A 恰好落在斜边的中点 F 处,则得到的图形(实线部分)中有 个等腰直角三角形.
B. 9
C. 12
D. 16
5
5
5
5
8.(2 分)如图,在边长为A 4 的等边三角形 ABC 中,AD 是 BC 边上的高,点 E、F 是 AD 上
的两点,则图中阴影部分的面积是( )
N
A.4 3
B.3 3
C.2 3
D. 3
B
M
C
9.(2 分)如图,在等边△ABC 中,BD、CE 分别是 AC、AB 上的高,它们相交于点 0,则
27.如图所示.可以作 8 个
28.设小正方形的边长为 1. ∵, AB2 = 12 + 22 = 5 , BC2 = 22 + 42 = 20 , AC2 = 32 + 42 = 25 ,∴ AB2 + BC2 = AC2 ,∴
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (352)

D.等腰三角形
6.(2 分)如图,为了测出湖两岸 A、B 间的距离.一个观测者在在 C 处设桩,使三角形
ABC 恰为直角三角形,通过测量得到 AC 的长为 160 m,BC 长为 l28 m,那么从点 A 穿过
湖到点 B 的距离为( )
A.86 mபைடு நூலகம்
B.90 m
C.96 m
D.l00 m
7.(2 分)如图,CD 是等腰直角三角形斜边 AB 上的中线,DE⊥BC 于 E,则图中等腰直角
10.D 11.D 12.C
评卷人
得分
二、填空题
13.1
14.(8,6)
15.25
16.95°
17.135°
18.AC=BD
19.(1)AD=BC,HL (2)BD=AC,HL (3)∠DAB=∠CBA,AAS (4)∠DBA=∠CAB,AAS
20.480 m
21.10
22.25°
23.240°
24.△ABD,△CBD,△ABC
浙教版初中数学试卷
2019-2020 年八年级数学上册《特殊三角形》测试卷
学校:__________ 姓名:__________ 班级:__________ 考号:__________
题号 一
二
三 总分
得分
评卷人 得分
一、选择题
1.(2 分)如图,在ΔABC 中,AC=DC=DB,∠ACD=100°,则∠B 等于( )
构成等腰三角形的有( )
A. ①④
B. ①②④
C. ②④
D. ①②
4.(2 分)已知一个三角形的周长为 l5 cm,且其中两边长都等于第三边的 2 倍,那么这个三
角形的最短边为( )
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (208)

(2)∵△ABD 和△ACE 都是等腰直角三角形,AB=AD,AC=AE,∠BAD=∠CAE=90°, ∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠BAE. 又∵AB=AC,∴AD=AB=AC=AE,∴△CAD≌△BAE,∴CD=BE. 22.6cm2 23.说明 Rt△ABE≌Rt△CDF 24.24m2
C.AB=AC=4,BC=5
D.AB=AC=6,BC=12
评卷人 得分
二、填空题
6.(2 分)若一个边三角形的边长为 6,则它的面积为 . 7.(2 分)如图,在 Rt△ABC 中,CD 是斜边上的中线,CE 是高.已知 AB=10cm, DE=2.5 cm,则∠BDC= 度,S△BCD= cm2
8.(2 分)如图,在长方形 ABCD 中,AB=6,BC=8,如果将该矩形沿对角线 BD 折叠,那 么图中重叠部分的面积是 .
25.略 26.(1)2 个等腰三角形:△BDF 和△CEF,理由略(2)BD=DE+CE,理由略 27.在△ABC 中.∵AB=AC,∠A=38,∴∠ABC=∠C= 1 ×(180°-∠A)=71°.
2 在△DBC 中,∵BD=BC,∴∠BDC=∠C=71°. ∴∠D8C=180°-∠BDC-∠C=180°-71°-71°=38°. 28.4 29.略 30.略
评卷人 得分
三、解答题
15.(7 分)根据下列条件,分别判断以 a,b,c 为边的三角形是不是直角三角形.
(1) a=8,b=15,c=17;
(2) a = 2 , b =1, c = 2
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (330)

答案:60°
16.(2 分)如图所示,在等腰三角形 ABC 中, AB = AC =12cm ,∠ABC = 30 ,那么底 边上的高 AD = cm.
17.(2 分)如图,在△ABC 中,AD⊥BC 于 D,AD 与 BE 相交于 H,且 BH=AC, DH=DC.那么∠ABC=
度.
18.(2 分)满足 a2 + b2 = c2 的三个正整数,称为 (2)6,8, (3)5,12, (4)8,15, .
角三角形,则这 3 条线段的长度分别是( )
A.5,7,8
B.7,8,11
C. 8,11,15
D. 8,15,17
2.(2 分)在△ABC 中,分析下列条件:①有一个角等于 60°的等腰三角形;②有两个角等
于 60°的三角形;③有 3 条对称钠的三角形;④有两边相的三角形. 其中能说明△ABC 是
等边三角形的有( )
B. 3 cm
C. 5 cm
D.4 cm
11.(2 分)下列说法错误的是( ) A.三个角都相等的三角形是等边三角形
B.有两个角是 60°的三角形是等边三角形
C.有一个角是 60°的等腰三角形是等边三角形
D.有两个角相等的等腰三角形是等边三角形
12.(2 分)等腰三角形的一边长是 8,周长是 l8,则它的腰长是( )
7.A 8.C 9.A 10.D 11.D 12.D
评卷人 得分
二、填空题
13.25 14.3 15. 16.6
17.45
18.勾股数(1)5(2)(2)10(3)13(4)17
19.625
20.30
21.40°
22.25°
23.△ABD,△CBD,△ABC
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (149)

∵AB=AC,∴△ABC 是等腰三角形.
∴AD 是△ABC 的 BC 边上的中线,∴BD=CD= 1 BC. 2
∵BD=6cm,∴BC=12(cm)
23.解:(1)作图略;
(2)在△ABC 中,AB=AC,AD 是△ABC 的中线,∴AD⊥BC,
BD = CD = 1 BC = 1 8 = 4 . 在 Rt△ABD 中,AB=10,BD=4, AD2 + BD2 = AB2 ,
16.(2 分)在 Rt△ABC 中,若∠C=90°,AB=c,BC=a,AC=b. (1)已知 a =3,b=4,则 c= ; (2)已知 a=6,c=10,则 b = ; (3)已知 b=5,c=13,则 a= . 17.(2 分)如图,在△ABC 中,∠ACB=90°,AC=BC,∠ACD=52°,则∠BDC= .
DBC= . 12.(2 分)如图,在△ABC 中,点 D 是 BC 上一点,∠BAD=80°,AB=AD=DC,则∠
C= .
13.(2 分)有一个角等于 70°的等腰三角形的另外两个角的度数是 . 14.(2 分)在△ABC 中,∠A=120°,∠B=30°,AB=4 cm,AC= cm. 15.(2 分)如图,点 D 是△ABC 内部一点,DE⊥AB 于 E,DF⊥BC 于 F,且 DE=DF,若 ∠ABD=26°,则∠ABC= .
浙教版初中数学试卷
2019-2020 年八年级数学上册《特殊三角形》测试卷
学校:__________ 姓名:__________ 班级:__________ 考号:__________
题号 一
二
三 总分
得分
评卷人 得分
一、选择题
1.(2 分)如图 ,在 Rt△ABC 中,∠B = 90°,ED 垂直平分 AC,交 AC 边于点 D,交 BC
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (973)

浙教版初中数学试卷2019-2020年八年级数学上册《特殊三角形》测试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.(2分)在△ABC 中,分析下列条件:①有一个角等于60°的等腰三角形;②有两个角等于60°的三角形;③有3条对称钠的三角形;④有两边相的三角形. 其中能说明△ABC 是等边三角形的有( ) A . ①B . ①②C . ①②③D . ①②③④2.(2分)有下列长度的三条线段:①3、3、1;②2、2、4;③4、5、6;④4、4、3. 其中能构成等腰三角形的有( ) A . ①④B . ①②④C . ②④D . ①②3.(2分)已知ABC △的三边长分别为5,13,12,则ABC △的面积为( ) A .30B .60C .78D .不能确定4.(2分)下列说法错误的是( ) A .三个角都相等的三角形是等边三角形 B .有两个角是60。
的三角形是等边三角形 C .有一个角是60°的等腰三角形是等边三角形 D .有两个角相等的等腰三角形是等边三角形 5.(2分)下列判断中,正确的是( ) A .顶角相等的两个等腰三角形全等 B .腰相等的两个等腰三角形全等C .有一边及锐角相等的两个直角三角形全等D .顶角和底边分别相等的两个等腰三角形全等6.(2分)如图AB=AC ,DE ⊥AB ,DF ⊥AC ,AD ⊥BC ,则图中的全等三角形有( ) A .1对B .2对C .3对D .4对7.(2分)已知Rt△ABC中,∠C=90°,若三角形的周长为24 cm ,斜边c为10 cm,则Rt △ABC的面积为()A.24 cm2 B.36 cm2 C.48 cm2 D.96 cm28.(2分)把等边三角形ABC一边AB延长一倍到D,则∠ADC是()A.等腰三角形B.直角三角形C.等边三角形D.不能确定9.(2分)要组成一个等边三角形,三条线段的长度可取()A.1,2,3 B.4,6,11 C.1,1,5 D.3.5,3.5,3.510.(2分)△ABC和△DEF都是等边三角形,若△ABC的周长为24 cm ,△DEF的边长比△ABC的边长长3 cm,则△DEF的周长为()A.27 cm B.30 cm C.33 cm D.无法确定11.(2分)等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高所在的直线C.顶角平分线所在的直线D.腰上的高所在的直线二、填空题12.(2分)如图,在平面直角坐标系中,OA=10,点B的坐标为(8,0),则点A 的坐标为 .13.(2分)在△ABC中,与∠A相邻的外角等于l35°,与∠B相邻的外角也等于l35°,则△ABC 是三角形.14.(2分)如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8,则AB的长为 .图1图2C3215.(2分)如图,若等腰三角形的两腰长分别为x 和26x ,则x 的值为________.16.(2分)如图,以直角三角形中未知边为边长的正方形的面积为 .17.(2分)已知一个三角形的三边长分别为3k ,4k ,5k (k 是为自然数),则这个三角形为 ,理由是 .18.(2分)在Rt △ABC 中,∠C=90°,AC=3cm ,BC=4cm ,则斜边AB= .三、解答题19.(7分)如图,AB=AC ,BD=BC. 若∠A = 38°,求∠DBC 的度数.20.(7分)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);.(2)证明:DC BE21.(7分)如图①所示是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高2 m,房间高2.6 m,所以不必从高度方面考虑方案的设计),按此方案,可使该家具通过图②中的长廊搬人房间,在图②中把你设计的方案画成草图,并通过近似计算说明按此方案可把家具搬人房间的理由.(注:搬运过程中不准拆卸家具,不准损坏墙壁)22.(7分)如图,在△ABC中,AB=AC,点P是边BC的中点,PD⊥AB,PE⊥AC,垂足分别为点D、E,说明PD=PE.23.(7分)如图,已知∠ABC、∠ADC都是直角,BC=DC.说明:DE=BE.24.(7分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图所示,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连结CC′,设AB=a,BC=b,AC=c,请用四边形BCC′D′的面积说明勾股定理:222+=.a b c25.(7分)有一块菜地,地形如图,试求它的面积s(单位:m).26.(7分)如图所示,Rt△ABC中,∠C=90,分别以AC、BC、AB为直径向外画半圆,这三个半圆的面积之间有什么关系?为什么?27.(7分)已知△ABC中,∠C=Rt∠,BC=a,AC=b.(1)若a=1,b=2,求c;(2)若a=15,c=17,求b.28.(7分)如图,已知Rt△ABC中,∠ACB=90°,AB=8 cm,D为AB中点,DE⊥AC于E,∠A=30°,求BC,CD和DE的长.29.(7分)如图,在等边△ABC所在平面内求一点,使△PAB、△PBC、△PAC都是等腰三角形,你能找到这样的点吗?30.(7分)如图,已知△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD.试判断△DEB是不是等腰三角形,并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C2.A3.A4.D5.D6.C7.A8.B9.D10.C11.C二、填空题12.(8,6)13.等腰直角14.15.616.10017.直角三角形;如果一个三角形较小的两边的平方和等于最大边的平方,那么这个三角形是直角三角形18.5 cm三、解答题19.在△ABC 中.∵AB=AC ,∠A=38,∴∠ABC=∠C=12×(180°-∠A)=71°. 在△DBC 中,∵BD=BC ,∴∠BDC=∠C=71°. ∴∠D8C=180°-∠BDC-∠C=180°-71°-71°=38°. 20.(1)解:图2中ABE ACD △≌△. 证明如下:ABC △与AED △均为等腰直角三角形, AB AC ∴=,AE AD =,90BAC EAD ∠=∠=.BAC CAE EAD CAE ∴∠+∠=∠+∠,即BAE CAD ∠=∠,ABE ACD ∴△≌△.(2)证明:由(1)ABE ACD △≌△知45ACD ABE ∠=∠=,又45ACB ∠=,90BCD ACB ACD ∴∠=∠+∠=,DC BE ∴⊥.21.如图放置,可求得 1.41 1.45≈<,所以能通过22.连接AP .说明AP 是角平分线,再利用角平分上的点到角两边的距离相等 23.先说明Rt △ADC ≌Rt △ABC ,再说明△DCE ≌△BCE 24.根据S 四边形BCC ′D ′=S △AC ′D ′+S △ABC +S △ACC ′,说明222a b c += 25.24m 226.设以AC 、AB 、BC 为直径的半圆面积分别为S 1、S 2、S 3:.则有S 1+S 3=S 2;理由略27.(12)828.BC=4cm ,CD=4 cm ,DE=2 cm29.共有10个,等边三角形共有三条对称轴,每条对称轴上有4个点,有3个点重合 30.△DEB 是等腰三角形.说明∠E=∠DBC=30°。
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (947)

浙教版初中数学试卷2019-2020年八年级数学上册《特殊三角形》测试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)一个三角形的周长为30cm ,且其中两条边长都等于第三条边长的2倍,那么这个三角形的最短边长为( )A . 4cmB . 5cmC . 6cmD .10cm2.(2分)如图,AD=BC=BA ,那么∠1与∠2之间的关系是( )A .∠l=2∠2B .2∠1+∠2=180°C .∠l+3∠2=180°D .3∠1-∠2=180°3.(2分)下列图形中,不是轴对称图形的是( )A .线段B .角C .直角三角形D .等腰三角形4.(2分)在△ABC 中,已知AC AB = ,DE 垂直平分AC ,50=∠A °,则DCB ∠的度数是( )A . 15°B .30°C . 50°D . 65°5.(2分)设M 表示直角三角形,N 表示等腰三角形,P 表示等边三角形,Q 表示等腰直角三角形,下图中能表示它们之间关系的是 ( )A .B .C .D .6.(2分)如图,两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北、向东驶去.如果自行车的速度为2.5 m/s,摩托车的速度为10 m/s,那么10 s后,两车大约相距()A.55 m B.l03 m C.125 m D.153 m7.(2分)已知等腰腰上的高线等于腰长的一半,那么这个等腰三角形的一个底角等于()A.15°B.75°C.15°或75°D.150°或30°8.(2分)下列说法错误的是()A.三个角都相等的三角形是等边三角形B.有两个角是60°的三角形是等边三角形C.有一个角是60°的等腰三角形是等边三角形D.有两个角相等的等腰三角形是等边三角形9.(2分)将两个完全一样的有一个角为30°的直角三角形拼成如图所示的图形,其中两条长直角边在同一直线上,则图中等腰三角形的个数有()A.4个B.3个C.2个D.1个10.(2分)在△ABC 中,AB =AC,∠A=70°,则∠B的度数是()A.l10°B.70°C.55°D.40°11.(2分)等腰三角形一腰上的高线与另一腰的夹角为30°,则顶角的度数为()A.60°B.120°C.60°或l50°D.60°或l20°评卷人得分二、填空题12.(2分)如图,在△ABC中,AB=AC,AD、CE 分别平分∠BAC 与∠ACB,AD 与 CE 相交于点 F .若∠B =62° , 则∠AFC = .13.(2分)等腰三角形的一个角为40°,则它的底角为 . 14.(2分)如图所示,在等腰三角形ABC 中,12cm AB AC ==,30ABC =∠,那么底边上的高AD = cm .15.(2分)如图,小红和弟弟同时从家中出发,小红以4 km /h 的速度向正南方向的学校走去,弟弟以3 km /h 的速度向正西方向的公园走去,lh 后,小红和弟弟相距 km .16.(2分)在Rt △ABC 中,∠C=90°,AC=3cm ,BC=4cm ,则斜边AB= .17.(2分)如图所示,等边三角形ABC 中,AD 、BE 、CF 分别是△ABC 的三条角平分线,它们相交于点O ,将△ABC 绕点0至少旋转 度,才能和原来的三角形重合.18.(2分)等边三角形三个角都是 .19.(2分)在△ABC 中,AB= AC= 6,BC= 5,AD ⊥BC 于 D ,则 CD= .20.(2分)如果等腰三角形的一个角为70°,那么另外两个角为 .评卷人得分 三、解答题21.(7分)如图,某人从点A 出发欲横渡一条河,由于水流影响,实际上岸地点C 偏离欲到达的地点B 有140 m (AB ⊥BC ),结果他在水中实际游了500 m ,求这条河的宽度为多少米?22.(7分)如图,在等边△ABC中,D、E分别是AB、AC上的一点,AD=CE,CD、BE交于点F.(1)试说明△ADC≌△CEB;(2)求∠CFE的度数.23.(7分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图所示,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连结CC′,设AB=a,BC=b,AC=c,请用四边形BCC′D′的面积说明勾股定理:222a b c+=.24.(7分)阅读下列解题过程:已知:a、b、c为△ABC一的三边,且满足222244−=−,试判定△ABC的形状.a cbc a b解:∵222244−=−(A)a cbc a b∴2222222()()()c a b a b a b−=+−,(B)∴222c a b=+, (C)∴△ABC是直角三角形.问:(1)上述解题过程中,从哪一步开始出现错误?请你写出该步的代号:.(2)错误的原因为:.(3)本题正确的结论是:.25.(7分)如图所示,正方形ABCD中,E是AD的中点,点F在DC上且DF=14DC,试判断BE与EF的关系,并作出说明.26.(7分)如图,在△ABC中,AB=AC=BC,D为BC边上的中点,DE上AC于E,试说明 CE=14 AC.27.(7分)在△ABC中,如果∠A=∠B=12∠C,试判断△ABC的形状,并说明理由.28.(7分)如图,∠A=∠B,CE∥DA,CE交AB于E,△CEB是等腰三角形吗?说明理由.29.(7分)如图,在△ABC 中,∠ABC= 50°,∠ACB=70°,延长 CB 至D使 BD=BA,延长 BC 至E使 CE=CA. 连结 AD、AE,求△ADE 各内角的度数.30.(7分)已知等腰三角形△ABC中,AB=AC,AC边上的中线BD将它的周长分成9 cm 和8 cm两部分,求腰长.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.C2.B3.C4.A5.A6.B7.C8.D9.B10.C11.D二、填空题12.121°13.70°或40°14.615.516.5 cm17.12018.60°19.2.520.70°,40°或55°,55°三、解答题21.480m22.(1)略;(2)60°23.根据S四边形BCC′D′=S△AC′D′+S△ABC+S△ACC′,说明222a b c+= 24.(1)C;(2)220a b−=可能成立;(3)△ABC为等腰三角形或直角三角形25.BE⊥EF.说明BE2+EP2=BF226.说明CE=12CD=14AC27.△ABC是等腰直角基角形28.是等腰三角形,说明∠CEB=∠B 29.∠D=25°,∠E=35°,∠DAF=120°30.6cm或163cm。
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (973)

浙教版初中数学试卷2019-2020年八年级数学上册《特殊三角形》测试卷学校:__________一、选择题1.(2分)在△ABC 中,分析下列条件:①有一个角等于60°的等腰三角形;②有两个角等于60°的三角形;③有3条对称钠的三角形;④有两边相的三角形. 其中能说明△ABC 是等边三角形的有( ) A . ①B . ①②C . ①②③D . ①②③④2.(2分)有下列长度的三条线段:①3、3、1;②2、2、4;③4、5、6;④4、4、3. 其中能构成等腰三角形的有( ) A . ①④B . ①②④C . ②④D . ①②3.(2分)已知ABC △的三边长分别为5,13,12,则ABC △的面积为( ) A .30B .60C .78D .不能确定4.(2分)下列说法错误的是( ) A .三个角都相等的三角形是等边三角形 B .有两个角是60。
的三角形是等边三角形 C .有一个角是60°的等腰三角形是等边三角形 D .有两个角相等的等腰三角形是等边三角形 5.(2分)下列判断中,正确的是( ) A .顶角相等的两个等腰三角形全等 B .腰相等的两个等腰三角形全等C .有一边及锐角相等的两个直角三角形全等D .顶角和底边分别相等的两个等腰三角形全等6.(2分)如图AB=AC ,DE ⊥AB ,DF ⊥AC ,AD ⊥BC ,则图中的全等三角形有( ) A .1对B .2对C .3对D .4对7.(2分)已知Rt△ABC中,∠C=90°,若三角形的周长为24 cm ,斜边c为10 cm,则Rt △ABC的面积为()A.24 cm2 B.36 cm2 C.48 cm2 D.96 cm28.(2分)把等边三角形ABC一边AB延长一倍到D,则∠ADC是()A.等腰三角形B.直角三角形C.等边三角形D.不能确定9.(2分)要组成一个等边三角形,三条线段的长度可取()A.1,2,3 B.4,6,11 C.1,1,5 D.3.5,3.5,3.510.(2分)△ABC和△DEF都是等边三角形,若△ABC的周长为24 cm ,△DEF的边长比△ABC的边长长3 cm,则△DEF的周长为()A.27 cm B.30 cm C.33 cm D.无法确定11.(2分)等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高所在的直线C.顶角平分线所在的直线D.腰上的高所在的直线评卷人得分二、填空题12.(2分)如图,在平面直角坐标系中,OA=10,点B的坐标为(8,0),则点A 的坐标为 .13.(2分)在△ABC中,与∠A相邻的外角等于l35°,与∠B相邻的外角也等于l35°,则△ABC 是三角形.14.(2分)如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1=4,S2=8,则AB的长为 .图1图2DC EA B3215.(2分)如图,若等腰三角形的两腰长分别为x 和26x −,则x 的值为________.16.(2分)如图,以直角三角形中未知边为边长的正方形的面积为 .17.(2分)已知一个三角形的三边长分别为3k ,4k ,5k (k 是为自然数),则这个三角形为 ,理由是 .18.(2分)在Rt △ABC 中,∠C=90°,AC=3cm ,BC=4cm ,则斜边AB= . 评卷人 得分三、解答题19.(7分)如图,AB=AC ,BD=BC. 若∠A = 38°,求∠DBC 的度数.20.(7分)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);⊥.(2)证明:DC BE21.(7分)如图①所示是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高2 m,房间高2.6 m,所以不必从高度方面考虑方案的设计),按此方案,可使该家具通过图②中的长廊搬人房间,在图②中把你设计的方案画成草图,并通过近似计算说明按此方案可把家具搬人房间的理由.(注:搬运过程中不准拆卸家具,不准损坏墙壁)22.(7分)如图,在△ABC中,AB=AC,点P是边BC的中点,PD⊥AB,PE⊥AC,垂足分别为点D、E,说明PD=PE.23.(7分)如图,已知∠ABC、∠ADC都是直角,BC=DC.说明:DE=BE.24.(7分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图所示,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连结CC′,设AB=a,BC=b,AC=c,请用四边形BCC′D′的面积说明勾股定理:222+=.a b c25.(7分)有一块菜地,地形如图,试求它的面积s(单位:m).26.(7分)如图所示,Rt△ABC中,∠C=90,分别以AC、BC、AB为直径向外画半圆,这三个半圆的面积之间有什么关系?为什么?27.(7分)已知△ABC中,∠C=Rt∠,BC=a,AC=b.(1)若a=1,b=2,求c;(2)若a=15,c=17,求b.28.(7分)如图,已知Rt△ABC中,∠ACB=90°,AB=8 cm,D为AB中点,DE⊥AC于E,∠A=30°,求BC,CD和DE的长.29.(7分)如图,在等边△ABC所在平面内求一点,使△PAB、△PBC、△PAC都是等腰三角形,你能找到这样的点吗?30.(7分)如图,已知△ABC是等边三角形,BD是AC边上的高,延长BC到E,使CE=CD.试判断△DEB是不是等腰三角形,并说明理由.【参考答案】***试卷处理标记,请不要删除一、选择题1.C2.A3.A4.D5.D6.C7.A8.B9.D10.C11.C二、填空题12.(8,6)13.等腰直角14.15.616.10017.直角三角形;如果一个三角形较小的两边的平方和等于最大边的平方,那么这个三角形是直角三角形18.5 cm三、解答题19.在△ABC 中.∵AB=AC ,∠A=38,∴∠ABC=∠C=12×(180°-∠A)=71°.在△DBC 中,∵BD=BC ,∴∠BDC=∠C=71°. ∴∠D8C=180°-∠BDC-∠C=180°-71°-71°=38°. 20.(1)解:图2中ABE ACD △≌△. 证明如下:ABC △与AED △均为等腰直角三角形, AB AC ∴=,AE AD =,90BAC EAD ∠=∠=.BAC CAE EAD CAE ∴∠+∠=∠+∠,即BAE CAD ∠=∠,ABE ACD ∴△≌△.(2)证明:由(1)ABE ACD △≌△知45ACD ABE ∠=∠=,又45ACB ∠=,90BCD ACB ACD ∴∠=∠+∠=,DC BE ∴⊥.21.如图放置,可求得2 1.41 1.45≈<,所以能通过22.连接AP .说明AP 是角平分线,再利用角平分上的点到角两边的距离相等 23.先说明Rt △ADC ≌Rt △ABC ,再说明△DCE ≌△BCE 24.根据S 四边形BCC ′D ′=S △AC ′D ′+S △ABC +S △ACC ′,说明222a b c += 25.24m 226.设以AC 、AB 、BC 为直径的半圆面积分别为S 1、S 2、S 3:.则有S 1+S 3=S 2;理由略 27.(152)828.BC=4cm ,CD=4 cm ,DE=2 cm29.共有10个,等边三角形共有三条对称轴,每条对称轴上有4个点,有3个点重合 30.△DEB 是等腰三角形.说明∠E=∠DBC=30°。
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (340)

浙教版初中数学试卷2019-2020年八年级数学上册《特殊三角形》测试卷学校:__________题号一二三总分得分评卷人得分一、选择题1.(2分)有6条线段,它们的长度分别为5、7、8、11、15、17,从中取出 3条组成一个直角三角形,则这 3条线段的长度分别是()A.5,7,8 B.7,8,11 C. 8,11,15 D. 8,15,172.(2分)在△ABC中,∠BAC=90°,AD⊥BC于D,若AB=3,BC=5,则DC的长度是()A.85B.45C.165D.2253.(2分)如图,在边长为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是()A.43B.33C.23D.34.(2分)设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,下图中能表示它们之间关系的是()A.B.C.D.5.(2分)已知Rt△ABC中,∠C=90°,若三角形的周长为24 cm ,斜边c为10 cm,则Rt △ABC的面积为()A.24 cm2 B.36 cm2 C.48 cm2 D.96 cm26.(2分)如图所示,已知直角三角形ABC中,∠ABC=90°,BD平分∠ABC,CE平分∠ACB,CE、BD相交于点F,∠EFB=65°,则∠A=()A.30°B.40°C.45°D.50°7.(2分)已知一个三角形的周长为39 cm,一边长为12 cm,另一边长为l5 cm,则该三角形是()A.直角三角形B.钝角三角形C.等腰三角形D.无法确定8.(2分)等腰三角形一腰上的高线与另一腰的夹角为30°,则顶角的度数为()A.60°B.120°C.60°或l50°D.60°或l20°评卷人得分二、填空题9.(2分)如图,∠ABC = 75°,∠A = 48°,AB的垂直平分线交AC于点D,则∠DBC= .10.(2分)等腰三角形的一个角为40°,则它的底角为.11.(2分)在△ABC中,到AB,AC距离相等的点在上.12.(2分)等腰三角形一边长为2 cm,另一边长为5cm,它的周长是 cm.13.(2分)如图,在△ABC中,AB=BC=2,∠ABC=900,D是BC的中点,且它关于AC的对称点是D′,则BD′= .14.(2分)如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条路,他们仅仅少走了步路(假设2步为l m),却踩伤了花草.15.(2分)在△ABC中,∠A=120°,∠B=30°,AB=4 cm,AC= cm.16.(2分)如图,阴影部分是一个正方形,则此正方形的面积为.图1 图2D CE AB17.(2分)如图,在△ABC 中,∠B=40°,∠C=20°,AD ⊥AC ,垂足为A ,交BC 于D ,若AB=4,则CD .18.(2分)如图,△ABC 是等边三角形,中线BD 、CE 相交于点0,则∠BOC= .19.(2分)在△ABC 中,∠A=48°,∠B=66°,AB=2.7 cm ,则AC= cm .20.(2分) 如图,在△ABC 中,AB=AD=DC ,∠BAD=26°,则∠C= .21.(2分)在△ABC 中,AB= AC= 6,BC= 5,AD ⊥BC 于 D ,则 CD= . 评卷人得分 三、解答题22.(7分)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母); (2)证明:DC BE .23.(7分)如图①所示是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高2 m,房间高2.6 m,所以不必从高度方面考虑方案的设计),按此方案,可使该家具通过图②中的长廊搬人房间,在图②中把你设计的方案画成草图,并通过近似计算说明按此方案可把家具搬人房间的理由.(注:搬运过程中不准拆卸家具,不准损坏墙壁)24.(7分)如图,已知AB=CD,AE⊥BC,DF⊥BC,CF=BE,则∠A=∠D,为什么?25.(7分)如图所示,正方形ABCD中,E是AD的中点,点F在DC上且DF=14DC,试判断BE与EF的关系,并作出说明.26.(7分)如图,在四边形ABCD中,BD⊥AD,AC⊥BC,E是AB的中点,试判断△CDE的形状并说明理由?27.(7分)如图,已知Rt△ABC中,∠ACB=90°,AB=8 cm,D为AB中点,DE⊥AC于E,∠A=30°,求BC,CD和DE的长.28.(7分)如图,在等边△ABC所在平面内求一点,使△PAB、△PBC、△PAC都是等腰三角形,你能找到这样的点吗?29.(7分)如图,在△ABC 中,∠ABC= 50°,∠ACB=70°,延长 CB 至D使 BD=BA,延长 BC 至E使 CE=CA. 连结 AD、AE,求△ADE 各内角的度数.30.(7分)如图,在△ABC 中,AB=AC,∠A= 50°,AB 的垂直平分线 ED 交AC于 D,交 AB 于 E,求∠DBC 的度数.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.D2.C3.C4.A5.A6.D7.C8.D评卷人得分二、填空题9.27°10.70°或40°11.∠A的平分线12.1213.答案:514.415.416.64 cm 217.818.120°19.2.720.38.5°21.2.5评卷人得分 三、解答题22.(1)解:图2中ABE ACD △≌△.证明如下:ABC △与AED △均为等腰直角三角形,AB AC ∴=,AE AD =,90BAC EAD ∠=∠=.BAC CAE EAD CAE ∴∠+∠=∠+∠,即BAE CAD ∠=∠,ABE ACD ∴△≌△.(2)证明:由(1)ABE ACD △≌△知45ACD ABE ∠=∠=,又45ACB ∠=, 90BCD ACB ACD ∴∠=∠+∠=,DC BE ∴⊥.23.如图放置,可求得2 1.41 1.45≈<,所以能通过24.说明Rt △ABE ≌Rt △DCF25.BE ⊥EF .说明BE 2+EP 2=BF 226.△CDE 为等腰三角形27.BC=4cm ,CD=4 cm ,DE=2 cm28.共有10个,等边三角形共有三条对称轴,每条对称轴上有4个点,有3个点重合29.∠D=25°,∠E=35°,∠DAF=120°30.15°。
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (225)

浙教版初中数学试卷2019-2020年八年级数学上册《特殊三角形》测试卷学校:__________题号一 二 三 总分 得分评卷人得分 一、选择题1.(2分)有6条线段,它们的长度分别为5、7、8、11、15、17,从中取出 3条组成一个直角三角形,则这 3条线段的长度分别是( )A .5,7,8B .7,8,11C . 8,11,15D . 8,15,172.(2分)若直角三角形的一条直角边长为 5,斜边上的中线长为 6.5,则另一条直角边长等于( )A . 3B .12C . 7D . 43.(2分)在△ABC 中,∠BAC=90°,AD ⊥BC 于D ,若AB=3,BC=5,则DC 的长度是( )A .85B .45C .165D .2254.(2分)如图,在Rt △ABC 中,CD 是斜边AB 上的中线,则图中与CD 相等的线段有( )A .AD 与BDB .BD 与BC C .AD 与BC D .AD ,BD 与BC5.(2分)在△ABC 中,已知AC AB = ,DE 垂直平分AC ,50=∠A °,则DCB ∠的度数是( )A . 15°B .30°C . 50°D . 65°6.(2分)如图,在等边ABC △中,9AC =,点O 在AC 上,且3AO =,点P 是AB 上一动点,连结OP ,将线段OP 绕点O 逆时针旋转60得到线段OD .要使点D 恰好落在BC 上,则AP 的长是( )A .4B .5C .6D .87.(2分)已知在△ABC 和△DFE 中,∠A=∠D=90°,则下列条件中不能判定△ABC 和△DEF 全等的是( )A .AB=DE ,AC=DFB .AC=EF,BC=DFC .AB=DE ,BC=FED .∠C=∠F ,BC=FE8.(2分)如图,在△ABC 中,∠BAC=90°,AD ⊥BC ,则图中与∠B 相等的角是( )A .∠BADB .∠C C .∠CAD D .没有这样的角9.(2分)下列条件中,不能判定两个直角三角形全等的是 ( )A .一条直角边和一个锐角分别相等B .两条直角边对应相等C .斜边和一条直角边对应相等D .斜边和一个锐角对应相等10.(2分)在一个直角三角形中,有两边长为6和8,下列说法正确的是( )A .第三边一定为10B .三角形周长为25C .三角形面积为48D .第三边可能为1011.(2分)如图,1l ∥2l ,△ABC 为等边三角形,∠ABD=25°,则∠ACE 的度数是( )A .45°B .35°C .25°D .15°12.(2分)等腰三角形的顶角为 80°,则一腰上的高与底边的夹角为( )A .1O °B. 40°C. 50°D. 80°13.(2分)在△ABC 中,AB =AC ,∠A=70°,则∠B 的度数是( )A.l10°B.70°C.55°D.40°14.(2分)等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高所在的直线C.顶角平分线所在的直线D.腰上的高所在的直线评卷人得分二、填空题15.(2分)在Rt△ABC中,∠C=90°,∠B=2∠A,CD⊥AB,交AB于D,若AB=a,则CD= .16.(2分)如图,在Rt△ABC中,CD是斜边上的中线,CE是高.已知AB=10cm,DE=2.5 cm,则∠BDC= 度,S△BCD= cm217.(2分)如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C= .18.(2分)如图,B、C是河岸两点,A是对岸一点,测得∠ABC=45°,BC=60m ,∠ACB=45°,则点A到岸边BC的距离是 m.19.(2分)在△ABC中,若AC2+AB2=BC2,则∠B+∠C= 度.20.(2分)如图,在△ABC中,AB=AC=BC,若AD⊥BC,BD=5 cm,则AB= cm.21.(2分)如图,∠A=36°,∠DBC=36°,∠C=72°,则图中的等腰三角形分别是.评卷人得分三、解答题22.(7分)你画一个等腰三角形,使它的腰长为 3cm.23.(7分)如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.(1)说明△BCE≌△ACD成立的理由;(2)说明CF=CH成立的理由;(3)判断△CFH的形状并说明理由.24.(7分)如图,在ΔABC中,AB=AC=10,BC=8.用尺规作图作BC边上的中线AD(保留作图痕迹,不要求写作法、证明),并求AD的长.AB C25.(7分)如图,某校把一块形状为直角三角形的荒地开辟为生物园,已知∠ACB=90°,AC=80 m.BC=60m.(1)若入口E在边AB上,且与A、B等距,求从入口E到出口C的最短路线的长;(2)若线段CD是一条水渠,且D点在边AB上,已知水渠的造价为l0元/米,则D点在距A点多远处此水渠的造价最低?最低造价是多少元?26.(7分)如图,在△ABC中,AB=AC,点P是边BC的中点,PD⊥AB,PE⊥AC,垂足分别为点D、E,说明PD=PE.27.(7分)根据下列条件,分别判断以a,b,c为边的三角形是不是直角三角形.(1) a=8,b=15,c=17;(2)23a=,1b=,23c=28.(7分)已知△ABC中,∠C=Rt∠,BC=a,AC=b.(1)若a=1,b=2,求c;(2)若a=15,c=17,求b.29.(7分)如图,在△ABC中,AB=AC=BC,D为BC边上的中点,DE上AC于E,试说明 CE=14 AC.30.(7分)如图,P、Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.【参考答案】***试卷处理标记,请不要删除评卷人得分一、选择题1.D2.B3.C4.A5.A6.C7.B8.C9.A10.D11.B12.B13.C14.C二、填空题1516.6017.25°18.3019.9020.1021.△ABD,△CBD,△ABC三、解答题22.略23.(1)略 (2) 略(3)△CFH是等边三角形,理由略24.解:(1)作图略;(2)在△ABC中,AB=AC,AD是△ABC的中线,∴AD⊥BC,118422BD CD BC ===⨯=. 在Rt △ABD 中,AB =10,BD =4,222AD BD AB +=,AD ∴===.25.(1)50 m(2)CD ⊥AB 时造价最低,即CD=48m,最低造价480元26.连接AP .说明AP 是角平分线,再利用角平分上的点到角两边的距离相等27.(1)是;(2)不是28.(12)829.说明CE=12CD=14AC30.120°。
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (108)

25.(7 分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方 法. 如图所示,火柴盒的一个侧面 ABCD 倒下到 AB′C′D′的位置,连结 CC′,设 AB=a,BC=b,AC=c,请用四边形 BCC′D′的面积说明勾股定理: a2 + b2 = c2 .
26.(7 分)如图,在四边形 ABCD 中,AC⊥DC,∠ADC 的面积为 30cm2,DC=12 cm , AB=3 cm ,BC=4 cm,求△ABC 的面积.
A.90°
B.75°
C.60°
D.45°
9.(2 分)等腰三角形的“三线合一”是指( )
A.中线、高、角平分线互相重合
B.腰上的中线、腰上的高、底角的平分线互相重合
C. 顶角的平分线、中线、高线三线互相重合
D. 顶角的平分线、底边上的高及底边上的中线三线互相重合
评卷人 得分
二、填空题
10.(2 分)如图,在△ABC 中,AB=AC,AD、CE 分别平分∠BAC 与∠ACB,AD 与 CE 相交于点 F .若∠B =62° , 则∠AFC = .
18.(2 分)如图,∠C=∠D=90°,请你再添加一个条件,使△ABD≌△BAC,并在添加的条 件后的( )内写出判定全等的依据. (1) ( ); (2) ( ); (3) ( ); (4) ( ).
19.(2 分)已知△ABC 的三边长分别是 8 cm,10 cm ,6 cm,则△ABC 的面积是 cm2. 20.(2 分)如图,是一长方形公园,如果要从景点 A 走到景点 C,那么至少要走 m.
15.(2 分)如图,以 Rt△ABC 的三边为边向外作正方形,其面积分别为 S1、S2、S3,且 S1=4,S2=8,则 AB 的长为 .
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (123)

24.184.5 cm2 25.10 km 26.DE=DF,理由略 27.BC=3.7 m,DE=1.85 m 28.△CDE 为等腰三角形 29.△DEB 是等腰三角形.说明∠E=∠DBC=30° 30.120°
28.(7 分)如图,在四边形 ABCD 中,BD⊥AD,AC⊥BC,E 是 AB 的中点,试判断 △CDE 的形状并说明理由?
29.(7 分)如图,已知△ABC 是等边三角形,BD 是 AC 边上的高,延长 BC 到 E,使 CE=CD.试判断△DEB 是不是等腰三角形,并说明理由.
30.(7 分)如图,P、Q 是△ABC 边 BC 上的两点,且 BP=PQ=QC=AP=AQ,求∠BAC 的度 数.
足,则∠A 与∠CED 的关系是( )
A. 相等
B. 互余
C. 互补
D.以上都有可能
2.(2 分)判断两个直角三角形全等,下列方法中,不能应用的是( )
A. AAS
B.HL
C.SAS
D. AAA
3.(2 分)下列判断中,正确的是( )
A.顶角相等的两个等腰三角形全等
B.腰相等的两个等腰三角形全等
C.有一边及锐角相等的两个直角三角形全等
D.顶角和底边分别相等的两个等腰三角形全等
4.(2 分)如图,在△ABC 中,∠BAC=90°,AD⊥BC,则图中与∠B 相等的角是( )
A.∠BAD
B.∠C
C.∠CAD
D.没有这样的角
5.(2 分)在全等三角形的判定方法中,一般三角形不具有,而直角三形形具有的判定方法
是()
A.SSS
B.SAS
C.ASA
评卷人 得分
三、解答题
21.(7 分)如图,∠BAC =∠ABD,AC = BD,点 0 是 AD、BC 的点,点 E 是 AB 边的中 点,试判断 OE 和 AB 的位置关系,并说明理由.
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (281)

足,则∠A 与∠CED 的关系是( )
A. 相等
B. 互余
C. 互补
D.以上都有可能
2.(2 分)如图,△ABC 中,AB=AC,过 AC 上一点作 DE⊥AC,EF⊥BC,若∠
BDE=140°,则∠DEF= ( )
A.55°
B.60
C.65°
D.70°
3.(2 分)已知 △ABC 的三边长分别为 5,13,12,则△ABC 的面积为( )
22.(7 分)如图,分别以 RtABC 的直角边 AC,BC 为边,在 RtABC 外作两个等边三角 形 ACE 和 BCF ,连结 BE,AF.
求证:BE=AF.
23.(7 分)如图,△ABC 和△DBC 都是直角三角形,∠A=∠D=90°,AB=DC.说明: △EBC 是等腰三角形.
24.(7 分)如图,某人欲横渡一条河,由于水流影响,实际上岸地点 C 偏离欲到达的地点 B 有 140 m,结果他在水中实际游了 500 m,求这条河的宽度为多少米?
13.(2 分)如图,剪四个与图①完全相同的直角三角形,然后将它们拼成如图②所示的图 形. (1)大正方形的面积可以表示为 . (2)大正方形的面积也可表示为 . (3)对比两种方法,你能得出什么结论?
14.(2 分)如图,在 Rt △ABC 中,∠ACB=90°,CD⊥AB 于点 D,点 M 平分 AB,已知
1.C 2.C 3.A 4.D 5.D 6.A 7.D
评卷人
得分
二、填空题
5
11.45 12.(1)AD=BC,HL (2)BD=AC,HL (3)∠DAB=∠CBA,AAS (4)∠DBA=∠CAB,AAS 13.(1)c2 ;(2) 4 1 ab + (b − a)2 ;(3) a2 + b2 = c2
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (220)

直角三角形全等;③有一边和锐角对应相等的两个直角形全等;④有一边相等的两个等腰
直角三角形全等;⑤有两直角边对应相等的两个直角三角形全等.其中正确的个数是
()
A.1 个
B.2 个
C.3 个
D.4 个
14.(2 分)我们知道,等腰三角形是轴对称图形,下列说法中,正确的是( )
A.等腰三角形顶角的平分线所在的直线是它的对称轴
24.(2 分)如图,△ABC 是等边三角形,中线 BD、CE 相交于点 0,则∠BOC= .
25.(2 分)如果等腰三角形的一个角为 70°,那么另外两个角为 .
评卷人 得分
三、解答题
26.(7 分)如图,在 6×6 的正方形网络中,有 A、B、C 三点.分别连接 AB、BC、AC,试 判断△ABC 的形状.
一动点,连结 OP ,将线段 OP 绕点 O 逆时针旋转 60 得到线段 OD .要使点 D 恰好落在
BC 上,则 AP 的长是( )
A.4
B.5
C.6
D.8
8.(2 分)如图,在ΔABC 中,AC=DC=DB,∠ACD=100°,则∠B 等于( )
A.50°
B.40°
C.25°
D.20°
9.(2 分)如图所示,在△ABC 中,AB=AC,∠B= 1 ∠BAC,AD⊥AB 垂足为 A,AD=1, 4
BDE=140°,则∠DEF= ( )
A.55°
B.60
C.65°
D.70°
6.(2 分)如图,在单位正方形组成的网格图中标有 AB、CD、EF、GH 四条线段,其中能
构成一个直角三角形三边的线段是( ) A.CD、EF、GH C.AB、CD、GH
B.AB、EF、GH D.AB、CD、EF
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (358)
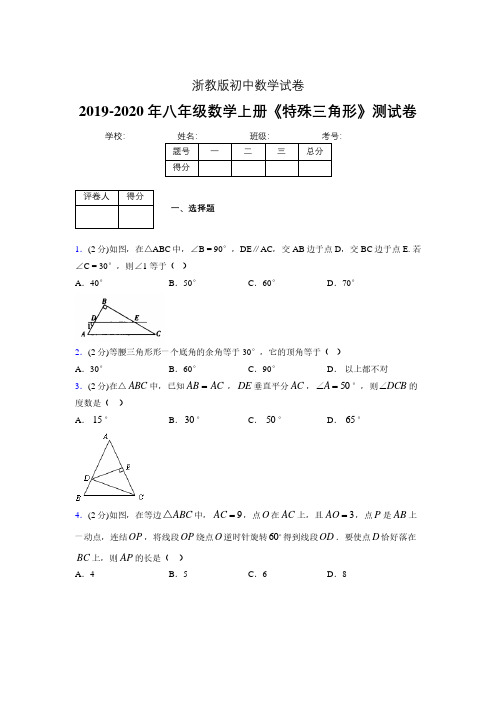
23.(7 分)已知:如图,∠AOB=∠AOC ,∠1=∠2. 试说明:(1)△ABC 是等腰三角形;(2)AO⊥BC.
24.(7 分)如图,∠A=36°,∠DBC=36°,∠C=72°,找出图中的一个等腰三角形,并给
予证明.
我找的等腰三角形是:
.
证明:
25.(7 分) 如图①所示是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高 2 m, 房间高 2.6 m,所以不必从高度方面考虑方案的设计),按此方案,可使该家具通过图② 中的长廊搬人房间,在图②中把你设计的方案画成草图,并通过近似计算说明按此方案可 把家具搬人房间的理由. (注:搬运过程中不准拆卸家具,不准损坏墙壁)
30.(7 分)如图,在△ABC 中,CA=CB,CD 是高,E、F 分别是 AB、BC 上的点,求作点 E、F 关于直线 CD 的对称点(只要求作出图形).
【参考答案】***试卷处理标记,请不要删除
评卷人 得分
一、选择题
1.C 2.B 3.A 4.C
5.B 6.C 7.D 8.A 9.B 10.B 11.C 12.D
A.3 个
B.4 个
C.5 个
D.6 个
7.(2 分)如图,在等腰△ABC 中,AB=AC,∠A=44°,CD⊥AB 于 D,则∠DCB 等于
()
A. 68°
B.46°
C.44°
D.22°
8.(2 分)如图,△ABC 是等边三角形,CD 是∠ACB 的平分线,过 D 作 BC 的平行线交
AC 于 E.已知评卷人得分二、填空题
13.AB=AD
14.8
15.6
16.勾股数(1)5(2)(2)10(3)13(4)17
17.5
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (20)

【参考答案】***试卷处理标记,请不要删除
评卷人 得分
一、选择题
1.B 2.B 3.A 4.C 5.B 6.C 7.B 8.C
DEF 全等的是( )
A.AB=DE,AC=DF B.AC=EF,BC=DF C.AB=DE,BC=FED.∠C=∠F,BC=FE
6.(2 分)如图所示,在△ABC 中,AB=AC,∠B= 1 ∠BAC,AD⊥AB 垂足为 A,AD=1, 4
则 BD=( )
A.1
B. 3
C.2
D.3
7.(2 分)如图,在△ABC 中,∠BAC=90°,点 D 是 AB 的中点,BC=14 cm,则 AD 的长
22.(7 分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方 法. 如图所示,火柴盒的一个侧面 ABCD 倒下到 AB′C′D′的位置,连结 CC′,设 AB=a,BC=b,AC=c,请用四边形 BCC′D′的面积说明勾股定理: a2 + b2 = c2 .
23.(7 分)有一块菜地,地形如图,试求它的面积 s(单位:m).
10.(2 分)如图,在平面直角坐标系中,OA=10,点 B 的坐标为(8,0),则点 A 的坐标 为.
11.(2 分)三角形中,和顶角相邻的外角的平分线和底边的位置关系是 .
12.(2 分)如图,已知 D 为等边三角形内一点,DB=DA,BF=AB,∠1=∠2,则∠ BFD= .
13.(2 分)在△ABC 中,若 AC2+AB2=BC2,则∠B+∠C= 度. 14.(2 分)已知△ABC 的三边长分别是 8 cm,10 cm ,6 cm,则△ABC 的面积是 cm2. 15.(2 分)如图,在 Rt△ABC 中,∠C=Rt∠,AC=6,AB=BC+2,则斜边 AB 长为 .
2019年秋浙教版初中数学八年级上册《特殊三角形》单元测试(含答案) (820)

浙教版初中数学试卷2019-2020年八年级数学上册《特殊三角形》测试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.(2分)下列说法中,错误的是( )A .等边三角形是特殊的等腰三角形B .等腰三角形底边上的中线是等腰三角形的对称铀C . 有一个角为 45°的直角三角形是等腰直角三角形D .等腰三角形的顶角可以是锐角、直角或钝角2.(2分)如图,△ABC 、△ADE 及△EFG 都是等边三角形,D 和G 分别为AC 和AE 的中点。
若AB =4时,则图形ABCDEFG 外围的周长是( )A .12B .15C .18D .213.(2分)如图,ABC △是等腰直角三角形,BC 是斜边,将ABP △绕点A 逆时针旋转后,能与ACP '△重合,如果3AP =,那么PP '的长等于( )A .B .C .D .4.(2分)下列判断中,正确的是( )A .顶角相等的两个等腰三角形全等B .腰相等的两个等腰三角形全等C .有一边及锐角相等的两个直角三角形全等D.顶角和底边分别相等的两个等腰三角形全等5.(2分)如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕A逆时针旋转后,能够与△ACP′重合,如果AP=3,那么2PP'等于()A.9 B.12 C.15 D.l86.(2分)等腰三角形一边长等于4,一边长等于9,它的周长是()A.17 B.22 C.17或22 D.137.(2分)满足下列条件的△ABC,不是直角三角形的是()A.222=-B.∠C=∠A一∠Bb a cC.∠A:∠B:∠C=3:4:5 D.a:b: c=12:13:58.(2分)连结等边三角形各边的中点所得到的三角形是()A.等边三角形B.直角三角形C.非等边三角形D.无法确定9.(2分)在下列几个说法中:①有一边相等的两个等腰三角形全等;②有一边相等的两个直角三角形全等;③有一边和锐角对应相等的两个直角形全等;④有一边相等的两个等腰直角三角形全等;⑤有两直角边对应相等的两个直角三角形全等.其中正确的个数是()A.1个B.2个C.3个D.4个10.(2分)等腰三角形的周长为l8 cm,其中一边长为8 cm,那么它的底边长为()A.2 cm B.8 cm C.2 cm或8 cm D.以上都不对11.(2分)等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高所在的直线C.顶角平分线所在的直线D.腰上的高所在的直线二、填空题12.(2分) 现有两根长度分别为 8cm和 l5cm的木棒,要钉成一个直角三角形木架,则所需要第三根木棒的长度为 .13.(2分)现用火柴棒摆一个直角三角形,两直角边分别用了7根、24根长度相同的火柴棒,则斜边需要用根相同的火柴棒.14.(2分)等腰三角形一边长为2 cm,另一边长为5cm,它的周长是 cm.15.(2分)如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3= .16.(2分)已知△ABC的三边长分别是8 cm,10 cm ,6 cm,则△ABC的面积是 cm2.17.(2分)如图,剪四个与图①完全相同的直角三角形,然后将它们拼成如图②所示的图形.(1)大正方形的面积可以表示为.(2)大正方形的面积也可表示为.(3)对比两种方法,你能得出什么结论?18.(2分) 等腰三角形△ABC 中,AB=AC,∠BAC=70°,D是BC的中点,则∠ADC= ,∠BAD= .19.(2分)等腰三角形的对称轴最多有条.20.(2分)等腰三角形的腰长与底边长之比为2;3,其周长为28 cm ,则底边长等于cm.三、解答题21.(7分)如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.(1)说明△BCE≌△ACD成立的理由;(2)说明CF=CH成立的理由;(3)判断△CFH的形状并说明理由.22.(7分)如图所示,一棵大树被龙卷风吹断了,折断点离地面9 m ,树顶端落在离树根12 m 处,问这棵大树原先高度是多少?23.(7分)如图,在ΔABC 中,AB=AC=10,BC=8.用尺规作图作BC 边上的中线AD (保留作图痕迹,不要求写作法、证明),并求AD 的长.24.(7分)如图,OD 平分∠AOB ,DC ∥A0交0B 于点C ,试说明△OCD 是等腰三角形的理由.25.(7分)如图,AD 、BE 分别是△ABC 的边BC 、AC 上的高,F 是DE 的中点,G 是AB 的中点,则FG ⊥DE ,请说明理由. A B C26.(7分)如图,Rt△ABC中,∠ACB=90°,D是AB的中点,过点D作DE⊥BC于E 点,F是BD的中点,连结EF.说明:CD=2EF.27.(7分)如图所示,小明在距山脚下C处500 m的D处测山高,测得∠ADB=15°,又测得∠ACB=30°,求山的高度AB.28.(7分)如图,∠A=∠B,CE∥DA,CE交AB于E,△CEB是等腰三角形吗?说明理由.29.(7分)如图,AC和BD相交于点0,且AB∥DC,OA=08,△0CD是等腰三角形吗?说明理由.30.(7分)如图,在△ABC中,∠1=∠2,AB=AC=10,BD=4,求△ABC的周长.【参考答案】***试卷处理标记,请不要删除一、选择题1.B2.B3.A4.D5.D6.B7.C8.A9.B10.C11.C二、填空题12.17cm cm13.2514.1215.135°16.2417.(1)c 2 ;(2)214()2ab b a ⨯+-;(3)222a b c +=18.90°,35°19.320.l2三、解答题21.(1)略 (2) 略(3)△CFH 是等边三角形,理由略22.24m23.解:(1)作图略;(2)在△ABC 中,AB=AC ,AD 是△ABC 的中线,∴AD ⊥BC , 118422BD CD BC ===⨯=. 在Rt △ABD 中,AB =10,BD =4,222AD BD AB +=,AD ∴===.24.说明∠OOC=∠BOD25.先说明EG=DG .再利用三线合一来说明26.说明EF=12BD=12CD27.250 m28.是等腰三角形,说明∠CEB=∠B29.是等腰三角形.说明∠C=∠D30.28。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
A
(1)请找出图 2 中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明: DC ⊥ BE .
B
CE
图1
图2
19.(7 分)如图,在等边△ABC 中,D、E 分别是 AB、AC 上的一点,AD=CE,CD、BE 交 于点 F. (1)试说明△ADC≌△CEB; (2)求∠CFE 的度数.
27.(7 分)将两块三角尺的直角顶点重合成如图的形状,若∠AOD=127°,则∠BOC 度数 是多少?
28.(7 分)在△ABC 中,如果∠A=∠B= 1 ∠C,试判断△ABC 的形状,并说明理由. 2
29.(7 分)如图,在等边△ABC 中,点 D、E 分别是边 AB,AC 的中点,说明 BC=2DE 的 理由.
评卷人
得分
三、解答题
17.在△ABC 中.∵AB=AC,∠A=38,∴∠ABC=∠C= 1 ×(180°-∠A)=71°. 2
在△DBC 中,∵BD=BC,∴∠BDC=∠C=71°. ∴∠D8C=180°-∠BDC-∠C=180°-71°-71°=38°.
18.(1)解:图 2 中△ABE ≌△ACD .
22.(7 分)如图,在四边形 ABCD 中,AC⊥DC,∠ADC 的面积为 30cm2,DC=12 cm , AB=3 cm ,BC=4 cm,求△ABC 的面积.
23.(7 分)一艘潜艇在水下 800 m 处用声纳测得水面上一艘静止的轮船与它的直线距离为 l000m,潜艇的速度为 20m/s,若它向这艘轮船方向驶去(深度保持不变),则经多少时间它 会位于轮船正下方?
浙教版初中数学试卷
2019-2020 年八年级数学上册《特殊三角形》测试卷
学校:__________ 姓名:__________ 班级:__________ 考号:__________
题号 一
二
三 总分
得分
评卷人 得分
一、选择题
1.(2 分)已知 △ABC 的三边长分别为 5,13,12,则△ABC 的面积为( )
BCD = ACB + ACD = 90 ,DC ⊥ BE .
19.(1)略;(2)60° 20.说明 Rt△ABC≌△Rt△DCF 21.根据 S 四边形 BCC′D′=S△AC′D′+S△ABC+S△ACC′,说明 a2 + b2 = c2 22.6cm2 23.30s 24.△CDE 为等腰三角形 25.BC=4cm,CD=4 cm,DE=2 cm 26.(1)利用△CBE≌△FBE 来说明;(2)利用 ASA 说明;(3)利用 CF=2CE 而 CF=BD 来 说明 27.53° 28.△ABC 是等腰直角基角形 29.说明△ADE 是等边三角形 30.等腰三角形,说明∠ABD=∠C′DB=∠BDC
24.(7 分)如图,在四边形 ABCD 中,BD⊥AD,AC⊥BC,E 是 AB 的中点,试判断 △CDE 的形状并说明理由?
25.(7 分)如图,已知 Rt△ABC 中,∠ACB=90°,AB=8 cm,D 为 AB 中点,DE⊥AC 于 E,∠A=30°,求 BC,CD 和 DE 的长.
26.(7 分)如图,已知等腰直角三角形 ABC 中,∠BAC=90°,∠ABC 的平分线交 AC 于 D,过 C 作 BD 的垂线交 BD 的延长线于 E,交 BA 的延长线于 F,请说明: (1)△BCF 是等腰三角形; (2)△ABD≌△ACF; (3)BD=2CE.
A.一条直角边和一个锐角分别相等
B.两条直角边对应相等
C.斜边和一条直角边对应相等
D.斜边和一个锐角对应相等
5.(2 分)已知等腰三角形一腰上的高线等于底边的一半,则这个等腰三角形的顶角等于
()
A.120°
B.90°
C. 60°
D.30°
6.(2 分)把等边三角形 ABC 一边 AB 延长一倍到 D,则∠ADC 是( )
A.30
B.60
C.78
D.不能确定
2.(2 分)已知等腰三角形的一个底角为80 ,则这个等腰三角形的顶角为( )
A. 20
B. 40
C. 50
D. 80
3.(2 分)如图,在△ABC 中,∠BAC=90°,AD⊥BC,则图中与∠B 相等的角是( )
A.∠BAD
B.∠C
C.∠CAD
D.没有这样的角
4.(2 分)下列条件中,不能判定两个直角三角形全等的是 ( )
30.(7 分)取出一张长方形的纸,沿一条对角线折叠,如图所示,问:重叠部分是一个什么 三角形?并说明理由.
【参考答案】***试卷处理标记,请不要删除
评卷人 得分
Hale Waihona Puke 一、选择题1.A2.A 3.C 4.A 5.A 6.B 7.D 8.B 9.C
评卷人
得分
二、填空题
10.45° 11. 12. 13.60° 14.90 15.8 16.60°
9.(2 分)已知等腰三角形的顶角为 l00°,则该三角形两腰的垂直平分线的交点位于( )
A.三角形内部
B.三角形的边上 C.三角形外部 D.无法确定
评卷人 得分
二、填空题
10.(2 分)E,F 分别是 Rt△ABC 的斜边 AB 上的两点,AF=AC,BE=BC,则∠ ECF= . 11.(2 分)如图,正方体的棱长为 1,用经过 A、B、C 三点的平面截这个正方体,所得截 面中∠CAB=_______度.
A.等腰三角形
B.直角三角形 C.等边三角形 D.不能确定
7.(2 分) 等腰三角形的一个外角为 140°,则顶角的度数为( )
A.40°
B. 40°或 70° C.70°
D. 40°或 100°
8.(2 分)等腰三角形的顶角为 80°,则一腰上的高与底边的夹角为( )
A.1O°B. 40°C. 50°D. 80°
20.(7 分)如图,△ABC 和△DBC 都是直角三角形,∠A=∠D=90°,AB=DC.说明: △EBC 是等腰三角形.
21.(7 分)一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方 法. 如图所示,火柴盒的一个侧面 ABCD 倒下到 AB′C′D′的位置,连结 CC′,设 AB=a,BC=b,AC=c,请用四边形 BCC′D′的面积说明勾股定理: a2 + b2 = c2 .
证明如下:
△ABC 与 △AED 均为等腰直角三角形,
AB = AC , AE = AD, BAC = EAD = 90 . BAC + CAE = EAD + CAE ,即 BAE = CAD ,△ABE ≌△ACD . (2)证明:由(1)△ABE ≌△ACD 知 ACD = ABE = 45 ,又 ACB = 45 ,
15.(2 分)在△ABC 中,∠A:∠B:∠C=1:2:3,BC=4,那么 AB= .
16.(2 分)等边三角形三个角都是 .
评卷人 得分
三、解答题
17.(7 分)如图,AB=AC,BD=BC. 若∠A = 38°,求∠DBC 的度数.
18.(7 分)两个大小不同的等腰直角三角形三角板如图 1 所示放置,图 2 是由它抽象出的几
答案:60°
12.(2 分)如图,以 Rt△ABC 的三边为边向外作正方形,其面积分别为 S1、S2、S3,且 S1=4,S2=8,则 AB 的长为 .
23
13.(2 分)已知等腰△ABC 中,AB=AC,∠B=60°,则∠A=_________.
14.(2 分)在△ABC 中,若 AC2+AB2=BC2,则∠B+∠C= 度.
