自控chapter2-1
自动控制原理与应用答案解析第二版_课后答案解析

第二章习题课 (2-11d)
2-11d 求系统的闭环传递函数 。
解: (1)
R(s) G1 + G2
C(s)
_
HG2
R(s)
_
C(s) G1 + G2
L1 H
C(s) R(s)
= (G1+G2
)
1 1+G2H
(2) L1=-G2H P1=G1 Δ1 =1
P2=G2 Δ2 =1
第二章习题课 (2-11e)
C(s)=
(s2+4s+2) (s+1)(s+2)
=1+
2 s+2
-
1 s+1
c(t)=δ (t)+2e-2t+e-t
第二章习题课 (2-10)
2式R-1(,s0) 试已- R画知(sG出)系1 -系统统G1的+2的G微G3G动1分G2G-2态G6方+3G结GG程-432GG构组46G图G5的3C并拉(s求)氏G传4变C递(s换) RC((函解ss))R=数:(s1)。+CRG- ((ss3)GX)X[GGX112(7(-1GX2(ssXs())3)s6=(=1--)s(G+GR{=s)=)R81GG((GGsGs(C2))3s236(]GG)G((s-ssG)1CG)4)1[[(XX=G2GXXsC7(3-)2Gs2((1G(5--2()ss(sGs+4G[))s8))(GG-)G1s-C3-15()7-GG(Gs(X+(1ss)GsGG)6)64[3)GG(3G(-3sG2sGG55G)G7)(4X2s(G8GG3GGG)s3(X3])5s7G86(573-)s(GC]s)4})]((8GsGG(s)14)7(C]s-C)(Gs(s)8))
自动控制原理第2版王划一课后习题答案

= 0.158 n = 3.16 % = 60.5%
加入比例微分和速度反馈后,阻尼比增大,使系统超调量减小,响应速度加
3-8 图 1 和图 2 系统均是稳定的。 3-9 (1)系统稳定。
(2)系统不稳定,s 右半平面有 2 个极点。 (3)系统不稳定,s 平面虚轴上有 2 对共轭极点。
3-10 (1)系统稳定。
带格式的: 字体: 小四, 降 低量 15 磅 带格式的: 缩进: 首行缩 进: 21.75 磅 带格式的: 行距: 多倍行距 1.25 字行 带格式的: 缩进: 首行缩 进: 7 字符, 行距: 多 倍行距 1.25 字行 带格式的: 字体: 小四, 降 低量 5 磅 带格式的: 缩进: 首行缩 进: 7.5 字符, 行距: 多 倍行距 1.25 字行 带格式的: 缩进: 首行缩 进: 4 字符, 行距: 多 倍行距 1.25 字行 带格式的: 行距: 多倍行距 1.25 字行 带格式的: 字体: 小四, 降 低量 5 磅 带格式的: 字体: 小四, 降 低量 5 磅 带格式的: 缩进: 首行缩 进: 1.5 字符, 行距: 多 倍行距 1.25 字行 带格式的: 行距: 多倍行距 1.25 字行 带格式的: 字体: 小四, 降 低量 5 磅 带格式的: 缩进: 首行缩 进: 0 字符, 行距: 多 倍行距 1.25 字行 带格式的: 行距: 多倍行距 1.25 字行 带格式的: 缩进: 首行缩 进: 0 字符 带格式的: 字体: 倾斜, 下 标 带格式的: 缩进: 首行缩 进: 2 字符 ... [1] ... [2] 带格式的: 字体: 小四 ... [3]
1
2
t
1
3
sin t
(3) ae nt cos n t
自动控制原理 答案 黄坚习题详解

第二章 自动控制系统的数学模型习题2-1 试建立图示电路的动态微分方程。
解:(a )解法一:直接列微分方程组法⎪⎩⎪⎨⎧-==+O i C O C C u u u Ru R u dt du C 21i i O O u CR dt du u R CR R R dt du 121211+=++⇒ 解法二: 应用复数阻抗概念求)()(11)(11s U s I Cs R Cs R s U O i ++= (1) 2)()(R s U s I O = (2) 联立式(1)、(2),可解得: Cs R R R R Cs R R s U s U i o 212112)1()()(+++= 微分方程为: i ioo u CR dt du u R CR R R dt du 121211+=++ (b )解法一:直接列微分方程组法⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧++=+===COC i O L C O L L L u R u dt du C R u u u u R u i dt di L u)(212 (a) (b) + u C -io oo u R u R R dt du C R R L dt u d LC R 22121221)()(=++++⇒解法二: 应用复数阻抗概念求⎪⎪⎩⎪⎪⎨⎧++=+=)(]1)()([)()()()(2122s U sC s U R s U R s U Ls R R s U s U CC O i O C)()()()()()(2212121s U R s U R R s sU C R R L s U LCs R io o o =++++⇒ 拉氏反变换可得系统微分方程:io o o u R u R R dt du C R R L dt u d LC R 22121221)()(=++++2-7 证明图示的机械系统(a)和电网络系统(b)是相似系统(即有相同形式的数学模型)。
解:(a)取A 、B 两点分别进行受力分析。
自动控制原理胡寿松主编课后习题答案详解

运动模态 e−t / 2 sin
3 2
t
所以: x(t) =
2 3
e
−t
/
2
sin
3 2
t
(3) &x&(t) + 2x&(t) + x(t) = 1(t)。
解:对上式两边去拉氏变换得:
(s 2
+ 2s + 1) X (s) = 1 → X (s) = s
s(s 2
1 + 2s + 1)
=
1 s(s + 1)2
(2)
iC 2
ห้องสมุดไป่ตู้
=
uC1
+ iC1R R
+
iC1
= uC1 R
+ 2iC1
= C2
duC 2 dt
= C2
d (u0 − iC1R) dt
(3)
4
胡寿松自动控制原理习题解答第二章
即:
uC1 R
+
2iC1
=
C2
d (u0
− iC1R) dt
(4)
将(1)(2)代入(4)得:
ui
− u0 R
+ 2C1
d (ui − u0 ) dt
y0
=
12.65
×
1.1y
0.1 0
= 13.915 ×1.1y00.1
2-8 设晶闸管三相桥式全控整流电路的输入量为控制角,输出量为空载整流电压,它们之间的关系为:
ed = Ed0 cosα
式中是整流电压的理想空载值,试推导其线性化方程式。 解:
设正常工作点为 A,这时 Ed = Ed 0 cosα 0
自动控制原理第2章ppt课件
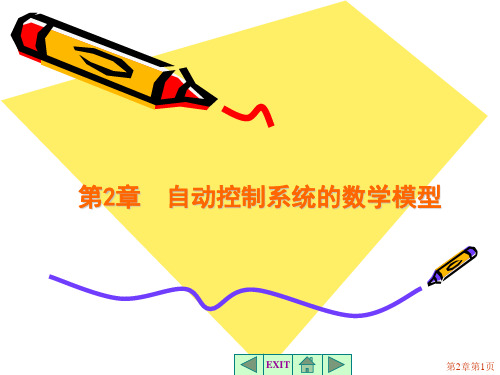
1 2 f 2! r12
(r1 r10)2
2 f r22
(r2
r20)2
yK1r1K2r2
函数变化与自变量变化成线性比例关系。
EXIT
第2章第21页
2.2.3 系统线性化的条件及步骤 1.条件 ① 系统工作在正常的工作状态,有一个稳定的工作 点; ② 在运行过程中偏离且满足小偏差条件; ③ 在工作点处,非线性函数各阶导数均存在,即函 数属于单值、连续、光滑的非本质非线性函数。
EXIT
第2章第14页
2.1.3 机电系统
图示为一他激直流电动机。 +
图中,ω为电动机角速度
〔rad/s ) ,Mc 为折 算到电
ua _
动机轴上的总负载力矩 +
〔N·m ) , ua 为 电 枢 电 压 〔V)。设激磁电流恒定, _
并忽略电枢反应。
ia La
ea Ra
Mc
负载
取ua为给定输入量, ω为输出量,Mc为扰动量,忽略电枢电感, 得:
因而,对于不太严重的非线性系统,可以在一定的工 作范围内线性化处理。工程上常用的方法是将非线性函数 在平衡点附近展开成泰勒级数,去掉高次项以得到线性函 数。
EXIT
第2章第19页
2.2.2 举例
y
① 一个自变量 y=f(r)
y0+△y
y0
r—元件的输入信号,y—元件的输出
AB
设信原号运行于某平衡点〔静态工作点)
频率特性
同一个系统,可以选用不同的数学模型, 如研究时域响应时可以用传递函数, 研究频域响应时则要用频率特性。
EXIT
第2章第5页
4.建立方法
a.分析计算法
分析计算法是根据支配系统的内在运动规律以 及系统的结构和参数,推导出输入量和输出量之间 的数学表达式,从而建立数学模型——适用于简单 的系统。
自动控制原理第二章课后习题答案(免费)

⾃动控制原理第⼆章课后习题答案(免费)⾃动控制原理第⼆章课后习题答案(免费)离散系统作业注明:*为选做题2-1 试求下列函数的Z 变换(1)()E z L =();n e t a = 解:01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ (2) ();at e t e -= 解:12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值:(1)112();(1)Tz E z z --=-解: 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- (2)2()(0.8)(0.1)z E z z z =--。
解:211(1)()(1)()0(0.8)(0.1)lim lim lim t z z z z f t z E z z z →∞→→-=-==--2-3* 已知()(())E z L e t =,试证明下列关系成⽴:(1)[()][];n z L a e t E a=证明:()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ (2)()[()];dE z L te t TzT dz=-为采样周期。
证明:11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以:()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。
自动控制原理第2章课后习题及解答
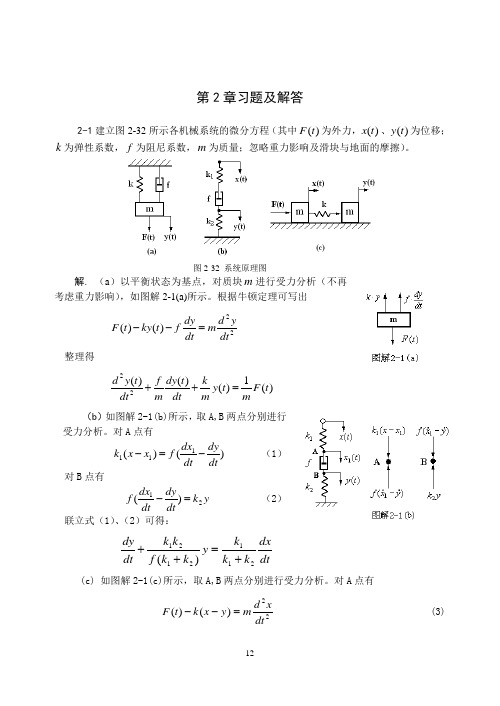
+
1 C2R2
uc
=
du
2 r
dt 2
+
2 CR
dur dt
+
1 C2R2
ur
(c) 由图解 2-2(c)可写出
Ur (= s) R1 [I1(s) + I2 (s)] + (Ls + R2 )I2 (s) (6)
1 Cs
I1
(s)
=
(Ls
+
R2
)I2
(s)
(7)
U c (s) = R2 I 2 (s)
第 2 章习题及解答
2-1 建立图 2-32 所示各机械系统的微分方程(其中 F (t) 为外力,x(t) 、y(t) 为位移; k 为弹性系数, f 为阻尼系数, m 为质量;忽略重力影响及滑块与地面的摩擦)。
图 2-32 系统原理图
解. (a)以平衡状态为基点,对质块 m 进行受力分析(不再
考虑重力影响),如图解 2-1(a)所示。根据牛顿定理可写出
2
2
X (s=)
e−s s2
(s
+
1) 2
−
e−3s s2
(2s
+
1) 2
(c) x(t) = a + (b − a)(t − t1 ) − (b − c)(t − t2 ) − c(t − t3 ) X (s) = 1 [a + (b − a)e−t1s − (b − c)e−t2s − ce−t3s ] s
k1k 2
k1 k2 k1
图解 2-3(a)
(b) 由图可写出
Uc (s) =
Ur (s)
R2
自动控制原理第二版课后答案第二章精选全文完整版

x kx ,简记为
y kx 。
若非线性函数有两个自变量,如 z f (x, y) ,则在
平衡点处可展成(忽略高次项)
f
f
z xv
|( x0 , y0 )
x y |(x0 , y0 )
y
经过上述线性化后,就把非线性关系变成了线性 关系,从而使问题大大简化。但对于如图(d)所示的 强非线性,只能采用第七章的非线性理论来分析。对于 线性系统,可采用叠加原理来分析系统。
Eb (s) Kbsm (s)
Js2 m(s) Mm fsm(s)
c
(s)
1
i
m
(s)
45
系统各元部件的动态结构图
传递函数是在零初始条件下建立的,因此,它只 是系统的零状态模型,有一定的局限性,但它有现 实意义,而且容易实现。
26
三、典型元器件的传递函数
1. 电位器
1 2
max
E
Θs
U s
K
U
K E
max
27
2. 电位器电桥
1
2
E
K1p1
K1 p 2
U
Θ 1
s
Θ
K1 p
Θ 2
s
U s
28
3.齿轮
传动比 i N2 N1
G2(s)
两个或两个以上的方框,具有同一个输入信号,并 以各方框输出信号的代数和作为输出信号,这种形
式的连接称为并联连接。
41
3. 反馈连接
R(s)
-
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后,得 到的输出再返回到这个方框的输入端,构成输 入信号的一部分。这种连接形式称为反馈连接。
自动控制原理(第二版)(赵四化)章 (2)

第2章 控制系统的数学模型 图2-3 直流电动机系统
第2章 控制系统的数学模型
(2) 建立输入、 输出量的动态联系。
在他励直流电动机系统中有机械运动及电磁 运动, 二者之间还存在耦合。 根据几种关系建立的输 入、 输出量的动态联系为
机械运动:
J d f M
dt
(2-7)
电磁运动:
u
Ea
La
dIa dt
图中, A点为工作点, y0=f(x0)。 x、 y在 工作点附近做小范围增量变化, 即当x=x0+Δx 时, 有 y=y0+Δy。 则函数y=f(x)在工作点附近可以展开成泰勒 级数:
y
f
(x0 )
f
(x0)x
1 2!
f
(x0 )x2
(2-13)
第2章 控制系统的数学模型
当Δx很小时, 可以忽略上式的高次项 , 则式(2-13)可以改写为
Ra Ia
(2-8)
第2章 控制系统的数学模型
机电之间的耦合关系:
Ea=CeΩ
(2-9)
M=CmIa
(2-10)
其中, Ce为电动机电势常数; Cm为电动机力矩常数。
第2章 控制系统的数学模型
(3) 消去中间变量, 得到系统的数学模型。 消去中间变量Ea、 Ia和M, 得
La CeCm
d 2
dt2
第2章 控制系统的数学模型
G(s) Uo(s) 1 Ui (s) Ts 1
(2-23)
这一关系可以用图2-6所示的方框图表示, 输入信号经过G(s)动态传递到输出, 故称G(s)为RC电路 的传递函数。
第2章 控制系统的数学模型 图2-6 RC电路方框图
自动控制原理第二章到第七章课后习题答案

自动控制原理第二章到第七章课后习题答案第二章2-1试求下图所示电路的微分方程和传递函数。
解:(a )根据电路定律,列写出方程组:001Li R c L R C di L u u dtu R i i dt Ci i i ⋅+==⋅==+⎰消除中间变量可得微分方程:20002i d u du L L C u u dt R dt⋅⋅+⋅+=对上式两边取拉氏变换得:2000()()()()i LL C U s s U s s U s U s R⋅⋅⋅+⋅⋅+= 传递函数为022()1()()1i U s R G s L U s R Ls LCRs s LCs R ===++++ (b )根据电路定律,列写出方程组:12011()i i u i R R idt C u u i R =++-=⎰消除中间变量可得微分方程:121012i R R Ru u idt R R C+=-⎰ 对上式两边取拉氏变换得:2012()(1)()(1)i U s R Cs U s R Cs R Cs +=++传递函数为0212()1()()1i U s R CsG s U s R Cs R Cs+==++2-3求下图所示运算放大器构成的电路的传递函数。
解:(a )由图(a ),利用等效复数阻抗的方法得22111(s)1(s)()1o i R U R Cs Cs G U s R R Cs ++==-=-+(b )由图(b ),利用等效复数阻抗的方法得222121211221211111(s)()1(s)1()1o i R U C s R R C C s R C R C s G U s R C s R C s R C s++++==-=-+2-5试简化下图中各系统结构图,并求传递函数()()C s R s 。
2-6试求下图所示系统的传递函数11()()C s R s ,21()()C s R s ,12()()C s R s 及22()()C s R s 。
自动控制原理_第2章 ppt课件

• “不怕太阳晒,也不怕那风雨狂,只怕先生骂我 笨,没有学问无颜见爹娘 ……”
• “太阳当空照,花儿对我笑,小鸟说早早早……”
与非线性系统相比,线性系统有如下特点:
叠加性
r1 ( t )
r2 (t )
线性系统
y1(t)
线性系统
y 2 (t)
r1(t) r2(t)
dy(t)ky(t)F(t) dt
设系统的工作点为 ( y 0 , F0 )
y(t)y0y(t) F(t)F0F(t)
m 20d 202 /[ 12y /10 7d t2 y ( t) ] fd [ y 0 d t py pt( 课t 件) ] k [ y 0 y ( t) ] F 0 F 9( t)
2020/12/17
线性系统
y1(t) y2(t)
ppt课件
5
齐次性 (比例性)
r (t)
y (t)
线性系统
r(t)
线性系统
y(t)
2020/12/17
ppt课件
6
非线性系统的线性化
在一定条件下,把非线性系统近似地处理成线性 系统的过程。
非线性特性的线性化
缩小问题的研究范围,把非线性方程近似地化为 线性方程的过程。
简记为:
y fx0x fx0x fx0x
2020/12/17
ppt课件
15
[例2-31] 将非线性方程式
yx1x2xx2 2
在原点附近线性化。
[解] 线性化后的方程式应该为:
y fx0x fx0x fx0x
2020/12/17
ppt课件
16
yx1x2xx2 2
自控第一二章习题
第一章自动控制的基本概念显示所有|| 隐藏所有•例1-1 一晶体稳压电源如图1-1所示。
试画出其方块图,并说明被控量、给定值、干扰量是什么,哪些元件起着测量、放大和执行作用。
•例1-2 图1-3中给出了一个反坦克导弹控制系统工作原理示意图。
试分析其工作原理并画出系统功能方块图。
解:该控制系统采取光学跟踪和有线制导。
由于采用光学制导系统(红外线、激光),射手只需将与光学跟踪器(如红外线测角仪)同步的瞄准镜的十字线对准目标,光学制导系统能测出目标与导弹的偏差角,产生偏差控制信号,操纵导弹自动修正它与瞄准线间的偏差而飞向目标。
该系统导弹是被控对象,导弹运动的航迹是被控量,光学瞄准具是测量比较装置,目标运动是给定输入信号,其功能方块图如图所示。
•例1-3 图1-5为发电机电压调节系统,该系统通过测量电枢回路电流i 产生附加的激励电压Ub来调节输出电压Uc。
试分析在电枢转速ω和激励电压Ug恒定不变而负载变化的情况下系统的工作原理并画出原理方框图。
•例1-4 某住宅楼水池水位控制系统如图1-7所示。
试简述系统各组成元件的作用及系统的工作原理,并画出系统的方块图。
解:该系统的控制任务是保持水池水位基本不变。
水池是被控对象,水位H是被控量,而Hr 是水位的希望值。
浮子随水位上下浮动,可以反映水位的实际高度H,也可以表示水位给定(希望)高度与实际高度的偏差Hr-H,相当于测量元件和比较元件。
浮子带动铰链机构控制进水阀开度,调节进水量,从而控制水位高度,故铰链和控制阀相当于放大元件和执行元件。
系统的工作原理:设系统原来处于进、出水量相等,水位高度等于给定值(即H = Hr)的工作状态下,如出水量Q2增大(而进水量一时没有改变),则Q1<Q2 ,水位高度H下降,使浮子下移,产生水位偏差Hr - H >0,铰链联动使进水阀门开度增大,进水量Q1增大,直至Q1 重新等于Q2 ,最后使水位高度H又恢复到或接近希望值Hr 。
自动控制理论答案(孙扬声版)
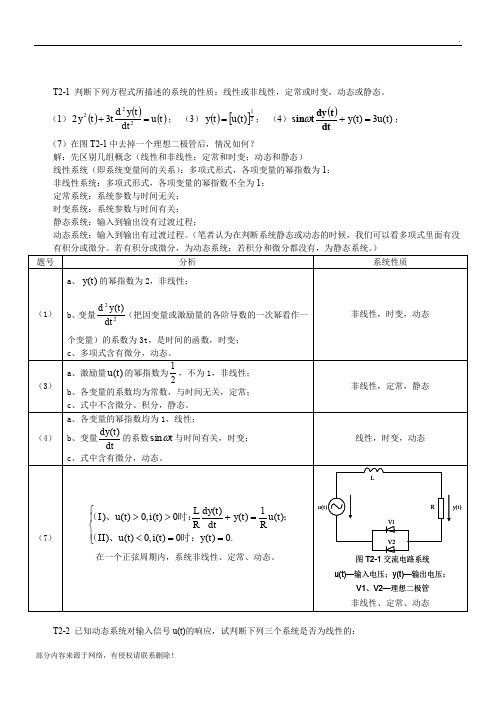
T2-1 判断下列方程式所描述的系统的性质:线性或非线性,定常或时变,动态或静态。
(1)()()()t u dt t y d t t y =+22232; (3)()[]21)(t u t y =; (4)())(3)(t u t y =+dtt dy t sin ω; (7)在图T2-1中去掉一个理想二极管后,情况如何?解:先区别几组概念(线性和非线性;定常和时变;动态和静态) 线性系统(即系统变量间的关系):多项式形式,各项变量的幂指数为1; 非线性系统:多项式形式,各项变量的幂指数不全为1; 定常系统:系统参数与时间无关;时变系统:系统参数与时间有关; 静态系统:输入到输出没有过渡过程; 动态系统:输入到输出有过渡过程。
(笔者认为在判断系统静态或动态的时候,我们可以看多项式里面有没T2-2 已知动态系统对输入信号u(t)的响应,试判断下列三个系统是否为线性的:(1)()⎰+=td u x t y 02)(0)(ττ;(2)()⎰+=td u x t y 0)(03)(ττ;(3)()⎰+--+=tt td u ex e t y 0)(0)(τττ。
解:先分清()0x 和()t u 这两个量:()0x 为状态变量(初始状态或初始条件);()t u 为输入变量。
零状态线性和零输入线性的判定方法:(I) 当()00=x 时,为零状态,对应的输出称为零状态响应,此时看输出()t y 与输入()t u 的关系是否满足线性,若满足,则为零状态线性;(II) 当()00=t u 时,为零输入,对应的输出称为零输入响应,此时看输出()t y 与初始状态()0x 的关系是否满足线性,若满足,则为零输入线性;T2-3 有一线性动态系统,分别用0≥t 时的输入()()()[],,0,,,321τ∈t t u t u t u 对其进行试验。
它们的初始状态都相同,且(),00≠x 三种试验中所得输出若为()()()。
自动控制原理电子版

第二章 自动控制系统的数学模型研究一个自动控制系统,除了对系统进行定性分析外,还必须进行定量分析,进而探讨改善系统稳态和动态性能的具体方法。
控制系统的运动方程式(也叫数学模型)是根据系统的动态特性,即通过决定系统特征的物理学定律,如机械﹑电气﹑热力﹑液压﹑气动等方面的基本定律而写成的。
它代表系统在运动过程中各变量之间的相互关系 ,既定性又定量地描述了整个系统的动态过程。
因此,要分析和研究一个控制系统的动态特性,就必须列写该系统的运动方程式,即数学模型。
第一节 系统动态微分方程模型常用的列写系统或环节的动态微分方程式的方法有两种﹕一种是机理分析法,即根据各环节所遵循的物理规律(如力学﹑电磁学﹑运动学﹑热学等)来编写。
另一种方法是实验辩识法,即根据实验数据进行整理编写。
在实际工作中,这两种方法是相辅相成的,由于机理分析法是基本的常用方法,本节着重讨论这种方法。
下面通过简单示例介绍机理分析法的一般步骤。
图2-1 RLC 网络[例2-1] 列写图2-1所示RLC 网络的微分方程。
解 1. 明确输入、输出量网络的输入量为电压)(t u r ,输出量为电压)(t u c 。
2.列出原始微分方程式。
根据电路理论得 )()(1)()(t Ri dt t i Cdt t di Lt u r ⎰++= (2-1) 而 ⎰=dt t i C t u c )(1)( (2-2) 式中)(t i 为网络电流,是除输入、输出量之外的中间变量。
3.消去中间变量将式(2-2)两边求导,得)(1)(t i C dt t du c = 或 dtt du C t i c )()(= (2-3) 代入式(2-1)整理为 )()()()(22t u t u dt t du RC dtt u d LC r c c c =++ (2-4) 显然,这是一个二阶线性微分方程,也就是2-1所示RLC 无源网络的数学模型。
[例2-2] 试列写图2-2所示电枢控制直流电动机的微分方程,要求取电枢电压)(t u a(V )为输入量,电动机转速)(t m ω)(s rad 为输出量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
④
u2 uc2
⑤
u1
C1
C2
u2
图2-4 RC组成的四端网络
由④、⑤得
i2
C2
duc2 dt
C2
du2 dt
由②导出
R1
U1
C1
i1
C1
duc1 dt
i2
C1
duc1 dt
C2
du2 dt
将i1、i2代入①、③,则得
u1 R1i1 R2i2 uc2
R2
C2
U2
一、建立系统微分方程的一般步骤
(3系)统消通除常中由间一变些量环,节写连出接输而入成、,输将出系变统中 的每量个的环微节分的方微程分;方程求出来,便可求出整个系 统的(微4)分将方式程子。标准化。
列写系将统与微输分入方量程有的关一的般项步写骤在:方程式等号右 (边1),与确输定出系量统有的关输的入项变写量在和等输号出的变左量边。
R1 (C1
duc1 dt
C2
du2 dt
)
R2C2
du2 dt
u2
R1[C1
d dt
(R2i2
u2 ) C2
du2 dt
]
R2C2
du2 dt
u2
R1C1R2C2
d 2u2 dt 2
R1C1
du2 dt
R1C2
du2 dt
R2C2
du2 dt
u2
R1R2C1C2
d 2u2 dt 2
(R1C1
R1C2
R2C2 )
du2 dt
u2
u1
这就是RC组成的四端网络的数学模型,是一 个二阶线性微分方程。
讨论:
假设系统是无负载,即假设负载阻抗为无穷大,则
可列写如下微分方程:
R1
R2
u1 R1i1 uc1
①
uc1
1 C1
i1dt
②
uc1 R2i2 uc2
duc2 dt
R2C2
duc2 dt
uc2
T1T2
d 2uc2 dt 2
(T1
T2 )
duc2 dt
uc2
与上面的结果相比,错在那里呢?
结论:根据无负载假设而导出的上述系统的微分 方程是不成立的。系统中负载效应的程度,决定了传 递函数的变化大小。
【例2-5】 下图是一个液体贮槽的示意图。 【例2-5】
质中量间变量弹关簧系式阻: 尼器
F(t)
(1) 确定F输K(t入) =和k输y出(t)
系输统F入工B量(t作)d=2过y输(f程t)d出:yd(t量t)
y(t)
m
(2) 初始a 微= 分d方t2程组
阻尼系数f
消变除量根中得据间:F牛m=顿md第2dayt(2二t) 定+律f dyd(tt) + ky(t) = F(t)
K2
1/C1
1/C2
• 机系统(a)和电系统(b)具有相同的数学模型,故这些物 理系统为相似系统(即电系统为即系统的等效网络)。
• 相似系统揭示了不同物理现象之间的相似关系。
• 为我们利用简单易实现的系统(如电的系统)去研究机械系 统......提供了方便。
• 因为一般来说,电的或电子的系统更容易,通过试验进行研 究。
5.由数学模型求取系统性能指标的主要途径
求解
观察
线性微分方程
时间响应
性能指标
傅 氏
拉氏变换
拉氏反变换 估算
估算
变
传递函数
换
S=jω
频率特性 计算 频率响应
2.2 线性系统的微分方程
一、建立微分方程的一般步骤 二、常见环节和系统的微分方程的建立 三、 线性微分方程式的求解
2.2 线性系统的微分方程
(5) 线性化
【例2-5】
原因
工程中大多数系统都是非线性的。非线性微分方
程式求解复杂,线性系统的理论和方法成熟。
条件 变量间关系在平衡点附近的小范围内是线性的,
把非线性方程局部线性化(增量化的理由)。
方法 泰勒级数展开法
描述函数法
相平面分析法
泰勒级数展开法
【例2-5】
将非线性函数y=f(x)在平衡点 ( x0 , y0 ) 附近展开成泰
勒级数,即
y
f (x0 )
f '( x0 )( x x0 )
f
'
'( x0 2!
)
(
x
x0
)2
由于增量Δ x = ( x x0 ) 很小,展开式 y
中增量的高次项可以忽略,则上式可近
似写成线性化方程:
y0
y f (x0 ) f '(x0 )( x x0 )
△y
△y △x △x
Qin
Qout
dV dt
A dh dt
Qout
………………(1)
(3) 消去中间变量Qout ,得到最终的方程
根据流体力学有
Qout f h
………………(2)
其中:f :阀的流通面积,
:阀的节流系数,设两者均为常数(β 为常数)。
A:水槽的横截面积。
dh Qin Qout A dt
3.建模方法
分析法 本课研究 实验法 系统辨识研究
4.常用数学模型
微分方程(differential equation)(或差分方程) 传递函数(transfer function) (或结构图block diagram ) 频率特性(frequency characteristics) 状态空间表达式(state space equation )
列出液位h对流入量Qin之间的关系式。
Qin
A h
步骤:
Qout 液体贮槽
(1) 确定输入(自变量)和输出变量(因变量)
输入(自变量):Qin ,输出(因变量):h
(2)利用物料(能量)平衡式:
Qin 【例2-3】
物料( 能量) 蓄存量的变化率 = 单位时间进入
A
的物料( 能量) - 单位时间流出的物料( 能量)h
8、GK . .e . n .en 等概念及求取。
9、脉冲响应函数及其应用。
重点与难点
重点
1、传递函数的概念及典型环节的传递函数
2、由动态结构图或信. 号流图求传递函数
3、
等概念及求取
.
.
难点
微分方程的列写与各种传递函数的求取
2.1 数学模型基础
1.定义:数学模型(mathematical model)是指出系统内 部物理量(或变量)之间动态关系的表达式。
-
(2) 建根R据立C基初d尔d始ut霍c微夫+分u定c方=律u程得r :组
ur= Ri + uc
i=C
duc dt
R(3C) 电消路除是中一间阶变常量系,数使线式性子微标分准方化程。
二、常见环节和系统微分方程的建立
2.机械位移系统
F(t) –系F统B(t组) –成F:K(t) = ma
弹簧系数k
把变量转换为增量形式,构成增量方程。
【例2-5】
A
Qout
如:
h h h0
• 益处: ①便于方程简化和求解,相当于设初始条件(稳
态条件)为零。
②便于线性化。
• 方法:
【例2-5】
1、把方程写成稳态方程(稳态的物料平衡式):
Qin0 Qout0 f h0
…………(1)
2、将原方程中的变量写成稳态值和增量值之和
Qout f h
【例2-3】 ………………(1)
………………(2)
把(2)代入(1)可得:
dh
Qin f
h
A dt
A dh f
dt
h Qin
是一个非线性一阶微分方程
(4) 增量化
Qin
• 目的:
h 主要关心被调参数在平衡点(设定值)附近
的变化情况,即参数偏离平衡点的变化量。因此,
............(1)
QQoouut t
Qout 0
Qout f hh h0........h..........................(2)
对(1)式中的非线性项线性化, 即(2)式线性化。并忽略
增量Δh的高次项, 则非线性的函数即近似为:
Qout f
h
Qout0
(2)-(1):
-
-
A
d(h0 dt
Ah)d(h0f
dt
hh0 )hf hf0
h0h
Qin0
Qin
……(2)
h h h0 整理
A dh f dt
h0 h f h0 Qin
Qout
Qout0
……(3)
注意: 在不引起混淆的场合,Δ号常常省略。
例2-4 图2-4为由一RC组成的四端无源网络。试列
写以U1(t)为输入量,U2(t)为输出量的网络微分方程。
解:设回路电流i1、i2,根据基尔霍夫定律,列写 方程如下:
u1 R1i1 uc1
①
R1
R2
uc1
1 C1
(i1 i2 )dt
②
uc1 R2i2 uc2
③
1
uc2 C2 i2dt
Qout h
hh0
(h
