【精品】第07讲解三角形-2009-2017全国高中数学联赛分类汇编

合集下载

三角函数、解三角形——2024届高考数学试题分类汇编(解析版)

2024高考复习·真题分类系列2024高考试题分类集萃·三角函数、解三角形
微专题总述：三角函数的图像与性质
【扎马步】2023高考三角函数的图像与性质方面主要考察“卡根法”的运用，是最为基础的表现
【雕龙头】在稳中求新的过程中，2023高考试题也透露出了新的风向，加强图像考察与其他知识点如几何、函数的结合，对称思想的隐含
微专题总述：正弦定理与余弦定理的应用
【扎马步】2023高考解三角形小题部分紧抓“教考衔接”基础不放，充分考察正余弦定理的运用
【雕龙头】在稳中求新的过程中，2023高考试题也透露出了新的风向，在考察正余弦定理时与角平分线定理结合（初中未涉及此定理）
微专题总述：解三角形综合问题
【扎马步】2023高考解三角形大题部分仍然与前几年保持一直模式，结构不良题型日益增多，但方向不变，均是化为“一角一函数”模式是达到的最终目的，考察考生基本计算与化简能力
【雕龙头】在稳中求新的过程中，2023高考试题也透露出了新的风向，如新高考卷中出现的数形结合可加快解题速度，利用初中平面几何方法快速求出对应参量在近几年高考题中频繁出现，可见初高中结合的紧密 2023年新课标全国Ⅰ卷数学
16．已知在ABC 中，
()3,2sin sin A B C A C B +=−=． (1)求sin A ；
(2)设5AB =，求AB 边上的高．
2023高考试题分类集萃·三角函数、解三角形参考答案
2。

高考数学全国卷分类汇编(解析几何)

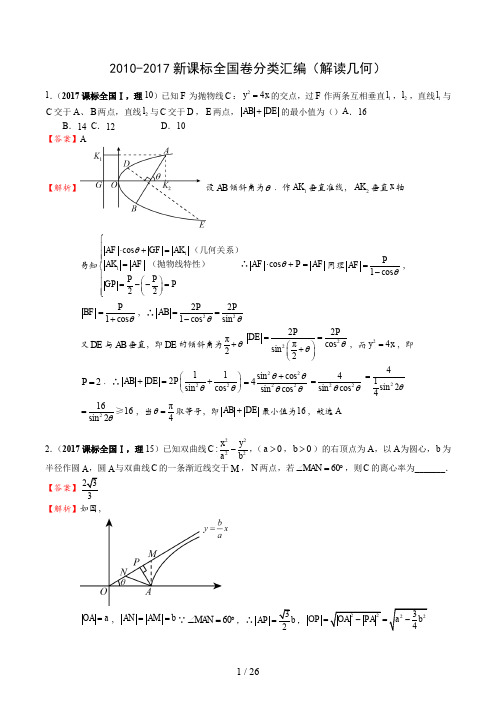
2010-2017新课标全国卷分类汇编（解读几何）1．（2017课标全国Ⅰ，理10）已知F 为抛物线C ：24y x =的交点，过F 作两条互相垂直1l ，2l ，直线1l 与C 交于A 、B 两点，直线2l 与C 交于D ，E 两点，AB DE +的最小值为（）A ．16B ．14C ．12D ．10【答案】A【解析】设AB 倾斜角为θ．作1AK 垂直准线，2AK 垂直x 轴易知11cos 22⎧⎪⋅+=⎪⎪=⎨⎪⎛⎫⎪=--= ⎪⎪⎝⎭⎩AF GF AK AK AF P P GP Pθ（几何关系）（抛物线特性）cos AF P AF θ⋅+=∴同理1cos PAF θ=-，1cos P BF θ=+，∴22221cos sin P PAB θθ==-又DE 与AB 垂直，即DE 的倾斜角为π2θ+2222πcos sin 2P PDE θθ==⎛⎫+ ⎪⎝⎭，而24y x =，即2P =．∴22112sin cos AB DE P θθ⎛⎫+=+ ⎪⎝⎭2222sin cos 4sin cos θθθθ+=224sin cos θθ=241sin 24=θ21616sin 2θ=≥，当π4θ=取等号，即AB DE +最小值为16，故选A2．（2017课标全国Ⅰ，理15）已知双曲线2222:x y C a b-，（0a >，0b >）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M ，N 两点，若60MAN ∠=︒，则C 的离心率为_______．【解析】如图，OA a =，AN AM b ==∵60MAN ∠=︒，∴AP =，OP =∴tan AP OP θ==又∵tan b aθ=b a =，解得223a b =∴e ==3．（2017课标全国Ⅰ，理20）（12分）已知椭圆C ：22221x y a b+=()0a b >>，四点()111P ，，()201P ，，31P ⎛- ⎝⎭，41P ⎛ ⎝⎭中恰有三点在椭圆C 上．（1）求C 的方程；（2）设直线l 不经过2P 点且与C 相交于A 、B 两点，若直线2P A 与直线2P B 的斜率的和为1-，证明：l 过定点．【解析】（1）根据椭圆对称性，必过3P 、4P 又4P 横坐标为1，椭圆必不过1P ，所以过234P P P ，，三点将()23011P P ⎛- ⎝⎭，，代入椭圆方程得222113141b ab ⎧=⎪⎪⎨⎪+=⎪⎩，解得24a =，21b = ∴椭圆C 的方程为：2214x y +=．（2）①当斜率不存在时，设()():A A l x m A m y B m y =-，，，，221121A A P A P B y y k k m m m----+=+==- 得2m =，此时l 过椭圆右顶点，不存在两个交点，故不满足． ②当斜率存在时，设()1l y kx b b =+≠∶，()()1122A x y B x y ，，，联立22440y kx bx y =+⎧⎨+-=⎩，整理得()222148440k x kbx b +++-=122814kb x x k -+=+，21224414b x x k -⋅=+，则22121211P A P By y k k x x --+=+()()21212112x kx b x x kx b x x x +-++-=222228888144414kb k kb kbk b k --++=-+()()()811411k b b b -==-+-，又1b ≠21b k ⇒=--，此时64k ∆=-，存在k 使得0∆>成立．∴直线l 的方程为21y kx k =--当2x =时，1y =-，所以l 过定点()21-，．4．（2017课标全国Ⅱ，理9）若双曲线)00(1:2222>>=-b a by a x C ，的一条渐近线被圆4)2(22=+-y x 所截得的弦长为2，则C 的离心率为A ．2B ．3C ．2D ．332 【答案】A【解读】由几何关系可得，双曲线()222210,0x y a b a b-=>>的渐近线方程为0bx ay ±=，圆心()2,0到渐近线距离为d =，则点()2,0到直线0b x a y +=的距离为2bd c=== 即2224()3c a c -=，整理可得224c a =，双曲线的离心率2e ===．故选A ．【考点】双曲线的离心率；直线与圆的位置关系，点到直线的距离公式【名师点睛】双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出a ，c ，代入公式ce a=；②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．5．（2017课标全国Ⅱ，理16）已知F 是抛物线x y C 8:2=的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则=FN . 【答案】6 【解读】试卷分析：如图所示，不妨设点M 位于第一象限，设抛物线的准线与x 轴交于点F'，作MB l ⊥与点B ，NA l ⊥与点A ，由抛物线的解读式可得准线方程为2x =-，则2,4A N F F '==，在直角梯形ANFF'中，中位线'32AN FF BM +==，由抛物线的定义有：3MF MB ==，结合题意，有3MN MF ==，故336FN FM NM =+=+=．【考点】抛物线的定义、梯形中位线在解读几何中的应用．【名师点睛】抛物线的定义是解决抛物线问题的基础，它能将两种距离(抛物线上的点到焦点的距离、抛物线上的点到准线的距离)进行等量转化．如果问题中涉及抛物线的焦点和准线，又能与距离联系起来，那么用抛物线定义就能解决问题．因此，涉及抛物线的焦半径、焦点弦问题，可以优先考虑利用抛物线的定义转化为点到准线的距离，这样就可以使问题简单化．6．（2017课标全国Ⅱ，理20）（12分）设O 为坐标原点，动点M 在椭圆12:22=+y x C 上，过M 作x 轴的垂线，垂足为N ，点P 满足= (1)求点P 的轨迹方程； (2)设点Q 在直线3-=x 上，且1=⋅. 证明：过点P 且垂直于OQ 的直线l 过C 的左焦点F .解：（1）设)(y x P ，，则)22(y x M ，，将点M 代入C 中得12222=+y x ，所以点P 的轨迹方程为222=+y x .（2）由题可知)01(，-F ，设)()3(n m P t Q ，，，-，则)1( )3(n m t ---=-=，，，， )3( )(n t m n m ---==，，，.由1=⋅得1322=-+--n tn m m ，由（1）有222=+n m ，则有033=-+tn m ，所以033 =-+=⋅tn m ，即过点P 且垂直于OQ 的直线l 过C 的左焦点F .7．（2017课标全国Ⅲ，理1）已知集合A={}22(,)1x y x y +=│，B={}(,)x y y x =│，则A ⋂B 中元素的个数为A ．3B ．2C ．1D ．0【答案】B【解读】A 表示圆221x y +=上所有点的集合，B 表示直线y x =上所有点的集合，故AB 表示两直线与圆的交点，由图可知交点的个数为2，即AB 元素的个数为2，故选B.8．（2017课标全国Ⅲ，理5）已知双曲线C 22221x y a b -= (a ＞0,b ＞0)的一条渐近线方程为y x =,且与椭圆221123x y +=有公共焦点，则C 的方程为A. 221810x y -=B. 22145x y -=C. 22154x y -=D. 22143x y -=【答案】B【解读】∵双曲线的一条渐近线方程为y，则b a =① 又∵椭圆221123x y +=与双曲线有公共焦点，易知3c =，则2229a b c +==②由①②解得2,a b =C 的方程为22145x y -=，故选B. 9．（2017课标全国Ⅲ，理10）已知椭圆C ：22221x y a b+=，（a >b >0）的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切，则C 的离心率为D.13【答案】A【解读】∵以12A A 为直径为圆与直线20bx ay ab -+=相切，∴圆心到直线距离d 等于半径，∴d a ==又∵0,0a b >>，则上式可化简为223a b = ∵222b ac =-，可得()2223a a c=-，即2223c a =∴c e a == A10．（2017课标全国Ⅲ，理12）在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为（） A ．3B．D ．2【答案】A【解读】由题意，画出右图．设BD 与C 切于点E ，连接CE ．以A 为原点，AD 为x 轴正半轴， AB 为y 轴正半轴建立直角坐标系，则C 点坐标为(2,1)． ∵||1CD =，||2BC =．∴BD = ∵BD 切C 于点E ． ∴CE ⊥BD ．∴CE 是Rt BCD △中斜边BD 上的高．()A O Dxy BP gCE12||||22||||||BCDBC CDSECBD BD⋅⋅⋅====△即C．∵P在C上．∴P点的轨迹方程为224(2)(1)5x y-+-=．设P点坐标00(,)x y，可以设出P点坐标满足的参数方程如下：21xyθθ⎧=⎪⎪⎨⎪=⎪⎩而00(,)AP x y=，(0,1)AB =，(2,0)AD =．∵(0,1)(2,0)(2,)AP AB ADλμλμμλ=+=+=∴112xμθ==+，1yλθ==+．两式相加得：112)2sin()3λμθθθϕθϕ+=+++=++=++≤(其中sinϕcosϕ=)当且仅当π2π2kθϕ=+-，k∈Z时，λμ+取得最大值3．11．（2017课标全国Ⅲ，理20）（12分）已知抛物线C：y2=2x，过点（2,0）的直线l交C与A,B 两点，圆M是以线段AB为直径的圆.（1）证明：坐标原点O在圆M上；（2）设圆M过点P（4，-2），求直线l与圆M的方程.解：（1）设()()11222A x,y,B x,y,l:x my=+由222x myy x=+⎧⎨=⎩可得212240则4y my,y y--==-又()22212121212==故=224y yy yx,x,x x=4因此OA 的斜率与OB 的斜率之积为1212-4==-14y y x x 所以OA ⊥OB故坐标原点O 在圆M 上.（2）由（1）可得()2121212+=2+=++4=24y y m,x x m y y m + 故圆心M 的坐标为()2+2，m m ，圆M 的半径r =由于圆M 过点P （4，-2），因此0AP BP =,故()()()()121244220x x y y --+++= 即()()121212124+2200x x x x y y y y -++++= 由（1）可得1212=-4，=4y y x x ，所以2210m m --=，解得11或2m m ==-.当m=1时，直线l 的方程为x-y-2=0，圆心M 的坐标为（3,1），圆M ，圆M 的方程为()()223110x y -+-=当12m =-时，直线l 的方程为240x y +-=，圆心M 的坐标为91，-42⎛⎫ ⎪⎝⎭，圆M 的半径为4，圆M 的方程为229185++4216x y ⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭12.（2016课标全国Ⅰ，理5）已知方程132222=--+nm y n m x 表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（A ）)3,1(-（B ）)3,1(-（C ）)3,0(（D ）)3,0(【解读】：222213x y m n m n-=+-表示双曲线，则()()2230m n m n +->，∴223m n m -<<由双曲线性质知：()()222234c m n m n m =++-=，其中c 是半焦距，∴焦距2224c m =⋅=，解得1m =∴13n -<<，故选A ．13.（2016课标全国Ⅰ，理10）以抛物线C 的顶点为圆心的圆交C 于B A ,两点，交C 的准线于ED ,两点，已知24=AB ,52=DE ，则C 的焦点到准线的距离为|||M N MN y y =- （A ）2 （B ）4 （C ）6 （D ）8【解读】：以开口向右的抛物线为例来解答，其他开口同理设抛物线为22y px =()0p >，设圆的方程为222x y r +=，如图：设(0A x ，2pD ⎛- ⎝，点(0A x 在抛物线22y px =上，∴082px =……①；点2pD ⎛- ⎝在圆222x y r +=上，∴2252p r ⎛⎫+= ⎪⎝⎭……②；点(0A x 在圆222x y r +=上，∴2208x r +=……③；联立①②③解得：4p =，焦点到准线的距离为4p =．故选B ．14.（2016课标全国Ⅰ，理20）（本小题满分12分）设圆015222=-++x y x 的圆心为A ，直线l 过点)0,1(B 且与x 轴不重合，l 交圆A 于D C ,两点，过B 作AC 的平行线交AD 于点E ．（Ⅰ）证明EB EA +为定值，并写出点E 的轨迹方程；（Ⅱ）设点E 的轨迹为曲线两点，求四边形MPNQ【解读】：⑴圆A 整理为(x BE AC Q ∥，则C =∠EBD D ∴=∠∠，则EB ⑵221:143x yC +=；设:l x 联立1l C 与椭圆：24x x =⎧⎪⎨⎪⎩圆心A 到PQ 距离d ==F所以||PQ==，()2212111||||2234MPNQmS MN PQm+⎡∴=⋅=⋅==⎣+15.（2016课标全国Ⅱ，理4）圆2228130x y x y+--+=的圆心到直线10ax y+-=的距离为1，则a=（）（A）43-（B）34-（C（D）216.（2016课标全国Ⅱ，理11）已知12,F F是双曲线2222:1x yEa b-=的左，右焦点，点M在E上，1MF与x轴垂直，211sin3MF F∠=,则E的离心率为（）（A（B）32（C（D）217.（2016课标全国Ⅱ，理20）（本小题满分12分）已知椭圆:E 2213x y t +=的焦点在x 轴上，A 是E 的左顶点，斜率为(0)k k >的直线交E 于,A M 两点，点N 在E 上，MA NA ⊥．（Ⅰ）当4,||||t AM AN ==时，求AMN ∆的面积；（Ⅱ）当2AM AN =时，求k 的取值范围．【答案】（Ⅰ）；（Ⅱ）.【解读】试卷分析：（Ⅰ）先求直线的方程，再求点的纵坐标，最后求的面积；（Ⅱ）设，，将直线的方程与椭圆方程组成方程组，消去，用表示，从而表示，同理用表示，再由求.试卷解读：（I ）设，则由题意知，当时，的方程为，.由已知及椭圆的对称性知，直线的倾斜角为.因此直线的方程为. 将代入得.解得或，所以.因此的面积.（II ）由题意，，.将直线的方程代入得. 由得，故.由题设，直线的方程为，故同理可得，由得，即.当时上式不成立，因此.等价于，即.由此得，或，解得.因此的取值范围是.考点：椭圆的性质，直线与椭圆的位置关系.18.（2016课标全国Ⅲ，理11）已知O为坐标原点，F是椭圆C：22221(0)x ya ba b+=>>的左焦点，,A B分别为C的左，右顶点.P为C上一点，且PF x⊥轴.过点A的直线l与线段PF交于点M，与y轴交于点E.若直线BM经过OE的中点，则C的离心率为（）（A）13（B）12（C）23（D）34【答案】A考点：椭圆方程与几何性质．【思路点拨】求解椭圆的离心率问题主要有三种方法：（1）直接求得,a c 的值，进而求得e 的值；（2）建立,,a b c 的齐次等式，求得ba 或转化为关于e 的等式求解；(3)通过特殊值或特殊位置，求出e ．19.（2016课标全国Ⅲ，理16）已知直线l ：30mx y m ++=与圆2212x y +=交于,A B 两点，过,A B 分别做l 的垂线与x 轴交于,C D 两点，若AB =||CD =__________________.【答案】4考点：直线与圆的位置关系．【技巧点拨】解决直线与圆的综合问题时，一方面，要注意运用解读几何的基本思想方法(即几何问题代数化)，把它转化为代数问题；另一方面，由于直线与圆和平面几何联系得非常紧密，因此，准确地作出图形，并充分挖掘几何图形中所隐含的条件，利用几何知识使问题较为简捷地得到解决．20.（2016课标全国Ⅲ，理20）（本小题满分12分）已知抛物线C ：22y x =的焦点为F ，平行于x 轴的两条直线12,l l 分别交C 于,A B 两点，交C 的准线于P Q ，两点．（I ）若F 在线段AB 上，R 是PQ 的中点，证明AR FQ ；（II ）若PQF ∆的面积是ABF ∆的面积的两倍，求AB 中点的轨迹方程.【答案】（Ⅰ）见解读；（Ⅱ）21y x =-．试卷解读：由题设)0,21(F .设b y l a y l ==:,:21，则0≠ab ，且)2,21(),,21(),,21(),,2(),0,2(22b a R b Q a P b b B a A +---.记过B A ,两点的直线为l ，则l 的方程为0)(2=++-ab y b a x . .....3分（Ⅰ）由于F 在线段AB 上，故01=+ab . 记AR 的斜率为1k ，FQ 的斜率为2k ，则222111k b a aba ab a b a a b a k =-=-==--=+-=，所以AR FQ . ......5分（Ⅱ）设l 与x 轴的交点为)0,(1x D ，则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆. 由题设可得221211b a x a b -=--，所以01=x （舍去），11=x . 设满足条件的AB 的中点为),(y x E . 当AB 与x 轴不垂直时，由DE ABk k =可得)1(12≠-=+x x yb a .而y ba =+2，所以)1(12≠-=x x y .当AB 与x 轴垂直时，E 与D 重合，所以，所求轨迹方程为12-=x y . ....12分考点：1、抛物线定义与几何性质；2、直线与抛物线位置关系；3、轨迹求法．【方法归纳】（1）解读几何中平行问题的证明主要是通过证明两条直线的斜率相等或转化为利用向量证明；（2）求轨迹的方法在高考中最常考的是直接法与代入法（相关点法），利用代入法求解时必须找准主动点与从动点．21.(2015课标全国Ⅰ，理5)已知00(,)M x y 是双曲线22:12x C y -=上的一点，12,F F 是C 的两个焦点，若120MF MF ⋅<,则0y 的取值范围是（A)((B)( (C)((D)( 答案：A解读：由条件知F1(－，0)，F2(，0)，＝(－－x0，－y0)，＝(－x0，－y0)，－3＜0.①又＝1，＝2+2.代入①得，∴－＜y0＜22.(2015课标全国Ⅰ，理14)一个圆经过椭圆221164x y+=的三个顶点，且圆心在x轴的正半轴上，则该圆的规范方程为答案：+y2＝解读：由条件知圆经过椭圆的三个顶点分别为(4，0)，(0，2)，(0，－2)，设圆心为(a，0)(a＞0)，所以＝4－a，解得a＝，故圆心为，此时半径r＝4－，因此该圆的规范方程是+y2＝23.(2015课标全国Ⅰ，理20)在直角坐标系xOy中，曲线2:4xC y=与直线:(0)l y kx a a=+>交于,M N两点。

2003-2017年全国高中数学联赛分类汇编(精编版)02

2003-2017年全国高中数学联赛分类汇编（精编版）02初等数论部分1、（2005一试6）记集合},4,3,2,1,|7777{},6,5,4,3,2,1,0{4433221=∈+++==i T a a a a a M T i 将M 中的元素按从大到小的顺序排列，则第2005个数是（）A ．43273767575+++B ．43272767575+++ C ．43274707171+++ D ．43273707171+++【答案】C2、（2006一试6）数码1232006,,,,a a a a 中有奇数个9的2007位十进制数12320062a a a a 的个数为（） A ．200620061(108)2+ B ．200620061(108)2- C ．20062006108+ D ．20062006108- 【答案】B3、(2008一试5) 方程组0,0,0x y z xyz z xy yz xz y ++=⎧⎪+=⎨⎪+++=⎩的有理数解(,,)x y z 的个数为（）。

（A ） 1 （B ） 2 （C ） 3 （D ）4 【答案】B4、（2004一试10）．设p 是给定的奇质数，正整数k 使得k 2－pk 也是一个正整数，则k= 【答案】14(p +1)2【解析】设k 2－pk=n ，则(k －p2)2－n 2=p 24，⇒(2k －p +2n )(2k －p －2n )=p 2，⇒k=14(p +1)2．5、(2005一试12) 如果自然数a 的各位数字之和等于7，那么称a 为“吉祥数”.将所有“吉祥数”从小到大排成一列,,,,321 a a a 若,2005=n a 则=n a 5 .∵2005是第1+7+28+28+1＝65个“吉祥数”，即.200565=a 从而.3255,65==n n又,210)5(,84)4(61069====CP C P 而∑==51.330)(k k P∴从大到小最后六个五位“吉祥数”依次是：70000，61000,60100,60010,60001,52000.∴第325个“吉祥数”是52000，即.520005=n a 6、（2006一试11）方程20062420042005(1)(1)2006x x x x x +++++=的实数解的个数为 . 【答案】17、（2010一试8）方程2010=++z y x 满足z y x ≤≤的正整数解(,,)x y z 的个数是. 【答案】336675易知 100420096100331⨯=+⨯+k ，所以110033*********-⨯-⨯=k200410052006123200910052006-⨯=-⨯+-⨯=，即3356713343351003=-⨯=k .从而满足z y x ≤≤的正整数解的个数为33667533567110031=++.8、（2011一试8）已知=n a C ())95,,2,1(2162003200=⎪⎪⎭⎫⎝⎛⋅⋅-n nnn ，则数列}{n a 中整数项的个数为．【答案】15 【解析】=n a C65400320020023n n n--⋅⋅．要使)951(≤≤n a n 为整数，必有65400,3200nn --均为整数，从而4|6+n ．当=n 2,8,14,20,26,32,38,44,50,56,62,68,74,80时，3200n -和65400n-均为非负整数，所以n a 为整数，共有14个．当86=n 时，=86a C 5388620023-⋅⋅，在C !114!86!20086200⋅=中，!200中因数2的个数为1972200220022002200220022002200765432=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡，同理可计算得!86中因数2的个数为82，!114中因数2的个数为110，所以C 86200中因数2的个数为511082197=--，故86a 是整数．当92=n 时，=92a C 10369220023-⋅⋅，在C !108!92!20092200⋅=中，同样可求得!92中因数2的个数为88,!108中因数2的个数为105,故C 86200中因数2的个数为410588197=--，故92a 不是整数．因此，整数项的个数为15114=+．9、（2015一试8）对四位数(19,0,,9)abcd a b c d ≤≤≤≤,若,,a b b c c d ><>,则称abcd 为P 类数,若,,a b b c c d <><,则称abcd 为Q 类数,用()N P 与()N Q 分别表示P 类数与Q 类数的个数,则()()N P N Q -的值为【答案】28511..dcba B dcba B A abcd A B ∈∈故反之，每个唯一对应于中的元素这建立了与之间的一一对应，因此有010()()||||||||||||.N P N Q A B A A B A -=-=+-=00||:0,0,19b,A abc A b ∈⋅⋅⋅下面计算对任一四位数可取，，，对其中每个99b a b c <≤<≤由及知，a 和c 分别有9-b 种取法，从而992200191019|=(9)26|85.b k b k ==⨯⨯-===∑∑A ()()285.N P N Q -=因此，10、（2016一试8）设4321,,,a a a a 是1，2，…，100中的4个互不相同的数，满足2433221242322232211)())((a a a a a a a a a a a a ++=++++则这样的有序数组),,,(4321a a a a 的个数为 . 【答案】40【解析】由柯西不等式知，2433221242322232211)())((a a a a a a a a a a a a ++≥++++，等号成立的充分必要条件是433221a a a a a a ==，即4321,,,a a a a 成等比数列.于是问题等价于计算满足{1,2,3,},,,{4321⊆a a a a …,100}的等比数列4321,,,a a a a 的个数.设等比数列的公比1≠q ，且q 为有理数.记mnq =，其中n m ,为互素的正整数，且n m ≠. 先考虑m n >的情况.此时331314)(m n a m n a a ==，注意到33,n m 互素，故31ma l =为正整数. 相应地，4321,,,a a a a 分别等于l n l mn nl m l m 3223,,,，它们均为正整数.这表明，对任意给定的1>=mnq ，满足条件并以q 为公比的等比数列4321,,,a a a a 的个数，即为满足不等式1003≤l n 的正整数l 的个数，即]100[3n . 由于10053>，故仅需考虑34,4,23,3,2=q 这些情况，相应的等比数列的个数为 20113312]64100[]64100[]27100[]27100[]8100[=++++=++++. 当m n <时，由对称性可知，亦有20个满足条件的等比数列4321,,,a a a a . 综上可知，共有40个满足条件的有序数组),,,(4321a a a a .11、（2017一试4）若一个三位数中任意两个相邻数码的差均不超过1，则称其为“平稳数”.平稳数的个数是. 【答案】7512、（2003二试2）设三角形的三边长分别是正整数l ，m ，n ．且l >m >n >0．已知⎩⎨⎧⎭⎬⎫3l104=⎩⎨⎧⎭⎬⎫3m104=⎩⎨⎧⎭⎬⎫3n104，其中{x }=x －[x ]，而[x ]表示不超过x 的最大整数．求这种三角形周长的最小值．∵ x=1，2，时3x ≡∕1(mod 10)，而34≡1(mod 10)，∴ x 必须是4的倍数；∵ x=4，8，12，16时3x ≡∕1(mod 102)，而320≡1(mod 102)，∴ x 必须是20的倍数；∵ x=20，40，60，80时3x ≡∕1(mod 103)，而3100≡1(mod 103)，∴ x 必须是100的倍数；∵ x=100，200，300，400时3x ≡∕1(mod 104)，而3500≡1(mod 104)．即，使3x ≡1(mod 104)成立的最小正整数x=500，从而l －n 、m －n 都是500的倍数，设l －n=500k ，m －n=500h ，(k ，h ∈N*，k >h )．由m +n >l ，即n +500h +n >n +500k ，⇒n >500(k －h )≥500，故n ≥501．取n=501，m=1001，l=1501，即为满足题意的最小三个值． ∴ 所求周长的最小值=3003．13、（2004二试3）对于整数n ≥4，求出最小的整数f (n )，使得对于任何正整数m ，集合{m ，m +1，…，m+n －1}的任一个f (n )元子集中，均至少有3个两两互素的元素．设对于n ≤k ，④成立，当n=k +1时，由于 M (m ，k +1)=M (m ，k －5)∪{m +k －5，m +k －4，…，m +k }．在{m +k －5，m +k －4，…，m +k }中，能被2或3整除的数恰有4个，即使这4个数全部取出，只要在前面的M (m ，k －5)中取出f (n )个数就必有3个两两互质的数．于是当n ≥4时，f (n +6)≤f (n )+4=f (n )+f (6)－1．故f (k +1)≤f (k －5)+f (6)－1=[k+22]+[k+23]－[k+26]+1，比较②，知对于n=k +1，命题成立． ∴对于任意n ∈N *，n ≥4，f (n )= [n+12]+[n+13]－[n+16]+1成立．又可分段写出结果：f (n )= 4k +1，(n=6k ， k ∈N*)，4k +2，(n=6k +1，k ∈N*)，4k +3，(n=6k +2，k ∈N*)，4k +4，(n=6k +3，k ∈N*)，4k +4，(n=6k +4，k ∈N*)，4k +5，(n=6k +5，k ∈N*)．14、（2005二试3）对每个正整数n ，定义函数⎪⎩⎪⎨⎧=.]}{1[,0)(不为平方数当为平方数当n n n n f（其中[x ]表示不超过x 的最大整数，]).[}{x x x -= 试求：∑=2401)(k k f 的值.示例如下：j则)]2()12([)]4()3()[1()]2()1([)()(1121n T n T T T n T T n j T a f ni ni kj +-+++-++==∑∑∑===……②由此，∑∑==+--=1512561)]()12()[16()(k k k T k T k k f ……③记,15,,2,1),2()12( =+-=k k T k T a k 易得k a 的取值情况如下：因此，∑∑===-=151161783)16()(k kk ak k f n……④15、（2006一试14）将2006表示成5个正整数12345,,,,x x x x x 之和. 记15i j i j S x x ≤<≤=∑. 问：（1）当12345,,,,x x x x x 取何值时，S 取到最大值；（2）进一步地，对任意1,5i j ≤≤有2i j x x -≤，当12345,,,,x x x x x 取何值时，S 取到最小值. 说明理由. 【解析】（1）首先这样的S 的值是有界集，故必存在最大值与最小值。

第08讲+解析几何-2009-2017全国高中数学联赛分类汇编

2009-2017全国高中数学联赛分类汇编第08讲：解析几何
1、（2009一试2）已知直线:90L x y +-=和圆22:228810M x y x y +---=，点A 在直线L 上，B ，C 为圆M 上两点，在ABC ∆中，45BAC ∠=︒，AB 过圆心M ，则点A 横坐标范围为．
【答案】[]36，
【解析】设()9A a a -，
，则圆心M 到直线AC 的距离sin45d AM =︒，由直线AC 与圆M 相交，得
d ．解得36a ≤≤．
2、（2009一试5）椭圆22
221x y a b
+=()0a b >>上任意两点P ，Q ，若OP OQ ⊥，则乘积OP OQ ⋅的最小值为．【答案】22
222a b a b
+ 【解析】设()cos sin P OP OP θθ，，ππcos sin 22Q OQ OQ θθ⎛⎫⎛⎫⎛⎫±± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝
⎭，．由P ，Q 在椭圆上，有
222221
cos sin a b OP θθ=+ ① 222221sin cos a b OQ θθ=+ ②
①+②得222211
11a b OP OQ +=+．于是当OP OQ =OP OQ 达到最小值22
222a b a b +．
3、（2010一试3）双曲线12
2=-y x 的右半支与直线100=x 围成的区域内部（不含边界）整点（纵横坐标均为整数的点）的个数是.
【答案】9800
4、（2011一试7）直线012=--y x 与抛物线x y 42=交于B A ,两点，C 为抛物线上的一点，︒=∠90ACB ，。

新课程标准十年(2007-2016)数学试卷分类汇编—三角

∆ABC 中， D 是 BC 上的点， AD 平分 ∠BAC ， ∆ABD 面积是 ∆ADC 面积的 2 倍． sin ∠B (Ⅰ ) 求； sin ∠C
(Ⅱ)若 AD = 1 ， DC =
2 ，求 BD 和 AC 的长． 2
3
新课程标准十年（2007-2016）数学试卷分类汇编—三角
2016 年 10 月 7 日
31．［2014 年高考全国新课标Ⅰ卷理数第 16 题］已知 a, b, c 分别为 ∆ABC 的三个内角 A, B, C 的对边， a =2，且 (2 + b)(sin A − sin B ) = (c − b ) sin C ，则 ∆ABC 面积的最大值为 .
32．［2014 年高考全国新课标Ⅰ卷文数第 2 题］若 tan α > 0 ，则 A. sin α > 0 B. cos α > 0 C. sin 2α > 0 D. cos 2α > 0
1
新课程标准十年（2007-2016）数学试卷分类汇编—三角
2016 年 10 月 7 日
7．［2016 年高考全国新课标Ⅲ卷数学（文）第 9 题］
π 1 , BC 边上的高等于 BC , 则 sin A = 3 （9）在 △ ABC 中，B= 4
3 (A) 10 10 (B) 10 5 (C) 5 3 10 (D) 10
1 3
⎡ ⎣
1⎤ ⎦
⎡ 1 1⎤ ⎣ ⎦
⎡ ⎣
1⎤ ⎦
15．［2016 年高考全国新课标Ⅰ卷数学（文）第 14 题］已知θ是第四象限角，且 sin(θ+
π 3 π )= ，则 tan(θ– )=__________. 4 5 4

第02讲初等数论20092017全国高中数学联赛分类汇编 (1)

2009-2017全国高中数学联赛分类汇编第02讲：初等数论1、（2010一试8）方程2010=++z y x 满足z y x ≤≤的正整数解(,,)x y z 的个数是. 【答案】336675易知 100420096100331⨯=+⨯+k ，所以110033*********-⨯-⨯=k200410052006123200910052006-⨯=-⨯+-⨯=，即3356713343351003=-⨯=k .从而满足z y x ≤≤的正整数解的个数为33667533567110031=++.2、（2011一试8）已知=n a C ())95,,2,1(2162003200=⎪⎪⎭⎫⎝⎛⋅⋅-n nnn ，则数列}{n a 中整数项的个数为．【答案】15 【解析】=n a C65400320020023n n n --⋅⋅．要使)951(≤≤n a n 为整数，必有65400,3200nn --均为整数，从而4|6+n ．当=n 2,8,14,20,26,32,38,44,50,56,62,68,74,80时，3200n -和65400n-均为非负整数，所以n a 为整数，共有14个．当86=n 时，=86a C 5388620023-⋅⋅，在C !114!86!20086200⋅=中，!200中因数2的个数为1972200220022002200220022002200765432=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡，同理可计算得!86中因数2的个数为82，!114中因数2的个数为110，所以C 86200中因数2的个数为511082197=--，故86a 是整数．当92=n 时，=92a C 10369220023-⋅⋅，在C !108!92!20092200⋅=中，同样可求得!92中因数2的个数为88,!108中因数2的个数为105,故C 86200中因数2的个数为410588197=--，故92a 不是整数．因此，整数项的个数为15114=+．3、（2015一试8）对四位数(19,0,,9)abcd a b c d ≤≤≤≤,若,,a b b c c d ><>,则称abcd 为P 类数,若,,a b b c c d <><,则称abcd 为Q 类数,用()N P 与()N Q 分别表示P 类数与Q 类数的个数,则()()N P N Q -的值为【答案】28599b a b c <≤<≤由及知，a 和c 分别有9-b 种取法，从而992200191019|=(9)26|85.b k b k ==⨯⨯-===∑∑A ()()285.N P N Q -=因此，学科@网4、（2016一试8）设4321,,,a a a a 是1，2，…，100中的4个互不相同的数，满足2433221242322232211)())((a a a a a a a a a a a a ++=++++则这样的有序数组),,,(4321a a a a 的个数为 . 【答案】40【解析】由柯西不等式知，2433221242322232211)())((a a a a a a a a a a a a ++≥++++，等号成立的充分必要条件是433221a a a a a a ==，即4321,,,a a a a 成等比数列.于是问题等价于计算满足{1,2,3,},,,{4321⊆a a a a …,100}的等比数列4321,,,a a a a 的个数.设等比数列的公比1≠q ，且q 为有理数.记mn q =，其中n m ,为互素的正整数，且n m ≠. 先考虑m n >的情况.此时331314)(m n a m n a a ==，注意到33,n m 互素，故31ma l =为正整数. 相应地，4321,,,a a a a 分别等于l n l mn nl m l m 3223,,,，它们均为正整数.这表明，对任意给定的1>=mnq ，满足条件并以q 为公比的等比数列4321,,,a a a a 的个数，即为满足不等式1003≤l n 的正整数l 的个数，即]100[3n.由于10053>，故仅需考虑34,4,23,3,2=q 这些情况，相应的等比数列的个数为20113312]64100[]64100[]27100[]27100[]8100[=++++=++++. 当m n <时，由对称性可知，亦有20个满足条件的等比数列4321,,,a a a a . 综上可知，共有40个满足条件的有序数组),,,(4321a a a a .5、（2017一试4）若一个三位数中任意两个相邻数码的差均不超过1，则称其为“平稳数”.平稳数的个数是. 【答案】756、（2009二试3）设k ，l 是给定的两个正整数．证明：有无穷多个正整数m k ≥，使得C k m 与l 互素．【解析】证法一：对任意正整数t ，令(!)m k t l k =+⋅⋅．我们证明()C 1k m l =，．设p 是l 的任一素因子，只要证明：p/|C k m ．若p /|k !，则由1!C ()kkmi k m k i ==-+∏1[((!)]ki i tl k =≡+∏1ki i =≡∏()1!mod k p α+≡．及|!p k α，且pα+1/|k !，知|!C k m p k α且1α+p /|!C k m k ．从而p/|C km ．证法二：对任意正整数t ，令2(!)m k t l k =+⋅⋅，我们证明()C 1k m l =，．设p 是l 的任一素因子，只要证明：p/|C k m ．若p /|k !，则由 1!C ()==-+∏kkmi k m k i 21[((!)]ki i tl k =≡+∏1ki i =≡∏()!mod k p ≡．即p 不整除上式，故p/|C k m ．若|!p k ，设1α≥使|!p k α，但1/|!p k α+．12|(!)p k α+．故由11!C ()k kmi k m k i -==-+∏21[((!)]ki i tl k =≡+∏1ki i =≡∏()1!mod k p α+≡,及|!p k α，且pα+1/|k !，知|!C k m p k α且1α+p /|!C k m k ．从而p/|C km ．7、（2009二试4）在非负数构成的39⨯数表中每行的数互不相同，前6列中每列的三数之和为1，1728390x x x ===，27x ，37x ，18x ，38x ，19x ，29x 均大于．如果P 的前三列构成的数表111213212223313233x x x S x x x x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭满足下面的性质()O ：对于数表P 中的任意一列123k k k x x x ⎛⎫⎪⎪ ⎪⎝⎭（1k =，2，…，9）均存在某个{}123i ∈，，使⑶{}123min ik i i i i x u x x x =≤，，．求证：（ⅰ）最小值{}123min i i i i u x x x =，，，1i =，2，3一定自数表S 的不同列．（ⅱ）存在数表P 中唯一的一列***123k k k x x x ⎛⎫⎪⎪ ⎪ ⎪⎝⎭，*1k ≠，2，3使得33⨯数表***111212122231323k k k x x x S x x x x x x ⎛⎫ ⎪'= ⎪ ⎪ ⎪⎝⎭仍然具有性质()O ．【解析】（ⅰ）假设最小值{}123min i i i i u x x x =，，，1i =，2，3不是取自数表S 的不同列．则存在一列不含任何i u ．不妨设2i i u x ≠，1i =，2，3．由于数表P 中同一行中的任何两个元素都不等，于是2i i u x <，1i =，2，3．另一方面，由于数表S 具有性质()O ，在⑶中取2k =，则存在某个{}0123i ∈，，使得002i i x u ≤．矛盾．（ⅱ）由抽届原理知，{}1112min x x ，，{}2122min x x ，，{}3132min x x ，中至少有两个值取在同一列．不妨设{}212222min x x x =，，{}313232min x x x =，．由前面的结论知数表S 的第一列一定含有某个i u ，所以只能是111x u =．同样，第二列中也必含某个i u ，1i =，2．不妨设222x u =．于是333u x =，即i u 是数表S 中的对角线上数字．下面证明33⨯数表***111212122231323k k k x x x S x x x x x x ⎛⎫ ⎪'= ⎪ ⎪ ⎪⎝⎭具有性质()O ．从上面的选法可知{}{}*1212:min min i i i i i ik u x x x x x '==，，，，(13)i =，．这说明{}*111211min k x x x u >，≥，{}*313233min k x x x u >，≥．又由S 满足性质()O ．在⑶中取*k k =，推得*22k x u ≤，于是{}**2212222min k k u x x x x '==，，．下证对任意的k M ∈，存在某个1i =，2，3使得i ik u x '≥．假若不然，则{}12min ik i i x x x >，，1i =，3且*22k k x x >．这与*2k x 的最大性矛盾．因此，数表S '满足性质()O ．下证唯一性．设有k M ∈使得数表111212122231323k k k x x x S x x x x x x ⎛⎫⎪= ⎪ ⎪⎝⎭具有性质()O ，不失一般性，我们假定⑷{}221222322min u x x x x ==，， 3231x x <．由于3231x x <，2221x x <及（ⅰ），有{}11112111min k u x x x x ==，，．又由（ⅰ）知：或者()a {}3313233min k k u x x x x ==，，，或者{}2212222()min k k b u x x x x ==，，．如果()a 成立，由数表S 具有性质()O ，则{}11112111min k u x x x x ==，，，⑸{}22122222min k u x x x x ==，，， {}3313233min k k u x x x x ==，，．由数表S 满足性质()O ，则对于3M ∈至少存在一个{}123i ∈，，使得*i ik u x ≥．由*k I ∈及⑷和⑹式知，*1111k x x u >=，*3323k x x u >=．于是只能有*222k k x u x =≤．类似地，由S '满足性质()O 及k M ∈可推得*222k k x u x '=≤．从而*k k =．学*科网 8、（2010一试11）证明：方程02523=-+x x 恰有一个实数根r ，且存在唯一的严格递增正整数数列}{n a ，使得+++=32152a a a r r r . 若存在两个不同的正整数数列 <<<<n a a a 21和 <<<<nb b b 21满足52321321=+++=+++ b b b a a a r r r r r r ，去掉上面等式两边相同的项，有 +++=+++321321t t t s s s r r r r r r，这里 <<<<<<321321,t t t s s s ，所有的i s 与j t 都是不同的. 不妨设11t s <，则 ++=++<21211t t s s s r r r r r，112111111121211=--<--=++≤++<--rr r r r s t s t ，矛盾.故满足题设的数列是唯一的.9、（2010二试2）设k 是给定的正整数，12r k =+．记(1)()()f r f r r r ==⎡⎤⎢⎥，()()l f r =(1)(()),2l f f r l -≥．证明：存在正整数m ，使得()()m f r 为一个整数．这里，x ⎡⎤⎢⎥表示不小于实数x 的最小整数，例如：112⎡⎤=⎢⎥⎢⎥，11=⎡⎤⎢⎥．【解析】记2()v n 表示正整数n 所含的2的幂次．则当2()1m v k =+时，()()m f r 为整数．下面我们对2()v k v =用数学归纳法．当0v =时，k 为奇数，1k +为偶数，此时()111()1222f r k k k k ⎛⎫⎡⎤⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎢⎥⎝⎭为整数．假设命题对1(1)v v -≥成立．对于1v ≥，设k 的二进制表示具有形式1212222v v v v v k αα++++=+⋅+⋅+，这里，0i α=或者1，1,2,i v v =++．于是 ()111()1222f r k k k k ⎛⎫⎡⎤⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎢⎥⎝⎭2122k k k =+++ 11211212(1)2()222v v v v v v v ααα-++++=+++⋅++⋅+++12k '=+， ① 这里1121122(1)2()22v v v v v v v k ααα-++++'=++⋅++⋅+++.显然k '中所含的2的幂次为1v -．故由归纳假设知，12r k ''=+经过f 的v 次迭代得到整数，由①知，(1)()v f r +是一个整数，这就完成了归纳证明．10、（2010二试4）一种密码锁的密码设置是在正n边形12nA A A的每个顶点处赋值0和1两个数中的一个，同时在每个顶点处涂染红、蓝两种颜色之一，使得任意相邻的两个顶点的数字或颜色中至少有一个相同．问：该种密码锁共有多少种不同的密码设置？设标有a的边有2i条，02ni⎡⎤≤≤⎢⎥⎣⎦，标有b的边有2j条，22n ij-⎡⎤≤≤⎢⎥⎣⎦．选取2i条边标记a的有2inC种方法，在余下的边中取出2j条边标记b的有22jn iC-种方法，其余的边标记c．由乘法原理，此时共有2inC22jn iC-种标记方法．对i，j求和，密码锁的所有不同的密码设置方法数为222222004n n ii jn n ii jC C-⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦-==⎛⎫⎪⎪⎪⎝⎭∑∑．①这里我们约定01C=．当n为奇数时，20n i->，此时2222122n ij n in ijC-⎡⎤⎢⎥⎣⎦---==∑．②代入①式中，得()()2222222221222000044222n n i n ni j i n i i n in n i n ni j i iC C C C-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦----====⎛⎫⎪==⎪⎪⎝⎭∑∑∑∑0022(1)(21)(21)n nk n k k n k k n nn nk kC C--===+-=++-∑∑31n=+．222222004n n ii jn n ii jC C-⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦-==⎛⎫⎪=⎪⎪⎝⎭∑∑()12221412ni n iniC⎡⎤-⎢⎥⎣⎦--=⎛⎫⎪⨯+⎪⎪⎝⎭∑()222124233ni n i nniC⎡⎤⎢⎥⎣⎦--==+=+∑．综上所述，这种密码锁的所有不同的密码设置方法数是：当n 为奇数时有31n +种；当n 为偶数时有33n +种．11、（2011二试2）证明：对任意整数4≥n ，存在一个n 次多项式具有如下性质：（1）110,,,-n a a a 均为正整数；（2）对任意正整数m ，及任意)2(≥k k 个互不相同的正整数k r r r ,,,21 ，均有)()()()(21k r f r f r f m f ≠．【解析】令 2)()2)(1()(++++=n x x x x f ， ①将①的右边展开即知)(x f 是一个首项系数为1的正整数系数的n 次多项式．下面证明)(x f 满足性质（2）．对任意整数t ，由于4≥n ，故连续的n 个整数n t t t +++,,2,1 中必有一个为4的倍数，从而由①知)4(mod 2)(≡t f ．因此，对任意)2(≥k k 个正整数k r r r ,,,21 ，有 )4(mod 02)()()(21≡≡k k r f r f r f ．但对任意正整数m ，有)4(mod 2)(≡m f ，故)4)(mod ()()()(21k r f r f r f m f ≡/，从而)()()()(21k r f r f r f m f ≠．所以)(x f 符合题设要求．学&科网12、（2011二试3）设)4(,,,21≥n a a a n 是给定的正实数，n a a a <<< 21．对任意正实数r ，满足)1(n k j i r a a a a j k ij ≤<<≤=--的三元数组),,(k j i 的个数记为)(r f n ．证明：4)(2n r f n <．因此，当n 为偶数时，设m n 2=，则有∑∑∑-=-=-=+==121212)()()()(m mj j m j j n j j n r g r g r g r f2)1(2)1()2()1(1212-+-=-+-≤∑∑-+==m m m m j m j m m j m j 4222n m m m =<-=．当n 为奇数时，设12+=m n ，则有∑∑∑+==-=+==mm j jmj j n j j n r gr g r g r f 21212)()()()(∑∑+==-++-≤mm j mj j m j 212)12()1(422n m <=．13、（2011二试4）设A 是一个93⨯的方格表，在每一个小方格内各填一个正整数．称A 中的一个)91,31(≤≤≤≤⨯n m n m 方格表为“好矩形”，若它的所有数的和为10的倍数．称A 中的一个11⨯的小方格为“坏格”，若它不包含于任何一个“好矩形”．求A 中“坏格”个数的最大值．【解析】首先证明A 中“坏格”不多于25个．用反证法．假设结论不成立，则方格表A 中至多有1个小方格不是“坏格”．由表格的对称性，不妨假设此时第1行都是“坏格”．设方格表A 第i 列从上到下填的数依次为9,,2,1,,, =i c b a i i i ．记9,,2,1,0,)(,11=+==∑∑==k c bT a S ki i ikk i ik ，这里000==T S ．即第2行至第3行、第1+m 列至第n 列组成一个“好矩形”，从而至少有2个小方格不是“坏格”，矛盾．类似地，也不存在90,,≤<≤n m n m ，使)10(mod n n m m T S T S +≡+．因此上述断言得证．故)10(mod 59210)(999≡++++≡+≡≡∑∑∑=== k k k k k k k T S T S ，所以 )10(mod 055)(99090≡+≡+≡+∑∑∑===k k k k k k k T S T S ，矛盾！故假设不成立，即“坏格”不可能多于25个．另一方面，构造如下一个93⨯的方格表，可验证每个不填10的小方格都是“坏格”，此时有25个“坏格”．综上所述，“坏格”个数的最大值是25．14、（2012二试2）试证明：集合{}22,2,,2,n A =满足b N *∈，若21b a <-，（１）对每个a A ∈，及则(1)b b +一定不是2a的倍数；（２）对每个a A ∈（其中A 表示A 在Ｎ中的补集），且1a ≠，必存在b N *∈，21b a <-，使(1)b b +是2a 的倍数．【解析】证明:对任意的a A ∈,设2,,ka k N *=∈则122,k a +=如果b 是任意一个小于21a -的正整数,则1 1 12 1 1 1 1 10 1 1 1 1 1 1 1 1 1 1111011112121b a+≤-则122ka m+=⋅下面给出(2)的三种证明方法:证法一:令1,12,kb mx b y+=+=消去b得12 1.k y mx+-=由于1(2,)1,k m+=这方程必有整数解;12kx x ty y mt+⎧=+⎪⎨=+⎪⎩其中00,(,)t z x y∈为方程的特解.把最小的正整数解记为(,),x y**则12kx*+<,故21,b mx a*=<-使(1)b b+是2a的倍数．证法二:由于1(2,)1,k m+=由中国剩余定理知,同余方程组10(mod2)1(mod)kxx m m+⎧=⎨=-⎩在区间1(0,2)k m+上有解,x b=即存在21,b a<-使(1)b b+是2a的倍数．证法三:由于(2,)1,m=总存在(,1),r r N r m*∈≤-使21(mod)r m=取,t N*∈使1,tr k>+则21(mod)tr m=存在1(21)(2)0,,tr kb q m q N+=--⋅>∈使021,b a<<-此时1,21,km b m++因而(1)b b+是2a的倍数．15.（2013二试4）（本题满分50分）设,n k为大于1的整数，2kn<.证明：存在2k个不被n整除的整数，若将它们任意分成两组，则总有一组若干个数的和被n整除.【证明】先考虑n为2的幂的情形.设2,1rn r=≥，则r k<.取3个12r-及23k-个1，显然这些数均不被n整除.将这2k个数任意分成两组，则总有一组中含2个12r-，它们的和为2r，被n整除.现在设n不是2的幂，取2k个数为22211,1,2,2,,2,1,2,2,,2k k-------，因为n不是2的幂，故上述2k个数均不被n整除.若可将这些数分成两组，使得每一组中任意若干个数的和均不能被n整除.不妨设1在第一组，由于（-1）+1=0，被n整除，故两个-1必须在第二组；因（-1）+（-1）+2=0，被n整除，故2在第一组，进而推出-2在第二组. 现归纳假设1,2,,2l 均在第一组，而1,1,2,,2l ----均在第二组，这里12l k ≤<-，由于()()()()1112220l l +-+-+-++-+=，被n 整除，故12l +在第一组，从而12l +-在第二组.故由数学归纳法可知，221,2,2,,2k -在第一组，221,1,2,2,,2k ------在第二组.最后，由于()()()()21112220k k ---+-+-++-+=，16、（2014二试4）（本题满分50分）设整数122014,,,2014x x x 模互不同余，122014,,,y y y 整数模2014也互不同余.证明：可将122014,,,y y y 重新排列为122014,,,z z z ，使得112220142014,,,x z x z x z +++模4028互不同余.【证明】(mod 2),12.,i i y i k i k i ≡≡≤≤记k=1007,不妨设x 对每个整数17、（2015二试4）(本题满分50分)求具有下述性质的所有正整数k :对任意正整数(1)1,2k n n -+不整除()!!kn n . 18、（2016二试3）（本题满分50分）给定空间中10个点，其中任意四点不在一个平面上，将某些点之间的线段相连，若得到的图形中没有三角形也没有空间四边形，试确定所连线段数目的最大值.【解析】以这10个点为顶点，所连线段为边，得到一个10界简单图G ，我们证明G 的边数不超过15.边，否则就形成三角形，所以，121,,,n v v v +⋅⋅⋅之间恰有n 条边.对每个j (210)n j +≤≤，j v 至多与21,,n v v +⋅⋅⋅中的一个顶点相邻（否则设j v 与,(21)s t v v s t n ≤<≤+）相邻，则1,,,s j t v v v v 就对应了一个空间四边形的四个顶点，这与题设条件矛盾，从而21,,n v v +⋅⋅⋅与210,,n v v +⋅⋅⋅之间的边数至多10(1)9n n -+=-条.在210,,n v v +⋅⋅⋅这9n -个顶点之间，由于没有三角形，由托兰定理，至多2(9)[]4n -条边，因此G 的边数22(9)(9)25(9)[]9[]9[]15444n n k n n --≤+-+=+≤+=百度文库 - 让每个人平等地提升自我11 如图给出的图共有15条边，且满足要求，综上所述，所求边数的最大值为15.学科*网19、（2017二试3）（本题满分50分）将33×33方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等，若相邻两个小方格的颜色不同，则称它们的公共边为“分隔边”.试求分隔边条数的最小值.解：记分隔边的条数为L ，首先，将方格纸按如图分成三个区域，分别染成三种颜色，粗线上均为分隔边，此时共有56个分隔边，即L=56.20、（2017二试4）（本题满分50分）设,m n 均是大于1的整数，12.,,,n m n a a a ≥是n 个不超过m 的互不相同的正整数，且12,,,n a a a 互素.证明：对任意实数x ，均存在一个(1)i i n ≤≤，使得2||||||||(1)i a x x m m ≥+，这里||||y 表示实数y 到它最近的整数的距离. 证明：首先证明以下两个结论.结论1:存在整数121122,,,,+++c 1,||,1.n n n i c c c c a c a a c m i n =≤≤≤满足并且由于121211221,,,+++c 1.1n n n n a a a c c c c a c a a ==（，，，），由裴蜀定理，存在整数，满足（）下面证明,通过调整,存在一组12,,,n c c c 满足（1），且绝对值均不超过m,记因为12S 与S 均是非负整数,故通过有限次上述的调整,可得到一组12,,,n c c c ，。

2011年—2017年新课标全国卷1文科数学分类汇编—三角函数、解三角形

新课标全国卷Ⅰ文科数学分类汇编——三角函数、解三角形（含解析）一、选择题【2017，11】△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ．已知sin sin (sin cos )0B A C C +-=，a=2，则C=( ) A ．π12B ．π6C ．π4D ．π3【2016，4】ABC △的内角A B C ,,的对边分别为a b c ,,．已知a =2c =，2cos 3A =，则b =（）A ．B C ．2 D ．3【2016，6】若将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期后，所得图像对应的函数为（）． A ．π2sin 24y x ⎛⎫=+⎪⎝⎭ B ．π2sin 23y x ⎛⎫=+ ⎪⎝⎭ C ．π2sin 24y x ⎛⎫=- ⎪⎝⎭ D ．π2sin 23y x ⎛⎫=- ⎪⎝⎭【2015，8】函数f (x )=cos(ωx +φ)的部分图像如图所示，则f (x )的单调递减区间为( )A ．13(,),44k k k Z ππ-+∈B ．13(2,2),44k k k Z ππ-+∈ C ．13(,),44k k k Z -+∈ D ．13(2,2),44k k k Z -+∈ 【2014，7】在函数① y=cos|2x|，②y=|cos x |，③)62cos(π+=x y ，④)42tan(π-=x y 中，最小正周期为π的所有函数为( )A ．①②③B ．①③④C ．②④D ．①③【2014，2】若tan 0α>，则（）A ． sin 0α>B ． cos 0α>C ． sin 20α>D ． cos 20α>【2013，10】已知锐角△ABC 的内角A ，B ，C 的对边分别为a ，b ，c,23cos 2A ＋cos 2A ＝0，a ＝7，c ＝6，则b ＝( )A ．10B ．9C ．8D ．5 【2012，9】9．已知0ω>，0ϕπ<<，直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴，则ϕ=（） A ．4π B ．3π C ．2πD ．34π 【2011，7】已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=（）．A ．45-B ．35-C ．35D ．45【2011，11】设函数ππ()sin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭，则（） A ．()f x 在π0,2⎛⎫⎪⎝⎭单调递增，其图象关于直线π4x =对称 B ．()f x 在π0,2⎛⎫⎪⎝⎭单调递增，其图象关于直线π2x =对称 C ．()f x 在π0,2⎛⎫⎪⎝⎭单调递减，其图象关于直线π4x =对称 D ．()f x 在π0,2⎛⎫⎪⎝⎭单调递减，其图象关于直线π2x =对称二、填空题【2017，15】已知0,2πα⎛⎫∈ ⎪⎝⎭，tan 2α=，则cos 4πα⎛⎫-= ⎪⎝⎭________．【2016，】14．已知θ是第四象限角，且π3sin 45θ⎛⎫+= ⎪⎝⎭，则πtan 4θ⎛⎫-= ⎪⎝⎭．【2013，16】设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝______．【2014，16】如图所示，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点．从A 点测得M 点的仰角60MAN ∠=︒，C 点的仰角 45CAB ∠=︒以及75MAC ∠=︒；从C 点测得60MCA ∠=︒．已知山高100BC m =，则山高MN = m ．【2011，15】ABC △中，120B =，7AC =，5AB =，则ABC △的面积为．三、解答题【2015，17】已知,,a b c 分别为ABC △内角,,A B C 的对边，2sin 2sin sin B A C =．（1）若a b =，求cos B ；（2）设90B ∠=，且a =ABC △的面积．【2012，17】已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，sin cos c C c A =-．（1）求A ；（2）若2a =，△ABC b ，c ．新课标全国卷Ⅰ文科数学分类汇编 4．三角函数、解三角形（解析版）一、选择题【2017，11】△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ．已知sin sin (sin cos )0B A C C +-=，a=2，则C=( ) A ．π12B ．π6C ．π4D ．π3【答案】B【解法】解法一：因为sin sin (sin cos )0B A C C +-=，sin sin()B A C =+，所以sin (sin cos )0C A A +=，又sin 0C >，所以sin cos A A =-，tan 1A =-，又0A π<<，所以34A π=，又a =2，c=即1sin 2C =．又02C π<<，所以6C π=，故选B ．解法二：由解法一知sin cos 0A A +=)04A π+=，又0A π<<，所以34A π=．下同解法一．【2016，4】ABC △的内角A B C ,,的对边分别为a b c ,,．已知a =2c =，2cos 3A =，则b =（） A ．BC ．2D ．3解析：选D ．由余弦定理得222cos 2b c a A bc +-=，即245243b b +-=，整理得()28113033b b b b ⎛⎫--=-+= ⎪⎝⎭，解得3b =．故选D ．【2016，6】若将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期后，所得图像对应的函数为（）． A ．π2sin 24y x ⎛⎫=+⎪⎝⎭ B ．π2sin 23y x ⎛⎫=+ ⎪⎝⎭ C ．π2sin 24y x ⎛⎫=- ⎪⎝⎭ D ．π2sin 23y x ⎛⎫=- ⎪⎝⎭解析：选D ．将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期，即向右平移π4个单位，故所得图像对应的函数为ππ2sin 246y x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦π2sin 23x ⎛⎫=- ⎪⎝⎭．故选D ．【2015，8】函数f (x )=cos(ωx +φ)的部分图像如图所示，则f (x )的单调递减区间为( ) A ．13(,),44k k k Z ππ-+∈ B ．13(2,2),44k k k Z ππ-+∈C ．13(,),44k k k Z -+∈ D ．13(2,2),44k k k Z -+∈ 解：选D ．依图，153++4242ππωϕωϕ==且，解得ω=π，=4πϕ， ()cos()4f x x ππ∴=+，224k x k πππππ<+<+由，，解得132244k x k -<<+，故选D ．【2014，7】在函数① y=cos|2x|，②y=|cos x |，③)62cos(π+=x y ，④)42tan(π-=x y 中，最小正周期为π的所有函数为( )A ．①②③B ．①③④C ．②④D ．①③解：选A ．由cos y x =是偶函数可知①y=cos|2x|=cos2x ，最小正周期为π；②y=|cos x |的最小正周期也是π；③中函数最小正周期也是π；正确答案为①②③，故选A【2014，2】若tan 0α>，则（）A ． sin 0α>B ． cos 0α>C ． sin 20α>D ． cos 20α>解：选C ．tan α>0，α在一或三象限，所以sin α与cos α同号，故选C【2013，10】已知锐角△ABC 的内角A ，B ，C 的对边分别为a ，b ，c,23cos 2A ＋cos 2A ＝0，a ＝7，c ＝6，则b ＝( )．A ．10B ．9C ．8D ．5解析：选D ．由23cos 2A ＋cos 2A ＝0，得cos 2A ＝125．∵A ∈π0,2⎛⎫⎪⎝⎭，∴cos A ＝15．∵cos A ＝2364926b b+-⨯，∴b ＝5或135b =-(舍)．【2012，9】9．已知0ω>，0ϕπ<<，直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴，则ϕ=（）A ．4πB ．3πC ．2π D ．34π【解析】选A ．由直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴，得()sin()f x x ωϕ=+的最小正周期52()244T πππ=-=，从而1ω=．由此()sin()f x x ϕ=+，由已知4x π=处()sin()f x x ϕ=+取得最值，所以sin()14πϕ+=±，结合选项，知ϕ=4π，故选择A ．【2011，7】已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=（）．A ．45-B ．35-C ．35D ．45【解析】设(,2)(0)P t t t ≠为角θ终边上任意一点，则cosθ=．当0t >时，cos 5θ=；当0t <时，cos 5θ=．因此223cos 22cos 1155θθ=-=-=-．故选B ．【2011，11】设函数ππ()sin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭，则（） A ．()f x 在π0,2⎛⎫⎪⎝⎭单调递增，其图象关于直线π4x =对称 B ．()f x 在π0,2⎛⎫⎪⎝⎭单调递增，其图象关于直线π2x =对称 C ．()f x 在π0,2⎛⎫⎪⎝⎭单调递减，其图象关于直线π4x =对称 D ．()f x 在π0,2⎛⎫⎪⎝⎭单调递减，其图象关于直线π2x =对称【解析】因为ππππ()sin 2cos 2224444f x x x x x ⎛⎫⎛⎫⎛⎫=+++=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，当π02x <<时，02πx <<，故()f x x =在π0,2⎛⎫⎪⎝⎭单调递减．又当π2x =π22⎛⎫⨯= ⎪⎝⎭π2x =是()y f x =的一条对称轴．故选D ．二、填空题【2017，15】已知0,2πα⎛⎫∈ ⎪⎝⎭，tan 2α=，则cos 4πα⎛⎫-= ⎪⎝⎭________．．0,2πα⎛⎫∈ ⎪⎝⎭，sin tan 22sin 2cos cos ααααα=⇒=⇒=，又22sin cos 1αα+=，解得sin 5α=，cos 5α=，cos (cos sin )4210πααα⎛⎫∴-=+= ⎪⎝⎭．【基本解法2】0,2πα⎛⎫∈ ⎪⎝⎭Q ，tan 2α=，∴角α的终边过(1,2)P ，故sin 5y r α==，cos x r α==r ==，cos (cos sin )42πααα⎛⎫∴-=+=⎪⎝⎭．【2016，】14．已知θ是第四象限角，且π3sin 45θ⎛⎫+= ⎪⎝⎭，则πtan 4θ⎛⎫-= ⎪⎝⎭．解析：43-．由题意sin sin 442θθπππ⎡⎤⎛⎫⎛⎫+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦3cos 45θπ⎛⎫=-= ⎪⎝⎭．因为2222k k θ3ππ+<<π+π()k ∈Z ，所以722444k k θ5ππππ+<-<π+()k ∈Z ，从而4sin 45θπ⎛⎫-=- ⎪⎝⎭，因此4tan 43θπ⎛⎫-=- ⎪⎝⎭．故填43-．方法2：还可利用ππtan tan 144θθ⎛⎫⎛⎫-+=- ⎪ ⎪⎝⎭⎝⎭来进行处理，或者直接进行推演，即由题意4cos 45θπ⎛⎫+= ⎪⎝⎭，故3tan 44θπ⎛⎫+= ⎪⎝⎭，所以tan 4θπ⎛⎫-= ⎪⎝⎭143tan 4θ-=-π⎛⎫+ ⎪⎝⎭．【2013，16】设当x ＝θ时，函数f (x )＝sin x －2cos x 取得最大值，则cos θ＝______．答案：解析：． ∵f (x )＝sin x －2cos xx －φ)，其中sin φcos φ当x －φ＝2k π＋π2(k ∈Z)时，f (x )取最大值．即θ－φ＝2k π＋π2(k ∈Z)，θ＝2k π＋π2＋φ(k ∈Z)．∴cos θ＝πcos 2ϕ⎛⎫+ ⎪⎝⎭＝－sin φ＝．【2014，16】16．如图所示，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点．从A 点测得M点的仰角60MAN ∠=︒，C 点的仰角45CAB ∠=︒以及 75MAC ∠=︒；从C 点测得60MCA ∠=︒．已知山高100BC m =，则山高MN = m ．解：在RtΔABC中，由条件可得AC =，在ΔMAC 中，∠MAC=45°；由正弦定理可得sin 60sin 45AM AC =︒︒，故310032AM =，在直角RtΔMAN 中，MN=AM sin60°=150．【2011，15】ABC △中，120B =，7AC =，5AB =，则ABC △的面积为．【解析】由余弦定理知2222cos120AC AB BC AB BC =+-⋅，即249255BC BC =++，解得3BC =．故11sin1205322ABC S AB BC =⋅=⨯⨯=△．．三、解答题【2015，17】已知,,a b c 分别为ABC △内角,,A B C 的对边，2sin 2sin sin B A C =．（1）若a b =，求cos B ；（2）设90B ∠=，且a =ABC △的面积．解析：（1）由正弦定理得，22b ac =．又a b =，所以22a ac =，即2a c =．则22222212cos 2422a a a a cb B a ac a ⎛⎫+- ⎪+-⎝⎭===⋅．（2）解法一：因为90B ∠=，所以()2sin 12sin sin 2sin sin 90B A C A A ===-，即2sin cos 1A A =，亦即sin 21A =．又因为在ABC △中，90B ∠=，所以090A <∠<，则290A ∠=，得45A ∠=．所以ABC △为等腰直角三角形，得a c ==，所以112ABC S ==△．解法二：由（1）可知22b ac =，①因为90B ∠=，所以222a cb +=，②将②代入①得()20a c -=，则a c =，所以112ABC S ==△．解：(Ⅰ) 因为sin 2B =2sin A sin C ．由正弦定理可得b 2=2ac ．又a =b ，可得a=2c ， b=2c ，由余弦定理可得2221cos 24a cb B ac +-==． (Ⅱ)由(Ⅰ)知b 2=2ac ．因为B=90°，所以a 2+c 2=b 2=2ac ．解得a =所以ΔABC 的面积为1．【2012，17】已知a ，b ，c 分别为△ABC 三个内角A ，B ，C的对边，sin cos c C c A =-．（1）求A ；（2）若2a =，△ABCb ，c ．【解析】（1）根据正弦定理2sin sin a cR A C==，得A R a sin 2=， C R c sin 2=，因为sin cos c C c A =-，所以2sin sin )sin 2sin cos R C R A C R C A =-⋅，化简得C C A C A sin sin cos sin sin 3=-，因为0sin ≠C ，所以1cos sin 3=-A A ，即21)6sin(=-πA ，而π<<A 0，6566πππ<-<-A ，从而66ππ=-A ，解得3π=A ．（2）若2a =，△ABC1）得3π=A ，则⎪⎪⎩⎪⎪⎨⎧==-+=43cos 233sin 21222a bc c b bc ππ，化简得⎩⎨⎧=+=8422c b bc ，从而解得2=b ，2=c ．。

第08讲解析几何-2009-2017全国高中数学联赛分类汇编含解析

2009-2017全国高中数学联赛分类汇编第08讲：解析几何1、（2009一试2)已知直线:90L x y +-=和圆22:228810M x y x y +---=，点A 在直线L 上，B ，C 为圆M 上两点，在ABC ∆中，45BAC ∠=︒，AB 过圆心M ，则点A横坐标范围为．【答案】[]36，【解析】设()9A a a -，，则圆心M 到直线AC 的距离sin 45d AM =︒，由直线AC 与圆M 相交，得d 36a ≤≤．2、（2009一试5)椭圆22221x y a b+=()0a b >>上任意两点P ，Q ,若OP OQ ⊥，则乘积OP OQ ⋅的最小值为．【答案】22222a b a b + 【解析】设()cos sin P OP OP θθ，，ππcos sin 22Q OQ OQ θθ⎛⎫⎛⎫⎛⎫±± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，．由P ，Q 在椭圆上，有222221cos sin a b OP θθ=+ ①222221sin cos a b OQ θθ=+ ②①+②得22221111a b OP OQ+=+．于是当OP OQ ==时，OP OQ 达到最小值22222a b a b +．3、(2010一试3）双曲线122=-y x 的右半支与直线100=x 围成的区域内部（不含边界)整点（纵横坐标均为整数的点）的个数是.【答案】98004、（2011一试7）直线012=--y x 与抛物线xy 42=交于B A ,两点,C 为抛物线上的一点,︒=∠90ACB ，则点C 的坐标为．【答案】)2,1(-或)6,9(-即0)(24)(21212212214=⋅++-+⋅++-y y t y y t x x t x x t ，即03161424=---t t t，即0)14)(34(22=--++t t t t．显然0142≠--t t，否则01222=-⋅-t t，则点C 在直线012=--y x 上,从而点C 与点A或点B 重合．所以0342=++t t，解得3,121-=-=t t．故所求点C 的坐标为)2,1(-或)6,9(-．5、（2012一试4)抛物线22(0)ypx p =>的焦点为F，准线为ｌ，,A B 是抛物线上的两个动点，且满足3AFB π∠=．设线段ＡＢ的中点M 在ｌ上的投影为N ，则||||MN AB 的最大值是.【答案】1【解析】由抛物线的定义及梯形的中位线定理得.2AF BFMN +=在AFB ∆中,由余弦定理得2222cos3ABAF BF AF BF π=+-⋅2()3AF BF AF BF =+-⋅22()3()2AF BF AF BF +≥+-22().2AF BF MN +==当且仅当AF BF =时等号成立。

计数原理-2009-2017全国高中数学联赛分类汇编(Word版含解析)

2009-2017全国高中数学联赛分类汇编第06讲：计数原理1、（2010一试8）方程2010=++z y x 满足z y x ≤≤的正整数解(,,)x y z 的个数是. 【答案】336675易知 100420096100331⨯=+⨯+k ，所以110033*********-⨯-⨯=k200410052006123200910052006-⨯=-⨯+-⨯=，即3356713343351003=-⨯=k .从而满足z y x ≤≤的正整数解的个数为33667533567110031=++.2、（2011一试5）现安排7名同学去参加5个运动项目，要求甲、乙两同学不能参加同一个项目，每个项目都有人参加，每人只参加一个项目，则满足上述要求的不同安排方案数为．（用数字作答）【答案】15000【解析】由题设条件可知，满足条件的方案有两种情形：（1）有一个项目有3人参加，共有3600!5!51537=⋅-⋅C C 种方案；（2）有两个项目各有2人参加，共有11400!5!5)(21252527=⋅-⋅⋅C C C 种方案；所以满足题设要求的方案数为15000114003600=+．3、（2011一试8）已知=n a C ())95,,2,1(2162003200=⎪⎪⎭⎫⎝⎛⋅⋅-n nnn ，则数列}{n a 中整数项的个数为．【答案】15 【解析】=n a C65400320020023n n n--⋅⋅．要使)951(≤≤n a n 为整数，必有65400,3200nn --均为整数，从而4|6+n ．当=n 2,8,14,20,26,32,38,44,50,56,62,68,74,80时，3200n -和65400n-均为非负整数，所以n a 为整数，共有14个．当86=n 时，=86a C 5388620023-⋅⋅，在C !114!86!20086200⋅=中，!200中因数2的个数为1972200220022002200220022002200765432=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡，同理可计算得!86中因数2的个数为82，!114中因数2的个数为110，所以C 86200中因数2的个数为511082197=--，故86a 是整数．当92=n 时，=92a C 10369220023-⋅⋅，在C !108!92!20092200⋅=中，同样可求得!92中因数2的个数为88,!108中因数2的个数为105,故C 86200中因数2的个数为410588197=--，故92a 不是整数．因此，整数项的个数为15114=+．4、（2013一试6）从1,2，…，20中任取5个不同的数，其中至少有两个是相邻数的概率为. 【答案】2323235、（2015一试8）对四位数(19,0,,9)abcd a b c d ≤≤≤≤,若,,a b b c c d ><>,则称abcd 为P 类数,若,,a b b c c d <><,则称a b c d 为Q 类数,用()N P 与()N Q 分别表示P 类数与Q 类数的个数,则()()N P N Q -的值为【答案】285【解析】分别记P 类数、Q 类数的全体为A,B ，再将个位数为零的P 类数全体记为0A ,个位数不等于零的P 类数全体记为1A .1,,,,1,abcd A dcba a b b c c d ∈><>≥对任一四位数将其对应到四位数注意到11..dcba B dcba B A abcd A B ∈∈故反之，每个唯一对应于中的元素这建立了与之间的一一对应，因此有010()()||||||||||||.N P N Q A B A A B A -=-=+-=00||:0,0,19b,A abc A b ∈⋅⋅⋅下面计算对任一四位数可取，，，对其中每个99b a b c <≤<≤由及知，a 和c 分别有9-b 种取法，从而992200191019|=(9)26|85.b k b k ==⨯⨯-===∑∑A ()()285.N P N Q -=因此，6、（2016一试8）设4321,,,a a a a 是1，2，…，100中的4个互不相同的数，满足2433221242322232211)())((a a a a a a a a a a a a ++=++++则这样的有序数组),,,(4321a a a a 的个数为 . 【答案】40先考虑m n >的情况.此时331314)(mn a m n a a ==，注意到33,n m 互素，故31m a l =为正整数. 相应地，4321,,,a a a a 分别等于l n l mn nl m l m 3223,,,，它们均为正整数.这表明，对任意给定的1>=mnq ，满足条件并以q 为公比的等比数列4321,,,a a a a 的个数，即为满足不等式1003≤l n 的正整数l 的个数，即]100[3n.由于10053>，故仅需考虑34,4,23,3,2=q 这些情况，相应的等比数列的个数为20113312]64100[]64100[]27100[]27100[]8100[=++++=++++. 当m n <时，由对称性可知，亦有20个满足条件的等比数列4321,,,a a a a . 综上可知，共有40个满足条件的有序数组),,,(4321a a a a .7、（2017一试4）若一个三位数中任意两个相邻数码的差均不超过1，则称其为“平稳数”.平稳数的个数是. 【答案】75【解析】考虑平稳数abc .若b=0,则a=1,{0,1},.c ∈有两个平稳数1,a {1,2},c {0,1,2},23=6.2b 8,a,c {b 1,b,b 1},733=63.9,a,c {8,9}22=4.2+6+63+4=75.b b =∈∈⨯≤≤∈-+⨯⨯=∈⨯若则有个平稳数若则有个平稳数若则，有个平稳数综上可知，平稳数的个数是个平稳数8、（2010二试4）一种密码锁的密码设置是在正n 边形12n A A A 的每个顶点处赋值0和1两个数中的一个，同时在每个顶点处涂染红、蓝两种颜色之一，使得任意相邻的两个顶点的数字或颜色中至少有一个相同．问：该种密码锁共有多少种不同的密码设置？同，标有a 和b 的边都是偶数条．所以这种密码锁的所有不同的密码设置方法数等于在边上标记a ，b ，c ，使得标有a 和b 的边都是偶数条的方法数的4倍．设标有a 的边有2i 条，02n i ⎡⎤≤≤⎢⎥⎣⎦，标有b 的边有2j 条，202n i j -⎡⎤≤≤⎢⎥⎣⎦．选取2i 条边标记a 的有2in C 种方法，在余下的边中取出2j 条边标记b 的有22jn i C -种方法，其余的边标记c ．由乘法原理，此时共有2in C 22j n i C -种标记方法．对i ，j 求和，密码锁的所有不同的密码设置方法数为 222222004n n i i j nn i i j C C -⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦-==⎛⎫ ⎪ ⎪ ⎪⎝⎭∑∑． ① 这里我们约定001C =．当n 为奇数时，20n i ->，此时22221202n i jn i n ij C-⎡⎤⎢⎥⎣⎦---==∑． ②代入①式中，得()()2222222221222000044222n n i n n i j i n i i n i nn i n n i j i i C C C C -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦----====⎛⎫ ⎪== ⎪ ⎪⎝⎭∑∑∑∑ 022(1)(21)(21)nnkn kk n kk n n nn k k C C --===+-=++-∑∑31n =+．当n 为偶数时，若2n i <，则②式仍然成立；若2ni =，则正n 边形的所有边都标记a ，此时只有一种标记方法．于是，当n 为偶数时，所有不同的密码设置的方法数为222222004n n i i j n n i i j C C -⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦-==⎛⎫ ⎪= ⎪⎪⎝⎭∑∑()122210412n i n i n i C ⎡⎤-⎢⎥⎣⎦--=⎛⎫ ⎪⨯+ ⎪ ⎪⎝⎭∑()2221024233n i n i nn i C ⎡⎤⎢⎥⎣⎦--==+=+∑．综上所述，这种密码锁的所有不同的密码设置方法数是：当n 为奇数时有31n +种；当n 为偶数时有33n+种．。

2017年高考全国卷数学分类汇编(三角与向量)

2017年高考数学全国卷分类汇编三角与向量全国1理（2小1大）9．已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结论正确的是 A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2 13．已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2 b |= .17．（12分） △ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求△ABC 的周长.全国1文（4小）8．函数sin21cos x y x=-的部分图像大致为11．△ABC 的内角A 、B 、C 的对边分别为a 、b 、c 。

已知sin sin (sin cos )0B A C C +-=，a =2，c 2，则C =A ．π12B ．π6C ．π4D ．π313．已知向量a =（–1，2），b =（m ，1）.若向量a +b 与a 垂直，则m =______________.15．已知π(0)2a ∈，,tan α=2，则πcos ()4α-=__________。

全国2理（2小1大）12.已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是（）A.2-B.32-C. 43- D.1-14.函数()23sin 4f x x x =-（0,2x π⎡⎤∈⎢⎥⎣⎦）的最大值是． 17.（12分）ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知2sin()8sin 2B AC +=． (1)求cos B(2)若6a c += , ABC ∆面积为2,求.b 全国2文（4小）3.函数()f x =πsin （2x+）3的最小正周期为A.4πB.2πC. πD.2π 4.设非零向量a ，b 满足+=-b b a a 则 A a ⊥b B. =b a C. a ∥b D. >b a13.函数()cos sin =2+f x x x 的最大值为 .16.△ABC 的内角A,B,C 的对边分别为a,b,c,若2b cosB=a cosC+c cosA,则B=全国3理（2小1大）6．设函数f (x )=cos(x +3π)，则下列结论错误的是 A ．f (x )的一个周期为−2π B ．y =f (x )的图像关于直线x =83π对称 C ．f (x +π)的一个零点为x =6π D ．f (x )在(2π,π)单调递减 12．在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP =λ AB +μAD ，则λ+μ的最大值为A ．3B ．22C ．5D ．217．（12分）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin A +3cos A =0，a =27,b =2．（1）求c ；（2）设D 为BC 边上一点，且AD ⊥ AC,求△ABD 的面积．全国3文（4小）4．已知4sin cos 3αα-=，则sin 2α= A ．79- B ．29- C ． 29 D ．796．函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为 A ．65B ．1C ．35D ．157．函数y =1+x +2sin x x 的部分图像大致为 A ． B ．C ．D ．13．已知向量(2,3),(3,)a b m =-=，且a ⊥b ，则m = .15．△ABC 的内角A ，B ，C 的对边分别为a ，b ，c 。

第01讲+不等式-2009-2017全国高中数学联赛分类汇编

2009-2017全国高中数学联赛分类汇编第01讲：不等式
1、（2009一试3）在坐标平面上有两个区域和，为ቤተ መጻሕፍቲ ባይዱ，是随变化的区域，它由不等式所确定，的取值范围是，则和的公共面积是函数．
【答案】
【解析】
由题意知
2、（2009一试4）使不等式对一切正整数都成立的最小正整数的值为．
以下考虑的情况，约定 ,由平均不等式得
,
所以 .
当时，上述不等式等号成立，且有，此时 .
综上所述，所求最大值为 .
16、（2017一试9）（本题满分16分）设为实数，不等式对所有成立，证明： .
证明：令
17、（2017一试10）（本题满分20分）设是非负实数，满足，求
的最小值和最大值.
解：由柯西不等式
【答案】2009
3、（2011一试3）设为正实数，，，则．
【答案】-1
【解析】由，得．又，
即于是
再由不等式中等号成立的条件，得．与联立解得或故．
4、（2012一试3）设，则的最大值是.
【答案】
【解析】不妨设则
因为
所以
当且仅当时上式等号同时成立.故
5、(2014一试2)设集合中的最大值与最小值分别为，则 =_________.
即，所以 .又，故 .
8、（2009一试11）求函数的最大和最小值．
又由柯西不等式得
所以．
由柯西不等式等号成立的条件，得，解得．故当时等号成立．因此的最大值为．
9、（2009二试2）求证不等式：，，2，…
【解析】证明：首先证明一个不等式：
⑴ ，．

第02讲初等数论20092017全国高中数学联赛分类汇编

2009-2017全国高中数学联赛分类汇编第02讲：初等数论1、（2010一试8）方程2010=++z y x 满足z y x ≤≤的正整数解(,,)x y z 的个数是. 【答案】336675易知 100420096100331⨯=+⨯+k ，所以110033*********-⨯-⨯=k200410052006123200910052006-⨯=-⨯+-⨯=，即3356713343351003=-⨯=k .从而满足z y x ≤≤的正整数解的个数为33667533567110031=++.2、（2011一试8）已知=n a C ())95,,2,1(2162003200=⎪⎪⎭⎫⎝⎛⋅⋅-n nnn ，则数列}{n a 中整数项的个数为．【答案】15 【解析】=n a C65400320020023n n n --⋅⋅．要使)951(≤≤n a n 为整数，必有65400,3200nn --均为整数，从而4|6+n ．当=n 2,8,14,20,26,32,38,44,50,56,62,68,74,80时，3200n -和65400n-均为非负整数，所以n a 为整数，共有14个．当86=n 时，=86a C 5388620023-⋅⋅，在C !114!86!20086200⋅=中，!200中因数2的个数为1972200220022002200220022002200765432=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡，同理可计算得!86中因数2的个数为82，!114中因数2的个数为110，所以C 86200中因数2的个数为511082197=--，故86a 是整数．当92=n 时，=92a C 10369220023-⋅⋅，在C !108!92!20092200⋅=中，同样可求得!92中因数2的个数为88,!108中因数2的个数为105,故C 86200中因数2的个数为410588197=--，故92a 不是整数．因此，整数项的个数为15114=+．3、（2015一试8）对四位数(19,0,,9)abcd a b c d ≤≤≤≤,若,,a b b c c d ><>,则称abcd 为P 类数,若,,a b b c c d <><,则称a b c d 为Q 类数,用()N P 与()N Q 分别表示P 类数与Q 类数的个数,则()()N P N Q -的值为【答案】28599b a b c <≤<≤由及知，a 和c 分别有9-b 种取法，从而992200191019|=(9)26|85.b k b k ==⨯⨯-===∑∑A ()()285.N P N Q -=因此，学科@网4、（2016一试8）设4321,,,a a a a 是1，2，…，100中的4个互不相同的数，满足2433221242322232211)())((a a a a a a a a a a a a ++=++++则这样的有序数组),,,(4321a a a a 的个数为 . 【答案】40【解析】由柯西不等式知，2433221242322232211)())((a a a a a a a a a a a a ++≥++++，等号成立的充分必要条件是433221a a a a a a ==，即4321,,,a a a a 成等比数列.于是问题等价于计算满足{1,2,3,},,,{4321⊆a a a a …,100}的等比数列4321,,,a a a a 的个数.设等比数列的公比1≠q ，且q 为有理数.记mn q =，其中n m ,为互素的正整数，且n m ≠. 先考虑m n >的情况.此时331314)(m n a m n a a ==，注意到33,n m 互素，故31ma l =为正整数. 相应地，4321,,,a a a a 分别等于l n l mn nl m l m 3223,,,，它们均为正整数.这表明，对任意给定的1>=mnq ，满足条件并以q 为公比的等比数列4321,,,a a a a 的个数，即为满足不等式1003≤l n 的正整数l 的个数，即]100[3n.由于10053>，故仅需考虑34,4,23,3,2=q 这些情况，相应的等比数列的个数为20113312]64100[]64100[]27100[]27100[]8100[=++++=++++. 当m n <时，由对称性可知，亦有20个满足条件的等比数列4321,,,a a a a . 综上可知，共有40个满足条件的有序数组),,,(4321a a a a .5、（2017一试4）若一个三位数中任意两个相邻数码的差均不超过1，则称其为“平稳数”.平稳数的个数是. 【答案】756、（2009二试3）设k ，l 是给定的两个正整数．证明：有无穷多个正整数m k ≥，使得C k m 与l 互素．【解析】证法一：对任意正整数t ，令(!)m k t l k =+⋅⋅．我们证明()C 1k m l =，．设p 是l 的任一素因子，只要证明：p/|C k m ．若p /|k !，则由1!C ()kkmi k m k i ==-+∏1[((!)]ki i tl k =≡+∏1ki i =≡∏()1!mod k p α+≡．及|!p k α，且pα+1/|k !，知|!C k m p k α且1α+p /|!C k m k ．从而p/|C km ．证法二：对任意正整数t ，令2(!)m k t l k =+⋅⋅，我们证明()C 1k m l =，．设p 是l 的任一素因子，只要证明：p/|C k m ．若p /|k !，则由 1!C ()==-+∏kkmi k m k i 21[((!)]ki i tl k =≡+∏1ki i =≡∏()!mod k p ≡．即p 不整除上式，故p/|C k m ．若|!p k ，设1α≥使|!p k α，但1/|!p k α+．12|(!)p k α+．故由11!C ()k kmi k m k i -==-+∏21[((!)]ki i tl k =≡+∏1ki i =≡∏()1!mod k p α+≡,及|!p k α，且pα+1/|k !，知|!C k m p k α且1α+p /|!C k m k ．从而p/|C km ．7、（2009二试4）在非负数构成的39⨯数表中每行的数互不相同，前6列中每列的三数之和为1，1728390x x x ===，27x ，37x ，18x ，38x ，19x ，29x 均大于．如果P 的前三列构成的数表111213212223313233x x x S x x x x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭满足下面的性质()O ：对于数表P 中的任意一列123k k k x x x ⎛⎫⎪⎪ ⎪⎝⎭（1k =，2，…，9）均存在某个{}123i ∈，，使⑶{}123min ik i i i i x u x x x =≤，，．求证：（ⅰ）最小值{}123min i i i i u x x x =，，，1i =，2，3一定自数表S 的不同列．（ⅱ）存在数表P 中唯一的一列***123k k k x x x ⎛⎫⎪⎪ ⎪ ⎪⎝⎭，*1k ≠，2，3使得33⨯数表***111212122231323k k k x x x S x x x x x x ⎛⎫ ⎪'= ⎪ ⎪ ⎪⎝⎭仍然具有性质()O ．【解析】（ⅰ）假设最小值{}123min i i i i u x x x =，，，1i =，2，3不是取自数表S 的不同列．则存在一列不含任何i u ．不妨设2i i u x ≠，1i =，2，3．由于数表P 中同一行中的任何两个元素都不等，于是2i i u x <，1i =，2，3．另一方面，由于数表S 具有性质()O ，在⑶中取2k =，则存在某个{}0123i ∈，，使得002i i x u ≤．矛盾．（ⅱ）由抽届原理知，{}1112min x x ，，{}2122min x x ，，{}3132min x x ，中至少有两个值取在同一列．不妨设{}212222min x x x =，，{}313232min x x x =，．由前面的结论知数表S 的第一列一定含有某个i u ，所以只能是111x u =．同样，第二列中也必含某个i u ，1i =，2．不妨设222x u =．于是333u x =，即i u 是数表S 中的对角线上数字．下面证明33⨯数表***111212122231323k k k x x x S x x x x x x ⎛⎫ ⎪'= ⎪ ⎪ ⎪⎝⎭具有性质()O ．从上面的选法可知{}{}*1212:min min i i i i i ik u x x x x x '==，，，，(13)i =，．这说明{}*111211min k x x x u >，≥，{}*313233min k x x x u >，≥．又由S 满足性质()O ．在⑶中取*k k =，推得*22k x u ≤，于是{}**2212222min k k u x x x x '==，，．下证对任意的k M ∈，存在某个1i =，2，3使得i ik u x '≥．假若不然，则{}12min ik i i x x x >，，1i =，3且*22k k x x >．这与*2k x 的最大性矛盾．因此，数表S '满足性质()O ．下证唯一性．设有k M ∈使得数表111212122231323k k k x x x S x x x x x x ⎛⎫⎪= ⎪ ⎪⎝⎭具有性质()O ，不失一般性，我们假定⑷{}221222322min u x x x x ==，， 3231x x <．由于323x x<，2221x x <及（ⅰ），有{}11112111min k u x x x x ==，，．又由（ⅰ）知：或者()a {}3313233m i n k k u x x x x ==，，，或者{}2212222()min k k b u x x x x ==，，．如果()a 成立，由数表S 具有性质()O ，则{}11112111min k u x x x x ==，，，⑸{}22122222min k u x x x x ==，，， {}3313233min k k u x x x x ==，，．由数表S 满足性质()O ，则对于3M ∈至少存在一个{}123i ∈，，使得*i ik u x ≥．由*k I ∈及⑷和⑹式知，*1111k x x u >=，*3323k x x u >=．于是只能有*222k k x u x =≤．类似地，由S '满足性质()O 及k M ∈可推得*222k k x u x '=≤．从而*k k =．学*科网 8、（2010一试11）证明：方程02523=-+x x 恰有一个实数根r ，且存在唯一的严格递增正整数数列}{n a ，使得+++=32152a a a r r r . 若存在两个不同的正整数数列 <<<<n a a a 21和 <<<<nb b b 21满足52321321=+++=+++ b b b a a a r r r r r r ，去掉上面等式两边相同的项，有 +++=+++321321t t t s s s r r r r r r，这里 <<<<<<321321,t t t s s s ，所有的i s 与j t 都是不同的. 不妨设11t s <，则 ++=++<21211t t s s s r r r r r，112111111121211=--<--=++≤++<--rr r r r s t s t ，矛盾.故满足题设的数列是唯一的.9、（2010二试2）设k 是给定的正整数，12r k =+．记(1)()()f r f r r r ==⎡⎤⎢⎥，()()l f r =(1)(()),2l f f r l -≥．证明：存在正整数m ，使得()()m f r 为一个整数．这里，x ⎡⎤⎢⎥表示不小于实数x 的最小整数，例如：112⎡⎤=⎢⎥⎢⎥，11=⎡⎤⎢⎥．【解析】记2()v n 表示正整数n 所含的2的幂次．则当2()1m v k =+时，()()m f r 为整数．下面我们对2()v k v =用数学归纳法．当0v =时，k 为奇数，1k +为偶数，此时()111()1222f r k k k k ⎛⎫⎡⎤⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎢⎥⎝⎭为整数．假设命题对1(1)v v -≥成立．对于1v ≥，设k 的二进制表示具有形式1212222v v v v v k αα++++=+⋅+⋅+，这里，0i α=或者1，1,2,i v v =++．于是 ()111()1222f r k k k k ⎛⎫⎡⎤⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎢⎥⎝⎭2122k k k =+++ 11211212(1)2()222v v v v v v v ααα-++++=+++⋅++⋅+++12k '=+， ① 这里1121122(1)2()22v v v v v v v k ααα-++++'=++⋅++⋅+++.显然k '中所含的2的幂次为1v -．故由归纳假设知，12r k ''=+经过f 的v 次迭代得到整数，由①知，(1)()v f r +是一个整数，这就完成了归纳证明．10、（2010二试4）一种密码锁的密码设置是在正n 边形12n A A A 的每个顶点处赋值0和1两个数中的一个，同时在每个顶点处涂染红、蓝两种颜色之一，使得任意相邻的两个顶点的数字或颜色中至少有一个相同．问：该种密码锁共有多少种不同的密码设置？设标有a 的边有2i 条，02n i ⎡⎤≤≤⎢⎥⎣⎦，标有b 的边有2j 条，202n i j -⎡⎤≤≤⎢⎥⎣⎦．选取2i 条边标记a 的有2inC 种方法，在余下的边中取出2j 条边标记b 的有22jn i C -种方法，其余的边标记c ．由乘法原理，此时共有2in C 22j n i C -种标记方法．对i ，j 求和，密码锁的所有不同的密码设置方法数为222222004n n i i j n n i i j C C -⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦-==⎛⎫ ⎪ ⎪ ⎪⎝⎭∑∑． ①这里我们约定001C =．当n 为奇数时，20n i ->，此时22221202n i j n i n ij C-⎡⎤⎢⎥⎣⎦---==∑． ②代入①式中，得()()2222222221222000044222n n i n n i j i n i i n i nn i n n i j i i C C C C -⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦----====⎛⎫ ⎪== ⎪ ⎪⎝⎭∑∑∑∑ 022(1)(21)(21)nnkn kk n kk n n nn k k C C --===+-=++-∑∑31n =+．222222004n n i i j n n i i j C C -⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦-==⎛⎫ ⎪= ⎪ ⎪⎝⎭∑∑()122210412n i n i n i C ⎡⎤-⎢⎥⎣⎦--=⎛⎫ ⎪⨯+ ⎪ ⎪⎝⎭∑()2221024233n i n i n n i C ⎡⎤⎢⎥⎣⎦--==+=+∑．综上所述，这种密码锁的所有不同的密码设置方法数是：当n 为奇数时有31n +种；当n 为偶数时有33n +种．11、（2011二试2）证明：对任意整数4≥n ，存在一个n 次多项式具有如下性质：（1）110,,,-n a a a 均为正整数；（2）对任意正整数m ，及任意)2(≥k k 个互不相同的正整数k r r r ,,,21 ，均有)()()()(21k r f r f r f m f ≠．【解析】令 2)()2)(1()(++++=n x x x x f ， ①将①的右边展开即知)(x f 是一个首项系数为1的正整数系数的n 次多项式．下面证明)(x f 满足性质（2）．对任意整数t ，由于4≥n ，故连续的n 个整数n t t t +++,,2,1 中必有一个为4的倍数，从而由①知)4(mod 2)(≡t f ．因此，对任意)2(≥k k 个正整数k r r r ,,,21 ，有 )4(mod 02)()()(21≡≡k k r f r f r f ．但对任意正整数m ，有)4(mod 2)(≡m f ，故)4)(mod ()()()(21k r f r f r f m f ≡/，从而)()()()(21k r f r f r f m f ≠．所以)(x f 符合题设要求．学&科网12、（2011二试3）设)4(,,,21≥n a a a n 是给定的正实数，n a a a <<< 21．对任意正实数r ，满足)1(n k j i r a a a a j k ij ≤<<≤=--的三元数组),,(k j i 的个数记为)(r f n ．证明：4)(2n r f n <．因此，当n 为偶数时，设m n 2=，则有∑∑∑-=-=-=+==121212)()()()(m mj j m j j n j j n r g r g r g r f2)1(2)1()2()1(1212-+-=-+-≤∑∑-+==m m m m j m j m m j m j 4222n m m m =<-=．当n 为奇数时，设12+=m n ，则有∑∑∑+==-=+==mm j jmj j n j j n r gr g r g r f 21212)()()()(∑∑+==-++-≤mm j mj j m j 212)12()1(422n m <=．13、（2011二试4）设A 是一个93⨯的方格表，在每一个小方格内各填一个正整数．称A 中的一个)91,31(≤≤≤≤⨯n m n m 方格表为“好矩形”，若它的所有数的和为10的倍数．称A 中的一个11⨯的小方格为“坏格”，若它不包含于任何一个“好矩形”．求A 中“坏格”个数的最大值．【解析】首先证明A 中“坏格”不多于25个．用反证法．假设结论不成立，则方格表A 中至多有1个小方格不是“坏格”．由表格的对称性，不妨假设此时第1行都是“坏格”．设方格表A 第i 列从上到下填的数依次为9,,2,1,,, =i c b a i i i ．记9,,2,1,0,)(,11=+==∑∑==k c bT a S ki i ikk i ik ，这里000==T S ．即第2行至第3行、第1+m 列至第n 列组成一个“好矩形”，从而至少有2个小方格不是“坏格”，矛盾．类似地，也不存在90,,≤<≤n m n m ，使)10(mod n n m m T S T S +≡+．因此上述断言得证．故)10(mod 59210)(999≡++++≡+≡≡∑∑∑=== k k k k k k k T S T S ，所以 )10(mod 055)(99090≡+≡+≡+∑∑∑===k k k k k k k T S T S ，矛盾！故假设不成立，即“坏格”不可能多于25个．另一方面，构造如下一个93⨯的方格表，可验证每个不填10的小方格都是“坏格”，此时有25个“坏格”．综上所述，“坏格”个数的最大值是25．14、（2012二试2）试证明：集合{}22,2,,2,n A =满足b N *∈，若21b a <-，（１）对每个a A ∈，及则(1)b b +一定不是2a 的倍数；（２）对每个a A ∈（其中A 表示A 在Ｎ中的补集），且1a ≠，必存在b N *∈，21b a <-，使(1)b b +是2a 的倍数．【解析】证明:对任意的a A ∈,设2,,ka k N *=∈则122,k a +=如果b 是任意一个小于21a -的正整数,则121b a +≤-则122k a m +=⋅下面给出(2)的三种证明方法: 证法一:令1,12,k b mx b y +=+=消去b 得12 1.k y mx +-=由于1(2,)1,k m +=这方程必有整数解;1002k x x ty y mt+⎧=+⎪⎨=+⎪⎩其中00,(,)t z x y ∈为方程的特解.把最小的正整数解记为(,),x y **则12k x *+<,故21,b mx a *=<-使(1)b b +是2a 的倍数．证法二:由于1(2,)1,k m +=由中国剩余定理知,同余方程组10(mod 2)1(mod )k x x m m +⎧=⎨=-⎩在区间1(0,2)k m +上有解,x b =即存在21,b a <-使(1)b b +是2a 的倍数．证法三:由于(2,)1,m =总存在(,1),r r N r m *∈≤-使21(mod )r m =取,t N *∈使1,tr k >+则21(mod )tr m =存在1(21)(2)0,,trk b q m q N +=--⋅>∈使021,b a <<-此时1,21,k m b m ++因而(1)b b +是2a 的倍数．15.（2013二试4）（本题满分50分）设,n k 为大于1的整数，2k n <.证明：存在2k 个不被n 整除的整数，若将它们任意分成两组，则总有一组若干个数的和被n 整除. 【证明】先考虑n 为2的幂的情形.设2,1r n r =≥，则r k <.取3个12r -及23k -个1，显然这些数均不被n 整除.将这2k 个数任意分成两组，则总有一组中含2个12r -，它们的和为2r ，被n 整除. 现在设n 不是2的幂，取2k 个数为22211,1,2,2,,2,1,2,2,,2k k -------，因为n 不是2的幂，故上述2k 个数均不被n 整除.若可将这些数分成两组，使得每一组中任意若干个数的和均不能被n 整除.不妨设1在第一组，由于（-1）+1=0，被n 整除，故两个-1必须在第二组；因（-1）+（-1）+2=0，被n 整除，故2在第一组，进而推出-2在第二组. 现归纳假设1,2,,2l 均在第一组，而1,1,2,,2l ----均在第二组，这里12l k ≤<-，由于()()()()1112220l l +-+-+-++-+=，被n 整除，故12l +在第一组，从而12l +-在第二组.故由数学归纳法可知，221,2,2,,2k -在第一组，221,1,2,2,,2k ------在第二组.最后，由于()()()()21112220k k ---+-+-++-+=，16、（2014二试4）（本题满分50分）设整数122014,,,2014x x x 模互不同余，122014,,,y y y 整数模2014也互不同余.证明：可将122014,,,y y y 重新排列为122014,,,z z z ，使得112220142014,,,x z x z x z +++模4028互不同余.【证明】(mod 2),12.,i i y i k i k i ≡≡≤≤记k=1007,不妨设x 对每个整数17、（2015二试4）(本题满分50分)求具有下述性质的所有正整数k :对任意正整数(1)1,2k n n -+不整除()!!kn n . 18、（2016二试3）（本题满分50分）给定空间中10个点，其中任意四点不在一个平面上，将某些点之间的线段相连，若得到的图形中没有三角形也没有空间四边形，试确定所连线段数目的最大值.【解析】以这10个点为顶点，所连线段为边，得到一个10界简单图G ，我们证明G 的边数不超过15.边，否则就形成三角形，所以，121,,,n v v v +⋅⋅⋅之间恰有n 条边.对每个j (210)n j +≤≤，j v 至多与21,,n v v +⋅⋅⋅中的一个顶点相邻（否则设j v 与,(21)s t v v s t n ≤<≤+）相邻，则1,,,s j t v v v v 就对应了一个空间四边形的四个顶点，这与题设条件矛盾，从而21,,n v v +⋅⋅⋅与210,,n v v +⋅⋅⋅之间的边数至多10(1)9n n -+=-条.在210,,n v v +⋅⋅⋅这9n -个顶点之间，由于没有三角形，由托兰定理，至多2(9)[]4n -条边，因此G 的边数22(9)(9)25(9)[]9[]9[]15444n n k n n --≤+-+=+≤+=如有帮助，欢迎下载支持11页脚内容如图给出的图共有15条边，且满足要求，综上所述，所求边数的最大值为15.学科*网19、（2017二试3）（本题满分50分）将33×33方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等，若相邻两个小方格的颜色不同，则称它们的公共边为“分隔边”.试求分隔边条数的最小值.解：记分隔边的条数为L ，首先，将方格纸按如图分成三个区域，分别染成三种颜色，粗线上均为分隔边，此时共有56个分隔边，即L=56.20、（2017二试4）（本题满分50分）设,m n 均是大于1的整数，12.,,,n m n a a a ≥是n 个不超过m 的互不相同的正整数，且12,,,n a a a 互素.证明：对任意实数x ，均存在一个(1)i i n ≤≤，使得2||||||||(1)i a x x m m ≥+，这里||||y 表示实数y 到它最近的整数的距离. 证明：首先证明以下两个结论.结论1:存在整数121122,,,,+++c 1,||,1.n n n i c c c c a c a a c m i n =≤≤≤满足并且由于121211221,,,+++c 1.1n n n n a a a c c c c a c a a ==（，，，），由裴蜀定理，存在整数，满足（）下面证明,通过调整,存在一组12,,,n c c c 满足（1），且绝对值均不超过m,记因为12S 与S 均是非负整数,故通过有限次上述的调整,可得到一组12,,,n c c c ，。

#2007年全国各地高考数学试题及解答分类汇编大全(09解三角形)

2007年高考中的“解三角形”试题汇编大全一、选择题：1.（2007重庆理）在ABC ∆中，,75,45,300===C A AB 则BC =（ A ）A .33- B.2 C.2 D.33+二、填空题：1.（2007北京文、理) 在ABC △中，若1tan 3A =，150C =，1BC =，则AB =210．2．（2007湖南理）在ABC △中，角A B C ，，所对的边分别为a b c ，，，若1a =，b，c =π3C =，则B = 5π6．3.（2007湖南文）在ABC ∆中，角A 、B 、C 所对的边分别为a b c 、、，若1,3a c π===，则A=π6.4.（2007重庆文）在△ABC 中，AB =1,B C =2,B =60°，则AC。

三、解答题：1.（2007福建文、理)（本小题满分12分）在△ABC 中，tan A =41,tan B =53. (I)求角C 的大小;(II)若AB 边的长为17，求BC 边的长1..本小题主要考查两角和差公式，用同角三角函数关系等解斜三角形的基本知识以及推理知运算能力.满分12分. 解：（I ）∵C ＝π-(A +B ),∴tan C =-tan(A +B )=，＝153·4115341--+ 又∵0<C<π,∴C=43π(II)由⎪⎪⎩⎪⎪⎨⎧=+==,1cos sin ,41cos sin tan 22A A A A 且A ∈（0，2π），得sinA=.1717 ∵,sin sin ABC C AB =∴BC ＝AB ·2sin sin =CA.所以，最小边BC =2．( 2007广东文)（本小题满分14分）已知ΔABC_三个顶点的直角坐标分别为A(3，4)、B(0，0)、C(c ，0)． (1)若0AB AC ⋅=,求c 的值； (2)若C=5，求sin ∠A 的值． 2.【解析】(1)(3,4),(3,4)AB AC c =--=--……… …4分由0AB AC ⋅=可得3(3)160c --+=………………6分,解得253c =………………8分 (2)当5c =时,可得5,5AB AC BC ===, ΔABC 为等腰三角形……10分过B 作BD AC ⊥交AC 于D ,可求得BD =12分故sin BD A AB ==……14分 (其它方法如①利用数量积AB AC ⋅求出cos A 进而求sin A ;②余弦定理正弦定理等!)3. (2007广东理)（本小题满分12分）已知△ABC 顶点的直角坐标分别为)0,()0,0()4,3(c C B A 、、. （1）若5=c ，求sin ∠A 的值;（2）若∠A 是钝角，求c 的取值范围.3. 解：(1) (3,4)AB =--, (3,4)AC c =--当c=5时，(2,4)AC =-cos cos ,A AC AB ∠=<>==进而sin 5A ∠==(2)若A 为钝角，则AB ﹒AC= -3(c -3)+( -4)2<0解得c>325显然此时有AB 和AC 不共线，故当A 为钝角时，c 的取值范围为[325，+∞)4．(2007海南、宁夏文、理)（本小题满分12分）如图，测量河对岸的塔高AB 时，可以选与塔底B 在同一水平面内的两个侧点C 与D ．现测得BCD BDC CD s αβ∠=∠==，，，并在点C 测得塔顶A 的仰角为θ，求塔高AB ．4．解：在BCD △中，πCBD αβ∠=--．由正弦定理得sin sin BC CDBDC CBD =∠∠．所以sin sin sin sin()CD BDC s BC CBD βαβ∠==∠+·．在ABC Rt △中，tan sin tan sin()s AB BC ACB θβαβ=∠=+·．5.（2007全国Ⅰ文）（本小题满分10分）设锐角三角形ABC 的内角A,B,C 的对边分别为a,b,c,a =2b sin A(Ⅰ)求B 的大小;(Ⅱ)若a =33,c =5,求b .5．解：（Ⅰ）由2sin a b A =，根据正弦定理得sin 2sin sin A B A =，所以1sin 2B =，由ABC △为锐角三角形得π6B =．（Ⅱ）根据余弦定理，得2222cos b a c ac B =+-272545=+-7=．所以，b =．6.（2007全国Ⅰ理）（本小题满分10分）设锐角三角形ABC 的内角A,B,C 的对边分别为a,b,c,a =2b sin A(Ⅰ)求B 的大小;(Ⅱ)求C A sin cos +的取值范围.6. 解：（Ⅰ）由2sin a b A =，根据正弦定理得sin 2sin sin A B A =，所以1sin 2B =，由ABC △为锐角三角形得π6B =．（Ⅱ）cos sin cos sin AC A A π⎛⎫+=+π-- ⎪6⎝⎭cos sin 6A A π⎛⎫=++ ⎪⎝⎭1cos cos 22A A A =++3A π⎛⎫=+ ⎪⎝⎭．由ABC △为锐角三角形知，2A 0π<<，πππ<+<6A 2．解得2A 3ππ<< 所以653A 32πππ<+<，所以1sin 23A π⎛⎫+< ⎪⎝⎭．3A π⎛⎫<+< ⎪⎝⎭ 所以，cos sin A C +的取值范围为32⎫⎪⎪⎝⎭，． 7．（2007山东文）（本小题满分12分）在ABC △中，角A B C ，，的对边分别为tan a b c C =，，，（1）求cos C ；（2）若52CB CA =，且9a b +=，求c ．7．解：（1）sin tan cos CC C=∴= 又22sin cos 1C C +=解得1cos 8C =±．tan 0C >，C ∴是锐角．1cos 8C ∴=．（2）52CB CA =，5cos 2ab C ∴=，20ab ∴=．又9a b += 22281a ab b ∴++=． 2241a b ∴+=．2222cos 36c a b ab C ∴=+-=． 6c ∴=．8.（2007山东理）(本小题满分12分)如图，甲船以每小时302海里的速度向正北方向航行，乙船按固定方向匀速直线航行.当甲船位于A 1处时，乙船位于甲船的北偏西105°方向的B 1处，此时两船相距20海里.当甲船航行20分钟到达A 1处时，乙船航行到甲船的北偏西120°方向的B 1处，此时两船相距102海里，问乙船每小时航行多少海里？8.【答案】解如图，连结12A B ，22A B=122060A A =⨯=， 122A A B ∆是等边三角形，1121056045B A B ∠=︒-︒=︒，在121A B B∆中，由余弦定理得2221211121112222cos 4520220200B B A B A B A B A B =+-⋅︒=+-⨯⨯=， 12B B=因此乙船的速度的大小为6020⨯= 答：乙船每小时航行.9．（2007上海文、理）（本题满分14分）在ABC △中，a b c ，，分别是三个内角A B C ，，的对边．若4π,2==C a ，5522cos =B ，求ABC △的面积S ．9．解：由题意，得3cos 5B B =，为锐角，54sin =B ，10274π3sin )πsin(sin =⎪⎭⎫ ⎝⎛-=--=B C B A ，由正弦定理得 710=c ， ∴ 111048sin 222757S ac B ==⨯⨯⨯=．10.（2007天津文）（本小题满分12分）在ABC △中，已知2AC =，3BC =，4cos 5A =-．（Ⅰ）求sinB 的值；（Ⅱ）求sin 26B π⎛⎫+⎪⎝⎭的值．10.本小题考查同角三角函数的基本关系式、两角和公式、倍角公式、正弦定理等的知识，考查基本运算能力．满分12分．（Ⅰ）解：在ABC △中，3sin 5A ===，由正弦定理，sin sin BC ACA B=．所以232sin sin 355AC B A BC ==⨯=．（Ⅱ）解：因为4cos A =-，所以角A 为钝角，从而角B 为锐角，于是cos 5B ===，217cos 22cos 121525B B =-=⨯-=，2sin 22sin cos 25515B B B ==⨯⨯=．sin 2sin 2cos cos 2sin 666B B B πππ⎛⎫+=+ ⎪⎝⎭171252252=+⨯1750=．11.（2007浙江文、理）（本题14分）已知ABC △1，且si n s i n 2s i A B C +=．（I ）求边AB 的长；（II ）若ABC △的面积为1sin 6C ，求角C 的度数．11.解：（I ）由题意及正弦定理，得1AB BC AC ++=，BC AC +=，两式相减，得1=．（II ）由ABC △的面积11sin sin 26BC AC C C =，得13BC AC =，由余弦定理，得222cos 2AC BC AB C AC BC+-=22()2122AC BC AC BC AB AC BC +--==，所以60C =．。

09级高三数学总复习讲义——解三角形X

09级高三数学总复习讲义——解三角形知识清单常用的主要结论有：(1)A+B+C=1800⑵任意两边之和大于第三边,任意两边之差小于第三边. ⑶等边对等角:a b A B =⇔=; 大边对大角:a b A B >⇔>. ⑷12A B CS =底×高=1()2r a b c ++(其中r 是内切圆半径)1sin 2ab C == ⑸2sin sin sin a b c R ABC===(正弦定理)⑹22222cos ,a b c bc A b =+-= (余弦定理)课前预习1．已知ab c b a c b a ABC 3,,222=-+∆且三边长分别为，求_____C ∠2.在ABC ∆中，如果sin A ∶sin B ∶sin C =5∶6∶8，那么此三角形最大角的余弦值是． 3．在ABC ∆中，a 、b 分别为角A 、B 的对边，若60B =︒，75C =︒，8a =，则边b 的长等于4．A B C ∆中，3A π∠=，3B C =，AB =，则C ∠= A ．6πB ．4πC ．34π D ．4π或34π5．已知：在⊿ABC 中，BC bc cos cos =，则此三角形为A. 直角三角形B. 等腰直角三角形C. 等腰三角形D. 等腰或直角三角形6．在△ABC 中，角A 、B 、C 的对边分别为,,,,1,3a b c A a b π===则c =（）．A ． 1 B. 2 C.3—1 D. 37．如图，测量河对岸的塔高A B 时，可以选与塔底B 在同一水平面内的两个测点C 与D ．测得153030BCD BDC CD ∠=∠==，，米，并在点C 测得塔顶A 的仰角为60, 则BC= 米, 塔高AB= 米。

8．在△ABC 中，a ,b ,c 分别是A ∠，B ∠，C ∠的对边，且222b c a ++=则A ∠等于（）A ．6πB ．3πC ．23π D ．56π9．在A B C V 中,45,B =5c b ==,则a 等于( )(A) (B) (C)5 (D)1010．在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为300,600,则塔高为( )(A)4003米 (B)3米 3(D)2003米A11．在ABC 中，,2,a x b ==，45B =,若这个三角形有两解，则x 的取值范围是（）()2A x >()2B x <()22C x << ()2D x <<12．在A B C ∆中，已知内角3A π=，边BC =.设内角B x =,面积为y .(1) 求函数()y f x =的解析式和定义域； (2) 求y 的最大值. 典型例题EG1．正弦定理与余弦定理在∆ABC 中，若 ()()3a b c c b a bc +++-=，则()A =．A ． 150B ．120C ． 60D ． 30变式1：在∆ABC 中，若 a =4c =，60A = ，则b =__________．变式2：在∆ABC 中，若 b =，30A = ，105C =，则此三角形的周长为__________．变式3：已知a 、b 、c 是△ABC 中∠A 、∠B 、∠C 的对边，S 是△ABC 的面积．若a =4，b =5，S =53，求c 的长度．EG2.三角形中的几何计算在∆ABC 中，3A B A C ==，2B C =，B ∠的平分线交过点A 且与B C 平行的线于点D ．求∆ABD 的面积．变式1：已知A B C △1，且sin sin A B C +=．（I ）求边A B 的长；（II ）若A B C △的面积为1sin 6C ，求角C 的度数．变式2：△ABC 中，,3,3A B C π==则△ABC 的周长为（）．A ．)33B π++ B ．)36B π++C ．6sin()33B π++ D ．6sin()36B π++变式3：在45,cos 5ABC B AC C ∆∠=︒==中，，求（1）?B C =（2）若点D AB 是的中点，求中线CD 的长度。

2009全国高中数学联赛另解

2009全国高中数学联赛另解一、如图，,M N 分别为锐角三角形ABC（A B ∠<∠）的外接圆Γ上弧 ,BC AC 的中点，过点C 作//PC MN 交圆Γ于P 点，I 为ABC 的内心，连接PI 并延长交圆Γ于T ．（I ）求证：MP MT NP NT ⋅=⋅；（II ）在弧 AB （不含点C ）上任取一点Q （,,Q A T B ≠），记,AQC QCB 的内心分别为12,I I ，求证：12,,,Q I I T 四点共圆．（I ）解法一（焦恩伟）：由,M N 为 ,BC AC 中点知,,;,,B I N C I M 分别共线．由//CP MN 知四边形CPMN 为等腰梯形，得,NP MC MP CN ==．故NCA ABN NBC NAC ∠=∠=∠=∠，于是NC NA =．于是NA MP =，得MI NP =．①又NTA NBA NBC NMC MNP MTI ∠=∠=∠=∠=∠=∠，且ANT AMT ∠=∠，有ANT ∽IMT ，则AN MINT MT=．又由①知MP NPNT MT=，即NP NT MT MP ⋅=⋅．解法二（白佳伟）：设NM 与PT 交于H ．连接,NI MI ．由于//CP MN ，四边形CPMN 为等腰梯形，得,NP MC MP CN ==．由MIC MAC ACI MCB BCI MCI ∠=∠+∠=∠+∠=∠，得MI MC NP ==．同理PM NI =，四边形PMIN 为平行四边形，故NH MH =．由于PMN PTN ∠=∠，TPN NMT ∠=∠，有PHM ∽NHT ，故NP PHMT MH= 同理MP PH NT HN =．因此MP NPNT MT =，即NP NT MT MP ⋅=⋅．解法三（刘晓艺）：由正弦定理，sin sin sin sin MI PI PC NCMPI PMI PNI NPC===∠∠∠∠．由于//PC MN ，1sin sin sin sin 21sin sin()sin sin 2BACNP NMP MPC MAC MP PNM NPC NBC ABCπ∠∠∠∠====∠-∠∠∠ sin sin sin sin sin sin sin sin IMPNT NT NPT NPI PNI IN PI IN MT TPM IPM PMI IMPMI PI∠⋅∠∠∠====⋅∠∠∠∠⋅ 故,,,P M T N 共圆，PNI PMI π∠+∠=．因此1sin sin sin sin 21sin sin sin sin 2ABCNT IN IMN AMN ABN MT IM INM BNM BAM BAC ∠∠∠∠=====∠∠∠∠ 所以NT MP MT NP =，即MP MT NP NT ⋅=⋅．（II ）类似标准解答．二、求证不等式：2111()ln ,1,2, (1)2nk k n n k =-<-≤=+∑解法一（李博杰）：首先用数学归纳法证明21ln nk n k =≤∑ ①当2n =时，1ln 2ln 412<⇔>成立．②假设命题对n m =成立．设11()(1)x f x x +=+，则11'()()(ln(1))f x f x x x=⋅-++．令'()11()ln(1)()f x g x f x x x==-++，则221111'()01x g x x x x x +=+-=>+，故()g x 单调递增，()lim ()0x g x g x →∞<=，又()0f x >，有'()()()0f x f x g x =⋅<，故()f x 单调递减．又11lim(1)n n e n +→∞=+，11(1)n e n ++>，所以11ln 1m m m+<+．由归纳假设，11ln mk m k=<∑，两式相加得1211ln ln ln(1)m k m m m k m +=+<+=+∑ 即命题对1n m =+也成立．③由①②可知命题对,2n N n +∈≥成立．故21ln 1nk kn k =-+∑ 221ln 21n k k n k ==+-+∑221ln 2n k k n k =≤+-∑ 2111ln 22n k n k =≤+-≤∑，等号当且仅当1n =时成立．下面用数学归纳法证明111ln 0n k n k-=->∑①当2n =时，1ln 2>，命题成立． ②当n m =时，由均值不等式易得11111111(1)1(1)1(1)...(1)(1)11n n n n n n n n n n ++⎛⎫⎛⎫+=⋅+<+++++=+ ⎪ ⎪++⎝⎭⎝⎭ 故数列1(1)n n +单调递增，由于1lim(1)n n e n →∞+=，有1(1)m e m+<．所以1ln(1)1m m +<，11ln m m m +>．由归纳假设，111ln m k m k -=>∑，两式相加得11ln(1)mk m k=>+∑，故命题对1n m =+也成立．③由①②可知，命题对,2n N n +∈≥都成立．因此21ln 1nk kn k =-+∑21ln n k k n k k =>-+∑11ln 1nk n k ==-+∑ 1111ln 1n k n k -=>-+->-∑，命题得证．解法二（刘晓艺）：由导数定义知，00ln(1)ln(1)ln1lim lim0x x x x x x →→++-=-为ln(1)x +在0x =处的导数，而ln(1)x +的导数为11x +，故0ln(1)lim1x x x→+=，即0lim(ln(1))0x x x →-+=．记()ln(1)g x x x =-+，则1'()1011x g x x x=-=>++，故()g x 单增．则0()lim(ln(1))0x g x x x →>-+=，111()0,()0ln k g x g k k k +>>⇒>．因此211111n nk k k k k ==>++∑∑12ln1nk k k =+>+∑ 12ln 1nk k k =+=+∏ 2ln ln(2)ln 22n n +==+-ln ln ln 1n e n >-=-．再记21()ln 1nk kf n n k ==-+∑，()ln(1)(0)1x h x x x x =+->+，则2211'()01(1)(1)xh x x x x =-=>+++，0()lim(ln(1))1x x h x x x →>+-+．又000(1)ln(1)ln(1)lim lim(1)lim 1x x x x x x x x x →→→+++=+⋅=，有lim(ln(1))01x x x x→∞+-=+，故111()0,()0ln 1k h x h k k k +>>⇒>+．因此22211n nk k k k k ==<+∑∑2ln1nk k k =<-∑ 2ln ln 1nk kn k ===-∏所以22()(1)ln 01nk kf n f n k =-=-<+∑，即1()(1)2f n f ≤=．证毕．解法三（姚博文）：先证明引理：当()0,x ∈+∞时，ln 1x x ≤-．事实上，令()()ln 1,0,f x x x x =-+∈+∞，则()11'1xf x x x-=-=．由下表可知，()()1f x f ≤，即．回到原题：当1n =时21111ln 122nk k n k =-<-=≤+∑成立；以下2,3,n = ．令()12,3,k x k k -== ，得111ln1k k k k k --≤-=-，即()1ln ln 1k k k--≥，所以()()221ln ln ln 1n nk k n k k k ===--≥∑∑，又 22121111n n nk k k k k k k k====<++∑∑∑， ∴ 212111ln 1122n n k k k n k k k===+<+++∑∑，即211ln 12nk k n k =-<+∑ 令1k x k =-，得1ln 1111k k k k k ≤-=---，即()1ln ln 11k k k --≤-，累加，得()()122111ln ln ln 11n n n k k k n k k k k -====--≤=-∑∑∑，∴11211111111111ln 1111n n n n n k k k k k k n k k k k k k +-======≥=->-≥-+++∑∑∑∑∑，即21ln 11nk kn k =->-+∑．综上所述，得2111ln ,1,2,12nk k n n k =-<-≤=+∑ ．解法四（杨蓉）：由图像知，1211ln n n k dx n k x =<=∑⎰，11111ln n n k dx n kx -=>=∑⎰，即121ln 1n k n k -=>-∑．以下类似解法一，用数学归纳法证明．三、设,k l 是给定的两个正整数．证明：有无穷多个正整数m k ≥，使得km C 与l 互素．解法一（李博杰）：令,a m k n l n N =+⋅∈，其中a 为充分大的正整数．考虑l 的任意一个素因子p ，由组合数定义，()(1) (1)(1) (1)aa a a k kmk n l k n l k n l n l C C k k +⋅+⋅-+⋅+⋅==-对1,2,...,i k =，设α是满足|p i α且1|p i α+的正整数．由于a 为充分大的正整数，且|p l ，有1|a p l α+，故|a p i l n α+⋅，1|a p i l n α++⋅，故i 与a i l n +⋅中所含素因子p 的幂次相同．故()(1)...(1)a a a k n l k n l n l +⋅-+⋅+⋅与!k 中所含素因子p 的幂次相同．因此k mC 的分子分母中的p 在约分时上下消去，有|k m p C ．对任意|p l ，都有(,)1k m p C =，故(,)1km l C =，而这样的n 有无穷多个，命题得证．解法二：令a m k l =+，其中a 为充分大的正整数．下同解法一．由于充分大的正整数a 有无穷多个，命题得证．解法三（焦恩伟）：设1212...rrp p p p ααα=，其中12,,...,r p p p 为素数，12,,...,r N ααα+∈．设k 在p 进制下有i a 位（1,2,...,i r =）．取(1,2,...,)i i n a i r ≥=，由孙子定理，满足11(mod )i i n n m p p -+≡的m 有无穷多个．记()p S m 为p 进制下m 的各位数字之和，类似地定义()p S m k -．令112(1)(...1)i i i n n n m a p p p p +--=⋅+-+++，于是121(...(1)...(1))i n p n m s s s p p -=--个．此时由于不发生进位，()()()p p p S m S m k S k =-+．由p 进制的性质知，!,()!,!m m k k -中含有p 的幂次分别为()()(),,111p p p m S m k S k m k S m k p p p --------．又因为()m m k k =-+，得()()()111p p p m S m k S k m k S m k p p p -----=+---，故!()!!km m C m k k =-中不含素因子p ．由于这样的a 有无穷多个，命题得证．解法四（姚博文）：当1l =，或1m =时，结论明显成立．以下设2k l ≥、，并作l 的素因数分解式1212s s l p p p ααα= ，并令1212s e e e s k A p p p =⋅ ，其中12s e e e N ∈ 、、、，*A N ∈，并且(),1A l =．任取*n N ∈且n A >，定义12121s e k e k e ks m n p p p +++=⋅- ，则m k ≥；以下称满足p n α的最大非负整数α为“正整数n 素数p 的次数”．记i 中j p 的次数为α，则j p i α，且j p i α≤．11je kk j j p m p m ++⇒+，01221j k i p C C C C αααααααα≥≥≥=++++≥+ ，∴ 11jp m α++．又 ()()1111!k k mi m m m k m iC k i =--++-==∏ ，∴ kmC 的分母和分子中素因数j p 的次数相等，从而 ()(),11,2,,k jmp C j s == ．又素数12,,,s p p p 互不相同，∴ (),1km l C =，故上述无穷多个正整数m 均满足条件．解法五（刘晓艺）：反证法．假设只有有限多个m 满足题意．由于m k =时，1k m C =显然成立，因此这样的m 存在．设m 为满足(,)1km l C =的最大者．设l 的素因子为12,,...,r p p p ．令a m >，a n m l =+．对,1,...,1t m m m k =--+，设||i p t α，由于a m α>≥，有1|a i p l α+，故t 与at l +中所含素因子i p 的幂次相同．而由于(1)...(1)|(1) (1)ki m m m m k p C k k --+=-，且t 中素因子i p 的幂次不少于t m k -+中素因子i p 的幂次，故t 与t m k -+中所含素因子i p 的幂次相同．因此t m k -+与a t l +中所含素因子i p 的幂次相同．因此()(1) (1)(1) (1)a a a knm l m l m k l C k k +-+-++=-中分子分母所含素因子i p 的幂次相同，有|kn p C ，而a n m l m =+>，与m 的最大性矛盾．因此存在无穷多个m 满足题意．解法六（马晓鹏）：Lucas 定理：设,m n 为正整数，p 是素数，且1110...k k k k m m p m p m p m --=++++，1110...k k k k n n p n p n p n --=++++．则0(mod )iikn n mm i C C p =≡∏．也就是说，|nm p C 当且仅当n 的p 进制表示中至少有一位大于m 的p 进制表示中对应的一位．证明：()(1)(1)mmkr r c rp rc m C x x ===+=+∑∏0(1)(mod )m mkp r m x p =≡+∏（由于(1)1(mod )mmp p x x p +≡+）00(mod )m m m m m m r ks s p r s m C x p ==⎛⎫≡ ⎪⎝⎭∑∏ 00(mod )m m k rs cr c m C x p ==⎛⎫≡∑ ⎪⎝⎭∑∏ 其中∑表示取遍所有满足00,km m m m m s c p s p c =≤≤<=∑的集合01(,,...,)k s s s ．如果对每个m ，都有m m c r ≤，则由于c 的p 进制表示是唯一的，至多存在一组01(,,...,)k s s s 使得m m s c =．若对某个m ，m m c r >，则内层∑=0．在上述两种情况中，对0,1,...,c r =，计算c x 的系数即可证明Lucas 定理．回到原题．对于给定的k ，设其p 进制表示中的最高位为r ．令(mod )r m k p ≡，则,n m 的p 进制表示中第0,1,...,r 位均相同，由Lucas 定理，|k m p C ．设l 的全部素因子为12,,...,t p p p ，则对每个i p ，均需满足(mod )i r i m k p ≡．由中国剩余定理，只需1212(mod ...)t r r r t m k p p p ≡，这样的m 有无穷多个，证毕．解法七（yunxiu ）：当1l =时，结论显然成立．下设1l >．设l 的全部素因子为12,,...,t p p p ，则对任意i p ，都存在唯一的非负整数i α使得1|!,|!i i i i p k p k αα+．对任意正整数12max{,,,...,}t a k ααα>，令1a m l =-，显然m k >．由于(1)(2)...()!a a a k ml l l k C k ---=，有!(1)!ka k m k C l x k =+-，其中x 为整数．整理得!((1))kk a m k C l x --=．对任意1i t ≤≤，由于|a a i p l ，i a α>，有|(1)k k i m p C --，故(,)1ki m p C =．因此(,)1k m l C =．这样的正整数a 有无穷多个，命题得证．解法八（Napoleon ）：设1212...s s l p p p ααα=，其中(1,2,...,)i p i s =为素数．而!m 中i p 的次数由勒让德函数有0(!)i p i m L m p αα≥⎡⎤=⎢⎥⎣⎦∑而()!m k -与!m 中i p 的次数同理写出：00(()!),(!)i i p p i i m k k L m k L k p p αααα≥≥⎡⎤⎡⎤--==⎢⎥⎢⎥⎣⎦⎣⎦∑∑由上述三式，若证(!)(()!)(!)i i i p p p L m L m k L k ≤-+，只需证0000i i i m k m k p p p αααααα≥≥≥⎡⎤⎡⎤⎡⎤---≤⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦∑∑∑ ①又当(mod )i m k p α≡时，设,i i m cp d k ep d αα=+=+，其中,,c d e 为整数且01i d p α≤≤-．又m k ≥，故c e ≥．故0(())0c e c e α≥---=∑，①成立，亦即(,)1km C p =．由中国剩余定理，存在无穷多个(mod )i m k p α≡，此时(,)1km C l =．解法九（sufangzai ）：当1k =或1l =时，命题显然成立．构造!1m n k l =⋅⋅-，其中n 为正整数．则1(1)...(1)!km C m m m k k =--+1!!!(!1)2(1)3(1)...(1)!23n k l n k l n k l n k l k k k⋅⋅⋅⋅⋅⋅=⋅⋅-⋅-⋅-⋅⋅- !!(!1)(1)...(1)2n k l n k ln k l k ⋅⋅⋅⋅=⋅⋅---显然!n k l ⋅⋅，!2n k l ⋅⋅，…，!n k lk⋅⋅为整数，且为l 的倍数，故!1n k l ⋅⋅-，!12n k l ⋅⋅-，…，!1n k l k ⋅⋅-分别与l 互质，因此kmC 与l 互质．四、在非负数构成的3×9数表111213141516171819212223242526272829313233343536373839x x x x x x x x x P x x x x x x x x x x x x x x x x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭中每行的数均不相同，前6列中每列的三数之和为1，1728390x x x ===，273718381929,,,,,x x x x x x 均大于1．如果P 的前三列构成的数表111213212223313233x x x S x x x x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭满足下面的性质（O ）：对于数表P 中的任意一列123k k k x x x ⎛⎫⎪⎪ ⎪⎝⎭(1,2,...,9)k =均存在某个{1,2,3}i ∈使得123min{,,}ik i i i i x u x x x ≤=．求证：（i ）最小值123min{,,},1,2,3i i i i u x x x i ==一定取自数表S 的不同列．（ii ）存在数表P 中唯一的一列1*2*3*,*1,2,3k k k x x k x ⎛⎫⎪≠ ⎪ ⎪⎝⎭使得3×3数表11121*21222*31323*'k k k x x x S x x x x x x ⎛⎫ ⎪= ⎪ ⎪⎝⎭仍然具有性质（O ）．另解（李博杰）：（i ）假设最小值123,,u u u 不是来自S 的不同列，则必有两个i u 属于同一列，不妨设12,u u 属于第1列．则不论3u 属于1、2、3中的哪一列，第2、3列中总有一列不包含任何i u ，不妨设为第3列．由于同行元素互不相同，113223333,,u x u x u x <<<．而对于3k =，不存在123min{,,}ik i i i i x u x x x ≤=，与性质（O ）矛盾．（ii ）首先证明存在性．假设不存在这样的*k 使得'S 满足性质（O ）．不妨设111222,u x u x ==，由（i ）知33*k u x =．由假设，对任意*4,5,6,7,8,9k = 都存在一列ik x ，使得对每个{1,2,3}i ∈，都有ik i x u >．取*k 为4,5,6,7,8,9中使得3*k x 最大者，则由于37381,1x x >>，有3*1k x >，而333*max{}1k k x u x >=>．若1,2,3,4,5,6k =，则这一列之和大于1，与每列和为1矛盾；若7,8,9k =，则33*k k x x >，与3*k x 的最大性矛盾．其次证明唯一性．假设存在两列,a b 同时满足性质（O ）．首先考虑a 列形成的数表S ．仍然不妨设111222333,,u x u x u x ===，且3231x x <．因为32312221,x x x x <<，11112111'min{,,}a u x x x x ==．由（i ）， 3313233'min{,,}a a u x x x x ==①或3212222'min{,,}a a u x x x x ==②若为情形①，由各列之和为1，有11122223','u x u x x ==<，3333'a u x x =≥．同理，由于选出b 列也满足性质（O ），有333a x x ≥．故333a x x =，3k =，矛盾．若为情形②，有11122332',','a u x u x u x ===．1111'b x x u >=，3323'b x x u >=，由各列之和为1，22b a x x ≤．同理，考虑选出b 列，可得22a b x x ≤．故22a b x x =，由于同行元素互不相同，有a b =，矛盾．综上，存在唯一的*k 使得'S 满足性质（O ）．。

第07讲解三角形-2009-2017全国高中数学联赛分类汇编

2009-2017全国高中数学联赛分类汇编第07讲：解三角形1、（2012一试2）设ABC ∆的内角,,A B C 的对边分别为,,a b c ，且满足3cos cos 5a B b A c -=，则t a n t a n AB的值是. 【答案】42、（2013一试3）在ABC ∆中，已知sin 10sin sin A B C =，cos 10cos cos A B C =,则tan A 的值为. 【答案】11.【解析】由于()()sin cos 10sin sin cos cos 10cos 10cos A A B C B C B C A -=-=-+=，所以sin 11cos A A =，故tan 11A =.3、（2014一试7）设等边三角形ABC 的内切圆半径为2，圆心为I .若点P 满足1=PI ，则AB C ∆与APC ∆的面积之比的最大值为__________.【答案】2【解析】1PI P I =由知点在以为圆心的单位圆k 上.000,BAP K P P ααα∠=设在圆上取一点，使得取到最大值，此时应落在000,3IAC K παα∠<≤<内，且是AP 与圆的切点，由于故001sin()sin sin sin 62,(1)1sin()sin()sin()sin()23336APB APC AP AB S S AP AC πθαααππππαααθ∆∆+⋅⋅==≤=⋅⋅----00=.6IAP πθα-=∠其中，0011sin ,cot 224IP AP I AI r πθθ∠=====由知，于是所以BABCMNPTIB1sin()cos 6sin()6πθθθπθ++===-012APB APC S P P S ∆∆=根据（）、（）可知，当时，4、（2009二试1）如图，M ，N 分别为锐角三角形ABC ∆（A B ∠<∠）的外接圆Γ上弧BC ⌒ 、AC ⌒的中点．过点C 作PC MN ∥交圆Γ于P 点，I 为ABC ∆的内心，连接PI 并延长交圆Γ于T ．⑴求证：MP MT NP NT ⋅=⋅；⑵在弧AB ⌒（不含点C ）上任取一点Q （Q A ≠，T ，B ），记AQC ∆，QCB △的内心分别为1I ，2I ，求证：Q ，1I ，2I ，T 四点共圆．【解析】⑴连NI ，MI．由于PC MN ∥，P ，C ，M ，N 共圆，于是NP MI =，PM NI =．故四边形MPNI 为平行四边形．因此PMT PNT S S =△△（同底，等高）．又P ，N ，T ，M 四点共圆，故180TNP PMT ∠+∠=︒，由三角形面积公式 1sin 2PMT S PM MT PMT =⋅∠△1sin 2PNT S PN NT PNT ==⋅∠△1sin 2PN NT PMT =⋅∠于是PM MT PN NT ⋅=⋅．⑵因为1111NCI NCA ACI NQC QCI CI N ∠=∠+∠=∠+∠=∠，所以1NC NI =，同理2MC MI =．由MP MT NP NT ⋅=⋅得NT MTMP NP=．由⑴所证MP NC =，NP MC =，故12NT MTNI MI =．又因12I NT QNT QMT I MT ∠=∠=∠=∠，有12I NT I MT ∆∆∽．故12NTI MTI ∠=∠，从而1212I QI NQM NTM I TI ∠=∠=∠=∠．因此Q ，1I ，2I ，T 四点共圆．5、（2010二试1）如图，锐角三角形ABC 的外心为O ，K 是边BC 上一点（不是边BC 的中点），D 是线段AK 延长线上一点，直线BD 与AC 交于点N ，直线CD 与AB 交于点M ．求证：若OK ⊥MN ，则A ，B ，D ，C 四点共圆．同理()()22222QK QO r KO r =-+-，所以2222PO PK QO QK -=-，故OK ⊥PQ ．由题设，OK ⊥MN ，所以PQ ∥MN ，于是AQ APQN PM=．① 由梅内劳斯（Menelaus ）定理，得1NB DE AQBD EA QN⋅⋅=，②M1MC DE APCD EA PM⋅⋅=．③ 由①，②，③可得NB MC BD CD =，所以ND MDBD DC=，故△DMN ∽△DCB ，于是DMN DCB ∠=∠，所以BC ∥MN ，故OK ⊥BC ，即K 为BC 的中点，矛盾！从而,,,A B D C 四点共圆. 注1：“2PK =P 的幂（关于⊙O ）+K 的幂（关于⊙O ）”的证明：延长PK 至点F ，使得PK KF AK KE ⋅=⋅，④则P ，E ，F ，A 四点共圆，故PFE PAE BCE ∠=∠=∠，从而E ，C ，F ，K 四点共圆，于是PK PF PE PC ⋅=⋅，⑤⑤-④，得2PK PE PC AK KE =⋅-⋅=P 的幂（关于⊙O ）+K 的幂（关于⊙O ）．注2：若点E 在线段AD 的延长线上，完全类似．6、（2011二试1）如图，Q P ,分别是圆内接四边形ABCD 的对角线BD AC ,的中点．若DPA BPA ∠=∠，证明：CQB AQB ∠=∠．FE QPONMK D CBA从而有BQ AC BD AC BD AC CD AB ⋅=⋅=⋅=⋅)21(21，即CDBQAC AB =．又ACD ABQ ∠=∠，所以△ABQ ∽△ACD ，所以DAC QAB ∠=∠．延长线段AQ 与圆交于另一点F ，则DAF CAB ∠=∠，故⋂⋂=DF BC ．又因为Q 为BD 的中点，所以DQF CQB ∠=∠．又DQF AQB ∠=∠，所以CQB AQB ∠=∠．7、（2012二试1）如图，在锐角ABC ∆中，,,AB AC M N >是BC 边上不同的两点，使得.BAM CAN ∠=∠设ABC ∆和AMN ∆的外心分别为12,O O ，求证：12,,O O A 三点共线.【解析】证明：如图.连接12,AO AO ,过A 点作1AO 的垂线AP 交BC 的延长线于点P ,则APABNC是1O 的切线.因此B PAC ∠=∠, 因为,BAM CAN ∠=∠ 所以AMP B BAM PAC CAN PAN ∠=∠+∠=∠+∠=∠因而AP 是AMN 的外接圆2O 的切线, 故2.AP AO ⊥所以12,,O O A 三点共线.8、（2013二试1）（本题满分40分）如图，AB 是圆ω的一条弦，P 为弧AB 内一点，E 、F 为线段AB 上两点，满足AE EF FB ==.连接PE PF 、并延长，与圆ω分别相交于点C D 、.求证：EF CD AC BD ⋅=⋅【证明】连接AD ，BC ，CF ，DE .由于AE=EF=FB ，从而sin =2sin BC BCE B CP BEAC ACE A CP AE⋅∠==⋅∠点到直线的距离点到直线的距离.○1 同样sin =2sin AD ADF A PD AFBD BDF B PD BF⋅∠==⋅∠点到直线的距离点到直线的距离.○2 另一方面，由于BCE BCP BDP BDF ∠=∠=∠=∠， ACE ACP ADP ADF ∠=∠=∠=∠，故将○1，○,2两式相乘可得4BC ADAC BD⋅=⋅，即4BC AD AC BD ⋅=⋅○3 ABCDEFPωωPFEDCBA由托勒密定理AD BC AC BD AB CD ⋅=⋅+⋅○4 故由○3，○4得3AB CD AC BD ⋅=⋅, 即EF CD AC BD ⋅=⋅.9、（2014二试2）（本题满分40分）如图，在锐角三角形ABC 中，∠BAC ≠60°，过点B,C 分别作三角形ABC 的外接圆的切线BD,CE,且满足BD=CE=BC,直线DE 与AB ，AC 的延长线分别交于点F,G ，设CF 与BD 交于点M,CE 与BG 交于点N ，证明：AM=AN.||,LN CG 同理，由此推出0180-BAL ABL +=∠ALM=∠ALB+∠BLM=∠ALB ∠∠0=180-CAL ALC ACL ALC CLN =+=+∠∠∠∠∠.ALN =∠||BC FG 再结合以及内角平分线定理得到1LM LM BF CG CL AB BC CL ABLN BF CG LN BC AC BL BL AC=⋅⋅=⋅⋅=⋅=及LM=LN. 故由AL=AL,∠ALM=∠ALN,LM=LN 得到△ALM 与△ALN 全等，因而AM=AN,证毕.10、(2015二试3)(本题满分50分)如图,ABC ∆内接于圆,O P 为 BC上一点,点K 在线段AP 上,使得BK 平分ABC ∠,过,,K P C 三点的圆Ω与边AC 交于点D ,连结BD 交圆Ω于点E ,连结PE 并延长与边AB 交于点F ,证明:2ABC FCB ∠=∠11、（2016一试9）（本题满分16分）在ABC ∆中，已知∙=∙+∙32.求C sin 的最大值.【解析】由数量积的定义及余弦定理知，2cos 222a c b A cb AC AB -+==∙.同理得，2222b c a BC BA -+=∙，2222c b a CB CA -+=∙.故已知条件化为)(3)(2222222222c b a b c a a c b -+=-++-+即22232c b a =+.等号成立当且仅当5:6:3::=c b a .因此C sin 的最大值是37.12、（2016二试2）（本题满分40分）如图所示，在△ABC 中，X,Y 是直线BC 上两点（X,B,C,Y 顺次排列），使得BX·AC=CY·AB. 设△ACX，△AB Y 的外心分别为12,O O ，直线12O O 与AB,AC 分别交于点U 、V.证明：△AUV 是等腰三角形.【证明】作∠BAC 的内角平分线交BC 于点P,设△ACX 和△ABY 的外接圆分别为1w 和2w ，由内角平分线的性质知，BP AB CP AC =,由条件可得BX ABCY AC =,从而 .PX BX BP AB BPPY CY CP AC CP+===+ 即CP·PX=BP·PY.故P 对圆1w 和2w 的幂相等，所以P 在1w 和2w 的根轴上. 于是AP⊥12O O ，这表明点U 、V 关于直线AP 对称，从而△AUV 是等腰三角形.13、（2017二试1）（本题满分40分）如图，在ABC ∆中，AB AC =，I 为ABC ∆的内心，以A 为圆心，AB 为半径作圆1T ，以I 为圆心，IB 为半径作圆2T ，过点B I 、的圆3T 与1T ,2T 分别交于点,P Q （不同于点B ），设IP 与BQ 交于点R .证明：BR CR ⊥.证明：连接,,,,.IB IC IQ PB PC 201,IBQ IPB..,I ABC IB IC,,1180,2360?IB IP Q T IB IQ IR IB IC IP AB AC IR ICBC BPC A BRC IRB IRC IBP ICP BIC BPC =∠=∠∆∆∠∠==∆==∆∆∠∠∠=-∠∠=∠+∠=∠+∠=-∠-∠= 由于点在圆上，故所以故IBP IRB,从而有IRB=IBP,且注意到且为的内心，故所以于是ICP IRC,故IRC=ICP.又点P 在圆T 的弧上，故因此0011°(90?22A A BR CR -∠--∠⊥）（）.故。

2008-2017全国卷解三角形部分(最新整理)

角度1.利用正弦、余弦定理解三角形1.（2008课标，3）如果等腰三角形的周长是底边长的5倍，那么它的顶角的余弦值为（）87.23.43.185.A D C B 2.（2016课标2，13）ABC 的内角A ，B ，C 的对边分别为a,b,c ，若，∆135cos ,54cos ==C A a=1，则b=_____________.角度2.应用正弦、余弦定理解决与三角形面积、范围及最值有关的问题1.（2014课标2，4）钝角三角形ABC 的面积是，AB=1，BC=，则AC =（）2121.2.5.5.A D C B 2.（2010课标，16）在ABC 中，D 为边BC 上一点，，AD=2.∆ 120ADB DC 21BD =∠=，若ADC 的面积为3-，则_____________.∆3=∠BAC 3.（2011课标，16）在ABC 中，，则AB+2BC 的最大值为_______.∆3AC 60B ==， 4.(2014课标1，16)已知a,b,c 分别为ABC 三个内角A ，B ，C 的对边，a=2，且(2+b)(sinA-∆sinB)=(c-b)sinC,则ABC 面积的最大值为_____________.∆5.（2015课标1，16）在平面四边形ABCD 中，，BC=2，则AB 的取 75C B A =∠=∠=∠值范围是_____________.题型3.利用正弦定理和余弦定理解三角形1.（2013课标1，17）在ABC 中，，BC=1，P 为ABC 内一点，∆3AB 90ABC ==∠， ∆。

90BPC =∠(1)若PB=，求PA ；21(2)若。

PBA ∠=∠tan 150APB ，求 2.（2015课标2，17）在ABC 中，D 是BC 上的点，AD 平分，ABD 面积是ADC ∆BAC ∠∆∆面积的2倍。

(1)求；CB sin sin(2)若AD=1，DC=，求BD 和AC 的长。

高中数学竞赛标准讲义：第七章：解三角形

2010高中数学竞赛标准讲义：第七章：解三角形一、基础知识在本章中约定用A , B , C 分别表示厶ABC 的三个内角，a, b, c 分别表示它们所对的各边长，p b c 为半周长。

2abc、.1.正弦定理：=2R (R ABC 外接圆半径)。

sin A sin B sin C1 1 1 1 ：△ ABC 的面积为 S ^ABC = absi nC bcsi nA ca si n B.2 2 2 2:在厶 ABC 中，有 bcosC+ccosB=a. 3:在厶ABC 中，A+B=二，解a 满足一a b，则a=A.si na sin (日—a) 推论推论推论正弦定理可以在外接圆中由定义证明得到，这里不再给出，下证推论。

先证推论1,由1正弦函数定义，BC 边上的高为bsinC ,所以S^BC =—absinC ;再证推论2,因为B+C=二-A ,2所以 sin(B+C)=sinA ，即 sinBcosC+cosBsinC=sinA ,两边同乘以 2R 得 bcosC+ccosB=a 再证推论 3,由正弦定理一a—，所以二 sin (r _a )，即 sinasin (二-A)=sin(—a)sinA ，等si nA si nB si nA sin (日-A)1 1价于 [cos( v -A+a)-cos( -A-a)]= [cos(二-a+A)-cos( -a-A)]，等价于cos(v-A+a)=cos(v-a+A)，因为 Ovr-A+a , —a+Av 二.所以只有 v-A+a=”a+A ，所以 a=A , 得证。

2 2 22.余弦定理：a 2=b 2+c 2-2bccosA= cosA=^ c —,下面用余弦定理证明几个常用的2bc结论。

(1)斯特瓦特定理：在△ ABC 中，D 是BC 边上任意一点，BD=p , DC=q ，贝U 2 2e 2 b p c q AD = pq.2 2 2 2 因为 c=AB =AD +BD -2AD • BDcos ADB , ①②(1) p q 【证明】所以 c 2=AD 2+p 2-2AD • pcos ADB.2 2 2 同理 b =AD +q -2AD • qcos ADC ,因为.ADB+ . ADC 二二，所以 cos_ ADB+cos _ ADC=0 , 所以q x ①+p x ②得2 2 2qc +pb=(p+q)AD +pq(p+q),即 A D= — 注：在(1)式中，若p=q .(2)海伦公式：因为S 2ABC则为中线长公式AD = 2b " 2c "-『1 2 2 2 1 2 2 2 1 2-bcsin A= bc (1-cos A)= bc 4 4 4 2 24b c1飞[(b+c)2-a2][a2-(b -c )2]=p (p-a )(p-b)(p-c).这里所以 S A ABC 二.p(p -a)( p-b)(p -c). 、方法与例题 1 •面积法。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2009-2017全国高中数学联赛分类汇编第07讲：解三角形1、（2012一试2）设A B C ∆的内角,,A B C 的对边分别为,,a b c ，且满足3c o s c o s 5a Bb Ac -=，则t an t an AB的值是. 【答案】42、（2013一试3）在A B C ∆中，已知sin 10sin sin A B C=，cos 10cos cos AB C=,则tanA的值为.【答案】11. 【解析】由于()()sinc o s 10sin sin c o s c o s 10c o s 10c o s A A B C B C B C A-=-=-+=，所以sin11cos A A=，故tan 11A =.3、（2014一试7）设等边三角形ABC 的内切圆半径为2，圆心为I .若点P 满足1=PI ，则ABC ∆与APC ∆的面积之比的最大值为__________.【答案】3+2【解析】1P I P I =由知点在以为圆心的单位圆k 上.000,B A P K P P ααα∠=设在圆上取一点，使得取到最大值，此时应落在000,3IA C K παα∠<≤<内，且是A P 与圆的切点，由于故001s in ()s in s in s in 62,(1)1s in ()s in ()s in ()s in ()23336A PB A P CA P AB S S A P AC πθαααππππαααθ∆∆+⋅⋅==≤=⋅⋅---- 00=.6IA P πθα-=∠其中，0011s in ,c o t 224IP A P I A Irπθθ∠=====由知，于是所以BABCMNPTIB1s in ()c o s in 6=2s in ()622πθθθπθ++===-03122A PB A PC S P P S ∆∆+=根据（）、（）可知，当时，的最大值为4、（2009二试1）如图，M ，N 分别为锐角三角形A B C ∆（A B∠<∠）的外接圆Γ上弧BC⌒ 、AC ⌒的中点．过点C 作P C M N ∥交圆Γ于P 点，I 为A B C ∆的内心，连接P I 并延长交圆Γ于T ．⑴求证：M P M TN P N T⋅=⋅；⑵在弧AB ⌒（不含点C ）上任取一点Q （QA≠，T ，B ），记A Q C ∆，Q C B △的内心分别为1I ，2I ，求证：Q ，1I ，2I ，T 四点共圆．【解析】⑴连N I ，M I ．由于P C M N ∥，P ，C ，M ，N 共圆，于是N PM I=，P MN I=．故四边形M P N I 为平行四边形．因此P M T P N TS S =△△（同底，等高）．又P ，N ，T ，M 四点共圆，故180T N PP M T ∠+∠=︒，由三角形面积公式1sin 2P M T S P M M T P M T =⋅∠△1sin 2P N T S P N N T P N T ==⋅∠△1sin 2P N N T P M T=⋅∠于是P MM T P N N T⋅=⋅．⑵因为1111N C I N C A A C I N Q C Q C I C I N∠=∠+∠=∠+∠=∠，所以1N CN I =，同理2M C M I =．由M P M T N P N T⋅=⋅得N T M T M PN P=．由⑴所证M PN C=，N PM C=，故12N T M T N I M I =．又因12I N T Q N T Q M T I M T∠=∠=∠=∠，有12I N TI M T∆∆∽．故12N T I M T I ∠=∠，从而1212I Q I N Q M N T M I T I ∠=∠=∠=∠．因此Q ，1I ，2I ，T 四点共圆．学/科网5、（2010二试1）如图，锐角三角形ABC 的外心为O ，K 是边BC 上一点（不是边BC 的中点），D 是线段AK 延长线上一点，直线BD 与AC 交于点N ，直线CD 与AB 交于点M ．求证：若OK ⊥MN ，则A ，B ，D ，C 四点共圆．同理()()22222Q KQ OrK Or=-+-，所以2222P O P KQ O Q K-=-，故O K ⊥P Q ．由题设，OK ⊥MN ，所以PQ ∥MN ，于是A Q A P Q NP M=．①由梅内劳斯（Menelaus ）定理，得1N B D E A Q B D E A Q N ⋅⋅=，②1M C D E A P C DE AP M⋅⋅=．③ 由①，②，③可得N B M C B DC D=，所以N D M D B DD C=，故△DMN ∽△DCB ，于是D M N D C B ∠=∠，所以BC ∥MN ，M故OK ⊥BC ，即K 为BC 的中点，矛盾！从而,,,A B D C 四点共圆. 注1：“2P K=P 的幂（关于⊙O ）+K 的幂（关于⊙O ）”的证明：延长PK 至点F ，使得P K K F A K K E ⋅=⋅，④则P ，E ，F ，A 四点共圆，故P F E P A E B C E ∠=∠=∠，从而E ，C ，F ，K 四点共圆，于是P K P F P E P C ⋅=⋅，⑤⑤-④，得2P KP E P C A K K E =⋅-⋅=P 的幂（关于⊙O ）+K 的幂（关于⊙O ）．注2：若点E 在线段AD 的延长线上，完全类似．6、（2011二试1）如图，QP ,分别是圆内接四边形ABCD 的对角线BDAC,的中点．若DPABPA∠=∠，证明：CQBAQB∠=∠．FE QPONMK DCBA从而有BQAC BD AC BD AC CD AB ⋅=⋅=⋅=⋅)21(21，即CDBQ ACAB =．又ACD ABQ∠=∠，所以△ABQ ∽△ACD ，所以DACQAB∠=∠．延长线段AQ 与圆交于另一点F ，则DAFCAB ∠=∠，故⋂⋂=DFBC．又因为Q 为BD 的中点，所以DQFCQB ∠=∠．又DQFAQB ∠=∠，所以CQBAQB∠=∠．7、（2012二试1）如图，在锐角A B C ∆中，,,A B A C M N >是B C 边上不同的两点，使得.B A M C A N ∠=∠设A B C ∆和A M N ∆的外心分别为12,O O ，求证：12,,O O A 三点共线.【解析】证明：如图.连接12,A O A O ,过A 点作1A O 的垂线A P 交B C 的延长线于点P ,则A P 是1O 的切线.因此B P A C ∠=∠, 因为,B A M C A N ∠=∠所以A M P B B A M P A C C A N P A N ∠=∠+∠=∠+∠=∠因而A P 是A M N 的外接圆2O 的切线, 故2.A P A O ⊥所以12,,O O A 三点共线.AB8、（2013二试1）（本题满分40分）如图，A B 是圆ω的一条弦，P 为弧A B 内一点，E 、F 为线段A B 上两点，满足AEEF FB==.连接P E P F 、并延长，与圆ω分别相交于点C D 、.求证：E F C D A C B D⋅=⋅【证明】连接AD ，BC ，CF ，DE .由于AE=EF=FB ，从而sin =2sin B C B C E B C P B E A C A C EA C P A E⋅∠==⋅∠点到直线的距离点到直线的距离. ○1 同样sin =2sin A D A D F A P D A F B D B D FB P D B F⋅∠==⋅∠点到直线的距离点到直线的距离. ○2 另一方面，由于B C E B C P B D P B D F ∠=∠=∠=∠， A C E A C P A D P A D F∠=∠=∠=∠，故将○1，○,2两式相乘可得4B C A D A C B D⋅=⋅，即 4BC AD AC BD⋅=⋅○3 由托勒密定理A DBC A C BD A B C D⋅=⋅+⋅ ○4 故由○3，○4得3A B C D A C B D⋅=⋅,即E F C D A C B D⋅=⋅.学科&网9、（2014二试2）（本题满分40分）如图，在锐角三角形ABC 中，∠BAC ≠60°，过点B,C 分别作三角形ABC 的外接圆的切线BD,CE,且满足BD=CE=BC,直线DE 与AB ，AC 的延长线分别交于点F,G ，设CF 与ABCDEFPωωPFEDCBABD 交于点M,CE 与BG 交于点N ，证明：AM=AN.||,L N C G 同理，由此推出0180-B A L A B L +=∠A L M =∠A L B +∠B L M =∠A L B ∠∠ 0=180-C A L A L C A C L A L C C L N =+=+∠∠∠∠∠.A L N =∠||B C F G 再结合以及内角平分线定理得到 1L M L M B F C G C L A B B C C L A B L NB FC GL NB CA CB LB LA C=⋅⋅=⋅⋅=⋅=及L M =L N.故由A L =A L ,∠A L M =∠A L N ,L M =L N 得到△A L M 与△A L N 全等，因而A M =A N ,证毕.10、(2015二试3)(本题满分50分)如图,A B C ∆内接于圆,O P 为B C 上一点,点K 在线段A P 上,使得B K 平。