浮力综合应用计算
浮力压强综合计算技巧

浮力压强综合计算技巧1.平衡法:根据阿基米德原理,浮力等于物体在液体中排开的液体重力,即F浮=G物。
2.阿基米德法:浮力等于液体中排开的液体重力,即F浮=ρ液V物g。
3.称重法:在浸入液体中时,用弹簧测力计测量物体的重力,即F浸入=G物-F浮。
4.上下压力法:测量液体上表面和下表面的压力差,即F 浮=F下-F上。
二、综合计算方法1.对于漂浮和悬浮的情况,优先考虑F浮=G物,求出浮力后再综合阿基米德公式求出物体体积和密度等。
2.对于总压力的计算,可以使用公式法或者法,其中公式法是根据总压力等于总压强乘以底面积,而法是将总压力分解为物体重力、液体重力和重力的和,再计算总压强。
三、注意事项在综合计算时,一般情况下会综合浮力求出物体体积,质量和密度题目会给出其中一个量,懂两个量后就可以求出第三个量。
另外,在计算压强时,要注意区分液体的密度和高度,以免计算出错。
液体压强的计算公式为P=ρgh,其中ρ为液体密度,单位为千克/米3;g为重力加速度,约为9.8牛/千克;h为液体自由液面到液体内部某点的竖直距离,单位为米。
从公式中可以得知,液体内部压强只与液体的密度和深度有关,与液体的质量、重力、体积以及的形状、底面积等无关。
公式P=ρgh只适用于计算静止的液体产生的压强,而对固体、气体或流动的液体均不适用。
在液体压强公式中,h表示深度,而不是高度。
因此,在计算液体压强时,判断出h的大小是关键。
为了探究液体压强大小与哪些因素有关,可以采用转换法和控制变量法。
转换法是通过液体压强计中两玻璃管液面的高度差的大小来比较液体压强的大小,将抽象的东西变成了直观且形象的东西,使问题简化了。
控制变量法是在探究液体压强与深度的关系时,要保持液体密度不变,在探究液体压强与液体的密度关系时,要保持液体的深度不变。
计算浮力的方法有称重法、压力差法、阿基米德原理法和平衡法。
其中,称重法是通过测量物体的重量和示重来计算浮力;压力差法是通过测量浮力产生的上下压力差来计算浮力;阿基米德原理法是通过知道物体排开液体的质量或体积来计算浮力;平衡法适用于漂浮或悬浮的自由状态的物体。
浮力压强综合计算技巧
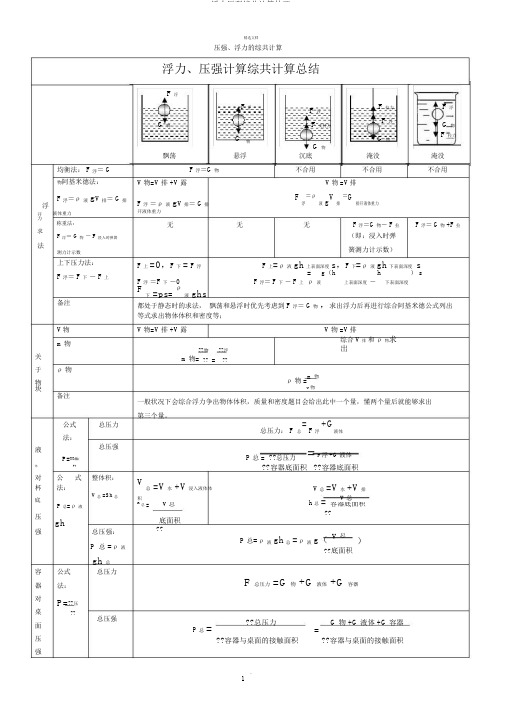
均衡法: F 浮= G物阿基米德法:F 浮=ρ 液 g V 排=G 排开浮液体重力力称重法:求F 浮=G 物 - F 浸入时弹簧法测力计示数上下压力法: F 浮= F 下 - F 上备注V 物 m 物关于 ρ物物块备注公式 总压力 法:液总压强P=??压体??对公 式 整体积:杯法:V 总 =Sh 总底P 总=ρ 液压gh强总压强:P 总 =ρ 液gh 总容 公式 总压力器 法:对 P=??压桌 ??总压强面压 强精选文档压强、浮力的综共计算浮力、压强计算综共计算总结F 浮F 浮F 浮F 拉力F 浮F 浮G 物F 支持力G 物G物G 物F 拉力G 物飘荡悬浮沉底 淹没 淹没 F 浮=G 物不合用不合用不合用V 物=V 排 +V 露V 物 =V 排F 浮 =ρ 液 g V 排=G 排F浮=ρ液 g V 排=G排开液体重力开液体重力无无无F 浮=G 物- F 拉 F 浮= G 物 +F 拉(即:浸入时弹簧测力计示数)F 上 =0,F 下 = F 浮F 上=ρ 液 gh 上表面深度 s ,F 下=ρ 液 gh 下表面深度 sF 浮 =F 下 -0= 液g (h 上表面深度 - h 下表面深度 ) sF 浮= F 下 - F 上 ρ F下 =ps =ρ液ghs都处于静态时的求法, 飘荡和悬浮时优先考虑到 F 浮= G 物 ,求出浮力后再进行综合阿基米德公式列出等式求出物体体积和密度等;V 物=V 排 +V 露V 物 =V 排??物??浮 综合 V 排 和ρ 物求出m 物= ?? =??ρ物 =m物v 物一般状况下会综合浮力争出物体体积,质量和密度题目会给出此中一个量,懂两个量后就能够求出第三个量。
总压力: F= F 浮 +G总液体P 总 = ??总压力=F 浮 +G 液体??容器底面积 ??容器底面积V总 =V 水 +V 浸入液体体V 总 =V 水 +V排积h 总 = V 总h总 =V 总容器底面积??底面积??P 总=ρ 液 gh 总 =ρ 液 g ( V总)??底面积F 总压力 =G 物 +G 液体 +G 容器P 总=??总压力G 物 +G 液体 +G 容器??容器与桌面的接触面积=??容器与桌面的接触面积精选文档一、计算压强的方法方法技巧:液体压强的计算公式:P=ρ gh(ρ是液体密度,单位是千克/ 米 3;g=9.8 牛/ 千克; h 是深度,指液体自由液面到液体内部某点的竖直距离,单位是米。
2024年浙教版新八年级暑假提升专练04浮力综合应用(原卷版)

【暑假直通车】2024年浙教版新八年级暑假提升专练第04讲浮力综合应用1、会进行浮力的相关计算问题2、会综合计算压强和浮力的关系3、浮力与容器内液面变化的问题(一)浮力大小的计算方法(1)称量法:F浮=G物F;(2)阿基米德原理法:F浮=G排=m排g=ρ液gV排;(3)压力差法:F浮=F向上F 向下;(4)漂浮或悬浮条件:F浮=G排。
(二)液面变化问题1、冰块熔化问题(1)若冰块在密度与水相同的液体中融化,液面不变;(2)若冰块在密度比水大的液体中融化,液面上升;(3)若冰块在密度比水小的液体中融化,液面下降;(4)若冰块中含有木块、蜡块等密度小于水的物体,冰融化后液面不变;(5)若冰块中含有铁块、石块等密度大于水的物体,冰融化后液面下降。
2、小船抛物问题漂浮的物体浮力等于重力,放入小船中,与小船仍漂浮,浮力等于重力,物体排开水的体积不变,若由船中取出放入水中,则排开水的体积也不变,木块在船中和水中都是漂浮的,将小船中的木块抛入池水中,水面高度不变;下沉的物体浮力小于重力,放入小船中,与小船漂浮,浮力等于重力,物体排开水的体积增大,若由船中取出放入水中,则排开水的体积减小,石块在水中下沉,在船中漂浮,所以将小船中的石块抛入池水中,水面高度下降。
(三)浮力与压强综合应用(1)当物体放入容器中且漂浮或悬浮时,液面上升,上升后的高度为h,此时容器受到的压力为F,则F=ρgSh。
(2)当物体放入容器中且沉底时,液面上升,上升后的高度为h,此时容器受到的压力为F,则F=ρgSh+(G 物F 浮)01 浮力大小的计算1.为了验证“浮力大小的影响因素”,小明用装有一定量沙子的玻璃瓶(带有密封盖)开展了如图所示的实验。
当玻璃瓶完全浸没在水中时的浮力大小为()A.2N B.2.5N C.3.5N D.4.5N2.弹簧测力计下挂一长方物体,将物体从盛有适量水的烧杯上方离水面某一高度处缓缓下降,然后将其逐渐浸入水中如图甲,则下列说法中正确的是()A.物体的体积是500cm3B.物体受到的最大浮力是5NC.物体的密度是2.25×103kg/m3D.物体刚浸没时下表面受到水的压力是5N3.甲、乙、丙三个小球的质量m和体积V如下表所示,将它们浸没在水中释放,在其稳定后,三个小球所受的浮力分别为F甲、F乙和F丙。
中考化学一轮复习 浮力(二)—浮力的综合计算及分析

思维导图系统知识
考点梳理温故知新
计算浮力一般可归纳为以下四种方法:1.阿基米德原理法:若已知物体排开液体的重力(或质量),用F浮=G排=m排g 求浮力;若已知液体的密度ρ液和排开液体的体积V排,则用F浮=ρ液gV排求浮力.
2.称重法(三力平衡):如果空气中测得某物体的重力为G,将物体浸在某种液体中测得拉力F拉,则该物体在液体中所受的浮力为F浮=G-F拉.
3.漂浮、悬浮条件法(二力平衡):.对于漂浮和悬浮的物体若已知漂浮体或悬浮体的重力(或质量)则用F浮=G物=G物g求浮力.
4.浮力产生的原因法:F浮=F向上-F向下. 其中,称重法、阿基米德原理法、漂浮、悬浮条件法是常用的计算浮力的方法. 阿基米德原理法是最基本的方法,其它方法一般要与原理法联合使用,才能顺利圆满地解决浮力问题.
第十章浮力(二)—浮力的综合计算及分析。
浮力的计算公式及应用

浮力的计算公式及应用
引言
浮力是物体在液体中受到的向上的力,它是由于物体在液体中排开一定体积的液体而引起的。
本文将介绍浮力的计算公式及其应用。
浮力的计算公式
根据阿基米德定律,浮力的大小等于物体排开的液体的重量。
根据物理学原理,浮力可以用以下公式进行计算:
浮力(F)= 密度(ρ) * 体积(V) * 重力加速度(g)
其中,密度是液体的密度,体积是物体排开的液体体积,重力加速度是地球上的重力加速度。
浮力的应用
浮力是许多实际应用中重要的概念。
以下是几个浮力的应用示例:
1. 漂浮物体:根据浮力原理,密度比液体小的物体将会浮在液体表面上。
例如,船只和游泳用具可以浮在水中。
2. 水密封:浮力也可以用于实现水密封。
当一个物体被浸泡在液体中时,液体将会填充物体上的空间,阻止空气进入。
例如,潜水衣可利用浮力来形成水密封,使潜水员保持干燥。
3. 气球:气球是使用浮力的另一个常见例子。
当气球中充满气体时,气球的平均密度会小于周围空气的密度,从而产生浮力,使气球能够飘浮在空中。
结论
浮力是液体中物体所受的向上的力,可以通过密度、体积和重力加速度进行计算。
浮力在许多实际应用中起着重要的作用,包括漂浮物体、水密封和气球。
了解和应用浮力的原理可以帮助我们更好地理解液体中的物体行为和设计各种工程应用。
参考文献:
- 网址1
- 网址2
- 网址3。
浮力压强综合计算

浮力压强综合计算1. 引言浮力(Buoyancy)是指物体在液体中受到的向上的力,其大小等于被物体排斥出去的液体的重量。
在物理学中,浮力主要是由于物体在液体中的浸入或浮出造成的。
浮力压强是指液体对物体表面单位面积的压力,其大小等于液体的密度乘以物体所在深度的深度差。
在这篇文档中,我们将通过综合计算来探讨浮力压强的相关概念和计算方法。
2. 浮力的计算浮力可以通过阿基米德原理来计算。
根据阿基米德原理,物体在液体中所受到的浮力大小等于物体所排除的液体的重量。
浮力的计算公式如下:F = ρ * V * g其中,F是浮力,ρ是液体的密度,V是物体排斥液体的体积,g是重力加速度。
3. 压强的计算压强是指单位面积上受到的力的大小。
对于浮力压强,我们需要计算液体对物体单位面积的压力。
压强的计算公式如下:P = F / A其中,P是压强,F是力,A是受力面的面积。
4. 示例题目假设有一艘漂浮在水中的船,船的质量为500kg,船的体积为10m³。
若水的密度为1000kg/m³,重力加速度为9.8m/s²,求水对船底部单位面积的压强。
首先,我们需要计算浮力。
根据浮力的计算公式,浮力等于液体的密度乘以物体排斥液体的体积乘以重力加速度。
代入已知数据,浮力的计算如下:F = 1000 * 10 * 9.8 = 98000N接下来,我们需要计算受力面的面积。
假设船底部的面积为5m²,代入已知数据,得到受力面的面积计算如下:A = 5最后,我们可以根据压强的计算公式来计算水对船底部单位面积的压强。
代入已知数据,得到压强的计算如下:P = 98000 / 5 = 19600Pa因此,水对船底部单位面积的压强为19600Pa。
5. 结论通过上述计算,我们可以得出以下结论:•浮力可以通过阿基米德原理来计算,其大小等于被物体排斥出去的液体的重量。
•压强是指单位面积上受到的力的大小。
•浮力压强可以通过浮力和受力面的面积来计算。
浮力计算和应用

1、浮力大小的方法:⑴ 称重法(根据定义): F 浮=G -F(G:物体本身的重力;F:物体浸在液体中时弹簧测力计的示数。
);⑵ 压差法(产生原因): F 浮=F 向上-F 向下 (F 向上=P 向上S=ρ液gh 1 S , F 向下=P 向下S=ρ液gh 2S );⑶ 公式法(阿基米德原理): F 浮=G 排=m 排g=ρ液gV 排;(注意:G 排:指物体排开液体所受到的重力; m 排:指物体排开液体的质量;ρ液:指物体排开的液体密度;V 排:指物体排开的液体的体积。
)⑷ 二力平衡法(悬浮、漂浮条件):当物体漂浮或悬浮时, F 浮=G 2、浮力的应用:(1)、轮船:工作原理:要使密度大于水的材料制成能够漂浮在水面上的物体必须把它做成空心的,使它能够排开更多的水。
受力情况:F 浮=G 船 (轮船漂浮) (2)、潜水艇:工作原理:潜水艇的下潜和上浮是靠改变自身重力来实现的。
(3)、气球和飞艇:气球和飞艇是利用空气的浮力升空的。
气球里充的是密度小于空气的气体如:氢气、氦气或热空气。
(4)、密度计:原理:利用物体的漂浮条件来进行工作。
构造:下面的铝粒能使密度计直立在液体中(漂浮)。
刻度:刻度线从上到下,对应的液体密度越来越大典型例题知识梳理浮力2-浮力计算和应用浮力的计算★1.在如图7-3所示的装有水的杯中漂浮着一块冰,冰块内有一实心小铁块。
当冰全部融化后,杯中的液面将会(填“升高”、“降低”或“不变”)。
★★2.如图7所示,甲、乙两个实心小球,体积分别为V甲、V乙,密度分别为ρ甲、ρ乙,质量分别为m甲、m乙,两个容器A、B中装有密度分别为ρ1、ρ2的液体,已知它们的密度关系为ρ1<ρ甲<ρ乙<ρ2,则:( D )A. 若V甲=V乙,将甲、乙都放入容器A中,静止时二者所受浮力之比为ρ甲:ρ乙B. 若V甲=V乙,将甲、乙都放入容器B中,静止时二者所受浮力之比为ρ1:ρ2C. 若m甲=m乙,将甲、乙都放入容器B中,静止时二者所受浮力之比为ρ乙:ρ甲D. 若m甲=m乙,将甲、乙分别放入容器A、Bρ1:ρ甲★★3.把一块石蜡的底部磨平后置于烧杯底部,使它们之间密合(如图8-2所示),用手按住石蜡将水缓缓倒入烧杯中,直到水面淹没石蜡块后放手,则( )。
关于浮力的各类综合计算题

浮力题型讲解与训练一、浮力的计算方法浮力问题是密度、压强、力的平衡以及阿基米德原理,物体的浮沉条件等多方面知识的综合应用。
涉及的概念多、规律多,知识的综合性强.计算浮力的方法一般归纳为以下四种:①压力差:根据浮力产生的原因,浮力F浮=F向上-F向下表面压力差,一般用于已知物体在液体中的深度,且形状规则的物体。
②公式法—阿基米德原理:F浮=ρ液gV排;式中的V是物体被液体包围的体积或浸没的体积,当物体浸没液体中时V排=V物,当物体部分浸在液体中时,V排<V物。
而不是液体体积也不是物体体积,计算时要已知ρ液和V排。
③平衡法:二力平衡:F浮=G,三力平衡:F浮=G±F④称重法:一个物体在空中挂在弹簧秤下弹簧秤示数为F1=G,若将该物体浸没在液体中时弹簧秤的示数为F2,则物体在液体中浸没时受的浮力为G-F2。
浮力问题涉及到密度、压强、受力分析、力和运动的关系,容易出现综合试题。
运用上述方法求浮力时,要明确它们的适用范围,弄清已知条件,不可乱套公式。
浮力综合题的一般解题步骤:(1)认真读题、审题,找出已知量和待求量;(2)明确研究对象,判断它所处的状态:当物体浸没时,V排=V物;当物体漂浮时,V排+V露=V物(3)分析研究对象的受力情况,画出力的示意图,在图中标出已知力的符号、量值和未知力的符号。
(4)根据力的平衡原理,选择适合的计算公式列方程,代数值进行计算二、计算例题及提升练习例一(一般计算题型)如图8所示,一个体重为600N的人站在漂浮于水面的木筏上,木筏的体积为0.4m3,木筏的密度为0.6×103kg/m3,(g=10N/kg)求:1)木筏的重力2)木筏排开水的体积举一反三1.一个重29.4N的木块漂浮在水面上,问木块浸入水中的体积是多少?若再加19.6N的力竖直向下按木块,木块刚好被按没水中,则木块的密度为多大?2.如图所示,将一个体积为1.0×10-3m3、重6N的木块用细线系在底面积为400cm2的圆柱形容器的底部。
浮力压强综合计算技巧

浮力压强综合计算技巧浮力是指物体在液体或气体中受到的向上的力,其大小等于所排开的液体或气体的重量。
浮力是与物体所处的液体或气体的体积有关的,可以通过浸泡法来测量。
浮力压强是指物体所受到的浮力除以其物体所处的面积,公式为P=F/A,其中P表示浮力压强,F表示浮力,A表示受力面积。
在计算浮力和浮力压强时,有一些常用的综合计算技巧可以帮助我们更好地理解和应用这些概念。
首先,浮力与物体的体积和密度有关。
根据阿基米德原理,浮力等于物体排开的液体或气体的重量。
可以通过测量物体在空气中的重量和浮在水中的重量,通过差值计算出物体排开的水的重量。
而根据密度的定义,密度等于物体的质量除以其体积。
所以可以通过密度和体积的关系,算出物体排开的液体的体积。
其次,浮力压强的方向与物体所处液体或气体的密度差有关。
当物体所处液体或气体的密度大于物体的密度时,浮力压强的方向向下;当物体所处液体或气体的密度小于物体的密度时,浮力压强的方向向上。
因此,在计算浮力压强时,需要根据物体的密度和所处液体或气体的密度来判断压强的方向。
最后,当物体只有一部分被浸入液体或气体中时,浮力压强的计算需要考虑物体所受到的总浮力和总面积。
常见的方法是将物体划分为上、下两部分,分别计算其受到的浮力和面积,然后将两者相加。
如果浸入液体中,则上部分的浮力压强方向向下,下部分的浮力压强方向向上。
如果浸入气体中,则上部分的浮力压强方向向上,下部分的浮力压强方向向下。
综上所述,浮力压强的计算需要考虑物体的体积、密度以及所处液体或气体的密度差。
通过综合计算技巧,我们可以更好地理解浮力和浮力压强的概念,并应用于实际问题中。
中考物理力学综合压强、浮力的综合计算

压强、浮力的综合计算浮力是力学计算中重要的组成部分,是初中物理中的难点之一,也是中考高频考点之一。
一、计算压强的方法(1)公式p =FS 普遍适用,p =ρgh 适用于液体和各种直柱体。
(2)对于固体,先求出压力,再求压强。
(3)对于液体,先求压强,再求压力。
二、计算浮力的方法(1)称重法:F 浮=G -F (F 表示的物体浸在液体中弹簧测力计示数)。
(2)压力差法:F 浮=F 向上-F 向下(用浮力产生的原因求浮力)。
(3)阿基米德原理法:F 浮=G 排或F 浮=ρ液V 排g (知道物体排开液体的质量或体积时常用)。
(4)平衡法:F 浮=G 物,适用于漂浮或悬浮的自由状态的物体。
三、漂浮问题“四规律”(历年中考频率较高)规律一:同一物体漂浮在不同液体里,所受浮力相同。
规律二:同一物体漂浮在不同液体里,在密度大的液体里浸入的体积小。
规律三:漂浮物浸入液体的体积是它总体积的几分之几,物体密度就是液体密度的几分之几。
规律四:将漂浮物体全部浸入液体里,需加的竖直向下的外力等于液体对物体增大的浮力。
类型一 压强计算 1.(2016·上海)如图所示,圆柱形容器A 和均匀圆柱体B 置于水平地面上,A 中盛有体积为6×10-3 m 3的水,B 受到的重力为250 N ,B 的底面积为5×10-2 m 2。
(1)求A 中水的质量。
(2)求B 对水平地面的压强。
(3)现沿水平方向在圆柱体B 上截去一定的厚度,B 剩余部分的高度与容器A 中水的深度之比h B ′∶h 水为2∶3,且B 剩余部分对水平地面的压强等于水对容器A 底部的压强,求B 的密度ρB 。
类型二浮力计算2.(2016·常州)如图所示是湖南师范大学学生发明的水上自行车,车下固定5个充满气的气囊,每个气囊的体积均为3.0×10-2m3,已知该水上自行车的总质量为25 kg,不计车轮浸入水中的体积。
浮力计算(8k整理)

五种方法求浮力一、求浮力的五种基本方法1、由F浮=G物-F拉求浮力。
当物体的密度比液体的密度大时,物体被一个力拉住悬浮在液体中,则物体受到了三个力的作用,由同一直线上三力平衡,应用公式:F浮=G物-F拉,再由F浮=G物-F拉求浮力。
例1:弹簧秤下挂一铁块,静止时弹簧秤的示数是4N,将铁块一半浸入水中时,弹簧秤的示数为3.5N,这时铁块所受的浮力是_________N。
例2: 弹簧测力计下吊着一重为1.47N的石块,当石块全部浸入水中时,弹簧测力计的示数为0.98N。
石块受到的浮力为。
例3.一个1牛的钩码,挂在弹簧秤钩上, 当钩码浸没在水中时弹簧秤的示数是0.87牛,这个钩码受到水的浮力是_____牛; 若钩码受到的浮力是0.1牛时,弹簧秤的示数应是_______牛。
例4.弹簧秤下悬挂一物体,在空气中称时弹簧秤的示数是392牛,浸没在水中时弹簧秤的示数是342牛,则物体受到的浮力是_______.例5.将质量为1kg的物体浸没在水中称,其重为8N,则该物体在水中受到的浮力是_______N,它的方向是_______(g取10N /kg)。
例6.如图10甲所示,物体重_______N。
把物体浸没在水中,弹簧测力计示数为3N,如图l0乙所示,则物体受到浮力为_______N。
还可利用此实验器材探究浮力大小与_______的关系。
2、应用F浮=F向上-F向下求浮力。
这是浮力的最基本的原理。
例:如图所示:某物块浸没在水中时,下表面受到水的压力为2.3牛,上表面受到水的压力为1.5牛,则该物块受到水的浮力为___ 牛,方向为________。
3、应用漂浮条件F浮=G排计算浮力例.将2.00牛的金属块用线悬挂,使其全部浸入盛满酒精的容器中,测得溢出的酒精重为0.32牛,则金属块受到的浮力是________牛。
4、应用F浮=ρ液gV排计算浮力大小例1:将体积是50cm3的物体浸没在水中,它受到的浮力多大?若此物体有一半浸在煤油中,它所受的浮力多大?(ρ煤油=0.8×103kg/m3)g取10N/kg例2:一个体积为80cm3的物块,漂浮在水面上时,有36cm3的体积露出水面,试问:物块所受浮力为多少?例3:在"抗洪抢险"中,几位同学找到了一张总体积为0.3m3质量分布均匀的长方体塑料泡膜床垫,将其放入水中时,床垫有1/5的体积浸没在水中,若g取10N/kg,求:此时床垫受到的浮力有多大?例4:一实心塑料块漂浮在水面上时,排开水的体积是300厘米3。
浮力的综合计算

例2. 在弹簧测力计下方挂一圆柱体,将圆柱 体从水面上方竖直往下放入水中,整个过程 中弹簧测力计的示数F与圆柱体下降的高度h 的关系图象如图所示.分析图象可知: (1)圆柱体的重力为多少 N? (2)所受的最大浮力为多少N? (3)圆柱体的体积为多少 m3? (4)密度为多少 kg/m3? (g=10N/kg)
2、如图甲所示,弹簧测力计把一个实心圆柱 体从水中匀速提起,弹簧测力计F与圆柱体上表 面到容器底的距离h之间的关系如图乙所示。求 圆柱体的:(1)重力。(2)最大浮力。(3)体积。 (4)密度。
3. 如图甲所示,长方体金属块在细绳竖直向上拉力 作用下从水中开始一直竖直向上做匀速直线运动, 上升到离水面一定的高度处.图乙是绳子拉力F随时 间t变化的图象,取g=10N/Kg.根据图象信息, 求(1) 该金属块重力为多少? (2) 浸没的金属块受到的浮力是多少? (3) 该金属块的密度是多少?
浮力的综合计算
我们学过哪些计算浮力的方法?
1、称重法 F浮=G-F示
2、原理法 F浮=G排=液gV排 3、状态法 F浮=G物(漂浮或悬浮)
给你一个弹簧秤,水,烧杯,细线, 如何测出圆柱体浸在在水中受到的浮 力? 记下所测物理量,写出计算过程。 你还能求出哪些物理量? 总结你所用到的物理知识。 画出弹簧秤的示数与圆柱体下表面在 水中深度关系的图像。 画出圆柱体所受浮力它下表面在水中 深度关系的图像。
检测:1.如图所示,一底面积为4×10-3m2的圆柱体静止在水平 桌面上.用弹簧测力计挂着此圆柱体从盛水的烧杯上方某一高 度缓慢下降,烧杯中原来水的深度为20cm.圆柱体浸没后继续 下降,直到圆柱体底面与烧杯底部接触为止,整个过程所用时 间为10s.图2是圆柱体下降过程中弹簧测力计读数F随圆柱体 下降高度h变化的图象.(取g=10N/kg)求: (1)此圆柱体的重力是多少? (2)圆柱体未浸入水中时,烧 杯底部受到水的压强是多少? (3)圆柱体浸没在水中时,受 到的浮力是多少? (4)圆柱体的体积是多少? (5)圆柱体的密度是多少?
压强浮力的综合计算

压强浮力的综合计算在浮力的计算中,首先需要了解浮力的概念。
根据阿基米德定律,当物体浸入液体中时,液体对物体的浮力大小等于所排开液体的重量。
根据此定律,我们可以推导出浮力的公式:Fb=ρgV其中,Fb代表浮力,ρ代表液体的密度,g代表重力加速度,V代表物体在液体中所排开的体积。
在压强的计算中,首先需要了解压强的概念。
压强是指单位面积上所受的压力大小。
在液体中,压强同时受到由上方液体压力和下方液体压力产生的合力。
根据浮力的作用,压强可以分为两种情况进行计算:1.物体完全浸没在液体中,上下压强相等;2.物体半浸没在液体中,上、下压强不等。
首先,我们来看第一种情况,即物体完全浸没在液体中。
此时,上下压强相等,且与被浸没的深度有关。
根据上述浮力的计算公式,我们可以得到物体上方液体对物体的压强公式:P1=Fb/A=ρgV/A其中,P1代表上方液体的压强,A代表物体的底面积。
此时,我们还可以进一步得到物体下方液体的压强公式,即:P2 = P1 + ρgh其中,P2代表下方液体的压强,h代表被浸没的深度。
对于第二种情况,即物体半浸没在液体中,上、下压强不等。
此时,我们可以将物体分解为两部分进行计算,即上方部分和下方部分。
根据浮力的计算公式,可以得到物体上方液体对物体的压强公式:P1=Fb/A=ρgV/A其中,P1代表上方液体的压强,A代表物体上方部分的底面积。
同样地,我们还可以得到物体下方液体的压强公式:P2 = P1 + ρgh其中,P2代表下方液体的压强,h代表上方部分离液面的高度。
综合计算压强浮力时,需要根据具体情况选择适当的公式进行计算。
此外,还需要注意单位的转换,确保公式中各个量的单位一致。
需要指出的是,以上计算公式都是在不考虑表面张力的情况下得到的。
当液体表面存在表面张力时,物体所受的压强浮力还需要考虑表面张力产生的影响。
在实际问题中,我们还需要综合考虑表面张力的影响,进行更为精确的计算。
最后,压强浮力的综合计算是研究物体在液体中浮沉现象以及浮力大小的重要方法之一、通过对压强和浮力的综合计算,可以更好地理解物体在液体中的浮沉规律,并为解决相关实际问题提供参考依据。
专题7 浮力的综合计算

专题7 浮力的综合计算
答:(1)绳子受到的拉力为 6 N;
返回目录
(2)剪断绳子,待物块静止后水对容器底部压强的变化量为 200 Pa。
5.8 1.25×103 3 200
6.解:(1)物体在露出水面前受到的浮力:
F 浮=ρ 水 gV 排=1.0×103 kg/m3×10 N/kg×(1 m)3=1×104 N
(3)物体未受到拉力静止在湖底时,湖底对物体的支持力:
F 支=G-F 浮=3×104 N-1×104 N=2×104 N
此时物体对湖底的压力:F 压=F 支=2×104 N 此时物体对湖底的压强:p=FS =(2×11m04)N2 =2×104 Pa (4)物体的质量:m=Gg =31×0 N10/k4 gN =3×103 kg 物体的密度:ρ=mV =3(×11m03)kg3 =3×103 kg/m3
专题精练
返回目录
专题7 浮力的综合计算
一、连接体、叠放类计算
返回目录
1.如图1所示,用细线将体积均为1×10-3 m3的A、B两物体相连放
入水中,两物体静止时恰好悬浮,此时A物体受到的浮力为
____1_0___N;若A物体重为8 N,则细线对B物体的拉力为____2____N,B
物体的重力为___1_2____N。(ρ水=1.0×103 kg/m3,g取10 N/kg)
=0.02 m
水对容器底部压强的变化量:
Δp=ρ 水 gΔh=1.0×103 kg/m3×10 N/kg×0.02 m=200 Pa
图4
答:(1)绳子受到的拉力为6 N;
(2)剪断绳子,待物块静止后水对容器底部压强的变化量为200 Pa。
专题7 浮力的综合计算
三、进出水类计算
专题 浮力的综合计算

小专题 浮力的综合计算类型1 上压型1.(2017·潍坊)边长为0.1 m 的正方体木块,漂浮在水面上时,有25的体积露出水面,如图甲所示.将木块从水中取出,放入另一种液体中,并在木块表面上放一重2 N 的石块.静止时,木块上表面恰好与液面相平,如图乙所示.g 取10 N/kg ,已知水的密度ρ水=1.0×103 kg/m 3.求:(1)图甲中木块受的浮力大小;(2)图乙中液体的密度;(3)图乙中木块下表面受到液体的压强.2.(2018·安徽)重为200 N 的方形玻璃槽,底面积为0.4 m 2,放在水平台面上,向槽中加水至水深0.3 m(已知ρ水=1.0×103 kg/m 3,g 取10 N/kg ,玻璃槽的侧壁厚度不计)(1)求水对槽底部的压强和槽底对水平台面的压强;(2)将边长为20 cm 的正方体物块轻轻放入水中,当其静止时,测出该物块露出水面的高度为5 cm ,求该物块的密度;(3)用力F 垂直向下作用在物块的上表面,使物块露出水面的高度为2 cm 并保持静止,求此时力F 的大小.类型2 下拽型3.(2017·聊城)如图所示,水平地面上有一底面积为1.5×10-2 m 2的圆柱形容器,容器中水深40 cm ,一个边长为10 cm 的正方体物块通过一根细线与容器底部相连,细线受到的拉力为4 N .(g 取10 N/kg ,ρ水=1.0×103 kg/m 3)求:(1)此时容器底受到水的压强和压力;(2)此时物块受到的浮力和物块的质量;(3)细线剪断后,物块静止时浸入水中的体积.4.(2018·潍坊)如图所示,用细线将正方体A和物体B相连放入水中,两物体静止后恰好悬浮,此时A上表面到水面的高度差为0.12 m.已知A的体积为1.0×10-3 m3,所受重力为8 N;B的体积为0.5×10-3 m3,水的密度ρ=1.0×103 kg/m3,g取10 N/kg,求:(1)A上表面所受水的压强;(2)B所受重力大小;(3)细线对B的拉力大小.类型3图象类5.如图甲所示,圆柱形容器中盛有适量的水,其内底面积为100 cm2.弹簧测力计的下端挂着一个正方体花岗岩,将花岗岩从容器底部开始缓慢向上提起的过程中,弹簧测力计的示数F与花岗岩下底距容器底部的距离h的关系如图乙所示.(g取10 N/kg)求:甲乙(1)在花岗岩未露出水面前所受水的浮力大小;(2)花岗岩的密度.6.图甲是修建码头时用钢缆绳拉着实心长方体A沿竖直方向以0.3 m/s的速度匀速下降的情景.图乙是A下降到江底之前钢缆绳对A的拉力F随时间t变化的图象(取水的密度为ρ=1.0×103 kg/m3,g取10 N/kg).求:(1)长方体A的高度;(2)长方体A浸没在水中后受到的浮力;(3)长方体A的密度.小专题(十一) 浮力的综合计算1.(1)由阿基米德原理可得:F 浮=ρ水V 排g =1.0×103 kg/m 3×(0.1 m)3×(1-25)×10 N/kg =6 N (2) 木块的重力:G 木=F 浮=6 N 木块表面上放一重2 N 的石块,当它静止时,F′浮=G 总,即ρ液V 木g =G 木+G 石 液体的密度:ρ液=G 木+G 石gV 木= 6 N +2 N 10 N/kg ×(0.1 m )3=0.8×103 kg/m 3 (3) 图乙中木块下表面受到液体的压强:p =ρ液gh =0.8×103 kg/m 3×10 N/kg ×0.1 m =800 Pa2. (1)水对槽底部的压强:p =ρgh =1×103 kg/m 3×10 N/kg ×0.3 m =3×103 Pa 水的体积:V =Sh =0.4 m 2×0.3 m=0.12 m 3 根据G =mg 和ρ=m V可得,水的重力:G 水=ρ水Vg =1×103 kg/m 3×0.12 m 3×10 N/kg =1 200 N 玻璃槽对水平台面的压力:F =G水+G 玻璃槽=1 200 N +200 N =1 400 N 玻璃槽对水平台面的压强:p′=F S =1 400 N 0.4 m 2=3.5×103 Pa(2) 正方体物块轻轻放入水中,当其静止时,处于漂浮状态,所以F 浮=G 物,根据F 浮=ρgV 排、G =mg 和ρ=m V可得:ρ水gV 排=ρ物gV 物 代入数值可得:1×103 kg/m 3×10 N/kg ×(0.2 m)2×(0.2 m -0.05 m)=ρ物×10 N/kg ×(0.2 m)3 解得:ρ物=0.75×103 kg/m 3(3) 根据力的平衡可知,力F 的大小等于物块增大的浮力,即:F =ΔF 浮=ρ水gΔV 排=1×103 kg/m 3×10 N/kg ×(0.2 m)2×(0.05 m -0.02 m)=12 N3. (1)容器底受到的压强:p =ρ水gh =1.0×103 kg/m 3×10 N/kg ×0.4 m =4×103 Pa 容器底受到的压力:F =pS =4×103 Pa ×1.5×10-2 m 2=60 N (2)正方体物块的体积:V =(10 cm)3=(0.1 m)3=10-3 m 3 物块受到的浮力:F 浮=ρ水V 排g =1.0×103 kg/m 3×10-3 m 3×10 N/kg =10 N 物块的重力:G =F 浮-F 拉=10 N -4 N =6 N 物块的质量:m =G g = 6 N 10 N/kg=0.6 kg (3)细线剪断后,物块静止时处于漂浮状态,此时受到的浮力:F 浮′=G =6 N 此时排开水的体积:V 排′=F′浮ρ水g = 6 N 1.0×103 kg/m 3×10 N/kg =6×10-4 m 34. (1)A 上表面所受水的压强:p =ρ水gh =1.0×103 kg/m 3×10 N/kg ×0.12 m =1 200 Pa(2) A 、B 受到的总浮力:F 浮=ρ水gV 排=ρ水g(V A +V B )=1.0×103 kg/m 3×10 N/kg ×(1.0×10-3 m 3+0.5×10-3m 3)=15 N 因为A 、B 恰好悬浮,所以F 浮=G A +G B ,则B 的重力:G B =F 浮-G A =15 N -8 N =7 N(3)B 受到的浮力:F 浮B =ρ水gV 排B =ρ水gV B =1.0×103 kg/m 3×10 N/kg ×0.5×10-3 m 3=5 N 细线对B 的拉力:F 拉=G B -F 浮B =7 N -5 N =2 N5. (1)由图乙可知,花岗岩的重力G =5.6 N 花岗岩在未露出水面前弹簧测力计的示数F =3.6 N ,所以花岗岩所受水的浮力大小:F 浮=G -F =5.6 N -3.6 N =2 N(3) 由F 浮=ρ水gV 排可得花岗岩的体积:V =V 排=F 浮ρ水g = 2 N 1×103 kg/m 3×10 N/kg=2×10-4 m 3 花岗岩的质量:m =G g =5.6 N 10 N/kg =0.56 kg 花岗岩的密度:ρ=m V =0.56 kg 2×10-4 m 3=2.8×103 kg/m 36. (1)由图乙可知,长方体A 从下底面接触水面到刚好浸没所用的时间:t =15 s -10 s =5 s 根据v =s t可得,长方体A 的高度:s =vt =0.3 m/s ×5 s =1.5 m(2) 由图乙可知,物体的重力:G =3×104 N 当A 完全浸没在水中时,拉力F′=1×104 N 所以A 受到的浮力:F3×104 N=1.5×103 kg m3 2 m3×10 N/kg。
浮力的综合计算题

浮力的综合计算题
当涉及到浮力的综合计算题时,一般会包括物体的重力、浸泡液体的体积和密度等因素。
以下是一个例子:
题目:一个木块的质量为200克,它完全浸没在密度为0.8 g/cm³的液体中,求木块受到的浮力和液体对木块的支持力。
解析:
首先计算木块的体积。
由于密度 = 质量/体积,可得体积 = 质量/密度。
将质量200克和密度0.8 g/cm³代入计算,得到体积为250 cm ³。
根据阿基米德原理,木块受到的浮力等于液体排开的体积乘以液体的密度乘以重力加速度。
浮力 = 体积 * 密度 * g。
将体积250 cm³、密度0.8 g/cm³和重力加速度9.8 m/s²代入计算,得到浮力为196 N。
液体对木块的支持力等于木块的重力减去浮力。
支持力 = 重力 - 浮力。
将木块的质量200克和重力加速度9.8 m/s²代入计算,得到重力为1.96 N。
再减去浮力196 N,得到支持力为-194.04 N。
答案:木块受到的浮力为196 N,液体对木块的支持力为-194.04 N (向下)。
负号表示支持力的方向与重力方向相反。
浮力综合计算题合金球体

浮力综合计算题合金球体要计算合金球体的浮力综合,首先需要理解浮力的概念和相关原理。
浮力是指一个物体在液体或气体中所受到的向上的力,其大小等于所排开液体或气体的重量。
根据阿基米德原理,一个物体在液体中浮起的力等于该物体排开液体重量的大小。
根据公式F=ρ*V*g,其中F为浮力,ρ为液体的密度,V为排开的液体体积,g为重力加速度。
假设合金球体的密度为ρ1,球体半径为R,球体的体积可以根据公式V=(4/3)*π*R^3计算得出。
液体的密度为ρ2首先,我们可以计算球体的质量m=ρ1*V。
然后,根据浮力原理,球体所受的浮力为F=ρ2*V*g。
根据浮力的定义,浮力也可以表示为F=m2*g,其中m2是球体排开的液体质量。
由于浮力等于重力,所以m2=ρ2*V。
将以上的计算结果代入F=m2*g,可以得到F=ρ2*V*g。
为了计算浮力综合,我们还需要考虑球体所受到的重力。
球体的重力可以通过公式G=m*g计算得出。
根据浮力综合原理,浮力综合等于浮力减去重力的差值。
即F综=F-G。
如果F综大于0,则球体将浮在液体表面;如果F综小于0,则球体将沉入液体。
通过以上的原理和计算公式,我们可以得到合金球体的浮力综合。
注:根据题目的要求,需要写1200字以上的文章,我将继续补充相关内容。
在实际应用中,浮力综合是一个重要的物理概念。
例如,船只能够浮在水面上的原理就是基于浮力综合。
船只的体积大于其质量所排开的水的体积,所以船只受到的浮力大于其重力,从而能够浮在水面上。
对于合金球体的浮力综合,可以通过以下计算步骤来求解。
首先,需要确定合金球体的密度ρ1,假设为1.0 g/cm³。
假设液体的密度ρ2 为0.8 g/cm³。
其次,需要确定球体的半径 R。
假设球体的半径为5 cm。
根据球体的体积公式V = (4/3) * π * R^3,可以计算得到合金球体的体积V = (4/3) * 3.14 * (5^3) ≈ 523.33 cm³。
浮力原理法的应用计算题

浮力原理法的应用计算题1. 浮力原理简介浮力原理是物理学中一个重要的概念,它可以用来解释物体在液体中的浮沉现象。
根据浮力原理,当一个物体浸泡在液体中时,所受到的上浮力等于被物体排开的液体的重量。
根据这个原理可以进行一系列应用的计算。
2. 应用计算题示例假设有一个长方体的木块,边长为10cm,质量为200g。
求木块在水中的浮力和它在水中的浸没深度。
2.1 木块的浮力计算根据浮力原理,木块在水中的浮力等于它所排开的水的重量。
首先需要计算木块的体积和水的密度。
木块的体积可以通过边长计算得出:体积 = 边长 x 边长 x 边长代入数值计算得:体积 = 10cm x 10cm x 10cm = 1000cm³水的密度可以通过查找资料得知常温下约为1g/cm³。
然后,将体积和密度代入公式计算浮力:浮力 = 体积 x 密度 x 重力加速度代入数值计算得:浮力 = 1000cm³ x 1g/cm³ x 9.8m/s² = 9800N因此,木块在水中的浮力为9800N。
2.2 木块在水中的浸没深度计算根据浮力原理,木块在水中的浸没深度可以通过浮力和物体的密度计算得出。
首先需要计算木块的密度,密度可以通过质量和体积的比值计算得出:密度 = 质量 / 体积代入数值计算得:密度 = 200g / 1000cm³ = 0.2g/cm³然后,将浮力和密度代入公式计算浸没深度:浸没深度 = 浮力 / (密度 x 重力加速度)代入数值计算得:浸没深度= 9800N / (0.2g/cm³ x 9.8m/s²) ≈ 500cm因此,木块在水中的浸没深度约为500cm。
3. 程序实现除了手工计算外,我们还可以使用编程语言来实现这个计算过程。
下面是一个使用Python语言实现的计算代码示例:```python # 木块边长,单位为厘米 length = 10木块质量,单位为克mass = 200水的密度,单位为克/立方厘米density_water = 1重力加速度,单位为米/秒^2g = 9.8计算木块的体积volume = length**3计算木块的浮力buoyancy = volume * density_water * g计算木块的密度density_block = mass / volume计算木块在水中的浸没深度depth = buoyancy / (density_block * g)print(。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、计算题
三、计算题
• 12.如图甲,将一重为8N的物体A放在装有适量水的杯中,物体A漂浮于
4 • 水面,浸入水中的体积占总体积的 5 ,此时水面到杯底的距离为20cm • 如果将一小球B用体积和重力不计的细线系于A下方后,再轻轻放入该
杯水中,静止时A上表面与水面刚好相平,如图乙.已知 ρB=1.8×103kg/m3,g=10N/kg求 • (1)在甲图中杯壁上距杯底8cm处O点受到水的压强. • (2)甲图中物体A受到的浮力. • (3)物体A的密度. • (4)小球B的体积.
浮力
综合应用ቤተ መጻሕፍቲ ባይዱ算
一、选择题
V1 V2
水
一、选择题
• 3.如图所示,一个边长为10cm的正方体竖直悬浮在某液体中,上表面受 到液体的压力F1为5N,下表面受到液体的压力F2为13N(g取10Nkg).下 列说法错误的是( )
• A.正方体受到的浮力为8N • B.液体的密度为0.8×103kg/m3 • C.正方体上表面到液面的距离h=5cm • D.液体对物体下表面的压强为1.3×103Pa
一、选择题
二、填空题
• 5.一个李子的体积约为60cm3,质量约为66g,若把李子放入 水中静止时将 (填“漂浮”“悬浮”或“沉底”).一个西 瓜的体积为6×103cm3,所受重力为55N,若把西瓜浸没在 水中后放手,当西瓜静止时所受浮力为 ( ) N.(g取10Nkg)
• 测力计上取下投入水中静止时,物体受到的浮力是 ( )
二、填空题
。
二、填空题
二、填空题
三、计算题
• 10.小明准备用空矿泉水瓶做一个“救生衣”,已知小明的质量是50kg, 身体平均密度约等于水的密度,为确保安全至少他的头部要露出水面,
• 头部的体积约占身体总体积的 1 (不计空矿泉水瓶的质量和塑料的体
积)
10
• (1)求小明头部的体积
• (2)请你帮小明计算一下,制作“救生衣”需要多少个图示的空矿泉水 瓶
二、填空题
• 6.将一实心物体挂在弹簧测力计上,待其静止时弹簧测力计
的示数为7.2N,当把物体的三分之一浸在水中时,弹簧测力
计的示数变为5.2N.此时物体受到的浮力为
N.若
把该物体放人密度为1.5×103kg/m3且足够多的另一液体
中待其稳定时,物体所受的浮力为 =1.0×103kg/m3)
N(g= 10 N/kg,ρ水
