第二章 弯矩-曲率关系
合集下载
利用弯矩-曲率(M-Φ)曲线评价截面性能
复制和粘贴
| 输入钢筋 |
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
11
05.任意形状截面性能评价
2. 弯矩-曲率关系曲线
计算已经输入了钢筋的矩形截面的弯矩－曲率曲线。
在主菜单中选择模型 > 材料和截面特性 > 弯矩－曲率曲线 1. 勾选“显示理想模型”选项 2. 在“用户自定义曲率(理想化模型)”选项中输入‘0.002’ 3. 点击“计算”键
1. 点击主菜单的文件> 打开项目打开名称为‘M-Phi_Model.mcb’ 的模型文件。 2. 点击主菜单的模型> 材料和截面特性 > 截面确认已定义的两个截面
| 确认矩形截面 |
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
| 确认任意形状截面 |
5
03.选择材料本构模型
1. 混凝土材料本构
2. 钢材 1) Menegotto-Pinto Model 2) Bilinear Model 3) Asymmetrical Bilinear Steel Model 4) Trilinear Steel Model
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
3
01.概要
利用下面的弯矩-曲率曲线计算截面的屈服和极限承载力、屈服和极限位移。 M
STEP 1. 选择非线性材料本构模型
STEP 2. 输入钢筋
STEP 3. 计算弯矩-曲率曲线
STEP 4. 利用弯矩-曲率曲线计算截面特性
STEP 5. 利用理想化的弯矩-曲率曲线评价截面性能
| 截面性能评价过程 |
操作例题 | 利用截面的弯矩-曲率(M-Φ)曲线评价截面性能
利用弯矩-曲率(M-Φ)曲线评价截面性能
1) Kent & Park Model 2) Japan Concrete Standard Specification Model 3) Japan Roadway Specification Model 4) Nagoya Highway Corporation Model 5) Trilinear Concrete Model 6) China Concrete Code (GB50010-02) 7) Mander Model 2. 钢材 1) Menegotto-Pinto Model 2) Bilinear Model 3) Asymmetrical Bilinear Steel Model 4) Trilinear Steel Model
3Байду номын сангаас
01.概要
利用下面的弯矩-曲率曲线计算截面的屈服和极限承载力、屈服和极限位移。 M
Mn
等항效복屈服点
极극限한状상태态点 (εcu=0.004)
Myi
초初기始항屈복服点
Φ yi
Φy
Φu
在此,
Mn : 极限状态时的弯矩 Myi : 初始屈服点的弯矩 Ø yi : 初始屈服时的曲率 Ø y : 等效屈服时的曲率 Ø u : 极限状态时的曲率 εcu : 混凝土极限应变
钢筋的材料特性如下：
材料标准强度 HRB335
项目 钢筋的屈服应变 钢筋的极限应变 钢筋的屈服强度 钢筋的极限强度
取值 0.0015
0.01 335 455
单位 -
MPa Mpa
Menegotto-Pinto Model中的参数说明如下： fy : 钢筋的屈服强度 E : 钢筋的初始弹性模量 b : 钢筋屈服后刚度与初始 刚度的比值 Ro, a1, a2 : 定义钢筋屈服 后应力-应变变化形状的 常数
3Байду номын сангаас
01.概要
利用下面的弯矩-曲率曲线计算截面的屈服和极限承载力、屈服和极限位移。 M
Mn
等항效복屈服点
极극限한状상태态点 (εcu=0.004)
Myi
초初기始항屈복服点
Φ yi
Φy
Φu
在此,
Mn : 极限状态时的弯矩 Myi : 初始屈服点的弯矩 Ø yi : 初始屈服时的曲率 Ø y : 等效屈服时的曲率 Ø u : 极限状态时的曲率 εcu : 混凝土极限应变
钢筋的材料特性如下：
材料标准强度 HRB335
项目 钢筋的屈服应变 钢筋的极限应变 钢筋的屈服强度 钢筋的极限强度
取值 0.0015
0.01 335 455
单位 -
MPa Mpa
Menegotto-Pinto Model中的参数说明如下： fy : 钢筋的屈服强度 E : 钢筋的初始弹性模量 b : 钢筋屈服后刚度与初始 刚度的比值 Ro, a1, a2 : 定义钢筋屈服 后应力-应变变化形状的 常数
梁纯弯曲变形
梁纯弯曲变形引言梁纯弯曲变形是工程力学中的一个重要概念。
在结构力学和土木工程中，梁是一种常见的结构元素，承受着各种外部荷载。
当外部荷载作用于梁上时，梁会发生变形。
本文将探讨梁在纯弯曲状态下的变形特性和相关的理论基础。
纯弯曲的概念纯弯曲是指梁所受的外部荷载仅产生弯矩作用，而不产生剪力作用。
在梁的纵轴上，上部受拉，下部受压，梁在这种状态下发生弯曲变形。
纯弯曲情况下，梁的截面仅发生弯矩引起的形状变化，并不会发生剪切变形。
纯弯曲对于大跨度的梁和悬臂梁等结构具有重要意义。
纯弯曲变形的理论基础梁纯弯曲变形的理论基础可以通过两种方法进行分析：理论分析和数值分析。
理论分析理论分析方法中，我们可以利用梁的弯矩-曲率关系来分析纯弯曲变形。
弯矩-曲率关系描述了梁截面上的弯矩和截面曲率之间的关系。
根据弯矩-曲率关系，我们可以计算出梁的曲率分布，从而得到梁的变形情况。
此外，利用材料力学中的应力-应变关系，还可以计算出梁截面上的应力分布。
数值分析数值分析方法中，我们可以使用有限元方法来模拟梁的纯弯曲变形。
有限元方法将梁划分为许多小的单元，通过求解弯矩和力的平衡方程，可以得到梁单元上的位移和应力分布。
通过将所有单元的位移组合起来，可以得到整个梁的变形情况。
纯弯曲变形的计算纯弯曲变形的计算依赖于梁的几何形状、材料特性和外部荷载。
常见的计算方法包括：基于梁理论的计算基于梁理论的计算方法适用于简单、均匀截面的梁。
在这种方法中，我们可以使用梁的截面形状和材料性质，通过弯矩-曲率关系计算出梁的曲率分布。
进一步，可以计算出梁的位移、剪力和应力等参数。
基于有限元分析的计算基于有限元分析的计算方法适用于复杂截面的梁。
在这种方法中，我们将梁划分为许多小的单元，并求解每个单元上的位移和应力分布。
通过将所有单元的位移组合起来，可以得到整个梁的变形情况。
梁纯弯曲变形的应用梁纯弯曲变形的应用广泛，特别是在土木工程和结构设计中。
通过对梁的纯弯曲变形进行分析，可以确定梁的合适截面形状和尺寸，以满足其承受的外部荷载要求。
UCfber在钢筋混凝土截面弯矩_曲率计算中的应用
3.3.2 衬砌混凝土改为钢筋混凝土。 3.3.3 拱底加设 Φ30cm 横向排水混凝土圆管， 进口设一层过滤网。
4 混凝土二次衬砌
为保证二次衬砌进度，并做到内实、外美，采用
2 台 9m 长整体钢模衬砌台车，台车总重量达 60t，主 骨架部分在厂家生产，现场安装后，焊接顶面钢板， 为保证模板周转使用不变形，采用 8mm 厚钢板，现 场安装需要一个月时间。二次衬砌要做到仰拱先行 创造环境，适时衬砌保安全。7 月初开始衬砌，在雨 季前完成进出口二次衬砌，施工安全得到保证。
Moment/kN*m Moment/kN*m
244800。如果该桥梁在罕遇地震顺桥向作用下，固定 墩墩底截面弯矩小于 92710，则说明固定墩墩底截 面处于弹性工作状态；如果固定墩墩底截面弯矩大 于 92710 但小于 476000，说明固定墩墩底截面已经 达到屈服状态但是尚未破坏，上述两种状态证明该
ρx，ρy—分别为箍筋在 x, y 的体积含筋率。由公
式（5）计算。
ρx
=
Asx s×dc
(5a)
ρy
=
Asy s×bc
(5b)
其中：
dc —矩形截面沿 Y 轴方向算到箍筋外缘的宽；
bc —矩形截面沿 X 轴方向算到箍筋外缘的宽；
S—纵向箍筋的间距。
算出 f′lx 和 f′ly 之后，就可以利用约束应力与约
开裂弯矩 /kN·m 28460 77040 67690 144900 92710 186300
表 1 各墩墩底截面弯矩 - 曲率计算结果
开裂曲率 /rad·m-1 1.237e-4 4.837e-5 1.124e-4 4.747e-5 9.684e-5 4.539e-5
屈服弯矩 /kN·m 90100 237500 171300 375000 223200 476000
4 混凝土二次衬砌
为保证二次衬砌进度，并做到内实、外美，采用
2 台 9m 长整体钢模衬砌台车，台车总重量达 60t，主 骨架部分在厂家生产，现场安装后，焊接顶面钢板， 为保证模板周转使用不变形，采用 8mm 厚钢板，现 场安装需要一个月时间。二次衬砌要做到仰拱先行 创造环境，适时衬砌保安全。7 月初开始衬砌，在雨 季前完成进出口二次衬砌，施工安全得到保证。
Moment/kN*m Moment/kN*m
244800。如果该桥梁在罕遇地震顺桥向作用下，固定 墩墩底截面弯矩小于 92710，则说明固定墩墩底截 面处于弹性工作状态；如果固定墩墩底截面弯矩大 于 92710 但小于 476000，说明固定墩墩底截面已经 达到屈服状态但是尚未破坏，上述两种状态证明该
ρx，ρy—分别为箍筋在 x, y 的体积含筋率。由公
式（5）计算。
ρx
=
Asx s×dc
(5a)
ρy
=
Asy s×bc
(5b)
其中：
dc —矩形截面沿 Y 轴方向算到箍筋外缘的宽；
bc —矩形截面沿 X 轴方向算到箍筋外缘的宽；
S—纵向箍筋的间距。
算出 f′lx 和 f′ly 之后，就可以利用约束应力与约
开裂弯矩 /kN·m 28460 77040 67690 144900 92710 186300
表 1 各墩墩底截面弯矩 - 曲率计算结果
开裂曲率 /rad·m-1 1.237e-4 4.837e-5 1.124e-4 4.747e-5 9.684e-5 4.539e-5
屈服弯矩 /kN·m 90100 237500 171300 375000 223200 476000
《弯矩曲率关系》课件
曲率的定义
曲率：描述曲线弯曲程度的量， 定义为曲线上任一点处切线方向 角的变化量与经过的弧长的比值
。
在数学上，曲率是用来衡量曲线 上某一点附近的小弧段弯曲程度
的量。
对于直线，其曲率为0；对于圆 ，其曲率是一个常数，等于圆的
半径倒数。
曲率的计算
曲率计算公式：K = lim(Δs->0) [Δs / (Δt)^2] / lim(Δt>0) [Δs / Δt]
在机械工程中的应用
传动系统设计
在机械传动系统中，弯矩曲率关系对于齿轮、轴等部件的设计和优化具有指导意义。了解弯矩与曲率的关系有助 于提高传动系统的效率和稳定性。
疲劳分析
在机械部件的疲劳分析中，弯矩曲率关系是评估其疲劳寿命的重要因素之一。通过对弯矩和曲率的变化规律进行 分析，可以预测部件的疲劳寿命和潜在的疲劳断裂风险。
在工程结构中，弯矩和曲率是密切相关的。例如，在桥梁、建筑和机械设计中，需 要考虑到结构的弯曲程度和弯矩之间的关系。
当结构受到外力作用时，会发生弯曲变形，曲率会发生变化，同时弯矩也会随之改 变。因此，在设计时需要考虑到结构的承载能力和稳定性。
了解弯矩与曲率的关系有助于工程师更好地设计结构，确保其安全性和稳定性。
需要研究弯矩曲率关系在不同温度、湿度等环境 条件下的变化规律。
需要探索弯矩曲率关系在复合材料、智能材料等 新型材料中的应用。
对学习者的建议
学习者应该深入理解弯矩和曲 率的定义及测量方法。
学习者应该掌握弹性力学和 材料力学的基本原理，以便 更好地理解弯矩曲率关系。
学习者可以通过实验和实践来 加深对弯矩曲率关系的理解和
应用。THANΒιβλιοθήκη S感谢观看详细描述
弯矩是材料力学中一个重要的概念，用于描述弯曲变形过程 中截面所受到的力矩作用。在材料受到弯曲时，截面上会产 生剪力和弯矩，弯矩的大小与剪力和中性轴距离有关。
第二章弯矩曲率关系
X 0,
n
i 1
ci
Ai s' As' s As N 0
n
2） 假定和 值
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )＝0 2 2
3） 由相容方程求出各条带混凝土的应变及钢筋的应变； 4） 由物理关系求出相应的应力，拉区混凝土条带的应变 超过其极限受拉应变时，应对其进行处理；
2） 假定 值
X 0,
n
i 1
ci
Ai s' As' s As N 0
n
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )＝0 2 2
3） 由相容方程求出各条带混凝土的应变及钢筋的应变； 4） 由物理关系求出相应的应力，拉区混凝土条带的应变 超过其极限受拉应变时，应对其进行处理；
5） 将各应力值代入第一平衡方程，判断是否满足平衡条件： 如不满足，需要调整 值直至满足为止，如满足平衡条件， 则由第二平衡方程求出M，然后重复步骤1～5
6） 当符合破坏条件时，停止计算。
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
M - 关系的计算方法之二 ：分级加荷载法
1） 取M＝M＋M
h h/2as
as b
n
As
对钢筋混凝土柱， 有时也可能会出现 s < 0
s s ( s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
as h/2as h h/2as as b 1 i Zi 截面中心线 n As As
n
i 1
ci
Ai s' As' s As N 0
n
2） 假定和 值
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )＝0 2 2
3） 由相容方程求出各条带混凝土的应变及钢筋的应变； 4） 由物理关系求出相应的应力，拉区混凝土条带的应变 超过其极限受拉应变时，应对其进行处理；
2） 假定 值
X 0,
n
i 1
ci
Ai s' As' s As N 0
n
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )＝0 2 2
3） 由相容方程求出各条带混凝土的应变及钢筋的应变； 4） 由物理关系求出相应的应力，拉区混凝土条带的应变 超过其极限受拉应变时，应对其进行处理；
5） 将各应力值代入第一平衡方程，判断是否满足平衡条件： 如不满足，需要调整 值直至满足为止，如满足平衡条件， 则由第二平衡方程求出M，然后重复步骤1～5
6） 当符合破坏条件时，停止计算。
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
M - 关系的计算方法之二 ：分级加荷载法
1） 取M＝M＋M
h h/2as
as b
n
As
对钢筋混凝土柱， 有时也可能会出现 s < 0
s s ( s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
as h/2as h h/2as as b 1 i Zi 截面中心线 n As As
梁的弯曲变形应用原理
梁的弯曲变形应用原理简介梁是一种常见的结构元素，用于承受和传递载荷。
在实际应用中，梁常常会发生弯曲变形，这种变形有着重要的应用原理和工程意义。
本文将介绍梁的弯曲变形的应用原理，以及它在工程领域中的具体应用。
梁的弯曲变形原理当梁受到外部载荷作用时，其会发生弯曲变形。
梁的弯曲变形主要是由内力矩引起的，内力矩是梁截面上的剪力和弯矩引起的。
弯曲变形原理可以用以下几个要点来描述：1.梁撑杆法：梁在弯曲时，可以看做由无数撑杆组成的系统。
每个撑杆受到不同大小的拉伸或压缩力，整个梁发生的弯曲变形是各撑杆弹性变形的综合效果。
2.中性轴和截面旋转：梁弯曲时，存在一个中性轴，该轴是在截面内法线应力为零的位置。
梁在弯曲时，截面内部会发生旋转，上部受拉，下部受压，截面的变形呈现出弯曲的形态。
3.弯矩与曲率关系：梁的弯曲变形与弯矩和曲率有关。
弯矩是横截面上的合力矩，而曲率则是截面内部形成的曲线的曲率半径的倒数。
根据弯矩和曲率之间的关系，可以计算出梁的变形情况。
梁的弯曲变形应用梁的弯曲变形在工程领域中有着广泛的应用。
下面列举了梁的弯曲变形应用在不同工程中的具体案例：1. 建筑结构设计在建筑结构设计中，梁的弯曲变形是必须考虑的因素之一。
通过合理的梁的尺寸和形状设计，可以满足建筑物的结构强度和刚度要求，保证建筑物的安全性和稳定性。
2. 桥梁工程在桥梁工程中，梁的弯曲变形对于桥梁的承载能力和结构安全性影响重大。
通过分析梁的弯曲变形情况，可以确定桥梁的设计参数，保证桥梁承受车辆和行人的荷载，确保桥梁的正常使用和运行。
3. 机械设计梁的弯曲变形在机械设计中也有着广泛的应用。
例如，在起重机设计中，梁的弯曲变形会导致起重机的运动效果失真，因此需要精确计算梁的弯曲变形，以确保起重机的稳定性和可靠性。
4. 航天器设计在航天器设计中，梁的弯曲变形是非常重要的考虑因素。
航天器需要承受巨大的重力和惯性力，梁的弯曲变形对于航天器的结构强度和稳定性至关重要。
【土木建筑】第十二章 弯矩-曲率关系
y
su
s
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct c
xn h0 h M
s
As b
c
b
sAs
采用线形的物理关系 c c E c
t t E c
s s E
s
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct c
xn h0 h M
s
2 E As 1 bh h xcr A 1 E s 2 bh
对一般钢筋混凝土梁 As / bh 0.5 ~ 2%,
xcr 0.5h
E 6 ~ 7
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
xn=n h0
c
ct
C M T
c
xn=xc
r
M 0
A
s
“拉伸硬 化”现象
三、截面尺寸和配筋构造
1. 梁
c c25mm d h h0=h-60 c b 净距25mm 钢筋直径d b h h0=h-35 c 净距30mm 钢筋直径d
净距30mm 钢筋直径d
h 2 ~ 3.5(矩形截面 ) b 2.5 ~ 4.0(T形截面 )
d 10 ~ 20mm(桥梁中 14 ~ 40mm)
u 0.0033 f cu 50105 u 0.0033 时，取 u 0.0033
五、受弯构件正截面受力分析
1. 基本假定
混凝土受拉时的应力-应变关系
t
ft
t=Ect
o t0
t
五、受弯构件正截面受力分析
1. 基本假定
钢筋的应力-应变关系
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
sAs
s
'
(
h 2
as
'
)
s
(h 2
a s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的物理方程（对物理方程的处理）
cic(ci) cic(ci)
s s
s ( s s (s )
)
as
( ci0) h/2-
( ci0) as
h h/2as
as
As
1
c1 s
As b
xn
sAs
（E-1）As
s t
s Ess E Ecst Et
用材料力学的方法求解
TsAsEAst
将钢筋等效成混凝土
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
当cb =tu时，认为拉区混凝土开裂并退出工作（约束受拉）
ct
ct
xn=n
c
h0
A
h0 h
M
s
s
t0
cb= tu
b
C xn=xc
As’
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
(1-n)h0
s
b c as
b
nh c t0ycnh0s 'as'(1sn)h0
五、受弯构件正截面受力分析
1. 基本假定
混凝土受压时的应力-应 变关系
当应力较小 c 时 0.3fc， 时如 ，可 c Ecc
n26 1(0fcu 5)0 当 , n2时， n2取
2~3.5(矩形截)面 2.5~4.0(T形截面 )
d1~ 02m 0(桥 m 1 梁 ~ 44m 中 0)m
三、截面尺寸和配筋构造
1. 板
c15mm d
分布钢筋
h0
h
d8~1m 2 m
h0 h20
板厚的模数为10mm
四、受弯构件的试验研究
1. 试验装置
试验 梁
荷载分 配梁 P
外加荷 载
应变 计
i
as h h/2-
Zi
as
截面b
c1 s ci M
N
sAs ci
sAs
ci > t0
该条带混 凝土开裂
ci > tu
该条带混凝 土退出工作
ci = 0
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
P
P
曲率
平均应变分布
即使在纯弯段也只可能在几个截面上出现裂 缝,裂缝间混凝土的拉应变不相等
c fc
c
fc 110c
n
o
0
00.0020.5fcu501 05
00.00时 2 ， 0取 0.002
c u
u 0.0033fcu50105
u 0.00时 33，u取 0.003
五、受弯构件正截面受力分析
1. 基本假定
混凝土受拉时的应力-应变关系
t ft
t=Ect
t
o t0
五、受弯构件正截面受力分析
一、概述
试验梁
荷载分配梁 P
外加荷载 应变计
数据采集系统
M
As
位移计
L/3
L/3
L
带定向滑 轮的千斤 顶
P
外加荷载
N
柱的竖向荷载
位移计
数据采集系统
h
As b
II I
O
As
试验柱
H
h
台座
b
超筋 平衡
III
适筋
最小配筋率
二、骨架曲线的弯矩-曲率关系
1. 基本假定
P
平截面假定----平均应变意义上
As’
n
X0 ,
c i A is 'A s ' sA sN 0
i 1
M 0 , M i n 1c i A iZ isA s(h 2 a s)sA s( a s h 2 ) ＝ 0
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
As
as 1
h/2-
结论
•适筋梁具有较好的变形能力，超筋梁和少筋梁的破坏具有突然性，设计 时应予避免
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢筋屈服的同 时，混凝土压碎
•界限配筋率、最小配筋率是区分适筋破坏、超筋破坏和少筋破坏的定量 指标
五、受弯构件正截面受力分析
1. 基本假定 P
平截面假定----平均应变意义上
位移
L/3
计
L/3
L
s
As bh 0
数据采集 系统
As
h
A bs
四、受弯构件的试验研究
2. 试验结果
适筋破坏
四、受弯构件的试验研究
2. 试验结果
超筋破坏
四、受弯构件的试验研究
2. 试验结果
超筋破坏
四、受弯构件的试验研究
2. 试验结果
平衡破坏（界限破坏，界 限配筋率）
四、受弯构件的试验研究
2. 试验结果
?
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理--Considère(1899)试验
N (kN)
200
混凝土：fc=30.8MPa; ft=1.97MPa;
Ec=25.1103MPa.
150
钢筋： fy=376MPa; fsu=681MPa; Es=205103MPa; As=284mm2.
i
ci M
Zi
N
截面中心线 s n
As
b
sAs ci
sAs
对钢筋混凝土柱， 有时也可能会出现
s < 0
s s(s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
As
as 1
h/2-
i
as h h/2-
Zi
as
截面中心线 s
n
as
As
b
c1 s ci M
N
sAs ci
sAs
r
T
c
sAs
为了计算方便用矩形应力 分布代替原来的应力分布
最小配筋率
四、受弯构件的试验研究
2. 试验结果 P
M
超筋 平衡
III
适筋
L/3 L
II 少筋 I O
最小配筋率
c
c
c
c
L/3
(c’<u) c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
sAs
s= fyAs
y
fyAs s>y
四、受弯构件的试验研究
2. 试验结果
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
as b
s
b c
(1-n)h0
忽略剪切变形对梁、柱构件变形的影响
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的相容关系
as h/2as h h/2as
as b
ci Zi
As
1
i
Zi
截面中心线 s n
As
c1 s ci M
N
sAs ci
1. 基本假定
钢筋的应力-应变关系
s
fy
s=Ess
y
s su
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
c
h0 h
M
s b c
As b
xn sAs
采用线形的物理关系
c c Ec
t t Ec
s s Es
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
c
h0 h
M
s b c
100 50 0
裸钢筋 152 混凝土中的钢筋 N
0.001
0.002
N 915
152
0.003
平均应变 0.004
“拉伸硬 化”现象
三、截面尺寸和配筋构造
1. 梁
c
c
净距30mm 钢筋直径d
净距30mm 钢筋直径d
h h0=h-60
c25mm d
c
b
净距25mm 钢筋直径d
h h0=h-35
b
h b
s
'
(
h 2
as
'
)
s
(h 2
a s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的物理方程（对物理方程的处理）
cic(ci) cic(ci)
s s
s ( s s (s )
)
as
( ci0) h/2-
( ci0) as
h h/2as
as
As
1
c1 s
As b
xn
sAs
（E-1）As
s t
s Ess E Ecst Et
用材料力学的方法求解
TsAsEAst
将钢筋等效成混凝土
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
当cb =tu时，认为拉区混凝土开裂并退出工作（约束受拉）
ct
ct
xn=n
c
h0
A
h0 h
M
s
s
t0
cb= tu
b
C xn=xc
As’
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
(1-n)h0
s
b c as
b
nh c t0ycnh0s 'as'(1sn)h0
五、受弯构件正截面受力分析
1. 基本假定
混凝土受压时的应力-应 变关系
当应力较小 c 时 0.3fc， 时如 ，可 c Ecc
n26 1(0fcu 5)0 当 , n2时， n2取
2~3.5(矩形截)面 2.5~4.0(T形截面 )
d1~ 02m 0(桥 m 1 梁 ~ 44m 中 0)m
三、截面尺寸和配筋构造
1. 板
c15mm d
分布钢筋
h0
h
d8~1m 2 m
h0 h20
板厚的模数为10mm
四、受弯构件的试验研究
1. 试验装置
试验 梁
荷载分 配梁 P
外加荷 载
应变 计
i
as h h/2-
Zi
as
截面b
c1 s ci M
N
sAs ci
sAs
ci > t0
该条带混 凝土开裂
ci > tu
该条带混凝 土退出工作
ci = 0
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
P
P
曲率
平均应变分布
即使在纯弯段也只可能在几个截面上出现裂 缝,裂缝间混凝土的拉应变不相等
c fc
c
fc 110c
n
o
0
00.0020.5fcu501 05
00.00时 2 ， 0取 0.002
c u
u 0.0033fcu50105
u 0.00时 33，u取 0.003
五、受弯构件正截面受力分析
1. 基本假定
混凝土受拉时的应力-应变关系
t ft
t=Ect
t
o t0
五、受弯构件正截面受力分析
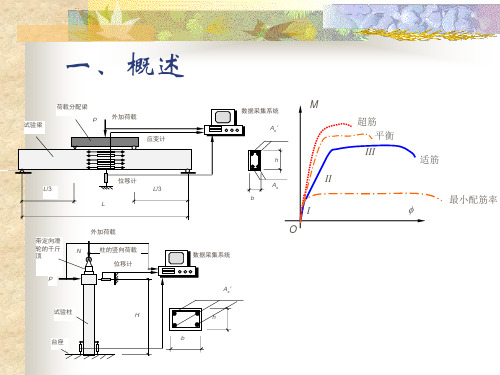
一、概述
试验梁
荷载分配梁 P
外加荷载 应变计
数据采集系统
M
As
位移计
L/3
L/3
L
带定向滑 轮的千斤 顶
P
外加荷载
N
柱的竖向荷载
位移计
数据采集系统
h
As b
II I
O
As
试验柱
H
h
台座
b
超筋 平衡
III
适筋
最小配筋率
二、骨架曲线的弯矩-曲率关系
1. 基本假定
P
平截面假定----平均应变意义上
As’
n
X0 ,
c i A is 'A s ' sA sN 0
i 1
M 0 , M i n 1c i A iZ isA s(h 2 a s)sA s( a s h 2 ) ＝ 0
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
As
as 1
h/2-
结论
•适筋梁具有较好的变形能力，超筋梁和少筋梁的破坏具有突然性，设计 时应予避免
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢筋屈服的同 时，混凝土压碎
•界限配筋率、最小配筋率是区分适筋破坏、超筋破坏和少筋破坏的定量 指标
五、受弯构件正截面受力分析
1. 基本假定 P
平截面假定----平均应变意义上
位移
L/3
计
L/3
L
s
As bh 0
数据采集 系统
As
h
A bs
四、受弯构件的试验研究
2. 试验结果
适筋破坏
四、受弯构件的试验研究
2. 试验结果
超筋破坏
四、受弯构件的试验研究
2. 试验结果
超筋破坏
四、受弯构件的试验研究
2. 试验结果
平衡破坏（界限破坏，界 限配筋率）
四、受弯构件的试验研究
2. 试验结果
?
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理--Considère(1899)试验
N (kN)
200
混凝土：fc=30.8MPa; ft=1.97MPa;
Ec=25.1103MPa.
150
钢筋： fy=376MPa; fsu=681MPa; Es=205103MPa; As=284mm2.
i
ci M
Zi
N
截面中心线 s n
As
b
sAs ci
sAs
对钢筋混凝土柱， 有时也可能会出现
s < 0
s s(s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
As
as 1
h/2-
i
as h h/2-
Zi
as
截面中心线 s
n
as
As
b
c1 s ci M
N
sAs ci
sAs
r
T
c
sAs
为了计算方便用矩形应力 分布代替原来的应力分布
最小配筋率
四、受弯构件的试验研究
2. 试验结果 P
M
超筋 平衡
III
适筋
L/3 L
II 少筋 I O
最小配筋率
c
c
c
c
L/3
(c’<u) c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
sAs
s= fyAs
y
fyAs s>y
四、受弯构件的试验研究
2. 试验结果
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
as b
s
b c
(1-n)h0
忽略剪切变形对梁、柱构件变形的影响
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的相容关系
as h/2as h h/2as
as b
ci Zi
As
1
i
Zi
截面中心线 s n
As
c1 s ci M
N
sAs ci
1. 基本假定
钢筋的应力-应变关系
s
fy
s=Ess
y
s su
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
c
h0 h
M
s b c
As b
xn sAs
采用线形的物理关系
c c Ec
t t Ec
s s Es
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
c
h0 h
M
s b c
100 50 0
裸钢筋 152 混凝土中的钢筋 N
0.001
0.002
N 915
152
0.003
平均应变 0.004
“拉伸硬 化”现象
三、截面尺寸和配筋构造
1. 梁
c
c
净距30mm 钢筋直径d
净距30mm 钢筋直径d
h h0=h-60
c25mm d
c
b
净距25mm 钢筋直径d
h h0=h-35
b
h b