QR码纠错码原理及实现
QR码编码原理二(编码)
编码就是把常见的数字、字符等转换成QR码的方法。
说具体的编码之前,先说一下QR码的最大容量问题。
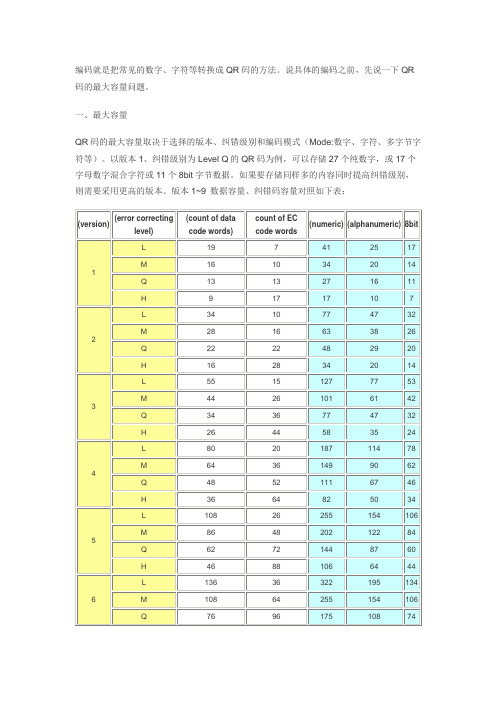
一、最大容量QR码的最大容量取决于选择的版本、纠错级别和编码模式(Mode:数字、字符、多字节字符等)。
以版本1、纠错级别为Level Q的QR码为例,可以存储27个纯数字,或17个字母数字混合字符或11个8bit字节数据。
如果要存储同样多的内容同时提高纠错级别,则需要采用更高的版本。
版本1~9 数据容量、纠错码容量对照如下表:下面,就举例说明将“ABCDE123”转换成为版本1、Level H的QR码转换方法。
二、模式标识符(Mode Indicator)QR码的模式(Mode)就是前文提到的数字、字符、8bit 字节码、多字节码等。
对于不同的模式,都有对应的模式标识符(Mode Indicator)来帮助解码程序进行匹配,模式标识符是4bit 的二进制数:1、数字模式(numeric mode ): 00012、混合字符模式(alphanumeric mode): 00103、8bit byte mode: 01004、日本汉字(KANJI mode): 10005、中国汉字(GB2312):1101由于示例文本串是混合字符,因此将选择alphanumeric mode,其标识码为:0010三、文本串计数标识符(Character count indicator)文本串计数标识符用来存储源内容字符串的长度,在版本1-9的QR码中,文本串长度标识符自身的长度被定义为:数字 : 10bit混合字符: 9bit8bit 字节码: 8bit多字节码: 8bit在本例中,源文本串的长度为8个字符,混合字符的长度为9bit,因此将字符个数8编码为9位二进制表示:000001000加上混合字符模式标识码,总的编码为0010 000001000四、数据内容编码1、数字模式下的编码在数字模式下,数据被限制为3个数字一段,分成若干段。
QR码纠错编码

Ie wrs Q c e Re- l r aot ; o fl Eoc r tg Ky o I R o ; d o n nl r m Glse ; r rcncd d d e S oo g i h ai d r - ei o r o e
条码技术是在计算机技术与信息技术基础 卜 发展起来的 们 集编码、印刷、i别、数据采集和处理于一 t : 体的新兴技 术。由J传统的 一 l 维条码信息容量很小, 信息的详细描述要 依赖数据库提供,囚而使其应用受到了一 定的限制。土世纪
G()的 元 另 求 成多 式 也 用 域 素 Fa 域 素, 外, 生 项 时 要 到 元 2上 a 因 , 们 求 G( 的 个 元 。 伽 华 的 , 此 我 先 出 F0 各 域 素 由 罗 域 2 )
性 知, a G() 本 元素, G() 每一 质可 若 是 F 的 原域 丫 则F 中 元 f
a (x( + 7 +a。 p6 6 ( 5 ( (+ (= x i a: ( )7 + )' a 1 ) ) 3 x ( X+ +
5 ( + t 4 ( + 3 ( + ) + )+ x a; ( ) + 5 3 “: ( ) + X i 3 “2 ( 、 x 1 之
( I pI ( n p0 a + ) a x 十 + ) 可见,两元素的相加的和就是对应多项式的系数相加后 所得的多项式。山 于系数取自 F ) 。与 ,校2 G ( ,故 1R是 相加, 2
第2卷 ,
V1 9 b. 2
第1 期
No了
计
算
机
工
程
2 )年1 (3 月 K
C mpt E g er g o ue ni ei r n n
文童编号:10-12( 0) - 03 1 01 48 03 1 - 9-f 1 2 0 0 〕 文献标识码:A
qr code 原理

qr code 原理
QR码的原理是利用二维编码来存储和传输信息。
它由黑白方块组成,可以被红外线扫描仪、激光扫描仪或手机相机等设备扫描并解码。
QR码的生成过程具体如下:首先,将需要编码的数据(例如文本、网址或其他信息)转换成二进制形式。
接下来,将二进制数据按照一定规律分配给QR码中的黑白方块,形成一个特定的二维编码模式。
每个方块代表一个数据单元,可以存储0或1的二进制值。
QR码的结构设计上采用了一种巧妙的纠错技术,即在编码中加入冗余信息,使得即使在一定程度的损坏或污损情况下,扫描仪仍然能够正确识别和解码信息。
这种纠错技术称为“Reed-Solomon”纠错码。
在扫描QR码时,扫描设备通过光源照射到码上,并接收反射回来的光信号。
然后,扫描设备解码接收到的信号,将其转换成二进制数据。
最后,通过解码软件将二进制数据解析为原始信息,例如网址、文本或其他数据。
由于QR码具有高密度存储信息、快速读取、纠错能力强等特点,广泛应用于商品包装、广告宣传、移动支付、票务管理等领域。
基于Reed_Solomon算法的QR码纠错编码

+α 2 x 2 +α 1 x+α 0
β(x)=β 7 x 7 +β 6 x 6 +β 5 x5 +β 4 x4 +β 3 x3
+β 2 x 2 +β 1 x+β 0 如元素10011010可表示为x 7 + x 4 + x 3 + x,则α,β
k-1
dk-1x +...+d
2
2x +d1x+d0,
则
可
用
多
项
式d(x)
表
示
待
编
码
的
数据。在编码中,我们要用到生成多项式的概念,由生成多
项式生成我们所要的编码。对于循环码的编码,有以下定
理: 定 理 1:GF(2m)上的[n,k]循环码中,存在唯一的n-k次
首 一 多 项 式g(x),每一码多项式 C(x)都是 g(x)的 倍 式 , 且 每
第 29卷 第 1期 Vol.29 № 1
计 算 机 工 程 Computer Engineering
2003年 1月 January 2003
·基金项目论文·
文章编号: 1000— 3428(2003)01 — 0093—03
文献标识码:A
中 图 分 类 号 : TP391.1
基于Reed-Solomon算法的QR码纠错编码
一个次数小于或等于n-1 的g(x)的倍式一定是码多项式(证明
参见参考文献2)。 我们所要进行的 Reed-Solomon编码是循环码的一种,因
此,我们可以这样构造生成多项式:设a∈GF(2m) 是 本 原 域 元素,mi (x)是ai 的最小多项式(I=0,1,...,r-1),则生成多项式
qr 编码逻辑 -回复

qr 编码逻辑-回复关于QR编码逻辑[qr 编码逻辑],指的是QR编码的原理和逻辑。
QR码(Quick Response code)是一种二维码,被广泛应用于商业和个人领域,方便快捷地扫描和解码。
本文将一步一步回答有关QR编码逻辑的问题,包括QR码的构成、编码方式、解码原理和应用等内容。
首先,我们来了解QR码的构成。
QR码由黑白方格组成,每个方格被称为一个模块。
QR码可以根据需求扩展到不同的尺寸,最小的QR码为21x21模块,最大的QR码可达177x177模块。
QR码中有三个特殊的模块:定位模块、对齐模块和校准模块。
定位模块用于确定QR码的位置和方向,对齐模块用于帮助解码器自动识别QR码的位置,而校准模块则用于对图像进行纠偏。
QR码的编码方式有多种,最常用的是数值、字母和字符的混合编码。
具体而言,QR码可以包含数字(0-9)、大写字母(A-Z)、ASCII字符和中文汉字等数据。
不同数据的编码方式也不同,数字使用4位二进制表示一个数字,字母使用11位二进制表示一个字母,而汉字使用13位二进制表示一个汉字。
编码后的数据以一定的格式和规则组织在QR码中,以实现正确的解码。
接下来,我们来探讨QR码的解码原理。
QR码的解码过程主要分为图像处理、数据提取和错误纠正三个步骤。
首先,需要对QR码的图像进行处理,包括二值化、去噪声和纠偏等操作,以提高解码的准确性。
然后,从处理后的图像中提取出QR码的模块,并计算模块的大小和位置关系,以确定QR码的结构。
最后,对提取出的模块进行解码,根据编码规则将模块的数据转换为原始数据,即可获得QR码中所含信息。
QR码的应用非常广泛,涵盖了商业和个人领域。
在商业方面,QR码可以用于商品标签、广告宣传、支付码等场景。
通过扫描QR码,用户可以获取商品信息、参与活动或完成支付等操作。
在个人领域,QR码可以用于个人名片、电子门票、WiFi连接等场景。
用户可以通过扫描QR码,轻松地获取联系方式、入场许可或快速连接到WiFi网络。
纠错编码的基本原理与性能

纠错编码的基本原理与性能
1.分组码的基本原理
(1)分组码的定义
分组码是指将信息码分组,为每组信码附加若干监督码(即差错控制码)的编码方式。
(2)分组码的结构
分组码一般用符号(n,k)表示,其中n是码组的总位数,又称码组的长度(码长),k 是码组中信息码元的数目,n-k=r为码组中的监督码元数目,又称监督位数目。
图11-1 分组码的结构
(3)分组码的参量
①码重
码重是指分组码中“1”的个数目。
②码距
码距是指两个码组中对应位上数字不同的位数,又称汉明距离。
③最小码距
最小码距是指编码中各个码组之间距离的最小值。
2.纠错编码的基本原理
最小码距d0的大小直接关系编码的检错和纠错能力:
(1)为检测e个错码,要求最小码距
(2)为纠正t个错码,要求最小码距
(3)为纠正t个错码,同时检测e个错码,要求最小码距
码距与纠错和检错能力的关系如图11-2所示。
图11-2 码距与检错和纠错能力的关系
纠错编码的性能
1.误码率的改善
采用纠错编码,误码率得到很大改善,改善的程度和所用的编码有关。
2.信噪比的改善
对于给定的传输系统,为
式中,R B为码元速率。
3.带宽增大
监督码元加入,发送序列增长,冗余度增大,若保持信息码元速率不变,则传输速率增大,系统带宽增大。
QR二维码的原理与识别方法

QR二维码的原理与识别方法一、QR码的原理:1.数据编码:QR码将信息编码为一系列黑白方块的模式。
它将输入的信息进行分段,并将每个字符转换为相应的二进制码,然后通过一系列的编码规则生成QR码的编码区域。
2. 误差校正:QR码通过内置的校验码来检测和纠正数据的错误。
它在编码区域中添加了一些特殊的模块,并使用Reed-Solomon纠错码来计算校验码,从而可以在一定程度上恢复和纠正编码中的错误。
3.定位模块:QR码中包含了多个定位模块,用来标识QR码的边界并帮助解码。
定位模块的位置和大小是固定的,解码器通过检测定位模块的位置和模式来确定QR码的边界。
4.数据密度:QR码的数据密度非常高,可以存储更多的信息。
通过增加编码区域的大小和模块的个数,可以有效提高QR码的存储容量和密度。
二、QR码的识别方法:2.定位模块检测:在图像中定位QR码的位置是识别QR码的重要步骤。
通常可以使用图像处理的方法,如边缘检测、轮廓检测等技术来检测QR码的定位模块,从而确定QR码的边界和角度。
4.数据解析与提取:在解码和校验码之后,可以将二进制数据转换为文本、数字或链接等特定的信息。
根据QR码的编码规则,将每个字符的二进制数据映射为相应的字符,从而提取和解析出最终的数据。
总结:QR码的原理是通过在二维平面上的黑白方块编码来存储信息,同时利用校验码和定位模块等机制来实现数据的校验和解析。
识别QR码的方法包括图像扫描、定位模块检测、解码校验码和数据解析与提取等步骤。
QR码已经在各个领域广泛应用,方便了信息的传递和存储。
纠错编码的方法

纠错编码的方法纠错编码(Error Correction Code,ECC)是一种在数字通信中用于检测和纠正错误的技术。
在数字通信中,由于噪声、干扰或其他原因,数据可能会发生错误。
纠错编码通过添加冗余信息来提高数据传输的可靠性,从而实现错误的检测和纠正。
1. 纠错编码的基本原理纠错编码的基本原理是通过在待传输数据中添加额外的冗余信息,并将这些冗余信息与原始数据一起传输。
接收方根据冗余信息对接收到的数据进行校验,并尝试恢复出原始数据。
常用的纠错编码方法包括海明码(Hamming Code)、卷积码(Convolutional Code)、低密度奇偶校验(Low-Density Parity Check, LDPC)等。
这些方法采用不同的算法和策略来实现错误检测和纠正。
2. 海明码海明码是一种最早被广泛应用于纠错编码中的方法。
它通过在待传输数据中添加冗余位来实现错误检测和纠正。
海明码采用了一种特殊的生成矩阵和校验矩阵来计算校验位,并将其添加到待传输数据中。
接收方根据接收到的数据和校验位计算出错误位,并进行纠正。
海明码的一个重要特点是可以检测和纠正多个错误。
通过添加足够数量的校验位,海明码能够检测到并纠正多达两个比特的错误。
3. 卷积码卷积码是一种基于状态机的纠错编码方法,它采用了一种特殊的编码器来生成冗余信息。
卷积码的编码器使用一个或多个移位寄存器和一个组合逻辑电路来生成冗余信息。
待传输数据经过编码器后,会产生一系列冗余比特,这些比特与原始数据一起传输。
接收方使用最大似然译码算法对接收到的数据进行解码,并根据冗余比特计算出错误位,并尝试进行纠正。
卷积码具有较高的编解码性能,但其复杂度较高。
为了降低复杂度,常常采用迭代译码算法(如Turbo译码)来提高性能。
4. 低密度奇偶校验低密度奇偶校验(LDPC)是一种近年来得到广泛关注和应用的纠错编码方法。
它采用了一种特殊的校验矩阵来生成冗余信息。
LDPC码的校验矩阵是一个稀疏矩阵,其中每一行和每一列的1的数量较少。
QRCODE纠错码的计算

2.3 计算自动纠错码Reed-solomon用于控制QRcode的误差首先,在先前的生成的块数据,根据数据RS块分隔的规则table5.例如,在RS区块号码为1时级别H是1,所以我们不需要划入。
接下来我们用table3的g(x)公式来计算修正的纠错码g(x)=x17 +α43x16 +α139x15 +α206x14 +α78x13 +α43x12+α239x11 +α123x10 +α206x9 +α214x8 +α147x7 +α24x6+α99x5 +α150x4 +α39x3 +α243x2 +α163x +α136以上的计算结果是GF(28)的一个基本元素GF(28)的特点有:1、四则运算的支持2、α255=13、我们可以转换成指数在α整数(反之亦然)参考table4现在多项式系数f(x),数据码字通过g(x)被划分f(x)=32x25 +65x24 +205x23 +69x22 +41x21 +220x20 +46x19 +128x18 +236x17 <—(1) 被g(x)所除引导f(x)的系数是32在table4 32是α5 , 所以我们用g(x)*(α5)*x8=α5*x25 +α5*α43*x24 +α5*α139*x23 +α5*α206*x22 +α5*α78*x21…..=α5*x25 +α48*x24 +α144*x23 +α211*x22 +α83*x21…..=32x25 +70x24 +168x23 +178x22 +187x21….. <—(2)然后计算出(1)与(2)的和f(x)’=7x24 +101x23 +247x22+146x21…..重复上面的过程直到这个结束. 接下来, 7 等于α198,我们使用g(x)*α198*x7如果指数a已经超过了255,我们让α255=1最后我们可以获得以下的结果R(x).R(x)=42x16 +159x15 +74x14 +221x13 +244x12 +169x11+239x10+150x9 +138x8 +70x7 +237x6 +85x5 +224x4 +96x3 +74x2 +219x +61(see table6)于是我们可以得到32 65 205 69 41 220 46 128 236 42 159 74 221 244 169 239 150 138 70 237 85 224 96 74 219 61表4、GF(28)αの指数と整数の対応表αの指数Exponent ofα整数Integer整数Integerαの指数Exponent ofα0 11 2 1 02 4 2 13 8 3 254 16 4 25 32 5 506 64 6 267 128 7 1988 29 8 39 58 9 22310 116 10 5111 232 11 23812 205 12 2713 135 13 10414 19 14 19915 38 15 7516 76 16 417 152 17 10018 45 18 22419 90 19 1420 180 20 5221 117 21 14122 234 22 23923 201 23 12924 143 24 2825 3 25 19326 6 26 10528 24 28 20029 48 29 830 96 30 7631 192 31 11332 157 32 533 39 33 13834 78 34 10135 156 35 4736 37 36 22537 74 37 3638 148 38 1539 53 39 3340 106 40 5341 212 41 14742 181 42 14243 119 43 21844 238 44 24045 193 45 1846 159 46 13047 35 47 6948 70 48 2949 140 49 18150 5 50 19451 10 51 12552 20 52 10653 40 53 3954 80 54 24955 160 55 18556 93 56 20157 186 57 15458 105 58 959 210 59 12060 185 60 7761 111 61 22862 222 62 11463 161 63 16664 95 64 665 190 65 19166 97 66 13967 194 67 9868 153 68 10270 94 70 4871 188 71 25372 101 72 22673 202 73 15274 137 74 3775 15 75 17976 30 76 1677 60 77 14578 120 78 3479 240 79 13680 253 80 5481 231 81 20882 211 82 14883 187 83 20684 107 84 14385 214 85 15086 177 86 21987 127 87 18988 254 88 24189 225 89 21090 223 90 1991 163 91 9292 91 92 13193 182 93 5694 113 94 7095 226 95 6496 217 96 3097 175 97 6698 67 98 18299 134 99 163 100 17 100 195 101 34 101 72 102 68 102 126 103 136 103 110 104 13 104 107 105 26 105 58 106 52 106 40 107 104 107 84 108 208 108 250 109 189 109 133 110 103 110 186111 206 111 61 112 129 112 202 113 31 113 94 114 62 114 155 115 124 115 159 116 248 116 10 117 237 117 21 118 199 118 121 119 147 119 43 120 59 120 78 121 118 121 212 122 236 122 229 123 197 123 172 124 151 124 115 125 51 125 243 126 102 126 167 127 204 127 87 128 133 128 7 129 23 129 112 130 46 130 192 131 92 131 247 132 184 132 140 133 109 133 128 134 218 134 99 135 169 135 13 136 79 136 103 137 158 137 74 138 33 138 222 139 66 139 237 140 132 140 49 141 21 141 197 142 42 142 254 143 84 143 24 144 168 144 227 145 77 145 165 146 154 146 153 147 41 147 119 148 82 148 38 149 164 149 184 150 85 150 180 151 170 151 124 152 73 152 17153 146 153 68 154 57 154 146 155 114 155 217 156 228 156 35 157 213 157 32 158 183 158 137 159 115 159 46 160 230 160 55 161 209 161 63 162 191 162 209 163 99 163 91 164 198 164 149 165 145 165 188 166 63 166 207 167 126 167 205 168 252 168 144 169 229 169 135 170 215 170 151 171 179 171 178 172 123 172 220 173 246 173 252 174 241 174 190 175 255 175 97 176 227 176 242 177 219 177 86 178 171 178 211 179 75 179 171 180 150 180 20 181 49 181 42 182 98 182 93 183 196 183 158 184 149 184 132 185 55 185 60 186 110 186 57 187 220 187 83 188 165 188 71 189 87 189 109 190 174 190 65 191 65 191 162 192 130 192 31 193 25 193 45 194 50 194 67195 100 195 216 196 200 196 183 197 141 197 123 198 7 198 164 199 14 199 118 200 28 200 196 201 56 201 23 202 112 202 73 203 224 203 236 204 221 204 127 205 167 205 12 206 83 206 111 207 166 207 246 208 81 208 108 209 162 209 161 210 89 210 59 211 178 211 82 212 121 212 41 213 242 213 157 214 249 214 85 215 239 215 170 216 195 216 251 217 155 217 96 218 43 218 134 219 86 219 177 220 172 220 187 221 69 221 204 222 138 222 62 223 9 223 90 224 18 224 203 225 36 225 89 226 72 226 95 227 144 227 176 228 61 228 156 229 122 229 169 230 244 230 160 231 245 231 81 232 247 232 11 233 243 233 245 234 251 234 22 235 235 235 235 236 203 236 122237 139 237 117 238 11 238 44 239 22 239 215 240 44 240 79 241 88 241 174 242 176 242 213 243 125 243 233 244 250 244 230 245 233 245 231 246 207 246 173 247 131 247 232 248 27 248 116 249 54 249 214 250 108 250 244 251 216 251 234 252 173 252 168 253 71 253 80 254 142 254 88 255 1 255 175table6calculation oferror corre ct code word s for sam ple x25x24x23x22x21x2x19x18x17x16x15x14x13x12x11x1x9x8x7x6x5x4x3x2x1x0coeff icients 326525694122461282360 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0=f(x) 7112471461542125948673481311423827252210 0 0 0 0 0 0 0=f(x)'6 1 36542391413632421562391351998814414633240 0 0 0 0 0 0141831641344374321551188166185952261911890 0 0 0 0 02261723928191363592212289769112931551250 0 0 0 074213122916921111366182914915145135321172450 0 0 023396152213464164219 0 622291621182332460 0 0711432918335222214193221152251861867261120 0911311661193183225128821286183218421597422124416923915138723785224967421961=R(x)。
QR二维码编解码原理

QR二维码编解码原理
一、信息编码:
编码过程主要包括以下几个步骤:
1.数据分割:将要编码的数据按一定规则进行拆分,每个数据块的长
度为8位,不足的用0补足。
2. 数据编码:将每个数据块转换为对应的二进制码,可以使用
ASCII码、Unicode等编码方式。
编码后的数据通常包括模式指示符、纠
错级别、编码方式等信息。
3.版本选择:根据需要编码的数据大小,选择合适的QR码版本,不
同版本的QR码可以存储不同数量的数据。
4.数据填充:将编码后的数据按照一定规则填充到QR码的矩阵中,
保证数据的可靠性和纠错能力。
二、错误纠正:
错误纠正的过程主要包括以下几个步骤:
1.创建生成多项式:根据QR码的版本和纠错级别,计算生成多项式。
生成多项式用于产生纠错码,以增强数据的纠错能力。
2.进行多项式除法:将消息多项式与生成多项式进行除法运算,得到
商和余数。
3.编码纠错码:将余数作为纠错码,与原数据组合成新的编码数据。
4.将纠错码填充到QR码的空白区域中,以实现数据的纠错功能。
三、解码:
QR码解码过程是编码过程的逆过程,主要包括以下几个步骤:
1.检测定位图案:通过识别定位图案,确认QR码的位置和方向。
6.数据恢复和纠错:根据纠错码进行恢复和纠错,得到原始的编码数据。
7.解码数据:将二进制数据按照事先约定的编码方式,转换为可识别的原始信息。
总结:。
QR码编码原理二(编码)
QR码编码原理二(编码)编码就是把常见的数字、字符等转换成QR码的方法。
说具体的编码之前,先说一下QR码的最大容量问题。
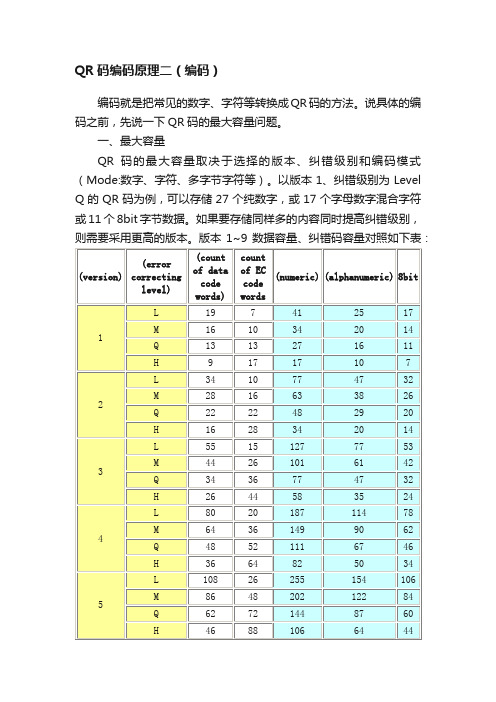
一、最大容量QR码的最大容量取决于选择的版本、纠错级别和编码模式(Mode:数字、字符、多字节字符等)。
以版本1、纠错级别为Level Q的QR码为例,可以存储27个纯数字,或17个字母数字混合字符或11个8bit字节数据。
如果要存储同样多的内容同时提高纠错级别,则需要采用更高的版本。
版本1~9 数据容量、纠错码容量对照如下表:如果要了解更详细的QR码容量信息,可以到电装的网站去看看。
下面,就举例说明将“ABCDE123”转换成为版本1、Level H的QR码转换方法。
二、模式标识符(Mode Indicator)QR码的模式(Mode)就是前文提到的数字、字符、8bit 字节码、多字节码等。
对于不同的模式,都有对应的模式标识符(Mode Indicator)来帮助解码程序进行匹配,模式标识符是4bit的二进制数:1、数字模式(numeric mode ): 00012、混合字符模式(alphanumeric mode) : 00103、8bit byte mode: 01004、日本汉字(KANJI mode) : 10005、中国汉字(GB2312):1101由于示例文本串是混合字符,因此将选择alphanumeric mode,其标识码为:0010三、文本串计数标识符(Character count indicator)文本串计数标识符用来存储源内容字符串的长度,在版本1-9的QR码中,文本串长度标识符自身的长度被定义为:数字 : 10bit混合字符 : 9bit8bit 字节码 : 8bit多字节码 : 8bit在本例中,源文本串的长度为8个字符,混合字符的长度为9bit,因此将字符个数8编码为9位二进制表示:000001000加上混合字符模式标识码,总的编码为0010 000001000四、数据内容编码1、数字模式下的编码在数字模式下,数据被限制为3个数字一段,分成若干段。
卷积码检纠错的原理

卷积码检纠错的原理
一、卷积码检纠错的原理
1、什么是卷积码检纠错
卷积码检纠错,也称作可纠错编码,是一种用于数据传输和存储系统中的错误检测和纠正技术。
它能够检测任何1个或多个位错误,并能够纠正误码。
卷积码检纠错利用传输/存储信息中冗余的方式来检测和纠正传输/存储信息中出现的错误。
它以一个特殊的编码序列或卷积码作为承载传输/存储信息的基础。
这种序列是由编码器产生的,在传输/
存储后由解码器检测和纠正被受干扰信息中出现的所有错误。
2、卷积码检纠错的原理
卷积码检纠错利用传输/存储信息冗余的特点,利用编码器和解码器在传输/存储数据过程中对原始信息进行加码、检验码计算、检测和纠错的过程实现错误检测和纠正。
(1) 编码器
编码器可以编码原始信息,原始信息乘以编码序列,生成编码序列。
编码后的信息由编码序列和检验码组成。
(2) 传输
接收者收到的信息将经过多次传输、存储和处理,可能会出现错误,这些错误可能是:一个位错误、多次传输错误、多个位错误或者多个位组错误。
(3) 解码器
解码器用于检测接收的信息是否出现错误,并且以信息中存在的冗余系数纠正错误。
如果解码器检测出有错误出现并且是可纠正的,解码器会消除错误,如果错误无法纠正就会报错。
3、卷积码检纠错的应用
卷积码检纠错可以应用于各种传输/存储系统中,如传输通信、存储器及控制系统等。
其中最广泛应用的是在无线电通信系统中,用于消除外界干扰所产生的错误。
基于DES改进算法的QR码防伪算法研究与实现

基于DES改进算法的QR码防伪算法研究与实现首先,了解QR码的基本原理。
QR码是一种二维条码,能够存储大量信息。
它由黑白像素组成,可以通过扫描或拍照的方式读取。
QR码包含了各种信息,如产品的批次、生产日期、生产地等。
这些信息可以帮助消费者验证产品的真伪。
其次,了解DES加密算法。
DES是一种对称密钥加密算法,具有高度的保密性和可靠性。
该算法将明文数据分组加密,然后通过多轮迭代进行混淆,并使用密钥进行加解密操作。
DES算法具有很高的安全性,但随着计算能力的提升,其破解难度逐渐降低。
针对QR码防伪的需求,我设计了一种基于DES改进算法的QR码防伪算法。
具体实现步骤如下:1.生成DES密钥:使用DES算法生成一个秘密密钥,并保存在服务器中。
2.QR码生成:根据产品的相关信息,生成对应的QR码。
将产品信息进行加密处理,然后嵌入到QR码中。
3.QR码扫描:用户使用手机等设备扫描QR码。
扫描后,将QR码中的信息传输到服务器上进行解密。
4.解密:服务器使用保存的DES密钥对加密的信息进行解密。
解密后得到产品的相关信息。
5.验证真伪:根据解密后的产品信息,与原始的产品信息进行对比。
如果两者一致,则验证为真实产品;如果不一致,则可能为伪劣产品。
基于DES改进算法的QR码防伪算法相较于传统的QR码防伪算法具有更高的安全性和准确性。
通过使用DES改进算法,增加了加密的难度,使得破解者更难以获取QR码中的信息。
在QR码扫描和解密过程中,信息已经经过了加密处理,确保了传输过程的安全性。
总结起来,QR码防伪算法的研究与实现是一个非常重要的课题。
通过使用基于DES改进算法的QR码防伪算法,能够提高QR码的安全性和可靠性,从而帮助消费者验证产品的真伪。
随着计算能力的不断提升,我们需要不断改进和更新防伪算法,以应对潜在的安全威胁。
QR二维码编解码原理

α0 α254 可用0000 0001 1111 1111 来表示
同时, α为P(X)=0的根。其中, P(X)是以GF(28)上8次首一既约多项式,以P(X)为 模的多项式剩余类环构成28阶伽罗华域。
编码
(c, k, r): c =码字总数 k =数据码字数 r =纠错容量
† 纠错容量小于纠错码字数的 一半,以减少错误译码的可能 性
生成多项式: g(x)=(x-α0)(x-α1)……(x-αn-1)
=(x-α0)(x-α1)……(x-α16)
其中n为生成多项式的次数, 也就是纠错码字数。本例中, 纠错码字数为17,生成多项式 如图所示。
排列规则
数据码字9个,纠错码字17个,共26个码字,就是26块码字区。 将码字,寻像图形,分隔符,校正图形按规则排列,放入二维码中即可
第13页/共24页
14
6.掩模:依次对符号的编码区域的位图进行掩模处理,评价所得结果,选择最优一种。
编码
例:对数字0123456789012345(16个数字字符)进行编码,生成QR码。
块的模块取反(浅色变成深色,或相反)。
3)对每个结果图形的不合要求的部分记分,以评估这些结果。
4)选择得分最低的图形。
i
j
版本1符号的所有的掩模图形,用掩模图形参 考000到111的掩模结果。
掩模图形参考
条件
000 (i + j) mod 2 = 0
001 i mod 2 = 0
010 j mod 3 = 0
c(α1)
QR二维码的原理与识别方法

QR二维码的原理与识别方法QR码呈正方形,只有黑白两色。
在3个角落,印有较小,像「回」字的的正方图案。
这三个是帮助解码软件定位的图案,使用者不需要对准,无论以任何角度拍摄,内容仍可正确被读取。
日本QR码的标准JIS X 0510在1999年1月发布,而其对应的ISO国际标准ISO/IEC18004,在2000年6月获得批准。
根据Denso Wave公司的资料,QR码是属于开放式的标准,QR码虽然由Denso Wave公司持有的专利,但不会被执行。
一、什么是二维码:二维码(2-dimensional bar code),是用某种特定的几何图形按一定规律在平面(二维方向上)分布的黑白相间的图形记录数据符号信息的。
在许多种类的二维条码中,常用的码制有:Data Matrix, Maxi Code, Aztec, QR Code, Vericode, PDF417, Ultracode, Code 49, Code 16K等。
1.堆叠式/行排式二维条码,如,Code 16K、Code 49、PDF417(如下图)等2.矩阵式二维码,最流行莫过于QR CODE 二维码的名称是相对与一维码来说的,比如以前的条形码就是一个“一维码”,它的优点有:二维码存储的数据量更大;可以包含数字、字符,及中文文本等混合内容;有一定的容错性(在部分损坏以后可以正常读取);空间利用率高等。
二、QR CODE 介绍QR(Q uick-R esponse) code是被广泛使用的一种二维码,解码速度快。
它可以存储多用类型1. 位置探测图形、位置探测图形分隔符:用于对二维码的定位,对每个QR码来说,位置都是固定存在的,只是大小规格会有所差异;这些黑白间隔的矩形块很容易进行图像处理的检测。
2. 校正图形:根据尺寸的不同,矫正图形的个数也不同。
矫正图形主要用于QR 码形状的矫正,尤其是当QR码印刷在不平坦的面上,或者拍照时候发生畸变等。
QR码纠错码原理及实现

QR码纠错码原理及实现QR码的纠错码原理主要基于汉明码(Hamming Code)或者BCH码(Bose-Chaudhuri-Hocquenhem Code)。
纠错码将原始数据编码为冗余结构,通过添加校验位来检测错误,并通过冗余信息纠正单个或多个错误。
以下是QR码纠错码的实现原理和过程:1.分组和编码:首先,将待编码的数据分成特定长度(例如8个比特)的块。
然后,通过使用特殊的编码算法将每个块编码为较长的编码块。
编码过程可以采用汉明码或BCH码实现。
2.创建纠错码字:对于每个编码块,生成一组纠错码字。
这些纠错码字是通过对编码块进行冗余计算来生成的。
纠错码字的长度通常比编码块长,以允许对单个或多个位错误进行纠正。
3.数据交错:将编码块和纠错码字进行交错,以使得数据在QR码中的分布更均匀。
交错的过程中,将编码块和纠错码字按照特定规则交错排列,以增加纠错能力。
```pythonimport qrcodeimport numpy as npdef generate_qr_code_with_error_correction(data,error_correction):# Generate QR code without error correctionqr_code = qrcode.QRCodeversion=2, # Version 2 is a 25x25 matrixerror_correction=qrcode.constants.ERROR_CORRECT_L,box_size=10,border=4,qr_code.add_data(data)qr_code.make(fit=True)# Embed error correction levelmatrix = np.array(qr_code.get_matrix()color = np.average(matrix) # Average color of the moduleserror_correction_value = 0 if error_correction == 'L' else 1 if error_correction == 'M' else 3qr_code_img = qr_code.make_image(fill_color=(color, color, color), back_color=(255, 255, 255))# Draw error correction levelqr_code_img.paste(error_correction_value, (10, 10))return qr_code_img# Generate QR code with error correction level 'L'qr_code_with_l =generate_qr_code_with_error_correction('Hello, World!', 'L') qr_code_with_l.show# Generate QR code with error correction level 'H'qr_code_with_h =generate_qr_code_with_error_correction('Hello, World!', 'H') qr_code_with_h.show```以上代码使用`qrcode`库生成QR码,并通过调整纠错级别和其他参数来实现纠错码的添加和绘制。
QR码纠错码原理及实现

S = Y1 ( X1 ) 2 + Y2 ( X2 ) 2 + … + Y r ( X r ) 2 2 S3 = Y1 ( X1 ) 3 + Y2 ( X2 ) 3 + … + Y r ( X r ) 3 S = Y ( X ) 2t + Y ( X ) 2t + …Y ( X ) 2t 2t 1 1 2 2 r r
中很容易受到污染、 涂痕、 撕裂等各种形式的破坏, 直接影响 因此采用一种好的检错与纠错算法尤为重要 。 目前在 识别, Solomon ) 错误控 二维条码中应用的最为广泛的是 RS ( ReedSolomon 码是一种重要的循环码, 制码。Reed是分组中纠错 能力最强的一种码, 在 QR 码中利用 RS 纠错码, 最高纠错等 [2 ] Solomon 码编译码 级能纠错 30% 的错误码字 。 但是 Reed算法比较复杂, 本文对 RS 纠错码算法在 QR 码中的应用进行 了相关研究。
n -1
R( x) =
∑r x
i i =0
i
= r0 x0 + r1 x1 + r2 x2 + … + r n - 2 x n - 2 + ( 3)
S3 … Sr S1 S2 S2 S3 S4 … S r + 1 T , B =[ 其中 A = σ x σ x -1 …σ t] S r S r + 1 S r + 2 … S2 r - 1 因此, 译码的关键是求解 σ( x) , 从而求出错误位置的值 。 系数 矩阵的行列式不为零时, 求解方程, 错误值的个数即为矩阵的 [5 ] 译码流程如图 2 。 秩 ,
QR码详解(下)

QR码详解(下)快速响应矩阵码(下)书接上回,继续下半场。
纠错码QR 码采⽤纠错算法⽣成⼀系列纠错码字,添加在数据码字序列之后,使得符号可以在遇到损坏时可以恢复。
这就是为什么⼆维码即使有残缺也可以扫出来。
没有残缺创造残缺也要把它扫出来,相信⼤家见过很多中间带图标的⼆维码吧。
纠错码字可以纠正两种类型的错误,拒读错误(错误码字的位置已知)和替代错误(错误码字位置未知)。
⼀个拒读错误是⼀个没扫描到或⽆法译码的符号字符,⼀个替代错误是错误译码的符号字符。
如果⼀个缺陷使深⾊模块变成浅⾊模块,或将浅⾊模块变成深⾊模块,将符号字符错误地译码为是另⼀个不同的码字,造成替代错误,这种数据替代错误需要两个纠错码字来纠正。
纠错等级纠错共有 4 个等级,对应 4 种纠错容量,如下表所⽰。
纠错等级L M Q H纠错容量,%(近似值)7152530⽤户应确定合适的纠错等级来满⾜应⽤需求。
从 L 到 H 四个不同等级所提供的检测和纠错的容量逐渐增加,其代价是对表⽰给定长度数据的符号的尺⼨逐渐增加。
例如,⼀个版本为 20-Q 的符号能包含 485 个数据码字,如果可以接受⼀个较低的纠错等级,则同样的数据也可⽤版本 15-L 的符号表⽰(准确数据容量为 523 个码字)。
纠错等级的选择与下列因素相关:1. 预计的符号质量⽔平:预计的符号质量等级越低,应⽤的纠错等级就应越⾼。
2. ⾸读率的重要性。
3. 在扫描误读失败后,再次扫描的机会。
4. 印刷符号的空间限制了使⽤较⾼的纠错等级。
纠错等级【L】适⽤于具有⾼质量的符号以及/或者要求使表⽰给定数据的符号尽可能最⼩的情况。
等级【M】被认为是“标准”等级,它具有较⼩尺⼨和较⾼的可靠性。
等级【Q】是具有“⾼可靠性”的等级,适⽤于⼀些重要的或符号印刷质量差的场合,等级【H】提供可实现的最⾼的可靠性。
纠错码字的⽣成纠错码字的⽣成多项式纠错码字是⽤数据码字除纠错码多项式所得到的余数。
纠错码多项式我们可以查表得出,⾸先查下表 3:QR码符号各版本的纠错特性。
QR码生成原理(一)

QR码生成原理(一)一、什么是QR码QR码属于矩阵式二维码中的一个种类,由DENSO(日本电装)公司开发,由JIS和ISO将其标准化。
QR码的样子其实在很多场合已经能够被看到了,我这还是贴个图展示一下:这个图如果被正确解码,应该看到我的名字和邮箱。
二、QR码的特点说到QR码的特点,一是高速读取(QR就是取自“Quick Response”的首字母),对读取速度的体验源自于我手机上的一个软件,象上面贴出的码图,通过摄像头从拍摄到解码到显示内容也就三秒左右,对摄像的角度也没有什么要求;二是高容量、高密度;理论上内容经过压缩处理后可以存7089个数字,4296 个字母和数字混合字符,2953个8位字节数据,1817个汉字;三是支持纠错处理;纠错处理相对复杂,目前我还没有深入了解,按照QR码的标准文档说明,QR码的纠错分为4个级别,分别是:•level L : 最大 7% 的错误能够被纠正;•level M : 最大 15% 的错误能够被纠正;•level Q : 最大 25% 的错误能够被纠正;•level H : 最大 30% 的错误能够被纠正;四是结构化;看似无规则的图形,其实对区域有严格的定义,下图就是一个模式2、版本1的QR图结构(关于QR码的"模式"、"版本"将在后面进行介绍):在上图21*21的矩阵中,黑白的区域在QR码规范中被指定为固定的位置,称为寻像图形(finder pattern)和定位图形(timing pattern)。
寻像图形和定位图形用来帮助解码程序确定图形中具体符号的坐标。
黄色的区域用来保存被编码的数据内容以及纠错信息码。
蓝色的区域,用来标识纠错的级别(也就是Level L到Level H)和所谓的"Mask pattern",这个区域被称为“格式化信息”(format information)。
五是扩展能力。
QR码的Structure Append特点,使一个QR码可以分解成多个QR码,反之,也可以将多个QR码的数据组合到一个QR码中来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
增刊 1
冯汉禄等: QR 码纠错码原理及实现
41
原始 信 息 v( x) 在 传 输 的 过 程 中 受 到 的 错 误 影 响 为 E( X) , 则实际接收到的信号 R( x) = v( x) + E( x) , 则原始信 息 v( x) = R( x) - E( x) , 设接收到的码字多项式为:
[4 ] r
σ( x) =
∏ ( 1 - x x) ; 0 ≤ r ≤ t
i i =1
( 7)
把 σ( x) 展开: σ ( x ) = ( 1 - x1 x ) ( 1 - x2 x ) ( 1 - x3 x ) … ( 1 - x t x ) = 1 - ( x1 + x2 + … + x t ) x + ( x1 x2 + x1 x3 + … + x t - 1 x t ) x2 - … + ( - 1 ) t x1 x2 … x t 令 σ1 = - ( x 1 + x 2 + … + x t ) ( 8)
1
RS 码编译算法
域是能够进行加与乘两种运算的非空元素的集合 。 伽罗 GF) 是一个有限域, 瓦域( Galois Field, 以素数 q 为模的整数 构成 q 阶的伽罗瓦域为 GF( q) 。 在 GF( q) 中, 某一个元素 a 满 q -1 a = 1 , a GF ( q ) 。 GF 足 称 为 的本原元 在任何 ( q) 中都能找 到一个本原元, 能够用它的幂次表示所有 q - 1 个非零元素, 0 a1 , a2 , a3 , a4 , …, a q -1 ,其 中 从而组 成 一 个 循 环 群 G( a) : a , q -1 a = 1。 [3 ] 可以纠正 t 个错误的 RS 码的生成多项式 为: 2 2t 2t g ( x ) = ( x - a ) ( x - a ) … ( x - a ) = x + g2 t - 1 x 2 t - 1 + g2 t - 2 x n - 2 + … + g1 x + g0 ( 1) 1, 2, …, 2 t - 1 ) 是 GF( q) 中元素, a 为 GF( q) 其中: g i ( i = 0 , 中的一个本原元。 1 2 若原始信息的多项式为 d( x) = d0 + d1 x + d2 x + … +
中很容易受到污染、 涂痕、 撕裂等各种形式的破坏, 直接影响 因此采用一种好的检错与纠错算法尤为重要 。 目前在 识别, Solomon ) 错误控 二维条码中应用的最为广泛的是 RS ( ReedSolomon 码是一种重要的循环码, 制码。Reed是分组中纠错 能力最强的一种码, 在 QR 码中利用 RS 纠错码, 最高纠错等 [2 ] Solomon 码编译码 级能纠错 30% 的错误码字 。 但是 Reed算法比较复杂, 本文对 RS 纠错码算法在 QR 码中的应用进行 了相关研究。
n -1
R( x) =
∑r x
i i =0
i
= r0 x0 + r1 x1 + r2 x2 + … + r n - 2 x n - 2 + ( 3)
S3 … Sr S1 S2 S2 S3 S4 … S r + 1 T , B =[ 其中 A = σ x σ x -1 …σ t] S r S r + 1 S r + 2 … S2 r - 1 因此, 译码的关键是求解 σ( x) , 从而求出错误位置的值 。 系数 矩阵的行列式不为零时, 求解方程, 错误值的个数即为矩阵的 [5 ] 译码流程如图 2 。 秩 ,
S = Y1 ( X1 ) 2 + Y2 ( X2 ) 2 + … + Y r ( X r ) 2 2 S3 = Y1 ( X1 ) 3 + Y2 ( X2 ) 3 + … + Y r ( X r ) 3 S = Y ( X ) 2t + Y ( X ) 2t + …Y ( X ) 2t 2t 1 1 2 2 r r
S j = R( a j ) = C( a j ) + E( a j ) = E( a j ) =
t
∑Y X
i i =1
li
= ( 5)
图2
RS 码译码流程
∑Y a
i i =1
li
2
RS 码在 QR 码中的编码过程
l 2, …, r) , 令 Xi = X i ( i = 1, 于是有 S1 = Y1 X1 + Y2 X2 + … + Yr Xr 。 同理用 a 的各次幂, 即式( 1 ) 的各个零点, 对差错 多项式( 5 ) 求值, 可得到 2 t 个方程的方程组。 S1 = Y1 X1 + Y2 X2 + … + Y r X r
∑Y X
i i =1
li
( 4)
l 其中 Y i ∈ GF( q) ,X i 称为错误位置, 说明错误发生在 R( x) n -1 中的第 n - l i ( x 的系数算第一位) 位, 错误值是 Y i 。 j 2, …, 2t) 对 用纠错码生成多项式 g( x) 的各个零点 a ( j = 1, j R( x) 求值, 其结果定义为伴随多项式 Sj 。 因为 C( a ) = 0, 故 t
0
引言
QR 二维条码又称为快速响应矩阵码, 相比于一维条码 它具有数据量大、 不依赖数据库、 应用方便、 纠错能力强等特 [1 ] 点 。也正因为二维条码的这些特点, 使二维条码比一维条 码的编码与解码技术更为复杂 。本文在对国内外的二维条码 进行对比研究之后, 论述了 QR 二维条码的编码与解码原理, Solomon 的原理。 并详尽阐述了二维码中所应用的 ReedQR 码如图 1 所示, 由正方形模块组成的一个正方形矩阵 列构成, 它包括编码区、 功能图形和空白区三部分 。编码区是 由文本信息转化的二进制码组成, 它包括格式信息、 版本信 息、 数据和纠错码字。功能图形包括位置探测图形 、 位置探测 定位图形和校正图形。 图形分隔符、
r n -1 x n -1
n -1 + e n - 2 x n - 2 + … + e1 x1 + e0 。 错误多项式 E( x) = e n -1 x 如果含有 r( 0 ≤ r ≤ t) 个错误, 它们发生在未知错误位置 i1 , i2 , …, i r 上, 则 t
E ( x ) = Y t X l t + Y t - 1 X l t - 1 + … + Y 1 X l1 =
第 31 卷增刊 1 2011 年 6 月 文章编号: 1001 - 9081 ( 2011 ) S1 - 0040 - 03
计算机应用 Journal of Computer Applications
Vol. 31 Suppl. 1 June 2011
QR 码纠错码原理及实现
冯汉禄, 黄颖为, 牛晓娇, 钱银超
摘
Principle and implementation of error correcting coding of QR code
FENG Hanlu, HUANG Yingwei, NIU Xiaojiao, QIAN Yinchao
( Faculty of Printing and Packaging Engineering,Xi'an University of Technology, Xi'an Shaanxi 710048,China)
σ t = ( - 1 ) x1 x2 … x t 则式( 8 ) 变为:
r 2 t σ t = 1 + σ1 x + σ2 x + … + σ t x = σ ( x ) =
{
QR 码多项式算法用位的模 2 算法和字节的模 100011101 算 8 8 4 3 这是伽罗华域 2 以 100011101 表示模块多项式: x + x + x + 法, 2 [7 ] x +1 。 数据码字为多项式各项的系数, 第一个数据码字为 最高次项的系数, 第一个纠错码字前的最后一个数据码字是 最低项的系数。 纠错码字是数据码字被纠错码字多项式 g( x) 除得的余 数。 余数的最高次系数为第一个纠错码字, 最低次项系数为最 后个纠错码字, 也是整个块的最后一个码字 。 格式信息是由 5 个数据位和 10 个纠错位组成的一个 15 QR 码中用 BCH( 15 , 5 ) 码纠错, 位序列, 以数据位串为系数的 [6 ] 10 8 G ( x ) = x + x + x5 + x4 + x2 + x + 1 多项式被生成多项式 除, 所得的剩余多项式的系数串追加到系数串上形成 ( 15 , 5 ) BCH 码字符串。 最后通过用 101010000010010 对位串进行 异或运算掩模, 来保证掩模图形和纠错等级的任意组合的格 式信息不全为 0 。 例: 纠错等级 M; 掩模图形参考 101 00101 二进制字符串: x2 + 1 生成多项式: 5 位信息组位长( 15 - 5) : x12 + x10 将次数升 15 位码字总长度, 10 8 5 4 2 2 7 被 G( x) 除后: = ( x + x + x + x + x + x + 1) x + ( x + 6 4 3 2 x +x +x +x ) 把上面的剩余多项式的系数字符串附加至格式信息数据串 00101 + 0011011100 → 001010011011100
