统计思维导图
统计思维导图

统计思维导图应用在统计学的教学工作中我们发现,学生普遍对统计方法的应用及创新存在困惑,究其根本的原因主要是对于知识的不理解,只是单纯地去记忆公式,违背了统计学的特点及规律。
为了解决这个问题,在课堂中引入统计学思维导图,经实践证明,有利于学生掌握统计知识,提高学习效率,增强应用能力及创新能力。
统计学是一门收集、分析、表述和解释数据的学科,在市场营销中有着十分广泛的应用.首先,变异是社会中普遍存在的现象,采用统计方法,可以发现不确定现象背后隐藏的规律,从而对营销过程中提出的理论假设加以科学的验证。
其次,结合统计学的知识,可以针对企业的特点,开展企业的市场营销管理工作,制定合理的营销策略,对产品的质量进行分析,对客户的需求进行定量化的描述,明确销售工作的重点和关键。
因此,在我国目前的医药市场营销的相关专业中,普遍开设了统计类的课程,但是在教学过程中我们发现,学生在学习统计学时经常不知从何入手,教学内容主要以记忆为主,违背了统计学科应用性的特点,不利于学生对知识的掌握和对方法的创新。
为了让学生更好的理解统计学,应用统计学,我们将思维导图应用于日常的教学工作中,取得了一定的经验效果。
1 统计思维导图统计学思维导图是表达发散性思维的有效的图形工具,是一种革命性的思维工具。
思维导图采用图文并重的方法,将各级各层的主题关系用相互隶属的层级图形表现出来,把关键词和图形、图像、颜色等建立记忆链接。
思维导图充分利用人脑的机能,利用记忆、思维等规律,协助人们对问题进行学习和理解,可以将其广泛地应用于统计学的教学工作中。
2统计学思维导图在教学中的应用随着多媒体技术的普及,很多高等医学院校都采用了PPT进行教学,这种教学方法比较直观,能通过生动的图像、声音等方法,调动学生的情绪,提高学习效率。
但是,由于其同样具有大信息量、大容量性的特点,使得学生在学习时感觉吃力,跟不上授课的进度.而且,多数幻灯片对于学习内容的排列方式是线式的,不符合人脑的发散性思维模式,不利于学生对知识的掌握和理解。
统计思维导图

第十一章 第一节统计与概率统计他们都是衡量一组数据波动大小的量 学习误区分不清集中趋势和离散趋势 总体弄不清三种统计图的表达意义的侧重点 个体总结升华统计的相关概念样本知能提升 样本容量扇形统计图样本估计总体的方法 条形统计图统计图表折线统计图数据的收集与整理频率分布图3.确定组距与组数; 直方图画频率分布直方图的步骤 普查 调查的方式画统计图抽样调查从总体中,抽取部分个体进行调查的方式统计 知识梳理//算数平均数画频数分布折线图的方法 学法指导平均数覘養i •踽矿加权平均数众数的大小只与数据中的部分数据有关 中位数分析数据众数 极差利用统计量解决实际问题 方差标准差数形结合法极差、方差与标准差 为了一定的目的,对考察对象进行全面的调查在统计中,所提取的样本个数平均数的大小与每一个数据有关,任一数据的变动都会引起平均数的变动取直方图中每个矩形上边的中点,把这些点用线段依次连接起来即可 在统计中,所有考察对象的全体在统计中,组成总体的每一个考察对象即通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况,常用于设计实际应用题 中位数只与数据的排列位置有关,某些数据的变动对它没有影响3.对事件提出合理化的建议这三个量越小,这组数据的波动越小,也越稳定;反之亦然 理解各个统计量的作用,使分析数据更具有方向性 5.列频率分布表;在统计中,实际观测或调查的那部分个体平均数、众数和中位数的区别一组数据中,最大与最小数据的差7.写出统计图的名称和数据来源 4.确定分点 6.画直方图 3.注意题目的侧重点来选取合适的知识解题 2.植物长势的判断 2.计算数据中的最大值与最小值的极差(2)根据已知条件,绘制或补全各类统计图n 个数据按大小顺序排列,处于中间位置的一个数据(或中间两个数据的平均数)1.认真理解各个基本概念的实质,找出区别与联系 (1)观察分析各类统计图表,解决相关问题1.比赛成绩的评估 1.收集数据;(放到统计图内)一组数据中,出现次数最多的那个数(注:有时会有多个)■s 常见的命题形式总体、样本的概念混乱。
心理统计学-描述统计思维导图_免费思维导图分享
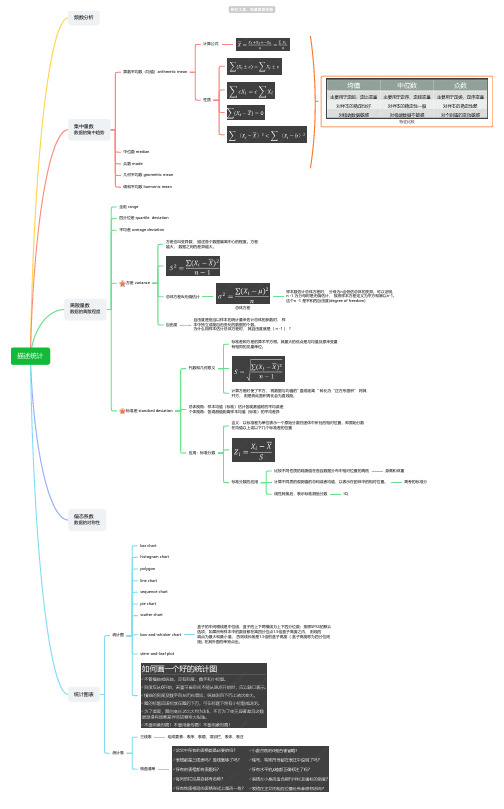
描述统计频数分析集中量数数据的集中趋势算数平均数(均值)arithmetic mean计算公式性质中位数 median众数 mode几何平均数 geometric mean调和平均数 harmonic mean特征比较离散量数数据的离散程度全距 range四分位差 quartile deviation平均差 average deviation方差 variance方差也叫变异数, 描述各个数据偏离中心的程度。
方差越大, 数据之间的差异越大。
总体方差&无偏估计总体方差样本数估计总体方差时, 分母为n会低估总体的变异。
可以证明,n -1 为分母时是无偏估计, 故将样本方差定义为平方和除以n-1。
这个n -1 是平和的自由度(degree of freedom)自由度自由度是指当以样本的统计量来估计总体的参数时, 样本中独立或能自由变化的数据的个数。
为什么用样本估计总体方差时, 其自由度就是( n -1 ) ?标准差 standard deviation代数和几何意义标准差即方差的算术平方根。
其最大的优点是与均值及原来变量有相同的见量单位。
计算方差时使了平方, 将数据与均值的" 直线距离“ 转化为“正方形面积” 将其开方, 则是将此面积再化会为直线距。
总体视角:样本均值(标准)估计各观测值时的平均误差个体视角:各观测值距离样本均值(标准)的平均差异应用:标准分数含义:以标准差为单位表示一个原始分数在团体中所处的相对位置,即原始分数在均值以上或以下几个标准差的位置标准分数的应用比较不同性质的观测值在各自数据分布中相对位置的高低身高和体重计算不同质的观测值的总和或者均值,以表示在团体中的相对位置。
高考的标准分线性转换后,表示标准测验分数IQ偏态系数数据的对称性统计图表统计图bar charthistogram chartpolygonline chartsequence chartpie chartscatter chartbox-and-whisker chart盒子的中间横线是中位线,盒子的上下两横线为上下四分位数;按照SPSS的默认选项,如果所有样本中的数目都在离四分位点1.5倍盒子高度之内, 则线的端点为最大和最小值, 否则线长就是1.5倍的盒子高度( 盒子高度称为四分位间距), 在其外面的单独点出。
统计思维导图

填写统计表,能进一步体会分段整理
数据的实际意义及其作用,这就为回顾解 决实际问题的方法与过程,反思分段整理 数据的技巧和要领作了准备
在分析数据的基础上,回顾收获, 从发展学生的数据分析观念
谢谢, 欢迎批评、指导,Leabharlann 回顾、反思,从而获得有关统计
表和统计图的基础知识以及初步的体 验。
从实际问题 引出分段整理数 据,既体现了整 理数据是解决实 际问题的需要, 又有利于学生联 系生活经验进行 数据的分段整理 活动。
在数据 较多的情况 下,用画 “正”字的 方法依次对 每一个数据 归类记录, 能避免遗漏 和重复。
苏教版四年级(上册)
《统计表和条形统计图》
例1、
中心主题 分支主题(子主题)
学生曾多次经历用自己的方法描述 数据的过程,并初步学会了用画“正” 字的方法记录数据,因此教材充分利用 学生已有经验创建了情境,.
引导学生通 过自主活动认识 统计表和统计图, 体会统计图表在 呈现数据时的作 用和价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章 统计与概率
第一节 统 计
统计
知识梳理
学法指导
总结升华
统计的相关概念
数据的收集与整理
分析数据
平均数
中位数
学习误区
1.认真理解各个基本概念的实质,找出区别与联系. 知能提升
理解各个统计量的作用,使分析数据更具有方向性. 样本估计总体的方法
画统计图
即通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况,常用于设计实际应用题.
画频率分布直方图的步骤
画频数分布折线图的方法
取直方图中每个矩形上边的中点,把这些点用线段依次连接起来即可.
平均数、众数和中位数的区别
极差、方差与标准差
利用统计量解决实际问题 数形结合法 总体 个体
样本
样本容量
统计图表
调查的方式
众数 极差
方差
标准差
总体、样本的概念混乱.
分不清集中趋势和离散趋势. 弄不清三种统计图的表达意义的侧重点. 3.注意题目的侧重点来选取合适的知识解题.
1.收集数据;(放到统计图内)
7.写出统计图的名称和数据来源.
常见的命题形式 (1)观察分析各类统计图表,解决相关问题.
(2)根据已知条件,绘制或补全各类统计图.
1.比赛成绩的评估.
2.植物长势的判断.
3.对事件提出合理化的建议.
他们都是衡量一组数据波动大小的量.这三个量越小,这组数据的波动越小,也越稳定;反之亦然.
平均数的大小与每一个数据有关,任一数据的变动都会引起平均数的变动.
众数的大小只与数据中的部分数据有关.
中位数只与数据的排列位置有关,某些数据的变动对它没有影响.
2.计算数据中的最大值与最小值的极差;
3.确定组距与组数;
4.确定分点;
5.列频率分布表;
6.画直方图;
在统计中,所有考察对象的全体.
在统计中,组成总体的每一个考察对象.
在统计中,实际观测或调查的那部分个体.
在统计中,所提取的样本个数.
扇形统计图.
条形统计图.
折线统计图. 频率分布图
直方图
普查
抽样调查
为了一定的目的,对考察对象进行全面的调查.
从总体中,抽取部分个体进行调查的方式.
算数平均数
加权平均数
n 个数据按大小顺序排列,处于中间位置的一个数据(或中间两个数据的平均数).
一组数据中,出现次数最多的那个数(注:有时会有多个).
一组数据中,最大与最小数据的差.。
