初二数学考试卷勾股定理与平方根

合集下载

【八年级】八年级上册第二章勾股定理与平方根单元试题(带答案)

【八年级】八年级上册第二章勾股定理与平方根单元试题（带答案）第二章勾股定理与平方根检测题【本试卷满分为100分，考试时间为90分钟】一、（每小题3分，共30分）1.以下陈述中正确的一项是（）a.已知是三角形的三边，则b、在直角三角形中，两边的平方和等于第三边的平方c.在rt△中，∠°，所以d、在RT Delta，∠ 是的，所以2.如图，在rt△中，∠°，c，c，则其斜边上的高为（）a、 6cb。

8.5摄氏度。

光盘C3.如图，在△中，∠°，，，点在上，且，，则的长为（）a、 6b。

7c。

8d。

九4.在下列各数中是无理数的有（），，，3，，（两个相邻的之间有10个），（小数部分由相继的正整数组成）.a、 3 b.4 C.5 d.65.下列结论正确的是（）a、 b。

c.d.6.如果已知平方根为，而64的立方根为，则的值为（）a.3b.7c.3或7d.1或77.以下陈述中正确的一项是（）a.两个无理数的和还是无理数b、两个不同的有理数之间肯定有无数个无理数c.在1和2之间的有理数有无数个，但无理数却没有d、如果是，它是一个有理数8.下列结论正确的是（）a、 27的立方根是Bc.的立方根是d.的立方根是9.以下陈述是正确的（）a.一个数的立方根有两个，它们互为相反数b、一个数字的立方根与这个数字有相同的符号c.如果一个数有立方根，那么它一定有平方根d、数字的立方根是一个非负数10.若，且，则的值为（）a、不列颠哥伦比亚省。

二、题(每小题3分,共24分)11.已知两条线段的长度分别为5C和12C。

当第三条线段的长度为_________;时，这三条线段可以形成一个直角三角形12.有一组勾股数，知道其中的两个数分别是17和8，则第三个数是.13.以下四组：① 5, 12, 13; ②7，24，25；③；④. 其中，可以形成直角三角形的边长是__________________14.36的平方根是；的算术平方根是.15.8的立方根是=16.比较大小:0.34____;____.17.如果正数的平方根分别为和，则正数为18.若、互为相反数，、互为负倒数，则=_______.三、回答问题（共46分）19.若△三边满足下列条件，判断△是不是直角三角形，并说明哪个角是直角：（1）;（2）.20.（12点）计算以下公式的值：（1）;（2）;（3）;（4）; （5）; （6）.21.（6分）比较下列各组数的大小:（1）和；（2）及22.（4分）已知，求的值.23.（6分）如图所示，台风过后，一所希望小学的旗杆在离地某处断裂，旗杆顶端距离旗杆底部8米。

八年级数学(上)第二章勾股定理与平方根单元测评卷(A)

第二章勾股定理与平方根单元测评卷（A）（附答案）（满分：100分时间：60分钟）一、选择题（每题4分，共28分）1．一个直角三角形的两边长分别为6 cm、8 cm，则这个三角形的斜边长为( )A．8 cm B．10 cm C．8 cm或10 cm D．10 cm或cm2．若等腰三角形中相等的两边长为10 cm，第三边长为16 cm，则第三边上的高为( ) A．6 cm B．8 cm C．10 cm D．12 cm3．若三角形的三边长分别为10、24、26，则它最长边上的中线长是( ) A．10 B．11 C．13 D．344．（2010．阜新）国家游泳中心——“水立方”是2008年北京奥运会标志性建筑物之一，其工程占地面积为62 828平方米，将62 828用科学记数法表示是（结果保留3个有效数字）( )A．6.28×103B．6.28×104C．6.282 8×l04D．0.628 28×1055( )A．5个B．4个C．3个D．2个6．如图，在四边形ABCD中，AB＝3 cm，BC＝4 cm，CD＝12 cm，DA＝13 cm，且∠ABC ＝90°，则四边形ABCD的面积是( )A．84 cm2B．36 cm2C．25.5 cm2D．无法确定7．如图，在由16个边长为1的小正方形拼成的图案中，有五条线段PA、PB、PC、PD、PE，其中长度是无理数的有( )A．1条B．2条C．3条D．4条二、填空题（每题4分，共28分）8．－4的绝对值是_______ ．81的平方根是______．9．如图，在数轴上点A和点B之间表示整数的点有_______个．10．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm，则A、B．C、D四个正方形的面积之和是______cm2．11．上海世博会的中国建筑外观以“东方之冠，鼎盛中华，天下粮仓，富庶百姓”为构思主题，建筑面积为4. 645 7万平方米，4.645 7保留2个有效数字是______万平方米．12．已知实数a 、b 10b -=，则a 2012＋b 2011＝______．13．如图，A 村到公路l 的距离AB ＝2 km ，C 村到公路l 的距离CD ＝6 km ，且BD ＝6 km现要在公路l 上取一点P ，使AP ＋CP 的值最小，则这个最小值为______．14．如图，△ABC 是直角边长为1的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，……依此类推，第n 个等腰直角三角形的斜边长是______．三、解答题（共44分）15．（6分）把下列各数填入相应的集合内：－6，0.45，0，2273π- 有理数集合：{ …}；无理数集合：{ …}．16．（6分）求下面各式中x 的值．(1)8－2(x －1)2＝－10；30-．17．（7分）如图，正方形网格中每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下面的要求画三角形．(1)在图①中画一个三角形，使它的三边长都是有理数；(2)在图②、图③中分别画一个直角三角形，使它们的三边长都是无理数，且所画的两个三角形不全等．18．（7分）如图，为了求出湖两岸的A、B两点之间的距离，一个观测者在点C设桩，使△ABC恰好为直角三角形，且∠ABC＝90°．通过测量，得到AC长为160米，BC长为128米．问从点A穿过湖到点B有多远？19．（9分）《中华人民共和国道路交通管理条例》规定：小汽车在城市街路上的行驶速度不得超过70 km/h．如图，一辆小汽车在一条城市街路上沿直道CB行驶，某一时刻刚好行驶到路对面车速检测仪A点正前方30 m的C点处，过了2s后，测得小汽车与车速检测仪之间的距离AB＝50 m．这辆小汽车超速了吗？20．（9分）如图，折叠长方形的一边AD，使点D落在BC边上的点F处．如果AB＝8 cm，BC＝10 cm，求EC的长．参考答案一、1．C 2．A 3．C 4．B 5．A 6．B 7．C二、8．4 ±9 9．4 10． 49 11．4.6 12．2 13．10 km 14．n三、 15．－6，0.45， 0，227 3π-16．(1)x ＝4或x ＝－2 (2)x ＝5或x ＝117．答案不惟一，(1)如图①所示 (2)如图②、③所示18．从点A 穿过湖到点B 有96米 19．这辆小汽车超速了20．EC 的长为3。

初二数学测试卷(勾股定理与平方根)

初二数学测试卷(勾股定理与平方根)初二数学测试卷（勾股定理与平方根）一、选择题1．一个直角三角形两直角边长分别为3和4，则下列说法正确的是（）．A、三角形面积为12B、三角形的周长为25C、斜边长为25D、斜边长为52．以下列各数为边长，不能组成直角三角形的是（）．A、3，4，5B、4，5，6C、5，12，13D、6，8，103．2(6)-的平方根是（）．A．6-B．36 C．±6D．6±4．下列判断中错误的是（）．A、△ABC中，若∠B＝∠C－∠A，则△ABC 是直角三角形B、△ABC中，若a2＝b2－c2，则△ABC是直角2三角形C、△ABC中，若∠A︰∠B︰∠C＝3︰4︰5，则△ABC是直角三角形D、△ABC中，若a︰b︰c＝5︰4︰3，则△ABC 是直角三角形5．下列命题正确的个数有：（1）33a a=，（2）2a a=，（3）无限小数都是无理数，（4）有限小数都是有理数，（5）实数分为正实数和负实数两类（）．A．1个B．2个C．3个D．4个6．若两条线段的长为8cm和15cm，则能组成一个直角三角形的第三条线段的长为（）．A、12cmB、13cmC、17cmD、17cm或161cm7．如图，在由单位正方形组成的网格图中标有AB CD EF GH，，，四条线段，其中能构成一个直角三角形三边的线段是（）．34A 、CD EF GH ，，B 、AB EF GH ，，C 、AB CD GH ，，D 、AB CD EF ，， 8．如图，有一块直角三角形纸片，两直角边AC ＝6cm ，BC ＝8cm ，现将直角边AC 沿AD 折叠，使它落在斜边AB 上，且与AE 重合，则BD ＝（）．A 、2cmB 、3cmC 、4cmD 、5cm（第7题图）（第8题图）9．在△ABC 中，AB ＝15，AC ＝13，高AD ＝12，则△ABC 的周长为（）．A 、42B 、32C 、42或32D 、不能确定A BE D C C E BH D F AG5 二、填空题1．算术平方根等于它本身的数有________，立方根等于本身的数有________．2．在Rt △ABC 中，∠C ＝90°，∠A ，∠B ，∠C的对边分别是a ，b ，c ．①若b ＝2a ，c ＝5，则a ＝________；②若a ︰b＝3︰4，c ＝10，则S △ABC ＝________．3．从电线杆高底面24m 处向地面拉一条长25m 的缆绳，则固定点B 到电线杆底部A 的距离为________m ．4．如果0)6(42=++-y x ，则=+y x ________．5．如果21a -和5a -是一个数m 的平方根，则.__________,==m a6．如图，所有的四边形都是正方形，所有三角形都是直角三角形，其中最大的正方形的边长是a ，则图中四个小正方形A B C D ，，，的面积之和是．A B C D a6 （第6题图）7．如图，将一根25cm 长的细木棒放入长、宽、高分别为8cm 、6cm 、和3的长方体无盖盒子中，则细木棒露在盒外面的最短长度是________cm ．8．一青蛙在如图8×8的正方形（每个小正方形的边长为1）网格的格点（小正方形的顶点）上跳跃，5，青蛙从点A 开始连续跳六次正好跳回到点A ，则所构成的封闭图形的面积的最大值是．（第7题图）（第8题图）三、解答题1．如图，滑杆在机械槽内运动，ACB ∠为直角，A EA已知滑杆AB长2．5米，顶端A在AC上运动，量得滑杆下端B距C点的距离为1．5米，当端点B向右移动0．5米时，求滑杆顶端A下滑多少米？2．△ABC中，D是BC上的一点，若AB＝10，BD＝6，AD＝8，AC＝17，求△ABC的面积．73．先观察下列表格：请你结合该表格及相关知识，求出b、c的值．列举猜想3、4、5 32＝4＋55、12、13 52＝12＋137、24、25 72＝24＋25…………35、b、c352＝b＋c894．如图（1）所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图（2）所示．已知展开图中每个正方形的边长为1．（1）求在该展开图中可画出最长线段的长度？这样的线段可画几条？（2）试比较立体图中BAC ∠与平面展开图中B A C '''∠的大小关系？5．在数轴上画出8-的点．CA BA 'C 'B '106．如图，△ABC 中，∠C ＝90°，D 是BC 上一点，AB ＝17，AD ＝10，BD ＝9，求CD 的长．7．已知：如图，︒=∠90C ，CM AM =，AB MP ⊥于P ．求证：222BC AP BP +=．AB CD8．已知：在ABC Rt ∆中，︒=∠90C ，D 、E 分别为BC 、AC 的中点，5=AD ，102=BE ．求AB 的长．测试卷答案一、选择题1．D ．2．B ．3．C ．4．C ．5．B ．6．D ．7．B ．8．D ． 9．C ．二、填空题1．0、1；0、1、－1． 2．①5；②24． 3．7．4．－2．5．－4，81． 6．2a ． 7．5． 8．12．三、解答题1．梯子下滑0．5米．2．84．3．612，613．4．（1）在平面展开图中可画出最长的线段长为104条；（2）连结线段B C ''，有∠BAC ＝∠B ，A ，C ，＝450． 5．略．6．6．7．∵在BMP Rt ∆中，AB MP ⊥，∴222PM BM BP-=．同理：在AMP Rt ∆中，222PMAM AP =-．在BCM Rt ∆中，222BMCM BC =+，又∵CM AM =，∴()()22222BP CM BC AM AP =+--．∴222AP BC BP +=．8．设c AB a BC b AC ===,,，∵AD 、BE 是中线，∴2b CE =，2a CD =． ∵∠C ＝90°，∴222222,CD AC AD BC CE BE +=+=． ∴2222225,2(210).2a b b a ⎧⎛⎫+=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩∴2252a b +=．∵在△ABC 中，︒=∠90C ∴2222252AB AC BC a b =+=+=．∴132=AB 52．。

八年级数学上册期末复习一勾股定理与平方根试题

创作；朱本晓勾股定理与平方根根本概念㈠、勾股定理：1．勾股定理 2．勾股定理的逆定理㈡、平方根立方根：1．平方根方 2．算术平方根 3．立方根㈢、实数：1．无理数 2．实数的分类㈣、近似数与有效数字：1．近似数 2.有效数字一、选择题 1、实数-1.732，2π，722，34…，01.0-中，无理数的个数有〔〕. A.2个 B. 3个 C.4个 D.5个 2、有以下四个说法：①1的算术平方根是1，②81的立方根是±21，③-27没有立方根，④互为相反数的两数的立方根互为相反数，其中正确的选项是〔〕.A .①②B .①③C .①④D .②④ 3、以下语句中正确的选项是〔〕A 、9的平方根是－3B 、－5是－25的平方根C 、－12是144的平方根D 、()23-的平方根是－34、三角形的三条边分别为22b a +、22b a -、２ab ，那么这个三角形是〔〕A、钝角三角形B、锐角三角形C、直角三角形D、不能确定5、有以下几组数据：①6、8、10 ②12、13、5 ③ 17、8 、15 ④4、11、9其中能构成直角三形的有：〔〕Ａ、４组Ｂ、３组Ｃ、２组Ｄ、１组46、如图，假设数轴上的点A，B，C，D表示数-2，1，2，3，那么表示7的点P应在线段〔〕创作；朱本晓创作；朱本晓A ．线段AB 上；B ．线段BC 上；C ．线段CD 上；D ．线段OB 上7、如图小方格都是边长为1的正方形,那么四边形ABCD 的面积是 ( ) A. 25 B. 12.5 C. 98、，如图长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，那么△ABE 的面积为〔〕 A 、3cm 2B 、4cm 2C 、6cm 2D 、12cm 29、，如图，一轮船以16海里/时的速度从港口A 出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行，分开港口2小时后，那么两船相距〔〕 A 、25海里 B 、30海里 C 、35海里 D 、40海里二、填空题10×105准确到位，有个有效数字。

勾股定理与平方根习题(附答案)

第二章勾股定理与平方根一、选择题1．下列几组数中不能作为直角三角形三边长度的是（）A ．7,24,25a b c ===B ． 1.5,2, 2.5a b c ===C ．25,2,34a b c ===D ．15,8,17a b c ===2．小强量得家里彩电荧屏的长为cm 58，宽为cm 46，则这台电视机尺寸是（）A ．9英寸（23cm ）B ．21英寸（54cm ）C ．29英寸（74cm ）D ．34英寸（87cm ）3．等腰三角形腰长10cm ，底边16cm ，则面积（）A ．296cmB ．248cmC ．224cmD ．232cm 4．三角形三边c b a ,,满足ab c b a 2)(22+=+，则这个三角形是（）A ．锐角三角形B ．钝角三角形C ．直角三角形D ．等腰三角形 5．2(6)-的平方根是（）A ．6-B ．36C ．±6D ．6±6．下列命题正确的个数有：a a a a ==233)2(,)1(（3）无限小数都是无理数（4）有限小数都是有理数（5）实数分为正实数和负实数两类（）A ．1个B ．2个C ．3个D ．4个 7．x 是2)9(-的平方根，y 是64的立方根，则=+y x（）A ．3B ．7C ．3，7D ．1，7 8．直角三角形两直角边长度为5，12，则斜边上的高（）A ．6B ．8C ．1813D ．60139．直角三角形边长为b a ,，斜边上高为h ，则下列各式总能成立的是（）A 、2h ab = B ．2222h b a =+C ．h b a 111=+D ．222111hb a =+ 10．如图一直角三角形纸片，两直角边cm BC cm AC 8,6==，现将直角边AC 沿直线AD折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于（） A ．cm 2 B ．cm 3C ．cm 4D ．cm 5二、填空题11．下列实数(1)3.1415926 .(2)0.3 22(3)7(5)(6)2π(7)0.3030030003...其中无理数有________，有理数有________．（填序号）12．49的平方根________，0.216的立方根________．13的平方根________的立方根________．14．算术平方根等于它本身的数有________，立方根等于本身的数有________． 15．若2256x =，则=x ________，若3216x =-，则=x ________．16．已知Rt ABC ∆两边为3，4，则第三边长________．17．若三角形三边之比为3：4：5，周长为24，则三角形面积________．18．已知三角形三边长n n n n n n ,122,22,1222++++为正整数，则此三角形是________三角形．19．如果0)6(42=++-y x ，则=+y x ________．20．如果21a -和5a -是一个数m 的平方根，则.__________,==m a 21．三角形三边分别为8，15，17，那么最长边上的高为________．AEBDC第10题图《同步课程》试卷八年级数学(上)22．直角三角形三角形两直角边长为3和4，三角形内一点到各边距离相等，那么这个距离为________．三、计算题23．求下列各式中x 的值2(1)16490x -=；2(2)(1)25x -=；3(3)(2)8x =-；3(4)(3)27x --=．四、作图题24．在数轴上画出8-的点．25．下图的正方形网格，每个正方形顶点叫格点，请在图中画一个面积为10的正方形．五、解答题26．已知如图所示，四边形ABCD中，3,4,13,A B c m A D c m B C c m C D c m==== 090A ∠=求四边形ABCD 的面积．第24题图第25题图A27．如图所示，在边长为c 的正方形中，有四个斜边为c 、直角边为b a ,的全等直角三角形，你能利用这个图说明勾股定理吗？写出理由．28．如图所示，15只空油桶（每只油桶底面直径均为60cm ）堆在一起，要给它盖一个遮雨棚，遮雨棚起码要多高？29．如图所示，在Rt ABC ∆中，090ACB ∠=，CD 是AB 边上高，若AD=8，BD=2，求CD ．30．如图，有一只小鸟从小树顶飞到大树顶上，请问它飞行的最短路程是多少米？（先画出示意图，然后再求解）．第27题图第29题图CADB第28题图《同步课程》试卷八年级数学(上)第二章勾股定理与平方根1．C 2．C 3．C 4．C 5．C 6．B 7．D 8．D 9．D 10．B 11． (4)(6)(7)；(1)(2)(3)(5) 12．23±,0.613．2±,2 14．0,1；0，1± 15．16±,-6 16．5 17．24 18．直角 19．-2 20．2或－4；9或81 21．1201722．1 23.(1) x=74±(2) x=6或x=－4 （3）x=-1 (4) x=024．略 25．如图 26．3627．2222222214(),22,2ab b a c ab a b ab c a b c ⨯+-=∴++-=∴+=28．h=60 29．4 30．13。

八年级数学(上)第二章勾股定理与平方根检测卷(含答案)

第二章勾股定理与平方根检测卷（附答案）（总分100分时间90分钟）一、选择题（每小题3分，共30分）1．下列各组数中，不能作为直角三角形三边长的是( )A．9，12，15 B．7，24，25 C．6，8，10 D．3，5，7 2．(－6)2的平方根是( )A．－6 B．36 C．±6 D3．下列说法中不正确的是( )A．－2是4的一个平方根B8的立方根C．立方根等于它本身的数只有1和0 D．平方根等于它本身的数只有0 4．下列说法正确的是( )A．无限小数是无理数B．带根号的数都是无理数C．无理数是无限小数D．无理数是开方开不尽的数5．下列说法中正确的有( )①0的平方根是0；②1的平方根是1；③－1是1的平方根；④－1是－1的平方根；⑤8A．1个B．2个C．3个D．4个6．如图一直角三角形纸片，两直角边AC＝6 cm，BC＝8 cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于( )A．2 cm B．3 cmC．4 cm D．5 cm7．把32. 982保留三个有效数字，并用科学记数法表示为( )A．3.92×10 B．3.2982×10 C．33.0 D．3.30×108．数轴上的任何一点表示( )A．有理数B．无理数C．实数D．正数和负数9．如果梯子的底端离建筑物5米，13米长的梯子可以达到该建筑物的高度是( ) A．12米B．13米C．14米D．15米10．要从电杆离地面4m处向地面拉—条长为5m的电缆，则地面电缆固定点与电线杆底部的距离应为( )A．5 m B．4 m C．3 m D．2 m二、填空题（每小题2分，共16分）11．直角三角形两条直角边的长分别为5、12，则斜边上的高为______．y+=，12_______()260则x＋y＝______．13．如图，在锐角三角形ABC中，AD⊥BC，AD＝12，AC＝13，BC＝14．则AB＝______．14．如图是一个育苗棚，棚宽a＝6 m，棚高b＝2.5 m，棚长d＝10 m，则覆盖在棚斜面上的塑料薄膜的面积为______m2．15．如图所示，15只空油桶(每只油桶底面直径均为60 cm)堆在一起，要给它盖一个遮雨棚，遮雨棚起码要_______cm 高．16．若一正数的两个平方根是2a －l 与－a ＋2，则a ＝______．17．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A 、B 、C 、D 的边长分别是3、5、2、3，则最大正方形E 的面积是______．18．如图，已知Rt △ABC 是直角边长为1的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，…，依此类推，第n 个等腰直角三角形的斜边长是______．三、解答题(19题8分，20题6分，其余每题各10分，共54分) 19．求下列各式中x 的值(1)5x 2－10＝0； (2)25(m ＋2)2－49＝0；20．把下列实数填在相应的集合中2273，0.1，－0.010010001…，－5．正整数集合{ }．正有理数集合{ }．无理数集合{ }．21．《中华人民共和国道路交通管理条例》规定：小汽车在城市街道上的行驶速度不得超过70千米／时．一辆“小汽车”在一条城市街道上直道行驶，如图某一时刻刚好行驶到路对面“车速检测仪A ”正前方50米C 处，过了6秒后，测得“小汽车”位置B 与“车速检测仪A ”之间的距离为130米，这辆“小汽车”超速了吗？请说明理由．22．如图，一张长方形纸片宽AB ＝8 cm ，长BC ＝10 cm ．现将纸片折叠，使顶点D 落在BC 边上的点F 处(折痕为AE)，求EC 的长．23．先观察下列等式，再回答问题：111111112=+-=+111112216=+-=+1111133112=+-=+…(1) (2)请按照上面各等式反映的规律，试写出用n(n 为正整数)表示的等式．24．在图中．正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE＝2b，且边AD和AE在同一直线上．操作示例当2b<a时，如图①，在BA上选取点G，使BG＝b，连接FG和CG，裁掉△FAG 和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH．思考发现小明在操作后发现：该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH 的位置，易知EH与AD在同一直线上，连接CH，由剪拼方法可得DH＝BG，故△CHD≌△CGB，从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置．这样，对于剪拼得到的四边形FGCH（如图①），过点F作FM⊥AE于点M(图略)，利用“SAS”可判断△HFM≌△CHD，易得FH＝HC＝GC＝FG，∠FHC＝90°．进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．实践探究(1)正方形FGCH的面积是______ ；（用含a，b的式子表示）(2)类比①的剪拼方法，请你就②～④的三种情形分别画出剪拼成一个新正方形的示意图．联想拓展小明通过探究后发现：当b≤a时，此类图形都能剪拼成正方形，且所选取的点G 的位置在BA方向上随着b的增大不断上移．当b>a时，如⑤的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．参考答案1．D 2．C 3．C 4．C 5．B 6．B 7．D 8．C 9．A 10．C 11．601312．±2，±1，0 －213．15 14．65 15．60) 16．－1 17．47 1819．(1)x (2)m ＝－35或－17520．正整数集合{．正有理数集合{227，0.1}．无理数集合3π，－0.010010001…}． 21．小汽车超速了． 22．EC 长3cm23．(1)1111144120+-=- (2) 11(1)n n =++ 24．(1)22a b +(2)剪拼方法如图联想拓展能；剪拼方法如图④。

八年级数学(上)第二章勾股定理与平方根单元测试卷

第2章勾股定理与平方根单元测试卷（附答案）满分：100分时间：60分钟一、选择题(每小题3分，共30分) 1．下列说法中，正确的是 ( )A ．B ．-a 2一定没有平方根C ．0.9的平方根是±0.3D ．a 2-1一定有平方根 2．下列各组数中，互为相反数的是 ( ) A ．2和12 B ．-2和-12C ．-2和|-2 | D3．下列数据：①王雨考试得了96分；②全班学生数学测试的平均分约为88.2分；③小红今天做了5道作业题；④珠穆朗玛峰高8 844米．其中，属于精确数据的有 ( ) A ．1个 B ．2个 C ．3个 D ．4个4．如图，火柴盒的一个侧面ABCD 倒下到．AB ’C ’D ’的位置，连接CC ’．设．AB=a ，BC=b ，AC=c ，这样可以用来说明我们学习过的定理或者公式是 ( ) A ．勾股定理 B ．平方差公式C ．完全平方公式D ．以上3个答案都可以5．如图，等边△ABC 的高AH 等于 ( )A ．B ．2C ．D ．46．已知等腰三角形的底边长为10，腰长为13，则一腰上的高为 ( ) A. 12 B ．6013C ．12013D ．13572=；②数轴上的点与实数一一对应；③-2根；④任何实数不是有理数就是无理数；⑤两个无理数的和还是无理数；⑥无理数都是无限小数．其中，正确的有 ( )A ．2个B ．3个C ．4个D ．5个8．三角形的三边长分别为22a b +，2ab ，22a b -(a 、b 都是正整数，且a>b)，则这个三角形是 ( )A ．直角三角形B ．钝角三角形C ．锐角三角形D ．不能确定 9．用四舍五入法按要求对846.31取近似值，下列四个结果中，错误的是 ( ) A ．846.3(保留4个有效数字) B ．846(精确到个位)C ．800(保留1个有效数字)D ．8.5×102(保留2个有效数字)10- 2的值 ( )A ．在1到2之间B ．在2到3之间C ．在3到4之间D ．在4到5之间二、填空题(每小题3分，共24分)11．平方根等于它本身的数是__________，算术平方根等于它本身的数是__________；12．__________开立方得__________．13．数学家发明了一个魔术盒，当任意实数对(a ，b)进入其中时，会得到一个新的实数：a 2+b+1．例如把(3，-2)放入其中，就会得到32+(-2)+l=8．现将实数对(-3)放入其中，得到实数m ，再将实数对(m ，1)放入其中后，得到的实数是__________．14 3.14，2，0.202 002 000 2…，227，1.56，π--中，正无理数是__________．15．如果直角三角形的两条边长分别是3和5，那么第三边长为__________．16．如图，在Rt △ABC 中，∠ABC=90°,BD ⊥AC 于D ，点E 为AC 的中点，若BC=7，AB=24，则BE= __________，BD=__________．17．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm ，则图中所有正方形的面积之和为__________cm 2．18．如图，把长方形纸片ABCD 折叠，B 、C 两点恰好重合落在AD 边上的点P 处．已知∠MPN=90°，且PM=3，PN=4，那么长方形纸片ABCD 的面积为__________．三、解答题(共46分)19．(6分)求下列各式中x 的值：(1) ()213430x --=； (2)25(x+2)2-36=0；(3)(2x+1)220．(10分)如图，在△ABC中，AC=8，BC=6,在△ABE中，DE为AB边上的高，DE=12，S△ABE=60；求△ABC的面积．21．(10分)如图①是单位长度均为1的方格图．(1)请把方格图中带阴影的图形适当剪开，重新拼成正方形(画出分割线与拼成正方形的草图)；(2)所拼成正方形的边长为多少?周长为多少?(3)利用这个例子，在图②的数轴上画出(2)中正方形边长表示的点(保留画图痕迹)．22．(10分)如图，点P是等边△ABC内的一点，分别连接PA、PB、PC，以BP为边作∠PBQ=60°，且BQ=BP，连接OQ．(1)观察并猜想AP与CQ之间的大小关系，并说明你的结论；(2)已知PA：PB：PC=3：4：5，连接PQ，试判断△PQC的形状，请说明理由．23．(10分)如图，长方体的长为2，宽为1，高为4．(1)求该长方体中能放入木棒的最大长度；(2)现有一只蚂蚁从点A处沿长方体的表面爬到点G处，求它爬行的最短路程．参考答案一、1．A 2．C 3．B 4．A 5．A 6．C 7．C 8．A 9．C 10．C 二、11．0 0、1 1213．2714．0.202 002 000 2… 15．416．25216825 17．147 18．1445三、19．(1)x=-6 (2)x=45-或165- (3)x=12或32-20．由于S △ABC =12×AB ×DE=60，所以12×AB ×12=60，解得AB=10．又因为AC 2+BC 2=82+62=100=AB 2，所以∠C=90°．从而S △ABC =12×AB ×DE=12×6×8=2421．(1)分割线如图①，拼成正方形如图②(2)设所拼成正方形的边长为x ，则x 2=5，所以(舍去负值)．所以拼成正方形的边长为(3)如图③22．(1)AP=CQ 理由：因为△ABC 为等边三角形，所以AB=BC ，∠ABC=60°．因为∠PBQ=60°，所以∠ABC=∠PBQ ，所以∠ABP=∠CBQ ．在△ABP 与△CBQ 中，,,,AB CB ABP CBQ BP BQ =⎧⎪∠=∠⎨⎪=⎩所以△ABP ≌△CBQ(SAS)．所以AP=CQ 。

八年级数学(上)第二章勾股定理与平方根课时练习：第10课时勾股定理的应用(1)

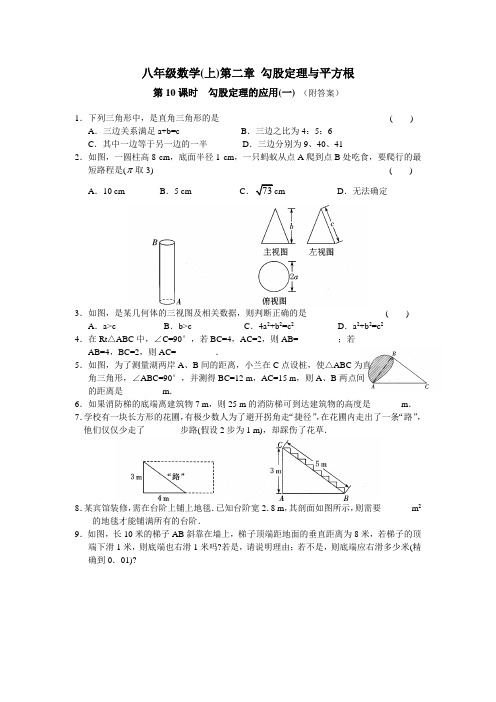
八年级数学(上)第二章勾股定理与平方根第10课时勾股定理的应用(一)（附答案）1．下列三角形中，是直角三角形的是( ) A．三边关系满足a+b=c B．三边之比为4：5：6C．其中一边等于另一边的一半D．三边分别为9、40、412．如图，一圆柱高8 cm，底面半径1 cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是( 取3) ( )A．10 cm B．5 cm C D．无法确定3．如图，是某几何体的三视图及相关数据，则判断正确的是( ) A．a>c B．b>c C．4a2+b2=c2D．a2+b2=c24．在Rt△ABC中，∠C=90°，若BC=4，AC=2，则AB=_________；若AB=4，BC=2，则AC=_________．5．如图，为了测量湖两岸A、B间的距离，小兰在C点设桩，使△ABC为直角三角形，∠ABC=90°，并测得BC=12 m，AC=15 m，则A、B两点间的距离是_________m．6．如果消防梯的底端离建筑物7 m，则25 m的消防梯可到达建筑物的高度是_______m．7．学校有一块长方形的花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了________步路(假设2步为1 m)，却踩伤了花草．8．某宾馆装修，需在台阶上铺上地毯．已知台阶宽2．8 m，其剖面如图所示，则需要_______m2的地毯才能铺满所有的台阶．9．如图，长10米的梯子AB斜靠在墙上，梯子顶端距地面的垂直距离为8米，若梯子的顶端下滑1米，则底端也右滑1米吗?若是，请说明理由；若不是，则底端应右滑多少米(精确到0．01)?10．小强家有一块三角形菜地，量得两边长分别为40 m、50 m，第三边上的高为30 m．请你帮小强计算这块菜地的面积(精确到0．01)．11．在一个底面直径为5 cm、高为12 cm的圆柱状水杯中，放了一根15 cm长的玻璃棒．问这根玻璃棒露出杯口至少有多长?12．一个正方体的棱长为3 cm，一只小蚂蚁想从A点爬到H点找食吃．已知蚂蚁每秒爬2 cm，则最少需要多少秒(精确到0．01)?13．《中华人民共和国道路交通安全法》规定：小汽车在城市道路上行驶速度不得超过70km ／h．如图，一辆小汽车在一条城市道路上直道行驶，某一时刻刚好行驶到路对面车速检测仪的正前方30 m处，过了2 s后，测得小汽车与车速检测仪之间的距离为50 m这辆小汽车超速了吗?参考答案1．D 2．C 3．D4．5．96．247．48．19．69．不是，底端向右滑1．41米10．996．86 m2或203．14 m211．2 cm12．3．3513．超速，小汽车速度为72 km／h，大于70 km／h。

【八年级数学试题】苏科版初二数学上册勾股定理与平方根单元测试(含答案)

苏科版初二数学上册勾股定理与平方根单元测试(含答案)
第二勾股定理与平方根提高测试
一、选择题
1．下列几组数中不能作为直角三角形三边长度的是（）
A． B．
c． D．
2．小强量得家里彩电荧屏的长为，宽为，则这台电视机尺寸是（）
A．9英寸（）B．21英寸（）
c．29英寸（）D．34英寸（）
3．等腰三角形腰长，底边，则面积（）
A． B． c． D．
4．三角形三边满足，则这个三角形是（）
A．锐角三角形B．钝角三角形c．直角三角形D．等腰三角形
5．的平方根是（）
A． B．36c．±6D．
6．下列命题正确的个数有（3）无限小数都是无理数（4）有限小数都是有理数（5）实数分为正实数和负实数两类（）A．1个B．2个c．3个D．4个
7．是的平方根，是64的立方根，则（）
A．3B．7c．3，7D．1，7
8．直角三角形两直角边长度为5，12，则斜边上的高（）
A．6B．8c． D．
9．直角三角形边长为，斜边上高为，则下列各式总能成立的是（）
A、 B．
c． D．
10．如图一直角三角形纸片，两直角边，现将直角边Ac沿直线。

第二章勾股定理与平方根单元复习试卷

第二章勾股定理与平方根复习卷班级：姓名：学号：一、选择题：1.下列实数中，是无理数的为（）A . 3.14B . 13 C . 3 D . 92．下列各数：2π,0·,227，0.30003… )A ．2 个B ．3 个C ．4 个D ．5 个3．下面说法中，正确的是（）A ．任何数的平方根有两个B ．一个正数的平方根的平方是它本身C ．只有正数才有平方根D ．正数的平方根是正数 4．4的平方根是（）A ．2B ．2±C ．4D ．4± 5．2的算术平方根是（）A ．4B ．4±C ．2D ．2±6．-8的立方根是（）A ．2B ． -2C ．12D ．12-7．64的立方根是（）A ．4B ．4±C ．8D ．8±8等于（）A ．3B ．3-C ．9D ．9- 9．下列计算正确的是（）Ａ．020=Ｂ．331-=- 3= +=10．下列式子中正确的是（）A ．525±= B ．332±= C ．525= D ．332-=11．下列式子中，正确的是（）A ．2=-B ．2(9=C 3=±D 3=12．－2是2的（）．A ．相反数B ．倒数C ．绝对值D ．算术平方根 13．比较2，）A．2<<B．2<C2<< D2<14．如图，数轴上点P 表示的数可能是（）．A．B． C ． 3.5- D ．15．下列各数中，在1与2之间的数是（）A ．1-BC ．12D ．316．估计）A ．在3与4之间B ．在4与5之间C ．在5与6之间D ．在6与7之间 17．估算2的值（）A ．在1和2之间B ．在2和3之间C ．在3和4之间D ．在4和5之间 18．实数2-，3-的大小关系是（）A ．3-<2-B ．3-<2-C ．2-<<3-D ．3-<2-< 19．给出四个数0，2，－12，0.3，其中最小的是（）A ．0B ． 2C ．－12D ．0.320. 在 -3 －1， 0 这四个实数中，最大的是（）A . -3B .－C . －1D . 0 21．下列说法中，正确的是（）A ．近似数1.70和1.7是一样的B ．近似数六百和近似数600的精确度是相同的C ．近似数35.0是精确到个位的数，它的有效数字是3和5两个数D ．近似数35.0是精确到十分位的数，它的有效数字是3,5,0三个数22．湖州市第11届房交会总成交金额约2.781亿元．近似数2.781亿元的有效数字的个数是（）A ．1B ．2C ．3D ．4 23．德州市2009年实现生产总值（GDP ）1545.35亿元，用科学记数法表示应是（结果保留3个有效数字）（）Ａ．81054.1⨯ 元Ｂ．1110545.1⨯元Ｃ．101055.1⨯元Ｄ．111055.1⨯元24．2010年4月20日晚，“支援青海玉树抗震救灾义演晚会”，热心企业和现场观众踊跃捐款31083.58元.将31083.58元保留两位有效数字可记为（）第7题图A．3.1×106元B．3.11×104元C．3.1×104元D．3.10×105元25．据统计，截止到5月31日上海世博会累计入园人数803.27万人．803.27万这个数字（保留两位有效数字）用科学记数法表示为（）A．8.0×102 B. 8.03×102 C. 8.0×106 D. 8.03×10626．由四舍五入法得到的近似数8.8×103，下列说法中正确的是（）．A．精确到十分位，有2个有效数字 B．精确到个位，有2个有效数字C．精确到百位，有2个有效数字 D．精确到千位，有4个有效数字27．图①是一个边长为()m n+的正方形，小颖将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是（）A．22()()4m n m n mn+--=B．222()()2m n m n mn+-+=C．222()2m n m n m n-+=+D．22()()m n m n m n+-=-28．把长为8cm的矩形按虚线对折，按图中的虚线剪出一个直角梯形，打开得到一个等腰梯形，剪掉部分的面积为6cm2，则打开后梯形的周长是（）A．（cm B．（）cm C．20cm D．18cm29.如图①，矩形ABCD，AB=12cm，AD=16cm，现将其按下列步骤折叠：（1）将边AB向AD折去，使AB落在AD上，得到折痕AF，如图②（2）将△AFB沿BF折叠，AF与DC交点G，如图③则所得梯形BDGF的周长等于（）A.12+22B.24+22C.24+42D.12+42C F CD ”①②③第28题图图①第27题图图②1．勾股定理：直角三角形两直角边的等于的平方．2．对一个近似数，从起，到止，所有的数字都称为这个近似数的有效数字． 3．下列各数：12，227，0.2020020002 （每两个2之间0的个数逐次加1），，3π，0.89- 无理数有．4．（1）无限不循环小数称为；（2）和统称为实数；（3）与数轴上的点一一对应．5．1-的相反数是，的绝对值是．6的倒数是，2-的绝对值是．7．正数的平方根有个，它们互为，零的平方根为，负数．8．因为42= ，（—4）2= ，所以4和—4都是的平方根． 9．如果62=x ，那么x 叫做6的，记作． 10．的平方根是0，的平方根是8±． 11．（1）8149的平方根为；（2）1.44的平方根为；（3）（—2）2的平方根为；（4）0.1-2的平方根为． 12．5的平方根是，算术平方根是．13．若24x =，则3x -的算术平方根是．14．（1）0．16的算术平方根为；（2）49的算术平方根为；（3）10-6的算术平方根为；（4）216()81-的算术平方根为．15．（1= ；（2）= ；（3）= ；（42= ． 16．求下列各数的平方根：81：；289：；0：；124：；2.56：；210-：．17．写出下列各数的算术平方根：0．01：；2516：；0：；10：；21()3-：．18．（1）100的平方根为，算术平方根为；（2）169的平方根为，算术平方根为；（3）0.25的平方根为，算术平方根为；（4）10-6的平方根为，算术平方根为．19．（1）= ；（2）= ；（3）= ；（4= ．20．求下列各数的平方根：（1）425：；（2）62-：；（3）4910⨯：．21．求下列各数的立方根：（1）8125：；（2）0.064-：；（3）0：；（4）17427：．22．0．001的立方根是，18-的立方根是．23= ，= ，= ．24．如果33(3)a =-，那么a = ，如果8=-，那么x = ．25．（1）= ；（2= ；（3）3= ；（4= ．26．写出下列各数的立方根： —27：；0.008：；1125：；—1：；0.064：；4：．27．求下列各数的立方根：（1）338-：；（2）62-：；（3）56.410-⨯：．28．求下列各式的值：3= ；= ；3= ；= ．29．比较下列数的大小：（1）；（2）2；（320.5．30．比较下列各组数的大小：（1）（2）π 3.142；（3）1.5．31．比较下列各组数的大小：（1）；（2 （3）3-；（4）1434．32．比较大小：（1）1；（2）1218+；（3．（1）精确到10kg ：；（2）精确到1kg ：；（3）精确到0.1kg ：．34．按要求用科学记数法表示下列各近似数：（1）33 400 000 000 000（保留2个有效数字）：；（2）361 000 000（精确到10 000 000）：．35．由四舍五入法得到的下列近似数，分别精确到哪一位？各有几个有效数字？（1）小明身高1.59m ；精确到位，有个有效数字，分别为；（2）地球的半径约为36.410km ⨯；精确到位，有个有效数字，分别为；（3）组成云的小水滴很小，最大的直径约为0.2mm ；精确到位，有个有效数字，分别为；36．3．45精确到位，有个有效数字，它们是；37．52.6710⨯精确到位，有个有效数字，它们是； 38．2.5万精确到位，有个有效数字，它们是． 39．按括号内的要求，用四舍五入法对下列各数取近似数：（1）2．0368（精确到0.001）≈ ；（2）3．987（保留2个有效数字）≈ ；（3）0．0155（保留2个有效数字）≈ ；（4）20549（保留3个有效数字）≈ ．40．已知直角三角形的两边长分别为3和5，则第三边的长为．41．直角三角形两直角边长分别是6和8，则斜边为，斜边上的高为． 42．在Rt △ABC 中，∠C =90°，AB =25，AC =7，则三角形面积为．43．已知：如图，在△ABC 中，AD ⊥BC ，AB =AC =5cm ，BC =6cm ．则AD = cm ，△ABC 的面积等于 cm 2．44．如图，等腰△ABC 的周长32cm ，底边长12cm ．则高AD = cm ；S △ABC = cm 2． 45．在等腰三角形ABC 中，AB=AC=17cm ，BC=30cm ，△ABC 的面积= cm 2． 46．如图，图中字母代表正方形的面积，那么A = ，B = ． 47．在Rt △ABC 中，∠C =90°．（1）如果BC =9，AC =12，那么AB = ；（2）如果BC =8，AB =10，那么AC = ；（3）如果AC =20，BC =15，那么AB = ；（4）如果AB =13，AC =12，那么BC = ；（5）如果AB =61，BC =11，那么AC = ． 48．在△ABC 中，∠C =90°．（1）若a=3，b=4，则c= ；（2）若c=13，b=5，则a= ；（3）若c=17，a=15，则b= ；（2）若a :c =3:5，且b=16，则a= ． 49．如图，一旗杆离地面6m 处折断，旗杆顶部落在离旗杆底部8m 处，144AB 1002536 第48题图ＡBCD第46题图50．如图，要建一个育苗棚，棚宽a 为2m ，高b 为1.5m ，长d 为10m ．则覆盖在顶上的塑料薄膜需 m 2．51．如图，要为一段高5m 、长13m 的楼梯铺上红地毯，红地毯至少需要 m ．52．如图是一张直角三角形的纸片，两直角边AC ＝6 cm 、BC ＝8 cm ，现将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则BE 的长为 cm .53．如图，三个直角三角形（Ⅰ，Ⅱ，Ⅲ）拼成一个直角梯形（两底分别为a 、b ，高为a +b ），利用这个图形，小明验证了勾股定理．请你填写计算过程中留下的空格：①，即（高下底）（上底梯形梯形).(21)()2121=+⋅+=⋅+=S b a b a SS 梯形=Ⅰ+Ⅱ+Ⅲ（罗马数字表式相应图形的面积） = + + ，即②梯形).(21=S由①、②，得222c b a =+．54．如图，等边三角形ABC 的边长为2，则它的高为．55．如图，四边形ABCD 的面积等于56．如图，两个阴影部分都是正方形，两个正方形的面积之比为1：2，这两个正方形的面积分别为．57．如图，BC 长为3cm ，AB 长为4cm ，AF 长为12cm ．正方形CDEF 的面积为 cm ． 58．有一张圆形铁片，面积为94πm 2，则半径为 m ．a bb cc ⅠⅡⅢa第53题图ABCD第54题图BCDEF第49题图13m5mABCDE第51题图第52题图ADB 4 12 3第55题图第57题图AB CD E FG59．把一张矩形纸片（矩形ABCD ）按如图方式折叠，使顶点B 和点D 重合，折痕为EF ．若AB = 3 cm ，BC = 5 cm ，则重叠部分△DEF 的面积是 cm 2．60．如图，在梯形ABCD 中，AB ∥CD ，AD ＝BC ，对角线AC ⊥BD ，垂足为O ．若CD ＝3，AB ＝5，则AC 的长为．61．如图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD 于点O ，AE ⊥BC ，DF ⊥BC ，垂足分别为E 、F ，AD ＝4，BC ＝8，则AE ＋EF 等于62．如图，以第①个等腰直角三角形的斜边长作为第②个等腰直角三角形的腰，以第②个等腰直角三角形的斜边长做为第③个等腰直角三角形的腰，依次类推，若第⑨个等腰直角三角形的斜边长为厘米，则第①个等腰直角三角形的斜边长为 _________厘米.63．已知△ABC 是边长为1的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，…，依此类推，第n 个等腰直角三角形的斜边长是．三、解答题：1．求下列各式中的x ：（1）216x =；（2）22549x =；（3）215x =；（4）2418x =；（5）1022=x ；（6）07532=-x ．ABCFE'A 第59题图（'B ）D 第64题图ABCDO第60题图第61题图第63题图2．求下列各式中的x ：（1）30.125x =-；（2）3827x =；（3）321x +=；（4）3(1)8x -=；（5）327343x =；（6）330.6480x +=．3．计算：（－1）2010－| －7 |＋ 9 ×（ 5 －π）0＋（ 15）－14.计算：（1）92|21|)3(12-+----；（2）)1()2010(40---+．5．在数轴上描出表示6．a -是否有平方根？为什么？7．若一个正数的平方根是12+x 和7-x ，则322+-x x 的平方根是什么？8．一个三角形三边长的比为3:4:5，它的周长是60cm ．求这个三角形的面积．9．如图，在△ABC 中，AB=26，BC=20，边BC 上的中线AD=24．求AC ．10．如图，在△ABC 中，AD 为边BC 上的高，AB=13，AD=12，AC=15．求BC 的长．ABCDA11．计算四边形ABCD 的面积．12．已知：如图，AD=4，CD=3，∠ADC=90°， AB=13，BC=12．求该图形的面积．13．如图，把火柴盒放倒，这个过程中也能验证勾股定理．你能利用下图验证勾股定理吗？14．做8个全等的直角三角形（两条直角边长分别为a 、b ，斜边长c ），再做3个边长分别为a 、b 、c 的正方形，把它们拼成两个正方形（如图）．你能利用这两个图形验证勾股定理吗？写出你的验证过程．15．如图，你能用它验证勾股定理吗？（提示：以斜边为边长的正方形的面积＋四个三角形的面积＝外正方形的面积）16．如图，以Rt △ABC 的三边为直径的3个半圆的面积之间有什么关系？请说明理由．17．如图，AD ⊥BC ，垂足为D ．如果CD =1，AD =3， BD =9，那么△ABC 是直角三角形吗？请说明理由．BC D Ea baabＡBCA BCDABCD- 11 -18．如图，在正方形ABCD 中，E 是边AD 的中点，点F 在边DC 上，且14D F D C ．试判断△BEF 的形状，并说明理由．19．如图，在四边形ABCD 中，∠B=90°，AB=BC=4，CD=6，DA=2．求∠DAB 的度数．20．如图，长为10m 的梯子AB 斜靠在墙上，梯子的顶端距地面的垂直距离为8m ．如果梯子的顶端下滑1m ，那么它的底端是否也滑动1m ？21．飞机在空中水平飞行，某一时刻刚好飞到一个男孩头顶正上方4000米处，过了20秒，飞机距离这个男孩5000米，飞机每小时飞行多少千米？22．某港口位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口1.5小时后相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？23．古希腊的哲学家柏拉图曾指出，如果m 表示大于1的整数，a =2m ，b =m 2-1，c = m 2+1，那么a 、b 、c 为勾股数．你认为正确吗？如果正确，请说明理由，并利用这个结论得出一些勾股数．BCB ACD EFABC D- 12 -24．学校计划用1000块统一规格的正方形地板砖铺设面积为250m 2的学生食堂地面．购买的地板砖的边长为多少时，才正好合适（即不浪费）？25．有两棵树，一棵高8m ，另一棵高2m ，它们相距8m ，一只小鸟从一棵树梢飞到另一棵树梢，要飞多少米？26．甲、乙两位探险者到沙漠进行探险．某日早晨8：00甲先出发，他以6km/h 的速度向东行走．1h 后乙出发，他以5km/h 的速度向北行进．上午10：00时，甲、乙两人相距有多远？27．在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形．在水池正中央有一根新生的芦苇，它高出水面1尺．如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面．请问这个水池的深度和这根芦苇的长度各是多少？28．如图，马路边一根电线杆高为5.4m ，被一辆卡车从离地面 1.5m 处撞断．倒下的电线杆顶部是否会落在离它的底部4m29．如图，有两只猴子在一棵树CD 高5m 的点B 处，它们都要到A 处的池塘去喝水，其中一只猴子沿树爬下走到离树10m 处的池塘A 处，另一只猴子爬到树顶D 后直线越向池塘的A 处．如果两只猴子所经过的路程相等，这棵树高有多少米？ABCD。

初二数学勾股定理和平方根练习题

10月15日周周练姓名___________班级________________一、选择题1.小强量得家里新购置的彩电荧光屏的长为58厘米,宽为46厘米,则这台电视机的尺寸是(实际测量的误差可不计) ( )A. 9英寸(23厘米)B. 21英寸(54厘米)C. 29英寸(74厘米)D. 34英寸(87厘米) 2.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( ) A. 12 cm B. 10 cm C. 8 cm D. 6 cm3.已知一个Rt △的两边长分别为3和4，则第三边长的平方是（） A 、25B 、14C 、7D 、7或254.已知，如图长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为（） A 、6cm 2B 、8cm 2C 、10cm 2D 、12cm 25.五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）15242520715202425157252024257202415(A)(B)(C)(D)6.已知一直角三角形的木版，三边的平方和为1800cm 2,则斜边长为（）.（A ）80cm (B)30cm (C)90cm (D120cm. 7. 图①是一个边长为()m n +的正方形，小颖将图①中的阴影部分拼成图②的形状，由图①和图② 能验证的式子是（）A ．22()()4m n m n mn +--=B ．222()()2m n m n mn +-+=C ．222()2m n mn m n -+=+D ．22()()m n m n m n +-=-二、填空题8. 如图是一张直角三角形的纸片，两直角边AC ＝6 cm 、BC ＝8 cm ，现将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则BE 的长为 cm .9.已知直角三角形斜边长为12㎝，周长为30㎝，则此三角形的面积为__ __。

八年级数学(上)第二章勾股定理与平方根课时练习：第11课时勾股定理的应用(2)

八年级数学(上)第二章勾股定理与平方根第11课时勾股定理的应用(二)（附答案）1．直角三角形中，以直角边为边长的两个正方形的面积为36 cm2和64 cm2，则以斜边为边长的正方形的面积为__________cm2．2．如图，在△ABC中，C D⊥AB于点D，且AD=BC=5，BD=3，则AC边的长为_________．3．如图，长方形网格中有△ABC，若小方格边长为1，求△ABC的面积是多少?4．等腰三角形的腰长为10，底边长为12，求其底边上的高．5．如图，在直角梯形ABCD中，AD∥BC，∠A=90°，∠C=45°，BC=2AD，CD 求梯形的面积．6．一个直角三角形的两直角边长分别为3和4，下列说法正确的是( ) A．斜边长为25 B．三角形的周长为25C．斜边长为5 D．三角形面积为207．在R t△ABC中，∠C=90°，AB=2，则AB2+BC2+CA2的值为( ) A．2 B．4 C．8 D．168．底边长为16，底边上的高为6的等腰三角形的腰长为( )A．8 B．9 C．10 D 139．如图，A C⊥CE于点C，AD=BE=13，BC=5，DE=7．试求AC的长．10．已知一直角三角形的三边长都是正整数，其中斜边长为13，并且周长为30．求这个直角三角形的面积．11．如图，长方体底面的长和宽分别为4和3，长方体的高为12．求长方体对角线的长．12．如图，小明先向东走1 m，然后向南走4 m，再向西走2 m，再向南走4 m，最后再向东走7 m，如图所示，求出发点到终点的距离．13．如图，每个小方格的边长为1，求图中以格点为端点的四边形AB C D的面积．14．第七届国际数学教育大会会徽的主题图案是由一连串如图所示的直角三角形演化而成的．设第一个Rt△OA1A2是等腰直角三角形，且OA1=A1A2=A2A3=A3A4=…=A n－1A n=1(n 为正整数)．请你先把图中其他7条线段的长计算出来．观察计算结果，猜想OA n－1和OA n的长．15．如图，A市接到台风警报时，台风中心位于A市正南方125 km的B处，正以15 km／h的速度沿BC方向移动．(1)已知A市到BC的距离AD=35 km，求台风中心从B处移到D处所需的时间．(2)如果在距台风中心40 km的圆形区域内都将受台风影响，那么A市受影响的时间是多长?(精确到1 min)参考答案1．100 2 3．13 4．8 5．150 6．C 7．C 8．C 9．在Rt △BCE 中，BE 2=CE 2+BC 2，132=CE 2+52，CE=12．∴DC=5．∵BC=5，∴BC=DC ．又∵AD=BE ， ∴Rt △ACD ≌Rt △ECB ．∴AC=EC ．∴AC=12 10．30 11．13 12．10 m 13．12．514．计算略猜想：1n OA -=n OA = 15．(1)在Rt △ABD 中，∠ADB=90°，∴120BD =(km)．∴120÷15=8 h (2)以A 为圆心，40 km 为半径作圆，交BD 于点E ，交BD 延长线于点F ．在Rt △ADE 中，∠ADB=90°，∴19.365DE ==(km)．∴EF=38．73 km ．∴38．73÷15≈2．582 h ，2．582×60≈155 min ．∴A 市受影响时间约为155 min。

2019-2020年八年级数学上册第二章勾股定理与平方根单元测试卷

2019-2020年八年级数学上册第二章勾股定理与平方根单元测试卷一、选择(每题3分，共30分)1．16的平方根是 ( ) A．4 B．±4 C．256 D．±2562．在所给的数：，，，，0．57．0．585 885 888 588 885…(相邻两个5之间的8的个数逐次增加1)中，无理数的个数是 ( )A．2 B．3 C．4 D．53．下列说法中，正确的是 ( ) A．64的平方根是8 B．4的平方根是2或－2C．(－3)2没有平方根 D．16的平方根是4和－44．地球七大洲的总面积约是149 480 000 km2，对这一数据保留3个有效数字可表示为( ) A．149 km B．1．5×108 km2 C．1．49×108 km2 D．1．50×108 km25．如图，若数轴上的点A、B、C、D表示数－2，1，2，3，则表示的点P应在线段( )A．AB上 B．BC上 C．CD上 D．OB上6．一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端 5 m，消防车的云梯最大升长为13 m，则云梯可以达到该建筑物的最大高度是 ( ) A．12 m B．13 m C．14 m D．15 m7．对于10．08与0．1008这两个近似数，它们的 ( ) A．有效数字与精确位数都不相同 B．有效数字与精确位数相同C．有效数字相同，精确位数不同 D．有效数字不同，精确位数相同8．下列各式中，正确的是 ( ) A． B．C．3 D．9．如图，在单位小正方形组成的网格图中有AB、CD、EF、GH四条线段．其中能构成一个直角三角形三边的线段是 ( )A．CD、FF、CH B．AB、FF、GHC．AB、CD、GH D．AB、CD、EF10．如图，已知1号、4号两个正方形的面积为为7，2号、3号两个正方形的面积和为4，则a，b，c三个方形的面积和为 ( )A．11 B．15 C．10 D．22二、填空(每题3分，共30分)11．的相反数是________．12．若一个偶数的立方根比2大，平方根比4小，则这个数一定是_________．13．近似数1．8×105精确到_________位，有__________个有效数字．14．写出一个3到4之间的无理数_________．15．比较下列实数的大小：___________．16．如图，阴影部分是以直角三角形的三边为直径的半圆，两个小半圆的直径之比是3：4，面积和为100．则大的半圆面积是__________．17．如图，将一根25 cm长的细术棒放入长、宽、高分别为8 cm、6 cm和cm的长方体无盖盒子中，则细木棒露在盒外面的最短长度是__________cm．18．若的整数部分为3，则a的取值范围是_________．19．若，且，则y=_________．20．用计算器计算：，，，…请你猜测__________．三、解答(每题8分，共40分)21．计算下列各题：(1)；(2)()()2232 2.53⎡⎤---⨯-⎣⎦．22．(1)如果3x+12的立方根是3，求2x+6的平方根；(2)已知一个正数的平方根是2a －1与－a+2．求a xx 的值．23．如图，在△ABC 中，AB=17 cm ，BC=16 cm ，BC 边上的中线AD=15 cm ，△ABC 是等腰三角形吗?为什么?24．下图是单位长度为1的网格．(1)在图1中画出长度为的线段AB；(2)在图2中画出以格点为顶点，面积为5的正方形．25．在解答“判断由线段长分别为，2，组成的三角形是不是直角三角形”一题中，小明是这样做的：因为2263610013625252525⎛⎫+=+=⎪⎝⎭，而222286468252555⎛⎫⎛⎫⎛⎫=+≠⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以这个三角形不是直角三角形．小明的做法对吗?为什么?参考答案1．B 2．C 3．D 4．C 5．B 6．A 7．C 8．D 9．B 10．B 11． 12．10或12或14 13．万 214．(答案不唯一) 15．>16．100 17．5 18．8<a<1519． 20． 21．(1)－1 (2)－622．(1)3x+12=27．x=52x+6=16所以2x+6的平方根是±4．(2)(2a－1)+(－a+2)=0∴ a=－1．∴所以a xx=－1．23．∵AD是BD上的中线，∴ BD=DC=8．∵ AD2+BD2=152+82=172=AB2，∴∠ADB=90°，即∠ADC=90°．在Rt△ADC中AC===．17∴AC=AB．即△ABC是等腰三角形．24．略25．小明的做法不正确，三角形是直角三角形，因为．。

人教版八年级数学下册二次根式、勾股定理综合测试卷 (含答案解析)

20.（1）已知y= ﹣ +8x，求的平方根．
（2）当﹣4＜x＜1时，化简 ﹣2 ．
21.一个25米长的梯子AB，斜靠在一竖直的墙AO上，这时的AO距离为24米，如果梯子的顶端A沿墙下滑4米，那么梯子底端B也外移4米，对吗？为什么？
22.综合题
（1）试比较与的大小；
（2）你能比较与的大小吗？其中k为正整数.
A. B. C. D.
2.若式子在实数范围内有意义，则x的取值范围是（）
A. x＞1 B. x＜1 C. x≥1 D. x≤1
3.下列变形中，正确的是（）
A.（2 ）2=2×3=6 B.
C. D.
4.下列组合哪个不是勾股数（）
A.30,40,50 B.7,24,25 C.5,12,13 D.1,2,3
【解析】【分析】（1）先根据二次根式有意义的条件可得x的值，进一步得到y的值，代入得到它的平方根；
（2）由于﹣4＜x＜1，根据完全平方公式和二次根式的性质得到 ﹣2 =|x+4|﹣2|x﹣1|，再去绝对值化简即可．
21.【答案】解：不对．
理由：如图，依题意可知
AB＝25(米)，AO＝24(米)，∠O＝90°，
22.【答案】（1）解：，
，
故＜
（2）解：，
，
故＜
【考点】二次根式的性质与化简，二次根式的乘除法
【解析】【分析】（1）比较两个二次根式的大小，用分母有理化的法则先将其化为最简二次根式，再比较大小即可；（2）方法同（1）.
23.【答案】解：如图，AB=28 ，∠P=45°，∠PAC=90°，∠ABQ=45°，∴∠ACP=45°，
5.下列二次根式中，与是同类二次根式的是（）

八年级数学下学期暑假作业勾股定理与平方根试题

卜人入州八九几市潮王学校勾股定理与平方根班级建议作业完成日期1建议完成时间是：20分钟1．假设一个数的算术平方根为a ，那么比这个数大2的数是〔〕22D.a 2+2 2．在数轴上表示1、2的对应点分别是A ，B ，点B 关于点A 的对应点为C ，那么点C 所表示的数是〔〕 A.2-1B.1-2C.2-2D.2-23．假设22441aab b ++=，那么a+2b=____________.4________，算术平方根是__________5．在Rt △ABC 中，有两条边为5cm 、12cm ，那么第三条边为.6．如图，∠C=∠ABD=90°，AC=4，BC=3，BD=12，那么AD 的长等于___________.第2题第6题第7题7.如图，正方形A 的面积是___________.8．位，有个有效数字.9．20211020≈〔保存两个有效数字〕；722≈〔准确到0.001〕. 10.以下各数是四舍五入得到的近似数，它们各有几个有效数字各准确到哪一位 (1)13亿；(2)560万；(3)7；(4)0.0070；×104； (6)6000.11．如图：等腰ABC ∆中，腰AB=AC=13cm ，底BC=24cm ，求ABC ∆的面积.12.:如图，在ΔABC 中，D 是BC 边上的一点，AB=15，AC=13，AD=12，CD=5.求：BC 的长.13.如图，在四边形ABCD 中，：AB ＝1，BC ＝2，CD ＝2，AD ＝3，且AB ⊥BC.试说明AC ⊥CD 的理由.14.五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的选项是〔〕A.B.C.D.15．x－2的平方根是 2，2x+y+7的立方根是3，求x2+y2的平方根和立方根.恭喜你顺利的HY完成作业，你不妨再仔细检查一下！作业实际完成时间是：月日家长检查签名〔章〕：。

人教版八年级上册第一学期数学期末专题复习卷三勾股定理与平方根(最新)

八年级数学期末专题复习卷三勾股定理与平方根（时间：60分钟满分：100分）一、选择题（每题2分，共20分）1．在三边长分别为下列长度的三角形中，是直角三角形的是( )．A ．2cm ，2 cm ，4 cmB ．8 cm ，14 cm ，10 cmC ．9 cm ，41 cm ，40 cmD ．6 cm ，6 cm ，6 cm2．(－6)2的平方根是( )．A ．－6B ．36C ．±6D 3．如图，矩形ABCD 边AD 沿拆痕AE 折叠，使点D 落在BC 上的F 处，已知AB ＝6，△ABF 的面积是24，则FC 等于( )．A ．1B ．2C ．3D ．4 4．直角三角形两直角边长为5，12，则斜边上的高( )．A ．6B ．8C ．1813D ．60135( )．A ．3B ．7C ．－3D ．－76．如图，若数轴上的点A 、B 、C 、D 表示数为－1，1，2，3，则表示4的点P 应在线段( )．A ．AB 上 B ．BC 上C ．CD 上 D ．OB 上7．下列命题：①如果a ，b ，c 为一组勾股数，那么4a ，4b ，4c 仍是勾股数；②如果直角三角形的两边是3，4，那么斜边必是5；③如果一个三角形的三边是12，25，21，那么此三角形必是直角三角形；④一个等腰直角三角形的三边是a ，b ，c （a>b ＝c ），那么a 2：b 2：c 2＝2：1：1，其中正确的是( )．A ．①②B ．①③C ．①④D ．②④8．某市在一次扶贫助残活动中，共捐款3185800元，将3185800元用科学记数法表示（精确到十万位）为( )．A ．3.1×106元B ．3.1×105元C ．3.2×106元D ．3.18×106元9，227，0.303030…，π0中，有理数的个数为( )． A ．3 B ．4 C ．5 D ．610．下列说法中不正确的是( )．A ．10B ．－2是4的一个平方根C ．49的平方根是23D ．0.01的算术平方根是0.1 二、填空题（每题3分，共24分）11．数组3，4，5；5，12，13；7，24，25；9，40，41；…都是勾股数，若n 为直角三角形的一较长直角边，用含n 的代数式表示斜边为_______．12．81的平方根是_______；1331的立方根是_______．13．对于四舍五入得到的近似数3.20×105，是精确到_______位．14．平方根节是数学爱好者的节日，这一天的月份和日期的数字正好是当年年份最后两位数字的平方根，例如：2009年的3月3日，2016年的4月4日，请你写出本世纪内你喜欢的一个平方根（题中所举例子除外）：_______年_______月_______日．15．若2a －1和5－a 是一个数m 的平方根，则a ＝_______，m ＝_______．16－3．173的相反数是_______，绝对值是_______．18．如图，在△ADC 中，∠ADC ＝90°，AD ＝DC ，三角形的顶点在相互平行的三条直线l 1，l 2，l 3上，且l 1，l 2之间的距离为2，l 2，l 3之间的距离为3，则AC 的长是_______．三、解方程和计算（每题5分，共10分）19．解方程：()21x -＝25．20．计算：(102123π-⎛⎫-⨯ ⎪⎝⎭．四、作图题（每题5分，共10分）2122．如图的正方形网格，每个正方形顶点叫格点，请在图中画一个面积为10的正方形．五、解答题（每题9分，共36分）23．陈平想知道学校旗杆的高，他发现旗杆上的绳子垂到地还多1m，当他把绳子的下端拉开5 m后，发现下端刚好接触地面，你能帮他求出旗杆的高吗？24．如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB＝5，DE＝1，BD＝8，设CD＝x．(1)用含x的代数式表示AC＋CE的长；(2)请问点C满足什么条件时，AC＋CE的值最小？(3)根据(2)中的规律和结论，值．25．如图为一直角三角形纸片，两直角边AC＝6，BC＝8，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长．26．[问题情境]勾股定理是一条古老的数学定理，它有很多种证明方法，我国汉代数学家赵爽根据弦图，利用面积法进行证明，著名数学家华罗庚曾提出把“数形关系”（勾股定理）带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．[定理表述]请你根据图(1)中的直角三角形叙述勾股定理（用文字及符号语言叙述）；[尝试证明]以图(1)中的直角三角形为基础，可以构造出以a ，b 为底，以a ＋b 为高的直角梯形(如图(2))，请你利用图(2)，验证勾股定理；[知识拓展]利用图(2)中的直角梯形，我们可以证明a b c+< ∵ BC ＝a ＋b ，AD ＝_______，又在直角梯形ABCD 中有BC_______AD （填大小关系），即_______，∴a b c+<参考答案1．C 2．C 3．B 4．D 5．A 6．B 7．C 8．C 9．B 10．C11．n ＋1 12．±9 1113．千14．答案不唯一，如：2001年1月1日15．－4 81 16．>17．33 1819．x ＝6或x ＝－420．原式＝－4＋3－3×1＝－4．21．点A22．略23．12 m ．24．(2)当A 、C 、E 三点共线时，AC ＋CE 的值最小．(3)如图所示 1326．略。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

求证：．
8．已知：在中， ,D、E分别为ＢC、AＣ的中点， , .
求AB的长.
测试卷答案
一、选择题
１．D．2.Ｂ.3.Ｃ.4.Ｃ.5．Ｂ．6．D.7.B．８．D.9．C．
二、填空题
１.０、1；0、１、-１．２.① ；②24.3．7．ﻩ４．-2．
5．－4，81.ﻩ６. .ﻩ7.5.８．12．
三、解答题
2．△ABC中,Ｄ是BC上的一点,若AB＝１0，BD=6,AD=8，ＡC=1７,求△ＡBＣ的面积.
3．先观察下列表格：请你结合该表格及相关知识，求出b、c的值．
列举
猜想
３、4、5
32＝4+5
5、12、13
５2=１２＋13
7、2４、25
72＝24+２５
……
……
3５、b、ｃ
３52=ｂ＋c
４.如图(１）所示为一上面无盖的正方体纸盒，现将其剪开展成平面图,如图（2）所示.
Ｃ、△ABC中,若∠A︰∠B︰∠C=３︰4︰5，则△ABC是直角三角形
D、△ABＣ中,若ａ︰b︰c=5︰4︰3，则△ＡBC是直角三角形
５．下列命题正确的个数有：（1） ,（2） ,（3)无限小数都是无理数,（4)有限小数都是有理数，(5)实数分为正实数和负实数两类（).
A.1个ﻩﻩB．2个ﻩﻩC．3个ﻩﻩD.4个
∵∠Ｃ＝90°,∴ .
∴
∴ ．
∵在△ABC中，
∴ .∴ （或 )．
Ａ、2cｍﻩＢ、３ｃmﻩﻩC、４cmﻩﻩﻩD、5cｍ
(第7题图)ﻩﻩ（第8题图)
９.在△ABＣ中，AB＝１５,AＣ＝１3，高AD＝１２，则△ABＣ的周长为（ﻩ）．
A、42ﻩﻩB、32ﻩﻩﻩC、42或32ﻩD、不能确定
二、填空题
1.算术平方根等于它本身的数有_＿____＿_，立方根等于本身的数有____＿___.
2．以下列各数为边长,不能组成直角三角形的是（)．
A、3,4，5B、４，5，6C、5,12，13D、6，8，１0
３．的平方根是(）．
A． ﻩﻩﻩＢ．36ﻩﻩC．±6ﻩﻩD．
４.下列判断中错误的是(）.
A、△AＢC中，若∠B＝∠C-∠A,则△AＢC是直角三角形
B、△AＢC中，若a２=ｂ２-ｃ2,则△ABC是直角三角形
1．梯子下滑0.5米．
2．8４.
３．6１２，６13.
4．(1)在平面展开图中可画出最长的线段长为 ,这样的线段可画４条;
（２)连结线段，有∠BAC=∠B，A，Ｃ，=４５0．
5.略．
6．６．
7．∵在中, ,∴ .
同理:在中, .
在中, ,
又∵ ,
∴ ．∴ ．
8．设，
∵数的平方根,则
6.如图，所有的四边形都是正方形，所有三角形都是直角三角形,其中最大的正方形的边长是 ,则图中四个小正方形的面积之和是.ﻩﻩﻩﻩﻩﻩﻩﻩﻩﻩﻩﻩﻩﻩ(第6题图)
7.如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、６cm、和 cm的长方体无盖盒子中，则细木棒露在盒外面的最短长度是____＿___ｃm．
6.若两条线段的长为8ｃm和1５ｃm，则能组成一个直角三角形的第三条线段的长为(ﻩ).
A、12cmﻩﻩﻩB、1３cmﻩﻩﻩC、17cmﻩﻩD、１7cｍ或 cm
７.如图，在由单位正方形组成的网格图中标有四条线段,其中能构成一个直角三角形三边的线段是(ﻩﻩ）.
A、Ｂ、 C、Ｄ、
8．如图,有一块直角三角形纸片，两直角边AC=６ｃm,BＣ＝8cm,现将直角边AC沿AD折叠,使它落在斜边AB上，且与ＡE重合,则BＤ=（）.
已知展开图中每个正方形的边长为1.（1)求在该展开图中可画出最长线段的长度？这样的线段可画几条?(2)试比较立体图中与平面展开图中的大小关系？
5．在数轴上画出的点.
6.如图，△ABC中，∠Ｃ＝90°,D是ＢC上一点,AB=17,AD=10,BD=9，求ＣＤ的长．
7.已知:如图, ，，于P.
8．一青蛙在如图８×８的正方形(每个小正方形的边长为1)网格的格点(小正方形的顶点)上跳跃，青蛙每次所跳的最远距离为 ,青蛙从点开始连续跳六次正好跳回到点 ,则所构成的封闭图形的面积的最大值是.
(第７题图)ﻩﻩ(第8题图)
三、解答题
1．如图,滑杆在机械槽内运动，为直角,已知滑杆长2．５米,顶端在上运动,量得滑杆下端距点的距离为1．5米,当端点向右移动０.５米时，求滑杆顶端下滑多少米？
2．在Rｔ△ABC中，∠Ｃ=9０°,∠Ａ,∠Ｂ，∠C的对边分别是a,b,ｃ.
①若b＝２ａ，c=5,则a=_＿＿__＿__;②若a︰b=３︰４,ｃ＝10，则S△ABC=________．
3.从电线杆高底面2４m处向地面拉一条长25m的缆绳,则固定点B到电线杆底部A的距离为______＿＿ｍ.
４．如果 ,则 ___＿＿_＿_．
初二数学测试卷(勾股定理与平方根)
———————————————————————————————— 作者：
———————————————————————————————— 日期：
初二数学测试卷(勾股定理与平方根)
一、选择题
１.一个直角三角形两直角边长分别为3和4,则下列说法正确的是(）．
A、三角形面积为12B、三角形的周长为25C、斜边长为25Ｄ、斜边长为５

初二数学考试卷勾股定理与平方根

最新初中八年级数学题库 八年级第二章勾股定理与平方根测试题

【八年级】八年级上册第二章勾股定理与平方根单元试题(带答案)

八年级数学(上)第二章 勾股定理与平方根 单元测评卷(A)

初二数学测试卷(勾股定理与平方根)

八年级数学上册期末复习一勾股定理与平方根试题

勾股定理与平方根习题(附答案)

八年级数学(上)第二章 勾股定理与平方根 检测卷(含答案)

八年级数学(上)第二章 勾股定理与平方根 单元测试卷

八年级数学(上)第二章 勾股定理与平方根 课时练习：第10课时 勾股定理的应用(1)

【八年级数学试题】苏科版初二数学上册勾股定理与平方根单元测试(含答案)

第二章 勾股定理与平方根单元复习试卷

初二数学勾股定理和平方根练习题

八年级数学(上)第二章 勾股定理与平方根 课时练习：第11课时 勾股定理的应用(2)

2019-2020年八年级数学上册第二章 勾股定理与平方根单元测试卷

人教版 八年级数学下册二次根式、勾股定理 综合测试卷 (含答案解析)