岩土体物理力学参数参考
(完整版)岩土力学参数大全
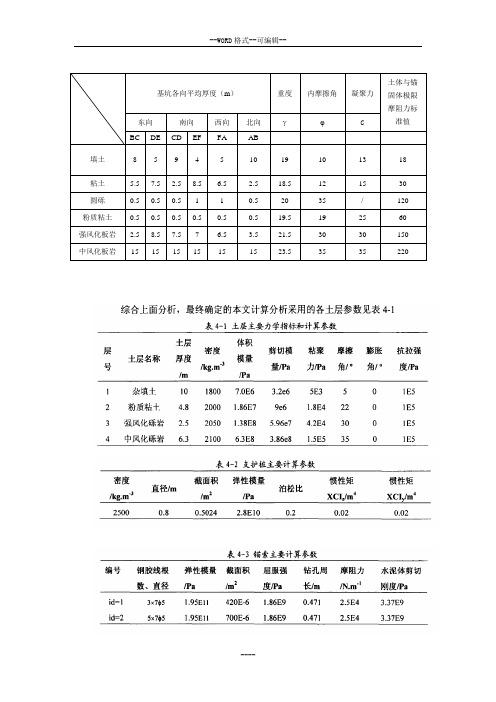
基坑各向平均厚度(m)重度内摩擦角凝聚力土体与锚固体极限摩阻力标准值东向南向西向北向γφ CBC DE CD EF FA AB填土8 5 9 4 5 10 19 10 13 18 粘土 5.5 7.5 2.5 8.5 6.5 2.5 18.5 12 15 30 圆砾0.5 0.5 0.5 1 1 0.5 20 35 / 120 粉质粘土0.5 0.5 0.5 0.5 0.5 0.5 19.5 19 25 60 强风化板岩 2.5 8.5 7.5 7 6.5 3.5 21.5 30 30 150 中风化板岩15 15 15 15 15 15 23.5 35 35 220常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.37.3 固有的强度特性在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:s 13N f φσσ=-+ (7.7)其中 )sin 1/()sin 1(N φφφ-+=1σ——最大主应力 (压缩应力为负); 3σ——最小主应力φ——摩擦角c ——粘聚力当0f s <时进入剪切屈服。
常用的岩土和岩石物理力学参数讲解

(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
岩土体物理力学参数

岩土体物理力学参数在边坡稳定性定量分析中,岩土体的物理力学参数往往直接控制着稳定系数和支护工程量。
常规的获取参数的方法主要有试验法、经验法、工程地质类比法、反演分析法等。
此外,当边坡稳定受成组结构面和岩桥共同控制时,仍常采用结构面连通率,即采用结构面和岩桥强度进行加权平均来求取潜在滑移面的综合抗剪强度。
以下对两种参数获取方法进行简单介绍。
1.试验法试验法一般可分为室内试验和现场试验两类。
现场试验试件尺寸一般较大,多为(50~70)cm×(50~70)cm,它能保持岩土体的原始状态,并能反映结构面二、三级起伏差对强度的影响,但加工困难,周期长,试验费用相对较高。
室内试验试件一般较小,多为扰动样,存在尺寸效应问题,但取样简单,可以开展各种不同工况下的试验,如三轴直剪试验、饱和固结快剪试验、饱和固结排水剪试验、慢剪试验等。
室内试验由于试验周期短,费用相对较低,可以大量开展。
目前,随着取样技术的发展,已具备取原状样的条件,且可在刚性伺服机上开展试验,能有效地确定有效正应力,控制剪切速度,试验成果较为真实可靠。
2.经验估算法可根据一些经验公式,如利用Hoek-Brown强度准则确定岩体的综合抗剪强度。
一般是在工程前期和缺乏试验的地区应用,该方法存在的问题是岩石强度权重偏大,应用在坚硬和极坚硬岩石中时,确定的抗剪强度常常偏高。
8.5.2 选择原则对于一些不重要或者工程前期缺乏试验资料的边坡,可通过经验法和工程地质类比法,初步确定岩土体的物理力学参数,以此估算边坡的稳定性和支护工程量。
对于一些已经失稳或正在变形的边坡,采用反演分析法来获取岩土体的物理力学参数是一种最有效的办法,但由于此时的抗剪强度已不是常规物理意义上的抗剪强度,而是岩土体抗剪强度参数、边界条件、地下水条件等因素的综合反映,因此,在应用时应严格注意条件的相似性。
同时,应考虑在工程有效期内工作条件的可能变化趋势对强度参数的影响,并适当进行调整。
附表2岩土工程物理力学指标表

表11-1 岩土参数建议值表岩土分层岩土名称时代与成因岩石地基承载力特征值土承载力特征值桩侧摩阻力特征值(钻孔灌注桩)桩端阻力特征值(钻孔灌注桩)桩极限侧阻力标准值(钻孔灌注桩)桩极限端阻力标准值(钻孔灌注桩)土体与锚固体极限摩阻力标准值岩石与锚固体极限摩阻力标准值地基系数的比例系数(灌注桩)岩层或土层水平基床系数岩层或土层垂直基床系数静止侧压力系数岩土泊桑比岩石质量指标基底摩擦系数边坡坡度高宽比允许值(1:n)土石可挖性分级f a f ak q sa q pa q sik q sik q s q s m K s Kc K0μRQD f(kPa) (kPa) (kPa) (kPa) (kPa) (kPa) (kPa) (MPa) (MPa/m2) (MPa/m) (MPa/m) (%)(1-1) 填土Q4ml60 18 18 12 0.40 0.29 0.28 支护Ⅰ~Ⅱ(3-4) 粗砂Q2al190 30 40 50 18.0 20 18 0.40 0.29 0.28 1.25 Ⅱ(4-2) 粉质粘土Q2el210 30 43 50 22.0 35 30 0.39 0.28 0.30 1 Ⅱ(11)-1 全风化板岩P t220 35 50 55 40.0 35 30 0.38 0.28 0.30 1 Ⅲ(11)-2 强风化板岩P t350 70 700 75 750 0.12 150 120 0.38 0.28 0.33 0.75 Ⅲ~Ⅳ(11)-3 中风化板岩P t800 130 1300 170 1600 0.30 170 135 0.28 0.22 10~150.38 0.5 Ⅳ(11)-4 微风化板岩P t1200 135 1500 180 1800 0.50 200 175 0.26 0.21 10~20 0.45 0.5 Ⅴ说明:1、本表的岩土参数值,是根据勘察结果,按工程类比(工程经验)的方法经过查阅有关规程、规范、手册或通过计算而提供的可用于设计的岩土参数。
岩土力学参数大全
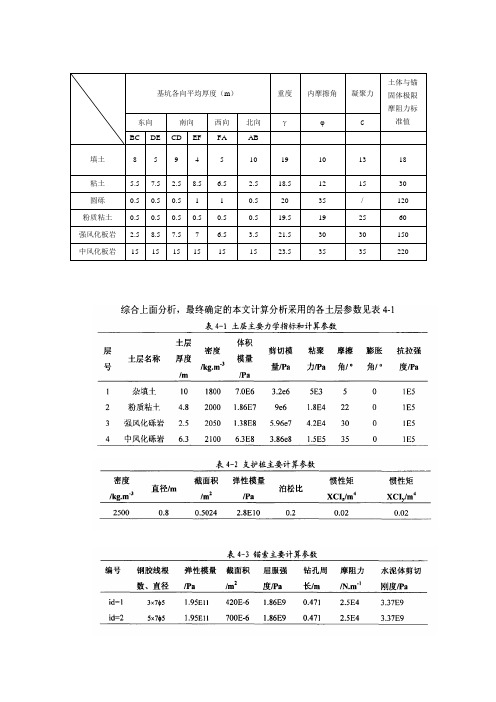
基坑各向平均厚度(m)重度内摩擦角凝聚力土体与锚固体极限摩阻力标准值东向南向西向北向γφ CBC DE CD EF FA AB填土8 5 9 4 5 10 19 10 13 18 粘土 5.5 7.5 2.5 8.5 6.5 2.5 18.5 12 15 30 圆砾0.5 0.5 0.5 1 1 0.5 20 35 / 120 粉质粘土0.5 0.5 0.5 0.5 0.5 0.5 19.5 19 25 60 强风化板岩 2.5 8.5 7.5 7 6.5 3.5 21.5 30 30 150 中风化板岩15 15 15 15 15 15 23.5 35 35 220常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.37.3 固有的强度特性在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:s 13N f φσσ=-+ (7.7)其中 )sin 1/()sin 1(N φφφ-+=1σ——最大主应力 (压缩应力为负); 3σ——最小主应力φ——摩擦角c ——粘聚力当0f s <时进入剪切屈服。
(水利水电)部分常用岩土物理力学参数经验数值

(水利水电)部分常用岩土物理力学参数经验数值-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN使用说明:1、资料涉及各行各业;2、资料出处为黄底加粗字体的为最新版本内容。
可按规范适用范围选择使用;3、资料出处非黄底加粗字体的为引用资料,很多为老版本,参考用。
水利水电工程部分岩土物理力学参数经验数值1岩土的渗透性(1)渗透系数《地下铁道、轻轨交通岩土工程勘察规范》GB50307-1999 139~140页土体的渗透系数值2《水利水电工程水文地质勘察规范》SL373-2007 62~63页岩土体渗透性分级Lu:吕荣单位,是1MPa压力下,每米试段的平均压入流量。
以L/min计摘自《水利水电工程地质勘察规范》GB50287-99 附录J 66页表F 岩土体渗透性分级3《水利水电工程地质勘察规范》(GB50487-2008)109页附录F (2)单位吸水量各种构造岩的单位吸水量(ω值)上表可以看出:同一断层内,一般碎块岩强烈透水;压碎岩中等透水;断层角砾岩弱透水;糜棱岩和断层泥不透水或微透水。
摘自高等学校教材天津大学《水利工程地质》第三版 113页坝基(肩)防渗控制标准4注:透水率1Lu(吕荣)相当于单位吸水量0.01摘自高等学校教材天津大学《水利工程地质》第三版 118页。
(3)简易钻孔抽注水公式1)简易钻孔抽水公式根据水位恢复速度计算渗透系数公式1.57γ(h2-h1)K= ———————t (S1+S2)式中:γ---- 井的半径;h1---- 抽水停止后t1时刻的水头值;h2---- 抽水停止后t2时刻的水头值;S1、S2---- t1或t2时刻从承压水的静止水位至恢复水位的距离;H---- 未抽水时承压水的水头值或潜水含水层厚度。
《工程地质手册》第三版 927页2)简易钻孔注水公式当l/γ<4时0.366Q 2lK= ———— lg ———Ls γ式中:K—渗透系数(m/d);l---试验段或过滤器长度(m);Q---稳定注水量(m3/d);s---孔中水头高度(m);γ---钻孔或过滤器半径(m)。
各土层物理力学性质指标平均值及承载力特征值确定一览表1
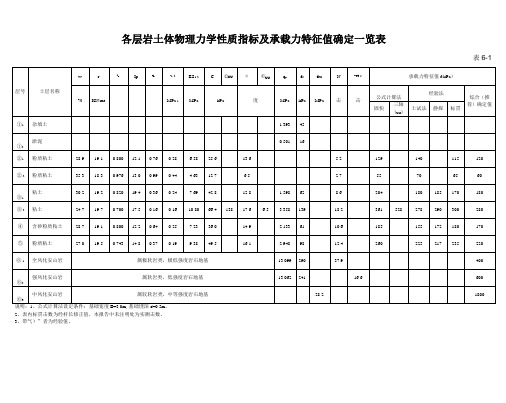
7.23
36.0
14.9
2.133
61
10.6
185
155
172
180
170
⑤
粉质粘土
27.0
19.5
0.743
14.8
0.37
0.19
9.38
49.5
16.1
2.948
98
12.4
260
225
217
235
220
⑥-1
全风化安山岩
属极软岩类,极低强度岩石地基
13.099
290
37.9
400
⑥2
0.36
0.24
7.69
42.8
12.8
1.598
62
8.6
204
180
185
170
180
③-2
粘土
24.719Βιβλιοθήκη 70.70017.5
0.16
0.16
10.80
66.4
138
17.6
6.5
3.358
139
18.2
361
528
278
290
300
280
④
含砂粉质粘土
28.7
19.1
0.800
12.2
0.64
强风化安山岩
属软岩类,低强度岩石地基
13.062
241
16.6
600
⑥3
中风化安山岩
属较软岩类,中等强度岩石地基
28.2
1800
说明:1、公式计算法设定条件:基础宽度B=3.0m,基础埋深d=0.5m。
2、表内标贯击数为经杆长修正值,本报告中未注明处为实测击数。
常用的岩土和岩石物理力学参数
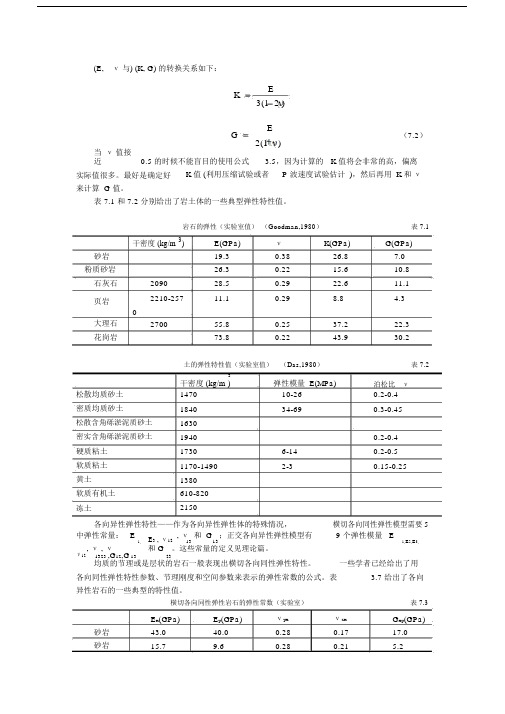
(E, ν与) (K, G) 的转换关系如下:KE3(1 2 )GE(7.2)2(1 )当 ν值接近0.5 的时候不能盲目的使用公式 3.5,因为计算的 K 值将会非常的高,偏离实际值很多。
最好是确定好K 值 (利用压缩试验或者P 波速度试验估计 ),然后再用 K 和 ν来计算 G 值。
表 7.1 和 7.2 分别给出了岩土体的一些典型弹性特性值。
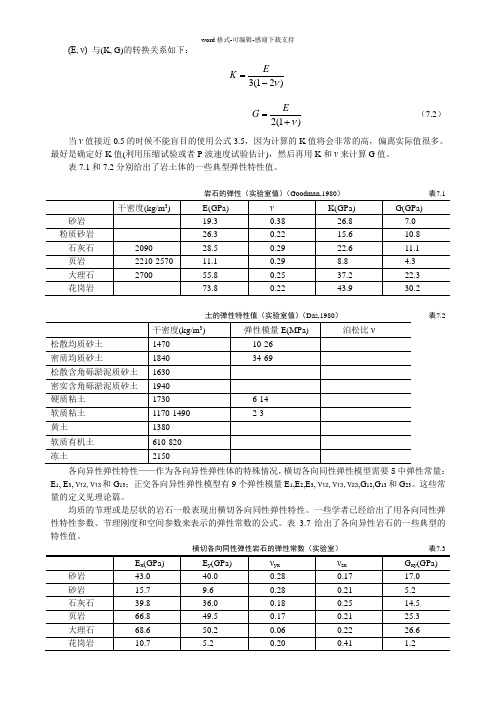
岩石的弹性(实验室值) (Goodman,1980) 表 7.1干密度 (kg/m 3)E(GPa) ν K(GPa)G(GPa)砂岩 19.3 0.38 26.8 7.0 粉质砂岩26.30.22 15.6 10.8石灰石 2090 28.5 0.29 22.6 11.1页岩 2210-25711.10.298.84.3大理石 270055.8 0.25 37.2 22.3花岗岩73.80.2243.930.2土的弹性特性值(实验室值) (Das,1980)表 7.2松散均质砂土 密质均质砂土松散含角砾淤泥质砂土 密实含角砾淤泥质砂土硬质粘土 软质粘土 黄土软质有机土冻土3弹性模量 E(MPa)泊松比 ν 干密度 (kg/m ) 1470 10-260.2-0.41840 34-690.3-0.45163019400.2-0.41730 6-14 0.2-0.5 1170-1490 2-30.15-0.251380610-820 2150各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5 中弹性常量: E E 3 , ν12 , ν 和 G 13 ;正交各向异性弹性模型有9 个弹性模量 E1, 131,E 2,E 3,ν12 , ν , ν 和 G 23。
这些常量的定义见理论篇。
1323 ,G 12,G 13均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
常用岩土材料参数和岩石物理力学性质一览表-附详细表格
(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f k K nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
(完整版)岩土力学参数大全

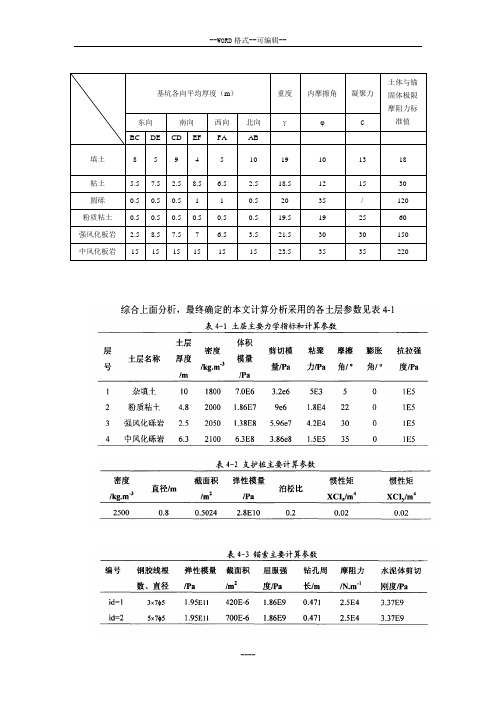
综合上面分析,最终确定的本文计算分析采用的各土层参数见表4-1表4-1土层主要力学指标和计算参数层号土层名称土层体积模量/Pa剪切模量/Pa粘聚力/Pa摩擦角/,膨胀角/。
抗拉强度/Pa厚度/m密度∕kg.m'3I 杂填土10 1800 7.0E6 3.2e6 5E3 5 0 IE52 粉质粘土 4.8 2000 I.86E7 9e6 1.8E4 22 0 IE53 强风化砾岩 2.5 2050 I.38E8 5.96e7 4.2E4 30 0 1E54 中风化砾岩 6.3 2100 6.3E8 3.86e8 1.5E5 35 0 1E5表4-2支护桩主要计算参数密度∕kg.m*3直径/m截面积∕m2弹性模量/Pa泊松比惯性矩XCI1Zm4惯性矩XCl√m42500 0.8 0.5024 2.8E10 0.2 0.02 0.02表4-3锚索主要计算参数编号钢胶线根数、直径弹性模量/Pa截面积∕m2屈服强度/Pa钻孔周长/m摩用力/N.m∙,水泥体剪切刚度/Paid=I 3×7φ5I.95E1I 420E-6 1.86E9 0.47] 2.5E4 3.37E9 id=2 5x7"5 1.95Eil 700E-6 1.86E9 0.471 2.5E4 3.37E9各层上的力学参数表5-2参数第一层土第一层十第二层土第四层十.泥岩厚度/m7 7 2 7 23 密度/(kgΛ113)1750 2000 1800 2000 2350 体枳模量/MPa0 38.9 8.0 83.3 136.5 切变模量/MPa0 13.0 4.8 17.9 20.0 内聚力ZkPa 3 5 0 5 14000 摩擦角/(。
)20 40 25 45 361.08 抗拉强度/MPa表4-1本次模拟中涉及到的土体的体积模量和剪切模■计算值常用岩土材料力学参数(E,V)与(K,G)的转换关系如下:E一E3(l-2v)(7.2)当V值接近0.5的时候不能盲目的使用公式3.5,因为计算的K值将会非常的高,偏离实际值很多。
岩土体工程地质类型及特征

一、岩土体工程地质类型及特征岩土体工程地质类型的划分根据岩土体形成条件、结构、岩性、力学特性及工程地质特征的差别,可分为松散松软堆积层岩类、碳酸盐岩类及碎屑岩类3个岩体类型6个工程地质岩组。
(一)土体工程地质类型及物理力学特征此岩类的划分根据其结构特征、力学性质及工程特性分为中偏高压缩粘性土类岩组和低压缩碎石土类岩组2个工程地质岩组。
1、中偏高压缩粘性土类岩组(1)残坡积土(Q el+dl)残坡积层主要分布于沿线丘陵沟谷坡脚一带,多为紫红色、棕红色粉砂质粘土或浅黄色、灰黄色砂土、亚粘土、粉土夹(含)碎石,沿线厚度不一。
残坡积亚粘土天然含水量W18.8~24.00%,天然孔隙比e0.600~0.697,塑性指数Ip 8.4~12.6,液性指数I L 0.46~0.60为软塑状,凝聚力C26.6~45.1Kpa,内摩擦角φ10.1~18.7度,压缩系数a0.25~0.40为中~偏高压缩土类。
残坡积层的主要工程地质问题是湿陷变形、压缩沉降变形、蠕滑变形。
(2)冲洪积土(Q4al+pl)冲洪积层主要分布于河床、河滩上,为灰色、浅灰色亚粘土、粘土及褐灰色细、粉砂土及砂砾卵石层,厚度不一。
亚粘土天然含水量W21.7~26.50%,天然孔隙比e0.619~0.838,塑性指数Ip 8.4~14.6,液性指数I L 0.46~0.87为可塑状,凝聚力C12.9~32.2Kpa,内摩擦角φ7.0~10.3度,压缩系数a0.31~0.47为中~偏高压缩土类。
粘土天然含水量W28.8~34.30%,天然孔隙比e0.838~0.978,塑性指数Ip 20.0~21.3,液性指数I L 0.54~0.77为软塑状,凝聚力C22.6~54.7Kpa,内摩擦角φ10.0~10.3度,压缩系数a0.24~0.605为中~高压缩土类。
冲洪积层的主要工程地质问题是湿陷变形、压缩沉降变形、蠕滑变形。
2、低压缩碎石土类岩组崩坡积土(Q4col+dl)崩坡积层主要分布于斜坡边缘、高陡斜坡的坡脚处,碎块石成份与地层岩性有关,为黄灰、红褐色亚粘土夹块石、碎石。
20191204岩体物理力学参数整理
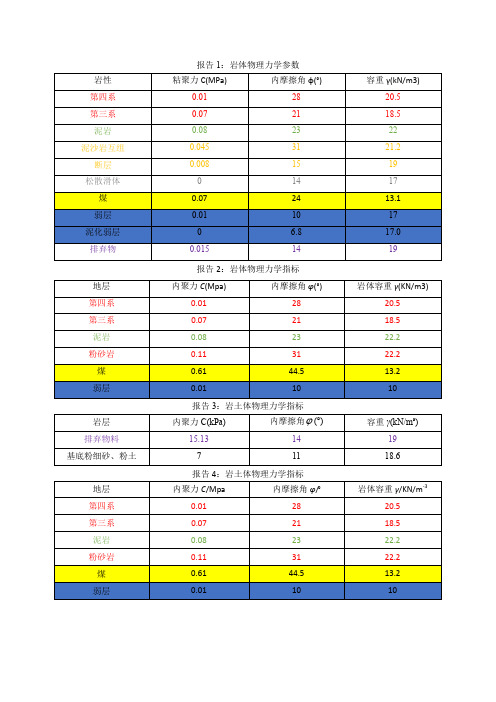
报告2:岩体物理力学指标
报告3:岩土体物理力学指标
注:报告1:《胜利东二露天矿内排土场与南帮变形成因与稳定性治理方案》,辽宁工程技术大学,2018年5月。
报告2:《胜利东二露天煤矿南帮边坡稳定性分析及治理》,辽宁工程技术大学,2011年5月。
报告3:《胜利东二号露天煤矿南排土场南帮边坡稳定性分析与控制技术研究报告》,辽宁工程技术大学,2015年1月。
报告4:《二〇一七年度评价胜利东二露天矿南北帮及内排土场边坡稳定性分析与评价》,辽宁工程技术大学,2017年10月。
报告5:《胜利东二号露天煤矿采场深部滑体清理采煤方案研究》,辽宁工程技术大学,2018年2月。
岩土体物理力学指标
需讨论:1、泥沙岩互组2、断层3、煤4、弱层。
岩土力学重要参数取值大全
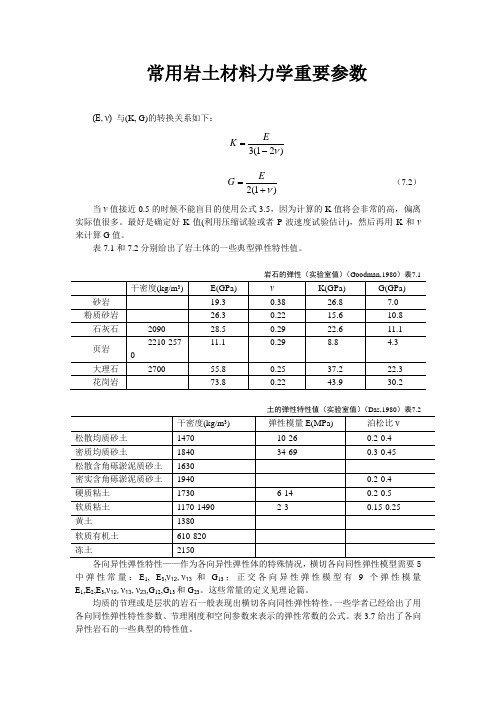
常用岩土材料力学重要参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=E K )1(2ν+=E G (7.2) 当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980)表7.1土的弹性特性值(实验室值)(Das,1980)表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3,ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3,ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室)表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK n t ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f 'K n m k C +=νν(7.4)其中3/4G K 1m +=ν f 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数 k ——渗透系数,单位和速度单位一样(如米/秒)f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
常用岩土材料参数和岩石物理力学性质一览表
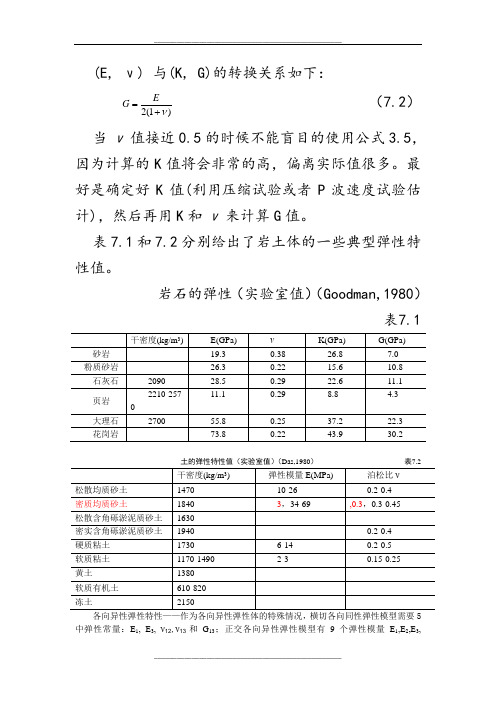
(E, ν) 与(K, G)的转换关系如下:)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980)表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3,ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
岩土物理力学性质指标

岩⼟物理⼒学性质指标1、塑性指数plasticity index塑性指数是液限和塑限之差称为塑性指数,⽤不带百分号的⼩数表⽰,符号为IP。
概述塑性是表征细粒⼟物理性能⼀个重要特征,⼀般⽤塑性指数来表⽰;液限与塑限的差值称为塑性指数IP,即IP=WL-WP。
过去的研究表明,细粒⼟的许多⼒学特性和变形参数均与塑性指数有密切的关系。
特征塑性指数可塑性是粘性⼟区别于砂⼟的重要特征。
可塑性的⼤⼩⽤⼟处在塑性状态的含⽔量变化范围来衡量,粘性⼟由⼀种状态过渡到另⼀种状态的分界含⽔量叫作界限含⽔量,也称为阿太堡界限,有缩限含⽔量、塑限含⽔量、液(流)限含⽔量、粘限含⽔量、浮限含⽔量五种,在建筑⼯程中常⽤前三种含⽔量。
固态与半固态间的界限含⽔量称为缩限含⽔量,简称缩限,⽤ω表⽰。
半固态与可塑状态间的含⽔量称为塑限含⽔量,简称塑限,⽤ωp表⽰。
可塑状态与流动状态间的含⽔量称为液(流)限含⽔量,简称液限,⽤ωl表⽰。
含⽔量⽤百分数表⽰。
天然含⽔量⼤于液限时⼟体处于流动状态;天然含⽔量⼩于缩限时,⼟体处于固态;天然含⽔量⼤于缩限⼩于塑限时,⼟体处于半固态;天然含⽔量⼤于塑限⼩于液限时,⼟体处于可塑状态。
塑性指数习惯上⽤不带%的数值表⽰。
塑性指数是粘⼟的最基本、最重要的物理指标之⼀,它综合地反映了粘⼟的物质组成,⼴泛应⽤于⼟的分类和评价。
因素由于塑性指数在⼀定程度上综合反映了影响粘性⼟特征的各种重要因素。
塑性指数愈⼤,表明⼟的颗粒愈细,⽐表⾯积愈⼤,⼟的粘粒或亲⽔矿物(如蒙脱⽯)含量愈⾼,⼟处在可塑状态的含⽔量变化范围就愈⼤。
也就是说塑性指数能综合地反映⼟的矿物成分和颗粒⼤⼩的影响。
因此,在⼯程上常按塑性指数对黏性⼟进⾏分类。
粉⼟为塑性指数⼩于等于10且粒径⼤于0.075的颗粒含量不超过总质量50%的⼟;黏性⼟为塑性指数⼤于10且粒径⼤于0.075的颗粒含量不超过总质量50%的⼟,其中:Ip>17 黏⼟Ip>10 粉质黏⼟Ip<10或Ip=10 粉⼟对黏性⼟来说,有⼀个指标叫液性指数,是判断⼟的软硬状态,表⽰天然含⽔率与界限含⽔率相对关系的指标。
常用岩土材料参数和岩石物理力学性质一览表

(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D 中用到的流动时间步长,∆ tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f k K nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K nm k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
最新常用岩土材料参数和岩石物理力学性质一览表

常用岩土材料参数和岩石物理力学性质一览表(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E1, E3,ν12,ν13和G13;正交各向异性弹性模型有9个弹性模量E1,E2,E3,ν12,ν13,ν23,G12,G13和G23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室)表7.3流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f,如果土粒是可压缩的,则要用到比奥模量M。
纯净水在室温情况下的K f值是2 Gpa。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f,不用折减。
这是由于对于大的K f流动时间步长很小,并且,力学收敛性也较差。
在FLAC3D中用到的流动时间步长, tf与孔隙度n,渗透系数k以及K f有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
f'K n m k C +=νν (7.4)其中3/4G K 1m +=νf 'k k γ=其中,'k ——FLAC 3D 使用的渗透系数k ——渗透系数,单位和速度单位一样(如米/秒) f γ——水的单位重量考虑到固结时间常量与νC 成比例,我么可以将K f 的值从其实际值(Pa 9102⨯)减少,利用上面得表达式看看其产生的误差。
岩土力学参数大全
常用岩土材料力学参数(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.37.3 固有的强度特性在FLAC 3D 中,描述材料破坏的基本准则是摩尔-库仑准则,这一准则把剪切破坏面看作直线破坏面:s 13N f φσσ=-+ (7.7)其中 )sin 1/()sin 1(N φφφ-+=1σ——最大主应力 (压缩应力为负);3σ——最小主应力φ——摩擦角c ——粘聚力当0f s <时进入剪切屈服。
这里的两个强度常数φ和c 是由实验室的三轴实验获得的。
当主应力变为拉力时,摩尔-库仑准则就将失去其物理意义。
简单情况下,当表面的在拉应力区域发展到3σ等于单轴抗拉强度的点时,tσ ,这个次主应力不会达到拉伸强度—例如;t 3t f σσ-= (7.8)当0f t >时进入拉伸屈服。
岩石和混凝土的抗拉强度通常有由西实验获得。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
50~150
24.23~28.81
100~250
破碎夹泥层Ⅰ(岩屑夹泥型)
<10
以碎块、岩屑为主,在碎块骨架间填有少量泥浆或次生泥质物,厚度常有变化
19.29~24.23
25-50
19.29~24.23
50~100
破碎夹泥层Ⅱ(泥夹岩屑型)
10~30
碎块岩屑间充填泥质物较多,呈泥包碎块状,有时上下层面附有断续的泥化层
3胶结或无充填的结构面抗剪断强度,应根据结构面的粗糙程度取大值或小值;
4当软弱夹层和断层有一定厚度时,应考虑充填物的影响。当厚度大于起伏差时,软弱层和断层应采用充填物的抗剪强度作为标注值;当厚度小于起伏差时,还应采用起伏差的最小爬坡角,提高充填物抗剪强度试验值作为标注值;
5当试件粘粒含量大于30%或有泥化镜面或粘土矿物以蒙脱石为主时,应采用流变强度作为标准值。
较软岩~软岩,结合一般
19~29
80~120
4
较坚硬~较软岩,结合差~结合很差;
软岩,结合差;软质岩的泥化面
13~19
8~50
5
较坚硬岩及全部软质岩,结合很差;
软质岩泥化层本身
<13
<50
——工程岩体分级标准(GB50218-94)
表5-14国内部分水电工程软弱结构面强度参数
结构面类型
结构面性状
抗剪强度
21.0
37.6
18.9
18.7
6.9
16°00′
永加线
褐红色含碎石粘土,碎石含量10~20%
21.10
20.35
8
18°00′
黄树岭滑坡
含碎石粘土
Hale Waihona Puke 1221°金钗湾南潜在滑移体
0.22-0.4
——小湾、溪落渡、糯扎渡、拉西瓦等水电站
表5-15国内部分滑坡滑带土物理力学参数
滑带土性质
天然
重度
(kN/m3)
含水量(%)
液限(%)
塑限(%)
塑性指数
计算指标
备注
C
(kPa)
φ
(°)
破碎岩层沿基岩面滑动(破碎岩层滑坡)
21.9
31.4
17.2
14.2
4.9
12°06′
酒店塘
砂岩沿泥岩顶面的泥化夹层滑动(岩石顺层滑坡)
φ(°)
C (MPa)
砾屑型断层
层状断层泥连续分布
11.9-14.4
0
岩屑砾型断层
层状断层泥断续分布
17.9-21.1
0.008-0.0413
小断层
起伏差数毫米(f),部分含泥
26.6-28.8
0.02-0.1
构造挤压带
破碎带部分泥化
27.2-32.3
0.004-0.022
裂隙
一般裂隙面
36.8-40.4
14.04~19.29
15~25
14.04~19.29
20~50
泥化夹层
(全泥型)
>30
薄层软弱岩石全部或大部分泥化而成,可塑状,以泥质物为主,夹于上、下硬岩之间,有时有次生泥质物充填
8.53~14.04
10~15
10.20~14.04
2~5
注:
1表中参数限于硬质岩中胶结或无充填的结构面;
2软质岩中的结构面应进行折减;
——中小型水利水电工程地质勘察规范(SL55-2005)
水利水电工程地质勘察规范(GB50287-99)
表5-13岩体结构面抗剪断峰值强度
序号
两侧岩体的坚硬程度及结构面的结合程度
φ(°)
c(kPa)
1
坚硬岩,结合好
>37
>220
2
坚硬~较坚硬岩,结合一般
29~37
120~220
3
坚硬~较坚硬岩,结合差;
表5-12结构面工程地质分类及参数取值表
类型
粘粒含量(%)
基本特征
抗剪强度参考值
抗剪断强度参考值
φ(°)
c(KPa)
φ'(°)
c' (KPa)
胶结的结构面
30.96~38.66
100~250
无充填的结构面
24.23~35
50~150
破碎夹层
(岩块岩屑型)
极少
薄层软弱岩层因构造挤压、错动而破碎,碎块形成层间骨架,碎块间很少有泥质物,碎块多成序排列
