昆明第一中学2018届高中新课标高三第一次摸底测试理科数学

合集下载

云南省昆明一中2018届高三考前适应性训练数学(理)试卷及答案

云南省昆明第一中学2018届高三第八次月考理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}ln A x y x ==，集合{}xB y y e==，则集合A 与B 的关系是（）A ． AB = B ．A B ≠⊂ C ．B A ≠⊂ D ．A B ∈2.在复平面内，复数z 与复数103i+对应的点关于实轴对称，则z =（） A ．3i + B ．3i - C ．3i -+ D ．3i --3.某班有50人，一次数学考试的成绩X 服从正态分布()110,100N ．已知()1001100.34P x <≤=，估计该班本次考试学生数学成绩在120分以上的有（） A ．5人 B ．6人 C ．7人 D ．8人4. ()62111x x ⎛⎫-+ ⎪⎝⎭展开式中3x 的系数为（） A ．14- B ．14 C. 15 D ．305.已知点F 是抛物线()2:20C x py p =>的焦点，O 为坐标原点，若以F 为圆心，FO 为半径的330x y -+=相切，则抛物线C 的方程为（）A ． 22x y = B ．24x y = C. 26x y = D ．28x y =6.已知函数()()()2sin 0f x x ωϕω=+>的部分图像如图所示，若图中在点,A D 处()f x 取得极大值，在点,B C 处()f x 取得极小值，且四边形ABCD 的面积为32，则ω的值是（） A ．18 B ．14 C. 8π D ．4π7.已知函数()f x x =，函数()2g x x =-，执行如图所示的程序框图，若输入的[]3,3x ∈-，则输出m 的值为()g x 的函数值的概率为（） A ．16 B ．14 C. 13 D ．128.设数列{}n a 的前n 项和为n S ，若()11,,*,2n n n S S S n N n -+∈≥构成等差数列，且122,4a a =-=-，则6a =（） A ． 64- B ．32- C. 16 D ． 649.已知双曲线()2222:10,0x y C a b a b -=>>的左、右焦点分别为12,F F ，点A 是双曲线C 底面右顶点，点M 是双曲线C 上一点，MA 平分12F MF ∠，且12:2:1MF MF =，则双曲线的离心率为（）A ．2B ．3 C. 2 D ．310.过正方体1111ABCD A B C D -的顶点A 的平面α与直线1AC 垂直，且平面α与平面11ABB A 的交线为直线l ，平面α与平面11ADD A 的交线为直线m ，则直线l 与直线m 所成角的大小为（）A ．6π B ．4π C. 3π D ．2π11.已知ABC ∆的面积为6，4cos 5A =-，P 为线段BC 上一点，2BP PC =u u u r u u u r ，点P 在线段,AB AC上的投影分别为,Q R ，则PQR ∆的面积为（） A ．625 B ．1225 C. 3225 D ．362512.已知定义在()0,+∞上的函数()()222,6ln 4f x x m h x n x nx =-=-，其中0n >，设两曲线()y f x =与()y h x =有公共点，且在公共点处的切线相同，则mn的最大值为（） A ．163e -B ．133e -C. 1332e D ．2313e第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若,x y 满足约束条件3020x y x y +-≥⎧⎨-≤⎩，则函数2z x y =+的最小值为．14.在数列{}n a 中，112a =，且()11*2n n a n N a +=∈-，设数列{}n a 的前n 项的积为n T ，则100T = ．15.定义符号函数()()()()1,00,01,0x g x x x >⎧⎪==⎨⎪-<⎩，若函数()()xf xg x e =⋅，则满足不等式()()233f a a f a +<+的实数a 的取值范围是．16.已知正方体1111ABCD A B C D -的棱长为4，点P 是1AA 的中点，点Q 是1BDC ∆内的动点，若1PQ BC ⊥，则点Q 到平面1111A B C D 的距离的范围是 .三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.在ABC ∆中，内角,,A B C 的对边分别为,,a b c ，设平面向量()()sin cos ,sin ,cos sin ,sin p A B A q B A B =+=-u r r ，且2cos p q C ⋅=u r r（Ⅰ）求C ；（Ⅱ）若c a b =+=ABC ∆中边上的高h .18.某学校研究性学习小组调查学生使用智能手机对学习成绩的影响，部分统计数据如下表：（Ⅰ）根据以上22⨯列联表判断，能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响？（Ⅱ）从学习成绩优秀的12名同学中，随机抽取2名同学，求抽到不使用智能手机的人数X 的分布列及数学期望.参考公式：()()()()()22=n ad bc a b c d a c b d κ-++++，其中=n a b c d +++参考数据：()0P K k ≥0.05 0,。

云南省昆明市2018届高三数学第一次摸底测试试题理2017110201121

云南省昆明市2018届高三数学第一次摸底测试试题理第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.x11.已知集合，集合，则（）A{x0}B{x N1x5}A Bx3A．{0,1,3,4,5}B．{0,1,4,5}C．{1,4,5}D．{1,3,4,5}2.如图，正方形ABCD内的图形来自宝马汽车车标的里面部分，正方形内切圆中的黑色部分和白色部分关于正方形对边中点连线成轴对称，在正方形内随机取一点，则此点取自黑色部分的概率是（）11A．B．C．D．42841z3.已知（其中是虚数单位），则（）i i1z1zA．1 B．0 C．2D．24.设函数f(x)x1x a的图象关于直线x1对称，则a的值为（）A．3 B．2 C. 1 D．-15.二项式(x x1)5展开式中的常数项为（）xA．10 B．-10 C. 5 D．-56.设数列{a}的前n项和为S，若2,S,3a成等差数列，则S的值是（）n n n n5A．-243 B．-242 C.-162 D．2437.执行如图所示的程序框图，若输出n的值为9，则判断框中可填入（）1A．S45?B．S36? C. S45?D．S55?8.设x,y为正数，且3x4y，当3x py时，p的值为（）A．B． C. D．log4log36log2log234339.一个正方体挖去一个多面体所得的几何体的三视图如图所示，其中正视图、左视图和俯视图均为边长等于2的正方形，这个几何体的表面积为（）A．1643B．1645 C. 2043D．204510.已知函数f(x)sin(x)sin(x)（0），且f()0，当取最小值时，623以下命题中假命题是（）A．函数f(x)的图象关于直线x对称12B．是函数的一个零点6C. 函数f(x)的图象可由g(x)3sin2x的图象向左平移个单位得到32D．函数f(x)在[0,]上是增函数1211.已知抛物线C:y24x的焦点为F，准线为l，点A l，线段AF交抛物线C于点B，若FA3FB，则AF（）A．3 B．4 C.6 D．712.已知数列{a}的前n项和为S，且，S 14a2，则数列{a}中的a为a12n n n n n12（）A．20480 B．49152 C. 60152 D．89150第Ⅱ卷二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知向量a(2,1)，a b10，a b52，则b．x3y3014.若实数x,y满足不等式组2x y30，则x y的最大值为．x y115.已知双曲线C的中心为坐标原点，点F(2,0)是双曲线C的一个焦点，过点F作渐近线的垂线l，垂足为M，直线l交y轴于点E，若FM3ME，则双曲线C的方程为．16.体积为183的正三棱锥A BCD的每个顶点都在半径为R的球O的球面上，球心O在此三棱锥内部，且R:BC2:3，点E为线段BD的中点，过点E作球O的截面，则所得截面圆面积的最小值是．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 在ABC中，a,b,c分别是角A,B,C的对边，且a2c23ac b2，3a2b （1）求3a2b的值；（2）若b6，求ABC的面积.18. 如图，在直三棱柱中，，，点分别为ABC A B C BAC900AB AC2M,N111A1C1,AB1的中点.3（1）证明：MN//平面BB C C；11（2）若CM MN，求二面角M CN A的余弦值.19. 某市为了解本市2万名学生的汉字书写水平，在全市范围内进行了汉字听写考试，发现其成绩服从正态分布N(69,49)，现从某校随机抽取了50名学生，将所得成绩整理后，绘制出如图所示的频率分布直方图.（1）估算该校50名学生成绩的平均值x（同一组中的数据用该组区间的中点值作代表）；（2）求这50名学生成绩在[80,100]内的人数；（3）现从该校50名考生成绩在[80,100]的学生中随机抽取两人，该两人成绩排名（从高到低）在全市前26名的人数记为X，求X的分布列和数学期望.参考数据：若X~N(,2)，则p(X)0.6826，p(2X2)0.9544p(3X3)0.997420. 已知动点M(x,y)满足：(x1)2y2(x1)2y222.4（1）求动点 M 的轨迹 E 的方程；（2）设过点 N (1, 0) 的直线l 与曲线 E 交于 A , B 两点，点 A 关于 x 轴的对称点为C （点C与点 B 不重合），证明：直线 BC 恒过定点，并求该定点的坐标.a21. 已知函数 f (x )e x ， g (x ) x 2x ，（其中 a R ， e 为自然对数的底数，2e 2.71828……）.（1）令 h (x )f (x )g ' (x ) ，若h (x )0对任意的 x R 恒成立，求实数 a 的值；nim（2）在（1）的条件下，设 m 为整数，且对于任意正整数 n ，( )m ，求的最小值.nni 1请考生在 22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修 4-4：坐标系与参数方程极坐标系中，O 为极点，半径为 2的圆C 的圆心坐标为 (2, ) .6（1）求圆C 的极坐标方程；（2）设直角坐标系的原点与极点O 重合， x 轴非负关轴与极轴重合，直线l 的参数方程为1 x t2 3y t 82（为参数），由直线上的点向圆引切线，求线线长的最小值.t l C23.选修 4-5：不等式选讲已知函数 f (x )x 2 x 3 .（1）求不等式 f (x ) 3的解集；（2）若不等式 f (x )a 26a 解集非空，求实数 a 的取值范围.5昆明一中全国联考第一期参考答案参考答案（理科数学）命题、审题组教师杨昆华李文清孙思应梁云虹王在方卢碧如凹婷波吕文芬陈泳序一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12答案 B C C A B B A C D C B B1.解析：集合A,1U3,，B0,1,2,3,4,5，所以A I B0,1,4,5，选B.2.解析：设正方形边长为2，则圆半径为1.此时正方形面积为224.图中黑色部分面积为2.则此点取自黑色部分的概率为2，选C.481izi3.解析：因为1i ，所以1z 2，选C.4.解析：12a1所以a 3，选A.r15511555r r r5.解析：通项T C x x C x221r 0，所以r 3，所以常，令r rr155x22数项为C5110，选B.336.解析：据题意得223a12；当n 2时，Sa，当n 1时，2S 23a，所以n n113333a S S a a a a ，即11n n n1n n1n n1222213aa a ，即3n 2，所以nn n122an1数列a是首项a ，公比q 3的等比数列，S5，所以12 n a 1q52135 2421q 13选B.7.解析：模拟执行如图所示的程序框图知，该程序的功能是计算S 12L 945，选A.8.解析：可令3x 4y t，则x log t，3y log t，由3x py 得4p3log t3log43，选C.t3log46l og233log t log34t19.解析：将三视图还原可得下图，所以S 5224252045，选D. 263310. 解析：f xxxxsin cos 3 sin2 23得，由f ( ) 0 3Z，即 3k 1，由 0 知的最小值是 2，当取得最小值时，kk3 33sin2f xx.由 f3 sin 2 3 sin 33 1212 32可得出：函数 f (x )的图象关于直线 x对称，A 为真； 12由 f3 sin 2 066 3可得出： x是函数 f (x ) 的一个零点，B 为真； 6将函数 g x 3 sin 2x 的图象向左平移6个单位得到3sin2f xx 的图象，所以3 C 为假；由复合函数单调性可得 f (x ) 在 0,上是增函数，所以 D 为真，选C.1211.解析：由已知B为AF的三等分点，作BH l于H（如图），则24BHFK，所以33BF BH 43，所以AF 3BF 4，选B.12.解析：由S a有2412a a a ，解得12412a ，故28a22a14，又aSSaa，于是aaaa ，因此数列aa是以n n n n n n n n n n n 221414221212127a 2 2a 14 为首项，公比为 2 的等比数列.得 1 24 2 1 2 1a a，于是nnnnaan 1n11， 22nn因此数列aanan.是以1为首项，1为公差的等差数列，解得1 1nnn ，2n22nnn所以 a 1249152 ，选 B.二、填空题13. 解析：因为 a b 5 2 ，所以2a b50 ，即2 2 2a b a b5 b20 50 250 ，所以所以 b 5 .14. 解析：如图， x y 在点 A (4, 5) 处取得最大值9 .15. 解析：设双曲线C 的方程为：xy2 2221 ，由已知得： FM b ，所以 a b24b 4 3， a 2b而 a 2 4 b 2 ，所以b 2 3 ， a 2 1，所以双曲线C 的方程：y2x 21 316. 设 BC 3k ，则 R 2k k0，因为体积为18 3 的正三棱锥 A BCD 的每个顶点都在半13径为R的球O的球面上，所以9k2h 18 3，得34h24.由2R2h R3k，2 k2得k 2或k 324（舍），所以R 4.由题意知点E为线段BD的中点，从而在△ODB中，OD OB 4，DB 6，解得OE 1697.所以当截面垂直于OE时，截面圆的半径为1673，故截面圆面积最小值为9.三、解答题17.解：（Ⅰ）由cos Ba2c2b23ac3得出：2ac2ac2B，6由3a 2b及正弦定理可得出：3sin A 2sin B，所以sin2sin1A，3638再由3a2b 知 a b ，所以 A 为锐角， cos1 12 2 A， 9 3所以sinsinsin sin coscos sin CA BA BA BA B3 226（Ⅱ）由b 6 及3a 2b 可得出 a 4 ，113 2 2所以Sab sin C46 2 3 2 2 . 2 2 618. 解：（Ⅰ）证明：连接 A B ， BC 1 ，点 M ， N 分别为 A 1C 1 ，A 1B 1的中点，所以 MN 为△ A BC 的一条中位线， MN //BC ，111MN平面 BB C C ， 1 1BC平面1BB C C ，1 1所以 MN // 平面 BB C C .1 12a 2 a 2 4 8（Ⅱ）设 AA 1 a ，则1 MN 1，CM， 2a24420CN5 ， 2a 2a 244由CMMN ，得CM 2MN 2CN 2 ，解得 a 2 ，由题意以点 A 为坐标原点， AB 为 x 轴， AC 为 y 轴，AA 为 z 轴建立空间直角坐标系.12可得 A (0,0,0) ，C (0, 2,0) ， N (1,0, ) ， M (0,1, 2) ，22 2 1 0故 AN （，，）， AC （0，2，0）， CN （1， 2，）， CM (0,1, 2），2 2 设 m （x ，y ，z ）为平面 ANC 的一个法向量，则 m m A C AN0 0，得 m （1，0，2），同理可得平面 MNC 的一个法向量为 n （3，2，2），设二面角 MCNA 的平面角为，cos m,n mnmn332155，15cos cos m,n5，15所以，二面角M CN A的余弦值为515.919.解：（Ⅰ）x450.08550.2650.32750.2850.12950.0868.2（Ⅱ）0.0080.012105010.10.9974（Ⅲ）P3X3=0.9974，则P X900.0013.20.00132000026.所以该市前26名的学生听写考试成绩在90分以上.上述50名考生成绩中90分以上的有0.08504人.随机变量X0,1,2.于是C12X6， P0==C3210C C811P X1==，64C15210C22P X2==.4C15210X的分布列：X012P 13815215182 4E X012.315155数学期望20.解：（Ⅰ）由已知，动点M到点P (1,0)，Q(1,0)的距离之和为22，且PQ 22，所以动点M的轨迹为椭圆，而a 2，c 1，所以b 1，所以，动点M的轨迹E的方程：x22y21.（Ⅱ）设A(x,y)，B(x,y)，则C(x ,y)，由已知得直线l的斜率存在，设斜率为k，则直11221110线l 的方程为： y k (x 1)y k (x 1)由2xy 122 得 (1 2k 2 )x 2 4k 2 x 2k 220，所以4k2xx12212k，2k 22x x1 2212k ，y yy y x yx y直线 BC 的方程为：21() y xy yx x ，所以211 22 122xxxxxx212121 ，x y x y2kx x k (xx ) 2x x(xx )令 y 0 ，则 x 1 22 11 2121 2122yyk (x x ) 2k(xx ) 2211 212，所以直线 BC 与 x 轴交于定点 D (2, 0) . 21. 解：（Ⅰ）因为 g (x )ax1所以 h (x ) e x ax1，由 h (x )0对任意的 xR 恒成立，即 h x ，( ) 0min由 h (x ) e x a ，（1）当 a 0 时， h (x ) e x a0 ， h (x )的单调递增区间为,，所以 x(,0) 时， h (x ) h (0) 0 ，所以不满足题意. （2）当 a 0 时，由 h(x ) e x a0 ，得 x ln axa 时， h (x ) 0 ， x (ln a,) 时， h (x ) 0 ，( ,ln )所以 h (x ) 在区间(,ln a ) 上单调递减，在区间 (ln a ,) 上单调递增，所以h(x)的最小值为h(ln a)a a ln a1.设(a)a a ln a1，所以(a)0，①因为(a)ln a令(a)ln a0得a1，所以(a)在区间(0,1)上单调递增，在区间(1,)上单调递减，所以(a)(1)0，②11由①②得(a)0，则a 1. （Ⅱ）由（Ⅰ）知e x x10，即1x e x，令xk kk （n N*，k0,1,2,,n1）则01 e，n n nkk所以(1)n(e n)n e k，nni12n1n所以()n()n()n()n()n e(n1)e(n2)e2e11 n n n nn i11e1e1n12，1e1e e1e111ni，所以()2nni1又(1)3(2)3(3)3 1，333所以m的最小值为2.第22、23题中任选一题做答，如果多做，则按所做的第一题记分.22.解：（Ⅰ）设M(,)是圆上任意一点，如图，连接OC，并延长与圆C交于点A，当点M异于O，A时，连接OM、MA，直角△MOA中，OM OA cos MOA，即4cos4cos()，66当点M与O，A重合时，也满足上式，所求圆C的极坐标方程为4cos().6（Ⅱ）直线l的普通方程为3x y80，圆心C(3,1)到直线l的距离为d，3318d3r，所以直线l与圆C相离，2故切线长的最小值为32225.23.解：（Ⅰ）由f(x)x2x33可化为：12xx 3 3 2或 x 2 x 3 3 x 2 x 3 3x 2或x 2 x 3 3 解得：x或 2 x 2 或 x2 ，所以，不等式解集为2,.（Ⅱ）因为 f (x )x 2x 3(x 2) (x 3)5所以 5 f (x ) 5，即 f (x ) 的最小值为 5 ，要不等式 f (x ) a 2 6a 解集非空，需 f (x )a 2 6a ，min从而 a 26a 5 0 ，解得 a1或 a 5 ，所以 a的取值范围为,1U5,.13昆明一中全国联考第一期参考答案参考答案（理科数学）命题、审题组教师杨昆华李文清孙思应梁云虹王在方卢碧如凹婷波吕文芬陈泳序一、选择题题号 1 2 3 4 5 6 7 8 9 10 1112答案BCCA B BA CDCB B 24. 解析：集合 A,1U3,， B0,1, 2, 3, 4, 5，所以 A I B0,1, 4, 5，选 B.25. 解析：设正方形边长为 2 ，则圆半径为 1.此时正方形面积为 2 2 4 .图中黑色部分面积为 2 .则此点取自黑色部分的概率为 2 ，选 C.4 81 iz i26. 解析：因为1 i，所以 1 z 2 ，选 C. 27. 解析：12 a1 所以 a 3 ，选 A.r15 55r1 r r15 528. 解析：通项TC x xC xr0 ，所以 r3 ，所以常1 ，令rr2 2 r 155x22数项为C，选 B.33511029. 解析：据题意得 22 3 12Sa ，当 n1时， 2S2 3a ，所以 a；当 n 2 时，nn113 3 3 3 a S Saaaa ，即1 1nnn 1nn 1n n 122 2 21 3 a a a ，即 3 n2，所以nnn 122an 1数列S5，a是首项a ，公比q 3的等比数列，所以12n a 1q 21355 24211q 13选B.30.解析：模拟执行如图所示的程序框图知，该程序的功能是计算S 12L 945，选A.31.解析：可令3x 4y t，则x logt，3y log t，由3x py得4p3log t3log43，选C.t3log46l og233log t log34t132.解析：将三视图还原可得右图，所以S 5224252142045，选D.3333.解析：f x sin x cos x3sin x223得，由f()03Z，即3k 1，由0知的最小值是2，当取得最小值时，kk333sin2f x x.由f3sin23sin33121232可得出：函数f(x)的图象关于直线x对称，A为真；12由f3sin20663可得出：x是函数f(x)的一个零点，B为真；6将函数g x 3sin2x的图象向左平移6个单位得到3sin2f x x的图象，所以3C为假；由复合函数单调性可得f(x)在0,12上是增函数，所以D为真，选C.A4334.解析：由已知B为AF的三等分点，作BH l于H（如图），则BH FK ，所以424BF BH333，所以AF 3BF 4，选B.H21B35. 解析：由 Sa 有 28 24 1 2 124 1 2 a，故aa a ，解得a 22a 1 4 ，K22O F又2 21 4 1 4 a2 2a 1 2 a12a ，因此aSS a a ，于是nnnnnnnnn1数列aa 是以，12a 2 2a 14 为首项，公比为 2 的等比数列.得n 1 n 1 aannn n12 4 2 2aa于是 11，因此数列nn22nnan2n 是以 1为首项， 1为公差的等差数列，解得a nn21 n1n ， an 2n .所以na ，选B.1249152二、填空题36. 解析：因为 a b 5 2 ，所以2a b50 ，即2 2 2a b2ab 505 b20 50 ，所以所以 b 5 .37. 解析：如图， x y 在点 A (4, 5) 处取得最大值9 .x -y +1=0yxy2 2 221，由已知得： FMb ，所abx +3y-3=0 32 12x-y -3=038. 解析：设双曲线 C 的方程为：–6 –5 –4 –3 –2 O–1–11 x23456–2 –315以24b4 ，而 3 a 2 ba 24 b 2 ，所以b 23 ， a 2 1，所以双曲线C 的方程：y2x 21 339. 设 BC 3k ，则 R 2kk0，因为体积为18 3 的正三棱锥 A BCD 的每个顶点都在半1 3径为 R 的球O 的球面上，所以 9k 2h18 3 ，得 34h24R 2h R3k ，.由22k2得 k 2 或 k 3 24 （舍），所以 R 4 .由题意知点 E 为线段 BD 的中点，从而在△ODB 中，OD OB ， DB 6 ，解得OE 16 9 7 .所以当截面垂直于OE 时，截面圆的半径4为 16 73，故截面圆面积最小值为9 .三、解答题 40. 解：（Ⅰ）由cos Ba 2 c 2b 2 3ac 3得出： 2ac 2ac 2B， (2)分 6由3a 2b 及正弦定理可得出：3sin A 2sin B ，所以 21sin A sin ，………4分3 6 3 再由3a2b 知 a b ，所以 A 为锐角， cos1 12 2 A， ………6分9 3所以 sinsinsin sin coscos sin CA BA BA BAB3 26………8分（Ⅱ）由b 6 及3a 2b 可得出 a 4 ，所以113 2 2S ab sin C462 3 2 2 .2 2 6………12分41. 解：（Ⅰ）证明：连接 A B ， BC 1 ，点 M ， N 分别为 A 1C 1 ，A 1B1的中点，所以 MN 为△ A BC 的一条中位线， MN //BC ，111MN平面 BB C C ， 1 1BC平面1BB C C ，1 1所以 MN // 平面 BB C C .………6分1 1162a 2a 2 4 8（Ⅱ）设 AA 1a ，则1CM， MN 1，2a244220CN5 ， 2a a 244由CMMN ，得CM 2 MN 2 CN 2 ，解得 a 2 ，由题意以点 A 为坐标原点， AB 为 x 轴， AC 为 y 轴，AA 为 z 轴建立空间直角坐标系.12可得 A (0,0,0) ，C (0, 2,0) ， N (1,0, ) ， M (0,1, 2) ，22 2故 AN （，，）， AC （0，2，0）， CN （1， 2，）， CM (0,1, 2），1 02 2 设 m （x ，y ，z ）为平面 ANC 的一个法向量，则m m A C AN0 0，得 m （1，0，2），同理可得平面 MNC 的一个法向量为 n （3，2，2），设二面角 M CNA 的平面角为，cos m , nmnmn3 3 0 2 15 5，15cos cos m , n5，15所以，二面角 M CNA 的余弦值为5 15. ………12分42. 解：（ Ⅰ ）x 45 0.08 55 0.2 65 0.32 75 0.2 85 0.12 95 0.08 68.2 ………4分（Ⅱ） 0.008 0.012105010 .………6分1 0.9974（Ⅲ）P 3 X3=0.9974 ，则P X 900.0013 .2 0.0013 20000 26 .所以该市前26名的学生听写考试成绩在90分以上.上述50名考生成绩中90分以上的有0.08504人.随机变量X0,1,2.于是C126， P X0==C321017C C118， P X1=64=C15210C224.P X2==C15210X的分布列：X012P138152151824数学期望E X12. ………12分31515543.解：（Ⅰ）由已知，动点M到点P (1,0)，Q(1,0)的距离之和为22，且PQ 22，所以动点M的轨迹为椭圆，而a 2，c 1，所以b 1，所以，动点M的轨迹E的方程：x22y2 1. (5)分（Ⅱ）设A(x,y)，B(x,y)，则C(x ,y)，由已知得直线l的斜率存在，设斜率为k，112211则直线l的方程为：y k(x 1)(1)y k x由2xy122得(12k2)x24k2x 2k220，所以4k2x x12212k，2k22x x12212k，………8分y y y y x yx y直线BC的方程为：y y 21(x x)，所以y 21x 122122x x x x x x212121，x y x y2kx x k(x x)2x x (xx)令y 0，则122112121212x2y y k(x x)2k(x x)2211212，所以直线BC与x轴交于定点D (2,0) (12)分44.解：（Ⅰ）因为g(x)ax 1所以h(x)e x ax 1，由h(x)0对任意的x R恒成立，即h x ，()0min18由h(x)e x a，（1）当a0时，h(x)e x a0，h(x)的单调递增区间为,，所以x(,0)时，h(x)h(0)0，所以不满足题意.（2）当a0时，由h(x)e x a0，得x ln ax a时，h(x)0，x(ln a,)时，h(x)0，(,ln)所以h(x)在区间(,ln a)上单调递减，在区间(ln a,)上单调递增，所以h(x)的最小值为h(ln a)a a ln a1.设(a)a a ln a1，所以(a)0，①因为(a)ln a令(a)ln a0得a1，所以(a)在区间(0,1)上单调递增，在区间(1,)上单调递减，所以(a)(1)0，②由①②得(a)0，则a 1. ………6分（Ⅱ）由（Ⅰ）知e x x10，即1x e x，令xk kk （n N*，k0,1,2,,n1）则01 e，n n nkk所以(1)(e)en n n k，nn i12n1n所以()n()n()n()n()n e(n1)e(n2)e2e11 n n n nn i11e1e1n12，1e1e e1e111ni，所以()n2ni1又(1)3(2)3(3)3 1，333所以m的最小值为2. ………12分19第 22、23 题中任选一题做答，如果多做，则按所做的第一题记分. 45. 解：（Ⅰ）设 M (,) 是圆上任意一点，如图，连接OC ，并延长与圆C 交于点 A ，当点 M 异于O ， A 时，连接OM 、 MA ，直角△ MOA 中，OM OAcos MOA ，即4 cos4 cos() ，66当点 M 与O ， A 重合时，也满足上式，所求圆C 的极坐标方程为4 cos() .………5分6（Ⅱ）直线l 的普通方程为 3x y 8 0 ，圆心C ( 3,1) 到直线l 的距离为 d ，3 318d3 r ，所以直线l 与圆C 相离，2故切线长的最小值为 32225 .………10分46. 解：（Ⅰ）由 f (x ) x 2 x 3 3 可化为：x 33 x 2或x 2 x 3 3 x 2 x 3 3x 2或 x 2 x 3 3 解得：x 或 2 x 2 或 x2 ，所以，不等式解集为2,. ………5分（Ⅱ）因为 f (x )x 2x 3(x 2) (x 3)5所以 5 f (x ) 5，即 f (x ) 的最小值为 5 ，要不等式 f (x ) a 2 6a 解集非空，需 f (x )a 2 6a ，min从而 a 26a 5 0 ，解得 a1或 a 5 ，所以 a的取值范围为,1U5,.………10分20。

云南省昆明市第一中学2018届高三上学期第一次摸底测试文综地理试题含解析

机密★启用前【考试时间：９月２日９∶００—１１∶３０】昆明第一中学２０１７届高中新课标高三第一次摸底测试文科综合试卷审题人：昆一中高三年级文科综合命题组本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分３００分，考试时间１５０分钟。

注意事项：１答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并请认真填涂准考证号。

２每小题选出答案后，用２Ｂ铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

答在试卷上的答案无效。

第Ⅰ卷（选择题，共１４０分）本卷共３５个小题，每小题４分，共１４０分，在每小题给出的四个选项中，只有一项是符合题目要求的。

读图１“北京及周边地区某月气象卫星遥感动态监测图”，完成１～２题。

１判断此时月份和风向可能是Ａ月偏东风Ｂ月偏西风Ｃ月偏东风Ｄ月偏西风２根据图示信息可知，北京及周边地区Ａ冷空气活动较强Ｂ水平气压梯度较小Ｃ近地面对流较强Ｄ大气湿度明显变小图２为我国新疆玛纳斯河流域２０００—２０１０年年均温、年降水和出山径流（河流由山区进入较平地区的径流量）变化图，读图完成３～４题。

３关于图中相关事项叙述正确的是Ａ出山径流量逐年递减Ｂ出山径流量与年降水量变化呈正相关Ｃ年降水量逐年递增Ｄ年均温变化能反映全球气候变化趋势４据图示信息可推测玛纳斯河山前段径流主要来自Ａ大气降水Ｂ地下水Ｃ湖泊水Ｄ冰雪融水阿富汗是一个内陆国，牧业是重要的经济支柱之一。

图３为阿富汗游牧业迁移路线图，读图完成５～６题。

５阿富汗的气候特征是Ａ终年温和湿润Ｂ终年炎热干燥Ｃ冬冷夏热，全年降水少Ｄ夏季炎热干燥，冬季温暖多雨６据图中信息，下列推测最有可能的是Ａ降水多少决定了游牧的迁移Ｂ游牧迁移的时间是春、秋季Ｃ甲为冬季牧场，乙为夏季牧场Ｄ游牧迁移路线一般沿山脊行进２０１６年３月，湄公河水位降至近９０年最低。

越南南部的湄公河三角洲正遭受百年来最严重旱情，中国政府应越南政府的请求向湄公河流域国家提供了“巨大帮助”。

2018届云南省昆明市高三摸底调研测试理科数学试题

2018届云南省昆明市高三摸底调研测试理科数学试题本试卷满分150分，考试用时120分钟。

注意事项:1.答卷前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一井交回。

一、选择题:本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

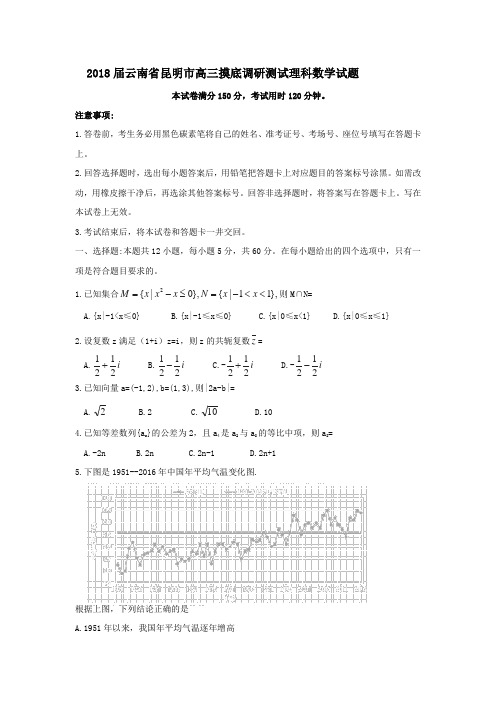
1.已知集合},11|{},0|{2<<-=≤-=x x N x x x M 则M ∩N=A.{x|-1<x ≤0}B.{x|-1≤x ≤0}C.{x|0≤x<1}D.{x|0≤x ≤1}2.设复数z 满足（1+i ）z=i ，则z 的共轭复数z = A.i 2121+ B.i 2121- C.-i 2121+ D.-i 2121- 3.已知向量a=(-1,2),b=(1,3),则|2a-b|= A.2 B.2 C.10 D.104.已知等差数列{a n }的公差为2，且a 4是a 2与a 8的等比中项，则a 8=A.-2nB.2nC.2n-1D.2n+15.下图是1951--2016年中国年平均气温变化图.根据上图，下列结论正确的是A.1951年以来，我国年平均气温逐年增高B.1951年以来，我国年平均气温在2016年再创新高C.2000年以来，我国年平均气温都高于1981-2010年的平均值D.2000年以来，我国年平均气温的平均值高于1981-2010年的平均值6.古人采取“用臼春米”的方法脱去稻谷的外壳，获得可供食用的大米，用于春米的“石臼”由一块正方体石料凿去一部分做成(凿去的部分可看作一个简单组合体).一个“石臼”的三视图如图所示，则凿去部分的体积为A.63πB.72πC.79πD.99π7.双曲线)0,0(1:2222>>=-b a by a x C 的左，右焦点分别为F 1,F 2,,以F 1F 2为直径的圆与C 在第一象限交于点P 。

2017-2018学年云南省昆明一中高三(上)第一次双基检测数学试卷(理科) Word版含解析

2017-2018学年云南省昆明一中高三（上）第一次双基检测数学试卷（理科）一、选择题（共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合A={x|x2﹣x≤0}，B={x|﹣2≤x≤0}，则A∩∁R B=（）A．∅B．{x∈R|x≠0} C．{x|0＜x≤1} D．R2．复数（i是虚数单位）在复平面上对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．对四组数据进行统计，获得以下散点图，关于其相关系数的比较，正确的是（）A．r2＜r4＜0＜r3＜r1B．r4＜r2＜0＜r1＜r3C．r4＜r2＜0＜r3＜r1D．r2＜r4＜0＜r1＜r34．已知双曲线﹣=1的一条渐近线与直线l：2x+y+2=0垂直，则此双曲线的离心率是（）A．B．C．D．45．有以下四个p1：∃x0∈（﹣∞，0），4＜5，p2：在锐角三角形ABC中，若tanA＞tanB，则A＞B；p3：∃x∈R，cosx0≥1；p4：∀x∈R，x2﹣x+1＞0其中假是（）A．p1B．p2C．p3D．p46．设x，y满足，则z=x+2y的最小值等于（）A．﹣3 B．3 C．6 D．127．已知数列{lg（a n+1）}为等差数列，且a1=9，a4=9999，则数列{a n}的前3项和S3=（）A．1113 B．1110 C．1107 D．9998．一个组合体的三视图如图所示，则该几何体的体积为（）A．16 B．20 C．D．9．执行如图所示的程序框图，若输出y=2，则输出的x的取值范围是（）A．B．（12，25]C．（14，26]D．10．已知四面体ABCD的棱长均为，则下列结论中错误的是（）A．AC⊥BDB．若该四面体的各顶点在同一球面上，则该球的体积为3πC．直线AB与平面BCD所成的角的余弦值为D．该四面体的体积为11．已知函数f（x）=|2x﹣2|，若m≠n，且f（m）=f（n），则m+n的取值范围是（）A．（1，+∞）B．（2，+∞）C．（﹣∞，1）D．（﹣∞，2）12．在△ABC中，D为BC边中点，O为△ABC内一点，且=2+，则=（）A．B．C．2 D．1二、填空题（共4小题，每小题5分，满分20分）13．已知函数f（x）=Asin（x+φ）（A＞0，|φ|＜），当x=π时，f（x）取最大值，则φ=．14．现有5人坐成一排，任选其中3人相互调整位置（着3人中任何一人不能做回原来的位置），其余2人位置不变，则不同的调整的方案的种数有．15．已知抛物线y2=2x，过焦点F的直线与抛物线交于A，B两点，过A，B分别作y轴的垂线，垂足分别为C，D，则|AC|+|BD|的最小值为．16．已知数列{a n}满足a1=2，a n+1=a n+n（n∈N*），则a n的最小值是．三、解答题（共6小题，解答时应写出必要的文字说明，证明过程或演算步骤）17．在△ABC中，已知BC=2，=，sinC=，求BC边上的中线AD的长．18．已知数列{a n}的前n项和S n=2a n﹣2（n∈N*），数列{b n}的前n项和为T n，且b n=2n+1．（1）求出数列{a n}的通项a n和数列{b n}的前n项和T n；（2）求数列{}的前n项和G n．19．有A，B，C，D，E五位同学参加英语口语竞赛培训，现分别从A，B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据，这两组数据的样本茎叶图如图所示．（1）现要从A，B中选派一人参加英语口语竞赛，从平均水平个方差的角度考虑，你认为派哪位同学参加较合适？请说明理由；（2）若从参加培训的5位同学中任选二人参加英语口语竞赛，求A，B二人都没有参加竞赛的概率．20．在三棱锥A﹣BCD中，底面BCD是正三角形，AC=BD=2，AB=AD=，O为BC的中点．（1）求证：AO⊥平面BCD；（2）求二面角A﹣DC﹣B的余弦值．21．已知椭圆C：+=1（a＞b＞0）的短轴长为2，且离心率为．（1）求椭圆C的方程；（2）设点F为椭圆C的右焦点，过点F的直线交该椭圆于P，Q两点（P，Q不是长轴的端点），线段PQ的垂直平分线交y轴于点M（0，y0），求y0的取值范围．22．已知函数f（x）=lnx+ax2﹣（2a+1）x﹣1（a为常数，且a≠0）．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）当x∈（0，e]时，f（x）≤0，求实数a的取值范围．2014-2015学年云南省昆明一中高三（上）第一次双基检测数学试卷（理科）参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知集合A={x|x2﹣x≤0}，B={x|﹣2≤x≤0}，则A∩∁R B=（）A．∅B．{x∈R|x≠0} C．{x|0＜x≤1} D．R考点：交、并、补集的混合运算．专题：集合．分析：分别求出关于集合A，集合B的补集，再取交集即可．解答：解：∵集合A={x|x2﹣x≤0}={x|0≤x≤1}，B={x|﹣2≤x≤0}，∁R B=（0，+∞）∪（﹣∞，﹣2），则A∩∁R B={x|0＜x≤1}，故选：C．点评：本题考查了集合的交、补集的混合运算，是一道基础题．2．复数（i是虚数单位）在复平面上对应的点位于（）A．第一象限B．第二象限C．第三象限D．第四象限考点：复数代数形式的乘除运算．专题：计算题．分析：将复数的分子分母同乘以1+i，利用多项式的乘法分子展开，求出对应的点的坐标，判断出所在的象限即可．解答：解：由题，所以在复平面上对应的点位于第一象限．故选A．点评：本题主要考查了复数代数形式的乘除运算，复数的除法运算法则：分子、分母同乘以分母的共轭复数，属于基础题．3．对四组数据进行统计，获得以下散点图，关于其相关系数的比较，正确的是（）A．r2＜r4＜0＜r3＜r1B．r4＜r2＜0＜r1＜r3C．r4＜r2＜0＜r3＜r1D．r2＜r4＜0＜r1＜r3考点：相关系数．专题：概率与统计．分析：根据题目给出的散点图，先判断是正相关还是负相关，然后根据点的集中程度分析相关系数的大小．解答：解：由给出的四组数据的散点图可以看出，图1和图3是正相关，相关系数大于0，图2和图4是负相关，相关系数小于0，图1和图2的点相对更加集中，所以相关性要强，所以r1接近于1，r2接近于﹣1，由此可得r2＜r4＜r3＜r1．故选：A点评：本题考查了两个变量的线性相关，考查了相关系数，散点分布在左下角至右上角，说明两个变量正相关；分布在左上角至右下角，说明两个变量负相关，散点越集中在一条直线附近，相关系数越接近于1（或﹣1），此题是基础题．4．已知双曲线﹣=1的一条渐近线与直线l：2x+y+2=0垂直，则此双曲线的离心率是（）A．B．C．D．4考点：双曲线的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：由双曲线的渐近线斜率即可计算该双曲线的离心率，本题中已知渐近线与直线2x+y+2=0垂直，故=，再利用c2=a2+b2，e=即可得双曲线的离心率．解答：解：双曲线﹣=1的一条渐近线方程为y=±x，∵渐近线与直线2x+y+2=0垂直，故渐近线的斜率为，∴=，即a2=4b2=4（c2﹣a2），即5a2=4c2，e2=双曲线的离心率e==故选：B．点评：本题考考查了双曲线的标准方程及其几何性质，双曲线渐近线与离心率间的关系，求双曲线离心率的一般方法．5．有以下四个p1：∃x0∈（﹣∞，0），4＜5，p2：在锐角三角形ABC中，若tanA＞tanB，则A＞B；p3：∃x∈R，cosx0≥1；p4：∀x∈R，x2﹣x+1＞0其中假是（）A．p1B．p2C．p3D．p4考点：的真假判断与应用．专题：简易逻辑．分析：根据全称和特称的性质分别进行判断即可．解答：解：p1：当x0∈（﹣∞，0），幂函数f（x）=x在（0，+∞）上为减函数，∴4＞5，错误．为假p2：在锐角三角形ABC中，函数y=tanx为增函数，若tanA＞tanB，则A＞B；正确，为真．p3：∃x=2kπ，k∈Z，有cosx0≥1成立；正确，为真．p4：∀x∈R，x2﹣x+1=（x﹣）2+＞0，正确，为真．故p1是假，故选：A点评：本题主要考查的真假判断，根据全称和特称的性质是解决本题的关键．6．设x，y满足，则z=x+2y的最小值等于（）A．﹣3 B．3 C．6 D．12考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用z的几何意义即可得到结论．解答：解：作出不等式组对应的平面区域，由z=x+2y，得y=，平移直线y=，由图象可知当直线经过点C时，直线y=的截距最小，此时z最小，由，得，即C（1，1）此时z=1+2×1=3．故选：B．点评：本题主要考查线性规划的应用，利用图象平行求得目标函数的最小值，利用数形结合是解决线性规划问题中的基本方法．7．已知数列{lg（a n+1）}为等差数列，且a1=9，a4=9999，则数列{a n}的前3项和S3=（）A．1113 B．1110 C．1107 D．999考点：等差数列的前n项和．专题：等差数列与等比数列．分析：根据等差数列的通项公式进行求解即可．解答：解：∵数列{lg（a n+1）}为等差数列，∴设数列{lg（a n+1）}为等差数列的公差为d，则lg（a4+1）=lg（a1+1）+3d，即lg10000=lg10+3d，则4=1+3d，解得d=1，则lg（a n+1）=lg10+n﹣1=1+n﹣1=n，则a n+1=10n，则a n=10n﹣1，则数列{a n}的前3项和S3=10﹣1+102﹣1+103﹣1=1110﹣3=1107，故选：C点评：本题主要考查数列求和的计算，根据等差数列求出数列的通项公式是解决本题的关键．8．一个组合体的三视图如图所示，则该几何体的体积为（）A．16 B．20 C．D．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：由已知中的三视图，可知该几何体是以俯视图为底面的四棱锥和四棱柱的组合体，求出它们的体积，相加可得答案．解答：解：由已知中的三视图，可知该几何体是以俯视图为底面的四棱锥和四棱柱的组合体，其底面面积S=2×2=4，棱柱的高h=4，棱锥的高h=5﹣4=1，∴棱柱的体积为4×4=16，棱锥体积为×4×1=，故组合体的体积V=16+=，故选：C点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．9．执行如图所示的程序框图，若输出y=2，则输出的x的取值范围是（）A．B．（12，25]C．（14，26]D．考点：程序框图．专题：图表型；算法和程序框图．分析：由框图知，此程序输出的y是循环次数，循环退出的条件是x＞51，由此关系得出不等式，求出x的取值范围即可．解答：解：当输出y=2时，应满足，得12＜x≤25．故选：B．点评：本题考查循环结构，解题的关键是根据框图得出其运算律，从而得到x所满足的不等式，解不等式求出要求的范围，由运算规则得出不等式组是本题的难点．10．已知四面体ABCD的棱长均为，则下列结论中错误的是（）A．AC⊥BDB．若该四面体的各顶点在同一球面上，则该球的体积为3πC．直线AB与平面BCD所成的角的余弦值为D．该四面体的体积为考点：棱锥的结构特征．专题：空间位置关系与距离．分析：分别对A、B、C、D各个选项进行判断即可．解答：解：对于A，如图②：在等边三角形BCD中，BM为CD边上的高，再在四面体ABCD中，过A作AH⊥平面BCD 于点H，则H为底面正三角形BCD的重心，∴DB⊥AH，BD垂直于过CH的直线，CH、AH交于H，∴BD⊥平面ACH，∴BD⊥AC，故A正确；对于选项B，如图①：，将四面体补成正方体，则正方体的棱长是1，正方体的对角线长为：，则此球的体积为：π×（）3=π，故B错误；对于选项C，如图②：在等边三角形BCD中，BM为CD边上的高，再在四面体ABCD中，过A作AH⊥平面BCD 于点H，则H为底面正三角形BCD的重心，则∠ABH=α，就是AB在平面BCD所成角，棱长为，由BM为CD边上的高，则BM=，在Rt△ABH中，则BH=BM=×=，∴cosα===，故C正确；对于D，如图②：由选项C得：AH==，S△BCD=×BM×DC=××=，V A﹣BCD=××=，故D正确；故选：B．点评：本题是中档题，考查空间想象能力，考查四面体的体积公式，选项B的判断较难，正四面体的外接球转化为正方体外接球，使得问题的难度得到降低，问题得到解决，注意正方体的对角线就是球的直径，也是比较重要的，选项D和选项C联合判断即可．11．已知函数f（x）=|2x﹣2|，若m≠n，且f（m）=f（n），则m+n的取值范围是（）A．（1，+∞）B．（2，+∞）C．（﹣∞，1）D．（﹣∞，2）考点：指数函数的图像变换．专题：函数的性质及应用；不等式的解法及应用．分析：由题意f（x）=|2x﹣2|，由f（m）=f（n），可得2﹣2m=2n﹣2，故2m+2n=4，再利用基本不等式求解．解答：解：不妨设m＜n，由f（m）=f（n），可得2﹣2m=2n﹣2，∴2m+2n=4，∴4=2m+2n=≥，当且仅当2m=2n时，即m=n时取等号，而m≠n，故上述等号不成立，∴2m+n＜4，∴m+n＜2∴m+n的取值范围是（﹣∞，2）故选：D．点评：此题考查了利用绝对值的性质脱去绝对值，同时考查基本不等式的应用，注意，利用基本不等式要验证等号成立的条件．12．在△ABC中，D为BC边中点，O为△ABC内一点，且=2+，则=（）A．B．C．2 D．1考点：向量在几何中的应用；向量加减混合运算及其几何意义．专题：平面向量及应用．分析：先根据所给的式子进行变形，再由题意和向量加法的四边形法则，得到，即：．结合三角形的面积关系判断四个小三角形的面积都相等即可．解答：解：由=2+，得﹣=2，即，∵D为BC边中点，∴，则，即O是AD的中点，则S△AOB=S△ODB，S△AOC=S△ODC，S△OBD=S△ODC，即四个小三角形的面积都相等，则=1，故选：D点评：本题主要考查向量在几何中的应用，根据向量的加法法则，求出O是AD的中点是解决本题的关键．二、填空题（共4小题，每小题5分，满分20分）13．已知函数f（x）=Asin（x+φ）（A＞0，|φ|＜），当x=π时，f（x）取最大值，则φ=﹣．考点：正弦函数的图象．专题：三角函数的图像与性质．分析：由题意可得+φ=2kπ+，k∈Z，再结合|φ|＜，可得φ的值．解答：解：由题意可得+φ=2kπ+，k∈Z，即φ=2kπ﹣，再结合|φ|＜，可得φ=﹣，故答案为：﹣．点评：本题主要考查正弦函数的最值，属于基础题．14．现有5人坐成一排，任选其中3人相互调整位置（着3人中任何一人不能做回原来的位置），其余2人位置不变，则不同的调整的方案的种数有20．考点：计数原理的应用．专题：排列组合．分析：先考虑从5人中任选3人的方法数，再考虑3人位置全调的方法数，利用分步计数原理可求．解答：解：从5人中任选3人有C53种，3人位置全调，由于不能是自己原来的位置，因此有A22种，故有C53A22=20种．故答案为：20．点评：本题主要考查排列组合知识，关键是问题的等价转化．15．已知抛物线y2=2x，过焦点F的直线与抛物线交于A，B两点，过A，B分别作y轴的垂线，垂足分别为C，D，则|AC|+|BD|的最小值为1．考点：抛物线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：求得抛物线的焦点和准线方程，由抛物线的定义，可得|AC|+|BD|=|AF|+|BF|﹣1=|AB|﹣1，求得|AB|的最小值即可．解答：解：抛物线y 2=2x 的焦点F （，0），准线方程为x=﹣，由抛物线的定义可得，|AF|=|AC|+，|BF|=|BD|+，即有|AC|+|BD|=|AF|+|BF|﹣1 =|AB|﹣1，当直线AB ⊥x 轴时，|AB|最小．令x=，则y 2=1，解得y=±1，即有|AB|min =2，则|AC|+|BD|的最小值为1．故答案为：1．点评：本题考查抛物线的定义、方程和性质，主要考查定义法及运算能力，属于中档题．16．已知数列{a n }满足a 1=2，a n+1=a n +n （n ∈N *），则a n 的最小值是 2 ．考点：数列递推式．专题：点列、递归数列与数学归纳法．分析：通过a n+1=a n +n 可知数列{a n }是递增数列，进而可得结论．解答：解：∵a n+1=a n +n ，∴a n+1﹣a n =n ＞0， ∴数列{a n }是递增数列， ∴a n 的最小值即为a 1=2，故答案为：2．点评：本题考查数列的简单性质，注意解题方法的积累，属于基础题．三、解答题（共6小题，解答时应写出必要的文字说明，证明过程或演算步骤） 17．在△ABC 中，已知BC=2，=，sinC=，求BC 边上的中线AD 的长．考点：解三角形．专题：解三角形．分析：首先利用余弦定理求出AC 和AB 的长度，然后在△ACD 中利用余弦定理求出AD 的长度．解答：解：因为sinC=，C 是三角形的内角，所以cosC=，设AB=3x ，AC=4x ，3x+4x＞2，则＜x ＜2，所以由余弦定理得到16x2+4﹣16x×=9x2，解得x=1或x=，所以AB=3，AC=4或者AB=，AC=；当AC=4时，在△ACD中，AD2=AC2+CD2﹣2AC×CDcosC=16+1﹣=，所以AD=；当AC=时，在△ACD中，AD2=AC2+CD2﹣2AC×CDcosC==，所以AD=．点评：本题主要考查了余弦定理在解三角形中的应用，关键是熟练运用余弦定理．18．已知数列{a n}的前n项和S n=2a n﹣2（n∈N*），数列{b n}的前n项和为T n，且b n=2n+1．（1）求出数列{a n}的通项a n和数列{b n}的前n项和T n；（2）求数列{}的前n项和G n．考点：数列的求和．专题：等差数列与等比数列．分析：（1）通过S n=2a n﹣2与S n+1=2a n+1﹣2作差、整理得a n+1=2a n，进而可知数列{a n}的通项a n=2n；利用等差数列的求和公式计算可得T n=n（n+2）；（2）通过（1）、裂项可知=（﹣），并项相加即得结论．解答：解：（1）∵S n=2a n﹣2（n∈N*），∴S n+1=2a n+1﹣2，两式相减得：a n+1=2a n+1﹣2a n，整理得：a n+1=2a n，又∵a1=2a1﹣2，即a1=2，∴a n=2•2n﹣1=2n；∵b n=2n+1，∴T n==n（n+2）；（2）由（1）得==（﹣），∴G n=（1﹣+﹣+﹣+…+﹣）=（1+﹣﹣）=﹣．点评：本题考查数列的通项及前n项和，考查运算求解能力，注意解题方法的积累，属于中档题．19．有A，B，C，D，E五位同学参加英语口语竞赛培训，现分别从A，B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据，这两组数据的样本茎叶图如图所示．（1）现要从A，B中选派一人参加英语口语竞赛，从平均水平个方差的角度考虑，你认为派哪位同学参加较合适？请说明理由；（2）若从参加培训的5位同学中任选二人参加英语口语竞赛，求A，B二人都没有参加竞赛的概率．考点：列举法计算基本事件数及事件发生的概率；茎叶图．专题：概率与统计．分析：（1）根据所给的数据做出两个人的平均数和方差，把平均数和方差进行比较，得到两个人的平均数相等，然后根据方差是反映稳定程度的，比较方差，越小说明越稳定；（2）从5人中任意派两人的可能情况有10种，每种结果出现的可能性相同，记“A，B二人都没有参加竞赛”为事件M，则M包含的结果有3种，由等可能事件的概率可求．解答：解：（1）派B参加比较合适．理由如下：=（75+80+80+83+85+90+92+95）=85，=（78+79+80+83+85+90+92+95）=85，S2A==41；S2B==35.5∵=，S2B＜S2A，∴B的成绩较稳定，派B参加比较合适．（2）从参加培训的5位同学中任派两个共有：（A，B），（A，C），（A，D），（A，E），（B，C），（B，D），（B，E），（C，D），（C，E），（D，E）共10种情况；A、B两人都不参加（C，D），（C，E），（D，E）有3种．所以A，B二人都没有参加竞赛的概率P=点评：对于两组数据，通常要求的是这组数据的方差和平均数，用这两个特征数来表示分别表示两组数据的特征，即平均水平和稳定程度．20．在三棱锥A﹣BCD中，底面BCD是正三角形，AC=BD=2，AB=AD=，O为BC的中点．（1）求证：AO⊥平面BCD；（2）求二面角A﹣DC﹣B的余弦值．考点：直线与平面垂直的判定；棱锥的结构特征．专题：空间位置关系与距离；空间角．分析：（1）由已知得AO⊥BD，AO⊥CO，由此能证明AO⊥平面BCD．（2）以O为原点，OB为x轴，OC为y轴，OA为z轴，建立空间直角坐标系，利用向量法能求出二面角A﹣DC﹣B的余弦值．解答：解：（1）证明：∵在三棱锥A﹣BCD中，底面BCD是正三角形，O为BD的中点，∴AO⊥BD，连结CO，∵AC=BD=2，AB=AD=，∴AO==1，CO=，∴AO2+CO2=AC2，∴AO⊥CO，又BD∩CO=O，∴AO⊥平面BCD．（2）解：以O为原点，OB为x轴，OC为y轴，OA为z轴，建立空间直角坐标系，A（0，0，1），D（﹣2，0，0），C（0，，0），B（1，0，0），=（﹣2，0，﹣1），=（0，，﹣1），设平面ADC的法向量=（x，y，z），则，取x=1，得=（1，﹣，﹣2），平面BDC的法向量=（0，0，1），cos＜，＞==﹣，∵二面角A﹣DC﹣B是锐二面角，∴二面角A﹣DC﹣B的余弦值为．点评：本题考查直线与平面垂直的证明，考查二面角的余弦值的求法，解题时要注意向量法的合理运用，属于中档题．21．已知椭圆C：+=1（a＞b＞0）的短轴长为2，且离心率为．（1）求椭圆C的方程；（2）设点F为椭圆C的右焦点，过点F的直线交该椭圆于P，Q两点（P，Q不是长轴的端点），线段PQ的垂直平分线交y轴于点M（0，y0），求y0的取值范围．考点：椭圆的简单性质．专题：直线与圆；圆锥曲线的定义、性质与方程．分析：（1）由题意可得b=，e==，a2﹣b2=c2，解方程可得a=2，进而得到椭圆方程；（2）分类讨论，设直线MN的方程为y=k（x﹣1）（k≠0），代入椭圆方程，求出线段MN的垂直平分线方程，令x=0，得y0==，利用基本不等式，即可求y的取值范围．解答：解：（1）由短轴长为2，且离心率为．可得b=，e==，a2﹣b2=c2，解得a=2，c=1．则椭圆的方程为+=1；（2）当PQ⊥x轴时，显然y0=0．当PQ与x轴不垂直时，可设直线PQ的方程为y=k（x﹣1）（k≠0）．由消去y整理得（3+4k2）x2﹣8k2x+4（k2﹣3）=0．设P（x1，y1），Q（x2，y2），线段PQ的中点为D（x3，y3），则x1+x2=．所以x3==，y3=k（x3﹣1）=，线段PQ的垂直平分线方程为y+=﹣（x﹣），在上述方程中令x=0，得y0==当k＜0时，+4k≤﹣4；当k＞0时，+4k≥4．所以﹣≤y0＜0，或0＜y0≤．综上y0的取值范围是．点评：本题考查椭圆的方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查基本不等式的运用，确定线段MN的垂直平分线方程是关键．22．已知函数f（x）=lnx+ax2﹣（2a+1）x﹣1（a为常数，且a≠0）．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）当x∈（0，e]时，f（x）≤0，求实数a的取值范围．考点：利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：导数的综合应用．分析：（Ⅰ）把a=1代入函数解析式，求其导函数，由导函数的符号确定原函数的单调区间；（Ⅱ）求出原函数的导函数，得到导函数的零点1和，然后分多种情况进行讨论，求出函数在（0，e]上的最大值，由最大值小于等于0求得a的范围，最后去并集得答案．解答：解：（Ⅰ）当a=1时，f（x）=lnx+x2﹣3x﹣1，=（x＞0），当x，（1，+∞）时，f′（x）＞0，当x时，f′（x）＜0．∴f（x）在上为增函数；在上为减函数；（Ⅱ）由f（x）=lnx+ax2﹣（2a+1）x﹣1，得==．令g（x）=（x﹣1）（2ax﹣1），当a=0时，x∈（0，1）时，f′（x）＞0．x∈（1，e）时f′（x）＜0，∴函数f（x）在（0，e]上有最大值为f（1）=﹣a﹣2．由﹣a﹣2≤0，得a≥﹣2，∴a=0；当，即时，g（x）≥0，f′（x）≥0，函数f（x）在（0，e]上得到递增，当x=e时函数有最大值为lne+ae2﹣（2a+1）e﹣1=ae2﹣2ae ﹣e，由ae2﹣2ae﹣e≤0，得a．∴；当＜0，即a＜0时，若x∈（0，1），f′（x）＞0，x∈（1，e），f′（x）＜0，∴在（0，e]上有最大值为f（1）=ln1+a﹣2a﹣1﹣1=﹣a﹣2．由﹣a﹣2≤0，得a≥﹣2．∴﹣2≤a＜0；当0＜＜1，即a时，x∈（0，），（1，e）时，f′（x）＞0．x∈时f′（x）＜0，∴函数f（x）在（0，e]上有最大值为f（）与f（e）的最大者，=．f（e）=ae2﹣2ae﹣e，f（e）＞，∴函数f（x）在（0，e]上有最大值为ae2﹣2ae﹣e，由ae2﹣2ae﹣e≤0，得a．∴；当1＜＜e，即＜a＜时，x∈（0，1），（，e）时，f′（x）＞0．x∈时f′（x）＜0，∴函数f（x）在（0，e]上有最大值为f（1）与f（e）的最大者，f（1）=ln1+a﹣2a﹣1﹣1=﹣a﹣2，f（e）=ae2﹣2ae﹣e，由，解得：，∴；当≥e，即0时，x∈（0，1）时，f′（x）＞0．x∈（1，e）时f′（x）＜0，∴函数f（x）在（0，e]上有最大值为f（1）=﹣a﹣2．由﹣a﹣2≤0，得a≥﹣2，∴0．综上，实数a的取值范围是．点评：本题考查了利用导数研究函数的单调性，考查了利用导数求函数的最值，考查了学生的计算能力，正确分类是解答该题的关键，属于难度较大的题目．。

云南省昆明一中高三上学期第一次摸底测试数学(理)试题 Word版含解析

昆明第一中学2018届高中新课标高三第一次摸底测试理科数学第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，集合，则（）A. B. C. D.【答案】B【解析】集合集合，故选B.2. 如图，正方形内的图形来自宝马汽车车标的里面部分，正方形内切圆中的黑色部分和白色部分关于正方形对边中点连线成轴对称，在正方形内随机取一点，则此点取自黑色部分的概率是（）A. B. C. D.【答案】C3. 已知（其中是虚数单位），则（）A. B. C. D.【答案】C【解析】,，故选C. 4. 设函数的图象关于直线对称，则的值为（）A. B. C. D.【答案】A【解析】若，因为函数的图象关于直线对称，所以若，因为函数的图象关于直线对称，所以（与前提条件矛盾）所以故选择A小提示：涉及绝对值的问题，一般都是将每个绝对值的零点作为分界点，进行讨论。

5. 二项式展开式中的常数项为（）A. B. C. D.【答案】B【解析】展开式的通项为，令得，所以展开式中的常数项为，故选B.【方法点晴】本题主要考查二项展开式定理的通项与系数，属于简单题. 二项展开式定理的问题也是高考命题热点之一，关于二项式定理的命题方向比较明确，主要从以下几个方面命题：（1）考查二项展开式的通项公式；（可以考查某一项，也可考查某一项的系数）（2）考查各项系数和和各项的二项式系数和；（3）二项展开式定理的应用.6. 设数列的前项和为，若成等差数列，则的值是（）A. B. C. D.【答案】B【解析】因为成等差数列，所以，当时，；当时，，即，即，数列是首项，公比的等比数列，，故选B.7. 执行如图所示的程序框图，若输出的值为，则判断框中可填入（）A. B. C. D.【答案】A【解析】模拟执行如图所示的程序框图知，该程序的功能是计算，选A.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.8. 设为正数，且，当时，的值为（）A. B. C. D.【答案】C【解析】令，则，由得，故选C.9. 一个正方体挖去一个多面体所得的几何体的三视图如图所示，其中正视图、左视图和俯视图均为边长等于的正方形，这个几何体的表面积为（）A. B. C. D.【答案】D【解析】由三视图可知，该几何体是棱长为的正方形的内部挖去一个底面为边长为的正四棱锥，将三视图还原可得如图，可得其表面积为，，故选D.【方法点睛】本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.10. 已知函数（），且，当取最小值时，以下命题中假命题是（）A. 函数的图象关于直线对称B. 是函数的一个零点C. 函数的图象可由的图象向左平移个单位得到D. 函数在上是增函数【答案】C【解析】，由得，即，由知的最小值是2，当取得最小值时，.由可得出：函数的图象关于直线对称，A为真；由可得出：是函数的一个零点，B为真；将函数的图象向左平移个单位得到的图象，所以C为假；由复合函数单调性可得在上是增函数，所以D为真，选C.【点睛】函数的性质(1).(2)周期(3)由求对称轴(4)由求增区间; 由求减区间11. 已知抛物线的焦点为，准线为，点，线段交抛物线于点，若，则（）A. B. C. D.【答案】B【解析】由已知为的三等分，作于，如图，则，，故选B.12. 已知数列的前项和为，且，，则数列中的为（）A. B. C. D.【答案】B【解析】由有，解得，故，又，于是，因此数列是以为首项，公比为的等比数列，得，于是，因此数列是以为首项，为公差的等差数列，解得，，故选B.【方法点晴】本题主要考查等差数列的定义以及已知数列的递推公式求通项，属于中档题.由数列的递推公式求通项常用的方法有：累加法、累乘法、构造法，已知数列前项和与第项关系，求数列通项公式，常用公式，将所给条件化为关于前项和的递推关系或是关于第项的递推关系，若满足等比数列或等差数列定义，用等比数列或等差数列通项公式求出数列的通项公式，否则适当变形构造等比或等数列求通项公式. 在利用与通项的关系求的过程中，一定要注意的情况.，进而得出的通项公式.第Ⅱ卷二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 已知向量，，，则__________．【答案】【解析】由可得，，即，，故答案为.14. 若实数满足不等式组，则的最大值为__________．【答案】【解析】画出不等式组所表示的可行域，如图，由图知平移直线，当直线经过点时，直线在轴上的截距最大，即在点处取得最大值，故答案为.【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.15. 已知双曲线的中心为坐标原点，点是双曲线的一个焦点，过点作渐近线的垂线，垂足为，直线交轴于点，若，则双曲线的方程为__________．【答案】【解析】设双曲线的方程为:，由已知得：由点到直线的距离公式可得由及勾股定理可得，又因为与渐近线垂直，结合可得双曲线的方程：，故答案为.16. 体积为的正三棱锥的每个顶点都在半径为的球的球面上，球心在此三棱锥内部，且，点为线段的中点，过点作球的截面，则所得截面圆面积的最小值是_________．【答案】三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 在中，分别是角的对边，且，（1）求的值；（2）若，求的面积.【答案】（1）；（2）.【解析】试题分析：（1）由余弦定理利用可得由，，再由正弦定理可得，从而可得，再利用三角形内角和定理、诱导公式、及两角和的正弦公式可得的值；（2）由及可得出，利用（1）的结论以及三角形面积公式可得结果.试题解析：（1）由得出：，由及正弦定理可得出：，所以，再由知，所以为锐角，，所以（2）由及可得出，所以.18. 如图，在直三棱柱中，，，点分别为的中点.（1）证明：平面；（2）若，求二面角的余弦值.【答案】（1）证明见解析；（2）.【解析】试题分析：（1）连接，，点，分别为，的中点，可得为△的一条中位线，，由线面平行的判定定理可得结论；（2）先利用勾股定理证明，由题意以点为坐标原点，为轴，为轴，为轴建立空间直角坐标系，分别求出平面与平面的一个法向量，根据空间向量夹角余弦公式，可得结果；试题解析：（1）证明：连接，，点，分别为，的中点，所以为△的一条中位线，，平面，平面，所以平面.（2）设，则，，，由，得，解得，由题意以点为坐标原点，为轴，为轴，为轴建立空间直角坐标系.可得，，，，故，，，，设为平面的一个法向量，则，得，同理可得平面的一个法向量为，设二面角的平面角为，，，所以，二面角的余弦值为.【方法点晴】本题主要考查线面平行的判定定理以及利用空间向量求二面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.19. 某市为了解本市万名学生的汉字书写水平，在全市范围内进行了汉字听写考试，发现其成绩服从正态分布，现从某校随机抽取了名学生，将所得成绩整理后，绘制出如图所示的频率分布直方图.（1）估算该校名学生成绩的平均值（同一组中的数据用该组区间的中点值作代表）；（2）求这名学生成绩在内的人数；（3）现从该校名考生成绩在的学生中随机抽取两人，该两人成绩排名（从高到低）在全市前名的人数记为，求的分布列和数学期望.参考数据：若，则，【答案】（1）；（2）；（3）.【解析】试题分析：（1）直方图中每个矩形的中点横坐标与该矩形的纵坐标相乘后求和，即可得到该校名学生成绩的平均值；（2）求出直方图中最后两个矩形的面积之和与总人数相乘即可求出这名学生成绩在内的人数；（3）的所有可能取值为分别求出各随机变量的概率，从而可得分布列，由期望公式可得结果.试题解析：（1）（2）.（3），则..所以该市前名的学生听写考试成绩在分以上.上述名考生成绩中分以上的有人.随机变量.于是，，.的分布列：数学期望.20. 已知动点满足：.（1）求动点的轨迹的方程；（2）设过点的直线与曲线交于两点，点关于轴的对称点为（点与点不重合），证明：直线恒过定点，并求该定点的坐标.【答案】（1）；（2）直线过定点，证明见解析.【解析】试题分析：（1）动点到点，的距离之和为，且，所以动点的轨迹为椭圆，从而可求动点的轨迹的方程；（2）直线的方程为：，由得，，根据韦达定理可得，直线的方程为，即可证明其过定点.试题解析：（1）由已知，动点到点，的距离之和为，且，所以动点的轨迹为椭圆，而，，所以，所以，动点的轨迹的方程：.（2）设，，则，由已知得直线的斜率存在，设斜率为，则直线的方程为：由得，所以，，直线的方程为：，所以，令，则，所以直线与轴交于定点.21. 已知函数，，（其中，为自然对数的底数，……）.（1）令，若对任意的恒成立，求实数的值；（2）在（1）的条件下，设为整数，且对于任意正整数，，求的最小值.【答案】（1）；（2）.【解析】试题分析：（1）由对任意的恒成立，即，利用导数讨论函数的单调性，求出最小值，即可得到实数的值；（2）由（1）知，即，令（，）则，所以，令，求和后利用放缩法可得，从而可得的最小值.所以，.试题解析：（1）因为所以，由对任意的恒成立，即，由，（i）当时，，的单调递增区间为，所以时，，所以不满足题意.(ii)当时，由，得时，，时，，所以在区间上单调递减，在区间上单调递增，所以的最小值为 .设，所以，①因为令得，所以在区间上单调递增，在区间上单调递减，所以，②由①②得，则.（2）由（1）知，即，令（，）则，所以，所以，所以，又，所以的最小值为.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. 选修4-4：坐标系与参数方程极坐标系中，为极点，半径为的圆的圆心坐标为.（1）求圆的极坐标方程；（2）设直角坐标系的原点与极点重合，轴非负关轴与极轴重合，直线的参数方程为（为参数），由直线上的点向圆引切线，求线线长的最小值.【答案】（1）；（2）.【解析】试题分析：（1）先确定圆心直角坐标，再写出圆的标准方程，最后将直角坐标方程化为极坐标方程（2）先根据加减消元法将直线的参数方程化为普通方程，再根据圆的几何意义得切线长最小时，直线上的点与圆心连线垂直直线，最后根据点到直线距离公式以及切线长公式求切线长最小值试题解析：解：（Ⅰ）设是圆上任意一点，如图，连接，并延长与圆交于点，当点异于，时，连接、，直角△中，，即，当点与，重合时，也满足上式，所求圆的极坐标方程为.（Ⅱ）直线的普通方程为，圆心到直线的距离为，，所以直线与圆相离，故切线长的最小值为.23. 选修4-5：不等式选讲已知函数.（1）求不等式的解集；（2）若不等式解集非空，求实数的取值范围.【答案】（1）；（2）.【解析】试题分析：（1）根据绝对值定义将不等式转化为三个不等式组，分别求解集，最后求并集（2）根据绝对值三角不等式得的最小值为，再解一元二次不等式得实数的取值范围.试题解析：解：（Ⅰ）由可化为：或或解得：或或，所以，不等式解集为.（Ⅱ）因为所以，即的最小值为，要不等式解集非空，需，从而，解得或，所以的取值范围为.点睛：含绝对值不等式的解法有两个基本方法，一是运用零点分区间讨论，二是利用绝对值的几何意义求解．法一是运用分类讨论思想，法二是运用数形结合思想，将绝对值不等式与函数以及不等式恒成立交汇、渗透，解题时强化函数、数形结合与转化化归思想方法的灵活应用，这是命题的新动向．。

2018届云南省昆明市高三上学期摸底调研测试理科数学试题及答案精品

昆明市2018届高三摸底调研测试理科数学试卷第I卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)设全集U=R，集合A={x| x(x -3)>0}，则C A=(A) [0，3] (B)(0，3)(C) (-∞,0) (3,+ ∞) (D) (-∞,0][3,+ ∞)(2) 设复数z满足(13)3,i z i z-=+=则(A)一i (B) i (C) 3455i-(D) 3455i+(3)设命题p：∀x∈R ，2x>0，则⌝p为(A) ∀x∈R, 2x<0(B) ∀x∈R, 2x<0(C) ∃xo∈R, 2 xo <0 (D)∃3xo∈R, 2xo <0(4) 一个几何体的三视图如图所示，则该几何体的体积等于(A) 8+4π(B) 8+2π(C) 8+43π(D) 8+23π(5)设a ，b ∈N*，记R(a\b)为a 除以b 所得的余数．执行如图所示的程序框图，若输入a= 243，b=45，则输出的值等于 (A) 0 (B) 1 (C) 9 (D) 18(6)已知ω>0，在函数y=sin ωx 与y=cos ωx 的图像的交点中，相邻两个交点的横坐标之差为1，则ω=(A)1 (B)2 (C)π (D) 2π(7)己知四边形ABCD 为正方形，3BP CP =，AP 与CD 交于点E ，若PE mCP nPD =+ 则m-n= (A)一23(B)23(C) —13(D) 13(8)己知a ∈（0，2π），cos(a +4π)= 一35，则tan a =(A) 17(B) 7 (C) 34(D) 43(9)四人进行一项游戏，他们约定：在一轮游戏中，每人掷一枚质地均匀的骰子1次，若某人掷出的点数为5或6，则此人游戏成功，否则游戏失败．在一轮游戏中，至少有2 人游戏成功的概率为(A) 127 (B) 827(C) 1127(D)89(10)已知F1，F2为双曲线C的左，右焦点，过F1的直线分别交C的左，右两支于A，B两点，若△AF2B为等腰直角三角形，且∠AF2B=90°，那么C的离心率为(11)已知曲线f(x)=e2x- 2e x+ax -1存在两条斜率为3的切线，则实数a的取值范围为(A)(3，+∞) (B) [3，72] (C) (一∞，72](D)(0，3)(12)棱长为a的正方体可任意摆放，则其在水平平面上投影面积的最大值为2：22 (D) 2a2第II卷本卷包括必考题和选考题两部分。

云南省昆明市2018届高三数学第一次摸底测试试题文.pdf

3
y
t8
2
23. 选修 4-5 ：不等式选讲
已知函数 f ( x) x 2 x 3 .
（1）求不等式 f (x) 3 的解集；
（2）若不等式 f ( x) a2 6a 解集非空，求实数 a 的取值范围 .
昆明一中全国联考第一期参考答案
5
1
为 1，则 C 的方程为（）
A． x 2 y2 1
B
． x2 y2 1
C.
2
x2 y 2 1
23
x2 y2
D．
1
33
6. 用一个平面去截正方体，则截面不可能是（
）
A．等边三角形
B ．直角三角形
C.
正方形
D ．正六边形
x y1 7. 若 x, y 满足约束条件 x y 1 ，则目标函数 z x 2 y 的最小值为（）
A1C1, AB1 的中点 .
3
（1）证明： MN // 平面 BB1C1C ；
（2）若 CM MN ，求三棱锥 M NAC 的体积 ..
19. 某市为了解本市 2 万名学生的汉字书写水平，在全市范围内进行了汉字听写考试，现从
某校随机抽取了 50 名学生，将所得成绩整理后，发现其成绩全部介于
[40,100] 之间，将其
[80,100] 的人数 .
4
20. 已知中心在原点 O ，焦点在 x 轴上的椭圆 E 过点 C (0,1) ，离心率为
2
.
2
（1）求椭圆 E 的方程；
（2）直线 l 过椭圆 E 的左焦点 F ，且与椭圆 E 交于 A, B 两点，若直线 l 的方程 .
OAB 的面积为 2 ，求 3
21. 已知函数 f ( x) ex ， g (x)

昆明市2018届高三摸底调研测试(理数试卷)

A．15 C． 45
B． 30 D． 60
11．若函数 f (x) 2x1 x2 2x 2 ，对于任意 x Z 且 x (, a) ， f (x) 0 恒成立，则实数
a 的取值范围是 A． (, 1]
B． (,0]
C． (,3]
D． (, 4]
12．在长方体 ABCD A1B1C1D1 中， AB AD 4，AA1 2 .过点 A1 作平面与 AB ， AD 分别交于 M ， N 两点.若 AA1 与平面所成角为 45 ，则截面 A1MN 面积的最小值是
．
15．已知函数
f
(x)
log2 (x 1) ,
x3
3x
1,
x 1, 则函数 f (x) 的零点个数为 x 1,
．
16．将数列an 中的所有项按每一行比上一行多 1 项的规则排成如下数阵：
a1 a2 , a3 a4 , a5 , a6 a7 , a8 , a9 , a10
记数阵中的第 1 列数 a1 ，a2 ，a4 ，，构成的数列为bn ，Sn 为数列bn 的前 n 项和.
D．x 0 x 1
2．设复数 z 满足 (1 i)z i ，则 z 的共轭复数 z
A． 1 1 i 22
C． 1 1 i 22
B． 1 1 i 22
D． 1 1 i 22
3．已知向量 a (1, 2) ， b (1,3) ，则 2a b
A． 2
B． 2
C． 10
D．10
4．已知等差数列{an} 的公差为 2，且 a4 是 a2 与 a8 的等比中项，则 an
8．定义[x] 表示不超过 x 的最大整数，例如[2] 2 ，[3.6] 3 ．右

云南省昆明市2018届高三数学第一次摸底测试试题文2017110201122

云南省昆明市2018届高三数学第一次摸底测试试题文第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.x11.已知集合，集合，则（）A{x0}B{x0x4}A Bx3A．(0,3)B．(0,3]C．(,4)D．(,4]2.若对于变量x的取值为3，4，5，6，7时，变量y对应的值依次分别为4.0，2.5，-0.5，-1，-2；若对于变量u的取值为1，2，3，4时，变量v对应的值依次分别为2，3，4，6，则变量x和y，变量u和v的相关关系是（）A．变量x和y是正相关，变量u和v是正相关B．变量x和y是正相关，变量u和v是负相关C．变量x和y是负相关，变量u和v是负相关D．变量x和y是负相关，变量u和v是正相关a2i3.已知复数为纯虚数（其中是虚数单位），则的值为（）i a1i11A．2 B．-2 C．D．224.如图，正方形ABCD内的图形来自宝马汽车车标的里面部分，正方形内切圆中的黑色部分和白色部分关于正方形对边中点连线成轴对称，在正方形内随机取一点，则此点取自黑色部分的概率是（）11 1A ．B ．C ．D ．42845.已知双曲线C 的中心为原点，点 F ( 2,0)是双曲线C 的一个焦点，点 F 到渐近线的距离为 1，则C 的方程为（）yxy222A ． x 2 y 2 1B ． x 2 1C.1D ．223 x y2213 36.用一个平面去截正方体，则截面不可能是（） A ．等边三角形B ．直角三角形C. 正方形D ．正六边形1x y7.若 x , y 满足约束条件 x y1 ，则目标函数 z x 2y 的最小值为（）2x y 2A ．2B ．1C. -2D ．-18. 执行如图所示的程序框图，若输出 n 的值为 9，则判断框中可填入（）A ． S 45?B ． S 36?C. S 45? D ． S 55?9.若函数 f (x ) x ，则函数 yf (x ) log x 的零点个数是（）1 2A ．5个B ．4个C. 3个D ．2个10. 已知函数 f (x )sin(x ) sin(x )（0 ），且 f ( ) 0 ，当取最小值时， 623以下命题中假命题是（）A．函数f(x)的图象关于直线x对称12B．是函数的一个零点x f(x)62C. 函数f(x)的图象可由g(x)3sin2x的图象向左平移个单位得到3D．函数f(x)在[0,]上是增函数1211.在ABC中，B600，AC43，AC边上的高为2，则ABC的内切圆半径r（）A．22B．2(21) C. 21D．2(21)12.设O为坐标原点，P是以F为焦点的抛物线y22px（p0）上任意一点，M是线段PF PM2MF OM上的点，且，则直线的斜率的最大值为（）223A．B． C. D．1233第Ⅱ卷二、填空题（每题5分，满分20分，将答案填在答题纸上）13.已知向量a(6,k)，向量b(3,1)，a b与b共线，则k．14.函数f(x)x2ln x在(1,1)处的切线方程为．315.已知，，则．sin()(,)tan454216.四面体A BCD中，AB CD10，AC BD234，AD BC241，则四面体A BCD外接球的表面积为．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 在等差数列{}中，公差，前5项和S，且成等比数列.a d01,3,7515a aa n（1）求数列{a}的通项公式；n（2）求（）的值.a a a ak N*28263k118. 如图，在直三棱柱中，，，点分别为ABC A B C BAC900AB AC2M,N111AC AB11,1的中点.3（1）证明：MN//平面BB C C；11（2）若CM MN，求三棱锥M NAC的体积..19. 某市为了解本市2万名学生的汉字书写水平，在全市范围内进行了汉字听写考试，现从某校随机抽取了50名学生，将所得成绩整理后，发现其成绩全部介于[40,100]之间，将其成绩按如下分成六组，得到频数分布表成绩[40,50)[50,60)[60,70)[70,80)[80,90)[90,100]人数 4 10 16 10 6 4（1）在答题卡上作出这些数据的频率分布直方图；（2）估算该校50名学生成绩的平均值x和中位数（同一组中的数据用该组区间的中点值作代表）；（3）以该校50名学生成绩的频率作为概率，试估计该市分数在[80,100]的人数.4220. 已知中心在原点O，焦点在x轴上的椭圆E过点C(0,1)，离心率为.2（1）求椭圆E的方程；（2）直线l过椭圆E的左焦点F，且与椭圆E交于A,B两点，若OAB的面积为2，求直3线l的方程.a21. 已知函数f(x)e x，g(x)x2x，（其中a R，e为自然对数的底数，2e 2.71828……）.（1）令h(x)f'(x)，求h(x)的单调区间；（2）已知f(x)在x 0处取得极小值，求实数a的取值范围.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程极坐标系中，O为极点，半径为2的圆C的圆心坐标为(2,).6（1）求圆C的极坐标方程；（2）设直角坐标系的原点与极点O重合，x轴非负关轴与极轴重合，直线l的参数方程为1x t23y t82（为参数），由直线上的点向圆引切线，求线线长的最小值.t l C23.选修4-5：不等式选讲已知函数f(x)x 2x 3.（1）求不等式f(x)3的解集；（2）若不等式f(x)a26a解集非空，求实数a的取值范围.昆明一中全国联考第一期参考答案5参考答案（文科数学）命题、审题组教师杨昆华李文清孙思应梁云虹王在方卢碧如凹婷波吕文芬陈泳序一、选择题题号 1 2 3 4 5 6 7 8 9 10 1112答案ADBC A BBADCB A1. 解析：集合 A1, 3， B0, 4 ，所以 A I B0,3，选 A.2. 解析：由正相关和负相关的定义知道，D 正确，选 D.3. 解析：因为a 2i (a 2) (a 2)i 1 i2，所以 a 2 ，选B.4. 解析：设正方形边长为 2 ，则圆半径为 1.此时正方形面积为 2 2 4 .图中黑色部分面积为 2 .则此点取自黑色部分的概率为 2 ，选C. 4 85. 解析：设 C 的方程为： x y2 22 2 1，由已知 b 1， c 2 ，所以 a 1，所以 C 的方程为 a bx 2 y 2 1，选 A .6. 解析：因为用一个平面去截正方体，若截面为三角形，则截面三角形只能是锐角三角形，选 B ．7. 解析：如图，目标函数 z 在点 A (1, 0) 处取得最小值，且 z1 ，选 B.8. 解析：模拟执行如图所示的程序框图知，该程序的功能是计算 S1 2 L 9 45 ，选A.9. 解析：如图：函数 f (x ) 与函数 g (x ) log x ，有 2 个交点，所以选D.1 263310. 解析：f xsin xcos x 3 sinx2 23得，由f ( ) 0 3Z，即 3k 1，由 0 知的最小值是 2，当取得最小值时，kk3 33sin2f x x3.由 f3 sin 2 3 sin312 12 32可得出：函数 f (x )的图象关于直线x对称，A 为真； 12由 f3 sin 26 6 3可得出： x是函数 f (x ) 的一个零点，B 为真；6将函数 gx3 sin 2x 的图象向左平移6个单位得到3 sin 2f xx3的图象，所以C 为假；由复合函数单调性可得 f (x ) 在 0,12上是增函数，所以 D 为真，选 C. 11. 解析：由1 1 S AB BC sin B 4 32 V 得 AB BC 16 ，又由余弦定理 ABC2 2AC 2AB 2 BC 2 2AB BC cos B (AB BC )2 3AB BC ，解得 AB BC4 6 ，从而V的周长为4( 63) ．由1 () ABCA得 Sr AB BC CAABC2r2S8 32( 21)ABCAB BC CA 4( 6 3)，选 B.12. 解析：由题意可得 ,0 ，设 F p 22yPy0 ,2p，当 y 00 ， K0 ；当OMy，0 K ．要OM求 K 的最大值，可设 OMy 00 ，则u u u r u u u ru u u ru u u r u u ru u u ru u u ru u u ru u u r u u u r21 112y p yOMOF FM OFFPOFOP OFOP OF, 3 3 3 36p 3 3，可得7KOMy1 123ypyp22 yp26p 32p y2p y．当且仅当 02 2 2yp 时取得等号，选A.二、填空题13. 解析：因为 a b (3, k 1) ，且 (a b )//b ，所以3(k1)3 ，所以 k2 .14. 解析：因为1，所以切线的斜率 k3，所以切线方程为3x y2 0 . f (x ) 2xx15. 解析：由,4 2得0,4 4 ，所以 cos 1 sin 2 4，所以 cos 1 sin 24 445，所以cos cos cos cos sin sin 4 4 4 44 4 1024 4 4 4 4410， 27 2sin 1 cos，10sin 所以 tan7 .cos16. 解析：由题意可采用割补法，考虑到四面体 A BCD 的四个面为全等的三角形，所以可在其每个面补上一个以10 ， 2 34 ， 2 41 为三边的三角形作为底面，分别以 x ， y ， z 为侧棱长且两两垂直的三棱锥，从而可得到一个长、宽、高分别为 x ， y ， z 的长方体，并且x 2 y 2 100 ， x 2 z 2 136 ， y 2 z 2 164 ．设球半径为 R ，则有2Rxyz200 ，所以 4R 2 200 ，得球的表面积为 200 ．2222三、解答题54 5a d 15117. 解：（Ⅰ）：据题意有22a 2da a 6d1113a12，解得3 d4 ，33所以数列a的通项公式为a an1 dn； nn14433 3（Ⅱ）由（Ⅰ）得：nn ，a3 133 1n44 4所以 aa a ……2826a3k 183 (3)3 33123k43 1 3k393 1k.4 1 3 8 33 3b另解：设，则b a3 1313 nN ，nn n n nn3 144 4b所以数列b 是首项为n9 4，公比为 3的等比数列，所以数列b 的前 k 项和Tnk91 3k943 1k1 3 8.18. 解：（ Ⅰ ）证明：连接 A B ， BC 1 ，点 M ， N 分别为 A 1C 1 ，AB 11的中点，所以 MN 为△ A BC 的一条中位线， 11MN //BC1MN平面 B B C C ， 1 1BC平面1BB C C ，1 1所以 MN // 平面 BB C C ．1 1（Ⅱ）设点D，E分别为AB，A A1的中点，AA1a，则CM2a21，222248205MN1，CN，由CM MN，得CM2MN2CN2，2aa2aa4444解得a 2，又NE 平面AA1C C，NE 1，1122111VV S AMC NEM NAC N AMC33223．所以三棱锥M NAC的体积为2 3.19.解：（Ⅰ）9（Ⅱ）x 450.08550.2650.32750.2850.12950.0868.2；由已知可设中位数为60x，则0.080.20.032x 0.5；所以x 6.875，所求中位数为x 66.875.（Ⅲ）该市分数在80,100的人数64200004000，故所求人数为4000人.5020.解：（Ⅰ）设椭圆E的方程为：x y22221(a b0)，a bb1c2由已知：a2a b c222得：a22，b21，所以，椭圆E的方程为：x22y21.（Ⅱ）由已知直线l过左焦点F (1,0)．当直线l与x轴垂直时，2A (1,)，22B (1,)，此时AB2，212则21S，不满足条件．OAB22当直线l与x轴不垂直时，设直线l的方程为：y k(x 1)y k (x 1) 由 2xy 122 得 (1 2k 2 )x 2 4k 2 x 2k 22 0所以4k2xx1 221 2k，2k2 2x x1 2212k， 11 而SOFyyyy ，OAB12122 2102由已知S得OAB34 yy ，123yy(yy )4y y2 12121 2[k (x x ) 2k ]4k (x1)(x1)221212， 4k4k22(1 2k )12k2 22所以4k4k16 22(1 2k ) 1 2k92 22，则 k 4k 2 2 0 ，所以 k1，所以直线l 的方程为： x y 1 0 或 x y 1 0 ．21. 解: (Ⅰ) 因为 f (x ) e x ax1，所以 h (x ) e x a ，当 a 0 时， h (x ) 0 ， h (x )的单调递增区间为,，当 a 0 时，由 h(x ) e x a 0 ，得 xln a ，xa 时， h (x ) 0 ， x (ln a ,) 时， h(x ) 0 ，( , ln )所以 h (x ) 的减区间为(, ln a ) ，增区间为 (ln a,)综上可得，当 a 0 时， h (x ) 在(,) 上单调递增当 a 0 时， h (x ) 的增区间为 (ln a ,) ，减区间为(,ln a ) .（Ⅱ）由题意得 f (x ) e x ax 1， f (0) 0 ，（1）当 a 0 时， f (x ) 在(,) 上单调递增，所以当 x 0 时， f (x ) f (0)0 ，当 x0 时， f (x ) f (0) 0 ，所以 f (x ) 在 x 0 处取得极小值，符合题意. （2）当 0 a1 时， ln a 0 ，由（Ⅰ）知 f (x ) 在 (ln a,) 单调递增，所以当x(ln a,0)时，f(x)f(0)0，当x(0,)时，f(x)f(0)0，所以f(x)在x0处取得极小值，符合题意.11（3）当a1时，由（Ⅰ）知f(x)在区间(,ln a)单调递减，f(x)在区间(ln a,)单调递增，所以f(x)在x ln a处取得最小值，即f(x)f(ln a)f(0)0，所以函数f(x)在R上单调递增，所以f(x)在x0处无极值，不符合题意.（4）当a1时，ln a0，由（Ⅰ）知f(x)的减区间为(,ln a)，所以当x(,0)时，f(x)f(0)0，当x(0,ln a)时，f(x)f(0)0，所以f(x)在x0处取得极大值，不符合题意，综上可知，实数a的取值范围为(,1).第22、23题中任选一题做答，如果多做，则按所做的第一题记分.22.解：（Ⅰ）设M(,)是圆上任意一点，如图，连接OC，并延长与圆C交于点A，当点M异于O，A时，连接OM、MA，直角△MOA中，OM OA cos MOA，即4cos4cos()，66当点M与O，A重合时，也满足上式，所求圆C的极坐标方程为4cos().6（Ⅱ）直线l的普通方程为3x y80，圆心C(3,1)到直线l的距离为d，3318d3r，所以直线l与圆C相离，2故切线长的最小值为32225.1223. 解：（Ⅰ）由 f (x ) x 2 x 3 3 可化为：xx 3 3 2或 x 2 x 3 3 x 2 x 3 3x 2或x 2 x 3 3 解得：x 或 2 x 2 或 x2 ，所以，不等式解集为2,.（Ⅱ）因为 f (x )x 2x 3(x 2) (x 3)5所以 5 f (x ) 5，即 f (x ) 的最小值为 5 ，要不等式 f (x ) a 2 6a 解集非空，需 f (x )a 2 6a ，min从而 a 26a 5 0 ，解得 a1或 a 5 ，所以 a的取值范围为,1U5,.13昆明一中全国联考第一期参考答案参考答案（文科数学）命题、审题组教师杨昆华李文清孙思应梁云虹王在方卢碧如凹婷波吕文芬陈泳序一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12答案 A D B C A B B A D C B A24.解析：集合A1,3，B0,4，所以A I B0,3，选A.25.解析：由正相关和负相关的定义知道，D正确，选D.26.解析：因为a 2i (a 2)(a2)i1i2，所以a 2，选B.27.解析：设正方形边长为2，则圆半径为1.此时正方形面积为224.图中黑色部分面积为2.则此点取自黑色部分的概率为2，选C.4828.解析：设C的方程为：x y22221，由已知b 1，c 2，所以a1，a b所以C的方程为x2y21，选A .yx-y=-1x+y=1329.解析：因为用一个平面去截正方体，若截面为三角形，则截面三角形22x-y=21只能是锐角三角形，选B．30.解析：如图，目标函数z在点A(1,0)处取得最小值，且z 1，选B. –5–4–3–2O–1–112345x 31.解析：模拟执行如图所示的程序框图知，该程序的功能是计算S 12L 945，选A.–2–332.解析：如图：函数f(x)与函数g(x)log x，有2个交点，所以选D.123333.解析：f x sin x cos x3sin x223得，由f()033yZ ，即3k 1，由0知的最小值是2，当k k332取得最小值时，3sin2f x x.由3–4–3–2–1O–1–21234xf3sin23sin3121232可得出：函数f(x)的图象–314关于直线 x对称，A 为真； 12由 f3 sin 2 066 3可得出： x是函数 f (x ) 的一个零点，B 为真；6将函数 g x3 sin 2x 的图象向左平移6个单位得到3 sin 2f x x3的图象，所以C 为假；由复合函数单调性可得 f (x ) 在 0,12上是增函数，所以 D 为真，选C. 34. 解析：由1 1 S AB BC sin B 4 32 V 得 AB BC 16 ，又由余弦定理 ABC2 2 AC 2AB 2 BC 2 2AB BC cos B (AB BC )2 3AB BC ，解得 AB BC4 6 ，从而V的周长为4( 63) ．由1 () ABCA得 Sr AB BC CAABC2r2S8 32( 21)ABCAB BC CA 4( 63)，选 B.35. 解析：由题意可得 ,0 ，设 F p 2y2 Py, 02p，当 y， 0 00 K；当 OMy ， 00 0 K．要OM求 K 的最大值，可设OMy，则00u u u r u u u r u u u r u u u r u u r u u u r u u u r u u u r u u u r u u u r21112y p yOM OF FM OF FP OF OP OF OP OF00,33336p33，可得KOMy1123y p y p22y p0026p32p y2p y00．当且仅当22y p时取得等号，选A.02二、填空题36.解析：因为a b (3,k 1)，且(a b)//b，所以3(k 1)3，所以k2.37.解析：因为1，所以切线的斜率k 3，所以切线方程为3x y20.f(x)2xx38.解析：由,42得0,44，所以cos 1sin24，所以cos 1sin24445，所以22cos cos cos cos sin sin44444410，1527 2sin 1 cos，10sin 所以 tan7 .cos39. 解析：由题意可采用割补法，考虑到四面体 A BCD 的四个面为全等的三角形，所以可在其每个面补上一个以10 ， 2 34 ， 2 41 为三边的三角形作为底面，分别以 x ， y ， z 为侧棱长且两两垂直的三棱锥，从而可得到一个长、宽、高分别为 x ， y ， z 的长方体，并且x 2 y 2 100 ， x 2 z 2 136 ， y 2 z 2 164 ．设球半径为 R ，则有2Rxyz 200 ，所以 4R 2 200 ，得球的表面积为 200 ．2222三、解答题54 5a d 15140. 解：（Ⅰ）：据题意有22a 2da a 6d1113a12，解得3 d4 ，………4分33所以数列a的通项公式为a a n 1 d n； ………6分 nn 14 433 3（Ⅱ）由（Ⅰ）得：a313 ，nn3 1n44 4所以 aa a ……2826a3k13333 ……12343k………9分313k3931k.4138………12分333b另解：设，则b a31313n nn n N，n nn31444b所以数列b是首项为n 94，公比为3的等比数列， (9)分所以数列b的前k项和Tn k 913k9431k138.………12分1641. 解：（ Ⅰ ）证明：连接A B ， BC 1 ，点 M ， N 分别为 A 1C 1 ， AB 11的中点，所以 MN 为△ A BC 的一条中位线， 11MN //BC1MN平面 B B C C ， 1 1BC平面1BB C C ，1 1所以 MN // 平面 BB C C ．………6分1 1（ Ⅱ ）设点 D ， E 分别为 AB ， A A 1 的中点， AA 1a ，则 CM 2a 21， 4820MN，CN 5，由CM MN ，得CM 2 MN 2CN 2 ，2a 2a 22a 2a 214444 解得 a 2 ，又 NE平面 AA 1C C ， NE1， 111 1 22 1VVSAMCNEM NAC N AMC33 2 2 3 ．所以三棱锥 M NAC 的体积为2 3. ………12分42. 解：（Ⅰ）………3分（Ⅱ）x45 0.08 55 0.2 65 0.32 75 0.2 85 0.12 95 0.08 68.2 ；………6分由已知可设中位数为 60 x ，则 0.08 0.2 0.032x 0.5；所以x 6.875 ，所求中位数为x 66.875. ………9分（Ⅲ）该市分数在80,100的人数64200004000，故所求人数5017为4000 人. ………12分43. 解：（Ⅰ）设椭圆 E 的方程为：xy2 222 1 (a b0) ， a b1 b2 c由已知：a 2abc222得： a 22 ，b 21，所以，椭圆 E 的方程为： x 22y 21. (4)分（Ⅱ）由已知直线l 过左焦点 F (1, 0) ．当直线l 与 x 轴垂直时，2 A (1, ) ，22 B (1, ) ，此时 AB2 ，212则2 1S，不满足条件．………5分OAB22当直线l 与 x 轴不垂直时，设直线l 的方程为： y k (x1)y k x(1)由 2x2y12 得 (1 2k 2 )x 24k 2 x 2k 22 0所以4k2xx12212k，2k 22x x1 2212k，………8分11 而SOFyyyy ，OAB1212222 由已知 S得OAB4yy ，123 3yy(yy )4y y212121 2[k (x x ) 2k ]4k (x1)(x1)221212， 4k4k22(1 2k )1 2k2 22所以4k4k16 22(1 2k ) 1 2k92 22，则 k 4k 2 2 0 ，所以 k1，所以直线l 的方程为： x y 1 0 或 x y 1 0 ． ………12分44. 解: (Ⅰ) 因为 f (x ) e x ax1，所以 h (x ) e x a ，18当 a 0 时， h (x ) 0 ， h (x ) 的单调递增区间为,，当 a 0 时，由 h(x ) e x a 0 ，得 xln a ，xa 时， h (x ) 0 ， x (ln a ,) 时， h(x ) 0 ，( , ln )所以 h (x ) 的减区间为 (, ln a ) ，增区间为 (ln a ,)综上可得，当 a 0 时， h (x ) 在 (,) 上单调递增当 a 0 时， h (x ) 的增区间为 (ln a ,) ，减区间为 (,ln a ) . ………5分（Ⅱ）由题意得 f (x ) e x ax 1， f (0) 0 ，（1）当 a 0 时， f (x ) 在 (,) 上单调递增，所以当 x 0 时， f (x ) f (0) 0 ，当 x0 时， f (x ) f (0) 0 ，所以 f (x ) 在 x 0 处取得极小值，符合题意.（2）当 0 a 1 时， ln a 0 ，由（Ⅰ）知 f (x ) 在 (ln a ,) 单调递增，所以当 x(ln a ,0) 时， f (x ) f (0) 0 ，当 x(0,) 时， f (x ) f (0) 0 ，所以 f (x ) 在 x 0 处取得极小值，符合题意.（3）当 a 1时，由（Ⅰ）知 f (x ) 在区间 (,ln a ) 单调递减， f (x ) 在区间 (ln a ,) 单调递增，所以 f (x ) 在 x ln a 处取得最小值，即 f (x ) f (ln a ) f (0) 0 ，所以函数 f (x ) 在 R 上单调递增，所以 f (x ) 在 x 0 处无极值，不符合题意.（4）当 a 1时， ln a0 ，由（Ⅰ）知 f (x ) 的减区间为 (,ln a ) ，所以当 x(,0) 时， f (x ) f (0) 0 ，当 x (0,ln a ) 时， f (x ) f (0) 0 ，所以 f (x ) 在 x 0 处取得极大值，不符合题意，19综上可知，实数 a 的取值范围为 (,1) . ………12分第 22、23题中任选一题做答，如果多做，则按所做的第一题记分. 45. 解：（Ⅰ）设 M (,) 是圆上任意一点，如图，连接OC ，并延长与圆C 交于点 A ，当点 M 异于O ， A 时，连接OM 、 MA ，直角△ MOA 中，OM OAcos MOA ，即4 cos4 cos() ，66当点 M 与O ， A 重合时，也满足上式，所求圆C 的极坐标方程为4 cos() .………5分6（Ⅱ）直线l 的普通方程为 3x y 8 0 ，圆心C ( 3,1) 到直线l 的距离为 d ，3 318d3 r ，所以直线l 与圆C 相离，2故切线长的最小值为 32225 .………10分46. 解：（Ⅰ）由 f (x ) x 2 x 3 3 可化为：33 x 2x或x 2 x 3 3x 2 x 33 x 2 或x 2 x 3 3解得：x或 2 x 2 或 x2 ，所以，不等式解集为2,. ………5分（Ⅱ）因为 f (x )x 2x 3(x 2) (x 3)5所以 5 f (x ) 5，即 f (x ) 的最小值为 5 ，要不等式 f (x ) a 2 6a 解集非空，需 f (x )a 2 6a ，min从而 a 26a 5 0 ，解得 a1或 a 5 ，所以 a的取值范围为,1U5,.………10分20。

2018-2019年云南省昆明市质检一：昆明市2018届高三第一次质量检测数学(理)试题-附答案精品

云南省昆明市2018届高三第一次质量检测理科数学一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.复数11212i i+++（其中i 为虚数单位）的虚部为（） A ．35 B ．35i C ．35- D ．35i - 2.若集合{|12}A x x =<<，{|,}B x x b b R =>∈，则A B ⊆的一个充分不必要条件是（）A ．2b ≥B ．12b <≤C ．1b ≤D ．1b <3.已知某7个数的平均数为4，方差为2，现加入一个新数据4，此时这8个数的平均数为x ，方差为2s ，则（）A ．4x =，22s <B ．4x =，22s >C ．4x >，22s <D ．4x >，22s > 4.已知椭圆C ：22221(0)x y a b a b+=>>，若长轴长为6，且两焦点恰好将长轴三等分，则此椭圆的标准方程为（）A ．2213632x y +=B ．22198x y +=C ．22195x y +=D ．2211612x y += 5.已知正项等比数列{}n a 满足31a =，5a 与432a 的等差中项为12，则1a 的值为（） A ．4 B ．2 C ．12 D ．14 6.已知变量x ，y 满足约束条件40221x y x y --≤⎧⎪-≤<⎨⎪≤⎩，若2z x y =-，则z 的取值范围是（）A ．[5,6)-B ．[5,6]-C ．(2,9)D ．[5,9]-7.七巧板是一种古老的中国传统智力游戏，被誉为“东方魔板”.如图，这是一个用七巧板拼成的正方形，其中1号板与2号板为两个全等的等腰直角三角形，3号板与5号板为两个全等的等腰直角三角形，7号板为一个等腰直角三角形，4号板为一个正方形，6号板为一个平行四边形.现从这个。

云南省2018-2019年高三一模考试数学（理）试题含答案

云南省2018-2019年⾼三⼀模考试数学（理）试题含答案⾼三下学期⼀模考试数学（理）试题第Ⅰ卷（共60分）⼀、选择题：本⼤题共12个⼩题,每⼩题5分,共60分.在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的. 1. 若复数z 满⾜()142i zi+=+，则z=（）A ．3i -+B ．32i- C ．3i + D ．1i +2.已知集合{}{}22,20A xx B x x x =<=-->，则A B ?=（）A ．{}22x x -<< B ．{}12xx -<<C ．{}21xx -<<- D ．{}12xx -<<3.若函数()xxf x aa>且1a ≠）在R 上为减函数，则函数() lo g 1ayx =-的图象可以是（）A． B． C．D ．4.已知,x y 满⾜约束条件10330210x y x y x y +-≥??-+≥??--≤?，则函数22zx y=+的最⼩值为（）A ．12B ．22C ．15.A B C ?的内⾓,,A B C 的对边分別为,,a b c ，已知()c o s 2c o s ,2,1b A c a B c a =-==，则A B C的⾯积是（） A ．12B ．32C ．1D ．36.对于实数,a b ，定义⼀种新运算“?”：ya b=?，其运算原理如程序框图所⽰，则5324=+（）A ．26B ．32C ．40D ．46 7.若函数()()3lo g 2,0,0x x f x g x x ->??=?3f g -=（）A ．3-B ．2-C ．1-D ．08.如图，⽹格纸上正⽅形⼩格的边长为1，粗实线画出的是某⼏何体的三视图，则该⼏何体的表⾯积为（）B ．24πC ．28πD ．32π 9.已知函数()()2s in 0,2f x x πω?ω??=+>< ?的最⼩正周期为4π，其图象关于直线23xπ=对称.给出下⾯四个结论：①函数()f x 在区间40,3π?上先增后减；②将函数()f x 的图象向右平移6π个单位后得到的图象关于原点对称；③点,03π-是函数()f x 图象的⼀个对称中⼼；④函数()f x 在[],2ππ上的最⼤值为1.其中正确的是（）A ．①②B ．③④C ．①③D ．②④10.甲、⼄、丙、丁四位同学参加⼀次数学智⼒竞赛，决出了第⼀名到第四名的四个名次.甲说:“我不是第⼀名”；⼄说:“丁是第⼀名”；丙说:“⼄是第⼀名”；丁说:“我不是第⼀名”.成绩公布后，发现这四位同学中只有⼀位说的是正确的.则获得第⼀名的同学为（） A ．甲 B ．⼄ C ．丙 D ．丁 11.双曲线210,0x y a b ab-=>>的左右焦点分别为12,F F ，过1F 的直线交曲线左⽀于,A B 两点,2F A B ?是以A 为直⾓顶点的直⾓三⾓形，且230A F B∠=?.若该双曲线的离⼼率为e ，则2e=（）A ．1143+ B ．1353+ C ．1663- D ．19103-12.函数()1yfx=+的图象关于直线1x=-对称，且()y f x =在[)0,+∞上单调递减.若[]1,3x ∈时，不等式()()()2ln 323ln 32f m x x f fx m x --≥-+-恒成⽴，则实数m 的取值范围为（）A ．1ln 66,26e +??B ．1ln 36,26e +??C ．1ln 66,6e +??D ．1ln 36,6e +??第Ⅱ卷（共90分）⼆、填空题（每题5分，满分20分，将答案填在答题纸上） 13. 实数,a b 满⾜22 21a b+=，则a b 的最⼤值为．14.()()5112x x+-展开式中2x 的系数为． (⽤数字填写答案）15．已知抛物线()20y a xa =>的准线为l ，若l 与圆()22:31C xy-+=相交所得弦长为3，则a16．正四棱柱1111A B C DA B C D -中，底⾯边长为2，侧棱11A A =，P 为上底⾯1111ABCD 上的动点，给出下列四个结论：①若3P D =，则满⾜条件的P 点有且只有⼀个；②若3P D =，则点P 的轨迹是⼀段圆弧；③若//P D 平⾯1A C B ，则P D 与平⾯11A C C A 所成⾓的正切的最⼤值为2；④若//P D 平⾯1A C B ，则平⾯B D P 截正四棱柱1111A B C DA B C D -的外接球所得图形⾯积最⼤值为2512π.其中所有正确结论的序号为．三、解答题（本⼤题共6⼩题，共70分.解答应写出⽂字说明、证明过程或演算步骤.） 17. 公差不为0的等差数列{}n a 的前n 项和为n S ，已知410S =，且139,,a a a 成等⽐数列.（1）求{}n a 的通项公式；（2）求数列3n n a的前n 项和n T .18.如图，直三棱柱111A B C A B C -中，14,2,22,45C C A B A C B A C ===∠=?，点M 是棱1A A 上不同于1,A A 的动点.⊥；（2）若平⾯1M B C 把此棱拄分成体积相等的两部分，求此时⼆⾯⾓1MB C A--的余弦值.19.某公司新上⼀条⽣产线，为保证新的⽣产线正常⼯作，需对该⽣产线进⾏检测.现从该⽣产线上随机抽取100件产品，测量产品数据，⽤统计⽅法得到样本的平均数14µ=，标准差2σ=，绘制如图所⽰的频率分布直⽅图.以频率值作为概率估计值.（1）从该⽣产线加⼯的产品中任意抽取⼀件，记其数据为X ，依据以下不等式评判（P 表⽰对应事件的概率）：①()0.6826P X µσµσ-<<+≥②()220.9544P X µσµσ-<<+≥ ③()330.9974P X µσµσ-<<+≥评判规则为：若⾄少满⾜以上两个不等式，则⽣产状况为优，⽆需检修；否则需检修⽣产线，试判断该⽣产线是否需要检修；（2）将数据不在()2,2µσµσ-+内的产品视为次品，从该⽣产线加⼯的产品中任意抽取2件，次品数记为Y ，求Y 的分布列与数学期望E Y . 20.如图，椭圆()2222:10x y Ca b ab+=>>的左右焦点分别为12,F F ，左右顶点分别为,,A B P 为椭圆C 上任⼀点（不与A B 、重合）.已知12P F F ?的内切圆半径的最⼤值为22.（1）求椭圆C 的⽅程；（2）直线l 过点B 且垂直于x 轴，延长A P 交l 于点N ，以B N 为直径的圆交B P 于点M ，求证:O M N 、、三点共线. 21.函数() ()()sin ,1c o s 2xxf x e x gx x x e==+-.（1）求()f x 的单调区间；（2）对120,,0,22x x ππ∈∈，使()()12f xg x m+≥成⽴，求实数m 的取值范围；（3）设()()2sin 2sin x h x fx n xx=-在0,2π?在平⾯直⾓坐标系xO y 中，直线l 的参数⽅程为1c o s s in x t y t αα=+??=?）（t 为参数，0απ≤<），在。

云南省昆明市2018届高三数学上学期第一次月考试题理

云南省昆明市2018届高三数学上学期第一次月考试题理第Ⅰ卷选择题（共60分）一．选择题（共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．已知集合A ＝{1，2，3，4}，B ＝{y |y ＝3x －2，x ∈A }，则A ∩B ＝( ) A ．{1} B ．{4} C ．{1，3} D ．{1，4}2.复数=+i12( ) A. 2-i B. 2-2i C. 1+i D. 1-i3. 函数f (x )＝2x－1＋1x －2的定义域为( ) A ．[0，2) B ．(2，＋∞) C ．[0，2)∪(2，＋∞) D ．(－∞，2)∪(2，＋∞)4.命题“若x 2＋y 2＝0，x ，y ∈R ，则x ＝y ＝0”的逆否命题是( )A ．若x ≠y ≠0，x ，y ∈R ，则x 2＋y 2＝0 B ．若x ＝y ≠0，x ，y ∈R ，则x 2＋y 2≠0 C ．若x ≠0且y ≠0，x ，y ∈R ，则x 2＋y 2≠0 D ．若x ≠0或y ≠0，x ，y ∈R ，则x 2＋y 2≠0 5.设f (x )＝ln x ，0＜a ＜b ，若p ＝f (ab )，q ＝f ⎝ ⎛⎭⎪⎫a ＋b 2，r ＝12(f (a )＋f (b ))，则下列关系式中正确的是( )A ．q ＝r ＜pB ．p ＝r ＜qC ．q ＝r ＞pD ．p ＝r ＞q6.已知幂函数f (x )＝x α的图象过点(4，2)，若f (m )＝3，则实数m 的值为( )A. 3 B ．± 3 C ．9 D ．±97.设x ∈R ，则“1＜x ＜2”是“|x －2|＜1”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件8.设a ＝0.60.6，b ＝0.61.5，c ＝1.50.6，则a ，b ，c 的大小关系是( )A ．a <b <cB ．a <c <bC ．b <a <cD ．b <c <a9.设函数f (x )＝⎩⎪⎨⎪⎧3x －b ，x <1，2x ，x ≥1.若f (f (56))＝4，则b ＝( )A ．12 B.78 C.34 D.110．设f (x )是周期为2的奇函数，当0≤x ≤1时，f (x )＝2x (1－x )，则f ⎝ ⎛⎭⎪⎫－52等于( )A ．－12B ．－14 C.14 D.1211．函数y ＝x 2－2|x |的图象是( )12．设集合A ＝{－1，0，1}，集合B ＝{0，1，2，3}，定义A *B ＝{(x ，y )|x ∈A ∩B ，y ∈A ∪B }，则A *B 中元素的个数是( )A ．7B ．10C ．25D ．52第Ⅱ卷非选择题（共90分）二、填空题（共4小题，每小题5分，共20分）13．命题“存在x 0∈R ，使得|x 0－1|－|x 0＋1|>3”的否定是_________________．14．已知f (x ＋1)＝x ＋2x ，则f (x )的解析式为f (x )＝__________．15．设二次不等式ax 2＋bx ＋1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－1<x <13，则ab 的值为________．16．已知集合A ＝{x |1≤x <5}，C ＝{x |－a <x ≤a ＋3}，若C ∩A ＝C ，则a 的取值范围是________．三．解答题（共6小题，第17小题10分，其余各小题12分，共70分.解答应写出必要的文字说明、证明过程或演算步骤）17.(1) lg 14－2lg 73＋lg 7－lg 18(2) (0.027)23＋⎝ ⎛⎭⎪⎫27125－13－⎝ ⎛⎭⎪⎫2790.518．已知集合A ＝{x |1<x <3}，集合B ＝{x |2m <x <1－m }．(1)当m ＝－1时，求A ∪B ； (2)若A ⊆B ，求实数m 的取值范围； (3)若A ∩B ＝∅，求实数m 的取值范围．19．已知函数f (x )＝log a (x ＋1)－log a (1－x )，a >0且a ≠1.(1)求f (x )的定义域；(2)判断f (x )的奇偶性并予以证明； (3)若a >1时，求使f (x )>0的x 的解集．20．已知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ，x ＞0，0，x ＝0，x 2＋mx ，x ＜0是奇函数．(1)求实数m 的值；(2)若函数f (x )在区间[－1，a －2]上单调递增，求实数a 的取值范围．21．已知c >0，且c ≠1，设p ：函数y ＝c x在R 上单调递减；q ：函数f (x )＝x 2－2cx ＋1在⎝ ⎛⎭⎪⎫12，＋∞上为增函数，若“p 且q ”为假，“p 或q ”为真，求实数c 的取值范围．22．设函数f(x)＝x2－2|x|－1(－3≤x≤3)(1)证明f(x)是偶函数；(2)画出这个函数的图象；(3)指出函数f(x)的单调区间，并说明在各个单调区间上f(x)是增函数还是减函数；(4)求函数的值域．昆明黄冈实验学校2017-2018学年上学期第一次月考高三理科数学参考答案与试题解析第Ⅰ卷选择题（共60分）二．选择题（共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一个选项是符合题目要求的）1．已知集合A ＝{1，2，3，4}，B ＝{y |y ＝3x －2，x ∈A }，则A ∩B ＝( )A ． {1}B ．{4}C ．{1，3}D ．{1，4}D [解析] 由题意得，B ＝{1，4，7，10}，所以A ∩B ＝{1，4}． 2.复数=+i12A. 2-iB. 2-2iC. 1+iD. 1-i 【答案】D【解析】，故选D.3. 函数f (x )＝2x－1＋1x －2的定义域为( ) A ．[0，2) B ．(2，＋∞)C ．[0，2)∪(2，＋∞)D ．(－∞，2)∪(2，＋∞)C [解析] 由题意得⎩⎪⎨⎪⎧2x－1≥0，x －2≠0，解得x ≥0且x ≠2.4.命题“若x 2＋y 2＝0，x ，y ∈R ，则x ＝y ＝0”的逆否命题是( D )A ．若x ≠y ≠0，x ，y ∈R ，则x 2＋y 2＝0 B ．若x ＝y ≠0，x ，y ∈R ，则x 2＋y 2≠0 C ．若x ≠0且y ≠0，x ，y ∈R ，则x 2＋y 2≠0 D ．若x ≠0或y ≠0，x ，y ∈R ，则x 2＋y 2≠0 5.设f (x )＝ln x ，0＜a ＜b ，若p ＝f (ab )，q ＝f ⎝ ⎛⎭⎪⎫a ＋b 2，r ＝12(f (a )＋f (b ))，则下列关系式中正确的是( )A ．q ＝r ＜pB ．p ＝r ＞qC ．q ＝r ＞pD ．p ＝r ＜q【答案】D 【解析】因为b ＞a ＞0，故a ＋b 2＞ab .又f (x )＝ln x (x ＞0)为增函数，所以f ⎝ ⎛⎭⎪⎫a ＋b 2＞f (ab )，即q ＞p .所以r ＝12(f (a )＋f (b ))＝12(ln a ＋ln b )＝ln ab ＝p .6.已知幂函数f (x )＝x α的图象过点(4，2)，若f (m )＝3，则实数m 的值为( )A. 3 B ．±3 C ．9 D ．±9 【答案】C【解析】由幂函数f (x )＝x α过点(4，2)可得4α＝22α＝2，所以α＝12，所以f (x )＝x 12＝x ，故f (m )＝m ＝3⇒m ＝9.7.设x ∈R ，则“1＜x ＜2”是“|x －2|＜1”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A 【解析】||x －2<1⇔1<x <3.由于{}x |1<x <2是{}x |1<x <3的真子集，所以“1<x <2”是“||x －2<1”的充分而不必要条件．8.设a ＝0.60.6，b ＝0.61.5，c ＝1.50.6，则a ，b ，c 的大小关系是( )A ．a <b <cB ．a <c <bC ．b <a <cD ．b <c <a 【答案】C【解析】因为函数y ＝0.6x 是减函数，0<0.6＜1.5，所以1>0.60.6＞0.61.5，即b ＜a <1.因为函数y ＝x 0.6在(0，＋∞)上是增函数，1＜1.5，所以1.50.6>10.6＝1，即c >1.综上，b ＜a ＜c .9.设函数f (x )＝⎩⎪⎨⎪⎧3x －b ，x <1，2x ，x ≥1.若f (f (56))＝4，则b ＝( )A ．12 B.78 C.34 D.1 【答案】A【解析】f (56)＝3×56－b ＝52－b ，若52－b <1，即b >32，则3×(52－b )－b ＝152－4b ＝4，解得b ＝78，不符合题意，舍去；若52－b ≥1，即b ≤32，则252－b ＝4，解得b ＝12. 10．设f (x )是周期为2的奇函数，当0≤x ≤1时，f (x )＝2x (1－x )，则f ⎝ ⎛⎭⎪⎫－52等于( ) A ．－12 B ．－14 C.14 D.12A [解析] 因为f (x )是周期为2的奇函数，所以f ⎝ ⎛⎭⎪⎫－52＝f ⎝ ⎛⎭⎪⎫－52＋2＝f ⎝ ⎛⎭⎪⎫－12＝－f ⎝ ⎛⎭⎪⎫12＝－2×12×⎝ ⎛⎭⎪⎫1－12＝－12.11．函数y ＝x 2－2|x |的图象是( )B [解析] 由y＝x2－2|x|知是偶函数，故图象关于y轴对称，排除C.当x≥0时，y ＝x2－2x＝(x－1)2－1.即当x＝0时，y＝0，当x＝1时，y＝－1，排除A、D，故选B.12．设集合A＝{－1，0，1}，集合B＝{0，1，2，3}，定义A*B＝{(x，y)|x∈A∩B，y∈A∪B}，则A*B中元素的个数是( )A．7 B．10 C．25 D．52【答案】B【解析】因为A＝{－1，0，1}，B＝{0，1，2，3}，所以A∩B＝{0，1}，A∪B＝{－1，0，1，2，3}．因为x∈A∩B，所以x可取0，1；因为y∈A∪B，所以y可取－1，0，1，2，3.则(x，y)的可能取值如下表所示：x0(0，－1)(0，0)(0，1)(0，2)(0，3)第Ⅱ卷非选择题（共90分）三．填空题（共4小题，每小题5分，共20分）13．命题“存在x0∈R，使得|x0－1|－|x0＋1|>3”的否定是______________．答案：对任意的x∈R，都有|x－1|－|x＋1|≤314．已知f(x＋1)＝x＋2x，则f(x)的解析式为f(x)＝__________．[解析] 法一：设t＝x＋1，则x＝(t－1)2(t≥1)；代入原式有f(t)＝(t－1)2＋2(t－1)＝t2－2t＋1＋2t－2＝t2－1.故f(x)＝x2－1(x≥1)．法二：因为x＋2x＝(x)2＋2x＋1－1＝(x＋1)2－1，所以f(x＋1)＝(x＋1)2－1(x＋1≥1)，即f(x)＝x2－1(x≥1)．[答案] x2－1(x≥1)15．设二次不等式ax 2＋bx ＋1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－1<x <13，则ab 的值为________．[解析] 由不等式ax2＋bx ＋1>0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－1<x <13，知a <0且ax 2＋bx ＋1＝0的两根为x 1＝－1，x 2＝13，由根与系数的关系知⎩⎪⎨⎪⎧－1＋13＝－b a ，－13＝1a ，所以a ＝－3，b ＝－2，ab ＝6.16．已知集合A ＝{x |1≤x <5}，C ＝{x |－a <x ≤a ＋3}，若C ∩A ＝C ，则a 的取值范围是________．[解析] 因为C ∩A ＝C ，所以C ⊆A .①当C ＝∅时，满足C ⊆A ，此时－a ≥a ＋3，得a ≤－32；②当C ≠∅时，要使C ⊆A ，则⎩⎪⎨⎪⎧－a <a ＋3，－a ≥1，a ＋3<5，解得－32<a ≤－1.综上，可得a 的取值范围是(－∞，－1]．三．解答题（共6小题，第17小题10分，其余各小题12分，共70分.解答应写出必要的文字说明、证明过程或演算步骤） 17.(1)lg 14－2lg 73＋lg 7－lg 18；(1)原式＝lg (2×7)－2(lg 7－lg 3)＋lg 7－lg(32×2) ＝lg 2＋lg 7－2lg 7＋2lg 3＋lg 7－2lg 3－lg 2＝0. (2) (0.027)23＋⎝ ⎛⎭⎪⎫27125－13－⎝ ⎛⎭⎪⎫2790.5 原式＝0.32＋⎝ ⎛⎭⎪⎫1252713－ 259＝9100＋53－53＝9100. 18．已知集合A ＝{x |1<x <3}，集合B ＝{x |2m <x <1－m }．(1)当m ＝－1时，求A ∪B ； (2)若A ⊆B ，求实数m 的取值范围； (3)若A ∩B ＝∅，求实数m 的取值范围． [解] (1)当m ＝－1时，B ＝{x |－2<x <2}，则A ∪B ＝{x |－2<x <3}． (2)由A ⊆B 知⎩⎪⎨⎪⎧1－m >2m ，2m ≤1，1－m ≥3，得m ≤－2，即实数m 的取值范围为(－∞，－2]． (3)由A ∩B ＝∅，得①若2m ≥1－m ，即m ≥13时，B ＝∅，符合题意；②若2m <1－m ，即m <13时，需⎩⎪⎨⎪⎧m <13，1－m ≤1或⎩⎪⎨⎪⎧m <13，2m ≥3，得0≤m <13或∅，即0≤m <13.综上知m ≥0，即实数m 的取值范围为[0，＋∞)．19．已知函数f (x )＝log a (x ＋1)－log a (1－x )，a >0且a ≠1.(1)求f (x )的定义域；(2)判断f (x )的奇偶性并予以证明； (3)若a >1时，求使f (x )>0的x 的解集．解 (1)f (x )＝log a (x ＋1)－log a (1－x )，则⎩⎪⎨⎪⎧x ＋1>0，1－x >0，解得－1<x <1.故所求函数f (x )的定义域为{x |－1<x <1}．……………………………………………(4分) (2)由(1)知f (x )的定义域为{x |－1<x <1}，且f (－x )＝log a (－x ＋1)－log a (1＋x ) ＝－[log a (x ＋1)－log a (1－x )]＝－f (x )，故f (x )为奇函数．…………………………………………………………(8分)(3)因为当a >1时，f (x )在定义域{x |－1<x <1}内是增函数，所以f (x )>0⇔x ＋11－x>1.解得0<x <1.所以使f (x )> 0的x 的解集是{x |0<x <1}．…………………………………(12分)20．已知函数f (x )＝⎩⎪⎨⎪⎧－x 2＋2x ，x ＞0，0，x ＝0，x 2＋mx ，x ＜0是奇函数．(1)求实数m 的值；(2)若函数f (x )在区间[－1，a －2]上单调递增，求实数a 的取值范围．[解] (1)设x ＜0，则－x ＞0，所以f (－x )＝－(－x )2＋2(－x )＝－x 2－2x .……………………(2分)又f (x )为奇函数，所以f (－x )＝－f (x )，……………………(4分)于是x ＜0时，f (x )＝x 2＋2x ＝x 2＋mx ，所以m ＝2.………………(5分)(2)由(1)知f (x )在[－1，1]上是增函数，要使f (x )在[－1，a －2]上单调递增．………(7分)结合f (x )的图象知⎩⎪⎨⎪⎧a －2＞－1，a －2≤1，……………………(9分)所以1＜a ≤3，……………………(11分)故实数a 的取值范围是(1，3]．……………………(12分)21．已知c >0，且c ≠1，设p ：函数y ＝c x 在R 上单调递减；q ：函数f (x )＝x 2－2cx ＋1在⎝ ⎛⎭⎪⎫12，＋∞上为增函数，若“p 且q ”为假，“p 或q ”为真，求实数c 的取值范围．【解】因为函数y ＝c x在R 上单调递减，所以0<c <1，即p ：0<c <1.因为c >0且c ≠1，所以綈p ：c >1. 又因为f (x )＝x 2－2cx ＋1在⎝ ⎛⎭⎪⎫12，＋∞上为增函数，所以c ≤12，即q ：0<c ≤12. 因为c >0且c ≠1，所以綈q ：c >12且c ≠1. 又因为“p 或q ”为真，“p 且q ”为假，所以p 真q 假或p 假q 真．①当p 真，q 假时，{c |0<c <1}∩⎩⎨⎧c ⎪⎪⎪⎭⎬⎫c >12，且c ≠1＝⎩⎨⎧c ⎪⎪⎪⎭⎬⎫12<c <1. ②当p 假，q 真时，{c |c >1}∩⎩⎨⎧⎭⎬⎫c ⎪⎪⎪0<c ≤12＝∅.综上所述，实数c 的取值范围是⎩⎨⎧c ⎪⎪⎪⎭⎬⎫12<c <1.22．设函数f (x )＝x 2－2|x |－1(－3≤x ≤3)(1)证明f (x )是偶函数；(2)画出这个函数的图象；(3)指出函数f (x )的单调区间，并说明在各个单调区间上f (x )是增函数还是减函数；(4)求函数的值域．解 (1)f (－x )＝(－x )2－2|－x |－1＝x 2－2|x |－1＝f (x )，即f (－x )＝f (x )．∴f (x )是偶函数．………………………………………………………(2分)(2)当x ≥0时，f (x )＝x 2－2x －1＝(x －1)2－2，当x <0时，f (x )＝x 2＋2x －1＝(x ＋1)2－2，即f (x )＝⎩⎪⎨⎪⎧ x －2－2， x ≥0，x ＋2－2， x <0.根据二次函数的作图方法，可得函数图象如下图．………………………………(6分)(3)由(2)中函数图象可知，函数f (x )的单调区间为[－3，－1]，[－1,0]， [0,1]，[1,3]．f (x )在区间[－3，－1]和[0,1]上为减函数，在[－1,0]，[1,3]上为增函数．……………(8分)(4)当x ≥0时，函数f (x )＝(x －1)2－2的最小值为－2，最大值为f (3)＝2；当x <0时，函数f (x )＝(x ＋1)2－2的最小值为－2，最大值为f (－3)＝2；故函数f (x )的值域为[－2,2]．………………………………………………………(12分)。

XXXX昆明一模：云南省昆明市2018届高三第一次模拟考试数)-

XXXX昆明一模：云南省昆明市2018届高三第一次模拟考试数）-199云南省昆明市2018年高中三年级第一次模拟考试理科数学多项选择题1题:此大题有12项，每项有5分，共60分。

在每个选项中给出的四个选项中，只有一个符合问题.11？(我是虚部)的虚部是()2？i1？2i3333A。

联邦调查局？d。

I 55551。

复杂2。

如果设置a？{x|1？x？2}、B？{x|x？b，b？然后呢？b的一个充分和不必要的条件是？2 B.1？b？2立方英尺？1d b？13。

假设7个数字的平均数是4，方差是2，则添加新的数据4。

此时，8个数字的平均数是x，方差是s，则()a。

x？4，s？2x？4，s？2x？4，s？2x？4，s？222222x2y24。

已知椭圆c: 2？2？1(a？b？0)，如果长轴是6，并且两个焦点正好平分长轴，则该椭圆的ab标准方程是()x2yx2yx2y 2？？1 B？？1摄氏度？？1 D？？1 A. 36329895161231A4等压项为，则a1值为()2211a.4b.2c.d.245。

已知的正项几何级数{an}符合a3？1、a5和？x？y。

4？0？6.已知变量x，y满足约束条件吗？？2？x？2，如果z？2x？y，z的取值范围是()？y。

1？七巧板是一种古老的中国传统智力游戏，被称为“东方魔板”。

如图所示，这是由拼图玩具制成的正方形，其中板1和板2是两个全等的等腰直角三角形，板3和板5是两个全等的等腰直角三角形，板7是等腰直角三角形，板4是正方形，板6是平行四边形。

从此。