化工原理例题分析
化工原理 第1章 流体流动 典型例题题解

化工原理典型例题题解第1章 流体流动例1 沿程阻力损失水在一段圆形直管内作层流流动,若其它条件不变,现流量及管径均减小为原来的二分之一,则此时因流动阻力产生的压力损失为原来的( )。
A 2倍 B .4倍 C .8 倍 D. 16 倍解:因管内流体流动处于层流状态,根据哈根(Hahen )-泊谡叶(poiseuille )公式 232dlu P f μ=∆(1) 将式中的流速u 用流量v q 和管径d 表示出来, 24dq u vπ=(2)将(2)式代入(1)式得 4128dlq P vf πμ=∆ (3) 现流量125.0v v q q =; 管径d 2=0.5d 1 , 根据(3)式,压力损失ΔP f2满足下式85.01/)5.0/(5.0//341141141142212====∆∆d q d q d q d q P P v v v v f f 故答案C 正确。
例2 流体在管内流动时剪应力的分布流体在管内流动的摩擦阻力,仅由流体与壁面之间的摩擦引起吗? 解:圆管中沿管截面上的剪应力分布式为 r lg Z P g Z P 2)()(2211ρρτ+-+=由该式推导条件可知,剪应力分布与流动截面的几何形状有关,而与流体种类,层流或湍流无关。
对于定常态流动体系,可见剪应力随圆管内流体半径的增大而增大,在壁面处,此剪应力达到最大。
故剪应力(磨擦阻力)并非仅产生于壁面处,而是在流体体内亦存在。
例3 并联管路中的阻力损失首尾相同的并联管路中,流体流经管径较小的支路时,总压头损失较大吗?例 4 附图解:A 为分支点,B 为汇合点。
并联管路Ⅰ、 Ⅱ、 Ⅲ具有相同的起始点A 和终点B ,分别利用柏努利方程式进行描述,得H f Ⅰ=H f Ⅱ=H f ⅢIIIIIIIII III IIIIII II III I gd u l gd u l gd u l 222222λλλ==因此,首尾相同的并联管路,各支路上总压头损失相等,并非仅取决于管径的大小,与各支路上的流速、管长均有关系。
化工原理固体干燥典型例题题解2-2022年学习资料

例4:两股气体的混合-气体1与气体2混合,则混合气体的状态点在状态点1与状态点2的连线上,-具体可以根据杠 规则确定混合气体的状态点。-L+L2=Lm-LH+LH2 Ln Hm-01-LI+L12 LmIm-LH=LzH2-H-H2 H---两股气流的混合-Lm-I1=L22-Im
例5:-已知:t=50°C,H0.016kg水/kg干气-求:I,p,0;td,tm=?-P,=101.3 10kpa-解:I-1.01+1.88Ht+2500H-=1.01+1.88×0.016×50+2500× .016-=92kJ/kg-Pw=2.5kPa-p,=ft-H=0.622-p=0.016→p=2.5kP -P-p-Hw=0.622-卫w'-9--=20.27%-P-Pw-ps-12.335-tn时的饱和水蒸气 印w-p=psta→t:=21.07C-t山.--试差得t=28.7℃
G=pu=1.02×6=6.12-kg-s·m-a=0.0143G0.8=0.0143×6.120.8=0 0609-k.J-m2.s.C-N4=t-t-0.0609×70-30.3)=0.995×10-2430·m2-2若t1=80C,查得此时tw=32.3C,rw=2420kJ/kg-N,-at-_00609x8 -323)-12x10-NA
例6:利用I-H图确定空气的状态参数:今测得空气=60℃,t=45C-求空气的H、p、I、ta。-空气的状 点-解:-I 212kJ/kg-为什么沿着等焓线-寻找状态点?-t=60°C-0=43%-p=1-tw=4 °C-A-ta=43°C
例7:空气状态变化过程的计算-注意:V=L,表示空气的kg-新鲜空气:t=18C,H1=0.006kg/k ,P=100kpa-废气:t=58℃,0=70%-混合气:H3=0.065kgkg-求:混合比、混合气的温 。-千燥器-预热器-解:(1-确定H2t2=58°C一P,=18.2kp。-P。=p,=0.70×18.2 12.7kp。H2=0.622-Pw—=0.0908kg1kg-P一pw-VH1+V,H2=V,+V2H3 H3-H1-0.065-0.006-=2.29-V H2-H3-0.0908-0.065
化工原理习题答案

化工原理习题答案问题一:质量守恒及干燥问题问题描述:一种含有30%水分的湿煤经过加热后,其水分含量降低到15%。
问:为了使1000kg湿煤的水分含量降到15%,需要排除多少千克水分?解答:根据质量守恒原则,该问题可以通过计算质量的变化来求解。
设湿煤的初始质量为m1,水分含量为w1,加热后的质量为m2,水分含量为w2。
根据题意可得到以下关系:m1 = m2 + m水分 w1 = (m水分 / m1) × 100% w2 = (m水分 / m2) × 100%根据题意可得到以下关系: w2 = 15% = 0.15 w1 = 30% = 0.30将以上关系代入计算,可得到: 0.15 = (m水分 / m2) × 100% 0.30 = (m水分 / m1) × 100%解得:m水分 = 0.15 × m2 = 0.30 × m1代入具体数值进行计算: m水分 = 0.15 × 1000kg = 150kg因此,需要排除150千克水分。
问题二:能量守恒问题问题描述:一个装有100升水的水箱,水温为20°C。
向该水箱中加热10000千卡的热量,水温升高到40°C。
问:热容量为1千卡/升·°C的水箱的温度升高了多少度?解答:根据能量守恒原理,可以通过计算热量的变化来求解。
热量的变化可表示为:Q = mcΔT其中,Q为热量的变化量,m为物体的质量,c为物体的比热容,ΔT为温度的变化。
根据题意可得到以下关系: Q = 10000千卡 = 10000 × 1000卡 m = 100升 = 100升 × 1千克/升 = 100 × 1千克 c = 1千卡/升·°C 代入公式计算温度的变化ΔT:10000 × 1000 = (100 × 1) × (ΔT) ΔT = (10000 × 1000) / (100 × 1) = 1000000 / 100 = 10000°C 因此,热容量为1千卡/升·°C的水箱的温度升高了10000度。
化工原理Ppt例题

xD
0.263
(2.61 1)
0.95
提馏段操作线与对角线交点坐标为
y x xw ,故 xw 0.0748
由两操作线交点 0.723x 0.263 1.25x
0.723x+0.263=1.25x-0.0187 解得 x 0.535
y 0.7230.535 0.263 0.65
因为露点下进料故 q 线为水平线,可得原料液组成 x F =y=0.65
4 80 1 (0.01415)2 d 29.81 d
hf
l d
u2 2g
d 5 2.041104
先假设摩擦系数λ,由试差方程求出d,然后计 算u、Re和λ ;若与原假设相符,则计算正确; 若不符,则需重新假设,直至查得的值与假设 值相符为止。
假设λ =0.023,由试差方程解得:
d 5 2.041104 来自Re 1.62105例:用某离心泵以40 m3/h的流量将贮 水池中65℃的热水输送到凉水塔顶, 并经喷头喷出而落入凉水池中,以达 到冷却的目的。已知水在进入喷头之 前需要维持49 kPa的表压强,喷头入 口较贮水池水面高8 m。吸入管路和 排出管路中压头损失分别为l m和5 m ,管路中的动压头可以忽略不计。试 选用合适的离心泵,并确定泵的安装
例
注意使用标 准单位
例题:某厂利用喷射泵输送氨。管中稀
氨水的质量流量为1×104kg/h,密度 为1000kg/m3,入口处的表压为147kPa 。管道的内径为53mm,喷嘴出口处内 径为13mm,喷嘴能量损失可忽略不计 ,试求喷嘴出口处的压力。
例题:用泵将水槽中水打到高位槽。泵入口处 真空表读数为31925Pa,管路阻力∑hf0-2=23u2, 管路阻力∑hf0-1=4u2 。 问题 (1)管内流速?
化工原理 第9章 液体精馏 典型例题题解(1)

第9章 精馏 典型例题例1:逐板法求理论板的基本思想有一常压连续操作的精馏塔用来分离苯-甲苯混合液,塔顶设有一平衡分凝器,自塔顶逸出的蒸汽经分凝器后,液相摩尔数为汽相摩尔数的二倍,所得液相全部在泡点下回流于塔,所得汽相经全凝器冷凝后作为产品。
已知产品中含苯0.95(摩尔分率),苯对甲苯的相对挥发度可取为2.5 。
试计算从塔顶向下数第二块理论板的上升蒸汽组成。
解: 884.095.05.15.295.05.115.20000=⨯-=→=+=x x x x y DR=L/D=2905.03/95.0884.0323/95.032:11=+⨯=+=+y x y n n 精馏段方程845.03/95.0793.032793.0905.05.15.2905.05.15.22111=+⨯==⨯-=-=y y y x例2:板数较少塔的操作型计算拟用一 3 块理论板的(含塔釜)的精馏塔分离含苯50%(摩尔分率,下同)的苯-氯苯混合物。
处理量F=100 Kmol/h ,要求 D=45 Kmol/h 且 x D >84%。
若精馏条件为:回流比R=1 ,泡点进料,加料位置在第二块理论板,α=4.10 ,问能否完成上述分离任务? 解:W=55kmol/h精馏段操作线方程:y n+1=0.5x n +0.42提馏段的操作线方程:Fq D R Wx x F q D R qFRD y w )1()1()1()1(--+---++=将相关数据代入得提馏段操作线方程:134.061.1-=x y 逐板计算:y 1=x D =0.84y 2=0.5×0.56+0.42=0.7057.0134.036.061.13=-⨯=y.22.05584.04550=⨯-=-=WDx Fx x Df w ()56.084.01.31.484.01111=⨯-=--=y y x αα36.07.01.31.470.02=⨯-=x22.024.057.01.31.457.03≥=⨯-=x所以不能完成任务。
化工原理精彩试题及其问题详解

化工原理试题与答案一、填空题1. 流体在一根圆形水平直管中流动,测得其平均流速为0.5 m ·s -1,雷诺数Re =1000,压降Δp =10 Pa ,问管中心处的最大流速为 m ·s -1。
若平均流速增大为1 m ·s -1,则压降Δp 为 Pa 。
2.反应器流体的混和按考察的尺度可划分为 混和和 混和。
3. 填料吸收塔正常操作时,若液气比增大,则吸收液的出塔浓度 ,吸收的推动力 。
4. 某间壁式换热器传热面积为2.5 m 2,传热平均温差为45 K ,传热速率为9000 W ,则该换热器此时的总传热系数K = 。
5. 气体的粘度值随温度的升高而 ;液体的粘度值随温度的升高而 。
6. 雷诺数Re 是流体流动 的判据。
流体在管道中流动,当Re 时为稳定层流;当Re 时,可以形成湍流;只有当Re 时,方可达到稳定的湍流。
7. 活塞流反应器的量纲一平均停留时间(无因次平均停留时间)θ等于 ;其停留时间的量纲一方差(无因次方差)为 。
8. 在连续接触的填料塔,进行定常等温吸收操作,填料层高度的计算,可由物料衡算式和吸收速率方程联列导出计算式, 填料层总高度等于 和 之乘积。
9. 列举四种工业上常用的间壁式热交换器: 、 、、 。
10.伯努利方程gZ 1+ρ1p +221u +W e =gZ 2+ρ2p +222u +)21(,-∑f H 适用的条件是在 流动时的 流体。
11. 从手册中查得某液体在25℃和1 atm 时的粘度为0.80 厘泊,试将其换算成国际单位制,粘度应为 。
12. 在研究流体流动规律时,要注意区分是定常(或称定态)流动和不定常(或称不定态)流动,稳定态和不稳定态。
如果所考察的流体流动过程或系统中任何一个部位或任何一个点上的流体性质和过程参数都不随时间而改变,则该过程为 过程,反之,则为 过程。
当流体流动过程的雷诺数大于1×104时,可以认为是 的湍流;当雷诺数在2000 ~4000 之间流体的流动型态为 的过渡区域。
化工原理颗粒的沉降和流态化典型例题题解

第5章颗粒的沉降和流态化【例1】落球粘度计。
使用光滑小球在粘性液体中的自由沉降测定液体的粘度。
现有密度为8010kg/m 3、直径0.16mm 的钢球置于密度为980kg/m 3的某液体中,盛放液体的玻璃管内径为20mm 。
测得小球的沉降速度为1.70mm/s ,试验温度为20℃,试计算此时液体的粘度。
测量是在距液面高度1/3的中段内进行的,从而免除小球初期的加速及管底对沉降的影响。
当颗粒直径d 与容器直径D 之比d/D <0.1,雷诺数在斯托克斯定律区内时,器壁对沉降速度的影响可用下式修正:—0.16x 10-3解:D ―2x 10-2=1.70x 10-31+2.104x 8x 10-3]=1.73X 10-3m/s可得d 2(p -p )g G.16x 10-3)(8010-980)x 9.81ILl=s =18u 18x 1.73x 10-3t=0.0567Pa •s校核颗粒雷诺数du 'p0.16x10-3x1.70x10-3x980tRet l 0.0567上述计算有效。
【例2】拟采用降尘室回收常压炉气中所含的球形固体颗粒。
降尘室底面积为10m 2,宽和高均为2m 。
操作条件下,气体的密度为0.75kg/m 3,粘度为 2.6X 10-5Pa •s ;固体的密度为3000kg/m 3;降尘室的生产能力为3m 3/s 。
试求:1)理论上能完全捕集下来的最小颗粒直径;2)粒径为40u m 的颗粒的回收百分率;3)如欲完全回收直径为10u m 的尘粒,在原降尘室内需设置多少层水平隔板?解:1)理论上能完全捕集下来的最小颗粒直径在降尘室中能够完全被分离出来的最小颗粒的沉降速度为V 3u =—r=——0.3t bl 10m/s由于粒径为待求参数,沉降雷诺准数Re t 无法计算,故需采用试差法。
假设沉降在滞流区,则可用斯托克斯公式求最小颗粒直径,即-18l u 18x 2.6x 10-5x 0.3d =t ==6.91x 10-5m =69.1|i mmin '.Ap -p )g\3000x 9.81s核算沉降流型u 1+2.104-I D J式中u't 为颗粒的实际沉降速度; u t 为斯托克斯定律区的计算值。
化工原理例题与解题指导

例题与解题指导【例2-1】某离心泵的叶轮外径D2为218mm,叶轮出口宽度b2为12.5mm,叶片出口流动角β2为35°,泵的转速n 为2900 r/min,试推导出该离心泵的理论压头与理论流量之间的关系式。
解:将题给数据分别代入式2-11及式2-12,经整理可得式2-13所示的具体线性关系式,即该式表明,对于后弯叶片,离心泵的流量增加,其压头随之降低。
【例2-2】在实验装置上,用20℃的清水于98.1kPa的条件下测定离心泵的性能参数。
泵的吸入管内径为80mm,排出管内径为50mm。
实验测得数据为:泵入口处真空度为72.0kPa,泵出口处表压强为253kPa,两测压表之间的垂直距离为0.4m,流量为19.0m3/h,电动机功率为2.3kw,泵由电动机直接带动,电动机传动效率为93%,泵的转速为2900r/min。
试求该泵在操作条件下的压头、轴功率和效率,并列出泵的性能参数。
解:(1) 泵的压头 在泵入口的真空表和泵出口压强表两截面之间列柏努利方程式,在忽略两测压口之间流动阻力下,可得测量泵压头的一般表达式为2201221()/2H h H H u u g =+++- (a) 式中h 0--泵的两测压截面之间的垂直距离,m ;H 1--与泵入口真空度对应的静压头,m ;H 1=p 1/(ρg) (p 1为真空度)H 2 --与泵出口表压对应的静压头,m ;H 2=p 2/(ρg)u 1、u 2--泵的入口和出口液体的流速,m/s ;m/sm/s取水的密度ρ=1000kg/m 3,将已知条件代入式a ,得m(2) 泵的轴功率0.93 2.3 2.139N =⨯= kW(3) 泵的效率η 泵的有效功率为31934.45109.8117843600Ne HQ g ρ==⨯⨯⨯= W 故 / 1.784/2.1390.834Ne N η=== 即83.4% 泵性能参数:转速n 为2900r/min ,流量Q 为19m 3/h ,压头H 为34.45m ,轴功率N 为2.139kw ,效率η为83.4%。
化工原理1-7章习题答案解析

目录第一章流体流动与输送机械 (2)第二章非均相物系分离 (32)第三章传热 (42)第四章蒸发 (69)第五章气体吸收 (73)第六章蒸馏 (95)第七章固体干燥 (119)第一章 流体流动与输送机械1. 某烟道气的组成为CO 2 13%,N 2 76%,H 2O 11%(体积%),试求此混合气体在温度500℃、压力101.3kPa 时的密度。
解:混合气体平均摩尔质量kg/mol 1098.2810)1811.02876.04413.0(33--⨯=⨯⨯+⨯+⨯=∑=i i m M y M ∴ 混合密度333kg/m 457.0)500273(31.81098.28103.101=+⨯⨯⨯⨯==-RT pM ρm m2.已知20℃时苯和甲苯的密度分别为879 kg/m 3和867 kg/m 3,试计算含苯40%及甲苯60%(质量%)的混合液密度。
解:8676.08794.012211+=+=ρρρa a m混合液密度 3kg/m 8.871=m ρ3.某地区大气压力为101.3kPa ,一操作中的吸收塔塔内表压为130kPa 。
若在大气压力为75 kPa 的高原地区操作该吸收塔,且保持塔内绝压相同,则此时表压应为多少?解:''表表绝+p p p p p a a =+=∴kPa 3.15675)1303.101)(''=-==+(-+真表a a p p p p4.如附图所示,密闭容器中存有密度为900 kg/m 3的液体。
容器上方的压力表读数为42kPa ,又在液面下装一压力表,表中心线在测压口以上0.55m ,其读数为58 kPa 。
试计算液面到下方测压口的距离。
解:液面下测压口处压力 ghp z g p p ρρ+=∆+=10题4 附图m 36.255.081.990010)4258(30101=+⨯⨯-=+ρ-=ρ-ρ+=∆∴h g p p g p gh p z5. 如附图所示,敞口容器内盛有不互溶的油和水,油层和水层的厚度分别为700mm 和600mm 。
化工原理 第9章 液体精馏 典型例题题解(1)

第9章 精馏 典型例题例1:逐板法求理论板的基本思想有一常压连续操作的精馏塔用来分离苯-甲苯混合液,塔顶设有一平衡分凝器,自塔顶逸出的蒸汽经分凝器后,液相摩尔数为汽相摩尔数的二倍,所得液相全部在泡点下回流于塔,所得汽相经全凝器冷凝后作为产品。
已知产品中含苯0.95(摩尔分率),苯对甲苯的相对挥发度可取为2.5 。
试计算从塔顶向下数第二块理论板的上升蒸汽组成。
解: 884.095.05.15.295.05.115.20000=⨯-=→=+=x x x x y DR=L/D=2905.03/95.0884.0323/95.032:11=+⨯=+=+y x y n n 精馏段方程845.03/95.0793.032793.0905.05.15.2905.05.15.22111=+⨯==⨯-=-=y y y x例2:板数较少塔的操作型计算拟用一 3 块理论板的(含塔釜)的精馏塔分离含苯50%(摩尔分率,下同)的苯-氯苯混合物。
处理量F=100 Kmol/h ,要求 D=45 Kmol/h 且 x D >84%。
若精馏条件为:回流比R=1 ,泡点进料,加料位置在第二块理论板,α=4.10 ,问能否完成上述分离任务? 解:W=55kmol/h精馏段操作线方程:y n+1=0.5x n +0.42提馏段的操作线方程:Fq D R Wx x F q D R qFRD y w )1()1()1()1(--+---++=将相关数据代入得提馏段操作线方程:134.061.1-=x y 逐板计算:y 1=x D =0.84y 2=0.5×0.56+0.42=0.7057.0134.036.061.13=-⨯=y.22.05584.04550=⨯-=-=WDx Fx x Df w ()56.084.01.31.484.01111=⨯-=--=y y x αα36.07.01.31.470.02=⨯-=x22.024.057.01.31.457.03≥=⨯-=x所以不能完成任务。
化工原理典型例题题解

第4章 流体通过颗粒层的流动典型例题例1:过滤机的最大生产能力用一板框压滤机对悬浮液进行恒压过滤,过滤20分钟得滤液 20m 3 ,过滤饼不洗涤,拆装时间为15分钟,滤饼不可压缩,介质阻力可略。
试求: (1) 该机的生产能力,以 m 3 (滤液)/h 表示(2)如果该机的过滤压力增加 20℅,该机的最大生产能力为多少 m 3(滤液)/h ? 解:(1)h m V Q D /3.34601520203=⨯+=+=θθ (2)根据恒压过滤方程V 2=KA 2θ202020222===θV KA为了得到最大生产能力,则应 min 15==D f θθ在原压力下对应的滤液量为 300152022=⨯==f opt KA V θ33.17m V opt = ΔP ’=1.2ΔPV ∝ΔP 1/2395.183.172.1m V opt =⨯=h m V Q Df opt/9.3760151595.183max =⨯+=+=θθ例2:滤饼的洗涤问题采用板框压过滤机进行恒压过滤,操作1小时后,得滤液 15m 3 ,然后用2m 3的清水在相同的压力下对滤饼进行横穿洗涤。
假设清水的粘度与滤液的粘度相同。
滤布阻力可略,试求: (1) 洗涤时间(2) 若不进行洗涤,继续恒压过滤1小时,可另得滤液多少 m 3 ? 解:V 2=KA 2θKA 2=152采用横穿洗涤法,则有:Ew d dV d dV ⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛θθ41 hr V KA V f w w 07.11521541224122=⨯⨯=⨯=θ 或者 hr Jf w 07.114115222=⨯⨯==θδθ''22θKA V = , 322.21215''m KA V =⨯==θ 32.6152.21m V =-=∆例3:操作压强对过滤机生产能力的影响用板框过滤机过滤某悬浮液,一个操作周期内过滤 20分钟后共得滤液 4m 3 (滤饼不可压缩,介质阻力可略)。
化工原理例题及解答(上)

例题及解答(上)一、如图所示,常温的水在管道中流过,两个串联的U 形管压差计中的指示液均为水银,密度为ρHg ,测压连接管内充满常温的水,密度为ρw ,两U 形管的连通管内充满空气。
若测压前两U 形管压差计内的水银液面均为同一高度,测压后两U 形管压差计的读数分别为R 1、R 2,试求a 、b 两点间的压力差b a p p -。
(10分)解: 11gh p p w a ρ+=,11gh p p w a ρ-=21p p =,132gR p p Hg ρ+=,43p p =,254gR p p Hg ρ+=55gh p p w b ρ+=52455gh gR p gh p p w Hg w b ρρρ--=-=()524113gh gR p gh gR p p p w Hg w Hg b a ρρρρ----+=-()5121gh gh R R g w w Hg ρρρ+-+=而 211R h h +=,225R h h -=所以 ()⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛--+=-222121R g gh R g gh R R g p p w w w w Hg b a ρρρρρ()()()g R R R R g R R g w Hg w Hg 2121212121+⎪⎭⎫⎝⎛-=+-+=ρρρρ二、用压缩空气将密度为1100kg/m 3的腐蚀性液体自低位槽送到高位槽,两槽的液面维持恒定。
管路直径均为φ60mm ⨯3.5mm ,其他尺寸见本题附图。
各管段的能量损失为2,2,,18.1,uh u h h BC f CD f AB f =∑=∑=∑。
两压差计中的指示液均为水银。
试求当mm h mm R 200,451==时:(1)压缩空气的压力p 1为若干(表压)?(2)U 形管压差计读数R 2为多少? 知:3/1100m kg =ρ mm d 535.3260=⨯-= 2,,u h h CD f AB f =∑=∑2,18.1u h BC f =∑ mm R 451= mm h 200= 求:(1)p 1 (2)R 2解:(1)在两槽液面间列柏努利方程:12,2222211122f h u p gz u p gz ∑+++=++ρρ由两槽液面为大液面,且2液面通大气, 得CDf BC f AB f h h h z zg p ,,,121)(∑+∑+∑+-=ρ所以 ()222212118.31018.1)(u g u u u z z g p ρρρ+=+++-= 又在BC 两截面间列柏努利方程: BC f C CC B BB h u p gz u p gz ,2222∑+++=++ρρ得BCf B C CB h z z g p p ,)(∑+-=-ρ所以 []2218.1518.1)(u g u z z g p p B C C B ρρρ+=+-=-而 g g R z z g g R p p Hg B C Hg C B ρρρρρρ5)()()(11+-=-+-=- 所以 g g R u g Hg ρρρρρ5)(18.1512+-=+18.1)(12gR u Hg ρρρ-=所以 18.1)(18.31011gR g p Hg ρρρ-+=)(3316.1227418.1807.9)110013600(045.018.3807.9110010表压Pa =⨯-⨯⨯+⨯⨯=(2) 在B2两截面间列柏努利方程:CD f BC f B BB h h u p gz u p gz ,,2222222∑+∑+++=++ρρ得222218.1)(2u u z z g up B B++-=+ρ所以22218.172u u g up B++=+ρ268.17u g p B ρρ+= 而 gh gR p Hg B ρρ+=2所以 2268.17u g gh gR Hg ρρρρ+=+ggR g h g ugh g R Hg Hg Hg ρρρρρρρρ18.1)(68.1)7(68.17122-+-=+-=mmm 609608885842.01360018.1)110013600(045.068.11100)2.07(≈=-⨯⨯+⨯-=三、在实验室用管道阻力测定装置对镀锌管(内径为27mm )阻力进行测定时,水的流量为2L/s ,水银U 形管压差计读数为400mm ,测压点间距为5290mm ,水的粘度为1cP ,密度为1000kg/m 3,水银的密度为13600kg/m 3。
化工原理第2章流体输送机械典型例题题解
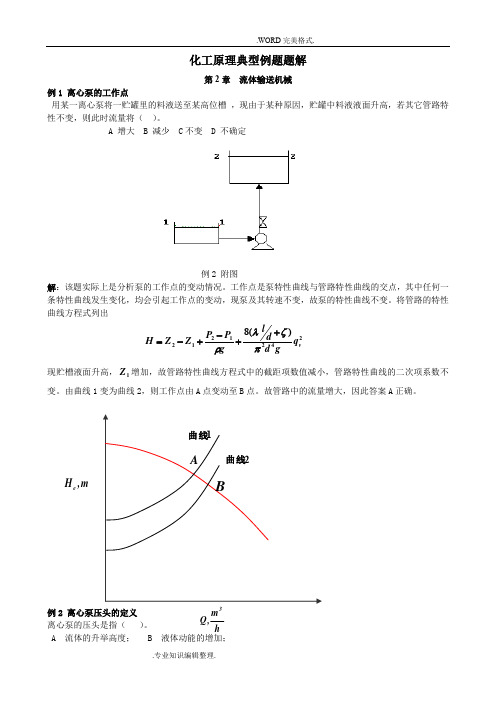
化工原理典型例题题解第2章 流体输送机械例1 离心泵的工作点用某一离心泵将一贮罐里的料液送至某高位槽 ,现由于某种原因,贮罐中料液液面升高,若其它管路特性不变,则此时流量将( )。
A 增大B 减少C 不变D 不确定例 2 附图例2 附图解:该题实际上是分析泵的工作点的变动情况。
工作点是泵特性曲线与管路特性曲线的交点,其中任何一条特性曲线发生变化,均会引起工作点的变动,现泵及其转速不变,故泵的特性曲线不变。
将管路的特性曲线方程式列出2421212)(8v q gd d l g P P Z Z H πζλρ++-+-= 现贮槽液面升高,1Z 增加,故管路特性曲线方程式中的截距项数值减小,管路特性曲线的二次项系数不变。
由曲线1变为曲线2,则工作点由A 点变动至B 点。
故管路中的流量增大,因此答案A 正确。
例2 离心泵压头的定义 离心泵的压头是指( )。
A 流体的升举高度; B 液体动能的增加; h m ,Q 3m,H eC 液体静压能的增加;D 单位液体获得的机械能。
解:根据实际流体的机械能衡算式H e =(Z 2-Z 1)+(P 2-P 1)+(u 22-u 12)/2g+ΣH f离心泵的压头可以表现为液体升举一定的高度(Z 2-Z 1),增加一定的静压能(P 2-P 1)/(g ρ),增加一定的动能(u 22-u 12)/(2g)以及用于克服流体流动过程中产生的压头损失ΣH f 等形式,但本质上离心泵的压头是施加给单位液体(单位牛顿流体)的机械能量J(J/N=m).故答案D 正确。
例3离心泵的安装高度H g 与所输送流体流量、温度之间的关系分析离心泵的安装高度H g 与所输送流体流量、温度之间的关系。
解:根据离心泵的必需汽蚀余量(NPSH)r ,计算泵的最大允许安装高度的计算公式为[][]5.0)()10(0+---=∑-r f vgNPSH H g P g P H ρρ (1) 首先分析离心泵的必需汽蚀余量(NPSH)r 的定义过程。
化工原理典型例题题解

第4章 流体通过颗粒层的流动典型例题例1:过滤机的最大生产能力用一板框压滤机对悬浮液进行恒压过滤,过滤20分钟得滤液 20m 3 ,过滤饼不洗涤,拆装时间为15分钟,滤饼不可压缩,介质阻力可略。
试求: (1) 该机的生产能力,以 m 3 (滤液)/h 表示(2)如果该机的过滤压力增加 20℅,该机的最大生产能力为多少 m 3(滤液)/h 解:(1)h m V Q D /3.34601520203=⨯+=+=θθ (2)根据恒压过滤方程V 2=KA 2θ202020222===θV KA为了得到最大生产能力,则应 min 15==D f θθ在原压力下对应的滤液量为 300152022=⨯==f opt KA V θ33.17m V opt = ΔP ’=ΔP V ∝ΔP 1/2395.183.172.1m V opt =⨯=h m V Q Df opt/9.3760151595.183max =⨯+=+=θθ例2:滤饼的洗涤问题采用板框压过滤机进行恒压过滤,操作1小时后,得滤液 15m 3 ,然后用2m 3的清水在相同的压力下对滤饼进行横穿洗涤。
假设清水的粘度与滤液的粘度相同。
滤布阻力可略,试求: (1) 洗涤时间(2) 若不进行洗涤,继续恒压过滤1小时,可另得滤液多少 m 3 解:V 2=KA 2θKA 2=152采用横穿洗涤法,则有:Ew d dV d dV ⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛θθ41 hr V KA V f w w 07.11521541224122=⨯⨯=⨯=θ 或者 hr Jf w 07.114115222=⨯⨯==θδθ ''22θKA V = , 322.21215''m KA V =⨯==θ 32.6152.21m V =-=∆例3:操作压强对过滤机生产能力的影响用板框过滤机过滤某悬浮液,一个操作周期内过滤 20分钟后共得滤液 4m 3 (滤饼不可压缩,介质阻力可略)。
化工原理典型例题题解

(2)若操作压强加倍,其它条件不变(物性、过滤面积、过滤时间与辅助时间),该机生产能力提高了多少?
解:滤饼不洗涤
(1)Q=4/(20+30)=0.08m3/min
(2)K∝ΔP
V’∝ΔP1/2
V’=21/2V=1.414×4=5.65m3
Q=5.65/50=0.113m3/min
例4:在9.81×103Pa的恒定压力差下过滤某种的悬浮液。悬浮液中固相为直径0.1mm的球形颗粒,固相体积分率为10%,过滤时形成空隙率为60%的不可压缩滤饼。已知水的粘度为1.0×10-3Pa·s,过滤介质阻力可以忽略,试求:(1)每平方米过滤面积上获得1.5m3滤液所需的过滤时间;(2)若将此过滤时间延长一倍,可再得滤液多少?
解:以1min为基准。由题给数据知
m3/min
(a)
s
(b)
滤饼体积 0.642×0.04=0.02568m3/min
取滤饼厚度,δ=7mm,于是得到
r/min
(c)
每分钟获得的滤液量为
m3/min
(d)
联立式a、b、c、d解得 m2, r/min。
例6若分别采用下列各项措施,试分析转筒过滤机的生产能力将如何变化。已知滤布阻力可以忽略,滤饼不可压缩。
(1)洗涤时间
(2)若不进行洗涤,继续恒压过滤1小时,可另得滤液多少m3?
解:V2=KA2θ
KA2=152
采用横穿洗涤法,则有:
或者
,
例3:操作压强对过滤机生产能力的影响
用板框过滤机过滤某悬浮液,一个操作周期内过滤20分钟后共得滤液4m3(滤饼不可压缩,介质阻力可略)。若在一个周期内共用去辅助时间30分钟,求:
(1)转筒尺寸按比例增大50%。
化工原理典型例题题解

第4章 流体通过颗粒层的流动典型例题例1:过滤机的最大生产能力用一板框压滤机对悬浮液进行恒压过滤,过滤20分钟得滤液 20m 3 ,过滤饼不洗涤,拆装时间为15分钟,滤饼不可压缩,介质阻力可略。
试求:(1) 该机的生产能力,以 m 3 (滤液)/h 表示(2)如果该机的过滤压力增加 20℅,该机的最大生产能力为多少 m 3(滤液)/h ?解:(1)h m V Q D /3.34601520203=⨯+=+=θθ (2)根据恒压过滤方程V 2=KA 2θ202020222===θV KA为了得到最大生产能力,则应 min 15==D f θθ在原压力下对应的滤液量为 300152022=⨯==f opt KA V θ33.17m V opt = ΔP ’=1.2ΔPV ∝ΔP 1/2395.183.172.1m V opt =⨯=h m V Q Df opt/9.3760151595.183max =⨯+=+=θθ例2:滤饼的洗涤问题采用板框压过滤机进行恒压过滤,操作1小时后,得滤液 15m 3 ,然后用2m 3的清水在相同的压力下对滤饼进行横穿洗涤。
假设清水的粘度与滤液的粘度相同。
滤布阻力可略,试求:(1) 洗涤时间(2) 若不进行洗涤,继续恒压过滤1小时,可另得滤液多少 m 3 ?解:V 2=KA 2θKA 2=152采用横穿洗涤法,则有:Ew d dV d dV ⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛θθ41 hr V KA V f w w 07.11521541224122=⨯⨯=⨯=θ 或者 hr J f w 07.114115222=⨯⨯==θδθ''22θKA V = , 322.21215''m KA V =⨯==θ32.6152.21m V =-=∆例3:操作压强对过滤机生产能力的影响用板框过滤机过滤某悬浮液,一个操作周期内过滤 20分钟后共得滤液 4m 3 (滤饼不可压缩,介质阻力可略)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-6.高位槽内的水面高于地面8m,水从108×4mm的管道中流出,管路出口高于地面2m。
在本题特定条件下,水流经系统的能量损失可按Σhf=6.5u2计算,其中u为水在管内的流速,m/s。
试计算:(1)A-A’截面处水的流速;(2)水的流量,以m3/h计。
1-7.20℃的水以2.5m/s的流速流经φ的水平管,此管以锥形管与另一53×3mm的水平管相连。
如本题附图所示,在锥形管两侧A、B处各插一垂直玻璃管以面察两截面的压强。
若水流经A、B两截面间的能量损失为1.5J/kg求两玻璃管的水面差(以mm计),并在本题附图中画出两玻璃管中水面的相对位置。
1-8.用离心泵把20℃的水从贮槽送至水洗塔顶部,槽内水位维持恒定。
各部分相对位置如本题附图所示。
管路的直径均为
φ76×2.5mm在操作条件下,泵入口处真空表的读数为
24.66×103Pa;水流经吸入管与排出管(不包括喷头)的能量损失可分别按Σhf,1=2u2与Σhf,2=10u2计算,由于管径不变,故式中u为吸入或排出管的流速m/s。
排水管与喷头连接处的压强为
98.07×103Pa(表压)。
试求泵的有效功率。
1 如图所示,槽内水位维持不变。
槽底部与内径为100mm钢管相连,管路上装有一个闸阀,阀前离管路入口端15m处安有一个指示液为汞的U形压差计,测压点与管路出口端之间距离为20m。
(1) 当闸阀关闭时测得R=600mm,h=1500mm;当闸阀部分开启时,测得R=400mm,
h=1400mm,管路摩擦系数取0.02,入口处局部阻力系数取0.5,问每小时从管中流出水量为多少m3。
(2)当阀全开时(取闸阀全开Le/d=15,λ=0.018),测压点B处的静压强为若干N/m2(表压)。
(13分)
2混合式冷凝器的真空度为78.48kPa,所需冷却水量为5×104 kg/h,冷水进冷凝器的入口比水池的吸水液面高15 m,用φ114×7 mm的管道输水,管长80 m,管路配有2个球形阀和5个90o弯头,已知阀门的阻力系数ζ= 3,90o弯头阻力系数ζ= 1.26,摩擦系数λ= 0.02。
现仓库中有四种规格离心泵如下:
编号 1 2 3 4
0.5 1 1 2
流量/
(m3/min)
扬程/ m 10 10 15 15
试问选用哪一号泵,并说明理由。
3由水库将水打入一水池,水池水面比水库水面高50m,两水面上的压力均为常压,要求的流量为90m3/h,输送管内径为156mm,在阀门全开时,管长和各种局部阻力的当量长度的总和为1000m,对所使用的泵在Q=65~135m3/h范围内属于高效区,在高效区中泵的性能曲线可用H=124.5-5.645×104Q2表示,此处H为泵的扬程m,Q为泵的流量m3/s,管子摩擦系数可取为λ=0.025,水的密度ρ=1000kg/m3。
求:
(1) 管路特性方程
(2) 核算此泵能否满足要求;
(3) 泵的实际流量和扬程。
解:(1) 在水库水面1-1和水池水面2-2间列伯努利方程式,以1-1面为基准面,则:
∑+++=+++f 2222e 211122H g u g p z H g u g p z ρρ ∵ 01=z ,m 502
=z ,021==p p (表), 021==u u 又 22e 2e f 421)(2)(⎪⎪⎪⎪⎭⎫ ⎝⎛+=+=∑∑∑d Q g d l l g
u d l l H πλλ 2422210238.2)156.0785.01(81.921156.01000
025.0Q Q ⨯=⨯⨯⨯⨯⨯=
∴ 管路特性方程:2
4f 2e 10238.250Q H z H ⨯+=+=∑ (Q —m 3/s )
(2) 当Q =90m 3/h=0.025m 3/s 时,H e =64.0m
又由泵的特性方程可得H =124.5-5.645×104×0.0252=89.22m 显然H >H e ,故此泵可用。
(3) 联立泵的特性方程和管路特性方程可得:
H =H e ,即 50+2.238×104Q 2=124.5-5.645×104Q 2
∴ Q =0.0307m 3/s=110.5m 3/h ,H e =71.1m
即泵的实际流量为110.5m 3/h ,扬程为71.1m 。
4 用泵将20℃水由贮槽打到某处,泵前后各装有真空表和压强表。
已知泵的吸入管路总阻力为2.3 mH 2O ,吸入管路速度头为0.2 mH 2O ,该泵的必需汽蚀余量为
5 m ,当地大气压为101.3 kPa 。
水在50℃时的饱和蒸汽压为12.31 kPa ,槽液面与吸入口位差2 m 。
试求:(1)真空表的读数为多少?(2)当水温由20℃变为50℃时发现真空表与压强表读数突然改变,流量骤然下降,此时出现了什么故障?原因何在?有何解决办法?
5 某离心泵输液自低位槽A 至高位槽B ,升扬高度为6m 。
p A =50kPa(真空度),p B =80kPa(表),液体密度1200kg/m 3,粘度与水相近。
(1) 阀全开时流量为36m 3/h ,扬程为28.2m ,且由水泵性能曲线图查得
N′=2.8kW。
求轴功率。
(2) 若关小阀使管路阻力比(1)时管路阻力大6mH2O,这时的流量为28m3/h,求轴功率,已知效率为0.60。
