浙教版八年级上册《2.6+直角三角形》2014年同步练习卷

合集下载

浙教版八年级数学上册 2.6 直角三角形同步测试题

2.6 直角三角形同步测试题（满分120分；时间：120分钟）真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！题号一二三总分得分一、选择题（本题共计10 小题，每题 3 分，共计30分，）1. 在中，，，则A. B. C. D.2. 如图，在中，，是边上的高，如果，则A. B. C. D.3. 如果直角三角形的一个锐角是另一个锐角的倍，那么这个直角三角形中一个锐角的度数可以是A. B. C. D.4. 如图，在中，，，是上一点，于点，于点，则的度数为（）A. B. C. D.5. 如图，在中，，为边上的高，且，则的度数为（）A. B. C. D.6. 如图，，，垂足为，下列结论错误的是（）A.图中有三个直角三角形B.C.和都是的余角D.7. 在一个直角三角形中，有一个锐角等于，则另一个锐角的度数是A. B. C. D.8. 中，，角平分线、中线、高线的大小关系是（）A. B.C. D.9. 如图，在中，，是边上的高，，那么度数为（）A. B.C. D.条件不足，无法计算10. 在直角三角形中，，，是的角平分线，交边于点，过点作中边上的高线，则的度数为（）A. B. C. D.二、填空题（本题共计10 小题，每题3 分，共计30分，）11. 当三角形中的一个内角是另一个内角的一半时，我们称此三角形为“特征三角形”，其中称为“特征角”．如果一个“特征三角形”的“特征角”为直角三角形，则这个“特征角”的度数为________．12. 在中，，如果，那么________．13. 中，，，，________．14. 如图，在中，，点在上，，，则________度．15. 如图，在中，，，，则________．16. 如图，在中，，是边上的一点，若，，则等于________度．17. 如图，，，，则________．18. 一个直角三角形的两锐角的差是，则其中较大的一个锐角是________．19. 如图，已知在中，，那么________度．20. 如图，中，，于，，，则________．三、解答题（本题共计6 小题共计60分，）21. 如图，，，过点作的垂线，垂足为，过作的垂线，垂足为，若，求、、的度数．22. 如图，在中，，是延长线上一点，，垂足为，与相交于点，．求的度数．23. 如图，在中，，于．求证：；若平分分别交、于、，求证：．24. 如图在直角三角形中，，斜边的高为，若，，，（1）求；（2）求．25. 如图，在直角三角形中，，作边上的高，图中出现多少个直角三角形？又作中边上的高，这时，图中共出现多少个直角三角形？按照同样的方法作下去，作，，…，当作出时，图中共出现多少个直角三角形？26. 在中，＝，点为直线上的一个动点（与点，不重合），分別作和的角平分线，两角平分线所在直线交于点．（1）若点在线段上，如图．①依题意补全图；②求的度数；（2）当点在直线上运动时，的度数是否变化？若不变，请说明理由；若变化，画出相应的图形，并直接写出的度数。

浙教版数学八年级上册2.6《直角三角形》同步练习

直角三角形练习1、填空题：（1）在△ABC 中，若∠A=∠B+∠C ，则△ABC 是（2）在△ABC 中，∠C=90°，∠A =2∠B ，则∠A= ，∠B= 。

（3）在△ABC 中，若∠A ∶∠B ∶∠C=1∶2∶3，则△ABC 是三角形。

（4）直角三角形两锐角之差是12度，则较大的一个锐角是度。

（5）已知：如图，∠BAC=90°，∠C=30°， A D⊥BC 于D ，DE⊥AB 于E ，BE=1，BC= 。

（6）在△ABC 中，如果∠A+∠B=∠C，且AC=21AB ，则∠B= 。

2选择题：（1）如果三角形的一个角等于其他两个角的差，那么这个三角形是（）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、以上都错（2）如果三角形的三个内角的比是3∶4∶7，那么这个三角形是（）A 、锐角三角形B 、直角三角形C 、钝角三角形D 、锐角三角形或钝角三角形（3）用两个完全相同的直角三角板，不能拼成下列图形的是（）A ．平行四边形B ．矩形C ．等腰三角形D ．梯形（4）.如图，EA⊥AB，BC⊥AB，AB=AE=2BC ，D 为AB 的中点，有以下判断：①DE=AC；②DE⊥AC；③∠CAB=30°； ④∠EAF=∠ADE；其中正确结论的个数是（）A 、1B 、2C 、3D 、4 3、解答题：（1）已知等腰三角形一腰上的高与底边成45°角，若腰长为2cm ，求它的面积。

（2）在△ABC 中，∠B=∠C ，D 、E 分别是BC 、AC 的中点，AB=6，求DE 的长。

ABCDEABC DEF（3）下面是小明同学在学了等腰三角形后所做的一道题，题目是这样的：“已知△ABC 是等腰三角形，BC 边上的高恰好等于BC 边长的一半，求∠BAC 的度数。

”解：如图，∵AD ⊥BC ，AD=21BC=BD=CD ，∴∠BAD=∠B=∠C=∠CAD=45°， ∴∠BAC=90° 你认为小明的解答正确吗？若不正确，请你将它补充完整。

直角三角形浙教版八年级数学上册同步练习(含答案)

浙教版数学八年级上册2.6《直角三角形》课时练习一、选择题1.使两个直角三角形全等的条件是（）A．一个锐角对应相等B．两个锐角对应相等C．一条边对应相等D．两条边对应相等2.具备下列条件的△ABC中，不是直角三角形的是( )A.∠A＋∠B=∠CB.∠A=2∠B=2∠CC.∠A∶∠B∶∠C=1∶2∶3D.∠A=∠B=3∠C3.如图，在△ABC中，∠ACB=90°，CD⊥AB于点D，则图中直角三角形有( )A.0个B.1个C.2个D.3个4.直角三角形两个锐角平分线相交所成的钝角的度数为( )A.120°B.135°C.150°D.120°或135°5.如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开.若测得AM的长为1.2 km，则M，C两点间的距离为( )A.0.5 kmB.0.6 kmC.0.9 kmD.1.2 km6.如图，在△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，E为AC的中点，连结DE，则△CDE的周长为( )A.12B.13C.14D.20二、填空题7.如图，在Rt △ABC 中，∠ACB =90°，DE 经过点C ，且DE ∥AB .若∠ACD =50°，则∠A =____，∠B = .8.如图，△ABC 绕点C 顺时针旋转35°得到△A ′B ′C ′，此时恰好A ′B ′⊥AC ，则∠A = .9.在△ABC 中，2∠B =∠A ＋∠C ，最小角∠A =30°，最长边中线为8 cm ，则最短边长为____cm ． 10.如图，在Rt △ABC 中，∠ACB =90°，AB 的垂直平分线DE 交AC 于点E ，交BC 的延长线于点F ．若∠F =30°，DE =1，则BE 的长是．11.直角三角形斜边上的高线长与中线长分别为5 cm 和6 cm ，则它的面积为 cm 2． 12.如图，PA ⊥OA 于点A ，PB ⊥OB 于点B ，D 是OP 的中点，则DA 与DB 的数量关系是 .13.等腰三角形一腰上的高线等于这条腰的一半，则这个等腰三角形的顶角的度数为． 14.如图，在等边三角形ABC 中，D ，E 分别为AB ，BC 边上的两动点，且总使AD =BE ，AE 与CD 交于点F ，AG ⊥CD 于点G ，则FGAF= ．三、解答题15.如图，CE⊥AD，垂足为E，∠A=∠C．求证：△ABD是直角三角形．16.如图，已知AB∥CD，直线EF分别交AB，CD于点E，F，∠BEF的平分线与∠DFE的平分线相交于点P．求证：△PEF是直角三角形．17.如图，在Rt△ABC中，∠C=90°，AB的中垂线DE交BC于点D，垂足为E，且∠CAD∶∠CAB=1∶3，求∠B的度数.18.如图，在△ABC中，∠ACB=90°，AC=BC，D为BC的中点，CE⊥AD于点E，BF∥AC 交CE的延长线于点F，连结DF．求证：AB垂直平分DF．参考答案1.答案为：D2.答案为：D .3.答案为：D .4.答案为：B .5.答案为：D .6.答案为：C .7.答案为：50°，40°；8.答案为：55°.9.答案为：8. 10.答案为：2. 11.答案为：30. 12.答案为：DA =DB . 13.答案为：30°或150°． 14.答案为：12．15.证明：∵CE ⊥AD ， ∴∠CED =90°， ∴∠C ＋∠D =90°．又∵∠A =∠C ， ∴∠A ＋∠D =90°， ∴△ABD 是直角三角形． 16.证明：∵AB ∥CD ， ∴∠BEF ＋∠DFE =180°．∵∠BEF 的平分线与∠DFE 的平分线相交于点P ， ∴∠PEF =12∠BEF ，∠PFE =12∠DFE ，∴∠PEF ＋∠PFE =12(∠BEF ＋∠DFE )=90°．∴△PEF 是直角三角形．17.解：设∠CAD =x °，则∠CAB =3x °，∠BAD =2x °. ∵DE 是AB 的中垂线， ∴DA =DB ， ∴∠B =∠BAD =2x °. ∵∠C =90°， ∴∠CAB ＋∠B =90°，即3x ＋2x =90，解得x =18， ∴∠B =2×18°=36°.18.证明：∵∠ACB =90°，AC =BC ，∴∠CAB =∠CBA =45°，∠CAD ＋∠CDE =90°． ∵CE ⊥AD ， ∴∠CED =90°． ∴∠CDE ＋∠DCE =90°．∴∠CAD =∠DCE ，即∠CAD =∠BCF ． ∵BF ∥AC ，∴∠CBF ＋∠ACB =180°， ∴∠CBF =180°－∠ACB =90°． ∴∠CBF =∠ACD ．在△ACD 和△CBF 中， ∵⎩⎪⎨⎪⎧∠ACD ＝∠CBF ，AC ＝CB ，∠CAD ＝∠BCF ， ∴△ACD ≌△CBF (ASA )． ∴CD =BF ． ∵D 为BC 的中点， ∴CD =BD ， ∴BD =BF ． ∵BF ∥AC ，∴∠ABF=∠CAB=∠DBA=45°．∴AB垂直平分DF．。

浙教版-数学-八年级上册-2.6.1 直角三角形练习

直角三角形(一)A组1．如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，则图中直角三角形有(D)A．0个 B．1个C．2个 D．3个(第1题)(第2题)2．如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开．若测得AM的长为1．2 km，则M，C两点间的距离为(D)A． 0．5 km B． 0．6 kmC． 0．9 km D． 1．2 km3．直角三角形两个锐角平分线相交所成的钝角的度数为(B)A． 120° B． 135°C． 150° D． 120°或135°4．如图，在△ABC中，AB＝AC＝10，BC＝8，AD平分∠BAC交BC于点D，E为AC的中点，连结DE，则△CDE的周长为(C)A． 12 B． 13C． 14 D． 20(第4题)(第5题)5．如图，在Rt△ABC中，∠ACB＝90°，DE经过点C，且DE∥AB．若∠ACD＝50°，则∠A ＝__50°__，∠B＝__40°__．6．如图，PA⊥OA于点A，PB⊥OB于点B，D是OP的中点，则DA与DB的数量关系是BA＝DB．，(第6题)) ，(第7题))7．如图，△ABC绕点C顺时针旋转35°得到△A′B′C′，此时恰好A′B′⊥AC，则∠A＝__55°__．8．如图，在Rt△ABC中，∠C＝90°，AB的中垂线DE交BC于点D，垂足为E，且∠CAD∶∠CAB＝1∶3，求∠B的度数．(第8题)【解】设∠CAD＝x°，则∠CAB＝3x°，∠BAD＝2x°．∵DE是AB的中垂线，∴DA＝DB，∴∠B＝∠BAD＝2x°．∵∠C＝90°，∴∠CAB＋∠B＝90°，即3x＋2x＝90，解得x＝18，∴∠B＝2×18°＝36°．(第9题)9．如图，在△ABC 中，AD ，BE 分别为边BC ，AC 上的高线，D ，E 为垂足，M 为AB 的中点，N 为DE 的中点．求证：(1)△MDE 是等腰三角形．(2)MN ⊥DE ．【解】 (1)∵AD ，BE 分别为边BC ，AC 上的高线，∴△ABD ，△ABE 均为直角三角形．∵M 是Rt △ABD 斜边AB 的中点，∴MD ＝12AB ．同理，ME ＝12AB ． ∴ME ＝MD ．∴△MDE 是等腰三角形．(2)∵ME ＝MD ，N 是DE 的中点，∴MN ⊥DE ．B 组(第10题)10．如图，在Rt △ABC 中，∠ACB ＝90°，将边BC 沿斜边上的中线CD 折叠到CB′．若∠B ＝50°，则∠ACB′＝__10°__．【解】 ∵∠ACB ＝90°，∠B ＝50°，∴∠A ＝40°．∵CD 是AB 边上的中线，∴CD ＝BD ＝AD ，∴∠BCD ＝∠B ＝50°，∠DCA ＝∠A ＝40°．由折叠可知∠B′CD＝∠BCD ＝50°，∴∠ACB′＝∠B′CD－∠DCA＝10°．(第11题)11．如图，在△ABC中，AD是高线，CE是中线，DC＝BE，DG⊥CE于点G．求证：(1)G是CE的中点．(2)∠B＝2∠BCE．【解】(1)连结DE．∵AD是高线，∴△ABD是直角三角形．∵CE是AB边上的中线，∴DE是Rt△ABD斜边上的中线．∴DE＝BE＝AE．∵DC＝BE，∴DE＝DC．又∵DG⊥CE，∴CG＝EG，即G是CE的中点．(2)∵DE＝BE，∴∠B＝∠BDE．∵DE＝DC，∴∠DEC＝∠BCE．∵∠BDE是△DCE的一个外角，∴∠BDE＝∠DEC＋∠BCE＝2∠BCE．∴∠B＝2∠BCE．(第12题)12．如图，在Rt△ABC中，∠ACB＝90°，M是边AB的中点，CH⊥AB于点H，CD平分∠ACB．(1)求证：∠1＝∠2．(2)过点M作AB的垂线交CD的延长线于点E，连结AE，BE．求证：CM＝EM．【解】(1)∵∠ACB＝90°，∴∠BCH ＋∠ACH ＝90°．∵CH ⊥AB ，∴∠CAH ＋∠ACH ＝90°，∴∠CAH ＝∠BCH ．∵M 是斜边AB 的中点，∴CM ＝AM ＝BM ，∴∠CAM ＝∠ACM ．∴∠BCH ＝∠ACM ．∵CD 平分∠ACB ，∴∠BCD ＝∠ACD ，∴∠BCD －∠BCH ＝∠ACD －∠ACM ，即∠1＝∠2．(2)∵CH ⊥AB ，ME ⊥AB ，∴ME ∥CH ，∴∠1＝∠MED ．∵∠1＝∠2，∴∠2＝∠MED ，∴CM ＝EM ．数学乐园(第13题)13．如图，在Rt △ABC 的场地上，∠B ＝90°，AB ＝BC ，∠CAB 的平分线AE 交BC 于点E ．甲、乙两人同时从A 处出发，以相同的速度分别沿AC 和A→B→E 线路前进，甲的目的地为C ，乙的目的地为E ．请你判断一下，甲、乙两人谁先到达各自的目的地？并说明理由．【解】同时到达．理由如下：过点E 作EF ⊥AC 于点F ．∵AB ＝BC ，∠B ＝90°，∴∠C ＝180°－∠B 2＝45°． ∵EF ⊥AC ，∴∠EFC ＝90°，∴∠CEF ＝90°－∠C ＝45°＝∠C ，∴EF ＝CF ．又∵AE 平分∠CAB ，∴EF ＝EB ．易证得△AEF≌△AEB，得AF＝AB，可知AB＋BE＝AF＋CF＝AC，故同时到达．。

浙教版八年级数学上册同步练习：2.6 直角三角形(2)

2.6 直角三角形（2）（巩固练习）姓名班级第一部分1、如图1，△ABC 中，∠A BC=45°，AD 是高，点E 在AD 上，且∠BED=∠C.试说明BE=AC的理由.2、如图2，△ACB 、△ECD 都是等腰直角三角形，且C 在AD 上，AE 的延长线与BD 交于F.请你在图中找出一对全等三角形，并写出它们全等的过程．3、如图3,在44⨯方格中作以AB 为一边的Rt ΔABC,要求点C 也在格点上,这样的Rt ΔABC 能作出……………………………（）A. 2个B. 3个C. 4个D. 5个4、如图4所示，每个小方格都是边长为1的正方形，点A B ，是方格纸的两个格点（即正方形的顶点），在这个66⨯的方格纸中，找出格点C ，使ABC △的面积为1个平方单位的直角三角形的个数是．图2 图3 图4AB图1图8图9第二部分1. 在Rt ABC △中，BAC ∠=90°，AD ⊥BC 于D,则图中共有个直角三角形.2. 在Rt ABC △中，BAC ∠=90°，若∠B=36°, 则∠C= 度.3.等腰直角三角形的底角等于度.4. Rt △ABC 中，∠C=Rt ∠，∠A ∶∠B=2∶3，则∠A= 度.5.如图8，一块等腰直角的三角板ABC ，在水平桌面上绕点C 按顺时针方向旋转到A B C ''的位置，使A C B '，，三点共线，那么旋转角度的大小为．6. 如图9，B 、C 是河岸边两点，A 是对岸岸边一点，测得ABC ∠=ACB ∠=45°，BC=60米，则点A 到岸边BC 的距离是________米.7.如图10, 已知CD ∥AE, ∠DCA 与∠CAE 的平分线相交于点B.判断ABC △是否直角三角形,并说明理由.8.如图11,已知ABC △是等腰直角三角形,把ABC △绕点A 逆时针旋转成ADE △,连接DB.求∠BDE 的度数.图10图119.如图12,在ABC △中，AB AC ，BAC ∠=90°，AD 是∠BAC 的平分线,且AD=4,求ABC △的面积.图12参考答案第一部分AB1个单位的两条平行线上.答案：14第二部分图8图91. 在Rt ABC △中，BAC ∠=90°，AD ⊥BC 于D,则图中共有个直角三角形.答案：32. 在Rt ABC △中，BAC ∠=90°，若∠B=36°, 则∠C= 度.答案：543.等腰直角三角形的底角等于度.答案：454. Rt △ABC 中，∠C=Rt ∠，∠A ∶∠B=2∶3，则∠A= 度.答案：365.如图8，一块等腰直角的三角板ABC ，在水平桌面上绕点C 按顺时针方向旋转到A B C ''的位置，使A C B '，，三点共线，那么旋转角度的大小为．答案：135°6. 如图9，B 、C 是河岸边两点，A 是对岸岸边一点，测得ABC ∠=ACB ∠=45°，BC=60米，则点A 到岸边BC 的距离是________米.答案：307.如图10, 已知CD ∥AE, ∠DCA 与∠CAE 的平分线相交于点B.判断ABC △是否直角三角形,并说明理由.解：∵BA 平分∠CAE , BC 平分∠DCA , ∴∠BAC =12∠CAE , ∠BCA =12∠DCA . ∵CD ∥AE , ∴∠CAE +∠DCA =180°,∴∠BAC +∠BCA =90°, 即△ABC 是直角三角形.8.如图11,已知ABC △是等腰直角三角形,把ABC △绕点A 逆时针旋转成ADE △,连接DB.求∠BDE 的度数.图10图11解：∵△ABC 绕点A 逆时针旋转成△ADE , ∴∠DAE =∠ADE =45°, AD=AB .∴∠ADB =67.5°, ∴∠BDE =∠ADB -∠ADE =22.5°.9.如图12,在ABC △中，AB AC ，BAC ∠=90°，AD 是∠BAC 的平分线,且AD=4,求ABC △的面积.解：∵AB=AC , ∠BAC =90°, ∴∠B=∠C =45°.∵AD 是∠BAC 的平分线, ∴∠BAD =∠CAD =45°. ∴∠B=∠BAD =∠CAD =∠C =45°, ∴BD =AD=DC =4. ∴BC =8. ∴S △ABC =12BC ·AD =16.图12。

八年级数学上2.6直角三角形(1)同步练习(含答案)

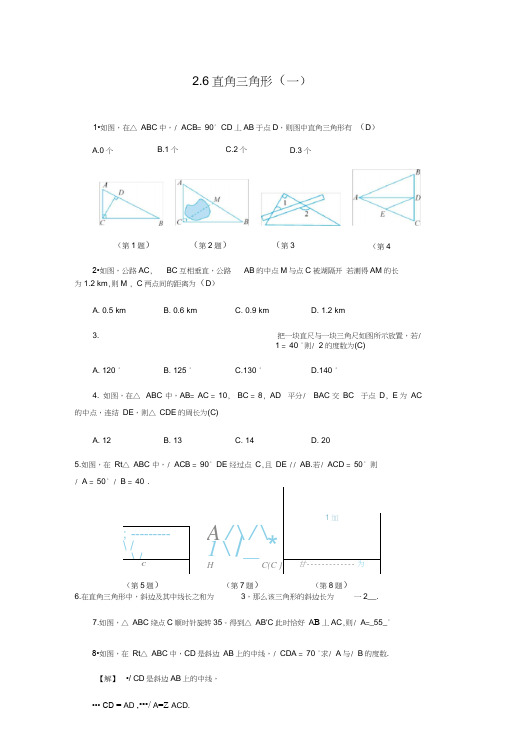
2.6直角三角形（一）1•如图，在△ ABC 中，/ ACB = 90° CD 丄AB 于点D ，则图中直角三角形有（D ）为1.2 km ,则M , C 两点间的距离为（D ）A. 0.5 kmB. 0.6 kmC. 0.9 kmD. 1.2 km 3.把一块直尺与一块三角尺如图所示放置，若/ 1 = 40 °则/ 2的度数为(C)A. 120 °B. 125 °C.130 °D.140 °4. 如图，在△ ABC 中，AB = AC = 10, BC = 8, AD 平分/ BAC 交 BC 于点 D , E 为 AC 的中点，连结 DE ，则△ CDE 的周长为(C)A. 12B. 13C. 14D. 205.如图，在 Rt △ ABC 中，/ ACB = 90° DE 经过点 C ,且 DE // AB.若/ ACD = 50° 则/ A = 50°/A / \ / \ 1 \ /_ *1加 ; --------- \ / \ / CH C(C } 甘 ------------- 为（第5题）（第7题）（第8题）6. 7.如图，△ ABC 绕点C 顺时针旋转35。

得到△ AB'C 此时恰好 A B 丄AC ,则/ A =_55_°8•如图，在 Rt △ ABC 中，CD 是斜边 AB 上的中线，/ CDA = 70 °求/ A 与/ B 的度数.【解】 •/ CD 是斜边AB 上的中线，••• CD = AD ,•••/ A =Z ACD.A.0个B.1个C.2个D.3个2•如图，公路AC , BC 互相垂直，公路 AB 的中点M 与点C 被湖隔开若测得AM 的长（第1题）（第2题）（第3（第4•••/ A+Z ACD + Z CDA = 180°/ 180 °-Z CDA 180。

八年级数学上册2.6直角三角形同步练习(新版)浙教版【含解析】

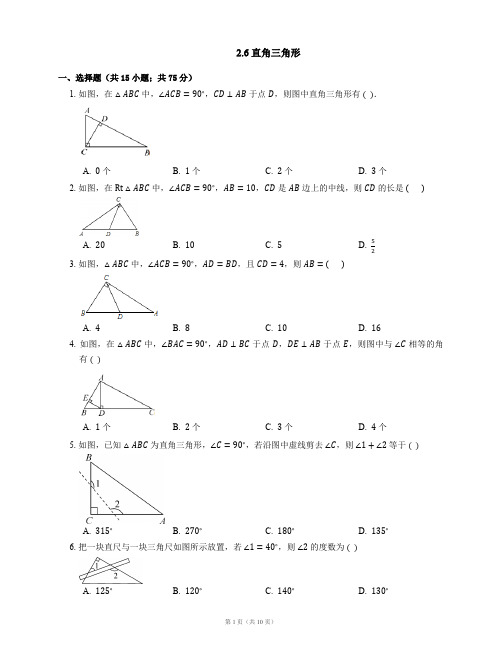
2.6 直角三角形一、选择题（共15小题；共75分）1. 如图，在△ABC中，∠ACB=90∘，CD⊥AB于点D，则图中直角三角形有( )．A. 0个B. 1个C. 2个D. 3个2. 如图，在Rt△ABC中，∠ACB=90∘，AB=10，CD是AB边上的中线，则CD的长是 ( )A. 20B. 10C. 5D. 523. 如图，△ABC中，∠ACB=90∘，AD=BD，且CD=4，则AB= ( )A. 4B. 8C. 10D. 164. 如图，在△ABC中，∠BAC=90∘，AD⊥BC于点D，DE⊥AB于点E，则图中与∠C相等的角有( )A. 1个B. 2个C. 3个D. 4个5. 如图，已知△ABC为直角三角形，∠C=90∘，若沿图中虚线剪去∠C，则∠1+∠2等于( )A. 315∘B. 270∘C. 180∘D. 135∘6. 把一块直尺与一块三角尺如图所示放置，若∠1=40∘，则∠2的度数为( )A. 125∘B. 120∘C. 140∘D. 130∘7. 若直角三角形的两条直角边的长分别为9 cm和12 cm，则斜边上的中线长为( )A. 4.5 cmB. 6 cmC. 7.5 cmD. 10 cm8. 如图，已知在Rt△ABC中，∠ABC=90∘，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径圆弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接AB中，一定BE，则下列结论：① ED⊥BC；② ∠A=∠EBA；③ EB平分∠AED；④ ED=12正确的是 ( )A. ①②③B. ①②④C. ①③④D. ②③④9. 如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于 ( )A. 25∘B. 30∘C. 45∘D. 60∘10. 如图，在Rt△ACB中，∠ACB=90∘,∠A=25∘，D是AB上一点，将Rt△ABC沿CD折叠，使B点落在AC边上的Bʹ处，则∠ADBʹ等于( )A. 25∘B. 30∘C. 35∘D. 40∘11. 如图，已知OP平分∠AOB，∠AOB=60∘，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果M是OP的中点，那么DM的长是( )A. 2B. √C. √3D. 2√312. 如图，已知点A(−1,0)和点B(1,2)，在坐标轴上确定点P，使得△ABP为直角三角形，则满足这样条件的点P共有 ( )A. 2个B. 4个C. 6个D. 7个13. 如图，在△ABC中，∠CAB=90∘，∠B<∠C，AD，AE，AF分别是△ABC的高、角平分线、中线．则∠DAE与∠FAE的大小关系是( )A. ∠DAE>∠FAEB. ∠DAE=∠FAEC. ∠DAE<∠FAED. 与∠C的度数有关，无法判断14. 如图，直角三角板的直角顶点落在直尺边上，若∠1=56∘，则∠2的度数为 ( )A. 56∘B. 44∘C. 34∘D. 28∘15. 如图，m∥n，直线l分别交m，n于点A、点B，AC⊥AB，AC交直线n于点C，若∠1=35∘，则∠2等于 ( )A. 35∘B. 45∘C. 55∘D. 65∘二、填空题（共15小题；共75分）16. 在Rt△ABC中，∠C=Rt∠，∠A=70∘，则∠B=．17. 在Rt△ABC中，锐角∠A=35∘，则另一个锐角∠B=18. 如图，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A，B能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来．若AB=20 cm，则画出的圆的半径为 cm．19. 如图，将一副三角尺叠放在一起，使直角的顶点重合于点O，则∠AOC+∠BOD=．20. 已知一个直角三角形的两条直角边长分别为3 cm和4 cm，则这个直角三角形斜边上的高线长为cm，斜边上的中线长为cm．21. 在直角三角形中，斜边及其中线长之和为3，那么该三角形的斜边长为．22. 如图，在Rt△ABC中，∠ACB=90∘，BC=6，AC=8，分别以点A，B为圆心，大于线段AB长度一半的长为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连接CD，则CD的长是．23. 如图，在△ABC中，∠ACB=90∘，CD是AB边上的高，则图中与∠A相等的角是．24. 如图，AB，CD相交于点O，AC⊥CD于点C．若∠BOD=38∘，则∠A=．25. 在△ABC中，2∠B=∠A+∠C，最小角∠A=30∘，最长边的中线为8cm，则最短边的长为cm．26. 如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为．27. 如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90∘．若∠1=25∘，∠2=70∘，则∠B=∘．28. 如图，△ABC中，CD⊥AB于D，E是AC的中点，若AD=6，CD=8，则DE的长等于．29. 如图，有一块含有60∘角的直角三角板的两个顶点放在矩形的对边上．如果∠1=15∘，那么∠2的度数是 .30. 已知边长为a的正三角形ABC，两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连结OC，则OC的长的最大值是．三、解答题（共5小题；共65分）31. 如图，在四边形ABCD中，∠ABC=∠ADC=90∘，M，N分别是AC，BD的中点，连接MN．Ⅰ试猜想MN与BD的位置关系，并证明你的结论．Ⅱ如果∠BCD=45∘，BD=2，求MN的长．32. 如图，O是等边三角形ABC内一点，∠AOB=110∘，∠BOC=α .将△BOC绕点C按顺时针方向旋转60∘得到△ADC，连接OD .Ⅰ求证：△COD是等边三角形．Ⅱ当α=150∘时，试判断△AOD的形状，并说明理由．Ⅲ探究：当α为多少度时，△AOD是等腰三角形?33. 如图，在Rt△ABC中，∠ACB=90∘，D是AB上一点，且∠ACD=∠B．求证：CD⊥AB．34. 如图，在Rt△ABC中，∠ACB=90∘，M是边AB的中点，CH⊥AB于点H，CD平分∠ACB．Ⅰ求证：∠1=∠2．Ⅱ过点M作AB的垂线交CD的延长线于点E，求证：CM=EM．35. 已知：如图，D为线段AB上一点（不与点A，B重合），CD⊥AB，且CD=AB，AE⊥AB，BF⊥AB，且AE=BD，BF=AD．Ⅰ如图 1，当点D恰是AB的中点时，请你猜想并证明∠ACE与∠BCF的数量关系；Ⅱ如图2，当点D不是AB的中点时，你在（1）中所得的结论是否发生变化，写出你的猜想并证明；Ⅲ若∠ACB=α，直接写出∠ECF的度数（用含α的式子表示）．答案第一部分1. D2. C3. B4. B5. B6. D7. C8. B9. B 10. D11. C 12. C 13. B 14. C 15. C第二部分16. 20∘17. 55 度18. 1019. 180∘20. 125；52 21. 222. 523. ∠BCD24. 52∘25. 826. 45∘27. 4528. 529. 15∘30.√3+12a第三部分31. （1） MN ⊥BD ．证明如下：连接 BM ，DM ．因为 ∠ADC =90∘，M 是 AC 的中点，所以 AC =2DM =2CM ．同理，AC =2BM =2CM ，所以 BM =DM ．因为 N 是 BD 的中点，所以 MN ⊥BD ．（2）由（1），得 BM =CM ，DM =CM ，所以 ∠BCM =∠CBM ，∠DCM =∠CDM ．因为 ∠AMB 是 △BCM 的一个外角，所以 ∠AMB =∠BCM +∠CBM =2∠BCM ．同理，∠AMD =2∠DCM ．因为∠BCD=45∘，所以∠BCM+∠DCM=45∘．所以∠BMD=∠AMB+∠AMD=2(∠BCM+∠DCM)=90∘．所以△BMD是直角三角形．因为N是BD的中点，BD=1．所以MN=1232. （1）∵将△BOC绕点C按顺时针方向旋转60∘得到△ADC，∴CO=CD，∠OCD=60∘，∴△COD是等边三角形．（2）当α=150∘时，△AOD是直角三角形．理由如下：∵△BOC≌△ADC，∴∠ADC=∠BOC=α=150∘ .∵△COD是等边三角形，∴∠ODC=60∘，∴∠ADO=90∘，∴△AOD是直角三角形．（3）分类讨论：①要使AO=AD，需∠AOD=∠ADO .∵∠AOD=190∘−α，∠ADO=α−60∘，∴190∘−α=α−60∘，∴α=125∘ .②要使AO=OD，需∠OAD=∠ADO .可得2(α−60∘)=180∘−(190∘−α)，∴α=110∘ .③要使OD=AD，需∠OAD=∠AOD .可得2(190∘−α)=180∘−(α−60∘)，∴α=140∘ .综上所述，当α的度数为125∘或110∘或140∘时，△ABC是等腰三角形．33. ∵∠ACB=90∘，∴∠A+∠B=90∘．∵∠ACD=∠B，∴∠A+∠ACD=90∘ .∴∠ADC=90∘ .∴CD⊥AB．34. （1）因为∠ACB=90∘，所以∠BCH+∠ACH=90∘ .因为CH⊥AB，所以∠CAH+∠ACH=90∘，所以∠CAH=∠BCH .因为M是斜边AB的中点，所以CM=AM=BM，所以∠CAM=∠ACM .所以∠BCH=∠ACM .因为CD平分∠ACB，所以∠BCD=∠ACD，所以∠BCD−∠BCH=∠ACD−∠ACM，即∠1=∠2 .（2）因为CH⊥AB，ME⊥AB，所以ME∥CH，所以∠1=∠MED .因为∠1=∠2，所以∠2=∠MED，所以CM=EM .35. （1）猜想：∠ACE=∠BCF．证明：∵D是AB中点，∴AD=BD，又AE=BD，BF=AD，∴AE=BF．∵CD⊥AB，AD=BD，∴CA=CB．∴∠1=∠2．∵AE⊥AB，BF⊥AB，∴∠3=∠4=90∘．∴∠1+∠3=∠2+∠4．即∠CAE=∠CBF．∴△CAE≌△CBF．∴∠ACE=∠BCF．（2）∠ACE=∠BCF仍然成立．证明：连接BE，AF．∵CD⊥AB，AE⊥AB，∴∠CDB=∠BAE=90∘．又BD=AE，CD=AB，△CDB≌△BAE．∴CB=BE，∠BCD=∠EBA．在Rt△CDB中，∵∠CDB=90∘，∴∠BCD+∠CBD=90∘．∴∠EBA+∠CBD=90∘．即∠CBE=90∘．∴△BCE是等腰直角三角形．∴∠BCE=45∘．同理可证：△ACF是等腰直角三角形．∴∠ACF=45∘．∴∠ACF=∠BCE．∴∠ACF−∠ECF=∠BCE−∠ECF．即∠ACE=∠BCF．（3）∠ECF的度数为90∘−α．。

浙教版八年级数学上册2.6直角三角形解答题专练(含答案)

∴∠FMC＝90°，
∵∠C＝30°，MF＝2，
∴FC＝2MF＝4，
∵DF＝FC，
∴DF＝4，
∵△ADF是等边三角形，
∴AF＝DF＝4，
∴AC＝AF+CF＝4+4＝8，
∵AB＝AC，
∴AB＝8．
7．如图1，在△ABC中，CD，BE分别是AB，AC边上的高线，M，N分别是线段BC，DE的中点． (1)求证：MN⊥DE. (2)连结DM，ME，猜想∠A与∠DME之间的关系，并说明理由． (3)若将锐角三角形ABC变为钝角三角形ABC，其余条件不变，如图2，则(1)(2)中的结论是否仍成立？请说明理由．
即∠FAD＝∠ADF＝∠AFD＝60°，
∴△ADF是正三角形；
6．如图，在△ABC中，AB＝AC，∠BAC＝120°，AD是BC边上的中线，且
BD＝BE，CD的垂直平分线MF交AC于F，交BC于M，MF的长为2．
（1）求∠ADE的度数；
（2）△ADF是正三角形吗？
（3）∵CD的垂直平分线MF，
（3）求AB的长．
2．如图，在△ABC中，∠ACB＝90°，D是BC延长线上一点，E是BD 垂直平分线与AB的交点，DE交AC于点F．求证：点E在AF的垂直平分线上．
【解析】证明：过E点作EG⊥BD，则EG 是线段BD的垂直平分线， ∴BE＝DE， ∴∠DEG＝∠BEG， ∵∠ACB＝90°， ∴AC∥EG， ∴∠AFE＝∠DEG，∠A＝∠BEG， ∴∠A＝∠AFE， ∴AE＝AF，即点E在AF的垂直平分线上．
4．已知：如图，四边形ABCD中，∠ABC＝90°，∠ADC＝90°，点 E为AC中点，点F为BD中点．求证：EF⊥BD．
【解析】证明：如图，连接BE、DE， ∵∠ABC＝90°，点E是AC的中点， ∴BE＝ AC，同理：DE＝ AC ∴BE＝DE，又∵点F是BD的中点， ∴EF⊥BD．

初中数学浙教版八年级上册《2.6直角三角形(1)》练习题

直角三角形（1）班级：___________姓名：___________得分：__________一、选择题1、直角三角形斜边上的中点是（）A．三条边中线的交点 B．三边高线的交点C．三个角平分线的交点 D．三边中垂线的交点2.△ABC为等腰直角三角形，∠C=90°，D为BC上一点，且AD=2CD，则∠DAB=（）A. 60°B. 45°C. 30°D. 15°3.如图，在把易拉罐中的水倒入一个圆水杯的过程中，若水杯中的水在点P与易拉罐刚好接触，则此时水杯中的水深为（）A．2cm B．4cm C．6cm D．8cm4.如果直角三角形的一个锐角是另一个锐角的4倍，那么这个直角三角形中一个锐角的度数是（）A．9° B．18° C．27° D．36°5.如图，AB⊥AC于A，BD⊥CD于D，若AC=DB，则下列结论中不正确的是（）A．∠A=∠D B．∠ABC=∠DCB C．OB=OD D．OA=OD二、填空题1、等腰三角形腰上的高等于腰长的一半，则这个等腰三角形的顶角为______度．2. 下图是屋架设计图的一部分，其中BC⊥AC，DE⊥AC，点D是AB的中点，∠A=30°，AB=7.4m，则BC=______m，DE=______m．3. 已知在△ABC中，∠ACB=90°，CD是AB边上的高，∠B=30°，AD=a，则AB=______．4. 如图，上午8时，一条船从A处测得灯塔C在北偏西30°，以15海里/时的速度向正北航行，9时30分到达B处，测得灯塔C在北偏西60°，那么当船继续航行，______时______分测得灯塔C在正西方向．三、证明题1. 如图，在△ABCC中，∠ACB=90°，CD⊥AB，AF是角平分线，交CD于点E．求证：∠1=∠2．2. 如图所示，△ABC中，AB=AC，∠BAC=120°，AP⊥AB交BC于点P。