“露天矿生产的车辆安排”的模型和评述
露天矿生产的车辆安排

露天矿生产的车辆安排金钟良,丁鲁明,岑志浩摘要本文建立了一个关于车辆安排的简化数学模型。
首先依据题目中的两个原则,将他们转化为一个整数的优化模型,对于同一个原则中的多个方面,我们将此转化为多目标的规划问题,并在计算中用线性加权的方法将多目标转化成单目标函数,而加权系数可以依据实际情况进行确定,(本文中使用了一种特殊情况),如此,本文就得到了一个统一的模型。
其次,本模型的计算采用了Lingo软件,得到第一原则下车辆的数目为13,第二原则下车辆总运量为8.52(吨)。
接着,本文根据计算所得的数据对车辆进行了安排。
(具体安排见表四、表六)本文附有本题的程序,如此,在微机上对给定数据可以实时得到结果,有很强的实用性,并可解决一定范围内同类型的问题。
1.问题重述某露天矿内有若干个铲位,铲位中已按铁含量将石料分为矿石和岩石(平均铁含量不低于25%的为矿石,否则为岩石)。
每个铲位至多能安置一台电铲,电铲的平均装车时间为5分钟。
卡车负责将铲位内的矿石和岩石运送到相应的卸货地点,卡车的平均卸车时间为3分钟。
卸货地点有卸矿石的矿石漏和2个铁路倒装场,卸岩石的岩石漏和岩场,总共五个卸点。
按要求,矿石卸点需要的铁含量品位限制都为29.5% 1%(在一个班次8小时内满足品位限制即可)。
km。
原则上在安排时不应发生卡所用卡车载重量为154吨,平均时速28h车等待的情况,电铲和卸点都不能同时为两辆及两辆以上卡车服务。
卡车每次都是满载运输,并且排除堵车现象。
一个班次的生产计划包含以下内容:出动几台电铲,分别在哪些铲位上;出动几辆卡车,分别在哪些路线上。
一个合格的计划要在卡车不等待条件下满足产量和质量(品位)要求。
一个好的计划应该考虑下面两条原则之一:1.总运量(吨*公里)最小,同时出动最少的卡车,从而运输成本最小;2.利用现有车辆运输,获得最大的产量(岩石产量优先;在产量相同的情况下,取总运量最小的解)。
问题一:就两条原则分别建立数学模型,并给出一个班次生产计划的快速算法。
露天矿生产的车辆安排模型大学论文

露天矿生产的车辆安排模型摘要本文成功引入了车次的概念。
在对时间进行合理假设之后,在约束条件下建立了对车次的全局最优的整数线性规划,利用lindo软件迅速解出全局最优的任务分配。
进一步,利用效率优先原则,对铲点进行优化,并根据物件可分的等容积装箱模型,最终得到了满足要求的计划安排。
根据原则一建立模型的解为:铲位:1、2、3、4、8、9、10,卡车数:13,总运量:8.56万吨·千米,车辆安排计划见表9;根据原则二建立模型的解为:铲位:1、2、3、4、8、9、10,卡车数:20,最大产量:10.35万吨,岩石量:4.93万吨,在最大产量下的最小运量:14.69万吨·千米车辆安排计划见表14。
一、问题的重述露天矿里有若干个爆破的铲位,已预先根据铁含量被分成矿石和岩石两种不同的石料。
每个铲位至多配备一台电动铲车进行装车,并由电动轮自卸卡车将矿石和岩石分别运送至各自的卸货地点,满足各卸点的产量和品位要求(29.5% 1%)。
卡车有其本身的平均速度,随机的装卸时间和载重。
根据所给定的条件,根据以下两条原则分别建立数学模型,并给出一个班次生产计划的快速算法,原则上在安排时不应发生卡车等待的情况。
1、总运量(吨公里)最小,同时出动最少的卡车,从而运输成本最小;2、利用现有车辆运输,获得最大的产量(岩石产量优先;在产量相同的情况下,取总运量最小的解)。
二、问题分析1、本题是一个有约束条件的组合优化问题,涉及到单车型多货种送货满载车辆的优化调度,因而属于NP难题(文献[1]),随着系统规模的扩大,问题的求解难度也大大增加,求解时间呈几何级数上升。
2、本问题最先应着重解决的是车辆的等待问题。
车辆在铲位和卸点的等待主要由三方面引起:(1) 随机因素造成运输和装卸时间不精确从而形成等待;(2) 由于车辆在不同道路上循环的周期不同所偶尔出现的在时间上的重叠。
这种交叉的可能性伴随着道路承载车辆数目的增加而增加,但也可以通过车辆自身的调整而加以避免,例如:改变路线、改变速度等;(3) 若车辆的密度超过了道路、铲点或卸点所能容纳的最大限,则在任意一个周期内都会出现的等待现象。
露天矿生产的车辆安排

露天矿生产的车辆安排摘要针对本问题的分析,我们按照“规划铲位到卸点的最优路线和次数→规划卸点回到铲位所需最优车辆资源数→根据以上两个规划寻求最优卡车调度方案”—三步走的方式,针对原则一和原则二分别建立数学模型如下:原则一:第一步:我们用整数规划的方法求取满足最优目标的由铲位到卸点的运输次数和路线,解决岩石和矿石的最优运输问题。
目标为总运量最小;第二步:根据第一步规划求得的运输路线及次数规划出卸点到铲位所需最优车辆资源数。
目标为空载时间最短,最小为吨公里;第三步:根据以上两个规划指导和求取相应调度问题。
目标为总发车次数最少。
对题目中的实际问题求得结果为:最少发车次数为13辆,铲车数为7。
原则二:目标1:最大的产量,并且满足产量、质量要求,同时优先考虑岩石产量并且总运量最小;由于问题已确定了车辆数,所以无需对车辆数范围的规划目标2:具体安排在解第二问时我们采用了一个快速算法,虽然不能保证每辆车都不等待,但避免了,大规模整数规划,所以我们认为这种简化是合理的。
最后,结合模型分析对模型进行了评价。
所用铲车数为7,卡车数为20,总运量:103488吨.一、问题的分析在满足对矿山采运资源的限制条件下,我们将该问题的两个目标转化为最优规化问题。
经分析后我们采用三步规划的方法,在可解的条件下,将问题划归为三个整数规划问题。
为达到问题的两个最优目标,我们采用目标到调度的逆向分析方法,以“规划铲位到卸点的最优路线和次数→规划卸点回到铲位所需最优车辆资源数→根据以上两个规划指导和求取相应调度问题”三步走的方式求解问题的最终目标。
首先我们用整数规划的方法求取满足最优目标的由铲位到卸点的运输次数和路线,解决岩石和矿石的最优运输问题。
其次,再根据第一步规划求得的运输路线及次数规划出卸点到铲位所需最优车辆资源数。
最后,根据前两步结果,指导和安排相应车辆的调度,达到第一步对最优目标的规划。
二、模型的假设及说明在已满足题目中所有假设条件的前提下,我们补充两点如下:1). 模型只考虑满足题目要求的调度计划本身,而不考虑如何保证一个计划的内容在现实过程中实现;2). 卡车在一个班次中始终保持正常运行,不出故障;3). 电铲和卸点都不能同时为两辆及两辆以上卡车服务。
2003(B) 论文

转载时请注明出处,并请保持文档完整性
-5-
2003 年“高教社杯”全国二等奖
li , j ---------第 i 个铲位到第 j 个卸点间的路程(单位:公里) ; f = (li , j ) = (l1,1 , l2,1 ,……,lm ,1 , l1, 2 , l2, 2 , ……,lm ,2 , ……,l1, n , l2, n , ……lm , n ) ------ 铲位 到 卸点 间的路程向量 xi , j --------第 i 个铲位到第 j 个卸点间线路的流量(单位:车) x = ( xi , j ) = ( x1,1 , x2,1 , ……xm,1 , x1, 2 , x2, 2 , ……,xm ,2 , ……,x1,n , x2, n , …… xm , n ) ------ 铲位 到 卸 点间的流量向量 ai ---------第 i 个铲位矿石的铁含量 Q j --------第 j 个卸点要求的产量(单位:车) amax j ------第 j 个卸点要求的矿石品位限制上界; amin j ------第 j 个卸点要求的矿石品位限制的下界; R1,i -------第 i 个铲位的矿石量; R2,i -------第 i 个铲位的岩石量; b1 ---------铲位工作的上限即电铲不停息地工作可装载的车数; b2 ---------卸点处工作的上限即自卸卡车不停息地工作可卸载的车数; v ---------卡车行驶的速度(单位: km / h ) ; T ---------一个班次的总时间(单位:小时) ; t1 ---------电铲装车的时间(单位:小时) ; t2 ---------自卸卡车的卸车时间(单位:小时) ; U --------卡车的载重量(单位:吨)
_露天矿生产的车辆安排_的模型和评述_方沛辰

同时运行 的卡 车数 是 有 限制 的 在
_
i
号 铲位 到j 号卸 点路 线 上运 行一 个 周期 平 均所需 时 间
,
。
二
、
X
j l ,
沼花 一
.
Z
~
_
+
3
.
十
( 分 ) 由 于 装 车 时 间 5 分 钟 大 于 卸 车 时 间 3 分 钟 所 以 可 分析 出 这 条 路线 5
。 容 易 用 线 性 模 型 实 现 一 种 简 单 的办 法 是 从 C 了 二
12 0
个 整 数 规划 中 取 最 优 的 即 得 到 最 佳
,
物 流 为完 成 第 全部计 算 定办得 到
。
;
7
条 由最 佳 物 流 算 出 各 条 路 线 上 的 最 少 派 出 车 辆数 再 给 出 具 体 安 排 即 完 成
卷
1
问题 分 析
从 题 目看 露 天 矿 生 产 主 要 是 运 石 料
) 2
3
4
,
。
它 与 典 型 的 运 输 问题 明 显 有 以 下 不 同
;
:
) 这 是 运 输 矿 石 与 岩 石 两 种 物 资 的 问题 1 ) 为 了完成 品位 约束 矿 石要 搭配运输
,
、 ,
属 于 产 量 大 于 销 量 的不 平 衡 运 输 问 题 ;
总之 深人研 究这 方面 问题 是很有 实际 意义 的
, , , 。 ,
由于 没有 详 细 确 定 的 资料 可 以参 考 所 以
。
比 较 适 合作 为 数 学 建 模 竞赛 的 题 目 做 题 时 没 有 框 框 能 留有 更 大 的 空 间 让 学 生 们 用 聪 明 才
露天矿生产的车辆安排数学建模

露天矿生产的车辆安排数学建模
随着采矿技术的不断发展,露天矿的生产模式也在不断完善。
在露天矿生产过程中,车辆的安排是一个重要的环节。
如何合理安排矿用车辆,提高生产效益,成为了矿山管理者的一个难题。
因此,本文将通过数学建模的方式,探讨露天矿生产的车辆安排问题。
首先,我们需要确定矿用车辆的数量。
根据不同的矿山规模和生产能力,车辆数量也会有所不同。
例如,对于一个小型露天矿山,可能只需要几辆矿用车辆,而对于一个大型矿山,可能需要数十辆甚至上百辆矿用车辆。
其次,我们需要确定车辆的工作时间。
矿山生产一般是24小时不间断进行的,因此车辆的工作时间也需要随之调整。
根据车辆的使用情况和维修保养的需要,我们可以将车辆的工作时间分为若干个时间段,如白班、夜班等。
然后,我们需要确定车辆的工作路线。
在露天矿生产中,车辆的工作路线会受到许多因素的影响,如矿山地形、矿石储量分布等。
因此,我们需要通过分析这些因素,确定车辆的工作路线,以提高生产效益。
最后,我们需要考虑车辆的调配问题。
在露天矿生产中,不同类型的矿用车辆具有不同的特点和用途,如大型矿用卡车适合运输大块矿石,而小型矿用车辆则适合在矿山内部进行小范围的转运。
因此,我们需要根据不同的工作任务和矿用车辆的特点,合理地调配车辆,以达到最优化的生产效益。
综上所述,通过数学建模的方式,可以帮助矿山管理者合理安排矿用车辆,提高生产效益,从而实现矿山的可持续发展。
露天矿生产车辆安排的数学模型

露天矿生产车辆安排的数学模型露天矿生产车辆安排的数学模型
露天矿的生产工作主要是靠机械运输车来完成的,为了确保生产流程的顺畅,
需要制定适当的机械运输车的调度和规划,以达到最佳的效率。
针对这种情况,专家们采取数学建模的方法来安排生产作业中机械运输车的安排。
这种数学模型能够在某一特定因素下求解最优调度方案,进而形成一条最优运输方案。
比如,在这种模型中,可以考虑到机械运输车的负载状况、运输时间、安全要
求以及运输成本等因素,以充分分析生产需求、客户需求等多种环境因素。
同时,它还可以考虑到多个任务之间的关系和约束,因为这些任务中都可能存在互斥关系,所以模型需要考虑到它们。
需要注意的是,该数学模型能够解决的问题,但是也无法解决生产现场的具体
实际问题,这仍需要生产人员的实际操作,以及适时的调整。
因为这些问题都涉及到机械运输车的调度安排,需要仔细考虑,作出恰当的判断和决定。
总的来说,采用数学模型安排露天矿生产中机械运输车的安排是有效的。
它能
够有效地解决机械运输车安排上出现的问题,为露天矿生产过程带来更加高效率高产量的效果,从而保证整个生产流程的顺利进行。
露天矿生产的车辆安排

露天矿生产的车辆安排 TPMK standardization office【 TPMK5AB- TPMK08- TPMK2C- TPMK18】露天矿生产的车辆安排(CMCM2003B)摘要本文要解决的问题主要围绕减少实际中的经济成本而展开的。
在经济运作中,减少成本是作为露天矿生产带来利润最大化的有效手段之一。
而合理安排有效路线和车次,成为了解决减少成本问题的关键。
鉴于铲点到卸点线路的复杂性,我们把问题分成两个层次加以解决。
首先我们采用了整体规划的算法,建立了数学模型以求得最小运输量。
其基本思想是提取重要的约束性条件,对于总产量达最小的目标函数进行约束,运用lingo程序求出其最优解,最后得出最小运输量为85628.62吨,且第5、6、7个铲点没有使用。
对于层次二,通过解决层次一所得出具体流量计算卡车在各个路线上一个班次最多可以运行的次数及各路线上需要的卡车数,从而得出所有路线要出动13辆卡车.问题重述此题类似与产地与销地的运输的整数规划问题。
10个矿位,5个卸点,运输矿石和岩石两种产品。
此题的重点在于限制条件的提取,由于题中所给条件较多如:每个铲位至多能安置一台电铲,电铲的平均装车时间为5分钟。
卸货地有卸矿石的矿石漏、2个铁路倒装场和卸岩石的岩石漏、岩场等。
每个卸点都有各自的产量要求,岩石卸点的品味限制都为29.5% 1%。
电铲和卸点都不能同时为两辆及两辆以上卡车服务。
卡车每次都是满载运输,且在一个班次中不存在卡车等待情况,卡车只在开始时点火一次。
卡车的平均卸车时间为3分钟。
一个班次为8小时等等。
总之,限制条件比较隐晦,需要从题中认真挖掘。
本文需要解决的问题是如何设计一个班次使得总运量(吨公里)最小,同时出动最少的卡车,从而运输成本最小。
一个班次的生产计划应该包含以下内容:出动几台电铲,分别在哪些铲位上;出动几辆卡车,分别在哪些路线上各运输多少次。
因此问题可转化为:1、如何在满足所有限制条件的条件下,使得一个班次内所有卡车的总运量最小。
露天矿生产的车辆安排模型

文 章 编 号 :0 6 4 1 (0 0)6 0 3 — 1 10 — 3 12 1 1— 10 0
1 问题 重 述 43考 虑 到 卡 车 等待 的费 用相 当可 观 ,故 我们 力求 保 证 卡 车 满 . 对 于 露 天 开采 的现 代 化 铁 矿 ,它 的 生 产 主 要 是 由 电 铲 装车 、 卡 足不等待条件。 考虑在 同~条运输 线上卡车不必等待 , 因为从铲位 i
关键词 : 露天 矿 生产; 辆安 排; 究 车 研
Ke y wor :o n ptmie p o cin v h ce ra g me t rs a c ds pe i n rdu to ; e ilsa rn e n ; e e rh
中 图分 类 号 :D T5
文 献 标 识 码 : A
A b tac :Thspa rc mb n d o r cia x e in e x lrd v hil ra g me t n o e pi mi e p o cin u d rt r mie fr s u c sr t i pe o i e fp a tc le p re c ,e poe e ce ar n e nsi p n~ t n rdu to n e wo p e s so e o re poe t n a d ma i m c n mi f ce y rtci n x mu e o o ce inc . o i
・10 ・ 3
价值 工程
露 天 矿 生产 的车 辆 安 排模 型
Ope tM i od to Ve ce r ng m e o e n Pi ne Pr uc i n hi lsAr a e ntM d l
张伟 Z a gW e; 智 鹏 Z a gZ ie g h n i张 h n hpn
数学建模:露天矿生产车辆安排之案的优化模型6模型的讨论、灵敏度分析与误差分析 高一上学期数学

模型的讨论、灵敏度分析与误差分析★1 模型的讨论就本题来说,题目中给出的两条原则是相互矛盾的,要想总运量最小,运输成本最小,其生产量必定不能达到最大;相反,若要想生产量获得最大,就不可能使得总运量和运输成本最小.下面讨论一下这两种情况.1.总运量最小,成本最少要获得总运量最小,主要取决于卡车的装载量、卡车数量、各卡车运输次数、各卸点的产量和总路程.对于本题来说,卡车的装载量是确定的,各卸点的产量也是确定的,所以影响总运量和成本的最大因素就是卡车的数量、各卡车运输次数和总路程.(1)铲车数量的影响讨论.模型Ⅰ、Ⅱ是针对原则1建立的模型,从结果来看我们出动6辆铲车就可以满足原则1的需求;模型II是针对原则2建立的模型,从结果来看需要7辆铲车全部出动才能满足要求.对于原则1,它主要是从总运量和成本最小来考虑的,所以在这种情况下,对产量要求就不十分苛刻,只要满足各卸点的产量要求即可.(2)卡车数量的影响讨论.模型Ⅰ、Ⅱ是针对原则1建立的模型,从结果来看我们出动13辆卡车就可以满足原则1的需求.2.产量最大要想获得生产量最大,主要取决于铲车数量、卡车数量、各卡车运输次数和卡车的装载量.同上,卡车的装载量也是已知的.(1)铲车数量的影响讨论.对于原则2,它主要是从总产量最大来考虑的,所以对总运量最小的考虑就相对减少.而铲车数量对开采铁矿来说,它主要是从影响卡车的运输来影响总产量,所以原则1的条件下求得的铲车数量上就不需要全部出动,而原则2的条件下求得的铲车数量上就必须全部出动.(2)卡车数量的影响讨论.模型Ⅲ是针对原则2建立的模型,从结果看来需要20辆卡车全部出动才能满足要求.同上,在原则1和原则2条件下,卡车所产生数量的影响有满足总运量最小的部分,也有满足最大产量的部分.★2灵敏度分析由于本题中对模型结果产生影响的因素有很多,我们在此取几个关键的参数进行了灵敏度分析.模型对这些参数的敏感性反映了各种因素影响结果的显著程度:反之,通过对模型参数的稳定性和敏感性分析,又可反映和检验模型的实际合理性.1.对模型Ⅱ卡车数量的灵敏度分析对模型Ⅱ卡车数量不仅关系到总运量的大小,而且原则1要求出动最少的卡车,这就要求我们在实际的规划中要充分考虑到卡车数量的变化对目标值的影响,假设在其他条件不变的情况下,通过逐个减少卡车的数量,计算得到相应的最小总运量,结果如表3.13和图3.7所示.由上面的计算结果我们可以知道,卡车的数量和总运量呈正比的关系,即卡车数量增加时总运量也增加;反之,则减少.从图3.7中我们可以很直观地看出,在卡车数为10、11、12时,总运量有一明显的增加.由此可知,我们在规划卡车数量时,如果不是矿产运输量有限的情况下,应尽量选择车辆数不小于11辆,当然其具体的数值应根据具体情况而定.2.对模型II的铲车数量以及品位限制的灵敏度分析(1)铲车数量.由于模型II铲车是关系到最大产量的重要因素,所以我们对模型Ⅱ铲车数量进行灵敏度分析,假设其他条件不变的情况下,逐个减少铲车的数量,得到相应的最大出车次数,其结果如表3.14和图3.8所示.从图3.8可以看出,铲车数和最大出车次数呈线性关系(也就是和产量呈线性关系),由此知铲车的数量对于产量来说是至关重要的,建议在开采矿产时,应对铲车的数量进行合理的规划,使铲车得到充分利用.(2)品位限制.同样,在考虑品位限制对产量的影响时,不考虑其他因素的影响,我们逐步对改变品位限制的范围,得到在一定的品位限制条件下的最大产量值(在本题中由于没有给出铲车确切的装填速度,所以无法计算精确的产量,所以用最大的出车量作为目标来代替产量).经过计算,得到的结果,如表3.15和图3.9所示.从上面的结果中可以看出,品质限制变化范围较小时,最大出车次数随品质限制范围的增加而快速上升,当增加到一定的范围时,最大出车次数就不再增长,也就是说,产量的上升也是依此规律上升的.★3 误差分析(数据近似误差)在建立模型的之前,为了满足卡车每次都是满载运输,考虑到卸点和矿位运输的实际,我们分两种情况对模型的数据进行了近似取值.(1)退零取整对矿位的最大运输车次近似取值.(2)进一法对卸点的最大运输车次近似取值.近似取值使模型的求解产生了数据误差,造成了模型求解结果的不精确,对三种参数的近似分别如表3.16、表3.17和表3.18所示.通过表3.16、表3.17和表3.18的近似取值可以看出表3.16数据的近似取值增大了卸点车次的下限,表3.17和表3.18数据的近似取值减小了运矿车次和运岩车次.卸点的车次下限、运矿车次和运岩车次都是目标函数的约束条件,增大或者减小了实际约束条件的范围,使总运量和产量的目标值都跟准确值有一定的误差.由于数据的近似取值对模型结果的影响,卸点所需车次下限的增大导致了总运量和产量目标值的增大;运矿和运岩车次的减小导致总运量和产量的减小.数据的近似取值是考虑了生产运输的实际,简化了模型的计算量.卸点车次下限和岩石矿石运输车次对模型结果影响有一定量相互调整,本章模型结果所得的运输车次与数据的近似值没有十分接近的情况,对目标值没有太大的影响,所以这个误差是可以接受的.针对本章的模型,调整模型数据误差,尽量不要使模型的结果和近似取值的数据贴近.。
露天煤矿开采车辆安排

露 天 煤 矿 的 车 辆 安 排摘 要本文用线性规划的方法,就在两条不同的原则要求下,分别给出了露天矿生产的车辆安排问题的数学模型。
利用Mathematcia 软件进行运算,得出了一组解,根据具体要求,通过对解的分析和比较、讨论,然后得出铲位、路线、车次、总运量、总产量等一组最优结果。
针对所给实例,我们分别计算出了①最小总运量为8.48292万 吨公里,出动的最小卡车数是13辆以及一个经过优化的具体卡车运输安排表;②最大产量为10.3488万吨,优化出另一个具体的卡车运输安排表。
而且我们验证了从各铲位到各卸点得石料场均满足题目所规定得要求。
关键字:目标规划、线性规划、铲位、卸点、品位、品位限制、总运量、总产量一、问题的提出:露天开采铁矿,有固定的若干爆破生成的石原料(铲位)、卸货地点(卸点)、工作于铲位的电动铲车(铲车)和负责从铲位运输矿料到卸点的电动轮自卸卡车(卡车)。
现在要求在一个班次(8小时)的时间内,计算要出动多少辆铲车,分布在哪些适当的铲位,通过那些合适的路线来运送石料,且这些矿料要满足每个不同的卸点所需的量和质(品位)的要求,使得:○1总运量(吨公里)最小,且出动的卡车数目最少,从而获得最低的运输成本;○2利用现有的若干车辆运输,获得最大的产量。
二、模型假设:1、当铲位固有石料量不足一车时,不可以再运输2、铲位上的岩石矿石都已分号,且数量、品位已知3、铲车在一个铲点即可铲岩石,也可铲矿石4、卡车每次都是满载运输(154吨/车次)5、在实际运行过程中,装、卸车时间间隔允许有一些细小的调整6、卡车可以在一个班次内跑不固定的铲位和卸点7、卡车平均时速28km/h ,不熄火情况下消耗功率均为81吨/小时8、铲车可以在铲位连续工作8小时不休息9、 因为无法排时,不考虑卡车会在各铲位或者是卸点发生等待 10、矿石的铁含量要满足品位限制的要求三、参数设置:1、X ij ——从第i(i=0,1,2,3……n)个铲位到第j 个卸点(j=1,2,……k )所运输岩石的次数,在本实例中,X oj 表示第10个铲位到第j 卸点所运输岩石的次数。
露天矿生产的车辆安排

露天矿生产的车辆安排露天矿生产的车辆安排(CMCM2003B)摘要本文要解决的问题主要围绕减少实际中的经济成本而展开的。
在经济运作中,减少成本是作为露天矿生产带来利润最大化的有效手段之一。
而合理安排有效路线和车次,成为了解决减少成本问题的关键。
鉴于铲点到卸点线路的复杂性,我们把问题分成两个层次加以解决。
首先我们采用了整体规划的算法,建立了数学模型以求得最小运输量。
其基本思想是提取重要的约束性条件,对于总产量达最小的目标函数进行约束,运用lingo程序求出其最优解,最后得出最小运输量为85628.62吨,且第5、6、7个铲点没有使用。
对于层次二,通过解决层次一所得出具体流量计算卡车在各个路线上一个班次最多可以运行的次数及各路线上需要的卡车数,从而得出所有路线要出动13辆卡车.问题重述此题类似与产地与销地的运输的整数规划问题。
10个矿位,5个卸点,运输矿石和岩石两种产品。
此题的重点在于限制条件的提取,由于题中所给条件较多如:每个铲位至多能安置一台电铲,电铲的平均装车时间为5分钟。
卸货地有卸矿石的矿石漏、2个铁路倒装场和卸岩石的岩石漏、岩场等。
每个卸点都有各自的产量要求,岩石卸点的品味限制都为29.5% 1%。
电铲和卸点都不能同时为两辆及两辆以上卡车服务。
卡车每次都是满载运输,且在一个班次中不存在卡车等待情况,卡车只在开始时点火一次。
卡车的平均卸车时间为3分钟。
一个班次为8小时等等。
总之,限制条件比较隐晦,需要从题中认真挖掘。
本文需要解决的问题是如何设计一个班次使得总运量(吨公里)最小,同时出动最少的卡车,从而运输成本最小。
一个班次的生产计划应该包含以下内容:出动几台电铲,分别在哪些铲位上;出动几辆卡车,分别在哪些路线上各运输多少次。
因此问题可转化为:1、如何在满足所有限制条件的条件下,使得一个班次内所有卡车的总运量最小。
2在总运量最小的情况下,如何设计卡车路线,使得出动的卡车数最少,从而使总成本最低。
数模论文——露天矿生产的车辆安排

摘要本文讨论对矿区开采点和加工厂进行物流配送,找出车站位置并求出最佳的车辆安排,是一个典型的车辆路径问题(VRP)。
对于第一题,用重心法进行求解。
首先通过聚类分析,将开采点分为四个区域,计算每个区域的开采点到所属加工厂的权重之和(权重是距离和产量的乘积),以此作为该加工厂的权重。
然后使得车站到四个加工厂的权重之和最小,最终通过Matlab工具箱中的Gatool函数求出车站坐标为(73.95,32.99),几乎与S2重合,因此直接把S2作为车站位置。
对于第二题,即对车辆路径进行安排。
首先将实际问题用数学规划模型抽象表示出来,然后通过综合运用扫描法和遗传算法相结合,并在第一问的基础上,对于已经分好的四个区域中的某些点做出调整,满足题设的各项条件,得出每个区域各个行车路径。
最终得出结论,在保证总路程最小(1085.04㎞)的情况下,至少需要3辆车参与运输便可按时完运输成任务。
对于第三题,即通过加大加工厂的日加工量以提高运输效率。
首先我们定义了评估运输效率的指标,包括行程利用率β,载重量利用率γ以及运输效率 。
在不调整平均聚类点的基础上,用第二题的方法计算出车辆路径的安排。
得到至少需要3辆车跑完全程的1032.30㎞。
最后计算上述的运输效率指标,增加S2,S3加工厂的最大日加工量,平均运输效率相对提高5.47%,明显提高了运输效率。
关键字:车辆路径问题(VRP)重心法线性规划扫描法运输效率一、问题重述某矿区有 4 个加工厂,65 个开采点,(单位:km )。
各加工厂每天有最大加工量,各开采点每天的开采量确定。
矿区位于一个平原地带,任意两点均可连通,它们之间的距离为几何距离。
现将这个矿区从开采点到加工厂的运输任务交给某运输队,运输队首先要根据运输任务大小及加工厂和开采点的分布确定一个车站位置,并建设车站的基础设施。
该车队所用运输车型最大载重量100t ,行驶速度31km/h 。
每天上午八点,运输车从车站出发,到达各个开采点并将开采点前一天开采的矿石运往加工厂。
露天矿生产的车辆安排问题的研究
露天矿生产的车辆安排问题的研究摘要本文建立了优化模型对露天矿生产的车辆安排问题进行了研究。
模型一的建立阶段建立了关于总运量最小,卡车数量最小的双目标线性规划模型。
模型一的求解阶段根据总运量最小的原则先建立了关于总运载量与运输距离的LINGO求解的目标函数—总运量:10511ij iji j m d==∑∑,将卡车数量最小与其他因素归结于LINGO求解的限制条件,将双目标规划模型转变为单目标规划模型求解。
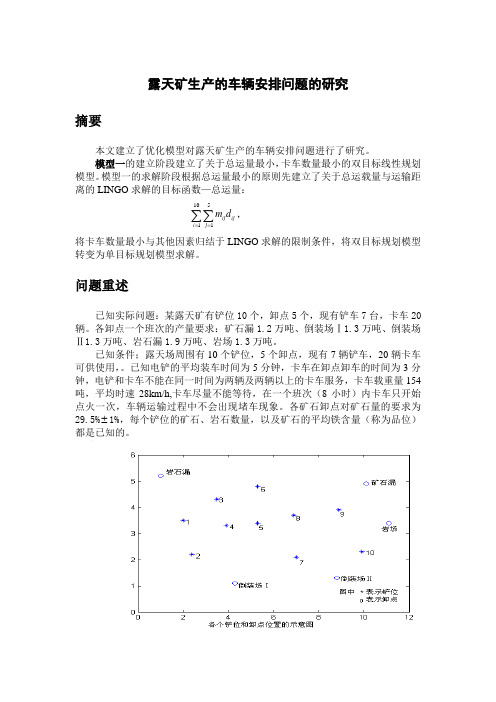
问题重述已知实际问题:某露天矿有铲位10个,卸点5个,现有铲车7台,卡车20辆。
各卸点一个班次的产量要求:矿石漏1.2万吨、倒装场Ⅰ1.3万吨、倒装场Ⅱ1.3万吨、岩石漏1.9万吨、岩场1.3万吨。
已知条件;露天场周围有10个铲位,5个卸点,现有7辆铲车,20辆卡车可供使用,。
已知电铲的平均装车时间为5分钟,卡车在卸点卸车的时间为3分钟,电铲和卡车不能在同一时间为两辆及两辆以上的卡车服务,卡车载重量154吨,平均时速28km/h,卡车尽量不能等待,在一个班次(8小时)内卡车只开始点火一次,车辆运输过程中不会出现堵车现象。
各矿石卸点对矿石量的要求为29.5%±1%,每个铲位的矿石、岩石数量,以及矿石的平均铁含量(称为品位)都是已知的。
现需要安排在一个班次内出动几台电铲,将其分布在哪些铲位,使用几辆卡车,分布在哪些线路上运行量又是多少?使得总运量最小,同时出动的卡车数量最小,从而运输成本最少。
模型假设:1.将矿石漏,倒装场1,倒装场2,岩石漏,岩场分别标记为卸点1,2,3,4,5.2.每个铲位至多能安置一台电铲3.卡车平均速度为28km/h,每次都是满载运输,且不会发生卡车等待的情况,电铲和卸点都不能同时为两辆及两辆以上卡车服务,卡车运输过程中无障碍。
4.电铲即可对岩石也可对矿石装载。
5.从长远看,卸点可以移动,但一个班次内不变。
符号说明:注:i表示铲位()i= ;j表示卸点,且j=1表示矿石漏,j=21,2,10表示倒装场1; j=3表示倒装场2;j=4表示岩场;j=5表示岩石漏。
露天矿生产的车辆安排-2003全国一等奖(第一组)

j=1,2……5
285≤ 0. 0.285
∑154 x c
ij i =1 n
ij
≤0.305, j = 1,2,3
∑154 x
i =1 n
5
ij
∑∑ n
i =1 j =1
5
ij
=N≤20
∑ 5x
j =1 n
ij
≤480
∑ 3x
i =1
ij
≤480
x
ij
=
8 × 60 × nij 2 × d ij 8+ v
4
(1)铲位的确定:
m
设 Xi= ∑ xij ,i=1,2,……n,其中 Xi 代表一个班次内第 i 个电铲装的车次数
j =1
那么,对 n 个电铲按照 Xi 值的大小进行排序,根据矿场的实际拥有铲车情况,选择 Xi 的值大的铲位设置铲车。 (2)运输系统路线的确定: 当铲位的数目和位置都已经确定,在原二部图 G(V,R) ,去掉不设置铲车的铲位 所代表的点以及与这些点相关联的边,这样得到简化的二部图 G’(V’,R’).再对目标函数 进行规划,求解出 Xij 的解集: 若 Xij=0,说明在 rij 这条线路上没有卡车通过,这条边是闲置的,舍弃。 若 Xij>0,说明在 rij 这条线路上有卡车通过,保留这条边。 由此,确定了该运输系统中卡车运行路线。 (3)卡车最小数量: 本题目要求卡车无论在铲位还是在卸位都不等待,因此,卡车周转一次所需时间 Tz 可 用下列公式计算:Tz=tz+ty+te tz…………..装车时间 min; min;
最小卡车的数量=
总时间 一个班次工作时间
Step6: 车流分配: 若规模大,采用计算机模拟。 若规模小,则运用自适应原则,人为排车。
CUMCM03B 露天矿生产的车辆安排(优秀论文)

题CUMCM03B 露天矿生产的车辆安排铁工业是国家工业的基础之一,铁矿是钢铁工业的主要原料基地。
许多现代化铁矿是露天开采的,它的生产主要是由电动铲车(以下简称电铲)装车、电动轮自卸卡车(以下简称卡车)运输来完成。
提高这些大型设备的利用率是增加露天矿经济效益的首要任务。
露天矿里有若干个爆破生成的石料堆,每堆称为一个铲位,每个铲位已预先根据铁含量将石料分成矿石和岩石。
一般来说,平均铁含量不低于25%的为矿石,否则为岩石。
每个铲位的矿石、岩石数量,以及矿石的平均铁含量(称为晶位)都是已知的。
每个铲位至多能安置一台电铲,电铲的平均装车时间为5分钟。
卸货地点(以下简称卸点)有卸矿石的矿石漏、2个铁路倒装场(以下简称倒装场)和卸岩石的岩石漏、岩场等,每个卸点都有各自的产量要求。
从保护国家资源的角度及矿山的经济效益考虑,应该尽量把矿石按矿石卸点需要的铁含量(假设要求都为29.5%1%,称为品位限制)搭配起来送到卸点,搭配的量在一个班次(8小时)内满足品位限制即可。
从长远看,卸点可以移动,但一个班次内不变。
卡车的平均卸车时间为3分钟。
所用卡车载重量为154吨,平均时速28。
卡车的耗油量很大,每个班次每台车消耗近1吨柴油。
发动机点火时需要消耗相当多的电瓶能量,故一个班次中只在开始工作时点火一次。
卡车在等待时所耗费的能量也是相当可观的,原则上在安排时不应发生卡车等待的情况。
电铲和卸点都不能同时为两辆及两辆以上卡车服务。
卡车每次都是满载运输。
每个铲位到每个卸点的道路都是专用的宽60的双向车道,不会出现堵车现象,每段道路的里程都是已知的。
一个班次的生产计划应该包含以下内容:出动几台电铲,分别在哪些铲位上;出动几辆卡车,分别在哪些路线上各运输多少次(因为随机因素影响,装卸时间与运输时间都不精确,所以排时计划无效,只求出各条路线上的卡车数及安排即可)。
一个合格的计划要在卡车不等待条件下满足产量和质量(品位)要求,而一个好的计划还应该考虑下面两条原则之一:1.总运量(吨公里)最小,同时出动最少的卡车,从而运输成本最小;2.利用现有车辆运输,获得最大的产量(岩石产量优先;在产量相同的情况下,取总运量最小的解)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(7)电铲数量约束:电铲数量约束无法用普通不等式表达,可以巧妙地引入10个。一l变
量来标志各个铲位是否有产量。这样做可以求出最优解,但算法运行时间增加了。当然也可用
其他方法解决该问题。
(8)车辆数量约束: xij 20, 其中考为各路线上运输量所需的实数卡车数。
环。参赛队逐年增加,解题能力、所用方法、使用软件和论文撰写的水平在不断提高都说明
了这一点。“露天矿生产的车辆安排”一题就是在这样的想法下设计的。
露天矿的生产调度,可以划分成许多种类型,但不论怎样最后都要牵涉到车辆的调度安
排这样一个组合问题,因此都是没有好算法的NP完全(NPC)问题。各国根据一些露天矿
出动卡车数最少,意味着出动的卡车利用率要最大。容易出现的一辆卡车为两个以上路
线服务的联合派车,可分为两种情况:(1)有共同铲位(或卸点)的联合派车(V字形或更复
杂);(2)不同铲位且不同卸点之间的联合派车(z字形或四边形或更复杂)。注意到派车方案
的空载路线应尽量安排在第一阶段规划的最佳物流路线内,即使有的超出也要保证超出的
6)铲位数多于铲车数意味着要最优的选择不多于7个产地作为最后结果中的产地;
7)不仅要求最佳物流,最后还要求出各条路线上的派出车辆数及安排。
每个运输问题对应着一个线性规划问题。以上不同点对它的影响不同,第1、2、3、4条
可通过变量设计、调整约束条件实现;第5条整数要求将使其变为整数线性规划;第6条不
Σ ≤7
为整数,i=1,?,10,J=1,?,5
为0—1变量,i=1,?,10
二.对最佳物流进行派车一第二阶段规划
这是一个组合优化中的一维装箱模型,又是一个NPC问题,针对快速பைடு நூலகம்法的要求,我们
用启发式方法求近优解。
维普资讯
第7期 “露天矿生产的车辆安排”的模型和评述 95
符号:
单位
z 从i号铲位到 号卸点的石料运量 车·次;
c 从i号铲位到 号卸点的距离 公里;
T 在i号铲位到 号卸点路线上运行一个周期平均所需时间 分;
A 从i号铲位到 号卸点最多能同时运行的卡车数 辆;
B 从i号铲位到 号卸点,一辆车一个班次中最多可以运行次数 次;
P : 号铲位的矿石铁含量乘以100 .
车·次大约为:Ld:Af,×B 总吨数大约为154×L
注:如果假设所有卡车的上班时间可以不是同一时刻,在此处应取B ,:L J,以下
U
的解法和结果也略有不同。
维普资讯
94 工程数学学报 第20卷
(2)电铲能力约束:还是因为~台电铲不能同时为两辆卡车服务,所以一台电铲在一个
的实际情况开发出许多实用软件,但都没有公开它们的算法。我国仅有几个露天矿用上了
智能化软件管理,水平还需要提高,应用面也需要扩大,矿业生产迫切需要这方面的成果。
总之,深入研究这方面问题是很有实际意义的。由于没有详细、确定的资料可以参考,所以
比较适合作为数学建模竞赛的题目,做题时没有框框,能留有更大的空间让学生们用聪明才
所有的e ,一Le ,J时把这些小数组合成最少的整数卡车数。所需总卡车数的下界显然是y :
rΣ ]。如果某种派车方案恰好派出Y 辆车实现了所有的 ,则其即为在第二阶段目标
l'J
意义下近优解的最优方案。但由于有联合派车而总公里数不一定最小,故不一定为全局意义
下的最佳方案,还需要进一步分析确定。
92 工程数学学报 第2O卷
1 问题分析
从题目看,露天矿生产主要是运石料。它与典型的运输问题明显有以下不同:
1)这是运输矿石与岩石两种物资的问题;
2)属于产量大于销量的不平衡运输问题;
3)为了完成品位约束,矿石要搭配运输;
4)产地、销地均有单位时间流量的限制;
5)运输车辆只有一种,每次都是满载运输,154吨/车·次;
T ,= +3+5(分)。由于装车时间5分钟大于卸车时间3分钟,所以可分析出这条路线
上在卡车不等待条件下最多能同时运行的卡车数A f= J。同样可分析出每辆卡车一个
班次中在这条路线上最多可以运行的次数B f:L 二 L J,其中(Au一1)×
5是开始装车 最后一辆车的延时时间。则一个班次中这条固定路线上最多可能运行的总
模型建立、算法设计与模型求解:
原则一、求运输成本最小的生产计划
一
. 以重载路程最小为目标函数求解最佳物流一第一阶段规划
目标函数与约束条件的分析:
(0)目标函数取为重载运输时的运量(吨公里)最小。
(1)道路能力约束:一个电铲(卸点)不能同时为两辆卡车服务,所以一条路线上最多能
同时运行的卡车数是有限制的。在i号铲位到 号卸点路线上运行一个周期平均所需时间
3.模型中应有道路能力约束,否则原则二的结果不可能正确。
4.派车问题本质为组合优化问题,如何快速得到最优解或近优解。
2 基本做法
模型假设:
维普资讯
第7期 “露天矿生产的车辆安排”的模型和评述 93
1.卡车在一个班次中不应发生等待或熄火后再启动的情况;
定办得到。从另一个角度看,这是两个阶段的规划问题,第一个阶段是确定各条路线上运输
石料的数量(车次),可以用整数规划建模;第二阶段是规划各条线路上的派车方案,是一个
组合优化问题。如果求最优解计算量较大,现成的各种算法都无能为力。于是问题可能变
为找一个寻求近优解的近似解法,例如可用启发式方法求解。
+
q-. 2C i 2
≤
q- Xi5
×
ckl~ 1000
cy 10000/3+ 4≤ × 154。/ 54J} , = ,?, 。
Σ ≥q , =1,?,5
Σ ×(p 一30.5)≤o1
。 }, =1,2,5
Σ ×(p 一28.5)≥oj
ΣΣ ≤20
i= 1 ,= 1 一U
化之后,使得学生在阅读过短短的几行之后,就对露天矿生产的情况有一个比较清晰的理
解。下面我们结合阅卷的一些情况,简述这一问题的基本模型和解法。
收稿日期:2003一l l一15 作者简介:方沛辰(1949年生),男、副教授,研究方向 随机过程、优化
维普资讯
可分忻出问题的主要难点有:
1.怎样处理在10个铲位选择安排7台电铲的问题。
2.从铲位i到卸点i的流量均为154吨的整数倍,即取为整数车·次数。这题的核心是如何
用近似算法求解NPC问题。整数规划的现有解法不是快速算法,无法保证在任何数据下都能在
短时间内算完,应该想办法巧妙地设计算法和使用数学软件减少运行整数规划耗费的时间。
容易用线性模型实现,一种简单的办法是从c7n=120个整数规划中取最优的即得到最佳
物流;为完成第7条由最佳物流算出各条路线上的最少派出车辆数再给出具体安排即完成
全部计算。然而这是个实际问题,为了及时指挥生产,题中要求算法是快速算法,而整数规
划的本质是NP完全(NPC)问题,短时间内计算含至少50个变量的整数规划来说就不一
况(2)。
根据最后派车方案,回代计算出各车辆在各路线的运输次数。由于整数部分已分配完运
输次数,小数乘以对应路线上的B 取整计算出小数部分对应的具体运输次数即可。
进一步计算出实际总运量与矿石和岩石的产量。
三 求解过程
(一)第一阶段规划
路程总和最小,这样才能实现重载路程最小且使卡车空载路程也最小。而情况(1)的路线不
会超出第一阶段规划的最佳物流路线。只有情况(2)才会有一部分不在第一阶段规划的最佳
物流路线内。
重申一下面前的问题:各路线都是小数的需车数,如何组合使总卡车数最少且如果出现
情况(2)时空载超出部分总和尽量小。
如果存在情况(1),则整体考虑情况(1)形路线需要的卡车数相加的和,先确定和的整数
智去发挥创造,充分地锻炼学生们解决实际问题的能力。
这道题是以国内某露天铁矿为背景,大幅度地简化难度和去掉许多实际要求而编制的
一个较理想的问题。特别是由于去掉了随机性,使得此题更接近露天矿生产的根本问题,也
更适于作为竞赛的题目。题目中要求给出各条路线上的车辆数及安排,即给出当班次生产
的一个宏观的计划,方法和结果对仍使用人工调度计划的单位有启发、指导的作用。做了简
标有:①重载路程最小;②总路程最小;③出动卡车数最少。仔细分析可得:①和②在第一阶
段,③在第二阶段;①与②基本等价,于是只用①于第一阶段,对其结果在第二阶段中派最少
的卡车,实现全局目标生产成本最小。第二个原则的主要目标有:④岩石产量最大,⑤矿石
产量最大和⑥运量最小,根据题意三者之间的关系应该理解为字典序。
“露天矿生产的车辆安排”的模型和评述
摘 要
关键词
分类号
方沛辰, 李磊
(吉林大学,长春130025)
结合今年全国大学生数学建模竞赛B题的评阅情况,该文叙述了一种基本解法和结果,并对审题
中的一些问题做出了回答。
完全问题:组合优化
AMS(2000)90C27 中图分类号:0221 文献标识码:A
P=(30,28,29,32,31,33,32,31,33,31);
q 号卸点任务需求,
Q =(1.2,1.3,1.3,1.9,1.3)×10000/154; 车·次;
ck :i号铲位的铁矿石储量 万吨;
cy :i号铲位的岩石储量 万吨;
:描述第i号铲位是否使用的开关变量,取1为使用;取0为关闭。
