回归方程在煤灰成分分析数理统计中的应用
灰色线性回归组合模型在黑龙江煤炭物流需求预测中应用

灰色线性回归组合模型在黑龙江煤炭物流需求预测中应用[摘要] 黑龙江省是煤炭资源大省,煤炭需求量的快速增长对物流体系提出了更高的发展要求。
利用灰色线性回归组合模型对黑龙江2006-2011年煤炭消费进行预量的结果与实际消费相对吻合,表明此模型具有较好的预测能力,可以证明对今后一个时期预测的可行性。
黑龙江省应根据煤炭物流需求量做出相应的应对对策,应加强煤炭生产,优化能源消费结构,加强黑龙江煤炭国际运输通道建设,建立黑龙江煤炭物流基地,满足经济社会快速发展的需要。
煤炭作为中国长期依赖的第一能源,在国家能源发展战略中处于极其重要p 灰色线性回归组合模型属于隐型灰色组合模型的一种,它改善了原线性回归模型中没有指数增长趋势和灰色GM(1,1)模型中没有线性因素的不足,因此该组合模型更适用于既有线性趋势又有指数增长趋势的序列。
对于灰色线性回归组合模型,其建模过程如下:设序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n))对X(0)进行一次累加生成处理,得到生成序列(5)计算相对误差表2 黑龙江省2006-2011年预测煤炭消费量相对误差从表2可以看出预测平均相对误差为1.939%,对于经济指标的预测,一般来讲相对误差达到5%,就算是比较精确了,因此本文所建立的灰色线性回归组合模型具有较好的预测能力。
(6)利用建立的灰色线性回归组合模型进行预测表3 黑龙江省2012-2015年煤炭消费量预测值表3的预测结果显示,黑龙江省煤炭物流预测的年增长率在7.91%左右,这与黑龙江省煤炭物流实际年增长率7.86%是相符合的。
三、相应对策到2015年黑龙江省煤炭消费量预计将达到17200.53万吨左右,煤炭需求量的快速增长对煤炭物流体系提出了更高的发展要求,要适时的根据煤炭物流需求量做出相应的应对对策。
1.加强煤炭生产,优化能源消费结构根据黑龙江煤炭实际生产情况及煤炭消费量预测可知,2015年煤炭物流需求量为17200.53万吨左右,是2006煤炭物流需求量9025.0万吨的1.9倍。
回归模型在统计分析中的应用

回归模型在统计分析中的应用摘要在人们研究对象的内在特性和个因素间的关系时,通常会建立数学模型。
在无法分析实际对象内在的因果关系时,往往会基于对数据的统计分析去建立模型。
回归分析作为统计数据寻求变量间关系的近似表达式的一种方法,其广泛用途使得回归模型成为了数据统计分析中的一种常见模型。
本论文分别从数学模型,回归分析,统计分析等的基本概念出发,进一步阐述了数学建模的基本方法和一般步骤,回归分析的基本模型、步骤和分类,以及统计分析的步骤。
最后借用MATLAB软件,以一个关于人们对某种品牌食品的评价的实例,用合理的步骤详细描述了在解决回归模型在统计分析中的应用的问题中该如何具体去做。
关键词:数学模型;统计分析;回归分析;回归模型;MATLAB软件APPLICATION OF REGRESSION MODEL INSTATISTICAL ANALYSISABSTRACTIn the process of researching the relationship between the inner characteristics and factors of the object,people usually build mathematical model. In the case of the inner causality that people can not analyse of actual object,we often to build model based on statistical analysis of data. As a method for seeking a approximate expressions of the statistical data,the wide applications of regression analysis made regression model become a common model in statistical analysis of data.This paper starts from the the basic concept such as the mathematicalmodel,regression analysis and statistical analysis.Then further elaborated the basic methods and general steps of mathematical modeling, the basic model, steps and classification of regression analysis, and the steps of statistical analysis. Finally, applying MATLAB software,using reasonable steps to describe how to solve the problem that the application of regression models in statistical analysis in detail,by using a example about people's evaluation towards a certain brand of food.Key words: mathematical model; statistical analysis; regression analysis;regression model; MATLAB software目录1 问题的提出-------------------------------------------------------- 12 数学模型与数学建模------------------------------------------------ 22.1 基本概念---------------------------------------------------- 22.2 数学建模的基本方法------------------------------------------ 22.2 数学建模的一般步骤------------------------------------------ 23 回归分析与回归模型------------------------------------------------ 43.1 基本概念---------------------------------------------------- 43.2 刻画回归模型------------------------------------------------ 43.3 回归分析的步骤---------------------------------------------- 43.4 回归分析的分类---------------------------------------------- 54 统计分析---------------------------------------------------------- 64.1 基本概念---------------------------------------------------- 64.2 统计分析的步骤---------------------------------------------- 65 一个线性回归模型实例---------------------------------------------- 75.1 问题的提出-------------------------------------------------- 75.2 分析与假设-------------------------------------------------- 75.3 模型建立---------------------------------------------------- 85.4 模型求解---------------------------------------------------- 85.5 结果分析---------------------------------------------------- 85.5.1 输出数据结果------------------------------------------- 95.5.2 模型检验----------------------------------------------- 95.5.3 解决提出的三个问题------------------------------------- 96 结论------------------------------------------------------------- 14 参考文献----------------------------------------------------------- 15附录--------------------------------------------------------------- 161 问题的提出当人们在研究对象的内在特性和各因素间的关系时,通常会寻求变量间的一个具体表达式,采用机理分析方法建立数学模型。
用二元线性回归法探讨煤炭发热量与全水分和灰分的关系
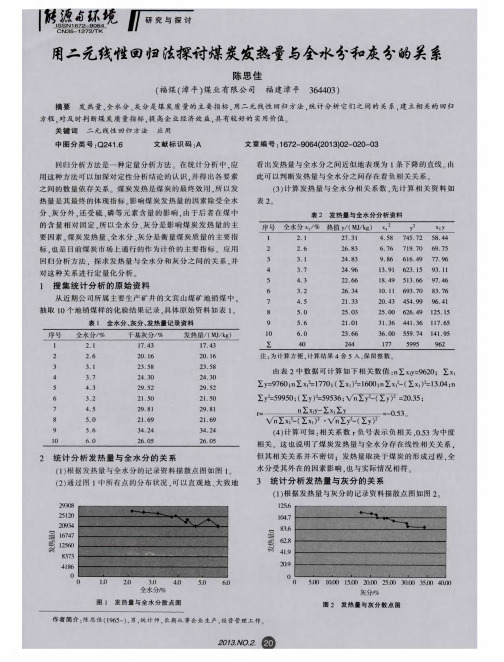
表 3 发热量与全水分分析资料
9 6 2 = 4 0 a + 1 7 7 b l + 1 o 4 1 b 2
5 9 5 9 = 2 4 8 a +1 4 1 0 b 1 + 6 4 0 0 b 2
( 4 )解 上 述 三 元 一 次 方 程 组 ,得 : b r = 一 0 . 4 8 , b l = O . 5 6 , a =
说明相关 程度密切 。这 也说 明构造 的回归方 程代表性 强 , 效
果 比较 好
性相关关 系。 在实践 中并经过检验 , 全水分 x 。 与灰分 X 2 不存在
相关关 系 , 更 不 是 线性 相关 关 系 , 由 此相 关 表 可整 理 如 表 4 。 ( 2 ) 设发 热量 与全水 分 、 灰 分 的二元线 性 回归方程 为 v =
r = : 二 墨 2 Y 一 09 1
.
1 V / 5 9 9 5 - 3 4 . 0 6 x 2 4 4 - 1 O 0 . 5 6 x 9 6 2 + O . 4 8 x 5 9 5 9 一
-
3
( 3 ) 再计算多元 线性 回归 的复判定 系数 :
R 乙旦 Y ! 墨 ! Y ± 2
1 5 李 _
( 2 ) 通 过 图 2中 所 有 点 的 分 布 状 况 , 可以直 观地 、 大致地
唬
Zx 2 y = a Zx z + b 1 ∑x l x b 2 ∑x 2 2
得:
2 4 4 =l O a + 4 0 b l + 2 4 8 b 2
看 出发热 量与灰分 之间近似 地表现为 1 条 下降的直 线 。 由此
( 1 ) 水冷壁 管 : 燃烧 区域 内水冷壁 管的高 温腐蚀情 况 、 磨 损 情况 、 胀粗 鼓胀 情 况 , 炉 膛人 孔 门管 子 、 打 焦孑 L 管子 的 腐
多元线性回归分析在动力煤低位发热量测定中的应用分析

多元线性回归分析在动力煤低位发热量测定中的应用分析发布时间:2021-01-28T11:40:50.530Z 来源:《中国电业》2020年28期作者:李凡女?[导读] 多元线性回归分析法,对当前煤炭发热量测定工作,李凡女?山东省济南市章丘区华电章丘发电有限公司??邮编:250200??摘要:多元线性回归分析法,对当前煤炭发热量测定工作,起到至关重要的作用。
本文以多元线性回归分析法在动力煤低位发热量测定的应用为主要研究对象,针对当前动力煤低位发热量测定工作进行多角度、多层次、多维度的内容分析,结合笔者在相关领域的科研经验,利用现代化计算软件SPSS进行测算和分析,从而将动力煤低位发热量测定问题进行解答和分析。
仅供参考。
关键词:多元线性回归分析法;动力煤;煤低位发热量引言:随着现代科学技术的发展,提升煤炭发热量不仅可以有效实现资源的高效化利用,同时还能够为相关企业提升煤炭资源的利用价值,实现二者的良性发展模式。
因此,利用多元线性回归分析法对动力煤进行煤低位发热量测定,可以进一步研究煤炭中相关成分的影响效应,从而实现动力煤发热量的精准对比。
一、多元线性回归分析法定义现代回归分析法则中,当出现两个或者两个以上自变量,可以称为多元回归,在实践案例中,通常会发现某种现象的组成是由于多个原因所导致,因此需要利用多个变量进行测算和分析,估计对应的变化量,该分析方法对比单一变量的分析方法更加科学和准确。
因此,在科学界通常将多元线性回归分析法作为某些事件或者现象的有效检测方式,具有极为广泛的现实意义。
基于动力煤低位发热量测定需求,利用多元线性回归分析法可以产生不可估量的测定效果,因此在实际应用过程中,利用多元线性回归分析法进行计算。
但是由于动力煤低位发热量测定需求需要多个自变量,在实际计算过程中会导致人为的主观计算问题,因此将PASS软件作为多元线性回归分析法应用的主要工具。
SPSS(Statistical Package for the Social Science)软件,自20世纪60年代开展逐步应用,在80年代左右成功应用到电脑系统中,并且已经在行业中占据重要的市场地位,针对自动统计、数据分析等相关方面的功能,起到极为显著的成效。
煤质检验数据分析及热值预测研究分析

煤质检验数据分析及热值预测研究分析【摘要】在煤炭电力企业的运营中,煤质数据信息在煤炭发电企业经营运行的各个环节都有涉及。
对煤质数据的分析与预测,能够使数据的作用发挥到最大。
本文使用数据相关性分析出主要指标对煤炭热值的相关性,并使用回归分析法以及神经网络模型进行了热值预测。
【关键词】煤质数据;分析;热值预测引言为了使煤炭资源利用率的得到提高,煤质数据分析是非常有效的技术手段。
所谓煤质分析就是指对收集的煤质资料进行分析,使数据能够得到充分的有效利用。
煤质分析时,计算机需要处理的数据较为庞大,所以,数据系统的全面、系统、科学是实现快速、准确、有效煤质数据处理的前提,能够大大提升企业的管理能力。
1 煤质检验数据分析及热值预测煤质检验数据分析就是通过对煤质数据的处理对企业所需要的煤质信息进行披露。
在煤质数据处理中,离群点分析、相关性分析是比较重要的两个内容。
在煤质数据中,煤炭热值的测量难度较大,因此对热值的预测的研究从未停止。
数据分析、数据预测都涉及大量的数据流操作,这就需要计算机系统来完成,建立系统化的数据分析处理方案,加强煤炭企业信息化建设,也是现代化企业发展的主要方向。
2 煤质数据中的主要分析指标2.1 水分水在煤中主要有三种存在形式:内外水分、水分解、结晶水。
在煤炭利用中,水分的存在是非常不利的,不仅影响了煤的加工利用,同时也造成了运输浪费,使得焦化周期变长,从而影响了焦化煤炭的产量。
煤质数据指标包括:全水分和空气干燥基水分。
2.2 灰分所谓煤炭灰分是指煤燃烧后残留物,也就是矿物质经过化学分解之后的残余物,包括内在灰分以及外在灰分。
灰分是一种有害物质,会使煤容易结渣。
动力煤中,若灰分增多,其排渣量就会增加,且发热量就会减少,煤就容易结渣了。
相关数据统计,每增加2%的灰分,相应就会降低发热量约0.42MJ/kg。
精煤冶炼中,灰分低则焦炭强度大,高炉利用系数就会降低,石灰石用量也会相应增加。
2.3 挥发分挥发分是指,在高温以及隔绝空气的条件下,煤中含有的有机物或者矿物质由于受热而分解出的液体或气体产物。
多元线性回归模型在火电厂煤炭质量监督中的应用

多元线性回归模型在火电厂煤炭质量监督中的应用摘要:为全面打造数字化燃料、智慧化电厂,本文利用公司“数字燃料”管控平台大量的化验数据,联系各个分析项目、燃煤的物理特性与发热量之间的关系,利用Excel建立模块化的发热量回归模型及预测模型,成为火电厂燃料创新发展的助推器。
0引言传统的燃料管理及业务流程在当前的社会发展中渐显不足,因此必须推进数字化的智慧燃料建设,充分利用大量的燃料数据,建立模块化的数据模型,挖掘燃料数据价值,将化验信息与煤质监督手段相结合,建立数学模型,从燃料生产现场煤质监督和煤化验室着手,全面提升企业风险防控能力。
1入厂煤发热量预测模型的建立入厂煤发热量预测模型利用直观、简单的物理因素,如光泽、矸石含量、粒度组成等,并且分析各因素与发热量的相关关系,同时与历史发热量相结合,建立发热量预测数据库并进行统计分析,得到发热量预测模型,应用到燃料生产现场进行煤质精准预测,对入厂燃煤达到准确预警。
1.1煤的物理特征与发热量之间的关系对于燃料生产现场的煤质监督,主要使用传统的“肉眼识煤”技能,该方法主要利用煤的物理性质与煤化程度之间的关系。
煤中矿物质含量越高,煤的光泽越暗;风化程度越深,煤的光泽也越暗,直到光泽完全消失。
可在构建评分系统时可将颜色与光泽相结合进行评价,将颜色按照煤炭的煤质变化程度从低到高给出0-100分的评分,表1为入厂煤光泽或颜色、评分及热值的对应表。
光泽/颜色评分热值(MJ/kg)光泽/颜色评分热值(MJ/kg)暗淡、土色02500黑色603500灰褐色202800亮黑色804000黑褐色403200似金属光泽105000表1 光泽(颜色)与热值对应表1.2矸石含量与发热量之间的关系对于同一矿区生产的煤炭,其矸石含量直接影响到灰分含量,也直接影响到煤炭发热量,通过现场进行洗煤,可通过掺配不同的矸石含量的煤样进行制样化验,从而得出矸石含量与收到基低位发热量之间的关系,如图1所示。
基于回归分析的煤炭价格预测模型

基于回归分析的煤炭价格预测模型华北电力大学(保定)武小莉热动0704王坤动力实07张帆电力实07基于回归分析的煤炭价格预测模型摘要:本文主要通过分析煤炭价格的变动趋势以及影响煤炭价格的因素,运用数据分析中的回归分析,分别建立了单变量非线性回归模型和多元线性回归预测模型,实现了对煤炭价格的预测。
首先通过对我国1985-2006年煤炭价格走势的分析,建立了以时间为自变量、煤炭价格为因变量的单变量非线性回归模型,拟合出了煤炭价格随时间的变化规律,此模型能在一定程度上预测出煤炭价格的变化趋势,但运用此模型预测出的2007年的煤炭价格与实际值有较大偏差。
对照国家相关政策的变动,对原模型产生偏差的原因进行深入分析,发现供求关系是影响煤炭价格的主要深层次因素。
选取1990-2006年间煤炭的生产量、消费量、进口量、出口量作为自变量,仍以煤炭价格作为因变量,建立了多元线性回归模型,并对此阶段的四个自变量做了时间序列分析,得到了2007年各个自变量的预测值,继而运用此模型较精确地预测出了2007年的煤炭价格。
关键词:单变量非线性回归分析、多元回归分析、价格预测一、问题的提出中国是当今世界上以煤为主要能源的少数几个国家之一,煤炭在中国经济社会发展中占有重要的地位。
它不仅是工业部门燃料动力的主要来源,也是重要的化工原料和民用能源,并已成为重要的出口商品。
目前,煤炭约占中国一次能源总产量的70%,约占一次能源中消费量的66%(国家统计局,2004d)。
未来较长时期内,煤炭仍将是中国能源的支柱,它在国民经济中具有重要的战略地位。
近十年来,我国的煤炭价格一直保持大幅度的波动,特别是近几年的煤炭价格上涨已经引起社会的广泛关注。
煤炭作为基础能源,需求缺口的拉大,必将导致作为市场信号的价格上扬。
客观分析和判定煤炭价格的影响因素,了解并能够预测未来煤炭价格,对于掌握决策的主动权,作出合理的决策,是非常必要的。
二、问题的分析对煤炭价格进行预测,需要掌握一定量的数据。
回归分析原理及其在煤炭企业管理中的应用(中)

=
。
:
假设 b
。
,
b
,
:
,
一
,
b`
分 别是 日
。 ,
日
:
:
,
一
,
, 日 的 最小
二 乘 估 计 值 ( 理论 上 可证 明这种 假设是 成 立的 )
b
。
则多元 线 性 回 归方程 为
“ “ “ ”
,
十
b
x
,
:
十
b
,
详 + .
b
: ,
:
” 十
,
b声 ,
。
一0
y y
式中
.
b
为常 数项
b
:
… b 为 回 归系 数
I
`
。
、 。
许多 客观现 象 之间 的联系 是 很复杂 的
:
、
,
许 多现象 的 变动 都涉 及到 多
,
例如
,
影 响生 产 掘进率 的 因素 ( 变量 ) 不 仅 有煤 层生产 能力 还 有采 掘
回 采工 作面 平 均长度 等等
。
。
采 掘工 作面 进度 比
研究 因变量
y
与多个 自变 t
之间 的定量 关系 问题
日
e
,
丫
因变量 y 的观察 值 向量
x ;
。
:
一
33
一
厂名
( (
。
一
b b
。
一
b b
一
b b
一
一b
. .
、
二
习
.
一
基于ARIMA和线性回归组合模型的煤炭价格预测

基于ARIMA和线性回归组合模型的煤炭价格预测作者:何文琪来源:《中国管理信息化》2021年第01期[摘要] 煤炭是国民经济发展的基础,对煤炭价格进行预测将有利于企业对将来的发展做出判断,同时有利于国家做出调控。
文章使用Eviews软件对2006-2020年每周的煤炭价格使用ARIMA(3,1,0)模型进行时间序列预测。
为综合考虑其他因素如原煤产量、原油进口量等对煤炭价格的影响,使用线性回归模型进行拟合,再使用预测误差平方和倒数法得到组合模型。
最终的预测结果误差为0.977%,预测效果较好,可为煤炭市场的经营和管理提供一定的理论依据。
[关键词] 煤炭价格;预测;ARIMA;线性回归doi : 10 . 3969 / j . issn . 1673 - 0194 . 2021. 01. 077[中图分类号] F713.54 [文献标识码] A [文章编号] 1673 - 0194(2021)01- 0187- 020 引言煤炭一直是我国重要的能源,其消费量占比相比于石油和天然气长期处于领先地位。
煤炭的市场价格不仅反映了煤炭市场的状况,也体现了我国的经济发展状况。
对煤炭价格进行精准预测能够帮助企业预估成本,做出决策,同时也为煤炭市场的平稳发展奠定了基础。
1 研究现状目前国内已有许多学者对煤炭价格的预测做出了研究。
向超[1]对煤炭价格进行了ARIMA 和SVR组合模型的预测,并比较各组合模型预测的精度,得到变权组合模型由于等权组合模型和单预测模型的结论。
孙福玉[2]对影响煤炭价格的因素使用层次分析法进行排序,并使用季节时间序列预测模型结合干预分析对煤炭价格进行综合预测。
宁晖[3]对从研究煤炭价格序列自身变化规律的角度,提出基于滚动时间窗的预测模型,将此模型应用于秦皇岛港5 500 kcal混煤价格的预测,分别得到1期、3期、6期、9期及12期的价格预测,达到预测结果的平均误差值不超过3%的良好效果。
金林等[4]综合考慮宏观经济、能源价格、气候环境和国际市场四方面因素,对市场中的煤炭交易价格建立指标体系,之后对广州煤炭交易市场价格使用BP神经网络进行预测。
-回归分析方法在江仓矿区煤质资料处理中的应用
-----------------------------------Docin Choose -----------------------------------豆 丁 推 荐↓精 品 文 档The Best Literature----------------------------------The Best Literature回归分析方法是处理变量之间相关关系的有利工具,它不仅提供建立变量间关系的数学表达式,而且利用概率统计知识进行分析讨论,从而判断取得方程式的正确性和合理性。
青海省木里煤田江仓矿区煤炭勘查前人的工作主要集中在1971年 ̄1981年间。
2004年,为经济发展的需要,上级部门决定对矿区进行补充详查和部分井田的勘探工作。
因此,江仓矿区的煤炭勘查工作可以分为两个阶段。
我国的煤炭分类方案到目前为止,也分为两个阶段,即1958年 ̄1986年为一个阶段,1986年以后为一个阶段;两个阶段煤炭分类的标准有所不同,1986年以前分类的主要指标为胶质层最大厚度(y),挥发份值的测定温度为850℃;而1986年以后分类的主要指标为粘结指数G值(GR.I),挥发份值的测定温度为900℃。
江仓矿区1981年以前的煤样除少数测定了粘结指数G值(GR.I)外,大部分样品没有测定。
对现阶段的工作来讲,怎样利用这部分没有测定粘结指数G值的样品分析成果,也是极为重要的内容。
参照《中国煤炭分类及其主要用途》中主要分类指标间的相关性利用回归分析法对挥发份值(Vdaf)和粘结指数G值进行处理。
1对挥发份值(Vdaf)的处理直接利用陈文敏采用最小二乘法的原理推导出的Vdaf(850℃)与Vdaf(900℃)间的回归方程换算得出,回归方程如下:Vr900℃=1.004×Vr850℃+0.8442对粘结指数G值的回归分析2.1对前人已有粘结指数G值和胶质层最大厚度(y)煤层做相应的散点图区内已有成果的煤层为20煤,16煤,13、15煤,12煤。
利用线性回归方程验证交易煤炭质量

利用线性回归方程验证交易煤炭质量标题:利用线性回归方程验证交易煤炭质量摘要:煤炭作为一种主要的能源来源,其质量的稳定及可靠性对于煤炭供需均衡有着十分重要的作用。
本研究以湖北省部分重要交易市场上交易的煤炭样本数据为基础,结合统计学与数理经济学的相关理论,利用线性回归方程,建立起质量指标及价格间的相关关系模型,通过定量分析得出可靠的煤炭质量判断结论。
关键词:煤炭;线性回归方程;质量评定;统计学正文:煤炭是实体经济中重要的能源来源,而煤炭的质量及可靠性对其应用与交易有着极大的影响。
随着能源成本的上涨,企业经营者希望以较低的价格获得合格的煤炭,而用户也希望能有办法确保所购煤炭质量合格。
因此,对煤炭质量的评定在当今依旧是非常必要的一项工作,尽管有时候会出现难以获得可靠结果的情况。
为此,本文将运用统计学和数理经济学的理论,尝试使用线性回归的方式,建立起质量指标与价格之间的相关性模型,进行定量分析,以得出可靠的煤炭质量预测结果。
首先,本文以湖北省部分重要交易市场上出售的煤炭测试样本为基础,结合煤炭质量指标,定义出煤炭质量、价格指标和相关联的变量。
然后,利用线性回归的方法,建立起模型,并应用数学统计学的方法,进行拟合分析,以获得质量与价格之间的相关关系模型。
最后,利用经过线性回归分析获得的数据,得出可靠的煤炭质量评定结论。
综上所述,本文以线性回归分析的方法,证明了煤炭质量指标与价格间存在一定的相关关系,并且可以根据这一模型,准确地预测煤炭质量水平。
该研究为今后煤炭管理和质量测试提供了参考。
本研究结果表明,价格是预测煤炭质量的重要参考因素之一。
煤炭质量高低与其价格间存在一定的正相关关系,舍去一些极端值后,其拟合度依然良好,这表明使用线性回归对煤炭质量及其价格进行定量分析是可行的。
本研究的结论可以为企业经营者、消费者、政府监管部门及学术界提供充足的参考,在实际工作中,利用数据分析技术,将能够进行精准的煤炭质量评估,有助于实现更有效率的经营管理,降低资源投入,提高企业效益并避免不必要的消费者损失。
线性回归方程在燃煤化验结果审核中的应用
2016年9月线性回归方程在燃煤化验结果审核中的应用赵亚兰(大唐华银攸县能源有限公司,湖南株洲412000)摘要:以研究煤化验审核校验数据为目的,建立弹筒发热量与灰水组合的数学模型,以最小二乘法为运算法则,总结弹筒发热量与灰水组合二者间的关系,利用一元线性回归曲线方程编制煤化验审核程序,更好的为煤化验结构的审核校验服务。
关键词:灰水组合;弹筒热值;灰水组合我国目前发电仍以煤炭发电为主,随着市场的不断发展进步,煤炭资源短缺程度的日益加剧,煤炭燃料的价格成为焦点,而确定煤炭价格的方式方法也在不断的发展更新。
传统煤炭的收购一般是按照市场平均价格进行的,即使出现高低的变化,其浮动范围也较小,因此经常出现煤炭生产商,为追求经济利益,降低煤炭的质量标准,为解决此问题的出现,发电厂便制定出了一种新的确定煤炭价格的方法:测定煤炭燃烧时所释放出的热量,根据所释放热量的多少来评定煤炭的价格,如此一来,测定煤炭燃烧时所释放热量的方法便成为了新的研究课题。
从电厂收购煤炭的角度进行考虑,对煤炭燃烧时所释放热量测量的越精准,定出的煤炭的价格也就越具有说服力。
面对新的挑战,电厂不仅对煤炭化验的设备、化验的方式方法做出更高的要求,还要对操作人员的自身素质做出更高标准的要求,并且加强了对煤炭化验结果的校验、审核、检测工作的重视程度,尽量的做到减小误差、减少纠纷,做到公平合理。
本文结合一元线性回归方程,对该方程进行关联性校验,并就该方程在化验结果的审核及应用加以论述。
1一元线性回归方程的确定日常电厂进行煤炭化验工作时,通常是把煤炭的样品(粉样:直径一般小于0.3mm)在电子秤上称重后进行常规化学检测分析,包括样品成分、水分百分比和挥发份等,然后再进行弹筒热值测量。
通过弹筒热值测量值得出低位热值,作为煤炭价格的结算标准,因此,弹筒热值的测量工作十分重要。
通过实验经验可知,弹筒热值和灰水组合存在着密切的联系,我们称之为线性关系。
建立一元线性回归方程涉及到几个量:①空气干燥条件下弹筒发热量(Qb.ab);②空气干燥条件下水份(Mad);③空气干燥条件下的灰份(Aad)。
线性回归方程在燃煤化验结果审核中的应用53

线性回归方程在燃煤化验结果审核中的应用摘要:燃煤化验的精准度,直接影响具体的使用情况,在各个行业中都会产生巨大影响,因此要不断提升煤炭化验的准确性。
实际操作中,其技术水平直接影响着煤质化验结果,采取有效措施解决这些问题,是降低化验误差的重要措施。
本文以某电厂为例,以研究煤化验审核校验数据为目的,建立弹筒发热量与灰水组合的数学模型,以最小二乘法为运算法则,总结弹筒发热量与灰水组合二者间的关系,利用一元线性回归曲线方程编制煤化验审核程序,更好地为煤化验结构的审核校验服务。
关键词:线性回归方程;燃煤化验;化验结果审核引言:在某2×660MW的火电厂运行中,通过对燃煤进行制样,并对其灰分、水分、发热量等进行化验。
在其结果的审核当中,采用了线性回归方程,以保证电厂运行更加稳定安全。
在实际化验工作中,要严格依照煤质化验各项控制指标,规范化验人员操作步骤,合理选用煤质化验技术来化验所选煤样。
煤炭化验工作操作步骤复杂,技术要求高,实际操作中任何环节出现错误,都会影响煤质检测结果。
社会经济发展中,煤质化验技术有一定的可靠性与准确性要求。
实际化验工作中,针对出现的问题要综合分析其原因,积极采取有效措施,尽可能降低人为与非人为操作引起的误差,对于煤炭化验管理,建立健全信息系统,确保煤质化验实现流程与信息化管理目标,以此获得更加准确的化验结果,为火电厂安全与稳定运行提供保障,从根本上实现可持续发展目标。
本文结合一元线性回归方程,对该方程进行关联性校验,并就该方程在化验结果的审核及应用加以论述。
1最小二乘法与线性回归方程1.1最小二乘法概述最小二乘法又称最小误差平方和法,即选择一个最佳函数,经过这个所选择函数的计算可以使实际数据与计算得出的数据之间误差平方和为最小。
最小二乘法通常用于解决一些优化问题和线性回归问题。
1.2线性回归方程概述线性回归方程是指一条近似直线,这条近似直线能最好地描述变量x与y之间的线性关系。
基于多元回归分析对煤炭能源消耗的研究

基于多元回归分析对煤炭能源消耗的研究作者:林刚于焱王同勋戴青松赵建强来源:《硅谷》2014年第09期摘要根据当今世界资源、能源紧缺,特别是煤炭资源是不可再生资源,必须对煤炭资源的消耗状况有足够的了解,才能够很好的控制未来的能源消耗。
文章主要根据优化模型,先对能源数据进行检验,然后根据最终的数据,建立优化模型,得到最终的煤炭能源消耗状况。
关键词煤炭能源;优化模型;能源紧缺中图分类号:TU443 文献标识码:A 文章编号:1671-7597(2014)09-0161-01当今世界的发展,能源是GDP增加直接关联的,能源的多少与经济的增长有着直接的相关性,煤炭更是必不可少的。
中国是世界上最大的煤炭生产国和煤炭消费国。
中国能源的自然特点是“富煤贫油少气”。
过去50年,煤炭在中国一次性能源消费总量中占70%以上,煤炭作为中国的主体能源,以后相当长时间内也不会发生根本性变化。
因此节约能源,使得单位GDP的增加能够减少能源的消耗[1],进而能够减少环境的危害。
因此在煤炭行业,确定影响洗煤厂洗出精煤数量的因素,并建立各洗煤厂的精煤产量模型显得很重要[2]。
1 过失误差的检验由于数据的波动范围较大,故此我们先对已给回收率和洗损率数据进行过失误差的检验。
计算包括可疑数据在内的平均值和及其标准偏差:;;其中为第次入洗原煤的回收率;为回收率算术平均值;为回收率的标准偏差;为已给回收率数据与其算术平均值的偏差;为第次入洗原煤的洗损率;为洗损率算术平均值;为洗损率的标准偏差;为已给回收率数据与其算术平均值的偏差。
2 多元线性回归在煤炭能源中的应用煤炭作为能源物质,在每个地区的消耗不同。
经济发达的地区,消耗的比较的多,因为需要大量的能源才能带动经济的发展,才能够带来GDOP的稳定增长。
但是在经济欠发达的地区,工业发展的相对缓慢,因此需要的能源也相对较少。
煤炭的消耗往往和很多因素有关,因此要能够很好的推算出煤炭的消耗情况,必须要能够建立起他们之间的相关性,可以利用多元回归分析,建立起它们之间的关系,得到煤炭的消耗情况。
线性回归方程在燃煤化验结果审核中的应用

线性回归方程在燃煤化验结果审核中的应用摘要:随着市场的进一步发展和进步,煤炭资源的短缺日益严重,煤炭价格受到整个社会广泛关注,特别是煤炭定价方法不断更新也影响着电厂的成本控制。
燃煤化验的精准度,直按影响煤炭的质量检验结果,因此要不断提升煤炭化验的准确性。
实际操作中,除了技术水平的提高还需采取有效措施来降低化验误差。
本文以某电厂为例,以研究煤化验审核校验数据为目的,通过一元线性回归方程对煤的发热量测定中发热量和灰分及水分的相关性进行了验证,并作为煤化验审核方程编制过程,使煤化验结果的准确性得到进一步提升。
关键词:线性回归方程;燃煤化验;发热量引言:燃料管理是火电企业安全生产和经济效益的一个关键因素,也是发电企业确保生产和降低成本的最有前景的挑战之一。
在燃煤成本占总成本的比重越来越大,风险防范和控制越来越困难的新形势下,加强对燃料入厂验收和检验的控制尤为重要。
电力公司非常重视燃料管理,在煤场质量控制建筑,如制样室、实验室和综合管理办公室。
为了从硬件升级到软件升级,他实践了质量和精细管理的概念。
煤质检测在质量建设中变得越来越重要,不准确的结果会对生产活动和企业绩效产生重大影响。
因此,加强煤质检验的详细管理是改善燃料管理的重要方面之一。
我国的电力生产仍以煤炭发电为重点,因为市场持续增长,煤炭资源日益短缺,煤炭价格成为一个令人关注的问题,煤炭定价方法和程序不断变化和更新。
传统煤炭的购买通常以平均市场价格进行。
即使在高低变化的情况下,浮动路径也很少,因此,煤炭生产商为解决问题,以获得经济效益,降低煤炭质量标准。
制定了一种稳定的买卖双方承认的煤炭定价方法:测量燃煤燃烧产生的热量排放,即发热量。
并根据发热量对煤炭价格进行评估。
所以燃煤所释放热量方式是一个新的研究方向。
发电厂购买煤炭释放热量测量越精确,在煤炭价格协商上就越有说服力。
面对新的挑战,发电厂不仅对煤炭测试设备和方法提出了更高的需求,而且对运营商的质量标准也提高了,而且更加注重煤炭测试结果的验证、审核和检验,以尽量减少煤化验误差。
回归分析在数理统计中的应用实例论文

福建农林大学计算机与信息学院(数学类课程)课程论文报告2011 年 6 月25 日福建农林大学计算机与信息学院数学类课程论文报告结果评定目录1、问题的提出 (4)2、问题的分析 (4)3、问题的解决 (4)问题重述 (4)建立模型 (4)模型求解 (5)模型检验 (7)4、小结 (9)参考文献 (9)附录10摘要:回归分析是数理统计中重要的一种数据统计分析的思想。
它是研究一个随机变量与一个或多个普通变量之间的相互关系的统计方法。
主要是解决从一组数据出发,确立变量间是否存在相关的关系,如果存在相关关系,确定他们之间合适的数学表达式即经验公式或回归方程,并对它的可信度作统计检验;还可以针对从共同影响一个变量的许多变量中,判断哪些变量的影响是显著的,哪些变量是不显著的,并利用所确定的回归方程进行预测和控制。
本文就是针对实际问题运用回归分析中一元线性回归分析的统计方法,来确定自变量与另一个变量的相关关系,并确立出较为合理的回归方程,再对其的可信度进行统计检验。
关键词:回归分析;回归方程;F检验法1、问题的提出根据以下9组关于营业税税收总额y和社会商品零售总额x的数据[1],确定出两者的关系。
表1 社会商品零售总额和营业税税收总额序号社会商品零售总额营业税税收总额1234567892、问题的分析营业税税收总额是受很多的因素所决定,但是题目中已经将主要的因素确定为社会商品零售总额,这就大大的减少了在对于自变量的多因素进行分析的过程,从而减少了在计算以及统计上的困难,但是这也在很大的程度上减少了结果的实际意义。
在针对本题所给的两个变量之间的关系,作出回归分析以及运用重要的数学软件的实现,从而来确定这两个变量之间的关系,并计算出两者之间的回归方程,再对方程的可信度进行检验。
3、问题的解决问题重述在本题目中已经明确地给出只有两个变量之间的关系,所有可以忽略影响营业税税收总额除社会商品零售总额之外的其他因素,这对于解决问题减少了难度。
煤质分析研究中回归方程实用价值的正确判断

2012年8月(中)工业技术科技创新与应用煤质分析研究中回归方程实用价值的正确判断贾志浩(黑龙江省煤炭质量监督检验五站,黑龙江哈尔滨150026)数理统计专著中,一般给出两个检验回归方程效果的手段,其一为检验因变量和自变量间的关系的密切程度,其二为计算推算值得误差。
对以求推算值为目的的回归方程来说,后者最具现实意义,因为根据推算值的准确度可以判断所得回归方程的实用价值,而前者则处于次要甚至无关紧要的地位。
本文拟通过煤质分析研究中常用的多个自变量的线性回归分析,阐明有关问题,并指出目前出现的一些似是而非的不正确做法。
1多个自变量的线性回归分析多个自变量线性回归分析也称为多元钱性回归分析。
下面是这种回归方程的通式:y=a+b1x1+b2x2+···+b k x k1.1相关系数和假单线性回归分析的相关系数相对应的多元钱性回归分析的相表示,以示区别于r。
前者的计算法和后者完全相似;(1)这里的R。
供做R的显著性检验的方差分析如表1所示。
表1多元线性回归的方差分析(2)全相关系数R的临界值Ra,(n-k-1)按下式计算:(3)表中k为自变量的数目,当k=1时,就成为简单线性回归分析,表中的R也就成为r了。
表2相关系数R的临界值摘录对应每个自由度的第1行数值相当于a=0.05,第2行数值相当于a=0.01。
在判断回归方程实用价值的实践中,常见只注重相关系数r而忽视推算值的误差的偏向———只要r具有显著性,就认为所得回归方程有实用价值,而不问推算值得准确度是否能满足实际需要。
前文已从理论上和用实例证明了这种判断方法的无效。
1.2近年来又出现一种更为明显不正确的判断方法———用F分布法检验推算值和实测值间是否存在显著性差异。
如果差异不具显著性,便认为所得回归方程有实用价值。
这种方法一旦广为流传,必将造成误解和消极后果。
下面对这种方法试做一下评述。
高维钺等在研究泥炭容重和元素成分C、H、N、S以及泥炭容重和苯萃取物B、易水解物还原糖r、腐植酸HA、黑棕腐植酸HZ、不被水解物P的相关关系的两篇文章中(分载于《煤炭分析及利用》第4卷第3期14~18页和第5卷第4期31~35页),在得出相应的简单回归式并据以得出相应的推算值之后,不是按常规计算推算值得误差并据以判断所得回归方程的实用价值,却用F分布法检验两组平行数据(即实测值和推算值)的离散程度S2y和S2y有无显著性差异。
