高等数学A(一)期末试题及答案
高等数学期末考试试题及答案(大一考试)
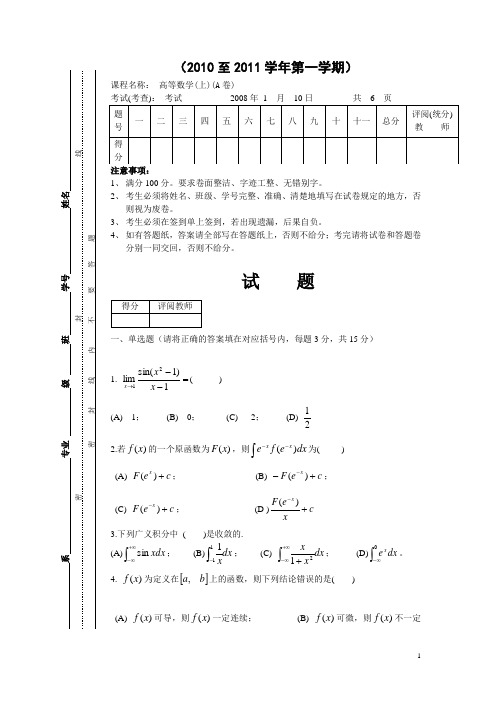
(2010至2011学年第一学期)课程名称: 高等数学(上)(A 卷)考试(考查): 考试 2008年 1 月 10日 共 6 页 注意事项:1、 满分100分。
要求卷面整洁、字迹工整、无错别字。
2、 考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方,否则视为废卷。
3、 考生必须在签到单上签到,若出现遗漏,后果自负。
4、 如有答题纸,答案请全部写在答题纸上,否则不给分;考完请将试卷和答题卷分别一同交回,否则不给分。
试 题一、单选题(请将正确的答案填在对应括号内,每题3分,共15分)1. =--→1)1sin(lim21x x x ( ) (A) 1; (B) 0; (C) 2; (D)212.若)(x f 的一个原函数为)(x F ,则dx e f e xx )(⎰--为( )(A) c e F x +)(; (B) c eF x+--)(;(C) c e F x+-)(; (D )c xe F x +-)( 3.下列广义积分中 ( )是收敛的. (A)⎰+∞∞-xdx sin ; (B)dx x⎰-111; (C) dx x x ⎰+∞∞-+21; (D)⎰∞-0dx e x。
4. )(x f 为定义在[]b a ,上的函数,则下列结论错误的是( )(A) )(x f 可导,则)(x f 一定连续; (B) )(x f 可微,则)(x f 不一定可导;(C) )(x f 可积(常义),则)(x f 一定有界; (D) 函数)(x f 连续,则⎰xadt t f )(在[]b a ,上一定可导。
5. 设函数=)(x f nn x x211lim++∞→ ,则下列结论正确的为( )(A) 不存在间断点; (B) 存在间断点1=x ; (C) 存在间断点0=x ; (D) 存在间断点1-=x二、填空题(请将正确的结果填在横线上.每题3分,共18分)1. 极限=-+→xx x 11lim 20 _____.2. 曲线⎩⎨⎧=+=321ty t x 在2=t 处的切线方程为______. 3. 已知方程xxe y y y 265=+'-''的一个特解为x e x x 22)2(21+-,则该方程的通解为 .4. 设)(x f 在2=x 处连续,且22)(lim2=-→x x f x ,则_____)2(='f5.由实验知道,弹簧在拉伸过程中需要的力F (牛顿)与伸长量s 成正比,即ks F =(k 为比例系数),当把弹簧由原长拉伸6cm 时,所作的功为_________焦耳。
大学《高等数学A》课后复习题及解析答案

大学数学A (1)课后复习题第一章一、选择题1.下列各组函数中相等的是. …….. ……..…………………………………………………………………………………….( ) A .2ln )(,ln 2)(x x g x x f ==B .0)(,1)(x x g x f ==C .1)(,11)(2-=-⋅+=x x g x x x f D .2)(|,|)(x x g x x f ==2.下列函数中为奇函数的是. ……. …….. …………………………………………………………………………………….( ). A .)1ln()(2++=x x x f B .||)(x e x f = C .x x f cos )(= D .1sin )1()(2--=x xx x f3.极限⎪⎭⎫⎝⎛+++∞→22221lim n n n n n 的值为………………………………………………………………………..…….( ) A .0 B .1 C .21D .∞ 4.极限xxx x sin lim+∞→的值为.. …….. ……..……………………………………………………………………………...…….( )A .0B .1C .2D .∞5.当0→x 时,下列各项中与 23x 为等价无穷小的是…………………………………………………….( )A .)1(3-xe x B .x cos 1- C .x x sin tan - D .)1ln(x + 6.设12)(-=xx f ,则当0→x 时,有…………………………………………………………………………..…….( ). A .)(x f 与x 是等价无穷小 B .)(x f 与x 同阶但非等价无穷小 C .)(x f 是比x 高阶的无穷小 D .)(x f 是比x 低阶的无穷小7.函数)(x f 在点x 0可导是)(x f 在点x 0连续的____________条件. ………...………………....…..( ) A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要8.设函数⎪⎩⎪⎨⎧<≤--<≤≤≤-=01,110,21,2)(2x x x x x x x f ,则下述结论正确的是……………………………………….( )A .在0=x ,1=x 处间断B .在0=x ,1=x 处连续C .在0=x 处间断,在1=x 处连续D .在1=x 处间断,在0=x 处连续 9.极限xx x 10)1(lim -→-的值为.. …….. ……..…………………………………………………………………………………….( )A .1B .e -C .e1D .e 二、填空题10.函数ln y x =的定义域为(用区间表示) . 11. 函数xxy -+=11的定义域为(用区间表示) . 12. 已知x xx f +=1)(,则=))((x f f . 13. 函数x x y 2353+-=的反函数为 .14. =→xx x 1sin lim 20 .15. 当________=α时,αx 与x 2sin 是0→x 时的同阶无穷小.16. 设21)1(lim e kx xx =+→,则=k .17. 设1sin lim0-=→xkxx ,则=k .18. =⎪⎭⎫ ⎝⎛+++∞→11232lim x x x x .9. 设⎪⎩⎪⎨⎧≤+>=0,0,1sin )(2x x a x xx x f 在点0=x 处连续,则=a . 三、解答与证明题20. 求下列数列极限 (1)⎪⎪⎭⎫⎝⎛+⨯++⨯+⨯∞→)1(1321211lim n n n (2))12(lim +-+∞→n n n n (3)⎪⎭⎫⎝⎛++++++∞→n n n n n n n n 22221lim (4)n n n nx 10...21lim +++∞→ 21. 求下列函数极限(1)15723lim 2323+++-∞→x x x x x (2)134lim 22++∞→x x x(3)503020)12()23()32(lim ++-∞→x x x x (4)11lim 31--→x x x (5)28lim 32--→x x x (6))1311(lim 31x x x ---→ (7))1(lim x x x -++∞→ (8)xx x x ln )1(lim1-→(9)xx x sin ln lim 0→ (10)x xx 3sin 2sin lim 0→(11)30sin tan lim xx x x -→ (12)x x x 10)51(lim -→ 22. 若432lim23=-+-→x ax x x ,求a 的值. 23. 若已知411lim21=-++→x b a x x ,求a,b 值. 24. 当 a 取何值时,函数)(x f 在 x =0 处连续:(1)⎩⎨⎧≥+<=0,0,)(x x a x e x f x . (2)⎪⎩⎪⎨⎧≤+>-+=0),cos(0,11)(x x a x xx x f . 25. 证明(1)方程01423=+-x x 在区间)1,0(内至少有一个根.(2)方程x e x 3=在)1,0(内至少有一个根.第二章一、选择题1、设函数)(x f 在点0x 可导,则=-+→hx f h x f h )()2(lim000( ).(A ) )(0x f '-; (B) )(0x f '; (C) )(20x f '; (D) )(20x f '-. 2、设函数)(x f 是可导函数,且13)1()1(lim-=--→xx f f x ,则曲线)(x f y =在点))1(,1(f 处切线的斜率是 ……………………………………………( ). (A) 3; (B) 1- ; (C) 13 ; (D) 3-.3、设)()()(x a x x f ϕ-=,其中)(x ϕ在a x =处连续,则)(a f '= ………( ). (A) )(a ϕ ; (B)0; (C)a ; (D))(a a ϕ.4、若0x 为函数)(x f 的极值点,则…………………………………………( ). (A)0)(0='x f ; (B)0)(0≠'x f ; (C)0)(0='x f 或不存在; (D))(0x f '不存在.5、设)0)(1ln(≠+=a ax y ,则y ''= ( ).(A)22)1(ax a +; (B)2)1(ax a +; (C)22)1(ax a +-; (D)2)1(ax a +-. 6、由方程5ln =-y xe y 确定的隐函数)(x y y =的导数=dxdy( ). (A)1-y y xe e ; (B)y y xe e -1; (C)yy e xe -1; (D)y y e xe 1-.7、)2sin sin (lim xx x x x +∞→= ……………………………………… ( ).(A)2; (B)1; (C)3; (D)极限不存在.8、设x x y =)0(>x 则='y ( ).(A)x x ; (B) x x x ln ; (C) 1-x x ; (D))1(ln +x x x .9、曲线x y sin 1+=在点)1,0(处的切线方程是…………………………( ). (A)01=--y x (B)01=+-y x (C)01=++y x (D)01=-+y x 10.下列函数在所给区间满足罗尔定理条件的是……………………( )(A) 2(),[0,3]f x x x =∈ (B) 21(),[1,1]f x x x=∈-(C) (),[1,1]f x x x =∈-(D) ()[0,3]f x x =∈ 二、填空题11、 设x x y 2sin 2+=,则=dy .12、已知x x y n ln )3(=-,(N n n ∈≥,3),则)(n y = .13、已知过曲线24y x =-上点P 的切线平行于直线x y =,则切点P 的坐标为 . 14. 已知2)1(='f ,则=-+-→2)1()(lim31x x f x f x .15. 设x a y =(0>a 且1≠a ),则=)(n y .16. 曲线3)1(-=x y 的拐点是 . 17.设函数)(x f 在0x 处可导,则xx x f x x f x ∆∆--∆+→∆)()(lim000= .18.设⎩⎨⎧≥+<=0)(x x a x e x f x ,当a =_____时,)(x f 在x = 0处可导.19.若函数5)(23-+-=x x ax x f 在),(+∞-∞上单调递增,则a 的取值范围为 .20. 设由参数方程⎩⎨⎧-=-=)cos 1()sin (t a y t t a x (其中0>a )确定的函数为)(x y y =,则=dxdy. 三、解答与证明题21.设e x x e y +=,求y '. 22.求下列函数的二阶导数.(1) 设x e y x sin =,求y ''. (2) 设1arctan1xy x-=+,求y ''23. 求曲线21x y =在点(4,2)处的切线方程和法线方程. 24. 讨论下列函数在点0=x 处的连续性和可导性:(1) 0 0 )1ln()(⎩⎨⎧<≥+=x x x x x f , (2) 0 tan 01sin )(2⎪⎩⎪⎨⎧≤>=x x x xx x f . 25. 求由方程ln xy x y x e -=所确定的隐函数y 的导数dxdy. 26. 求极限: (1)]1)1ln(1[lim 0x x x -+→; (2)30sin tan lim xx x x -→; (3))arctan 2(lim x x x -+∞→π; (4)x x x +→0lim ;(5))1sin 1(lim 0x x x -→; (6)200sin lim xdt t xx ⎰→. 27. 设函数)(x y y =由参数方程⎩⎨⎧-=+=tt y t x arctan )1ln(2所确定,求22dx yd .28.求函数()(f x x =-. 29. 求函数32332y x x x =-++的凹凸区间、拐点. 30. 已知点)3,1(为曲线1423+++=bx ax x y 的拐点. (1) 求b a ,的值; (2)求函数1423+++=bx ax x y 的极值. 31. 设11xy x-=+,求()n y 32.设b a <<0,证明:a b ab ba a --<+ln ln 222. 33. 设0,()(0)0,x f x f ≥=连续,0'()x f x >当时,存在且'()f x 单调增加,证明:当0x >时函数()f x x 单调增加.34. 证明:当0>x 时,x x x x<+<+)1ln(1. 35. 证明:当0x >时,有1x x x e xe <-<成立.第三章一、选择题:1.下列凑微分正确的一个是 ( ) A .)2(sin cos x d xdx = ; B. )11(arctan 2xd xdx += C .)1(ln x d xdx = D. )1(12x d dx x -=2.若⎰+=,)(c x dx x f 则⎰-dx x f )32(= ( )A .2-3x+c ; B. c x +-31; C. x+c ; D. c x +-2)32(213.在以下等式中,正确的一个是 ( ) A .⎰=')()(x f dx x f B. ⎰=')(])([x f dx x f C .⎰=)(])([x f dx x f d D. ⎰='')(])([x f dx x f 4. 设x x f 3sin )(=',则⎰dx x f )(是 ( )A .cos3x ; B. cos3x+c ; C.c x +-3cos 31; D.2193sin c x c x++- 5. 若,0(),0x x x f x e x ≥⎧=⎨<⎩,则21()d f x x -=⎰( ). A. 13e -- B. 13e -+ C. 3e - D. 3e + 6. 下列定积分是负数的是( )(A )dx x ⎰20sin π(B)dx x ⎰20cos π(C)dx x ⎰ππ2sin (D)dx x ⎰ππ2cos7. 若4)12(1=+⎰dx x a,则a = ( )(A) 3 (B) 2 (C) 0 (D) 48.若⎰∞-=31dx e kx ,则k=( ) (A)31 (B)-31(C) 3 (D)-3 9.=+⎰)1(212x dt t t dx d ( ) (A )x x+12(B) 212-+x x(C) 241x x + (D) 2512x x +10.若,21)(21)(0-=⎰x f dt t f x且1)0(=f ,则=)(x f ( ) (A)2x e (B)x e 21 (C)x e 2 (D)x e 221 二、填空题: 1.x d xdx 3(arcsin ________312=-).2.⎰=+________________912dx x .3.若⎰+=,3cos )(c x dx x f 则f (x )= .4. ⎰='____________________)()(22dx x f x xf . 5. F(x ) =dt t x ⎰+223,则=')1(F _________.6. 极限020cos d limxx t t x→⎰= ;7. 23423sin 1x e xdx x x -++⎰= 8.设()f x 连续,(0)1f =,则曲线0()d xy f x x =⎰在()0,0处的切线方程是 ;三、解答题:1、2x dx 2、⎰-+322x x dx3、⎰+dx x x214、422331.1x x dx x ⎛⎫++ ⎪+⎝⎭⎰ 5、cos 2.cos sin xdx x x -⎰6、dx x x ⎰-42 7、⎰-+211xdx8、⎰xdx x arctan 29、1x ⎰10、10d e ex xx-+⎰11、10x ⎰12、22()e d xx x x --+⎰;13.40d 1cos2xx xπ+⎰;14.41x ⎰;15.1d ln x x x+∞⎰16.2203sin d limx x t t x→⎰;17.求曲线xxe y e y -==,及直线1=x 所围成的平面图形的面积.18. 求由曲线)cos 2(2θ+=a r 所围图形的面积19. 由曲线2y x =和2x y =所围成的图形绕y 轴旋转后所得旋转体体积. 20. 计算曲线)3(31x x y -=上相应于31≤≤x 的一段弧的弧长大学数学A (1)复习题参考答案第一章一、选择题1、D2、A3、C4、B5、C6、B7、A8、C9、D二、填空题10、]3,0( 11、)1,1[- 12、x x21+ 13、)23(2353≠-+=x x x y 14、0 15、1 16、2 17、-1 18、e 19、0三、解答与证明题20(1)⎪⎪⎭⎫⎝⎛+⨯++⨯+⨯∞→)1(1321211lim n n n )1113121211(lim +-++-+-=∞→n n n 1)111(lim =+-=∞→n n . (2)2111211lim12lim )12(lim=+++=+++=+-+∞→∞→∞→nn n n n n n n n n n . (3)因为 1212222222+≤++++++≤+n n n n n n n n n n n n ,而 11lim lim 2222=+=+∞→∞→n n n n n n n , 所以121lim 222=⎪⎭⎫⎝⎛++++++∞→n n n n n n nn . (4)因为n nn n n nn n n nn 101010...101010...211010=+++<+++<=,110lim 10lim 1==∞→∞→nn nn ,故1010...21lim =+++∞→n n n n n .21(1)15723lim2323+++-∞→x x x x x 33115723lim x xx x x +++-=∞→53=.(2)331341lim 134lim 2222=++=++∞→∞→xx x x x x . (3)503020)12()23()32(lim ++-∞→x x x x 503020122332lim ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=∞→x x x x 503020)02()03()02(++-=3023⎪⎭⎫⎝⎛=. (4)11lim31--→x x x 1)1)(1(lim333231-++-=→x x x x x 3)1(lim 3321=++=→x x x .(5)12)42(lim 28lim2232=++=--→→x x x x x x . (6)112lim 131lim )1311(lim 2132131-=+++-=--++=---→→→xx x x x x x x x x x . (7))1(lim x x x -++∞→011lim=++=+∞→xx x .(8)11)1(lim ln )1(lim11=--=-→→x x x x x x x x .(9)0sin lim ln sin lnlim 00==→→xxx x x x . (10)x xx 3sin 2sin lim0→3232lim 32lim 00===→→x x x x . (11)30sin tan limx x x x -→30)cos 1(tan lim x x x x -⋅=→3202lim x x x x ⋅=→21=. (12)xx x 1)51(lim -→ xt 51-== tt t 511lim -∞→⎪⎭⎫ ⎝⎛+511lim -∞→⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=t t t 5-=e .22 解 由题意知 0)2(lim 23=+-→a x x x ,即06232=+⨯-a ,从而3-=a .23 解 因1→x 时, 012→-x , 而函数极限存在, 则)1(0→→++x b a x即 0lim 1=++→b a x x从而01=++b a (1)故原式=)1)(1)(1(1lim 11lim121a a x x x x x a a x x x ++++--=-+-+→→ aa a x x x +=++++=→141)1)(1(1lim1即41141=+a(2) 由(1)(2)解得1,0-==b a .24 解 (1)因为 a x a x f x x =+=++→→)(lim )(lim 0,1lim )(lim 0==--→→x x x e x f ,而 ,)0(a f = 故要使 )(lim 0x f x -→)(lim 0x f x +→=)0(f =,须且只须 1=a .所以当且仅当1=a 时,函数)(x f 在0=x 处连续.(2)因为 21111lim 11lim )(lim 00=++=-+=+++→→→x xx x f x x x , a x a x f x x cos )cos(lim )(lim 00=+=--→→,而 ,cos )0(a f = 故要使 )(lim 0x f x -→)(lim 0x f x +→=)0(f =, 须且只须 21cos =a ,即32ππ±=k a )(Z k ∈. 所以当且仅当32ππ±=k a )(Z k ∈时,函数)(x f 在0=x 处连续.25 证 (1)令14)(23+-=x x x f ,则)(x f 在[0,1]上连续, 且,02)1(,01)0(<-=>=f f由零点定理知,),1,0(∈∃ξ使,0)(=ξf 即01423=+-ξξ,所以方程01423=+-x x 在(0,1)内至少有一个根.(2)设x e x f x3)(-=,则)(x f 在]1,0[上连续,且03)1(,01)0(<-=>=e f f ,故由零点定理知方程在)1,0(内至少有一个根.第二章一、选择题1、C2、D3、A4、C5、C6、B7、A8、D9、B 10、D 二、填空题11、dx x x )2cos 2(2+ 12、21x -13、)415,21(- 14、1215、n x a a )(ln 16、(1,0) 17、)(20x f ' 18、1. 19、),31(+∞ 20、t tcos 1sin -.三、解答与证明题21、解:1-+='e x ex e y .22、解:(1)(sin cos )xy e x x '=+,(sin cos )(cos sin )2cos x x x y e x x e x x e x ''=++-=.(2) 2111111x y x x x '-⎛⎫'=⎪+⎝⎭-⎛⎫+ ⎪+⎝⎭()()2222(1)1(1)(1)(1)1x x x x x x -+--+=⋅+++- 22212(1)(1)x x --==++()1211y x -'⎡⎤''=-+⎢⎥⎣⎦()()22222121x x x x -=+⋅=+23、解:2121-='x y ,所以4121)4(421=='=-x x y , 所以切线方程为)4(412-=-x y ,法线方程为)4(42--=-x y . 24、解:(1)因为0)(lim 0=+→x f x ,0)(lim 0=-→x f x ,所以,0)(lim 0=→x f x .且0)0(=f ,因此,函数在0=x 处连续.10lim 0)0()(lim )0(00'=--=--=++→→+x x x f x f f x x ,10)1ln(lim 0)0()(lim )0(00'=--+=--=+-→→-x x x f x f f x x ,所以函数在0=x 处可导. (2)因为0)(lim 0=+→x f x ,0)(lim 0=-→x f x ,所以,0)(lim 0=→x f x .且0)0(=f ,因此,函数在0=x 处连续.01sin lim 001sinlim 0)0()(lim )0(0200'==--=--=+++→→→+xx x x x x f x f f x x x , 10tan lim 0)0()(lim )0(00'=--=--=--→→-x x x f x f f x x ,所以函数在0=x 处不可导.25、解:两边同时对x 求导得,11ln ()xy y x y e y xy x ''--=+,所以,1ln xyxy yye x y x xe--'=+. 26、解:(1)原式=)1ln()1ln(limx x x x x ++-→=20)1ln(lim xx x x +-→=xx x 2111lim 0+-→=)1(21lim 0x x +→=21.(2)30sin tan lim x x x x -→=30)1cos 1(sin lim xx x x -→=x x x x x cos )cos 1(sin lim 30⋅-→121lim 320⋅⋅=→x x x x =21. (3))arctan 2(lim x x x -+∞→πx x x 1)arctan 2(lim -=+∞→π22111limxx x -+-=+∞→11lim 22=+=+∞→x x x .(4)xx x +→0lim =xx xx x x eeln lim ln 00lim +→+=→,0ln lim 0=+→x x x ,所以原极限10=e .(5))1sin 1(lim 0x x x -→ x x x x x sin sin lim 0-=→20sin lim xx x x -=→x x x 2cos 1lim 0-=→2sin lim 0x x →=0=. (6)2sin lim x dt t x x ⎰→=x x x 2sin lim 0→=21.27、解:22111221dy dy t dt t dx t dx dt t -+===+, 22221()12241d dy d y t dt dx dx t dx t dt t +===+.28、解:函数定义域为),(+∞-∞.'()f x =,令'()0f x =,得驻点1=x ,1x =-为不可导点.由上表可以看出,函数在),1(),1,(+∞--∞上单调上升,函数在(1,1)-上单调下降;函数在1-=x 处取得极大值0)1(=-f ,在1=x 处取得极小值343)1(-=f , 29、解:函数定义域为),(+∞-∞.2363y x x '=-+,666(1)y x x ''=-=-, 令0y ''=,得x =1.当1x >时,0y ''>;当1x <时,0y ''<,所以函数的拐点为(1,3),在(-∞,1)上是凸的;在(1,+∞)上是凹的. 30、解:(1)b ax x y ++='232,a x y 26+=''.由条件,有⎩⎨⎧+=+++=ab a 2601413,解得9,3-=-=b a .(2)149323+--=x x x y ,函数定义域为),(+∞-∞.)3)(1(3963)(2-+=--='x x x x x f ,)1(666)(-=-=''x x x f .令0)(='x f ,得稳定点 11-=x ,32=x . 又012)1(<-=-''f ,012)3(>=''f故149323+--=x x x y 在点1-=x 处取极大值,极大值为19)1(=-f , 在点3=x 处取极小值,极小值为13)3(-=f .31. 解:122111x y x x--+==-+++()2121(1)y x '=-+,()()()312121y x ''=--+ ()()()41212(3)1y x '''=---+…… ()n y()()1121!1nn n x +=-+32. 证明:令x x f ln )(=, 则)(x f 在],[b a 上连续,在),(b a 内可导.所以由Lagrange 中值定理知,),(b a ∈∃ξ,使)()()(ξf ab a f b f '=--,即ξ1ln ln =--a b a b .又由),(b a ∈ξ,故22211ba ab +>>ξ.. 即222ln ln ba aa b a b +>--. 33. 证明:1)令()(0)f x F x x x=>()2'()()(2)'()xf x f x F x x-=2(0)0'()[()(0)]f xf x f x f x =-- 2'()'()(0)xf x xf x xξξ-<<微分中值定理 '()'()f x f xξ-=当0x >时,'()f x 单调增加 ∴'()'(),'()'()0f f x f x f ξξ<->即故有()'()0.(0,)f x F x x>+∞即在单调增加 34. 证明:令)1ln()(u u f +=,则)(u f 在],0[x 上满足Lagrange 中值定理条件,故),0(x ∈∃ξ,使)0)(()0()(-'=-x f f x f ξ,即)0(11)01ln()1ln(-+=+-+x x ξ,即ξ+=+1)1ln(x x . 又由),0(x ∈ξ,故x xx x <+<+ξ11,即x x xx <+<+)1ln(1. 35. 证明:令()[],0,t f t e t x =∈,()t f t e =在[]0,x 应用拉格朗日中值定理 ()00,0x e e e x x ξ-=-<ξ<x e 是单调增函数,0x e e e ξ∴<<,故有1xxx e xe <-<,0x > 证毕第三章一、选择题1-5 DCBDA 6-10 CBCDC 二、填空题 1.3 2. 11arctan 33x C + 3. -3sin3x 4. 221()+C 4f x5. -2 6. -1 7. 0 8.y x =三、解答题1. 572222=557x dx x dx dx x x C --=-+⎰⎰2.2111=23(3)(1)41311ln ||43dx dx dx dx x x x x x x x Cx ⎛⎫=- ⎪+-+--+⎝⎭-=++⎰⎰⎰⎰3. 22221(1)1=ln |1|+C 1212x d x dx x x x +=+++⎰⎰ 4. 42232233113arctan .11x x dx x dx x x C x x ⎛⎫++⎛⎫=+=++ ⎪ ⎪++⎝⎭⎝⎭⎰⎰5.22cos 2cos sin (cos sin )sin cos .cos sin cos sin x x x dx dx x x dx x x C x x x x-==+=-+--⎰⎰⎰ 6.dx x x ⎰-42=c xx +--)2arccos 24(tan 227.⎰-+211xdx =cxx x +-+-211arcsin8.⎰xdx x arctan 2=c x x x x +++-)1ln(6161arctan 312239.令t x tan =,则1x ⎰=3344111cos d ln sin 21cos t t t t ππππ-=+⎰=10. 10d e e x x x -+⎰=112200e 1d de e 1e 1x x x x x =++⎰⎰1arctan(e )arctan e 4xπ==-11.10x ⎰=102⎰2121216π===⎰12. 22()e d xx x x --+⎰=22220002e d 2de 2e2e d xxx x x x x x x ----=-=-+⎰⎰⎰262e =-13.40d 1cos2x x x π+⎰=442001d d tan 2cos 2x x x x x ππ=⎰⎰ 444000111ln 2tan tan d lncos 228284x x x x x πππππ=-=+=-⎰14. 41x⎰412ln x =⎰4112x x ⎤=-⎥⎦⎰124ln 2x ⎡⎤=-⎢⎥⎣⎦⎰ 14218ln 22d x x -=-⎰8ln24=-15. ee 11d d(ln )ln(ln )ln ln e x x x x xx +∞+∞+∞===+∞⎰⎰ 16. 22220322000sin d 2sin 22(2)8=333lim lim lim x x x x t t x x x x x →→→==⎰17.如图所示,解方程组xxy e y e -⎧=⎨=⎩,得交点(0,1),所求面积为11100()d []2x x x x A e e x e e e e---=-=+=+-⎰18.解:∵1D :⎩⎨⎧+<<<<)cos 2(200θπθa r∴12220141122[2(2cos3)]4[4(sin 3sin 6)1823212D D S S a d a a ππθθπθθθπ==+=+++=⎰19. 思路: 该平面图形绕y 轴旋转而成体积V 可看作1D :⎩⎨⎧≤≤≤≤yx y 010绕y 轴旋转而成的体积1V ,减去2D :⎩⎨⎧≤≤≤≤2010y x y 绕y 轴旋转而成的立体体积2V 所得,见图解: πππ103)()(102221021=-=-=⎰⎰dy y dy y V V V20.解:12y '==, ∴3432322(21)214)1(113123313122-=+=+=-+='+=⎰⎰⎰x x dx x x dx x x dx y s ba。
《高等数学(一)》期末考试试卷(A卷)

《高等数学(一)》期末考试试卷(A 卷)适用班级:一、填空题(每空2分,共20分)函数211x y x -=-的连续区间是 ,1x =是 间断点.设()f x 在(),-∞+∞上连续,且()13f =,则()01lim ln 1x f x x →⎡⎤+=⎢⎥⎣⎦.函数1xy e =当x → 时为无穷大量,当x → 时为无穷小量. 若()12f '=,则极限()()11limh f h f h→--= .5.函数22ln y x x =-的极小值为 .若()()f x dx F x C =+⎰,则()sin cos f d θθθ=⎰.已知()f x 的一个原函数是ln x ,则()=f x .= .二、单项选择题(每小题3分,共30分) 1.下列函数对中不为同一个函数的是( ).A.x x x f ⋅=)(,3)(x x g =B.x e x f ln )(=,x x g =)(C.()0()1f x x =-,22()sin cos g x x x =+ D. x x f ln 3)(=,3ln )(x x g = 2.下列等式正确的是 ( ) A. sin lim1x x x →∞= B. 0sin lim 1x xx→=C. 01lim sin 1x x x →=D. 1lim sin 0x x x→∞=3. 下列叙述正确的是( )A. 若函数()y f x =在点x 处可导,则函数()y f x =在点x 处必连续.B. 若函数()y f x =在点x 处连续,则函数()y f x =在点x 处必可导.C. 若函数()y f x =在点x 处不可导,则函数()y f x =在点x 处不连续.D. 若曲线()y f x =在点x 处有切线,则函数()y f x =在点x 处必可导. 4. 当0x →时,无穷小量2sin x x -是x 的( ) A. 高阶无穷小 B. 低阶无穷小 C. 同阶无穷小但不是等价无穷小 D. 等价无穷小 5. 0x =是sgn x 的( ).A. 连续点B. 可去间断点C. 无穷间断点D. 跳跃间断点 6.下列等式成立的是( )A. d=B. ()()cos cos d d cos x x e e x =C. ()22d d ln 11xx x ⎡⎤-=⎣⎦- D. ()d +1d x x x = 7.下列结论正确的是( )A. 驻点一定是极值点B. 极大值一定大于极小值C. 可导函数的极值点一定是驻点D. 二阶导数等于零的点一定不是极值点8. d x e x -=⎰( )A. x e -B. x e C -+C. x e --D. x e C --+9. ln d 2xx =⎰( )A. ln 2x x x C -+B. ln 42xx x C -+C. ln 22x x x C -+D. ln 2xx x C ++10. 已知()()F x f x '=,则下列等式正确的是( ) A.()()d f x dx f x dx dx ⎡⎤=⎣⎦⎰ B. ()()d F x dx f x dx ⎡⎤=⎣⎦⎰C. ()()f x dx F x C '=+⎰D. ()()f x dx F x C =+⎰三、解答题(每小题7分,共42分) 1.计算011lim 1x x x e →⎛⎫- ⎪-⎝⎭. 2. 计算()()2ln 1lim ln 1x x x →+∞++3. 设)4ln(2x x y -+=,求d y .4. 计算34cos d sin x x x⎰.5.计算x . 6. 计算3d x xe x ⎰.四、讨论题(8分)求()213sin cos ,00,0x x x f x xx ⎧+≠⎪=⎨⎪=⎩的导函数()f x '.。
高数a大一期末考试题简单及答案

高数a大一期末考试题简单及答案一、选择题(每题4分,共40分)1. 极限的定义中,如果对于任意的正数ε,存在正数δ,使得当0<|x-a|<δ时,有|f(x)-L|<ε,则称函数f(x)当x趋近于a时的极限为L。
以下哪个选项不是极限的定义?A. 函数f(x)在某点a处的极限B. 函数f(x)在某点a的左极限C. 函数f(x)在某点a的右极限D. 函数f(x)在某点a处的连续性答案:D2. 以下哪个函数是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = |x|答案:B3. 以下哪个函数是偶函数?A. f(x) = x^3B. f(x) = x^2C. f(x) = x^4D. f(x) = |x|答案:B4. 以下哪个函数在x=0处不可导?A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = x^4答案:B5. 以下哪个选项是正确的不定积分?A. ∫x dx = x^2 + CB. ∫x^2 dx = x^3 + CC. ∫1/x dx = ln|x| + CD. ∫e^x dx = e^x + C答案:C6. 以下哪个选项是正确的定积分?A. ∫[0,1] x dx = 1/2B. ∫[0,1] x^2 dx = 1/3C. ∫[0,1] x^3 dx = 1/4D. ∫[0,1] x^4 dx = 1/5答案:B7. 以下哪个选项是正确的微分方程的通解?A. y' = 2y => y = Ce^(2x)B. y' = 3y => y = Ce^(3x)C. y' = 4y => y = Ce^(4x)D. y' = 5y => y = Ce^(5x)答案:A8. 以下哪个选项是正确的二阶导数?A. y = x^3, y'' = 6xB. y = x^2, y'' = 2C. y = x^4, y'' = 12x^2D. y = x^5, y'' = 20x^3答案:B9. 以下哪个选项是正确的洛必达法则的应用?A. ∫0/0 型不定式,分子分母同时乘以分母的导数B. ∫∞/∞ 型不定式,分子分母同时乘以分子的导数C. ∫0/0 型不定式,分子分母同时除以分子的导数D. ∫∞/∞ 型不定式,分子分母同时除以分母的导数答案:D10. 以下哪个选项是正确的泰勒级数展开?A. e^x = 1 + x + x^2/2! + x^3/3! + ...B. sin(x) = x - x^3/3! + x^5/5! - ...C. cos(x) = 1 - x^2/2! + x^4/4! - ...D. ln(1+x) = x - x^2/2 + x^3/3 - ...答案:A二、填空题(每题4分,共20分)11. 函数f(x) = x^2 + 3x + 2的导数是________。
高数必不挂-高等数学A(一)2010-2011(A)解答

第 1 页 共 6 页上 海 海 事 大 学 试 卷2010 — 2011 学年第一学期期末考试 《 高等数学A (一)》(A 卷)解答一、单项选择题(在每个小题四个备选答案中选出一个正确答案,填在题末的括号中) (本大题分3小题, 每小题4分, 共12分).)( ;)(;2)( ; 0)(2coslim 120不存在,但不是无穷大为无穷大 等于 等于)(的值为、D C ••B A •••A••••••••••••••••xx x +→个不同的实根 有 有三个不同的实根 有唯一实根 无实根 )(则方程适合、设5)()()()(0432,,53,,2352D C •••B A ••••B•••••c bx ax x b a b a =+++< 为正常数 恒为零 为负常数 不为常数 )(则、设)()()()()(,)(32sin D C •••B A •••D•••••••••••x F dt e x F •x •xt ⎰+=π二、填空题(将正确答案填在横线上)(本大题分2小题, 每小题4分, 共8分)1、的值为201lim x x e x x --→ 212、设a b c ,,均为非零向量,满足c b a a c b b a c ⨯=⨯=⨯=,,,b ++三 计算题(必须有解题过程,否则不给分) (本大题分10小题,每题6分,共 60分)1、极限xx xx 2)4(lim +∞→ 884)41(lim e xxx =+=⋅∞→原式 6分2、)0(,)cos()(y y xy e x y y xy '=+=求确定由方程设--------------------------------------------------------------------------------------装 订线第 2 页 共 6 页解:y xy y x y y x y e xy '='+-'+)sin()()(, 4分2)0(,2.,0='==y y x 时当 6分3、.求dx xx••⎰--1145 解:令 ,541452-==-x t x t () 1分 原式=-⎰185213()t dt4分 =166分 4、.d )1(arctan x x x x⎰+求解:x x x xd )1(arctan ⎰+)d(arctan arctan 2x x ⎰= 3分C x +=2)(arctan 6分(遗留C 扣1分)5、.点处的连续性和可导性在试讨论,,已知 0)( , 00cos )(20=⎪⎩⎪⎨⎧≤>=⎰x x f x •••x x tdt t x f •x •解:0)0(0lim )(lim )0(0cos lim )0(200====-==+--+→→→⎰f x x f f tdt t f x x xx 又 2分∴= 在点处连续f x x ()0 3分lim )0()(lim )0(0)cos (lim cos lim )0()(lim )0(200000==-='===-='--+++→→-→→→+⎰x x xf x f f x x xtdt t xf x f f x x x xx x 5分第 3 页 共 6 页'==f f x x ()()000,在点处可导. 6分.,试求: 斜率等于处的切线,且它在原点通过原点具有连续导数,又曲线、设函数xx dtt f •••x f y x f •x•x sin )(lim100)()(60⎰→=解:,,由题意知,1)0(0)0(='=f f 2分lim()sin lim ()sin cos x xx f t dt x x f x x x x→→⎰=+000 4分='-→lim()cos sin x f x x x x 02 5分='=12012f () 6分7、)为驻点,,使得点(中的试确定442,,,,23-+++=d c b a d cx bx ax y(1,—10)为拐点。
高等数学期末考试试题及答案(大一考试)

高等数学期末考试试题及答案(大一考试)姓名:__________ 班级:__________ 学号:__________课程名称:高等数学(上)(A卷) 考试日期:2008年1月10日注意事项:1.本试卷满分100分,要求卷面整洁、字迹工整、无错别字。
2.考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方,否则视为废卷。
3.考生必须在签到单上签到,若出现遗漏,后果自负。
4.如有答题纸,请将答案全部写在答题纸上,否则不给分。
考完请将试卷和答题卷分别一同交回,否则不给分。
一、单选题(每题3分,共15分)1.lim(sin(x^2-1)/(x-1)),x趋近于1,等于()A)1;(B)0;(C)2;(D)不存在。
2.若f(x)的一个原函数为F(x),则∫e^(-x)f(e^x)dx等于()A)F(e^x)+c;(B)-F(e^-x)+c;(C)F(e^-x)+c;(D)F(e^-x^2/2)+c。
3.下列广义积分中()是收敛的。
A)∫sinxdx,从负无穷到正无穷;(B)∫1/|x|dx,从-1到1;(C)∫x/(1+x^2)dx,从负无穷到正无穷;(D)∫e^x dx,从负无穷到0.4.f(x)为定义在[a,b]上的函数,则下列结论错误的是()A)f(x)可导,则f(x)一定连续;(B)f(x)可微,则f(x)不一定可导;(C)f(x)可积(常义),则f(x)一定有界;(D)函数f(x)连续,则∫f(x)dx在[a,b]上一定有定义。
5.设函数f(x)=lim(n→∞)(1+x^2n)^2,则下列结论正确的是()A)不存在间断点;(B)存在间断点x=1;(C)存在间断点x=0;(D)存在间断点x=-1.二、填空题(每题3分,共18分)1.极限lim(x→∞)(x^2+1-1)/x=______。
2.曲线y=3t在t=2处的切线方程为y=______。
3.已知方程y''-5y'+6y=xe^(2x)的一个特解为-1/2(x+2x)e^(2x),则该方程的通解为______。
1112高等数学A(一)试题解答

等价无穷小, a ___ . 则
知识点:无穷小的比较,等价无穷小性质, 无穷小替换定理.
1 2
1 2 解 当x 0时,-cos x x ,ax sin x ax 2 1 2 1 2 x 1- cos x 1 1 2 lim lim 2 1 a . x 0 ax sin x x 0 ax 2 2a
6
方法2 利用求导公式. 令g( x) ( x 1)( x 2)( x 3), 则y( x ) xg( x )
f ( x ) ( x) g( x) xg( x ) g( x) xg( x ) f (0) g(0) 0 ( 1) ( 2)( 3) 6
2. 设是可微函数,则df (cos2 x)=
D .
( A) 2 f (cos2 x)dx; ( B) 2 f (cos2 x)sin2 xd 2 x; (C ) 2 f (cos2 x)sin2 xdx; ( D) 2 f (cos2 x)sin2 xdx.
知识点:函数的微分,复合函数的微分法则.
四、应用:
1.证明不等式 : 利用lagrange定理.单调性凹凸性及最值等证法 . ; 2.研究方程根的问题 : 利用Rolle定理.单调性及介值定理等 ; 3.实际应用中的最值问题 (求驻点等) .
CH4-6 一元函数积分学
定义、性质(定)、意义、常用恒等式 一、基本概念: 二、计算:
基 本 积 分 公 式 凑微分 1.不 定 积 分 三 角 代 换 (注意结果中的常数C) 分部积分
( A) (C )
+
1 1
0
《高等数学(一)》期末复习题(答案)

《高等数学(一)》期末复习题一、选择题1. 极限)x x →∞的结果是 ( C ).(A )0 (B ) ∞ (C ) 12(D )不存在 2. 设()xxx f +-=11ln,则)(x f 是 ( A ). (A )奇函数 (B) 偶函数 (C )非奇非偶函数 (D )既奇又偶函数 3. 极限21lim sinx x x→= ( A ) . (A )0 (B) 1 (C )+∞ (D )-∞ 4. 方程3310x x -+=在区间(0,1)内( B ).(A )无实根 (B )有唯一实根 (C )有两个实根 (D )有三个实根 5. 设()()ln 1f x x =+,g (x )=x ,则当0x →时,()f x 是()g x 的( A ).(A )等价无穷小 (B) 低阶无穷小(C )高阶无穷小 (D) 同阶但非等价无穷小 6. 下列变量中,是无穷小量的为( A ).(A ))1(ln →x x (B ))0(1ln +→x x (C )cos (0)x x → (D ))2(422→--x x x 7. 极限011lim(sinsin )x x x x x→- 的结果是( C ).(A )0 (B ) 1 (C ) 1- (D )不存在8. 下列函数中满足罗尔定理条件的是( D ).(A )()2,[0,1]f x x x =-∈ (B) 3(),[0,1]f x x x =∈ (C )(),[1,1]f x x x =∈- (D)4(),[1,1]f x x x =∈-9. 函数1cos sin ++=x x y 是( C ).(A )奇函数 (B )偶函数 (C )非奇非偶函数 (D )既是奇函数又是偶函数 10. 当0→x 时, 下列是无穷小量的是( B ).(A )1+x e (B) )1ln(+x (C) )1sin(+x (D) 1+x11. 当x →∞时,下列函数中有极限的是( A ).(A )211x x +- (B) cos x (C) 1xe(D)arctan x 12. 方程310(0)x px p ++=>的实根个数是 ( B ).(A )零个 (B )一个 (C )二个 (D )三个 13.21()1dx x '=+⎰( B ).(A )211x + (B )211C x++ (C ) arctan x (D ) arctan x c + 14. 定积分()f x dx ⎰是( A ).(A )一个函数族 (B )()f x 的的一个原函数 (C )一个常数 (D )一个非负常数15.函数(ln y x =+是( A ).(A )奇函数 (B )偶函数 (C ) 非奇非偶函数 (D )既是奇函数又是偶函数 16. 设函数在区间上连续,在开区间内可导,且,则( B ).(A) (B) (C) (D) 17. 设曲线221x y e-=-,则下列选项成立的是( C ). (A) 没有渐近线 (B) 仅有铅直渐近线 (C) 既有水平渐近线又有铅直渐近线 (D) 仅有水平渐近线 18. 设是的一个原函数,则等式( D )成立.(A )(B) (C ) (D)19. 设⎰+=C x dx x xf arcsin )(,则⎰=dx x f )(1( B ). (A )C x +--32)1(43 (B )C x +--32)1(31 (C )C x +-322)1(43 (D )C x +-322)1(32()f x []0,1()0,1()0f x '>()00f <()()10f f >()10f >()()10f f <F x ()f x ()dd d x f x x F x (())()⎰='=+⎰F x x f x c()()d '=⎰F x x F x ()()d dd d xf x x f x (())()⎰=20. 数列})1({nn n-+的极限为( A ).(A )1(B) 1-(C) 0(D) 不存在21. 下列命题中正确的是( B ).(A )有界量和无穷大量的乘积仍为无穷大量(B )有界量和无穷小量的乘积仍为无穷小量 (C )两无穷大量的和仍为无穷大量 (D )两无穷大量的差为零 22. 若()()f x g x ''=,则下列式子一定成立的有( C ).(A)()()f x g x = (B)()()df x dg x =⎰⎰(C)(())(())df x dg x ''=⎰⎰(D)()()1f x g x =+ 23. 下列曲线有斜渐近线的是 ( C ).(A)sin y x x =+ (B)2sin y x x =+ (C)1siny x x =+ (D)21sin y x x=+ 24. 函数)1,0(11)(≠>+-=a a a a x x f x x ( B ).(A )是奇函数 (B )是偶函数(C )既奇函数又是偶函数 (D )是非奇非偶函数 25. 下列函数中满足罗尔定理条件的是( D ).(A )]1,0[,1)(∈-=x x x f (B)]1,0[,)(2∈=x x x f (C )()sin ,[1,1]f x x x =∈- (D)]1,1[,)(2-∈=x x x f26. 若函数221)1(xx x x f +=+,则=)(x f ( B ). (A )2x (B )22-x (C )2)1(-x (D )12-x 27. 设函数,ln )(x x x f =则下面关于)(x f 的说法正确的是( A ).(A )在(0,e 1)内单调递减 (B)在(+∞,1e)内单调递减 (C )在(0,+∞)内单调递减 (D)(0,+∞)在内单调递增28. 设1)(+=x x f ,则)1)((+x f f =( D ).(A )x (B )x + 1 (C )x + 2 (D )x + 329. 已知0)1(lim 2=--+∞→b ax x x x ,其中a ,b 是常数,则( C ).(A )1,1==b a , (B )1,1=-=b a (C )1,1-==b a (D )1,1-=-=b a 30. 下列函数在指定的变化过程中,( B )是无穷小量.(A ) (B )(C ) (D )31. 设函数(),2x xe ef x -+=则下面关于)(x f 的说法正确的是( B ) .(A )在(0,)+∞内单调递减 (B)在(,0)-∞内单调递减 (C )在(,0)-∞内单调递增 (D)在(,)-∞+∞内单调递增32. 下列函数中,在给定趋势下是无界变量且为无穷大的函数是( C ).(A ))(1sin∞→=x xx y (B )())(1∞→=-n n y n (C ))0(ln +→=x x y (D ))0(1cos 1→=x xx y33. 设⎪⎩⎪⎨⎧≤>=0,0,1sin )(x x x xx x f ,则)(x f 在0=x 处( B ). (A )连续且可导(B )连续但不可导 (C )不连续但可导(D )既不连续又不可导34. 在下列等式中,正确的是( C ).(A )()()f x dx f x '=⎰ (B) ()()df x f x =⎰(C )()()df x dx f x dx=⎰ (D)[()]()d f x dx f x =⎰ 35. 曲线x x y -=3在点(1,0)处的切线是( A ).(A )22-=x y(B )22+-=x ye 1xx ,()→∞sin ,()xxx →∞ln(),()11+→x x x xx +-→110,()(C )22+=x y(D )22--=x y36. 已知441x y =,则y ''=( B ). (A ) 3x (B )23x (C )x 6 (D ) 6 37. 若x xf =)1(,则=')(x f ( D ).(A )x 1 (B )21x (C )x 1- (D )21x-38. 下列各组函数中,是相同的函数的是( B ).(A )()()2ln 2ln f x x g x x == 和 (B )()||f x x = 和 ()g x =(C )()f x x = 和 ()2g x =(D )()||x f x x=和 ()g x =1 39. 函数()()20ln 10x f x x a x ≠=+⎨⎪=⎩ 在0x =处连续,则a =( B ).(A )0 (B )14(C )1 (D )240. 曲线ln y x x =的平行于直线10x y -+=的切线方程为( A ).(A )1y x =- (B )(1)y x =-+ (C )()()ln 11y x x =-- (D )y x = 41. 设函数()||f x x =,则函数在点0x =处( C ).(A )连续且可导 (B )连续且可微 (C )连续不可导 (D )不连续不可微 42. 设()f x 可微,则0()(2)limh f x f x h h→--=( D ).(A )()f x '- (B)1()2f x ' (C )2()f x '- (D)2()f x '43. 点0x =是函数4y x =的( D ).(A )驻点但非极值点 (B )拐点 (C )驻点且是拐点 (D )驻点且是极值点 44. 曲线1||y x =的渐近线情况是( C ). (A )只有水平渐近线 (B )只有垂直渐近线(C )既有水平渐近线又有垂直渐近线 (D )既无水平渐近线又无垂直渐近线45.211f dx x x⎛⎫' ⎪⎝⎭⎰的结果是( D ). (A )1f C x ⎛⎫-+ ⎪⎝⎭(B )1f C x ⎛⎫--+ ⎪⎝⎭(C )1f C x ⎛⎫+ ⎪⎝⎭(D )1f C x ⎛⎫-+ ⎪⎝⎭46.x x dxe e -+⎰的结果是( A ).(A )arctan x e C + (B )arctan x e C -+ (C )x x e e C --+ (D )ln()x x e e C -++47. 下列各组函数中,是相同函数的是( C ).(A) ()f x x =和()g x =()211x f x x -=-和1y x =+(C) ()f x x =和()22(sin cos )g x x x x =+ (D) ()2ln f x x =和()2ln g x x =48. 设函数()()2sin 21112111x x x f x x x x -⎧<⎪-⎪⎪==⎨⎪->⎪⎪⎩,则()1lim x f x →=( D ).(A) 0 (B) 1 (C) 2 (D)不存在49. 设函数22456x y x x -=-+,则2x =是函数的( A ).(A) 可去间断点 (B) 跳跃间断点 (C) 无穷间断点 (D) 振荡间断点 50. 设函数()y f x =在点0x 处可导,且()f x '>0, 曲线则()y f x =在点()()00,x f x 处的切线的倾斜角为( C ). (A) 0 (B)2π(C)锐角 (D)钝角 51. 曲线ln y x =上某点的切线平行于直线23y x =-,则该点坐标是( D ).(A) 12,ln2⎛⎫ ⎪⎝⎭ (B) 12,ln 2⎛⎫- ⎪⎝⎭ (C) 1,ln 22⎛⎫ ⎪⎝⎭ (D) 1,ln 22⎛⎫- ⎪⎝⎭52. 函数2x y x e -=及图象在()1,2内是( B ).(A)单调减少且是凸的 (B)单调增加且是凸的 (C)单调减少且是凹的 (D)单调增加且是凹的 53. 以下结论正确的是( C ).(A) 若0x 为函数()y f x =的驻点,则0x 必为函数()y f x =的极值点. (B) 函数()y f x =导数不存在的点,一定不是函数()y f x =的极值点. (C) 若函数()y f x =在0x 处取得极值,且()0f x '存在,则必有()0f x '=0. (D) 若函数()y f x =在0x 处连续,则()0f x '一定存在.54. 设函数22132x y x x -=-+,则1x =是函数的( A ).(A )可去间断点 (B) 跳跃间断点 (C) 无穷间断点 (D) 振荡间断点 55. 设函数()y f x =的一个原函数为12x x e ,则()f x =( A ).(A) ()121x x e - (B)12xx e - (C) ()121x x e + (D) 12xxe56. 若()()f x dx F x c =+⎰,则()sin cos xf x dx =⎰( D ).(A) ()sin F x c + (B) ()sin F x c -+ (C) ()cos F x c + (D) ()cos F x c -+57. 函数21,0e ,0xx x y x ⎧+<=⎨≥⎩在点0x =处( D ).(A )连续且可导 (B) 不连续且不可导 (C) 不连续但可导 (D) 连续但不可导 58. 函数 2)1ln(++-=x x y 的定义域是( C ).(A ) []1,2- (B ) [)1,2- (C )(]1,2- (D )()1,2- 59. 极限x x e ∞→lim 的值是( D ).(A )∞+ (B ) 0 (C )∞- (D )不存在 60. =--→211)1sin(limx x x ( C ).(A )1 (B ) 0 (C )21-(D )2161. 曲线 23-+=x x y 在点)0,1(处的切线方程是( B ).(A ) )1(2-=x y (B ))1(4-=x y (C )14-=x y (D ))1(3-=x y62. 函数, 0,0xx x y e x <⎧=⎨≥⎩在点0x =处( B ). (A )连续且可导 (B) 不连续且不可导 (C) 不连续但可导 (D) 连续但不可导 63. 下列各微分式正确的是( C ).(A ))(2x d xdx = (B ))2(sin 2cos x d xdx = (C ))5(x d dx --= (D )22)()(dx x d = 64. 设⎰+=C xdx x f 2cos 2)( ,则 =)(x f ( B ). (A )2sin x (B ) 2sin x - (C )C x +2sin (D )2sin 2x-65. 设()f x 可微,则0(2)()limh f x h f x h→+-=( D ).(A )()f x '- (B)1()2f x ' (C)2()f x '- (D)2()f x ' 66.⎰=+dx x xln 2( B ).(A )Cx x ++-22ln 212 (B )C x ++2)ln 2(21(C )C x ++ln 2ln (D )C xx++-2ln 1 67. 函数)1lg(12+++=x x y 的定义域是( B ).(A )()()+∞--,01,2 (B )()),0(0,1+∞- (C )),0()0,1(+∞- (D )),1(+∞-68. 设0tan 4()lim6sin x x f x x →+=,则0()lim x f x x→=( B ) .(A )1 (B )2 (C )6 (D )24 69. 下列各式中,极限存在的是( A ).(A ) x x cos lim 0→ (B )x x arctan lim ∞→ (C )x x sin lim ∞→ (D )x x 2lim +∞→70. =+∞→xx xx )1(lim ( D ). (A )e (B )2e (C )1 (D )e1 71. 设0sin 4()lim5sin x x f x x →+=,则0()lim x f x x→=( B ) .(A )0 (B )1 (C )5 (D )2572. 曲线x x y ln =的平行于直线01=+-y x 的切线方程是( C ).(A )x y = (B ))1)(1(ln --=x x y (C )1-=x y (D ))1(+-=x y73. 已知x x y 3sin = ,则=dy ( B ).(A )dx x x )3sin 33cos (+- (B )dx x x x )3cos 33(sin + (C )dx x x )3sin 3(cos + (D )dx x x x )3cos 3(sin + 74. 下列等式成立的是( C ).(A )⎰++=-C x dx x 111ααα (B )⎰+=C x a dx a x x ln (C )⎰+=C x xdx sin cos (D )⎰++=C xxdx 211tan 75. 极限01lim sinx x x→= ( A ) . (A ) 0 (B) 1 (C )+∞ (D) -∞ 76. 设()1cos f x x =-,()2g x x =,则当0x →时,()f x 是()g x 的( D ).(A )等价无穷小 (B) 低阶无穷小 (C ) 高阶无穷小 (D) 同阶但非等价无穷小 77. 计算⎰xdx x e x cos sin sin 的结果中正确的是( D ).(A )C e x +sin (B )C x e x +cos sin (C )C x e x +sin sin (D )C x e x +-)1(sin sin78. 5lg 1)(-=x x f 的定义域是( D ).(A )()),5(5,+∞∞- (B )()),6(6,+∞∞-(C )()),4(4,+∞∞- (D )())5,4(4, ∞- ()),6(6,5+∞79. 如果函数f (x )的定义域为[1,2],则函数f (x )+f (x 2)的定义域是( B ).(A )[1,2] (B )[1,2] (C )]2,2[- (D )]2,1[]1,2[ --80. 函数)1lg()1lg(22x x x x y -++++=( D ).(A )是奇函数,非偶函数 (B )是偶函数,非奇函数 (C )既非奇函数,又非偶函数 (D )既是奇函数,又是偶函数 81. 设()sin f x x x =,则)(x f 是( C ).(A )非奇非偶函数 (B) 奇函数 (C)偶函数 (D) 既奇又偶函数 82. 函数)10(1)(2≤≤--=x x x f 的反函数=-)(1x f( C ).(A )21x - (B )21x --(C ))01(12≤≤--x x (D ))01(12≤≤---x x 83. 下列数列收敛的是( C ).(A )1)1()(1+-=+n n n f n (B )⎪⎩⎪⎨⎧-+=为偶数为奇数n nn n n f ,11,11)((C )⎪⎩⎪⎨⎧+=为偶数为奇数n n n n n f ,11,1)( (D )⎪⎪⎩⎪⎪⎨⎧-+=为偶数为奇数n n n f nn n n ,221,221)(84. 设1111.0个n n y =,则当∞→n 时,该数列( C ).(A )收敛于0.1 (B )收敛于0.2 (C )收敛于91(D )发散 85. 下列极限存在的是( A ).(A )2)1(lim x x x x +∞→ (B )121lim -∞→x x (C )x x e 10lim → (D )x x x 1lim 2++∞→ 86. xx xx x x sin 2sin 2lim 22+-+∞→=( A ).(A )21(B )2 (C )0 (D )不存在 87. =--→1)1sin(lim 21x x x ( B ).(A )1 (B )2 (C )21(D )0 88. 下列极限中结果等于e 的是( B ).(A )xx x x x sin 0)sin 1(lim +→ (B )x xx x x sin )sin 1(lim +∞→ (C )xxx xxsin )sin 1(lim -∞→- (D )xxx xxsin 0)sin 1(lim +→89. 函数||ln 1x y =的间断点有( C )个. (A )1 (B )2 (C )3 (D )4 90. 下列结论错误的是( A ).(A )如果函数f (x )在点x =x 0处连续,则f (x )在点x =x 0处可导; (B )如果函数f (x )在点x =x 0处不连续,则f (x )在点x =x 0处不可导; (C )如果函数f (x )在点x =x 0处可导,则f (x )在点x =x 0处连续; (D )如果函数f (x )在点x =x 0处不可导,则f (x )在点x =x 0处也可能连续。
人教A版高一数学上学期期末测试卷(带答案)

高一数学本卷共三大题,时量120分钟,满分120分,试卷总页4页一.选择题:(本大题共10个小题,每小题4分,共40分,每小题都有四个不同的答案,其中只有一个是正确的,请把正确的答案选出来) 1.函数f(x)=x x ln 1+-的定义域为( )A.]1,(-∞B.(0,+∞)C.(0,1]D.(0,1)),1(+∞⋃2.下列函数中,既是奇函数,又是增函数的是( )A . y=-2xB . x y 2= C. x y lg = D . 3x y = 3. 已知空间直角坐标系中一点A(-3,1,-4),则点A 关于x 轴对称点的坐标为( )A .(-3,-1,4) B.(-3,-1,-4) C.(3,1,4) D.(3,-1,-4) 4.函数()3log 82f x x x =-+的零点一定位于区间( ) A. ()5,6 B. ()3,4 C. ()2,3 D. ()1,2 5.下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是( )A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)6.半径为R 的球的内接正方体的表面积是( )A.234R B.22R C.24R D.28R7.已知,αβ,γ是三个不同的平面, m,n 是两条不同的直线 ,下列命题中正确..的是( ) A.若m//α,n//α,则m//n B. 若m//α,m//β,则α//β C.若γα⊥,γβ⊥则α//βD .若α⊥β,m ⊥β,m ⊄α,则m ∥α8、若0,0ac bc <<,则直线0ax by c ++=不经过( ) A .第一象限 B.第二象限 C.第三象限 D.第四象限 9、若直线L :ax+by=1与圆C :122=+y x 相切,则点P (a,b)与圆C 的位置关系是 ( )A.在圆上B.在圆外C.在圆内D.以上皆有可能 10、如图,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为( )A.3B.5C.5D.5二.填空题(本大题共5个小题,每小题4分,共20分) 11.圆心在(2,-1)且与y 轴相切的圆的标准方程为 。
大学高等数学期末考试题A卷(答案)

广东海洋大学2006 —— 2007 学年第 二学期《高等数学》试题答案(A 卷)一、填空题。
(每小题3分,共24分) 1.曲线2x y =与直线xy 2= 所围成的平面图形面积为A= 34;2.设向量{}2,3,1-=a,{}2,2,1-=b,则a·b= -3 ;3. 函数221yx z--=的定义域为 }1),({22≤+y x y x ;4.过点(3, 0, -1)且与平面3x -7y +5z -12=0平行的平面方程为: 3x -7y +5z -4=0 ;5.设函数x y Z cos =,则yx Z ∂∂∂2= -sinx ;6.改变累次积分I=⎰⎰102),(xx dy y x f dx 的次序为I = ⎰⎰10),(X yy d y x f dy ;7. 设曲线方程为⎩⎨⎧=+-=++0380422222z y x z y x ,该曲线在Oxy 面上的投影方程为: ⎩⎨⎧==+0042z y x .8. 写出函数x x f sin )(=的幂级数展开式,并注明收敛域:x sin = )(,)!12()1(!5!312153R x n xxxx n n ∈+--+-+---二、选择题。
(每小题3分,共15分)1.函数z f x y =(,)在点(,)x y 00处连续是它在该点偏导数存在的( D )(A)必要而非充分条件 (B)充分而非必要条件(C)充分必要条件 (D)既非充分又非必要条件 2.下列方程中,通解为12e e x x y C C x =+的微分方程是( A ). (A) 02=+'-''y y y (B) ''+'+=y y y 21; (C) '+=y y 0 (D) '=y y . 3. 设函数),(v x f Z=,),(y x v ϕ=,其中ϕ,f 都有一阶连续偏导数,则xZ ∂∂等于( B )班级:姓名:学号:试题共 页加白纸张密封线(A)xf ∂∂ ;(B)vf xf ∂∂+∂∂·x∂∂ϕ ; (C)xxf ∂∂+∂∂ϕ ; (D)xf ∂∂·x∂∂ϕ4.设函数),(y x f Z=在点(1,2)处有)2,1(='x f ,)2,1(='y f ,且1)2,1(="xx f ,0)2,1(="xy f ,2)2,1(="yy f ,则下列结论正确的是( D )(A ))2,1(f 不是极大值; (B ))2,1(f 不是极小值; (C ))2,1(f 是极大值; (D ))2,1(f 是极小值。
大学高等数学A1期末综合测试1试题与答案

1《高等数学A1》测试题1一、填空、选择题(24%)1. 21lim __________;1xx x x →∞-⎛⎫= ⎪+⎝⎭2.若0(),0x f x a x ⎧≠==⎩在0x =处连续,则______;a =3. 设函数()f x 可导,且(1)2f '=,则0(1)(1)lim()2x f x f x∆→-∆-=∆(A) 1; (B) 1-; (C) 2; (D) 2-。
4. 223_______________;310x dx x x +=++⎰5.22(cos )__________;2x xe ex dx ππ---+=⎰6. 设21()txF x te dt =⎰,则()_______________;dF x = 7. 若12lim (),lim (),x ax af x k f x k +-→→==其中12,k k 是确定的常数,则x a =不可能是()f x 的( )(A) 连续点; (B) 可去间断点; (C) 跳跃间断点; (D) 无穷间断点。
8.设曲线()y f x =上任一点切线斜率为这点横坐标的3次方,并且曲线经过点(1,1),则该曲线方程为( ) (A) 41344y x =+(B) 41344y x =-(C) 443y x =+ (D) 443y x =-二、解答下列各题(30%) 1. 3tan sin lim;1xx x x e→--2. 0limxx →3. 21sinxy e=,求y ';4. 3();(1).tx f t y f e π=-⎧⎨=-⎩其中f 可导,且(0)0f '≠,求0t dydx =;5. y e xy e +=,求(0)y ''.三、解答下列题(30%) 1. 22322x dxx x +++⎰; 2. 1arctan x xdx ⎰;3. 设(0)(3)(3)3f f f '===,()f x 二阶导数连续,求3()xf x dx ''⎰;4.求微分方程2321xy y x x '+=++的通解;5.求微分方程32x y y y xe '''-+=的通解. 四、解答下列各题(16%)1.已知函数32()f x x ax bx =++在1x =处有极小值2-,(1).求a 与b 的值; (2). 求()f x 的极大值点与极大值。
高数(A卷)+答案+评分标准

武夷学院期末考试试卷( 2012 级 建设 专业2012~2013 学 年 第 一 学 期) 课程名称 高等数学 A 卷 考试形式 闭卷 考核类型 考试 本试卷共 四 大题,卷面满分100分,答题时间120分钟。
一、选择题:(本大题共10小题,每小题2分,共20分。
)(注:请将选项填在下面表格里。
)1、dx x)11(⎰-=A .21x C x -+ B .21x C x++ C .ln ||x x C -+ D .ln ||x x C ++ 2、以下函数奇偶性不同于其他三项的是( )A .33)(x x x f +=;B . )1)(1()(+-=x x x x f ;C .35)(x x x f -=;D . x x e e x f -+=)(。
3、若'F (x)=f(x),则⎰=)(x dF ( )A .f(x);B .F(x); C. f(x)+C ;D .F(x)+C 。
4、3232lim x x x +∞→= ( )A .∞;B .0;C .31; D .-1。
5、设函数)(x f 在),(+∞-∞内二阶可导,且)()(x f x f -=如果当0>x 时,,0)('>x f 且,0)(">x f 则当0<x 时,曲线)(x f y =( )。
A .递减,凸的; B.递减,凹的;C. 递增,凹的;D. 递增,凸的。
6、下列命题正确的是( )A. 驻点一定是极值点;B.驻点不是极值点;C. 驻点不一定是极值点;D. 驻点是函数的零点。
7、设22z x y xy =+,则zx ∂=∂A .22xy y +B .22x xy +C .4xyD .22x y +8、下面函数相同的一组是( ) A.x y x y 2cos 1,sin -==; B. 2ln ,ln 2x y x y ==; C.x y x y lg 4,lg 4==; D.x x y y 23,3==。
高数a上册期末试题及答案

高数a上册期末试题及答案一、选择题(每题5分,共20题)1. 设函数 $f(x) = \sqrt{3x-2}$,则其定义域为A. $(-\infty, \frac{2}{3}]$B. $\left[ \frac{2}{3}, \infty \right)$C. $[\frac{2}{3}, \infty)$D. $(-\infty, \frac{2}{3}) \cup [\frac{2}{3}, \infty)$答案:C2. 函数 $y = \sin^2 x + \cos^2 x$ 的值域为A. $(-\infty, 1]$B. $[0, 1]$C. $[1, \infty)$D. $[\frac{1}{2}, 1]$答案:B3. 设函数 $f(x) = e^x \ln x$,则 $f'(x) = $A. $e^x \ln x$B. $e^x \left( \frac{1}{x} + \ln x \right)$C. $e^x \left( \ln x - \frac{1}{x} \right)$D. $e^x \left( \frac{1}{x} - \ln x \right)$答案:B4. 若直线 $y = 3x + b$ 与抛物线 $y = ax^2 + bx + 1$ 相切,则 $a + b = $A. 2B. 3C. 4D. 5答案:D5. 函数 $f(x) = \frac{x-1}{\sqrt{x^2 + 1}}$ 的渐近线为A. $y = x - 1$B. $y = x + 1$C. $y = -x + 1$D. $y = -x - 1$答案:A6. 函数 $f(x) = \ln(1 + e^{2x})$ 的反函数为A. $f^{-1}(x) = \ln(x) - \ln(1 - x^2)$B. $f^{-1}(x) = \ln(x^2 - 1)$C. $f^{-1}(x) = \frac{e^x - 1}{2}$D. $f^{-1}(x) = \frac{1}{2} \ln(x) + \ln(1 - x)$答案:D7. 设函数 $f(x) = \arcsin (\sin x)$,则当 $x = \frac{5\pi}{6}$ 时,$f(x) =$A. $\frac{5\pi}{6}$B. $\frac{\pi}{6}$C. $\frac{\pi}{3}$D. $\frac{2\pi}{3}$答案:C8. 函数 $f(x) = \frac{\sin x}{\cos^2 x}$ 的最大值为A. 1B. $\sqrt{3}$C. 2D. $2\sqrt{3}$答案:D9. 函数 $f(x) = x^2 + 2x + 1$ 在区间 $[-1, 1]$ 上的最大值为A. 0B. 1C. 2答案:D10. 函数 $f(x) = \frac{x^2 - 1}{x^2 + 1}$ 的图像关于直线 $x = a$ 对称,则 $a = $A. 1B. 0C. -1D. 2答案:B11. 设 $\sin \alpha = \frac{1}{4}$,$\cos \beta = \frac{4}{5}$,且$\alpha$ 和 $\beta$ 都是第二象限角,则下列四个式子中成立的是A. $\sin (\alpha - \beta) = -\frac{3}{4}$B. $\sin (\alpha + \beta) = \frac{3}{8}$C. $\cos (\alpha - \beta) = \frac{1}{5}$D. $\cos (\alpha + \beta) = \frac{2}{5}$答案:C12. 如果点 $A(1, 2)$ 在抛物线 $y = -x^2 + 3x + k$ 上,那么 $k = $A. -3B. -5D. -9答案:B13. 设函数 $f(x) = x^3 - 3x^2 - 4x + 12$,则 $f'(x)$ 的零点有A. -2, 2B. -1, 3C. -4, 3D. -1, 4答案:A14. 设点 $P(x, y)$ 满足 $y^2 = px$,其中 $p > 0$ 是常数,则焦点所在的直线方程为A. $y = -\frac{p}{2}$B. $x = -\frac{p}{2}$C. $y = \frac{p}{2}$D. $x = \frac{p}{2}$答案:B15. 函数 $f(x) = x^3 - 3x + 1$ 在区间 $[0, 2\pi]$ 上的最小值为A. -1B. 0D. 2答案:A16. 设直线 $y = 2x + 1$ 与曲线 $y = x^2 + bx + c$ 相切,则 $b + c = $A. 0B. $\frac{1}{2}$C. 1D. 2答案:C17. 设函数 $f(x) = (1 - x^2) \cos x$,则 $f''(x)$ 的一个零点在A. $(0, \frac{\pi}{2})$B. $(0, \pi)$C. $(\pi, 2\pi)$D. $(\pi, 3\pi)$答案:B18. 设函数 $f(x) = \sin^2 x - \sqrt{3} \sin x \cos x + \cos^2 x$,则$f(x)$ 的最大值为A. 2B. $2\sqrt{2}$C. 3D. $2 + \sqrt{3}$答案:C19. 设函数 $f(x) = e^x$,$g(x) = x^2$,则 $f(x) \cdot g(x) = $A. $e^{x^2}$B. $x^2 e^x$C. $x^2 e^{x^2}$D. $x^2 + e^x$答案:B20. 设 $a > 0$,则 $\lim\limits_{x \to +\infty} \frac{x^a}{e^x}$ 的值为A. 0B. $\frac{1}{e}$C. 1D. $+\infty$答案:A二、计算题(每题10分,共4题)1. 求函数 $f(x) = \frac{2x^2 - 3x + 1}{x - 1}$ 的极限 $\lim\limits_{x\to 1} f(x)$.解:使用“分子分母可约”的性质,可将函数 $f(x)$ 化简为 $f(x) = 2x - 1$,则 $\lim\limits_{x \to 1} f(x) = \lim\limits_{x \to 1} (2x - 1) = 2(1) - 1 = 1$.答案:12. 求曲线 $y = e^x$ 与直线 $y = kx$ 相交的两个点的坐标,其中 $k > 0$ 是常数.解:将曲线 $y = e^x$ 和直线 $y = kx$ 代入方程中,得到 $e^x = kx$,然后可以使用迭代法或图像法求得相交点的坐标.答案:相交点的坐标为 $(x_1, e^{x_1})$ 和 $(x_2, e^{x_2})$,其中$x_1$ 和 $x_2$ 是满足方程 $e^x = kx$ 的两个解.3. 求曲线 $y = \sin x$ 与直线 $y = x$ 相交的点的个数,并说明理由.解:将曲线 $y = \sin x$ 和直线 $y = x$ 代入方程中,得到 $\sin x = x$,然后可以通过分析函数的周期性和图像来确定相交点的个数.答案:方程 $\sin x = x$ 的解存在无穷个,但相交点的个数取决于给定的区间. 在区间 $[0, \pi]$ 上,方程有一个解;在区间 $[2\pi, 3\pi]$ 上,方程又有一个解. 因此,相交点的个数是不确定的.4. 求函数 $y = x^2 + x$ 在区间 $[-2, 2]$ 上的最大值和最小值,并求出取得最大值和最小值的点.解:首先求导数 $y' = 2x + 1$,然后令 $y' = 0$,解得 $x = -\frac{1}{2}$,将 $x = -2, -\frac{1}{2}, 2$ 代入函数 $y = x^2 + x$,得到对应的 $y$ 值. 最大值为 $y = y_{\text{max}}$ 对应的点为 $(-\frac{1}{2},y_{\text{max}})$,最小值为 $y = y_{\text{min}}$ 对应的点为 $(-2,y_{\text{min}})$ 和 $(2, y_{\text{min}})$.答案:最大值为 $y_{\text{max}} = \frac{5}{4}$,取得最大值的点为 $(-\frac{1}{2}, \frac{5}{4})$;最小值为 $y_{\text{min}} = -2$,取得最小值的点为 $(-2, -2)$ 和 $(2, -2)$.三、证明题(每题20分,共2题)1. 证明函数 $f(x) = \frac{x^3}{3} - x^2 + 2x$ 的导数 $f'(x)$ 恒大于零.证明:求导数 $f'(x) = x^2 - 2x + 2$,我们可以通过判别式来判断 $f'(x)$ 的正负性.判别式为 $\Delta = (-2)^2 - 4(1)(2) = 4 - 8 = -4$,由于 $\Delta < 0$,所以判别式小于零,即 $f'(x)$ 的二次项系数小于零,说明二次项的系数是正的,从而导数 $f'(x)$ 恒大于零.证毕.2. 证明函数 $f(x) = x^3 - 3x^2 + 3$ 的图像关于直线 $x = 1$ 对称.证明:要证明函数的图像关于直线 $x = 1$ 对称,需证明对于任意$x$ 值,函数 $f(x)$ 和 $f(2 - x)$ 的函数值相等.将 $f(x) = x^3 - 3x^2 + 3$ 代入 $f(2 - x)$,得到 $f(2 - x) = (2 - x)^3 -3(2 - x)^2 + 3$,对其进行展开和化简得到 $f(2 - x) = (2 - x)^3 - 3(2 -x)^2 + 3 = x^3 - 3x^2 + 3 = f(x)$,即 $f(x) = f(2 - x)$,证明了函数的图像关于直线 $x = 1$ 对称.证毕.四、应用题(每题50分,共1题)1. 求函数 $f(x) = x^3 + x^2 - 3x$ 的驻点及其对应的极值.解:求导函数 $f'(x) = 3x^2 + 2x - 3$,令 $f'(x) = 0$,求得驻点的 $x$ 坐标,然后将其代入原函数求得对应的 $y$ 坐标.求导的一阶导数方程为 $f'(x) = 3x^2 + 2x - 3 = 0$,通过求根公式求得 $x = -1$ 和 $x = \frac{1}{3}$,将其代入原函数 $f(x)$ 得到对应的$y$ 坐标.将 $x = -1$ 代入 $f(x)$,得到 $f(-1) = (-1)^3 + (-1)^2 - 3(-1) = -1 + 1+ 3 = 3$,将 $x = \frac{1}{3}$ 代入 $f(x)$,得到 $f(\frac{1}{3}) =(\frac{1}{3})^3 + (\frac{1}{3})^2 - 3(\frac{1}{3}) = \frac{1}{27} +\frac{1}{9} - 1 = 0$.因此,函数 $f(x) = x^3 + x^2 - 3x$ 的驻点及其对应的极值为 $(-1, 3)$ 和 $(\frac{1}{3}, 0)$.答案:驻点为 $(-1, 3)$ 和 $(\frac{1}{3}, 0)$,分别对应极大值和极小值.。
《高等数学A1》2018-2019学年第一学期期末试卷A卷

浙江大学2018—2019学年第一学期期末试卷课程:《高等数学A1》浙江大学2018—2019学年第一学期期末教学质量检测《高等数学A1》课程期末试卷A注:1.本次测试满分100分,考试时间为90分钟。
2.考试期间允许使用计算器,不得东张西望,抓到一次警告或交卷,第二次直接处分退学。
3.考试期间必须履行《浙江海洋学院考试条例》,监考教师必须履行《浙江海洋学院监考条例》。
4.考试结束前30分钟允许交卷,考试结束前10分钟不允许交卷。
5.考试结束后监考老师会收试卷和答题卷,试卷和答题卷一律不得带出考场,否则按作弊处理。
题号 一(25%)二(16%)三(21%)四(16%)五(22%)总分(100%)审核(100%)得分 评卷人一、选择题(本题共5小题,每小题5分,共25分)1.设f x ()有连续的导数,f =(0)0,f ≠'(0)0,()()()220F x x t f t dt x=-⎰,且当x →0时,F x '()与x k 是同阶无穷小,则k 等于A.1B.2C.3D.4 2.若+=f x af x (1)()总成立,且'(0)=f b ,a ,b 为非零实数,则f x ()在x =1处 A.不可导 B.可导且'(1)=f a C.可导且'(1)=f b D.可导且'(1)=f ab 3.设对任意的x ,总有ϕ≤≤x f x g x ()()(),且ϕx g x x →∞-=lim ()()0][,则→∞x f x lim ()A.存在且一定等于0B.存在但不一定为0C.一定不存在D.不一定存在4.曲线x y ex x x x =++-+212arctan1(1)(2)的渐近线有 A.1条 B.2条 C.3条 D.4条…………………………………………装………………………………………………订………………………………………………线…………………………………………院系:班级:姓名: 学号: 考场:5.设a x b x c x d e x x →-+--+-=02limtan (1cos )In(12)(1)2,其中a c +≠220,则必有A.=4b dB.=-4b dC.=4a cD.=-4a c二、填空题(本题共4小题,每小题4分,共16分)1.x x x x x x 02lim3sin cos1(1cos )In(1)→+++= . 2.设函数=y y x ()由方程+=+23In()sin x y x y x 确定,则dy dxx 0== .3.xe exx12⎰-=)( .4.曲线L :y x x =≤≤202)(,则xds 02=⎰.(s 表示弧长)三、计算题(本题共3小题,每小题7分,共21分) 1.求不定积分dxx x13+⎰)(2.求极限μμ→⎰⎰+⎡⎣⎢⎤⎦⎥-x xt dt d x x 200lim arctan(1)(1cos )3.求定积分t t x dt 01-⎰四、解答题(本题共2小题,每小题8分,共16分) 1.试确定积分dxx a 1+∞⎰在a 取什么值时收敛,取什么值时发散。
高数A期末试卷A试卷答案

1. limxa
n
等价于( D )
(A)对任给的0,在(a,a)内有数列{xn}的无穷多项;
(B)对任给的0,在(a,a)内只有数列{xn}的有限多项;
(C)对任给的0,在(a,a)外有数列{xn}的无穷多项;
(D)对任给的0,在(a,a)外只有数列{xn}的有限多项.
2. x为函数f(x)的( C)
1siny0确定隐函数yf(x),求
2
d2y
.
dx2
d2y
dx2
(2cosy)2
===========================教材103页例4===================================
xtsint
4.计算由摆线的参数方程y1cost所确定的函数yy(x)的一阶导数.
8.设函数f(x)连续,且满足f(x)3x2x1f(x)dx,求f(x).
0
令1f(x)dxA,则f(x)3x2Ax,两边积分,得
0
1AA
f(x)dx(3x2Ax)dxx3x2|11
00
202
即A1A,得A2.故f(x)3x22x.
2
四、证明题(本大题16分,每小题8分,共2小题)
1.证明:若函数f(x)在(,)内满足关系式f(x)f(x),且有f(0)1,则f(x)ex.
x1ln(1x))elimx(x1)ln(x1)e.
x0x
x0
x(1x)x2
x0
x2(x1)2
=====================(单元测验用题)===========================================
2.已知yln(x1x2),求dy.
湖南大学高数A1试题(期末试卷)

诚信应考,考试作弊将带来严重后果!
湖南湖南大学课程考试试卷
第 2 页(共 3 页)
4。
当时,与是同阶无穷小, 则【】
(A) (B) (C ) (D )
5. 设且,记则下列不等式成立的是 【】
三、计算题(每小题5分,共20分)
四、(11分)设试问为何值时,在处二阶导数存在?
五、(7分)若记(即在上的最大值),求。
六、(8分)(融化立方体冰块)某地为了解决干旱问题,需将极地水域拖来的冰山融化提供淡水。
假设冰山为巨大
的立方体,其表面积成正比。
如果在最初的一小时里冰被融化掉九分之一的部分需多少小时?(结果精确到小数点
后一位,不能使用计算器)
七、(10分)过点作曲线的切线. 试求(1)切线的方程;(2)与所围平面图形的面积;(3)图形的的部分绕
湖南大学课程考试试卷
湖
南大学课程考试试卷
第 3 页(共 3 页)
此结论推广到满足在上连续且关于为偶函数 (即对中的任何有)的任意函数的情形, 请叙述并证明你的结论.
九、(6分)设在上连续, 在内可导,且,试证: 至少存在一点, 使得.。
A5AB.大一高等期末试题(参考答案)

因此设 f ( x, y) x 2 g( y) ,从而
(t ,1)
2xydx
( 0,0 )
f (x , y)dy
t
0dx
0
12
2
[ t g ( y )] dy t
0
1
g( y)dy ,( 5 分)
0
(1, t )
2 xydx
( 0,0 )
f ( x, y)dy
1
0dx
0
t
t
[1 g( y )]dy t
0,
2z
2
4 ,可知在驻点 (0, 2) 与 (0, 16 ) 有 H
y 1 2z 8y
7
0 。( 5 分)
在 (0, 2) 点, z 1 ,因此
2z
2
4
0 ,所以 (0, 2) 为极小值点,极小值为
z 1 ;( 6 分)
x 15
在 (0, 16 ) 点, z 7
2
8 ,因此
z
2
7
x
4
0 ,所以
(0,
; 美高梅mgm4688 https:// 美高梅mgm4688 ;
; 美高梅在线登录网址 https:// 美高梅在线登录网址 ;
1
2
0 2
34
(7 分)
7.
解
:L所
围
区
域D
:
2
x
2
y
2
a
,由
格
林
公
式
,
可
得
2
xy d y
L
( xy 2 ) (
x
D
( x 2 y) )dxdy =
y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学2013~2014学年第一学期课程考试试卷(A 卷) 课 程 考试时间
………………注:请将答案全部答在答题纸上,直接答在试卷上无效。
………………
一、填空题(每小题2分,共10分) (1) =-∞→x x x )11(lim e
1 . (2) 设)tan(2x x y +=,则=dy dx x x x )(sec )21(22++ .
(3) 曲线36223+++=x x x y 的拐点是 )6,1(- . (4) =-⎰
10211dx x 2π . (5) =⎰∞
+121dx x
1 . 二、选择题(每小题2分,共10分) (1) =∞→x x x 2sin lim (A) (A) 0. (B) 1. (C) 2. (D)
21. (2) 设x
x x f tan )(=,则0=x 是函数)(x f 的(A) (A) 可去间断点. (B) 跳跃间断点. (C) 第二类间断点. (D) 连续点.
(3) 当0→x 时,下列变量中与x 是等价无穷小的是(B)
(A) x 3sin . (B) 1-x e . (C) x cos . (D) x +1.
(4) 函数)(x f 在0x 点可导是它在该点连续的(C)
(A) 充分必要条件. (B) 必要条件. (C) 充分条件. (D) 以上都不对.
(5) 设)(x f 在),(∞+-∞内有连续的导数,则下列等式正确的是(D)
(A) ⎰=')()(x f dx x f . (B)
C x f dx x f dx d +=⎰)()(. (C) )0()())((0f x f dt t f x
-='⎰. (D) )())((0x f dt t f x ='⎰.
三、计算下列极限、导数(每小题6分,共18分) (1) 213lim 21-++--→x x x x x .解: )13)(2()13)(13(lim 213lim 2121x x x x x x x x x x x x x x ++--+++-+--=-++--→→ 6
2)13)(2(1lim 2)13)(2)(1(22lim 11-=++-+-=++-+--=→→x x x x x x x x x x
(2) 22)2(sin ln lim x x x -→ππ.解:)2(4sin cos lim )2(sin ln lim 2
22x x x
x x x x --=-→→ππππ 812sin lim 41sin 12cos lim 412
2-=---=⋅--=→→x x x x x x πππ (3) 设函数)(x y y =由方程0ln =+-y x y y 所确定,求:dx
dy 和22dx y d . 两边对x 求导得:01)1(ln ='+-'+y y y
所以得; y
y ln 21+=' y
y ln 21+=
'
四、计算下列积分(每小题8分,共32分)
(1) ⎰-dx x x )2sin(2. 解:C x x d x dx x x +-=---=-⎰⎰)2cos(2
1)2()2sin(21)2sin(2222 (2) ⎰-dx x 21. 解:令t x sin =,2||π≤
t ,则:⎰⎰=-tdt dx x 22cos 1 C t t t C t t dt t ++=++=+=
⎰cos sin 2
122sin 412)2cos 1(21 C x x x +-+=2121arcsin 21 (3) ⎰1
0arctan xdx . 解:⎰⎰+-=1
0210101]arctan [arctan dx x x x x xdx 2ln 2
14)]1ln(21[4102-=+-=ππx (4) ⎰1
0dx e x . 解:令x t =,则2t x =,tdt dx 2=,⎰⎰=1
0102dt te dx e t x 22][221
0101
0=-==⎰⎰dt e te tde t t t 五、综合题(每小题10分,共20分)
(1) 设函数)(x y y =由参数方程⎪⎩
⎪⎨⎧=++=⎰22031t u du e y t t x 所确定,求函数)(x y y =的极值. 解:23124t te dx dy t +=,令0=dx
dy ,得0=t ,代入得:1=x 。
当1<x 时,0<t ,所以0<dx dy ;当1>x 时,0>t ,所以0>dx
dy 。
函数)(x y y =的极大值为0)1(=y 。
(2) 过点)0,0(O 做曲线L :x e y =的切线,切点为A ;由曲线L ,直线OA 和y 轴所围成的图形记为D . 求:
(Ⅰ) OA 的直线方程;
(Ⅱ) D 绕x 轴旋转一周所得旋转体的体积.
解:(Ⅰ)设A 点的横坐标为0x 。
由于x
e y =',所以00
0x x e x e =,即10=x , A 点的坐标为),1(e ,OA 的直线方程为ex y =。
(Ⅱ) 26)(21
0222π
ππ-=-=⎰e dx x e e V x
六、证明题(10分)设函数)(x f 在闭区间]1,0[上连续,在开区间)1,0(内可导,且0)0(=f ,1)1(=f .证明:(Ⅰ) 存在一点)1,0(0∈x ,使得21)(0=
x f ; (Ⅱ) 在)1,0(内存在两点1x 和2x ,使得2)
(1)(121='+'x f x f . 证:(Ⅰ)由于)(x f 在闭区间]1,0[上连续,且)1(2
1)0(f f <<,有介值定理,存在一点)1,0(0∈x ,使得2
1)(0=x f 。
(Ⅱ)由于)(x f 在闭区间]1,0[上连续,在开区间)1,0(内可导,则在),0(0x 内存在一点1x ,使得0001210)0()()(x x f x f x f =--=';又在)1,(0x 内存在一点2x ,使得)
1(211)()1()(0002x x x f f x f -=--='。
所以:
2)1(22)(1)(10021=-+='+'x x x f x f。
