专题17 圆问题-决胜2018中考数学压轴题全揭秘精品(原卷版)

合集下载

2018年中考数学押轴题解析-文档资料

2018年中考数学押轴题解析以下是查字典数学网为您推荐的 2018年中考数学押轴题解析，希望本篇文章对您学习有所帮助。

2018年中考数学押轴题解析一、选择题1. (2018福建龙岩4分)如图，矩形ABCD中，AB=1，BC=2，把矩形ABCD 绕AB所在直线旋转一周所得圆柱的侧面积为【】A. B. C. D.2【答案】B。

【考点】矩形的性质，旋转的性质。

【分析】把矩形ABCD 绕AB所在直线旋转一周所得圆柱是以BC=2为底面半径，AB=1为高。

所以，它的侧面积为。

故选B。

2. (2018福建南平4分)如图，正方形纸片ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别和AE、AF折叠，点B、D恰好都将在点G处，已知BE=1，则EF的长为【】A. B. C. D.3【答案】B。

【考点】翻折变换(折叠问题)，正方形的性质，折叠的性质，勾股定理。

【分析】∵正方形纸片ABCD的边长为3，C=90，BC=CD=3。

根据折叠的性质得：EG=BE=1，GF=DF。

设DF=x，则EF=EG+GF=1+x，FC=DC-DF=3-x，EC=BC-BE=3-1=2。

在Rt△EFC中，EF2=EC2+FC2，即(x+1)2=22+(3-x)2，解得：。

DF= ，EF=1+ 。

故选B。

3. (2018福建宁德4分)如图，在矩形ABCD中，AB=2，BC=3，点E、F、G、H分别在矩形ABCD的各边上，EF∥HG，EH∥FG，则四边形EFGH的周长是【】A.10B.13C.210D.2134. (2018福建莆田4分)如图，在平面直角坐标系中，A(1，1)，B(-1，1)，C(-1，-2)，D(1，-2).把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处，并按ABC-DA一的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是【】A.(1，-1)B.(-1，1)C.(-1，-2)D.(1，-2)【答案】B。

2018中考数学挑战压轴题[含答案解析]

2017 挑战压轴题中考数学精讲解读篇因动点产生的相似三角形问题1．如图，在平面直角坐标系xOy中，将抛物线y=x2的对称轴绕着点P（0，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上一点．（1）求直线AB的函数表达式；（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；（3）如图②，若点Q在y轴左侧，且点T（0，t）（t＜2）是射线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值．2．如图，已知BC是半圆O的直径，BC=8，过线段BO上一动点D，作AD⊥BC交半圆O于点A，联结AO，过点B作BH⊥AO，垂足为点H，BH的延长线交半圆O 于点F．（1）求证：AH=BD；（2）设BD=x，BE•BF=y，求y关于x的函数关系式；（3）如图2，若联结FA并延长交CB的延长线于点G，当△FAE与△FBG相似时，求BD的长度．3．如图，在平面直角坐标系xOy中，直线AB过点A（3，0）、B（0，m）（m＞0），tan∠BAO=2．（1）求直线AB的表达式；（2）反比例函数y=的图象与直线AB交于第一象限内的C、D两点（BD＜BC），当AD=2DB时，求k1的值；（3）设线段AB的中点为E，过点E作x轴的垂线，垂足为点M，交反比例函数y=的图象于点F，分别联结OE、OF，当△OEF∽△OBE时，请直接写出满足条件的所有k2的值．4．如图，在Rt△ABC中，∠ACB=90°，AC=1，BC=7，点D是边CA延长线的一点，AE⊥BD，垂足为点E，AE的延长线交CA的平行线BF于点F，连结CE交AB于点G．（1）当点E是BD的中点时，求tan∠AFB的值；（2）CE•AF的值是否随线段AD长度的改变而变化？如果不变，求出CE•AF的值；如果变化，请说明理由；（3）当△BGE和△BAF相似时，求线段AF的长．5．如图，平面直角坐标系xOy中，已知B（﹣1，0），一次函数y=﹣x+5的图象与x轴、y轴分别交于点A、C两点，二次函数y=﹣x2+bx+c的图象经过点A、点B．（1）求这个二次函数的解析式；（2）点P是该二次函数图象的顶点，求△APC的面积；（3）如果点Q在线段AC上，且△ABC与△AOQ相似，求点Q的坐标．6．已知：半圆O的直径AB=6，点C在半圆O上，且tan∠ABC=2，点D为弧AC上一点，联结DC（如图）（1）求BC的长；（2）若射线DC交射线AB于点M，且△MBC与△MOC相似，求CD的长；（3）联结OD，当OD∥BC时，作∠DOB的平分线交线段DC于点N，求ON的长．7．如图，已知二次函数y=x2+bx+c（b，c为常数）的图象经过点A（3，﹣1），点C（0，﹣4），顶点为点M，过点A作AB∥x轴，交y轴与点D，交该二次函数图象于点B，连结BC．（1）求该二次函数的解析式及点M的坐标；（2）若将该二次函数图象向上平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包含△ABC的边界），求m的取值范围；（3）点P时直线AC上的动点，若点P，点C，点M所构成的三角形与△BCD相似，请直接写出所有点P的坐标（直接写出结果，不必写解答过程）．因动点产生的等腰三角形问题8．如图1，在△ABC中，∠ACB=90°，∠BAC=60°，点E是∠BAC角平分线上一点，过点E作AE的垂线，过点A作AB的垂线，两垂线交于点D，连接DB，点F是BD的中点，DH⊥AC，垂足为H，连接EF，HF．（1）如图1，若点H是AC的中点，AC=2，求AB，BD的长；（2）如图1，求证：HF=EF；（3）如图2，连接CF，CE．猜想：△CEF是否是等边三角形？若是，请证明；若不是，说明理由．9．已知，一条抛物线的顶点为E（﹣1，4），且过点A（﹣3，0），与y轴交于点C，点D是这条抛物线上一点，它的横坐标为m，且﹣3＜m＜﹣1，过点D作DK ⊥x轴，垂足为K，DK分别交线段AE、AC于点G、H．（1）求这条抛物线的解析式；（2）求证：GH=HK；（3）当△CGH是等腰三角形时，求m的值．10．如图，已知在Rt△ABC中，∠ACB=90°，AB=5，sinA=，点P是边BC上的一点，PE⊥AB，垂足为E，以点P为圆心，PC为半径的圆与射线PE相交于点Q，线段CQ与边AB交于点D．（1）求AD的长；（2）设CP=x，△PCQ的面积为y，求y关于x的函数解析式，并写出定义域；（3）过点C作CF⊥AB，垂足为F，联结PF、QF，如果△PQF是以PF为腰的等腰三角形，求CP的长．11．如图（1），直线y=﹣x+n交x轴于点A，交y轴于点C（0，4），抛物线y=x2+bx+c 经过点A，交y轴于点B（0，﹣2）．点P为抛物线上一个动点，过点P作x轴的垂线PD，过点B作BD⊥PD于点D，连接PB，设点P的横坐标为m．（1）求抛物线的解析式；（2）当△BDP为等腰直角三角形时，求线段PD的长；（3）如图（2），将△BDP绕点B逆时针旋转，得到△BD′P′，当旋转角∠PBP′=∠OAC，且点P的对应点P′落在坐标轴上时，请直接写出点P的坐标．12．综合与探究如图，在平面直角坐标系中，已知抛物线y=ax2+bx﹣8与x轴交于A，B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（﹣2，0），（6，﹣8）．（1）求抛物线的函数表达式，并分别求出点B和点E的坐标；（2）试探究抛物线上是否存在点F，使△FOE≌△FCE？若存在，请直接写出点F 的坐标；若不存在，请说明理由；（3）若点P是y轴负半轴上的一个动点，设其坐标为（0，m），直线PB与直线l交于点Q，试探究：当m为何值时，△OPQ是等腰三角形．因动点产生的直角三角形问题13．已知，如图1，在梯形ABCD中，AD∥BC，∠BCD=90°，BC=11，CD=6，tan∠ABC=2，点E在AD边上，且AE=3ED，EF∥AB交BC于点F，点M、N分别在射线FE和线段CD上．（1）求线段CF的长；（2）如图2，当点M在线段FE上，且AM⊥MN，设FM•cos∠EFC=x，CN=y，求y 关于x的函数解析式，并写出它的定义域；（3）如果△AMN为等腰直角三角形，求线段FM的长．14．如图，在矩形ABCD中，点O为坐标原点，点B的坐标为（4，3），点A、C 在坐标轴上，点P在BC边上，直线l1：y=2x+3，直线l2：y=2x﹣3．（1）分别求直线l1与x轴，直线l2与AB的交点坐标；（2）已知点M在第一象限，且是直线l2上的点，若△APM是等腰直角三角形，求点M的坐标；（3）我们把直线l1和直线l2上的点所组成的图形为图形F．已知矩形ANPQ的顶点N在图形F上，Q是坐标平面内的点，且N点的横坐标为x，请直接写出x的取值范围（不用说明理由）．因动点产生的平行四边形问题15．如图，在平面直角坐标系xOy中，抛物线y=ax2﹣2ax﹣3a（a＜0）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：y=kx+b与y轴交于点C，与抛物线的另一个交点为D，且CD=4AC．（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；（2）点E是直线l上方的抛物线上的一点，若△ACE的面积的最大值为，求a 的值；（3）设P是抛物线对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．16．如图，在矩形OABC中，OA=5，AB=4，点D为边AB上一点，将△BCD沿直线CD折叠，使点B恰好落在OA边上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．（1）求点E坐标及经过O，D，C三点的抛物线的解析式；（2）一动点P从点C出发，沿CB以每秒2 个单位长的速度向点B运动，同时动点Q从E点出发，沿EC以每秒1个单位长的速度向点C运动，当点P到达点B时，两点同时停止运动．设运动时间为t秒，当t为何值时，DP=DQ；（3）若点N在（2）中的抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使得以M，N，C，E为顶点的四边形是平行四边形？若存在，请求出M点的坐标；若不存在，请说明理由．17．如图，抛物线y=﹣x2+2x+3与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D和点C关于抛物线的对称轴对称，直线AD与y轴交于点E．（1）求直线AD的解析式；（2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH 平行于x轴交直线AD于点H，求△FGH周长的最大值；（3）点M是抛物线的顶点，点P是y轴上一点，点Q是坐标平面内一点，以A，M，P，Q为顶点的四边形是以AM为边的矩形．若点T和点Q关于AM所在直线对称，求点T的坐标．18．如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O．点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F，使DF=CD，以DE，DF为邻边作矩形DEGF．设AQ=3x．（1）用关于x的代数式表示BQ，DF．（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长．（3）在点P的整个运动过程中，①当AP为何值时，矩形DEGF是正方形？②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案）．19．在平面直角坐标系xOy（如图）中，经过点A（﹣1，0）的抛物线y=﹣x2+bx+3与y轴交于点C，点B与点A、点D与点C分别关于该抛物线的对称轴对称．（1）求b的值以及直线AD与x轴正方向的夹角；（2）如果点E是抛物线上一动点，过E作EF平行于x轴交直线AD于点F，且F 在E的右边，过点E作EG⊥AD与点G，设E的横坐标为m，△EFG的周长为l，试用m表示l；（3）点M是该抛物线的顶点，点P是y轴上一点，Q是坐标平面内一点，如果以点A、M、P、Q为顶点的四边形是矩形，求该矩形的顶点Q的坐标．20．如图，直线y=mx+4与反比例函数y=（k＞0）的图象交于点A、B，与x轴、y轴分别交于D、C，tan∠CDO=2，AC：CD=1：2．（1）求反比例函数解析式；（2）联结BO，求∠DBO的正切值；（3）点M在直线x=﹣1上，点N在反比例函数图象上，如果以点A、B、M、N为顶点的四边形是平行四边形，求点N的坐标．21．如图，在平面直角坐标系中，抛物线y=ax2+bx+c的顶点坐标为（2，9），与y轴交于点A（0，5），与x轴交于点E、B．（1）求二次函数y=ax2+bx+c的表达式；（2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P 在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD 的面积最大？并求出最大面积；（3）若点M在抛物线上，点N在其对称轴上，使得以A、E、N、M为顶点的四边形是平行四边形，且AE为其一边，求点M、N的坐标．因动点产生的梯形问题22．如图，在平面直角坐标系xOy中，二次函数y=+bx+c的图象与y轴交于点A，与双曲线y=有一个公共点B，它的横坐标为4，过点B作直线l∥x轴，与该二次函数图象交于另一个点C，直线AC在y轴上的截距是﹣6．（1）求二次函数的解析式；（2）求直线AC的表达式；（3）平面内是否存在点D，使A、B、C、D为顶点的四边形是等腰梯形？如果存在，求出点D坐标；如果不存在，说明理由．23．如图，矩形OMPN的顶点O在原点，M、N分别在x轴和y轴的正半轴上，OM=6，ON=3，反比例函数y=的图象与PN交于C，与PM交于D，过点C作CA⊥x轴于点A，过点D作DB⊥y轴于点B，AC与BD交于点G．（1）求证：AB∥CD；（2）在直角坐标平面内是否若存在点E，使以B、C、D、E为顶点，BC为腰的梯形是等腰梯形？若存在，求点E的坐标；若不存在请说明理由．因动点产生的面积问题24．如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A，C间的一个动点（含端点），过点P作PF⊥BC 于点F，点D、E的坐标分别为（0，6），（﹣4，0），连接PD、PE、DE．（1）请直接写出抛物线的解析式；（2）小明探究点P的位置发现：当P与点A或点C重合时，PD与PF的差为定值，进而猜想：对于任意一点P，PD与PF的差为定值，请你判断该猜想是否正确，并说明理由；（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE周长最小时“好点”的坐标．25．如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连接CP，过点P作PM⊥CP交AB于点D，且PM=CP，过点M作MN∥OA，交BO于点N，连接ND、BM，设OP=t．（1）求点M的坐标（用含t的代数式表示）．（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由．（3）当t为何值时，四边形BNDM的面积最小．26．在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD 与边长为2的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG 在同一直线上．（1）小明发现DG⊥BE，请你帮他说明理由．（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG 上时，请你帮他求出此时BE的长．（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．27．在平面直角坐标系中，O为原点，直线y=﹣2x﹣1与y轴交于点A，与直线y=﹣x交于点B，点B关于原点的对称点为点C．（1）求过A，B，C三点的抛物线的解析式；（2）P为抛物线上一点，它关于原点的对称点为Q．①当四边形PBQC为菱形时，求点P的坐标；②若点P的横坐标为t（﹣1＜t＜1），当t为何值时，四边形PBQC面积最大？并说明理由．28．如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD⊥x轴于点D，交线段OB于点E，已知CD=8，抛物线经过O、E、A三点．（1）∠OBA= °．（2）求抛物线的函数表达式．（3）若P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形面积记作S，则S取何值时，相应的点P有且只有3个？29．如图1，关于x的二次函数y=﹣x2+bx+c经过点A（﹣3，0），点C（0，3），点D为二次函数的顶点，DE为二次函数的对称轴，E在x轴上．（1）求抛物线的解析式；（2）DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由；（3）如图2，DE的左侧抛物线上是否存在点F，使2S△FBC=3S△EBC？若存在求出点F的坐标，若不存在请说明理由．30．已知抛物线y=mx2+（1﹣2m）x+1﹣3m与x轴相交于不同的两点A、B（1）求m的取值范围；（2）证明该抛物线一定经过非坐标轴上的一点P，并求出点P的坐标；（3）当＜m≤8时，由（2）求出的点P和点A，B构成的△ABP的面积是否有最值？若有，求出该最值及相对应的m值．31．问题提出（1）如图①，已知△ABC，请画出△ABC关于直线AC对称的三角形．问题探究（2）如图②，在矩形ABCD中，AB=4，AD=6，AE=4，AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．问题解决（3）如图③，有一矩形板材ABCD，AB=3米，AD=6米，现想从此板材中裁出一个面积尽可能大的四边形EFGH部件，使∠EFG=90°，EF=FG=米，∠EHG=45°，经研究，只有当点E、F、G分别在边AD、AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能，求出裁得的四边形EFGH部件的面积；若不能，请说明理由．32．如图，在平面直角坐标系中，矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上，OC=8，OE=17，抛物线y=x2﹣3x+m与y轴相交于点A，抛物线的对称轴与x轴相交于点B，与CD交于点K．（1）将矩形OCDE沿AB折叠，点O恰好落在边CD上的点F处．①点B的坐标为（、），BK的长是，CK的长是；②求点F的坐标；③请直接写出抛物线的函数表达式；（2）将矩形OCDE沿着经过点E的直线折叠，点O恰好落在边CD上的点G处，连接OG，折痕与OG相交于点H，点M是线段EH上的一个动点（不与点H重合），连接MG，MO，过点G作GP⊥OM于点P，交EH于点N，连接ON，点M从点E开始沿线段EH向点H运动，至与点N重合时停止，△MOG和△NOG的面积分别表示为S1和S2，在点M的运动过程中，S1•S2（即S1与S2的积）的值是否发生变化？若变化，请直接写出变化范围；若不变，请直接写出这个值．温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．33．如图，已知▱ABCD的三个顶点A（n，0）、B（m，0）、D（0，2n）（m＞n＞0），作▱ABCD关于直线AD的对称图形AB1C1D（1）若m=3，试求四边形CC1B1B面积S的最大值；（2）若点B1恰好落在y轴上，试求的值．因动点产生的相切问题34．如图，已知在平面直角坐标系xOy中，抛物线y=ax2+2x+c与x轴交于点A （﹣1，0）和点B，与y轴相交于点C（0，3），抛物线的对称轴为直线l．（1）求这条抛物线的关系式，并写出其对称轴和顶点M的坐标；（2）如果直线y=kx+b经过C、M两点，且与x轴交于点D，点C关于直线l的对称点为N，试证明四边形CDAN是平行四边形；（3）点P在直线l上，且以点P为圆心的圆经过A、B两点，并且与直线CD相切，求点P的坐标．35．如图，在Rt△ABC中，∠C=90°，AC=14，tanA=，点D是边AC上一点，AD=8，点E是边AB上一点，以点E为圆心，EA为半径作圆，经过点D，点F是边AC 上一动点（点F不与A、C重合），作FG⊥EF，交射线BC于点G．（1）用直尺圆规作出圆心E，并求圆E的半径长（保留作图痕迹）；（2）当点G的边BC上时，设AF=x，CG=y，求y关于x的函数解析式，并写出它的定义域；（3）联结EG，当△EFG与△FCG相似时，推理判断以点G为圆心、CG为半径的圆G与圆E可能产生的各种位置关系．36．如图，线段PA=1，点D是线段PA延长线上的点，AD=a（a＞1），点O是线段AP延长线上的点，OA2=OP•OD，以O为圆心，OA为半径作扇形OAB，∠BOA=90°．点C是弧AB上的点，联结PC、DC．（1）联结BD交弧AB于E，当a=2时，求BE的长；（2）当以PC为半径的⊙P和以CD为半径的⊙C相切时，求a的值；（3）当直线DC经过点B，且满足PC•OA=BC•OP时，求扇形OAB的半径长．37．如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD 向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，0.8cm为半径作⊙O，点P与点O同时出发，设它们的运动时间为t（单位：s）（0＜t＜）．（1）如图1，连接DQ平分∠BDC时，t的值为；（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；（3）请你继续进行探究，并解答下列问题：①证明：在运动过程中，点O始终在QM所在直线的左侧；②如图3，在运动过程中，当QM与⊙O相切时，求t的值；并判断此时PM与⊙O 是否也相切？说明理由．38．如图，抛物线y=﹣x2+mx+n的图象经过点A（2，3），对称轴为直线x=1，一次函数y=kx+b的图象经过点A，交x轴于点P，交抛物线于另一点B，点A、B 位于点P的同侧．（1）求抛物线的解析式；（2）若PA：PB=3：1，求一次函数的解析式；（3）在（2）的条件下，当k＞0时，抛物线的对称轴上是否存在点C，使得⊙C 同时与x轴和直线AP都相切，如果存在，请求出点C的坐标，如果不存在，请说明理由．因动点产生的线段和差问题39．如图，抛物线y=x2﹣4x与x轴交于O，A两点，P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q．（1）这条抛物线的对称轴是，直线PQ与x轴所夹锐角的度数是；（2）若两个三角形面积满足S△POQ=S△PAQ，求m的值；（3）当点P在x轴下方的抛物线上时，过点C（2，2）的直线AC与直线PQ交于点D，求：①PD+DQ的最大值；②PD•DQ的最大值．40．抛物线y=ax2+bx+4（a≠0）过点A（1，﹣1），B（5，﹣1），与y轴交于点C．（1）求抛物线的函数表达式；（2）如图1，连接CB，以CB为边作▱CBPQ，若点P在直线BC上方的抛物线上，Q为坐标平面内的一点，且▱CBPQ的面积为30，求点P的坐标；（3）如图2，⊙O1过点A、B、C三点，AE为直径，点M为上的一动点（不与点A，E重合），∠MBN为直角，边BN与ME的延长线交于N，求线段BN长度的最大值．41．如图，在每一个四边形ABCD中，均有AD∥BC，CD⊥BC，∠ABC=60°，AD=8，BC=12．（1）如图①，点M是四边形ABCD边AD上的一点，则△BMC的面积为；（2）如图②，点N是四边形ABCD边AD上的任意一点，请你求出△BNC周长的最小值；（3）如图③，在四边形ABCD的边AD上，是否存在一点P，使得cos∠BPC的值最小？若存在，求出此时cos∠BPC的值；若不存在，请说明理由．42．如图，把△EFP按图示方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上，已知EP=FP=4，EF=4，∠BAD=60°，且AB＞4．（1）求∠EPF的大小；（2）若AP=6，求AE+AF的值；（3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值．43．如图，在平面直角坐标系中，抛物线y=﹣x2﹣x+2与x轴交于B、C两点（点B在点C的左侧），与y轴交于点A，抛物线的顶点为D．（1）填空：点A的坐标为（，），点B的坐标为（，），点C的坐标为（，），点D的坐标为（，）；（2）点P是线段BC上的动点（点P不与点B、C重合）①过点P作x轴的垂线交抛物线于点E，若PE=PC，求点E的坐标；②在①的条件下，点F是坐标轴上的点，且点F到EA和ED的距离相等，请直接写出线段EF的长；③若点Q是线段AB上的动点（点Q不与点A、B重合），点R是线段AC上的动点（点R不与点A、C重合），请直接写出△PQR周长的最小值．44．如图，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM 对折，得到△ANM．（1）当AN平分∠MAB时，求DM的长；（2）连接BN，当DM=1时，求△ABN的面积；（3）当射线BN交线段CD于点F时，求DF的最大值．45．如图，半圆O的直径AB=4，以长为2的弦PQ为直径，向点O方向作半圆M，其中P点在上且不与A点重合，但Q点可与B点重合．发现：的长与的长之和为定值l，求l：思考：点M与AB的最大距离为，此时点P，A间的距离为；点M与AB的最小距离为，此时半圆M的弧与AB所围成的封闭图形面积为；探究：当半圆M与AB相切时，求的长．（注：结果保留π，cos35°=，cos55°=）46．（1）发现：如图1，点A为线段BC外一动点，且BC=a，AB=b．填空：当点A位于时，线段AC的长取得最大值，且最大值为（用含a，b的式子表示）（2）应用：点A为线段BC外一动点，且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE．①请找出图中与BE相等的线段，并说明理由；②直接写出线段BE长的最大值．（3）拓展：如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，请直接写出线段AM长的最大值及此时点P的坐标．47．如图，直线l：y=﹣3x+3与x轴、y轴分别相交于A、B两点，抛物线y=ax2﹣2ax+a+4（a＜0）经过点B．（1）求该抛物线的函数表达式；（2）已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值；（3）在（2）的条件下，当S取得最大值时，动点M相应的位置记为点M′．①写出点M′的坐标；②将直线l绕点A按顺时针方向旋转得到直线l′，当直线l′与直线AM′重合时停止旋转，在旋转过程中，直线l′与线段BM′交于点C，设点B、M′到直线l′的距离分别为d1、d2，当d1+d2最大时，求直线l′旋转的角度（即∠BAC的度数）．48．如图，在平面直角坐标系xOy中，将二次函数y=x2﹣1的图象M沿x轴翻折，把所得到的图象向右平移2个单位长度后再向上平移8个单位长度，得到二次函数图象N．（1）求N的函数表达式；（2）设点P（m，n）是以点C（1，4）为圆心、1为半径的圆上一动点，二次函数的图象M与x轴相交于两点A、B，求PA2+PB2的最大值；（3）若一个点的横坐标与纵坐标均为整数，则该点称为整点．求M与N所围成封闭图形内（包括边界）整点的个数．49．如图，顶点为A（，1）的抛物线经过坐标原点O，与x轴交于点B．（1）求抛物线对应的二次函数的表达式；（2）过B作OA的平行线交y轴于点C，交抛物线于点D，求证：△OCD≌△OAB；（3）在x轴上找一点P，使得△PCD的周长最小，求出P点的坐标．2017 挑战压轴题中考数学精讲解读篇参考答案与试题解析一．解答题（共36小题）1．如图，在平面直角坐标系xOy中，将抛物线y=x2的对称轴绕着点P（0，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上一点．（1）求直线AB的函数表达式；（2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；（3）如图②，若点Q在y轴左侧，且点T（0，t）（t＜2）是射线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值．【分析】（1）根据题意易得点M、P的坐标，利用待定系数法来求直线AB的解析式；（2）如图①，过点Q作x轴的垂线QC，交AB于点C，再过点Q作直线AB的垂线，垂足为D，构建等腰直角△QDC，利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答；（3）根据相似三角形的对应角相等推知：△PBQ中必有一个内角为45°；需要分类讨论：∠PBQ=45°和∠PQB=45°；然后对这两种情况下的△PAT是否是直角三角形分别进行解答．另外，以P、B、Q为顶点的三角形与△PAT相似也有两种情况：△Q″PB∽△PAT、△Q″BP∽△PAT．【解答】解：（1）如图①，设直线AB与x轴的交点为M．∵∠OPA=45°，∴OM=OP=2，即M（﹣2，0）．设直线AB的解析式为y=kx+b（k≠0），将M（﹣2，0），P（0，2）两点坐标代入，得，解得．故直线AB的解析式为y=x+2；（2）如图①，过点Q作x轴的垂线QC，交AB于点C，再过点Q作直线AB的垂线，垂足为D，根据条件可知△QDC为等腰直角三角形，则QD=QC．设Q（m，m2），则C（m，m+2）．∴QC=m+2﹣m2=﹣（m﹣）2+，QD=QC=[﹣（m﹣）2+]．故当m=时，点Q到直线AB的距离最大，最大值为；（3）∵∠APT=45°，∴△PBQ中必有一个内角为45°，由图知，∠BPQ=45°不合题意．①如图②，若∠PBQ=45°，过点B作x轴的平行线，与抛物线和y轴分别交于点Q′、F．此时满足∠PBQ′=45°．∵Q′（﹣2，4），F（0，4），∴此时△BPQ′是等腰直角三角形，由题意知△PAT也是等腰直角三角形．（i）当∠PTA=90°时，得到：PT=AT=1，此时t=1；（ii）当∠PAT=90°时，得到：PT=2，此时t=0．②如图③，若∠PQB=45°，①中是情况之一，答案同上；先以点F为圆心，FB为半径作圆，则P、B、Q′都在圆F上，设圆F与y轴左侧的抛物线交于另一点Q″．则∠PQ″B=∠PQ′B=45°（同弧所对的圆周角相等），即这里的交点Q″也是符合要求．设Q″（n，n2）（﹣2＜n＜0），由FQ″=2，得n2+（4﹣n2）2=22，即n4﹣7n2+12=0．解得n2=3或n2=4，而﹣2＜n＜0，故n=﹣，即Q″（﹣，3）．可证△PFQ″为等边三角形，所以∠PFQ″=60°，又PQ″=PQ″，所以∠PBQ″=∠PFQ″=30°．则在△PQ″B中，∠PQ″B=45°，∠PBQ″=30°．（i）若△Q″PB∽△PAT，则过点A作y轴的垂线，垂足为E．则ET=AE=，OE=1，所以OT=﹣1，解得t=1﹣；（ii）若△Q″BP∽△PAT，则过点T作直线AB垂线，垂足为G．设TG=a，则PG=TG=a，AG=TG=a，AP=，∴a+a=，解得PT=a=﹣1，∴OT=OP﹣PT=3﹣，∴t=3﹣．综上所述，所求的t的值为t=1或t=0或t=1﹣或t=3﹣．2．如图，已知BC是半圆O的直径，BC=8，过线段BO上一动点D，作AD⊥BC交半圆O于点A，联结AO，过点B作BH⊥AO，垂足为点H，BH的延长线交半圆O于点F．（1）求证：AH=BD；（2）设BD=x，BE•BF=y，求y关于x的函数关系式；（3）如图2，若联结FA并延长交CB的延长线于点G，当△FAE与△FBG相似时，求BD的长度．【分析】（1）由AD⊥BC，BH⊥AO，利用垂直的定义得到一对直角相等，再由一对公共角，且半径相等，利用AAS得到三角形ADO与三角形BHO全等，利用全等三角形对应边相等得到OH=OD，利用等式的性质化简即可得证；（2）连接AB，AF，如图1所示，利用HL得到直角三角形ADB与直角三角形BHA 全等，利用全等三角形对应角相等得到一对角相等，再由公共角相等得到三角形ABE与三角形AFB相似，由相似得比例即可确定出y与x的函数解析式；（3）连接OF，如图2所示，利用两对角相等的三角形相似得到三角形AFO与三角形FOG相似，由相似得比例求出BD的长即可．【解答】（1）证明：∵AD⊥BC，BH⊥AO，∴∠ADO=∠BHO=90°，在△ADO与△BHO中，，∴△ADO≌△BHO（AAS），∴OH=OD，。

决胜2018中考数学压轴题全揭秘精品：(压轴题)专题22 动态几何之动点形成的四边形存

（3）在（2）的条件下，过点 P 作 PF⊥x 轴于点 F，G 为抛物线上一动点，M 为 x 轴上一动点，N 为直线 PF 上一
动点，当以
F、M、G
为顶点的四边形是正方WW.ziyua nku.co m
16．（2016 内蒙古呼伦贝尔市，第 26 题，13 分）如图，抛物线 y x2 2x 3 与 x 轴相交的于 A，B 两点（点 A
在点 B 的左侧），与 y 轴相交于点 C，顶点为 D．（1）直接写出 A，B，C 三点的坐标和抛物线的对称轴；（2）连接 BC，与抛物线的对称轴交于点 E，点 P 为线段 BC 上的一个动点（P 不与 C，B 两点重合），过点 P 作 PF∥DE 交抛物线于点 F，设点 P 的横坐标为 m． ①用含 m 的代数式表示线段 PF 的长，并求出当 m 为何值时，四边形 PEDF 为平行四边形． ②设△BCF 的面积为 S，求 S 与 m 的函数关系式；当 m 为何值时，S 有最大值．
4
11．（2016 山东省东营市）在平面直角坐标系中，平行四边形 ABOC 如图放置，点 A、C 的坐标分别是（0，4）、（﹣1，0），将此平行四边形绕点 O 顺时针旋转 90°，得到平行四边形 A′B′OC′．（1）若抛物线经过点 C、A、A′，求此抛物线的解析式；（2）点 M 是第一象限内抛物线上的一动点，问：当点 M 在何处时，△AMA′的面积最大？最大面积是多少？并求出此时 M 的坐标；（3）若 P 为抛物线上一动点，N 为 x 轴上的一动点，点 Q 坐标为（1，0），当 P、N、B、Q 构成平行四边形时，求点 P 的坐标，当这个平行四边形为矩形时，求点 N 的坐标．
C 三点，其中点 A 的坐标为（0，8），点 B 的坐标为（﹣4，0）．（1）求该二次函数的表达式及点 C 的坐标；（2）点 D 的坐标为（0，4），点 F 为该二次函数在第一象限内图象上的动点，连接 CD、CF，以 CD、CF 为邻边作平行四边形 CDEF，设平行四边形 CDEF 的面积为 S．$来&源： ①求 S 的最大值； ②在点 F 的运动过程中，当点 E 落在该二次函数图象上时，请直接写出此时 S 的值．

2018年中考数学压轴题之圆题例题

广东中考数学专题训练（二）：几何综合题（圆题）例题训练1．如图，⊙O 为∆ABC 外接圆，BC 为⊙O 直径，BC =4．点D 在⊙O 上，连接OA 、CD 和BD ，AC 与BD 交于点E ，并作AF ⊥BC 交BD 于点G ，点G 为BE 中点，连接OG ．（1）求证：OA ∥CD ；（2）若∠DBC =2∠DBA ，求BD 的长；（3）求证：FG =2DE ．2．如图，⊙O 为∆ABC 外接圆，AB 为⊙O 直径，AB =4．⊙O 切线CD 交BA 延长线于点D ，∠ACB 平分线交⊙O 于点E ，并以DC为边向下作∠DCF =∠CAB 交⊙O 于点F ，连接AF ．（1）求证：∠DCF =∠D +∠B ；（2）若AF =32，AD =52，求线段AC 的长；（3）若CEAB ⊥CF ．3．如图，⊙O为 ABC外接圆，BC为⊙O直径．作»AD=»AC，连接AD、CD和BD，AB与CD交于点E，过点B作⊙O 切线，并作点E作EF⊥DC交切线于点G．（1）求证：∠DAC=∠G+90°；（2）求证：CF=GF；（3）若EFBD=23，求证：AE=DE．4．如图，⊙O 为 ABC 外接圆，AB 为⊙O 直径．连接CO ，并作AD ∥CO 交⊙O 于点D ，过点D 作⊙O 切线DE 交CO 延长线于点E ，连接BE ，作AF ⊥CO 交BC 于点G ，交BE 于点H ，连接OG ．（1）若CF =2，OF =3，求AC 的长；（2）求证：BE 是⊙O 的切线；（3）若2AF AHDE g =23，求证：OG ⊥AB ．。

2018全国各地中考数学试题《圆》试题汇编(解答题)

2018全国各地中考数学试题《圆》试题汇编(解答题)2018全国各地中考数学试题《圆》解答题汇编1. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．求证：∠CBP=∠ADB．若OA=2，AB=1，求线段BP的长．2.如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O 于点D．已知⊙O的半径为6，∠C=40°．求∠B的度数．求AD的长．3.如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．求证：AD⊥CD；若∠CAD=30°，⊙O的半径为3，一只蚂蚁从点B出发，沿着BE-EC-CB爬回至点B，求蚂蚁爬过的路程．第 1 页共 27 页4. 如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．求证：OP ⊥CD；连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5. 如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O 于点F，AC平分∠BAD，连接BF．求证：AD⊥ED；若CD=4，AF=2，求⊙O的半径．6. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE 丄AB，交AB的延第 2 页共 27 页长线于点E．求证：CB平分∠ACE；若BE=3，CE=4，求⊙O的半径．7.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB 于点F．求证：BC是⊙O的切线；若⊙O的半径是2cm，E 是AD的中点，求阴影部分的面积8.已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，如图①，若D为AB的中点，求∠ABC和∠ABD的大小；如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，第 3 页共 27 页求∠OCD的大小．9. 如图，D是△ABC外接圆上的动点，且B，D位于AC 的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG ⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．求证：BG∥CD；设△ABC外接圆的圆心为O，若AB=3DH，∠OHD=80°，求∠BDE的大小．10. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．求证：AE与⊙O相切于点A；若AE∥BC，BC=27，AC=22，求AD的长．第 4 页共 27 页11.如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．求证：DA=DE；若AB=6，CD=43，求图中阴影部分的面积．13.如图，△ABC中，AB=AC，以AB为直径的⊙O交BC 于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．求证：DF是⊙O的切线；已知BD=25 第 5 页共27 页25. 如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D．过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F．求证：PC是⊙O的切线；若∠ABC=60°，AB=10，求线段CF的长．26. 如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．试判断直线DE与⊙O的位置关系，并说明理；若⊙O的半径为2，∠B=50°，AC=，求图中阴影部分的面积．第 11 页共 27 页27.如图，AB是⊙O的直径，点C为⊙O上一点，CN为⊙O的切线，OM⊥AB于点O，分别交AC、CN于D、M两点．求证：MD=MC；若⊙O的半径为5，AC=45，求MC的长．27. 如图，在⊙O中，AB为直径，AC为弦．过BC延长线上一点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．判断CM与⊙O的位置关系，并说明理；若∠ECF=2∠A，CM=6，CF=4，求MF的长．第 12 页共 27 页28.如图，在△ABC中，AB=AC，以AB为直径的圆交AC 于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC．求证：四边形ABFC是菱形；若AD=7，BE=2，求半圆和菱形ABFC的面积．29.如图，已知A、B、C、D、E是⊙O上五点，⊙O的直径BE=23，∠BCD=120°，A为BE的中点，延长BA到点P，使BA=AP，连接PE．求线段BD的长；求证：直线PE是⊙O的切线．第 13 页共 27 页30.如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F．求证：EF是⊙O的切线；若AC=4，CE=2，求 BD的长度．31.已知：如图，AB是⊙O的直径，AB=4，点F，C是⊙O上两点，连接AC，AF，OC，弦AC平分∠FAB，∠BOC=60°，过点C作CD⊥AF交AF的延长线于点D，垂足为点D．求扇形OBC的面积；求证：CD是⊙O的切线．32.已知：如图，以等边△ABC的边BC为直径作⊙O，分别交AB，AC于点D，E，过点D作DF⊥AC交AC于点F．求证：DF是⊙O的切线；若等边△ABC的边长为8，求第 14 页共 27 页DE、DF、EF围成的阴影部分面积．33.如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．求证：AE=ED；若AB=10，∠CBD=36°，求AC的长．34.如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D，OB与⊙O相交于点E．求证：AC是⊙O 的切线；若BD=3，BE=1．求阴影部分的面积．第 15 页共 27 页35.如图，已知⊙O是等边三角形ABC的外接圆，点D在圆上，在CD的延长线上有一点F，使DF=DA，AE∥BC交CF于E．求证：EA是⊙O的切线；求证：BD=CF．36. 如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点C．若∠ADE=25°，求∠C的度数；若AB=AC，CE=2，求⊙O半径的长．37. 如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，点D是AM上一点，连接OD，过点B作BE∥OD交⊙O于点E，连接DE并延长交BN于点C．求证：DE是⊙O的切线；第 16 页共 27 页若AD=l，BC=4，求直径AB的长．38. 如图所示，PB是⊙O的切线，B为切点，圆心O在PC上，∠P=30°，D为弧BC的中点．求证：PB=BC；试判断四边形BOCD的形状，并说明理．39. 某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径．如图，若这个输水管道有水部分的水面宽AB=16cm，水最深的地方的高度为4cm，求这个圆形截面的半径．40. 如图，AB是⊙O的直径，弦CD⊥AB于点E，过点C 的切线交AB的延长线于点F，连接DF．求证：DF是⊙O的切线；连接BC，若∠BCF=30°，BF=2，求CD的长．第 17 页共 27 页41. 已知，如图AB是⊙O的直径，点P在BA的延长线上，弦BC平分∠PBD，且BD⊥PD于点D．求证：PD是⊙O 的切线．若AB=8cm，BD=6cm，求CD的长．42. 如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC 是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．求证：CF是⊙O的切线；若∠F=30°，EB=8，求图中阴影部分的面积．43.如图，已知△ABC内接于⊙O，AB是直径，OD∥AC， AD=OC．求证：四边形OCAD是平行四边形；第 18 页共 27 页探究：①当∠B= °时，四边形OCAD是菱形；②当∠B满足什么条件时，AD与⊙O相切？请说明理．43. 如图，AB是⊙O的一条弦，OD⊥AB，垂足为点C，交⊙O于点D，点E在⊙O上．若∠AOD=52°，求∠DEB的度数；若OC=3，OA=5，求AB的长．44.如图，在⊙O中，弦AD、BC相交于点E，连接OE，已知AD=BC，AD⊥CB．求证：AB=CD；如果⊙O的半径为5，DE=1，求AE的长．第 19 页共 27 页45.如图，⊙O的直径AB=12，弦AC=6，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于点E，连接AD，BD． AB，BD，AD围成的阴影部分的面积是；求线段DE的长．46.如图，在△ABC中，AB=AC，O为边AC上一点，以OC 为半径的圆分别交边BC，AC于点D，E，过点D作DF⊥AB于点F．求证：直线DF是⊙O的切线；若∠A=45°，OC=2，求劣弧DE的长．第 20 页共 27 页2018全国各地中考数学试题《圆》解答题汇编1. 如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P，过B点的切线交OP于点C．求证：∠CBP=∠ADB．若OA=2，AB=1，求线段BP的长．2.如图，AB是⊙O的直径，AC切⊙O于点A，BC交⊙O 于点D．已知⊙O的半径为6，∠C=40°．求∠B的度数．求AD的长．3.如图，AB是⊙O的直径，直线CD与⊙O相切于点C，且与AB的延长线交于点E，点C是BF的中点．求证：AD⊥CD；若∠CAD=30°，⊙O的半径为3，一只蚂蚁从点B出发，沿着BE-EC-CB爬回至点B，求蚂蚁爬过的路程．第 1 页共 27 页4. 如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．求证：OP ⊥CD；连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．5. 如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O 于点F，AC平分∠BAD，连接BF．求证：AD⊥ED；若CD=4，AF=2，求⊙O的半径．6. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE 丄AB，交AB的延第 2 页共 27 页长线于点E．求证：CB平分∠ACE；若BE=3，CE=4，求⊙O的半径．7.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，点O在AB上，⊙O经过A、D两点，交AC于点E，交AB 于点F．求证：BC是⊙O的切线；若⊙O的半径是2cm，E是AD的中点，求阴影部分的面积8.已知AB是⊙O的直径，弦CD与AB相交，∠BAC=38°，如图①，若D为AB的中点，求∠ABC和∠ABD的大小；如图②，过点D作⊙O的切线，与AB的延长线交于点P，若DP∥AC，第 3 页共 27 页求∠OCD的大小．9. 如图，D是△ABC外接圆上的动点，且B，D位于AC 的两侧，DE⊥AB，垂足为E，DE的延长线交此圆于点F．BG ⊥AD，垂足为G，BG交DE于点H，DC，FB的延长线交于点P，且PC=PB．求证：BG∥CD；设△ABC外接圆的圆心为O，若AB=3DH，∠OHD=80°，求∠BDE的大小．10. 如图，BD为△ABC外接圆⊙O的直径，且∠BAE=∠C．求证：AE与⊙O相切于点A；若AE∥BC，BC=27，AC=22，求AD的长．第 4 页共 27 页11.如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．12.如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E为⊙O上一点，过点E作直线DC分别交AM，BN于点D，C，且CB=CE．求证：DA=DE；若AB=6，CD=43，求图中阴影部分的面积．13.如图，△ABC中，AB=AC，以AB为直径的⊙O交BC 于点D，交AC于点E，过点D作DF⊥AC于点F，交AB的延长线于点G．求证：DF是⊙O的切线；已知BD=25 第 5 页共27 页。

2018挑战中考数学压轴题全套含答案及解析

第一部分函数图象中点的存在性问题§1．1 因动点产生的相似三角形问题例1 2014年市中考第28题例2 2014年市中考第21题例3 2015年湘西州中考第26题例4 2015年市中考第25题例5 2016年市中考第26题例6 2016年市中考第24题例7 2016年市崇明县中考模拟第25题例8 2016年市黄浦区中考模拟第26题§1．2 因动点产生的等腰三角形问题例9 2014年市中考第26题例10 2014年市第25题例11 2014年市中考第26题例12 2014年市中考第27题例13 2015年市中考第22题例14 2015年市中考第26题例15 2016年市中考第26题例16 2016年市长宁区金山区中考模拟第25题例17 2016年省中考第23题§1．3 因动点产生的直角三角形问题例19 2015年市中考第21题例20 2015年市中考第26题例21 2016年市中考第26题例22 2016年市松江区中考模拟第25题例23 2016年义乌市市中考第24题§1．4 因动点产生的平行四边形问题例24 2014年市中考第24题例25 2014年市中考第20题例26 2014年市中考第25题例27 2015年市中考第25题例28 2015年黄冈市中考第24题例29 2016年市中考第26题例30 2016年市嘉定区宝山区中考模拟中考第24题例31 2016年市徐汇区中考模拟第24题§1．5 因动点产生的面积问题例32 2014年市中考第25题例33 2014年永州市中考第25题例35 2015年市中考第26题例36 2015年株洲市中考第23题例37 2015年市中考第28题例38 2016年市中考第22题例39 2016年永州市中考第26题例40 2016年市中考第26题例41 2016年省中考第25题§1．6 因动点产生的相切问题例42 2014年市中考第27题例43 2014年株洲市中考第23题例44 2015年市中考第25题例45 2015年湘西州中考第25题例46 2016年市中考第25题例47 2016年市中考第26题例48 2016年市闵行区中考模拟第24题例49 2016年市普陀区中考模拟中考第25题§1．7 因动点产生的线段和差问题例50 2014年市中考第26题例51 2014年湘西州中考第25题例53 2015年市中考第28题例54 2015年市中考第25题例55 2016年市中考第26题例56 2016年市中考第24题例57 2016年市中考第21题第二部分图形运动中的函数关系问题§2．1 由比例线段产生的函数关系问题例1 2014年市中考第26题例2 2014年市中考第25题例3 2014年市中考第25题例4 2015年市中考第25题例5 2015年市中考第26题例6 2015年市中考第25题例7 2015年市中考第26题例8 2016年市中考第25题例9 2016年湘西州中考第26题例10 2016年市静安区青浦区中考模拟第25题例11 2016年市中考第27题第三部分图形运动中的计算说理问题§3．1 代数计算及通过代数计算进行说理问题例1 2014年市中考第25题例2 2014年市中考第23题例3 2014年市中考第26题例4 2014年株洲市中考第24题例5 2015年市中考第27题例6 2015年市中考第25题例7 2015年永州市中考第26题例8 2015年市中考第25题例9 2015年株洲市中考第24题例10 2016年市中考第22题例11 2016年市中考第25题例12 2016年株洲市中考第26题例13 2016年市中考第25题例14 2016年市中考第26题§3．2 几何证明及通过几何计算进行说理问题例15 2014年市中考第26题例16 2014年市中考第26题例17 2014年市中考第23题例18 2015年市中考第26题例19 2015年市中考第20题例20 2015年永州市中考第27题例21 2015年市中考第23题例22 2016年市中考第25题例23 2016年市中考第25题例24 2016年永州市中考第27题例25 2016年市中考第23题例26 2016年株洲市中考第25题例27 2016年市中考第25题第四部分图形的平移、翻折与旋转§4．1 图形的平移例1 2015年市中考第15题例2 2015年市中考第14题例3 2015年株洲市中考第14题例4 2016年市虹口区中考模拟第18题§4．2 图形的翻折例5 2016年市奉贤区中考模拟第18题例6 2016年市静安区青浦区中考模拟第18题例7 2016年市闵行区中考模拟第18题例8 2016年市浦东新区中考模拟第18题例8 2016年市普陀区中考模拟第18题例10 2016年市中考第15题例11 2016年市中考第14题例12 2016年市中考第18题例13 2016年市中考第15题例14 2016年市中考第12题§4．3 图形的旋转例15 2016年昂立教育中学生三模联考第18题例16 2016年市崇明县中考模拟第18题例17 2016年市黄浦区中考模拟第18题例18 2016年市嘉定区宝山区中考模拟第18题例19 2016年市闸北区中考模拟第18题例20 2016年市中考第13题例21 2016年株洲市中考第4题§4．4 三角形例22 2016年省中考第10题例23 2016年市中考第10题例24 2016年省中考第16题例25 2016年市中考第10题例27 2016年市中考第10题例28 2016年省中考第14题例29 2016年江市中考第11题例30 2016年市中考第18题§4．5 四边形例31 2016年湘西州中考第11题例32 2016年市中考第4题例33 2016年市中考第6题例34 2016年市中考第16题例35 2016年市中考第14题例36 2016年市中考第13题例37 2016年市中考第18题例38 2016年市中考第17题例39 2016年市中考第15题§4．6 圆例40 2016年滨州市中考第16题例41 2016年市中考第17题例42 2016年市中考第16题例43 2016年市中考第17题例45 2016年市中考第18题例46 2016年市中考第9题例47 2016年宿迁市中考第16题例48 2016年市中考第17题例49 2016年市中考第18题例50 2016年湘西州中考第18题例51 2016年永州市中考第20题§4．7 函数的图象及性质例52 2015年荆州市中考第9题例53 2015年市中考第12题例54 2015年市中考第12题例55 2015年市中考第10题例56 2015年市中考第10题例57 2015年呼和浩特市中考第10题例58 2016年市中考第18题例59 2016年市中考第19题例60 2016年市中考第15题例61 2016年株洲市中考第9题例62 2016年永州市中考第19题例63 2016年市中考第8题例64 2016年市中考第16题例65 2016年市中考第14题例66 2016年株洲市中考第10题例67 2016年株洲市中考第17题例68 2016年东营市中考第15题例69 2016年市中考第13题例70 2016年市中考第16题例71 2016年宿迁市中考第15题例72 2016年市中考第14题例73 2016年义乌市市中考第9题例74 2016年市中考第12题例75 2016年市中考第16题§1．1 因动点产生的相似三角形问题课前导学相似三角形的判定定理有3个，其中判定定理1和判定定理2都有对应角相等的条件，因此探求两个三角形相似的动态问题，一般情况下首先寻找一组对应角相等．判定定理2是最常用的解题依据，一般分三步：寻找一组等角，分两种情况列比例方程，解方程并检验．如果已知∠A ＝∠D ，探求△ABC 与△DEF 相似，只要把夹∠A 和∠D 的两边表示出来，按照对应边成比例，分AB DE AC DF =和AB DF AC DE=两种情况列方程．应用判定定理1解题，先寻找一组等角，再分两种情况讨论另外两组对应角相等．应用判定定理3解题不多见，根据三边对应成比例列连比式解方程（组）．还有一种情况，讨论两个直角三角形相似，如果一组锐角相等，其中一个直角三角形的锐角三角比是确定的，那么就转化为讨论另一个三角形是直角三角形的问题．求线段的长，要用到两点间的距离公式，而这个公式容易记错．理解记忆比较好．如图1，如果已知A 、B 两点的坐标，怎样求A 、B 两点间的距离呢？我们以AB 为斜边构造直角三角形，直角边与坐标轴平行，这样用勾股定理就可以求斜边AB 的长了．水平距离BC 的长就是A 、B 两点间的水平距离，等于A 、B 两点的横坐标相减；竖直距离AC 就是A 、B 两点间的竖直距离，等于A 、B 两点的纵坐标相减．图1例 1 2014年省市中考第28题二次函数y ＝a x 2＋b x ＋c （a ≠0）的图象与x 轴交于A (－3, 0)、B (1, 0)两点，与y 轴交于点C (0,－3m )（m ＞0），顶点为D ．（1）求该二次函数的解析式（系数用含m 的代数式表示）；（2）如图1，当m ＝2时，点P 为第三象限抛物线上的一个动点，设△APC 的面积为S ，试求出S 与点P 的横坐标x 之间的函数关系式及S 的最大值；（3）如图2，当m 取何值时，以A 、D 、C 三点为顶点的三角形与△OBC 相似？图1 图2动感体验请打开几何画板文件名“1428”，拖动点P 运动，可以体验到，当点P 运动到AC 的中点的正下方时，△APC 的面积最大．拖动y 轴上表示实数m 的点运动，抛物线的形状会改变，可以体验到，∠ACD 和∠ADC 都可以成为直角．思路点拨1．用交点式求抛物线的解析式比较简便．2．连结OP ，△APC 可以割补为：△AOP 与△COP 的和，再减去△AOC ．3．讨论△ACD 与△OBC 相似，先确定△ACD 是直角三角形，再验证两个直角三角形是否相似．4．直角三角形ACD 存在两种情况．图文解析（1）因为抛物线与x 轴交于A (－3, 0)、B (1, 0)两点，设y ＝a (x ＋3)(x －1)．代入点C (0,－3m )，得－3m ＝－3a ．解得a ＝m ．所以该二次函数的解析式为y ＝m (x ＋3)(x －1)＝mx 2＋2mx －3m ．（2）如图3，连结OP ．当m ＝2时，C (0,－6)，y ＝2x 2＋4x －6，那么P (x , 2x 2＋4x －6)．由于S △AOP ＝1()2P OA y ⨯-＝32-(2x 2＋4x －6)＝－3x 2－6x ＋9， S △COP ＝1()2P OC x ⨯-＝－3x ，S △AOC ＝9，所以S ＝S △APC ＝S △AOP ＋S △COP －S △AOC ＝－3x 2－9x ＝23273()24x -++．所以当32x =-时，S 取得最大值，最大值为274．图3 图4 图5（3）如图4，过点D 作y 轴的垂线，垂足为E ．过点A 作x 轴的垂线交DE 于F ．由y ＝m (x ＋3)(x －1)＝m (x ＋1)2－4m ，得D (－1,－4m )．在Rt △OBC 中，OB ∶OC ＝1∶3m ．如果△ADC 与△OBC 相似，那么△ADC 是直角三角形，而且两条直角边的比为1∶3m ．①如图4，当∠ACD ＝90°时，OA OC EC ED =．所以331m m =．解得m ＝1．此时3CA OC CD ED ==，3OC OB =．所以CA OC CD OB =．所以△CDA ∽△OBC ． ②如图5，当∠ADC ＝90°时，FA FD ED EC =．所以421m m=．解得2m =．此时222DA FD DC EC m===，而3232OC m OB ==．因此△DCA 与△OBC 不相似．综上所述，当m ＝1时，△CDA ∽△OBC ．考点伸展第（2）题还可以这样割补：如图6，过点P 作x 轴的垂线与AC 交于点H ．由直线AC ：y ＝－2x －6，可得H (x ,－2x －6)．又因为P (x , 2x 2＋4x －6)，所以HP ＝－2x 2－6x ．因为△PAH 与△PCH 有公共底边HP ，高的和为A 、C 两点间的水平距离3，所以S ＝S △APC ＝S △APH ＋S △CPH＝32(－2x 2－6x ) ＝23273()24x -++．图6例2 2014年省市中考第21题如图1，在直角梯形ABCD中，AB//CD，AD⊥AB，∠B＝60°，AB＝10，BC＝4，点P沿线段AB从点A向点B运动，设AP＝x．2·1·c·n·j·y（1）求AD的长；（2）点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由；（3）设△ADP与△PCB的外接圆的面积分别为S1、S2，若S＝S1＋S2，求S的最小值.动感体验图1请打开几何画板文件名“1421”，拖动点P在AB上运动，可以体验到，圆心O的运动轨迹是线段BC的垂直平分线上的一条线段．观察S随点P运动的图象，可以看到，S有最小值，此时点P看上去象是AB的中点，其实离得很近而已．思路点拨1．第（2）题先确定△PCB是直角三角形，再验证两个三角形是否相似．2．第（3）题理解△PCB的外接圆的圆心O很关键，圆心O在确定的BC的垂直平分线上，同时又在不确定的BP的垂直平分线上．而BP与AP是相关的，这样就可以以AP 为自变量，求S的函数关系式．图文解析（1）如图2，作CH⊥AB于H，那么AD＝CH．在Rt△BCH中，∠B＝60°，BC＝4，所以BH＝2，CH＝23．所以AD＝23．（2）因为△APD是直角三角形，如果△APD与△PCB相似，那么△PCB一定是直角三角形．①如图3，当∠CPB＝90°时，AP＝10－2＝8．所以APAD ＝23＝43，而PCPB＝3．此时△APD与△PCB不相似．图2 图3 图4 ②如图4，当∠BCP＝90°时，BP＝2BC＝8．所以AP＝2．所以AP AD ＝23＝3．所以∠APD ＝60°．此时△APD ∽△CBP ．综上所述，当x ＝2时，△APD ∽△CBP ．（3）如图5，设△ADP 的外接圆的圆心为G ，那么点G 是斜边DP 的中点．设△PCB 的外接圆的圆心为O ，那么点O 在BC 边的垂直平分线上，设这条直线与BC 交于点E ，与AB 交于点F ．设AP ＝2m ．作OM ⊥BP 于M ，那么BM ＝PM ＝5－m ．在Rt △BEF 中，BE ＝2，∠B ＝60°，所以BF ＝4．在Rt △OFM 中，FM ＝BF －BM ＝4－(5－m )＝m －1，∠OFM ＝30°，所以OM ＝3(1)m -．所以OB 2＝BM 2＋OM 2＝221(5)(1)3m m -+-．在Rt △ADP 中，DP 2＝AD 2＋AP 2＝12＋4m 2．所以GP 2＝3＋m 2．于是S ＝S 1＋S 2＝π(GP 2＋OB 2)＝22213(5)(1)3m m m π⎡⎤++-+-⎢⎥⎣⎦＝2(73285)3m m π-+．所以当167m =时，S 取得最小值，最小值为1137π．图5 图6考点伸展关于第（3）题，我们再讨论个问题．问题1，为什么设AP ＝2m 呢？这是因为线段AB ＝AP ＋PM ＋BM ＝AP ＋2BM ＝10．这样BM ＝5－m ，后续可以减少一些分数运算．这不影响求S 的最小值．问题2，如果圆心O 在线段EF 的延长线上，S 关于m 的解析式是什么？如图6，圆心O 在线段EF 的延长线上时，不同的是FM ＝BM －BF ＝(5－m )－4＝1－m ．此时OB 2＝BM 2＋OM 2＝221(5)(1)3m m -+-．这并不影响S 关于m 的解析式．例 3 2015年省湘西市中考第26题如图1，已知直线y ＝－x ＋3与x 轴、y 轴分别交于A 、B 两点，抛物线y ＝－x 2＋bx ＋c 经过A 、B 两点，点P 在线段OA 上，从点O 出发，向点A 以每秒1个单位的速度匀速运动；同时，点Q 在线段AB 上，从点A 出发，向点B 以每秒2个单位的速度匀速运动，连结PQ ，设运动时间为t 秒．（1）求抛物线的解析式；（2）问：当t 为何值时，△APQ 为直角三角形；（3）过点P 作PE //y 轴，交AB 于点E ，过点Q 作QF //y 轴，交抛物线于点F ，连结EF ，当EF //PQ 时，求点F 的坐标；（4）设抛物线顶点为M ，连结BP 、BM 、MQ ，问：是否存在t 的值，使以B 、Q 、M 为顶点的三角形与以O 、B 、P 为顶点的三角形相似？若存在，请求出t 的值；若不存在，请说明理由．图1动感体验请打开几何画板文件名“15湘西26”，拖动点P 在OA 上运动，可以体验到，△APQ 有两个时刻可以成为直角三角形，四边形EPQF 有一个时刻可以成为平行四边形，△MBQ 与△BOP 有一次机会相似．思路点拨1．在△APQ 中，∠A ＝45°，夹∠A 的两条边AP 、AQ 都可以用t 表示，分两种情况讨论直角三角形APQ ．2．先用含t 的式子表示点P 、Q 的坐标，进而表示点E 、F 的坐标，根据PE ＝QF 列方程就好了．3．△MBQ 与△BOP 都是直角三角形，根据直角边对应成比例分两种情况讨论．图文解析（1）由y ＝－x ＋3，得A (3, 0)，B (0, 3)．将A (3, 0)、B (0, 3)分别代入y ＝－x 2＋bx ＋c ，得930,3.b c c -++=⎧⎨=⎩ 解得2,3.b c =⎧⎨=⎩ 所以抛物线的解析式为y ＝－x 2＋2x ＋3．（2）在△APQ 中，∠PAQ ＝45°，AP ＝3－t ，AQ ＝2t ．分两种情况讨论直角三角形APQ ：①当∠PQA ＝90°时，AP ＝2AQ ．解方程3－t ＝2t ，得t ＝1（如图2）．②当∠QPA ＝90°时，AQ ＝2AP ．解方程2t ＝2(3－t )，得t ＝1.5（如图3）．图2 图3（3）如图4，因为PE //QF ，当EF //PQ 时，四边形EPQF 是平行四边形．所以EP ＝FQ ．所以y E －y P ＝y F －y Q ．因为x P ＝t ，x Q ＝3－t ，所以y E ＝3－t ，y Q ＝t ，y F ＝－(3－t )2＋2(3－t )＋3＝－t 2＋4t ．因为y E －y P ＝y F －y Q ，解方程3－t ＝(－t 2＋4t )－t ，得t ＝1，或t ＝3（舍去）．所以点F 的坐标为(2, 3)．图4 图5（4）由y ＝－x 2＋2x ＋3＝－(x －1)2＋4，得M (1, 4)．由A (3, 0)、B (0, 3)，可知A 、B 两点间的水平距离、竖直距离相等，AB ＝2．由B (0, 3)、M (1, 4)，可知B 、M 两点间的水平距离、竖直距离相等，BM 2 所以∠MBQ ＝∠BOP ＝90°．因此△MBQ 与△BOP 相似存在两种可能： ①当BM OB BQ OP =23322t t=-．解得94t =（如图5）． ②当BM OP BQ OB =23322t t =-．整理，得t 2－3t ＋3＝0．此方程无实根．考点伸展第（3）题也可以用坐标平移的方法：由P (t , 0)，E (t , 3－t )，Q(3－t , t )，按照P →E 方向，将点Q 向上平移，得F (3－t , 3)．再将F (3－t , 3)代入y ＝－x 2＋2x ＋3，得t ＝1，或t ＝3．§1．2 因动点产生的等腰三角形问题课前导学我们先回顾两个画图问题：1．已知线段AB ＝5厘米，以线段AB 为腰的等腰三角形ABC 有多少个？顶点C 的轨迹是什么？2．已知线段AB ＝6厘米，以线段AB 为底边的等腰三角形ABC 有多少个？顶点C 的轨迹是什么？已知腰长画等腰三角形用圆规画圆，圆上除了两个点以外，都是顶点C ．已知底边画等腰三角形，顶角的顶点在底边的垂直平分线上，垂足要除外．在讨论等腰三角形的存在性问题时，一般都要先分类．如果△ABC 是等腰三角形，那么存在①AB ＝AC ，②BA ＝BC ，③CA ＝CB 三种情况．解等腰三角形的存在性问题，有几何法和代数法，把几何法和代数法相结合，可以使得解题又好又快．几何法一般分三步：分类、画图、计算．哪些题目适合用几何法呢？如果△ABC 的∠A （的余弦值）是确定的，夹∠A 的两边AB 和AC 可以用含x 的式子表示出来，那么就用几何法．①如图1，如果AB ＝AC ，直接列方程；②如图2，如果BA ＝BC ，那么1cos 2AC AB A =∠；③如图3，如果CA ＝CB ，那么1cos 2AB AC A =∠．代数法一般也分三步：罗列三边长，分类列方程，解方程并检验．如果三角形的三个角都是不确定的，而三个顶点的坐标可以用含x 的式子表示出来，那么根据两点间的距离公式，三边长（的平方）就可以罗列出来．图1 图2 图3例 9 2014年市中考第26题如图1，抛物线y ＝ax 2＋bx ＋c （a 、b 、c 是常数，a ≠0）的对称轴为y 轴，且经过(0,0)和1(,)16a 两点，点P 在该抛物线上运动，以点P 为圆心的⊙P 总经过定点A (0, 2)．（1）求a 、b 、c 的值；（2）求证：在点P 运动的过程中，⊙P 始终与x 轴相交；（3）设⊙P 与x 轴相交于M (x 1, 0)、N (x 2, 0)两点，当△AMN 为等腰三角形时，求圆心P 的纵坐标．图1动感体验请打开几何画板文件名“1426”，拖动圆心P 在抛物线上运动，可以体验到，圆与x 轴总是相交的，等腰三角形AMN 存在五种情况．思路点拨1．不算不知道，一算真奇妙，原来⊙P 在x 轴上截得的弦长MN ＝4是定值．2．等腰三角形AMN 存在五种情况，点P 的纵坐标有三个值，根据对称性，MA ＝MN 和NA ＝NM 时，点P 的纵坐标是相等的．图文解析（1）已知抛物线的顶点为(0,0)，所以y ＝ax 2．所以b ＝0，c ＝0．将1(,)16a 代入y ＝ax 2，得2116a =．解得14a =（舍去了负值）．（2）抛物线的解析式为214y x =，设点P 的坐标为21(,)4x x ．已知A (0, 2)，所以222411(2)4416PA x x x =+-+＞214x ．而圆心P 到x 轴的距离为214x ，所以半径PA ＞圆心P 到x 轴的距离．所以在点P 运动的过程中，⊙P 始终与x 轴相交．（3）如图2，设MN 的中点为H ，那么PH 垂直平分MN ．在Rt △PMH 中，2241416PM PA x ==+，22411()416PH x x ==，所以MH 2＝4．所以MH ＝2．因此MN ＝4，为定值．等腰△AMN 存在三种情况：①如图3，当AM ＝AN 时，点P 为原点O 重合，此时点P 的纵坐标为0．图2 图3 ②如图4，当MA ＝MN 时，在Rt △AOM 中，OA ＝2，AM ＝4，所以OM ＝23．此时x ＝OH ＝232+．所以点P 的纵坐标为22211(232)(31)42344x =+=+=+．如图5，当NA ＝NM 时，根据对称性，点P 的纵坐标为也为423+．图4 图5③如图6，当NA ＝NM ＝4时，在Rt △AON 中，OA ＝2，AN ＝4，所以ON ＝23．此时x ＝OH ＝232-．所以点P 的纵坐标为22211(232)(31)42344x =-=-=-．如图7，当MN ＝MA ＝4时，根据对称性，点P 的纵坐标也为423-．图6 图7考点伸展如果点P 在抛物线214y x =上运动，以点P 为圆心的⊙P 总经过定点B (0, 1)，那么在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．这是因为：设点P 的坐标为21(,)4x x ．已知B (0, 1)，所以2114PB x ==+．而圆心P 到直线y ＝－1的距离也为2114x +，所以半径PB ＝圆心P 到直线y ＝－1的距离．所以在点P 运动的过程中，⊙P 始终与直线y ＝－1相切．例 10 2014年省市中考第25题如图1，在平面直角坐标系中，O 为坐标原点，抛物线y ＝ax 2＋bx ＋c （a ≠0）过O 、B 、C 三点，B 、C 坐标分别为(10, 0)和1824(,)55-，以OB 为直径的⊙A 经过C 点，直线l 垂直x 轴于B 点．（1）求直线BC 的解析式；（2）求抛物线解析式及顶点坐标；（3）点M 是⊙A 上一动点（不同于O 、B ），过点M 作⊙A 的切线，交y 轴于点E ，交直线l 于点F ，设线段ME 长为m ，MF 长为n ，请猜想mn 的值，并证明你的结论；（4）若点P 从O 出发，以每秒1个单位的速度向点B 作直线运动，点Q 同时从B 出发，以相同速度向点C 作直线运动，经过t （0＜t ≤8）秒时恰好使△BPQ 为等腰三角形，请求出满足条件的t 值．图图1 动感体验请打开几何画板文件名“1425”，拖动点M 在圆上运动，可以体验到，△EAF 保持直角三角形的形状，AM 是斜边上的高．拖动点Q 在BC 上运动，可以体验到，△BPQ 有三个时刻可以成为等腰三角形．思路点拨1．从直线BC 的解析式可以得到∠OBC 的三角比，为讨论等腰三角形BPQ 作铺垫．2．设交点式求抛物线的解析式比较简便．3．第（3）题连结AE 、AF 容易看到AM 是直角三角形EAF 斜边上的高．4．第（4）题的△PBQ 中，∠B 是确定的，夹∠B 的两条边可以用含t 的式子表示．分三种情况讨论等腰三角形．图文解析（1）直线BC 的解析式为31542y x =-．（2）因为抛物线与x 轴交于O 、B (10, 0)两点，设y ＝ax (x －10)．代入点C 1824(,)55-，得241832()555a -=⨯⨯-．解得524a =．所以2255255125(10)(5)2424122424y x x x x x =-=-=--．抛物线的顶点为125(5,)24-．（3）如图2，因为EF 切⊙A 于M ，所以AM ⊥EF ．由AE ＝AE ，AO ＝AM ，可得Rt △AOE ≌Rt △AME ．所以∠1＝∠2．同理∠3＝∠4．于是可得∠EAF ＝90°．所以∠5＝∠1．由tan ∠5＝tan ∠1，得MA ME MF MA=．所以ME ·MF ＝MA 2，即mn ＝25．图2（4）在△BPQ 中，cos ∠B ＝45，BP ＝10－t ，BQ ＝t ．分三种情况讨论等腰三角形BPQ ： ①如图3，当BP ＝BQ 时，10－t ＝t ．解得t ＝5．②如图4，当PB ＝PQ 时，1cos 2BQ BP B =∠．解方程14(10)25t t =-，得8013t =． ③如图5，当QB ＝QP 时，1cos 2BP BQ B =∠．解方程14(10)25t t -=，得5013t =．图3 图4 图5考点伸展在第（3）题条件下，以EF 为直径的⊙G 与x 轴相切于点A ．如图6，这是因为AG 既是直角三角形EAF 斜边上的中线，也是直角梯形EOBF 的中位线，因此圆心G 到x 轴的距离等于圆的半径，所以⊙G 与x 轴相切于点A ．图6例11 2014年省市中考第26题在平面直角坐标系中，抛物线y＝x2－(m＋n)x＋mn（m＞n）与x轴相交于A、B两点（点A位于点B的右侧），与y轴相交于点C．（1）若m＝2，n＝1，求A、B两点的坐标；（2）若A、B两点分别位于y轴的两侧，C点坐标是(0,－1)，求∠ACB的大小；（3）若m＝2，△ABC是等腰三角形，求n的值．动感体验请打开几何画板文件名“1426”，点击屏幕左下方的按钮（2），拖动点A在x轴正半轴上运动，可以体验到，△ABC保持直角三角形的形状．点击屏幕左下方的按钮（3），拖动点B在x轴上运动，观察△ABC的顶点能否落在对边的垂直平分线上，可以体验到，等腰三角形ABC有4种情况．思路点拨1．抛物线的解析式可以化为交点式，用m，n表示点A、B、C的坐标．2．第（2）题判定直角三角形ABC，可以用勾股定理的逆定理，也可以用锐角的三角比．3．第（3）题讨论等腰三角形ABC，先把三边长（的平方）罗列出来，再分类解方程．图文解析（1）由y＝x2－(m＋n)x＋mn＝(x－m)(x－n)，且m＞n，点A位于点B的右侧，可知A(m, 0)，B(n, 0)．若m＝2，n＝1，那么A(2, 0)，B(1, 0)．．（2）如图1，由于C(0, mn)，当点C的坐标是(0,－1)，mn＝－1，OC＝1．若A、B两点分别位于y轴的两侧，那么OA·OB＝m(－n)＝－mn＝1．所以OC2＝OA·OB．所以OC OB．OA OC所以tan ∠1＝tan ∠2．所以∠1＝∠2．又因为∠1与∠3互余，所以∠2与∠3互余．所以∠ACB ＝90°．图1 图2 图3（3）在△ABC 中，已知A (2, 0)，B (n , 0)，C (0, 2n )．讨论等腰三角形ABC ，用代数法解比较方便：由两点间的距离公式，得AB 2＝(n －2)2，BC 2＝5n 2，AC 2＝4＋4n 2．①当AB ＝AC 时，解方程(n －2)2＝4＋4n 2，得43n =-（如图2）． ②当CA ＝CB 时，解方程4＋4n 2＝5n 2，得n ＝－2（如图3），或n ＝2（A 、B 重合，舍去）．③当BA ＝BC 时，解方程(n －2)2＝5n 2，得51n +=-（如图4），或51n -=（如图5）．图4 图5考点伸展第（2）题常用的方法还有勾股定理的逆定理．由于C (0, mn )，当点C 的坐标是(0,－1)，mn ＝－1．由A (m , 0)，B (n , 0)，C (0,－1)，得AB 2＝(m －n )2＝m 2－2mn ＋n 2＝m 2＋n 2＋2， BC 2＝n 2＋1，AC 2＝m 2＋1．所以AB 2＝BC 2＋AC 2．于是得到Rt △ABC ，∠ACB ＝90°．第（3）题在讨论等腰三角形ABC 时，对于CA ＝CB 的情况，此时A 、B 两点关于y轴对称，可以直接写出B (－2, 0)，n ＝－2．例 12 2014年省市中考第27题如图1，在△ABC 中，∠ACB ＝90°，AC ＝4cm ，BC ＝3cm ．如果点P 由点B 出发沿BA 方向向点A 匀速运动，同时点Q 由点A 出发沿AC 方向向点C 匀速运动，它们的速度均为1cm/s ．连结PQ ，设运动时间为t （s ）（0＜t ＜4），解答下列问题：（1）设△APQ 的面积为S ，当t 为何值时，S 取得最大值？S 的最大值是多少？（2）如图2，连结PC ，将△PQC 沿QC 翻折，得到四边形PQP ′C ，当四边形PQP ′C 为菱形时，求t 的值；（3）当t 为何值时，△APQ 是等腰三角形？图1 图2动感体验请打开几何画板文件名“1427”，拖动点Q 在AC 上运动，可以体验到，当点P 运动到AB 的中点时，△APQ 的面积最大，等腰三角形APQ 存在三种情况．还可以体验到，当QC ＝2HC 时，四边形PQP ′C 是菱形．思路点拨1．在△APQ 中，∠A 是确定的，夹∠A 的两条边可以用含t 的式子表示．2．四边形PQP ′C 的对角线保持垂直，当对角线互相平分时，它是菱形，．图文解析（1）在Rt △ABC 中，AC ＝4，BC ＝3，所以AB ＝5，sin A ＝35，cos A ＝45．作QD ⊥AB 于D ，那么QD ＝AQ sin A ＝35t ．所以S ＝S △APQ ＝12AP QD ⋅＝13(5)25t t -⨯＝23(5)10t t --＝23515()+1028t --．当52t =时，S 取得最大值，最大值为158．（2）设PP ′与AC 交于点H ，那么PP ′⊥QC ，AH ＝AP cos A ＝4(5)5t -．如果四边形PQP ′C 为菱形，那么PQ ＝PC ．所以QC ＝2HC ．解方程4424(5)5t t ⎡⎤-=⨯--⎢⎥⎣⎦，得2013t =．图3 图4（3）等腰三角形APQ 存在三种情况：①如图5，当AP ＝AQ 时，5－t ＝t ．解得52t =． ②如图6，当PA ＝PQ 时，1cos 2AQ AP A =．解方程14(5)25t t =-，得4013t =． ③如图7，当QA ＝QP 时，1cos 2AP AQ A =．解方程14(5)25t t -=，得2513t =．图5 图6 图7考点伸展在本题情境下，如果点Q 是△PP ′C 的重心，求t 的值．如图8，如果点Q 是△PP ′C 的重心，那么QC ＝23HC ．解方程2444(5)35t t ⎡⎤-=⨯--⎢⎥⎣⎦，得6023t =．图8例 13 2015年省市中考第22题如图1，已知Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，点P 以每秒1个单位的速度从A 向C 运动，同时点Q 以每秒2个单位的速度从A →B →C 方向运动，它们到C 点后都停止运动，设点P 、Q 运动的时间为t 秒．（1）在运动过程中，求P 、Q 两点间距离的最大值；（2）经过t 秒的运动，求△ABC 被直线PQ 扫过的面积S 与时间t 的函数关系式；（3）P ，Q 两点在运动过程中，是否存在时间t ，使得△PQC 为等腰三角形．若存在，求出此时的t 值，若不存在，请说明理由．（24.25≈，结果保留一位小数）图1动感体验请打开几何画板文件名“1522”，拖动点P 在AC 上运动，可以体验到，PQ 与BD 保持平行，等腰三角形PQC 存在三种情况．思路点拨1．过点B 作QP 的平行线交AC 于D ，那么BD 的长就是PQ 的最大值．2．线段PQ 扫过的面积S 要分两种情况讨论，点Q 分别在AB 、BC 上．3．等腰三角形PQC 分三种情况讨论，先罗列三边长．图文解析（1）在Rt △ABC 中，AC ＝8，BC ＝6，所以AB ＝10．如图2，当点Q 在AB 上时，作BD //PQ 交AC 于点D ，那么22AB AQ t AD AP t===．所以AD ＝5．所以CD ＝3．如图3，当点Q 在BC 上时，16228CQ t CP t-==-．又因为623CB CD ==，所以CQ CB CP CD =．因此PQ //BD ．所以PQ 的最大值就是BD ．在Rt △BCD 中，BC ＝6，CD ＝3，所以BD ＝35．所以PQ 的最大值是35．图2 图3 图4（2）①如图2，当点Q 在AB 上时，0＜t ≤5，S △ABD ＝15．由△AQP ∽△ABD ，得2()AQPABDS AP S AD =△△．所以S ＝S △AQP ＝215()5t ⨯＝235t ． ②如图3，当点Q 在BC 上时，5＜t ≤8，S △ABC ＝24．因为S △CQP ＝12CQ CP ⋅＝1(162)(8)2t t --＝2(8)t -，所以S ＝S △ABC －S △CQP ＝24－(t －8)2＝－t 2＋16t －40．（3）如图3，当点Q 在BC 上时，CQ ＝2CP ，∠C ＝90°，所以△PQC 不可能成为等腰三角形．当点Q 在AB 上时，我们先用t 表示△PQC 的三边长：易知CP ＝8－t ．如图2，由QP //BD ，得QP AP BD AD =，即535t =．所以35QP t =．如图4，作QH ⊥AC 于H ．在Rt △AQH 中，QH ＝AQ sin ∠A ＝65t ，AH ＝85t ．在Rt △CQH 中，由勾股定理，得CQ ＝22QH CH +＝2268()(8)55t t +-．分三种情况讨论等腰三角形PQC ：（1）①当PC ＝PQ 时，解方程358t t -=，得6510t =-≈3.4（如图5所示）． ②当QC ＝QP 时，226835()(8)55t t t +-=．整理，得2111283200t t -+=．所以(11t －40)(t －8)＝0．解得4011t =≈3.6（如图6所示），或t ＝8（舍去）． ③当CP ＝CQ 时，22688()(8)55t t t -=+-．整理，得25160t t -=．解得165t =＝3.2（如图7所示），或t ＝0（舍去）．综上所述，当t 的值约为3.4，3.6，或等于3.2时，△PQC 是等腰三角形．图5 图6 图7考点伸展第（1）题求P 、Q 两点间距离的最大值，可以用代数计算说理的方法：①如图8，当点Q 在AB 上时，PQ ＝22QH PH +＝2268()()55t t t +-＝35t ．当Q 与B 重合时，PQ 最大，此时t ＝5，PQ 的最大值为35．②如图9，当点Q 在BC 上时，PQ ＝22CQ CP +＝22(2)CP CP +＝5(8)t -．当Q 与B 重合时，PQ 最大，此时t ＝5，PQ 的最大值为35．综上所述，PQ 的最大值为35．图8 图9§1．3 因动点产生的直角三角形问题课前导学我们先看三个问题：1．已知线段AB ，以线段AB 为直角边的直角三角形ABC 有多少个？顶点C 的轨迹是什么？2．已知线段AB ，以线段AB 为斜边的直角三角形ABC 有多少个？顶点C 的轨迹是什么？3．已知点A (4,0)，如果△OAB 是等腰直角三角形，求符合条件的点B 的坐标．图1 图2 图3如图1，点C 在垂线上，垂足除外．如图2，点C 在以AB 为直径的圆上，A 、B 两点除外．如图3，以OA为边画两个正方形，除了O、A两点以外的顶点和正方形对角线的交点，都是符合题意的点B，共6个．解直角三角形的存在性问题，一般分三步走，第一步寻找分类标准，第二步列方程，第三步解方程并验根．一般情况下，按照直角顶点或者斜边分类，然后按照三角比或勾股定理列方程．有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便．解直角三角形的问题，常常和相似三角形、三角比的问题联系在一起．如果直角边与坐标轴不平行，那么过三个顶点作与坐标轴平行的直线，可以构造两个新的相似直角三角形，这样列比例方程比较简便．如图4，已知A(3, 0)，B(1,－4)，如果直角三角形ABC的顶点C在y轴上，求点C的坐标．我们可以用几何的方法，作AB为直径的圆，快速找到两个符合条件的点C．如果作BD⊥y轴于D，那么△AOC∽△CDB．设OC＝m，那么341mm-=．这个方程有两个解，分别对应图中圆与y轴的两个交点．图4例19 2015年省市中考第21题如图1，已知抛物线E1：y＝x2经过点A(1,m)，以原点为顶点的抛物线E2经过点B(2,2)，点A、B关于y轴的对称点分别为点A′、B′．（1）求m的值及抛物线E2所表示的二次函数的表达式；（2）如图1，在第一象限，抛物线E1上是否存在点Q，使得以点Q、B、B′为顶点的三角形为直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由；（3）如图2，P为第一象限的抛物线E1上与点A不重合的一点，连结OP并延长与抛物线E2相交于点P′，求△PAA′与△P′BB′的面积之比．。

2018年全国各地中考数学真题汇编圆(图片版)

2018年全国各地中考数学真题汇编圆（图片版）2018年全国各地中考数学真题汇编圆（图片版）2018^中考数学真题汇编;同（填空催择46題！1”已却00：的半轻为玄巧O0丄的半径力丄伽，圖匚也06=站心则©6吕00的位羞矣系*处离E.外切c. ffiS氏內切【笞莉R乩如◎」効0。

的直径，CD^ O6?的弦，止亠.几贝1 ＜住的度塹为（A- S5E・亦G 55*b.6亍【薛肮虫已却半妙s葩e是ZUBC前外接戲若Z1BC=254 "噸焕啲长为（）18【答和C4.如图，衽SiSUD中，丄5 =眄,O匚的半轻対禺则国中阴崔部廿的面乘罡（：）【答秦】cS •如图N 是圆0的弦,X 丄AB,交圆0于点C,连接(^,佃』6若厶心20°测厶・0B 的度数是〈)CA.40° E. 50° C. 70° D.80°【答案】D 匕•如图，荡占旦丁近彳烤作生圆椎和圆柱绢必若用毛也苔建一个底面圆面枳为找开丫，圆乜高为叽同稚高为加白障占包.贝I 需要毛玷爭面枳杲()址3 0+5 炳)ndB. dOXn^CI3O+5^21)^in-D.557Tn ;【答案】A匚如虱从一块直疑为加的郎:•铁支上商出一个凰心争为90 °的扇形•则此扇形的曲积为＜A. T 加c. m2D ・2oPrwi A8•用反证法证明呵，假设结论“点在圆外”不成立，那么点与圆的位砂系只能罡＜＞A. •旦右内E.点存同上上【答案】D 匚・，点在匡心 D.点在區上或国内 9•如西AD 是圆锥昭线，氏为底面言径，已知DSGg 圆锥们面积为15b/ 、则轴厶攵旳值旳C.【答案】C血如图所示，AB 是O )的直空"切6于点亀线段F0交Go 于点S 曲BC ，若ZP=33^ ,则NE 爷于( ＞。

B. 32*C. 36・D. 54*【答亲】人11•如图，GU 过点0(0 0)，dTLo), zXo.l),点万定'轴下方Q •｛上的一点，洼授万6 BD, 则z OBZ)的克迫足( )A 1>B・30・ C. 45*D・ 60°【笞案】BJL2 •如團，AC^Cu的言径，弦创丄AU于E,连^BU, 11*0作5一氏于F,若EWNs, AE=Zcm,则OF 的长度是（）【筈秦】D13•如西在ZSA3C中，ZACB=90° ,厶咖。

中考数学试题-2018年全国中考数学压轴题精选精析(5份) 最新

2018年全国中考数学压轴题精选精析（二）14（18江苏常州）（本题答案暂缺）28.如图,抛物线24y x x =+与x 轴分别相交于点B 、O ,它的顶点为A ,连接AB,把AB 所的直线沿y 轴向上平移,使它经过原点O,得到直线l ,设P 是直线l 上一动点.(1) 求点A 的坐标; (2) 以点A 、B 、O 、P 为顶点的四边形中,有菱形、等腰梯形、直角梯形,请分别直接写出这些特殊四边形的顶点P 的坐标;(3) 设以点A 、B 、O 、P 为顶点的四边形的面积为S,点P 的横坐标为x,当46S +≤≤+,求x 的取值范围.13（18江苏淮安）（本题答案暂缺）28．(本小题14分)如图所示，在平面直角坐标系中．二次函数y=a(x-2)2-1图象的顶点为P ，与x 轴交点为 A 、B ，与y 轴交点为C ．连结BP 并延长交y 轴于点D. (1)写出点P 的坐标；(2)连结AP ，如果△APB 为等腰直角三角形，求a 的值及点C 、D 的坐标； (3)在(2)的条件下，连结BC 、AC 、AD ，点E(0，b)在线段CD(端点C 、D 除外)上,将△BCD 绕点E 逆时针方向旋转90°，得到一个新三角形．设该三角形与△ACD 重叠部分的面积为S ，根据不同情况，分别用含b 的代数式表示S ．选择其中一种情况给出解答过程，其它情况直接写出结果；判断当b 为何值时,重叠部分的面积最大?写出最大值．14（18江苏连云港）24．（本小题满分14分）如图，现有两块全等的直角三角形纸板Ⅰ，Ⅱ，它们两直角边的长分别为1和2．将它们分别放置于平面直角坐标系中的AOB △，COD △处，直角边OB OD ，在x 轴上．一直尺从上方紧靠两纸板放置，让纸板Ⅰ沿直尺边缘平行移动．当纸板Ⅰ移动至PEF △处时，设PE PF ，与OC 分别交于点M N ，，与x 轴分别交于点G H ，．(第28题）（第24题图）（1）求直线AC 所对应的函数关系式；（2）当点P 是线段AC （端点除外）上的动点时，试探究：①点M 到x 轴的距离h 与线段BH 的长是否总相等？请说明理由；②两块纸板重叠部分（图中的阴影部分）的面积S 是否存在最大值？若存在，求出这个最大值及S 取最大值时点P 的坐标；若不存在，请说明理由．（18江苏连云港24题解析）24．解：（1）由直角三角形纸板的两直角边的长为1和2，知A C ，两点的坐标分别为(12)(21)，，，．设直线AC 所对应的函数关系式为y kx b =+． ················ 2分有221k b k b +=⎧⎨+=⎩，．解得13k b =-⎧⎨=⎩，．所以，直线AC 所对应的函数关系式为3y x =-+． ·············· 4分（2）①点M 到x 轴距离h 与线段BH 的长总相等．因为点C 的坐标为(21)，，所以，直线OC 所对应的函数关系式为12y x =．又因为点P 在直线AC 上，所以可设点P 的坐标为(3)a a -，．过点M 作x 轴的垂线，设垂足为点K ，则有MK h =．因为点M 在直线OC 上，所以有(2)M h h ，． ······ 6分因为纸板为平行移动，故有EF OB ∥，即EF GH ∥．又EF PF ⊥，所以PH GH ⊥．法一：故Rt Rt Rt MKG PHG PFE △∽△∽△，从而有12GK GH EF MK PH PF ===．得1122GK MK h ==，11(3)22GH PH a ==-．（第24题答图）所以13222OG OK GK h h h =-=-=．又有13(3)(1)22OG OH GH a a a =-=--=-． ··············· 8分所以33(1)22h a =-，得1h a =-，而1BH OH OB a =-=-，从而总有h BH =． ···························· 10分法二：故Rt Rt PHG PFE △∽△，可得12GH EF PH PF =-．故11(3)22GH PH a ==-．所以13(3)(1)22OG OH GH a a a =-=--=-．故G 点坐标为3(1)02a ⎛⎫-⎪⎝⎭，．设直线PG 所对应的函数关系式为y cx d =+，则有330(1)2a ca d c a d -=+⎧⎪⎨=-+⎪⎩，．解得233c d a =⎧⎨=-⎩ 所以，直线PG 所对的函数关系式为2(33)y x a =+-． ············ 8分将点M 的坐标代入，可得4(33)h h a =+-．解得1h a =-．而1BH OH OB a --=-，从而总有h BH =． ················ 10分 ②由①知，点M 的坐标为(221)a a --，，点N 的坐标为12a a ⎛⎫ ⎪⎝⎭，．ONH ONG S S S =-△△1111133(1)222222a NH OH OG h a a a -=⨯-⨯=⨯⨯-⨯⨯- 22133133224228a a a ⎛⎫=-+-=--+ ⎪⎝⎭． ···················12分当32a =时，S 有最大值，最大值为38． S 取最大值时点P 的坐标为3322⎛⎫⎪⎝⎭，． ···················· 14分15（18江苏连云港）25．（本小题满分12分）我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段AB 的最小覆盖圆就是以线段AB 为直径的圆．（1）请分别作出图1中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写AA作法）；（2）探究三角形的最小覆盖圆有何规律？请写出你所得到的结论（不要求证明）；（3）某地有四个村庄E F G H ，，，（其位置如图2所示），现拟建一个电视信号中转站，为了使这四个村庄的居民都能接收到电视信号，且使中转站所需发射功率最小（距离越小，所需功率越小），此中转站应建在何处？请说明理由．（18江苏连云港25题解析）25．解：（1）如图所示： ············· 4分（注：正确画出1个图得2分，无作图痕迹或痕迹不正确不得分）（2）若三角形为锐角三角形，则其最小覆盖圆为其外接圆； ··········· 6分若三角形为直角或钝角三角形，则其最小覆盖圆是以三角形最长边（直角或钝角所对的边）为直径的圆． ······························· 8分（3）此中转站应建在EFH △的外接圆圆心处（线段EF 的垂直平分线与线段EH 的垂直平分线的交点处）． ················ 10分理由如下：由47.835.182.9HEF HEG GEF ∠=∠+∠=+=，50.0EHF ∠=，47.1EFH ∠=，G49.8F53.8 44.0 47.1 35.1 47.8 50.0 （第25题图2） 80 100 （第25题答图1）32.4 49.8 F53.8 44.047.135.147.8 50.0故EFH △是锐角三角形，所以其最小覆盖圆为EFH △的外接圆，设此外接圆为O ，直线EG 与O 交于点E M ，，则50.053.8EMF EHF EGF ∠=∠=<=∠．故点G 在O 内，从而O 也是四边形EFGH 的最小覆盖圆．所以中转站建在EFH △的外接圆圆心处，能够符合题中要求．························ 12分16（18江苏南京）28．（10分）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为(h)x ，两车之间的距离．．．．．．．为(km)y ，图中的折线表示y 与x 之间的函数关系．根据图象进行以下探究：信息读取（1）甲、乙两地之间的距离为 km ；（2）请解释图中点B 的实际意义；图象理解（3）求慢车和快车的速度；（4）求线段BC 所表示的y 与x 之间的函数关系式，并写出自变量x 的取值范围；问题解决（5）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？（18江苏南京28题解析）28．（本题10分）解：（1）900； ······························· 1分（2）图中点B 的实际意义是：当慢车行驶4h 时，慢车和快车相遇． ······· 2分（3）由图象可知，慢车12h 行驶的路程为900km ，所以慢车的速度为90075(km /h)12=； ···················· 3分当慢车行驶4h 时，慢车和快车相遇，两车行驶的路程之和为900km ，所以慢车和快车行驶的速度之和为900225(km /h)4=，所以快车的速度为150km/h ． ········· 4分（4）根据题意，快车行驶900km 到达乙地，所以快车行驶9006(h)150=到达乙地，此时两车之间的距离为675450(km)⨯=，所以点C 的坐标为(6450)，．设线段BC 所表示的y 与x 之间的函数关系式为y kx b =+，把(40)，，(6450)，代入得 044506.k b k b =+⎧⎨=+⎩，（第28题）y解得225900.k b =⎧⎨=-⎩，所以，线段BC 所表示的y 与x 之间的函数关系式为225900y x =-． ······ 6分自变量x 的取值范围是46x ≤≤． ····················· 7分（5）慢车与第一列快车相遇30分钟后与第二列快车相遇，此时，慢车的行驶时间是4.5h ．把 4.5x =代入225900y x =-，得112.5y =．此时，慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km ，所以两列快车出发的间隔时间是112.51500.75(h)÷=，即第二列快车比第一列快车晚出发0.75h ． · 10分 17（18江苏南通）（第28题14分） 28．已知双曲线k y x =与直线14y x =相交于A 、B 两点．第一象限上的点M （m ，n ）（在A 点左侧）是双曲线ky x=上的动点．过点B 作BD ∥y 轴交x 轴于点D ．过N （0，－n ）作NC ∥x 轴交双曲线ky x=于点E ，交BD 于点C ．（1）若点D 坐标是（－8，0），求A 、B 两点坐标及k 的值．（2）若B 是CD 的中点，四边形OBCE 的面积为4，求直线CM 的解析式．（3）设直线AM 、BM 分别与y 轴相交于P 、Q 两点，且MA =pMP ，MB =qMQ ，求p －q 的值．（18江苏南通28题解析）28．解：（1）∵D （－8，0），∴B 点的横坐标为－8，代入14y x =中，得y =－2．∴B 点坐标为（－8，－2）．而A 、B 两点关于原点对称，∴A （8，2）．从而8k =⨯．……………………………………………………………………3分（2）∵N （0，－n ），B 是CD 的中点，A 、B 、M 、E 四点均在双曲线上，∴mn k =，B （－2m ，－2n ），C （－2m ，－n ），E （－m ，－n ）． ……………4分（第28题）S 矩形DCNO 22mn k ==，S △DBO =1122mn k =，S △OEN =1122mn k =， ………………7分∴S 四边形OBCE = S 矩形DCNO －S △DBO － S △OEN =k ．∴4k =． …………………………8分由直线14y x =及双曲线4y x=，得A （4，1），B （－4，－1）， ∴C （－4，－2），M （2，2）．………………………………………………………9分设直线CM 的解析式是y ax b =+，由C 、M 两点在这条直线上，得 42,2 2.a b a b -+=-⎧⎨+=⎩ 解得23a b ==． ∴直线CM 的解析式是2233y x =+．………………………………………………11分（3）如图，分别作AA 1⊥x 轴，MM 1⊥x 轴，垂足分别为A 1、M 1．设A 点的横坐标为a ，则B 点的横坐标为－a ．于是111A M MA a mp MP M O m-===．同理Bm q Qm=13分∴2a m m ap q m m-+-=-=-．……………………14分18（18江苏宿迁）27．（本题满分12分）如图，⊙O 的半径为1，正方形ABCD 顶点B 坐标为)0,5(，顶点D 在⊙O 上运动． (1)当点D 运动到与点A 、O 在同一条直线上时,试证明直线CD 与⊙O 相切；(2)当直线CD 与⊙O 相切时，求CD 所在直线对应的函数关系式；(3)设点D 的横坐标为x ，正方形ABCD 的面积为S ，求S 与x 之间的函数关系式，并求出S 的最大值与最小值．（18江苏宿迁27题解析）27．解：(1) ∵四边形ABCD 为正方形 ∴CD AD ⊥ ∵A 、O 、D 在同一条直线上 ∴︒=∠90ODC ∴直线CD 与⊙O 相切； (2)直线CD 与⊙O 相切分两种情况:①如图1, 设1D 点在第二象限时,过1D 作x E D ⊥11轴于点1E ,设此时的正方形的边长为a ,则2225)1(=+-a a ,解得4=a 或3-=a (舍去)．由BOA Rt ∆∽11OE D Rt ∆ 得OBOD BA E D OA OE 1111== ∴54,53111==E D OE ∴)54,53(1-D ，故直线OD 的函数关系式为x y 34-=；②如图2, 设2D 点在第四象限时,过2D 作x E D ⊥22轴于点2E ,设此时的正方形的边长为b ,则2225)1(=++b b ,解得3=b 或4-=b (舍去)．由BOA Rt ∆∽22OE D Rt ∆得OBOD BA E D OA OE 2222==第27题图1第27题图2∴53,54222==E D OE ∴)53,54(2-D ，故直线OD 的函数关系式为x y 43-=. (3)设),(0y x D ,则201x y -±=,由)0,5(B 得x x x DB 1026)1()5(22-=-+-=∴x x BD S 513)1026(21212-=-==∵11≤≤-x∴851318513=-==+=最小值最大值，S S .19（18江苏泰州）29．已知二次函数)0(21≠++=a c bx ax y 的图象经过三点（1，0），（-3，0），（0，23-）。

决胜2018中考数学压轴题全揭秘精品：(压轴题)专题25动态几何之定值(恒等)问题(原卷版)

连接 ON，点 M 从点 E 开始沿线段 EH 向点 H 运动，至与点 N 重合时停止，△MOG 和△NOG 的面积分别表示为
S1 和 S2，在点 M 的运动过程中，S1S2（即 S1 与 S2 的积）的值是否发生变化？若变化，请直接写出变化范围；若不
变，请直接写出这个值．
温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．
19．（2015 河南）已知：如图 1，在面积为 3 的正方形 ABCD 中，E、F 分别是 BC 和 CD 边上的两点，AE⊥BF 于点 G，且 BE=1．（1）求证：△ABE≌△BCF；（2）求出△ABE 和△BCF 重叠部分（即△BEG）的面积；（3）现将△ABE 绕点 A 逆时针方向旋转到△AB′E′（如图 2），使点 E 落在 CD 边上的点 E′处，问△ABE 在旋转前后与△BCF 重叠部分的面积是否发生了变化？请说明理由．
（2）如图 2，已知直线 PA，PB 与 y 轴分别交于 E、F 两点．当点 P 运动时， OE OF 是否为定值？若是，试求 OC
出该定值；若不是，请说明理由．
9．（2016 贵州省黔南州）如图，在四边形 OABC 是边长为 4 的正方形，点 P 为 OA 边上任意一点（与点 O、A 不重合），连接 CP，过点 P 作 PM⊥CP 交 AB 于点 D，且 PM=CP，过点 M 作 MN∥AO，交 BO 于点 N，连结 ND、 BM，设 OP=t．（1）求点 M 的坐标（用含 t 的代数式表示）；
．
三、解答题资 *源%库 ziy 1
5．（2016 广东省深圳市）如图，已知⊙O 的半径为 2，AB 为直径，CD 为弦．AB 与 CD 交于点 M，将 CD 沿 CD
翻折后，点 A 与圆心 O 重合，延长 OA 至 P，使 AP=OA，连接 PC．（1）求 CD 的长；（2）求证：PC 是⊙O 的切线；

2018年中考数学圆压轴题专题复习

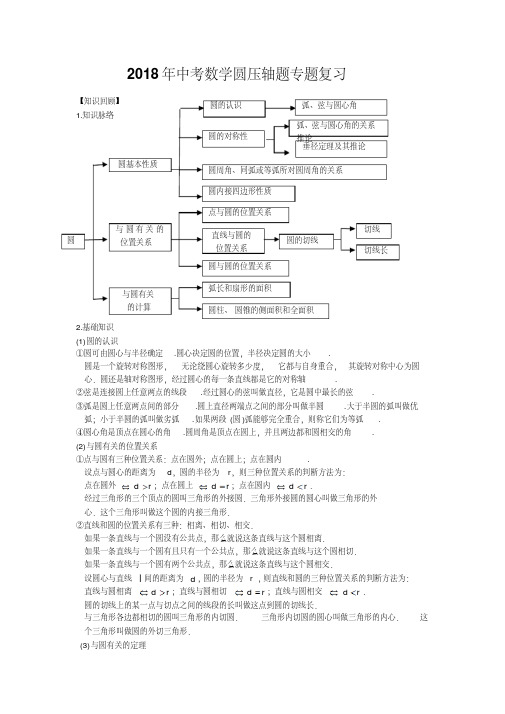
如图，△ ABC 是⊙ O 的内接三角形， AD ⊥BC 于 D 点， AE 是直径 .
说明： (1) AB·AC=AD ·AE；
(2) 延长 AD 交圆于点 F ，连结 BE， CF，则 BE=CF．
A
O
B
DC
E
如图，已知 AB 是⊙ O 的弦， OB=2，∠ B=30°， C 是弦 AB 上的任意一点 ( 不与点 A、 B
.
设点与圆心的距离为 d，圆的半径为 r，则三种位置关系的判断方法为：
点在圆外 d r ；点在圆上 d r ；点在圆内 d r ．
经过三角形的三个顶点的圆叫三角形的外接圆．三角形外接圆的圆心叫做三角形的外
心．这个三角形叫做这个圆的内接三角形．
②直线和圆的位置关系有三种：相离、相切、相交．
如果一条直线与一个圆没有公共点，那么就说这条直线与这个圆相离．
重合 ) ，连接 CO 并延长 CO 交⊙ O 于点 D ，连接 AD．
(1) 弦长 AB 等于
(
结果保留根号 ) ；
(2) 当∠ D=20°时，求∠ BOD 的度数；
(3) 当 AC 的长度为多少时，以 A， C， D 为顶点的三角形与以 B，C， O 为顶点的三角形
相似？请写出解答过程．
D
O
AC
弧长和扇形的面积圆柱、圆锥的侧面积和全面积
2.基础知识
(1) 圆的认识 ①圆可由圆心与半径确定 .圆心决定圆的位置，半径决定圆的大小 .
圆是一个旋转对称图形，无论绕圆心旋转多少度，它都与自身重合，其旋转对称中心为圆
心．圆还是轴对称图形，经过圆心的每一条直线都是它的对称轴
.
②弦是连接圆上任意两点的线段 .经过圆心的弦叫做直径，它是圆中最长的弦 .

2018天津市中考数学17题、圆、二次函数专项训练

1、如图，正方形ABCD，点E，F分别在AD，CD上，BG⊥EF，点G为垂足，AB=5，AE=1，CF=2，则BG= ．3、如图2，如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积为4，则阴影部分的面积为_________ ．4、如图，将Rt△ABC绕点A逆时针旋转40°，得到Rt△AB'C'，点C'恰好落在斜边AB上，连接BB'，则∠BB'C'＝_______．5、如图，正方形ABCD的面积为25，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为．6、如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=5，AC=2，则DF的长为________．8、如图，正三角形的边长为12cm，剪去三个角后成为一个正六边形，则这个正六边形的内部任意一点到各边的距离和为cm．10、如图，直线l过正方形ABCD的顶点B，点A，C到直线l的距离分别是2和3，则EF的长为__________．11、如图，在△ABC中，∠BAC=45°，AB=4 cm，将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′，则阴影部分的面积为：1、如图1，△ABC内接于⊙O，AC是直径，点D是AC延长线上一点，且∠DBC＝∠BAC，.(1)求证：BD是⊙O的切线；(2)求的值；(3) 如图2，直径AC=5，，求△ABF面积2、已知抛物线y=(m－1)x2＋(m－2)x－1与x轴交于A、B两点.(Ⅰ)求m的取值范围;(Ⅱ)若m＜0,且点A在点B的左侧,OA:OB=3:1,试确定抛物线的解析式;4、如图,在平面直角坐标系中,已知点A的坐标为(0,2),△ABO为等边三角形,P是x轴上的一个动点(不与O点重合),将线段AP绕A点按逆时针方向旋转60°,P点的对应点为点Q.(Ⅰ)求点B的坐标;(Ⅱ)当点P在x轴负半轴运动时,求证:∠ABQ=90°; (Ⅲ)连接OQ,在点P运动的过程中,当OQ平行AB时,求点P 的坐标.5、在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC 于点E.(Ⅰ)如图①,过点D作DF⊥AC,垂足为F,求证:直线DF与⊙O 相切;(Ⅱ)如图②,过点B作⊙O的切线,与AC的延长线交于点G,若∠BAC=35°,求∠CBG的大小.6、四边形ABCD 内接于⊙O ,AC 为其中一条对角线. (Ⅰ)如图①,若∠BAD =70°,BC =CD ,求∠BAC 的大小; (Ⅱ)如图②,若AD 经过圆心O ,连接OC ,AB =BC ,OC ∥AB ,求∠OCD 的大小.7、如图，AB 是⊙O 的直径，点P 在AB 的延长线上，弦CE 交AB 于点D ，连接OE ，AC ，且∠P ＝∠E ，∠POE ＝2∠CAB . (1)求证：CE ⊥AB ； (2)求证：PC 是⊙O 的切线；3．（丰台18期末26）在平面直角坐标系xOy 中，抛物线2y x bx c =-++经过点（2，3），对称轴为直线x =1.（1）求抛物线的表达式；（2）如果垂直于y 轴的直线l 与抛物线交于两点A （1x ，1y ），B （2x ，2y ），其中01<x ，02>x ，与y 轴交于点C ，求BC -AC 的值；（3）将抛物线向上或向下平移，使新抛物线的顶点落在x 轴上，原抛物线上一点P 平移后对应点为点Q ，如果OP =OQ ，直接写出点Q 的坐标.4．（昌平18期末26）在平面直角坐标系xOy 中，抛物线y=mx 2－2mx －3 (m ≠0)与y 轴交于点A ，其对称轴与x 轴交于点B 顶点为C 点．（1）求点A 和点B 的坐标；（2）若∠ACB =45°，求此抛物线的表达式；（3）在（2）的条件下，垂直于y 轴的直线l 与抛物线交于点P （x 1，y 1）和Q （x 2，y 2），与直线AB 交于点N （x 3，y 3），若x 3<x 1<x 2，结合函数的图象，直接写出x 1+x 2+x 3的取值范围为 .5．（朝阳18期末27）已知抛物线l 1与l 2形状相同，开口方向不同，其中抛物线l 1：2782--=ax ax y 交x 轴于A ，B两点（点A 在点B 的左侧），且AB ＝6；抛物线l 2与l 1交于点A 和点C （5，n ）.（1）求抛物线l 1，l 2的表达式；（2）当x 的取值范围是时，抛物线l 1与l 2上的点的纵坐标同时随横坐标的增大而增大；（3）直线MN ∥y 轴，交x 轴，l 1，l 2分别相交于点P （m ，0），M ，N ，当1≤m ≤7时，求线段MN 的最大值. 16．（顺义18期末28）在平面直角坐标系xOy 中，抛物线219y x bx =+经过点A （-3，4）．（1）求b 的值；（2）过点A 作x 轴的平行线交抛物线于另一点B ，在直线AB 上任取一点P ，作点A 关于直线OP 的对称点C ；①当点C 恰巧落在x 轴时，求直线OP 的表达式； ②连结BC ，求BC 的最小值．x yAO。

专题17 圆问题-决胜2018中考数学压轴题全揭秘精品(解析版)

一、选择题1．（2017临沂，第10题，3分）如图，AB是⊙O的直径，BT是⊙O的切线，若∠ATB=45°，AB=2，则阴影部分的面积是（）A．2B．3124π-C．1D．1124π+【答案】C．【分析】设AT交⊙O于D，连结BD，先根据圆周角定理得到∠ADB=90°，则可判断△ADB．△BDC都是等腰直角三角形，所以AD=BD=CD=22AB=2，然后利用弓形AD的面积等于弓形BD的面积得到阴影部分的面积=S△BTD．点睛：本题考查了切线的性质，等腰直角三角形的性质，解决本题的关键是利用等腰直角三角形的性质把阴影部分的面积转化为三角形的面积．考点：切线的性质；扇形面积的计算．2．（2017广西百色市，第11题，3分）以坐标原点O为圆心，作半径为2的圆，若直线y=﹣x+b与⊙O相交，则b的取值范围是（）A ．022b ≤<B ．2222b -≤≤C ．2323b -<<D ．2222b -<<【答案】D ．【分析】求出直线y =﹣x +b 与圆相切，且函数经过一、二、四象限，和当直线y =﹣x +b 与圆相切，且函数经过二、三、四象限时b 的值，则相交时b 的值在相切时的两个b 的值之间．【解析】当直线y =﹣x +b 与圆相切，且函数经过一、二、四象限时，如图．在y =﹣x +b 中，令x =0时，y =b ，则与y 轴的交点是（0，b ），当y =0时，x =b ，则A 的交点是（b ，0），则OA =OB ，即△OAB 是等腰直角三角形．连接圆心O 和切点C ．则OC =2，则OB =2OC =22．即b =22；同理，当直线y =﹣x +b 与圆相切，且函数经过二、三、四象限时，b =﹣22．则若直线y =﹣x +b 与⊙O 相交，则b 的取值范围是2222b -<<．故选D ．点睛：本题考查了切线的性质，正确证得直线y =﹣x +b 与圆相切时，可得△OAB 是等腰直角三角形是关键．考点：直线与圆的位置关系；一次函数图象与系数的关系．3．（2017江苏省无锡市，第9题，3分）如图，菱形ABCD 的边AB =20，面积为320，∠BAD ＜90°，⊙O 与边AB ，AD 都相切，AO =10，则⊙O 的半径长等于（）A ．5B ．6C ．25D ．32【答案】C ．【分析】如图作DH ⊥AB 于H ，连接BD ，延长AO 交BD 于E ．利用菱形的面积公式求出DH ，再利用勾股定理求出AH ，BD ，由△AOF ∽△DBH ，可得OA OF BD BH =，延长即可解决问题．【解析】如图作DH ⊥AB 于H ，连接BD ，延长AO 交BD 于E ．∵菱形ABCD 的边AB =20，面积为320，∴AB •DH =32O ，∴DH =16，在Rt △ADH 中，AH =22AD DH - =12，∴HB =AB ﹣AH =8，在Rt △BDH 中，BD =22DH BH +=85，设⊙O 与AB 相切于F ，连接AF ．∵AD =AB ，OA 平分∠DAB ，∴AE ⊥BD ，∵∠OAF +∠ABE =90°，∠ABE +∠BDH =90°，∴∠OAF =∠BDH ，∵∠AFO =∠DHB =90°，∴△AOF ∽△DBH ，∴OA OF BD BH =，∴885OF =，∴OF =25．故选C ．点睛：本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．考点：切线的性质；菱形的性质；综合题．学科.网4．（2017河北，第16题，2分）已知正方形MNOK 和正六边形ABCDEF 边长均为1，把正方形放在正六边形中，使OK 边与AB 边重合，如图所示，按下列步骤操作：将正方形在正六边形中绕点B 顺时针旋转，使KM 边与BC 边重合，完成第一次旋转；再绕点C 顺时针旋转，使MN 边与CD 边重合，完成第二次旋转；…在这样连续6次旋转的过程中，点B ，M 间的距离可能是（）A ．1.4B ．1.1C ．0.8D ．0.5【答案】C ．【分析】如图，在这样连续6次旋转的过程中，点M 的运动轨迹是图中的红线，观察图象可知点B ，M 间的距离大于0.5小于等于1，由此即可判断．【解析】如图，在这样连续6次旋转的过程中，点M 的运动轨迹是图中的红线，观察图象可知点B ，M 间的距离大于0.5小于等于1，故选C ．点睛：本题考查正六边形、正方形的性质等知识，解题的关键作出点M 的运动轨迹，利用图象解决问题，题目有一定的难度．考点：正多边形和圆；旋转的性质；操作型；综合题．5．（2017湖北省武汉市，第9题，3分）已知一个三角形的三边长分别为5、7、8，则其内切圆的半径为（）A ．23B ．23 C ．3 D ．32 【答案】C ．【分析】如图，AB =7，BC =5，AC =8，内切圆的半径为r ，切点为D 、E 、F ，作AD ⊥BC 于D ，设BD =x ，则CD =5﹣x ．由AD 2=AB 2﹣BD 2=AC 2﹣CD 2，可得72﹣x 2=82﹣（5﹣x ）2，解得x =1，推出AD =43，由12•BC •AD =12（AB +BC +AC ）•r ，列出方程即可解决问题．【解析】如图，AB =7，BC =5，AC =8，内切圆的半径为r ，切点为D 、E 、F ，作AD ⊥BC 于D ，设BD =x ，则CD =5﹣x ．由勾股定理可知：AD 2=AB 2﹣BD 2=AC 2﹣CD 2，即72﹣x 2=82﹣（5﹣x ）2，解得x =1，∴AD =43∵12•BC •AD =12（AB +BC +AC ）•r ，12×5×4312×20×r ，∴r 3C ．点睛：本题考查三角形的内切圆与内心、勾股定理、三角形的面积等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用面积法求内切圆的半径，属于中考常考题型．考点：三角形的内切圆与内心．6．（2017湖北省随州市，第10题，3分）如图，在矩形ABCD中，AB＜BC，E为CD边的中点，将△ADE 绕点E顺时针旋转180°，点D的对应点为C，点A的对应点为F，过点E作ME⊥AF交BC于点M，连接AM、BD交于点N，现有下列结论：①AM=AD+MC；②AM=DE+BM；③DE2=AD•CM；④点N为△ABM的外心．其中正确的个数为（）A．1个B．2个C．3个D．4个【答案】B．【分析】根据全等三角形的性质以及线段垂直平分线的性质，即可得出AM=MC+AD；根据当AB=BC时，四边形ABCD为正方形进行判断，即可得出当AB＜BC时，AM=DE+BM不成立；根据ME⊥FF，EC⊥MF，运用射影定理即可得出EC2=CM×CF，据此可得DE2=AD•CM成立；根据N不是AM的中点，可得点N不是△ABM的外心．【解析】∵E为CD边的中点，∴DE=CE，又∵∠D=∠ECF=90°，∠AED=∠FEC，∴△ADE≌△FCE，∴AD=CF，AE=FE，又∵ME⊥AF，∴ME垂直平分AF，∴AM=MF=MC+CF，∴AM=MC+AD，故①正确；当AB=BC时，即四边形ABCD为正方形时，设DE=EC=1，BM=a，则AB=2，BF=4，AM=FM=4﹣a，在Rt △ABM中，22+a2=（4﹣a）2，解得a=1.5，即BM=1.5，∴由勾股定理可得AM=2.5，∴DE+BM=2.5=AM，又∵AB＜BC，∴AM=DE+BM不成立，故②错误；∵ME⊥FF，EC⊥MF，∴EC2=CM×CF，又∵EC=DE，AD=CF，∴DE2=AD•CM，故③正确；∵∠ABM=90°，∴AM是△ABM的外接圆的直径，∵BM＜AD，∴当BM∥AD时，MN BMAN AD＜1，∴N不是AM的中点，∴点N不是△ABM的外心，故④错误．综上所述，正确的结论有2个，故选B．点睛：本题主要考查了相似三角形的判定与性质，全等三角形的判定与性质，矩形的性质以及旋转的性质的综合应用，解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例，解题时注意：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心，故外心到三角形三个顶点的距离相等．考点：相似三角形的判定与性质；全等三角形的判定与性质；矩形的性质；三角形的外接圆与外心；旋转的性质；综合题．7．（2017陕西省，第9题，3分）如图，△ABC是⊙O的内接三角形，∠C=30°，⊙O的半径为5，若点P 是⊙O上的一点，在△ABP中，PB=AB，则P A的长为（）A．5B．532C．52D．53【答案】D．【分析】连接OA、OB．OP，根据圆周角定理求得∠APB=∠C=30°，进而求得∠P AB=∠APB=30°，∠ABP=120°，根据垂径定理得到OB⊥AP，AD=PD，∠OBP=∠OBA=60°，即可求得△AOB是等边三角形，从而求得PB=OA=5，解直角三角形求得PD，即可求得P A．【解析】连接OA、OB、OP，∵∠C=30°，∴∠APB=∠C=30°，∵PB=AB，∴∠P AB=∠APB=30°∴∠ABP=120°，∵PB=AB，∴OB⊥AP，AD=PD，∴∠OBP=∠OBA=60°，∵OB=OA，∴△AOB是等边三角形，∴AB=OA=5，则Rt△PBD中，PD=cos30°•PB=32×5=53，∴AP=2PD=53，故选D．点睛：本题考查了圆周角定理、垂径定理、等边三角形的判定和性质以及解直角三角形等，作出辅助性构建等边三角形是解题的关键．考点：三角形的外接圆与外心；等腰三角形的性质．8．（2017山东省莱芜市，第12题，3分）如图，正五边形ABCDE的边长为2，连结AC、AD、BE，BE分别与AC和AD相交于点F、G，连结DF，给出下列结论：①∠FDG=18°；②FG=35；③（S四边形CDEF）2=9+5DF2﹣DG2=7﹣5）A．1B．2C．3D．4【答案】B．【分析】①先根据正五方形ABCDE的性质得：∠ABC=180°﹣3605=108°，由等边对等角可得：∠BAC=∠ACB=36°，再利用角相等求BC=CF=CD，得∠CDF=∠CFD=（180°-72°）÷2=54°，可得∠FDG=18°；②证明△ABF∽△ACB，得AB EGAC ED=，代入可得FG的长；③如图1，先证明四边形CDEF是平行四边形，根据平行四边形的面积公式可得：（S四边形CDEF）2= 10+5④如图2，▱CDEF是菱形，先计算EC=BE=4﹣FG=15S四边形CDEF=12FD•EC=210254+，可得FD2=10﹣5【解析】①∵五方形ABCDE是正五边形，∴AB=BC，∠ABC=180°﹣3605=108°，∴∠BAC=∠ACB=36°，∴∠ACD=108°﹣36°=72°，同理得：∠ADE=36°，∵∠BAE=108°，AB=AE，∴∠ABE=36°，∴∠CBF=108°﹣36°=72°，∴BC=FC，∵BC=CD，∴CD=CF，∴∠CDF=∠CFD=（180°-72°）÷2=54°，∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°；所以①正确；②∵∠ABE=∠ACB=36°，∠BAC=∠BAF，∴△ABF∽△ACB，∴AB EGAC ED=，∴AB•ED=AC•EG，∵AB=ED=2，AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG，EG=BG﹣FG=2﹣FG，∴22=（2﹣FG）（4﹣FG），∴FG=352（舍），FG=35所以②正确；③如图1，∵∠EBC=72°，∠BCD=108°，∴∠EBC+∠BCD=180°，∴EF∥CD，∵EF=CD=2，∴四边形CDEF是平行四边形，过D作DM⊥EG于M，∵DG=DE，∴EM=MG=12EG=12（EF﹣FG）=12（2﹣35=512-，由勾股定理得：DM=22DE EM-=22512()2-- =10254+，∴（S四边形CDEF）2=EF2×DM2=4×10254+=10+25；所以③不正确；④如图2，连接EC，∵EF=ED，∴▱CDEF是菱形，∴FD⊥EC，∵EC=BE=4﹣FG=4﹣（3﹣5）=1+5，∴S四边形CDEF=12FD•EC=2×10254+，12×FD×（1+5）=1025+，FD2=10﹣25，∴DF2﹣DG2=10﹣25﹣4=6﹣25，所以④不正确；本题正确的有两个，故选B．点睛：本题考查了相似三角形的判定和性质，勾股定理，正五边形的性质、平行四边形和菱形的判定和性质，有难度，熟练掌握正五边形的性质是解题的关键．考点：正多边形和圆；相似三角形的判定与性质；综合题．9．（2017四川省凉山州，第12题，4分）如图，一个半径为1的⊙O1经过一个半径为2的⊙O的圆心，则图中阴影部分的面积为（）A．1B．12C2D．22【答案】A．【分析】连接OA，OB，OO1，求出∠AOB=90°，进而利用S阴影部分=S半圆AB﹣S弓形AB=S半圆AB﹣（S扇形OAB﹣S △OAB）=S半圆AB﹣S扇形OAB+S△OAB求出答案即可．【解析】如图，⊙O 的半径为2，⊙O 1的半径为1，点O 在⊙O 1上，连接OA ，OB ，OO 1，∵OA =2，O 1A =O 1O =1，则有（2）2=12+12，∴OA 2=O 1A 2+O 1O 2，∴△OO 1A 为直角三角形，∴∠AOO 1=45°，同理可得∠BOO 1=45°，∴∠AOB =90°，∴AB 为⊙O 1的直径，∴S 阴影部分=S 半圆AB ﹣S 弓形AB =S 半圆AB ﹣（S 扇形OAB ﹣S △OAB ）=S 半圆AB ﹣S 扇形OAB +S △OAB =12π×12﹣902360π⨯ +12×2×2=1．故选A ．点睛：本题主要考查了相交两圆的性质以及扇形面积的计算，解题的关键是正确作出辅助线，此题有一定的难度．考点：相交两圆的性质；扇形面积的计算．10．（2016陕西省）如图，⊙O 的半径为4，△ABC 是⊙O 的内接三角形，连接OB 、OC ，若∠ABC 和∠BOC 互补，则弦BC 的长度为（）A ．33B ． 34C ． 35D ． 36【答案】B ．【分析】首先过点O 作OD ⊥BC 于D ，由垂径定理可得BC =2BD ，又由圆周角定理，可求得∠BOC 的度数，然后根据等腰三角形的性质，求得∠OBC 的度数，利用余弦函数，即可求得答案．【解析】过点O 作OD ⊥BC 于D ，则BC =2BD ，∵△ABC 内接于⊙O ，∠BAC 与∠BOC 互补，∴∠BOC =2∠A ，∠BOC +∠A =180°，∴∠BOC =120°，∵OB =OC ，∴∠OBC =∠OCB =12（180°-∠BOC ）=30°，∵⊙O 的半径为4，∴BD =OB •cos ∠OBC =342⨯=23BC =34．故选B ．考点：垂径定理；圆周角定理；解直角三角形．学科.网11．（2016山东省泰安市）如图，△ABC 内接于⊙O ，AB 是⊙O 的直径，∠B =30°，CE 平分∠ACB 交⊙O 于E ，交AB 于点D ，连接AE ，则S △ADE ：S △CDB 的值等于（）A ．12B ．13C ．1：2D ．2：3【答案】D ．【分析】由AB 是⊙O 的直径，得到∠ACB =90°，根据已知条件得到33AC AB =，根据三角形的角平分线定理得到3AC AD AB BD ==AD 333+，BD 33+AB ，过C 作CE ⊥AB 于E ，连接OE ，由CE 平分∠ACB 交⊙O 于E ，得到OE ⊥AB ，求出OE =12AB ，CE 3，根据三角形的面积公式即可得到结论．【解析】∵AB 是⊙O 的直径，∴∠ACB =90°，∵∠B =30°，∴3AC AB =，∵CE 平分∠ACB 交⊙O 于E ，∴33AC AD AB BD ==，∴AD 333+，BD 33+AB ，过C 作CE ⊥AB 于E ，连接OE ，∵CE 平分∠ACB 交⊙O 于E ，∴AE DE =，∴OE ⊥AB ，∴OE =12AB ，CE =34AB ，∴S △ADE ：S △CDB =（12AD •OE ）：（12BD •CE ）=（1312233AB AB ⋅+）：（132433AB AB ⋅+）=2：3．故选D ．考点：相似三角形的判定与性质；圆周角定理．12．（2016内蒙古呼和浩特市）如图，△ABC 是一块绿化带，将阴影部分修建为花圃，已知AB =15，AC =9，BC =12，阴影部分是△ABC 的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为（）A ．16 B ．6π C ．8π D ．5π【答案】B ．【分析】由AB =15，BC =12，AC =9，得到222AB BC AC =+，根据勾股定理的逆定理得到△ABC 为直角三角形，于是得到△ABC 的内切圆半径=（12+9-15）÷2=3，求得直角三角形的面积和圆的面积，即可得到结论．考点：几何概率；三角形的内切圆与内心．13．（2016浙江省丽水市）如图，已知⊙O 是等腰Rt △ABC 的外接圆，点D 是AC 上一点，BD 交AC 于点E ，若BC =4，AD =45，则AE 的长是（）A ．3B ．2C ．1D ．1.2 【答案】C ．【分析】利用圆周角性质和等腰三角形性质，确定AB 为圆的直径，利用相似三角形的判定及性质，确定△ADE 和△BCE 边长之间的关系，利用相似比求出线段AE 的长度即可．【解析】∵等腰Rt △ABC ，BC =4，∴AB 为⊙O 的直径，AC =4，AB =4，∴∠D =90°，在Rt △ABD 中，AD =45，AB =42，∴BD =285，∵∠D =∠C ，∠DAC =∠CBE ，∴△ADE ∽△BCE ，∵AD ：B C =45：4=1：5，∴相似比为1：5，设AE =x ，∴BE =5x ，∴DE =285﹣5x ，∴CE =28﹣25x ，∵AC =4，∴x +28﹣25x =4，解得：x =1．故选C ．考点：三角形的外接圆与外心．14．（2016浙江省台州市）如图，在△ABC 中，AB =10，AC =8，BC =6，以边AB 的中点O 为圆心，作半圆与AC 相切，点P ，Q 分别是边BC 和半圆上的动点，连接PQ ，则PQ 长的最大值与最小值的和是（）A ． 6B ． 1132C ． 9D ． 332【答案】C ．【分析】如图，设⊙O 与AC 相切于点E ，连接OE ，作OP 1⊥BC 垂足为P 1交⊙O 于Q 1，此时垂线段OP 1最短，P 1Q 1最小值为OP 1﹣OQ 1，求出OP 1，如图当Q 2在AB 边上时，P 2与B 重合时，P 2Q 2最大值=5+3=8，由此不难解决问题．【解析】如图，设⊙O 与AC 相切于点E ，连接OE ，作OP 1⊥BC 垂足为P 1交⊙O 于Q 1，此时垂线段OP 1最短，P 1Q 1最小值为OP 1﹣OQ 1，∵AB =10，AC =8，BC =6，∴AB 2=AC 2+BC 2，∴∠C =90°，∵∠OP 1B =90°，∴OP 1∥AC∵AO =OB ，∴P 1C =P 1B ，∴OP 1=12AC =4，∴P 1Q 1最小值为OP 1﹣OQ 1=1，如图，当Q 2在AB 边上时，P 2与B 重合时，P 2Q 2最大值=5+3=8，∴PQ 长的最大值与最小值的和是9．故选C ．考点：切线的性质；最值问题．15．（2016贵州省遵义市）如图，矩形ABCD 中，AB =4，BC =3，连接AC ，⊙P 和⊙Q 分别是△ABC 和△ADC 的内切圆，则PQ 的长是（）A ．52B ．5C ．52D ．22【答案】B ．【分析】根据矩形的性质可得出⊙P 和⊙Q 的半径相等，利用直角三角形内切圆半径公式即可求出⊙P 半径r 的长度．连接点P 、Q ，过点Q 作QE ∥BC ，过点P 作PE ∥AB 交QE 于点E ，求出线段QE 、EP 的长，再由勾股定理即可求出线段PQ 的长，此题得解．【解析】∵四边形ABCD 为矩形，∴△ACD ≌△CAB ，∴⊙P 和⊙Q 的半径相等．在Rt △BC 中，AB =4，BC =3，∴AC =22AB BC +=5，∴⊙P 的半径r =2AB BC AC +-=3452+-=1．连接点P 、Q ，过点Q 作QE ∥BC ，过点P 作PE ∥AB 交QE 于点E ，则∠QEP =90°，如图所示．在Rt △QEP 中，QE =BC ﹣2r =3﹣2=1，EP =AB ﹣2r =4﹣2=2，∴PQ 22QE EP +2212+5B ．考点：三角形的内切圆与内心；矩形的性质．16．（2016黑龙江省龙东地区）若点O 是等腰△ABC 的外心，且∠BOC =60°，底边BC =2，则△ABC 的面积为（）A ．23+B ．233C ．23+或23-D ．423+或23- 【答案】C ．【分析】根据题意可以画出相应的图形，然后根据不同情况，求出相应的边的长度，从而可以求出不同情况下△ABC 的面积，本题得以解决．【解析】由题意可得，如右图所示，存在两种情况，当△ABC 为△A 1BC 时，连接OB 、OC ，∵点O 是等腰△ABC 的外心，且∠BOC =60°，底边BC =2，OB =OC ，∴△OBC 为等边三角形，OB =OC =BC =2，OA 1⊥BC于点D ，∴CD =1，OD =2221-=3，∴1ΔA BC S =12BC •A 1D =12(23)2⨯⨯-=23-；当△ABC 为△A 2BC 时，连接OB 、OC ，∵点O 是等腰△ABC 的外心，且∠BOC =60°，底边BC =2，OB =OC ，∴△OBC 为等边三角形，OB =OC =BC =2，OA 1⊥BC 于点D ，∴CD =1，OD =2221-=3，∴S △A 2BC =12BC •A 2D =12(23)2⨯⨯+=23+，由上可得，△ABC 的面积为23-或23+，故选C ．考点：三角形的外接圆与外心；等腰三角形的性质；分类讨论．17．（2016湖北省鄂州市）如图所示，AB 是⊙O 的直径，AM 、BN 是⊙O 的两条切线，D 、C 分别在AM 、BN 上，DC 切⊙O 于点E ，连接OD 、OC 、BE 、AE ，BE 与OC 相交于点P ，AE 与OD 相交于点Q ，已知AD =4，BC =9，以下结论： ①⊙O 的半径为132 ，②OD ∥BE ，③PB =181313， ④tan ∠CEP =23其中正确结论有（）A ．1个B ．2个C ．3个D ．4个【答案】C ．【分析】作DK ⊥BC 于K ，连接OE ，①错误，在RT △CDK 中，利用勾股定理求得DK =12，故错误．②正确．可以证明AQ =QE ，AO =OB ，由此得出结论．③正确．根据PB=BC OBOC⋅计算即可．④正确．根据tan ∠CEP =tan ∠CBP =BPPC计算即可．【解析】作DK ⊥BC 于K ，连接OE ．∵AD 、BC 是切线，∴∠DAB =∠ABK =∠DKB =90°，∴四边形ABKD 是矩形，∴DK =AB ，AD =BK =4，∵CD 是切线，∴DA =DE ，CE =CB =9，在RT △DKC 中，∵DC =DE +CE =13，CK =BC ﹣BK =5，∴DK =22DC CK -=12，∴AB =DK =12，∴⊙O 半径为6．故①错误，∵DA =DE ，OA =OE ，∴OD 垂直平分AE ，同理OC 垂直平分BE ，∴AQ =QE ，∵AO =OB ，∴OD ∥BE ，故②正确．在RT △OBC 中，PB =BC OBOC ⋅=69313⨯=181313，故③正确，∵CE =CB ，∴∠CEB =∠CBE ，∴tan ∠CEP =tan ∠CBP =BP PC =181313271313=23，故④正确，∴②③④正确，故选C ．考点：切线的性质；圆周角定理．学科.网18．（2016四川省广安市）如图，AB 是圆O 的直径，弦CD ⊥AB ，∠BCD =30°，CD =43，则S 阴影=（）A．2πB．83πC．43πD．38π【答案】B．【分析】根据垂径定理求得CE=ED=23，然后由圆周角定理知∠DOE=60°，然后通过解直角三角形求得线段OD、OE的长度，最后将相关线段的长度代入S阴影=S扇形ODB﹣S△DOE+S△BE C．【解析】如图，假设线段CD、AB交于点E，∵AB是⊙O的直径，弦CD⊥AB，∴CE=ED=23，又∵∠BCD=30°，∴∠DOE=2∠BCD=60°，∠ODE=30°，∴OE=DE•cot60°=23×33=2，OD=2OE=4，∴S阴影=S扇形ODB﹣S△DOE+S△BEC=260360ODπ⨯﹣12OE×DE+12BE•CE=823233π-+=83π．故选B．考点：圆周角定理；垂径定理；扇形面积的计算．19．（2016山东省滨州市）如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是（）A．②④⑤⑥B．①③⑤⑥C．②③④⑥D．①③④⑤【答案】D．【分析】①由直径所对圆周角是直角，②由于∠AOC是⊙O的圆心角，∠AEC是⊙O的圆内部的角角，③由平行线得到∠OCB=∠DBC，再由圆的性质得到结论判断出∠OBC=∠DBC；④用半径垂直于不是直径的弦，必平分弦；⑤用三角形的中位线得到结论；⑥得不到△CEF和△BED中对应相等的边，所以不一定全等．【解析】①、∵AB是⊙O的直径，∴∠ADB=90°，∴AD⊥BD，②、∵∠AOC是⊙O的圆心角，∠AEC 是⊙O的圆内部的角角，∴∠AOC≠∠AEC，③、∵OC∥BD，∴∠OCB=∠DBC，∵OC=OB，∴∠OCB=∠OBC，∴∠OBC=∠DBC，∴CB平分∠ABD，④、∵AB是⊙O的直径，∴∠ADB=90°，∴AD⊥BD，∵OC∥BD，∴∠AFO=90°，∵点O为圆心，∴AF=DF，⑤、由④有，AF=DF，∵点O为AB中点，∴OF是△ABD的中位线，∴BD=2OF，⑥∵△CEF和△BED中，没有相等的边，∴△CEF与△BED不全等，故选D．考点：圆的综合题．20．（2016四川省资阳市）在Rt△ABC中，∠ACB=90°，AC=23，以点B为圆心，BC的长为半径作弧，交AB于点D，若点D为AB的中点，则阴影部分的面积是（）A．2233πB．2433πC．4233πD．23π【答案】A．【分析】根据点D为AB的中点可知BC=BD=12AB，故可得出∠A=30°，∠B=60°，再由锐角三角函数的定义求出BC的长，根据S阴影=S△A B C﹣S扇形C B D即可得出结论．【解析】∵D为AB的中点，∴BC=BD=12AB，∴∠A=30°，∠B=60°．∵AC=23，∴BC=AC•tan30°=323=2，∴S阴影=S△A B C﹣S扇形C BD =216022322360π⨯⨯-=2233π-．故选A．考点：扇形面积的计算．21．（2016山东省潍坊市）如图，在Rt△ABC中，∠A=30°，BC=23AC为直径作⊙O交AB 于点D，则图中阴影部分的面积是（）A ．153342π- B ．153322π- C ．7346π- D ．7326π- 【答案】A ．【分析】连接连接OD 、CD ，根据S 阴=S △ABC ﹣S △ACD ﹣（S 扇形OCD ﹣S △OCD ）计算即可解决问题．【解析】如图连接OD 、CD ．∵AC 是直径，∴∠ADC =90°，∵∠A =30°，∴∠ACD =90°﹣∠A =60°，∵OC =OD ，∴△OCD 是等边三角形，∵BC 是切线，∴∠ACB =90°，∵BC =23，∴AB =43，AC =6，∴S 阴=S △ABC ﹣S △ACD ﹣（S扇形OCD﹣S △OCD ）=22116033623333(3)22360π⨯⨯⨯-⨯⨯--⨯=15332π-．故选A ．考点：扇形面积的计算；含30度角的直角三角形．22．（2015甘南州）⊙O 过点B ，C ，圆心O 在等腰直角△ABC 内部，∠BAC =90°，OA =1，BC =6，则⊙O 的半径为（）A 10B ．3C 13D ．32【答案】C ．【解析】试题分析：过A 作AD ⊥BC ，由题意可知AD 必过点O ，连接OB ，∵△BAC 是等腰直角三角形，AD ⊥BC ，∴BD =CD =AD =3，∴OD =AD ﹣OA =2，Rt △OBD 中，根据勾股定理，得：OB 22BD OD +13故选C ．考点：1．垂径定理；2．勾股定理；3．等腰直角三角形．23．（2015龙东）如图，⊙O的半径是2，AB是⊙O的弦，点P是弦AB上的动点，且1≤OP≤2，则弦AB 所对的圆周角的度数是（）A．60°B．120° C．60°或120° D．30°或150°【答案】C．考点：1．圆周角定理；2．含30度角的直角三角形；3．垂径定理；4．分类讨论．24．（2015南通）如图，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，AB=6，AD=5，则AE的长为（）A．2.5 B．2.8 C．3 D．3.2【答案】B．考点：1．相似三角形的判定与性质；2．勾股定理；3．圆周角定理；4．综合题．25．（2015扬州）如图，若锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），则下列三个结论：①sin∠C＞sin∠D；②cos∠C＞cos∠D；③tan∠C＞tan∠D中，正确的结论为（）A．①② B．②③ C．①②③ D．①③【答案】D．考点：1．锐角三角函数的增减性；2．圆周角定理．26．（2015南宁）如图，AB 是⊙O 的直径，AB =8，点M 在⊙O 上，∠MAB =20°，N 是弧MB 的中点，P 是直径AB 上的一动点．若MN =1，则△PM N 周长的最小值为（）A ．4B ．5C ．6D ．7 【答案】B ．考点：1．轴对称-最短路线问题；2．圆周角定理；3．综合题．学科.网27．（2015雅安）如图所示，MN 是⊙O 的直径，作AB ⊥MN ，垂足为点D ，连接AM ，AN ，点C 为AN 上一点，且AC AM =，连接CM ，交AB 于点E ，交AN 于点F ，现给出以下结论：①AD =BD ；②∠MAN =90°；③AM BM =；④∠ACM +∠ANM =∠MOB ；⑤AE =12MF ．其中正确结论的个数是（）A ．2B ．3C ．4D ．5 【答案】D ．【解析】试题分析：∵MN 是⊙O 的直径，AB ⊥MN ，∴AD =BD ，AM BM =，∠MAN =90°，故①②③正确； ∵AC AM =，∴AC AM BM ==，∴∠ACM +∠ANM =∠MOB ，故④正确； ∵∠MAE =∠AME ，∴AE =ME ，∠EAF =∠AFM ，∴AE =EF ，∴AE =12MF ，故⑤正确．正确的结论共5个．故选D ．考点：1．圆周角定理；2．垂径定理；3．压轴题．28．（2015贵港）如图，已知P 是⊙O 外一点，Q 是⊙O 上的动点，线段PQ 的中点为M ，连接OP ，OM ．若⊙O 的半径为2，OP =4，则线段OM 的最小值是（）A ．0B ．1C ．2D ．3 【答案】B ．考点：1．点与圆的位置关系；2．三角形中位线定理；3．最值问题；4．轨迹．29．（2015宜昌）如图，圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为O，三角尺的直角顶点C落在直尺的10cm处，铁片与直尺的唯一公共点A落在直尺的14cm处，铁片与三角尺的唯一公共点为B，下列说法错误的是（）A．圆形铁片的半径是4cm B．四边形AOBC为正方形C．弧AB的长度为4πcm D．扇形OAB的面积是4πcm2【答案】C．考点：1．切线的性质；2．正方形的判定与性质；3．弧长的计算；4．扇形面积的计算；5．应用题；6．综合题．30．（2015河池）我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：=+与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA y kx43上运动时，使得⊙P成为整圆的点P个数是（）A ．6B ．8C ．10D ．12 【答案】A ．【解析】试题分析：∵直线l ：43y kx =+与x 轴、y 轴分别交于A 、B ，∴B （0，43），∴OB =43，在RT △AOB 中，∠OAB =30°，∴OA =3OB =343⨯=12，∵⊙P 与l 相切，设切点为M ，连接PM ，则PM ⊥AB ，∴PM =12P A ，设P （x ，0），∴P A =12﹣x ，∴⊙P 的半径PM =12P A =162x -，∵x 为整数，PM 为整数，∴x 可以取0，2，4，6，8，10，共6个数，∴使得⊙P 成为整圆的点P 个数是6．故选A ．考点：1．切线的性质；2．一次函数图象上点的坐标特征；3．新定义；4．动点型；5．综合题． 31．（2015南京）如图，在矩形ABCD 中，AB =4，AD =5，AD ，AB ，BC 分别与⊙O 相切于E ，F ，G 三点，过点D 作⊙O 的切线BC 于点M ，切点为N ，则DM 的长为（）A ．133 B ．92 C 4133D ．5【答案】A ．考点：1．切线的性质；2．矩形的性质；3．综合题．32．（2015义乌）在Rt△ABC中，∠C=90°，BC=3，AC=4，点P在以C为圆心，5为半径的圆上，连结P A，PB．若PB=4，则P A的长为．【答案】3或73．考点：1．点与圆的位置关系；2．勾股定理；3．垂径定理；4．分类讨论．33．（2015苏州）如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD．若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为（）A．433π-B．4233π-C．3π-D．233π-【答案】A．【解析】试题分析：过O点作OE⊥CD于E，∵AB为⊙O的切线，∴∠ABO=90°，∵∠A=30°，∴∠AOB=60°，∴∠COD=120°，∠OCD=∠ODC=30°，∵⊙O的半径为2，∴OE=1，CE=DE=3，∴CD=23，∴图中阴影部分的面积为：2120211233602⋅π⋅-⨯⨯=433π-．故选A．考点：1．扇形面积的计算；2．切线的性质．二、填空题34．（2017四川省宜宾市，第15题，3分）如图，⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G，AE=2，则EG的长是．51．【分析】在⊙O 的内接正五边形ABCDE 中，设EG =x ，易知：∠AEB =∠ABE =∠EAG =36°，∠BAG =∠AGB =72°，推出AB =BG =AE =2，由△AEG ∽△BEA ，可得AE 2=EG •EB ，可得22=x （x +2），解方程即可．【解析】在⊙O 的内接正五边形ABCDE 中，设EG =x ，易知：∠AEB =∠ABE =∠EAG =36°，∠BAG =∠AGB =72°，∴AB =BG =AE =2，∵∠AEG =∠AEB ，∠EAG =∠EBA ，∴△AEG ∽△BEA ，∴AE 2=EG •EB ，∴22=x （x +2），解得x =15-或15-EG 5151．点睛：本题考查正多边形与圆、相似三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是正确寻找相似三角形解决问题，学会构建方程解决问题，属于中考填空题中的压轴题．考点：正多边形和圆；压轴题．35．（2017四川省广元市，第14题，3分）已知⊙O 的半径为10，弦AB ∥CD ，AB =12，CD =16，则AB 和CD 的距离为．【答案】14或2．【分析】分两种情况：①当AB 、CD 在圆心O 的两侧时，如图1，作辅助线，构建两个直角三角形，先由垂径定理得出BF 和ED 的长，再利用勾股定理计算出OE 和OF 的长，相加即可求出距离EF 的长； ②当AB 、CD 在圆心O 的同侧时，如图2，同理求得距离EF 的长．【解析】分两种情况：①当AB 、CD 在圆心O 的两侧时，如图1，过O 作OE ⊥CD 于E ，延长EO 将AB 于F ，连接OD 、OB ，∵AB ∥CD ，∴EF ⊥AB ，∴ED =12CD ，BF =12AB ，∵AB =12，CD =16，∴ED =12×16=8，BF =12×12=6，由勾股定理得：OE 22OD ED -22108-6，OF 22OB BF -22106-=8，∴EF =OE +OF =6+8=14； ②当AB 、CD 在圆心O 的同侧时，如图2，同理得：EF =OF ﹣OE =8﹣6=2．综上所述，AB 和CD 的距离为14或2．点睛：本题考查了垂径定理和两平行线的距离，熟练掌握垂径定理，应用了垂直弦的直径平分这条弦，恰当地作辅助线构建半径和弦心距，这是圆中常作的辅助线，要熟练掌握；本题还采作了分类讨论的思想，分别求出弦心距作和与差得出两平行线的距离．考点：垂径定理；平行线之间的距离；分类讨论．36．（2017四川省达州市，第16题，3分）如图，矩形ABCD 中，E 是BC 上一点，连接AE ，将矩形沿AE 翻折，使点B 落在CD 边F 处，连接AF ，在AF 上取点O ，以O 为圆心，OF 长为半径作⊙O 与AD 相切于点P ．若AB =6，BC =33，则下列结论：①F 是CD 的中点；②⊙O 的半径是2；③AE =92CE ；④3S =阴影．其中正确结论的序号是．【答案】①②④．【分析】①易求得DF 长度，即可判定；②连接OP ，易证OP ∥CD ，根据平行线性质即可判定； ③易证AE =2EF ，EF =2EC 即可判定；④连接OG ，作OH ⊥FG ，易证△OFG 为等边△，即可求得S 阴影即可解题；【解析】①∵AF 是AB 翻折而来，∴AF =AB =6，∵AD =BC =33DF 22AF AD -3，∴F 是CD 中点；∴①正确；②连接OP ，∵⊙O 与AD 相切于点P ，∴OP ⊥AD ，∵AD ⊥DC ，∴OP ∥CD ，∴AO OPAF DF=，设OP =OF =x ，则636x x -=，解得：x =2，∴②正确；③∵RT △ADF 中，AF =6，DF =3，∴∠DAF =30°，∠AFD =60°，∴∠EAF =∠EAB =30°，∴AE =2EF ； ∵∠AFE =90°，∴∠EFC =90°﹣∠AFD =30°，∴EF =2EC ，∴AE =4CE ，∴③错误；④连接OG ，作OH ⊥FG ，∵∠AFD =60°，OF =OG ，∴△OFG 为等边△；同理△OPG 为等边△； ∴∠POG =∠FOG =60°，OH =32OG =3，S 扇形OPG =S 扇形OGF ，∴S 阴影=（S 矩形OPDH ﹣S 扇形OPG ﹣S △OGH ）+（S 扇形OGF﹣S △OFG ）=S 矩形OPDH ﹣32S △OFG =3123(23)22⨯-⨯⨯⨯=32．∴④正确；故答案为：①②④．点睛：本题考查了矩形面积的计算，正三角形的性质，平行线平分线段的性质，勾股定理的运用，本题中熟练运用上述考点是解题的关键．考点：切线的性质；矩形的性质；扇形面积的计算；翻折变换（折叠问题）；综合题．学科.网37．（2017山东省威海市，第18题，3分）如图，△ABC 为等边三角形，AB =2．若P 为△ABC 内一动点，且满足∠P AB =∠ACP ，则线段PB 长度的最小值为．【答案】233．【分析】由等边三角形的性质得出∠ABC =∠BAC =60°，AC =AB =2，求出∠APC =120°，当PB ⊥AC 时，PB 长度最小，设垂足为D ，此时P A =PC ，由等边三角形的性质得出AD =CD =12AC =1，∠P AC =∠ACP =30°，∠ABD =12∠ABC =30°，求出PD =AD •tan30°=33AD =33，BD =3AD =3，即可得出答案．【解析】∵△ABC 是等边三角形，∴∠ABC =∠BAC =60°，AC =AB =2，∵∠P AB =∠ACP ，∴∠P AC +∠ACP =60°，∴∠APC =120°，当PB ⊥AC 时，PB 长度最小，设垂足为D ，如图所示：此时P A =PC ，则AD =CD =12AC =1，∠P AC =∠ACP =30°，∠ABD =12∠ABC =30°，∴ PD =AD •tan30°=33AD =33，BD =3AD =3，∴PB =BD ﹣PD =3﹣33=233．故答案为：233．点睛：本题考查了等边三角形的性质、等腰三角形的性质、三角形内角和定理、勾股定理、三角函数等知识；熟练掌握等边三角形的性质是解决问题的关键．考点：点与圆的位置关系；等边三角形的性质；最值问题；圆周角定理；动点型．38．（2017德州，第17题，4分）某景区修建一栋复古建筑，其窗户设计如图所示．圆O 的圆心与矩形ABCD 对角线的交点重合，且圆与矩形上下两边相切（E 为上切点），与左右两边相交（F ，G 为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m ，根据设计要求，若∠EOF =45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为．(2)2π+．【分析】把透光部分看作是两个直角三角形与四个45°的扇形的组合体，其和就是透光的面积，再计算矩形的面积，相比可得结果．【解析】设⊙O与矩形ABCD的另一个交点为M，连接OM、OG，则M、O、E共线，由题意得：∠MOG=∠EOF=45°，∴∠FOG=90°，且OF=OG=1，∴S透明区域=21801360π⨯+2×12×1×1=2π+1，过O作ON⊥AD 于N，∴ON=12FG=122，∴AB=2ON=2×122=2，∴S矩形=2×2=22，∴SS透光区域矩形=1222π+=(2)28π+．故答案为：(2)28π+．点睛：本题考查了矩形的性质、扇形的面积、直角三角形的面积，将透光部分化分为几个熟知图形的面积是关键．考点：扇形面积的计算；综合题．39．（2017济宁，第15题，3分）如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2，如此继续下去，则正六边形A4B4C4D4E4F4的面积是．【答案】318．【分析】由正六边形的性质得：∠A1B1B2=90°，∠B1A1B2=30°，A1A2=A2B2，由直角三角形的性质得出B1B231B13，A2B2=12A1B2=B1B23A2B2C2D2E2F2的面积：。

决胜2017中考数学压轴题全揭秘精品(原卷版)

《中考压轴题全揭秘》第二辑原创模拟预测题专题35：动态几何之动点形成的全等、相似三角形存在性问题数学因运动而充满活力，数学因变化而精彩纷呈．动态题是近年来中考的的一个热点问题，以运动的观点探究几何图形的变化规律问题，称之为动态几何问题，随之产生的动态几何试题就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题，就其运动对象而言，有点动、线动、面动三大类，就其运动形式而言，有轴对称（翻折）、平移、旋转（中心对称、滚动）等，就问题类型而言，有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等．解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况．以动态几何问题为基架而精心设计的考题，可谓璀璨夺目、精彩四射．动态几何形成的存在性问题是动态几何中的基本类型，包括等腰（边）三角形存在问题；直角三角形存在问题；平行四边形存在问题；矩形、菱形、正方形存在问题；梯形存在问题；全等三角形存在问题；相似三角形存在问题；其它存在问题等．本专题原创编写动点形成的全等、相似三角形存在性问题模拟题．在中考压轴题中，动点形成的全等、相似三角形存在性问题的重点和难点在于应用数形结合的思想准确地进行分类．原创模拟预测题1．如图，一次函数4y x =-+的图象与x 轴、y 轴分别相交于点A 、B ，过点A 作x 轴的垂线l ，点P 为直线l 上的动点，点Q 为直线AB 与△OAP 外接圆的交点，点P 、Q 与点A 都不重合．（1）写出点A 的坐标；（2）当点P 在直线l 上运动时，是否存在点P 使得△OQB 与△APQ 全等？如果存在，求出点P 的坐标；如果不存在，请说明理由．（3）若点M 在直线l 上，且∠POM =90°，记△OAP 外接圆和△OAM 外接圆的面积分别是1S 、2S ，求2111S S +的值．原创模拟预测题2．如图，已知抛物线252y ax ax =-+（0a ≠）与y 轴交于点C ，与x 轴交于点A （1，0）和点B ．（1）求抛物线的解析式；（2）求直线BC 的解析式；（3）若点N 是抛物线上的动点，过点N 作NH ⊥x 轴，垂足为H ，以B ，N ，H 为顶点的三角形是否能够与△OBC 相似？若能，请求出所有符合条件的点N 的坐标；若不能，请说明理由．原创模拟预测题3．如图，已知二次函数的图象M 经过A （﹣1，0），B （4，0），C （2，﹣6）三点．（1）求该二次函数的解析式；（2）点G 是线段AC 上的动点（点G 与线段AC 的端点不重合），若△ABG 与△ABC 相似，求点G 的坐标；（3）设图象M 的对称轴为l ，点D （m ，n ）（(12)m -<<）是图象M 上一动点，当△ACD 的面积为278时，点D 关于l 的对称点为E ，能否在图象M 和l 上分别找到点P 、Q ，使得以点D 、E 、P 、Q 为顶点的四边形为平行四边形？若能，求出点P 的坐标；若不能，请说明理由．原创模拟预测题4．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D为边CB上的一个动点（点D 不与点B重合），过D作DO⊥AB，垂足为O，点B′在边AB上，且与点B关于直线DO对称，连接DB′，AD．（1）求证：△DOB∽△ACB；（2）若AD平分∠CAB，求线段BD的长；（3）当△AB′D为等腰三角形时，求线段BD的长．原创模拟预测题5．已知：⊙O上两个定点A，B和两个动点C，D，AC与BD交于点E．（1）如图1，求证：EA•EC=EB•ED；AB BC，AD是⊙O的直径，求证：AD•AC=2BD•BC；（2）如图2，若=（3）如图3，若AC⊥BD，点O到AD的距离为2，求BC的长．原创模拟预测题6．如图1，矩形ABCD 的两条边在坐标轴上，点D 与坐标原点O 重合，且AD =8，AB =6．如图2，矩形ABCD 沿OB 方向以每秒1个单位长度的速度运动，同时点P 从A 点出发也以每秒1个单位长度的速度沿矩形ABCD 的边AB 经过点B 向点C 运动，当点P 到达点C 时，矩形ABCD 和点P 同时停止运动，设点P 的运动时间为t 秒．（1）当t =5时，请直接写出点D 、点P 的坐标；（2）当点P 在线段AB 或线段BC 上运动时，求出△PBD 的面积S 关于t 的函数关系式，并写出相应t 的取值范围；（3）点P 在线段AB 或线段BC 上运动时，作PE ⊥x 轴，垂足为点E ，当△PEO 与△BCD 相似时，求出相应的t 值．原创模拟预测题7．如图，已知直线3y x =-+与x 轴、y 轴分别交于A ，B 两点，抛物线2y x bx c =-++经过A ，B 两点，点P 在线段OA 上，从点O 出发，向点A 以1个单位/秒的速度匀速运动；同时，点Q 在线段AB 上，从点A 出发，向点B 2个单位/秒的速度匀速运动，连接PQ ，设运动时间为t 秒．（1）求抛物线的解析式；（2）问：当t 为何值时，△APQ 为直角三角形；（3）过点P 作PE ∥y 轴，交AB 于点E ，过点Q 作QF ∥y 轴，交抛物线于点F ，连接EF ，当EF ∥PQ 时，求点F 的坐标；（4）设抛物线顶点为M ，连接BP ，BM ，MQ ，问：是否存在t 的值，使以B ，Q ，M 为顶点的三角形与以O ，B ，P 为顶点的三角形相似？若存在，请求出t 的值；若不存在，请说明理由．。

2018全国各地中考数学压轴题精选(含详细答案).docx

一．解答（共30 小）1．（区）如，直l1：y=kx+b 平行于直y=x 1，且与直l2：相交于点P（ 1， 0）．（1）求直l1、 l2的解析式；（2）直 l1与 y 交于点A．一点 C 从点 A 出，先沿平行于x 的方向运，到达直l2上的点 B1后，改垂直于 x 的方向运，到达直l1上的点 A1后，再沿平行于x 的方向运，到达直l2上的点 B2后，又改垂直于x 的方向运，到达直 l 1上的点 A2后，仍沿平行于x 的方向运，⋯照此律运，点 C 依次点 B1， A1， B2， A2， B3，A3，⋯， B n， A n，⋯①求点 B1， B2， A1， A2的坐；②你通得出点 A、B 的坐；并求当点 C到达 A ，运的路径的？n n n2．（莆田）如1，在平面直角坐系xOy 中，矩形 OABC的 OA 在 y 的正半上，OC在x 的正半上， OA=1， OC=2，点 D 在 OC 上且 OD= ．（1）求直AC 的解析式；（2）在 y 上是否存在点P，直 PD与矩形角AC交于点 M，使得△ DMC 等腰三角形？若存在，直接写出所有符合条件的点P 的坐；若不存在，明理由．（3）抛物y= x 怎平移，才能使得平移后的抛物点 D 和点 E（点 E 在 y 的正半上），且△ ODE沿DE折叠后点O 落在 AB 上 O′ ．3．（阳）已知 Z 市某种生活必需品的年需求量y1（万件）、供量 y2（万件）与价格x （元 / 件）在一定范内分近似足下列函数关系式：y= 4x+190，y =5x 170．当 y =y1212，称商品的价格定价格，需求量定需求量；当y1＜ y2，称商品的供求关系供于求；当y1＞ y2，称商品的供求关系供不求．（1）求商品的定价格和定需求量；（2）当价格为45（元 / 件）时，该商品的供求关系如何？为什么？4．（哈尔滨）如图 1，在平面直角坐标系中，点 O 是坐标原点，四边形 ABCO是菱形，点 A 的坐标为（﹣ 3，4），点 C 在 x 轴的正半轴上，直线 AC 交 y 轴于点 M，AB 边交 y 轴于点 H．（1）求直线AC 的解析式；（2）连接 BM，如图 2，动点 P 从点 A 出发，沿折线ABC方向以 2 个单位 / 秒的速度向终点C 匀速运动，设△ PMB 的面积为S（ S≠0），点 P 的运动时间为 t 秒，求 S 与 t 之间的函数关系式（要求写出自变量t 的取值范围）；（3）在（ 2）的条件下，当t 为何值时，∠ MPB 与∠ BCO互为余角，并求此时直线OP与直线 AC 所夹锐角的正切值．5．（桂林）如图已知直线L： y= x+3，它与x 轴、 y 轴的交点分别为A、 B 两点．（1）求点 A、点 B 的坐标．F（不（2）设 F 为 x 轴上一动点，用尺规作图作出⊙P，使⊙ P 经过点 B 且与 x 轴相切于点写作法，保留作图痕迹）．（3）设（ 2）中所作的⊙ P 的圆心坐标为 P（ x， y），求 y 关于 x 的函数关系式．（4）是否存在这样的⊙ P，既与 x 轴相切又与直线 L 相切于点 B？若存在，求出圆心 P 的坐标；若不存在，请说明理由．6．（防城港）如图，在平面直角坐标系，直线y=﹣（x﹣6）与x 轴、 y 轴分别相交于A、D 两点，点 B 在 y 轴上，现将△ AOB 沿 AB 翻折 180 °，使点 O 刚好落在直线AD 的点 C 处．（1）求 BD 的长；（2）设点 N 是线段 AD 上的一个动点（与点 A、D 不重合）， S△NBD=S1，S△NOA=S2，当点 N 运动到什么位置时，S1?S2的值最大，并求出此时点N 的坐标；（3）在 y 轴上是否存在点M ，使 △ MAC 为直角三角形？若存在，请写出所有符合条件的点M 的坐标，并选择一个写出其求解过程；若不存在，简述理由．7．（大兴安岭）直线 y=kx+b （ k ≠0）与坐标轴分别交于 A 、 B 两点， OA 、 OB 的长分别是方程 x 2﹣ 14x+48=0 的两根（ OA ＞ OB ），动点 P 从 O 点出发，沿路线 O?B?A 以每秒 1 个单位长度的速度运动，到达 A 点时运动停止．（ 1）直接写出 A 、 B 两点的坐标；（ 2）设点 P 的运动时间为 t （秒）， △ OPA 的面积为 S ，求 S 与 t 之间的函数关系式（不必写出自变量的取值范围）；（3）当 S=12 时，直接写出点P 的坐标，此时，在坐标轴上是否存在点M ，使以 O 、 A 、 P 、M 为顶点的四边形是梯形？若存在，请直接写出点 M 的坐标；若不存在，请说明理由．8．（云南）如图，在直角坐标系中，半圆直径为 OC ，半圆圆心 D 的坐标为（ 0， 2），四边形 OABC 是矩形，点 A 的坐标为（ 6， 0）．（1）若过点 P （ 2，0）且与半圆 D 相切于点 F 的切线分别与 y 轴和 BC 边交于点 H 与点E ，求切线 PF 所在直线的解析式；（2）若过点 A 和点 B 的切线分别与半圆相切于点P 1 和 P 2（点 P 1、 P 2 与点 O 、 C 不重合），请求 P 1、 P 2 点的坐标并说明理由．（注：第（2）问可利用备用图作答）．9．（厦门）如图，在直角梯形 OABD 中， DB ∥ OA ，∠ OAB=90°，点 O 为坐标原点，点 A 在 x 轴的正半轴上，对角线 OB ， AD 相交于点 M ． OA=2， AB=2 ，BM ： MO=1 ： 2．（1）求 OB 和 OM 的值；（2）求直线OD 所对应的函数关系式；（3）已知点P 在线段 OB 上（ P 不与点 O，B 重合），经过点 A 和点 P 的直线交梯形OABD的边于点E（ E 异于点 A），设 OP=t，梯形 OABD 被夹在∠ OAE内的部分的面积为S，求 S关于 t 的函数关系式．10．（天门）如图①，在平面直角坐标系中， A 点坐标为（ 3，0），B 点坐标为（ 0，4）．动点 M 从点 O 出发，沿OA 方向以每秒 1 个单位长度的速度向终点 A 运动；同时，动点N 从点 A 出发沿 AB 方向以每秒个单位长度的速度向终点 B 运动．设运动了x 秒．（1）点 N 的坐标为（_________，_________）；（用含x 的代数式表示）（2）当 x 为何值时，△ AMN 为等腰三角形；（3）如图②，连接 ON 得△ OMN，△ OMN 可能为正三角形吗？若不能，点M 的运动速度不变，试改变点N 的运动速度，使△ OMN为正三角形，并求出点N 的运动速度．11．（乐山）如图，在平面直角坐标系中，△ABC的边 AB 在 x 轴上，且 OA＞ OB，以 AB 为直径2的圆过点 C．若点 C 的坐标为（ 0， 2）， AB=5，A，B 两点的横坐标 x A， x B是关于 x 的方程 x﹣（ m+2） x+n﹣1=0 的两根．（1）求 m， n 的值；（2）若∠ ACB 平分线所在的直线l 交 x 轴于点 D，试求直线l 对应的一次函数解析式；（3）过点 D 任作一直线l 分′别交射线CA，CB（点 C 除外）于点M，N．则的是否为定值？若是，求出该定值；若不是，请说明理由．12．（黄冈）已知：如图，在直角梯形 COAB中， OC∥ AB，以 O 为原点建立平面直角坐标系， A，B，C 三点的坐标分别为 A（8 ，0）， B（ 8，10）， C（ 0，4），点 D 为线段 BC的中点，动点P 从点 O 出发，以每秒 1 个单位的速度，沿折线 OABD 的路线移动，移动的时间为 t 秒．（1）求直线 BC的解析式；（2）若动点 P 在线段 OA 上移动，当 t 为何值时，四边形 OPDC的面积是梯形 COAB面积的；（3）动点 P 从点 O 出发，沿折线OABD 的路线移动过程中，设△ OPD的面积为S，请直接写出 S 与 t 的函数关系式，并指出自变量t 的取值范围；（4）试探究：当动点 P 在线段 AB 上移动时，能否在线段OA 上找到一点Q，使四边形CQPD 为矩形？并求出此时动点P 的坐标．13．（遵义）如图，已知一次函数的图象与x 轴， y 轴分别相交于A， B 两点，点 C 在 AB 上以每秒 1 个单位的速度从点 B 向点 A 运动，同时点 D 在线段 AO 上以同样的速度从点 A 向点 O 运动，运动时间用t（单位：秒）表示．（1）求 AB 的长；（2）当 t 为何值时，△ ACD与△ AOB 相似并直接写出此时点 C 的坐标；（3）△ ACD 的面积是否有最大值？若有，此时t 为何值；若没有，请说明理由．14．（株洲）已知 Rt△ABC，∠ ACB=90°， AC=4， BC=3， CD⊥AB 于点 D，以 D 为坐标原点，CD 所在直线为 y 轴建立如图所示平面直角坐标系．（1）求 A， B， C 三点的坐；（2）若⊙ O1，⊙ O2分△ACD，△ BCD的内切，求直O1O2的解析式；（3）若直 O1O2分交 AC，BC 于点 M，N，判断 CM 与 CN的大小关系，并明你的．15．（江）探索、研究：下是按照一定的律画出的一列“ 型” ，下表的n 表示“型” 的序号， a n表示第 n 个“ 型” 中“ 枝”的个数．：表：n 2 3 4⋯13 7 1⋯a n15（1）根据“ ”、“表”可以出a n关于 n 的关系式_________．若直 l1点（ a1， a2）、（ a2， a3），求直 l 1的函数关系式，并明任意的正整数 n，点（ a n，a n+1）都在直 l1上．（2）直l2： y= x+4 与 x 相交于点A，与直l1相交于点M ，双曲 y=（x＞0）点 M，且与直l2相交于另一点N．①求点 N 的坐，并在如所示的直角坐系中画出双曲及直l 1、 l2．② H 双曲在点 M、 N 之的部分（不包括点 M 、N）， P H 上一个点，点 P 的横坐 t ，直 MP 与 x 相交于点 Q，当 t 何，△ MQA 的面等于△ PMA 的面的2 倍又是否存在 t 的，使得△ PMA 的面等于 1？若存在，求出 t 的；若不存在，明理由．③在 y 上是否存在点G，使得△GMN 的周最小？若存在，求出点G的坐；若不存在，明理由．16．（咸宁）如，在平面直角坐系 xoy 中，已知矩形 ABCD的 AB、AD 分在 x 、 y 上，点 A 与坐原点重合，且 AB=2， AD=1．操作：将矩形ABCD折叠，使点 A 落在 DC 上．探究：（1）我们发现折痕所在的直线与矩形的两边一定相交，那么相交的情形有几种请你画出每种情形的图形；（只要用矩形草稿纸动手折一折你会有发现的！）（2）当折痕所在的直线与矩形的边 OD 相交于点 E，与边 OB 相交于点 F 时，设直线的解析式为y=kx+b．①求 b 与 k 的函数关系式；②求折痕 EF的长（用含k 的代数式表示），并写出k 的取值范围．17．（厦门）已知点 P（m， n）（ m＞ 0）在直线 y=x+b（0＜ b＜ 3）上，点 A、 B 在 x 轴上（点 A 在点 B 的左边），线段 AB 的长度为 b，设△ PAB的面积为 S，且 S= b 2+ b．（1）若 b= ，求 S 的值；（2）若 S=4，求 n 的值；（3）若直线 y=x+b（ 0＜ b＜ 3）与 y 轴交于点 C，△PAB是等腰三角形，当 CA∥ PB 时，求 b的值．18．（乌鲁木齐）如图1，在平面直角坐标系中，O 为坐标原点，点 A 的坐标为（ 0， 6），点 B 坐标为，BC∥ y轴且与x轴交于点C，直线 OB 与直线 AC 相交于点P．（1）求点 P 的坐标；（2）若以点 O 为圆心， OP 的长为半径作⊙ O（如图 2），求证：直线 AC与⊙ O 相切于点 P；（3）过点 B 作 BD∥ x 轴与 y 轴相交于点 D，以点 O 为圆心， r 为半径作⊙ O，使点 D 在⊙ O内，点 C 在⊙ O 外；以点 B 为圆心， R 为半径作⊙ B，若⊙ O 与⊙ B 相切，试分别求出 r， R 的取值范围．19．（随州）如图，直角梯形 ABCD的腰 BC 所在直线的解析式为 y=﹣ x﹣ 6 ，点 A 与坐标原点 O重合，点 D 的坐标为（ 0，﹣ 4 ），将直角梯形 ABCD绕点 O 顺时针旋转 180°，得到直角梯形OEFG（如图 1）．（1）直接写出E， F 两点的坐标及直角梯形OEFG的腰 EF所在直线的解析式；（2）将图 1 中的直角梯形ABCD先沿 x 轴向右平移到点 A 与点 E 重合的位置，再让直角顶点 A 紧贴着 EF，向上平移直角梯形ABCD（即梯形ABCD向上移动时，总保持着AB∥ FG），当点 A 与点 F 重合时，梯形 ABCD停止移动．观察得知：在梯形ABCD移动过程中，其腰 BC始终经过坐标原点 O．（如图 2）①设点 A 的坐标为（ a， b），梯形 ABCD与梯形 OEFG重合部分的面积为S，试求 a 与何值时， S的值恰好等于梯形 OEFG面积的；②当点 A 在 EF上滑动时，设AD 与 x 轴的交点为 M，试问：在 y 轴上是否存在点 P，使得△PAM 是底角为 30 °的等腰三角形？如果存在，请求出所有符合条件的点P 的坐标；如果不存在，请说明理由．（利用图 3 进行探索）20．（邵阳）如图，直线y=﹣x+2 与 x 轴， y 轴分别相交于点A， B．将△ AOB 绕点 O 按顺时针方向旋转α角（ 0°＜α≤ 360）°，可得△ COD．（1）求点 A， B 的坐标；（2）当点 D 落在直线 AB 上时，直线 CD 与 OA 相交于点 E，△ COD和△ AOB 的重叠部分为△ODE（图①）．求证：△ ODE∽△ ABO；（3）除了（ 2）中的情况外，是否还存在△ COD和△ AOB 的重叠部分与△ AOB 相似，若存在，请指出旋转角α的度数；若不存在，请说明理由；（4）当α=30时°（图②）， CD与 OA， AB 分别相交于点 P，M ， OD 与 AB 相交于点 N，试求△ COD与△ AOB 的重叠部分（即四边形 OPMN）的面积．21．（韶关）如图，在平面直角坐标系中，四边形OABC是矩形，OA=4，AB=2，直线与坐标轴交于D、 E．设 M 是 AB 的中点， P 是线段 DE上的动点．（1）求 M、 D 两点的坐标；（2）当 P 在什么位置， PA=PB求出此 P 点的坐；（3） P 作 PH⊥ BC，垂足 H，当以 PM 直径的⊙ F 与 BC 相切于点 N ，求梯形 PMBH的面．22．（衢州）如，点 B1（1， y1）， B2（2， y2）， B3（ 3， y3）⋯， B n（ n， y n）（ n 是正整数）依次一次函数 y= x+ 的象上的点，点 A1（ x1，0），A2（ x2，0），A3（ x3，0），⋯，A n（ x n， 0）（ n 是正整数）依次是x 正半上的点，已知x1=a（ 0＜a＜ 1），△ A1B1A2，△A2B2A3，△ A3B3A4⋯△ A n B n A n+1分是以B1， B2，B3，⋯， B n点的等腰三角形．（1）写出 B2， B n两点的坐；（2）求 x2， x3（用含 a 的代数式表示）；分析形中各等腰三角形底度之的关系，写出你成立的两个；是否存在直角三角形？若存在，（3）当 a（ 0＜ a＜ 1）化，在上述所有的等腰三角形中，求出相的 a 的；若不存在，明理由．23．（黔南州）某商厦一种成本 50 元 / 件的商品，定的售价不低于成本，又不高于 80 元/ 件，中售量 y（件）与售价 x（元 / 件）的关系可近似的看作一次函数（如）．（1）求 y 与 x 的关系式；（2）商厦得的毛利（毛利 =售成本） s（元），售价定多少，商厦利最大，最大利是多少？此的售量是多少件？24．（牡丹江）如图，在平面直角坐标系中，已知点A（﹣ 3， 6），点 B，点 C 分别在 x 轴2的负半轴和正半轴上，OB， OC的长分别是方程x ﹣4x+3=0 的两根（ OB＜ OC）．（1）求 B， C 两点的坐标；（2）在坐标平面内是否存在点Q 和点 P（点 P 在直线 AC 上），使以 O、P、C、Q 为顶点的四边形是正方形？若存在，请直接写出Q 点的坐标；若不存在，请说明理由；（3）若平面内有 M（ 1，﹣ 2）， D 为线段 OC上一点，且满足∠ DMC=∠ BAC，∠ MCD=45°，求直线 AD 的解析式．25．（梅州）如图，直角梯形ABCD中， AB∥ CD，∠ A=90°， AB=6， AD=4，DC=3，动点 P从点 A 出发，沿A→D→C→B方向移动，动点Q 从点 A 出发，在AB 边上移动．设点P 移动的路程为x，点 Q 移动的路程为y，线段 PQ 平分梯形ABCD的周长．（1）求 y 与 x 的函数关系式，并求出x，y 的取值范围；（2）当 PQ∥ AC 时，求 x，y 的值；（3）当 P 不在 BC 边上时，线段PQ能否平分梯形ABCD的面积？若能，求出此时x 的值；若不能，说明理由．26．（聊城）某市为了进一步改善居民的生活环境，园林处决定增加公园 A 和公园 B 的绿化面积．已知公园 A， B 分别有如图1，图 2 所示的阴影部分需铺设草坪，在甲、乙两地分别有同种草皮 1608m 2和 1200m2出售，且售价一样．若园林处向甲、乙两地购买草皮，其路程和运费单价见下表：公园 A公园 B路程（千米）运费单价（元）路程（千米）运费单价（元）甲地300.25320.25乙地220.3300.3（注：运费单价指将每平方米草皮运送 1 千米所需的人民币）（1）分别求出公园 A ，B 需铺设草坪的面积；（结果精确到 1m 2）（2）请设计出总运费最省的草皮运送方案，并说明理由．27．（佳木斯）如图，在平面直角坐标系中，已知点 A （﹣ 3， 6），点 B ，点 C 分别在 x 轴的负半轴和正半轴上， OB ， OC 的长分别是方程 x 2﹣4x+3=0 的两根（ OB ＜ OC ）．（ 1）求点 B ，点 C 的坐标；（ 2）若平面内有 M （ 1，﹣ 2）， D 为线段 OC 上一点，且满足∠ DMC=∠ BAC ，求直线 MD 的解析式；（ 3）在坐标平面内是否存在点Q 和点 P （点 P 在直线 AC 上），使以 O ，P ，C ，Q 为顶点的四边形是正方形？若存在，请直接写出Q 点的坐标；若不存在，请说明理由．28．（济南）已知：如图，在平面直角坐标系中，△ ABC 是直角三角形，∠ ACB=90°，点 A ，C 的坐标分别为 A （﹣ 3， 0）， C （1， 0）， tan ∠ BAC= ．（1）求过点 A ， B 的直线的函数表达式；（2）在 x 轴上找一点 D ，连接 DB ，使得 △ ADB 与 △ ABC 相似（不包括全等），并求点 D 的坐标；（3）在（ 2）的条件下，如 P ，Q 分别是 AB 和 AD 上的动点，连接 PQ ，设 AP=DQ=m ，问是否存在这样的 m ，使得 △ APQ 与 △ ADB 相似？如存在，请求出 m 的值；如不存在，请说明理由．29．（黑龙江）如图，点＜OB ）的长分别是关于（1）求∠ ABC 的度数；A 为 x 轴负半轴上一点，点B 为 x 轴正半轴上一点， OA ， OB （ OAx 的一元二次方程 22的两根， C （ 0，3），且 S △ABC =6x ﹣4mx+m +2=0（2）过点 C 作 CD⊥ AC 交 x 轴于点 D，求点 D 的坐标；（3）在第（ 2）问的条件下， y 轴上是否存在点 P，使∠ PBA=∠ ACB？若存在，请直接写出直线 PD 的解析式；若不存在，请说明理由．AD 平行于x 轴，下底BC 交y 30．（哈尔滨）如图，梯形ABCD在平面直角坐标系中，上底轴于点E，点C（ 4，﹣ 2），点D（ 1， 2）， BC=9， sin∠ ABC=．（1）求直线AB 的解析式；（2）若点 H 的坐标为（﹣ 1，﹣ 1），动点 G 从 B 出发，以 1 个单位 / 秒的速度沿着BC边向C 点运动（点G 可以与点 B 或点 C 重合），求△ HGE的面积 S（ S≠0）随动点 G 的运动时间t′秒变化的函数关系式（写出自变量t′的取值范围）；（3）在（ 2）的条件下，当秒时，点G 停止运动，此时直线GH 与y 轴交于点N．另一动点 P 开始从 B 出发，以 1 个单位 / 秒的速度沿着梯形的各边运动一周，即由 B 到 A，然后由 A 到 D，再由 D 到 C，最后由 C 回到 B（点 P 可以与梯形的各顶点重合）．设动点P 的运动时间为t 秒，点 M 为直线 HE 上任意一点（点M 不与点 H 重合），在点P 的整个运动过程中，求出所有能使∠PHM 与∠ HNE相等的 t 的值．答案与分准一．解答（共30 小）1．（区）如，直l1：y=kx+b 平行于直y=x 1，且与直l2：相交于点P （ 1， 0）．（1）求直l1、 l2的解析式；（2）直 l1与 y 交于点A．一点 C 从点 A 出，先沿平行于x 的方向运，到达直l2上的点 B1后，改垂直于 x 的方向运，到达直l1上的点 A1后，再沿平行于x 的方向运，到达直l2上的点 B2后，又改垂直于x 的方向运，到达直 l 1上的点 A2后，仍沿平行于x 的方向运，⋯照此律运，点 C 依次点B1， A1， B2， A2， B3，A3，⋯， B n， A n，⋯①求点 B1， B2， A1， A2的坐；②你通得出点A n、B n的坐；并求当点C到达 A n，运的路径的？考点：一次函数合。

(完整版)2018年中考数学挑战压轴题(含答案)

2017 挑战压轴题中考数学精讲解读篇因动点产生的相似三角形问题1．如图,在平面直角坐标系xOy中，将抛物线y=x2的对称轴绕着点P（0，2)顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上一点．(1)求直线AB的函数表达式;(2）如图①，若点Q在直线AB的下方,求点Q到直线AB的距离的最大值；（3）如图②，若点Q在y轴左侧,且点T（0，t)（t＜2）是射线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值．2．如图，已知BC是半圆O的直径,BC=8,过线段BO上一动点D，作AD⊥BC交半圆O于点A，联结AO，过点B作BH⊥AO，垂足为点H,BH的延长线交半圆O于点F．（1)求证：AH=BD;（2）设BD=x，BE•BF=y，求y关于x的函数关系式；(3）如图2，若联结FA并延长交CB的延长线于点G，当△FAE与△FBG相似时，求BD的长度．3．如图，在平面直角坐标系xOy中，直线AB过点A（3,0）、B（0，m)（m＞0）,tan∠BAO=2．（1）求直线AB的表达式;（2）反比例函数y=的图象与直线AB交于第一象限内的C、D两点(BD＜BC），当AD=2DB时，的值；求k1（3）设线段AB的中点为E，过点E作x轴的垂线，垂足为点M，交反比例函数y=的图象于的值．点F,分别联结OE、OF,当△OEF∽△OBE时，请直接写出满足条件的所有k24．如图，在Rt△ABC中，∠ACB=90°,AC=1,BC=7，点D是边CA延长线的一点，AE⊥BD，垂足为点E，AE的延长线交CA的平行线BF于点F,连结CE交AB于点G．（1)当点E是BD的中点时，求tan∠AFB的值;（2）CE•AF的值是否随线段AD长度的改变而变化？如果不变，求出CE•AF的值；如果变化，请说明理由；（3）当△BGE和△BAF相似时，求线段AF的长．5．如图，平面直角坐标系xOy中，已知B（﹣1，0），一次函数y=﹣x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=﹣x2+bx+c的图象经过点A、点B．（1）求这个二次函数的解析式;(2）点P是该二次函数图象的顶点，求△APC的面积;(3）如果点Q在线段AC上，且△ABC与△AOQ相似,求点Q的坐标．6．已知：半圆O的直径AB=6,点C在半圆O上，且tan∠ABC=2，点D为弧AC上一点，联结DC（如图）（1）求BC的长；（2）若射线DC交射线AB于点M，且△MBC与△MOC相似，求CD的长；（3）联结OD,当OD∥BC时，作∠DOB的平分线交线段DC于点N，求ON的长．7．如图,已知二次函数y=x2+bx+c(b，c为常数）的图象经过点A（3,﹣1），点C（0，﹣4），顶点为点M，过点A作AB∥x轴，交y轴与点D，交该二次函数图象于点B，连结BC．(1)求该二次函数的解析式及点M的坐标；（2）若将该二次函数图象向上平移m（m＞0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包含△ABC的边界)，求m的取值范围；（3）点P时直线AC上的动点，若点P，点C，点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标（直接写出结果，不必写解答过程）．因动点产生的等腰三角形问题8．如图1,在△ABC中，∠ACB=90°,∠BAC=60°，点E是∠BAC角平分线上一点，过点E作AE 的垂线，过点A作AB的垂线，两垂线交于点D，连接DB,点F是BD的中点，DH⊥AC，垂足为H，连接EF，HF．(1）如图1，若点H是AC的中点，AC=2，求AB，BD的长；（2）如图1，求证：HF=EF；（3）如图2，连接CF，CE．猜想:△CEF是否是等边三角形?若是，请证明；若不是，说明理由．9．已知，一条抛物线的顶点为E（﹣1，4）,且过点A（﹣3,0）,与y轴交于点C，点D是这条抛物线上一点，它的横坐标为m，且﹣3＜m＜﹣1,过点D作DK⊥x轴，垂足为K,DK分别交线段AE、AC于点G、H．（1）求这条抛物线的解析式；（2)求证：GH=HK；(3)当△CGH是等腰三角形时,求m的值．10．如图，已知在Rt△ABC中，∠ACB=90°,AB=5，sinA=，点P是边BC上的一点，PE⊥AB，垂足为E，以点P为圆心，PC为半径的圆与射线PE相交于点Q,线段CQ与边AB交于点D．（1）求AD的长；（2）设CP=x，△PCQ的面积为y，求y关于x的函数解析式，并写出定义域；（3）过点C作CF⊥AB,垂足为F，联结PF、QF，如果△PQF是以PF为腰的等腰三角形，求CP 的长．11．如图（1），直线y=﹣x+n交x轴于点A，交y轴于点C（0,4），抛物线y=x2+bx+c经过点A，交y轴于点B（0,﹣2）．点P为抛物线上一个动点，过点P作x轴的垂线PD，过点B作BD ⊥PD于点D，连接PB,设点P的横坐标为m．（1）求抛物线的解析式;（2）当△BDP为等腰直角三角形时，求线段PD的长；（3)如图(2)，将△BDP绕点B逆时针旋转，得到△BD′P′，当旋转角∠PBP′=∠OAC，且点P 的对应点P′落在坐标轴上时，请直接写出点P的坐标．12．综合与探究如图，在平面直角坐标系中,已知抛物线y=ax2+bx﹣8与x轴交于A,B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为（﹣2，0），(6，﹣8）．（1)求抛物线的函数表达式，并分别求出点B和点E的坐标；（2）试探究抛物线上是否存在点F，使△FOE≌△FCE？若存在，请直接写出点F的坐标;若不存在，请说明理由；（3）若点P是y轴负半轴上的一个动点，设其坐标为（0,m)，直线PB与直线l交于点Q，试探究：当m为何值时,△OPQ是等腰三角形．因动点产生的直角三角形问题13．已知，如图1,在梯形ABCD中,AD∥BC，∠BCD=90°，BC=11，CD=6，tan∠ABC=2，点E在AD边上，且AE=3ED，EF∥AB交BC于点F,点M、N分别在射线FE和线段CD上．（1）求线段CF的长；（2)如图2,当点M在线段FE上，且AM⊥MN，设FM•cos∠EFC=x，CN=y，求y关于x的函数解析式，并写出它的定义域；（3）如果△AMN为等腰直角三角形，求线段FM的长．14．如图，在矩形ABCD 中,点O 为坐标原点，点B 的坐标为（4，3）,点A 、C 在坐标轴上，点P 在BC 边上，直线l 1:y=2x+3，直线l 2:y=2x ﹣3．（1）分别求直线l 1与x 轴，直线l 2与AB 的交点坐标；（2）已知点M 在第一象限，且是直线l 2上的点，若△APM 是等腰直角三角形，求点M 的坐标；（3）我们把直线l 1和直线l 2上的点所组成的图形为图形F ．已知矩形ANPQ 的顶点N 在图形F 上,Q 是坐标平面内的点，且N 点的横坐标为x ，请直接写出x 的取值范围（不用说明理由）．因动点产生的平行四边形问题15．如图，在平面直角坐标系xOy 中,抛物线y=ax 2﹣2ax ﹣3a(a ＜0）与x 轴交于A ，B 两点(点A 在点B 的左侧），经过点A 的直线l ：y=kx+b 与y 轴交于点C ，与抛物线的另一个交点为D ，且CD=4AC ．（1)直接写出点A 的坐标,并求直线l 的函数表达式（其中k ，b 用含a 的式子表示）；（2）点E 是直线l 上方的抛物线上的一点，若△ACE 的面积的最大值为，求a 的值;（3）设P 是抛物线对称轴上的一点,点Q 在抛物线上，以点A ，D ，P ，Q 为顶点的四边形能否成为矩形？若能，求出点P 的坐标；若不能,请说明理由．16．如图，在矩形OABC中，OA=5，AB=4,点D为边AB上一点，将△BCD沿直线CD折叠，使点B 恰好落在OA边上的点E处，分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系．（1）求点E坐标及经过O，D，C三点的抛物线的解析式；（2)一动点P从点C出发，沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动．设运动时间为t秒，当t为何值时,DP=DQ；（3）若点N在（2）中的抛物线的对称轴上，点M在抛物线上，是否存在这样的点M与点N，使得以M，N，C，E为顶点的四边形是平行四边形？若存在，请求出M点的坐标；若不存在,请说明理由．17．如图，抛物线y=﹣x2+2x+3与x轴交于A、B两点（点A在点B的左边）,与y轴交于点C,点D和点C关于抛物线的对称轴对称，直线AD与y轴交于点E．（1）求直线AD的解析式;(2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH周长的最大值；（3)点M是抛物线的顶点,点P是y轴上一点，点Q是坐标平面内一点，以A，M，P,Q为顶点的四边形是以AM为边的矩形．若点T和点Q关于AM所在直线对称，求点T的坐标．18．如图，点A和动点P在直线l上，点P关于点A的对称点为Q,以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4,作△ABQ的外接圆O．点C在点P右侧，PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D，交AB右侧的圆弧于点E．在射线CD上取点F,使DF=CD,以DE，DF为邻边作矩形DEGF．设AQ=3x．(1）用关于x的代数式表示BQ，DF．(2)当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长．（3）在点P的整个运动过程中，①当AP为何值时,矩形DEGF是正方形?②作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长（直接写出答案)．19．在平面直角坐标系xOy（如图）中，经过点A(﹣1，0）的抛物线y=﹣x2+bx+3与y轴交于点C，点B与点A、点D与点C分别关于该抛物线的对称轴对称．（1)求b的值以及直线AD与x轴正方向的夹角；（2）如果点E是抛物线上一动点，过E作EF平行于x轴交直线AD于点F，且F在E的右边，过点E作EG⊥AD与点G，设E的横坐标为m，△EFG的周长为l，试用m表示l；（3)点M是该抛物线的顶点，点P是y轴上一点，Q是坐标平面内一点,如果以点A、M、P、Q为顶点的四边形是矩形，求该矩形的顶点Q的坐标．20．如图，直线y=mx+4与反比例函数y=（k＞0）的图象交于点A、B，与x轴、y轴分别交于D、C，tan∠CDO=2，AC：CD=1：2．(1）求反比例函数解析式；（2）联结BO，求∠DBO的正切值；（3）点M在直线x=﹣1上,点N在反比例函数图象上,如果以点A、B、M、N为顶点的四边形是平行四边形，求点N的坐标．21．如图,在平面直角坐标系中，抛物线y=ax2+bx+c的顶点坐标为（2,9），与y轴交于点A（0，5）,与x轴交于点E、B．（1）求二次函数y=ax2+bx+c的表达式;（2）过点A作AC平行于x轴，交抛物线于点C,点P为抛物线上的一点（点P在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；(3）若点M在抛物线上，点N在其对称轴上，使得以A、E、N、M为顶点的四边形是平行四边形，且AE为其一边,求点M、N的坐标．因动点产生的梯形问题22．如图，在平面直角坐标系xOy中，二次函数y=+bx+c的图象与y轴交于点A,与双曲线y=有一个公共点B，它的横坐标为4，过点B作直线l∥x轴，与该二次函数图象交于另一个点C，直线AC在y轴上的截距是﹣6．（1）求二次函数的解析式；（2)求直线AC的表达式;(3）平面内是否存在点D，使A、B、C、D为顶点的四边形是等腰梯形？如果存在，求出点D坐标；如果不存在，说明理由．23．如图，矩形OMPN的顶点O在原点，M、N分别在x轴和y轴的正半轴上,OM=6，ON=3，反比例函数y=的图象与PN交于C，与PM交于D，过点C作CA⊥x轴于点A，过点D作DB⊥y轴于点B，AC与BD交于点G．（1）求证：AB∥CD；（2）在直角坐标平面内是否若存在点E,使以B、C、D、E为顶点，BC为腰的梯形是等腰梯形？若存在，求点E的坐标；若不存在请说明理由．因动点产生的面积问题24．如图，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，点P是抛物线上点A，C间的一个动点（含端点），过点P作PF⊥BC于点F,点D、E的坐标分别为（0,6），（﹣4，0),连接PD、PE、DE．（1)请直接写出抛物线的解析式；（2)小明探究点P的位置发现:当P与点A或点C重合时，PD与PF的差为定值，进而猜想：对于任意一点P，PD与PF的差为定值，请你判断该猜想是否正确，并说明理由；（3）小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点"，且使△PDE的周长最小的点P也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE周长最小时“好点"的坐标．25．如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连接CP,过点P作PM⊥CP交AB于点D,且PM=CP，过点M作MN∥OA，交BO于点N,连接ND、BM，设OP=t．（1）求点M的坐标（用含t的代数式表示)．（2)试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由．（3)当t为何值时，四边形BNDM的面积最小．26．在数学兴趣小组活动中,小明进行数学探究活动，将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．（1）小明发现DG⊥BE,请你帮他说明理由．（2）如图2，小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时，请你帮他求出此时BE的长．（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转,线段DG与线段BE将相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．27．在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B，点B关于原点的对称点为点C．（1）求过A,B，C三点的抛物线的解析式；（2)P为抛物线上一点，它关于原点的对称点为Q．①当四边形PBQC为菱形时,求点P的坐标；②若点P的横坐标为t（﹣1＜t＜1),当t为何值时，四边形PBQC面积最大？并说明理由．28．如图，在平面直角坐标系中，点A（10,0）,以OA为直径在第一象限内作半圆，B为半圆上一点，连接AB并延长至C，使BC=AB，过C作CD⊥x轴于点D,交线段OB于点E，已知CD=8，抛物线经过O、E、A三点．（1）∠OBA= °．（2）求抛物线的函数表达式．（3）若P为抛物线上位于第一象限内的一个动点，以P、O、A、E为顶点的四边形面积记作S，则S取何值时,相应的点P有且只有3个?29．如图1，关于x的二次函数y=﹣x2+bx+c经过点A(﹣3，0),点C（0，3)，点D为二次函数的顶点，DE为二次函数的对称轴,E在x轴上．（1)求抛物线的解析式；（2)DE上是否存在点P到AD的距离与到x轴的距离相等？若存在求出点P，若不存在请说明理由;（3）如图2,DE的左侧抛物线上是否存在点F，使2S△FBC =3S△EBC？若存在求出点F的坐标，若不存在请说明理由．30．已知抛物线y=mx2+（1﹣2m）x+1﹣3m与x轴相交于不同的两点A、B（1）求m的取值范围；（2）证明该抛物线一定经过非坐标轴上的一点P，并求出点P的坐标；(3）当＜m≤8时，由（2)求出的点P和点A，B构成的△ABP的面积是否有最值?若有，求出该最值及相对应的m值．31．问题提出（1）如图①,已知△ABC，请画出△ABC关于直线AC对称的三角形．问题探究（2）如图②,在矩形ABCD中，AB=4,AD=6，AE=4,AF=2，是否在边BC、CD上分别存在点G、H，使得四边形EFGH的周长最小?若存在,求出它周长的最小值；若不存在,请说明理由．问题解决（3)如图③，有一矩形板材ABCD,AB=3米，AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=米,∠EHG=45°，经研究，只有当点E、F、G分别在边AD、AB、BC上，且AF＜BF，并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形EFGH部件？若能,求出裁得的四边形EFGH 部件的面积；若不能，请说明理由．32．如图，在平面直角坐标系中，矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上，OC=8，OE=17，抛物线y=x2﹣3x+m与y轴相交于点A，抛物线的对称轴与x轴相交于点B,与CD交于点K．（1）将矩形OCDE沿AB折叠，点O恰好落在边CD上的点F处．①点B的坐标为（、）,BK的长是，CK的长是；②求点F的坐标；③请直接写出抛物线的函数表达式；（2）将矩形OCDE沿着经过点E的直线折叠，点O恰好落在边CD上的点G处，连接OG，折痕与OG相交于点H，点M是线段EH上的一个动点（不与点H重合），连接MG,MO，过点G作GP⊥OM 于点P，交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动，至与点N重合时停止，△MOG和△NOG的面积分别表示为S1和S2，在点M的运动过程中，S1•S2（即S1与S2的积）的值是否发生变化？若变化,请直接写出变化范围；若不变，请直接写出这个值．温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．33．如图，已知▱ABCD的三个顶点A(n,0）、B（m，0）、D(0，2n）（m＞n＞0)，作▱ABCD关于直线AD的对称图形AB1C 1 D（1）若m=3,试求四边形CC1B1B面积S的最大值；（2)若点B1恰好落在y轴上,试求的值．因动点产生的相切问题34．如图，已知在平面直角坐标系xOy中，抛物线y=ax2+2x+c与x轴交于点A（﹣1，0）和点B,与y轴相交于点C（0，3），抛物线的对称轴为直线l．（1）求这条抛物线的关系式，并写出其对称轴和顶点M的坐标；（2)如果直线y=kx+b经过C、M两点，且与x轴交于点D，点C关于直线l的对称点为N,试证明四边形CDAN是平行四边形；（3）点P在直线l上,且以点P为圆心的圆经过A、B两点，并且与直线CD相切，求点P的坐标．35．如图，在Rt△ABC中，∠C=90°,AC=14，tanA=,点D是边AC上一点，AD=8，点E是边AB 上一点,以点E为圆心，EA为半径作圆，经过点D，点F是边AC上一动点（点F不与A、C重合），作FG⊥EF，交射线BC于点G．（1）用直尺圆规作出圆心E，并求圆E的半径长（保留作图痕迹）；（2）当点G的边BC上时，设AF=x，CG=y，求y关于x的函数解析式，并写出它的定义域；（3）联结EG，当△EFG与△FCG相似时，推理判断以点G为圆心、CG为半径的圆G与圆E可能产生的各种位置关系．36．如图，线段PA=1,点D是线段PA延长线上的点,AD=a（a＞1），点O是线段AP延长线上的点，OA2=OP•OD，以O为圆心，OA为半径作扇形OAB,∠BOA=90°．点C是弧AB上的点，联结PC、DC．(1）联结BD交弧AB于E,当a=2时，求BE的长;（2)当以PC为半径的⊙P和以CD为半径的⊙C相切时，求a的值；（3）当直线DC经过点B,且满足PC•OA=BC•OP时，求扇形OAB的半径长．37．如图，在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD 上，点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，0.8cm为半径作⊙O，点P与点O同时出发,设它们的运动时间为t（单位:s）（0＜t＜）．（1）如图1，连接DQ平分∠BDC时，t的值为；（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；（3）请你继续进行探究，并解答下列问题：①证明：在运动过程中,点O始终在QM所在直线的左侧;②如图3,在运动过程中，当QM与⊙O相切时，求t的值；并判断此时PM与⊙O是否也相切？说明理由．38．如图,抛物线y=﹣x2+mx+n的图象经过点A（2，3），对称轴为直线x=1，一次函数y=kx+b 的图象经过点A,交x轴于点P，交抛物线于另一点B,点A、B位于点P的同侧．（1）求抛物线的解析式；(2)若PA：PB=3：1，求一次函数的解析式；(3）在（2)的条件下，当k＞0时，抛物线的对称轴上是否存在点C,使得⊙C同时与x轴和直线AP都相切，如果存在，请求出点C的坐标，如果不存在,请说明理由．因动点产生的线段和差问题39．如图，抛物线y=x2﹣4x与x轴交于O，A两点，P为抛物线上一点，过点P的直线y=x+m与对称轴交于点Q．(1）这条抛物线的对称轴是，直线PQ与x轴所夹锐角的度数是；（2）若两个三角形面积满足S△POQ =S△PAQ，求m的值;（3）当点P在x轴下方的抛物线上时,过点C（2，2)的直线AC与直线PQ交于点D,求:①PD+DQ 的最大值；②PD•DQ的最大值．40．抛物线y=ax2+bx+4(a≠0）过点A（1,﹣1），B（5,﹣1)，与y轴交于点C．(1）求抛物线的函数表达式；（2）如图1，连接CB，以CB为边作▱CBPQ，若点P在直线BC上方的抛物线上,Q为坐标平面内的一点，且▱CBPQ的面积为30，求点P的坐标；（3)如图2，⊙O1过点A、B、C三点，AE为直径，点M为上的一动点(不与点A，E重合），∠MBN为直角，边BN与ME的延长线交于N,求线段BN长度的最大值．41．如图，在每一个四边形ABCD中，均有AD∥BC，CD⊥BC，∠ABC=60°，AD=8，BC=12．（1）如图①，点M是四边形ABCD边AD上的一点,则△BMC的面积为；(2）如图②，点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值；(3）如图③，在四边形ABCD的边AD上，是否存在一点P，使得cos∠BPC的值最小？若存在，求出此时cos∠BPC的值;若不存在,请说明理由．42．如图，把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC 上，已知EP=FP=4，EF=4，∠BAD=60°，且AB＞4．（1)求∠EPF的大小；(2）若AP=6，求AE+AF的值；(3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值．43．如图，在平面直角坐标系中，抛物线y=﹣x2﹣x+2与x轴交于B、C两点(点B在点C的左侧），与y轴交于点A，抛物线的顶点为D．（1）填空：点A的坐标为（，），点B的坐标为( ，），点C的坐标为（，），点D的坐标为（，）；（2）点P是线段BC上的动点(点P不与点B、C重合）①过点P作x轴的垂线交抛物线于点E,若PE=PC,求点E的坐标；②在①的条件下，点F是坐标轴上的点，且点F到EA和ED的距离相等，请直接写出线段EF的长；③若点Q是线段AB上的动点(点Q不与点A、B重合），点R是线段AC上的动点（点R不与点A、C重合)，请直接写出△PQR周长的最小值．44．如图，矩形ABCD中，AB=4,AD=3，M是边CD上一点，将△ADM沿直线AM对折,得到△ANM．（1)当AN平分∠MAB时，求DM的长;（2)连接BN,当DM=1时，求△ABN的面积；（3)当射线BN交线段CD于点F时，求DF的最大值．45．如图,半圆O的直径AB=4，以长为2的弦PQ为直径，向点O方向作半圆M，其中P点在上且不与A点重合,但Q点可与B点重合．发现：的长与的长之和为定值l，求l：思考：点M与AB的最大距离为,此时点P，A间的距离为;点M与AB的最小距离为，此时半圆M的弧与AB所围成的封闭图形面积为；探究：当半圆M与AB相切时，求的长．(注：结果保留π，cos35°=，cos55°=）46．（1）发现：如图1，点A为线段BC外一动点,且BC=a,AB=b．填空：当点A位于时，线段AC的长取得最大值，且最大值为（用含a，b的式子表示)（2）应用:点A为线段BC外一动点,且BC=3，AB=1，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD,BE．①请找出图中与BE相等的线段，并说明理由；②直接写出线段BE长的最大值．（3）拓展:如图3,在平面直角坐标系中，点A的坐标为(2，0），点B的坐标为(5，0）,点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标．47．如图，直线l：y=﹣3x+3与x轴、y轴分别相交于A、B两点，抛物线y=ax2﹣2ax+a+4(a＜0）经过点B．（1)求该抛物线的函数表达式；（2)已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式，并求出S的最大值;（3)在（2）的条件下，当S取得最大值时,动点M相应的位置记为点M′．①写出点M′的坐标；②将直线l绕点A按顺时针方向旋转得到直线l′，当直线l′与直线AM′重合时停止旋转，在旋转过程中,直线l′与线段BM′交于点C，设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时，求直线l′旋转的角度(即∠BAC的度数)．48．如图,在平面直角坐标系xOy中，将二次函数y=x2﹣1的图象M沿x轴翻折，把所得到的图象向右平移2个单位长度后再向上平移8个单位长度，得到二次函数图象N．（1）求N的函数表达式；(2）设点P（m，n）是以点C（1，4）为圆心、1为半径的圆上一动点，二次函数的图象M与x 轴相交于两点A、B，求PA2+PB2的最大值；（3）若一个点的横坐标与纵坐标均为整数,则该点称为整点．求M与N所围成封闭图形内（包括边界）整点的个数．49．如图，顶点为A(，1)的抛物线经过坐标原点O，与x轴交于点B．（1）求抛物线对应的二次函数的表达式；（2)过B作OA的平行线交y轴于点C，交抛物线于点D,求证:△OCD≌△OAB;（3)在x轴上找一点P，使得△PCD的周长最小，求出P点的坐标．2017 挑战压轴题中考数学精讲解读篇参考答案与试题解析一．解答题（共36小题)1．如图，在平面直角坐标系xOy中，将抛物线y=x2的对称轴绕着点P（0，2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点．（1）求直线AB的函数表达式；(2）如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;（3）如图②,若点Q在y轴左侧，且点T(0，t)（t＜2)是射线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值．【分析】(1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式;（2)如图①,过点Q作x轴的垂线QC，交AB于点C,再过点Q作直线AB的垂线,垂足为D,构建等腰直角△QDC，利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答;（3）根据相似三角形的对应角相等推知：△PBQ中必有一个内角为45°；需要分类讨论:∠PBQ=45°和∠PQB=45°；然后对这两种情况下的△PAT是否是直角三角形分别进行解答．另外,以P、B、Q为顶点的三角形与△PAT相似也有两种情况：△Q″PB∽△PAT、△Q″BP∽△PAT．【解答】解：（1）如图①,设直线AB与x轴的交点为M．∵∠OPA=45°，∴OM=OP=2，即M（﹣2，0）．设直线AB的解析式为y=kx+b（k≠0），将M（﹣2，0），P(0,2）两点坐标代入，得，解得．故直线AB的解析式为y=x+2；（2）如图①,过点Q作x轴的垂线QC,交AB于点C，再过点Q作直线AB的垂线，垂足为D，根据条件可知△QDC为等腰直角三角形，则QD=QC．设Q（m，m2),则C(m，m+2）．∴QC=m+2﹣m2=﹣（m﹣）2+,QD=QC=[﹣（m﹣）2+]．故当m=时，点Q到直线AB的距离最大,最大值为;（3）∵∠APT=45°，∴△PBQ中必有一个内角为45°，由图知，∠BPQ=45°不合题意．①如图②,若∠PBQ=45°，过点B作x轴的平行线，与抛物线和y轴分别交于点Q′、F．此时满足∠PBQ′=45°．∵Q′（﹣2，4），F（0，4),∴此时△BPQ′是等腰直角三角形,由题意知△PAT也是等腰直角三角形．(i）当∠PTA=90°时，得到：PT=AT=1，此时t=1;（ii）当∠PAT=90°时，得到：PT=2，此时t=0．②如图③，若∠PQB=45°，①中是情况之一,答案同上;先以点F为圆心，FB为半径作圆，则P、B、Q′都在圆F上，设圆F与y轴左侧的抛物线交于另一点Q″．则∠PQ″B=∠PQ′B=45°（同弧所对的圆周角相等），即这里的交点Q″也是符合要求．设Q″（n，n2）（﹣2＜n＜0），由FQ″=2，得n2+(4﹣n2)2=22,即n4﹣7n2+12=0．解得n2=3或n2=4,而﹣2＜n＜0，故n=﹣，即Q″（﹣,3）．可证△PFQ″为等边三角形，所以∠PFQ″=60°，又PQ″=PQ″，所以∠PBQ″=∠PFQ″=30°．则在△PQ″B中，∠PQ″B=45°，∠PBQ″=30°．(i）若△Q″PB∽△PAT，则过点A作y轴的垂线,垂足为E．则ET=AE=,OE=1，所以OT=﹣1，解得t=1﹣；(ii)若△Q″BP∽△PAT,则过点T作直线AB垂线，垂足为G．设TG=a,则PG=TG=a,AG=TG=a，AP=,∴a+a=，解得PT=a=﹣1，∴OT=OP﹣PT=3﹣，∴t=3﹣．综上所述，所求的t的值为t=1或t=0或t=1﹣或t=3﹣．2．如图，已知BC是半圆O的直径，BC=8,过线段BO上一动点D，作AD⊥BC交半圆O于点A，联结AO,过点B作BH⊥AO，垂足为点H,BH的延长线交半圆O于点F．（1）求证：AH=BD；（2）设BD=x，BE•BF=y，求y关于x的函数关系式；（3）如图2,若联结FA并延长交CB的延长线于点G，当△FAE与△FBG相似时，求BD的长度．【分析】（1)由AD⊥BC，BH⊥AO,利用垂直的定义得到一对直角相等，再由一对公共角,且半径相等，利用AAS得到三角形ADO与三角形BHO全等，利用全等三角形对应边相等得到OH=OD，利用等式的性质化简即可得证；（2)连接AB，AF，如图1所示，利用HL得到直角三角形ADB与直角三角形BHA全等,利用全等三角形对应角相等得到一对角相等,再由公共角相等得到三角形ABE与三角形AFB相似，由相似得比例即可确定出y与x的函数解析式；（3)连接OF,如图2所示，利用两对角相等的三角形相似得到三角形AFO与三角形FOG相似，由相似得比例求出BD的长即可．【解答】（1）证明：∵AD⊥BC，BH⊥AO,∴∠ADO=∠BHO=90°,在△ADO与△BHO中,，∴△ADO≌△BHO（AAS），∴OH=OD，又∵OA=OB，∴AH=BD；(2）解：连接AB、AF，如图1所示，∵AO是半径，AO⊥弦BF，。

专题07 反比例函数问题-决胜2018中考数学压轴题全揭秘精品(原卷版)

一、选择题1．（2017滨州，第12题，3分）在平面直角坐标系内，直线AB垂直于x轴于点C（点C在原点的右侧），并分别与直线y=x和双曲线1yx=相交于点A、B，且AC+BC=4，则△OAB的面积为（）A．23+3或23﹣3B．2 +1或2﹣1C．23﹣3D．2﹣12．（2017广西桂林市，第11题，3分）一次函数y=﹣x+1（0≤x≤10）与反比例函数1yx=（﹣10≤x＜0）在同一平面直角坐标系中的图象如图所示，点（x1，y1），（x2，y2）是图象上两个不同的点，若y1=y2，则x1+x2的取值范围是（）A．﹣8910≤x≤1B．﹣8910≤x≤899C．﹣899≤x≤8910D．1≤x≤89103．（2017新疆乌鲁木齐市，第10题，4分）如图，点A（a，3），B（b，1）都在双曲线3yx=上，点C，D，分别是x轴，y轴上的动点，则四边形ABCD周长的最小值为（）A．52B．62C．21022D．24．（2017江苏省泰州市，第6题，3分）如图，P为反比例函数kyx=（k＞0）在第一象限内图象上的一点，过点P分别作x轴，y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B．若∠AOB=135°，则k的值是（）A ．2B ．4C ．6D ．8 5．（2017湖北省十堰市，第10题，3分）如图，直线36y x =-分别交x 轴，y 轴于A ，B ，M 是反比例函数ky x=（x ＞0）的图象上位于直线上方的一点，MC ∥x 轴交AB 于C ，MD ⊥MC 交AB 于D ，AC •BD =43，则k 的值为（）A ．﹣3B ．﹣4C ．﹣5D ．﹣66．（2017湖北省咸宁市，第8题，3分）在平面直角坐标系xOy 中，将一块含有45°角的直角三角板如图放置，直角顶点C 的坐标为（1，0），顶点A 的坐标为（0，2），顶点B 恰好落在第一象限的双曲线上，现将直角三角板沿x 轴正方向平移，当顶点A 恰好落在该双曲线上时停止运动，则此时点C 的对应点C ′的坐标为（）A ．（32，0） B ．（2，0） C ．（52，0） D ．（3，0）7．（2017湖北省荆州市，第10题，3分）规定：如果关于x 的一元二次方程20ax bx c ++=（a ≠0）有两个实数根，且其中一个根是另一个根的2倍，则称这样的方程为“倍根方程”．现有下列结论： ①方程2280x x +-=是倍根方程；②若关于x 的方程220x ax ++=是倍根方程，则a =±3；③若关于x 的方程260ax ax c -+=（a ≠0）是倍根方程，则抛物线26y ax ax c =-+与x 轴的公共点的坐标是（2，0）和（4，0）； ④若点（m ，n ）在反比例函数4y x=的图象上，则关于x 的方程250mx x n ++=是倍根方程．上述结论中正确的有（）A ．①②B ．③④C ．②③D ．②④8．（2017湖北省荆门市，第12题，3分）已知：如图，在平面直角坐标系xOy 中，等边△AOB 的边长为6，点C 在边OA 上，点D 在边AB 上，且OC =3BD ，反比例函数ky x=（k ≠0）的图象恰好经过点C 和点D ，则k 的值为（）A ．813 B ． 813 C ． 813 D ．8139．（2017怀化，第10题，4分）如图，A ，B 两点在反比例函数1k yx的图象上，C ，D 两点在反比例函数2k yx的图象上，AC ⊥y 轴于点E ，BD ⊥y 轴于点F ，AC =2，BD =1，EF =3，则12k k 的值是（）A．6B．4C．3D．210．（2017辽宁省营口市，第8题，3分）如图，在菱形ABOC中，∠A=60°，它的一个顶点C在反比例函数kyx=的图象上，若将菱形向下平移2个单位，点A恰好落在函数图象上，则反比例函数解析式为（）A．33yx=-B．3yx=-C．3yx=-D．3yx=11．（2017辽宁省锦州市，第8题，2分）如图，矩形OABC中，A（1，0），C（0，2），双曲线kyx=（0＜k＜2）的图象分别交AB，CB于点E，F，连接OE，OF，EF，S△OEF=2S△BEF，则k值为（）A．23B．1C．43D．212．（2017贵州省黔西南州，第10题，4分）如图，点A是反比例函数1yx=（x＞0）上的一个动点，连接OA，过点O作OB⊥OA，并且使OB=2OA，连接AB，当点A在反比例函数图象上移动时，点B也在某一反比例函数kyx=图象上移动，则k的值为（）A．﹣4B．4C．﹣2D．213．（2017四川省乐山市，第10题，3分）如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数xy6=的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（）A．52-B．211-C．51-D．241-14．（2017四川省达州市，第10题，3分）已知函数()()123xxyxx⎧->⎪⎪=⎨⎪<⎪⎩的图象如图所示，点P是y轴负半轴上一动点，过点P作y轴的垂线交图象于A，B两点，连接OA、OB．下列结论：①若点M1（x1，y1），M2（x2，y2）在图象上，且x1＜x2＜0，则y1＜y2；②当点P坐标为（0，﹣3）时，△AOB是等腰三角形；③无论点P在什么位置，始终有S△AOB=7.5，AP=4BP；④当点P移动到使∠AOB=90°时，点A的坐标为（26，6-）．其中正确的结论个数为（）A．1B．2C．3D．415．（2017临沂，第14题，3分）如图，在平面直角坐标系中，反比例函数kyx=（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N两点，△OMN的面积为10．若动点P在x轴上，则PM+PN的最小值是（）A ．62 B ．10 C ．226 D ．22916．（2017山东省威海市，第12题，3分）如图，正方形ABCD 的边长为5，点A 的坐标为（﹣4，0），点B 在y 轴上，若反比例函数xky =（k ≠0）的图象过点C ，则该反比例函数的表达式为（）A ．x y 3=B ．x y 4=C ． x y 5=D ．xy 6= 17．（2016吉林省长春市）如图，在平面直角坐标系中，点P （1，﹣4）、Q （m ，n ）在函数ky x =（x ＞0）的图象上，当m ＞1时，过点P 分别作x 轴、y 轴的垂线，垂足为点A ，B ；过点Q 分别作x 轴、y 轴的垂线，垂足为点C 、D ．QD 交PA 于点E ，随着m 的增大，四边形ACQE 的面积（）A ．减小B ．增大C ．先减小后增大D ．先增大后减小 18．（2016天津市）若点A （﹣5，1y ），B （﹣3，2y ），C （2，3y ）在反比例函数3y x=的图象上，则1y ，2y ，3y 的大小关系是（）A ．132y y y <<B ．123y y y <<C ．321y y y <<D ．213y y y << 19．（2016宁夏）正比例函数11y k x =的图象与反比例函数22k y x=的图象相交于A ，B 两点，其中点B 的横坐标为﹣2，当12y y <时，x 的取值范围是（）A ．x ＜﹣2或x ＞2B ．x ＜﹣2或0＜x ＜2C ．﹣2＜x ＜0或0＜x ＜2D ．﹣2＜x ＜0或x ＞220．（2016四川省乐山市）如图，在反比例函数2y x=-的图象上有一动点A ，连接AO 并延长交图象的另一支于点B ，在第一象限内有一点C ，满足AC =BC ，当点A 运动时，点C 始终在函数ky x=的图象上运动．若tan ∠CAB =2，则k 的值为（）A ．2B ．4C ．6D ．821．（2016山东省临沂市）如图，直线y =﹣x +5与双曲线ky x=（x ＞0）相交于A ，B 两点，与x 轴相交于C 点，△BOC 的面积是52．若将直线y =﹣x +5向下平移1个单位，则所得直线与双曲线ky x=（x ＞0）的交点有（）A ．0个B ．1个C ．2个D ．0个，或1个，或2个 22．（2016山东省日照市）正比例函数11y k x =（1k ＞0）与反比例函数22k y x=（2k ＞0）图象如图所示，则不等式21k k x x>的解集在数轴上表示正确的是（）A ．B ．C ．D ．23．（2016山东省济宁市）如图，O 为坐标原点，四边形OACB 是菱形，OB 在x 轴的正半轴上，sin ∠AOB =45，反比例函数48y x=在第一象限内的图象经过点A ，与BC 交于点F ，则△AOF 的面积等于（）A ．60B ．80C ．30D ．40 24．（2016山东省淄博市）反比例函数a y x =（a ＞0，a 为常数）和2y x=在第一象限内的图象如图所示，点M在ayx=的图象上，MC⊥x轴于点C，交2yx=的图象于点A；MD⊥y轴于点D，交2yx=的图象于点B，当点M在ayx=的图象上运动时，以下结论：①S△ODB=S△OCA；②四边形OAMB的面积不变；③当点A是MC的中点时，则点B是MD的中点．其中正确结论的个数是（）A．0B．1C．2D．325．（2016山东省烟台市）反比例函数16tyx-=的图象与直线y=﹣x+2有两个交点，且两交点横坐标的积为负数，则t的取值范围是（）A．t＜16B．t＞16C．t≤16D．t≥1626．（2016湖北省十堰市）如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线kyx=上（k＞0，x＞0），则k的值为（）A．3B．183C．93D．927．（2016湖北省宜昌市）函数21yx=+的图象可能是（）A ．B ．C ．D ．28．（2016湖南省株洲市）已知，如图一次函数1y ax b =+与反比例函数2ky x=的图象如图示，当12y y <时，x 的取值范围是（）A ．x ＜2B ．x ＞5C ．2＜x ＜5D ．0＜x ＜2或x ＞529．（2016甘肃省兰州市）如图，A ，B 两点在反比例函数1k y x =的图象上，C 、D 两点在反比例函数2ky x=的图象上，AC⊥x 轴于点E ，BD⊥x 轴于点F ，AC=2，BD=3，EF=103，则21k k -=（）A ．4B ．143 C ．163D ．630．（2016湖北省荆州市）如图，在Rt △AOB 中，两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上，将△AOB 绕点B 逆时针旋转90°后得到△A ′O ′B ．若反比例函数ky x=的图象恰好经过斜边A ′B的中点C ，S △ABO =4，tan ∠BAO =2，则k 的值为（）A ．3B ．4C ．6D ．831．（2016辽宁省抚顺市）如图，矩形ABCD 的顶点D 在反比例函数ky x=（x ＜0）的图象上，顶点B ，C 在x 轴上，对角线AC 的延长线交y 轴于点E ，连接BE ，若△BCE 的面积是6，则k 的值为（）A ．﹣6B ．﹣8C ．﹣9D ．﹣1232．（2016黑龙江省大庆市）已知A （1x ，1y ）、B （2x ，2y ）、C （3x ，3y ）是反比例函数2y x=上的三点，若123x x x <<，213y y y <<，则下列关系式不正确的是（） A ．12x x ＜0 B ．13x x ＜0 C ．23x x ＜0 D ．12x x +＜033．（2015宿迁）在平面直角坐标系中，点A ，B 的坐标分别为（﹣3，0），（3，0），点P 在反比例函数xy 2=的图象上，若△P AB 为直角三角形，则满足条件的点P 的个数为（） A ．2个 B ．4个 C ．5个 D ．6个 34．（2015眉山）如图，A 、B 是双曲线xky =上的两点，过A 点作AC ⊥x 轴，交OB 于D 点，垂足为C ．若△ADO 的面积为1，D 为OB 的中点，则k 的值为（） A ．34 B ．38C ．3D ．435．（2015内江）如图，正方形ABCD位于第一象限，边长为3，点A在直线y=x上，点A的横坐标为1，正方形ABCD的边分别平行于x轴、y轴．若双曲线kyx=与正方形ABCD有公共点，则k的取值范围为（）A．1＜k＜9 B．2≤k≤34 C．1≤k≤16 D．4≤k＜1636．（2015孝感）如图，△AOB是直角三角形，∠AOB=90°，OB=2OA，点A在反比例函数1yx=的图象上．若点B在反比例函数kyx=的图象上，则k的值为（）A．﹣4B．4C．﹣2D．237．（2015宜昌）如图，市煤气公司计划在地下修建一个容积为410m3的圆柱形煤气储存室，则储存室的底面积S（单位：m2）与其深度d（单位：m）的函数图象大致是（）A ．B ．C ．D ．38．（2015三明）如图，已知点A 是双曲线2y x=在第一象限的分支上的一个动点，连接AO 并延长交另一分支于点B ，过点A 作y 轴的垂线，过点B 作x 轴的垂线，两垂线交于点C ，随着点A 的运动，点C 的位置也随之变化．设点C 的坐标为（m ，n ），则m ，n 满足的关系式为（）A ．2n m =-B ．2n m =-C ．4n m =-D ．4n m=- 39．（2015乌鲁木齐）如图，在直角坐标系xOy 中，点A ，B 分别在x 轴和y 轴，34OA OB =．∠AOB 的角平分线与OA 的垂直平分线交于点C ，与AB 交于点D ，反比例函数ky x=的图象过点C ．当以CD 为边的正方形的面积为27时，k 的值是（）A ．2B ．3C ．5D ．740．（2015重庆市）如图，在平面直角坐标系中，菱形ABCD 在第一象限内，边BC 与x 轴平行，A ，B 两点的纵坐标分别为3，1．反比例函数3y x=的图象经过A ，B 两点，则菱形ABCD 的面积为（）A ．2B ．4C ．22D ．4241．（2015临沂）在平面直角坐标系中，直线2y x =-+与反比例函数1y x=的图象有唯一公共点，若直线y x b =-+与反比例函数1y x=的图象有2个公共点，则b 的取值范围是（）A ．b ＞2B ．﹣2＜b ＜2C ．b ＞2或b ＜﹣2D ．b ＜﹣242．（2015滨州）如图，在x 轴的上方，直角∠BOA 绕原点O 按顺时针方向旋转，若∠BOA 的两边分别与函数1y x=-、2y x =的图象交于B 、A 两点，则∠OAB 的大小的变化趋势为（）A ．逐渐变小B ．逐渐变大C ．时大时小D ．保持不变二、填空题43．（2017云南省，第6题，3分）已知点A （a ，b ）在双曲线5y x=上，若a 、b 都是正整数，则图象经过B （a ，0）、C （0，b ）两点的一次函数的解析式（也称关系式）为．44．（2017内蒙古通辽市，第17题，3分）如图，直线333--=x y 与x ，y 轴分别交于点A ，B ，与反比例函数xky =的图象在第二象限交于点C ，过点A 作x 轴的垂线交该反比例函数图象于点D ．若AD =AC ，则点D 的坐标为．45．（2017四川省成都市，第24题，4分）在平面直角坐标系xOy 中，对于不在坐标轴上的任意一点P （x ，y ），我们把点P （1x，1y ），称为点P 的“倒影点”，直线1y x =-+ 上有两点A 、B ，它们的倒影点A ′，B ′均在反比例函数ky x=的图象上，若AB =22 ，则k = ． 46．（2017山东省日照市，第16题，4分）如图，在平面直角坐标系中，经过点A 的双曲线ky x=（x ＞0）同时经过点B ，且点A 在点B 的左侧，点A 的横坐标为2，∠AOB =∠OBA =45°，则k 的值为．47．（2017江苏省南通市，第18题，3分）如图，四边形OABC 是平行四边形，点C 在x 轴上，反比例函数ky x=（x ＞0）的图象经过点A （5，12），且与边BC 交于点D ．若AB =BD ，则点D 的坐标为．48．（2017江苏省宿迁市，第16题，3分）如图，矩形ABOC 的顶点O 在坐标原点，顶点B ，C 分别在x ，y 轴的正半轴上，顶点A 在反比例函数ky x=（k 为常数，k ＞0，x ＞0）的图象上，将矩形ABOC 绕点A 按逆时针方向旋转90°得到矩形AB ′O ′C ′，若点O 的对应点O ′恰好落在此反比例函数图象上，则COBO 的值是．49．（2017江苏省常州市，第18题，2分）如图，已知点A 是一次函数12y x =（x ≥0）图象上一点，过点A 作x 轴的垂线l ，B 是l 上一点（B 在A 上方），在AB 的右侧以AB 为斜边作等腰直角三角形ABC ，反比例函数ky x=（x ＞0）的图象过点B ，C ，若△OAB 的面积为6，则△ABC 的面积是．50．（2017江苏省盐城市，第16题，3分）如图，曲线l 是由函数6yx在第一象限内的图象绕坐标原点O 逆时针旋转45°得到的，过点A （42-，42），B （22，22）的直线与曲线l 相交于点M 、N ，则△OMN 的面积为．51．（2017江苏省连云港市，第15题，3分）设函数3y x 与y =﹣2x ﹣6的图象的交点坐标为（a ，b ），则12a b的值是．52．（2017江苏省连云港市，第16题，3分）如图，已知等边三角形OAB与反比例函数kyx=（k＞0，x＞0）的图象交于A、B两点，将△OAB沿直线OB翻折，得到△OCB，点A的对应点为点C，线段CB交x轴于点D，则BDDC的值为．（已知sin15°=624）53．（2017浙江省宁波市，第17题，4分）已知△ABC的三个顶点为A（﹣1，﹣1），B（﹣1，3），C（﹣3，﹣3），将△ABC向右平移m（m＞0）个单位后，△ABC某一边的中点恰好落在反比例函数3yx的图象上，则m的值为．54．（2017浙江省温州市，第15题，5分）如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）．若AB=1，反比例函数kyx=（k≠0）的图象恰好经过点A′，B，则k的值为．55．（2017浙江省湖州市，第16题，4分）如图，在平面直角坐标系xOy中，已知直线y=kx（k＞0）分别交反比例函数1yx=和9yx=在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交1yx=的图象于点C，连结AC．若△ABC是等腰三角形，则k的值是．56．（2017金华，第15题，4分）如图，已知点A（2，3）和点B（0，2），点A在反比例函数kyx=的图象上，做射线AB，再将射线AB绕点A按逆时针方向旋转45°，交反比例函数图象于点C，则点C的坐标为．57．（2017湖北省孝感市，第16题，3分）如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数kyx=（x＞0）的图象经过A，B两点．若点A的坐标为（n，1），则k的值为．58．（2017湖北省荆州市，第18题，3分）如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在x 轴的负半轴、y轴的正半轴上，点B在第二象限．将矩形OABC绕点O顺时针旋转，使点B落在y轴上，得到矩形ODEF，BC与OD相交于点M．若经过点M的反比例函数kyx=（x＜0）的图象交AB于点N，S矩形OABC =32，tan∠DOE=12，则BN的长为．59．（2017湖北省鄂州市，第15题，3分）如图，AC ⊥x 轴于点A ，点B 在y 轴的正半轴上，∠ABC =60°，AB =4，BC =23，点D 为AC与反比例函数ky x=的图象的交点．若直线BD 将△ABC 的面积分成1：2的两部分，则k 的值为．60．（2017湖南省株洲市，第17题，3分）如图所示是一块含30°，60°，90°的直角三角板，直角顶点O 位于坐标原点，斜边AB 垂直于x 轴，顶点A 在函数11k y x =（x ＞0）的图象上，顶点B 在函数22ky x=（x ＞0）的图象上，∠ABO =30°，则12k k = ．61．（2017贵州省遵义市，第18题，4分）如图，点E ，F 在函数2y x=的图象上，直线EF 分别与x 轴、y 轴交于点A 、B ，且BE ：BF =1：3，则△EOF 的面积是．62．（2017辽宁省盘锦市，第16题，3分）在平面直角坐标系中，点P的坐标为（0，﹣5），以P为圆心的圆与x轴相切，⊙P的弦AB（B点在A点右侧）垂直于y轴，且AB=8，反比例函数kyx=（k≠0）经过点B，则k= ．63．（2017黑龙江省齐齐哈尔市，第18题，3分）如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=43，反比例函数kyx=的图象经过点C，与AB交于点D，若△COD的面积为20，则k的值等于．64．（2017山东省济南市，第20题，3分）如图，过点O的直线AB与反比例函数kyx=的图象交于A，B两点，A（2，1），直线BC∥y轴，与反比例函数3kyx-=（x＜0）的图象交于点C，连接AC，则△ABC的面积为．65．（2017山东省莱芜市，第15题，4分）直线y=kx+b与双曲线6yx=-交于A（﹣3，m），B（n，﹣6）两点，将直线y=kx+b向上平移8个单位长度后，与双曲线交于D，E两点，则S△ADE= ．66．（2016云南省昆明市）如图，反比例函数kyx=（k≠0）的图象经过A，B两点，过点A作AC⊥x轴，垂足为C，过点B作BD⊥x轴，垂足为D，连接AO，连接BO交AC于点E，若OC=CD，四边形BDCE 的面积为2，则k的值为．67．（2016内蒙古包头市）如图，在平面直角坐标系中，点A在第二象限内，点B在x轴上，∠AOB=30°，AB=BO，反比例函数kyx=（x＜0）的图象经过点A，若S△ABO=3，则k的值为．68．（2016内蒙古呼和浩特市）已知函数1yx=-，当自变量的取值为﹣1＜x＜0或x≥2，函数值y的取值．69．（2016四川省内江市）如图，点A在双曲线5yx=上，点B在双曲线8yx=上，且AB∥x轴，则△OAB的面积等于．70．（2016四川省眉山市）如图，已知点A是双曲线6yx=在第三象限分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边三角形ABC，点C在第四象限内，且随着点A的运动，点C的位置也在不断变化，但点C始终在双曲线kyx=上运动，则k的值是．71．（2016四川省达州市）如图，在平面直角坐标系中，矩形ABCD的边AB：B C=3：2，点A（3，0），B（0，6）分别在x轴，y轴上，反比例函数kyx=（x＞0）的图象经过点D，且与边BC交于点E，则点E的坐标为．72．（2016山东省滨州市）如图，已知点A、C在反比例函数y=的图象上，点B，D在反比例函数y=的图象上，a＞b＞0，AB∥CD∥x轴，AB，CD在x轴的两侧，AB=，CD=，AB与CD间的距离为6，则a ﹣b的值是．73．（2016广东省深圳市）如图，四边形ABCO是平行四边形，OA=2，AB=6，点C在x轴的负半轴上，将▱ABCO绕点A逆时针旋转得到▱ADEF，AD经过点O，点F恰好落在x轴的正半轴上，若点D在反比例函数kyx=（x＜0）的图象上，则k的值为．74．（2016广西南宁市）如图所示，反比例函数k y x =（k ≠0，x ＞0）的图象经过矩形OABC 的对角线AC 的中点D ．若矩形OABC 的面积为8，则k 的值为．75．（2016江西省）如图，直线l ⊥x 轴于点P ，且与反比例函数11k y x =（x ＞0）及22k y x=（x ＞0）的图象分别交于点A ，B ，连接OA ，OB ，已知△OAB 的面积为2，则12k k -= ．76．（2016陕西省）已知一次函数y =2x +4的图象分别交x 轴、y 轴于A 、B 两点，若这个一次函数的图象与一个反比例函数的图象在第一象限交于点C ，且AB =2BC ，则这个反比例函数的表达式为．77．（2016江苏省宿迁市）如图，在平面直角坐标系中，一条直线与反比例函数8y x=（x ＞0）的图象交于两点A 、B ，与x 轴交于点C ，且点B 是AC 的中点，分别过两点A 、B 作x 轴的平行线，与反比例函数2y x =（x ＞0）的图象交于两点D 、E ，连接DE ，则四边形ABED 的面积为．78．（2016江苏省扬州市）如图，点A 在函数4y x =（x ＞0）的图象上，且OA =4，过点A 作AB ⊥x 轴于点B ，则△ABO 的周长为．79．（2016浙江省丽水市）如图，一次函数y =﹣x +b 与反比例函数4y x=（x ＞0）的图象交于A ，B 两点，与x 轴、y 轴分别交于C ，D 两点，连结OA ，OB ，过A 作AE ⊥x 轴于点E ，交OB 于点F ，设点A 的横坐标为m ．（1）b = （用含m 的代数式表示）；（2）若4OAF EFBC S S +=△四边形，则m 的值是．80．（2016浙江省宁波市）如图，点A 为函数9y x =（x ＞0）图象上一点，连结OA ，交函数1y x =（x ＞0）的图象于点B ，点C 是x 轴上一点，且AO =AC ，则△ABC 的面积为．81．（2016浙江省绍兴市）如图，已知直线l：y=﹣x，双曲线1yx=，在l上取一点A（a，﹣a）（a＞0），过A作x轴的垂线交双曲线于点B，过B作y轴的垂线交l于点C，过C作x轴的垂线交双曲线于点D，过D作y轴的垂线交l于点E，此时E与A重合，并得到一个正方形ABCD，若原点O在正方形ABCD的对角线上且分这条对角线为1：2的两条线段，则a的值为．82．（2016浙江省温州市）如图，点A，B在反比例函数kyx=（k＞0）的图象上，AC⊥x轴，BD⊥x轴，垂足C，D分别在x轴的正、负半轴上，CD=k，已知AB=2AC，E是AB的中点，且△BCE的面积是△ADE 的面积的2倍，则k的值是．83．（2016浙江省湖州市）已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P 向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．（1）k的值是；（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数4yx-=图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若1279SS=，则b的值是．84．（2016浙江省衢州市）如图，正方形ABCD的顶点A，B在函数kyx=（x＞0）的图象上，点C，D分别在x轴，y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．（1）当k=2时，正方形A′B′C′D′的边长等于．（2）当变化的正方形ABCD与（1）中的正方形A′B′C′D′有重叠部分时，k的取值范围是．85．（2016贵州省黔东南州）如图，点A是反比例函数11yx=（x＞0）图象上一点，过点A作x轴的平行线，交反比例函数2kyx=（x＞0）的图象于点B，连接OA、OB，若△OAB的面积为2，则k的值为．86．（2016湖北省荆门市）如图，已知点A（1，2）是反比例函数kyx=图象上的一点，连接AO并延长交双曲线的另一分支于点B，点P是x轴上一动点；若△P AB是等腰三角形，则点P的坐标是．87．（2016湖北省鄂州市）如图，已知直线1y k x b =+与x 轴、y 轴相交于P 、Q 两点，与2k y x =的图象相交于A （﹣2，m ）、B （1，n ）两点，连接OA 、OB ，给出下列结论：①12k k ＜0；②m +12n =0；③S △AOP =S △BOQ ；④不等式21k k x b x+>的解集是x ＜﹣2或0＜x ＜1，其中正确的结论的序号是．88．（2016湖北省随州市）如图，直线y =x +4与双曲线k y x=（k ≠0）相交于A （﹣1，a ）、B 两点，在y 轴上找一点P ，当P A +PB 的值最小时，点P 的坐标为．89．（2016湖北省孝感市）如图，已知双曲线k y x=与直线y =﹣x +6相交于A ，B 两点，过点A 作x 轴的垂线与过点B 作y 轴的垂线相交于点C ，若△ABC 的面积为8，则k 的值为．90．（2016辽宁省葫芦岛市）如图，在△AOB中，∠AOB=90°，点A的坐标为（2，1），BO=25，反比例函数kyx=的图象经过点B，则k的值为．91．（2016黑龙江省齐齐哈尔市）如图，已知点P（6，3），过点P作PM⊥x轴于点M，PN⊥y轴于点N，反比例函数kyx=的图象交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k= ．92．（2015南宁）如图，点A在双曲线23yx=（0x>）上，点B在双曲线kyx=（0x>）上（点B在点A的右侧），且AB∥x轴．若四边形OABC是菱形，且∠AOC=60°，则k= ．93．（2015桂林）如图，以▱ABCO 的顶点O 为原点，边OC 所在直线为x 轴，建立平面直角坐标系，顶点A 、C 的坐标分别是（2，4）、（3，0），过点A 的反比例函数k y x =的图象交BC 于D ，连接AD ，则四边形AOCD 的面积是．94．（2015贵港）如图，已知点A 1，A 2，…，A n 均在直线1y x =-上，点B 1，B 2，…，B n 均在双曲线1y x=-上，并且满足：A 1B 1⊥x 轴，B 1A 2⊥y 轴，A 2B 2⊥x 轴，B 2A 3⊥y 轴，…，A n B n ⊥x 轴，B n A n +1⊥y 轴，…，记点A n 的横坐标为a n （n 为正整数）．若11a =-，则a 2015= ．95．（2015南京）如图，过原点O 的直线与反比例函数1y ，2y 的图象在第一象限内分别交于点A ，B ，且A 为OB 的中点，若函数11y x=，则2y 与x 的函数表达式是．96．（2015攀枝花）如图，若双曲线k y x =（0k >）与边长为3的等边△AOB （O 为坐标原点）的边OA 、AB 分别交于C 、D 两点，且OC =2BD ，则k 的值为．97．（2015荆门）如图，点1A ，2A 依次在93(0)y x x=＞的图象上，点1B ，2B 依次在x 轴的正半轴上，若11A OB △，212A B B △均为等边三角形，则点2B 的坐标为．98．（2015烟台）如图，矩形OABC 的顶点A 、C 的坐标分别是（4，0）和（0，2），反比例函数k y x =（x ＞0）的图象过对角线的交点P 并且与AB ，BC 分别交于D ，E 两点，连接OD ，OE ，DE ，则△ODE 的面积为．三、解答题99．（2017内蒙古呼和浩特市，第23题，7分）已知反比例函数21k y x--=（k 为常数）．（1）若点P 1（13-，y 1）和点P 2（12-，y 2）是该反比例函数图象上的两点，试利用反比例函数的性质比较y 1和y 2的大小；（2）设点P （m ，n ）（m ＞0）是其图象上的一点，过点P 作PM ⊥x 轴于点M ．若tan ∠POM =2，PO =5（O为坐标原点），求k 的值，并直接写出不等式210k kx x++>的解集． 100．（2017内蒙古赤峰市，第21题，10分）如图，一次函数31y x =-+的图象与x 轴、y 轴分别交于点A 、B ，以线段AB 为边在第一象限作等边△ABC ．（1）若点C 在反比例函数ky x=的图象上，求该反比例函数的解析式；（2）点P （23，m ）在第一象限，过点P 作x 轴的垂线，垂足为D ，当△P AD 与△OAB 相似时，P 点是否在（1）中反比例函数图象上？如果在，求出P 点坐标；如果不在，请加以说明．101．（2017四川省自贡市，第24题，10分）[探究函数xx y 4+=的图象与性质] （1）函数xx y 4+=的自变量x 的取值范围是；（2）下列四个函数图象中函数xx y 4+=的图象大致是；（3）对于函数xx y 4+=，求当x ＞0时，y 的取值范围．请将下列的求解过程补充完整．解：∵x ＞0 ∴x x y 4+==22()()x x + =2()x x -+ ． ∵2()x x-≥0，∴y ≥ ． [拓展运用]（4）若函数259x x y x-+=，则y 的取值范围．102．（2017宁夏，第24题，8分）直线y =kx +b 与反比例函数6y x=（x ＞0）的图象分别交于点 A （m ，3）和点B （6，n ），与坐标轴分别交于点C 和点D ．（1）求直线AB 的解析式；（2）若点P 是x 轴上一动点，当△COD 与△ADP 相似时，求点P 的坐标．103．（2017济宁，第22题，11分）定义：点P 是△ABC 内部或边上的点（顶点除外），在△P AB ，△PBC ，△PCA 中，若至少有一个三角形与△ABC 相似，则称点P 是△ABC 的自相似点．例如：如图1，点P 在△ABC 的内部，∠PBC =∠A ，∠PCB =∠ABC ，则△BCP ∽△ABC ，故点P 是△ABC 的自相似点．请你运用所学知识，结合上述材料，解决下列问题：在平面直角坐标系中，点M是曲线33yx=（x＞0）上的任意一点，点N是x轴正半轴上的任意一点．（1）如图2，点P是OM上一点，∠ONP=∠M，试说明点P是△MON的自相似点；当点M的坐标是（3，3），点N的坐标是（3，0）时，求点P的坐标；（2）如图3，当点M的坐标是（3，3），点N的坐标是（2，0）时，求△MON的自相似点的坐标；（3）是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由．104．（2017山东省淄博市，第22题，8分）如图，在直角坐标系中，Rt△ABC的直角边AC在x轴上，∠ACB=90°，AC=1，反比例函数kyx=（k＞0）的图象经过BC边的中点D（3，1）．（1）求这个反比例函数的表达式；（2）若△ABC与△EFG成中心对称，且△EFG的边FG在y轴的正半轴上，点E在这个函数的图象上．①求OF的长；②连接AF，BE，证明四边形ABEF是正方形．105．（2017山东省聊城市，第23题，8分）如图，分别位于反比例函数1yx=，kyx=在第一象限图象上的两点A、B，与原点O在同一直线上，且13 OAOB=．（1）求反比例函数kyx=的表达式；（2）过点A作x轴的平行线交kyx=的图象于点C，连接BC，求△ABC的面积．106．（2017江苏省苏州市，第25题，8分）如图，在△ABC中，AC=BC，AB⊥x轴，垂足为A．反比例函数kyx=（x＞0）的图象经过点C，交AB于点D．已知AB=4，BC=52．（1）若OA=4，求k的值；（2）连接OC，若BD=BC，求OC的长．107．（2017湖北省恩施州，第21题，8分）如图，∠AOB=90°，反比例函数2yx（x＜0）的图象过点A（﹣1，a），反比例函数kyx=（k＞0，x＞0）的图象过点B，且AB∥x轴．（1）求a和k的值；（2）过点B作MN∥OA，交x轴于点M，交y轴于点N，交双曲线kyx=于另一点，求△OBC的面积．108．（2017黄冈，第23题，12分）月电科技有限公司用160万元，作为新产品的研发费用，成功研制出了一种市场急需的电子产品，已于当年投入生产并进行销售．已知生产这种电子产品的成本为4元/件，在销售过程中发现：每年的年销售量y（万件）与销售价格x（元/件）的关系如图所示，其中AB为反比例函数图象的一部分，BC为一次函数图象的一部分．设公司销售这种电子产品的年利润为s（万元）．（注：若上一年盈利，则盈利不计入下一年的年利润；若上一年亏损，则亏损计作下一年的成本．）（1）请求出y（万件）与x（元/件）之间的函数关系式；（2）求出第一年这种电子产品的年利润z（万元）与x（元/件）之间的函数关系式，并求出第一年年利润的最大值．（3）假设公司的这种电子产品第一年恰好按年利润s（万元）取得最大值时进行销售，现根据第一年的盈亏情况，决定第二年将这种电子产品每件的销售价格x（元）定在8元以上（x＞8），当第二年的年利润不低于103万元时，请结合年利润z（万元）与销售价格x（元/件）的函数示意图，求销售价格x（元/件）的取值范围．109．（2017湖南省株洲市，第24题，8分）如图所示，Rt△P AB的直角顶点P（3，4）在函数kyx=（x＞0）的图象上，顶点A、B在函数tyx=（x＞0，0＜t＜k）的图象上，P A∥x轴，连接OP，OA，记△OP A的面积为S△OP A，△P AB的面积为S△P AB，设w=S△OP A﹣S△P AB．①求k的值以及w关于t的表达式；②若用w max和w min分别表示函数w的最大值和最小值，令T=w max+a2﹣a，其中a为实数，求T min．110．（2017四川省攀枝花市，第21题，8分）如图，在平面直角坐标系中，坐标原点O是菱形ABCD的对称中心．边AB与x轴平行，点B（1，-2），反比例函数kyx=（k≠0）的图象经过A，C两点．（1）求点C的坐标及反比例函数的解析式．（2）直线BC与反比例函数图象的另一交点为E，求以O，C，E为顶点的三角形的面积．111．（2017山东省济南市，第26题，9分）如图1，▱OABC的边OC在y轴的正半轴上，OC=3，A（2，1），反比例函数kyx=（x＞0）的图象经过的B．（1）求点B的坐标和反比例函数的关系式；（2）如图2，直线MN分别与x轴、y轴的正半轴交于M，N两点，若点O和点B关于直线MN成轴对称，求线段ON的长；（3）如图3，将线段OA延长交kyx=（x＞0）的图象于点D，过B，D的直线分别交x轴、y轴于E，F两点，请探究线段ED与BF的数量关系，并说明理由．。

专题30 代数几何综合问题-决胜2018中考数学压轴题全揭秘精品(原卷版)

一、选择题1．（2017四川省乐山市，第10题，3分）如图，平面直角坐标系xOy 中，矩形OABC 的边OA 、OC 分别落在x 、y 轴上，点B 坐标为（6，4），反比例函数x y 6=的图象与AB 边交于点D ，与BC 边交于点E ，连结DE ，将△BDE 沿DE 翻折至△B 'DE 处，点B '恰好落在正比例函数y =kx 图象上，则k 的值是（）A ．52-B ．211-C ．51-D ．241- 2．（2017四川省内江市，第11题，3分）如图，在矩形AOBC 中，O 为坐标原点，OA 、OB 分别在x 轴、y 轴上，点B 的坐标为（0，33），∠ABO =30°，将△ABC 沿AB 所在直线对折后，点C 落在点D 处，则点D 的坐标为（）A ．（32，332）B ．（2，332）C ．（332，32）D ．（32，3﹣332） 3．（2017临沂，第14题，3分）如图，在平面直角坐标系中，反比例函数k y x=（x ＞0）的图象与边长是6的正方形OABC 的两边AB ，BC 分别相交于M ，N 两点，△OMN 的面积为10．若动点P 在x 轴上，则PM +PN 的最小值是（）A ．62B ．10C ．226D ．2294．（2017山东省威海市，第12题，3分）如图，正方形ABCD 的边长为5，点A 的坐标为（﹣4，0），点B 在y 轴上，若反比例函数xk y =（k ≠0）的图象过点C ，则该反比例函数的表达式为（）A ．x y 3=B ．x y 4=C ． x y 5=D ．xy 6= 5．（2017新疆乌鲁木齐市，第10题，4分）如图，点A （a ，3），B （b ，1）都在双曲线3y x =上，点C ，D ，分别是x 轴，y 轴上的动点，则四边形ABCD 周长的最小值为（）A ．52B ．62C ． 21022D ．26．（2017江苏省泰州市，第6题，3分）如图，P 为反比例函数k y x=（k ＞0）在第一象限内图象上的一点，过点P 分别作x 轴，y 轴的垂线交一次函数y =﹣x ﹣4的图象于点A 、B ．若∠AOB =135°，则k 的值是（）A．2B．4C．6D．87．（2017甘肃省兰州市，第15题，4分）如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是25，则矩形ABCD的面积是（）A．235B．5C．6D．2548．（2017甘肃省天水市，第10题，4分）如图，在等腰△ABC中，AB=AC=4cm，∠B=30°，点P从点B 出发，以3c m/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1c m/s的速度沿BA﹣AC 方向运动到点C停止，若△BPQ的面积为y（cm2），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是（）A．B．C ．D ．9．（2016山东省济南市）如图，在四边形ABCD 中，AB ∥CD ，∠B =90°，AB =AD =5，BC =4，M 、N 、E 分别是AB 、AD 、CB 上的点，AM =CE =1，AN =3，点P 从点M 出发，以每秒1个单位长度的速度沿折线MB ﹣BE 向点E 运动，同时点Q 从点N 出发，以相同的速度沿折线ND ﹣DC ﹣CE 向点E 运动，当其中一个点到达后，另一个点也停止运动．设△APQ 的面积为S ，运动时间为t 秒，则S 与t 函数关系的大致图象为（）A ．B ．C ．D ．10．（2016山东省济宁市）如图，O 为坐标原点，四边形OACB 是菱形，OB 在x 轴的正半轴上，sin ∠AOB =45，反比例函数48y x=在第一象限内的图象经过点A ，与BC 交于点F ，则△AOF 的面积等于（）A ．60B ．80C ．30D ．4011．（2016广西梧州市）如图所示，抛物线2y ax bx c =++（a ≠0）与x 轴交于点A （﹣2，0）、B （1，0），直线x =﹣0.5与此抛物线交于点C ，与x 轴交于点M ，在直线上取点D ，使MD =MC ，连接AC 、BC 、AD 、BD，某同学根据图象写出下列结论：①a﹣b=0；②当﹣2＜x＜1时，y＞0；③四边形ACBD是菱形；④9a﹣3b+c＞0你认为其中正确的是（）A．②③④B．①②④C．①③④D．①②③12．（2016浙江省湖州市）如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（）A．4B．174C．32D．2513．（2015邵阳）如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C 点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y 与t的函数关系的图象是（）A．B．C．D．14．（2015河池）我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l：43y kx=+与x轴、y轴分别交于A、B，∠OAB=30°，点P在x轴上，⊙P与l相切，当P在线段OA 上运动时，使得⊙P成为整圆的点P个数是（）A．6B．8C．10D．1215．（2015乐山）如图，已知直线334y x=-与x轴、y轴分别交于A、B两点，P是以C（0，1）为圆心，1为半径的圆上一动点，连结P A、PB．则△P AB面积的最大值是（）A．8 B．12 C．212D．172二、填空题16．（2017江苏省南通市，第18题，3分）如图，四边形OABC是平行四边形，点C在x轴上，反比例函数kyx=（x＞0）的图象经过点A（5，12），且与边BC交于点D．若AB=BD，则点D的坐标为．17．（2017浙江省温州市，第16题，5分）小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，水流路线呈抛物线，把手端点A，出水口B和落水点C恰好在同一直线上，点A至出水管BD的距离为12cm，洗手盆及水龙头的相关数据如图2所示，现用高10.2cm的圆柱型水杯去接水，若水流所在抛物线经过点D和杯子上底面中心E，则点E到洗手盆内侧的距离EH为cm．18．（2017浙江省湖州市，第16题，4分）如图，在平面直角坐标系xOy中，已知直线y=kx（k＞0）分别交反比例函数1yx=和9yx=在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交1yx=的图象于点C，连结AC．若△ABC是等腰三角形，则k的值是．19．（2017金华，第16题，4分）在一空旷场地上设计一落地为矩形ABCD的小屋，AB+BC=10m，拴住小狗的10m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S （m2）（1）如图1，若BC=4m，则S= m2．（2）如图2，现考虑在（1）中矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域，使之变成落地为五边形ABCED的小屋，其他条件不变，则在BC的变化过程中，当S取得最小值时，边BC的长为m．20．（2016四川省眉山市）如图，已知点A是双曲线6yx=在第三象限分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边三角形ABC，点C在第四象限内，且随着点A的运动，点C的位置也在不断变化，但点C始终在双曲线kyx=上运动，则k的值是．21．（2016浙江省湖州市）已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P 向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．（1）k的值是；（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数4yx-=图象交于C，D 两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若1279SS=，则b的值是．22．（2016浙江省衢州市）如图，正方形ABCD的顶点A，B在函数kyx=（x＞0）的图象上，点C，D分别在x轴，y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．（1）当k=2时，正方形A′B′C′D′的边长等于．（2）当变化的正方形ABCD与（1）中的正方形A′B′C′D′有重叠部分时，k的取值范围是．23．（2016湖北省鄂州市）如图，直线l：43y x=-，点A1坐标为（﹣3，0）．过点A1作x轴的垂线交直线l于点B1，以原点O为圆心，OB1长为半径画弧交x轴负半轴于点A2，再过点A2作x轴的垂线交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴负半轴于点A3，…，按此做法进行下去，点A2016的坐标为．24．（2016福建省龙岩市）如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10= ．25．（2016辽宁省葫芦岛市）如图，点A1（2，2）在直线y=x上，过点A1作A1B1∥y轴交直线12y x=于点B1，以点A1为直角顶点，A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1，再过点C1作A2B2∥y轴，分别交直线y=x和12y x=于A2，B2两点，以点A2为直角顶点，A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…，按此规律进行下去，则等腰直角△A n B n C n的面积为．（用含正整数n的代数式表示）26．（2016黑龙江省齐齐哈尔市）如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=2，OC=1．在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的32倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大32倍，得到矩形A2OC2B2…，以此类推，得到的矩形A n OC nB n的对角线交点的坐标为．27．（2015庆阳）如图，定点A（﹣2，0），动点B在直线y x=上运动，当线段AB最短时，点B的坐标为．28．（2015凉山州）菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P 是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．三、解答题29．（2017江苏省连云港市，第26题，12分）如图，已知二次函数23yax bx （a ≠0）的图象经过点A（3，0），B （4，1），且与y 轴交于点C ，连接AB 、AC 、BC ．（1）求此二次函数的关系式；（2）判断△ABC 的形状；若△ABC 的外接圆记为⊙M ，请直接写出圆心M 的坐标；（3）若将抛物线沿射线BA 方向平移，平移后点A 、B 、C 的对应点分别记为点A 1、B 1、C 1，△A 1B 1C 1的外接圆记为⊙M 1，是否存在某个位置，使⊙M 1经过原点？若存在，求出此时抛物线的关系式；若不存在，请说明理由．30．（2017河南省，第23题，11分）如图，直线23y x c =-+与x 轴交于点A （3，0），与y 轴交于点B ，抛物线243y x bx c =-++经过点A ，B ．（1）求点B 的坐标和抛物线的解析式；（2）M （m ，0）为x 轴上一动点，过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P ，N ． ①点M 在线段OA 上运动，若以B ，P ，N 为顶点的三角形与△APM 相似，求点M 的坐标；②点M 在x 轴上自由运动，若三个点M ，P ，N 中恰有一点是其它两点所连线段的中点（三点重合除外），则称M ，P ，N 三点为“共谐点”．请直接写出使得M ，P ，N 三点成为“共谐点”的m 的值．31．（2017浙江省台州市，第24题，14分）在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根．比如对于方程2520x x -+=，操作步骤是：第一步：根据方程的系数特征，确定一对固定点A （0，1），B （5，2）；第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A ，另一条直角边恒过点B ；第三步：在移动过程中，当三角板的直角顶点落在x 轴上点C 处时，点C 的横坐标m 即为该方程的一个实数根（如图1）；第四步：调整三角板直角顶点的位置，当它落在x 轴上另一点D 处时，点D 的横坐标n 即为该方程的另一个实数根．（1）在图2中，按照“第四步”的操作方法作出点D （请保留作出点D 时直角三角板两条直角边的痕迹）；（2）结合图1，请证明“第三步”操作得到的m 就是方程2520x x -+=的一个实数根；（3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程20ax bx c ++= （a ≠0，24b ac -≥0）的实数根，请你直接写出一对固定点的坐标；（4）实际上，（3）中的固定点有无数对，一般地，当m 1，n 1，m 2，n 2与a ，b ，c 之间满足怎样的关系时，点P （m 1，n 1），Q （m 2，n 2）就是符合要求的一对固定点？32．（2017浙江省宁波市，第25题，12分）如图，抛物线21144y x x c 与x 轴的负半轴交于点A ，与y轴交于点B ，连结AB ，点C （6，152）在抛物线上，直线AC 与y 轴交于点D ．（1）求c 的值及直线AC 的函数表达式；（2）点P 在x 轴正半轴上，点Q 在y 轴正半轴上，连结PQ 与直线AC 交于点M ，连结MO 并延长交AB 于点N ，若M 为PQ 的中点．①求证：△APM ∽△AON ；②设点M 的横坐标为m ，求AN 的长（用含m 的代数式表示）．33．（2017浙江省湖州市，第24题，12分）如图，在平面直角坐标系xOy 中，已知A ，B 两点的坐标分别为（﹣4，0），（4，0），C （m ，0）是线段A B 上一点（与 A ，B 点不重合），抛物线L 1：211y ax b x c =++（a ＜0）经过点A ，C ，顶点为D ，抛物线L 2：222y ax b x c =++（a ＜0）经过点C ，B ，顶点为E ，AD ，BE 的延长线相交于点F ．（1）若a =12-，m =﹣1，求抛物线L 1，L 2的解析式；（2）若a =﹣1，AF ⊥BF ，求m 的值；（3）是否存在这样的实数a （a ＜0），无论m 取何值，直线AF 与BF 都不可能互相垂直？若存在，请直接写出a 的两个不同的值；若不存在，请说明理由．34．（2017浙江省绍兴市，第24题，14分）如图1，已知□ABCD ，AB ∥x 轴，AB =6，点A 的坐标为（1，-4），点D 的坐标为（-3，4），点B 在第四象限，点P 是□ABCD 边上一个动点．（1）若点P 在边BC 上，PD =CD ，求点P 的坐标．（2）若点P 在边AB 、AD 上，点P 关于坐标轴对称的点Q ，落在直线1y x =-上，求点P 的坐标．（3）若点P 在边AB ，AD ，CD 上，点G 是AD 与y 轴的交点，如图2，过点P 作y 轴的平行线PM ，过点G 作x 轴的平行线GM ，它们相交于点M ，将△PGM 沿直线PG 翻折，当点M 的对应点落在坐标轴上时，求点P 的坐标（直接写出答案）．35．（2017衢州，第24题，12分）在直角坐标系中，过原点O 及点A （8，0），C （0，6）作矩形OABC 、连结OB ，点D 为OB 的中点，点E 是线段AB 上的动点，连结DE ，作DF ⊥DE ，交OA 于点F ，连结EF ．已知点E 从A 点出发，以每秒1个单位长度的速度在线段AB 上移动，设移动时间为t 秒．（1）如图1，当t =3时，求DF 的长．（2）如图2，当点E 在线段AB 上移动的过程中，∠DEF 的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan ∠DEF 的值．（3）连结AD ，当AD 将△DEF 分成的两部分的面积之比为1：2时，求相应的t 的值．36．（2017金华，第24题，12分）如图1，在平面直角组坐标系中，四边形OABC 各顶点的坐标分别为O （0，0），A （3，33、B （9，53），C （14，0），动点P 与Q 同时从O 点出发，运动时间为t 秒，点P 沿OC 方向以1单位长度/秒的速度向点C 运动，点Q 沿折线OA ﹣AB ﹣BC 运动，在OA 、AB 、BC 上运动的速度分别为3，3，52（单位长度/秒），当P 、Q 中的一点到达C 点时，两点同时停止运动．（1）求AB 所在直线的函数表达式；（2）如图2，当点Q 在AB 上运动时，求△CPQ 的面积S 关于t 的函数表达式及S 的最大值；（3）在P 、Q 的运动过程中，若线段PQ 的垂直平分线经过四边形OABC 的顶点，求相应的t 值．37．（2017海南省，第24题，16分）抛物线23y ax bx =++ 经过点A （1，0）和点B （5，0）．（1）求该抛物线所对应的函数解析式；（2）该抛物线与直线335y x =+ 相交于C 、D 两点，点P 是抛物线上的动点且位于x 轴下方，直线PM ∥y 轴，分别与x 轴和直线CD 交于点M 、N ．①连结PC 、PD ，如图1，在点P 运动过程中，△PCD 的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；②连结PB ，过点C 作CQ ⊥PM ，垂足为点Q ，如图2，是否存在点P ，使得△CNQ 与△PBM 相似？若存在，求出满足条件的点P 的坐标；若不存在，说明理由．38．（2017天门，第25题，12分）如图，在平面直角坐标系中，四边形ABCD 的边AD 在x 轴上，点C 在y 轴的负半轴上，直线BC ∥AD ，且BC =3，OD =2，将经过A 、B 两点的直线l ：y =﹣2x ﹣10向右平移，平移后的直线与x 轴交于点E ，与直线BC 交于点F ，设AE 的长为t （t ≥0）．（1）四边形ABCD 的面积为；（2）设四边形ABCD 被直线l 扫过的面积（阴影部分）为S ，请直接写出S 关于t 的函数解析式；（3）当t =2时，直线EF 上有一动点，作PM ⊥直线BC 于点M ，交x 轴于点N ，将△PMF 沿直线EF 折叠得到△PTF ，探究：是否存在点P ，使点T 恰好落在坐标轴上？若存在，请求出点P 的坐标；若不存在，请说明理由．39．（2017湖北省十堰市，第25题，12分）抛物线2y x bx c =++与x 轴交于A （1，0），B （m ，0），与y 轴交于C ．（1）若m =﹣3，求抛物线的解析式，并写出抛物线的对称轴；（2）如图1，在（1）的条件下，设抛物线的对称轴交x 轴于D ，在对称轴左侧的抛物线上有一点E ，使103ACE ACD S S ∆∆=，求点E 的坐标；（3）如图2，设F （﹣1，﹣4），FG ⊥y 于G ，在线段OG 上是否存在点P ，使∠OBP =∠FPG ？若存在，求m 的取值范围；若不存在，请说明理由．40．（2017湖北省咸宁市，第24题，12分）如图，抛物线212y x bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ，其对称轴交抛物线于点D ，交x 轴于点E ，已知OB =OC =6．（1）求抛物线的解析式及点D 的坐标；（2）连接BD ，F 为抛物线上一动点，当∠F AB =∠EDB 时，求点F 的坐标；（3）平行于x 轴的直线交抛物线于M 、N 两点，以线段MN 为对角线作菱形MPNQ ，当点P 在x 轴上，且PQ =12MN 时，求菱形对角线MN 的长．41．（2017湖北省恩施州，第24题，12分）如图，已知抛物线2y ax c 过点（﹣2，2），（4，5），过定点F （0，2）的直线l ：y =kx +2与抛物线交于A 、B 两点，点B 在点A 的右侧，过点B 作x 轴的垂线，垂足为C ．（1）求抛物线的解析式；（2）当点B 在抛物线上运动时，判断线段BF 与BC 的数量关系（＞、＜、=），并证明你的判断；（3）P 为y 轴上一点，以B 、C 、F 、P 为顶点的四边形是菱形，设点P （0，m ），求自然数m 的值；（4）若k =1，在直线l 下方的抛物线上是否存在点Q ，使得△QBF 的面积最大？若存在，求出点Q 的坐标及△QBF 的最大面积；若不存在，请说明理由．42．（2017湖北省武汉市，第24题，12分）已知点A （﹣1，1）、B （4，6）在抛物线2y ax bx =+上．（1）求抛物线的解析式；（2）如图1，点F 的坐标为（0，m ）（m ＞2），直线AF 交抛物线于另一点G ，过点G 作x 轴的垂线，垂足为H ．设抛物线与x 轴的正半轴交于点E ，连接FH 、AE ，求证：FH ∥AE ；（3）如图2，直线AB 分别交x 轴、y 轴于C 、D 两点．点P 从点C 出发，沿射线CD 方向匀速运动，速度2个单位长度；同时点Q 从原点O 出发，沿x 轴正方向匀速运动，速度为每秒1个单位长度．点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM=2PM，直接写出t的值．43．（2017湖北省荆州市，第25题，12分）如图在平面直角坐标系中，直线334y x=-+与x轴、y轴分别交于A、B两点，点P、Q同时从点A出发，运动时间为t秒．其中点P沿射线AB运动，速度为每秒4个单位长度，点Q沿射线AO运动，速度为每秒5个单位长度．以点Q为圆心，PQ长为半径作⊙Q．（1）求证：直线AB是⊙Q的切线；（2）过点A左侧x轴上的任意一点C（m，0），作直线AB的垂线CM，垂足为M．若CM与⊙Q相切于点D，求m与t的函数关系式（不需写出自变量的取值范围）；（3）在（2）的条件下，是否存在点C，直线AB、CM、y轴与⊙Q同时相切？若存在，请直接写出此时点C的坐标；若不存在，请说明理由．44．（2017湖北省荆门市，第24题，12分）已知：如图所示，在平面直角坐标系xOy中，∠C=90°，OB=25，OC=20，若点M是边OC上的一个动点（与点O、C不重合），过点M作MN∥OB交BC于点N．（1）求点C的坐标；（2）当△MCN的周长与四边形OMNB的周长相等时，求CM的长；（3）在OB上是否存在点Q，使得△MNQ为等腰直角三角形？若存在，请求出此时MN的长；若不存在，请说明理由．45．（2017湖北省襄阳市，第25题，13分）如图，矩形OABC 的两边在坐标轴上，点A 的坐标为（10，0），抛物线24y ax bx =++过点B ，C 两点，且与x 轴的一个交点为D （﹣2，0），点P 是线段CB 上的动点，设CP =t （0＜t ＜10）．（1）请直接写出B 、C 两点的坐标及抛物线的解析式；（2）过点P 作PE ⊥BC ，交抛物线于点E ，连接BE ，当t 为何值时，∠PBE =∠OCD ？（3）点Q 是x 轴上的动点，过点P 作PM ∥BQ ，交CQ 于点M ，作PN ∥CQ ，交BQ 于点N ，当四边形PMQN 为正方形时，请求出t 的值．46．（2017湖北省鄂州市，第22题，9分）如图，已知BF 是⊙O 的直径，A 为⊙O 上（异于B 、F ）一点，⊙O 的切线MA 与FB 的延长线交于点M ；P 为AM 上一点，PB 的延长线交⊙O 于点C ，D 为BC 上一点且P A =PD ，AD 的延长线交⊙O 于点E ．（1）求证：BE CE =；（2）若ED 、EA 的长是一元二次方程0552=+-x x 的两根，求BE 的长；（3）若MA =62sin ∠AMF =13，求AB 的长．47．（2017湖北省鄂州市，第24题，12分）已知，抛物线23y ax bx =++（a ＜0）与x 轴交于A （3，0）、B 两点，与y 轴交于点C ，抛物线的对称轴是直线x =1，D 为抛物线的顶点，点E 在y 轴C 点的上方，且CE =12．（1）求抛物线的解析式及顶点D 的坐标；（2）求证：直线DE 是△ACD 外接圆的切线；（3）在直线AC 上方的抛物线上找一点P ，使ACD PAC S S ∆∆=21，求点P 的坐标；（4）在坐标轴上找一点M ，使以点B 、C 、M 为顶点的三角形与△ACD 相似，直接写出点M 的坐标．48．（2017湖北省随州市，第25题，12分）在平面直角坐标系中，我们定义直线y =ax ﹣a 为抛物线 2y ax bx c =++（a 、b 、c 为常数，a ≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y 轴上的三角形为其“梦想三角形”．已知抛物线2234323y x x =--+与其“梦想直线”交于A 、B 两点（点A 在点B 的左侧），与x 轴负半轴交于点C ．（1）填空：该抛物线的“梦想直线”的解析式为，点A 的坐标为，点B 的坐标为；（2）如图，点M 为线段CB 上一动点，将△ACM 以AM 所在直线为对称轴翻折，点C 的对称点为N ，若△AMN 为该抛物线的“梦想三角形”，求点N 的坐标；（3）当点E 在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F ，使得以点A 、C 、E 、F 为顶点的四边形为平行四边形？若存在，请直接写出点E 、F 的坐标；若不存在，请说明理由． 49．（2017黄冈，第24题，14分）已知：如图所示，在平面直角坐标系xoy 中，四边形OABC 是矩形，OA =4，OC =3，动点P 从点C 出发，沿射线CB 方向以每秒2个单位长度的速度运动；同时，动点Q 从点O 出发，沿x 轴正半轴方向以每秒1个单位长度的速度运动．设点P 、点Q 的运动时间为t （s ）．（1）当t =1s 时，求经过点O ，P ，A 三点的抛物线的解析式；（2）当t =2s 时，求tan ∠QP A 的值；（3）当线段PQ 与线段AB 相交于点M ，且BM =2AM 时，求t （s ）的值；（4）连接CQ ，当点P ，Q 在运动过程中，记△CQP 与矩形OABC 重叠部分的面积为S ，求S 与t 的函数关系式．50．（2017湖北省黄石市，第25题，10分）如图，直线l ：y =kx +b （k ＜0）与函数4y x=（x ＞0）的图象相交于A 、C 两点，与x 轴相交于T 点，过A 、C 两点作x 轴的垂线，垂足分别为B 、D ，过A 、C 两点作y 轴的垂线，垂足分别为E 、F ；直线AE 与CD 相交于点P ，连接DE ，设A 、C 两点的坐标分别为（a ，4a）、（c ，4c），其中a ＞c ＞0．（1）如图①，求证：∠EDP =∠ACP ；（2）如图②，若A 、D 、E 、C 四点在同一圆上，求k 的值；（3）如图③，已知c =1，且点P 在直线BF 上，试问：在线段AT 上是否存在点M ，使得OM ⊥AM ？请求出点M 的坐标；若不存在，请说明理由．51．（2017湖南省岳阳市，第24题，10分）如图，抛物线223y x bx c =++经过点B （3，0），C （0，﹣2），直线l ：2233y x =--交y 轴于点E ，且与抛物线交于A ，D 两点，P 为抛物线上一动点（不与A ，D 重合）．（1）求抛物线的解析式；（2）当点P 在直线l 下方时，过点P 作PM ∥x 轴交l 于点M ，PN ∥y 轴交l 于点N ，求PM +PN 的最大值．（3）设F 为直线l 上的点，以E ，C ，P ，F 为顶点的四边形能否构成平行四边形？若能，求出点F 的坐标；若不能，请说明理由．52．（2016四川省自贡市）抛物线()240y x ax b a =-++>与x 轴相交于O 、A 两点（其中O 为坐标原点），过点P （2，2a ）作直线PM ⊥x 轴于点M ，交抛物线于点B ，点B 关于抛物线对称轴的对称点为C （其中B 、C 不重合），连接AP 交y 轴于点N ，连接BC 和PC ．（1）32a =时，求抛物线的解析式和BC 的长；（2）如图1a >时，若AP ⊥PC ，求a 的值；（3）是否存在实数a ，使12AP PN =，若存在，求出a 的值；若不存在，请说明理由．53．（2016山东省泰安市）如图，在平面直角坐标系中，抛物线2y ax bx c =++的顶点坐标为（2，9），与y 轴交于点A （0，5），与x 轴交于点E 、B ．（1）求二次函数2y ax bx c =++的表达式；（2）过点A 作AC 平行于x 轴，交抛物线于点C ，点P 为抛物线上的一点（点P 在AC 上方），作PD 平行与y 轴交AB 于点D ，问当点P 在何位置时，四边形APCD 的面积最大？并求出最大面积；（3）若点M 在抛物线上，点N 在其对称轴上，使得以A 、E 、N 、M 为顶点的四边形是平行四边形，且AE 为其一边，求点M 、N 的坐标．54．（2016山东省济南市）如图1，▱OABC 的边OC 在x 轴的正半轴上，OC =5，反比例函数my x=（x ＞0）的图象经过点A （1，4）．（1）求反比例函数的关系式和点B 的坐标；（2）如图2，过BC 的中点D 作DP ∥x 轴交反比例函数图象于点P ，连接AP 、OP ． ①求△AOP 的面积；②在▱OABC 的边上是否存在点M ，使得△POM 是以PO 为斜边的直角三角形？若存在，请求出所有符合条件的点M 的坐标；若不存在，请说明理由．55．（2016山东省济宁市）已知点P （0x ，0y ）和直线y =kx +b ，则点P 到直线y =kx +b 的距离证明可用公式d 0021kx y b k-++计算．例如：求点P （﹣1，2）到直线y =3x +7的距离．解：因为直线y =3x +7，其中k =3，b =7．所以点P （﹣1，2）到直线y =3x +7的距离为：d 0021kx y b k -++23(1)271k ⨯--++1010．根据以上材料，解答下列问题：（1）求点P （1，﹣1）到直线y =x ﹣1的距离；（2）已知⊙Q 的圆心Q 坐标为（0，5），半径r 为2，判断⊙Q 与直线39y x =+的位置关系并说明理由；（3）已知直线y =﹣2x +4与y =﹣2x ﹣6平行，求这两条直线之间的距离．56．（2016广西河池市）在平面直角坐标系中，抛物线223y x x =--+与x 轴交于A ，B 两点（A 在B 的左侧），与y 轴交于点C ，顶点为D ．（1）请直接写出点A ，C ，D 的坐标；（2）如图（1），在x 轴上找一点E ，使得△CDE 的周长最小，求点E 的坐标；（3）如图（2），F 为直线AC 上的动点，在抛物线上是否存在点P ，使得△AFP 为等腰直角三角形？若存在，求出点P 的坐标，若不存在，请说明理由．57．（2016广西百色市）正方形OABC 的边长为4，对角线相交于点P ，抛物线L 经过O 、P 、A 三点，点E 是正方形内的抛物线上的动点．（1）建立适当的平面直角坐标系，①直接写出O 、P 、A 三点坐标； ②求抛物线L 的解析式；（2）求△OAE 与△OCE 面积之和的最大值．58．（2016广西贵港市）如图，抛物线25y ax bx =+-（a ≠0）与x 轴交于点A （﹣5，0）和点B （3，0），与y 轴交于点C ．（1）求该抛物线的解析式；（2）若点E 为x 轴下方抛物线上的一动点，当S △ABE =S △ABC 时，求点E 的坐标；（3）在（2）的条件下，抛物线上是否存在点P ，使∠BAP =∠CAE ？若存在，求出点P 的横坐标；若不存在，请说明理由．59．（2016广西贺州市）如图，矩形的边OA 在x 轴上，边OC 在y 轴上，点B 的坐标为（10，8），沿直线OD 折叠矩形，使点A 正好落在BC 上的E 处，E 点坐标为（6，8），抛物线2y ax bx c =++经过O 、A 、E 三点．（1）求此抛物线的解析式；（2）求A D 的长；（3）点P 是抛物线对称轴上的一动点，当△PAD 的周长最小时，求点P 的坐标．60．（2016内蒙古呼伦贝尔市，第26题，13分）如图，抛物线223y x x =-++与x 轴相交的于A ，B 两点（点A 在点B 的左侧），与y 轴相交于点C ，顶点为D ．（1）直接写出A ，B ，C 三点的坐标和抛物线的对称轴；（2）连接BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点（P 不与C ，B 两点重合），过点P 作PF ∥DE 交抛物线于点F ，设点P 的横坐标为m ．①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形．②设△BCF的面积为S，求S与m的函数关系式；当m为何值时，S有最大值．61．（2016内蒙古赤峰市）（12分）如图，在平面直角坐标系中，O（0，0），A（0，﹣6），B（8，0）三点在⊙P上．（1）求圆的半径及圆心P的坐标；（2）M为劣弧OB的中点，求证：AM是∠OAB的平分线；（3）连接BM并延长交y轴于点N，求N，M点的坐标．62．（2016内蒙古赤峰市）（14分）在平面直角坐标系中，已知点A（﹣2，0），B（2，0），C（3，5）．（1）求过点A，C的直线解析式和过点A，B，C的抛物线的解析式；（2）求过点A，B及抛物线的顶点D的⊙P的圆心P的坐标；（3）在抛物线上是否存在点Q，使AQ与⊙P相切，若存在请求出Q点坐标．63．（2016吉林省）如图1，在平面直角坐标系中，点B 在x 轴正半轴上，OB 的长度为2m ，以OB 为边向上作等边三角形AOB ，抛物线l ：2y ax bx c =++经过点O ，A ，B 三点．（1）当m =2时，a = ，当m =3时，a = ；（2）根据（1）中的结果，猜想a 与m 的关系，并证明你的结论；（3）如图2，在图1的基础上，作x 轴的平行线交抛物线l 于P 、Q 两点，PQ 的长度为2n ，当△APQ 为等腰直角三角形时，a 和n 的关系式为；（4）利用（2）（3）中的结论，求△AOB 与△APQ 的面积比．64．（2016天津市）在平面直角坐标系中，O 为原点，点A （4，0），点B （0，3），把△ABO 绕点B 逆时针旋转，得△A ′BO ′，点A ，O 旋转后的对应点为A ′，O ′，记旋转角为α．（1）如图①，若α=90°，求AA ′的长；（2）如图②，若α=120°，求点O ′的坐标；（3）在（2）的条件下，边OA 上的一点P 旋转后的对应点为P ′，当O ′P +BP ′取得最小值时，求点P ′的坐标（直接写出结果即可）65．（2016四川省凉山州）如图，已知抛物线2y ax bx c =++（a ≠0）经过A （﹣1，0）、B （3，0）、C （0，﹣3）三点，直线l 是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P 是直线l 上的一个动点，当点P 到点A 、点B 的距离之和最短时，求点P 的坐标；。

专题19 几何变换综合题-决胜2018中考数学压轴题全揭秘精品(原卷版)

一、选择题1．（2017四川省达州市，第9题，3分）如图，将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置，继续绕右下角的顶点按顺时针方向旋转90°至图②位置，以此类推，这样连续旋转2017次．若AB=4，AD=3，则顶点A在整个旋转过程中所经过的路径总长为（）A．2017πB．2034πC．3024πD．3026π2．（2017临沂，第14题，3分）如图，在平面直角坐标系中，反比例函数kyx=（x＞0）的图象与边长是6的正方形OABC的两边AB，BC分别相交于M，N两点，△OMN的面积为10．若动点P在x轴上，则PM+PN的最小值是（）A．62B．10C．226D．2293．（2017新疆乌鲁木齐市，第10题，4分）如图，点A（a，3），B（b，1）都在双曲线3yx=上，点C，D，分别是x轴，y轴上的动点，则四边形ABCD周长的最小值为（）A．52B．62C．21022D．24．（2017湖北省恩施州，第12题，3分）如图，在平面直角坐标系中2条直线为l1：y=﹣3x+3，l2：y=﹣3x+9，直线l1交x轴于点A，交y轴于点B，直线l2交x轴于点D，过点B作x轴的平行线交l2于点C，点A、E 关于y轴对称，抛物线2y ax bx c过E、B、C三点，下列判断中：①a﹣b+c=0；②2a+b+c=5；③抛物线关于直线x=1对称；④抛物线过点（b，c）；⑤S四边形ABCD=5，其中正确的个数有（）A．5B．4C．3D．25．（2017湖北省咸宁市，第8题，3分）在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标为（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（）A．（32，0）B．（2，0）C．（52，0）D．（3，0）6．（2017辽宁省营口市，第8题，3分）如图，在菱形ABOC中，∠A=60°，它的一个顶点C在反比例函数kyx的图象上，若将菱形向下平移2个单位，点A恰好落在函数图象上，则反比例函数解析式为（）A．33yx=-B．3yx=-C．3yx=-D．3yx=7．（2016浙江省湖州市）如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（）A．4B．174C．32D．258．（2016湖北省鄂州市）如图，菱形ABCD的边AB=8，∠B=60°，P是AB上一点，BP=3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点A′．当CA′的长度最小时，CQ的长为（）A．5B．7C．8D．13 29．（2016四川省广元市）如图．在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B 的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E．那么点D的坐标为（）A．（45-，125）B．（25-，135）C．（12-，135）D．（35-，125）10．（2016江苏省镇江市）如图，在平面直角坐标系中，坐标原点O是正方形OABC的一个顶点，已知点B 坐标为（1，7），过点P（a，0）（a＞0）作PE⊥x轴，与边OA交于点E（异于点O、A），将四边形ABCE 沿CE翻折，点A′、B′分别是点A、B的对应点，若点A′恰好落在直线PE上，则a的值等于（）A．54B．43C．2D．311．（2015北海，第12题，3分）如图，在矩形OABC中，OA=8，OC=4，沿对角线OB折叠后，点A与点D重合，OD与BC交于点E，则点D的坐标是（）A．（4，8）B．（5，8）C．（245，325）D．（225，365）12．（2015南宁，第11题，3分）如图，AB是⊙O的直径，AB=8，点M在⊙O上，∠MAB=20°，N是弧MB的中点，P是直径AB上的一动点．若MN=1，则△PMN周长的最小值为（）A．4B．5C．6D．713．（2015无锡，第10题，2分）如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为（）A．35B．45C．23D．3214．（2015泸州，第11题，3分）如图，在△ABC中，AB=AC，BC=24，tanC=2，如果将△ABC沿直线l 翻折后，点B落在边AC的中点E处，直线l与边BC交于点D，那么BD的长为（）A．13 B．152C．272D．1215．（2015绵阳，第12题，3分）如图，D是等边△ABC边AB上的一点，且AD：DB=1：2，现将△ABC 折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=（）A ．34B ．45C ．56D ．6716．（2015鄂州，第8题，3分）如图，在矩形ABCD 中，AB =8，BC =12，点E 是BC 的中点，连接AE ，将△ABE 沿AE 折叠，点B 落在点F 处，连接FC ，则sin ∠ECF =（）A ．43B ．34C ．53D ．5417．（2015绥化，第9题，3分）如图，在矩形ABCD 中，AB =10，BC =5．若点M 、N 分别是线段ACAB 上的两个动点，则BM +MN 的最小值为（）A ．10B ．8C ．53D ．618．（2015泰安，第20题，3分）如图，矩形ABCD 中，E 是AD 的中点，将△ABE 沿直线BE 折叠后得到△GBE ，延长BG 交CD 于点F ．若AB =6，BC =46，则FD 的长为（）A ．2B ．4C 6D ．2319．（2015淄博，第11题，4分）如图，在一张矩形纸片的一端，将折出的一个正方形展平后，又折成了两个相等的矩形，再把纸片展平，折出小矩形的对角线，并将小矩形的对角线折到原矩形的长边上．设MN 的长为251）线段的有（）A ．0种B ．1种C ．2种D ．3种20．（2015宁波，第10题，4分）如图，将△ABC 沿着过AB 中点D 的直线折叠，使点A 落在BC 边上的A 2处，称为第1次操作，折痕DE 到BC 的距离记为h 1；还原纸片后，再将△ADE 沿着过AD 中点D 1的直线折叠，使点A 落在DE 边上的A 2处，称为第2次操作，折痕D 1E 1到BC 的距离记为h 2；按上述方法不断操作下去…，经过第2015次操作后得到的折痕D 2014E 2014到BC 的距离记为h 2015，到BC 的距离记为h 2015．若h 1=1，则h 2015的值为（）A ．201521B ．201421C ．2015211- D ．2014212-21．（2015本溪，第9题，3分）如图，在平面直角坐标系中，直线AB 与x 轴交于点A （﹣2，0），与x 轴夹角为30°，将△ABO 沿直线AB 翻折，点O 的对应点C 恰好落在双曲线k y x=（0k ≠）上，则k 的值为（）A ．4B ．﹣2C 3D ．322．（2015武汉，第10题，3分）如图，△ABC ，△EFG 均是边长为2的等边三角形，点D 是边BC 、EF 的中点，直线AG 、FC 相交于点M ．当△EFG 绕点D 旋转时，线段BM 长的最小值是（）A ．23B 31C 2D 3123．（2015庆阳，第12题，3分）在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1关于点B2成中心对称，如此作下去，则△B2n A2n+1B2n+1（n是正整数）的顶点A2n+1的坐标是（）A．（4n﹣1，3）B．（2n﹣1，3）C．（4n+1，3）D．（2n+1，3）24．（2015枣庄，第9题，3分）如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1，边B1C1与CD交于点O，则四边形AB1OD的面积是（）A．34B．716C．212-D．21-25．（2015抚顺，第10题，3分）如图，将矩形ABCD绕点A旋转至矩形AB′C′D′位置，此时AC的中点恰好与D点重合，AB′交CD于点E．若AB=3，则△AEC的面积为（）A ． 3B ． 1.5C ． 23D ．326．（2015广元，第9题，3分）如图，把RI △ABC 放在直角坐标系内，其中∠CAB =90°， BC =5．点A 、B 的坐标分别为（1，0）、（4，0）．将△ABC 沿x 轴向右平移，当点C 落在直线26y x =-上时，线段BC 扫过的面积为（）A ．4B ．8C ．16D ．8227．（2015黔西南州，第10题，4分）在数轴上截取从0到3的对应线段AB ，实数m 对应AB 上的点M ，如图1；将AB 折成正三角形，使点A 、B 重合于点P ，如图2；建立平面直角坐标系，平移此三角形，使它关于y 轴对称，且点P 的坐标为（0，2），PM 的延长线与x 轴交于点N （n ，0），如图3，当m =3时，n 的值为（）A ．423-B ．432-C ．332-D ．332二、填空题28．（2017湖南省常德市，第16题，3分）如图，有一条折线A 1B 1A 2B 2A 3B 3A 4B 4…，它是由过A 1（0，0），B 1（2，2），A 2（4，0）组成的折线依次平移4，8，12，…个单位得到的，直线y =kx +2与此折线恰有2n （n ≥1，且为整数）个交点，则k 的值为．29．（2017山东省菏泽市，第14题，3分）如图，AB⊥y轴，垂足为B，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线33y x=-上，再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置，使点O1的对应点O2落在直线33y x=-上，依次进行下去…若点B的坐标是（0，1），则点O12的纵坐标为．30．（2017湖南省张家界市，第14题，3分）如图，在正方形ABCD中，AD=23，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为．31．（2017四川省内江市，第25题，6分）如图，已知直线l1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=430，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且P A+AB+BQ最小，此时P A+BQ= ．32．（2017安徽省，第14题，5分）在三角形纸片ABC中，∠A=90°，∠C=30°，AC=30cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），减去△CDE后得到双层△BDE（如图2），再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为cm．33．（2017山东省东营市，第15题，4分）如图，已知菱形ABCD的周长为16，面积为83，E为AB的中点，若P为对角线BD上一动点，则EP+AP的最小值为．34．（2017山东省泰安市，第24题，3分）如图，∠BAC=30°，M为AC上一点，AM=2，点P是AB上的一动点，PQ⊥AC，垂足为点Q，则PM+PQ的最小值为．35．（2017浙江省温州市，第15题，5分）如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）．若AB=1，反比例函数kyx（k≠0）的图象恰好经过点A′，B，则k的值为．36．（2016福建省南平市）如图，等腰△ABC中，CA=CB=4，∠ACB=120°，点D在线段AB上运动（不与A、B重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ，给出下列结论：①CD=CP=CQ；②∠PCQ的大小不变；③△PCQ面积的最小值为435；④当点D在AB的中点时，△PDQ是等边三角形，其中所有正确结论的序号是．37．（2016山东省济南市）如图1，在矩形纸片ABCD中，AB=83，AD=10，点E是CD中点，将这张纸片依次折叠两次；第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME/NE；第二次折叠纸片使点N与点E重合，如图3，点B落到B′处，折痕为HG，连接HE，则tan∠EHG= ．38．（2016福建省宁德市4分）如图，在Rt△ABC中，∠BAC=90°，AB=4，AC=3，点D、E分别是AB、AC的中点，点G、F在BC边上（均不与端点重合），DG∥EF．将△BDG绕点D顺时针旋转180°，将△CEF绕点E逆时针旋转180°，拼成四边形MGFN，则四边形MGFN周长l的取值范围是39．（2016福建省宁德市4分）如图，在Rt△ABC中，∠BAC=90°，AB=4，AC=3，点D、E分别是AB、AC的中点，点G、F在BC边上（均不与端点重合），DG∥EF．将△BDG绕点D顺时针旋转180°，将△CEF绕点E逆时针旋转180°，拼成四边形MGFN，则四边形MGFN周长l的取值范围是40．（2016内蒙古呼伦贝尔市，第17题，3分）如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，把△ABC 绕AB边上的点D顺时针旋转90°得到△A′B′C′，A′C′交AB于点E，若AD=BE，则△A′DE的面积是．41．（2015宁夏，第14题，3分）如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线45y x上一点，则点B与其对应点B′间的距离为．42．（2015泰州，第16题，3分）如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP 翻折至△EBP，PE与CD相交于点O，且OE=OD，则AP的长为．43．（2015攀枝花，第15题，4分）如图，在边长为2的等边△ABC中，D为BC的中点，E是AC边上一点，则BE+DE的最小值为．44．（2015宜宾，第15题，3分）如图，一次函数的图象与x轴、y轴分别相交于点A、B，将△AOB沿直线AB翻折，得△ACB．若C（32，32），则该一次函数的解析式为．45．（2015达州，第14题，3分）如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上，点D落在D′处，C′D′交AE于点M．若AB=6，BC=9，则AM的长为．46．（2015凉山州，第26题，5分）菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．47．（2015内江，第14题，5分）如图，在四边形ABCD中，AD∥BC，∠C=90°，E为CD上一点，分别以EA，EB为折痕将两个角（∠D，∠C）向内折叠，点C，D恰好落在AB边的点F处．若AD=2，BC=3，则EF的长为．48．（2015孝感，第16题，3分）如图，四边形ABCD是矩形纸片，AB=2．对折矩形纸片ABCD，使AD 与BC重合，折痕为EF；展平后再过点B折叠矩形纸片，使点A落在EF上的点N，折痕BM与EF相交于点Q；再次展平，连接BN，MN，延长MN交BC于点G．有如下结论：①∠ABN=60°；②AM=1；③QN=33；④△BMG是等边三角形；⑤P为线段BM上一动点，H是BN的中点，则PN+PH的最小值是3．其中正确结论的序号是．49．（2015鄂州，第16题，3分）如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，四边形PMON的面积为．50．（2015随州，第16题，3分）在▱ABCD中，AB＜BC，已知∠B=30°，AB=23，将△ABC沿AC翻折至△AB′C，使点B′落在▱ABCD所在的平面内，连接B′D．若△AB′D是直角三角形，则BC的长为．51．（2015梅州，第14题，3分）如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB=4，BC=2，那么线段EF的长为．52．（2015河南省，第15题，3分）如图，正方形ABCD的边长是16，点E在边AB上，AE=3，点F是边BC上不与点B，C重合的一个动点，把△EBF沿EF折叠，点B落在B′处．若△CDB′恰为等腰三角形，则DB′的长为．53．（2015牡丹江，第20题，3分）矩形纸片ABCD，AB=9，BC=6，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E，F，则EF长为．54．（2015绥化，第21题，3分）在矩形ABCD中，AB=4，BC=3，点P在AB上．若将△DAP沿DP折叠，使点A落在矩形对角线上的A'处，则AP的长为__________．+的菱形ABCD中，∠A=60°，点E，F分别在AB，55．（2015包头，第19题，3分）如图，在边长为31AD上，沿EF折叠菱形，使点A落在BC边上的点G处，且EG⊥BD于点M，则EG的长为．56．（2015天津市，第18题，3分）在每个小正方形的边长为1的网格中．点A，B，D均在格点上，点E、F分别为线段BC、DB上的动点，且BE=DF．（1）如图①，当BE=52时，计算AE+AF的值等于；（2）当AE+AF取得最小值时，请在如图②所示的网格中，用无刻度的直尺，画出线段AE，AF，并简要说明点E和点F的位置如何找到的（不要求证明）．57．（2015山西省，第16题，3分）如图，将正方形纸片ABCD沿MN折叠，使点D落在边AB上，对应点为D′，点C落在C′处．若AB=6，AD′=2，则折痕MN的长为．58．（2015西宁，第20题，2分）如图，△ABC是边长为1的等边三角形，BD为AC边上的高，将△ABC 折叠，使点B与点D重合，折痕EF交BD于点D1，再将△BEF折叠，使点B于点D1重合，折痕GH交BD1于点D2，依次折叠，则BD n= ．59．（2015滨州，第17题，4分）如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后端点D恰好落在边OC上的点F处．若点D的坐标为（10，8），则点E的坐标为．60．（2015杭州，第16题，4分）如图，在四边形纸片ABCD 中，AB =BC ，AD =CD ，∠A =∠C =90°，∠B =150°．将纸片先沿直线BD 对折，再将对折后的图形沿从一个顶点出发的直线裁剪，剪开后的图形打开铺平．若铺平后的图形中有一个是面积为2的平行四边形，则CD = ．61．（2015盘锦，第17题，3分）如图，直线33y x =-+与x 轴交于点B ，与y 轴交于点A ，以线段AB 为边，在第一象限内作正方形ABCD ，点C 落在双曲线k y x =（0k ≠）上，将正方形ABCD 沿x 轴负方向平移a 个单位长度，使点D 恰好落在双曲线k y x=（0k ≠）上的点D 1处，则a = ．62．（2015绵阳，第18题，3分）如图，在等边△ABC 内有一点D ，AD =5，BD =6，CD =4，将△ABD 绕A 点逆时针旋转，使AB 与AC 重合，点D 旋转至点E ，则∠CDE 的正切值为．63．（2015孝感，第16题，3分）如图，四边形ABCD是矩形纸片，AB=2．对折矩形纸片ABCD，使AD 与BC重合，折痕为EF；展平后再过点B折叠矩形纸片，使点A落在EF上的点N，折痕BM与EF相交于点Q；再次展平，连接BN，MN，延长MN交BC于点G．有如下结论：①∠ABN=60°；②AM=1；③QN=33；④△BMG是等边三角形；⑤P为线段BM上一动点，H是BN的中点，则PN+PH的最小值是3．其中正确结论的序号是．64．（2015福州，第16题，4分）如图，在Rt△ABC中，∠ABC=90°，AB=BC=2，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，则BM的长是．65．（2015大庆，第18题，3分）在Rt△ABC中，∠C=90°，AC=BC=1，将其放入平面直角坐标系，使A 点与原点重合，AB在x轴上，△ABC沿x轴顺时针无滑动的滚动，点A再次落在x轴时停止滚动，则点A 经过的路线与x轴围成图形的面积为．66．（2015重庆市，第18题，4分）如图，在矩形ABCD中，AB=46，AD=10．连接BD，∠DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△BC′E′．当射线BE′和射线BC′都与线段AD相交时，设交点分别为F，G．若△BFD为等腰三角形，则线段DG长为．67．（2015朝阳，第16题，3分）如图，在Rt△AOB中，∠AOB=90°，AO=3，BO=1，AB的垂直平分线交AB于点E，交射线BO于点F．点P从点A出发沿射线AO以每秒23个单位的速度运动，同时点Q 从点O出发沿OB方向以每秒1个单位的速度运动，当点Q到达点B时，点P、Q同时停止运动．设运动的时间为t秒．（1）当t= 时，PQ∥EF；（2）若P、Q关于点O的对称点分别为P′、Q′，当线段P′Q′与线段EF有公共点时，t的取值范围是．68．（2015沈阳，第16题，4分）如图，正方形ABCD 绕点B 逆时针旋转30°后得到正方形BEFG ，EF 与AD 相交于点H ，延长DA 交GF 于点K ．若正方形ABCD 边长为3，则AK = ．三、解答题69．（2017四川省宜宾市，第24题，12分）如图，抛物线2y x bx c =-++与x 轴分别交于A （﹣1，0），B （5，0）两点．（1）求抛物线的解析式；（2）在第二象限内取一点C ，作CD 垂直X 轴于点D ，链接AC ，且AD =5，CD =8，将Rt △ACD 沿x 轴向右平移m 个单位，当点C 落在抛物线上时，求m 的值；（3）在（2）的条件下，当点C 第一次落在抛物线上记为点E ，点P 是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q ，使以点B 、E 、P 、Q 为顶点的四边形是平行四边形？若存在，请出点Q 的坐标；若不存在，请说明理由．70．（2017山东省潍坊市，第24题，12分）边长为6的等边△ABC 中，点D 、E 分别在AC 、BC 边上，DE ∥AB ，EC =23（1）如图1，将△DEC 沿射线方向平移，得到△D ′E ′C ′，边D ′E ′与AC 的交点为M ，边C ′D ′与∠ACC ′的角平分线交于点N ，当CC ′多大时，四边形MCND ′为菱形？并说明理由．（2）如图2，将△DEC 绕点C 旋转∠α（0°＜α＜360°），得到△D ′E ′C ，连接AD ′、BE ′．边D ′E ′的中点为P ．①在旋转过程中，AD ′和BE ′有怎样的数量关系？并说明理由； ②连接AP ，当AP 最大时，求AD ′的值．（结果保留根号）71．（2017内蒙古赤峰市，第25题，12分）△OP A 和△OQB 分别是以OP 、OQ 为直角边的等腰直角三角形，点C 、D 、E 分别是OA 、OB 、AB 的中点．（1）当∠AOB =90°时如图1，连接PE 、QE ，直接写出EP 与EQ 的大小关系；（2）将△OQB 绕点O 逆时针方向旋转，当∠AOB 是锐角时如图2，（1）中的结论是否成立？若成立，请给出证明；若不成立，请加以说明．（3）仍将△OQB 绕点O 旋转，当∠AOB 为钝角时，延长PC 、QD 交于点G ，使△ABG 为等边三角形如图3，求∠AOB 的度数．72．（2017四川省南充市，第25题，10分）如图1，已知二次函数2y ax bx c =++（a 、b 、c 为常数，a ≠0）的图象过点O （0，0）和点A （4，0），函数图象最低点M 的纵坐标为38-，直线l 的解析式为y =x ．（1）求二次函数的解析式；（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．73．（2017四川省自贡市，第25题，12分）如图1，在平面直角坐标系，O为坐标原点，点A（﹣1，0），点B（0，3）．（1）求∠BAO的度数；（2）如图1，将△AOB绕点O顺时针得△A′OB′，当A′恰好落在AB边上时，设△AB′O的面积为S1，△BA′O的面积为S2，S1与S2有何关系？为什么？（3）若将△AOB绕点O顺时针旋转到如图2所示的位置，S1与S2的关系发生变化了吗？证明你的判断．74．（2017天津，第24题，10分）将一个直角三角形纸片ABO放置在平面直角坐标系中，点A3，0），点B（0，1），点O（0，0）．P是边AB上的一点（点P不与点A，B重合），沿着OP折叠该纸片，得点A的对应点A'．（1）如图①，当点A'在第一象限，且满足A'B⊥OB时，求点A'的坐标；（2）如图②，当P为AB中点时，求A'B的长；（3）当∠BP A'=30°时，求点P的坐标（直接写出结果即可）．75．（2017临沂，第25题，11分）数学课上，张老师出示了问题：如图1，AC，BD是四边形ABCD的对角线，若∠ACB=∠ACD=∠ABD=∠ADB=60°，则线段BC，CD，AC三者之间有何等量关系？经过思考，小明展示了一种正确的思路：如图2，延长CB到E，使BE=CD，连接AE，证得△ABE≌△ADC，从而容易证明△ACE是等边三角形，故AC=CE，所以AC=BC+CD．小亮展示了另一种正确的思路：如图3，将△ABC绕着点A逆时针旋转60°，使AB与AD重合，从而容易证明△ACF是等边三角形，故AC=CF，所以AC=BC+CD．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图4，如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小颖提出的问题，请你写出结论，并给出证明．（2）小华提出：如图5，如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”，其它条件不变，那么线段BC，CD，AC三者之间有何等量关系？针对小华提出的问题，请你写出结论，不用证明．76．（2017山东省烟台市，第23题，10分）【操作发现】（1）如图1，△ABC为等边三角形，现将三角板中的60°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于30°），旋转后三角板的一直角边与AB交于点D，在三角板斜边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=30°，连接AF，EF．①求∠EAF的度数；②DE与EF相等吗？请说明理由；【类比探究】（2）如图2，△ABC为等腰直角三角形，∠ACB=90°，先将三角板的90°角与∠ACB重合，再将三角板绕点C按顺时针方向旋转（旋转角大于0°且小于45°），旋转后三角板的一直角边与AB交于点D，在三角板另一直角边上取一点F，使CF=CD，线段AB上取点E，使∠DCE=45°，连接AF，EF，请直接写出探究结果：①求∠EAF的度数；②线段AE，ED，DB之间的数量关系．77．（2017山东省青岛市，第23题，10分）数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题．下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．探究一：求不等式|x ﹣1|＜2的解集（1）探究|x ﹣1|的几何意义如图①，在以O 为原点的数轴上，设点A ′对应的数是x ﹣1，有绝对值的定义可知，点A ′与点O 的距离为|x ﹣1|，可记为A ′O =|x ﹣1|．将线段A ′O 向右平移1个单位得到线段AB ，此时点A 对应的数是x ，点B 对应的数是1．因为AB =A ′O ，所以AB =|x ﹣1|，因此，|x ﹣1|的几何意义可以理解为数轴上x 所对应的点A 与1所对应的点B 之间的距离AB ．（2）求方程|x ﹣1|=2的解因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2，所以方程的解为3，﹣1．（3）求不等式|x ﹣1|＜2的解集因为|x ﹣1|表示数轴上x 所对应的点与1所对应的点之间的距离，所以求不等式解集就转化为求这个距离小于2的点对应的数x 的范围．请在图②的数轴上表示|x ﹣1|＜2的解集，并写出这个解集．探究二：探究22)()(b y a x -+-的几何意义（1）探究22y x +的几何意义如图③，在直角坐标系中，设点M 的坐标为（x ，y ），过M 作MP ⊥x 轴于P ，作MQ ⊥y 轴于Q ，则P 点坐标为（x ，0），Q 点坐标为（0，y ），OP =|x |，OQ =|y |，在Rt △OPM 中，PM =OQ =|y |，则MO =222222||||y x y x PM OP MO +=+=+=，因此，22y x + 的几何意义可以理解为点M （x ，y ）与点O （0，0）之间的距离MO ．（2）探究22)5()1(-+-y x 的几何意义如图④，在直角坐标系中，设点A ′的坐标为（x ﹣1，y ﹣5），由探究二（1）可知，A ′O =22)5()1(-+-y x ，将线段A ′O 先向右平移1个单位，再向上平移5个单位，得到线段AB ，此时点A 的坐标为（x ，y ），点B 的坐标为（1，5），因为AB =A ′O ，所以AB =22)5()1(-+-y x ，因此22)5()1(-+-y x 的几何意义可以理解为点A （x ，y ）与点B （1，5）之间的距离AB ．（3的几何意义请仿照探究二（2）的方法，在图⑤中画出图形，并写出探究过程．（4）22)()(b y a x -+-的几何意义可以理解为：．拓展应用：（1）22)1()2(++-y x +22)5()1(+++y x 的几何意义可以理解为：点A （x ，y ）与点E （2，﹣1）的距离和点A （x ，y ）与点F （填写坐标）的距离之和．（2）22)1()2(++-y x +22)5()1(+++y x 的最小值为（直接写出结果）78．（2017南京，第27题，11分）折纸的思考．【操作体验】用一张矩形纸片折等边三角形．第一步，对折矩形纸片ABCD （AB ＞BC ）（图①），使AB 与DC 重合，得到折痕EF ，把纸片展平（图②）．第二步，如图③，再一次折叠纸片，使点C 落在EF 上的P 处，并使折痕经过点B ，得到折痕BG ，折出PB ，PC ，得到△PBC ．（1）说明△PBC 是等边三角形．【数学思考】（2）如图④，小明画出了图③的矩形ABCD 和等边三角形PBC ，他发现，在矩形ABCD 中把△PBC 经过图形变化，可以得到图⑤中的更大的等边三角形，请描述图形变化的过程．（3）已知矩形一边长为3cm ，另一边长为a cm ，对于每一个确定的a 的值，在矩形中都能画出最大的等边三角形，请画出不同情形的示意图，并写出对应的a 的取值范围．【问题解决】（4）用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片，所需正方形铁片的边长的最小值为cm．79．（2017江苏省徐州市，第27题，9分）如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠，展平后，得折痕AD，BE（如图①），点O为其交点．（1）探求AO到OD的数量关系，并说明理由；（2）如图②，若P，N分别为BE，BC上的动点．①当PN+PD的长度取得最小值时，求BP的长度；②如图③，若点Q在线段BO上，BQ=1，则QN+NP+PD的最小值= ．80．（2017河南省，第22题，10分）如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．（1）观察猜想图1中，线段PM与PN的数量关系是，位置关系是；（2）探究证明把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；（3）拓展延伸把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出△PMN面积的最大值．81．（2017湖北省十堰市，第24题，10分）已知O为直线MN上一点，OP⊥MN，在等腰Rt△ABO中，∠BAO=90°，AC∥OP交OM于C，D为OB的中点，DE⊥DC交MN于E．（1）如图1，若点B在OP上，则：①AC OE（填“＜”，“=”或“＞”）；②线段CA、CO、CD满足的等量关系式是；（2）将图1中的等腰Rt△ABO绕O点顺时针旋转α（0°＜α＜45°），如图2，那么（1）中的结论②是否成立？请说明理由；（3）将图1中的等腰Rt△ABO绕O点顺时针旋转α（45°＜α＜90°），请你在图3中画出图形，并直接写出线段CA、CO、CD满足的等量关系式．82．（2017湖北省襄阳市，第24题，10分）如图，在△ABC中，∠ACB=90°，CD是中线，AC=BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E，F，DF 与AC交于点M，DE与BC交于点N．（1）如图1，若CE=CF，求证：DE=DF；（2）如图2，在∠EDF绕点D旋转的过程中：①探究三条线段AB，CE，CF之间的数量关系，并说明理由；②若CE=4，CF=2，求DN的长．83．（2017湖南省岳阳市，第23题，10分）问题背景：已知∠EDF的顶点D在△ABC的边AB所在直线上（不与A，B重合），DE交AC所在直线于点M，DF交BC所在直线于点N，记△ADM的面积为S1，△BND 的面积为S2．（1）初步尝试：如图①，当△ABC是等边三角形，AB=6，∠EDF=∠A，且DE∥BC，AD=2时，则S1S2= ；（2）类比探究：在（1）的条件下，先将点D沿AB平移，使AD=4，再将∠EDF绕点D旋转至如图②所示位置，求S1S2的值；（3）延伸拓展：当△ABC是等腰三角形时，设∠B=∠A=∠EDF=α．（Ⅰ）如图③，当点D在线段AB上运动时，设AD=a，BD=b，求S1S2的表达式（结果用a，b和α的三角函数表示）．（Ⅱ）如图④，当点D在BA的延长线上运动时，设AD=a，BD=b，直接写出S1S2的表达式，不必写出解答过程．84．（2017湖南省郴州市，第26题，12分）如图1，△ABC是边长为4cm的等边三角形，边AB在射线OM 上，且OA=6cm，点D从O点出发，沿OM的方向以1c m/s的速度运动，当D不与点A重合时，将△ACD 绕点C逆时针方向旋转60°得到△BCE，连结DE．（1）求证：△CDE 是等边三角形；（2）如图2，当6＜t ＜10时，△BDE 的周长是否存在最小值？若存在，求出△BDE 的最小周长；若不存在，请说明理由；（3）如图3，当点D 在射线OM 上运动时，是否存在以D 、E 、B 为顶点的三角形是直角三角形？若存在，求出此时t 的值；若不存在，请说明理由．85．（2017辽宁省大连市，第25题，12分）如图1，四边形ABCD 的对角线AC ，BD 相交于点O ，OB =OD ，OC =OA +AB ，AD =m ，BC =n ，∠ABD +∠ADB =∠ACB ．（1）填空：∠BAD 与∠ACB 的数量关系为；（2）求nm 的值；（3）将△ACD 沿CD 翻折，得到△A ′CD （如图2），连接BA ′，与CD 相交于点P ．若CD =512 ，求PC 的长．86．（2017辽宁省盘锦市，第25题，14分）如图，在Rt △ABC 中，∠ACB =90°，∠A =30°，点O 为AB 中点，点P 为直线BC 上的动点（不与点B 、点C 重合），连接OC 、OP ，将线段OP 绕点P 顺时针旋转60°，得到线段PQ ，连接BQ ．（1）如图1，当点P 在线段BC 上时，请直接写出线段BQ 与CP 的数量关系．（2）如图2，当点P 在CB 延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P 在BC 延长线上时，若∠BPO =15°，BP =4，请求出BQ 的长．。

专题24 几何综合问题-决胜2018中考数学压轴题全揭秘精品(解析版)

一、选择题1．（2017内蒙古包头市，第12题，3分）如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF 平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（）A．32B．43C．53D．85【答案】A．【分析】根据三角形的内角和定理得出∠CAF+∠CF A=90°，∠F AD+∠AED=90°，根据角平分线和对顶角相等得出∠CEF=∠CFE，即可得出EC=FC，再利用相似三角形的判定与性质得出答案．点睛：本题考查了直角三角形性质、等腰三角形的性质和判定，三角形的内角和定理以及相似三角形的判定与性质等知识，关键是推出∠CEF=∠CFE．考点：相似三角形的判定与性质；勾股定理；角平分线的性质；综合题．2．（2017四川省内江市，第12题，3分）如图，过点A（2，0）作直线l：3y x的垂线，垂足为点A1，过点A 1作A 1A 2⊥x 轴，垂足为点A 2，过点A 2作A 2A 3⊥l ，垂足为点A 3，…，这样依次下去，得到一组线段：AA 1，A 1A 2，A 2A 3，…，则线段A 2016A 2107的长为（）A ．20153()2B ．20163()2C ．20173()2D ．20183()2 【答案】B ．【分析】根据含30°的直角三角形的性质结合图形即可得到规律“OA n =3()n OA =2×3()n ”，依此规律即可解决问题．【解析】由3y x ，得l 的倾斜角为30°，点A 坐标为（2，0），∴OA =2，∴OA 1=32OA =3， OA 2=32OA 1=32，OA 3=32OA 2=334，OA 4=32OA 3=98，…，∴OA n =3()2n OA =2×3()2n ，∴OA 2016=2×20163()2，A 2016A 2107的长12×2×20163()2=20163()2，故选B ．点睛：本题考查了规律型中点的坐标以及含30度角的直角三角形，利用“在直角三角形中，30°角所对的直角边等于斜边的一半”结合图形找出变化规律OA n =3()n OA =2×3()n 是解题的关键．考点：一次函数图象上点的坐标特征；规律型；综合题．3．（2017四川省泸州市，第11题，3分）如图，在矩形ABCD 中，点E 是边BC 的中点，AE ⊥BD ，垂足为F ，则tan ∠BDE 的值是（）A ．24B ．14C ．13D ．23【答案】A ．【分析】证明△BEF ∽△DAF ，得出EF =12AF ，EF =13AE ，由矩形的对称性得：AE =DE ，得出EF =13DE ，设EF =x ，则DE =3x ，由勾股定理求出DF =22DE EF -=22x ，再由三角函数定义即可得出答案．【解析】∵四边形ABCD 是矩形，∴AD =BC ，AD ∥BC ，∵点E 是边BC 的中点，∴BE =12BC =12AD ，∴△BEF ∽△DAF ，∴EF BE AF AD ==12，∴EF =12AF ，∴EF =13AE ，∵点E 是边BC 的中点，∴由矩形的对称性得：AE =DE ，∴EF =13DE ，设EF =x ，则DE =3x ，∴DF =22DE EF -=22x ，∴tan ∠BDE =22EF DF x = =2；故选A ．点睛：本题考查了相似三角形的判定和性质，矩形的性质，三角函数等知识；熟练掌握矩形的性质，证明三角形相似是解决问题的关键．考点：矩形的性质；解直角三角形；综合题．学.科.网4．（2017四川省绵阳市，第11题，3分）如图，直角△ABC 中，∠B =30°，点O 是△ABC 的重心，连接CO 并延长交AB 于点E ，过点E 作EF ⊥AB 交BC 于点F ，连接AF 交CE 于点M ，则MO MF的值为（）A ．12B 5C ．23D 3【答案】D ．【分析】根据三角形的重心性质可得OC =23CE ，根据直角三角形的性质可得CE =AE ，根据等边三角形的判定和性质得到CM =12CE ，进一步得到OM =16CE ，即OM =16AE ，根据垂直平分线的性质和含30°的直角三角形的性质可得EF 3AE ，MF =12EF ，依此得到MF 3AE ，从而得到MO MF的值．【解析】∵点O 是△ABC 的重心，∴OC =23CE ，∵△ABC 是直角三角形，∴CE =BE =AE ，∵∠B =30°，∴∠F AE =∠B =30°，∠BAC =60°，∴∠F AE =∠CAF =30°，△ACE 是等边三角形，∴CM =12CE ，∴OM =23CE ﹣12CE =16CE ，即OM =16AE ，∵BE =AE ，∴EF =33AE ，∵EF ⊥AB ，∴∠AFE =60°，∴∠FEM =30°， ∴MF =12EF ，∴MF =3AE ，∴MO MF =163AE AE =3．故选D ．点睛：考查了三角形的重心，等边三角形的判定和性质，垂直平分线的性质，含30°的直角三角形的性质，关键是得到OM =16AE ，MF =3AE ．考点：三角形的重心；相似三角形的判定与性质；综合题．5．（2017四川省达州市，第9题，3分）如图，将矩形ABCD 绕其右下角的顶点按顺时针方向旋转90°至图①位置，继续绕右下角的顶点按顺时针方向旋转90°至图②位置，以此类推，这样连续旋转2017次．若AB =4，AD =3，则顶点A 在整个旋转过程中所经过的路径总长为（）A ．2017πB ．2034πC ．3024πD ．3026π【答案】D ．【分析】首先求得每一次转动的路线的长，发现每4次循环，找到规律然后计算即可．【解析】∵AB =4，BC =3，∴AC =BD =5，转动一次A 的路线长是：904180π⨯ =2π，转动第二次的路线长是：905180π⨯ =52π，转动第三次的路线长是：903180π⨯ =32π，转动第四次的路线长是：0，以此类推，每四次循环，故顶点A 转动四次经过的路线长为：52π+32π+2π=6π，∵2017÷4=504…1，∴顶点A 转动四次经过的路线长为：6π×504+2π=3026π，故选D ．点睛：本题主要考查了探索规律问题和弧长公式的运用，掌握旋转变换的性质、灵活运用弧长的计算公式、发现规律是解决问题的关键．考点：轨迹；矩形的性质；旋转的性质；规律型；综合题．6．（2017德州，第11题，3分）如图放置的两个正方形，大正方形ABCD 边长为a ，小正方形CEFG 边长为b （a ＞b ），M 在BC 边上，且BM =b ，连接AM ，MF ，MF 交CG 于点P ，将△ABM 绕点A 旋转至△ADN ，将△MEF 绕点F 旋转至△NGF ，给出以下五个结论：①∠MAD =∠AND ；②CP =2b b a-；③△ABM ≌△NGF ；④22AMFN S a b =+；⑤A ，M ，P ，D 四点共圆，其中正确的个数是（）A ．2B ．3C ．4D ．5【答案】D ．【分析】①根据正方形的性质得到∠BAD =∠ADC =∠B =90°，根据旋转的性质得到∴∠NAD =∠BAM ，∠AND =∠AMB ，根据余角的性质得到∠DAM +∠NAD =∠NAD +∠AND =∠AND +∠NAD =90°，等量代换得到∠DAM =∠AND ，故①正确；②根据正方形的性质得到PC ∥EF ，根据相似三角形的性质得到CP =2b b a-；故②正确； ③根据旋转的性质得到GN =ME ，等量代换得到AB =ME =NG ，根据全等三角形的判定定理得到△ABM ≌△NGF ；故③正确；④由旋转的性质得到AM =AN ，NF =MF ，根据全等三角形的性质得到AM =NF ，推出四边形AMFN 是矩形，根据余角的想知道的∠NAM =90°，推出四边形AMFN 是正方形，于是得到S 四边形AMFN =AM 2=a 2+b 2；故④正确；⑤根据正方形的性质得到∠AMP =90°，∠ADP =90°，得到∠ABP +∠ADP =180°，于是推出A ，M ，P ，D 四点共圆，故⑤正确．【解析】①∵四边形ABCD 是正方形，∴∠BAD =∠ADC =∠B =90°，∴∠BAM +∠DAM =90°，∵将△ABM 绕点A 旋转至△ADN ，∴∠NAD =∠BAM ，∠AND =∠AMB ，∴∠DAM +∠NAD =∠NAD +∠AND =∠AND +∠NAD =90°，∴∠DAM =∠AND ，故①正确；②∵四边形CEFG 是正方形，∴PC ∥EF ，∴△MPC ∽△EMF ，∴PC CM EF ME=，∵大正方形ABCD 边长为a ，小正方形CEFG 边长为b （a ＞b ），BM =b ，∴EF =b ，CM =a ﹣b ，ME =（a ﹣b ）+b =a ，∴PC a b b a -=，∴CP =2b b a-；故②正确；③∵将△MEF绕点F旋转至△NGF，∴GN=ME，∵AB=a，ME=a，∴AB=ME=NG，在△ABM与△NGF中，∵AB=NG=a，∠B=∠NGF=90°，GF=BM=b，∴△ABM≌△NGF；故③正确；④∵将△ABM绕点A旋转至△ADN，∴AM=AN，∵将△MEF绕点F旋转至△NGF，∴NF=MF，∵△ABM ≌△NGF，∴AM=NF，∴四边形AMFN是矩形，∵∠BAM=∠NAD，∴∠BAM+DAM=∠NAD+∠DAN=90°，∴∠NAM=90°，∴四边形AMFN是正方形，∵在Rt△ABM中，a2+b2=AM2，∴S四边形AMFN=AM2=a2+b2；故④正确；⑤∵四边形AMFN是正方形，∴∠AMP=90°，∵∠ADP=90°，∴∠ABP+∠ADP=180°，∴A，M，P，D 四点共圆，故⑤正确．故选D．点睛：本题考查了四点共圆，全等三角形的判定和性质，相似三角形的判定和性质，正方形的性质，旋转的性质，勾股定理，正确的理解题意是解题的关键．考点：四点共圆；相似三角形的判定与性质；正方形的性质；旋转的性质；综合题．7．（2017山东省淄博市，第12题，4分）如图，在Rt△ABC中，∠ABC=90°，AB=6，BC=8，∠BAC，∠ACB的平分线相交于点E，过点E作EF∥BC交AC于点F，则EF的长为（）A．52B．83C．103D．154【答案】C．【分析】延长FE交AB于点D，作EG⊥BC、作EH⊥AC，由EF∥BC可证四边形BDEG是矩形，由角平分线可得ED=EH=EG、∠DAE=∠HAE，从而知四边形BDEG是正方形，再证△DAE≌△HAE、△CGE≌△CHE得AD=AH、CG=CH，设BD=BG=x，则AD=AH=6﹣x、CG=CH=8﹣x，由AC=10可得x=2，即BD=DE=2、AD =4，再证△ADF ∽△ABC 可得DF 的长，据此得出EF =DF ﹣DE =103．【解析】如图，延长FE 交AB 于点D ，作EG ⊥BC 于点G ，作EH ⊥AC 于点H ，∵EF ∥BC 、∠ABC =90°，∴FD ⊥AB ，∵EG ⊥BC ，∴四边形BDEG 是矩形，∵AE 平分∠BAC 、CE 平分∠ACB ，∴ED =EH =EG ，∠DAE =∠HAE ，∴四边形BDEG 是正方形，在△DAE 和△HAE 中，∵∠DAE =∠HAE ，AE =AE ，∠ADE =∠AHE ，∴△DAE ≌△HAE （SAS ），∴AD =AH ，同理△CGE ≌△CHE ，∴CG =CH ，设BD =BG =x ，则AD =AH =6﹣x 、CG =CH =8﹣x ，∵AC =22AB AC +=2268+=10，∴6﹣x +8﹣x =10，解得：x =2，∴BD =DE =2，AD =4，∵DF ∥BC ，∴△ADF ∽△ABC ，∴AD DF AB BC =，即468DF =，解得：DF =163，则EF =DF ﹣DE =163﹣2=103，故选C ．点睛：本题主要考查相似三角形的判定与性质、全等三角形的判定与性质及正方形的判定与性质，熟练掌握角平分线的性质和正方形的判定与性质、相似三角形的判定与性质是解题的关键．考点：相似三角形的判定与性质；角平分线的性质；等腰三角形的判定与性质；综合题．8．（2017广东省深圳市，第12题，3分）如图，正方形ABCD 的边长是3，BP =CQ ，连接AQ ，DP 交于点O ，并分别与边CD ，BC 交于点F ，E ，连接AE ，下列结论：①AQ ⊥DP ；②OA 2=OE •OP ；③S △AOD =S 四边形OECF ；④当BP =1时，tan ∠OAE =1316，其中正确结论的个数是（）A ．1B ．2C ．3D ．4【答案】C ．【分析】由四边形ABCD 是正方形，得到AD =BC ，∠DAB =∠ABC =90°，根据全等三角形的性质得到∠P =∠Q ，根据余角的性质得到AQ ⊥DP ；故①正确；根据相似三角形的性质得到AO 2=OD •OP ，由OD ≠OE ，得到OA2≠OE•OP；故②错误；根据全等三角形的性质得到CF=BE，DF=CE，于是得到S△ADF﹣S△DFO=S△DCE ﹣S△DOF，即S△AOD=S四边形OECF；故③正确；根据相似三角形的性质得到BE，QE，QO，OE，由三角函数的定义即可得到结论．【解析】∵四边形ABCD是正方形，∴AD=BC，∠DAB=∠ABC=90°，∵BP=CQ，∴AP=BQ，在△DAP与△ABQ中，∵AD=AB，∠DAP=∠ABQ，AP=BQ，∴△DAP≌△ABQ，∴∠P=∠Q，∵∠Q+∠QAB=90°，∴∠P+∠QAB=90°，∴∠AOP=90°，∴AQ⊥DP；故①正确；∵∠DOA=∠AOP=90，∠ADO+∠P=∠ADO+∠DAO=90°，∴∠DAO=∠P，∴△DAO∽△APO，∴AO OPOD OA=，∴AO2=OD•OP，∵AE＞AB，∴AE＞AD，∴OD≠OE，∴OA2≠OE•OP；故②错误；在△CQF与△BPE中，∵∠FCQ=∠EBP，∠Q=∠P，CQ=BP，∴△CQF≌△BPE，∴CF=BE，∴DF=CE，在△ADF与△DCE中，∵AD=CD，∠ADC=∠DCE，DF=CE，∴△ADF≌△DCE，∴S△ADF﹣S△DFO=S△DCE ﹣S△DOF，即S△AOD=S四边形OECF；故③正确；∵BP=1，AB=3，∴AP=4，∵△AOP∽△DAP，∴43PB PAEB DA==，∴BE=34，∴QE=134，∵△QOE∽△P AD，∴1345QO OE QEPA AD PD===，∴QO=135，OE=3920，∴AO=5﹣QO=125，∴tan∠OAE=OEOA=1316，故④正确．故选C．点睛：本题考查了相似三角形的判定和性质，全等三角形的判定和性质，正方形的性质，三角函数的定义，熟练掌握全等三角形的判定和性质是解题的关键．考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质；解直角三角形；综合题．9．（2017广西贵港市，第12题，3分）如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC 边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是12，其中正确结论的个数是（）A．2B．3C．4D．5【答案】D．【分析】根据正方形的性质，依次判定△CNB≌△DMC，△OCM≌△OBN，△CON≌△DOM，△OMN∽△OAD，根据全等三角形的性质以及勾股定理进行计算即可得出结论．【解析】∵正方形ABCD中，CD=BC，∠BCD=90°，∴∠BCN+∠DCN=90°，又∵CN⊥DM，∴∠CDM+∠DCN=90°，∴∠BCN=∠CDM，又∵∠CBN=∠DCM=90°，∴△CNB≌△DMC（ASA），故①正确；根据△CNB≌△DMC，可得CM=BN，又∵∠OCM=∠OBN=45°，OC=OB，∴△OCM≌△OBN（SAS），∴OM=ON，∠COM=∠BON，∴∠DOC+∠COM=∠COB+∠BPN，即∠DOM=∠CON，又∵DO=CO，∴△CON ≌△DOM（SAS），故②正确；∵∠BON+∠BOM=∠COM+∠BOM=90°，∴∠MON=90°，即△MON是等腰直角三角形，又∵△AOD是等腰直角三角形，∴△OMN∽△OAD，故③正确；∵AB=BC，CM=BN，∴BM=AN，又∵Rt△BMN中，BM2+BN2=MN2，∴AN2+CM2=MN2，故④正确；∵△OCM≌△OBN，∴四边形BMON的面积=△BOC的面积=1，即四边形BMON的面积是定值1，∴当△MNB的面积最大时，△MNO的面积最小，设BN=x=CM，则BM=2﹣x，∴△MNB的面积=12x（2﹣x）=﹣12x2+x，∴当x=1时，△MNB的面积有最大值12，此时S△OMN的最小值是1﹣12=12，故⑤正确；综上所述，正确结论的个数是5个，故选D．点睛：本题属于四边形综合题，主要考查了正方形的性质、全等三角形的判定与性质，相似三角形的判定以及勾股定理的综合应用，解题时注意二次函数的最值的运用．考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质；二次函数的最值；最值问题；综合题．10．（2017江苏省无锡市，第9题，3分）如图，菱形ABCD的边AB=20，面积为320，∠BAD＜90°，⊙O与边AB，AD都相切，AO=10，则⊙O的半径长等于（）A．5B．6C．25D．32【答案】C．【分析】如图作DH⊥AB于H，连接BD，延长AO交BD于E．利用菱形的面积公式求出DH，再利用勾股定理求出AH ，BD ，由△AOF ∽△DBH ，可得OA OF BD BH =，延长即可解决问题．【解析】如图作DH ⊥AB 于H ，连接BD ，延长AO 交BD 于E ．∵菱形ABCD 的边AB =20，面积为320，∴AB •DH =32O ，∴DH =16，在Rt △ADH 中，AH =22AD DH - =12，∴HB =AB ﹣AH =8，在Rt △BDH 中，BD =22DH BH +=85，设⊙O 与AB 相切于F ，连接AF ．∵AD =AB ，OA 平分∠DAB ，∴AE ⊥BD ，∵∠OAF +∠ABE =90°，∠ABE +∠BDH =90°，∴∠OAF =∠BDH ，∵∠AFO =∠DHB =90°，∴△AOF ∽△DBH ，∴OA OF BD BH =，∴885OF =，∴OF =25．故选C ．点睛：本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．考点：切线的性质；菱形的性质；综合题．11．（2017浙江省台州市，第10题，4分）如图，矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上，BE =BF ，将△AEH ，△CFG 分别沿边EH ，FG 折叠，当重叠部分为菱形且面积是菱形ABCD 面积的116时，则AE EB为（）A ． 53B ．2C ． 52D ．4 【答案】A ．【分析】设重叠的菱形边长为x ，BE =BF =y ，由矩形和菱形的对称性以及折叠的性质得：四边形AHME 、四边形BENF 是菱形，得出EN =BE =y ，EM =x +y ，由相似的性质得出AB =4MN =4x ，求出AE =AB ﹣BE =4x ﹣y ，得出方程4x ﹣y =x +y ，得出x =23y ，AE =53y ，即可得出结论．点睛：本题考查了折叠的性质、菱形的判定与性质、矩形的性质、相似多边形的性质等知识；熟练掌握菱形的判定与性质是解决问题的关键．考点：翻折变换（折叠问题）；菱形的性质；矩形的性质；综合题．学.科.网12．（2017浙江省杭州市，第10题，3分）如图，在△ABC中，AB=AC，BC=12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD=x，tan∠ACB=y，则（）A．x﹣y2=3B．2x﹣y2=9C．3x﹣y2=15D．4x﹣y2=21【答案】B．【分析】过A作AQ⊥BC于Q，过E作EM⊥BC于M，连接DE，根据线段垂直平分线求出DE=BD=x，根据等腰三角形求出BD=DC=6，求出CM=DM=3，解直角三角形求出EM=3y，AQ=6y，在Rt△DEM中，根据勾股定理求出即可．【解析】过A作AQ⊥BC于Q，过E作EM⊥BC于M，连接DE，∵BE的垂直平分线交BC于D，BD=x，∴BD=DE=x，∵AB=AC，BC=12，tan∠ACB=y，∴EM AQMC CQ=y，BQ=CQ=6，∴AQ=6y，∵AQ⊥BC，EM⊥BC ，∴AQ ∥EM ，∵E 为AC 中点，∴CM =QM =12CQ =3，∴EM =3y ，∴DM =12﹣3﹣x =9﹣x ，在Rt △EDM 中，由勾股定理得：x 2=（3y ）2+（9﹣x ）2，即2x ﹣y 2=9，故选B ．点睛：本题考查了线段垂直平分线性质，等腰三角形的性质，勾股定理，解直角三角形等知识点，能正确作出辅助线是解此题的关键．考点：解直角三角形；线段垂直平分线的性质；等腰三角形的性质；综合题． 13．（2017衢州，第9题，3分）如图，矩形纸片ABCD 中，AB =4，BC =6，将△ABC 沿AC 折叠，使点B 落在点E 处，CE 交AD 于点F ，则DF 的长等于（）A ． 53B ． 35C ． 37D ． 45 【答案】B ．【分析】根据折叠的性质得到AE =AB ，∠E =∠B =90°，易证Rt △AEF ≌Rt △CDF ，即可得到结论EF =DF ；易得FC =F A ，设F A =x ，则FC =x ，FD =6﹣x ，在Rt △CDF 中利用勾股定理得到关于x 的方程x 2=42+（6﹣x ）2，解方程求出x ．【解析】∵矩形ABCD 沿对角线AC 对折，使△ABC 落在△ACE 的位置，∴AE =AB ，∠E =∠B =90°，又∵四边形ABCD 为矩形，∴AB =CD ，∴AE =DC ，而∠AFE =∠DFC ，在△AEF 与△CDF 中，∵∠AFE =∠CFD ，∠E =∠D ，AE =CD ，∴△AEF ≌△CDF （AAS ），∴EF =DF ；∵四边形ABCD 为矩形，∴AD =BC =6，CD =AB =4，∵Rt △AEF ≌Rt △CDF ，∴FC =F A ，设F A =x ，则FC =x ，FD =6﹣x ，在Rt △CDF 中，CF 2=CD 2+DF 2，即x 2=42+（6﹣x ）2，解得x =133，则FD =6﹣x =35．故选B ．点睛：本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应边相等．也考查了矩形的性质和三角形全等的判定与性质以及勾股定理．考点：翻折变换（折叠问题）；矩形的性质；综合题．14．（2017湖北省武汉市，第10题，3分）如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（）A．4B．5C．6D．7【答案】D．【分析】①以B为圆心，BC长为半径画弧，交AB于点D，△BCD就是等腰三角形；②以A为圆心，AC长为半径画弧，交AB于点E，△ACE就是等腰三角形；③以C为圆心，BC长为半径画弧，交AC于点F，△BCF就是等腰三角形；④作AC的垂直平分线交AB于点H，△ACH就是等腰三角形；⑤作AB的垂直平分线交AC于G，则△AGB是等腰三角形；⑥作BC的垂直平分线交AB于I，则△BCI是等腰三角形．⑦以C为圆心，BC长为半径画弧，交AB于点K，△BCK就是等腰三角形；【解析】如图：故选D．点睛：本题考查了等腰三角形的判定的应用，主要考查学生的理解能力和动手操作能力．考点：等腰三角形的判定与性质；分类讨论；综合题；操作型．15．（2017湖北省随州市，第10题，3分）如图，在矩形ABCD中，AB＜BC，E为CD边的中点，将△ADE 绕点E顺时针旋转180°，点D的对应点为C，点A的对应点为F，过点E作ME⊥AF交BC于点M，连接AM、BD交于点N，现有下列结论：①AM=AD+MC；②AM=DE+BM；③DE2=AD•CM；④点N为△ABM的外心．其中正确的个数为（）A．1个B．2个C．3个D．4个【答案】B．【分析】根据全等三角形的性质以及线段垂直平分线的性质，即可得出AM=MC+AD；根据当AB=BC时，四边形ABCD为正方形进行判断，即可得出当AB＜BC时，AM=DE+BM不成立；根据ME⊥FF，EC⊥MF，运用射影定理即可得出EC2=CM×CF，据此可得DE2=AD•CM成立；根据N不是AM的中点，可得点N不是△ABM的外心．【解析】∵E为CD边的中点，∴DE=CE，又∵∠D=∠ECF=90°，∠AED=∠FEC，∴△ADE≌△FCE，∴AD =CF ，AE =FE ，又∵ME ⊥AF ，∴ME 垂直平分AF ，∴AM =MF =MC +CF ，∴AM =MC +AD ，故①正确；当AB =BC 时，即四边形ABCD 为正方形时，设DE =EC =1，BM =a ，则AB =2，BF =4，AM =FM =4﹣a ，在Rt △ABM 中，22+a 2=（4﹣a ）2，解得a =1.5，即BM =1.5，∴由勾股定理可得AM =2.5，∴DE +BM =2.5=AM ，又∵AB ＜BC ，∴AM =DE +BM 不成立，故②错误；∵ME ⊥FF ，EC ⊥MF ，∴EC 2=CM ×CF ，又∵EC =DE ，AD =CF ，∴DE 2=AD •CM ，故③正确；∵∠ABM =90°，∴AM 是△ABM 的外接圆的直径，∵BM ＜AD ，∴当BM ∥AD 时，MN BM AN AD =＜1，∴N 不是AM 的中点，∴点N 不是△ABM 的外心，故④错误．综上所述，正确的结论有2个，故选B ．点睛：本题主要考查了相似三角形的判定与性质，全等三角形的判定与性质，矩形的性质以及旋转的性质的综合应用，解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例，解题时注意：三角形外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心，故外心到三角形三个顶点的距离相等．考点：相似三角形的判定与性质；全等三角形的判定与性质；矩形的性质；三角形的外接圆与外心；旋转的性质；综合题． 16．（2017湖南省长沙市，第12题，3分）如图，将正方形ABCD 折叠，使顶点A 与CD 边上的一点H 重合（H 不与端点C ，D 重合），折痕交AD 于点E ，交BC 于点F ，边AB 折叠后与边BC 交于点G ．设正方形ABCD 的周长为m ，△CHG 的周长为n ，则mn 的值为（）A ．22B ．21 C ．215- D ．随H 点位置的变化而变化【答案】B ．【分析】设CH =x ，DE =y ，则DH =4m ﹣x ，EH =4m ﹣y ，然后利用正方形的性质和折叠可以证明△DEH ∽△CHG ，利用相似三角形的对应边成比例可以把CG ，HG 分别用x ，y 分别表示，△CHG 的周长也用x ，y 表示，然后在Rt △DEH 中根据勾股定理可以得到222m m x x y -=，进而求出△CMG 的周长．【解析】设CH =x ，DE =y ，则DH =4m ﹣x ，EH =4m ﹣y ，∵∠EMG =90°，∴∠DME +∠CMG =90°．∵∠DME + ∠DEM =90°，∴∠DEM =∠CMG ，又∵∠D =∠C =90°△DEM ∽△CMG ，∴CG CM MG DM DE EM ==，即 44CG x MG m m y x y ==--，∴CG =()4m x x y -，MG =()4m x y y -，△CMG 的周长为n =CM +CG +MG =22mx x y -，在Rt △DEM 中，DM 2+DE 2=EM 2，即（4m ﹣x ）2+y 2=（4m ﹣y ）2，整理得222m m x x y -=，∴ n =CM +MG +CG =22mx x y -=2my y =2m ，∴m n =21．故选B ．点睛：本题考查翻折变换及正方形的性质，正方形的有些题目有时用代数的计算证明比用几何方法简单，甚至几何方法不能解决的用代数方法可以解决．本题综合考查了相似三角形的应用和正方形性质的应用．考点：翻折变换（折叠问题）；综合题．17．（2017甘肃省兰州市，第14题，4分）如图，在正方形ABCD 和正方形DEFG 中，点G 在CD 上，DE =2，将正方形DEFG 绕点D 顺时针旋转60°，得到正方形DE ′F ′G ′，此时点G ′在AC 上，连接CE ′，则CE ′+CG ′=（）A 26B 31C 32D 36【答案】A ．【分析】解法一：作G ′I ⊥CD 于I ，G ′R ⊥BC 于R ，E ′H ⊥BC 交BC 的延长线于H ．连接RF ′．则四边形RCIG ′是正方形．首先证明点F ′在线段BC 上，再证明CH =HE ′即可解决问题．解法二：首先证明CG ′+CE ′=AC ，作G ′M ⊥AD 于M ．解直角三角形求出DM ，AM ，AD 即可；【解析】解法一：作G ′I ⊥CD 于I ，G ′R ⊥BC 于R ，E ′H ⊥BC 交BC 的延长线于H ．连接RF ′．则四边形RCIG ′是正方形．∵∠DG ′F ′=∠IGR =90°，∴∠DG ′I =∠RG ′F ′，在△G ′ID 和△G ′RF 中，∵G ′D = G ′F ，∠D G ′I =∠R G ′F ′，G ′I = G ′R ，∴△G ′ID ≌△G ′RF ，∴∠G ′ID =∠G ′RF ′=90°，∴点F ′在线段BC上，在Rt△E′F′H中，∵E′F′=2，∠E′F′H=30°，∴E′H=12E′F′=1，F′H=3，易证△RG′F′≌△HF′E′，∴RF′=E′H，RG′RC=F′H，∴CH=RF′=E′H，∴CE′=2，∵RG′=HF′=3，∴CG′=2RG′=6，∴CE′+CG′=26．故选A．解法二：作G′M⊥AD于M．易证△DAG'≌△DCE'，∴AG'=CE'，∴CG′+CE′=AC，在Rt△DMG′中，∵DG′=2，∠MDG′=30°，∴MG′=1，DM=3，∵∠MAG′=45°，∠AMG′=90°，∴∠MAG′=∠MG′A=45°，∴AM=MG′=1，∴AD=1+3，∵AC=2AD，∴AC=26．故选A．点睛：本题考查旋转变换、正方形的性质、全等三角形的判定和性质、勾股定理、等腰直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．考点：旋转的性质；正方形的性质；综合题．学.科.网18．（2017黑龙江省龙东地区，第20题，3分）如图，在边长为4的正方形ABCD中，E、F是AD边上的两个动点，且AE=FD，连接BE、CF、BD，CF与BD交于点G，连接AG交BE于点H，连接DH，下列结论正确的个数是（）①△ABG∽△FDG②HD平分∠EHG③AG⊥BE④S△H S△HBG=tan∠DAG⑤线段DH的最小值是252．A．2B．3C．4D．5【答案】C ．【分析】首先证明△ABE ≌△DCF ，△ADG ≌△CDG （SAS ），△AGB ≌△CGB ，利用全等三角形的性质，等高模型、三边关系一一判断即可．【解析】∵四边形ABCD 是正方形，∴AB =CD ，∠BAD =∠ADC =90°，∠ADB =∠CDB =45°，在△ABE 和△DCF 中，∵AB =CD ，∠BAD =∠ADC ，AE =DF ，∴△ABE ≌△DCF （SAS ），∴∠ABE =∠DCF ，在△ADG 和△CDG 中，∵AD =CD ，∠ADB =∠CDB ，DG =DG ，∴△ADG ≌△CDG （SAS ），∴∠DAG =∠DCF ，∴∠ABE =∠DAG ，∵∠DAG +∠BAH =90°，∴∠BAE +∠BAH =90°，∴∠AHB =90°，∴AG ⊥BE ，故③正确，同法可证：△AGB ≌△CGB ，∵DF ∥CB ，∴△CBG ∽△FDG ，∴△ABG ∽△FDG ，故①正确，∵S △H S △HBG =BG =BC =CD =tan ∠FCD ，又∵∠DAG =∠FCD ，∴S △H S △HBG =tan ∠FCD ，tan ∠DAG ，故④正确取AB 的中点O ，连接OD 、OH ，∵正方形的边长为4，∴AO =OH =12×4=2，由勾股定理得，OD =2242+ =25，由三角形的三边关系得，O 、D 、H 三点共线时，DH 最小，DH 最小=252-．无法证明DH 平分∠EHG ，故②错误，故①③④⑤正确，故选C ．点睛：本题考查了正方形的性质，全等三角形的判定与性质，三角形的三边关系，勾股定理、等高模型等知识，解题的关键是灵活运用所学知识解决问题，难点在于⑤作辅助线并确定出DH 最小时的情况．考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质；解直角三角形；综合题．19．（2017四川省攀枝花市，第10题，3分）如图，正方形ABCD 中．点E ，F 分别在BC ，CD 上，△AEF 是等边三角形．连接AC 交EF 于点G ．过点G 作GH ⊥CE 于点H ．若3EGH S ∆=，则ADF S ∆=（）A ．6B ．4C ．3D ．2【答案】A ．【分析】通过条件可以得出△ABE ≌△ADF ，从而得出∠BAE =∠DAF ，BE =DF ，由正方形的性质就可以得出EC =FC ，就可以得出AC 垂直平分EF ，得到EG =GF ，根据相似三角形的性质得到S △EFC =12，设AD =x ，则DF =x ﹣26，根据勾股定理得到AD =632+，DF =326-，根据三角形的面积公式即可得到结论．【解析】∵四边形ABCD 是正方形，∴AB =BC =CD =AD ，∠B =∠BCD =∠D =∠BAD =90°．∵△AEF 等边三角形，∴AE =EF =AF ，∠EAF =60°，∴∠BAE +∠DAF =30°．在Rt △ABE 和Rt △ADF 中，∵AE =AF ，AB =AD ，∴Rt △ABE ≌Rt △ADF （HL ），∴BE =DF ，∵BC =CD ，∴BC ﹣BE =CD ﹣DF ，即CE =CF ，∴△CEF 是等腰直角三角形，∵AE =AF ，∴AC 垂直平分EF ，∴EG =GF ，∵GH ⊥CE ，∴GH ∥CF ，∴△EGH ∽△EFC ，∵S △EGH =3，∴S △EFC =12，∴CF =26，EF =43，∴AF =43，设AD =x ，则DF =x ﹣26，∵AF 2=AD 2+DF 2，∴（43）2=x 2+（x ﹣26）2，∴x =632+，∴AD =632+，DF =326-，∴S △ADF =12AD •DF =6．故选A ．点睛：本题考查了正方形的性质的运用，全等三角形的判定及性质的运用，相似三角形的判定和性质，勾股定理的运用，等边三角形的性质的运用，解答本题的关键是运用勾股定理的性质．考点：正方形的性质；等边三角形的性质；综合题．20．（2017四川省雅安市，第12题，3分）如图，四边形ABCD 中，AB =4，BC =6，AB ⊥BC ，BC ⊥CD ，E 为AD 的中点，F 为线段BE 上的点，且FE =13BE ，则点F 到边CD 的距离是（）A ．3B ．103 C ．4 D ．143【答案】C ．【分析】过点D 作DG ⊥AB ，交BA 的延长线于点G ，过点E 作EH ⊥BG 于点H ，过点F 作FP ⊥BG 于点P ，延长PF 交CD 于点M ，则FM 即为点F 到边CD 的距离，则四边形BCDG ，四边形BCMP 为矩形，得到PM 的长．再由三角形中位线定理得EH 的长，再由相似三角形的性质得到PF 的长，从而得到结论．点睛：作出恰当的辅助线是解答本题的关键．考点：矩形的判定与性质；三角形中位线定理；相似三角形的判定与性质；综合题．21．（2017山东省莱芜市，第12题，3分）如图，正五边形ABCDE的边长为2，连结AC、AD、BE，BE 分别与AC和AD相交于点F、G，连结DF，给出下列结论：①∠FDG=18°；②FG=3﹣5；③（S四边形CDEF）2=9+25；④DF2﹣DG2=7﹣25．其中正确结论的个数是（）A．1B．2C．3D．4【答案】B．【分析】①先根据正五方形ABCDE的性质得：∠ABC=180°﹣3605=108°，由等边对等角可得：∠BAC=∠ACB=36°，再利用角相等求BC=CF=CD，得∠CDF=∠CFD=（180°-72°）÷2=54°，可得∠FDG=18°；②证明△ABF∽△ACB，得AB EGAC ED=，代入可得FG的长；③如图1，先证明四边形CDEF是平行四边形，根据平行四边形的面积公式可得：（S四边形CDEF）2= 10+5④如图2，▱CDEF是菱形，先计算EC=BE=4﹣FG=15S四边形CDEF=12FD•EC=210254+，可得FD2=10﹣5【解析】①∵五方形ABCDE是正五边形，∴AB=BC，∠ABC=180°﹣3605=108°，∴∠BAC=∠ACB=36°，∴∠ACD=108°﹣36°=72°，同理得：∠ADE=36°，∵∠BAE=108°，AB=AE，∴∠ABE=36°，∴∠CBF=108°﹣36°=72°，∴BC=FC，∵BC=CD，∴CD=CF，∴∠CDF=∠CFD=（180°-72°）÷2=54°，∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°；所以①正确；②∵∠ABE=∠ACB=36°，∠BAC=∠BAF，∴△ABF∽△ACB，∴AB EGAC ED=，∴AB•ED=AC•EG，∵AB=ED=2，AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG，EG=BG﹣FG=2﹣FG，∴22=（2﹣FG）（4﹣FG），∴FG=3+5＞2（舍），FG=3﹣5；所以②正确；③如图1，∵∠EBC=72°，∠BCD=108°，∴∠EBC+∠BCD=180°，∴EF∥CD，∵EF=CD=2，∴四边形CDEF是平行四边形，过D作DM⊥EG于M，∵DG=DE，∴EM=MG=12EG=12（EF﹣FG）=12（2﹣3+5）=512-，由勾股定理得：DM=22DE EM-=22512()2-- =10254+，∴（S四边形CDEF）2=EF2×DM2=4×1025+=10+25；所以③不正确；④如图2，连接EC，∵EF=ED，∴▱CDEF是菱形，∴FD⊥EC，∵EC=BE=4﹣FG=4﹣（3﹣5）=1+5，∴S四边形CDEF=12FD•EC=2×10254+，12×FD×（1+5）=1025+，FD2=10﹣25，∴DF2﹣DG2=10﹣25﹣4=6﹣25，所以④不正确；本题正确的有两个，故选B．点睛：本题考查了相似三角形的判定和性质，勾股定理，正五边形的性质、平行四边形和菱形的判定和性质，有难度，熟练掌握正五边形的性质是解题的关键．考点：正多边形和圆；相似三角形的判定与性质；综合题．学.科.网22．（2017辽宁省鞍山市，第8题，3分）如图，在矩形ABCD中，点E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②DF=DC；③S△DCF=4S△DEF；④tan∠CAD=22．其中正确结论的个数是（）A．4B．3C．2D．1【答案】A．【分析】①正确．只要证明∠EAC=∠ACB，∠ABC=∠AFE=90°即可；②根据已知条件得到四边形BMDE是平行四边形，求得BM=DE=12BC，根据线段垂直平分线的性质得到DM垂直平分CF，于是得到结论，③根据三角形的面积公式即可得到结论；④设AE=a，AB=b，则AD=2a，根据相似三角形的性质即可得到结论．【解析】如图，过D作DM∥BE交AC于N，∵四边形ABCD是矩形，∴AD∥BC，∠ABC=90°，AD=BC，S△DCF=4S△DEF∵BE⊥AC于点F，∴∠EAC=∠ACB，∠ABC=∠AFE=90°，∴△AEF∽△CAB，故①正确；②∵DE∥BM，BE∥DM，∴四边形BMDE是平行四边形，∴BM=DE=12BC，∴BM=CM，∴CN=NF，∵BE⊥AC于点F，DM∥BE，∴DN⊥CF，∴DM垂直平分CF，∴DF=DC，故②正确；③∵点E是AD边的中点，∴S△DEF=12S△ADF，∵△AEF∽△CBA，∴AF：CF=AE：BC=12，∴S△CDF=2S△ADF=4S△DEF，故③正确；④设AE=a，AB=b，则AD=2a，由△BAE∽△ADC，有2b aa b=，即b2a，∴tan∠CAD=2CD bAD a=2．故④正确；故选A．点睛：本题主要考查了相似三角形的判定和性质，矩形的性质，图形面积的计算以及解直角三角形的综合应用，正确的作出辅助线构造平行四边形是解题的关键．解题时注意：相似三角形的对应边成比例．考点：相似三角形的判定与性质；矩形的性质；解直角三角形；综合题．23．（2016山东省潍坊市）关于x 的一元二次方程22sin 0x x a -+=有两个相等的实数根，则锐角α等于（）A ．15°B ．30°C ．45°D ．60° 【答案】B ．【分析】由方程有两个相等的实数根，结合根的判别式可得出sin α=12，再由α为锐角，即可得出结论．【解析】∵关于x 的一元二次方程22sin 0x x a -+=有两个相等的实数根，∴△=2(2)4sin 0α--=，解得：sin α=12，∵α为锐角，∴α=30°．故选B ．考点：根的判别式；特殊角的三角函数值．24．（2016福建省莆田市）如图，在△ABC 中，∠ACB =90°，AC =BC =4，将△ABC 折叠，使点A 落在BC 边上的点D 处，EF 为折痕，若AE =3，则sin ∠BFD 的值为（）A ．13 B 22 C 2 D ．35【答案】A ．【分析】由题意得：△AEF ≌△DEF ，故∠EDF =∠A ；由三角形的内角和定理及平角的知识问题即可解决．【解析】∵在△ABC 中，∠ACB =90°，AC =BC =4，∴∠A =∠B ，由折叠的性质得到：△AEF ≌△DEF ，∴∠EDF =∠A ，∴∠EDF =∠B ，∴∠CDE +∠BDF +∠EDF =∠BFD +∠BDF +∠B =180°，∴∠CDE =∠BFD ．又∵AE =DE =3，∴CE =4﹣3=1，∴在直角△ECD 中，sin ∠CDE =13CE ED =．故选A ．考点：翻折变换（折叠问题）；等腰直角三角形；锐角三角函数的定义．。