七年级数学下全等三角形证明题精选
七年级下册数学全等三角形证明题

七年级下册数学全等三角形证明题
1. 给定三角形ABC,其中∠BAC=90度,AD是BC上的中线。
证明:△ABD≌△ACD。
证明:
因为∠BAD=∠CAD,而又AD=AD(公共边),所以△ABD≌△ACD (SAS)。
2. 给定四边形ABCD,其中AB=BC,CD=DA,BD是AC的中线。
证明:△ABD≌△CBD,△BCD≌△DAB。
证明:
因为BD是AC的中线,所以BD=1/2AC。
又因为AB=BC,CD=DA,所以△ABD≌△CBD(SAS),△BCD≌△DAB(SAS)。
3. 给定三角形ABC和点D,使得∠BAD=∠ACD。
证明:
△ABD≌△ACD。
证明:
因为∠BAD=∠ACD,而又共有一边AD,所以△ABD≌△ACD(AAS)。
4. 给定三角形ABC和点D,使得AC=CD,∠ACB=∠ADB。
证明:△ACB≌△ADB。
证明:
由AC=CD可知∠ADC=∠ACD。
所以
∠ADB=∠ACB+∠ACD=∠ADB+∠ADC,即∠ADC=0。
因此,D与B重合,且AB=AB,AC=AD,所以△ACB≌△ADB(SSS)。
5. 给定三角形ABC和点D,使得AB=BD,CD是BC的中线。
证明:△ABD≌△ACD。
证明:
因为CD是BC的中线,所以CD=1/2BC。
又因为AB=BD,所以
∠ABD=∠ADB。
因此,△ABD≌△ACD(SAS)。
最新北师大版七年级下册三角形全等(SSS)的证明试题以及答案(共41道证明题)
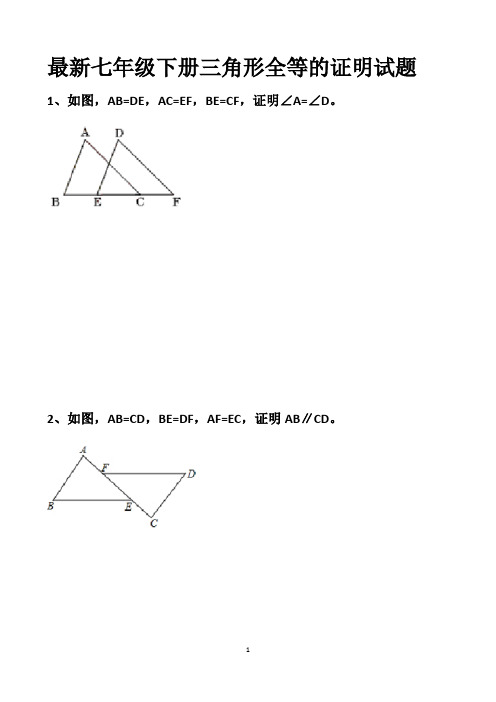
最新七年级下册三角形全等的证明试题1、如图,AB=DE,AC=EF,BE=CF,证明∠A=∠D。
2、如图,AB=CD,BE=DF,AF=EC,证明AB∥CD。
3、如图,AC=DF,EF=BC,AD=BE,证明∠F=∠C。
4、如图,AB=AC,AD=AE,BE=DC,证明∠ABD=∠AEC。
5、如图,AB=AD,AE=AC,BC=ED,证明∠ABE=∠ACD。
6、如图,AD=AB,DC=BC,证明∠B=∠D。
7、如图,AB=AC,BD=DC,证明∠1=∠2.8、如图,∠C=90°,AD=BD,DE=DC,AE=BC,说明AB和DE的关系。
9、如图,AB=DE,BC=EF,AF=CD,证明AB∥DE。
10、如图,AB=AC,D是BC的中点,证明AD⊥BC。
11、如图,AE=DF,AB=CD,CE=BF,证明AE∥DF。
12、如图,AB=AD,AE=AC,BC=DE,证明∠E=∠C。
13、如图,BC=BE,DE=DC,∠C=90°,证明(1)DE⊥AB(2)BD是∠ABC的角平分线。
14、如图,AB=EF,AD=CF,DE=BC,证明∠B=∠E。
15、如图,OA=OB,AC=BD,AD=BC,证明∠ACB=∠ADB。
16、如图,AD=BC,A0=OB,OC=OD,证明∠BAD=∠ABC。
17、如图,AD=BD,BE=AC,AD+DE=BC,AD⊥BC,证明BE⊥AC。
18、如图,AD=BC,AF=EC,DE=BF,证明DE∥BF,AD∥BC。
19、如图,AB=DC,AC=BD,AO=OD,证明∠B=∠C。
20、如图,AB=AD,AE=AC,BC=DE,证明∠1=∠2.21、如图,AC⊥CE,AC=CE,AB=CD,且AB+DE=BD,AB∥DE。
22、如图,AE=AB,AC=AF,EC=BF,证明∠BAE=∠CAF。
23、如图,AD=BC,AC=BD,证明∠ADO=∠BCO。
24、如图,AB=AC,BD=CE,AD=AE,证明∠ABC=∠ADE。
七年级数学下---全等三角形证明题精选

七年级数学下---全等三角形证明题精选1、已知:如图,四边形ABCD 中,AC 平分角BAD ,CE 垂直AB 于E ,且∠B+∠D=180°,求证:AE=AD+BEABDCE 122、已知:如图,AB 、CD 交于O 点,CE//DF ,CE=DF ,AE=BF 。
求证:∠ACE=∠BDF 。
3. 已知:如图,△ABC 中,AD ⊥BC 于D ,E 是AD 上一点,BE 的延长线交AC 于F ,若BD=AD ,DE=DC 。
求证:BF ⊥AC 。
4. 已知:如图,△ABC 和△A 'B 'C '中,∠BAC=∠B 'A 'C ',∠B=∠B ',AD 、A 'D '分别是∠BAC 、∠B 'A 'C '的平分线,且AD=A 'D '。
求证:△ABC ≌△A ’B ’C ’。
ABCDEFOAB CDEFAB C D A' B'C'D' 1 23 45、已知:如图,AB=CD ,AD=BC ,O 是AC 中点,OE ⊥AB 于E ,OF ⊥D 于F 。
求证:OE=OF 。
A BCDE F O6.已知:如图,AC ⊥OB ,BD ⊥OA ,AC 与BD 交于E 点,若OA=OB ,求证:AE=BE 。
OB ACDE7.已知:如图,AB//DE ,AE//BD ,AF=DC ,EF=BC 。
求证:△AEF ≌△DBC 。
A BDEF8.如图,B ,E 分别是CD 、AC 的中点,AB ⊥CD ,DE ⊥AC 求证:AC=CD (连接AD )9.已知:如图,PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线,•它们交于点P ,PD ⊥BM 于D ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.10、如图,已知AD 是∠BAC 的平分线, DE ⊥AB 于E , DF ⊥AC 于F , 且BE=CF , 求证: (1)AD 是△ABC 的中线;(2)AB=AC .11.在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E . (1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE =AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE =AD -BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.CBAE D图1NMABCDEMN图2ACBEDN M 图3 A1 2 EF CDB12、如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE ⊥AD 交AB 于E . 求证∠CDA =∠EDB .(作CF ⊥AB )13、在Rt △ABC 中,∠B AC =90°,CE 是角平分线,和高AD 相交于F ,作FG ∥BC 交AB 于G , 求证:AE =BG (平行四边形对边相等).14、如图,已知△ABC 是等边三角形,∠BDC =120º,说明AD=BD+CD 的理由15、如图,在△ABC 中,AD 是中线,BE 交AD 于F,且AE=EF,说明AC=BF 的理由。
最新北师大版七年级下册三角形全等(AAS或ASA)的证明试题以及答案 (共50道)

最新七年级下册三角形全等的证明试题两角一边的证明题如下图模型。
1、如图,AB∥CD,且AB=CD,证明O是AD、BC的公共中点。
2、如图,CA⊥OM,CB⊥ON,OC平分∠MON,证明(1)OA=OB(2)连接AB,证明AB⊥OC。
3、如图,∠B=∠C,AD=AE,证明BD=CE。
4、如图,AC平分∠BAD,AB⊥BC,AD⊥DC,证明CA平分∠BCD。
5、如图,AB∥DE,BF=CE,∠A=∠D,试着说明AC和DF的关系。
6、如图,AB=CD,∠A=∠D,证明∠1=∠2.7、如图,∠A=∠D,∠BCE=∠ACD,CB=CE,证明AB=ED。
8、如图,DE⊥AB,DF⊥AC,D是BC的中点,∠BDF=∠CDE,证明AB=AC。
9、如图,∠1=∠2,AB=AE,∠B=∠E,证明∠D=∠C。
10、如图,AB⊥BC,DC⊥BC,BE=CF,∠BED=∠ACF,证明AF⊥DE。
11、如图,CE、BD分别是三角形的两条高线,且AB=AC,证明∠CBD=∠BCE。
12、如图,BE=CF,∠A=∠D,AB∥DE,说明AC和DF的关系。
13、如图,∠C=∠D,∠ABD=∠BAC,证明DE=CE。
14、如图,AB∥CF,AD=CF,证明E是AC的中点。
15、如图,AF=CE,AD∥BC,DF∥BE,说明AB和CD关系。
16、如图,BE⊥CE,AD⊥CE,AC⊥BC,且AC=BC,说明线段BE、AD、DE之间的关系。
17、如图,∠A+∠C=180°,BD平分∠ABC,证明AD=CD。
18、如图,∠1=∠2,∠E=∠D,AE=AD,证明EC=BD。
19、如图,AD=BC,∠A=∠C,说明A、C的连线和B、D的连线的关系。
20、如图,∠1=∠2,∠D=∠E,AB=AC,证明BD=CE。
21、如图,BD平分∠ABC,∠A=∠C,证明A、C的连线和BD垂直。
22、如图,△ABD是以AB为斜边的等腰直角三角形,∠C与∠AEB互补,说明BE和AC的关系。
全等三角形证明中考题精选(有答案)

全等三角形证明中考题精选(有答案)work Information Technology Company.2020YEAR七年级数学下---全等三角形证明题1.如图,已知AD是△ABC的中线,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.2.如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现:如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:①线段DE与AC的位置关系是_________;②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是_________.(2)猜想论证当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.(3)拓展探究已知∠ABC=60°,点D是角平分线上一点,BD=CD=4,DE∥AB交BC于点E(如图4).若在射线BA上存在点F,使S△DCF =S△BDE,请直接写出相应的BF的长.3.如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB 边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;(2)求出∠FHG的度数.4.如图所示,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,如图①,然后将△ADE绕A点顺时针旋转一定角度,得到图②,然后将BD、CE分别延长至M、N,使DM=BD,EN=CE,得到图③,请解答下列问题:(1)若AB=AC,请探究下列数量关系:①在图②中,BD与CE的数量关系是_________ ;②在图③中,猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系,并证明你的猜想;(2)若AB=k•AC(k>1),按上述操作方法,得到图④,请继续探究:AM与AN的数量关系、∠MAN与∠BAC的数量关系,直接写出你的猜想,不必证明.4.(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.6.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE _________ CF;EF _________ |BE﹣AF|(填“>”,“<”或“=”);②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_________ ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).7.如图,已知AB=AC,(1)若CE=BD,求证:GE=GD;(2)若CE=m•BD(m为正数),试猜想GE与GD有何关系.(只写结论,不证明)8.(1)已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=60°,求证:①AC=BD;②∠APB=60度;(2)如图②,在△AOB和△COD中,若OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系式为_________ ;∠APB的大小为_________ ;(3)如图③,在△AOB和△COD中,若OA=k•OB,OC=k•OD(k>1),∠AOB=∠COD=α,则AC与BD 间的等量关系式为_________ ;∠APB的大小为10.已知:EG∥AF,AB=AC,DE=DF;求证:BE=CF参考答案与试题解析2.解:(1)①∵△DEC绕点C旋转点D恰好落在AB边上,∴AC=CD,∵∠BAC=90°﹣∠B=90°﹣30°=60°,∴△ACD是等边三角形,∴∠ACD=60°,又∵∠CDE=∠BAC=60°,∴∠ACD=∠CDE,∴DE∥AC;②∵∠B=30°,∠C=90°,∴CD=AC=AB,∴BD=AD=AC,根据等边三角形的性质,△ACD的边AC、AD上的高相等,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;故答案为:DE∥AC;S1=S2;(2)如图,∵△DEC是由△ABC绕点C旋转得到,∴BC=CE,AC=CD,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°﹣90°=90°,∴∠ACN=∠DCM,∵在△ACN和△DCM中,,∴△ACN≌△DCM(AAS),∴AN=DM,∴△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2;3、解答:(1)证明:∵在△CBF和△DBG中,,∴△CBF≌△DBG(SAS),∴CF=DG;(2)解:∵△CBF≌△DBG,∴∠BCF=∠BDG,又∵∠CFB=∠DFH,∴∠DHF=∠CBF=60°,∴∠FHG=180°﹣∠DHF=180°﹣60°=120°.4、解答:解:(1)①结论:BD=CE,BD⊥CE;②结论:BD=CE,BD⊥CE;理由如下:∵∠BAC=∠DAE=90°∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE在△ABD与△ACE中,∵∴△ABD≌△ACE(SAS)∴BD=CE延长BD交AC于F,交CE于H.在△ABF与△HCF中,∵∠ABF=∠HCF,∠AFB=∠HFC;∴∠CHF=∠BAF=90°∴BD⊥CE(2)结论:乙.AB:AC=AD:AE,∠BAC=∠DAE=90°解答:解:(1)①BD=CE;②AM=AN,∠MAN=∠BAC,∵∠DAE=∠BAC,∴∠CAE=∠BAD,在△BAD和△CAE中∵∴△CAE≌△BAD(SAS),∴∠ACE=∠ABD,∵DM=BD,EN=CE,∴BM=CN,在△ABM和△ACN中,∵∴△ABM≌△ACN(SAS),∴AM=AN,∴∠BAM=∠CAN,即∠MAN=∠BAC;(2)AM=k•AN,∠MAN=∠BAC.5.6.解答:解:(1)①∵∠BCA=90°,∠α=90°,∴∠BCE+∠CBE=90°,∠BCE+∠ACF=90°,∴∠CBE=∠ACF,∵CA=CB,∠BEC=∠CFA;∴△BCE≌△CAF,∴BE=CF;EF=|BE﹣AF|.②所填的条件是:∠α+∠BCA=180°.证明:在△BCE中,∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α.∵∠BCA=180°﹣∠α,∴∠CBE+∠BCE=∠BCA.又∵∠ACF+∠BCE=∠BCA,∴∠CBE=∠ACF,又∵BC=CA,∠BEC=∠CFA,∴△BCE≌△CAF(AAS)∴BE=CF,CE=AF,又∵EF=CF﹣CE,∴EF=|BE﹣AF|.(2)EF=BE+AF.7.解答:证明:(1)过D作DF∥CE,交BC于F,则∠E=∠GDF.∵AB=AC,∴∠ACB=∠ABC∵DF∥CE,∴∠DFB=∠ACB,∴∠DFB=∠ACB=∠ABC.∴DF=DB.∵CE=BD,∴DF=CE,在△GDF和△GEC中,,∴△GDF≌△GEC(AAS).∴GE=GD.(2)GE=m•GD.9.解答:解:(1)①∵∠AOB=∠COD=60°,∴∠AOB+∠BOC=∠COD+∠BOC.即:∠AOC=∠BOD.又∵OA=OB,OC=OD,∴△AOC≌△BOD.∴AC=BD.②由①得:∠OAC=∠OBD,∵∠AEO=∠PEB,∠APB=180°﹣(∠BEP+∠OBD),∠AOB=180°﹣(∠OAC+∠AEO),∴∠APB=∠AOB=60°.(2)AC=BD,α(3)AC=k•BD,180°﹣α.。
七年级数学全等三角形证明精选题

七年级数学全等三角形证明精选题先做几道基础题:1、如图(1):AD ⊥BC ,垂足为D ,BD=CD 。
求证:△ABD ≌△ACD 。
2. 如图(8):A 、B 、C 、D 四点在同一直线上,AC=DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
3、如图(10)∠BAC=∠DAE ,∠ABD=∠ACE ,BD=CE 。
求证:AB=AC 。
(图1)D CB A F E (图8)DC B A E (图10)D CB A2.如图,在Rt△ABC中,∠ACB=90°,AC=BC,D 是斜边AB上的一点,AE⊥CD于E,BF⊥CD交CD 的延长线于F.求证:△ACE≌△CBF.3.如图,点E在△ABC外部,点D在BC边上,DE 交AC于点F,若∠1=∠2=∠3,AC=AE.试说明下列结论正确的理由:(1)∠C=∠E;(2)△ABC≌△ADE.4.如图:DF=CE,AD=BC,∠D=∠C.求证:△AED≌△BFC.5.如图,在△ABC中,AB=AC,D是BC的中点,连接AD,在AD的延长线上取一点E,连接BE,CE.△ABE 与△ACE全等吗?为什么?6.(2010•顺义区)已知:如图,AB=AC,点D是BC 的中点,AB平分∠DAE,AE⊥BE,垂足为E.求证:AD=AE.7.(2010•十堰)如图,△ABC中,AB=AC,BD⊥AC,CE⊥AB.求证:BD=CE.8.(2008•南宁)如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.(1)图中有几对全等的三角形请一一列出;(2)选择一对你认为全等的三角形进行证明.9.(2005•新疆)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.10.如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.求证:△ADE≌△BEC.11.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足.AE=CF,求证:∠ACB=90°.12.(2002•湛江)如图,有一池塘.要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长,就是A、B的距离.请说明DE的长就是A、B的距离的理由.13.(2010•广安)已知:如图,在矩形ABCD中,BE=CF,求证:AF=DE.14.(2005•三明)已知:如图,∠1=∠2,BD=BC.求证:∠3=∠4.15.如图,△ABC和△ADE都是等腰直角三角形,CE 与BD相交于点M,BD交AC于点N.证明:(1)BD=CE;(2)BD⊥CE.16.如图所示,△ABD,△ACE都是等边三角形,求证:CD=BE.答案与评分标准一.解答题(共16小题)1.如图,已知AB∥DE,AB=DE,AF=DC.(1)求证:△ABF≌△DEC;(2)请你找出图中还有的其他几对全等三角形.(只要直接写出结果,不要证明)考点:全等三角形的判定。
七年级数学下---全等三角形证明题精选

七年级数学下---全等三角形证明题精选9.已知:如图,PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线,•它们交于点P ,PD ⊥BM 于D ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.10、如图,已知AD 是∠BAC 的平分线, DE ⊥AB 于E , DF ⊥AC 于F , 且BE=CF , 求证: (1)AD 是△ABC 的中线;(2)AB=AC .11.在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E . (1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE =AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE =AD -BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.C BAE D 图N M ABCDEM N图AC BE D N M图A 1 2E CD B12、如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE ⊥AD 交AB 于E . 求证∠CDA =∠EDB .(作CF ⊥AB )13、在Rt △ABC 中,∠B AC =90°,CE 是角平分线,和高AD 相交于F ,作FG ∥BC 交AB 于G , 求证:AE =BG (平行四边形对边相等).14、如图,已知△ABC 是等边三角形,∠BDC =120º,说明AD=BD+CD 的理由15、如图,在△ABC 中,AD 是中线,BE 交AD 于F,且AE=EF,说明AC=BF 的理由。
C12ABCDEGF EDCB A注意:(等腰三角形两底角相等)16、如图,在△ABC 中,∠ABC=100º,AM=AN,CN=CP,求∠MNP 的度数。
七年级全等三角形的证明110道经典练习题附带答案
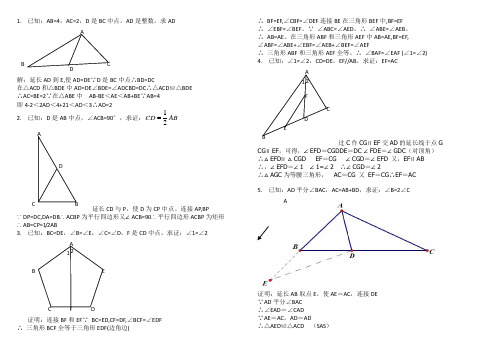
1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADCBD=DC ∴△ACD ≌△BDE ∴AC=BE=2∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4 即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP ,BP∵DP=DC,DA=DB ∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形 ∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF 连接BE 在三角形BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2) 4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC ∠FDE =∠GDC (对顶角) ∴△EFD ≌△CGD EF =CG ∠CGD =∠EFD 又,EF ∥AB ∴,∠EFD =∠1 ∠1=∠2 ∴∠CGD =∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC5. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:延长AB 取点E ,使AE =AC ,连接DE ∵AD 平分∠BAC ∴∠EAD =∠CAD ∵AE =AC ,AD =AD∴△AED ≌△ACD (SAS )A BC DEF 21 ADBCDABCBA CDF2 1 EA∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF ∴AE=AF+FE=AD+BE12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学下---全等三角形证明题精选
1、已知:如图,四边形ABCD 中,AC 平分角BAD ,CE 垂直AB 于E ,且∠B+∠D=180°,求证:AE=AD+BE
2、已知:如图,AB 、CD 交于O 点,CE//DF ,CE=DF ,AE=BF 。
求证:∠ACE=∠BDF 。
3. 已知:如图,△ABC 中,AD ⊥BC 于D ,E 是AD 上一点,BE 的延长线交AC 于F ,若BD=AD ,DE=DC 。
求证:BF ⊥AC 。
4. 已知:如图,△ABC 和△A 'B 'C '中,∠BAC=∠B 'A 'C ',∠B=∠B ',AD 、A 'D '分别是∠BAC 、∠B 'A 'C '的平分线,且AD=A 'D '。
求证:△ABC ≌△A ’B ’C ’。
5、已知:如图,AB=CD ,AD=BC ,O 是AC 中点,OE ⊥AB 于E ,OF ⊥D 于F 。
求证:OE=OF 。
6.已知:如图,AC ⊥OB ,BD ⊥OA ,AC 与BD 交于E 点,若OA=OB ,求证:AE=BE。
7.已知:如图,AB//DE ,AE//BD ,AF=DC ,EF=BC 。
求证:△AEF ≌△DBC 。
8.如图,B ,E 分别是CD 、AC 的中点,AB ⊥CD ,DE ⊥AC 求证:AC=CD (连接AD ) 9.已知:如图,PA 、PC 分别是△ABC 外角∠MAC 和∠NCA 的平分线,•它们交于点P ,PD ⊥BM 于D ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.
10、如图,已知AD 是∠BAC 的平分线, DE ⊥AB 于E , DF ⊥AC 于F , 且BE=CF , 求证:
(1)AD 是△ABC 的中线;(2)AB=AC . 11.在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .
(1)当直线MN 绕点C 旋转到图1的位置时,求证:①△ADC ≌△CEB ;②DE =AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE =AD -BE ;
(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 具有怎样的等量关系?请写出这个等量关系,并加以证明.
12、如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE ⊥AD 交AB 于E .
求证∠CDA =∠EDB .(作CF ⊥AB )
C
B
A
E D
图1
N M
A
B
C D
E
M
N
图2
A C
B
E
D N M 图3
1
2
C
D
A
B C D
E F
A 1 2 E
C D B
G
F
E
D
C
B A 13、在Rt △AB
C 中,∠B AC =90°,CE 是角平分线,和高A
D 相交于F ,作FG ∥BC 交AB 于G ,
求证:AE =BG (平行四边形对边相等).
14、如图,已知△ABC 是等边三角形,∠BDC =120o ,说明
15、如图,在△ABC 中,AD 是中线,BE 交AD 于F,且注意:(等腰三角形两底角相等)
16、如图,在△ABC 中,∠ABC=100o ,AM=AN,CN=CP,求∠17、如图,在△ABC 中,AB=BC,M,N 为BC 边上的两点,并且∠BAM=∠CAN,MN=AN,求∠MAC 的度数.
18、如图,已知∠BAC=90o,AD ⊥BC, ∠1=∠2,EF ⊥BC, FM ⊥AC,说明FM=FD 的理由。
19、如图D C B A 、、、四点在同一直线上,请你从下面四项中选出三个作为条件,其余一个作为结论,构成一个真命题,并进行证明.
①D ACE ∠=∠,②CD AB =,③ BF AE =,④ FBG EAG ∠=∠
20、已知:如图,△ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且
BE ⊥AC 于E ,与CD 相交于点F ,H 是BC 边的中点,连结DH 与BE 相交于点G 。
(1) BF =AC (2) CE =
1
2
BF 。
21、如图,△ACB 和△ECD 都是等腰直角三角形,A ,C ,D 三点在同一直线上,连结BD ,AE ,
并延长AE 交BD 于F .求证:(1)△ACE ≌△BCD (2)直线AE 与BD 互相垂直 22、如图,在四边形ABCD 中,AB=BC ,BF 是∠ABC 的平分线,AF ∥DC ,连接AC 、CF , 求证:CA 是∠DCF 的平分线。
23、已知:如图,AB ⊥BC ,AD ⊥DC ,AB=AD ,CB=CD ,若E 是AC 任意上一点。
求证:EB=ED 。
C
D。
