空间向量和立体几何练习题及答案.
高中数学-空间向量和立体几何练习试题[附答案及解析]
![高中数学-空间向量和立体几何练习试题[附答案及解析]](https://img.taocdn.com/s3/m/1a58087426d3240c844769eae009581b6bd9bd6e.png)
空间向量练习题1. 如下图,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD的中点,P A ⊥底面ABCD ,P A =2. 〔Ⅰ〕证明:平面PBE ⊥平面P AB ;〔Ⅱ〕求平面P AD 和平面PBE 所成二面角〔锐角〕的大小.如下图,以A 为原点,建立空间直角坐标系.那么相关各点的 坐标分别是A 〔0,0,0〕,B 〔1,0,0〕,33(2C 13(2D P 〔0,0,2〕,3E 〔Ⅰ〕证明 因为3BE =, 平面P AB 的一个法向量是0(0,1,0)n =, 所以0BE n 和共线.从而BE ⊥平面P AB . 又因为BE ⊂平面PBE , 故平面PBE ⊥平面P AB .(Ⅱ)解 易知3(1,0,2),(0,02PB BE =-=), 13(0,0,2),(,22PA AD =-= 设1111(,,)n x y z =是平面PBE 的一个法向量,那么由110,n PB n BE ⎧=⎪⎨=⎪⎩得111122020,3000.2x y z x y z +⨯-=⎧⎪⎨⨯++⨯=⎪⎩所以11110,2.(2,0,1).y x z n ===故可取 设2222(,,)n x y z =是平面PAD 的一个法向量,那么由220,0n PA n AD ⎧=⎪⎨=⎪⎩得2222220020,1300.22x y z x y z ⨯+⨯-=⎧⎪⎨++⨯=⎪⎩所以2220,3.z x ==-故可取2(3,1,0).n =-于是,1212122315cos ,52n n n n n n <>===⨯故平面PAD 和平面PBE 所成二面角〔锐角〕的大小是152. 如图,正三棱柱ABC -A 1B 1C 1的所有 棱长都为2,D 为CC 1中点。
〔Ⅰ〕求证:AB 1⊥面A 1BD ;〔Ⅱ〕求二面角A -A 1D -B 的大小; 〔Ⅲ〕求点C 到平面A 1BD 的距离;〔Ⅰ〕证明 取BC 中点O ,连结AO . ABC △为正三角形,AO BC ∴⊥.在正三棱柱111ABC A B C -中,平面ABC ⊥平面11BCC B ,AD ∴⊥平面11BCC B .取11B C 中点1O ,以O 为原点,OB ,1OO ,OA 的方向为x y z ,,轴的正方向建立空间直角坐标系,那么(100)B ,,,(110)D -,,,1(023)A ,,,(003)A ,,,1(120)B ,,, 1(123)AB ∴=-,,,(210)BD =-,,,1(123)BA =-,,.12200AB BD =-++=,111430AB BA =-+-=, 1AB BD ∴⊥,11AB BA ⊥.1AB ∴⊥平面1A BD .〔Ⅱ〕解 设平面1A AD 的法向量为()x y z =,,n .(113)AD =--,,,1(020)AA =,,.AD ⊥n ,1AA ⊥n ,100AD AA ⎧=⎪∴⎨=⎪⎩,,n n 3020x y z y ⎧-+-=⎪∴⎨=⎪⎩,,03y x z =⎧⎪∴⎨=-⎪⎩,.令1z =得(301)=-,,n 为平面1A AD 的一个法向量. 由〔Ⅰ〕知1AB ⊥平面1A BD ,1AB ∴为平面1A BD 的法向量.cos <n ,1113364222AB AB AB -->===-n n .∴二面角1A A D B --的大小为6arccos4. xzAB CD1A1C1BO F y〔Ⅲ〕解 由〔Ⅱ〕,1AB 为平面1A BD 法向量,1(200)(12BC AB =-=,,,,.∴点C 到平面1A BD的距离1122BC AB d AB -===. 3.如图,在四面体ABCD 中,O 、E 分别是BD 、BC 的中点,2,CA CB CD BD AB AD ======〔1〕求证:AO ⊥平面BCD ;〔2〕求异面直线AB 与CD 所成角的余弦值; 〔3〕求点E 到平面ACD 的距离.⑴ 证明 连结OC,,.BO DO AB AD AO BD ==∴⊥ ,BO DO BC CD ==,CO BD ⊥.在AOC ∆中,由可得1,AO CO == 而2AC =, 222,AO CO AC ∴+=90,o AOC ∴∠=即.AO OC ⊥,BD OC O = ∴AO ⊥平面BCD .(2)解 以O为原点,如图建立空间直角坐标系, 那么(1,0,0),(1,0,0),B D -1(0,0,1),((1,0,1),(1,2C A E BA CD =-=-2cos ,4BA CD BA CD BA CD⋅∴<>==⋅ ∴ 异面直线AB 与CD 所成角的余弦值为4. ⑶解 设平面ACD 的法向量为(,,),n x y z =那么(,,)(1,0,1)0(,,)(0,3,1)0n AD x y z n AC x y z ⎧⋅=⋅--=⎪⎨⋅=⋅-=⎪⎩, ∴030x z y z +=⎧⎪⎨-=⎪⎩,令1,y =得(3,1,3)n =-是平面ACD 的一个法向量. 又13(,,0),22EC =- ∴点E 到平面ACD 的距离 32177EC n h n⋅===. 4.三棱锥P -ABC 中,PA ⊥ABC ,AB ⊥AC ,PA=AC=½AB ,N 为AB 上一点,AB=4AN,M,S分别为PB,BC 的中点.〔Ⅰ〕证明:CM ⊥SN ;〔Ⅱ〕求SN 与平面CMN 所成角的大小.证明:设PA=1,以A 为原点,射线AB ,AC ,AP 分别为x ,y ,z 轴正向建立空间直角坐标系如图。
空间向量和立体几何练习题及答案

1如图,在四棱锥P- ABCD中,底面ABCD为正方形,平面PAD丄平面ABCD ,点 M 在线段 PB 上 , PD // 平面 MAC , PA = PD = 7 , AB= 4 .(1)求证:M为PB的中点;(2)求二面角B - PD - A的大小;(3)求直线MC与平面BDP所成角的正弦值.【分析】(1)设AC n BD=O,则0为BD的中点,连接OM,利用线面平行的性质证明OM // PD,再由平行线截线段成比例可得 M为PB的中点;(2)取AD中点G,可得PG丄AD,再由面面垂直的性质可得 PG丄平面ABCD,则PG丄AD,连接OG,贝U PG丄OG,再证明OG丄AD .以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系,求出平面 PBD 与平面PAD的一个法向量,由两法向量所成角的大小可得二面角 B- PD - A的大小;(3)求出P的坐标,由与平面PBD的法向量所成角的余弦值的绝对值可得直线MC与平面BDP所成角的正弦值.【解答】(1)证明:如图,设ACn BD=O ,••• ABCD为正方形,二O为BD的中点,连接 OM ,••• PD//平面 MAC, PD?平面 PBD,平面 PBDn 平面 AMC=OM ,••• PD// OM,则丄-二,即卩M为PB的中点;BD BP(2)解:取AD中点G,••• PA=PD,二 PG 丄 AD , •••平面PAD 丄平面ABCD ,且平面 PAD G 平面 ABCD=AD , ••• PG 丄平面ABCD ,贝U PG 丄AD ,连接OG ,贝U PG 丄OG , 由G 是AD 的中点,O 是AC 的中点,可得 OG // DC,贝U OG 丄AD .以G 为坐标原点,分别以GD 、GO 、GP 所在直线为x 、y 、z 轴距离空间直角坐 标系, 由 PA=PD=V^,AB=4,得 D( 2, 0,0),A (- 2, 0, 0),P (0,0,讥),C (2, 4, 0) , B (- 2, 4, 0), M (- 1, 2,平),设平面PBD 的一个法向量为|— ■-. ■,-. ■,取平面PAD 的一个法向量为::,L II : •二面角B- PD - A 的大小为60 ° ; (3)解—:=,平面BDP 的一个法向量为,,1. 1.-•直线 MC 与平面 BDP 所成角的正弦值为| cos < r i' > =| 」.|=| - |=:Imllml @+4+护1 9【点评】本题考查线面角与面面角的求法,训练了利用空间向量求空间角,属中 档题.2.如图,在三棱锥 P- ABC 中,PA 丄底面ABC, / BAC=90° .点D , E, N 分 别为棱PA,m*DP=0则由,二工f ,得」L ID*DB=O7:y0,取 z=^,得&(i.--cos < 二:!>PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2 .(I)求证:MN //平面BDE ;(U)求二面角C- EM - N的正弦值;(川)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为二,求-W-丄线段AH的长.【分析】(I)取AB中点F,连接MF、NF,由已知可证 MF //平面BDE,NF//平面BDE .得至U平面 MFN //平面BDE,贝U MN //平面BDE ;(U)由PA丄底面ABC,/ BAC=90°.可以A为原点,分别以 AB、AC、AP 所在直线为x、y、z轴建立空间直角坐标系.求出平面 MEN与平面CME的一个法向量,由两法向量所成角的余弦值得二面角c-EM-N的余弦值,进一步求得正弦值;(川)设AH=t,则H (0, 0, t),求出而、瓦的坐标,结合直线NH与直线 BE所成角的余弦值为」列式求得线段AH的长.21【解答】(I)证明:取AB中点F,连接MF、NF,••• M 为 AD 中点,二 MF // BD,••• BD?平面 BDE,MF?平面 BDE,二 MF // 平面 BDE .••• N 为 BC 中点,二 NF // AC,又 D、E 分别为 AP、PC 的中点,二 DE // AC,贝U NF // DE .v DE?平面 BDE , NF?平面 BDE,二 NF // 平面 BDE .又 MF A NF=F .•••平面 MFN //平面BDE,贝U MN //平面BDE ;(U)解:v PA丄底面ABC, / BAC=90°.•••以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.v PA=AC=4, AB=2,• A (0, 0, 0), B (2, 0, 0), C (0, 4, 0) , M (0, 0, 1) , N (1, 2, 0), E(0, 2, 2),则叮…..一,「...一,设平面MEN的一个法向量为.1 「,Q •袖二0 Z0f x+2y-z=0 左•远d得I沁二0取 z=2,得-b :.由图可得平面CME的一个法向量为:.Im [ | n | XI 21•••二面角C- EM - N 的余弦值为] ,则正弦值为;21 21(川)解:设 AH=t ,则 H (0, 0, t ),而二(七 -2, t ),祝二(七厶 2). •••直线NH 与直线BE 所成角的余弦值为」,21 | = | | ='.|NH||BE| 晶 I 迈 21 '解得:t=或t=±.52•••当H 与P 重合时直线NH 与直线BE 所成角的余弦值为」,此时线段AH 的21【点评】本题考查直线与平面平行的判定, 考查了利用空间向量求解空间角, 考 查计算能力,是中档题.3.如图,几何体是圆柱的一部分,它是由矩形 ABCD (及其内部)以AB 边所 在直线为旋转轴旋转120 °得到的,G 是-的中点.(I )设P 是卜上的一点,且 AP 丄BE ,求/ CBP 的大小; (U )当AB=3 , AD=2时,求二面角E - AG - C 的大小.D••• coy=:二 2t-2•••1 cosv 忙],1 =| 长为一或].【分析】(I)由已知利用线面垂直的判定可得 BE丄平面ABP,得到BE丄BP, 结合/EBC=120。
高中数学选修2-1 第三章《空间向量与立体几何》单元测试题(含答案)

这时Q ⎝ ⎛⎭⎪⎫43,43,83.答案:C二、填空题:本大题共4小题,每小题5分,共20分.13.若A (x,5-x,2x -1),B (1,x +2,2-x ),则当|AB →|取最小值时,x 的值等于________.解析:AB →=(1-x,2x -3,-3x +3),则 |AB →|=1-x2+2x -32+-3x +32=14x 2-32x +19=14⎝⎛⎭⎪⎫x -872+57,故当x =87时,|AB →|取最小值.答案:8714.正方体ABCD -A 1B 1C 1D 1中,直线BC 1与平面A 1BD 夹角的正弦值是________. 解析:如图,以DA 、DC 、DD 1分别为x 轴、y 轴、z 轴建立空间直角坐标系,设正方体的棱长为1,则A (1,0,0),B (1,1,0),C 1(0,1,1), 易证AC 1→是平面A 1BD 的一个法向量.AC 1→=(-1,1,1),BC 1→=(-1,0,1). cos 〈AC 1→,BC 1→〉=1+13×2=63. 所以BC 1与平面A 1BD 夹角的正弦值为63.答案:63设AC ∩BD =N ,连结NE ,则N ⎝ ⎛⎭⎪⎫22,22,0,E (0,0,1), ∴NE →=⎝ ⎛⎭⎪⎫-22,-22,1. 又A (2,2,0),M ⎝ ⎛⎭⎪⎫22,22,1, ∴AM →=⎝ ⎛⎭⎪⎫-22,-22,1. ∴NE →=AM →,且NE 与AM 不共线.∴NE ∥AM .又NE ⊂平面BED ,AM ⊄平面BDE ,∴AM ∥平面BDE .(2)设P (t ,t,0)(0≤t ≤2),则PF →=(2-t ,2-t,1),CD →=(2,0,0).又∵PF →与CD →所成的角为60°,|2-t ·2|2-t2+2-t 2+1·2=12, 解之得t =22,或t =322(舍去). 故点P 为AC 的中点.22.(本小题满分12分)如图,在圆锥PO 中,已知PO =2,⊙O 的直径AB =2,C 是AB 的中点,D 为AC 的中点.。
高二数学选修2-1第三章 空间向量与立体几何练习题及答案

第三章 空间向量与立体几何空间向量的数乘运算 测试题姓名:_________班级:________ 得分:_______ 1. 下列命题中不正确的命题个数是( )①若A 、B 、C 、D 是空间任意四点,则有AB +BC + CD +DA =0;②对空间任意点O 与不共线的三点A 、B 、C ,若OP =x OA +y OB +z OC (其中x 、y 、z ∈R ),则P 、A 、B 、C 四点共面;③若a 、b 共线,则a 与b 所在直线平行。
A .1B .2C .3D .42.设OABC 是四面体,G 1是△ABC 的重心,G 是OG 1上一点,且OG =3GG 1,若OG =x OA +y OB +z OC ,则(x ,y ,z )为( )A .(41,41,41) B .(43,43,43) C .(31,31,31) D .(32,32,32) 3.在平行六面体ABCD -EFGH 中,AG xAC y AF z AH =++,________.x y z ++=则4.已知四边形ABCD 中,AB =a -2c ,CD =5a +6b -8c ,对角线AC 、BD 的中点分别为E 、F ,则EF =_____________.5.已知矩形ABCD ,P 为平面ABCD 外一点,且P A ⊥平面ABCD ,M 、N 分别为PC 、PD 上的点,且M 分PC 成定比2,N 分PD 成定比1,求满足MN xAB y AD z AP =++的实数x 、y 、z 的值.§3.1.3空间向量的数量积运算1.已知正四棱柱1111ABCD A B C D -中,1AA =2AB ,E 为1AA 重点,则异面直线BE 与1CD 所形成角的余弦值为( ) A .1010 B . 15 C .31010 D . 352.如图,设A ,B ,C ,D 是空间不共面的四点,且满足0AB AC ⋅=,0AC AD ⋅=,0AB AD ⋅=,则△BCD 的形状是( )A .钝角三角形B .锐角三角形C .直角三角形D .不确定的_ C _ D _ A _ P_ N _ B_ M3.已知ABCD -A 1B 1C 1D 1 为正方体,则下列命题中错误的命题为__________.;221111111①(A A+A D +A B )=3(A B )()0;C ⋅-=1111②A A B A A 60;︒11向量与向量的夹角为AD A B ③ ⋅⋅11111立方体ABCD-A B C D 的体积为|AB AA AD |;④4.如图,已知:平行六面体ABCD -A 1B 1C 1D 1的底面ABCD 是菱形,且∠C 1CB =∠C 1CD =∠BCD =60° (1)证明:C 1C ⊥BD ; (2)当1CDCC 的值为多少时,能使A 1C ⊥平面C 1BD ?请给出证明. §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1.已知向量(2,2,3)OA =-,(,1,4)OB x y z =-,且平行四边形OACB 的对角线的中点坐标为M 31(0,,)22-,则(,,)x y z =( ) A .(2,4,1)--- B .(2,4,1)-- C .(2,4,1)-- D .(2,4,1)--2.已知(2,2,4)a =-,(1,1,2)b =-,(6,6,12)c =--,则向量、、a b c ( ) A .可构成直角三角形 B .可构成锐角三角形 C .可构成钝角三角形 D .不能构成三角形3.若两点的坐标是A (3cosα,3sinα,1),B (2cosθ,2sinθ,1),则|AB |的取值范围是( )A .[0,5]B .[1,5]C .(1,5)D .[1,25] 4.设点C (2a +1,a +1,2)在点P (2,0,0)、A (1,-3,2)、B (8,-1,4)确定的平面上,则a 的值为 . 5.如图,正三棱柱ABC -A 1B 1C 1的底边长为a ,侧棱长为2a .建立适当的坐标系,⑴写出A ,B ,A 1,B 1的坐标;⑵求AC 1与侧面ABB 1A 1所成的角.3.2立体几何中的向量方法1.到一定点(1,0,1)的距离小于或等于2的点的集合为( ) A .222{(,,)|(1)(1)4}x y z x y z -++-≤ B .222{(,,)|(1)(1)4}x y z x y z -++-= C .222{(,,)|(1)(1)2}x y z x y z -++-≤ D .222{(,,)|(1)(1)2}x y z x y z -++-=C 1 B 1 A 1B A2. 正方体ABCD —A 1B 1C 1D 1中,直线BC 1与平面A 1BD 所成角的余弦值为( ) A .42 B .32 C .33 D .23 3. 已知斜三棱柱111ABC A B C -,90BCA ∠=,2AC BC ==,1A 在底面ABC 上的射影恰为AC 的中点D ,又知11BA AC ⊥.(1)求证:1AC ⊥平面1A BC ; (2)求1C 到平面1A AB 的距离; (3)求二面角1A A B C --余弦值的大小.B 4. 如图,在直三棱柱111ABC A B C -中, AB =1,13AC AA ==,∠ABC =60°. (1)证明:1AB A C ⊥;(2)求二面角A —1A C —B 的大小.5. 如右图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱S D 上的点. (1)求证:AC ⊥SD ;(2)若SD ⊥平面P AC ,求二面角P-AC-D 的大小 (3)在(2)的条件下,侧棱S C 上是否存在一点E , 使得BE ∥平面P AC .若存在,求S E :EC 的值; 若不存在,试说明理由.参考答案第三章 空间向量与立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算§3.1.2空间向量的数乘运算1.A2.A3.324.3a +3b -5c5.如图所示,取PC 的中点E ,连结NE ,则MN EN EM =-.∵1122EN CD BA ===12AB -,CBA C 1B 1 A1 D 1C 1B 1A 1DABC_ C_ D_ A_S_ F_ B_ P_ N_ EEN PM PE =-=211326PC PC PC -=,连结AC ,则PC AC AP AB AD AP =-=+- ∴11()26MN AB AB AD AP =--+-=211366AB AD AP --+,∴211,,366x y z =-=-=.§3.1.3空间向量的数量积运算1.C2.B3. ③④4.(1)设1,,CB a CD b CC c === ,则||||a b =,BD CD CB b a =-=- ,所以1()||||cos 60||||cos 600CC b a c b c a c b c a c ⋅=-⋅=⋅-⋅=︒-︒=BD ,11BD CC BD CC ∴⊥⊥即 ;(2)1,2,CD x CD CC ==1设则 2CC =x, 111,BD AA C C BD A C ⊥∴⊥ 面 ,11:0x AC CD ∴⋅= 只须求满足, 设1,,A A a AD b DC c ===,11,A C a b c C D a c =++=-,2211242()()6A C C D a b c a c a a b b c c xx ∴⋅=++⋅-=+⋅-⋅-=+-, 令24260x x+-=,则2320x x --=,解得1x =,或23x =-(舍去),111,.A C C BD ∴=⊥1CD时能使平面CC §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1.A2.D3.B4.165. (1)建系如图,则A (0,0,0) B (0,a ,0)A 1(0,0,2a ),C 1(-23a ,a 2,2a) (2)解法一:在所建的坐标系中,取A 1B 1的中点M , 于是M (0,a 2,2a),连结AM ,MC 1 则有1(,0,0)2MC =-(0,,0)AB a=,1)AA =, ∴10MC AB ⋅=,110MC AA ⋅=,所以,MC 1⊥平面ABB 1A 1.因此,AC 1与AM 所成的角就是AC 1与侧面ABB 1A 1所成的角.1(,)2a AC =-,(0,)2aAM =,A∴2194a AC AM ⋅=,而|13||3,||2AC a AM a ==,由cos<1,AC AM >=1132||||AC AM AC AM ⋅=,∴ <1,AC AM >=30°.∴AC 1与侧面ABB 1A 1所成的角为30°.3.2立体几何中的向量方法1.A2.C3.(1)如右图,取AB 的中点E ,则//DE BC ,因为BC AC ⊥, 所以DE AC ⊥,又1A D ⊥平面ABC , 以1,,DE DC DA 为,,x y z 轴建立空间坐标系, 则()0,1,0A -,()0,1,0C ,()2,1,0B ,()10,0,A t ,()10,2,C t ,()10,3,AC t =,()12,1,BA t =--,()2,0,0CB =,由10AC CB ⋅=,知1A C CB ⊥, 又11BA AC ⊥,从而1AC ⊥平面1A BC .(2)由1AC ⋅2130BA t =-+=,得3t = 设平面1A AB 的法向量为(),,n x y z =,(13AA =,()2,2,0AB =,所以130220n AA y z n AB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩,设1z =,则()3,3,1n =-, 所以点1C 到平面1A AB 的距离1AC n d n⋅==221. (3)再设平面1A BC 的法向量为(),,m x y z =,(10,3CA =-,()2,0,0CB =, 所以13020m CA y z m CB x ⎧⋅=-+=⎪⎨⋅==⎪⎩,设1z =,则()0,3,1m =, 故cos ,m n m n m n⋅<>==⋅77-,根据法向量的方向, 可知二面角1A A B C --7. 4.(1)三棱柱111ABC A B C -为直三棱柱,11AB AA AC AA ∴⊥⊥,,Rt ABC ∆,1,3,60AB AC ABC ==∠=︒,由正弦定理030ACB ∠=.090BAC ∴∠=AB AC ⊥即 .如右图,建立空间直角坐标系,则 1(0,0,0),(1,0,0)(0,3,0),(0,0,3)A B C A1(1,0,0),(0,3,3)AB AC ∴==, 110030(3)0AB AC ⋅=⨯+⨯+⨯-=, 1AB A C ∴⊥.(2) 如图可取(1,0,0)m AB ==为平面1AA C 的法向量, 设平面1A BC 的法向量为(,,)n l m n =, 则10,0,130BC n AC n BC ⋅=⋅==-又(,,), 303,330l m l m n m m n ⎧-+=⎪∴∴==⎨-=⎪⎩. 不妨取1,(3,1,1)m n ==则,22222231101015cos ,5(3)11100m n m n m n ⋅⨯+⨯+⨯<>===⋅++⋅++.1A AC BD ∴--15二面角的大小为arccos 5. 5. (1)连结BD ,设AC 交于BD 于O ,由题意知SO ABCD ⊥平面.以O 为坐标原点,OB OC OS ,,分别为x 轴、y 轴、z 轴正方向,建立坐标系O xyz -如右图.设底面边长为a ,则高62SO a =.于是 62(0,0,),(,0,0)22S a D a -,2(0,,0)2C a ,2(0,,0)2OC a =,26(,0,)2SD a =-,0OC SD ⋅= ,故OC SD ⊥.从而 AC SD ⊥. _ C_ A_S_ F_ BO(2)由题设知,平面PAC 的一个法向量(,0,)22DS a a =,平面DAC 的一个法向量002OS =(,,),设所求二面角为θ,则cos 2OS DS OS DSθ⋅==,得所求二面角的大小为30°. (3)在棱SC 上存在一点E 使//BE PAC 平面.由(2)知DS 是平面PAC 的一个法向量,且,0,),(0,,)2222DS a a CS a a ==-(.设,CE tCS = 则(,(1),)222BE BC CE BC tCS a t at =+=+=--,而 103BE DC t ⋅=⇔=.即当:2:1SE EC =时,BE DS ⊥.而BE 不在平面PAC 内,故//BE PAC 平面.(完)。
高中数学空间向量与立体几何练习题附答案
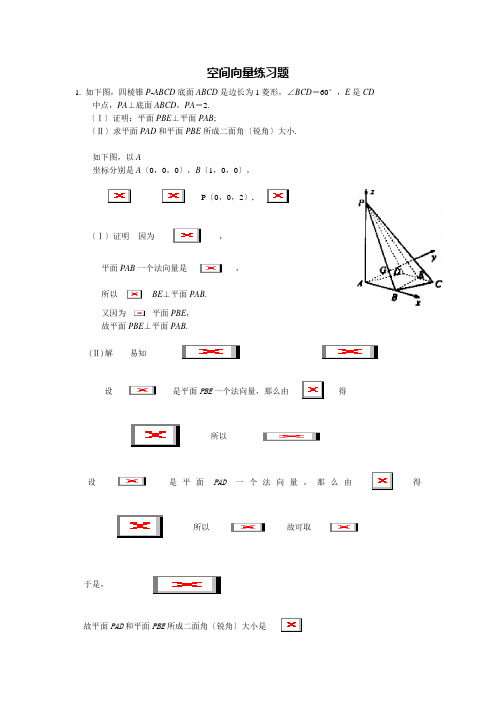
空间向量练习题1. 如下图,四棱锥P-ABCD底面ABCD是边长为1菱形,∠BCD=60°,E是CD中点,PA⊥底面ABCD,PA=2.〔Ⅰ〕证明:平面PBE⊥平面PAB;〔Ⅱ〕求平面PAD和平面PBE所成二面角〔锐角〕大小.如下图,以A坐标分别是A〔0,0,0〕,B〔1,0,0〕,P〔0,0,2〕,〔Ⅰ〕证明因为,平面PAB一个法向量是,所以BE⊥平面PAB.又因为平面PBE,故平面PBE⊥平面PAB.(Ⅱ)解易知设是平面PBE一个法向量,那么由得所以设是平面PAD一个法向量,那么由得所以故可取于是,故平面PAD和平面PBE所成二面角〔锐角〕大小是2. 如图,正三棱柱ABC-A1B1C1全部棱长都为2,D为CC1中点。
〔Ⅰ〕求证:AB1⊥面A1BD;〔Ⅱ〕求二面角A-A1D-B大小;〔Ⅲ〕求点C到平面A1BD间隔;〔Ⅰ〕证明取中点,连结.为正三角形,.在正三棱柱中,平面平面,平面.取中点,以为原点,,,方向为轴正方向建立空间直角坐标系,那么,,,,,,,.,,,.平面.〔Ⅱ〕解设平面法向量为.,.,,令得为平面一个法向量.由〔Ⅰ〕知平面,为平面法向量.,.二面角大小为.xzABCDOFy〔Ⅲ〕解由〔Ⅱ〕,为平面法向量,.点到平面间隔.3.如图,在四面体ABCD中,O、E分别是BD、BC中点,〔1〕求证:平面BCD;〔2〕求异面直线AB与CD所成角余弦值;〔3〕求点E到平面ACD间隔.⑴证明连结OC,.在中,由可得而,即∴平面.(2)解以O为原点,如图建立空间直角坐标系,那么,∴异面直线AB与CD 所成角余弦值为.⑶解设平面ACD 法向量为那么ACDOBEzxACDOBEzx,∴,令得是平面ACD一个法向量.又∴点E到平面ACD间隔.4.三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC中点.〔Ⅰ〕证明:CM⊥SN;〔Ⅱ〕求SN与平面CMN所成角大小.证明:设PA=1,以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图。
空间向量与立体几何测试题及答案

空间向量与立体几何测试题及答案(总10页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--高中 数学选修(2-1)空间向量与立体几何测试题一、选择题1.若把空间平行于同一平面且长度相等的所有非零向量的始点放置在同一点,则这些向量的终点构成的图形是( ) A.一个圆 B.一个点 C.半圆 D.平行四边形 答案:A2.在长方体1111ABCD A B C D -中,下列关于1AC 的表达中错误的一个是( ) A.11111AA A B A D ++ B.111AB DD D C ++ C.111AD CC D C ++D.11111()2AB CD AC ++答案:B3.若,,a b c 为任意向量,∈R m ,下列等式不一定成立的是( ) A.()()a b c a b c ++=++ B.()a b c a c b c +=+··· C.()a b a b +=+m m m D.()()a b c a b c =···· 答案:D4.若三点,,A B C 共线,P 为空间任意一点,且PA PB PC αβ+=,则αβ-的值为( ) A.1 B.1- C.12D.2-答案:B5.设(43)(32)a b ==,,,,,x z ,且∥a b ,则xz 等于( ) A.4-B.9C.9-D.649答案:B6.已知非零向量12e e ,不共线,如果1222122833e e e e e e =+=+=-,,AB AC AD ,则四点,,,A B C D ( )A.一定共圆B.恰是空间四边形的四个顶点心 C.一定共面 D.肯定不共面 答案:C7.如图1,空间四边形ABCD 的四条边及对 角线长都是a ,点E F G ,,分别是AB AD CD ,, 的中点,则2a 等于( )A.2BA AC · B.2AD BD ·C.2FGCA ·D.2EFCB · 答案:B8.若123123123=++=-+=+-,,a e e e b e e e c e e e ,12323d e e e =++,且x y z =++d a b c ,则,,x y z 的值分别为( )A.51122--,, B.51122-,,C.51122--,,D.51122,,答案:A9.若向量(12)λ=,,a 与(212)=-,,b 的夹角的余弦值为89,则λ=( ) A.2B.2- C.2-或255D.2或255-答案:C10.已知ABCD 为平行四边形,且(413)(251)(375)A B C --,,,,,,,,,则顶点D 的坐标为( )A.7412⎛⎫- ⎪⎝⎭,,B.(241),, C.(2141)-,,D.(5133)-,,答案:D11.在正方体1111ABCD A B C D -中,O 为AC BD ,的交点,则1C O 与1A D 所成角的( )A.60°B.90° C.D. 答案:D12.给出下列命题:①已知⊥a b ,则()()a b c c b a b c ++-=···;②,,,A B M N 为空间四点,若BABM BN ,,不构成空间的一个基底,那么A B M N ,,,共面;③已知⊥a b ,则,a b 与任何向量都不构成空间的一个基底; ④若,a b 共线,则,a b 所在直线或者平行或者重合. 正确的结论的个数为( ) A.1 B.2 C.3 D.4答案:C二、填空题13.已知(315)(123)==-,,,,,a b ,向量c 与z 轴垂直,且满足94==-,··c a c b ,则c = .答案:2221055⎛⎫- ⎪⎝⎭,,14.已知,,A B C 三点不共线,O 为平面ABC 外一点,若由向量1253OP OA OB OC λ=++确定的点P 与AB C ,,共面,那么λ= . 答案:21515.已知线段AB ⊥面α,BC α⊂,CD BC ⊥,DF ⊥面α于点F ,30DCF ∠=°,且D A ,在平面α的同侧,若2AB BC CD ===,则AD 的长为 .答案:16.在长方体1111ABCD A B C D -中,1B C 和1C D 与底面所成的角分别为60°和45°,则异面直线1B C 和1C D 所成角的余弦值为 . 答案:6三、解答题17.设123423223325=-+=+-=-+-=++,,,a i j k a i j k a i j k a i j k ,试问是否存在实数λμν,,,使4123a a a a λμν=++成立?如果存在,求出λμν,,;如果不存在,请写出证明.答案:解:假设4123a a a a λμν=++成立.1234(211)(132)(213)(325)a a a a =-=-=--=,,,,,,,,,,,∵, (22323)(325)λμνλμνλμν+--++--=,,,,∴. 22332235λμνλμνλμν+-=⎧⎪-++=⎨⎪--=⎩,,,∴解得213λμν=-⎧⎪=⎨⎪=-⎩,,. 所以存在213v λμ=-==-,,使得412323a a a a =-+-. 理由即为解答过程.18.如图2,正三棱柱111-ABC A B C 的底面边长为a ,侧棱长为2a ,求1AC 与侧面11ABB A 所成的角.解:建立如图所示的空间直角坐标系,则113(000)(00)(002)22⎛⎫-⎪ ⎪⎝⎭,,,,,,,,,,,aA B a A a C a a . 由于(100)=-,,n 是面11ABB A 的法向量,1111312cos 6023aAC AC AC a AC ===⇒=,,·°n n n n.故1AC 与侧面11ABB A 所成的角为30°.19.如图3,直三棱柱111ABC A B C -中,底面是等腰直角三角形,90ACB ∠=°,侧棱12AA D E =,,分别是1CC 与1A B 的中点,点E 在平面ABD 上的射影是ABD △的重心G ,求点1A 到平面AED 的距离. 解:建立如图所示的空间直角坐标系,设2CA a =, 则1221(200)(020)(001)(202)(1)333a a A a B a D A a E a a G ⎛⎫⎪⎝⎭,,,,,,,,,,,,,,,,,.从而2(021)333a a GE BD a ⎛⎫==- ⎪⎝⎭,,,,,. 由0GE BD GEBD ⊥⇒=·,得1a =, 则1(202)(200)(111)A A E ,,,,,,,,.自1A 作1A H ⊥面AED 于M ,并延长交xOy 面于H ,设(0)H x y ,,,则1(22)A H x y =--,,. 又(201)AD =-,,,(111)AE =-,,. 由112(2)20(2)20A H AD x A H AE x y ⊥---=⎧⎧⇒⎨⎨⊥--+-=⎩⎩,,11x y =⎧⇒⎨=⎩,,得(110)H ,,.又1111cos A M A A A A A M =,·11126cos 226A AA A A H ==⨯=,·.20.已知正方体1111ABCD A B C D -的棱长为2,P Q ,分别是BC CD ,上的动点,且2PQ =,确定P Q ,的位置,使11QB PD ⊥.解:建立如图所示的空间直角坐标系,设BP t =, 得22(2)CQ t =--,222(2)DQ t =---.那么211(202)(022)(20)(22(2)20)B D P t Q t ---,,,,,,,,,,,,从而21(2(2)22)QB t =---,,,1(222)PD t =--,,, 由11110QB PD QB PD ⊥⇒=·, 即222(2)2(2)401t t t -----+=⇒=. 故P Q ,分别为BC CD ,的中点时,11QB PD ⊥.21.如图4,在底面是直角梯形的四棱锥S ABCD -中,90ABC ∠=°,SA ⊥面ABCD ,112SA AB BC AD ====,,求面SCD 与面SBA 所成二面角的正切值.解:建立如图所示的空间直角坐标系,则1(000)(100)(110)00(001)2A B C D S ⎛⎫-- ⎪⎝⎭,,,,,,,,,,,,,,.延长CD 交x 轴于点F ,易得(100)F ,,,作AE SF ⊥于点E ,连结DE ,则DEA ∠即为面SCD 与面SBA 所成二面角的平面角.又由于SA AF =且SA AF ⊥,得11022E ⎛⎫⎪⎝⎭,,, 那么102EA ⎛⎫=-- ⎪⎝⎭,,12,111222ED ⎛⎫=-- ⎪⎝⎭,,, 从而6cos EA ED EA ED EA ED ==,·, 因此2tan EAF ED =,. 故面SCD 与面SBA 所成二面角的正切值为2.22.平行六面体1111ABCD A B C D -的底面ABCD 是菱形,且11C CB C CD BCD ∠=∠=∠,试问:当1CDCC 的值为多少时,1A C ⊥面1C BD 请予以证明.解:欲使1A C ⊥面1C BD ,只须11AC C D ⊥,且11AC C B ⊥. 欲证11AC C D ⊥,只须证110CA C D =·, 即11()()0CA AA CD CC +-=·,也就是11()()0CD CB CC CD CC ++-=·, 即22111cos cos 0CD CC CB CD BCD CB CC C CB -+∠-∠=. 由于1C CB BCD ∠=∠,显然,当1CD CC =时,上式成立; 同理可得,当1CD CC =时,11AC C B ⊥. 因此,当11CDCC =时,1A C ⊥面1C BD .一.选择题:(10小题共40分)1.已知A 、B 、C 三点不共线,对平面ABC 外的任一点O,下列条件中能确定点M与点A 、B 、C 一定共面的是 ( ) A.OC OB OA OM ++=B.OC OB OA OM --=2C.3121++=D.313131++=2.直三棱柱ABC —A 1B 1C 1中,若====B A C CC b CB a CA 11,,,则 ( )A.-+B.+-C.++-D.-+-3.若向量λμλμλ且向量和垂直向量R ∈+=,(,、则)0≠μ ( )A.n m //B.n m ⊥C.也不垂直于不平行于,D.以上三种情况都可能4.以下四个命题中,正确的是( ) A.若OB OA OP 3121+=,则P 、A、B三点共线 B.设向量},,{是空间一个基底,则{+,+,+}构成空间的另一个基底C.b a ⋅⋅=⋅(D.△ABC 是直角三角形的充要条件是0=⋅ 5.对空间任意两个向量//),(,≠的充要条件是( )A.=B.-=C.λ=D.λ= 6.已知向量与则),2,1,1(),1,2,0(--==的夹角为 ( )° °°°7.在平行六面体1111D C B A ABCD -中,M 为AC 与BD 的交点,若A D AB A ===11111,,,则下列向量中与B 1相等的是 ( )A.212121++-B.212121++C.+-2121 +-21218.已知的值分别为与则若μλμλλ,//),2,12,6(),2,0,1(b a b a -=+= ( )A.21,51 ,2C.21,51--,-29.已知与则35,2,23+-=-+= ( )10.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是( )A.52-B.52 C.53 D.1010 二.填空题: (4小题共16分)11.若A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线,则m+n= . 12.已知A (0,2,3),B (-2,1,6),C (1,-1,5),若则向量且,,,3||⊥⊥= 的坐标为 .13.已知b a ,是空间二向量,若b ab ab a 与则,7||,2||,3||=-==的夹角为 .14.已知点G 是△ABC 的重心,O 是空间任一点,若的值则λλ,OG OC OB OA =++为 . 三.解答题:(10+8+12+14=44分)15.如图:ABCD 为矩形,PA ⊥平面ABCD ,PA=AD ,M 、N 分别是PC 、AB 中点, (1)求证:MN ⊥平面PCD ;(2)求NM 与平面ABCD 所成的角的大小.16.一条线段夹在一个直二面角的两个面内,它和两个面所成的角都是300,求这条线段与这个二面角的棱所成的角的大小.17.正四棱锥S —ABCD 中,所有棱长都是2,P 为SA 的中点,如图. (1)求二面角B —SC —D 的大小;(2)求DP 与SC 所成的角的大小.18.如图,直三棱柱ABC —A 1B 1C 1,底面△ABC 中,CA=CB=1,∠BCA=90°,棱AA 1=2,M 、N 分别是A 1B 1,A 1A 的中点;(1)求;的长BN(2)求;,cos 11的值><CB BA (3).:11M C B A ⊥求证(4)求CB 1与平面A 1ABB 1所成的角的余弦值.高中数学选修2-1测试题(10)—空间向量(1)参考答案DDBB DCDA AB 12.(1,1,1)15.(1)略 (2)450 17.(1) 13- (2) π 18.(1)3 (2)30 (3) 略 (4)310 18.如图,建立空间直角坐标系O —xyz.(1)依题意得B (0,1,0)、N (1,0,1)∴|BN |=3)01()10()01(222=-+-+-.(2)依题意得A 1(1,0,2)、B (0,1,0)、C (0,0,0)、B 1(0,1,2)∴1BA ={-1,-1,2},1CB ={0,1,2,},1BA ·1CB =3,|1BA |=6,|1CB |=5∴cos<1BA ,1CB >=30101||||1111=⋅⋅CB BA CB BA . (3)证明:依题意,得C 1(0,0,2)、M (21,21,2),B A 1={-1,1,2},M C 1={21,21,0}.∴B A 1·M C 1=-2121++0=0,∴B A 1⊥M C 1,∴A 1B ⊥C 1M. 评述:本题主要考查空间向量的概念及运算的基本知识.考查空间两向量垂直的充要条件.图。
(完整word版)空间向量与立体几何测试题及答案

高中 数学选修(2-1)空间向量与立体几何测试题一、选择题1 •若把空间平行于同一平面且长度相等的所有非零向量的始点放置在同一点,则这些向量 的终点构成的图形是()A. —个圆 E. —个点 C.半圆 D.平行四边形答案:A2 .在长方体 ABCD -ABQD i 中,下列关于 AG 的表达中错误的一个是( )答案:E3.若a , b, c 为任意向量, A. (a 亠b ) c =a - (b c )B. (a 亠b )・c =a ・c b-cC.m(a 亠 b ) =m a 亠 m bD. (a ・b )・c=a ・( b-c ) 答案:D1A. 1B. -1C.丄D -22答案:BA.B. AB DD^ De lC. AD CC 1 DC 1D.1(AB i CD i ) - AC im R ,下列等式不一定成立的是(4.若三点A B , e 共线,P 为空间任意一点, 且 PA 叱iPB = 1 PC ,^y - 的值为5. 设 a =(x,4,3), b= (3,2, z),且 a II b , A. -4 B. 9 C. -9答案:B6 . 已知非零向量 e b e 2不共线, 如果A B, C , D ( )A. 一定共圆则四点亠A DB.恰是空间四边形的四个顶点心C. 一定共面D. 肯定不共面答案:C则xz 等于(AB = e AC =2 e 2 8 e AD =3 e -3 e 2,答案:B则x, y , z 的值分别为( )9 .若向量a =(1, ,2)与b= (2, -1,2)的夹角的余弦值为答案:c答案:D12.给出下列命题:① 已知 a _b ,则 a-(b c ) c-(b a ) =b c ;② A, B, M , N 为空间四点,若BA,B M ,BN 不构成空间的一个基底, 那么A , B, M , N 共面; ③ 已知a_b ,则a , b 与任何向量都不构成空间的一个基底; ④ 若a, b 共线,则a, 正确的结论的个数为(A. 1B. 2 答案:C 二、填空题13.已知 a =(3,15), b = (1,2,3),向量 c 与 z 轴垂直,且满足 c-a = 9, c-b - -4,则 c =7.如图1空间四边形 ABCD 的四条边及对 角线长都是a ,点E , F , G 分别是AB, AD , CD 的中点,贝U a 2等于() B. 2AD-BD C. 2FG-CAD. 8 .右 a = e e 2 - e 3, b =e ^ - e 2 ■ e 3, c =e<i • e 2 — e 3,d =e 2 e 2 3 e ,且 d = x a y b z c ,1.1,2 5 厶D1 - 1「25 /1 - 1「2 5 ~1 - 2-A. 2B. -2C.-2或—55D. 2 或-5510 •已知ABCD 为平行四边形,且A(413),A. -,4,12答案:DB. (2,4,1) 11 .在正万体 ABCD - A| B 1C 1D 1 中,A. 60°B. 90°B(2,— 5,1), C(3,7, -5),则顶点D 的坐标为(C. (24,1)D. (513, -3)O 为AC , BD 的交点,则 C品C. arccos ——3GO 与AD 所成角的(D. arccos ——6b 所在直线或者平行或者重合.)D. 4A. 2EF-CB答案:22, -21 , 0 5 514.已知A B, C 三点不共线,O 为平面ABC 外一点,若由向量 ■ OC 确5 3 定的点P 与A, B, C 共面,那么,二 ____________ . 答案:-1515.已知线段 AB_面〉,BC 二卅,CD _BC , DF _ 面〉于点 F , / DCF =30°,且 D , A 在平面:-的同侧,若 AB =BC 二CD =2,则AD 的长为 ____________________ . 答案:2 216.在长方体ABCD —ABQ i D i 中,BQ 和CQ 与底面所成的角分别为 60°和45°,则异面直 线BC 和CQ 所成角的余弦值为 _____________________ . 答案:—4 三、解答题17 .设 a t =2i - j +K 逊=i +3 j -2 k 爲=-2 i + j 弋 k a =3 i +2 j +5 k,试问是否存在实 数-,7,使a 4 a 「;[_a 2 •a 3成立?如果存在,求出 \ ;如果不存在,请写出证明.答案:解:假设a 4 = ■ a^ ''a 2亠、.①成立. •- a 1 =(2, -1,1), a 2 =(13, -2), a 3 =(-21,3), a^(3,2,5), ••• (2 •-2、,-,3二朕:,• -2」- 3、)=(3,2,5).◎人+4-2v=3, j\ = -2, •. -2,解得」=1,■ -2」-3.. =5,- -3.所以存在,=-2, " =1 , v = -3 使得 a 4 = -2a 1 a 2 -3a 3. 理由即为解答过程.18 .如图2,正三棱柱AB^ -A 1B 1C 1的底面边长为a ,侧棱长为 所成的角.解:建立如图所示的空间直角坐标系,则 A(0,0, 0, B(0 , a , 0, A (0,0, V2a) , C 「一亟 a, - , ,7a2 2 由于n = ( -1,0, 0)是面ABB 1A ]的法向量,1*122a ,求AC 1与侧面ABB 1A\故AC i与侧面ABB i A所成的角为30°.19 •如图3,直三棱柱ABC- ABC中,底面是等腰直角三角形, .ACB 二90°,侧棱AA i =2, D, E分别是CC i与AB的中点,点E在平面ABD上的射影是求点A i到平面AED的距离. △ ABD的重心G ,解:建立如图所示的空间直角坐标系,设CA=2a ,则A(2a,0,0, B(0,2a,0, D(0,0,1), A(2a,0,2) E(a, a,),-(0 , -2a,1).由GE_BD=GE・BD=0,得a=1,则A i(2,0,2) A(2,0,0) E(1,1,1).自A1作AH —面AED于M,并延长交xOy面于H,设H (x, y,0), —I则AH =(x —2, y, -2).又AD =(-2,0,1) , AE =(—1,1,1).丄AH _AD, —2(x—2)—2=0, x =1, ZR由1得H (1,1,0)."H _ AE -(x -2) y -2 =0 y =1,又AM =A1A90s A1AAM = AA^cos A1AAH =2 —=20.已知正方体ABCD -ABGD1的棱长为2, P, Q分别是BC, CD上的动点,且PQ = . 2 ,确定P, Q的位置,使QB1 _PD . 解:建立如图所示的空间直角坐标系,设BP =t ,得CQ = 2 -(2 -t)2, DQ =2 - 2 -(2 -t)2.那么B(2,0, 2) D1(0,2,2, P(2 , , 0) Q(2 - 2-(2-t)2,2,0),从而QB =( 2 -(2 -t)2, -2 ,2) , PD1 =(22 -t,2),T —+由QB _ PD = QB^PD t =0 ,即-2 2 -(2 -t)2 -2(2 -t) 4 =0二t =1 .故P, Q分别为BC, CD的中点时,QB i _PD i .21.如图4,在底面是直角梯形的四棱锥S—ABCD中,.ABC=90°,SA_面ABCD ,1SA二AB二BC =1, AD ,求面SCD与面SBA所成二面角的正切2值.解:建立如图所示的空间直角坐标系,(1\则A(0,0,0, B(—1,0,0, C(—1,1,0) D .0, 2 0 , S(0,0,1).延长CD交x轴于点F ,易得F(1,0, 0),作AE _SF于点E ,连结DE ,则ZDEA即为面SCD与面SBA所成二面角的平面角.又由于SA二AF且SA_AF,得E -€5那么从而乩一1,°,」,ED…丄,1,V 2 2 丿V 2 2cos EA, EDEA-ED因此tan EAF , ED 二彳.故面SCD与面SBA所成二面角的正切值为22.平行六面体ABCD -A1B1C1D1的底面ABCD是菱形,且.GCB =. GCD = BCD ,试问:CD的值为多少时,AQ _面GBD ?请予以证明.当CG解:欲使AQ _面GBD ,只须AC _GD ,且AC _GB .欲证AC丄GD ,只须证CA・CD =0 ,t —t T 即(CA AA)・(CD -CG) =0 ,也就是(CD CB CC)(CD _CCJ =0,|C^2 -|C CJ2+|CB|C D|COS^BCD由于• GCB =/BCD , 显然,当CD |CC1时,上式成立;cos _GCB = 0 .同理可得,当时,AC —GB .CD因此,当时, AC _面G BD ..选择题:(10小题共40分)定共面的是2.直三棱柱 ABC — A B i G 中,若 CA = a, CB = b, CC r = C,则 A )B =3.若向量m 垂直向量a 和b ,向量n = ■ a h :b(',」:=只且■、,北0)则A. m 〃 nB. m _ nC. mi 不平行于n,m 也不垂直于nD.以上三种情况都可台匕 冃匕4.以下四个命题中,正确的是C. (a b)c5.对空间任意两个向量 a,b(b o),a//b 的充要条件是6.已知向量a =(0,2,1),b =(-1,1,-2),则a 与b 的夹角为A B i = a, A i D i = b, A A = c ,则下列向量中与B 1M 相等的是1.已知A B C 三点不共线,对平面ABC 外的任一点O,下列条件中能确定点 M 与点A. OM = OA 亠 OB 亠 OCB . OM = 2OA _ OB _ OCC . OM =OA !OB !OC2 3D.OM =1OA 」0B -OC3 3 3A. a b —cB. a — b eC. 一 a b cD. - a b - cA.若00=丄0入+丄0目 则P 、 2 3 'A 、E 三点共线 B.设向量{a,b,c }是空间一个基底,c + a }构成空间的另一个基底D. △ ABC 是直角三角形的充要条件是 AB AC =0A. a 二 bB. a - -bC. b - ■ aA.0 °B.45C.90o.D.180 °7.在平行六面体 ABCD - A 1B 1C 1D 1中,M 为AC 与 BD 的A. -lalb lc B. la 」b 」c C. 2 2 2 28.已知 a =(• 1,0,2 Jb =(6,2」 -1,2),若a 〃b,则•与•啲值分别为9.已知a =3i 2j - k,b = i - j 2k,则5a 与3b 勺数量积等于10.在棱长为1的正方体ABC —A i B i CD 中,M 和N 分别为AB 和BB 的中点,那么直线CN所成角的余弦值是二.填空题:(4 小题共16分)11.若 A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9) 12.已知 A(0, 2, 3), B(-2 , 1, 6), C( 1, -1 , 5),若|a |二.3,且a _ AB,a _ AC,则向量 a的坐标为13.已知a,b 是空间二向量,若心|=3,闪|=2扁4卜.7,则a 与b 的夹角为 14.已知点 G 是厶ABC 的重心,O 是空间任一点,若 OA • OB • OC 」OG,贝,的值三.解答题:(10+8+12+14=44 分)15. 如图:ABCD 为矩形,PAL 平面 ABCD PA=AD M N 分别是PC AB 中点,16. 一条线段夹在一个直二面角的两个面内, 它和两个面所成的角都是300,求这条线段与这个二面角的棱所成的角的大小B.5, 2D.-5 , -2-b c 2A.-15B.-5C.-3D.-1AM 与2 B.-5C.35 D 」10三点共线,则 m+n= (1)求证:MN L 平面PCD (2)求NM 与平面 ABCD 所成的角的大小•17. 正四棱锥S—ABCD中,所有棱长都是2, P为SA的中点,如图(1) 求二面角B—SC- D的大小;(2)求DP与SC所成的角的大小18. 如图,直三棱柱ABC-A1B1C1,底面△ ABC中,CA=CB=1 / BCA=90,棱AA=2, M N分别是A1B1, AA的中点;(1)求BN的长;⑵求cos ::: BA1,CB1的值;⑶求证:AB _CM•(4)求CB与平面AABB所成的角的余弦值高中数学选修2-1测试题(10)—空间向量⑴参考答案DDBB DCDA AB 11.0 12.(1 ,1 , 1) 13.60 0 14.315.(1) 略⑵45 016.45 0 17.(1) 1 3⑵18.(1) 3 (2) ■ 30(3) 略(4) 3 1010 1018.如图,建立空间直角坐标系O—xyz. (1 )依题意得B ( 0, 1, 0)、N( 1, 0, 1) •••I BN |= .(1 一0)2(0 一1)2 (1 - 0)2「3.(2) 依题意得A1 (1, 0, 2)、B ( 0, 1 , 0)、C (0, 0, 0)、B…BA ={ —1, —1, 2}, CB1 ={0, 1, 2, }, BA| • CB1 =3,BA. CB 11CB 1 |= J5 ••• cos< BA 1 , CB 1 >=(3)证明:依题意,得 G (0, 0, 2)、M( 1,1,2), A 1B ={ - 1 , 1 , 2} , CM,2 2 1 2 2评述:本题主要考查空间向量的概念及运算的基本知识 .考查空间两向量垂直的充要条件——-1 . 30. |BAJ|CB i |102‘20}. • A , B • C 1M =-1 12+ 2+0=0,AB 丄 C 1M ,• AB 丄CM.。
(完整word版)空间向量与立体几何测试题及答案

高中 数学选修(2-1)空间向量与立体几何测试题、选择题1 •若把空间平行于同一平面且长度相等的所有非零向量的始点放置在同一点,则这些向量的终点构成的图形是()A. —个圆E. —个点 C.半圆 D.平行四边形答案:AUUJU2 .在长方体 ABCD A 1B 1C 1D 1中,下列关于 AC ,的表达中错误的一个是( )C. 一定共面D. 肯定不共面A. UUL T AA LUUIT AB UUU TA D C.UUL T AD UUUU CC 1 ULU U D 1C 1 B. D. UUU UlUULUJUJAB DD D G1 uma ujun uuuir-(AB 1 CD 1) AC 13.若 A. B. a , (a (a b, c 为任意向量, b) c a b )・c F 列等式不一定成立的是( a-c C. D.m(a b) (a-b)-c 答案:Dma a-(b-c)(b c) b-cmb4.若二点A B, C 共线,P 为空1 间任意一占八、且 PAPB A. 1B. 1C.- 1D. 22答案:B5.设 a (x,4,3), b (3,2, z),且 a II b , 则xz:等于()A. 4B. 9C. 9D. 649答案:B6 .已: 知非 零向量 e 〔,e2不共线,如果UJUAB UUT e e 2, AC 2A B, C , D ()uuuPC ,则UULT8©,, AD3e 的值为则四点答案: B uni uu mA. —定共圆B. 恰是空间四边形的四个顶点心答案:C7.如图1,空间四边形 ABCD 的四条边及对 角线长都是a ,点E , 的中点,贝U a 2等于( uuu uurA. 2BA AC F , G 分别是 AB, AD , CDB. uuu UJU 2AD-BD uur uuuC. 2FG-CAD. uuu UJU 2EF-CB答案:B &若a则 x, y , e 1 e 2 e ® z 的值分别为 b e 1 e2e3,c e1)e2e3, e i2e 2 3是,且 d xa ybzc ,A. 5 2, 答案:AB.C.D. 2 J'19.若向量a (1 ,2)与 b (2, 1,2)的夹角的余弦值为 8,则 9A. 2B. 2C. 2或— 55D.2或—55答案:C 10 •已知ABCD 为平行四边形,且A(413), ” 7A. —,4, 1 2答案:D B. (2,4,1) B(2, 5,1), C(3,7,C. ( 214,1) 11 .在正方体ABCD AB 1C 1D1 中, 5),则顶点D 的坐标为(D. (513, 3)A. 60°B. 90° O 为AC , BD 的交点,则 C 43C. arccos -3 GO 与AD 所成角的(arccos 6 D. 答案:D 12.给出下列命题: b ,贝U a-(b ①已知a c) c ・(b a) b-c ; ② A, B, uuu uuuu uuirM , N 为空间四点,若BABM ,BN 不构成空间的一个基底, 那么A , B, M , N 共面; b ,则a , b 与任何向量都不构成空间的一个基底; ④若a, b 共线,则a, 正确的结论的个数为( A. 1 B. 2 答案:C ③已知a b 所在直线或者平行或者重合. ) C. 3D. 4二、填空题 13.已知 a (3,15), b(1,2, 3),向量c 与z 轴垂直,且满足c-a 9, c-b4,则c所成的角. 解:建立如图所示的空间直角坐标系,则 A(0,0,0, B(0, a ,0, A(0,0,&a), G — a<a 虽a 2 2 由于n ( 1,0,0)是面ABB 1A ]的法向量,答案:22 21,05 5 UlU 1 UUU 2 UUU 14.已知A B, C 三点不共线,O 为平面ABC 外一点,若由向量OP OA OB 5 3 LULT ” OC 确 定的点P 与A, B, C 共面,那么 _______________ 答案:- 15 15.已知线段 AB 面,BC ,CD BC ,DF 面 于点F ,在平面 的同侧,若 AB BC CD 2,则AD 的长为 _________________ . DCF 30°,且 D , A 答案:2 2 16 .在长方体ABCD A 1B 1C 1D 1中,BQ 和CQ 与底面所成的角分别为 线BC 和CQ 所成角的余弦值为 _______________ . 60°和45° ,则异面直 答案: 17 .设 a 1 2i j k , a 2 i 3j 2k , a a 2i j 3k , a 4 3i 2j 5k ,试问是否存在实 数,, ,a 4 a 1 a 2 a 3成立? 如果存在,求出 ,,;如果不存在,请写出 证明. 答案:解: 假设 a 4 a 1 a 2 a 3成立. ••• a 1 (2, 1,1), a 2(13, 2) , a 3 ( 21, 3) , a 4 (3,2,5),•- (2 2 ,3 , 2 3 ) (3,2,5).2 232 ,32,解得1,2 3 5,3.所以存在 2, 1, v3使得a 4 2a 1 a 2 3a 3.三、解答题 理由即为解答过程. 18.如图2,正三棱柱ABC A 1B 1C 1的底面边长为 a ,侧棱长为 2a ,求AC 1与侧面ABB 1AI ;20.已知正方体 ABCD AB1GD 1的棱长为2 , P, Q 分别是BC , CD 上的动点,且PQ 2 , 确定P, Q 的位置,使QB 1 PD 1 . 解:建立如图所示的空间直角坐标系,设BP t ,得 CQ 2 (2 t)2 , DQ 2 2 (2 t)2 ..uuuu cos AG , nUJIHAC/nJJUIAG n故AC i 与侧面ABB i A 所成的角为30°.19 •如图 3,直三棱柱 ABC ABQ i 中,底面是等腰直角三角形, ACB 90°,侧棱AA 2,D ,E 分别是CC i 与AB 的中点,点 E 在平面 ABD 上的射影是 求点A 到平面AED 的距离.解:建立如图所示的空间直角坐标系,设CA 2a ,'""2a 2a 1 则 A(2a,0,0, B(0,2a,0, D(0,0,1), A(2a,0,2) E(a, a,1), G 一,一,-. 33 3切 a a 2 uuu从而 GE — _ ,BD (0, 2a,1).3 3 3 uuu uur△ ABD 的重心G ,则 A !(2,0,2) A(2,0,0) E(1,1,1).自A 作AH 面AED 于M ,并延长交xOy 面于H ,设H (x, y ,0), uuuu则 AH (x 2, y ,2).uuu uuu 又 AD ( 2,0,) , AE ( 1,1,1).A 1H AD , A 1H AE2(x22) 220 0 % 1,得 H(1,1,0) (x 2) y 2 0y 1 ,又AMA 1A 'cos JUTULULTA A AMjUULT LULU. AA ・cos A 1A AH2 4 22.6那么 B(2,0,2) D(0,2 -2, P(2 , , 0) Q(22 (2 t)2 ,2 - 0),从而QR ( 2 (2 t)2 - 2 -2),PD 1 (2,2 t , 2),由 QB PD 1 uuuu uuuuQB/PD ! 0,1 21 图X即 2 2 (2 t)22(2 t) 4 0 t 1 .故P, Q 分别为BC , CD 的中点时,QB i PD i .21.如图4,在底面是直角梯形的四棱锥 S ABCD 中, ABC 90°,SA 面 ABCD , 1 SA AB BC 1, AD ,求面SCD 与面SBA 所成二面角的正切 2 值. 解:建立如图所示的空间直角坐标系, 戸, 1 则 A(0,0,0, B( 1,0, 0, C( 1,1,0) D 0,0 , S(0,0,1). 延长CD 交x 轴于点F ,易得F(1,0, 0), 作AE SF 于点E ,连结DE , 则 DEA 即为面SCD 与面SBA 所成二面角的平面角. 1 1 又由于 SA AF 且 SA AF ,得 E - , 0 ,-, 2 2uur 1 那么EA 2,01 uur ED 2从而 uuu uuu.EA ,.uu u UUUI. ED |1 1 2,2 6 3uur umr.因此 tan EAF , ED 故面SCD 与面SBA 所成二面角的正切值为 22 .平行六面体 ABCD A 1B 1C 1D 1的底面ABCD 是菱形,且 GCB GCD BCD ,试问:CD当一一的值为多少时, AQ 面GBD ?请予以证明. CG 解:欲使AQ 面GBD ,只须AC C 1D ,且AC GB . uuir uuun欲证AC GD ,只须证CAGD 0 , uur uur uuu uuur 即(CA AA )• (CD CG ) 0 , uur uuu 也就是(CD CB ujuu uur uuur CC)(CD CCJ 0,uuu 2 .uuuu 2 uuu u uu 即 CD ICC 1CB CD cos BCD uuu uuui CB CC 1 cos 由于 C 1CB BCD , C 1CB 0.显然,uur CDuuuuCC 1时,上式成立; 同理可得,当 因此,当CDCC 1uur CD iuuu CC 1AC1 时,AC 面 GBD ..选择题:(10小题共40分)ABC 外的任一点 O,下列条件中能确定点 M 与点A B C定共面的是()A. OM OA OB ' OCB . OM2OA OB OCC. OMOA 1 ^OB1 ^OCD. OM^OA ^OB -OC233 3 3 2.直三棱柱ABC-A 1B 1G 中, 若CAa,CB bgC,则 AB()A. a b— c B. a ■ — b cC. a■ — b cD. a b c3.若向量m 垂直向量a 和b ,向量n—» a b(,R 且、0)则(能4.以下四个命题中,正确的是—1 —1 —-A.若OP OA OB ,则P 、A 、E 三点共线2 3B.设向量{a,b,c }是空间一个基底,则{ a + b , b +c , c + a }构成空间的另一个基底—► —*—► fC . (a b )c a b cA 1B 1 a, A 1D 1 b, AA c ,则下列向量中与B 1M 相等的是 ()1.已知A B C 三点不共线,对平面 A. m 〃 n B. mn C.qp •*m 不平行于n,m 也不垂直于D.以上三种情况都可D. △ ABC 是直角三角形的充要条件是 AB AC 0 5.对空间任意两个向量 a,b (bo ),a//b 的充要条件是A . a bB . aC. b aD. a6.已知向量a(0,2,1),b ( 1,1, 2),则a 与b 的夹角为A.0 °B.45C.90o.D.1807.在平行六面体 ABCD A 1B 1C 1D 1中,M 为 AC 与 BD2B.5C.35 D 」10二.填空题:(4 小题共16分)11.若 A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线,则 m+n=12.已知 A( 0,2,3),B( -2,1 , 6), C( 1,-1 ,5),若 |a| 3,且a AB,a AC,则向量a的坐标为13.已知a,b 是空间二向量,若|a| 3,|b| 2,| a b| 7,则a 与b 的夹角为 14.已知点 G 是厶ABC 的重心,O 是空间任一点,若OA OB OC OG,则 的值为.三.解答题:(10+8+12+14=44 分)15.如图:ABCD 为矩形,PAL 平面 ABCD PA=AD M N 分别是PC AB 中点, (1)求证:MNL 平面PCD (2)求NM 与平面 ABCD 所成的角的大小.16. 一条线段夹在一个直二面角的两个面内,它和两个面所成的角都是 300,求这条线段与这个二面角的棱所成的角的大小 .10.在棱长为1的正方体ABC —A 1B 1CD 中,M 和N 分别为AB 和BB 的中点,那么直线 AM 与CN所成角的余弦值是A.1 1「 1 11 11111 a b C B. a b -C C. a b c D.- a b c2 2 22 2 2 2 22 28.已知a (1,0,2 ),b(6,21,2),若 a//b,则的值分别为A.1,jB.5, 2D.-5 , -29.已知 a 3i 2j k,b iA.-15B.-5C.-3D.-1C. 117.正四棱锥S—ABCD中,所有棱长都是2, P为SA的中点,如图•(1)求二面角B—SC- D的大小;(2)求DP与SC所成的角的大小•518.如图,直三棱柱ABC-A1B1C1,底面△ ABC中,CA=CB=1 / BCA=90,棱AA=2, M N分别是A1B1, AA的中点;(1)求BN的长;⑵求cos BA,CB1的值;(3)求证:AB C1M .(4)求CB与平面AABB所成的角的余弦值高中数学选修2-1测试题(10)—空间向量 ⑴ 参考答案•-1 BN |= (1 0)2 (0 1)2 (1 0)2 3.DDBB DCDA AB 11.0 12.(1 ,1 , 1)13.6014.315.(1) 略⑵4516.4517.(1)1 3⑵18.(1)3(2)30 (3) 略(4)3 10101018.如图,建立空间直角坐标系O — xyz.(1 )依题意得B ( 0,(2)依题意得 A 1 (1, 0, 2)、B ( 0, 1 , 0)、 • BA ={ —1 , — 1 , 2} , CB 1 ={0 , 1 , 2, }, C (0, 0, 0)、B (0, 1 , 2)BA| • CB 1 =3, | BA |=4 g1J齐■二4 Z图1,0)、N (1,0,1)I CB i |= 5二cos<BA i ,CB i >=BA CB1—-:'30 .IBA i I |CB i|10(3)证明:依题意,得G(0, 0, 2)、M( 1,1,22 2 ),A>{ -1,1,2}, C j M={-,-,1 2 20}. • A B • C i M =—11+0=0,••• AB 丄CM ,••• A i B丄CM.评述:本题主要考查空间向量的概念及运算的基本知识.考查空间两向量垂直的充要条件。
空间向量与立体几何【题集】(教师版)

空间向量与立体几何【题集】1. 空间向量的直角坐标运算空间向量的坐标运算A.B.C.D.1.【解析】【标注】设,,,若,则点坐标为( ).【答案】C设点的坐标为;则,,则由,得,,,解得,,,,所以选项是正确的.【知识点】空间向量线性运算的坐标表示A.,B.,C.,D.,2.【解析】【标注】已知,,若,则实数,的值分别为( ).【答案】A 由,且,∴解得.故选.【知识点】空间向量线性运算的坐标表示A.B.C.D.3.已知向量 , ,且,那么的值是【解析】【标注】【答案】A ∵,∴.∴ ,∴.故选.【知识点】空间向量线性运算的坐标表示空间向量平行和垂直的坐标表示A.B.C.D.4.【解析】【标注】已知向量,则下列向量中与平行的是( ).【答案】B两向量平行,则对应坐标或比例,∵,∴与平行.故选.【知识点】空间向量线性运算的坐标表示A.B.C.D.5.【解析】【标注】已知两个向量,,若,则的值为( ).【答案】C ∵,∴存在实数使得,∴,解得,,,则.故选:.【知识点】空间向量线性运算的坐标表示A. B. C. D.6.【解析】【标注】已知向量,,其中.若,则的值为( ).【答案】A由知存在,使,即.∴.解得.故选.【知识点】空间向量线性运算的坐标表示A.()()B.()()C.()()D.()()7.【解析】【标注】以下四组向量中,互相平行的是( ).(),;(),;(),;(),.【答案】D选项中,对应坐标不成比例,故此两个向量不平行,选项中有:,选项中与向量平行,选项,事实上对应坐标不成比例,故此两个向量不平行,以下四组向量中,互相平行的是()().故选.【知识点】空间向量线性运算的坐标表示A.相交B.垂直C.平行D.以上都不对8.若向量,,则向量与( ).【答案】C【解析】【标注】∵向量,,则与平行.故选.【知识点】空间向量线性运算的坐标表示9.【解析】【标注】已知,,若和相互垂直,则 .【答案】,所以.【知识点】空间向量的数量积及其坐标表示;空间向量线性运算的坐标表示两个向量夹角与模长的坐标计算公式A. B. C. D.10.【解析】【标注】已知向量,,则等于( ).【答案】C∵,,,∴.故选.【知识点】空间向量线性运算的坐标表示A. B. C. D.11.已知向量,,则等于( ).【答案】B【解析】【标注】,,.故选:.【知识点】空间向量线性运算的坐标表示A. B. C. D.12.【解析】【标注】若,,则( )【答案】C,,,.故选:.【知识点】向量的模;空间向量线性运算的坐标表示13.【解析】【标注】若,,,则 .【答案】,,,,,故答案为:.【知识点】空间向量的线性运算(非坐标);空间向量线性运算的坐标表示A. B. C. D.14.【解析】若,,且,则实数的值是( ).【答案】D因为,,所以,【标注】又因为,所以,解得,故选.【知识点】空间向量的数量积及其坐标表示15.【解析】【标注】已知向量,,则与的夹角为 .【答案】设与的夹角为,则.故答案为:.【知识点】反三角函数;空间向量的数量积及其坐标表示2. 直线的方向向量1.直线的方向向量是唯一确定的.( )2.平面的单位法向量是唯一确定的.( )3.若两平面的法向量平行,则两平面平行.( )4.若两直线的方向向量不平行,则两直线不平行.( )5.若,则所在直线与所在直线平行.( )6.若空间向量平行于平面,则所在直线与平面平行.( )16.【标注】判断下列结论是否正确(请在括号中打“√”或“”).【答案】××✓✓××【知识点】向量法解决异面直线所成角问题;直线的方向向量与平面的法向量;向量法解决空间中的平行问题A. B. C. D.17.【解析】若,在直线上,则直线的一个方向向量为( ).【答案】A由题意可得:直线的一个方向向量,【标注】又∵,∴是直线的一个方向向量.故选.【知识点】直线的方向向量与平面的法向量;空间向量的线性运算(非坐标)A.B.C.D.18.【解析】【标注】直线的一个方向向量是( ).【答案】D直线的斜率为,∴直线的一个方向向量,或.故选.【知识点】直线的方向向量与平面的法向量19.【解析】【标注】经过点且方向向量为的直线的点方向式方程是 .【答案】∵过点,方向向量,∴直线方程为:,转化为点方向式方程,得:.【知识点】向量的概念;直线方程的五种形式的联系和使用范围的区别;直线的点斜式方程3. 平面的法向量平面法向量的求解步骤A.B.C.D.20.点,,,平面的一个法向量为( ).【解析】【标注】设为平面的法向量,则,即,解得不妨取,则.【知识点】直线的方向向量与平面的法向量A. B. C. D.21.【解析】【标注】已知平面上的两个向量,,则平面的一个法向量为( ).【答案】C显然与不平行,设平面的一个法向量为,则∴令,得,,∴.【知识点】直线的方向向量与平面的法向量;空间向量的数量积及其坐标表示直线与平面垂直的判定定理的向量证明A. B. C. D.22.【解析】已知平面的法向量为,直线与平面相交但不垂直,则向量的坐标可以是( ).【答案】D选项:,则面,不符;选项:,则面,不符;选项:,则面,不符;选项:,且与不平行,符合.【标注】【知识点】向量法解决空间中的垂直问题;向量法解决空间中的平行问题;直线的方向向量与平面的法向量23.【解析】如图所示,正三棱柱(底面为正三角形的直三棱柱)的所有棱长都为,为的中点.求证:平面.【答案】证明见解析.如图所示,取的中点,连接.因为为正三角形,所以.因为在正三棱柱中,平面平面,所以平面.取的中点,连,以为原点,分别以,,所在直线为轴,轴,轴建立空间直角坐标系,则,,,,.设平面的法向量为,,.因为,,故,【标注】令,则,,故为平面的一个法向量,而,所以,所以,故平面.【知识点】向量法解决空间中的垂直问题;直线的方向向量与平面的法向量24.方法一:【解析】在正方体中,,分别是,的中点,求证:平面.【答案】证明见解析.设正方体的棱长为,如图,建立空间直角坐标系,则,,,,,∴,,.∴.,∴,.又,∴平面.【备注】【教师可见】请老师带领学生,着重用方法一练习本题.方法二:【标注】设,,,则,如图,连接,则.∵,∴,∴,即.同理.又,∴平面.【知识点】建立空间直角坐标系;向量法解决空间中的垂直问题;向量法解决空间中的平行问题;空间向量的数量积及其坐标表示用法向量证明平面与平面垂直25.平面、的法向量分别为,,若,则等于 .【答案】【解析】【标注】知,.即,解得.【知识点】向量法解决空间中的垂直问题26.【解析】【标注】已知平面的法向量是,平面的法向量是,且,则实数的值为 .【答案】或,整理得:,解得:或,故答案为:或.【知识点】向量法解决空间中的垂直问题;直线的方向向量与平面的法向量27.【解析】已知:在正方体中,、分别是、的中点.求证:平面平面.【答案】证明见解析.如图所示,建立空间直角坐标系.令,则有,,,,,.设,分别是平面,平面的法向量,则,,所以,所以,【标注】令,得.同理可得.所以,知.所以平面平面.【知识点】向量法解决空间中的垂直问题;向量法解决二面角问题;直线的方向向量与平面的法向量28.【解析】如图,在正三棱柱中,,,分别是,上的点,且,.求证:平面平面.【答案】证明见解析.以为坐标原点,建立如图所示的空间直角坐标系,则,,,,,∴,,设平面的法向量为,则,,由,得,解得,令,得,∴平面的一个法向量为,【标注】由题意可知,平面的一个法向量为,∴,∴平面平面.【素养】数学运算【知识点】向量法解决二面角问题。
人教版高中数学选修2-1第三章-空间向量与立体几何练习题及答案

第三章 空间向量及立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算 §3.1.2空间向量的数乘运算1. 下列命题中不正确的命题个数是( ) ①若A 、B 、C 、D 是空间任意四点,则有AB +BC + CD +DA =0;②对空间任意点O 及不共线的三点A 、B 、C ,若OP =x OA +y OB +z OC (其中x 、y 、z ∈R ),则P 、A 、B 、C 四点共面;③若a 、b 共线,则a 及b 所在直线平行。
A .1 B .2 C .3 D .42.设OABC 是四面体,G 1是△ABC 的重心,G 是OG 1上一点,且OG =3GG 1,若OG =x OA +y OB +z OC ,则(x ,y ,z )为( )A .(41,41,41) B .(43,43,43) C .(31,31,31) D .(32,32,32) 3.在平行六面体ABCD -EFGH 中,AG xAC y AF z AH =++,________.x y z ++=则4.已知四边形ABCD 中,AB =a -2c ,CD =5a +6b -8c ,对角线AC 、BD 的中点分别为E 、F ,则EF =_____________.5.已知矩形ABCD ,P 为平面ABCD 外一点,且PA ⊥平面ABCD ,M 、N 分别为PC 、PD 上的点,且M 分PC 成定比2,N 分PD 成定比1,求满足MN xAB y AD z AP =++的实数x 、y 、z 的值.§3.1.3空间向量的数量积运算1.已知正四棱柱1111ABCD A B C D -中,1AA =2AB ,E 为1AA 重点,则异面直线BE 及1CD 所形成角的余弦值为( )A .1010 B . 15C .31010 D . 352.如图,设A ,B ,C ,D 是空间不共面的四点,且满足0AB AC ⋅=,0AC AD ⋅=,0AB AD ⋅=,则△BCD 的形状是( )A .钝角三角形B .锐角三角形C .直角三角形D .不确定的3.已知ABCD -A 1B 1C 1D 1 为正方体,则下列命题中错误的命题为__________.4.如图,已知:平行六面体ABCD -A 1B 1C 1D 1的底面ABCD 是菱形,且∠C 1CB =∠C 1CD =∠BCD =60° (1)证明:C 1C ⊥BD ;_C_D_A_P_ N_B_M(2)当1CDCC 的值为多少时,能使A 1C ⊥平面C 1BD ?请给出证明. §3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示1.已知向量(2,2,3)OA =-,(,1,4)OB x y z =-,且平行四边形OACB 的对角线的中点坐标为M 31(0,,)22-,则(,,)x y z =( ) A .(2,4,1)--- B .(2,4,1)-- C .(2,4,1)-- D .(2,4,1)--2.已知(2,2,4)a=-,(1,1,2)b =-,(6,6,12)c =--,则向量、、a b c ( )A .可构成直角三角形B .可构成锐角三角形C .可构成钝角三角形D .不能构成三角形3.若两点的坐标是A (3cosα,3sinα,1),B (2cosθ,2sinθ,1),则|AB |的取值范围是( ) A .[0,5] B .[1,5] C .(1,5) D .[1,25]4.设点C (2a +1,a +1,2)在点P (2,0,0)、A (1,-3,2)、B (8,-1,4)确定的平面上,则a 的值为 .5.如图,正三棱柱ABC -A 1B 1C 1的底边长为a ,侧棱长为2a .建立适当的坐标系,⑴写出A ,B ,A 1,B 1的坐标;⑵求AC 1及侧面ABB 1A 1所成的角.3.2立体几何中的向量方法1.到一定点(1,0,1)的距离小于或等于2的点的集合为( ) A .222{(,,)|(1)(1)4}x y z x y z -++-≤ B .222{(,,)|(1)(1)4}x y z x y z -++-= C .222{(,,)|(1)(1)2}x y z x y z -++-≤ D .222{(,,)|(1)(1)2}x y z x y z -++-=2. 正方体ABCD —A 1B 1C 1D 1中,直线BC 1及平面A 1BD 所成角的余弦值为( ) A .42 B .32 C .33 D .23 3. 已知斜三棱柱111ABC A B C -,90BCA ∠=,2AC BC ==,1A 在底面ABC 上的射影恰为AC 的中点D ,又知11BA AC ⊥.(1)求证:1AC ⊥平面1A BC ;D 1C 1B 1A 1DABCC 1 B 1 A 1B A(2)求1C 到平面1A AB 的距离;(3)求二面角1A A B C --余弦值的大小.B 4. 如图,在直三棱柱111ABC A B C -中, AB =1,1AC AA ==(1)证明:1ABA C ⊥; (2)求二面角A —1A C —B 的大小.5. 如右图,四棱锥S-ABCD 棱S D 上的点. (1)求证:AC ⊥SD ;(2)若SD ⊥平面PAC ,求二面角P-AC-D 的大小 (3)在(2)的条件下,侧棱S C 上是否存在一点E , 使得BE ∥平面PAC .若存在,求S E :EC 的值; 若不存在,试说明理由.参考答案第三章 空间向量及立体几何3.1空间向量及其运算§3.1.1空间向量及其加减运算 §3.1.2空间向量的数乘运算1.A2.A3.324.3a +3b -5c5.如图所示,取PC 的中点E ,连结NE ,则MN EN EM =-. 连结AC ,则§3.1.3空间向量的数量积运算1.C2.B3. ③④4.(1)设1,,CB a CD b CC c === ,则||||a b =,BD CD CB b a =-=- ,所以1()||||cos 60||||cos 600CC b a c b c a c b c a c ⋅=-⋅=⋅-⋅=︒-︒=BD ,11BD CC BD CC ∴⊥⊥即 ; (2)1,2,CD x CD CC ==1设则 2CC =x, 设1,,A A a AD b DCc ===,11,A C a b c C D a c =++=-,2211242()()6A C C D a b c a c a a b b c c xx ∴⋅=++⋅-=+⋅-⋅-=+-,令24260xx +-=,则2320x x --=,解得1x =,或23x =-(舍去),_C_D _A_P_ N _B _M _EA 1§3.1.4空间向量的正交分解及其坐标表示§3.1.5空间向量运算的坐标表示 1.A 2.D 3.B 4.165. (1)建系如图,则A (0,0,0) B (0,a ,0)A 1(0,0,2a ),C 1(-23a ,a 2,2a) (2)解法一:在所建的坐标系中,取A 1B 1的中点M , 于是M (0,a 2,2a),连结AM ,MC 1则有所以,MC 1⊥平面ABB 1A 1.因此,AC 1及AM 所成的角就是AC 1及侧面ABB 1A 1所成的角.∴2194a AC AM ⋅=,而|13||3,||2AC a AM a ==,由cos<1,AC AM >=1132||||AC AM AC AM ⋅=,∴ <1,AC AM >=30°. ∴AC 1及侧面ABB 1A 1所成的角为30°. 3.2立体几何中的向量方法 新 课 标 第 一网1.A2.C3. (1)如右图,取AB 的中点E ,则//DE BC ,因为BC AC ⊥,所以DEAC ⊥,又1A D ⊥平面ABC ,以1,,DE DC DA 为,,x y z 轴建立空间坐标系, 则()0,1,0A -,()0,1,0C ,()2,1,0B ,()2,0,0CB =,由10AC CB ⋅=,知1A C CB ⊥, 又11BA AC ⊥,从而1AC ⊥平面1A BC .(2)由1AC ⋅2130BA t =-+=,得t =.设平面1A AB 的法向量为(),,n x y z =,(1AA =,()2,2,0AB =,所以10220n AA y n AB x y ⎧⋅=+=⎪⎨⋅=+=⎪⎩,设1z =,则()3,n =-,所以点1C 到平面1A AB 的距离1AC n d n⋅==7. (3)再设平面1A BC 的法向量为(),,m x y z =,(10,CA =-,()2,0,0CB =,所以13020m CA y z m CB x ⎧⋅=-+=⎪⎨⋅==⎪⎩,设1z =,则()0,3,1m =,故cos ,m n m n m n⋅<>==⋅77-,根据法向量的方向,可知二面角1A A B C --的余弦值大小为77. 4.(1)三棱柱111ABC A B C -为直三棱柱,由正弦定理030ACB∠=.如右图,建立空间直角坐标系, 则1(0,0,0),(1,0,0)(0,3,0),(0,0,3)A B C A(2) 如图可取(1,0,0)m AB ==为平面1AA C 的法向量,设平面1A BC 的法向量为(,,)n l m n =,则10,0,130BC n AC n BC ⋅=⋅==-又(,,), 不妨取1,(3,1,1)mn ==则,1A AC BD ∴--15二面角的大小为arccos 5. 5. (1)连结BD ,设AC 交于BD 于O ,由题意知SO ABCD ⊥平面.以O 为坐标原点,OB OC OS ,,分别为x 轴、y 轴、z 轴正方向,建立坐标系O xyz -如右图.设底面边长为a ,则高62SO a =.于是 62(0,0,),(,0,0)22S a D a -,2(0,,0)2C a ,2(0,,0)2OC a =,26(,0,)22SD a a =--,0OC SD ⋅= ,故OC SD ⊥.从而 AC SD ⊥. (2)由题设知,平面PAC 的一个法向量26()2DSa =,平面DAC 的一个法向量600aOS =(,,,设所求二面角为θ,则3cos OS DS OS DSθ⋅==,得所求二面角的大小为30°._C_A_S_F_BO(3)在棱SC 上存在一点E 使//BE PAC 平面.由(2)知DS 是平面PAC 的一个法向量,且),(0,)DS CS ==.设,CEtCS = 则((1)BE BC CE BC tCS t =+=+=-,而 103BE DC t ⋅=⇔=.即当:2:1SE EC =时,BE DS ⊥.而BE 不在平面PAC 内,故//BE PAC 平面. 作 者 于华东 责任编辑 庞保军。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.
(1)求证:M为PB的中点; (2)求二面角B﹣PD﹣A的大小; (3)求直线MC与平面BDP所成角的正弦值.
【分析】(1)设AC∩BD=O,则O为BD的中点,连接OM,利用线面平行的性质证明OM∥PD,再由平行线截线段成比例可得M为PB的中点; (2)取AD中点G,可得PG⊥AD,再由面面垂直的性质可得PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG,再证明OG⊥AD.以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系,求出平面PBD与平面PAD的一个法向量,由两法向量所成角的大小可得二面角B﹣PD﹣A的大小; (3)求出的坐标,由与平面PBD的法向量所成角的余弦值的绝对值可得直线MC与平面BDP所成角的正弦值. 【解答】(1)证明:如图,设AC∩BD=O, ∵ABCD为正方形,∴O为BD的中点,连接OM, ∵PD∥平面MAC,PD⊂平面PBD,平面PBD∩平面AMC=OM, ∴PD∥OM,则,即M为PB的中点; (2)解:取AD中点G, ∵PA=PD,∴PG⊥AD, ∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD, ∴PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG, 由G是AD的中点,O是AC的中点,可得OG∥DC,则OG⊥AD. 以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系, 由PA=PD=,AB=4,得D(2,0,0),A(﹣2,0,0),P(0,0,),C(2,4,0),B(﹣2,4,0),M(﹣1,2,), ,. 设平面PBD的一个法向量为,
则由,得,取z=,得. 取平面PAD的一个法向量为. ∴cos<>==. ∴二面角B﹣PD﹣A的大小为60°; (3)解:,平面BDP的一个法向量为.
∴直线MC与平面BDP所成角的正弦值为|cos<>|=||=||=.
【点评】本题考查线面角与面面角的求法,训练了利用空间向量求空间角,属中档题.
2.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2. (Ⅰ)求证:MN∥平面BDE; (Ⅱ)求二面角C﹣EM﹣N的正弦值; (Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长. 【分析】(Ⅰ)取AB中点F,连接MF、NF,由已知可证MF∥平面BDE,NF∥平面BDE.得到平面MFN∥平面BDE,则MN∥平面BDE; (Ⅱ)由PA⊥底面ABC,∠BAC=90°.可以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.求出平面MEN与平面CME的一个法向量,由两法向量所成角的余弦值得二面角C﹣EM﹣N的余弦值,进一步求得正弦值; (Ⅲ)设AH=t,则H(0,0,t),求出的坐标,结合直线NH与直线BE
所成角的余弦值为列式求得线段AH的长. 【解答】(Ⅰ)证明:取AB中点F,连接MF、NF, ∵M为AD中点,∴MF∥BD, ∵BD⊂平面BDE,MF⊄平面BDE,∴MF∥平面BDE. ∵N为BC中点,∴NF∥AC, 又D、E分别为AP、PC的中点,∴DE∥AC,则NF∥DE. ∵DE⊂平面BDE,NF⊄平面BDE,∴NF∥平面BDE. 又MF∩NF=F. ∴平面MFN∥平面BDE,则MN∥平面BDE; (Ⅱ)解:∵PA⊥底面ABC,∠BAC=90°. ∴以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系. ∵PA=AC=4,AB=2, ∴A(0,0,0),B(2,0,0),C(0,4,0),M(0,0,1),N(1,2,0),E(0,2,2), 则,, 设平面MEN的一个法向量为, 由,得,取z=2,得. 由图可得平面CME的一个法向量为. ∴cos<>=. ∴二面角C﹣EM﹣N的余弦值为,则正弦值为; (Ⅲ)解:设AH=t,则H(0,0,t),,. ∵直线NH与直线BE所成角的余弦值为,
∴|cos<>|=||=||=. 解得:t=或t=. ∴当H与P重合时直线NH与直线BE所成角的余弦值为,此时线段AH的长为或.
【点评】本题考查直线与平面平行的判定,考查了利用空间向量求解空间角,考查计算能力,是中档题.
3.如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是的中点. (Ⅰ)设P是上的一点,且AP⊥BE,求∠CBP的大小; (Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小. 【分析】(Ⅰ)由已知利用线面垂直的判定可得BE⊥平面ABP,得到BE⊥BP,结合∠EBC=120°求得∠CBP=30°; (Ⅱ)法一、取的中点H,连接EH,GH,CH,可得四边形BEGH为菱形,取AG中点M,连接EM,CM,EC,得到EM⊥AG,CM⊥AG,说明∠EMC为所求二面角的平面角.求解三角形得二面角E﹣AG﹣C的大小. 法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.求出A,E,G,C的坐标,进一步求出平面AEG与平面ACG的一个法向量,由两法向量所成角的余弦值可得二面角E﹣AG﹣C的大小. 【解答】解:(Ⅰ)∵AP⊥BE,AB⊥BE,且AB,AP⊂平面ABP,AB∩AP=A, ∴BE⊥平面ABP,又BP⊂平面ABP, ∴BE⊥BP,又∠EBC=120°, 因此∠CBP=30°; (Ⅱ)解法一、 取的中点H,连接EH,GH,CH, ∵∠EBC=120°,∴四边形BECH为菱形, ∴AE=GE=AC=GC=. 取AG中点M,连接EM,CM,EC, 则EM⊥AG,CM⊥AG, ∴∠EMC为所求二面角的平面角. 又AM=1,∴EM=CM=. 在△BEC中,由于∠EBC=120°, 由余弦定理得:EC2=22+22﹣2×2×2×cos120°=12, ∴,因此△EMC为等边三角形, 故所求的角为60°. 解法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系. 由题意得:A(0,0,3),E(2,0,0),G(1,,3),C(﹣1,,0), 故,,. 设为平面AEG的一个法向量,
由,得,取z1=2,得; 设为平面ACG的一个法向量, 由,可得,取z2=﹣2,得. ∴cos<>=. ∴二面角E﹣AG﹣C的大小为60°.
【点评】本题考查空间角的求法,考查空间想象能力和思维能力,训练了线面角的求法及利用空间向量求二面角的大小,是中档题.
4.如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D﹣AF﹣E与二面角C﹣BE﹣F都是60°. (Ⅰ)证明平面ABEF⊥平面EFDC; (Ⅱ)求二面角E﹣BC﹣A的余弦值.
【分析】(Ⅰ)证明AF⊥平面EFDC,利用平面与平面垂直的判定定理证明平面ABEF⊥平面EFDC; (Ⅱ)证明四边形EFDC为等腰梯形,以E为原点,建立如图所示的坐标系,求出平面BEC、平面ABC的法向量,代入向量夹角公式可得二面角E﹣BC﹣A的余弦值. 【解答】(Ⅰ)证明:∵ABEF为正方形,∴AF⊥EF. ∵∠AFD=90°,∴AF⊥DF, ∵DF∩EF=F, ∴AF⊥平面EFDC, ∵AF⊂平面ABEF, ∴平面ABEF⊥平面EFDC; (Ⅱ)解:由AF⊥DF,AF⊥EF, 可得∠DFE为二面角D﹣AF﹣E的平面角; 由ABEF为正方形,AF⊥平面EFDC, ∵BE⊥EF, ∴BE⊥平面EFDC 即有CE⊥BE, 可得∠CEF为二面角C﹣BE﹣F的平面角. 可得∠DFE=∠CEF=60°. ∵AB∥EF,AB⊄平面EFDC,EF⊂平面EFDC, ∴AB∥平面EFDC, ∵平面EFDC∩平面ABCD=CD,AB⊂平面ABCD, ∴AB∥CD, ∴CD∥EF, ∴四边形EFDC为等腰梯形. 以E为原点,建立如图所示的坐标系,设FD=a, 则E(0,0,0),B(0,2a,0),C(,0,a),A(2a,2a,0),
∴=(0,2a,0),=(,﹣2a,a),=(﹣2a,0,0)
设平面BEC的法向量为=(x1,y1,z1),则,
则,取=(,0,﹣1). 设平面ABC的法向量为=(x2,y2,z2),则, 则,取=(0,,4). 设二面角E﹣BC﹣A的大小为θ,则cosθ= ==﹣, 则二面角E﹣BC﹣A的余弦值为﹣.
【点评】本题考查平面与平面垂直的证明,考查用空间向量求平面间的夹角,建立空间坐标系将二面角问题转化为向量夹角问题是解答的关键. 5.如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=,EF交于BD于点H,将△DEF沿EF折到△D′EF的位置,OD′=.
