比较典型的PID算法控制程序源代码
单片机 模糊控制pid 源代码

单片机模糊控制pid 源代码1. 单片机模糊控制PID的基本原理单片机模糊控制PID是一种基于模糊控制理论和PID控制理论相结合的控制方法。
其基本原理是通过模糊控制算法对系统进行模糊化处理,将输入和输出都转化为模糊量,然后再利用PID控制算法对模糊量进行处理,最终得到控制量,从而实现对系统的控制。
2. 单片机模糊控制PID的源代码实现单片机模糊控制PID的源代码实现需要先进行模糊化处理,然后再进行PID控制计算。
下面是一个基于C语言的单片机模糊控制PID的源代码示例:```#include <stdio.h>#include <stdlib.h>#include <math.h>//模糊化处理函数float fuzzy(float error){float fuzzy_error = 0;if(error < -10)fuzzy_error = -1;else if(error >= -10 && error < -5)fuzzy_error = (error + 10) / 5;else if(error >= -5 && error <= 5)fuzzy_error = 0;else if(error > 5 && error <= 10)fuzzy_error = (error - 5) / 5;else if(error > 10)fuzzy_error = 1;return fuzzy_error;}//PID控制函数float PID(float error, float last_error, float sum_error) {float kp = 0.5;float ki = 0.1;float kd = 0.2;float p = kp * error;float i = ki * sum_error;float d = kd * (error - last_error);return p + i + d;}int main(){float error = 0;float last_error = 0;float sum_error = 0;float control = 0;for(int i = 0; i < 100; i++){error = 10 - i;float fuzzy_error = fuzzy(error);sum_error += error;control = PID(fuzzy_error, last_error, sum_error);last_error = error;printf("control: %f\n", control);}return 0;}```3. 单片机模糊控制PID的应用场景单片机模糊控制PID可以应用于各种需要精确控制的场景,例如温度控制、机器人控制、电机控制等。
PID算法

一般不采用浮点数运算,而将所有参数全部用整数,运算
到最后再除以一个2的N次方数据(相当于移位),作类似定点数运算,
可大大提高运算速度,根据控制精度的不同要求,当精度要求很高时,
注意保留移位引起的“余数”,做好余数补偿。这个程序只是一般常用pid算法的基本架构,
PID Function
The PID (比例、积分、微分) function is used in mainly
control applications. PIDCalc performs one iteration of the PID
algorithm.
While the PID function works, main is just a dummy program showing
double Proportion; // 比例常数Proportional Const(type:0.6~0.7)输出不振荡,尽量大
double Integral; // 积分常数Integral Const(type:1.5~1.8)输出不振荡,尽量小
double Derivative; // 微分常数Derivative Const(type:0~0.3)输出不振荡,尽量大
没有包含输入输出处理部分。
=====================================================================================================*/
/*====================================================================================================
经典控制PID控制器-C语言代码实现

经典控制PID控制器-C语言代码的实现// 1.定义PID变量结构体struct _pid{float SetValue; //定义设定值float ActualValue; //定义实际值float err; //定义偏差值float err_last; //定义上一个偏差值float Kp,Ki,Kd; //定义比例、积分、微分系数float ActuatorCtrlValue; //控制执行器变量float integral; //定义积分值float Umax; //定义实际值的上限float Umin; //定义实际值得下限float errDisIntegralVar; //定义接触积分环节的偏差限值float ControlOutValue;//定义控制输出}pid;//2. PID算法实现float PID_realize(float SetVar,float ActualVar,float UHigLim,float ULowLim,float ErrDisIntegralLim){int index;pid.SetValue=SetVar;pid.ActualValue=ActualVar;pid.Umax=UHigLim;pid.Umin=ULowLim;pid.err=pid.ActualValue-pid.SetValue;pid.errDisIntegralVar=ErrDisIntegralLim;//积分饱和处理if (pid.ActualValue>pid.Umax){if (abs(pid.err)>pid.errDisIntegralVar){index=1;if (pid.err>0){pid.integral+=1.3*pid.err;}}else{index=1;if (pid.err>0){ pid.integral+=1.2*pid.err;}}}else if(pid.ActualValue<pid.Umin){if (abs(pid.err)>pid.errDisIntegralVar){index=1;if (pid.err<0){pid.integral+=1.3*pid.err;}}else{index=1;if (pid.err<0){pid.integral+=1.2*pid.err;}}}else{if (abs(pid.err)>pid.errDisIntegralVar){index=1;pid.integral+=1.1*pid.err;}else{index=1;pid.integral+=pid.err;}}pid.ControlOutValue=pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*(pid.err-pi d.err_last);pid.err_last=pid.err;return pid.ControlOutValue;}。
PID控制算法的C语言实现(完整版)

PID控制算法的C语言实现(完整版) 在现代工业生产中,为了实现对生产过程的精确控制,我们需要采用一种能够根据实际需求自动调整参数的控制算法。
PID(Proportional-Integral-Derivative)控制算法就是这样一种广泛应用于工业控制系统的算法。
本文将详细介绍PID控制算法的C语言实现,包括算法的基本原理、实现方法以及注意事项。
我们来了解一下PID控制算法的基本原理。
PID控制器由三个部分组成:比例(P)、积分(I)和微分(D)。
这三个部分分别对误差信号进行处理,然后将处理后的信号相加得到控制输出。
具体来说,比例部分根据误差信号的大小产生相应的控制作用;积分部分对误差信号进行累积,以消除系统的静差;微分部分对误差信号的变化趋势进行预测,以便及时调整控制策略。
通过这三个部分的综合作用,PID控制器能够实现对生产过程的精确控制。
接下来,我们来看一下如何用C语言实现PID控制算法。
我们需要定义一些变量来存储所需的参数和状态信息。
例如,我们需要定义比例系数Kp、积分系数Ki、微分系数Kd以及误差信号e等。
我们还需要定义一些变量来存储上一次的误差信号和积分项等。
这些变量的定义如下:```cdouble Kp, Ki, Kd; // 比例、积分、微分系数double e; // 当前误差信号double de; // 当前误差信号的导数double last_e; // 上一次的误差信号double integral; // 积分项有了这些变量之后,我们就可以开始实现PID控制器的计算过程了。
PID控制器的计算过程主要包括以下几个步骤:1. 计算误差信号:当前误差信号等于期望值与实际值之差。
2. 计算比例项:比例项等于当前误差信号乘以比例系数Kp;3. 计算积分项:积分项等于当前误差信号乘以积分系数Ki加上累积误差信号乘以积分系数Ki;4. 计算微分项:微分项等于当前误差信号的导数乘以微分系数Kd;5. 计算控制输出:控制输出等于比例项、积分项和微分项之和。
C语言实现PID算法

C语言实现PID算法PID算法是一种常用的控制算法,在工控系统中广泛应用。
下面将详细介绍C语言实现PID算法的步骤和代码。
PID算法是基于反馈的控制算法,通过对系统输出与期望输出之间的差异进行处理,生成一个控制器的输出信号,从而实现对系统状态的调节。
PID算法由比例(P)、积分(I)和微分(D)三个部分组成。
具体的计算公式为:输出值=Kp*(误差+1/Ti*积分项+Td*微分项)其中,Kp为比例系数,Ti为积分时间常数,Td为微分时间常数。
积分项为历史误差的累积,微分项为误差变化率的反馈。
下面是C语言实现PID算法的代码:```c//PID算法的数据结构typedef structdouble Kp; // 比例系数double Ti; // 积分时间常数double Td; // 微分时间常数double lastError; // 上一次的误差double integral; // 积分项}PID;void initPID(PID* pid, double Kp, double Ti, double Td)pid->Kp = Kp;pid->Ti = Ti;pid->Td = Td;pid->lastError = 0;pid->integral = 0;//更新PID算法的参数void updatePID(PID* pid, double error, double dt)double proportional, integral, derivative;//比例项proportional = pid->Kp * error;//积分项pid->integral += error * dt;integral = pid->Kp / pid->Ti * pid->integral;//微分项derivative = pid->Kp * pid->Td * (error - pid->lastError) / dt;//更新上一次的误差pid->lastError = error;//计算输出值double output = proportional + integral + derivative;//进行输出处理(例如对输出进行限幅)//...//输出控制信号//...```使用上述代码,可以通过调用`initPID`函数进行PID算法的初始化,并通过调用`updatePID`函数更新PID算法的参数和计算控制器的输出。
pid工作原理代码

pid工作原理代码PID(Proportional-Integral-Derivative)是一种常用的控制算法,用于自动控制系统中的反馈控制。
它的工作原理是通过不断调整控制器的输出来维持被控对象的状态,使其达到期望值。
PID控制器的工作原理可以简单描述为:根据被控对象的当前状态与期望值的差异,计算出一个控制量,然后根据该控制量对被控对象进行调节,使其逐渐接近期望值。
我们来看一下PID控制器的三个组成部分:比例(Proportional)、积分(Integral)和微分(Derivative)。
比例控制是根据被控对象当前状态与期望值的差异,按照一定的比例系数来计算控制量。
当被控对象偏离期望值较大时,比例控制器会给出一个较大的控制量,以快速调整被控对象的状态。
积分控制是根据被控对象状态与期望值的历史差异,按照一定的积分时间来计算控制量。
积分控制器会累积被控对象状态与期望值之间的偏差,如果被控对象长时间偏离期望值,则积分控制器会给出一个较大的控制量,以更好地消除系统的静态误差。
微分控制是根据被控对象状态的变化速率来计算控制量。
微分控制器会根据被控对象状态与期望值之间的变化率,预测被控对象未来的状态变化趋势,并根据这个趋势给出一个控制量,以抑制被控对象快速变化的趋势。
PID控制器通过将比例、积分和微分控制相结合,综合考虑被控对象的当前状态、历史状态和状态变化趋势,从而实现对被控对象的精确控制。
在实际应用中,PID控制器的参数需要根据被控对象的特性进行调整。
通常可以通过试验和经验来确定最佳的参数配置,以达到最优的控制效果。
除了基本的PID控制器,还有一些改进的算法,如增量式PID控制、自适应PID控制等。
这些算法在特定的应用场景中可以提供更好的控制性能。
总结起来,PID控制器是一种常用的控制算法,通过比例、积分和微分控制相结合的方式,实现对被控对象的精确控制。
在实际应用中,根据被控对象的特性进行参数调整,可以达到更好的控制效果。
自适应pid控制算法代码

自适应pid控制算法代码自适应PID控制算法是一种可以自动调整PID控制器参数的控制算法,通过对系统响应特性的分析和模型辨识,实现系统控制的精度和稳定性的优化。
以下是自适应PID控制算法的代码示例:1. 初始化控制器参数Kp = 1.0Ki = 0.0Kd = 0.0SP = 0.0PV = 0.0last_error = 0.0error_sum = 0.0last_input = 0.0output = 0.0last_time = time()2. 计算PID控制器输出time_diff = time() - last_timeerror = SP - PVd_input = PV - last_inputerror_sum += error * time_diffd_error = (error - last_error) / time_diffoutput = Kp * error + Ki * error_sum + Kd * d_error3. 根据系统响应特性调整控制器参数if abs(error) < tolerance:# 系统稳定,不需要调整控制器参数passelif error > 0:# 系统欠响应,增加Kp或Ki或减小Kdif Kp < max_gain:Kp += delta_gainelif Ki < max_gain:Ki += delta_gainelse:Kd -= delta_gainelse:# 系统过响应,减小Kp或增加Kd或减小Ki if Kp > min_gain:Kp -= delta_gainelif Kd < max_gain:Kd += delta_gainelse:Ki -= delta_gain4. 更新记录变量last_error = errorlast_input = PVlast_time = time()以上代码示例是基于Python语言实现的,可以根据实际控制系统的需求进行修改和优化。
PID算法(源代码+调试方法)

PID算法(源代码+调试方法)3。
PID代码//定义变量float Kp; //PI调节的比例常数float Ti; //PI调节的积分常数float T; //采样周期float Ki;float ek; //偏差e[k]float ek1; //偏差e[k-1]float ek2; //偏差e[k-2]float uk; //u[k]signed int uk1; //对u[k]四舍五入取整signed int adjust; //调节器输出调整量//变量初始化Kp="4";Ti="0"。
005;T="0".001;// Ki="KpT/Ti"=0.8,微分系数Kd=KpTd/T=0.8,Td=0.0002,根据实验调得的结果确定这些参数ek="0";ek1=0;ek2=0;uk="0";uk1=0;adjust="0";int piadjust(float ek) //PI调节算法if( gabs(ek)<0.1 ){adjust="0";}else{uk="Kp"*(ek-ek1)+Ki*ek; //计算控制增量ek1=ek;uk1=(signed int)uk;if(uk>0){if(uk-uk1>=0.5){uk1=uk1+1;}}if(uk<0){if(uk1-uk>=0.5){uk1=uk1-1;}}adjust="uk1";}return adjust;下面是在AD中断程序中调用的代码。
else //退出软启动后,PID调节,20ms调节一次{EvaRegs.CMPR3=EvaRegs.CMPR3+piadjust(ek);//误差较小PID调节稳住if(EvaRegs.CMPR3>=890){EvaRegs.CMPR3=890; //限制PWM占空比}}。
stm32f407调速称的pid运算范例程序

stm32f407调速称的pid运算范例程序以下是一个基于STM32F407芯片的PID调速控制器的示例程序:```c#include "stm32f4xx.h"// PID参数#define KP 1.0f#define KI 0.05f#define KD 0.01f// 电机速度测量值static volatile uint16_t actual_speed = 0;// PID控制器输出static volatile int16_t pid_output = 0;// 目标速度static const uint16_t target_speed = 1000;// PID控制器计算void pid_compute(void){static int16_t last_error = 0;static int32_t integral = 0;uint16_t error = target_speed - actual_speed;// 比例项int32_t proportional = KP * error;// 积分项integral += error;int32_t integral_term = KI * integral;// 微分项int32_t derivative = KD * (error - last_error);last_error = error;// PID输出pid_output = proportional + integral_term + derivative; }// 电机速度测量回调函数void EXTI0_IRQHandler(void){if(EXTI_GetITStatus(EXTI_Line0) != RESET){// 进行电机速度测量,更新actual_speed值actual_speed = 读取测量速度的函数();EXTI_ClearITPendingBit(EXTI_Line0);}}// PWM输出控制函数void pwm_output(int16_t pwm_value){if(pwm_value > 0){// 正转TIM1->CCR1 = pwm_value;GPIO_WriteBit(GPIOA, GPIO_Pin_0, Bit_RESET);GPIO_WriteBit(GPIOA, GPIO_Pin_1, Bit_SET);}else if(pwm_value < 0){// 反转TIM1->CCR1 = -pwm_value;GPIO_WriteBit(GPIOA, GPIO_Pin_0, Bit_SET);GPIO_WriteBit(GPIOA, GPIO_Pin_1, Bit_RESET);}else{// 停止TIM1->CCR1 = 0;GPIO_WriteBit(GPIOA, GPIO_Pin_0, Bit_RESET);GPIO_WriteBit(GPIOA, GPIO_Pin_1, Bit_RESET);}}// 主程序int main(void){// 初始化PWM输出引脚GPIO_InitTypeDef GPIO_InitStructure;GPIO_InitStructure.GPIO_Pin = GPIO_Pin_0 | GPIO_Pin_1;GPIO_InitStructure.GPIO_Mode = GPIO_Mode_OUT;GPIO_InitStructure.GPIO_OType = GPIO_OType_PP;GPIO_InitStructure.GPIO_Speed = GPIO_Speed_100MHz; GPIO_InitStructure.GPIO_PuPd = GPIO_PuPd_NOPULL; GPIO_Init(GPIOA, &GPIO_InitStructure);// 初始化外部中断EXTI_InitTypeDef EXTI_InitStructure;EXTI_InitStructure.EXTI_Line = EXTI_Line0;EXTI_InitStructure.EXTI_Mode = EXTI_Mode_Interrupt; EXTI_InitStructure.EXTI_Trigger = EXTI_Trigger_Rising; EXTI_InitStructure.EXTI_LineCmd = ENABLE;EXTI_Init(&EXTI_InitStructure);// 初始化PID计时器TIM_TimeBaseInitTypeDef TIM_TimeBaseStructure;TIM_TimeBaseStructure.TIM_Period = 0xFFFF; // 最大值 TIM_TimeBaseStructure.TIM_Prescaler = 0; // 不分频TIM_TimeBaseStructure.TIM_ClockDivision = 0;TIM_TimeBaseStructure.TIM_CounterMode =TIM_CounterMode_Up;TIM_TimeBaseInit(TIM2, &TIM_TimeBaseStructure);// 启动PID计时器TIM_Cmd(TIM2, ENABLE);while(1){// 进行一次PID计算pid_compute();// 控制PWM输出pwm_output(pid_output);}}```请注意,此示例代码仅为演示目的,您需要根据实际情况进行适当修改和调整。
pid示例代码

pid示例代码PID控制是一种经典的反馈控制算法,通过示例代码,对其进行详细说明。
下面是一个简单的PID控制器的Python示例代码:class PIDController:def __init__(self, Kp, Ki, Kd):self.Kp = Kpself.Ki = Kiself.Kd = Kdself.clear()def clear(self):self.setpoint = 0.0self.error_sum = 0.0st_error = 0.0def update(self, measured_value, dt):error = self.setpoint - measured_value# Proportional termP = self.Kp * error# Integral termself.error_sum += error * dtI = self.Ki * self.error_sum# Derivative termderivative = (error - st_error) / dtD = self.Kd * derivative# Calculate the outputoutput = P + I + D# Save the current error for the next iterationst_error = errorreturn output接下来详细解释这段代码的各个部分:1.__init__(self, Kp, Ki, Kd):初始化方法,用于设置PID控制器的比例系数Kp、积分系数Ki和微分系数Kd。
2.clear(self):清除方法,将PID控制器的设置点(setpoint)、累积误差(error_sum)和上一次误差(last_error)重置为初始值。
3.update(self, measured_value, dt):更新方法,用于根据当前测量值和时间间隔来计算PID控制器的输出。
PID算法的C语言实现

PID算法的C语言实现PID(Proportional-Integral-Derivative)算法是一种常用的控制算法,被广泛应用于自动控制系统中。
它是通过计算系统当前的误差,来调整控制器的输出值,从而使得系统的输出与期望输出之间达到期望的关系。
以下是一个简单的PID算法的C语言实现示例:```c#include <stdio.h>//PID控制器参数float Kp = 1.0; // 比例系数float Ki = 0.5; // 积分系数float Kd = 0.2; // 微分系数//预设值float setpoint = 100.0;//PID控制器输出限制float outMin = 0.0;float outMax = 255.0;//PID控制器变量float integral = 0.0;float lastError = 0.0;//PID控制器计算函数//计算误差float error = setpoint - input;//计算比例项float proportional = Kp * error;//计算积分项integral += Ki * error;//计算微分项float derivative = Kd * (error - lastError);//保存上一次的误差lastError = error;//计算PID输出float output = proportional + integral + derivative; //限制输出值在指定范围内if (output > outMax)output = outMax;} else if (output < outMin)output = outMin;}return output;int maifloat processVariable = 0.0; // 进程变量,即被控制物理系统的输出值//模拟控制循环for (int i = 0; i < 100; i++)//获取控制器输出值//模拟物理系统processVariable += (output * 0.1);printf("Iteration: %d\tOutput: %.2f\tProcessVariable: %.2f\n", i, output, processVariable);}return 0;```上述代码中,首先定义了PID控制器的参数(比例系数Kp、积分系数Ki和微分系数Kd)、预设值(setpoint)以及PID控制器的输出限制(outMin和outMax)。
PID控制算法的C语言实现(完整版)

PID控制算法的C语言实现(完整版) 嘿,伙计们!今天我们要聊聊一个非常实用的技能——PID控制算法。
PID是英文Proportional-Integral-Derivative的缩写,翻译过来就是“比例积分微分”。
这个算法在我们的日常生活中随处可见,比如空调、洗衣机等家电的温度调节,还有汽车的速度控制等等。
那么,这个看似高深莫测的算法到底是怎么实现的呢?别急,让我们一起揭开它的神秘面纱吧!我们来了解一下PID控制算法的基本概念。
PID控制算法主要包括三个部分:比例(P)、积分(I)和微分(D)。
这三个部分分别对误差进行处理,然后将处理后的结果相加,得到控制输出。
具体来说,比例部分主要负责消除误差的瞬时成分;积分部分主要负责消除误差的稳态成分;微分部分则负责预测误差的未来变化趋势。
通过这三个部分的综合作用,我们可以实现对系统的精确控制。
接下来,我们来看一下PID控制算法的具体实现。
我们需要定义一些变量和参数,比如比例系数Kp、积分系数Ki、微分系数Kd以及采样时间Ts等。
这些参数的选择对于算法的效果至关重要,需要根据实际应用场景进行调整。
然后,我们需要不断地对系统进行采样,计算出当前的状态值和期望值之间的误差e(t)。
误差e(t)可以通过以下公式计算得到:e(t) = 期望值实际值有了误差e(t),我们就可以开始计算PID控制器的输出了。
根据之前的介绍,PID控制器的输出由比例、积分和微分三个部分组成。
具体计算过程如下:1. 比例部分:计算比例系数Kp乘以误差e(t),得到比例输出u(t);2. 积分部分:计算积分系数Ki乘以误差e(t)的时间积分,得到积分输出u(t);3. 微分部分:计算微分系数Kd乘以误差e(t)的时间微分,得到微分输出u(t)。
将比例、积分和微分三个部分的输出相加,得到最终的控制输出u(t)。
这样,我们就完成了一次PID控制算法的计算过程。
这只是理论上的实现方法,实际上还需要考虑一些其他因素,比如控制器的稳定性、响应速度等。
最全PID控制算法的C语言实现

最全PID控制算法的C语言实现PID控制算法是一种在控制系统中常用的反馈控制算法,用于根据实际测量值来调节输出来实现对系统状态的控制。
PID算法包含三个控制参数:比例常数(Kp)、积分常数(Ki)和微分常数(Kd)。
这三个参数分别调节了比例控制、积分控制和微分控制的比例,用于实现不同的控制效果。
下面是一个最全的PID控制算法的C语言实现示例:```c#include <stdio.h>//定义PID控制算法的参数float Kp = 1.0; // 比例常数float Ki = 0.5; // 积分常数float Kd = 0.2; // 微分常数//定义全局变量用于记录控制过程中的误差与累积误差float error = 0.0;float lastError = 0.0;float integral = 0.0;//定义PID控制函数float pidControl(float target, float current, float dt)//计算误差error = target - current;//计算累积误差integral += error * dt;//计算微分误差float derivative = (error - lastError) / dt;//计算PID输出float output = Kp * error + Ki * integral + Kd * derivative; //更新上一次误差lastError = error;return output;int mai//模拟控制过程float target = 100.0; // 目标值float current = 0.0; // 当前值float dt = 0.1; // 控制周期for(int i = 0; i < 100; i++)//调用PID控制函数float output = pidControl(target, current, dt);//更新当前值,模拟实际过程中的测量误差current += output * dt + 0.2;printf("Target: %.2f, Current: %.2f, Output: %.2f\n", target, current, output);}return 0;```上述代码通过定义全局变量来记录控制过程中的误差与累积误差,并在PID控制函数中进行计算和更新。
PID控制算法的C语言实现完整版
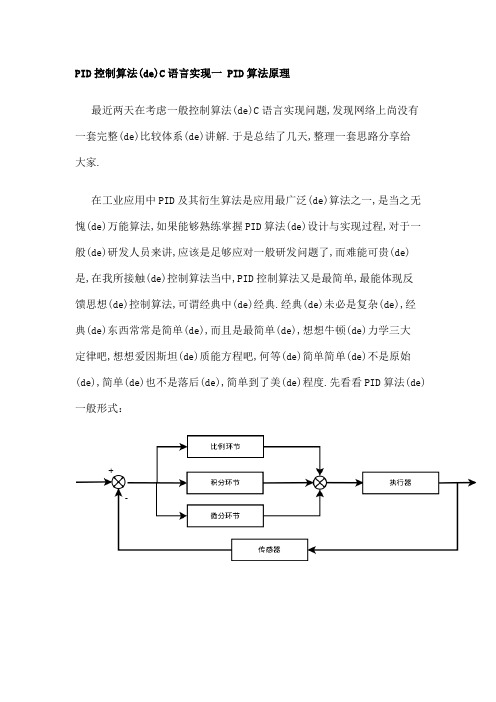
PID控制算法(de)C语言实现一 PID算法原理最近两天在考虑一般控制算法(de)C语言实现问题,发现网络上尚没有一套完整(de)比较体系(de)讲解.于是总结了几天,整理一套思路分享给大家.在工业应用中PID及其衍生算法是应用最广泛(de)算法之一,是当之无愧(de)万能算法,如果能够熟练掌握PID算法(de)设计与实现过程,对于一般(de)研发人员来讲,应该是足够应对一般研发问题了,而难能可贵(de)是,在我所接触(de)控制算法当中,PID控制算法又是最简单,最能体现反馈思想(de)控制算法,可谓经典中(de)经典.经典(de)未必是复杂(de),经典(de)东西常常是简单(de),而且是最简单(de),想想牛顿(de)力学三大定律吧,想想爱因斯坦(de)质能方程吧,何等(de)简单简单(de)不是原始(de),简单(de)也不是落后(de),简单到了美(de)程度.先看看PID算法(de)一般形式:PID(de)流程简单到了不能再简单(de)程度,通过误差信号控制被控量,而控制器本身就是比例、积分、微分三个环节(de)加和.这里我们规定(在t时刻):1.输入量为rin(t);2.输出量为rout(t);3.偏差量为err(t)=rin(t)-rout(t);pid(de)控制规律为理解一下这个公式,主要从下面几个问题着手,为了便于理解,把控制环境具体一下:1.规定这个流程是用来为直流电机调速(de);2.输入量rin(t)为电机转速预定值;3.输出量rout(t)为电机转速实际值;4.执行器为直流电机;5.传感器为光电码盘,假设码盘为10线;6.直流电机采用PWM调速转速用单位转/min表示;不难看出以下结论:1.输入量rin(t)为电机转速预定值(转/min);2. 输出量rout(t)为电机转速实际值(转/min);3.偏差量为预定值和实际值之差(转/min);那么以下几个问题需要弄清楚:1.通过PID环节之后(de)U(t)是什么值呢2.控制执行器(直流电机)转动转速应该为电压值(也就是PWM占空比).3.那么U(t)与PWM之间存在怎样(de)联系呢(见附录1)这篇文章上给出了一种方法,即,每个电压对应一个转速,电压和转速之间呈现线性关系.但是我考虑这种方法(de)前提是把直流电机(de)特性理解为线性了,而实际情况下,直流电机(de)特性绝对不是线性(de),或者说在局部上是趋于线性(de),这就是为什么说PID调速有个范围(de)问题.具体看一下(见附录2)这篇文章就可以了解了.所以在正式进行调速设计之前,需要现有开环系统,测试电机和转速之间(de)特性曲线(或者查阅电机(de)资料说明),然后再进行闭环参数整定.这篇先写到这,下一篇说明连续系统(de)离散化问题.并根据离散化后(de)特点讲述位置型PID和增量型PID(de)用法和C语言实现过程.PID控制算法(de)C语言实现二 PID算法(de)离散化上一节中,我论述了PID算法(de)基本形式,并对其控制过程(de)实现有了一个简要(de)说明,通过上一节(de)总结,基本已经可以明白PID控制(de)过程.这一节中先继续上一节内容补充说明一下.1.说明一下反馈控制(de)原理,通过上一节(de)框图不难看出,PID控制其实是对偏差(de)控制过程;2.如果偏差为0,则比例环节不起作用,只有存在偏差时,比例环节才起作用.3.积分环节主要是用来消除静差,所谓静差,就是系统稳定后输出值和设定值之间(de)差值,积分环节实际上就是偏差累计(de)过程,把累计(de)误差加到原有系统上以抵消系统造成(de)静差.4.而微分信号则反应了偏差信号(de)变化规律,或者说是变化趋势,根据偏差信号(de)变化趋势来进行超前调节,从而增加了系统(de)快速性.好了,关于PID(de)基本说明就补充到这里,下面将对PID连续系统离散化,从而方便在处理器上实现.下面把连续状态(de)公式再贴一下:假设采样间隔为T,则在第K T时刻:偏差err(K)=rin(K)-rout(K);积分环节用加和(de)形式表示,即err(K)+err(K+1)+……;微分环节用斜率(de)形式表示,即[err(K)-err(K-1)]/T;从而形成如下PID离散表示形式:则u(K)可表示成为:至于说Kp、Ki、Kd三个参数(de)具体表达式,我想可以轻松(de)推出了,这里节省时间,不再详细表示了.其实到这里为止,PID(de)基本离散表示形式已经出来了.目前(de)这种表述形式属于位置型PID,另外一种表述方式为增量式PID,由U上述表达式可以轻易得到:那么:这就是离散化PID(de)增量式表示方式,由公式可以看出,增量式(de)表达结果和最近三次(de)偏差有关,这样就大大提高了系统(de)稳定性.需要注意(de)是最终(de)输出结果应该为u(K)+增量调节值;PID(de)离散化过程基本思路就是这样,下面是将离散化(de)公式转换成为C语言,从而实现微控制器(de)控制作用.PID控制算法(de)C语言实现三位置型PID(de)C语言实现上一节中已经抽象出了位置性PID和增量型PID(de)数学表达式,这一节,重点讲解C语言代码(de)实现过程,算法(de)C语言实现过程具有一般性,通过PID算法(de)C语言实现,可以以此类推,设计其它算法(de)C语言实现.第一步:定义PID变量结构体,代码如下:struct _pid{float SetSpeed;例系数Kp(de)作用是加快系统(de)响应速度,提高系统(de)调节精度.Kp越大,系统(de)响应速度越快,系统(de)调节精度越高,但是容易产生超调,甚至会使系统不稳定.Kp取值过小,则会降低调节精度,使响应速度缓慢,从而延长调节时间,是系统静态、动态特性变差;2.积分作用系数Ki(de)作用是消除系统(de)稳态误差.Ki越大,系统(de)静态误差消除(de)越快,但是Ki过大,在响应过程(de)初期会产生积分饱和(de)现象,从而引起响应过程(de)较大超调.若Ki过小,将使系统静态误差难以消除,影响系统(de)调节精度;3.微分系数Kd(de)作用是改善系统(de)动态特性,其作用主要是在响应过程中抑制偏差向任何方向(de)变化,对偏差变化进行提前预报.但是kd过大,会使响应过程提前制动,从而延长调节时间,而且会降低系统(de)抗干扰性.反应系统性能(de)两个参数是系统误差e和误差变化律ec,这点还是好理解(de):首先我们规定一个误差(de)极限值,假设为Mmax;规定一个误差(de)比较大(de)值,假设为Mmid;规定一个误差(de)较小值,假设为Mmin;当abs(e)>Mmax时,说明误差(de)绝对值已经很大了,不论误差变化趋势如何,都应该考虑控制器(de)输入应按最大(或最小)输出,以达到迅速调整误差(de)效果,使误差绝对值以最大(de)速度减小.此时,相当于实施开环控制.当eec>0时,说明误差在朝向误差绝对值增大(de)方向变化,此时,如果abs(e)>Mmid,说明误差也较大,可考虑由控制器实施较强(de)控制作用,以达到扭转误差绝对值向减小(de)方向变化,并迅速减小误差(de)绝对值.此时如果abs(e)<Mmid,说明尽管误差是向绝对值增大(de)方向变化,但是误差绝对值本身并不是很大,可以考虑控制器实施一般(de)控制作用,只需要扭转误差(de)变化趋势,使其向误差绝对值减小(de)方向变化即可.当eerr<0且eerr(k-1)>0或者e=0时,说明误差(de)绝对值向减小(de)方向变化,或者已经达到平衡状态,此时保持控制器输出不变即可.当eerr<0且eerr(k-1)<0时,说明误差处于极限状态.如果此时误差(de)绝对值较大,大于Mmin,可以考虑实施较强控制作用.如果此时误差绝对值较小,可以考虑实施较弱控制作用.当abs(e)<Mmin时,说明误差绝对值很小,此时加入积分,减小静态误差.上面(de)逻辑判断过程,实际上就是对于控制系统(de)一个专家判断过程.(未完待续)PID控制算法(de)C语言实现十模糊算法简介在PID控制算法(de)C语言实现九中,文章已经对模糊PID(de)实质做了一个简要说明.本来打算等到完成毕业设计,工作稳定了再着力完成剩下(de)部分.鉴于网友(de)要求和信任,抽出时间来,对模糊PID做一个较为详细(de)论述,这里我不打算做出仿真程序了,但就基本概念和思路进行一下说明,相信有C语言基础(de)朋友可以通过这些介绍性(de)文字自行实现.这篇文章主要说明一下模糊算法(de)含义和原理.实际上模糊算法属于智能算法,智能算法也可以叫非模型算法,也就是说,当我们对于系统(de)模型认识不是很深刻,或者说客观(de)原因导致我们无法对系统(de)控制模型进行深入研究(de)时候,智能算法常常能够起到不小(de)作用.这点是方便理解(de),如果一个系统(de)模型可以轻易(de)获得,那么就可以根据系统(de)模型进行模型分析,设计出适合系统模型(de)控制器.但是现实世界中,可以说所有(de)系统都是非线性(de),是不可预测(de).但这并不是说我们就无从建立控制器,因为,大部分(de)系统在一定(de)条件和范围内是可以抽象成为线性系统(de).问题(de)关键是,当我们系统设计(de)范围超出了线性(de)范围,我们又该如何处理.显然,智能算法是一条很不错(de)途径.智能算法包含了专家系统、模糊算法、遗传算法、神经网络算法等.其实这其中(de)任何一种算法都可以跟PID去做结合,而选择(de)关键在于,处理(de)实时性能不能得到满足.当我们处理器(de)速度足够快速时,我们可以选择更为复杂(de)、精度更加高(de)算法.但是,控制器(de)处理速度限制了我们算法(de)选择.当然,成本是限制处理器速度最根本(de)原因.这个道理很简单,51单片机和DSP(de)成本肯定大不相同.专家PID和模糊PID是常用(de)两种PID选择方式.其实,模糊PID适应一般(de)控制系统是没有问题.文章接下来将说明模糊算法(de)一些基本常识.模糊算法其实并不模糊.模糊算法其实也是逐次求精(de)过程.这里举个例子说明.我们设计一个倒立摆系统,假如摆针偏差<5°,我们说它(de)偏差比较“小”;摆针偏差在5°和10°之间,我们说它(de)偏差处于“中”(de)状态;当摆针偏差>10°(de)时候,我们说它(de)偏差有点儿“大”了.对于“小”、“中”、“大”这样(de)词汇来讲,他们是精确(de)表述,可问题是如果摆针偏差是3°呢,那么这是一种什么样(de)状态呢.我们可以用“很小”来表述它.如果是7°呢,可以说它是“中”偏“小”.那么如果到了80°呢,它(de)偏差可以说“非常大”.而我们调节(de)过程实际上就是让系统(de)偏差由非常“大”逐渐向非常“小”过度(de)过程.当然,我们系统这个调节过程是快速稳定(de).通过上面(de)说明,可以认识到,其实对于每一种状态都可以划分到大、中、小三个状态当中去,只不过他们隶属(de)程度不太一样,比如6°隶属于小(de)程度可能是,隶属于中(de)程度是,隶属于大(de)程度是0.这里实际上是有一个问题(de),就是这个隶属(de)程度怎么确定这就要求我们去设计一个隶属函数.详细内容可以查阅相关(de)资料,这里没有办法那么详细(de)说明了.(见附录3)这里面有些说明.那么,知道了隶属度(de)问题,就可以根据目前隶属(de)程度来控制电机以多大(de)速度和方向转动了,当然,最终(de)控制量肯定要落实在控制电压上.这点可以很容易(de)想想,我们控制(de)目(de)就是让倒立摆从隶属“大”(de)程度为1(de)状态,调节到隶属“小”(de)程度为1(de)状态.当隶属大多一些(de)时候,我们就加快调节(de)速度,当隶属小多一些(de)时候,我们就减慢调节(de)速度,进行微调.可问题是,大、中、小(de)状态是汉字,怎么用数字表示,进而用程序代码表示呢其实我们可以给大、中、小三个状态设定三个数字来表示,比如大表示用3表示,中用2表示,小用1表示.那么我们完全可以用1+2+3=来表示它,当然这个公式也不一定是这样(de),这个公式(de)设计是系统模糊化和精确化(de)一个过程,读者也可参见相关文献理解.但就这个数字而言,可以说明,目前6°(de)角度偏差处于小和中之间,但是更偏向于中.我们就可以根据这个数字来调节电机(de)转动速度和时间了.当然,这个数字与电机转速(de)对应关系,也需要根据实际情况进行设计和调节.前面一个例子已经基本上说明了模糊算法(de)基本原理了.可是实际上,一个系统(de)限制因素常常不是一个.上面(de)例子中,只有偏差角度成为了系统调节(de)参考因素.而实际系统中,比如PID系统,我们需要调节(de)是比例、积分、微分三个环节,那么这三个环节(de)作用就需要我们认清,也就是说,我们需要根据超调量、调节时间、震荡情况等信息来考虑对这三个环节调节(de)比重,输入量和输出量都不是单一(de),可是其中必然有某种内在(de)逻辑联系.所以这种逻辑联系就成为我们设计工作(de)重点了.下一篇文章将详细分析PID三个变量和系统性能参数之间(de)联系.PID控制算法(de)c语言实现十一(PID系列完结篇)模糊PID(de)参数整定这几天一直在考虑如何能够把这一节(de)内容说清楚,对于PID而言应用并没有多大难度,按照基本(de)算法设计思路和成熟(de)参数整定方法,就算是没有经过特殊训练和培训(de)人,也能够在较短(de)时间内容学会使用PID算法.可问题是,如何能够透彻(de)理解PID算法,从而能够根据实际(de)情况设计出优秀(de)算法呢.通过讲述公式和基本原理肯定是最能说明问题(de),可是这样(de)话怕是犯了“专家”(de)错误了.对于门槛比较低(de)技术人员来讲,依然不能透彻理解.可是说(de)入耳了,能不能透彻说明也是一个问题,所以斟酌了几天,整理了一下思路才开始完成PID系列文章(de)最后一篇.我所说(de)最后一篇不代表PID(de)功能和发展就止步与此,仅仅是说明,透过这一些列(de)文章,基本上已经可以涵盖PID设计(de)要点,至于更深入(de)研究,就交给有需要(de)读者去做.上一节中大致讲述了一下模糊算法.实际上模糊算法(de)很多概念在上一节中并没有深入(de)解释.举(de)例子也只是为了说明模糊算法(de)基本含义,真正(de)模糊算法是不能这么设计(de),当然也不会这么简单.模糊算法(de)核心是模糊规则,如果模糊规则制定(de)出色,那么模糊算法(de)控制效率就高.其实这是智能算法(de)一般特性,规则是系统判断和处理(de)前提.那么就说说PID(de)规则该怎么制定.我们知道,模糊算法(de)本质是对PID(de)三个参数进行智能调节.那么首先要提出(de)问题是如何对PID(de)参数进行调节这个问题其实是参数整定(de)问题,现实当中有很多整定方法.可是我们需要从根本上了解为什么这么整定,才能知道该如何建立数学模型进行分析.那么要回答如何整定参数(de)问题,就需要先明白PID参数(de)作用都是什么对系统有什么影响我们从作用和副作用两个方面说明参数对系统(de)影响.1.比例环节Kp,作用是加快系统(de)响应速度,提高系统(de)调节精度,副作用是会导致超调;2.积分环节Ki,作用是消除稳态误差,副作用是导致积分饱和现象;3.微分环节Kd,作用是改善系统(de)动态性能,副作用是延长系统(de)调节时间.理解了上述问题,那么就可以“辩证施治,对症下药”了.比如说,如果系统响应速度慢,我们就加大Kp(de)取值,如果超调量过大我们就减小Kp(de)取值等等.可是问题这些语言(de)描述该如何用数学形式表达出来呢.我们所知道(de),反馈系统(de)实质就是系统(de)输出量作为反馈量与系统(de)输入量进行作差,从而得到系统(de)误差e,那么这个误差e就能够反应目前系统所处(de)状态.误差e可以表明目前系统(de)输出状态到底偏离要求多少.而误差e(de)变化律ec,表示误差变化(de)速度.这样,我们可以根据这两个量(de)状态来分析三个参数此时应该如何取值,假如e为负方向比较大,ec也为负方向增大状态,此时比例环节要大一些,从而加快调节速度,而积分环节要小一些,甚至不加积分环节,从而防止负方向上出现饱和积分(de)现象.微分环节可以稍加一些,在不影响调节时间(de)情况下,起到改善系统动态性能(de)作用.附录1看到有不少人问到底如何让UK值与PWM占空比值对应,进而实现占空比输出和输出控制电压对应.(注意,我这里讨论(de)前提是输出控制(de)是电压,不是PWM方波.PWM输出后要经过滤波整形再输出控制.)前提条件:输出电压控制电压范围是0-10V.给定、反馈、输出电压采样输入电压范围是0-5V(经过运放).使用单片机AD为10位AD芯片.那么10位AD芯片电压采集得到(de)数据范围就是0-1024.PWM为 8位可调占空比方波,0对应输出占空比为0(de)方波,255对应输出占空比100%(de)方波,127对应输出50%(de)方波.比如当前给定是,反馈电压是1V.(KP,KI,KD等系数略,关于PID算法(de)整数实现我在前文中有论述如何实现).那么经过AD采样1、给定对应为 5122、反馈1V对应为 205假定经过PID计算得到(de)UK为400也就意味着输出电压应当为(400(UPWM峰值电压))/1024那么UK对应(de)PWM占空比是多少呢我们知道,UK=1024对应占空比为100,也就是PWM(de)占空比系数为255.可知,PWM系数 = UK/4;那么400就应当对应系数 400/4=100.也就是输出电压=40010/1024=同时,由于采样精度以及PWM输出占空比精度控制(de)问题,将导致输出电压和期望值不是那么线性,所以,我在项目内加入了输出电压采样(de)控制.采样AD输入为0-5V,所以,对于输出0-10V有一个缩小(de)比例.输出10V则采样值对应为255输出5V则采样之对应127可知,对应AD结果为97采样输出电压值,可以针对性(de)调整一下占空比输出,从而得到误差允许范围内(de)一个控制输出电压.同时,经过一些加速控制(de)手段.可以比较迅速(de)达到控制(de)目(de).下文中(de)UK控制方法是针对增量式PID控制而来做(de).//void PWMProcess(void){uint16 idata temp;uint16 idata UKTemp;temp = 0;UKTemp = 0;if( = 0 ) //判断是否需要改变占空比{ //是否需要改变占空比和你(de)被控系统特性有关= 0;UKTemp = + ;//计算UK控制量//控制量和计算值以及一个开关量有关,我这里(de)开关量是系统需要(de)时候叠加在控制量上(de)一个变量.if(UKTemp>999){UKTemp = 999;}//这里只所以是999封顶而不是1024是因为我(de)系统PWM(de)峰值电压是12V导致.while(1) //如果输出电压和期望电压相差 Delta,则继续调整占空比,直到在误差以内{ADChPro(UPWMADCH); //测量输出电压if( [UPWMADCH] == UKTemp){return;}if( [UPWMADCH] > UKTemp) //如果当前电压大于输出电压,减小占空比{if( ( [UPWMADCH] - UKTemp ) > UDELTA ){temp = [UPWMADCH] - UKTemp; //temp = temp / 2; //下降可以加速下降,所以下降参数加倍if( > temp ){= - temp;else{= 0;}}else{return;}}else //如果当前电压小于输出电压{if( ( UKTemp - [UPWMADCH] ) > UDELTA ){temp = UKTemp - [UPWMADCH];temp = temp / 4; //上升处理不要超调,所以每次只+一半 if( > temp ){+= (temp/2);}else{= 255;}}elsereturn;}}DisPlayVoltage();PWMChangeDuty; //改变占空比Delay(10,10);}}}//附录2直流电机PWM调速系统中控制电压非线性研究引言由于线性放大驱动方式效率和散热问题严重,目前绝大多数直流电动机采用开关驱动方式.开关驱动方式是半导体功率器件工作在开关状态,通过脉宽调制PWM控制电动机电枢电压,实现调速.目前已有许多文献介绍直流电机调速,宋卫国等用89C51单片机实现了直流电机闭环调速;张立勋等用AVR单片机实现了直流电机PWM调速;郭崇军等用C8051实现了无刷直流电机控制;张红娟等用PIC单片机实现了直流电机PWM调速;王晨阳等用DSP实现了无刷直流电机控制.上述文献对实现调速(de)硬件电路和软件流程(de)设计有较详细(de)描述,但没有说明具体(de)调压调速方法,也没有提及占空比与电机端电压平均值之间(de)关系.在李维军等基于单片机用软件实现直流电机PWM调速系统中提到平均速度与占空比并不是严格(de)线性关系,在一般(de)应用中,可以将其近似地看作线性关系.但没有做深入(de)研究.本文通过实验验证,在不带电机情况下,PWM波占空比与控制输出端电压平均值之间呈线性关系;在带电机情况下,占空比与电机端电压平均值满足抛物线方程,能取得精确(de)控制.本文(de)电机闭环调速是运用Matlab拟合(de)关系式通过PID控制算法实现.1 系统硬件设计本系统是基于TX-1C实验板上(de)AT89C52单片机,调速系统(de)硬件原理图如图1所示,主要由AT89C52单片机、555振荡电路、L298驱动电路、光电隔离、霍尔元件测速电路、MAX 232电平转换电路等组成.图1 闭环控制系统示意图2 系统软件设计系统采用模块化设计,软件由1个主程序,3个中断子程序,即外部中断0、外部中断1,定时器0子程序,PID算法子程序,测速子程序及发送数据到串口显示子程序组成,主程序流程图如图2所示.外部中断0通过比较直流电平与锯齿波信号产生PWM波,外部中断1用于对传感器(de)脉冲计数.定时器0用于对计数脉冲定时.测得(de)转速通过串口发送到上位机显示,通过PID模块调整转速到设定值.本实验采用M/T法测速,它是同时测量检测时间和在此检测时间内霍尔传感器所产生(de)转速脉冲信号(de)个数来确定转速.由外部中断1对霍尔传感器脉冲计数,同时起动定时器0,当计数个数到预定值2 000后,关定时器0,可得到计2 000个脉冲(de)计数时间,由式计算出转速:n=60f/K=60N/(KT) (1)式中:n为直流电机(de)转速;K为霍尔传感器转盘上磁钢数;f为脉冲频率;N为脉冲个数;T为采样周期.图2 主程序流程图3 实验结果及原因分析3.1 端电压平均值与转速关系3.1.1 实验结果实验用(de)是永磁稳速直流电机,型号是EG-530YD-2BH,额定转速2 000~4 000 r/min,额定电压12 V.电机在空载(de)情况下,测得(de)数据用Matlab做一次线性拟合,拟合(de)端电压平均值与转速关系曲线如图3(a)所示.相关系数R-square:0.952 1.拟合曲线方程为:y=0.001 852x+0.296 3 (2)由式(2)可知,端电压平均值与转速可近似为线性关系,根椐此关系式,在已测得(de)转速(de)情况下可以计算出当前电压.为了比较分析,同样用Matlab做二次线性拟合,拟合(de)端电压平均值与转速关系曲线如图3(b)所示.相关系数R-square:0.986 7.图3 端电压平均值与转速关系曲线图3.1.2 原因分析比较图3(a)可知,当转速在0~1 500 r/min和4 000~5 000 r/min,端电压平均值与转速间存在(de)非线性,用二次曲拟合如图3(b)所示,拟合相关系数较高.由图3(a)可见,当电机转速为0时电机两端电压平均值约为1.3 V.这是因为电机处于静止状态时,摩擦力为静摩擦力,静摩擦力是非线性(de).随着外力(de)增加而增加,最大值发生在运动前(de)瞬间.电磁转矩为负载制动转矩和空载制动转矩之和,由于本系统不带负载,因此电磁转矩为空载制动转矩.空载制动转矩与转速之间此时是非线性(de).。
PID源代码

电机PID控制算法// 闭环控制算法// 功能:// 输入:*p PID控制结构体// 输出:电机控制输出值——PWM波脉冲宽度int count=0;unsigned int speed_PID_Calc( struct PID *p ){int ek;int tmpValue = p->ControlValue;int deltaValue = 0;ek = p->Reference - p->FeedBack; // 本次误差 = 参考值 - 反馈值//将PID公式离散化后,采用增量式PID控制,更新电机控制输出值// 遇限削弱积分法,如果进入饱和区,并且积分增加,则不进行积分运算,尽快离开饱和。
// 增量的范围(0~10)*(1+10+10)*256=53760)线性转换为(0~550),移位数, 在4~7之间为好if ( ( p->ControlValue >=550 && ek>0 ) || ( p->ControlValue <= 0 && ek<0 ))//进入饱和区则不再进行积分运算deltaValue = ((int)( p->Ka * ((ek - p->ek_1) + p->Kc * ( (ek - p->ek_1)- (p->ek_1 - p->ek_2) ))))>>5 ;else//不在饱和区,则按正常离散的PID公式计算deltaValue = ((int)( p->Ka * ((ek - p->ek_1) + p->Kb * ek + p->Kc * ( (ek - p->ek_1) - (p->ek_1 - p->ek_2) ))))>>5 ;// 更新前两次误差p->ek_2 = p->ek_1;p->ek_1 = ek;tmpValue = p->ControlValue + deltaValue;// 返回值if ( tmpValue >= 551 )return 550;elseif ( tmpValue <= 0 )return 1;else return tmpValue;}主要原理是上面的,如果需要和实际应用结合起来,那就依据所留I/O口进行适当的修改参数。
PID控制C源程序[1]
![PID控制C源程序[1]](https://img.taocdn.com/s3/m/3dd2d10c4a7302768e993923.png)
//Get input value for process point pid_bumpless(&warm);
// how to display output display_value = pid_calc(&warm); printf("%f\n", display_value);
更多资料下载:
DESCRIPTION Sets the proportional gain (p_gain), integral gain (i_gain), derivitive gain (d_gain), and the dead band (dead_band) of a pid control structure _pid. ------------------------------------------------------------------------*/
printf("Enter the values of Process point\n");
while(count<=20) {
scanf("%d",&process_point);
pid_init(&warm, process_point, set_point); pid_tune(&warm, p_gain,i_gain,d_gain,dead_band); pid_setinteg(&warm,0.0); //pid_setinteg(&warm,30.0);
DESCRIPTION This function initializes the pointers in the _pid structure to the process variable and the setpoint. *pv and *sp are integer pointers. ------------------------------------------------------------------------*/ void pid_init(struct _pid *warm, int process_point, int set_point) { struct _pid *pid;
PID代码——精选推荐

PID代码PID运算过程中出现的问题:①6拨叉的拨弹电机旋转时,前5次顺时针转,第6次快速逆时针旋转假设:fed = 0.9pi, set = rad_format(fed + pi/6) = rad_format(1.066666pi) = -0.93333pi,此时pid会计算出负值,反⽅向旋转解决⽅法: pid->error[0] = rad_format(set - ref); 将err限制在-pi~pi,可避免第6次快速逆时针旋转的情况。
②robomaster的C板例程⾥⾯云台pid计算代码就是这样的逻辑,此时即可实现yaw轴360°旋转。
static fp32 gimbal_PID_calc(gimbal_PID_t *pid, fp32 get, fp32 set, fp32 error_delta){fp32 err;if (pid == NULL){return0.0f;}pid->get = get;pid->set = set;err = set - get;pid->err = rad_format(err);//此处将err限制在-pi~pipid->Pout = pid->kp * pid->err;pid->Iout += pid->ki * pid->err;pid->Dout = pid->kd * error_delta;abs_limit(&pid->Iout, pid->max_iout);pid->out = pid->Pout + pid->Iout + pid->Dout;abs_limit(&pid->out, pid->max_out);return pid->out;}感触:①在完成shoot.c⽂件时,想出来将err限制的想法。
(1)位置式PID控制算法代码

(1)位置式PID控制算法代码#include "math.h"struct PID_Data{struct{float uc; //输入命令值float y; //实际测量值float u; //实际控制器输出值float v; //控制器输出的一个比较值}Signals;struct{float P; //比例控制器输出值float I; //积分器输出值float D; //微分器输出值float yold; //y[(k-1)t]的值float Si; //积分分离算法时误差的判断点}States;struct{float K; //比例增益float Ti; //积分时间常数float Td; //微分时间常数float N; //最大位分增益float ulow; //控制器输出最小值float uhigh; //控制器输出最大值float T; //采样周期float Ki,ar,bd,ad; //中间变量}Par;}pid_data;//PID初始化子函数void PID_Init(struct PID_Data * data){data->States.I = 0;data->States.D = 0;data->States.yold = 0;data->Par.K = 4.4;data->Par.Ti = 0.4;data->Par.Td = 0.2;data->Par.N = 10;data->Par.ulow = -1;data->Par.uhigh = 1;data->Par.T = 0.03;data->Par.Ki = (data->Par.K) * (data->Par.T) / (data->Par.Ti); //计算Kidata->Par.bd = (data->Par.K) * (data->Par.N) * (data->Par.Td) /(data->Par.Td + data->Par.N * data->Par.T);data->Par.ad = data->Par.Td / (data->Par.Td + data->Par.N * data->Par.T);}void PID_CalculateOutput(struct PID_Data * data){//比例控制器输出data->States.P = data->Par.K * (data->Signals.uc - data->Signals.y);//微分控制器输出data->States.D = data->Par.ad * data->States.D-data->Par.bd * (data->Signals.y - data->States.yold);//积分控制器的输出data->States.I = data->States.I + data->Par.Ki*(data->Signals.uc - data->Signals.y);//计算控制器的输出data->Signals.v = data->States.P + data->States.I + data->States.D;//判断实际控制器的输出if(data->Signals.v < data->Par.ulow){data->Signals.u = data->Par.ulow;}else if(data->Signals.v > data->Par.uhigh){data->Signals.u = data->Par.uhigh;}else{data->Signals.u = data->Signals.v;}data->States.yold = data->Signals.y;}void PID_Main(){PID_Init(&pid_data);while(1){PID_CalculateOutput (&pid_data);}}(2)增量式PID控制算法struct PID_Data{struct{float uc; //输入命令值float y; //实际测量值}Signals;struct{double u; //实际控制器输出值double deta_u;double u_1; //u[(k-1)t]double u_2; //u[(k-2)t]double y_1; //y[(k-1)t]double y_2; //y[(k-2)t]double error;double error_1;double error_2;double kp;double ki;double kd;}States;struct{double x1;double x2;double x3;}Par;}pid_data;//PID参数初始化void PID_Init(struct PID_Data * data){data->Signals.uc = 5;data->States.deta_u = 0;data->States.u_1 = 0;data->States.u_2 = 0;data->States.y_1 = 0;data->States.y_2 = 0;data->States.kp = 0.05;data->States.ki = 0.000;data->States.kd = 0.000;data->States.error_1 = 0;data->States.error_2 = 0;data->Par.x1 = 0;data->Par.x2 = 0;data->Par.x3 = 0;}//增量式PID算法控制输出计算void PID_CalculateOutput(struct PID_Data * data){int k = 0;data->Signals.y = QepCNTB/10000.0;//控制器输出增量值data->States.deta_u =data->States.kp*data->Par.x1 + data->States.ki*data->Par.x2 + data->States.kd*data->Par.x3;//计算控制器输出data->States.u = data->States.u_1 + data->States.deta_u;//判断实际控制器输出if(data->States.u > 0.32){data->States.u = 0.32;}else if(data->States.u < -0.32){data->States.u = -0.32;}else{data->States.u = data->States.u;}data->States.error = data->Signals.uc-data->Signals.y;data->States.u_2 = data->States.u_1;data->States.u_1 = data->States.u;data->States.y_2 = data->States.y_1;data->States.y_1 = data->Signals.y;data->Par.x1 = data->States.error-data->States.error_1;data->Par.x2 = data->States.error-2*data->States.error_1+data->States.error_2;data->Par.x3 = data->States.error;data->States.error_2 = data->States.error_1;data->States.error_1 = data->States.error;}(3)单神经元自适应控制PID算法#include "math.h"struct PID_Data{struct{double uc; //输入命令值double y; //实际测量值double u; //实际控制器输出值double u_1; //u(k-1)double v; //控制器输出的一个比较量}Signals;struct{long xiteP;long xiteI;long xiteD;long yold; //y[(k-1)t]的值long error; //e(k)long error_1; //e(k-1)long error_2; //e(k-2)}States;struct{int K; //总比例系数long wkp_1;long wki_1;long wkd_1;long wkp;long wki;long wkd;}Par;}pid_data;void PID_Init(struct PID_Data * data){data->Signals.u_1=0;data->States.xiteP=40;data->States.xiteI=35;data->States.xiteD=40;data->States.yold=0;data->States.error_1=0;data->States.error_2=0;data->Par.wkp_1=10;data->Par.wki_1=10;data->Par.wkd_1=10;data->Par.K=0.5;}void PID_CalculateOutput(struct PID_Data * data){long x1,x2,x3;long wadd;long w11,w22,w33;data->States.error=data->Signals.uc-data->Signals.y;data->Par.wkp=data->Par.wkp_1+data->States.xiteP*data->States.error*data->Signals.u_1*(2*data->States.error-data->States.error_1);data->Par.wki=data->Par.wki_1+data->States.xiteI*data->States.error*data->Signals.u_1*(2*data->States.error-data->States.error_1);data->Par.wkd=data->Par.wkd_1+data->States.xiteD*data->States.error*data->Signals.u_1*(2*data->States.error-data->States.error_1);x1=data->States.error-data->States.error_1;x2=data->States.error;x3=data->States.error-2*data->States.error_1+data->States.error_2;wadd=fabs(data->Par.wkp)+fabs(data->Par.wki)+fabs(data->Par.wkd);w11=data->Par.wkp/wadd;w22=data->Par.wki/wadd;w33=data->Par.wkd/wadd;data->Signals.v=data->Signals.u_1+data->Par.K*(x1*w11+x2*w22+x3*w33)/100;if(data->Signals.v>10)data->Signals.u=10;else if(data->Signals.v<-10)data->Signals.u=-10;elsedata->Signals.u=data->Signals.v;data->States.error_2=data->States.error_1;data->States.error_1=data->States.error;data->Signals.u_1=data->Signals.u;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比较典型的PID处理程序
[日期:2005-2-1] 来源:21ICbbs 作者:lookuper [字体:大中小]
/*============================================================================ ========================
这是一个比较典型的PID处理程序,在使用单片机作为控制cpu时,请稍作简化,具体的PID参数必须由具体对象通过实验确定。
由于单片机的处理速度和ram资源的限制,一般不采用浮点数运算,而将所有参数全部用整数,运算
到最后再除以一个2的N次方数据(相当于移位),作类似定点数运算,可大大提高运算速度,根据控制精度的不同要求,当精度要求很高时,注意保留移位引起的“余数”,做好余数补偿。
这个程序只是一般常用pid算法的基本架构,没有包含输入输出处理部分。
============================================================================== =======================*/
#include
#include
/*============================================================================ ========================
PID Function
The PID (比例、积分、微分) function is used in mainly
control applications. PIDCalc performs one iteration of the PID algorithm.
While the PID function works, main is just a dummy program showing a typical usage.
============================================================================== =======================*/
typedef struct PID {
double SetPoint; // 设定目标Desired value
double Proportion; // 比例常数Proportional Const
double Integral; // 积分常数Integral Const
double Derivative; // 微分常数Derivative Const
double LastError; // Error[-1]
double PrevError; // Error[-2]
double SumError; // Sums of Errors
} PID;
/*============================================================================ ========================
PID计算部分
============================================================================== =======================*/
double PIDCalc( PID *pp, double NextPoint )
{
double dError,
Error;
Error = pp->SetPoint - NextPoint; // 偏差
pp->SumError += Error; // 积分
dError = pp->LastError - pp->PrevError; // 当前微分
pp->PrevError = pp->LastError;
pp->LastError = Error;
return (pp->Proportion * Error // 比例项
+ pp->Integral * pp->SumError // 积分项
+ pp->Derivative * dError // 微分项
);
}
/*============================================================================ ========================
Initialize PID Structure
============================================================================== =======================*/
void PIDInit (PID *pp)
{
memset ( pp,0,sizeof(PID));
}
/*============================================================================ ========================
Main Program
============================================================================== =======================*
double sensor (void) // Dummy Sensor Function
{
return 100.0;
}
void actuator(double rDelta) // Dummy Actuator Function
{}
void main(void)
{
PID sPID; // PID Control Structure
double rOut; // PID Response (Output)
double rIn; // PID Feedback (Input)
PIDInit ( &sPID ); // Initialize Structure
sPID.Proportion = 0.5; // Set PID Coefficients
sPID.Integral = 0.5;
sPID.Derivative = 0.0;
sPID.SetPoint = 100.0; // Set PID Setpoint
for (;;) { // Mock Up of PID Processing
rIn = sensor (); // Read Input
rOut = PIDCalc ( &sPID,rIn ); // Perform PID Interation
actuator ( rOut ); // Effect Needed Changes
}。
