量子物理之氢原子的角向概率密度和径向概率密度
量子力学中的力学量3

的本征值方程
l 表征角动量的大小,称为角量子数 m 表征角动量在 z 轴的投影,称为磁量子数 简并:对应于同一个本征值,有一个以上的本征函数; 本征函数的数目称为简并度。 的本征值是 2l + 1 度 简并的 称 l = 0, 1, 2, 3, … 的态依次为 s, p, d, f, … 态。处于这 些态的粒子,依次称为 s, p, d, f, … 粒子
√
算符的对易关系(4/7)
力学量的完全集合:一组完全确定体系状态的力学量。集 合中力学量的数目一般等于体系自由度的数目 例:三维空间的自由粒子(不考虑自旋) 对易的力学量算符组: 共同本征函数:平面波函数 力学量的完全集合: 自由度:3
例:氢原子中的电子 对易的力学量算符组: 共同本征函数:氢原子的定态波函数 力学量的完全集合: 自由度:3
内部运动方程
√
三维氢原子(2/5)
解
分析
能级依赖于径向量子数 nr 和角量子数 l 的特殊组合 nr+l+1 能级 En 存在 l 简并,简并度 n2 不同于一般中心力场(三维空间几何对称性 O3 )的简并度 2l+1,反映了 -1/r 具有更高的对称性( O4 )
√
三维氢原子(3/5)
电离能:E 与电子基态能量之差
跃迁:电子由 En 跃迁到 Em
√
氢原子(4/5)
波函数(内部结构)
径向概率密度 :节点数目为 n-l-1
√
氢原子(5/5)
角向概率密度 :与 无关
√
厄密算符本征函数(1/3)
正交
14.10量子物理之氢原子的电子云图和概率密度等值面图

对于4d态电子,当m = 0时, 概率密度分为上下双峰,上下 还有两包,左右还有四双包。 彩色电子云图分上下左右八片, 上下的中间两片比较鲜艳。 概率密度的等值面是六个曲面,上下 四个是封闭曲面,中间两个是环面。
对于4d态电子,当m = ±1时,概 率密度分为对称的四峰和四包。 彩色电子云图分为四角对称的八片。 概率密度的等值面是 上下四个分立的环面。
对于4f态电子,当m =±2时,概率 密度分为上下左右四峰和左右两包。 彩色电子云图分上下左右 六片,上下四片比较鲜艳。 概率密度的等值面是三个曲面,上下 两个是封闭曲面,中间一个是环面。
对于4f态电子,当m = ±2时, 概率密度分为对称的四峰,与m = ±1的3d态电子类似。 彩色电子云图分为四角对称的四片。 概率密度的等值面是上下两个分 立的环面,其形状与3d态(m = ±1)电子的概率密度形状相似。
MATLAB可视化 大学物理学
第十四章结束 湖南大学物电院 子,当磁量子数m = 0时,概 率密度曲面形成上下双峰,峰顶比较圆。 上下两片电子云是双峰的投影, 等值线分别围绕着两个峰。 概率密度的等值面是两个分立的闭合曲 面,由此可知:上下两片电子云是分立。
对于2p态电子,当m = ±1时,概 率密度曲面分为左右双峰。 在彩色电子云图中,左右 两片电子云是双峰的投影。 概率密度的等值面是中间空心的环面, 左右两片电子云是绕z轴联成一体的。
对于4p态电子,当m = 0时,概率密度 除了上下双峰之外,还有四个波包, 比m = 0的3p态电子多两个波包。 彩色电子云图分为上下六片,相 邻的波峰和波包是分开的,等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上 下六个分立的闭合曲面。
对于4p态电子,当m = ±1时,概 率密度分为左右双峰和四个波包, 比m = ±1的4p态电子多一对波包。 彩色电子云图分为左右对称的六片。 概率密度的等值面是三个 空心的环面,环面层层相 套,三个环面是相似的。
用基础量子力学解释氢原子

用基础量子力学解释氢原子四川师范大学本科毕业论文用基本量子力学解释氢原子——量子力学与氢原子的相遇相知相交学生姓名黄兰院系名称物理与电子工程学院专业名称物理学班级2008级 2 班学号2008070219指导教师侯邦品四川师范大学教务处二○一二年五月用基本量子力学解释氢原子本科生:黄兰指导老师:侯邦品内容摘要:主要从以下几个方面来运用基本量子力学解释氢原子。
1、氢原子的能级和能量本征函数。
首先介绍在量子力学中的波函数,再利用薛定谔方程来导出氢原子的能量本征函数,最后再分析它的物理含义。
2、氢原子的四个量子数的物理意义。
解释它们其与氢原子的能级的关系。
3、径向波函数和角度波函数。
主要是得出径向波函数和角度波函数同时给出它的物理意义。
4、简并性破除与量子激光。
氢原子的内部结构中电子在原子中受到的磁场的作用所产生的正常塞曼效应和反常塞曼效应,以及可能引起的电子跃迁。
5、氢原子的Stark效应。
氢原子在外场的作用下表现的Stark 效应,这部分将作简单的介绍。
关键词:量子量子力学氢原子 stark效应Schr?dinger方程Using quantum mechanics to explain the physical phenomena in hydrogen atomsAbstract:we shall use quantum mechanics to explain the physicalphenomena in the hydrogen atoms as follows: 1, the energy eigenfunctions for hydrogen are obtained after introducing the wave function in quantum mechanics . 2 , physical significance of the four quantum numbers in the hydrogen atoms.Here we shall focus on the hydrogen atom electron spin and its physical meaning of the four quantum numbers . 3, the radial wave function and the angle wave function . Coming to the radial wave function and the angle of the wave function at the same time we will get its physical significance. 4, the degeneracy is broken by magnetic fields. The normal and the anomalous Zeeman effect induced by magnetic field are introduced. 5, Finally, the the Stark effect in the hydrogen atomis briefly introduced.Key Words:Quantum Quantum mechanics Hydrogen atoms stark effect Schr?dinger equation目录引言 (4)1氢原子的能级和能量本征函数 (6)1.1波函数与Shr?dinger方程 (6)1.1.1波函数 (6)1.1.2波函数的归一化 (6)1.2 Shr?dinger方程 (7)1.2.1不含时Shr?dinger方程 (7)1.2.2 Shr?dinger方程的一般形式 (7)1.3中心力场中角动量守恒与径向方程 (7)1.4氢原子的能级与本征函数波函数 (8)2氢原子四个量子数 (11)2.1氢原子的定态薛定谔方程 (11)2.2 三个量子数 (12)2.3电子的自旋与第四量子数 (15)2.3.1斯特恩--盖拉赫实验(1921年) (15)3径向波函数和角度波函数 (17)3.1径向几率分布 (17)3.2电子的几率密度随角度的变化 (19)4氢原子四个量子数 ................................................................ 错误!未定义书签。
半导体物理氢原子中电子的分布几率

4.6.2 电子的角向几率分布 在θ→θ+dθ,φ→φ+dφ立体角内找到电子的几
率
R无论何值,在(θφ)附近立体角dΩ中找到 电子的几率密度为 l,ml ,
l,ml
d
0 l,ml ,nd
R Y r0 n,l l,ml
无论θ、φ如何,电子在r→r+dr中的几率密度为: ρn,l 几率dωnl=ρnl·dr ρnl-径向几率密度
nl r dr
nlml d 0
2 R 2 2 2 r 2 sindrdd
0
nl (r)dr
2
d
0
0
|
Rnl (r)Ylm
( ,)
|2
r2
s in drd
Rnl 2 (r)r 2dr
2
d
0
0
|
Ylm
(
,
)
|2
s in d
Rnl2 (r)r2dr
n,l
r
dn,l
dr
Rn,l 2 * r 2
例,求氢原子中1s态电子的径向几率密度及极值
R1,0 r
3
a2 0
r
2 e a0
1,0 r
R nl r
r 2
2
r
a e3 2
r a0
0
2
4
a03
2r
r 2e a0
③l=1
m=0
Y2 10
3
4
cos2
θ=0 │Y10│2=3/4π 最大(z轴) θ=π/2 │Y10│2=0 最小
4.7 正常塞曼效应
量子物理之氢原子的电子云图和概率密度等值面图2
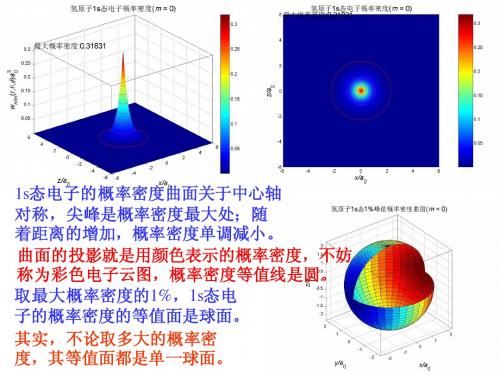
概率密度的等值面是三个曲面,上下 两个是封闭曲面,中间一个是环面。
对于4f态电子,当m = ±2时, 概率密度分为对称的四峰,与m = ±1的3d态电子类似。 彩色电子云图分为四角对称的四片。 概率密度的等值面是上下两个分 立的环面,其形状与3d态(m = ±1)电子的概率密度形状相似。
对于4f态电子,当m = ±3时, 概率密度分为左右双峰。 彩色电子云图分为左右两片。 概率密度的等值面是一个环 面,其形状与2p态(m = ±1) 电子的概率密度形状相似。
彩色电子云图分为左右对称的四片。
概率密度的等值面是两个空 心的环面,并且外环面套着 内环面,两个环面是相似的。
对于3d态电子,当m = 0时,概率 密度分为上下双峰和左右双包。
彩色电子云图分上下左右 四片,上下两片比较鲜艳。 概率密度的等值面是三个曲面,上下 两个是封闭曲面,中间一个是环面。
对于3d态电子,当m = ±1时, 概率密度分为对称的四峰。 彩色电子云图分为四角对称的四片。 概率密度的等值面是 上下两个分立的环面。
对于4p态电子,当m = 0时,概率密度 除了上下双峰之外,还有四个波包, 比m = 0的3p态电子多两个波包。 彩色电子云图分为上下六片,相 邻的波峰和波包是分开的,等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上 下六个分立的闭合曲面。
对于4p态电子,当m = ±1时,概 率密度分为左右双峰和四个波包, 比m = ±1的4p态电子多一对波包。
对于3p态电子,当m = 0时,概率密度 除了上下双峰之外,还有两个波包。 由于波包的概率密度相对于 波峰较小,所以颜色较暗。 彩色电子云图分为上下四片,相 邻的波峰和波包是分开的,等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上下四个分立的闭合曲面。
量子物理之氢原子的角向概率密度和径向概率密度

*{范例14.9} 氢原子的角向概率密度和径向概率密度
(2)当氢原子主量子数n一定时,各种角量子数 的径向概率密度随距离分布的规律是什么?
n阶拉盖尔 多项式为
(1)k (n!) 2 k L n ( x) x 2 k 0 (k !) (n k !
n
n + l 阶拉盖尔L ( x) (1) [(n l )!] xk n l 2 k 0 (k !) (n l k )! 多项式为
当 l = 1, m = 0时,氢 原子中p态 电子的角 向概率密 度wlm之一 呈纺锤状, 其剖面是 直立的双 纽线。
当l = 1,m = ±1时,氢原子中p态 电子的角向概率密度wlm之一呈轮 胎状,其剖面是横置的双纽线。
当 l = 2, m = 0时,氢 原子中d态 电子的角向 概率密度 wlm之一呈 带盘的纺锤 状,其剖面 是带叶的双 纽线。
在氢原子中取一个体积元dV = r2sinθdrdθdφ = r2drdΩ, dΩ = sinθdθdφ是立体角。 电子出现在距核为r,纬度为θ,经度为φ处的体积元dV中的概 率为wnlmdV = |ψnlm|2dV = |Rnl|2|Θlm|2|Φm|2dV。 电子出现在φ到φ + dφ之间的概率为wmdφ = |Φm|2dφ。 根据经度分布函数可知:|Φm|2是常量,因 此概率的角分布关于z轴具有旋转对称性。 电子出现在立体角 dΩ之内的概率为
*{范例14.9} 氢原子的角向概率密度和径向概率密度
(1)求氢原子角向概率密度,说明角向概率密度的变化规律。 (2)当氢原子主量子数n一定时,说明各种角量子数的径向概 率密度的分布规律。 为了简单起见,用m表示轨道磁量子数ml。
[解析](1)求氢原子薛定谔方程可得到电子的波函数ψnlm(r,θ,φ)。 每一组量子数(n,l,m),都有一组波函数描述一个确定的状态 ψnlm(r, θ, φ) = Rnl(r)Θlm(θ)Φm(φ), 这里,Φm(φ)是氢原子的经度分布函数,Θlm(θ)是纬 度分布函数,Rnl(r)是径向分布函数。 氢原子的经度 ( ) 1 exp(im ), m 2π 分布函数为
3-6量子力学对氢原子的描述jm

(r
2
dR dr
)[
2m
2
(E
e
2
4 0 r
2
)
r
2
]R 0(1)
径向方程
sin
(sin
Y
)
1 sin
2
Y
2
Y
(2) 角向方程
) 1
2
2 ˆ 2 角 动 量 算 符 : L [
1
sin
(sin
z
l 0 ml o
x
r a0
r
r a0
1s
r / a0
12
3p电子 (n=3,l=1) m=+1
l 1
z
3 p ( m l 1)
电子的空间几率:电子在核外不是按一定轨道运动,量子 力学不能断言电子一定出现在核外某确切位置,而只给出 电子在核外各处出现的概率,其形象描述——“电子云”
r sin
1 r r
2
(r
2
u r
)
1
2
r sin
(sin
u
)
1
2 2
u
2 2
r sin
2m
(E
e
2
4 0 r
)u 0
2
1 r r
2
(r
2
u r
)
1
2
r sin
(sin
u
)
磁 量 子 数 : m 0, 1, 2, 3..., l
Ylm ( , )= lm ( ) m ( )
原子物理学中的波函数:氢原子波函数和角动量

原子物理学中的波函数:氢原子波函数和角动量波函数是原子物理学中重要的概念之一,它用于描述原子或分子系统的量子状态。
在氢原子中,波函数被广泛应用于分析和理解氢原子的性质和行为。
此外,波函数还与角动量密切相关,它提供了有关原子的角动量信息。
在本文中,我们将详细探讨氢原子的波函数以及与之相关的角动量。
1. 波函数简介波函数是量子力学中描述自旋态和位置的函数。
它通常用希腊字母Ψ(Psi)表示,Ψ(r,t),其中r是位置向量,t是时间。
波函数描述了一个量子系统的全部信息,包括能量、动量、自旋等。
波函数的模的平方,|Ψ(r,t)|²,给出了在给定时刻在某个位置找到该量子系统的概率。
2. 氢原子波函数氢原子是原子物理学中最简单的原子,由一个质子和一个电子组成。
氢原子的波函数可以由薛定谔方程得到,它是描述量子力学体系的基本方程。
氢原子波函数相当复杂,主要由径向部分和角向部分构成。
2.1 径向波函数氢原子的径向波函数,记作R(r),描述了电子在原子核周围的运动方式。
径向波函数取决于主量子数n、角量子数l和磁量子数m。
主量子数n决定了能级,角量子数l确定了角动量大小,磁量子数m描述了角动量在空间中的方向。
径向波函数展示了电子和原子核之间的相互作用。
2.2 角向波函数氢原子的角向波函数,记作Y(theta, phi),展示了电子在球坐标系中的分布情况。
角向波函数取决于角量子数l和磁量子数m。
角向波函数是球谐函数的一种特殊形式,它给出了电子在不同方向上的概率分布。
3. 角动量与波函数在原子物理学中,角动量是一个重要的物理量,描述了物体旋转的性质。
角动量分为轨道角动量(L)和自旋角动量(S)两部分。
波函数与角动量之间存在紧密的联系。
3.1 定态波函数与角动量定态波函数是不随时间变化的波函数,描述了量子系统的固有状态。
在氢原子中,定态波函数与角动量之间具有简洁的关系。
根据定态波函数的表达式,能够计算出氢原子的角动量大小和方向。
氢原子的概率密度分布

0 4
0 3
( 1 . 5 )
0 2
0 ,
注意( 1 . 5 ) 式 给 出 的径 向概率 密度 是 指半 径 r 到r — r + d r 球 壳 内找 到 电 子 的概 率 , 而 并不 是 说在 半 径
为r 的球面上真实空 间的概率密度. 比如我们熟知 的玻 尔半径 , 是指在 l '  ̄ - C t 的球面上总的概率取极大值 ,
关键 词 : 氢原子 ; 概 率 密度 ; 数 值 计 算
中 图分类 号 : 04 1 3 . 1 文献 标 志码 : A 文章 编 号 : 1 6 7 3 —1 8 O 8 ( 2 0 1 5 ) 0 3 -0 0 1 0 -0 6
作为 量子 力 学 的一 个 经典 问题 , 氢 原 子一 直是 人们 关 注 的对 象 , 近 年来 关 于氢原 子 概率 密度 在 空 间分
0
= 2 ( r ) r 2 d r
( 1 . 2 )
粒子 的径 向函数为
e
( r 2 1 + ( r ) ,
1
( 1 . 3 )
式 中 , 是归 一化 常数 . 归一 化常 数为
, 3 、2
===
)
j 一
4
[ 收稿 日期 ] 2 0 1 5 - 0 5 - 1 1
{ ’ 。 {
图 1 . 2 分别取 n =2 , 0 ,n =2 , l =1 时 的 2 ( r) 。
【 实线 ) 和R 2( : r ) ( 点线 ) 分布 曲线 。
t ●
、
f \ 1 O }
而不是在 r = 0 的空间点上取极值. 而空间沿径向真实的概率密度值应该 由R : ( r ) 给出. 为了考察氢原子的
氢原子的量子理论作业含答案

氢原⼦的量⼦理论作业含答案第26章氢原⼦的量⼦理论习题 (初稿)⼀、填空题1. 氢原⼦的波函数可以写成如下形式(,,)()(,)l l nlm nl lm r R r Y ψθ?θ?=,请给出电⼦出现在~r r dr +球壳内的概率为___________,电⼦出现在(),θ?⽅向⽴体⾓d Ω内的概率为_______________。
2. 泡利不相容原理是指 ______________,原⼦核外电⼦排布除遵循泡利不相容原理外,还应遵循的物理规律是 __________ 。
3. 可以⽤⽤ 4 个量⼦数描述原⼦中电⼦的量⼦态,这 4 个量⼦数各称和取值范围怎样分别是:(1) (2) (3) (4) 。
4. 根据量⼦⼒学原理,如果不考虑电⼦⾃旋,对氢原⼦当n确定后,对应的总量⼦态数⽬为_ _个,当n 和l 确定后,对应的总量⼦态数⽬为__ __个5. 给出以下两种元素的核外电⼦排布规律:钾(Z=19): 铜(Z=29): ___ __6. 设有某原⼦核外的 3d 态电⼦,其可能的量⼦数有个,分别可表⽰为 ____________________________。
7. 电⼦⾃旋与其轨道运动的相互作⽤是何种性质的作⽤。
8. 类氢离⼦是指___________________,⾥德伯原⼦是指________________。
9. 在主量⼦数为n=2,⾃旋磁量⼦数为s=1/2的量⼦态中,能够填充的最⼤电⼦数是________。
10. 1921年斯特恩和格拉赫实验中发现,⼀束处于s 态的原⼦射线在⾮均匀磁场中分裂为两束,对于这种分裂⽤电⼦轨道运动的⾓动量空间取向量⼦化难于解释,只能⽤_________来解释。
⼆、计算题11. 如果⽤13.0 eV 的电⼦轰击处于基态的氢原⼦,则: (1)氢原⼦能够被激发到的最⾼能级是多少?(2)氢原⼦由上⾯的最⾼能级跃迁到基态发出的光⼦可能波长为多少? (3)如果使处于基态的氢原⼦电离,⾄少要多⼤能量的电⼦轰击氢原⼦?12. 写出磷的电⼦排布,并求每个电⼦的轨道⾓动量。
量子力学专题氢原子

3. 几率密度随角度变化
对 r ( 0∞) 积分
Wnlm (r, , )d | nlm (r, , ) |2 r 2dr sindd
Wlm ( , )d
Rnl(r)已归一
| Ylm ( , ) |2
d
|
0
Rnl (r )r 2dr
电子在 (θ,) 附近立体角
d =
sin d d 内的几率
| Ylm ( , ) |2 d
8r a04
(a0 r )e 2r / a0
0r
a0
a0Wn l(r)
0.6 0.5 0.4 0.3 0.2 0.1
Wn l (r) ~ r 的函数关系
[n,l]
[1,0]
Rn l (r) 的节点数 n r = n – – 1
[2,0]
[3,0]
[4,0]
03 6
9 12 15 18 21 24 27 30 33 36
2. 径向几率分布
1.氢原子的波函数 将上节给出的波函数取 Z=1,
μ用电子折合质量,就得到 当氢原子处于ψnlm(r,θ,)时,
氢原子的波函数:
电子在(r,θ,)点附近体积元
n1
对空间立体角积
d = r2sin drdd 内的几率
R e 2 r / a0 10 a03/ 2
n2
分后得到在半径 r r+dr 球壳内找到电子
r
(r 2
r
)
Lˆ2 2r 2
Ze2 r
R(r)Ylm ( , )
ER(r)Ylm ( , )
并令 R(r) = u(r) / r 代入上式得u(r)的方程
径向部分:
d 2u dr 2
15-9 氢原子的量子理论简介

nl表示电子态 表示电子态
如 1s 2p
3 角动量空间量子化和磁量子数 角动量空间量子化和磁量子数 空间量子化 当原子置于外磁场中, 当原子置于外磁场中 , 角动量 L 在空间 取向只能取一些特 定的方向, 在外磁场方 取向只能取一些 特 定的方向 , L在外磁场方 向的投影必须满足量子化条件
Lz = ml ℏ
7Q 2(7s) 6(7p) 10(7d) 14(7f) 18(7g) 22(7h) 26(7i) 98
(二)能量最小原理 原子系统处于正常态时, 原子系统处于正常态时,每个电子总是尽先 占据能量最低的能级。 占据能量最低的能级。
1 s → 2 s → 2 p → 3 s → 3 p → 4 s → 3d → 4 p → 5 s → 4 d → 5 p → 6 s → 4 f → 5d → 6 p
z
LZ
h h Lz = 0, , − 2π 2π
ℏ = h / 2π
L= 2ℏ
z
L ħ o ħ
第十五章
量子物理
4
空间量子化示意图 (ℏ ) z
(ℏ ) z 1 0
(ℏ ) 3
z
2 1
0
2 1
0
−1
l =1
L = 2ℏ
−1 −2
l=2
L = 6ℏ
−1
−2 −3
l=3
L = 12ℏ 对于一个给定的 l =0, ml=0, ± 1, ± 2,... ± l, 取向。 这时 L 在空间可以有 (2l+1) 个可能取向。
s=1/2 对所有的电子是相同的,不能成为区别 对所有的电子是相同的, 电子态的参数。 电子态的参数。
(2)自旋角动量在外磁场方向上只有两个分量 )自旋角动量在外磁场方向上只有两个分量: h S z = ms ms称为自旋磁量子数 2π
氢原子中电子的概率分布

1
对分布函数的一阶导数等于零求得
d dr
wnl
(r)
d dr
[r 2 Rn2l
(r)]
0
(r为最概然半径 )
可以证明,对于n-l-1 = 0的所有量子态的最概然半
径可以表示为
rn n2a , n 1, 2,
这与玻尔理论中各能级所对应的圆形轨道半径公式 完全一致 。
与无关,所以角度分布 函数wlm (, )是以z轴为
旋转对称轴的。
一些低量子数态 的角分布曲线。
3
立体角d = sin d d内发现电子的概率为
wlm (,)d
0
Rபைடு நூலகம்l
(r)Ylm (,)
2 r 2dr
sin
d
d
Ylm (,) 2 sin d d = Ylm (,) 2 d
式中wlm (, )是电子出现在相应立体角内的概率密
度,称为电子概率的角度分布函数。 2
在上式中,由于
Ylm(,) 2 Nl2m[Plm (cos)]2 e-im eim Nl2m[Plm (cos)]2
量子力学中的量子力学中的量子力学中的概率幅与概率密度

量子力学中的量子力学中的量子力学中的概率幅与概率密度量子力学中的概率幅与概率密度量子力学是一门研究微观世界的科学学科,它提供了一种描述和解释原子、分子以及更小尺度下的微观粒子行为的理论框架。
在量子力学中,我们经常会涉及到概率幅和概率密度这两个概念,它们在描述粒子行为和计算测量结果时非常重要。
一、概率幅在量子力学中,概率幅是描述粒子状态的数学量。
根据量子力学的基本原理,一个粒子的状态可以由一个波函数来描述,而概率幅就是波函数的系数。
具体来说,对于一个处于定态的量子系统,其波函数可以表示为一个无边界的平面波乘以一个相位因子,即Ψ(x, t) =Ae^(i(kx-ωt))。
在这个表达式中,A 是概率幅,表示粒子被观测到的概率振幅。
概率幅的模的平方就是概率密度。
也就是说,|A|^2 = P(x, t),其中P(x, t) 表示在时刻 t 处测量到粒子在位置 x 处的概率。
二、概率密度概率密度是描述粒子存在于不同位置的概率分布。
在量子力学中,我们关注的是粒子被观测到在某一位置上的概率,而不是具体的位置值。
因此,概率密度的概念在这里变得尤为重要。
根据量子力学的基本原理,粒子的概率密度可以通过概率幅的模的平方来计算。
具体来说,对于一个处于定态的量子系统,其概率密度可以表示为|Ψ(x, t)|^2 = |A|^2 = P(x, t)。
这个公式告诉我们,概率密度与概率幅的模的平方成正比。
概率密度在实际计算中起到了至关重要的作用。
它提供了一种将概率幅的数学抽象转化为实际可测量的概率的方式。
我们可以通过测量粒子位置的概率密度来得到粒子出现在不同位置上的概率信息。
三、应用实例概率幅和概率密度在量子力学中有着广泛的应用。
例如,在粒子穿过一个势垒的问题中,我们可以使用概率幅来描述粒子的传播行为,通过计算概率密度来确定粒子被观测到在不同位置上的概率。
另一个例子是电子的波粒二象性。
在电子的双缝实验中,我们可以观察到电子显示出波动和粒子性质。
p14_10氢原子的电子云图和概率密度等值面图1

氢原子中的电子在体积元dV之中出现的概率为
wnlmdV = |ψnlm|2dV = |Rnl|2|Θlm|2|Φm|2dV, 由于|Φm(φ)|2 = 1/2π,所以电子出 现在原子核周围的概率密度为
w n lm (r ,,) |R n l(r )|22 1 π | lm ()|2 r 1 2w n l(r )w lm ()
wlm(θ) = |Θlm(θ)|2/2π是角向概率密度, wnl = |Rnl(r)r|2是径向概率密度。
当主量子数和角量子数确定之后,径向概率密度就
20确21/7定/1 了,磁量子数不同,概率密度的分布就不同。
7
2021/7/1
8
2021/7/1
9
2021/7/1
10
2021/7/1
11
2021/7/1
12
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解,求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图? (2)氢原子的概率密度曲面是什么形状?彩色电子云图是 如何分布的?通过氢原子最大概率密度的百分之一的等 值曲面,说明概率密度的三维形状。
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解,求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图? (2)氢原子的概率密度曲面是什么形状?彩色电子云图是 如何分布的?通过氢原子最大概率密度的百分之一的等 值曲面,说明概率密度的三维形状。
26 氢原子量子论

赖曼系
开始电离,基态电子能量
E1 13.60eV
电离能
E 13.60eV
13.60 E (eV)
(4)电子跃迁时辐射光的频率
Em En 1 1 v Rc( 2 2 ) h n m
2.氢原子中电子的波函数和能级简并度 氢原子中电子的稳定状态由一组量子数 n, l, ml 决定, 即每组量子数确定一个波函数,描述一个稳定的状态。
l =1
2
l =2
三、氢原子能级与光谱
1.能级
离散值
n 4 3 2
巴耳末系
14
me 1 En 2 2 2 8 0 h n
4
帕邢系
0 0.89 1.51 3.39
(1)能级 En 随 n 的增加而增高; (2)能级间距随 n 增加而减小; (3)当
n E 0
d 2 2 ml 0 2 d
(3)
7
ml2 1 d d sin 2 0 (4) sin d d sin
解方程(3)
z
P
Ae ( ) ( 2 )
iml 由自然周期条件
O
N lm (l m)! 2l 1 (l m)! 4π
正交,归一
1 d 2 dR 2m e2 l (l 1) 2 R 0 r 2 E 2 r dr dr 4 0 r r
10
(1)
把一定的 l 值代入方程 (1) 求解,分两种情况求解: (1) E > 0,电子已不再受氢核的束缚,E 可取连续值。
L x , L y i L z L y , L z i L x 角动量算符的对易关系 L2 , L x L2 , L y L2 , L z 0 z , L x i L y L
近代3(氢原子 四个量子数)
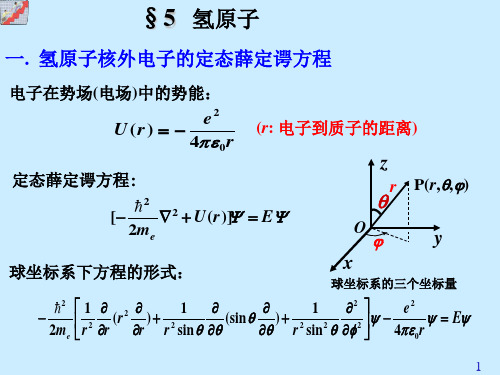
m l = 0、 ± 1、 ±2
LZ = 0,± ,±2
6
z ml=2 Lz = 2 O − − 2 ml=1 Lz = ml=0 Lz = 0 ml=-1 ml=-2
11
5.本征波函数
ψ n ,l ,m ( r ,θ , ϕ ) = Rn ,l ( r )Θ l ,m (θ )Φ m (ϕ ) = Rn ,l ( r )Yl ,m (θ , ϕ )
ν =
Ei − E j h
7
例:处于第三激发态的氢原子,可能发出的光谱线有多少?
其中可见光谱线几条?
解:第三激发态 n = 4
喇曼系3条 ——紫外线 六条谱线 巴耳末系2条 ——可见光 帕邢系1条 ——红外线 n=1 n=4 n=3 n=2
h = 6.63 × 10 −34 J ⋅ S hν = E n − E k − 13.6 En = n2
−
r a0
求电子处于半径为 a0 的球面内的概率P0。 解:概率密度P100=|ψ 100 |2,电子处于半径为r 、厚度 为dr 的壳层内的概率为 dP= P100 4πr2dr 在半径为 a0 的球面内的概率
P0 =
∫
a0
0
ψ 100 4π r 2 dr
4 e 3 a0
− 2r a0
2
=
∫
a0
0
d 2Φ 2 + m Φ =0 l 2 dϕ
ml 只能取整数,ml=0,±1, ±2 …
1, 2, 3,) −13.6 2 (eV ) (n = 能根据氢原子能级讨论氢原子光谱特征 En =
1 n
15
§6 电子的自旋 四个量子数
斯特恩-盖拉赫实验(1921年) e L • 轨道运动⇒磁矩 µ = −
§3 氢原子

Rl (r) ~ r s
从而有
Rl ~ r l,r (l1)
由此给出 l (r) r 0 rRl ~ rl1 或 r l
但对后一解,有界条件要求 s<3/2
但l的取值范围 l 0,1,2,
决定了这一解不符合要求,故去掉,所以
l (r)~ rl1
即
Rl ~ r l
64
7
(2)当r→∞时 方程化为
64
33
氢原子的激发态 2s态: n=2, l=0, m=0
E2s
-
2.179 10-18 22
-0.544810-15 J
2s
1 8a03
(2
-
r a0
)e-r / 2a0
1 4π
1 =
1 ( 2 - r ) e -r/a0
4
2a
3 0
a0
64
34
(a) 2s的 2 r
64 图及电子云
nr和l
但库仑场中,En只依赖于n,但是 n=nr+l+ 故 能级En除了对m简并,对l也是简1 并的。 所以库仑场具有更高的对称性。对称元素越多,
对称性越高,简并度越大
从径向方程的求解过程可以看出,这是
V (r) 1 导致的。
64
r
22
En 的本征函数 nlm (r,,) Rnl (r)Ylm (,)
为
V (r) e2
64
r
1
径向波函数满足方程
d 2 Rl dr 2
2 r
dRl dr
2
2
(E
Ze2 ) r
l(l 1)
r2
Rl
0
(0 r )
径向概率密度

径向概率密度径向概率密度是概率论和统计学中的一个重要概念,描述了随机变量与原点(或其他指定点)之间的距离的概率分布。
下面我将以人类的视角为出发点,用生活中的例子来解释径向概率密度的概念。
【引言】每个人都有自己的圈子,这个圈子可以是朋友、家人,也可以是工作、学习环境。
我们与这些不同的圈子之间的距离可以用径向概率密度来描述。
不同的圈子之间的距离远近不同,我们与某个圈子的距离越近,参与其中的概率就越大。
【圈子一:家庭】家庭是我们最亲近的圈子之一。
无论是在城市还是农村,家庭始终是我们的港湾。
在这个圈子里,我们与父母、兄弟姐妹之间的距离最近,参与其中的概率最大。
我们与父母之间的距离可以用径向概率密度来衡量,这个概率密度是一个钟形曲线,表明我们与父母的距离越近,概率越大,越远则概率越小。
在这个圈子中,我们与父母的交流、互动更加频繁,我们能够分享彼此的喜怒哀乐,共同度过美好的时光。
【圈子二:朋友】朋友是我们生活中的另一个重要圈子。
与家庭不同,我们可以选择朋友,而他们也选择与我们相处。
在这个圈子中,我们与不同朋友之间的距离也不尽相同。
与最好的朋友之间的距离最近,参与其中的概率最大。
这个概率密度也是一个钟形曲线,表明我们与最好的朋友之间的距离越近,概率越大,越远则概率越小。
在这个圈子中,我们可以相互倾诉、分享生活中的点滴,彼此之间建立起深厚的情感纽带。
【圈子三:工作】工作是我们每个人都必须面对的现实。
我们与同事、上司之间的距离也可以用径向概率密度来描述。
在这个圈子中,我们与最亲近的同事之间的距离最近,参与其中的概率最大。
这个概率密度同样是一个钟形曲线,表明与最亲近的同事之间的距离越近,概率越大,越远则概率越小。
在这个圈子中,我们与同事之间的合作、沟通更加频繁,我们可以共同解决问题,推动工作的进展。
【结语】径向概率密度不仅可以用于描述我们与不同圈子之间的距离,还可以帮助我们理解人际关系的复杂性。
通过了解不同圈子之间的距离分布,我们可以更好地把握人际关系的发展规律,建立更加紧密和谐的人际关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当l = 2,m = ±1时,氢原子中d态 电子的角向概率密度wlm之一呈双 钵状,其剖面是四叶玫瑰线。
当l = 2,m = ±2时,氢原子 中d态电子的角向概率密度 wlm之一呈轮胎状。
与l = 1,m = ±1的图形相 比,这种轮胎形状更扁。
当氢原子 角量子数 l = 3时, 磁量子数 m可取0, ±1,±2, ±3,角 向概率密 度如图所 示。
当m = 0 时,角 向概率 密度呈 带盘的 纺锤状;
当m = l时,角向概 率密度呈轮胎状;
当m是其他数整数时, 角向概率密度呈双钵状 和带盘的双钵状。
*{范例14.9} 氢原子的角向概率密度和径向概率密度
(2)当氢原子主量子数n一定时,各种角量子数 的径向概率密度随距离分布的规律是什么? [解析](2)氢原子薛定谔方 R (r ) M exp( Z r )( 2Z r )l L2l 1 ( 2Z r ) nl nl n l na0 na0 na0 程的径向分布函数为
n l
设k - 2l – 1 = i,即k = i + 2l + 1,可得 氢原子中的电子出现 i +1 2 n l 1 在r到dr之间的概率为 ( 1) [( n + l )!] 2l 1 i 2r2dr L n l ( x) x w d r = | R | nl nl (n l 1 i)!(2l +1+i)!i !
i 0
径向概率 w (r ) | R (r )r |2 M 2 [exp( Z r )( 2Z r )l L2l 1 ( 2Z r )r ]2 . nl nl nl n l 密度为 na0 na0 na0
当氢原子主量子数n为1时,角量子数l 只能取0,径向概率密度wnl随距离的增 加先增后减,其峰值出现在r = a0处。
n l k 2
k ! k n 对于幂函数y = xk, ( n) y k (k 1)...(k n 1) x k n x (k n)! 其n阶导数为
因此缔合拉盖 尔多项式为
d 2l 1 2l 1 Lnl ( x) k [(n+l )!]2 x k 2l 1 k 2l 1 k !( n l k )! (k 2l 1)!
wlmdΩ =
|Θlm|2|Φm|2dΩ
1 | lm ( ) |2 d 2π
根据纬度分布函数 w ( ) 1 | ( ) |2 1 [ N P|m| (cos )]2 . lm lm l 可得角向概率密度 lm 2π 2π
当氢原子角量子数为0时(l = 0),磁量子 数只能取0(m = 0),氢原子中s态电子的 角向概率密度wlm呈球状,其剖面是圆。
*{范例14.9} 氢原子的角向概率密度和径向概率密度
(2)当氢原子主量子数n一定时,各种角量子数 的径向概率密度随距离分布的规律是什么?
n阶拉盖尔 多项式为
(1)k (n!) 2 k L n ( x) x 2 k 0 (k !) (n k )!
n
n + l 阶拉盖尔L ( x) (1) [(n l )!] xk n l 2 k 0 (k !) (n l k )! 多项式为
Z为原子序数(氢原子Z = 1),a0是第一玻 2Z 3 (n l 1)! M nl ( ) 尔半径, Mnl是归一化常数(以区别Nlm) na0 2n[(n l )!]3 设 x
2Z r, na0
1 L2nl l ( x)
是缔合(连带)拉盖尔多项式。
下标n + l表示拉盖尔多项式阶数,即n + l阶拉盖尔多项 式Ln+l(x);上标2l + 1表示对Ln + l(x)求2l + 1阶导数。
当n = 4时,曲 线族如图所示。
当n = 5时,曲 线族如图所示。
当n = 6时,曲 线族如图所示。
当n = 7时,曲 线族如图所示。
比较这些图可知: 对于主量子数n来 说,角量子数l可取 0,1,...,n – 1, 共n个值,每条曲 线有n - l个峰。当l = n – 1时,峰值出 现在r = n2a0处,这 个峰比其他曲线的 最高峰还要高一些。
当主量子数n为2时,如果l为 0,径向概率密度有两个峰, 两峰之间有一个节点;如果l 为1,径向概率密度只有一 个峰,峰值出现在r = 4a0处。
当主量子数n为3时,如果l为 0,曲线有3个峰,随着距离 增加,一个峰比一个峰高, 曲线共有2个节点;如果l为1, 曲线有2个峰,1个节点;如 果l为2,曲线只有1个峰,峰 值出现在r = 9a0处。
*{范例14.9} 氢原子的角向概率密度和径向概率密度
(1)求氢原子角向概率密度,说明角向概率密度的变化规律。 (2)当氢原子主量子数n一定时,说明各种角量子数的径向概 率密度的分布规律。 为了简单起见,用m表示轨道磁量子数ml。
[解析](1)求氢原子薛定谔方程可得到电子的波函数ψnlm(r,θ,φ)。 每一组量子数(n,l,m),都有一组波函数描述一个确定的状态 ψnlm(r, θ, φ) = Rnl(r)Θlm(θ)Φm(φ), 这里,Φm(φ)是氢原子的经度分布函数,Θlm(θ)是纬 度分布函数,Rnl(r)是径向分布函数。 氢原子的经度 ( ) 1 exp(im ), m 2π 分布函数为
当 l = 1, m = 0时,氢 原子中p态 电子的角 向概率密 度wlm之一 呈纺锤状, 其剖面是 直立的双 纽线。
当l = 1,m = ±1时,氢原子中p态 电子的角向概率密度wlm之一呈轮 胎状,其剖面是横置的双纽线。
当 l = 2, m = 0时,氢 原子中d态 电子的角向 概率密度 wlm之一呈 带盘的纺锤 状,其剖面 是带叶的双 纽线。
1/ 2π 是归一化常数。
纬度分布函数为
lm ( ) Nlm Pl|m| (cos ),
Nlm (2l 1)(l | m |)! . 2(l | m |) !
Plm(x)是缔合(连带)勒让德 多项式,Nlm是归一化常数
*{范例14.9} 氢原子的角向概率密度和径向概率密度
在氢原子中取一个体积元dV = r2sinθdrdθdφ = r2drdΩ, dΩ = sinθdθdφ是立体角。 电子出现在距核为r,纬度为θ,经度为φ处的体积元dV中的概 率为wnlmdV = |ψnlm|2dV = |Rnl|2|Θlm|2|Φm|2dV。 电子出现在φ到φ + dφ之间的概率为wmdφ = |Φm|2dφ。 根据经度分布函数可知:|Φm|2是常量,因 此概率的角分布关于z轴具有旋转对称性。 电子出现在立体角 dΩ之内的概率为
