拓扑排序C语言代码
拓扑排序 代码 C语言

/* 用邻接表表示图的拓扑排序算法*/#include<stdio.h>#include<stdlib.h>#define MAXVEX 100#define TRUE 1#define FALSE 0typedef struct EdgeNode EdgeNode;typedef struct EdgeNode * PEdgeNode;typedef struct EdgeNode * EdgeList;struct EdgeNode{int endvex; /* 相邻顶点字段 */PEdgeNode nextedge; /* 链字段 */}; /* 边表中的结点 */typedef struct{/*VexType vertex;*/ /* 顶点信息 */EdgeList edgelist; /* 边表头指针 */} VexNode; /* 顶点表中的结点 */typedef struct{int n; /* 图的顶点个数 */VexNode vexs[MAXVEX];} GraphList;typedef struct{int vexsno[MAXVEX]; /* 顶点在顶点表中的下标值 */ /*VexType vexs[MAXVEX];*/ /* 顶点信息 */} Topo;/* 求出图中所有顶点的入度 *//* 方法是搜索整个邻接表 */void findInDegree(GraphList* g, int *inDegree){int i; PEdgeNode p;for (i = 0; i < g->n; i++)inDegree[i] = 0;for (i = 0; i < g->n; i++){p = g->vexs[i].edgelist;while (p){++inDegree[p->endvex];p = p->nextedge;}}}int topoSort(GraphList * paov, Topo * ptopo){EdgeList p;int i, j,k, nodeno = 0, top = -1;int indegree[MAXVEX];findInDegree(paov, indegree); /* 求出图中所有顶点的入度 */for (i = 0; i < paov->n; i++)if (indegree[i] == 0){ /* 将入度为零的顶点入栈 */indegree[i] = top;top = i;}while (top != -1){ /* 栈不为空 */j = top;top = indegree[top]; /* 取出当前栈顶元素 */ptopo->vexsno[nodeno++] = j;p = paov->vexs[j].edgelist; /* 取该元素边表中的第一个边结点 */ while (p){ /* 删除以该顶点为起点的边 */k = p->endvex;indegree[k]--;if (indegree[k] == 0){ /* 将新的入度为零的边入栈 */indegree[k] = top;top = k;}p = p->nextedge;}}if (nodeno < paov->n){ /* AOV网中存在回路 */printf("The aov network has a cycle\n");return FALSE;}return TRUE;}/* 边的插入算法*/void insert(GraphList* p,int a,int b){EdgeList pp;PEdgeNode temp;temp = (PEdgeNode)malloc(sizeof(EdgeNode)); temp->endvex = b;temp->nextedge = NULL;pp = p->vexs[a].edgelist;if (pp == NULL)p->vexs[a].edgelist = temp;else{while (pp->nextedge != NULL)pp = pp->nextedge;pp->nextedge = temp;}}/* 实例邻接表的构造 */GraphList * makeList(){GraphList* p;int i;p = (GraphList*)malloc(sizeof(GraphList)); p->n = 9;for (i = 0; i < p->n; i++)p->vexs[i].edgelist = NULL;insert(p, 0, 2);insert(p, 0, 7);insert(p, 1, 2);insert(p, 1, 3);insert(p, 1, 4);insert(p, 2, 3);insert(p, 3, 5);insert(p, 3, 6);insert(p, 4, 5);insert(p, 7, 8);insert(p, 8, 6);return p;}void main(){GraphList *p;Topo topo;int i;p = makeList();if (topoSort(p, &topo) == TRUE){printf("邻接表表示图的拓扑排序结果如下:\n"); for (i = 0; i < p->n; i++)printf("%d ", topo.vexsno[i]);}printf("\n");}欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
拓扑排序序列的步骤

拓扑排序序列的步骤拓扑排序是一种常用的有向图排序算法,它可以用来解决依赖关系的排序问题。
拓扑排序序列指的是通过拓扑排序算法得到的图中节点的一个线性排序。
在本文中,我们将深入探讨拓扑排序的步骤并给出实现示例。
一、拓扑排序简介拓扑排序适用于有向无环图(DAG)。
它的基本思想是将有向图中的节点按照依赖关系排序,使得每个节点的所有前驱节点都在它的前面。
如果存在环路,则无法进行拓扑排序。
二、拓扑排序步骤1. 初始化一个队列,用于储存入度为0的节点。
2. 遍历图中的所有节点,并统计每个节点的入度,将入度为0的节点加入队列。
3. 从队列中取出一个节点,将其输出,并将其所有邻接节点的入度减1。
4. 如果邻接节点的入度变为0,则将其加入队列。
5. 重复步骤3和步骤4,直到队列为空。
6. 如果输出的节点数量与图中节点的数量相同,则拓扑排序成功;否则,说明图中存在环路,无法进行拓扑排序。
示例代码如下:```pythondef topological_sort(graph):indegree = [0] * len(graph)queue = []# 统计每个节点的入度for node in graph:for adjacent in graph[node]: indegree[adjacent] += 1 # 将入度为0的节点加入队列 for i in range(len(indegree)):if indegree[i] == 0:queue.append(i)result = []while queue:node = queue.pop(0)result.append(node)# 将邻接节点的入度减1 for adjacent in graph[node]:indegree[adjacent] -= 1if indegree[adjacent] == 0: queue.append(adjacent) # 判断是否成功拓扑排序if len(result) == len(graph):return resultelse:return []# 图的邻接表表示graph = {0: [1, 2],1: [3, 4],2: [3],3: [],4: [3]}result = topological_sort(graph)if result:print("拓扑排序序列为:", result)else:print("图中存在环路,无法进行拓扑排序")```以上代码实现了拓扑排序的步骤,可以根据具体需求进行调用和扩展。
C语言常用算法程序汇总

C语言常用算法程序汇总C语言是一门广泛应用于计算机编程的语言,具有较高的效率和灵活性。
在C语言中,常见的算法程序包括排序算法、查找算法、递归算法等等。
以下是一些常用的C语言算法程序的汇总:1.排序算法:-冒泡排序:通过多次迭代比较相邻元素并交换位置,将最大的元素逐渐移动到正确的位置。
-插入排序:将待排序的元素与已排序的部分依次比较并插入到正确的位置。
-选择排序:每次从待排序的元素中选择最小的元素并与已排序的部分交换位置。
-快速排序:通过选择一个基准元素,将数组划分为两个子数组进行递归排序。
2.查找算法:-顺序查找:逐个比较数组中的元素,直到找到目标元素或到数组末尾。
-二分查找:通过比较目标元素与数组中间元素的大小,逐步缩小范围,直到找到目标元素。
-哈希查找:通过散列函数将目标元素映射到哈希表的索引位置进行查找。
3.递归算法:-阶乘:通过递归调用自身计算一个正整数的阶乘。
-斐波那契数列:通过递归调用自身计算斐波那契数列的第n个数。
-二叉树遍历:通过递归调用自身遍历二叉树的各个节点。
4.图算法:- 最短路径算法:如Dijkstra算法和Floyd算法,用于计算图中两个节点之间的最短路径。
-拓扑排序:通过对有向无环图进行排序,使得所有的边从排在前面的节点指向排在后面的节点。
- 最小生成树:如Prim算法和Kruskal算法,用于找到图中连接所有节点的最小子树。
5.动态规划:-最长公共子序列:通过寻找两个字符串中的最长公共子序列,解决字符串匹配问题。
-背包问题:通过动态规划解决在给定容量下选取物品使得总价值最大的问题。
-最大子序列和:通过动态规划解决一个数组中选取连续子序列使得和最大的问题。
以上只是一些C语言中常用的算法程序的汇总,实际上,还有很多其他的算法,如逆波兰表达式、霍夫曼编码、最小割等等。
通过学习这些算法,可以更好地理解C语言的应用和开发。
图基本算法拓扑排序(基于dfs)

图基本算法拓扑排序(基于dfs) 拓扑排序,是对有向⽆回路图进⾏排序,以期找到⼀个线性序列,这个线性序列在⽣活正可以表⽰某些事情完成的相应顺序。
如果说所求的图有回路的话,则不可能找到这个序列。
在⼤学数据结构课上,我们知道求拓扑排序的⼀种⽅法。
⾸先⽤⼀个⼊度数组保存每个顶点的⼊度。
在进⾏拓扑排序时,我们需要找到⼊度为0的点,将其存⼊线性序列中,再将其从图中删除(与它相关的边都删除,相邻的顶点的⼊度均减1),再重复上⾯的操作,直⾄所有的顶点都被找到为⽌。
如果不对每次找⼊度为0的顶点的⽅法进⾏处理,⽽直接去遍历⼊度数组,则该算法的时间复杂度为O(|V|2),如果使⽤⼀个队列来保存⼊度为0的顶点,则可以将这个算法的复杂度降为O(V+E)。
今天在算法导论上看了⽤dfs来求拓扑排序的算法,才发现其⾼深之处,膜拜之Orz…下⾯是算法导论的叙述: 本节说明了如何运⽤深度优先搜索,对⼀个有向⽆回路图(dag)进⾏拓扑排序。
对有向⽆回路图G=(V,E)进⾏拓扑排序后,结果为该图顶点的⼀个线性序列,满⾜如果G包含边(u, v),则在该序列中,u就出现在v的前⾯(如果图是有回路的,就不可能存在这样的线性序列)。
⼀个图的拓扑排序可以看成是图中所有顶点沿⽔平线排列⽽成的⼀个序列。
使得所有的有向边均从左指向右。
因此,拓扑排序不同于通常意义上的排序。
在很多应⽤中,有向⽆回路图⽤于说明时间发⽣的先后次序,下图1即给出⼀个实例,说明Bumstead教授早晨穿⾐的过程。
他必须先穿好某些⾐服,才能再穿其他⾐服(如先穿袜⼦后穿鞋),其他⼀些⾐服则可以按任意次序穿戴(如袜⼦和裤⼦),在图1中,有向边<u,v>表⽰⾐服u必须先于⾐服v穿戴。
因此,该图的拓扑排序给出了⼀个穿⾐的顺序。
图2说明了对该图进⾏拓扑排序后,将沿⽔平线⽅向形成⼀个顶点序列,使得图中所有有向边均从左指向右。
拓扑排序算法具体步骤如下:1、调⽤dfs_travel();2、在dfs_travel()每次调⽤dfs()的过程中,都记录了顶点s的完成时间,将顶点s按完成顺序保存在存放拓扑排序顺序的数组topoSort[]中。
数据结构之拓扑排序算法详解

数据结构之拓扑排序算法详解拓扑排序算法是一种常用于有向无环图(DAG)的排序算法,它可以将图中的顶点按照一定的顺序进行排序,使得图中任意一条有向边的起点在排序结果中都排在终点的前面。
在实际应用中,拓扑排序算法常用于解决任务调度、依赖关系分析等问题。
本文将详细介绍拓扑排序算法的原理、实现方法以及应用场景。
### 一、拓扑排序算法原理拓扑排序算法的原理比较简单,主要包括以下几个步骤:1. 从DAG图中选择一个入度为0的顶点并输出。
2. 从图中删除该顶点以及以该顶点为起点的所有有向边。
3. 重复步骤1和步骤2,直到图中所有顶点都被输出。
### 二、拓扑排序算法实现下面以Python语言为例,给出拓扑排序算法的实现代码:```pythondef topological_sort(graph):in_degree = {v: 0 for v in graph}for u in graph:for v in graph[u]:in_degree[v] += 1queue = [v for v in graph if in_degree[v] == 0] result = []while queue:u = queue.pop(0)result.append(u)for v in graph[u]:in_degree[v] -= 1if in_degree[v] == 0:queue.append(v)if len(result) == len(graph):return resultelse:return []# 测试代码graph = {'A': ['B', 'C'],'B': ['D'],'C': ['D'],'D': []}print(topological_sort(graph))```### 三、拓扑排序算法应用场景拓扑排序算法在实际应用中有着广泛的应用场景,其中包括但不限于以下几个方面:1. 任务调度:在一个任务依赖关系图中,拓扑排序可以确定任务的执行顺序,保证所有任务按照依赖关系正确执行。
详解C++实现拓扑排序算法

详解C++实现拓扑排序算法⽬录⼀、拓扑排序的介绍⼆、拓扑排序的实现步骤三、拓扑排序⽰例⼿动实现四、拓扑排序的代码实现五、完整的代码和输出展⽰⼀、拓扑排序的介绍拓扑排序对应施⼯的流程图具有特别重要的作⽤,它可以决定哪些⼦⼯程必须要先执⾏,哪些⼦⼯程要在某些⼯程执⾏后才可以执⾏。
为了形象地反映出整个⼯程中各个⼦⼯程(活动)之间的先后关系,可⽤⼀个有向图来表⽰,图中的顶点代表活动(⼦⼯程),图中的有向边代表活动的先后关系,即有向边的起点的活动是终点活动的前序活动,只有当起点活动完成之后,其终点活动才能进⾏。
通常,我们把这种顶点表⽰活动、边表⽰活动间先后关系的有向图称做顶点活动⽹(Activity On Vertex network),简称AOV⽹。
⼀个AOV⽹应该是⼀个有向⽆环图,即不应该带有回路,因为若带有回路,则回路上的所有活动都⽆法进⾏(对于数据流来说就是死循环)。
在AOV⽹中,若不存在回路,则所有活动可排列成⼀个线性序列,使得每个活动的所有前驱活动都排在该活动的前⾯,我们把此序列叫做拓扑序列(Topological order),由AOV⽹构造拓扑序列的过程叫做拓扑排序(Topological sort)。
AOV⽹的拓扑序列不是唯⼀的,满⾜上述定义的任⼀线性序列都称作它的拓扑序列。
⼆、拓扑排序的实现步骤1.在有向图中选⼀个没有前驱的顶点并且输出2.从图中删除该顶点和所有以它为尾的弧(⽩话就是:删除所有和它有关的边)3.重复上述两步,直⾄所有顶点输出,或者当前图中不存在⽆前驱的顶点为⽌,后者代表我们的有向图是有环的,因此,也可以通过拓扑排序来判断⼀个图是否有环。
三、拓扑排序⽰例⼿动实现如果我们有如下的⼀个有向⽆环图,我们需要对这个图的顶点进⾏拓扑排序,过程如下:⾸先,我们发现V6和v1是没有前驱的,所以我们就随机选去⼀个输出,我们先输出V6,删除和V6有关的边,得到如下图结果:然后,我们继续寻找没有前驱的顶点,发现V1没有前驱,所以输出V1,删除和V1有关的边,得到下图的结果:然后,我们⼜发现V4和V3都是没有前驱的,那么我们就随机选取⼀个顶点输出(具体看你实现的算法和图存储结构),我们输出V4,得到如下图结果:然后,我们输出没有前驱的顶点V3,得到如下结果:然后,我们分别输出V5和V2,最后全部顶点输出完成,该图的⼀个拓扑序列为:v6–>v1—->v4—>v3—>v5—>v2四、拓扑排序的代码实现下⾯,我们将⽤两种⽅法来实现我么的拓扑排序:1.Kahn算法2.基于DFS的拓扑排序算法⾸先我们先介绍第⼀个算法的思路:Kahn的算法的思路其实就是我们之前那个⼿动展⽰的拓扑排序的实现,我们先使⽤⼀个栈保存⼊度为0 的顶点,然后输出栈顶元素并且将和栈顶元素有关的边删除,减少和栈顶元素有关的顶点的⼊度数量并且把⼊度减少到0的顶点也⼊栈。
使用C#代码实现拓扑排序

使⽤C#代码实现拓扑排序0.参考资料尊重他⼈的劳动成果,贴上参考的资料地址,本⽂仅作学习记录之⽤。
1.介绍⾃⼰之前并没有接触过拓扑排序,顶多听说过拓扑图。
在写前⼀篇⽂章的时候,看到 Abp 框架在处理模块依赖项的时候使⽤了拓扑排序,来确保顶级节点始终是最先进⾏加载的。
第⼀次看到觉得很神奇,看了⼀下维基百科头也是略微⼤,⾃⼰的⽔平也是停留在冒泡排序的层次。
ヽ(≧□≦)ノ看了第⼆篇参考资料才⼤致了解,在此记录⼀下。
2.原理先来⼀个基本定义:在图论中,拓扑排序(Topological Sorting)是⼀个有向⽆环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。
且该序列必须满⾜下⾯两个条件:每个顶点出现且只出现⼀次。
若存在⼀条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前⾯。
有向⽆环图(DAG)才有拓扑排序,⾮DAG图没有拓扑排序⼀说。
例如,有⼀个集合它的依赖关系如下图:可以看到他有⼀个依赖关系:Module D 依赖于 Module E 与 Module B 。
Module E 依赖于 Module B 与 Module C 。
Module B 依赖于 Module A 与 Module C 。
Module C 依赖于 Module A 。
Module A ⽆依赖。
这个就是⼀个 DAG 图,我们要得到它的拓扑排序,⼀个简单的步骤如下:从 DAG 图中选择⼀个没有前驱的顶点并输出。
从 DAG 图中删除该顶点,以及以它为起点的有向边。
重复步骤 1、2 直到当前的 DAG 图为空,或者当前图不存在⽆前驱的顶点为⽌。
按照以上步骤,我们来进⾏⼀个排序试试。
最后的排序结果就是:Module D -> Module E -> Module B -> Module C -> Module Aemmmm,其实⼀个有向⽆环图可以有⼀个或者多个拓扑序列的,因为有的时候会存在⼀种情况,即以下这种情况:这个时候你就可能会有这两种结果D->E->B->C->F->AD->E->B->F->C->A因为 F 与 C 是平级的,他们初始化顺序即便不同也没有什么影响,因为他们的依赖层级是⼀致的,不过细⼼的朋友可能会发现这个顺序好像是反的,我们还需要将其再反转⼀次。
C语言常用算法大全

C语言常用算法大全1.排序算法-冒泡排序:依次比较相邻的两个元素,如果顺序不对则交换,每轮找出一个最大或最小的元素-选择排序:从未排序的元素中选择最小或最大的放到已排序的最后,以此类推-插入排序:将未排序的元素插入到已排序的合适位置,从后向前进行比较和交换-快速排序:选择一个基准元素,将小于基准元素的放在左边,大于基准元素的放在右边,然后对左右两边递归地进行快速排序-归并排序:将待排序的序列不断划分为左右两部分,分别排序后再将排序好的左右两部分按顺序合并-堆排序:构建大顶堆,将堆顶元素与末尾元素交换,然后重新调整堆,重复这个过程直到排序完成2.查找算法-顺序查找:从给定的元素序列中逐个比较,直到找到目标元素或遍历完整个序列-二分查找:对于有序序列,在序列的中间位置比较目标元素和中间元素的大小关系,通过每次缩小一半的范围来查找目标元素-插值查找:根据目标元素与有序序列的最小值和最大值的比例推测目标元素所在的位置,然后递归地进行查找-斐波那契查找:根据斐波那契数列的性质来确定目标元素所在的位置,然后递归地进行查找3.图算法-深度优先(DFS):从图的一些顶点出发,依次访问其未被访问过的邻接顶点,直到所有顶点都被访问过为止-广度优先(BFS):从图的一些顶点出发,逐层遍历图的顶点,直到所有顶点都被访问过为止- 最小生成树算法:Prim算法和Kruskal算法,用于找到连接图中所有顶点的最小权值边,构成一棵包含所有顶点的生成树- 最短路径算法:Dijkstra算法和Floyd-Warshall算法,用于找到图中两个顶点之间的最短路径-拓扑排序:用于有向无环图(DAG)中的顶点排序,确保排序后的顶点满足所有依赖关系-关键路径算法:找出网络中的关键路径,即使整个工程完成的最短时间4.字符串算法- KMP算法:通过预处理模式串构建next数组,利用next数组在匹配过程中跳过一部分不可能匹配的子串- Boyer-Moore算法:从模式串的末尾开始匹配,利用坏字符和好后缀规则进行跳跃匹配- Rabin-Karp算法:利用哈希函数对主串和匹配串的子串进行哈希计算,然后比较哈希值是否相等- 字符串匹配算法:BM算法、Shift-And算法、Sunday算法等,用于寻找模式串在主串中的出现位置5.动态规划算法-最长公共子序列(LCS):用于寻找两个序列中最长的公共子序列-最长递增子序列(LIS):用于寻找给定序列中最长的递增子序列-0-1背包问题:将有限的物品放入容量为C的背包中,使得物品的总价值最大-最大子数组和:用于求解给定数组中连续子数组的最大和-最大正方形:在给定的0-1矩阵中,找出只包含1的最大正方形的边长这些算法是在C语言中常用的算法,它们涵盖了排序、查找、图、字符串和动态规划等多个领域。
数据结构C语言版_拓扑排序

}
}
p=p->nextarc;
}
printf("\n");
}
}
// 求顶点的入度,算法7.12、7.13调用
void FindInDegree(ALGraph G,int indegree[])
exit(0); // 存储分配失败
(*S).top = (*S).base; // 栈底与栈顶相同表示一个空栈
(*S).stacksize = STACK_INIT_SIZE;
return 1;
}
// 若栈S为空栈(栈顶与栈底相同的),则返回1,否则返回0。
int StackEmpty(SqStack S)
{
int i,j,k;
int w; // 权值
VertexType va,vb;
ArcNode *p;
printf("请输入图的类型(有向图:0,有向网:1,无向图:2,无向网:3): ");
scanf("%d",&(*G).kind);
printf("请输入图的顶点数和边数:(空格)\n");
break;
case DN: printf("有向网\n");
break;
case AG: printf("无向图\n");
break;
case AN: printf("无向网\n");
}
printf("%d个顶点:\n",G.vexnum);
C语言常用的入门算法

C语言常用的入门算法C语言是一门广泛应用于计算机科学和软件开发领域的编程语言。
作为一门通用的编程语言,C语言提供了丰富的算法和数据结构库,使得开发人员能够解决各种不同类型的问题。
下面是C语言入门算法的一些常见示例:1.排序算法:-冒泡排序:通过不断比较相邻的元素,并交换它们的位置来排序。
-插入排序:将未排序的元素逐一插入已排序的列表中。
-选择排序:通过重复找到最小的元素并将其放置在已排序序列的末尾来排序。
-快速排序:通过选择一个基准元素,将列表划分成较小和较大的两部分,然后对其进行递归排序。
-归并排序:将列表分成较小的子列表,然后逐个合并这些子列表。
2.查找算法:-顺序查找:逐个比较列表中的元素,直到找到匹配的元素为止。
-二分查找:在已排序的列表中通过递归或循环的方式,将待查找的元素与中间元素进行比较,以确定它可能在哪一半中。
-哈希表:通过散列函数将元素映射到一个较小的固定大小的数组(哈希表)中,并通过索引快速查找。
3.字符串算法:-字符串长度:使用循环逐个字符遍历,直到遇到字符串结束符'\0'为止,统计字符个数。
-字符串比较:逐个字符比较两个字符串的对应位置,直到遇到不相等的字符或字符串结束符。
-字符串拼接:将一个字符串的字符逐个复制到另一个字符串的末尾,直到遇到字符串结束符'\0'。
-子字符串匹配:在一个较长的字符串中查找一个较短的子字符串,常用的算法有朴素算法和KMP算法。
4.数值算法和运算:-求和、平均值、最大/最小值:循环遍历列表,累加求和,计算平均值,找出最大/最小值。
-阶乘和斐波那契数列:使用循环或递归计算给定数字的阶乘和斐波那契数列。
-幂运算和开方:通过循环或递归计算给定数字的幂和开方。
- 线性方程求解:求解形如ax + b = 0的一元线性方程。
5.图算法:-广度优先(BFS):通过遍历图的邻居节点来逐层扩展区域,通常用于查找最短路径。
-深度优先(DFS):通过遍历图的邻居节点来递归到达所有可能的节点,通常用于查找所有路径、拓扑排序等。
拓扑排序简单的例子

拓扑排序简单的例子拓扑排序是一种对有向无环图(Directed Acyclic Graph, DAG)进行排序的方法,它可以帮助我们确定图中所有节点的线性顺序。
拓扑排序在实际应用中非常有用,例如任务调度、编译顺序等场景。
下面将从不同的角度给出10个简单的拓扑排序的例子,以展示其用途和特点。
标题1:拓扑排序概述拓扑排序是一种对有向无环图进行排序的方法,它可以帮助我们确定图中所有节点的线性顺序。
拓扑排序的基本原理是通过不断删除入度为0的节点,直到所有节点都被删除或没有入度为0的节点为止。
拓扑排序可以应用于各种实际场景,例如任务调度、编译顺序等。
标题2:任务调度的拓扑排序在任务调度中,我们需要确定任务的执行顺序,以保证所有任务都能按照正确的顺序运行。
拓扑排序可以帮助我们解决这个问题。
例如,假设有一组任务,它们之间存在依赖关系,我们可以使用拓扑排序确定它们的执行顺序,从而保证任务能够按照正确的顺序完成。
标题3:编译顺序的拓扑排序在编译过程中,我们需要确定源代码文件的编译顺序,以保证所有文件都能正确地被编译。
拓扑排序可以帮助我们解决这个问题。
例如,假设有一组源代码文件,它们之间存在依赖关系,我们可以使用拓扑排序确定它们的编译顺序,从而保证文件能够按照正确的顺序被编译。
标题4:拓扑排序的应用举例除了任务调度和编译顺序外,拓扑排序还可以应用于其他许多场景。
例如,在学校的课程安排中,拓扑排序可以帮助我们确定课程的学习顺序。
在软件工程中,拓扑排序可以用于解决模块的依赖关系。
在交通规划中,拓扑排序可以用于确定道路的修建顺序。
总之,拓扑排序在各个领域都有重要的应用。
标题5:拓扑排序的算法步骤拓扑排序的算法步骤如下:1. 找到图中入度为0的节点,将其加入结果集中。
2. 删除该节点以及与其相连的边。
3. 重复步骤1和步骤2,直到所有节点都被删除。
4. 如果还有剩余的节点没有被删除,则说明图中存在环,无法进行拓扑排序。
标题6:用邻接表表示图在拓扑排序中,我们通常使用邻接表来表示图。
C语言经典算法大全精选

C语言经典算法大全精选1.排序算法1.1冒泡排序:通过不断交换相邻元素的位置,将最大(最小)值“冒泡”到序列的末尾(开头)。
1.2插入排序:将未排序的元素逐个插入已排序的序列中,保持序列始终有序。
1.3选择排序:每次从未排序的元素中选择最小(最大)的元素,放到已排序序列的末尾(开头)。
1.4快速排序:通过递归地将序列分割为较小和较大的两部分,然后分别对两部分进行排序。
1.5归并排序:将序列递归地分割为两个子序列,分别排序后再将结果合并。
1.6堆排序:构建最大(最小)堆,然后逐步将堆顶元素与最后一个元素交换,并调整堆结构。
2.查找算法2.1顺序查找:逐个比较元素,直到找到目标元素或遍历完整个序列。
2.2二分查找:在有序序列中,通过不断缩小查找范围,找到目标元素。
2.3插值查找:根据目标元素与序列中最大、最小元素的关系,按比例选择查找范围。
2.4哈希查找:利用哈希函数将目标元素映射到一个唯一的位置,从而快速定位目标元素。
3.字符串算法3.1字符串匹配算法:在文本串中查找给定的模式串,并返回匹配位置。
3.2字符串翻转:将一个字符串逆序输出。
3.3字符串压缩:将连续出现多次的字符压缩为一个字符,并输出压缩后的字符串。
3.4字符串拆分:按照指定的分隔符将字符串拆分为多个子串,并返回子串列表。
3.5字符串反转单词:将一个句子中的单词顺序逆序输出。
4.图算法4.1深度优先:从起始顶点出发,递归地访问所有能到达的未访问顶点。
4.2广度优先:从起始顶点出发,逐层地访问与当前层相邻的未访问顶点。
4.3最小生成树:找到连接所有顶点的具有最小权值的无环边集合。
4.4最短路径:找到两个顶点之间最短路径的权值和。
4.5拓扑排序:找到一个顶点的线性序列,满足所有有向边的起点在终点之前。
5.数学算法5.1质数判断:判断一个数是否为质数(只能被1和自身整除)。
5.2求最大公约数:找到两个数的最大公约数。
5.3求最小公倍数:找到两个数的最小公倍数。
c语言排序与查找代码

c语言排序与查找代码在程序设计中,排序和查找是非常常见的操作。
排序是将一组数据按照特定规则进行重新排列的过程,而查找则是在已经排列好的数据中寻找某个特定的元素。
C语言提供了丰富的函数和算法来实现这两个操作。
一、排序代码实现:C语言中有多种排序算法可以选择,其中最常见和经典的有冒泡排序、选择排序、插入排序和快速排序等。
1. 冒泡排序代码实现:冒泡排序是一种简单直观的排序算法,它通过不断交换相邻元素的位置,将较大的元素逐渐往后移动。
具体实现代码如下:```cvoid bubbleSort(int arr[], int n) {for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}```2. 选择排序代码实现:选择排序是一种简单的排序算法,它每次从待排序的数据中选出最小(或最大)的元素,放到已排序序列的末尾。
具体实现代码如下:```cvoid selectionSort(int arr[], int n) {int i, j, minIndex, temp;for (i = 0; i < n - 1; i++) {minIndex = i;for (j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}```3. 插入排序代码实现:插入排序是一种简单直观的排序算法,它将待排序的数据分为已排序和未排序两部分,每次从未排序部分取出一个元素插入到已排序部分的适当位置。
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)
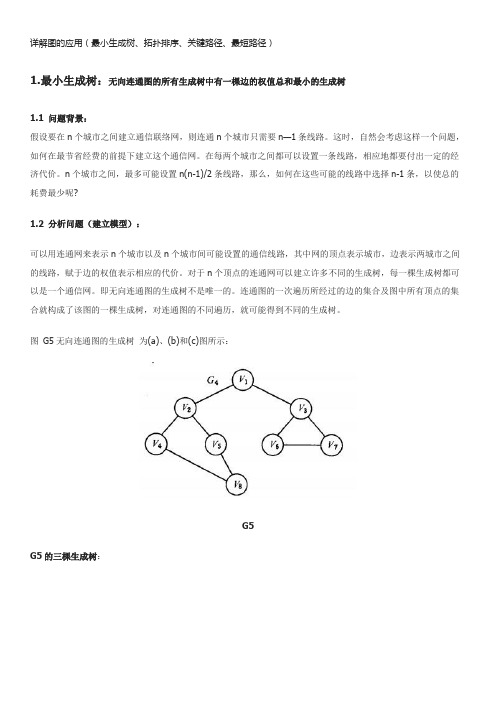
详解图的应用(最小生成树、拓扑排序、关键路径、最短路径)1.最小生成树:无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景:假设要在n个城市之间建立通信联络网,则连通n个城市只需要n—1条线路。
这时,自然会考虑这样一个问题,如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路,相应地都要付出一定的经济代价。
n个城市之间,最多可能设置n(n-1)/2条线路,那么,如何在这些可能的线路中选择n-1条,以使总的耗费最少呢?1.2 分析问题(建立模型):可以用连通网来表示n个城市以及n个城市间可能设置的通信线路,其中网的顶点表示城市,边表示两城市之间的线路,赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树,每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树,对连通图的不同遍历,就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示:G5G5的三棵生成树:可以证明,对于有n 个顶点的无向连通图,无论其生成树的形态如何,所有生成树中都有且仅有n-1 条边。
1.3最小生成树的定义:如果无向连通图是一个网,那么,它的所有生成树中必有一棵边的权值总和最小的生成树,我们称这棵生成树为最小生成树,简称为最小生成树。
最小生成树的性质:假设N=(V,{ E}) 是个连通网,U是顶点集合V的一个非空子集,若(u,v)是个一条具有最小权值(代价)的边,其中,则必存在一棵包含边(u,v)的最小生成树。
1.4 解决方案:两种常用的构造最小生成树的算法:普里姆(Prim)和克鲁斯卡尔(Kruskal)。
他们都利用了最小生成树的性质1.普里姆(Prim)算法:有线到点,适合边稠密。
时间复杂度O(N^2)假设G=(V,E)为连通图,其中V 为网图中所有顶点的集合,E 为网图中所有带权边的集合。
课程设计实现拓扑排序算法

课程设计实现拓扑排序算法一、课程目标知识目标:1. 学生能理解拓扑排序的概念,掌握拓扑排序算法的基本原理和应用场景。
2. 学生能描述有向无环图(DAG)的特点,并识别出给定图中的关键路径。
3. 学生能运用所学知识,对实际问题进行拓扑排序,解决项目管理、任务调度等实际问题。
技能目标:1. 学生能通过分析问题,构建出相应的有向无环图,并进行拓扑排序。
2. 学生能运用编程语言实现拓扑排序算法,解决具体问题。
3. 学生能通过实例分析,培养解决问题的能力和逻辑思维能力。
情感态度价值观目标:1. 学生通过学习拓扑排序算法,体验算法在实际问题中的应用价值,增强学习兴趣和动力。
2. 学生在团队协作中,培养沟通能力、合作精神和集体荣誉感。
3. 学生在学习过程中,树立正确的价值观,认识到科学技术的进步对社会发展的重要意义。
课程性质:本课程属于数据结构与算法领域,旨在帮助学生掌握拓扑排序这一重要算法,提高解决实际问题的能力。
学生特点:学生具备一定的编程基础和图论知识,具有一定的抽象思维和逻辑分析能力。
教学要求:结合学生特点和课程性质,教师应注重启发式教学,引导学生通过实例分析、编程实践等方式,掌握拓扑排序算法,提高实际应用能力。
同时,关注学生的情感态度价值观培养,激发学生的学习兴趣和动力。
在教学过程中,将课程目标分解为具体的学习成果,以便进行有效的教学设计和评估。
二、教学内容1. 图的基本概念复习:介绍图的相关术语,如顶点、边、邻接点、度等,回顾有向图和无向图的特点。
2. 有向无环图(DAG)的判定:讲解DAG的定义,引导学生识别DAG及其在实际问题中的应用。
3. 拓扑排序的概念与算法:介绍拓扑排序的定义,阐述拓扑排序的算法步骤,分析拓扑排序与DAG的关系。
4. 拓扑排序算法的实现:结合教材,教授编程语言实现拓扑排序算法,包括邻接表和邻接矩阵两种表示方法。
5. 拓扑排序的应用案例:分析拓扑排序在项目管理、任务调度等领域的应用,结合实际案例进行讲解。
拓扑排序的实现

拓扑排序的实现拓扑排序是一种常见的图排序算法,用于解决有向无环图(DAG)中节点的依赖关系排序问题。
在实际应用中,拓扑排序可以应用于任务调度、编译顺序、依赖管理等方面。
本文将介绍拓扑排序的实现及其应用场景。
拓扑排序的实现通常使用深度优先搜索(DFS)或宽度优先搜索(BFS)算法。
这里我们以DFS算法为例进行介绍。
首先,我们需要定义一个有向图,表示节点之间的依赖关系。
每个节点表示一个任务或一个实体,图中的边表示节点之间的依赖关系。
接下来,我们定义一个栈用于存储已经排序完成的节点。
在进行拓扑排序时,我们从一个没有前置依赖的节点开始遍历,将该节点标记为已排序,并将其加入栈中。
然后,我们递归地访问该节点的后继节点,并将后继节点的前置依赖数减一。
如果某个后继节点的前置依赖数减为零,表示该节点的所有前置节点都已排序完成,我们将其标记为已排序,将其加入栈中。
重复以上步骤,直到图中的所有节点都被遍历。
最后,我们可以从栈中依次弹出节点,即可得到拓扑排序的结果。
拓扑排序的实现在某些场景下非常有效。
例如,在任务调度中,可以根据任务之间的依赖关系使用拓扑排序确定任务的执行顺序;在编译顺序中,可以根据源代码文件之间的依赖关系使用拓扑排序确定编译的顺序;在依赖管理中,可以根据软件包之间的依赖关系使用拓扑排序确定软件包的安装顺序。
总结起来,拓扑排序是一种有效的图排序算法,可以解决有向无环图中节点的依赖关系排序问题。
通过深度优先搜索或宽度优先搜索算法,可以实现拓扑排序。
拓扑排序在任务调度、编译顺序、依赖管理等方面具有广泛的应用。
希望本文对读者理解和运用拓扑排序有所帮助。
参考文献:1. Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms. MIT Press.2. Sedgewick, R., & Wayne, K. (2011). Algorithms (4th Edition). Addison-Wesley Professional.。
拓扑排序c++代码

什么是拓扑排序拓扑排序是对一个有向图构造拓扑序列的过程,使得该序列满足:每个顶点出现且只出现一次;若存在一条从顶点A到顶点B的路径,那么在序列中顶点A出现在顶点B的前面。
拓扑排序可以用来判断一个有向图是否为DAG (有向无环图)。
如果一个有向图可以被拓扑排序,那么这个有向图就是DAG。
拓扑排序的应用场景是什么?拓扑排序通常用来“排序”具有依赖关系的任务。
比如,如果用一个DAG图来表示一个工程,其中每个顶点表示工程中的一个任务,用有向边A→B表示在做任务B之前必须先完成任务A。
那么这个DAG图就是一个合法的任务安排,而且它的拓扑序列就是合法的任务执行顺序。
拓扑排序还可以用来检测一个有向图是否有环。
如果有环,则该有向图不可能拓扑排序,反之,可以拓扑排序。
另外,拓扑排序还可以用于解决一些实际问题,如编译器的依赖关系分析、工程项目的任务调度等。
拓扑排序时间复杂度对于有n个顶点和e条边的图来说,拓扑排序的时间复杂度为O(n+e)拓扑排序C++代码实现#include<bits/stdc++.h>using namespace std;const int N=100010;int n,m;int h[N],e[N],ne[N],idx;int d[N];void add(int a,int b){e[idx]=b,ne[idx]=h[a],h[a]=idx++;d[b]++;}void topsort(){queue<int>q;for(int i=1;i<=n;i++)if(!d[i])q.push(i);while(q.size()){int t=q.front();q.pop();cout<<t<<'';for(int i=h[t];~i;i=ne[i]){int j=e[i];if(--d[j]==0)q.push(j);}}}int main(){memset(h,-1,sizeof h);cin>>n>>m;while(m--){int a,b;cin>>a>>b;add(a,b);}topsort();return0;}拓扑排序Python代码实现from collections import dequedef topo_sort(graph):in_degree=dict((u,0)for u in graph) for u in graph:for v in graph[u]:in_degree[v]+=1q=deque()for u in in_degree:if in_degree[u]==0:q.appendleft(u)l=[]while q:u=q.pop()l.append(u)for v in graph[u]:in_degree[v]-=1if in_degree[v]==0:q.appendleft(v)return l。
拓扑排序的原理及其实现

拓扑排序的原理及其实现取材自以下材料:/wiki/Topological_sorting/wiki/Hamiltonian_path定义和前置条件:定义:将有向图中的顶点以线性方式进行排序。
即对于任何连接自顶点u到顶点v的有向边uv,在最后的排序结果中,顶点u总是在顶点v的前面。
如果这个概念还略显抽象的话,那么不妨考虑一个非常非常经典的例子——选课。
我想任何看过数据结构相关书籍的同学都知道它吧。
假设我非常想学习一门“机器学习”的课程,但是在修这么课程之前,我们必须要学习一些基础课程,比如:计算机科学概论,C语言程序设计,数据结构,算法等等。
那么这个制定选修课程顺序的过程,实际上就是一个拓扑排序的过程,每门课程相当于有向图中的一个顶点,而连接顶点之间的有向边就是课程学习的先后关系。
只不过这个过程不是那么复杂,从而很自然的在我们的大脑中完成了。
将这个过程以算法的形式描述出来的结果,就是拓扑排序。
那么是不是所有的有向图都能够被拓扑排序呢?显然不是。
继续考虑上面的例子,如果告诉你在选修“计算机科学概论”这门课之前需要你先学习“机器学习”,你是不是会被弄糊涂?在这种情况下,就无法进行拓扑排序,因为它中间存在互相依赖的关系,从而无法确定谁先谁后。
在有向图中,这种情况被描述为存在环路。
因此,一个有向图能被拓扑排序的充要条件就是它是一个有向无环图(DAG:Directed Acyclic Graph)。
偏序/全序关系:偏序和全序实际上是离散数学中的概念。
这里不打算说太多形式化的定义,形式化的定义教科书上或者上面给的链接中就说的很详细。
还是以上面选课的例子来描述这两个概念。
假设我们在学习完了算法这门课后,可以选修“机器学习”或者“计算机图形学”。
这个“或者”表示,学习“机器学习”和“计算机图形学”这两门课之间没有特定的先后顺序。
因此,在我们所有可以选择的课程中,任意两门课程之间的关系要么是确定的(即拥有先后关系),要么是不确定的(即没有先后关系),绝对不存在互相矛盾的关系(即环路)。
【洛谷日报#157】快速入手拓扑排序

【洛⾕⽇报#157】快速⼊⼿拓扑排序⽬录1. 前⾔2. 基本思路3. 模拟思路4.代码实现5. 例题6. 参考⽂献与鸣谢1.前⾔在正式讲拓扑排序之前,我们来引⼊⼀下,以便各位更好理解。
(所有有向图出品于Xmind)⾸先,你想学习计算机的原理怎么办?(⽩⼿起家)肯定有很多前置知识啊!流程图就像下⾯:很明显,此时你需要按⼀定顺序(这个顺序叫 “拓扑序列”)学习才能彻底了解计算机原理。
那么这个顺序怎么求呢?拓扑排序帮你忙!前置知识:图的基本概念以及建图编程能⼒。
2.基本思路 & 实现⾸先,对于点的关系,⼤致分为2种关系:1. 先后关系,如上图的 “数学” 与 “物理学” 的关系。
2. 并列关系(应该叫做“没有关系”),如上图的 ”物理学“ 和 “计算机发展史” 的关系。
不难发现,因为有了并列关系,拓扑序列不⼀定是唯⼀的。
如上图,可以得到很多个拓扑序列,这⾥只举⼀个例⼦,其他的相信⼤家都会看。
上图的⼀个拓扑序列:12345678那么⼤家不难发现,拓扑排序的时候,⼤家总会找⼊度为0的点,因为这是你不⽤学习的点,可以直接解锁。
找到了之后,你就可以把这个点放到序列⾥,那么随之就有新的点的⼊度为0,然后重复上述知道图空。
以上就是拓扑排序的基本思路!我们可以简述为:1. 从图中,选择⼀个⼊度为0的点,并输出该顶点;2. 从图中,删除该顶点,以及相关联的边;3. 重复上述步骤,知道输出所有点。
(原来如此简单!)下⾯带⼤家模拟⼀遍拓扑排序的过程(⼤家觉得烦可以跳过)。
3. 模拟思路⾸先,可以轻易发现,只有点1是⼊度为0,因此,把它输出,删除点1和边A、B。
如下图:糟了,有4个点的⼊度为0怎么办?不着急,由于拓扑序列不⽌⼀个的原因,怎样都⾏,我就按照从⼩到⼤来。
但是为了加快进度,我们直接删掉4个点,并从⼩到⼤⼊拓扑序列,同时删除H、C、E、F、D、G六条边!现在就很明了啦,把点6、7和相关的边删掉,⼊队,再把点8删掉就完⼯!最终拓扑序列:12345678关键来了,怎么⽤代码实现呢?(其实也不考码⼒(>_<)啦)4. 代码实现拓扑排序⼀般有三种实现⽅法(建图是必不可少的):1. 算法设置⼀个队列(⽅便使⽤优先队列,从⼩到⼤输出),将所有⼊度为0的顶点⼊队。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
return 0; //存储分配失败
}
s.top=s.base;
s.stacksize=STACK_INIT_SIZE;
return 1;
}
int Push(SqStack &s,SElemType e){ //元素的入栈
if(s.top-s.base>=s.stacksize)//栈满,追加存储控件
}
}
Status TopologicalSort(ALGraph g){
//有向图G采用的临界表存储结构
//若G无回路,则输出G的顶点的一个拓扑序列并返回OK,否则返回ERROR
int i;int count;int k;
ArcNode *p;
int indegree[MAX]={0};SqStack s;
{
printf("请输入第%d个顶点的值:",i);
scanf("%d",&g.vertices[i].data);
getchar();
g.vertices[i].firstarc=NULL;
}
printf("输入边的信息(输入格式为:i,j)\n");
for(i=1;i<=g.arcnum;i++) /* 输入弧的信息 */
//****************栈的使用函数*********************
int InitStack(SqStack &s){//栈的初始化
s.base=(SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));
if(!s.base)
FindInDegree(g,indegree);//对各个顶点求入度indegree[1..vexnum]
InitStack(s);
for(i=1;i<=g.vexnum;i++) //建零入度顶点栈S
if(!indegree[i]) Push(s,i);//入度为零者进栈
count=0; //对输出顶点计数
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<iomanip>
//----------------公共的-----------------
#define TRUE 1
#define FALSE 0
#define OK 1
if(!(--indegree[k])) Push(s,k);
}//for
}//while
printf("\n");
if(count<g.vexnum) return ERROR;
else return OK;
}
void main()
{
A};
struct ArcNode *nextarc; //指向下一条弧的指针
}ArcNode;
typedef int VertexType;//每个顶点的值的类型
typedef struct VNode//邻接表的顶点
{
VertexType data;
ArcNode *firstarc;
}VNode,AdjList[MAX_VERTEX_NUM];
typedef struct{
AdjList vertices; //邻接表
int vexnum,arcnum;//图的当前顶点数和弧数
int kind; //图的种类标志 0为无向图 1为有向图
}ALGraph;
typedef int Boolean;
typedef int Status;
typedef char InfoType;
typedef struct ArcNode{ //邻接表的弧
int adjvex; //该弧所指向的顶点的位置
InfoType *info; //该弧相关信息的指针(如:权值等)
ArcNode *p;
int i;int j;
for(i=1;i<=g.vexnum;i++)
{
j=0;
p=g.vertices[i].firstarc;
while(p)
{
indegree[p->adjvex]++;
p=p->nextarc;
}
while(!StackEmpty(s)){
Pop(s,i);
printf("%d ",g.vertices[i].data);++count;//输出i号顶点并计数
for(p=g.vertices[i].firstarc;p;p=p->nextarc){
k=p->adjvex; //对i号顶点的每个邻接点入度减1
{
printf("请输入第%d条边的信息:",i);
scanf("%d,%d",&j,&k);
getchar();
p=(ArcNode *)malloc(sizeof(ArcNode));
p->adjvex=k;
p->nextarc=g.vertices[j].firstarc;
int i,j,k;
ArcNode *p;
printf("请输入顶点数和边数(格式为:顶点数,边数):");
scanf("%d,%d",&i,&j);
getchar();
g.vexnum=i;g.arcnum=j;
for(i=1;i<=g.vexnum;i++)//输入顶点
#define STATCKINCREMENT 10
//**********************************************
//*************栈的元素类型***************
typedef int SElemType;
typedef struct SqStack
s.stacksize+=STATCKINCREMENT;
}
*(s.top)++=e;
return 1;
}
int Pop(SqStack &s,SElemType &e){//元素的出栈
if(s.top==s.base) return 0;
e=*--s.top;
return 1;
g.vertices[j].firstarc=p;
}
return OK;
}
int FirstAdjVex(ALGraph g,int v){
//获取邻接表g的第v个顶点的第一个邻接点
//返回第v个顶点的第一个邻接点的位置
if(g.vertices[v].firstarc!=NULL)
CreateDG(g);
printf("其中一条有效的拓扑排序为:");
TopologicalSort(g);
system("pause");
}
{
SElemType *base;
SElemType *top;
SElemType stacksize;
}SqStack;
//****************************************
#define MAX_VERTEX_NUM 20
#define MAX 20
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
//---------------------------------------
//*************栈的初始大小和增量***************
#define STACK_INIT_SIZE 100
}
int StackEmpty(SqStack s){//若S为为空战,则返回1,否则返回0
if(s.top==s.base) return 1;
else return 0;
}
//*************************************************
Status CreateDG(ALGraph &g){ /* 邻接表建立有向图 */
for(p=g.vertices[v].firstarc;p!=NULL;p=p->nextarc)
if(p->adjvex==w && p->nextarc!=NULL)
return p->nextarc->adjvex;
return -1;
}
void FindInDegree(ALGraph g,int indegree[MAX]){//找出图g的入度数组
{
s.base=(SElemType *)realloc(s.base,(s.stacksize+STATCKINCREMENT)*sizeof(SElemType));
if(!s.base) return 0;//存储分配失败
