MATLAB神经网络实验
Matlab神经网络工具箱介绍与数值试验
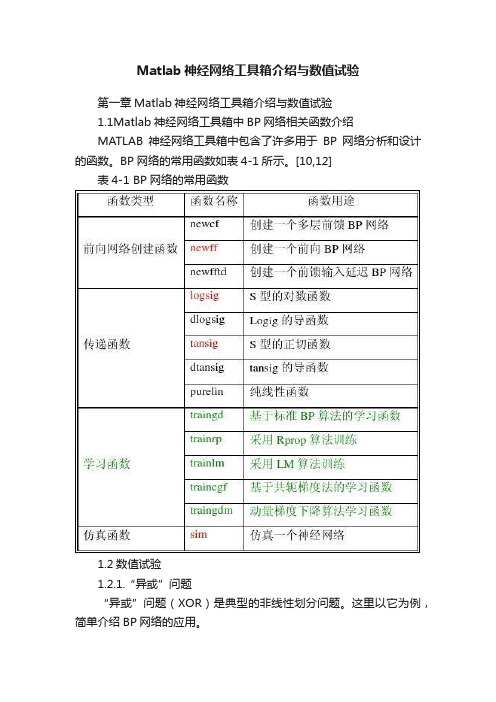
Matlab神经网络工具箱介绍与数值试验第一章Matlab神经网络工具箱介绍与数值试验1.1Matlab神经网络工具箱中BP网络相关函数介绍MATLAB神经网络工具箱中包含了许多用于BP网络分析和设计的函数。
BP网络的常用函数如表4-1所示。
[10,12]表4-1 BP网络的常用函数1.2数值试验1.2.1.“异或”问题“异或”问题(XOR)是典型的非线性划分问题。
这里以它为例,简单介绍BP网络的应用。
在Matlab7.0环境下,建立一个三层的BP神经网络,其中输入层和隐层分别各有两个神经元,输出层有一个神经元。
现要求训练这一网络,使其具有解决“异或”问题的能力。
“异或”问题的训练输入和期望输出如表5-1。
表5-1 异或问题的训练输入和期望输出1)基于标准BP 算法结果如下及图5.1所示:横轴表示迭代次数,纵轴表示误差。
迭代到第240次时达到预设精度。
迭代停止时,误差为9.97269e-005,此时的梯度为0.00924693。
5010015020010-410-310-210-110101240 EpochsT r a i n i n g -B l u e G o a l -B l a c kPerformance is 9.97269e-005, Goal is 0.0001图5.1 基于标准BP 算法的“异或”问题2)基于共轭梯度法结果如下及图5.2所示:横轴表示迭代次数,纵轴表示误差。
迭代到第16次时达到预设精度。
迭代停止时,误差为9.0770e-005,此时的梯度为0.00318592。
024681012141610-410-310-210-11010116 EpochsT r a i n i n g -B l u e G o a l -B l a c k Performance is 9.07705e-005, Goal is 0.0001图5.2 基于共轭梯度法的“异或”问题3)基于LM 算法结果如下及图5.3所示:横轴表示迭代次数,纵轴表示误差。
如何进行MATLAB神经网络的训练和预测

如何进行MATLAB神经网络的训练和预测【第一章】MATLAB神经网络的基础知识神经网络是一种模拟人类神经系统运行方式的计算模型,它通过模拟人类的感知、学习和决策过程,可以对复杂的问题进行处理和求解。
在实际应用中,MATLAB是一个常用的工具来进行神经网络的训练和预测。
本章将介绍MATLAB 神经网络的基础知识,包括神经网络的原理、MATLAB的神经网络工具箱以及神经网络训练和预测的一般步骤。
1.1 神经网络的原理神经网络由神经元(neuron)组成,每个神经元接收多个输入并产生一个输出。
神经网络的基本单元是感知器(perceptron),它由权重、偏置和激活函数组成。
权重决定了输入对输出的影响程度,偏置用于调整输出的偏移量,激活函数用于处理神经元的输出。
通过调整权重和偏置,神经网络可以学习和适应不同的输入输出模式。
常见的神经网络包括前馈神经网络(feedforward neural network)、循环神经网络(recurrent neural network)和卷积神经网络(convolutional neural network)。
前馈神经网络是最基本的神经网络类型,信息只能在网络中的一个方向流动,即从输入层到输出层。
循环神经网络具有反馈连接,可以记忆之前的状态信息,适用于序列数据的处理。
卷积神经网络则主要用于图像和语音等二维数据的处理。
1.2 MATLAB神经网络工具箱MATLAB提供了一个神经网络工具箱(Neural Network Toolbox),用于设计、训练和模拟神经网络。
该工具箱包括多种神经网络类型、各种激活函数、训练算法和性能函数等各种功能模块。
使用MATLAB神经网络工具箱可以方便地进行神经网络的建模和仿真。
在MATLAB神经网络工具箱中,神经网络被表示为一个网络对象(network object)。
网络对象由一系列图层(layer)组成,每个图层由若干个神经元组成。
网络对象还包括连接权重矩阵、偏置向量和训练参数等属性。
实验六 MATLAB神经网络工具箱汇总

实验七 MATLAB 神经网络工具箱一、实验目的1、掌握Matlab 对感知器网络的构建与训练方法。
2、掌握Matlab 对线性神经网络的构建与训练方法。
3、掌握Matlab 对BP 神经网络的构建与训练方法。
二、实验原理1、感知器的MATLAB 仿真感知器(Pereceptron)是一种特殊的神经网络模型,是由美国心理学家F.Rosenblatt 于1958年提出的,一层为输入层,另一层具有计算单元,感知器特别适合于简单的模式分类问题,也可用于基于模式分类的学习控制和多模态控制中。
(一)感知器神经元模型感知器神经元通过对权值的训练,可以使感知器神经元的输出能代表对输入模式进行的分类,图1.1为感知器神经元模型。
图1.1 感知器神经元模型感知器神经元的每一个输入都对应于一个合适的权值,所有的输入与其对应权值的加权和作为阀值函数的输入。
由于阀值函数的引入,从而使得感知器可以将输入向量分为两个区域,通常阀函数采用双极阶跃函数,如:⎩⎨⎧<≥=0,00,1)(x x x f (1.1) 而感知器神经元模型的实际输出为⎪⎭⎫⎝⎛-=∑-=R ii i b x w f o 1 (1.2)其中b 为阀值(二)感知器的网络结构图1.2所描述的是一个简单的感知器网络结构,输入层有R 个输入,Q 个输出,通过权值w ij 与s 个感知器神经元连接组成的感知器神经网络。
根据网络结构,可以写出感知器处理单元对其输入的加权和操作,即:∑==Rj j ij i p w n 1(1.3)而其输出a i 为a i =f (n i +b i ) (1.4)由式2.1易知⎩⎨⎧<+≥+=0001i i i i i b n b n a (1.5) 则当输入n i +b i 大于等于0,即有n i ≥-b i 时,感知器的输出为1;否则输出为0。
上面所述的单层感知器神经网络是不可能解决线性不可分的输入向量分类问题,也不能推广到一般的前向网络中去。
基于MATLAB的BP神经网络实现研究

方法与实验设计
基于MATLAB的BP神经网络实现主要包括以下几个步骤:
1、数据预处理:首先需要对数据进行预处理,包括数据清洗、归一化等操 作。
2、网络设计:根据问题特点选择合适的网络结构,并确定输入层、输出层 和隐藏层的节点数。
3、训练模型:使用MATLAB中的神经网络工具箱进行模型训练。
2、在防止过拟合方面,可以研究更有效的正则化方法和技术,以避免模型 在训练过程中产生过拟合问题。
3、在网络结构设计方面,可以研究更加智能的自适应网络结构设计方法, 以简化人工设计网络的复杂度。
4、可以进一步拓展BP神经网络在其他领域的应用研究,例如自然语言处理、 生物信息学等。
谢谢观看
结论与展望
本次演示研究了基于MATLAB的BP神经网络实现方法,通过实验设计和实验结 果分析,可以得出以下结论:
1、BP神经网络在解决分类、逼近和优化等问题方面具有较好的性能,证实 了其在实际应用中的价值。
2、在超参数调整方面,学习率和迭代次数对模型性能具有重要影响,需要 根据实际问题进行调整。
2、函数逼近:BP神经网络可以用于逼近复杂的非线性函数。例如,在控制 系统、信号处理等领域,可以利用BP神经网络对系统进行建模和预测。
3、优化问题:BP神经网络可以应用于求解各种优化问题。例如,利用BP神 经网络实现函数的最小化、多目标优化等。
然而,目前的研究还存在着一些问题。首先,由于BP神经网络的训练速度较 慢,可能需要进行大量的迭代才能得到较好的结果。其次,BP神经网络的训练过 程中容易出现过拟合问题,这可能导致模型的泛化能力下降。最后,BP神经网络 的性能受到初始参数的影响较大,如何选择合适的参数也是亟待解决的问题。
4、模型评估与优化:通过验证数据集评估模型的性能,并进行参数调整和 优化。
MATLAB中的神经网络模型构建与训练

MATLAB中的神经网络模型构建与训练神经网络模型是一种模拟人脑神经元活动的数学模型,其可以用于进行各种复杂的数据分析和问题求解。
在MATLAB中,我们可以利用其强大的工具和函数来构建和训练神经网络模型。
本文将介绍MATLAB中神经网络模型的构建过程及其相关训练方法。
一、神经网络模型简介神经网络模型是由一系列相互连接的神经元组成的网络结构。
每个神经元都有多个输入和一个输出,输入通过权重被加权后,经过激活函数激活输出。
神经网络可以分为三层:输入层、隐藏层和输出层。
输入层接收原始数据,隐藏层进行信息处理和特征提取,而输出层给出最终结果。
二、神经网络构建在MATLAB中,可以通过Neural Network Toolbox来构建神经网络。
首先,我们需要确定网络结构,包括输入层神经元数、隐藏层神经元数和输出层神经元数。
接下来,我们调用network函数来创建一个空的神经网络对象。
```matlabnet = network;```然后,我们可以通过net的属性来设置神经网络的各个参数,如输入层的大小、隐藏层的大小、激活函数等。
```matlabnet.numInputs = 1; % 设置输入层神经元数net.numLayers = 2; % 设置网络层数net.biasConnect = [1; 1]; % 设置偏置net.inputConnect = [1; 0]; % 设置输入连接yerConnect = [0 0; 1 0]; % 设置层连接net.outputConnect = [0 1]; % 设置输出连接yers{1}.size = 10; % 设置隐藏层神经元数yers{1}.transferFcn = 'tansig'; % 设置激活函数yers{2}.transferFcn = 'purelin'; % 设置激活函数```上述代码中,我们设置了一个具有10个隐藏层神经元的神经网络,其输入和输出分别为1个。
如何利用Matlab进行神经网络训练

如何利用Matlab进行神经网络训练神经网络训练是机器学习领域中不可或缺的一环,而Matlab作为一种功能强大的数值计算和科学研究工具,提供了丰富的神经网络训练相关函数和工具箱,为我们提供了便利。
本文将介绍如何利用Matlab进行神经网络训练,从基础概念到具体实现的技巧,希望能够给读者一些启发和指导。
一、神经网络概述神经网络是一种由神经元和连接它们的权重构成的模型,其模拟了人类大脑的信息处理方式。
在神经网络中,神经元接收来自输入层或其他神经元的输入,并通过激活函数计算输出。
神经元之间的连接权重决定了信号在网络中的传递和加权。
二、神经网络的训练神经网络的训练是通过调整连接权重,使得网络对给定输入能够产生期望的输出。
训练的目标是最小化网络的误差,并提高网络的泛化能力。
在神经网络训练中,最常用的方法是反向传播算法(Backpropagation),即基于链式法则计算误差对连接权重的偏导数,并利用梯度下降算法进行权重的更新。
三、Matlab中的神经网络工具箱Matlab提供了用于神经网络建模和训练的专用工具箱,包括网络创建与配置、数据预处理、训练算法、性能评估等功能。
在开始使用神经网络工具箱前,需要先安装并加载工具箱,可以通过运行命令"neural network toolbox"进行加载。
四、神经网络的建模和配置在利用Matlab进行神经网络训练前,首先需要对网络进行建模和配置。
首先确定网络的拓扑结构,包括输入层、隐藏层和输出层的神经元数量和连接方式。
可以使用Matlab提供的"feedforwardnet"函数创建前馈神经网络,或者"patternnet"函数创建模式识别神经网络。
然后,需要对网络的参数进行配置,包括激活函数、训练算法、训练参数等。
Matlab提供了多种激活函数和训练算法的选择,可以根据具体任务的需求进行调整。
例如,可以使用sigmoid或ReLU激活函数,可以使用反向传播、Levenberg-Marquardt等训练算法。
BP神经网络实验详解(MATLAB实现)

BP神经网络实验详解(MATLAB实现)BP(Back Propagation)神经网络是一种常用的人工神经网络结构,用于解决分类和回归问题。
在本文中,将详细介绍如何使用MATLAB实现BP神经网络的实验。
首先,需要准备一个数据集来训练和测试BP神经网络。
数据集可以是一个CSV文件,每一行代表一个样本,每一列代表一个特征。
一般来说,数据集应该被分成训练集和测试集,用于训练和测试模型的性能。
在MATLAB中,可以使用`csvread`函数来读取CSV文件,并将数据集划分为输入和输出。
假设数据集的前几列是输入特征,最后一列是输出。
可以使用以下代码来实现:```matlabdata = csvread('dataset.csv');input = data(:, 1:end-1);output = data(:, end);```然后,需要创建一个BP神经网络模型。
可以使用MATLAB的`patternnet`函数来创建一个全连接的神经网络模型。
该函数的输入参数为每个隐藏层的神经元数量。
下面的代码创建了一个具有10个隐藏神经元的单隐藏层BP神经网络:```matlabhidden_neurons = 10;net = patternnet(hidden_neurons);```接下来,需要对BP神经网络进行训练。
可以使用`train`函数来训练模型。
该函数的输入参数包括训练集的输入和输出,以及其他可选参数,如最大训练次数和停止条件。
下面的代码展示了如何使用`train`函数来训练模型:```matlabnet = train(net, input_train, output_train);```训练完成后,可以使用训练好的BP神经网络进行预测。
可以使用`net`模型的`sim`函数来进行预测。
下面的代码展示了如何使用`sim`函数预测测试集的输出:```matlaboutput_pred = sim(net, input_test);```最后,可以使用各种性能指标来评估预测的准确性。
使用Matlab进行神经网络优化问题求解的方法

使用Matlab进行神经网络优化问题求解的方法一、引言在当今信息时代,神经网络已经成为解决复杂问题的重要工具。
随着计算能力的提升,神经网络优化问题的求解变得越来越重要。
而Matlab作为一种强大的科学计算软件,能够提供丰富的工具和函数来解决神经网络优化问题。
本文将介绍如何使用Matlab来解决神经网络优化问题。
二、神经网络优化问题的建模在使用Matlab解决神经网络优化问题之前,首先需要对问题进行建模。
通常来说,神经网络优化问题可以分为两类:单目标优化问题和多目标优化问题。
单目标优化问题是指希望优化网络的某个特定输出,常见的问题有回归问题和分类问题。
而多目标优化问题则是希望在多个指标上获得最优解,常见的问题有多目标分类和多目标回归问题。
在建模过程中,需要确定网络的结构和参数。
神经网络的结构通常由输入层、隐藏层和输出层组成。
输入层接受原始数据,隐藏层进行特征提取,输出层给出最终的结果。
而参数则包括权重和偏置,这些参数需要进行调整以达到最优解。
三、使用Matlab解决单目标优化问题1. 数据准备在解决单目标优化问题之前,首先需要准备好数据集。
数据集应该包含输入值和对应的目标值。
2. 网络训练使用Matlab的神经网络工具箱,可以方便地进行网络训练。
首先,需要创建一个神经网络对象,并设置好网络的结构和参数。
然后,使用训练函数对网络进行训练,常见的训练函数有Levenberg-Marquardt算法和梯度下降算法。
通过训练函数,可以不断调整网络的权重和偏置,直到达到最优解。
3. 网络评估训练完网络后,需要对网络进行评估。
可以使用测试数据集来评估网络的性能,通常采用预测误差、准确率等指标来评估网络的表现。
四、使用Matlab解决多目标优化问题解决多目标优化问题与解决单目标优化问题的方法类似,只是目标变成了多个。
可以使用多种方法来解决多目标优化问题,如加权法、约束法和分级法等。
1. 加权法加权法是一种常用的解决多目标优化问题的方法。
MATLAB中的深度神经网络设计与训练技巧分享

MATLAB中的深度神经网络设计与训练技巧分享深度学习是近年来机器学习领域的一大热门话题,而神经网络是深度学习的核心。
在深度神经网络的设计与训练过程中,MATLAB是一款非常强大的工具,它提供了丰富的函数和工具箱,能够帮助我们快速而有效地进行模型构建和训练。
本文将分享一些在MATLAB中设计和训练深度神经网络时的一些技巧,希望对正在学习和实践深度学习的读者有所帮助。
1. 数据预处理在训练深度神经网络之前,对数据进行预处理是非常重要的一步。
数据预处理的目的是将原始数据转换为适合神经网络处理的形式,这样能够提高网络的训练效果和泛化能力。
在MATLAB中,可以使用Datastore对象来管理和处理大规模数据集,例如使用ImageDatastore对象来处理图像数据集。
除了数据转换外,数据预处理还包括数据清洗和标准化。
对于图像数据,可以使用MATLAB提供的图像增强工具箱对图像进行清洗,例如去噪、调整亮度和对比度等操作。
对于其他类型的数据,可以使用MATLAB的统计工具箱对数据进行标准化,例如z-score标准化或min-max标准化。
2. 网络架构设计在设计深度神经网络的时候,需要考虑网络的层数和每层的神经元数量。
一般来说,网络的深度和宽度都会影响网络的性能。
较深的网络可以学习更复杂的特征,但也会增加网络的训练时间和计算资源。
而较宽的网络可以提高网络的表达能力,但也会增加网络的参数数量和过拟合的风险。
在网络的设计过程中,可以使用MATLAB提供的Deep Network Designer工具来进行可视化设计。
该工具可以帮助我们快速搭建网络结构,并进行参数设置和网络调试。
另外,还可以使用MATLAB的神经网络工具箱提供的命令行接口,通过编程方式创建和训练自定义的网络模型。
3. 激活函数选择激活函数在神经网络中起到了非常重要的作用,它可以引入非线性,增加网络的表达能力。
在选择激活函数时,需要考虑网络的性质和任务的特点。
(完整版)BP神经网络matlab实例(简单而经典)

p=p1';t=t1';[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); %原始数据归一化net=newff(minmax(pn),[5,1],{'tansig','purelin'},'traingdx');%设置网络,建立相应的BP网络net.trainParam.show=2000; % 训练网络net.trainParam.lr=0.01;net.trainParam.epochs=100000;net.trainParam.goal=1e-5;[net,tr]=train(net ,pn,tn); %调用TRAINGDM算法训练BP 网络pnew=pnew1';pnewn=tramnmx(pnew,minp,maxp);anewn=sim(net,pnewn); %对BP网络进行仿真anew=postmnmx(anewn,mint,maxt); %还原数据y=anew';1、BP网络构建(1)生成BP网络=net newff PR S S SNl TF TF TFNl BTF BLF PF(,[1 2...],{ 1 2...},,,)PR:由R维的输入样本最小最大值构成的2R⨯维矩阵。
S S SNl:各层的神经元个数。
[ 1 2...]{ 1 2...}TF TF TFNl:各层的神经元传递函数。
BTF:训练用函数的名称。
(2)网络训练[,,,,,] (,,,,,,)=net tr Y E Pf Af train net P T Pi Ai VV TV(3)网络仿真=[,,,,] (,,,,)Y Pf Af E perf sim net P Pi Ai T{'tansig','purelin'},'trainrp'2、BP网络举例举例1、%traingdclear;clc;P=[-1 -1 2 2 4;0 5 0 5 7];T=[-1 -1 1 1 -1];%利用minmax函数求输入样本范围net = newff(minmax(P),T,[5,1],{'tansig','purelin'},'trainrp');net.trainParam.show=50;%net.trainParam.lr=0.05;net.trainParam.epochs=300;net.trainParam.goal=1e-5;[net,tr]=train(net,P,T);net.iw{1,1}%隐层权值net.b{1}%隐层阈值net.lw{2,1}%输出层权值net.b{2}%输出层阈值sim(net,P)举例2、利用三层BP神经网络来完成非线性函数的逼近任务,其中隐层神经元个数为五个。
Matlab中的神经网络建模与训练方法

Matlab中的神经网络建模与训练方法引言神经网络在机器学习和人工智能领域中扮演着重要的角色。
它们被用于各种应用,包括图像识别、语音识别、自然语言处理等。
在神经网络的研究和开发过程中,Matlab是一个非常流行的工具,提供了丰富的功能和库,方便了对神经网络的建模和训练。
本文将详细介绍Matlab中神经网络建模与训练的方法。
1. 神经网络建模神经网络模型的构建是神经网络研究的第一步。
在Matlab中,我们可以使用neural network toolbox来构建神经网络模型。
首先,我们需要定义网络的结构,包括输入层、隐藏层和输出层的节点数量、激活函数等。
接下来,我们可以选择不同类型的网络模型,如前馈神经网络、递归神经网络、卷积神经网络等。
每种网络模型都有不同的特点和适用场景。
一旦定义了网络结构,我们可以使用Matlab中的函数来创建并初始化网络。
常用的函数包括feedforwardnet、fitnet和patternnet等。
通过这些函数,我们可以方便地创建各种类型的神经网络,并设置参数,如学习率、权重衰减等。
2. 数据预处理在进行神经网络建模之前,通常需要进行数据预处理。
数据预处理的目的是将原始数据转化为适合神经网络输入的形式。
在Matlab中,我们可以使用各种函数来实现数据预处理,包括数据平滑、标准化、归一化等。
数据平滑可以减少数据中的噪声,并提高神经网络的泛化能力。
Matlab中提供了smoothdata函数来实现数据平滑处理。
标准化可以将数据转化为均值为0、方差为1的形式,以便神经网络更好地处理。
Matlab中的zscore函数可以方便地实现标准化处理。
归一化可以将数据转化为指定的区间范围内,常用的归一化方法包括min-max scaling和z-score normalization。
3. 神经网络训练神经网络的训练是指通过一定的输入数据和对应的输出结果,调整网络的权重和偏置,以获得更好的模型预测能力。
如何使用MATLAB进行神经网络建模

如何使用MATLAB进行神经网络建模使用MATLAB进行神经网络建模神经网络是一种模拟人脑神经系统运作的数学模型,它能够模拟人类的感知、学习和决策过程。
在现代科学和工程领域,神经网络被广泛应用于诸如模式识别、图像处理、时间序列预测等问题的解决中。
而MATLAB作为科学计算和数据分析的常用工具,也提供了一系列强大的神经网络建模工具。
接下来,我们将介绍如何使用MATLAB进行神经网络建模。
一、准备工作在使用MATLAB进行神经网络建模之前,我们需要准备一些必要的工作。
首先,需要安装MATLAB软件,并确保安装的是最新版本。
其次,需要了解MATLAB中神经网络建模的基本原理和概念。
二、数据准备与预处理在进行神经网络建模之前,我们首先需要准备好用于训练和测试的数据集。
通常情况下,我们需要将数据集分为训练集和测试集两部分。
训练集用于神经网络的训练,而测试集则用于评估神经网络的性能。
在准备好数据集后,我们还需要对数据进行一些预处理操作,例如数据归一化、数据标准化等。
这些操作有助于提高神经网络的性能和收敛速度。
三、神经网络建模使用MATLAB进行神经网络建模的核心步骤包括网络设计、网络训练和网络评估。
首先,我们需要确定神经网络的结构,包括输入层、隐藏层和输出层的神经元数量。
这需要根据具体问题的需求和特点进行调整。
然后,我们可以使用MATLAB提供的神经网络工具箱来建立神经网络模型。
根据问题的不同,有多种神经网络模型可供选择,例如前馈神经网络、递归神经网络、自适应神经网络等。
在建立好神经网络模型后,我们还需要选择合适的训练算法对网络进行训练。
常用的训练算法包括误差逆传播算法(Backpropagation)、Levenberg-Marquardt算法等。
最后,我们使用测试集对训练好的神经网络进行评估,得到模型的性能指标,如准确率、误差等。
四、模型调优与改进神经网络建模是一个不断调优与改进的过程。
在建立好初始模型后,我们可以通过修改网络结构、调整训练参数等方式来改进模型的性能。
MATLAB中的神经网络算法和实现方法

MATLAB中的神经网络算法和实现方法简介:神经网络是一种模仿生物神经系统活动的数学模型,广泛应用于机器学习和模式识别领域。
MATLAB作为一种功能强大的科学计算软件,提供了丰富的工具箱和函数,用于神经网络的设计、训练和应用。
本文将介绍MATLAB中的神经网络算法和实现方法。
1. 神经网络的基本原理神经网络由多个神经元组成的网络结构,每个神经元都有多个输入和一个输出。
神经网络的基本原理是通过对输入和权重的加权求和,经过激活函数的处理得到输出。
神经网络的学习过程就是通过调整权重的数值和选择合适的激活函数,使网络能够逼近目标函数。
2. MATLAB中的神经网络工具箱MATLAB提供了神经网络工具箱(Neural Network Toolbox),用于快速实现各种类型的神经网络。
神经网络工具箱包含了各种神经网络算法和函数,可用于网络的创建、训练和应用。
3. 神经网络的创建与配置在MATLAB中创建神经网络可以通过网络构建函数(newff、newcf、newp等)来实现。
可以根据网络的拓扑结构、层数和节点数目来创建神经网络。
配置神经网络可以通过设置网络的参数,如网络输入、目标输出、激活函数、训练算法等。
4. 神经网络的训练神经网络的训练过程是调整网络的权值和偏置,使网络能够对输入进行正确的分类或预测输出。
在MATLAB中,可以使用train函数进行神经网络的训练。
train函数提供了多种训练算法,如梯度下降、Levenberg-Marquardt算法等。
训练过程中,可以设置训练次数、学习率、误差目标等参数。
5. 神经网络的应用神经网络可以用于各种应用领域,如模式识别、数据挖掘、图像处理等。
在MATLAB中,可以使用已经训练好的神经网络对新的输入进行分类或预测。
可以使用sim函数对训练好的网络进行模拟,并根据输出结果进行判断。
6. 神经网络的性能评估与改进在使用神经网络进行建模和预测时,需要对网络的性能进行评估。
matlab神经网络43个案例分析

matlab神经网络43个案例分析MATLAB神经网络是一种广泛使用的机器学习工具,可以应用于多种问题的解决。
下面为大家介绍43个用MATLAB神经网络解决的案例分析。
1. 基于神经网络的股票市场预测通过分析历史数据,建立神经网络模型,预测未来股票市场走势。
2. 神经网络分类器建模分析通过建立分类模型,对不同类型数据进行分类处理。
3. 基于神经网络的信用评估模型通过收集客户的基本信息和信用历史,建立神经网络模型,对客户的信用进行评估。
4. 神经网络医学图像分析通过医学图像数据,建立神经网络模型,进行疾病诊断与分析。
5. 基于神经网络的机器人动作控制通过神经网络,训练机器人进行动作控制,提高机器人的智能化水平。
6. 神经网络预测库存需求通过分析历史销售数据,建立神经网络模型,预测未来库存需求,提高企业的运作效率。
7. 基于神经网络的人脸识别通过收集人脸数据,建立神经网络模型,实现人脸识别功能。
8. 神经网络垃圾邮件过滤通过建立神经网络模型,对邮件进行分类,筛选出垃圾邮件。
9. 基于神经网络的语音识别通过收集语音数据,建立神经网络模型,实现语音识别功能。
10. 神经网络飞机失速预测通过分析飞机数据和空气动力学知识,建立神经网络模型,预测飞机发生失速的概率。
11. 基于神经网络的目标识别通过收集目标数据,建立神经网络模型,实现目标识别功能。
12. 神经网络电力负荷预测通过历史电力数据,建立神经网络模型,预测未来电力负荷。
13. 基于神经网络的网络入侵检测通过建立神经网络模型,检测网络攻击行为。
14. 神经网络手写数字识别通过收集手写数字数据,建立神经网络模型,实现手写数字识别功能。
15. 基于神经网络的情感分析通过对情感文本数据进行分析,建立神经网络模型,实现情感分析功能。
16. 神经网络自然语言处理通过对自然语言文本数据进行处理和分析,建立神经网络模型,实现自然语言处理功能。
17. 基于神经网络的物体识别通过收集物体数据,建立神经网络模型,实现物体识别功能。
MATLABBP神经网络用法的总结(试用于初学者)

MATLABBP神经网络用法的总结(试用于初学者)MATLAB是一种高级编程语言和环境,适用于各种科学和工程应用。
其中的BP神经网络(Backpropagation Neural Network)是一种最常用的人工神经网络类型,用于解决分类和回归问题。
对于初学者来说,使用MATLAB的BP神经网络可能会感到有些困惑,但通过一些基本的了解和指导,可以帮助他们尽快入门并开始应用该技术。
一、MATLAB中BP神经网络的基本原理BP神经网络是一种多层的前馈神经网络,其学习算法基于误差反向传播原理。
它由输入层、隐藏层和输出层组成,每个神经元都与前一层的所有神经元相连。
具体来说,它的训练过程包括四个主要步骤:初始化权重、前向传播、计算误差、反向传播。
通过迭代这四个步骤,神经网络可以根据样本数据不断调整权重,以最小化预测输出与实际输出之间的误差。
二、使用MATLAB创建BP神经网络在MATLAB中,可以使用Neural Network Toolbox(神经网络工具箱)来创建和训练BP神经网络。
可以按照以下步骤创建一个简单的BP神经网络模型。
1.定义输入和输出数据:首先,需要准备输入数据和对应的输出数据。
输入和输出数据的维度应该匹配,且数据应该以矩阵的形式表示。
2. 配置神经网络:使用‘newff’函数来创建一个新的BP神经网络对象。
可以指定隐藏层的数量和每个隐藏层的神经元数。
3. 训练神经网络:使用‘train’函数来训练神经网络。
可以指定训练算法、迭代次数、误差目标等参数。
4.预测和评估:使用已经训练好的神经网络对新的输入数据进行预测,并对预测结果进行评估。
三、MATLAB中BP神经网络的常见问题和解决方法1.数据预处理:在使用BP神经网络之前,需要对输入数据进行预处理,如归一化、标准化等,以确保数据在合理的范围内。
2.过拟合问题:BP神经网络容易过拟合数据,即在训练数据上表现较好,但在未知数据上表现较差。
matlab神经网络实例(超级简单)

介绍神经网络算法在机械结构优化中的应用的例子(大家要学习的时候只需要把输入输出变量更改为你自己的数据既可以了,如果看完了还有问题的话可以加我微博“极南师兄”给我留言,与大家共同进步)。
把一个结构的8个尺寸参数设计为变量,如上图所示,对应的质量,温差,面积作为输出。
用神经网络拟合变量与输出的数学模型,首相必须要有数据来源,这里我用复合中心设计法则构造设计点,根据规则,八个变量将构造出81个设计点。
然后在ansys workbench中进行81次仿真(先在proe建模并设置变量,将模型导入wokbench中进行相应的设置,那么就会自动的完成81次仿真,将结果导出来exceel文件)Matlab程序如下P=[20 2.5 6 14.9 16.5 6 14.9 16.515 2.5 6 14.9 16.5 6 14.9 16.525 2.5 6 14.9 16.5 6 14.9 16.520 1 6 14.9 16.5 6 14.9 16.520 4 6 14.9 16.5 6 14.9 16.520 2.5 2 14.9 16.5 6 14.9 16.520 2.5 10 14.9 16.5 6 14.9 16.520 2.5 6 10 16.5 6 14.9 16.520 2.5 6 19.8 16.5 6 14.9 16.520 2.5 6 14.9 10 6 14.9 16.520 2.5 6 14.9 23 6 14.9 16.520 2.5 6 14.9 16.5 2 14.9 16.520 2.5 6 14.9 16.5 10 14.9 16.520 2.5 6 14.9 16.5 6 10 16.520 2.5 6 14.9 16.5 6 19.8 16.520 2.5 6 14.9 16.5 6 14.9 1020 2.5 6 14.9 16.5 6 14.9 2317.51238947 1.75371684 4.009911573 12.46214168 13.26610631 4.00991157312.46214168 19.7338936922.48761053 1.75371684 4.009911573 12.46214168 13.26610631 4.00991157312.46214168 13.2661063117.51238947 3.24628316 4.009911573 12.46214168 13.26610631 4.00991157322.48761053 3.24628316 4.009911573 12.46214168 13.26610631 4.00991157317.33785832 13.2661063117.51238947 1.75371684 7.990088427 12.46214168 13.26610631 4.00991157317.33785832 19.7338936922.48761053 1.75371684 7.990088427 12.46214168 13.26610631 4.00991157317.33785832 13.2661063117.51238947 3.24628316 7.990088427 12.46214168 13.26610631 4.00991157312.46214168 19.7338936922.48761053 3.24628316 7.990088427 12.46214168 13.26610631 4.00991157312.46214168 13.2661063117.51238947 1.75371684 4.009911573 17.33785832 13.26610631 4.00991157317.33785832 13.2661063122.48761053 1.75371684 4.009911573 17.33785832 13.26610631 4.00991157317.33785832 19.7338936917.51238947 3.24628316 4.009911573 17.33785832 13.26610631 4.00991157312.46214168 13.2661063122.48761053 3.24628316 4.009911573 17.33785832 13.26610631 4.00991157312.46214168 19.7338936917.51238947 1.75371684 7.990088427 17.33785832 13.26610631 4.00991157312.46214168 13.2661063122.48761053 1.75371684 7.990088427 17.33785832 13.26610631 4.00991157312.46214168 19.7338936917.51238947 3.24628316 7.990088427 17.33785832 13.26610631 4.00991157317.33785832 13.2661063122.48761053 3.24628316 7.990088427 17.33785832 13.26610631 4.00991157317.33785832 19.7338936917.51238947 1.75371684 4.009911573 12.46214168 19.73389369 4.00991157317.33785832 13.2661063122.48761053 1.75371684 4.009911573 12.46214168 19.73389369 4.00991157317.33785832 19.7338936917.51238947 3.24628316 4.009911573 12.46214168 19.73389369 4.00991157312.46214168 13.2661063122.48761053 3.24628316 4.009911573 12.46214168 19.73389369 4.00991157312.46214168 19.7338936917.51238947 1.75371684 7.990088427 12.46214168 19.73389369 4.00991157312.46214168 13.2661063122.48761053 1.75371684 7.990088427 12.46214168 19.73389369 4.00991157312.46214168 19.7338936917.51238947 3.24628316 7.990088427 12.46214168 19.73389369 4.00991157317.33785832 13.2661063122.48761053 3.24628316 7.990088427 12.46214168 19.73389369 4.00991157317.33785832 19.7338936917.51238947 1.75371684 4.009911573 17.33785832 19.73389369 4.00991157322.48761053 1.75371684 4.009911573 17.33785832 19.73389369 4.00991157312.46214168 13.2661063117.51238947 3.24628316 4.009911573 17.33785832 19.73389369 4.00991157317.33785832 19.7338936922.48761053 3.24628316 4.009911573 17.33785832 19.73389369 4.00991157317.33785832 13.2661063117.51238947 1.75371684 7.990088427 17.33785832 19.73389369 4.00991157317.33785832 19.7338936922.48761053 1.75371684 7.990088427 17.33785832 19.73389369 4.00991157317.33785832 13.2661063117.51238947 3.24628316 7.990088427 17.33785832 19.73389369 4.00991157312.46214168 19.7338936922.48761053 3.24628316 7.990088427 17.33785832 19.73389369 4.00991157312.46214168 13.2661063117.51238947 1.75371684 4.009911573 12.46214168 13.26610631 7.99008842717.33785832 13.2661063122.48761053 1.75371684 4.009911573 12.46214168 13.26610631 7.99008842717.33785832 19.7338936917.51238947 3.24628316 4.009911573 12.46214168 13.26610631 7.99008842712.46214168 13.2661063122.48761053 3.24628316 4.009911573 12.46214168 13.26610631 7.99008842712.46214168 19.7338936917.51238947 1.75371684 7.990088427 12.46214168 13.26610631 7.99008842712.46214168 13.2661063122.48761053 1.75371684 7.990088427 12.46214168 13.26610631 7.99008842712.46214168 19.7338936917.51238947 3.24628316 7.990088427 12.46214168 13.26610631 7.99008842717.33785832 13.2661063122.48761053 3.24628316 7.990088427 12.46214168 13.26610631 7.99008842717.33785832 19.7338936917.51238947 1.75371684 4.009911573 17.33785832 13.26610631 7.99008842712.46214168 19.7338936922.48761053 1.75371684 4.009911573 17.33785832 13.26610631 7.99008842712.46214168 13.2661063117.51238947 3.24628316 4.009911573 17.33785832 13.26610631 7.99008842717.33785832 19.7338936922.48761053 3.24628316 4.009911573 17.33785832 13.26610631 7.99008842717.33785832 13.2661063117.51238947 1.75371684 7.990088427 17.33785832 13.26610631 7.99008842717.33785832 19.7338936922.48761053 1.75371684 7.990088427 17.33785832 13.26610631 7.99008842717.33785832 13.2661063117.51238947 3.24628316 7.990088427 17.33785832 13.26610631 7.99008842722.48761053 3.24628316 7.990088427 17.33785832 13.26610631 7.99008842712.46214168 13.2661063117.51238947 1.75371684 4.009911573 12.46214168 19.73389369 7.99008842712.46214168 19.7338936922.48761053 1.75371684 4.009911573 12.46214168 19.73389369 7.99008842712.46214168 13.2661063117.51238947 3.24628316 4.009911573 12.46214168 19.73389369 7.99008842717.33785832 19.7338936922.48761053 3.24628316 4.009911573 12.46214168 19.73389369 7.99008842717.33785832 13.2661063117.51238947 1.75371684 7.990088427 12.46214168 19.73389369 7.99008842717.33785832 19.7338936922.48761053 1.75371684 7.990088427 12.46214168 19.73389369 7.99008842717.33785832 13.2661063117.51238947 3.24628316 7.990088427 12.46214168 19.73389369 7.99008842712.46214168 19.7338936922.48761053 3.24628316 7.990088427 12.46214168 19.73389369 7.99008842712.46214168 13.2661063117.51238947 1.75371684 4.009911573 17.33785832 19.73389369 7.99008842717.33785832 13.2661063122.48761053 1.75371684 4.009911573 17.33785832 19.73389369 7.99008842717.33785832 19.7338936917.51238947 3.24628316 4.009911573 17.33785832 19.73389369 7.99008842712.46214168 13.2661063122.48761053 3.24628316 4.009911573 17.33785832 19.73389369 7.99008842712.46214168 19.7338936917.51238947 1.75371684 7.990088427 17.33785832 19.73389369 7.99008842712.46214168 13.2661063122.48761053 1.75371684 7.990088427 17.33785832 19.73389369 7.99008842712.46214168 19.7338936917.51238947 3.24628316 7.990088427 17.33785832 19.73389369 7.99008842717.33785832 13.2661063122.48761053 3.24628316 7.990088427 17.33785832 19.73389369 7.99008842717.33785832 19.73389369]';%注意因为本人做了81组仿真试验,这里的矩阵后面有转置符号,在神经网络模型中,输入P的是8X81的矩阵(把程序复制过来之后格式没对齐,大家自己调整一下啦),对应的下面的输出T的是3x81的矩阵。
MATLAB神经网络应用设计

MATLAB神经网络应用设计
详细报告
一、背景
自20世纪80年代以来,神经网络已经广泛应用于各种领域,例如模式识别,认知科学,信息处理,机器人控制,图像处理等。
MATLAB具有强大的图形用户界面(GUI),有助于用户实施神经网络设计和应用。
MATLAB有助于神经网络的处理,同时也可以帮助开发者设计神经网络应用。
二、目标
本文的目的是讨论使用MATLAB实现神经网络应用设计的方法。
三、过程
1.开发者首先需要根据目标定义神经网络模型或者使用已有的神经网络模型,并设计其输入输出结构.
2.然后,开发者开发一个MATLAB神经网络应用程序,该程序负责收集数据,训练神经网络,预测结果等。
3.然后,开发者需要使用MATLAB提供的一些工具,如神经网络工具箱(NNTB),建立训练数据的输入和输出模型,调整训练参数,以便获得更好的建模结果。
5.最后,开发者可以使用MATLAB中的其他工具(如神经网络应用编程界面(NNAPI)),将训练的模型部署到实际的应用场景中,以实现实时预测和模型的可重复使用。
MATLAB神经网络应用实验.

• 该函数用来初始化一个前馈网络,函数输入参数含义如下: • PR :一个R 行2 列的矩阵,第i 行是R 维输入向量的第i 个分
• • • •
• • •
量取值区间的端点值. Si :第i 层包含的结点个数. TFi :第i 层的传输函数,缺省值为函数tansig. BTF :反向传播网络的训练函数,缺省值为函数trainlm. BLF :反向传播权值P阀值的学习函数,缺省值为函数 learngdm. PF :执行函数,缺省值为函数mse. newff () 函数返回一个多层前馈反向传播网络. 与该函数 对应的老版本函数为 [w1 ,b1 ,w2 ,b2 ,w3 ,b3 ] = initff (p ,s1 ,f1 ,s2 ,f2 ,s3 ,f3) .
.
• 三、 过程离线辩识的实验步骤 • 例:辩识以下非线性仿真对象 • 1) 初步确定网络的层数,各层结点数和各层传输函数等结
构参数,然后以它们为参数调用newff () 或initff () 初始化 一个网络net . 对于该仿真对象可预设网络结构为:5 ×20 ×10 ×1
• 2) 调用u = random(’unif’, - 5 ,5 ,1 ,100) 产生均匀分布白
y (5) ⋯y (100) 构成网络在输入p 下的输出
• • •
步数、训练误差、学习率取为(5000 0. 02 0. 0015) , (15000 0. 015 0. 0011) 或(20000 0. 015 0. 0008) 均可. 5) 观察、检验网络在其它输入下和被辩识过程在相同输入 下的输出逼近情况. 6)将训练好的网络和仿真对象或实际系统在工况输入,如 su = 5 *sin (2*pi 3 k/50) 下的输出一同绘图. 注:若发现网络输出不能很好地逼近仿真对象或实际系统 的输出时,则要增加学习样本个数、增加输入延时序列长 度或者调整(1) 、(3) 中的参数,重复上述步骤.
MATLAB神经网络实验

神经元模型
Neuron Model: 多输入,单输出,带偏置
输入:R维列向量
p [ p1,
pR ]T
w1R ]
阈值:标量 b
权值:R维行向量 w [w11 , 求和单元 n p w b i 1i
i 1 R
传递函数 f 输出
a f ( wp b)
参数含义
训练步数 显示训练结果的间隔步数
默认值
100 25
net.trainParam.goal
net.trainParam.time net.trainParam.lr
训练目标误差
训练允许时间 学习率
0
INf 0.01
BP网络的设计(1)
网络层数
已经证明,单隐层的BP网络可以实现任意非线性映射. BP网络的隐层数一般不超过两层.
n = 10; net = newff(minmax(p), [n,1], {'tansig' 'purelin'}, 'trainlm'); % 对于该初始网络,可以应用sim()函数观察网络输出 y1 = sim(net,p); % 同时绘制网络输出曲线,并与原函数相比较 figure; plot(p,t,'-',p,y1,'--') title('未训练网络的输出结果'); xlabel('时间'); ylabel('仿真输出 - - 原函数 -');
对数Sigmoid函数 1 a f (n) 1 e n
正切Sigmoid函数
en e n a tanh(n) n n e e
神经网络的MATLAB实现(苏析超)

神经网络的MATLAB实现
%% 网络结构初始化 innum=24; midnum=25; outnum=4; %权值初始化 w1=rands(midnum,innum); b1=rands(midnum,1); w2=rands(midnum,outnum); b2=rands(outnum,1);
input_train=input(n(1:1500),:)'; output_train=output(n(1:1500),:)'; input_test=input(n(1501:2000),:)'; output_test=output(n(1501:2000),:)'; %输入数据归一化 [inputn,inputps]=mapminmax(input_train);
%画出预测语音种类和实际语音种类的分类图 figure(1) plot(output_fore,'r') hold on plot(output1(n(1501:2000))','b') legend('预测语音类别','实际语音类别')
神经网络的MATLAB实现
%画出误差图 figure(2) plot(error) title('BP网络分类误差','fontsize',12) xlabel('语音信号','fontsize',12) ylabel('分类误差','fontsize',12)
神经网络的MATLAB实现
%% 权值阀值修正 %计算误差 e=output_train(:,i)-yn; E(ii)=E(ii)+sum(abs(e));
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因为使用newff()函数建立网 络时,权值和阈值的初始化 是随机的,所以网络输出的 结果很差,根本达不到函数 逼近的目的,并且每次运行 结果也有所不同。
• Step 3: 网络训练 • 应用函数train()对网络进行训练之前,要先设置训练 参数。将训练时间设置为50,精度设置为0.01,其余 用缺省值。 • 训练后得到的误差变化过程如图:
2.反向传播
反向传播时,把误差信号按原来正向传播的通路反向传回,并对每个 隐层的各个神经元的权系数进行修改,以望误差信号趋向最小。
BP算法实质是求取误差函数的最小值问题。这种算法采用非 线性规划中的最速下降方法,按误差函数的负梯度方向修改 权系数。
BP网络的快速学习算法与选择
MATLAB神经网络工具箱对常规BP算法进行改进,提供 了一系列快速算法,以满足不同问题的需要
t = sin(k*pi*p);
plot(p,t,'-')
title('要逼近的非线性函数');
xlabel('时间'); ylabel('非线性函数');
• Step 2: 网络建立 应用函数newff()建立BP网络结构,为二层BP 网络。隐层神经元数目n可以改变,暂设为 10,输出层有一个神经元。选择隐层和输 出层神经元传递函数分别为tansig函数和 purelin函数,网络训练算法采用trainlm
模式分类
函数拟合 模式分类 函数拟合
收敛最快
收敛较快 性能稳定 收敛较快
较小
中等
较大
模式分类
收敛较慢
较小
BP网络的训练
利用已知的”输入—目标”样本向量数据对网络进行训练, 采用train 函数来完成. 训练之前, 对训练参数进行设置 net = train(net, P, T)
训练参数
net.trainParam.epochs net.trainParam.show
输入层的节点数
输入层接收外部的输入数据, 节点数取决于输入向量 的维数
输出层的节点数
输出层的节点数取决于输出数据类型和该类型所需 的数据大小. 对于模式分类问题,节点数为 log 2 m
BP网络的设计(2)
隐层的节点数
隐层的节点数与求解问题的要求,输入输出单元数多 少有关. 对于模式识别/分类的节点数可按下列公式设计
MATLAB神经网络工具箱 介绍及实验要求
神经元模型
Neuron Model: 多输入,单输出,带偏置
输入:R维列向量
p [ p1, pR ]T
阈值:标量 b
权值:R维行向量 w [w11 , w1R ] 求和单元 n p w b i 1i
i 1 R
传递函数 f 输出
%定义训练样本 p=[-1 -1 3 1;-1 1 5 -3]; t=[-1 -1 1 1]; %创建一个新的BP网络 net=newff(minmax(p),[3 1],{'tansig','purelin'},'traingdm'); %设置训练参数 net.trainParam.epochs=1000; net.trainParam.goal=0.001; net.trainParam.show=50; net.trainParam.lr=0.05; net.trainParam.mc=0.9;%动量因子,缺省为0.9 net=train(net,p,t); % 训练网络 A=sim(net,p) %网络仿真
a f ( wp b)
常用传递函数
阈值函数
1 (n 0) MATLAB函数: hardlim a f (n) hardlim(n) 0 (n 0)
a 1 -1
-b
Wp
1 (n 0) a f (n) hard lim s(n) 1 (n 0)
学习算法 trainlm 适用问题类型
函数拟合
收敛性能
收敛快,误差小
占用存储空间
大
其他特点
性能随网络规模 增大而变差 性能随网络训练 误差减小而变差 尤其适用于网络 规模较大的情况 计算量岁网络规 模的增大呈几何 增长 适用于提前停止 的方法
trainrp
trainscg trainbfg traingdx
n ni n0 a
其中 n 为隐层节点数, ni 为输入节点数, a 为1~10之间的整数
传递函数
隐层传递函数采用S型函数, 输出层采用S型函数或 线性函数
训练方法及其参数选择
针对不同应用, BP网络提供了多种训练学习方法.
BP网络设计实例
采用动量梯度下降算法训练BP网络. 训练样本
训练误差变化曲线(每次不同)
训练误差变化曲线
目标线
实验2: BP网络用于曲线拟合
• 要求设计一个简单的BP网络,实现对非线性函数 的逼近。通过改变该函数的参数以及BP网络隐层 神经元的数目,来观察训练时间以及训练误差的 变化情况。
Step1: 将要逼近的非线性函数设为正弦函数
k = 1; p = [-1:.05:1];
MATLAB函数: hardlims
线性函数
Purelin Transfer Function :
a f (n) n
a
n
MATLAB函数: purelin
Sigmoid函数
Sigmoid
特性:
Function :
值域a∈(0,1) 非线性,单调性 无限次可微 |n|较小时可近似线性 函数 |n|较大时可近似阈值 函数
BP网络
多层前馈网络
传递函数:隐层采用S形函数,输出层S形函数或线性函数
主要功能: 函数逼近, 模式识别, 信息分类
BP网络的生成
newff
函数newff用来生成一个BP网络
net=newff(PR,[S1 S2...SN],{TF1 TF2... TFN},BTF,BLF,PF) PR: 一个R×2矩阵, 由R维输入向量的每维最小值和最大值组成 Si: 第i层的神经元个数 TFi: 第i层的传递函数, 默认为tansig BTF: 训练函数, 默认为trainlm BLF: 学习函数, 默认为learngdm PF: 性能函数, 默认为mse net=newff([0,10;-1,2],[5,1],{‘tansig’,’purelin’},’trainlm’);
%生成一个两层BP网络,隐层和输出层神经的个数为5和1, 传递函数分别为 tansig和purelin, 训练函数为trainlm, 其他默认
BP网络的初始化
newff 函数在建立网络对象的同时, 自动调用初始化函数, 根据缺省的参数设置网络的连接权值和阈值. 使用函数init可以对网络进行自定义的初始化. 通过选择 初始化函数, 可对各层连接权值和阈值分别进行不同的初始 化.
net.trainParam.epochs = 50; net.trainParam.goal = 0.01; net = train(net,p,t);
Stet 4: 网络测试 对于训练好的网络进行仿真 并绘制网络输出曲线,与原始非线性函数曲线以及未训 练网络的输出结果曲线相比较
y2 = sim(net,p); figure; plot(p,t,'-',p,y1,'--',p,y2,'-.') title('训练后网络的输出结果'); xlabel('时间'); ylabel('仿真输出'); 从图中可以看出,得到的曲 线和原始的非线性函数曲线 很接近。这说明经过训练后, BP网络对非线性函数的逼近 效果相当好。
对数Sigmoid函数 1 a f (n) 1 e n
正切Sigmoid函数
en e n a tanh(n) n n e e
MATLAB函数: logsig(对数), tansig(正切)
前馈神经网络
前馈神经网络(feed
forward NN):各神经元 接受前级输入,并输出到下一级,无反馈, 可用一有向无环图表示。 前馈网络通常分为不同的层(layer),第i层的 输入只与第i-1层的输出联结。 可见层:输入层(input layer)和输出层(output layer) 隐藏层(hidden layer) :中间层
n = 10; net = newff(minmax(p), [n,1], {'tansig' 'purelin'}, 'trainlm'); % 对于该初始网络,可以应用sim()函数观察网络输出 y1 = sim(net,p); % 同时绘制网络输出曲线,并与原函数相比较 figure; plot(p,t,'-',p,y1,'--') title('未训练网络的输出结果'); xlabel('时间'); ylabel('仿真输出 - - 原函数 -');
BP网络的学习规则
权值和阈值的调节规则采用误差反向传播算法(back propagation). 反向 传播算法分二步进行,即正向传播和反向传播。
1.正向传播
输入的样本从输入层经过隐单元一层一层进行处理,通过所有的隐层 之后,则传向输出层;在逐层处理的过程中,每一层神经元的状态只对 下一层神经元的状态产生影响。在输出层把现行输出和期望输出进行比 较,如果现行输出不等于期望输出,则进入反向传播过程。
参数含义
训练步数 显示训练结果的间隔步数
默认值
100 25
net.trainParam.goal
net.trainParam.time net.trainParam.lr
