2008年高考数学试题分类汇编——函数与导数(二)

2008年高考数学导数汇编

导数1．设函数1()(01)ln f x x x x x=>≠且（Ⅰ）求函数()f x 的单调区间；（Ⅱ）已知12a xx >对任意(0,1)x ∈成立，求实数a 的取值范围。

2．设函数sin ()2cos x f x x=+．（Ⅰ）求()f x 的单调区间；（Ⅱ）如果对任何0x ≥，都有()f x ax ≤，求a 的取值范围．3．设函数2()(0),f x ax bx c a =++≠曲线y=f(x)通过点（0，2a+3），且在点（-1，f （-1））处的切线垂直于y轴.（Ⅰ）用a 分别表示b 和c ；（Ⅱ）当bc 取得最小值时，求函数g(x)=-f(x)e-x 的单调区间.4．已知函数22()(1)x b f x x -=-，求导函数()f x '，并确定()f x 的单调区间．5．已知函数321()23f x x x =+-，设{a n }是正数组成的数列，前n 项和为S n ，其中a 1=3.若点211(,2)n n n a a a ++-(n ∈N*)在函数y =f ′(x )的图象上。

求证：点（n , S n ）也在y =f ′(x )的图象上。

6．设k ∈R，函数111()1x x f x x ⎧<⎪-=⎨⎪⎩，≥，()()F x f x kx =-，x ∈R ，试讨论函数()F x 的单调性．7．水库的蓄水量随时间而变化，现用t 表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于t 的近似函数关系式为V （t ）=⎪⎩⎪⎨⎧≤<+--≤<+-+-1210,50)413)(10(4,100,50)4014(412t t t t e t t t（Ⅰ）该水库的蓄水量小于50的时期称为枯水期.以i －1＜t ＜i 表示第i 月份（i=1,2,…,12）,问一年内哪几个月份是枯水期？（Ⅱ）求一年内该水库的最大蓄水量（取e=2.7计算）.8．已知函数f (x )=ln 2(1+x)－21x x +. （Ⅰ）求函数f (x )的单调区间; （Ⅱ）若不等式1(1)n a e n ++≤对任意的N*n ∈都成立（其中e 是自然对数的底数），求α的最大值.9．设函数ln ()ln ln(1)1x f x x x x=-+++．（Ⅰ）求f (x )的单调区间和极值；（Ⅱ）是否存在实数a ，使得关于x 的不等式()f x a ≥的解集为（0，+∞）？若存在，求a 的取值范围；若不存在，试说明理由．10．设函数1()(,)f x ax a b Z x b=+∈+，曲线()y f x =在点(2,(2))f 处的切线方程为3y =。

2008届全国百套高考数学模拟试题分类汇编-022函数填空题

2008届全国百套高考数学模拟试题分类汇编02函数二、填空题1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)三位同学在研究函数 f (x ) = x1 + | x |(x ∈R ) 时，分别给出下面三个结论：① 函数 f (x ) 的值域为 (－1,1)② 若x 1≠x 2，则一定有f (x 1)≠f (x 2)③ 若规定 f 1(x ) = f (x )，f n +1(x ) = f [ f n (x )]，则 f n (x ) = x 1 + n | x |对任意 n ∈N *恒成立. 你认为上述三个结论中正确的个数有答案：3.2、(江苏省启东中学2008年高三综合测试一)已知函数()3x f x =的反函数是1()f x -且1(18)23a f a -=+则=______________答案：23、(江苏省启东中学高三综合测试二)给出下列图象其中可能为函数f (x )＝x 4＋ax 3＋bx 2＋cx ＋d (a ，b ，c ，d ∈R)的图象的是_____. 答案：①③4、(江苏省启东中学高三综合测试二)已知f (x )=a ｘ（ａ＞1），ｇ（ｘ）＝ｂｘ（ｂ＞1），当f (x 1)＝g (ｘ2)＝2时，有ｘ1＞ｘ2，则a,ｂ的大小关系是 . 答案：a ＜b5、(江苏省启东中学高三综合测试四)已知函数⎩⎨⎧≤>=)0(2)0(log )(3x x x x f x ，则 )]91([f f =答案：146、(江西省五校2008届高三开学联考)设{x }表示离x 最近的整数，即若x m <-21≤21+m (m ∈Z )，则{x } = m ．给出下列关于函数|}{|)(x x x f -=的四个命题： ①函数)(x f y =的定义域是R ，值域是[0，21]； ②函数)(x f y =的图像关于直线2kx =(k ∈Z )对称； ③函数)(x f y =是周期函数，最小正周期是1； ④函数)(x f y =是连续函数，但不可导．其中真命题是 __________ ．答案：①②③④7、(四川省巴蜀联盟2008届高三年级第二次联考)已知函数y =[0,)+∞，则实数m 的取值范围是答案：(0,1][9,)+∞8、(陕西长安二中2008届高三第一学期第二次月考)函数)1lg ()(2--=ax x x f 在区间),1(+∞上单调增函数，则a 的取值范围是________。

2008年高考数学章节分类(试题)(1-10)章目录

2008年高考数学章节分类试题文科使用（共16章242页）2008年9月整理2008年高考数学章节分类试题目录第一章《集合与函数概念》 (1)第二章《基本初等函数（幂函数、指数函数、对数函数）》 (11)第三章《空间几何体》.......................................................... . (17)第四章《点、直线、平面之间的位置关系》、《空间向量与立体几何》 (22)第五章《直线与圆及其方程》............................................................ (57)第六章《算法初步》 (62)第七章《统计与概率》..................................................................... ..71 第八章《三角函数与恒等变形》.. (77)第九章《平面向量》 (91)第十章《解三角形》 (95)第十一章《数列》 (102)第十二章《不等式与简单的线性》 (120)第十三章《常用逻辑用语》 (125)第十四章《圆锥曲线（抛物线、椭圆与双曲线）》 (128)第十五章《导数及其应用》 (163)第十六章《数系的扩充与复数的引入》 (186)答案第一章《集合与函数概念》 (187)第二章《基本初等函数（幂函数、指数函数、对数函数）》 (193)第三章《空间几何体》.......................................................... . (196)第四章《点、直线、平面之间的位置关系》、《空间向量与立体几何》 (199)第五章《直线与圆及其方程》............................................................ (204)第六章《算法初步》 (207)第七章《统计与概率》..................................................................... (209)第八章《三角函数与恒等变形》 (212)第九章《平面向量》 (217)第十章《解三角形》 (221)第十一章《数列》 (223)第十二章《不等式与简单的线性》 (226)第十三章《常用逻辑用语》 (229)第十四章《圆锥曲线（抛物线、椭圆与双曲线）》 (231)第十五章《导数及其应用》 (338)第十六章《数系的扩充与复数的引入》 (341)。

2008年高考数学试题分类汇编——函数与导数

2008年高考数学试题分类汇编函数与导数一．选择题：1.（全国一1）函数y =的定义域为（ C ） A ．{}|0x x ≥B ．{}|1x x ≥C ．{}{}|10x x ≥D ．{}|01x x ≤≤2.（全国一2）汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图像可能是（ A ）3.（全国一6）若函数(1)y f x =-的图像与函数1y =的图像关于直线y x =对称，则()f x =（ B ） A ．21x e -B ．2x eC ．21x e +D ．22x e +4.（全国一7）设曲线11x y x +=-在点(32)，处的切线与直线10ax y ++=垂直，则a =（ D ） A ．2B ．12C ．12-D ．2-5.（全国一9）设奇函数()f x 在(0)+∞，上为增函数，且(1)0f =，则不等式()()0f x f x x --<的解集为（ D ）A ．(10)(1)-+∞，， B ．(1)(01)-∞-，， C ．(1)(1)-∞-+∞，， D ．(10)(01)-，， 6.（全国二3）函数1()f x x x=-的图像关于（ C ） A ．y 轴对称B ．直线x y -=对称A ．B ．C ．D ．C ．坐标原点对称D ．直线x y =对称8.（全国二4）若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ C ） A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a9.（北京卷2）若0.52a =，πlog 3b =，22πlog sin 5c =，则（ A ）A ．a b c >>B ．b a c >>C ．c a b >>D ．b c a >> 10.（北京卷3）“函数()()f x x ∈R 存在反函数”是“函数()f x 在R 上为增函数”的（ B ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件11.（四川卷10）设()()sin f x x ωϕ=+，其中0ω>，则()f x 是偶函数的充要条件是( D ) （Ａ）()01f = （Ｂ）()00f = （Ｃ）()'01f = （Ｄ）()'00f = 12.（四川卷11）设定义在R 上的函数()f x 满足()()213f x f x ⋅+=，若()12f =，则()99f =( C )（Ａ）13 （Ｂ）2 （Ｃ）132 （Ｄ）21313.（天津卷3）函数1y =+04x ≤≤）的反函数是A（A ）2(1)y x =-（13x ≤≤）（B ）2(1)y x =-（04x ≤≤）（C ）21y x =-（13x ≤≤）（D ）21y x =-（04x ≤≤）14.（天津卷10）设1a >，若对于任意的[,2]x a a ∈，都有2[,]y a a ∈满足方程lo g lo g 3a ax y +=，这时a 的取值集合为B （A ）2{|1}a a <≤ （B ）{|}2a a ≥ （C ）3|}2{a a ≤≤ （D ）{2,3} 15.（安徽卷7）0a <是方程2210ax x ++=至少有一个负数根的（ B ）A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件16.（安徽卷9）在同一平面直角坐标系中，函数()y g x =的图象与x y e =的图象关于直线y x =对称。

2008年全国各地高考数学试题及解答分类汇编大全(02常用逻辑用语)

2008 年全国各地高考数学试题及解答分类汇编大全
（02 常用逻辑用语）
一.选择题：
1．（2008 安徽文、理） a 0 是方程 ax2 2x 1 0 至少有一个负数根的（ B ）
A．必要不充分条件
B．充分不必要条件
C．充分必要条件
D．既不充分也不必要条件
2.(2008 北京理)“函数 f (x)(x R) 存在反函数”是“函数 f (x) 在 R 上为增函数”的
第 1 页（共 3 页）
9．(2008 湖北理)若非空集合 A,B,C 满足 A∪B=C，且 B 不是 A 的子集，则（B ）
A.“x∈C”是“x∈A”的充分条件但不是必要条件 B. “x∈C”是“x∈A”的必要条件但不是充分条件 C. “x∈C”是“x∈A”的充分条件 D. “x∈C”是“x∈A”的充分条件也不是“x∈A”必要条件
12．(2008 江西文) “ x y ”是“ x y ”的（B ）
A．充分不必要条件 B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
13.(2008 山东文)给出命题：若函数 y f (x) 是幂函数，则函数 y f (x) 的图象不过第四
象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是（ C ）
A. a ， b 方向相同
B. a ， b 两向量中至少有一个为零向量
C. R ， b a
D. 存在不全为零的实数 1 ， 2 ， 1a 2 b 0
8. (2008 湖北文)若集合 P {1, 2,3, 4},Q {x 0 x 5, x R},则（ A ） A. “ x R ”是“ x Q ”的充分条件但不是必要条件 B. “ x R ”是“ x Q ”的必要条件但不是充分条件 C. “ x R ”是“ x Q ”的充要条件 D. “ x R ”既不是“ x Q ”的充分条件也不是“ x Q ”的必要条件

2008年高考试题分类(3)(数学-导数)(2)

03 导数的应用一、选择题 1．（福建11）如果函数y=f (x )的图象如右图，那么导函数/()y f x =的图象可能是（ A ）2．（辽宁6）设P 为曲线C ：223y x x =++上的点，且曲线C 在点P 处切线倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦，，则点P 横坐标的取值范围为（ A ）A ．112⎡⎤--⎢⎥⎣⎦，B ．[]10-，C ．[]01，D ．112⎡⎤⎢⎥⎣⎦，3．（全国Ⅰ4）曲线324y x x =-+在点(13)，处的切线的倾斜角为（ B ） A ．30°B ．45°C ．60°D ．120°4．（全国Ⅱ）设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ A ）A ．1B ．12C ．12-D ．1-二、填空题1．（北京13）如图，函数()f x 的图象是折线段ABC ，其中A B C ，，的坐标分别为(04)(20)(64)，，，，，，则((0))f f =_________；2函数()f x 在1x =处的导数(1)f '=_________．2-2．（江苏14）13)(3+-=x ax x f 对于[]1,1-∈x 总有0)(≥x f 成立，则a = 42 BCAyx1 O 3 4 5 612 3 4三、解答题 1．（安徽20）（本小题满分12分）设函数323()(1)1,32a f x x x a x a =-+++其中为实数。

（Ⅰ）已知函数()f x 在1x =处取得极值，求a 的值；（Ⅱ）已知不等式'2()1f x x x a >--+对任意(0,)a ∈+∞都成立，求实数x 的取值范围。

解: (1) '2()3(1)f x ax x a =-++，由于函数()f x 在1x =时取得极值，所以 '(1)0f =即 310,1a a a -++==∴ (2) 方法一由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立设 22()(2)2()g a a x x x a R =+--∈, 则对任意x R ∈，()g a 为单调递增函数()a R ∈ 所以对任意(0,)a ∈+∞，()0g a >恒成立的充分必要条件是(0)0g ≥ 即 220x x --≥，20x -≤≤∴ 于是x 的取值范围是}{|20x x -≤≤方法二由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立于是2222x x a x +>+对任意(0,)a ∈+∞都成立，即22202x xx +≤+ 20x -≤≤∴于是x 的取值范围是}{|20x x -≤≤2．（北京17）（本小题共13分）已知函数32()3(0)f x x ax bx c b =+++≠，且()()2g x f x =-是奇函数．（Ⅰ）求a ，c 的值；（Ⅱ）求函数()f x 的单调区间．解：（Ⅰ）因为函数()()2g x f x =-为奇函数，所以，对任意的x ∈R ，()()g x g x -=-，即()2()2f x f x --=-+．又32()3f x x ax bx c =+++所以32323232x ax bx c x ax bx c -+-+-=----+．所以22a a c c =-⎧⎨-=-+⎩，．解得02a c ==，．（Ⅱ）由（Ⅰ）得3()32f x x bx =++．所以2()33(0)f x x b b '=+≠．当0b <时，由()0f x '=得x b =±-．x 变化时，()f x '的变化情况如下表：x()b -∞--，b --()b b ---，b - b -+∞（，）()f x '+-+所以，当0b <时，函数()f x 在()b -∞--，上单调递增，在()b b ---，上单调递减，在()b -+∞，上单调递增．当0b >时，()0f x '>，所以函数()f x 在()-∞+∞，上单调递增． 3．(福建21)（本小题满分12分）已知函数32()2f x x mx nx =++-的图象过点（-1，-6），且函数()()6g x f x x '=+的图象关于y 轴对称. (Ⅰ)求m 、n 的值及函数y =f (x )的单调区间；(Ⅱ)若a ＞0，求函数y =f (x )在区间（a -1,a +1）内的极值. 解：（1）由函数f (x )图象过点（－1，－6），得m -n =-3, ……① 由f (x )=x 3+mx 2+nx -2，得f ′（x ）=3x 2+2mx +n , 则g (x )=f ′(x )+6x =3x 2+(2m +6)x +n ; 而g (x )图象关于y 轴对称，所以－3262⨯+m ＝0，所以m =-3, 代入①得n =0.于是f ′(x )＝3x 2-6x =3x (x -2). 由f ′(x )>得x>2或x <0,故f (x )的单调递增区间是（－∞，0），（2，＋∞）；由f ′(x )<0得0<x <2,故f (x )的单调递减区间是（0，2）.(Ⅱ)由（Ⅰ）得f ′(x )＝3x (x -2), 令f ′(x )＝0得x =0或x=2.当x 变化时，f ′(x )、f (x )的变化情况如下表： X (-∞.0) 0 (0,2) 2 (2,+ ∞) f ′(x ) + 0 － 0 ＋ f (x )极大值极小值由此可得：当0<a <1时，f (x )在（a -1,a +1）内有极大值f (O )=-2,无极小值；当a =1时，f (x )在（a -1,a +1）内无极值；当1<a <3时，f (x )在（a -1,a +1）内有极小值f (2)＝－6，无极大值；当a ≥3时，f (x )在（a -1,a +1）内无极值.综上得：当0<a <1时，f (x )有极大值－2，无极小值，当1<a <3时，f (x )有极小值－6，无极大值；当a=1或a ≥3时，f (x )无极值. 4．（宁夏）（本小题满分12分）设函数()bf x ax x=-， ()y f x =在点(2(2))f ，处的切线方程为74120x y --=．（Ⅰ）求()f x 的解析式；（Ⅱ）证明：曲线()y f x =上任一点处的切线与直线0x =和直线y x =所围成的三角形面积为定值，并求此定值．．解：（Ⅰ）方程74120x y --=可化为734y x =-．当2x =时，12y =． ················································································································· 2分又2()b f x a x '=+，于是1222744b a b a ⎧-=⎪⎪⎨⎪+=⎪⎩，，解得13.a b =⎧⎨=⎩，故3()f x x x=-． ······················································································································· 6分（Ⅱ）设00()P x y ，为曲线上任一点，由231y x'=+知曲线在点00()P x y ，处的切线方程为002031()y y x x x ⎛⎫-=+- ⎪⎝⎭，即00200331()y x x x x x ⎛⎫⎛⎫--=+- ⎪ ⎪⎝⎭⎝⎭．令0x =得06y x =-，从而得切线与直线0x =的交点坐标为060x ⎛⎫- ⎪⎝⎭，．令y x =得02y x x ==，从而得切线与直线y x =的交点坐标为00(22)x x ，． ················ 10分所以点00()P x y ，处的切线与直线0x =，y x =所围成的三角形面积为016262x x-=．故曲线()y f x =上任一点处的切线与直线0x =，y x =所围成的三角形的面积为定值，此定值为6． ····················································································································································· 12分 5．（江西21）已知函数4322411()(0)43f x x ax a x a a =+-+> （1）求函数()y f x =的单调区间；（2）若函数()y f x =的图像与直线1y =恰有两个交点，求a 的取值范围．解：（1）因为322()2(2)()f x x ax a x x x a x a '=+-=+- 令()0f x '=得1232,0,x a x x a =-== 由0a >时，()f x '在()0f x '=根的左右的符如下表所示x(,2)a -∞-2a -(2,0)a - 0(0,)a a (,)a +∞ ()f x ' -+-+()f x极小值极大值极小值所以()f x 的递增区间为(2,0)(,)a a -+∞与()f x 的递减区间为(2)(0)a a -∞-，与，（2）由（1）得到45()(2)3f x f a a =-=-极小值，47()()12f x f a a ==极小值 4()(0)f x f a ==极大值要使()f x 的图像与直线1y =恰有两个交点，只要44571312a a -<<或41a <，即4127a >或01a ≤<.6．（湖南21）已知函数43219()42f x x x x cx =+-+有三个极值点。

【VIP专享】2008年高考数学试题分类汇编——函数与导数

A． a b c
B． b a c
11.（北京卷 5）函数 f (x) (x 1)2 1(x 1) 的反函数为（ B ）
A． f 1(x) 1 x 1(x 1)
C． f 1(x) 1 x 1(x ≥1) D． f 1(x) 1 x 1(x ≥1)
12.（福建卷 11）如果函数 y=f(x)的图象如右图，那么导函数 y=f(x)的图象可能是 A
s
O
A
．
tO
s
B．
3.（全国一 4）曲线 y x3 2x 4 在点 (1，3) 处的切线的倾斜角为（
A．30°
B．45°
C．60°
tO
4.（全国一 8）若函数 y f (x) 的图象与函数 y ln x 1的图象关于直线 y x 对称，
则 f (x) （ A ）
A． e2x2
B． e2x
一．选择题：
2008 年高考数学试题分类汇编函数与导数
1.(全国一 1)函数 y 1 x x 的定义域为（ D ）
A．{x | x ≤1}
C．{x | x ≥或1 ≤x 0}
B．{x | x ≥ 0}
D．{x | 0 ≤≤x 1}
2.（全国一 2）汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程 s 看作时间 t 的函数，其图像可能是（ A ）
D．120°
D．
s
tO
D
．
D． b < c < a
t
B）
A． f 1(x) 1 x 1(x 1)
C． f 1(x) 1 x 1(x 2)
9.（安徽卷 9）．设函数 f (x) 2x 1 1(x 0), 则 f (x) （ A ） x

2008年全国各地高考试题归类评析——函数与导数

的（砉（１，Ｊ在线＝的侧实点，，，直ｙ同，数）２｝ …）均则
。的取值范围是（０８年上海市数学高考理科试题）２０评析本题通过对函数图像的分析，而找到确定量从的约束条件：由题意知方程＋Ｏ４＝．Ｘ一０的解可转化为函数，）＝＋ｏ与ｇ（（）＝的图像交点来处理，函数而
学潜能方面都作了比较深入的考查．
１试题特点
１１客观题考查与命题．
（）１以函数之要素为背景，考查函数定义或对应关系．
Ｙ＝与Ｙ ÷的交点坐标为Ａ２２，（２一）若，）＝（，）Ｂ一，２．（
与ｇ）（图像的交点记为Ｃ，则Ｃ（ｃ＋口，，＋Ｄ，ｘ，３）Ｄ（ｃｎ．ＣＤ要在Ｙ＝）若，直线同侧，可以分为２类：第１类：，ＣＤ在Ｙ＝直线上方，则有
科试题Ｉ９；国数学高考理ຫໍສະໝຸດ 试题 Ⅱ ３第题全第题．
（）３函数的图像及应用在２００８年的试题中有一定的
＞Ｉ２；
Ｊ＜一；２
量，并也有一定难度．例如，京市数学高考理科试题第８北
题；国数学高考理科试题Ｉ２题．全第函数图像主要考查考生的作图、识图和用图能力，而用图能力实际上要求考生有
例如全国数学高考理科试题Ｉ的第１题和第６题；上海市
数学高考理科试题第４题；京市数学高考理科试题第３北题；湖北省数学高考理科试题第４题．

2008年高考数学试题分类汇编

2008年高考数学试题分类汇编立体几何过点A作AH⊥PB于H，由（Ⅰ）知平面PBE⊥平面P AB,所以AH⊥平面PBE.在Rt△ABF中，因为∠BAF＝60°，所以，AF=2AB=2=AP.在等腰Rt△P AF中，取PF的中点G，连接AG.则AG⊥PF.连结HG，由三垂线定理的逆定理得，PF⊥HG.所以∠AGH是平面P AD和平面PBE所成二面角的平面角（锐角）.在等腰Rt△P AF中，2AG PA==在Rt△P AB中，AP ABAHPB====所以，在Rt△AHG中，sinAHAGHAG∠===故平面P AD和平面PBE所成二面角（锐角）的大小是解法二: 如图所示，以A为原点，建立空间直角坐标系.则相关各点的坐标分别是A（0，0，0），B（1，0，0），3 ( 2C1(2D P（0，0，2）,E（Ⅰ）因为(0,,0)2BE=，平面P AB的一个法向量是(0,1,0)n=，所以BE n和共线.从而BE⊥平面P AB.又因为BE⊂平面PBE，故平面PBE⊥平面P AB.(Ⅱ)易知(1,0,2),(0,0PB BE=-=），1(0,0,2),(,2PA AD=-=设1111(,,)n x y z=是平面PBE的一个法向量，则由110,n PBn BE⎧=⎪⎨=⎪⎩得111122020,000.x y z x y z +⨯-=⎧⎪⎨⨯+⨯=⎪⎩所以11110,2.(2,0,1).y x z n ===故可取设2222(,,)n x y z =是平面PAD 的一个法向量，则由220,0n PA n AD ⎧=⎪⎨=⎪⎩得2222220020,100.2x y z x y z ⨯+⨯-=⎧⎪⎨+⨯=⎪⎩所以2220,.z x ==故可取2(3,1,0).n =-于是，12121223cos ,5n n n n n n <>===⨯故平面PAD 和平面PBE 所成二面角（锐角）的大小是陕西卷19．（本小题满分12分）三棱锥被平行于底面ABC 的平面所截得的几何体如图所示，截面为111A B C ，90BAC ∠=，1A A ⊥平面ABC ，1A A =，AB =，2AC =，111AC =，12BD DC =．（Ⅰ）证明：平面1A AD ⊥平面11BCC B ；（Ⅱ）求二面角1A CC B --的大小．解法一：（Ⅰ）1A A ⊥平面ABC BC ⊂，平面ABC ，∴1A A BC ⊥．在Rt ABC △中，2AB AC BC ==∴，， :1:2BD DC =，BD ∴=，又BD ABAB BC==， DBA ABC ∴△∽△，90ADB BAC ∴∠=∠=，即AD BC ⊥．又1A AAD A =，BC ∴⊥平面1A AD ，BC ⊂平面11BCC B ，∴平面1A AD ⊥平面11BCC B ．（Ⅱ）如图，作1AE C C ⊥交1C C 于E 点，连接BE ，由已知得AB ⊥平面11ACC A ．AE ∴是BE 在面11ACC A 内的射影．A 1 A C 1B 1BDC由三垂线定理知1BE CC ⊥，AEB ∴∠为二面角1A CC B --的平面角．过1C 作1C F AC ⊥交AC 于F 点，则1CF AC AF =-=，11C F A A =160C CF ∴∠=．在Rt AEC △中，sin 6022AE AC ==⨯= 在Rt BAE △中，tan AB AEB AE ===．arctanAEB ∴∠= 即二面角1A CC B --为解法二：（Ⅰ）如图，建立空间直角坐标系，则11(000)0)(020)(00A B C A C ，，，，，，，，，，:1:2BD DC =，13BD BC ∴=． D ∴点坐标为203⎫⎪⎪⎝⎭，，． ∴2203AD ⎛⎫= ⎪⎪⎝⎭，，，1(220)(00BC AA =-=，，，．10BC AA =，0BC AD =，1BC AA ∴⊥，BC AD ⊥，又1A A AD A =，BC ∴⊥平面1A AD ，又BC ⊂平面11BCC B ，∴平面1A AD ⊥平面11BCC B ．（Ⅱ）BA ⊥平面11ACC A ，取(20)AB ==，，m 为平面11ACC A 的法向量，设平面11BCC B 的法向量为()l m n =，，n ，则100BC CC ==，n n ．200m m ⎧+=⎪∴⎨-+=⎪⎩，，l n∴==，，如图，可取1m =，则=⎭n ， A 1 AC 1B 1BD CFE（第19题，解法一）（第19题，解法二）22010cos5(2)1⨯+<>==+，m n，即二面角1A CC B--为15arccos5．重庆卷（19）（本小题满分13分，（Ⅰ）小问6分，（Ⅱ）小问7分.）如题（19）图，在ABC中，B=90,AC=152,D、E两点分别在AB、AC上.使2AD AEDB EC==,DE=3.现将ABC沿DE折成直二角角，求：（Ⅰ）异面直线AD与BC的距离；（Ⅱ）二面角A-EC-B的大小（用反三角函数表示）.解法一：（Ⅰ）在答（19）图1中，因AD AEDB CE=，故BE∥BC.又因B＝90°，从而AD⊥DE.在第（19）图2中，因A-DE-B是直二面角，AD⊥DE,故AD⊥底面DBCE，从而AD⊥DB.而DB⊥BC,故DB为异面直线AD与BC的公垂线.下求DB之长.在答（19）图1中，由2ADAECB BC==，得2.3DE ADBC AB==又已知DE=3,从而39.22BC DE==6.AB===因1, 2.3DBDBAB=故＝（Ⅱ）在第（19）图2中，过D作DF⊥CE,交CE的延长线于F，连接AF.由（1）知，AD⊥底面DBCE,由三垂线定理知AF ⊥FC,故∠AFD为二面角A-BC-B的平面角.在底面DBCE中，∠DEF=∠BCE,11552,,322DB EC===因此4sin.5DBBCEEC==从而在Rt△DFE中，DE=3,412sin sin3.55DF DE DEF DE BCE====在5Rt ,4,tan .3AD AFD AD AFD DF ∆===中因此所求二面角A -EC -B 的大小为arctan 5.3解法二：（Ⅰ）同解法一.（Ⅱ）如答（19）图3.由（Ⅰ）知，以D 点为坐标原点，DB DE DA 、、的方向为x 、y 、z 轴的正方向建立空间直角坐标系，则D （0，0，0），A （0，0，4），9202C ⎛⎫⎪⎝⎭，，，E （0，3，0）.302AD AD ⎛⎫ ⎪⎝⎭＝-2，-，，＝（0，0，-4）.过D 作DF ⊥CE ,交CE 的延长线于F ，连接AF .设00(,,0),F x y 从而00(,,0),DF x y = 00(,3,0).EF x y DF CE =-⊥由，有0030,20.2DF CE x y =+=即 ① 又由003,.22x y CE EF -=得 ②联立①、②，解得00364836483648,.,,0,,4.252525252525x y F AF ⎛⎫⎛⎫=-=-=-- ⎪ ⎪⎝⎭⎝⎭即，得因为36483(2)025252A F C E ⎛⎫⎛⎫=--+-= ⎪ ⎪⎝⎭⎝⎭,故AF CE ⊥,又因D F C E ⊥,所以D F A ∠为所求的二面角A-EC-B 的平面角.因3648,,0,2525DF ⎛⎫=- ⎪⎝⎭有22364812,4,5DF AD ⎛⎫⎛⎫=-+== ⎪ ⎪所以5tan .3AD AFD DF ==因此所求二面角A-EC-B 的大小为5arctan .3福建卷（18）（本小题满分12分）如图，在四棱锥P-ABCD 中，则面PAD⊥底面ABCD ，侧棱P A =PD ABCD 为直角梯形，其中BC ∥AD ,AB ⊥AD ,AD =2AB =2BC =2,O 为AD 中点.（Ⅰ）求证：PO ⊥平面ABCD ；（Ⅱ）求异面直线PD 与CD 所成角的大小；（Ⅲ）线段AD 上是否存在点Q ，使得它到平面PCD 求出AQQD的值；若不存在，请说明理由.本小题主要考查直线与平面的位置关系、异面直线所成角、点到平面的距离等基本知识，考查空间想象能力、逻辑思维能力和运算能力.满分12分.解法一：（Ⅰ）证明：在△P AD 中P A =PD ,O 为AD 中点，所以PO ⊥AD ,又侧面P AD ⊥底面ABCD ,平面PAD ⋂平面ABCD =AD , PO ⊂平面P AD ，所以PO ⊥平面ABCD .（Ⅱ）连结BO ，在直角梯形ABCD 中、BC ∥AD ，AD =2AB =2BC ,有OD ∥BC 且OD =BC ,所以四边形OBCD 是平行四边形，所以OB ∥DC .由（Ⅰ）知，PO ⊥OB ,∠PBO 为锐角，所以∠PBO 是异面直线PB 与CD 所成的角.因为AD =2AB =2BC =2,在Rt △AOB 中，AB =1,AO =1,所以OB在Rt △POA 中，因为AP AO ＝1，所以OP ＝1，在Rt △PBO 中，tan ∠PBO ＝PG PBO BC ==∠=所以异面直线PB 与CD 所成的角是arctan2.（Ⅲ）假设存在点Q ，使得它到平面PCD设QD ＝x ，则12DQC S x ∆=，由（Ⅱ）得CD =OB在Rt △POC 中， PC ==所以PC =CD =DP , 2(2)42PCD S ∆== 由V p-DQC =V Q-PCD ,得2，所以存在点Q 满足题意，此时13AQ QD =. 解法二：(Ⅰ)同解法一.(Ⅱ)以O 为坐标原点，OC OD OP 、、的方向分别为x 轴、y 轴、z 轴的正方向，建立空间直角坐标系O-xyz ,依题意，易得A (0,-1,0),B (1,-1,0),C (1,0,0),D (0,1,0),P (0,0,1),所以110111CD PB ---＝（，，），＝（，，）.所以异面直线PB 与CD 所成的角是(Ⅲ)假设存在点Q ，使得它到平面PCD由(Ⅱ)知(1,0,1),(1,1,0).CP CD =-=- 设平面PCD 的法向量为n =(x 0,y 0,z 0).则0,0,n CP n CD ⎧=⎪⎨=⎪⎩所以00000,0,x z x y -+=⎧⎨-+=⎩即000x y z ==，取x 0=1,得平面PCD 的一个法向量为n =(1,1,1). 设(0,,0)(11),(1,,0),Q y y CQ y -≤≤=-由3CQ n n=，得=解y =-12或y =52(舍去)，此时13,22AQ QD ==，所以存在点Q 满足题意，此时13AQ QD =. 广东卷20．（本小题满分14分）。

2008高考试卷分类汇编02----函数与导数2

2008高考试卷分类汇编02----函数与导数2三、解答题80.（安徽理20）（本小题满分12分）设函数1()(01)ln f x x x x x=>≠且（Ⅰ）求函数()f x 的单调区间；（Ⅱ）已知12ax x >对任意(0,1)x ∈成立，求实数a 的取值范围。

解（Ⅰ） '22ln 1(),ln x f x x x+=-若 '()0,f x = 则 1x e=列表如下（Ⅱ）在 12ax x > 两边取对数, 得1ln 2ln a x x>,由于01,x <<所以1ln 2ln a x x>(*)由(1)的结果可知,当(0,1)x ∈时, 1()()f x f e e≤=-,为使(*)式对所有(0,1)x ∈成立,当且仅当ln 2a e >-,即ln 2a e >-设函数323()(1)1,32a f x x x a x a =-+++其中为实数。

（Ⅰ）已知函数()f x 在1x =处取得极值，求a 的值；（Ⅱ）已知不等式'2()1f x x x a >--+对任意(0,)a ∈+∞都成立，求实数x 的取值范围。

解: (1)'2()3(1)f x ax x a =-++，由于函数()f x 在1x =时取得极值，所以 '(1)0f = 即 310,1a a a -++==∴ (2) 方法一由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立设 22()(2)2()g a a x x x a R =+--∈, 则对任意x R ∈，()g a 为单调递增函数()a R ∈ 所以对任意(0,)a ∈+∞，()0g a >恒成立的充分必要条件是(0)0g ≥ 即 220x x --≥，20x -≤≤∴，于是x 的取值范围是}{|20x x -≤≤ 方法二由题设知：223(1)1ax x a x x a -++>--+对任意(0,)a ∈+∞都成立即22(2)20a x x x +-->对任意(0,)a ∈+∞都成立于是2222x x a x +>+对任意(0,)a ∈+∞都成立，即22202x x x +≤+20x -≤≤∴，于是x 的取值范围是}{|20x x -≤≤已知函数22()(1)x b f x x -=-，求导函数()f x '，并确定()f x 的单调区间．解：242(1)(2)2(1)()(1)x x b x f x x ----'=- 3222(1)x b x -+-=-32[(1)](1)x b x --=--．令()0f x '=，得1x b =-．当11b -<，即2b <时，()f x '的变化情况如下表：当11b ->，即2b >时，()f x '的变化情况如下表：所以，当2b <时，函数()f x 在(1)b -∞-，上单调递减，在(11)b -，上单调递增，在(1)+∞，上单调递减．当2b >时，函数()f x 在(1)-∞，上单调递减，在(11)b -，上单调递增，在(1)b -+∞，上单调递减．当2b =时，2()1f x x =-，所以函数()f x 在(1)-∞，上单调递减，在(1)+∞，上单调递减．已知函数32()3(0)f x x ax bx c b =+++≠，且()()2g x f x =-是奇函数．（Ⅰ）求a ，c 的值；（Ⅱ）求函数()f x 的单调区间．解：（Ⅰ）因为函数()()2g x f x =-为奇函数，所以，对任意的x ∈R ，()()g x g x -=-，即()2()2f x f x --=-+．又32()3f x x ax bx c =+++所以32323232x ax bx c x ax bx c -+-+-=----+．所以22a a c c =-⎧⎨-=-+⎩，．解得02a c ==，．（Ⅱ）由（Ⅰ）得3()32f x x bx =++．所以2()33(0)f x x b b '=+≠．当0b <时，由()0f x '=得x =x 变化时，()f x '的变化情况如下表：所以，当0b <时，函数()f x 在(-∞-，上单调递增，在(上单调递减，在)+∞上单调递增．当0b >时，()0f x '>，所以函数()f x 在()-∞+∞，上单调递增．已知函数321()23f x x x =+-.（Ⅰ）设}{n a 是正数组成的数列，前n 项和为n S ，其中13a =.若点211(,2)n n n a a a ++-(n ∈N*)在函数'()y f x =的图象上，求证：点(,)n n S 也在'()y f x =的图象上；（Ⅱ）求函数()f x 在区间(1,)a a -内的极值.解：(Ⅰ)证明：因为321()2,3f x x x =+-所以'2()2f x x x =+，由点211(,2)(N )n n n a a a n +++-∈在函数'()y f x =的图象上,221122n n n n a a a a ++-=+ 所以12n n a a +-=，}{n a 是13,2a d ==的等差数列所以2(1)32=22n n n S n n n -=+⨯+,又因为'2()2f n n n =+,所以()n S f n '=,故点(,)n n S 也在函数'()y f x =的图象上.(Ⅱ)解:2()2(2)f x x x x x '=+=+,令()0,f x '=得02x x ==-或. 当x 变化时,()f x '﹑()f x 的变化情况如下表:注意到(1)12a a --=<,从而①当212,21,()(2)3a a a f x f -<-<-<<--=-即时的极大值为,此时()f x 无极小值；②当10,01,()a a a f x -<<<<即时的极小值为(0)2f =-,此时()f x 无极大值； ③当2101,()a a a f x ≤--≤≤≥或或时既无极大值又无极小值.已知函数()ln(1)f x x x =+- （Ⅰ）求()f x 的单调区间；（Ⅱ）记()f x 在区间[]0,n （n ∈N*）上的最小值为n b 令ln(1)n n a n b =+- ①如果对一切nc <c 的取值范围；②求证：1313211224242 1.n na a a a a a a a a a a a -+++<解：（I ）因为()ln(1)f x x x =+-，所以函数定义域为(1,)-+∞，且'1()111x f x xx-=-=++。

2008年高考数学导数汇编答案

参考答案 1．解(1)'22ln 1(),x f x +=-若 '()0,f x =则1x =列表如下(2)在12ax x > 两边取对数, 得1ln 2ln a x x>,由于01,x <<所以1ln 2ln a x x>(1)由(1)的结果可知,当(0,1)x ∈时, 1()()f x f e e≤=-, 为使(1)式对所有(0,1)x ∈成立,当且仅当ln 2a e >-,即ln 2a e >-2．解：（Ⅰ）22(2cos )cos sin (sin )2cos 1()(2cos )(2cos )x x x x x f x x x +--+'==++．当2π2π2π2π33k x k -<<+（k ∈Z ）时，1cos 2x >-，即()0f x '>；当2π4π2π2π33k x k +<<+（k ∈Z ）时，1cos 2x <-，即()0f x '<．因此()f x 在每一个区间2π2π2π2π33k k ⎛⎫-+⎪⎝⎭，（k ∈Z ）是增函数， ()f x 在每一个区间2π4π2π2π33k k ⎛⎫++ ⎪⎝⎭，（k ∈Z ）是减函数．（Ⅱ）令()()g x ax f x =-，则22cos 1()(2cos )x g x a x +'=-+2232cos (2cos )a xx =-+++211132cos 33a x ⎛⎫=-+- ⎪+⎝⎭．故当13a ≥时，()0g x '≥．又(0)0g =，所以当0x ≥时，()(0)0g x g =≥，即()f x ax ≤．当103a <<时，令()sin 3h x x ax =-，则()c o s 3h x x a'=-．故当[)0arccos 3x a ∈，时，()0h x '>．因此()h x 在[)0arccos 3a ，上单调增加．故当(0arccos 3)x a ∈，时，()(0)0h x h >=，即sin 3x ax >．于是，当(0arccos 3)x a ∈，时，sin sin ()2cos 3x x f x ax x=>>+．当0a ≤时，有π1π0222f a ⎛⎫=>∙ ⎪⎝⎭≥．因此，a 的取值范围是13⎡⎫+∞⎪⎢⎣⎭，．3．解：(Ⅰ)因为2(),()2.f x a x b x cf x a x b '=++=+所以又因为曲线()y f x =通过点（0，2a +3）,故(0)23,(0),2 3.f a f c c a =+==+而从而又曲线()y f x =在（-1，f (-1)）处的切线垂直于y 轴，故(1)0,f '-=即-2a +b =0,因此b=2a .(Ⅱ)由(Ⅰ)得2392(23)4(),44bc a a a =+=+-故当34a =-时，bc 取得最小值-94.此时有33,.22b c =-=从而233333(),(),42222f x x x fx x '=--+=--2333()()()422x xg x f x c x x e--=-=+-所以23()(()()(4).4xxg x f x f x e x e--''=-=--令()0g x '=，解得122, 2.x x =-= 当(,2),()0,()(,2)x g x g x x '∈-∞-<∈-∞-时故在上为减函数；当(2,2)()0,()(2,).x g x g x x '∈->∈+∞时，故在上为减函数当(2,)()0()(2,)x g x g x x '∈+∞<∈+∞时，，故在上为减函数.由此可见，函数()g x 的单调递减区间为（-∞，-2）和（2，+∞）；单调递增区间为（-2，2）.4．解：242(1)(2)2(1)()(1)x x b x f x x ----'=- 3222(1)x b x -+-=-32[(1)](1)x b x --=--．令()0f x '=，得1x b =-．当11b -<，即2b <时，()f x '的变化情况如下表：当11b ->，即2b >时，()f x '的变化情况如下表：所以，当2b <时，函数()f x 在(1)b -∞-，上单调递减，在(11)b -，上单调递增，在(1)+∞，上单调递减．当2b >时，函数()f x 在(1)-∞，上单调递减，在(11)b -，上单调递增，在(1)b -+∞，上单调递减．当11b -=，即2b =时，2()1f x x =-，所以函数()f x 在(1)-∞，上单调递减，在(1)+∞，上单调递减．5．(Ⅰ)证明：因为321()2,3f x x x =+-所以f ′(x )=x 2+2x ,由点211(,2)(N )n n n a a a n +++-∈在函数y =f ′(x )的图象上,得221122n n n n a a a a ++-=+，即11()(2)0,n n n n a a a a -+---=又0(N ),n a n +>∈所以12n n a a +-=，又因为13a =，所以2(1)32=22n n n S n n n -=+⨯+,又因为f ′(n )=n 2+2n ,所以()n S f n '=,故点(,)n n S 也在函数y=f ′(x )的图象上.(Ⅱ)解:2()2(2)f x x x x x '=+=+,由()0,f x '=得02x x ==-或. 当x 变化时,()f x '﹑()f x 的变化情况如下表: 注意到(1)12a a --=<,从而①当212,21,()(2)3a a a f x f -<-<-<<--=-即时的极大值为,此时()f x 无极小值；②当10,01,()a a a f x -<<<<即时的极小值为(0)2f =-,此时()f x 无极大值； ③当2101,()a a a f x ≤--≤≤≥或或时既无极大值又无极小值.6．解1,1,1()(),1,kx x xF x f x kx kx x ⎧-<⎪-=-=⎨⎪≥⎩，21,1,(1)'(),1,k x x F x k x ⎧-<⎪-⎪=⎨⎪≥⎪⎩对于1()(1)1F x kx x x=-<-，当0k ≤时，函数()F x 在(,1)-∞上是增函数；当0k >时，函数()F x在1(,1-∞-上是减函数，在(1-上是增函数；对于()(1)F x k x =-≥，当0k ≥时，函数()F x 在[)1,+∞上是减函数；当0k <时，函数()F x 在211,14k ⎡⎫+⎪⎢⎣⎭上是减函数，在211,4k ⎡⎫++∞⎪⎢⎣⎭上是增函数。

2008年高考试题分类(2)(数学-函数)

02 函数一、选择题1．（安徽6）．函数2()(1)1(0)f x x x =-+≤的反函数为（ C ）A ．1()11)fx x -=≥ B ． 1()11)fx x -=≥C ．1()12)f x x -=≥ D ． 1()12)f x x -=≥2．（安徽9）．设函数1()21(0),f x x x x=+-< 则()f x （ A ） A ．有最大值B ．有最小值C ．是增函数D ．是减函数3．（北京2）若372log πlog 6log 0.8a b c ===，，，则（ A ） A ．a b c >>B ．b a c >>C ．c a b >>D ．b c a >>4．（北京5）函数2()(1)1(1)f x x x =-+<的反函数为（ B ）A ．1()11)fx x -=+>B ．1()11)fx x -=>C ．1()11)f x x -=≥D ．1()11)f x x -=≥5．（福建4）函数f (x )=x 3+sin x +1(x ∈R)，若f (a )=2, 则f (-a )的值为（ B ） A.3 B.0 C.-1 D.-2 6．（湖南4）函数)0()(2≤=x x x f 的反函数是 ( B ))0()(.1≥=-x x x f A )0()(.1≥-=-x x x fB)0()(.1≤--=-x x x fC )0()(.21≤-=-x x x fD7．（湖南6）下面不等式成立的是 ( A )A ．322log 2log 3log 5<<B ．3log 5log 2log 223<<C ．5log 2log 3log 232<<D ．2log 5log 3log 322<< 8．（江西3）若函数()y f x =的定义域是[0,2]，则函数(2)()1f xg x x =-的定义域是（ B ） A ．[0,1] B ．[0,1) C ． [0,1)(1,4] D ．(0,1)9．（江西4）若01x y <<<，则（ C ）A ．33y x <B ．log 3log 3x y <C ．44log log x y <D ．11()()44x y <10．（江西12）已知函数2()2(4)4f x x m x m =+-+-，()g x mx =，若对于任一实数x ，()f x 与()g x 的值至少有一个为正数，则实数m 的取值范围是（ C ）A ． [4,4]-B ．(4,4)-C ． (,4)-∞D ．(,4)-∞-11．（辽宁2）若函数(1)()y x x a =+-为偶函数，则a =（ C ） A ．2-B ．1-C ．1D ．212．（辽宁4）已知01a <<，log log a a x =1log 52a y =，log log a a z =，则（ C ） A ．x y z >> B ．z y x >> C ．y x z >>D ．z x y >>13．（全国Ⅰ1）函数y = D ）A ．{|1}x x ≤B ．{|0}x x ≥C ．{|10}x x x ≥或≤D ．{|01}x x ≤≤14．（全国Ⅰ2）汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s 看作时间t 的函数，其图像可能是（ A ）15．（全国Ⅰ8）若函数()y f x =的图象与函数ln 1y =的图象关于直线y x =对称，则()f x =（ A ）A ．22ex -B ．2e xC ．21ex +D ．2+2ex16．（全国Ⅱ4）1()f x x x=-的图像关于（ C ） A ．y 轴对称 B ．直线x y -=对称 C ．坐标原点对称 D ．直线x y =对称17．（全国Ⅱ）若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ C ） A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a18．(山东3) 函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是（ A ）19．(山东5) 设函数2211()21x x f x x x x ⎧-⎪=⎨+->⎪⎩，，，，≤则1(2)f f ⎛⎫⎪⎝⎭的值为（ A ）xxA ． B． C ．D ．A ．B ．C ．D ．A ．1516B ．2716-C ．89D ．1820．(山东12) 已知函数()log (21)(01)xa f xb a a =+->≠，的图象如图所示，则a b ，满足的关系是（ A ） A ．101a b -<<<B ．101b a -<<<C ．101ba -<<<-D ．1101ab --<<<21．(天津3 )函数14)y x =≤≤的反函数是（ A ）A ．2(1)(13)y x x =-≤≤ B ．2(1)(04)y x x =-≤≤ C ．21(13)y x x =-≤≤D ．21(04)y x x =-≤≤22．(天津10) 设1a >，若对于任意的[]2x a a ∈，，都有2y a a ⎡⎤∈⎣⎦，满足方程log log 3a a x y +=，这时a 的取值的集合为（ B ）A ．{}12a a <≤B ．{}2a a ≥C ．{}23a a ≤≤D ．{}23，23．(重庆6)函数y =10x 2-1 (0＜x ≤1＝的反函数是 ( D )(A)1)10y x =＞(B)y =x ＞110)(C) y =110＜x ≤)1(D) y =110＜x ≤)1 24．(湖北6).已知()f x 在R 上是奇函数，且2(4)(),(0,2)()2,(7)f x f x x f x x f +=∈==当时，则 ( A ) A.-2 B.2 C.-98 D.98 25．(湖北8).函数1()1f x n x=( D ) A.(,4][2,)-∞-+∞ B. (4,0)(0,1)-⋃ C.[4,0)(0,1]- D.[4,0)(0,1]-⋃ 26．(陕西) 已知函数3()2x f x +=，1()fx -是()f x 的反函数，若16mn =（m n ∈+R ，），则11()()f m f n --+的值为（ D ）A ．10B ．4C ．1D ．2-27．(陕西) 定义在R 上的函数()f x 满足()()()2f x y f x f y xy +=++（x y ∈R ，），(1)2f =，则(2)f -等于（ A ）A ．2B ．3C ．6D ．9二、填空题1．（安徽13）函数2()f x =的定义域为．[3,)+∞2．（北京13）如图，函数()f x 的图象是折线段ABC ，其中A B C ，，的坐标分别为(04)(20)(64)，，，，，，则((0))f f =_________；2函数()f x 在1x =处的导数(1)f '=_________．2-3．（北京14）．已知函数2()cos f x x x =-，对于ππ22⎡⎤-⎢⎥⎣⎦，上的任意12x x ，，有如下条件：①12x x >； ②2212x x >； ③12x x >．其中能使12()()f x f x >恒成立的条件序号是_________．②4．（湖南15）设[]x 表示不超x 的最大整数，（如[]145,22=⎥⎦⎤⎢⎣⎡=）。

2008年高考数学全国卷2

选择题：1. 若函数f(x) = x^2 + 2x + 1，则f(-1)的值为：a) -2b) 0c) 2d) 42. 若a和b是实数，且a ≠ 0，那么方程ax^2 + bx + c = 0有两个不相等的实根的条件是：a) b^2 - 4ac < 0b) b^2 - 4ac = 0c) b^2 - 4ac > 0d) b^2 - 4ac ≠ 03. 一辆汽车以每小时60公里的速度行驶，行驶了2小时，其行驶的路程是：a) 60公里b) 120公里c) 240公里d) 360公里4. 若在某个区间上，函数f(x) = x^3 + 2x^2 + x + 1是增函数，那么该区间的可能取值为：a) (-∞, -1)b) (0, ∞)c) (-1, 0)d) (1, ∞)5. 若函数f(x) = (x + 1)^2 - 4，则f(x)与x轴交点的个数为：a) 0b) 1c) 2d) 3填空题：1. 一瓶药水中溶有6克的盐，溶液的浓度是每升_________克。

答案：6克2. 若a^2 - b^2 = 16，且a - b = 4，则a + b的值是_________。

答案：83. 已知函数f(x) = 3x - 4，解方程f(x) = 5的解为_________。

答案：34. 若对所有的x，有f(x) = f(x + 1)，则函数f(x)的周期是_________。

答案：15. 若a:b = 2:3，且b:c = 5:7，则a:c的比值是_________。

答案：10:21应用题：1. 某学校有1000名学生，其中男生占总人数的60%，女生占总人数的40%。

男生中有20%是高三年级的学生，求高三男生的人数。

答案：高三男生的人数是120人。

2. 在一个等差数列中，第1项是3，第10项是15，求该等差数列的公差及第15项的值。

答案：公差为1，第15项的值为29。

3. 在一个等比数列中，第1项是2，公比是3，求该等比数列的第5项及总和。

2008年数学高考题分类总汇编详解(下)【超全超详细】【强烈推荐】

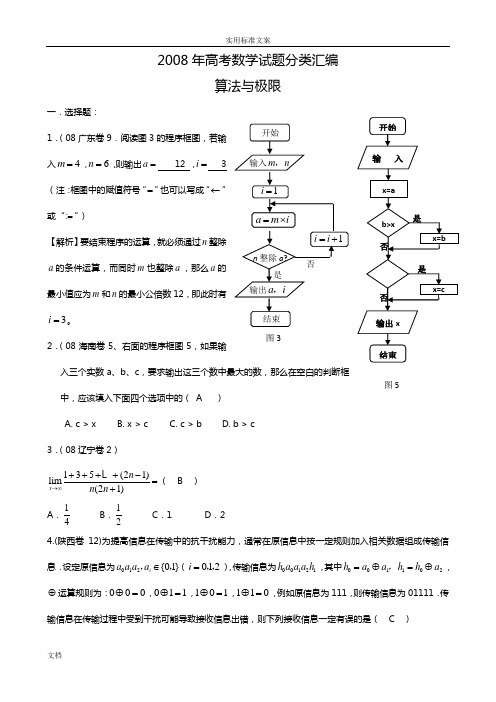
开始 1i =n 整除a ?是输入m n ，结束 a m i =⨯输出a i ，1i i =+图3否2008年高考数学试题分类汇编算法与极限一．选择题：1．（08广东卷9．阅读图3的程序框图，若输入4m =，6n =，则输出a = 12 ，i = 3（注：框图中的赋值符号“=”也可以写成“←”或“:=”）【解析】要结束程序的运算，就必须通过n 整除a 的条件运算，而同时m 也整除a ，那么a 的最小值应为m 和n 的最小公倍数12，即此时有3i =。

2．（08海南卷5、右面的程序框图5，如果输入三个实数a 、b 、c ，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（ A ） A. c > xB. x > cC. c > bD. b > c3．（08辽宁卷2）135(21)lim(21)x n n n →∞++++-=+L （ B ）A ．14B ．12C ．1D ．24.(陕西卷12)为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入相关数据组成传输信息．设定原信息为012i a a a a ，{01}∈，（012i =，，），传输信息为00121h a a a h ，其中001102h a a h h a =⊕=⊕，，⊕运算规则为：000⊕=，011⊕=，101⊕=，110⊕=，例如原信息为111，则传输信息为01111．传输信息在传输过程中受到干扰可能导致接收信息出错，则下列接收信息一定有误的是（ C ）是否开始输入x=ab>x 输出x结束 x=b x=c否是图5A ．11010B ．01100C ．10111D ．00011二．填空题：1．（08湖南卷11）211lim ______34x x x x →-=+-.15 2．（08江西卷11）211lim ______34x x x x →-=+-.153．（08山东卷13）执行右边的程序框图6，若p ＝0.8，则输出的n ＝ 4 .4．（08陕西卷13）(1)1lim2n a n n a∞++=+→，则a = ．15．（08重庆卷12）已知函数f(x)=(当x ≠0时) ，点在x =0处连续，则2221lim x an a n n →∞+=+ . 13图62008年高考数学试题分类汇编直线与圆一．选择题：1．（08上海卷15）如图，在平面直角坐标系中，Ω是一个与x 轴的正半轴、y 轴的正半轴分别相切于点C 、D 的定圆所围成的区域（含边界），A 、B 、C 、D 是该圆的四等分点．若点()P x y ，、点()P x y '''，满足x x '≤且y y '≥，则称P 优于P '．如果Ω中的点Q 满足：不存在Ω中的其它点优于Q ，那么所有这样的点Q 组成的集合是劣弧（ D ）Ａ．弧AB B ．弧BC C ．弧CD D ．弧DA2．（08全国一10）若直线1x ya b+=通过点(cos sin )M αα，，则（ D ） A ．221a b +≤ B ．221a b +≥ C ．22111a b +≤ D ．22111a b +≥3．（08全国二5）设变量x y ，满足约束条件：222y x x y x ⎧⎪+⎨⎪-⎩，，．≥≤≥，则y x z 3-=的最小值（ D ）A ．2-B ．4-C ．6-D ．8-4．（08全国二11）等腰三角形两腰所在直线的方程分别为20x y +-=与740x y --=，原点在等腰三角形的底边上，则底边所在直线的斜率为（ A ）A ．3B ．2C ．13-D ．12- 5．（08北京卷5）若实数x y ，满足1000x y x y x ⎧-+⎪+⎨⎪⎩，，，≥≥≤则23x yz +=的最小值是（ B ）AB CD O xyΩA ．0B ．1C ．3D ．96．（08北京卷7）过直线y x =上的一点作圆22(5)(1)2x y -+-=的两条切线12l l ，，当直线12l l ，关于y x =对称时，它们之间的夹角为（ C ）A ．30oB ．45oC ．60oD ．90o7．（08四川卷４）直线3y x =绕原点逆时针旋转090，再向右平移１个单位，所得到的直线为( A ) （Ａ）1133y x =-+ （Ｂ）113y x =-+ （Ｃ）33y x =- （Ｄ）113y x =+ 8．（08天津卷2）设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x ，则目标函数y x z +=5的最大值为D（A ）2 （B ）3 （C ）4 （D ）59．（08安徽卷8）．若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点，则直线l 的斜率的取值范围为（ C ）A ．[3,3]-B ．(3,3)-C ．33[,]33-D ．33(,)33-10．（08山东卷11）已知圆的方程为08622=--+y x y x .设该圆过点（3，5）的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为B（A ）106 （B ）206 （C ）306 （D ）40611．（08山东卷12）设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142,080192y x y x y x ，所表示的平面区域为M ，使函数y ＝a x (a ＞0，a ≠1)的图象过区域M 的a 的取值范围是C（A ）[1,3] (B)[2,10] (C)[2,9] (D)[10,9]12．（08湖北卷9）过点(11,2)A 作圆22241640x y x y ++--=的弦，其中弦长为整数的共有CA.16条B. 17条C. 32条D. 34条13．（08湖南卷3）已知变量x 、y 满足条件1,0,290,x x y x y ≥⎧⎪-≤⎨⎪+-≤⎩则x y +的最大值是( C )A.2B.5C.6D.814．（08陕西卷5）直线30x y m -+=与圆22220x y x +--=相切，则实数m 等于（ C ）A ．3或3-B ．3-或33C ．33-或3D ．33-或3315．（08陕西卷10）已知实数x y ，满足121y y x x y m ⎧⎪-⎨⎪+⎩≥，≤，≤．如果目标函数z x y =-的最小值为1-，则实数m 等于（ B ） A ．7B ．5C ．4D ．316．（08重庆卷3)圆O 1:0222=-x y x ＋和圆O 2: 0422=-y y x ＋的位置关系是B(A)相离(B)相交(C)外切 (D)内切17．（08辽宁卷3）圆221x y +=与直线2y kx =+没有．．公共点的充要条件是（ C ） A ．(22)k ∈-， B ．(2)(2)k ∈--+U ∞，，∞ C ．(33)k ∈-，D ．(3)(3)k ∈--+U ∞，，∞ 二．填空题：1．（08天津卷15）已知圆C 的圆心与点(2,1)P -关于直线1y x =+对称．直线34110x y +-=与圆C 相交于B A ,两点，且6=AB ，则圆C 的方程为__________________．22(1)18x y ++=2．（08全国一13）若x y ，满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩，，，≥≥≤≤则2z x y =-的最大值为．93．（08四川卷14）已知直线:40l x y -+=与圆()()22:112C x y -+-=，则C 上各点到l 的距离的最小值为_______。

2008年高考数学试题分类汇编——三角函数 (2)

2008年高考数学试题分类汇编三角函数一．选择题：1.（全国一8）为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像，只需将函数sin 2y x =的图像（ A ）A ．向左平移5π12个长度单位 B ．向右平移5π12个长度单位 C ．向左平移5π6个长度单位 D ．向右平移5π6个长度单位 2.（全国二8）若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ B ）A ．1BCD ．23.（四川卷３）()2tan cot cos x x x +=( D )（Ａ）tan x （Ｂ）sin x （Ｃ）cos x （Ｄ）cot x4.（四川卷５）若02,sin απαα≤≤>，则α的取值范围是：( C )（Ａ）,32ππ⎛⎫ ⎪⎝⎭ （Ｂ）,3ππ⎛⎫ ⎪⎝⎭ （Ｃ）4,33ππ⎛⎫ ⎪⎝⎭ （Ｄ）3,32ππ⎛⎫⎪⎝⎭5.（天津卷6）把函数sin y x =（x R ∈）的图象上所有点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是C（A ）sin(2)3y x π=-，x R ∈ （B ）sin()26x y π=+，x R ∈（C ）sin(2)3y x π=+，x R ∈ （D ）sin(2)32y x π=+，x R ∈6.（天津卷9）设5sin7a π=，2cos 7b π=，2tan 7c π=，则D （A ）c b a << （B ）a c b << （C ）a c b << （D ）b a c <<7.（安徽卷5）将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中心对称，则向量α的坐标可能为（ C ） A ．(,0)12π-B ．(,0)6π-C ．(,0)12πD ．(,0)6π8.（山东卷5）已知cos （α-6π）+sin α=的值是则)67sin(,354πα- （A ）-532 （B ）532 (C)-54 (D) 549.（湖北卷5）将函数3sin()y x θ=-的图象F 按向量(,3)3π平移得到图象F ',若F '的一条对称轴是直线4x π=,则θ的一个可能取值是AA.π125 B. π125- C. π1211D. 1112π-10.（湖南卷6）函数2()sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( C )A.1B.12+ C.3211.（重庆卷10)函数f(x)(02x π≤≤) 的值域是B（A ）[-2] (B)[-1,0] （C ）] （D ）]12.（福建卷9)函数f (x )=cos x (x )(x ∈R )的图象按向量(m,0) 平移后，得到函数y =-f ′(x )的图象，则m 的值可以为AA.2πB.πC.－πD.－2π 13.（浙江卷5）在同一平面直角坐标系中，函数])20[)(232cos(ππ，∈+=x x y 的图象和直线21=y 的交点个数是C （A ）0 （B ）1 （C ）2 （D ）4 14.（浙江卷8）若,5sin 2cos -=+a a 则a tan =B （A ）21 （B ）2 （C ）21- （D ）2- 15.（海南卷1）已知函数y=2sin(ωx+φ)(ω>0)在区间[0，2π]的图像如下：那么ω=（ B ） A. 1B. 2C. 1/2D. 1/316.（海南卷7）0203sin 702cos 10--=（ C ）A. 12B.22C. 2D.32二．填空题：1.（上海卷6）函数f (x )＝3sin x +sin(2+x )的最大值是 22.（山东卷15）已知a ，b ，c 为△ABC 的三个内角A ，B ，C 的对边，向量m ＝（1,3-），n ＝（cos A ,sin A ）.若m ⊥n ，且a cos B +b cos A =c sin C ，则角B ＝ 6π. 3.（江苏卷1）()cos 6f x x πω⎛⎫=- ⎪⎝⎭的最小正周期为5π，其中0ω>，则ω= ．104.（广东卷12）已知函数()(sin cos )sin f x x x x =-，x ∈R ，则()f x 的最小正周期是．π5.（辽宁卷16）已知()sin (0)363f x x ff ωωπππ⎛⎫⎛⎫⎛⎫=+>= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，且()f x 在区间63ππ⎛⎫⎪⎝⎭，有最小值，无最大值，则ω＝__________．143三．解答题：1.（全国一17）．（本小题满分10分）（注意：在试题卷上作答无效．．．．．．．．．）设ABC △的内角A B C ，，所对的边长分别为a b c ，，，且3cos cos 5a Bb Ac -=．（Ⅰ）求tan cot A B 的值；（Ⅱ）求tan()A B -的最大值．解析：（Ⅰ）在ABC △中，由正弦定理及3cos cos 5a Bb Ac -=可得3333sin cos sin cos sin sin()sin cos cos sin 5555A B B A C A B A B A B -==+=+即sin cos 4cos sin A B A B =，则tan cot 4A B =；（Ⅱ）由tan cot 4A B =得tan 4tan 0A B =>2tan tan 3tan 3tan()1tan tan 14tan cot 4tan A B B A B A B B B B --===+++≤34当且仅当14tan cot ,tan ,tan 22B B B A ===时，等号成立，故当1tan 2,tan 2A B ==时，tan()A B -的最大值为34.2.（全国二17）．（本小题满分10分）在ABC △中，5cos 13B =-，4cos 5C =．（Ⅰ）求sin A 的值；（Ⅱ）设ABC △的面积332ABC S =△，求BC 的长．解：（Ⅰ）由5cos 13B =-，得12sin 13B =，由4cos 5C =，得3sin 5C =．所以33sin sin()sin cos cos sin 65A B C B C B C =+=+=． ········· 5分（Ⅱ）由332ABC S =△得133sin 22AB AC A ⨯⨯⨯=，由（Ⅰ）知33sin 65A =，故65AB AC ⨯=， ························ 8分又sin 20sin 13AB B AC AB C ⨯==，故2206513AB =，132AB =．所以sin 11sin 2AB A BC C ⨯==． ····················10分 3.（北京卷15）．（本小题共13分）已知函数2π()sin sin 2f x x x x ωωω⎛⎫=+ ⎪⎝⎭（0ω>）的最小正周期为π．（Ⅰ）求ω的值；（Ⅱ）求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦，上的取值范围．解：（Ⅰ）1cos 2()22x f x x ωω-=112cos 222x x ωω=-+π1sin 262x ω⎛⎫=-+ ⎪⎝⎭．因为函数()f x 的最小正周期为π，且0ω>，所以2ππ2ω=，解得1ω=．（Ⅱ）由（Ⅰ）得π1()sin 262f x x ⎛⎫=-+ ⎪⎝⎭．因为2π03x ≤≤，所以ππ7π2666x --≤≤，所以1πsin 2126x ⎛⎫-- ⎪⎝⎭≤≤，因此π130sin 2622x ⎛⎫-+ ⎪⎝⎭≤≤，即()f x 的取值范围为302⎡⎤⎢⎥⎣⎦，．4.（四川卷17）．（本小题满分12分）求函数2474sin cos 4cos 4cos y x x x x =-+-的最大值与最小值。

2008年高考试题——数学理(全国卷2)

绝密★启用前【考试时间：6月7日 15:00—17:00】2008年普通高等学校招生全国统一考试理科数学本试卷分第Ⅰ（选择题）卷和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页，第Ⅱ卷3至4页。

考试结束后，将本试卷和答题卡一并交回。

满分150分，考试用时120分钟。

第Ⅰ卷（选择题，共60分）注意事项：1．答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚，并认真核准条形码的准考证号码、姓名、考场号、座位号及科目，在规定的位置贴好条形码。

2．每小题选出答案后，用2B 铅笔吧答题卡上对应题目的答案涂黑。

如需改动用橡皮擦擦干净后，再选涂其它答案标号。

答在试卷上的答案无效。

参考公式：如果事件A 、B 互斥，那么P （A+B ）=P （A ）+P （B ）如果事件A 、B 相互独立，那么P （A ·B ）=P （A ）·P （B ）如果事件A 在一次试验中发生的概率是P ，那么 n 次独立重复试验中恰好发生k 次的概率P n (k)=C k nP k (1－P)n －k本卷12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

一．选择题（1）设集合}23{<<-∈=m Z m M ,}31{≤≤-∈=n Z n N ,则=⋂N MA ．}1,0{ B. }1,0,1{- C. }2,1,0{ D }2,1,0,1{- (2)设a ，b ∈R 且b ≠0，若复数3bi)(a +是实数，则A ． 223a b = B. 223b a = C. 229a b = D.229b a =球的表面积公式S=42R π其中R 表示球的半径，球的体积公式V=334R π，其中R 表示球的半径(3)函数x xx f -=1)(的图像关于 A ． y 轴对称 B.直线y=-x C.坐标原点对称 D.直线y=x (4)若)1,(1-∈e x ，x ln =a ,x ln 2=b ,x 3ln =c ,则A ．c b a << B. b a c << C. c a b << D. a c b <<（5）设变量x,y 满足约束条件：2,22,-≥≤+≥x y x x y 则y x z 3-=的最小值为：A ．-2 B.-4 C. -6 D.-8（6）从20名男同学，10名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为 A ．299 B. 2910 C. 2919 D. 2920 （7）()()4611x x+-的展开式中x 的系数是A ．-4 B.-3 C.3 D.4（8）若动直线a x =与函数x x f sin )(=和x x g cos )(=的图像分别交于M 、N 两点，则MN 的最大值为A ．1 B. 2 C.3 D.2（9）设1>a ，则双曲线22221(1)x y a a -=+的离心率e 的取值范围是 A ．)2,2( B. )5,2( C. )5,2( D. )5,2(（10）已知正四棱锥S-ABCD 的侧棱长与底面边长都相等，E 是SB 的中点，则AE 、SD 所成的角的余弦值为 A ．31 B. 32 C. 33 D. 32 （11）等腰三角形两腰所在直线的方程分别为02=-+y x 和047=--y x ，原点在等腰三角形的底边上，则底边所在直线的斜率为 A ．3 B. 2 C. 31-D. 21-（12）已知球的半径为2，相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2，则两圆的圆心距等于A ．1 B. 2 C. 3 D. 2第Ⅱ卷（非选择题，共90分）二．填空题：（本大题共4个小题，每小题5分，共20分。