书人教育五年级奥数资料-斐波那契专题
斐波那契数的规律

斐波那契数的规律嘿,朋友们!今天咱来聊聊那神奇的斐波那契数呀!这斐波那契数啊,就像是数学世界里的一串神秘密码。
你看啊,从 1,1 开始,后面的每个数都等于前两个数的和。
就好像是一级一级的台阶,让我们不断往上爬,去探索更奇妙的数学天地。
咱可以把斐波那契数想象成是生活中的一些有趣现象。
比如说,兔子的繁殖!一对小兔子长大以后,每个月能生出一对小兔子,那兔子的数量增长不就有点像斐波那契数的增长嘛!刚开始可能就那么一两只,慢慢地越来越多,越来越多。
再想想大自然中的那些美丽图案,有些花朵的花瓣数,不也常常和斐波那契数有关系嘛!这难道不是大自然在向我们展示斐波那契数的神奇魅力吗?这多有意思呀!斐波那契数还有一个特别神奇的地方,就是它在很多领域都有出现呢!不只是数学,在艺术、建筑等方面也都能看到它的影子。
就好像它是一把万能钥匙,能打开各种不同领域的大门。
而且哦,斐波那契数的规律有时候还能帮我们解决一些实际问题呢!比如说在设计一些图案或者排列东西的时候,按照斐波那契数的规律来,可能会让整个布局看起来更加和谐、美观。
你说这斐波那契数是不是很神奇?它就像是一个隐藏在数学世界里的宝藏,等着我们去不断挖掘、发现。
我们在生活中不也常常会遇到这样看似简单却蕴含着大道理的事情吗?就像斐波那契数,一开始可能觉得不就是几个数字嘛,但深入了解后才发现它的奥秘无穷无尽。
那我们是不是也应该像对待斐波那契数一样,对生活中的各种事物都保持着好奇心和探索精神呢?不要轻易地就忽略那些看似普通的东西,说不定它们背后都有着让人惊叹的一面呢!斐波那契数,真的是让我们感受到了数学的魅力和神奇。
它不仅仅是一些数字的组合,更是一种智慧的体现,一种对世界的独特解读。
所以啊,朋友们,可别小看了这斐波那契数哦!。
斐波那契数列资料

斐波那契数列斐波那契数列一、简介斐波那契数列(Fibonacci),又称黄金分割数列,由数学家斐波那契最早以“兔子繁殖问题”引入,推动了数学的发展。
故斐波那契数列又称“兔子数列”。
斐波那契数列指这样的数列:1,1,2,3,5,8,13,……,前两个数的和等于后面一个数字。
这样我们可以得到一个递推式,记斐波那契数列的第i项为F i,则F i=F i-1+F i-2.兔子繁殖问题指设有一对新生的兔子,从第三个月开始他们每个月都生一对兔子,新生的兔子从第三个月开始又每个月生一对兔子。
按此规律,并假定兔子没有死亡,10个月后共有多少个兔子?这道题目通过找规律发现答案就是斐波那契数列,第n个月兔子的数量是斐波那契数列的第n项。
二、性质如果要了解斐波那契数列的性质,必然要先知道它的通项公式才能更简单的推导出一些定理。
那么下面我们就通过初等代数的待定系数法计算出通项公式。
令常数p,q满足F n-pF n-1=q(F n-1-pF n-2)。
则可得:F n-pF n-1=q(F n-1-pF n-2)=q2(F n-2-pF n-3)=…=q n-2(F2-pF1)又∵F n-pF n-1=q(F n-1-pF n-2)∴F n-pF n-1=qF n-1-pqF n-2F n-1+F n-2-pF n-1-qF n-1+pqF n-2=0(1-p-q)F n-1+(1+pq)F n-2=0∴p+q=1,pq=-1是其中的一种方程组∴F n-pF n-1= q n-2(F2-pF1)=q n-2(1-p)=q n-1F n=q n-1+pF n-1=q n-1+p(q n-2+p(q n-3+…))=q n-1+pq n-2+p2q n-3+…+p n-1不难看出,上式是一个以p/q为公比的等比数列。
将它用求和公式求和可以得到:而上面出现了方程组p+q=1,pq=-1,可以得到p(1-p)=-1,p2-p-1=0,这样就得到了一个标准的一元二次方程,配方得p2-p+0.25=1.25,(p-0.5)2=1.25,p=±√1.25+0.5。
斐波那契原理的应用

斐波那契原理的应用1. 什么是斐波那契序列斐波那契序列是指从0和1开始,后面的每一项都是前面两项的和。
即,序列的第一项为0,第二项为1,第三项为0+1=1,第四项为1+1=2,第五项为1+2=3,以此类推。
2. 斐波那契原理的应用场景斐波那契原理在各个领域都有广泛的应用。
以下是一些常见的应用场景:2.1. 财务规划斐波那契原理可以用于财务规划中的资产分配和投资管理。
通过斐波那契序列,可以制定合理的资产配置比例,帮助投资者平衡风险和回报。
2.2. 项目管理斐波那契原理可以应用于项目管理中的时间估算和资源分配。
根据斐波那契数列,可以合理预估项目的进度和完成时间,以及确定合适的资源分配策略。
2.3. 自然科学斐波那契序列在自然科学中的应用非常广泛。
例如,在植物学中,斐波那契序列可以用来描述植物的分枝规律;在动物学中,斐波那契序列可以用来解释动物的进化规律。
2.4. 编程算法斐波那契序列也经常被用于编程算法中。
例如,在动态规划算法中,可以利用斐波那契序列来解决一些问题,如爬楼梯问题和切割钢条问题等。
3. 斐波那契原理的优点斐波那契原理具有以下几个优点:3.1. 简单易懂斐波那契原理的定义简单,易于理解和应用。
只需要知道前两项的值,就可以通过简单的加法运算来计算后面的项。
3.2. 可预测性强斐波那契序列具有较强的可预测性。
根据前面的项,可以准确地预测出后面的项的值,这对于一些需要进行长期规划和决策的场景非常有用。
3.3. 应用广泛斐波那契原理在不同领域都有广泛的应用。
无论是财务规划、项目管理还是自然科学,都可以通过斐波那契原理来解决一些问题。
4. 斐波那契原理的局限性然而,斐波那契原理也存在一些局限性:4.1. 高度理想化的假设斐波那契原理的应用基于一些理想化的假设,比如每一项都是前两项的和,但在实际情况中,可能存在其他因素的影响,使得序列的规律不完全符合斐波那契原理。
4.2. 信息局限性斐波那契原理只能根据已知的前面的项来计算后面的项,无法考虑其他可能的因素。
费波那契数列

斐波拉契数列(又译作“斐波那契数列”或“斐波那切数列”)是一个非常美丽、和谐的数列,它的形状可以用排成螺旋状的一系列正方形来说明(如右词条图),起始的正方形(图中用灰色表示)的边长为1,在它左边的那个正方形的边长也是1 ,在这两个正方形的上方再放一个正方形,其边长顺次加上边长为3、5、8、13、21……等等的正方形。
这些数字每一个都等于前面两个数之和,它们正好构成了斐波那契数列。
斐波拉契数列的简介:“斐波那契数列”的发明者,是意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci,生于公元1170年,卒于1240年。
籍贯大概是比萨)。
他被人称作“比萨的列昂纳多”。
1202年,他撰写了《珠算原理》(Liber Abaci)一书。
他是第一个研究了印度和阿拉伯数学理论的欧洲人。
他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。
他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。
斐波那契数列指的是这样一个数列:1,1,2,3,5,8,13,21,34……这个数列从第三项开始,每一项都等于前两项之和。
它的通项公式为:(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}(√5表示5的算术平方根)(19世纪法国数学家敏聂(Jacques Phillipe Marie Binet 1786-1856) 很有趣的是:这样一个完全是自然数的数列,通项公式居然是用无理数来表达的。
斐波拉契数列之闻名,可能还跟美国悬疑作家丹·布朗有关,他在他的小说《达芬奇密码》之中巧妙地运用了该数列。
其实,我国现行的高中教材中提及了杨辉三角,斐波拉契数列可在其中寻得。
13世纪初,欧洲最好的数学家是斐波拉契;他写了一本叫做《算盘书》的著作,是当时欧洲最好的数学书。
书中有许多有趣的数学题,其中最有趣的是下面这个题目:“如果一对兔子每月能生1对小兔子,而每对小兔在它出生后的第3个月裏,又能开始生1对小兔子,假定在不发生死亡的情况下,由1对初生的兔子开始,1年后能繁殖成多少对兔子?”斐波拉契把推算得到的头几个数摆成一串:1,1,2,3,5,8……这串数里隐含着一个规律:从第3个数起,后面的每个数都是它前面那两个数的和。
斐班那切数列

斐班那切数列斐波那契数列(Fibonacci sequence)是一个典型的数学问题,也是一个非常有趣的数列。
它是通过前两个数字的和得到下一个数字的一种规律,起始数字常为0和1。
斐波那契数列的定义很简单,就是从1开始,每一项都等于前两项之和,公式表示为:F(n)=F(n-1)+F(n-2),其中F(n)表示数列的第n项。
斐波那契数列的前几项依次为:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,以此类推。
可以看出,这个数列是个无限数列,每一项都是前两项的和。
斐波那契数列最早是由13世纪的意大利数学家斐波那契(Fibonacci)研究得出的。
他在其著作《算盘书》中介绍了斐波那契数列,并且用兔子繁殖作为实例来说明这个数列的应用。
斐波那契数列有着许多有趣的性质和应用。
首先,它是一个递归数列,可以通过递归的方式来生成。
其次,斐波那契数列的增长速度非常快,后面的数字会迅速增大。
这也使得它在金融学、自然科学、计算机科学等领域有着广泛的应用。
在金融学中,斐波那契数列出现在黄金分割比例中。
黄金分割比例是一个数学上的常数,被广泛应用在艺术、建筑、美学等领域。
它可以用斐波那契数列的比值逼近得到,即相邻两项的比例会越来越接近黄金分割比例1.618。
在自然科学中,斐波那契数列也有着一些有趣的应用。
例如,它出现在植物的排列方式中。
在一些植物的叶子、花瓣、果实等排列中,可以发现它们的数量往往是斐波那契数列的某一项。
这种规律被称为植物的斐波那契序列。
在计算机科学中,斐波那契数列常常被用来展示递归算法的实现。
由于斐波那契数列的递归定义,可以使用递归算法来计算数列的某一项。
然而,递归算法在计算大量项时会遇到效率问题,结果需要大量的重复计算。
因此,可以使用动态规划等方法来优化算法,避免重复计算。
斐波那契数列还和黄金矩形、黄金螺旋等有着紧密的联系。
黄金矩形是一种长宽比例接近黄金分割比例的矩形,黄金螺旋则是由一系列黄金矩形组成的螺旋形状。
斐波那契---一个天才数学计算专家(斐波那契线的奥秘所在)

斐波那契---一个天才数学计算专家(斐波那契线的奥秘所在)斐波那契---一个天才数学计算专家(斐波那契线的奥秘所在)斐波那契,十二世纪意大利的天才数字研究专家,那时候,罗马数字和阿拉伯数字正好风靡欧洲。
斐波那契醉心数字,因为发明斐波那契数列而闻名全世界。
闲话少说。
请看数列:1+1=2 13+21=34 自己另加:233+377=6101+2=3 21+34=55 377+610=9872+3=5 34+55=89 610+987=15973+5=8 35+89=144 987+1597=25845+8=13 89+144=233 1597+2584=41818+13=21 144+233=377 2584+4181=6765直到无穷要知道一个数字天才发现的东西,肯定不是一个简单的东西。
如果你简单一看,你就看明白了,那你也是天才。
如果如我般看不明白才是真正的蠢才,那是非常正常的。
不可能人人都是天才。
对天才的东西加以利用,至少我们可以从蠢才变成人才、地才。
天才就免了吧。
1、从上面得出一组数据:1、3、5、8、13、21、34、55、89、144、233、377.......2、随便取一组数据:34+55=89.做除法得出几个相同且重要的数据:55除以34,结果等于1.618.34除以55,结果等于0.618.34除以89,结果等于0.382.无论你用数组中哪一个数字那出来,都会得到这几个数字,于是6个数字你是必须记住的:0.382、0.50、0.618、0.786、1.27、1.618.你可能马上想:0.50、0.786、1.27怎么冒出来的?将三个数字之和除以2就是0.5,0.786是0.618的平方根,1.27是1.618的平方根。
所有这些在市场交易中非常重要。
智者宝之,无谓者哂之。
3、0.382、0.50、0.618、0.786是回调数。
1.27和1.618就是扩展数。
上涨回调一般是按依次23.6、38.2、50、61.8依次回调。
裴波那契数列

把一对老兔子用
表示,一对小兔子用
表示。
兔子繁殖有规律哟 啊
1月 1
2月 1
3月 2
4月 3
5月 5
6月 8
7月 13
8月 21
9月 34
10 月 55
11 月 89
12 月 144
数列规律: 数列规律: 即从第三项起,每一项都等于前两项之和。 即从第三项起,每一项都等于前两项之和。
首先将一对刚出生的小兔放到围墙里,一 个月后就能长成大兔,再过一个月便能生下一 对小兔,并且此后每个月都生一对小兔。随着 时间的推移,小兔子长成大兔子并且继续繁殖。 假如一年内没有发生死亡,则一对小兔子在一 年内能繁殖成多少对兔子呢?(新生的小兔第 二个月变为成熟的兔子)
①一对大兔生过一对小兔后,下个月会接着 生,无死亡。
2、松果和菠萝一片片的鳞片在整粒松果上顺着两组螺线排 列:一组呈顺时针旋转,另一组呈反时针。仔细瞧瞧,顺 时针螺线的排列数目是 8,反时针方向则为 13。向日葵常 见的螺线数目为“21和34”还有螺线数目为“89和144”, 更大的甚至还有“144和233”。这些全都是裴波那契数列 中相邻两项的数值
3、如蜘蛛网、水流的旋涡、蜗牛壳的螺纹以及星 系内星球的分布等也是按照裴波那契螺旋排列的。 4、美国还于1963年创办了《裴波那契季刊》这一 数学杂志,定期发表一些与裴波那契数列有关系 的研究成果。
一个楼梯共有10台阶,我们规定上楼梯时,每次只能跨上 一个台阶或两个台阶。从地面到最上层共有多少种不同的 跨法? • 提示: 如果只有一阶台阶,那么只有一种跨法, 如果只有两节台阶,那么只有两种跨法。即每次跨一级或 一次跨两级。 如果只有三节台阶,就有三种跨法。即每次跨一级或先跨 一级再跨两级或先跨两级在跨一级。 如果只有四节台阶,就有五种跨法。
斐波那契_精品文档

斐波那契斐波那契数列是一种非常有趣且重要的数学序列,由意大利数学家列奥纳多·斐波那契(Leonardo Fibonacci)在13世纪提出。
斐波那契数列的定义非常简单,就是从0和1开始,后续的每个数都是前面两个数的和。
斐波那契序列的前几个数字依次为0、1、1、2、3、5、8、13、21、34、55等等。
可以看出,斐波那契序列中的每个数都是前面两个数的和,这是斐波那契数列的重要特点。
斐波那契数列在数学上有很多有意义的应用,也在编程领域中被广泛使用。
下面我们将对斐波那契序列的一些性质进行详细讨论。
1. 斐波那契数列的递推关系斐波那契数列的递推关系非常简单,即 F(n) = F(n-1) + F(n-2),其中F(n)表示第n个斐波那契数。
这个递推关系可以很容易地用递归函数来实现,也可以使用迭代的方式进行求解。
2. 斐波那契数列的公式推导斐波那契数列还可以通过一个公式来计算,这个公式被称为斐波那契公式。
斐波那契公式是通过对斐波那契数列的递推关系进行推导得到的,其表达式如下:F(n) = (pow(1+sqrt(5),n) - pow(1-sqrt(5),n)) / (pow(2,n) * sqrt(5))其中,pow表示幂运算,sqrt表示平方根运算。
3. 斐波那契数列的性质斐波那契数列具有很多有趣的性质,下面我们介绍其中的一些:(1)黄金分割斐波那契数列中,每个数与它的前一个数的比值趋近于黄金分割比例0.618,也就是说,当 n 足够大时,F(n) / F(n-1) ≈ 0.618。
黄金分割在艺术、建筑和自然界中广泛应用,被认为是最具美感的比例之一。
(2)兔子繁殖问题斐波那契数列最初是用来描述兔子繁殖问题的。
假设一对兔子从出生开始,每个月都可以繁殖一对新的兔子。
新生的兔子在出生后第二个月开始繁殖,且每对兔子都不会死亡。
那么经过n个月,有多少对兔子呢?根据斐波那契数列的定义和递推关系,我们可以得到答案,即第n个月有F(n)对兔子。
裴波那契数列

裴波那契数列裴波那契数列800年前,意⼤利的数学家斐波纳契出版了惊世之作《算盘书》。
在《算盘书》⾥,他提出了著名的“兔⼦问题”:假定⼀对兔⼦每个⽉可以⽣⼀对兔⼦,⽽这对新兔⼦在出⽣后第⼆个⽉就开始⽣另外⼀对兔⼦,这些兔⼦不会死去,那么⼀对兔⼦⼀年内能繁殖多少对兔⼦?答案是⼀组⾮常特殊的数字:1,1,2,3,5,8,13,21,34,55,89……不难发现,从第三个数起,每个数都是前两数之和,这个数列则称为“斐波纳契数列”,其中每个数字都是“斐波纳契数”。
这个数列从第三项开始,每⼀项都等于前两项之和。
它的通项公式为:斐波拉契数列是⼀个⾮常美丽、和谐的数列,它的形状可以⽤排成螺旋状的⼀系列正⽅形来说明起始的正⽅形(图中⽤灰⾊表⽰)的边长为1,在它左边的那个正⽅形的边长也是1 ,在这两个正⽅形的上⽅再放⼀个正⽅形,其边长为2,以后顺次加上边长为3、5、8、13、21……等等的正⽅形。
这些数字每⼀个都等于前⾯两个数之和,它们正好构成了斐波那契数列。
斐波纳契数列还暗含着许多有趣的数字规律,如从第3个数开始每隔两个必是2的倍数,从第4个数开始每隔3个必是3的倍数,从第5个数开始每隔4个必是5的倍数……另外,这个数列最具有和谐之美的地⽅是,越往后,相邻两项的⽐值会⽆限趋向于黄⾦⽐0.61803……。
⽣活中的裴波那契数列斐波拉契数列⽆处不在,以下仅举⼏条常见的例⼦:1.杨辉三⾓对⾓线上各数之和构成斐波拉契数列.2.多⽶诺牌(可以看作⼀个2×1⼤⼩的⽅格)完全覆盖⼀个n×2的棋盘,覆盖的⽅案数等于斐波拉契数列。
3.从蜜蜂的繁殖来看,雄蜂只有母亲,没有⽗亲,因为蜂后产的卵,受精的孵化为雌蜂,未受精的孵化为雄峰。
⼈们在追溯雄峰的祖先时,发现⼀只雄峰的第n代祖先的数⽬刚好就是斐波拉契数列的第n项Fn。
4.钢琴的13个半⾳阶的排列完全与雄蜂第六代的排列情况类似,说明⾳调也与斐波拉契数列有关。
5.⾃然界中⼀些花朵的花瓣数⽬符合于斐波拉契数列,也就是说在⼤多数情况下,⼀朵花花瓣的数⽬都是3,5,8,13,21,34,……(有6枚是两套3枚;有4枚可能是基因突变)。
斐波那契数列

斐波那契数列与黄金分割
黄金分割
黄金分割是一种比例关系,即将一条线段分为两部分,使得较长部分与原线段的比例等于较短部分与较长部分 的比。在斐波那契数列中,每一项都是前一项与前前一项的比值,这个比值趋近于黄金分割的比值(√5 - 1) /2约等于0.618034。
应用
斐波那契数列和黄金分割在艺术、音乐、建筑等领域都有广泛的应用,如绘画、雕塑、音乐节奏等。
• 优点:可以适用于较大的n值,且代码相对简洁。 • 缺点:相对于递归和迭代算法,其计算效率较低。 • 示例代码 • function fibonacci(n) • A = {{0, 1}, {1, 1}} • x = {0, 1} • for i from 2 to n do • x = {x[1] + x[2], x[0]} • return x[0] • · 矩阵乘法算法是通过将斐波那契数列视为矩阵的方式来计算的。矩阵乘法算法的时间复杂度为O(n^2),相
2023
斐波那契数列
汇报人:
目录
• 斐波那契数列简介 • 斐波那契数列的算法 • 斐波那契数列的数学性质 • 斐波那契数列的计算机实现 • 斐波那契数列的优化与扩展 • 斐波那契数列的相关问题与挑战
01
斐波那契数列简介
定义与特性
特性
除了前两个数字外,每个数字都 是正整数。
定义:斐波那契数列是一系列数 字,从0和1开始,后面的每个数 字是前两个数字的和。
矩阵乘法的优化
要点一
矩阵乘法优化概述
要点二
分布式计算
矩阵乘法是计算量较大的运算之一, 因此对其进行优化可以提高计算效率 。
使用分布式计算框架如Apache Spark,将矩阵乘法运算分布到多个 计算节点上,从而加快计算速度。
斐波那契资料

比萨的列奥纳多,又称斐波那契(Leonardo Pisano ,Fibonacci, Leonardo Bigollo,1175年-1250年),意大利数学家,西方第一个研究斐波那契数,并将现代书写数和乘数的位值表示法系统引入欧洲。
螺旋斐波那契(Leonardo Fibonacci, 约1175-约1240)也许是在生活在丢番图(Diophantos)之后费尔马(Pierre de Fermat)之前这2000年间欧洲最杰出的数论学家。
我们对他的生平知道得很少。
他出生在意大利那个后来因为伽里略做过落体实验而著名的斜塔所在的城市里,现在那里还有他的一座雕像。
他年轻是跟随经商的父亲在北非和欧洲旅行,大概就是由此而学习到了世界各地不同的算术体系。
在他最重要的著作《算盘书》(Liber Abaci,写于1202年)中,引进了印度-阿拉伯数码(包括0)及其演算法则。
数论方面他在丢番图方程和同余方程方面有重要贡献。
坐落在意大利比萨的斐波那契雕像数学中有一个以他的名字命名的著名数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ……从第三项开始每一项都是数列中前两项之和。
这个数列是斐波那契在他的《算盘书》的“兔子问题”中提出的。
在问题中他假设如果一对兔子每月能生一对小兔(一雄一雌),而每对小兔在它出生后的第三个月,又能开始生小兔,如果没有死亡,由一对刚出生的小兔开始,一年后一共会有多少对兔子?将问题一般化后答案就是,第n个月时的兔子数就是斐波那契数列的第n项。
斐波那契数列和黄金分割数有很密切的联系。
斐波那契并没有把这个问题和这个数列看得特别重要,在《算盘书》中兔子问题只不过是书里许多问题中并不特别的其中一个罢了。
但是在此后的岁月中,这个数列似乎和题中的高产兔子一样,引发了为数众多的数学论文和介绍文章(本文似乎也在步此后尘)。
不过在这里我不想介绍浩如烟海的有关斐波那契数列的数学文章,只想欣赏大自然的造化。
斐波那契数列的

斐波那契数列的斐波那契数列是一个有趣而又复杂的数学问题,它可以用一组有规则的数字序列来描述,并且在各个领域都有广泛的应用。
斐波那契数列是从第三项开始的一个等比数列,每一项的值都是前两项的和。
由于它有很多有趣的性质,因此受到了众多学者的关注和研究,而且被广泛应用到工程、经济学、生物学等不同领域。
首先,让我们来看一下斐波那契数列的定义,它是由以下等式定义的:f(n)=f(n-1)+f(n-2),其中n≥3,f(1)=f(0)=1。
从这里可以看出,斐波那契数列是一个等比数列,每一项的值都是前两项之和。
斐波那契数列也可以用图表来表示:1,1,2,3,5,8,13,21,34,55,89,144,233……斐波那契数列有很多有趣的性质,其中最常见的一个就是每个数字都是前面两个数字的和。
由此可以推出后面的数字,这样就可以生成一个无限的等比数列。
此外,斐波那契数列还有一种特殊的性质,就是其中每两个相邻的数字都是有一定比例关系的,这个比例称为黄金分割比,即前后两个数字的比值约为1.618,被称为黄金分割比。
此外,斐波那契数列还有一个很有趣的性质,就是它的前面的数字中,每次出现的数字都是它的因数,例如:144的因数有1,2,3,4,6,8,9,12,16,18,24,36,48,72,144,而斐波那契数列前面的几个数字正是这些因数,即1,1,2,3,5,8,13,21,34,55,89。
斐波那契数列不仅有着许多独特的性质,而且也因其强大的应用性而受到了学术界的广泛研究。
斐波那契数列在工程,经济,生物学等各个领域都有广泛的应用,比如在工程中,我们可以使用斐波那契数列来分析结构物的稳定性,在经济学中,它可以帮助我们了解货币市场的变化趋势,而在生物学领域,它可以帮助我们研究突变和定型等诸多问题。
总之,斐波那契数列是一个具有深远影响的数学问题,它的出现不仅创造了许多有趣的数学性质,而且还被广泛应用到了工程、经济学、生物学等多个领域,成为了研究突变和定型等各种问题的重要工具。
斐波那契数列的奥秘

斐波那契数列的奥秘1. 什么是斐波那契数列斐波那契数列(Fibonacci Sequence)又称黄金分割数列,因13世纪的意大利数学家斐波那契(Leonardoda Fibonacci)而得名。
这个数列从0和1开始,之后的每一个数都由前两个数相加得到:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ……以此类推。
2. 斐波那契数列的应用斐波那契数列并不只是一种数学上的抽象概念,它在现实世界中有着广泛的应用。
其中一个典型的例子就是菠萝的结构。
菠萝的鳞片排列呈现出斐波那契数列的规律,这种规律使得菠萝更加紧密地生长。
同时,在生物学领域,许多植物的花朵、树叶等都呈现出斐波那契树形态,这种形态美感十足,而且有助于植物的生长和传播。
3. 斐波那契数列的几何意义斐波那契数列还与黄金分割密切相关。
黄金分割是指把一条线段分割成两部分,使其中一部分与全长之比等于另一部分与这部分之比。
这个比例即为金子比(约1.618),也被称为黄金分割点。
如果我们取斐波那契数列中相邻两个数的比值,会发现随着数列增长,这个比值越来越逼近黄金分割点。
这说明斐波那契数列具有很强的几何意义,与自然界中许多规律相吻合。
4. 斐波那契数列在艺术中的运用除了在自然界中呈现,斐波那契数列还被广泛运用在艺术领域。
许多艺术作品中都能看到斐波那契数列的身影,如建筑设计、绘画作品等。
艺术家们通过运用这种神秘而美妙的数字序列,使作品更加富有节奏感和动态美。
5. 斐波那契数列在计算机科学中的应用在计算机科学领域,斐波那契数列也有着重要的应用价值。
它被广泛应用在算法设计、数据结构等方面。
特别是在递归算法中,经常会看到斐波那契数列的身影。
6. 斐波那契数列与金融市场斐波那契数列还被运用于金融市场的技术分析中。
通过观察股票或者外汇市场走势图表上出现的斐波那契比例线(Fibonacci Retracement Levels),交易者可以预测价格可能出现支撑或阻力,并做出相应交易决策,提高投资成功率。
斐波那契数列通项公式推导讲解

斐波那契数列通项公式推导讲解斐波那契数列是一个非常有趣且广泛应用的数列。
它的定义非常简单,第一个和第二个数都是1,从第三个数开始,每个数都是前两个数的和。
也就是说,斐波那契数列的前几个数分别是1,1,2,3,5,8,13,21,34,55,以此类推。
我们知道,斐波那契数列的递推关系为Fn=Fn-1+Fn-2,其中Fn代表第n个斐波那契数。
那么,如何推导出斐波那契数列的通项公式呢?下面,我将详细讲解。
假设斐波那契数列的通项公式为Fn=a^n,其中a是一个实数。
将通项公式带入递推关系式中,得到:a^n=(a^n-1)+(a^n-2)。
接下来,我们将两边都除以a^n-2,得到方程:a^2=a+1这是一个二次方程,我们可以将其转化为标准形式,得到:a^2-a-1=0。
接下来,我们需要求解这个二次方程的解。
通过求根公式,得到:a=(1±√(1+4))/2简化后a1=(1+√5)/2≈1.618a2=(1-√5)/2≈-0.618因此,斐波那契数列的通项公式可以写为:Fn=(1+√5)/2^n-(1-√5)/2^n值得注意的是,由于二次方程存在两个根,因此斐波那契数列的通项公式将会有两个部分。
但在实际应用中,虽然有两个部分,但是通常只考虑第一个部分,因为这个部分是一个递增的函数,与斐波那契数列的增长趋势相一致。
以上就是斐波那契数列通项公式的推导过程。
通过这个通项公式,我们可以直接计算任意位置的斐波那契数,而不需要进行逐步迭代计算。
这大大简化了计算的复杂度,使得斐波那契数列的计算更加高效。
同时,斐波那契数列的通项公式也在很多领域有着广泛的应用。
书人教育五年级奥数资料-斐波那契专题
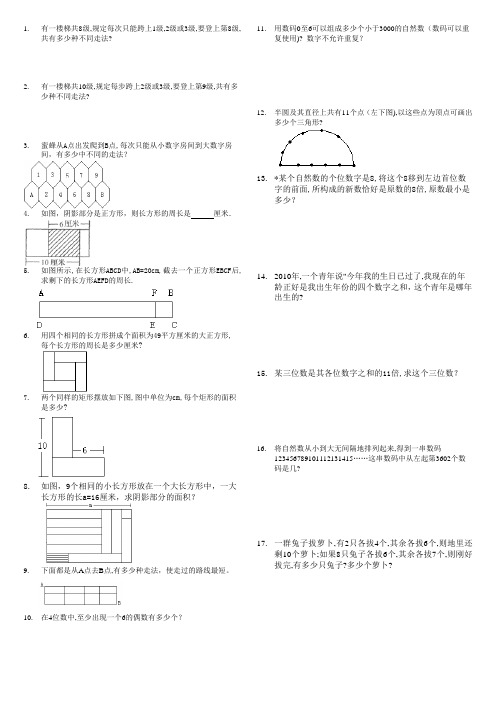
1.有一楼梯共8级,规定每次只能跨上1级,2级或3级,要登上第8级,共有多少种不同走法?2.有一楼梯共10级,规定每步跨上2级或3级,要登上第9级,共有多少种不同走法?3.蜜蜂从A点出发爬到B点,每次只能从小数字房间到大数字房间,有多少中不同的走法?4.如图,阴影部分是正方形,则长方形的周长是厘米.5.如图所示,在长方形ABCD中,AB=20cm,截去一个正方形EBCF后,求剩下的长方形AEFD的周长.6.用四个相同的长方形拼成个面积为49平方厘米的大正方形,每个长方形的周长是多少厘米?7.两个同样的矩形摆放如下图,图中单位为cm,每个炬形的面积是多少?8.如图,9个相同的小长方形放在一个大长方形中,一大长方形的长a=16厘米,求阴影部分的面积?9.下面都是从A点去B点,有多少种走法,使走过的路线最短。
10.在4位数中,至少出现一个6的偶数有多少个?11.用数码0至6可以组成多少个小于3000的自然数(数码可以重复使用)? 数字不允许重复?12.半圆及其直径上共有11个点(左下图),以这些点为顶点可画出多少个三角形?13.*某个自然数的个位数字是8,将这个8移到左边首位数字的前面,所构成的新数恰好是原数的8倍,原数最小是多少?14.2010年,一个青年说"今年我的生日已过了,我现在的年龄正好是我出生年份的四个数字之和,这个青年是哪年出生的?15.某三位数是其各位数字之和的11倍,求这个三位数?16.将自然数从小到大无间隔地排列起来,得到一串数码123456789101112131415……这串数码中从左起第3602个数码是几?17.一群兔子拔萝卜,有2只各拔4个,其余各拔6个,则地里还剩10个萝卜;如果8只兔子各拔6个,其余各拔7个,则刚好拔完,有多少只兔子?多少个萝卜?。
(完整版)小学奥数斐波那契数列典型例题

拓展目标:一:周期问题的解决方法(1)找出排列规律,确定排列周期。
(2)确定排列周期后,用总数除以周期。
①如果没有余数,正好有整数个周期,那么结果为周期里的最后一个②如果有余数,即比整数个周期多n个,那么结果为下一个周期的第n个。
例1:(1)1,2,1,2,1,2,…那么第18个数是多少?这个数列的周期是2,1829÷=,所以第18个数是2.(2)1,2,3,1,2,3,1,2,3,…那么第16个数是多少?这个数列的周期是3,16351÷=⋅⋅⋅,所以第16个数是1.二:斐波那契数列斐波那契是的有关兔子的问题:假设一对刚出生的小兔,一个月后就能长成大兔,再过一个月便能生下一对小兔,并且此后每个月都生一对小兔。
一年内没有发生死亡。
那么,由一对刚出生的兔子开始,12个月后会有多少对斐波那契数列(兔子数列)1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …你看出是什么规律:。
【前两项等于1,而从第三项起,每一项是其前两项之和,则称该数列为斐波那契数列】【巩固】(1)2,2,4,6,10,16,(),()(2)34,21,13,8,5,(),2,()例1:有一列数:1,1,2,3,5,8,13,21,34…..这个有趣的“兔子”数列,在前120个数中有个偶数?个奇数?第2004个数是数(奇或偶)?【解析】120÷3=40 2004÷3=668【巩固】有一列数按1、1、2、3、5、8、13、21、34……的顺序排列,第500个数是奇数还是偶数?例2:(10秒钟算出结果!)(1)1+1+2+3+5+8+13+21+34+55=(2)1+2+3+5+8+13+21+34+55+89=数学家发现:连续 10个斐波那契数之和,必定等于第 7个数的 11 倍!巩固:34+55+89+144+233+377+610+987+1597+2584==例3:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …(1)这列数中第2013个数的个位数字是几?分析:相加,只管个位,发现60个数一循环个位数F1 - F30:1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 61 7 8 5 3 8 1 9 0F31-F60:9 9 8 7 5 2 7 9 6 5 1 6 7 3 0 3 3 6 9 5 49 3 2 5 7 2 9 1 0F61-F81:1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 6 2013 = 60*33 + 33,第33个个位为8巩固:这列数中第2003个数的个位数字是几?(2)这列数中第2003个数除以5的余数是几?规律:发现20个数一循环、。
斐波那契数列解题技巧

斐波那契数列解题技巧斐波那契数列,又称黄金分割数列、兔子数列,是数学领域中一道著名的难题。
它的定义如下:第一个数和第二个数均为1,从第三个数开始,每个数都是前两个数之和。
例如:1, 1, 2, 3, 5, 8,以此类推。
本文将介绍斐波那契数列的解题技巧及其应用。
斐波那契数列的通项公式为:F(n) = (1 / sqrt(5)) * [((1 + sqrt(5)) / 2)^n - ((1 - sqrt(5)) / 2)^n]。
通过这个公式,我们可以快速计算出斐波那契数列的任意一项。
此外,斐波那契数列还具有以下性质:从第三项开始,每一项与前一项的比值趋近于黄金分割比例0.618。
在求解斐波那契数列时,有多种方法可供选择。
以下列举四种常见方法:1.迭代法:通过不断迭代计算,求出斐波那契数列的每一项。
这种方法简单易懂,但计算速度较慢,适用于小范围数值计算。
2.递归法:利用斐波那契数列的定义,编写递归函数来求解。
这种方法在计算过程中会产生大量重复计算,效率较低,但在某些场景下可以简化代码。
3.矩阵求幂法:将斐波那契数列表示为矩阵形式,通过矩阵求幂来计算。
这种方法具有较高的计算效率,适用于大规模数值计算。
4.循环迭代法:在迭代法的基础上,采用循环结构提高计算速度。
这种方法结合了迭代法和递归法的优点,适用于一般场景。
斐波那契数列在实际应用中具有广泛的应用价值。
例如,在金融领域,斐波那契数列可以用于预测价格走势;在计算机科学领域,斐波那契数列可用于查找最优路径;在生物学领域,斐波那契数列可以用于研究生物种群的增长规律。
此外,斐波那契数列还有一些拓展问题,如:寻找斐波那契数列的规律,预测未来项;研究斐波那契数列的数列极限;探讨斐波那契数列与其他数列的关系等。
总之,斐波那契数列是一道具有丰富内涵的数学问题。
通过掌握解题技巧,我们能更好地应对与之相关的题目。
同时,了解斐波那契数列的应用场景,能使我们更好地将其运用到实际问题中。
菲波拉契数列公式

菲波拉契数列公式菲波拉契数列是一种非常有趣且重要的数学数列,它以数学家列昂纳多·斐波那契的名字命名。
斐波那契数列的特点是每个数字都是前两个数字的和。
这个数列以0和1作为开头,接下来的数字依次是1、2、3、5、8、13、21……以此类推。
菲波拉契数列公式可以用数学符号表示为:F(n) = F(n-1) + F(n-2),其中F(n)表示第n个斐波那契数。
菲波拉契数列在数学、自然科学、经济学等领域都有广泛的应用。
在数学中,斐波那契数列可以用来解决各种复杂的问题,例如在数论中用于证明黄金分割比例的存在性。
在自然科学中,斐波那契数列常常出现在自然界的各种规律中,例如植物的分枝、螺旋壳的形状等。
在经济学中,斐波那契数列可以用来分析金融市场的波动和趋势。
斐波那契数列不仅在数学领域引起了广泛的关注,它还具有一些有趣的性质。
首先,斐波那契数列的增长是呈指数级别的,也就是说随着n的增加,数列中的数字会迅速增大。
其次,斐波那契数列中的数字有一种奇妙的对称性。
例如,如果将数列倒过来排列,数字的对称性会变得非常明显。
这种对称性在数学的研究中也有很多有趣的应用。
除了数学和科学领域,斐波拉契数列还经常出现在艺术和设计中。
许多艺术家和设计师喜欢使用斐波那契数列的比例和对称性来创作作品。
例如,在建筑设计中,斐波那契数列的比例可以用来设计具有美感和和谐感的建筑物。
在绘画和雕塑中,斐波那契数列的对称性可以用来创造出独特而迷人的艺术作品。
斐波那契数列的应用还不仅限于数学、科学和艺术领域。
在生活中,我们也可以通过斐波那契数列来解决一些实际问题。
例如,斐波那契数列可以用来计算兔子繁殖的数量,或者用来估计人口的增长。
斐波那契数列还可以用来制定合理的投资策略,预测股市的走势。
菲波拉契数列是一种非常有趣且重要的数学数列,它在数学、自然科学、经济学和艺术设计等领域都有广泛的应用。
通过研究和了解斐波那契数列,我们可以更好地理解和解决各种复杂的问题,同时也可以将其应用于实际生活中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有一楼梯共8级,规定每次只能跨上1级,2级或3级,要登上第8级,共有多少种不同走法? 2. 有一楼梯共10级,规定每步跨上2级或3级,要登上第9级,共有多少种不同走法?
3.
蜜蜂从A点出发爬到B点,每次只能从小数字房间到大数字房间,有多少中不同的走法?
4.
如图,阴影部分是正方形,则长方形的周长是
厘米.
5.
如图所示,在长方形ABCD中,AB=20cm,截去一个正方形EBCF后,求剩下的长方形AEFD的周长
.
6.
用四个相同的长方形拼成个面积为49平方厘米的大正方形,每个长方形的周长是多少厘米?
7.
两个同样的矩形摆放如下图
,图中单位为cm,每个炬形的面积是多少
?
8. 如图,9个相同的小长方形放在一个大长方形中,一大
长方形的长a=16厘米,求阴影部分的面积?
9. 下面都是从A点去B点,有多少种走法,使走过的路线最短。
10. 在4位数中,至少出现一个6的偶数有多少个?
11. 用数码0至6可以组成多少个小于3000的自然数(数码可以重
复使用)? 数字不允许重复?
12. 半圆及其直径上共有11个点(左下图),以这些点为顶点可画出
多少个三角形
?
13. *某个自然数的个位数字是8,将这个8移到左边首位数
字的前面,所构成的新数恰好是原数的8倍,原数最小是多少?
14. 2010年,一个青年说"今年我的生日已过了,我现在的年
龄正好是我出生年份的四个数字之和,这个青年是哪年出生的?
15. 某三位数是其各位数字之和的11倍,求这个三位数?
16. 将自然数从小到大无间隔地排列起来,得到一串数码123456789101112131415……这串数码中从左起第3602个数码是几?
17. 一群兔子拔萝卜,有2只各拔4个,其余各拔6个,则地里还
剩10个萝卜;如果8只兔子各拔6个,其余各拔7个,则刚好拔完,有多少只兔子?多少个萝卜?。
