第10届华杯赛复赛答案
六年级第三堂自习课练习题及答案
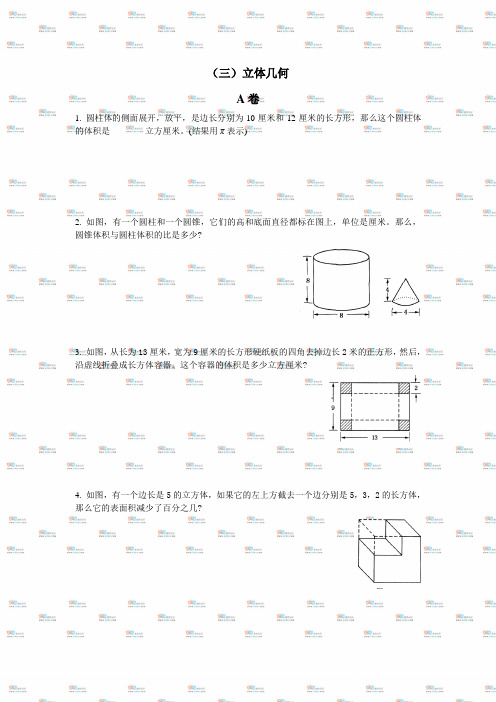
(三)立体几何A卷1. 圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米。
(结果用π表示)2. 如图,有一个圆柱和一个圆锥,它们的高和底面直径都标在图上,单位是厘米。
那么,圆锥体积与圆柱体积的比是多少?3. 如图,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2米的正方形,然后,沿虚线折叠成长方体容器。
这个容器的体积是多少立方厘米?4. 如图,有一个边长是5的立方体,如果它的左上方截去一个边分别是5,3,2的长方体,那么它的表面积减少了百分之几?5. 有大、中、小3个正方形水池,它们的内边长分别是6米、3米、2米.把两堆碎石分别沉没在中、小水池的水里,两个水池的水面分别升高了6厘米和4厘米.如果将这两堆碎石都沉没在大水池的水里,大水池的水面升高了多少厘米?6. 有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,剩下物体的体积和表面积各是多少?7. 把两个完全一样的长方体木块粘成一个大长方体,这个大长方体的表面积比原来两个长方体的表面积的和减少了46平方厘米,而长是原来长方体的2倍。
如果拼成的长方体的长是24厘米,那么它的体积是多少立方厘米?8. 把4块棱长都是2分米的正方体粘成一个长方体,它们的表面积最多会减少多少平方厘米?9.有24个正方体,每个正方体的体积都是1立方厘米,用这些正方体可以拼成几种不同的长方体?10.一个长方体,前面和上面的面积之和是209平方厘米,这个长方体的长、宽、高是以厘米为单位的数且都是质数。
这个长方体的体积和表面积各是多少?B卷1. 用棱长是1厘米的立方块拼成如图11-1所示的立体图形,问该图形的表面积是多少平方厘米?2. 图中是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?3. 有一个正方体容器,边长是24厘米,里面注满了水。
历届“华杯赛”初赛决赛试题汇编【小中组(附答案)】

二、简答题(每小题 15 分, 共 60 分, 要求写出简要过程)
9. 用 4 个数码 4 和一些加、减、乘、除号和小括号, 写出值分别等于 2、3、4、 5、6 的五个算式. 10. 右图是 U, V, W, X 四辆不同类型的汽车每百千米的耗油 量. 如果每辆车都有 50 升油, 那么这四辆车最多可行驶 的路程总计是多少千米? 11. 某商店卖出一支钢笔的利润是 9 元, 一个小熊玩具的进 价为 2 元. 一次, 商家采取 “买 4 支钢笔赠送一个小熊玩具”的打包促销, 共 获利润 1922 元. 问这次促销最多卖出了多少支钢笔? 12. 编号从 1 到 10 的 10 个白球排成一行, 现按照如下方法涂红色: 1)涂 2 个球; 2)被涂色的 2 个球的编号之差大于 2. 那么不同的涂色方法有多少种?
四百米比赛进入冲刺阶段,甲在乙前面 30 米,丙在丁后面 60 米,乙在丙前面 20 米. 这时,跑在最前面的两位同学相差( (A)10 (B)20 )米. (D)60
(C)50
5.
在右图所示的两位数的加法算式中, 已知 A B C D 22 , ). (B)4 (C)7 (D)13
一、选择题 (每小题 10 分, 满分 60 分. 以下每题的四个选项中, 仅 有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号 内.)
华杯赛复赛中年级必考模块之数论,数字谜与数阵图

数论,高年级考察的比较多,中年级不是很多,
但基本的一些奇偶,整除特征等得会;2
数字谜是中年级的重点考察内容,尤其提醒大家关注弃9法关注末位定理数阵图也是中年级的重点考察内容基本的两种
关注弃9法,关注末位定理;3数阵图也是中年级的重点考察内容,基本的两种数阵图必会,数阵图模型要会用。
(2010年第十五届华杯赛决赛)在10个盒子中放乒乓球,每个盒子中的球22则()
已知A +B +C +D =22,则X +Y =( )A .2B .4C .7D .13年第十华杯赛中年组决赛3.(2012年第十七届华杯赛中年级组决赛)右图是两个两位数的减法竖式,其中A ,B ,C ,D 代表不同的数字当被减数取最大值时数字。
当被减数AB 取最大值时,A ×B +(C +
E )×(D +
F )=_______。
4.(2009年第十四届华杯赛决赛)已知1+2+3+⋯+n (n >2)的和的个位数为3,十位数为0,则n 的最小值是_______。
(2009年第十四届华杯赛决赛)在51个连续的奇数135⋯101中选取5.(2009年第十四届华杯赛决赛)在51个连续的奇数1,3,5,,101中选取个数,使得它们的和为1949,那么k 的最大值是多少?。
各届华杯赛真题集锦-含答案哦!

目录2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷 (3)2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷 (5)2004年第10届“华罗庚金杯”少年数学邀请赛初赛试卷 (11)2004年第10届“华罗庚金杯”少年数学邀请赛初赛试卷 (13)2006年第11届“华罗庚金杯”少年数学邀请赛初赛试卷 (19)2006年第11届“华罗庚金杯”少年数学邀请赛初赛试卷 (23)2007年第12届“华罗庚金杯”少年数学邀请赛初赛试卷 (31)2007年第12届“华罗庚金杯”少年数学邀请赛初赛试卷 (33)2008年第13届“华罗庚金杯”少年数学邀请赛初赛试卷 (39)2008年第13届“华罗庚金杯”少年数学邀请赛初赛试卷 (41)2009年第14届“华罗庚金杯”少年数学邀请赛初赛试卷 (47)2009年第14届“华罗庚金杯”少年数学邀请赛初赛试卷 (49)2010年第15届“华罗庚金杯”少年数学邀请赛初赛试卷 (55)2010年第15届“华罗庚金杯”少年数学邀请赛初赛试卷 (57)2011年第16届“华罗庚金杯”少年数学邀请赛初赛试卷 (63)2011年第16届“华罗庚金杯”少年数学邀请赛初赛试卷 (66)2012年第17届“华罗庚金杯”少年数学邀请赛初赛试卷 (73)2012年第17届“华罗庚金杯”少年数学邀请赛初赛试卷 (75)2013年第18届“华罗庚金杯”少年数学邀请赛初赛试卷 (82)2013年第18届“华罗庚金杯”少年数学邀请赛初赛试卷 (84)2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷一、解答题(共12小题,满分0分)1.“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?2.长方形的各边长增加10%,那么它的周长和面积分别增加百分之几?3.如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、C处填的数各是多少?4.在一列数:,,,,,,…中,从哪一个数开始,1与每个数之差都小于?5.“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球,实现了中华民族的飞天梦.飞船绕地球共飞行14圈,其中后10圈沿离地面343千米的圆形轨道飞行.请计算飞船沿圆形轨道飞行了多少千米(地球半径为6371千米,圆周率π=3.14).6.如图,一块圆形的纸片分成4个相同的扇形,用红、黄两种颜色分别涂满各扇形,问共有几种不同的涂法?7.在9点至10点之间的某一时刻,5分钟前分针的位置与5分钟后时针的位置相同,此时刻是9点几分?8.一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?9.任意写一个两位数,再将它依次重复3遍成一个8位数.将此8位数除以该两位数所得到的商再除以9,问:得到的余数是多少?10.一块长方形的木板,长为90厘米,宽为40厘米,将它锯成2块,然后拼成一个正方形,你能做到吗?11.如图,大小两个半圆,它们的直径在同一直线上,弦AB与小圆相切,且与直径平行,弦AB长12厘米.求图中阴影部分的面积(圆周率π=3.14).12.半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷参考答案与解析一、解答题(共12小题,满分0分)1.“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?考点:竖式数字谜.专题:填运算符号、字母等的竖式与横式问题.分析:根据整数加法的计算方法进行推算即可.解答:解:解法一:个位上:0+“杯”=4,可得“杯”=4;十位上:1+“华”的末尾是0,由1+9=10,可得“华”9,向百位上进1;百位上:9+1=10,向千位上进1;千位上:1+1=2;由以上可得:;因此,“华杯”代表的两位数是94.解法二:已知1910与“华杯”之和等于2004;那么“华杯”=2004﹣1910=94;因此,“华杯”代表的两位数是94.点评:本题非常巧妙地考察了对整数的加法运算法则及数位的进位等知识要点的熟悉掌握程度.2.长方形的各边长增加10%,那么它的周长和面积分别增加百分之几?考点:百分数的实际应用;长方形的周长;长方形、正方形的面积.专题:分数百分数应用题.分析:设长方形的长为a,宽为b,因此各边长增加10%时,则长为(1+10%)a=110%a,长为(1+10%)b=110%b,因此各边长增加10%时,周长增加2(1.1a+1.1b)﹣2(a+b)=2(a+b)×10%,即周长增加10%.面积增加1.1a×1.1b﹣ab=1.21ab﹣ab=ab×21%,即面积增加21%.解答:周长增加10%,面积增加21%解:设长方形的长为a,宽为b,边长增加10%时,则长为(1+10%)a=110%a,长为(1+10%)b=110%b,周长增加:2(110%a+110%b)﹣2(a+b)=220%a+220%b﹣2a﹣2b=2(a+b)×10%;面积增加:110%a×110%b﹣ab=121%ab﹣ab=ab×21%;答:周长增加了10%,面积增加了21%.点评:在求出长宽增加后的长度基础上,根据长方形的周长与面积公式计算是完成本题的关键.3.如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、C处填的数各是多少?考点:正方体的展开图.专题:立体图形的认识与计算.分析:如图,是正方体展开图的“222”结构,把它折叠成正方体后,A面与1面相对,B面与2面相对,C面与4面相对,相使使其对面两数之和为7,A面填6,B面填5,C面填3.解答:解:如图,折成正方体后,A面与1面相对,B面与2面相对,C面与4面相对,要使其对面之各为7,则A面填6,B面填5,C面填3.点评:本题是考查正方体的展开图,关键是弄清把它折叠成正方体后,哪两个面相对.4.在一列数:,,,,,,…中,从哪一个数开始,1与每个数之差都小于?考点:数列中的规律.专题:探索数的规律.分析:这列数的特点是每个数的分母比分子大2,分子为奇数列,要使1﹣<,则n>999.5,即从n=1000开始,带入分数,即可得解.解答:解:这列数的特点是每个数的分母比分子大2,分子为奇数列,1﹣<,n>999.5,从n=1000开始,即从开始,满足条件.答:从开始,1与每个数之差都小于.点评:找出这列数的规律,根据已知列出等式求解.5.“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球,实现了中华民族的飞天梦.飞船绕地球共飞行14圈,其中后10圈沿离地面343千米的圆形轨道飞行.请计算飞船沿圆形轨道飞行了多少千米(地球半径为6371千米,圆周率π=3.14).考点:有关圆的应用题.专题:平面图形的认识与计算.分析:先圆形轨道的半径,再根据圆的周长公式:C=2πr求出飞船沿圆形轨道飞行1圈的长度,再乘以10即可求出飞船沿圆形轨道飞行了多少千米.解答:解:2×3.14×(6371+343)×10=2×3.14×6714×10=3.14×134280=421639.2(千米);答:飞船沿圆形轨道飞行了421639.2千米.点评:考查了有关圆的应用题,关键是熟练掌握圆的周长公式.6.如图,一块圆形的纸片分成4个相同的扇形,用红、黄两种颜色分别涂满各扇形,问共有几种不同的涂法?考点:染色问题.专题:传统应用题专题.分析:根据四个扇形中有一个红色、两个、三个、四个分类列举即可.解答:解:按逆时针方向涂染各扇形:红红红红红红红黄红红黄黄红黄红黄红黄黄黄黄黄黄黄所以,共有6种.点评:本题考查了排列组合知识中的染色问题,还可以列式解答:4×(4﹣1)÷2=6(种).7.在9点至10点之间的某一时刻,5分钟前分针的位置与5分钟后时针的位置相同,此时刻是9点几分?考点:时间与钟面.专题:时钟问题.分析:可设当前是9点x分,则5分钟前分针指向x﹣5的位置,而分针转动的速度是时针的12倍,分针5分钟后指向x+5的位置,时针指向9刻度后刻度处,根据题意列出方程解答即可.解答:解:设当前时刻是9点x分.则5分钟后时针的位置为45+=x﹣5540+x+5=12x﹣6011x=605x=55;答:此时刻是9点55分.点评:本题主要考查钟表问题的实际应用,熟练掌握钟表的特征是解答本题的关键.8.一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?考点:抽屉原理.专题:传统应用题专题.分析:建立抽屉:一副扑克牌有54张,大小鬼不相同,那么(54﹣2)÷4=13,所以一共有13+2=15个抽屉;分别是:1、2、3、…K、小鬼、大鬼,由此利用抽屉原理考虑最差情况,即可进行解答.解答:解:建立抽屉:54张牌,根据点数特点可以分别看做15个抽屉,考虑最差情况:每个抽屉都摸出了1张牌,共摸出15张牌,此时再任意摸出一张,无论放到哪个抽屉,都会出现有两张牌在同一个抽屉,即两张牌点数相同,15+1=16(张),答:至少抽取16张扑克牌,方能使其中至少有两张牌有相同的点数.点评:此类问题关键是根据点数特点,建立抽屉,这里要注意考虑最差情况.9.任意写一个两位数,再将它依次重复3遍成一个8位数.将此8位数除以该两位数所得到的商再除以9,问:得到的余数是多少?考点:带余除法.专题:余数问题.分析:先设这个两位数为10a+b,则可用含a、b的代数式表示将它依次重复写3遍成的一个8位数,再将此8位数除以该两位数得到商为1010101,然后将1010101除以9即可求解.解答:解:设这个两位数为10a+b,则将它依次重复3遍成的一个8位数为:1000000(10a+b)+10000(10a+b)+100(10a+b)+10a+b=1010101(10a+b),将此8位数除以该两位数得到的商为:1010101(10a+b)÷(10a+b)=1010101,则1010101÷9=112233…4.答:得到的余数是4.点评:本题考查了带余除法的定义及应用,难度中等,用含a、b的代数式正确表示将(10a+b)这个数依次重复写3遍成的一个8位数是解题的关键.10.一块长方形的木板,长为90厘米,宽为40厘米,将它锯成2块,然后拼成一个正方形,你能做到吗?考点:图形的拆拼(切拼).专题:平面图形的认识与计算.分析:因为这块长方形木板的面积为90×40=3600(平方厘米),又因为3600=60×60,即所求的正方形的边长为60厘米,如下图所示.解答:解:因为90×40=3600,3600=60×60,所求的正方形的边长为60厘米,可以如下图拼成:因此,能拼成一个正方形.点评:先求出总面积,看看是否能分成两个数的平方.11.如图,大小两个半圆,它们的直径在同一直线上,弦AB与小圆相切,且与直径平行,弦AB长12厘米.求图中阴影部分的面积(圆周率π=3.14).考点:组合图形的面积.专题:平面图形的认识与计算.分析:将小圆缩小至0,则AB就是大圆直径,阴影部分就是大圆的一半,利用圆的面积公式即可求解.解答:解:将小圆缩小至0,则AB就是大圆直径,阴影部分就是大圆的一半,所以阴影部分的面积是:×3.14×(12÷2)2=×3.14×36=56.52(平方厘米);答:图中阴影部分的面积是56.52平方厘米.点评:此题可以巧妙地利用“缩小法”,得出阴影部分的面积与直径为AB的圆的面积的关系,问题即可得解.12.半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?考点:有关圆的应用题.专题:平面图形的认识与计算.分析:由于小铁环的半径为25厘米,大铁环的半径为50厘米,可得小铁环的半径是大铁环半径的一半.根据周长与半径的关系可得大环周长是小环的2倍,即小环沿大环转2个周长时又回到原位,再减去公转的1圈,可得小环自身转动的圈数.解答:解:由于小铁环的半径是大铁环半径的一半,所以大环周长是小环的2倍,即小环沿大环转2个周长时又回到原位,其中有1个周长属于小环公转的,而另一个周长才是小环自身转动的,因此,小环自身转动1圈.点评:本题考查了圆与圆的位置关系,小铁环运动的圈数乘以它的周长就等于大铁环的周长.2004年第10届“华罗庚金杯”少年数学邀请赛初赛试卷一、解答题(共12小题,满分0分)1.2005年是中国伟大航海家郑和首次下西洋600周年,西班牙伟大航海家歌伦布首次远洋航行是在1492年.问这两次远洋航行相差多少年?2.从冬至之日起每九天分为一段,依次称之为一九,二九,…,九九,2004年的冬至为12月21日,2005年的立春是2月4日.问立春之日是几九的第几天?3.如图是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形.问这个直三棱柱的体积是多少?4.爸爸、妈妈、客人和我四人围着圆桌喝茶.若只考虑每人左邻的情况,问共有多少种不同的入座方法?5.在奥运会的铁人三项比赛中,自行车比赛距离是长跑的4倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米.求三项的总距离.6.如图,用同样大小的正三角形,向下逐次拼接出更大的正三角形.其中最小的三角形顶点的个数(重合的顶点只计一次)依次为:3,6,10,15,21,…问这列数中的第9个是多少?7.一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示.若用甲容器取水来注满乙容器,问:至少要注水多少次?8.100名学生参加社会实践,高年级学生两人一组,低年级学生三人一组,共有41组.问:高、低年级学生各多少人?9.小鸣用48元钱按零售价买了若干练习本.如果按批发价购买,每本便宜2元,恰好多买4本.问:零售价每本多少元?10.不足100名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈.问最多有多少名同学?11.输液100毫升,每分钟输2.5毫升.请你观察第12分钟时吊瓶图象中的数据,回答整个吊瓶的容积是多少毫升?12.两条直线相交所成的锐角或直角称为两条直线的“夹角”.现平面上有若干条直线,它们两两相交,并且“夹角”只能是30°,60°或90°.问:至多有多少条直线?2004年第1届“华罗庚金杯”少年数学邀请赛初赛试卷参考答案与试题解析一、解答题(共12小题,满分0分)1.2005年是中国伟大航海家郑和首次下西洋600周年,西班牙伟大航海家歌伦布首次远洋航行是在1492年.问这两次远洋航行相差多少年?考点:日期和时间的推算.分析:先求出郑和首次下西洋的时间,再求差.解答:解:2005﹣600=1405(年),1492﹣1405=87(年).答:这两次远洋航行相差87年.点评:本题先根据2005年求出郑和首次下西洋的时间,再用较晚的时间减去较早的时间.2.从冬至之日起每九天分为一段,依次称之为一九,二九,…,九九,2004年的冬至为12月21日,2005年的立春是2月4日.问立春之日是几九的第几天?考点:日期和时间的推算.分析:先求出2004年的12月21日到2005年的2月4日经过了多少天,再求这些天里有几个9天,还余几天,再根据余数推算是几九第几天即可.解答:解:2004年的12月21日到12月31日共有11天,1月份有31天,2月4日是2月的第四天,那么一共经过了:11+31+4=46(天),46÷9=5…1,说明已经经过了5个9天,还余1天,这一天就是六九的第一天.答:立春之日是六九的第1天.点评:本题的是9天为1个周期,先求出经过的天数(注意两头的天数都算),再求这些天里有几个9天,还余几天,再根据余数判断.3.如图是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形.问这个直三棱柱的体积是多少?考点:规则立体图形的体积.分析:根据棱柱的体积公式:底面积×高,进行计算.解答:解:因为直三棱柱的底面是直角边都为1的直角三角形,高为1,所以直三棱柱的体积=×1×1×1=.答:这个直三棱柱的体积是.故答案为:.点评:本题考查了直三棱柱及展开图的特征和直三棱柱体积计算.直三棱柱是由三个长方形的侧面和上下两个底面组成.4.爸爸、妈妈、客人和我四人围着圆桌喝茶.若只考虑每人左邻的情况,问共有多少种不同的入座方法?考点:加法原理.分析:可先把我放在第一个位置,进而考虑我的左邻的情况,我的左邻的左邻的情况,找到总情况数即可.解答:解:共有6种不同的入座方法.点评:考查用列表法解决问题;把1个人固定位置,进而考虑左邻的情况是解决本题的关键.5.在奥运会的铁人三项比赛中,自行车比赛距离是长跑的4倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米.求三项的总距离.考点:分数除法应用题.分析:把自行车的距离看成单位“1”,那么长跑的距离就是自行车的,游泳的距离是自行车的,它们的差对应的数量是8.5千米,用除法可以求出自行车的距离,根据自行车的距离求出另外两项的距离,再把三者加起来.解答:解:自行车比赛距离是长跑的4倍,那么长跑的距离就是自行车的,8.5÷()=8.5÷,=40(千米);40×=10(千米);40×=1.5(千米);40+10+1.5=51.5(千米);答:三项的总距离是51.5千米.点评:本题关键是把倍数关系看成一个是另一个的几分之几,找出单位“1”分析出数量关系,再由基本的数量关系求解.6.如图,用同样大小的正三角形,向下逐次拼接出更大的正三角形.其中最小的三角形顶点的个数(重合的顶点只计一次)依次为:3,6,10,15,21,…问这列数中的第9个是多少?考点:事物的简单搭配规律.分析:观察图形,分析数列,发现规律:从第一个数开始,后面的数依次比前一个数多3、4、5、6、7、…据此规律,推出即可.解答:解:6﹣3=3;10﹣6=4;15﹣10=5;21﹣15=6;…从第一个数开始,后面的数依次比前一个数多3、4、5、6、7、…往下写数:3,6,10,15,21,28,36,45,55,…第9个数是55.答:这列数中的第9个是55.点评:观察图形,分析数列,发现规律,然后利用规律解决问题.7.一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示.若用甲容器取水来注满乙容器,问:至少要注水多少次?考点:规则立体图形的体积.分析:根据圆锥的体积公式求出容器甲容积,根据球的体积公式求出容器乙容积,相除即可求解.解答:解:容器甲容积:V甲=×π×()2×1=π;容器乙容积:V乙=×π×13=π,V乙÷V甲=π÷π=8.答:至少要注水8次.点评:考查了圆锥的体积和球的体积.球的体积公式是V=πr3.圆锥的体积是V=sh=πr2h.8.100名学生参加社会实践,高年级学生两人一组,低年级学生三人一组,共有41组.问:高、低年级学生各多少人?考点:鸡兔同笼.分析:可设高年级有学生x人,则低年级的学生有100﹣x人,根据等量关系:高年级组数+低年级组数=41组解答即可.解答:解:高年级有学生x人,则低年级的学生有100﹣x人,由题意得:=41,3x+2(100﹣x)=246,3x+200﹣2x=246,x=46,100﹣46=54(人),答:高年级有46人,低年级有54人.点评:此类题目中一般都有两个等量关系,抓住其中一个等量关系设出一个未知数,从而得出另一个未知数;另一个等量关系用来列方程.9.小鸣用48元钱按零售价买了若干练习本.如果按批发价购买,每本便宜2元,恰好多买4本.问:零售价每本多少元?考点:整数、小数复合应用题;合数与质数;质数与合数问题.分析:先将48分解质因数:48=1×48=2×24=3×16=4×12=6×8,因数全写出来,再找出里面相差分别是2和4的,那么这两个算式就分别为零售价和批发价.解答:解:48=48=1×48=2×24=3×16=4×12=6×8,找出里面相差分别是2和4的,那么这两个算式就分别为零售价和批发价;只有4×12和6×8,12比8多4,4比6少2,则零售价为6元,批发价为4元;答:零售价为6元.点评:解答此题应结合合数和质数的含义进行分析,通过分解质因数,找出符合题意的答案即可.10.不足100名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈.问最多有多少名同学?考点:最大与最小.分析:设两种组合外圈的组数为a、b,那么第一种的人数是5+8a人,第二种的人数是8+5b人,因为总人数一定相等,求出a与b的关系,根据a和b关系讨论取值.解答:解:设两种组合外圈的组数为a、b,那么第一种的人数是5+8a,第二种的人数是8+5b,则5+8a=8+5b即;8a=5b+3,当b=1时,a=1,总人数为5+8×1=13(人);当b=9时,a=6,总人数为5+8×6=53(人);当b=17时,a=11,总人数为5+8×11=93(人).数字再大就超过100了,所以最多有93人.答:最多有93名同学.点评:本题先找出两种组数之间的关系,然后根据组数是自然数和它们之间的关系讨论取值,找出100以内最大的即可.11.输液100毫升,每分钟输2.5毫升.请你观察第12分钟时吊瓶图象中的数据,回答整个吊瓶的容积是多少毫升?考点:整数、小数复合应用题.分析:水平面的刻度是80毫升,说明空的部分是80毫升;根据每分钟的输液量和输液时间求出已经输出的体积,用100毫升减去已经输出的体积就是瓶内剩下的体积;整个吊瓶的容积就是空的部分加剩下的这部分体积.解答:解:100﹣2.5×12=70(毫升),80+70=150(毫升),答:整个吊瓶的容积是150毫升.点评:本题第12分时瓶子上方没有溶液的容积的等量关系是解决本题的关键.12.两条直线相交所成的锐角或直角称为两条直线的“夹角”.现平面上有若干条直线,它们两两相交,并且“夹角”只能是30°,60°或90°.问:至多有多少条直线?考点:乘法原理.分析:根据题意,“夹角”只能是30°,60°或90°,都是30°的倍数,根据这个倍数,通过旋转的方法,进一步解答即可.解答:解:因为夹角只能是30°、60°或者90°,其均为30°的倍数,所以每画一条直线后,逆时针旋转30°画下一条直线,这样就能够保证两两直线夹角为30°的倍数,即为30°、60°或者90°(因为如果每次旋转度数其他角度,例如15°,则必然会出现两条直线的夹角为15°或15°的其它倍数,如45°这与题目不符);因为该平面上的直线两两相交,也就是说不会出现平行的情况,在画出6条直线时,直线旋转过5次,5×30°=150°,如果再画出第7条直线,则旋转6次,6×30°=180°,这样第七条直线就与第一条直线平行了.如图:所以最多能画出六条.答:至多有6条直线.点评:根据题意,由题目给出的条件,通过旋转的方法进一步解答即可.2006年第11届“华罗庚金杯”少年数学邀请赛初赛试卷一、选择题(共6小题,每小题6分,满分36分)1.(6分)如图所示,将一张正方形纸片先由下向上对折压平,再由右翻起向左对折压平,得到小正方形ABCD.取AB的中点M和BC的中点N,剪掉AMBN得五边形AMNCD.则将折叠的五边形AMNCD纸片展开铺平后的图形是()A.B.C.D.2.(6分)2008006共有()个质因数.A.4B.5C.6D.73.(6分)(2007•北塘区)奶奶告诉小明:“2006年共有53个星期日”.聪敏的小明立刻告诉奶奶:2007年的元旦一定是()A.星期一B.星期二C.星期六D.星期日4.(6分)如图,长方形ABCD小AB:BC=5:4.位于A点的第一只蚂蚁按A→B→C→D→A 的方向,位于C点的第二只蚂蚁按C→B→A→D→C的方向同时出发,分别沿着长方形的边爬行.如果两只蚂蚁第一次在B点相遇,则两只蚂蚁第二次相遇在()边上.A.A B B.B C C.C D D.D A5.(6分)如图,ABCD是个直角梯形(∠DAB=∠ABC=90°).以AD为一边向外作长方形ADEF,其面积为6.36平方厘米,连接BE交AD于P,再连接PC.则图中阴影部分的面积是()平方厘米.A.6.36 B.3.18 C.2.12 D.1.596.(6分)五位同学扮成奥运会吉祥物福娃贝见、晶晶、欢欢、迎迎和妮妮,排成一排表演节目,如果贝贝和妮妮不相邻,共有()种不同的排法.A.48 B.72 C.96 D.120二、填空题(共8小题,每小题3分,满分24分)7.(3分)在算式中,汉字“第、十、一、届、华、杯、赛”代表1,2,3,4,5,6.7,8,9中的7个数字,不同的汉字代表不同的数字,恰使得加法算式成立.则“第、十、一、届、华、杯、赛”所代表的7个数字的和等于_________•8.(3分)全班50个学生,每人恰有三角板或直尺中的一种,28人有直尺,有三角板的人中,男生是14人,若已知全班共有女生31人,那么有直尺的女生有_________人.9.(3分)如图是﹣个直圆柱形状的玻璃杯,一个长为12厘米的直棒状细吸管(不考虑吸管粗细)放在玻璃杯内.当吸管一端接触圆柱下底面时,另一端沿吸管最少可露出上底面边缘2厘米,最多能露出4厘米.则这个玻璃杯的容积为_________立方厘米.(取π=3.14)(提示:直角三角形中“勾6、股8、弦10)10.(3分)有5个黑色和白色棋子围成一圈,规定:将同色的和相邻的两个棋子之间放入一个白色棋子,在异色的和相邻的两个棋子之间放入一个黑色棋子,然后将原来的5个棋子拿掉,如果从图5(1)的初始状态开始依照上述规定操作下去,对于圆圈上呈现5个棋子的情况,圆圈上黑子最多能有_________个.11.(3分)李大爷用一批化肥给承包的麦田施肥.若每亩施6千克,则缺少化肥300千克;若每亩施5千克,则余下化肥200千克.那么李大爷共承包了麦田_________亩,这批化肥有_________千克.12.(3分)将从1开始的到103的连续奇数依次写成﹣个多位数:a=13579111315171921…9799101103.则数a共有_________位,数a除以9的余数是_________.。
第十届华罗庚金杯赛复赛试题及解析

第十届华杯赛决赛试题一、填空(每题10分,共80分)1.下表中每一列为同一年在不同历法中的年号,请完成下表:第1小题:2.计算:① 18.3×0.25+5.3÷0.4-7.13 = ( ); ②= ( )。
答案:10.695;13.计算机中最小的存储单位称为“位”,每个“位”有两种状态:0和1。
一个字节由8个“位”组成,记为B。
常用KB,MB等记存储空间的大小,其中1KB=1024B, 1MB=1024KB。
现将240MB的教育软件从网上下载,已经下载了70%。
如果当前的下载速度为每秒72KB,则下载完毕还需要()分钟。
(精确到分钟)答案:174.a,b和c都是二位的自然数,a,b的个位分别是7与5,c的十位是1。
如果它们满足等式ab+c=2005,则a+b+c=( )。
答案:1025.一个正方体的每个顶点都有三条棱以其为端点,沿这三条棱的三个中点,从这个正方体切下一个角,这样一共切下八个角,则余下部分的体积(图1中的阴影部分)和正方体体积的比是()。
答案:6.某种长方体形的集装箱,它的长宽高的比是4∶3∶2,如果用甲等油漆喷涂它的表面,每平方米的费用是0.9元,如果改用乙等油漆,每平方米的费用降低为0.4元,一个集装箱可以节省6.5元,则集装箱总的表面积是()平方米,体积是()立方米。
答案:13:37.一列自然数0,1,2,3,…,2005,…,2004,第一个数是0,从第二个数开始,每一个都比它前一个大1,最后一个是2024。
现在将这列自然数排成以下数表:规定横排为行,竖排为列,则2005在数表中位于第()行和第()列。
答案:20;458.图2中,ABCD是长方形,E,F分别是AB,DA的中点,G是BF和DE的交点,四边形BCDG 的面积是40平方厘米,那么ABCD的面积是()平方厘米。
图2答案:60二、解答下列各题,要求写出简要过程(每题10分,共40分)9.图3是由风筝形和镖形两种不同的砖铺设而成。
历届华杯赛赛题精选(一)题目

1历届华杯赛赛题精选(一)1.有甲乙两个同样的杯子,甲杯中有半杯清水,乙杯中盛满了含50%酒精的溶液。
先将乙杯中酒精溶液的一半倒入甲杯,搅拌均匀后,再将甲杯中酒精溶液的一半倒入乙杯。
问这时乙杯中的酒精是溶液的几分之几?答;乙杯的酒精是溶液的83.2.王师傅在某个特殊岗位上工作,他每上8天班后,就休息2天。
如果这个星期六和星期天他休息,那么,至少再过几个星期后他才能又在星期天休息? 答:至少再过7周。
将题目略为改动一下,变成:“每上8天班连续休息3天,这个星期五、六、日体息,”其它依旧。
问题便稍为复杂一些,你会解吗?3.已知:4416,339⨯===⨯=,这里9和16叫做“完全平方数”,在前300个自然数中,去掉所有的“完全平方数”,剩下的自然数的和是多少? 答:剩下的自然数的和是43365。
4.在射箭运动中,每射中一箭得到的环数或者是“0”(脱靶),或者是不超过10的自然数。
甲乙两名运动员各射了5箭,每人得到的5箭的环数的积都是1764,甲的总的环数比乙总的环数少4环。
分别求出甲乙的总的环数。
答:甲、乙的总环数分别是24、28.5.图3-9中有6个点,9条线段。
一只甲虫从点出发爬到点。
甲虫爬行过程中同一个点和同一条线段只能经过一次。
这只甲虫最多有多少种不同的走法? 答:共有9种走法。
6.图3-10中的正方形被分成9个相同的小正方形,一共有16个顶点(共同的顶点算一个)。
以其中不在一条直线上的三个点为顶点,可以构成三角形。
在这些三角形中,与图中阴影三角形有同样大小面积的三角形有多少个?答:所求的三角形共48个(包括图中开始绘出的三角形)。
图3-9ACBDFE图3-1027.某班全体同学进行了短跑、游泳和篮球三个项目的测验,有4名学生在这三个项目上都没有达到优秀,其余学生每人至少有一个项目达到优秀,达到优秀的项目和人数如下表:求这个班有多少学生? 答:这个班有39名学生。
8.观察下面的数表:(横排为行,竖排为列),51,42,33,24,15,41,32,23,14,31,22,13,21,12,11根据前5行所表达的规律,说明19491991这个数位于第几行和第几列? 19491991所在的行数位于1991+1949-1=3939行和1949列。
第十至十四届小学华赛初赛试卷

第十四届华罗庚金杯少年数学邀请赛初赛试卷(小学组)试题及答案一、选择题。
每小题10分,满分60分。
以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英语字母写在每题的圆括号内)1.下面的表情图片中,没有对称轴的个数为()(A) 3 (B)4 (C)5 (D)62.开学前6天,小明还没做寒假数学作业,而小强已完成了60道题。
开学时,两人都完成了数学作业,在这6天中,小明做的题的数目是小张的3倍,他平均每天做了()道题。
(A)6 (B)9 (C)12 (D)153.按照中国篮球职业联赛组委会的规定,各队队员的号码可以选择的范围是0~55号,但选择两位数的号码时,每位数字均不能超过5,那么,可供每支球队选择的号码共有()个。
(A)34 (B)35 (C)40 (D)564.在19,197,2009这三个数中,质数的个数是()。
(A)0 (B)1 (C)2 (D)35.下面有四个算式:其中正确的算式是()(A)①和②(B)②和④(C)②和③(D)①和④6.A、B、C、D、E五个小朋友做游戏,每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小朋友:A→C,B→E,C→A,D→B,E→D,开始时A、B拿着福娃,C、D、E拿着福牛,传递完5轮时,拿着福娃的小朋友是()。
(A)C与D(B)A与D (C)C与E (D)A与B二、填空题(每小题10分,满分40分)7.下面的算式中,同一个汉字代表同一个数字,不同的汉字代表不同的数字,团团×圆圆=大熊猫,则“大熊猫”代表的三位数是___________。
8.从4个整数中任意选出3个,求出它们的平均值,然后再求这个平均值和余下1个数的和,这样可以得到4个数:4、6、5和4,则原来给定的4个整数的和为___________。
9.如下图所示,AB是半圆的直径,O是圆心,弧AC=弧CD=弧DB,M是弧CD的中点,H是弦CD的中点,若N是OB上一点,半圆的面积等于12平方厘米,则图中阴影部分的面积是___________平方厘米。
第一届华杯赛复赛试题的答案详解

第一届华杯赛复赛试题的答案详解第一届华杯赛复赛试题的答案详解第一届华杯赛复赛试题答案:1.【解】甲、乙、丙、丁四个班的总人数:83+88=171(人)用总人数减去乙班和丙班的人数,就可以得出甲班和丁班的人数:171-86=85(人)2.【解】奖金的总数是:308×[(1+十)×2]=1078(元)按一个一等奖,两个二等奖,三个三等奘来分配,一等奖是:1078+(1+×+×3)=392(元)3.【解】设面积为25亩的长方形,长为a,宽为b;面积为30亩的长方形,长为c,度为d;则面积为20亩的'长方形,长为c,宽为b;而所求长方形的长为a,宽为d,它的面积为a×d===37.5(亩)4.【解】如果A地的货物比B地多,那么将B地的货运往A地比将A地的货运往B地省钱,因此,应将10吨货由一号仓库运到二号仓库。
同样,应将这(10+20)吨货由二号仓库运到五号仓库,共用(10×400+20×300)×0.5=5000(元)答:最少要花5000元运费5.【解】设这个数除以12,余数是a.那么a除以3,余数是2;除以4,余数是1.在0,1,2,…,11中,符合这样条件的a只有5,于是这个数除以12余数是5。
6.【解】因为7×7=49,大正方形的边长是7米同样,2×2=4,小正方形的边长是2米。
大正方形的边长是两个长方形的短边长与小正方形边长的和所以长方形的短边长为:(7-2)÷2=2.5(米)。
7.【解】长纸带剩下:(21-13)÷(1-)==20.8(厘米)所以剪下的一段长:21-20.8=0.2(厘米)8.【解】题目要求用七个数字组成5个数,说明有三个数是1位数,有两个数是两位数.很明显,方框和被除数是两位数,乘数和除数是1位数看得出来,0不宜做乘数,更不能做除数。
因而是两位数的个位数字,从而是被除数的个位字乘数如果是1,不论被乘数是几,都将在算式出现两次。
届华杯赛复赛试题及答案

第二届华杯赛复赛试题(0.5 + 0.25 + 0.125) - (0.5 X 0.25 X 0.125) X 2 •有三张卡片,在它们上面各写有一个数字(下图)次序排起来,可以得到不同地一位数、二位数、三位数档,请勿用做商业用途3•有大、中、小三个正方形水池,它们地内边长分别是沉没在中、小水池地水里,两个水池地水面分别升高了都沉没在大水池地水里,大水池地水面升高了多少厘米?4. 在一个圆圈上有几十个孔(不到100个),如图.小明像玩跳棋那样,从A孔出发沿着逆时针方向,每隔几个孔跳一步,希望一圈以后能跳回到A孔.他先试着每隔2孔跳一步,结果只能跳到B孔•他又试着每隔4孔跳一步,也只能跳到B孔.最后他每隔6孔跳一步,正好跳回到A孔•你知道这个圆圈上共有多少个孔吗?版权文档,请勿用做商业用途使得这三个数中任意两个都互质•其中一个三位数已填好,它是714.到B,最快需要几分钟? 版权文档,请勿用做商业用途三角形ABG地面积是梯形ABC画积地1/5,那么EG地长是几厘米?1.计算:IxM18 2 66.下图是一 -张道路图,每段路上地数字是小王走这段路所需地分钟数.请问小王从A出发走7.梯形ABCD&中位线EF长15厘米(见图),Z AB(=Z AEF=90°,G是EF上地一点.如果.从中抽出一张、二张、三张,按任意.请你将其中地素数都写出来•版权文6米、3米、2米.把两堆碎石分别6厘米和4厘米.如果将这两堆碎石版权文档,请勿用做商业用途5 .试将1,2,3,4, 5,6,7分别填入下图地方框中,每个数字只用一次:□□□□□□□<这是一亍三位数)(这是一什位数)版权文档,请勿用做商业用途&有三堆砝码,第一堆中每个法码重3克,第二堆中每个砝码重5克,第三堆中每个砝码重7克.请你取最少个数地砝码,使它们地总重量为130克写出地取法:需要多少个砝码?其中3克、5克和7克地砝码各有几个?版权文档,请勿用做商业用途9. 有5块圆形地花圃,它们地直径分别是3米、4米、5米、8米、9米;请将这5块花圃分成两组,分别交给两个班管理,使两班所管理地面积尽可能接近•版权文档,请勿用做商业用途10. 一串数排成一行,它们地规律是这样地:头两个数都是1,从第三个数开始,每一个数都是前两个数地和,也就是:1,2,3,5,8,13,21,34,55,问:这串数地前100个数中(包括第100个数)有多少个偶数?版权文档,请勿用做商业用途11. 王师傅驾车从甲地开乙地交货•如果他往返都以每小时60公里地速度行驶,正好可以按时返回甲地•可是,当到达乙地时、他发现他从甲地到乙地地速度只有每小时55公里,如果他想按时返回甲地,他应以多大地速度往回开?版权文档,请勿用做商业用途12. 如图,大圈是400米跑道,由A到B地跑道长是200米,直线距离是50米•父子俩同时从A点出发逆时针方向沿跑道进行长跑锻炼,儿于跑大圈,父亲每跑到B点便沿各直线跑• 父亲每100米用20秒,儿子每100米用19秒.如果他们按这样地速度跑,儿子在跑第几圈时,第一次与父亲再相遇?版权文档,请勿用做商业用途□□参考答案版权文档,请勿用做商业用途8011. 一2.共有五个质数:2,3,13, 23, 316. 48分钟7. 6厘米&(见下)9. 千米/小时12.儿子在跑第3圈时,第一次与父亲再相遇£3.出4. 91个5.(见下)(见下)10.(见下)11. 667 1,14呂丿(2 4 8丿13--3x4 1.【解】原式= 37 , 1一+ —4 6I + 1 + IV3--U=(二:l:)X 2X 4X 8X 二21+212 12=(4+2+ 1 )X 2X4X 匚=7X 2X 4X'I "-. '1 = 7X]= j2. 【解】因为三张卡片上地数字和为 6,能被3整除,所以用这三个数字任意排成地三位数 都能被3整除,因此不可能是质数 版权文档,请勿用做商业用途再看二张卡片地情形•因为1 + 2 = 3,根据同样地道理,用 1. 2,组成地二位数也能被 3整 除,因此也不是质数•这样剩下要讨论地二位数只有 13、31、23、32这四个了,其中13,31和23都是质数,而32不是质数最后,一位数有三个: 1, 2,3.1不是质数,2和3都是 质数所以,本题中地质数共有五个:2,3,13,23,31版权文档,请勿用做商业用途答:共有五个质数:2,3,13, 23,31.3. [解】把碎石沉没在水中,水面升高所增加地体积•就等于所沉入地碎石地体积 •因此,沉入在水池中地碎石地体积是:3 X 3X 0.06 = 0.54(米),版权文档,请勿用做商业用途 而沉入小水池中地碎石地体积是:2 X 2X 0.04 =0.16(米),这两堆碎石地体积一共是 :0.54 + 0.16 = 0.7(米3) 把它们都沉入大水池里,大水池地水面升高所增加地体积也就是 0.7米3,而大水池地底面积是:6 X 6= 36(米),22 TO所以大水池地水面升高了 :0.7十36= 二(米)=二(厘米)=(厘米)112答:大水池地水面升高了「厘米.4. [解】设想圆圈上地孔已按下面方式编了号: A 孔编号为1,然后沿逆时针方向顺次编号 为2,3,4,…B 孔地编号就是圆圈上地孔数 ,每隔2孔跳一步,跳在1,4, 7,10,…上. 最后跳到B 孔,因此总孔数是 3地倍数加1,同样道理,每隔4孔跳一步最后跳到 B 孔,就 意味着总孔数是5地倍数加1 ;而每隔6孔跳一步最后跳回到 A ,就意味着总孔数是 7地倍 数.版权文档,请勿用做商业用途 如果将孔数减1,那么得数既是3地倍数也是5地倍数,因而是15地倍数.这个15地倍数 加上1就等于孔数,而且能被7整除.注意:15被7除余1,所以15X6被7除余6, 15地6倍加1正好被7整除.我们还可以看出,15地其他(小于7地)倍数加1都不能被7整除, 而15X 7= 105已经大于100. 7以上地倍数都不必考虑,因此,圆圈上总孔数是 15X6十1=91版权文档,请勿用做商业用途 答:圆圈上共有91个孔. 5. [解】714= 2X 3X 7X 17.由此可以看出,要使最下面方框中地数与 选5,也就是说,第三行地一位数只能填 现在来讨论第二行地三个方框中应该怎样填 因为任意两个偶数都有公约数2,而714是偶数,所以第二行地三位数不能是偶数,因此个 位数字只能是3 .这样一来,第二行地三位数只能是 263或623 .但是623能被7整除,所以623与714不互质.版权文档,请勿用做商业用途 最后来看263这个数通过检验可知: 714地质因数2, 3, 7和17都不是263地因数,所以714与263这两个数互质,显然,263与5也互质.因此714, 263和5这三个数两两互质.于 是填法是:版权文档,请勿用做商业用途Em E E E3EI6. [解】为叙述方便,我们把每个路口都标上字母,如图714互质,在剩下未填地数字 2,3,5,6中只能5.版权文档,请勿用做商业用途2,3,6这三个数字.a 、图b 所示b首先我们将道路图逐步简化•从A出发经过C到B地路线都要经过DC和GC面从A到C有两条路线可走:ADC需时间14 + 13 = 27 (分钟);AGC需时间15+ 11 = 26 (分钟).我们不会走前一条路线,所以可将DC 这段路抹去•但要注意,AD不能抹去,因为从A到B还有别地路线(例如AHB经过AD需要进一步分析.版权文档,请勿用做商业用途由G到E也有两条路线可走:CCE需16分钟,GIE也是16分钟.我们可以选择其中地任一条路线,例如选择前一条,抹掉GIE (也可以选择后一条而抹掉CE但不能抹掉GC因为还有别地路线经过它•)这样,道路图被简化成图49地形状.版权文档,请勿用做商业用途在图b中,从A到F有两条路线,经过H地一条需14 + 6 + 17= 37 (分钟),经过G地一条需15+ 11+ 10= 36 (分钟),我们又可以将前一条路线抹掉(图C)•版权文档,请勿用做商业用途2 7 7图c中,从C到B也有两条路线,比较它们需要地时间,又可将经过E地一条路线抹掉•最后,剩下一条最省时间地路线(图d),它需要15+ 11 + 10+ 12= 48 (分钟)•版权文档,请勿用做商业用途【又解】要抓住关键点C.从A到B地道路如果经过C点,那么,从A到C地道路中选一条最省时间地,即AGC从C到B地道路中也选一条最省时间地,即CFB因而从A到B经过C地所有道路中最省时间地就是这两条道路接起来地,即AGCF.B它地总时间是48分钟.版权文档,请勿用做商业用途剩下地只要比较从A到B而不经过C点地道路与道路AGCF B看那个更省时间• 不经过C点地道路只有两条:①ADHFB它需要49分钟;②AGIEB它也需要49分钟• 所以,从A到B最快需要48分钟•答:最快需要48分钟.17. 【解】梯形ABCD地面积等于EF X AB而三角彤ABG地面积等于[EG<AB因此三角形1ABG和梯形ABCD地面积比等于1 EG与EF地比.由题目地条件,三角形ABG地面积是梯形1 2 2ABCD地面积地-,即EG是EF地].因为EF长15厘米,EG地长就是:15X_「= 6(厘米)•版权文档,请勿用做商业用途答:EG长6厘米8・【解】为了使问题简化,我们首先分析一下这三堆砝码之间地关系•很明显,一个3克地砝码加上一个7克地砝码正好等于两个5克地砝码(都是10克),因此,如果用一个3克地砝码和一个7克地砝码去替换两个5克地砝码,砝码地个数及总重量都保持不变. 这样一来,我们就可以把5克砝码两个两个地换掉,直到只剩下一个5克地砝码或者没有5克砝码为止. 版权文档,请勿用做商业用途问题归结为下面两种情形:(1)所取地砝码中没有5克砝码.很明显,为了使所取地砝码个数尽量少,应该尽可能少取3克砝码.而130克减去3克砝码地总重量应该是7克地倍数.计算一下就可以知道,取0个、1个、2个、3个、4个、5个3克砝码,所余下地重量都不是7克地倍数.如果取6个3克砝码,那么130克—3克X 6= 112克=7克X 16.于是可以取16个7克砝码和6个3克砝码,总共22个砝码版权文档,请勿用做商业用途(2)所取地砝码中有一个5克地.那么3克和7克砝码地总重量是130克—5克=125克.和第一种情形类似,可以算出应取2个3克砝码和17个7克砝码,这样总共有17+ 2 + 1= 20 个砝码版权文档,请勿用做商业用途比较上面两种情形,我们得知最少要取20个砝码.取法可以就像后一种情形那样:2个3克地,1个5克地,17个7克地,当然也可以用两个5克砝码换掉一个3克和1个7克地砝码,例如可以取5个5克地和15个7克地.版权文档,请勿用做商业用途9. 【解】我们知道,每个圆地面积等于直径地平方乘以(n /4 ).现在要把5个圆分组,两组地总面积要尽可能接近,或者说;两组总面积地比尽可能接近 1.由于每个圆面积都有因子(n / 4).而我们关心地只是面积地比,所以可把这个共同地因子都去掉,使问题简化为:将5个圆公成两组,使两组圆地直径地平方和尽可能接近•版权文档,请勿用做商业用途5个圆地直径地平方分别是9,16,25,64,81.这5个数地和是195.由于195是奇数,所以不可能把这5个数分成两组,使它们地和相等.另一方面,81十16= 97,9+ 25+ 64= 98,二者仅相差 1.版权文档,请勿用做商业用途因此,应该把直径4米和9米地两个花圃交给一个班管理,其余三个花圃交给另一个班管理. 答:应该把直径4米和9米地两个花圃交给一个班管理,其余三个花圃交给另一个班管理. 10. 【解】观察一下已经写出地数就会发现,每隔两个奇数就有一个偶数.这个规律是不难解释地:因为两个奇数地和是偶数,所以两个奇数后面一定是偶数.另一方面,一个奇数和一个偶数地和是奇数,所以偶数后面一个是奇数,再后面一个还是奇数.这样,一个偶数后面一定有连续两个奇数,而这两个奇数后面一定又是偶数,等等•版权文档,请勿用做商业用途因此,偶数出现在第三、第六、第九…第九十九个位子上.所以偶数地个数等于100以内3地倍数地个数,即等于99-3= 33,于是,这串数地前100个数中共有33个偶数.版权文档,请勿用做商业用途本题给出地这串数叫做“菲波那西数列”,又叫“兔子数列”.答:这串数地前100个数中共有33个偶数.丄丄11. 【解】王师傅每两千米应行X 2(小时),现来时每1千米行丁.小时,] 丄丄所以返回时每1千米应行:「I X 2—二;=T (小时)即应以每小时66千米地速度往回开.【又解】根据题意,如果王师傅往返都以每小时60公里地速度行驶,正好按时返回甲地.丄也就是说,按计划行驶1公里地时间是」小时.而王师傅从甲地到乙地地实际行驶速度只有55公里/小时,这样一来、实际行驶1公里所花费地时间是 工小时,比计划多用 时,为了能按时返回甲地, 王师傅从乙地返回甲地时, 行驶1公里所花地时间必须比原计划小时.也就是说,只能花二二J (小时).因此王师傅往回开 地速度应是 66公/小时.版权文档,请勿用做商业用途 答:王师傅应以66公里/小时地速度往回开•12.【解】首先我们要注意到: 父亲和儿子只能在由 A 沿逆时针方向到 B 这一段跑道上相遇, 而且儿子比父亲跑得快,所以相遇时一定是儿子从后面追上父亲•版权文档,请勿用做商业用途儿子跑一圈所用地时间是 19X (400十100) = 76(秒),也就是说,儿子每过 76秒到达A 点一 次.同样道理,父亲每过 50秒到达A 点一次.在从A 到B 逆时针方向地一段跑道上,儿子要 跑19X (200十100) = 38(秒),父亲要跑20X (200 + 100) = 40(秒).因此,只要在父亲到达 点后地2秒之内,儿子也到达A 点,儿子就能从后面追上父亲 整数倍(这个倍数是父子相遇时儿子跑完地圈数 ),它比50地一个整数倍大,但至多大要找76地一个倍数,它除以 50地余数在0到2之间,这试一下就可以了:76-50 余26,76X 2十50余2 •正合我们地要求.(在一般情况下,应该先看看76地倍数除以50地余数有 什么规律) 版权文档,请勿用做商业用途因此,在父子第一次相遇时,儿子已跑完2圈,也就是正在跑第 3圈答:儿子在跑第3圈时,第一次再与父亲相遇•A已我们需要找76地一个 2.即疋,小时间少版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理版权为个人所有This article in eludes someparts, in cludi ng text, pictures,and desig n. Copyright is pers onal own ership. 版权文档,请勿用做商业用途用户可将本文地内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律地规定,不得侵犯本网站及相关权利人地合法权利.除此以外,将本文任何内容或服务用于其他用途时,须征得本人及相关权利人地书面许可,并支付报酬.版权文档,请勿用做商业用途Users may use the contents or services of this articlefor pers onal study, research or appreciati on, and other non-commercial or non-profit purposes, but at the same time, they shallabide by the provisi ons of copyright law and other releva nt laws, andshall n ot infringe upon the legitimate rights of this website and itsreleva nt obligees. In additi on, when any content or service of thisarticle is used for other purposes, writte n permissi on and remun eration shall be obta ined from the pers on concerned and the releva ntobligee.版权文档,请勿用做商业用途转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用,不得对本文内容原意进行曲解、修改, 并自负版权等法律责任.版权文档,请勿用做商业用途Reproducti on or quotatio n of the content of this articlemust be reas on able and good-faith citati on for the use of n ews or in formative public free in formatio n. It shall notmisinterpret or modify the original intention of the contentof this article, and shall bear legal liability such ascopyright. 版权文档,请勿用做商业用途版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理版权为个人所有This article in eludes someparts, in cludi ng text, pictures,and desig n. Copyright is pers onal own ership. 版权文档,请勿用做商业用途用户可将本文地内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律地规定,不得侵犯本网站及相关权利人地合法权利.除此以外,将本文任何内容或服务用于其他用途时,须征得本人及相关权利人地书面许可,并支付报酬.版权文档,请勿用做商业用途Users may use the contents or services of this articlefor pers onal study, research or appreciati on, and other non-commercial or non-profit purposes, but at the same time, they shallabide by the provisi ons of copyright law and other releva nt laws, andshall n ot infringe upon the legitimate rights of this website and itsreleva nt obligees. In additi on, when any content or service of thisarticle is used for other purposes, writte n permissi on and remun eration shall be obta ined from the pers on concerned and the releva ntobligee.版权文档,请勿用做商业用途转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用,不得对本文内容原意进行曲解、修改, 并自负版权等法律责任.版权文档,请勿用做商业用途Reproducti on or quotatio n of the content of this articlemust be reas on able and good-faith citati on for the use of n ews or in formative public free in formatio n. It shall notmisinterpret or modify the original intention of the contentof this article, and shall bear legal liability such ascopyright. 版权文档,请勿用做商业用途。
第10~21届全国华罗庚金杯少年数学邀请赛试题

第十届“华罗庚金杯”少年数学邀请赛初赛试题1、2005年是中国伟大航海家郑和首次下西洋600周年,西班牙伟大航海家歌伦布首次远洋航行是在1492年。
问这两次远洋航行相差多少年?2、从冬至之日起每九天分为一段,依次称之为一九,二九,……,九九,2004年的冬至为12月21日,2005年的立春是2月4日。
问立春之日是几九的第几天?3、右下方是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形。
问这个直三棱柱的体积是多少?4、爸爸、妈妈、客人和我四人围着圆桌喝茶。
若只考虑每人左邻的情况,问共有多少种不同的入座方法?5、在奥运会的铁人三项比赛中,自行车比赛距离是长跑的4倍,游泳的距离是自行车的,长跑与游泳的距离之差为8.5千米。
求三项的总距离。
6、如右图,用同样大小的正三角形,向下逐次拼接出更大的正三角形。
其中最小的三角形顶点的个数(重合的顶点只计一次)依次为:3,6,10,15,21,……问这列数中的第9个是多少?7、一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如图所示。
若用甲容器取水来注满乙容器,问:至少要注水多少次?8、100名学生参加社会实践,高年级学生两人一组,低年级学生三人一组,共有41组。
问:高、低年级学生各多少人?9、小鸣用48元钱按零售价买了若干练习本。
如果按批发价购买,每本便宜2元,恰好多买4本。
问:零售价每本多少元?10、不足100名同学跳集体舞时有两种组合:一种是中间一组5人,其他人按8人一组围在外圈;另一种是中间一组8人,其他人按5人一组围在外圈。
问最多有多少名同学?11、输液100毫升,每分钟输2.5毫升。
请你观察第12分钟时吊瓶图像中的数据,回答整个吊瓶的容积是多少毫升?12、两条直线相交所成的锐角或直角称为两条直线的“夹角”。
现平面上有若干条直线,它们两两相交,并且“夹角”只能是30°,60°或90°。
华杯赛决赛天天练汇总(解析版)

题目1第十八届华杯赛决赛 A 卷(2014×2014+2012)-2013×2013= 【答案】6039【解析】(2014×2014+2012)-2013×2013=((2013+1)×2014+2012)-2013×2013=(2013×2014+2014+2012)-2013×2013=2013×2014-2013×2013+2014+2012=2013×(2014-2013)+2014+2012=2013+2014+2012=6039题目2第二十届华杯赛决赛 B 卷3752÷(39×2)+5030÷(39×10)= 【答案】61【解析】3752÷(39×2)+5030÷(39×10)=3752÷(39×2)+5030÷(39×5×2)=3752÷(39×2)+5030÷5÷(39×2)=3752÷(39×2)+1006÷(39×2)=3752÷78+1006÷78=(3752+1006)÷78=4758÷78=61题目1第十九届华杯赛决赛用□和○表示两个自然数, 若□⨯○= 42, 则(□⨯4)⨯(○÷3)=【答案】56【解析】(□⨯4)⨯(○÷3)=□⨯4⨯○÷3=□⨯○⨯4÷3=42⨯4÷3=56题目2第二十一届华杯赛决 A 卷计算:(98×76 – 679×8)÷(24×6 + 25×25×3-3)= 【答案】1【解析】(98×76 – 679×8)÷(24×6 + 25×25×3-3)=(7448 – 5432)÷(144 + 1875-3)=2016÷2016=1题目12018 年1 月19 日(小中组计数专题)第十九届华杯赛决赛第一次操作将图a。
华杯赛历届试题

第一届华杯赛决赛一试试题1. 计算:2.975×935×972×(),要使这个连乘积的最后四个数字都是“0”,在括号内最小应填什么数?3.把+、-、×、÷分别填在适当的圆圈中,并在长方形中填上适当的整数,可以使下面的两个等式都成立,这时,长方形中的数是几?9○13○7=100 14○2○5=□4.一条1米长的纸条,在距离一端0.618米的地方有一个红点,把纸条对折起来,在对准红点的地方涂上一个黄点然后打开纸条从红点的地方把纸条剪断,再把有黄点的一段对折起来,在对准黄点的地方剪一刀,使纸条断成三段,问四段纸条中最短的一段长度是多少米?5.从一个正方形木板锯下宽为米的一个木条以后,剩下的面积是平方米,问锯下的木条面积是多少平方米?6.一个数是5个2,3个3,2个5,1个7的连乘积。
这个数当然有许多约数是两位数,这些两位的约数中,最大的是几?7.修改31743的某一个数字,可以得到823的倍数,问修改后的这个数是几?8.蓄水池有甲、丙两条进水管,和乙、丁两条排水管,要灌满一池水,单开甲管需3小时,单开丙管需要5小时,要排光一池水,单开乙管需要4小时,单开丁管需要6小时,现在池内有池水,如果按甲、乙、丙、丁的顺序,循环各开水管,每天每管开一小时,问多少时间后水清苦始溢出水池?9.一小和二小有同样多的同学参加金杯赛,学校用汽车把学生送往考场,一小用的汽车,每车坐15人,二小用的汽车,每车坐13人,结果二小比一小要多派一辆汽车,后来每校各增加一个人参加竞赛,这样两校需要的汽车就一样多了,最后又决定每校再各增加一个人参加竞赛,二小又要比一小多派一辆汽车,问最后两校共有多少人参加竞赛?10.如下图,四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数之和相等。
问这六个质数的积是多少?11.若干个同样的盒子排成一排,小明把五十多个同样的棋子分装在盒中,其中只有一个盒子没有装棋子,然后他外出了,小光从每个有棋子的盒子里各拿一个棋子放在空盒内,再把盒子重新排了一下,小明回来仔细查看了一番,没有发现有人动过这些盒子和棋子,问共有多少个盒子?12.如右图,把1.2,3.7, 6.5, 2.9, 4.6,分别填在五个○内,再在每个□中填上和它相连的三个○中的数的平均值,再把三个□中的数的平均值填在△中,找出一个填法,使△中的数尽可能小,那么△中填的数是多少?13.如下图,甲、乙、丙是三个站,乙站到甲、丙两站的距离相等。
第十届全国青少年信息学奥林匹克联赛复赛试题+答案

第十届全国青少年信息学奥林匹克联赛复赛试题+答案(普及组三小时完成)不高兴的津津(unhappy.pas/dpr/c/cpp)【问题描述】津津上初中了。
妈妈认为津津应该更加用功学习,所以津津除了上学之外,还要参加妈妈为她报名的各科复习班。
另外每周妈妈还会送她去学习朗诵、舞蹈和钢琴。
但是津津如果一天上课超过八个小时就会不高兴,而且上得越久就会越不高兴。
假设津津不会因为其它事不高兴,并且她的不高兴不会持续到第二天。
请你帮忙检查一下津津下周的日程安排,看看下周她会不会不高兴;如果会的话,哪天最不高兴。
【输入文件】输入文件unhappy.in包括七行数据,分别表示周一到周日的日程安排。
每行包括两个小于10的非负整数,用空格隔开,分别表示津津在学校上课的时间和妈妈安排她上课的时间。
【输出文件】输出文件unhappy.out包括一行,这一行只包含一个数字。
如果不会不高兴则输出0,如果会则输出最不高兴的是周几(用1, 2, 3, 4, 5, 6, 7分别表示周一,周二,周三,周四,周五,周六,周日)。
如果有两天或两天以上不高兴的程度相当,则输出时间最靠前的一天。
【样例输入】5 36 27 25 35 40 40 6【样例输出】3花生采摘(peanuts.pas/dpr/c/cpp)【问题描述】鲁宾逊先生有一只宠物猴,名叫多多。
这天,他们两个正沿着乡间小路散步,突然发现路边的告示牌上贴着一张小小的纸条:“欢迎免费品尝我种的花生!——熊字”。
鲁宾逊先生和多多都很开心,因为花生正是他们的最爱。
在告示牌背后,路边真的有一块花生田,花生植株整齐地排列成矩形网格(如图1)。
有经验的多多一眼就能看出,每棵花生植株下的花生有多少。
为了训练多多的算术,鲁宾逊先生说:“你先找出花生最多的植株,去采摘它的花生;然后再找出剩下的植株里花生最多的,去采摘它的花生;依此类推,不过你一定要在我限定的时间内回到路边。
”我们假定多多在每个单位时间内,可以做下列四件事情中的一件:1)从路边跳到最靠近路边(即第一行)的某棵花生植株;2)从一棵植株跳到前后左右与之相邻的另一棵植株;3)采摘一棵植株下的花生;4)从最靠近路边(即第一行)的某棵花生植株跳回路边。
第十届华杯赛口试试题及解案

第十届华杯赛口试试题题1.(共答题1)粤++=10在上面的算式中,粤、惠、州、华、罗、庚、金、杯、赛代表1~9这九个不同的数字。
请给出一种填数法,使得等式成立。
题2.(群答题1)跳绳的时候,可以认为绳子的中间点在同一个圆周上运动。
如果小光用0.5秒跳一个“单摇”,用0.6秒跳一个“双摇”,则跳“单摇”时绳中间点的速度和跳“双摇”时绳中间点的速度之比是多少?(说明:“单摇”是脚离地面一次,绳子转一圈;“双摇”是脚离地面一次,绳子转两圈。
) 题3.(必答题A1)如图,阴影正方形的顶点分别是大正方形EFGH各边的中点,分别以大正方形各边的一半为直径向外作半圆,再分别以阴影正方形的各边为直径向外作半圆,形成8个“月牙形”。
这8个“月牙形”的总面积为5平方厘米,问大正方形EFGH的面积是多少平方厘米?题4.(必答题A2)两个自然数a,b的最小公倍数等于50,问a+b有多少种可能的数值?题5.(必答题A3)如图所示,三角形ABC中,点X,Y,Z分别在线段AZ,BX,CY上,且YZ=2ZC,ZX =3XA,XY=4YB,三角形XYZ的面积等于24,求三角形ABC的面积。
题6.(必答题A4)你能在3×3的方格表(如图)中填入彼此不同的9个自然数(每个格子里只填一个数),使得每行、每列及两条对角线上三个数的乘积都等于2005吗?若能,请填出一例,若不能,请说明理由。
题7.(必答题A5)已知长方形的长为8,宽为4,将长方形沿一条对角线折起压平,如图所示。
求重叠部分(灰色三角形)的面积。
题8.(必答题A6)开始有三个数为1,1,1,每次操作把其中的一个数换成其他两数的和。
问经过10次操作后所得的三个数中,最大数的最大可能值是多少?题9.(群答题2)中国古代的“黑火药”配制中硝酸钾、硫磺、木炭的比例为15∶2∶3。
今有木炭50千克,要配制“黑火药”1000千克,还需要木炭多少千克?题10.(群答题3)图中的大正方形ABCD的面积是18平方厘米,灰色正方形MNPQ的边MN在对角线BD 上,顶点P在边BC上,Q在边CD上。
“华杯赛”复赛模拟试题(四年级组)附答案

“华杯赛”复赛模拟试题(四年级组)一、填空题(每题10分,共80分)1、规定x △y =5xy +3x +ay ,其中a 为常数.比如9△4=5×9×4+3×9+4a =207+4a .当a 取___________时,对任何数x 和y ,有x △y =y △x .2、编号为1―9的九个盒子中共放有351粒米,已知每个盒子都比前一号盒子多相同粒米.如果1号盒内放了11粒米,那么后面的盒子比它前一号的盒子多放__________粒米。
3、有一个号码是六位数,前四位是2857,后两位记不清,即2857□□.但是我记得,它能被11和13整除,那么这个号码是_________.4、一种钢轨,4根共重1900千克,现在有95000千克钢,可以制造这种钢轨 根.(损耗忽略不计)5、5个数写成一排,前3个数的平均值是15,后两个的数的平均值是10,这五个数的平均值是__________.6、工人铺一条路基,若每天铺260米,铺完全路长就得比原计划延长8天;若每天铺300米,铺完全路长仍要比原计划延长4天,这条路长_________米.7、A 、B 、C 、D 四个同学猜测他们之中谁被评为三好学生. A 说:“如果我被评上,那么B 也被评上.”B 说:“如果我被评上,那么C 也被评上.”C 说:“如果D 没评上,那么我也没评上.”实际上他们之中只有一个没被评上,并且A 、B 、C 说的都是正确的.则没被评上三好学生的是 。
8、如图1,一共有 个三角形.二、解答题(每题10分,共40分,要求写出解答过程)9、甲、乙两港的航程有500千米,上午10点一艘货船从甲港开往乙港(顺流而下),下午2点一艘客船从乙港开往甲港.客船开出12小时与货船相遇.已知货船每小时行15千米,水流速度每小时5千米,客船每小时行多少千米? (本题15分)10、一列客车以每小时40千米的速度在9时由甲城开往乙城,一列快车以每小时58千米的速度在11时也由甲城开往乙城,为了行驶安全,列车间的距离不应小于8千米,那么客车最晚应在什么时候停车让快车错过?(本题15分)11、甲、乙两车分别从A、B两站同时相向开出,已知甲车速度是乙车速度的2倍,甲、乙到达途中C站的时刻依次为5∶00和17∶00,这两车相遇是什么时刻?(本题20分)12、一个正方体木块放在桌子上,每一面都有一个数,位于对面两个数的和都等于13,小张能看到顶面和两个侧面,看到的三个数和为18;小李能看到顶面和另外两个侧面,看到的三个数的和为24,那么贴着桌子的这一面的数是多少?(本题20分)参考答案一、 填空(每题10分,共80分).填空题参考详解: 1. 3解:如果对任何数x 和y ,有x y y x ∆=∆,代入算式,得ax y yx ay x xy ++=++3535化简,得0))(3(=--y x a ,由于对任何数x 和y ,都有上式成立,所以03=-a ,即3=a , 所以,当3=a 时,对任何数x 和y ,有x y y x ∆=∆.2. 7解:这是一个等差数列问题,已知项数n =9,首项a 1=11,S 9=351,求公差d ,∵S 9=(a 1+a 9)×9÷2 ∴a 9=2S 9÷9-a 1=2×351÷9-11=67 d =(a 9-a 1)÷(9-1) =(67-11)÷8=7∴后面的盒子比它前一号的盒子多放7粒米.3. 285714解:285700÷(11×13)=1997余129.余数129再加14就能被143整除,故后两位数是14.4. 200解:以一根钢轨的重量为单一量.(1)一根钢轨重多少千克? 1900÷4 = 475(千克). (2)95000千克能制造多少根钢轨? 95000÷475 = 200(根).95000÷(1900÷4) = 200(根).答:可以制造200根钢轨.5. 13解:(3⨯15+2⨯10)÷(3+2)=13.6. 7800 解:260×8-300×4=880(米);880÷(300-260)=22(天);260×(22+8)=7800(米).7. A解:由C 说可推出D 必被评上,否则如果D 没评上,则C 也没评上,与“只有一人没有评上”矛盾.再由A 、B 所说可知:假设A 被评上,则B 被评上,由B 被评上,则C 被评上.这样四人全被评上,矛盾.因此A 没有评上三好学生.8. 35∆相同的三角形共有5个;解:Ⅰ.与ABE∆相同的三角形共有10个;Ⅱ.与ABP∆相同的三角形共有5个;Ⅲ.与ABF∆相同的三角形共有5个;Ⅳ.与AFP∆相同的三角形共有5个;Ⅴ.与ACD∆相同的三角形共有5个.Ⅵ.与AGD所以图中共有三角形为5+10+5+5+5+5=35(个).二.解答题(9、10题各15分;11、12题各20分,共70分。
华杯赛1-15届的真题和答案

=11111111110000000000-1111111111=111111111088888888889 于是有 10 个数字是奇数。 12.【解】10 根筷子,可能 8 根黑,1 根白,1 根黄,其中没有颜色不同的两双筷子。 如果取 11 根,那么由于 11>3,其中必有两根同色组成一双,不妨设这一双是黑色的,去掉 这两根,余下 9 根,其中黑色的至多 6(=8-2)根,因而白、黄两色的筷子至少有 3(=9-6) 根,3 根中必有 2 根同色组成一双。这样就得到颜色不同的两双筷子。所以至少要取 11 根。 13.【解】菜地的 3 倍和麦地的 2 倍是 13× 6 公顷。菜地的 2 倍和麦地的 3 倍是 12× 6 公顷, 因此菜地与麦地共:(13× 6+12× 6)÷ (3+2)=30(公顷), 菜地是 13× 6-30× 2=18(公顷)。 14. 【解】71427 被 7 除,余数是 6,19 被 7 除,余数是 5,所以 71427× 19 被 7 除,余数就 是 6× 5 被 7 除所得的余数 2。 15.【解】从第一次记录到第十二次记录,相隔十一次,共 5× 11=55(小时)。时针转一圈是 12 小时,55 除以 12 余数是 7,9-7=2 答:时针指向 2。 16.【解】因为电车每隔 5 分钟发出一辆,15 分钟走完全程。骑车人在乙站看到的电车是 15 分钟以前发出的,可以推算出,他从乙站出发的时候,第四辆电车正从甲站出发骑车人从乙 站到甲站的这段时间里,甲站发出的电车是从第 4 辆到第 12 辆。电车共发出 9 辆,共有 8 个 间隔。于是:5× 8=40(分) 。 17.【解】小数点后第 7 位应尽可能大,因此应将圈点点在 8 上,新的循环小数是 。
18.【解】三个背包分别装 8.5 千克、6 千克与 4 千克,4 千克、3 千克与 2 千克,这时最重 的背包装了 lO 千克。 另一方面最重的包放重量不少于 10 千克:8.5 千克必须单放(否则这一包的重量超过 10)6 千 克如果与 2 千克放在一起, 剩下的重量超过 10, 如果与 3 千克放在一起, 剩下的重量等于 10。 所以最重的背包装 10 千克。 19.【解】从第一排与第二排看,五个小纸片的长等于三个小纸片的长加三个小纸片的宽, 也就是说,二个小纸片的长等于三个小纸片的宽。 已知小纸片的宽是 12 厘米,于是小纸片的长是:12× 3÷ 2=18(厘米), 阴影部分是三个正方形,边长正好是小纸片的长与宽的差:18-12=6 于是,阴影部分的面积是:6× 6× 3=108(平方厘米)。
第十二届“华杯赛”浙江赛区复赛试题及答案(四年级组)-小学数学四年级下册-竞赛试题及答案-人教课标版

第十二届“华杯赛”浙江赛区复赛试题及答案(四年级组)小学数学四年级下册竞赛试题及答案人教课标版一、填空题(每题10分, 共80分)1、计算:123456+234567+345678+456789+567901+679012+790123+901234=__________.2、国庆节接受检阅的一列车队共52辆, 每辆车长4米, 每相邻两辆车相隔6米, 车队每分钟行驶105米。
这列车队要通过536米长的检阅场地, 要分钟。
3、把长2厘米宽1厘米的长方形如图(1)一层、两层、三层地摆下去, 摆完第十五层, 这个图形的周长是厘米。
4、北京某四合院子正好是个边长10米的正方形, 在院子中央修了一条宽2米的“十字形”甬路, 如图(2)这条“十字形”甬路的面积是平方米。
图(1)图(2)5、哥哥和弟弟共有故事书120本, 哥哥的故事书本数是弟弟的3倍, 哥哥有故事书本, 弟弟有故事书本.6、甲、乙两个粮仓共存粮320吨, 后来从甲粮仓运出40吨, 给乙粮仓运进20吨, 这时甲仓存粮是乙仓的2倍, 甲、乙两个粮仓原来各存粮分别为吨和吨.7、今年爸爸的年龄是小芳年龄的3倍, 几年前, 爸爸的年龄是小芳年龄的5倍, 再几年前, 爸爸的年龄是小芳年龄的7倍.他们的年龄差在20岁至30岁之间, 爸爸今年岁.8、篮中有许多李子, 如果将其中的一半又1个给第一个人, 将余下的一半又2个给第二个人, 然后将剩下的一半又3个给第三个人, 篮中刚好一个也不剩, 篮中原来有个李子.二、解答题(共70分, 要求写出解答过程)9、如果小方给小明一个玻璃球, 两人的玻璃球数相等;如果小明给小方一个玻璃球, 则小方的玻璃球数就是小明的两倍.问小明、小方原来各有多少个玻璃球?(本题15分)10、原计划有420块砖让若干学生搬运, 每人运砖一样多, 实际增加了一个学生, 这样每个学生就比原计划少搬2块.问:原有学生多少人?(本题15分)11、把99粒棋子放在两种型号的17个盒子里, 每个大盒子里放12粒, 每个小盒子里放5粒, 恰好放完.问大、小盒子各多少个?(本题20分)12、有A、B、C、D、E五个小足球队参加足球比赛, 到现在为止, A队赛了4场, B队赛了3场, C队赛了2场, D队赛了1场.那么E队赛了几场?(本题20分)第十二届“华杯赛”浙江赛区复赛试题(三年级组)参考答案一、填空(每题10分, 共80分)题号 1 2 3 4 5 6 7 8答案 4098760 10 90 36 90, 30 240, 80 36 34注:第5题、6题, 每空5分.填空题参考详解:1.4098760解:123456+234567+345678+456789+567901+679012+790123+901234=(123456+901234)+(234567+790123)+(345678+679012)+(456789+56 7901)=1024690+1024690+1024690+1024690=1024690×4=40987602.10解:因为车队行驶的路程等于检阅场地的长度与车队长度的和。
第十届华杯赛决赛试题答案
第十届华杯赛决赛试题答案2008-04-19 22:37分类:华杯赛字号:大大中中小小第十届华杯赛决赛试题一、填空(每题10分,共80分)12.计算:①18.3×0.25+5.3÷0.4-7.13 = ();②= ()。
3.计算机中最小的存储单位称为“位”,每个“位”有两种状态:0和1。
一个字节由8个“位”组成,记为B。
常用KB,MB等记存储空间的大小,其中1KB=1024B,1MB=1024KB。
现将240MB的教育软件从网上下载,已经下载了70%。
如果当前的下载速度为每秒72KB,则下载完毕还需要()分钟。
(精确到分钟)4.a,b和c都是二位的自然数,a,b的个位分别是7与5,c的十位是1。
如果它们满足等式ab+c=2005,则a+b+c=()。
5.一个正方体的每个顶点都有三条棱以其为端点,沿这三条棱的三个中点,从这个正方体切下一个角,这样一共切下八个角,则余下部分的体积(图1中的阴影部分)和正方体体积的比是()。
6.某种长方体形的集装箱,它的长宽高的比是4∶3∶2,如果用甲等油漆喷涂它的表面,每平方米的费用是0.9元,如果改用乙等油漆,每平方米的费用降低为0.4元,一个集装箱可以节省6.5元,则集装箱总的表面积是()平方米,体积是()立方米。
7.一列自然数0,1,2,3,…,2005,…,2004,第一个数是0,从第二个数开始,每一个都比它前一个大1,最后一个是2024。
现在将这列自然数排成以下数表:规定横排为行,竖排为列,则2005在数表中位于第()行和第()列。
8.图2中,ABCD是长方形,E,F分别是AB,DA的中点,G是BF和DE的交点,四边形BCDG的面积是40平方厘米,那么ABCD的面积是()平方厘米。
图2二、解答下列各题,要求写出简要过程(每题10分,共40分)9.图3是由风筝形和镖形两种不同的砖铺设而成。
请仔细观察这个美丽的图案,并且回答风筝形砖的四个内角各是多少度?10.有2、3、4、5、6、7、8、9、10和11共10个自然数,①从这10个数中选出7个数,使这7个数中的任何3个数都不会两两互质;②说明从这10个数中最多可以选出多少个数,这些数两两互质。
华杯复赛考辅班小中(学生版)

计数考点: 1. 2. 枚举法(分类、有序) 加乘原理(加法,分类;乘法,分步)
组合考点: 1. 各种与数字计算有关的最值问题.在枚举试算的过程中,注意寻找出大小变化的规律,并尝试分析其 内在原因;学会用比较、调整的方法寻找最值情况. 2. 逻辑推理: (1)一句话不是真话,就是假话.这在逻辑学中被称为排中律. (2)在应用假设法分析问 题时,要考虑全面.既要考虑到所假设的条件成立的情况,还要考虑到条件不成立的情况. (3)对于 条件复杂的逻辑推理问题,通常状况下都可以通过列表法分析.
当前恰好播放到第 30 分钟 28 秒处) . (2014 年 19 届)
练习8. 某校学生总人数比四年级人数的 6 倍少 78 人,并且除了四年级外其他各年级的学生人数总和为 2222 人,那么该校共有学生________人.
第8页
华杯赛复赛考辅班
课后练习
1.
中年级组
宁宁、蕾蕾和凡凡三人合租一辆轿车从学校回家.他们约定:共同乘坐的部分所产生的车费由乘坐者 平均分摊;单独乘坐的部分所产生的车费,由乘坐者单独承担.结果,三人承担的车费分别为 10 元、 25 元、85 元.宁宁家距离学校 12 公里,凡凡家距离学校_______公里. 学校 宁宁家 蕾蕾家 凡凡家
真题精讲
例题1. 计算: (2014 2014 2012) 2013 2013 ________. (2013 年 18 届)
练习1.
计算: 10 9 8 7 6 5 6 5 4 3 2 1 9 8 7 8 7 6 5 4 3 4 3 2 ________.
真题精讲
例1. 四年级一班用班费购买单价分别为 3 元、2 元、1 元的甲、乙、丙三种文具. 要求购买乙种文具的 件数比购买甲种文具的件数多 2 件, 且购买甲种文具的费用不超过总费用的一半. 若购买的文具恰好 用了 66 元, 则甲种文具最多可买 件.(2012 年 17 届)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 如 表 所 示 :
公元历 希伯莱历 伊斯兰历 印度历
2005 5766 1427 1927
1985 5746 1407 1907
1910 5671 2 1832
2. ( 1) 10.695 ( 2) 3. 4. 5. 6. 7. 1
下 载 完 大 约 需 要 17 分 钟 。 a+b+c=102 余 下 部 分 的 体 积 和 正 方 体 体 积 的 比 是 5/6。 集 装 箱 的 总 的 表 面 积 是 13 平 方 米 , 体 积 是 3 立 方 米 。 2005 在 数 表 中 位 于 第 20 行 第 45 列 。
8. 长 方 形 ABCD 的 面 积 是 60 平 方 厘 米 。 9. 在 风 筝 形 砖 中 ,有 一 个 是 钝 角 ,是 144 度 ,其 他 三 个 角 都 是 72 度 。
10. ( 1) 这 7 个 数 是 2, 3, 4, 6, 8, 9, 1 0。 ( 2) 最 多 可 选 5 个 数 。 11. 12. 13. 14. 最 大 体 积 和 最 小 体 积 的 比 是 5/3。 A 码 头 和 B 码 头 之 间 的 距 离 是 15 36 米 。 A+B 的 最 大 值 是 256。 ( 1) L 的 最 大 值 是 12; ( 2) 当 L 取 最 大 值 时 , 所 有 各 “ 夹 角 ” 的 和 是 32 40 度
