2016北京市普通高中会考数学模拟试题九
2016年北京市普通高中春季会考数学试题 及答案

2016年北京市普通高中春季会考数学试题及答案核准通过,归档资料。
未经允许,请勿外传~2015年北京市春季普通高中会考数学试卷1. 考生要认真填写考场号和座位序号。
204页,分为两部分,第一部分选择题,2. 本试卷共60个小题(共分);第二部分非选择题,二道大题(共考40分)。
生3(试题所有答案必须填涂或书写在答题卡上,在试须卷上作答无效。
第一部分必须用2B铅笔作答;第二知部分必须用黑色的签字笔作答。
4(考试结束后,考生应将试卷、答题卡及草稿纸放在桌面上,待监考员收回。
360第一部分选择题(每小题分,共分)一、在每个小题给出的四个备选答案中,只有一个是符合题目要求的. ,,,,A,3,5,6,8,B,1,3,5AB:1.已知集合,那么等于( ),,,,,,1,3,5,6,86,83,5A. B. C. D.- 1 -,,1,6,8,(1,1)2. 平面向量a,b满足b=2a如果a,那么b等于( ),(2,2)(,2,,2)(2,,2)(2,2)A. B. C. D.f(x),lg(x,1)f(x)3. 已知函数,那么的定义域是 3主视图( ) 左视图 5,,,,,,xx,1xx,1xx,0R 2A B C D俯视图4.一个几何体的三视图如图所示,该集合体的体积是( )30405060A. B. C. D.1a,,2a,0a,那么的最小值为( ) 5.如果32224A. B. C. D.A(,1,1),B(4,a)a16.已知过两点的直线斜率为,那么的值是( ),66,44A. B. C. D.,5tan67. 等于( )23,32,11A(; B(; C(; D((f(x)R8. 已知定义在上的函数的图像是一条连续不断地曲线,f(x)且有部分对应值如表所示,那么函数一定存在零点的区间是( ) (,,,1)(1,2)(2,3)(3,,,)A. B. C. D. x31233,1 f(x), 22- 2 -1y,2xy,logx(0,,,)y,xy,3x29.函数,,,中,在区间上单调递减的是( ) 1y,2xy,logxy,xy,3x2A B C Dx,y,2,0mx,y,0m10.已知直线与直线垂直,那么的值是( ),2,112A. B. C. D.1xy,()xy,3311. 在同一坐标系中,函数的图与的图象( )yx轴对称; B(关于轴对称; A(关于y,xy,xC(关于原点对称; D(关于直线对称(,,,,aaa,1,a,85nn1412. 在等比数列中,,那么的前项和是( ),31153163A( B ( C( D(x,y,2,0,,x,y,2,0,,y,0x,yz,x,2y,13.已知实数满足条件,那么目标函数的最小值是( ),6,4,24A. B. C. D.14. 某程序框图如图所示,执行该程序后输出的S的值是( )234345A. B. C.- 3 -56D.2y,(sinx,cosx)15. 函数的最小正周期是:( ),,32,22,( ,(,(; ,(; ,(; 8f(x)[,4,0):(0,4]16. 已知函数是定义在64f(x)上的奇函数,当时,的图像如图所示,2f(x)那么的值域是( )1510551015O4(,4,4)[,6,6]2A. B.4(,4,4):(4,6][,6,,4):(4,6]C. D.66217.边长为的正三角形的顶点和各边的中点共个点,从中任1选两点,所选出的两点之间距离大于的概率是( )112325 A. B. C. D.35,b,a18. 设,是两条不同的直线,、是两个不同的平面,给出下列四个命题: ,ab//,//,,ab//a? 如果,那么 ; ?如果? ,,bab//,a,,, ,那么 ;,,,a,,a,,ab//,a,?如果 , , 那么 ; ?如果,,,,,b,,, 那么其中正确命题的序号是( )A. ?B. ?C. ?- 4 -D. ?AB,5,AC,3,BC,4,ABCAB,AC19. 在中,如果,那么角等于:9152012( ),(; ,(; ,(; ,((f(x),ax,1g(x),(a,1)x20. 已知函数与的图像没有交点,那么实数的取值范围是( )11(0,)[,1)(,,,0][1,,,)22A. B. C. D.40第二部分非选择题(共分)二、填空题(共4个小题,每小题3分,共12分)129,log4,2 ( 21.计算22.一家电讯公司在某大学对学生每月的手机话费进行抽样调查,随机抽取了100名学生,将他们的手机话费情况进行统计分析,绘制成频率分布直方图(如图所示)。
2016北京市普通高中会考数学模拟试题五

北京市普通高中会考数学模拟试题数学试卷一、选择题(共20个小题,每小题3分,共60分)1.设全集}4,3{},5,4{},6,5,4,3,2,1{===B A U ,则=⋃)(C U B A}5,4,3.{A }6,4,3,2,1.{B }6,2,1.{c }6,5,3,2,1.{D2.过点(O ,4)且平行于直线032=--y x 的直线方程是042.=--y x A 042.=+-y x B 042.=-+y x c 042.=++y x D3.下列四组函数中,表示同一函数的是2)1(1.-=-=x y x y A 与 111..--=-=⋅x x y x y B 与 2lg 2lg 4.x y x y c ==与 100lg2lg .x y x y D =-=与 4.已知向量),2,1(=a 向量),2,(-=x b 且)(b a a -⊥,则实数x 等于A. -4B.4C.0D.95.给出四个条件:;0a b >>①,②b a >>0;0b a >>③,0>>b a ④其中能使ba 11<成立的条件是 ②③④.A ①③④.B ①②④.c ①②③④.D6.已知直线0=-y ax 与直线0132=++y x 平行,则a 等于 32.A 32.-B 23.c 23-.D 25sin 20sin 65sin 70sin .7-o 的值等于21.A23.B 22.c 22.-D 8.若m ,n 表示不同的直线,a 表示平面,则下列命题中,正确的个数为αα⊥⇒⎭⎬⎫⊥n m n m //① n m n m //⇒⎭⎬⎫⊥⊥αα② n m n m ⊥⇒⎭⎬⎫⊥αα//③ αα⊥⇒⎭⎬⎫⊥ n n m m //④ A.1 B.2 C.3 D.49.函数x x y 2cos 2sin 2=是 A.周期为2π的奇函数 B .周期为2π的偶函数 C .周期为4π的奇函数 D .周期为4π的偶函数10.如图,表示图中阴影部分的平面区域的不等式组是⎩⎨⎧-≥+≤11.A y x y ⎩⎨⎧-≤+≤11.y x y B ⎩⎨⎧-≥+≥11.y x y c ⎩⎨⎧-≤+≥11.y x y D 11.设,6.5log ,3.4log ,7.6log 225.0===c b a 则a ,b ,c 的大小关系为a cb A <<. bc a B <<. c b a c <<. a b c D <<.12.某程序框图如图所示,该程序运行后输出的k 的值是A.4B.5C.6D.713.过点A(2,1)的直线交圆04222=+-+y x y x 于B ,C 两点,当||BC 最大时,直线BC 的方程是053.=--y x A 073.=-+y x B 053.=-+y x c 053.=+-y x D14.函数)622sin(5π+=x y 图象的一条对称轴方程是 12.π-=x A 0.=x B 6.π=x c 3.π=x D15.在ABC ∆中,A ,B ,C 所对的边分别为a ,b ,c ,且,2,2,13==+=c b a 那么角C 的大小是6.πA 4.πB 3.πC 32.πD 16.设,833)(-+=x x f x 用二分法求方程0833=-+x x 在)2,1(∈x 内近似解的过程中得0)25.1(,0)5.1(,0)1(<><f f f 则方程的根所在的区间是)25.1,1.(A )5.1,25.1.(B )75.1,5.1.(c )2,75.1.(D17.小船以h km /310的静水速度按垂直于对岸的方向行驶,同时河水的流速为,/10h km 则小船实际航行速度的大小为h km A /220. h km B /20. h km C /210. h km D /10.18.已知直线)0(0=/=++abc c by ax 与圆122=+y x 相切,则三条边长分别为|||,||,|c b a 的三 角形 ( ) A.是锐角三角形 B .是直角三角形 C .是钝角三角形 D .不存在19.为鼓励节约用水,某地对居民用水实施如下计费方式:每户月用水量z (单位:立方米)与应交水费y(单位:元)按下式计算.⎪⎩⎪⎨⎧>-≤<-≤≤=.30,2.314.2,3022,2.138.1,220,2.1 x x x x x x y 如果甲、乙两户某月用水量分别为20立方米、40立方米,那么该月乙户应比甲户多交水费( )A .24.O 元B .40.8元C .48.O 元D .64.8元20.在区间]1,1[-上随机取一个数2cos ,xx π的值介于O 到21之间的概率为 31.A π2.B 21.c 32.D 二、填空题(共4个小题,每小题3分,共12分)21.圆1)1(22=-+y x 的圆心到直线2=x 的距离是22.函数2)3lg(--=x x y 的定义域是 23.已知数列}{n a 的前n 项和,12-=n s n 其中,,3,2,1 =n 那么=5a 24.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在]3000,2700(的频率为三、解答题(共3个小题,共28分)25.(8分)在中,A ,B ,C 所对的边分别为a ,b ,c .已知ABC ∆(1)求角C 的大小;.61,5,4===c b a(2)求的面积.ABC ∆26.(10分)已知圆C 与y 轴交于两点),2,0(),2,0(N M -且圆心C 在直线062=--y x 上.(1)求圆C 的方程;(2)过圆C 的圆心C 作一直线,使它夹在两直线022;1=--y xl 和03:2=-+F y x l 间的线段AB 恰好被点C 所平分,求此直线的方程.27. (10分)数列}{n a 满足,2,021==a a ,3,2,1,2sin 4)2cos 1(222=++=+n n a n a n n ππ (1)求,,43a a 并求数列}{n a 的通项公式;(2)设,1231-+++=k k a a a S ,.242k k a a a T +-+= *),(22N k T S W kk k ∈+=求使1>k W 的所有k 的值,并说明理由,。
2016北京市普通高中会考数学模拟试题一

北京市普通高中会考数学模拟试题一数学试卷一、选择题(共20个小题,每小题3分,共60分)1.已知集合}4|{},0|{<=>=x x B x x A 那么集合=B A∅.A }0|.{>x x B }4|.{<x x C }40|.{<<x x D2.如果函数c y x +=2的图象经过点(2,5),则c=A.1B.0.C. -1D. -2D. -23.下列函数中,在),0(+∞上是减函数的是xy A 1.=1.2+=x y B x y C2.= x y D 3log .= 4.函数)652cos(π-=x y 的最小正周期是 2.πA π.B π2.C π4.D 5.已知过点)4,(),,2(m B m A -的直线与直线012=-+y x 平行,则m 的值为A.O B .-8 C .2 D .106.若一条直线同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是(A .异面B .相交C .平行D .不能确定7.函数x y 3=的图象与x y -=3的图象A .关于z 轴对称B .关于y 轴对称C .关于直线y=x 对称D .关于直线y=-z 对称8.下面四个命题中,正确的是A .平行于同一条直线的两条直线互相平行B .垂直于同一条直线的两条直线互相垂直C .平行于同一个平面的两条直线互相平行D .垂直于同一个平面的两条直线互相垂直9.已知向量),1,2(),4,3(-==b a 如果向量xb a +与b 垂直,则=x323.A 233.B 2.C 52.-D 10.圆012222=+--+y x y x 上的点到直线2=-y x 的距离最大值是2.A 21.+B 221.+C 221.+D 11.已知),5,2(),1,3(-==b a 则=-b a 23)7,2.(A )7,13.(-B )7,2.(-C )13,13.(D12.在等差数列}{n a 中,已知,13,2321=+=a a a 则=++654a a aA.40B.42C.43D.4513.已知53sin =α,且),,2(ππα∈那么α2sin 等于 2512.A 2512.-B 2524.C 2524.-D 14.在ABC ∆中,222bc c b a ++=则角A 为o A 30. 45.B 120.C 150.D15.从数字1,2,3,4,5中,随机抽取两个数字(不允许重复),则这两个数字之和 为奇数的概率54.A 53.B 52.C 51.D 16.已知角α的终边经过点),3,4(-p 则)2sin(απ+的值为53.A 53.-B 54.c 54.-D 17.将函数x y 2cos =的图象向右平移4π个单位,所得图象的函数解析式为 )42cos(.π+=x y A )42cos(.π-=x y B x y C 2sin .= x y D 2sin .-= 18.下边程序框图表示的算法是A.输出c ,b ,a B .输出最大值C .输出最小值D .比较a ,b ,c 的大小 ‘19.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )π9.A π10.B π11.c π12.D20.为改善生态环境,某城市对排污系统进行了整治.如果经过三年整治,城市排污量由原来每年排放125万吨降到27万吨,那么排污量平均每年降低的百分率是 ( )%50.A %40.B %30.C %20.D二、填空题(共4个小题,每小题3分,共计12分)。
北京市2016届高三下学期普通高中毕业会考数学试卷

2016年北京市季普通高中会考 考生须知 1. 考生要认真填写考场号和座位序号。
2. 本试卷共页,分为两个部分,第一部分为选择题,个小题(共分);第二部分为解答题,个小题(共分)。
3.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用铅笔作答;第二部分必须用黑色字迹的签字笔作答。
4.第一部分选择题(每小题3分,共75分) 在每个小题给出的四个备选答案中,只有一个是符合题目要求的. .的最小正周期是 A. B. C. D. .,,如果,那么实数等于 A. B. C. D. 3.,,那么等于 A. B. C. D. 4.中,函数与的图象之间的关系是 A.对称 B.轴对称 C.对称2 D.对称 5..时,输出的值为 A. B. C. D. .经过点,且与直线平行,那么直线的方程是 A. B. C. D. . A. B. C. D. 8.中,,AC=2,BC=3,那么AB等于 A. B. C. D. . A. B. C. D. .等于 A. B. C. D. 11.,其后每天产生的数据量都是前一天的倍,那么训练天产生的总数据量为 A. B. C. D. .,那么等于 A. B. C. D. .①;②;③;④中,图象经过点(1,1)的函数的序号是 A.① B.② C.③ D.④ 14. A. B. C. D. 15. A. B. C. D. .,且,那么在不等式①;②;③; ④中,一定成立的不等式的序号是 A.① B.② C.③ D.④ 17.中,E,F,G分别是,,的中点,给出下列四个推断: ①FG平面;②EF平面; ③FG平面;④平面EFG平面 其中推断正确的序号是 A.①③ B.①④ C.②③ D.②④ 18.的方程为,圆的方程为,如果这两个圆有且只有一个公共点,那么的所有取值构成的集合是 A. B. C. D. .中,已知点和满足,那么的值为 A.3 B. C. D. 20.,其中,且,如果以,为端点的线段的中点在轴上,那么等于 A.1 B. C. D. .,动点的坐标满足,那么的最小值是 A. B. C. D. 22.,关于的性质,有以下四个推断: ①的定义域是;②的值域是; ③是奇函数;④是区间上的增函数. A.1 B. C. D. 23. A. B. C. D. 24.,其中,,如果对任意,都有,那么在不等式①;②;③;④中,一定成立的不等式的序号是 A.① B.② C.③ D.④ 25.的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是 A.9 B. C. D. 第二部分解答题(每小题5分,共25分) 26. 已知,且. ;(将结果直接填写在答题卡的相应位置上) (Ⅱ)求的值. . 如图,在三棱柱中,平面ABC,,AB=2,,D是棱上一点. ; (Ⅱ)求三棱锥的体积. . 已知直线与轴交于点P,圆O的方程为(). 与圆O相切,那么 ;(将结果直接填写在答题卡的相应位置上) (Ⅱ)如果直线与圆O交于A,B两点,且,求的值. .5分) 数列满足,,2,3,,的前项和记为. 时, ;(将结果直接填写在答题卡的相应位置上) (Ⅱ)数列是否可能为等比数列?证明你的推断; (Ⅲ)如果,证明: 30.5分) 已知函数,其中,. 时,的零点为 ;(将结果直接填写在答题卡的相应位置上) (Ⅱ)当时,如果存在,使得,试求的取值范围; (Ⅲ)如果对于任意,都有成立,试求的最大值. 2016年 数学试卷答案及评分参考 [说明] 1.. 2..... (每小题3分共75) 题号 1 2 3 4 5 6 7 8 9 答案 D C A CA B C D 题号 1 11 12 13 14 15 16 17 18答案 D B A B C D A C 题号 1 20 21 2223 24 25 ------- 答案 A B C B D B 第二部分解答题 (每题5分,共25) 26. …………2分 (Ⅱ) …………5分 27. (Ⅱ) …………5分 28. …………1分 (Ⅱ)的值为或 …………5分 29. …………1分 (Ⅱ)数列不可能为等比数列 …………3分 (Ⅲ)略 …………5分 30.的零点为0, …………1分 (Ⅱ)的取值范围是 …………3分 (Ⅲ)的最大值是2 …………5分。
新课标2016年北京市普通高中会考(数学春季B卷)

新课标2016年北京市普通高中会考(数学春季B 卷)一、单选题(每小题3分,共60分)1.已知集合A={1,2,3},B={2,3,4,},那么集合AB =( )A. {2}B. {2,3}C.{1,2,3}D. {1,2,3,4} 2.不等式220x x -<的解集是( )A.{}02x x << B. {}20x x -<< C.{}0,2x x x <>或 D. {}2,0x x x <->或3.一个空间几何体的三视图如图所示,那么这个空间几何体是( ) A. 球 B. 圆锥 C.正方体 D.圆柱 4.已知直线l 经过点A(0,4),且与直线230x y --=垂直, 那么直线l 的方程是( ).A .280x y +-=B .280x y ++=C .240x y --=D .240x y -+=5.某校有学生1000人,其中高一学生400人.为调查学生了解消防知识的现状,采用按年级分层抽样的方法,从该校学生中抽取一个40人的样本,那么样本中高一学生的人数为( ).A . 8B . 12C . 16D . 206.已知四个函数233,,3,log xy x y x y y x ====,其中奇函数是( )A.3y x =B. 2y x = C. 3xy = D. 3log y x =7.如图,正方体ABCD-A 1B 1C 1D 1的棱长为a ,那么四棱锥D 1-ABCD 的体积是( )A.312a B. 313a C. 314a D. 316a 8.已知函数()sin f x x =,那么()f x π-等于( ) A. sin x B. cos x C. sin x - D. cos x - 9.函数22,0()1,0x x f x x x +<⎧=⎨->⎩的零点个数是( ) A. 0个 B. 1个 C. 2个 D. 3个10.已知3tan 4θ=,那么tan()4πθ+等于( ) A. 7- B. 17- C. 7 D. 1711.在△ABC 中,D 是BC 的中点,那么AB AC +等于( ) A. BD B. AD C. 2BD D. 2AD12. 不等式组114x y x y ≥⎧⎪≥⎨⎪+≤⎩,所表示的平面区域的面积为( ).A . 1B .2C . 3D . 4 13. 在ABC ∆中,3A π=,BC =1AC =,那么AB 等于( )A .1 BC.214.上海世博会期间,某日13时至21时累计..入园人数的折线图如图所示,那么在13时~14时,14时~15时,……,20时~21时八个时段中,入园人数最多的时段是( )A. 13时~14时B. 16时~ 17时C. 18时~19时D. 19时~20时 15. 已知两条直线,m n 和平面α,那么下列命题中的真命题为( )A.若m ∥n,n ⊂α,则m ∥αB.若m n ⊥,n ⊂α,则m ⊥αC.若m ∥n ,n ⊂α,m α⊄,则m ∥αD.若m n ⊥ ,n ⊂α,m α⊄,则m ⊥α16.已知3sin 5α=,那么cos2α等于( ) A. 725B. 725-C. 2425D. 2425-17.已知0a >,且4ab =,那么a b +的最小值是( ) A. 2 B. 4 C. 6 D. 818.某校高二年级开设三门数学选修课程。
北京市西城区2016届九年级下学期第一次中考模拟考试数学试题解析(解析版)

北京市西城区2016届九年级下学期第一次中考模拟考试数学试题一、选择题(本题共30分,每小题3分)1.64的立方根是( )A. ±8B. ±4C. 8D. 4【答案】D【解析】试题分析:根据34=64,则64的立方根为4.考点:立方根的计算.2.2014年11月北京主办了第二十二届APEC (亚太经合组织)领导人会议,“亚太经合组织”联通太平洋两岸,从地理概念上逐渐变成了一个拥有280000000人口的经济合作体,把“280000000”用科学记数法表示正确的是( )A .82810.⨯B .92810.⨯C .82810⨯D .72810⨯【答案】A【解析】试题分析:科学计数法是指a ×10n ,且1≤a <10,n 为原数的整数位数减一.考点:科学计数法.3.如右图是由四个相同的小正方体组成的立体图形,它的俯视图为( )A B C D【答案】D【解析】试题分析:根据三视图的法则可得,这个立体图形的俯视图为D.考点:三视图.4.一名射击爱好者5次射击的中靶环数依次为:6,7,9,8,9,这5个数据的中位数是( )A .6B .7C .8D .9【答案】C【解析】试题分析:将这些数字从小到大排列起来则为6,7,8,9,9,则中位数为8.考点:中位数的计算.5.下列图形中,是中心对称图形的是( )A .B .C .D .【答案】A【解析】试题分析:中心对称图形是指将图形围绕一点旋转180°之后能与原图形完全重合.根据定义可得A 为中心对称图形.考点:中心对称图形.6.在函数y =中,自变量x 的取值范围是( )A .3x >B .3x ≥C .3x <D . 3x ≤【答案】B【解析】试题分析:二次根式的被开方数为非负数,则x -3≥0,解得:x ≥3.考点:二次根式的性质.7.一个不透明的口袋中,装有4个红球,3个黄球,1个白球,这些球除颜色外其余都相同,从口袋中随机摸一个球,则摸到红球的概率为( )A .18B .38C .21D .34【答案】C【解析】试题分析:摸到红球的概率=红球的数量÷球的总数量.考点:概率的计算.8.如图,⊙O 的半径为5,AB 为⊙O 的弦,OC ⊥AB 于点C .若3OC ,则弦AB 的长为( )A .4B .6C .8D .10 A BCO【答案】C【解析】试题分析:连接OB ,则OB=5,根据Rt △OBC 的勾股定理得出BC=4,则AB=2BC=8.考点:垂径定理.9.若正多边形的一个外角为60º,则这个正多边形的中心角的度数是( )A .30°B .60°C .90°D .120°【答案】B【解析】试题分析:根据外角可得这个多边形为六边形,则正多边形的中心角的度数为60°.考点:正多边形的性质.10.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,AC=6,BD=8,动点P 从点B 出发,沿着B-A-D 在菱形ABCD的边上运动,运动到点D 停止,点'P 是点P 关于BD 的对称点,'PP 交BD 于点M ,若BM=x ,'OPP △的面积为y ,则y 与x 之间的函数图象大致为( )M O P'PDB ACx y x y x y xyO O O OD A B C 483333848448【答案】D【解析】试题分析:根据题意可得:当x=0,x=4和x=8时,y=0,则排除A 和C ,当0<x <4和4<x <8时为抛物线,则选择D.考点:二次函数的性质.二、填空题(本题共18分,每小题3分)11.若2(2)0m ++= 则m n -= .【答案】-3考点:非负数的性质.12.质量检测部门对甲、乙两工厂生产的同样产品抽样调查,计算出甲厂的样本方差为0.99,乙厂的样本方差为1.22.由此可以推断出生产此类产品,质量比较稳定的是 厂.【答案】甲【解析】试题分析:方差越小,则说明成绩越稳定.考点:方差的作用.13.在综合实践课上,小明同学设计了如图测河塘宽AB 的方案:在河塘外选一点O ,连结AO ,BO ,测得18AO =m ,21BO =m ,延长AO ,BO 分别到D ,C 两点,使6OC =m ,7OD =m ,又测得5CD =m ,则河塘宽AB= m .DCB AO【答案】15【解析】 试题分析:根据题意可得:13OC OD AO BO ==,∠DOC=∠BOA ,则△OCD ∽△OAB ,则13CD AB =,则AB=15m. 考点:三角形相似的应用14.写出一个当自变量0x 时,y 随x 的增大而增大的反比例函数表达式 _____.【答案】y=-1x(答案不唯一) 【解析】试题分析:对于反比例函数,当k <0时,在每个象限内,y 随x 的增大而增大.考点:反比例函数的增减性.15.居民用电计费实行“一户一表”政策,以年为周期执行阶梯电价,即:一户居民全年不超过2880度的电量,执行第一档电价标准为0.48元/度;全年用电量在2880度到4800度之间(含4800),超过2880度的部分,执行第二档电价标准为0.53元/度;全年用电量超过4800度,超过4800度的部分,执行第三档电价标准为0.78元/度.小敏家2014年用电量为3000度,则2014年小敏家电费为 元.【答案】1446元.【解析】试题分析:本题需要将3000度点分成两部分进行计算,得出最后的答案.2880×0.48+(3000-2880)×0.53=1382.4+63.6=1446元考点:分段计算.16.规定:在平面直角坐标系xOy 中,“把某一图形先沿x 轴翻折,再沿y 轴翻折”为一次变化.如图,已知正方形ABCD ,顶点A(1,3),C(3,1).若正方形ABCD 经过一次上述变化,则点A 变化后的坐标为 ,如此这样,对正方形ABCD 连续做2015次这样的变化,则点D 变化后的坐标为 .yxA BC D O 1133【答案】(-1,-3);(-3,-3)【解析】试题分析:一次变换实际上就是做了中心对称,两次变换后回到原来的位置.则一次变换后A 的坐标为(-1,-3);经过2015次变换后点D 的坐标为(-3,-3)考点:规律题.三、解答题(本题共30分,每小题5分)17.计算:1012015452-⎛⎫+-︒ ⎪⎝⎭. 【答案】3【解析】试题分析:首先根据幂和二次根式、三角函数的计算法则求出各式的值,然后进行实数的加减法计算. 试题解析:原式==21+-=3考点:实数的计算.18.解不等式组:()4156,30.x x x ⎧->-⎨+>⎩【答案】-3<x <2【解析】试题分析:首先分别求出每个不等式的解,然后求出不等式组的解.试题解析:解不等式①得x <2 解不等式②得x >-3∴原不等式的解集为-3<x <2考点:不等式组的解法.19.如图,C ,D 为线段AB 上两点,且AC=BD ,AE ∥BF .AE=BF .求证:∠E=∠F .FA BCD E【答案】证明过程见解析【解析】试题分析:根据AC=BD 得出AD=BC ,根据平行线得出∠A=∠B ,结合AE=BF 得出△EAD 和△FBC 全等,从而得出答案.试题解析:∵AC=BD , ∴AD=BC .∵AE ∥BF , ∴∠A=∠B .又∵AE=BF ,∴△EAD ≌△FBC ,∴∠E=∠F .考点:三角形全等.20.已知3b a =-,求代数式22112aba b a ab b ⎛⎫⋅- ⎪-+⎝⎭的值. 【答案】-13【解析】 试题分析:首先将括号里面的分式进行通分,将分式的分子和分母进行因式分解,然后将除法改成乘法进行约分化简,最后利用整体代入的思想进行求解.试题解析:原式=()2abb a aba b -=⋅-1b a =- ∵3b a =-,∴3b a -=-, ∴原式1b a =-13=-. 考点:分式的化简求值. 21.已知关于x 的一元二次方程2320kx x --=有两个不相等的实数根.(1)、求k 的取值范围;(2)、若k 为小于2的整数,且方程的根都是整数,求k 的值.【答案】(1)、98k >-且0k ≠;(2)、k=-1. 【解析】试题分析:(1)、根据根的判别式和一元二次方程的定义求出k 的取值范围;(2)、根据取值范围得出k 的值,然后分别进行计算得出k 的值.试题解析:(1)、△=9+8k ∵方程2320kx x --=有两个不相等的实数根,∴9+80,0.k k >⎧⎨≠⎩ ∴98k >-且0k ≠ (2)、∵k 为不大于2的整数, ∴1k =-,1k =∴当1k =-时,方程2320x x ---=的根-1,-2都是整数;当1k =时,方程2320x x --= 综上所述,1k =-.考点:(1)、解一元二次方程;(2)、根的判别式.22.列方程或方程组解应用题:在练习100米跑步时,小丽为了帮助好朋友小云提高成绩,让小云先跑7.5秒后自己再跑,结果两人同时到达终点,这次练习中小丽的平均速度是小云的1.6倍,求小云这次练习中跑100米所用的时间.【答案】20秒.【解析】试题分析:首先设小云的时间为x 秒,则小丽的时间为(x -7.5)秒,根据题意列出分式方程进行求解,最后将得出的解进行验根得出答案.试题解析:设小云这次练习跑100米的时间为x 秒,则小丽的时间为(x -7.5)秒. 依题意,得1001001.67.5x x ⨯=-. 解得20x =. 经检验:20x =是所列方程的根,且符合实际意义答:小云这次练习跑100米的时间为20秒.考点:分式方程的应用.四、解答题(本题共20分,每小题5分)23.如图,平行四边形ABCD 中,点E 是AD 边上一点,且 CE ⊥BD 于点F ,将△DEC 沿从D 到A 的方向平移,使点D 与点A 重合,点E 平移后的点记为G .(1)、画出△DEC 平移后的三角形; (2)、若BC=BD=6,CE=3,求AG 的长.DCEB A F【答案】(1)、答案见解析;(2)考点:(1)、三角形全等;(2)、勾股定理;(3)、图像的平移.24.为了提倡“绿色”出行,顺义区启动了公租自行车项目,为了解我区居民公租自行车的使用情况,某校的社团把使用情况分为A (经常租用)、B (偶尔租用)、C (不使用)三种情况.先后在2015年1月底和3月底做了两次调查,并根据调查结果绘制成了如下两幅不完整的统计图:根据以上信息解答下列问题:(1)在扇形统计图中,A(经常租用)所占的百分比是;(2)求两次共抽样调查了多少人;并补全折线统计图;(3)根据调查的结果,请你谈谈从2015年1月底到2015年3月底,我区居民使用公租自行车的变化情况.【答案】(1)、20%;(2)、100人;答案见解析;(3)、常使用公租自行车的人数明显增多,从不使用的人数明显减少,说明大家越来越认识公租自行车的好处.【解析】试题分析:(1)、根据扇形统计图得出A所占的百分比;(2)、根据B的人数和比例求出总人数,然后画出图形;(3)、根据图形得出结论,只要符合题意即可.试题解析:(1)、20%;(2)、(24+32)÷56%=100(人)两次调查公租自行车使用情况折线统计图2015年3月底2015年1月底使用情况A B C20841216人数242832(3)、经常使用公租自行车的人数明显增多,从不使用的人数明显减少,说明大家越来越认识公租自行车的好处.考点:统计图.25.如图,AB 是⊙O 的直径,C 是⊙O 上一点,D 是BC 的中点,过点D 作⊙O 的切线,与AB ,AC 的延长线分别交于点E ,F ,连结AD .(1)求证:AF ⊥EF ; (2)若1tan 2CAD ∠=,AB=5,求线段BE 的长. EF DABCO【答案】(1)、证明过程见解析;(2)、53【解析】试题分析:(1)、连接OD 根据切线得出OD ⊥EF ,根据OA=OD 得出∠1=∠3,根据弧的中点得出∠1=∠2,则∠2=∠3,说明OD ∥AF ,得到切线;(2)、连接BD ,根据tan ∠CAD 的值得出tan ∠1的值,根据Rt △ADB 得出BD 和AD 的长度,根据平行得出△EDO 与△EFA 相似,设BE=x ,根据相似比得出x 的值. 试题解析:(1)、连结OD . ∵直线EF 与⊙O 相切于点D , ∴OD ⊥EF .∵OA = OD ,∴∠1=∠3.∵点D 为BC 的中点, ∴∠1=∠2,∴∠2=∠3,∴OD ∥AF ,∴AF ⊥EF .(2)、连结BD .∵1tan 2CAD ∠=, ∴1tan 12∠=在Rt △ADB 中,AB=5,∴AD=, 在Rt △AFD 中,可得DF=2,AF=4,∵OD ∥AF ,∴△EDO ∽△EFA ,∴OD OEAF AE=,又∵OD=2.5,设BE=x , ∴2.5 2.545x x +=+,∴53x =,即BE=53. 321OCBADF E EFDABCO123考点:(1)、圆的基本性质;(2)、三角形相似.26.阅读、操作与探究:小亮发现一种方法,可以借助某些直角三角形画矩形,使矩形邻边比的最简形式(如4:6的最简形式为2:3)为两个连续自然数的比,具体操作如下:如图1,Rt △ABC 中,BC ,AC ,AB 的长分别为3,4,5,先以点B 为圆心,线段BA 的长为半径画弧,交CB 的延长线于点D ,再过D ,A 两点分别作AC ,CD 的平行线,交于点E .得到矩形ACDE ,则矩形ACDE 的邻边比为 .请仿照小亮的方法解决下列问题:(1)如图2,已知Rt △FGH 中,GH :GF :FH= 5:12:13,请你在图2中画一个矩形,使所画矩形邻边比的最简形式为两个连续自然数的比,并写出这个比值;(2)若已知直角三角形的三边比为()()()2221:2+2:2+21n n n n n ++(n 为正整数),则所画矩形(邻边比的最简形式为两个连续自然数的比)的邻边比为 .图2图1HGFEDAB C【答案】(1)、1:2;2:3;(2)、n:(n+1). 【解析】试题分析:(1)、根据题意中的画法得出矩形的邻边之比;根据题意画出图形得出比值;(2)、根据直角三角形的三边长进行化简,得出比值. 试题解析:(1)、1:2;NMFG H 图22:3; (2)、()1n n +:考点:(1)、规律题;(2)、作图;(3)、操作与探究.五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.在平面直角坐标系xOy 中,抛物线21212y ax x a =+-+与y 轴交于C 点,与x 轴交于A ,B 两点(点A 在点B 左侧),且点A 的横坐标为-1. (1)求a 的值;(2)设抛物线的顶点P 关于原点的对称点为'P ,求点'P 的坐标;(3)将抛物线在A ,B 两点之间的部分(包括A , B 两点),先向下平移3个单位,再向左平移m (0m >)个单位,平移后的图象记为图象G ,若图象G 与直线'PP 无交点,求m 的取值范围.xyO22-2-2【答案】 (1)、a=-2;(2)、P ′(-1,-4);(3)、m >154【解析】试题分析:(1)、将点A 的坐标代入解析式求出a 的值;(2)、根据a 的值得出函数解析式,然后求出顶点坐标,根据原点对称的性质求出点P ′的坐标;(3)、根据题意得出直线PP ′的解析式,图象向下平移3个单位后,得出A ′和B ′的坐标,若图象G 与直线PP ′无交点,则B ′要左移到M 及左边,将y=3代入一次函数得出点M 的坐标,然后求出m 的取值范围. 试题解析:(1)、∵A (-1,0)在抛物线21212y ax x a =+-+上,∴12102a x a --+=,∴解得2a =- (2)、∴抛物线表达式为223y x x =-++. ∴抛物线223y x x =-++的顶点P 的坐标为(1,4). ∵点P 关于原点的对称点为'P ,∴'P 的坐标为(-1,-4). (3)、直线'PP 的表达式为4y x =,图象向下平移3个单位后,'A 的坐标为(-1,-3),'B 的坐标为(3,-3),若图象G 与直线'PP 无交点,则'B 要左移到M 及左边,令3y =-代入'PP ,则34x =-,M 的坐标为3,34⎛⎫-- ⎪⎝⎭xyMA'B'OP C B A P'∴315344B'M=⎛⎫--=⎪⎝⎭,∴154m >.考点:二次函数的综合应用.28.如图,△ABC 中,AB=AC ,点P 是三角形右外一点,且∠APB=∠ABC .(1)如图1,若∠BAC=60°,点P 恰巧在∠ABC 的平分线上,PA=2,求PB 的长; (2)如图2,若∠BAC=60°,探究PA ,PB ,PC 的数量关系,并证明; (3)如图3,若∠BAC=120°,请直接写出PA ,PB ,PC 的数量关系.图3图1图2ABCPABCPABC P【答案】(1)、BP=4;(2)、PA+PC=PB ,证明过程见解析;(3)PA+PC=PB 【解析】试题分析:(1)、根据题意得出△ABC 为等边三角形,根据点P 在∠ABC 的平分线上,则∠ABP=30°,根据∠PAB=90°得出BP=2AP ;(2)、在在BP 上截取PD ,使PD=PA ,连结AD ,证明△ABD 和△ACP 全等,从而得出PC=BD ,得出所求的答案;(3)、根据同样的方法得出线段之间的关系.试题解析:(1)、∵AB=AC ,∠BAC=60°,∴△ABC 是等边三角形,∠APB=∠ABC ,∴∠APB=60°, 又∵点P 恰巧在∠ABC 的平分线上,∴∠ABP=30°∴∠PAB=90°.∴BP=2AP ,∵AP=2,∴BP=4. (2)、结论:PA+PC=PB .在BP 上截取PD ,使PD=PA ,连结AD .12DABPC∵∠APB =60°,∴△ADP 是等边三角形,∴∠DAP =60°,∴∠1=∠2,PA=PD ,又∵AB=AC ,∴△ABD ≌△ACP ,∴PC=BD ,∴PA+PC=PB . (3)PA+PC=PB .12FDABCP考点:三角形全等.29.已知:如图1,抛物线的顶点为M ,平行于x 轴的直线与该抛物线交于点A ,B (点A 在点B 左侧),根据对称性△AMB 恒为等腰三角形,我们规定:当△AMB 为直角三角形时,就称△AMB 为该抛物线的“完美三角形”.(1)①如图2,求出抛物线2y x =的“完美三角形”斜边AB 的长;②抛物线21y x +=与2y x =的“完美三角形”的斜边长的数量关系是 ; (2)若抛物线24y ax +=的“完美三角形”的斜边长为4,求a 的值;(3)若抛物线225y mx x+n =+-的“完美三角形”斜边长为n ,且225y mx x+n =+-的最大值为-1,求m ,n 的值.xyxyxyy =x 2备用图1O图2(M )ABO 图1MBAO【答案】(1)、AB=2;相等;(2)、a=±12;(3)、34m =-,∴83n =. 【解析】试题分析:(1)、过点B 作BN ⊥x 轴于N ,由题意可知△AMB 为等腰直角三角形,设出点B 的坐标为(n ,-n),根据二次函数得出n 的值,然后得出AB 的值;(2)、根据抛物线的性质相同得出抛物线的完美三角形全等,从而得出点B 的坐标,得出a 的值;(3)、根据最大值得出mn -4m -1=0,根据抛物线的完美三角形的斜边长为n 得出点B 的坐标,然后代入抛物线求出m 和n 的值.试题解析:(1)、①过点B 作BN ⊥x 轴于N ,由题意可知△AMB 为等腰直角三角形,AB ∥x 轴, 易证MN=BN ,设B 点坐标为(n ,-n ),代入抛物线2y x =,得2n n =, ∴1n =,0n =(舍去),∴抛物线2y x =的“完美三角形”的斜边2AB = ②相等;(2)、∵抛物线2y ax =与抛物线24y ax =+的形状相同, ∴抛物线2y ax =与抛物线24y ax =+的“完美三角形”全等,∵抛物线24y ax +=的“完美三角形”斜边的长为4,∴抛物线2y ax =的“完美三角形”斜边的长为4, ∴B 点坐标为(2,2)或(2,-2),∴12a=±. (3)、∵225y mx x+n =+-的最大值为-1,∴()45414m n m--=-,∴410mn m --=,∵抛物线225y mx x+n =+-的“完美三角形”斜边长为n , ∴抛物线2y mx =的“完美三角形”斜边长为n ,∴B 点坐标为,22n n ⎛⎫- ⎪⎝⎭,∴代入抛物线2y mx =,得222n n m ⎛⎫⋅=- ⎪⎝⎭,∴2mn =-(不合题意舍去), ∴34m =-,∴83n =考点:(1)、二次函数的综合应用;(2)、直角三角形的性质.。
2016年北京市春季会考数学模拟考试试题印

中医附中2015~2016第一学期高三数学文科月考 2015年12月7日第一部分 选择题(每题3分共75分)姓名:一、在每个小题给出的四个备选答案中,只有一个是符合题目要求的.1.已知集合{}{}5,3,1,8,6,5,3==B A ,那么A B 等于( ) A. {}8,6,5,3,1 B. {}8,6 C. {}5,3 D. {}8,6,1 2 .已知过两点),4(),1,1(a B A -的直线斜率为1,那么a 的值是( ) A. 6- B. 4- C. 4 D. 6 3. lg4+2lg5的值为( )A . 2B . 5C . 18D . 20 4 .函数()2sin3cos3f x x x =⋅的最小正周期为( )A. πB. 2πC. 3πD. 6π5.函数21,lg ,cos ,y e y x y x y x -====中,奇函数是( )A. cos y x =B. x y e =C. lg y x =D. 1y x -=6.已知函数2,0()2,0x x f x x x ⎧≥=⎨-<⎩,如果0()4f x =,那么实数0x 的值为( )A. 2B. 0C. 2或2-D. 1或2-7.为了解某停车场中车辆停放的状况,在工作日(周一至周五)期间随机选取了一天,对该停车场内的1000辆汽车的停放时间进行了统计分析,绘制出车辆停放时间的频率分布直方图(如图所示),那么这1000辆汽车中停放时间不多于...4小时的汽车有( )A.700辆 B. 350辆 C. 300辆 D. 70辆8.盒子里装有大小完全相同且分别标有数字1,2,3,4的四个小球,从盒子里随机摸出两个小球,那么事件“摸出的小球上标有的数字之和为5”的概率是( )A.16 B. 13 C. 12 D. 23 9.已知平面向量(1,2),(2,)a b x =-=,且0a b ⋅=,那么b 等于( )A. B. C. 20 D. 5 10.已知某三棱锥的三视图如右图所示,那么三棱锥的体积是( )A.13 B. 1 C. 32 D. 9211在边长为2的正方形ABCD 内随机取一点P ,那么点P 到顶点A 的距离大于1的概率是( )A.16π B. 116π- C. 4π D. 14π- 12.在△ABC 中,角A 、B 、C 所对的边分别为,,a b c ,且1,60a b B ===,那么c 等于( )A. 1B. 2C. 3D. 4 13.函数()25ln f x x x =-+的零点所在的区间是( )A. (1,2)B. (2,3)C. (3,4)D. (4,5) 14.已知函数()x a x f sin ⋅=,如果()x f 在区间⎥⎦⎤⎢⎣⎡20π,上的最大值为3,那么a 的值为( ) A .0B .1C .2D .315已知实数y x ,满足条件⎪⎩⎪⎨⎧≤≥++≤--00202y y x y x ,那么目标函数y x z 2+=的最小值是( )A. 6-B. 4-C. 2-16. 在等比数列{}n a 中,,11=a a A .31- B .15 C 17.函数()xx x f 22+=()0>x A .1 B .2 18 已知函数)(x f 是定义在)0,4[-如图所示,那么)(x f A. )4,4(- B. ]6,6[- C. (19.国际能源署研究发现,在2000年发电量为a 度,那么经过12(61.06=A. 2aB. 3a 20.给定函数①x x f 2=)(;②f (任意的1x ,2x ,满足等式“)()()(2121x f x f x x f ⋅=+”的函数的序号是( )A .①B .②C .③D .④21.执行如图所示的程序框图,如果输出S=15,那么框图中①处关于k 的不等式应为( ) A .k<2 B .k<3 C .k<4 D .k<522.设,m n 是两条不同的直线,,αβ是两个不同的平面,给出下列四个命题: ①如果//,m n αα⊂,那么//m n ;②如果,m m αβ⊥⊥,那么//αβ;③如果,m αβα⊥⊥,那么//m β;④如果,,m m n αβαβ⊥⋂=⊥,那么n β⊥. 其中正确的命题是( )A. ①B. ②C. ③D. ④23 在ABC ∆中,如果4,3,5===BC AC AB ,那么角AC AB ∙等于:( )A.9; B.12; C.15; D.20.24.如果两点(-1,1),(0,-1)在直线kx-y=0的同一侧,那么实数k 的取值范围是() A .()1-∞-, B .()11,- C .(]20, D .()+∞,1 25.在直角坐标系xOy 中,对于点P (x ,y ),定义变换σ:将点P (x ,y )变换为P /(x /,y /),其中⎩⎨⎧-='+='byax y by ax x (a ,b 为常数).如果变换σ将直线y=2x 上的各点均变换为该点自身,则a +b 等于( ) A .43 B .45 C .49 D .411 第二部分解答题 (本小题满分5分共25分)26. (本小题满分5分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c .且3,2,32π===A b a (1)求角B 的大小; (2)如果函数),2sin(sin )(B x x x f +-=求函数)(x f 的单调递增区间。
北京市房山区2016届九年级数学4月毕业会考(一模)试卷

房山区2016年九年级数学综合练习(一)一、 选择题(本大题共30分,每小题3分):1.为了减少燃煤对大气的污染,北京实施煤改电工程.每年冬季采暖季期间可压减燃煤约608000吨,将608000用科学记数法表示应为A.460.810⨯ B.46.0810⨯ C. 60.60810⨯ D. 56.0810⨯2.如图,数轴上有A ,B ,C ,D 四个点,其中表示2的相反数的点是A .点AB .点BC .点CD .点D3.有五张形状、大小、质地都相同的卡片,这些卡片上面分别画有下列图形:①正方形;②等边三角形;③平行四边形;④等腰三角形;⑤圆.将卡片背面朝上洗匀,从中随机抽取一张,抽出的纸片正面图形是轴对称图形,但不是中心对称图形的概率是 A. 51 B.52 C. 53 D. 54 4.如图,在△ABC 中,∠C =90°,点D 在AC 边上,DE ∥AB ,如果∠ADE =46°,那么∠B 等于 A .34° B.54° C .46° D .44°5.象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种。
由于用具简单,趣味性强,成为流行极为广泛的棋艺活动。
如图是一方的棋盘,如果“帅”的坐标是(0,1),“卒”的坐标是(2,2),那么“马”的坐标是A .(-2,1)B .(2,-2)C .(-2,2)D .(2,2)6.为了估算河的宽度,我们可以在河对岸的岸边选定一个目标记为点A ,再在河的这一边选点B 和点C ,使得AB ⊥BC ,然后再在河岸上选点E ,使得EC ⊥BC ,设BC 与AE 交于点D ,•如图所示,测得BD=120米,DC=60米,EC=50米,那么这条河的大致宽度是B4题图A12345-1-2-3-46A.75米 B.25米 C.100米 D.120米7. 在“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩的A. 中位数B. 众数C.平均数D. 方差8. 下列几何体中,主视图相同的是A.①② B.①④ C.①③ D.②④9.如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为A. 23π B.83π C.6π D.103π10.如图,在正方形ABCD中,AB=3cm,动点M自点A出发沿AB方向以每秒1厘米的速度运动,同时动点N自点A出发沿折线AD—DC—CB以每秒3厘米的速度运动,到达点B时运动同时停止.设△AMN的面积为y (厘米2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是二、填空题(本大题共18分,每小题3分):NMD CBA211. 分解因式:3a a -=________________.12.已知反比例函数的图象经过A(2,-3),那么此反比例函数的关系式为______.13. 2016年3月12日“植树节”前夕,某小区为绿化环境,购进200棵柏树苗和120棵枣树苗,且两种树苗所需费用相同.每棵枣树苗的进价比每棵柏树苗的进价的2倍少5元,求这两种树苗的进价分别是多少元.如果设每棵柏树苗的进价是x 元,那么可列方程为______________.14.关于x 的一元二次方程mx 2+4x +1=0有两个实数根,那么m 的取值范围是 .15. 二次函数y=ax 2+bx+c(a ≠0)图象经过A(-1,m),B(2,m).写出一组满足条件的a 、b 的值:a=_____,b=______. 16.如图,已知∠AOB . 小明按如下步骤作图:① 以点O 为圆心,任意长为半径画弧,交OA 于点D ,交OB 于点E . ② 分别以D ,E 为圆心,大于12DE 长为半径画弧,在∠AOB 的内部两弧交于点C .③ 画射线OC .所以射线OC 为所求∠AOB 的平分线. 根据上述作图步骤,回答下列问题:(1)写出一个正确的结论:________________________. (2)如果在OC 上任取一点M ,那么点M 到OA 、OB 的距离相等.依据是:_______________________________________________________.三、解答题(本大题共72分,其中第17—26题,每小题5分,第27题7分,第28题7分,第29题8分):17. 计算:1)21(31)-(2016+3tan30 -+-+︒π.18.已知07432=--a a ,求代数式22))(()12(b b a b a a --+--的值.19. 解分式方程:2212+=--x x x .20.已知:如图,在△ABC 中,∠ABC = 90°,BD 为AC 边的中线,过点C 作 CE∥AB 与BD 延长线交于点E .EB4求证:∠A =∠E .21.列方程(组)解应用题:为提高饮用水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A 、B 两种型号家用净水器共160台,A 型号家用净水器进价为每台150元,B 型号家用净水器进价为每台350元,购进两种型号的家用净水器共用去36000元.求A 、B 两种型号家用净水器各购进了多少台.22. 如图,在ABCD 中,E 为BC中点,过点E 作 AB EG ⊥于G ,连结DG ,延长DC ,交GE 的延长线于点H.已知10BC =,45GDH ∠=︒,DG =求 CD 的长.23 .如图,在平面直角坐标系中,点A (2,0),B (0,3),C (0,2),点D 在第二象限,且△AOB ≌△OCD .(1) 请在图中画出△OCD ,并直接写出点D 的坐标; (2) 点P 在直线AC 上,且△PCD 是等腰直角三角形.坐标.24.如图,AB 为⊙O 的直径,点C 在⊙O 上, 且∠CAB=30°,点D 为弧AB 的中点, AC=求CD 的长.25. “PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,也称可入肺颗粒物.公众对于大气环境质量越来越关注,某市为了了解市民对于“PM 2.5浓度升高时,对于户外活动的影响”的态度,随机抽取了部分市民进行调查.根据调查的相关数据,绘制的统计图表如下:Ax根据以上信息解答下列问题:(1)直接写出统计表中m 的值; (2)根据以上信息,请补全条形统计图;(3)如果该市约有市民400万人,根据上述信息,请你估计一下持有“影响很大,尽可能不去户外活动”这种态度的约有多少万人.26.如图,在平面直角坐标系xOy 中,双曲线12y x=(1)当x 时,1y >0;(2)直线2y x b =-+,当b =线有唯一公共点,问:b 时,直线与双曲线有两个公共点;(3)如果直线2y x b =-+与双曲线12y x=交于A 、B 两点,且点A 的坐标为(1,2),点B 的纵坐标为1.设E 为线段AB 的中点,过点E 作x 轴的垂线EF ,交双曲线于点F .求线段EF 的长.27. 如图,二次函数c bx x ++-=2y 的图象(抛物线)与x 轴交于A(1,0), 且当0x =和2x -=时所对2% 42% C6% E30% BDA PM2.5浓度升高时对于户外活动 公众的态度的扇形统计图PM2.5浓度升高时对于户外活动 公众的态度的条形统计图应的函数值相等.(1)求此二次函数的表达式;(2)设抛物线与x轴的另一交点为点B,与y轴交于点C,在这条抛物线的对称轴上是否存在点D,使得△DAC的周长最小?如果存在,求出D点的坐标;如果不存在,请说明理由. (3)设点M在第二象限,且在抛物线上,如果△MBC的面积最大,求此时点M的坐标及△MBC 的面积.28.如图1,在四边形ABCD中,BA=BC,∠ABC=60°,∠ADC=30°,连接对角线BD.(1)将线段CD绕点C顺时针旋转60°得到线段CE,连接AE.①依题意补全图1;②试判断AE与BD的数量关系,并证明你的结论;(2)在(1)的条件下,直接写出线段DA、DB和DC之间的数量关系;(3)如图2,F是对角线BD上一点,且满足∠AFC=150°,连接FA和FC,探究线段FA、FB和FC 之间的数量关系,并证明.(图1)(图2)29.在平面直角坐标系xoy中,对于任意三点A,B,C给出如下定义:如果正方形的任何一条边均与某条坐标轴平行,且A,B,C三点都在正方形的内部或边界上,那么称该正方形为点A,B,C的外延正方形,在点A,B,C所有的外延正方形中,面积最小的正方形称为点A,B,C的最佳外延正方形.例如,图1中的正方形A1B1C1D1,A2B2C2D2,A3B3CD3都是点A,B,C 的外延正方形,正方形A3B3CD3是点A,B,C的最佳外延正方形.(图1)(图2)(1)如图1,点A(-1,0),B(2,4),C(0,t)(t为整数).①如果t=3,则点A,B,C的最佳外延正方形的面积是;②如果点A,B,C的最佳外延正方形的面积是25,且使点C在最佳外延正方形的一边6上,请写出一个符合题意的t值;(图3 )(图4)(2)如图3,已知点M(3,0),N(0,4),P(x,y)是抛物线y=x2-2x-3上一点,求点M,N,P的最佳外延正方形的面积以及点P的横坐标x的取值范围;(3)如图4,已知点E(m,n)在函数x6y (x>0)的图象上,且点D的坐标为(1,1),设点O,D,E的最佳外延正方形的边长为a,请直接写出a的取值范围.8房山区2016年九年级数学综合练习(一)参考答案及评分标准 三、 选择题(本大题共30分,每小题3分):四、 填空题(本大题共18分,每小题3分):11.()()11a a a +-. 12. y=x6-. 13. ()20012025x x =-. 14.4≤m 且0≠m . 15. a=1,b=-1. 答案不唯一(全对给3分).16. (1) OD=OE 或DC=EC 或OC 平分∠AOB 等等均可;--------------------------1分(2)角平分线上的点到角两边距离相等. --------------------------3分三、解答题(本大题共72分,其中第17—26题,每小题5分,第27题7分,第28题7分,第29题8分): 17.解: 1)21(31)-(2016+3tan30 -+-+︒π=2131333+-++⨯----------------------------4分 =232+ ----------------------------5分18.解:法1:22))(()12(b b a b a a --+--=2222)(144b b a a a ---+- ---------------------------2分 =2222144b b a a a -+-+-=1432+-a a ----------------------------3分∵07432=--a a ,∴7432=-a a , -----------------------------4分 当7432=-a a 时原式=17+=8 --------------------------5分 法2:22))(()12(b b a b a a --+--=2222)(144b b a a a ---+- ---------------------------2分=2222144b b a a a -+-+-=1432+-a a ----------------------------3分∵07432=--a a , ∴11-=a ,372=a -----------------------------4分 当11-=a 时,原式=8 当372=a 时,原式=8 ------------------------------5分19.解: x x x x x 2)2()2)(2(=+-+- ---------------------------1分x x x x 22422=--- ----------------------------2分解得:1-=x------------------------------------------------3分经检验1-=x 是原方程的解.------------------------------------------------4分 ∴原方程的解是1-=x .-------------------------------------------------5分20.证明:法1:∵在△ABC 中, ∠ABC = 90°,BD 为AC 边的中线.∴BD=AD =21AC .---------------------------------------------1分∴∠A= ∠ABD ,---------------------------------------------3分∵CE∥AB , ∴∠ABD=∠E .--------------------------------------------4分∴∠A=∠E . ---------------------------------------------5分法2:∵CE∥AB ,∴∠ABC+∠EC B=180°.---------------------------------------------1分10∵∠ABC = 90°, ∴∠EC B= 90°.---------------------------------------------2分∴∠A +∠ACB =90°,∠E +∠EBC= 90°.∵在△ABC 中, ∠ABC = 90°,BD 为AC 边的中线,∴CD=BD =21AC .---------------------------------------------3分∴∠ACB =∠EBC ,-----------------------------------------------4分∴∠A=∠E .------------------------------------------------5分法3:∵CE∥AB ,∴∠ABC+∠EC B=180°.---------------------------------------------1分∵∠ABC = 90°,∴∠EC B= 90°.----------------------------------------------2分∴∠ABC =∠EC B .∵在△ABC 中, ∠ABC = 90°,BD 为AC 边的中线,∴CD=BD =21AC .--------------------------------------------3分∴∠ACB =∠EBC ,--------------------------------------------4分∴△ABC∽△ECB .∴∠A=∠E . --------------------------------------------5分法4:∵在△ABC 中, ∠ABC = 90°,BD 为AC 边的中线,∴CD=BD =21AC .---------------------------------------------1分∴∠DCB = ∠DBC ,-------------------------------------------2分∵CE∥AB ,∴∠ABC+∠EC B=180°.----------------------------------------------3分∵∠ABC = 90°,∴∠EC B =90°. ∴∠ABC =∠ECB .----------------------------------------------4分∵BC=CB∴△ABC ≌△ECB .∴∠A=∠E . ----------------------------------------------5分法5:∵在△ABC 中, ∠ABC = 90°,BD 为AC 边的中线,∴BD=CD =21AC .---------------------------------------------1分∴∠DBC=∠DCB ,---------------------------------------------2分∵CE∥AB ,∴∠ABC+∠EC B=180°.--------------------------------------------3分∵∠ABC = 90°,∴∠EC B =90°. ∴∠ABC =∠EC B .---------------------------------------------4分∴∠ABC-∠DBC =∠EC B-∠DCB .即:∠ABD =∠ECD ∵∠ADB =∠EDC .∴∠A=∠E . --------------------------------------------5分21.解:设购进A 型号净水器每台x 元,B 型号净水器每台y 元,-----------------------1分根据题意,得:---------------------------3分解得:⎩⎨⎧==60100y x ----------------------------5分答:A 种型号家用净水器购进了100台,B 种型号家用净水器购进了60台.22.解:∵四边形ABCD 是平行四边形∴AB ∥CD ,12∵E G ⊥AB 于点G , ∴.90︒=∠=∠EHC BGE在△DHG 中,︒=∠90GHD ,45GDH ∠=︒,DG =∴8DH GH ==. -------------------------1分 ∵E 为BC 中点,10BC =,∴5BE EC ==. ------------------------2分 ∵BEG CEH ∠=∠ ∴△BEG ≌△CEH . ∴142GE HE GH ===. ------------------------3分 在△EHC 中,90H ∠=︒,5CE =,4EH =,∴3CH =. -----------------------4分∴5=CD -------------------------5分23.(1)图1,正确画出△COD ---------------------------1分(图1) (图2) (图3)点D 的坐标为:D (-3,2). -----------------------2分 (2) 由OC =OA =2,∠AOC =90°, ∴∠OAC =45°. ∵A (2,0),C (0,2)∴过A 、C 两点的一次函数的关系式为:2+-=x y ------------------3分当CD 为直角边时,如图2,此时,点P 的横坐标为-3.∴P(-3,5). --------------------------------------4分 ② 当CD 为斜边时,如图,此时3,点P 的横坐标为32-. ∴P(32-72). ---------------------------------------5分 x∴在直线AC 上,使△PCD 是等腰直角三角形的点P 坐标为:(-3,5)或(32-,72).24.解法1:连结BC∵AB 为⊙O 的直径,点C 在⊙O 上, ∴∠ACB =90°. -------------1分 ∵∠CAB =30°,∴∠D =60°. ---------------2分∵点D 为弧AB 的中点,∴∠ACD =45°.过点A 作AE ⊥CD , ∵AC=∴AE=CE =分 ∴DE =. ------------------------4分 ∴CD =分解法2:∵AB 为⊙O 的直径,点D 为弧AB 的中点,∴∠DAB =∠ACD =45°. ------------1分∵∠CAB =30°,∴弧BC=60°,弧AC =120°.∴∠ADC =60°. ------------------2分 过点A 作AE ⊥CD , ∵AC=∴AE=CE =. -----------------------3分 ∴DE =分 ∴CD =分25. 解:(1)20%; ----------------------------------1分 (2)如图 -----------------------3分B AB A(3)400×20%=80(万人). -----------------------5分26.解:(1)x >0 -----------1分(2)当b <22-或b >22,-----3分(3)∵点B 的纵坐标为1,∴点B 的横坐标为2,∵点E 为AB 中点,∴点E 坐标为()23,23 ---------4分∴点F 的坐标为(23,34)∴EF=613423=- -------------5分27.解:(1)∵二次函数c bx x ++-=2y , 当0x =和2x -=时所对应的函数值相等,∴二次函数c bx x ++-=2y 的图象的对称轴是直线1-=x . ∵二次函数c bx x ++-=2y 的图象经过点A (1,0),∴⎪⎩⎪⎨⎧-=++-=1210bc b ----------------------------------------1分解得⎩⎨⎧=-=32c b∴二次函数的表达式为:32y 2+--=x x . ---------------------------------------2分(2)存在 由题知A 、B 两点关于抛物线的对称轴x=﹣1对称∴连接BC ,与x=﹣1的交于点 D ,此时△DAC 周长最小----------------------3分 ∵32y 2+--=x x∴C 的坐标为:(0,3)直线BC 解析式为:y=x+3 --------------------4分 ∴D (﹣1,2); ---------- 5分(3) 设M 点(x ,322+--x x )(﹣3<x <0) 作过点M 作ME ⊥x 轴于点E ,则E(x,0)∵S △MBC =S 四边形BMCO ﹣S △BOC =S 四边形BMCO ﹣29,S 四边形BMCO =S △BME +S 四边形MEOC)(2121OC ME OE ME BE +⨯⨯+⨯⨯==21(x+3)(322+--x x )+21(﹣x )(322+--x x +3)=8272923232++⎪⎭⎫ ⎝⎛+-x∵要使△MBC 的面积最大,就要使四边形BMCO 面积最大 当x=23-时,四边形BMCO 在最大面积=82729+ ∴△BMC最大面积=8272982729=-+--------------------------------6分 当x=23-时,32y 2+--=x x =415 ∴点M坐标为(23-,415 )--------------------------------7分 28.(1)①补全图形,如图1---------------------------------1分 ②判断:AE =BD---------------------------------2分 证明:如图2,连接ACB16∵BA =BC ,且∠ABC =60° ∴△ABC 是等边三角形 ∴∠ACB =60°,且CA =CB∵将线段CD 绕点C 顺时针旋转60°得到线段CE ∴CD =CE ,且∠DCE =60° ∴∠BCD =∠ACE∴△BCD ≌△ACE (SAS )∴AE =BD(2)判断:222DA DC DB +=(3)判断:222FA FC FB +=证明:如图3,连接AC∵BA =BC ,且∠ABC =60° ∴△ABC 是等边三角形 ∴∠ACB =60°,且CA =CB将线段CF 绕点C 顺时针旋转60°得到线段CE ,连接EF 、EA ∴CE =CF ,且∠FCE =60°, ∴△CEF 是等边三角形 ∴∠CFE =60°,且FE =FC ∴∠BCF =∠ACE∴△BCF ≌△ACE (SAS )∴AE =BF ∵∠AFC =150°, ∠CFE =60° ∴∠AFE =90°在Rt △AEF 中, 有:222FA FE AE += ∴222FA FC FB +=.---------------------------------7分 29.解:(1)①16;B28-图3CBD---------------------------------2分②5或-1;----------------------------------3分(2)以ON 为一边在第一象限作正方形OKIN ,如图3①点M 在正方形OKIN 的边界上,抛物线一部分在正方形OKIN 内,P 是抛物线上一点, ∴正方形OKIN 是点M ,N ,P 的一个面积最小的最佳外延正方形 ∴点M ,N ,P 的最佳外延正方形的面积的最小值是16;∴点M ,N ,P 的最佳外延正方形的面积S 的取值范围是:S ≥16 -----------------5分满足条件的点P 的横坐标x 的取值范围是≠x 3 ------------------------------6分(3)6≥a----------------------------------8分。
2016年北京春季普通高中会考

2016年北京市春季普通高中会考数 学 试 卷第一部分 选择题(每小题3分,共60分)在每个小题给出的四个备选答案中,只有一个是符合题目要求的. 1.函数2sin 3)(+=x x f 的最小正周期是A. 1B. 2C. πD. 2π2. 已知集合{}{}3,,1,2,1m B A ==,如果A B A = ,那么实数m 等于( ) A. 1- B. 0 C. 2 D. 4 3. 如果向量a =(1,2),b =(4,3),那么a 2-b 等于( )A .)(8,9 B. ),(4-7- C. ),(47 D. )(8-,9- 4.在同一直角坐标系xOy 中,函数x y cos =与x y cos -=的图像之间的关系是( ) A .关于x 轴对称 B. 关于y 轴对称 C. 关于直线x y =对称 D. 关于直线y -=5.执行如图所示的程序框图.当输入2-时,输出的y A .2- B. 0 C. 2 D. 2±6.已知直线l 经过点)1,2(P ,且与直线022=+-y x 平行,那么直线l 的方程是A . 032=--y x B. 042=-+y x C. 042=--y x D.042=--y x7. 某市共有初中学生270000人,其中初一年级,初二年级,初三年级学生人数分别为99000,90000,81000.为了解该市学生参加“开放性科学实践活动”的意向,现采用分层抽样的方法从中抽取一个容量为3000的样本,那么应抽取初三学生的人数为( ) A . 800 B. 900 C. 1000 D. 11008.在ABC ∆中,3,2,600===∠BC AC C ,那么AB 的值是( )A .5 B.6 C.7 D. 229.口袋中装有大小和材质都相同的6个小球,其中有3个红球,2个黄球和1个白球.从中随机摸出1个小球,那么摸到红球或白球的概率是 A .61 B. 31 C. 21 D. 32 10.如果正方形的边长为1,那么AB AC ∙等于 A .1 B.2 C.3 D. 211.2015年9月3日,纪念中国人民抗日战争暨世界反法西斯战争胜利70周年大会在北京天安门广场隆重举行.大会的阅兵活动向全世界展示了我军威武文明之师的良好形象,展示了科技强军的伟大成就以及维护世界和平的坚定决心.在阅兵活动的训练工作中,不仅使用了北斗导航、电子沙盘、仿真系统、激光测距机、迈速表和高清摄像头等新技术装备,还通过信息管理中心对每天产生的大数据进行存储、分析,有效保证了阅兵活动的顺利进行.假如训练过程第一天产生的数据量为a ,其后每天产生的数据量都是前一天的)1( q q 倍,那么训练n 天产生的总数据量为( ) A .1-n aqB. naq C. q q a n ---1)1(1 D. qq a n --1)1(12.已知21cos =α,那么)α2cos(-等于( ) A .23-B. 21-C. 21D. 2313.在函数①1-=x y ;②x y 2=;③x y 2log =;④x y tan =中,图像经过点)1,1(的函数的序号是( )A .① B. ② C. ③ D. ④14. 8log 2log 44-等于( )A .2- B. 1- C. 1 D. 215.A .32 B. 24 C. 2124+ D. 21216.如果0 b a ,且1=+b a ,那么在不等式①1 b a ;② a b 11 ;③abb a 111+;④41ab 中,一定成立的不等式的序号是( ) A .① B. ② C. ③ D. ④17.在正方体1111D C B A ABCD -中,G F E ,,分别是11111,,BB C B B A 的中点.给出下列四个推断:①FG ∥平面D D AA 11;②EF ∥平面11D BC ;③FG ∥平面④平面EFG ∥平面11D BC ,其中推断正确的序号是( ) A .① ③ B. ① ④ C. ② ③ D. ②④18.已知圆1O 的方程为422=+y x ,圆2O 的方程为)(22=+-y a x .如果这两个圆有且只有一个公共点,那么a 的所有取值构成的集合是( ) A . {}1,1- B. {}3,3- C. {}3,3,1,1-- D.{}3,3,5,5--19.在直角坐标系xOy 中,已知点)2,4(A 和),0(b B 满足BA BO =,那么的b 值为( ) A. 3 B. 4 C. 5 D. 620.已知函数x a x f =)(,其中0 a ,且1≠a .如果以))(,(11x f x P ))(,((22x f x f Q 为端点的线段的中点在y 轴上,那么)((21x f x f ∙)等于 A. 1 B. a C. 2 D. 2a21. 已知点)1,0(A ,动点),(y x P 的坐标满足x y ≤,那么PA 的最小值是( )A .21B. 22C.23 D. 122. 已知函数1(2+=x xx f ).关于)x f (的性质,有以下四个推断:①)x f (的定义域是),∞+∞-(;②)x f (的值域是⎥⎦⎤⎢⎣⎡2121-,;③)x f (是奇函数;④)x f (是区间)2,0(上的增函数,其中推断正确的个数是( )A . 1 B. 2 C. 3 D. 423.为应对我国人口老龄化问题,某研究院设计了延迟退休方案.第一步:2017年女干部和女工人退休年龄统一规定为55岁;第二步:从2018年开始,女性退休年龄每3年延迟1岁,至2045年时,退休年龄统一规定为65岁.小明母亲是出生于1964年的女干部,据此方案,她退休的年份是( )A .2019 B. 2020 C. 2021 D. 202224. 已知函数x b x a x f cos sin (+=),其中R b R a ∈∈,.如果对任意R x ∈,都有2(≠)x f ,那么在不等式①44 b a +-;②44 b a --;③222 b a +;④422 b a +中,一定成立的不等式的序号是( )A .① B. ② C. ③ D. ④25.我国古代数学名著《续古摘奇算法》(杨辉)亿书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入33⨯的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示).我们规定,只要两个幻方的对应位置(如第一行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( ) A . 9 B. 8 C. 6 D. 4n n=1是a 结束开始第二部分 解答题(每小题5分,共25分)26.(本小题满分5分) 已知),(ππθ2∈,且53sin =θ. (Ⅰ)=θtan ;(将结果直接填写在答题卡...的相应位置上) (Ⅱ)求)3cos(πθ+的值.27.(本小题满分5分) 如图,在三棱柱中111C B A ABC -,⊥1BB 平面ABC ,D BB BC AB ABC ,1,2,9010====∠是棱上11B A 一点.(Ⅰ)证明:AD BC ⊥; (Ⅱ)求三棱锥ACD B -的体积.28.(本小题满分5分)已知直线1:=+y x l 与y 轴交于点,圆O 的方程为)(0222 r r y x =+.(Ⅰ)如果直线l 与圆O 相切,那么=r ;(将结果直接填写在答题卡...的相应位置上) (Ⅱ)如果直线l 与圆O 交于B A ,两点,且21=PBPA ,求r 的值. 29.(本小题满分5分) 数列{}n a 满足,,3,2,1,121 =+=+n a a a n nn {}n a 的前n 项和记为n S . (Ⅰ)当21=a 时,=2a ;(将结果直接填写在答题卡...的相应位置上) (Ⅱ)数列{}n a 是否可能....为等比数列?证明你的推断; (Ⅲ)如果01≠a ,证明:1111++-=n n n a a a a S .30.(本小题满分5分)已知函数12(2+-+=a bx ax x f ),其中R b R a ∈∈,. (Ⅰ)当1==b a 时,)x f (的零点为 ;(将结果直接填写在答题卡...的相应位置上) (Ⅱ)当34=b 时,如果存在R x ∈0,使得0)(0 x f ,试求a 的取值范围;(Ⅲ)如果对于任意[]1,1-∈x ,都有0)(≥x f 成立,试求b a +的最大值.参考答案:1-25 DCBAC ABCDA DBABC DACCA BCBDB 26.(Ⅰ)43-(Ⅱ)10334+-27. (Ⅰ)略(Ⅱ)3128. (Ⅰ)22(Ⅱ)35或529. (Ⅰ)52(Ⅱ)不可能(Ⅲ)略30. (Ⅰ)21-0,(Ⅱ)),(),(∞+∞3231- (Ⅲ)2。
2016北京市夏季会考数学试题 Word版含答案

2016北京市夏季会考数学试题 Word版含答案2016年北京市夏季普通高中会考数学试卷1. 考生要认真填写考场号和座位序号。
考2. 本试卷共6页,分为两个部分,第一部分为选择题,25个小题(共75分);生第二部分为解答题,5个小题(共25分)。
须3(试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必知须用铅笔作答;第二部分必须用黑色字迹的签字笔作答。
2B4(考试结束后,考生应将试卷、答题卡放在桌面上,待监考员收回。
3第一部分选择题(每小题分,共75分) 在每个小题给出的四个备选答案中,只有一个是符合题目要求的.A:B1(已知集合,那么等于 ,,,,A,,1,0,1,B,0,1,2B. C. D. A. ,,,,,,,,010,1,1,0,1,2侧(左)视图正(主)视图2. 已知某几何体的三视图如图所示,那么该几何体是( ) A(球 B. 圆锥 C. 圆台 D. 圆柱20001404003.某市有超市家,其中大型超市家,中型超市家,1460100小型超市家.现采用分层抽样的方法从中抽取一个容量为俯视图的样本,那么应抽取中型超市的数量为7204073A( B. C. D.4(等于 sin(,,,)sin,,sin,A. B. C. D. cos,,cos, 5(在长方体中,.该长方体的表面积为ABCD,ABCDAB,BC,2,AC,31111816412A( B. C. D.00,ABCAC6(在中,,那么等于( ) ,A,60,,B,45,BC,32612A( B. C. D. 2(,2,m)7(如果向量a=,b=(1,2),且a?b,那么实数等于( ) m,11,44A( B. C. D.8(在空间中,给出下列四个命题:? 平行于同一直线的两条直线平行; ?平行于同一平面的两条直线平行;?垂直于同一直线的两条直线平行; ?垂直于同一平面的两个平面平行. 其中正确命题的序号A(? B. ? C. ? D. ?9.直线的倾斜角的大小是 3x,y,1,00000A( 45 B. 60 C. 120 D. 135,,an10. 在数列中,,那么等于 a,1,a,a,2,(n,1,2,3,?,)a1nn,18A( ,2 B.C. D. ,11277717cos2,11.已知,,那么等于 sin,6366671175555A( B. C. D. ,,3399444412.函数的图像大致是 3333y22yy22y111110864221048668410212142468101214xx10864224681012141086422468101214xx 1111A( B. C. D. 22223,13.3函数3的单调递增区间是f(x),sinx,x,[0,]3324444,3,,,A( B. C. D. [0,][,,][,][0,,]22222xy,cosx14.在函数中,偶函数的个数是 y,2xy,xy,2,,0312A( B. C. D.MNM(0,,1)N(2,3)ax,2y,3,015.已知点,.如果直线垂直于直线,那么实数a 等于,4,2,11A( B. C. D.116.如果函数,那么等于 f(x),logxf()3311,11A( B. C. D. ,2217.每年的3月5日是“青年志愿者服务日”,共青团中央号召全国青年积极参加志愿服务活动.甲、乙2人随机参加“文明交通”和“邻里互助”两项活动中的一项,那么2人参加的活动恰好相同的概率是1111A( B. C. D. 643218.在区间内随机选一个实数,该实数恰好在区间内的概率是 x[0,4][1,3]1113A( B. C. D. 43242n19.已知,那么等于 f(4)f(n),2,2,?,2A( 15 B. 30 C. 55 D. 126222220.已知圆的方程为,圆的方程为,那么这两个圆x,y,4(x,a),(y,1),1OO12的位置关系不可能是 (((A( 外离 B. 外切 C. 内含 D. 内切2x,3y,,0,,21.已知实数满足,那么的最大值是 x,yz,y,xx,0,,y,0,35A( 12 B. C. D.22.2012年我国环境保护部批准《环境空气质量指数(AQI)技术规定(试行)》为国家环境保护标准,其中“空气质量指数(Air Quality Index,简称AQI)”是定量描述空气质量状况的无量纲指数,其类别如下表所示:0-50 51-100 101-150 151-200 201-300 AQI数据 301以上 AQI类别优良轻度污染中度污染重度污染严重污染根据北京市2014年和2015年的AQI数据,得到下图:根据上述信息,从统计学角度分析,下列结论中不正确的是 (((A. 2014年有9个月的AQI类别属于“轻度污染”B.2015年12月份AQI类别为“优”的天数一定为0C. 2014年上半年 AQI数据标准差大于2015年上半年 AQI数据标准差D. 每年的第二、第三季度空气质量较好*23.我国南宋数学家秦九韶(约公园1202-1261年)给出了求次多项式n(n,N) 1nn,的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,ax,ax,?,ax,a110nn,其程序开始框图如图所示.432输入 x,0.4当时,多项式的值为 x,0.6x,x,2.56x,1a,a,?,a,n,x12n100.21.589441.261762.248A( B. C. D. k,1,S,anC24. 已知点,,如果点在函数的图像上, A(,1,0)B(1,0)S,x,S,an,1,ABCC那么使得为直角三角形的点的个数为 88642A( B. C. D.是 22,,25.对于集合, M,aa,x,y,x,Z,y,Zk,k,1 k,n否给出如下三个结论:其中正确结论的个数是 6输出 SP,M? 如果,那么; ,,P,bb,2n,1,n,Z结束 c,M?如果,那么; c,4n,2,n,Z4? 如果,那么. a,Ma,Maa,M,1212第二部分解答题(每小题5分,共25分) 26.(本小题满分5分) 2 ,1已知函数的部分图像如图所示. f(x),sin(,x,)(,,0)6(?) ;(将结果直接填写在答题卡的相应位置上) ,,(((3π5π2π3πππππ3π2π5π3πOx0(?)求的值. x0222222 BDC27.(本小题满分5分)正方体被平面截去 ABCD,ABCD1111112一部分后得到几何体. 如图所示 ABD,ABCD11468101.在几何体的面上画出一条线段, ABD,ABCDAD1111EB1使该线段所在的直线平行于平面; BDC112.设为的中点,求证:平面. EBDBD,AECA11111ADBC 28.(本小题满分5分)5已知是公比为的等比数列,. a,1,a,a,,,qa112n3(?)当;(将结果直接填写在答题卡的相应位置上) q,(((n,2(?)在和之间插入个数,其中,使这个数成等差数列.anan,1,2,3,?,n,11记插入的个数的和为,求的最大值. SSnnn29.(本小题满分5分)22M已知圆的方程是. x,6x,y,16,0M(?)圆的半径是 ;(将结果直接填写在答题卡的相应位置上) (((lC,MBCMB(?)设斜率为的直线交圆于和点,交轴于点.如果的yk(k,0)A(,2,0) 4kk面积是,求的值.30.(本小题满分5分)2已知函数,其中.b,c,Rf(x),x,bx,cx,1b,(?)当的图像关于直线对称时, ;(将结果直接填写在答题卡的相应f(x)(((位置上)x,R(?)如果在区间不是单调函数,证明:对任意,都有; ,,,1,1f(x)f(x),c,1((2(?)如果在区间上有两个不同的零点. 求的取值范围.f(x)(0,1)c,(1,b)c 参考答案:1-25 C CBBD BC A BD DBACD ADCBC CB A BD,26.(?)(?)2 327. (?)略(?)略21028. (?)(?)的最大值q, Sn39429. (?)(?)或5 263130. (?)(?)略(?)(0,)-2 16。
2016年北京市高级中等学校招生考试数学试卷及答案
2016年北京市高级中等学校招生考试数学试卷学校 姓名 准考证号 考生须知1. 本试卷共8页,共三道大题,29道小题,满分120分。
考试时间120分钟。
2. 在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3. 试题答案一律填涂在答题卡上,在试卷上作答无效。
4. 在答题卡上,选择题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5. 考试结束后,将本试卷、答题卡和草稿纸一并交回。
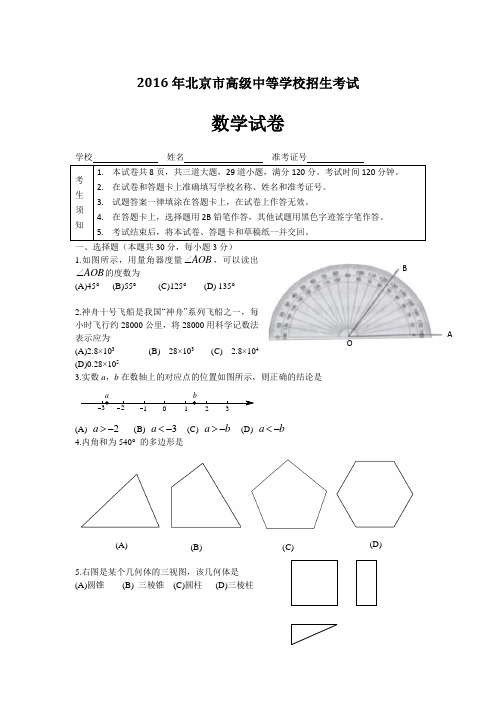
一、选择题(本题共30分,每小题3分)1.如图所示,用量角器度量AOB ∠,可以读出AOB ∠的度数为 (A)45° (B)55° (C)125° (D) 135°2.神舟十号飞船是我国“神舟”系列飞船之一,每小时飞行约28000公里,将28000用科学记数法表示应为 (A)2.8×103 (B) 28×103 (C) 2.8×104 (D)0.28×1053.实数a ,b 在数轴上的对应点的位置如图所示,则正确的结论是ba 3210123(A) 2a >- (B) 3a <- (C) a b >- (D) a b <- 4.内角和为540° 的多边形是5.右图是某个几何体的三视图,该几何体是 (A)圆锥 (B) 三棱锥 (C)圆柱 (D)三棱柱(A) (B) (C)(D)BAO6.如果2a b +=,那么代数式2b aa a ab ⎛⎫- ⎪-⎝⎭的值是 (A) 2 (B) -2 (C)12 (D)12-7.甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,不是..轴对称的是ABCD8.在1~7月份,某种水果的每斤进价与每斤售价的信息如图所示,则出售该种水果每斤利润最大的月份是(A)3月份 (B) 4月份 (C)5月份 (D)6月份第8题图 第9题图9.如图,直线m n ⊥,在某平面直角坐标系中,x 轴∥m ,y 轴∥n ,点A 的坐标为42-(,),点B 的坐标为24-(,),则坐标原点为 (A)1O (B) 2O (C) 3O (D) 4O10.为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增.计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%.为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:3m ),绘制了统计图,如图所示.下面有四个推断: ①年用水量不超过1803m 的该市居民家庭按第一档水价交费②年用水量不超过2403m 的该市居民家庭按第三档水价交费③该市居民家庭年用水量的中位数在150~180之间④该市居民家庭年用水量的平均数不超过180其中合理的是(A) ①③(B)①④(C) ②③(D)②④二、填空题(本题共18分,每小题3分)11.如果分式21x有意义,那么x的取值范围是.12.右图中四边形均为矩形,根据图形,写出一个正确的等式:.13.林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组统计数据:移植的棵数n1000 1500 2500 4000 8000 15000 20000 30000 成活的棵数m865 1356 2220 3500 7056 13170 17580 26430成活的频率mn0.865 0.904 0.888 0.875 0.882 0.878 0.879 0.881估计该种幼树在此条件下移植成活的概率为__________.14.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯小的影长分别为1.8m、1.5m,已知小军、小珠的身高分别为1.8m、1.5m,则路灯的高为__________m15.百子回归图是由1,2,3,...,100无重复排列而成的正方形数表,它是一部数化的澳门简史,如:中央四位“19 99 12 20”标示澳门回归日期,最后一行中间两位“23 50”标示澳门面积,……,同时它也是十阶幻方,其每行10个数之和、每列10个数之和、每条对角线10个数之和均相等,则这个和为________。
2016北京市普通高中会考数学模拟试题七

北京市普通高中会考数学模拟试题七数学试卷一、选择题(共20个小题,每小题3分,共60分)1.如果集合},1|{->=x x X 那么 ( )X A ⊆0. X B ∈}0.{ X x c ∈. X D ⊆}0.{2.以下四组函数中,表示同一个函数的是 ( )||)(.x x f A =与x x f =)( 1.+=x y B 与112--=x x y 1.+=x y c 与112--=x x y 1.-=x y D 与122+-=x x y 3.直线122=+y x 的倾斜角为 ( ) 45.A 60.B 135.c 150.D4.过点(0,1)并且与直线32+-=x y 垂直的直线方程是 ( )012.=--y x A 022.=+-y x B 012.=+-y x c 022.=--y x D5.已知偶函数)(x f y =在区间]4,0[上是增函数,则)3(-f 与)(πf 的关系是 ( ))()3(.πf f A >- )()3(.πf f B <- )()3(.πf f c =- )()3(.πf f D ≥-6.在区间],2[ππ上x y A sin .=单调递增,x y cos =单调递减B .x y sin =单调递减,x y cos =单调递增x y c sin .=单调递增,x y cos =单调递增x y D sin .=单调递减,x y cos =单调递减7.若,54sin =α且α为锐角,则α2sin 的值等于 ( ) 2512.A 2524.B 251.2-C 2524.-D 8.已知数列}{n a 满足,21+=+n n a a 且,21=a 那么=5a ( )7.A 8. B 9.c 10.D 9.已知M B A ),4,3(),0,1(是线段AB 的中点,那么向量AM 的坐标是 ( ))2,1.(A )2,1.(--B )1,2.(c )1,2.(--D10.圆心在点(2,O),且与y 轴相切的圆的方程为 ( )2)2.(22=+-y x A 2)2.(22=++y x B 4)2.(22=+-y x c 4)2.(22=++y x D11.已知数列}{n a 中,n n n S n a a a ),,4,3,2(,211 =-==-是其前n 项和,那么下列关系式中成立的是( )21.a a A < 54.a a B > 43.s S C > 65.S s D <12.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工为7人,则样本容量为 ( )7.A 15.B 25.c 35.D13.已知,0<<b a 那么下列不等式中一定成立的是 ( )0.<ab A 22.b a B < ||||.b a c < b a D 1.1.> 14.在同一坐标系中,x y )21(=与x y 2log =的图象都正确的是 ( )15.若函数⎩⎨⎧>+-≤+=,1,9,1,53)(x x x x x f 则)(x f 的最大值为 ( ) 9.A 8.B 7.c 6.D16.若某空间几何体的三视图如图所示,则该几何体的体积是 ( )2.A 1.B 32.c 31.D 17.将一枚质地均匀的硬币连续抛掷2次,记事件A 为“出现一次正面,一次反面”,则=)(A P ( )41.A 31.B 21.c 32.D18.在某项体育比赛中,七位裁判为一选手打出的分数如下:90 89 90 95 93 94 93去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )2,92.A 8.2,92.B 2,93.c 8.2,93.D19.某工厂为了治理污染,保护环境,拟投入资金用于对污染物进行处理.该厂计划一月份投资16万元,以后每个月比上个月投资减少l 万元,那么该厂当年12个月的投资总额为 ( )A.126万元 B .138万元 C .150万元 D .162万元20.下列函数关系中,可以看作是一次函数b ax y +=模型的是 ( )A.某个细胞分裂时,,第一次分裂为2个,第二次分裂为4个,第三次分裂为8个……这样所得到的细胞个数与细胞分裂次数之间的函数关系B .小球做自由落体运动,下降的高度与时间的关系(不计空气阻力)C .汽车的耗油量与行驶公里数的关系D .物体做简谐振动时位移与时间的关系二、填空题(共4个小题,每小题3分,共12分)21.函数2cos 2sin x x y =的最小正周期为_________ 22.已知),,2(),3,1(k b a ==且a 与b 垂直,则实数=k ______23.已知圆C 的圆心在第一象限,其半径小于5,那么圆C 的方程是__________.(只要求写出满足条件的一个方程)24.某程序框图如图所示,该程序运行后输出的结果是__________三、解答题(共3小题,共28分)25.(7分)如图,四棱柱1111.D C B A ABC 中,底面ABCD 是正方形,侧棱⊥A A 1底面E ABCD ,为A A 1的中点,求证:EBD C A 平面//1.26.(10分)已知函数b a bx ax x f ,(1)(2++=为实数),,R x ∈(1)若,0)1(=-f 且函数0)(≥x f 恒成立,求)(x f 表达式;(2)在(1)的条件下,当]2,2[-∈x 时,kx x f x g -=)()(是单调函数,求实数k 的取值范围;(3)设0>a 且)(x f 为偶函数,记⎩⎨⎧<->=).0)((),0)(()(x x f x x f x F 若,0.,0>+<n m mn 判断+)(m F )(n F 与0的大小. 27.(10分)设x 轴、y 轴正方向上的单位向量分别是i 、j ,坐标平面上点列*)(N n B A n n ∈、分别满足下列两个条件:①;11j i A A OA n n +==+且②.3)32(311i B B i OB n n n ⨯==+且 (1)求32OA OA 及的坐标,并证明点n A 在直线1+=x y 上;(2)若四边形11++n n n n A B B A 的面积是,n a 求*)(N n a n ∈的表达式;(3)对于(2)中的,n a 是否存在最小的自然数M ,对一切*N n ∈都有M a n <成立?若存在,求M;若不存在,说明理由,答案。
2016年北京市普通高中夏季会考数学试卷与解析word

2016年北京市普通高中夏季会考数学试卷一、在每个小题给出的四个备选答案中,只有一个是符合题目要求的.1.(3分)已知集合A={﹣1,0,1},B={0,1,2},那么A∩B等于()A.{0}B.{1}C.{0,1}D.{﹣1,0,1,2}2.(3分)已知某几何体的三视图如图所示,那么该几何体是()A.球B.圆锥C.圆台D.圆柱3.(3分)某市有超市2000家,其中大型超市140家,中型超市400家,小型超市1460家.现采用分层抽样的方法从中抽取一个容量为100的样本,那么应抽取中型超市的数量为()A.7 B.20 C.40 D.734.(3分)sin(π+α)等于()A.sinα B.﹣sinαC.cosαD.﹣cosα5.(3分)在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1=3.该长方体的表面积为()A.4 B.8 C.12 D.166.(3分)在△ABC中,∠A=60°,∠B=45°,BC=,那么AC等于()A.B.C.1 D.7.(3分)如果向量=(﹣2,m),=(1,2),且∥,那么实数m等于()A.﹣1 B.1 C.﹣4 D.48.(3分)在空间中,给出下列四个命题:①平行于同一直线的两条直线平行;②平行于同一平面的两条直线平行;③垂直于同一直线的两条直线平行;④垂直于同一平面的两个平面平行.其中正确命题的序号()A.①B.②C.③D.④9.(3分)直线x﹣y+1=0的倾斜角的大小是()A.45°B.60°C.120° D.135°10.(3分)在数列{a n}中,a1=1,a n•a n﹣1=2,(n=2,3,…,),那么a8等于()A.﹣2 B.﹣1 C.1 D.211.(3分)已知sinα=,那么cos2α等于()A.B.C.D.12.(3分)函数y=x的图象大致是()A.B. C.D.13.(3分)函数的单调递增区间是()A.B.[0,π]C.D.14.(3分)在函数y=2x,y=x2,y=2x,y=cosx中,偶函数的个数是()A.0 B.1 C.2 D.315.(3分)已知点M(0,﹣1),N(2,3).如果直线MN垂直于直线ax+2y﹣3=0,那么实数a等于()A.﹣4 B.﹣2 C.﹣1 D.116.(3分)如果函数f(x)=log3x,那么f()等于()A.﹣1 B.C.D.117.(3分)每年的3月5日是“青年志愿者服务日”,共青团中央号召全国青年积极参加志愿服务活动.甲、乙2人随机参加“文明交通”和“邻里互助”两项活动中的一项,那么2人参加的活动恰好相同的概率是()A.B.C.D.18.(3分)在区间[0,4]内随机选一个实数x,该实数恰好在区间[1,3]内的概率是()A .B .C .D .19.(3分)已知f(n)=2+22+…+2n,那么f(4)等于()A.15 B.30 C.55 D.12620.(3分)已知圆O1的方程为x2+y2=4,圆O2的方程为(x﹣a)2+(y﹣1)2=1,那么这两个圆的位置关系不可能是()A.外离B.外切C.内含D.内切21.(3分)已知实数x,y 满足,那么z=y﹣x的最大值是()A.1 B.2 C.3 D.522.(3分)2012年我国环境保护部批准《环境空气质量指数(AQI)技术规定(试行)》为国家环境保护标准,其中“空气质量指数(Air Quality Index,简称AQI)”是定量描述空气质量状况的无量纲指数,其类别如表所示:根据北京市2014年和2015年的AQI数据,得到如图:根据上述信息,从统计学角度分析,下列结论中不正确的是()A.2014年有9个月的AQI类别属于“轻度污染”B.2015年12月份AQI类别为“优”的天数一定为0C.2014年上半年AQI数据标准差大于2015年上半年AQI数据标准差D.每年的第二、第三季度空气质量较好23.(3分)我国南宋数学家秦九韶(约公园1202﹣1261年)给出了求n(n∈N*)次多项式a n x n+a n﹣1x n﹣1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2﹣2.56x+1的值为()A.0.2 B.1.58944 C.1.26176 D.2.24824.(3分)已知点A(﹣1,0),B(1,0),如果点C在函数y=﹣3x2+2的图象上,那么使得△ABC为直角三角形的点C的个数为()A.8 B.6 C.4 D.225.(3分)对于集合M={a|a=x2﹣y2,x∈Z,y∈Z},给出如下三个结论:其中正确结论的个数是()①如果P={b|b=2n+1,n∈Z},那么P⊆M;②如果c=4n+2,n∈Z,那么c∉M;③如果a1∈M,a2∈M,那么a1a2∈M.A.1 B.2 C.3 D.0二、解答题(每小题5分,共25分)26.(5分)已知函数f(x)=sin(ωx﹣)(ω>0)的部分图象如图所示.(Ⅰ)ω=;(将结果直接填写在答题卡的相应位置上)(Ⅱ)求x0的值.27.(5分)正方体ABCD﹣A 1B1C1D1被平面B1D1C截去一部分后得到几何体AB1D1﹣ABCD.如图所示.(1)在几何体AB1D1﹣ABCD的面上画出一条线段,使该线段所在的直线平行于平面B1D1C.(2)设E为B1D1的中点,求证:B1D1⊥平面A1ECA.28.(5分)已知{a n}是公比为q的等比数列,a1=1,a1+a2=.(Ⅰ)当q=;(Ⅱ)在a1和a n之间插入n个数,其中n=1,2,3,…,使这n+2个数成等差+1数列.记插入的n个数的和为S n,求S n的最大值.29.(5分)已知圆M的方程是x2﹣6x+y2﹣16=0.(Ⅰ)圆M的半径是;(Ⅱ)设斜率为k(k>0)的直线l交圆M于A(﹣2,0)和点B,交y轴于点C.如果△MBC的面积是4k,求k的值.30.(5分)已知函数f(x)=x2+bx+c,其中b,c∈R.(Ⅰ)当f(x)的图象关于直线x=1对称时,b=;(Ⅱ)如果f(x)在区间[﹣1,1]不是单调函数,证明:对任意x∈R,都有f(x)>c﹣1;(Ⅲ)如果f(x)在区间(0,1)上有两个不同的零点.求c2+(1+b)c的取值范围.2016年北京市普通高中夏季会考数学试卷参考答案与试题解析一、在每个小题给出的四个备选答案中,只有一个是符合题目要求的.1.(3分)已知集合A={﹣1,0,1},B={0,1,2},那么A∩B等于()A.{0}B.{1}C.{0,1}D.{﹣1,0,1,2}【解答】解:集合A={﹣1,0,1},B={0,1,2},那么A∩B={﹣1,0,1}∩{0,1,2}={0,1},故选:C.2.(3分)已知某几何体的三视图如图所示,那么该几何体是()A.球B.圆锥C.圆台D.圆柱【解答】解:由俯视图得到几何体为圆台;故选:C.3.(3分)某市有超市2000家,其中大型超市140家,中型超市400家,小型超市1460家.现采用分层抽样的方法从中抽取一个容量为100的样本,那么应抽取中型超市的数量为()A.7 B.20 C.40 D.73【解答】解:某市有超市2000家,其中大型超市140家,中型超市400家,小型超市1460家.现采用分层抽样的方法从中抽取一个容量为100的样本,则应抽取中型超市的数量为:100×=20.故选:B.4.(3分)sin(π+α)等于()A.sinα B.﹣sinαC.cosαD.﹣cosα【解答】解:利用诱导公式可得:sin(π+α)=﹣sinα.故选:B.5.(3分)在长方体ABCD﹣A 1B1C1D1中,AB=BC=2,AC1=3.该长方体的表面积为()A.4 B.8 C.12 D.16【解答】解:连结AC,∵在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1=3,∴AC===2,∴CC1===1,∴长方体ABCD﹣A1B1C1D1的表面积为:S=2S 正方形ABCD+4=2×(2×2)+4×(2×1)=16.故选:D.6.(3分)在△ABC中,∠A=60°,∠B=45°,BC=,那么AC等于()A.B.C.1 D.【解答】解:在△ABC中,由正弦定理得⇒=⇒AC=.故选:B7.(3分)如果向量=(﹣2,m),=(1,2),且∥,那么实数m等于()A.﹣1 B.1 C.﹣4 D.4【解答】解:∵∥,∴﹣2×2﹣m=0,得m=﹣4,故选:C.8.(3分)在空间中,给出下列四个命题:①平行于同一直线的两条直线平行;②平行于同一平面的两条直线平行;③垂直于同一直线的两条直线平行;④垂直于同一平面的两个平面平行.其中正确命题的序号()A.①B.②C.③D.④【解答】解:在①中,由平行公理得平行于同一直线的两条直线平行,故①正确;在②中,平行于同一平面的两条直线平行、相交或异面,故②错误;在③中,垂直于同一直线的两条直线平行、相交或异面,故③错误;在④中,垂直于同一平面的两个平面平行或相交,故④错误.故选:A.9.(3分)直线x﹣y+1=0的倾斜角的大小是()A.45°B.60°C.120° D.135°【解答】解:直线x﹣y+1=0即为y=x+1,则斜率为,设倾斜角为α,则tanα=,可得α=60°,故选:B.10.(3分)在数列{a n}中,a1=1,a n•a n﹣1=2,(n=2,3,…,),那么a8等于()A.﹣2 B.﹣1 C.1 D.2【解答】解:∵a1=1,a n•a n﹣1=2,∴a n•a n﹣1=a n+1•a n=2,=a n﹣1,则a n+1则a n=a n,+2即a8=a6=a4=a2,∵a1=1,a n•a n﹣1=2,∴a2•a1=2,得a2=2,即a8=2,故选:D.11.(3分)已知sinα=,那么cos2α等于()A.B.C.D.【解答】解:∵sinα=,那么cos2α=1﹣2sin2α=1﹣2•=,故选:D.12.(3分)函数y=x的图象大致是()A.B. C.D.【解答】解:函数是幂函数,定义域为:{x|x≥0},排除选项C,D,因为x>1时,,所以排除选项A.故选:B.13.(3分)函数的单调递增区间是()A.B.[0,π]C.D.【解答】解:对于函数f(x)=sinx,它的单调增区间为[2kπ﹣,2kπ+],k∈Z,再结合x∈[0,],可得它的增区间为[0,],故选:A.14.(3分)在函数y=2x,y=x2,y=2x,y=cosx中,偶函数的个数是()A.0 B.1 C.2 D.3【解答】解:在函数y=2x,y=x2,y=2x,y=cosx中,它们的定义域都是R,其中,满足f(﹣x)=f(x)的只有y=x2 和y=cosx,故偶函数有y=x2 和y=cosx.而满足f(﹣x)=﹣f(x)的只有y=2x,故函数y=2x为奇函数,而y=2x,不满足f(﹣x)=f(x),也不满足f(﹣x)=﹣f(x),故y=2x为非奇非偶函数,故选:C.15.(3分)已知点M(0,﹣1),N(2,3).如果直线MN垂直于直线ax+2y﹣3=0,那么实数a等于()A.﹣4 B.﹣2 C.﹣1 D.1【解答】解:根据题意,M(0,﹣1),N(2,3);则K MN==2,而直线ax+2y﹣3=0的斜率k=﹣,若直线MN垂直于直线ax+2y﹣3=0,则有2×(﹣)=﹣1,解可得a=1,故选:D.16.(3分)如果函数f(x)=log3x,那么f()等于()A.﹣1 B.C.D.1【解答】解:∵函数f(x)=log3x,∴f()==﹣1.故选:A.17.(3分)每年的3月5日是“青年志愿者服务日”,共青团中央号召全国青年积极参加志愿服务活动.甲、乙2人随机参加“文明交通”和“邻里互助”两项活动中的一项,那么2人参加的活动恰好相同的概率是()A.B.C.D.【解答】解:甲、乙2人随机参加“文明交通”和“邻里互助”两项活动中的一项,基本事件总数n=2×2=4,2人参加的活动恰好相同包含的基本事件个数m==2,∴2人参加的活动恰好相同的概率p=.故选:D.18.(3分)在区间[0,4]内随机选一个实数x,该实数恰好在区间[1,3]内的概率是()A.B.C.D.【解答】解:在区间[0,4]内随机选一个实数x,区间长度为4,而该实数恰好在区间[1,3]内的区间长度为2,所以所求概率是;故选:C.19.(3分)已知f(n)=2+22+…+2n,那么f(4)等于()A.15 B.30 C.55 D.126【解答】解:∵f(n)=2+22+…+2n,∴f(4)=2+22+23+24==30.故选:B.20.(3分)已知圆O1的方程为x2+y2=4,圆O2的方程为(x﹣a)2+(y﹣1)2=1,那么这两个圆的位置关系不可能是()A.外离B.外切C.内含D.内切【解答】解:圆O1的方程为x2+y2=4,圆心(0,0),半径为2;圆O2的方程为(x﹣a)2+(y﹣1)2=1,圆心(a,0)半径为:1,圆心距为:≥1=2﹣1,所以两个圆的位置关系不可能是内含.故选:C.21.(3分)已知实数x,y满足,那么z=y﹣x的最大值是()A.1 B.2 C.3 D.5【解答】解:画出实数x,y满足的可行域如图:将z=y﹣x变形为y=x+z作直线y=x将其平移至A(﹣3,0)时,直线的纵截距最大,最大为:3.故选:C.22.(3分)2012年我国环境保护部批准《环境空气质量指数(AQI)技术规定(试行)》为国家环境保护标准,其中“空气质量指数(Air Quality Index,简称AQI)”是定量描述空气质量状况的无量纲指数,其类别如表所示:根据北京市2014年和2015年的AQI数据,得到如图:根据上述信息,从统计学角度分析,下列结论中不正确的是()A.2014年有9个月的AQI类别属于“轻度污染”B.2015年12月份AQI类别为“优”的天数一定为0C.2014年上半年AQI数据标准差大于2015年上半年AQI数据标准差D.每年的第二、第三季度空气质量较好【解答】解:由图可得A,D正确,2014年上半年AQI数据波动比2015年上半年AQI数据波动小,故C正确,2015年12月份AQI类别为“优”的天数不一定为0,故B错误,故选:B.23.(3分)我国南宋数学家秦九韶(约公园1202﹣1261年)给出了求n(n∈N*)次多项式a n x n+a n﹣1x n﹣1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2﹣2.56x+1的值为()A.0.2 B.1.58944 C.1.26176 D.2.248【解答】解:模拟程序框图的运行,可得a0=1,a1=﹣2.56,a2=1,a3=0.6,a4=1,n=4,x=0.4,k=1,S=1,S=0.4×1+0.6=1,满足条件k<4,执行循环体,k=2,S=1×0.4+1=1.4,满足条件k<4,执行循环体,k=3,S=1.4×0.4﹣2.56=﹣2,满足条件k<4,执行循环体,k=4,S=(﹣2)×0.4+1=0.2,不满足条件k<4,退出循环,输出S的值为0.2.故选:A.24.(3分)已知点A(﹣1,0),B(1,0),如果点C在函数y=﹣3x2+2的图象上,那么使得△ABC为直角三角形的点C的个数为()A.8 B.6 C.4 D.2【解答】解:∵点A(﹣1,0),B(1,0),如果点C在函数y=﹣3x2+2的图象上,则设点C(a,﹣3a2+2),∵△ABC为直角三角形,①若A为直角顶点,则有AC⊥AB,此时,a=﹣1,点C的坐标为(﹣1,﹣1);②若B为直角顶点,则有BC⊥AB,此时,a=1,点C的坐标为(1,﹣1);③若C为直角顶点,则有AC⊥BC,此时,=(﹣1﹣a,3a2﹣2)•(1﹣a,3a2﹣2)=(﹣1﹣a)•(1﹣a)+(3a2﹣1)2=a2﹣1+9a4﹣12a2+4=9a4﹣11a2+3=0,求得a2=,或a2=,故此时,a的不同的值共有4个,此时,点C共有4个.综上可得,满足条件的点C共有6个,故选:B.25.(3分)对于集合M={a|a=x2﹣y2,x∈Z,y∈Z},给出如下三个结论:其中正确结论的个数是()①如果P={b|b=2n+1,n∈Z},那么P⊆M;②如果c=4n+2,n∈Z,那么c∉M;③如果a1∈M,a2∈M,那么a1a2∈M.A.1 B.2 C.3 D.0【解答】解:集合M={a|a=x2﹣y2,x∈Z,y∈Z},对于①,b=2n+1,n∈Z,则恒有2n+1=(n+1)2﹣n2,∴2n+1∈M,即P={b|b=2n+1,n∈Z},则P⊆M,①正确;对于②,c=4n+2,n∈Z,若4n+2∈M,则存在x,y∈Z使得x2﹣y2=4n+2,∴4n+2=(x+y)(x﹣y),又x+y和x﹣y同奇或同偶,若x+y和x﹣y都是奇数,则(x+y)(x﹣y)为奇数,而4n+2是偶数;若x+y和x﹣y都是偶数,则(x+y)(x﹣y)能被4整除,而4n+2不能被4整除,∴4n+2∉M,即c∉M,②正确;对于③,a1∈M,a2∈M,可设a 1=x12﹣y12,a2=x22﹣y22,x i、y i∈Z;则a1a2=(x12﹣y12)(x22﹣y22)=(x1x2)2+(y1y2)2﹣(x1y2)2﹣(x2y1)2=(x1x2+y1y2)2﹣(x1y2+x2y1)2∈M那么a1a2∈M,③正确.综上,正确的命题是①②③.故选:C.二、解答题(每小题5分,共25分)26.(5分)已知函数f(x)=sin(ωx﹣)(ω>0)的部分图象如图所示.(Ⅰ)ω=2;(将结果直接填写在答题卡的相应位置上)(Ⅱ)求x0的值.【解答】解:(Ⅰ)由五点对应法得•ω﹣=0.得ω=2.(Ⅱ)由(Ⅰ)得f(x)=sin(2x﹣),函数的周期是T==π,则x0﹣==,则x0=+=,故答案为:2,27.(5分)正方体ABCD﹣A1B1C1D1被平面B1D1C截去一部分后得到几何体AB1D1﹣ABCD.如图所示.(1)在几何体AB1D1﹣ABCD的面上画出一条线段,使该线段所在的直线平行于平面B1D1C.(2)设E为B1D1的中点,求证:B1D1⊥平面A1ECA.【解答】解:(1)如图,连接BD,则BD∥平面B1D1C,证明:∵由已知可得:BD∥B1D1,且BD⊄平面AB1D1,∴BD∥平面B1D1C.(2)证明:在等腰A1B1D1中,E为B1D1的中点,所以,B1D1⊥A1E,由已知可得:AA1⊥平面A1B1D1,所以,AA1⊥B1D1,所以,B1D1⊥平面A1ECA.28.(5分)已知{a n}是公比为q的等比数列,a1=1,a1+a2=.(Ⅰ)当q=;(Ⅱ)在a1和a n之间插入n个数,其中n=1,2,3,…,使这n+2个数成等差+1数列.记插入的n个数的和为S n,求S n的最大值.【解答】解:(Ⅰ)∵{a n}是公比为q的等比数列,a1=1,a1+a2=,∴,解得q=.故答案为:.(Ⅱ),∴=,依题意得S n==,∵S n﹣S n=﹣=.﹣1∴S1<S2,S2=S3,S3>S4>S5>…∴S n的最大值为S2=S3=.29.(5分)已知圆M的方程是x2﹣6x+y2﹣16=0.(Ⅰ)圆M的半径是5;(Ⅱ)设斜率为k(k>0)的直线l交圆M于A(﹣2,0)和点B,交y轴于点C.如果△MBC的面积是4k,求k的值.【解答】解:(Ⅰ)由x2﹣6x+y2﹣16=0,得(x﹣3)2+y2=25,∴圆M的半径是5.故答案为:5;(Ⅱ)设B(x0,y0),C(0,y1),直线l的方程为y=k(x+2)(k>0).联立,得(1+k2)x2+(4k2﹣6)x+4k2﹣16=0.∴,即.∴.在y=k(x+2)中,令x=0可得y1=2k.∴=.∵S=4k,且k>0,∴,解得k=或k=.30.(5分)已知函数f(x)=x2+bx+c,其中b,c∈R.(Ⅰ)当f(x)的图象关于直线x=1对称时,b=﹣2;(Ⅱ)如果f(x)在区间[﹣1,1]不是单调函数,证明:对任意x∈R,都有f (x)>c﹣1;(Ⅲ)如果f(x)在区间(0,1)上有两个不同的零点.求c2+(1+b)c的取值范围.【解答】解:(Ⅰ)函数f(x)=x2+bx+c的对称轴为x=﹣,由f(x)的图象关于直线x=1对称,可得﹣=1,解得b=﹣2,故答案为:﹣2.(Ⅱ)证明:由f(x)在[﹣1,1]上不单调,可得﹣1<﹣<1,即﹣2<b<2,对任意的x∈R,f(x)≥f(﹣)=﹣+c=c﹣,由﹣2<b<2,可得f(x)≥c﹣>c﹣1;(Ⅲ)f(x)在区间(0,1)上有两个不同的零点,设为r,s,(r≠s),r,s∈(,1),可设f(x)=(x﹣r)(x﹣s),由c2+(1+b)c=c(1+b+c)=f(0)f(1)=rs(1﹣r)(1﹣s),且0<rs(1﹣r)(1﹣s)<[]2•[]2=,则c2+(1+b)c∈(0,).赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD内接于⊙O,对角线AC⊥BD于P,设⊙O的半径是2。
2016北京市普通高中会考数学模拟试题二

北京市普通高中会考数学模拟试题二数学试卷一、选择题:(共20个小题,每小题3分,共60分)1.设全集},3,2,1,0{=I 集合},3,2,0{},2,1,0{==N M 则=)C (IN M }1.{A }3,2.{B }2,1,0.{c ∅.D2.在等比数列}{n a 中,,8,1685=-=a a 则=11aA. -4B.±4C. -2D.±23.下列四个函数中,在区间),0(+∞上是减函数的是x y A 3log .= x y B 3.= 21.x y c = x y D 1.=4.若,54sin =α且α为锐角,则αtan 的值等于 53.A 53.-B 34.c 34.-D 5.在C AB ∆中,,4,2,2π===A b a 则=B 3.πA 6.πB 656.ππ或c 323.ππ或D 6.在等差数列}{n a 中,若,99=S 则=+64a aA.0B.1C.2D.37.若,,,,b a R c b a >∈则下列不等式成立的是b a A 11.< 22.b a B > 1c 1.22+>+b c a c ||||.c b c a D > 8.已知二次函数,1)2()(2+-=x x f 那么)0()3()2(.f f f A << )3()2()0(.f f f B << )2()3()0(.f f f C << )3()0()2(.f f f D <<9.若函数⎩⎨⎧>+-≤+=1;91;53)(x x x x x f 则)(x f 的最大值为 A.9 B .8 C .7 D .610.在下列命题中,正确的是.A.垂直于同一个平面的两个平面互相平行 B .垂直于同一个平面的两条直线互相平行C .平行于同一个平面的两条直线互相平行D .平行于同一条直线的两个平面互相平行11.已知,0>x 函数xx y 1+=的最小值是 A.1 B .2 C .3 D .412.这50个学生“六一”节午餐费的平均值和方差分别是56.0,2.4.A 56.0,2.4.B 6.0,4.C 6.0,4.D13.下列命题中正确命题个数为;.a b b a =⋅① ;00,0=⇒=/=⋅b a b a ②;c ,0,0.==/=/=⋅a b a c b b a 则且③,0,0=/=/b a ④)()(,0c b a c b a c ⋅⋅=⋅⋅=/则A.0B.1C.2D.3 14.函数x x y 2cos 2sin =是A.周期为2π的奇函数 B .周期为2π的偶函数 C .周期为π的奇函数 D .周期为π的偶函数15.如图,一个空间几何体的正视图(主视图)与侧视图(左视图)为全等的等边三角形,俯视图为一个半径为1的圆,那么这个几何体的全面积为 ( )π.A π3.B π2.c 3.+πD16.已知实数x ,y 满足不等式组⎪⎩⎪⎨⎧≤-+≥≥,022,0,0y x y x 则y x z +=的最大值是A.1.B.1C.2D.317.以点(2,-1)为圆心且与直线3x-4y+5=0相切的圆的方程为3)1.()2.(22=++-y x A 3)1()2.(22=-++y x B9)1()2.(C 22=++-y x 9)1()2.(22=-++y x D18.已知),1,2(),4,3(-==b a 且⋅-⊥+)()(b a xb a 则x 等于23.A 223.B 323.c 423.D 19.要得到函数)42sin(π-=x y 的图象,只要将函数x y 2sin =的图象 A .向左平移4π个单位 B .向右平移4π个单位 C .向左平移8π个单位 D .向右平移8π个单位 20 猜商品的价格游戏观众甲:2000!主持人:高了!观众甲:1000!主持人:低了!.观众甲:1500! 主持人:高了!观众甲:1250!主持人:低了!观众甲:1375!主持人:低了!则此商品价格所在的区间是A. (1000,1250)B.(1250,1375)C. (1375,1500)D. (1500,2000)二、填空题(本大题共4小题,每小题3分,共12分)21.某个容量为100的样本的频率分布直方图如右图,则在区间[4,5)上的数据的频数为22.函数)1(log )(2x x f a -=的定义域为23.一个质地均匀的骰子连续投2次,点数和为4的概率24.阅读程序框图,若输入的n 是100,则输出的变量=S =T ,三、解答题(本大题共3小题,共28分).25.(8分)如图,在正四棱柱1111C D B A ABCD -中,AC 为底面ABCD 的对角线,E 为D D 1的中点(1)求证:;1AC B D ⊥(2)求证://1B D 平面.AEC26. (10分)已知等差数列}n{a 的前n 项和为.0,2,52==S a S n (1)求数列}{n a 的通项公式;(2)当n 为何值时n S 取得最大值.27.(10分)已知函数**∈∈=N y N x x f y ,),(,满足:①对任意,,,b a N b a =/⋅∈都有);()()()(a bf b af b bf a af +>+ ②对任意⋅∈N n 都有.3)]([n n f f =(1)试证明*N )(:为x f 上的单调增函数;(2)求);28()6()1(f f f ++(3)令,),3(⋅∈=N n f a n n 试证明⋅<+++41111:21n a a a。
2016北京市普通高中会考数学模拟试题三

北京市普通高中会考数学模拟试题三数学试卷一、选择题(共20个小题,每小题3分,共60分)1.若集合},31|{≤≤=x x A 集合},2|{<=x x B 则=B A}21|.{<≤x x A }21|.{<<x x B }3|.{≤x x c }32|.{≤<x x D=o 330tan .23.A 33.B3.-c 33.-D 3.已知,3lg ,2lg b a ==则=23lg b a A - . a b B -. a b c . ba D . 4.函数x x x f cos sin 2)(=的最大值为A.2B. -2C.1D. -15.随机投掷1枚骰子,掷出的点数恰好是3的倍数的概率为21.A 31.B 51.c 61.D 6.在等比数列}{n a 中,若23=a ,则=⋅54321a a a a a8.A 16.B 32.c 24.D7.已知点O(o ,0)与点A(O ,2)分别在直线m x y +=的两侧,那么m 的取值范围是02.<<-m A 20.<<m B 20.><m m c 或 20.-<>m m D 或8.如果直线012=++y ax 与直线023=-+y x 互相垂直,那么a 的值等于6.A 23.-B2.-c 6.-D 9.函数)62sin(π+=x y 图象的一个对称中心是)0,12.(π-A )0,6.(π-B )0,6.(πc )0,3.(πD 10.若函数c bx x x f ++=2)(对任意的实数t 都有)2()2(t f t f -=+,则)4(f )1()2(.<<f f A )4()2()1(.f f f B <<)1()4()2(.f f f C << )1()2()4(.f f f D <<11.点P 在直线04=-+y x 上,0为原点,则||OP 的最小值为2.-A 22.B 6.c 10.D12.函数x y 2cos =在下列哪个区间是减函数]4,4.[ππ-A ]43,4.[ππ-B ]2,0.[πC ],2.[ππD 13.如图,D 是△ABC 的边AB 的三等分点,则向量D C 等于A 32.+B 31.+c 32.+ D 31.+ 14.有四个幂函数:;)(1-=x x f ① ;)(2-=x x f ② ;)(3x x f =③ .)(31x x f =④某同学研究了其中的一个函数,他给出这个函数的两个性质:(1)定义域是}01,|{=/∈x f R x x (2)值域是⋅=/∈}0,|{y R y y 且如果这个同学给出的两个性质都是正确的,那么他研究的函数是A.① B.② C.③ D.④15.如果执行下面的程序框图,那么输出的S 等于A.45B.55C.90D.11016.将函数x y cos =的图象上的所有点的纵坐标不变,横坐标缩小到原来的一半,然后再将图象沿x 轴负方向平移4π个单位,则所得图象的解析式为 x y A sin .= x y B 2sin .-= )42cos(.C π+=x y )42cos(.π+=x y D 17.某住宅小区有居民2万户,从中随机抽取200户,调查是否已接入宽带.调查结果如下表所示:则该小区已接入宽带的住户估计有A.3000户 B .6500户 C .9500户 D .19000户18.在ABC ∆中,127,4,ππ==B A 角A 的对边2=a ,则角C 的对边c 等于 2.A 3.B 2.c 1.D19.半径是20cm 的轮子按逆时针方向旋转,若轮周上一点转过的弧长是40cm ,则轮子转过的弧度数是 ( )2.A π2.B 4.C π4.D20.如果方程.03422=+-a ax x 的一根小于1,另一根大于1,那么实数a 的取值范围是( )131.<<a A1.>a B 31.<a c 1.=a D 二、填空题(共4个小题,每小题3分,共12分)21.函数21)(x x f -=的定义域为22.在-1和4之间插入两个数,使这四个数顺次构成等差数列,则插入的两个数的和为23.把函数x y 2sin =的图象向左平移⋅6π个单位,得到的函数解析式为 24.不等式021>-+x x 的解集 三、解答题(共3个小题,共28分)25.(8分)已知⋅=<<54sin ,20απα (1)求αtan 的值;(2)求)2sin(2cos παα++的值.26.(10分)设二次方程)(0112⋅∈=+-+N n x a x a n n 有两根α和β且满足.3626=+-βαβα(1)试用n a 表示 1+n a(2)求证}32{-n a 是等比数列;(3)当671=a 时,求数列}{n a 的通项公式.27. (10分)已知点)1,0(A ,B ,C 是x 轴上两点,且6||=BC (点B 在C 的左侧).设ABC ∆的外接圆的圆心为M.(1)已知,4-=⋅试求直线AB 的方程;(2)当圆M 与直线y=9相切时,求圆M 的方程;(3)设,||,||21l AC l AB ==1221i l l l s +=试求s 的最大值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市普通高中会考数学模拟试题九
数学试卷
一、选择题(共20个小题,每小题3分,共60分)
1.已知集合},0)1)(2(|{=-+=x x x A 那么下列结论正确的是 ( )
A A ∈-2. A
B ∉1. A
C ∈2. A
D ∈-1.
2.如果直线012=-+y x 和kx y =互相平行,则实数k 的值为 ( )
2.A ⋅21.B 2.-c 2
1.-D 3.下列函数中,最小正周期为兀的是 ( ) x y A 4cos .= x y B 2sin .= 2sin
.x y c = 4cos .x y D = 4.下列函数中,在区间)2,0(π
上是减函数的是 ( )
x y A cos .= 2sin
.x y B = 2.x y C = 12.+=x y D 5.函数1
3+-=x x y 的定义域是 ( ) ),3[)1,.(+∞--∞u A ]3,1.(-B ),3[]1,.(+∞--∞u c ]3,1.[-D
6.实数5lg 24lg 4
1log 3922123
3++⋅-og 的值为 ( ) 25.A 28.B 32.c 33.D
7.设,3lg )(-+=x x x f 用二分法求方程03lg =-+x x 在(2,3)内近似解的过程中得)2.2(5f ,0)75.2(,0><f ,0)3(,0)5.2(><f f 则方程的根落在区间 ( )
)25.2,2.(A )5.2,25.2.(B )75.2,5.2.(c )3,75.2.(D
8.函数|
|3x y =为 ( ) A .偶函数且在),0(+∞上是减函数 B .偶函数且在),0(∞
+ 上是增函数 C .奇函数且在)0,(-∞上是减函数 D .奇函数且在)0,(-∞上是增函数
9.在空间中,a 、b 是不重合的直线,βα、是不重合的平面,则下列条件中可推出b a //的是( )
αα⊥⊥b a A ,. αα⊂b a B ,//. βαβα//,,.⊂⊂b a c αα⊂⊥b a D ,.
10.如图,在平行四边形ABCD 中,下列结论中正确的是 ( )
CD AB A =. BD AD AB B =-. AC AB AD C =+. 0.=+BC AD D
11.从l ,2,3,4这4个数中,不放回地任意取两个数,两个数都是奇数的概率是 ( )
61
.A 41.B 31.c 21
.D
12.数列}{n a 中,如果*),(21N n a a n n ∈=+且,21
1=a 那么数列}{n a 的前5项的和等于 ( )
431
.A 231.B 431.-c 231
.-D
13.圆心在点C(-2,1),并经过点A (2,-2)的圆的方程是 ( )
5)1()2.(22=++-y x A 25)1()2.(22=++-y x B
5)1()2.(22=-++y x c 25)1()2.(22=-++y x D
14.按照程序框图(如下图)执行,第3个输出的数是 ( )
7.A 6.B 5.c 4.D
15.已知实数x 、y 满足约束条件⎪⎩⎪⎨⎧≤+≥≥,
6,2,
2y x y x 则y x z 42+=的最大值为 ( )
24.A 20.B 16.c 12.D
16.已知向量),sin ,cos (.),2,4(αα=-=b a 且,b a ⊥则 ( )
34
.-A 34
.B 54
.-c 54
.D
17.如图为函数x m y n log +=的图象,其中m 、n 为常数,则下列结论正确的是
( )
1,0.><n m A 1,0.>>n m B 10,0.<<>n m c 10,0.<<<n m D
18.已知棱长为2的正方体的八个顶点都在同一个球面上,若在球内任取一点,则这一点恰在正方体内的概率为 ( )
π43.A π223.B π332.c .31.π
D 19.在金秋的苹果节上,某商家将参展的苹果摆成16层,从上到下每层的苹果数是一个等差数列,已知第
8层和第9层共有苹果40个,则此商家参展的苹果共有 ( )
A .300个
B .320个
C .340个
D .360个
20.已知某种笔筒,其三视图如图所示(单位:cm ).现要为100个这种相同规格的笔筒涂色(笔筒内外均
要涂色,笔筒厚度忽略不计).如果每0.5 kg 涂料可以涂,12m 那么为这批笔筒涂色约需涂料 ( )
kg A 23.1. kg B 76.1. kg C 46.2. kg D 52.3.
二、填空题(共4个小题,每小题3分,共12分)
21.已知.2||,3||==b a 若,3=⋅b a 则a 与b 夹角的大小为________
22. -个社会调查机构要了解某地区8000名教师的月收入情况,从中随机抽取400名进行调查,调查结果
则该地区月收入在]4000,2000[的教师估计有_______名.
23.在R 上定义运算.bc ad d c b a -=若,53)sin(-=-θπ则θθ
θθcos sin sin cos 的值是______ 24.已知圆C 的方程为,08222=--+x y x 写出一条与圆C 相切的直线的方程____________________
(写出一个满足题意的直线方程即可)
三、解答题(共3个小题,共28分)
25.(8分)如图,在四棱锥ABCD S -中,⊥SB 底面ABCD ,底面为ABCD 矩形,E 点为SB 的中点.
(1)求证:;SC AB ⊥
(2)求证://AD 平面.AEC
26.(10分)如图,某货轮在A 处看灯塔B 在货轮北偏东,75 距离为;1612e nmi 在A 处看灯塔C 在货轮的北偏西,30 距离为.138e nmi 货轮由A 处向正北航行到D 处时,再看灯塔B 在北偏东.120 求:
(1)A 处与D 处之间的距离;
(2)灯塔C 与D 处之间的距离.
27. (10分)定义函数:)(x f y =对于任意整数m ,当实数)2
1,21(+-∈m m x 时,有.)(m x f = (1)设函数的定义域为D ,画出函数)(x f 在]4,0[ D x ∈上的图象;
(2)若数列*),()5
2
(102N n a n n ∈+=记),()()(21n n a f a f a f s +++= 求;n s (3)若等比数列}{n b 的首项是,11=b 公比为),0(>q q 又,4)()()(321=++b f b f b f 求公比q 的取值范围.
答案。
