实变3-4
实变函数第四章答案

实变函数第四章▉▉第4章 Lebesgue (习题及参考解答)E E A 1.设是)(x f 上的可积函数,如果对于上的任意可测子集,有()0Af x dx =∫,试证:=0,)(x f ].[.E e a }1)(|{}0)(|{1kx f x E x f x E k ≥=≠∞=∪k ∀∈ 证明 因为,,而}1)(|{kx f x E ≥}1)(|{}1)(|{k x f x E k x f x E −≤≥=∪,由已知,有111{||()|}{|()}{|()}()()()E x f x E x f x E x f x kkkf x dx f x dx f x dx ≥≥≤−=+∫∫∫000=+=.又因为11{|(){|()}1110(){|()}E x f x E x f x kkf x dx dx mE x f x k k k≥≥0=≥=≥∫∫≥ 并且11{|()}{|()1110(){|()E x f x E x f x kkf x dx dx mE x f x k k k ≥−≥−⎛⎞=≤−−≤⎜⎟⎝⎠∫∫}0−≤ 所以,0}1)(|{}1)(|{=−≤=≥kx f x mE k x f x mE .故,0}1)(|{}1)(|{}1|)(|{=−≤+≥=≥kx f x mE k x f x mE k x f x mE因此,11{|()0}[{|()|}k mE x f x m E x f x k∞=≠=≥∪111{|()|}00k k mE x f x k ∞∞==≤≥==∑∑0)(=x f .从而,,.].[.E e a2. 设,f g 都是E 上的非负可测函数,并且对任意常数,都有a })(|{})(|{a x g x mE a x f x mE ≥=≥)()(x g x f =,试证:,从而,()Ef x dx =∫()Eg x dx ∫.证明 我们证与f g 是同一个简单函数序列的极限函数. ∞=1){m m ψ对于及,令m ∀∈ 12,,1,0−=mm k }21)(2|{,m m k m k x f k x E E +≤≤= })(|{2,m x f x E E mm m ≥=并且再令,则是互不相交的可测集,并且. 定义简单函数k m E ,k m m k E E m ,21==∪∑==mk m m k E m m x kx 20)(2)(,χψ. E x ∈)()(lim x f x m m =∞→ψ.下面证明:,m ∀∈ m m m E x 2,0∈E x ∈∀0+∞=)(0x f , 若. 事实上,,则,有)()(0∞→∞→=m m x m ψ)()(lim 00x f x m n =∞→ψ. 即, .所以, +∞<)(0x f 若,则可取正整数,当)(00x f m >0m m ≥∀时, 有}21)(2|{})(0|{1210mm m k k x f k x E m x f x E x m +<≤=<≤∈−=∪ 故,存在使得)120(−≤≤mm k k }21)(2|{0mm k x f k x E x +<≤∈ mm k x f k 21)(20+<≤. 因此, 即,m m k E m m kx k x mk m 2)(2)(20,==∑=χψ. 故000|()()|()()m m 0f x x f x x ψψ−=− 011()02222m m m m k k k f x +−<−=→=)()(lim 00x f x m n =∞→ψ.从而,实变函数第四章▉▉同理,对m ∀∈ ,定义简单函数列∑==mkm m k E m m x kx 20)(2)(*,χψ,其中:}21)(2|{*,mm k m k x g k x E E +<≤=,. 12,,1,0−=mm k 并且.})(|{*,m x g x E E k m ≥=E x ∈)()(lim 0x g x m n =∞→ψ.,同上一样,我们可以证明:因,有a ∀∈ })(|{})(|{a x g x mE a x f x mE ≥=≥,则,a ∀∈ })(|{b x f a x mE <≤})(|{b x g a x mE <≤=.从而,,有)120(−≤≤∀m m k k,1{|()}22m k m mk k mE mE x f x +=≤< *,1{|()}22m k m m k k mE x g x mE +=≤<=并且.即,,mm m m m m mEm x g x mE m x f x mE mE 2,*2,})(|{})(|{=≥=≥=N m ∈∀=)(x m ψ)(x m ϕ.)()(lim )(lim )(x g x x x f m m m m ===∞→∞→ϕψ.因此,⎪⎩⎪⎨⎧=为有理数,当为无理数,当x x x x x f 31)(3. 若,计算.∫1,0[)(dx x f x x E |]1,0[{0∈=01]1,0[E E −=为有理数},解 设,则∫]1,0[)(dx x f +=∫∫1)()(]1,0[E dx x f dx x f∫∫∫+==0111E EE dx xdx xdx x10E E E ==+∫∫∫ 2]2[11101]1,0[====∫∫x dx xdx x .4. 设是中n 个可测集,若内每一点至少属于个集中的个集,证明:中至少有一个测度不小于n 1,,n E E ]1,0[]1,0[nq 1,,q n E E . 证明 令,其中:∑==ni E x x f i1)()(χi E χ为上的特征函数并且,有i E ]1,0[∈∀x q x x f ni E i≥=∑=1)()(χ所以,. 又因为q qdx dx x f =≥∫∫]1,0]1,0[)(1[0,1][0,1]()()inE i q f x dx x χ=≤=∑∫∫dx1n.1110,1()()i i nnnE E i i i i E i x dx x dx mE χχ=======∑∑∑∑∫∫nqmE i <,则 如果每个∑∑===⋅=>ni n i i q nq n n qmE 11nqmE i ≥这与矛盾. 从而,存在∑=≤ni i mE q 1(1)i i n ≤≤. 使得5. 设与都是f g E 上的可积函数,试证明:22g f +E 也是上可积函数.E 证明:(1)先证:设与都是)(x f )(xF 0()f x ≤上的可测函数并且E E ()F x ≤ ,若在].[.E e a )(x F 可积,则在)(x f 可积.N m l ∈∀,)()(0x F x f ≤≤ ,故].[.E e a ,因为事实上,l l x F x f )}({)}({0≤≤.因此,+∞<≤≤≤∫∫∫EE llE ldx x f dx x F dx x F dx x f mm)()}({)}({)}({,其中:m m S E E ∩=,}||||{∞<=x x S m . 从而,是∞=∫1})}({{l l E dx x F m实变函数第四章▉▉单调递增有上界的数列,故∫Edx x F )(∫∫∫≤=∞→EE ll E dx x F dx x f dx x f mm)()}({lim )(.又因单调递增有上界,所以存在,并且∫∞=mE m dx x f 1})({∫∞→mE l dx x f )(lim∫∫∫+∞<≤=∞→EE ll Edx x F dx x f dx x f m)()}({lim )(即. 所以,在+∞<≤∫dx x f E)(∫∞→∞→mE l l m dx x f )}({lim lim E )(x f 可积.E (2上可积.在E E 事实上,因为与在f g 上都可积. 所以, 与在||f ||g 上可积. 从而, +在E ||f ||g 上可积.||||f g ≤+E ,由(1)上可积.在6. 设+∞<mE ,是)(x f E 上的非负可测函数,,∞+<∫Edx x f )(})(|{k x f x E E k >=0lim =⋅∞→dx mE k k l .,试证明:k ∀∈ 证明 ,因为+∞<≤≤≤∫∫EE k dx x f dx x f kmE k)()(0所以)(0)(10∞→→≤≤∫k dx x f k mE Ek lim 0k k mE →∞=.故,又因为,由积分的绝对连续性(即,P85,定理4), 对于∫+∞<Edx x f )(δ<mA 0>∀ε0>∃δE A ⊂,,使得对于任何可测集,恒有,∫Adx x f |)(|∫<=Adx x f ε)(.0>δN k ∈0对于,根据,存在0lim =∞→k k mE ,0k k ≥∀时,δ<k mE ,有ε<≤⋅≤∫dx x f mE k kE k )(0.0lim =⋅∞→k k mE k .从而, +∞<mE E E 7. 设为可测集,并且,为)(x f 上的非负可测函数,,试证:在}1)(|{+<≤=∧k x f k x E E k E )(x f 上可积当且仅当级数收敛.∧∞=∑kk Ekm 1证明 设,k }1)(|{+<≤=∧k x f k x E E k ∈ )(⇒,因为在)(x f E 可积,故111()()kkk k k k EE E f x dx f x dx k dx k mE ∞∞∞====≥=∑∑∑∫∫∫⋅即,级数收敛.∑∞=∧⋅1k kEm k k ∀∈ )(⇐, 因为,则}1)(|{+<≤=k x f k x E E k k E k k E mE kmE mE k dx k dx x f kk+=+=+≤∫∫)1()1()(.又因并且,根据Lebesgue 基本定理,有∑∞==1)()()(k E x x f x f k χdx x x f dx x f m kE EE )()()(χ∫∫=1()()()kE k EE f x dx f x x dx χ∞==∑∫∫11()()kk k k k E f x dx kmE mE ∞∞===≤+∑∑∫+∞<+=+=∑∑∑∞=∞=∞=k k k k k k k mE kmE mE kmE 111.E 从而,在)(x f 上可积.8. 设是 上的可积函数,证明:.∫=−+→],[00|)()(|limb a k dx x f b x f f实变函数第四章▉▉R ′0>∀ε)(x ϕ证明 (1)先证:,使得,存在时直线上的连续函数∫<−+→],[0|)()(|limb a k dx x f b x f ε.对于,记:N ∀∈ ⎪⎩⎪⎨⎧−<−>≤=N x f N N x f N N x f x f x f n )(,)(,|)(|,)()]([],[b a E x =∈,其中则0,|()|()[()](),()(),()N f x N f x f x f x N f x N f x N f x N≤⎧⎪−=−>⎨⎪+<−⎩因此,[,]|()[()]|N a b f x f x d −∫x=+dx x f x f N f E n|)]([)(|)|(|∫≤−dx x f x f N f E n|)]([)(|)|(|∫>−(||)|()[()]|N E f N f x f x d >−∫x =dx N x f N f E |)(|)|(|∫>+≤dx x f N f E |)(|)|(|∫>≤.0>∀ε0>∃δ因为在上是Lebesgue 可积的,故对于)(x f ],[b a ,,使∀δ<mA E A ⊂,恒有:Adx x f Aε<∫|)(|又因是单调的集列并且,则)|(|)|(|1+∞==>∞=f E n f E n ∩∞=1|)}(|{n f E =>=>∞→∞→)]|(|lim [)|(|lim n f E m n f mE n n 0)|(|=+∞=f mE .4|)(|)|(|ε<∫>dx x f N f E 0>δN ∃∈ .所以,对于,使得现在对于,取04>=NεηN x f )]([,由连续扩张定理,存在闭集F [,]a b ⊂)(x ϕ以及 上的连续函数,使得F F N x x f |)(|)]([ϕ=(A ); NF E m 4)(ε<−(B );N x ≤|)(|ϕ(C ). 因此,[,][]||[]|N N a b E Ff dx f dx ϕϕ−−=−∫∫([]||)|2()242N E Ff dx N m E F N Nεεϕ−≤+≤⋅−<⋅∫=从而,[,][,]()()||()[()]||[]()|N N a b a b f x x dx f x f x dx f x dx ϕϕ−≤−+−∫∫εεεϕ=+⋅≤−+≤∫∫>242|)(][||)(|2],[)|(|dx x f dx x f b a N N f E (2)再证:.0|)()(lim],[0=−+∫→dx x f b x f b a h 0>∀ε)(x ϕ,由(1)知,存在上的连续函数 使得对于3|)()(]1,1[εϕ<−∫+−dx x x f b a .)(x ϕ因为在上一致连续,则]1,1[+−b a )1(0<>∃δδ使得,当],[b a x ∈∀)1(||<<δh 时,恒有)(3|)()(|a b x h x −<−+εϕϕ.又因为[,]|()()|a b f x h f x dx +−≤∫[,]|()()|a b f x h x h dx ϕ+−+∫++dx x h x b a |)()(|],[∫−+ϕϕdx x f x b a |)()(|],[∫−ϕ],[b a x ∈(||1)h h δ∀<<(1,1x h a b )+∈−+,故并且对于,,有3|)()(|]1,1[εϕ<−≤∫+−dx x x f b a dx h x h x f b a |)()(|],[∫+−+ϕ所以,实变函数第四章▉▉≤−+∫dx x f h x f b a |)()(|],[[1,1]|()()|a b f x x d ϕ−+−∫xεεεε=++<333dx x x f dx x h x b a b a |)()(||)()(|],[],[∫∫−+−+ϕϕϕ+.从而,.0|)()(|lim],[0=−+∫→dx x f h x f b a h9. 设是f E 上的非负可积函数,是任意常数,满足c ∫≤≤Edx x f c )(0试证:存在,使得.c dx x f E =∫1)(E E ⊂1证明:设常数,合于,当时,存在,使得. 不妨设.∫≤≤Edx x f c )(0∫=Edx x f c )(c ∫≤≤Edx x f c )(0c dx x f E =∫1)(E E =1我们先证:在∫−=Et t dx x f t F ∩],[)()(),0[0+∞∈∀t),0[+∞上连续,,事事实上,对于0t t >∀,因为000[,][,]0()()()()t t Et t EF t F t f x dx f x dx −−≤−=−∫∫∩∩00[,][,]()()t t Et t Ef x dx f x dx −−=+∫∫∩∩δ<mA 0>∃δE A ⊂∀由积分的绝对连续性(p.85,定理4),,有,,2)(|)(|ε<=∫∫AAdx x f dx x f .δ<−≤∀00:t t t δ<−≤−00)),([t t E t t m ∩,故故,对于,因为εεε=+=+=−≤∫∫−−22)()()()(0],[],[000Ety t Et t dx x f dx x f t F t F ∩∩.)()(lim 00t F t F t t =+→. 所以,),0[0+∞∈∀t 同理,对,用上述完全类似方法可得.故,在)()(lim 00t F t F t t =−→)(t F ),0[+∞上连续.又因为(根据p.89的定义4), 则,使得c dx x f dx x f EEt t t >=∫∫−+∞→)()(lim],[∩00>∃t c dx x f t F Et t >=∫−∩],[0)()(.)()0(0t F c F <<.故由于在闭区间上连续,由连续函数的介值定理,∃],0[0t 1t ∈)(t F E E t t E ⊂−=∩],[1110(0,)t ,有,使得c t F dx x f dx x f Et t E ===∫∫−)()()(1],[01∩.E 10. 设是g 上的可测函数,是大于1的数,是的共轭数,即p q p 111=+qp . 如果对任意,都有)(E L f P ∈1()fg L E ∈,试证:. )(E L g q∈11. 试证:1)1(1lim),0(1=+∫+∞∞→dt tkt kk k (i ).dx x e dx x n x x n k ∫∫+∞−+∞−∞→=−),0(),0(11(lim αα(ii) .2≥∀k 证明:(i )时,(寻找控制函数) )10(≤<t t 时,因为当tttttktt f kkk k 4111)1(1)(2111≤=≤≤+=;而当时,1>t 112111()(1)1((1)()2!k k k kk f t t k k t t k t t k k k=≤=−+⋅+++实变函数第四章▉▉224)211(2t t =−≤令⎪⎪⎩⎪⎪⎨⎧+∞≤<≤<=t t t tt F 1,410,4)(2从而,),0(+∞∈∀t ,并且在)()(t F t f k ≤)(t F ),0(+∞是R-可积的,故在)(t F ),0(+∞是L-可积的. 又因为tt kk tt kk kk k k k e etkt t ktt f −∞→∞→∞→∞→==⋅+=+=11lim])1[(1lim)1(1lim)(lim 11则由Lebesgue 控制收敛定理,∫∫∫∞∞→∞∞→∞∞→==+),0(),0(),0(1)(lim )(lim)1(1limdt t fdt t fdt tkt kk kk kk k10==∫+∞−dt e t ∫∞−=),0(dt et.(ii), 定义n ∀∈ 1(1),(0,]()0,(n n x ,)xx n f x nx n α−⎧−∈⎪=⎨⎪∈+∞⎩, 并且,1)(−−=αx ex F x),0(+∞∈x ),0(+∞∈∀x , 则对于,有)(1(lim )(lim 11x F x e x nxx f x n n n n ==−=−−−∞→∞→αα. N n ∈∀,.)()(1x f x f n n +≤下面证明:ttx t G )1()(−=),0(+∞∈∀x ),1[+∞∈t ,取 事实上,,令,1ln()(ln txt t G −=,则▉▉第四章习题参考解答x t xt x t x t x t txt G t G −+−=−+−=′)1ln(11)1ln()()(2. x t xt x t h −+−=′)1ln()(,又因 又记222)()()(11)(x t xx t t x x t x t x tx t h −−−=−−−=′0)()()(222<−−=−−−=x t t x x t t tx x t x .xt xt x t G t G t h −+−=′=)1ln()()()(所以,关于单调递减并且故,t 0)(lim =∞→t h t ),1[+∞∈∀t ,有. 因此,0)(>t h 0)()()(>⋅=′t h t G t G .即, 在)(t G ),1[+∞n ∀∈ 单调增加. 从而,,)1(11()1()(1+=+−<−=+n G n x n x n G n n .所以,)()11()1()(1111x f x n x x n x x f n n n n +−+−=+−<−=αα.因此, ,n ∀∈ 1)()(|)(|−−=≤=αx e x F x f x f x n n ),0(+∞∈x,因为在1)(−−=αx e x F x ),0(+∞上可积,由Lebesgue 控制收敛定理,有∫∫∫+∞−−+∞∞→−∞→===−),0(1),0(),0(1)(lim )1(limdx x e dx x f dx x n x x n n n n n αα.+∞<mE 12. 设,试证明:在E 上当且仅当0⇒k f 0||1||lim =+∫∞→dx f f Ek k k . k ∀∈ 0>∀σ)(⇒,因为证明 ,实变函数第四章▉▉)1|(|]||1||[σσσ−≥=≥+k k k f E f f E 并且(在0⇒k f E 上),则我们有01|(|lim )||1||{lim =−≥=≥+∞→∞→σσσk k k k k f mE f f mE .0||1||⇒+k k f f E .故在上,1||1||≤+k k f f k ∀∈ +∞<mE ,由Lebesgue又因为对于,并且有界收敛定理,有00||1||lim ==+∫∫∞→E E k k k dx dx f f .0>∀σ)(⇐,因为对于(||)0(||)11kk E f EmE f dx σσσσσσ≥≤≥=++∫ ∫≥+Ef E k k k dx f f )|(|||1||σ≤)(0∞→→k . 则有0)|(|lim 10≤≥−≤∞→δσσk k f mE . 从而,0)|(|lim =≥∞→δk k f mE . 即.0⇒k f。
实变函数复习题

复习题1 一、判断1、若N 是自然数集,e N 为正偶数集,则N 与e N 对等。
(对)2、由直线上互不相交的开间隔所成之集是至多可列集。
(对)3、若12,,,n A A A 是1R 上的有限个集,则下式()1212n n A A A A A A ''''+++=+++成立。
(对)4、任意多个开集的交集一定是开集。
(错)5、有限点集和可列点集都可测。
(对)6、可列个零测集之并不是零测集。
(对)7、若开集1G 是开集2G 的真子集,则一定有12mG mG <。
(错) 8、对于有界集1ER ⊆,必有*m E <+∞。
(对)9、任何点集E 上的常数函数()f x =C ,x E ∈是可测函数。
(错)10、由()f x 在()1,2,k E k = 上可测可以推出()f x 在1kk E E ∞==∑上可测。
(对)二、填空1、区间(0,1)和全体实数R 对等,只需对每个()0,1x ∈,令 ()tan()2x x πϕπ=-2、任何无限集合都至少包含一个 可数子集3、设12,S S 都可测,则12S S ⋃也可测,并且当12S S ⋂为空集时,对于任意集合T 总有***1212[()]()()m T S S m T S m T S ⋂⋃=⋂+⋂4、设E 是任一可测集,则一定存在F ∂型集F ,使F E ⊂,且 ()0m E F -=5、可测集n ER ⊂上的 连续函数 是可测函数。
6、设E 是一个有界的无限集合,则E 至少有一 个聚点。
7、设π是一个与集合E 的点x 有关的命题,如果存在E 的子集M ,适合mM=0,使得π在E\M 上恒成立,也就是说,E\E[π成立]= 零测度集 ,则我们称π在E 上几乎处处成立。
8、E 为闭集的充要条件是'(E E)E E ⊂∂⊂或 。
9、设A 、B 是两个非空集合,若,A B B A ≤≤,则有 A =B。
三、证明 1、证明:若A B ⊂,且~A A C ⋃,则有~B B C ⋃。
实变函数论习题集选解

《实变函数论》习题选解一、集合与基数1.证明集合关系式:(1))()()()(B D C A D C B A --⊂--- ; (2))()()()(D B C A D C B A -=--; (3)C B A C B A )()(-⊆--;(4)问)()(C B A C B A --=- 成立的充要条件是什么?证 (1)∵cB A B A =-,cc c B A B A =)((对偶律),)()()(C A B A C B A =(交对并的分配律), ∴)()()()()()(D C B A D C B A D C B A c c cc c==---第二个用对偶律)()()()()()(B D C A D B C A D B A C B A c c c c c --=⊆=交对并分配律.(2))()()()()()(c c c cD B C A D C B A D C B A ==--交换律结合律)()()()(D B C A D B C A c-==第二个用对偶律.(3))()()()()(C A B A C B A C B A C B A c ccc ===--分配律C B A C B A c )()(-=⊆.(4)A C C B A C B A ⊆⇔--=-)()( . 证 必要性(左推右,用反证法):若A C ⊄,则C x ∈∃ 但A x ∉,从而D ∀,)(D A x -∉,于是)(C B A x --∉; 但C B A x )(-∈,从而左边不等式不成立,矛盾! 充分性(右推左,显然):事实上,∵A C ⊆,∴C C A = ,如图所示:故)()(C B A C B A --=- .2.设}1 ,0{=A ,试证一切排列A a a a a n n ∈ ),,,,,(21所成之集的势(基数)为c .证 记}}1 ,0{),,,,,({21=∈==A a a a a a E n n 为所有排列所成之集,对任一排列}1 ,0{ ),,,,,(21=∈=A a a a a a n n ,令 n a a a a f 21.0)(=,特别,]1 ,0[0000.0)0(∈== f ,]1 ,0[1111.0)1(∈== f ,即对每一排列对应于区间]1 ,0[上的一个2进小数]1 ,0[.021∈ n a a a ,则f 是一一对应(双射),从而集合E 与集合]1 ,0[对等(即E ~]1 ,0[),而对等的集合有相同的基数,故c E ==]1 ,0[.3.证明:整系数多项式的全体是可列的(可数的).证 对任一N ∈n ,n 次多项式n n n x a x a x a a P ++++= 2210对应于一个序列:n a a a a ,,,,210 ,而每个)0(n i a i ≤≤取自可数集N N Z }0{-=,因此,全体n 次整系数多项式n P 是有限个(1+n 个)可数集之并集,仍是可数的.故全体整系数多项式所构成的集合 N∈=n n P P 就是可数个可数集之并集,由定理1.3.8可知:它仍是可数的.4.设]1,0[C 表示区间]1,0[上一切连续函数所成之集,试证它的势为c .证 首先,对任意实数R ∈k ,看作常值连续函数,]1 ,0[C k ∈,∴ ]1 ,0[C ≤R ,即 ]1 ,0[C c ≤;另一方面,实数列全体之集}),,,,,{(21R ∈=i n a a a a E 的基数c E =,为证c C ≤]1 ,0[,只需证]1,0[C 与E 的一个子集对等即可.事实上,把]1 ,0[中的有理数]1 ,0[ Q 排列成 ,,,,21n r r r .对任何]1 ,0[C f ∈,则f 由它在 ,,,,21n r r r 处的值 ),(,),(),(21n r f r f r f 所完全确定.这是因为]1 ,0[ 在Q 中是稠密的,即对任何]1 ,0[∈x ,存在上述有理数列的一个子列)(∞→→k x r k n ,由f 的连续性知:)(lim )(k n k r f x f ∞→=.现在,作映射E C →]1 ,0[:ϕ,)),(,),(),(()(21 n r f r f r f x f ,则ϕ是单射,而集E C f r f r f r f A n ⊂∈=}]1 ,0[)),(,),(),({(21 是全体实数列E 的一个子集,故]1 ,0[C ~E A ⊂,即 c C ≤]1 ,0[.综上可知:c C =]1 ,0[.附注 ①若∅=21A A ,∅=21B B ,又1f :1A ~1B ,2f :2A ~2B .则存在f :21A A ~21B B ;假如21A A ⊂,21B B ⊂,21,f f 的意义同前,问是否存在 12A A -到12B B -的一一对应?解 若∅=21A A ,∅=21B B ,令⎩⎨⎧∈∈=,),(,),()(2211A x x f A x x f x f 则)(x f 就是21A A 到21B B 的一一对应.若21A A ⊂,21B B ⊂,则12A A -与12B B -之间不一定存在一一对应.例如:} , ,,2 ,1{ , }, ,4 ,3{ , },, ,3 ,2{2211 n B A n B n A ====,),3 ,2( 1:1 =+n n n f ,),2,1( :2 =n n n f ,则1f 是1A 到1B 的一一对应,2f 是2A 到2B 的一一对应.但}2 ,1{ },1{1212=-=-B B A A ,显然12A A -与12B B -之间不存在任何一一对应.②几个常见的一一对应:(ⅰ)) ,(b a ~R ,()) ,( , tan )(2b a x x f a b ax ∈-⋅=--ππ; )1 ,0(~R ,)1 ,0( , 1)(2∈-=x xxx f ; (ⅱ))1 ,0(~]1 ,0[,将)1 ,0(中的有理数排列为 , , , ,21n r r r ,而]1 ,0[中的有理数排列为 , , , , ,1 ,021n r r r .作其间的对应f 如下:⎪⎪⎩⎪⎪⎨⎧>====+,中无理数时是当当当当)1 ,0(, ),2( ,,,1 , ,0 )(221x x n r x r r x r x x f n n 则)(x f 是)1 ,0(与]1 ,0[间的一一对应. 注意 这种)(x f 一定不是连续的(为什么?).(ⅲ)N N ⨯~N ,()N N ⨯∈-=-),( , )12(2),(1j i j j i f i .这是因为任一自然数均可唯一表示为q n p⋅=2(p 非负整数,q 正奇数),而对非负整数p ,正奇数q ,又有唯一的N ∈j i ,使得12 ,1-=-=j q i p . (ⅳ)}]1 ,0[)()({上的一切实函数为x f x f F =,则c F 2=. 证 1.c F 2≥;设E 为]1 ,0[的任一子集,)(x E χ为E 的特征函数,即⎩⎨⎧-∈∈=.]1,0[ ,0, ,1)(E x E x x E χ当21 E E 、均为]1 ,0[的子集,21 E E ≠时,)(1x E χ≠)(2x E χ.记}]1 ,0[{⊂=E E M ,}]1 ,0[)({⊂=X E x E χ,则M ~X ,c M 2==X .而F ⊂X ,从而有F ≤X ,即F c ≤2.2.cF 2≤.对每一F x f ∈)(,有平面上一点集 }]1 ,0[ ),(),{(∈==x x f y y x G f (即f 的图形)与之对应.记 })({F x f G G f F ∈=,则F ~F G ,F G F = . F G 为平面上一切点集全体B 的子集,而cB 2=,从而有cF G F 2≤=.综合 1, 2立知 cF 2=.附注 此题提供了证明两个无限集对等的一般方法,这便是Cantor-Bernstein 定理. 其特殊情况是:若C B A ⊂⊂,而A ~C ,则B ~C (此结果更便于应用).5.试证任何点集的内点全体组成的集是开集.证 设集F 的内点集为0F (称为F 的内部),下证0F 为开集.F x ∈∀,由内点的定义,存在x 的邻域F I x x x ⊆=),(βα.现作集 Fx x I G ∈=,则显然G 为开集,且G F⊆0.另一方面,对任意G y ∈,存在0x I ,使得F I y x ⊆∈0,所以,y 为F 的内点,即0F y ∈,也就是说0F G ⊆.综上有G F =0为开集. 6.开映射是否连续?连续映射是否开?解 开映射未必连续.例:在每个区间) ,2 ,1 ,0( ]1 ,[ ±±=+n n n 上作Cantor 三分集n P ,且令n n P n n G -+=]1 ,[,而 +∞-∞==n n P P , +∞-∞==n n G G ,则G 为开集.又设G 的构成区间为} ,3 ,2 ,1 ), ,{( =k b a k k .(教材P21例1中的Cantor 集P 即本题中的0P )现在R 上定义函数 ⎪⎩⎪⎨⎧∈=∈---=, ,0 , ,3 ,2 ,1 ), ,( )],21(tan[)(P x k b a x a b x b x f k k kk k π 则f 在R 上映开集为开集,但f 并不连续.事实上,若开区间) ,(βα含于某个构成区间) ,(k k b a 内,则f 就映) ,(βα为开区间) )]21(tan[ )],21(tan[ (kk k k k k a b b a b b ------βπαπ;若开区间) ,(βα中含有P 中的点,则f 就映) ,(βα为R .然而P 中的每个点都是)(x f 的不连续点.又连续映射未必为开映射.例:2)(x x f =在R 上连续,但开集)1 ,1(-的像为)1 ,0[非开非闭.7.设E 是Cantor 集P 的补集中构成区间的中点所成的集,求E '.解 P E ='.分以下三步:①设Cantor 集为P ,其补集(或叫余集)为G ,则 ),(),(),(989792913231=G . 考察]1 ,0[中的点的三进制表示法,设 ⎩⎨⎧=,2,0i a ⎪⎩⎪⎨⎧=,2,1,0i b ( ,3 ,2 ,1=i ).由Cantor 集的构造知:当P y ∈时,y 的小数点后任一位数字都不是1,因而可设n a a a y 21.0=;当G x ∈时,可设 2121.0++=n n n b b a a a x ;特别,对于G 的构成区间的右端点右y 有0200.021n a a a y =右;对于G 的构成区间的左端点左y 有 20222.021n a a a y =左.由此可见,G E ⊆,且当E z ∈时,有 111.0)(2121n a a a y y z =+=右左.②下证Cantor 集P 中的点都是E 的极限点:对P y ∈∀,由于 n a a a y 21.0=,取E z k ∈,则 111.021n k a a a z =. 由于y 与k z 的小数点后前k 位小数相同,从而k k k k k y z 3131********1<⋅=++≤-+++ , 故,0 ,0>∃>∀N ε当N k >时,有ε<k 31,即ε<-y z k , ∴)( ∞→→k y z k ,即 E y '∈.③下证G x ∈∀,有E x '∉.事实上,有两种情况:10.若E x ∈,则只能是G 的构成区间的中点,即 111.021n a a a x =.由Cantor集的构造知:对)( x z E z ≠∈∀,都有 n x z 31≥-,所以,E x '∉; 20.若E x ∉且G x ∈,则)1(,111.0121+>=+n m b a a a a x m m n ,于是,E z ∈∀,有m x z 31>-,所以,E x '∉. 故G 中的点不属于E '.综上所述,我们有:P 中的点都是E 的极限点,不在P 中的点都不是E 的极限点,从而P E ='.8.设点集列}{k E 是有限区间],[b a 中的非空渐缩闭集列(降列),试证∅≠∞= 1k k E .证 用反证法:若∅=∞= 1k k E ,则()] ,[\] ,[\] ,[11b a E b a E b a k k k k ==∞=∞= ,从而} ,\] ,[{N ∈=k E b a E k c k 为有界渐张开集列(升列),且覆盖],[b a ,由数学分析中的“有限覆盖定理”(Borel )可知:存在子覆盖} , ,2 ,1:{n k E c k=,使得] ,[1b a E nk ck ⊇= ,即()] ,[\] ,[1b a E b a n k k == . ∴ ] ,[\] ,[1b a E b a n k k == ,从而∅== nk k E 1,故∅=n E ,矛盾!附注 更一般地,若非空闭集套}{n E : ⊃⊃⊃⊃n E E E 21满足0sup )(,−−→−-=∞→∈n E y x n y x E nρ,则存在唯一的 ∞=∈10n n E x .(这等价于“分析学”或“拓扑学”中著名的“压缩映像原理”) 证 由n E 非空,取) ,3 ,2 ,1( =∈n E x n n ,则}{n x 为Cauchy 基本收敛列.事实上,由于1+⊃n n E E ,所以,) ,2 ,1 ,0( =⊂∈++m E E x n m n m n ,从而0)(sup ,−−→−=-≤-∞→∈+n n E y x n m n E y x x x nρ,由极限存在的Cauchy 准则知:存在唯一的0x 使得0x x n n −−→−∞→.又由n E 为闭集立知n E x ∈0,从而 ∞=∈10n n E x .存在性得证.下证唯一性:若另有 ∞=∈10n n E y ,则) ,2 ,1( 00 =∈n E y x n 、,而0)(00→≤-n E y x ρ,所以,00x y =.这就证明了唯一性.9.若] ,[)(b a C x f ∈,则 ()αα≥∈∀f E , R 为闭集.证 只要证:若0x 为()α≥f E 的极限点(即聚点),必有E x ∈0.由0x 为()α≥f E 的极限点,故有点列) ,2 ,1( =∈n E x n ,满足0lim x x n n=;又由于诸 ] ,[ b a E x n ⊂∈以及)(x f 的连续性,从而有] ,[ ,)(0b a x x f n ∈≥α 以及 α≥=)(lim )(0n nx f x f .这就证明了E x ∈0.9*.若在],[b a 上,)()(lim x f x f n n=,记}],[ ,)({)(b a x x f x E n n ∈>=αα,}],[ ,)({)(b a x x f x E ∈>=αα,证明:() ∞=∞→+=11lim )(k kn n E E αα. 证 一方面,当)(αE x ∈时,α>)(x f ⇒, k ∃使得kx f 1)(+>α,即kn nx f 1)(lim +>α, N ∃⇒当N n >时,kn x f 1)(+>α()() ∞=∞→∞→+∈⇒+∈⇒111lim lim k kn n kn n E x E x αα. 另一方面,() ∞=∞→+∈11lim k kn n E x αk ∃⇒,使()k n n E x 1lim +∈∞→α, N ∃⇒当N n >时, ()k n E x 1+∈α. 即 kn x f 1)(+>α(N n >)k n nx f x f 1)(lim )(+≥=⇒α, α>⇒)(x f ,从而)(αE x ∈. 综上可得 () ∞=∞→+=11lim )(k kn n E E αα. 10.每一个闭集是可数个开集的交集.证 设F 为闭集,作集) ,2 ,1( }),( {1 =<=n F x x G nn ρ,其中),(F x ρ表示点x 到集F 的距离,则n G 为开集.下证: nn G F =.事实上,由于对任意N ∈n 有n G F ⊂,故有 nn G F ⊂;另一方面,对任意 nn G x ∈0,有 ) ,2 ,1( ),(010 =<≤n F x nρ,令∞→n 有0),(0=F x ρ.所以,F x ∈0(因F 为闭集),从而F G nn ⊂ .综上可知: nn G F =.附注 此题结果也说明:可数个开集的交不一定是开集,因而才引出了δG -型集的概念.11.证明:开区间不能表示成两两互不相交的可数个闭集的并集.证 可有两种证法(很麻烦):一种是反证法,即若 nn F b a I ==) ,(0,其中}{n F 为两两互不相交的闭集列,我们设法找到一点) ,(0b a x ∈,但 nn F x ∉0,从而得出矛盾;另一种证法是:记) ,(b a =∆,证明下述更强的结果:若}{n F 为含于∆内的任一组两两互不相交的闭集列,则 nn F -∆的势(基数)等于连续势c ,从而立知不可能有nn F b a ==∆) ,(.取1F ,令1010sup , inf F b F a ==,由1F 为闭集,故100 , F b a ∈,且100000] ,[ , F b a I b b a a ⊃=<≤<.又记) ,( , ) ,(0201b b a a =∆=∆(非空),则有两种情况: ①若)2 , 1( 2=∆∞=i F n n i中至少有一个空集,比如 21∅=∆∞= n n F ,而∅=∆⊂∆0111I F ,所以, 11∅=∆∞= n n F , 11∆⊃-∆∞= n n F .因此,c F nn=∆≥-∆1 .问题得证.②)2 , 1( 1=∆∞=i F n n i均不为空集,对)2 , 1( =∆i i ,在 , ,32F F 中存在最小的下标)(1i n 使∅≠∆i n i F )(1,显然,2},min{)2(1)1(11≥=n n n 以及)(1, , ,00i n F b b a a ∉,从而i n i n i i F F ∆=∆ )(1)(1为含于开区间i ∆内的闭集,对此闭集仿上作出两个闭区间)2 ,1( )(1=i I i ,它们满足:(ⅰ))2(1)1(10 , ,I I I 互不相交; (ⅱ)21121)(101===⊃⊃i i n i i i i F F I I .对在∆中挖去)2(1)1(10 , ,I I I 后余下的四个开区间重复上述步骤,以此类推,用归纳法假设第N 步作出闭区间)2 , ,2 ,1( )(N k N k I =,它们满足:(ⅰ)) , ,2 ,1 ; 2 , ,2 ,1( ,)(0N n j I I n j n ==互不相交;(ⅱ)111121)(0)]([+====⊃⊃N i i n i i N n j j n F F I I N n(因为1+≥N n N ).在开区间∆中挖去闭区间) , ,2 ,1 ; 2 , ,2 ,1( ,)(0N n j I I n j n ==后余下的12+N 个开区间中,如果至少有一个开区间比如0i ∆与2+≥N n n F 的交为空集,则由(ⅱ)知与 ∞=1n n F 的交也为空集,从而c F i nn=∆≥-∆0 .问题得证.若不然,则这12+N 个开区间均与2+≥N n n F 相交,重复上述步骤得到一列闭区间} ,{)(0j n I I ,再利用完备集的结构定理可知它关于] ,[b a 的余集为非空完备集,又在(ⅱ)中令∞→N ,得∞=∞==⊃1121)(0)]([i i n j j n F I I n所以,集 ∞=-1) ,(i i F b a 的势(基数)等于连续势c .附注 ①我们知道:可数个闭集的并集不一定是闭集,而此题结果又说明了“开区间(是开集)却不能表示成可数个互不相交的闭集的并集”,所以又引出了σF -集. ②任何闭区间不可能表示成可数个疏集的并集(提示:用反证法,若 ii F b a =],[,其中),2,1( =i F i 为疏集,可构造一闭区间套,则导出矛盾!)12.证明:用十进位小数表示]1 ,0[中的数时,其用不着数字7的一切数成一完备集.证 对]1 ,0[中的任一数x 均可表示为) ,2 ,1 },9 , ,2 ,1 ,0{( 101=∈=∑∞=k a a x k k k k(x的这种表示法不一定唯一),而如此表示的级数其值都在]1 ,0[内. 记G 表示]1 ,0[中数的十进位可能表示101∑∞=k k ka 中必有某一个7=k a 的那些数的全体,从而只要证明G 关于]1 ,0[的余集G P -=∆]1 ,0[为完备集.作开区间()1081070,=δ,),2 ,1( 10810 , 1071011111=⎪⎪⎭⎫⎝⎛++=+=+=∑∑n a a n n k k k n n k k k aa nδ其中n a a ,,1 为不等于7而小于10的非负整数.显见这些开区间为]1 ,0[中可数无穷个无公共端点的互不相交的开区间,其内点用十 进位数表示时至少有一个7=n a ,而端点用十进位数表示时可使所有7≠k a .作这些开 区间的并集记为U ,则U 为开集,且根据完备集的结构定理知U 关于]1 ,0[的余集为一 完备集,于是,只要证明U G =即可.由U 的定义显见G U ⊂;另一方面,若G x ∈,则在x 的所有可能的十进位表示101∑∞=k k ka 中均必有一个7=n a ,且不妨设此n 为满足等式的最小整数即11,,-n a a 均不等于7.首先证明下述两种情况不能发生:①) ,2 ,1( 0 ++==n n m a m ,此时x 表示 区间11-n a a δ的左端点,它有另一十进位表示:∑∑+≥-=++11110910610n i in n i iia ,在此表示中一 切7≠n a ,因此x 不可能是这种情况;②) ,2 ,1( 7 ++==n n m a m ,此时x 表示区 间11-n a a δ的右端点,它有另一十进位表示:n n i i ia 1081011+∑-=,在此表示中一切7≠n a ,因此x 也不可能是这种情况.由此可知U x n aa ⊂∈-11δ.综上所证可知U G =.证毕!附注 ①c P =; ②P 在]1 ,0[中不稠密(因∅=)7.0 , 28.0( P ).13.试在]1 ,0[上定义一个函数,它在任一有理点不连续,但在任一无理点连续.解 ①设∑∞=1n n a 为一收敛的正级数,因]1 ,0[上全体有理数可数,故可记为},,,,{21 n r r r Q =.对]1 ,0[∈∀x ,定义函数∑<=xr n n a x f )(,其中和式是对x r n <的那些相应的n a 求和.则)(x f 为]1 ,0[上单调递增函数且在无理点连续,有理点不连续其跃度为000)()(n n n a r f r f =--+. 事实上,因为对任意x y >,0)()(≥=-∑<≤y r x n n a x f y f ,所以,)(x f 为增函数;又记}{y r x r E n n y x <≤=,当x 为无理数时,∅=+→y x xy E lim ,所以,)()0(x f x f =+. 同理可证)()0(x f x f =-,所以,)(x f 在无理点连续;当x 为有理数0n r 时,有0lim n y x x y r E =+→,所以,0)()0(n a x f x f =-+,且此时类似亦有)()0(x f x f =-(0n r x =),从而 000)()(n n n a r f r f =--+0>. ②微积分中熟知的Riemann 函数 ⎪⎩⎪⎨⎧≥==中无理数,为,,互素正整数]1,0[0),,( ,)(1x q p q p x x R p q p亦为所求函数.附注 ①不存在]1 ,0[上这样的函数,它在每一有理点连续,而在每一无理点不连续; (提示:只要证任何在]1 ,0[中有理点连续的函数)(x f ,至少在一个无理点上连续.可利用闭区间套定理).②设B A ,为非空不交闭集(可无界),则存在) ,()(∞+-∞∈C x f 满足:1)(0≤≤x f ,且当A x ∈时,0)(=x f ,而当B x ∈时,1)(=x f ; (提示:),( , ),(),(),()(+∞-∞∈+=x B x A x A x x f ρρρ,其中),(A x ρ为点x 到集A 的距离.再证分子连续,分母大于0连续,从而)(x f 连续.而满足条件显然)更一般地,此结果可推广到n 个非空不交闭集上:设),,2,1(n k A k =为n 个非空不交 闭集,∃连续函数)(x f 使得k A x ∈时,k C x f =)((k C 为常数,n k ,,2,1 =),则⎪⎪⎪⎩⎪⎪⎪⎨⎧∉=∈====∑∑. ,),(1),(,,,2,1 , ,)(111 n k k nk k nk kk k k A x A x A x C n k A x C x f ρρ即可. 二、勒贝格(Lebesgue )测度1.设1E 、2E 均为有界可测集,试证()()212121E E m mE mE E E m -+=.证 因1E 、2E 可测,则21E E 可测,212E E E -可测,且)()(212212E E m mE E E E m -=-.又由()∅=-2121E E E E ,得()()()2121212121E E m mE mE E E E m mE E E m -+=-+=.2.试证可数个零测度集的并仍是零测度集.证 设 ∞====1, ,2 ,1 ,0n n n E E n mE ,则E 可测,且有0011=≤⎪⎪⎭⎫ ⎝⎛=≤∑∞=∞=n n n n mE E m mE ,∴ 0=mE .3.设有两个开集21G G 、,且21G G ⊆,那么是否一定有21mG mG <?解 不一定成立.例:)2 ,1()1 ,0(1 =G ,)2 ,0(2=G ,则21G G ⊂,但212mG mG ==.4.对任意开集G ,是否一定有mG G m =成立?解 不一定.例 :对]1 ,0[中的所有有理数} , , , ,{21 n r r r ,作开集如下:∞=++⎪⎭⎫ ⎝⎛+-=12221 ,21n n n n n r r G ,则G 为开集,且2121*11=≤=∑∞=+n n G m mG .但由]1 ,0[⊇G ,可得1]1 ,0[=≥m G m .故mG G m ≠.5.设n A A A 、、、 21是]1 0[,中n 个可测集,且满足11->∑=n mA nk k ,试证01>⎪⎪⎭⎫ ⎝⎛= n k k A m .证 由1题可知:)()(212121E E m mE mE E E m -+=.又∵]1 ,0[⊆i A ,∴ 1≤i mA ,n i , ,2 ,1 =,而cn i c i ni i A A ⎪⎪⎭⎫⎝⎛=== 11,∴∑∑====--=-≥⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛n i i n i ci n i c i n i i mA m mA A m A m 1111)]1 ,0[(1110)1(111>--=+-=∑∑==n mA mA n n i i n i i .(由已知11->∑=n mA nk k )6*.设0*>=q E m ,则对任何) ,0(q p ∈,存在E E ⊂0,使得p E m =0*(称为“外测度的介值定理”).(以下证明最好能看懂,否则Pass !)证 ①先设E 是有界集,即] ,[b a E ⊆,0*>=q E m .令()] ,[**)(x a E m E m x f x ==,] ,[b a x ∈,则)(x f 是] ,[b a 上单调不减的连续函数.事实上,10.因∅==或}{}{a a E E a ,E b a E E b ==] ,[ ,则0)(=a f ,0)(>=q b f ;当21x x <,且] ,[21b a x x ∈、时,21] ,[] ,[21x x E x a E x a E E =⊆= ,由外测度的单调性,有)(**)(2121x f E m E m x f x x =≤=.所以,)(x f 是] ,[b a 上的单调不减函数.20.因()1112*]),[(***)()(2112x x x x E m x x E E m E m E m x f x f -=-=-()122121],[*],[*x x x x m x x E m -=≤≤ ;同理,当12x x <时,2121)()(x x x f x f -≤-. ∴ 2121)()(x x x f x f -≤-.于是,让1x 为] ,[b a 上任意一点x ,而] ,[2b a x x x ∈∆+=,则有x x f x x f ∆≤-∆+)()(,故当0→∆x 时,)()(x f x x f →∆+,即] ,[)(b a C x f ∈.②由] ,[)(b a C x f ∈,) ,0(q p ∈∀,即)()(b f p a f <<,由闭区间上连续函数的介值定理,] ,[0b a x ∈∃,使得p x f =)(0,即()p x a E m =] ,[*0 . ③当E 无界时,令] ,[][n n E E n -= ,N ∈n ,则n E ][可测,满足⊆⊆⊆⊆n E E E ][][][21,且有 ∞==1][n n E E ,∴ 0*][*lim >>==∞→p q E m E m n n .由极限的保号性,N ∈∃0n ,使得p E m n >0][*.记)( ][*00p p E m n >=,而0][n E 为有界集:] ,[] ,[][000n n n n E E n -⊆-= .如前两步所证,作函数()] ,[][**)(00x n E m E m x f n x -==则)(x f 在] ,[0n n -上连续不减,且000)(0)(p n f n f =<=-.由00p p <<,) ,( 00n n x -∈∃,使得p x f =)(0,即p E m x =0*.附注 若E 可测,0>=q mE ,则 q p p <<∀0 ,,∃可测集E E ⊂1,使p mE =1.7.试作一闭集]1 ,0[⊂F ,使F 中不含任何开区间,但21=mF . 解 仿照Cantor 集的方法构造闭集F : 第一步:将]1 ,0[作12等份,挖去中央的开区间1)127,125(G =,长度为61; 第二步:将余下的两个闭区间]125,0[和]1 ,127[再各12等份,分别挖去中央的开区间2)7259,7255()7217,7213(G = ,各长6131⨯,共长61312⨯⨯; ……第n 步:在余下的12-n 个闭区间中,分别挖去其中央处长为()61131⨯-n 的开区间,记这12-n个互不相交的开区间之并为n G ,其长度为12-n ()()1326161131--⨯=⨯⨯n n ;将这手续无限进行下去,得一串开集 ,, , , ,321n G G G G . 令 ∞==1n n G G ,则G 为开集,且G F \]1 ,0[=有与Cantor 集类似的性质:①F 为闭集且是完备集; ②F 不含任何开区间(疏集); ③F 可测,且由于()21132611132611=-===∑∑∞=-∞=n n n n mG mG , 故21211]1 ,0[=-=-=mG m mF . 附注 ①当第n 次去掉的12-n 个开区间的长度为n51时,则32115121525111=--=⋅-=∑∞=-n n n mF ;②对任何10 ,<<αα,当第n 次去掉的12-n 个开区间的长度为()13131--⋅n α时,所得开集G 的测度为()ααα-=-⋅==-∞=--∑1113231113231n n mG ,则 α=-=mG mF 1,这可作为一般公式来应用.8.试证定义在) ,(∞+-∞上的单调函数的不连续点集至多可数,因而是0测度集.证 设)(x f 为) ,(∞+-∞上的单增函数,则间断点必为第一类间断点,即若0x 为)(x f 的间断点,则0)0()0(00>--+x f x f .记}0)0()0({>--+=x f x f x E ,则E x ∈∀,))0( ),0((+-x f x f 为y 轴上的一个开区间,每个开区间中可取一有理数x r ,则E 中每个元x 与有理数集中一元x r 相对应,即E 与Q 的一个真子集一一对应,故Q ≤E ,即E 至多可数,故0=mE .9.设N ∈n E n },{为可测集列,且∞<∑∞=1n n mE ,则0lim =⎪⎭⎫ ⎝⎛∞→n n E m .证 ∵∞<∑∞=1n n mE ,∴ , ,0N ∃>∀ε使ε<∑∞=Nn n mE .而∞=∞=∞=∞→⊆=Nn n k k n n n n E E E 1lim ,∴ε<≤⎪⎪⎭⎫ ⎝⎛≤⎪⎭⎫ ⎝⎛∑∞=∞=∞→N n n N n n n n mE E m E m lim . 故 0lim =⎪⎭⎫ ⎝⎛∞→n n E m .10.试举出一列可测集}{n E ,含在一个有限区间中,而且n n mE ∞→lim 存在,但⎪⎭⎫ ⎝⎛≠⎪⎭⎫ ⎝⎛∞→∞→n n n n E m E m lim lim .解 考察如下集列 ⎪⎩⎪⎨⎧=+=--=), ,6 ,4 ,2( )1 ,0[),,5 ,3 ,1( ]0 ,1(11 n n E n n n显然 ),3,2,1( )2 ,2( =-⊂n E n .又 ()()]1 ,1[1 ,1 1 ,1 lim 1111111-=⎥⎥⎦⎤⎢⎢⎣⎡+--⎥⎥⎦⎤⎢⎢⎣⎡+--==++∞=∞= 为偶数为奇数n nn n n n n n k k n nE E , }0{}0{lim 11 ===∞=∞=∞= n n nk k n n E E .(从而n nE lim 不存在) 所以,0lim 2lim =⎪⎭⎫ ⎝⎛≠=⎪⎭⎫ ⎝⎛∞→∞→n n n n E m E m .虽然n nE lim 不存在,但}{n mE 存在极限:()11lim lim 1=+=nnn nmE . 附注 一般,若}{n E 为可测集列,且∞=1n n E 有界,则n n n n mE E m ∞→∞→≤⎪⎭⎫ ⎝⎛lim lim ,n n n n mE E m ∞→∞→≥⎪⎭⎫ ⎝⎛lim lim .(不妨一证) 11*.设N ∈n En },{为R 中互不相交的点集列, ∞==1n n E E,则∑∞=≥1**n n E m E m .证 因 ∞==1n n E E ,且n E 互不相交,则对每个n E ,有σF 型集n F ,使n n E F ⊂,且n n E m mF *=.∴ ∞=1n n F 仍为σF 型集.又对于E 的σF 型集E F ⊂,且E m mF *=.但F F n n ⊂∞= 1,故有∑∞=≥1**n n E m E m .三、可测函数1.证明)(x f 是E 上可测函数的充要条件是:对任一有理数r ,集)(r f E >恒可测.如果集)(r f E =恒可测,问)(x f 是否一定可测? 证 必要性:显然,∵ 有理数属实数集.充分性:设对任一有理数r ,集)(r f E >恒可测,则对R ∈∀α,∃有理数列∞=1}{n n r ,α>n r ,使得α=∞→n n r lim .从而 ∞=>=>1)()(n n r f E f E α为可测集.又如果对任何有理数r ,集)(r f E =恒可测,则f 不一定是可测的.例如:R =E ,F 是E 中的不可测集(它是存在的,尽管不容易构造,教材P65定理2.5.7),对任意F x ∈,3)(=x f ;F x ∉,2)(=x f .则对任何有理数r ,∅==)(r f E 恒可测,但F f E =>)2(是不可测集,从而f 不可测.2.设)(x f 是E 上的可测函数,F G 、分别为R 中的开集和闭集,试问)(G f E ∈和)(F f E ∈是否可测?这里记号})(:{)(A x f E x A f E ∈∈=∈.答 )(G f E ∈和)(F f E ∈均可测. 证 令 ∞==1) ,(n n n b a G ,j i ≠时,∅=) ,() ,(j j i i b a b a ,即) ,(n n b a (N ∈n )为开集G 的构成区间.∵)(x f 是E 上的可测函数,∴)(n n b f a E <<是E 中的可测集,从而∞=<<=∈1)()(n n n b f a E G f E 仍为可测集.又对R 中的闭集F ,令F G \R =,则G 为开集.由上面证明可知)(G f E ∈可测,故)(\)(G f E E F f E ∈=∈仍可测.3.(1)证明:)(lim lim n n n n A S A S -=-∞→∞→;(2)设n A 是下述点集:当n 为奇数时,)1 ,0(1n n A -=;当n 为偶数时,)1 ,(1nn A =.证明:∞=1}{n n A 有极限,并求此极限.证 (1))(lim )(lim 111n n k kn n k k n n k k n n n n A S A S A S A S A S -=-=⎪⎪⎭⎫ ⎝⎛-=-=-∞→∞=∞=∞=≥∞=∞=∞→ .(2))1 ,0()1 ,0(lim 11===∞=∞=≥∞→ k k kn n n n A A ,())1 ,0(1 ,lim 1111=-==∞=∞=≥∞→ k kk k kn n n n A A , ∴ )1 ,0(lim =∞→n n A .4.试作]1 ,0[=E 上的可测函数)(x f ,使对任何连续函数)(x g 有0)(≠≠g f mE .此结果与鲁金(Lusin )定理是否矛盾?解 作函数⎩⎨⎧=∞+∈=,0 , ],1 ,0( , )(1x x x f x 则显然)(x f 是]1 ,0[=E 上的可测函数.设)(x g 是]1 ,0[=E 上的任一连续函数,则)(x g 在]1 ,0[=E 上有界,于是,∃0>N ,使得N x g ≤)((]1 ,0[∈x ).而在] ,0[1N 上,N x f >)(,所以有]) ,0[( )()(1N x x g x f ∈≠.故0] ,0[)(11>=≥≠NN m g f mE .这就是说,]1 ,0[=E 上任何连续函数)(x g 都有0)(≠≠g f mE .此结果与鲁金定理并不矛盾.事实上,0>∀ε,可取闭集E F ⊂=]1 ,[2ε,则 εε<=2)\(F E m ,而所作的函数)(x f 在F 上显然是连续的.此题也说明鲁金定理结论中的0>ε可任意小,但都0≠.5.设)(x f 是) , (∞+-∞上的连续函数,)(x g 是] , [b a 上的可测函数,试证明:)]([x g f 是可测函数.证 R ∈∀α,由)(x f 在R 上连续可知:)(α>f R 是开集,设其构成区间为) ,(i i βα ( ,2 ,1=i ).于是,N ∈∀i ,当) ,()(i i x g βα∈时,α>)]([x g f ;反之,若α>)]([x g f ,则必有N ∈i ,使) ,()(i i x g βα∈.所以,()()() ii i ii i x g E x g E x g f E βαβαα<<=∈=>)() ,()()]([.但由题设:)(x g 在] , [b a 上可测,则()i i x g E βα<<)(可测,故()α>)]([x g f E 可测.6.设函数列∞=1)}({n n x f 在E 上依测度收敛于)(x f (即f f n−→−μ),且在E 上几乎处处有)( )()(N ∈≤n x g x f n .试证在E 上几乎处处有 )()(x g x f ≤.证 ∵ f f n −→−μ,由黎斯(Riesz )定理,∃子列)}({)}({x f x f n n k ⊆,使f f k n →,a.e.于E (∞→k ),即E E ⊂∃0,f f kn →于0E ,且0)(0=-E E m .令()()f f E g f E A k n n n →/⎪⎪⎭⎫⎝⎛>= ,则()0=→/f f mE k n ;而由题设:g f n ≤,a.e.于E (N ∈n )可知,nn g f mE 2)( ,0εε<>>∀(N ∈n ),则有()()()εε=<+><→/+⎪⎪⎭⎫ ⎝⎛>≤∑∑∞=∞=1120n n n n n n n g f mE f f mE g f E m mA , 即0=mA ,而在A E -上有g f n ≤(0E x ∈∀)且f f k n →(0E x ∈∀).故)()(lim )(x g x f x f k n k ≤=∞→(0E x ∈∀),即)()(x g x f ≤,a.e.于E .7.设函数列∞=1)}({n n x f 在E 上依测度收敛于)(x f ,且在E 上几乎处处有)()(1x f x f n n +≤)( N ∈n ,则)(x f n 在E 上几乎处处收敛于)(x f (即f f n →,a.e.于E ).证 ∵ f f n −→−μ,由黎斯(Riesz )定理,∃子列)}({)}({x f x f n n k ⊆,使 f f kn →,a.e.于E (∞→k );再由)()(1x f x f n n +≤,a.e.于E ,则必有f f n →,a.e.于E .8.设函数列∞=1)}({n n x f 在E 上依测度收敛于)(x f ,而)(x f n ~)(x g n )( N ∈n (称为对等,也即n n g f =,a.e.于E ),则)(x g n 在E 上也依测度收敛于)(x f .证 ∵ f f n −→−μ,且n n g f =,a.e.于E ,则0>∀ε,()0lim =≥-∞→εf f mE n n 且()0=≠n n g f mE .∵ f f f g f g n n n n -+-≤-,∴ ()()()εεε≥-≥-⊆≥-f f E f g E f g E n n n n .又()()()()0−−→−≥-≤≥-+≥-≤≥-∞→n n n n n n f f E f f E f g mE f g mE εεεε∴ ()0−−→−≥-∞→n n f g mE ε,即 f g n −→−μ.9.试举例说明:对于叶果洛夫(Egorov )定理,不能加强为除掉一个0测度集外,)(x f n一致收敛于)(x f .解 构造函数列)}({x f n 如下:()⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤<≤-⋅+-<≤<<+==+++++,1 ,0 , ,)1(1, ,1 ,0 ,)2( ,0 ,0 )(111111112121x x x n n x x x n x x f n n n n n n n n 则)(x f n 是]1 ,0[=E 上的连续函数列,必可测,且 )(0)(lim x f x f n n ==∞→于]1 ,0[=E .下面证明:对任一0 ,00=⊂mE E E 时,)}({x f n 在0E E -上不会一致收敛. 取210=ε,无论N 取得多么大,总可取N N n >+=1,令[)02131 ,E A n n -=++,则显然A 非空(为什么?).但A x x f N ∈=+ ,1)(1, A x x f x f x f N N ∈>==-++ ,1)()()(011ε.所以,)}({x f n 在0E E -上不一致收敛.由此可知:叶果洛夫定理不能加强为:除掉一个0测度集外,)(x f n 一致收敛于)(x f .10.几乎处处有限的可测函数列)}({x f n )(x f −→−μ的充要条件是:对任何正数σ和ε,存在N ,当N m N n >> ,时,()εσ<≥-m n f f mE (即它是依测度的Cauchy 列). 证 必要性由)()(x f x f n −→−μ,则N n N >∃>>∀ , ,0 ,0εσ时,()22εσ<≥-f f mE n . 又易知:()()()22σσσ≥-≥-⊂≥-f f E f f E f f E m n m n ,则 ()()()22σσσ≥-+≥-≤≥-f f E f f E f f mE m n m n ,从而当N m N n >> ,时,()εσ<≥-m n f f mE .下证充分性:先找出一个子序列f x f k n k −−→−∞→)}({,a.e.于E .任取数列+∞<>∑∞=1,0 },{i i i i ηηη.由题设条件可知:存在k n ,使得()) ,2 ,1 ; ,2 ,1( 21==<≥-+m k f f mE km n n kk k η,从而可取+∞↑kn ,且有 ()kn n kkk f f mE η<≥-+211.对这串}{kn 作P Q ,:() ∞=∞=≥-=+1211i ik n n kk k f f E Q ,() ∞=∞=<-=-=+1211i ik n n kk k f fE Q E P .令() ∞=≥-=+ik n ni kk k f f E R 211,则 ⊃⊃⊃⊃⊃+121n n R R R R, ∞==1i i R Q .因此,()0lim limlim 211=≤≥-≤=∑∑∞=∞→∞=∞→∞→+ik ki ik n ni i i kk k f f mE mR mQ η,所以,0=mQ .下面证明)}({x f k n 是P 上的收敛基本列.记 () ∞=∞=∞==<-=+11211i ii ik n nA f f E P kk k ,则 ⊂⊂⊂++21i i iA AA .若P x ∈,则存在0i ,使得 ⊂⊂∈+100i i A A x .对任给的0>ε,必有0i i >,使得ε<-121i ,故对一切 ,2 ,1 ,=>m i l ,有 ε<=≤-≤-≤--∞=∞==∑∑∑+++1212111i i j j ij n n m ij n n n n j j j j m l l f f f f f f . 所以,)}({x f kn 在P 上的收敛于)(x f ,其中)( )(lim )(P x x f x f k n k ∈=∞→.显然,f f k n −→−μ,于是,对任何正数σ和ε,存在N ,当N n N n k >> ,时,()22εσ<≥-k n n f f mE ,()22εσ<≥-f f mE kn . 而()⊂>-σf f E n () 2σ≥-k n n f f E ()2σ≥-f f E k n ,所以,当N n >时, ()εσ<>-f f mE n ,即 f f n −→−μ于E .四、Lebesgue 积分1.设)()(x g x f 、都是E 上的可测函数,)()(E L x g ∈,且在E 上几乎处处成立)()(x g x f ≤,问在E 上)(x f 是否一定可积?解 )(x f 未必可积,因)(x f 不一定满足非负性.例如:取]1 ,0[=E ,0)(=x g ,⎪⎪⎪⎩⎪⎪⎪⎨⎧=∈-∈-∈-=-.0 ,0 ], ,( ,2, ], ,( ,4],1 ,( ,2)(12121214121x x x x x f n n n 则显然 )()(E L x g ∈,)()(x g x f ≤,但-∞=⋅-=∑⎰∞=1]1 ,0[ 21)2(d )(n n n m x f 不可积. 2.设在Cantor 集P 上定义函数)(x f 为零,而在P 的补集中长为n31的构成区间上定义)(x f 为n (N ∈n ),试证L x f ∈)(,并求积分值. 解 令 n e 为P 的补集G 中长为n 31的各构成区间之并,则 ∞==1n n e G ,n me n n 321-=.令 ⎪⎩⎪⎨⎧-∈=∈==, ]1 ,0[ ,0),, ,2 ,1( ,)(1 n i i i n e x n i e x i x ϕ 则简单函数列)}({x n ϕ满足 )()()()(021x f x x x n ≤≤≤≤≤≤ ϕϕϕ,且 f x n →)(ϕ.∴ 33232lim d )( lim d )( 1111]1 ,0[ ]1 ,0[ =⋅=⋅==∑∑⎰⎰∞=-=-∞→∞→n n n ni i i n n n n i m x m x f ϕ.即 ]1 ,0[L f ∈,且3d )( ]1 ,0[ =⎰m x f .3.设0)(≥x f 为可测函数,令 ⎩⎨⎧>≤=,)( ,0 ,)( ),()]([N x f N x f x f x f N 若若 试证明⎰⎰=EEN Nm x f m x f d )( d )]([ lim .证 由题设知: ≤≤≤≤≤N f f f ][][][021,且 f f N N −−→−∞→][,则由勒维(Levi )定理可知 ⎰⎰=E E N Nm x f m x f d )( d )]([ lim.4.设从]1 ,0[中取n 个可测子集n E E E 、、、 21,假定]1 ,0[中任一点至少属于这n 个子集中的p 个.试证:必有一集,它的测度不小于np.证 令 i E 的特征函数为)(x iE χ,则⎰⎰⎰+++=+++11 01 021d )(d )(d )(21x x x x x x mE mE mE n E E E n χχχp x p x x ni E i =≥⎪⎪⎭⎫⎝⎛=⎰⎰∑=1 0 1 0 1d d )(χ. 令 } , , , m ax {21n mE mE mE mE =,则 1≤mE ,从而 p mE mE mE mE n n ≥+++≥⋅ 21, ∴ npmE ≥.5.勒维(Levi )定理中去掉函数列的非负性假定,结论是否成立?解 Levi 定理中函数列的非负性条件是必要的,不可去,否则结论未必成立.例如: ,2 ,1 ,0 ,0 ],1 ,1[,0 ,)(11=⎩⎨⎧=-∈≠-=n x x x x f nx n , ⎩⎨⎧=-∈≠=,0,0 ],1 ,1[,0 , )(1x x x x f x则 0)(≠x f ,a.e.于]1 ,1[-,且有≤≤≤≤)()()(21x f x f x f n ,)()(lim x f x f n n =∞→.但()+∞=-⎰-01 11d x x n ,故 ⎰-1 1 d )(x x f n 不存在;同理,⎰-11 d )(x x f 也不存在. 因此,Levi 定理不成立.容易证明:若存在)()(E L x g ∈,满足 ≤≤≤≤≤)()()()(21x f x f x f x g n ,则Levi 定理成立(不妨一证).6.设0>mE ,又设E 上的可积函数)()(x g x f 、满足)()(x g x f <,试证⎰⎰<E E m x g m x f d )( d )( .证 ∵ 0)()(>-x f x g ,∴ 由L 积分的单调性(3L )可知0d )]()([d )(d )( ≥-=-⎰⎰⎰E E E m x f x g m x f m x g .(设法去掉等号!) 若0d )()(d )]()([ =-=-⎰⎰E E m x f x g m x f x g ,则由命题3.2.5的(ⅲ)可知0)()(=-x f x g ,a.e.于E ,与)()(x g x f <矛盾!故0d )(d )( >-⎰⎰E E m x f m x g .7.设)(x f 为E 上的可积函数,如果对任何有界可测函数)(x ϕ,都有0d )()( =⎰Em x x f ϕ,则0=f ,a.e.于E ,试证明之.证 由 )(x ϕ的任意性,不妨设⎪⎩⎪⎨⎧=∈<∈->∈=),0( ,0 ),0( ,1),0( ,1 )(f E x f E x f E x x ϕ 则)(x ϕ为E 上的有界可测函数,由题设,应有0d d )()( )0( ==⎰⎰>f E E m f m x x f ϕ.而()()()0d d d d 0 0 0 ==+=⎰⎰⎰⎰>=>f E f E f E E m f m f m f m f ,故由命题3.2.5的(ⅲ)可知:0=f ,a.e.于E .8 设)(x f 为]1 ,0[上的可积函数,若对任何)1 ,0(∈a ,恒有0d )( ),0( =⎰a m x f ,则0=f ,a.e.于]1 ,0[.证 用反证法:设在]1 ,0[上)(x f 不是几乎处处为零,令 )1 ,0(=E ,)0(1>=f E E , )0(2<=f E E ,则21 mE mE 、中至少有一个大于0.不妨设01>mE ,则存在闭集 )1 ,0(1⊂⊂E F ,满足0>mF ,从而0d )( >⎰F m x f .令}sup{ },inf{F x x F x x ∈=∈=βα,则 10<<<βα.现取)1 ,(β∈r ,并令F r G -=) ,0(,则G 为开集.由于对任何)1 ,0(∈a ,恒有0d )( ) ,0( =⎰a m x f ,于是有0d )( ) ,0( =⎰r m x f ,所以,0d )(0d )(d )(d )( ) ,0( <-=-=⎰⎰⎰⎰F F r G m x f m x f m x f m x f . (*)又设 ∞==1) ,(i i i b a G ,其中) ,(i i b a 为互不相交的构成区间,则必存在某个G b a k k ⊂) ,(,使得0d )(),( <⎰k k b a m x f (否则必有0d )( ≥⎰Gm x f 而与(*)式矛盾!).但000d )(d )(d )() ,0( ) ,0( ) ,( =-=-=⎰⎰⎰kkkka b b a m x f m x f m x f ,为此矛盾!故 0=f ,a.e.于]1 ,0[.9.设]) ,([)(b a L x f ∈,试证:对每个N ∈n ,)]([x nf (取整函数)可积且有等式⎰⎰=∞→),( ),( 1d )( d )]([ limb a b a n n m x f m x nf.证 当n k n k x f 1)(+<≤(Z ∈k )时,1)(+<≤k x nf k ,k x nf =)]([,nkn x nf =)]([1. ∴ ][)(1nf x nn =ϕ 为简单函数列,且 )()(lim x f x n n =∞→ϕ. 故 ⎰⎰⎰==∞→∞→),( ) ,( 1),( 1d )(d )]([lim d )]([limb a b a nn b a n n m x f m x nf m x nf.10.设对每个N ∈n ,)(x f n 在E 上可积,f f n →,a.e.于E ,且一致有K m x f En ≤⎰ d )(,K 为常数,则)(x f 在E 上可积.试证明之.证 设()f f E E n →=0,由f f n →于0E ,得 f f n →于0E . 由法都(Fatou )定理,得K m f m f m f En n E n n E≤≤=⎰⎰⎰∞→∞→0d limd lim d .∵ ()00=-E E m ,∴0d 0=⎰-EE m f ,于是有∞<≤=⎰⎰K m f m f E E 0d d ,即 f 在E 上可积,从而 )(x f 在E 上可积.11.设)(x f ,)(x f n (N ∈n )均是E 上的可积函数,f f n →,a.e.于E ,且⎰⎰=∞→EEn n m x f m x f d )( d )( lim.试证:在任意可测子集E e ⊂上,有 ⎰⎰=∞→een n m x f m x f d )( d )( lim .证 由法都(Fatou )定理,有 ⎰⎰⎰∞→∞→≤=en n e n n e m f m f m f d lim d lim d ①;同理有⎰⎰-∞→-≤eE n n eE m f m f d limd ;运用性质若()n n ny x +lim 存在,则()n n n n ny x y x lim lim lim+=+,(*)则有⎰⎰⎰⎰⎰---=-=eE En neE Ee mf m f m f m f m f d d lim d d d。
实变函数论作业部分习题解(参考)

《实变函数论》作业部分习题解(参考)说明:1. 本题解是视频课体置的全部习题,只是作业1~作业4的部分习题。
2.题序为“章——节——题号”作业1(第一章~第二章)1-1-1 证明(B —A ) A=B 的充要条件是A ⊂B.证:必要性显然,事实上A 为B 的子集,因而A ⊂B. 充分性:由A ⊂B 知B-A ⊂B ,所以(B-A ) A ⊂B. 但(B-A ) A ⊃B 恒成立,于是得证. 1-1-2 证明A-B=A BC证:B A x -∈∀,即A x ∈且B x ∈,亦即c B x A x ∈∈且,于是c B A x ∈.再c B A x ∈∀ ,即A x ∈且c B x ∈. 亦即B x A x ∈∈且,边就是B A x -∈.综上述得证. 1-1-3 证明定理4中的(3),(4),定理6中第二式。
证:定理4(3):00,λλλλB x B x ∈∈∀∧∈使必存在 ,从而0λA x ∈,当然有 ∧∈∈λλA x ,又,由上述c x ∈显然成立. 证毕.定理4(4):∈∀x 左边,必存在000λλλB A x ∈有, 由0λA x ∈,当然有 ∧∈∈λλ0A x ,由0λB x ∈,当然有 ∧∈∈λλB x . 所以∈x 右边. 再∈∀x 右边,则 ∧∈∈λλA x 或 ∧∈∈λλB x ,由 ∧∈∈λλA x ,则存在某λ使λA x ∈,又由 ∧∈∈λλB x ,也存在某λλB x ∈使,从而λλB A x ∈,故 ∧∈∈λλλ)(B A x =左边. 综上述,命题得证 定理6(第二式):∈∀x 左边,解 ∧∈∈λλA x ,必存在某λ使λA x ∈,即cA x λ∈,从而 ∧∈∈λλcA x 显然成立.再,∈∀x 右边,存在某λ使cA x λ∈,即λA x ∈,当然满足 ∧∈∈λλA x ,即有cA x )( ∧∈∈λλ综上述,得证.1-1-4 证明(A-B ) B=(A B )—B 的充要条件是B=φ. 证:充分性显然,现证必要性:用反证法,若φ≠B ,则可令B x ∈,从而)(B A B x -∈ .但由题设又有B B A x -∈)( 推到B x ∈产生矛盾证毕.1-2-1 用解析式给出(-1,1)和(),+∞-∞之间的一个1-1对应。
肺部的解剖结构
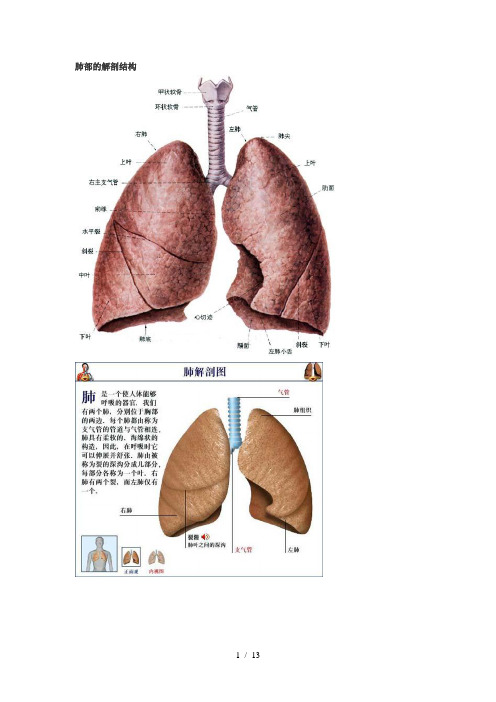
肺部的解剖结构呼吸系统正常X线影像表现胸片是由胸内外组织形成前后重迭的复合影像。
必须熟悉X线片上各种影像的正常及其变异,以免误诊。
分为胸廓、纵隔障、横膈、胸膜和肺五部分描述。
一、胸廓由软组织及骨骼构成(一)软组织(图3-1)图3-1 胸壁的软组织及骨骼部分可能诊断错误的情况(附叶间裂的变异)1.颈肋2 .胸锁乳突肌3. 第一、二肋骨的伴随阴影4 . 奇叶裂5.肋骨前端骨桥关节形成6.肋骨联合7.叉状肋8.上中叶间裂(水平叶裂)9.(略)10. 下副叶裂11.乳头12 .乳房13.锁骨下动脉14. 肋软骨钙化15. 肋骨沟16.左副中叶裂17.胸大肌18.肩胛骨边缘19.菱形窝1.胸锁乳突肌与锁骨上皮肤皱褶,胸锁乳突肌是从两侧颈部向下方斜行,附着于胸骨柄和锁骨内端,遮盖肺尖内侧形成外缘清楚的密度均匀影。
其下端与锁骨上缘的横行皮肤皱褶相连,后者表现为锁骨上缘3~5mm宽的薄层软组织影,系锁骨上皮肤及皮下组织的投影。
2.胸大肌胸大肌发达者,在两胸中部外带显示扇形淡薄影,下界清楚,密度较浓,由内下向外上斜行,与腋前皱壁相连续,右侧常较明显,勿误为肺内病变。
3.女性乳房和乳头乳房在两肺下野形成下缘清楚、上缘不清、且密度逐渐变淡的半圆形致密影,其下缘向外与腋部皮肤连续。
随着乳房形状、大小、下垂与否而有变异。
乳头有时在两肺下部大致相当于第五肋间处形成小结节状影,年龄较大的妇女多见,有时亦见于男性,勿误为肺内病变。
(二)骨骼肋骨:肋骨位于胸椎两侧,后段呈水平向外走行,前段自外上向内下倾斜形成肋弓,后段较前段厚故显影较前段致密。
第1~10肋骨前端有肋软骨与胸骨相连,软骨不显影故胸片上肋骨前端似游离状。
20~30岁第一对肋软骨首先钙化,随着年龄增长,其它肋骨也自下而上逐条钙化,表现为不规则的斑片、斑点状致密影,勿误认为肺内病变。
肋骨有多种先天性变异,常见的有颈肋,自第七颈椎发出,表现为短小较直的小肋骨,可一侧或两侧。
实变函数(程其襄版)第一至四章课后习题答案

,再由极限的唯一性,
上下极限还有用交集与并集来表示。
定理3
⑴ ; ⑵
证明我们利用
来证明⑴式.记 , .设 ,则对任意取定的 ,总有 ,使 ,即对任何 ,总有 ,故 .反之,设 ,则对任意的 ,总有 ,即总存在 ,有 ,所以 ,因此 ,即 .
2.集合的包含关系
若集合A和B满足关系:对任意 ∈A,可以得到x∈B,则成A是B的子集,记为A B或B A,若A B但A并不与B相同,则称A是B的真子集.
例7. 若 在R上定义,且在[a,b]上有上界M,即任意对
∈[a,b]有 M.用集合语言表示为:[a,b] { : M}.
用集合语言描述函数性质,是实变函数中的常用方法,请在看下例.
(1)单射:对任意 ,若 ,使得 ;
(2)满射:对任意 ,存在 ,使得 .
则称A和B对等,记为 ,规定 .
例1 我们可给出有限集合的一个不依赖与于元素个数概念的定义:集合A称为有限合,如果 或者A和正整数的某截断 对等。
注:有限集合的一个不依赖与于元素个数概念的定义,例如A的总个数与正整数的某个截断相对应。
⑵式可同样证明.
用定理3,例12中的⑴式和⑵式可分别简写为
,
.
如果 ,则称 收敛,记为 .若极限允许取 ,则单调数列总有极限,在集合论中也有类似的结论.
5.单调系列
如果集列 满足 , ,则称 为增加(减少)系列.增加与减少的集列统称为单调集列.容易证明:单调集列是收敛的.如果 增加,则 ,如果 减少,则 .请读者自证.
第一章 集合
早在中学里我们就已经接触过集合的概念,以及集合的并、交、补的运算,因此这章的前两节具有复习性质,不过,无限多个集合的并和交,是以前没有接触过的,它是本书中常常要用到,是学习实变函数论时的一项基本功。
实变函数试题库参考答案

实变函数试题库参考答案(共37页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《实变函数》试题库及参考答案(完整版)选择题1,下列对象不能构成集合的是:( )A 、全体自然数B 、0,1 之间的实数全体C 、[0, 1]上的实函数全体D 、全体大个子2、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{全体小个子}D 、{x :x>1}3、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{x :x>1}D 、{全体胖子}4、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体整数}C 、{x :x>1}D 、{全体瘦子}5、下列对象不能构成集合的是:( )A 、{全体小孩子}B 、{全体整数}C 、{x :x>1}D 、{全体实数}6、下列对象不能构成集合的是:( )A 、{全体实数}B 、{全体大人}C 、{x :x>1}D 、{全体整数}7、设}1:{ααα≤<-=x x A , I 为全体实数, 则ααA I∈⋃= ( ) A 、(-1, 1) B 、(-1, 0) C 、(-∞, +∞) D 、(1, +∞)8、设}1111:{ix i x A i -≤≤+-=, N i ∈, 则i i A ∞=⋃1= ( ) A 、(-1, 1) B 、(-1, 0) C 、[0, 1] D 、[-1, 1]9、设}110:{ix x A i +≤≤=, N i ∈, 则i i A ∞=⋂1= ( ) A 、(0, 1) B 、[0, 1] C 、[0, 1] D 、(0, +∞)10、设}1211:{ix i x A i +<<-=, N i ∈, 则i i A ∞=⋃1= ( ) A 、[1, 2] B 、(1, 2) C 、 (0, 3) D 、(1, 2)11、设}23:{+≤≤=i x i x A i , N i ∈, 则i i A ∞=⋂1= ( ) A 、(-1, 1) B 、[0, 1] C 、Φ D 、{0}12、设}11:{ix i x A i <<-=, N i ∈, 则i i A ∞=⋂1= ( ) A 、(-1, 1) B 、[0, 1] C 、Φ D 、{0}13、设]1212,0[12--=-n A n , ]211,0[2nA n +=, N n ∈,则=∞→n n A lim ( )A 、[0, 2]B 、[0, 2]C 、[0, 1]D 、[0, 1]14、设]1212,0[12--=-n A n , ]211,0[2nA n +=, N n ∈, 则=∞→n n A lim ( ) A 、[0, 2]B 、[0, 2]C 、[0, 1]D 、[0, 1]15、设),0(n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、[0, n]C 、RD 、(0, ∞)16、设)1,0(nA n =, N n ∈, 则=∞→n n A lim ( ) A 、(0, 1)B 、(0, n1) C 、{0} D 、Φ 17、设)1,0(12nA n =-, ),0(2n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、(0, n1) C 、(0, n) D 、(0, ∞) 18、设)1,0(12nA n =-, ),0(2n A n =, N n ∈, 则=∞→n n A lim ( )A 、ΦB 、(0, n1) C 、(0, n) D 、(0, ∞) 19、设A 、B 、C 是三个集合, 则A-(A-B)= ( )A 、B B 、AC 、A ⋂BD 、A ⋃B20、设A 、B 、C 是三个集合, 则A-(B ⋃C)= ( )A 、(A-B)⋂(A-C)B 、(A-B)⋃(A-C)C 、A ⋂BD 、A ⋂C21、设A 、B 、C 是三个集合, 则A-(B ⋂C)= ( )A 、(A-B)⋂(A-C)B 、(A-B)⋃(A-C)C 、A ⋂BD 、A ⋂C22、设A 、B 、S 是三个集合, 且S A ⊂, S B ⊂, 则)(B A C s -= ( )A 、BC A C s s ⋃ B 、B C A C s s ⋂ C 、B A C s ⋃D 、B A C s ⋂23、设A 、B 、S 是三个集合, 且S A ⊂, S B ⊂, 则)(B A C s ⋃= ( )A 、BC A C s s ⋃ B 、B C A C s s ⋂ C 、B A C s ⋃D 、B C A s ⋃24、设A 、B 、C 是三个集合, 则A-(B-C) = ( )A 、 A ⋃C-B B 、 A-B-C C 、 (A-B)⋃(A ⋂C)D 、 C-(B-A)25、集合E 的全体内点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包26、集合E 的全体聚点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包27、集合E 的全体边界点和内点所成的集合是E 的 ( )A 、开核B 、边界C 、导集D 、闭包28、E-E '所成的集合是 ( )A 、开核B 、边界C 、外点D 、{E 的全体孤立点}29、E 的全体边界点所成的集合称为E 的 ( )A 、开核B 、边界C 、导集D 、闭包30、设点P 是集合E 的边界点, 则 ( )A 、P 是E 的聚点B 、P 是E 的孤立点C 、P 是E 的内点D 、P 是CE 的边界点31、设)3,2()1,0(⋃=G , 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(21, 1) C 、[0, 1] D 、(0, 2) 32、设)1,0(1=G , )2,21()0,1(2⋃-=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 2)C 、(-1, 21) D 、(-1, 2) 33、设)4,0(1=G , )4,3()1,0(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(3, 4)C 、(0, 4)D 、 (1, 4)34、设)1,0(1=G , )4,3()2,1(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 3)C 、(0, 4)D 、(1, 4)35、设)2,0(1=G , )4,3()2,1(2⋃=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(0, 1)B 、(0, 2)C 、(1, 2)D 、(1, 4)36、设)2,1()1,0(1⋃=G , )23,21()0,1(2⋃-=G 21G G G ⋃=, 则下列那一个是G 的构成区间: ( )A 、(21, 23) B 、(1, 2) C 、(0, 1) D 、(-1, 0) 37、若B A ⊂ ,则下列命题错误的是: ( )A 、B A ⊂ B 、A '⊂B 'C 、B A ∂⊂∂D 、B A ⊂38、若C B A =⋃, 则下列命题正确的是:( )A 、 CB A =⋃ B 、 A '⋃B '=C ' C 、C B A ∂=∂⋃∂D 、{A 的孤立点}⋃{B 的孤立点}={C 的孤立点}39、若C B A =⋂, 则下列命题错误的是:( )A 、 CB A =⋂ B 、C '⊂ A '⋂B ' C 、C B A =⋂D 、{A 的孤立点}⋂{B 的孤立点}={C 的孤立点}40、设CA 是A 的余集,则下列命题正确的是:( )A 、 )()(CA A C =B 、)(CA A ∂=∂C 、C(A ')=(CA )'D 、CA A C =)(41、设A -B=C, 则下列命题正确的是:( )A 、CB A ∂=∂-∂ B 、C B A =- C 、A '-B '=C 'D 、{A 的孤立点}-{B 的孤立点}={C 的孤立点}42、 (2-4-1-2) 下列命题错误的是:( )A 、A 是闭集B 、A '是闭集C 、A ∂是闭集D 、 A 是闭集43、若A 是闭集,B 是开集,则A -B 是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断44、若A 是开集,B 是闭集,则A -B 是:( )A 、开集B 、闭集C 、既非开集又非闭集D 、无法判断45、若}{n A 是一开集列,则n n A ∞=⋃1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断46、若}{n A 是一开集列,则n n A ∞=⋂1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断47、若}{n A 是一闭集列,则n n A ∞=⋃1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断48、若}{n A 是一闭集列,则n n A ∞=⋂1是:( ) A 、开集 B 、闭集 C 、既非开集又非闭集 D 、无法判断49、若]1,0[ Q E =,则=mE ( )A 、0B 、1C 、2D 、350、下述结论( )正确.A 、E m E m **>B 、E m E m *≥*C 、E m E m **<D 、E m E m **≤51、下列说法正确的是( )A 、xx f 1)(=在(0,1)有限 B 、xx f 1)(=在)1,21(无界 C 、⎪⎩⎪⎨⎧=∞+∈=0,]1,0(,1)(x x x x f ,在[0,1]有限 D 、⎪⎩⎪⎨⎧=∈=0,1]1,0(,1)(x x x x f ,在[0,1]有界 52、函数列n n x x f =)(在[0,1]上( )于0.A 、a ,e 一致收敛B 、收敛C 、一致收敛D 、基本上一致收敛53、设E 是[0,1]中的不可测集,⎩⎨⎧-∈-∈=E x E x x f ]1,0[,1,1)( 则下列函数在[0,1]上可测的是( ).A 、)(x fB 、)(x f +C 、|)(|x fD 、)(x f -54、若)(x f 可测,则它必是( ).A 、连续函数B 、单调函数C 、简单函数D 、简单函数列的极限55、若Q E -=]1,0[,则=mE ( )A 、0B 、1C 、2D 、356、下列说法不正确的是( )A 、E 的测度有限,则E 必有界B 、E 的测度无限,则E 必无界C 、有界点集的测度有限D 、n R 的测度无限57、(4-4-2-1)下述论断正确的是( )A 、x x f tg )(=在)4,0(π无界 B 、⎪⎩⎪⎨⎧=∞+∈=2,)2,0[,tg )(ππx x x x f 在]2,0[π有限 C 、⎪⎩⎪⎨⎧=∈=2,1)2,0[,tg )(ππx x x x f 在]2,0[π有界 D 、x x f tg )(=在)2,0(π有限58、函数列n n x x f )21()(=在[0, 2]上( )于0. A 、收敛 B 、一致收敛 C 、基本上一致收敛 D 、.一致收敛59、设⎩⎨⎧-∈-∈=Ex x E x x x f ]1,0[,,)(其中E 是[0,1]的不可测集,则下列函数在[0, 1]可测的是( ).A 、|)(|x fB 、)(x fC 、)(x f +D 、)(x f -60、一个函数在其定义域中的( )点处都是连续的.A 、边界点B 、内点C 、聚点D 、孤立点.61、0P 是康托尔(cantor )集,则=0mP ( )A 、0B 、1C 、2D 、362、设A 是B 的真子集,则( )A 、B m A m **< B 、B m A m **≤C 、B m A m **>D 、B m A m **≥63、下列说法正确的是( )A 、x x f ctg )(=在)2,4(ππ无界 B 、⎪⎩⎪⎨⎧=∞+∈=0,]2,0(ctg )(x x x x f π在]2,0[π有限C 、⎪⎩⎪⎨⎧=∈=0,1]2,0(ctg )(x x xx f π在]2,0[π有界 D 、x x f ctg )(=在)2,0(π有限64、函数列n n n x x f 2)(=在]21,0[上( )于0. A 、收敛 B 、一致收敛、 C 、基本上一致收敛 D 、a. e.一致收敛65、设E 是[0, 1]上的不可测集,⎩⎨⎧-∈-∈=Ex xE x x x f ]1,0[)(22则下列函数在[0, 1]可测的是( ). A 、)(x f B 、)(x f + C 、|)(|x f D 、)(x f -66、设E 为可测集,则下列结论中正确的是( )A 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n 一致收敛于)(x fB 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n 基本上一致收敛于)(x fC 、若)}({x f n 在E 上a , e 收敛于一个a , e 有限的可测函数)(x f ,则)(x f n ⇒)(x fD 、若)}({x f n 在E 上基本上一致收敛于)(x f ,则)(x f n a , e 收敛于)(x f67、G 表示康托尔(cantor )集在[0,1]中的余集,则mG=( ) A 、0 B 、1 C 、2 D 、368、设21,S S 都可测,则21S S ( )A 、可测B 、不可测C 、可能可测也可能不可测D 、以上都不对 69、下列说法正确的是( ) A 、x x f sec )(=在)4,0(π上无界B 、x x f sec )(=在)4,0(π上有限C 、⎪⎩⎪⎨⎧=∞+∈=2)2,0[sec )(ππx x xx f 在]2,0[π上有限 D 、⎪⎩⎪⎨⎧=∈=21)2,0[sec )(ππx x x x f 在]2,0[π上有界 70、函数列n n n x x f 3)(=在]31,0[上( )于0 A 、收敛 B 、一致收敛 C 、基本上一致收敛 D 、a. e.一致收敛71、设⎩⎨⎧-∈∈-=E x x Ex x x f ]1,0[,,)(33,其中E 是[0, 1]上的不可测集,则( )在[0, 1]可测.A 、)(x f 、B 、)(x f +C 、)(x f -D 、|)(|x f 72、关于连续函数与可测函数,下列论述中正确的是( )A 、它们是同一概念B 、a , e 有限的可测函数是连续函数C 、a , e 有限的可测函数是基本上连续的函数D 、a , e 有限的可测函数是a , e 连续的函数 73、()=-)2,1()1,0( m ( ) A 、1、 B 、2 C 、3 D 、4 74、A 可测,B 是A 的真子集,则( )A 、mB mA ≥ B 、B m mA *≥C 、B m mA *=D 、以上都不对 75、下列说法正确的是( ) A 、21)(x x f =在(0, 1)有限、 B 、21)(xx f =在]1,21[无界C 、⎪⎩⎪⎨⎧=∞+∈=0,]1,0(,1)(2x x x x f 在[0, 1]有限D 、⎪⎩⎪⎨⎧=∈=1,1]1,0(,1)(2x x x x f 在[0, 1]有界76、函数列x x f n n sin )(=在]2,0[π上( )于0.A 、收敛B 、基本上一致收敛C 、一致收敛D 、a. e.一致收敛77、设⎩⎨⎧-∈∈-=Ex x Ex x x f ]1,0[,,)(22其中E 是[0, 1]上的不可测集,则( )在[0, 1]上是可测的.A 、|)(|x fB 、)(x fC 、)(x f +D 、)(x f - 78、关于简单函数与可测函数下述结论不正确的是( )A 、简单函数一定是可测函数B 、简单函数列的极限是可测函数C 、简单函数与可测函数是同一概念D 、简单函数列的极限与可测函数是同一概念79、()=-]3,2()1,1[ m ( ) A 、1 B 、2 C 、3 D 、4 80、L 可测集类,对运算( )不封闭.A 、可数和B 、有限交C 、单调集列的极限D 、任意和. 81、下列说法正确的是( ) A 、31)(x x f =在)1,21(无界 B 、31)(xx f =在)1,0(有限C 、⎪⎩⎪⎨⎧=∞+∈=0]1,0(1)(3x x xx f 在[0, 1]有限 D 、⎪⎩⎪⎨⎧=∈=01]1,0(1)(3x x xx f 在[0, 1]有界82、函数列x x f n n cos )(=在]2,0[π上( )于0.A 、基本一致收敛B 、收敛C 、一致收敛D 、a. e.一致收敛83、设E 是]2,0[π中的不可测集,⎪⎩⎪⎨⎧-∈-∈=E x x E x x x f ]2,0[,sin ,sin )(π则下列函数在]2,0[π上可测的是( ).A 、)(x fB 、|)(|x fC 、)(x f +D 、)(x f - 84、关于依测度收敛,下列说法中不正确的是( )A 、依测度收敛不一定一致收敛B 、依测度收敛不一定收敛C 、若)}({x f n 在E 上.收敛于.有限的可测函数)(x f ,则)()(x f x f n ⇒D 、若)()(x f x f n ⇒,则存在子列)}({x f i n a. e.收敛于)(x f85、设)(x f 是可测集E 上的非负可测函数,则)(x f ( )A 、必可积B 、必几乎处处有限C 、必积分确定D 、不一定积分确定 86、设)(x f 在可测集E 上可积,则在E 上( )A 、)(x f +与)(x f -只有一个可积B 、)(x f +与)(x f -皆可积C 、)(x f +与)(x f -不一定可积D 、)(x f +与)(x f -至少有一个不可积 87、设0=mE (Φ≠E ),)(x f 是E 上的实函数,则下面叙述正确的是( )A 、)(x f 在E 上不一定可测B 、)(x f 在E 上可测但不一定可积C 、)(x f 在E 上可积且积分值为0D 、)(x f 在E 上不可积 88、)(x f 在可测集E 上)(L 可积的必要条件是,)(x f 为( )A 、连续函数B 、几乎处处连续函数C 、单调函数D 、几乎处处有限的可测函数89、设)(x D 为狄立克雷函数,则⎰=10)()(dx x D L ( )A 、 0B 、 1C 、1/2D 、不存在 90、设)(x f 为Cantor 集的特征函数,则⎰=10)()(dx x f L ( )A 、 0B 、 1/3C 、2/3D 、 1 填空题1、设A 为一集合,B 是A 的所有子集构成的集合;若A =n, 则B =2、设A 为一集合,B 是A 的所有子集构成的集合;若A 是一可数集, 则B =3、若c A =, c B =, 则=⋃B A4、若c A =, B 是一可数集, 则=⋃B A5、若c A =, n B =, 则=⋃B A6、若}{n A 是一集合列, 且c A n =, =⋃∞=n n A 17、若I A ∈αα}{是任意集族, 其中I 是指标集, 则ααA I∈⋂=8、若I A ∈αα}{是任意集族, 其中I 是指标集, 则ααA I∈⋃=9、若I A ∈αα}{是任意集族, 其中I 是指标集, S 是一集合, 则)(ααA C IS ∈⋂=10、若I A ∈αα}{是任意集族, 其中I 是指标集, S 是一集合, 则)(ααA C IS ∈⋃=11、若}{n A 是任意一个集合列, 则=∞→n n A lim12、若}{n A 是任意一个集合列, 则=∞→n n A lim13、欧氏空间n R 中, 任意两点),,(21n x x x x =, ),,(21n y y y y =的距离d(x, y)=14、C[a, b]空间中,任意两元素x(t), y(t) 的距离 d(x, y)= 15、2l 空间中, 任意两元素 ),,,(21 n x x x x =, ),,(21 n y y y y =的距离 d(x, y)=16、欧氏空间2R 中, 任意两点),(21x x x =, ),(21y y y =的距离 d(x, y)= 17、欧氏空间3R 中, 任意两点),,(321x x x x =, ),,(321y y y y =的距离d(x, y)=18、欧氏空间4R 中, 任意两点),,,(4321x x x x x =, ),,,(4321y y y y y =的距离d(x,y)=19、设2R X =,}1:),{(22<+=y x y x E ,则E =20、设3R X =, }1:),,{(222<++=z y x z y x E , 则E =21、设2R X =,}1:),{(22<+=y x y x E ,则E ∂= 22、设2R X =,}1:),{(22<+=y x y x E ,则E '=23、设3R X =, }1:),,{(222<++=z y x z y x E , 则 E ∂= 24、设3R X =, }1:),,{(222<++=z y x z y x E , 则E '= 25、设A= [0, 1] , B = [3, 4] , 则 d(A, B) = 26、设C 是康托完备集, G= [0, 1]-C , 则d (C, G) = 27、设C 是康托完备集, 则C 的半径)(C δ=28、两个非空集合A, B 距离的定义为 d (A, B ) = 29、一个非空集合A 的直径的定义为)(A δ= 30、设A = [0, 1] ⋂Q, 则)(A δ=31、nR E ⊂,对每一列覆盖E 的开区间 ∞=⊃1i i E I ,定义=E m *________。
实变函数课后答案

实变函数课后答案以下是十道实变函数的课后试题及答案:1.计算函数f(x)=2x+3在x=4处的取值。
答案:f(4)=2(4)+3=112.证明函数f(x)=x^2在定义域内是增函数。
答案:对于任意x1<x2,在区间(x1,x2)内有f(x1)<f(x2)。
证明:f(x2)-f(x1)=x2^2-x1^2=(x2+x1)(x2-x1)>0,其中x2+x1>0且x2-x1>0。
因此,f(x)=x^2在定义域内是增函数。
3. 求函数f(x) = ln(x)的定义域。
答案:由于ln(x)的定义域是(0, +∞),所以函数f(x) = ln(x)的定义域是(0, +∞)。
4.求函数f(x)=,x-3,的值域。
答案:由于,x-3,的值域是[0,+∞),所以函数f(x)=,x-3,的值域是[0,+∞)。
5.计算函数f(x)=e^x在x=2处的导数。
答案:f'(x)=e^x,所以f'(2)=e^26. 计算函数f(x) = sin(x)在x = π/4处的导数。
答案:f'(x) = cos(x),所以f'(π/4) = cos(π/4) = 1/√27.证明函数f(x)=x^3是奇函数。
答案:对于任意x,f(-x)=(-x)^3=-x^3=-f(x),所以函数f(x)=x^3是奇函数。
8. 证明函数f(x) = sin(x)在定义域内是周期函数。
答案:sin(x)的周期是2π,对于任意实数x,有sin(x + 2π) = sin(x),所以函数f(x) = sin(x)在定义域内是周期函数。
9.求函数f(x)=e^x的反函数。
答案:令y = e^x,解得x = ln(y),所以函数f(x) = e^x的反函数是f^(-1)(x) = ln(x)。
10.计算函数f(x)=1/x在x=2处的极限。
答案:lim(x→2)(1/x) = 1/2。
(完整版)《实变函数》第四章可测函数

第四章 可测函数(总授课时数 14学时)由于建立积分的需要,我们还必须引进一类重要的函数——Lebesgue 可测函数,并讨论其性质和结构。
§1 可测函数及其性质教学目的 本节将给出可测函数的定义并讨论其基本性质教学要点 可测函数有若干等价的定义. 它是一类范围广泛的函数, 并且有很好的运算封闭性. 可测函数可以用简单函数逼近, 这是可测函数的构造性特征。
本节难点 可测函数与简单函数的关系。
授课时数 4学时———---—-——-——-—-—--——-——————-—1可测函数定义定义:设()f x 是可测集E 上的实函数(可取±∞),若[],f a a R E>∀∈可测,则称()f x 是E 上的可测函数。
2可测函数的性质性质1 零集上的任何函数都是可测函数。
注:称外测度为0的集合为零集;零集的子集,有限并,可数并仍为零集性质2 简单函数是可测函数若1nii E E ==⋃ (iE 可测且两两不交),()f x 在每个iE 上取常值ic ,则称()f x 是E 上的简单函数;1()()i ni E i f x c x χ==∑ 其中1()0ii E i x E x x E E χ∈⎧=⎨∈-⎩注:Dirichlet 函数是简单函数性质3 可测集E 上的连续函数()f x 必为可测函数 设()f x 为E 上有限实函数,称()f x 在0x E ∈处连续00(,)((),)0,0,()x f x f OE Oδεεδ∀>∃>⋂⊂若使得对比:设()f x 为(),a b 上有限实函数,0()(,)f x x a b ∈在处连续lim ()()x x f x f x →=若0,0,|||()()|x x f x f x εδδε∀>∃>-<-<即当时,有00(,)((),)0,0,()x f x x Of x O δεεδ∀>∃>∈∈即当时,有00(,)((),)0,0,()x f x f OOδεεδ∀>∃>⊂即使得()f x 在0[,]x a b ∈处连续(对闭区间端点则用左或右连续)证明:任取[]x E f a ∈>, 则()f x a >,由连续性假设知, 对(),0,xf x a εδ=-∃>使得(,)((),)()(,)x x f x f OE Oa δε⋂⊂⊂+∞即(,)[]x x f a OE Eδ>⋂⊂。
实变函数论4 n维空间中的点集、聚点、内点、界点(课堂PPT)

E 的 内 点 必 为 E 的 聚 点 , 但 E 的 聚 点 未 必 是 E 的 内 点 .
E 的 聚 点 可 能 属 于 E 也 可 能 不 属 于 E , 但 E 的 孤 立 点 一 定 属 于 E . E 的 边 界 点 不 是 聚 点 E 便 是 孤 立 点 .
U(x,)U(xi,i), i 1,2. (iv)若x y,存在U(x,)和U(y,),使U(x,) U(y,)
( i) i y U ( x ,) , 0 使 U ( y ,) U ( x ,);
证仅 明证 i) i ( 令 (y,x)则 , 0.若 z U (y,)则 , (z,y),从(而 z,x)(z,y)(y,x) (),故 z U (x,),于U 是 (y,) U (x,).6
( 1)
称为开区间, 记作(a1,b1;a2,b2; ;aN,bN). 若把(1)中的诸不等式换成 ai xi bi, i 1,2,
称I 为闭区间, 记作[a1,b1;a2,b2; ;aN,bN]. 若把(1)中的诸不
, N, 则
等式换成 ai xi bi, i 1,2, , N,则 称I 为半开区间,记作(a1,b1;a2,b2; ;aN,bN].
22
*定理4 (波尔察诺-外尔斯特拉斯(Bolzano-
Weierstrass)定理)若 E是 R n 中一 个有界的无穷集合,则 E 至少有一个 聚点 P ,即 E。 *定理5 若E,ERn, 则 E 至少有一个 界点,即 E 。
p 0
证明:(3) (2) (1)显然,下证 (1)(3) 16
命 题 1x 0是 E 的 聚 点 E 中 存 在 着 一 列 异 于 x 0的 点 x 1 ,x 2 ,x 3 , 收 敛 于 x 0 .
肺炎-医学课件

(5)X线:可见双肺散在小片状或点状阴影
并发症
(1)呼吸衰竭 (2)心力衰竭 (3)肺脓肿、脓胸 (4)支气管扩张
病原菌
大叶性肺炎 多为肺炎球菌
小叶性肺炎 化脓菌
发病年龄
青壮年
小儿,年老体弱者
病变特点
纤维素性炎
化脓性炎
病变范围
肺段或肺叶
灰色肝样变期
灰色肝样变期
灰 色 肝 样 变 期
肉眼: 肺叶肿胀,充血消退, 灰白色,切面干燥, 颗粒状,质实如肝。
临床病理联系
发绀,呼吸困难症状减轻 泡沫状稀薄黏液脓痰 肺实变体征与红肝期基本相同 肺炎球菌不易检出
4)溶解消散期(7-10天)
镜下:中性粒细胞大多变性坏死, 纤维蛋白网减少, 肺泡壁毛细血管由贫血状态恢复正常
脱落崩解的粘膜上皮细胞
肺泡间隔毛细血管扩张充血 肺泡腔内充满浆液,中性粒,脓细胞
脱落崩解的肺泡上皮细胞
病灶周围肺组织呈代偿性肺气肿
4.病理与临床联系
(1)发热、咳嗽、咳痰
(2)呼吸困难及紫绀 病灶内细支气管及肺泡内有多量渗出物, 使肺泡通气量减少及换气障碍
(3)实变体征不明显: 病变大于3-4cm可出现实变体征
肉眼:肺叶肿胀,重量↑,暗红色, 切面可挤出带泡沫的血性浆液
•
(图)
临床病理联系
毒血症—寒战,高热,外周血白细胞升高 咳嗽,咳痰—淡红色泡沫痰,稀薄或带血丝
痰检:可检出肺炎球菌
听诊:湿罗音 X线:模糊,片状分布的阴影
2)红色肝样变期(3-4天)
镜下: 肺泡壁毛细血管扩张充血 肺泡腔充满大量纤维素及红细胞,少量中性粒 细胞、巨噬细胞 纤维素连接成网 渗出物中检出多量肺炎球菌
实变函数论课后答案第三版

1. 证明:()B A A B -=的充要条件是A B ⊂.证明:若()B A A B -=,则()A B A A B ⊂-⊂,故A B ⊂成立. 反之,若A B ⊂,则()()B A A B A B B -⊂-⊂,又x B ∀∈,若x A ∈,则()x B A A ∈-,若x A ∉,则()x B A B A A ∈-⊂-.总有()x B A A ∈-.故()B B A A ⊂-,从而有()B A A B -=。
证毕2. 证明c A B A B -=.证明:x A B ∀∈-,从而,x A x B ∈∉,故,c x A x B ∈∈,从而x A B ∀∈-, 所以c A B A B -⊂.另一方面,c x A B ∀∈,必有,c x A x B ∈∈,故,x A x B ∈∉,从而x A B ∈-, 所以 c A B A B ⊂-.综合上两个包含式得c A B A B -=. 证毕3. 证明定理4中的(3)(4),定理6(De Morgan 公式)中的第二式和定理9.证明:定理4中的(3):若A B λλ⊂(λ∈∧),则A B λλλλ∈∧∈∧⊂.证:若x A λλ∈∧∈,则对任意的λ∈∧,有x A λ∈,所以A B λλ⊂(∀λ∈∧)成立知x A B λλ∈⊂,故x B λλ∈∧∈,这说明A B λλλλ∈∧∈∧⊂.定理4中的(4):()()()A B A B λλλλλλλ∈∧∈∧∈∧=.证:若()x A B λλλ∈∧∈,则有'λ∈∧,使 ''()()()x A B A B λλλλλλ∈∧∈∧∈⊂.反过来,若()()x A B λλλλ∈∧∈∧∈则x A λλ∈∧∈或者x B λλ∈∧∈.不妨设x A λλ∈∧∈,则有'λ∈∧使'''()x A A B A B λλλλλλ∈∧∈⊂⊂.故()()()A B A B λλλλλλλ∈∧∈∧∈∧⊂.综上所述有()()()A B A B λλλλλλλ∈∧∈∧∈∧=.定理6中第二式()c c A A λλλλ∈∧∈∧=.证:()c x A λλ∈∧∀∈,则x A λλ∈∧∉,故存在'λ∈∧ ,'x A λ∉所以'c c x A A λλλ∈∧∉⊂从而有()c c A A λλλλ∈∧∈∧⊂.反过来,若c x A λλ∈∧∈,则'λ∃∈∧使'c x A λ∉,故'x A λ∉,x A λλ∈∧∴∉,从而()c x A λλ∈∧∈()c c A A λλλλ∈∧∈∧∴⊃. 证毕定理9:若集合序列12,,,,n A A A 单调上升,即1n n A A +⊂(相应地1n n A A +⊃)对一切n 都成立,则 1lim n n n A ∞→∞==(相应地)1lim n n n A ∞→∞==.证明:若1n n A A +⊂对n N ∀∈成立,则i m i mA A ∞==.故从定理8知11liminf n i m n m i mm A A A ∞∞∞→∞=====另一方面,m n ∀,令m i i mS A ∞==,从1m m A A +⊂对m N ∀∈成立知11111()()m i mi m i i m i mi m i m i m S A A A A A A S ∞∞∞∞++==+=+=+==⊂==.故定理8表明1111limsup liminf n i m m n n n m i mm m A A S S A A ∞∞∞∞→∞→∞=========故1lim limsup liminf n n n m n n n m A A A A ∞→∞→∞→∞====.4. 证明()()A B B A B B -=-的充要条件是B =∅. 证:充分性若B =∅,则()()A B B A A A A A -=-∅∅=-∅==∅=∅-∅必要性 若()()A B B A B B -=-,而B ≠∅则存在x B ∈.所以()()x A B B A B B ∈-=-即所以,x A B x B ∈∉这与x B ∈矛盾, 所以x B ∈.4. 设{}{}{}{}1,2,3,4,1,2,3,4S A ==,求()F A .又如果1;1,2,3,,S n n⎧⎫==⎨⎬⎩⎭01;A n ⎧⎫=⎨⎬⎩⎭为奇数,{}1111,,,,321A i ⎧⎫⎧⎫⎧⎫=⎨⎨⎬⎨⎬⎬-⎩⎭⎩⎭⎩⎭,问()()01,F A F A 是什么. 解:若{}{}{}{}1,2,3,4,1,2,3,4S A ==,则(){}{}{}{},1,2,3,4,1,2,3,4F A =∅.若011111;1,2,3,,;1,,,,3521S n A nni ⎧⎫⎧⎫⎧⎫====⎨⎬⎨⎬⎨⎬-⎩⎭⎩⎭⎩⎭为奇数, 则从1111111,,,,,,,3521242ci i ⎧⎫⎧⎫=⎨⎬⎨⎬-⎩⎭⎩⎭, 易知()111111,,1,,,,,,,,3521242F A S i i ⎧⎫⎧⎫⎧⎫=∅⎨⎨⎬⎨⎬⎬-⎩⎭⎩⎭⎩⎭. {}1111,,,,321A i ⎧⎫⎧⎫⎧⎫=⎨⎨⎬⎨⎬⎬-⎩⎭⎩⎭⎩⎭. 令11;1,2,,;1,2,212B i C i i i⎧⎫⎧⎫====⎨⎬⎨⎬-⎩⎭⎩⎭. {}{}{}1,F A S AK A B K C K A =∅==∅为的子集,或.证明: 因为{}111,,,,,321A B i ⎧⎫⎧⎫∈⎨⎬⎨⎬-⎩⎭⎩⎭的任何子集()1F A .所以有()1B F A ∈,而c B C =,故()1C F A ∈,又()1F A ∅∈. 任取B 的一子集A ,()1A A F A ∅=∈,且()1A C F A ∈. 显S A ∈,故只用证A 的确是一个σ-域.(1) ,c c S S A ∅==∅∈,且B ∀的子集A ,若K =∅,则,c KA A A C ∅==(B A -是B 的子集,故()()cc A A C F A ∅=∈) 又B ∀的子集A ,()cc c c A C A C A B ==. 显然是B 的子集,所以()()cc A C A B A =∅∈.又若n A 为B 的子集()1,2,3,,n n K C ==或∅.则()111nn n n n n n A K A K A K ∞∞∞===⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭.这里1n n A A B ∞==⊂是B 的子集.1n n K K C ∞===或∅.所以()1n n n A K A ∞=∈.若n A 中除B 的子集外,还有S ,则()1n n n A K S A ∞==∈.若n A 中有∅,不影响1n n A B ∞=⊂.故A 是σ-域,且()1F A A =. 证毕.6.对于S 的子集A ,定义A 的示性函数为()10A x Ax x A ϕ∈⎧=⎨∉⎩证明:(1)()()liminf liminf nnA A x x ϕϕ=(2)()()limsup limsup nnA A x x ϕϕ=证明:x S ∀∈,若()liminf nA x x ϕ∈则()liminf 1nA x ϕ=。
实变函数论课后答案第三版

1. 证明:()B A A B -=的充要条件是A B ⊂.证明:若()B A A B -=,则()A B A A B ⊂-⊂,故A B ⊂成立. 反之,若A B ⊂,则()()B A A B A B B -⊂-⊂,又x B ∀∈,若x A ∈,则()x B A A ∈-,若x A ∉,则()x B A B A A ∈-⊂-.总有()x B A A ∈-.故()B B A A ⊂-,从而有()B A A B -=。
证毕2. 证明c A B A B -=.证明:x A B ∀∈-,从而,x A x B ∈∉,故,c x A x B ∈∈,从而x A B ∀∈-, 所以c A B A B -⊂.另一方面,c x A B ∀∈,必有,c x A x B ∈∈,故,x A x B ∈∉,从而x A B ∈-, 所以 c A B A B ⊂-.综合上两个包含式得c A B A B -=. 证毕3. 证明定理4中的(3)(4),定理6(De Morgan 公式)中的第二式和定理9.证明:定理4中的(3):若A B λλ⊂(λ∈∧),则A B λλλλ∈∧∈∧⊂.证:若x A λλ∈∧∈,则对任意的λ∈∧,有x A λ∈,所以A B λλ⊂(∀λ∈∧)成立知x A B λλ∈⊂,故x B λλ∈∧∈,这说明A B λλλλ∈∧∈∧⊂.定理4中的(4):()()()A B A B λλλλλλλ∈∧∈∧∈∧=.证:若()x A B λλλ∈∧∈,则有'λ∈∧,使 ''()()()x A B A B λλλλλλ∈∧∈∧∈⊂.反过来,若()()x A B λλλλ∈∧∈∧∈则x A λλ∈∧∈或者x B λλ∈∧∈.不妨设x A λλ∈∧∈,则有'λ∈∧使'''()x A A B A B λλλλλλ∈∧∈⊂⊂.故()()()A B A B λλλλλλλ∈∧∈∧∈∧⊂.综上所述有()()()A B A B λλλλλλλ∈∧∈∧∈∧=.定理6中第二式()c c A A λλλλ∈∧∈∧=.证:()c x A λλ∈∧∀∈,则x A λλ∈∧∉,故存在'λ∈∧ ,'x A λ∉所以'c c x A A λλλ∈∧∉⊂从而有()c c A A λλλλ∈∧∈∧⊂.反过来,若c x A λλ∈∧∈,则'λ∃∈∧使'c x A λ∉,故'x A λ∉,x A λλ∈∧∴∉,从而()c x A λλ∈∧∈()c c A A λλλλ∈∧∈∧∴⊃. 证毕定理9:若集合序列12,,,,n A A A 单调上升,即1n n A A +⊂(相应地1n n A A +⊃)对一切n 都成立,则 1lim n n n A ∞→∞==(相应地)1lim n n n A ∞→∞==.证明:若1n n A A +⊂对n N ∀∈成立,则i m i mA A ∞==.故从定理8知11liminf n i m n m i mm A A A ∞∞∞→∞=====另一方面,m n ∀,令m i i mS A ∞==,从1m m A A +⊂对m N ∀∈成立知 11111()()m i mi m i i m i mi m i m i m S A A A A A A S ∞∞∞∞++==+=+=+==⊂==.故定理8表明1111limsup liminf n i m m n n n m i mm m A A S S A A ∞∞∞∞→∞→∞=========故1lim limsup liminf n n n m n n n m A A A A ∞→∞→∞→∞====.4. 证明()()A B B A B B -=-的充要条件是B =∅. 证:充分性若B =∅,则()()A B B A A A A A -=-∅∅=-∅==∅=∅-∅必要性 若()()A B B A B B -=-,而B ≠∅则存在x B ∈.所以()()x A B B A B B ∈-=-即所以,x A B x B ∈∉这与x B ∈矛盾, 所以x B ∈.4. 设{}{}{}{}1,2,3,4,1,2,3,4S A ==,求()F A .又如果1;1,2,3,,S n n⎧⎫==⎨⎬⎩⎭01;A n ⎧⎫=⎨⎬⎩⎭为奇数,{}1111,,,,321A i ⎧⎫⎧⎫⎧⎫=⎨⎨⎬⎨⎬⎬-⎩⎭⎩⎭⎩⎭,问()()01,F A F A 是什么. 解:若{}{}{}{}1,2,3,4,1,2,3,4S A ==,则(){}{}{}{},1,2,3,4,1,2,3,4F A =∅.若011111;1,2,3,,;1,,,,3521S n A nni ⎧⎫⎧⎫⎧⎫====⎨⎬⎨⎬⎨⎬-⎩⎭⎩⎭⎩⎭为奇数, 则从1111111,,,,,,,3521242ci i ⎧⎫⎧⎫=⎨⎬⎨⎬-⎩⎭⎩⎭, 易知()111111,,1,,,,,,,,3521242F A S i i ⎧⎫⎧⎫⎧⎫=∅⎨⎨⎬⎨⎬⎬-⎩⎭⎩⎭⎩⎭. {}1111,,,,321A i ⎧⎫⎧⎫⎧⎫=⎨⎨⎬⎨⎬⎬-⎩⎭⎩⎭⎩⎭. 令11;1,2,,;1,2,212B i C i i i⎧⎫⎧⎫====⎨⎬⎨⎬-⎩⎭⎩⎭. {}{}{}1,F A S AK A B K C K A =∅==∅为的子集,或.证明: 因为{}111,,,,,321A B i ⎧⎫⎧⎫∈⎨⎬⎨⎬-⎩⎭⎩⎭的任何子集()1F A .所以有()1B F A ∈,而c B C =,故()1C F A ∈,又()1F A ∅∈. 任取B 的一子集A ,()1A A F A ∅=∈,且()1A C F A ∈. 显S A ∈,故只用证A 的确是一个σ-域.(1) ,c c S S A ∅==∅∈,且B ∀的子集A ,若K =∅,则,c KA A A C ∅==(B A -是B 的子集,故()()cc A A C F A ∅=∈) 又B ∀的子集A ,()cc c c A C A C A B ==. 显然是B 的子集,所以()()cc A C A B A =∅∈.又若n A 为B 的子集()1,2,3,,n n K C ==或∅.则()111nn n n n n n A K A K A K ∞∞∞===⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭.这里1n n A A B ∞==⊂是B 的子集.1n n K K C ∞===或∅.所以()1n n n A K A ∞=∈.若n A 中除B 的子集外,还有S ,则()1n n n A K S A ∞==∈.若n A 中有∅,不影响1n n A B ∞=⊂.故A 是σ-域,且()1F A A =. 证毕.6.对于S 的子集A ,定义A 的示性函数为()10A x Ax x A ϕ∈⎧=⎨∉⎩证明:(1)()()liminf liminf nnA A x x ϕϕ=(2)()()limsup limsup nnA A x x ϕϕ=证明:x S ∀∈,若()liminf nA x x ϕ∈则()liminf 1nA x ϕ=。
实变函数与泛函分析郭懋正答案.docx

实变函数与泛函分析郭懋正答案【篇一:北京大学数学科学学院双学位课程介绍 (4)】课程类型:数、统/必修课每周3学时,3学分先修要求:高等数学(两学期)基本目的:1. 实数与极限的理论、函数的可积性、函数列与函数级数一致收敛性的基本知识。
2. 培养学生的抽象思维和推理能力,加深学生对微积分的理论基础的了解,为进一步学习后续数学课程作必要的理论准备。
内容提要:一. 实数与极限的理论1.实数理论初步。
2.确界存在定理,区间套定理,聚点。
3.紧性定理(序列紧,有限覆盖,一致连续)。
4.完备性(哥西基本列,实数的另一种定义)。
5.上极限与下极限。
二.连续函数1. 连续函数的基本性质2. 闭区间上连续函数的性质3.一致连续。
三. 函数的可积性1. 达布和,上积分与下积分。
2. 函数可积分的充要条件。
四. 函数列与函数级数的一致收敛性北京大学数学科学学院*双学位课程介绍*---------------1. 一致收敛性及其判别法。
2. 一致收敛函数列极限函数的性质。
教学方式:课堂讲授教材或参考书:1.教材:?数学分析?(双学位)讲义伍胜健2.参考书:?数学分析简明教程? 邓东皋等高等教育出版社课程编号:00136810 课程名称:实变函数课程类型:数、统/必修课每周2学时,2学分先修要求:高等数学,线性代数基本目的:1.熟悉欧氏空间中lebesgue 测度,lebesgue 积分的基本理论。
2.掌握l2(rn)空间理论。
3.熟悉hilbert空间,banach空间的基本理论。
内容提要:1.lebesgue测度与lebesgue 积分:lebesgue 可测集,可测函数,lebesgue 积分,lebesgue积分的极限定理。
2.l2(rn)空间:l2 空间的基本理论教学方式:课堂讲授教材:《实变函数与泛函分析》郭懋正北京大学出版学生成绩评定:平时作业15分,期中考试25分,期末考试60分。
北京大学数学科学学院*双学位课程介绍*---------------课程编号:00136350 课程名称:概率论课程类型:数、统/必修课每周4+1学时,5学分先修要求:微积分,线性代数(或相当高等数学)基本目的:1. 本课程的目的是引导学生学习用数学的语言,来刻划、表达与抽象随机现象,着重在随机现象的“建模”。
周民强《实变函数》解答 第四章 lebesgue积分

fE
m(E0) = 0,
E = E0 ∪ E1 ∪ E2,
1 ´ µ ~ [f(x)]1/kdx = [f(x)]1/kdx + [f(x)]1/kdx,
E
E1
E2
E1
[f (x)]1/k ≤ f (x), Lebesgue
1 1 G H | } ¾ ¸ ~ | } ~ lim [f(x)]1/kdx =
678
E
E
lim fk(x)dx = lim fk(x)dx.
k→∞ E
E k→∞
j k B l m n 1 o p w q r 1 G H s t p w q Ek = {x : fk(x) > fk+1(x)}
r u v w r 1 o t u x y x y z 1E{ r s | } ~ W )
m(E2) = 0,
E f (x)dx = E1 f (x)dx +
m(E) = m(E1) + m(E2) = 0.
Ek ⊂ E, m(E\Ek) < 1/k(k = 1, 2, · · ·),,
` a 1 6 7 8 a ' f W f(x) E
lim f (x)dx
k→∞ Ek
9A@CBEg FIh E˜1
678
lim fk(x) = f (x), lim gk(x) = g(x),
k→∞
k→∞
lim
k→∞
gk(x)dx =
E
g(x)dx < ∞,
E
lim
k→∞
fk(x)dx =
E
f (x)dx.
3-4解析函数的高阶导数

19
1 1 3 ( z 2)2 z dz 3 2 dz z ( z 2) C1 C2
2i 1 2 2! ( z 2 )
z 0
2i 1 3 1! z
z 2
3i 3i 8 8 0.
20
例5
设C表示圆周x 2 y 2 3,并且
27
2
, 则有
z z z z
所以有
2
f ( ) M 2 ML C ( z )2 ( z z ) d 2 L 3 2
5
于是有
f ( z z ) f ( z ) 1 f ( )d 2 ML z 3 2 z 2i C ( z ) 2
23
练习:计算下面积分
cos z (1) dz 3 C C1 C 2 z
其中C1 : z 3, C2 : z 1
cos z ( 2) dz 3 C C 1 C 2 ( z 2)
其中C1 : z 3, C2 : z 1
24
从高阶导数公式我们还可以推导出柯西不等式:
解
1 函数 有两个奇点 z 2 和 z 0, 2 3 ( z 2) z
1 (1) z 3 2, 仅包含奇点 z 2, 取 f ( z ) 3 , z 1 3 3 i 1 2i 1 z ; 3 2 3 dz 2 dz 8 ( z 2) z 1! z ( z 2) C C
16
课堂练习
设 C 是不通过 z0 的简单闭曲线 , z4 z2 求 g ( z0 ) 3 dz . ( z z0 ) C
实变函数 (4)

第三节 开集,闭集,完备集
1. 开集、闭集 若Eº= E , 则称E为开集(E中每个点都为内点) 若 E E ,则称E为闭集(与E紧挨的点不跑到E外)
P0为 E的接触点: 0, 有O( p0 , ) E P0为 E的聚点: 0, 有O( p0 , ) (E { p0}) P0为 E的内点: 0, 使得O( p0 , ) E
则{Ui : i I}中存在可数个开集U1 ,U2, … ,Un ,… ,它同样覆盖F
提示:利用空间中以有理点为中心,正有理数为半径 的圆全体为可数集,开集中的点都为内点,以及有理 点全体在Rn中稠密
7 自密集和完备集的定义
自密集:设 E Rn ,如果 E E' ,则称E
为自密集,也即集合中每点都是这个集 合的聚点,或没有孤立点的集合为自密 集。
bx
从而[a,b]是闭集。
说明: 要证E是闭集,只要证
E ' E或Ec (E' )c 或E E或Ec (E)c (因为E E显然)
注:闭集为对极限运算封闭的点集
即:A为闭集当且仅当A中的任意收敛点列收敛于A中的点
若 E E (或 E' E),则称E为闭集。 (与E接近的点不跑到E外)
从而{yni
}的子列{ yni j
},使lim j
yni j
y
又B为闭集,故y∈B,
另外对
d
(
A,
B)
d
(
xni j
,
yni
j
)
d
(
A,
B)
1 ni j
两边关于j取极限得d(x,y)=d(A,B)
实变函数论课后答案第四章4

实变函数论课后答案第四章4第四章第四节习题 1.设()()n f x f x ⇒于E ,()()n g x g x ⇒于E ,证明:()()()n n f x g x f x g x +⇒+于E证明:0ε∀>,[||()()(()())|][||()()|][||()()|]22n n n n E x f x g x f x g x E x f x f x E x g x g x εεε+-+≥⊂-≥⋃-≥ A B εε⋃(否则,若[||()()(()())|n n x E x f x g x f x g x ε∈+-+≥,而x A B εε∉⋃,()c c c x A B A B εεεε∈⋃=⋂|()()||()()|22n n f x f x g x g x εε⇒-<-<|()()(()())||()()||()()|22n n n n f x g x f x g x f x f x g x g x εεεε⇒≤+-+≤-+-<+=矛盾),则[||()()(()())|][||()()|][||()()|]022n n n n mE x f x g x f x g x mE x f x f x mE x g x g x εεε+-+≥≤-≥+-≥→(()(),()()n n f x f x g x g x ⇒⇒) 从而()()()()n n f x g x f x g x +⇒+ 2.设|()|n f x K ≤.a e 于E ,1n ≥,且()()n f x f x ⇒于E ,证明|()|f x K ≤.a e于E证明:由本节定理2(Riesz 定理)从()()n f x f x ⇒知∃{}()n f x 的子列{}()kn fx 使()lim ()k n k f x f x →∞=.a e 于E设A E ⊂,(\)0m E A =,()()kn f x f x →于A ,从条件|()|kn f x K ≤.a e 于E ,设k n B E ⊂,(\)0k n m E B =,|()|k n f x K ≤.a e 于k n B 上令1()kn k B B A +∞==⋂ ,则B K ⊂,且11(\)()(()(())k k ccccc n n k k m E B m E B m E B A m E A B E +∞+∞===⋂=⋂⋃=⋂⋃⋂111()()(\)(\)00k k ccn n k k k m E A m E B m E A m E B +∞+∞+∞===≤⋂+⋂=+=+∑∑∑故(\)0m E B =,,k n x B k B B A ∀∈∀⊂⋂,则|()|k n f x K ≤令k →∞,|()|f x K ≤故x B ∀∈有|()|f x K ≤,从而命题得证 3.举例说明mE =+∞时定理不成立解:取(0,)E =+∞,作函数列1(0,](){0(,)n x n f x x n ∈=∈+∞ 1,2,n =显然()1n f x →于E 上,但当01ε<<时[;|1|](,)n E x f n ε->=+∞,[;|1|](,)n mE x f m n ε->=+∞=+∞不0→故mE =+∞时定理不成立,即n f f →.a e 于E 不能推出()()n f x f x ⇒于E周民强《实变函数》P108Th2.25 若:n n T R R →是非奇异线性变换,n E R ⊂,则**(())|det |()m T E T m E =⋅ (2.8)|det |T 表示矩阵T 的行列式的绝对值.证明:记{}012(,,,);01,1n i I x i n ξξξξ==≤<≤≤{}12(,,,);02,1k n i I x i n ξξξξ-==≤<≤≤显然0I 是2nk 个I 的平移集{}j I x +(1,2,2nk j = )的并集,0()T I 是2nk个{}()j T I x +(1,2,2nk j = )的并集,且有{}{}***()()()j j m T I x m TI T x m TI +=+=,{}()()j mT I x m TI += 1,2,2nk j =现在假定(2.8)式对于0I 成立00(())|det |()|det |m T I T m I T =⋅= (2.9)则 0|det |(())2(())nk T m T I m T I ==因为()2nk m I -=,所以得到()2|det ||det |()nk m TI T T m I -=⋅=⋅这说明(2.8)式对于I 以及I 的平移集成立,从而可知(2.8)式对可数个互不相交的二进方体的并集是成立的(对任意方体0a ∀>,{}12(,,,);0a n iI x a ξξξξ==≤< 000(())()|det()|()|det ||det ||det |()n a m T I m T aI T aE m I T aE a T m I =⋅=⋅== 0|det |()|det |()aT m aE I T m I =⋅=) 对一般开集G ,1i i G I +∞== ,i I 为二进方体,i I 互补相交则111()()()|det |()|det |i i i i i i m TG m TI m TI T m I T mG +∞+∞+∞=======∑∑T 1-1 1i i TG TI +∞== ,T 连续,1T -连续 G 开,则()T G 开,从而可测于是应用等测包的推理方法立即可知,对一般点集(2.8)式成立 设G 为有界G δ集1i i G G +∞== ,i G 开,1nn i i S G == ,则n S 开,1n n G S +∞== 且不妨设11S G =有界,否则令1S G U =⊂ U 有界,令 1G G U =⋂即可. 1T -连续,则i TG 开,n TS 开,TG 可测(1n n T G T S +∞== ),12TS TS ⊃⊃ ,12n S S S ⊃⊃⊃⊃故1()()lim ()lim |det |()n n n n n n m TG m TS m TS T m S +∞→+∞→+∞====⋅1|det |lim ()|det |()|det |n n n n T m S T m S T mG +∞→+∞==== (n S 开)若G 为无界G δ集,令{};||m E x x m =<,则1m m G G E +∞==⋂ ,m G E ⋂为有界G δ集1()(())lim (())m m n m m TG m T G E m T G E +∞→+∞==⋂=⋂1lim |det |()|det |lim ()|det |()|det |m m m n n m T m G E T m G E T m G E T mG+∞→+∞→+∞==⋅⋂=⋂=⋂= n E R ∀⊂,T 线性,则n E R ∀⊂若0mE =,则(())0m T E =(后面证) n E R ∀⊂,则由注释书P69定理3,存在G δ集G E ⊃,*mG m E =,若E 有界,*m E <+∞则*(\)0m G E =,故**0((\))(\))m T G E m TG TE == (T 1-1)****()(\))()0()()m TG m TG TE m TE m TE m TG ≤+=+≤则*()()m TE m TG =,故**()()|det ||det |m TE m TG T mG T m E ===若E 无界,{};||m E x x m =<则1m m E E E +∞==⋂ ,m E E ⋂****1()(())lim (())lim |det |()m m m n n m m TE m T E E m T E E T m E E +∞→+∞→+∞==⋂=⋂=⋂**11|det |lim ()|det |()|det |(())m m m n m m T m E E T m G E T m E E +∞+∞→+∞===⋂=⋂=⋂*|det |()T m E =:n n T R R ∀→线性,若*()0m E =,则*()0m TE =证明:(0,,1,0,,0)n i e R =∈ 为n R 的基,()i i T e x =,n x R ∀∈,12(,,,)n x ξξξ= ,1122n n Tx x x x ξξξ=+++ ,令1221(||)i i M x +∞==∑,则112222112211|()|||||||||||||(||)(||)||nnn n i i i i T x x x x x M x ξξξξ==≤+++≤=∑∑则|()()|||,,n T x T y M x y x y R -≤-∀∈(即T 是Lipschitz 连续的)∀一边平行于坐标平面的开超矩体{}121122(,,,),(,)(,)(,)n i i i n n I x a b a b a b a b ξξξξ==<<=⨯⨯⨯ 于12n I I I ⨯⨯⨯ 221()(||)n ni i i diamI b a +∞==-∑12n TI TI TI TI =⨯⨯⨯ ,(,)i i i I a b =开,1T -连续,则i TI 是1R 中开集从而可测,从而12TI TI ⨯是2R 中可测集,由归纳法知12n TI TI TI ⨯⨯⨯ 是可测集若(2.9)式成立*0()|det |()o m TI T m I =,则∀矩体{},i i iI x a b ξ=<< , 1ni i I I == ,iI 为正方体,则对开集G 也有()|det |()m TG T m G =,特别对开区间{},i i i I x a b ξ=<<这一开集有*()|det |()m TI T m I =则可知n E R ∀∈,若*()0m E =,则*()0m TE =事实上,0ε∀>,{}1i i I +∞=∃开区间,1i i E I ∞=⊂ ,1||i i I ε∞=<∑****111()(())()()i i i i i i m TE m T I m TI m TI ∞∞∞===≤=≤∑111|det |()|det |()|det ||||det |i i i i i i T m I T m I T I T ε∞∞∞======<∑∑∑令0ε→知*()0m TE =若(2.9)成立,则T 将可测集映为可测集,还要看(2.8)证明过程是否用到T 将可测集映为可测集或*()0m E =推出*()0m TE =这一性质!下面证(2.9)成立.任一线性变换至多可分解为有限个初等变换的乘积(i )坐标12,,,n ξξξ 之间的交换 (ii )11,i i ξβξξβξ→→ (2,,)i n = (iii) 112,i i ξξξξξ→+→ (2,,)i n = 在(i )的情形显然00|det |1,T TI I ==(2.9)成立在(ii )的情形下,T 矩阵可由恒等矩阵在第一行乘以β而得到{}1211()(,,,),01,2,3,,,0(0),0(0)o n i T I x i n ξξξξξβββξβ==≤<=≤<><≤< 当当 从而可知0(())||m T I β= (2.9)式成立在(iii )的情形,此时det 1T = (1100010000100001T ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦) 而且{}01212()(,,,),01(1),01n i T I x i ξξξξξξ==≤<≠≤-< X ({}{}00122();,(,,,),01,1n i T I y x I y Tx i n ξξξξξ=∃∈==+≤<≤≤01221221(),(,,,),01,01n i y T I y ξξξξξξξξξ∀∈=+≤<≤+-=<则{}01212()(,,,),01(1),01n i T I x i ξξξξξξ⊂=≤<≠≤-< 反过来,12(,,,)n y X ξξξ∀=∈ ,01(1)i i ξ≤<≠则1201ξξ≤-<令122(,,,)n x ξξξξ=- 则0x I ∈,12(,,,)n Tx y ξξξ==则0()y T I ∈,0()X T I ⊂ ) 记{}1201(,,,)(),1n A x T I ξξξξ==∈< {}012()(,,,),01(1)n i T I x i ξξξξ==≤<≠10(1,0,,0),()\e B T I A == ,则{}12021(,,,),n A x I Y ξξξξξ==∈≤ {}112012\(,,,),n B e x I C ξξξξξ==∈<(12(,,,)n x Y ξξξ∀=∈ ,则01,1i i n ξ≤<≤≤,21ξξ≤,则12001,()x T I ξξ≤-<∈,且11ξ<,则x A ∈反过来,y A ∀∈,则存在120(,,,)n x I ξξξ=∈ ,01i ξ≤<,使122(,,,)n y Tx ξξξξ==+ ,12001,y I ξξ≤+<∈,且212,y YOK ξξξ≤+∈!1y B e ∀∈-,存在00()\z T I A ∈,使1\y z e =, 0x I ∃∈,122(,,,)01n i z Tx ξξξξξ==+≤<121z A ξξ∉+≥,,1122\(1,,,)n z e ξξξξ=+- , 12210011,\z e I ξξξ≤+-≤<∈1221111,\y z e C ξξξξ+-≤⇔<=∈反过来,y C ∀∈,12012(,,,),,01,1n i y I i n ξξξξξξ=∈<≤<≤≤112(1,,,)n z y e ξξξ=+=+ ,则 1212011(,01)i ξξξξξ≤-+<<≤<则0()z T I ∈,又10111,()\,\,z A z T I A B z e y z B ξ+≥∉∈==∈, 则11\,\,y B e C B e C B ∈∈=得证)由此得到0011(),{(),()T I A B A B I A B e A B e =⋃⋂=∅=⋃-⋂-=∅010(())(\)1|det |m T I mA mB mA m B e mI T =+=+===故(2.9)式成立 这里用到A,B可测,(),(,)(,)(A TIHH =⋂=-∞+∞⨯-∞+∞,0()T I 可测,H 开,则A 可测,0()\T I A B =可测故还是需要:若:n n T R R →为非奇异线性变换,则Borel ∀集n E R ⊂,()T E 是可测集,从而∀方块I ,()T I 可测,0()T I 可测有了,这就有(2.9),从(2.9)知T 将零测集E 变为零测集,从而有T 将可测集变为可测集1:n f R R →可测11()BorelB R f B -⇔∀⊂为可测集(江则坚P109习题10)现设:n n f R R →连续,则∀开集n O R ⊂,1()f O -是开集, 记{}1|()n n B R f B R -=⊂是中的可测子集1B ,可证1B 是一个σ-代数,且包含全部开集,从而包含全部Borel 集证1)1()f -∅∈∅=∅,1B 可测2)若A ∈1B ,则1111()()()()c n n f A f R A f R f A ----=-=-显然也可测,c A ∈1B3)若,(1,23,)i A i ∈= 1B ,则i ∀,1()i f A -可测,1111()()i i i i f A f A +∞+∞--=== 可测1B 是σ-代数 f 连续,则1()open Of O -∀∈1B ,1B 包含全部开集,从而包含全部Borel 集:n n T R R →为非奇异线性,1T -显然连续I ∀方体半开半闭(显然为Borel 集),11()T I TI --=可测 1[,)n i i i I a b ==∏为Borel ,111[,)ni i i m I a b m+∞===-∏ 事实上,0ε∀>从()()mkm m n f x g x →(当k →+∞)知00(,)N N m ε∃=,使当0k N ≥时|()()|m km m n f x g x ε→<而当0m a x (,(,))k m N m ε≥时,k mk k n n ≥,故|()()|k km m n f x g x ε→< (kkn 是{}1m k k n+∞=的子列中的一个元,故,m kk m k k l n n +=,0l ≥则0(,)k N m ε≥时,0m k k l N +≥ 则,|()()||()()|k mkk l m km m m m n nf xg x f x g x ε+→=→<)()k m f x 收敛于1()m g x R ∈,即k f 在E 上收敛.若条件改为:F 是一族一致有界的[,]a b 上的函数族,则结论成立 令{}123,,,[,]E x x x a b =⊂ 则0,|()|,[,]M f x M x a b ∃>≤∀∈, {}11()|x f x f =∈F F ,则1x F 是1R 中的有界集,由聚点原理∃一列n f ∈F 和1()g x R ∈,11()()kn f g x n →→∞同样令{}11(2)2()|1,2,kx n f x k == F (n f 为上述取定的一列n f ∈F )故12|()|kn f x M ≤,由聚点原理,存在1kn f 的子列2kn f 和1()g x R ∈(21k k n n k ≥≥)使22()kn f g x →,由此用归纳法可作出m N ∀∈,{}1mkn k f +∞=⊂F (m kn f 为1m kn f -的子列)使1()m km n f g x R →∈令k kk n f f =,则n f ∈F 且m ∀有()k km n f g x →故由Berstein 定理即知(0,1)B C c ≤≤=,C c =方法②建立十进位小数的展式中缺7的所有无尽十进位小数之集A 和(0,1)上一切无尽九进位小数之集B 之间的一一对应.集A 中每个十进位小数对应B 中这样的小数,该小数是前一个小数中凡是数字9都有数字7代替后而得到的,这个对应是一一的(九进小数中不含9,而A 中不含7,将9 7,而其他不动)显然(0,1),B c A c === 周民强书P35思考题:6.设F 是定义在[,]a b 上的实值函数族,[,]E a b ⊂是可数集,则存在n f ∈F (1,2,n = )使得{}()n f x 在E 上收敛.我怀疑本题有错:若不假设F 是[,]a b 上一致有界的,会有反例: 令[,]a b =[0,1],设{}|1,2,m f m == F 这里(),[,]m f x m x a b =∀∈,则显然任取无穷个(1,2,)()kkk n n f k f x n ∈==→+∞ F 于[,]x a b ∀∈,故()n f x 不会收敛!0a =时,{}111|lim ()0[|()]n j n k n i n j iE x f x E x f x k +∞+∞+∞+∞→∞====>=>故还有:[|lim ()][|lim(())][|lim(())]n n n n n n E x f x a E x f x a E x f x a →∞→∞→∞<=--<=->- 111111[|()][|()]j j k n i n j ik n i n j i E x f x a E x f x a k k +∞+∞+∞+∞+∞+∞+∞+∞=========->-+=<-鄂强91:介于0与1之间,而十进展开式中数字7的一切实数所成立之集具有什么势?证明:①从江则坚CH1§4.3题知2N c =,且从证明中知2N A ∀⊂与之1-1对应的是(1)(2)0.(0,1)A A χχ∈ ,故(0,1)中小数点全是0,1两位数字构成的数组成的集合,(0,1)B 满足(0,1)2N B c ==,而十进展开式中缺数字7的一切实数之集C 满足(0,1)B C ⊂⊂附加题:徐森林书P15.8设()(1,2,)i f x i = 为定义在n R 上的实函数列,适用点集 1{|()},1,2,i x f x i j j ≥= 表示点集[|lim ()0]n n x f x →∞> 证明:江则坚书第一章第一节习题8:若()()n f x f x →于E ,则1a R ∀∈有11[|()]liminf [|()]n k E x f x a E x f x a k +∞=≤=≤+ 111111[|()]liminf [|()][|()]cn i k k k n i n E x f x a E x f x a E x f x a k k +∞+∞+∞+∞+∞=====⎛⎫>=≤+=>+ ⎪⎝⎭ 即111[|lim ()][|()]n i n k n i n E x f x a E x f x a k+∞+∞+∞→∞===>=>+ 另一方面,{}()n f x ∀易知{}|sup ()[|()]m m m n m n E x f x a E x f x a +∞≥=>=> 故{}1|lim ()[|inf sup ()]n m n n m n E x f x a E x f x a →∞≥≥>=> 111111[|limsup ()][|sup ()][|()]m m m n m n m i k n i n k n i n m i E x f x a E x f x a E x f x a k k +∞+∞+∞+∞+∞+∞+∞→∞≥≥========>=>+=>+思考:若A 不可测, B 也不可测,且(,)0A B ρ>,则A B ⋃不可测? ((,)0A B ρ=显然不对, 1,,(,)0,R Q B R Q R Q R R ρ===⋃=可测 至少当,A B 有一个有界时,结论是对的? 若存在开集G 使G A ⊂,G B ⋂=∅,不妨设A 有界, mG <+∞,则若A B ⋃可测,则****(())(())()c mG m G A B m G A B m A m G A =⋂⋃+⋂⋃=+- )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m( limE n) limm( E n )。 ≥
n →∞ n →∞
证明: En = ∩ ∪ En,由于{ ∪ En:k ∈ N }为递减集列,则 lim
n →∞ k ≥1 n ≥ k n ≥k k ≥1 n ≥ k
∩ ∪ En = lim ∪ En;而当k充分大时(k ≥ k 0),m( ∪ En) m( ∪ En) +∞, ≤ <
k →∞ n ≥ k n≥k n ≥ k0 n →∞ k →∞ n ≥ k k →∞ n ≥ k k ≥k 0
⇒ 由可测集列的上连续性知:m( limEn) m( lim ∪ En ) = m( lim ∪ En ) = = lim m( ∪ En ) = limm( ∪ En ) ≥ limm( Ek ) = limm( En ).
n →∞ n →∞ n →∞ n →∞
9.
设E ⊆ R,则m( E ) > 0, 则存在x0 , x1 ∈ E使得:x1 − x0.为无理数。 证明:显然E不是至多可数集, G = {x − x0. | x ∈ E}, ⇒ 显然, = E > ℵ0 , 故G中至少含一个无理数y,即∃x1 ∈ E , x1 − x0. = y. G
而由习题 2 知: m ( G 1 ∪ G 2 ) + m ( G 1 ∩ G 2 ) = m ( G 1 ) + m ( G 2 );
∗ 而 m( A ∪ B ) m ∗ ( A ∩ B ) +
≤ m (G1 ∪ G 2 ) + m (G1 ∩ G 2 ) = m (G1 ) + m (G 2 )
2.R n空间中lebesgue测度的常见性质: 空间中lebesgue测度的常见性质: (定义中10条除外) (定义中10条除外)
(1)单调性:
若A,B均可测,A ⊂ B,则mA ≤ mB.
(2)可减性:
若 A,B可测, A ⊂ B, mA < +∞, A,B可测 可测, 则 m ( B − A) = mB − mA
n →∞ n →∞
= = 证明:m(lim E n) m( ∪ ∩ E n) lim m( ∩ E n)
n →∞ k ≥1 n ≥ k k →∞ n ≥k
= lim m( ∩ E n) lim m( E k) lim m( E n ). ≤ =
k →∞ n ≥k k →∞ n→∞
8
设E n 为可测集(n = 1, L),若存在k 0,使得:m( ∪ E n) +∞, 则 ,2 <
n→ ∞ n→ ∞
m(lim An ) = lim mAn
n →∞ n →∞
mA1 < +∞
则 m ( lim An ) = lim mA n
3.R n空间中lebesgue测度的等价条件: 空间中lebesgue测度的等价条件:
(1) E可测 ⇔ ∀ε > 0, ∃开集G, 使得E ⊂ G且m(G − E ) < ε。
2 设A,B是Rn的子集,A可测,证明等式 的子集, 可测,
m ( A ∪ B) + m ( A ∩ B ) = m ( A) + m ( B)
证明: 证明: 由于A可测,
故∀T ⊂ R ,有m T = m (T ∩ A) + m (T ∩ A )
n c ∗ ∗ ∗
∗
∗
∗
∗
取T = A ∪ B,有m A ∪ B) m ( A) + m ( B ∩ A ) ( =
(3)次可数可( ∪ An ) ≤ ∑ m( An );
n =1 n =1
2)若{A i }为两两不交的可测集列,则 m ( ∪ 1 A i ) = i=
∞
∑
∞
mA
i=1
i
(4)测度的下连续性与上连续性: (a) 若An是递增的可测集列,则 (b) 若An 是递减的可测集列且
1)µ (φ ) = 0; 2)可数可加性,
定义1:设X为空间,ϑ为X中一个σ − 代数,µ:ϑ → [0,+∞], 满足:
称µ为(X , ϑ)上的一个测度,(X , ϑ,µ)为测度空间。 若(X , ϑ,µ)还满足:µ(A) = 0,则∀B ⊆ A,有B ∈ ϑ, 则称µ为完备测度。
定义2:设(X , ϑ,µ)为测度空间,µ(X) +∞, < 则称µ为有限测度。 定义3:设(X , ϑ,µ)为测度空间,µ(X) 1, = 则称µ为概率测度。其中,X为样本空间,ϑ为所有的事件。
证明:m( lim E n) m(lim E n) lim m( E n ) ≤ limm( E n ) ≤ m( limE n) m( lim E n) = ≤ = .
n →∞ n →∞ n →∞ n →∞ n →∞ n →∞
⇒ m( lim E n) lim m( E n ) = limm( E n ) = lim m( E n )。 =
例(计数测度):设X ≠ φ , ϑ = 2 X , 事实上,µ(φ) 0;若{ An }互不相交,且An 有限时(n = 1, L),µ( ∪ An) ∞ = ∑ µ(An) = 2, = ;
n
二、习题选讲。
m∗ E > 0 ,则对任意小 1 设E是直线上的一有界集, 是直线上的一有界集, ∗ ∗ 的正数c 恒有子集E 于 m E 的正数c,恒有子集E1,使 m E1 = c
n =1 n =1 ∞ ∞
注:
若m( E ) = ∞,则E必为无界集。(否则为有界集,测度闭有限) 反之不对,E必为无界集,m( E )不一定为∞(如有理数集)。 即:有界集,测度必有限;测度有限未必就是有界集。
7
设E n 为可测集(n = 1, L),则 ,2 m(lim E n) lim m( E n ). ≤
证明:由于 有界 有界, 证明:由于E有界,故不妨令 E ⊂ [a, b] 令f(x)=m*(E∩[a,x]),则f(a)=0,f(b)=m*E, , 则f(x)在[a,b]上(一致)连续(以前已证); 在 上 一致)连续(以前已证); 界值定理知 存在ξ 由界值定理知,存在 ∈[a,b] ,使f(ξ)=c, 使 令E1=E ∩[a, ξ],则E1满足要求. , 满足要求
第三章 测度论
小结与习题讲解
一、 小结与补充 1.R n空间中lebesgue测度的公理化定义 空间中lebesgue测度的公理化定义
若存在集族µ及集函数m:µ → [0,+∞] 使得:
( P1 )φ ∈ µ; ( P2 )若{E n }为µ中的集族, 则 ∪ E n ∈ µ;
n
( P3 )E ∈ µ , 则E C ∈ µ ; ( P4 )G为开集, 则G ∈ µ。 (Q1 )m(φ ) = 0; (Q2 )正则性:m([0,1]n ) = 1; (Q3 )可数可加性(σ − 可加性) ; (Q4 )完备性:m(E) = 0,则∀E 0 ⊆ E , 有E 0 ∈ µ; (Q5 )平移不变性:E ∈ µ,x0 ∈ R n,则E + {x0 } ∈ µ,且m( E + {x0 }) = m( E ). (Q6 )逼近性质:E ∈ µ,∀ε > 0, 存在开集G,及闭集F使得: F ⊆ E ⊆ G, 且m(G − F ) < ε .
k →∞ n ≥k k →∞ n≥k k →∞ n →∞
注:运用7、8可以证明: 运用 、 可以证明
设En为可测集(n = 1, L), En 存在,且若存在k 0, ,2 lim
n →∞
使得:m( ∪ En) +∞, 则m( lim En) lim m( En )。 < =
n≥k 0 n →∞ n →∞
6(正可测集与区间的关系) 正可测集与区间的关系)
设E为R n中可测集,且m( E ) > 0,0 < λ < 1, 则存在区间I 使得:
λ | I |< m(I ∩ E )。
证明:若m( E ) = ∞,则E必为无界集,显然任取区间I 就有:λ | I |< m(I ∩ E ), 1 不妨设m( E ) < +∞, 取ε为小于( − 1)m( E )的正数,
∞
证明:令 O = ∩ B n,则 E ⊂ O , O 为可测集,
n =1
且 m (O − E ) ≤ m ( Bn − E ) → 0( n → ∞ )
* *
从而m (O − E ) = 0
*
说明: 说明:也可通过
令 H = ∪
∞ n =1
故 O − E为可测集,
进一步 E = O − (O − E )
A
n
E = H ∪ (E − H ) 为可测集。 为可测集。 来证明
5 直线上可测集全体A的势为 2 ℵ 直线上可测集全体A 证明: 集为P, 由于Cantor的测度为 , 的测度为0, 证明:令Cantor集为 , 由于 集为 的测度为 从而它的子集都可测, 从而它的子集都可测,故 2 P ⊂ A ⊂ 2 R 又P,R的势都为 ℵ , 的势都为 从而 2 ℵ = 2 P ≤ A ≤ 2 R = 2 ℵ 再由Bernstein定理知 A = 2 ℵ 定理知 再由
∗ ∗
3 设A,B是Rn的子集,证明不等式 的子集,
m ( A ∪ B ) + m ( A ∩ B ) ≤ m ( A) + m ( B )
证明: 证明:作 G δ 型集 G 1,使 A ⊂ G 1 且 mG
1 2
∗
∗
∗
∗
= m ∗A, = m ∗B,
作 G δ 型集 G 2,使 B ⊂ G 2 且 mG
ε
, 存在可测集A,A为覆盖E,且m( A) < c + . 2 2
