结构轴力—扭转屈曲变形中的精确动力刚度
弯曲与扭转力学分析

弯曲与扭转力学分析弯曲与扭转是材料力学中非常重要的概念和研究方向。
弯曲通常是指材料的一个部分受到外力作用,导致该部分发生形变的过程。
而扭转是指材料整体在一个点处受到外力扭矩作用,导致整体发生旋转的过程。
本文将深入探讨弯曲与扭转的力学分析。
一、弯曲力学分析弯曲是在横截面内发生的,通常发生在杆件之类的结构中。
弯曲过程中,材料上的顶点处的应变是最大的,而中性轴附近的应变较小。
弯曲时,杆件上各点的应力呈现梯度状,越靠近顶点的应力越大,越靠近中性轴的应力越小。
为了分析弯曲问题,常用的方法是欧拉-伯努利理论和斯格米定理。
欧拉-伯努利理论是假设杆件在受到外力时,各截面处的纤维保持笔直,未发生剪切形变。
斯格米定理则是假设截面上所有的纤维在应力状态和平衡方面相同。
在弯曲力学分析中,常涉及到杆件的截面性质,如惯性矩和截面模量。
惯性矩是描述截面抵抗物体弯曲的能力,而截面模量则表示物体抵抗拉伸和压缩的能力。
这些参数对弯曲性能的分析和设计至关重要。
二、扭转力学分析扭转是材料整体或部分在某个轴上产生转动的过程,通常出现在轴类结构和圆形截面杆件中。
扭转产生的力矩和角度之间的关系由杨氏模量决定。
杨氏模量描述了材料在受到扭转作用时变形和应力之间的关系。
扭转力学分析中,将杆件视为薄壁的圆筒,应用薄壁圆筒的形变和应力理论进行分析。
扭转力矩和扭转角之间的关系可以通过圆筒壁的剪切应力和圆筒半径来计算。
在扭转过程中,圆筒壁上的剪切应力是非常重要的参数,也是设计和分析的关键指标。
结论弯曲与扭转力学分析是研究材料力学中的重要方向。
通过对弯曲和扭转过程中的力学特性进行分析和计算,可以为工程设计和材料选择提供有力的依据。
在实际应用中,需要结合材料的力学性能参数和实际的工程需求,进行适当的材料选择和设计。
弯曲和扭转力学分析在许多工程领域具有广泛的应用,如建筑结构、机械设计和航空航天等。
深入理解弯曲和扭转的原理和力学特性,对于工程师和研究人员来说是非常重要的。
四三一简答填空选择

一、单项选择:第四章1. 设H1、H2、H3、H4分别为框架、框架—剪力墙、框架—筒体、筒体结构适用的最大高度,若在同一设防烈度下,均采用现浇结构,下式正确的是(A)A.H1<H2<H3<H4 B.H1<H3<H2<H4C.H1<H4<H3<H2 D.H1<H2=H3<H42. 关于框架、剪力墙及框架—剪力墙在水平荷载作用下的变形曲线,下列叙述错误..的是(D)A.框架的变形曲线呈剪切型B.剪力墙的变形曲线呈弯曲型C.当λ在1-6之间时,框架—剪力墙的变形曲线呈弯剪型D.当λ≤1时,框架-剪力墙的变形曲线接近于剪切型3. 在确定高层建筑各种结构体系所适用的房屋最大高度时,房屋高度是指(A)A.室外地面至房屋檐口的高度B.基础顶面至房屋檐口的高度C.室外地面至房屋最高点的高度D.基础顶面至房屋最高点的高度4. 剪力墙斜截面受剪承载力计算公式建立的依据是(D)A.斜拉破坏B.斜压破坏C.剪拉破坏D.剪压破坏5. 在水平力作用下,单榀壁式框架的变形曲线是(B)A.弯曲型B.剪切型C.弯剪型D.剪弯型6. 在确定高层建筑防震缝最小宽度时,不需要...考虑的因素是(C)A.结构类型B.设防烈度C.结构最大层高D.屋面高度7.在确定剪力墙有效翼缘宽度时,除考虑至洞口边缘的距离及墙间距外,还应考虑的因素有(D) A.腹板厚度、总高B.腹板厚度、层高C.翼缘厚度、层高D.翼缘厚度、总高8. 框架-剪力墙结构中,根据协同工作分析结果,综合框架柱的剪力最小值(C)A.最顶层B.中部附近C.最底层D.顶部附近9. 计算高层建筑的风荷载时,不需要...考虑(D)A.建筑体型B.建筑总高度C.地面粗糙度D.基础形式10. 对于需要考虑风振的高层建筑(A)A.建筑物刚度越小,自振周期越长,风振系数越大B.建筑物刚度越小,自振周期越短,风振系数越小C.建筑物刚度越大,自振周期越长,风振系数越小D.建筑物刚度越大,自振周期越短,风振系数越大11. 与壁式框架相比,双肢墙(A)A.整体性较弱,墙肢一般不出现反弯点B.整体性较弱,墙肢一般会出现反弯点C.整体性较强,墙肢一般会出现反弯点D.整体性较强,墙肢一般不出现反弯点12. 高层建筑的基础埋置深度,当采用天然地基时,基础埋置深度最小值为建筑高度的(D)A.1/8 B.1/12C.1/14 D.1/1513. 高层钢筋混凝土剪力墙墙肢截面设计时,下列说法中正确的是(A)A.如墙肢是小偏心受压,则需要按轴心受压构件验算平面外的承载力B.如墙肢是大偏心受压,则需要按轴心受压构件验算平面外的承载力C.如墙肢是大偏心受拉,则需要按轴心受拉构件验算平面外的承载力D.如墙肢是小偏心受拉,则需要按轴心受拉构件验算平面外的承载力14. 为建立双肢墙连梁未知竖向剪力q(x)的微分方程,需要分析连梁跨中切口处的竖向变形协调条件,切口处的竖向相对位移由三部分组成,其中不包括...(A)A.连梁的轴向变形产生的竖向相对位移B.墙肢弯曲变形产生的竖向相对位移C.墙肢的轴向变形产生的竖向相对位移D.连梁的弯曲变形和剪切变形产生的竖向相对位移15. 在风荷载作用下,高层建筑顶部的水平位移一般与建筑总高度H成(D)A.线性关系B.平方关系C.三次方关系D.四次方关系16. 在框架-剪力墙结构设计中,下列关于剪力墙的布置原则中不正确...的是( A )A.纵向剪力墙宜布置在同一温度区段的两端B.剪力墙的最大间距应按规定予以限制C.剪力墙的合理数量既要保证承载力和刚度要求,又要让框架发挥应有作用D.横向剪力墙宜均匀、对称布置17. 在用力法求解双肢墙连梁切口处的竖向剪力时,引入了一些基本假定,下列四条中不正确...的是(B)A.各层连梁简化为沿高度连续分布的等厚度弹性薄片B.假定墙肢承受的局部弯矩不超过总弯矩的15%C.两墙肢在同一水平标高处的水平侧移和转角是相等的D.假定连梁的反弯点在其跨度中央18. 在下列提高双肢剪力墙延性的措施中,不正确...的是()A.减小墙肢的轴压比B.在墙肢截面端部设置约束边缘构件并按要求配筋C.设置跨高比l0/h<2.0的连梁D.在连梁中加配交叉斜筋19. 高层建筑对风的动力作用比较敏感( A )A.建筑物越柔,自振周期越长,风的动力作用越显著B.建筑物越柔,自振周期越短,风的动力作用越显著C.建筑物越刚,自振周期越长,风的动力作用越显著D.建筑物越刚,自振周期越短,风的动力作用越显著20. 下列关于整体墙的描述中不正确...的是( C )A.洞口总立面面积不大于总墙面立面面积的15%B.洞口间的净距要大于洞口的长边尺寸C.洞口对结构计算的影响可以忽略D.洞口至墙边的净距大于洞口长边尺寸21. 我国在《高层建筑混凝土结构技术规程》(JGJ3-2002)中,规定10层及10层以上或房屋高度超过某值的建筑物为高层建筑,此值为( B )A.26m B.28m C.30m D.35m22. 关于框架-剪力墙结构的刚度特征值λ,下列说法中正确的是(A )A.λ越大,结构侧移曲线越接近于框架的侧移曲线B.λ越大,剪力墙承担的层间剪力越多C.λ越小,结构侧移越呈现剪切型的特点D.λ越小,框架承担的层间剪力越多23. 剪力墙结构的侧移曲线为( A )A.弯曲型B.剪切型C.弯剪型D.剪弯型24. 用力法分析双肢墙连梁切口处产生的竖向相对位移 (x)时,下列各项变形中不产生竖向相对位移的是( A )A.连梁的轴向变形B.连梁的弯曲变形和剪切变形C.墙肢的轴向变形D.墙肢的弯曲变形25. 下列有关小开口剪力墙的叙述中,不正确...的是(B )A.洞口立面面积大于墙总立面面积的15%B.各层墙肢大部分出现反弯点c.墙肢承受的整体弯矩不低于总弯矩的85%D.墙肢承受的局部弯矩不超过总弯矩的15%26. 剪力墙一般不允许...发生( D ) A .小偏心受压破坏 B .大偏心受压破坏 C .大偏心受拉破坏 D .小偏心受拉破坏 27. .以下高层建筑结构体系中,应设置转换层楼盖的是( ) A .框架结构 B .剪力墙结构 C .框支剪力墙结构 D .框架—剪力墙结构 28. 以下墙体中不属于...剪力墙的是( D ) A .整体墙 B .小开口墙 C .联肢墙 D .填充墙29. 关于框架结构、剪力墙结构在水平荷载作用下的受力及变形特点,下列说法中错误..的是( B )A .框架的侧向变形曲线呈剪切型B .框架柱子一般不出现反弯点C .剪力墙的侧向变形曲线呈弯曲型D .剪力墙的连梁会出现反弯点30. 高度超过150米的高层建筑混凝土结构应满足舒适度要求,对住宅和办公楼,结构顶点最大加速度分别不应..大于( A ) A .0.15m/s 2和0.25m/s 2 B .0.05m/s 2和0.01m/s 2 C .0.25m/s 2和0.15m/s 2D .0.01m/s 2和0.05m/s 231. 整体小开口墙的判别条件是(注:为肢强系数限值为整体系数][,ζα)( C ) A .10],[<≤αζζ B .10],[≥>αζζ C .10],[≥≤αζζD .10],[<>αζζ32. 关于框筒结构的剪力滞后现象,下列说法中错.误.的是( C ) A .腹板框架中,角柱轴力大于中柱轴力B .腹板框架中,柱子轴力沿筒体边缘呈曲线分布C .翼缘框架中,柱子轴力沿筒体边缘呈直线分布D .翼缘框架中,柱子轴力沿筒体边缘呈曲线分布33. 对大偏心受压剪力墙进行正截面承载力计算时,达到屈服强度并参加工作的竖向分布钢筋是(注:x 为名义受压区高度)( D ) A .受压区范围内的全部竖向分布钢筋B .受拉区范围内的全部竖向分布钢筋C .距受压区边缘1.5x 范围以内的竖向分布钢筋D .距受压区边缘1.5x 范围以外的竖向分布钢筋34. 采用桩基础时,高层建筑基础的埋置深度可取房屋高度的( C ) A .1/5 B .1/10 C .1/18D .1/2035. A 级高度钢筋混凝土高层建筑中适用高度最大的结构体系是( D ) A .框架 B .框架-剪力墙 C .剪力墙D .筒中筒36. 框架结构的弹性层间位移与层高之比h u /∆的最大限值为( B ) A .1/800 B .1/550 C .1/500D .1/45037. 墙肢斜截面受剪承载力计算是基于防止( A ) A .剪压破坏 B .斜压破坏 C .剪拉破坏D .斜拉破坏38. 符合下列条件的可判定为联肢剪力墙(α为整体系数,[]ζ为肢强系数限值)( A ) A .[]10,<αζ≤ζ B .[]10,≥αζ>ζ C .[]10,<αζ>ζ D .[]10,≥αζ≤ζ39. 下列叙述正确的是( C ) A .框架的变形曲线呈弯曲型 B .剪力墙的变形曲线呈剪切型C .当λ在l~6之间时,框架-剪力墙的变形曲线呈弯剪型D .当λ≤1时,框架-剪力墙的变形曲线接近于剪切型40. 高度不超过150m 的一般剪力墙结构,其底部加强部位高度为( C ) A .底部两层的高度 B .墙肢总高度的1/8C .墙肢总高度的1/8和底部两层高度二者的较大值D .墙肢总高度的1/10,并不小于底层层高 41. .剪力墙内的分布钢筋不应..采用( A ) A .单排配筋 B .双排配筋 C .三排配筋D .四排配筋42. 我国《高层建筑混凝土结构技术规程》(JGJ3-2002)对高层建筑的定义是( D ) A .8层以上建筑物 B .8层及8层以上建筑物 C .10层以上建筑物D .10层及10层以上或高度超过28m 的建筑物43. 高度不大于150m 的剪力墙结构,其层间弹性位移与层高之比Δu/h 的限值为( D ) A.5501 B.8001 C.9001 D.1000144. 有关壁式框架的描述,下列说法中不正确...的是( A ) A.计算时不考虑剪切变形的影响 B.可采用D 值法进行近似计算 C.比双肢墙的整体系数大D.其受力特点基本上与一般框架相似45. 若要降低框架-剪力墙结构中的系数λ,可采取的措施是( C ) A.增加框架的数量 B.增加剪力墙的数量 C.增加剪力墙的配筋 D.增大框架柱的截面尺寸46. 剪力墙墙肢截面设计时,下列说法中不正确...的是( C ) A.墙肢正截面承载力计算时,应考虑受拉屈服竖向分布筋的作用 B.一般不允许发生小偏心受拉破坏C.如墙肢是大偏心受压,则需要按轴心受压构件验算其平面外承载力D.验算平面外承载力时,不考虑竖向分布钢筋的作用47. .关于框架—剪力墙结构的刚度特征值λ,下列说法中错误..的是( A ) A.λ越大,剪力墙数量越多B.λ越小,框架数量越少C.λ越大,结构侧移曲线越接近剪切形D.λ越小,结构侧移曲线越接近弯曲形48. 框架—剪力墙结构铰接体系中,C f 是综台框架的侧向刚度,即框架产生单位剪切角所需要的剪力,EI e0为综合剪力墙等效抗弯刚度,p f 为作用于综合框架的分布力。
2017年电大建筑结构试验习题及答案
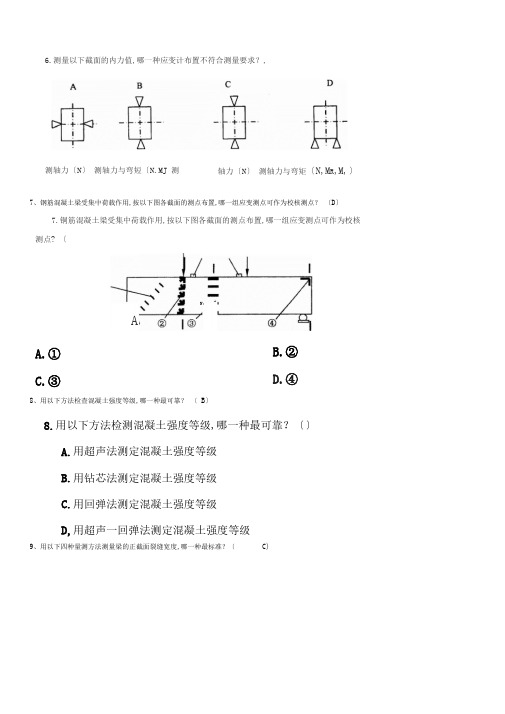
6.测量以下截面的内力值,哪一种应变计布置不符合测量要求?,测轴力〔N〕测轴力与弯短〔N.MJ 测轴力〔N〕测轴力与弯矩〔N,M R,M,〕7、钢筋混凝土梁受集中荷载作用,按以下图各截面的测点布置,哪一组应变测点可作为校核测点?〔D〕7.铜筋混凝土梁受集中荷载作用,按以下图各截面的测点布置,哪一组应变测点可作为校核测点? 〔N:AA.①B.②C.③D.④8、用以下方法检查混凝土强度等级,哪一种最可靠?〔B〕8.用以下方法检测混凝土强度等级,哪一种最可靠?〔〕A.用超声法测定混凝土强度等级B.用钻芯法测定混凝土强度等级C.用回弹法测定混凝土强度等级D,用超声一回弹法测定混凝土强度等级9、用以下四种量测方法测量梁的正截面裂缝宽度,哪一种最标准?〔C)9.用以下四种量测方法测量梁的正截面裂缝宽度,哪一种最标准?〔〕A,取侧面三条最大裂缝的平均宽度区取底面三条最大裂缝的平均宽度C取受拉主钢筋重心处的最大裂缝宽度D.取侧面和底面三条最大裂缝平均宽度1、结构静力试验加载分级是为了便于观察变形与荷载的关系〔对〕.4、结构静力实验时,安装在结构上的仪表,要求刚度小,不影响被测结构的工作性能.〔对〕5、测量结构振动时,安装在结构上的振动传感器的质量尽可能大,才能不影响结构的振动特性.〔错〕2、生产检验性试验与研究性试验,荷载分级有哪些不相同的?2,答事①生产检验性试般当加载至破坏荷载计算值的90%后,每级应取不大于承载力检监荷载值的5%逐级加荷至结构破坏F②研究性试验当加载至计算破坏荷载的9.%后•为了求得精确的破晶荷载值,每级应取不大于标准荷载的5%逐级加荷至结构破坏13、静力试验中,各级荷载下的恒载持续时间是如何规定的?工答土①混凝土结构的级间停留时间不得少于10〜15min,例结构取lOmin,物体和木结构也可参照执行.②在正常使用极限状态标准荷载作用下的持续时间不应少于30向力,钢结构也不宜少于30min,砌体为30小时#木结构不小于24小时[拱式矿石结构或混凝土结构不小于72小时工③对于预应力混廉土构件的研究性试验,到达开裂荷载计算值仍未开裂,应持续30向口〔检验性构件不受此限制建④对于果用新材料、新工艺、新结梅形式的结构构件,或肾度较大〔大于12m〕的屋架.桁架等结构构件,为了保证使用期间的平安,要求在正常使用极限状态短期试验荷载作用下的持续时间不宜少于12h,在这段时间内变形继续增长而无稳定趋势时+还应延长持续时间直至变形开展稳定为止.4、样确定开裂荷载实测值?4.答;①如果在规定的荷载持载时间结束后出现裂缝,那么将此级荷载定为开裂荷载实测值.②如果在规定的荷载持载时间内出现裂缝,那么将此级荷载与前一级荷载的平均值定为开裂荷载实测值.③如果没有及时发现第一条裂健,可取荷载一挠度曲线上的转折点〔曲线第一弯转段两端点切线的交点〕的荷载值作为构件的开裂荷载实测值,5、一个截面对称的构件,承受弯矩与轴力共同作用,如下图,用电阻应变仪测量弯矩引起的最大应变.试拟定一个测试方案,并列出应变仪读书与实际应变的关系?S. 一个截面对称的构件,承受弯矩与轴力共同作用,如下图,用电阻应变仪测也弯矩弓起的最大应变.试拟定一个测试方案,并列出应变仪读数与实际应变的关系?答:①如图,在截面的受拉及受压边缘各贴一片电阻片*②按半桥接法,将受拉边缘电阻片接于电桥端,将受压边缀电阻片接于电桥B、C 端*③Ei ~ 2e *〔或:①如右图,在裁面的受拉及受压边缀各贴两片电阻片।②按全桥接法•将受拉边煤电阻片接于电桥A、B及端,将受压边缘电阻片接于电桥B、C及D、A端,③七L=4E,〕6、测定结构的动力特性的方法有哪几种?6.答:①自由振动法;②共振法;③脉动法.7、下面为低周反复荷载试验的结果.试说明图中所示四点的强度的定义.7,以下图为低周反复荷载试验的结果.试说明图中所示四点的强度的定义.M( /V.7,答:①开裂强度试件出现垂直裂缝或斜裂建时的截面内力〔防,%〕或应力㈤,口〕值.②屈服强度试件刚度开始明显变化时的截面内力〔My,N「V\〕或施力〔八,八〕值&③极限强度试件到达最大承载水平时的截面内力〔Ma.NwiWmJ或应力值1t④破损强度试件经历最大承载水平后,到达某一辆余承载水平时的截面内力〔Mp,Np,%>〕或应力〔仃,门〕值.目前试验标准和规程规定可取极限强度的既%.,,… q —3E1 ',, _ ,_S F=jF = Tjta = r _ _8、一根端部作用着荷载的悬臂梁,按最大挠度相似设计模型,设已经确定上o简述确定相似常数的过程.8.一根端部作用着荷载的悬臂梁,按最大挠度〔看钻〕相似设计模型,设已经确定$E =】"=0.1 *0=1.篇述确定相似常数的过程,乱答:①按公式求相似判据心由最大挠度公式可得西=假设=3②将相似判据换算成相似指标,并令其为1,即:组J L=I 町③确定相应的相似常数:设材料相同介=1闻=0,1,最大挠度相同$p=h那么可求得士Si ~10试卷代号:1142中央播送电视大学2006 2007学年度第一学期“开放本科〞期末测试土木工程专业建筑结构试验试题一、选择题〔每题3分,共45分〕1.建筑结构模型试验的优点,做如下表述中.〔〕是不对的.A.制作容易,节省材料、时间、人力8.可以根据试验目的,突出主要因素,针对性强C.可以严格限制其主要参数,防止许多外界因素干扰,保证数据准确D.能表达实体的一切特征9.按试验的目的可将建筑结构试验分为〔〕.A.生产检验性试验和科学研究性试验B.真型试验和模型试验C.短期荷载试验和长期荷载试验D.静力试验与动力试验10以下〔〕方法属于动荷加载方法.A.液压加载B.重物加载C.激振器加载D .机械式加载11〔〕和限制系统投资较大,维修费用较高,使川条件比拟苛刻,对试验人员的试验技能要求较高,因此,它的使用受到一定限制.A.电液伺服作动器B.单向作用液压加载器C.双向作用液压加载器D.液压千斤顶12贴电阻片处的应变为1500 vf电阻片的灵敏系数K=2.0,在这个电阻片上应产生的电阻变化率应是〔〕.A. 0. 2%B. 0. 4%C. 0. 1%D. 0. 3%6.在轴向拉压状态下,〔〕布置应变片的形式和测量桥路的特点是:消除了温度的影响,使用的应变片较少,不能消除偏心荷载的影响和不能提升测量灵敏度.A.外设补偿片的半桥测试方案B.测量应变片互相补偿的半桥测试方案C.外设补偿片的全桥测试方案D.测量应变片互相补偿的全桥测试方案7.用非破损检测混凝土强度等级,〔〕是不当的.A.用超声法测定混凝土强度等级8.用钻芯法测定混凝土强度等级C.用回弹法测定混凝土强度等级D.用超声一回弹法测定混凝土强度等级8.利用〔〕检测技术,可在混凝土结构中用于检测混凝土的强度、检测裂缝的深度、检测混凝土内部的缺陷,即混凝土结合面的质量检测和混凝土内部空洞和疏松等缺陷的检测.A.超声法B.钻芯法C.回弹法D.扁顶法9.结构试验包括〔〕等主要环节.I .结构试验设计口 .结构试验准备m.结构试验实施iv.结构试验分析A. I、口、WB. I、口、IVC. I、W. IVD. I、口、皿、IV10.以下〔〕不包括在建筑结构试验设计内容之内.A.试件设计B.试验加载设计C.试验观测设计D.试件制作与安装11.以下钢筋混凝土结构的承载力极限标志中,〔〕条不正确.A.跨中最大挠度到达跨度的1/50B.受拉主筋重心处裂缝宽度到达2. OmmC.剪力区,受压混凝土剪压破坏或斜压破坏D.主筋端部相对混凝土滑移达0. 2mm12.以下〔〕项不是测量振动参数一般采用的仪器组合方案.A.加速度计+电荷放大器+记录仪B.磁电式拾振器十电压放大器+记录仪C.微型计算机+A/D转换卡D.电阻应变计+应变仪+微机13.疲劳试验过程中要进行四种形式的试验.〔〕的加载值为最大荷载的20%,以消除支座等连接件之间的不良接触,检查仪器工作是否正常.A.预加载B.静载试验C.疲劳试]金D.破坏试验14.受弯构件的正截面疲劳破坏标志有〔〕.I .纵向主筋疲劳断裂口.受压区混凝土疲劳破坏m.与临界斜裂缝相交的腹筋疲劳断裂iv.混凝土剪压疲劳破坏A.I、口B.口、mC.皿、IVD. I、IV15.以下〔〕不是低周反复试验的优点.A.设备比拟简单,耗资较少B.在逐步加载过程中可以停下来仔细观察反复荷蛾下结构的变形和破坏现象C.能做比拟大型的结构试验及各种类型的结构试验D.能与任一次确定性的非线性地震反响结果相比二、判断〔将判断结果填入括甄,以,表示正确,以X表示错误.每小3分,共15分〕1.在“钢筋混凝土结构〞及“砖石结构〞课程中讲到的试验研究绝大多数是用模型试验做出来的.〔〕2.静荷加载的方法有:重物加载,机械式加载.气压加载、液压加载.〔〕3.被测物理量的单位变化引起测试系统输出值变化量的大小称为灵敏度,灵敏度的表示方法是:输出量与输入量之比.〔〕4.研究结构在荷载作用下的弹性、弹塑性直至破坏各阶段全过程的工作性能,应取弹性模型进行试验.〔〕5.移动荷载作用下结构所产生的动挠度往往比静挠度大.〔〕三、简答〔共40分〕1.结构试验按试验的目的,对象、荷载性质、试验场所以及试验持续时间可将结构分为哪几类?〔5分〕答:2.重物加载有什么优、缺点?〔6分〕答,3.应变测量主要有哪几种方法?〔6分〕答:4.超声波检测混凝土强度的根本原理是什么?〔6分〕答;5.建筑结构试验设计包括哪些内容?’6分〕答:6.何谓加载图式?〔5分〕答:7.钢筋混凝土梁校核测点的作用是什么?应布置在彳f么位置?〔5分〕答:试卷代号:1142中央播送电视大学2006 2007学年度第一学期“开放本科〞期末测试土木工程专业建筑结构试验试题答案及评分标准〔供参考〕2007年1月一、选择题〔每小3分,共45分〕1 . D2,A3.C4.A5,D6. A7,B8.A9.D10,D11. B12.D13.A14.A15,D二、判断题〔将判断结果填入括,以,表示正确,以X表示错误.每题3分,共15分〕1 . V2. V 3. X4. X 5. V三、简做题〔每小5分,共40分〕1.〔6分〕答:结构试验按试验的目的、对象,荷载性质、试验场所以及试验持续时间可将结构分为生产检验性试验和科学研究性试验,真型试验与模型试验;静力试验与动力试验;短期荷载试验与长期荷载试验.2.〔6分〕答:重物加载的优点是:〔1〕适于长时期的建筑结构试验,并能保持荷载值的稳定;〔2〕荷载重物容易获取,加载方法简单方便,经济可靠.其缺点是:在加载过程中费时、费力,砂子、砖块等材料含水量容易变化.3.〔6分〕答:应变测量主要有:电阻应变测量方法;手持式应变仪测量方法与振弦式应变计测量方法.4.〔6分〕答:混凝土抗压强度〔o与超声波在其内部传播时的速度有一定的相关性,这就是超声法检测混凝土强度的根本原理.混凝土强度越高,超声波在混凝土中传播的波速也越大,反之波速就小.5.〔6分〕答:建筑结构试验设计内容包括:试件设计,试验加载设计,试验观测设计,试验误差限制举措和试验平安举措等内容.6.〔5分〕答:试验荷载在试验结构构件上的布置形式〔包括荷载类型和分布情况〕称为加载图式.7.〔5分〕答:校核测点的作用是:校核试验的正确性,便于整理试验结果时进行修正.校核测点经常布置在梁的端部凸角上的零应力处.2006018.结构静力试验加载分级是为了限制加载速度.〔对〕4、结构静力试验时,安装在结构上的仪表,要求刚度小,不影响被测结构的工作性能.〔对〕2、研究性试验,荷载如何分级?2.答:①到达标准荷载之前,每级加载值不应大于标准值的2.%,一般分五级加至标准荷载, ②标准荷载之后,每级不宜大于标准荷载的1.%1③当加载至计算破坏荷载的9.%后,为了求得精确的破探荷载值,每级应取不大于标推荷载的5%逐级加荷至结构破坏*④对于钢筋混凝土或预应力构件*加载到开裂荷载的9.%后,也应改为不大于标准值的5%施加,直至第一条裂犍出现,开裂后再恢复到正常加载程序.4怎样确定承载力极限荷载实测值?4.答:①当在规定的荷载持载时间内出现上述承载力检验标志之一时,应将本级荷载与前一级荷载的平均值做为承载力检验荷载实测值,②如果在规定的荷载持载时间结束后出现上述检验标志之一时,应将本级荷载做为承乳力检验荷载实测值05一个截面对称的受弯构件,如下图,用电阻应变仪测量截面应变变化规律,试拟定一个测试方案.5.答】①在梁的一个截面上等距离地贴5-7个电阻应变片作工作片,如左图所示:②另取与梁同一材料的试块作补偿块,贴一片电阻应变片作补偿片;③补偿片依次与工作片组成半桥测点,测出各点应变;7、低周反复加载试验的目的是什么?7.答:用静力加载方法来近似模拟地震作用,获得结构构件超过弹性极限后的荷载变形工作性能〔恢复力特性〕和破坏特征,也可以用来比拟或脸证抗震构造举措的有效性和确定结构的抗震极限承载水平.进而为建立数学模型,通过计算机进行结构抗震非线性分析效劳,为改良现行抗震设计方法和修订设计标准提供依据.—1_ 1 _1【尸J L史〕距-1:汕=筋;% = 1 8、一根承受均布荷载的简支梁,要求最大挠度股4瑁相似设计试验模型.设已经确定iU简述求的过程.8. 一根承受均布荷载的筒支梁,要求最大挠度〔/==嘉假设〕相似设计试验模型,设已经确■ J c5 4 ,匕I定式一点I Jq - lr简述求界的过程.8,答】①按公式求相似判据m心且叱7 384 E1由上式可得广程J=3;4②将相似判据换算成相似指标,并令其为!,即:且_A_ %比f③确定相应的相似常数:材料相同配=1,均布荷载g相同Sq = h那么可求得:2005074、怎样确定开裂荷载实测值?。
工程力学第8章 变形及刚度计算

结构构件在满足强度要求条件下,若其变形过大, 会影响正常使用。本章将学习杆件的变 形及刚度计算。
1
8.1 轴向拉压杆的变形
杆件在发生轴向拉伸或轴向压缩变形时,其纵向尺 寸和横向尺寸一般都会发生改变,现分别予以讨论。 8.1.1 轴向变形 图8.1所示一等直圆杆,变形前原长为l,横向直径 为d;变形后长度为l′,横向直径为d′,则称
8.8 题8.8图所示一直径为d的圆轴,长度为l,A端 固定,B端自由,在长度方向受分布力偶m 作用发生扭 转变形。已知材料的切变模量为G,试求B端的转角。
56
8.9 某传动轴,转速 n=150 r/min,传递的功率 P =60 kW,材料的切变模量为 G =80GPa,轴的单位长度 许用扭转角[θ]=0.5(°)/m,试设计轴的直径。
30
例 8.9 简支梁受力如图 8.11所示
31
8.4 简单超静定问题
8.4.1 超静定问题的概念 前面几章所研究的杆或杆系结构,其支座反力和内 力仅仅用静力平衡条件即可全部求解出来,这类问题称 为静定问题(staticallydeterminateproblem)。例如,图 8.12所示各结构皆为静定问题。在工程实际中,有时为 了提高强度或控制位移,常常采取增加约束的方式,使 静定问题变成了超静定问题或静不定问题 (staticallyindeterminateproblem)。超静定问题的特点 是,独立未知力的数目大于有效静力平衡方程式的数目, 仅仅利用静力平衡条件不能求出全部的支座反力和内力。
52
8.5 高为l的圆截面锥形杆直立于地面上,如题8.5图 所示。已知材料的重度γ和弹性模量E,试求杆在自重作 用下的轴向变形Δl。
53
54
材料力学扭转刚度课件

d
v
V V
d
1
1
1
对于线弹性材料,或者 p
d
1
v
V V
d
1
1
d
v 由剪切胡Biblioteka 定 律,1 2 G
2
剪切应变能密度等于切应力-切应变 曲线下方图形的面积。
v
G 2
2 2G
2
二、等直圆杆扭转时的应变能
T 显然 GI P
圆轴扭转刚度条件为:
单位长度扭转角的许可值
m
0
已知:阶梯轴尺寸如图 已知 mA 3.0 N m, mB 1.8 N m, mC 1.2 N m
d1 50 mm, d 2 75mm
圆轴扭转刚度条件为:
FS
α
2、簧丝的直径 d 远小于弹簧的中径 D, 簧丝由平面圆周曲杆 直杆 D
簧丝横截面上的应 力: 1、剪力 F S 引起的 1 近似 认为是均匀分布 2、扭矩 T 引起的 圆轴扭转计算 按照
1
2 max
2
簧丝横截面上的应 力:
1
F
d 4
2
4F d 2
1
A d
2 max
GI
l
T
P
dx
GI P
对于阶梯轴,以及等直圆轴但扭矩为阶梯形变化的情况, 分段计算,求代数和
对于等直圆轴,T为常数时
Tl GI P
φ 相距 l 的两个截面之间的相对扭转角
第4章杆件的变形和刚度

拉刚度为EA,B点处受F作用,试求B点位移B。
a
【解】 M A 0,
F
L
1 2
L
cos
FCD
FNCD
2F
cos
FNCD
A
C
C
αD
F
B
LCD
FNCD LCD EA
2Fa
EAcos2
C1
L/2
L/2
B1
CC1
CC LCD
cos cos
B
BB1
2CC1
形。实验结果表明,若在弹性范围内加载,轴向应变x与 横向应变y之间存在下列关系:
y x
为材料的一个弹性常数,称为泊松比(Poisson ratio)。
第4章 杆件的变形和刚度
拉压杆件 的变形分析
【例4-1】 变截面直杆,ADE段为铜制,EBC段为钢制;
在A、D、B、C等4处承受轴向载荷。已知:ADEB段杆的
第4章 杆件的变形和刚度
拉压杆件 的变形分析
【例4-2】 已知杆长L=2m,杆直径d=25mm,=300,材料
的 弹 性 模 量 E=2.1×105MPa , 设 在 结 点 A 处 悬 挂 一 重 物
F=100kN,试求结点A的位移A。
【解】 1. 求轴力
Fx 0,
FNAC sin FNAB sin 0
B1
2C
FNAB FNAC
αα
Fy 0,
FNAC cos FNAB cos F 0
FNAC
FNAB
F
2 cos
A
扭转刚度(材料力学)

109mm
12
2、由刚度条件确定所需外直径D
jm ax
Tmax GIp
180 π
G
Tmax πD4 (1
4
)
180 π
[j]
32
D
4
32Tmax
Gπ(1 -
4
)
180 π
1
[j ]
4
32 9.56 106 80103 π 1 0.54
180 π
0.3
1 103
125.5mm
d D 0.5125.5 63.75mm
等直圆轴扭转时的变形•刚度条件
Ⅰ、扭转时的变形 ——两个横截面的相对扭转角j
Me
Me j
a
b
T
T
O1
O2
A g D dj
D'
a dx b
扭转角沿杆长的变化率 dj T
d x GI p
dj T d x
GIp
1
Me
Me j
相距l 的两横截面间相对扭转角为
lT
j dj
dx
l
0 GI p
等直圆杆仅两端截面受外力偶矩 Me 作用时
T2l AC GIP
637103 500 80103 π 704
1.69103 rad
32
jCB j AB jCA [1.52 (1.69)]103 0.17 103 rad
5
例 图示空心圆杆 AB,A端固定,底板 B为刚性杆, 在其中心处焊一直径为d2的实心圆杆CB。空心杆的 内、外径分别为 D1和 d1,外力偶矩 Me、两杆的长 度l1、l2 及材料的切变模量G 均为已知。试求:
2、非等直杆扭转、扭矩沿杆长变化、或端面有约束 不能自由翘曲时
结构力学名词解释

结构力学名词解释弹性模量(Elastic modulus)弹性模量是材料的物理性质之一,它表征了材料在受到力作用后能够恢复原始形状和大小的能力。
它是应力与应变之间的比率,通常用于衡量材料的刚度和变形的程度。
弹性模量越高,材料的刚度越大。
线弹性(Linear elasticity)线弹性是指在一定应力范围内,材料的应变与应力呈线性关系。
当施加的力或压力小到足够接近零时,材料的应变也趋近于零,直线关系成立。
线弹性是结构力学中常用的假设,用于简化计算和分析。
屈服强度(Yield strength)屈服强度是指材料在受到力作用后开始发生可观的不可逆变形的应力水平。
在这个应力水平以上,材料会开始产生塑性变形,超过该水平则可能发生永久性变形。
屈服强度是评估材料抗变形能力的重要指标。
破坏强度(Ultimate strength)破坏强度是指材料承受极限荷载后发生完全破坏的应力水平。
当材料受到超过破坏强度的荷载时,会发生断裂、裂纹扩展或其他形式的破坏。
破坏强度通常用于评估材料的极限承载能力。
弯曲刚度(Bending stiffness)弯曲刚度是指材料在承受弯曲力矩时抵抗变形的能力。
它与材料的几何形状、尺寸和材料的弹性模量相关。
弯曲刚度越大,材料的抵抗弯曲变形的能力越强。
位移(Displacement)位移是指物体在受到外力作用后位置的改变量。
在结构力学中,位移常用来描述结构件的变形情况。
位移可以是线性的、旋转的、平移的或非线性的,取决于受到的外力和材料的性质。
拉伸应变(Tensile strain)拉伸应变是指材料在受到拉伸力作用时产生的相对长度变化。
它是单位长度的变形量,通常表示为一个小数或百分数。
拉伸应变可以用于评估材料的延展性和可塑性。
状态方程(Equilibrium equation)状态方程是指描述物体或系统受力平衡的方程。
在结构力学中,状态方程可以用来求解物体的受力分布,并判断系统是否处于平衡状态。
扭转刚度的概念

扭转刚度的概念扭转刚度是结构物或材料产生扭转变形时所表现出的抗扭转程度的物理量。
它用于衡量结构或材料在受到扭转力矩作用下的变形情况和承载能力。
扭转刚度是描述结构或材料在扭转运动中抵抗扭转变形的能力。
扭转刚度的概念可以通过以下几个方面进行回答:1. 宏观层面定义:扭转刚度是指结构或材料在单位扭转力矩作用下的变形程度。
具体来说,扭转刚度是扭转角度和所施加扭转力矩之间的比值。
扭转刚度表示了材料或结构在受到扭转力矩作用时的稳定性和抵抗力。
2. 微观层面定义:在微观尺度上,扭转刚度可以理解为材料的分子或原子之间的相互作用力。
当物体受到外界扭转力矩时,这些相互作用力会抵抗变形,从而使结构或材料具有抗扭转变形的能力。
扭转刚度是由材料自身的特性和分子结构决定的。
3. 应用领域:扭转刚度的概念在工程学领域中具有重要的应用。
例如,在建筑和桥梁设计中,扭转刚度是评估结构对地震和风力等外力的响应能力的关键参数。
在机械工程中,扭转刚度是制造旋转部件和连接装置时必须考虑的因素。
扭转刚度也被广泛应用于材料科学和纳米技术领域。
4. 影响因素:结构或材料的扭转刚度受到多个因素的影响。
首先,材料的组成、结构和性质对其扭转刚度起着重要作用。
材料的硬度、弹性模量以及分子间的键合强度都会影响其扭转刚度。
其次,结构或材料的几何形状和尺寸也是影响扭转刚度的重要因素。
扭转刚度还与材料的温度和湿度等环境因素有关。
5. 评价方法:扭转刚度的评价可以使用实验方法和数值模拟方法。
在实验中,可以通过施加已知的扭转力矩并测量相应的扭转角度来确定扭转刚度。
数值模拟方法可以使用有限元分析等技术来计算结构或材料的扭转刚度。
这些方法可用于确定结构或材料的设计参数并评估其扭转性能。
总结起来,扭转刚度是描述结构或材料在扭转运动中抵抗扭转变形的能力的物理量。
它是宏观上和微观上描述结构或材料特性的数值,并且在工程学中具有广泛的应用。
通过实验和数值模拟方法,我们可以评价和优化结构或材料的扭转刚度,以提高其抗扭转性能。
机械结构的弯曲与扭转分析研究

机械结构的弯曲与扭转分析研究机械结构的弯曲与扭转分析是研究结构在外力作用下的变形和应力分布规律的重要课题。
在工程实践中,了解和掌握结构的弯曲与扭转特性可以帮助我们设计和优化机械系统,提高其性能和可靠性。
一、弯曲分析弯曲是指结构在外力作用下产生的纵向变形。
当结构受到弯曲时,不同位置的截面将产生不同大小的弯矩和弯曲应力。
弯曲分析的主要目的是确定结构中各个截面的弯曲应力和变形情况。
在弯曲分析中,我们可以使用弯曲方程来描述结构的变形和应力分布。
常见的弯曲方程包括欧拉—伯努利梁理论和蒸汽液体力学梁理论。
这些方程可以通过假设结构为线弹性材料、截面平面保持平直以及截面变形小等条件来推导得出。
通过这些方程,我们可以计算出结构中各个截面的弯曲应力和变形量,为结构的设计和分析提供依据。
二、扭转分析扭转是指结构在外力作用下产生的截面旋转。
在扭转分析中,我们主要关注结构中截面的扭转角度和扭转应力分布。
与弯曲分析类似,我们也可以使用扭转方程来分析结构的扭转特性。
扭转方程主要适用于圆杆等截面对称的结构。
通过应用扭转方程,我们可以计算出结构中截面的扭转角度和扭转应力。
在扭转分析中,还要考虑截面的剪切变形。
剪切变形会导致截面形状变化,进而影响扭转应力分布。
因此,扭转分析需要综合考虑截面的剪切变形和扭转变形,以获得更精确的结果。
三、弯曲与扭转的耦合效应在实际工程中,结构通常会同时受到弯曲和扭转的作用。
弯曲和扭转的耦合效应会导致结构变形和应力分布的复杂性增加。
为了研究弯曲与扭转的耦合效应,我们可以使用杆件有限元方法来建立结构的数值模型,并通过数值求解获得结构的变形和应力分布。
有限元方法可以将结构离散为多个小单元,在每个单元上建立位移和应力的关系,然后通过求解整个结构的平衡方程得到最终结果。
通过弯曲与扭转的耦合分析,我们可以得到结构在实际工作条件下的应力和变形情况。
这对于结构的设计和优化非常重要,可以帮助我们改进结构的设计方案,提高结构的性能和可靠性。
混凝土梁的扭转刚度检测标准

混凝土梁的扭转刚度检测标准一、前言混凝土梁是建筑结构中常用的构件,其扭转刚度是评估其受力性能的重要参数。
因此,制定混凝土梁扭转刚度检测标准对于保障建筑结构的安全具有重要意义。
本文将从混凝土梁扭转刚度检测的基本原理、检测方法、检测设备、检测过程等方面,详细介绍混凝土梁扭转刚度检测标准。
二、基本原理混凝土梁的扭转刚度是指在扭转作用下,梁的抗扭能力大小的参数。
根据材料力学原理,梁的扭转刚度可以通过检测梁的扭转角度和所施加的扭矩大小来计算得出。
梁的扭转刚度与梁的几何尺寸、截面形状、材料特性、受力形式等多方面因素有关。
三、检测方法1.试验法试验法是目前最常用的混凝土梁扭转刚度检测方法。
该方法将混凝土梁固定在试验台上,通过施加一定的扭矩,测量梁的扭转角度,从而计算出梁的扭转刚度。
试验法具有检测精度高、适用范围广等优点,但需要较为复杂的试验设备和专业的技术人员进行操作。
2.计算法计算法是通过计算混凝土梁的几何尺寸、截面形状、材料特性等参数,来推算出梁的扭转刚度。
该方法操作简单,但需要对梁的参数有较为准确的了解,并且考虑到混凝土梁在实际使用中可能会存在的缺陷和损伤等情况,计算法的精度可能会有所下降。
四、检测设备1.扭转试验机扭转试验机是进行试验法混凝土梁扭转刚度检测所必需的设备。
该设备由主机、计算机、控制器、传感器等部分组成,可以实现对混凝土梁的扭转角度和扭矩的测量和控制。
2.测量仪器测量仪器包括测角仪、测力计、千分尺等设备。
这些设备可以用于对混凝土梁的几何尺寸、扭转角度和扭矩的测量,以及对试验过程中的数据进行记录和分析。
五、检测过程1.准备工作进行混凝土梁扭转刚度检测前,需要对试验设备进行检查和校准,并对试验样品进行加工和制备。
同时,还需要对试验环境进行调整,保证试验过程中的稳定性和准确性。
2.试验操作试验操作包括将混凝土梁固定在试验台上,施加一定的扭矩,测量梁的扭转角度和扭矩大小等步骤。
在试验过程中,需要对试验数据进行记录和分析,以保证试验的准确性和可靠性。
工程力学中的刚度与结构稳定性分析

工程力学中的刚度与结构稳定性分析工程力学是研究物体受力、变形和运动规律的一门学科。
在工程力学中,刚度和结构稳定性分析是非常重要的概念和计算方法。
本文将从理论和实际应用的角度,探讨工程力学中的刚度和结构稳定性分析。
一、刚度分析刚度是指物体对外力的相对抗力能力。
在工程力学中,刚度通常分为结构刚度和材料刚度两个方面。
1. 结构刚度结构刚度是指物体在受力作用下,对力的反抗能力。
它与结构的几何形状、材料性质和连接方式等密切相关。
常见的刚度计算方法有有限元法、刚度矩阵法等。
2. 材料刚度材料刚度是指材料本身的抵抗外力的性质。
材料刚度可以通过拉伸试验、压缩试验等实验方法来确定。
常见的刚度参数有弹性模量、泊松比等。
二、结构稳定性分析结构稳定性是指结构在受力作用下,保持平衡的能力。
结构稳定性分析是指判断和评估结构在外力作用下是否会出现不稳定的现象。
1. 屈曲分析屈曲是指结构由于受到压力或挠度等因素作用下,失去原有的稳定性。
屈曲分析是为了确定结构的最大承载能力和防止结构失稳的措施。
2. 延性分析延性是指结构在发生变形或受到外力作用时,能够发生一些延长现象而不破坏的能力。
延性分析是为了评估结构在受力过程中的耐久性和安全性。
三、应用案例工程力学中的刚度和结构稳定性分析在实际工程中有着广泛的应用。
1. 桥梁工程刚度和稳定性是桥梁工程设计中的关键问题。
通过对桥梁结构进行刚度分析和结构稳定性分析,可以确保桥梁的安全可靠性。
同时,刚度和稳定性的分析结果也对桥梁的维护和加固提供了重要的依据。
2. 高层建筑对于高层建筑而言,刚度和稳定性是保证建筑物整体结构牢固稳定的基础。
通过刚度和稳定性分析,可以评估建筑物在发生自然灾害或强风等外力作用下的抗压能力和稳定性,为建筑物的设计和施工提供可靠参考。
3. 航天工程航天工程需要考虑各种复杂的受力情况和环境条件,在设计和制造过程中,刚度和结构稳定性分析是确保航天器在高速飞行和重力环境中保持稳定的重要手段。
工程力学中的弯曲刚度与刚度优化设计

工程力学中的弯曲刚度与刚度优化设计工程力学中的弯曲刚度是指材料、结构或系统在受到弯曲作用时的抵抗变形的能力。
弯曲刚度是工程设计中非常重要的一个参数,影响着结构的稳定性、安全性和使用寿命。
本文将详细介绍工程力学中的弯曲刚度的概念、计算方法以及刚度优化设计的应用。
一、弯曲刚度的概念与计算方法1. 弯曲刚度的概念弯曲刚度是指材料或结构在受到弯曲作用时所表现出的抵抗变形的能力。
一般来说,弯曲刚度可以通过弯曲刚度系数(bending stiffness)来表示,它是弯曲力矩对应的曲率和截面惯性矩的比值。
2. 弯曲刚度的计算方法计算弯曲刚度的方法根据不同的工程问题和结构类型而有所不同。
对于一维梁的弯曲刚度计算,可以使用梁的基本弯曲理论,根据梁的几何形状、材料的力学性质以及施加载荷的形式进行计算。
对于复杂的结构或系统,可以使用有限元分析等数值方法进行计算。
二、刚度优化设计的概念与方法1. 刚度优化设计的概念刚度优化设计是指在满足工程要求的前提下,通过合理设计结构的尺寸和布局,以提高结构的弯曲刚度。
刚度优化设计可以使结构在承受荷载时变形较小,增强结构的稳定性和抗震性能,提高结构的使用寿命。
2. 刚度优化设计的方法刚度优化设计的方法分为直接优化方法和参数化优化方法两种。
直接优化方法主要是通过对结构的形状、截面和材料等进行优化,以提高结构的弯曲刚度。
参数化优化方法则是通过对结构的参数进行调整,以实现刚度的优化设计。
常用的优化算法有遗传算法、蚁群算法等。
三、刚度优化设计的应用案例1. 建筑结构的刚度优化设计在建筑结构设计中,刚度优化设计可以减少结构的变形和振动,提高结构的整体稳定性和抗震性能。
通过对结构的布局、尺寸和材料等进行优化,可以达到节约材料、降低成本的效果。
2. 机械结构的刚度优化设计在机械结构设计中,刚度优化设计可以提高机械系统的精度和稳定性,减少机械运动过程中的变形和振动。
通过优化机械结构的刚度,可以提高机械系统的工作效率和使用寿命。
2023年度结构扭矩计算

2023年度结构扭矩计算
首先,为了计算结构扭矩,需要了解以下几个概念:
1. 扭转角度
扭转角度是指结构在受力的作用下,发生扭转时的旋转
角度。
扭转角度可以通过测量结构的两个端点之间的角度
变化来确定。
2. 惯性矩
惯性矩是指结构所具有的抵抗力的大小,它是由结构的
形状和截面积决定的。
惯性矩越大,结构抵抗力越强。
3. 扭转刚度
扭转刚度是指结构受到扭转作用时,对扭转产生的反力
的大小。
扭转刚度越大,结构对扭转力的抵抗能力越强。
有了以上的概念基础,可以进行结构扭矩的计算。
下面
以几何形状简单的圆柱体为例,介绍结构扭矩的计算方法。
首先,需要测量圆柱体的长度L和直径D,计算出其截
面积A:
A = π * D^2 / 4
接着,需要确定圆柱体的惯性矩I,公式如下:
I = π * D^4 / 64
然后,可以计算出圆柱体的扭转刚度k,公式如下:
k = G * I / L
其中,G是圆柱体的杨氏模量,可以通过材料的性质进
行确定。
最后,可以根据受力情况和结构刚度,计算出结构扭矩τ,公式如下:
τ = k * θ
其中,θ是圆柱体的扭转角度。
需要注意的是,以上的计算方法仅适用于几何形状简单
的结构,对于复杂的结构,需要采用更加精细的计算方法。
此外,还需要根据具体材料的性质进行修正,以确保计算
的准确性和可靠性。
833结构力学

833结构力学一、引言结构力学是一门研究物体在外力作用下的力学性质和变形行为的学科。
它是工程力学的重要分支,涉及到各种材料的结构设计和力学分析。
本文将介绍和探讨833结构力学的相关内容。
二、基本概念1. 外力:指作用在结构上的力,可以是静力、动力或其他形式的力。
2. 内力:指结构内部的力,包括受力构件的轴力、剪力、弯矩等。
3. 应变:指结构受到外力作用后所产生的形变,它可以分为线性应变和非线性应变。
4. 应力:指单位面积上受到的力的大小,它是由外力作用引起的应变产生的内力所引起的。
5. 变形:指结构受到外力作用后所发生的形状改变。
6. 刚度:指结构在外力作用下所表现出的抵抗变形的能力。
三、结构力学的基本原理1. 平衡条件:结构在外力作用下处于平衡状态时,受力构件所受合力与合力矩必须为零。
2. 支反力原理:结构的支持系统对结构的力学行为有重要影响,通过计算支反力可以进一步分析结构的受力情况。
3. 变形条件:结构在外力作用下会发生变形,变形引起内力的变化,内力又进一步引起变形。
通过这种相互作用,可以确定结构的受力状态和变形情况。
4. 包络原理:在结构力学分析中,常常采用极大和极小包络原理,即通过取不同外载作用下的最大和最小值来确定结构的边界条件和极限状态。
四、典型结构的力学分析1. 梁的力学分析:梁是结构力学中最基本的构件之一,主要受到弯矩和剪力的作用。
通过梁的力学分析,可以确定梁的支反力和内力分布情况。
2. 桁架的力学分析:桁架是由杆件和节点组成的平面或空间结构,常用于大跨度建筑物和桥梁等工程中。
桁架的力学分析可以确定各杆件的内力和节点的位移。
3. 刚架的力学分析:刚架是由刚性杆件和铰接节点组成的平面或空间结构,常用于建筑物和机械设备中。
刚架的力学分析可以确定各杆件的内力和节点的位移。
4. 平面钢架的力学分析:平面钢架是由钢杆件和节点组成的平面结构,常用于厂房和航空航天领域。
平面钢架的力学分析可以确定各杆件的内力和节点的位移。
结构中的各种刚度

结构中的各种刚度刚度:结构或构件抵抗变形的能力,包括构件刚度和截面刚度,按受力状态不同可分为轴向刚度、弯曲刚度、剪变刚度和扭转刚度等。
对于构件刚度,其值为施加于构件上的力(力矩)与它引起的线位移(角位移)之比。
对于截面刚度,在弹性阶段,其值为材料弹性模量或剪变模量与截面面积或惯性矩的乘积。
首先得从刚度说起。
刚度是指:单位变形条件下,结构或构件在变形方向所施加的力的大小。
在结构静力或动力分析时需要用到。
如用位移法分析结构内力时要用到刚度矩阵,计算地震作用或风振影响时需要用到结构的刚度参数。
还有在设计动力机器基础时也需要用到结构刚度参数。
可以看有关结构力学或结构动力学的书。
举个两个简单的例子以方便理解:用力弯折直径和长度相等的实心钢管和木头,哪个费劲哪个刚度(弯曲刚度)就大。
很显然是钢管的大,你有可能把木头弯折,但要弯折钢管就很难吧!用力弯折长度相等而直径不等的实心钢管,当然是直径小的容易弯折吧,那就是直径小的刚度小了。
所以刚度是和材料特性及截面特性直接相关,当然线刚度还和长度有关了!一般能满足F=k△,F为作用力,△为位移,k即为刚度,所以刚度物理意义为单位位移时所产生的力。
k可以是某些量的函数,即可为表达式。
由F的不同,叫法不同。
另外就是我们要说的刚度叫线刚度,即单位长度上的刚度。
比如,我们在用反弯点法计算多层框架水平荷载作用下内力近似计算时。
计算柱的水平剪力时,剪力与柱层间水平位移△的关系为V=(12ic/h2)△那么d=(12ic/h2)就叫柱的侧移刚度,表示柱上下两端相对有单位侧移时柱中产生的剪力。
其中ic表示柱的线刚度(即ic=EI/h),h为楼层高,EI是柱的抗弯刚度(M=EI(1/p),M为弯矩,(1/p)为曲率,也满足F=k△形式)。
另外还可用D值法,即考虑了梁柱的刚度比变化,因为柱两端梁的刚度不同,即对柱的约束不同,那么它的反弯点,即M=0的点会随之移动,那端强,反弯点离它越远。
变形及刚度计算_图文_图文

一、基本概念(挠度、转角、挠曲线)
度量梁变形后横截面位移的两个基本量 2、转角() :横截面对其原来位置的角位移(横截面 绕中性轴转动的角度) , 称为该截面的转角。
A
C
B
x
y挠度
C'
y
转角
转角方程:一般各横截面的转角是不相同的,是位置x的 函数,称为转角方程,记做= (x)
4、挠度和转角的关系
注意:位移边界条件在支座处
变形连续条件中间在分段点
三、 用积分法求梁的变形 注意
当梁上的外力将梁分为数段时,由于各段梁 的弯矩方程不同,因而梁的挠曲线近似微分方程 需分段列出。相应地各段梁的转角方程和挠曲线 方程也随之而异。
F
A
a
D
B
b
三、 用积分法求梁的变形 步骤
1、正确分段,分别列弯矩方程; 2、分段列近似微分方程,一次积分得转角方程,再此积 分得挠度方程; 3、由位移边界条件和变形连续条件求得积分常数。
纵向伸长量: 横向缩短量:
轴向压缩:
F
F
纵向缩短、横向伸长
纵向缩短量: 横向伸长量:
注:绝对变形量不足以描述变形的程度,尤其对于长度不 一的杆件,因此引入应变的概念。
§ 8-1 轴向拉压杆的变形
二、线应变
线应变:将绝对伸长量除以杆件的初始尺寸,即得单位伸长 ,称之为线应变。
1、纵(轴)向变形量: F
即 该式表明,某截面的转角等于挠曲线在该截面处的 一阶导数
A
挠曲线
y
C
C'
转角
B
x
y挠度
5、挠度和转角的符号约定
挠度:向下为正,向上为负。 转角:自x 转至切线方向,顺时针转为正,逆时针转为负。
扭转刚度单位

扭转刚度单位我们知道扭转刚度是描述物体抗扭刚度的一个特征量。
对于轴对称结构,该刚度与荷载、截面形状无关。
轴对称结构的扭转刚度可以根据荷载作用下,弯矩、剪力与轴力的比值表示出来。
我们说扭转刚度是物体弯曲变形或抵抗变形的能力,那么一般情况下我们把物体的整体对外弯曲变形而又不发生断裂的最大限度叫做物体抵抗弯曲变形的极限。
因此,物体抵抗弯曲变形的极限越大,它就具有较大的扭转刚度,反之就小。
可见,弯曲刚度大,变形就小,抵抗弯曲变形的极限就大;扭转刚度大,变形就小,抵抗扭转变形的极限就小。
扭转刚度对于我们来说并不陌生,我们通常都会使用扭转刚度来进行材料的有限元分析和结构设计工作。
特别是在多跨连续梁桥的分析中,通过对扭转刚度的测试和研究,为连续梁桥提供一个准确的扭转刚度计算公式,避免了由于不同的施工误差导致的相邻跨不均匀扭转的产生。
由于在有限元法的材料本构关系中引入了轴对称扭转刚度的概念,所以在实际应用中往往需要在不同的节点上测量扭转刚度,分析得到的轴对称扭转刚度才能作为有限元计算的依据。
所以,扭转刚度的测试在有限元法的材料本构关系中至关重要。
扭转刚度在结构分析中有着重要作用,所以在使用前必须经过严格的验算。
一般地说,在设计时按照扭转刚度和刚度折减系数两项指标来考虑是比较合理的。
这里需要强调的是,采用有限元法建立的结构模型仅仅是一种近似模型,它不能完全代替实际结构的受力情况。
对于结构来说,如果在同样的边界条件下,对比不同模型的计算结果,就可以明显看出不同模型的预估误差和预估精度。
所以,在使用有限元法进行结构分析时,应当严格遵守有限元法的规定和原则,认真验算模型的正确性,包括验算模型是否满足材料本构关系和基本假定。
对于扭转刚度的验算,也可以采用与材料的轴对称线弹性本构关系类似的方法,即采用边界条件与相应的简化模型一起通过力一位移平衡条件来确定模型中的扭转刚度,再按照相应的求解方法进行结构的稳态计算和分析。
总之,在进行结构分析时,只有充分地了解结构在实际工作状态下各个构件的内力和变形情况,并且将其合理地叠加起来,形成完整的受力体系,才能真正揭示结构的内部特性,达到设计要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( T) 基 于 GB 的梁 有 限 元 ; 构 整 体 屈 曲 性 GB ; T 结
C B a l . as g i a,D.Ca mot a d N. S le te i m n i s r v
能; 节点 翘 曲传 递
Ab ta t T i p p r r p rs r s a c wor c c r ig t e sr c : h s a e e o t e e r h k on e n n h
cu e ny t e frtf u r i— o y e o main mo e ld s o l h i o r( i d b d )d f r t d  ̄ s g o
n mey n e c ie )t e kn ma ia o esd v lp d a l,o e d s rb s j h ie t l c m d l e eo e
u eofG n r l e e m h o y( T)t n ls h lb s e e ai d B a T e r GB s o a ay e tego —
a lbuc l g b avi a e an a c hi— al r e ki eh n ourofpln d sp e t n w l ed fam s. F l ig a b i ol ow n refover e h ai n ept n pr e— viw oft e m n c c o s a d oc d e n ur s ivol n t e p ror a c ved i h e f m n e ofa GBT b ki g a al uc ln n y— ss,on r e s i t i t or ulton a um erca m . i e p es nt n de a I he f m a i nd n i li pl e a i of a G BT- s d b am fnie elm e t ha i em nt ton ba e e i t e n t t n.
构 件 的整 体 屈 曲分 析
Gl oba lBuc l g A n l i an n a e ki ayss of Pl e a d Sp c n
由度 和节 点广 义位 移 之 间 的联 系 。最 后 , 绍 并 讨 介
论 数值 结 果 , 其可 能 有 助 于 基 于 广 义 梁 理 论 的有 限 元 公 式 的制定 和 实 施 。并 将 基 于 GB 分 析 的结 果 T
i h rc d rs a o t d t a de t e e fc s se mig i e po e u e d p e o h n l h fe t tm )t n
f o t e on c ncden e rm h n . oi i c of h m e b c n r dal a t e m er e t oi nd
( 临界屈 曲载 荷 和模态 ) ANS 与 YS程 序 中壳单 元 和
梁 单元 的建模 分析 结果 进 行 了对 比验 证 。 关 键 词 : 面 薄壁 结 构 ; 间 薄 壁结 构 ; 义 梁 理 论 平 空 广
Thn. ai d F a s i h i W l r me n t e Cont e extofGBT
结 构 轴 力 一 扭 转 屈 曲变 形 中 的 精 确 动 力 刚 度
Exa tDyn m i if e s f c a c Stf n s orAxilTor on a- si a
B c l g o t u t r lF a s u ki fS r c u a r me n
维普资讯
非 线性有 限元建 模 ; 强度 和延 性
和剪 力 中心轴 ( 截 面 非 双 向对 称 ) 重 合 的效 应 ; 横 不
i ) 点 构 件 的定 义 , 些节 点 可 提供 连 接构 件 的 自 i节 i 这
对 广 义 梁 理 论 中的 平 面 和 空 间 薄 壁
o e o n lss t u t r l p s d f r a ay i n s r c u a i me h nc . S c n o d r c a is e o d re
e f t h a al or e nd or e fec s of t e xi f c a t qu ar c e onsder i ed. Th e o sit ntna ur c n s e t alboun r m om e s an or e e gi n da y nt d f c s ar ve t s e t ym m e r h o en ur he s t y oft e dyn m i tf n s m a rx i a c s if es ti n f flig t e ulil he r quiem en h e pr a h n r toft e r ci oc lt eor m . The e e x- a td c yna i if es a rx i m cstf n sm t i sobt n ort is i e u- aied f he frttm sig o w er eres n p s i exp n on. Gen al dit i t a al a si er l y s rbu ed xi f c a b a al ed w ihou difcul or e c n e n yz t t fi t y. I i i e ou t s p nt d o t t t n - nior s c i s ha on u f m e ton m a n b f tvey n y ed y ot e efec i l a alz du t t c ver n pr e . Th it a i digr m s e o he on ge t oblm e n ercton a a du o b a i r qu e t vi r ton f e enc y, a alf c nd t q— e i n de aI ed i t i s. K e wo d y r s: Be am c um n; P ol ower eres; E c d a i s i xa t yn m c s if s tfne s; I er c i xilt si alb nt a tve a a—or on uckig l n
A.Y.T. L eun g
t i l e t e wapn rn mi in a f os mua h r i ta s s o t 怕me j it o - t g s on s c n
ne tn w o or n c ig t orm e on- l ed U-an - e i e b s, ai gn d Is cton m m er Ab ta t sr c :A dyn m i axilt si b k ig he y i pr a c a-or on uc ln t or s o-
