九年级数学圆周角和圆心角的关系练习题.doc
鲁教版2020九年级数学圆周角与圆心角课后作业题3(附答案)

鲁教版2020九年级数学圆周角与圆心角课后作业题3(附答案)一.选择题(共10小题)1.如图,在半圆⊙O中,直径AB=4,点C、D是半圆上两点,且∠BOC=84°,∠BOD =36°,P为直径上一点,则PC+PD的最小值为()A.4B.2C.2D.22.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是()A.=B.=C.=D.不能确定3.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,则α取值范围是()A.36°≤α≤45°B.45°≤α≤54°C.54°≤α≤72°D.72°≤α≤90°4.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为()A.4cm B.3cm C.5cm D.4cm5.如图,A、B、C在⊙O上,∠A=50°,则∠OBC的度数是()A.50°B.40°C.100°D.80°6.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC、BD,若∠AOC=110°,则∠ABD的度数是()A.35°B.46°C.55°D.70°7.如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是()A.AC=CD B.+=C.OD⊥AB D.CD平分∠ACB 8.如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为()A.50°B.60°C.70°D.80°9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是()A.120°B.80°C.100°D.60°10.如图,点A,B,C,D,E都是⊙O上的点,=,∠B=122°,则∠D=()A.58°B.116°C.122°D.128°二.填空题(共10小题)11.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是.12.如图,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:①∠CBA=30°,②OD⊥BC,③OE=AC,④四边形AODC是菱形.正确的个数是.13.如图是两个半圆,点O为大半圆的圆心,AB平行于半圆的直径且是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积是.14.已知⊙O的弦AB把圆分成两部分的比为1:5,若AB=3cm,则⊙O的半径等于cm.15.如图,五边形ABCDE内接于⊙O,BC=CD=DE,若∠B=98°,∠E=116°,则∠A =°.16.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD=.17.如图,四边形ABCD内接于⊙O,∠BOD=120°,则∠DCE=.18.如图,在圆内接四边形ABCD中,∠B=100°,则∠D的度数为.19.如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC=.20.如图,点A,B,C,D都在⊙O上,C是的中点,AB=CD.若∠ODC=50°,则∠ABC的度数为°.三.解答题(共8小题)21.如图,弦AB和弦CD相交于⊙O内一点E,AD=CB,求证:AB=CD.22.如图,在⊙O中,=,∠A=40°,求∠D的度数.23.如图,在⊙O中,=(1)若∠C=75°,求∠A的度数;(2)若AB=13,BC=10,求⊙O的半径.24.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD.求证:P A=PC.25.如图1,AB、EF是⊙O的直径,点C、F在AB上,且F是的中点,弦BC与FE交于点D,连接AC、BC、FC、FB、AE.(1)求证:AC∥EF;(2)如图2,过点C作FB的平行线,交EF于点N,M为线段CF的中点,连接MD并延长MD交AB于点H,连接FH.若EN=2,AB=6,求FH的长.26.如图,AB为圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F (1)请写出三条与BC有关的正确结论;(2)当∠D=30°,CD=2时,求圆中阴影部分的周长.27.已知:四边形ABCD是⊙O的内接四边形.求证:∠ABC+∠ADC=180°.(用两种方法)28.如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形;(2)连接OA,OB,当点P位于什么位置时,四边形PBOA是菱形?并说明理由;(3)已知P A=a,PB=b,求PC的长(用含a和b的式子表示).参考答案与试题解析一.选择题(共10小题)1.如图,在半圆⊙O中,直径AB=4,点C、D是半圆上两点,且∠BOC=84°,∠BOD =36°,P为直径上一点,则PC+PD的最小值为()A.4B.2C.2D.2【解答】解:作点D关于AB的对称点DE,连接CE,交AB于点P,过点O作OF⊥CE,垂足为F,∵∠BOC=84°,∠BOD=36°,∴∠BOE=36°,∠COE=120°,∴∠C=30°,∵AB=4,∴OC=2,∴OF=1,CF=,∴CE=2,∴PC+PD的最小值为2,故选:B.2.如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,恰好经过点O,则与的关系是()A.=B.=C.=D.不能确定【解答】解:连接OC,BC,过O作OE⊥AC于D交圆O于E,∵把半圆沿弦AC折叠,恰好经过点O,∴OD=OE,∵AB是半圆O的直径,∴∠ACB=90°,∴OD∥BC,∵OA=OB,∴OD=BC,∴BC=OE=OB=OC,∴∠COB=60°,∴∠AOC=120°,∴=,故选:A.3.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,则α取值范围是()A.36°≤α≤45°B.45°≤α≤54°C.54°≤α≤72°D.72°≤α≤90°【解答】解:∵在△AOB中,OA=OB,∠OAB=α∴∠OBA=α,∠AOB=180°﹣2α∴当α=36°时,∠AOB=180°﹣2×36°=108°108×5=540°∵转360°恰好位于点A,540°﹣360°=180°>108°∴此时不位于弧AB上,A错误;当α=60°时,∠AOB=60°,60×5=300°∴此时小华还没到达点A,故C错误;当α=60°时,∠AOB=60°,60×5=300°当α=90°时,点B在圆外,不符合题意,故D错误;故选:B.4.如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为()A.4cm B.3cm C.5cm D.4cm【解答】解:连接OD,OC,作DE⊥AB于E,OF⊥AC于F,∵∠CAD=∠BAD,∴=,∴∠DOB=∠OAC=2∠BAD,在△AOF和△ODE中,,∴△AOF≌△ODE,∴OE=AF=AC=3,在Rt△DOE中,DE==4,在Rt△ADE中,AD==4,故选:A.5.如图,A、B、C在⊙O上,∠A=50°,则∠OBC的度数是()A.50°B.40°C.100°D.80°【解答】解:∵∠BAC=50°,∴∠BOC=100°,∵BO=CO,∴∠OBC=(180°﹣100°)÷2=40°,故选:B.6.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC、BD,若∠AOC=110°,则∠ABD的度数是()A.35°B.46°C.55°D.70°【解答】解:连接BC,∵∠AOC=110°,∴∠ABC=∠AOC═55°,∵CD⊥AB,∴=,∴∠ABD=∠ABC=55°,故选:C.7.如图,在⊙O中,点C在优弧上,将弧沿BC折叠后刚好经过AB的中点D,连接AC,CD.则下列结论中错误的是()A.AC=CD B.+=C.OD⊥AB D.CD平分∠ACB 【解答】解:A、过D作DD'⊥BC,交⊙O于D',连接CD'、BD',由折叠得:CD=CD',∠ABC=∠CBD',∴AC=CD'=CD,故①正确;B、∵AC=CD',∴,由折叠得:,∴=,故②正确;C、∵D为AB的中点,∴OD⊥AB,故③正确;D、延长OD交⊙O于E,连接CE,∵OD⊥AB,∴∠ACE=∠BCE,∴CD不平分∠ACB,故④错误;故选:D.8.如图,四边形ABCD是⊙O内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD的度数为()A.50°B.60°C.70°D.80°【解答】解:由圆周角定理得,∠CAD=∠CBD=80°,∴∠BAD=80°+30°=110°,∵四边形ABCD是⊙O内接四边形,∴∠BCD=180°﹣∠BAD=70°,故选:C.9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是()A.120°B.80°C.100°D.60°【解答】解:∵四边形ABCD为⊙O的内接四边形,∴∠A=180°﹣∠BCD=60°,由圆周角定理得,∠BOD=2∠A=120°,故选:A.10.如图,点A,B,C,D,E都是⊙O上的点,=,∠B=122°,则∠D=()A.58°B.116°C.122°D.128°【解答】解:连接AC、CE,∵点A、B、C、E都是⊙O上的点,∴∠AEC=180°﹣∠B=58°,∵=,∴∠ACE=∠AEC=58°,∴∠CAE=180°﹣58°﹣58°=64°,∵点A、C、D、E都是⊙O上的点,∴∠D=180°﹣64°=116°,故选:B.二.填空题(共10小题)11.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是51°.【解答】解:如图,∵==,∠COD=34°,∴∠BOC=∠EOD=∠COD=34°,∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°.又∵OA=OE,∴∠AEO=∠OAE,∴∠AEO=×(180°﹣78°)=51°.故答案为:51°.12.如图,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:①∠CBA=30°,②OD⊥BC,③OE=AC,④四边形AODC是菱形.正确的个数是①②③④.【解答】:如图,连接CD、AD、CO,,∵点C,D是半圆上的三等分点,∴∠AOC=∠COD=∠BOD=180°÷3=60°,∴∠CBA=∠AOC÷2=60°÷2=30°,即①正确;∵∠BEO=180°﹣∠BOD﹣∠CBA=180°﹣60°﹣30°=90°∴OD⊥BC,即②正确.∵OB=OC,OD⊥BC,∴E是BC的中点,又∵O是AB的中点,∴OE是△ABC的中位线,∴OE=AC,即③正确.∵AC⊥BC,OD⊥BC,∴AC∥OD,∵∠DCB=∠BOD÷2=60°÷2=30°,∠CBA=30°∴∠DCB=∠CBA,∴CD∥AB,∴四边形AODC是平行四边形,∵∠AOC=60°,OA=OC,∴△AOC是等边三角形,∴AO=AC,又∵四边形AODC是平行四边形,∴AO=OD=DC=CA,∴四边形AODC是菱形,即④正确.综上,可得正确的结论有:①②③④.故答案为①②③④.13.如图是两个半圆,点O为大半圆的圆心,AB平行于半圆的直径且是大半圆的弦且与小半圆相切,且AB=24,则图中阴影部分的面积是72π.【解答】解:将小圆向右平移,使两圆变成同心圆,如图,连OB,过O作OC⊥AB于C点,则AC=BC=12,∵AB是大半圆的弦且与小半圆相切,∴OC为小圆的半径,∴S阴影部分=S大半圆﹣S小半圆=π•OB2﹣π•OC2=π(OB2﹣OC2)=πBC2=72π.故答案为72π.14.已知⊙O的弦AB把圆分成两部分的比为1:5,若AB=3cm,则⊙O的半径等于3cm.【解答】解:∵弦AB将圆分成的两段弧所对的圆心角度数之比为1:5,∴∠AOB=×360°=60°,∵OA=OB,∴△AOB为等边三角形,∵⊙O的半径为3cm,∴AB=3cm.故答案为:3.15.如图,五边形ABCDE内接于⊙O,BC=CD=DE,若∠B=98°,∠E=116°,则∠A =102°.【解答】解:连接AC,AD,∵BC=CD=DE,∴==,∴设∠BAC=∠CAD=∠DAE=α,∵∠B=98°,∠E=116°,∴∠B+∠E﹣α=98°+116°﹣α=180°,∴α=34°,∴∠BAE=3α=102°,故答案为:102°.16.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD=40°.【解答】解:连接OD,∵AD∥OC,∴∠DAB=∠BOC=50°,∵OA=OD∴∠AOD=180°﹣2∠DAB=80°,∴∠ACD=∠AOD=40°故答案为40°17.如图,四边形ABCD内接于⊙O,∠BOD=120°,则∠DCE=120°.【解答】解:∵∠BOD=120°,∴∠BCD==60°.∴∠DCE=180°﹣60°=120°.故答案为:120°.18.如图,在圆内接四边形ABCD中,∠B=100°,则∠D的度数为80°.【解答】解:∵四边形ABCD是圆内接四边形,∴∠B+∠D=180°,∵∠B=100°,∴∠D=80°,故答案为80°.19.如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC=25°.【解答】解:∵AD∥BC,∴=,∴∠PBC=∠PCB,∵∠APB=50°,∴∠PBC=25°,故答案为:25°.20.如图,点A,B,C,D都在⊙O上,C是的中点,AB=CD.若∠ODC=50°,则∠ABC的度数为100°.【解答】解:∵C是的中点,AB=CD.∴==,∵∠ODC=50°,∴∠A=∠ACB=∠COD=×(180°﹣2∠ODC)=×(180°﹣50°×2)=40°,∴∠ABC=180°﹣∠A﹣∠ACB=180°﹣40°×2=100°.故答案为:100.三.解答题(共8小题)21.如图,弦AB和弦CD相交于⊙O内一点E,AD=CB,求证:AB=CD.【解答】证明:∵AD=BC,∴=,∴=,∴CD=AB.22.如图,在⊙O中,=,∠A=40°,求∠D的度数.【解答】解:∵∠A=40°,∴劣弧BC的度数为80°,则优弧BC的度数为:360°﹣80°=280°,∴∠D=140°.23.如图,在⊙O中,=(1)若∠C=75°,求∠A的度数;(2)若AB=13,BC=10,求⊙O的半径.【解答】解:(1)∵在⊙O中,=,∴AB=AC.∴∠B=∠C=75°.∴∠A=180°﹣2×75°=30°;(2)如图,延长AO交BC于D,则AD⊥BC,BD=CD=BC=5,∴在直角△ABD中,由勾股定理,得AD===12.在直角△OBD中,由勾股定理,得OB2=(12﹣OB)2+52,解得OB=,即⊙O的半径是.24.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD.求证:P A=PC.【解答】证明:连接AC,∵AB=CD,∴=,∴+=+,即=,∴∠C=∠A,∴P A=PC.25.如图1,AB、EF是⊙O的直径,点C、F在AB上,且F是的中点,弦BC与FE交于点D,连接AC、BC、FC、FB、AE.(1)求证:AC∥EF;(2)如图2,过点C作FB的平行线,交EF于点N,M为线段CF的中点,连接MD并延长MD交AB于点H,连接FH.若EN=2,AB=6,求FH的长.【解答】(1)证明:∵点F是的中点,∴∠BAC=∠BOC=∠BOF,∴AC∥EF;(2)解:如图2,∵CN∥FB,OA=OE=OB=OF,∴∠CNF=∠OFB=∠OBF=∠E,∴AE∥FB,∴CN∥AE,∵AC∥EF,∴四边形AENC是▱AENC,∴AC=EN=2,∵OC=OB,∠COF=∠BOF,∴DC=DB,OD⊥BC于点D,∵OD是△ABC的中位线,∴OD=AC=1,∵OB=3,∴BD=2,又∵MD是△BCE的中位线,∴MH∥FB,∴∠ODH=∠OFB=∠OBF=∠DHO,∴OD=OH,又∠DOH为公共角,∴△FOH≌△BOD,∴FH=BD=2.26.如图,AB为圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F (1)请写出三条与BC有关的正确结论;(2)当∠D=30°,CD=2时,求圆中阴影部分的周长.【解答】解:(1)答案不唯一,只要合理均可.例如:①BC=BD;②OF∥BC;③∠BCD=∠A;④△BCE∽△OAF;⑤BC2=BE•AB;⑥BC2=CE2+BE2;⑦△ABC是直角三角形;⑧△BCD是等腰三角形.(2)∵CD=2,∴CE=,∵∠D=∠A=30°,∴AC=2,AB=4,∴==π,∴周长为:+227.已知:四边形ABCD是⊙O的内接四边形.求证:∠ABC+∠ADC=180°.(用两种方法)【解答】证法1:连接OA,OC,∵∠B=∠1,∠D=∠2,∴∠B+∠D=(∠1+∠2)=×360°=180°;证法2:如图2,连接CA,BD,∵∠1=∠2,∠3=∠4,∴∠ADC=∠1+∠3=∠2+∠4,∴∠ADC+∠ABC=∠2+∠4+∠ABC=180°.28.如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形;(2)连接OA,OB,当点P位于什么位置时,四边形PBOA是菱形?并说明理由;(3)已知P A=a,PB=b,求PC的长(用含a和b的式子表示).【解答】(1)证明:∵∠BAC=∠CPB=60°,∴∠ABC=∠APC=60°,∴∠ABC=∠BAC=∠ACB=60°,∴△ABC为等边三角形;(2)解:当点P位于的中点时,四边形PBOA是菱形.理由如下:连接OP,如图1,∵∠AOB=2∠ACB=120°,而P是的中点,∴∠AOP=∠BOP=60°,又∵OA=OP=OB,∴△OAP和△OBP都为等边三角形,∴OA=AP=OB=PB,∴四边形PBOA是菱形;(3)解:如图2,在PC上截取PD=P A,又∵∠APC=60°,∴△APD是等边三角形,∴P A=DA,∠DAP=60°,∵∠P AB+∠BAD=∠BAD+∠DAC,∴∠P AB=∠DAC,在△APB和△ADC中,∴△APB≌△ADC(ASA),∴PB=DC,又∵P A=PD,∴PC=PD+DC=P A+PB=a+b.。
圆心角圆周角练习题

圆心角圆周角练习题圆心角和圆周角是圆内角的一种特殊形式,它们在几何学中具有重要的地位。
本文将介绍关于圆心角和圆周角的一些练习题,帮助读者加深对这一概念的理解。
一、选择题1. 在同一个圆中,圆心角和对应的圆周角的关系是:A. 圆心角大于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角小于对应的圆周角2. 已知在同一个圆中,圆心角的度数为56°,则对应的圆周角的度数为:A. 56°B. 112°C. 224°3. 在圆O中,∠ACB是圆心角,则它所对应的圆周角的度数为:A. 30°B. 60°C. 120°4. 若∠ACD是圆O中的圆心角,且其度数为72°,则弧AB所对应的圆周角的度数为:A. 72°B. 144°C. 288°5. 在同一个圆中,圆心角和对应的弧所对应的圆周角之间的关系是:A. 圆心角小于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角大于对应的圆周角二、填空题1. 在同一圆中,一条弧的度数等于其所对应的圆周角的度数,则这条弧所对应的圆心角的度数为________。
2. 在圆O中,已知∠ACB是圆心角,则它所对应的圆周角的度数为________。
3. 在同一个圆中,圆心角的度数等于所对应的弧所对应的圆周角的度数,则该弧所对应的圆周角的度数为________。
三、解答题1. 在同一个圆中,圆心角和对应的圆周角的关系是什么?为什么?2. 已知在同一个圆中,圆心角的度数为60°,则对应的圆周角的度数是多少?并通过计算或推理进行解答。
3. 在圆O中,∠ACB是圆心角,则它所对应的圆周角的度数是多少?并通过计算或推理进行解答。
4. 若∠ACD是圆O中的圆心角,且其度数为90°,则弧AB所对应的圆周角的度数是多少?并通过计算或推理进行解答。
总结:本文通过选择题、填空题和解答题的形式,对圆心角和圆周角的概念进行了练习和探讨。
圆周角定理练习题

圆周角定理练习题在数学中,圆周角定理是一个非常重要的定理,它关于圆周角和圆心角的关系进行了阐述。
理解和掌握这个定理对于解决与圆相关的问题非常有帮助。
那么,现在我们来进行一些圆周角定理的练习题,以便加深对该定理的理解和运用能力。
练习题一:已知半径为r的圆上的弧AB所对的圆周角为θ,求弧AB的长度。
解答:根据圆周角定理可知,圆周角θ所对的弧的长度等于半径r乘以圆周角的弧度。
即弧AB的长度为rθ。
练习题二:已知弧CD的长度为s,求弧CD所对的圆周角。
解答:根据圆周角定理可知,弧CD所对的圆周角的弧度等于弧长s除以半径r。
即圆周角θ等于s/r。
练习题三:已知圆O的半径为r,圆弧AB所对的圆周角为θ,求圆O的周长。
解答:根据圆周角定理可知,圆周角θ所对的弧AB的长度为rθ。
因为圆O的周长等于圆周率π乘以直径d,而直径d等于半径r的两倍,所以圆O的周长为2πr。
练习题四:已知半径为r的圆上的弧AB的长度为s,求弧AB所对的圆周角。
解答:根据圆周角定理可知,弧AB所对的圆周角的弧度等于弧长s除以半径r。
即圆周角θ等于s/r。
练习题五:已知圆O的半径为r,圆上的弧AB所对的圆周角为θ,求弧AB所对的圆心角。
解答:根据圆周角定理可知,圆周角θ所对的圆心角的度数为360°乘以θ/2π。
通过以上练习题,我们可以更好地理解和应用圆周角定理。
掌握这个定理对于解决与圆有关的各种问题非常重要。
希望通过练习能够加深你对圆周角定理的理解,并培养你的数学思维和解题能力。
初中数学 圆周角和圆心角的关系同步练习及答案

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:在同圆中,同弦所对的圆周角 ( )A.相等 B.互补 C.相等或互补 D.互余试题2:如图3-63所示,A,B,C,D在同一个圆上,四边形ABCD的两条对角线把四个内角分成的8个角中,相等的角共有 ( )A.2对 B.3对 C.4对D.5对试题3:如图3-64所示,⊙O的半径为5,弦AB=,C是圆上一点,则∠ACB的度数是.试题4:如图,四边形 ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为()A.50° B.80° C.100° D.130°试题5:如图是中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是() A.180° B.15 0° C.135° D.120°试题6:下列命题中,正确的命题个数是()①顶点在圆周上的角是圆周角;②圆周角度数等于圆心角度数的一半;③900的圆周角所对的弦是直径;④圆周角相等,则它们所对的弧也相等。
A、1个B、2个C、3个D、4个试题7:如图3-65所示,在⊙O中,∠AOB=100°,C为优弧ACB的中点,则∠CAB=.试题8:如图3-66所示,AB为⊙O的直径,AB=6,∠CAD=30°,则弦DC=.试题9:如图3-67所示,AB是⊙O的直径,∠BOC=120°,CD⊥AB,求∠ABD的度数.试题10:如图,已知AB是⊙O的直径,AD ∥ OC弧AD的度数为80°,则∠BOC=_________ 试题11:如图,⊙O内接四边形ABCD中,AB=CD则图中和∠1相等的角有______。
2022-2023学年北师大版九年级数学下册《3-4圆周角与圆心角的关系》同步练习题(附答案)

2022-2023学年北师大版九年级数学下册《3.4圆周角与圆心角的关系》同步练习题(附答案)一.选择题1.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是()A.10°B.20°C.30°D.40°2.如图,AB是⊙O的弦,OC⊥AB交⊙O于点C,点D是⊙O上一点,∠ADC=30°,则∠BOC的度数为()A.30°B.40°C.50°D.60°3.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB =60°,则点C的纵坐标为()A.+B.2+C.4D.2+24.如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为()A.50°B.60°C.80°D.90°5.如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为()A.45°B.50°C.55°D.60°6.如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是()A.OC∥BD B.AD⊥OC C.△CEF≌△BED D.AF=FD7.如图,BC是半圆O的直径,D,E是上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为()A.35°B.38°C.40°D.42°8.已知⊙O的半径为3,AB、AC是⊙O的两条弦,AB=3,AC=3,则∠BAC的度数是()A.75°或105°B.15°或105°C.15°或75°D.30°或90°二.填空题9.如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC=.10.如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若AP:PB=1:4,CD=8,则AB =.11.如图,四边形ABCD为⊙O的内接四边形,∠A=100°,则∠DCE的度数为.12.如图,A、B、C是⊙O上的三点,且四边形OABC是菱形.若点D是圆上异于A、B、C的另一点,则∠ADC的度数是.13.如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE =.14.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=.15.如图,在⊙O中,四边形OABC为菱形,点D在上,则∠ADC的度数是.16.已知:如图,等腰三角形ABC中,AB=AC=4,若以AB为直径的⊙O与BC相交于点D,DE∥AB,DE与AC相交于点E,则DE=.三.解答题17.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且=.(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.18.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.19.如图,AC是⊙O的直径,弦BD交AC于点E.(1)求证:△ADE∽△BCE;(2)如果AD2=AE•AC,求证:CD=CB.20.已知:如图.△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O 于点D,DE⊥AB于点E,且交AC于点P,连接AD.(1)求证:∠DAC=∠DBA;(2)求证:P是线段AF的中点;(3)若⊙O的半径为5,AF=,求tan∠ABF的值.21.如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.(1)求证:△CBE∽△AFB;(2)当时,求的值.22.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的边于G,F,E点.求证:(1)F是BC的中点;(2)∠A=∠GEF.参考答案一.选择题1.解:连接BC,延长ED交⊙O于N,连接OD,并延长交⊙O于M,∵∠AOC=80°,∴的度数是80°,∵点D为弦AC的中点,OA=OC,∴∠AOD=∠COD,∴=,即M为的中点,∴和的度数都是80°=40°,∵>,∴40°<的度数<80°,∴20°<∠CED<40°,∴选项C符合题意;选项A、选项B、选项D都不符合题意;故选:C.2.解:如图,∵∠ADC=30°,∴∠AOC=2∠ADC=60°.∵AB是⊙O的弦,OC⊥AB交⊙O于点C,∴=.∴∠AOC=∠BOC=60°.故选:D.3.解:连接P A,PB,PC,过P作PD⊥AB于D,PE⊥OC于E,∵∠ACB=60°,∴∠APB=120°,∵P A=PB,∴∠P AB=∠PBA=30°,∵A(﹣5,0),B(1,0),∴AB=6,∴AD=BD=3,∴PD=,P A=PB=PC=2,∵PD⊥AB,PE⊥OC,∠AOC=90°,∴四边形PEOD是矩形,∴OE=PD=,PE=OD=2,∴CE===2,∴OC=CE+OE=2+,∴点C的纵坐标为2+,故选:B.4.解:如图,∵A、B、D、C四点共圆,∴∠GBC=∠ADC=50°,∵AE⊥CD,∴∠AED=90°,∴∠EAD=90°﹣50°=40°,延长AE交⊙O于点M,∵AO⊥CD,∴,∴∠DBC=2∠EAD=80°.故选:C.5.解:∵四边形ABCD内接于⊙O,∠ABC=105°,∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.∵=,∠BAC=25°,∴∠DCE=∠BAC=25°,∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.故选:B.6.解:∵AB是⊙O的直径,BC平分∠ABD,∴∠ADB=90°,∠OBC=∠DBC,∴AD⊥BD,∵OB=OC,∴∠OCB=∠OBC,∴∠DBC=∠OCB,∴OC∥BD,选项A成立;∴AD⊥OC,选项B成立;∴AF=FD,选项D成立;∵△CEF和△BED中,没有相等的边,∴△CEF与△BED不全等,选项C不成立;故选:C.7.解:连接CD,如图所示:∵BC是半圆O的直径,∴∠BDC=90°,∴∠ADC=90°,∴∠ACD=90°﹣∠A=20°,∴∠DOE=2∠ACD=40°,故选:C.8.解:分为两种情况:①当圆心O在∠BAC的内部时,如图所示,过O作OE⊥AB于E,OD⊥AC于D,连接OA,∵OE⊥AB,OE过圆心O,AB=3,∴AE=BE=,由勾股定理得:OE===,即OE=AE,∴∠BAO=45°,∵OD⊥AB,OD过圆心O,AC=3,∴AD=CD=,∵OA=3,∴AD=OA,∴∠AOD=30°,∴∠CAO=60°,∴∠BAC=∠BAO+∠CAO=45°+60°=105°;②当O在∠BAC的外部时,由①得:∠CAO=60°,∠BAO=45°,所以∠BAC=∠CAO﹣∠BAO=60°﹣45°=15°;故选:B.二.填空题9.解:∵OA=OB,OA=AB,∴OA=OB=AB,即△OAB是等边三角形,∴∠AOB=60°,∵OC⊥OB,∴∠COB=90°,∴∠COA=90°﹣60°=30°,∴∠ABC=15°,故答案为:15°10.解:∵AB是⊙O的直径,弦CD⊥AB,CD=8,∴CP=4,根据相交弦定理得,16=AP×4AP,解得AP=2,∴AB=10.11.解:∵四边形ABCD为⊙O的内接四边形,∴∠DCE=∠A=100°,故答案为:100°12.解:连接OB,∵四边形OABC是菱形,∴AB=OA=OB=BC,∴△AOB是等边三角形,∴∠ADC=60°,∠AD′C=120°.故答案为:60°或120°.13.解:∵∠BOD=120°,∴∠A=∠BOD=60°.∵四边形ABCD是圆内接四边形,∴∠DCE=∠A=60°.故答案为:60°.14.解:∵∠A=55°,∠E=30°,∴∠EBF=∠A+∠E=85°,∵∠A+∠BCD=180°,∴∠BCD=180°﹣55°=125°,∵∠BCD=∠F+∠CBF,∴∠F=125°﹣85°=40°.故答案为40°.15.解:∵四边形ABCD内接于⊙O,∴∠B+∠D=180°,∵四边形OABC为菱形,∴∠B=∠AOC,∴∠D+∠AOC=180°,∵∠AOC=2∠D,∴3∠D=180°,∴∠ADC=60°,故答案为60°.16.解:连接AD,∵AB为直径,∴∠ADB=90°,又∵AB=AC,∴D为BC的中点,又∵DE∥AB,∴DE为△ABC的中位线,∴DE=AB=×4=2.三.解答题17.解:(1)△ABC为等腰三角形.理由如下:连接AE,如图,∵=,∴∠DAE=∠BAE,即AE平分∠BAC,∵AB为直径,∴∠AEB=90°,∴AE⊥BC,∴△ABC为等腰三角形;(2)∵△ABC为等腰三角形,AE⊥BC,∴BE=CE=BC=×12=6,在Rt△ABE中,∵AB=10,BE=6,∴AE==8,∵AB为直径,∴∠ADB=90°,∴AE•BC=BD•AC,∴BD==,在Rt△ABD中,∵AB=10,BD=,∴AD==,∴sin∠ABD===.18.解:(1)∵AB是半圆O的直径,∴∠ACB=90°,又∵OD∥BC,∴∠AEO=90°,即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°,∠AOD=∠B=70°.∵OA=OD,∴∠DAO=∠ADO===55°∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;(2)在直角△ABC中,BC===.∵OE⊥AC,∴AE=EC,又∵OA=OB,∴OE=BC=.又∵OD=AB=2,∴DE=OD﹣OE=2﹣.19.证明:(1)如图,∵∠A与∠B是对的圆周角,∴∠A=∠B,又∵∠1=∠2,∴△ADE∽△BCE;(2)如图,∵AD2=AE•AC,∴,又∵∠A=∠A,∴△ADE∽△ACD,∴∠AED=∠ADC,又∵AC是⊙O的直径,∴∠ADC=90°,即∠AED=90°,∴直径AC⊥BD,∴=,∴CD=CB.20.(1)证明:∵BD平分∠CBA,∴∠CBD=∠DBA,∵∠DAC与∠CBD都是弧CD所对的圆周角,∴∠DAC=∠CBD,∴∠DAC=∠DBA;(2)证明:∵AB为直径,∴∠ADB=90°,∵DE⊥AB于E,∴∠DEB=90°,∴∠ADE+∠EDB=∠ABD+∠EDB=90°,∴∠ADE=∠ABD=∠DAP,∴PD=P A,∵∠DF A+∠DAC=∠ADE+∠PDF=90°,且∠ADB=90°,∴∠PDF=∠PFD,∴PD=PF,∴P A=PF,即:P是AF的中点;(3)解:∵∠DAF=∠DBA,∠ADB=∠FDA=90°,∴△FDA∽△ADB,∴=,由题意可知圆的半径为5,∴AB=10,∴===,∴在Rt△ABD中,tan∠ABD==,即:tan∠ABF=.21.(1)证明:∵AE=EB,AD=DF,∴ED是△ABF的中位线,∴ED∥BF,∴∠CEB=∠ABF,又∵∠C=∠A,∴△CBE∽△AFB.(2)解:由(1)知,△CBE∽△AFB,∴,又AF=2AD,∴.22.证明一:(1)连接DF,∵∠ACB=90°,D是AB的中点,∴BD=DC=AB,∵DC是⊙O的直径,∴DF⊥BC,∴BF=FC,即F是BC的中点;(2)∵D,F分别是AB,BC的中点,∴DF∥AC,∴∠A=∠BDF,∵∠BDF=∠GEF(圆周角定理),∴∠A=∠GEF.证明二:(1)连接DF,DE,∵DC是⊙O直径,∴∠DEC=∠DFC=90°.∵∠ECF=90°,∴四边形DECF是矩形.∴EF=CD,DF=EC.∵D是AB的中点,∠ACB=90°,∴EF=CD=BD=AB.∴△DBF≌△EFC.∴BF=FC,即F是BC的中点.(2)∵△DBF≌△EFC,∴∠BDF=∠FEC,∠B=∠EFC.∵∠ACB=90°(也可证AB∥EF,得∠A=∠FEC),∴∠A=∠FEC.∵∠FEG=∠BDF(同弧所对的圆周角相等),∴∠A=∠GEF.(此题证法较多,大纲卷参考答案中,又给出了两种不同的证法,可供参考.)。
初三数学圆心角试题

初三数学圆心角试题1.在同一个圆中,同弧所对的圆周角和圆心角的关系是.【答案】圆周角度数等于圆心角度数的一半【解析】直接根据圆周角定理填空即可.在同一个圆中,同弧所对的圆周角和圆心角的关系是圆周角度数等于圆心角度数的一半.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,难度一般.2.如图,直径垂直于弦,垂足为,,则的度数为,的度数为,的度数为,的度数为.【答案】,,,【解析】根据垂径定理及圆周角定理依次分析即可得到结果.∵直径垂直于弦,∴弧AD的度数等于弧AC的度数等于∴弧CBD的度数等于∴=,的=.【考点】垂径定理,圆周角定理点评:垂径定理是圆中极为重要的知识点,一般与勾股定理结合使用,因而是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.3.如图,是半圆的直径,为圆心,是半圆上一点,且,是延长线上一点,与半圆相交于点,如果,则,,.【答案】,,【解析】设∠A=x,由AB=OC,得到∠BOA=x,根据三角形外角性质得到∠EBO=2x,而OB=OE,得∠AEO=2x,则x+2x=93°,得到x=31°,再根据三角形的内角和定理即可求得∠EOB、∠ODE.设∠A=x,∵AB=OC,∴∠BOA=x,∴∠EBO=2x,而OB=OE,∴∠AEO=2x,∴∠EOD=∠A+∠AEO,而∠EOD=93°,∴x+2x=93°,∴x=31°,∴∠EOB=180°-4x=180°-124°=56°,∴∠ODE=(180°-93°)÷2=.【考点】圆的基本性质,等腰三角形的性质,三角形内角和定理,三角形的外角性质点评:本题知识点多,综合性强,在中考中比较常见,在各种题型中均有出现,一般难度不大,需特别注意.4.如图,,则,,,.【答案】,,,【解析】在同一个圆中,同弧或等弧所对的圆周角度数等于圆心角度数的一半.∵弧ACB:弧ADB=5:4,弧ACB+弧ADB=360°∴弧ACB=200°,弧ADB=160°∴,,,.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,难度一般.5.如图,△内接于,,点,分别在和上,若,则,.【答案】,【解析】由可得弧AC的度数,由可得弧AB的度数,即可得到弧BFC的度数,从而求得结果.∵,∴弧AC的度数等于弧AB的度数等于100°∴弧BFC的度数等于160°,弧BAC的度数等于200°∴,.【考点】圆周角定理点评:圆周角定理是圆中极为重要的知识点,在中考中比较常见,在各种题型中均有出现,一般难度不大,需熟练掌握.6.在同圆中,同弦所对的两个圆周角()A.相等B.互补C.相等或互补D.互余【答案】C【解析】根据圆周角定理及圆的基本性质即可判断.在同圆中,同弦所对的两个圆周角相等或互补,故选C.【考点】圆周角定理,圆的基本性质点评:圆周角定理是圆中极为重要的知识点,在中考中比较常见,在各种题型中均有出现,一般难度不大,需熟练掌握.7.在中,弦所对的劣弧为圆的,有以下结论:①为,②,③,④△为等边三角形,⑤弦的长等于这个圆的半径.其中正确的是()A.①②③④⑤B.①②④⑤C.①②D.②④⑤【答案】B【解析】根据圆周角定理及圆的基本性质依次分析各小题即可判断.∵弦所对的劣弧为圆的∴弧AB为60°,,△为等边三角形,弦的长等于这个圆的半径故选B.【考点】圆周角定理,圆的基本性质点评:圆周角定理是圆中极为重要的知识点,在中考中比较常见,在各种题型中均有出现,一般难度不大,需熟练掌握.8.,,,,依次是上的四个点,,弦,的延长线交于点,若,则等于()A.B.C.D.【答案】C【解析】根据圆周角的度数等于它所对的弧的度数的一半得到弧AD的度数,从而得到弧ABCD的度数,根据弧AB=弧CB=弧CD,即可求得弧BC的度数,从而求得结果.如图:∵∠ABD=60°,∴弧AD的度数=2×60°=120°,∴弧ABCD的度数=360°-120°=240°,又∵弧AB=弧CB=弧CD,∴弧BC的度数=×240°=80°,∴∠BDC=40°,而∠ABD=∠P+∠BDP,∴∠P=60°-40°=20°.故选C.【考点】圆的基本性质,等腰三角形的性质,三角形内角和定理,三角形的外角性质点评:本题知识点多,综合性强,在中考中比较常见,在各种题型中均有出现,一般难度不大,需特别注意.9.如图,△为锐角三角形,△内接于圆,,是△的垂心,是的直径.求证:.【答案】见解析【解析】易得△BCD为含30°的直角三角形,则CD=BD,利用H是垂心及直径所对的圆周角是直角可得四边形AHCD是平行四边形,则AH=CD,可得所证.连接AD,CD,CH∵BD是⊙O直径,∴∠BAD=∠BCD=90°,又∠BAC=60°,∴∠CAD=30°,∠DBC=∠CAD=30°,在Rt△BCD中,CD=BD,H是△ABC的垂心,AH⊥BC,CH⊥AB,又DC⊥BC,DA⊥AB,∴四边形AHCD为平行四边形,∵AH=CD,∴.【考点】与圆有关的证明点评:辅助线问题是初中数学的难点,能否根据题意准确作出适当的辅助线很能反映一个学生的对图形的理解能力,因而是中考的热点,尤其在压轴题中比较常见,需特别注意.10.如图,已知是外任意一点,过点作直线,,分别交于点,,,.求证:(的度数的度数).【答案】见解析【解析】先由三角形外角的性质得∠BCD=∠P+∠ABC,再由圆周角定理即可得出结论.∵的度数等于弧BD的度数,的度数等于弧AC的度数(弧BD的度数-弧AC的度数).【考点】三角形外角的性质,圆周角定理点评:辅助线问题是初中数学的难点,能否根据题意准确作出适当的辅助线很能反映一个学生的对图形的理解能力,因而是中考的热点,尤其在压轴题中比较常见,需特别注意.。
北师大版九年级下册数学 3.4圆周角和圆心角之间的关系 同步练习(含解析)

3.4圆周角和圆心角之间的关系同步练习一.选择题1.如图,AB是⊙O的直径,AC是弦,若∠ACO=30°,则sin∠COB的等于()A.B.C.D.2.⊙O中,∠AOB=100°,若C是上一点,则∠ACB等于()A.80°B.100°C.120°D.130°3.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于()A.50°B.60°C.70°D.75°4.如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP =∠CAP=10°,若的度数是40°,则的度数是()A.10°B.15°C.20°D.25°5.AB为半圆O的直径,弦AD,BC相交于点P,若CD=3,AB=4,则tan∠BPD等于()A.B.C.D.6.如图所示,AB是直径,点E是弧AB中点,弦CD∥AB且平分OE,连AD,∠BAD度数为()A.45°B.30°C.15°D.107.如图,AB是圆O的直径,点C是半圆O上不同于A,B的一点,点D为弧AC的中点,连结OD,BD,AC,设∠CAB=β,∠BDO=α,则()A.α=βB.α+2β=90°C.2α+β=90°D.α+β=45°8.如图,已知A、B、C、D、E是⊙O上的五个点,圆心O在AD上,∠BCD=110°,则∠AEB的度数为()A.70°B.35°C.40°D.20°9.如图,⊙O中,若OA⊥BC、∠AOB=66°,则∠ADC的度数为()A.33°B.56°C.57°D.66°10.如图,四边形ABCD内接于⊙O,AC为⊙O的直径,D为弧AC的中点,过点D作DE ∥AC,交BC的延长线于点E.若⊙O的半径为5,AB=8,则CE的长为()A.4B.C.D.二.填空题11.如图所示,⊙O的直径CD过弦EF的中点G,∠GEO=46°,则∠DCF=.12.如图,AD是⊙O的直径,若∠B=40°,则∠DAC的度数为.13.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是.14.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=70°,则∠BAE=°.15.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM 的最小值为.三.解答题16.如图,以△ABC的一边为直径的半圆与其它两边AC、BC分别交于点D、E,=.(1)求证;AC=AB;(2)若BC=8,BA=6,求CD的长.17.如图,在⊙O中.(1)若=,∠ACB=80°,求∠BOC的度数;(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.18.如图,⊙O的直径AB=12,半径OC⊥AB,D为弧BC上一动点(不包括B、C两点),DE⊥OC,DF⊥AB,垂足分别为E.F.(1)求EF的长.(2)若点E为OC的中点,①求弧CD的度数.②若点P为直径AB上一动点,直接写出PC+PD的最小值.参考答案一.选择题1.解:∵OA=OC,∠ACO=30°,∴∠OAC=∠ACO=30°,∵∠COB是△AOC的外角,∴∠COB=∠ACO+∠OAC=60°,∴sin∠COB=sin60°=.故选:C.2.解:如图:在优弧上取点D,连接AD,BD,∵⊙O中,∠AOB=100°,∴∠ADB=∠AOB=50°,∵四边形ACBD是⊙O的内接四边形,∴∠ACB=180°﹣∠ADB=130°.故选:D.3.解:连接OA,OB,OC,OD,∵∠BAD=50°,==,∴∠BOD=2∠BAD=100°,∵==,∴AOB=∠BOC=∠COD=∠BOD=50°,∴∠AOD=∠AOB+∠BOC+∠COD=150°,∴∠AED=∠AOD=75°.故选:D.4.解:∵的度数是40°,∴∠ACM=40°∵∠CBP=∠CAP=10°,∴A、C、P、B四点共圆,∴∠ACM=∠ABP=40°,∵∠CPB=10°,∴∠ABC=40°﹣10°=30°,∵AC=BC,∴∠CAB=∠ABC=30°,∴∠ACB=120°,∴∠BCN=180°﹣∠ACM﹣∠ACB=20°,∴的度数是20°.故选:C.5.解:连接BD.则∠CDA=∠ABC.(同圆中同弧AC所对的圆周角相等)同理∠DCB=∠DAB,所以△PCD∽△P AB,==.∵AB直径,∴∠ADB=90°.∴∠PDB=∠ADB=90°,在Rt△PDB中,cos∠DPB==,∴sin∠DPB=.(sin2∠DPB+cos2∠DPB=1)tan∠BPD==.故选:A.6.解:设CD与OE交于P,则连接OC,∵CD∥AB且平分OE,∴OP=•OC,∴sin∠PCO=,∴∠PCO=30°,又∵CD∥AB,∴∠COA=∠PCO=30°,∴∠BAD=∠BOD=15°.故选:C.7.解:如图,设AC与DO交点为E,如图,∵OD=OB,∴∠OBD=∠BDO=α,∴∠DOA=2∠OBD=2α,又∵D为中点,AB为⊙O直径,∴OD⊥AC,∴∠EAO+∠EOA=90°,即2α+β=90°.故选:C.8.解:如图,连接DE,数学∵四边形BCDE是⊙O的内接四边形,∴∠BCD+∠BED=180°,∵∠BCD=110°,∴∠BED=70°,∵AD是⊙O的直径,∴∠AED=90°,∴∠AEB=∠AED﹣∠BED=90°﹣70°=20°,故选:D.9.解:如图,连接OC,OB.∵OA⊥BC,∴=,∴∠AOC=∠AOB=66°,∴∠ADC=∠AOC=33°,数学故选:A.10.解:∵⊙O的半径为5,∴AC=10,∴AD=CD=5,∵AC为⊙O的直径,∴∠ABC=90°,∵AB=8,∴BC=6,∵∠BAD=∠DCE,∵∠ABD=∠CDE=45°,∴△ABD∽△CDE,∴,∴,∴CE=,故选:B.二.填空题11.解:∵CD是直径,EG=GF,∴CD⊥EF,∴=,∴∠CDF=∠EOD,∵∠OGE=90°,∠GEO=46°,∴∠EOD=44°,∴∠DCF=22°.故答案为:22°.12.解:连接CD.∵AD是直径,∴∠ACD=90°,∵∠D=∠B=40°,∴∠DAC=90°﹣40°=50°.故答案为50°.13.解:连结OA、OB,作△ABC的外接圆D,如图1,∵OA=OB=2,AB=2,∴△OAB为等边三角形,∴∠AOB=60°,∴∠APB=∠AOB=30°,∵AC⊥AP,∴∠C=60°,∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,∵∠ACB=60°,点C在⊙D上,∴∠ADB=120°,如图2,当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,∴△ABC的最大面积为.故答案为:.14.解:∵四边形ABCD是平行四边形,∠D=70°,∴∠DCB=(180°﹣∠D)=110°,∵四边形AECD是圆内接四边形,∴∠AEB=∠D=70°,∠B=180°﹣∠BCD=70°∴∠BAE=180°﹣70°﹣70°=40°,故答案为:4015.解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.∵=,∴OM⊥PD,∴∠MOD=90°,∴∠MCD=∠MOD=45°,∵∠ACB=90°,∴∠ACT=45°,∵AT⊥CT,∴∠ATC=90°,∵AC=10,∴AT=AC•sin45°=5,∵AM≥AT,∴AM≥5,∴AM的最小值为5,故答案为5.三.解答题16.(1)证明:∵=,∴∠CAE=∠BAE,∵AB为直径,∴∠AEB=90°,∵∠ABE+∠BAE=90°,∠C+∠CAE=90°,∴∠ABC=∠C,∴AC=AB;(2)解:∵∠CAE=∠CBD,∠ACE=∠BCD,∴△CAE∽△CBD,∴=,即=,∴CD=.17.解:(1)∵=,∴∠ABC=∠ACB=80°,∴∠A=180°﹣80°﹣80°=20°,∴∠BOC=2∠A=40°;(2)作OH⊥BC于H,如图,则BH=CH=BC=5,在Rt△OBH中,OH===12,即点O到BC的距离为12.18.解:(1)连接OD,∵⊙O的直径AB=12,∴圆的半径为12÷2=6,∵OC⊥AB,DE⊥OC,DF⊥AB,∴四边形OFDE是矩形,∴EF=OD=6;(2)①∵点E为OC的中点,∴OE=OC=OD,∴∠EDO=30°,∴∠DOE=60°,∴弧CD的度数为60°;②延长CO交⊙O于G,l连接DG交AB于P,则PC+PD的最小值=DG,∵∠G=∠COD=30°,∵EG=9,数学∴DG===6,∴PC+PD的最小值为6.。
九年级数学下册练习圆周角和圆心角的关系

3.4 圆周角和圆心角的关系 第1课时 圆周角定理及其推论1基础题 知识点1 圆周角的概念1.下列四个图中,∠x 是圆周角的是( )A B C D知识点2 圆周角定理2.(2018·衢州)如图,点A ,B ,C 在⊙O 上,∠ACB =35°, 则∠AOB 的度数是( )A .75°B .70°C .65°D .35°3.如图,已知CD 是⊙O 的直径,过点D 的弦DE 平行于半径OA.若∠D 的度数是50°,则∠C 的度数是( )A .25°B .30°C .40°D .50°4.(2017·兰州)如图,在⊙O 中,AB ︵=BC ︵,点D 在⊙O 上,∠CDB =25°, 则∠AOB =( )A .45°B .50°C .55°D .60°5.(2018·广东)同圆中,已知弧AB 所对的圆心角是100°,则弧AB 所对的圆周角是 .6.如图,⊙O 是△ABC 的外接圆,∠AOB =70°,AB =AC ,则∠ABC = . 知识点3 圆周角定理的推论17.(教材P80练习T2变式)(2017·柳州)如图,在⊙O 中与∠1一定相等的角是( ) A .∠2 B .∠3 C .∠4 D .∠58.(2017·哈尔滨)如图,⊙O 中,弦AB ,CD 相交于点P ,∠A =42°,∠APD =77°,则∠B 的大小是( )A .43°B .35°C .34°D .44°9.如图,⊙O 的直径AB 过弦CD 的中点E.若∠C =25°,则∠D = .10.如图,已知A ,B ,C ,D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD ,AD.求证:DB 平分∠ADC. 证明:易错点 忽略弦所对的圆周角不唯一而致错11.在直径为4的⊙O 中,弦AB =23,点C 是圆上不同于A ,B 的点,那么∠ACB 的度数为 中档题12.(2018·菏泽)如图,在⊙O 中,OC ⊥AB ,∠ADC =32°,则∠OBA 等于( ) A .64° B .58° C .32° D .26° 13.(2017·泰安)如图,点A ,B ,C 是⊙O 上的三点,且四边形ABCO 是平行四边形,OF ⊥OC 交圆O 于点F ,则∠BAF 等于( ) A .12.5° B .15° C .20° D .22.5°14.(2017·贵港)如图,A ,B ,C ,D 是⊙O 上的四个点,B 是AC ︵的中点,M 是半径OD 上任意一点.若∠BDC =40°,则∠AMB 的度数不可能是( ) A .45° B .60° C .75° D .85° 15.(2018·泰安)如图,⊙O 是△ABC 的外接圆,∠A =45°,BC =4, 则⊙O 的直径为 .17.如图,在⊙O 中,AB =AC ,∠CBD =30°,∠BCD =20°,试求∠BAC 的度数. 解:连接OB ,OC ,OD.第2课时圆周角定理的推论2,3基础题知识点1圆周角定理的推论21.如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是(C)A.35°B.45°C.55°D.65°2.(教材P83练习T2变式)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是(B)3.(2018·南充)如图,BC是⊙O的直径,点A是⊙O上的一点,∠OAC=32°,则∠B的度数是(A)A.58°B.60°C.64°D.68°4.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8 cm,ON=6 cm,则该圆玻璃镜的半径是(B)A.10 cmB.5 cmC.6 cmD.10 cm5.如图,A,D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=(B)A.64°B.58°C.72°D.55°6.如图,在半径为5 cm的⊙O中,AB为直径,∠ACD=30°,求弦BD的长.解:∵AB为直径,∴∠ADB=90°.又∵∠ABD=∠ACD=30°,∴BD=AB·cos∠ABD=10×32=53(cm).知识点2圆周角定理的推论37.圆内接四边形ABCD中,已知∠A=70°,则∠C=(D)A.20°B.30°C.70°D.110°8.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点. 若∠BAD=105°,则∠DCE的大小是(B)A.115°B.105°C.100°D.95°9.(2018·邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是(B)A.80°B.120°C.100°D.90°10.(2017·淮安)如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是120°.易错点对圆内接四边形的概念理解不清导致错误11.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.中档题12.如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)A.30°B.45°C.60°D.70°13.(2017·牡丹江)如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于(B)A.100°B.112.5°C.120°D.135°14.(2018·白银)如图,⊙A过点O(0,0),C(3,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是(B)A.15°B.30°C.45°D.60°15.如图,四边形ABCD内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°.求证:(1)AD=CD;(2)AB是⊙O的直径.证明:(1)∵四边形ABCD内接于⊙O,∴∠D=180°-∠B=130°.∵∠ACD=25°,∴∠DAC=180°-∠D-∠ACD=180°-130°-25°=25°.∴∠DAC=∠ACD.∴AD=CD.(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,∠B=50°,∴∠ACB=180°-∠B-∠BAC=180°-50°-40°=90°.∴AB是⊙O的直径.16.(2018·宜昌)如图,在△ABC中,AB=AC.以AB为直径的半圆交AC于点D,交BC于点E.延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.解:(1)证明:∵AB为半圆的直径,∴∠AEB=90°,∵AB=AC,∴CE=BE,又∵EF=AE,∴四边形ABFC是平行四边形.又∵AB=AC(或∠AEB=90°),∴平行四边形ABFC是菱形.(2)连接BD.∵AD=7,BE=CE=2,设CD=x,则AB=AC=7+x.∵AB为半圆的直径,∴∠ADB=90°,∴AB2-AD2=CB2-CD2.∴(7+x)2-72=42-x2.∴x1=1或x2=-8(舍去).∴AB=8.∴S半圆=12×π×42=8π.∴BD=15.∴S菱形ABFC=815.综合题17.如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O 的半径为2 3.(1)求证:△CDE∽△CBA;(2)求DE的长.解:(1)证明:∵四边形ABED为⊙O的内接四边形,∴∠A+∠BED=180°.又∵∠BED+∠CED=180°,∴∠CED=∠A.又∵∠C=∠C,∴△CDE∽△CBA.(2)连接AE.由(1)得DEBA=CECA,∵AB为⊙O的直径,⊙O的半径为23,∴∠AEB=∠AEC=90°,AB=4 3.在Rt△AEC中,∵∠C=60°,∴∠CAE=30°.∴DEBA=CECA=12,即DE=2 3.3.4 圆周角和圆心角的关系 答案 第1课时 圆周角定理及其推论1基础题 知识点1 圆周角的概念1.下列四个图中,∠x 是圆周角的是(C)A B C D知识点2 圆周角定理2.(2018·衢州)如图,点A ,B ,C 在⊙O 上,∠ACB =35°, 则∠AOB 的度数是(B)A .75°B .70°C .65°D .35°3.如图,已知CD 是⊙O 的直径,过点D 的弦DE 平行于半径OA.若∠D 的度数是50°,则∠C 的度数是(A)A .25°B .30°C .40°D .50°4.(2017·兰州)如图,在⊙O 中,AB ︵=BC ︵,点D 在⊙O 上,∠CDB =25°, 则∠AOB =(B)A .45°B .50°C .55°D .60°5.(2018·广东)同圆中,已知弧AB 所对的圆心角是100°,则弧AB 所对的圆周角是50°.6.如图,⊙O 是△ABC 的外接圆,∠AOB =70°,AB =AC ,则∠ABC =35°. 知识点3 圆周角定理的推论17.(教材P80练习T2变式)(2017·柳州)如图,在⊙O 中与∠1一定相等的角是(A) A .∠2 B .∠3 C .∠4 D .∠58.(2017·哈尔滨)如图,⊙O 中,弦AB ,CD 相交于点P ,∠A =42°,∠APD =77°,则∠B 的大小是(B)A .43°B .35°C .34°D .44°9.如图,⊙O 的直径AB 过弦CD 的中点E.若∠C =25°,则∠D =65°.10.如图,已知A ,B ,C ,D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD ,AD.求证:DB 平分∠ADC. 证明:∵AB =BC , ∴AB ︵=BC ︵. ∴∠ADB =∠BDC. ∴DB 平分∠ADC.易错点 忽略弦所对的圆周角不唯一而致错11.在直径为4的⊙O 中,弦AB =23,点C 是圆上不同于A ,B 的点,那么∠ACB 的度数为60°或120°. 中档题12.(2018·菏泽)如图,在⊙O 中,OC ⊥AB ,∠ADC =32°,则∠OBA 等于(D) A .64° B .58° C .32° D .26° 13.(2017·泰安)如图,点A ,B ,C 是⊙O 上的三点,且四边形ABCO 是平行四边形,OF ⊥OC 交圆O 于点F ,则∠BAF 等于(B) A .12.5° B .15° C .20° D .22.5°14.(2017·贵港)如图,A ,B ,C ,D 是⊙O 上的四个点,B 是AC ︵的中点,M 是半径OD 上任意一点.若∠BDC =40°,则∠AMB 的度数不可能是(D) A .45° B .60° C .75° D .85° 15.(2018·泰安)如图,⊙O 是△ABC 的外接圆,∠A =45°,BC =4, 则⊙O 的直径为42.17.如图,在⊙O 中,AB =AC ,∠CBD =30°,∠BCD =20°,试求∠BAC 的度数. 解:连接OB ,OC ,OD.∵∠BOD =2∠BCD ,∠COD =2∠CBD ,∠CBD =30°, ∠BCD =20°,∴∠COD =60°,∠BOD =40°. ∴∠BOC =100°, ∠BAC =12∠BOC =50°.综合题18.如图,四边形ABCD 内接于⊙O ,点E 在对角线AC 上,EC =BC =DC. (1)若∠CBD =39°,求∠BAD 的度数; (2)求证:∠1=∠2. 解:(1)∵BC =DC , ∴BC ︵=DC ︵.∴∠BAC =∠CAD =∠CBD. ∵∠CBD =39°, ∴∠BAC =∠CAD =39°.∴∠BAD =∠BAC +∠DAC =78°. (2)证明:∵EC =BC , ∴∠CBE =∠CEB.∵∠CBE =∠1+∠CBD ,∠CEB =∠2+∠BAC , ∴∠1+∠CBD =∠2+∠BAC. 又∵∠BAC =∠CBD ,∴∠1=∠2.第2课时圆周角定理的推论2,3基础题知识点1圆周角定理的推论21.如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是(C)A.35°B.45°C.55°D.65°2.(教材P83练习T2变式)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是(B)3.(2018·南充)如图,BC是⊙O的直径,点A是⊙O上的一点,∠OAC=32°,则∠B的度数是(A)A.58°B.60°C.64°D.68°4.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8 cm,ON=6 cm,则该圆玻璃镜的半径是(B)A.10 cmB.5 cmC.6 cmD.10 cm5.如图,A,D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=(B)A.64°B.58°C.72°D.55°6.如图,在半径为5 cm的⊙O中,AB为直径,∠ACD=30°,求弦BD的长.解:∵AB为直径,∴∠ADB=90°.又∵∠ABD=∠ACD=30°,∴BD=AB·cos∠ABD=10×32=53(cm).知识点2圆周角定理的推论37.圆内接四边形ABCD中,已知∠A=70°,则∠C=(D)A.20°B.30°C.70°D.110°8.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点. 若∠BAD=105°,则∠DCE的大小是(B)A.115°B.105°C.100°D.95°9.(2018·邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是(B)A.80°B.120°C.100°D.90°10.(2017·淮安)如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是120°.易错点对圆内接四边形的概念理解不清导致错误11.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.中档题12.如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)A.30°B.45°C.60°D.70°13.(2017·牡丹江)如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于(B)A.100°B.112.5°C.120°D.135°14.(2018·白银)如图,⊙A过点O(0,0),C(3,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是(B)A.15°B.30°C.45°D.60°15.如图,四边形ABCD内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°.求证:(1)AD=CD;(2)AB是⊙O的直径.证明:(1)∵四边形ABCD内接于⊙O,∴∠D=180°-∠B=130°.∵∠ACD=25°,∴∠DAC=180°-∠D-∠ACD=180°-130°-25°=25°.∴∠DAC=∠ACD.∴AD=CD.(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,∠B=50°,∴∠ACB=180°-∠B-∠BAC=180°-50°-40°=90°.∴AB是⊙O的直径.16.(2018·宜昌)如图,在△ABC中,AB=AC.以AB为直径的半圆交AC于点D,交BC于点E.延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.解:(1)证明:∵AB为半圆的直径,∴∠AEB=90°,∵AB=AC,∴CE=BE,又∵EF=AE,∴四边形ABFC是平行四边形.又∵AB=AC(或∠AEB=90°),∴平行四边形ABFC是菱形.(2)连接BD.∵AD=7,BE=CE=2,设CD=x,则AB=AC=7+x.∵AB为半圆的直径,∴∠ADB=90°,∴AB2-AD2=CB2-CD2.∴(7+x)2-72=42-x2.∴x1=1或x2=-8(舍去).∴AB=8.∴S半圆=12×π×42=8π.∴BD=15.∴S菱形ABFC=815.综合题17.如图,在△ABC中,∠C=60°,以AB为直径的半圆O分别交AC,BC于点D,E,已知⊙O 的半径为2 3.(1)求证:△CDE∽△CBA;(2)求DE的长.解:(1)证明:∵四边形ABED为⊙O的内接四边形,∴∠A+∠BED=180°.又∵∠BED+∠CED=180°,∴∠CED=∠A.又∵∠C=∠C,∴△CDE∽△CBA.(2)连接AE.由(1)得DEBA=CECA,∵AB为⊙O的直径,⊙O的半径为23,∴∠AEB=∠AEC=90°,AB=4 3.在Rt△AEC中,∵∠C=60°,∴∠CAE=30°.∴DEBA=CECA=12,即DE=2 3.3.4 圆周角和圆心角的关系第1课时 圆周角定理及其推论1基础题知识点1 圆周角的概念1.下列四个图中,∠x 是圆周角的是(C)A B C D知识点2 圆周角定理2.(2018·衢州)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,则∠AOB 的度数是(B)A .75°B .70°C .65°D .35°3.如图,已知CD 是⊙O 的直径,过点D 的弦DE 平行于半径OA.若∠D 的度数是50°,则∠C 的度数是(A)A .25°B .30°C .40°D .50°4.(2019·兰州)如图,在⊙O 中,AB ︵=BC ︵,点D 在⊙O 上,∠CDB=25°,则∠AOB=(B)A .45°B .50°C .55°D .60°5.(2018·广东)同圆中,已知弧AB 所对的圆心角是100°,则弧AB 所对的圆周角是50°.6.如图,⊙O 是△ABC 的外接圆,∠AOB=70°,AB =AC ,则∠ABC=35°.知识点3 圆周角定理的推论17.(教材P80练习T2变式)(2019·柳州)如图,在⊙O 中与∠1一定相等的角是(A)A .∠2B .∠3C .∠4D .∠58.(2019·哈尔滨)如图,⊙O 中,弦AB ,CD 相交于点P ,∠A=42°,∠APD=77°,则∠B 的大小是(B)A .43°B .35°C .34°D .44°9.如图,⊙O 的直径AB 过弦CD 的中点E.若∠C=25°,则∠D=65°.10.如图,已知A ,B ,C ,D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD ,AD.求证:DB 平分∠ADC. 证明:∵AB=BC ,∴AB ︵=BC ︵.∴∠ADB=∠BDC.∴DB 平分∠ADC.易错点 忽略弦所对的圆周角不唯一而致错11.在直径为4的⊙O 中,弦AB =23,点C 是圆上不同于A ,B 的点,那么∠ACB 的度数为60°或120°.中档题12.(2018·菏泽)如图,在⊙O 中,OC ⊥AB ,∠ADC=32°,则∠OBA 等于(D)A .64°B .58°C .32°D .26°13.(2019·泰安)如图,点A ,B ,C 是⊙O 上的三点,且四边形ABCO 是平行四边形,OF⊥OC 交圆O 于点F ,则∠BAF 等于(B)A .12.5°B .15°C .20°D .22.5°14.(2019·贵港)如图,A ,B ,C ,D 是⊙O 上的四个点,B 是AC ︵的中点,M 是半径OD 上任意一点.若∠BDC=40°,则∠AMB 的度数不可能是(D)A .45°B .60°C .75°D .85°15.(2018·泰安)如图,⊙O 是△ABC 的外接圆,∠A=45°,BC =4,则⊙O 的直径为16.如图,AB 是⊙O 的一条弦,OD⊥AB,垂足为点C ,交⊙O 于点D ,点E 在⊙O 上.(1)若∠AOD=52°,求∠DEB 的度数;(2)若OC =3,OA =6,求tan∠DEB 的值.解:(1)连接OB.∵OD⊥AB,∴AD ︵=BD ︵.∴∠BOD=∠AOD=52°.∴∠DEB=12∠BOD=26°. (2)∵OD⊥AB,OC =3,OA =6,∴OC=12OA ,即∠OAC=30°. ∴∠AOC=60°.∴∠DEB=12∠AOC=30°. ∴tan∠DEB=33. 17.如图,在⊙O 中,AB =AC ,∠CBD=30°,∠BCD=20°,试求∠BAC 的度数.解:连接OB ,OC ,OD.∵∠BOD=2∠BCD,∠COD=2∠CBD,∠CBD=30°,∠BCD=20°,∴∠COD=60°,∠BOD=40°.∴∠BOC=100°,∠BAC=12∠BOC=50°. 综合题18.如图,四边形ABCD 内接于⊙O,点E 在对角线AC 上,EC =BC =DC.(1)若∠CBD =39°,求∠BAD 的度数;(2)求证:∠1=∠2.解:(1)∵BC=DC ,∴BC ︵=DC ︵.∴∠BAC=∠CAD=∠CBD.∵∠CBD=39°,∴∠BAC=∠CAD=39°.∴∠BAD=∠BAC+∠DAC=78°.(2)证明:∵EC=BC ,∴∠CBE=∠CEB.∵∠CBE=∠1+∠CBD,∠CEB=∠2+∠BAC,∴∠1+∠CBD=∠2+∠BAC.又∵∠BAC=∠CBD,∴∠1=∠2.第2课时圆周角定理的推论2,3基础题知识点1 圆周角定理的推论21.如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是(C)A.35°B.45°C.55°D.65°2.(教材P83练习T2变式)从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是(B)3.(2018·南充)如图,BC是⊙O的直径,点A是⊙O上的一点,∠OAC=32°,则∠B的度数是(A)A.58°B.60°C.64°D.68°4.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM =8 cm,ON=6 cm,则该圆玻璃镜的半径是(B)A.10 cmB.5 cmC.6 cmD.10 cm5.如图,A,D是⊙O上的两个点,BC是直径.若∠D=32°,则∠OAC=(B)A.64°B.58°C.72°D.55°6.如图,在半径为5 cm的⊙O中,AB为直径,∠ACD=30°,求弦BD的长.解:∵AB为直径,∴∠ADB=90°.又∵∠ABD=∠ACD=30°,∴BD=AB·cos∠ABD=10×32=53(cm).知识点2 圆周角定理的推论37.圆内接四边形ABCD中,已知∠A=70°,则∠C=(D)A.20°B.30°C.70°D.110°8.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点.若∠BAD=105°,则∠DCE的大小是(B)A.115°B.105°C.100°D.95°9.(2018·邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是(B)A.80°B.120°C.100°D.90°10.(2019·淮安)如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为4∶3∶5,则∠D的度数是120°.易错点对圆内接四边形的概念理解不清导致错误11.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.中档题12.如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)A.30°B.45°C.60°D.70°13.(2019·牡丹江)如图,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC等于(B)A.100°B.112.5°C.120°D.135°14.(2018·白银)如图,⊙A过点O(0,0),C(3,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO,BD,则∠OBD的度数是(B)A.15°B.30°C.45°D.60°15.如图,四边形ABCD内接于⊙O,∠B=50°,∠ACD=25°,∠BAD=65°.求证:(1)AD=CD;(2)AB是⊙O的直径.证明:(1)∵四边形ABCD内接于⊙O,∴∠D=180°-∠B=130°.∵∠ACD=25°,∴∠DAC=180°-∠D-∠ACD=180°-130°-25°=25°.∴∠DAC=∠ACD.∴AD=CD.(2)∵∠BAC=∠BAD-∠DAC=65°-25°=40°,∠B=50°,∴∠ACB=180°-∠B-∠BAC=180°-50°-40°=90°.∴AB是⊙O的直径.16.(2018·宜昌)如图,在△ABC中,AB=AC.以AB为直径的半圆交AC于点D,交BC于点E.延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.解:(1)证明:∵AB为半圆的直径,∴∠AEB=90°,∵AB=AC,∴CE=BE,又∵EF=AE,∴四边形ABFC是平行四边形.又∵AB=AC(或∠AEB=90°),∴平行四边形ABFC 是菱形.(2)连接BD.∵AD=7,BE =CE =2,设CD =x ,则AB =AC =7+x.∵AB 为半圆的直径,∴∠ADB=90°,∴AB 2-AD 2=CB 2-CD 2.∴(7+x)2-72=42-x 2.∴x 1=1或x 2=-8(舍去).∴AB=8.∴S 半圆=12×π×42=8π. ∴BD=15.∴S 菱形ABFC =815.综合题17.如图,在△ABC 中,∠C=60°,以AB 为直径的半圆O 分别交AC ,BC 于点D ,E ,已知⊙O 的半径为2 3.(1)求证:△CDE∽△CBA;(2)求DE 的长.解:(1)证明:∵四边形ABED 为⊙O 的内接四边形,∴∠A+∠BED=180°.又∵∠BED+∠CED=180°,∴∠CED=∠A.又∵∠C=∠C,∴△CDE∽△CBA.(2)连接AE.由(1)得DE BA =CE CA, ∵AB 为⊙O 的直径,⊙O 的半径为23,∴∠AEB=∠AEC=90°,AB =4 3.在Rt△AEC 中,∵∠C=60°,∴∠CA E =30°.∴DE BA =CE CA =12,即DE =2 3.北师大版初中数学九年级下3.3圆周角和圆心角的关系练习卷(带解析)一、填空题1.如图,等边三角形ABC的三个顶点都在⊙O上,D是上任一点(不与A、C重合),则∠ADC的度数是________.【答案】120°【解析】试题分析:根据等边三角形的性质及圆内接四边形的性质即可求得结果.∵等边三角形ABC∴∠ABC=60°∴∠ADC=180°-∠ABC=120°.考点:等边三角形的性质,圆内接四边形的性质点评:特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.2.如图,四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中有_________对全等三角形;________对相似比不等于1的相似三角形.【答案】3,1【解析】试题分析:根据圆内接四边形的性质及圆周角定理即可得到结果.由题意得△ABE≌△DCE,△ABD≌△DCA,△ABC≌△DCB有3对全等三角形相似比不等于1的相似三角形有△ADE∽△DCB这一对.考点:圆内接四边形的性质,圆周角定理点评:全等三角形的判定和性质的应用贯穿于整个初中学习,是平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.3.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC=_______度.【答案】160°【解析】试题分析:由∠BAD=100°可得∠BAC的度数,再根据圆周角定理即可求得结果.∵∠BAD=100°∴∠BAC=80°∴∠BOC=160°.考点:邻补角定理,圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.4.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.【答案】44°【解析】试题分析:连接OB,根据圆的基本性质可得∠AOB的度数,再根据圆周角定理即可求得结果.连接OB∵∠OAB=46°,OA=OB∴∠AOB=88°∴∠ACB=44°.考点:圆的基本性质,圆周角定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.5.如图,AB是⊙O的直径, ,∠A=25°,则∠BOD的度数为________.【答案】50°【解析】试题分析:圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.∵,∠A=25°∴∠BOD=50°.考点:圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.6.如图,AB是半圆O的直径,AC="AD,OC=2,∠CAB=30°," 则点O到CD的距离OE=____.【答案】【解析】试题分析:由AC=AD,∠CAB=30°可得∠CDO的度数,即可得到∠EOD、∠COE的度数,判断出△COE的形状再结合勾股定理即可求得结果.∵AC=AD,∠CAB=30°,OA=OC∴∠CDO=75°,∠COD=60°∴∠EOD=15°∴∠COE=45°∴△COE为等腰直角三角形∵OC=2∴OE=.考点:三角形内角和定理,勾股定理点评:特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.二、选择题1.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )A.50° B.100° C.130° D.200°【答案】A【解析】试题分析:圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.∵∠BOC=100°∴∠BAC=50°故选A.考点:圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.2.如图,A、B、C、D四个点在同一个圆上,四边形ABCD的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对【答案】C【解析】试题分析:圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.相等的角有∠ADB=∠ACB,∠BAC=∠BDC,∠CAD=∠CBD,∠ACD=∠ABC4对,故选C.考点:圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.3.如图,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A.4个 B.3个 C.2个 D.1个【答案】B【解析】试题分析:圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.∵D是弧AC的中点∴∠ABD=∠ACD=∠CBD=∠CAD故选B.考点:圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.4.如图, ,则∠A+∠B等于( )A.100° B.80° C.50° D.40°【答案】C【解析】试题分析:连接CO并延长交圆于点D,根据圆周角定理即可得到结果.连接CO并延长交圆于点D由图可得∠A+∠B=∠AOD+∠BOD=∠AOB=50°故选C.考点:圆周角定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.5.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )A.30° B.30°或150° C.60° D.60°或120°【答案】B【解析】试题分析:根据圆的性质可得这条弦与半径围成的三角形为等边三角形,再根据圆周角定理即可求得结果.由题意得这条弦与半径围成的三角形为等边三角形则该弦所对的圆周角的度数是30°或150°故选B.考点:圆周角定理点评:特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.6.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC="140°," ∠CBD的度数是( )A.40°B.50°C.70°D.110°【答案】C【解析】试题分析:先求得弧ABC所对的圆周角的度数,再根据圆内接四边形的对角互补可得∠ABC的度数,即可求得结果.∵∠AOC=140°∴弧ABC所对的圆周角的度数为70°∴∠ABC=110°∴∠CBD=70°故选C.考点:圆周角定理,圆内接四边形的性质点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.三、解答题1.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.【答案】4cm【解析】试题分析:连接OC、OD,根据圆周角定理可得∠COD=60°,即可得到△COD是等边三角形,根据等边三角形的性质即可求得结果.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD=4cm.考点:圆周角定理,等边三角形的判定和性质点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.2.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC=∠CAD,求弦AC的长.【答案】3【解析】试题分析:连接DC,根据圆周角定理可得∠ADC=∠ABC=∠CAD,即可得到AC=CD,由AD是直径可得∠ACD=90°,再根据勾股定理即可求得结果.连接DC,则∠ADC=∠ABC=∠CAD,故AC=CD.∵AD是直径,∴∠ACD=90°,∴AC2+CD2=AD2,即2AC2=36,AC2=18,AC=3.考点:圆周角定理,勾股定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.3.如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tan∠BPD的值【答案】【解析】试题分析:连接BD, 根据圆周角定理可得∠ADB=90°,证得△PCD ∽△PAB,根据相似三角形的性质结合余弦的定义可得∠BPD的余弦值,再结合勾股定理即可求得结果.连接BD,∵AB是直径,∴∠ADB=90°.∵∠C=∠A,∠D=∠B,∴△PCD ∽△PAB,∴.在Rt△PBD中,cos∠BPD==,设PD=3x,PB=4x,则BD=,∴tan∠BPD=.考点:圆周角定理,相似三角形的判定和性质,勾股定理,三角函数点评:本题综合性强,知识点较多,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.4.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.【答案】(1)相等;(2)∠CP′D+∠COB=180°【解析】试题分析:(1)连接OD,根据垂径定理可得∠COB=∠DOB,再结合圆周角定理即可得到结果;(2)连接P′P,则可得∠P′CD=∠P′PD,∠P′PC=∠P′D C.即可得∠P′CD+∠P′DC=∠CPD,从而可以得到结果.从而∠CP′D+∠COB=180°.(1)连接OD,∵AB⊥CD,AB是直径,∴,∴∠COB= ∠DOB.∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.(2)连接P′P,则∠P′CD=∠P′PD,∠P′PC=∠P′DC.∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,从而∠CP′D+∠COB=180°.考点:垂径定理,圆周角定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.5.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)【答案】让乙射门较好【解析】试题分析:根据圆周角定理结合三角形外角的性质分析即可得到结论.迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A<MCN=∠B,即∠B>∠A, 从而B处对MN的张角较大,在B处射门射中的机会大些.考点:圆周角定理,三角形外角的性质点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.6.钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母, 问下料时至少要用直径多大的圆钢?【答案】a【解析】试题分析:根据圆内接正方形的性质结合勾股定理即可求得结果.由题意得则下料时至少要用直径为的圆钢.考点:圆内接正方形的性质,勾股定理点评:特殊四边形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.。
人教版 九年级数学上册 第24章 圆的概念及弧、弦、圆心角和圆周角 专题练习(含答案)

圆的概念及弧、弦、圆心角和圆周角专题练习(含答案)例1. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于()A.160°B.150°C.140°D.120°例2. 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE CE=1.则弧BD 的长是()B C D例3.如图,已知A,B,C在⊙O上,ACB为优弧,下列选项中与∠AOB相等的是()A.2∠C B.4∠B C.4∠A D.∠B+∠C例4. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是()A.6 B.5 C.4 D.3巩固练习1.如下图,(1)若点O为⊙O的圆心,则线段__________是圆O的半径;线段________是圆O的弦,其中最长的弦是______;______是劣弧;______是半圆.(2)若∠A=40°,则∠ABO=______,∠C=______,∠ABC=______.2.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为________.3.⊙O中,∠AOB=100°,若C是AB上一点,则∠ACB等于( ).A.80°B.100°C.120°D.130°4.已知:如图,在同心圆中,大圆的弦AB交小圆于C,D两点.(1)求证:∠AOC=∠BOD;(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.5. 已知:如图,AB为⊙O的直径,C,D为⊙O上的两点,且C为AD的中点,若∠BAD=20°,求∠ACO的度数6.如图,以ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC、AD于E、F,交BA的延长线于G,试说明弧EF和弧FG相等.7. ⊙O中,M为AB的中点,则下列结论正确的是( ).A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定8. 如图,⊙O中,AB为直径,弦CD交AB于P,且OP=PC,试猜想AD与CB之间的关系,并证明你的猜想.9. 如图,⊙O中,直径AB=15cm,有一条长为9cm的动弦CD在ANB上滑动(点C与A,点D与B不重合),CF⊥CD交AB于F,DE⊥CD交AB于E.(1)求证:AE=BF;(2)在动弦CD滑动的过程中,四边形CDEF的面积是否为定值?若是定值,请给出证明并求这个定值;若不是,请说明理由.10.如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=______,∠ABE=______,∠ADC=______,∠ABC=______.10题图11题图12题图11.如图,若六边形ABCDEF是⊙O的内接正六边形,则∠AED=______,∠FAE=______,∠DAB=______,∠EFA=______.12.如图,ΔABC是⊙O的内接正三角形,若P是AB上一点,则∠BPC=______;若M是BC上一点,则∠BMC=______.13.在⊙O中,若圆心角∠AOB=100°,C是AB上一点,则∠ACB等于( ).A.80°B.100°C.130°D.140°14.在圆中,弦AB,CD相交于E.若∠ADC=46°,∠BCD=33°,则∠DEB等于( ).A.13°B.79°C.38.5°D.101°15.如图,AC 是⊙O 的直径,弦AB ∥CD ,若∠BAC =32°,则∠AOD 等于( ).A .64°B .48°C .32°D .76°16.如图,弦AB ,CD 相交于E 点,若∠BAC =27°,∠BEC =64°,则∠AOD 等于( ).A .37°B .74°C .54°D .64°17.如图,四边形ABCD 内接于⊙O ,则x = 。
2019-2020【提分必做】九年级数学下册 第二章 2.2 圆心角、圆周角练习 (新版)湘教版

2.2 圆心角、圆周角2.2.1 圆心角基础题知识点1 认识圆心角1.下面四个图中的角,是圆心角的是(D)A B C D2.将一个圆分成四个扇形,它们的圆心角的度数比为4∶4∶5∶7,则这四个扇形中,圆心角最大的是(D) A .54° B .72°C .90°D .126°知识点2 圆心角、弧、弦之间的关系 3.下列说法中,正确的是(B) A .等弦所对的弧相等 B .等弧所对的弦相等 C .圆心角相等,所对的弦相等 D .弦相等所对的圆心角相等4.如图,在⊙O 中,AB ︵=AC ︵,∠AOB=122°,则∠AOC 的度数为(A) A .122°B .120°C .61°D .58°5.如图,A ,B ,C ,D 是⊙O 上的四点,且AD =BC ,则AB 与CD 的大小关系为(B) A .AB>CD B .AB =CD C .AB<CDD .不能确定6.如图,已知在⊙O 中,BC 是直径,AB ︵=DC ︵,∠AOD=80°,则∠ABC 等于(B) A .40°B .65°C .100°D .105°7.如图所示,在⊙O 中,AC ,BC 是弦,根据条件填空: (1)若AC =BC ,则AC ︵=BC ︵,∠AOC=∠BOC; (2)若AC ︵=BC ︵,则AC =BC ,∠AOC=∠BOC; (3)若∠AOC=∠BOC,则AC ︵=BC ︵,AC =BC .8.如图,在⊙O 中,点C 是AB ︵的中点,∠OAB=50°,则∠BOC 等于40°.9.如图所示,在⊙O 中,AB ︵=AC ︵,∠B=70°,则∠A =40°.10.(教材P49练习T2变式)如图所示,AB 是⊙O 的直径,BC ︵=CD ︵=DE ︵,∠COD=34°,求∠AEO 的度数.解:∵BC ︵=CD ︵=DE ︵, ∠COD=34°, ∴∠BOE=102°. ∵OA=OE ,∴∠AEO=∠EAO=12∠BOE=51°.中档题11.如图,AB 是⊙O 的直径,BC ,CD ,DA 是⊙O 的弦,且BC =CD =DA.则∠BCD 等于(C) A .100°B .110°C .120°D .135°12.如图,在⊙O 中,已知弦AB =DE ,OC⊥AB,OF⊥DE,垂足分别为C ,F ,则下列说法中,正确的个数为(D)①∠DOE=∠AOB;②AB ︵=DE ︵;③OF=OC ;④AC=EF. A .1B .2C .3D .413.已知AB ︵,CD ︵是同圆的两段弧,且AB ︵=2CD ︵,则弦AB 与2CD 之间的关系为(B)A .AB =2CD B .AB <2CDC .AB >2CD D .不能确定提示:如图,在圆上截取DE ︵=CD ︵,连接DE ,CE ,则有AB ︵=CE ︵.∴AB=CE.又CD +DE =2CD>CE =AB ,∴AB<2CD ,故选B.14.如图,A ,B ,C 是⊙O 上的三点,且有AB ︵=BC ︵=CA ︵. (1)求∠AOB,∠BOC,∠AOC 的度数; (2)连接AB ,BC ,CA ,试确定△ABC 的形状.解:(1)∵AB ︵=BC ︵=CA ︵, ∴∠AOB=∠BOC=∠AOC.又∵∠AOB+∠BOC+∠COA=360°, ∴∠AOB=∠BOC=∠AOC=120°. (2)∵AB ︵=BC ︵=CA ︵, ∴AB=BC =CA.∴△ABC 是等边三角形.15.如图,AB ,CD 是⊙O 的两条直径,过点A 作AE∥CD 交⊙O 于点E ,连接BD ,DE ,求证:BD =DE.证明:连接OE , ∵OA=OE , ∴∠A=∠OEA. ∵AE∥CD,∴∠BOD=∠A,∠DOE=∠OEA. ∴∠BOD=∠DOE. ∴BD=DE.16.如图,已知AB 是⊙O 的直径,M ,N 分别是AO ,BO 的中点,CM⊥AB,DN⊥AB.求证:AC ︵=BD ︵.证明:连接OC ,OD ,∵AB 是⊙O 的直径,M ,N 分别是AO ,BO 的中点, ∴OM=ON.∵CM⊥AB,DN⊥AB, ∴∠OMC=∠OND=90°.在Rt△OMC 和Rt△OND 中,⎩⎪⎨⎪⎧OM =ON ,OC =OD ,∴Rt△OMC≌Rt△OND(HL). ∴∠COM=∠DON. ∴AC ︵=BD ︵. 综合题17.如图,在⊙O 中,AB ,CD 是两条弦,OE⊥AB,OF⊥CD,垂足分别为E ,F. (1)如果∠AOB=∠COD,那么OE 与OF 的大小有什么关系?为什么? (2)如果OE =OF ,那么AB ︵与CD ︵的大小有什么关系?为什么?解:(1)OE =OF.理由:∵OE⊥AB,OF⊥CD,OA =OB ,OC =OD ,∴∠OEB=∠OFD=90°,∠EOB=12∠AOB,∠FOD=12∠COD.∵∠AOB=∠COD,∴∠EOB=∠FOD. 在△EOB 和△FOD 中, ⎩⎪⎨⎪⎧∠OEB=∠OFD,∠EOB=∠FOD,OB =OD ,∴△EOB≌△FOD(AAS). ∴OE=OF. (2)AB ︵=CD ︵.理由:∵OE⊥AB,OF⊥CD,AO =BO ,CO =DO , ∴∠OEB=∠OFD=90°.∴点E ,F 分别是AB ,CD 的中点.在Rt△BEO 和Rt△DFO 中,⎩⎪⎨⎪⎧OB =OD ,OE =OF ,∴Rt△BEO≌Rt△DFO(HL). ∴BE=DF.∵AB=2BE ,CD =2DF , ∴AB=CD. ∴AB ︵=CD ︵.2.2.2 圆周角第1课时圆周角定理及其推论1基础题知识点1 认识圆周角1.下列四个图中,∠x是圆周角的是(C)知识点2 圆周角定理2.(2018·衢州)如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是(B)A.75° B.70° C.65° D.35°3.如图,△ABC内接于⊙O.若∠A=α,则∠OBC等于(D)A.180°-2αB.2αC.90°+αD.90°-α4.如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A,B两点,P是优弧AB上任意一点(与A,B不重合),则∠APB=30°.5.(2018·广东)在同圆中,已知弧AB所对的圆心角是100°,则弧AB所对的圆周角是50°.知识点3 圆周角定理推论16.如图,点A ,B ,C ,D 都在⊙O 上,AC ,BD 相交于点E ,则∠ABD=(A) A .∠ACD B .∠ADB C .∠AEDD .∠ACB7.如图,已知AB ,CD 是⊙O 的两条直径,∠ABC=28°,那么∠BAD=(A) A .28°B .42°C .56°D .84°8.(教材P52练习T3变式)如图,在⊙O 中,弦AB ,CD 相交于点P.若∠A=30°,∠APD=70°,则∠B 等于(C) A .30°B .35°C .40°D .50°9.如图,BD 是⊙O 的直径,点A ,C 在⊙O 上,AB ︵=BC ︵,∠AOB=60°,则∠BDC 的度数是(D) A .60°B .45°C .35°D .30°10.如图所示,弦AB ,CD 相交于点O ,连接AD ,BC ,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是答案不唯一,如:∠A=∠C,∠B=∠D,∠AOD=∠BOC,∠AOC=∠BOD.11.如图,已知A ,B ,C ,D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD ,AD.求证:DB 平分∠ADC.证明:∵AB=BC , ∴AB ︵=BC ︵. ∴∠BDC=∠ADB. ∴DB 平分∠ADC.易错点 忽略弦所对的圆周角不唯一而致错12.已知某个圆的弦长等于它的半径,则这条弦所对的圆周角的度数为30°或150°. 中档题13.如图,P 是⊙O 外一点,PA ,PB 分别交⊙O 于C ,D 两点,已知AB ︵和CD ︵所对的圆心角分别为90°和50°,则∠P=(D) A .45°B .40°C .25°D .20°14.(2018·菏泽)如图,在⊙O 中,OC⊥AB,∠ADC=32°,则∠OBA 等于(D) A .64°B .58°C .32°D .26°15.如图,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上,则∠AED 的正弦516.如图所示,在⊙O 中,已知∠BAC=∠CDA=20°,则∠ABO 的度数为50°.17.(教材P52练习T3变式)如图,在⊙O 中,A ,B 是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC ,则∠BAC=35°.18.如图,点A ,B ,C 三点在⊙O 上,过C 作CD∥AB 与⊙O 相交于D 点,E 是CD ︵上一点,且满足AD =DE ,连接BD 与AE 相交于点F.求证:△AFD∽△ABC.证明:∵AB∥CD, ∴∠BAC=∠ACD. ∵AD=DE ,∴AD ︵=DE ︵. ∴∠DAE=∠AED.∴∠DAE=∠AED=∠ACD=∠BAC.∵∠ADF=∠ACB,∠DAE=∠BAC, ∴△AFD∽△ABC. 综合题19.如图,⊙O 的半径为1,A ,P ,B ,C 是⊙O 上的四个点,∠APC=∠CPB=60°. (1)判断△ABC 的形状,并证明你的结论;(2)试探究线段PA ,PB ,PC 之间的数量关系,并证明你的结论.证明:(1)△A BC 是等边三角形. 在⊙O 中,∵∠BAC 与∠CPB 是BC ︵所对的圆周角, ∠ABC 与∠APC 是AC ︵所对的圆周角, ∴∠BAC=∠CPB,∠ABC=∠APC. 又∵∠APC=∠CPB=60°, ∴∠ABC=∠BAC=60°. ∴△ABC 为等边三角形.(2)在PC 上截取PD =AP ,连接AD , ∵∠APC=60°, ∴△APD 是等边三角形. ∴AD=AP =PD ,∠ADP=60°, 即∠ADC=120°.又∵∠APB=∠APC+∠B PC =120°, ∴∠ADC=∠APB. 在△APB 和△ADC 中,⎩⎪⎨⎪⎧∠APB=∠ADC,∠ABP=∠ACD,AP =AD ,∴△APB≌△ADC(AAS). ∴BP=CD. 又∵PD=AP.∴CP=CD +PD =BP +AP.第2课时圆周角定理推论2及圆内接四边形的性质基础题知识点1 圆周角定理推论21.(2017·福建)如图,AB是⊙O的直径,C,D是⊙O上位于AB异侧的两点.则下列四个角中,一定与∠ACD互余的角是(D)A.∠A DC B.∠ABDC.∠BAC D.∠BAD2.如图,小华同学设计了一个量直径的测量器,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位长度,OF=6个单位长度,则圆的直径为(B)A.12个单位长度B.10个单位长度C.4个单位长度D.15个单位长度3.如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为(C)A.20° B.40° C.50° D.70°4.如图,CD是⊙O的直径,已知∠1=30°,则∠2=(C)A.30° B.45° C.60° D.70°5.如图,把直角三角形的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M,N,量得OM=8 cm,ON=6 cm,则该圆玻璃镜的半径是(B)A.10 cmB.5 cmC.6 cmD.10 cm6.如图,AB是⊙O的直径,点D在⊙O上,∠AOD=130°,BC∥OD交⊙O于C,求∠A的度数.解:∵∠AOD=130°,∴∠BOD=50°.∵BC∥OD,∴∠B=∠BOD=50°.∵AB是⊙O的直径,∴∠ACB=90°.∴∠A=90°-∠B=40°.知识点2 圆内接四边形对角互补7.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点.若∠BAD=105°,则∠DCE的大小是(B)A.115° B.105° C.100° D.95°8.(教材P55例4变式)(2018·邵阳)如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是(B)A.80° B.120° C.100° D.90°9.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70°.10.如图,已知∠EAD是圆内接四边形ABCD的一个外角,并且BD=DC.求证:AD平分∠EAC.证明:∵∠EAD+∠BAD=180°,∠DCB+∠BAD=180°,∴∠EAD=∠DCB.∵BD=DC,∴∠DBC=∠DCB.又∵∠DBC=∠DAC,∴∠EAD=∠DAC,即AD平分∠EAC.易错点对圆内接四边形的概念理解不清导致错误11.如图,在⊙O中,点A,B,C在⊙O上,且∠ACB=110°,则∠α=140°.中档题12.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶5,则∠D等于(B)A .60°B .120°C .140°D .150°13.如图,AB 为⊙O 的直径,关于角p ,q ,r ,s 之间的关系:①p=2q ;②q=r ;③p+s =180°中,正确的是(A) A .只有①和② B .只有①和③ C .只有②和③D .①②③14.(2018·白银)如图,⊙A 过点O(0,0),C(3,0),D(0,1),点B 是x 轴下方⊙A 上的一点,连接BO ,BD ,则∠OBD 的度数是(B) A .15°B .30°C .45°D .60°15.(2018·北京)如图,点A ,B ,C ,D 在⊙O 上,CB ︵=CD ︵,∠CAD=30°,∠ACD=50°,则∠ADB =70°.16.如图,已知点A ,B ,C ,D 均在⊙O 上,CD 为∠ACE 的平分线. (1)求证:△ABD 为等腰三角形;(2)若∠DCE =45°,BD =6,求⊙O 的半径.解:(1)证明: ∵CD 平分∠ECA,∴∠ECD=∠DCA.∵∠ECD+∠DCB=180°,∠DCB+∠BAD=180°,∴∠ECD=∠DAB.又∵∠DCA=∠DBA,∴∠DBA=∠DAB.∴DB=DA.∴△ABD是等腰三角形.(2)∵∠DCE=∠DCA=45°,∴∠ECA=∠ACB=90°.∴∠BDA=90°.∴AB是直径.∵BD=AD=6,∴AB=BD2+DA2=62+62=6 2.∴⊙O的半径为3 2.17.(2018·宜昌)如图,在△ABC中,AB=AC.以AB为直径的半圆交AC于点D,交BC于点E.延长AE至点F,使EF=AE,连接FB,FC.(1)求证:四边形ABFC是菱形;(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.解:(1)证明:∵AB为半圆的直径,∴∠AEB=90°,∵AB=AC,∴CE=BE.又∵EF=AE,∴四边形ABFC是平行四边形.又∵AB=AC,(或∠AEB=90°)∴平行四边形ABFC是菱形.(2)连接BD.∵AD=7,BE =CE =2, 设CD =x ,则AB =AC =7+x. ∵AB 为半圆的直径, ∴∠ADB=90°. ∴AB 2-AD 2=CB 2-CD 2. ∴(7+x)2-72=42-x 2. ∴x 1=1或x 2=-8(舍去). ∴S 半圆=12×π×42=8π.∴BD=15. ∴S 菱形ABFC =815. 综合题18.如图,在⊙O 中,直径AB 的两侧有定点C 和动点P ,点P 在AB ︵上运动(不与A ,B 重合),过点C 作CP 的垂线,与PB 的延长线交于点Q.(1)试猜想:△PCQ 与△ACB 具有何种关系?(不要求证明) (2)当点P 运动到什么位置时,△ABC≌△PCB?并给出证明.解:(1)△PCQ∽△ACB. (2)当CP ︵为半圆时, △ABC≌△PCB. 证明:∵AB 是直径, ∴∠ACB=90°. ∵CP ︵为半圆,∴CP是直径.∴∠PBC=90°,AB=CP.∵CB是公共边,∴Rt△ABC≌Rt△PCB(HL).。
圆周角与圆心角的关系

2.思考与讨论 (1)观察上图,在画出的无数个圆周角中, 这些圆周角与圆心O有几种位置关系? (2)设BC所对的圆周角为∠BAC,除了圆 心O在∠BAC的一边上外,圆心O与∠BAC
还系有,哪结几论种∠B位A置C=关系?对∠B于O1这C还几成种立位吗置?关 2
试证明之.
温馨提示:为更好地满足您的学习和使用需求,课件在下载后可以自由编辑,请您根据实际情况进行调整!Thank you for
2.第二种情况:
证明:连接AO并延长交⊙O
A
于点D,由第1种情况得
O
∠BAD=
1 2
∠
BOD
B
C
D
∠CAD= 1 ∠ COD
2
∠BAD+∠CAD= 1∠ BOD+ 1∠COD
2
2
即∠BAC= 1 ∠BOC 2
3.第三种情况: 证明:作射线AO交⊙O于D。
由第1种情况得 ∠CAD= 1 ∠ COD
温故而知新
1.什么叫圆心角?
顶点在圆心的角叫圆心角
O.
2.在同圆或等圆中,圆心 A
B
角的度数等于它所对的
____弧_的______度数
活动一:动手操作
圆心角的顶点发生变化时,可能出现几 种情况?动手画一画。
O
O
O
请说说我们是如何给 圆心角下定义的,试回答?
顶点在圆心的角叫圆心角。
考考你:你能仿照圆心角的定义, 给下图中象∠ACB 这样的角下个定义吗?
顶点在圆上,并且两边都和 圆相交的角叫做圆周角.
探索:判断下列各图中,哪些是圆周角,为什么?
活动二 观察与思考
如图,AB为⊙O的直径,∠BOC、∠BAC分 别是BC所对的圆心角、圆周角,求出图 (1)、(2)、(3)中∠BAC的度数.
2021-2022学年北师大版九年级数学下册《3-4圆周角与圆心角的关系》自主达标测试(附答案)
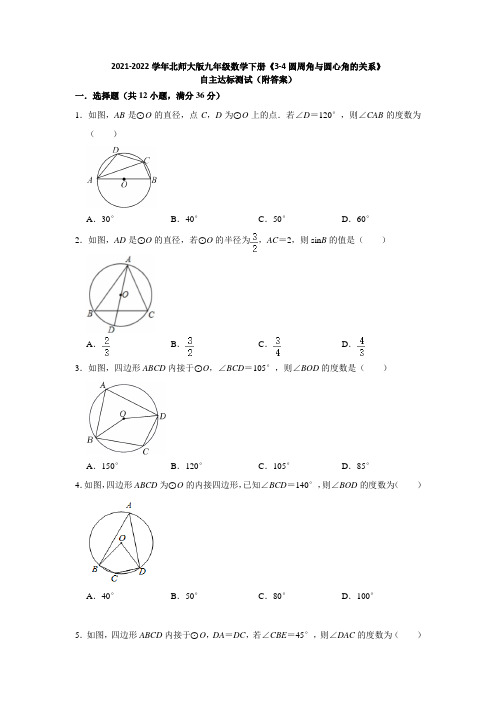
2021-2022学年北师大版九年级数学下册《3-4圆周角与圆心角的关系》自主达标测试(附答案)一.选择题(共12小题,满分36分)1.如图,AB是⊙O的直径,点C,D为⊙O上的点.若∠D=120°,则∠CAB的度数为()A.30°B.40°C.50°D.60°2.如图,AD是⊙O的直径,若⊙O的半径为,AC=2,则sin B的值是()A.B.C.D.3.如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠BOD的度数是()A.150°B.120°C.105°D.85°4.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=140°,则∠BOD的度数为()A.40°B.50°C.80°D.100°5.如图,四边形ABCD内接于⊙O,DA=DC,若∠CBE=45°,则∠DAC的度数为()A.70°B.67.5°C.62.5°D.65°6.如图,A,B,C,D都是⊙O上的点,OA⊥BC,垂足为E,若∠ADC=35°,则∠OBC =()A.15°B.20°C.30°D.35°7.如图,四边形ABCD内接于⊙O,对角线BD垂直平分半径OC,若∠ABD=50°,则∠ADC的大小为()A.130°B.120°C.110°D.100°8.如图,四边形ABCD内接于⊙O,AC、BD为其两条对角线,CB=CD,∠CAD=30°,∠ACD=45°,连接OA,OB,则∠OAB的大小为()A.15°B.20°C.22.5°D.25°9.如图,四边形ABCD内接于⊙O,点P为边AD上任意一点(点P不与点A,D重合)连接CP.若∠B=120°,则∠APC的度数可能为()A.30°B.45°C.50°D.65°10.如图,四边形ABCD内接于⊙O,AB为直径,AD=CD,过点D作DE⊥AB于点E.连接AC交DE于点F.若cos∠CBA=,EF=3.则AB的长为()A.10B.12C.16D.2011.如图,四边形ABCD内接于⊙O,若∠A=80°,则∠C的度数是()A.80°B.100°C.110°D.120°12.如图,正方形ABCD内接于⊙O,点P在劣弧AB上,连接DP,交AC于点Q.若QP =QO,则的值为()A.B.C.D.二.填空题(共8小题,满分24分)13.如图,AB是⊙O的直径,O为圆心,点C是半圆O上的点,若∠CAB=4∠CBA,点D 是上任意一点,则∠BDC的度数为度.14.⊙O内一点P,OP=3cm,过点P的最短的弦AB=6cm,Q是⊙O上除AB两点之外的任一点,则∠AQB=.15.如图,AB是⊙O的直径,∠BAC=30°,D是弧AC上任意一点,则∠D=.16.如图,AB是半圆O的直径,AB=4,点C,D在半圆上,OC⊥AB,=2,点P 是OC上的一个动点,则BP+DP的最小值为.17.如图,点A、B、C是半径为4的⊙O上的三个点,若∠BAC=45°,则弦BC的长等于.18.如图,在⊙O中,∠BOC=80°,则∠BAC的度数是.19.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于.20.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP=.三.解答题(共10小题,满分60分)21.如图,AB为⊙O的直径,点C为的中点,CD⊥AE交直线AE于D点.(1)求证:OC∥AD;(2)若DE=1,CD=2,求⊙O的直径.22.如图,AB是⊙O的直径,弦CD⊥AB于E,∠A=15°,AB=4.求弦CD的长.23.如图,在⊙O中,弦AB、CD相交于点P,且PD<PC.(1)求证:△P AD∽△PCB;(2)若P A=3,PB=8,CD=10,求PD.24.如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.(1)求证:AB=CD;(2)如果⊙O的直径为10,DE=1,求AE的长.25.如图,已知圆O,弦AB、CD相交于点M.(1)求证:AM•MB=CM•MD;(2)若M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.26.如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4,求EC的长.27.如图,在⊙O中,过弦AB的中点E作弦CD,且CE=2,DE=4,求弦AB的长.28.如图,已知圆O,弦AB、CD相交于点M.(1)求证:AM•MB=CM•MD;(2)若M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.29.如图,(1)已知:P为半径为5的⊙O内一点,过P点最短的弦长为8,则OP=(2)在(1)的条件下,若⊙O内有一异于P点的Q点,过Q点的最短弦长为6,且这两条弦平行,求PQ的长.(3)在(1)的条件下,过P点任作弦MN、AB,试比较PM•PN与P A•PB的大小关系,且写出比较过程.你能用一句话归纳你的发现吗?(4)在(1)的条件下,过P点的弦CD=,求PC、PD的长.30.如图,已知BC是⊙O的直径,AH⊥BC,垂足为D,点A为的中点,BF交AD于点E,且BE•EF=32,AD=6.(1)求证:AE=BE;(2)求DE的长;(3)求BD的长.参考答案一.选择题(共12小题,满分36分)1.解:∵∠D+∠B=180°,∠D=120°,∴∠B=60°,∵AB是直径,∴∠ACB=90°,∴CAB=90°﹣∠B=30°,故选:A.2.解:连接CD,∵AD是⊙O的直径,∴∠ACD=90°,∵⊙O的半径为,AC=2,∴AD=3,∴sin D==,∵∠B=∠D,∴sin B=.故选:A.3.解:如图,四边形ABCD内接于⊙O,∠BCD=105°,则∠A=180°﹣∠BCD=180°﹣105°=75°.∴∠BOD=2∠A=2×75°=150°,故选:A.4.解:∵四边形ABCD为⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠BCD=140°,∴∠A=40°,∵圆周角∠A和圆心角∠BOD都对着,∴∠A=BOD,∴∠BOD=2×40°=80°,故选:C.5.解:∵∠CBE=45°,∴∠ABC=180°﹣∠CBE=135°,∵四边形ABCD是⊙O的内接四边形,∴∠D+∠ABC=180°,∴∠D=45°,∵AD=CD,∴∠DAC=∠DCA=(180°﹣∠D)=67.5°,故选:B.6.解:如图所示:∵∠ADC=35°,∴的度数是70°,∵OA⊥BC,OA过圆心O,∴=,∴的度数是70°,∴∠AOB=70°,∵OA⊥BC,∴∠OEB=90°,∴∠OBC=90°﹣∠AOB=90°﹣70°=20°,故选:B.7.解:设BD交OC于E,连接OD,OA,∵BD垂直平分OC,∴OE=OC=OD,∠OED=90°,∴∠ODE=30°,∴∠DOC=90°﹣30°=60°,∵OC=OD,∴△OCD是等边三角形,∴∠ODC=60°,∵∠ABD=50°,∴∠AOD=2∠ABD=100°,∵OA=OD,∴∠ADO=∠OAD=(180°﹣∠AOD)=40°,∴∠ADC=∠ADO+∠ODC=40°+60°=100°,故选:D.8.解:∵∠CAD=30°,∴所对的圆心角的度数是60°,∵CB=CD,∴=,∴所对的圆心角的度数也是60°,∵∠ACD=45°,∴所对的圆心角的度数是90°,∴所对的圆心角的度数是360°﹣60°﹣60°﹣90°=150°,∴∠AOB的度数是150°,∵OA=OB,∴∠OAB=∠OBA=(180°﹣∠AOB)=(180°﹣150°)=15°,故选:A.9.解:∵四边形ABCD内接于⊙O,∴∠B+∠D=180°,∵∠B=120°,∴∠D=180°﹣∠B=60°,∵∠APC为△PCD的外角,∴∠APC>∠D,只有D满足题意.故选:D.10.解:连接BD,∵DE⊥AB,∴∠AED=∠BED=90°,∠ABD+∠BDE=90°,∵AB为直径,∴∠ADB=∠ACB=90°,∴∠EF A=∠CBA,∵cos∠CBA=,EF=3,∴AF==5,∴AE=4,∵AD=CD,∴∠DAC=∠DCA,而∠DCA=∠ABD,∴∠DAC=∠ABD,而∠ADE+∠BDE=90°,∴∠ABD=∠ADE,∴∠ADE=∠DAC,∴DF=AF=5,∴DE=5+3=8,∵∠ADE=∠DBE,∠AED=∠BED,∴△ADE∽△DBE,∴DE:BE=AE:DE,即8:BE=4:8,∴BE=16,∴AB=4+16=20.故选:D.11.解:∵四边形ABCD内接于⊙O,∴∠A+∠C=180°,∵∠A=80°,∴∠C=100°,故选:B.12.解:如图,设⊙O的半径为r,QO=m,则QP=m,QC=r+m,QA=r﹣m.在⊙O中,根据相交弦定理,得QA•QC=QP•QD.即(r﹣m)(r+m)=m•QD,所以QD=.连接DO,由勾股定理,得QD2=DO2+QO2,即,解得所以,故选:D.二.填空题(共8小题,满分24分)13.解:∵AB是直径,∴∠ACB=90°,∴∠A+∠ABC=90°,∵∠CAB=4∠ABC,∴5∠ABC=90°,∴∠ABC=18°,∠A=72°,∵∠CDB+∠A=180°,∴∠BDC=108°,故答案为:108.14.解:如图,连接OA,OB,∵过点P的最短的弦AB=6cm,∴OP⊥AB,∴AP=BP=AB=3(cm),∵OP=3cm,∴tan∠AOP===,∴∠AOP=60°,∴∠AOB=120°,∴∠AQB=AOB=60°,∴∠AQ′B=180°﹣∠AQB=120°,故∠AQB=60°或120°,故答案为:60°或120°.15.解:∵AB是直径,∴∠ACB=90°,∵∠BAC=30°,∴∠ABC=60°,∵∠ADC+∠ABC=180°,∴∠ADC=180°﹣60°=120°,故答案为:120°.16.解:如图,连接AD,P A,PD,OD.∵OC⊥AB,OA=OB,∴P A=PB,∠COB=90°,∵=2,∴∠DOB=×90°=60°,∵OD=OB,∴△OBD是等边三角形,∴∠ABD=60°∵AB是直径,∴∠ADB=90°,∴AD=AB•sin∠ABD=2,∵PB+PD=P A+PD≥AD,∴PD+PB≥2,∴PD+PB的最小值为2,故答案为:2.17.解:连接OB,OC.∵∠BOC=2∠BAC,∠BAC=45°,∴∠BOC=90°,∵OB=OC=4,∴BC==4,故答案为:4.18.解:∵∠BOC与∠BAC是同弧所对的圆心角与圆周角,∠BOC=80°,∴∠BAC=∠BOC=40°.故答案为:40°.19.解:∵∠BOD=138°,∴∠A=∠BOD=69°,∴∠BCD=180°﹣∠A=111°,∴∠DCE=180°﹣∠BCD=69°.故答案为:69°.20.解:由相交弦定理得,AP•BP=CP•DP,则DP==6,故答案为:6.三.解答题(共10小题,满分60分)21.(1)证明:连接BE.∵AB是直径,∴∠AEB=90°,即AD⊥BE,∵点C为的中点,∴=,∴OC⊥EB,∴OC∥AD;(2)解:设BE交OC于点T.∵CD⊥AD,∴∠D=∠DET=∠CTE=90°,∴四边形DETC是矩形,∴CD=ET=2,DE=CT=1,∵OC⊥EB,∴BT=TE=2,设OB=OC=r,则r2=(r﹣1)2+22,∴r=,∴AB=2r=5,即⊙O的直径为5.22.解:∵∠A=15°,∴∠COB=30°.∵AB=4,∴OC=2.∵弦CD⊥AB于E,∴CE=CD.在Rt△OCE中,∠CEO=90°,∠COB=30°,OC=2,∴CE=1.∴CD=2.23.(1)证明:∵∠A=∠C,∠D=∠B(在同圆或等圆中,同弧所对的圆周角相等),∴△P AD∽△PCB;(2)解:∵△P AD∽△PCB,∴=,∵P A=3,PB=8,CD=10,∴=,解得:PD=4或6,当PD=4时,PC=6,当PD=6时,PC=4,∵PD<PC,∴PD=4.24.(1)证明:如图,∵AD=BC,∴=,∴﹣=﹣,即=,∴AB=CD;(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.则AF=FD,BG=CG.∵AD=BC,∴AF=CG.在Rt△AOF与Rt△COG中,,∴Rt△AOF≌Rt△COG(HL),∴OF=OG,∴四边形OFEG是正方形,∴OF=EF.设OF=EF=x,则AF=FD=x+1,在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,解得x=3.则AF=3+1=4,即AE=AF+3=7.25.解:(1)连接AD、BC.∵∠A=∠C,∠D=∠B,∴△ADM∽△CBM∴即AM•MB=CM•MD.(2)连接OM、OC.∵M为CD中点,∴OM⊥CD在Rt△OMC中,∵OC=3,OM=2∴CD=CM===由(1)知AM•MB=CM•MD.∴AM•MB=•=5.26.解:设EC=x,则ED=CD﹣CE=4﹣x,根据题意得AE•BE=CE•DE,所以x(4﹣x)=5•1,整理得x2﹣4x+5=0,解得x=2±,即EC的长为2+或2﹣.27.解:∵过弦AB的中点E作弦CD,CE=2,DE=4,∴CE×DE=AE×BE,∴2×4=AE2,解得:AE=2,∴弦AB的长为:AB=2AE=4.28.解:(1)∵∠A=∠C,∠D=∠B,∴△ADM∽△CBM∴,即AM•MB=CM•MD.(2)连接OM、OC.∵M为CD中点,∴OM⊥CD在Rt△OMC中,∵OC=3,OM=2∴CM=DM=,由(1)知AM•MB=CM•MD.∴AM•MB=•=5.29.解:(1)连接OP,过点P作CD⊥OP于点P,连接OD.根据题意,得CD=8,OD=5.根据垂径定理,得PD=4,根据勾股定理,得OP=3;(2)根据平行线的性质和垂线的性质,知O、P、Q三点共线.根据(1)的求解方法,得OQ=4,则PQ=1或7;(3)连接AM、BN.∵∠A=∠N,∠M=∠B,∴△APM∽△NPB,∴,即PM•PN=P A•PB;(4)作直径AB,根据相交弦定理,得PC•PD=P A•PB=(5﹣3)(5+3)=16,又CD=,设PC=x,则PD=﹣x,则有x(﹣x)=16,解得x=3或x=.即PC=3或,PD=或3.30.(1)证明:连AF,AB,AC.因为A是的中点,∴∠ABE=∠AFB.又∠AFB=∠ACB,∴∠ABE=∠ACB.∵BC为直径,∴∠BAC=90°,AH⊥BC.∴∠BAE=∠ACB.∴∠ABE=∠BAE.∴AE=BE.(3分)(2)解:设DE=x(x>0),由AD=6,BE•EF=32,AE•EH=BE•EF,则(6﹣x)(6+x)=32,解得x=2,即DE的长为2;(5分)(3)解:由(1)、(2)有:BE=AE=6﹣2=4,在Rt△BDE中,BD==.(7分)。
北京四中九年级下册数学圆周角和圆心角的关系—巩固练习(基础)

圆周角和圆心角的关系—巩固练习(基础)【巩固练习】一、选择题1.如图,△ABC内接于⊙O,∠A=50°,∠ABC=60°,BD是⊙O的直径,BD交AC于点E,连结DC,则∠AEB等于( ).A.70°B.90°C.110°D.120°(第1题图)(第2题图)2.如图所示,∠1,∠2,∠3的大小关系是().A.∠1>∠2>∠3 B.∠3>∠1>∠2 C.∠2>∠1>∠3 D.∠3>∠2>∠13.如图,AC是⊙O的直径,弦AB∥CD,若∠BAC=32°,则∠AOD等于( ).A.64°B.48°C.32°D.76°4.如图,弦AB,CD相交于E点,若∠BAC=27°,∠BEC=64°,则∠AOD等于( ).A.37°B.74°C.54°D.64°(第3题图)(第4题图)(第5题图)5.如图,四边形ABCD内接于⊙O,若∠BOD=138°,则它的一个外角∠DCE等于( ).A.69°B.42°C.48°D.38°6.在半径等于5cm的圆内有长为53cm的弦,则此弦所对的圆周角为().A.120oB.30o或120oC.60oD.60o或120o二、填空题7.在同圆或等圆中,两个圆心角及它们所对的两条弧、两条弦中如果有一组量相等,那么_ _________.8.在圆中,圆心与弦的距离(即自圆心作弦的垂线段的长)叫做弦心距,不难证明,在同圆或等圆中,如果两条弦相等,那么它们的弦心距也______.反之,如果两条弦的弦心距相等,那么___________________.9.如图,AB是⊙O的直径,弦CD⊥AB于H,BD∥OC,则∠B的度数是 .ODA BC(第10题图)10.如图,△ABC 内接于⊙O ,AB =BC ,∠BAC =30°,AD 为⊙O 的直径,AD =2 3 ,则BD = .11.如图,已知⊙O 的直径MN =10,正方形ABCD 四个顶点分别在半径OM 、OP 和⊙O 上,且∠POM =45°,则AB = .(第11题图) (第12题图)12.如图,已知A 、B 、C 、D 、E 均在⊙O 上,且AC 为直径,则∠A+∠B+∠C=________度.三、解答题13. 如图所示,AB ,AC 是⊙O 的弦,AD ⊥BC 于D ,交⊙O 于F ,AE 为⊙O 的直径,试问两弦BE 与CF 的大小有何关系,说明理由.14.如图,AB 是半圆O 的直径,C 、D 是半径OA 、OB 的中点且OA ⊥CE 、OB ⊥DF ,求证:⌒AE =⌒EF =⌒FB .15.如图,⊙O 中,直径AB =15cm ,有一条长为9cm 的动弦CD 在上滑动(点C 与A ,点D 与B 不重合),CF ⊥CD 交AB 于F ,DE ⊥CD 交AB 于E .(1)求证:AE =BF ;(2)在动弦CD 滑动的过程中,四边形CDEF 的面积是否为定值?若是定值,请给出证明并求这个定值;若不是,请说明理由.【答案与解析】一、选择题1.【答案】C;【解析】因为∠A=50°,∠ABC=60°,BD是⊙O的直径,所以∠D=∠A=50°,∠DBC=40°,∠ABD=60°-40°=20°,∠ACD=∠ABD=20°,∠AED=∠ACD+∠D=20°+50°=70°,∠AEB=180°-70°=110°.2.【答案】D;【解析】圆内角大于圆周角大于圆外角.3.【答案】A;【解析】∵弦AB∥CD,∠BAC=32°,∴∠C=∠A=32°,∠AOD=2∠C=64°.4.【答案】B;【解析】∠ACD=64°-27°=37°,∠AOD=2∠ACD=74°.5.【答案】A;【解析】∠BAD=12∠BOD=69°,由圆内接四边形的外角等于它的内对角得∠DCE=∠BAD=69°.6.【答案】D;【解析】一条弦所对的圆周角有两个,这两个角互补.二、填空题7.【答案】它们所对应的其余各组量也分别相等;8.【答案】相等,这两条弦也相等;9.【答案】60°;10.【答案】3;11.【答案】;【解析】如图,设AB=x,在Rt⊿AOD 中:x²+(2x)²=5², x=, 即 AB的长=.第11题第12题12.【答案】90°;【解析】如图,连结AB、BC,则∠CAD + ∠EBD +•∠ACE=∠CBD +∠EBD +•∠ABE=∠ABC=90°.三、解答题13.【答案与解析】BE=CF.理由:∵AE为⊙O的直径,AD⊥BC,∴∠ABE=90°=∠ADC,又∠AEB=∠ACB,∴∠BAE=∠CAF,∴»»BE CF.∴BE=CF.14.【答案与解析】如图,连接OE、OF,∵D是半径OB的中点OB⊥DF,∴OD=12OF,∴∠OFD=30°,即∠FOD=60°,同理∠EOA=60°,∴∠FOD=∠EOA=∠EOF,∴⌒AE=⌒EF=⌒FB.15.【答案与解析】(1)如图,作OH⊥CD于H,利用梯形中位线易证OF=OE,OA=OB,所以AF=BE,AF+EF=BE+EF,即AE=BF.(2)四边形CDEF 的面积是定值. 连结OC ,则22215OC -CH =-=6229()()2, 11()2O 6922S CF DE CD H CD =+⋅=⋅⋅⋅=⨯=54(cm 2).。
鲁教版2020九年级数学圆周角与圆心角的关系课后练习题4(附答案)

鲁教版2020九年级数学圆周角与圆心角课后练习题4(附答案)一.选择题(共10小题)1.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法,其中正确说法的个数是()(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)=;(4)DE>DG,A.0B.1C.2D.32.如图,圆心角∠AOB=25°,将AB旋转n°得到CD,则∠COD等于()A.25°B.25°+n°C.50°D.50°+n°3.如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为()A.40°B.50°C.60°D.70°4.如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是()个①AB=2BC②=2③∠ACB=2∠CAB④∠ACB=∠BOC.A.1B.2C.3D.45.如图,等腰直角三角板ABC的斜边AB与量角器的直径重合,点D是量角器上60°刻度线的外端点,连接CD交AB于点E,则∠CEB的度数为()A.60°B.65°C.70°D.75°6.如图,点A、B、C都是圆O上的点,在四边形ABCO中,∠AOC=140°,则∠B的度数为()A.110°B.70°C.140°D.100°7.如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=26°,则∠CAB的度数为()A.26°B.74°C.64°D.54°8.如图,点A,B,C,D都在⊙O上,BD为直径,若∠A=65°,则∠DBC的值是()A.15°B.25°C.35°D.65°9.四边形ABCD是圆的内接四边形,若∠ABC=70°,则∠ADC的度数是()A.70°B.90°C.110°D.120°10.在圆内接四边形ABCD中,∠ACB=∠ACD=60°,对角线AC、BD交于点E.已知BC=3,CD=2,则线段CE的长为()A.B.C.D.二.填空题(共10小题)11.如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且+=,M是AB上一点,则MC+MD的最小值是.12.如图,在△ABC中,∠C=90°,∠B=22°,以C为圆心,CA长为半径的圆交AB于点D,交BC于点E,则的度数是.13.AB是⊙O的直径,C,D是上两点,且,,的比为3:2:5(,,弧长之和为),则∠AOC=.14.如图所示,点A是半圆上一个三等分点,点B是的中点,点P是直径MN上一动点,若⊙O的直径为2,则AP+BP的最小值是.15.如图,在⊙O中,AB是直径,C是圆上一点,且∠BOC=40°,则∠ACO=.16.如图,已知点C是以AB为直径的半圆的中点,D为弧AC上任意一点,过点C作CE ⊥BD于点E,连接AE,若AB=4,则AE的最小值为.17.如图,已知⊙O的半径为2,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为.18.如图,四边形ABCD内接于⊙O,连结AC,若∠BAC=35°,∠ACB=40°,则∠ADC =°.19.如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=45°,∠E=30°,则∠F=.20.如图,四边形ABCD为⊙O的内接四边形,若∠BOD=150°,则∠A=°.三.解答题(共8小题)21.如图,AB是⊙O的直径.OC,OD是半径,且OD∥AC,求证:=.22.如图,在⊙O中,,∠B=70°(Ⅰ)若⊙O的半径为3,求⊙O的周长(精确到0.1);(Ⅱ)求∠A的度数.23.已知:在⊙O中,弦AB=AC,AD是⊙O的直径.求证:BD=CD.24.如图,⊙O中,OA⊥BC,∠AOB=50°,求∠ADC的度数.25.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AC,BC.(1)求证:∠A=∠BCD;(2)若AB=10,CD=6,求BE的长.26.如图,AB为⊙O的直径,点C在⊙O上,连接BC并延长至点D,使DC=CB.连接DA并延长,交⊙O于另一点E,连接AC,CE.(1)求证:∠E=∠D(2)若AB=4,BC﹣AC=2,求CE的长.27.已知四边形ABCD是圆内接四边形,∠1=112°,求∠CDE.28.已知四边形ABCD内接于⊙O,∠DAB=90°(1)如图①,若∠ACB=60°,AB=4,求⊙O的直径;(2)如图②,若AD≠AB,点C为弧DB的中点且AD=m,AB=n,求AC的长.参考答案与试题解析一.选择题(共10小题)1.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法,其中正确说法的个数是()(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)=;(4)DE>DG,A.0B.1C.2D.3【解答】解:连接DG、AG,作GH⊥AD于H,连接OD,如图,∵G是BC的中点,∴AG=DG,∴=;∴HG⊥AD,∵OG=OD,∴点O不是HG的中点,∴圆心O不是AC与BD的交点;而四边形AEFD为⊙O的内接矩形,∴AF与DE的交点是圆O的圆心;∵∠DAB=90°,∴DE是⊙的直径,∴DE>DG,∴(1)错误,(2)(3)(4)正确.故选:D.2.如图,圆心角∠AOB=25°,将AB旋转n°得到CD,则∠COD等于()A.25°B.25°+n°C.50°D.50°+n°【解答】解:∵将AB旋转n°得到CD,∴=,∴∠COD=∠AOB=25°,故选:A.3.如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,则的度数为()A.40°B.50°C.60°D.70°【解答】解:连结OD,如图,∵扇形OAB沿过点B的直线折叠,点O恰好落在上的点D处,折痕交OA于点C,∴BC垂直平分OD,∴BD=BO,∵OB=OD,∴△OBD为等边三角形,∴∠DOB=60°,∴∠AOD=∠AOB﹣∠DOB=110°﹣60°=50°,∴的度数为为50°,故选:B.4.如图,OA、OB、OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC,则下列结论正确的是()个①AB=2BC②=2③∠ACB=2∠CAB④∠ACB=∠BOC.A.1B.2C.3D.4【解答】解:取的中点D,连接AD,BD,∵∠AOB=2∠BOC,∴=2,故②正确,∴==,∴AD=BD=BC,∵AB<AD+BD,∴AB<2BC.故①错误,∵∠AOB=2∠BOC,∠BOC=2∠CAB,∴∠AOB=4∠CAB,∵∠AOB=2∠ACB,∴∠ACB=∠BOC=2∠CAB,故③④正确.故选:C.5.如图,等腰直角三角板ABC的斜边AB与量角器的直径重合,点D是量角器上60°刻度线的外端点,连接CD交AB于点E,则∠CEB的度数为()A.60°B.65°C.70°D.75°【解答】解:如图,∵一块直角三角板ABC的斜边AB与量角器的直径重合,∴点A、B、C、D都在以AB为直径的圆上,∵点D是量角器上60°刻度线的外端点,即∠BOD=120°,∴∠BCD=∠BOD=60°,∴∠CEB=180°﹣∠BCD﹣∠ABC=75°.故选:D.6.如图,点A、B、C都是圆O上的点,在四边形ABCO中,∠AOC=140°,则∠B的度数为()A.110°B.70°C.140°D.100°【解答】解:如图所示,在优弧AOC上取一点D,连接AD,CD,∵∠AOC=140°,∴∠ADC=70°,∵四边形ABCD是圆内接四边形,∴∠B=180°﹣70°=110°.故选:A.7.如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=26°,则∠CAB的度数为()A.26°B.74°C.64°D.54°【解答】解:由圆周角定理得,∠ABC=∠ADC=26°,∵AB为⊙O的直径,∴∠ACB=90°,∴∠CAB=90°﹣∠ABC=64°,故选:C.8.如图,点A,B,C,D都在⊙O上,BD为直径,若∠A=65°,则∠DBC的值是()A.15°B.25°C.35°D.65°【解答】解:∵BD为直径,∴∠BCD=90°,由圆周角定理得,∠D=∠A=65°,∴∠DBC=90°﹣65°=25°,故选:B.9.四边形ABCD是圆的内接四边形,若∠ABC=70°,则∠ADC的度数是()A.70°B.90°C.110°D.120°【解答】解:∵四边ABCD是圆的内接四边形,∠ABC=70°,∴∠ADC=180°﹣70°=110°.故选:C.10.在圆内接四边形ABCD中,∠ACB=∠ACD=60°,对角线AC、BD交于点E.已知BC=3,CD=2,则线段CE的长为()A.B.C.D.【解答】解:作BM⊥AC于M,DN⊥AC于N,如图所示:则BM∥DN,∴△BME∽△DNE,∴=,∵∠ACB=∠ACD=60°,∴∠CBM=∠CDN=30°,∴CM=BC=,CN=CD=,∴BM=CM=,DN==,∴MN=CM﹣CN=,∴=,∴EN=MN=,∴CE=CN+EN=+=;故选:C.二.填空题(共10小题)11.如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且+=,M是AB上一点,则MC+MD的最小值是.【解答】解:过D作DD′⊥AB于H交⊙O于D′,∴=,∵+=,∴+=,∴∠COD′=120°,连接CD′交AB于M,则CD′=MC+MD的最小值,过O作ON⊥CD′于N,∵OC=OD′,∴CD′=2NC,∠C=30°,∵OC=AB=1,∴CN=,∴CD′=,∴MC+MD的最小值是,故答案为:.12.如图,在△ABC中,∠C=90°,∠B=22°,以C为圆心,CA长为半径的圆交AB于点D,交BC于点E,则的度数是46°.【解答】解:连接CD,∵∠C=90°,∠B=22°,∴∠A=90°﹣22°=68°,∵CD=CA,∴∠CDA=∠A=68°,∴∠ACD=44°,∴∠BCD=90°﹣44°=46°,∴的度数是46°,故答案为:46°.13.AB是⊙O的直径,C,D是上两点,且,,的比为3:2:5(,,弧长之和为),则∠AOC=54°.【解答】解:∵,,的比为3:2:5(,,弧长之和为),∴∠AOC:∠COD:∠BOD=3:2:5,∴∠AOC=×180°=54°.故答案为54°.14.如图所示,点A是半圆上一个三等分点,点B是的中点,点P是直径MN上一动点,若⊙O的直径为2,则AP+BP的最小值是.【解答】解:作点B关于MN的对称点B′,连接AB′交MN于点P,连接BP,此时AP+BP=AB′最小,连接OB′,如图所示.∵点B和点B′关于MN对称,∴PB=PB′.∵点A是半圆上一个三等分点,点B是的中点,∴∠AON=180°÷3=60°,∠B′ON=∠AON÷2=30°,∴∠AOB′=∠AON+∠B′ON=90°.∵OA=OB′=1,∴AB′=.故答案为:.15.如图,在⊙O中,AB是直径,C是圆上一点,且∠BOC=40°,则∠ACO=20°.【解答】解:∵∠BOC=40°,∴∠A=∠BOC=20°,∵OA=OC,∴∠ACO=∠A=20°.故答案为:20°.16.如图,已知点C是以AB为直径的半圆的中点,D为弧AC上任意一点,过点C作CE ⊥BD于点E,连接AE,若AB=4,则AE的最小值为﹣.【解答】解:连接OC、BC,P点为BC的中点,作PH⊥AB于H,如图,∵点C是以AB为直径的半圆的中点,∴OC⊥OB,∴△BOC、△BPH为等腰直角三角形,∴BC=OB=2,BP=,PH=1,∵CE⊥BD,∴∠BEC=90°,∴点E在⊙P上,连接AP交⊙P于E′,此时AE′的长为AE的最小值,在Rt△APH中,AH=3,PH=1,∴AP==,∴AE′=﹣,∴AE的最小值为﹣.故答案为﹣.17.如图,已知⊙O的半径为2,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为2.【解答】解:把∠COD饶点O顺时针旋转,使点C与D重合,∵∠AOB与∠COD互补,∴∠AOD=180°∵⊙O的半径为2,∴AD=4,∵弦CD=6,∠ABD=90°,∴AB==2.故答案是:2.18.如图,四边形ABCD内接于⊙O,连结AC,若∠BAC=35°,∠ACB=40°,则∠ADC =75°.【解答】解:∠ABC=180°﹣∠BAC﹣∠ACB=105°,∵四边形ABCD内接于⊙O,∴∠ADC=180°﹣∠ABC=75°,故答案为:75.19.如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=45°,∠E=30°,则∠F=60°.【解答】解:∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣∠A=135°,有三角形的外角性质可知,∠EDC=∠BCD﹣∠E=105°,∴∠F=∠EDC﹣∠A=60°,故答案为:60°.20.如图,四边形ABCD为⊙O的内接四边形,若∠BOD=150°,则∠A=105°.【解答】解:∵∠BOD=150°,∠BOD=2∠C∴∠C=75°∵四边形ABCD为⊙O的内接四边形,∴∠A+∠C=180°∴∠A=105°故答案为:105三.解答题(共8小题)21.如图,AB是⊙O的直径.OC,OD是半径,且OD∥AC,求证:=.【解答】证明:∵OA=OC,∴∠OCA=∠A,∵OD∥AC,∴∠BOD=∠A,∠COD=∠OCA,∴∠COD=∠BOD,∴=.22.如图,在⊙O中,,∠B=70°(Ⅰ)若⊙O的半径为3,求⊙O的周长(精确到0.1);(Ⅱ)求∠A的度数.【解答】解:(Ⅰ)∵⊙O的半径为3,∴⊙O的周长=2×π×3≈18.8;(Ⅱ)∵,∴∠C=∠B=70°,∴∠A=180°﹣∠C﹣∠B=40°.23.已知:在⊙O中,弦AB=AC,AD是⊙O的直径.求证:BD=CD.【解答】证明:∵AB=AC,∴=,∴∠ADB=∠ADC,∵AD是⊙O的直径,∴∠B=∠C=90°,∴∠BAD=∠DAC,∴=,∴BD=CD.24.如图,⊙O中,OA⊥BC,∠AOB=50°,求∠ADC的度数.【解答】解:∵⊙O中,OA⊥BC,∴=,∴∠ADC=∠AOB=×50°=25°.25.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接AC,BC.(1)求证:∠A=∠BCD;(2)若AB=10,CD=6,求BE的长.【解答】(1)证明:∵直径AB⊥弦CD,∴弧BC=弧BD.∴∠A=∠BCD;(2)连接OC∵直径AB⊥弦CD,CD=6,∴CE=ED=3.∵直径AB=10,∴CO=OB=5.在Rt△COE中,∵OC=5,CE=3,∴OE==4,∴BE=OB﹣OE=5﹣4=1.26.如图,AB为⊙O的直径,点C在⊙O上,连接BC并延长至点D,使DC=CB.连接DA并延长,交⊙O于另一点E,连接AC,CE.(1)求证:∠E=∠D(2)若AB=4,BC﹣AC=2,求CE的长.【解答】(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,即AC⊥BC,∵DC=CB,∴AD=AB.∴∠B=∠D,∵∠E=∠B,∴∠E=∠D;(2)解:∵∠E=∠D,∴DC=CE,∵DC=CB,∴CB=CE,在Rt△ABC中,AC2+BC2=AB2,即(BC﹣2)2+BC2=42解得,BC1=1+,BC1=1﹣(舍去),∴CE=1+,即CE的长为1+.27.已知四边形ABCD是圆内接四边形,∠1=112°,求∠CDE.【解答】解:由圆周角定理得,∠A=∠1=56°,∵四边形ABCD是圆内接四边形,∴∠CDE=∠A=56°.28.已知四边形ABCD内接于⊙O,∠DAB=90°(1)如图①,若∠ACB=60°,AB=4,求⊙O的直径;(2)如图②,若AD≠AB,点C为弧DB的中点且AD=m,AB=n,求AC的长.【解答】解:(1)如图,连接BD,∵∠DAB=90°∴BD是直径,∵∠DAB=90°,∠ACB=∠ADB=60°,AB=4,∴sin∠ADB=∴DB==8∴⊙O的直径为8(2)如图,连接BD,过点D作DE⊥AC于点E,∵∠DAB=90°∴BD是直径,∴∠BCD=90°∵点C为弧DB的中点∴∠DAC=∠CAB=45°∴CD=BC,∴DB=CD∵∠DCA=∠ABD,∠DEC=∠DAB=90°∴△DEC∽△DAB∴∴=∴DE=m,EC=n,∵∠DAC=45°,DE⊥AC∴AE=DE=m∴AC=AE+EC=m+n。
3.4 圆周角和圆心角的关系(1)(数学北师大版九年级下册)

[归纳总结] 对“同弧或等弧所对的圆周角相等”的理解: (1)“同弧”指“在同一个圆中”;(2)“等弧”指“在同圆或等 圆中”;(3)“同弧或等弧”不能改为“同弦或等弦”.
∠ABC 与圆心角∠AOC,它们的大小有什么关系?
图 3-4-1
在探讨圆周角与圆心角的大小关系时,首先考虑了一种特
殊情况(圆心在圆周角的一边上),如图 3-4-1①所示.
∵∠AOC 是△ABO 的外角, ∴∠AOC=∠ABO+__∠__O_A_B__. 又∵OA=OB,
∴∠OAB=__∠__A_B_O____, ∴∠AOC=_2_∠__A_B_C__, 即∠ABC=21∠AOC. 如果∠ABC 的两边都不经过圆心,如图 3-4-1②、③, 那么结论会怎样?请你说明理由.
总结反思
知识点一 圆周角 圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角. 由定义可知圆周角具备两个特征:一是顶点必须在圆上,二是 角的两边都和圆相交.
知识点二 圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的___一__半___.
知识点三 圆周角定理推论1 同弧或等弧所对的圆周角__相__等____.
图 3-4-2
[解析] 根据△AOB 是等腰三角形,由∠ABO=55°,可 得∠AOB=70°,再利用圆周角定理即可求解.
解:∵OA=OB,∴△AOB 是等腰三角形. 又∵∠ABO=55°, ∴∠AOB=180°-∠ABO-∠OAB=180°- 55°-55°=70°, ∴∠BCA=21∠AOB=12×70°=35°.
初三上册圆的圆周角练习题

初三上册圆的圆周角练习题在初三数学的课程中,圆的相关概念和性质是学生们需要掌握的重要内容之一。
其中,圆周角作为圆的一个重要性质,在解题过程中起着至关重要的作用。
本文将为大家提供一些圆周角练习题,帮助大家巩固和提升对圆周角的理解和运用。
1.已知半径为r的圆上有两条弧AB和CD,弧AB对应的圆心角为α,弧CD对应的圆心角为β。
如果α+β=90°,求证:弧AB和弧CD的长度相等。
解答:由于α+β=90°,根据圆周角和的性质可知,弧AB和弧CD所对应的弧度和为π/2,即AB+CD=π/2。
又由于AB和CD是同一圆上的两条弧,因此它们的弧长相等,即AB=CD。
2.已知圆心角θ对应的圆弧长度为s,圆的半径为r。
求证:θ的度数等于s/r的弧度数。
解答:根据圆周等分的原理,360°对应于2π的弧度数。
假设θ对应的弧度数为x,那么x/2π=θ/360°。
根据题目已知条件,s/r=x/2π,两边乘以360°得到s/r=θ。
3.已知直径为d的圆上的两条弧AB和CD,弧AB对应圆心角为α,弧CD对应圆心角为β。
如果α和β的度数之和等于180°,求证:弧AB和弧CD的长度之和等于圆周长的一半。
解答:由题意可知,α+β=180°,根据圆周角和的性质可得,AB+CD=π,即弧AB和弧CD的长度之和等于圆周长的一半。
通过以上的练习题,我们可以更深入地了解和应用圆的圆周角的性质。
在解题过程中,需要灵活运用和转化弧度和度数的关系、圆周角和的性质等概念。
只有真正理解并掌握这些概念,才能在数学问题中正确地运用它们。
圆周角作为圆的一个重要性质,不仅存在于初三数学中,也在实际生活中有着广泛的应用。
比如,在建筑中,为了保证圆形构件的连接稳定,需要正确地计算和设计圆周角。
因此,对圆周角的学习不仅仅是应试的需要,更是培养学生逻辑思维和数学运算能力的重要一环。
通过不断练习和巩固,相信大家在初三数学中的圆的圆周角问题上将能够得心应手,取得良好的成绩。
九年级数学圆心角与圆周角的关系

切两种情况.
例2:已知△ABC 的三边分别是 a、b、c,两圆的半径 r1
=a,r2=b,圆心距 d=c,则这两个圆的位置关系是__________.
解析:∵△ABC 的三边分别是a、b、c,∴a+b>c,即r1 +r2>d,∴两圆相交.
专题三
求与圆有关的阴影部分的面积
求圆中不规则阴影图形的面积,通常用割补法,将其面积 用规则图形(如扇形、三角形、矩形等)的面积的和或差表示. 例 3:如图 24-2,将△ABC 绕点 B 逆时针旋转到A′BC′
又∵△ABC 是等边三角形,∴∠ADE=∠C=60°.
∴△ADE 是等边三角形.
(2)解:易知∠B=60°, 又∵DO=BO,∴△BDO 是等边三角形,∴∠DOB=60°.
同理,∠EOC=60°.即∠DOE=60°.
∵等边△ABC 边长为 2,∴DO=OE=1.
nπr2 60·π·1 π π ∴扇形 ODE 的面积 S= 360 = 360 =6, DC 的长度 l=3. 1 且圆锥底面半径 r=6.
图 24-7
D.y=
8.(2010 年广东)如图 24-8,PA 与⊙O 相切于点 A,弦 AB
⊥OP,垂足为 C,OP 与⊙O 相交于 D 点,已知 OA=2,OP=4.
(1)求∠POA 的度数;
(2)计算弦 AB 的长.
图 24-8
解:(1)60° (2)AB= 2
3
9.(1)如图 24-9(1),已知△ABC 是边长为 2 的等边三角形, 以 BC 为直径的⊙O 交 AB、AC 于 D、E.求证:△ADE 是等边三
O2 相切.
图 24-5
5.(2010 年广东湛江)已知两圆的半径分别为 3 cm 和 4 cm, 两个圆的圆心距为 8 cm,则两圆的位置关系是( C ) A.内切 B.相交 C.外离 D.外切
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题:
1 •如图1,等边三角形ABC 的三个顶点都在OO 上,D 是AC 上任一点(不与A 、C 重合),则ZADC 的度数是 _______
(1) (2) (3) (4)
2•如图2,四边形ABCD 的四个顶点都在OO 上,且AD 〃BC,对角线AC 与BC 相交于点E,那么图
(10)
8•如图&A 、B. C> D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中, 相等的角有()
A.2对
B.3对
C.4对
D.5对 9•如图9,D 是AC 的中点,则图中与ZABD 相等的角的个数是
()
中有__________ 对全等三角
似三角形. 3•已知,如图3,ZBAC 的对角
形; _______ 对相似比不等于1的相
ZBAD=100°,则 ZBOC 二 ______ 度.
(9) r
D
4•如图4,A、B、C 为OO 上三点,若ZOAB=46°,则ZACB二 _____ 度.
5•如图5,AB是OO的直径,BC = BD,ZA=25。
,则ZBOD的度数为 ________ ・
6•如图6,AB是半圆O的直径,AC=AD,OC=2,ZCAB= 30 °,则点O到CD的距离OE二
7•如图7,已知圆心角ZBOC=1(M)。
,则
二、选择题:
A.50°
B.100°
C.130°
D.200°
(7)
周角ZBAC的度数是(
A・4个B・3个C・2个D・1个
10•如图10,ZAOB=100°,则ZA+ZB 等于()
A.100°
B.80°
C.50°
D.40° 11 •在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是()
A30° B.30。
或150。
C-60° D.60。
或120° 12•如图,A. B. C三点都在OO上点D是AB延长线上一点,ZAOC=140%
ZCBD的度数是()
A.40。
B.50。
C.70。
D4100
三、解答题:
13•如图,G)O的直径AB=8cm,ZCBD=30°,求弦DC的长.
B
14•如图,A、B、C、D四点都在(DO上,AD是0O的直径,且AD=6cm,若ZABC二ZCAD,求弦AC 的长.
A
15•如图,AB为半圆O的直径,弦AD. BC相交于点P,若CD=3,AB=4,求tanZBPD的值.
C
P
16•如图,在OO中,AB是直径,CD是弦,AB丄CD.
(1)P是GW上一点(不与C、D重合),试判断ZCPD与ZCOB的大小关系,并说明理由.
(2)点P,在劣弧CD上(不与C、D重合时),ZCP9与ZCOB有什么数量关系?请证明你的结
论.
A
17•在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻•当甲带球部到A点时,乙随后冲
到B点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不
考虑其他因素)
18•钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母,问下料时至少要用直径多大的圆钢?
3.3圆周角和圆心角的关系同步练习
一、填空题:
1 •如图1,等边三角形ABC 的三个顶点都在OO 上,D 是AC 上任一点(不与A 、C 重合), 则ZADC 的度数是 _________
2•如图2,四边形ABCD 的四个顶点都在(DO 上,且AD 〃BC,对角线AC 与BC 相交于 点E,那么图中有 __________ 对全等三角形; ________ 对相似比不等于1的相似三角 形.
3•已知,如图3,ZBAC 的对角ZBAD=100°,则ZBOC 二 _______ 度.
4•如图 4,A 、B 、C 为OO 上三点,若ZOAB=46°,则ZACB= _______ 度. 5•如图5,AB 是OO 的直径,BC = BD ,Z225。
,则ZBOD 的度数为 ___________ ・
6•如图6,AB 是半圆O 的直径,AC=AD,OC=2,ZCAB 二30。
,则点O 到CD 的距离
OE= _____ ・
二、选择题
:
⑷
r
B
7•如图7,已知圆心角ZBOC=100°,则圆周角ZBAC 的度数是()
10•如图 10,ZAOB=100°,则ZA+ZB 等于()
A.100。
B.80°
C.50°
D.40° 11 •在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是(
A.30°
B.3O 0 或 150°
C.60°
D.60。
或 120°
12•如图,A 、B 、C 三点都在OO 上,点D 是AB 延长线上一点,ZAOC=140°, ZCBD 的 度数是()
A.40°
B.50°
C.70°
D.110°
三、解答题:
13•如图QO 的直径AB=8cm,ZCBD=30°,求弦DC 的长.
A.500
B.100°
C.130。
D.200°
(7) 8•如图 &A 、B 、 的八个角中,相等的角有()
A.2对 (8)
C 、
D 四个点在同一个圆上,四边形ABCD B.3对 C.4对 D.5对
的对角线把四个内角分成 9•如图9,D 是AC 的中点,则图中与ZABD 相等的角的个数是(A
A.4个
B.3个
C.2个 D ・1个
B D D C
14•如图,A、B、C、D四点都在OO上,AD是(DO的直径,且AD=6cm,若ZABC= ZCAD, 求弦AC的长.
A
15•如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tanZBPD的值.
16•如图,在OO中,AB是直径,CD是弦,AB丄CD.
(1)P是CAD±一点(不与C、D重合),试判断ZCPD与ZCOB的大小关系,并说
明理由.
⑵点P,在劣弧CD上(不与C、D重合时),ZCPD与ZCOB有什么数量关系?请
证明你的结论.
17•在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻•当甲带球部到A 点 时,乙随后冲到B 点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让 乙射门好呢?为什么?(不考虑其他因素)
多大的圆钢?
钳工车间用圆钢做方形螺母,现要做边长为
的方形螺母,问下料时至少要用直径
D
\! -------------- N
答案:
1.120°
2.3 1
3.160°
4.44°
5.50° 6・" 7.A 8.C 9.B 10.C ll.B 12.C
13•连接OC、OD,则OC=OD=4cm,ZCOD=60。
,故厶COD是等边三角形,从而CD= 4cm. 14•连接DC,贝(JZADC二ZABC二ZCAD,故AC=CD・
VAD 是直径,・・・ZACD=90°, /. AC2+CD2=AD2,B卩2AC2=36,AC2=18,AC=3 "・15•连接BD,则・・AB是直径,・・・ZADB=90°.
PD CD
V ZC=ZA,ZD=ZB,.\ APCD ^APAB,/.—=—・
PB AB
PD CD 3
在RtA PBD 中,cosZBPD=——=—二一,
PB AB 4
设PD=3x,PB=4x,
贝I) BD二J PB? _ PD? = &4歼 _ (3X)2 =岳,
AtanZBPD=^ = ^ = ^.
PD 3x 3
16.(1)相等.理由如下涟接OD,T AB丄CD,AB是直径,
・・・ BC = BD,:・ ZCOB= ZDOB・
V ZCOD=2ZP,.\ ZCOB=ZP,即ZCOB二ZCPD・
(2)ZCP r D+ZCOB=180°.
理由如下:连接PT,
则ZP r CD=ZP r PD,ZPTC=ZP r DC.
A ZP r CD+ZP r DC=ZPTD+ZPTC=ZCPD・
.•.ZCP,D=180°-(ZP,CD+ZP,DC)=180°-ZCPD=180°-ZCOB,
从而ZCP r D+ZCOB=180°.
17•迅速回传乙,让乙射门较好,在不考虑其他因素的情况下,如果两个点到球门的距离相差不大,要确定较好的射门位置•关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越尢如图所示,则ZA<MCN=ZB,即ZB>ZA,从而B处对MN的张角较大,在B处射门射中的机会大些.
18.72 a.。
