圆中点Bresenham算法
案例3圆中点Bresenham算法

效果图
图3-1 效果图
原理算法
MFC提供的CDC类的成员函数Ellipse()函数用于绘制椭
圆,而圆是一种特殊的椭圆。本案例中,由于圆心的位置是 直线的中点,而直线的位置是变化的,所以需要将主教材《 计算机图形学基础教程(Visual C++版)》中讲解的圆中点 Bresenham算法,根据直线的位置进行整体平移。
计算机图形学实践教程(VisualC++版)(第2版)
案例3 圆中点Bresenham算法
孔令德 太原工业学院计算机工程系 2017.1.10
知识点
八分法画圆算法。 中点Bresenham画圆算法。 以直线为圆的直径绘制圆。 鼠标按键消息映射方法。
案例描述
在窗口客户区内按下鼠标左键选择直线
原理
y
Pi Q Pu
③ ② ④ ⑤ ① ⑥ ⑧ ⑦
M Pd
O
x
图3-2 八分之一绘制原理
算法
圆心在坐标系原点的1/8圆中点Bresenham算法如下: (1)根据鼠标选择的直线端点计算圆的半径R。 (2)定义圆当前点坐标x,y、定义中点误差项d、定义像素 点颜色clr。 (3)计算 ,x=0,y=R,clr=RGB(0,0,255)。 (4)绘制点(x,y)及其在八分圆中的另外7个对称点。 (5)判断d的符号。若d<0,则(x,y)更新为(x+1,y) ,d更新为d+2x+3;否则(x,y)更新为(x+1,y-1), d更新为d+2(x-y)+5。 (6)当x小于等于y,重复步骤(4)与(5),否则结束。
总结
本案例由于可以使用鼠标任意指定直线段,所以圆心的位 置会发生变化。在八分法画圆子函数中,对圆心位置进行了平 移,使得直线段成为圆的直径。请在八分法画圆子函数 CirclePoint()中添加以下语句绘制起点为p0、终点为p1的直线段 ,该直线段成为圆的直径。
中点bresenham算法过程

中点Bresenham算法是一种用于计算在直线上的格点的算法。
它是由Bresenham在1965年提出的,是一种高效的计算机图形学算法,通常用于直线、圆、椭圆等形状的绘制。
通过这篇文章,我们将详细介绍中点Bresenham算法的过程。
1. 背景知识在计算机图形学中,我们经常需要在屏幕上绘制直线、圆、椭圆等形状。
而计算机屏幕上的图像是由像素组成的,因此我们需要一种算法来计算出这些形状上的像素坐标,从而进行绘制。
中点Bresenham算法就是用来解决这个问题的。
2. 中点Bresenham算法的原理中点Bresenham算法的原理是通过巧妙的数学推导,找到离直线最近的像素点,从而确定需要绘制的像素坐标。
该算法通过利用误差项来判断下一个像素点的位置,具有高效、简洁的特点。
3. 中点Bresenham算法的过程中点Bresenham算法的过程可以分为以下几个步骤:3.1 初始化变量:首先需要确定直线的起点和终点,并初始化相关变量,如起点坐标(x0, y0)、终点坐标(x1, y1)、误差项d和增量变化量dx、dy等。
3.2 计算斜率k和误差项初始值:通过计算直线的斜率k,并根据斜率确定误差项的初始值。
3.3 循环计算像素点的坐标:根据误差项的大小,确定下一个像素点的位置,并更新误差项的值,直到绘制完整条直线。
4. 中点Bresenham算法的优势* 算法简洁高效:中点Bresenham算法通过简单的数学计算,即可确定直线上的像素坐标,避免了直接计算斜率导致的浮点数运算,因此在计算速度上具有较大优势。
* 适用范围广泛:中点Bresenham算法不仅适用于直线,还可以用于绘制圆、椭圆等图形,具有良好的通用性。
5. 中点Bresenham算法的应用中点Bresenham算法广泛应用于计算机图形学中的直线、圆、椭圆等图形的绘制。
其高效、简洁的特点使得它成为了计算机图形学中不可或缺的算法之一。
中点Bresenham算法是计算机图形学中的重要算法之一,通过巧妙的数学计算,实现了高效、简洁的直线绘制。
bresenham圆生成算法

bresenham圆生成算法Bresenham圆生成算法是一种经典的计算机图形学算法,用于在计算机屏幕上绘制圆形。
该算法是由美国计算机科学家Jack E. Bresenham于1965年发明的。
这个算法非常简单,但是它却非常有效,因为它只需要使用整数运算。
Bresenham圆生成算法的基本思想是使用一个叫做“决策参数”的变量来决定下一个像素点的位置。
该变量根据当前像素点到圆心的距离和半径之间的差异进行调整。
如果该差异小于0,则移动到右上方的像素点;否则,移动到右上方和正上方之间的像素点。
具体来说,Bresenham圆生成算法可以通过以下步骤来实现:1. 输入圆心坐标和半径。
2. 初始化x和y坐标为0,并计算出初始决策参数d=3-2r。
3. 在每个步骤中,检查当前像素点是否在圆内。
如果是,则将该像素点绘制出来;否则,不绘制。
4. 计算下一个像素点的位置。
如果d小于0,则移动到右上方;否则,移动到右上方和正上方之间。
5. 更新决策参数d。
Bresenham圆生成算法的优点是它非常快速和有效。
它只需要使用整数运算,因此可以在计算机上非常快速地执行。
此外,该算法还可以轻松地扩展到三维空间中的球体和其他形状。
尽管Bresenham圆生成算法已经有几十年的历史了,但它仍然是计算机图形学中最常用的算法之一。
它被广泛应用于游戏开发、计算机辅助设计、虚拟现实等领域。
此外,该算法还被用于许多其他领域,如数字信号处理和图像处理。
总之,Bresenham圆生成算法是一种简单而有效的计算机图形学算法。
它可以快速地绘制出圆形,并且可以轻松地扩展到其他形状。
尽管这个算法已经有几十年的历史了,但它仍然是计算机图形学中最常用的算法之一,并且在许多其他领域也得到了广泛应用。
Bresenham 画圆算法_计算机图形学实用教程(第3版)_[共3页]
![Bresenham 画圆算法_计算机图形学实用教程(第3版)_[共3页]](https://img.taocdn.com/s3/m/5c9f4c2e0242a8956aece48f.png)
55 01e r =− (3-39) 这样,由于判别式的初值为整数,增量也为整数,因此判别式始终为整数,即中点画圆算法可用整数加减运算来计算圆周上所有像素的位置。
中点画圆算法的描述如下。
(1)输入圆的半径r 和圆心坐标(x c , y c ),先计算以原点为圆心、r 为半径的圆周上的点,令初始点为00(,)(0,)x y r =。
(2)求初始判别式d ,1d r =−。
(3)在每一个x n 的位置,从n = 0开始,进行下列检测:如果d <0,则圆心在原点的圆的下一个点为(x n +1, y n ),且23n d d x =++;否则,圆的下一个点为(x n +1, y n −1),且2()5nn d dx y =+−+。
(4)确定(x n+1, y n +1)在其余7个八分圆中的对称点位置。
(5)将计算出的每个像素位置(x , y )平移到圆心位于(x c , y c )的圆的轨迹上,即分别沿水平和垂直方向平移x c 和y c ,平移后的坐标值为(x', y' ),c x x x ′=+,c y y y ′=+。
(6)重复第(3)至(5)步,直到x ≥y 时为止。
下面以半径r = 10、圆心在原点的圆为例来说明按上述算法计算第一八分圆上的像素位置的过程。
首先求出初始点(x 0, y 0) = (0, 10),判别式d 0 = 1−r =1−10 = −9,其后续的判别式计算结果和生成的像素位置如表3-1所示。
经过计算最后生成的从(x 0, y 0)到(x 7, y 7)第一八分圆上的8个像素位置如图3-8所示。
表3-1以原点为圆心r =10的第一八分圆的判别式的值和像素位置 n d 2x n + 32x n − 2y n + 5 (x n , y n ) 0 −9 3- (0, 10) 1 −6 5- (1, 10) 2 −1 7- (2, 10) 3 6 -−9 (3, 10) 4 −3 11- (4, 9) 5 8 -−3 (5, 9) 6 5 -1 (6, 8) 7 6 - - (7, 7)3.2.4 Bresenham 画圆算法与中点画圆算法一样,Bresenham 画圆算法也是先考虑圆心在原点、半径为r 的第一四分圆的生成,即取(0, r )为起点,按顺时针方向生成第一四分圆,然后根据圆的对称特性通过对称变换生成整圆。
像素画圆算法范文

像素画圆算法范文一、引言像素画圆算法是一种用于计算机图形学中绘制圆的常用算法。
在计算机图形学中,圆是一个非常基本的图形元素,无论是在2D还是3D图形中,圆都是最直观的图形之一、因此,能够高效绘制圆形对于计算机图形学来说是非常重要的。
在本篇文章中,我们将介绍两种常用的像素画圆算法:Bresenham算法和中点画圆算法。
这两种算法都是基于直线绘制算法的思想发展而来,通过巧妙的数学推导,将直线绘制算法应用到圆形的绘制过程中。
二、Bresenham算法Bresenham算法是一种经典的像素画圆算法,它是由Jack E. Bresenham于1962年发明的。
该算法通过计算以像素为单位的数学判定来绘制圆形。
该算法的基本思想是,对于给定的圆心坐标和半径长度,我们从一个点开始,根据圆的对称性,计算出其他8个对称特殊点的坐标,并选择最接近圆的边缘的点绘制。
接着,根据选择的点计算下一个边缘点,并反复迭代这一过程,直到找到了整个圆的边缘点。
具体的Bresenham算法如下:1.初始化半径r和圆心坐标(x,y);2.设置两个变量x1和y1分别为0和r;3.计算判别式d=3-2*r;4.在每次迭代中,绘制八个对称点中最接近圆边缘的点,并更新判别式d和坐标x和y的值:-如果d<0,选择右偏移的点(x+1,y),d的值不变;-如果d>=0,选择右上偏移的点(x+1,y+1),d的值减去Δd;-更新判别式d=d+4*x+6;5.重复步骤4,直到x>y。
这里的Δd是一个关于x和y的常数,它的值预先计算得出,使得可以在循环中快速计算判别式d的变化。
通过这种方式,Bresenham算法能够高效地计算出整个圆的边缘点,从而实现圆形的绘制。
三、中点画圆算法中点画圆算法(Midpoint Circle Drawing Algorithm)是另一种常用的像素画圆算法,它是由Jack E. Bresenham于1977年发展而来的。
画圆形(Bresenham算法)

画圆形(Bresenham算法)下⾯先简要介绍常⽤的画圆算法(Bresenham算法),然后再具体阐述笔者对该算法的改进。
⼀个圆,如果画出了圆上的某⼀点,那么可以利⽤对称性计算余下的七段圆弧:Plot(x,y),Plot(y,x),Plot(y,-x),Plot(x,-y),Plot(-x,-y),Plot(-y,-x),Plot(-y,x),Plot(-x,y)。
1、Bresenham 画圆算法。
Bresenham算法的主要思想是:以坐标原点(0,0)为圆⼼的圆可以通过0度到45°的弧计算得到,即x从0增加到半径,然后利⽤对称性计算余下的七段圆弧。
当x从0增加到时,y从R递减到。
设圆的半径为R,则圆的⽅程为:f(x,y)=(x+1)2+y2-R2=0 (1)假设当前列(x=xi列)中最接近圆弧的像素已经取为P(xi,yi),根据第⼆卦限1/8圆的⾛向,下⼀列(x=xi+1列)中最接近圆弧的像素只能在P的正右⽅点H(xi+1,yi)或右下⽅点L(xi+1,yi-1)中选择,如图1所⽰。
Bresenham画圆算法采⽤点T(x,y)到圆⼼的距离平⽅与半径平⽅之差D(T)作为选择标准,即D(T)=(x+1)2+y2-R2 (2)通过⽐较H、L两点各⾃对实圆弧上点的距离⼤⼩,即根据误差⼤⼩来选取,具有最⼩误差的点为绘制点。
根据公式(2)得:对H(xi+1,yi)点有:D(H)=(xi+1)2+yi2-R2;对L(xi+1,yi-1)点有:D(L)=(xi+1)2+(yi-1)2-R2;根据Bresenham画圆算法,则选择的标准是:如果|D(H)|<|D(L)|,那么下⼀点选取H(xi+1,yi);如果|D(H)|>|D(L)|,那么下⼀点选取L(xi+1,yi-1);如果|D(H)|=|D(L)|,那么下⼀点可以取L(xi+1,yi-1),也可以选取H(xi+1,yi),我们约定选取H(xi+1,yi)。
bresenham画圆算法原理

bresenham画圆算法原理宝子!今天咱们来唠唠这个Bresenham画圆算法的原理,可有趣儿啦!你想啊,画圆这个事儿,在计算机里可不像咱们拿个圆规在纸上画那么简单。
计算机就知道一个个的像素点,它得想办法把这些像素点组合起来,看起来像个圆才行。
Bresenham画圆算法就像是一个超级聪明的小工匠,在像素的世界里一点点雕琢出圆的形状。
那这个算法是咋开始的呢?咱们先得知道圆的方程,一般的圆方程是(x - a)^2+(y - b)^2 = r^2,这里的(a,b)是圆心坐标,r是半径。
但是这个算法可不会直接用这个方程来一个点一个点地找。
为啥呢?因为计算起来太麻烦啦,计算机可不喜欢干这么费劲的事儿。
这个算法呀,它很聪明地利用了圆的对称性。
圆多对称呀,关于x轴、y轴还有原点都对称。
所以呢,只要算出圆的八分之一部分的像素点,其他部分就可以根据对称关系得到啦。
就好像你有一个小拼图块,通过对称翻转,就能拼出整个大图案一样。
咱就拿第一象限里的八分之一圆来说吧。
这个算法开始的时候,先确定一个初始点。
这个初始点呢,是在x = 0的时候,y = r。
这就像是在圆的最上面的那个点,就像圆的小脑袋一样。
然后呢,它就要开始一步一步地找下一个点啦。
它怎么找下一个点呢?这里面就有个很妙的决策。
它会比较两个可能的下一个点到圆的距离。
你可以想象成有两个小蚂蚁,都想朝着圆的方向走,但是哪条路更近呢?算法就要判断这个。
它会根据一些简单的计算,这些计算都是基于整数的哦,计算机就喜欢整数计算,快得很。
它会看如果选择一个点,和选择另一个点,哪个会让这个点更接近真正的圆。
如果一个点离圆更近,那就选这个点作为下一个点。
然后呢,每确定一个新的点,就像在这个像素的世界里又铺了一块小砖头,慢慢地,这个八分之一圆的形状就出来了。
等这个八分之一圆的像素点都确定好了,就可以根据对称关系,把整个圆的像素点都找出来啦。
这个算法的好处可多啦。
它计算速度快,因为都是整数运算,不用做那些复杂的浮点数计算。
中点bresenham算法过程描述

中点Bresenham算法是一种在计算机图形学中用于绘制直线的算法。
它是由Bresenham在1965年提出的,经过研究和改良后,成为一种非常高效的直线绘制算法。
1. 算法描述中点Bresenham算法的基本思想是利用线的对称性来进行计算,通过计算线上的各个像素点与理想直线的距离来确定下一个要绘制的像素点,从而高效地绘制直线。
2. 算法过程具体来说,中点Bresenham算法的计算过程如下:1) 首先确定直线的起点(x0, y0)和终点(x1, y1),并计算直线的斜率k = (y1 - y0) / (x1 - x0)。
2) 然后计算直线的斜率误差delta = |k| - 0.5。
3) 初始化绘制像素点的坐标(x, y),初始误差值为0。
4) 对于直线斜率绝对值小于1的情况:a) 如果斜率k大于0,则初始误差值为0.5,否则为-0.5。
b) 从x0到x1的范围内,依次计算每个像素点的y坐标,并根据误差值确定下一个像素点的位置,并更新误差值。
c) 如果误差值大于0,表示下一个像素点在直线的下边,否则在上边。
5) 对于直线斜率绝对值大于1的情况,可以通过将直线绘制区域进行旋转并交换x和y坐标来处理。
6) 最终绘制直线时,可以根据具体的应用场景选择存储像素点的方式,比如直接在屏幕上绘制,或者存储在像素数组中后再一次性绘制等。
3. 算法优势中点Bresenham算法相对于其他直线绘制算法的优势在于:它避免了复杂的浮点数计算,减少了计算量,提高了绘制的效率。
尤其在早期计算机硬件性能有限的情况下,该算法表现出了明显的优势,成为了广泛使用的直线绘制算法。
4. 算法应用中点Bresenham算法不仅仅局限于直线的绘制,它还可以应用于其他图形的绘制,比如圆、椭圆、矩形等。
在计算机图形学和图像处理领域,Bresenham算法及其改进版本被广泛应用于各种图形的绘制和处理中。
5. 算法总结中点Bresenham算法是一种非常经典且高效的直线绘制算法,它通过简单的整数运算和位操作实现了高效的直线绘制,成为了计算机图形学中不可或缺的重要工具之一。
§3.2圆、圆弧的生成—Bresenham算法

§3.2圆的生成——Bresenham算法条件:给定圆心(x c,y c)和半径R约定:只考虑圆心在原点,半径为整数R的圆x2+y2.=R2。
对于圆心不在原点的圆,可先通过平移转换,化为圆心在原点的圆,再进行扫描转换,把所得到的像素集合加上一个位移量,就可以把目标圆光栅化。
在众多圆的生成算法,如逐点比较法、角度DDA法、Bresenham算法中,Bresenham画圆法是一种最简单有效的的方法。
首先注意到只要生成一个八分圆,那么,圆的其它部分就可以通过一系列的对成变换得到。
12345678由算法生成y=x第一八分圆关于y=x对称变换第一四分圆关于x=0对称变换上半圆关于y=0对称变换如果以点x=0,y=R为起点按顺时针方向生成圆,则在第一象限内y是x 的单调递减函数。
要在这三个像素中选择一个使其与理想圆的距离的平方达到最小,即下列数值中的最小者。
R(0,R)(R,0)xy这样,从圆上任一点出发,按顺时针方向生成圆时,为了最佳逼近该圆,对于下一像素的取法只有三种可能的选择,即正右方像素、正下方像素和右下角像素,分别记作:m H、m V、m D。
(x i,y i)(x i,y i-1)(x i+1,y i)(x i+1,y i-1)m Hm Dm Vm H=|(x i+1)2+(y i)2-R2|m V=|(x i)2+(y i+1)2-R2|m D=|(x i+1)2+(y I-1)2-R2|m H(x i,y i)(x i+1,y i)(x i+1,y i+1)(x i+1,y i-1)(x i-1,y i-1)(x i,y i-1)m Vm D12354圆与点(x i,y i)附近光栅格网的相交关系只有五种可能。
从圆心到右下角像素(x i+1,y i-1)的距离平方m D与圆心到圆上点的距离平方R2之差等于:Δi=(x i+1)2+(y i-1)2-R2如果Δi<0,那么右下角像素(x i+1,y i-1)在该圆内(图中①、②),显然这时只能取像素(x i+1,y i),即m H;或像素(x i+1,y i-1),即m D。
bresenham中点画圆原理介绍

1.中点Bresenham 算法的原理圆心在原点、半径为R 的圆方程的隐函数表达式为:圆将平面划分成三个区域:对于圆上的点,F(x ,y)=0;对于圆外的点,F (x ,y )>0;对于圆内的点,F (x ,y )<0。
事实上,考虑到圆在第一象限内的对称性,本算法可以进一步简化。
用四条对称轴x =0,y =0, x =y,x =-y 把圆分成8等份。
只要绘制出第一象限内的1/8圆弧,根据对称性就可绘制出整圆,这称为八分法画圆算法。
假定第一象限内的任意点为P (x,y ),可以顺时针确定另外7个点:P (y ,x ),P (y ,-x ),P (x,- y ),P (-x ,-y ),P (-y ,-x ),P (-y ,x ),P (-x ,y )。
2.构造中点偏差判别式从P (xi ,yi )开始,为了进行下一像素点的选取,需将Pu 和Pd 的中点M (x i+1,y i-0.5)代入隐函数,构造中点偏差判别式:⑴当d<0时,下一步的中点坐标为:M (xi +2,yi -0.5)。
下一步中点偏差判别式为:⑵当d ≥0时,下一步的中点坐标为:M (xi +2,yi -1.5)。
),(222=-+=R y x y xF )5.0,1(),(-+==i i M M y x F y x F d ⎩⎨⎧≥<=+)0( 1-)0(1d y d y y i i i 2221)5.0()2()5.0,2(R y x y x F d i i i i i --++=-+=+3232)5.0()1(222++=++--++=i i i i i x d x R yx2221)5.1()2()5.1,2(R y x y x F d i i i i i --++=-+=+。
生成圆的bresenham算法原理描述详细

生成圆的bresenham算法原理描述详细Bresenham算法是计算机图形学中非常重要的算法之一,可以生成各种形状的图像。
其中,生成圆形图像的Bresenham算法也是应用比较广泛的算法之一。
本文将详细描述生成圆的Bresenham算法原理。
1. 圆的数学表示圆是一个几何图形,其数学表示为:x² + y² = r²,其中,x、y是圆上点的坐标,r是圆的半径。
因此,生成圆的Bresenham算法需要计算出符合该数学表示的所有点的坐标。
2. Bresenham算法的核心思想Bresenham算法的核心思想是利用对称性和递推式来快速计算出每个点的坐标。
对于圆而言,其有四分之一的区域可以通过对称性计算出来,而另外四分之三的区域可以通过递推式来得出。
3. 圆的对称性对于圆而言,其具有对称性,即当坐标为(x,y)在圆上时,也必然存在(y,x)、(y,-x)、(x,-y)、(-x,-y)、(-y,-x)、(-y,x)、(-x,y)在圆上的点,也就是说,直接通过圆的对称性可以得到大约四分之一的在圆上的点。
4. 圆的递推式对于圆的另外四分之三的部分,我们可以使用递推式来获得。
根据圆的坐标表示式x² + y² = r²,我们可以得到下届式:x² + y² - r² = 0根据这个方程,可以计算出下一个点的坐标为:x + 1, y 或 x + 1, y - 1如果采用当前点(x,y)的对称点来计算,比如(y,x),那么坐标可以改成:y + 1, x 或 y + 1, x - 1通过这种方式,就可以逐个计算出每个点的坐标了。
5. 算法步骤生成圆的Bresenham算法的步骤如下:1)确定圆的中心点的坐标和半径;2)以圆心为原点建立坐标系,以x轴为基准线向右,y轴向上;3)通过圆的对称性计算出直径上的点的坐标;4)使用递推式计算出剩余的坐标;5)根据得到的坐标渲染圆的边缘。
中点画圆和Bresehnm画圆算法

二、中点画圆算法
void huayuan(int x0,int y0,int r,int color) { int x,y,d; x=0;y=r;d=1.25-r; while(y>=x) { huadian(x0,y0,x,y,color); if(d<0) {d=d+2*x+3;x++;} else {d=d+2*(x-y)+5;x++;y--;} } } void main() { int r, c=RGB(255,0,0); initgraph(640,480); huayuan(200,200,100,c); if(getch()==1) exit; closegraph(); }
四、两种画圆算法的优劣
算法比较和启发: 通过实际的程序运行比较分析,是中点画圆法速度快.就算法本身而言,该算 法仍可在某些方面进行改进,如将其中的浮点运算改为整数运算等,执行速度 将更快。 生成直线和圆这类基础算法在编程时要被无数次的调用,可能每生成一帧画面 就要被调用成百上千次,因此其执行速度是至关重要的.而这类基础算法的长 度都很短,即使多用一些分支,多用一些变量和语句,一般来说只不过增加几 十个语句.这样的空间增加与算法极重要的速度要求来比较是相对次要的因素, 因此在开发图形学的基础算法时,如果有可能提高算法的速度,应不惜多占一 些存储空间.
三、 Bresenham 画圆算法原理
算法原理: Bresenham画圆算法与Bresenham 直线算法一样,其基本的方法是利用判别变 量来判断选择最近的像素点,判别变量的数值仅仅用一些加、减和移位运算就 可以计算出来。为了简便起见,考虑一个圆 心在坐标原点的圆,而且只计算八 分圆周上的点,其余圆周上的点利用对称性就可得到。
中点bresenham算法的基本原理与递推公式

中点Bresenham算法是一种用于绘制直线的光栅化算法,它可以在计算机图形学中高效地绘制直线,尤其适用于嵌入式系统和低性能设备。
本文将介绍中点Bresenham算法的基本原理和递推公式。
一、中点Bresenham算法的基本原理1.1 数值方式直线的差值算法在了解中点Bresenham算法之前,我们需要先了解数值方式直线的差值算法。
通过计算两个端点的坐标差值,可以得到直线的斜率和步长,从而在光栅化的像素网格上绘制直线。
然而,这种算法需要进行浮点数运算,对于嵌入式系统和低性能设备来说,性能较差。
1.2 中点Bresenham算法的优势中点Bresenham算法通过整数运算和递推公式来高效地绘制直线,避免了浮点数运算的开销,因此在嵌入式系统和低性能设备上具有很高的应用价值。
它利用了直线的对称性和整数坐标的特点,通过逐个像素的递推计算来实现直线的绘制。
1.3 算法的基本思想中点Bresenham算法的基本思想是从直线的起点到终点,在每一步选择最接近直线的像素作为下一个像素,从而逐步绘制整条直线。
通过比较像素的位置和理想直线的位置关系,选择最接近直线的像素进行绘制,从而得到了中点Bresenham算法的递推过程。
二、中点Bresenham算法的递推公式2.1 直线斜率的计算我们需要计算直线的斜率m。
对于给定的两个端点P1(x1, y1)和P2(x2, y2),直线的斜率可以通过以下公式计算得到:m = (y2 - y1) / (x2 - x1)2.2 中点Bresenham算法的关键递推公式中点Bresenham算法通过比较像素的位置和理想直线的位置关系,选择最接近直线的像素进行绘制。
其关键递推公式如下:对于斜率0 ≤ m ≤ 1的直线:d = 2 * (y - y0) - (x - x0)若d < 0,则选择(x, y)为下一个像素,d = d + 2 * (y1 - y0)若d ≥ 0,则选择(x, y)为下一个像素,d = d + 2 * (y1 - y0) - 2 * (x1 - x0)对于斜率m > 1的直线:d = 2 * (x - x0) - (y - y0)若d < 0,则选择(x, y)为下一个像素,d = d + 2 * (x1 - x0)若d ≥ 0,则选择(x, y)为下一个像素,d = d + 2 * (x1 - x0) - 2 * (y1 - y0)2.3 递推过程通过以上递推公式,我们可以在每一步选择最接近直线的像素进行绘制,从而逐步绘制整条直线。
中点bresenham算法负斜率

一、概述Bresenham算法是一种用于计算直线、圆和椭圆等图形的算法,是由Jack Elton Bresenham在1962年提出的。
在计算机图形学领域,Bresenham算法广泛应用于直线绘制,它可以高效地计算出直线上的像素点,是图形绘制中不可缺少的重要算法之一。
二、Bresenham算法原理Bresenham算法通过计算像素点的坐标,来实现直线绘制。
对于一条从点P0(x0, y0)到点P1(x1, y1)的直线,我们需要找出直线经过的所有像素点,Bresenham算法便是通过斜率的计算和递推关系,来确定每个像素点的位置并进行绘制。
三、Bresenham算法计算流程1. 根据P0和P1计算出直线的斜率k。
2. 根据斜率k的值,分为正斜率和负斜率两种情况进行处理。
3. 在具体实现中,我们可以通过判断斜率k的绝对值来确定直线画法的不同情况,细分为0<k<1、k>1、-1<k<0和k<-1四个基本情况,以简化直线绘制的过程。
四、Bresenham算法负斜率情况分析对于Bresenham算法而言,处理负斜率直线是一个非常重要且复杂的情况。
当直线的斜率k小于0时,我们需要根据不同的取值范围采用不同的算法流程来确定像素点的位置并进行绘制。
五、Bresenham算法负斜率实现1. 我们需要对直线的起点和终点进行判断,确定起点和终点的坐标值。
2. 根据斜率k的负值来分情况处理。
当-1<k<0时,我们需要沿着主方向y自增,次方向x自减;当k<-1时,则需要沿着主方向x自减,次方向y自增。
3. 确定像素点的位置后,进行像素绘制。
六、Bresenham算法负斜率实例演示以具体数值为例,对一条直线上的像素点位置进行计算和绘制演示,以便更好地理解Bresenham算法在处理负斜率直线时的实现流程和细节。
七、Bresenham算法负斜率应用Bresenham算法在计算机图形学中的应用非常广泛,尤其是在直线绘制和图形显示领域。
Bresenham画圆算法与中点画圆法

Bresenham画圆算法与中点画圆法Bresenham画圆算法不失⼀般性,假设圆的圆⼼位于坐标原点(如果圆⼼不在原点,可以通过坐标平移使其与原点重合),半径为R。
以原点为圆⼼的圆C有四条对称轴:x = 0, y = 0, x = y和x = -y。
若已知圆弧上⼀点P1=C(x, y),利⽤其对称性便可以得到关于四条对称轴的其它7个点,即: P2=C(x,-y), P3=C(-x, y), P4=C(-x,-y), P5=C(y,x), P6=C(-y,x), P7=C(y,-x), P8=C(-y,-x)。
这种性质称为⼋对称性。
因此,只要扫描转换⼋分之⼀圆弧,就可以通过圆弧的⼋对称性得到整个圆。
【Bresenham算法】简单图形的扫描转换常⽤算法是Bresenham算法。
它的思想在于⽤误差量来衡量点选取的逼近程度。
其过程如下:以平⾯⼆维图形的扫描转换为例,设要画的图形⽅程为F(x, y)=0,要画的区域为[x0, x](不妨设x⽅向是最⼤位移⽅向,即△x > △y),则F(x,y) 也是⼀个误差度量函数,我们拿离散的点值代⼊如果⼤于0则正向偏离,否则负向偏离,等于0的情况⽐较少,它表⽰的是不偏离即恰好与真实点重合。
既然x是最⼤位移⽅向,那每次对x⾃增1,相应的y可以选择不增或增1(或-1,具体问题具体分析),选择的⽅法就是d = F(x + 1, y ± 0.5)的正负情况进⾏判断从⽽选择y的值。
实际情况中还要考虑到浮点数的计算问题,因为基本的图形扫描转换算法最好能够硬件实现,所以摆脱浮点数是最好的,常⽤的⽅法是对d 进⾏递推,⽽不是直接由F(x,y)给出(直接给出速度会慢)。
【圆的扫描转换算法】以画圆为例,给出圆⼼的坐标(0, 0)和半径R,求圆图像的最佳逼近点。
圆是中⼼对称的特殊图形,所以可以将圆⼋等分,则只须对⼋分之⼀圆孤求解,其它圆孤可以由对称变换得到,我们求的⼋分之⼀圆孤为(0, R) -(R√2,R√2),可知最⼤位移⽅向是x⽅向,x0 = 0, y0 = R,每次对x⾃增,然后判断y是否减1,直到x >= y为⽌(从点(0, R)到圆的⼋分之⼀处就有这种情况)。
bresenham圆弧算法

bresenham圆弧算法Bresenham圆弧算法Bresenham圆弧算法是一种用于绘制圆弧的算法,该算法基于Bresenham直线算法,通过在二维平面上绘制一系列点的方式来逼近圆弧的形状。
与传统的圆弧绘制算法相比,Bresenham圆弧算法具有较高的效率和精度。
Bresenham圆弧算法的核心思想是利用圆的对称性,将圆弧的绘制问题转化为直线的绘制问题。
通过逐步迭代,计算出每个绘制点的坐标,从而绘制出整个圆弧。
该算法在绘制过程中,只需进行简单的加减运算和比较判断,不需要复杂的三角函数运算,因此具有较高的效率。
其基本原理是:首先确定圆弧的起点和终点,然后计算圆弧所在的圆的半径和圆心坐标。
接下来,在一个辅助的正方形区域内,按照Bresenham直线算法的思想,逐步迭代计算出每个绘制点的坐标。
通过判断与圆弧的距离,确定每个点应该绘制在圆弧内还是外部。
最后,根据需要,可以进行平移、旋转和缩放等变换操作,以实现对圆弧的精确绘制。
Bresenham圆弧算法的优点在于其简洁性和高效性。
由于该算法只需进行简单的加减运算和比较判断,因此在计算机中的实现非常方便。
而且,该算法的绘制结果具有较高的精度,可以满足大部分绘制需求。
此外,由于Bresenham圆弧算法基于对称性,因此可以减少计算量,提高绘制速度,特别适用于实时绘制和动画效果的生成。
然而,Bresenham圆弧算法也存在一些局限性。
首先,该算法只适用于绘制位于正方形区域内的圆弧,无法直接绘制超出该区域的圆弧。
其次,由于该算法是通过逼近的方式来绘制圆弧,因此在绘制过程中可能会产生一些误差。
特别是对于较大的圆弧或高分辨率要求较高的场景,这种误差可能会导致绘制结果的不准确。
Bresenham圆弧算法是一种简洁高效的圆弧绘制算法,通过利用圆的对称性和Bresenham直线算法的思想,可以快速、准确地绘制圆弧。
该算法在计算机图形学和计算机游戏等领域得到广泛应用,为实时绘制和动画效果的生成提供了重要的支持。
易懂的Bresenham布雷森汉姆算法画圆的原理与Python编程实现教程

易懂的Bresenham布雷森汉姆算法画圆的原理与Python编程实现教程Bresenham 布雷森汉姆算法画圆的原理与编程实现教程注意:Bresenham的圆算法只是中点画圆算法的优化版本。
区别在于Bresenham的算法只使⽤整数算术,⽽中点画圆法仍需要浮点数。
注意:不要因为我提到了中点画圆法你就去先看完再看Bresenham算法,这样是浪费时间。
中点画圆法和Bresenham画圆法只是思想⼀样,但是思路并没有很⼤关联。
所以直接看Bresenham算法就可以。
看下⾯这个图,这就是⼀个像素⼀个像素的画出来的。
我们平常的圆也是⼀个像素⼀个像素的画出来的,你可以试试在“画图”这个软件⾥⾯画⼀个圆然后放⼤很多倍,你会发现就是⼀些像素堆积起来的。
我们看出来圆它是⼀个上下左右都对称,⽽且也是中⼼对称的。
所以我们只⽤画好⼋分之⼀圆弧就可以,其他地⽅通过对称复制过去就好。
看下⾯这幅图,绿线夹住的那部分就是⼋分之⼀圆弧。
注意我们是逆时针画圆的(即从⽔平那个地⽅即(r,0)开始画因为⼀开始我们只知道⽔平位置的像素点该放哪其他地⽅我们都不知道)。
Bresenham 算法画完⼀个点(x,y)后注意x,y都是整数。
他们代表的是x,y⽅向上的第⼏个像素。
,它下⼀步有两个选择(x,y+1),(x-1,y+1)。
也就是说y⼀定增加,但是x要么保持不变要么减⼀(你也可以让x⼀定增加y要么不变要么加⼀,其实差不多的)。
当程序画到粉红⾊那个像素点的时候,程序选择下⼀步要绘制的点为(x-1,y+1)。
当程序画到黄⾊的那个像素点时候,程序选择下⼀步要绘制的点为(x,y+1)。
我们看看粉⾊的那个点的下⼀步是如何抉择的。
Bresenham是根据待选的两个点哪个离圆弧近就下⼀步选哪个。
那它是怎么判断的呢?这两个点⼀定有⼀个在圆弧内⼀个在圆弧外。
到底选哪个?Bresenham的⽅法就是直接计算两个点离圆弧之间的距离,然后判断哪个更近就选哪个。
Bresenham算法画圆
bresenham画圆算法bresenham画圆算法中点画圆算法在一个方向上取单位间隔,在另一个方向的取值由两种可能取值的中点离圆的远近而定。
实际处理中,用决策变量的符号来确定象素点的选择,因此算法效率较高。
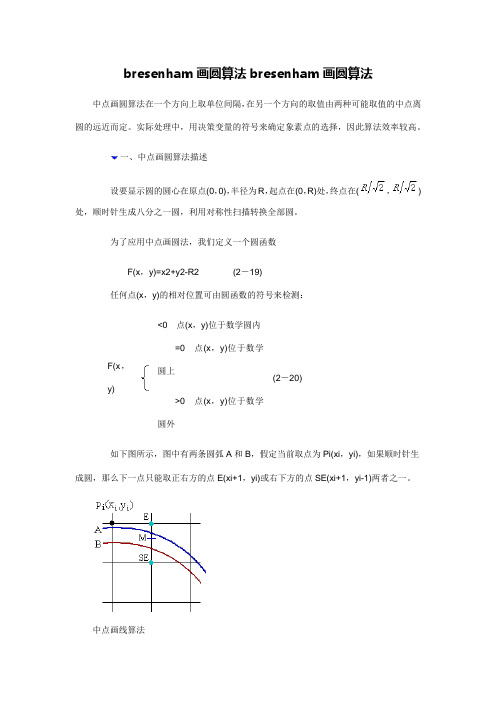
一、中点画圆算法描述设要显示圆的圆心在原点(0,0),半径为R,起点在(0,R)处,终点在(,)处,顺时针生成八分之一圆,利用对称性扫描转换全部圆。
为了应用中点画圆法,我们定义一个圆函数F(x,y)=x2+y2-R2 (2-19)任何点(x,y)的相对位置可由圆函数的符号来检测:F(x,y) <0点(x,y)位于数学圆内=0点(x,y)位于数学圆上>0点(x,y)位于数学圆外(2-20)如下图所示,图中有两条圆弧A和B,假定当前取点为Pi(xi,yi),如果顺时针生成圆,那么下一点只能取正右方的点E(xi+1,yi)或右下方的点SE(xi+1,yi-1)两者之一。
中点画线算法假设M是E和SE的中点,即,则:1、当F(M)<0时,M在圆内(圆弧A),这说明点E距离圆更近,应取点E作为下一象素点;2、当F(M)>0时,M在圆外(圆弧B),表明SE点离圆更近,应取SE点;3、当F(M)=0时,在E点与SE点之中随便取一个即可,我们约定取SE点。
二、中点画圆算法思想因此,我们用中点M的圆函数作为决策变量d i,同时用增量法来迭代计算下一个中点M的决策变量d i+1。
(2-21)下面分两种情况来讨论在迭代计算中决策变量d i+1的推导。
1、见图(a),若d i <0,则选择E点,接着下一个中点就是,这时新的决策变量为:(2-22)(a)(di<0) 中点画线算法式(2-22)减去(2-21)得:d i+1=d i+2x i+3(2-23)2、见图(b),若di≥0,则选择SE点,接着下一个中点就是,这时新的决策变量为:(2-24)(b)(d i ≥0) 中点画线算法式(2-24)减去(2-21)得:d i+1=d i+2(x i-y i)+5(2-25)我们利用递推迭代计算这八分之一圆弧上的每个点,每次迭代需要两步处理:(1)用前一次迭代算出的决策变量的符号来决定本次选择的点。
Bresenham直线算法与画圆算法

Bresenham直线算法与画圆算法文章分类:Java编程计算机是如何画直线的?简单来说,如下图所示,真实的直线是连续的,但我们的计算机显示的精度有限,不可能真正显示连续的直线,于是我们用一系列离散化后的点(像素)来近似表现这条直线。
(上图来自于互联网络,《计算机图形学的概念与方法》柳朝阳,郑州大学数学系)接下来的问题就是如何尽可能高效地找到这些离散的点,Bresenham直线算法就是一个非常不错的算法。
Bresenham直线算法是用来描绘由两点所决定的直线的算法,它会算出一条线段在 n 维光栅上最接近的点。
这个算法只会用到较为快速的整数加法、减法和位元移位,常用于绘制电脑画面中的直线。
是计算机图形学中最先发展出来的算法。
(引自wiki百科布雷森漢姆直線演算法)这个算法的流程图如下:可以看到,算法其实只考虑了斜率在 0 ~ 1 之间的直线,也就是与 x 轴夹角在 0 度到 45 度的直线。
只要解决了这类直线的画法,其它角度的直线的绘制全部可以通过简单的坐标变换来实现。
下面是一个C语言实现版本。
Java代码1.view sourceprint?2. // 交换整数 a 、b 的值3.4.inline void swap_int(int *a, int *b)5.{6. *a ^= *b;7. *b ^= *a;8. *a ^= *b;9.}10.11.// Bresenham's line algorithm12.13.void draw_line(IMAGE *img, int x1, int y1, int x2, int y2, unsigned long c)14.{15. // 参数 c 为颜色值16. int dx = abs(x2 - x1),17. dy = abs(y2 - y1),18. yy = 0;19.20. if(dx < dy)21. {22. yy = 1;23. swap_int(&x1, &y1);24. swap_int(&x2, &y2);25. swap_int(&dx, &dy);26. }27.28. int ix = (x2 - x1) > 0 ? 1 : -1,29. iy = (y2 - y1) > 0 ? 1 : -1,30. cx = x1,31. cy = y1,32. n2dy = dy * 2,33. n2dydx = (dy - dx) * 2,34. d = dy * 2 - dx;35.36.// 如果直线与 x 轴的夹角大于45度37. if(yy)38. {39. while(cx != x2)40. {41. if(d < 0)42. {43. d += n2dy;44. }45. else46. {47. cy += iy;48. d += n2dydx;49. }50.51. putpixel(img, cy, cx, c);52.53. cx += ix;54. }55. }56.57.// 如果直线与 x 轴的夹角小于度58. else59. {60. while(cx != x2)61. {62. if(d < 0)63. {64. d += n2dy;65. }66. else67. {68. cy += iy;69. d += n2dydx;70. }71.72. putpixel(img, cx, cy, c);73.74. cx += ix;75. }76. }77.}可以看到,在画线的循环中,这个算法只用到了整数的加法,所以可以非常的高效。
bresenham圆弧算法

bresenham圆弧算法Bresenham圆弧算法Bresenham圆弧算法是一种用于绘制圆弧的算法,它是Bresenham 线算法的扩展。
Bresenham线算法是一种用于绘制直线的算法,而Bresenham圆弧算法则是在此基础上实现的。
圆弧是一个弧线段,它是由圆的一部分组成。
绘制圆弧的方法有很多种,但Bresenham圆弧算法是一种简单而高效的方法。
它通过使用离散的像素点来逼近圆弧的曲线,从而实现圆弧的绘制。
Bresenham圆弧算法的核心思想是利用圆的对称性和连续性,在每个象限内只绘制其中一部分弧线,然后通过变换和旋转来得到其他象限的弧线。
具体来说,算法通过计算每个象限内的像素点与理想圆弧曲线的差距,然后选择最接近理想曲线的像素点来绘制圆弧。
为了实现Bresenham圆弧算法,我们需要知道圆心坐标、半径和起始角度。
首先,我们需要确定圆弧的起始点和终止点,这可以通过圆心坐标、半径和起始角度来确定。
然后,我们可以使用Bresenham线算法来绘制起始点和终止点之间的线段。
接下来,我们需要计算每个象限内的像素点与理想圆弧曲线的差距,并选择最接近理想曲线的像素点来绘制圆弧。
Bresenham圆弧算法的优点是效率高,绘制的圆弧曲线非常接近理想曲线。
这是因为算法利用了圆的对称性和连续性,只需绘制部分弧线即可得到完整的圆弧。
此外,算法的实现较为简单,只需使用基本的数学运算和判断即可完成绘制。
然而,Bresenham圆弧算法也存在一些局限性。
首先,算法只适用于绘制在屏幕上呈现为直线的圆弧。
对于曲线较为复杂的圆弧,Bresenham圆弧算法可能无法得到准确的结果。
此外,算法对圆心坐标和半径的限制较大,不适用于所有情况。
Bresenham圆弧算法是一种用于绘制圆弧的高效算法。
它通过使用离散的像素点来逼近圆弧的曲线,实现了圆弧的绘制。
虽然算法具有一定的局限性,但在满足条件的情况下,它可以得到准确且高效的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章本案例知识要点●掌握八分法中点Bresenham 算法绘制圆的原理 ●设计八分法绘制圆的中点Bresenham 算法 ●编写八分法绘制圆的CirclePoint(x,y) 子函数 ● 编写绘制整圆的Mbcircle()子函数一、案例需求1.案例描述使用中点Bresenham 算法绘制圆心位于屏幕客户区中心的圆。
2.案例效果图案例输入对话框及效果如图3-1所示。
(a )输入对话框 (b )效果图3-1 圆中点Bresenham 算法效果图 3.功能说明(1)要求使用对话框输入圆的半径。
(2)圆的颜色为蓝色。
三、算法设计1. 输入圆的半径R 。
2. 定义圆当前点坐标x ,y 、定义中点偏差判别式d 、定义像素点颜色rgb 。
3. 计算R d -=25.1,x=0,y=R ,rgb =RGB(0,0,255)。
案例三 圆中点Bresenham 算法4.绘制点(x,y)及其在八分圆中的另外7个对称点。
5.判断d的符号。
若d<0,则(x,y)更新为(x+1,y),d更新为d+2x+3;否则(x,y)更新为(x+1,y-1),d更新为d+2(x-y)+5。
6.当x小于等于y,重复步骤⑷和⑸,否则结束。
四、案例实现1.CTestView.h文件// TestView.h : interface of the CTestView class/////////////////////////////////////////////////////////////////////////////#if !defined(AFX_TESTVIEW_H__A75FDCFB_621C_4E38_A154_C344803E6372__INCLUDED_)#define AFX_TESTVIEW_H__A75FDCFB_621C_4E38_A154_C344803E6372__INCLUDED_#if _MSC_VER > 1000#pragma once#endif // _MSC_VER > 1000#include "InputDlg.h"//包含对话框头文件class CTestView : public CView{protected: // create from serialization onlyCTestView();DECLARE_DYNCREATE(CTestView)// Attributespublic:CTestDoc* GetDocument();// Operationspublic:void GetMaxY();//获得屏幕的最大x值函数void GetMaxX();//获得屏幕的最大y值函数void CirclePoint(double x,double y);//八分法画圆子函数void Mbcircle();//圆中点Bresenham算法// Overrides// ClassWizard generated virtual function overrides//{{AFX_VIRTUAL(CTestView)public:virtual void OnDraw(CDC* pDC); // overridden to draw this viewvirtual BOOL PreCreateWindow(CREATESTRUCT& cs);protected:virtual BOOL OnPreparePrinting(CPrintInfo* pInfo);virtual void OnBeginPrinting(CDC* pDC, CPrintInfo* pInfo);virtual void OnEndPrinting(CDC* pDC, CPrintInfo* pInfo);//}}AFX_VIRTUAL// Implementationpublic:virtual ~CTestView();#ifdef _DEBUGvirtual void AssertValid() const;virtual void Dump(CDumpContext& dc) const;#endifprotected:int MaxX,MaxY; //屏幕x和y的最大坐标double R; //圆的半径// Generated message map functionsprotected://{{AFX_MSG(CTestView)afx_msg void OnMENUMbcircle();//}}AFX_MSGDECLARE_MESSAGE_MAP()};#ifndef _DEBUG // debug version in TestView.cppinline CTestDoc* CTestView::GetDocument(){ return (CTestDoc*)m_pDocument; }#endif///////////////////////////////////////////////////////////////////////////////{{AFX_INSERT_LOCATION}}// Microsoft Visual C++ will insert additional declarations immediately before the previous line.#endif // !defined(AFX_TESTVIEW_H__A75FDCFB_621C_4E38_A154_C344803E6372__INCLUDED_) 2.CTestView. cpp文件// TestView.cpp : implementation of the CTestView class#include "stdafx.h"#include "Test.h"#include "TestDoc.h"#include "TestView.h"#define ROUND(a) int(a+0.5) //四舍五入#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif///////////////////////////////////////////////////////////////////////////// // CTestViewIMPLEMENT_DYNCREATE(CTestView, CView)BEGIN_MESSAGE_MAP(CTestView, CView)//{{AFX_MSG_MAP(CTestView)ON_COMMAND(ID_MENU_Mbcircle, OnMENUMbcircle)//}}AFX_MSG_MAP// Standard printing commandsON_COMMAND(ID_FILE_PRINT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_DIRECT, CView::OnFilePrint)ON_COMMAND(ID_FILE_PRINT_PREVIEW, CView::OnFilePrintPreview)END_MESSAGE_MAP()///////////////////////////////////////////////////////////////////////////// // CTestView construction/destructionCTestView::CTestView(){// TODO: add construction code here}CTestView::~CTestView(){}BOOL CTestView::PreCreateWindow(CREATESTRUCT& cs){// TODO: Modify the Window class or styles here by modifying// the CREATESTRUCT csreturn CView::PreCreateWindow(cs);}///////////////////////////////////////////////////////////////////////////// // CTestView drawingvoid CTestView::OnDraw(CDC* pDC){CTestDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data here}///////////////////////////////////////////////////////////////////////////// // CTestView printingBOOL CTestView::OnPreparePrinting(CPrintInfo* pInfo){// default preparationreturn DoPreparePrinting(pInfo);}void CTestView::OnBeginPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add extra initialization before printing}void CTestView::OnEndPrinting(CDC* /*pDC*/, CPrintInfo* /*pInfo*/){// TODO: add cleanup after printing}///////////////////////////////////////////////////////////////////////////// // CTestView diagnostics#ifdef _DEBUGvoid CTestView::AssertValid() const{CView::AssertValid();}void CTestView::Dump(CDumpContext& dc) const{CView::Dump(dc);}CTestDoc* CTestView::GetDocument() // non-debug version is inline{ASSERT(m_pDocument->IsKindOf(RUNTIME_CLASS(CTestDoc)));return (CTestDoc*)m_pDocument;}#endif //_DEBUG///////////////////////////////////////////////////////////////////////////// // CTestView message handlersvoid CTestView::GetMaxX()//得到客户区的最大横坐标{CRect Rect;GetClientRect(&Rect);MaxX=Rect.right;}void CTestView::GetMaxY()//得到客户区最大纵坐标{R=dlg.m_R;}AfxGetMainWnd()->SetWindowText("基本图形扫描转换:Mbcircle");RedrawWindow();GetMaxX();GetMaxY();Mbcircle();}五、案例说明因为设备坐标系的原点在屏幕左上角,所以为了在屏幕中心绘制圆,定义了GetMaxX()和GetMaxY()函数来获得屏幕的MaxX和MaxY,参见案例1的实现部分。
