练3_二次函数的应用(沪科版)(原卷版)

二次函数的实际应用题专项训练卷(3)

二次函数的实际应用题专项训练卷（3）1．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫降价1元，商场平均每天可多售出2件．若设每件衬衫降价x元，解答下列问题：（1）当每件衬衫降价5元，则每件利润元，平均每天可售出件．（2）若平均每天获利为Q元，请求出Q与x的函数关系式．（3）若商场想平均每天盈利1200元，每件衬衫应降价多少元？2．某超市销售一种商品，成本价为20元/千克，经市场调查，每天销售量y（千克）与销售单价x（元/千克）之间的关系如图所示，规定每千克售价不能低于30元，且不高于80元．设每天的总利润为w元．（1）根据图象求出y与x之间的函数关系式；（2）请写出w与x之间的函数关系式，并写出自变量x的取值范围；（3）当销售单价定为多少元时，该超市每天的利润最大？最大利润是多少元？3．普洱茶是中国十大名茶之一，也是中华古老文明中的一颗瑰宝．某公司经销某种品牌普洱茶，每千克成本为50元．经市场调查发现：每周销售量y（千克）与销售单价x（元/千克）满足一次函数关系，部分数据如下表所示，销售单价x（元/千克）566575销售量y（千克）12811090解答下列问题：（1）求y与x的函数关系式；（2）求这一周销售这种品牌普洱茶获得的利润W元的最大值；（3）物价部门规定茶叶销售单价不得高于90元/千克，公司想获得不低于2000元周利润，请计算销售单价范围．4．为了研究飞机着陆后滑行的距离s（单位：米）与滑行的时间t（单位：秒）之间的关系，测得一些数据如表：滑行的时间t02468滑行的距离s0114216306384（1）若滑行的距离和时间之间是一个一次函数或二次函数关系，用你学过的知识进行判断并求出这个函数关系式；（2）飞机着陆后滑行多远才能停下来？5．有一如图所示的纸片，拱形边缘呈抛物线形状，MN＝8米，抛物线顶点到边MN的距离是8米．点A和点D是抛物线上的两动点，且AD∥BC，过点A作AB⊥BC作DC⊥BC，过点B作DC⊥BC，点B、C在边MN上．（1）四边形ABCD是否可能为正方形？试说明明理由；（2）试求四边形ABCD周长的最大值．6．小明同学利用寒假30天时间贩卖草莓，了解到某品种草莓成本为10元/千克，在第x天的销售量与销售单价如下（每天内单价和销售量保持一致）：销售量m（千克）m＝40﹣x销售单价n（元/千克）当1≤x≤15时，n＝20+x当16≤x≤30时，n＝10+设第x天的利润w元．（1）请计算第几天该品种草莓的销售单价为25元/千克？（2）这30天中，该同学第几天获得的利润最大？最大利润是多少？注：利润＝（售价﹣成本）×销售量（3）在实际销售的前15天中，草莓生产基地为刺激销售，鼓励销售商批发草莓，每多批发1千克就发给a（a≥2）元奖励．通过销售记录发现，前8天中，每天获得奖励后的利润随时间x（天）的增大而增大，试求a的取值范围．7．受我国经济刺激政策和全球经济复苏的影响，2009年我国房地产市场开始回暖，下图反映08年7月至09年6月我国70个大城市房价同比增长率变化情况（注：同比增长率是指房价与上一年同时期相比增长的百分比）（1）看图分析：2008年7月房价比2007年7月的房价；2008年8月的房价比2008年7月的房价；（填“高”、“相等”、“低”、“不能确定”．）（2）从图上可以看出：同比增长率与月份之间折线图可以“近似”的看成一段抛物线，以2008年7月的坐标为（0，7.0）建立平面直角坐标系．请你根据图中信息求出同比增长率与月份之间“近似”的函数关系式，并据此推算2009年9月同比增长率会达到多少？（3）若从2008年7月到2008年9月房价持平，求从2009年7月开始到2009年9月房价月平均增长率．（结果精确到0.01，可能用到数据：）8．现有边长为180厘米的正方形铁皮，准备将它设计并制成一个开口的水槽，使水槽能通过的水的流量最大．某校九年级（2）班数学兴趣小组经讨论得出结论：在水流速度一定的情况下，水槽的横截面面积越大，则通过水槽的水的流量越大．为此，他们对水槽的横截面，进行了如下探索：（1）方案①：把它折成横截面为矩形的水槽，如图．若∠ABC＝90°，设BC＝x厘米，该水槽的横截面面积为y厘米2，请你写出y关于x的函数关系式（不必写出x的取值范围），并求出当x取何值时，y的值最大，最大值又是多少？方案②：把它折成横截面为等腰梯形的水槽，如图．若∠ABC＝120°，请你求出该水槽的横截面面积的最大值，并与方案①中的y的最大值比较大小．（2）假如你是该兴趣小组中的成员，请你再提供一种方案，使你所设计的水槽的横截面面积更大．画出你设计的草图，标上必要的数据（不要求写出解答过程）．9．襄阳市精准扶贫工作已进入攻坚阶段．贫困户张大爷在某单位的帮扶下，把一片坡地改造后种植了优质水果蓝莓，今年正式上市销售．在销售的30天中，第一天卖出20千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出4千克．第x天的售价为y 元/千克，y关于x的函数解析式为y＝，且第12天的售价为32元/千克，第26天的售价为25元/千克．已知种植销售蓝莓的成本是18元/千克，每天的利润是W元（利润＝销售收入﹣成本）．（1）m＝，n＝；（2）求销售蓝莓第几天时，当天的利润最大？最大利润是多少？（3）在销售蓝莓的30天中，当天利润不低于870元的共有多少天？10．近年来，西部某民族聚居区扶贫工作小组结合当地实际，大力开发乡村旅游扶贫项目，积极挖掘乡村生态休闲、旅游观光、文化教育价值，发展乡村民宿．某民宿建有40个房间供游客居住，当每个房间的定价为每天180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆每天需对每个房间支出40元的各种费用，设每个房间的定价为x元，相应的住房数为y间．（1）求y与x的函数关系式；（2）求每个房间定价为多少元时，该民宿当天利润W最大？最大利润是多少？11．某服装经销商甲，库存有进价每套400元的A品牌服装1200套，正常销售时每套600元，每月可卖出100套，一年内刚好卖完，现在市场上流行B品牌服装，此品牌服装进价每套200元，售出价每套500元，每月可卖出120套（两套服装的市场行情互不影响）．目前有一可进B品牌的机会，若这一机会错过，估计一年内进不到这种服装，可是，经销商手头无流动资金可用，只有低价转让A品牌服装，经与经销商乙协商，达成协议，转让价格（元/套）与转让数量（套）有如下关系：转让数量120011001000900800700600500400300200100（套）240250260270280290300310320330340350价格（元/套）方案1：不转让A品牌服装，也不经销B品牌服装；方案2：全部转让A品牌服装，用转让来的资金购B品牌服装后，经销B品牌服装；方案3：部分转让A品牌服装，用转让来的资金购B品牌服装后，经销B品牌服装，同时经销A品牌服装．问：①经销商甲选择方案1与方案2一年内分别获得利润各多少元？②经销商甲选择哪种方案可以使自己一年内获得最大利润？若选用方案3，请问他转让给经销商乙的A品牌服装的数量是多少（精确到百套）？此时他在一年内共得利润多少元？12．一辆电瓶车在实验过程中，前10秒行驶的路程s（米）与时间t（秒）满足关系式s＝at2，第10秒末开始匀速行驶，第24秒末开始刹车，第28秒末停在离终点20米处．下图是电瓶车行驶过程中第2秒记录一次的图象．（1）求电瓶车从出发到刹车时的路程s（米）与时间t（秒）的函数关系式．（2）如果第24秒末不刹车继续匀速行驶，那么出发多少秒后通过终点？（3）如果10秒后仍按s＝at2的运动方式行驶，那么出发多少秒后通过终点？（参考数据：≈2.24，≈2.45，计算结果保留两个有效数字．）Array 13．如图，正方形ABCD是一次函数y＝x+1图象的其中一个伴侣正方形．（1）若某函数是一次函数y＝x+1，求它的图象的所有伴侣正方形的边长；（2）若某函数是反比例函数，它的图象的伴侣正方形为ABCD，点D（2，m）（m＜2）在反比例函数图象上，求m的值及反比例函数解析式；（3）若某函数是二次函数y＝ax2+c（a≠0），它的图象的伴侣正方形为ABCD，C、D中的一个点坐标为（3，4）．写出伴侣正方形在抛物线上的另一个顶点坐标，写出符合题意的其中一条抛物线解析式，并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数？．（本小题只需直接写出答案）14．如图，隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y＝﹣x2+bx+c表示，且抛物线的点C到墙面OB的水平距离为3m时，到地面OA的距离为m．（1）求该抛物线的函数关系式，并计算出拱顶D到地面OA的距离；（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向行车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？15．【问题实验】如图①，在地面BD上有两根等长立柱AB，CD之间悬挂一根近似成抛物线y＝x2﹣x+3的绳子．（1）求绳子最低点到地面的距离；（2）如图②，因实际需要，需用一根立柱MN撑起绳子．①若在离AB为4米的位置处用立柱MN撑起，使立柱左侧的抛物线的最低点距MN为1米，离地面1.8米，求MN的长；②将立柱MN来回移动，移动过程中，在一定范围内，总保持立柱MN左侧抛物线的形状不变，其函数表达式为y＝x2﹣mx+3，当抛物线最低点到地面距离为0.5米时，求m 的值．【问题抽象】如图③，在平面直角坐标系中，函数y＝﹣mx+3（x＜0）的图象记为M1，函数y＝﹣mx+3（x≥0）的图象记为M2，其中m是常数，图象M1、M2合起来得到的图象记为M．设M在﹣3≤x≤2上的最低点纵坐标为y0，当﹣6≤y0≤2时，直接写出m的取值范围．16．某水果超市以每千克6元的价格购进了一批水果，经测算，此水果超市每天需支出固定费用（包括房租，水电费，员工工资等）为600元．若该种水果的销售单价不超过10元，则日销售量为300千克；若该种水果的销售单价超过10元，则每超过1元，日销售就减少12千克．设该种水果的销售单价为x（x＞6，且x为整数）元，日净收入为y元（日净收入＝日销售利润﹣每天固定支出的费用）．（1）求y与x之间的函数关系式；（2）此水果超市销售该种水果的日净收入能否达到1560元？否能，请求出此时的销售单价．17．我市一家电子计算器专卖店每只进价12元，售价20元，多买优惠；凡是一次买10只以上的，每多买1只，所买的全部计算器每只就降低0.10元，例如，某人买20只计算器，于是每只降价0.10×（20﹣10）＝1（元），因此，所买的全部20只计算器都按照每只19元计算，但是最低价为每只16元．（1）求一次至少买多少只，才能以最低价购买；（2）求该专卖店当一次销售x只时（x＞10），所获利润y（元）与x（只）之间的函数关系式，并写出自变量x的取值范围；（3）若店主一次卖的只数在10至50只之间，问一次卖多少只获得的利润最大？其最大利润为多少元？18．某电视机生产厂家去年销往农村的某品牌电视机每台的售价y（元）与月份x之间满足函数关系y＝﹣50x+2600，去年的月销售量p（万台）与月份x之间成一次函数关系，其中两个月的销售情况如下表：月份1月5月销售量 3.9万台 4.3万台（1）求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？（2）由于受国际金融危机的影响，今年1，2月份该品牌电视机销往农村的售价都比去年12月份下降了m%，且每月的销售量都比去年12月份下降了1.5m%．国家实施“家电下乡”政策，即对农村家庭购买新的家电产品，国家按该产品售价的13%给予财政补贴．受此政策的影响，今年3至5月份，该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下，平均每月的销售量比今年2月份增加了1.5万台．若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元，求m的值（保留一位小数）．（参考数据：≈5.831，≈5.916，≈6.083，≈6.164）。

专题02 二次函数的实际应用(30题)(原卷版)

专题第02讲二次函数的实际应用（30题）1．（2022秋•泰兴市期末）一水果店售卖一种水果，以8元/千克的价格进货，经过往年销售经验可知：以12元/千克售卖，每天可卖60千克；若每千克涨价0.5元，每天要少卖2千克；若每千克降价0.5元，每天要多卖2千克，但不低于成本价．设该商品的价格为x元/千克时，一天销售总质量为y千克．（1）求y与x的函数关系式．（2）若水果店货源充足，每天以固定价格x元/千克销售（x≥8），试求出水果店每天利润W与单价x的函数关系式，并求出当x为何值时，利润达到最大．2．（2023•朝阳）某超市以每件10元的价格购进一种文具，销售时该文具的销售单价不低于进价且不高于19元．经过市场调查发现，该文具的每天销售数量y（件）与销售单价x（元）之间满足一次函数关系，部分数据如下表所示：销售单价x/元…121314……363432…每天销售数量y/件（1）直接写出y与x之间的函数关系式；（2）若该超市每天销售这种文具获利192元，则销售单价为多少元？（3）设销售这种文具每天获利w（元），当销售单价为多少元时，每天获利最大？最大利润是多少元？3．（2023•海淀区校级开学）电缆在空中架设时，两端挂起的电缆下垂可以近似的看成抛物线的形状．如图，在一个斜坡BD上按水平距离间隔60米架设两个塔柱，每个塔柱固定电缆的位置离地面高度为27米（AB ＝CD＝27米），以过点A的水平线为x轴，水平线与电缆的另一个交点为原点O建立平面直角坐标系，如图所示．经测量，AO＝40米，斜坡高度12米（即B、D两点的铅直高度差）．结合上面信息，回答问题：（1）若以1米为一个单位长度，则D点坐标为，下垂电缆的抛物线表达式为．（2）若电缆下垂的安全高度是13.5米，即电缆距离坡面铅直高度的最小值不小于13.5米时，符合安全要求，否则存在安全隐患．（说明：直线GH⊥x轴分别交直线BD和抛物线于点H、G．点G距离坡面的铅直高度为GH的长），请判断上述这种电缆的架设是否符合安全要求？请说明理由．4．（2023春•江岸区校级月考）如图，在斜坡底部点O处安装一个的自动喷水装置，喷水头（视为点A）的高度（喷水头距喷水装置底部的距离）是1.8米，自动喷水装置喷射出的水流可以近似地看成抛物线．当喷射出的水流与喷水装置的水平距离为8米时，达到最大高度5米．以点O为原点，自动喷水装置所在的直线为y轴，建立平面直角坐标系．（1）求抛物线的解析式；（2）斜坡上距离O水平距离为10米处有一棵高度为1.75米的小树NM，MN垂直水平地面且M点到水平地面的距离为2米．①记水流的高度为y1，斜坡的高度为y2，求y1﹣y2的最大值（斜坡可视作直线OM）；②如果要使水流恰好喷射到小树顶端的点N，直接写出自动喷水装置应向后平移（即抛物线向左）多少米？5．（2023•武汉模拟）如图，灌溉车为绿化带浇水，喷水口H离地竖直高度OH为1.2m．可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象；把绿化带横截面抽象为矩形DEFG，其水平宽度DE＝3m，竖直高度EF＝0.5m．下边缘抛物线是由上边缘抛物线向左平移得到，上边抛物线最高点A离喷水口的水平距离为2m，高出喷水口0.4m，灌溉车到绿化带的距离OD为d（单位：m）．（1）求上边缘抛物线的函数解析式，并求喷出水的最大射程OC；（2）求下边缘抛物线与x轴的正半轴交点B的坐标；（3）要使灌溉车行驶时喷出的水能浇灌到整个绿化带，直接写出d的取值范围．6．（2022秋•华容区期末）农户销售某农产品，经市场调查发现：若售价为6元/千克，日销售量为40千克，若售价每提高1元/千克，日销售量就减少2千克．现设售价为x元/千克（x≥6且为正整数）．（1）若某日销售量为24千克，求该日产品的单价；（2）若政府将销售价格定为不超过18元/千克．设每日销售额为w元，求w关于x的函数表达式，并求w的最大值和最小值；（3）市政府每日给农户补贴a元后（a为正整数），发现最大日收入（日收入＝销售额+政府补贴）还是不超过450元，并且只有5种不同的单价使日收入不少于440元，请直接写出所有符合题意的a的值．7．（2023春•蔡甸区月考）如图，抛物线AB，AC是某喷水器喷出的水抽象而成，抛物线AB由抛物线AC 向左平移得到，把汽车横截面抽象为矩形DEFG，其中DE＝米，DG＝2米，OA＝h米，抛物线AC表达式为y＝a（x﹣2）2+h+，h＝，且点A，B，D，G，C均在坐标轴上．（1）求抛物线AC表达式．（2）求点B的坐标．（3）要使喷水器喷出的水能洒到整个汽车，记OD长为d米，直接写出d的取值范围．8．（2022秋•华容区期末）如图，足球场上守门员在O处开出一高球，球从离地面1米的A处飞出（A在y 轴上），运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M，距地面约4米高．球第一次落地点后又一次弹起．据实验，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．（1）求足球开始飞出到第一次落地时，该抛物线的表达式．（2）运动员乙要抢到第二个落点D，他应再向前跑多少米？（取，）9．（2023•淮安一模）某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售y（件）与销售单价x（元）之间存在一次函数关系，如图所示．（1）求y与x之间的函数关系式；（2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？10．（2023•盘锦）某工厂生产一种产品，经市场调查发现，该产品每月的销售量y（件）与售价x（万元/件）之间满足一次函数关系，部分数据如表：每件售价x/万元…2426283032…月销售量y/件…5248444036…（1）求y与x的函数关系式（不写自变量的取值范围）．（2）该产品今年三月份的售价为35万元/件，利润为450万元．①求：三月份每件产品的成本是多少万元？②四月份工厂为了降低成本，提高产品质量，投资了450万元改进设备和革新技术，使每件产品的成本比三月份下降了14万元．若四月份每件产品的售价至少为25万元，且不高于30万元，求这个月获得的利润w（万元）关于售价x（万元/件）的函数关系式，并求最少利润是多少万元．11．（2023春•江都区月考）某企业生产并销售某种产品，假设销售量与产量相等，图中的线段AB表示该产品每千克生产成本y1（单位：元）与产量x（单位：kg）之间的函数关系；线段CD表示该产品销售价y2（单位：元）与产量x（单位：kg）之间的函数关系，已知0＜x≤120，m＞60．（1）求线段AB所表示的y1与x之间的函数表达式；（2）若m＝90，该产品产量为多少时，获得的利润最大？最大利润是多少？（3）若60＜m＜70，该产品产量为多少时，获得的利润最大？最大利润是多少？12．（2023•梁溪区模拟）为加强劳动教育，各校纷纷落实劳动实践基地．某校学生在种植某种高产番茄时，经过试验发现：①当每平方米种植2株番茄时，平均单株产量为8.4千克；②在每平方米种植的株数不超过10的前提下，以同样的栽培条件，株数每增加1株，平均单株产量减少0.8千克．（1）求平均单株产量y（千克）与每平方米种植的株数x（x为整数，且2≤x＜10）之间的函数关系式；（2）已知学校劳动基地共有10平方米的空地用于种植这种番茄．问：当每平方米种植多少株时，该学校劳动基地能获得最大的产量？最大产量为多少千克？13．（2023春•仓山区校级期末）根据以下素材，探索完成任务．如何设计大棚苗木种植方案？素材1：图1中有一个大棚苗木种植基地及其截面图，其下半部分是一个长为20m，宽为1m的矩形，其上半部分是一条抛物线，现测得，大棚顶部的最高点距离地面5m．素材2：种植苗木时，每棵苗木高1.76m，为了保证生长空间，相邻两棵苗木种植点之间间隔1m，苗木顶部不触碰大棚，且种植后苗木成轴对称分布．（1）任务1：确定大棚上半部分形状．根据图2建立的平面直角坐标系，通过素材1提供的信息确定点的坐标，求出抛物线的函数关系式；（2）任务2：探究种植范围．在图2的坐标系中，在不影响苗木生长的情况下，确定种植点的横坐标的取值范围．14．（2023•岳麓区校级二模）从2020年开始，越来越多的商家向线上转型发展，“直播带货”已经成为商家的一种促销的重要手段．某商家在直播间销售一种进价为每件10元的日用商品，经调查发现，该商品每天的销售量y（件）与销售单价x（元）满足y＝﹣10x+400，设销售这种商品每天的利润为W（元）．（1）求W与x之间的函数关系式；（2）该商家每天想获得1250元的利润，又要减少库存，应将销售单价定为多少元？（3）若销售单价不低于28元，且每天至少销售50件时，求W的最大值．15．（2022秋•蜀山区校级期末）某超市经销甲、乙两种商品．商品甲每千克成本为20元，经试销发现，该种商品每天销售量y（千克）与销售单价x（元/千克）满足如图所示的一次函数关系，商品乙的成本为4元/千克，销售单价为10元/千克，但每天供货总量只有80千克，且能当天销售完．为了让利消费者，超市开展了“买一送一”活动，即买1千克的商品甲，免费送1千克的商品乙．（1）直接写出销售量y与销售单价x之间的函数表达式；（2）设这两种商品的每天销售总额为S元，求出S（元）与x（元/千克）的函数关系式；（注：商品的销售额＝销售单价×销售量）（3）设这两种商品销售总利润为W，若商品甲的售价不低于成本，不超过成本的150%，当销售单价定为多少时，才能使当天的销售总利润最大？最大利润是多少？（注：销售总利润＝两种商品的销售总额﹣两种商品的总成本）16．（2023春•莲池区校级期中）为促进学生德智体美劳全面发展，推动文化学习与体育锻炼协调发展，某校举办了学生趣味运动会．该校计划用不超过5900元购买足球和篮球共36个，分别作为运动会团体一、二等奖的奖品．已知足球单价170元，篮球单价160元．（1）学校至多可购买多少个足球？（2）受卡塔尔世界杯的影响，学校商议决定按（1）问的结果购买足球作为一等奖奖品，以鼓励更多学生热爱足球，同时商场也对足球和篮球的价格进行调整，足球单价下降了a%，篮球单价上涨了，最终学校购买奖品的经费比计划经费的最大值节省了155元，求a的值．17．（2023春•宜都市期末）某公司分别在A，B两城生产同种产品，共100件．A城生产产品的总成本y（万元）与产品数量x（件）之间具有一次函数关系：y＝ax+b．当x＝5时，y＝40；当x＝30时，y＝140．B 城生产产品的每件成本为7万元．（1）求a，b的值；（2）当A，B两城生产这批产品的总成本之和为660万元时，求A，B两城各生产产品多少件？（3）从A城把该产品运往C，D两地的费用分别为m万元/件和3万元/件；从B城把该产品运往C，D 两地的费用分别为1万元/件和2万元/件．C地需要90件，D地需要10件，在（2）的条件下，若A，B 两城总运费之和的最小值为150万元，求m的值．18．（2023•海淀区校级四模）某公园修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安装一个可调节角度的喷水头，从喷水头喷出的水柱形状是一条抛物线．建立如图所示的平面直角坐标系，抛物线形水柱的竖直高度y（单位：m）与到池中心的水平距离x（单位：m）满足的关系式近似为y＝a （x﹣h）2+k（a＜0）．（1）在某次安装调试过程中，测得x与y的部分对应值如下表：水平距离x/m00.51 1.52 2.53竖直高度y/m 2.25 2.81253 2.8125 2.25 1.31250根据表格中的数据，解答下列问题：①水管的长度是m；②求出y与x满足的函数解析式y＝a（x﹣h）2+k（a＜0）；（2）安装工人在上述基础上进行了下面两种调试：①不改变喷水头的角度，将水管长度增加1m，水柱落地时与池中心的距离为d1；②不改变水管的长度，调节喷水头的角度，使得水柱满足y＝﹣0.6（x﹣1.5）2+3.6，水柱落地时与池中心的距离为d2．则比较d1与d2的大小关系是：d1d2（填“＞”或“＝”或“＜”）19．（2023•罗山县三模）实心球是中考体育项目之一．在掷实心球时，实心球被掷出后的运动路线可以看作是抛物线的一部分．已知小军在一次掷实心球训练中，第一次投掷时出手点距地面1.8m，实心球运动至最高点时距地面3.4m，距出手点的水平距离为4m．设实心球掷出后距地面的竖直高度为y（m），实心球距出手点的水平距离为x（m）．如图，以水平方向为x轴，出手点所在竖直方向为y轴建立平面直角坐标系．（1）求第一次掷实心球时运动路线所在抛物线的表达式．（2）若实心球投掷成绩（即出手点与着陆点的水平距离）达到12.4m为满分，请判断小军第一次投掷实心球能否得满分．（3）第二次投掷时，实心球运动的竖直高度y与水平距离x近似满足函数关系y＝﹣0.08（x﹣5）2+3.8记小军第一次投掷时出手点与着陆点的水平距离为d1，第二次投掷时出手点与着陆点的水平距离为d2，则d1d2．（填“＞”“＜”“＝”）20．（2023•花溪区校级一模）过山车是一项富有刺激性的娱乐工具，在乘坐过山车的过程中能够亲身体验由能量守恒、加速度和力交织在一起产生的效果，那感觉真是妙不可言．如图是合肥某乐园中部分过山车滑道所抽象出来的函数图象，线段AB是一段直线滑道，且AB长为米，点A到地面距离OA＝6米，点B到地面距离BE＝3米，滑道B﹣C﹣D可以看作一段抛物线，最高点为C（8，4）．（1）求滑道B﹣C﹣D部分抛物线的函数表达式；（2）当小车（看成点）沿滑道从A运动到D的过程中，小车距离x轴的垂直距离为2.5米时，它到出发点A的水平距离是多少？（3）现在需要对滑道C﹣D部分进行加固，建造某种材料的水平和竖直支架CF，PH，PG．已知这种材料的价格是75000元/米，为了预算充足，至少需要申请多少元的资金．21．（2022秋•丰都县期末）抛实心球是丰都中考体育考试项目之一，如图1是一名男生投实心球情境，实心球行进路线是一条抛物线，行进高度y（m）与水平距离x（m）之间的函数关系如图2所示，掷出时，起点处高度为1.9m，当水平距离为4m时，实心球行进至最高点3.5m处．（1）求y关于x的函数表达式；（2）根据中考体育考试评分标准（男生版），投掷过程中，实心球从起点到落地点的水平距离大于等于9.7m时，即可得满分10分．该男生在此项考试中能否得满分，请说明理由．22．（2022秋•建昌县期末）2022年11月，“中国传统制茶技艺及其相关习俗”申遗成功，弘扬茶文化，倡导“和美雅静”的生活方式已成时尚．某茶商经销某品牌茶，成本为50元/千克，经市场调查发现，每周的销量y（千克）与销售单价x（元/千克）满足一次函数关系，部分数据列表如下：566575…销售单价x（元/千克）销量y（千克）12811090…（1）求y与x的一次函数关系式；（2）求该茶商这一周销售该品牌茶叶所获利润w（元）的最大值．23．（2023•锦州二模）近年来国家出台政策要求电动车上牌照，“保安全、戴头盔”出行．某头盔专卖店购进一批单价为36元的头盔．在销售中，通过分析销售情况发现这种头盔的月销售量y（个）与售价x（元/个）（42≤x≤72）满足一次函数关系，下表是其中的两组对应值．售价x（元/个）…5055…月销售量y（个）…10090…（1）求y与x之间的函数关系式；（2）专卖店的优惠活动：若购买一个这种头盔，就赠送一个成本为6元的头盔面罩．请问这种头盔的售价定为多少元时，月销售利润最大，最大月销售利润是多少元？24．（2023•金湖县三模）某超市购进甲、乙两种商品，已知购进5件甲商品和2件乙商品，需80元：购进3件甲商品和4件乙商品，需90元．（1）甲、乙两种商品的进货单价分别是多少？（2）设甲商品的销售单价为x（单位：元/件），在销售过程中发现：当12≤x≤18时，甲商品的日销售量y（单位：件）与销售单价x之间存在一次函数关系，x、y之间的部分数值对应关系如表：销售单价x（元/件）1218日销售量y（件）164请写出当12≤x≤18时，y与x之间的函数关系式；（3）在（2）的条件下，设甲商品的日销售利润为w元，当甲商品的销售单价x（元/件）定为多少时，日销售利润最大？最大利润是多少？25．（2022秋•新抚区期末）疫情防控常态化，全国人民同心抗疫．某商家决定将一个月获得的利润全部捐赠给社区用于抗疫．已知商家购进一批产品，成本为10元/件，拟采取线上和线下两种方式进行销售，市场调查发现，线下的月销量y（件）与线下售价x（元/件，且12≤x≤16）之间满足一次函数关系，部分数据如下表：x（元/件）12131415y（件）1000900800700（1）求y与x之间的函数关系式；（2）若线上售价始终比线下每件便宜2元，且线上的月销量固定为600件．当x为何值时，线上和线下销售月利润总和W达到最大？最大利润是多少？（3）要使（2）中月利润总和W不低于4400元，请直接写出x的取值范围．26．（2023•嘉鱼县模拟）为巩固扶贫攻坚成果，我县政府督查各部门和单位对口扶贫情况．某单位的帮扶对象种植的农产品在某月（按30天计）的第x天（x为正整数）的销售价格p（元/千克）关于x的函数关系为p＝，销售量y（千克）与x之间的关系如图所示．（1）直接写出y与x之间的函数关系式和x的取值范围；（2）求该农产品的销售量有几天不超过60千克？（3）当月第几天，该农产品的销售额最大，最大销售额是多少？（销售额＝销售量×销售价格）27．（2023•云梦县校级三模）李丽大学毕业后回家乡创业，开了一家服装专卖店代理品牌服装的销售．已知该品牌服装进价每件40元，日销售y（件）与销售价x（元/件）之间的关系如图所示（实线），每天付员工的工资每人82元，每天应支付其他费用106元．（1）直接写出日销售y（件）与销售价x（元/件）之间的函数关系式；（2）当某天的销售价为48元/件时，收支恰好平衡（收入＝支出），求该店员工人数；（3）若该店只有2名员工，则每天能获得的最大利润是多少元？此时，每件服装的价格应定为多少元？28．（2023•卧龙区二模）如图，在斜坡底部点O处安装一个自动喷水装置，喷水头（视为点A）的高度（喷水头距喷水装置底部的距离）是1.8米，自动喷水装置喷射出的水流可以近似地看成抛物线．当喷射出的水流与喷水装置的水平距离为8米时，达到最大高度5米．以点O为原点，自动喷水装置所在的直线为y轴，建立平面直角坐标系．（1）求抛物线的函数关系式；（2）斜坡上距离O水平距离为10米处有一棵高度为1.75米的小树NM，MN垂直水平地面，且M点到水平地面的距离为2米，绿化工人向左水平移动喷水装置后，水流恰好喷射到小树顶端的点N，求自动喷水装置向左水平平移（即抛物线向左）了多少米？29．（2023•竞秀区二模）过山车是一项富有刺激性的娱乐工具，深受年轻游客的喜爱．某游乐场修建了一款大型过山车．如图所示，A→B→C为这款过山车的一部分轨道（B为轨道最低点），它可以看成一段抛物线，其中OA＝16.9米，OB＝13米（轨道厚度忽略不计）．（1）求抛物线A→B→C的函数表达式；（2）在轨道上有两个位置P和C到地面的距离均为n米，当过山车运动到C处时，又进入下坡段C→E （接口处轨道忽略不计，E为轨道最低点），已知轨道抛物线C→E→F的形状与抛物线A→B→C完全相同，E点坐标为（33，0），求n的值；（3）现需要对轨道下坡段A→B进行安全加固，建造某种材料的水平和竖直支架GD、GM、HI、HN，且要求MN＝2OM，已知这种材料的价格是100000元/米，请计算OM多长时，造价最低？最低造价为多少元？30．（2023•利辛县模拟）如图，某小区的景观池中安装一雕塑OA，OA＝2米，在点A处安装喷水装置，喷出两股水流，两股水流可以抽象为平面直角坐标系中的两条抛物线（图中的C1，C2）的部分图象，两条抛物线的形状相同且顶点的纵坐标相同，且经测算发现抛物线C2的最高点（顶点）C距离水池面2.5米，且与OA的水平距离为2米．（1）求抛物线C2的解析式；（2）求抛物线C1与x轴的交点B的坐标；（3）小明同学打算操控微型无人机在C1，C2之间飞行，为了无人机的安全，要求无人机在竖直方向上的活动范围不小于0.5米，设无人机与OA的水平距离为m，求m的取值范围．。

21.4 二次函数的应用沪科版数学九年级上册课后练习(含答案解析)

二次函数的应用一、单选题1．如图，小明以抛物线y=x2-2x+4为灵感设计了一款杯子，若AB=4，DE=2，则杯子的高CE为（）A．4B．5C．6D．72．如图，一边靠墙（墙有足够长），其它三边用12m长的篱笆围成一个矩形（ABCD）花园，这个花园的最大面积是（）A．18m2B．12 m2C．16 m2D．22 m23．苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑，“门”的造型是东方之门的立意基础，“门”的内侧曲线呈抛物线型，如图1，两栋建筑第八层由一条长60m的连桥连接，在该抛物线两侧距连桥150m处各有一窗户，两窗户的水平距离为30m，如图2，则此抛物线顶端O到连桥AB距离为（）A．180m B．200m C．220m D．240m4．如图是抛物线型拱桥，当拱顶离水面时，水面宽．若水面再下降，水面宽度为（）．A．B．C．D．5．一人一盔安全守规，一人一带平安常在！某商店销售一批头盔，售价为每顶80元，每月可售出200顶．在“创建文明城市”期间，计划将头盔降价销售，经调查发现：每降价1元，每月可多售出20顶．已知头盔的进价为每顶50元，则该商店每月获得最大利润时，每顶头盔的售价为（）元．A．60B．65C．70D．756．将进货价为35元的商品按单价40元售出时，能卖出200个，已知该商品单价每上涨1元，其销售量就减少5个，设这种商品的售价为元时，获得的利润为元，则下列关系式正确的是（）A．B．C．D．7．在中考体育训练期间，小宇对自己某次实心球训练的录像进行分析，发现实心球飞行高度y （米）与水平距离x（米）之间的关系式为，由此可知小宇此次实心球训练的成绩为（）A．米B．8米C．10米D．2米8．如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y＝a（x﹣k）2+h．已知球与D点的水平距离为6m时，达到最高2.6m，球网与D点的水平距离为9m．高度为2.43m，球场的边界距O点的水平距离为18m，则下列判断正确的是（）A．球不会过网B．球会过球网但不会出界C．球会过球网并会出界D．无法确定9．如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线．图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌架底部的距离）是1米．当喷射出的水流距离喷水头20米时．达到最大高度11米，现将喷灌架置于坡度为1：10的坡地底部点O处，草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB，因为刚刚被喷洒了农药，近期不能被喷灌．下列说法正确的是（）A．水流运行轨迹满足函数y＝﹣x2﹣x+1B．水流喷射的最远水平距离是40米C．喷射出的水流与坡面OA之间的最大铅直高度是9.1米D．若将喷灌架向后移动7米，可以避开对这棵石榴树的喷灌10．共享单车为市民出行带来了方便，某单车公司第一个月投放辆单车，计划第三个月投放单车辆，若第二个月的增长率是，第三个月的增长率是第二个月的两倍，那么与的函数关系是（）A．B．C．D．11．汽车在刹车后，由于惯性作用还要继续向前滑行一段距离才能停下，我们称这段距离为“刹车距离”，刹车距离往往跟行驶速度有关，在一个限速35km/h的弯道上，甲、乙两辆汽车相向而行，发现情况不妙，同时刹车，最后还是相撞了事发后，交警现场测得甲车的刹车距离略超过12m，乙车的刹车距离略超过10m，又知甲、乙两种车型的刹车距离s（m）与车速x（km/h）的关系大致如下：S甲，S乙．由此可以推测（）A．甲车超速B．乙车超速C．两车都超速D．两车都未超速12．如图，菱形的边长是，，动点P从点A出发，以的速度沿运动至点C，动点Q从点A出发，以的速度沿运动至点C．若P，Q同时出发，设运动时间为，的面积为（当B，P，Q三点共线时，不妨设），则下面图象中能表示S与t之间的函数关系的是（）A．B．B．C．D．二、填空题13．如图，要在夹角为30°的两条小路与形成的角状空地上建一个三角形花坛，分别在边和上取点和点，并扎起篱笆将花坛保护起来（篱笆的厚度忽略不计）．若和两段篱笆的总长为8米，则当______米时，该花坛的面积最大．14．如图，一座悬索桥的桥面OA与主悬钢索MN之间用垂直钢索连接，主悬钢索是抛物线形状，两端到桥面的距离OM与AN相等．小强骑自行车从桥的一端0沿直线匀速穿过桥面到达另一端A，当他行驶18秒时和28秒时所在地方的主悬钢索的高度相同，那么他通过整个桥面OA共需_____________秒．15．某快餐店销售A、B两种快餐，每份利润分别为12元、8元，每天卖出份数分别为40份、80份．该店为了增加利润，准备降低每份A种快餐的利润，同时提高每份B种快餐的利润．售卖时发现，在一定范围内，每份A种快餐利润每降1元可多卖2份，每份B种快餐利润每提高1元就少卖2份．如果这两种快餐每天销售总份数不变，那么这两种快餐一天的总利润最多是______元．16．为了在体育中考中取得更好的成绩，小明积极训练，体育老师对小明投掷铅球的录像进行技术分析，如图，发现铅球在行进过程中高度y（m）与水平距离x（m）之间的关系为，由此可知小明此次投掷的成绩是___．17．如图，在Rt△ACB中，∠ACB＝90°，AC＝BC，D是AB上的一个动点，连接CD，将△BCD 绕点C顺时针旋转90°得到△ACE，连接DE，则△ADE面积的最大值等于____________．三、解答题18．用规格长为6m，宽为0.1m的铝合金型材，恰好制作成一个“日”字型窗子的边框（如图1，不计耗损），中间装长x m，宽y m完全一样的两张玻璃．这个窗子要装入最大边长为1.5m的正方形墙洞（如图2）中．（1）求y与x之间的函数关系式，并求出x的取值范围．（2）这个窗子的采光面积（两张玻璃面积之和）存在最大值吗？如果有，请求出来；如果没有，请说明理由．19．一个圆形喷水池的中央竖直安装了一个高为9米的柱形喷水装置OA，A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，如果抛物线的最高点M离柱形喷水装置1米，离地面12米，若不计其他因素，水池的半径OB至少为多少米时，才能使喷出的水流不落在池外？20．某商场将一种每件成本价为10元的商品连续加价两次后，以每件24元作为定价售出．已知第二次加价的增长率比第一次加价的增长率多．（1）求第一次加价的增长率；（2）该商场在试销中发现，如果以定价售出，则每天可售出100个．如果销售单价每降低1元，销售量就可以增加10件．那么当销售单价为多少元时，该商场每天销售该商品获得的利润最大？最大利润是多少？21．在“学习一项体育技能”活动中，小明作为学生代表去观看“青岛黄海足球队”的训练．他看到队员们在做掷界外球训练，甲球员要将足球掷给离他7.5米远的乙球员，掷出足球的运行轨还是一条抛物线，足球行进的高度y（米）与水平距离x（米）之间的关系如图所示，足球出手时离地面的高度为2米，在距离甲球员4米处达到最大高度3.6米．若不计其他因素，身高1.85米的乙球员要能触到足球，他垂直起跳的高度至少要达到多少米？22．如图，是等腰直角三角形，，，点P是边上一动点，沿的路径移动，过点P作于点D，设，的面积为y．（1）当时，求y的值；（2）在这一变化过程中，写出y关于x的函数解析式及x的取值范围；（3）当x取何范围时，（直接写出结果即可）．参考答案1．C解：∵=（x-1）2+3，∴抛物线的顶点D的坐标为（1，3），∵AB=4，∴BC=2，点B的横坐标为x =3，把x =3代入得y=7，∴CD=7-3=4，∴CE=CE+DE=4+2=6，故选：C.2．A解：设与墙垂直的矩形的边长为xm，则这个花园的面积是：S=x（12-2x）=，∴当x=3时，S取得最大值，此时S=18，故选：A．3．B解：以所在的直线为轴，以线段的垂直平分线所在的直线为轴建立平面直角坐标系：，，，设抛物线的解析式为，将代入，得：，解得：，，抛物线顶端的坐标为，此抛物线顶端到连桥距离为．故选：B．4．D解：如图，以AB所在直线为x轴，以过拱顶C且垂直于AB的直线为y轴，建立平面直角坐标系，则由题意可知A（-2，0），B（2，0），C（0，2），设该抛物线的解析式为y=ax2+2，将B（2，0）代入得：0=a×4+2，解得：a=-．∴抛物线的解析式为y=-x2+2，∴若水面再下降1.5m，则有-1.5=-x2+2，解得：x=±．∵-（-）=2，∴水面宽度为2m．故选：D．5．C解：每顶头盔降价x元，利润为w元，由题意可得，w＝（80﹣x﹣50）（200+20x）＝﹣20（x﹣10）2+8000，∴当x＝10时，w取得最大值，此时80﹣x＝70，即该商店每月获得最大利润时，每顶头盔的售价为70元，故选：C．6．B解：设这种商品的售价为x元时，获得的利润为y元，根据题意可得：即y=（x-35）（400-5x），故选：B．7．B解：当y＝0时，即＝0，解得：x1＝﹣2（舍去），x2＝8，所以小宇此次实心球训练的成绩为8米，故选：B．8．C解：根据题意,将点A(0,2)代入得：36a+2.6=2，解得：∴y与x的关系式为当x=9时,∴球能过球网，当x=18时,∴球会出界.故选C.9．D解：A、设石块运行的函数关系式为y=a（x-20）2+11，把（0，1）代入解析式得：400a+11=1，解得：，∴解析式为；故A不符合题意；B、当y=0时，；解得x=2+20，∴水流喷射的最远水平距离是2+20米；故B不符合题意；C、当x=20时，y=11，∴11-2=9∴喷射出的水流与坡面OA之间的最大铅直高度是9米故C不符合题意；D、向后平移后的解析式为，当x=37时，y=8.58.5-3=5.5＞2.3，∴可以避开对这棵石榴树的喷灌；故选：D10．A解：第二个月的增长率是，第三个月的增长率是第二个月的两倍，第三个月的增长率为第一个月投放辆单车，第二个月投放辆第三个月投放量故选：A．11．B解：由，先求出，x的解也就是二次函数的图象与x轴的两个交点的横坐标：从图象可得，x是在A点的左侧以及B点的右侧，即或．由，先求出，x的解也就是二次函数的图象与x轴的两个交点的横坐标：从图象可得，x是在C点的左侧以及D点的右侧，即或．由于，从而可得：，．经比较：乙车超过限速．故选：B．12．B解：当0≤t≤2时，BQ=4﹣2t，AP= t,点P到AB的距离为t，S＝（4﹣2t）×t＝﹣（t﹣1）2+，∴该函数图象开口向下，当2＜t≤4时，BQ=4﹣2t，点P在AD上，到BC的距离为×4，S＝×（2t﹣4）××4＝2t﹣4，∴该函数图象是线段，且y随x的增大而增大，当4＜t≤8时，S＝×4××（8﹣t）＝8﹣t，∴该函数图象是线段，且y随x的增大而减小．故选：B．13．4解：设OP=x，则OQ=8-x，过点P作PM⊥OQ,交OQ于点M，如图，∵∴∴∵∴函数图象开口向下，有最大值，为4，故当OP=4时，花坛的面积最大．故答案为：4．14．46解：∵主悬钢索是抛物线形状，两端到桥面的距离OM与AN相等，且小强骑行18秒时和28秒时所在地方的主悬钢索的高度相同，∴MN的对称轴为直线x==23，∴他通过整个桥面OA共需23×2=46（秒）．故答案为：46．15．1264解：设种快餐的总利润为，种快餐的总利润为，两种快餐的总利润为，设快餐的份数为份，则B种快餐的份数为份．据题意：∴∵∴当的时候，W取到最大值1264，故最大利润为1264元故答案为：126416．7m解：由题意，得当y＝0时，，化简，得：，解得：（舍去），故答案为：7m．17．解：如图，△BCD绕点C顺时针旋转90°得到△ACE，∴△BDC≌△AEC，∴∠B=∠CAE，∵BC=AC=，△ABC为等腰直角三角形，∴∠B=∠CAE=∠BAC=45°，∴∠DAE=∠BAC+∠CAE=90°，在Rt△ABC中，由勾股定理AB=，设BD=AE=x，则AD=（2-x），∴，∵，函数开口向下，函数有最大值，当x=1时，．故答案为：．18．（1）y＝﹣0.75x+1.35，1≤x≤1.3；（2）这个窗子的采光面积有最大值，最大值为1.2m2，见解析．解：（1）由题意，得3x+2（2y+0.1×3）＝6，整理，得3x+4y＝5.4，∴y＝﹣0.75x+1.35，∴y与x之间的函数关系式为y＝﹣0.75x+1.35，由题意，得，解得1≤x≤1.3，即x的取值范围是1≤x≤1.3；（2）设这个窗子的采光面积为Sm2，由题意，得S＝2xy＝2x（﹣0.75x+1.35）＝﹣1.5x2+2.7x，配方，得S＝﹣1.5（x﹣0.9）2+1.215，∵a＝﹣1.5＜0，对称轴为x＝0.9，∴当x＞0.9时，y随x的增大而减小，∵1≤x≤1.3，∴当x＝1时，S有最大值，S最大＝1.2，答：这个窗子的采光面积有最大值，最大值为1.2m2．19．3米解：由题意可得：抛物线顶点坐标为（1，12），A点坐标为（0，9），故设抛物线解析式为：，则，解得：a＝﹣3，故抛物线解析式为：，当y＝0时，解得：x1＝﹣1，x2＝3，则水池的半径OB至少为3米时，才能使喷出的水流不落在池外．20．（1）50%；（2）当销售单价为22元/个时，该商场每天销售该商品获得的利润最大，最大利润是1440元解：（1）解：设第一次加价的增长率为x，由题意得解得：（不合题意，舍去）答：第一次加价的增长率为．（2）解：当销售单价为m元/个时，获得的利润为y元，由题意得∵∴当时，y可取得最大值为1440答：当销售单价为22元/个时，该商场每天销售该商品获得的利润最大，最大利润是1440元．21．他垂直起跳的高度至少要达到米解：根据题意可知抛物线的顶点坐标为，与抛出点的坐标为，设抛物线的解析式为：，顶点坐标代入得：，抛出点坐标代入得：，解得：，∴抛物线得解析式为：，当时，，米，故他垂直起跳的高度至少要达到米．22．（1）；（2）；（3）x的取值范围为：或解：（Ⅰ）是等腰直角三角形，则，因为PD⊥BC ，则为等腰直角三角形，故，则，当时，；（Ⅱ）当点在上运动时，由（1）知，，当点在上运动时，同理可得为等腰直角三角形，则，则，故；（Ⅲ）①当时，则，当时，即，解得（舍去负值），当时，即，解得（舍去负值），故；②当时，则，当时，即=，解得：，当时，即，解得：，故；综上，x的取值范围为：或．。

初中数学沪科版九年级上册第二十一章《二次函数的应用》练习题(解析版)

初中数学沪科版九年级上册第二十一章21.4二次函数的应用练习题一、选择题1.如图是王阿姨晚饭后步行的路程s(单位：m)与时间t(单位：min)的函数图象，其中曲线段AB是以B为顶点的抛物线一部分．下列说法不正确的是()A. 25min～50min，王阿姨步行的路程为800mB. 线段CD的函数解析式为s=32t+400(25≤t≤50)C. 5min～20min，王阿姨步行速度由慢到快D. 曲线段AB的函数解析式为s=−3(t−20)2+1200(5≤t≤20)2.二次函数y=x2−8x+15的图象与x轴相交于M，N两点，点P在该函数的图象上运动，能使△PMN的面积等于1的点P共有()2A. 1个B. 2个C. 3个D. 4个3.某畅销书的售价为每本30元，每星期可卖出200本，书城准备开展“读数节活动”，决定降价促销，经调研，如果调整书籍的售价，每降价2元，每星期可多卖出40本，设每件商品降价x元后，每星期售出此畅销书的总销售额为y元，则y与x之间的函数关系式为()A. y=(30−x)(200+40x)B. y=(30−x)(200+20x)C. y=(30−x)(200−40x)D. y=(30−x)(200−20x)4.某农产品市场经销一种销售成本为40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨一元，月销售量就减少10千克．设销售单价为每千克x元，月销售利润为y元，则y与x的函数关系式为()A. y=(x−40)(500−10x)B. y=(x−40)(10x−500)C. y=(x−40)[500−10(x−50)]D. y=(x−40)[500−10(50−x)]5.进入夏季后，某电器商场为减少库存，对电热取暖器连续进行两次降价．若设平均每次降价的百分率是x，降价后的价格为y元，原价为a元，则y与x之间的函数关系式为()A. y=2a(x−1)B. y=2a(1−x)C. y=a(1−x2)D. y=a(1−x)26.为解决药价虚高给老百姓带来的求医难问题，国家决定对药品价格分两次降价，若设平均每次降价的百分率为x，该药品的原价是18元/盒，降价后的价格为y元/盒，则y与x之间的函数关系式是()A. y=36(1−x)B. y=36(1+x)C. y=18(1−x)2D. y=18(1+x2)7.在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形，如果设剩余部分的面积为y，那么y关于x的函数解析式是()A. y=x2B. y=4−x2C. y=x2−4D. y=4−2x8.矩形的周长为12cm，设其一边长为xcm，面积为ycm2，则y与x的函数关系式及其自变量x的取值范围均正确的是()A. y=−x2+6x(3<x<6)B. y=−x2+6x(0<x<6)C. y=−x2+12x(6<x<12)D. y=−x2+12x(0<x<12)9.长方形的周长为24cm，其中一边为xcm(其中x>0)，面积为ycm2，则这样的长方形中y与x的关系可以写为()A. y=x2B. y=(12−x)2C. y=(12−x)xD. y=2(12−x)10.广场上喷水池中的喷头微露水面，喷出的水线呈一条抛物线，水线上水珠的高度y(x2+6x(0≤x≤4)，米)关于水珠和喷头的水平距离x(米)的函数解析式是y=−32那么水珠的高度达到最大时，水珠与喷头的水平距离是()A. 1米B. 2米C. 5米D. 6米二、填空题11.某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=________．12.据权威部门发布的消息，2021年第一季度安徽省城镇居民人均可支配收入约为0.75万元，若第三季度安徽省城镇居民人均可支配收人为y万元，平均每个季度城镇居民人均可支配收入增长的百分率为x，则y与x之间的函数表达式是____．13.如图，用一段长为40m的篱笆围成一个一边靠墙的矩形菜园ABCD，墙长为18m，设AD的长为x m，菜园ABCD的面积为y m2，则y关于自变量x的函数关系式是___________________________．14.某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件，商品进价为每件40元，若设涨价x(x>0)元，总利润为y元，则y与x的函数关系式为______．15.某工厂今年一月份生产防疫护目镜的产量是20万件，计划之后两个月增加产量，如果月平均增长率为x，那么第一季度防疫护目镜的产量万件与x之间的关系应表示为______．三、解答题16.已知抛物线y=−x2+bx+c的对称轴为直线x=1，其图象与x轴相交于A，B两点，与y轴相交于点C(0,3)．(1)求b，c的值；(2)直线1与x轴相交于点P．①如图1，若l//y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x=1的对称点为点D，求四边形CEDF面积的最大值；②如图2，若直线1与线段BC相交于点Q，当△PCQ∽△CAP时，求直线1的表达式．17.如图1，在平面直角坐标系中，已知抛物线y=ax2+bx−5与x轴交于A(−1,0)，B(5,0)两点，与y轴交于点C．(1)求抛物线的函数表达式；(2)如图2，CE//x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标；(3)若点K为抛物线的顶点，点M(4,m)是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．18.在平面直角坐标系中，函数y=x2−2ax−1(a为常数)的图象与y轴交于点A．(1)求点A的坐标．(2)当此函数图象经过点(1,2)时，求此函数的表达式，并写出函数值y随x的增大而增大时x的取值范围．(3)当x≤0时，若函数y=x2−2ax−1(a为常数)的图象的最低点到直线y=2a的距离为2，求a的值．(4)设a<0，Rt△EFG三个顶点的坐标分别为E(−1,−1)、F(−1,a−1)、G(0,a−1).当函数y=x2−2ax−1(a为常数)的图象与△EFG的直角边有交点时，交点记为点P.过点P作y轴的垂线，与此函数图象的另一个交点为P′(P′与P不重合)，过点A 作y轴的垂线，与此函数图象的另一个交点为A′.若AA′=2PP′，直接写出a的值．答案和解析1.【答案】C【解析】【分析】本题考查了二次函数的应用，一次函数的应用，正确的识别图象、数形结合是解题的关键.根据函数图象中的信息，利用数形结合求相关线段的解析式解答即可．【解答】解：A.25min ～50min ，王阿姨步行的路程为2000−1200=800m ，故A 正确；B .设线段CD 的函数解析式为s =kt +b ，把(25,1200)，(50,2000)代入得，{1200=25k +b 2000=50k +b，解得：{k =32b =400， ∴线段CD 的函数解析式为s =32t +400(25≤t ≤50)，故B 正确；C .在A 点的速度为5255=105m/min ，在B 点的速度为1200−52520−5=67515=45m/min ，速度从快变慢，故C 错误；D .当t =5，20时，由图象可得s =525，1200m ，将t =5，20分别代入s =−3(t −20)2+1200(5≤t ≤20)得s =525，s =1200，故D 正确．故选C ．2.【答案】D【解析】【分析】本题结合图象的性质考查二次函数的综合应用，难度中等．要注意函数求出的各个解是否符合实际．由题可求出MN 的长，即△MNP 的底边已知，要求面积为12，那么根据面积即可求出高，只要把相应的y 值代入即可解答．【解答】解：y =x 2−8x +15的图象与x 轴交点(3,0)和(5,0)，|MN|=2，设p 点(x,y)，y =x 2−8x +15，面积=12=12|MN|⋅|y|，可得y 1=12，或者y 2=−12，当y =12时，x =8±√62；当y =−12时，x =8±√22，所以共有四个点．故选：D ．3.【答案】B【解析】【分析】本题考查由实际问题列二次函数关系式，解答本题的关键是明确题意，列出相应的函数关系式．根据降价x 元，则售价为(30−x)元，销售量为(200+20x)本，由题意可得等量关系：总销售额为y =销量×售价，根据等量关系列出函数解析式即可．【解答】解：设每本降价x 元，则售价为(30−x)元，销售量为(200+20x)本，根据题意得，y =(30−x)(200+20x)，故选B ．4.【答案】C【解析】【分析】此题主要考查了根据实际问题抽象出二次函数关系式，正确表示出销量是解题关键．直接利用每千克利润×销量=总利润，进而得出关系式．【解答】解：设销售单价为每千克x 元，月销售利润为y 元，则y 与x 的函数关系式为：y =(x −40)[500−10(x −50)]．故选：C ．5.【答案】D【解析】解：由题意得第二次降价后的价格是a(1−x)2．则函数解析式是y=a(1−x)2．故选D．原价为a，第一次降价后的价格是a×(1−x)，第二次降价是在第一次降价后的价格的基础上降价的，为a×(1−x)×(1−x)=a(1−x)2．本题需注意第二次降价是在第一次降价后的价格的基础上降价的．6.【答案】C【解析】【分析】此题主要考查了根据实际问题抽象出二次函数关系式，本题需注意第二次降价是在第一次降价后的价格的基础上降价的．原价为18，第一次降价后的价格是18(1−x)，第二次降价是在第一次降价后的价格的基础上降价的为：18(1−x)×(1−x)=18(1−x)2，则函数关系式即可求得．【解答】解：原价为18，第一次降价后的价格是18(1−x)；第二次降价是在第一次降价后的价格的基础上降价的为：18(1−x)×(1−x)=18(1−x)2．则函数解析式是：y=18(1−x)2．故选C．7.【答案】B【解析】解：设剩下部分的面积为y，则：y=−x2+4(0<x<2)，故选：B．根据剩下部分的面积=大正方形的面积−小正方形的面积得出y与x的函数关系式即可．此题主要考查了根据实际问题列二次函数关系式，利用剩下部分的面积=大正方形的面积−小正方形的面积得出是解题关键．8.【答案】B【解析】【分析】此题主要考查了根据实际问题列二次函数关系式的知识，解题的关键是用x表示出矩形的另一边，此题难度一般．已知一边长为xcm，则另一边长为(6−x)cm，根据矩形的面积公式即可解答．【解答】解：已知一边长为xcm，则另一边长为(6−x)．则y=x(6−x)化简可得y=−x2+6x，(0<x<6)，故选：B．9.【答案】C【解析】【分析】本题考查列二次函数关系式，得到长方形的另一边长是解决本题的关键点．先得到长方形的另一边长，那么面积=一边长×另一边长．【解答】解：∵长方形的周长为24cm，其中一边为x(其中x>0)，∴长方形的另一边长为12−x，∴y=(12−x)⋅x．故选C．10.【答案】B【解析】【分析】本题考查了二次函数的应用，解决本题的关键是掌握二次函数的顶点式．根据二次函数的顶点式即可求解．【解答】解：方法一：根据题意，得y=−32x2+6x(0≤x≤4)，=−32(x−2)2+6所以水珠的高度达到最大时，水珠与喷头的水平距离是2米．方法二：因为对称轴x=−62×(−32)=2，所以水珠的高度达到最大时，水珠与喷头的水平距离是2米．故选：B．11.【答案】a(1+x)2【解析】【分析】本题考查根据实际问题列二次函数关系式，关键是由一月份新产品的研发资金为a元，根据题意可以得到2月份研发资金为a×(1+x)，而三月份在2月份的基础上又增长了x，那么三月份的研发资金也可以用x表示出来，由此即可确定函数关系式．【解答】解：∵一月份新产品的研发资金为a元，二月份起，每月新产品的研发资金与上月相比增长率都是x，∴二月份新产品的研发资金为a(1+x)元，∴三月份新产品的研发资金为a(1+x)(1+x)=a(1+x)2元，即y=a(1+x)2．12.【答案】y=0.75(1+x)2【解析】【分析】此题主要考查了根据实际问题列二次函数关系式，属于中考常考题型．第一季度安徽省城镇居民人均可支配收入约为0.75万元，第二季度安徽省城镇居民人均可支配收入是0.75(1+x)元，第三季度安徽省城镇居民人均可支配收人为0.75(1+x)2元，则函数解析式即可求得．【解答】解：平均每个季度城镇居民人均可支配收入增长的百分率为x，根据题意可得：y与x之间的函数关系为：y=0.75(1+x)2．故答案为y=0.75(1+x)2．13.【答案】y=−2x2+40x(11≤x<20)【解析】【分析】本题考查了根据实际问题列二次函数关系式、矩形的面积公式的运用，利用篱笆的总长用含x的代数式表示出平行于墙的边长是解题的关键．先用含x的代数式表示出平行于墙的边长，再由矩形的面积公式就可以得出结论；【解答】解：根据题意，AD边的长为x米，则AB边的长为(40−2x)米，∴y=x(40−2x)，即y与x之间的函数关系式为y=−2x2+40x；0<40−2x≤18，11≤x<20，故答案为y=−2x2+40x(11≤x<20)．14.【答案】y=10x2−500x+6000【解析】解：设涨价x(x>0)元，总利润为y元，则y与x的函数关系式为：y=(60−40−x)(300−10x)=10x2−500x+6000．故答案为：y=10x2−500x+6000．直接利用销量×每件利润=总利润，进而得出函数关系式．此题主要考查了根据实际问题列二次函数关系式，正确表示出销量和每件利润是解题关键．15.【答案】y=20+20(x+1)+20(x+1)2【解析】解：y与x之间的关系应表示为：y=20+20(x+1)+20(x+1)2．故答案为：y=20+20(x+1)+20(x+1)2．根据平均增长问题，可得答案．本题考查了根据实际问题列二次函数关系式，利用增长问题获得函数解析式是解题关键． 16.【答案】解：(1)由题意得：{b2=1c =3， ∴b =2，c =3，(2)①如图1，∵点C 关于直线x =1的对称点为点D ，∴CD//OA ，∴3=−x 2+2x +3，解得：x 1=0，x 2=2，∴D(2,3)，∵抛物线的解析式为y =−x 2+2x +3，∴令y =0，解得x 1=−1，x 2=3，∴B(−1,0)，A(3,0)，设直线AC 的解析式为y =kx +b ，∴{3k +b =0b =3，解得：{k =−1b =3， ∴直线AC 的解析式为y =−x +3，设F(a,−a 2+2a +3)，E(a,−a +3)，∴EF =−a 2+2a +3+a −3=−a 2+3a ，四边形CEDF 的面积=S △EFC +S △EFD =12EF ⋅CD =12×(−a 2+3a)×2=−a 2+3a =−(a −32)2+94， ∴当a =32时，四边形CEDF 的面积有最大值，最大值为94．②当△PCQ∽△CAP 时，∴∠PCA =∠CPQ ，∠PAC =∠PCQ ，∴PQ//AC ，∵C(0,3)，A(3,0)，∴OA =OC ，∴∠OCA=∠OAC=∠PCQ=45°，∴∠BCO=∠PCA，如图2，过点P作PM⊥AC交AC于点M，∴tan∠PCA=tan∠BCO=OBOC =13，设PM=b，则CM=3b，AM=b，∵AC=√OC2+OA2=3√2，∴b+3b=3√2，∴b=34√2，∴PA=34√2×√2=32，∴OP=OA−PA=3−32=32，∴P(32,0)，设直线l的解析式为y=−x+n，∴−32+n=0，∴n=32．∴直线l的解析式为y=−x+32．【解析】(1)根据抛物线的对称轴及抛物线与y轴的交点坐标可求出b、c的值；(2)由题意先求出D点坐标为(2,3)，求出直线AC的解析式，设F(a,−a2+2a+3)，E(a,−a+3)，则EF=−a2+3a，四边形CEDF的面积可表示为12EF⋅CD，利用二次函数的性质可求出面积的最大值；(3)当△PCQ∽△CAP时，可得∠PCA=∠CPQ，∠PAC=∠PCQ=∠OCA=45°，则PQ//AC，∠BCO=∠PCA，过点P作PM⊥AC交AC于点M，可求出PM、PA、OP的长，用待定系数法可求出函数解析式．本题考查了二次函数的综合题：熟练掌握二次函数的性质和轴对称的性质；会利用待定系数法求函数解析式；理解坐标与图形性质，会利用相似三角形的性质解题；要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度是解题的关键．17.【答案】解：(1)∵点A(−1,0)，B(5,0)在抛物线y =ax 2+bx −5上，∴{a −b −5=025a +5b −5=0，解得{a =1b =−4，∴抛物线的表达式为y =x 2−4x −5，(2)设H(t,t 2−4t −5)，∵CE//x 轴，∴点E 的纵坐标为−5，∵E 在抛物线上，∴x 2−4x −5=−5，∴x =0(舍)或x =4，∴E(4,−5)，∴CE =4，∵B(5,0)，C(0,−5)，∴直线BC 的解析式为y =x −5，∴F(t,t −5)，∴HF =t −5−(t 2−4t −5)=−(t −52)2+254，∵CE//x 轴，HF//y 轴，∴CE ⊥HF ，∴S 四边形CHEF =12CE ⋅HF =−2(t −52)2+252，∴H(52,−354)；(3)如图2，∵K 为抛物线的顶点，∴K(2,−9)，∴K 关于y 轴的对称点K′(−2,−9)，∵M(4,m)在抛物线上，∴M(4,−5)，∴点M关于x轴的对称点M′(4,5)，∴直线K′M′的解析式为y=73x−133，∴P(137,0)，Q(0,−133).【解析】(1)根据待定系数法直接确定出抛物线解析式；(2)先求出直线BC的解析式，进而求出四边形CHEF的面积的函数关系式，即可求出；(3)利用对称性找出点P，Q的位置，进而求出P，Q的坐标．此题是二次函数综合题，主要考查了待定系数法，四边形的面积的计算方法，对称性，解的关键是利用对称性找出点P，Q的位置，是一道中等难度的题目．18.【答案】解：(1)当x=0时，y=x2−2ax−1=−1，∴点A的坐标为：(0,−1)；(2)将点(1,2)代入y=x2−2ax−1，得：2=1−2a−1，解得：a=−1，∴函数的表达式为：y=x2+2x−1，∵y=x2+2x−1=(x+1)2−2，∴抛物线的开口向上，对称轴为x=−1，如图1所示：∴当x>−1时，y随x的增大而增大；(3)抛物线y=x2−2ax−1=(x−a)2−a2−1的对称轴为：x=a，顶点坐标为：(a,−a2−1)，当a>0时，对称轴在y轴右侧，如图2所示：∵x≤0，∴最低点就是A(0,−1)，∵图象的最低点到直线y=2a的距离为2，∴2a−(−1)=2，解得：a=12；当a<0，对称轴在y轴左侧，顶点(a,−a2−1)就是最低点，如图3所示：∴2a −(−a 2−1)=2，整理得：(a +1)2=2，解得：a 1=−1−√2，a 2=−1+√2(不合题意舍去)；综上所述，a 的值为12或−1−√2；(4)∵a <0，Rt △EFG 三个顶点的坐标分别为E(−1,−1)、F(−1,a −1)、G(0,a −1)， ∴直角边为EF 与FG ，∵抛物线y =x 2−2ax −1=(x −a)2−a 2−1的对称轴为：x =a ，A(0,−1)， ∴AA′=−2a ，当点P 在EF 边上时，如图4所示：则x p =−1，∵EA =OA =1，∴点P 在对称轴x =a 的左侧，∴PP′=2(a +1)，∵AA′=2PP′，∴−2a =2×2(a +1)，解得：a =−23；当点P 在FG 边上时，如图5所示：则y p =a −1，∴x 2−2ax −1=a −1，解得：x 1=a +√a 2+a ，x 2=a −√a 2+a ，∴PP′=a +√a 2+a −(a −√a 2+a)=2√a 2+a ，∵AA′=2PP′，∴−2a =4√a 2+a ，解得：a 1=−43，a 2=0(不合题意舍去)；综上所述，a 的值为−23或−43．【解析】(1)当x =0时，代入y =x 2−2ax −1，即可得出结果；(2)将点(1,2)代入y =x 2−2ax −1，得a =−1，则函数的表达式为y =x 2+2x −1，由y =x 2+2x −1=(x +1)2−2，得出抛物线的开口向上，对称轴为x =−1，则当x >−1时，y 随x 的增大而增大；(3)抛物线y =x 2−2ax −1=(x −a)2−a 2−1的对称轴为x =a ，顶点坐标为(a,−a 2−1)，当a >0时，对称轴在y 轴右侧，最低点就是A(0,−1)，则2a −(−1)=2，即可得出结果；当a <0，对称轴在y 轴左侧，顶点(a,−a 2−1)就是最低点，则2a −(−a 2−1)=2，即可得出结果；(4)易证直角边为EF 与FG ，由抛物线的对称轴为x =a ，A(0,−1)，则AA′=−2a ，当点P 在EF 边上时，PP′=2(a +1)，则−2a =2×2(a +1)，即可得出结果；当点P 在FG 边上时，求出PP′=2√a 2+a ，则−2a =4√a 2+a ，即可得出结果．本题是二次函数综合题，主要考查了二次函数图象与性质、待定系数法求解析式、直角三角形的性质、解一元二次方程、分类讨论等知识；熟练掌握二次函数图象与性质是解题的关键．1、最困难的事就是认识自己。

沪科版-数学-九年级上册-九上22.5二次函数的应用同步练习及答案

22.5二次函数的应用同步练习第1题. 用8m 长木条，做成如图的窗框（包括中间棱），若不计损耗，窗户的最大面积为2m ．答案：43第2题. 在底边长20cm BC =，高12cm AM =的三角形铁板ABC 上，要截一块矩形铁板EFGH ，如图所示．当矩形的边EF =cm 时，矩形铁板的面积最大，其最大面积为2cm ．答案：6 60ＡＥＭＣＨＮ第3题. 如图，用20m 长的铁丝网围成一个一面靠墙的矩形养殖场，其养殖场的最大面积为（）2m Ａ．45 Ｂ．50Ｃ．60Ｄ．65答案：Ｂ第4题. 用长8m 的铝合金条制成如图形状的矩形窗框，为了使窗户的透光面积最大，那么这个窗户的最大透光面积是（）Ａ．264m 25 Ｂ．24m 3Ｃ．28m 3Ｄ．24m答案：Ｃ第5题. 用长8m 的铝合金条制成如图形状的矩形窗框，为了使窗户的透光面积最大，那么这个窗户的最大透光面积是（）Ａ．264m 25Ｂ．24m 3 Ｃ．28m 3Ｄ．24m答案：Ｃ第6题. 如图，用长10m 的铝合金条制成下部为矩形、上部为半圆的窗框（包括窗棱CD ），若使此窗户的透光面积最大，则最大透光面积为（）2mＡ．50πＢ．504+π Ｃ．508+πＤ．5016+π答案：Ｃ第7题. 图是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图，横截面的地平线为x 轴，横断面的对称轴为y 轴，桥拱的DGD '部分为一段抛物线，顶点G 的高度为8m ，AD 和A D ''是两侧高为5.5m 的支柱，OA 和OA '为两个方向的汽车通行区，宽都为15m ，线段CD 和C D ''为两段对称的上桥斜坡，其坡度为1:4（即:1:4DA AC =）．（1）求桥拱DGD '所在抛物线的函数表达式．（2）BE 和B E ''为支撑斜坡的立柱，其高都为4m ，为相应的AB 和A B ''两个方向的行人及非机动车通行区，试求AB 和A B ''的宽．（3）按规定，汽车通过桥下时，载货最高处和桥拱间的距离不得小于0.4m ，今有一大型运货汽车，装载某大型设备后，其宽为4m ，设备的顶部与地面距离为7m ，它能否从OA （或OA '）区域安全通过，请说明理由．ＤＣＢD 'E ''B ' A 'ＯＡＢＣxyＧＤＥ答案：（1）设DGD '所在抛物线为2(0)y ax c a =+<，(08)G ，，(15)D ，5.5，8225 5.5c a c =⎧∴⎨+=⎩，，190a =-，8c =，21890y x ∴=-+．（2）14EB BC =，4BE =，16BC =，22166AB AC BC =-=-=，AB ∴和A B ''宽都为6m ．（3）在21890y x =-+中，当4x =时，137********y =-⨯+=．37197(70.4)04545∴-+=>，∴该货车可以从OA （或OA '）区域安全通过．第8题. 如图所示，公园要建造圆形的喷水池，在水池中央垂直于水面处安装一个柱子OA ，O 恰在水面中心， 1.25m OA =，由A 处的喷头向外喷水，水流在各个方向沿形状相同的抛物线路线落下，为使水流形状较为漂亮，要求设计成水流离OA 距离为1m 处达到距水面最大高度2.25m ．（1）以O 为坐标轴原点，OA 为y 轴建立直角坐标系，求抛物线ACB 的函数表达式；（2）水池半径至少要多少米，才能使喷出的水流不致落到池外？（3）若水池的半径为3.5m ，要使水流不落到池外，此时水流高度应达多少米（精确到0.1m ）？ＣＡＯy答案：（1）依题意可知(01.25)A ，，(12.25)C ，．抛物线开口向下，∴表达式为22(1) 2.252 1.25y x x x =--+=-++（2）令2(1) 2.250x --+=，得10.5x =-（舍去），2 2.5x =，∴水池半径至少2.5m ．（3）由于抛物线形状与上面相同，即二次项系数为1-，故可设此抛物线为2()y x h k =--+，求得117h =，1413 3.7(m)196k =≈，水流的最大高度为3.7m ．第9题. 如图，在△ABC 中，6AC =，12AB =，3cos 5A =，点M 在AB 上运动，MP AC ∥交BC 于P ，MQ AC ⊥于Q ，设AM x =，梯形MPCQ 的面积为y ．（1）求y 关于x 的函数表达式及自变量x 的取值范围；（2）当梯形MPCQ 的面积为4时，求x 的值；（3）梯形MPCQ 的面积是否有最大值，如果有，求出最大值；如果没有，请说明理由．答案：（1）由MP AC ∥，得△MBP ∽△ABC ，MP MB AC AB =，162MP x =-．在Rt AQM △中，3cos 5A =，35AQ x =，365CQ x =-，45MQ x =．1()2y MP CQ MQ =+1134662255x x x ⎛⎫=-+- ⎪⎝⎭，ＰＢＱ21124255y x x ∴=-+，06x <<．（2）当1011x =时，4y =．（3）当6011x =时，梯形面积最大，为14411．第10题. 某农场种植一种蔬菜，销售员张平根据往年的销售情况，对今年这种蔬菜的销售价格进行了预测，预测情况如图，图中的抛物线（部分）表示这种蔬菜销售价与月份之间的关系．观察图象，你能得到关于这种蔬菜销售情况的哪些信息？答题要求：（1）请提供四条信息；（2）不必求函数的表达式．答案：（1）2月份每千克销售价是3.5元（2）7月份每千克销售价是0.5元（3）1月到7月的销售价逐月下降（4）7月到12月的销售价逐月上升（5）2月与7月的销售差价是3元／kg （6）7月份销售价最低，1月份销售价最高（7）6月与8月、5月与9月、4月与10月、3月与11月、2月与12月的销售价相同（答案不唯一）第11题. 用12m 长的木条，做一个有一条横档的矩形窗子，为使透进的光线最多，则窗子的横档长为 m ．1 2 3 4 5 6 7 8 9 11112 3 45月份每千克销售价/元答案：2第12题. 如图，用12m 长的木方，做一个有一条横档的矩形窗子，为使透进的光线最多，应选择窗子的长、宽各为 m ．答案：3、2第13题. 如图，在矩形ABCD 中，6cm AB =，12cm BC =，点P 从A 出发沿AB 边向点B 以1cm/s 的速度移动，同时点Q 从点B 出发沿BC 边以2cm/s 的速度移动，分别到达B ，C 两点后就停止运动．（1）设运动开始后第s t 时，五边形APQCD 的面积为2cm S ，试写出S 与t 的函数关系式，并指出自变量t 的取值范围．（2）第几秒五边形APQCD 的面积最小？是多少？答案：（1）第s t 时，AP t =，6PB t =-，2BQ t =，故21(6)262PBQSt t t t =⨯-=-+． 61272ABCD S =⨯=矩形，272672(06)PBQS St t t ∴=-=-+≤≤．ＤＣＱＢＡ（2）2(3)63S t =-+，故当3t =时，S 有最小值63，即第3s 时，五边形APQCD 的面积最小，为263cm ．第14题. 如图，有长为24m 的篱笆，现一面利用墙（墙的最大可用长度a 为10m ）围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB 为cm x ，面积为2m S ．（1）求S 与x 的函数关系式．（2）要围成面积为245m 的花圃，AB 的长是多少米？（3）能围成面积比245m 还大的花圃吗？如果能，求出最大面积，并说明围法；如果不能，请说明理由．答案：（1）243BC x =-，故214(243)32483S x x x x x ⎛⎫=-=-+<⎪⎝⎭≤．（2）由已知得232445x x -+=，即28150x x -+=，解得13x =，25x =，当3x =时，24331510BC =-⨯=>，不合题意，故5x =，即5m AB =．（3）2223243(8)3(4)48S x x x x x =-+=--=--+．1483x <≤，1443>，S ∴随着x 的增大而减小．故当143x =时，S 有最大值22142483446(m )33⎛⎫--= ⎪⎝⎭．∴能围成面积比245m 还大的花圃．围法：42431031-⨯=，花圃的长BC 为10m ，宽为4m 32．这时花圃面积最大，为2246m 3．第15题. 如图，在Rt△ABC 中，90C ∠=，4BC =，8AC =，点D 在斜边AB 上，分别作DE AC ⊥于E ，DF BC ⊥于F ，设DE x =，DF y =．（1）求y 与x 之间的函数关系，并求出x 的取值范围．（2）设四边形DECF 的面积为S ，试求S 的最大值．答案：（1）由已知得DECF 是矩形，故EC DF y ==，88AE EC y =-=-．由DE BC ∥得△ADE ∽△ABC ，DE AE BC AC ∴=，即848x y-=，82(04)y x x ∴=-<<．（2）2(82)2(2)8S xy x x x ==-=--+．当2x =时，S 有最大值8．第16题. 某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元．在销售过程中发现，年销售量y （万件）与销售单位x （元）之间存在着如图所示的一次函数关系．（1）求y 关于x 的函数关系式；（2）试写出该公司销售该种产品的年获利z （万元）关于销售单价x （元）的函数关系式（年获利＝年销售额－年销售产品总进价－年总开支）．当销售单价x 为何值时，年获利最大？并求这个最大值；（3）若公司希望该种产品一年的销售获利不低于40万元，借助（2）中函数的图象，请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？ＡＣＤ答案：解：（1）设y kx b =+，它过点(605)(804)，，，560480k b k b =+⎧⎨=+⎩解得：1208k b ⎧=-⎪⎨⎪=⎩1820y x =-+∴．（2）21140120(8)(40)120104402020z yx y x x x x =--=-+--=-+- ∴当100x =元时，最大年获利为60万元．（3）令40z =，得21401044020x x =-+-，整理得：220096000x x -+= 解得：180x =，2120x =由图象可知，要使年获利不低于40万元，销售单价应在80元到120元之间．又因为销售单价越低，销售量越大，所以要使销售量最大，又要使年获利不低于40万元，销售单价应定为80元．第17题. 如图9，在平行四边形ABCD 中，AD =4 cm ，∠A =60°，BD ⊥AD . 一动点P 从A 出发，以每秒1 cm 的速度沿A →B →C 的路线匀速运动，过点P 作直线PM ，使PM ⊥AD .(1) 当点P 运动2秒时，设直线PM 与AD 相交于点E ，求△APE 的面积；0 20 4060 8012 3 4 5 6 y (万件)x (元4060 080 100 120x (元)z (万元)(2) 当点P 运动2秒时，另一动点Q 也从A 出发沿A →B →C 的路线运动，且在AB 上以每秒1 cm 的速度匀速运动，在BC 上以每秒2 cm 的速度匀速运动. 过Q 作直线QN ，使QN ∥PM . 设点Q 运动的时间为t 秒(0≤t ≤10)，直线PM 与QN 截平行四边形ABCD 所得图形的面积为S cm 2 .① 求S 关于t 的函数关系式；② (附加题) 求S 的最大值.答案：(1) 当点P 运动2秒时，AP =2 cm ，由∠A =60°，知AE =1，PE =3.∴ S ΔAPE =23. (2) ① 当0≤t ≤6时，点P 与点Q 都在AB 上运动，设PM 与AD 交于点G ，QN 与AD 交于点F ，则AQ =t ，AF =2t ，QF =t 23，AP =t +2，AG =1+2t ，PG =t 233+. ∴ 此时两平行线截平行四边形ABCD 的面积为S =2323+t . 当6≤t ≤8时，点P 在BC 上运动，点Q 仍在AB 上运动. 设PM 与DC 交于点G ，QN 与AD 交于点F ，则AQ =t ，AF =2t，DF =4-2t ，QF =t 23，BP =t-6，CP =10-t ，PG =3)10(t -，而BD =34，故此时两平行线截平行四边形ABCD 的面积为S =3343108352-+-t t . 当8≤t ≤10时，点P 和点Q 都在BC 上运动. 设PM 与DC 交于点G ，QN 与DC 交于点F ，则CQ =20-2t ，QF =(20-2t )3，CP =10-t ，PG =3)10(t -.∴ 此时两平行线截平行四边形ABCD 的面积为S =31503302332+-t t .故S 关于t 的函数关系式为2233(06)53103343(68)33303150 3.(810)t t S t t t t t t ⎧+⎪⎪⎪⎪=-+-⎨⎪⎪-+⎪⎪⎩，≤≤，≤≤≤≤ ②(附加题)当0≤t ≤6时，S 的最大值为237；当6≤t ≤8时，S 的最大值为36；当8≤t ≤10时，S 的最大值为36；所以当t =8时，S 有最大值为36第18题. 在青岛市开展的创城活动中，某居民小区要在一块一边靠墙（墙长15m ）的空地上修建一个矩形花园ABCD ，花园的一边靠墙，另三边用总长为40m 的栅栏围成（如图所示）．若设花园的BC x 边长为（m ），花园的面积为y （m 2）．（1）求y 与x 之间的函数关系式，并写出自变量x 的取值范围；（2）满足条件的花园面积能达到200 m 2吗？若能，求出此时x 的值；若不能，说明理由；（3）根据(1)中求得的函数关系式,描述其图象的变化趋势；并结合题意判断当x 取何值时，花园的面积最大？最大面积为多少？解：（1）（2）A BCD（3）答案：解：（1）根据题意得：(40)2x y x-= 2120(015)2y x x x =-+<∴≤ （2）当200y =时，即21202002x x -+= ∴2404000x x -+=解得：2015x =>015x <∵≤∴此花园的面积不能达到200m 2（3）21202y x x =-+的图像是开口向下的抛物线，对称轴为20x =． ∴当015x <≤时，y x 随的增大而增大∴当15x y =时，有最大值21152015187.52y =-⨯+⨯=最大值（m 2）即：当15x =时，花园面积最大，最大面积为187.5m 2第19题. 市政府为改善居民的居住环境，修建了环境幽雅的环城公园，为了给公园内的草评定期喷水，安装了一些自动旋转喷水器，如图所示，设喷水管AB 高出地面1.5m ，在B 处有一个自动旋转的喷水头，一瞬间喷出的水流呈抛物线状．喷头B 与水流最高点C 的连线与地平面成45的角，水流的最高点C 离地平面距离比喷水头B 离地平面距离高出2m ，水流的落地点为D ．在建立如图所示的直角坐标系中：（１）求抛物线的函数解析式；（２）求水流的落地点D 到A 点的距离是多少m ？答案：解：在如图所建立的直角坐标系中，由题意知，B 点的坐标为(01.5)，， 45CBE BEC ∠=∴，△为等腰直角三角形， 2BE ∴=，C ∴点坐标为(23.5)，（1）设抛物线的函数解析式为2(0)y ax bx c a =++≠，则抛物线过点(01.5)，顶点为(23.5)，，∴当0x =时， 1.5y c ==由22ba -=，得4b a =-，由24 3.54ac b a -=，得2616 3.54a a a -=解之，得0a =（舍去），1422a b a =-∴=-=，．所以抛物线的解析式为213222y x x =-++．（２）D 点为抛物线213222y x x =-++的图象与x 轴的交点，∴当0y =时，即：2132022x x -++=，解得27x =±，27x =-不合题意，舍去，取27x =+． D ∴点坐标为()(2727AD ∴=+，，（m ）．答：水流的落地点D 到A 点的距离是(27+m ．ＥＣＦＡ(Ｏ)x D 1.5m45 B。

2023年二轮复习解答题专题十七：二次函数的应用(销售利润问题)(原卷版)

2023年二轮复习解答题专题十七：二次函数的应用——销售利润问题方法点睛二次函数解决销售问题是我们生活中经常遇到的问题，这类问题通常是根据实际条件建立二次函数关系式，然后利用二次函数的最值或自变量在实际问题中的取值解决利润最大问题.典例分析例1：（2022青岛中考）李大爷每天到批发市场购进某种水果进行销售，这种水果每箱10千克，批发商规定：整箱购买，一箱起售，每人一天购买不超过10箱；当购买1箱时，批发价为8.2元/千克，每多购买1箱，批发价每千克降低0.2元．根据李大爷的销售经验，这种水果售价为12元/千克时，每天可销售1箱；售价每千克降低0.5元，每天可多销售1箱．（1）请求出这种水果批发价y（元/千克）与购进数量x（箱）之间的函数关系式；（2）若每天购进的这种水果需当天全部售完，请你计算，李大爷每天应购进这种水果多少箱，才能使每天所获利润最大？最大利润是多少？专题过关1. （2022鄂尔多斯中考）（10分）某超市采购了两批同样的冰墩墩挂件，第一批花了6600元，第二批花了8000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进50个．（1）求第二批每个挂件的进价；（2）两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？2．（2022荆门中考）（10分）某商场销售一种进价为30元/个的商品，当销售价格x（元/个）满足40＜x ＜80时，其销售量y （万个）与x 之间的关系式为y ＝﹣x +9．同时销售过程中的其它开支为50万元．（1）求出商场销售这种商品的净利润z （万元）与销售价格x 函数解析式，销售价格x 定为多少时净利润最大，最大净利润是多少？（2）若净利润预期不低于17.5万元，试求出销售价格x 的取值范围；若还需考虑销售量尽可能大，销售价格x 应定为多少元？3. （2022宁波中考）为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y 千克与每平方米种植的株数x （28x ££，且x 为整数）构成一种函数关系．每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克．（1）求y 关于x 的函数表达式．（2）每平方米种植多少株时，能获得最大产量？最大产量为多少千克？4. （2022广元中考）为推进“书香社区”建设，某社区计划购进一批图书．已知购买2本科技类图书和3本文学类图书需154元，购买4本科技类图书和5本文学类图书需282元．（1）科技类图书与文学类图书的单价分别为多少元？（2）为了支持“书香社区”建设，助推科技发展，商家对科技类图书推出销售优惠活动（文学类图书售价不变）：购买科技类图书超过40本但不超过50本时，每增加1本，单价降低1元；超过50本时，均按购买50本时的单价销售．社区计划购进两种图书共计100本，其中科技类图书不少于30本，但不超过60本．按此优惠，社区至少要准备多少购书款？4. （2022滨州中考）某种商品每件的进价为10元，若每件按20元的价格销售，则每月能卖出360件；若每件按30元的价格销售，则每月能卖出60件．假定每月的销售件数y 是销售价格x （单位：元）的一次函数．（1）求y 关于x 的一次函数解析式；（2）当销售价格定为多少元时，每月获得的利润最大？并求此最大利润．5. （2022营口中考）某文具店最近有A ，B 两款纪念册比较畅销，该店购进A 款纪念册5本和B 款纪念册4本共需156元，购进A 款纪念册3本和B 款纪念册5本共需130元．在销售中发现：A 款纪念册售价为32元/本时，每天的销售量为40本，每降低1元可多售出2本；B 款纪念册售价为22元/本时，每天的销售量为80本，B款纪念册每天的销售量与售价的之间满足一次函数关系，其部分对应数据如下表所示：售价（元/本）…22232425…每天销售量（本）…80787674…（1）求A ，B 两款纪念册每本的进价分别为多少元；（2）该店准备降低每本A 款纪念册的利润，同时提高每本B 款纪念册的利润，且这两款纪念册每天销售总数不变，设A 款纪念册每本降价m 元．①直接写出B 款纪念册每天的销售量（用含m 的代数式表示）；②当A 款纪念册售价为多少元时，该店每天所获利润最大，最大利润多少？6. （2022盘锦中考）某商场新进一批拼装玩具，进价为每个10元，在销售过程中发现．，日销售量y （个）与销售单价x （元）之间满足如图所示的一次函数关系．（1）求y 与x 的函数关系式（不要求写出自变量x 的取值范围）；（2）若该玩具某天的销售利润是600元，则当天玩具的销售单价是多少元？（3）设该玩具日销售利润为w 元，当玩具的销售单价定为多少元时，日销售利润最大？最大利润是多少元？7. （2022抚顺中考）某超市以每件13元的价格购进一种商品，销售时该商品的销售单价不低于进价且不高于18元．经过市场调查发现，该商品每天的销售量y （件）与销售单价x （元）之间满足如图所示的一次函数关系．是（1）求y 与x 之间的函数关系式；（2）销售单价定为多少时，该超市每天销售这种商品所获的利润最大？最大利润是多少？8．（2022葫芦岛中考）（12分）某蔬菜批发商以每千克18元的价格购进一批山野菜，市场监督部门规定其售价每千克不高于28元．经市场调查发现，山野菜的日销售量y （千克）与每千克售价x （元）之间满足一次函数关系，部分数据如表：每千克售价x （元）……202224……日销售量y （千克）……666054……（1）求y 与x 之间的函数关系式；（2）当每千克山野菜的售价定为多少元时，批发商每日销售这批山野菜所获得的利润最大？最大利润为多少元？9. （2022铜仁中考）为实施“乡村振兴”计划，某村产业合作社种植了“千亩桃园”．2022年该村桃子丰收，销售前对本地市场进行调查发现：当批发价为4千元/吨时，每天可售出12吨，每吨涨1千元，每天销量将减少2吨，据测算，每吨平均投入成本2千元，为了抢占市场，薄利多销，该村产业合作社决定，批发价每吨不低于4千元，不高于5.5千元．请解答以下问题：（1）求每天销量y （吨）与批发价x （千元/吨）之间的函数关系式，并直接写出自变量x 的取值范围；（2）当批发价定为多少时，每天所获利润最大？最大利润是多少？10．（2022天门中考）（10分）某超市销售一种进价为18元/千克的商品，经市场调查后发现，每天的销售量y （千克）与销售单价x （元/千克）有如下表所示的关系：销售单价x （元/千…2022.52537.540…克）销售量y （千克）…3027.52512.510…（1）根据表中的数据在如图中描点（x ，y ），并用平滑曲线连接这些点，请用所学知识求出y 关于x 的函数关系式；（2）设该超市每天销售这种商品的利润为w （元）（不计其它成本）．①求出w 关于x 的函数关系式，并求出获得最大利润时，销售单价为多少；②超市本着“尽量让顾客享受实惠”的销售原则，求w ＝240（元）时的销售单价．11. （2022荆州中考）某企业投入60万元（只计入第一年成本）生产某种产品，按网上订单生产并销售（生产量等于销售量）．经测算，该产品网上每年的销售量y （万件）与售价x （元/件）之间满足函数关系式y ＝24－x ，第一年除60万元外其他成本为8元/件．（1）求该产品第一年的利润w （万元）与售价x 之间的函数关系式；（2）该产品第一年利润为4万元，第二年将它全部作为技改资金再次投入（只计入第二年成本）后，其他成本下降2元/件．①求该产品第一年的售价；②若第二年售价不高于第一年，销售量不超过13万件，则第二年利润最少是多少万元？12. （2022十堰中考）某商户购进一批童装，40天销售完毕．根据所记录的数据发现，日销售量y （件）与销售时间x （天）之间的关系式是203062403040x x y x x <£ì=í-+<£î，，，销售单价p （元/件）与销售时间x （天）之间的函数关系如图所示．（1）第15天的日销售量为_________件；（2）当030x <£时，求日销售额的最大值；（3）在销售过程中，若日销售量不低于48件的时间段为“火热销售期”，则“火热销售期”共有多少天？13 .（2022大庆中考）果园有果树60棵，现准备多种一些果树提高果园产量．如果多种树，那么树之间的距离和每棵果树所受光照就会减少，每棵果树的平均产量随之降低．根据经验，增种10棵果树时，果园内的每棵果树平均产量为75kg ．在确保每棵果树平均产量不低于40kg 的前提下，设增种果树x （0x >且x 为整数）棵，该果园每棵果树平均产量为kg y ，它们之间的函数关系满足如图所示的图象．（1）图中点P 所表示的实际意义是________________________，每增种1棵果树时，每棵果树平均产量减少____________kg ；（2）求y 与x 之间的函数关系式，并直接写出自变量x 的取值范围；（3）当增种果树多少棵时，果园的总产量(kg)w 最大？最大产量是多少？14. （2022贺州中考） 2022年在中国举办的冬奥会和残奥会令世界瞩目，冬奥会和残奥会的吉祥物冰墩墩和雪容融家喻户晓，成为热销产品，某商家以每套34元的价格购进一批冰墩墩和雪容融套件，若该产品每套的售价是48元时，每天可售出200套；若每套售价提高2元，则每天少卖4套．（1）设冰墩墩和雪容融套件每套售价定为x 元时，求该商品销售量y 与x 之间的函数关系式；（2）求每套售价定为多少元时，每天销售套件所获利润W 最大，最大利润是多少元？15. （2022北部湾中考）打油茶是广西少数民族特有的一种民俗，某特产公司近期销售一种盒装油茶，每盒的成本价为50元，经市场调研发现，该种油茶的月销售量y （盒）与销售单价x （元）之间的函数图像如图所示．（1）求y 与x 的函数解析式，并写出自变量x 的取值范围；（2）当销售单价定为多少元时，该种油茶月销售利润最大求出最大利润．16.（2022郑州一模）某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，某村组织村民加工包装土特产销售给游客，以增加村民收入，试销的30天中，该村第一天卖出土特产42千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出6千克，第x 天的售价为y 元/千克，y 关于x 的函数解析式为y ＝()()821202030mx m x n x ì-£<ïí££ïî，x 为正整数，且第14天的售价为34元/千克，第27天的售价为27元/千克．已知土特产的成本是21元/千克，每天的利润是W 元（利润＝销售收入﹣成本）．（1）m ＝，n ＝；（2）求每天的利润W 元与销售的天数x （天）之间的函数关系式；（3）在销售土特产的30天中，当天利润不低于1224元的共有多少天？17. （2022河南天一大联考）某体育用品专卖店新进一批篮球和足球，已知每个篮球的进的价比每个足球的进价多30元，用6000元购进篮球的数量与用4800元购进足球的数量相同．（1）求篮球、足球每个进价分别为多少元？（2）专卖店准备在进价基础上，篮球加价60%作为售价，足球加价50%作为售价．该专卖店平均每天卖出篮球120个，足球100个．为回馈顾客，减少库存，专卖店准备搞活动促销．经调查发现，篮球、足球的销售单价每降低10元，这两种商品每天都可多销售20个，为了使每天获取更大的利润，该专卖店决定把篮球、足球的销售单价都下降a 元．请通过计算说明，如何定价，专卖店才能获取最大利润．18. （2022河南商水二模）小强经营的网店以特色小吃为主，其中一品牌茶饼的进价为6元/袋，拟采取线上和线下两种方式进行销售．调查发现，线下的月销量y （单位：袋）与线下的售价x （单位：元/袋，1016x ££，且x 为整数）满足一次函数的关系，部分数据如下表所示．x （元/袋）1011121314y （袋）10090807060（1）求y 与x 的函数关系式．（2）若线上的售价始终比线下的售价每袋便宜1元，且线上的月销量固定为60袋．问当x 为多少时，线上和线下的月利润总和达到最大？并求出此时的最大利润．19.（2022河南虞城二模）铁棍山药上有像铁锈一样的痕迹．故得名铁棍山药．某网店购进铁根山药若干箱．物价部门规定其销售单价不高于80元/箱，经市场调查发现：销件单价定为80元/箱时，每日销售20箱；如调整价格，每降价1元/箱，每日可多销售2箱．（1）已知某天售出铁棍山药70箱，则当天的销售单价为______元/箱．（2）该网店现有员工2名．每天支付员工的工资为每人每天100元，每天平均支付运费及其他费用250元，当某天的销售价为45元/箱时，收支恰好平衡．①铁棍山药的进价；②若网店每天的纯利润(收入-支出)全部用来偿还一笔15000元的贷款，则至少需多少天才能还清贷款？20. （2022平顶山一模）基商场以30元/台的价格购进500台新型电子产品，在销售过程中发现，其日销售量y （单位∶台）与销售单价x （单位∶元）之间存在如图所示的函数关系．（1）求y 与x 的函数关系式；（2）按物价部门规定，产品的利润率不得超过 80%，该电子产品每台最高售价为元，此时的日销售量为台；（3）若按照日销售获得最大利润时的售价，计算商场销售完这批电子产品获得的总利润．21. （2022开封二模）“慈母手中线，游子身上衣”，为感恩母亲，许多子女选择用康乃馨这种鲜花来表达对母亲的祝福．某花店采购了一批康乃馨，进价是每支8元．当每支售价为12元时，可销售30支；当每支售价为10元时，可销售40支．在销售过程中，发现这种康乃馨的销售量y （支）是每支售价x （元）的一次函数()030x £<．（1）求y 与x 之间的函数关系式；（2）设此花店这种康乃馨的销售利润是w 元，根据题意：当销售单价为多少元时，商家获得利润最大．22. （2022河南安阳县一模）疫情期间，为满足市民防护需求，某药店想要购进A 、B 两种口罩，B 型口罩的每盒进价是A 型口罩的两倍少10元．用6000元购进A 型口罩的盒数与用10000元购进B 型口罩盒数相同．（1）A 、B 型口罩每盒进价分别为多少元？（2）经市场调查表明，B 型口罩受欢迎，当每盒B 型口罩售价为60元时，日均销量为100盒，B 型口罩每盒售价每增加1元，日均销量减少5盒．当B 型口罩每盒售价多少元时，销售B 型口罩所得日均总利润最大？最大日均总利润为多少元？23. （2022河南汝州一模）小明大学毕业回家乡创业，第一期培植盆景与花卉各50盆．已知2盆盆景与1盆花卉的利润共330元，1盆盆景与3盆花卉的利润共240元．（1）求1盆盆景和1盆花卉的利润各为多少元？（2）调研发现：盆景每增加1盆，盆景的平均每盆利润减少2元；每减少1盆，盆景的平均每盆利润增加2元；花卉的平均每盆利润始终不变．小明计划第二期培植盆景与花卉共100盆，设培植的盆景比第一期增加x 盆，第二期盆景与花卉售完后的利润分别为1W ，2W （单位：元）．①含x 的代数式分别表示1W ，2W ；②当x 取何值时，第二期培植的盆景与花卉售完后获得的总利润W 最大，最大总利润是多少元？。

沪科版九年级上册数学《二次函数应用题》试题

沪科版九年级上册数学二次函数应用题要点提示1. 二次函数的解析式：（1）一般式：；（2）顶点式：2. 顶点式的几种特殊形式.⑴ ， ⑵ ， ⑶ ，（4） .3．二次函数c bx ax y ++=2通过配方可得224()24b ac b y a x a a -=++，其抛物线关于直线x = 对称，顶点坐标为（，）.⑴ 当0a >时，抛物线开口向，有最（填“高”或“低”）点,当x = 时，y 有最（“大”或“小”）值是； ⑵ 当0a <时，抛物线开口向，有最（填“高”或“低”）点,当x = 时，y 有最（“大”或“小”）值是．典例分析1. 橘子洲头要建造一个圆形的喷水池，并在水池中央垂直安装一个柱子OP ，柱子顶端P 处装上喷头，由P 处向外喷出的水流（在各个方向上）沿形状相同的抛物线路径落下（如图所示）.若已知OP ＝3米，喷出的水流的最高点A 距水平面的高度是4米，离柱子OP 的距离为1米.（1）求这条抛物线的解析式；（2）若不计其它因素，水池的半径至少要多少米，才能使喷出的水流不至于落在池外？2.随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润1y 与投资量x 成正比例关系，如图（1）所示；种植花卉的利润2y 与投资量x 成二次函数关系，如图（2）所示（注：利润与投资量的单位：万元）⑴ 分别求出利润1y 与2y 关于投资量x 的函数关系式；⑵ 如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润？他能获取的最大利润是多少？（1）（2）3.某广告公司设计一幅长为12米的矩形广告牌，广告设计费为每平方米1000元。

设矩形的一边长为x 米，面积为s 平方米.(1)求出s 与x 之间的函数关系式；(2)请你设计一个方案，使获得的设计费用最多，并求出这个费用；(3)为使广告牌美观大方，要求做成黄金矩形.请你按要求设计，并计算出可获得的设计费是多少（精确到元）？基础强化1.恒利商厦九月份的销售额为200万元，十月份的销售额下降了20%，商厦从十一月份起加强管理，改善经营，使销售额稳步上升，十二月份的销售额达到了193.6万元，求这两个月的平均增长率.2.某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染．请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？3.益群精品店以每件21元的价格购进一批商品，该商品可以自行定价，若每件商品售价a 元，则可卖出（350－10a）件，但物价局限定每件商品的利润不得超过20%，商店计划要盈利400元，需要进货多少件？每件商品应定价多少？4.国家为了加强对香烟产销的宏观管理,对销售香烟实行征收附加税政策. 现在知道某种品牌的香烟每条的市场价格为70元,不加收附加税时, 每年产销100万条,若国家征收附加税,每销售100元征税x元(叫做税率x%), 则每年的产销量将减少10x万条.要使每年对此项经营所收取附加税金为168万元,并使香烟的产销量得到宏观控制,年产销量不超过50万条,问税率应确定为多少?5.一块长和宽分别为40厘米和250厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体纸盒，使它的底面积为450平方厘米.那么纸盒的高是多少？6.某农场要建一个长方形的养鸡场，鸡场的一边靠墙（墙长18m），另三边用木栏围成，木栏长35m。

沪科新版九年级(上) 中考题同步试卷：21.4 二次函数的应用(13)

沪科新版九年级（上）中考题同步试卷：21.4 二次函数的应用（13）一、解答题（共30小题）1．如图，抛物线y＝x2﹣2mx（m＞0）与x轴的另一个交点为A，过P（1，﹣m）作PM⊥x 轴于点M，交抛物线于点B．点B关于抛物线对称轴的对称点为C．（1）若m＝2，求点A和点C的坐标；（2）令m＞1，连接CA，若△ACP为直角三角形，求m的值；（3）在坐标轴上是否存在点E，使得△PEC是以P为直角顶点的等腰直角三角形？若存在，求出点E的坐标；若不存在，请说明理由．2．如图，抛物线y＝﹣x2+x﹣2交x轴于A，B两点（点A在点B的左侧），交y轴于点C，分别过点B，C作y轴，x轴的平行线，两平行线交于点D，将△BDC绕点C逆时针旋转，使点D旋转到y轴上得到△FEC，连接BF．（1）求点B，C所在直线的函数解析式；（2）求△BCF的面积；（3）在线段BC上是否存在点P，使得以点P，A，B为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．3．如图，在平面直角坐标系中，四边形ABCD是等腰梯形，AD∥BC，AB＝DC，BC在x轴上，点A在y轴的正半轴上，点A，D的坐标分别为A（0，2），D（2，2），AB＝2，连接AC．（1）求出直线AC的函数解析式；（2）求过点A，C，D的抛物线的函数解析式；（3）在抛物线上有一点P（m，n）（n＜0），过点P作PM垂直于x轴，垂足为M，连接PC，使以点C，P，M为顶点的三角形与Rt△AOC相似，求出点P的坐标．4．如图，已知一次函数y1＝x+b的图象l与二次函数y2＝﹣x2+mx+b的图象C′都经过点B（0，1）和点C，且图象C′过点A（2﹣，0）．（1）求二次函数的最大值；（2）设使y2＞y1成立的x取值的所有整数和为s，若s是关于x的方程＝0的根，求a的值；（3）若点F、G在图象C′上，长度为的线段DE在线段BC上移动，EF与DG始终平行于y轴，当四边形DEFG的面积最大时，在x轴上求点P，使PD+PE最小，求出点P的坐标．5．如图，抛物线y＝ax2+bx+2与x轴交于点A（1，0）和B（4，0）．（1）求抛物线的解析式；（2）若抛物线的对称轴交x轴于点E，点F是位于x轴上方对称轴上一点，FC∥x轴，与对称轴右侧的抛物线交于点C，且四边形OECF是平行四边形，求点C的坐标；（3）在（2）的条件下，抛物线的对称轴上是否存在点P，使△OCP是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．6．如图，抛物线y＝﹣x2+2x+3与x轴相交于A、B两点，与y轴交于点C，顶点为D，抛物线的对称轴DF与BC相交于点E，与x轴相交于点F．（1）求线段DE的长；（2）设过E的直线与抛物线相交于点M（x1，y1），N（x2，y2），试判断当|x1﹣x2|的值最小时，直线MN与x轴的位置关系，并说明理由；（3）设P为x轴上的一点，∠DAO+∠DPO＝∠α，当tan∠α＝4时，求点P的坐标．7．如图，过A（1，0）、B（3，0）作x轴的垂线，分别交直线y＝4﹣x于C、D两点．抛物线y＝ax2+bx+c经过O、C、D三点．（1）求抛物线的表达式；（2）点M为直线OD上的一个动点，过M作x轴的垂线交抛物线于点N，问是否存在这样的点M，使得以A、C、M、N为顶点的四边形为平行四边形？若存在，求此时点M 的横坐标；若不存在，请说明理由；（3）若△AOC沿CD方向平移（点C在线段CD上，且不与点D重合），在平移的过程中△AOC与△OBD重叠部分的面积记为S，试求S的最大值．8．如图，在平面直角坐标系xOy中，一次函数y＝x+m的图象与x轴交于A（﹣1，0），与y轴交于点C．以直线x＝2为对称轴的抛物线C1：y＝ax2+bx+c（a≠0）经过A、C两点，并与x轴正半轴交于点B．（1）求m的值及抛物线C1：y＝ax2+bx+c（a≠0）的函数表达式．（2）设点D（0，），若F是抛物线C1：y＝ax2+bx+c（a≠0）对称轴上使得△ADF 的周长取得最小值的点，过F任意作一条与y轴不平行的直线交抛物线C1于M1（x1，y1），M2（x2，y2）两点，试探究+是否为定值？请说明理由．（3）将抛物线C1作适当平移，得到抛物线C2：y2＝﹣（x﹣h）2，h＞1．若当1＜x ≤m时，y2≥﹣x恒成立，求m的最大值．9．综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（﹣2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．（1）求抛物线W的解析式及顶点D的坐标；（2）将抛物线W和▱OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和▱O′A′B′C′，在向下平移的过程中，设▱O′A′B′C′与▱OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x 轴上的动点，点N是抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．10．如图，直线y＝2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y＝﹣x2+bx+c与直线BC交于点D（3，﹣4）．（1）求直线BD和抛物线的解析式；（2）在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；（3）在直线BD上方的抛物线上有一动点P，过点P作PH垂直于x轴，交直线BD于点H，当四边形BOHP是平行四边形时，试求动点P的坐标．11．复习课中，教师给出关于x的函数y＝2kx2﹣（4k+1）x﹣k+1（k是实数）．教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上．学生思考后，黑板上出现了一些结论．教师作为活动一员，又补充一些结论，并从中选出以下四条：①存在函数，其图象经过（1，0）点；②函数图象与坐标轴总有三个不同的交点；③当x＞1时，不是y随x的增大而增大就是y随x的增大而减小；④若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数．教师：请你分别判断四条结论的真假，并给出理由．最后简单写出解决问题时所用的数学方法．12．如图1，在菱形OABC中，已知OA＝2，∠AOC＝60°，抛物线y＝ax2+bx+c（a≠0）经过O，C，B三点．（Ⅰ）求出点B、C的坐标并求抛物线的解析式．（Ⅱ）如图2，点E是AC的中点，点F是AB的中点，直线AG垂直BC于点G，点P 在直线AG上．（1）当OP+PC的值最小时，求出点P的坐标；（2）在（1）的条件下，连接PE、PF、EF得△PEF，问在抛物线上是否存在点M，使得以M，B，C为顶点的三角形与△PEF相似？若存在，请求出点M的坐标；若不存在，请说明理由．13．如图，在平面直角坐标系中，抛物线与x轴交于点A（﹣1，0）和点B（1，0），直线y ＝2x﹣1与y轴交于点C，与抛物线交于点C、D．（1）求抛物线的解析式；（2）求点A到直线CD的距离；（3）平移抛物线，使抛物线的顶点P在直线CD上，抛物线与直线CD的另一个交点为Q，点G在y轴正半轴上，当以G、P、Q三点为顶点的三角形为等腰直角三角形时，求出所有符合条件的G点的坐标．14．如图1，矩形ABCD的边AD在y轴上，抛物线y＝x2﹣4x+3经过点A、点B，与x轴交于点E、点F，且其顶点M在CD上．（1）请直接写出下列各点的坐标：A，B，C，D；（2）若点P是抛物线上一动点（点P不与点A、点B重合），过点P作y轴的平行线l 与直线AB交于点G，与直线BD交于点H，如图2．①当线段PH＝2GH时，求点P的坐标；②当点P在直线BD下方时，点K在直线BD上，且满足△KPH∽△AEF，求△KPH面积的最大值．15．已知抛物线C1：y＝a（x+1）2﹣2的顶点为A，且经过点B（﹣2，﹣1）．（1）求A点的坐标和抛物线C1的解析式；（2）如图1，将抛物线C1向下平移2个单位后得到抛物线C2，且抛物线C2与直线AB 相交于C，D两点，求S△OAC：S△OAD的值；（3）如图2，若过P（﹣4，0），Q（0，2）的直线为l，点E在（2）中抛物线C2对称轴右侧部分（含顶点）运动，直线m过点C和点E．问：是否存在直线m，使直线l，m 与x轴围成的三角形和直线l，m与y轴围成的三角形相似？若存在，求出直线m的解析式；若不存在，说明理由．16．如图，在矩形AOCD中，把点D沿AE对折，使点D落在OC上的F点，已知AO＝8．AD ＝10．（1）求F点的坐标；（2）如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点，我们把这条直线称为抛物线的切线，已知抛物线过点O，F，且直线y＝6x﹣36是该抛物线的切线，求抛物线的解析式；（3）直线y＝k（x﹣3）﹣与（2）中的抛物线交于P、Q两点，点B的坐标为（3，﹣），求证：+为定值．（参考公式：在平面直角坐标系中，若M（x1，y1），N （x2，y2），则M，N两点间的距离为|MN|＝）17．如图，已知抛物线y＝x2﹣x﹣3与x轴的交点为A、D（A在D的右侧），与y轴的交点为C．（1）直接写出A、D、C三点的坐标；（2）若点M在抛物线对称轴上，使得MD+MC的值最小，并求出点M的坐标；（3）设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．18．如图，直角梯形ABCO的两边OA，OC在坐标轴的正半轴上，BC∥x轴，OA＝OC＝4，以直线x＝1为对称轴的抛物线过A，B，C三点．（1）求该抛物线的函数解析式；（2）已知直线l的解析式为y＝x+m，它与x轴交于点G，在梯形ABCO的一边上取点P．①当m＝0时，如图1，点P是抛物线对称轴与BC的交点，过点P作PH⊥直线l于点H，连结OP，试求△OPH的面积；②当m＝﹣3时，过点P分别作x轴、直线l的垂线，垂足为点E，F．是否存在这样的点P，使以P，E，F为顶点的三角形是等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．19．在平面直角坐标系xOy中，抛物线y＝x2﹣（m+n）x+mn（m＞n）与x轴相交于A、B 两点（点A位于点B的右侧），与y轴相交于点C．（1）若m＝2，n＝1，求A、B两点的坐标；（2）若A、B两点分别位于y轴的两侧，C点坐标是（0，﹣1），求∠ACB的大小；（3）若m＝2，△ABC是等腰三角形，求n的值．20．如图①，在平面直角坐标中，点A的坐标为（1，﹣2），点B的坐标为（3，﹣1），二次函数y＝﹣x2的图象为l1．（1）平移抛物线l1，使平移后的抛物线经过点A，但不过点B．①满足此条件的函数解析式有个．②写出向下平移且经点A的解析式．（2）平移抛物线l1，使平移后的抛物线经过A，B两点，所得的抛物线l2，如图②，求抛物线l2的函数解析式及顶点C的坐标，并求△ABC的面积．（3）在y轴上是否存在点P，使S△ABC＝S△ABP？若存在，求出点P的坐标；若不存在，请说明理由．21．如图，抛物线y＝ax2+bx+c（a，b，c是常数，a≠0）的对称轴为y轴，且经过（0，0）和（，）两点，点P在该抛物线上运动，以点P为圆心的⊙P总经过定点A（0，2）．（1）求a，b，c的值；（2）求证：在点P运动的过程中，⊙P始终与x轴相交；（3）设⊙P与x轴相交于M（x1，0），N（x2，0）（x1＜x2）两点，当△AMN为等腰三角形时，求圆心P的纵坐标．22．已知抛物线y＝x2﹣（k+2）x+和直线y＝（k+1）x+（k+1）2．（1）求证：无论k取何实数值，抛物线总与x轴有两个不同的交点；（2）抛物线于x轴交于点A、B，直线与x轴交于点C，设A、B、C三点的横坐标分别是x1、x2、x3，求x1•x2•x3的最大值；（3）如果抛物线与x轴的交点A、B在原点的右边，直线与x轴的交点C在原点的左边，又抛物线、直线分别交y轴于点D、E，直线AD交直线CE于点G（如图），且CA•GE ＝CG•AB，求抛物线的解析式．23．如图，抛物线y＝ax2﹣8ax+12a（a＞0）与x轴交于A、B两点（A在B的左侧），与y 轴交于点C，点D的坐标为（﹣6，0），且∠ACD＝90°．（1）请直接写出A、B两点的坐标；（2）求抛物线的解析式；（3）抛物线的对称轴上是否存在点P，使得△P AC的周长最小？若存在，求出点P的坐标及周长的最小值；若不存在，说明理由；（4）平行于y轴的直线m从点D出发沿x轴向右平行移动，到点A停止．设直线m与折线DCA的交点为G，与x轴的交点为H（t，0）．记△ACD在直线m左侧部分的面积为s，求s关于t的函数关系式及自变量t的取值范围．24．已知：抛物线y＝ax2+bx+c（a≠0）经过点A（1，0），B（3，0），C（0，﹣3）．（1）求抛物线的表达式及顶点D的坐标；（2）如图①，点P是直线BC上方抛物线上一动点，过点P作y轴的平行线，交直线BC于点E．是否存在一点P，使线段PE的长最大？若存在，求出PE长的最大值；若不存在，请说明理由；（3）如图②，过点A作y轴的平行线，交直线BC于点F，连接DA、DB．四边形OAFC 沿射线CB方向运动，速度为每秒1个单位长度，运动时间为t秒，当点C与点B重合时立即停止运动．设运动过程中四边形OAFC与四边形ADBF重叠部分面积为S，请求出S与t的函数关系式．25．如图，在平面直角坐标系中，已知点O（0，0），A（5，0），B（4，4）．（1）求过O、B、A三点的抛物线的解析式．（2）在第一象限的抛物线上存在点M，使以O、A、B、M为顶点的四边形面积最大，求点M的坐标．（3）作直线x＝m交抛物线于点P，交线段OB于点Q，当△PQB为等腰三角形时，求m的值．26．如图，在平面直角坐标系中，已知点P（0，4），点A在线段OP上，点B在x轴正半轴上，且AP＝OB＝t，0＜t＜4，以AB为边在第一象限内作正方形ABCD；过点C、D 依次向x轴、y轴作垂线，垂足为M，N，设过O，C两点的抛物线为y＝ax2+bx+c．（1）填空：△AOB≌△≌△BMC（不需证明）；用含t的代数式表示A点纵坐标：A（0，）；（2）求点C的坐标，并用含a，t的代数式表示b；（3）当t＝1时，连接OD，若此时抛物线与线段OD只有唯一的公共点O，求a的取值范围；（4）当抛物线开口向上，对称轴是直线x＝2﹣，顶点随着t的增大向上移动时，求t 的取值范围．27．如图，抛物线经过点A（1，0），B（5，0），C（0，）三点，设点E（x，y）是抛物线上一动点，且在x轴下方，四边形OEBF是以OB为对角线的平行四边形．（1）求抛物线的解析式；（2）当点E（x，y）运动时，试求平行四边形OEBF的面积S与x之间的函数关系式，并求出面积S的最大值？（3）是否存在这样的点E，使平行四边形OEBF为正方形？若存在，求E点，F点的坐标；若不存在，请说明理由．28．给定直线l：y＝kx，抛物线C：y＝ax2+bx+1，b≠2k．（1）当b＝1时，l与C相交于A，B两点，其中A为C的顶点，B与A关于原点对称，求a的值；（2）若把直线l向上平移k2+1个单位长度得到直线l′，则无论非零实数k取何值，直线l′与抛物线C都只有一个交点．①求此抛物线的解析式；②若P是此抛物线上任一点，过P作PQ∥y轴且与直线y＝2交于Q点，O为原点．求证：OP＝PQ．29．如图，抛物线y＝ax2+x+c与x轴交于点A（4，0）、B（﹣1，0），与y轴交于点C，连接AC，点M是线段OA上的一个动点（不与点O、A重合），过点M作MN∥AC，交OC于点N，将△OMN沿直线MN折叠，点O的对应点O′落在第一象限内，设OM＝t，△O′MN与梯形AMNC重合部分面积为S．（1）求抛物线的解析式；（2）①当点O′落在AC上时，请直接写出此时t的值；②求S与t的函数关系式；（3）在点M运动的过程中，请直接写出以O、B、C、O′为顶点的四边形分别是等腰梯形和平行四边形时所对应的t值．30．在平面直角坐标系中，一次函数y＝kx+b的图象与x轴、y轴分别相交于A（﹣3，0），B（0，﹣3）两点，二次函数y＝x2+mx+n的图象经过点A．（1）求一次函数y＝kx+b的解析式；（2）若二次函数y＝x2+mx+n图象的顶点在直线AB上，求m，n的值；（3）当﹣3≤x≤0时，二次函数y＝x2+mx+n的最小值为﹣4，求m，n的值．沪科新版九年级（上）中考题同步试卷：21.4 二次函数的应用（13）参考答案一、解答题（共30小题）1．；2．；3．；4．；5．；6．；7．；8．；9．；10．；11．；12．；13．；14．（0，3）；（4，3）；（4，﹣1）；（0，﹣1）；15．；16．；17．；18．；19．；20．无数；y＝﹣x2﹣1；21．；22．；23．；24．；25．；26．DNA或△DPA；4﹣t；27．；28．；29．；30．；。

初中数学沪科版九年级上册第二十一章《二次函数的应用》练习题(解析版)

初中数学沪科版九年级上册第二十一章21.4二次函数的应用练习题一、选择题1.如图是王阿姨晚饭后步行的路程s(单位：m)与时间t(单位：min)的函数图象，其中曲线段AB是以B为顶点的抛物线一部分．下列说法不正确的是()A. 25min～50min，王阿姨步行的路程为800mB. 线段CD的函数解析式为s=32t+400(25≤t≤50)C. 5min～20min，王阿姨步行速度由慢到快D. 曲线段AB的函数解析式为s=−3(t−20)2+1200(5≤t≤20)2.二次函数y=x2−8x+15的图象与x轴相交于M，N两点，点P在该函数的图象上运动，能使△PMN的面积等于1的点P共有()2A. 1个B. 2个C. 3个D. 4个3.某畅销书的售价为每本30元，每星期可卖出200本，书城准备开展“读数节活动”，决定降价促销，经调研，如果调整书籍的售价，每降价2元，每星期可多卖出40本，设每件商品降价x元后，每星期售出此畅销书的总销售额为y元，则y与x之间的函数关系式为()A. y=(30−x)(200+40x)B. y=(30−x)(200+20x)C. y=(30−x)(200−40x)D. y=(30−x)(200−20x)4.某农产品市场经销一种销售成本为40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨一元，月销售量就减少10千克．设销售单价为每千克x元，月销售利润为y元，则y与x的函数关系式为()A. y=(x−40)(500−10x)B. y=(x−40)(10x−500)C. y=(x−40)[500−10(x−50)]D. y=(x−40)[500−10(50−x)]5.进入夏季后，某电器商场为减少库存，对电热取暖器连续进行两次降价．若设平均每次降价的百分率是x，降价后的价格为y元，原价为a元，则y与x之间的函数关系式为()A. y=2a(x−1)B. y=2a(1−x)C. y=a(1−x2)D. y=a(1−x)26.为解决药价虚高给老百姓带来的求医难问题，国家决定对药品价格分两次降价，若设平均每次降价的百分率为x，该药品的原价是18元/盒，降价后的价格为y元/盒，则y与x之间的函数关系式是()A. y=36(1−x)B. y=36(1+x)C. y=18(1−x)2D. y=18(1+x2)7.在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形，如果设剩余部分的面积为y，那么y关于x的函数解析式是()A. y=x2B. y=4−x2C. y=x2−4D. y=4−2x8.矩形的周长为12cm，设其一边长为xcm，面积为ycm2，则y与x的函数关系式及其自变量x的取值范围均正确的是()A. y=−x2+6x(3<x<6)B. y=−x2+6x(0<x<6)C. y=−x2+12x(6<x<12)D. y=−x2+12x(0<x<12)9.长方形的周长为24cm，其中一边为xcm(其中x>0)，面积为ycm2，则这样的长方形中y与x的关系可以写为()A. y=x2B. y=(12−x)2C. y=(12−x)xD. y=2(12−x)10.广场上喷水池中的喷头微露水面，喷出的水线呈一条抛物线，水线上水珠的高度y(x2+6x(0≤x≤4)，米)关于水珠和喷头的水平距离x(米)的函数解析式是y=−32那么水珠的高度达到最大时，水珠与喷头的水平距离是()A. 1米B. 2米C. 5米D. 6米二、填空题11.某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=________．12.据权威部门发布的消息，2021年第一季度安徽省城镇居民人均可支配收入约为0.75万元，若第三季度安徽省城镇居民人均可支配收人为y万元，平均每个季度城镇居民人均可支配收入增长的百分率为x，则y与x之间的函数表达式是____．13.如图，用一段长为40m的篱笆围成一个一边靠墙的矩形菜园ABCD，墙长为18m，设AD的长为x m，菜园ABCD的面积为y m2，则y关于自变量x的函数关系式是___________________________．14.某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件，商品进价为每件40元，若设涨价x(x>0)元，总利润为y元，则y与x的函数关系式为______．15.某工厂今年一月份生产防疫护目镜的产量是20万件，计划之后两个月增加产量，如果月平均增长率为x，那么第一季度防疫护目镜的产量万件与x之间的关系应表示为______．三、解答题16.已知抛物线y=−x2+bx+c的对称轴为直线x=1，其图象与x轴相交于A，B两点，与y轴相交于点C(0,3)．(1)求b，c的值；(2)直线1与x轴相交于点P．①如图1，若l//y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x=1的对称点为点D，求四边形CEDF面积的最大值；②如图2，若直线1与线段BC相交于点Q，当△PCQ∽△CAP时，求直线1的表达式．17.如图1，在平面直角坐标系中，已知抛物线y=ax2+bx−5与x轴交于A(−1,0)，B(5,0)两点，与y轴交于点C．(1)求抛物线的函数表达式；(2)如图2，CE//x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标；(3)若点K为抛物线的顶点，点M(4,m)是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．18.在平面直角坐标系中，函数y=x2−2ax−1(a为常数)的图象与y轴交于点A．(1)求点A的坐标．(2)当此函数图象经过点(1,2)时，求此函数的表达式，并写出函数值y随x的增大而增大时x的取值范围．(3)当x≤0时，若函数y=x2−2ax−1(a为常数)的图象的最低点到直线y=2a的距离为2，求a的值．(4)设a<0，Rt△EFG三个顶点的坐标分别为E(−1,−1)、F(−1,a−1)、G(0,a−1).当函数y=x2−2ax−1(a为常数)的图象与△EFG的直角边有交点时，交点记为点P.过点P作y轴的垂线，与此函数图象的另一个交点为P′(P′与P不重合)，过点A 作y轴的垂线，与此函数图象的另一个交点为A′.若AA′=2PP′，直接写出a的值．答案和解析1.【答案】C【解析】【分析】本题考查了二次函数的应用，一次函数的应用，正确的识别图象、数形结合是解题的关键.根据函数图象中的信息，利用数形结合求相关线段的解析式解答即可．【解答】解：A.25min ～50min ，王阿姨步行的路程为2000−1200=800m ，故A 正确；B .设线段CD 的函数解析式为s =kt +b ，把(25,1200)，(50,2000)代入得，{1200=25k +b 2000=50k +b，解得：{k =32b =400， ∴线段CD 的函数解析式为s =32t +400(25≤t ≤50)，故B 正确；C .在A 点的速度为5255=105m/min ，在B 点的速度为1200−52520−5=67515=45m/min ，速度从快变慢，故C 错误；D .当t =5，20时，由图象可得s =525，1200m ，将t =5，20分别代入s =−3(t −20)2+1200(5≤t ≤20)得s =525，s =1200，故D 正确．故选C ．2.【答案】D【解析】【分析】本题结合图象的性质考查二次函数的综合应用，难度中等．要注意函数求出的各个解是否符合实际．由题可求出MN 的长，即△MNP 的底边已知，要求面积为12，那么根据面积即可求出高，只要把相应的y 值代入即可解答．【解答】解：y =x 2−8x +15的图象与x 轴交点(3,0)和(5,0)，|MN|=2，设p 点(x,y)，y =x 2−8x +15，面积=12=12|MN|⋅|y|，可得y 1=12，或者y 2=−12，当y =12时，x =8±√62；当y =−12时，x =8±√22，所以共有四个点．故选：D ．3.【答案】B【解析】【分析】本题考查由实际问题列二次函数关系式，解答本题的关键是明确题意，列出相应的函数关系式．根据降价x 元，则售价为(30−x)元，销售量为(200+20x)本，由题意可得等量关系：总销售额为y =销量×售价，根据等量关系列出函数解析式即可．【解答】解：设每本降价x 元，则售价为(30−x)元，销售量为(200+20x)本，根据题意得，y =(30−x)(200+20x)，故选B ．4.【答案】C【解析】【分析】此题主要考查了根据实际问题抽象出二次函数关系式，正确表示出销量是解题关键．直接利用每千克利润×销量=总利润，进而得出关系式．【解答】解：设销售单价为每千克x 元，月销售利润为y 元，则y 与x 的函数关系式为：y =(x −40)[500−10(x −50)]．故选：C ．5.【答案】D【解析】解：由题意得第二次降价后的价格是a(1−x)2．则函数解析式是y=a(1−x)2．故选D．原价为a，第一次降价后的价格是a×(1−x)，第二次降价是在第一次降价后的价格的基础上降价的，为a×(1−x)×(1−x)=a(1−x)2．本题需注意第二次降价是在第一次降价后的价格的基础上降价的．6.【答案】C【解析】【分析】此题主要考查了根据实际问题抽象出二次函数关系式，本题需注意第二次降价是在第一次降价后的价格的基础上降价的．原价为18，第一次降价后的价格是18(1−x)，第二次降价是在第一次降价后的价格的基础上降价的为：18(1−x)×(1−x)=18(1−x)2，则函数关系式即可求得．【解答】解：原价为18，第一次降价后的价格是18(1−x)；第二次降价是在第一次降价后的价格的基础上降价的为：18(1−x)×(1−x)=18(1−x)2．则函数解析式是：y=18(1−x)2．故选C．7.【答案】B【解析】解：设剩下部分的面积为y，则：y=−x2+4(0<x<2)，故选：B．根据剩下部分的面积=大正方形的面积−小正方形的面积得出y与x的函数关系式即可．此题主要考查了根据实际问题列二次函数关系式，利用剩下部分的面积=大正方形的面积−小正方形的面积得出是解题关键．8.【答案】B【解析】【分析】此题主要考查了根据实际问题列二次函数关系式的知识，解题的关键是用x表示出矩形的另一边，此题难度一般．已知一边长为xcm，则另一边长为(6−x)cm，根据矩形的面积公式即可解答．【解答】解：已知一边长为xcm，则另一边长为(6−x)．则y=x(6−x)化简可得y=−x2+6x，(0<x<6)，故选：B．9.【答案】C【解析】【分析】本题考查列二次函数关系式，得到长方形的另一边长是解决本题的关键点．先得到长方形的另一边长，那么面积=一边长×另一边长．【解答】解：∵长方形的周长为24cm，其中一边为x(其中x>0)，∴长方形的另一边长为12−x，∴y=(12−x)⋅x．故选C．10.【答案】B【解析】【分析】本题考查了二次函数的应用，解决本题的关键是掌握二次函数的顶点式．根据二次函数的顶点式即可求解．【解答】解：方法一：根据题意，得y=−32x2+6x(0≤x≤4)，=−32(x−2)2+6所以水珠的高度达到最大时，水珠与喷头的水平距离是2米．方法二：因为对称轴x=−62×(−32)=2，所以水珠的高度达到最大时，水珠与喷头的水平距离是2米．故选：B．11.【答案】a(1+x)2【解析】【分析】本题考查根据实际问题列二次函数关系式，关键是由一月份新产品的研发资金为a元，根据题意可以得到2月份研发资金为a×(1+x)，而三月份在2月份的基础上又增长了x，那么三月份的研发资金也可以用x表示出来，由此即可确定函数关系式．【解答】解：∵一月份新产品的研发资金为a元，二月份起，每月新产品的研发资金与上月相比增长率都是x，∴二月份新产品的研发资金为a(1+x)元，∴三月份新产品的研发资金为a(1+x)(1+x)=a(1+x)2元，即y=a(1+x)2．12.【答案】y=0.75(1+x)2【解析】【分析】此题主要考查了根据实际问题列二次函数关系式，属于中考常考题型．第一季度安徽省城镇居民人均可支配收入约为0.75万元，第二季度安徽省城镇居民人均可支配收入是0.75(1+x)元，第三季度安徽省城镇居民人均可支配收人为0.75(1+x)2元，则函数解析式即可求得．【解答】解：平均每个季度城镇居民人均可支配收入增长的百分率为x，根据题意可得：y与x之间的函数关系为：y=0.75(1+x)2．故答案为y=0.75(1+x)2．13.【答案】y=−2x2+40x(11≤x<20)【解析】【分析】本题考查了根据实际问题列二次函数关系式、矩形的面积公式的运用，利用篱笆的总长用含x的代数式表示出平行于墙的边长是解题的关键．先用含x的代数式表示出平行于墙的边长，再由矩形的面积公式就可以得出结论；【解答】解：根据题意，AD边的长为x米，则AB边的长为(40−2x)米，∴y=x(40−2x)，即y与x之间的函数关系式为y=−2x2+40x；0<40−2x≤18，11≤x<20，故答案为y=−2x2+40x(11≤x<20)．14.【答案】y=10x2−500x+6000【解析】解：设涨价x(x>0)元，总利润为y元，则y与x的函数关系式为：y=(60−40−x)(300−10x)=10x2−500x+6000．故答案为：y=10x2−500x+6000．直接利用销量×每件利润=总利润，进而得出函数关系式．此题主要考查了根据实际问题列二次函数关系式，正确表示出销量和每件利润是解题关键．15.【答案】y=20+20(x+1)+20(x+1)2【解析】解：y与x之间的关系应表示为：y=20+20(x+1)+20(x+1)2．故答案为：y=20+20(x+1)+20(x+1)2．根据平均增长问题，可得答案．本题考查了根据实际问题列二次函数关系式，利用增长问题获得函数解析式是解题关键． 16.【答案】解：(1)由题意得：{b2=1c =3， ∴b =2，c =3，(2)①如图1，∵点C 关于直线x =1的对称点为点D ，∴CD//OA ，∴3=−x 2+2x +3，解得：x 1=0，x 2=2，∴D(2,3)，∵抛物线的解析式为y =−x 2+2x +3，∴令y =0，解得x 1=−1，x 2=3，∴B(−1,0)，A(3,0)，设直线AC 的解析式为y =kx +b ，∴{3k +b =0b =3，解得：{k =−1b =3， ∴直线AC 的解析式为y =−x +3，设F(a,−a 2+2a +3)，E(a,−a +3)，∴EF =−a 2+2a +3+a −3=−a 2+3a ，四边形CEDF 的面积=S △EFC +S △EFD =12EF ⋅CD =12×(−a 2+3a)×2=−a 2+3a =−(a −32)2+94， ∴当a =32时，四边形CEDF 的面积有最大值，最大值为94．②当△PCQ∽△CAP 时，∴∠PCA =∠CPQ ，∠PAC =∠PCQ ，∴PQ//AC ，∵C(0,3)，A(3,0)，∴OA =OC ，∴∠OCA=∠OAC=∠PCQ=45°，∴∠BCO=∠PCA，如图2，过点P作PM⊥AC交AC于点M，∴tan∠PCA=tan∠BCO=OBOC =13，设PM=b，则CM=3b，AM=b，∵AC=√OC2+OA2=3√2，∴b+3b=3√2，∴b=34√2，∴PA=34√2×√2=32，∴OP=OA−PA=3−32=32，∴P(32,0)，设直线l的解析式为y=−x+n，∴−32+n=0，∴n=32．∴直线l的解析式为y=−x+32．【解析】(1)根据抛物线的对称轴及抛物线与y轴的交点坐标可求出b、c的值；(2)由题意先求出D点坐标为(2,3)，求出直线AC的解析式，设F(a,−a2+2a+3)，E(a,−a+3)，则EF=−a2+3a，四边形CEDF的面积可表示为12EF⋅CD，利用二次函数的性质可求出面积的最大值；(3)当△PCQ∽△CAP时，可得∠PCA=∠CPQ，∠PAC=∠PCQ=∠OCA=45°，则PQ//AC，∠BCO=∠PCA，过点P作PM⊥AC交AC于点M，可求出PM、PA、OP的长，用待定系数法可求出函数解析式．本题考查了二次函数的综合题：熟练掌握二次函数的性质和轴对称的性质；会利用待定系数法求函数解析式；理解坐标与图形性质，会利用相似三角形的性质解题；要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度是解题的关键．17.【答案】解：(1)∵点A(−1,0)，B(5,0)在抛物线y =ax 2+bx −5上，∴{a −b −5=025a +5b −5=0，解得{a =1b =−4，∴抛物线的表达式为y =x 2−4x −5，(2)设H(t,t 2−4t −5)，∵CE//x 轴，∴点E 的纵坐标为−5，∵E 在抛物线上，∴x 2−4x −5=−5，∴x =0(舍)或x =4，∴E(4,−5)，∴CE =4，∵B(5,0)，C(0,−5)，∴直线BC 的解析式为y =x −5，∴F(t,t −5)，∴HF =t −5−(t 2−4t −5)=−(t −52)2+254，∵CE//x 轴，HF//y 轴，∴CE ⊥HF ，∴S 四边形CHEF =12CE ⋅HF =−2(t −52)2+252，∴H(52,−354)；(3)如图2，∵K 为抛物线的顶点，∴K(2,−9)，∴K 关于y 轴的对称点K′(−2,−9)，∵M(4,m)在抛物线上，∴M(4,−5)，∴点M关于x轴的对称点M′(4,5)，∴直线K′M′的解析式为y=73x−133，∴P(137,0)，Q(0,−133).【解析】(1)根据待定系数法直接确定出抛物线解析式；(2)先求出直线BC的解析式，进而求出四边形CHEF的面积的函数关系式，即可求出；(3)利用对称性找出点P，Q的位置，进而求出P，Q的坐标．此题是二次函数综合题，主要考查了待定系数法，四边形的面积的计算方法，对称性，解的关键是利用对称性找出点P，Q的位置，是一道中等难度的题目．18.【答案】解：(1)当x=0时，y=x2−2ax−1=−1，∴点A的坐标为：(0,−1)；(2)将点(1,2)代入y=x2−2ax−1，得：2=1−2a−1，解得：a=−1，∴函数的表达式为：y=x2+2x−1，∵y=x2+2x−1=(x+1)2−2，∴抛物线的开口向上，对称轴为x=−1，如图1所示：∴当x>−1时，y随x的增大而增大；(3)抛物线y=x2−2ax−1=(x−a)2−a2−1的对称轴为：x=a，顶点坐标为：(a,−a2−1)，当a>0时，对称轴在y轴右侧，如图2所示：∵x≤0，∴最低点就是A(0,−1)，∵图象的最低点到直线y=2a的距离为2，∴2a−(−1)=2，解得：a=12；当a<0，对称轴在y轴左侧，顶点(a,−a2−1)就是最低点，如图3所示：∴2a −(−a 2−1)=2，整理得：(a +1)2=2，解得：a 1=−1−√2，a 2=−1+√2(不合题意舍去)；综上所述，a 的值为12或−1−√2；(4)∵a <0，Rt △EFG 三个顶点的坐标分别为E(−1,−1)、F(−1,a −1)、G(0,a −1)， ∴直角边为EF 与FG ，∵抛物线y =x 2−2ax −1=(x −a)2−a 2−1的对称轴为：x =a ，A(0,−1)， ∴AA′=−2a ，当点P 在EF 边上时，如图4所示：则x p =−1，∵EA =OA =1，∴点P 在对称轴x =a 的左侧，∴PP′=2(a +1)，∵AA′=2PP′，∴−2a =2×2(a +1)，解得：a =−23；当点P 在FG 边上时，如图5所示：则y p =a −1，∴x 2−2ax −1=a −1，解得：x 1=a +√a 2+a ，x 2=a −√a 2+a ，∴PP′=a +√a 2+a −(a −√a 2+a)=2√a 2+a ，∵AA′=2PP′，∴−2a =4√a 2+a ，解得：a 1=−43，a 2=0(不合题意舍去)；综上所述，a 的值为−23或−43．【解析】(1)当x =0时，代入y =x 2−2ax −1，即可得出结果；(2)将点(1,2)代入y =x 2−2ax −1，得a =−1，则函数的表达式为y =x 2+2x −1，由y =x 2+2x −1=(x +1)2−2，得出抛物线的开口向上，对称轴为x =−1，则当x >−1时，y 随x 的增大而增大；(3)抛物线y =x 2−2ax −1=(x −a)2−a 2−1的对称轴为x =a ，顶点坐标为(a,−a 2−1)，当a >0时，对称轴在y 轴右侧，最低点就是A(0,−1)，则2a −(−1)=2，即可得出结果；当a <0，对称轴在y 轴左侧，顶点(a,−a 2−1)就是最低点，则2a −(−a 2−1)=2，即可得出结果；(4)易证直角边为EF 与FG ，由抛物线的对称轴为x =a ，A(0,−1)，则AA′=−2a ，当点P 在EF 边上时，PP′=2(a +1)，则−2a =2×2(a +1)，即可得出结果；当点P 在FG 边上时，求出PP′=2√a 2+a ，则−2a =4√a 2+a ，即可得出结果．本题是二次函数综合题，主要考查了二次函数图象与性质、待定系数法求解析式、直角三角形的性质、解一元二次方程、分类讨论等知识；熟练掌握二次函数图象与性质是解题的关键．1、最困难的事就是认识自己。

二次函数图象性质与综合应用(44题)(原卷版)

二次函数图象性质与综合应用（44题）一、单选题A．抛物线的对称轴为直线C．A，B两点之间的距离为2．（2023·浙江台州·统考中考真题）抛物线若120x x+<，则直线A．4个4．（2023·四川自贡·统考中考真题）经过为自变量）与x轴有交点，则线段A．4个B6．（2023·四川泸州·统考中考真题）已知二次函数函数值y均为正数，则aA ．．．．．（2023·四川广安·统考中考真题）如图所示，二次函数2y ax bx =++轴交于点()()3,0,1,0AB −0；②若点()12,y −和(50a b c −+=；④4a c + ）A．1个B．212．（2023·四川眉山·统考中考真题）如图，二次函数()1,0，对称轴为直线=1x−，2A．1个B．213．（2023·浙江宁波·统考中考真题）已知二次函数A．点(1,2)在该函数的图象上B．当1−≤≤时，a=且13xC．该函数的图象与x轴一定有交点解；③若()11,t −，()24,t 是抛物线上的两点，则12t t <；④对于抛物线，223y ax bx =+−，当23x −<<时，2y 的取值范围是205y <<．其中正确结论的个数是（）A ．4个B ．3个C ．2个D ．1个二、填空题417．（2023·四川宜宾物线与y 轴的交点B①当31x −≤≤时，1y ≤；②当ABM 的面积为32③当ABM 为直角三角形时，在AOB 内存在唯一点1893+．三、解答题(1)求抛物线的解析式；(2)设点P是直线BC上方抛物线上一点，求出PBC的最大面积及此时点(3)若点M是抛物线对称轴上一动点，点N为坐标平面内一点，是否存在以点的四边形是菱形，若存在，请直接写出点N的坐标；若不存在，请说明理由．(1)求该抛物线的解析式；(2)点F是该抛物线上位于第一象限的一个动点，直线=时，求CD的长；①当CD CE②若CAD，CDE，CEF△的面积分别为，ABC外接圆的圆心为(1)求抛物线的函数解析式；(2)若直线()50x m m =−<<与抛物线交于点E ，与直线BC 交于点F ． ①当EF 取得最大值时，求m 的值和EF 的最大值； ②当EFC 是等腰三角形时，求点E 的坐标．27．（2023·四川成都·统考中考真题）如图，在平面直角坐标系xOy 中，已知抛物线2y ax c =+经过点3(4,)P −，与y 轴交于点(0,1)A ，直线(0)y kx k =≠与抛物线交于B ，C 两点．(1)求抛物线的函数表达式；(2)若ABP 是以AB 为腰的等腰三角形，求点B 的坐标；(3)过点(0,)M m 作y 轴的垂线，交直线AB 于点D ，交直线AC 于点E ．试探究：是否存在常数m ，使得OD OE ⊥始终成立？若存在，求出m 的值；若不存在，请说明理由．28．（2023·浙江·统考中考真题）已知点(),0m −和()3,0m 在二次函数23,(y ax bx a b =++是常数，0)a ≠的图像上．(1)当1m =−时，求a 和b 的值；时，求OBD与△(1)如图2，若抛物线经过原点O ．①求该抛物线的函数表达式；②求BE EC的值． (2)连接,PC CPE ∠与BAO ∠能否相等？若能，求符合条件的点P 的横坐标；若不能，试说明理由．(1)求抛物线的解析式；(2)如图1，当:3:5BM MQ =时，求点N 的坐标；(3)如图2，当点Q 恰好在y 轴上时，P 为直线1l 下方的抛物线上一动点，连接设OQE 的面积为1S ，PQE 的面积为2S ．求21S S 的最大值．(1)求点A，B的坐标；(1)求抛物线的表达式；(2)当点P在直线AC上方的抛物线上时，连接BP交AC于点D．如图标及PDDB的最大值；≌；．求证：ACB BDEx(1)如果四个点()()()()0,00,21,11,1−、、、中恰有三个点在二次函数2y ax =（a 为常数，且0a ≠）的图象上． ①=a ________；②如图1，已知菱形ABCD 的顶点B 、C 、D 在该二次函数的图象上，且AD y ⊥轴，求菱形的边长； ③如图2，已知正方形ABCD 的顶点B 、D 在该二次函数的图象上，点B 、D 在y 轴的同侧，且点B 在点D 的左侧，设点B 、D 的横坐标分别为m 、n ，试探究n m −是否为定值．如果是，求出这个值；如果不是，请说明理由．(2)已知正方形ABCD 的顶点B 、D 在二次函数2y ax =（a 为常数，且0a >）的图象上，点B 在点D 的左侧，设点B 、D 的横坐标分别为m 、n ，直接写出m 、n 满足的等量关系式．38．（2023年重庆市中考数学真题（A 卷））如图，在平面直角坐标系中，抛物线22y ax bx =++过点()1,3，(1)求抛物线的表达式；(2)点P是直线BC上方抛物线上的一动点，点E，求PDE△周长的最大值及此时点(3)在（2）中PDE△周长取得最大值的条件下，将该抛物线沿射线点，与y 轴交于点C ．(1)求抛物线的解析式；(2)点P 在抛物线上，点Q 在x 轴上，以B ，C ，P ，Q 为顶点的四边形为平行四边形，求点P 的坐标；(3)如图2，抛物线顶点为D ，对称轴与x 轴交于点E ，过点()1,3K 的直线（直线KD 除外）与抛物线交于G ，H 两点，直线DG ，DH 分别交x 轴于点M ，N ．试探究EM EN ⋅是否为定值，若是，求出该定值；若不是，说明理由．40．（2023·四川宜宾·统考中考真题）如图，抛物线2y ax bx c =++与x 轴交于点()4,0A −、()2,0B ，且经过点()2,6C −．(1)求抛物线的表达式；(2)在x 轴上方的抛物线上任取一点N ，射线AN 、BN 分别与抛物线的对称轴交于点P 、Q ，点Q 关于x 轴的对称点为Q '，求APQ '△的面积；(3)点M 是y 轴上一动点，当AMC ∠最大时，求M 的坐标．41．（2023·四川广安·统考中考真题）如图，二次函数2y x bx c =++的图象交x 轴于点A B ，，交y 轴于点C ，点B 的坐标为()1,0，对称轴是直线=1x −，点P 是x 轴上一动点，PM x ⊥轴，交直线AC 于点M ，交抛物线于点N ．(1)求这个二次函数的解析式．(2)若点P 在线段AO 上运动（点P 与点A 、点O 不重合），求四边形ABCN 面积的最大值，并求出此时点P 的坐标．(3)若点P 在x 轴上运动，则在y 轴上是否存在点Q ，使以M 、N C Q 、、为顶点的四边形是菱形？若存在，请直接写出所有满足条件的点Q 的坐标；若不存在，请说明理由．42．（2023·江苏连云港·统考中考真题）如图，在平面直角坐标系xOy 中，抛物线21:23L y x x =−−的顶点为P ．直线l 过点()()0,3M m m ≥−，且平行于x 轴，与抛物线1L 交于A B 、两点（B 在A 的右侧）．将抛物线1L 沿直线l 翻折得到抛物线2L ，抛物线2L 交y 轴于点C ，顶点为D ．(1)当1m =时，求点D 的坐标；(2)连接BC CD DB 、、，若BCD △为直角三角形，求此时2L 所对应的函数表达式；(3)在（2）的条件下，若BCD △的面积为3,E F 、两点分别在边BC CD 、上运动，且EF CD =，以EF 为一边作正方形EFGH ，连接CG ，写出CG 长度的最小值，并简要说明理由．43．（2023·云南·统考中考真题）数和形是数学研究客观物体的两个方面，数（代数）侧重研究物体数量方面，具有精确性、形（几何）侧重研究物体形的方面，具有直观性．数和形相互联系，可用数来反映空间形式，也可用形来说明数量关系．数形结合就是把两者结合起来考虑问题，充分利用代数、几何各自的优势，数形互化，共同解决问题．同学们，请你结合所学的数学解决下列问题．在平面直角坐标系中，若点的横坐标、纵坐标都为整数，则称这样的点为整点．设函数2(42)(96)44y a x a x a =++−−+（实数a 为常数）的图象为图象T ．(1)求证：无论a 取什么实数，图象T 与x 轴总有公共点；(2)是否存在整数a ，使图象T 与x 轴的公共点中有整点？若存在，求所有整数a 的值；若不存在，请说明理由．44．（2023·湖南怀化·统考中考真题）如图一所示，在平面直角坐标系中，抛物线28y ax bx =+−与x 轴交于(4,0)(2,0)A B −、两点，与y 轴交于点C ．(1)求抛物线的函数表达式及顶点坐标；(2)点P为第三象限内抛物线上一点，作直线AC，连接PA 标；(3)设直线135 :4l y kx k=+−交抛物线于点M、N，求证：无论存在一点E，使得MEN∠为直角．。

2019-2020学年数学沪科版九年级上册21.4 二次函数的应用(3) 同步练习D卷

2019-2020学年数学沪科版九年级上册21.4 二次函数的应用（3）同步练习D卷姓名:________ 班级:________ 成绩:________一、选择题 (共9题；共18分)1. （2分）某品牌钢笔进价8元，按10元1支出售时每天能卖出20支，市场调查发现如果每支每涨价1元，每天就少卖出2支，为了每天获得最大利润，其售价应定为（）A . 11元B . 12元C . 13元D . 14元2. （2分）为了改善居民住房条件，某市计划用未来两年的时间，将城镇居民的住房面积由现在的人均约为20平方米提高到28.8平方米，若每年的年增长率相同，设年增长率为x,则下面列出的方程中正确的是（）A .B .C .D .3. （2分）某企业是一家专门生产季节性产品的企业，当产品无利润时，企业会自动停产，经过调研预测，它一年中每月获得的利润y（万元）和月份n之间满足函数关系式y=﹣n2+14n﹣24，则企业停产的月份为（）A . 2月和12月B . 2月至12月C . 1月D . 1月、2月和12月4. （2分）某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映，如果调整商品售价，每降价1元，每星期可多卖出20件．设每件商品降价x元后，每星期售出商品的总销售额为y元，则y与x的关系式为（）A . y=60（300+20x）B . y=（60﹣x）（300+20x）C . y=300（60﹣20x）D . y=（60﹣x）（300﹣20x）5. （2分）某大学生利用课余时间在网上销售一种成本为50元/件的商品，每月的销售量y（件）与销售单价x（元/件）之间的函数关系式为y=–4x+440，要获得最大利润，该商品的售价应定为（）A . 60元B . 70元C . 80元D . 90元6. （2分）某产品进货单价为90元，按100元一件出售时能售出500件．若每件涨价1元，则销售量就减少10件．则该产品能获得的最大利润为（）A . 5000元B . 8000元C . 9000元D . 10000元7. （2分）某超市有一种商品，进价为2元，据市场调查，销售单价是13元时，平均每天销售量是50件，而销售价每降低1元，平均每天就可以多售出10件．若设降价后售价为x元，每天利润为y元，则y与x之间的函数关系为（）A . y=10x2﹣100x﹣160B . y=﹣10x2+200x﹣360C . y=x2﹣20x+36D . y=﹣10x2+310x﹣23408. （2分）如图，正△ABC的边长为4，点P为BC边上的任意一点（不与点B、C重合），且∠APD=60°，PD交AB于点D．设BP=x，BD=y，则y关于x的函数图象大致是（）A .B .C .D .9. （2分）已知面包店的面包一个15元，小明去此店买面包，结账时店员告诉小明：“如果你再多买一个面包就可以打九折，价钱会比现在便宜45元”，小明说：“我买这些就好了，谢谢．”根据两人的对话，判断结账时小明买了多少个面包？（）A . 39B . 40C . 41D . 42二、填空题 (共6题；共6分)10. （1分）某纸箱厂第1年的利润为50万元，如果每一年比上一年的利润增长率相同，都是x，则第3年的利润为________万元。

沪科版九年级数学习题-二次函数的应用(第2课时)

第2課時二次函數的應用(2)1．圖①是泰州某河上一座古拱橋的截面圖，拱橋橋洞上沿是拋物線形狀，拋物線兩端點與水面的距離都是1 m，拱橋的跨度為10 m，橋洞與水面的最大距離是5 m，橋洞兩側壁上各有一盞距離水面4 m的景觀燈．若把拱橋的截面圖放在平面直角坐標系中(如圖②)．(1)求拋物線的解析式；(2)求兩盞景觀燈之間的水準距離．2．跳繩時，繩甩到最高處時的形狀是拋物線．正在甩繩的甲、乙兩名同學拿繩的手間距AB為6米，到地面的距離AO和BD均為0.9米，身高為1.4米的小麗站在距點O的水準距離為1米的點F處，繩子甩到最高處時剛好通過她的頭頂點E.以點O為原點建立如圖所示的平面直角坐標系，設此拋物線的解析式為y＝ax2＋bx＋0.9.(1)求該拋物線的解析式；(2)如果小華站在OD之間，且離點O的距離為3米，當繩子甩到最高處時剛好通過他的頭頂，請你算出小華的身高；(3)如果身高為1.4米的小麗站在OD之間，且離點O的距離為t米，繩子甩到最高處時超過她的頭頂，請結合圖象，求t的取值範圍．3．在NBA籃球大賽中，一位運動員在距籃下4 m處跳起投籃，球運行的路線是拋物線，當球運行的水準距離是2.5 m時，達到最大高度3.5 m，然後準確落入籃圈．已知籃圈中心到地面的距離為3.05 m.(1)建立如圖所示的平面直角坐標系，求拋物線的解析式；(2)該運動員身高1.8 m，在這次跳投中，球在頭頂上方0.25 m處出手，問球出手時，他距離地面的高度是多少？4．如圖所示，一單杠高2.2 m，兩立柱間的距離為1.6 m，將一根繩子的兩端拴於立柱與鐵杠的結合處A、B，繩子自然下垂，呈拋物線狀，一個身高0.7 m的小孩站在距立柱0.4 m處，其頭部剛好觸上繩子的D處，求繩子的最低點O到地面的距離．5．如圖，某隧道橫截面的上下輪廓線分別由拋物線對稱的一部分和矩形的一部分構成，最大高度為6米，底部寬度為12米．現以O點為原點，OM所在直線為x軸建立直角坐標系．(1)直接寫出點M及拋物線頂點P的座標；(2)求出這條拋物線的函數解析式；(3)若要搭建一個矩形“支撐架”AD-DC-CB，使C、D點在拋物線上，A、B點在地面OM上，則這個“支撐架”總長的最大值是多少？6．(創新應用)某水產品養殖企業為指導該企業某種水產品的養殖和銷售，對歷年市場行情和水產品養殖情況進行了調查．調查發現這種水產品的每千克售價y1(元)與銷售月份x(月)滿足關係式y＝38x＋36，而其每千克成本y2(元)與銷售月份x(月)滿足的函數關係如圖所示．(1)試確定b、c的值；(2)求出這種水產品每千克的利潤y(元)與銷售月份x(月)之間的函數關係式；(3)“五·一”之前，幾月份出售這種水產品每千克的利潤最大？最大利潤是多少？參考答案1.解：(1)拋物線的頂點座標為(5,5)，與y軸交點座標是(0,1)．設拋物線的解析式是y＝a(x－5)2＋5(a≠0)，把點(0,1)代入y＝a(x－5)2＋5，得a＝4 25 -.∴y＝425-(x－5)2＋5(0≤x≤10)．(2)由已知，得兩景觀燈的縱坐標都是4，∴4＝425-(x－5)2＋5.∴425(x－5)2＝1.∴x1＝152，x2＝52.∴兩景觀燈間的距離為|x1－x2|＝15522-＝5(m)．2.解：(1)小麗頭頂處E點的座標為E(1,1.4)，B的座標為(6,0.9)，代入解析式，得0.91.4 3660.90.9 a ba b⎧⎨⎩＋＋＝，＋＋＝，解得0.10.6ab⎧⎨⎩＝－，＝，∴函數解析式為y＝－0.1x2＋0.6x＋0.9(0≤x≤6)．(2)由y＝－0.1x2＋0.6x＋0.9，配方，得y＝－0.1(x－3)2＋1.8，當x＝3時，y＝1.8，∴小華的身高為1.8米．(3)當y＝1.4時，得－0.1x2＋0.6x＋0.9＝1.4，解得x1＝1，x2＝5，∴當y＞1.4時，1＜t＜5.3.解：(1)由題圖知，頂點為(0,3.5)，籃圈座標為(1.5,3.05)，設函數解析式為y＝ax2＋3.5(a≠0)，將(1.5,3.05)代入，得a＝－0.2，故籃球運行軌跡所在的拋物線的解析式為y＝－0.2x2＋3.5.(2)當x＝－2.5時，y＝－0.2×(－2.5)2＋3.5＝2.25，故跳投時，距地面的高度為2.25－1.8－0.25＝0.2(m)．4.解：如圖所示，以O為座標原點，水準方向為x軸，垂直方向為y軸，建立直角坐標系，設拋物線的解析式為y＝ax2(a≠0)．設A 、B 、D 三點座標依次為(x A ，y A )、(x B ，y B )、(x D ，y D )，由題意，得AB ＝1.6，∴x A ＝－0.8，x B ＝0.8，得x D ＝1 1.60.42⎛⎫-⨯- ⎪⎝⎭＝－0.4. ∴當x ＝－0.8時，y A ＝a ·(－0.8)2＝0.64a ；當x ＝－0.4時，y D ＝a ·(－0.4)2＝0.16a . ∴y A －y D ＝2.2－0.7＝1.5.∴0.64a －0.16a ＝1.5.∴a ＝258. ∴拋物線解析式為y ＝2258x . 當x ＝－0.4時，y D ＝258×(－0.4)2＝0.5， ∴0.7－0.5＝0.2(m)．答：繩子的最低點距地面0.2 m.5. 解：(1)M (12,0)，P (6,6)．(2)設此函數關係式為y ＝a (x －6)2＋6(a ≠0)， ∵函數y ＝a (x －6)2＋6經過點(0,3)，∴3＝a (0－6)2＋6，即a ＝112-. ∴此函數解析式為y ＝112-(x －6)2＋6＝2112x -＋x ＋3(0≤x ≤12)． (3)設A (m,0)，則B (12－m,0)、2112,312C m m m ⎛⎫--++ ⎪⎝⎭、21,312D m m m ⎛⎫-++ ⎪⎝⎭， ∴“支撐架”總長AD ＋DC ＋CB ＝21312m m ⎛⎫-++ ⎪⎝⎭＋(12－2m )＋21312m m ⎛⎫-++ ⎪⎝⎭＝216m -＋18. ∵此二次函數的圖象開口向下，∴當m ＝0時，AD ＋DC ＋CB 有最大值為18.6. 解：(1)由題意，得2212533,812444,8b c b c ⎧=⨯++⎪⎪⎨⎪=⨯++⎪⎩解得15,859.2b c ⎧=-⎪⎪⎨⎪=⎪⎩ (2)y ＝y 1－y 2＝2311559368882x x x ⎛⎫-+--+ ⎪⎝⎭ ＝21313822x x -++. (3)y ＝21313822x x -++ ＝18-(x 2－12x ＋36)＋91322+ ＝18-(x －6)2＋11. ∵a ＝18-＜0， ∴拋物線開口向下．在對稱軸x ＝6左側y 隨x 值的增大而增大．由題意x ＜5，∴在4月份出售這種水產品每千克的利潤最大．最大利潤＝18-(4－6)2＋11＝212(元)．。

沪科版-数学-九年级上册- 21.4 二次函数的应用第3课时

第3课时二次函数的应用(3)练习1．如图，在Rt△ABC中，∠BAC＝90°，∠C＝60°，BC＝24.点P是BC边上的动点(点P与点B、C不重合)，过动点P作PD∥BA交AC于点D．试问：当PC等于多少时，△APD 的面积最大？最大面积是多少？2．学校计划用地面砖铺设教学楼前的矩形广场的地面ABCD，已知矩形广场地面的长为100米，宽为80米，图案设计如图所示，广场的四角为小正方形，阴影部分为四个矩形，四个矩形的宽都是小正方形的边长，阴影部分铺设绿色地面砖，其余部分铺设白色地面砖．(1)要使铺设白色地面砖的面积为5 200平方米，那么矩形广场四角的小正方形的边长为多少米？(2)如图，铺设白色地面砖的费用为每平方米30元，铺设绿色地面砖的费用为每平方米20元，当广场四角小正方形的边长为多少米时，铺设广场地面的总费用最少？最少费用是多少？3．已知某型号汽车在干燥的路面上，汽车停止行驶所需的刹车距离与刹车时的车速之速度v(km/h)48648096112…刹车距离s(m)22.53652.57294.5…(1)请你以汽车刹车时的车速v为自变量，刹车距离s为函数，在下图所示的坐标系中描点连线，画出函数的图象；(2)观察所画的函数的图象，你发现了什么？(3)若把这个函数的图象看成是一条抛物线，请根据表中所给的数据，选择三对数据，求出它的函数关系式；(4)用你留下的两对数据，验证一下你所得到的结论是否正确．4．为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系．随着补贴款额x 的不断增大，销售量也不断增加，但每台彩电的收益Z(元)会相应降低且Z与x之间也大致满足如图②所示的一次函数关系．(1)在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？(2)在政府补贴政策实施后，分别求出该商场销售彩电台数y和每台家电的收益Z与政府补贴款额x之间的函数关系式；(3)要使该商场销售彩电的总收益W(元)最大，政府应将每台补贴款额x定为多少？并求出总收益W的最大值．5．(创新应用)某数学研究所门前有一个边长为4米的正方形花坛，花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案，图案中AE＝MN.准备在形如Rt△AEH的四个全等三角形内种植红色花草，在形如Rt△MEH的四个全等三角形内种植黄色花草，在正方形MNPQ内种植紫色花草，每种花草的价格如下表：品种红色花草黄色花草紫色花草价格(元/米2)6080120设AE的长为x米，正方形EFGH的面积为S平方米，买花草所需的费用为W元，解答下列问题：(1)S与x之间的函数关系式为S＝____________；(2)求W与x之间的函数关系式，并求所需的最低费用是多少元；(3)当买花草所需的费用最低时，求EM的长．参考答案1.解：设PC＝x，∵PD∥BA，∠BAC＝90°，∴∠PDC＝90°.又∵∠C＝60°，∴∠B＝30°.∴AC＝12，CD＝12 x.∴AD＝12－12 x.而PD＝221322x x x⎛⎫-=⎪⎝⎭，∴S△APD＝12PD·AD＝13112222x x⎛⎫⨯-⎪⎝⎭＝3-(x2－24x)＝3-(x－12)2＋183.∴PC等于12时，△APD的面积最大，最大面积是183.2解：(1)设矩形广场四角的小正方形的边长为x米，根据题意，得4x2＋(100－2x)(80－2x)＝5 200，整理得x2－45x＋350＝0，解得x1＝35，x2＝10，经检验x1＝35，x2＝10均适合题意，所以，要使铺设白色地面砖的面积为5 200平方米，则矩形广场四角的小正方形的边长为35米或者10米．(2)设铺设矩形广场地面的总费用为y元，广场四角的小正方形的边长为x米，则y＝30＋20，即y＝80x2－3 600x＋240 000，配方得y＝80(x－22.5)2＋199 500，当x＝22.5时，y 的值最小，最小值为199500，所以当矩形广场四角的小正方形的边长为22.5米时，所铺设矩形广场地面的总费用最少，最少费用为199 500元．3解：(1)函数的图象如图所示．(2)图象可看成一条抛物线，这个函数可看作二次函数．(3)设所求函数关系式为s＝a v2＋b v＋c.把v1＝48，s1＝22.5；v2＝64，s2＝36；v3＝96，s3＝72分别代入s＝a v2＋b v＋c，得222484822.5646436969672a b c a b c a b c ⎧⎪⎨⎪⎩＋＋＝，＋＋＝，＋＋＝，解得3,5123,160,a b c ⎧=⎪⎪⎪=⎨⎪=⎪⎪⎩∴s ＝23351216v v +. (4)当v ＝80时，233351216512v v +=×802＋316×80＝52.5；当v ＝112时，233351216512v v +=×1122＋316×112＝94.5. 经检验，所得结论是正确的．4解：(1)该商场销售家电的总收益为800×200＝160 000(元)．(2)依题意可设y ＝k 1x ＋800，Z ＝k 2x ＋200.∴有400k 1＋800＝1 200,200k 2＋200＝160.解得k 1＝1，k 2＝15-. ∴y ＝x ＋800，Z ＝15x -＋200. (3)W ＝yZ ＝(x ＋800)12005x ⎛⎫-+ ⎪⎝⎭＝15-(x －100)2＋162 000. 政府应将每台补贴款额x 定为100元，总收益有最大值，其最大值为162 000元． 5解：(1)x 2＋(4－x )2或2x 2－8x ＋16(2)W ＝60×4S △AEH ＋80(S 正方形EFGH －S 正方形MNPQ )＋120S 正方形MNPQ ＝60×4×12x (4－x )＋80＋120x 2＝80x 2－160x ＋1 280.配方，得W ＝80(x －1)2＋1 200.∴当x ＝1时，W 最小值＝1 200元．(3)设EM ＝a 米，则MH ＝(a ＋1)米．在Rt △EMH 中，a 2＋(a ＋1)2＝12＋32，解得a ＝1192-±，∵a ＞0， ∴a ＝1192-.∴EM 的长为12-米．。

沪科版九年级数学习题-二次函数的应用(第3课时)

第3課時二次函數的應用（3）1．如圖，在Rt△ABC中，∠BAC＝90°，∠C＝60°，BC＝24.點P是BC邊上的動點(點P與點B、C不重合)，過動點P作PD∥BA交AC於點D．試問：當PC等於多少時，△APD的面積最大？最大面積是多少？2．學校計畫用地面磚鋪設教學樓前的矩形廣場的地面ABCD，已知矩形廣場地面的長為100米，寬為80米，圖案設計如圖所示，廣場的四角為小正方形，陰影部分為四個矩形，四個矩形的寬都是小正方形的邊長，陰影部分鋪設綠色地面磚，其餘部分鋪設白色地面磚．(1)要使鋪設白色地面磚的面積為5 200平方米，那麼矩形廣場四角的小正方形的邊長為多少米？(2)如圖，鋪設白色地面磚的費用為每平方米30元，鋪設綠色地面磚的費用為每平方米20元，當廣場四角小正方形的邊長為多少米時，鋪設廣場地面的總費用最少？最少費用是多少？3．已知某型號汽車在乾燥的路面上，汽車停止行駛所需的刹車距離與刹車時的車速之間有下表所示的對應關係.(1)請你以汽車刹車時的車速為引數，刹車距離為函數，在下圖所示的坐標系中描點連線，畫出函數的圖象；(2)觀察所畫的函數的圖象，你發現了什麼？(3)若把這個函數的圖象看成是一條拋物線，請根據表中所給的數據，選擇三對數據，求出它的函數關係式；(4)用你留下的兩對數據，驗證一下你所得到的結論是否正確．4．為了擴大內需，讓惠於農民，豐富農民的業餘生活，鼓勵送彩電下鄉，國家決定對購買彩電的農戶實行政府補貼．規定每購買一臺彩電，政府補貼若干元，經調查某商場銷售彩電台數y(臺)與補貼款額x(元)之間大致滿足如圖①所示的一次函數關係．隨著補貼款額x的不斷增大，銷售量也不斷增加，但每臺彩電的收益Z(元)會相應降低且Z與x之間也大致滿足如圖②所示的一次函數關係．(1)在政府未出臺補貼措施前，該商場銷售彩電的總收益額為多少元？(2)在政府補貼政策實施後，分別求出該商場銷售彩電台數y和每臺家電的收益Z與政府補貼款額x之間的函數關係式；(3)要使該商場銷售彩電的總收益W(元)最大，政府應將每臺補貼款額x定為多少？並求出總收益W的最大值．5．(創新應用)某數學研究所門前有一個邊長為4米的正方形花壇，花壇內部要用紅、黃、紫三種顏色的花草種植成如圖所示的圖案，圖案中AE＝MN.準備在形如Rt△AEH的四個全等三角形內種植紅色花草，在形如Rt△MEH的四個全等三角形內種植黃色花草，在正方形MNPQ內種植紫色花草，每種花草的價格如下表：設AE的長為x米，正方形EFGH的面積為S平方米，買花草所需的費用為W元，解答下列問題：(1)S與x之間的函數關係式為S＝____________；(2)求W與x之間的函數關係式，並求所需的最低費用是多少元；(3)當買花草所需的費用最低時，求EM的長．參考答案1.解：設PC ＝x ，∵PD ∥BA ，∠BAC ＝90°，∴∠PDC ＝90°.又∵∠C ＝60°，∴∠B ＝30°.∴AC ＝12，CD ＝12x . ∴AD ＝12－12x .而PD =，∴S △APD ＝12PD ·AD ＝1112222x x ⎛⎫⨯- ⎪⎝⎭＝x 2－24x )＝8-(x －12)2＋∴PC 等於12時，△APD 的面積最大，最大面積是2解：(1)設矩形廣場四角的小正方形的邊長為x 米，根據題意，得4x 2＋(100－2x )(80－2x )＝5 200，整理得x 2－45x ＋350＝0，解得x 1＝35，x 2＝10，經檢驗x 1＝35，x 2＝10均適合題意，所以，要使鋪設白色地面磚的面積為5 200平方米，則矩形廣場四角的小正方形的邊長為35米或者10米．(2)設鋪設矩形廣場地面的總費用為y 元，廣場四角的小正方形的邊長為x 米，則y ＝30[4x 2＋(100－2x )(80－2x )]＋20[2x (100－2x )＋2x (80－2x )]，即y ＝80x 2－3 600x ＋240 000，配方得y ＝80(x －22.5)2＋199 500，當x ＝22.5時，y 的值最小，最小值為199 500，所以當矩形廣場四角的小正方形的邊長為22.5米時，所鋪設矩形廣場地面的總費用最少，最少費用為199 500元．3解：(1)函數的圖象如圖所示．(2)圖象可看成一條拋物線，這個函數可看作二次函數．(3)設所求函數關係式為s ＝av 2＋bv ＋c .把v 1＝48，s 1＝22.5；v 2＝64，s 2＝36；v 3＝96，s 3＝72分別代入s ＝av 2＋bv ＋c ，得222484822.5646436969672a b c a b c a b c ⎧⎪⎨⎪⎩＋＋＝，＋＋＝，＋＋＝，解得3,5123,160,a b c ⎧=⎪⎪⎪=⎨⎪=⎪⎪⎩∴s ＝23351216v v +. (4)當v ＝80時，233351216512v v +=×802＋316×80＝52.5；當v ＝112時，233351216512v v +=×1122＋316×112＝94.5. 經檢驗，所得結論是正確的．4解：(1)該商場銷售家電的總收益為800×200＝160 000(元)．(2)依題意可設y ＝k 1x ＋800，Z ＝k 2x ＋200.∴有400k 1＋800＝1 200,200k 2＋200＝160.解得k 1＝1，k 2＝15-. ∴y ＝x ＋800，Z ＝15x -＋200. (3)W ＝yZ ＝(x ＋800)12005x ⎛⎫-+ ⎪⎝⎭＝15-(x －100)2＋162 000. 政府應將每臺補貼款額x 定為100元，總收益有最大值，其最大值為162 000元． 5解：(1)x 2＋(4－x )2或2x 2－8x ＋16(2)W ＝60×4S △AEH ＋80(S 正方形EFGH －S 正方形MNPQ )＋120S 正方形MNPQ ＝60×4×12x (4－x )＋80[x 2＋(4－x )2－x 2]＋120x 2＝80x 2－160x ＋1 280.配方，得W ＝80(x －1)2＋1 200.∴當x ＝1時，W 最小值＝1 200元．(3)設EM ＝a 米，則MH ＝(a ＋1)米．在Rt △EMH 中，a 2＋(a ＋1)2＝12＋32，解得a＝12-±，∵a ＞0， ∴a.∴EM 的長為12-米．。

沪科版九年级上册数学小专题(二) 二次函数的应用练习

沪科版九年级上册数学小专题(二) 二次函数的应用练习类型1二次函数与代数的结合1.抛物线y=x2-2x-1与x轴的交点坐标是(C)A.(0,-1)B.(1,0)C.(1+√2,0),(1-√2,0)D.(-1+√2,0),(-1-√2,0)2.已知抛物线y=x2-5x-6.(1)若该抛物线与y轴交于点C,求点C的坐标;(2)若该抛物线与x轴交于点A和点B(点A在点B左侧),求点A、点B的坐标.解:(1)当x=0时,y=-6,所以点C坐标为(0,-6).(2)当y=0时,x2-5x-6=0,解得x1=-1,x2=6,因为点A 在点B左侧,所以点A坐标为(-1,0),点B坐标为(6,0).3.(绵阳中考)将二次函数y=x2的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数y=2x+b的图象有公共点,则实数b的取值范围是(D)A.b>8B.b>-8C.b≥8D.b≥-84.求证:函数y=mx2-(3m-1)x+2m-2的图象与x轴必有交点.证明:①当m=0时,函数为一次函数y=x-2,其图象与x轴有交点(2,0);②当m≠0,函数为二次函数,∵Δ=(3m-1)2-4m(2m-2)=m2+2m+1=(m+1)2≥0,∴抛物线y=mx2-(3m-1)x+2m-2与x轴必有交点.5.如图,抛物线y=-2x2+nx-6与x轴交于点A(m,0),B(3,0).(1)求m,n的值;(2)点D是该抛物线在第一象限部分上的一动点,△ABD的面积是否能等于6?若能,求出点D的坐标;若不能,请说明理由.解:(1)抛物线y=-2x2+nx-6经过点B(3,0),所以0=-18+3n-6,n=8;抛物线为y=-2x2+8x-6,当y=0时,即-2x2+8x-6=0,解得x=1或x=3,所以点A坐标为(1,0),m=1.(2)不能.理由:设点D 的横坐标为m ,则点D 的纵坐标为-2m 2+8m-6,由(1)得点A 坐标为(1,0),点B 坐标为(3,0),所以AB=2,又点D 在第一象限,结合三角形面积公式有12×2·(-2m 2+8m-6)=6,整理为m 2-4m+6=0,由于Δ=(-4)2-24=-8<0,此方程无实数解,所以△ABD 的面积不能等于6.类型2 二次函数与三角形的结合6.如图,二次函数y=-35x 2+bx+c 的图象经过点A (5,0)与B (0,3).(1)试确定该二次函数;(2)若点C 是该二次函数图象的顶点,试确定点C 的坐标;(3)点P 是该二次函数对称轴上一动点,若以点P ,点O ,点B 为顶点的三角形是等腰三角形,请直接写出点P 的坐标(不用说理).解:(1)根据题意,得{c =3,-35×52+5b +3=0,解得{b =125,c =3,所以二次函数表达式为y=-35x 2+125x+3.(2)y=-35x 2+125x+3=-35(x 2-4x )+3=-35(x-2)2+275,所以顶点C 的坐标为(2,275). (3)点P 坐标为(2,32)或(2,√5)或(2,-√5)或(2,3-√5)或(2,3+√5).类型3 二次函数与四边形的结合7.(湖南岳阳)如图,抛物线y=23x 2+bx+c 经过点B (3,0),C (0,-2),直线l :y=-23x-23交y 轴于点E ,且与抛物线交于A ,D 两点.P 为抛物线上一动点(不与A ,D 重合).(1)求抛物线的表达式;(2)当点P 在直线l 下方时,过点P 作PM ∥x 轴交l 于点M ,PN ∥y 轴交l 于点N.求PM+PN 的最大值;(3)设F 为直线l 上的点,以E ,C ,P ,F 为顶点的四边形能否构成平行四边形?若能,求出点F 的坐标;若不能,请说明理由.解:(1)将B (3,0),C (0,-2)代入y=23x 2+bx+c ,得{6+3b +c =0,c =-2,解得(b =-43,c =-2, ∴抛物线的表达式为y=23x 2-43x-2. (2)设P (a ,23a 2-43a -2)(-1<a<2),则N (a ,-23a -23), ∴PN=-23a 2+23a+43=-23(a -12)2+32≤32,∵M ,N 在直线l :y=-23x-23上,PM ∥x ,PN ∥y ,∴PN PM =23,∴PM+PN=52PN ≤154. 即PM+PN 的最大值为154. (3)能.F 点的坐标为(1,-43),(-1,0),(1+√172,-3+√173),(1-√172,3-√173).类型4 最值问题8.如图,直线y=kx+b (k ,b 为常数)分别与x 轴、y轴交于点C (-3,0),D (0,3),抛物线y=-23x 2+43x+2与x 轴交于点A 和点B (点A 在点B 的左侧).(1)求直线y=kx+b 的表达式;(2)求点A 和点B 的坐标;(3)若直线l 与x 轴垂直,在点A 与点B 之间移动,且与直线y=kx+b (k ,b 为常数)交于点E ,与抛物线y=-23x 2+43x+2交于点F ,求EF 的最小值. 解:(1)∵直线y=kx+b 经过点C (-3,0),D (0,3), ∴{-3k +b =0,b =3,解得{k =1,b =3,∴直线的表达式是y=x+3.(2)当y=0时,即-23x 2+43x+2=0,解得x 1=-1,x 2=3,又点A 在点B 的左侧,所以点A 坐标为(-1,0),点B 坐标为(3,0).(3)令点E ,F 的横坐标为a ,EF=s ,点F 的纵坐标为-23a 2+43a+2,点E 的纵坐标为a+3,所以s=(a+3)-(-23a 2+43a +2)=23a 2-13a+1(-1<a<3), 又s=23a 2-13a+1=23(a 2-12a )+1=23(a-14)2+2324,由于23>0,所以抛物线的开口向上,又-1<a<3,所以当a=14时,s 有最小值2324,且最小值为2324,即EF 的最小值为2324. 类型5 利润问题9.已知老王一个月销售某种服装x (件)与获得利润y (元)满足表达式:y=-x 2+1200x-120190,则当一个月卖出600件衣服时,获得最大利润240000元.10.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=-2x+80.设这种产品每天的销售利润为y(元).(1)求y与x之间的函数表达式;(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?解:(1)y=(x-20)(-2x+80)=-2x2+120x-1600.(2)y=-2x2+120x-1600=-2(x-30)2+200,∴当x=30时,y有最大值200,即当销售价定为30元/千克时,每天可获最大销售利润200元.(3)当y=150时,可得方程-2(x-30)2+200=150,解得x1=25,x2=35,根据题意,x2=35不合题意,应舍去,∴当销售价定为25元/千克时,该农户每天可获得销售利润150元.类型6几何图形面积问题11.用长为6 m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是(C) m2 B.1 m2A.23m2 D.3 m2C.3212.如图,用长20 m的篱笆,一面靠墙(墙足够长)围成一个长方形的园子,园子的最大面积是50 m2.13.如图所示,某学校拟建一个含内接矩形的菱形花坛.矩形的四个顶点分别在菱形的四条边上,菱形的边长AB=4米,∠ABC=60°.设AE=x米(0<x<4),矩形的面积为S平方米.(1)求S与x的函数表达式;(2)学校准备在矩形内种植红色花草,四个三角形内种植黄色花草,已知红色花草的价格为20元/平方米,黄色花草的价格为40元/平方米.当x为何值时,购买花草所需的总费用最低,最低总费用是多少?(结果保留根号)解:(1)连接AC,BD,AC与EH交于点M.∵花坛为菱形,∠ABC=60°,∴△ABC,△BEF是等边三角形,AC⊥EH.∴EF=BE=AB-AE=4-x.x,在Rt△AEM中,∠AEM=30°,易得EM=√32∴EH=2EM=√3x.∴S=EH·EF=√3x·(4-x),即S=-√3x2+4√3x. (2)∵红色花草价格比黄色花草便宜,∴当矩形面积最大时,购买花草的总费用最低.又∵S=-√3x2+4√3x=-√3(x-2)2+4√3,∴当x=2时,S最大=4√3.易得S=8√3,菱形ABCD此时四个三角形的面积为8√3-4√3=4√3.∴最低总费用为20×4√3+40×4√3=240√3(元).类型7 分段函数问题14.(达州中考)宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x 天生产的产品数量为y 件,y 与x 满足如下关系:y={7.5x (0≤x ≤4),5x +10(4<x ≤14),(1)工人甲第几天生产的产品数量为70件?(2)设第x 天生产的产品成本为P 元/件,P 与x 的函数图象如图.工人甲第x 天创造的利润为W 元,求W 与x 的函数表达式,并求出第几天时,利润最大,最大利润是多少?解:(1)当0≤x ≤4,当x=4时,7.5×4=30<70,当4<x ≤14时,70=5x+10,解得x=12,∴工人甲第12天生产的产品数量为70件.(2)当0≤x ≤4时,W=(60-40)×7.5x=150x ,当x=4时,w 有最大值为600元;当4<x ≤14,设成本与x 之间的函数表达式为P=kx+b ,代入点(4,40),(14,50)得{4k +b =40,14k +b =50,解得k=1,b=36,∴P=x+36. ∴W=[60-(x+36)](5x+10)=-5(x-11)2+845, ∴当x=11时,W 有最大值为845.∴第11天时,利润为最大,最大值为845元.15.某超市以每件20元的价格新进一批商品,经市场调研发现:该商品每天的销售量y (件)与销售价格x (元/件)(20≤x ≤60)的关系如下图所示.(1)试确定y 与x 之间的函数表达式(写出自变量的取值范围);(2)若超市一天销售该商品的利润为w (元),写出w 与商品的售价x (元/件)之间的函数表达式;(3)求(2)中当销售价格x 定为多少时,一天的利润w 最大,最大利润是多少?解:(1)分两种情况:①当20≤x ≤30时,设y=ax+b ,根据题意得{20+b =200,30a +b =400,解得{a =20,b =-200,∴y=20x-200;②当30<x ≤60时,设y=mx+n ,根据题意得{30m +n =400,60m +n =100,解得{m =-10,n =700,∴y=-10x+700,故y 与x 之间的函数表达式是y={20x -200(20≤x ≤30),-10x +700(30<x ≤60).(2)当20≤x ≤30时,w=(x-20)(20x-200)=20x 2-600x+4000; 当30<x ≤60时,w=(x-20)(-10x+700)=-10x 2+900x-14000.w={20x 2-600x +4000(20≤x ≤30),-10x 2+900x -14000(30<x ≤60).(3)当20≤x ≤30时,w=20x 2-600x+4000=20(x 2-30x )+4000=20(x-15)2-500,抛物线开口向上,x>15时,y 随x 的增大而增大,又20≤x ≤30,所以当x=30时,w 最大值=20(30-15)2-500=4000;当30<x ≤60时,w=-10x 2+900x-14000=-10(x 2-90x )-14000=-10(x-45)2+6250,抛物线开口向下,当x=45时,w 最大值=6250.综上所述,当定价为45元/件时,一天的利润w 最大,最大值为6250元.类型8建立函数模型问题16.(恩施中考)宜万铁路开通后,给恩施州带来了很大方便.恩施某工厂拟用一节容积是90立方米、最大载重量为50吨的火车皮运输购进的A,B 两种材料共50箱.已知A种材料一箱的体积是1.8立方米、重量是0.4吨;B种材料一箱的体积是1立方米、重量是1.2吨.不计箱子之间的空隙,设A种材料进了x箱.(1)求厂家共有多少种进货方案?(不要求列举方案)(2)若工厂用这两种材料生产出来的产品的总利润y(万元)与x(箱)的函数关系大致如下表,请先根据下表画出简图,猜想函数类型,求出函数表达式(求函数表达式不取近似值),确定采用哪种进货方案能让厂家获得最大利润,并求出最大利润.x1520253038404550y10约27.5840约48.20约49.10约47.1240约26.99解:(1)38.(2)图略,该函数为二次函数,y=-0.1x2+7x-72.5,A种材料购进35箱,B种材料购进15箱时,能让厂家获得最大利润,最大利润为50万元.。

练3_二次函数的应用(沪科版)(原卷版)

二次函数的实际应用题专项训练卷(3)

专题02 二次函数的实际应用(30题)(原卷版)

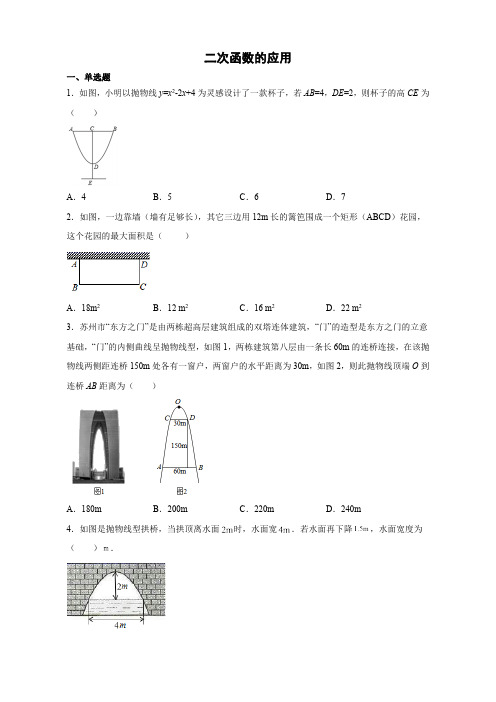
21.4 二次函数的应用 沪科版数学九年级上册课后练习(含答案解析)

初中数学沪科版九年级上册第二十一章《二次函数的应用》练习题(解析版)

沪科版-数学-九年级上册-九上22.5二次函数的应用同步练习及答案

2023年二轮复习解答题专题十七：二次函数的应用(销售利润问题)(原卷版)

沪科版九年级上册数学《二次函数应用题》试题

沪科新版九年级(上) 中考题同步试卷：21.4 二次函数的应用(13)

初中数学沪科版九年级上册第二十一章《二次函数的应用》练习题(解析版)

二次函数图象性质与综合应用(44题)(原卷版)

2019-2020学年数学沪科版九年级上册21.4 二次函数的应用(3) 同步练习D卷

沪科版九年级数学习题-二次函数的应用(第2课时)

沪科版-数学-九年级上册- 21.4 二次函数的应用第3课时

沪科版九年级数学习题-二次函数的应用(第3课时)

沪科版九年级上册数学 小专题(二) 二次函数的应用练习

21.4 二次函数的应用沪科版数学九年级上册课后练习(含答案解析)

沪科版九年级上册数学小专题(二) 二次函数的应用练习