2017西安交通大学网络学院《高等数学》选择题答案
《2017年成人高考专升本《高等数学一》真题及答案

一、选择题:1~10 小题。每小题 4 分,共 40 分.在每个小题给出的四个选 项 中,只有一项是符合题目要求的。把所选项前的字母填在题后的括号内。
第1题
答案:C 第2题
答案:C
第 1 页 共 11 页
第3题
答案:D 第4题
答第 21 题
答案:
第 22 题 答案:
第 7 页 共 11 页
第 23 题 答案:
第 8 页 共 11 页
第 23 题 答案:
第 24 题 答案:
第 9 页 共 11 页
第 25 题 答案:
第 26 题 答案:
第 10 页 共 11 页
第 27 题 答案:
第 28 题 答案:
第 11 页 共 11 页
答案:0 第 15 题
答案: 第 16 题 答案:8
第 5 页 共 11 页
第 17 题 答案: 第 18 题 答案: 第 19 题
答案: 第 20 题 答案:
第 6 页 共 11 页
三、解答题:21~28 题,前 5 小题各 8 分,后 3 小题各 10 分。共 70 分.解答 应写出推理、演算步骤。
答案:B 第6题
答案:B 第7题
答案:A 第8题
答案:A
第 3 页 共 11 页
第9题
答案:C 第 10 题
答案:C 二、填空题:11~20 小题。每小题 4 分,共 40 分.把答案填在题中横线上。
第 11 题 答案:
第 4 页 共 11 页
第 12 题
答案:y=1 第 13 题
答案:f(-2)=28 第 14 题
西安交通大学网络教育学院《高等数学-学习指南》(专升本) (徐文雄)

《高等数学》——学习指南一、解答下列各题 (1)求0011lim (sinsin)x y x y yx→→+。
(2) 判断级数+1∞∑(3) 求函数cos()xyz e x y =+的全微分dz 。
(4)求曲线3z t ⎧⎪⎨⎪=⎩2x =t y =t 上的点,使在该点的切线平行于平面24x y z ++=。
(5)解方程()()0x yx yyxe edx e e dy ++-++=。
(6)计算二重积分Dσ⎰⎰,其中D是由两条抛物线y =,2y x=所围成的闭区域。
(7)证明:00lim x y x yx y →→+-不存在。
(8)证明:级数211nn e∞-=∑发散。
(9)设22()u xy ϕ=+,求证:0u u xyyx∂∂-=∂∂。
(10)求曲线3z t ⎧⎪⎨⎪=⎩2x =t y =t 在点(1,1,1)处的切线及法平面方程。
(11)解方程22dy ydxxy x=-。
(12)计算二重积分Dσ⎰⎰,其中D是由两条抛物线y =,2y x=所围成的闭区域。
(13)求21lim2x x x →-+-(14)证明:级数 ()()1112n n n n ∞=++∑收敛。
(15)求函数:()(),,sin x z f x y z e x y +=+的全微分df 。
(16)求过点(1,2,1)-且与直线2431x ty t z t =-⎧⎪=-+⎨⎪=-+⎩垂直的平面方程。
(17)解微分方程()320y x dx xdy --=。
(18)计算二重积分()Dx y dxdy+⎰⎰,其中D :222x y ax +≤。
二、设22()y z f x y =-,其中()f u 为可导函数,验证:211z z z x xy yy∂∂+=∂∂。
三、计算对坐标的曲线积分22()-(-)Lx y dx x y dyx y++⎰ ,其中L 是圆周222x y a+= (按逆时针方向绕行)。
四、计算曲面积分2Ix dS∑=⎰⎰,其中∑是球面2222x y z R++=。
高数下期末考试试题及答案解析

WORD 格式整理⋯⋯⋯⋯⋯⋯⋯名⋯姓⋯⋯⋯⋯.⋯号⋯学⋯⋯线封号序密过超号班要学教不纸题卷试答⋯学⋯大峡.三⋯⋯⋯⋯⋯⋯⋯⋯2017 学年春季学期《高等数学Ⅰ(二)》期末考试试卷(A)注意:1、本试卷共3页;2、考试时间110 分钟; 3 、姓名、学号必须写在指定地方题号一二三四总分得分阅卷人得分一、单项选择题( 8 个小题,每小题 2 分,共 16 分)将每题的正确答案的代号 A、 B、 C或 D 填入下表中.题号12345678答案1.已知 a 与 b都是非零向量,且满足a b a b ,则必有().(A)a b0(B) a b0(C) a b0(D)a b02. 极限 lim( x2y2 )sin212().x0x yy0(A) 0(B) 1(C) 2(D)不存在3.下列函数中, df f 的是 ().( A) f (x, y)xy( B) f (x, y)x y c0 ,c0为实数( C) f (x, y)x2y2( D) f (x, y)e x y4.函数 f ( x, y)xy (3x y) ,原点 (0,0)是 f (x, y) 的 ().( A)驻点与极值点( B)驻点,非极值点( C)极值点,非驻点( D)非驻点,非极值点5 .设平面区域 D : (x1)2( y 1)2 2 ,若 I 1x yd, I 2x y d ,D4D4I 33x yd,则有() .4D( A) I1I2I3( B) I 1I 2I 3( C) I 2I1I 3( D) I 3 I 1I 26.设椭圆 L :x2y 21的周长为 l ,则(3x2 4 y2 )ds() .43Ll3l4l12l(A)(B)(C)(D)7.设级数a n为交错级数, a n0 (n) ,则() .n 1(A) 该级数收敛(B)该级数发散(C) 该级数可能收敛也可能发散(D)该级数绝对收敛8. 下列四个命题中,正确的命题是() .( A)若级数a n发散,则级数a n2也发散n 1n 1( B)若级数an2发散,则级数a n也发散n 1n 1( C)若级数an2收敛,则级数a n也收敛n 1n 1( D)若级数| a n |收敛,则级数an2也收敛n 1n 1阅卷人得分二、填空题 (7 个小题,每小题 2 分,共 14 分) .3x 4 y2z60a 为.1. 直线3y z a与 z 轴相交,则常数x02.设 f ( x, y)ln( xy ), 则 fy(1,0)___________.x3.函数 f (x, y)x y 在 (3, 4) 处沿增加最快的方向的方向导数为.4.设 D : x2y22x ,二重积分( x y)d=.D5.设 f x 是连续函数,{( x, y , z) | 0z9x2y2 } , f (x 2y 2 )dv 在的三次积分为.6. 幂级数( 1)n 1x n的收敛域是.n!n 17. 将函数 f ( x)1,x0为周期延拓后,其傅里叶级数在点1x2,0 x以 2于.专业资料值得拥有--学习资料分享----⋯⋯⋯⋯⋯⋯⋯名⋯姓⋯⋯⋯⋯.⋯号⋯学⋯⋯线封号序密过超号班要学教不纸题卷试答⋯学⋯大峡.三⋯⋯⋯⋯⋯⋯⋯⋯阅卷人得分三、综合解答题一( 5 个小题,每小题7 分,共 35 分,解答题应写出文字说明、证明过程或演算步骤)1.设 u xf ( x, x) ,其中 f 有连续的一阶偏导数,求u ,u.y x y解:4.设是由曲面z xy, y x, x 1 及 z 0 所围成的空间闭区域,求 I xy2 z3dxdydz .解:2.求曲面 e z z xy 3 在点 (2,1,0) 处的切平面方程及法线方程.解:5.求幂级数nx n 1的和函数 S(x) ,并求级数n n的和.n 1n 1 2解:3. 交换积分次序,并计算二次积分dxxsin y dy.y解:专业资料值得拥有--学习资料分享----⋯⋯⋯⋯⋯⋯⋯名⋯姓⋯⋯⋯⋯.⋯号⋯学⋯⋯线封号序密过超号班要学教不纸题卷试答⋯学⋯大.峡三⋯⋯⋯⋯⋯⋯⋯⋯阅卷人得分四、综合解答题二( 5 个小题,每小题7 分,共 35 分,解答题应写出文字说明、证明过程或演算步骤)1.从斜边长为 1 的一切直角三角形中,求有最大周长的直角三角形.解4.计算xdS ,为平面x y z 1在第一卦限部分.解:2.计算积分( x2y2 )d s,其中 L 为圆周 x2y2ax ( a0 ) .L解:5.利用高斯公式计算对坐标的曲面积分蝌dxdy + dydz + dzdx,S其中为圆锥面 z2x2y2介于平面 z0 及 z 1之间的部分的下侧解:3.利用格林公式,计算曲线积分 I(x2y 2)d x (x 2xy)dy ,其中 L 是由抛物线 y x2和Lx y2所围成的区域 D 的正向边界曲线.yy x2x y2D专业资料值得拥有O x--学习资料分享----2017 学年春季学期《高等数学Ⅰ(二)》期末考试试卷(A)答案及评分标准一、单项选择题(8 个小题,每小题 2 分,共 16 分)题号12345678答案D A B B A D C D1.已知 a 与 b 都是非零向量,且满足a b a b ,则必有(D)(A) a b0 ;(B)a b 0 ;(C) a b0 ; (D) a b0 .2. 极限 lim( x2y2 )sin212( A )x0x yy0(A) 0;(B) 1;(C) 2;(D)不存在 .3.下列函数中, df f 的是 ( B );( A) f ( x, y)xy ;( B) f ( x, y)x y c0 , c0为实数;( C) f (x, y)x2y2;( D) f (x, y)e x y.4.函数 f ( x, y)xy (3x y) ,原点 (0,0)是 f (x, y) 的 ( B).(A)驻点与极值点;(B)驻点,非极值点;(C)极值点,非驻点;( D)非驻点,非极值点 .5 .设平面区域 D: ( x 1)2( y 1)2 2 ,若 I1x y d , I2x ydD4D4WORD 格式整理3 x yd ,则有( A)I 34D(A) I 1I2I 3;(B) I 1I2I 3;( C) I 2I1I 3;(D) I 36.设椭圆 L :x2y 21的周长为 l ,则(3 x24y 2 )ds( D)43L(A) l ;(B)3l;(C)4l ;(D)12l7.设级数a n为交错级数, a n0(n) ,则(C)n 1(A) 该级数收敛;(B)该级数发散;(C) 该级数可能收敛也可能发散;(D)该级数绝对收敛.8. 下列四个命题中,正确的命题是(D)( A)若级数a n发散,则级数an2也发散;n1n 1( B)若级数an2发散,则级数a n也发散;n1n 1( C)若级数an2收敛,则级数a n也收敛;n1n 1( D)若级数| a n |收敛,则级数a n2也收敛.n1n 1二、填空题 (7 个小题,每小题 2 分,共 14 分 ) .3x 4 y2z60a 为31. 直线3y z a与 z 轴相交,则常数。
2017数学二真题

2017数学二真题一、选择题(每小题4分,共32分) (1)若函数21cos ,0(),0xx f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续,则( )。
A. 12ab =B. 12ab =-C. 0ab =D. 2ab =【答案】A【解析】由连续的定义可知:-00lim ()lim ()(0),x x f x f x f +→→==其中-0(0)lim ()x f f x b →==,2000112lim ()lim lim 2x x x f x ax a+++→→→===,从而12b a =,也即12ab =,故选A.【试题点评】本题考查函数的连续性。
此知识点在冲刺阶段的数学冲刺串讲班中第一部分高等数学有重点讲解,在强化阶段数学强化班高等数学第一章函数、极限、连续和强化阶段数学重点题型精讲班也均有涉及。
(2)设二阶可导函数()f x 满足(1)(1)1,(0)1f f f =-==-,且''()0f x >,则( )。
【答案】D【解析】limsin )sin nn x x x a a→∞+=+(,而要使sin 0a a +=,只有a=0,故D 正确。
【试题点评】本题考查级数收敛性。
此知识点在冲刺阶段的数学冲刺串讲班中第一部分高等数学有重点讲解,在强化阶段数学强化班高等数学第九章级数和强化阶段数学重点题型精讲班也均有涉及。
(4)微分方程()'''2481cos2xy y y e x -+=+的特解可设为ky=( )。
A. ()22cos2sin2xx Aee B x C x ++ B. ()22cos2sin 2xx Axe e B x C x ++ C. ()22cos2sin 2xx Aexe B x C x ++ D. ()22cos2sin 2xx Axexe B x C x ++【答案】C【解析】齐次方程的特征根为22r i =±,原方程可分解为两个非齐次方程:2''4'8xy y y e -+=和2''4'8cos2x y y y e x-+=,可知第一个方程的特解为2xAe ,第二个方程的特解为2(cos2sin 2)xxeB xC x +,故选C.【试题点评】本题考查微分方程的解。
2017西安交通大学网络学院《高等数学》选择题答案

《高等数学》(专升本)(2017)秋试卷总分:100 测试时间:--一、单选题(共40 道试题,共80 分。
)V1. 如题:A. AB. BC. CD. D2. 如题:A. AB. BC. CD. D3. 如题:A. AB. BC. CD. D4. 如题:A. AB. BC. CD. D5. 如题:A. AB. BC. CD. D6. 如题:A. AB. B7. 如题:A. AB. BC. CD. D8. 如题:A. AB. BC. CD. D9. 如题:A. AB. BC. CD. D10. 如题:A. AB. BC. CD. D11. 如题:A. AB. BC. CD. D12. 如题:A. AB. BC. CD. D13. 如题:A. AB. BC. CD. D14. 如题:A. AB. BC. CD. D15. 如题:A. AB. BC. CD. D16. 如题:A. AB. BC. CD. D17. 如题:A. AB. BC. CD. D18. 如题:A. AB. BC. CD. D满分:2 分19. 如题:A. AB. BC. CD. D20. 如题:A. AB. BC. CD. D21. 如题:A. AB. BC. CD. D满分:2 分22. 如题:A. AB. BC. CD. D满分:2 分23. 如题:A. AB. BC. CD. D满分:2 分24. 如题:A. AB. BC. C25. 如题:A. AB. BC. CD. D满分:2 分26. 如题:A. AB. BC. CD. D满分:2 分27. 如题:A. AB. BC. CD. D满分:2 分28. 如题:A. AB. BC. CD. D满分:2 分29. 如题:A. AB. BC. CD. D满分:2 分30. 如题:A. AB. BC. C31. 如题:A. AB. BC. CD. D满分:2 分32. 如题:A. AB. BC. CD. D满分:2 分33. 如题:A. AB. BC. CD. D满分:2 分34. 如题:A. AB. BC. CD. D满分:2 分35. 如题:A. AB. BC. CD. D满分:2 分36.如题:A. AB. BC. C请同学及时保存作业,如您在20分钟不作操作,系统将自动退出。
西安交通大学《高等数学上》作业集问题详解

文案大全第一章 函数与极限作业参考答案第一节 函数(作业一)一、1. C .2.A .3.B .4. B .5.A .6. B .7.A . B .9.B .10. D .二、填空:11.322333a a b ab b +++;12.(12)xxa +;13.sin cos cos sin x y x y +;;14.1;15.2sec x ; 16.22()()a b a ab b -++;17.(1)(21)6n n n ++.三、18.(1) (,0)-∞;(2) [4,][0,]ππ-; (3) ]0,1[-和1=x ;(4)]11,2[]2,11[ --.第一节 函数(作业二)一、1.D .2.C .3.D .4.A .5.A .6.D .7.D .8.B .9.A .10.D . 二、11.1[sin()sin()]2x y x y ++-; 12.1[cos()cos()]2x y x y ++-;13.2sin cos x x ; 14.22cos sin x x -;15...222x x ++; 18.[,]66ππ-; 19.2cos y x =;20.内点.三、计算题:21.πk x x f 2)(-=,当ππ)12()12(+<≤-k x k 时,Z k ∈.22.⎩⎨⎧><+-=.0,0,,)(22x x x x x x x f 23.(1) 3u y =,υu sin =,x v 1=;(2) u y 2=,υarcsin =u ,2x υ=;(3)u y lg =,υu lg =,ωυlg =,21xω=;(4)u y arctan =,υe u =,x cos =υ.第二节 数列的极限(作业一 )一、1. D .2.C .3.C .4.A .5.B .二、6.0;7.1;8.12; 9.0;10.1;11.0;12.0;13.1n;14.1;15.1. 三、计算题:17. (1) 0 ; (2)1;(3) 2 ;(4)13.第二节 数列的极限(作业二 )一、1.A .2.A .3.D .4.B .5.C .6.D .7. B .二、计算下列各题:8;9.1 ;10.12 ;11.32;12. e . 三、计算题:13.(1) 1; (2) ,1;31,1;1,1;1,1-=-=-<>x x x x 发散.14. (1)正确;(2)不正确,如nn a )1(-=;(3)正确;(4)正确;(5)不正确,如!1n a n =,0lim =∞→n n a ,但10lim1≠=+∞→nn n a a ;(6)正确.设A A a a n n n n =⋅=⋅=>∞→∞→ααααα1)1(lim lim ,0.119第三节 函数的极限(作业一)一、1.A .2.A .3. D .4.B .D .6. A .π- 二、计算下列各题:7.27;8; 9.1;10.32;11.3;12.13;13.0;14.1.三、计算题:15.3)(lim 3=-→x f x ,8)(lim 3=+→x f x ;16.不存在;17. 7. 第三节 函数的极限(作业二)一、单项选择题 :1.B .2.B .3.C .4.C .5.C .二、计算下列各题:6.32;7.1;8.94; 9.ln 2;10.1;11.(1)2n n +12.12;13.2;14.3;15.1;16.2e ;17.2;18.1;19.3e -.三、计算题:.第四节 无穷小量与无穷大量一、单项选择题 :1. B .2.A .3.C .4.C .5.B .6.D .7.A .8.B .9.B .二、10.0;11.1;12.29;13.1;14.ae ;15.12;16.12 ;17.1;18.cos a ;19.1;20.0. 三、22.∞→x 时是无穷小,3→x 时是无穷大.23.x ,sin x ,2tan x ,1)-是等价无穷小量.24.1x e -,ln(1)x +1-是与x 同阶的无穷小量.cos 1x -, 2sin x ,2(sin )x 是比x 更高阶的无穷小量.第五节 函数的连续性与间断点(作业一)一、单项选择题 :1.B .2.A .3.A .4.B. 二、填空:5.0;6.0;7.1;8.0;9.12e-.三、10. )(x f 在0=x 不连续;11.1=K ;12.⎪⎩⎪⎨⎧≥<≤<≤=150,6.015050,7.0500,8.0x x x x x x yy 不是x 的连续函数;13.s=332.01.第五节 函数的连续性与间断点(作业二)一、单项选择题:1. B .2.D .3.B .4.D .二、计算下列各题:5.0;6.3;7.1-;8.12e -;9.2π.三、10.(1) 2=x ,无穷型 (2) 1=x ,可去型,2=x ,无穷型 (3) 0=x ,可去型 (4)1-=x ,2-=x ,无穷型 .12.1=a ,1-=b . 13. 可去型.14.无界,非无穷大.第一章 综合练习题1.01=)(f ,02=-)(f ,224=⎪⎭⎫⎝⎛πf ,224=⎪⎭⎫ ⎝⎛-πf ;2.(1) 偶,π=T ; (2) 1=T ;文案大全(3) 偶;3.(1) ↓-∞)0,(,↓+∞),0(,无界; (2) ↑+∞-∞),(,有界; (2) ↑+∞-),1(,无界;(4) ↑-]0,[a ,↓],0(a ,有界;.4.(1))1,0(,1log 2∈-=x xx y ;(2) 0),(21≥-=-x e e y x x;5.)1arcsin()(2x x -=ϕ; 6.21)(2-=x x f ;7..4,0,0,4,,1,ln ))((2>=≠≤⎪⎩⎪⎨⎧=x x x x x x x f ϕ;8.2. 10. 求下列各极限.(1) 1;(2) 3 ;(3) 61;(4) 1;(5) 201032; (6) 0;(7) 1;(8) 0;(9) 4e ;(10)23 ;(11) 43;(12) 1;(13) 25;(14) 4; (15) 2;(16) x ;(17)16-;(18) 1-; (19) 2e -;(20) 2e ;(21) e ;(22) 3e -;(23) 2e -;(24) 16e - ;(25) 4e -(26) 2-. 11.(1) 1=x ,可去型 (2) 1=x ,跳跃型.第二章 导数与微分作业参考答案第一节 导数概念一、单项选择题 :1. B .2.B .3.D .4.C .5.B .C .6.D .7.C . 8.C .9.B .二、填空10.11ln 2xx +;11.2ln 2x xe +;12.cos sin x x -; 1321x-;14. ln x y y ;15.1x xy -;16.1-;17. 2cos a -;18.2ln 2x -;19.()()f a a ϕ'=.三、20. 连续、可导 0)0(='f ; 21. 连续、可导 1)0(='f ;22. 连续、不可导;3. 连续、不可导.第二节 导数的计算 (四则运算)一、 1.D .2.C .3.A .4.B .二、5. 23464y x x '=++;6.323(3y x '=++ 7. 566cos sin y x x x x '=- ;8. (sin cos )sin x x y e x x x xe x '=-+; 9. 2tan sec 3sec tan y x x x x x '=+-;10.1421123333341cos sin cot cos csc cos cos 33y x x x x x x x x x x x x -'=--++; 11. 52323322y x x x --'=--;12.y '=.222121x x y x +-'=+(); 14.22(sin cos )(1tan )sin sec 1tan x x x x x x xy x ++-'=+(); 15. 32322(1)sec tan 6sec 1x x x x xy x +-'=+();12116.2222(1)(2(ln )(2ln 22)2x x x x x x x x x y x x ++-++'=+)(). 17.6x y π='=213+,4x y π='=2 ;18.(0)f '=253,(2)f '=1517;19.4x y π='=8)2(2+π三、 20.切线方程02=-y x ,法线方程02=+y x . 21.ea 21=,切线方程为:022=--e y e x ,法线方程为:01222=+-+)(e y x e .第二节 导数的计算 (复合函数求导法)一、单项选择题 1. C . 2.D .3.B .4.C . 二、5.'tan y x =-;6.2'y =;7.'2sec2tan 2y x x =;8.22222sin 2cos 2sin sin 'cos x x x x x y x +=;9.2211'secy x x =- ;10.'cot y x =; 11.2'2csc 2y x =-;12.'3csc3cot 3y x x =-;13.1'ln (ln 1)x n x y a a nx x x -=+++;14.2'y =;15.'y =;16.y '=412x x+;17.y '=212arcsin xx x x -+; 18.y '=xx x 2ln 1ln arcsin 2-;19.y '=xx e x)1(2arctan+;20.y '=x arccos ;21.y '=x x x 22sec tan 3sin 1+;22.y '=211x +-; 23. y '=xx --1854; 24. y '=x x x x x xxln ln ln 1ln 1ln 22ln 2ln --⋅⋅;25.y '=211x+; 26.y '=x e xe x xx⋅⋅---2ln 2)ln 1(21;27. y '=211x +-;28.y '=22111xx -+-; 29.y '=x e x x1sin 222sin 1-;30.y '=222cos sin 2sin 2sin x x x x x +.第三节 高阶导数一、单项选择题:1.D .2.D .48.3.A .二 填空:4.sin(),1,2,2n x n π+= ; 5.1(1),1,2,n n n x --= ;6.0 ; 7.cos(),1,2,2n x n π+= ;8.,1,2,x e n = ;9.1 . 10. 2cos 2cos sin ln x y x x x x '=-⋅+ ,y ''=22cos 2sin 2ln 2cos 2x xx x x x ---;文案大全11.2y '=+,y ''=252)1(3--x x ;12.y '=,y ''=23222)(x a a --;13.221x y x -'=-,y ''=222)1()1(2x x -+-; 14.2arctan 1y x x '=+,y ''=212arctan 2xxx ++ ; 15.y '=,y ''=232)1(x x +-; 16.2323(1)x y x -'=+,y ''=333)1()12(6+-x x x ; 17. )sin (sin )sin ()cos 1(2x x f x x x f x +'⋅-+''+;18. )()]([)()(22x f x f x f x f '-'';19.322222)](1[)]()([)(1)]()()]([[)(1)()(2x f x f x f x x f x f x f x f x x f x f x f +'-+''+'++'; 20.)()(3)(32xx x x x x e f e e f e e f e ''+'+.三、 21. )(n x e x+; 22.)2(!)2()1(1≥---n x n n n ; 23.n m x n m m m m -++---1)1)(11()21)(11(1 , 24.)212sin(21π-+-n x n .第四节 其他形式下函数求导问题一、1.B .2. B .3. D .4. B .5. C .6.C . 7.A . 二、8.切线方程0222=-+y x ,法线方程0142=--y x ;9.线方程01234=-+y x ,法线方程0643=+-y x三、10.t tan - ; 11. 23-; 12.;2- ;13. π3232e -.四、 14. xy x y xy --; 15.12-y xy ;16. yx y x -+ ; 17.)sin()sin(1xy x xy y +-.第五节 函数的微分一、1.C .2.C .3. C . 4. C .5. C .6. C . 7. C .8. B .9.C . 10.A .二、11.2111sec tan dy dx x x x=-;12.22tan sec dy x xdx =;13.111(sin cos )dy dx x x x =- 14.211dy dx x =-+;15.dy = ;16.22sec ()1sec ()x y dy dx x y +=-+;17.33(2)12t t dy dx t -=-; 18.dy =;19.0t dy dx ==;20.(2sin cos )cos sin t t t t dy dx t t t+=-.三、 21.dx x x x dy )2cos 22(sin += ;22.dx x x e dy x)]3sin()3[cos(----=-;12323. ⎪⎪⎩⎪⎪⎨⎧<<--<<--=10101122x xdx x x dx dy ;24.dx x x x dy )21(sec )31tan(123222+⋅+=;25.dx x dy 232)1(-+=; 26.dx x x x dy 232)1(1)11(32++--=-.第六节 导数在经济分析中的应用1.边际成本5, 边际收入x 02.010-,边际利润x 02.05-;2. 300(单位);3.bp -;4. ⑴ 边际成本x +3,边际收入x50,边际利润x50x --3 ⑵ 1-.5.⑴ 当6190<<p 时,低弹性,当4619<<p 时,高弹性;⑵ 当30ap <<时,低弹性,当a p a<<3时,高弹性; 6. ⑴边际利润 xx 120310--;⑵ 收益的价格弹性p p --10310; 7. ⑴利润函数⎪⎩⎪⎨⎧<<-≤≤--=646402213)(2x x x x x x L ;⑵边际利润⎩⎨⎧<<-≤≤-='641403)(x x x x L . 第二章 综合练习题一、1. D .2. D . 二、3. ⑴ )(0x f '- ⑵)0(f ' ⑶)(20x f ';4. ⑴ t g gt ∆--21100; ⑵ 010gt -; 5. )(x f 在α=x 处可导,且)()(αϕα='f 6. )0(-'f 存在,且='-)0(f )0(+'f ;7.)(0x N ',当劳动力为0x 时,增加一个劳动力时该商品增加)(0x N '(劳动生产率); 8.96%,1.6%;9. 切线方程032=-+y x ,法线方程012=--y x ;10. (1) )111(ln )1(x x x x x x ++++; (2) ])2(3251[25512532+--+-x xx x x ; (3)]1534)2(21[)1()3(254+---++-+x x x x x x ;(4)])1(2sin cos 1[1sin 21x x x e e x x x e x x --+-.11.⑴ 32)2()3(y y e y -- ;⑵ )(cot )(csc 232y x y x ++-; 14.⑴3-t ; ⑵αθθ3csc sec 4;15. )/(1442s m π;文案大全16.当11181==∆=∆dy y x 时, 当0.1 1.161, 1.1x y dy ∆=∆==时,当0.010.110601,0.11x y dy ∆=∆==时.17. 21x y +;18. ⑴ 87476.0;⑵74300' ; ⑶ 9867.9; ⑷ 0052.2 ; ⑸ 96509.0-; ⑹2600'.21. )()(a f a f e '.22. 不一定成立,例⎪⎩⎪⎨⎧>≤=1132)(23x xx xx f ,⎩⎨⎧>≤≠'1212)(2x xx xx f ,⎪⎩⎪⎨⎧>=<='12112)(2x xx x x x f 不存在. 23. R a b A ∈==00;24. 12=±=b a ,.25. x x f xx f ln 1==')(,)(. 26. 0=-y x .27. 111=-=-=c b a .28. 08215=+-y x .29.122-x .30.+---)!3()1(21n n +---)!2()1(21n n )!1()1(1---n n .31. ⑴5.0 当价格4=p 时,如果价格上涨%1,收益增加%5.0⑵64.0- 当价格6=p 时,如果价格上涨%1,收益减少%636.0;如果价格下降%1,收益增加%636.0,应下调价格至16.5.第三章 微分中值定理与导数的应用作业参考答案第一节 微分中值定理一、1. D .2. B . 3. A .4. A .5. B .6.C .7. A .8.C .9.A .10. B .第二节 洛必达(L ’Hospital )法则一、 1. B . 2. B .3. C .4.A .5. B .6. C .二、7.2- ;8.13; 9.a ; 10.0;11.2(3)f '-;12.24a π-;13.12;14.16;15.216.32;17.1 ;18.1;19.31;20.0;21 ∞ ;22.61-e ;23.0;24 π2-e ;19.21;25.a ;26. 21-e;27. 1-e ;28.31e ;29. 41-;30. 21; 31. 2e- .第三节 泰勒(Taylor )公式一、⑴31,⑵ 21-. 二、⑴ ])1[()1()1()1(11332+++-+-+--=x o x x x x;⑵])4[()4(5121)4(641)4(412332-+-+---+=x o x x x x ;125⑶ )(31tan 33x o x x x ++=;⑷ )(21132sin x o x x e x +++= 三、4523)(cos 3]2)()[sin sin(31tan x x x x x x x θθθ+++=, 10<<θ.四、)()!1(!232n n x x o n x x x x xe +-++++= . 五、⑴ 10724.3303≈; 51088.1-⨯≤E ; ⑵ 1827.02.1ln ≈; 4104-⨯≤E第四节 函数性态的研究一、1. B .2. D .3.A .4. B .5. B .6.B .7.C .. B . 9.A .10. B .二、11. 4;12.2-;13.单调增加;14.'(0)0f =,"(0)0f <;15.'0y ≥;16.1p =; 四、19.1)2(=极大y ;20.4)2(-=-极大y ,0)0(=极小y ;21.205101)512(=极大y ;22.无极值. 第五节 函数作图一、1. D .2.C .3. C .4.A .5. C .6.A .7. B .8. C .9.C .10.A . 二、11.0,1y x ==;12. (,0)π; 13.(22-;14.有一个拐点;15.2π+=x y ,2π-=x y ; 16.22049x y -=;17.y x =. 第六节 最大最小值问题及在经济管理中的应用一、⑴ 0)0(=最大y , 16)4(-=最小y ⑵ 45)43(=最大y , 56)5(-=-最小y 二、设半径为32πVr =, 高为34πV h =时, 表面积最小三、产量140=x , 平均成本104=c , 边际成本104='c 四、出售3000=x 件时,收益最高.五、101=p (元), 3920=Q , 167080=最大L (元)第三章 综合练习3.(1)↓)2,0(↑∞+),2(;(2)11(,),(,)22-∞↓+∞↑; (3)↓-∞)0,(↓)21,0(↑)1,21(↓∞+),1(;(4)↑-∞)32,(a ↓),32(a a ↑∞+),(a .4.(提示: 设那条直线为b kx y +=).5. (提示: 设()()nF x x f x =) ;6.2-<a , 无根; 2-=a ,唯一根2-=x ; 2->a ,在),(a -∞和),(∞+a 内各有一根.文案大全7. ⎪⎩⎪⎨⎧=-''≠+-+'='--0,21)0(0,)()()(2x g x x e x g xe x g x x f xx , )(x f '在),(∞+-∞处处连续.9. 驻点1=x , 1)1(=极小y .10. 设)1,0(∈x ,证明:22(1)ln (1)x x x ++<. 11.2)0(=极大f , 21()e f e e--=极小.12.当n 为奇数时, 在0x 无极值,当n 为偶数时, f 在0x 有极值 13.一段为ππ+4a , 另一段为π+44a. 14.当)(0bc a cbp -<<时, 随单价p 的增加,相应的销售额也增加; 当)(bc a c bp ->时, 随单价p 的增加,相应的销售额减少; 当)(bc a c bp -=时, 销售额最大, 2max )(bc a R -=15.定价a b p 2185+=(元)时, 的最大利润: 2)45(16a b bcL -=(元).第四章 不定积分作业参考答案第一节 不定积分的概念及性质一、1. B . 2. D .3. B .4. C .5.C .6.A .7. B .8. C . 9. C .二、10.3tan x c +;11.2arctan x c +;12.ln(x c++;13.tan x x c -+;14.ln x c ++;15.31ln 3x x e c ++;16.cot tan x x c --+;17.1arctan x c x-++; 18.2sincot x x c ++;19.3arcsin x c +;20.ln(x c ++;21.cot x x c --+;22.2ln 2x xe c ++;23.sin cos x x c -+;24.sin 2x xc -+;25.sin x c +; 26.1(sin cos )2x x x c --+;27.1(tan )2x x c ++;28.tan cot x x c -+.第二节 基本积分法 (换元积分法)一、1. C .2.B .3. B .4. B . 5. C . 6.A . 7.A . 8. D .二、9.c x ++)1ln(2;10.212x e c --+;11.c u +-232)5(31; 12.c e x +-1;13.c x x +-arcsin )(arcsin 515;14.c x x +-ln 1;15.1arccos ||c x +;16.c x x +-sec sec 313;12717.c x x ++3tan 31tan ;183arcsin 2x c ++;19.c x x +-⋅9912; 20.c x a a x ++222;21.c x x ++-+2325)1(32)1(52;22.2c +; 23.11cos cos5210x x c -+;24.ln |c -+;25.arcsin x c -; 26.2ln |tan c +.第二节 基本积分法(分部积分法)一、 1.A .2.A . 3.A . 4.A . 二、5.2(22)x e x x c -++;6.c x ex+-)1(2;7.2sin 2cos 2sin x x x x x c +-+.8.ln x x x c -+;9.21arccot(2)ln(14)4x x x c -++;10.2(arccos )2x x x x c +++. 118ln(3x c -++;12.1(sin 22cos 2)5x e x x c --++; 13. 1211cos sin n n n n I x x I n n---=+.第三节 有理函数的积分一、单项选择题: 1. B .2. C .3. D .4. B . 5. A .二、6.c x x +--2)1(; 7.c x x x ++-++33)23ln(2;8.c xx x x ++++2)1(ln 1;9.c x x ++1ln2; 10.21arctan 22(1)x x c x +++;11c +. 122xc +;13.ln |1tan |2x c ++;14.cos 1ln |tan |2sin 22x x c x -++; 15.1ln |sin cos |2x x x c -++..16.1)c +;17.ln ||c +;18.1)x c -+.第四节 不定积分在经济领域的应用1.12212-+=x x y ;2.23252s t t =-+;3.()100()50100,()50C x C x x C x x x =+==+; 4.2()50100P t t t =+; 5.10000.5pQ =⋅文案大全第四章 综合练习一、单项选择题 :1. D . 2. C . 二、3.323c +;4.1ln |cos |c x+;5.c x +;6.137ln |5|ln |2|33x x c ---+; 7.13ln |1|2ln |2|ln |3}22x x x c -+++-++;8.11ln |sec tan |c x x -++;9.1x x e c ++;10.1x x xe c -+;11.12(ln |23|)923x c x++++.三、12.c x x e x +++--)22(2; 13.c x x x ++-2sin 412cos 21;14.3311()ln 39x x x x x c +--+; 15.ln(1)1x xx e c e ---+++; 16.21tan ln |cos |2x x x x c -+++; 17.11cos 2sin 248x x x c -++;18.(cosln sin ln )2x x x c ++; 19.321(ln 3ln 6ln 6)x x x c x-++++.五、23|c -++;24.2(1)arcsin 22x x c -++; 25.11ln ||x c x x ---+;26.c x x ++)ln (2122;27.c e e x x ++-ln ;28.c x++-tan 11;29.ln(1)x x e c -++;30.c x x x ++-cos 2sin ln 2; 31.1(arcsin 2x c -+;32.c x x ++-+4549)32(53)32(91;33.1c +;34.c x x++-)1(ln 1;35.c x f x xf +-)()(';36.c x x x x +-sin 2cos ;37.26ln 11x c x x ++++;38.c x x x x +-++-+312arctan 33)1()1(ln 6122;39.x x c +;40.1x x c ++.41、22(21)x x e c --++.42、()2ln(1)x dx x x c ϕ=-++⎰.43、2211,122max(1,||)0111122x c x x dx x cx x cx ⎧--+<⎪⎪=+≤≤⎨⎪⎪++>⎩⎰. 第五章 定积分及其应用作业参考答案129第一节 定积分的概念与性质一、1. B . 2. C . 3. D . 4.C . 5.A . 6.A .7.C . 二、8.3;9. 3;10.12;11.1;12. 2π;13.76;14. 4. 三、15.⎰⎰>202sin ππxdx xdx ; 16.⎰⎰<-55dx e dx e x x ;17.⎰⎰>20422sin sin ππxdx xdx ; 18.⎰⎰<-202sin sin ππxdx xdx .四、19.a dx eaeaax a 2222≤≤⎰---; 20.ππππ2)sin 1(4542≤+≤⎰dx x ;21.2ln sin 2124≤≤⎰ππdx x x; 22.2arctan 8333ππ≤≤⎰xdx x .第三节 微积分学基本定理一、1. C . 2. B . 3.A .4. B . 5. D . 6. B . 7.A . 8. B . 二、9. (())()f x x ϕϕ';10.2221x x x -++;11.()sin 2x d p x e x dx =; 12.sin cos xx e x e ---;13.1()sin 2sin(2)x x e x d p x e x e e dx--+=-.14.2e ;15.12;16.1;17.1;18.0;19.13-.20.3;21.32;22.3ln 22-;23.2021ln 21;24.23e -.第四节 定积分的换元积分法与分部积分法一、1. B . 2.A . 3.A .34.4. C . 5. C . 6. C . 二、7.0;8.0;9.1;10.8-;11.4ln 3;12.43;13.2;14.21(1)4e --;15.4π;16.51(1)5e -;17.43;18.1596π;19.32π;20.24π.第五节 反常积分初步与Γ函数一、1. D .2.A .3. B .4. D . 5. C . 6. C . 7.A . 8. C .9.A . 10.A .二、11.2;12.4π;13.2π;14.ln 2;15.2;16.0. 17. 18 ;18. π52;19.)1(1n n Γ, (0>n ) ;20.)21(21+Γn 21->n .三、21.0α≥ 发散;0α< 收敛于 1α-; 22.1α≥- 发散;1α<- 收敛于11α-+;文案大全23.1α≥- 发散;1α<- 收敛于11α-+; 24.1α≥- 发散;1α<- 收敛于2)1(1+α;25.2π; 26.发散;27.83;28.1-. 第六节 定积分的几何应用一、单项选择题 1. D .二、2.1132; 3.1132;4.1172; 5.1; 6.1; 7.1132;8.2a π;9.232a π三、10.=x V 2pa π; 11.=x V 312a π;12.=x V π; 13.=x V 24π;14.=x V e e π)52(-;15.=x V 2(1)4e π- =y V 310π; 16.=x V 1287π, =y V π8.12.第七节 定积分的经济应用1.585585058505≈⨯+-e;2.10100QR Qe-=;3.1999331666=;4.(1)9950;(2)19600;5.(1)400台(2)5000元.第五章 综合习题一、1.21;2.22π-;3.2arctan 2-;4.1;5.2ln 27+;6.105584;7.8π;8.13;9.14;10.2;11.1(1ln 2)2-;12.14π-; 14.π-4;15.122;16.154;17.2(1ln 2)-;18.ln 2;19.απsin 2;20.1718-;21.2ln 264π-;22.23;23.8π;24.23ln 211+;25.21(1)2e +;26.21ln 28-;27.21)π;28.9655;29.62ln 2-;30.2;31.2ln 32ln 3-;32.12ln 2-;33.ln 222π+-;34.214e -;35.8(2)e -;36.214e -;37.)1(10-e e .三、不一定;四、16;五、最大值为:3ln 32-;最小值为:0 .六、 1x =为极大值点,2x =为极小值点.七、 ()cos sin f x x x =-.十、在)1,(-∞单减,在),1(∞+单增,在)251,(--∞),251(∞++ 上凸,在)251,251(+-上凹。
西安交通大学网络学院《高等数学》选择题答案
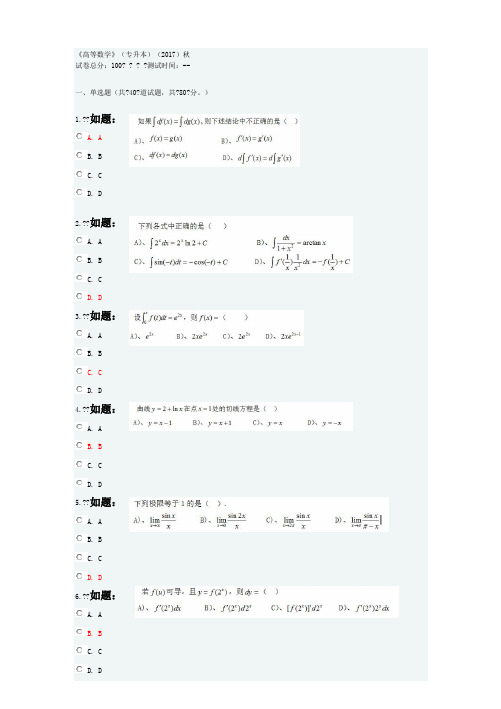
《高等数学》(专升本)(2017)秋试卷总分:100? ? ? ?测试时间:--一、单选题(共?40?道试题,共?80?分。
)1.??如题:A. AB. BC. CD. D2.??如题:A. AB. BC. CD. D3.??如题:A. AB. BC. CD. D4.??如题:A. AB. BC. CD. D5.??如题:A. AB. BC. CD. D6.??如题:A. AB. B7.??如题:A. AB. BC. CD. D8.??如题:A. AB. BC. CD. D9.??如题:A. AB. BC. CD. D10.??如题:A. AB. BC. CD. D11.??如题:A. AB. BC. CD. D12.??如题:A. AB. BC. CD. D13.??如题:A. AB. BC. CD. D14.??如题:A. AB. BC. CD. D15.??如题:A. AB. BC. CD. D16.??如题:A. AB. BC. CD. D17.??如题:A. AB. BC. CD. D18.??如题:A. AB. BC. CD. D ??????满分:2??分19.??如题:A. AB. BC. CD. D20.??如题:A. AB. BC. CD. D21.??如题:A. AB. BC. CD. D ??????满分:2??分22.??如题:A. AB. BC. CD. D ??????满分:2??分23.??如题:A. AB. BC. CD. D ??????满分:2??分24.??如题:A. AB. BC. C25.??如题:A. AB. BC. CD. D ??????满分:2??分26.??如题:A. AB. BC. CD. D ??????满分:2??分27.??如题:A. AB. BC. CD. D ??????满分:2??分28.??如题:A. AB. BC. CD. D ??????满分:2??分29.??如题:A. AB. BC. CD. D ??????满分:2??分30.??如题:A. AB. BC. C31.??如题:A. AB. BC. CD. D ??????满分:2??分32.??如题:A. AB. BC. CD. D ??????满分:2??分33.??如题:A. AB. BC. CD. D ??????满分:2??分34.??如题:A. AB. BC. CD. D ??????满分:2??分35.??如题:A. AB. BC. CD. D ??????满分:2??分36.??如题:A. AB. BC. C请同学及时保存作业,如您在20分钟内不作操作,系统将自动退出。
西安交通大学14春学期《高等数学(上)》离线作业

第一章 函数与极限本章要点:1.函数极限的概念(对极限的N -ε、δε-定义可在学习过程中逐步加深理解,对于给出ε求N 或δ不作过高要求。
)2.极限四则运算法则。
3.两个极限存在准则(夹逼准则和单调有界准则),会用两个重要极限求极限。
4.无穷小、无穷大,以及无穷小的阶的概念。
会用等价无穷小求极限。
5.函数在一点连续的概念。
6.间断点的概念,并会判别间断点的类型。
7.初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理.)本章目标:1.理解函数的概念的理解复合函数的概念,了解反函数的概念。
2.了解函数的奇偶性、单调性、周期性和有界性。
3.掌握基本初等函数的性质及其图形。
4.会建立简单实际问题中的函数关系式。
5.理解极限的概念(对于给出ε求N 或δ不作过高要求。
)6.掌握极限的四则运算法则。
7.了解极限存在准则(夹逼准则和单调有界准则),会用两个重要极限求极限。
8.了解无穷小、无穷大,以及无穷小的阶的概念。
会用等价无穷小求极限。
9.理解函数在一点连续的概念。
10.了解间断点的概念,并会判别间断点的类型。
11.了解初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理。
) 本章重点:1.函数极限的概念,会求一些简单函数的极限。
2.函数在一点连续的概念,会判断一些简单函数间断点的类型。
本章难点1.两个极限存在准则;2.判别间断点的类型。
第一章 总结本章主要介绍了极限的概念、极限存在的判定准则,极限的求法以及连续函数的定义与性质. 利用极限的定义证明函数(或数列)以某确定常数为极限,是本章的难点之一。
极限存在性问题是本章的重点,也是难点.一般地,常用以下方法判定一个极限是否存在:(1)利用单调有界准则;(2)利用夹逼准则;(3)利用柯西准则;(4)利用左右极限是否存在且相等;(5)利用子数列或部分极限。
掌握好求极限的方法是学好高等数学所必须的,这是本章的重点内容。
目前为止,我们可以(1)利用定义验证极限;(2)利用极限四则运算法则求极限;(3)利用重要极限求极限;(4)利用无穷小量等价代换求极限;(5)利用夹逼准则求极限;(6)利用单调有界数列必有极限准则求极限;(7)利用函数连续性求极限等等.在后面的章节中,我们还会陆续介绍其它一些求极限的方法。
西安交通大学现代远程教育(精)

西安交通大学现代远程教育 2007年专升本入学考试复习题高等数学复习题(一)注:答案一律写在答题卷上,写在试题上无效考生注意:根据国家要求,试卷中正切函数、余切函数、反正切函数、反余切函数分别用tan ,cot ,arctan ,arccot x x x x 来表示。
一、 单项选择题 (本大题共20小题,每小题3分,共40分)1.设)(x f 是奇函数,)(x g 是偶函数,则)]([x g f 是【 】A .即不是奇函数,又不是偶函数B .偶函数C .有可能是奇函数,也可能是偶函数D .奇函数 2.极限03limtan4x xx→=【 】A .0B .3C .43D .4 3.因为e n nn =⎪⎭⎫ ⎝⎛+∞→11lim ,那么=xe 【 】A .xn n n x ⎪⎭⎫ ⎝⎛+∞→1lim B .n n n x ⎪⎭⎫ ⎝⎛+∞→1lim C .nxn n x ⎪⎭⎫ ⎝⎛+∞→1lim D .xn n n ⎪⎭⎫ ⎝⎛+∞→11lim 4.若2)(2+=xe xf ,则=)0('f 【 】A .1B .eC .2D .2e 5.设1)(-=x e xf ,用微分求得(0.1)f 的近似值为【 】A .11.0-e B .1.1 C .1.0 D .2.0 6.设⎩⎨⎧==2bt y at x ,则=dy dx【 】 A .a b 2 B .bt a 2 C .abt 2 D .bt 2)()('x f de x f 7.设0=-yxe y ,则=dxdy 【 】 A .1-y y xe e B .y y xe e -1 C .y y e xe -1 D .yy exe 1- 8.下列函数中,在闭区间]1,1[-上满足罗尔定理条件的是【 】A .x eB .21x - C .x D .x ln9.函数x x y ln =在区间【 】A .),0(+∞内单调减B .),0(+∞内单调增C .)1,0(e 内单调减D .),1(+∞e内单调减10.不定积分⎰=dx x x )cos(2【 】A .C x +)sin(212 B .21sin 2x C + C .C x +-)sin(212 D .C x +-)sin(2211.不定积分⎰=+dx exx ln 32【 】 A .C ex +233 B .C e x +236 C .C e x +2331 D .C e x +236112.已知()f x 在0x =某邻域内连续,且(0)0f =,0()lim21cos x f x x→=-,则在 0x =处()f x 【 】A .不可导B .可导但()0f x '≠C .取得极大值D .取得极小值 13.广义积分221dx x +∞=⎰【 】 A .0 B .∞+ C .21-D .2114.函数223y x z -=在)0,0(点为【 】A .驻点B .极大值点C .极小值点D .间断点 15.定积分122121ln1xx dx x-+=-⎰【 】 A .1- B .0 C .∞- D .116.设在区间[],a b 上()0,()0,()0f x f x f x '''><>,令 1 ()baS f x dx =⎰,2()()S f b b a =-,31(()())()2S f a f b b a =+-。
17-18(2)《高等数学》(下)半期试题解答(1)

则直线
l1与
l2
的夹角
0
2
为:
班级
密封装订线
( ) cos = cos s 1 , s 2
= s1 • s2 =
−1 + 2 + 2
= 1 = arccos 1 = ,故应选(C).
s1 • s2 1+4+1 • 1+1+4 2
23
3.二元函数
f
( x,
y)
=
xy x2 + y2
,
(
x
−0
=
0−0 lim x→0 x
=
lim 0 = 0 ,
x→0
f
y
(
0
,
0
)
=
lim
y→0
f
(0 , 0 + y) −
y
f
(0 , 0)
=
lim
y→0
0 • y
02 + (y)2
y
−0
=
0−0 lim y→0 y
=
lim 0 = 0 ,
y→0
所以函数
f (x, y) 在点 (0 , 0) 处的两个偏导数都存在,且
西南交通大学 2017-2018 学年第(2)学期半期测试题解答
课程代码 1272005 课程名称 《高等数学》BII 考试时间 90 分钟
一、选择题(每小题 5 分,共 6 个小题,共 30 分)
密封装订线
1.曲面 x2 − y2 − z2 = 3 是【 A 】 4
(A) xoy 面上的双曲线绕 x 轴旋转一周所得;
4
4
4
所以曲面
x2 4
西安交通大学高等数学(上册)期终考题汇编

西安交通大学往届高等数学(上册)期终考题汇编一.填空题:(4分*4=16分)1. ()sin ,,22 032 0xx f x x x x k x ⎧<⎪=⎨⎪-+≥⎩在0x =处连续,则常数k = ________.2. (221x x -+=⎰___________.3.设1nn n a x ∞=∑的收敛半径为3,则()111n n n na x ∞-=-∑的收敛半径R =_____________.4. sin cos 220d d d 1x tt x t=+⎰___________.二.单项选择题(4分*4=16分)1.设周期函数()f x 在(),-∞+∞内可导,其周期为4,且()()lim1112x f f x x→--=-,则曲线()y f x =在点()(),55f 处的切线的斜率为 ( ) A. 2. B.-2. C. 1. D.-1.2.对于常数0k >,级数()tan 12111n n k n n ∞-=⎛⎫-+ ⎪⎝⎭∑ ( )A. 绝对收敛.B.条件收敛.C. 发散.D.收敛性与k 的取值相关.3.()()()ln sin221+1x x x x f x x =-的可去间断点的个数是 ( ) A. 0. B. 1. C. 2. D. 3.4.设tan 410d x I x x π=⎰,tan 420d xI x xπ=⎰,则 ( )A. 121I I >>.B. 121I I >>.C. 211I I >>.D. 211I I >>.三. 计算下列各题(6分*9):1.求极限()arctan lim ln 3012x x xx →-+. 2. 计算积分sin cos 5d x x x x ⎰. 3.求定积分41x ⎰. 4. 设ln ,ln 21122d 1d t t x u u ut y u u u⎧=⎪>⎨⎪=⎩⎰⎰,求22d d y x . 5.求微分方程43x xy y x e '-=的通解.6.将函数()f x x =,x π≤展开成傅里叶级数.7. 在抛物线()208y x x =≤≤上求一点,使得过此点所作切线与直线8x =及x 轴所围图形面积最大.8. 将函数()24253x f x x x +=--在1x =处展开成1x -的幂级数并指出其收敛域.9.(说明:学习《工科分析》者做(1),其余的做(2))(1)设广义积分()21d fx x +∞⎰收敛,证明广义积分()1d f x x x+∞⎰绝对收敛. (2) 计算arctan 31d x x x +∞⎰.四.(8分)求幂级数 112n n n x n -∞=∑的收敛域及和函数.五.(6分)设函数()f x ''存在,且()lim 101x f x x →=-,记()()1011d x f x t t ϕ'=++⎡⎤⎣⎦⎰,求()x ϕ在1x =的某个邻域内的导数,并讨论()x ϕ'在1x =处的连续性.2010-1-19一.填空题:(5分*3=15分)1.在抛物线2y x =上与直线20x y +=垂直的切线方程是______________________.2. 设()(),,21 0ax e x f x b x x ≤⎧⎪=⎨->⎪⎩在(),-∞+∞上可微,则a =_______,b =___________. 3.设()f x 的定义域为(),0+∞,已知()(),2311f f x x '==,则()4f =_____________.二.单项选择题(5分*3=15分)1.设()f x 在x a =处取得极值且满足()()()12x f taf x f x e dt +'''+=⎰,则()f x 在x a =处()A. 必取极大值.B.必取极小值.C. 不可能取极值.D.是否取极值不能确定.2.设a 为常数,则级数()sin 211n na n∞=⎡⎤⎢⎣∑ ( ) A. 绝对收敛. B.条件收敛. C. 发散. D.收敛性与数a 取值有关.3.设()()ln 21f x x x =-,()sin 2g x x =,则当0x →时,()f x 是()g x 的 ( )A. 同阶但非等价无穷小.B. 等价无穷小.C. 高阶无穷小.D. 低阶无穷小. 三. 解答下列各题(6分*4): 1.设()arctan1y x =>,求lim 1d d x yx +→. 2. 设()2022d 1tu t x e u y e t --⎧=⎪⎨=+⎪⎩⎰,求221d d t y x =.3. 求不定积分()ln 1d x x e e x +⎰.4.求微分方程222xy y x '=+的通解.四. 解答下列各题(8分*4):1.(说明:学习《工科分析》者做(1),其余的做(2))(1)讨论级数12nxn n ∞-=∑在[)(),0δδ+∞>上的一致收敛性,并求和.(2)求幂级数1112n nn x n ∞-=∑的收敛域及和函数. 2. 设函数(),,1 012 12x f x x ≤≤⎧=⎨<<⎩在[],02上将()f x 展成以4为周期的正弦级数,并指出级数在5x =处的值.3. 设函数()sin sin ,,201d 00 0x t t x f x x x ⎧⎛⎫⋅≠⎪ ⎪=⎝⎭⎨⎪=⎩⎰,求()f x ',并讨论()f x '在0x =处的连续性. 4.计算反常积分()20d 1xx xe I x e -+∞-=+⎰. 5. 一抛物线2y ax bx c =++通过()(),,,0012A B 两点,且0a <.(1) 确定,,a b c 的值使得抛物线与x 轴所围图形D 的面积最小. (2) 求此图形D 绕y 轴旋转一周所得旋转体的体积.五.(6分)设函数()f x 在闭区间[],a b 上连续,在开区间(),a b 内可导,且()0f x '>. 若极限()lim 2x a f x a x a +→--存在,证明在(),a b 内存在点ξ,使得()()222d b ab a f f x xξξ-=⎰.2009-01-12一.解答下列各题(6分*10): 1.求极限)1ln(lim 1xx e x ++→. 2.设⎪⎭⎫ ⎝⎛++++=22222ln a x x a a x x y ,求y d .3.设⎪⎩⎪⎨⎧-=-=3232tt y tt x ,求22d d x y .4.判定级数()()0!12≥-∑∞=λλλn nn n n e 的敛散性.5.求反常积分()⎰-10d 1arcsinx x x x.6.求⎰x x x d arctan .7.⎰-π03d sin sin x x x .8.将⎪⎩⎪⎨⎧≤≤<=πππx x x x f 2,02,)(在[]ππ,-上展为以π2为周期的付里叶级数,并指出收敛于()x f 的区间. 9.求微分方程0d )4(d 2=-+y x x x y 的解.10.求曲线1=xy 与直线0,2,1===y x x 所围平面图形绕y 轴旋转一周所得旋转体的体积. 二.(8分)将()()54ln -=x x f 展开为2-x 的幂级数,并指出其收敛域.三.(9分)在曲线()10sin 2≤≤=x x y 上取点()()10,sin ,2≤≤a a a A ,过点A 作平行于ox 轴的直线L ,由直线L ,oy 轴及曲线()a x x y ≤≤=0sin 2所围成的图形记为1S ,由直线L ,直线1=x 及曲线()1sin 2≤≤=x a x y 所围成的图形面积记为2S ,问a 为何值时,21S S S +=取得最小值.四.(9分)冷却定律指出,物体在空气中冷却的速度与物体和空气温度之差成正比,已知空气温度为30℃时,物体由100℃经15分钟冷却至70℃,问该物体冷却至40℃需要多少时间? 五.(8分)(学习《工科数学分析》的做(1),其余的做(2)) (1)证明级数∑∞=-02n nx e x 在[),0+∞上一致收敛.(2)求幂级数()∑∞=-----122121212)1(n n n n x n 的收敛域及和函数.六.(6分)设()[]b a C x f ,2∈,试证存在[]b a ,∈ξ,使()()()()⎰''-+⎪⎭⎫⎝⎛+-=ba f ab b a f a b dx x f ξ324122008年1月一、解答下列各题(每小题6分,共60分)1.计算极限xx x e x x 30sin 2)2(lim ++-→ 2.设.,5arctan log 22π+-=x x e y x求.dy 3.设).20(cos sin cos ln π<<⎩⎨⎧-==t t t t y t x 求.322π=t dx y d 4.判定级数∑∞=123n n nn 的敛散性. 5.计算反常积分.ln 12dx x x ⎰∞+ 6.计算不定积分.cos sin 23dx xxx ⎰ 7.计算定积分.)1(102⎰+x e dx8.求微分方程0)()1(32=++++dy y y x dx y 的通解.9.将函数⎩⎨⎧<<≤≤=21,210,1)(x x x f 在]2,0[上展成以4为周期的正弦级数.10.求由曲线72+=x y 及532+=x y 所围成的图形绕ox 轴旋转一周而成的旋转体的体积. 二、(9分)证明:当0≥x 时,有).1ln(2arctan 41]1)1ln(2[)1(22x x x x x +-≥+-++三、(9分)设抛物线)0(2<+=a bx ax y 通过点)3,1(M ,为了使此抛物线与直线x y 2=所围成的平面图形的面积最小,试确定a 和b 的值. 四、(8分)设一车间空间容积为10000立方米,空气中含有%12.0的二氧化碳(以容积计算),现将含二氧化碳%04.0的新鲜空气以1000立方米每分钟的流量输入该车间,同时按1000立方米每分钟的流量抽出混合气体,问输入新鲜空间10分钟后,车间内二氧化碳的浓度降到多少? 五、(8分)求幂级数∑∞=+0!21n nnx n n 的收敛域及其和函数. 六、(6分)设函数)(x f 在0=x 的邻域内有连续的一阶导数,且)0()(lim>=→a a xx f x , 证明:∑∞=--11)1()1(n n n f 条件收敛.2007年1月一、解答下列各题1.计算极限02lim.1cos 2x x→- 2.设cos(3)x y e x -=-,求dy .3.求曲线20213(2)123ln(1)t x du u y t t ⎧=++⎪+⎨⎪=-++⎩⎰在3x =处的切线方程. 4.判定级数143nn n∞=+∑的敛散性. 5.计算反常积分1+∞⎰ 6.计算不定积分. 7.将10/2()0/2x f x x πππ≤≤⎧=⎨<≤⎩展开成以2π为周期的傅里叶正弦级数,并求此级数分别在32x π=和52x π=两点的收敛值.8.将函数()ln f x x =展开为2x -的幂级数,并指出其收敛域.9.求微分方程7/2(1)2(1)x y y x '+-=+的通解. 10.求抛物线25x y =与21x y =+所围图形的面积.二、设2301(),0(),0x t f t dt x F x x k x ⎧≠⎪=⎨⎪=⎩⎰,其中()f t 是可导函数,为了使()F x 在0x =点处连续,试确定k 值,并对所确定的k 值,讨论()F x 在0x =点的可导性. 三、(9分)在曲线(0)x y e x -=≥上求一点00(,)x x e -,使得过该点的切线与两个坐标轴所围平面图形的面积最大,并求出此最大面积.四、半径为R 的半球形水池充满水,将水从池中抽出,并抽出的水所作的功为将水全部抽出所作的功的一半时,试问此时水面下降的深度H 为多少?五、求函数项级数20(1)nn xx ∞=+∑收敛性及和函数,并证明对任意0αβ<<,此级数在闭区间[,]αβ上一致收敛,但在其收敛域内不一致收敛.六、已知函数()f x 在[0,)+∞上可导,且(0)1f =并满足等式01()()()0,1xf x f x f t dt x '+-=+⎰求()f x '并证明:()1(0).x e f x x -≤≤≥2006年1月一、解答下列各题1.计算极限30tan sin lim .x x xx →- 2.设1arctan(tan )22x y =,求dy . 3.设2,0(),1,0xe xf x x x -⎧≥=⎨+<⎩求21(1).f x dx --⎰ 4.判定级数221112n n n n n ∞=+⎛⎫⎪⎝⎭∑的敛散性.5.设()y y x =由方程tan()y x y =+所确定,求y '.6.计算不定积分22(1).1x xe dx e ++⎰ 7.将()2||,[,]f x x x ππ=+∈-展开成以2π为周期的傅里叶级数.8.将函数21()32f x x x =++展成4x +的幂级数,并指出收敛区间.9.求微分方程43x xy y x e '-=的通解.10.设曲线2(0,0)y ax a x =>≥与21y x =-交于点A ,过坐标原点O 和点A 的直线与曲线2y ax =围成一个平面图形,问a 为何值时,该图形绕x 轴旋转一周所产生的旋转体的体积最大.二、试证明不等式:当0x >时,1(01).x x αααα-≤-<<三、设221()x t f x e dt -=⎰,求1().xf x dx ⎰四、一物体在某一介质中按3x ct =作直线运动,已知介质的阻力与物体速度的平方成正比,计算物体由0x =移动到x a =时克服阻力所作的功. 五、(注意:学习《工科分析》者做第(1)题,其余的做第(2)题) (1)证明:级数1nx n ∞-=在区间[,)(0)δδ+∞>上一致收敛,而在(0,)+∞上不一致收敛.(2)求级数01(1)3nn n ∞=+∑的和. 六、设()0,[,],f x x a b ''>∈证明:1()()()().22b a a b f a f b f f x dx b a ++≤≤-⎰2005年1月一、、解答下列各题1. 计算极限()0sin 1lim sin x x e x x x x x →-+-. 2。
高数2017-2018 学年第 1 学期半期测试卷解答

西南交通大学2017-2018学年第1学期半期测试卷 课程代码1271046 课程名称 高等数学BI 考试时间90分钟参 考 评 分 标 准一. 选择题(每小题4分,共20分)1、下列结论中正确的是( C ).(A )有界数列必然收敛;(B )发散数列必然无界;(C )若2lim n n x a →∞=,21lim n n x a +→∞=,则lim n n x a →∞=;(D )若3lim n n x a →∞=,31lim n n x a +→∞=,则lim n n x a →∞=.2、已知0→x 时2ln(1)ax +与1x e x --等价无穷小,则a =( B ).(A )1;(B )12;(C )1-; (D )12-.3、若函数()()(1)x e bf x x a x -=--有无穷型间断点10x =和可去间断点21x =,则( A). (A )0,a b e ==; (B ),0a e b ==; (C )0,1a b ==; (D )1,0a b ==.4、设函数()f x 在点0x 处可导,则( D ).(A )()f x 在点0x 处不一定有极限; (B )()f x 在点0x 处不一定连续;(C )()f x 在点0x 处不一定可微; (D )()f x 在点0x 处不一定二阶可导.5、函数(1)(2)(3)(4)y x x x x x =----的导函数有( C )个零点.(A )1;(B )2;(C )4; (D )5.二. 填空题(每小题5分,共25分)1、已知为常数,且23lim()1ax x x e x →∞+=+,则a =1.2、若(1)(1)2f f '==,则220(1)(1)lim x f x f x →+-=8.3、设函数1(arctan )y f x =,其中()f x 为可导函数,则d y =211-(arctan )d +1f x x x '.4、函数sin (0)x y x x =>的导函数为sin sin (cos ln )x xx x x x +.5、函数ln(12)y x =-在0x =处的n 阶导数()(0)n y =2(1)!n n --.三. 计算题(每小题7分,共21分)注意:解题方法不唯一1、求20lim x x x +→解:原极限00lim lim x x x e ++→→=⋅(3分)20212lim 12x x x +→=1=(7分) 2、求tan 01lim ()x x x+→; 解:原极限0lim tan ln tan ln 0lim x x x x x x e e +→+--→==(2分) 其中000021ln lim tan ln lim ln lim lim 011x x x x x x x x x x x x++++→→→→====-(6分) 所以原极限01e ==(7分)3、求2011lim()tan x x x x→-. 解:原极限2300tan tan limlim tan x x x x x x x x x →→--==(3分) 220sec 1lim 3x x x→-=(5分) 220tan 1lim 33x x x →==(7分) 四. 解答题(每小题9分,共27分)注意:解题方法不唯一1、求曲线方程()sin ln()xy y x x +-=在点()0,1处的切线方程.解:方程两边对x 求导得:()()1cos (1)1xy y xy y y x''++-=-(1)(4分) 将0,1x y ==代入(1)式得:(0)1y '=(6分)所求切线方程为:1y x =+.(9分)2、求由参数方程2ln(1)arctan x t t y t⎧=-+⎨=⎩确定的函数的一阶导数d d y x 和二阶导数22d d y x . 解:22221d (arctan )112d (ln(1))(1)11y t t t x t t t t '+==='-+--+(4分) 考虑参数方程22d 1d (11)ln()x t y x t t ⎧=-+=-⎪⎨⎪⎩,求导得: 2232225212(ln(112()d 2()(1)(1)d (1)))11y t t x t t t t t t -+'-+-'---===-+.(9分) 3、已知32ln(1-),0()1sin ,0x x f x x x x ⎧≤⎪=⎨>⎪⎩,求()f x '. 解:当0x >时,2111()(sin )2sin cos f x x x x x x''==-.(2分) 当0x <时,233()1-x f x x-'=.(4分) 当0x =时,2001sin ()(0)lim lim 0x x x f x f x x x ++→→-==;(6分)300()(0)ln(1)lim lim 0x x f x f x x x--→→--==,(8分) 所以(0)0f '=.(9分)五. 证明题(共7分)设函数()f x 在[0,1]上连续,在()0,1上可导,且(0)(1)1f f =-=,证明:存在()0,1ξ∈,使得()3()0f f ξξξ'+=.证明:设3()()F x x f x =,则32()()3()F x x f x x f x ''=+.(3分)因为(0)(1)1f f =-=,由零点定理,存在()0,1η∈,使得()0f η=,即()0F η=.(5分) 又因为(0)0F =,所以由中值定理,存在()()0,0,1ξη∈∈,使得()0F ξ'=,即()3()0f f ξξξ'+=.(7分)。
西安交通大学高等数学(上)小抄总结

《高等数学(上)》——学习指南一、选择题1.函数lg(1)y x =-的反函数是【 】A. 1x y e =+B. 101x y =+C.101y x =-D. 101y x -=+ 参考答案:B对等式两边做e 的指数,得到101y x =-,变换一下因变量和自变量得到:101x y =-。
即:101x y =+2.极限1111lim 122334(1)n n n →∞⎡⎤++++=⎢⎥⨯⨯⨯⨯+⎣⎦【 】 A. 1 B. 0 C.23 D. 32参考答案:A由题目知通项n S 有如下的形式:()1111+12233411111111122334111111111223341111n S n n n n n n n =+++⨯⨯⨯⨯+⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭=-+-+-++-+=-+ ()11111lim +lim 1112233411n n n n n →∞→∞⎡⎤⎡⎤+++=-=⎢⎥⎢⎥⨯⨯⨯⨯++⎣⎦⎣⎦3.若33222lim 3x x x a→-=-,则a =【 】 A. 1 B. 2 C. 3 D. 4参考答案:D()()()332233222222lim 3lim 230lim 383223834x x x x x ax x a x x a a a →→→-=-⇔---=⇔-=-⇒-=-⇒=4.当1x →时,21()1f x x =-【 】 A. 极限不存在 B. 是无穷大量 C. 是无穷小量 D. 是未定式参考答案:B当x 趋向于1时,分母趋向于0,任意常数除以0都是无穷大量。
所以原式是一个无穷大量。
5.设函数2sin(2)()32x f x x x +=-+, 那么函数的所有间断点是【 】A. 0B. 1和2C.2-D.1-和3参考答案:B()()()()()2sin 2sin 23212x x f x x x x x ++==-+--,当1x =或者2时,分式的分母等于零,方程没有意义。
西交2017《高等数学(上)》在线作业

西交2017《高等数学(上)》在线作业一、单选题共40题,80分12分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:22分•A A•B B•C C•D D2正确答案:C学生答案:C得分:2分解析:32分•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:42分•A A•B B•C C•D D3正确答案:A学生答案:A得分:2分解析:52分•A A•B B•C C•D D正确答案:C学生答案:C得分:2分解析:62分•A A4•C C•D D正确答案:A学生答案:A得分:2分解析:72分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:82分5•B B•C C•D D正确答案:C学生答案:C得分:2分解析:92分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:102分6•A A•B B•C C•D D正确答案:C学生答案:C得分:2分解析:112分•A A•B B•C C•D D7正确答案:C学生答案:C得分:2分解析:122分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:132分8•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:142分•A A•B B•C C•D D9正确答案:D学生答案:D得分:2分解析:152分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:162分•A A•B B•C C•D D10正确答案:C学生答案:C得分:2分解析:172分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:182分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:192分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:202分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:212分•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:222分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:232分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:242分•A A•B B•C C•D D正确答案:C学生答案:C得分:2分解析:252分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:262分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:272分•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:282分•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:292分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:302分•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:312分•A A•B B•C C•D D正确答案:C学生答案:C得分:2分解析:322分•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:332分1•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:342分•A A•B B•C C•D D正确答案:C学生答案:C得分:2分解析:352分•A A•B B•C C•D D正确答案:C学生答案:C得分:2分解析:362分•A A•B B•C C•D D正确答案:A学生答案:A得分:2分解析:372分•A A•B B•C C•D D正确答案:D学生答案:D得分:2分解析:382分•A A•B B•C C正确答案:C学生答案:C得分:2分解析:392分•A A•B B•C C•D D正确答案:B学生答案:B得分:2分解析:402分•A A•B B•D D正确答案:A学生答案:A得分:2分解析:二、判断题共10题,20分12分如果函数f(x)在[a,b]上连续,f(x)在[a,b]上的定积分存在•A错误•B正确正确答案:B学生答案:B得分:2分解析:22分函数在某点连续则函数在该点可导•A错误•B正确正确答案:A学生答案:A得分:2分解析:32分两个函数和的不定积分等于两个函数不定积分的和•A错误•B正确正确答案:B学生答案:B得分:2分解析:42分函数在某点极限存在的充要条件是函数在该点的左右极限存在且相等•A错误•B正确正确答案:B学生答案:B得分:2分解析:52分函数在一点处极限存在的充要条件是函数在该点的左极限等于右极限。
中国大学mooc《高等数学(二)(西安交大)(高等理工课程中心) 》满分章节测试答案

title高等数学(二)(西安交大)(高等理工课程中心) 中国大学mooc答案100分最新版content第一周测验一1、答案:2、答案:3、答案:4、答案:5、答案:6、答案:7、答案:8、答案:9、答案:10、答案: 11、答案:12、答案:13、答案:14、答案: 15、答案:16、答案:17、答案: 错误18、答案: 错误19、答案: 正确20、答案: 错误21、答案: 正确22、答案: 正确23、答案: 正确24、答案: 错误25、答案: 错误26、答案: 正确27、答案: 错误28、答案: 错误29、答案: 正确30、答案: 错误31、答案: 正确第二周测验二1、答案:2、答案:3、答案:4、答案:5、答案:6、答案:7、答案:8、答案: 9、答案: 10、答案: 11、答案: 12、答案: 13、答案:14、答案: 15、答案:16、答案:17、答案: 18、答案: 19、答案:20、答案:21、答案: 22、答案: 23、答案: 24、答案:25、答案:26、答案: 27、答案:28、答案: 正确29、答案: 正确30、答案: 错误31、答案: 错误32、答案: 正确33、答案: 正确34、答案: 错误35、答案: 正确36、答案: 正确37、答案: 正确38、答案: 错误39、答案: 错误40、答案: 错误41、答案: 正确42、答案: 错误43、答案: 错误44、答案: 正确45、答案: 错误46、答案: 正确47、答案: 正确48、答案: 错误49、答案: 正确50、答案: 正确51、答案: 错误52、答案: 正确53、答案: 错误54、答案: 错误第三周测验三1、答案:2、答案:3、答案:4、答案:5、答案:6、答案:7、答案: 8、答案:9、答案: 10、答案:11、答案: 12、答案: 13、答案: 14、答案: 15、答案: 16、答案:17、答案: 18、答案:19、答案: 正确20、答案: 错误21、答案: 正确22、答案: 错误23、答案: 正确24、答案: 错误25、答案: 正确26、答案: 正确27、答案: 错误28、答案: 正确29、答案: 正确30、答案: 错误31、答案: 错误32、答案: 错误33、答案: 错误34、答案: 错误35、答案: 正确36、答案: 正确第四周测验四1、答案:2、答案:3、答案:4、答案:5、答案:6、答案:7、答案:8、答案:9、答案:10、答案:11、答案:12、答案:13、答案:14、答案: 15、答案:16、答案:17、答案: 18、答案: 19、答案:20、答案: 错误21、答案: 错误22、答案: 正确23、答案: 错误24、答案: 错误25、答案: 错误26、答案: 正确27、答案: 错误28、答案: 正确29、答案: 错误30、答案: 错误31、答案: 错误32、答案: 正确33、答案: 正确34、答案: 错误35、答案: 错误36、答案: 错误37、答案: 正确38、答案: 错误39、答案: 正确40、答案: 正确41、答案: 正确42、答案: 错误第五周测试五1、答案:2、答案:3、答案:4、答案:5、答案:6、答案: 7、答案: 8、答案:9、答案: 10、答案: 11、答案:12、答案: 13、答案: 14、答案: 15、答案:16、答案: 17、答案: 18、答案: 19、答案: 20、答案: 正确21、答案: 错误22、答案: 错误23、答案: 错误24、答案: 正确25、答案: 错误26、答案: 正确27、答案: 正确28、答案: 错误29、答案: 正确30、答案: 错误31、32、答案: 错误33、答案: 正确34、答案: 错误35、答案: 正确36、答案: 错误37、答案: 错误第六周测试六1、2、答案:3、答案:4、答案:5、答案:6、答案:7、答案:8、答案: 9、答案:10、答案:11、答案:12、答案:13、答案: 14、答案: 15、答案:16、答案:17、答案: 18、答案: 19、答案: 20、答案: 21、答案:22、答案:23、答案: 24、答案: 25、答案:26、答案: 27、答案:28、答案:29、答案:30、答案: 31、答案: 32、答案: 33、答案: 34、答案: 35、答案: 36、答案: 错误37、答案: 错误38、答案: 正确39、答案: 正确40、答案: 正确41、答案: 错误42、答案: 正确43、答案: 正确44、答案: 正确45、答案: 正确第七周测试七1、答案:2、答案:3、答案:4、答案:5、答案:6、答案:7、答案: 8、答案: 9、答案: 10、答案:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等数学》(专升本)(2017)秋
试卷总分:100 测试时间:--
一、单选题(共40 道试题,共80 分。
)V
1. 如题:
A. A
B. B
C. C
D. D
2. 如题:
A. A
B. B
C. C
D. D
3. 如题:
A. A
B. B
C. C
D. D
4. 如题:
A. A
B. B
C. C
D. D
5. 如题:
A. A
B. B
C. C
D. D
6. 如题:
A. A
B. B
C. C
7. 如题:
A. A
B. B
C. C
D. D
8. 如题:
A. A
B. B
C. C
D. D
9. 如题:
A. A
B. B
C. C
D. D
10. 如题:
A. A
B. B
C. C
D. D
11. 如题:
A. A
B. B
C. C
D. D
12. 如题:
A. A
B. B
C. C
D. D
13. 如题:
A. A
B. B
C. C
D. D
14. 如题:
A. A
B. B
C. C
D. D
15. 如题:
A. A
B. B
C. C
D. D
16. 如题:
A. A
B. B
C. C
D. D
17. 如题:
A. A
B. B
C. C
D. D
18. 如题:
A. A
B. B
C. C
D. D
满分:2 分
19. 如题:
A. A
B. B
C. C
D. D
20. 如题:
A. A
B. B
C. C
D. D
21. 如题:
A. A
B. B
C. C
D. D
满分:2 分22. 如题:
A. A
B. B
C. C
D. D
满分:2 分23. 如题:
A. A
B. B
C. C
D. D
满分:2 分24. 如题:
A. A
B. B
C. C
25. 如题:
A. A
B. B
C. C
D. D
满分:2 分26. 如题:
A. A
B. B
C. C
D. D
满分:2 分27. 如题:
A. A
B. B
C. C
D. D
满分:2 分28. 如题:
A. A
B. B
C. C
D. D
满分:2 分29. 如题:
A. A
B. B
C. C
D. D
满分:2 分30. 如题:
A. A
B. B
C. C
31. 如题:
A. A
B. B
C. C
D. D
满分:2 分32. 如题:
A. A
B. B
C. C
D. D
满分:2 分33. 如题:
A. A
B. B
C. C
D. D
满分:2 分34. 如题:
A. A
B. B
C. C
D. D
满分:2 分35. 如题:
A. A
B. B
C. C
D. D
满分:2 分36.
如题:
A. A
B. B
C. C
请同学及时保存作业,如您在20分钟内不作操作,系统将自动退出。
37. 如题:
A. A
B. B
C. C
D. D
满分:2 分
38. 如题:
A. A
B. B
C. C
D. D
满分:2 分
39. 如题:
A. A
B. B
C. C
D. D
满分:2 分
40. 如题:
A. A
B. B
C. C
D. D
满分:2 分。
