初中数学一元二次方程复习专题
一元二次方程专题复习

一元二次方程专题复习(一)直接开平方法→配方法要点一、一元二次方程的解法---配方法1.配方法解一元二次方程: (1)配方法解一元二次方程: 将一元二次方程配成的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.(2)配方法解一元二次方程的理论依据是公式:.(3)用配方法解一元二次方程的一般步骤: ①把原方程化为的形式;②将常数项移到方程的右边;方程两边同时除以二次项的系数,将二次项系数化为1;③方程两边同时加上一次项系数一半的平方;④再把方程左边配成一个完全平方式,右边化为一个常数;⑤若方程右边是非负数,则两边直接开平方,求出方程的解;若右边是一个负数,则判定此方程无实数解. 要点诠释:(1)配方法解一元二次方程的口诀:一除二移三配四开方; (2)配方法关键的一步是“配方”,即在方程两边都加上一次项系数一半的平方. (3)配方法的理论依据是完全平方公式.类型一、用配方法解一元二次方程1.用配方法解方程x 2-7x-1=0.【答案与解析】将方程变形为x 2-7x =1,两边加一次项的系数的一半的平方,得x 2-7x+=1+,所以有=1+.直接开平方,得x-=或x-=-.所以原方程的根为x =+或x =-.【总结升华】一般地,用先配方,再开平方的方法解一元二次方程,应按以下步骤进行: (1)把形如ax 2+bx+c =0(a ≠0)的方程中二次项的系数化为1; (2)把常数项移到方程的右边;2222()a ab b a b ±+=±(3)方程的两边都加“一次项系数一半的平方”,配方得形如(x+m)2=n(n ≥0)的方程; (4)用直接开平方的方法解此题.举一反三:【变式】用配方法解方程.(1)x 2-4x-2=0; (2)x 2+6x+8=0.要点二、配方法的应用1.用于比较大小:在比较大小中的应用,通过作差法最后拆项或添项、配成完全平方,使此差大于零(或小于零)而比较出大小.2.用于求待定字母的值:配方法在求值中的应用,将原等式右边变为0,左边配成完全平方式后,再运用非负数的性质求出待定字母的取值.3.用于求最值:“配方法”在求最大(小)值时的应用,将原式化成一个完全平方式后可求出最值. 4.用于证明:“配方法”在代数证明中有着广泛的应用,我们学习二次函数后还会知道“配方法”在二次函数中也有着广泛的应用. 要点诠释:“配方法”在初中数学中占有非常重要的地位,是恒等变形的重要手段,是研究相等关系,讨论不等关系的常用技巧,是挖掘题目当中隐含条件的有力工具,一定要学好.类型二、配方法在代数中的应用2.若代数式,,则的值( )A .一定是负数B .一定是正数C .一定不是负数D .一定不是正数【答案】B ;【解析】(作差法).故选B.【总结升华】本例是“配方法”在比较大小中的应用,通过作差法最后拆项、配成完全平方,使此差大于零而比较出大小.221078Ma b a =+-+2251N a b a =+++M N -22221078(51)M N a b a a b a -=+-+-+++2222107851a b a a b a =+-+----29127a a =-+291243a a =-++2(32)30a =-+>3.用配方法说明:代数式x2+8x+17的值总大于0.【答案与解析】x2+8x+17= x2+8x+42-42+17=(x+4)2+1∵(x+4)2≥0,∴(x+4)2+1>0,故无论x取何实数,代数式 x2+8x+17的值总大于0.【总结升华】利用配方法将代数式配成完全平方式后,再分析代数式值得符号.举一反三:【变式】求代数式 x2+8x+17的最小值4.(2014春•滦平县期末)已知x2+y2﹣4x+6y+13=0,求(x+y)2013的值.【思路点拨】采用配方法求出x、y的值,代入计算即可得到答案.【答案与解析】解:x2+y2﹣4x+6y+13=0,x2﹣4x+4+y2﹣+6y+9=0,(x﹣2)2+(y+3)2=0∴x﹣2=0,y+3=0,解得,x=2,y=﹣3,(x+y)2013=﹣1.【总结升华】本题考查的是配方法的应用和非负数的性质的应用,掌握配方法的步骤和几个非负数的和为0,每个非负数都为0是解题的关键.1.一元二次方程的求根公式 一元二次方程,当时,.2.一元二次方程根的判别式 一元二次方程根的判别式:. ①当时,原方程有两个不等的实数根;②当时,原方程有两个相等的实数根;③当时,原方程没有实数根.3.用公式法解一元二次方程的步骤 用公式法解关于x 的一元二次方程的步骤:①把一元二次方程化为一般形式;②确定a 、b 、c 的值(要注意符号); ③求出的值;④若,则利用公式求出原方程的解;若,则原方程无实根.要点诠释:(1)虽然所有的一元二次方程都可以用公式法来求解,但它往往并非最简单的,一定要注意方法的选用.(2)一元二次方程,用配方法将其变形为:①当时,右端是正数.因此,方程有两个不相等的实根:② 当时,右端是零.因此,方程有两个相等的实根: ③ 当时,右端是负数.因此,方程没有实根.20 (0)ax bx c a ++=≠2224()24b b ac x a a -+=240b ac ∆=->1,22b x a-±=240b ac ∆=-=1,22b x a=-240b ac ∆=-<5. 用公式法解下列方程.(1); (2).【总结升华】 用公式法解一元二次方程的关键是对a 、b 、c 的确定.用这种方法解一元二次方程的步骤是:(1)把方程化为一元二次方程的一般形式;(2)确定a ,b ,c 的值并计算的值;(3)若是非负数,用公式法求解.举一反三:【变式】用公式法解方程6.用公式法解下列方程:(1); (2) .【总结升华】首先把每个方程化成一般形式,确定出a 、b 、c 的值,在的前提下,代入求根公式可求出方程的根.23310x x --=2241x x =-24b ac -24b ac -2341x x =+2100x -+=(1)(1)x x +-=240b ac -≥举一反三:【变式】(2014秋•泽州县校级期中)用公式法解方程:5x 2﹣4x ﹣12=0.【巩固练习】 一、选择题1.已知关于x 的一元二次方程,用配方法解此方程,配方后的方程是( )A .B .C .D . 2.用配方法解下列方程时,配方有错误的是( )A .化为B .化为C .化为D .化为3.(2015春•张家港市校级期中)若M=2x 2﹣12x+15,N=x 2﹣8x+11,则M 与N 的大小关系为( ) A .M ≥N B . M >N C . M ≤N D . M <N 4.不论x 、y 为何实数,代数式的值 ( )A .总小于2B .总不小于7C .为任何实数D .不能为负数 5.已知,则的值等于( )A.4B.-2C.4或-2D.-4或2 6.若t 是一元二次方程的根,则判别式和完全平方式的关系是( )A.△=MB. △>MC. △<MD. 大小关系不能确定二、填空题 7.(1)x 2-x+ =( )2; (2)x 2+px+ =( )2. 220x x m --=2(1)1x m -=+2(1)1x m +=+22(1)1x m -=+22(1)1x m +=+22990x x --=2(1)100x -=22740t t --=2781416t ⎛⎫-= ⎪⎝⎭2890x x ++=2(4)25x +=23420x x --=221039x ⎛⎫-= ⎪⎝⎭22247x y x y ++-+438.已知,则的值为 . 9.已知4x 2-ax+1可变为(2x-b )2的形式,则ab=_______.10.将一元二次方程x 2-2x-4=0用配方法化成(x+a )2=b 的形式为____ ___,∴所以方程的根为_________. 11.把一元二次方程3x 2-2x-3=0化成3(x+m)2=n 的形式是___ ________;若多项式x 2-ax+2a-3是一个完全平方式,则a=_________. 12.(2015春•重庆校级期中)a 2+b 2﹣4a+2b+5=0,则b a 的值为 .三、解答题 13. 用配方法解方程.(1) 3x 2-4x-2=0; (2)x 2-4x+6=0.14. 用公式法解下列方程:(2) .15.(2014•甘肃模拟)用配方法证明:二次三项式﹣8x 2+12x ﹣5的值一定小于0.16.已知在⊿ABC 中,三边长a 、b 、c ,满足等式a 2-16b 2-c 2+6ab+10bc=0,求证:a+c=2b223730216b a a b -+-+=a -2(1)210x ax --=;22222(1)()ab x a x b x a b +=+>一元二次方程专题复习(二)温故知新:1.直接开平方法2.配方法3.公式法一、因式分解法因式分解法就是利用因式分解的手段,求出方程的解的方法,这种方法简单易行,是解一元二次方程最常用的方法。
初中数学一元二次方程复习专题

初中数学一元二次方程复习专题一、一元二次方程的定义及基本形式一元二次方程是指形如ax²+bx+c=0的方程,其中a、b、c为已知实数,且a≠0。
其中,a是二次项系数,b是一次项系数,c是常数项。
二、一元二次方程的解法1.利用因式分解法解方程当一元二次方程可以进行因式分解时,可以利用因式分解法来解方程。
即将方程两边同时化简为一个或多个数相乘的形式,并使方程中至少一个因子为0,解出方程。
例如:求解方程x²-5x+6=0可以进行因式分解,得到(x-2)(x-3)=0,因此,x-2=0或x-3=0,解得x=2或x=32.利用求根公式解方程对于一元二次方程ax²+bx+c=0,可以利用求根公式解方程。
求根公式有二次根公式和贝努力公式两种形式。
二次根公式:对于方程ax²+bx+c=0,当Δ=b²-4ac≥0时,方程有两个实根,即x₁=(-b+√Δ)/2a和x₂=(-b-√Δ)/2a。
当Δ<0时,方程无实根。
例如:求解方程x²-5x+6=0根据二次根公式,可以得到Δ=(-5)²-4×1×6=1,因为Δ≥0,所以方程有两个实根。
代入公式得到x₁=(-(-5)+√1)/2×1=3和x₂=(-(-5)-√1)/2×1=2三、一元二次方程的判别式及性质1. 判别式Δ=b²-4ac的意义判别式Δ表示方程ax²+bx+c=0的二次项系数、一次项系数和常数项的平方差。
Δ的值可以判断方程的解的情况:a)当Δ>0时,方程有两个不相等的实根;b)当Δ=0时,方程有两个相等的实根;c)当Δ<0时,方程没有实根。
2.一元二次方程的性质a)当a>0时,方程的图像开口向上,最低点为最小值;b)当a<0时,方程的图像开口向下,最高点为最大值;c)当c>0时,方程的图像与x轴在两个交点之间有交点;d)当c<0时,方程的图像与x轴在两个交点之外有交点。
中考数学复习 一元二次方程专练 公式法解一元二次方程专项练习106题-人教版初中九年级全册数学试题

word公式法解一元二次方程1.2x2﹣7x+3=0(公式法)2.2t2﹣t﹣3=0,3.2x2﹣7x+4=0.4.2x2+2x=15.5y+2=3y2.6.x2+3x﹣4=0 7. 2x2﹣4x﹣1=08.2x2﹣x﹣2=0.9.2x2﹣5x+1=0.10.x2﹣1=4x.11.x2+3x﹣3=0 12.3x2﹣4x﹣2=0.13.x2+x﹣4=0.14.2x2﹣6x+3=0.15.2x2﹣3x﹣1=0.16.2x2﹣2x﹣1=0 17.3x2﹣4x﹣1=0.18.2x2﹣x﹣4=0 19.2x2+x﹣2=0 20.3x2+6x﹣4=0 21.x2﹣x﹣3=0.22.3x2+4x﹣4=0,23.(3x﹣1)(x+2)=11x ﹣4.24.2x2﹣5x﹣1=0.25..26.3x2+4x+5=0.28.x2﹣x﹣4=0.29..30.2x2﹣2x﹣1=031.3x2+7x+10=1﹣8x.32.5x2﹣3x+2=0.34.x2+3x+1=0,35.4x2=2x+136.5x2﹣3x=x+1.37.3x2+7x+4=038.2x2﹣3x﹣1=0(用公式法)39.3x2+5x+1=0;40.x2﹣4x+1=041. x2﹣4x+5=042. x2+5x+3=043.2x2﹣3x﹣6=0.44.3x2+4x+1=045.x2﹣4x﹣8=046.2x2﹣x﹣2=047.3x2+2(x﹣1)=0.48.x2﹣4x﹣7=049.y2﹣2y﹣4=050.x2﹣3x=2 51.2x2+x﹣=0.52.x2x+1=053.2x2﹣9x+8=0;55. x2+x﹣1=0;56. 2x2﹣6x+3=0;57.2x(x+4)=158.3x2+5(2x+1)=0.59.2x2﹣4x﹣1=060.3x2﹣6x﹣4=061.x2+2x﹣5=0 62.x2﹣4x﹣3=063.4x2﹣3x﹣1=063. x2+2x﹣2=0;65. x2+3=2x.66.x2﹣4x=﹣367. 3x2﹣2x﹣1=0;68.;69. 2x2﹣7x+5=0;70. 2x2﹣7x﹣18=0.71. (x+1)(x+3)=6x+4;73. x2﹣(2m+1)x+m=0.74. x(x+8)=16,76. 2x2﹣2x+1=0,77. 5x2+2x﹣1=078. 6y2+13y+6=079. 3•x2+6x+9=780. 2x2﹣3x+1=0;81. 2y(y﹣1)+3=(y+1)2.82. x2=3x+1;83. (t+1)(t﹣3)=﹣t(3﹣3t).84.x2﹣2ax﹣b2+a2=0.85. 3x2=2﹣5x;87. (x+1)(x﹣1)=2x.88.(2x﹣1)2﹣7=3(x+1);89.x2﹣6x+11=090 .5x2﹣8x+2=0.91.x2﹣3x+1=0.92.x2=5﹣12x93. x2+x﹣1=094.3x2﹣4x﹣1=095.3x2+2(x﹣1)=0,97.3x2﹣4x﹣1=098.99. .101.2x2+5x﹣1=0.102.2x2﹣x﹣1=0.103..104.3x2+5x﹣1=0.105.5x2﹣8x+2=0,106.3x2+7x+10=1﹣8x,公式法解一元二次方程106题参考答案:1.2x2﹣7x+3=0(公式法)a=2,b=﹣7,c=3,∴b2﹣4ac=(﹣7)2﹣4×2×3=49﹣24=25>0,方程有两个不相等的实数根,即:,x1=3,2.2t2﹣t﹣3=0,∵a=2,b=﹣1,c=﹣3,∴x===,3.2x2﹣7x+4=0.∵a=2,b=﹣7,c=4,b2﹣4ac=49﹣32=17,∴x==,∴,∴x1=,x2=4.2x2+2x=1由原方程,得2x2+2x﹣1=0,∴该方程的二次项系数a=2,一次项系数b=2,常数项c=﹣1;∴x===,5.5y+2=3y2.移项,3y2﹣5y﹣2=0,a=3,b=﹣5,c=﹣2,b2﹣4ac=(﹣5)2﹣4×3×(﹣2)=49>0,∴x=,∴x1=2,x2=﹣;6.x2+3x﹣4=0a=1,b=3,c=﹣4,△=9+4×1×4=25>0,∴x==,∴x1=﹣4,x2=1.7. 2x2﹣4x﹣1=0a=2,b=﹣4,c=﹣1,△=16+4×2=24>0,∴x==1±,∴x1=1+,x2=1﹣8.2x2﹣x﹣2=0.∵a=2,b=﹣1,c=﹣2,∴b2﹣4ac=17>0∴x=.即x1=,x2=9.2x2﹣5x+1=0.∵a=2,b=﹣5,c=1,∴b2﹣4ac=17,∴x=,∴x1=,x2=2原方程化为一般式:x2﹣4x﹣1=0.∵a=1,b=﹣4,c=﹣1,∴△=b2﹣4ac=(﹣4)2﹣4×1×(﹣1)=20,∴x===2±,∴x1=2+,x2=2﹣11.x2+3x﹣3=0a=1,b=3,c=﹣3;∵b2﹣4ac=9+12=21>0∴=∴,12.3x2﹣4x﹣2=0.a=3,b=﹣4,c=﹣2,△=b2﹣4ac=(﹣4)2﹣4×3×(﹣2)=40>0,x==,x1=,x2=13.x2+x﹣4=0.∴x==,∵x1=﹣2,x2=.14.2x2﹣6x+3=0.∵a=2,b=﹣6,c=3∴x=∴x1=,x2=;15.2x2﹣3x﹣1=0.a=2,b=﹣3,c=﹣1,∴△=9+8=17,x1=,x2=16.2x2﹣2x﹣1=0a=2,b=﹣2,c=﹣1,∴b2﹣4ac=12,∴x==,∴x1=,x2=17.3x2﹣4x﹣1=0.∵一元二次方程3x2﹣4x﹣1=0的二次项系数a=3,一次项系数b=﹣4,常数项c=﹣1,∴x===,∴x1=,x2=18.2x2﹣x﹣4=0∵2x2﹣x﹣4=0,∴=,∴x 1=,19.2x2+x﹣2=0∵a=2,b=1,c=﹣2(1分)∵b2﹣4ac=12﹣4×2×(﹣2)=17>0(2分)∴(4分)∴,20.3x 2+6x﹣4=0∵a=3,b=6,c=﹣4,∴b2﹣4ac=62﹣4×3×(﹣4)=84,∴x==,21.x2﹣x﹣3=0.∵a=1,b=﹣1,c=﹣3,∴△=(﹣1)2﹣4×1×(﹣3)=13>0,∴x==,∴x1=,x2=.22.3x2+4x﹣4=0,这里a=3,b=4,c=﹣4,b2﹣4ac=42﹣4×3×(﹣4)=64,x=,x1=,x2=﹣223.(3x ﹣1)(x+2)=11x﹣4.3x 2+6x﹣x﹣2=11x﹣4,整理得3x2﹣6x+2=0,∵△=(﹣6)2﹣4×3×2=12,∴x==∴x1=,x2=24.2x2﹣5x﹣1=0.2x2﹣5x﹣1=0,∵b2﹣4ac=(﹣5)2﹣4×2×(﹣1)=33,∴x=,即x 1=,x2=25..∵a=1,b=,c=﹣20,b2﹣4ac=()2﹣4×1×(﹣20)=100>0,∴x=,x=,解得x1=﹣+5,x2=﹣﹣5.26.3x2+4x+5=0.∵△=42﹣4×3×5=﹣44<0,∴方程没有实数根.27.x2﹣4x﹣2=0.∵a=1,b=﹣4,c=﹣2,∴△=(﹣4)2﹣4×1×(﹣2)=4×6,∴x===2±,∴x1=2+,x2=2﹣.28.x2﹣x﹣4=0.a=1,b=﹣1,c=﹣4.b2﹣4ac=1+16=17>0.∴=∴x1=,x2=29..由原方程,得t2+2t﹣2=0,这里a=1,b=2,c=2.则t===﹣,即t1=t 2=﹣30.2x2﹣2x﹣1=0∵a=2,b=﹣2,c=﹣1,∴b2﹣4ac=(﹣2)2﹣4×2×(﹣1)=12,∴x1=,x2=31.3x2+7x+10=1﹣8x.原方程可化为x2+5x+3=0,解得:32.5x2﹣3x+2=0.∵b2﹣4ac=(﹣3)2﹣4×5×2<0,∴此方程无解33. 5x2﹣3x=x+11(公式法)5x2﹣3x=x+11,整理得:5x2﹣4x﹣11=0,这里a=5,b=﹣4,c=﹣11,∵△=16+220=236,∴x==,则x1=,x2=34.x2+3x+1=0,这里a=1,b=3,c=1,∵△=b 2﹣4ac=9﹣4=5,∴x=,则x1=,x2=35.4x2=2x+1移项得:4x2﹣2x﹣1=0,∵b2﹣4ac=(﹣2)2﹣4×4×(﹣1)=20,∴x==,∴x1=,x2=36.5x2﹣3x=x+1.方程化简为:5x2﹣4x﹣1=0,这里a=5,b=﹣4,c=﹣1,∴x==,∴x1=1,x2=﹣.37.3x2+7x+4=03x2+7x+4=0,∵a=3,b=7,c=4,∴b2﹣4ac=49﹣48=1>0,∴x=,∴x 1=﹣1,x2=﹣.38.2x2﹣3x﹣1=0(用公式法)∵a=2,b=﹣3,c=﹣1,∴△=(﹣3)2﹣4×2×(﹣1)=17,∴x==,所以x1=,x2=39.3x2+5x+1=0;∵原方程的二次项系数a=3,一次项系数b=5,常数项c=1,∴原方程的根是:x==,即x=;40.x2﹣4x+1=0a=1,b=﹣4,c=1,∴x====2±;41. x2﹣4x+5=0a=1,b=﹣4,c=5,∵△=b2﹣4ac=16﹣20=﹣4<0,42. x2+5x+3=0a=1,b=5,c=3,∴x===43.2x2﹣3x﹣6=0.这里a=2,b=﹣3,c=﹣6,∵△=b2﹣4ac=9+48=57,∴x=,则x1=,x2=44.3x2+4x+1=0(用公式法)∵二次项系数a=3,一次项系数b=4,常数项c=1,∴△=b 2﹣4ac=42﹣4×3×1=4>0∴x==∴x1=﹣1 x2=﹣;45.x2﹣4x﹣8=0(公式法)∵方程x2﹣4x﹣8=0的二次项系数a=1、一次项系数b=﹣4、常数项c=﹣8,∴x===2±2,∴x1=2+2,x2=2﹣2;46.2x2﹣x﹣2=0a=2,b=﹣1,c=﹣2,∵b2﹣4ac=(﹣1)2﹣4×2×(﹣2)=1+16=17>0,∴x==,∴x1=,x2=47.3x2+2(x﹣1)=0.2∵a=3,b=2,c=﹣2,△=b2﹣4ac=4+24=28,x==,解得x1=,x2=48.x2﹣4x﹣7=0∵x2﹣4x﹣7=0的二次项系数是a=1、一次项系数是b=﹣4、常数项是c=﹣7,∴x===2±,∴x1=2+,x2=2﹣49.y2﹣2y﹣4=0(公式法)由原方程知,二次项系数a=1,一次项系数b=﹣2,常数项c=﹣4,∴x==,∴,∴x1=1+,x2=1﹣;50.x2﹣3x=2x2﹣3x﹣2=0,∵a=1,b=﹣3,c=﹣2,∴x===,∴x1=,x2=51.2x2+x﹣=0.∵关于x的一元二次方程2x2+x﹣=0的二次项系数a=2,一次项系数b=1,常数项c=﹣,∴原方程的根是:=,即x=52.x2x+1=0这里a=1,b=﹣2,c=1,∵△=8﹣4=4,∴x==±1,则x1=+1,x2=﹣153.2x2﹣9x+8=0;∵a=2,b=﹣9,c=8∴x=,x1=,x2=;54. x2﹣6x+1=0;∵a=1,b=﹣6,c=1∴x=,∴x1=3+2,x2=3﹣2;55. x2+x﹣1=0;∵a=1,b=1,c=﹣1,∴x==;56. 2x2﹣6x+3=0;∵a=2,b=﹣6,c=3,∴x===;57.2x(x+4)=12x2+8x﹣1=0,∵a=2,b=8,c=﹣1,△=b2﹣4ac=64+8=72,∴x===.即x1=,x2=58.3x2+5(2x+1)=0.3x2+5(2x+1)=0,整理得:3x2+10x+5=0,∵a=3,b=10,c=5,∴b2﹣4ac=100﹣60=40>0,∴x==,则原方程的解为x1=,x2=59.2x2﹣4x﹣1=0(公式法)解:这里a=2,b=﹣4,c=﹣1,∵b2﹣4ac=(﹣4)2﹣4×2×(﹣1)=24,∴x==,∴x1=,x2=60.3x2﹣6x﹣4=0(公式法)3x2﹣6x﹣4=0,这里a=3,b=﹣6,c=﹣4,∵b2﹣4ac=36+48=84>0,∴x==,则x1=,x2=61.x2+2x﹣5=0∵a=1,b=2,c=﹣5,b2﹣4ac=24,∴x==﹣1,即x1=,x2=﹣1.62.x2﹣4x﹣3=0由题意得:a=1,b=﹣4,c=﹣3,∴x====2±63.4x2﹣3x﹣1=0a=4,b=﹣3,c=﹣1,△=9+16=25x==∴x1=1,x2=﹣.63. x2+2x﹣2=0;这里a=1,b=2,c=﹣2,∵b2﹣4ac=22﹣4×1×(﹣2)=12>0,∴x==﹣1,∴x1=﹣1+,x2=﹣1﹣;64. y2﹣3y+1=0;这里a=1,b=﹣3,c=1.∵b2﹣4ac=(﹣3)2﹣4×1×1=5>0,∴y=,∴y1=,y 2=;65. x2+3=2x.移项,得x2﹣2x+3=0,这里a=1,b=﹣2,c=3.∵b2﹣4ac=(﹣2)2﹣4×1×3=﹣4<0.∴原方程没有实数根66.x2﹣4x=﹣3移项,得x2﹣4x+3=0.∵a=1,b=﹣4,c=3,∴b2﹣4ac=(﹣4)2﹣4×1×3=4>0,∴x==,∴x1=1,x2=367. 3x2﹣2x﹣1=0;∵a=3,b=﹣2,c=﹣1,∴b2﹣4ac=(﹣2)2﹣4×3×(﹣1)=16,∴x===,∴x1=1,x2=﹣.68.;∵a=2,b=﹣1,c=﹣,∴b2﹣4ac=(﹣1)2﹣4×2×(﹣)=5,∴x==,∴x1=,x2=.69. 2x2﹣7x+5=0;∵a=2,b=﹣7,c=5,∴b 2﹣4ac=(﹣7)2﹣4×2×5=9,∴x==,∴x1=,x2=1.70. 2x2﹣7x﹣18=0.∵a=2,b=﹣7,c=﹣18,∴b2﹣4ac=(﹣7)2﹣4×2×(﹣18)=193,∴x==,∴x1=,x2=71. (x+1)(x+3)=6x+4;去括号,移项方程化为一般式为:x2﹣2x﹣1=0,∵a=1,b=﹣2,=﹣1,∴b2﹣4ac=(﹣2)2﹣4×1×(﹣1)=8∴x===1±,∴x1=1+,x2=1﹣;72. x2+2(+1)x+2=0;∵a=1,b=2(+1),c=2,∴b2﹣4ac=[2(+1)]2﹣4×1×2=16,∴x===﹣(+1)±2,∴x 1=﹣﹣3,x2=﹣+1;73. x2﹣(2m+1)x+m=0.∵a=1,b=﹣(2m+1),c=m,∴b2﹣4ac=[﹣(2m+1)]2﹣4×1×m=4m2+1,∴x=,∴x1=,x2=74. x(x+8)=16,x2+8x﹣16=0,a=1,b=8,c=﹣16,b2﹣4ac=82﹣4×1×(﹣16)=128>0,x=,x1=﹣4+4,x2=﹣4﹣4;75. x2﹣4x=4;x 2﹣4x﹣4=0;a=,b=﹣4,c=﹣4,b 2﹣4ac=(﹣4)2﹣4××(﹣4)=48>0,x==±,x1=+,x2=﹣;76. 2x2﹣2x+1=0,a=2,b=﹣2,c=1,b2﹣4ac=(﹣2)2﹣4×2×1=0,x1=x2=.77. 5x2+2x﹣1=0 ∵a=5,b=2,c=﹣1,∴△=b2﹣4ac=4+4×5×1=24>0∴x1•x2=∴x1=.78. 6y2+13y+6=0∵a=6,b=13,c=6,∴△=b2﹣4ac=169﹣4×6×6=25>0 ∴x=∴x1=﹣,x2=﹣.79. 3•x2+6x+9=7整理,得:x2+6x+2=0∴a=1,b=6,c=2∴△=b2﹣4ac=36﹣4×1×2=28>0 ∴x1•2==﹣3±∴x1=﹣3+,x2=﹣3﹣.80. 2x2﹣3x+1=0;根据原方程,得a=2,b=﹣3,c=1,∵b2﹣4ac=9﹣4×2×1=1>0,∴x=,x==.∴x1=1,x2=;81. 2y(y﹣1)+3=(y+1)2.由原方程,得2y2﹣2y+3=y2+2y+1,即y2﹣4y+2=0,∴a=1,b=﹣4,c=2.b2﹣4ac=(﹣4)2﹣4×1×2=8>0.∴x=x==∴x1=2+,x2=2﹣.82. x2=3x+1;方程化为x2﹣3x﹣1=0,∴a=1,b=﹣3,c=﹣1,b2﹣4ac=(﹣3)2﹣4×1×(﹣1)=13.∴x1=.83. (t+1)(t﹣3)=﹣t(3﹣3t).方程化为2t2﹣t+3=0,a=2,b=﹣1,c=3b2﹣4ac=1﹣4×2×3=﹣23<0,∴原方程无实数根84.x2﹣2ax﹣b2+a2=0.∵a=1,b=﹣2a,c=﹣b2+a2∴b2﹣4ac=4a2+4b2﹣4a 2=4b2∴x==a±|b|.85. 3x2=2﹣5x;a=3,b=5,c=﹣2b2﹣4ac=52﹣4×3×(﹣2)=25+24=49>0.x==.所以x1=﹣2,x 2=.86. y2﹣4y=1;原方程变形为:3y2﹣8y﹣2=0.a=3,b=﹣8,c=﹣2.b2﹣4ac=(﹣8)2﹣4×3×(﹣2)=64+24=88.x==.所以x 1=,x2=.87. (x+1)(x﹣1)=2x.原方程变形x2﹣2x﹣1=0.a=1,b=﹣2,c=﹣1.b2﹣4ac=(﹣2)2﹣4×1×(﹣1)=8+4=12>0.所以x==.故x1=+,x2=﹣.88.(2x﹣1)2﹣7=3(x+1);整理,得4x2﹣7x﹣9=0,因为a=4,b=﹣7,c=﹣9.所以x=89.x2﹣6x+11=0由原方程,知a=,b=﹣6,c=11将其代入求根公式x=,得x=,∴原方程的根是:x1=4,x2=90 .5x2﹣8x+2=0.这里a=5,b=﹣8,c=2,∵b2﹣4ac=64﹣40=24>0,∴x==,则x1=,x2=.91.x2﹣3x+1=0.x2﹣3x+1=0,这里a=1,b=﹣3,c=1,∵b2﹣4ac=(﹣3)2﹣4×1×1=9﹣4=5>0,∴x==,则x1=,x2=92.x2=5﹣12x方程化为一般形式为:x 2+12x﹣5=0,∴a=1,b=12,c=﹣5,∴△=122﹣4×1×(﹣5)=4×41>0,∴x===﹣6±,所以x1=﹣6+,x2=﹣6﹣.93. x2+x﹣1=0解:x2+x﹣1=0,b2﹣4ac=12﹣4×1×(﹣1)=5,∴x=,∴x1=,x2=.94.3x2﹣4x﹣1=0解:3x2﹣4x﹣1=0,这里a=3,b=﹣4,c=﹣1,b2﹣4ac=(﹣4)2﹣4×3×(﹣1)=28,∴x==,∴原方程的解是:x1=,x2=,这里a=2,b=﹣2,c=1,∴b2﹣4ac=﹣4×2×1=4,∴x==,∴x1=,x2=,∴原方程的解是x1=,x2=95.3x 2+2(x﹣1)=0,整理得:3x2+2x ﹣2=0,这里a=3,b=2,c=﹣2,∵△=b2﹣4ac=4+24=28,∴x==,则x1=,x2=96.方程整理得:x2﹣2x+1=0,这里a=1,b=﹣2,c=1,∵△=8﹣4=4,∴x==±1,则x1=+1,x2=﹣1.97.3x2﹣4x﹣1=03x2﹣4x﹣1=0,这里a=3,b=﹣4,c=﹣1,∵b2﹣4ac=(﹣4)2﹣4×3×(﹣1)=16+12=28>0,∴x==,则x1=,x 2=98.2x2﹣x+1=0a=2,b=﹣,c=1△=10﹣8=2x=∴x1=,x2=99. .解:整理得:x2﹣2x﹣1=0,∴b2﹣4ac=﹣4×1×(﹣1)=12,∴x==±,∴x1=+,x2=﹣100.3x2﹣4x﹣1=0.3x2﹣4x﹣1=0,a=3,b=﹣4,c=﹣1,b2﹣4ac=(﹣4)2﹣4×3×(﹣1)=28,∴x==,∴x 1=,x2=101.2x2+5x﹣1=0.∵a=2,b=5,c=﹣1,△=b 2﹣4ac=25+8=33,∴x===.即x 1=,x2=102.2x2﹣x﹣1=0.∵原方程的二次项系数a=2,一次项系数b=﹣1,常数项c=﹣1,∴x===,∴x1=1,x2=﹣.103..∵a=2,b=﹣,c=﹣,∴△=(﹣)2﹣4×2×(﹣)=6>0,x==.104.3x2+5x﹣1=0.∵一元二次方程3x2+5x﹣1=0的二次项系数a=3,一次项系数b=5,常数项c=﹣1,∴x===,∴x 1=,x2=.105.5x2﹣8x+2=0,a=5,b=﹣8,c=2,b2﹣4ac=(﹣8)2﹣4×5×2=24>0,x==,x1=,x2=.106.3x2+7x+10=1﹣8x,整理得:x 2+5x+3=0,解得:x==,即:x1=,x2=;。
初中数学 一元二次方程解法 专题练习

一元二次方程解法巩固复习
1.公式法解下列方程
x x 3232=+ 012=-+x x 02342
=+-x x
23x =25x + 1)53)(2(=--x x 0223422=-+x x
2. 不解方程,你能判断下列方程根的情况吗?
0=8-2x +(1)x 2 4-4x =(2)x 2 -3=3x -(3)x 2
0=12-x +x )4(2 11+2x =8+4x +x )5( 2
3.已知关于x 的方程()()0212
2=-+++m x m x 有两个相等的实数根。
① 求m 的值;② 求出这时方程的根。
4.若关于x的一元二次方程042=--m x x 有两个不相等的实数根,则实数m的取值范围是
5. 若关于x 的一元二次方程()01412=++-x x k 有实数根,则k 的取值范围是
6. 用因式分解法解下列方程:
(x-2)·(x -3)=0 0=11x -4x 2 02)2(=-+-x x x 4
3241252
2
+
-=--x x x x
7.解一元二次方程时,要根据方程的特点,灵活选用适当的方法求解.
222)5(2
3)32)(3)(4(6
6)3(0
32)2(9)2)(1(2222=+-+=+-=-=--=-y y x x x x x x x x
8.无论p 取何值,方程0=p -2)-3)(x -(x 2总有两个不等的实数根吗?给出你的答案并说明理由.。
初中数学一元二次方程知识点总结(含习题)

初中数学一元二次方程知识点总结(含习题)一元二次方程知识点的总结知识结构梳理:1、概念1) 一元二次方程含有一个未知数。
2) 未知数的最高次数是2.3) 是方程。
4) 一元二次方程的一般形式是ax²+bx+c=0.2、解法1) 因式分解法,适用于能化为(x+m)(x+n)=0的一元二次方程。
2) 公式法,即把方程变形为ax²+bx+c=0的形式,一元二次方程的解为x=[-b±√(b²-4ac)]/(2a)。
3) 完全平方式,其中求根公式是(x±a)²=b,当时,方程有两个不相等的实数根。
4) 配方法,其中求根公式是(x±a)(x±b)=0,当时,方程有两个实数根。
5) 二次函数图像法,当时,方程有没有实数根。
3、应用1) 一元二次方程可用于解某些求值题。
2) 一元二次方程可用于解决实际问题的步骤包括:列方程、化简方程、解方程、检验答案。
知识点归类:考点一:一元二次方程的定义如果一个方程通过移项可以使右边为0,而左边只含有一个未知数的二次多项式,那么这样的方程叫做一元二次方程。
一元二次方程必须同时满足以下三点:①方程是整式方程。
②它只含有一个未知数。
③未知数的最高次数是2.考点二:一元二次方程的一般形式一元二次方程的一般形式为ax²+bx+c=0,其中a、b、c分别叫做二次项系数、一次项系数、常数项。
要准确找出一个一元二次方程的二次项系数、一次项系数和常数项,必须把它先化为一般形式。
考点三:解一元二次方程的方法一元二次方程的解也叫一元二次方程的根。
解一元二次方程的方法包括因式分解法、公式法、完全平方式、配方法和二次函数图像法。
解一元二次方程有四种常用方法:直接开平方法、配方法、因式分解法和公式法。
选择哪种方法要根据具体情况而定。
直接开平方法是解形如x²=a的方程的方法,解为x=±√a。
配方法是将方程的左边加上一次项系数一半的平方,再减去这个数,使得含未知数的项在一个完全平方式里,然后用因式分解法或直接开平方法解方程。
人教版初中数学-学年九年级上学期期末专题复习 专题1:一元二次方程 解析版

人教版初中数学2019-2020学年九年级上学期期末专题复习专题1:一元二次方程一、单选题1.下列方程中,关于x的一元二次方程是()A. x2+2y=1B. ﹣2=0C. ax2+bx+c=0D. x2+2x=12.一元二次方程x2-x-4=0的一次项系数和常数项分别是()A. 1,-1B. 1,-4C. -1,-4D. -1,43.将一元二次方程化为一般形式,正确的是()A. B. C. D.4.方程的解是()A. B. C. , D.5.关于x的一元二次方程kx2-2x-1=0有实数根,则k的取值范围是( )A. k>-1或k≠0B. k≥-1C. k≤-1或k≠0D. k≥-1且k≠06.一元二次方程x2+4x+2=0的根的判别式的值为()A. 8B. 24C.D.7.已知x1、x2、是一元二次方程x2+x-2=0的两个根,则x1+x2+x1x2的值为()A. 1B. -3C. 3D. -2二、填空题8.方程x2-2ax+3=0有一个根是1,a的值是________。
9.若代数式可化为,则=________,=________.10.定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a,如:min{1,-2)=-2,min{-3,-2)=-3,则方程min{x,-x}=x2-1的解是________.三、计算题11.解下列方程。
(1)x2-5x+6=0(2)(2x+1)(x-4)=5.12.(1)先化简,再求值:(x-2y)2-x(x+3y)-4y2,其中x=-4,y= .(2)已知:x+y=6,xy=4,求下列各式的值x2+y213.按要求解一元二次方程(1)4x2﹣8x+1=0(配方法)(2)7x(5x+2)=6(5x+2)(因式分解法)(3)3x2+5(2x+1)=0(公式法)(4)x2﹣2x﹣8=0.(5)(6x-1)2=25;四、解答题14.如图,在宽为20m,长为27m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为450 ,求道路的宽.15.要组织一次篮球邀请比赛,参赛的队伍每两个队都要比赛一场.赛程安排7天,每天比赛4场,问组织者应该邀请多少个队参赛?五、综合题16.已知关于x的一元二次方程x2+x+m﹣1=0.(1)当m=0时,求方程的实数根.(2)若方程有两个不相等的实数根,求实数m的取值范围.17.在一次聚会上,规定每两个人见面必须握手,且握手1次.(1)若参加聚会的人数为3,则共握手________次;若参加聚会的人数为5,则共握手________次;(2)若参加聚会的人数为n(n为正整数),则共握手________次;(3)若参加聚会的人共握手28次,请求出参加聚会的人数.(4)嘉嘉由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A,B),线段总数为多少呢?请直接写出结论.答案解析部分一、单选题1. D解:A、含有两个未知数,不是一元二次方程,故本选项不符合题意;B、分母中含有未知数,是分式方程,故本选项不符合题意;C、当a=0时不是一元二次方程,故本选项不符合题意;D、是一元二次方程,故本选项符合题意;故答案为:D.【分析】一元二次方程是指含有一个未知数,并且所含未知数的项的最高次数是2次的整式方程,根据定义判断即可.2. C解:一元二次方程x2-x-4=0的一次项系数时-1,常数项是-4,故C正确。
初中数学解一元二次方程经典练习题(含答案)

初中数学解一元二次方程经典练习题(含答案)解下列解一元二次方程:1、x2=121;2、(2x+3)2=9;3、3(4x+5)2-147=0;4、(2x−7)2+9 =6(2x-7);5、7x(x-6)=3(12-2x);6、(3x-5)(2x+5)= x+7;7、3(3x-4)+ x(4-3x)=0;8、x(2x+5)=4(2x-1)+3;9、(x−3)2+4=5(3-x);10、4x2+7x +1=0;11、512x2+ 13= x;12、(x−1)(x−2)2 -1 = (x+1)(x−3)3;13、14[12(x+1)+13(x+2)+2] =x2;14、(x+1)(x+2)+(x+3)(x+4)=(x+2)(x+3)+32;15、x= 2(0.3x+21)3 - (0.2x−1)(x+2)2;16、x2+(1+ 2√5)x +( 4+√5)=0;参考答案1、x2=121;解:x2=121等式两边同时开平方x= 11故原方程的根是:x1=11,x2= -112、(2x +3)2=9;解:(2x +3)2=9等式两边同时开平方(2x +3)=±3令2x +3 = 3,即2x=0,解得x=0令2x +3 =-3,即2x=-6,解得x=-3故原方程的根是:x 1=0,x 2=-33、3(4x +5)2-147=0;解:3(4x +5)2-147=03(4x +5)2=147等式两边同时除以3(4x +5)2= 49等式两边同时开平方4x+5=±7令4x+5=7, 解得x= 12 令4x+5= -7,解得x=-3故原方程的根是:x 1= 12,x 2=-34、(2x −7)2+9 =6(2x-7);解:(2x −7)2 +9 =6(2x-7)右边的项移到等号左边(2x−7)2-6(2x-7)+9 =0(2x−7)2 -2・3・(2x-7)+32=0[(2x−7)−3 ]2=0令(2x−7)−3 =0,解得 x=5故原方程的根是:x1=x2=55、7x(x-6)=3(12-2x);解:7x(x-6)=3(12-2x)等号左边提取-27x(x-6)=-6(x-6)右边的项移到等号左边7x(x-6)+6(x-6)=0提取公因式(x-6)(x-6)(7x+6)=0令x-6=0,解得x=6令7x+6=0,解得x= - 67故原方程的根是:x1=6,x2=- 676、(3x-5)(2x+5)= x+7;解(3x-5)(2x+5)= x+7等号左边去括号6x2+15x-10x-25 =x+76x2+5x-25=x+76x2+4x-32=03x2+2x-16=0(3x+8)(x-2)=0令3x+8=0,解得x= - 83令x-2 =0,解得x=2故原方程的根是:x1=- 8,x2=237、3(3x-4)+ x(4-3x)=0;解:3(3x-4)+ x(4-3x)=0 3(3x-4)- x(3x-4)=0 提取公因式(3x-4)(3x-4)(3- x)=0令3x-4=0,解得x= 43令3- x =0,解得x=3,x2=3 故原方程的根是:x1= 438、x(2x+5)=4(2x-1)+3;解:x(2x+5)=4(2x-1)+3 2x2 +5x =8x-4+32x2 +5x =8x-12x2 -3x +1=0(2x-1)(x-1)=0令2x-1=0,解得x= 12 令x-1=0,解得x=1故原方程的根是:x 1= 12 ,x 2=19、(x −3)2 +4=5(3-x );解:(x −3)2 +4= 5(3-x )等号左边提取-1(x −3)2 +4= -5(x-3)右边的项移到等号左边(x −3)2 +5(x-3)+4=0[(x -3)+1][(x-3)+4]=0(x-2)(x+1)=0令x-2=0,解得x=2令x+1=0,解得x=-1故原方程的根是:x 1=2,x 2=-110、4x 2+7x +1=0;解:4x 2+7x +1=0判别式△=72 -4×4×1 =33x= −7 ±√332×4 = −7 ±√338故原方程的根是:x 1=−7 +√338,x 2=−7 −√33811、512x 2 + 13 = x ; 解:512x 2 + 13 = x等式两边同时乘以125x 2 +4 =12x5x 2 +4 -12x =0(5x-2)(x-2)=0令5x-2=0,解得x= 25 令x-2=0,解得x=2故原方程的根是:x 1= 25,x 2=212、(x−1)(x−2)2-1 = (x+1)(x−3)3 ; 解:(x−1)(x−2)2 -1 = (x+1)(x−3)3 等式两边分子去括号x 2−3x+22 -1 = x 2−2x−33等式两边同时乘以63(x 2−3x +2)-6 =2(x 2−2x −3) 3x 2 -9x+6 -6= 2x 2 -4x −6x 2 -5x +6=0(x-2)(x-3)=0令x-2=0,解得x=2令x-3=0,解得x=3故原方程的根是:x 1=2,x 2=313、 14[12(x+1)+13(x+2)+2] =x 2;解:14[12(x+1)+13(x+2)+2] =x 2等号两边同时乘以412(x+1)+13(x+2)+2 =4x 2等号两边同时乘以63(x+1)+2(x+2)+12 =24x 23x+3+2x+4+12=24x 224x 2-5x-19=0(24x+19)(x-1)=0令24x+19=0,解得x= −1924令x-1=0,解得x= 1故原方程的根是:x 1=−1924,x 2= 114、(x+1)(x+2)+(x+3)(x+4)=(x+2)(x+3)+32;解:(x+1)(x+2)+(x+3)(x+4)=(x+2)(x+3)+32 等号两边去括号x 2+3x+2+x 2+7x+12 =x 2+5x+6+32整理得x 2+5x-24=0(x+8)(x-3)=0令x+8=0,解得x= -8令x-3=0,解得x= 3故原方程的根是:x 1=-8,x 2= 315、x=2(0.3x+21)3 - (0.2x−1)(x+2)2 ; 解:x= 2(0.3x+21)3 - (0.2x−1)(x+2)2等号两边同时乘以66x=4(0.3x+21)-3(0.2x-1)(x+2) 去括号6x=1.2x+84-0.6x 2+1.8x+6整理得0.6x 2+3x-90=0等号两边同时乘以10,然后再除以6 x 2+5x-150=0(x+15)(x-10)=0令x+15=0,解得x= -15令x-10=0,解得x= 10故原方程的根是:x 1= -15,x 2= 1016、x 2+(1+ 2√5)x +( 4+√5)=0; 解:x 2+(1+ 2√5)x +( 4+√5)=0 判别式△=(1+ 2√5)2-4・1・( 4+√5)=1+4√5+20-16-4√5=5x= −(1+ 2√5)±√52∙1即x= −(1+ 2√5)+√52=−(1+ √5)2或 x= −(1+ 2√5)−√52=−(1+3 √5)2故原方程的根是:x1=−(1+ √5)2,x2= −(1+3 √5)2。
一元二次方程综合复习(含知识点和练习)(含答案)

一元二次方程本章内容“一元二次方程”是《课程标准》“数与代数”的重要内容,也是方程中重点内容,是学习二次函数等内容的基础,本节是本章的起始内容,主要学习下列三个内容:建立一元二次方程此内容是本节课的难点之一,在后续的内容中将继续学习,为此设计较易的[拓展应用]的例4及其变式题,[课时作业]的第6、7题。
1.一元二次方程的概念此内容是本节课的重点,是学习一元二次方程的基础,为此设计[拓展应用]的例1、例3,[当堂检测]的第1、2、4题,[课时作业]的第1—5题。
2.一元二次方程的解的含义利用方程解的含义,可求方程中的待定系数,也可由此把二次三项式变形求值,为此设计[拓展应用]的例2,[当堂检测]的第3题,[选做题]和[备选题目]的问题。
点击一:一元二次方程的定义答案:(5)针对练习。
答案:一元二次方程二次项的系数不等于零。
故m≠-3点击二:一元二次方程的一般形式元二次方程的一般形式是ax2+bx+c=0(a≠0),其中ax2是二次项,bx是一次项,c是常数项,a是二次项系数,b是一次项系数,c是常数.任何一个一元二次方程都可以通过整理转化成一般形式.由此,对于一个方程从形式上,应先将这个方程进行整理,看是否符合ax2+bx+c=0(a≠0)的一般形式.其中,尤其注意a≠0的条件,有了a≠0的条件,就能说明ax2+bx+c=0是一元二次方程.若不能确定a≠0,并且b≠0,则需分类讨论:当a≠0时,它是一元二次方程;当a=0时,它是一元一次方程.针对练习3:答案:原方程化为一般形式是:5x2+8x-2=0(若写成-5x2-8x+2=0,则不符合人们的习惯),其中二次项是5x2,二次项系数是5,一次项是8x,一次项系数是8,常数项是-2(因为一元二次方程的一般形式是三个单项式的和,所以不能漏写单项式系数的负号).点击三:一元二次方程的根的定义的意义一元二次方程的根的定义可以当作性质定理使用,即若有实数m是一元二次方程ax 2+bx +c =0(a ≠0)的根,则m 必然满足该方程,将m 代入该方程,便有am 2+bm +c =0(a ≠0);定义也可以当作判定定理使用,即若有数m 能使am 2+bm +c =0(a ≠0)成立,则m 一定是ax 2+bx +c =0的根.我们经常用定义法来解一些常规方法难以解决的问题,能收到事半功倍的效果.针对练习答案: m 3+2m 2+2009=m 3+ m 2+m 2+2009=m (m 2+ m )+ m 2+2009=m+ m 2+2009=1+2009=2010.类型之一:一元二次方程的定义例1.关于x 的方程2322+-=-mx x x mx 是一元二次方程,m 应满足什么条件? 【解析】先把这个方程变为一般形式,只要二次项的系数不为0即可.【解答】由mx 2-3x=x 2-mx+2得到(m -1)x 2+(m -3)x -2=0,所以m -1≠0,即m≠1.所以关于x 的方程2322+-=-mx x x mx 是一元二次方程,m 应满足m≠1.【点评】要特别注意二次项系数a≠0这一条件,当a=0时,上面的方程就不是一元二次方程了.当b=0或c=0时,上面的方程在a≠0的条件下,仍是一元二次方程,只不过是不完全的一元二次方程.类型之二:考查一元二次方程一般形式一元二次方程的一般形式是ax 2+bx+c=0(a 、b 、c 是已知数,a≠0),其中a 叫做二次项系数,b 叫做一次项系数c 叫做常数项.只有将方程化为一般形式之后,才能确定它的二次项系数、一次项系数和常数项.这里特别要注意各项系数的符号。
(完整版)初中数学一元二次方程复习专题

一元二次方程专题复习韦达定理:如一元二次方程20(0)ax bx c a ++=≠的两根为12,x x ,则12b x x a +=-,12cx x a⋅=适用题型:(1)已知一根求另一根及未知系数;(2)求与方程的根有关的代数式的值;(3)已知两根求作方程;(4)已知两数的和与积,求这两个数;(5)确定根的符号:(12,x x 是方程两根);(6)题目给出两根之间的关系,如两根互为相反数、互为倒数、两根的平方和或平方差是多少、两根是Rt ∆的两直角边求斜边等情况.注意:(1)222121212()2x x x x x x +=+-⋅(2)22121212()()4x x x x x x -=+-⋅;12x x -=(3)①方程有两正根,则121200x x x x ∆≥⎧⎪+>⎨⎪⋅>⎩;②方程有两负根,则1212000x x x x ∆≥⎧⎪+<⎨⎪⋅>⎩ ;③方程有一正一负两根,则120x x ∆>⎧⎨⋅<⎩;④方程一根大于1,另一根小于1,则120(1)(1)0x x ∆>⎧⎨--<⎩(4)应用韦达定理时,要确保一元二次方程有根,即一定要判断根的判别式是否非负;求作一元二次方程时,一般把所求作得方程的二次项系数设为1,即以12,x x 为根的一元二次方程为21212()0x x x x x x -++⋅=;求字母系数的值时,需使二次项系数0a ≠,同时满足∆≥0;求代数式的值,常用整体思想,把所求代数式变形成为含有两根之和12x x +,•两根之积12x x ⋅的代数式的形式,整体代入。
4.用配方法解一元二次方程的配方步骤: 例:用配方法解24610x x -+= 第一步,将二次项系数化为1:231024x x -+=,(两边同除以4) 第二步,移项: 23124x x -=- 第三步,两边同加一次项系数的一半的平方:2223313()()2444x x -+=-+ 第四步,完全平方:235()416x -=第五步,直接开平方:344x -=±,即:1344x =++,2344x =-+一元二次方程的定义与解法➢ 【要点、考点聚焦】1. 加深理解一元二次方程的有关概念及一元二次方程的一般形式20(0)ax bx c a ++=≠;2.熟练地应用不同的方法解方程;直接开平方法、配方法、公式法、因式分解法;并体会“降幂法”在解方程中的含义.(其中配方法很重要) ➢ 【课前热身】1. 当a =____________时,方程2310ax x ++=是一元二次方程.2. 已知1x =是方程220x ax ++=的一个根,则方程的另一根为__________. 3.一元二次方程(1)x x x -=的解是_____________.4. 若关于x 的一元二次方程20(0)ax bx c a ++=≠,且0a b c ++=,则方程必有一根为____________.5. 用配方法解方程2420x x -+=,则下列配方正确的是( )A.2(2)2x -= B.2(2)2x += C.2(2)2x -=- D.2(2)6x -=➢ 【典型例题解析】1、关于x 的一元二次方程2(1)(2)26ax ax x x --=-+中,求a 的取值范围.2、已知:关于x 的方程226350x x m m -+--=的一个根是1-,求方程的另一个根及m 的值。
初中数学一元二次方程全章复习与巩固(基础)
《一元二次方程》全章复习与巩固(基础)【学习目标】1.了解一元二次方程及有关概念2.掌握通过配方法、公式法、因式分解法降次──解一元二次方程3.掌握依据实际问题建立一元二次方程的数学模型的方法【知识网络】【要点梳理】要点一、一元二次方程的有关概念1.一元二次方程的概念:通过化简后,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的整式方程,叫做一元二次方程.2.一元二次方程的一般式:3.一元二次方程的解:使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解,也叫做一元二次方程的根. 要点诠释:判断一个方程是否为一元二次方程时,首先观察其是否是整式方程,否则一定不是一元二次方程;其次再将整式方程整理化简使方程的右边为0,看是否具备另两个条件:①一个未知数;②未知数的最高次数为2.对有关一元二次方程定义的题目,要充分考虑定义的三个特点,不要忽视二次项系数不为0. 要点二、一元二次方程的解法 1.基本思想一元二次方程⎯⎯⎯→降次一元一次方程 2.基本解法直接开平方法、配方法、公式法、因式分解法. 要点诠释:解一元二次方程时,根据方程特点,灵活选择解题方法,先考虑能否用直接开平方法和因式分解法,再考虑用公式法.要点三、一元二次方程根的判别式及根与系数的关系 1.一元二次方程根的判别式一元二次方程)0(02≠=++a c bx ax 中,ac b 42−叫做一元二次方程)0(02≠=++a c bx ax 的根的判别式,通常用“∆”来表示,即ac b 42−=∆(1)当△>0时,一元二次方程有2个不相等的实数根. (2)当△=0时,一元二次方程有2个相等的实数根. (3)当△<0时,一元二次方程没有实数根.2.一元二次方程的根与系数的关系如果一元二次方程)0(02≠=++a c bx ax 的两个实数根是21x x ,,那么a b x x −=+21,a cx x =21.注意它的使用条件为a ≠0, Δ≥0. 要点诠释:1.一元二次方程的根的判别式正反都成立.利用其可以解决以下问题:(1)不解方程判定方程根的情况. (2)根据参系数的性质确定根的范围. (3)解与根有关的证明题.2. 一元二次方程根与系数的应用很多:(1)已知方程的一根,不解方程求另一根及参数系数.(2)已知方程,求含有两根对称式的代数式的值及有关未知数系数. (3)已知方程两根,求作以方程两根或其代数式为根的一元二次方程.要点四、列一元二次方程解应用题 1.列方程解实际问题的三个重要环节:一是整体地、系统地审题. 二是把握问题中的等量关系. 三是正确求解方程并检验解的合理性. 2.利用方程解决实际问题的关键是寻找等量关系. 3.解决应用题的一般步骤:审 (审题目,分清已知量、未知量、等量关系等). 设 (设未知数,有时会用未知数表示相关的量). 列 (根据题目中的等量关系,列出方程).解 (解方程,注意分式方程需检验,将所求量表示清晰). 验 (检验方程的解能否保证实际问题有意义). 答 (写出答案,切忌答非所问). 4.常见应用题型数字问题、平均变化率问题、利息问题、利润(销售)问题、形积问题等. 要点诠释:列方程解应用题就是先把实际问题抽象为数学问题(列方程),然后由数学问题的解决而获得对实际问题的解决.【典型例题】类型一、一元二次方程的有关概念1.下列方程中是关于x 的一元二次方程的是( )A .2210x x+=B .20ax bx c ++= C .(1)(2)1x x −+=D .223250x xy y −−=【答案】C【解析】A :不是整式方程,故本选项错误.B :当a =0时,即ax 2+bx +c =0的二次项系数是0时,该方程就不是一元二次方程,故本选项错误.C :由原方程,得x 2+x-3=0,符号一元二次方程的要求;故本选项正确.D :方程3x 2-2xy -5y 2=0中含有两个未知数;故本选项错误.故选C .【总结升华】一元二次方程必须满足四个条件:(1)未知数的最高次数是2 (2)二次项系数不为0 (3)是整式方程(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.举一反三:【变式】关于x 的方程22(28)(2)10a a x a x −−++−=,当a 时为一元一次方程;当a 时为一元二次方程.【答案】a =4;a ≠4且a ≠-2.类型二、一元二次方程的解法2.用适当的方法解一元二次方程 (1) 0.5x 2-=0 (2) (x+a)2=(3) 2x 2-4x-1=0 (4) (1-)x 2=(1+)x【答案与解析】 (1)原方程可化为0.5x 2=∴x 2=用直接开平方法,得方程的根为 ∴x 1=,x 2=-(2)原方程可化为x 2+2ax+a 2=4x 2+2ax+∴x 2=a 2用直接开平方法,得原方程的根为 ∴ x 1=a ,x 2=-a .(3) a=2,b=-4,c=-1b 2-4ac=(-4)2-4×2×(-1)=24>0x=∴x1=,x2=.(4)将方程整理,得(1-)x2-(1+)x=0用因式分解法,得x[(1-)x-(1+)]=0∴ x1=0,x2=-3-2.【总结升华】在以上归纳的几种解法中,因式分解法是最简便、最迅捷的方法,但只有一部分方程可以运用这种方法,所以要善于及时观察标准的二次三项式在有理数范围内是否能直接因式分解,凡能直接因式分解的,应首先采取这种方法.公式法是可以解任何类型的一元二次方程,但是计算过程较繁琐,所以只有选择其他解法不顺利时,才考虑用这种解法.虽然先配方,再开平方的方法也适用于任何类型的一元二次方程,但是对系数复杂的一元二次方程,配方的过程比运用公式更繁琐,所以,配方法适用于系数简单的一元二次方程的求解.举一反三:【变式】解方程. (1)(3x-2)2+(2-3x)=0 (2)2(t-1)2+t=1【答案】(1)原方程可化为:(3x-2)2-(3x-2)=0,∴ (3x-2)(3x-2-1)=0∴ 3x-2=0或3x-3=0,∴12 3x=,21x= (2)原方程可化为:2(t-1)2+(t-1)=0∴ (t-1)[2(t-1)+1]=0∴ (t-1)(2t-1)=0,∴ t-1=0或2t-1=0∴11t=,21 2t=类型三、一元二次方程根的判别式的应用3.(2020•荆门)若关于x的一元二次方程x2﹣4x+5﹣a=0有实数根,则a的取值范围是()A.a≥1 B.a>1 C.a≤1 D.a<1【答案】A【解析】∵关于x的一元二次方程x2﹣4x+5﹣a=0有实数根∴△=(﹣4)2﹣4(5﹣a )≥0 ∴a ≥1 故选A .【总结升华】本题考查的是一元二次方程根的判别式,根据方程有两个实数根,得到判别式大于等于零,求出a 的取值范围.类型四、一元二次方程的根与系数的关系4.已知x 1、x 2是关于x 的方程2220x x t −++=的两个不相等的实数根,(1)求t 的取值范围;(2)设2212s x x =+,求s 关于t 的函数关系式. 【答案与解析】(1)因为一元二次方程有两个不相等的实数根.所以△=(-2)2-4(t+2)>0,即t <-1. (2)由一元二次方程根与系数的关系知:122x x +=,122x x t =+,从而2212s x x =+21212()2x x x x =+−222(2)2t t =−+=−,即2(1)s t t =−<−.【总结升华】利用根与系数关系求函数解析式综合题. 举一反三:【变式】已知关于x 的一元二次方程222(1)x m x m =−−的两实数根为1x ,2x .(1)求m 的取值范围;(2)设12y x x =+,当y 取得最小值时,求相应m 的值,并求出最小值.【答案】(1)将原方程整理为222(1)0x m x m +−+=. ∵ 原方程有两个实数根.∴ 22[2(1)]4840m m m =−−=−+≥△,∴ 12m ≤. (2) 1222y x x m =+=−+,且12m ≤. 因为y 随m 的增大而减小,故当12m =时,取得最小值1.类型五、一元二次方程的应用5.如图所示,在长为10cm ,宽为8cm 的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去的小正方形的边长.【答案与解析】设小正方形的边长为xcm,由题意得4x2=10×8×(1-80%).解得x1=2,x2=-2.经检验,x1=2符合题意,x2=-2不符合题意舍去.∴ x=2.答:截去的小正方形的边长为2cm.【总结升华】设小正方形的边长为x cm,因为图中阴影部分面积是原矩形面积的80%,所以4个小正方形面积是原矩形面积的20%.举一反三:【变式】(2020春•启东市月考)如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在欲砌50m长的墙,砌成一个面积300m2的矩形花园,则BC的长为多少m?【答案】解:设AB=x米,则BC=(50﹣2x)米.根据题意可得,x(50﹣2x)=300解得:x1=10,x2=15当x=10,BC=50﹣10﹣10=30>25故x1=10(不合题意舍去)50﹣2x=50﹣30=20答:BC的长为20m.6.某旅行社有100张床位,每床每晚收费10元,空床可全部租出;若每床每晚提高2元,则减少10张床位租出;若每床每晚收费再提高2元,则再减少10张床位租出.以每次提高2元的这种方法变化下去,为了每晚获得1120元的利润,每床每晚应提高多少元?【答案与解析】设每床每晚提高x个2元,则每床每晚收费为(10+2x)元,每晚出租出去的床位为(100-10x)张,根据题意,得(10+2x)(100-10x)=1120.整理,得x2-5x+6=0解得,x1=2,x2=3∴当x=2时,2x=4当x=3时,2x=6答:每床每晚提高4元或6元均可.【总结升华】这是商品经营问题,总利润=每张床费×床数.可设每床每晚提高x个2元,则床费为(10+2x)元,由于每晚每床提高2元,出租出去的床位减少10张,则出租出去的总床位为(100-10x)张,据此可列方程.【巩固练习】 一、选择题1.已知1是关于x 的一元二次方程(m ﹣1)x 2+x+1=0的一个根,则m 的值是( )A.1B.﹣1C.0D.无法确定2.若一元二次方程式ax (x +1)+(x +1)(x +2)+bx (x +2)=2的两根为0.2,则|3a +4b |之值为何( )A .2B .5C .7D .83.(2020•濠江区一模)某机械厂一月份生产零件50万个,三月份生产零件72万个,则该机械厂二、三月份生产零件数量的月平均增长率为( ) A .2%B . 5%C . 10%D . 20%4.将代数式x 2+4x-1化成(x+p )2+q 的形式( )A.(x-2)2+3 B.(x+2)2-4 C.(x+2)2-5 D.(x+2)2+45.若关于x 的一元二次方程2210kx x ++=有实数根,则k 的取值范围是( ). A .k <0 B .k ≤0 C .k ≠1且k ≠0 D .k ≤1且k ≠06.从一块正方形的铁片上剪掉2 cm 宽的长方形铁片,剩下的面积是48 cm 2,则原来铁片的面积是( )A.64 cm 2B.100 cm 2C.121 cm 2D.144 cm 27.若t 是一元二次方程的根,则判别式和完全平方式的关系是( )A.△=MB. △>MC. △<MD. 大小关系不能确定 8.如果关于x 的方程ax 2+x-1=0有实数根,则a 的取值范围是( ) A . B . C .且 D .且二、填空题9.已知关于x 的方程x 2+mx ﹣6=0的一个根为2,则m = ,另一个根是 .10.(2020秋•青海校级期末)有一间长20m ,宽15m 的矩形会议室,在它的中间铺一块地毯,地毯的面积是会议室面积的一半,四周未铺地毯的留空宽度相同,则地毯的长、宽分别为 和 . 11.关于x 的一元二次方程22(1)10a x x a −++−=有一个根为0,则a = .12.阅读材料:设一元二次方程似20ax bx c ++=(a ≠0)的两根为x 1,x 2,则两根与方程系数之间有如下关系:12bx x a+=−,12c x x a=,根据该材料填空:已知x 1,x 2是方程2630x x ++=的两实数根,则2112x x x x +的值为________. 13.已知两个连续奇数的积是15,则这两个数是___________________.14.设x 1,x 2是一元二次方程x 2-3x-2=0的两个实数根,则2211223x x x x ++的值为________. 15.问题1:设a 、b 是方程x 2+x -2012=0的两个实数根,则a 2+2a +b 的值为 ;问题2:方程x 2-2x -1=0的两个实数根分别为x 1,x 2,则(x 1―1)(x 2―1)= ; 问题3:已知一元二次方程x 2-mx +m -2=0的两个实数根为x 1、x 2且x 1x 2(x 1+x 2)=3,则m 的值是 ;问题4:已知一元二次方程x 2-2x+m=0,若方程的两个实数根为X 1,X 2,且X 1+3X 2=3,则m 的值是 . 16.某校2010年捐款1万元给希望工程,以后每年都捐款,计划到2012年共捐款4.75万元,则该校捐款的平均年增长率是 .三、解答题17.某两位数的十位数字与个位上的数字之和是5,把这个数的个位上的数字与十位上的数字对调后,所得的新两位数与原两位数的乘积为736,求原来的两位数.18. 恒利商厦九月份的销售额为200万元,十月份的销售额下降了20%,商厦从十一月份起加强管理,改善经营,使销售额稳步上升,十二月份的销售额达到了193.6万元,求这两个月的平均增长率.19.(2020•十堰)已知关于x 的一元二次方程x 2﹣(2m+3)x+m 2+2=0. (1)若方程有实数根,求实数m 的取值范围;(2)若方程两实数根分别为x 1、x 2,且满足x 12+x 22=31+|x 1x 2|,求实数m 的值.20.某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件. (1)求商场经营该商品原来一天可获利润多少元? (2)设后来该商品每件降价x 元,商场一天可获利润y 元.①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?②求出y 与x 之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当x取何值时,商场获利润不少于2160元?【答案与解析】一、选择题1.【答案】B;【解析】解:根据题意得:(m﹣1)+1+1=0,解得:m=﹣1.故选B.2.【答案】B;【解析】先根据一元二次方程式ax(x+1)+(x+1)(x+2)+bx(x+2)=2的根确定a.b的关系式.然后根据a.b的关系式得出3a+4b=-5.用求绝对值的方法求出所需绝对值.3.【答案】D;【解析】设平均每月增长的百分率为x,根据题意,得50(1+x)2=72,解得x1=0.2=20%,x2=﹣2.2(不合题意,舍去)故选D.4.【答案】C;【解析】根据配方法,若二次项系数为1,则常数项是一次项系数的一半的平方,若二次项系数不为1,则可先提取二次项系数,将其化为1后再计算.x2+4x-1=x2+4x+4-4-1=(x+2)2-5,故选C.5.【答案】D;【解析】因为方程是一元二次方程,所以k≠0,又因为一元二次方程有实数根,所以△≥0,即△=4-4k≥0,于是有k≤1,从而k的取值范围是k≤1且k≠0.6.【答案】A;【解析】本题用间接设元法较简便,设原铁片的边长为xcm.由题意,得x(x-2)=48,解得x1=-6(舍去),x2=8.∴x2=64,即正方形面积为64 cm2.7.【答案】A;【解析】由t是方程的根得at2+bt+c=0,M=4a2t2+4abt+b2=4a(at2+bt)+b2= b2-4ac=△.8.【答案】B;【解析】注意原方程可能是一元二次方程,也可能是一元一次方程.二、填空题9.【答案】1;﹣3.【解析】根据一元二次方程的解定义,将x =2代入关于x 的方程x 2+mx ﹣6=0,然后解关于m 的一元一次方程;再根据根与系数的关系x 1+x 2=﹣b a解出方程的另一个根. 10.【答案】 15m ,10m ;【解析】设留空宽度为xm ,则(20﹣2x )(15﹣2x )=20×15×,整理得:2x 2﹣35x+75=0,即(2x ﹣5)(x ﹣15)=0,解得x 1=15,x 2=2.5,∵20﹣2x >0,∴x<10,∴x=2.5, ∴20﹣2x=15,15﹣2x=10.∴地毯的长、宽分别为15m 和10m .11.【答案】-1;【解析】把x=0代入方程得1a =±,因为10a −≠,所以1a =−.12.【答案】10;【解析】此例首先根据阅读部分,明确一元二次方程根与系数的关系, 然后由待求式2112x x x x +变形为2221212121212()2x x x x x x x x x x ++−=,再整体代换. 具体过程如下:由阅读材料知 x 1+x 2=-6,x 1x 2=3.而222221121212121212()2(6)23103x x x x x x x x x x x x x x ++−−−⨯+====. 13.【答案】3和5或-3和-5;【解析】注意不要丢解.14.【答案】7;【解析】∵ x 1,x 2是一元二次方程2320x x −−=的两实数根,∴ x 1+x 2=3,x 1x 2=-2∴ 222222112211221212123(2)()3(2)7x x x x x x x x x x x x x x ++=+++=++=+−=15.【答案】2011;-2;m=-1或3;m=34.【解析】由于a,b是方程x2+x-2012=0的两个实数根,根据根与系数的关系可以得到a+b=-1,并且a2+a-2012=0,然后把a2+2a+b可以变为a2+a+a+b,把前面的值代入即可求出结果.16.【答案】50%;【解析】设该校捐款的平均年增长率是x,则,整理,得,解得,答:该校捐款的平均年增长率是50%.三、解答题17.【答案与解析】设原两位数的十位数字为x,则个位数字为(5-x),由题意,得[10x+(5-x)][10(5-x)+x]=736.整理,得x2-5x+6=0,解得x1=2,x2=3.当x=2时5-x=3,符合题意,原两位数是23.当x=3时5-x=2符合题意,原两位数是32.18.【答案与解析】设这两个月的平均增长率是x.,则根据题意,得200(1-20%)(1+x)2=193.6,即(1+x)2=1.21,解这个方程,得x1=0.1,x2=-2.1(舍去).答:这两个月的平均增长率是10%.19.【答案与解析】解:(1)∵关于x的一元二次方程x2﹣(2m+3)x+m2+2=0有实数根,∴△≥0,即(2m+3)2﹣4(m2+2)≥0,∴m≥﹣;(2)根据题意得x1+x2=2m+3,x1x2=m2+2,∵x12+x22=31+|x1x2|,∴(x1+x2)2﹣2x1x2=31+|x1x2|,即(2m+3)2﹣2(m2+2)=31+m2+2,解得m=2,m=﹣14(舍去),∴m=2.20.【答案与解析】⑴若商店经营该商品不降价,则一天可获利润100×(100-80)=2000(元)⑵①依题意得:(100-80-x)(100+10x)=2160即x2-10x+16=0解得:x1=2,x2=8经检验:x1=2,x2=8都是方程的解,且符合题意.答:商店经营该商品一天要获利润2160元,则每件商品应降价2元或8元.②依题意得:y=(100-80-x)(100+10x)∴y=-10x2+100x+2000=-10(x-5)2+2250画草图(略)观察图像可得:当2≤x≤8时,y≥2160∴当2≤x≤8时,商店所获利润不少于2160元.。
九年级数学一元二次方程总复习资料

九年级数学一元二次方程总复习资料一、知识扫描1.只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程.因此,由一元二次方程的定义可知,即一元二次方程必须满足满足以下三个条件:①方程的两边都是关于未知数的整式;②只含有一个未知数;③未知数的最高次数是2。
这样的方程才是一元二次方程,不满足其中任何一个条件的方程都不是一元二次方程。
例如:535,53,02,3422222+===-+-x x x x x x x 都是一元二次方程。
而03132=-+x x不是一元二次方程,原因是x1是分式。
2.任何关于x 的一元二次方程的都可整理成)0(02≠=++a c bx ax 的形式.这种形式叫做一元二次方程的一般形式,它的特征是方程左边是一个关于未知数的二次三项式,方程右边是零,其中2ax 叫二次项,a 叫做二次项系数;bx 叫做一次项,b 叫做一次项系数;c 叫做常数项。
注意b 、c 可以是任何实数,但a 绝对不能为零,否则,就不是一元二次方程了。
化一元二次方程为一般形式的手段是去分母、去括号、移项、合并同类项,整理后的方程最好按降幂排列,二次项系数化为正数。
注意任何一个一元二次方程不可缺少二次项,担可缺少一次项和常数项,即b 、c 均可以为零。
如方程013x 023x 02222=-=-=、、x x 都是一元二次方程。
3.一元二次方程的解. 使一元二次方程左、右两边相等的未知数的值,叫一元二次方程的解,又叫一元二次方程的根。
如x=1时,022=-+x x成立,故x=1叫022=-+x x的解。
4.一元二次方程的解法解一元二次方程的基本思想是通过降次转化为一元一次方程,本节共介绍了四种解法。
(1)直接开平方法:方程)0(2≥=a a x的解为a x ±=,这种解一元二次方程的方法叫直接开平方法。
它是利用了平方根的定义直接开平方,只要形式能化成()a =2的一元二次方程都可以采用直接开平方法来解。
初中数学一元二次方程根与系数关系专项复习题(附答案详解)

初中数学一元二次方程根与系数关系专项复习题(附答案详解)1.已知关于x 的一元二次方程2210ax x --=有两个不相等的实数根,则二次项系数a 的取值范围是( ) A .1a >-B .2a >-C .1a >且0a ≠D .1a >-且0a ≠2.若关于x 的一元二次方程x 2-2x+k=0有两个不相等的实数根,那么k 的取值范围是( )A .k <1B .k≠0C .k >1D .k <03.一元二次方程ax 2+x ﹣2=0有两个不相等实数根,则a 的取值范围是( ) A .a 18<B .a= 18-C .a 18>-且a≠0 D .a 18> 且a≠0 4.下列方程中,两根是﹣2和﹣3的方程是( ) A .x 2﹣5x+6=0 B .x 2﹣5x ﹣6=0 C .x 2+5x ﹣6=0 D .x 2+5x+6=05.关于x 的一元二次方程260x mx +-=的一个根是3,则另一个根是( ) A .-1B .1C .-2D .26.已知方程x 2+2x-1=0,则此方程( )A .无实数根B .两根之和为2C .两根之积为-1D .有一个根为21+7.已知方程x 2﹣4x +k =0有一个根是﹣1,则该方程的另一根是( ) A .1B .0C .﹣5D .58.已知关于x 的一元二次方程x 2-6x +k +1=0的两个实数根是x 1,x 2,且x +x =24,则k 的值是(). A .8B .-7C .6D .59.关于x 的方程的022=+-a ax x 两个根的平方和5是,则a 的值是( )A .-1或5B . 1C .5D .-110.已知一元二次方程2310x x -+=的两根是1x 、2x ,则12x x +的值是( ) A .3B .1C .3-D .1-11.若方程25320x x --=的两个实数根为,m n ,则11m n+的值为__________. 12.若方程x 2+(m+1)x ﹣2n=0的两根分别为2和﹣5,则m=_____,n=_____. 13.已知a ,b 是一元二次方程220180x x --=的两个实数根,则22________a a b--=;14.方程2x2+4x﹣1=0的两根为x1,x2,则x1+x2=____.15.若关于x的方程的两根互为倒数,则= .16.如果一元二次方程2x2﹣5x+m=0有两个实数根,那么实数m的取值范围为_____.17.写出一个二次项系数为2,一个根比1大,另一个根比1小的一元二次方程__________.18.若-2是一元二次方程x2―2x―a=0的一个根,则a的值为____.19.若关于的方程有两个相等的实数根,则k的值为▲ . 20.如果方程x2﹣2x+m=0的两实根为a,b,且a,b,1可以作为一个三角形的三边之长,则实数m的取值范围是___________________.21.已知关于的方程.(1)若该方程有两个不相等的实数根,求实数的取值范围;(2)若该方程的一个根为1,求的值及该方程的另一根.22.已知关于x的一元二次方程x2+(2m+3)x+m2=0有两个不相等的实数根,(1)求m的取值范围(2)若α,β是方程的两个实数根,且满足11αβ+=﹣1,求m的值.23.阅读材料:材料1 若一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2则x1+x2=﹣ba,x1x2=ca.材料2 已知实数m,n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求n mm n+的值.解:由题知m,n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得m+n=1,mn =﹣1,所以222()2121n m m n m n mn m n mn mn ++-++===-=﹣3. 根据上述材料解决以下问题:(1)材料理解:一元二次方程5x 2+10x ﹣1=0的两个根为x 1,x 2,则x 1+x 2= ,x 1x 2= .(2)类比探究:已知实数m ,n 满足7m 2﹣7m ﹣1=0,7n 2﹣7n ﹣1=0,且m ≠n ,求m 2n +mn 2的值:(3)思维拓展:已知实数s 、t 分别满足19s 2+99s +1=0,t 2+99t +19=0,且st ≠1.求41st s t++的值.24.已知关于x 的一元二次方程(k ﹣1)x 2+(2k+1)x+k =0. (1)依据k 的取值讨论方程解的情况.(2)若方程有一根为x =﹣2,求k 的值及方程的另一根.25.已知关于x 的方程230x x a ++=①的两个实数根的倒数和等于3,且关于x 的方程2(1)320k x x a -+-=②有实数根,又k 为正整数,求代数式2216k k k -+-的值.26.已知关于的一元二次方程x 2-4x +k +1=0(1)若=-1是方程的一个根,求k 值和方程的另一根;(2)设x 1,x 2是关于x 的方程x 2-4x +k +1=0的两个实数根,是否存在实数k ,使得x 1x 2>x 1+x 2成立?请说明理由.27.已知关于x 的一元二次方程2104x x m -+=有两个实数根. ()1若m 为正整数,求此方程的根.()2设此方程的两个实数根为a 、b ,若2221y ab b b =-++,求y 的取值范围.28.已知关于x 的一元二次方程x 2+(4m+1)x+2m-1=O . (1)求证:不论m 为任何实数,方程总有两个不相等的实数根; (2)若方程两根为x 1、x 2,且满足12111+?=2x x ,求m 的值.29.关于的一元二次方程(1)求证:方程有两个不相等的实数根; (2)为何整数时,此方程的两个根都为正整数.30.已知关于x的一元二次方程01)1(22=-+++k x k kx 有两个实数根,求k 的取值范围.参考答案1.D【解析】【分析】由关于x的一元二次方程ax2-2x-1=0有两个不相等的实数根,即可得判别式△>0且二次项系数a≠0,继而可求得a的范围.【详解】∵一元二次方程ax2-2x-1=0有两个不相等的实数根,∴△=(-2)2-4×a×(-1)>0,且a≠0,解得:a>-1且a≠0,故选D.【点睛】此题考查了一元二次方程根的判别式的知识.此题比较简单,注意掌握一元二次方程有两个不相等的实数根,即可得△>0.2.A【解析】∵关于x的一元二次方程x2−2x+k=0有两个不相等的实数根,∴△=(−2)2−4k>0,解得:k<1.故选:A.3.C【解析】【分析】根据已知得出b2-4ac=12-4a•(-2)>0,求出即可.【详解】∵一元二次方程ax2+x-2=0有两个不相等实数根,∴b2-4ac=12-4a•(-2)>0,解得:a>-18且a≠0,故选:C.【点睛】本题考查了根的判别式的应用,注意:一元二次方程ax2+bx+c=0(a、b、c为常数,a≠0)的根的判别式是b 2-4ac ,当b 2-4ac >0时,方程有两个不相等的实数根,当b 2-4ac=0时,方程有两个相等的实数根,当b 2-4ac <0时,方程没有实数根. 4.D . 【解析】试题分析:设两根是﹣2和﹣3的方程为:x 2+ax+b=0,根据根与系数的关系,可得(﹣2)+(﹣3)=﹣a=5,(﹣2)×(﹣3)=b=6,故方程为:x 2+5x+6=0.故选D . 考点:根与系数的关系. 5.C 【解析】 【分析】设该一元二次方程的另一根为t ,则根据根与系数的关系得到36t =-,由此易求t 的值. 【详解】解:设关于x 的一元二次方程260x mx +-=的另一个根为t ,则36t =-, 解得2t =-. 故选:C . 【点睛】本题考查了根与系数的关系.若二次项系数为1,常用以下关系:1x ,2x 是方程20x px q ++=的两根时,12x x p +=-,12x x q =,反过来可得12()p x x =-+,12q x x =,前者是已知系数确定根的相关问题,后者是已知两根确定方程中未知系数. 6.C . 【解析】试题解析:A 、△=22-4×1×(-1)=8>0,则该方程有两个不相等的实数根.故本选项错误; B 、设该方程的两根分别是α、β,则α+β=-2.即两根之和为2,故本选项错误; C 、设该方程的两根分别是α、β,则αβ=-1.即两根之积为-1,故本选项正确;D 、根据求根公式1=-±1-+1-.故本选项错误; 故选C .考点:1.根与系数的关系;2.根的判别式.【解析】 【分析】利用根与系数的关系,即可求出. 【详解】设该方程的另一根为m , 利用根与系数的关系:12b x x a+=- 得:m ﹣1=4, 解得:m =5. 故选:D . 【点睛】本题考查一元二次方程的解的定义以及根数系数的关系,熟练掌握相关知识点是解题关键. 8.D 【解析】 【分析】根据一元二次方程根与系数的关系,即韦达定理进行作答. 【详解】 由韦达定理,即,x 1·x 2=.而x +x =24=()2-2 x 1·x 2=36-2(k +1),解出k =5.所以,答案选D. 【点睛】本题考查了一元二次方程根与系数的关系,即韦达定理的运用,熟练掌握一元二次方程根与系数的关系,即韦达定理是本题解题关键. 9.D 【解析】试题分析:设,αβ是方程022=+-a ax x 的两个根,则,2a a αβαβ+==,又225αβ+=,所以22()245a a αβαβ+-=-=,解得a =-1或5,当a=-1时,9=V >0,当a=5时,16=-V <0,所以a=5不合题意舍去,所以选:D . 考点:根与系数的关系.【解析】 【分析】根据根与系数的关系得到x 1+x 2=3,即可得出答案. 【详解】解:∵x 1、x 2是一元二次方程x 2−3x+1=0的两个根, ∴x 1+x 2=3, 故选A.. 【点睛】本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx+c=0(a≠0)的两根时,x 1+x 2=b a -,x 1x 2=c a. 11.32-【解析】 【分析】因为方程25320x x --=的两个实数根为m 、n ,所以32,55m n mn +==-,而11m n +=m nnm +,将所得的式子代入计算即可. 【详解】解:∵方程25320x x --=的两个实数根为m 、n ,∴32,55m n mn +==-, ∴11m n +=m n n m +=3525-=32-.故答案为32-.【点睛】本题考查的是一元二次方程的根与系数的关系,对于此类题目,一般的思路和方法是先写出两根之和与两根之积,再将所求的式子变形成两根和与积的形式,整体代入求解. 12. 2 5【解析】∵方程x 2+(m+1)x ﹣2n=0的两根分别为2和﹣5,∴由一元二次方程“根与系数的关系”可得:2+(﹣5)=﹣(m+1),2×(﹣5)=﹣2n,解得:m=2,n=5.故答案为2,5.13.2017【解析】【分析】先根据一元二次方程解的定义得到a2=a+2018,所以a2-2a-b化简为-(a+b)+2018,再利用根与系数的关系得到a+b=1,然后利用整体代入的方法计算.【详解】∵a为方程x2-x-2018=0的根,∴a2-a-2018=0,即a2=a+2018,∴a2-2a-b=a+2018-2a-b=-(a+b)+2018,∵a、b是一元二次方程x2-x-2018=0的两个实数根,∴a+b=1,所以原式=-1+2018=2017.故答案是:2017.【点睛】考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-ba,x1x2=ca.也考查了一元二次方程解的定义.14.﹣2 【解析】试题解析:根据一元二次方程根与系数的关系可得:x1+x2=4-=-2 2.15.-1.【解析】试题分析:设已知方程的两根分别为m,n,由题意得:m与n互为倒数,即mn=1,由方程有解,得到,解得:,又mn=,∴=1,解得:=1(舍去)或=-1,则=-1.故应填为:-1.考点:根与系数的关系.点评:此题要求熟练掌握一元二次方程ax 2+bx+c=0(a ≠0),当b 2-4ac≥0时,方程有解,然后利用韦达定理得出,.16.m≤258【解析】 【分析】此题根据方程有实数根,可得25420,m -⨯≥解这个不等式即可得出答案. 【详解】解:关于x 的一元二次方程2250x x m -+=有两个实数根,由一元二次方程根的判别式,得25420,m -⨯≥解得:25.8m ≤ 故答案为:25.8m ≤ 【点睛】一元二次方程根的判别式:△>0时,一元二次方程有两个不等实根; △=0时,一元二次方程有两个相等实根; △<0时,一元二次方程没有实根; △≥0时,方程有实数根.17.2240x x -=(答案不唯一) 【解析】 【分析】根据题意可设一根为2,另一根为0,再计算出2+0=2,2×0=0,然后根据根与系数的关系写出新方程,再把二次项系数化为2即可. 【详解】解:设一根为2,另一根为0, ∵2+0=2,2×0=0,∴以2和0为根的一元二次方程可为x 2-2x=0, 当二次项系数为2时,方程变形为2x 2-4x=0. 故答案为2240x x -=. 【点睛】本题考查了根与系数的关系:若x 1,x 2是方程ax 2+bx+c=0的两根时,12bx x a +=-,12c x x a=. 18.8【解析】解析:把x=-2代入方程得:4+4-a=0, 解得:a=8.考点:一元二次方程的解. 19.8 【解析】若一元二次方程有两个相等的实数根,则根的判别式△=b 2-4ac=0,建立关于k 的等式,求出k 的值.解:由题意知方程有两相等的实根, ∴△=b 2-4ac=36-4k-4=0, 解得k=8. 20.34<m≤1. 【解析】 【分析】若一元二次方程有两根,则根的判别式△=b 2-4ac≥0,建立关于m 的不等式,求出m 的取值范围.再根据根与系数的关系和三角形中三边的关系来再确定m 的取值范围,最后综合所有情况得出结论. 【详解】∵方程x 2-2x+m=0的两实根为a ,b , ∴有△=4-4m≥0, 解得:m≤1,由根与系数的关系知:a+b=2,a•b=m , 若a ,b ,1可以作为一个三角形的三边之长, 则必有a+b >1与|a-b|<1同时成立,故只需(a-b )2<1即可, 化简得:(a+b )2-4ab <1,把a+b=2,a•b=m 代入得:4-4m <1, 解得:m >34, ∴34<m≤1, 故本题答案为:34<m≤1. 【点睛】主要考查一元二次方程的根的判别式与根的关系和一元二次方程根与系数的关系、三角形中三边的关系. 21.(1);(2)的值是,该方程的另一根为.【解析】试题分析:(1)利用根的判别式列出不等式求解即可; (2)利用根与系数的关系列出有关的方程(组)求解即可.试题解析:(1)∵b 2﹣4ac=22﹣4×1×(a ﹣2)=12﹣4a >0, 解得:a <3, ∴a 的取值范围是a <3;(2)设方程的另一根为x 1,由根与系数的关系得:111x 21x 2a +=-⎧⎨⋅=-⎩,解得:11x 3a =-⎧⎨=-⎩, 则a 的值是﹣1,该方程的另一根为﹣3.22.(1)m >﹣34;(2)m =3. 【解析】 【分析】(1)根据方程有两个相等的实数根可知△>0,求出m 的取值范围即可; (2)根据根与系数的关系得出α+β与αβ的值,代入代数式进行计算即可. 【详解】(1)∵关于x 的一元二次方程x 2+(2m +3)x +m 2=0有两个不相等的实数根,∴△>0,即△=(2m +3)2﹣4m 2>0,解得m >﹣34; (2)∵α,β是方程的两个实数根, ∴α+β=﹣(2m +3),αβ=m 2. ∵211(23)1m mαβαβαβ+-++===-, ∴﹣(2m +3)=﹣m 2,解得m 1=3,m 2=﹣1(舍弃). ∴m =3. 【点睛】考查的是根与系数的关系,熟知x 1,x 2是一元二次方程ax 2+bx +c =0(a ≠0)的两根时,x 1+x 2=﹣b a ,x 1x 2=ca是解答此题的关键. 23.(1)-2,-15;(2)﹣17;(3)﹣15.【解析】 【分析】(1)直接利用根与系数的关系求解;(2)把m 、n 可看作方程7x 2﹣7x ﹣1=0,利用根与系数的关系得到m +n =1,mn =﹣17,再利用因式分解的方法得到m 2n +mn 2=mn (m +n ),然后利用整体的方法计算;(3)先把t 2+99t +19=0变形为19•(1t )2+99•1t +1=0,则把实数s 和1t可看作方程19x 2+99x +1=0的两根,利用根与系数的关系得到s +1t =﹣9919,s •1t =119,然后41st s t ++变形为s +4•s t +1t,再利用整体代入的方法计算. 【详解】解:(1)x 1+x 2=﹣105=﹣2,x 1x 2=﹣15;故答案为﹣2;﹣15;(2)∵7m 2﹣7m ﹣1=0,7n 2﹣7n ﹣1=0,且m ≠n , ∴m 、n 可看作方程7x 2﹣7x ﹣1=0, ∴m +n =1,mn =﹣17,∴m2n+mn2=mn(m+n)=﹣17×1=﹣17;(3)把t2+99t+19=0变形为19•(1t)2+99•1t+1=0,实数s和1t可看作方程19x2+99x+1=0的两根,∴s+1t=﹣9919,s•1t=119,∴41st st++=s+4•st+1t=﹣9919+4×119=﹣15.【点睛】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=﹣ba,x1x2=ca.也考查了解一元二次方程.24.(1)k>﹣18且k≠1时,原方程有两个不相等的实数根;k=﹣18时,原方程有两个相等的实数根;k<﹣18时,原方程没有实数根;(2)k=6,方程的另一根为﹣35.【解析】【分析】(1)根据方程的系数可得出根的判别式△=8k+1,进而可得出方程解得情况;(2)将x=﹣2代入原方程可求出k值,再利用两根之和等于ba-及方程的一根为x=﹣2,可求出方程的另一根.【详解】解:(1)a=k﹣1,b=2k+1,c=k,∵△=b2﹣4ac=(2k+1)2﹣4×(k﹣1)×k=8k+1,∴当k>﹣18且k≠1时,原方程有两个不相等的实数根;当k=﹣18时,原方程有两个相等的实数根;当k<﹣18时,原方程没有实数根.(2)将x=﹣2代入原方程,得:(k﹣1)×(﹣2)2+(2k+1)×(﹣2)+k=0,解得:k=6,∴原方程为5x2+13x+6=0,∴方程的另一根为x =﹣135﹣(﹣2)=﹣35. 【点睛】本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根”;(2)代入x=-2求出k 值. 25.0. 【解析】 【分析】由于关于x 的方程x 2+3x +a =0的两个实数根的倒数和等于3,利用根与系数的关系可以得到关于a 的方程求出a ,又由于关于x 的方程(k -1)x 2+3x -2a =0有实数根,分两种情况讨论,该方程可能是一次方程、有可能是一元二次方程,又k 为正整数,利用判别式可以求出k ,最后代入所求代数式计算即可求解. 【详解】解:设方程①的两个实数根分别为x 1、x 2则12123940x x x x a a +-⎧⎪⎨⎪-≥⎩V=== , 由条件,知12121211x x x x x x ++==3, 即33a -=,且94a ≤, 故a =-1,则方程②为(k -1)x 2+3x +2=0,Ⅰ.当k -1=0时,k =1,x =23-,则22106k k k -=+-.Ⅱ.当k -1≠0时,∆=9-8(k -1)=17-6-8k ≥0,则178k ≤, 又k 是正整数,且k≠1,则k =2,但使2216k k k -+-无意义.综上,代数式2216k k k -+-的值为0【点睛】本题综合考查了根的判别式和根与系数的关系,在解方程时一定要注意所求k 的值与方程判别式的关系.要注意该方程可能是一次方程、有可能是一元二次方程, 26.(1)k=" -6" ,方程的另一根是5. (2)不存在.理由见解析. 【解析】试题分析:(1)把已知的根代入原方程,求出k ,然后根据根与系数的关系,求得另一根; (2)根据一元二次方程的跟的判别式求出k 的范围,然后再根据根与系数的关系表示出x 1+x 2=4,x 1·x 2=k +1,根据已知的不等式求出k 的范围,从判断是否存在. 试题解析:(1)k="-6" ,方程的另一根是5. ( 2 ) 不存在.理由:由题意得Δ=16-4(k +1)≥0,解得k≤3. ∵x 1,x 2是一元二次方程的两个实数根, ∴x 1+x 2=4,x 1x 2=k +1, 由x 1x 2>x 1+x 2得k +1>4, ∴k >3,∴不存在实数k 使得x 1x 2>x 1+x 2成立.考点:一元二次方程根的判别式,根与系数的关系 27.()11m =,1212x x ==.()724y ≤. 【解析】 【分析】(1)根据方程的系数结合根的判别式,即可得出114m 1m 04=-⨯=-≥V ,由此吉可求得m 的取值范围,根据m 为正整数,可得出m 的值,将m 代入原方程求出x 的值即可; (2)根据根与系数的关系以及一元二次方程根的定义可得1ab m 4=,21b b m 04-+=,由此可得3y m 14=+,根据m 的取值范围进行求解即可. 【详解】()1∵一元二次方程21x x m 04-+=有两个实数根,∴114m 1m 04=-⨯=-≥V , ∴m 1≤.∵m 为正整数, ∴m 1=,当m 1=时,此方程为21x x 04-+=, ∴此方程的根为121x x 2==; ()2∵此方程的两个实数根为a 、b ,∴1ab m 4=,21b b m 04-+=, ∴()22113y ab 2b 2b 1ab 2b b 1m 2m 1m 1444⎛⎫=-++=--+=--+=+ ⎪⎝⎭, ∵()4m y 13=-, 又∵m 1≤, ∴()4m y 113=-≤, ∴y 的取值范围为7y 4≤. 【点睛】本题考查了一元二次方程根的判别式、根与系数的关系、一元二次方程的根等,综合性较强,正确理解题意,熟练运用相关知识是解题的关键. 28.(1)相交线;(2)m=110-. 【解析】 【分析】(1)要证明方程总有两个不相等的实数根,那么只要证明△>0即可; (2)首先利用根与系数的关系可以得到x 1+x 2,x 1x 2,接着利用根与系数的关系得到关于m 的方程,解方程即可解决问题. 【详解】(1)证明:因为一元二次方程x 2+(4m+1)x+2m-1=O 的根的判别式 △=(4m+1)2-4(2m-1)=16m 2+8m+1-8m+4=16m 2+5.因为不论m 取何值时,m 2≥0,所以16m 2+5总大于0,即不论m 为任何实数,方程总有两个不相等的实数根;(2)因为方程两根为x 1、x 2,所以x 1+x 2=-(4m+1),x 1x 2=2m -1, 因为12111+=,2x x 所以121212x x x x +=,所以()411212m m -+=-,所以m=110-.【点睛】本题考查了一元二次方程根的判别式及根与系数的关系,掌握(1) △>0,方程有两个不相等的实数根;(2) △=0,方程有两个相等的实数根;(3) △<0,方程没有实数根,是解答本题的关键. 29.(1)证明见解析;(2)2或3. 【解析】试题分析:(1)表示出根的判别式,得到根的判别式大于0,进而确定出方程总有两个不相等的实数根;(2)由(1)得到方程有两个不相等的实数根,利用求根公式表示出方程的两根:x 1=,x 2=1,要使原方程的根是整数,必须使得x 1==1+为正整数,则m-1=1或2,进而得出符合条件的m 的值.解:(1)∵△=b 2-4ac=(-2m )2-4(m-1)(m+1)=4>0, ∴方程有两个不相等的实数根; (2)由求根公式,得x=, ∴x 1==,x 2==1;∵m 为整数,且方程的两个根均为正整数, ∴x 1==1+,必为正整数,∴m-1=1或2, ∴m=2或m=3.考点:根的判别式;一元二次方程的定义. 30.k≥-13且k≠0. 【解析】试题分析:若一元二次方程有两不等实数根,则根的判别式△=b 2-4ac≥0,建立关于k 的不等式,求出k 的取值范围.还要注意二次项系数不为0. 试题解析:∵a=k ,b=2(k+1),c=k-1,∴△=[2(k+1)]2-4×k×(k-1)=12k+4≥0,解得:k≥-13,∵原方程是一元二次方程,∴k≠0.所以:k的取值范围为:k≥-13且k≠0.考点:根的判别式.。
初中数学-一元二次方程复习题及答案

初中数学-一元二次方程复习题及答案一元二次方程1.一元二次方程 x(x-1)=0 的解是(B)x=1.2.用配方法解一元二次方程 x-4x=5 的过程中,配方正确的是(D)(x-2)2=9.3.如果关于 x 的一元二次方程 x2+px+q=0 的两根分别为x1=2,x2=1,那么 p,q 的值分别是(A)-3,2.4.若分式 (x-3)/(x-3) 为零,则 x 的值为(A)3.5.已知 3 是关于 x 的方程 x2-5x+c=0 的一个根,则这个方程的另一个根是(B)-1.6.若 a+b+c=0,则关于 x 的一元二次方程 ax2+bx+c=0(a≠0)有一根是(C)2.7.方程 2x(x-1)=x-1 的解是(A)x1=1.8.关于 x 的一元二次方程 x+(m-2)x+m+1=0 有两个相等的实数根,则 m 的值是(D)-3.9.如果 x2+x-1=0,那么代数式 x3+2x2-7 的值是(B)8.10.已知关于 x 的一元二次方程 (a-1)x2-2x+1=0 有两个不相等的实数根,则 a 的取值范围为(C)a<2且a≠1.11.三角形两边的长是 3 和 4,第三边的长是方程 x2-12x+35 的根,则该三角形的周长为(A)14.填空题12.方程 (x-1)2=4 的解是 3.1.若$x=2$是关于$x$的方程$x-x-a+5=0$的一个根,则$a$的值为______.2.已知关于$x$的一元二次方程的一个根是1,写出一个符合条件的方程:3.某城市居民最低生活保障在20XX年是240元,经过连续两年的增加,到20XX年提高到345.6元,则该城市两年来最低生活保障的平均年增长率是_______________.17.已知2是关于$x$的一元二次方程$x^2+4x-p=0$的一个根,则该方程的另一个根是______.18.如果关于$x$的方程$x^2-2x+m=0$有两个相等实数根,那么$m$=______.19.已知一元二次方程$x^2-6x-5=0$的两根为$a$、$b$,则$\frac{a+b}{ab}$的值是______.20.解下列方程:1)$2x-2x-2=0$;2)$(x-3)^2+4x(x-3)=0$.21.已知$|a-1|+b+2=0$,求方程$\frac{a}{x}+bx=1$的解.22.已知关于$x$的一元二次方程$x+kx-1=0$:1)求证:方程有两个不相等的实数根;2)设方程的两根分别为$x_1$,$x_2$,且满足$x_1+x_2=x_1x_2$,求$k$的值.23.为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.20XX年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到20XX年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.1)求每年市政府投资的增长率;2)若这两年内的建设成本不变,求到20XX年底共建设了多少万平方米廉租房.24.商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价$x$元.据此规律,请回答:1)商场日销售量增加$2x+60$件,每件商品盈利$50-x$元;2)在上述条件不变、销售正常情况下,每件商品降价$10$元时,商场日盈利可达到2100元.25.由于受甲型H1N1流感(起初叫猪流感)的影响,4月初某地猪肉价格大幅度下调,下调后每斤猪肉价格是原价格的$80\%$.经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.1.求4月初猪肉价格下调后每斤多少元?答:4月初猪肉价格下调后每斤10元。
一元二次方程专题复习资料

一元二次方程专题复习 知识盘点1.方程中只含有 个未知数,并且整理后未知数的最高次数是 ,这样的 方程叫做一元二次方程。
通常可写成如下的一般形式 ( a 、b 、c 、为常数,a )。
2. 一元二次方程的解法:(1)直接开平方法:当一元二次方程的一边是一个含有未知数的 的平方,而另一边是一个 时,可以根据 的意义,通过开平方法求出这个方程的解。
(2)配方法:用配方法解一元二次方程()02≠=++a o c bx ax 的一般步骤是:①化二次项系数为 ,即方程两边同时除以二次项系数;②移项,使方程左边为 项和 项,右边为 项;③配方,即方程两边都加上 的平方;④化原方程为2()x m n +=的形式,如果n 是非负数,即0n ≥,就可以用 法求出方程的解。
如果n <0,则原方程 。
(3)公式法: 方程20(0)ax bx c a ++=≠,当24b ac -_______ 0时,x = ________(4)因式分解法:用因式分解法解一元二次方程的一般步骤是:①将方程的右边化为 ;②将方程的左边化成两个 的乘积;③令每个因式都等于 ,得到两个 方程;④解这两个方程,它们的解就是原方程的解。
3.一元二次方程的根的判别式 .(1)ac b 42->0⇔一元二次方程()002≠=++a c bx ax 有两个 的实数根,即-----=-----=2,1x x(2)ac b 42-=0⇔一元二次方程有两个 的实数根,即-----==21x x ,(3)ac b 42-<0⇔一元二次方程()002≠=++a c bx ax 实数根。
4. 一元二次方程根与系数的关系如果一元二次方程20ax bx c ++=(0)a ≠的两根为12,x x ,则12x x += ,12x x =提示:在应用一元二次方程根与系数的关系时,一定要保证元二次方程有实数根。
5. 列一元二次方程解应用题列一元二次方程解应用题的步骤和列一元一次方程解应用题的步骤一样,即审、找、设、列、解、答六步。
初中数学一元二次方程知识点总结(含方法技巧归纳,易错辨析)

初中数学⼀元⼆次⽅程知识点总结(含⽅法技巧归纳,易错辨析)
考情分析⾼频考点考查频率所占分值
1.元⼆次⽅程的概念★7~12分
2.⼀元⼆次⽅程的解法★★★
3.⼀元⼆次⽅程根的判别式★★
4.⼀元⼆次⽅程根与系数的关系★
5.利⽤⼀元⼆次⽅程解决实际问题★★★
1⼀元⼆次⽅程的定义及⼀般形式
定义:等号两边都是整式,只含有⼀个未知数(⼀元),并且未知数的最⾼次数是2(⼆次)的⽅程,
叫作⼀元⼆次⽅程.
点拨
对定义的理解抓住三个条件:“⼀元”“⼆次”“整式⽅程”,缺⼀不可,同时强调⼆次项的系数不为0.
⽤公式法解⼀元⼆次⽅程的记忆⼝诀
要⽤公式解⽅程,⾸先化成⼀般式.
调整系数随其后,使其成为最简⽐.
确定参数
,计算⽅程判别式.
判别式值与零⽐,有⽆实根便得知.
若有实根套公式,若⽆实根要告之.
3因式分解法
通过因式分解,使⼀元⼆次⽅程化为两个⼀次式的乘积等于0的形式,再使这两个⼀次式分别等
于0,从⽽实现降次,这种解⼀元⼆次⽅程的⽅法叫作因式分懈法.
因式分解法体现了将⼀元⼆次⽅程“降次”转化为⼀元⼀次⽅程来解的思想,运⽤这种⽅法的步
骤:
(1)将所有项移到⽅程的左边,将⽅程的右边化为0;
(2)将⽅程左边分解为两个⼀次因式的乘积;
(3)令每个因式分别等于零,得到两个⼀元⼀次⽅程;
(4)解这两个⼀元⼀次⽅程,他们的解就是原⽅程的解.。
一元二次方程专题复习资料

一元二次方程专题复习资料一元二次方程专题复知识盘点:1.一元二次方程是指方程中只含有一个未知数,且整理后未知数的最高次数为2的方程。
通常可写成如下的一般形式:ax^2+bx+c=0(a、b、c为常数,且a≠0)。
2.一元二次方程的解法:1)直接开平方法:当一元二次方程的一边是一个含有未知数的平方,而另一边是一个常数时,可以根据平方的意义,通过开平方法求出这个方程的解。
2)配方法:用配方法解一元二次方程ax^2+bx+c=0(a≠0)的一般步骤是:①化二次项系数为1,即方程两边同时除以二次项系数;②移项,使方程左边为一次项和常数项,右边为零项;③配方,即方程两边都加上b/2a的平方;④化原方程为(x+m)^2=n的形式,如果n是非负数,即n≥0,就可以用开平方法求出方程的解。
如果n<0,则原方程无实数解。
3)公式法:方程ax^2+bx+c=0(a≠0),当b^2-4ac>0时,x=(-b±√(b^2-4ac))/2a;当b^2-4ac=0时,x=-b/2a;当b^2-4ac<0时,方程无实数解。
4)因式分解法:用因式分解法解一元二次方程的一般步骤是:①将方程的右边化为零;②将方程的左边化成两个一次项的乘积;③令每个因式都等于零,得到两个一次方程;④解这两个一次方程,它们的解就是原方程的解。
3.一元二次方程的根的判别式:1)b^2-4ac>0,即一元二次方程ax^2+bx+c=0(a≠0)有两个不相等的实数根,即x1=(-b+√(b^2-4ac))/2a,x2=(-b-√(b^2-4ac))/2a;2)b^2-4ac=0,即一元二次方程有两个相等的实数根,即x1=x2=-b/2a;3)b^2-4ac<0,即一元二次方程ax^2+bx+c=0(a≠0)无实数根。
4.一元二次方程根与系数的关系:如果一元二次方程ax^2+bx+c=0(a≠0)的两根为x1和x2,则x1+x2=-b/a,x1x2=c/a。
一元二次方程复习专题.docx

一.知识梳理1.一元二次方程的定义一元二次方程:只含有一个未知数,未知数的最高次数是2,且系数不为0,这样的方程叫一元二次方程.一般形式:ax'+bx+c二0(aH0)。
注意:判断某方程是否为-•元二次方程时,应首先将方程化为一般形式。
2.一元二次方程的解法:⑴直接开平方法:对形如(x+m) 5M0)的方程两边直接开平方而转化为两个一元一次方程的方法。
例:(x+1) 2 =4(2)配方法:用配方法解一元二次方程ax2+bx + c = O(a^O)的一-般步骤是:①化二次项系数为1,即方程两边同时除以二次项系数;②移项,使方程左边为二次项和一次项,右边为常数项;③配方,即方程两边都加上一次项系数一半的平方;④化原方程为(x + m)2=n的形式;⑤如果M>0,就可以用直接开平方求出方程的解,如果水0,则原方程无解.例:4#-8对1=0⑶公式法:公式丫•缪用或根公式求出一元二次方程的解的方法.它是通过配方推导出来的.一元二次方程的求—b 土 Jb' — 4ac根公式是" ——(b2-4ac^0)o步骤:①把方程转化为一般形式;②确定a, b, c的值;③求出恋一4ac的值,当b2—4ac>0吋代入求根公式。
⑷因式分解法:用因式分解的方法求一元二次方程的根的方法叫做因式分解法.理论根据:若ab=O,则沪0或b 二0。
步骤是:①将方程右边化为0;②将方程左边分解为两个一次因式的乘枳;③令每个因式等于0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解.因式分解的方法:提公因式、公式法、十字相乘法。
例:A-5X~6=0;33 一元二次方程的注意事项:(1)在一元二次方程的一般形式屮要注意,强调aHO.因当a二0时,不含有二次项,即不是一元二次方程.如关于x的方程(m2—4) x2+2mx+l=0中,当m二土2时就是一元一次方程了.⑵应用求根公式解一元二次方程时应注意:①先化方程为一般形式再确定a, b, c的值;②若b2-4a<0,则方程无解.⑶ 利川因式分解法解方程时,方程两边绝不能随便约去含有未知数的代数式.如一2(x+4)~3 (x+4)中,不能随便约去x+4o⑷注意:解一元二次方程时一般不使用配方法(除特别要求外)但又必须熟练掌握,解一元二次方程的一般顺序是:开平方法一因式分解法一公式法.丄+丄/+花。
中考一轮复习 数学专题05 一元二次方程(学生版)

专题05 一元二次方程一、单选题1.(2022·甘肃兰州)关于x 的一元二次方程2210kx x +-=有两个相等的实数根,则k =( ) A .-2B .-1C .0D .12.(2022·湖南郴州)一元二次方程2210x x +-=的根的情况是( ) A .有两个不相等的实数根 B .有两个相等的实数根 C .只有一个实数根D .没有实数根3.(2022·黑龙江哈尔滨)某种商品原来每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x ,根据随意,所列方程正确的是( )A .()2150196x -=B .150(1)96x -=C .2150(1)96x -=D .150(12)96x -=4.(2022·山东泰安)我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,遣人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株楼后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x 株,则符合题意的方程是( ) A .()316210x x -= B .()316210x -= C .()316210x x -=D .36210x =5.(2022·浙江温州)若关于x 的方程260x x c ++=有两个相等的实数根,则c 的值是( ) A .36B .36-C .9D .9-6.(2021·辽宁丹东)若实数k 、b 是一元二次方程(3)(1)0x x +-=的两个根,且k b <,则一次函数y kx b =+的图象不经过( ) A .第一象限B .第二象限C .第三象限D .第四象限7.(2021·贵州毕节)某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排15场比赛,则八年级班级的个数为( ) A .5B .6C .7D .88.(2021·贵州毕节)已知关于x 的一元二次方程2410ax x --=有两个不相等的实数根,则a 的取值范围是( )A .4a ≥-B .4a >-C .4a ≥-且0a ≠D .4a >-且0a ≠9.(2021·内蒙古赤峰)一元二次方程2820x x --=,配方后可形为( ) A .()2418x -= B .()2414x -= C .()2864x -=D .()241x -=10.(2020·内蒙古)下列命题正确的是( ) A .若分式242x x --的值为0,则x 的值为±2.B .一个正数的算术平方根一定比这个数小.C .若0b a >>,则11a ab b ++>.D .若2c ≥,则一元二次方程223x x c ++=有实数根.11.(2020·山东泰安)将一元二次方程2850x x --=化成2()x a b +=(a ,b 为常数)的形式,则a ,b 的值分别是( ) A .4-,21B .4-,11C .4,21D .8-,6912.(2020·四川攀枝花)若关于x 的方程20x x m --=没有实数根,则m 的值可以为( ). A .1-B .14-C .0D .113.(2022·青海西宁)关于x 的一元二次方程220x x k +-=没有实数根,则k 的取值范围是( )A .18k <-B .18k ≤-C .18k >-D .18k ≥-14.(2022·贵州黔东南)已知关于x 的一元二次方程220x x a --=的两根分别记为1x ,2x ,若11x =-,则2212a x x --的值为( )A .7B .7-C .6D .6-15.(2022·辽宁大连)若关于x 的一元二次方程260x x c ++=有两个相等的实数根,则c 的值是( ) A .36B .9C .6D .9-16.(2022·山东聊城)用配方法解一元二次方程23610x x +-=时,将它化为()2x a b +=的形式,则a b +的值为( )A .103 B .73C .2D .4317.(2022·广西贵港)若2x =-是一元二次方程220x x m ++=的一个根,则方程的另一个根及m 的值分别是( ) A .0,2-B .0,0C .2-,2-D .2-,018.(2021·山东潍坊)若菱形两条对角线的长度是方程x 2﹣6x +8=0的两根,则该菱形的边长为( ) 本**号资料皆来源#于微信:数学A B .4 C .25 D .519.(2021·广西贵港)已知关于x 的一元二次方程x 2-kx +k -3=0的两个实数根分别为12,x x ,且22125x x +=,则k 的值是( ) A .-2B .2C .-1D .120.(2021·山东济宁)已知m ,n 是一元二次方程220210x x +-=的两个实数根,则代数式22m m n ++的值等于( ) A .2019B .2020C .2021D .202221.(2020·四川巴中)关于x 的一元二次方程x 2+(2a ﹣3)x +a 2+1=0有两个实数根,则a 的最大整数解是( ) A .1B .1-C .2-D .022.(2020·四川雅安)如果关于x 的一元二次方程2310kx x -+=有两个实数根,那么k 的取值范围是( ) A .94kB .94k -且0k ≠C .94k且0k ≠ D .94k -23.(2020·湖北省直辖县级单位)关于x 的方程222(1)0x m x m m +-+-=有两个实数根α,β,且2212αβ+=,那么m 的值为( ) A .1-B .4-C .4-或1D .1-或424.(2022·湖北恩施)已知抛物线212y x bx c =-+,当1x =时,0y <;当2x =时,0y <.下列判断: ①22b c >;①若1c >,则32b >;①已知点()11,A m n ,()22,B m n 在抛物线212y x bx c =-+上,当12m m b <<时,12n n >;①若方程2102x bx c -+=的两实数根为1x ,2x ,则123x x +>.其中正确的有( )个.A .1B .2C .3D .425.(2022·湖北武汉)若关于x 的一元二次方程222410x mx m m -+--=有两个实数根1x ,2x ,且()()121222217x x x x ++-=,则m =( )A .2或6B .2或8C .2D .626.(2022·天津)已知抛物线2y ax bx c =++(a ,b ,c 是常数,0a c <<)经过点(1,0),有下列结论: 本号资料皆来源于微信:数*#学①20a b +<;①当1x >时,y 随x 的增大而增大;①关于x 的方程2()0ax bx b c +++=有两个不相等的实数根. 其中,正确结论的个数是( ) A .0B .1C .2D .327.(2021·四川绵阳)关于x 的方程20ax bx c ++=有两个不相等的实根1x 、2x ,若212x x =,则49b ac -的最大值是( )A .1BC D .228.(2021·山东枣庄)在平面直角坐标系xOy 中,直线AB 垂直于x 轴于点C (点C 在原点的右侧),并分别与直线y x =和双曲线2y x=相交于点A ,B ,且4AC BC +=,则OAB 的面积为( )A .22B .2或2C .2D .229.(2020·湖北随州)将关于x 的一元二次方程20x px q -+=变形为2x px q =-,就可以将2x 表示为关于x 的一次多项式,从而达到“降次”的目的,又如32()x x x x px q =⋅=-=…,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知:210x x --=,且0x >,则4323x x x -+的值为( )A .1B .3C .1D .3二、填空题30.(2022·广西梧州)一元二次方程()()270x x -+=的根是_________.31.(2022·湖南娄底)已知实数12,x x 是方程210x x +-=的两根,则12x x =______.32.(2021·江苏泰州)关于x 的方程x 2﹣x ﹣1=0的两根分别为x 1、x 2则x 1+x 2﹣x 1•x 2的值为 ___. 33.(2021·江苏宿迁)若关于x 的一元二次方程x 2 +ax -6=0的一个根是3,则a =34.(2021·湖北黄冈)若关于x 的一元二次方程2x 2x m 0-+=有两个不相等的实数根,则m 的值可以是____.(写出一个即可)35.(2020·山东淄博)已知关于x 的一元二次方程x 2﹣x+2m =0有两个不相等的实数根,则实数m 的取值范围是_____.36.(2022·青海)如图,小明同学用一张长11cm ,宽7cm 的矩形纸板制作一个底面积为221cm 的无盖长方体纸盒,他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计).设剪去的正方形边长为x cm ,则可列出关于x 的方程为______.37.(2022·上海)已知x -+m =0有两个不相等的实数根,则m 的取值范围是_____.38.(2022·黑龙江绥化)设1x 与2x 为一元二次方程213202x x ++=的两根,则()212x x -的值为________.39.(2022·湖南永州)我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,则AE =______.40.(2021·贵州黔西)三角形两边的长分别为2和5,第三边的长是方程28150x x -+=的根,则该三角形的周长为 _____.41.(2021·江苏南通)若m ,n 是一元二次方程2310x x +-=的两个实数根,则3231m m n m +-的值为___________.42.(2020·山东枣庄)已知关于x 的一元二次方程(a ﹣1)x 2﹣2x +a 2﹣1=0有一个根为x =0,则a =___.43.(2020·内蒙古呼伦贝尔)已知关于x 的一元二次方程21(1)104m x x --+=有实数根,则m 的取值范围是___________.44.(2022·四川内江)已知x 1、x 2是关于x 的方程x 2﹣2x +k ﹣1=0的两实数根,且2112x x x x +=x 12+2x 2﹣1,则k 的值为 _____.45.(2022·四川眉山)设1x ,2x 是方程2230x x +-=的两个实数根,则2212x x +的值为________.46.(2022·四川凉山)已知实数a 、b 满足a -b 2=4,则代数式a 2-3b 2+a -14的最小值是________.47.(2021·湖南娄底)已知2310t t -+=,则1t t+=________.48.(2020·山东济南)如图,在一块长15m 、宽10m 的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m 2,则修建的路宽应为_____米.49.(2020·贵州黔南)对于实数a ,b ,定义运算“*”,22()*()a ab a b a b ab b a b ⎧->=⎨-⎩例如4*2,因为42>,所以24*24428=-⨯=.若12,x x 是一元二次方程28160x x -+=的两个根,则12*x x =_________.50.(2020·江苏南通)若x 1,x 2是方程x 2﹣4x ﹣2020=0的两个实数根,则代数式x 12﹣2x 1+2x 2的值等于_____. 51.(2020·黑龙江大庆)已知关于x 的一元二次方程220x x a --=,有下列结论: ①当1a >-时,方程有两个不相等的实根; ①当0a >时,方程不可能有两个异号的实根; ①当1a >-时,方程的两个实根不可能都小于1;①当3a >时,方程的两个实根一个大于3,另一个小于3. 以上4个结论中,正确的个数为_________.52.(2020·辽宁辽宁)如图,在Rt ABC ∆中,90ACB ∠=︒,2AC BC =,分别以点A 和B 为圆心,以大于12AB 的长为半径作弧,两弧相交于点M 和N ,作直线MN ,交AC 于点E ,连接BE ,若3CE =,则BE 的长为_________.53.(2020·湖北孝感)如图1,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.在此图形中连接四条线段得到如图2的图案,记阴影部分的面积为1S ,空白部分的面积为2S ,大正方形的边长为m ,小正方形的边长为n ,若12S S ,则nm的值为______.54.(2020·湖南)阅读理解:对于x 3﹣(n 2+1)x +n 这类特殊的代数式可以按下面的方法分解因式: x 3﹣(n 2+1)x +n =x 3﹣n 2x ﹣x +n =x (x 2﹣n 2)﹣(x ﹣n )=x (x ﹣n )(x +n )﹣(x ﹣n )=(x ﹣n )(x 2+nx ﹣1).理解运用:如果x 3﹣(n 2+1)x +n =0,那么(x ﹣n )(x 2+nx ﹣1)=0,即有x ﹣n =0或x 2+nx ﹣1=0, 因此,方程x ﹣n =0和x 2+nx ﹣1=0的所有解就是方程x 3﹣(n 2+1)x +n =0的解. 解决问题:求方程x 3﹣5x +2=0的解为_____.三、解答题55.(2022·四川凉山)解方程:x 2-2x -3=056.(2020·黑龙江齐齐哈尔)解方程:x 2﹣5x +6=057.(2020·江苏南京)解方程:2230x x --=.58.(2022·广东广州)已知T =()()()2232323a b a b a b a +++-+ (1)化简T ;(2)若关于x 的方程2210x ax ab +-+=有两个相等的实数根,求T 的值.59.(2022·江苏常州)第十四届国际数学教育大会(ICME -14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统,有0~7共8个基本数字.八进制数3745换算成十进制数是3210387848582021⨯+⨯+⨯+⨯=,表示ICME -14的举办年份.(1)八进制数3746换算成十进制数是_______;(2)小华设计了一个n 进制数143,换算成十进制数是120,求n 的值.60.(2022·贵州贵阳)(1)a ,b 两个实数在数轴上的对应点如图所示.用“<”或“>”填空:a _______b ,ab _______0;(2)在初中阶段我们已经学习了一元二次方程的三种解法,他们分别是配方法、公式法和因式分解法,请从下列一元二次方程中任选两个,并解这两个方程. ①x 2+2x −1=0;①x 2−3x =0;①x 2−4x =4;①x 2−4=0.61.(2022·湖北随州)已知关于x 的一元二次方程()222110x k x k ++++=有两个不等实数根1x ,2x .(1)求k 的取值范围; (2)若125x x =,求k 的值.62.(2021·山东淄博)为更好地发展低碳经济,建设美丽中国.某公司对其生产设备进行了升级改造,不仅提高了产能,而且大幅降低了碳排放量.已知该公司去年第三季度产值是2300万元,今年第一季度产值是3200万元,假设公司每个季度产值的平均增长率相同.(1)求该公司每个季度产值的平均增长率;(2)问该公司今年总产值能否超过1.6亿元?并说明理由.63.(2021·湖北黄石)已知关于x 的一元二次方程2220x mx m m +++=有实数根. 本号资料皆来源于@微信公*众号:数学(1)求m 的取值范围;(2)若该方程的两个实数根分别为1x 、2x ,且221212x x +=,求m 的值.64.(2021·山西)2021年7日1日建党100周年纪念日,在本月日历表上可以用一个方框圈出4个数(如图所示),若圈出的四个数中,最小数与最大数的乘积为65,求这个最小数(请用方程知识解答). 本号资料皆来源*于#微信:数#学65.(2021·山东菏泽)列方程(组)解应用题端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:小王:该水果的进价是每千克22元;小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?66.(2021·浙江嘉兴)小敏与小霞两位同学解方程()()2333-=-的过程如下框:x x你认为他们的解法是否正确?若正确请在框内打“√”;若错误请在框内打“×”,并写出你的解答过程.67.(2020·河北)用承重指数W 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W 与木板厚度x (厘米)的平方成正比,当3x =时,3W =. (1)求W 与x 的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x (厘米),Q W W =-厚薄.①求Q 与x 的函数关系式; ①x 为何值时,Q 是W 薄的3倍?【注:(1)及(2)中的①不必写x 的取值范围】68.(2020·四川南充)已知1x ,2x 是一元二次方程2220x x k -++=的两个实数根.(1)求k 的取值范围; (2)是否存在实数k ,使得等式12112k x x +=-成立?如果存在,请求出k 的值,如果不存在,请说明理由.69.(2022·江苏无锡)某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m ),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1:2的矩形,已知栅栏的总长度为24m ,设较小矩形的宽为x m (如图).(1)若矩形养殖场的总面积为362m ,求此时x 的值;(2)当x 为多少时,矩形养殖场的总面积最大?最大值为多少?70.(2022·贵州毕节)2022北京冬奥会期间,某网店直接从工厂购进A 、B 两款冰嫩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)(1)网店第一次用850元购进A 、B 两款钥匙扣共30件,求两款钥匙扣分别购进的件数;(2)第一次购进的冰墩嫩钥匙扣售完后,该网店计划再次购进A 、B 两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?(3)冬奥会临近结束时,网店打算把B 款钥匙扣调价销售.如果按照原价销售,平均每天可售4件.经调查发现,每降价1元,平均每天可多售2件,将销售价定为每件多少元时,才能使B 款钥匙扣平均每天销售利润为90元?71.(2022·湖北荆州)某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y (万件)与售价x (元/件)之间满足函数关系式y =24-x ,第一年除60万元外其他成本为8元/件.(1)求该产品第一年的利润w (万元)与售价x 之间的函数关系式;(2)该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;①若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?72.(2022·湖北十堰)已知关于x 的一元二次方程22230x x m --=. (1)求证:方程总有两个不相等的实数根; 本*号资料皆来源于微信:数学 (2)若方程的两个实数根分别为α,β,且25αβ+=,求m 的值.73.(2022·湖北宜昌)某造纸厂为节约木材,实现企业绿色低碳发展,通过技术改造升级,使再生纸项目的生产规模不断扩大.该厂3,4月份共生产再生纸800吨,其中4月份再生纸产量是3月份的2倍少100吨. (1)求4月份再生纸的产量;(2)若4月份每吨再生纸的利润为1000元,5月份再生纸产量比上月增加%m .5月份每吨再生纸的利润比上月增加%2m,则5月份再生纸项目月利润达到66万元.求m 的值; (3)若4月份每吨再生纸的利润为1200元,4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同,6月份再生纸项目月利润比上月增加了25%.求6月份每吨再生纸的利润是多少元?74.(2021·山东日照)某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量y (桶)与每桶降价x (元)(020x <<)之间满足一次函数关系,其图象如图所示:(1)求y 与x 之间的函数关系式;(2)在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?75.(2021·辽宁盘锦)某工厂生产并销售A ,B 两种型号车床共14台,生产并销售1台A 型车床可以获利10万元;如果生产并销售不超过4台B 型车床,则每台B 型车床可以获利17万元,如果超出4台B 型车床,则每超出1台,每台B 型车床获利将均减少1万元.设生产并销售B 型车床x 台. (1)当4x >时,完成以下两个问题: ①请补全下面的表格:①若生产并销售B 型车床比生产并销售A 型车床获得的利润多70万元,问:生产并销售B 型车床多少台? (2)当0<x ≤14时,设生产并销售A ,B 两种型号车床获得的总利润为W 万元,如何分配生产并销售A ,B 两种车床的数量,使获得的总利润W 最大?并求出最大利润.76.(2021·湖北荆门)已知关于x 的一元二次方程26210x x m -+-=有1x ,2x 两实数根. (1)若11x =,求2x 及m 的值;(2)是否存在实数m ,满足()()126115x x m --=-?若存在,求出求实数m 的值;若不存在,请说明理由.77.(2021·辽宁本溪)某网店销售一款市场上畅销的蒸蛋器,进价为每个40元,在销售过程中发现,这款蒸蛋器销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x 元,每星期销售量为y 个. (1)请直接写出y (个)与x (元)之间的函数关系式;(2)当销售单价是多少元时,该网店每星期的销售利润是2400元?(3)当销售单价是多少元时,该网店每星期的销售利润最大?最大利润是多少元?78.(2020·贵州黔南)在2020年新冠肺炎疫情期间,某中学响应政府有“停课不停学”的号召,充分利用网络资源进行网上学习,九年级1班的全体同学在自主完成学习任务的同时,彼此关怀,全班每两个同学都通过一次电话,互相勉励,共同提高,如果该班共有48名同学,若每两名同学之间仅通过一次电话,那么全同学共通过多少次电话呢?我们可以用下面的方式来解决问题.用点12348A A A A ⋯、、分表示第1名同学、第2名同学、第3名同学…第48名同学,把该班级人数x 与通电话次数y 之间的关系用如图模型表示:(1)填写上图中第四个图中y 的值为_______,第五个图中y 的值为_______.(2)通过探索发现,通电话次数y 与该班级人数x 之间的关系式为________,当48x =时,对应的y =________.(3)若九年级1班全体女生相互之间共通话190次,问:该班共有多少名女生?79.(2020·内蒙古赤峰)阅读理解:材料一:若三个非零实数x ,y ,z 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数x ,y ,z 构成“和谐三数组”. 本号资料皆来源于微信:@数学材料二:若关于x 的一元二次方程ax 2+bx +c = 0(a ≠0)的两根分别为1x ,2x ,则有12b x x a +=-,12c x x a⋅=. 问题解决:(1)请你写出三个能构成“和谐三数组”的实数 ;(2)若1x ,2x 是关于x 的方程ax 2+bx +c = 0 (a ,b ,c 均不为0)的两根,3x 是关于x 的方程bx +c =0(b ,c 均不为0)的解.求证:x 1,x 2,x 3可以构成“和谐三数组”;(3)若A (m ,y 1) ,B (m + 1,y 2) ,C (m +3,y 3)三个点均在反比例函数4y x=的图象上,且三点的纵坐标恰好构成“和谐三数组”,求实数m 的值.80.(2022·辽宁锦州)某商场新进一批拼装玩具,进价为每个10元,在销售过程中发现.,日销售量y (个)与销售单价x (元)之间满足如图所示的一次函数关系.(1)求y 与x 的函数关系式(不要求写出自变量x 的取值范围);(2)若该玩具某天的销售利润是600元,则当天玩具的销售单价是多少元?(3)设该玩具日销售利润为w 元,当玩具的销售单价定为多少元时,日销售利润最大?最大利润是多少元?。
(完整版)一元二次方程知识点总结和例题——复习,推荐文档
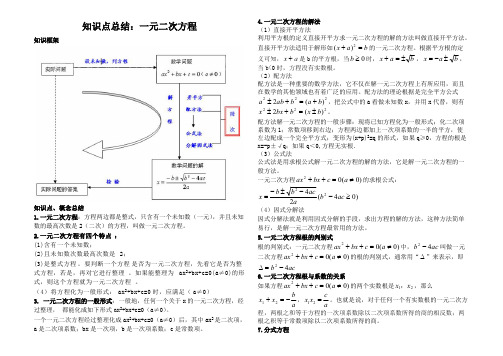
配方法解一元二次方程的一般步骤:现将已知方程化为一般形式;化二次项 系数为 1;常数项移到右边;方程两边都加上一次项系数的一半的平方,使 左边配成一个完全平方式;变形为(x+p)2=q 的形式,如果 q≥0,方程的根是 x=-p±√q;如果 q<0,方程无实根. (3)公式法 公式法是用求根公式解一元二次方程的解的方法,它是解一元二次方程的一 般方法。
一个一元二次方程经过整理化成 ax2+bx+c=0(a≠0)后,其中 ax2 是二次项,
程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两 根之积等于常数项除以二次项系数所得的商。
a 是二次项系数;bx 是一次项,b 是一次项系数;c 是常数项。
7.分式方程
分母里含有未知数的方程叫做分式方程。
c a
。
温馨提示:利用根与系数的关系解题时,一元二次方程必须有实数根。
例题:
1、关于 x 的一元二次方程 x2 kx 4k 2 3 0 的两个实数根分别是 x1, x2 ,
且满足 x1 x2 x1x2 ,则 k 的值为:
()
(A) 1或 3 4
(B) 1
3
(C)
4
(D)不存在
2、已知 , 是关于 x 的一元二次方程 x2 2m 3x m2 0 的两个不相
12、当 x =
时,代数式 x2 3x 比代数式 2x2 x 1的值大 2 .
13、某商品原价每件 25 元,在圣诞节期间连续两次降价,现在商品每件 16
A.2 B.3 C.-2 或 3 D.2 或-3
建议收藏下载本文,以便随时学习! 一元二次方程综合复习
10、若(m+1) xm(m2)1 +2mx-1=0 是关于 x 的一元二次方程,则 m 的值是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程专题复习韦达定理:如一元二次方程20(0)ax bx c a ++=≠的两根为12,x x ,则12b x x a +=-,12cx x a⋅=适用题型:(1)已知一根求另一根及未知系数;(2)求与方程的根有关的代数式的值;(3)已知两根求作方程;(4)已知两数的和与积,求这两个数;(5)确定根的符号:(12,x x 是方程两根);(6)题目给出两根之间的关系,如两根互为相反数、互为倒数、两根的平方和或平方差是多少、两根是Rt ∆的两直角边求斜边等情况.注意:(1)222121212()2x x x x x x +=+-⋅(2)22121212()()4x x x x x x -=+-⋅;12x x -=(3)①方程有两正根,则121200x x x x ∆≥⎧⎪+>⎨⎪⋅>⎩;②方程有两负根,则1212000x x x x ∆≥⎧⎪+<⎨⎪⋅>⎩ ;③方程有一正一负两根,则120x x ∆>⎧⎨⋅<⎩;④方程一根大于1,另一根小于1,则12(1)(1)0x x ∆>⎧⎨--<⎩(4)应用韦达定理时,要确保一元二次方程有根,即一定要判断根的判别式是否非负;求作一元二次方程时,一般把所求作得方程的二次项系数设为1,即以12,x x 为根的一元二次方程为21212()0x x x x x x -++⋅=;求字母系数的值时,需使二次项系数0a ≠,同时满足∆≥0;求代数式的值,常用整体思想,把所求代数式变形成为含有两根之和12x x +,•两根之积12x x ⋅的代数式的形式,整体代入。
4.用配方法解一元二次方程的配方步骤:例:用配方法解24610x x -+= 第一步,将二次项系数化为1:231024x x -+=,(两边同除以4) 第二步,移项: 23124x x -=- 第三步,两边同加一次项系数的一半的平方:2223313()()2444x x -+=-+ 第四步,完全平方:235()416x -=第五步,直接开平方:344x -=±,即:1344x =++,2344x =-+一元二次方程的定义与解法➢ 【要点、考点聚焦】1. 加深理解一元二次方程的有关概念及一元二次方程的一般形式20(0)ax bx c a ++=≠;2.熟练地应用不同的方法解方程;直接开平方法、配方法、公式法、因式分解法;并体会“降幂法”在解方程中的含义.(其中配方法很重要) ➢ 【课前热身】1. 当a =____________时,方程2310ax x ++=是一元二次方程.2. 已知1x =是方程220x ax ++=的一个根,则方程的另一根为__________. 3.一元二次方程(1)x x x -=的解是_____________.4. 若关于x 的一元二次方程20(0)ax bx c a ++=≠,且0a b c ++=,则方程必有一根为____________.5. 用配方法解方程2420x x -+=,则下列配方正确的是( )A.2(2)2x -= B.2(2)2x += C.2(2)2x -=- D.2(2)6x -= ➢ 【典型例题解析】1、关于x 的一元二次方程2(1)(2)26ax ax x x --=-+中,求a 的取值范围.2、已知:关于x 的方程226350x x m m -+--=的一个根是1-,求方程的另一个根及m 的值。
3、用配方法解方程:2210x x --=【考点训练】1、关于x 的一元二次方程22(1)10a x x a -++-=的一个根是0,则a 的值为( )A. 1 B.1- C.1或1- D.122、解方程23(121)4(121)x x -=-的最适当的方法( )A. 直接开平方法B. 配方法C. 因式分解法D. 公式法3、若0a b c -+=,则一元二次方程20ax bx c ++=有一根是( ) A.2B.1C.0 D. -14、当k __________时,22(9)(5)30k x k x -+--=不是关于x 的一元二次方程.5、已知方程23214x x -+=,则代数式21283x x -+=_____________.一元二次方程根的判别式➢ 【要点、考点聚焦】1.一元二次方程20(0)ax bx c a ++=≠根的情况与∆的关系;2.一元二次方程根的判别式的性质反用也成立,即已知根的情况,可以得到一个等式或不等式,从而确定系数的值或取值范围. ➢ 【课前热身】1.若关于x 的一元二次方程2210x x -+=有实数根,则m 的取值范围是( )A.1m <B. 1m <且0m ≠C.m ≤1D. m ≤1且0m ≠2. 一元二次方程2210x x --=的根的情况为( )A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D. 没有实数根3.已知关于x 的一元二次方程2410x x m ++-=.请你为m 选取一个合适的整数,当m =____________时,得到的方程有两个不相等的实数根;4.若关于x 的方程227(21)04x k x k +-+-=有两个相等的实数根,求k 的取值范围➢ 【典型考题】1.已知关于x 的方程2(2)2(1)10m x m x m ---++=,当m 为何非负整数时: (1)方程只有一个实数根; (2)方程有两个相等的实数根; (3)方程有两个不等的实数根.2.已知,,a b c 是三角形的三条边,求证:关于x 的方程222222()0b x b c a x c ++-+=没有实数根.【课时训练】1、一元二次方程的根的情况为( )A.有两个相等的实数根B.有两个不相等的实数根C.只有一个实数根D.没有实数根2、已知关于x 的一元二次方程22x m x -=有两个不相等的实数根,则m 的取值范围是( )A.1m >-B.2m <- C.m ≥0 D.0m <3、一元二次方程2(1)210k x x ---=有两个不相等的实数根,则k 的取值范围是__________. 4、求证:关于x 的方程2(21)10x k x k +++-=有两个不相等的实数根。
课后练习 一、填空题1、关于x的方程2(3)20m x --=是一元二次方程,则m 的取值范围是 ____ .2、若(0)b b ≠是关于x 的方程220x cx b ++=的根,则2b c +的值为 ____ .3、方程2310x x -+=的根的情况是____________________.4、写出一个既能直接开方法解,又能用因式分解法解的一元二次方程是.5、在实数范围内定义一种运算“*”,其规则为)(b a a b a -=*,根据这个规则,方程(2)50x +*=的解为_________________.6、如果关于x 的一元二次方程2210kx x --=有两个实数根,则k 的取值范围是_____________。
7、设12,x x 是一元二次方程20ax bx c ++=的两个根,则代数式3322121212()()()0a x x b x x c x x +++++=的值为___________.8、 a 是整数,已知关于x 的一元二次方程01)12(2=-+-+a x a ax 只有整数根,则a =__________. 二、选择题1、关于x 的方程220x kx k -+-=的根的情况是( )A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.不能确定2、已知方程有一个根是,则下列代数式的值恒为常数的是( )A 、 B 、C 、D 、3、方程23270x +=的解是( )A. B. C. D. 无实数根4、若关于x 的一元二次方程22(4)60x kx x --+=没有实数根,那么k 的最小整数值是( )A.1B.2 C.3 D. 5、如果a 是一元二次方程230x x m -+=的一个根,a -是一元二次方程230x x m +-=的一个根,那么a 的值是( )A 、1或2B 、0或3-C 、1-或2-D 、0或3 6、设m 是方程250x x +=的较大的一根,n 是方程2320x x -+=的较小的一根,则m n +=( )A.B.C.1 D. 2三、解答题1、用配方法解下列方程:2()0(0)a x b c a -+=≠2、已知方程222(9)(34)0x k x k k +-+++=有两个相等的实数根,求k 值,并求出方程的根。
3、已知,,a b c 是ABC ∆的三条边长,且方程222()210a b x cx +-+=有两个相等的实数根,试判断ABC ∆的形状。
4、 已知关于x 的一元二次方程2223840x mx m m --+-=. (1)求证:原方程恒有两个实数根;(2)若方程的两个实数根一个小于5,另一个大于2,求m 的取值范围.5、方程2(2008)2007200910x x -⨯-=的较大根为a ,方程020*******=--x x 的较小根为b ,求2009)(b a +的值.。
