xx省xx县中学201X-201x学年高一数学下学期期末考试试题
高中高一第二学期数学期末考试试卷

高中高一第二学期数学期末考试试卷高中2021年高一第二学期数学期末考试试卷【】高中生各科考试,各位考生都在厉兵秣马,枕戈待旦,把自己调整到最正确作战形状。
在这里查字典数学网为各位考生整理了高中2021年高一第二学期数学期末考试试卷,希望可以助各位考生一臂之力,祝各位考生金榜题名,前程似锦!!一、填空题:本大题共14小题,每题5分,合计70分.请把答案填写在答题卡相应位置上.1.集合,那么2.在△ABC中,假设(a+b+c)(b+c-a)=3bc,那么角A等于___ __ __.3.数列是等差数列,且,那么等于___ __ __.4. 向量,,那么 .5. 假定,那么 =_ _____.6.两点、区分在直线的异侧,那么的取值范围是__ _.7.函数最小正周期为 .8.点A为周长等于3的圆周上的一个定点,假定在该圆周上随机取一点B,那么劣弧 AB的长度小于1的概率为 .9.为了解高中生用电脑输入汉字的水平,随机抽取了局部先生停止每分钟输入汉字个数测试,以下图是依据抽样测试后的数据绘制的频率散布直方图,其中每分钟输入汉字个数的范围是[50,150],样本数据分组为[50,70),[70,90), [90,110),[110,130),[130,150],样本中每分钟输入汉字个数小于90的人数是36,那么样本中每分钟输入汉字个数大于或等于70个并且小于130个的人数是 .10.运转如下图顺序框图后,输入的结果是 .11. 等比数列为递增数列,且,,那么 _ _____.12.点O为的外心,且 ,那么 ___ __ __.13.函数假定,那么实数a的取值范围是 .14. 假定等差数列的首项为公差为,前项的和为,那么数列为等差数列,且通项为 .相似地,假定各项均为正数的等比数列的首项为,公比为,前项的积为,那么数列为等比数列,通项为 .二、解答题(本大题共6小题,共90分,解答时应写出文字说明、证明进程或演算骤.)15.解不等式16.为了了解«中华人民共和国路途交通平安法»在先生中的普及状况,调查部门对某校6名先生停止问卷调查,6人得分状况如下:5,6,7,8,9,10.把这6名先生的得分看成一个总体.(1)求该总体的平均数;(2)用复杂随机抽样方法从这6名先生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的相对值不超越0.5的概率.17.设的三个内角所对的边区分为,且满足 .(Ⅰ)求角的大小;(Ⅱ)假定,试求的最小值.18. 函数 ( ).(Ⅰ)当时,求函数的最小正周期和图象的对称轴方程; (Ⅱ)当时,在的条件下,求的值.19. 某市环保研讨所对市中心每天环境污染状况停止调查研讨后,发现一天中环境综合污染指数与时间x(小时)的关系为,其中a与气候有关的参数,且,假定用每天的最大值为当天的综合污染指数,并记作 .(1)令,求t的取值范围;(2)求函数 ;(3)市政府规则,每天的综合污染指数不得超越2,试问目前市中心的综合污染指数是多少?能否超标?20. 数列,设,数列。
高一下学期期末考试数学试题 (有答案)

高一下学期期末考试数学试题 (有答案)一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、)1560cos( -的值为( )A.23-B. 21- C. 21 D. 23 2、如果31)sin(-=-απ,那么)23cos(απ-的值为( ) 31.A 31-.B 322.C 322-.D3、函数)252sin(π+=x y 的一条对称轴方程是 ( )A .2π-=xB .4π-=xC .8π=xD .45π=x4、函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示,则函数表达式为( )A .)48sin(4π-π-=x yB .)48sin(4π-π=x yC .)48sin(4π+π=x yD .)48sin(4π+π-=x y5、下列说法正确的是( )A .方向相同或相反的向量是平行向量B .零向量是0C .长度相等的向量叫做相等向量D .共线向量是在一条直线上的向量 60=( )A 1B 2CD 7、 在ABC ∆中,若22tan tan b a B A =,则ABC ∆的形状是( ) A 直角三角形 B 等腰或直角三角形 C 不能确定 D 等腰三角形8、在ABC ∆中,点P 是BC 上的点,AC AB AP PC BP μλ+==,2,则( )3231.12.====μλμλ,,C A3132.21.====μλμλ,,D B 9、对于非零向量b a ,,下列命题中正确的是( )a b a A ⇒//.在b 上的投影为||a 00.=⇒=∙a b a B 或0=b2)(.b a b a b a C ∙=∙⇒⊥b ac b c a D =⇒∙=∙.10、若,是一组基底,向量),,(R y x y x ∈+=则称),(y x 为向量在基底,下的坐标,现已知向量a 在基底)1,2(),1,1(=-=q p 下的坐标为)2,2-(,则向量a 在另一组基底)2,1(),1,1(=-=n m 下的坐标为( ))0,2.(A )2,0.(-B )0,2.(-C )2,0.(D二、填空题:(本大题共4小题,每小题5分,共20分.)11、将300-化为弧度为12、如图,单摆从某点开始来回摆动,离开平衡位置O 的位移)(cm y 和时间)(s t 的函数关系为)62sin(6ππ+=t y ,那么单摆来回摆动一次所需的时间为 13、在AB C ∆中,角C B A ,,所对的边分别为c b a ,,,角A 为锐角,且B a b sin 3=,则=A 2tan 错误!未找到引用源。
高一数学下学期期末考试试题含解析试题

【解析】由题意有:此人每天所走的路程形成等比数列 ,其中公比 ,那么 ,解出 ,所以 ,选C.
11. 正四面体 中, 是 的中点,那么异面直线 与 所成角的余弦值为
A. B. C. D.
【答案】B
【解析】试题分析:如图,取 中点 ,连接 ,因为 是 中点,那么 , 或者其补角就是异面直线 所成的角,设正四面体棱长为1,那么 , , .应选B.
点睛:两角用正弦定理求解
3. 以下命题正确的个数为
①梯形一定是平面图形;
②假设两条直线和第三条直线所成的角相等,那么这两条直线平行;
③两两相交的三条直线最多可以确定三个平面;
假如两个平面有三个公一共点,那么这两个平面重合.
A. 0 B. 1 C. 2 D. 3
【答案】C
【解析】分析:逐一判断每个命题的真假,得到正确命题的个数.
A. B. C. D.
【答案】A
【解析】平面四边形ABCD中,AB=AD=CD=2,BD=2 ,BD⊥CD,将其沿对角线BD折成四面体A'﹣BCD,
使平面A'BD⊥平面BCD.四面体A'﹣BCD顶点在同一个球面上,△BCD和△A'BC都是直角三角形,
BC的中点就是球心,所以BC=2 ,球的半径为: ;
点睛:(1)此题主要考察空间直线平面的位置关系,意在考察学生对这些根底知识的掌握程度和空间想象才能.(2)对于类似这种空间直线平面位置关系的命题的判断,一般可以利用举反例的方法和直接证明法,大家要灵敏选择方法判断.
4. 在数列 中, ,那么 等于
A. B. C. D.
【答案】D
【解析】分析: 逐一求解 。
A. B. C. D.
【答案】A
高一数学下学期期末考试试题含解析 28

沁县中学2021-2021学年度第二学期期末考试高一数学一、选择题(本大题一一共12小题,每一小题5分,一共60分,在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的)的一个通项公式是〔〕A. B.C. D.【答案】C【解析】【分析】观察数列分子为以0为首项,2为公差的等差数列,分母是以1为首项,2为公差的等差数列,故可得数列的通项公式.【详解】观察数列分子为以0为首项,2为公差的等差数列,分母是以1为首项,2为公差的等差数列,故可得数列的通项公式a n=〔n∈Z*〕.应选:C.【点睛】此题考察了数列的概念及简单表示法,考察了数列的通项公式的求法,是根底题.2.设集合A={x|x2-4x+3<0},B={x|2x-3>0},那么A∩B=( )A. (,3)B. (-3,)C. (1,)D. (-3,)【答案】A【解析】【分析】解不等式求出集合A,B,结合交集的定义,可得答案.【详解】∵集合A={x|x2﹣4x+3<0}=〔1,3〕,B={x|2x﹣3>0}=〔,+∞〕,∴A∩B=〔,3〕,应选:A.【点睛】此题考察的知识点是集合的交集及其运算,难度不大,属于根底题.中,,那么〔〕A. B. C. 或者 D. 或者【答案】C【解析】【分析】由正弦定理可求得sinB==,结合范围,即可解得B的值.【详解】∵∴由正弦定理可得:sinB===,,∴解得:B=或者π.应选:C.【点睛】此题主要考察了正弦定理的应用,属于根本知识的考察.的前项和为,假设,那么=〔〕A. B. C. D.【答案】B【解析】【分析】设出公差d,由a8+a10=28求出公差d,求利用前n项和公式求解S9得答案.【详解】等差数列的首项为a1=2,设公差为d,由a8=a1+7d,a10=a1+9d,∵a8+a10=28即4+16d=28得d=,那么S9==72.应选:B.【点睛】此题考察了等差数列的通项公式,考察了等差数列的前n项和,是根底题.,那么以下说法正确的选项是〔〕A. 假设,,那么B. 假设,那么C. 假设,那么D. 假设,那么【答案】D【解析】【分析】根据不等式的根本性质以及特殊值法判断即可.【详解】A.取a=1,b=-3,c=2,d=1,可知不成立,B.取c=0,显然不成立,C.取a=-3,b=﹣2,显然不成立,D.根据不等式的根本性质,显然成立,综上可得:只有B正确.应选:D.【点睛】此题考察了不等式的根本性质、举反例否认一个命题的方法,考察了推理才能,属于根底题.的三个内角满足,那么〔〕A. 一定是锐角三角形;B. 一定是直角三角形;C. 一定是钝角三角形;D. 可能是锐角三角形,也可能是钝角三角形.【答案】A【解析】【分析】先根据正弦定理及题设,推断a:b:c=7:11:13,再通过余弦定理求得cosC的值小于零,推断C为钝角.【详解】∵根据正弦定理,又sinA:sinB:sinC=7:11:13∴a:b:c=7:11:13,设a=7t,b=11t,c=13t〔t≠0〕∵c2=a2+b2﹣2abcosC∴cosC===>0∴角C为锐角.又角C为最大角,故一定是锐角三角形应选:A.【点睛】由边角关系判断三角形形状,可以灵敏应用“角化边〞或者“边化角〞两个途径,其中方法一综合应用正弦定理完成边向角的转化,应用和差角公式进展三角变形,得出角之间的关系,最终确定三角形的形状。
高一数学下学期期末考试试题含解析_3

一中2021~2021年度第二学期高一年级期末考试数学试卷〔文科〕一、选择题:每一小题给出的四个选项里面只有一项是哪一项符合题目要求的. a b >,那么以下不等式成立的是〔 〕A.11a b< B. 22ax bx > C. 22a b > D.33x x a b > 【答案】D 【解析】 【分析】取特殊值检验,利用排除法得答案。
【详解】因为a b >,那么当1,1a b ==-时11a b>,故A 错;当0x =时22ax bx =,故B 错; 当1,1a b ==-时,22a b =,故C 错;因为a b >且103x >,所以33x x a b>应选D.【点睛】此题考察不等式的根本性质,属于简单题。
ABC △中,3A π∠=,6,BC AB ==C ∠=〔 〕A.4π或者34πB.34πC.4π D.6π 【答案】C 【解析】 【分析】由正弦定理计算即可。
【详解】由题根据正弦定理可得sin sin BC AC A C = sin C =,解得sin 2C = , 所以C ∠为4π或者34π,又因为3A π∠=,所以C ∠为4π应选C.【点睛】此题考察正弦定理,属于简单题。
}{na 满足11a==,那么10a =〔 〕A. 10B. 20C. 100D. 200【答案】C 【解析】 【分析】由题可得数列是以1为首相,1为公差的等差数列,求出数列的通项公式,进而求出10100a =【详解】因为11a ==,所以数列是以1为首相,1为公差的等差数列()111n n =+-⨯=10=,那么10100a =【点睛】此题考察由递推公式证明数列是等差数列以及等差数列的通项公式,属于一般题。
x 的不等式0ax b ->的解集是(1,)+∞,那么关于x 的不等式()(3)0ax b x +->的解集是〔 〕 A. (,1)(3,)-∞-+∞ B. (1,3)- C. (1,3) D. (,1)(3,)-∞+∞【答案】A【解析】 【分析】由不等式的解集可知0a >且1ba=;从而可解得()()30ax b x +-=的根,根据二次函数图象可得所求不等式的解集.【详解】由0ax b ->的解集为()1,+∞可知:0a >且1ba= 令()()30ax b x +-=,解得:11x =-,23x =0a > ()()30ax b x ∴+->的解集为:()(),13,-∞-+∞此题正确选项:A【点睛】此题考察一元二次不等式的求解问题,关键是可以通过一次不等式的解集确定方程的根和二次函数的开口方向.5.我国古代名著?九章算术?中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤,斩末一尺,重二斤.〞意思是:“现有一根金锤,长5尺,头部1尺,重4斤,尾部1尺,重2斤〞,假设该金锤从头到尾,每一尺的重量构成等差数列,该金锤一共重多少斤?〔 〕 A. 6斤 B. 7斤C. 9斤D. 15斤【答案】D 【解析】【分析】直接利用等差数列的求和公式求解即可.【详解】因为每一尺的重量构成等差数列{}n a ,14a =,52a =,156a a ∴+=,数列的前5项和为155553152a a S =⨯=⨯=+.即金锤一共重15斤, 应选D .【点睛】此题主要考察等差数列求和公式的应用,意在考察运用所学知识解答实际问题的才能,属于根底题.}{na 前n 项和为nS,满足1020S S =,那么以下结论中正确的选项是〔 〕A. 15S 是n S 中的最大值B. 15S 是n S 中的最小值C. 150S =D. 300S =【答案】D 【解析】此题考察等差数列的前n 项和公式,等差数列的性质,二次函数的性质. 设公差为,d 那么由等差数列前n 项和公式1(1)2n n n S na d -=+知:n S 是n 的二次函数;又1020S S =知对应二次函数图像的对称轴为102015;2n +==于是对应二次函数为2()(15);f n a n b =-+无法确定000;a a a =><或或所以根据条件无法确定n S 有没有最值;但是根据二次函数图像的对称性,必有(0)(30)0,f f ==即300.S =应选D}{na 中,23711440aa a -+=,数列}{nb 是等比数列,且77b a =,那么68b b =〔 〕A. 4B. 8C. 16D. 64【答案】D 【解析】 【分析】根据等差数列性质可求得7a ,再利用等比数列性质求得结果.【详解】由等差数列性质可得:()222371131177744480a a a a a a a a -+=+-=-=又{}n a 各项不为零 78a ∴=,即78b =由等比数列性质可得:268764b b b ==此题正确选项:D【点睛】此题考察等差数列、等比数列性质的应用,属于根底题.ABC ∆中,内角,,A B C 所对应的边分别为,,a b c ,假设sin cos 0b A B -=,且三边,,a b c 成等比数列,那么2a cb+的值是〔 〕B.2C. 2D. 1【答案】D 【解析】 【分析】由正弦定理整理可得tan B =,进而可知在三角形中3B π=,由,,a b c 成等比数列得2b ac =,再根据余弦定理化简配方,从而得出答案。
河北省xx县xx中学201X-201x学年高一数学下学期期末考试试题
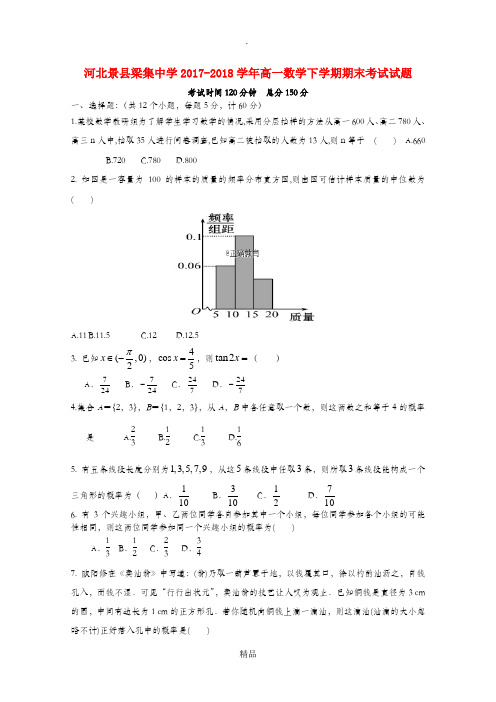
河北景县梁集中学2017-2018学年高一数学下学期期末考试试题考试时间120分钟 总分150分一、选择题:(共12个小题,每题5分,计60分)1.某校数学教研组为了解学生学习数学的情况,采用分层抽样的方法从高一600人、高二780人、高三n 人中,抽取35人进行问卷调查,已知高二被抽取的人数为13人,则n 等于 ( ) A.660B.720C.780D.8002. 如图是一容量为100的样本的质量的频率分布直方图,则由图可估计样本质量的中位数为 ( )A.11B.11.5C.12D.12.53. 已知(,0)2x π∈-,4cos 5x =,则=x 2tan ( ) A .247 B .247- C .724 D .724- 4.集合A ={2,3},B ={1,2,3},从A ,B 中各任意取一个数,则这两数之和等于4的概率是A.23B.12C.13D.165. 有五条线段长度分别为1,3,5,7,9,从这5条线段中任取3条,则所取3条线段能构成一个三角形的概率为( )A .101 B .103 C .21 D .1076. 有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )A .13B .12C .23D .347. 欧阳修在《卖油翁》中写道:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.已知铜钱是直径为3 cm 的圆,中间有边长为1 cm 的正方形孔.若你随机向铜钱上滴一滴油,则这滴油(油滴的大小忽略不计)正好落入孔中的概率是( )A .9π4B .94πC .4π9D .49π8. 已知角α的终边经过点(1,2)P -),则tan 4πα⎛⎫+ ⎪⎝⎭的值是( ). A .3 B .3- C .13 D .13- 9. =-40cos 40sin 5sin 5cos 22( ) A .1 B .21C .2D .1-10. 若3)tan(=+βα,5)tan(=-βα,则α2tan =( )A .74B. 74-C. 21 D. 21-11. 函数)cos[2()]y x x ππ=-+是 A.周期为4π的奇函数B.周期为4π的偶函数C.周期为2π的奇函数D.周期为2π的偶函数12.已知cos 23θ=,则44sin cos θθ+的值为A .1813 B .1811C .97D .1-二、填空题:(共4个小题,每题5分,计20分)13. 求值:0tan 20tan 4020tan 40+=_____________。
xx市201X-201x学年高一数学下学期期末大联考试题

2017-2018学年度高一年级第二学期期末教学质量检测试卷数学第Ⅰ卷一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知数列{}n a 为等差数列,2812a a +=,则5a =( )A .5B .6C .7D .82.在正方体1111ABCD A B C D -中,1BC 与1D C 所成角的大小为( )A .30°B .45°C .60°D .90°3.若2x >,则42x x +-的最小值为( ) A .2 B .4 C .6 D . 84.已知数列{}n a 是公比为正数的等比数列,若11a =,515a =,则数列{}n a 的前7项和为( )A .63B .64 C.127 D .1285.已知23600x y x y y +≤⎧⎪-≥⎨⎪≥⎩,则3z x y =-的最大值为( )A .9B .0 C.125D .9- 6.关于利用斜二侧法得到的直观图有下列结论:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形。
以上结论正确的是( )A .①②B .① C.③④ D .①②③④7.把边长为a 的正方形ABCD 沿对角线AC 折起,当B 、D 两点距离为a 时,二面角B AC D --的大小为( )A .30°B .45° C.60° D .90°8.某几何体的三视图如图所示,则该几何体的表面积为( )A .(32)π+B .(42)π+ C.(342)π+ D .(422)π+9.直线l 过点(1,0)P ,且与以(2,1)A ,3)B 为端点的线段总有公共点,则直线l 斜率的取值范围是( )A .3,1⎡⎤⎣⎦B .(,3][1,)-∞+∞ C.(,3]-∞ D .[1,)+∞ 10.直线210x y -+=关于直线1x =对称的直线方程是( )A .210x y +-=B .210x y +-= C.230x y +-=D .230x y +-=11.已知(3,1)A -,(5,2)B -,点P 在直线0x y +=上,若使||||PA PB +取最小值,则点P 的坐标是( )A .(1,1)-B .(1,1)- C.1313(,)55- D .(2,2)- 12.已知正ABC ∆中,点D 为BC 的中点,把ABD ∆沿AD 折起,点B 的对应点为点'B ,当三棱锥'B ADC -体积的最大值为36时,三棱锥'B ADC -的外接球的体积为( ) A 33 B .34π C.56π D 55 第Ⅱ卷二、填空题(共4小题,每小题5分,满分20分)13.已知直线1l :210ax y ++=与直线2l :(3)0a x y a --+=,若12l l ⊥,则实数a 的值为 或 .14.在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知503b =,150c =,30B =︒,则边长a = 或 .15.已知α为锐角,且5cos()313πα+=,则cos α= . 16.给出下列命题:①如果a ,b 是两条直线,且a b ,那么a 平行于经过b 的任何平面;②如果直线a 和平面α满足a α,那么直线a 与平面α内的任何直线平行;③如果直线a ,b 和平面α满足a α,b α,那么a b ;④如果直线a ,b 和平面α满足a b ,a α,b α⊄,那么b α;⑤如果平面α,β,γ满足αγ,βγ,那么αβ. 其中正确命题的序号是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 求满足下列条件的直线的方程:(1)直线l 经过点(2,3)A -,并且它的倾斜角等于直线13y x =的倾斜角的2倍,求直线l 的方程;(2)直线l 过点(2,4)P ,并且在x 轴上的截距是y 轴上截距的12,求直线l 的方程.18. 若函数2()cos 2cos 1f x x x x m =++-在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值为-2. (1)求m 的值及()f x 的最小正周期;(2)求()f x 的单调递增区间.19. 已知正方形的中心为直线10x y -+=和直线220x y ++=的交点,其一边所在直线方程为320x y +-=,求其它三边所在直线的方程.20. 设ABC ∆的内角A ,B ,C 所对的边分别为a ,b ,c ,且3cos 32a C b c =-.(1)求sin A 的值;(2)若b B =,求a 的值;(3)若a =ABC ∆面积的最大值.21. 如图,在三棱柱111ABC A B C -中,1AB AC AA ==,平面11AA C C ⊥平面11AA B B ,1160CAA BAA ∠=∠=︒,点D 是1AA 的中点.(1)求证:BD ⊥平面11AAC C ;(2)求直线1BC 与平面11AAC C 所成角的正弦值.22. 在数列{}n a 中,12a =,121n n n a a +=++(1)求证:数列{}2n n a -为等差数列;(2)若数列{}n b 满足2log (1)n n b a n =+-,求证:1324351111134n n b b b b b b b b +++++<.试卷答案一、选择题1-5:BCCCA 6-10:ADABD 11、12:CD二、填空题13.1或214.16.④⑤ 三、解答题 17.解:(1)设直线13y x =的倾斜角为α,则1tan 3α= ∴22122tan 33tan 211tan 41()3ααα⨯===-- ∴直线l 的斜率为34 又∵直线l 经过点(2,3)A -∴直线l 的方程为:33(2)4y x +=-即34180x y --= (2)若直线l 在两轴上的截距均不为0,设直线l 在x 轴上的截距为a (0a ≠),则直线l 在y 轴上的截距为2a ,可设l :12x y a a +=(0a ≠),将点(2,4)P 代入,得4a = ∴直线l :148x y +=即280x y +-= 若直线l 在两轴上的截距均为0,由直线l 过点(2,4)P ,∴直线l 的方程是:280x y +-=或2y x =.18.解:(1)()2sin 26f x x m π⎛⎫=++ ⎪⎝⎭∵0,2x π⎡⎤∈⎢⎥⎣⎦,∴72666x πππ≤+≤ ∴当7266x ππ+=即2x π=时,min 1()222f x m ⎛⎫=⨯-+=- ⎪⎝⎭∴1m =-,此时()2sin 216f x x π⎛⎫=+- ⎪⎝⎭ ∴()f x 的最小正周期为π(2)由222262k x k πππππ-+≤+≤+,k Z ∈ 可得:36k x k ππππ-+≤≤+,k Z ∈∴()f x 的单调递增区间为,36k k ππππ⎡⎤-++⎢⎥⎣⎦,k Z ∈ 19.解:由10220x y x y -+=⎧⎨++=⎩,得:10x y =-⎧⎨=⎩即中心坐标为(1,0)- ∵正方形一边所在直线方程为320x y +-=∴可设正方形与其平行的一边所在直线方程为30x y m ++=(2m ≠-) ∵正方形中心到各边距离相等,=∴4m =或2m =-(舍)∴这边所在直线方程为340x y ++=设与320x y +-=垂直的两边所在直线方程为30x y n -+=∵正方形中心到各边距离相等=∴6n =或0n =∴这两边所在直线方程为30x y -=,360x y -+=∴其它三边所在直线的方程为340x y ++=,30x y -=,360x y -+=20.解:(1)ABC ∆中,3cos 32a C b c =-由正弦定理得:3sin cos 3sin 2sin A C B C =-∴3sin cos 3sin()2sin A C A C C=+-∴3cos sin 2sin A C C =∵sin 0C ≠,∴2cos 3A =∵(0,)A π∈,∴sin A =(2)由b B =,得sin b B=∴sin a A=a ==(3)由(1)知sin 3A =1sin 26ABC S bc A ∆==由余弦定理得:222cos 2b c a A bc+-=,a =∴2246263bc b c bc =+-≥- ∴9bc ≤(当且仅当b c =时取“=”号)9ABC S ∆=≤=即ABC ∆21.解:(1)证明:连接1A B ,∵1AB A A =,160BAA ∠=︒, ∴1BAA ∆为正三角形∵D 是1AA 的中点,∴1BD AA ⊥,又∵平面11AA C C ⊥平面11AA B B ,且平面11AAC C 平面111AA B B AA =,BD ⊂平面11AA B B∴BD ⊥平面11AAC C(2)连接1DC ,(1)中已证BD ⊥平面11AAC C ,所以1BC D ∠为直线1BC 与平面11AAC C 所成的角设2AB a =,则正三角形1BAA ∆中,3BD a =, 11A DC ∆中,1A D a =,112AC a =,11120DA C ∠=︒∴22221(2)22cos1207DC a a a a a =+-⨯⨯⨯︒= ∴17DC a =∴1RT BDC ∆中,2213710BC a a a =+= ∴11330sin 1010BD a BC D BC a ∠=== 即直线1BC 与平面11AAC C 所成角的正弦值为301022.解:(1)∵121n n n a a +=++.∴111(2)(2)21n n n n n n n a a a a +++---=--= 又∵12a =,∴120a -=∴数列{}2n n a -为首项为0,公差为1的等差数列.(2)由(1)知:21n n a n -=-,∴12n n a n +-=∴22log (1)log 2n n n b a n n =+-== ∴13243521111n n b b b b b b b b +++++⋅ 11111111111232435112n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦111112212n n ⎛⎫=+-- ⎪++⎝⎭31114212n n ⎛⎫=-+ ⎪++⎝⎭∵*n N ∈ ∴1110212n n ⎛⎫+> ⎪++⎝⎭∴3111342124n n ⎛⎫-+< ⎪++⎝⎭ ∴1324352111134n n b b b b b b b b +++++<⋅如有侵权请联系告知删除,感谢你们的配合!。
高一数学下期期末考试试题含解析

2021—2021学年第二学期期末考试试卷高一数学一:选择题。
1.假设sin 0α<,且tan 0α>,那么α是〔 〕 A. 第一象限角 B. 第二象限角C. 第三象限角D. 第四象限角 【答案】C 【解析】sin 0α<,那么α的终边在三、四象限;tan 0α>那么α的终边在三、一象限, sin 0α<,tan 0α>,同时满足,那么α的终边在三象限。
2.4sin()3π-的值等于( )A.12 B. -12D. 【答案】C 【解析】 【分析】利用诱导公式把4sin()3π-化简成sin 3π.【详解】44sin()sin()sin 3332πππ-=-==【点睛】此题考察诱导公式的应用,即把任意角的三角函数转化成锐角三角函数,考察根本运算求解才能.3.(3,0)AB =,那么AB 等于( )A. 2B. 3C. 4D. 5【答案】B 【解析】【详解】因为(3,0)AB =, 所以903AB =+=, 应选B.4.如图是某体育比赛现场上评委为某位选手打出的分数的茎叶图,去掉一个最高分和一个最低分,所剩数据的平均数和方差分别是( )A. B. 85和 C. D.【答案】B 【解析】 【分析】去掉最低分79分,最高分93分,利用平均数的计算公式求得85x =,利用方差公式求得2 1.6s =.【详解】去掉最低分79分,最高分93分,得到数据84,84,84,86,87, 该组数据的平均数8484848687855x ++++==,222222(8485)(8485)(8485)(8685)(8785) 1.65s -+-+-+-+-==.【点睛】此题考察从茎叶图中提取信息,并对数据进展加工和处理,考察根本的运算求解和读图的才能.5.函数y=2cos 1x -的最大值、最小值分别是( ) A. 2,-2 B. 1,-3C. 1,-1D. 2,-1【答案】B 【解析】 【分析】根据余弦函数有界性确定最值.【详解】因为1cos 1x -≤≤,所以2cos 1[3,1]y x =-∈-,即最大值、最小值分别是1,-3,选B.【点睛】此题考察余弦函数有界性以及函数最值,考察根本求解才能,属基此题.6.sin 20︒cos 40︒+cos 20°sin 40°的值等于A.14C.12【答案】B 【解析】由题可得,000002040+2040=60sin cos cos sin sin =.应选B.7.向量(4,2)a =-,向量,)5(b x =,且//a b ,那么x 等于( ) A. 10B. 5C. 52-D. 10-【答案】D【解析】 【分析】由两向量平行,其向量坐标穿插相乘相等,得到452x ⨯=-. 【详解】因为//a b ,所以452x ⨯=-,解得:10x =-.【点睛】此题考察向量平行的坐标运算,考察根本运算,注意符号的正负.8.从装有5个红球和3个白球的口袋内任取3个球,那么,互斥而不对立的事件是( ) A. 至少有一个红球与都是红球 B. 至少有一个红球与都是白球 C. 至少有一个红球与至少有一个白球 D. 恰有一个红球与恰有两个红球 【答案】D 【解析】【详解】试题分析:从装有5个红球和3个白球的口袋内任取3个球,不同的取球情况一共有以下几种:3个球全是红球;2个红球1个白球;1个红球2个白球;3个球全是白球. 选项A 中,事件“都是红球〞是事件“至少有一个红球〞的子事件, 不是互斥事件; 选项B 中,事件“至少有一个红球〞与事件“都是白球〞是对立事件;选项C 中,事件“至少有一个红球〞与事件“至少有一个白球〞的交事件为“2个红球1个白球〞与“1个红球2个白球〞, 不是互斥事件;选项D 中,事件“恰有一个红球〞与事件“恰有二个红球〞互斥不对立 考点:互斥事件与对立事件9.函数()y Asin x ωϕ=+的局部图象如下图,那么〔 〕A. 2sin 26y x π⎛⎫=-⎪⎝⎭B. 2sin 23y x π⎛⎫=-⎪⎝⎭C. 2sin 26y x π⎛⎫=+ ⎪⎝⎭D. 2sin 23y x π⎛⎫=+⎪⎝⎭【答案】A 【解析】 【分析】由函数的图象的顶点坐标求出A ,由周期求出w ,由五点法作图求出ϕ的值,可得函数的解析式.【详解】根据函数()y Asin x ωϕ=+的局部图象,可得2A =,236T πππω==+,解得2w =,再根据五点法作图,可得232ππϕ⨯+=,解得6πϕ=-,故()226f x sin x π⎛⎫=- ⎪⎝⎭, 应选:A .【点睛】此题主要考察由函数()y Asin x ωϕ=+的局部图象求解析式,其中解答中函数的图象的顶点坐标求出A ,由周期求出w ,由五点法作图求出ϕ的值是解答的关键,着重考察了推理与运算才能,属于根底题.10.设函数()sin(2)2f x x π=-〔x ∈R 〕,那么()f x 是A. 最小正周期为π的奇函数B. 最小正周期为π的偶函数C. 最小正周期为2π的奇函数 D. 最小正周期为2π的偶函数 【答案】B 【解析】 ∵f (x )=sin 22x π⎛⎫-⎪⎝⎭=-cos2x , ∴f (x )为偶函数,周期T =π.11.假设将一个质点随机投入长方形ABCD 中,其中2,1AB BC ==,那么质点落在以AB 为直径的半圆内的概率为〔 〕A. 8πB. 6πC. 4πD.2π 【答案】C 【解析】 【分析】质点落在以AB 为直径的半圆内的概率等于半圆面积与长方形面积比. 【详解】如下图:2,1AB BC ==,2112214S P S ππ⋅⋅===⋅半圆长方形.【点睛】此题考察几何概型的概率计算,注意概率值是半圆面积与长方形面积的比值,与单个图形面积的大小无关.12.[2021·沙中学期末]在四边形ABCD 中,AB =a +2b ,BC =-4a -b ,CD =-5a -3b ,其中a ,b 不一共线,那么四边形ABCD 为( ) A. 平行四边形 B. 矩形C. 梯形D. 菱形【答案】C 【解析】∵AD =AB +BC +CD =-8a -2b =2BC ,AB 与CD 不平行,∴四边形ABCD 为梯形.二、填空题.13.角α的终边经过点()3,4P ,那么cos α的值是____________. 【答案】35【解析】 【分析】由题意和任意角的三角函数的定义求出cos a 的值即可. 【详解】由题意得角α的终边经过点()3,4P ,那么5OP =, 所以3cos 5x a OP ==,故答案为35. 【点睛】此题考察任意角的三角函数的定义,属于根底题.14.向量a =(3,2),b =(0,-1),那么向量3b -a 的坐标是 . 【答案】(3,5)-- 【解析】试题分析:因为(3,2),(0,1)a b ==-,所以33(0,1)(3,2)(3,5)b a -=--=--. 考点:向量坐标运算.15.ABC ∆三个顶点的坐标分别为(1,0),(1,2),(0,)A B C c -,假设AB ⊥BC ,那么c 的值是______. 【答案】3 【解析】 【分析】求出(2,2),(1,2)AB BC c ==--,再利用AB ⋅0BC =,求得3c =. 【详解】(2,2),(1,2)AB BC c ==--,因为AB ⊥BC ,所以2(1)2(2)0c ⨯-+⨯-=,解得:3c =.【点睛】此题考察向量的坐标表示、数量积运算,要注意向量坐标与点坐标的区别.16.一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下列图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出80人作进一步调查,那么在[1 500,2 000)(元)月收入段应抽出 人.【答案】16 【解析】试题分析:由频率分布直方图知,收入在1500--2000元之间的概率为0.0004×500=0.2,所以在[1 500,2 000〕〔元〕月收入段应抽出80×0.2=16人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沁县中学2017-2018学年度第二学期期末考试高一数学答题时间:120分钟,满分:150分一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1. 数列2460,,,357的一个通项公式是( )A .1)1n n a n N n *-=∈+(B .1)21n n a n N n *-=∈+(C .21)21n n a n N n *-=∈-()(D .2)21n na n N n *=∈+(2.设集合A ={x |x 2-4x +3<0},B ={x |2x -3>0},则A ∩B =( )A. (23,3) B. (-3,23) C. (1,23)D. (-3,23-)3.在ABC ∆中,3,6,sin a b A ===,则B =( ) A .3π B. 23π C. 3π或23π D. 6π或56π4.已知等差数列{}n a 的前n 项和为n S ,若18102,28a a a =+=,则9S =( )A .36 B.72 C.144 D.2885.若R c b a ∈,,,则下列说法正确的是( )A.若b a >,c d >,则ac bd >B. 若b a >,则22bc ac >C.若0a b <<,则11a b< D. 若b a >,则c b c a ->- 6.若ABC ∆的三个内角满足sin :sin :sin 7:11:13A B C =,则ABC ∆( )A.一定是锐角三角形;B. 一定是直角三角形;C. 一定是钝角三角形;D. 可能是锐角三角形,也可能是钝角三角形. 7.在各项都为正数的数列{}n a 中,首项12a =,且点221(,)(,2)n n a a n N n *-∈≥在直线90x y -=上,则数列{}n a 的前n 项和n S 为( )A. 1(3)2n --B. 31n -C. 132n +D. 232n n +8.若两个正实数,x y 满足211x y+=,则2x y +的最小值为( )A. 8B. 6C. 4D. 29.已知ABC ∆中,,,A B C ∠∠∠的对边分别是,,a b c ,2=33ABC A b S π∆=,=1,,则2=sin sin 2sin a b cA B C+-+-( )A .239B .39 C . 27 D .4710. 等差数列{}n a 中, 135105a a a ++=,24699a a a ++=,{}n a 的前n 项和为n S ,则使n S 达到最大值的n 值为( )A .21B .20 C. 19 D .1811.若不等式组033x y x y x y a ->⎧⎪+<⎨⎪+>⎩表示一个三角形内部的区域,则实数a 的取值范围是( )A . 3,4⎛⎫+∞ ⎪⎝⎭B .3,2⎛⎫+∞ ⎪⎝⎭ C. 3,4⎛⎫-∞ ⎪⎝⎭ D . 3,2⎛⎫-∞ ⎪⎝⎭12.在锐角ABC ∆中,B A 2=,则ACAB的取值范围是( ) A .0,3() B .)2,1( C .)3,2( D .)3,1(二、填空题(本大题共4小题,每小题5分,共20分)二、填空题:13. 数列满足1112,1(2,3,4)n n a a n a -==-=,则14a = . 14. 已知20ax x b ++>的解集为()-2,3,则=a b + .15.如图,为了测量,A C 两点间的距离,选取同一平面上的,B D 两点,测出四边形ABCD 各边的长度:5,8,3,5AB km BC km CD km DA km ====,且B ∠与D ∠互补,则AC 的长为 .16.设数列{}n a 的前n 项和为n S ,且21n S n n =-+,正项等比数列{}n b 的前n 项和为n T ,且22b a =,45b a =, 数列{}n c 中,11c a =,且1n n n c c T +=-,则{}n c 的通项公式为 .三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17. (10分)如图,在四边形ABCD 中,已知AD CD ⊥,=10AD ,=14AB ,=60BDA ∠,=135BCD ∠,求BC 的长度。
18.(12分)共享单车给市民出行带来了诸多便利,某公司购买了一批单车投放到某地给市民使用,据市场分析,每辆单车的营运累计利润y (单位:元)与营运天数()x x N *∈满足函数关系式21608002y x x =-+-. (1)要使营运累计利润高于800元,求营运天数的取值范围; (2)每辆单车营运多少天时,才能使每天的平均营运利润yx的值最大?最大值为多少?19.(12分)已知公差不为0的等差数列}{n a 的首项21=a ,且1,1,1421+++a a a 成等比数列.(1)求数列}{n a 的通项公式; (2)设11+=n n n a a b ,*N n ∈,求数列}{n b 的前n 项和n S .20. (12分)某工艺厂有铜丝5万米,铁丝9万米,准备用这两种材料编制成花篮和花盆出售,已知一只花篮需要用铜丝200米,铁丝300米;编制一只花盆需要铜丝100米,铁丝300米,设该厂用所有材料编制个花篮x 个, 花盆y 个.(1)列出,x y 满足的关系式,并画出相应的平面区域;(2)若出售一个花篮可获利300元,出售一个花盆可获利200元,那么怎样安排花篮与花盆的编制个数,可使得所得利润最大,最大利润是多少?21.(12分)设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且sin cos b A B =. (1)求角B 的大小;(2)若3,sin 2sin b C A ==,求,a c 的值及ABC ∆的周长.22.(12分)已知数列{a n }的前n 项和为S n ,且S n =2a n -2(n ∈N *) ,在数列{b n }中,b 1=1,点P (b n ,b n +1)在直线x -y +2=0上.(1)求数列{a n },{b n }的通项公式; (2)记T n =a 1b 1+a 2b 2+…+a n b n ,求T n .沁县中学2017-2018学年度第二学期期末考试高一数学答案一、 选择题: 1—5 CACBD 6—10 ABACB 11——12 DB二、填空题:13.1214. 5 15. 7m k 16.2n n c n =- 17.解:在ABD ∆中 ,由余弦定理得222=AD 2cos AB BD AD BD ADB +-⋅∠220-96=0BD BD ∴-,解得=16BD 或=-6BD (舍) …………… 5分AD CD ⊥,=60BDA ∠,=30BDC ∴∠在BCD ∆中 ,由正弦定理得sin sin BD BCBCD BDC =∠∠12BC =解得BC …………… 10分 18.解:(1)要使营运累计收入高于800元,令80080060212>-+-x x , ……1分 解得8040<<x .所以营运天数的取值范围为40到80天之间 .………………………………4分(2)6080021+--=x x xy 6020≤-= …………………………………9分 当且仅当18002x x=时等号成立,解得400x = (10)分所以每辆单车营运400天时,才能使每天的平均营运利润最大,最大值为每天20元. …………………… 12分19.解:(Ⅰ)设数列{}n a 的公差为d ,则2(1)n a n d =+-,*N n ∈.由 11a +,21a +,41a +成等比数列,得()()()2214111a a a +=++, …………2分 即()()23333d d +=+,得0d =(舍去)或3d =. ……………… 4分所以数列{}n a 的通项公式为31n a n =-,*N n ∈. ………………6分 (Ⅱ)因为()()111111313233132n n n b a a n n n n +⎡⎤===-⎢⎥-+-+⎣⎦, ………………8分所以()111111111111325358331323232232n nS n n n n ⎡⎤⎡⎤⎡⎤⎡⎤=-+-++-=-=⎢⎥⎢⎥⎢⎥⎢⎥-+++⎣⎦⎣⎦⎣⎦⎣⎦. ………………12分 20.解:(1)由已知x 、y 满足的关系式为2001005000030030090000 ,00x y x y x y +⎧⎪+⎪⎨⎪⎪⎩等价于250030000x y x y x y +⎧⎪+≤⎪⎨⎪⎪⎩ …………………4分该二元一次不等式组所表示的平面区域如图中的阴影部分. …………………7分 (2)设该厂所得利润为z 元,则目标函数为z=300x+200y 将z=300x+200y 变形为32200z y x =-+,这是斜率为32-,在y 轴上截距为200z、随z 变化的一族平行直线.又因为x 、y 满足约束条件,所以由图可知,当直线32200zy x =-+经过可行域上的点M 时,截距200z最大,即z 最大. …………………9分 解方程组2500{33900x y x y +=+=得点M 的坐标为(200,100)且恰为整点,即x=200,y=100. …………………10分所以, 30020020010080000max z =⨯+⨯=. …………11分答:该厂编制200个花篮,100花盆所获得利润最大,最大利润为8万元. …………12分 21.解: (1)sin 3cos b A a B=由正弦定理得sin sin cos B A A B = 在ABC ∆中,sin 0,0A B π≠<<tan B ∴=,即=3B π; …………5分(2)sin 2sin C A = ,由正弦定理得 2c a =又222=2cos ,3,3b ac ac B b B π+-==229=422cos3a a a a π∴+-⋅解得a =,2c a ∴==∴ ABC ∆的周长=3a b c ++=+ …………12分22.解: (1)由S n =2a n -2,得S n -1=2a n -1-2(n ≥2), 两式相减得a n =2a n -2a n -1,即 1-n na a =2(n ≥2), 又a 1=2a 1-2,∴a 1=2,∴{a n }是以2为首项,以2为公比的等比数列,∴a n =2n .∵点P (b n ,b n +1)在直线 x -y +2=0上,∴b n -b n +1+2=0,即b n +1-b n =2, ∴{b n }是以2为公差的等差数列,∵b 1=1,∴b n =2n -1. ……………6分(2)∵T n =1×2+3×22+5×23+…+(2n -3)2n -1+(2n -1)2n ①∴2T n = 1×22+3×23+5×24+ … +(2n -3)2n +(2n -1)·2n +1 ② ①-②得:-T n =1×2+2(22+23+…+2n )-(2n -1)·2n +1=2+2·212222-⋅-n -(2n -1)2n +1=2+4·2n -8-(2n -1)2n +1=(3-2n )·2n +1-6∴T n =(2n -3)·2n +1+6. …………………………12分如有侵权请联系告知删除,感谢你们的配合!如有侵权请联系告知删除,感谢你们的配合!。
