找规律经典
五年级找规律(经典30道)

五年级找规律一.选择题1.按的方式摆放在桌面上.8个按这种方式摆放,有()个面露在外面.A.20B.23C.26D.292.按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8B.32C.363.将一些小圆球如图摆放,第六幅图有()个小圆球.A.30B.36C.424.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10B.25=9+16C.36=15+21D.49=18+315.找规律填空3、5、8、10、13、()、18、20.A.14B.15C.16D.176.按规律填数:2,3,5,9,(),33,…….A.13B.15C.17D.307.找规律:19.8,18.6,17.4,()A.17.2B.16.8C.16.2D.15.28.按如图规律摆放三角形则第⑥个图三角形的个数为()A.15B.17C.20D.249.观察下面的点阵图,按规律,第(9)个点阵图中有()个点.A.27B.30C.33D.54二.填空题(共19小题)10.摆一个需要4根小棒,摆需要7根小棒,摆需要10根小棒…,像这样摆n个正方形需要根小棒,当n=20时,需要根小棒.11.如图方式摆放桌子和椅子,一张桌子能坐6人,3张桌子能坐人.12.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为3,6,9,12.按这个规律.由100个小等边三角形拼成的图形,周长为.13.如图,它是由火柴棒拼成的图案,如果在这个图案中用了51根火柴棒,可拼成个三角形.14.找规律填数.(1)1,4,7,10,,,.(2)2,4,6,8,,,.(3)1,1,2,3,5,8,,.(4)2,5,4,7,6,9,8,,.(5)1,﹣4,9,﹣16,25,,.15.△□□△□□△□□…,这一组图形中第16个是,第21个是.16.●●〇●〇〇〇●●〇●〇〇〇…,黑白两色棋子是按的规律摆放的,第51枚棋子是,前20枚棋子中,白色棋子有枚.17.按规律填数:,,,,,,.18.先找规律,再填数:1,,,,,,.19.照下图排列的规律,第10幅图有个圆点,第n个图有个圆点.20.用同样长的小木棒摆成如图,照这样摆下去,第6幅图需要根这样的小木棒.21.下图是小亮在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第7个小房子用了块石子.22.将一些▲按一定的规律摆放,(如图所示).图中▲的个数依次是6、10、16、24……第10个图形共有个▲.第m个图形中共有个▲.23.用边长为1的小三角形按如图方式摆图形.摆第7个图形需要个小三角形,第7个图形的周长是.24.将一些半径相同的小圆按如图所示的規律摆放:第1个图形中有6个小圆,第2个形中有10个小圆,第3个图形中有16个小圆,第4个图形中有24个小圆,…依此律,第6个图形有个小圆.25.仔细观察如图,照这样排列下去,第六个图形中共有个三角形,其中涂色的三角形有个.26.数形结合是一种重要的数学思想.请你仔细观察,找出下面图形与算式的关系,再直接填空.(1)推算:1+3+5+…+19=2(2)概括:=2(3)拓展应用:1+3+5+7+9+11+13+15+13+11+9+7+5+3+1=27.奇思用小棒这样摆三角形:…,一共用了27根小棒,摆出了个三角形.28.如图,每个图案都是由若干个棋子摆成,依照此规律,第100个图案中棋子的总个数是.三.解答题(共2小题)29.学校准备了40000元,够不够?30.摆放易拉罐,(如图)看图回答问题.(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有个.摆五层一共有个.摆六层一共有个.…(2)用n表示摆的层数,你能总结出一个计算公式吗?.五年级找规律参考答案与试题解析一.选择题(共9小题)1.按的方式摆放在桌面上.8个按这种方式摆放,有()个面露在外面.A.20B.23C.26D.29【解】根据题干分析可得,n个正方体有5+(n﹣1)×3=3n+2;所以8个小正方体时,露在外部的面有:3n+2=3×8+2=26(个)故选:C.2.按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8B.32C.36【解】1+2+3+4+5+6+7+8,=(1+8)+(2+7)+(3+6)+(4+5),=9×4,=36;答:第8副图案有36个笑脸.故选:C.3.将一些小圆球如图摆放,第六幅图有()个小圆球.A.30B.36C.42【解】观察图形可知:第一个图形中有1×2=2个小圆球,第二个图形中有2×3=6个小圆球,第三个图形中有3×4=12个小圆球,第四个图形中有4×5=20个小圆球,…所以第六幅图有6×7=42个小圆球.故选:C.4.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10B.25=9+16C.36=15+21D.49=18+31【解】这些三角形数的规律是1,3,6,10,15,21,28,36,45,…,且正方形数是这串数中相邻两数之和,很容易看到:恰有36=15+21.故选:C.5.找规律填空3、5、8、10、13、()、18、20.A.14B.15C.16D.17【解】10+5=15故选:B.6.按规律填数:2,3,5,9,(),33,…….A.13B.15C.17D.30【解】2×9﹣1=18﹣1=17所以:2,3,5,9,17,33,…….故选:C.7.找规律:19.8,18.6,17.4,()A.17.2B.16.8C.16.2D.15.2【解】17.4﹣1.2=16.2.故选:C.8.按如图规律摆放三角形则第⑥个图三角形的个数为()A.15B.17C.20D.24【解】图①三角形的个数:2×3﹣1=5(个)图②三角形的个数:3×3﹣1=8(个)图③三角形的个数:4×3﹣1=11(个)……图n三角形的个数:3(n+1)﹣1=(3n+2)个……第⑥个图三角形的个数为:3×6+2=18+2=20(个)答:第⑥个图三角形的个数为20个.故选:C.9.观察下面的点阵图,按规律,第(9)个点阵图中有()个点.A.27B.30C.33D.54【解】由分析可知,第n项是(3n+3)个点3×9+3=27+3=30答:第(9)个点阵图中有30个点.故选:B.二.填空题(共19小题)10.摆一个需要4根小棒,摆需要7根小棒,摆需要10根小棒…,像这样摆n个正方形需要3n+1根小棒,当n=20时,需要61根小棒.【解】第一个正方形由四根火柴摆成,以后加三根就可加一个正方形,摆n个正方形需要3n+1根小棒,当n=20时,需要3×20+1=61根小棒.故答案为:3n+1,61.11.如图方式摆放桌子和椅子,一张桌子能坐6人,3张桌子能坐14人.【解】有1张桌子时有6把椅子,有2张桌子时有10把椅子,10=6+4×1,有3张桌子时有14把椅子,14=6+4×2,答:3张桌子可以坐14人.故答案为:14.12.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为3,6,9,12.按这个规律.由100个小等边三角形拼成的图形,周长为30.【解】因为:100=102所以由100个小等边三角形拼成的图形编号为(10),所以周长为:3×10=30.故答案为:30.13.如图,它是由火柴棒拼成的图案,如果在这个图案中用了51根火柴棒,可拼成25个三角形.【解】第一个三角形有1+2=3根火柴棒组成,以后每多一个三角形就多用2根火柴棒,所以组成n个三角形就需要1+2n根火柴棒;当1+2n=51时2n=50n=25答:可拼成25个三角形.故答案为:25.14.找规律填数.(1)1,4,7,10,13,16,19.(2)2,4,6,8,10,12,14.(3)1,1,2,3,5,8,13,21.(4)2,5,4,7,6,9,8,11,10.(5)1,﹣4,9,﹣16,25,49,﹣64.【解答】解(1)10+3=1313+3=1616+3=19(2)8+2=1010+2=1212+2=14(3)5+8=138+13=21(4)72=49﹣16×4=﹣64故答案为:13,16,19;10,12,14,13,21,49,﹣64.15.△□□△□□△□□…,这一组图形中第16个是△,第21个是□.【解】16÷3=5…1,所以这一组图形中第16个是△;21÷3=7,所以这一组图形中第21个是□;故答案为:△,□.16.●●〇●〇〇〇●●〇●〇〇〇…,黑白两色棋子是按●●〇●〇〇〇的规律摆放的,第51枚棋子是黑色的,前20枚棋子中,白色棋子有11枚.【解】51÷7=7(周)…2(个)第51枚棋子是黑色的.20÷7=2(周)…6(个)2×4+3=11(个)所以前20枚中一共有11个白色的.答:第51枚棋子是黑色的,前20枚棋子中,白色棋子有11枚.故答案为:黑色的,11.17.按规律填数:,,,,,,.【解】==故答案为:;.18.先找规律,再填数:1,,,,,,.【解】1=,由前几个分数可知,分子是从1开始的连续奇数,分母是项数的平方;所以,第6项的分子是11,分母是62=36,是.故答案为:.19.照下图排列的规律,第10幅图有33个圆点,第n个图有(3n+3)个圆点.【解】第一幅图圆点个数:1+2+3=6(个)第二副图圆点个数:2+3+4=9(个)第三幅图圆点个数:3+4+5=12(个)……第10幅图圆点个数:10+11+12=33(个)……第n幅图圆点的个数:n+(n+1)+(n+2)=(3n+3)个答:第10幅图有33个圆点,第n个图有(3n+3)个圆点.故答案为:33;(3n+3).20.用同样长的小木棒摆成如图,照这样摆下去,第6幅图需要34根这样的小木棒.【解】由分析可得:第n幅图需要小棒:4+6(n﹣1)根.所以第6幅图需要小棒:4+6(n﹣1)=4+6×(6﹣1)=4+30=34(根)答:第6幅图需要34根这样的小木棒.故答案为:34.21.下图是小亮在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第7个小房子用了77块石子.【解】第一个图形有5块小石子,5=1×(1+4)第二个图形有12块小石子,12=2×(2+4)第三个图形由21块小石子,21=3×(3+4)……由此推出:第n个图形有n(n+4)块石子7×(7+4)=7×11=77(块)答:第7个小房子用了77块石子.故答案为:77.22.将一些▲按一定的规律摆放,(如图所示).图中▲的个数依次是6、10、16、24……第10个图形共有114个▲.第m个图形中共有m(m+1)+4个▲.【解】∵第1个图形有1×2+4=6个三角形,第2个图形有4+2×3=10个三角形,第3个图形有4+3×4=16个三角形,…,∴第m个图形中有m(m+1)+4个三角形,∴第10个图形棋子的颗数为:10×(10+1)+4=10×11+4=110+4=114(个)故答案为:114,m(m+1)+4.23.用边长为1的小三角形按如图方式摆图形.摆第7个图形需要49个小三角形,第7个图形的周长是21.【解】根据题干分析可得:第一个图形是12=1个三角形,边长是1;第二个图形是22=4个三角形,边长是2;第三个图形是32=9个三角形,边长是3;…,第七个图形是72=49个三角形,边长是7,周长是7×3=21.答:摆第7个图形需要49个小三角形,第7个图形的周长是21.故答案为:49;21.24.将一些半径相同的小圆按如图所示的規律摆放:第1个图形中有6个小圆,第2个形中有10个小圆,第3个图形中有16个小圆,第4个图形中有24个小圆,…依此律,第6个图形有44个小圆.【解】第1个图形中有6个小圆第2个形中有10个小圆第3个图形中有16个小圆第4个图形中有24个小圆……第n个图形为:[n(n+1)+4]个小圆所以,第6个图形小圆的个数为:6×7+4=42+2=44(个)答:第6个图形有44个小圆.故答案为:44.25.仔细观察如图,照这样排列下去,第六个图形中共有49个三角形,其中涂色的三角形有21个.【解】根据题干分析可得:第n个图形涂色的小三角形个数为1+2+3+…+n,没有涂色的小三角形个数为1+2+3+…+n+n+1,当n=6时,1+2+3+4+5+6=21(个)没有涂色小三角形有1+2+3+4+5+6+7=28(个)21+28=49(个)故答案为:49,21.26.数形结合是一种重要的数学思想.请你仔细观察,找出下面图形与算式的关系,再直接填空.(1)推算:1+3+5+…+19=102(2)概括:=n2(3)拓展应用:1+3+5+7+9+11+13+15+13+11+9+7+5+3+1=113【解】(1)1+3+5+…+19=(19+1)÷2=10(个),即1+3+5+…+19由10个加数其和是102即1+3+5+…+19=102(2)=n2(3)1+3+5+7+9+11+13+15+13+11+9+7+5+3+1=(1+3+5+7+9+11+13+15)+(1+3+5+7+9+11+13)=82+72=64+49=113故答案为:10,n,113.27.奇思用小棒这样摆三角形:…,一共用了27根小棒,摆出了13个三角形.【解】当有n个三角形时小棒的数量就是:3+2(n﹣1)=3+2n﹣2=2n+1(根);当有27根小棒时:2n+1=272n=26n=13;答:摆27根小棒能摆出13个三角形.故答案为:13.28.如图,每个图案都是由若干个棋子摆成,依照此规律,第100个图案中棋子的总个数是10100.【解】由分析可得:每个图案的纵队棋子个数是:n,每个图案的横队棋子个数是:n+1,那么第n个图案中棋子的总个数与n的关系式为:总个数=n(n+1).那么第100个图案中棋子的总个数:100×(100+1)=100×101=10100(个)答:第100个图案中棋子的总个数是10100个.故答案为:10100.三.解答题(共2小题)29.学校准备了40000元,够不够?【解】172×42+328×45=7224+14760=21984(元)21984<40000答:学校准备了40000元,够.30.摆放易拉罐,(如图)看图回答问题.(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有1+2+3+4=10个.摆五层一共有1+2+3+4+5=15个.摆六层一共有1+2+3+4+5+6=21个.…(2)用n表示摆的层数,你能总结出一个计算公式吗?n(n+1).【解】(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有1+2+3+4=10个.摆五层一共有1+2+3+4+5=15个.摆六层一共有1+2+3+4+5+6=21个(2)用n表示摆的层数:n(n+1)故答案为:1+2+3+4=10;1+2+3+4+5=15;1+2+3+4+5+6=21;n(n+1)。
找规律记忆法的经典例子

找规律记忆法的经典例子找规律记忆法是一种通过寻找事物之间的规律和联系来进行记忆的方法。
下面列举了十个经典例子,帮助读者更好地理解和运用这种记忆方法。
1. 天干地支记年份:天干有甲、乙、丙、丁、戊、己、庚、辛、壬、癸,地支有子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥。
通过记忆天干地支的顺序,可以记住中国农历的年份。
2. 数字规律记密码:通过将数字和字母进行对应,例如A对应1,B对应2,以此类推,就可以通过数字来记忆密码,避免忘记。
3. 英文单词拼写规律:英文单词的拼写通常遵循一定的规律,例如“i”在大多数情况下后面跟随的是“e”,通过记忆这些规律,可以更好地拼写英文单词。
4. 数学公式推导:数学公式中存在一些常用的推导规律,例如平方差公式、三角函数的和差化积等,通过记忆这些规律,可以在解题时更快地推导出正确的结果。
5. 物理公式应用:物理学中存在一些常用的公式,例如速度等于位移除以时间,通过记忆这些公式,可以在实际问题中更准确地应用。
6. 化学元素周期表:化学元素周期表按照一定的规律排列,通过记忆这种规律,可以更好地记住元素的名称和性质。
7. 历史事件时间顺序:通过记忆历史事件发生的时间顺序,可以更好地理解历史发展的脉络和演变过程。
8. 音乐音阶记忆:音乐中的音阶通常遵循一定的规律,例如大调音阶的音程是全全半全全全半,通过记忆这种规律,可以更好地演奏音乐。
9. 生物分类系统:生物学中存在一套完整的分类系统,通过记忆这个系统的规律,可以更好地理解不同生物之间的关系。
10. 艺术作品风格记忆:不同的艺术家和艺术时期有着不同的风格,通过记忆这些风格的规律,可以更好地辨别和欣赏艺术作品。
总结:找规律记忆法可以帮助我们更好地记忆各种知识和信息。
通过寻找事物之间的规律和联系,我们可以更轻松地掌握和运用这些知识。
以上列举的十个经典例子,展示了找规律记忆法在不同领域的应用,希望能够对读者在学习和记忆中有所帮助。
初中数学中经典的找规律题

初中数学中经典的找规律题这类问题没有丽的知识方法可真7在现在的教科书上而顷虫及这类问 一 题。
这类题目主要考查学生的综合分析问题和解决问题的能力。
下面就解 决这类问题作一个初步的探究。
中考数学探索题训练一找规律1、 我们平常用的数是十进制数,如2639=2X 103+6 X 102+3 X101+9 X10°,表示十进制的数要用 10个数 码(又叫数字):0, 1 , 2, 3, 4, 5, 6,乙8, 9。
在电子数字计算机中用的是二进制,只要两个 数码:0 和 1。
如二进制中 101=1X22+0 X 2〔+1 X20等于十进制的数 5, 10111=1 X24+0 X23 + 1 X22+ 1 X21 + 1X20等于十进制中的数 23,那么二进制中的1101等于十进制的数 。
2、 从1开始,将连续的奇数相加,和的情况有如下规律:1=1=12; 1+3=4=22; 1+3+5=9=3 2;1+3+5+7=16=42; 1+3+5+7+9=25=5 2;…按此规律请你猜想从 1开始,将前10个奇数(即当最后一 个奇数是19时),它们的和是。
4、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要Q o o °& O o o O。
fl O O(1) (2) 第4题5、如下右图是某同学在沙滩上用石子摆成的小房子, 观察图形的变化规律, 写出第n 个小房子用了 块石子。
6、如下图是用棋子摆成的“上”字:第一个“上”字 第二个“上”字 第三个“上”字OCIG。
如果按照以上规律继续摆下去,那么通过观察,可以发现:( 1)第四、第五个“上” 字分别需用 和 枚棋子;(2)第n 个“上”字需用 枚棋子。
7、 如图一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分, 、则这串珠子被盒子遮住的部分有 颗.( 18、 根据下列5个图形及相应点的个数的变化规律:猜想第 6个图形有 ,、个点,第n 个图形中有 个点。
七年级数学找规律经典题型

七年级数学找规律经典题型一、数字规律1. 数列规律例1:观察数列1,3,5,7,9,…,求第n个数。
解析:首先观察这个数列,发现相邻两个数的差值都是2。
第1个数是1 = 2×1 1;第2个数是3 = 2×2 1;第3个数是5 = 2×3 1;第4个数是7 = 2×4 1;第5个数是9 = 2×5 1。
所以可以得出第n个数为2n 1。
例2:观察数列2,4,8,16,32,…,求第n个数。
解析:这个数列中,后一个数都是前一个数的2倍。
第1个数是2 = 2^1;第2个数是4 = 2^2;第3个数是8 = 2^3;第4个数是16 = 2^4;第5个数是32 = 2^5。
所以第n个数为2^n。
2. 数字循环规律例:有一组数按照1, 1,1, 1,…的规律排列,求第n个数。
解析:观察这组数字,发现数字是1和 1交替出现。
当n为奇数时,第n个数为1;当n为偶数时,第n个数为 1。
可以用(-1)^(n + 1)来表示,当n = 1时,(-1)^(1+1)=1;当n = 2时,(-1)^(2 + 1)= 1。
二、图形规律1. 图形数量规律例1:用火柴棒搭三角形,搭1个三角形需要3根火柴棒,搭2个三角形需要5根火柴棒,搭3个三角形需要7根火柴棒,…,求搭n个三角形需要多少根火柴棒。
解析:搭1个三角形需要3根火柴棒,即2×1+1;搭2个三角形时,第二个三角形和第一个三角形共用一条边,所以需要3 + 2 = 5根火柴棒,即2×2+1;搭3个三角形时,第三个三角形和前面的三角形共用两条边,所以需要3+2×2 = 7根火柴棒,即2×3 + 1。
所以搭n个三角形需要2n+1根火柴棒。
例2:观察下列图形的点数规律:第1个图形有1个点;第2个图形有1 + 3 = 4个点;第3个图形有1+3 + 5 = 9个点;第4个图形有1+3+5 + 7 = 16个点;求第n个图形的点数。
十道初中数学找规律的题型及解题思路

十道初中数学找规律的题型及解题思路这里有10道初中数学找规律的题目,涵盖了常见的数列、图形等多种类型,希望能帮助学生更好地掌握找规律的技巧:数列找规律1.等差数列:1.1, 4, 7, 10, ... 下一个数是多少?2.100, 97, 94, ... 第10个数是多少?2.等比数列:1.2, 4, 8, 16, ... 第8个数是多少?2.81, 27, 9, ... 第6个数是多少?3.混合数列:1.1, 4, 9, 16, 25, ... 下一个数是多少?(提示:考虑每个数的平方)2.2, 5, 10, 17, ... 下一个数是多少?(提示:观察相邻两数的差)4.周期数列:1.1, 2, 3, 1, 2, 3, ... 第20个数是多少?2.A, B, C, A, B, C, ... 第100个数是多少?图形找规律图形的变化:1.一组图形,每个图形由小方块组成,观察图形的变化规律,画出下一个图形。
图形的旋转:1.一个图形不断旋转,观察旋转的规律,画出旋转后的图形。
图形的翻转:1.一个图形不断翻转,观察翻转的规律,画出翻转后的图形。
数字与图形结合数字与图形对应:1.一组图形,每个图形对应一个数字,找出数字与图形之间的对应关系。
图形中的数字规律:1.一个图形中包含多个数字,找出数字之间的规律。
综合题型1.数字和图形的综合:1.一组图形和数字交替出现,找出数字和图形之间的关系。
解题技巧:•观察:仔细观察数列或图形的变化规律,找出其中的共同点和差异点。
•比较:比较相邻的数或图形,找出它们的递增、递减或其他变化关系。
•联想:将题目与以前学过的知识联系起来,寻找解题思路。
•归纳:根据观察和比较的结果,归纳出一般性的规律。
•验证:将得到的规律代入后面的数或图形中进行验证,确保规律的正确性。
注意事项:•找规律题的答案可能不唯一,只要找到一种合理的规律即可。
•遇到困难时,可以尝试从不同的角度去观察和分析。
初一找规律经典题型(含部分答案)

初一找规律经典题型(含部分答案)初一数学规律题应用知识汇总有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
因此,将变量和序列号放在一起比较,就更容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索:一、基本方法——看增幅一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为:a1+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅。
然后再简化代数式a+(n-1)b。
例如,对于数列4、10、16、22、28……,求第n位数。
我们可以发现,从第二位数开始,每位数都比前一位数增加6,增幅都是6.因此,第n位数是4+(n-1)6=6n-2.二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
例如,古希腊数学家把数1,3,6,10,15,21,……,叫做三角形数,它们之间有一定的规律性。
要求第24个三角形数与第22个三角形数的差,我们可以通过求出第24个和第22个三角形数的值,再相减得到答案。
除了基本方法外,还可以用分析观察的方法求解。
例如,在一个面积为S的等边三角形中,我们将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形。
当n=5时,共向外作出了4个小等边三角形;当n=k时,共向外作出了k-2个小等边三角形。
中考规律类试题在素材选取、文字表述、题型设计等方面都别具一格,旨在考察学生的创新意识与实践能力。
找规律知识点文字总结

找规律知识点文字总结一、数列的规律在数列中,我们常常需要找到数列中的规律,进而可以推断出数列的通项公式。
在找规律时,我们可以根据数列中相邻项的关系、公差的规律、首项和末项的关系等来进行分析。
常见的数列有等差数列、等比数列、斐波那契数列等,它们的规律各不相同,需要我们对数列有深入的了解才能进行准确的推断。
1. 等差数列的规律等差数列是指数列中相邻两项之差是一个常数的数列,常用的表示方法为an=a1+(n-1)d。
其中,an表示数列的第n项,a1为首项,d为公差,n为项数。
在找等差数列的规律时,我们可以根据公差的规律来进行推断,一般来说,如果数列中相邻两项的差是一个常数,那么就可以判断它是等差数列。
另外,我们还可以通过首项和末项之间的关系来进行判断,例如首项和末项的和是数列项数的两倍减一。
2. 等比数列的规律等比数列是指数列中相邻两项之比是一个常数的数列,常用的表示方法为an=a1*r^(n-1)。
其中,an表示数列的第n项,a1为首项,r为公比,n为项数。
在找等比数列的规律时,我们可以根据相邻两项之比是一个常数的规律来进行推断。
另外,我们还可以通过首项和末项的关系来进行判断,例如首项和末项的乘积是公比的项数次方。
3. 斐波那契数列的规律斐波那契数列是指数列中每一项都是前两项之和的数列,常用的表示方法为an=an-1+an-2。
在找斐波那契数列的规律时,我们可以通过每一项都是前两项之和的规律来进行推断。
例如,我们可以利用递推公式来计算斐波那契数列的任意项,另外,还可以通过黄金分割比例来推断斐波那契数列的性质。
二、函数的规律函数是数学中一个非常重要的概念,它描述了数学世界中各种关系的规律。
通过找函数的规律,我们可以了解函数的性质和特点,进而可以解决各种问题。
常见的函数有线性函数、二次函数、指数函数、对数函数等,它们的规律各不相同,需要我们对函数有深入的了解才能进行准确的分析。
1. 线性函数的规律线性函数是指函数的图像是一条直线的函数,常用的表示方法为y=kx+b。
数学找规律公式大全

数学找规律公式大全一、数字规律。
1. 等差数列。
- 定义:如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列。
- 通项公式:a_n=a_1+(n - 1)d,其中a_n表示第n项的数值,a_1是首项(数列的第一项),n是项数,d是公差(相邻两项的差值)。
- 例如:数列1,3,5,7,·s,a_1=1,d = 2,那么第n项a_n=1+(n - 1)×2=2n - 1。
2. 等比数列。
- 定义:如果一个数列从第二项起,每一项与它的前一项的比值等于同一个常数,这个数列就叫做等比数列。
- 通项公式:a_n=a_1q^n - 1,其中a_n表示第n项的数值,a_1是首项,n是项数,q是公比(相邻两项的比值)。
- 例如:数列2,4,8,16,·s,a_1=2,q = 2,则第n项a_n=2×2^n - 1=2^n。
3. 数字规律中的其他常见类型。
- 平方数数列:1,4,9,16,·s,通项公式为a_n=n^2。
- 立方数数列:1,8,27,64,·s,通项公式为a_n=n^3。
- 斐波那契数列:1,1,2,3,5,8,·s,从第三项起,每一项都等于前两项之和,即a_n=a_n - 1+a_n - 2(n≥slant3)。
二、图形规律。
1. 点的规律。
- 在平面直角坐标系中,如果点的坐标呈现一定规律。
例如,点(1,1),(2,4),(3,9),(4,16)·s,横坐标为n,纵坐标为n^2。
2. 多边形边数与内角和的规律。
- 多边形内角和公式:(n - 2)×180^∘,其中n为多边形的边数。
例如三角形(n = 3)内角和为(3 - 2)×180^∘=180^∘;四边形(n = 4)内角和为(4 -2)×180^∘=360^∘。
3. 图形数量规律。
- 例如,用小棒摆三角形,摆1个三角形需要3根小棒,摆2个三角形需要5根小棒(共用一条边),摆3个三角形需要7根小棒。
初中数学之10大找规律方法总结

初中数学之10大找规律方法总结
找规律是数学研究过程中十分重要的一个环节,下面总结了初
中数学中常用的10种找规律方法,希望能够对同学们的研究有所
帮助。
1. 相邻两项间的关系:找出相邻两个数之间的规律,如公差、
倍数关系等。
2. 累加法:将所求的数字列出来累加,看其和与第几项相关。
3. 累乘法:将所求的数字列出来累乘,看其积与第几项相关。
4. 因式分解法:将数字进行因式分解,观察其因子,找出规律。
5. 奇偶性法:观察数字的奇偶性和结尾数字的规律。
6. 交错相加法:在一串数字中,用加减交替的方法,找出数字
之间的规律。
7. 格式法:观察数字的表达方式,如小数、分数等,找到其规律。
8. 取整型列举法:将数字取整后列举出来进行分析找规律。
9. 归纳法:根据前几项找出规律,得到通项公式,推导出后面
的答案。
10. 逆向思维法:找出已知答案与所求数的关系。
以上10种方法可以根据题目的不同特点和难度灵活组合使用,既可以单独使用其中一种方法,也可以多种方法结合使用,找出有
用的部分,最终得出正确答案。
希望以上总结能够帮助同学们更好地理解并掌握找规律的方法,提高数学解题能力。
初一找规律经典题型(含部分问题详解)

图1 图2 图3初一数学规律题应用知识汇总“有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索:一、基本方法——看增幅(一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n 个数可以表示为:a1+(n-1)b ,其中a 为数列的第一位数,b 为增幅,(n-1)b 为第一位数到第n 位的总增幅。
然后再简化代数式a+(n-1)b 。
例:4、10、16、22、28……,求第n 位数。
分析:第二位数起,每位数都比前一位数增加6,增幅都是6,所以,第n 位数是:4+(n-1)6=6n -2例1、已知一个面积为S 的等边三角形,现将其各边n (n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示).(1)当n = 5时,共向外作出了 个小等边三角形(2)当n = k 时,共向外作出了 个小等边三角形(用含k 的式子表示).例2、如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,……,则在第n 个图形中,互不重叠的三角形共有 个(用含n 的代数式表示)。
(二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差n =3 n =4 n =5 ……数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察的方法求出,方法就简单的多了。
初一找规律经典题带答案

初一找规律经典题带答案一、数字排列1、按照题目给出的规律,可以猜想1+3+5+7+…+2005+2007的值为1004×1004=xxxxxxx。
推广式子为1+3+5+7+9+…+(2n-1)+(2n+1)=n(2n+1)。
2、数列后两位应该填上22,因为每个数都是前两个数之和。
3、横线上的数字应该填13,因为每个数都是前两个数之和。
4、这串数的排列规律为1、2、3、2、3、4、3、4、5、4、5、6、…,即从1开始,每次增加1,到达一个峰值后再减少1.第100个数为13.二、几何图形变化1、实心球和空心球交替出现,每两个球中有一个实心球。
因此,2004个球中实心球的个数为1002个。
2、第一个图形是正方形,按照规律,每隔两个图形就循环一次□○△。
因此,第2008个图形是○。
三、数、式计算1、根据题目给出的等式,可以得出第5个等式为13+23+33+43+53=225.2、根据规律,1+2+3+…+n=(1+n)×n/2,因此1+2+3+…+99+100+99+…+3+2+1=2×(1+2+3+…+99)+100=.3、根据题目给出的规律,可以得出10+ =102×,因此a+b=22.规律发现:1.第n个图案中有白色地砖n-1块。
2.将正方形沿着对角线对折,可以得到两个直角三角形,其斜边长均为1.因此,将矩形纸片按照斜边长度从小到大排列,可以拼成一个直角三角形,其面积为1/2.根据等差数列求和公式,可以得到1/2×(1+1/4+1/9+…+1/n^2)=1/2×π^2/6=π^2/12.4.将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线)。
继续对折,每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕。
那么对折四次可以得到几条折痕?如果对折n次,可以得到多少条折痕?答案:对折四次可以得到15条折痕,对折n次可以得到2^n-1条折痕。
四年级奥数:找规律

找规律(一)知识要点在三年级的时候我们已经学习了一些简单算式规律,有些算式看上去很复杂,很难找出它们的排列规律。
但我们可以从相隔数的关系、排列的变化等找出它们的规律。
经典范例同学们,有一个阿拉伯的故事:在很久很久以前的一个王国里,老国王为了选择一个头脑聪明的人作为接班人,就出了一道数学题。
谁能解出这道题谁就是老国王的继承人。
于是全国人都放下了手中的事情来解这道题。
奇怪的是没有一个人能解出来。
题目时这样的:在下列括号内填上适当的数5、8、13、21、34、()、()你们也来试试吧?例1 找出下列各列数的规律,并按此规律在()内填上适当的数。
(1)1、2、2、3、3、4、()、()(2)4、6、10、16、26、()、()(3)15、6、13、7、11、8、()、()思路解析:(1)把这列数按照(1、2)、(2、3)、(3、4)分组(2)从第三项10开始没项都等于前两项和。
(3)奇数项是15、13、11----,偶数项是6、7、8解:(1) 1、2、2、3、3、4、(4)、(5)(2)4、6、10、16、26、(42)、(68)(3)15、6、13、7、11、8、(9)、(9)例2 根据下列数的变化规律,填出括号里的数12 43 6 94 8 12 16() 10 ()() 25()( ) ()()24 ()()思路解析:最左的一斜列式按照1、2、3、4、5、6、---规律排列的;每一行后面你的数依次是第一个数的2倍、3倍、4倍、5倍-----解:12 43 6 94 8 12 16(5) 10 (15)(20) 25(6)(12) (18) 24(30(36)例3 观察下列算式,再填出正确的数(1)123456789×9=111111111 (2)123456789×18=222222222(3)123456789×()×9=333333333 (4)123456789×()=444444444(5)123456789×5×9=()(6)123456789×54=()思路解析:在这组算式中,第一个因数不变,第二因数与积都在变化,第二因数扩大几倍,积就扩大几倍。
中考数学找规律经典题目

1 11 1 1 1 1 11 1 12 3 3 4 4 5 5 10 a 10 AC 1PC2B 2B 1B 3C 3CB找规律问题1. 阳阳和明明玩上楼梯游戏,规定一步只能上一级或二级台阶,玩着玩着两人发现:当楼梯的台级数为一级、二级、三级、……逐步增加时,楼梯的上法依次为:1,2,3,5,8,13,21,……(这就是著名的斐波拉契数列).请你仔细观察这列数的规律后回答:上10级台阶共有 种上法.2.把若干个棱长为a 的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层共有4个立方体, 摆三层共有10个立方体,那么摆五层共有 个立方体.3.下面由“*”拼出的一列形如正方形的图案,每条边上(包括两个顶点)有n (n>1)个“*”,每个图形“*”的总数是S :n=2,S=4 n=3,S=8 n=4,S=12 n=5,S=16 通过观察规律可以推断出:当n=8时,S= .4.下面由火柴杆拼出的一列图形中,第n 个图形由n 个正方形组成: ……n=1 n=2 n=3 n=4 …… 通过观察发现:第n 个图形中,火柴杆有 根. 5.已知P 为△ABC 的边BC 上一点,△ABC 的面积为a , B 1、C 1分别为AB 、AC 的中点,则△PB 1C 1的面积为4a, B 2、C 2分别为BB 1、CC 1的中点,则△PB 2C 2的面积为163a,B 3、C 3分别为B 1B 2、C 1C 2的中点,则△PB 3C 3的面积为647a,按此规律……可知:△PB 5C 5的面积为 . 6.如图的三角形数组是我国古代数学家杨辉发现的, 称为杨辉三角形.根据图中的数构成的规律可得: 图中a 所表示的数是 . 7.观察下列等式:13+23=32;13+23+33=62;13+23+33+43=102……;根据前面各式规律可得:13+23+33+43+53+63+73+83= .8.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第 1个图案需 7根火柴,第 2 个图案需 13 根火柴,…,依此规律,第 11 个图案需( )根火柴.A. 156B. 157C. 158D. 159* * * * * * * * * * * * * * ** * * * * * * * * * * * ** * * * * ** * ** * * • • • • • •• • •• • • • • • • • • • • • • • • • • • • • • • • •9.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M 与m 、n 的关系是A . M =mnB . M =n (m +1)C .M =mn +1D .M =m (n +1)10.如图9所示,图中每一个小方格的面积为1,则可根据面积计算得到如下算式:()127531-+⋅⋅⋅++++n = . (用n 表示,n 是正整数)2n -15 12 347 1 1 2 43 3 n图911.用大小相同的小三角形摆成如图所示的图案,按照这样的规律摆放,则第n 个图案中共用小三角形的个数是 .12.当白色小正方形个数n 等于1,2,3…时,由白色小正方形和黑色小正方形组成的图形分别如图所示.则第n 个图形中白色小正方形和黑色小正方形的个数总和等于________.(用n 表示,n 是正整数)13.观察下列图形:(3)(2)(1)C 3B 3A 3A 2C 1B 1A 1C B AC 2B 2B 2C 2A B C A 1B 1C 1A 2C 1B 1A 1C B A … 图4它们是按一定规律排列的,依照此规律,第9个图形中共有 个14. 如图4,在图(1)中,A 1、B 1、C 1分别是△ABC 的边BC 、CA 、AB 的中点,在图(2)中,A 2、B 2、C 2分别是△A 1B 1C 1的边B 1C 1、C 1 A 1、 A 1B 1的中点,…,按此规律,则第n 个图形中平行四边形的个数共有 个.15.挪动珠子数(颗)2 3 4 5 6 …… 对应所得分数(分)26122030……则挪动的珠子数为 颗16.如图,菱形ABCD 中,AB =2 ,∠C =60°,菱形ABCD 在直线l 上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作菱形中心O 所经过的路径总长为(结果保留π) .17.如图:已知AB =10,点C 、D 在线段AB 上且AC =DB =2; P 是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ,连结EF ,设EF 的中点为G ;当点P 从点C 运动到点D 时,则点G 移动路径的长是________.318.(6分)观察下面的变形规律:211⨯ =1-12; 321⨯=12-31;431⨯=31-41;…… 解答下面的问题:ABD EF GO B C(第16题) lD⑴ 1+8=? 1+8+16=? ⑵⑶ 1+8+16+24=? 第20题图 …… (1)若n 为正整数,请你猜想)1(1+n n = ;(2)证明你猜想的结论; (3)求和:211⨯+321⨯+431⨯+…+201020091⨯ . 19. 右图为手的示意图,在各个手指间标记字母A 、B 、C 、D 。
(完整版)找规律(含答案)

练习一:先找出下列各列数的排列规律,然后在括号里填上适当的数。
年级:日期:(1)2,6,10,14,(),22,26找规律(2)3,6,9,12,(),18,21专题简介:(3)33,28,23,(), 13,(),3 观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规(4)55,49,43,(), 31,(),19律,在一般情况下,我们可以从以下几个方面来找规律:(5)3,6,12,(),48,(),192 1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;(6)2,6,18,(),162,()2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;(7)128,64,32,(),8,(),23.要善于从整体上把握数据之间的联系,从而很快找出规律;(8)19,3,17,3,15,3,(),(),11,34.数之间的联系往往可以从不同的角度来理解,只要言之有理,所例 2:先找出下列数排列的规律,然后在括号里填上适当的数。
得出的规律都可以认为是正确的。
1,2,4,7,(),16,22例 1:先找出下列数排列的规律,并根据规律在括号里填上适当的数。
分析:在这列数中,前 4 个数每相邻的两个数的差依次是1,2,3。
1 ,,,,(),,19由此可以推算 7 比括号里的数少4,括号里应填: 7+4=11。
4 7 10 16分析:在这列数中,相邻的两个数的差都是 3,即每一个数加上 3 都经验证,所填的数是正确的。
等于后面的数。
根据这一规律,括号里应填的数为:应填的数为: 7+4=11 或 16-5=11 10+3=13 或 16-3=13 练习二:先找出下列数排列的规律,然后在括号里填上适当的数。
像上面按照一定的顺序排列的一串数叫做数列。
(1)10,11,13,16,20,(),31(2)1,4,9,16,25,(),49,64(3)3,2,5,2,7,2,(),(),11,2(4)53,44,36,29,(),18,(),11,9,8(5)81,64,49,36,(),16,(),4,1,0(6)28,1,26,1,24,1,(),(),20,1(7)30,2,26,2,22,2,(),(),14,2(8)1,6,4,8,7,10,(),(),13,14例 3:先找出规律,然后在括号里填上适当的数。
找规律试题几道经典题目含答案

数学试题分类汇编一一找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有 8个小圆圈,第100个图中有 ___________ 个小圆圈.(1) (2) (3)2、找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 _______ 个菱形,第n 幅图中有 个菱形.C.::> <沐〉<3:«「> …二•…123n3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 ________ 枚(用含n 的代数式表示)4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为 ________________•••••第2个图 第3个图L3 42 4 6 苦3 6 9 1343 12 Id---1821 C71第1个图5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个 2 2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3 3的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个4 4的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1 0 10的正方形图案,则其中完整的圆共有个--:l6、如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子______________ 枚(用含有n的代数式表示,并写成最简形式).0^0 O • • O O • • • O O O OO O O OO • • • OO O O O O7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第 334个图形需 ______ 根火柴棒。
run fuxq 厂ajb? ic )8将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排, 从左到右第m 个数,如(4 ,2)表示实数9,则表示实数17的有序实数对是O OO-2 3 -4 5 -6 7 -8 9 -1011、下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,一 4101 3□ 2 5 9 口 8第一排 第二排 第三排 第四排9、如图 2,用n 表示等边三角形边上的小圆圈,f (n )表示这个三角形中小圆圈的总数,那么 f (n )和n 的关系是10、观察图4的三角形数阵, 则第 50行的最后一个数是( )第n 个图案中白色正方形的个数为12、观察下列各式:13=1213 23 = 32 13 23 32 = 6213 23 33 4亠102猜想:13 23 33 ||II|| 103 二 _____________ .答案解析:1解析:n=1时,m=5 n 再每增加一个数时,m 就增加3个数.解答:根据所给的具体数据,发现:8=5+3, 1仁5+3X 2, 14=5+3X 3,….以此类推,第 n 个圈中,m=5+3( n-1 ) =3n+2.2解析:分析可得:第1幅图中有1X2-1=1个,第2幅图中有2X 2-1=3个,第3幅图中有3X2-1=5个,…, 故第n 幅图中共有2n-1个3解析:在4的基础上,依次多3个,得到第n 个图中共有的棋子数.观察图形,发现:在4的基础上,依次多3个.即第n 个图中有4+3 (n-1) =3n+1 .当n=6时,即原 式=19 .故第6个图形需棋子19枚4解析:此题只要找出截取表一的那部分,并找出其规律即可解. 解答:解:表二截取的是其中的一列:上下两个数字的差相等,所以a=15+3=18 .表三截取的是两行两列的相邻的四个数字:右边一列数字的差应比左边一列数字的差大 1,所b=24+25-20+1=30 .表四中截取的是两行三列中的 6个数字:18是3的6倍,则c 应是4的7倍,即28. 故选D.第一个认真观察表格,熟知各个数字之间的关系:第一列是 1 , 2, 3,…;第二列是对应第一列的2倍;等三列是对应第一列的3倍5解析:据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方,每四个小正方形组成一个完整的圆,从而可得这样的圆是大正方形边长减1的平方,从而可得若这样铺成一个10X10的正方形图案,则其中完整的圆共有102+ (10-1 )2=181 个.解答:解:分析可得完整的圆是大正方形的边长减1的平方,从而可知铺成一个10X10的正方形图案中,完整的圆共有102+ (10-1)2=181个.点评:本题难度中等,考查探究图形的规律.本题也只可以直接根据给出的四个图形中计数出的圆的个数,找出数字之间的规律得出答案.6解析:解:第1个正方形图案有棋子共32=9枚,其中黑色棋子有12=1枚,白色棋子有(32-12)枚; 第2个正方形图案有棋子共42=16枚,其中黑色棋子有22=4枚,白色棋子有(42-22)枚;…由此可推出想第n个图案的白色棋子数为(n+2)2-n2=4 (n+1).故第n个图案的白色棋子数为(n+2)2-n2=4 (n+1).点评:根据图形提供的信息探索规律,是近几年较流行的一种探索规律型问题.解决这类问题首先要从简单图形入手,抓住随着编号”或序号”曾加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论7解析:根据题意分析可得:搭第1个图形需12根火柴;搭第2个图形需12+6X1=18根;搭第3个图形需12+6X2=24根;搭第n个图形需12+6 (n-1)=6n+6根.解答:解:搭第334个图形需6X334+6=2010根火柴棒8解析:寻找规律,然后解答.每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.解答:解:观察图表可知:每排的数字个数就是排数;且奇数排从左到右,从小到大,而偶数排从左到右,从大到小.实数15=1+2+3+4+5,则17在第6 排,第5个位置,即其坐标为(6,5).故答案填:(6,5).对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.一 1 29解析:根据题意分析可得:第n行有n个小圆圈.故f (n)和n的关系是?(n)= -(n +n).(n —l)xn10解析:根据题意可得:第n 行有n 个数;且第n 行第一个数的绝对值为-—+1,最后一个数的(n —1)X71绝对值为 —2— +n ;奇数为正,偶数为负;故第50行的最后一个数是1275 .奇数为正,偶数为负, 第50行的最后一个数是1275第一个图中白色正方形的个数为 3X 3-1 ; 第二个图中白色正方形的个数为 3X5-2 第三个图中白色正方形的个数为 3X 7-3 ;当其为第n 个时,白色正方形的个数为 3 (2n+1) -n=5n+312解析:根据所给的等式,可以发现右边的底数是前边的底数的和,指数是平方,则最后的底数是 1+2+3+..+10=5 X 11=55,则原式=552.解答:解:根据分析最后的底数是1+2+3+..+10=5 X 11=55,则原 式=552. 故答案552解答:解:第n 行第一个数的绝对值为 (n —ljxn""2+1 , 最后一个数的绝对值为(n —ljxn3 +n ,。
找规律方法与技巧

找规律方法与技巧
1. 嘿,找规律啊,那可得好好睁大眼瞧!比如说数字1、3、5、7、9,这不是很明显的奇数序列嘛!你看,只要细心观察,规律不就出来啦。
2. 哇塞,找规律有时候就像玩捉迷藏!像图形的变化,方的、圆的、三角的,总有它的特点在里面呀,你得把它揪出来!比如那些按颜色交替的图形,这规律不就显而易见了嘛。
3. 哎呀呀,找规律可别马虎!看那一堆物品的排列,大的小的高的矮的,这不就能发现个子高矮的规律嘛!就像排队的小朋友,谁高谁矮一目了然呀。
4. 嘿哟,找规律也得有点小聪明嘞!比如音乐的节奏,哒哒哒,咚咚咚,节奏的快慢不就是规律嘛!这不就跟心跳一样,有快有慢有规律呀。
5. 哇哦,找规律要细心又耐心呀!像季节的更替,春夏秋冬,这多明显的规律呀!你难道感觉不到每个季节的不同嘛。
6. 哈哈,找规律可有意思啦!比如车来车往,一辆红的一辆黑的,颜色的规律就出来啦!这就像彩虹的颜色一样丰富多彩呀。
7. 哎哟喂,找规律不难呀!像走路的脚步,左一步右一步,这不就是左右的规律嘛!就跟跳舞的步伐似的。
8. 嘿嘿,找规律只要用心就会有发现!像星星的闪烁,一亮一暗,这闪烁的规律多好玩呀!就好像在跟我们眨眼睛呢。
总之,找规律就是要多留意身边的事物,善于观察,规律自然就会被你找到啦!。
找规律小学奥数题100道及答案(完整版)

找规律小学奥数题100道及答案(完整版)题目1:1,3,5,7,9,()答案:11(相邻两个数的差为2,依次递增)题目2:2,4,6,8,10,()答案:12(相邻两个数的差为2,依次递增)题目3:5,10,15,20,25,()答案:30(相邻两个数的差为5,依次递增)题目4:1,4,9,16,25,()答案:36(分别是1、2、3、4、5 的平方,下一个是 6 的平方)题目5:3,6,9,12,15,()答案:18(相邻两个数的差为3,依次递增)题目6:1,2,4,8,16,()答案:32(后一个数是前一个数的2 倍)题目7:2,6,12,20,30,()答案:42(相邻两个数的差依次为4、6、8、10、12)题目8:1,1,2,3,5,8,()答案:13(前两个数相加等于后一个数)题目9:3,4,7,11,18,()答案:29(前两个数相加等于后一个数)题目10:1,3,7,13,21,()答案:31(相邻两个数的差依次为2、4、6、8、10)题目11:2,5,10,17,26,()答案:37(相邻两个数的差依次为3、5、7、9、11)题目12:9,16,25,36,()答案:49(分别是3、4、5、6 的平方,下一个是7 的平方)题目13:1,8,27,64,()答案:125(分别是1、2、3、4 的立方,下一个是5 的立方)题目14:5,12,19,26,33,()答案:40(相邻两个数的差为7,依次递增)题目15:3,8,15,24,()答案:35(相邻两个数的差依次为5、7、9、11)题目16:2,3,5,8,13,()答案:21(前两个数相加等于后一个数)题目17:1,4,10,22,46,()答案:94(相邻两个数的差依次为3、6、12、24、48)题目18:1,5,14,30,55,()答案:91(相邻两个数的差依次为4、9、16、25、36)题目19:2,6,18,54,()答案:162(后一个数是前一个数的3 倍)题目20:7,14,28,56,()答案:112(后一个数是前一个数的2 倍)题目21:1,2,6,24,120,()答案:720(后一个数依次是前一个数乘2、3、4、5、6)题目22:3,5,9,17,33,()答案:65(相邻两个数的差依次为2、4、8、16、32)题目23:1,3,8,19,42,()答案:89(相邻两个数的差依次为2、5、11、23、47,这些差依次增加3、6、12、24)题目24:2,4,10,28,82,()答案:244(相邻两个数的差依次为2、6、18、54、162,后一个差是前一个差的 3 倍)题目25:5,9,17,33,65,()答案:129(相邻两个数的差依次为4、8、16、32、64)题目26:1,4,27,256,()答案:3125(分别是1、2、3、4 的1、2、3、4 次方,下一个是5 的 5 次方)题目27:1,6,21,66,201,()答案:606(相邻两个数的差依次为5、15、45、135、405,后一个差是前一个差的3 倍)题目28:3,8,15,24,35,()答案:48(相邻两个数的差依次为5、7、9、11、13)题目29:2,3,7,18,47,()答案:123(7 = 3×2 + 1,18 = 7×2 + 4,47 = 18×2 + 11,下一个数应为47×2 + 16 = 123)题目30:1,2,5,14,41,()答案:122(相邻两个数的差依次为1、3、9、27、81,后一个差是前一个差的3 倍)题目31:2,5,11,23,47,()答案:95(相邻两个数的差依次为3、6、12、24、48)题目32:4,9,16,25,36,()答案:49(分别是2、3、4、5、6 的平方,下一个是7 的平方)题目33:6,12,20,30,42,()答案:56(相邻两个数的差依次为6、8、10、12、14)题目34:1,3,7,15,31,()答案:63(相邻两个数的差依次为2、4、8、16、32)题目35:3,9,27,81,()答案:243(后一个数是前一个数的3 倍)题目36:5,13,25,41,()答案:61(相邻两个数的差依次为8、12、16、20)题目37:2,8,32,128,()答案:512(后一个数是前一个数的4 倍)题目38:7,16,29,46,()答案:67(相邻两个数的差依次为9、13、17、21)题目39:1,5,13,25,()答案:41(相邻两个数的差依次为4、8、12、16)题目40:6,18,54,162,()答案:486(后一个数是前一个数的3 倍)题目41:8,18,32,50,()答案:72(相邻两个数的差依次为10、14、18、22)题目42:1,4,13,40,()答案:121(相邻两个数的差依次为3、9、27、81)题目43:3,10,21,36,()答案:55(相邻两个数的差依次为7、11、15、19)题目44:5,15,45,135,()答案:405(后一个数是前一个数的3 倍)题目45:2,6,14,30,()答案:62(相邻两个数的差依次为4、8、16、32)题目46:9,25,49,81,()答案:121(分别是3、5、7、9 的平方,下一个是11 的平方)题目47:7,19,37,61,()答案:91(相邻两个数的差依次为12、18、24、30)题目48:4,12,36,108,()答案:324(后一个数是前一个数的3 倍)题目49:1,6,15,28,()答案:45(相邻两个数的差依次为5、9、13、17)题目50:8,20,36,56,()答案:80(相邻两个数的差依次为12、16、20、24)题目51:3,11,23,39,()答案:59(相邻两个数的差依次为8、12、16、20)题目52:6,15,35,77,()答案:143(相邻两个数的差依次为9、20、42、66,差依次增加11、22、24)题目53:2,9,28,65,()答案:126(分别是1、2、3、4 的立方加1,下一个是5 的立方加1)题目54:1,7,19,37,()答案:61(相邻两个数的差依次为6、12、18、24)题目55:5,16,29,46,()答案:67(相邻两个数的差依次为11、13、17、21)题目56:3,12,27,48,()答案:75(相邻两个数的差依次为9、15、21、27)题目57:7,18,33,52,()答案:77(相邻两个数的差依次为11、15、19、25)题目58:2,10,30,68,()答案:130(相邻两个数的差依次为8、20、38、62,差依次增加12、18、24)题目59:4,15,32,55,()答案:84(相邻两个数的差依次为11、17、23、29)题目60:6,21,42,72,()答案:106(相邻两个数的差依次为15、21、30、34)题目61:1,9,25,49,()答案:81(分别是1、3、5、7 的平方,下一个是9 的平方)题目62:8,24,48,80,()答案:120(相邻两个数的差依次为16、24、32、40)题目63:3,13,31,57,()答案:91(相邻两个数的差依次为10、18、26、34)题目64:5,19,41,71,()答案:105(相邻两个数的差依次为14、22、30、34)题目65:2,11,26,47,()答案:76(相邻两个数的差依次为9、15、21、29)题目66:9,27,51,81,()答案:117(相邻两个数的差依次为18、24、30、36)题目67:7,17,33,55,()答案:83(相邻两个数的差依次为10、16、22、28)题目68:4,14,30,52,()答案:78(相邻两个数的差依次为10、16、22、26)题目69:6,18,36,60,()答案:90(相邻两个数的差依次为12、18、24、30)题目70:1,11,27,51,()答案:81(相邻两个数的差依次为10、16、24、30)题目71:5,17,33,53,()答案:77(相邻两个数的差依次为12、16、20、24)题目72:3,14,31,58,()答案:91(相邻两个数的差依次为11、17、27、33)题目73:8,22,42,70,()答案:106(相邻两个数的差依次为14、20、28、36)题目74:2,13,30,53,()答案:84(相邻两个数的差依次为11、17、23、31)题目75:9,29,55,91,()答案:133(相邻两个数的差依次为20、26、36、42)题目76:7,20,39,64,()答案:95(相邻两个数的差依次为13、19、25、31)题目77:4,16,36,64,()答案:100(分别是2、4、6、8 的平方,下一个是10 的平方)题目78:3,15,33,57,()答案:87(相邻两个数的差依次为12、18、24、30)题目79:6,22,44,74,()答案:110(相邻两个数的差依次为16、22、30、36)题目80:1,13,29,53,()答案:89(相邻两个数的差依次为12、16、24、36)题目81:5,21,41,67,()答案:99(相邻两个数的差依次为16、20、26、32)题目82:8,26,50,82,()答案:118(相邻两个数的差依次为18、24、32、36)题目83:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目84:7,23,45,73,()答案:107(相邻两个数的差依次为16、22、28、34)题目85:2,14,32,56,()答案:88(相邻两个数的差依次为12、18、24、32)题目86:9,31,59,95,()答案:139(相邻两个数的差依次为22、28、36、44)题目87:6,24,48,84,()答案:126(相邻两个数的差依次为18、24、36、42)题目88:1,15,33,57,()答案:87(相邻两个数的差依次为14、18、24、30)题目89:5,23,47,77,()答案:113(相邻两个数的差依次为18、24、30、36)题目90:8,28,52,82,()答案:118(相邻两个数的差依次为20、24、30、36)题目91:3,19,41,69,()答案:105(相邻两个数的差依次为16、22、28、36)题目92:7,27,51,81,()答案:117(相邻两个数的差依次为20、24、30、36)题目93:4,18,38,66,()答案:100(相邻两个数的差依次为14、20、28、34)题目94:6,26,50,80,()答案:116(相邻两个数的差依次为20、24、30、36)题目95:2,16,36,60,()答案:90(相邻两个数的差依次为14、20、24、30)题目96:9,33,63,99,()答案:141(相邻两个数的差依次为24、30、36、42)题目97:8,28,56,92,()答案:136(相邻两个数的差依次为20、28、36、44)题目98:5,21,43,71,()答案:105(相邻两个数的差依次为16、22、28、34)题目99:3,17,37,67,()答案:107(相邻两个数的差依次为14、20、30、40)题目100:7,25,49,79,()答案:115(相邻两个数的差依次为18、24、30、36)。
找规律试题几道经典题目(含答案)--2012116
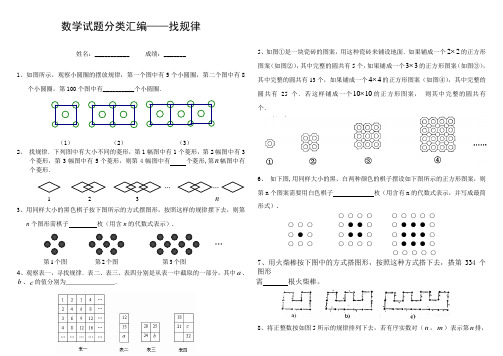
数学试题分类汇编——找规律姓名:___________ 成绩:_______1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有__________个小圆圈.(1) (2) (3) 2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为______________.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要用白色棋子 枚(用含有n 的代数式表示,并写成最简形式).○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○ ○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○ ○ ○ ○ ○ ○ 7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需 根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排,1 2 3n … … 第1个图 第2个图 第3个图 …从左到右第m个数,如(4,2)表示实数9,则表示实数17的有序实数对是.9、如图2,用n表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n的关系是10、观察图4的三角形数阵,则第50行的最后一个数是()1-2 3-4 5 -67 -8 9 -10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(2009年江苏省)下面是按一定规律排列的一列数:
第1个数:11122-⎛⎫-+ ⎪⎝⎭; 第2个数:2311(1)(1)1113234⎛⎫⎛⎫---⎛⎫-++
+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭
; 第3个数:234511(1)(1)(1)(1)11111423456⎛⎫⎛⎫⎛⎫⎛⎫
-----⎛⎫-++
+++ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭
;…… 第n 个数:232111(1)(1)(1)111112342n n n -⎛⎫⎛⎫⎛⎫
----⎛⎫-++++ ⎪⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭
.
那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是( )
A .第10个数
B .第11个数
C .第12个数
D .第13个数 【答案】A 2.(2009年重庆)观察下列图形,则第n 个图形中三角形的个数是( )
A .22n +
B .44n +
C .44n -
D .4n
【答案】D .
3.(2009年河北)古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”. 从图7中可以发现,任何一个大于1 的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
A .13 = 3+10
B .25 = 9+16
C .36 = 15+21
D .49 = 18+31
【答案】C
4.(2009武汉)14.将一些半径相同的小圆按如
图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.
【答案】46
5.(2009重庆綦江)观察下列等式:
221.4135-=⨯; 222.5237-=⨯; 223.6339-=⨯ 224.74311-=⨯;…………
则第n (n 是正整数)个等式为________. 【答案】2
2
(3)3(23)n n n +-=⨯+
6.(2009年娄底)王婧同学用火柴棒摆成如下的三个“中”字形图案,依此规律,第n 个
“中”字形图案需 根火柴棒.
【答案】6n +3或9+6(n -1)
第1个图形
第2个图形
第3个图形
第4个图形
…
……
第1个 第2个 第3个
4=1+3 9=3+6
16=6+10
图7
…
7(2009恩施市)观察数表
根据表中数的排列规律,则字母A 所表示的数是____________. 【答案】-10 8.(2009年广西南宁)正整数按图8的规律排列.请写出第20行,第21列的数字 .
【答案】420
9.(2009年牡丹江市)有一列数12
34251017--,,
,,…,那么第7个数是 .【答案】750
- 10.(2009年益阳市)图6是一组有规律的图案,第1个 图案由4个基础图形组成,第2
个图案由7个基础图形组成,……,第n (n 是正整数)个图案中由 个基础图形组成.
-
【答案】3n+1
11.(2009年济宁市)观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个 . 【答案】121 第一行 第二行 第三行 第四行 第五行 第一列 第二列
第三列 第四列 第五列 1 2 5 10 17 ... 4 6 11 18 ... 9 8 7 12 19 ... 16 15 14 13 20 (25)
23 22
21
…
…… 图8
1 1 1 1
1 1 1 1 1-1-1-6-6-2
-3-5-4-
4-3 6 10 15 15 5 A 20- 1 图6
(1) (2)
(3) ……
第1个第2个第3个
12.(2009年广西钦州)一组按一定规律排列的式子:-2
a ,52a ,-83a ,11
4a ,…,(a ≠0)
则第n 个式子是_▲_(n 为正整数). 【答案】31(1)n n a
n
--
13.(2009年广西梧州)图(3)是用火
柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = ★ . (用n 的代数式表示s ) 【答案】2(1)n n +
14.(2009肇庆)15.观察下列各式:
1
11113
23⎛⎫
=- ⎪⨯⎝⎭
,111135235⎛⎫=- ⎪⨯⎝⎭,111157257⎛⎫
=- ⎪⨯⎝⎭
,…,根据观察计算:1111
133557(21)(2
1)
n n ++++⨯⨯⨯-+ = .(n 为正整数) 【答案】
21
n n + 15.(2009年咸宁市)如图所示的运算程序中,若开始输入的x 值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,……第2009次输出的结果为___________. 【答案】3
16.(2009年广东省)用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则
第(3)个图形中有黑色瓷砖 __________块,第n 个图形中需要黑色瓷砖__________块(用含n 的代数式表示).
【答案】10,31n +
17.(2009年山西省)下列图案
是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第n 个图中所贴
剪纸“○”的个数为 .
【答案】23+n
18.(2009年铁岭市)如图所示,把
同样大小的黑色
棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是 .
……
n =1 n =2
n
=3
(1) (2) (3) ……
……
(1)
(2)
(3)
【答案】(2)n n +或2
2n n +或2(1)1n +-
19.(2009年青海)观察下面的一列单项式:x ,2
2x -,
34x ,48x -,…根据你发现
的规律,第7个单项式为 ;第n 个单项式为 【答案】7
64x ;1(2)n n x --
20.(2009年龙岩)观察下列一组数:21,43,65,8
7,…… ,它们是按一定规律排列的. 那
么这一组数的第k 个数是 .【答案】
k
k 21
2- 34.(2009年抚顺市)观察下列图形(每幅图中最小..的三角形都是全等的),请写出第n 个图中最小..的三角形的个数有 个.
20. (2009年
梅州市)如图5,
每一幅图中有
若干个大小不
同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第4幅图中有 个,第n 幅图中共有 个. 22.(2009年台州市)将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则
①n = ;②第i 行第j 列的数为 (用i ,j 表示).
第1列
第2列
第3列
… 第n 列 第1行 1 2 3 … n
第2行 1+n 2+n 3+n … n 2 第3行 12+n
22+n
32+n
… n 3
…
…
…
…
…
…
【答案】10,1010-+j i (第一空2分,第二空3分;答j i +-)1(10给3分,答j
i n +-)1(给2分)
第1个图 第2个图 第3个图 第4个图
… … 第1幅 第2幅 第3幅 第n 幅 图
5。
