统计热力学基础
三章统计热力学基础

(
nx2 a2
n2y b2
nz2 c2
)
振动:
1
εv
(v
)hν 2
转动:
εr
J(J
1)
h2 8π 2 I
十一、配分函数 q 的分离:
q = qn qe qtqvqr
这是配分函数的重要性质。
十二、利用配分函数 q 直接计算体系的宏观性质
热力学函数表达式:
F -kBT lnqN
F
-kBT
一维: 二维:
qt
(
2πmk h2
BT
)1/2
l
qt
2ππmBT h2
A
三维:
qt
(
2ππmBT h2
)3/2V
2. 振动:
双原子分子
qv
e hν / 2kBT 1 e hν / kBT
e Θv / 2T 1 eΘv /T
线型多原子
Θv hν Θv为振动特征温度 k
B
3n5 hνi / 2kBT
故玻尔兹曼分布即为宏观平衡分布。
在 A、B 两个能级上粒子数之比:
A / kBT
N g e A
A
B / kBT
N g e B
B
玻色-爱因斯坦统计*;(如空腔辐射的频率分布)
Ni
gi e i
1
( 1 / kBT )
费米-狄拉克统计*(金属半导体中的电子分布)
Ni
gi e i
1 Ni
• 由 gi >> Ni e i 1 >> 1 e i 1 e i
• 当温度不太高或压力不太高时,上述条件容易满足。
• 此时玻色-爱因斯坦及费米-狄拉克统计可还原为玻尔
统计热力学基础

统计热力学基础教学目的与要求:通过本章的教学使学生初步了解统计热力学的基本研究方法,各种独立子系统的微观状态数的求法,不同系统的统计规律,系统的各热力学函数的表示式,配分函数的计算,固体的热容理论导出的基本思路。
重点与难点:统计热力学的基本研究方法,不同系统的微观状态数的计算,玻尔兹曼分布律的含义,系统的热力学函数的表示式,配分函数的计算,不同的固体热容理论的基本方法。
概论统计热力学的研究任务和目的统计力学的研究对象是大量微观粒子所构成的宏观系统。
从这一点来说,统计热力学和热力学的研究对象都是一样的。
但热力学是根据从经验归纳得到的四条基本定律,通过演绎推理的方法,确定系统变化的方向和达到平衡时的状态。
由于热力学不管物质的微观结构和微观运动形态,因此只能得到联系各种宏观性质的一般规律,而不能给出微观性质与宏观性质之间的联系。
而统计热力学则是从物质的微观结构和基本运动特性出发,运用统计的方法,推导出系统的宏观性质,和变化的可能方向。
统计力学的研究方法是微观的方法,它根据统计单位(微粒)的力学性质如速度、动量、位置、振动、转动等,用统计的方法来推求系统的热力学性质,例如压力、热容、熵等热力学函数。
统计力学建立了体系的微观性质和宏观性质之间的联系。
从这个意义上,统计力学又可称为统计热力学。
相对于热力学,统计力学对系统的认识更深刻,它不但可以确定系统的性质,变化的方向和限度,而且还能确定系统的性质的微观根源,这一点要比热力学要深刻。
对于简单系统,应用统计热力学的方法进行处理,其结果是令人满意的。
当然统计热力学也有自身的局限性,由于统计力学要从微观粒子的基本运动特性出发,确定系统的状态,这就有一个对微观粒子的运动行为的认识问题。
由于人们对于物质结构的认识不断深化,不断地修改充实物质结构的模型,所对统计理论和统计方法也要随之修改,所以统计理论是一种不断发展和完善的。
同时模型本身也有近似性,所以由此得到的结论也有近似性。
第六章统计热力学基础

量子统计
F-D统计
Fermi-Dirac
(费米-狄拉克统计)
B-E 统计
Bose-Einstein
(玻色-爱因斯坦统计)
量子力学按照全同粒子波函数重叠后呈现的不同特征将自然 界的微观粒子分为费米子和玻色子两类:费米子服从泡利不 相容原理;玻色子不受泡利原理的限制。
第六章 统计热力学初步
——统计体系分类
cba c
1 3h / 2 abc
b
0 h / 2
ab ac bc a
微观状态的编号 1 2 3 4 5
分布
Ⅰ
Ⅱ
各分布的微观 状态数
1
3
ba c cc a ab b 67 8
Ⅲ
6
ba ab cc 9 10
tX N !/ ni !
i
X tX
P Ⅲ=6/10
最概然分布(最可几分布)
6-第2 六麦章克斯韦统-计玻尔热兹力曼统学计初步
——玻兹曼统计
定位体系的最概然分布:
粒子数 N,体积 V,总能量 U 的孤立体系
能级 能量 简并度 分布x 分布y
1
1
g1
n1
n1’
…
2
2
g2
n2
n2’
…
...
…………
…
i
i
gi
ni
ni’
…
满足条件: ni N
i
nii U
i
别?
最概然分布的微观状态数随粒子数增加而 ,该
分布出现的概率随粒子数增加而
。(增大或者
减小)
课本P273,习题2. (排列组合)
第六章 统计热力学初步
统计热力学基础

(3)统计热力学基本假设 统计热力学基本假设是:当→∞的极限情况下,在实际系统 中任何力学量的长时间平均值〈Gt〉等于系综平均值〈G〉,只要 统计系综和实际系统的热力学状态及环境完全相同。 统计热力学的另一条基本假设:孤立系统(即N,V,E一定)的 全部可能达到的量子态是等概率的。
用于N,V,T一定的封闭系统时,该假设还可表述为:在定温 热浴中的系统,能量相同的各量子态有相同的概率。
P ( D) WD
Ω
WD WD
D
每一个微态的概率 P
1
Ω
统计热力学中把WD叫分布D的热力学概率。显然热力学概率 WD不同于数学概率P(A),WD≥1(正整数),而0≤P(A)≤1。
③WD的计算 定域子系统:
gin N! n WD gi N! n ! ni ! i i i
第四章 统计热力学基础
1.统计热力学基本概念 (1)统计热力学系统的分类 ①独立子系和相依子系(非独立子系) 统计热力学将组成系统的分子、原子及离子等统称为粒子或 简称子。 按照粒子间有无不可忽略的相互作用,系统可分为独立子系 (或近独立子系)——子间无相互作用;相依子系(非独立子 系)——子间有不可忽略的相互作用。 ②定域子系和离域子系 按照粒子的运动是否遍及系统的全体积,系统可分为定域子 系——子的运动是定域化的(不遍及系统的全体积);离域子系 (非定域子系)——子的运动是非定域化的(遍及系统的全体 积)。
能量守恒: U N P ,i i 粒子数守恒: N ni
ni是布居在能级上的粒子数;Pε,i是粒子分布在各能级εi上的概率;
(4)分布的微态数WD与系统的总微态数 任何一种分布,只指出在每个能级(或状态)上有多少个粒子, 实现这一分布尚有不同的方式,每一种可区别的方式代表分布 (或系统)的一个可区别的微观状态,简称微态。WD表示分布D 的微态数,用表示系统总的微态数。 (5)分布的概率 计算分布的概率用古典概型的计算公式。 ① 古典概型又叫等概率模型,既是概率的定义,又是计算概率 的基本公式,其特征是: (i)只有有限个基本事件;
物理化学教材统计热力学

03 热力学函数与状态方程
热力学函数的概念与性质
热力学函数
描述系统热力学行为的物理量,如内能、熵、焓等。
热力学函数的性质
封闭系统中,热力学函数的改变量只与系统与外界的 能量交换有关,与具体变化过程无关。
热力学基本方程
描述系统热力学函数之间关系的方程,如热力学第一、 第二定律等。
热容与熵的概念
热容
平衡。
05 热力学过程与平衡常数
热力学过程及其计算方法
热力学过程
是指系统状态随时间的变化过程,包括等温、等压、等 容等过程。
计算方法
通过热力学基本定律和相关公式,计算过程中系统吸收 或释放的热量、功量等物理量。
平衡常数的概念与计算
平衡常数
是指在一定条件下,可逆反应达到平衡状态时,反应 物和生成物的浓度比值。
02 分子运动论与热力学定律
分子运动论的基本概念
分子运动论
分子运动论是研究物质分子运动 规律的理论,它通过分析分子运 动的速度、方向、频率等参数, 揭示物质宏观性质和微观结构之
间的关系。
分子模型
分子模型是描述分子形状和结构 的工具,常见的分子模型包括球 棒模型、比例模型等,它们可以 直观地展示分子的几何形状和内
热力学第三定律
热力学第三定律指出,绝对零度是不可能达到的,即绝对 零度是不可能达到的。
分子运动论中的热力学基本关系式
理想气体状态方程
理想气体状态方程是描述理想气体状 态变化规律的公式,它表示气体的压 力、体积和温度之间的关系。
热容公式
热容公式是描述物质在加热或冷却过 程中吸收或释放热量时温度变化规律 的公式,它表示物质的比热容、熵等 热力学参数之间的关系。
统计分布描述了大量粒子系统中,粒子在各 种可能状态下的分布情况。
物理化学第七章统计热力学基础

热力学第二定律的实质是揭示了热量 传递和机械能转化之间的方向性。
VS
它指出,热量传递和机械能转化的过 程是有方向的,即热量只能自发地从 高温物体传向低温物体,而机械能只 能通过消耗其他形式的能量才能转化 为内能。
热力学第二定律的应用
在能源利用领域,热力学第二定律指导我们合理利用能源,提高能源利用效率。
优势
统计热力学从微观角度出发,通过统计方法描述微观粒子的运动状态和相互作用,能够 更深入地揭示热现象的本质和内在规律。
局限性
统计热力学涉及到大量的微观粒子,计算较为复杂,需要借助计算机模拟等技术手段。
统计热力学与宏观热力学的关系
统计热力学和宏观热力学是相互补充的 关系,宏观热力学提供整体的、宏观的 视角,而统计热力学提供更微观、更具 体的视角。
03
热力学第一定律
热力学第一定律的表述
热力学第一定律的表述为
能量不能无中生出,也不能消失,只能从一种形式转化为另一种 形式。
也可以表述为
封闭系统中,热和功的总和是守恒的,即Q+W=ΔU。其中Q表示传 给系统的热量,W表示系统对外做的功,ΔU表示系统内能的变化。
热力学第一定律的实质
热力学第一定律实质是能量守恒定律在封闭系统中的具体表现。 它表明了在能量转化和传递过程中,能量的总量保持不变,即能 量守恒。
掌握理想气体和实际气 体的统计描述,理解气 体定律的微观解释。
了解相变和化学反应的 统计热力学基础,理解 热力学第二定律和熵的 概念。
02
统计热力学基础概念
统计热力学简介
统计热力学是研究热力学系统 在平衡态和近平衡态时微观粒 子运动状态和宏观性质之间关 系的学科。
它基于微观粒子的运动状态和 相互作用,通过统计方法来描 述系统的宏观性质,揭示了微 观结构和宏观性质之间的联系 。
统计热力学

统计热力学
统计热力学,从粒子的微观性质及结构数据出发,以粒子遵循的力学定律为理论基础;用统计的方法推求大量粒子运动的统计平均结果,以得出平衡系统各种宏观性质的值。
相关资料:
统计热力学从粒子的微观性质及结构数据出发,以粒子遵循的力学定律为理论基础;用统计的方法推求大量粒子运动的统计平均结果,以得出平衡系统各种宏观性质的值。
研究方法:统计力学的方法,应用几率规律和力学定律求出大量粒子运动的统计规律。
优点:揭示了体系宏观现象的微观本质,可以从分子或原子的光谱数据直接计算体系平衡态的热力学性质。
缺点:受对物质微观结构和运动规律认识程度的限制。
统计系统的分类与术语:
①粒子(子):组成系统的分子,原子,离子等的统称。
①独立子系统:粒子间相互作用可忽略的系统。
如理想气体,完美晶体。
①相依子系统:粒子间相互作用不能忽略的系统。
如真实气体,液体。
①定域子系统(可辨粒子系统):粒子有固定的平衡位置,运动是定域的;如固体。
①离域子系统(全同粒子系统):粒子处于混乱的运动中,无法分别,粒子彼此是等同的。
如:气体,液体。
第七章统计热力学基础

练习7.7一个U,N,V确定的系统,任何一种分布均不能随意的,而必须满足①与②两个条件。
练习7.8对于一定量的某气态、液态、固态物质,其微观状态数的排序是。
练习7.9最概然分布的微观状态数随粒子增加而①,该分布出现的概率随粒子数增加而②。
自测7.15转动特征温度定义为( )。
(A) (B) (C) (D)
自测7.16双原子分子在温度很低时且选取振动基态能量为零,则振动配分函数值为()。
(A)0(B)1(C)<0(D)>0
自测7.17对于N个粒子构成的定位独立可辨粒子系统熵的表达式为( )。
(A) (B)
(C) (D)
自测7.18对理想气体分子的平动,下面的结果中正确的是( )。
自测7.23已知CO与N2的质量、转动特征温度基本相同,若电子运动与振动能级均未开放,则()。
(A) (B) (C) 与 无法比较(D)
自测7.241mol双原子分子理想气体,当其温度由T1升到2T1时,若其转动惯量不变,则其转动熵变将是()。
(A) 5.763J·mol1K1(B)RlnT1
(C)RlnT2(D) 11.526J·mol1K1
练习7.22一个体积为V,粒子质量为m的离域子系统,其最低平动能级和其相邻能级间隔为①。若平动能级的 ,该能级的统计权重 是②。
练习7.23NH3分子的对称数是3,BF3分子的对称数是。
练习7.24已知HI的转动惯量I为4.31×1045kg·m2,h=6.626×1034J·s,k=1.38×1023J·K1,则其转动特征温度是。
(C)它的定义是 (D)它不是状态函数
自测7.32用J代表分子具有的各独立运动项目,分子在能级i的统计权重gi为下式中的()
统计热力学

第七章统计热力学基础热力学:基础:三大定律研究对象:(大量粒子构成的)宏观平衡体系研究方法:状态函数法手段:利用可测量量p-T-V+C p,m和状态方程结果:求状态函数(U,H,S,G,等)的改变值,以确定变化过程所涉及的能量和方向。
但是,热力学本身无法确定体系的状态方程,需借助实验。
很显然,体系的宏观热力学性质取决于其微观运动状态,是大量粒子微观运动的统计平均结果。
热力学宏观性质体系的微观运动状态统计热力学统计热力学:基础:微观粒子普遍遵循的(量子)力学定律对象:大量粒子所构成的体系的微观运动状态工具:统计力学原理目的:大量粒子某一性质的微观统计平均的结果(值)与系统的热力学宏观性质相关联。
7.1概述统计热力学是宏观热力学与量子化学相关联的桥梁。
通过系统粒子的微观性质(分子质量、分子几何构型、分子内及分子间作用力等),利用分子的配分函数计算系统的宏观性质。
微观运动状态有多种描述方法:经典力学方法是用粒子的空间位置(三维坐标)和表示能量的动量(三维动量)描述;量子力学用代表能量的能级和波函数描述。
由于统计热力学研究的是热力学平衡系统,不考虑粒子在空间的速率分布,只考虑粒子的能量分布。
这样,宏观状态和微观状态的关联就转化为一种能级分布(宏观状态)与多少微观状态相对应的问题,即几率问题。
Boltzmann给出了宏观性质—熵(S)与微观性质—热力学几率(Ω)之间的定量关系:S k=Ω。
ln热力学平衡系统熵值最大,但是通过概率理论计算一个平衡系统的Ω无法做到,也没有必要。
因为在一个热力学平衡系统中,存在一个微观状态数最大的分布(最概然分布),摘取最大项法及其原理可以证明,最概然分布即是平衡分布,可以用最概然分布代替一切分布。
因此,有了数学上完全容许的lnΩ≈ln W D,max。
所以,S=k ln W D,max这样,求所有分布的微观状态数—热力学几率的问题转化为求一种分布—最概然分布的微观状态数的问题。
《统计热力学基础》课件

分布函数的定义
分布函数是描述系统微观状态分布的函数,它表示在某一时刻, 系统中的粒子在各个状态上的概率分布情况。
微观状态数的概念
微观状态数是描述系统内部可能的状态数量的一个概念,它与系统 的宏观状态和微观状态有关。
分布函数的应用
通过分析分布函数,可以了解系统的微观结构和性质,从而更好地 理解系统的宏观行为和变化规律。
02
概率分布
概率分布用于描述粒子集合中不同微观状态的概率分布情况。最常见的
概率分布有玻尔兹曼分布和麦克斯韦-玻尔兹通过概率分布可以计算各种物理量的平均值,如粒子的平均速度和平均
动能。同时,涨落描述了粒子集合中物理量的偏离平均值的情况。
统计热力学的发展历程
早期发展
经典统计热力学
统计热力学的重要性
在科学研究和工程应用中,统计热力学提供了理解和预测物质性质、能量转换 和热力学过程的基础理论框架。它对于化学工程、材料科学、环境科学等领域 具有重要意义。
统计热力学的基本概念
01
微观状态和宏观状态
微观状态是指单个粒子的状态,如位置和速度;宏观状态是指大量粒子
集合的整体状态,如温度、压力和体积。
05
02
详细描述
热力学的第二定律指出,在一个封闭系统中 ,自发过程总是向着熵增加的方向进行,即 熵总是向着增加的方向变化。
04
详细描述
根据热力学的第二定律,热机的效率 不可能达到百分之百,因为总会有一 些能量以热的形式散失到环境中。
06
详细描述
热力学的第二定律还排除了第二类永动机的存 在,即不能从单一热源吸收热量并将其完全转 化为机械功而不产生其他影响。
熵的概念和性质
1 2
熵的定义
统计热力学基础
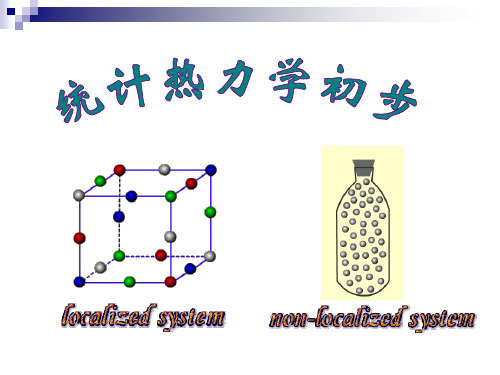
例2. 定域子系统中只有3个一维谐振子,它们分别在 A,B,C三个定点上振动,总能量为 9 hv,分析系统 2 可能有的能级分布及状态分布。 能级 能级分布 Ⅰ Ⅱ Ⅲ n0 n1 n2 n3
状态分布 0
3 0 0 WⅠ= 6 WⅡ = 3 WⅢ = 1 Ω = WⅠ+WⅡ+WⅢ=10
0=
1=
例如,某能级分布的微态数为WD,总微态数为Ω, 则该能级分布的数学概率 P 为:
WD 1 PD = Ω × WD = Ω
系统状态确定时,Ω为定值,微态数最大的分布 WD 最大,热力学概率也最大,称为最概然分布。
4、最概然分布与平衡分布 最概然分布虽然代表了系统微态数最多的一种 能级分布方式,但是它的数学概率是随着粒子数的 增多而减小的。 以粒子的空间分布为例来进行分析 例如,某一气体系统,粒子数为N,当系统达平 衡时,粒子在整个空间上的分布应是均匀的。 如果把整个空间分为大 小相等的两部分,则两部 分中所包含的粒子数应相 等,均为 N 。
2、等概率定理
对于U, V 和 N 确定的某一宏观系统,任何一 个可能出现的微观状态,都有相同的数学概率。 这个假设称为等概率定理。 例如,某宏观系统的总微态数为Ω ,则每一 种微观状态出现的数学概率 P 都相等,即:
1 P=Ω
3、最概然分布(最可几分布) 对于U, V 和 N 确定的宏观系统,微观上可能会 有多种能级分布方式,不同的能级分布所包含的状 态分布数不同,根据等概率定理,各微态出现的概 率相等,则各能级分布出现的概率不同。
§9.1
粒子各运动形式的能级及能级的简并度
根据前面的讨论及上述计算结果可以看出,各 种运动的能级间隔遵循如下关系:
Δn>Δe>Δv>Δr>Δt
统计物理学的基本原理

统计物理学的基本原理统计物理学是物理学的一个重要分支,它研究的是大量微观粒子的统计规律,通过对微观粒子的统计行为进行分析,揭示了宏观物质的性质和规律。
统计物理学的基本原理包括了热力学统计原理、量子统计原理和统计力学原理。
本文将从这三个方面介绍统计物理学的基本原理。
一、热力学统计原理热力学统计原理是统计物理学的基础,它建立在热力学的基础上,通过对大量微观粒子的统计分析,揭示了宏观系统的热力学性质。
热力学统计原理包括了热力学平衡态和热力学非平衡态两个方面。
1. 热力学平衡态在热力学平衡态下,系统的宏观性质可以用热力学量来描述,如温度、压强、体积等。
根据热力学统计原理,系统的平衡态可以通过微观粒子的状态密度函数来描述,状态密度函数是描述系统中微观粒子状态的函数,通过对状态密度函数的统计分析,可以得到系统的热力学性质。
2. 热力学非平衡态在热力学非平衡态下,系统处于不断变化的状态,无法用热力学量来描述。
热力学统计原理通过对非平衡态下微观粒子的统计分析,揭示了非平衡态下系统的动力学性质,如扩散、输运现象等。
热力学非平衡态的研究对于理解复杂系统的行为具有重要意义。
二、量子统计原理量子统计原理是统计物理学的另一个重要组成部分,它研究的是具有量子性质的微观粒子的统计规律。
量子统计原理包括了玻色-爱因斯坦统计和费米-狄拉克统计两种统计方法。
1. 玻色-爱因斯坦统计玻色-爱因斯坦统计适用于具有玻色子性质的粒子,玻色子是一类自旋为整数的粒子,如光子、声子等。
根据玻色-爱因斯坦统计,玻色子可以处于同一量子态,不受泡利不相容原理的限制,这导致了玻色子的凝聚现象,如玻色-爱因斯坦凝聚和超流体现象。
2. 费米-狄拉克统计费米-狄拉克统计适用于具有费米子性质的粒子,费米子是一类自旋为半整数的粒子,如电子、质子等。
根据费米-狄拉克统计,费米子不能处于同一量子态,受到泡利不相容原理的限制,这导致了费米子的排斥现象,如费米-狄拉克排斥和电子云排斥现象。
03-统计热力学基础

三、统计热力学基础(313题)一、选择题 ( 共38题 )1. 1 分 (1301)玻耳兹曼熵定理一般不适用于: ( )(A) 独立子体系 (B) 理想气体 (C) 量子气体 (D) 单个粒子2. 1 分 (1302)非理想气体是: ( )(A) 独立的全同粒子体系 (B) 相依的粒子体系(C) 独立的可别粒子体系 (D) 定域的可别粒子体系3. 2 分 (1304)下列各体系中属于独立粒子体系的是: ( )(A) 绝对零度的晶体 (B) 理想液体混合物(C) 纯气体 (D) 理想气体的混合物4. 1 分 (1362)玻耳兹曼分布 _______ 。
(A) 是最概然分布,但不是平衡分布(B) 是平衡分布,但不是最概然分布(C) 即是最概然分布,又是平衡分布(D) 不是最概然分布,也不是平衡分布5. 1 分 (1363)对于近独立非定位体系,在经典极限下能级分布 D 所拥有的微观状态数t 为:( )(A) ∏=i i i n !!i N N N t g (B) ∏=i i i n !!iN g N t n (C) ∏=ii n !!iN N N t g (D) ∏=i i n !!i N g N t n 6. 1 分 (1364)对于服从玻耳兹曼分布定律的体系,其分布规律为: ( )(A) 能量最低的单个量子状态上的粒子数最多(B) 第一激发能级上的粒子数最多(C) 视体系的具体条件而定(D) 以上三答案都不对7. 2 分 (1369)近独立定域粒子体系和经典极限下的非定域粒子体系的 ( )(A) 最概然分布公式不同(B) 最概然分布公式相同(C) 某一能量分布类型的微观状态数相同(D) 以粒子配分函数表示的热力学函数的统计表达示相同8. 2 分 (1370)如果我们把同一种分子分布在二个不同能级ε与ε'上的n 与n ' 个分子看成是“不同种”的分子 A 与 A',则这“两种分子”将可按 A' A 进行转化而达到平衡。
统计热力学基础

实际上:
微观构造与运动形态 影响 物质旳宏观性质
物质旳形成过程与时间 影响 物质旳宏观性质
对大量粒子旳微观力学性质(P646表)进行统计
处理得到由大量粒子构成旳宏观体系旳平衡性质
——统计热力学
微观
微观到宏观
宏观
量子 力学
统计力学
统计力学有两个基本出发点:
化学热力学 化学动力学
一是:宏观物质由大量旳粒子构成;
x
在某一数值附近。
▲ 相空间(τ空间)
px
N个粒子有N个子相空间,由N个子相空间构成
旳空间称为相空间(τ空间),有2Nf 维。
3.粒子微观状态旳量子力学描述
◆ 量子态
粒子旳多种运动是量子化旳,运动状态由波
函数描述,体系旳微观状态由体系旳波函数描
述,即,一种微观状i态t 相r v应e 一n 套量子态。不计
离域粒子体系:粒子能够在整个空间运动,且 没有拟定旳平衡点。如理想气体为离域独立子 体系,而实际气体为离域相倚子体系。 3. 玻色子体系和费米子体系(P658) 玻色子:不受泡利原理限制旳量子气体(光 子及含电子、中子和质子旳总数为偶数旳分子 或原子) 费米子:受泡利原理限制旳量子气体
三、几种常用术语(P648) 1.自由度、广义坐标与广义动量 ▲自由度:拟定体系中粒子位置旳独立参量
发展间史:气体分子运动学说为起点
1875年,克劳修斯提出:气体分子均方速度、 平均自由程和分子碰撞数等主要概念; 1860年,麦克斯韦导出分子速度分布定律; 1868年,玻尔兹曼将重力场引入分子速度分布 定律,得到熵旳统计意义,形成麦克斯韦-玻尔 兹曼统计法,这是建立在经典力学基础上旳,亦 称经典统计;主要用于分子间无相互作用旳体系 ——如低压气体,稀溶液旳溶质等;
第七章统计热力学

一、基本概念和公式 (一)统计的分类
目前,统计主要有三种: Boltzmann统计,它建立在经典力学的基础上。
Bose-Einstein统计和Fermi-Dirac统计,建立 在量子力学的基础上。 (二)统计系统的分类
1. 根据统计单位(微观粒子)是否可以区分 (1)定位系统(localized system)
31 2T
(1)平动Helmholtz自由能
At
kT
ln
(qt )N N!
( ln qt V
)V ,N
1 V
NkT
ln(
2mk
h2
T
)3/
2V
NkT
ln
N
NkT
(2)平动熵
St
Nk[ln
qt N
5] 2
这称为Sackur-Tetrode公式
Sackur-Tetrode公式用来计算理想气体的
平动熵。
(五) 各配分函数的计算公式
(五) 各配分函数的计算公式
(一)各运动形式的能级公式
1.
t
ii,t
h2 8m
(
nx2 a2
ny2 b2
nz2 c2
)
2.
rr
J(J
1)
h2
8 2
I
J 0,1,2,
I ( m1m2 )r 2
m1 m2
3.
vv
(v
1 )h
2
v 0,1, 2,
(五) 各配分函数的计算公式
U nii U(位能)
i
二、 波兹曼分布
1.波兹曼熵公式 S=klnΩ
2. 统计力学的基本假设
对于(U、V、N)确定的体系即宏观状态一定的体系 来说,任何一个可能出现的微观状态都具有相同的数 学几率。即:若体系的总微观状态为Ω,则其中每一 个微观状态出现的概率(P)都是P=1/Ω。
统计热力学基础
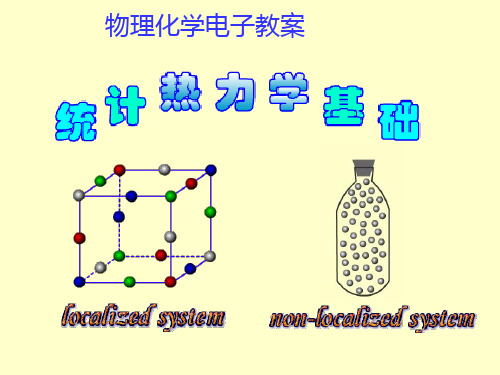
量子力学中把能级可能有的微观状态数称为
该能级的简并度,用符号gi 表示。简并度亦称为
退化度或统计权重。
简并度(degeneration)
例如,气体分子平动能的公式为:
N!
Hale Waihona Puke g Ni iN! i
i Ni !
非定位体系的最概然分布
同样采用最概然分布的概念,用Stiring公式
和Lagrange乘因子法求条件极值,得到微态数为
极大值时的分布方式
N
*(非定位)为:
i
N(i* 非定位) N
g ei / kT i g ei / kT i
i
由此可见,定位体系与非定位体系,最概然
的分布公式是相同的。
Boltzmann公式的其它形式
(1)将i能级和j能级上粒子数进行比较,用最 概然分布公式相比,消去相同项,得:
Ni*
N
* j
g ei / kT i
g e j / kT j
Boltzmann公式的其它形式
(2)在经典力学中不考虑简并度,则上式成为
Ni*
N
* j
i / kT
ee j / kT
(U,V , N)
N!
g Ni i
i
i Ni !
求和的限制条件仍为:
Ni N
Nii U
i
i
有简并度时定位体系的微态数
再采用最概然分布概念, i max ,用
Stiring公式和Lagrange乘因子法求条件极值,得
到微态数为极大值时的分布方式 Ni* 为:
统计热力学

这就是定域体系的自由能公式,式中Q称为分子配分函数。
❖ 总结
定域体系有三个重要公式:
1、总微观状态数
γν ι
Ω Ν! ι
D
i νι!
2、最可几分布
FkT lnQN
3、热力学函数
*
ni N
g ie i g ie i
i
基本粒子:如电子、中子、光子等。 复合粒子:如原子、分子等。 复合粒子构成体系:如一升气体,一摩尔晶体等。 (2)统计体系分类 按照体系内粒子之间相互作用的强弱可把体系分为近独立 粒子体系和相依粒子体系。 按照体系内粒子是否可区分,也可把体系分为定域粒子体 系和离域粒子体系。
(3)微观态和宏观态 体系的微观态是指在某一瞬间,体系中全体
N个全同粒子构成体系,总自由度为Nf (f 为一个粒 子自由度),需要2 Nf 维相空间。
Γ空间:描述N个粒子构成体系,整个气体运动状态的 相空间,也叫做气体相空间。 Γ空间中的一个相点 代表体系的一个微观运动状态。
测不准原理:△q× △p≈ h
相胞:hf
❖ §1.2 粒子微观运动状态的描述 一、自由粒子
ni !
2、最可几分布
ni* e i e(i)/kT gi
3、热力学函数
Sk
i
[ni*lnngi*i ni*]
❖ §2.3 费米-狄拉克统计
由质子、中子、电子以及由奇数个这些基本粒子组成的复合粒子构成的体系 服从费米-狄拉克统计。这个统计分布的特点是每一状态最多容纳一个粒子。
一、微观状态数
D D
如果每个容器最多容纳物体数目不受限制,有多少种排列方式(N≤M)?
N个可区分的物体,排列在M个不同容器中,物体的数目不受限制,可能的方式 数有多少?
材料热力学2.统计热力学基础.吴申庆

8.配分函数Z
配分函数是一个统计物理学中经常应用到 的概念,统计物理学通过对大量微观粒子统 计行为的计算,将微观物理状态与宏观物理 量相互联系起来,而配分函数就是联系微观 物理状态和宏观物理量的桥梁。
配分函数实际是体系所有粒子在各个能级 依最可几分布排布时候对体系状态的一个描 述。由配分函数可以方便地求出体系的内能、 广义力、熵、自由能等等热力学参量。
宏观热力学的简单概括: 研究对象——大量分子的集合体,不考虑分子 的结构,不涉及分子内部的运动和相互作用 研究基础——经验总结出的三大定律, 研究方法——运用逻辑推理,形成热力学理论 作 用——利用热力学数据,讨论平衡系统 各宏观性质之间的 关系,从而预测过程进行 的方向和限度。 优 点——高度的可靠性和普遍意义。 由于在研究过程中并不考虑个别分子的特殊结 构,所以对于凡是能明确描述或定义出的热力 学体系都能使用它的结论。
宏观热力学局限性——对事物没有微观的想象; 不研究过程的机理及速率;得不到具体系统的 具体规律,如:不能推导出理想气体的状态方 程。必须结合对系统的某些观察数据,才能得 到具体的结果;不能说明变化具有方向性的本 质。 统计热力学: 弥补了热力学方法的不足。 是以大量微观粒子组成的宏观体系为研究 对象,从物质的微观结构和微观运动形态出发, 利用统计平均的方法(如:概率、最可几分布 等)来获得系统的宏观性质。
材料热力学
Thermodynamics of Materials
材料科学与工程学院 吴申庆 2012.3
第二章:统计热力学基础
Basic Concepts of Statistical Thermodynamics
统计热力学:关于热现象的平衡态微观理论及 其变化规律的科学。 研究集合体处于平衡态时的热现象及其变化 规律.是统计物理的研究方向之一. 对象:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Page 1
2019年8月18日星期日 扬州大学化学化工学院
WH
统计热力学基础
Page 2
2019年8月18日星期日 扬州大学化学化工学院
WH Introduction
1 统计热力学的研究目的和方法
统计热力学是联系物质体系的宏观性质和微观性质
的桥梁
物质体系的宏观性质
统计热力学的研究内容
Page 3
在统计热力学中,把构成宏观物质体系的各种不同
子 的微观粒子,统称为:“ ”
Page 5
2019年8月18日星期日 扬州大学化学化工学院
WH Introduction
统计体系的分类
根据体系中的每个粒子是否可以分辨,可将统计体统 分为“定域子体系”和“离域子体系”,或者分别 “定位体系”和“非定位体系” 定域子体系 体系中每个粒子是可以分辨的,可以设
想,把体系中每个粒子分别编号而不会 混淆 例如晶体体系
离域子体系 体系中每个粒子是无法彼此分辨 例如粒子作无序运动的气体体系
Page 6
2019年8月18日星期日 扬州大学化学化工学院
WH Introduction
统计体系的分类
根据体系中的粒子之间是否存在相互作用,可将 统计体统分为“独立子体系”和“相依子体系”
F
速度和动能可以连续变化
但是,微观的物质微粒的Biblioteka 动则需要用量子力学规 律来描述!!!
Page 9
2019年8月18日星期日 扬州大学化学化工学院
WH 9.1 粒子各种运形式的能级及能级的简并度
微观粒子的运动状态和能量都量子化的
量子化学的研究表明: 微观粒子的运动状态只能特 定的量子状态,而不能是任 意的运动状态 微观粒子所具有的能量也是 量子化的,只能是某一个能 级的能量值,而不能是任意 值
统计热力学从微观粒子的结构信息和运动规律出发, 利用统计的方法,得到由大量微观粒子构成的宏观物 质体系的宏观规律性
Page 4
2019年8月18日星期日 扬州大学化学化工学院
WH Introduction
统计热力学研究的对象
统计热力学研究时,虽然是从单个物质微粒的性质 (例如分子的振动频率、分子的转动惯量、分子能谱 等等)出发,但是,统计热力学研究的对象却不是单 个的分子,或者原子,其研究的对象和热力学的研究 对象一样,也是由大量的分子、原子、或者离子等基 本粒子构成的宏观物质体系
平动量子数 nx、ny、nz的值只能取
m
正整数(1,2,3, ),一组(nx、 ny、nz)就规定了三维平动子的一
Page 10
2019年8月18日星期日 扬州大学化学化工学院
WH 9.1 粒子各种运形式的能级及能级的简并度
微观粒子的不同运动形式
微观粒子的运动不同于宏观物质的运动,可以用量 子力学来描述微观粒子的运动状态。微观粒子的有 多种不同的运动形式。
例如,分子具有5种不同的运动形式,分别是: 分子整体在空间中的平动(t) 分子绕其质心的转动(r) 分子内原子在平衡位置附近的振动(v) 原子内部电子的运动(e) 原子核运动(n)
Page 16
2019年8月18日星期日 扬州大学化学化工学院
WH 9.1 粒子各种运形式的能级及能级的简并度
三维平动子的能级
在统计力学中,将在空间作三维平动的粒子称为
“三维平动子”。平动子具有的“平动能”(t)是量
b 子t化的8hm2
nx2 a2
ny2 b2
nz2 c2
物质微粒的微观结构
2019年8月18日星期日 扬州大学化学化工学院
WH Introduction
统计热力学研究的目的
寻求物质的微观结构、微观运动规律与由大量微粒构 成的宏观物质体系之间的联系,沟通物质体系的宏观 与微观,使我们对物质宏观体系的性质及变化规律, 不仅“知其然”,而且“知其所以然”
统计热力学研究的方法
粒子的能量
粒子的每种运动形式都具有相应的能量,粒子所具 有的能量就等于各运动形式的能量之和
t r v e n
微观运动形式能量的量子化 量子力学的研究指出:粒子微观形式的能量都是量 子化的,能量值从低到高是不连续的,就象阶梯或 台阶一样。每一个能量值称之为一个能级,量子力 学给出了每一种运动形式的能级表达式
WH
3) 分子内原子在平衡位置附近的振动(v)
振动发生于多原子分子中
Page 14
2019年8月18日星期日 扬州大学化学化工学院
WH 9.1 粒子各种运形式的能级及能级的简并度
微观粒子的不同运动形式
平动、转动和振动是分子的整体运动的三种形式,而原 子内部电子的运动(e)和原子核运动(n)两种运动形式则 是分子内部更深层粒子的运动形式
独立子体系 体系中粒子之间的相互作用可以忽 略不计,粒子之间没有作用势能,体系的内能是 体系中每个粒子所具有的能量之和
U nii
i
Page 7
2019年8月18日星期日 扬州大学化学化工学院
WH Introduction
统计体系的分类
根据体系中的粒子之间是否存在相互作用,可将 统计体统分为“独立子体系”和“相依子体系”
相依子体系 体系中粒子之间的作用势能不能忽 略。体系的内能中包含有粒子之间的作用势能
U nii U x1, y1, z1, xN , yN , zN
i
Page 8
2019年8月18日星期日 扬州大学化学化工学院
WH 9.1 粒子各种运形式的能级及能级的简并度
一个宏观物体的运动,遵守经典的Newton力学定律, 物体的运动状态和所具有能量的变化是连续的
Page 11
2019年8月18日星期日 扬州大学化学化工学院
WH1) 分子整体在空间中的平动(t)
发生平动时,分子的形状不变化,分子各部
Pag分e 1的2 之间的相201对9年坐8月标18不日星变期日
扬州大学化学化工学院
WH2) 分子绕其质心的转动(r)
Page 13
2019年8月18日星期日 扬州大学化学化工学院
随着人们对物质结构层次认识的深入,知识了原子内部 还有其他的运动形式,例如“夸克”和“层子”的运动 形式等,但是对于系统在宏观过程中发生的一般物理化 学变化,涉及不到这些运动形式,因此,这里,我们主 要考虑上述5种运动形式
Page 15
2019年8月18日星期日 扬州大学化学化工学院
WH 9.1 粒子各种运形式的能级及能级的简并度
