Sallen―Key低通滤波器高频馈通现象的原因及解决-4页word资料
滤波器在无线通信系统中的信号解调

滤波器在无线通信系统中的信号解调无线通信系统在传输信号时,常常会受到多种干扰和噪声的影响,这些干扰和噪声会降低信号质量,导致通信过程中出现误码或丢包等问题。
为了解决这些问题,滤波器在无线通信系统中起到了重要的作用。
本文将探讨滤波器在无线通信系统中的信号解调方面的应用。
一、滤波器的基本原理滤波器是一种能够根据信号频率响应的电子设备,它可以将特定频段的信号通过,而将其他频段的信号抑制。
滤波器通过选择合适的滤波器类型和参数来实现信号的解调和去噪。
常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
低通滤波器可以允许低频信号通过,而抑制高频信号;高通滤波器则相反。
带通滤波器则可以选择一定范围内的频率通过,而抑制其他频率;带阻滤波器则可选择一定频率范围的信号抑制,而放行其他频率的信号。
二、滤波器在信号解调中的应用1. 降低多径干扰无线通信系统中,信号会通过多条路径传播,由于路径的差异性,导致信号叠加在一起时产生多径干扰。
这种干扰会导致信号失真,影响信号的解调。
通过在接收端添加适当的滤波器,可以抑制多径干扰,提高信号的解调性能。
2. 去除噪声在无线通信中,信号往往会受到各种噪声的干扰,如热噪声、频率选择性衰落噪声等。
这些噪声会使信号的信噪比降低,影响信号的解调。
选择合适的滤波器,可以通过抑制噪声频率分量,提高信号的信噪比,从而改善信号的解调性能。
3. 解调频率选择性衰落信号无线通信系统中,由于不同路径的传播特性,信号在传输过程中会出现频率选择性衰落现象。
这种现象会导致部分频率分量的失真和衰减,影响信号的解调。
为了解决这个问题,可以通过在解调之前采用带通滤波器来补偿频率选择性衰落的效果。
带通滤波器可以去除衰落频率范围之外的部分,使信号在解调之前的频谱特性更加均衡,提高解调效果。
4. 抑制干扰信号无线通信系统中,常常会受到外部干扰信号的影响,如其他信号源发射的干扰信号、信号的反射和散射等。
这些干扰信号会降低接收信号的质量,导致信号解调的困难。
低通滤波器衰减

低通滤波器衰减1. 什么是低通滤波器低通滤波器是一种信号处理工具,用于将高频信号从输入信号中滤除,只保留低频成分。
它可以通过改变信号的频率响应来实现这一目标。
在数字信号处理中,低通滤波器是一种线性时不变系统,其传递函数在正常工作频率范围内对低频信号具有较高的增益,而对高频信号有较低的增益。
这意味着它会使输入信号中的高频成分衰减,并保留较低频成分。
2. 为什么需要低通滤波器在许多实际应用中,我们可能只对某些特定频率范围内的信号感兴趣。
例如,在音频处理中,我们可能只对人类可听到的声音感兴趣,而不关心超出此范围的高频噪声。
此时,使用低通滤波器可以有效地去除不需要的高频噪声。
另一个常见的应用是图像处理中的平滑操作。
通过使用低通滤波器,我们可以去除图像中的高频细节部分,从而实现平滑效果。
此外,低通滤波器还可用于信号采样过程中的抗混叠滤波。
在模拟信号转换为数字信号时,由于采样频率限制,可能会产生混叠现象。
通过在采样之前应用低通滤波器,我们可以限制输入信号的频率范围,以防止混叠。
3. 低通滤波器的衰减特性低通滤波器的衰减特性是指它对高频信号的抑制程度。
一般来说,我们希望低通滤波器在截止频率之后能够迅速衰减高频成分,以确保只保留所需的低频成分。
常见的低通滤波器类型包括巴特沃斯、切比雪夫和椭圆等。
这些滤波器都具有不同的衰减特性和相应的设计参数。
•巴特沃斯低通滤波器:巴特沃斯低通滤波器是一种具有最平坦幅度响应的低通滤波器。
它在截止频率处有最小的衰减,并且随着频率增加而逐渐增加衰减。
•切比雪夫低通滤波器:切比雪夫低通滤波器是一种具有更快衰减特性的低通滤波器。
它可以通过调整设计参数来实现不同的衰减程度,但在截止频率附近会出现振铃效应。
•椭圆低通滤波器:椭圆低通滤波器是一种具有最快衰减特性的低通滤波器。
它可以提供更高的衰减程度,但在频率响应上会出现过渡带的振荡。
4. 低通滤波器的设计方法设计一个低通滤波器需要确定以下关键参数:•截止频率:决定了过渡带和阻带的频率范围。
影响高频载波通道水平的几个因素及解决方法
影响高频载波通道水平的几个因素及解决方法陈志光广东省电力中心调度所,广州510600在电力系统中,尤其是超高压系统,出现故障时要求保护快速、可靠、有选择地将故障切除。
出现故障概率最高的应属电力线路,所以,在广东电力系统中,220 kV及以上的线路均配备了双高频保护,实现全线速动保护。
高频保护能否正确动作,除取决于保护和收发信机能否正常工作外,还与高频通道的工作状况有关。
当通道水平不理想,遇到天气不好或其它因素干扰时,出现故障的可能性就较大,造成高频保护误动或拒动。
本文就实际运行中影响高频载波通道工作水平的几个因素作简要分析。
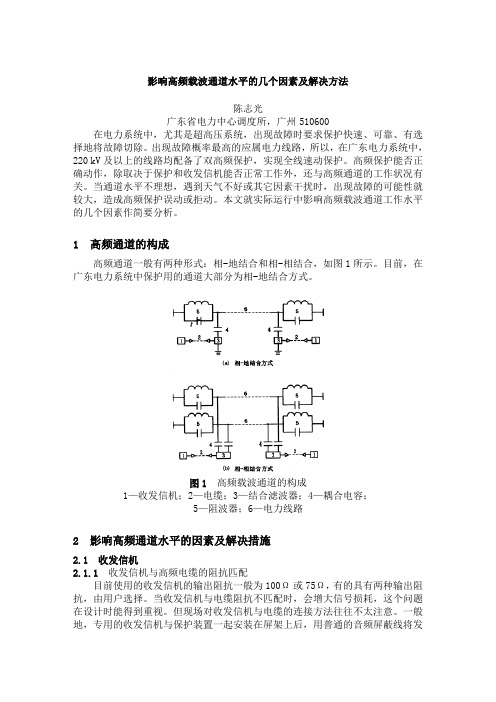
1 高频通道的构成高频通道一般有两种形式:相-地结合和相-相结合,如图1所示。
目前,在广东电力系统中保护用的通道大部分为相-地结合方式。
图1 高频载波通道的构成1—收发信机;2—电缆;3—结合滤波器;4—耦合电容;5—阻波器;6—电力线路2 影响高频通道水平的因素及解决措施2.1 收发信机2.1.1 收发信机与高频电缆的阻抗匹配目前使用的收发信机的输出阻抗一般为100Ω或75Ω,有的具有两种输出阻抗,由用户选择。
当收发信机与电缆阻抗不匹配时,会增大信号损耗,这个问题在设计时能得到重视。
但现场对收发信机与电缆的连接方法往往不太注意。
一般地,专用的收发信机与保护装置一起安装在屏架上后,用普通的音频屏蔽线将发信输出的高频信号接至屏后的端子排上,再与高频电缆相接。
这样带来的问题是音频屏蔽线对高频信号的衰减作用很大,且不能满足阻抗匹配要求,尤其给频率较高的信号的传输带来不良影响。
2.1.2 解决办法在保护屏后安装高频电缆转接插座,步骤如下:a)将视频插座装在金属板上,把与收发信机输出阻抗匹配的高频电缆同插座连接好,如图2(a),电缆的另一端和收发信机的发信输出端相连。
b)将视频插头与上通道的高频电缆接好,如图2(b)。
c)完成视频插头与插座的转接,如图2(c)。
图2 高频电缆的转接2.2 高频电缆收发信机与结合滤波器间的连接馈线通常采用高频电缆,目前采用最广泛的是SYV-100-7,SYV-75-9,SYV-75-18三种型号。
滤波器的基本原理

滤波器的基本原理1.滤波器是由电感和电容组成的低通滤波电路所构成,它允许有用信号的电流通过,对频率较高的干扰信号则有较大的衰减。
由于干扰信号有差模和共模两种,因此滤波器要对这两种干扰都具有衰减作用。
其基本原理有三种:A)利用电容通高频隔低频的特性,将火线、零线高频干扰电流导入地线(共模),或将火线高频干扰电流导入零线(差模);B)利用电感线圈的阻抗特性,将高频干扰电流反射回干扰源;C)利用干扰抑制铁氧体可将一定频段的干扰信号吸收转化为热量的特性,针对某干扰信号的频段选择合适的干扰抑制铁氧体磁环、磁珠直接套在需要滤波的电缆上即可2 电源滤波器高频插入损耗的重要性尽管各种电磁兼容标准中关于传导发射的限制仅到30MHz(旧军标到50MHz,新军标到10MHz),但是对传导发射的抑制绝不能忽略高频的影响。
因为,电源线上高频传导电流会导致辐射,使设备的辐射发射超标。
另外,瞬态脉冲敏感度试验中的试验波形往往包含了很高的频率成份,如果不滤除这些高频干扰,也会导致设备的敏感度试验失败。
电源线滤波器的高频特性差的主要原因有两个,一个是内部寄生参数造成的空间耦合,另一个是滤波器件的不理想性。
因此,改善高频特性的方法也是从这两个方面着手。
内部结构:滤波器的连线要按照电路结构向一个方向布置,在空间允许的条件下,电感与电容之间保持一定的距离,必要时,可设置一些隔离板,减小空间耦合。
电感:按照前面所介绍的方法控制电感的寄生电容。
必要时,使用多个电感串联的方式。
差模滤波电容:电容的引线要尽量短。
要理解这个要求的含义:电容与需要滤波的导线(火线和零线)之间的连线尽量短。
如果滤波器安装在线路板上,线路板上的走线也会等效成电容的引线。
这时,要注意保证时机的电容引线最短。
共模电容:电容的引线要尽量短。
对这个要求的理解和注意事项同差模电容相同。
但是,滤波器的共模高频滤波特性主要靠共模电容保证,并且共模干扰的频率一般较高,因此共模滤波电容的高频特性更加重要。
低通滤波器怎么用

低通滤波器怎么用在信号处理领域,低通滤波器是一种常用的工具,用于去除信号中的高频部分,保留低频成分。
低通滤波器的使用可以帮助我们实现信号去噪、平滑、降采样等多种功能。
在本文中,我们将介绍低通滤波器的类型、工作原理以及如何正确地应用低通滤波器。
低通滤波器类型低通滤波器根据其截止频率的不同可以分为不同类型,常见的有理想低通滤波器、巴特沃斯低通滤波器、切比雪夫低通滤波器等。
每种类型的低通滤波器在频域和时域的特性都不同,选择合适的类型取决于具体的信号处理需求。
低通滤波器工作原理低通滤波器通过设计滤波器的频率响应来实现信号频域的选择性处理。
在频域中,低通滤波器将信号中高于截止频率的部分滤除,保留低频成分。
这样可以去除高频噪声、平滑信号,并且有助于降低信号的采样频率。
低通滤波器应用1.信号去噪:低通滤波器常用于去除信号中的高频噪声,提高信号的清晰度和质量。
2.信号平滑:对于包含较多高频成分的不稳定信号,可以通过低通滤波器平滑信号,使其更易于分析和处理。
3.信号恢复:在某些情况下,信号可能因传输或处理过程中丢失部分频谱信息,可以通过低通滤波器对信号进行恢复。
4.降采样:在需要降低信号采样率的情况下,先使用低通滤波器滤除高频部分,然后再进行下采样操作。
低通滤波器使用注意事项在使用低通滤波器时,需要根据具体情况选择合适的滤波器类型和参数。
需要注意以下几点:1.截止频率选择:截止频率应该根据信号的频率特性来确定,选择过高或过低的截止频率都可能导致滤波效果不佳。
2.滤波器阶数:滤波器的阶数会影响滤波器的性能,通常情况下,阶数越高,滤波器的性能越好,但计算复杂度也会增加。
3.信号延迟:滤波器会引入信号延迟,应根据应用场景考虑延迟对系统性能的影响。
4.实时处理:在实时处理中,需要考虑滤波器的计算效率,避免引入过大的延迟。
综上所述,低通滤波器是信号处理中常用的一种滤波器,可以在去噪、平滑、恢复信号等多个方面起到关键作用。
正确地选择和应用低通滤波器可以提高信号处理的效果和质量,有效地改善系统性能。
低通滤波器工作原理和应用实例

低通滤波器工作原理和应用实例低通滤波器容许低频信号通过,但减弱(或减少)频率高于截止频率的信号的通过。
对于不同滤波器而言,每个频率的信号的减弱程度不同。
当使用在音频应用时,它有时被称为高频剪切滤波器,或高音消除滤波器。
高通滤波器则相反,而带通滤波器则是高通滤波器同低通滤波器的组合.低通滤波器概念有许多不同的形式,其中包括电子线路(如音频设备中使用的hiss滤波器、平滑数据的数字算法、音障(acoustic barriers)、图像模糊处理等等。
低通滤波器在信号处理中的作用等同于其它领域如金融领域中移动平均数(moving average)所起的作用;这两个工具都通过剔除短期波动、保留长期发展趋势提供了信号的平滑形式。
低通滤波器实例RC电路实现的一个低通电子滤波器一个固体屏障就是一个声波的低通滤波器。
当另外一个房间中播放音乐时,很容易听到音乐的低音,但是高音部分大部分被过滤掉了。
类似的情况是,一辆小汽车中非常大的音乐声在另外一个车中的人听来却是低音节拍,因为这时封闭的汽车(和空气间隔)起到了低通滤波器的作用,减弱了所有的高音。
电子低通滤波器用来驱动重低音喇叭(subwoofer)和其它类型的扩音器、并且阻塞它们不能有效传播的高音节拍。
无线电发射机使用低通滤波器阻塞可能引起与其它通信发生干扰的谐波发射。
DSL分离器使用低通和高通滤波器分离共享使用双绞线的DSL和POTS信号。
低通滤波器也在如Roland公司这样的模拟合成器(synthesiser)合成的电子音乐声音处理中发挥着重要的作用。
参见subtractive synthesis.[编辑]理想与实际滤波器一个理想的低通滤波器能够完全剔除高于截止频率的所有频率信号并且低于截止频率的信号可以不受影响地通过。
实际上的转换区域也不再存在。
一个理想的低通滤波器可以用数学的方法(理论上)在频域中用信号乘以矩形函数得到,作为具有同样效果的方法,也可以在时域与sinc函数作卷积得到。
基于CMOS的Sallen-Key型二阶低通滤波器设计1

摘要低通滤波器是一个通过低频信号而衰减或抑制高频信号的部件。
在数据处理、数据传输、抑制干扰、自动化、通信以及大部分的电子系统中得到了广泛的应用。
随着现代科学技术的发展,传统的滤波器在体积、功耗、滤波等方面逐渐显现出劣势,为了满足高精度、高稳定性、高可靠性的要求,出现了有源滤波器、数字滤波器和开关电容滤波器等类型的产品。
随后新型滤波器也被广泛应用于各种集成电路系统中,提高了产品的性能,降低了生产成本,并使得产品在实际应用更加简单、便捷。
本文主要设计了一种基于CMOS的低功耗、截止频率为2KHz的二阶低通滤波器,电路为Sallen-Key结构,Sallen-Key电路具有输出阻抗低、原件差值范围小、放大能力高等优点。
本文利用Multisim软件对整个电路进行了设计及仿真,最后利用Tanner 软件完成了对整个滤波器的版图设计,设计采用0.5nm CMOS工艺。
经过实验验证,本次设计的滤波器能够满足设计要求,在一定频率范围内能很好地实现滤波功能。
关键词CMOS;低通滤波器;Multisim;TannerAbstractLow pass filter is a high frequency signal attenuation or inhibited by the low-frequency signal components. Has been widely used in data processing, data transmission, interference suppression, automation, communication and electronic system in most. With the development of modern science and technology, the traditional filter in the volume, power consumption, filter and so on gradually shows disadvantages, in order to meet the requirements of high precision, high stability, high reliability requirements, the active power filter, digital filter and a switched capacitor filter and other types of products. The new filter has been widely used in various integrated circuit system, improving the performance of the products, reduce the production cost, and makes the product more simple, convenient in practical application.In this paper, based on the design of a low power consumption, the CMOS cutoff frequency of two order 2KHz low-pass filter, circuit for the Sallen-Key structure, the Sallen-Key circuit has low output impedance, the original small, difference amplifying ability etc.. The whole circuit is designed and simulated with Multisim software, and finally completed the layout design of the filter by using the Cadence software, designed by 0.5nm CMOS process. After experimental verification, the designed filter can meet the design requirements, to achieve a good filtering function within a certain frequency range.Key wordsCMOS;Low pass filter; Multisim;Tanner目录摘要 (I)Abstract (II)第一章滤波器简介 (1)1.1 课题背景及研究意义 (1)1.2 滤波器概述 (1)1.3 滤波器国内外研究现状 (4)1.4 主要研究内容 (5)第二章滤波器总体方案设计 (6)2.1 滤波器方案选择及分析 (6)2.1.1 一阶有源滤波电路 (6)2.1.2 二阶有源滤波电路 (7)2.1.3 压控电压源(Sallen-Key)二阶有源滤波电路 (8)2.2 电路结构的选择 (10)2.3 滤波器电路的确定 (12)2.3 低功耗CMOS运算放大器的设计 (13)2.5 本章小结 (14)第三章滤波器版图设计 (15)3.1 版图设计中寄生效应的影响 (15)3.1.1 焊盘的寄生效应 (15)3.1.2 CMOS闩锁效应 (15)3.1.3 衬底耦合 (16)3.2 运算放大器的版图设计 (17)3.3 低通滤波器版图 (18)3.4 本章小结 (19)第四章二阶低通滤波电路仿真与结果分析 (20)4.1 Multisim仿真软件介绍 (20)4.2 滤波器的仿真 (20)4.3 仿真结果分析 (23)4.4 本章小结 (24)结论 (25)参考文献 (26)致谢 ......................................................................................................... 错误!未定义书签。
基于AFSA-WNN的Sallen-Key滤波器电路软故障诊断

收稿日期:2018-08-20修回日期:2018-11-05作者简介:王春兰(1986-),女,陕西宝鸡人,硕士研究生。
研究方向:电子信息处理。
摘要:为提高对Sallen-Key 滤波器的软故障诊断能力,提出一种基于多分辨率变换与小波神经网络(WNN )的软故障诊断方法。
该方法先引入多分辨率变换提取Sallen-Key 滤波器电路的软故障特征,在此基础上,采用人工鱼群算法优化的WNN 构建电路软故障诊断模型。
仿真结果表明,与单纯的WNN 相比,所提出方法对电路软故障的诊断性能更好,总正确率达到94.1%。
从而证明该方法用于Sallen-Key 滤波器软故障诊断是可行的,也是有效的。
关键词:Sallen-Key 滤波器,多分辨率变换,小波神经网络,人工鱼群算法,软故障诊断中图分类号:TP181;TM930文献标识码:ADOI :10.3969/j.issn.1002-0640.2019.10.034引用格式:王春兰,郭峰.基于AFSA-WNN 的Sallen-Key 滤波器电路软故障诊断[J ].火力与指挥控制,2019,44(10):173-177.基于AFSA-WNN 的Sallen-Key 滤波器电路软故障诊断王春兰,郭峰(西京学院,西安710123)Soft Fault Diagnosis for Sallen-Key Filter Circuit Based on AFSA-WNNWANG Chun-lan ,GUO Feng (Xijing University ,Xi ’an 710123,China )Abstract :In order to improve the capability of soft fault diagnosis for Sallen-Key filter ,a soft faultdiagnosis method based on multi-resolution transform and wavelet neural network (WNN )is proposed.Firstly ,the soft fault feature of Sallen-Key filter circuit is extracted by multi-resolution transform ,and then ,on the basis of this ,WNN optimized by artificial fish swarm algorithm is used to establish the soft fault diagnosis model of the circuit.The simulation results show that ,compared with the simple WNN ,the proposed method has better diagnosis performance for circuit soft fault ,the total correct rate is 94.1%.So it is proved that the method is feasible and effective in soft fault diagnosis for Sallen-Key filter.Key words :Sallen-Key filter ,multi-resolution transform ,wavelet neural network ,artificial fish swarm algorithm ,soft fault diagnosisCitation format :WANG C L ,GUO F.Soft fault diagnosis for Sallen-Key filter circuit based on AFSA-WNN [J ].Fire Control &Command Control ,2019,44(10):173-177.0引言Sallen-Key 滤波器是1955年R P Sallen 与E L Key 提出的一种由单个运算放大器和电阻、电容组成的低通滤波器,也是军事装备中应用最广泛的滤波器之一。
sallen-key低通滤波计算

Sallen-Key低通滤波器是一种常见的滤波器电路,用于电子电路中对信号进行滤波和去噪。
它具有简单的结构和良好的性能,因此在各种电子设备中被广泛应用。
本文将对Sallen-Key低通滤波器的计算方法进行详细介绍,帮助读者更深入地理解这一电路的工作原理和设计过程。
1. Sallen-Key低通滤波器的基本结构Sallen-Key低通滤波器由两个电容和两个电阻组成,其基本结构如下图所示:其中,R1和R2分别为电阻,C1和C2分别为电容,Vin为输入信号,Vout为输出信号。
通过调节电阻和电容的数值,可以实现对输入信号的滤波效果,将高频噪声和干扰信号滤除,从而获得干净的输出信号。
2. Sallen-Key低通滤波器的频率响应Sallen-Key低通滤波器的频率响应是描述其滤波特性的重要参数之一。
在设计和使用滤波器时,需要了解其在不同频率下的响应情况,以便选择合适的参数和进行性能评估。
Sallen-Key低通滤波器的频率响应可以通过其传递函数来描述。
传递函数H(jω)定义为输出信号与输入信号之间的复数比值,其中jω为频率参数。
Sallen-Key低通滤波器的传递函数一般形式为:H(jω) = Vo/Vin = K/((1+jω/ω1)(1+jω/ω2))其中,Vo为输出信号,Vin为输入信号,K为传递函数的增益,ω1和ω2为滤波器的角频率。
通过传递函数,可以分析Sallen-Key低通滤波器在不同频率下的幅频特性和相频特性,进而评估其滤波效果和应用范围。
3. Sallen-Key低通滤波器的参数选择与计算在实际应用中,需要根据具体的滤波要求和电路条件来选择Sallen-Key低通滤波器的参数,并进行相应的计算。
一般来说,需要确定以下几个参数:截止频率、增益、品质因数和中心频率。
(1)截止频率截止频率是指Sallen-Key低通滤波器在该频率下对输入信号的幅度进行衰减的频率。
一般情况下,截止频率是根据滤波要求和系统性能来确定的。
数字图像处理之频率滤波

数字图像处理之频率滤波
频率滤波是数字图像处理中的一种常用技术,用于改变图像中不同频率的成分,以达到图像增强、去噪等目的。
频率滤波可以分为低通滤波和高通滤波。
低通滤波器允许低频成分通过,而抑制高频成分。
它可以用于去除图像中的高
频噪声,平滑图像,使图像变得模糊。
常见的低通滤波器有均值滤波器、高斯滤波器等。
高通滤波器允许高频成分通过,而抑制低频成分。
它可以用于增强图像的边缘、细节等高频特征。
常见的高通滤波器有拉普拉斯滤波器、Sobel滤波器等。
频率滤波的基本原理是将图像转换到频域,通过对频域图像进行滤波操作,再
将滤波后的频域图像转换回空域,得到滤波后的图像。
常用的频率滤波方法有傅里叶变换、小波变换等。
在实际应用中,频率滤波常用于图像增强、去噪、边缘检测等领域。
通过选择
不同的滤波器和调整滤波参数,可以实现不同的滤波效果。
但是需要注意的是,频率滤波也可能引入一些副作用,如图像模糊、失真等,因此在应用时需要根据具体情况进行选择和调整。
优译低通滤波器解释及定义解析

低通滤波(Low-pass filter) 是一种过滤方式,规则为低频信号能正常通过,而超过设定临界值的高频信号则被阻隔、减弱。
但是阻隔、减弱的幅度则会依据不同的频率以及不同的滤波程序(目的)而改变。
它有的时候也被叫做高频去除过滤(high-cut filter)或者最高去除过滤(treble-cut filter)。
低通过滤是高通过滤的对立。
低通滤波可以简单的认为:设定一个频率点,当信号频率高于这个频率时不能通过,在数字信号中,这个频率点也就是截止频率,当频域高于这个截止频率时,则全部赋值为0。
因为在这一处理过程中,让低频信号全部通过,所以称为低通滤波。
低通过滤的概念存在于各种不同的领域,诸如电子电路,数据平滑,声学阻挡,图像模糊等领域经常会用到。
低通滤波器:电感阻止高频信号通过而允许低频信号通过,电容的特性却相反。
信号能够通过电感的滤波器、或者通过电容连接到地的滤波器对于低频信号的衰减要比高频信号小,称为低通滤波器。
低通滤波器原理很简单,它就是利用电容通高频阻低频、电感通低频阻高频的原理。
对于需要截止的高频,利用电容吸收电感、阻碍的方法不使它通过;对于需要放行的低频,利用电容高阻、电感低阻的特点让它通过。
如图所示,低频率允许通过,高频率不允许通过(抑制)。
对于不同滤波器而言,每个频率的信号的减弱程度不同。
低通滤波器概念有许多不同的形式,其中包括电子线路(如音频设备中使用的hiss 滤波器、平滑数据的数字算法、音障(acoustic barriers)、图像模糊处理等等,这两个工具都通过剔除短期波动、保留长期发展趋势提供了信号的平滑形式。
常用的滤波电路有无源滤波和有源滤波两大类。
若滤波电路元件仅由无源元件(电阻、电容、电感)组成,则称为无源滤波电路。
无源滤波的主要形式有电容滤波、电感滤波和复式滤波(包括倒L型、LC滤波、LCπ型滤波和RCπ型滤波等)。
若滤波电路不仅有无源元件,还有有源元件(双极型管、单极型管、集成运放)组成,则称为有源滤波电路。
基于Sallen-Key滤波器的核脉冲成形电路研究

基于Sallen-Key滤波器的核脉冲成形电路研究1李东仓1,杨磊1,田勇2,袁树林21兰州大学核科学与技术学院,兰州(730000)2 兰州大学信息科学与工程学院,兰州(730000)摘要:将Sallen-Key滤波器应用于核脉冲信号的成形中,采用较少的级数就可以达到准高斯波形的输出,文中仿真了基于Sallen-Key滤波器的滤波成形电路的特性,并给出了最佳的滤波器参数,采用宽带高速运算放大器设计和实现了该电路,通过实验测量证明了该电路的优越性。
关键词:Sallen-Key滤波器,核脉冲,高斯波形,成形中图分类号:TN722.7文献标识码:A在核电子学系统中,为了将核探测器输出的脉冲信号的幅度信息无失真的进行放大和成形,通常要在前置放大器之后的线性放大器中采用滤波成形电路,如极零相消电路,微分电路,多级积分电路等,以满足后级电路对信号波形的需要,提高信号噪声比。
通过最佳滤波器的讨论可知[1],对称无限宽尖顶脉冲具有最佳的信噪比,而高斯型波形即具有以上的特征,同时脉冲顶部比较平坦,弹道亏损小,所以,核脉冲的成形一般以成形为高斯型(准高斯型)波形为目标,通常由多级无源积分或有源积分电路组成[2]。
Sallen-Key滤波器(S-K滤波器,下同)是一种信号处理中常用的有源滤波电路[3,4],1955年由R. P. Sallen 和E. L. Key 提出了该电路,有高通S-K滤波器和低通S-K滤波器之分,该滤波器由于采用了部分正反馈而具有较大的品质因数。
将其应用于核脉冲的滤波成形,可以在较少的级数下得到准高斯波形,本文设计了一种基于S-K滤波器的采用高速集成运算放大器的准高斯滤波成形电路,通过电路仿真给出最佳参数,并进行了实验的验证。
1 准高斯滤波成形电路原理核探测器输出的电流脉冲信号经过电荷灵敏前置放大器,变换为以大的时间常数衰减的指数衰减信号,极零相消电路将信号变换为较小时间常数的指数衰减信号,并消除下冲,后面的两级S-K滤波器完成准高斯滤波成形,并获得一定的电压放大倍数。
实验报告5基于正反馈结构的高通滤波器的设计
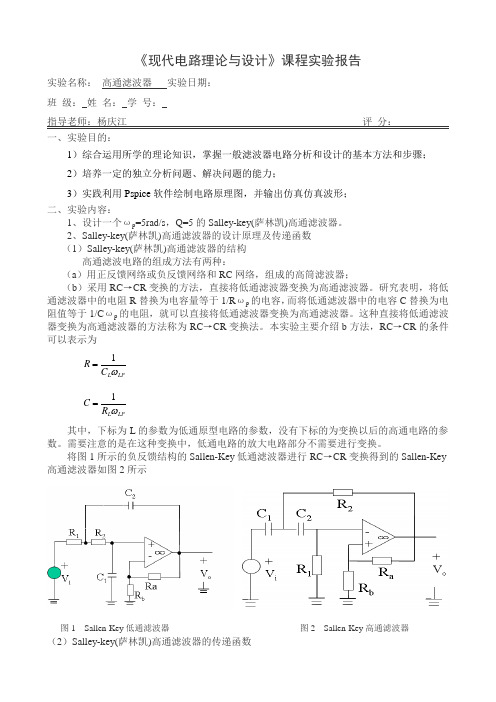
《现代电路理论与设计》课程实验报告实验名称: 高通滤波器 实验日期: 班 级: 姓 名: 学 号:指导老师:杨庆江 评 分: 一、实验目的:1)综合运用所学的理论知识,掌握一般滤波器电路分析和设计的基本方法和步骤;2)培养一定的独立分析问题、解决问题的能力;3)实践利用Pspice 软件绘制电路原理图,并输出仿真仿真波形;二、实验内容:1、设计一个ωp =5rad/s ,Q=5的Salley-key(萨林凯)高通滤波器。
2、Salley-key(萨林凯)高通滤波器的设计原理及传递函数 (1)Salley-key(萨林凯)高通滤波器的结构高通滤波电路的组成方法有两种:(a )用正反馈网络或负反馈网络和RC 网络,组成的高筒滤波器;(b )采用RC →CR 变换的方法,直接将低通滤波器变换为高通滤波器。
研究表明,将低通滤波器中的电阻R 替换为电容量等于1/R ωp 的电容,而将低通滤波器中的电容C 替换为电阻值等于1/C ωp 的电阻,就可以直接将低通滤波器变换为高通滤波器。
这种直接将低通滤波器变换为高通滤波器的方法称为RC →CR 变换法。
本实验主要介绍b 方法,RC →CR 的条件可以表示为 1L L PR C ω=1L L PC R ω=其中,下标为L 的参数为低通原型电路的参数,没有下标的为变换以后的高通电路的参数。
需要注意的是在这种变换中,低通电路的放大电路部分不需要进行变换。
将图1所示的负反馈结构的Sallen-Key 低通滤波器进行RC →CR 变换得到的Sallen-Key 高通滤波器如图2所示图1 Sallen-Key 低通滤波器 图2 Sallen-Key 高通滤波器(2)Salley-key(萨林凯)高通滤波器的传递函数对电路的节点列写方程如下:电路的转移函数为:传递函数转化为了:三、实验过程:1、理论计算(1)推导p ω 和Q 的表达式将高通滤波器电路的转移函数与标准的高通滤波函数相比较得:(2)计算p ω 和Q 的灵敏度根据灵敏度的定义,由式1和式2可以求得p ω 和Q 的灵敏度为()()()1211222 110b i o o a bR sC sC V s sC V V s sC V s R R R R ⎡⎤++---=⎢⎥+⎣⎦()()2221110sC V s sC V s R ⎡⎤+-=⎢⎥⎣⎦21b o oa bR V V V R R K==+()2211221121211111[) (]o iVK sK V s s R C C R C R R C C HS =-++++=222H (s)ppS Kss Qωω=++p ω=式1)121122)()(1)Q R R C K R C =++-式0H K =12120.5p p p pR R C C s s s s ωωωω====-20.5QR s Q =-+10.5QC s Q =-20.5[(QR s Q K =+--()1a b Q QR R s s K Q=-=-(3)元件值的设计根据所求得的表达式,令R 1 = R 2=R ,C 1=C 2=C 。
二阶 Sallen-Key

24
• 基本上一個 n-bit的轉換器就會有n個數 位輸出位元,此位元數是等效於A/D轉 換器輸入端的類比大小特性值,若所要 輸入的電壓或是電流量較大時,所需轉 換後的位元數也相對較多。 • 一典型A/D轉換器的基本腳位配置圖如 圖4.18所示。
25
圖4-18 A/D轉換器的基本腳位配置圖
26
類比數位轉換器類型
21
2.解析度
– 解析度係指A/D轉換器所能分辨的最小類比 輸入量,通常以可用於轉換數值的位元數 來表示,如8-bit、10-bit、12-bit與16-bit等, 位元數越高,解析度也越高。
22
3.轉換誤差
– 通常以相對誤差的形式輸出,用以表示A/D 轉換器實際輸出的數位值與理想輸出的數 位值之間的差異量,使用最低有效位LSB 的倍數表示。
18
類比與數位轉換
• 類比與數位轉換主要是將類比訊號轉換 成微處理器或電腦可以處理的數位訊號。
19
類比數位轉換器
• 顧名思義,A/D轉換器就是一個具有將 類比訊號 (電壓或是電流的形式) 轉換成 數位訊號的晶片,一般A/D轉換器的選 用因素大致是以解析度與轉換速度等兩 方面來加以考量。 • 完整的類比數位轉換過程中,必須包括 取樣、保持、量化、編碼等幾部分電路。
4-39
6
− ( nm ω RC ) 2 (1 +
RA ) RB
• 將 (4-39)式套入二階高通濾波器的轉換 通式如 (4-40)式,此處的Q亦為純數:
H = H DC − ( f fo )2 1 + ( j / Q)( f f o ) − ( f f o ) 2
4-40
• 可得其解如 (4-41)式,並畫出振幅響應 如圖4.14(b)。
有源滤波器Sallen-key拓扑介绍

做嵌入式系统,信号滤波是一个重要且复杂的话题,滤波的本质就是设计一个系统对不同频率带增益的控制。
不管是数字滤波器还是模拟滤波器,都是基于系统的传递函数对其幅频响应、相频响应等维度的设计应用。
Sallen-key拓扑的特点是:a. 高输入阻抗;b. 增益容易被配置;c. 运放被配置为电压跟随(Voltage Follower)模式;通用 Sallen-key 拓扑图 1 显示了采用单位增益运算放大器实现的通用单位增益 Sallen–Key 滤波器拓扑。
下面的分析基于假设运算放大器是理想的。
图 1 Sallen-key拓扑因为运算放大器(OA)是在一负反馈配置,根据虚短原则,其 V+ = V-。
并且,反相输入端V-直接连接到输出Vout,所以(1)根据电流节点方程(KCL)应用于Vx节点(2)通过结合方程式(1)和(2),在 OA 的非反相输入应用等式(1)和 KCL,可得意思就是(3)结合方程式(2)和(3)可得出(4)重新排列方程式(4)给出传递函数(5)分支阻抗通过选择不同的无源元件(例如,电阻器和电容器)Z1,Z2,Z4 和 Z3,该滤波器可以具有低通,带通和高通特性。
在下面的例子,回想与电阻器的电阻R有阻抗ZR的=RZR并与电容器的电容C有阻抗 CR的这里s = jw = 2πjf(这里 j表示虚数单位)是复角频率,并且f是纯正弦波输入的频率。
也就是说,电容器的阻抗与频率有关,而电阻器的阻抗与频率无关。
应用举例以下图 2、图 3、图 4 分别为 Sallen-key 拓扑下的单位增益低通滤波器、单位增益高通滤波器、放大倍数 G = 1+Rb/Ra 的带通滤波器。
图 2 Sallen-key拓扑的单位增益低通滤波器图 3 Sallen-key拓扑的单位增益高通滤波器图 4 Sallen-key拓扑的带通滤波器其中图2给出了单位增益低通配置的示例。
此处,运算放大器用作缓冲器,尽管发射级跟随器也很有效。
滤波器的原理

2.2滤波器的原理为了能准确的恢复信号/(/),必须以超过/(/)最高频率分量两倍的频率对其进行采样,实际上许多信号包含了频率分量的全部频谱,即从有用的频谱到白噪声的频谱,要精确的恢复这些信息,要求系统具有无法实现的高采样速率。
通过预处理输入信号,可以很容易的克服这个困难,其方法是在采样数据输入之前,采取措施限制带宽或则进行频率滤除。
前置滤波器通常称为抗混叠保证滤波器,例如在低通滤波器情况,数据釆样系统接受到的模拟信号,其频谱内容不比滤波器允许的那些频率高。
所以在考虑语音信号的干扰信号的频谱时,可以釆用限制宽带的方法,如果低通滤波器预先限制带宽,产生于语音信号的噪声的研究将得到简化。
2.2.1设计要点要得到一个完全理想的滤波器是无法用一个运放组成的。
即使可能,山于各个元件之间的复杂互感而导致设计者要用非常复杂的计算才能完成滤波器的设计。
通常对波形的控制要求越复杂就意味者需要更多的运放,这将根据设计者可以接受的最大畸变来决定。
或者可以通过儿次实验而最终确定下来。
如果设计者希望用最少的元件来实现滤波器,那么就别无选择,只能使用传统的滤波器,通过计算就可以得到了。
这里主要考虑以下儿点:1.滤波器的拐点(中心)频率2.滤波器电路的增益3.低通和高通滤波器的类型(Butterworth、Chebyshev、Bessel)2.2.2滤波器的原理及论证理想滤波电路的频响在通带内应具有一定幅值和线形相移,而在阻带内其幅值为0,实际中滤波器的设汁往往难以在幅频和相频响应都能达到理想的要求,因此只能根据实际情况设计不同的滤波器来寻求最佳的效果,这里对常见的三种滤波电路做个简单的比较。
下图给出了巴特沃斯与贝塞尔(Bessel)、契比雪夫(Chebyshev)滤波器的特性差异。
可以看出,巴特沃斯滤波器在线性相位、衰减斜率和加载特性三个方面具有特性均衡的优点,因此在本设计中,巴特沃斯滤波器列为首选。
图2.3滤波器特性差异图巴特沃斯(Butterworth)滤波器是一种具有最大平坦幅度响应的低通滤波器, 它在通信领域里已有广泛应用,在电测中也具有广泛的用途,可以作检测信号。
多重反馈型低通滤波器

多重反馈型低通滤波器
另一种常见的二阶低通滤波器的形式如图 1 所示。这种形式的滤波器比 Sallen-Key 型要多一个电阻,但是它在高频端的衰减特性要好的多,并且大 信号输入时失真也小。 图 1: 多重反馈型低通滤波器 列写电路方程如下: 化简后可得到: 当 R1 = R2 = R3 = R 时,上面的式子可以化简为: 可以看出输入输出关系是典型的二阶低通滤波器。 因此,设 C =sqrt(C1*C2),则根据品质因数 Q 可以确定两个电容的容值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Sallen―Key低通滤波器高频馈通现象的原因及解决
1.引言
Sallen-Key二阶低通滤波器是工程上应用最广泛的滤波器之一,其电路原型是利用电压反馈运算放大器及RC元件构成,优点是电路结构简单,通带增益、极点角频率和品质因数的表达式简洁,而且品质因数调节方便,可调范围大。
当设计一个模拟低通抗混叠滤波器时,通常希望它的幅度增益在滤波器的转折频率后一直下降。
对于Sallen-Key滤波器的确可以衰减转折频率和某个频点(这个频点比转折频率更高)间的信号,但在该高频点后,滤波器的幅度增益开始随着频率的增加而增加,即高频馈通现象。
本文分析了Sallen-Key低通滤波器产生的高频馈通现象的原因,并且通过TI公司的SPICE仿真软件Tina-TI进行仿真验证,快速且直观的反应出了这种高频馈通现象。
通过给出的三种常见解决方法,有效的抑制了高频馈通现象。
2.Sallen-Key低通滤波器高频馈通现象产生的原因
以OPA227运放为例,如图1所示,为一个典型的Sallen-Key低通滤波器。
图1 典型Sallen-Key低通滤波器
该电路的增益曲线如图2所示。
图2 典型Sallen-Key低通滤波器增益曲线
考虑到Sallen-Key型滤波器的拓扑结构,实际上有两条路径产生了Vout,一条是忽略了输出阻抗的运放输出,它主宰了前半部分“正常”的
增益曲线;另一条是流过R1和C2的电流注入到运放闭环输出阻抗Zo上的结果,它主宰了“上扬”的后半部分增益曲线。
在100K频率附近前,既是理想的滤波器增益曲线。
我们知道放大器的特性:随着频率的升高,放大器的开环增益下降,它的闭环输出阻抗开始增加。
所以随着闭环输出电阻Zo的增加,当其上的电压等于运放的正向输出电压,此时开始Zo上的电压将占主导地位(因为运放的增益持续降低,信号难以通过运放,将选择更容易到达输出端的路径),此时开始,增益曲线的斜率将跟随着Zo增加的斜率。
直到运放的开环增益降为0的频率开始,Zo保持恒定,增益曲线保持稳定。
我们可以用等效电路来推倒上面的结论,假设到某一频点(转折频率附近),导致C1,C2都交流短路,则可以得到:
OPA227的开环输出阻抗约为20欧姆,所以Zo最大也就是20欧姆,远小于R1,因此可以简化得到:
这里R1为2.4K。
查看OPA277的开环增益曲线可知,在主极点140mHz 后,OPA277的开环增益以-20dB/decade的速率下降,相反地闭环输出阻抗将以20dB/decade的速度增大,所以,闭环增益曲线将随Zo的
20dBde/decade斜率上升而上升,并在运放的开环增益为0时,闭环增益降等于Zo/R1。
由图2,可以清楚地看到,在C1,C2短路前,滤波器的开环增益曲线,以-40dB/decade的速度下降;C1,C2短路后,滤波器的闭环增益随着Zo
的上升斜率20dB/decade开始上升,直到8MHz附近,OPA277开环增益降为0dB,Zo=20欧姆,此时,Vout/Vin=20/2.4K=0.008≈40dB。
3.解决Sallen-Key低通滤波器高频馈通的常用方法
基于对以上高频馈通原因的分析,下面给出三种常用的解决方法:
(1)如果可能,选择FET或者CMOS型放大器作为为有源滤波器,他们拥有pA级的输入偏置电流,这是的可以将R1和R2增大10倍,C1,C2减小10倍。
增大R1,可以大大减少流过Zo的电流;减小C,可以节约尺寸和成本。
(2)在滤波后再加一个RC滤波抑制高频,如图3所示。
(3)在C2和Zo间添加一个缓冲器隔离,使得C2上的电流不再流入Zo。
图3 加入RC滤波后的Sallen-Key低通滤波器
图4 加入RC滤波后的Sallen-Key低通滤波器增益曲线
图5 加入缓冲隔离后的Sallen-Key低通滤波器
图6 加入缓冲隔离后的Sallen-Key低通滤波器增益曲线
需要注意的是为了减少运放偏置电流对系统频率的影响,隔离C2和Zo的运放应该选择FET或CMOS输入的放大器。
加入隔离运放后,我们看到系统较第二种方法将拥有更好的滤波响应。
4.结论
通过分析Sallen-Key低通滤波器的高频馈通现象产生的原因,本文给出了三种可行的解决方法并加以比较,通过Tina-TI软件仿真,验证了文中所提的三种方法能够有效的解决Sallen-Key低通滤波器的高频馈通。
希望以上资料对你有所帮助,附励志名言3条:
1、生命对某些人来说是美丽的,这些人的一生都为某个目标而奋斗。
2、推销产品要针对顾客的心,不要针对顾客的头。
3、不同的信念,决定不同的命运。
