2017-2018学年高中数学人教A版必修三同步训练题库几何概型与均匀随机数的产生练习
2017-2018学年人教A版数学必修3习题精选:第三章 概率 3-3-2 含解析 精品

3.3.2均匀随机数的产生课后篇巩固探究A组1.与均匀随机数特点不符的是()A.是区间内的任何一个实数B.是随机的C.是等可能的D.是随机数的平均数解析:A,B,C是均匀随机数的定义,均匀随机数的“均匀”是“等可能”的意思,并不是“随机数的平均数”.答案:D2.设x是[0,1]内的一个均匀随机数,经过变换,y=2x+3,则x=错误!未找到引用源。
对应变换成的均匀随机数是()A.0B.2C.4D.5解析:当x=错误!未找到引用源。
时,y=2×错误!未找到引用源。
+3=4.答案:C3.把[0,1]内的均匀随机数x分别转化为[0,4]和[-4,1]内的均匀随机数y1,y2,需实施的变换分别为()A.y1=-4x,y2=5x-4B.y1=4x-4,y2=4x+3C.y1=4x,y2=5x-4D.y1=4x,y2=4x+3解析:∵x∈[0,1],∴4x∈[0,4],5x-4∈[-4,1].故选C.答案:C4.在边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为错误!未找到引用源。
,则阴影区域的面积约为()A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.无法计算解析:在正方形中随机撒一粒豆子,它落在阴影区域内的概率为错误!未找到引用源。
,∵S正方形=4,∴S阴影≈错误!未找到引用源。
.答案:B5.下列关于用转盘进行随机模拟的说法正确的是()A.旋转次数的多少不会影响估计的结果B.旋转次数越多,估计的结果越精确C.旋转时可以按规律旋转D.转盘的半径越大,估计的结果越精确答案:B6.已知利用计算机产生[0,1]上的均匀随机数x=0.2,则利用伸缩和平移变换后,得到在[2,4]内的均匀随机数为.解析:利用计算机产生[0,1]上的均匀随机数后,由伸缩和平移变换公式x=x1×(b-a)+a,得到[2,4]上的均匀随机数0.2×(4-2)+2=2.4.答案:2.47.一鱼缸盛有a升水,内有b条鱼苗,用一个水杯从鱼缸中取出c(c<a)升水,用随机模拟的方法判断这杯水中大约含有条鱼苗.解析:设含有x条鱼苗,错误!未找到引用源。
人教A版高中数学必修三试卷-高中同步练测:3.3几何概型.docx

高中数学学习材料鼎尚图文*整理制作第3章 3.3 几何概型 同步测试试卷(数学人教A 版必修3)一、选择题(本题包括5小题,每小题5分,共25分)1. 在面积为S 的△ABC 的边AB 上任取一点P ,则△PBC 的面积大于S4的概率是( )A.14B.12C.34D.232. 在半径为1的圆周上有一定点A ,以A 为端点连一弦,另一端点在圆周上等可能的选取(即在单位长度的弧上等可能选取),则弦长超过3的概率为( ) A.14 B.23 C.13 D.333.向如图所示的方砖上随机投掷一粒豆子,则该豆子落在阴影部分的概率是( )A.18B.29 C.79 D.7164.已知实数x 、y ,可以在0<x <2,0<y <2的条件下随机取数,那么取出的数对(x ,y )满足(x -1)2+(y -1)2<1的概率是( ) A.π4 B.4πC .π2D.π35.在1万 km 2的海域中有40 km 2的大陆架贮藏着石油,假如在海域中任意一点钻探,钻到油层面的概率是( )A.2511B.2491C.2501 D.2521二、填空题(本题包括4小题,每小题5分,共20分)6. 点A 为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B ,则劣弧AB 的长度小于1的概率为________.7. 广告法对插播广告时间有规定,某人对某台的电视节目作了长期的统计后得出结论,他任意时间打开电视机看该台节目,看不到广告的概率约为910,那么该台每小时约有________分钟广告.8. 如下图,在半径为1的半圆内,放置一个边长为21的正方形ABCD ,向半圆内任投一点,该点落在正方形内的概率为_________.A BCD9. 如下图,在直角坐标系内,射线OT 落在60°的终边上,任作一条射线OA ,则射线落在∠xOT建议用时 实际用时满分 实际得分45分钟100分内的概率是________.三、计算题(本题共3小题,共55分)10.(18分)一海豚在水池中自由游弋,水池为长30 m、宽20 m的长方形,求此海豚嘴尖离岸边不超过2 m的概率.11.(18分)如图,在等腰直角三角形ABC中,过直角顶点C在∠ACB内部作一条射线CM,与线段AB交于点M.求AM<AC的概率.12.(19分)在转盘游戏中,假设有三种颜色红、绿、蓝.在转盘停止时,如果指针指向红色为赢,绿色为平,蓝色为输,问若每种颜色被平均分成四块,不同颜色相间排列,要使赢的概率为15,输的概率为13,则每个绿色扇形的圆心角为多少度(假设转盘停止位置都是等可能的)?第3章 3.3 几何概型同步测试试卷(数学人教A版必修3)答题纸得分:一、选择题题号 1 2 3 4 5答案二、填空题6. 7. 8. 9.二、计算题10.11.12.第3章 3.3 几何概型 同步测试试卷(数学人教A 版必修3)答案一、选择题1.C 解析:如右图所示,在边AB 上任取一点P ,因为△ABC 与△PBC 是等高的,所以事件“△PBC的面积大于S 4”等价于事件“|BP |∶|AB |>14”.即P (△PBC 的面积大于S 4)=|P A ||BA |=34.2.C 解析:如图,另一端落在圆周上任一点,可用圆周长来度量.圆内接正三角形ABC 的边长为3.若任一端点落在劣弧上,则弦长超过3,而落在劣弧之外,则弦长不超过 3.劣弧之长为圆周的13.事件A=“弦长超过3”意味着另一端点落在劣弧上,A 可用弧长来度量,故P (A )==13.故选C.3.B 解析:符合面积型几何概型问题,故选B.4.A 解析: 0<x <2,0<y <2表示图形为正方形内部点,(x -1)2+(y -1)2<1表示圆内部点,此圆内切于正方形,由几何概型概率计算公式知,概率值等于面积比,即π2×2=π4.5.C 解析:. 二、填空题6. 解析:圆周上使的长度为1的点M 有两个,设为M 1,M 2,则过A 的圆弧的长度为2,B 点落在优弧上就能使劣弧的长度小于1,所以劣弧的长度小于1的概率为23.7.解析:这是一个与时间长度有关的几何概型,这人看不到广告的概率为910,则看到广告的概率约为110,故60×110=6. 8.π21解析:=. 9. 解析:P =.三、解答题10.解:如图,四边形ABCD 是长30 m 、宽20 m 的长方形.图中的阴影部分表示事件A :海豚嘴尖离岸边不超过2 m .问题可化为求海豚嘴尖出现在阴影部分的概率.∵ S 长方形ABCD =30×20=600(m 2),S 长方形A ′B ′C ′D ′=(30-4)×(20-4)=416(m 2), ∴ S 阴影部分=S 长方形ABCD -S 长方形A ′B ′C ′D ′=600-416=184(m 2),根据几何概型的概率公式,得P (A )=184600=2375≈0.31.11.解:这是几何概型问题且射线CM 在∠ACB 内部.在AB 上取AC ′=AC ,则∠ACC ′=180°-45°2=67.5°.设A ={在∠ACB 内部作一条射线CM ,与线段AB 交于点M ,AM <AC }.则所有可能结果的区域角度为90°,事件A 的区域角度为67.5°,∴ P (A )=67.590=34.12.解:由于转盘旋转停止位置都是等可能的,并且位置是无限多的,所以符合几何概型的特点,问题转化为求圆盘角度或周长问题.因为赢的概率为15,所以红色所占角度为周角的15,即α1=360°5=72°.同理,蓝色占周角的13,即α2=360°3=120°,所以绿色所占角度α3=360°-120°-72°=168°. 将α3分成四等份, 得α3÷4=168°÷4=42°.即每个绿色扇形的圆心角为42°.。
2017-2018学年高中数学人教A版必修三课时作业:第3章 概率 3.3 习题课 Word版含答案

课时目标
的正方形中有一封闭曲线围成的阴影区域.在正方形中随机撒一粒豆子,它落在阴影区域内的概率为
.如图所示,在直角坐标系内,射线
落在∠xOT内的概率是
落在直角坐标系的每个位置可能性是一样的,这是与角度有关的几何概型问题.因为周角是
为事件A,其概率为
BP BA
的面积大于S
4)|BA|4
.如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为
假设每次都能击中木板,且击中木板上每个点的可能性都一样,
()。
2017-2018学年高中数学必修三教材用书:第三章 概率 3

3.3.2 均匀随机数的产生[导入新知]1.均匀随机数的产生(1)计算器上产生[0,1]的均匀随机数的函数是RAND 函数. (2)Excel 软件产生[0,1]区间上均匀随机数的函数为“rand(_)”. 2.用模拟的方法近似计算某事件概率的方法(1)试验模拟的方法:制作两个转盘模型,进行模拟试验,并统计试验结果.(2)计算机模拟的方法:用Excel 的软件产生[0,1]区间上均匀随机数进行模拟.注意操作步骤.[化解疑难]整数随机数与均匀随机数的异同二者都是随机产生的随机数,在一定的区域长度上出现的概率是均等的.但是整数随机数是离散的单个整数值,相邻两个整数随机数的步长为1;而均匀随机数是小数或整数,是连续的小数值,相邻两个均匀随机数的步长是人为设定的.[例1] 得两段的长都不小于2 m 的概率有多大?[解] 设剪得两段的长都不小于2 m 为事件A .法一:(1)利用计算器或计算机产生n 个0~1之间的均匀随机数,x =RAND ; (2)作伸缩变换:y =x *(5-0),转化为[0,5]上的均匀随机数; (3)统计出[2,3]内均匀随机数的个数m ; (4)概率P (A )的近似值为mn .法二:(1)做一个带有指针的转盘,把圆周五等分,标上刻度[0,5](这里5和0重合); (2)固定指针转动转盘或固定转盘旋转指针,记下指针在[2,3]内(表示剪断绳子位置在[2,3]范围内)的次数m 及试验总次数n ;(3)概率P (A )的近似值为m n .[类题通法]利用随机模拟计算概率的步骤(1)确定概率模型;(2)进行随机模拟试验,即利用计算器等以及伸缩和平移变换得到[a ,b ]上的均匀随机数; (3)统计计算;(4)得出结论,近似求得概率. [活学活用]已知米粒等可能地落入如图所示的四边形ABCD 内,如果通过大量的试验发现米粒落入△BCD 内的频率稳定在49附近,那么点A 和点C 到直线BD 的距离之比约为________.解析:设米粒落入△BCD 内的频率为P 1,米粒落入△BAD 内的频率为P 2,点C 和点A 到直线BD 的距离分别为d 1,d 2,根据题意得,P 2=1-P 1=1-49=59,又∵P 1=S △BCDS 四边形ABCD =12×BD ×d 1S 四边形ABCD ,P 2=S △BADS 四边形ABCD =12×BD ×d 2S 四边形ABCD ,∴P 2P 1=d 2d 1=54. 答案:54[例2] 面画了小、中、大三个同心圆,半径分别为3 cm ,6 cm,9 cm.某人站在3 m 之外向此板投镖,假设投镖击在线上或没有投中木板不算,可重投,用随机模拟的方法估计:(1)“投中小圆内”的概率是多少?(2)“投中小圆与中圆形成的圆环”的概率是多少? [解] 记事件A ={}投中小圆内, 事件B ={}投中小圆与中圆形成的圆环.按如下步骤进行:第一步,用计算机产生两组[0,1]上的均匀随机数,a 1=RAND ,b 1=RAND ;第二步,经过伸缩和平移变换,a =a 1·32-16,b =b 1·32-16,得到两组[-16,16]上的均匀随机数;第三步,统计投在小圆内的次数N 1(即满足a 2+b 2<9的点(a ,b )的个数),投中小圆与中圆形成的圆环的次数N 2(即满足9<a 2+b 2<36的点(a ,b )的个数),投中木板的总次数N (即满足-16<a <16,-16<b <16的点(a ,b )的个数);第四步,计算频率f n (A )=N 1N ,f n (B )=N 2N ,即分别为概率P (A ),P (B )的近似值. [类题通法]用随机模拟方法估计长度型与面积型几何概型的概率的联系与区别 (1)联系:二者模拟试验的方法和步骤基本相同,都需产生随机数;(2)区别:长度型几何概型只要产生一组均匀随机数即可,所求事件的概率为表示事件的长度之比,对面积型几何概型问题,一般需要确定点的位置,而一组随机数是不能在平面上确定点的位置的,故需要利用两组均匀随机数分别表示点的横纵坐标,从而确定点的位置,所求事件的概率为点的个数比.[活学活用]现向图中所示正方形内随机地投掷飞镖,试用随机模拟的方法求飞镖落在阴影部分的概率.解:第一步,利用计算器或计算机产生两组0至1区间内的均匀随机数a 1、b 1(共N 组);第二步,经过平移和伸缩变换,a =(a 1-0.5)*2, b =(b 1-0.5)*2;第三步,数出满足不等式b <2a -43,即6a -3b >4的数组数N 1.所求概率P ≈N 1N .可以发现,试验次数越多,概率P 越接近25144.机撒一粒豆子,它落在阴影区域内的概率为23,则阴影区域的面积为( )A.43 B .83C.23D .无法计算(2)利用随机模拟的方法近似计算图中阴影部分(抛物线y =2-2x -x 2与x 轴围成的图形)的面积.[解析] (1)选B 由几何概型的公式可得S 阴影S 正方形=23,又S 正方形=4,∴S 阴影=4×23=83.(2)第一步,利用计算机产生两组[0,1]上的均匀随机数,a 1=RAND ,b 1=RAND ; 第二步,经过平移和伸缩变换,a =a 1·4-3,b =b 1·3,得到一组[-3,1]和一组[0,3]上的均匀随机数;第三步,统计试验总次数N 和落在阴影部分的点数N 1(满足条件b <2-2a -a 2的点(a ,b )的个数);第四步,计算频率N 1N 就是点落在阴影部分的概率的近似值;第五步,设阴影部分的面积为S ,由几何概型概率公式得点落在阴影部分的概率为S12,所以S 12≈N 1N ,故S ≈12N 1N 即为阴影部分面积的近似值. [类题通法]利用随机模拟法估计图形面积的步骤(1)把已知图形放在平面直角坐标系中,将图形看成某规则图形(长方形或圆等)内的一部分,并用阴影表示;(2)利用随机模拟方法在规则图形内任取一点,求出落在阴影部分的概率P (A )=N 1N; (3)设阴影部分的面积是S ,规则图形的面积是S ′,则有S S ′=N 1N ,解得S =N 1N S ′,即已知图形面积的近似值为N 1N S ′.[活学活用]利用随机模拟的方法近似计算图中阴影部分(曲线y =2x 与直线x =±1及x 轴围成的图形)的面积.解:设事件A 为“随机向正方形内投点,所投的点落在阴影部分”,操作步骤如下:第一步,用计数器n 记录做了多少次试验,用计数器m 记录其中有多少次(x ,y )满足-1<x <1,0<y <2x (即点落在图中阴影部分),首先设置n =0,m =0;第二步,用变换rand( )*2-1产生-1~1之间的均匀随机数x 表示所投点的横坐标,用变换rand( )*2产生0~2之间的均匀随机数y 表示所投点的纵坐标;第三步,判断点是否落在阴影部分,即是否满足y <2x ,如果是,则计数器m 的值加1,即m =m +1,如果不是,m 的值保持不变;第四步,表示随机试验次数的计数器n 的值加1,即n =n +1,如果还要试验,则返回步骤第二步继续执行,否则结束.程序结束后事件A 发生的频率mn作为事件A 的概率的近似值.设阴影部分的面积为S ,正方形面积为4,由几何概型概率计算公式得,P (A )=S 4,所以mn ≈S 4,故4mn 可作为阴影部分面积S 的近似值.9.几何概型中的会面问题[典例] 甲、乙两人约定晚上6点到7点之间在某地见面,并约定先到者要等候另一人一刻钟,过时即可离开.求甲、乙能见面的概率.[解题流程][规范解答]法一(利用几何概型的概率公式): 如图所示:[类题通法]利用几何概型求解会面问题会面问题是利用数形结合转化为面积型几何概型的问题解决的,步骤如下: (1)将时间分别用x ,y 两个坐标表示,构成平面内的点(x ,y ); (2)找出会面关系,用式子表示出能够会面的条件;(3)在平面直角坐标系里,画出所有可能的结果表示的区域,并求出面积; (4)用阴影部分表示出能够会面的区域,并求面积; (5)代入几何概型的概率公式求解. [活学活用]两艘轮船都要停靠同一个泊位,它们可能在一昼夜的任意时刻到达,设甲、乙两艘轮船停靠泊位的时间分别是2小时与4小时,求有一艘轮船停靠泊位时必须等待一段时间的概率.解:如图所示,以x 和y 分别表示甲、乙两船到达泊位的时间,则有一艘船停靠泊位时必须等待一段时间的等价条件是甲先到:y ≤x +2,乙先到:x ≤y +4.在平面直角坐标系内,(x ,y )的所有可能结果是边长为24的正方形,而事件A “有一艘船停靠泊位时必须等待一段时间”的所有可能结果由图中的阴影部分来表示,μA =242-12×222-12×202=134,μΩ=242=576,所以P (A )=μA μΩ=134576=67288.故有一艘轮船停靠泊位时必须等待一段时间的概率为67288.[随堂即时演练]1.要产生[-3,3]上的均匀随机数y ,现有[0,1]上的均匀随机数x ,则y 不可取为( ) A .-3x B .3x C .6x -3D .-6x -3解析:选D 法一:利用伸缩和平移变换进行判断, 法二:由0≤x ≤1,得-9≤-6x -3≤-3, 故y 不能取-6x -3.2.设x ,y 是两个[0,1]上的均匀随机数,则0≤x +y ≤1的概率为( ) A.12 B .14C.29D .316解析:选A 如图所示,所求的概率为 P =S 阴影S 正方形=12. 3.b 1是[0,1]上的均匀随机数,b =6(b 1-0.5),则b 是________上的均匀随机数. 解析:∵b 1∈[0,1], ∴b 1-0.5∈[-0.5,0.5], ∴6(b 1-0.5)∈[-3,3]. 答案:[-3,3]4.(全国甲卷改编)从区间[0,1]随机抽取2n 个数x 1,x 2,…,x n ,y 1,y 2,…,y n ,构成n 个数对(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为________.(用m ,n 表示)解析:因为x 1,x 2,…,x n ,y 1,y 2,…,y n 都在区间[0,1]内随机抽取,所以构成的n 个数对(x 1,y 1),(x 2,y 2),…,(x n ,y n )都在边长为1的正方形OABC 内(包括边界),如图所示.若两数的平方和小于1,则对应的数对在扇形OAC 内(不包括扇形圆弧上的点所对应的数对),故在扇形OAC 内的数对有m 个.用随机模拟的方法可得S 扇形S 正方形=m n ,即π4=mn ,所以π=4m n .答案:4m n5.如图所示,向边长为2的大正方形内投飞镖,利用随机模拟的方法求飞镖落在中央边长为1的小正方形中的概率.(假设飞镖全部落在大正方形内)解:用几何概型概率计算公式得P =S 小正方形S 大正方形=14.用计算机随机模拟这个试验,步骤如下:第一步,用计数器n 记录做了多少次投飞镖的试验,用计数器m 记录其中有多少次投在中央的小正方形内,设置n =0,m =0;第二步,用函数rand( )*4-2产生两个-2~2之间的均匀随机数x ,y ,x 表示所投飞镖的横坐标,y 表示所投飞镖的纵坐标;第三步,判断(x ,y )是否落在中央的小正方形内,也就是看是否满足|x |<1,|y |<1,如果是,则m 的值加1,即m =m +1,否则m 的值保持不变;第四步,表示随机试验次数的计数器n 加1,即n =n +1,如果还需要继续试验,则返回步骤第二步继续执行,否则,程序结束.程序结束后飞镖投在小正方形内的频率mn作为所求概率的近似值.[课时达标检测]一、选择题1.若-4≤x ≤2,则x 是负数的概率是( ) A.14 B .34C.13 D .23答案:D2.已知函数f (x )=log 2x ,x ∈⎣⎡⎦⎤12,2,则在区间⎣⎡⎦⎤12,2上任取一点x 0,使f (x 0)≥0的概率为( )A .1B .12C.23 D .34答案:C3.设一直角三角形两直角边的长均是区间[0,1]上的随机数,则斜边的长小于1的概率为( )A.12 B .34C.π4 D .3π16答案:C4.欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为1.5 cm 的圆,中间有边长为0.5 cm 的正方形孔,随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为( )A.49π B .94π C.4π9 D .9π4答案:A5.如图,在△AOB 中,已知∠AOB =60°,OA =2,OB =5,在线段OB 上任取一点C ,求△AOC 为钝角三角形的概率.( )A .0.6B .0.4C .0.2D .0.1答案:B 二、填空题6.如图的矩形,长为5 m ,宽为2 m ,在矩形内随机撒300粒黄豆,数得落在阴影部分的黄豆数为138,则我们可以估计出阴影部分的面积为________m 2.解析:由题意得:138300=S 阴影5×2,S 阴影=235.答案:2357.一个投针试验的模板如图所示,AB 为半圆O 的直径,点C 在半圆上,且CA =CB .现向模板内任投一针,则该针恰好落在△ABC 内(图中的阴影区域)的概率是________.解析:设半圆O 的半径为r , 则半圆O 的面积S 半圆=12πr 2,在△ABC 中,AB =2r ,CA =CB =2r , ∴S △ABC =12·2r ·2r =r 2.据题意可知该概率模型是几何概型,所以所求的概率为P =S △ABC S 半圆=r 212πr 2=2π.答案:2π8.小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若此点到圆心的距离大于12,则周末去看电影;若此点到圆心的距离小于14,则去打篮球;否则,在家看书.则小波周末不在家看书的概率为________.解析:由题意画出示意图,如图所示.表示小波在家看书的区域如图中阴影部分所示,则他在家看书的概率为⎝⎛⎭⎫122π-⎝⎛⎭⎫142ππ=316, 因此他不在家看书的概率为 1-316=1316. 答案:1316三、解答题9.利用随机模拟方法计算图中阴影部分(曲线y =2x 与x 轴、x =±1围成的部分)的面积. 解:(1)利用计算机产生两组[0,1]上的均匀随机数,a 1=RAND ,b 1=RAND.(2)经过平移和伸缩变换,a =(a 1-0.5)*2,b =b 1]N 1,N ),即为点落在阴影部分的概率的近似值.(3)统计试验总次数N 和落在阴影内的点数N 1. (4)计算频率N 1N,即为点落在阴影部分的概率的近似值.(5)用几何概型的概率公式求得点落在阴影部分的概率为P =S 4,N 1N =S 4,∴S ≈4N 1N ,即为阴影部分的面积值.10.对某人某两项指标进行考核,每项指标满分100分,设此人每项得分在[0,100]上是等可能出现的.若单项80分以上,且总分170分以上才合格,求他合格的概率.解:设某人两项的分数分别为x 分、y 分, 则0≤x ≤100,0≤y ≤100, 某人合格的条件是:80<x ≤100, 80<y ≤100,x +y >170.在同一平面直角坐标系中,作出上述区域(如图中阴影部分所示).由图可知:0≤x ≤100,0≤y ≤100构成的区域面积为100×100=10 000,合格条件构成的区域面积为S 五边形BCDEF =S 矩形ABCD -S △AEF =400-12×10×10=350, 所以所求概率为P =35010 000=7200. 答:该人合格的概率为7200. 11.已知甲、乙两人约定到羽毛球馆去打球,两人都在9:30~11:30的任意时刻到达,若两人的到达时刻相差20分钟以内,两人可以一起打球,否则先到者就和别人在一起打球,求甲、乙两人没在一起打球的概率.解:设甲的到达时刻为x ,乙的到达时刻为y ,由(x ,y )构成的区域Ω={(x ,y )|0≤x ≤2,0≤y ≤2},此区域面积S =2×2=4,令两人没在一起打球的事件为A ,则事件A 构成区域A =(x ,y )|x -y |>13,0≤x ≤2,0≤y ≤2,区域A 的面积为S A =⎝⎛⎭⎫532=259, ∴P (A )=S A S =2536.。
人教A版高中数学必修3第三章3.3几何概型同步练习(II)卷

人教A版高中数学必修3 第三章3.3 几何概型同步练习(II)卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题;共12分)1. (2分)一个游戏转盘上有四种颜色:红、黄、蓝、黑,并且它们所占面积的比为6∶2∶1∶4,则指针停在红色或蓝色的区域的概率为()A .B .C .D .2. (2分)在[0,π]上随机取一个数x,则事件“2sin cos+cosx≥”发生的概率为()A .B .C .D .3. (2分)(2017·安庆模拟) 已知单位圆有一条长为的弦AB,动点P在圆内,则使得≥2的概率为()A .B .C .4. (2分)一只蚂蚁在边长为5的等边三角形的边上爬行,某时刻该蚂蚁距离三角形的三个顶点的距离均超过1的概率为()A .B .C .D .5. (2分)(2018·鞍山模拟) 《九章算术》是我国古代数学名著,也是古代东方数学的代表作.书中有如下问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“已知直角三角形两直角边长分别为5步和12步,问一边在勾上的内接正方形边长为多少步?”现向此三角形内投一粒豆子,则豆子落在这个内接正方形内的概率是()A .B .C .D .6. (2分) (2018高一下·临沂期末) 在边长为的等边三角形的边上任取一点,使成立的概率为()A .B .D .二、填空题 (共4题;共6分)7. (1分)(2017·渝中模拟) 已知Ω1是集合{(x,y)|x2+y2≤1}所表示的区域,Ω2是集合{(x,y)|y≤|x|}所表示的区域,向区域Ω1内随机的投一个点,则该点落在区域Ω2内的概率为________.8. (3分)判断下列每对事件是不是互斥事件:①将一枚硬币抛掷两次,记事件A:两次出现正面;事件B:只有一次出现正面.________②某人射击一次,记事件A:中靶;事件B:射中9环.________③某人射击一次,记事件A:射中环数大于5;事件B:射中环数小于5.________.9. (1分) (2018高二下·晋江期末) 任取两个小于1的正数x、y ,若x、y、1能作为三角形的三条边长,则它们能构成钝角三角形三条边长的概率是________.10. (1分)抛掷一粒骰子,观察掷出的点数,设事件A为出现奇数,事件B为出现2点,已知P(A)=,P(B)=,则出现奇数点或2点的概率是________三、解答题 (共2题;共15分)11. (10分) (2017高一下·新余期末) 设关于x的一元二次方程x2+ax﹣ +1=0.(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程中有实根的概率;(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.12. (5分)如图,在圆心角为直角的扇形OAB中,分别以OA、OB为直径作两个半圆,在扇形OAB内随机取一点,求此点取自阴影部分的概率.参考答案一、单选题 (共6题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共4题;共6分)7-1、8-1、9-1、10-1、三、解答题 (共2题;共15分)11-1、11-2、12-1、。
2017-2018学年高中数学人教A版必修3练习:3-3 几何概

1.下面关于几何概型的说法错误的是( )A .几何概型也是古典概型的一种B .几何概型中事件发生的概率与位置、形状无关C .几何概型在一次试验中可能出现的结果有无限个D .几何概型中每个结果的发生具有等可能性解析:古典概型属有限等可能性,而几何概型是无限等可能,所以几何概型不能划到古典概型之列.答案:A2.一个红绿灯路口,红灯亮的时间为30秒,黄灯亮的时间为5秒,绿灯亮的时间为45秒,当你到达路口时,恰好看到黄灯亮的概率是( )A.112B.38C.116D.56 解析:530+45+5=580=116. 答案:C3.一只蚂蚁在如图所示的地板砖(除颜色不同外,其余全部相同)上爬来爬去,它最后停留在黑色地板砖(阴影部分)上的概率是( )A.13B.23C.14D.18解析:地板砖共有3×4=12块,黑色有4块.∴412=13. 答案:A4.一条河上有一个渡口,每隔一小时有一趟渡船,河的上游还有一座桥,某人到这个渡口等候渡船,他准备等候20分钟,如果20分钟渡船不到,他就要绕到上游从桥上过河.则他乘船过河的概率是__________.解析:2060=13. 答案:135.在如图所示的正方形中随机撒入1 000粒芝麻,则撒入圆内的芝麻数大约为________ (结果保留整数).解析:设正方形边长为2a ,则S 正=4a 2,S 圆=πa 2.因此芝麻落入圆内的概率为P =πa 24a 2=π4,大约有1 000×π4≈785粒. 答案:7856.将一长为 18 cm 的线段随机地分成三段,则这三段能组成一个三角形的概率是多少?解:假设x 与y 表示三个长度中的两个,因为是长度,所以应有:x >0,y >0和x +y <18,即所有x 和y 值必须在如图所示的以(0,18),(0,0)和(18,0)为顶点的三角形内.要组成三角形,由组成三角形的条件知,x 和y 都小于9,且x +y >9(如图所示的阴影部分),又因为阴影部分三角形的面积占大三角形面积的14,故能够组成三角形的概率为0.25.。
人教A版高中数学必修3同步检测第3章3.3几何概型.docx

人教 A 版高中数学必修 3 同步检测第三章3.3几何概型3.3.1几何概型3.3.2均匀随机数的产生A 级基础巩固一、选择题1.下列关于几何概型的说法中,错误的是()A.几何概型是古典概型的一种,基本事件都具有等可能性B.几何概型中事件发生的概率与它的位置或形状无关C.几何概型在一次试验中可能出现的结果有无限多个D.几何概型中每个结果的发生都具有等可能性解析:几何概型和古典概型是两种不同的概率模型.答案: A2.有下列四个游戏盘,将它们水平放稳后,向上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是 ()311解析: A 中奖概率为8, B 中奖概率为4,C 中奖概率为3,D 中1.奖概率为3答案: A人教 A 版高中数学必修 3 同步检测3.在 400 毫升自来水中有一个大肠杆菌,今从中随机取出 2 毫升水样放到显微镜下观察,则发现大肠杆菌的概率为() A.0.008B.0.004C.0.002D.0.005答案: D4.在 2016 年春节期间, 3 路公交车由原来的每15 分钟一班改为现在的每 10 分钟一班,在车站停 1 分钟,则乘客到达站台立即乘上车的概率是 ()A.1B.1C.1D.91091110解析:记“乘客到达站台立即乘上车”为事件 A,则 A 所占时间区域长度为 1 分钟,而整个区域的时间长度为 10 分钟,故由几何1概型的概率公式,得P(A)=10.答案: A5.在腰长为 2 的等腰直角三角形内任取一点,则该点到此三角形的直角顶点的距离小于 1 的概率为 ()ππππA.16B.8C.4D.2解析:该点到此三角形的直角顶点的距离小于1,则此点落在以1直角顶点为圆心、 1 为半径的14ππ4圆内.所以所求的概率为1=8.× 2×22答案: B二、填空题6.在正方体 ABCD- A1B1C1D1内随机抽取一点,则该点在三棱锥 A1- ABC 内的概率是 ________.2VA1-ABC1解析: P==6.VABCD-A1B1C1D11答案:67.某人对某台的电视节目进行了长期的统计后得出结论,他任9意时间打开电视机看该台节目时,看不到广告的概率为10,那么该台每小时约有 ________分钟的广告.9解析: 60× 1-10=6(分钟 ).答案: 68.有一根长度为 3 m 的绳子,拉直后在任意位置剪断,那么剪得的两段的长度都不小于 1 m 的概率是 ________.解析:从每一个位置剪断都是一个基本事件,剪断位置可以是长度为 3 m 的绳子上的任意一点.如上图,记“剪得两段的长都不小于 1 m”为事件 A.把绳子三等分,于是当剪断位置处在中间一段上时,事件 A 发生.由于中间一11段的长度等于绳长的3,于是事件 A 发生的概率 P(A)=3.1答案:3三、解答题9.一海豚在水池中自由游弋,水池为长30 m、宽 20 m 的长方形,求此刻海豚嘴尖离岸边不超过 2 m 的概率.解:如下图所示,四边形 ABCD 是长 30 m、宽 20 m 的长方形.图中的阴影部分表示事件A“海豚嘴尖离岸边不超过 2 m”.可化求海豚嘴尖出在阴影部分的概率.因 S 长方形ABCD=30×20= 600(m2),S 长方形=(30-4)× (20-4)=416(m2),A′B′C′D′所以 S 阴影部分=S 长方形-S长方形=600-416=184(m2),ABCD A′B′C′D ′184 23根据几何概型的概率公式,得P(A)=600=75≈0.31.10.一个路口的灯亮的30 秒,黄灯亮的 5 秒,灯亮的40 秒,当你到达路口,看下列三种情况的概率各是多少?(1)灯亮;(2)黄灯亮;(3)不是灯亮.解:在 75 秒内,每一刻到达路口亮灯的是等可能的,属于几何概型.( 1)P=灯亮的302全部=++=5.30405黄灯亮的51(2)P=全部=75=15.不是灯亮的黄灯亮或灯亮的=45=3,(3)P=全部=全部75 5 2 3或P=1- P(灯亮 )=1-5=5.B能力提升1.(2016 ·全国Ⅱ卷)从区 [0,1]随机抽取 2n 个数 x1,x2,⋯,x n,y1,y2,⋯, y n,构成 n 个数 (x1,y1),(x2, y2),⋯, (x n,y n),其中两数的平方和小于 1 的数共有 m 个,用随机模的方法得到的周率π的近似 ()4n2n4m2mA. mB.mC. nD. n答案: C2.小波通做游的方式来确定周末活,他随机地往位1内投一点,若此点到心的距离大于2,周末去看影;若此点1到心的距离小于4,去打球;否,在家看.小波周末不在家看的概率 ________.解析:“小波周末去看影” 事件A,1 2π·23P(A)= 1-π=4,“小波周末去打球” 事件B,1 2π·411P(B)=π=16,点到心的距离大于2与点到心的距离小于14不可能同生,所以事件 A 与事件 B 互斥,小波周末不在家看3 113事件 A+B.P(A+ B)=P(A)+P(B)=4+16=16.13答案:163.如所示,已知AB 是半 O 的直径, AB=8,M,N,P 是将半周四等分的三个分点.(1)从 A,B,M ,N,P 这 5 个点中任取 3 个点,求这 3 个点组成直角三角形的概率;(2)在半圆内任取一点 S,求△ SAB 的面积大于 8 2的概率.解:(1)从 A,B,M ,N,P 这 5 个点中任取 3 个点,一共可以组成 10 个三角形:△ABM,△ABN,△ABP,△AMN ,△AMP ,△ANP,△ BMN,△BMP ,△BNP,△ MNP ,其中是直角三角形的3只有△ABM,△ ABN,△ABP 3 个,所以组成直角三角形的概率为10.(2)如下图所示,连接MP ,取线段 MP 的中点 D,则 OD⊥MP .易求得 OD= 2 2.1当点 S 在线段 MP 上时, S△ABS=2×2 2×8=8 2,所以只有当点 S 落在阴影部分时,△SAB 的面积才能大于8 2,1π1而 S 阴影=S 扇形MOP-S△OMP=2·2·42-2×42=4π-8,所以由几何概4π-8π-2型的概率公式得△SAB 的面积大于 8 2的概率为8π=2π.。
2017_2018学年高中数学第三章概率3.3几何概型3.3.2均匀随机数的产生优化练习新人教A版必

3.3.2 均匀随机数的产生[课时作业] [A 组 学业水平达标]1.用随机模拟方法求得某几何概型的概率为m ,其实际概率的大小为n ,则( ) A .m >n B .m <nC .m =nD .m 是n 的近似值解析:用随机模拟方法求得几何概型的概率是实际概率的近似值. 答案:D2.设x 是[0,1]内的一个均匀随机数,经过变换y =2x +3,则x =12对应变换成的均匀随机数是( ) A .0 B . 2 C .4D .5解析:当x =12时,y =2×12+3=4.答案:C3.已知函数f (x )=log 2x ,x ∈⎣⎢⎡⎦⎥⎤12,2,在区间⎣⎢⎡⎦⎥⎤12,2上任取一点x 0,则使f (x 0)≥0的概率为( ) A .1 B.12 C.23D.34解析:由log 2x 0≥0,得x 0≥1,又x 0∈⎣⎢⎡⎦⎥⎤12,2,所以1≤x 0≤2,所以P =2-12-12=132=23,故选C. 答案:C4.如图,曲线OB 的方程为y 2=x (0≤x ≤1),为估计阴影部分的面积,采用随机模拟方法产生x ∈(0,1),y ∈(0,1)的200个点(x ,y ),经统计,落在阴影部分的点共134个,则估计阴影部分的面积是( )A .0.47B .0.57C .0.67D .0.77解析:根据题意,落在阴影部分的点的概率是134200=0.67,矩形的面积为1,阴影部分的面积为S ,所以S =0.67. 答案:C5.将[0,1]内的均匀随机数转化为[-2,6]内的均匀随机数,需实施的变换为( )解析:将[0,1]内的随机数转化为[a ,b ]内的随机数,需进行的变换为答案:C6.若x 可以在-4≤x ≤2的条件下任意取值,则x 是负数的概率是________.解析:记事件A 为“x 是负数”,则A 的长度为0-(-4)=4,整个事件长度为2-(-4)=6,则P (A )=46=23.答案:237.假设你在如图所示的图形上随机撒一粒黄豆,则它落在阴影部分(等腰三角形)的概率是__________.解析:设圆的半径为R ,则圆的面积为πR 2,等腰三角形的面积为12×2R ×R=R 2,∴所求概率为P =R 2πR 2=1π. 答案:1π8.利用随机模拟法近似计算图中阴影部分(曲线y =log 3x 与x =3及x 轴围成的图形)的面积.解析:设事件A :“随机向正方形内投点,所投的点落在阴影部分”. (1)利用计算器或计算机产生两组 [0,1]上的均匀随机数,x 1=RAND ,y 1=RAND. (2)经伸缩变换x =3x 1,y =3y 1,得一组[0,3],一组[0, 3]上的均匀随机数. (3)统计试验总次数N 和落在阴影部分的点的个数为N 1.(4)设阴影部分的面积为S ,正方形的面积为9,由几何概率公式得P (A )=S 9,所以N 1N ≈S9.所以S ≈9N 1N即为阴影部分面积的近似值.9.利用随机模拟的方法近似计算边长为2的正方形内切圆面积,并估计π的近似值. 解析: (1)利用计算机产生两组[0,1]上的均匀随机数,a 1=RAND ,b 1=RAND.(2)经过平移和伸缩变换,a =(a 1-0.5)*2,b =(b 1-0.5)*2,得到两组[-1,1]上的均匀随机数.(3)统计试验总次数N 和点落在圆内的次数N 1(满足a 2+b 2≤1的点(a ,b )数). (4)计算频率N 1N,即为点落在圆内的概率的近似值. (5)设圆面积为S ,则由几何概型概率公式得P =S4.∴S 4≈N 1N ,即S ≈4N 1N, 即为正方形内切圆面积的近似值. 又S 圆=πr 2=π,∴π=S ≈4N 1N,即为π的近似值.[B 组 应考能力提升]1.如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为23,则阴影区域的面积为( )A.43B.83C.23 D .无法计算解析:∵S 阴影S 正方形=23,∴S 阴影=23S 正方形=83. 答案:B2.如图,在直角坐标系内,射线OC 落在120°角的终边上,任作一条射线OA (OA 在平面直角坐标系内的分布是等可能的),那么射线OA 落在∠xOC 内的概率为( ) A.12 B.23 C.13D.34解析:射线OA 落在∠xOC 内的概率只与∠xOC 的大小有关,故所求概率为120360=13.答案:C3.用计算器生成两个[0,1]上的均匀随机数,问这两个随机数的差小于0.5的概率为________.解析:设x ,y 为计算器生成的[0,1]上的两个均匀随机数,则0≤x ≤1,0≤y ≤1,所有的可能(x ,y )构成边长为1的正方形,如图,设事件A ={两随机数的差小于0.5},则当|x -y |<0.5时事件A 发生,条件(x ,y )构成图中的阴影部分. ∴P (A )=S 阴影S 正方形=1-2×12×1221=34. 答案:344.如图,一不规则区域内,有一边长为1米的正方形,向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数400颗,以此实验数据为依据可以估计出该不规则图形的面积为________m 2.(用分数作答).解析:∵向区域内随机地撒1 000颗黄豆,数得落在正方形区域内(含边界)的黄豆数为400颗,记“黄豆落在正方形区域内”为事件A ,∴P (A )=4001 000=1S 不规则图形,∴S 不规则图形=52 m 2.答案:525.甲、乙两辆班车都要停在同一停车位,它们可能在一天中的任意时刻到达.如果这两辆班车的停车时间都是一个小时,求有一辆班车停车时必须等待一段时间的概率.解析:记事件A ={有一辆班车停泊时必须等待一段时间}.(1)用计算器或计算机产生两组[0,1]区间上的均匀随机数,a =RAND ,b =RAND ;(2)经过伸缩变换x =a *24,y =b *24,得到[0,24]区间上的两组均匀随机数; (3)统计试验次数N 和事件A 发生对应的次数N 1(满足|x -y |≤1的点(x ,y )的个数); (4)计算频率f n (A )=N 1N,即有一辆班车停泊时必须等待一段时间的概率.6.假设小霞、小倩和小珍所在的班级共有 65名学生,并且这65名学生早上到校先后的可能性是相同的.设计模拟方法估计下列事件的概率: (1)小倩比小珍先到校;(2)小倩比小珍先到校,小珍比小霞先到校.解析:因为早上到校先后的可能性是相同的,所以假设每人到校的时间是某一个时间段内的任一时刻,可以分别用三组随机数x 、y 、z 表示,因而可以随机模拟.设事件A :“小倩比小珍先到校”;设事件B :“小倩比小珍先到校,小珍比小霞先到校”. (1)利用计算器或计算机产生一组[0,1]内的均匀随机数,a =RAND ,b =RAND ,c =RAND 分别表示小霞、小倩和小珍三人早上到校的时间;(2)统计出试验总次数N 以及其中满足b <c 的次数N 1,满足b <c <a 的次数N 2; (3)计算频率f n (A )=N 1N ,f n (B )=N 2N ,即分别为事件A ,B 的概率的近似值.附:什么样的考试心态最好大部分学生都不敢掉以轻心,因此会出现很多过度焦虑。
人教A版高中数学必修三试卷高中3.3.2《均匀随机数的产生》同步测试新.docx

3-3-2均匀随机数的产生一、选择题1.下列关于几何概型的说法中,错误的是( )A.几何概型是古典概型的一种,基本事件都具有等可能性B.几何概型中事件发生的概率与它的位置或形状无关C.几何概型在一次试验中可能出现的结果有无限多个D.几何概型中每个结果的发一都具有等可能性[答案] A[解析]几何概型和古典概型是两种不同的概率模型.几何概型中的基本事件有无限多个,古典概型中的基本事件有有限个.2.用均匀随机数进行随机模拟,可以解决( )A.只能求几何概型的概率,不能解决其他问题B.不仅能求几何概型的概率,还能计算图形的面积C.不但能估计几何概型的概率,还能估计图形的面积D.最适合估计古典概型的概率[答案] C[解析]很明显用均匀随机数进行随机模拟,不但能估计几何概型的概率,还能估计图形的面积,但得到的是近似值,不是精确值,用均匀随机数进行随机模拟,不适合估计古典概型的概率.3.用随机模拟方法求得某几何概型的概率为m,其实际概率的大小为n,则( ) A.m>n B.m<nC.m=n D.m是n的近似值[答案] D4.如下四个游戏盘(各正方形边长和圆的直径都是单位1),如果撒一粒黄豆落在阴影部分,则可中奖.小明希望中奖,则应选择的游戏盘是( )[答案] A[解析] P (A )=38,P (B )=26=13,P (C )=1-π41=1-π4,P (D )=1π. 5.将[0,1]内的均匀随机数转化为[-2,6]内的均匀随机数,需实施的变换为( )[答案] C[解析] 将[0,1]内的随机数转化为[a ,b ]内的随机数,需进行的变换为a =a 1] 6.设x 是[0,1]内的一个均匀随机数,经过变换y =2x +3,则x =12对应变换成的均匀随机数是( )A .0B .2C .4D .5[答案] C[解析] 当x =12时,y =2×12+3=4.7.在矩形ABCD 中,长AB =4,宽BC =2(如图所示),随机向矩形内丢一粒豆子,则豆子落入圆内的概率是( )A.14B.12C.π4D.π8[答案] D8.把[0,1]内的均匀随机数分别转化为[0,4]和[-4,1]内的均匀随机数,需实施的变换分别为( )A.y=-4x,y=5-4 B.y=4x-4,y=4x+3C.y=4x,y=5x-4 D.y=4x,y=4x+3[答案] C9.一个路口的红绿灯,红灯亮的时间为30 s,黄灯亮的时间为5 s,绿灯亮的时间为40 s,当你到达路口时,事件A为“看见绿灯”、事件B为“看见黄灯”、事件C为“看见不是绿灯”的概率大小关系为( )A.P(A)>P(B)>P(C) B.P(A)>P(C)>P(B)C.P(C)>P(B)>P(A) D.P(C)>P(A)>P(B)[答案] B10.如图所示,在墙上挂着一块边长为16cm的正方形木块,上面画了小、中、大三个同心圆,半径分别为2cm,4cm,6cm,某人站在3 m之外向此板投镖,设镖击中线上或没有投中木板时不算,可重投,记事件A={投中大圆内},事件B={投中小圆与中圆形成的圆环内},事件C={投中大圆之外}.(1)用计算机产生两组[0,1]内的均匀随机数,a 1=RAND ,b 1=RNAD.(2)经过伸缩和平移变换,a =16a 1-8,b =16b 1-8,得到两组[-8,8]内的均匀随机数. (3)统计投在大圆内的次数N 1(即满足a 2+b 2<36的点(a ,b )的个数),投中小圆与中圆形成的圆环次数N 2(即满足4<a 2+b 2<16的点(a ,b )的个数),投中木板的总次数N (即满足上述-8<a <8,-8<b <8的点(a ,b )的个数).则概率P (A )、P (B )、P (C )的近似值分别是( ) A.N 1N ,N 2N ,N -N 1NB.N 2N ,N 1N ,N -N 2NC.N 1N ,N 2-N 1N ,N 2ND.N 2N ,N 1N ,N 1-N 2N[答案] A[解析] P (A )的近似值为N 1N ,P (B )的近似值为N 2N ,P (C )的近似值为N -N 1N. 二、填空题11.设函数y =f (x )在区间[0,1]上的图像是连续不断的一条曲线,且恒有0≤f (x )≤1,可以用随机模拟方法近似计算由曲线y =f (x )及直线x =0,x =1,y =0所围成部分的面积S .先产生两组(每组N 个)区间[0,1]上的均匀随机数x 1,x 2,…,x N 和y 1,y 2,…,y N ,由此得到N 个点(x i ,y i )(i =1,2,…N ).再数出其中满足y i ≤f (x i )(i =1,2,…,N )的点数N 1,那么由随机模拟方法可得到S 的近似值为________.[答案]N 1N[解析] 这种随机模拟的方法,是在[0,1]内生成了N 个点,而满足几条曲线围成的区域内的点是N 1个,所以根据比例关系SS 矩形=N 1N,而矩形的面积为1,所以随机模拟方法得到的面积为N 1N.12.设A 为圆周上一定点,在圆周上等可能任取一点与A 连接,则弦长超过半径2倍的概率为________.[答案] 12[解析] 如图所示,在圆周上过定点A 作弦AB =AC =2r ,则BC 是圆的一条直径.当取的点在BC 上方时满足了弦长大于半径的2倍,所以P =12.13.在等腰直角三角形ABC 中,在斜边AB 上任取一点M ,则AM >AC 的概率是________. [答案] 1-22[解析] 设CA =CB =m (m >0),则AB =2m . 设事件M :AM >AC ,即P (M )=AB -AC AB =2m -m 2m=1-22. 14.某人从甲地去乙地共走了500 m ,途中要过一条宽为x m 的河流,他不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品不掉在河里,则能找到,已知该物品能被找到的概率为45,则河宽为________m.[答案] 100[解析] 已知河宽为x m ,由题意得1-x 500=45,则x =100.三、解答题15.在长为14cm 的线段AB 上任取一点M ,以A 为圆心,以线段AM 为半径作圆.用随机模拟法估算该圆的面积介于9πcm 2到16πcm 2之间的概率.[分析] 圆的面积只与半径有关,故此题为与长度有关的几何概型.解答本题时只需产生一组均匀随机数.[解析]设事件A表示“圆的面积介于9π cm2到16π cm2之间”.(1)利用计算器或计算机产生一组[0,1]上的均匀随机数a1=RAND;(2)经过伸缩变换a=14a1得到一组[0,14]上的均匀随机数;(3)统计出试验总次数N和[3,4]内的随机数个数N1(即满足3≤a≤4的个数);(4)计算频率f n(A)=N1N,即为概率P(A)的近似值.16.设有一个正方形网格,其中每个最小正方形的边长都等于6cm,现用直径等于2cm的硬币投掷到网格上,用随机模拟方法求硬币落下后与格线有公共点的概率.[解析]记事件A={硬币与格线有公共点},设硬币中心为B(x,y).步骤:(1)利用计算机或计算器产生两组0到1之间的均匀随机数,x1=RAND,y1=RAND.(2)经过平移,伸缩变换,则x=(x1-0.5)*6,y=(y1-0.5)*6,得到两组[-3,3]内的均匀随机数.(3)统计试验总次数N及硬币与格线有公共点的次数N1(满足条件|x|≥2或|y|≥2的点(x,y)的个数).(4)计算频率N1N,即为硬币落下后与格线有公共点的概率.17.用随机模拟方法求函数y=x与x轴和直线x=1围成的图形的面积.[分析] 将问题转化为求在由直线x=1,y=1和x轴,y轴围成的正方形中任取一点,该点落在已知图形内的概率.用随机模拟方法来估计概率即可.[解析]如图所示,阴影部分是函数y=x的图象与x轴和直线x=1围成的图形,设阴影部分的面积为S.随机模拟的步骤:(1)利用计算机产生两组[0,1]内的均匀随机数,x 1=RAND ,y 1=RAND ;(2)统计试验总次数N 和落在阴影内的点数N 1(满足条件y <x 的点(x ,y )的个数); (3)计算频率N 1N,即为点落在阴影部分的概率的近似值;(4)直线x =1,y =1和x ,y 轴围成的正方形面积是1,由几何概型公式得点落在阴影部分的概率为S1=S .则S =N 1N ,即阴影部分面积的近似值为N 1N.18.现向如图所示正方形内随机地投掷飞镖,用随机模拟的方法计算飞镖落在阴影部分的概率,阴影部分由直线6x -3y -4=0和x =1,y =-1围成.[分析] 要确定飞镖落点位置,需要确定两个坐标x 、y ,可用两组均匀随机数来表示点的坐标.[解析]记事件A={飞镖落在阴影部分}.(1)用计算机或计算器产生两组[0,1]上的均匀随机数,x1=RAND,y1=RAND.(2)经过平移和伸缩变换,x=2(x1-0.5),y=2(y1-0.5)得到两组[-1,1]上的均匀随机数.(3)统计试验总次数N及落在阴影部分的点数N1(满足6x-3y-4>0的点(x,y)的个数).(4)计算频率f n(A)=N1N即为飞镖落在阴影部分的概率的近似值.。
新人教A版高中数学必修333几何概型同步测试题

几何概型一、选择题一、取一根长度为3cm的绳索,拉直后在任意位置剪断,那么间的两段的长都不小于m的概率是()A、23B、13C、14D、不能确信2、某人睡午觉醒来,觉察表停了,他打开收音机想听电台整点报时,则他等待的时刻小于10分钟的概率是()A、16B、112C、160D、1723、在线段[0,3]上任取一点,则此点坐标大于1的概率是()A、34B、23C、12D、134、在1万平方千米的海域中有40平方千米的大陆架贮藏着石油,假若在海域中任意一点钻探,那么钻到油层面的概率是()A、140B、125C、1250D、1500二、填空题5、已知地铁列车每10分钟一班,在车站停1分钟,则乘客抵达站台当即乘上车的概率是__________________________。
6、边长为2a的正方形及其内切圆,随机向正方形内丢一粒豆子,则豆子落在圆及正方形夹的部份的概率是__________________________。
7、在等腰直角三角形ABC中,在斜线段AB上任取一点M,则AM的长小于AC的长的概率是_______________________。
8、几何概率的两个特点:(1)________________________________________________________。
(2)________________________________________________________。
9、在400ml自来水中有一个大肠杆菌,今从中随机掏出2ml水样放到显微镜下观看,则发觉大肠杆菌的概率是________________________________。
10、关于几何概率,概率为0的事件是不是可能发生?_________________。
11、在线段[0,a]上随机地投三个点,试求由点O到三个点的线段能组成一个三角形的概率是_____________________________________。
高中数学人教A版必修三习题:第三章3.3几何概型含答案

第三章3.3几何概型3.3.1几何概型3.3.2均匀随机数的产生-----------------高效演练知能提升------------------A级基础巩固一、选择题1.下列关于几何概型的说法中,错误的是()A.几何概型是古典概型的一种,基本事件都具有等可能性B.几何概型中事件发生的概率与它的位置或形状无关C.几何概型在一次试验中可能出现的结果有无限多个D.几何概型中每个结果的发生都具有等可能性解析:几何概型和古典概型是两种不同的概率模型.答案:A2-有下列四个游戏盘,将它们水平放稳后,向上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是()A B C D解析:A中奖概率为B中奖概率为C中奖概率为?,D中奖概率对.答案:A3.在400毫升自来水中有一个大肠杆菌,今从中随机取出2毫升水样放到显微镜F观察,则发现大肠杆菌的概率为()A.0.008B.0.004C.0.002D.0.005答案:D4-在2016年春节期间,3路公交车由原来的每15分钟一班改为现在的每10分钟一班,在车站停1分钟,则乘客到达站台立即乘上车的概率是()A.±B i C-J-D旦土10%U1110解析:记“乘客到达站台立即乘上车”为事件扇则/所占时间区域长度为1分钟,而整个区域的时间长度为10分钟,故由几何概型的概率公式,得PC4)=佥.答案:A5.在腰长为2的等腰直角三角形内任取一点,则该点到此三角形的直角顶点的距离小于1的概率为()北北刀g氏诟B.石C.J D.万解析:该点到此三角形的直角顶点的距离小于1,则此点落在以宜角顶点为圆心、1为半径的i圆内.所以所求的概率一=喜5x2x2答案:B二、填空题6.在正方体ABCAJ&5内随机抽取一点,则该点在三棱锥A-ABC内的概率是y VA.-ABC_1解"VABCIbA^CJk~^答案:*7.某人对某台的电视节目进行了长期的统计后得出结论,他任意时间打开电视机看该台节目时,看不到广告的概率璟,那么该台每小时约有分钟的广告.解析:60乂(1一制=6(分钟).答案:68.有一根长度为3m的绳子,拉直后在任意位置剪断,那么剪得的两段的长度都不小于1m的概率是.解析;从每一个位置剪断都是一个基本事件,剪断位置可以是长度为3m的绳子上的任意一点.MHl・—3一4如上图,记“乾得两段的长都不小于1m w为事件4把绳子三等分,于是当剪断位置处在中间一段上时,事件/发生.由于中间一段的长度等于绳长的§于是事件/发生的概率心=§答案::三、解答题9.-海豚在水池中自由游弋,水池为长30m、宽20m的长方形,求此刻海豚嘴尖离岸边不超过2m的概率.解:如下图所示,四边形球是长30m、宽20m的长方形.图中的阴影部分表示事件为“海豚嘴尖离岸边不超过2 m.问题可化为求海豚嘴尖出现在阴影部分的概率.因为S长方形g=30X20=600(m)Ss…。
人教A版高中数学 必修3 第三章3.3 几何概型 同步练习A卷

人教A版高中数学必修3 第三章3.3 几何概型同步练习A卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题;共12分)1. (2分) (2016高一下·三原期中) ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为()A .B .C .D .2. (2分)已知,若向区域内随机投一点P,则点P落在区域A内的概率为()A .B .C .D .3. (2分) (2018高一下·商丘期末) 在区域内任意取一点,则的概率是()A . 0B .C .4. (2分)空间直角坐标系中,已知原点为O,A(1,0,0),B(0,1,0),C(0,0,1),在三棱锥O﹣ABC 中任取一点P(x,y,z),则满足的概率是()A .B .C .D .5. (2分) (2018高一下·伊通期末) 已知定义在上的偶函数在上单调递增,若,则不等式成立的概率是()A .B .C .D .6. (2分) (2017高一下·平顶山期末) 如图,点A为周长为3的圆周上的一定点,若在该圆周上随机取一点B,则劣弧AB的长度小于1的概率为()A .C .D .二、填空题 (共4题;共4分)7. (1分) (2017高二下·烟台期中) 如图,设D是图中边长为4的正方形区域,E是D内函数y=x2图象下方的点构成的区域.向D中随机投一点,则该点落入E中的概率为________.8. (1分) (2018高一下·河南月考) 甲、乙两支足球队进行比赛,根据赛前的数据分析,甲队赢球的概率为0.55,乙队赢球的概率为0.2,则两支球队踢成平局的概率为________.9. (1分)(2013·山东理) 在区间[﹣3,3]上随机取一个数x使得|x+1|﹣|x﹣2|≥1的概率为________.10. (1分)抽查10件产品,设事件A:至少有两件次品,则A的对立事件为________三、解答题 (共2题;共25分)11. (15分) (2016高一下·和平期末) 一个路口的红绿灯,红灯亮的时间为40秒,黄灯亮的时间为5秒,绿灯亮的时间为50秒(没有两灯同时亮),当你到达路口时,看见下列三种情况的概率各是多少?(1)红灯;(2)黄灯;(3)不是红灯.12. (10分) (2016高二上·潮阳期中) 已知向量 =(﹣2,1), =(x,y)(1)若x,y分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足 =﹣1的概率;(2)若x,y在连续区间[1,6]上取值,求满足<0的概率.参考答案一、单选题 (共6题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共4题;共4分)7-1、8-1、9-1、10-1、三、解答题 (共2题;共25分)11-1、11-2、11-3、12-1、12-2、。
人教A版高中数学必修3课后练习第三章、几何概型均匀随机数的产生
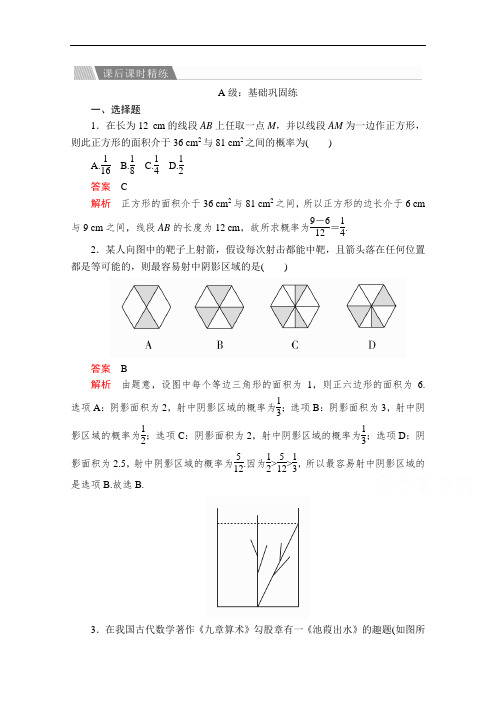
A 级:基础巩固练一、选择题1.在长为12 cm 的线段AB 上任取一点M ,并以线段AM 为一边作正方形,则此正方形的面积介于36 cm 2与81 cm 2之间的概率为( )A.116B.18C.14D.12 答案 C解析 正方形的面积介于36 cm 2与81 cm 2之间,所以正方形的边长介于6 cm 与9 cm 之间,线段AB 的长度为12 cm ,故所求概率为9-612=14.2.某人向图中的靶子上射箭,假设每次射击都能中靶,且箭头落在任何位置都是等可能的,则最容易射中阴影区域的是( )答案 B解析 由题意,设图中每个等边三角形的面积为1,则正六边形的面积为 6.选项A :阴影面积为2,射中阴影区域的概率为13;选项B :阴影面积为3,射中阴影区域的概率为12;选项C :阴影面积为2,射中阴影区域的概率为13;选项D :阴影面积为2.5,射中阴影区域的概率为512.因为12>512>13,所以最容易射中阴影区域的是选项B.故选B.3.在我国古代数学著作《九章算术》勾股章有一《池葭出水》的趣题(如图所示):“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思是:有一个正方形的池子,边长为1丈,池中心有一株芦苇,露出水面1尺,将芦苇拉至池边,它的顶端正好与水面一样平,问水有多深?该植物有多长?(“丈”和“尺”都是旧制长度单位,现已停止使用,1丈=10尺,1米=3尺).若从该芦苇上随机取一点,则该点取自水下的概率是()A.910 B.1213 C.1314 D.1415答案 B解析设水深为x尺,则(x+1)2=x2+52,解得x=12,即水深12尺,芦苇长13尺,则所求概率P=12 13.4.分别在区间[1,6],[1,4]内各任取一个实数,依次记为m,n,则m>n的概率是()A.0.3 B.0.6 C.0.7 D.0.8答案 C解析画出图形(如图所示),m,n所满足的区域为矩形ABCD,而m>n所满足的区域为梯形ABCE,所以m>n的概率P=S梯形ABCES矩形ABCD=15-9215=0.7.故选C.5.在区间[0,2]上随机地取一个数x,则事件“-1≤log 12⎝⎛⎭⎪⎫x+12≤1”发生的概率为()A.34 B.23 C.13 D.14答案 A解析由-1≤log 12⎝⎛⎭⎪⎫x+12≤1得log122≤log12⎝⎛⎭⎪⎫x+12≤log1212,所以12≤x+12≤2,解得0≤x ≤32,故事件“-1≤log 12⎝ ⎛⎭⎪⎫x +12≤1”发生的概率为322=34.二、填空题6.一只蚂蚁在三边长分别为3、4、5的三角形面上自由爬行,某时刻该蚂蚁距离三角形的三个顶点的距离不超过1的概率为________.答案 π12解析 由已知得到三角形为直角三角形,三角形ABC 的面积为12×3×4=6, 离三个顶点距离都不大于1的地方如图三角形的阴影部分,它的面积为半径为1的半圆面积S =12π×12=π2,所以其恰在离三个顶点距离不超过1的概率为 P =π26=π12.7.记函数f (x )=6+x -x 2的定义域为D .在区间[-4,5]上随机取一个数x ,则x ∈D 的概率是________.答案 59解析 由6+x -x 2≥0,解得-2≤x ≤3,则D =[-2,3],则所求概率为3-(-2)5-(-4)=59.8.“丁香”和“小花”是好朋友,她们相约本周末去爬歌乐山,并约定周日早上8:00至8:30之间(假定她们在这一时间段内任一时刻等可能地到达)在歌乐山健身步道起点处会合,若“丁香”先到,则她最多等待“小花”15分钟.若“小花”先到,则她最多等待“丁香”10分钟.若在等待时间内对方到达,则她俩就一起快乐地爬山,否则,她们均不再等候对方而独自去爬山,则“丁香”和“小花”快乐地一起爬歌乐山的概率是________(用数字作答).答案4772解析 由题意知本题是一个几何概型.设“小花”和“丁香”到达的时间分别为(8+x )时和(8+y )时,则0≤x ≤12,0≤y ≤12,若两人见面,则0≤x -y ≤1560=14,或者0≤y -x ≤1060=16,如图,正方形的面积为14,落在两直线之间部分的面积为14-118-132, 所以“丁香”和“小花”快乐地一起爬歌乐山的概率是14-118-13214=4772.故答案为4772.三、解答题9.在转盘游戏中,假设有红、绿、蓝三种颜色.在转盘停止时,如果指针指向红色为赢,绿色为平,蓝色为输,问:若每种颜色被平均分成四块,不同颜色相间排列,要使赢的概率为15,输的概率为13,则每个绿色扇形的圆心角为多少度?(假设转盘停止位置都是等可能的)解 因为赢的概率为15. 所以红色所占角度为周角的15, 即α1=360°5=72°.同理,蓝色占周角的1 3,即α2=360°3=120°,所以绿色所占角度α3=360°-120°-72°=168°.将α3分成四等份,得α3÷4=168°÷4=42°,即每个绿色扇形的圆心角为42°.B级:能力提升练10.如图所示,在地上画一个正方形方框,其边长等于一枚硬币直径的2倍,向方框中投硬币,硬币完全落在正方形外的情况不计,求硬币完全落在正方形内的概率.解如图所示,设正方形ABCD的边长为4a,硬币的半径r=a,则正方形O1O2O3O4的面积为4a2,曲边多边形EFGHIJKL的面积为16a2+4×(4a×r)+4×1 4πr2=32a2+πa2.记“硬币完全落入正方形内”为事件A,则硬币完全落入正方形内的概率应等于正方形O1O2O3O4的面积与曲边多边形EFGHIJKL的面积比,即P(A)=4a232a2+πa2=432+π.。
人教A版高中数学必修三第3章 3.3.2 均匀随机数的产生 同步训练(1)D卷

人教A版高中数学必修三第3章 3.3.2 均匀随机数的产生同步训练(1)D卷姓名:________ 班级:________ 成绩:________一、单选题 (共6题;共12分)1. (2分)在Excel中产生[0,1]区间上均匀随机数的函数为“rand()”,在用计算机模拟估计函数y=sinx的图象、直线x=和x轴在区间[0,]上部分围成的图形面积时,随机点(a1 , b1)与该区域内的点(a,b)的坐标变换公式为()A . a=a1+, b=b1B . a=2(a1﹣0.5),b=2(b1﹣0.5)C . a[0,1],b∈[0,1]D . a=,b=b12. (2分)设x是[0,1]内的一个均匀随机数,经过变换,y=2x+3,则x= 对应变换成的均匀随机数是()A . 0B . 2C . 4D . 53. (2分)对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A={两次都击中飞机},B={两次都没击中飞机},C={恰有一次击中飞机},D={至少有一次击中飞机},下列关系不正确的是()A . A⊆DB . B∩D=C . A∪C=DD . A∪B=B∪D4. (2分) (2018高二上·马山期中) 甲、乙、丙三位同学站成一排照相,则甲、丙相邻的概率为()A .B .C .D .5. (2分)用样本频率分布估计总体频率分布的过程中,下列说法正确的是()A . 总体容量越大,估计越精确B . 总体容量越小,估计越精确C . 样本容量越大,估计越精确D . 样本容量越小,估计越精确6. (2分) (2018高二上·宾县期中) 一颗质地均匀的正方体骰子,其六个面上的点数分别为1,2,3,4,5,6,将这颗骰子连续抛掷三次,观察向上的点数,则三次点数依次构成等差数列的概率为()A .B .C .D .二、填空题 (共5题;共5分)7. (1分)甲、乙两支篮球队进行一局比赛,甲获胜的概率为0.6,若采用三局两胜制举行一次比赛,现采用随机模拟的方法估计乙获胜的概率.先利用计算器或计算机生成0到9之间取整数值的随机数,用0,1,2,3,4,5表示甲获胜;6,7,8,9表示乙获胜,这样能体现甲获胜的概率为0.6.因为采用三局两胜制,所以每3个随机数作为一组.例如,产生30组随机数.034 743 738 636 964 736 614 698 637 162 332 616 804 560 111 410 959 774 246 762 428 114 572 042 533 237 322 707 360 751据此估计乙获胜的概率为________.8. (1分)一鱼缸盛有a升水,内有b条鱼苗,用一个水杯从鱼缸中取出c(c<a)升水,用随机模拟的方法判断这杯水中大约含有________条鱼苗.9. (1分)在用随机(整数)模拟求“有个男生和个女生,从中取个,求选出个男生个女生”的概率时,可让计算机产生的随机整数,并用代表男生,用代表女生.因为是选出个,所以每个随机数作为一组.若得到的一组随机数为“ ”,则它代表的含义是________.10. (1分) (2018高一下·苏州期末) 袋中装有5个大小相同的球,其中3个黑球,2个白球,从中一次摸出2个球,则摸出1个黑球和1个白球的概率等于________.11. (1分)(2017·大庆模拟) 某校高三年级要从5名男生和2名女生中任选3名代表参加数学竞赛(每人被选中的机会均等),则在男生甲被选中的情况下,男生乙和女生丙至少一个被选中的概率是________.三、解答题 (共4题;共25分)12. (5分)一个学生在一次竞赛中要回答道题是这样产生的:从道物理题中随机抽取道;从道化学题中随机抽取道;从道生物题中随机抽取道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为,化学题的编号为,生物题的编号为 .13. (10分) (2019高二上·田阳月考) 某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.(1)将频率视为概率,估计该校900名学生中“读书迷”有多少人?(2)从已抽取的7名“读书迷”中随机抽取男、女“读书迷”各1人,参加读书日宣传活动.(i)共有多少种不同的抽取方法?(ii)求抽取的男、女两位“读书迷”月均读书时间相差不超过2小时的概率.14. (5分)一个学生在一次竞赛中要回答道题是这样产生的:从道物理题中随机抽取道;从道化学题中随机抽取道;从道生物题中随机抽取道.使用合适的方法确定这个学生所要回答的三门学科的题的序号(物理题的编号为,化学题的编号为,生物题的编号为 .15. (5分)一个体育代表队共有名水平相当的运动员.现从中任意抽取人参加某场比赛,其中运动员甲必须参加,写出利用随机模拟抽取的过程.参考答案一、单选题 (共6题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、二、填空题 (共5题;共5分)7-1、8-1、9-1、10-1、11-1、三、解答题 (共4题;共25分)12-1、13-1、13-2、14-1、15-1、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何概型与均匀随机数的产生练习班级:姓名:A级基础巩固一、选择题1.下列关于几何概型的说法中,错误的是( )A.几何概型是古典概型的一种,基本事件都具有等可能性B.几何概型中事件发生的概率与它的位置或形状无关C.几何概型在一次试验中可能出现的结果有无限多个D.几何概型中每个结果的发生都具有等可能性2.有下列四个游戏盘,将它们水平放稳后,向上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是( )3.在400毫升自来水中有一个大肠杆菌,今从中随机取出2毫升水样放到显微镜下观察,则发现大肠杆菌的概率为( )A.0.008 B.0.004 C.0.002 D.0.0054.在2016年春节期间,3路公交车由原来的每15分钟一班改为现在的每10分钟一班,在车站停1分钟,则乘客到达站台立即乘上车的概率是( )A.110B.19C.111D.9105.在腰长为2的等腰直角三角形内任取一点,则该点到此三角形的直角顶点的距离小于1的概率为( )A.π16B.π8C.π4D.π2二、填空题6.在正方体ABCD-A1B1C1D1内随机抽取一点,则该点在三棱锥A1-ABC内的概率是________.7.某人对某台的电视节目进行了长期的统计后得出结论,他任意时间打开电视机看该台节目时,看不到广告的概率为910,那么该台每小时约有________分钟的广告.8.有一根长度为3 m的绳子,拉直后在任意位置剪断,那么剪得的两段的长度都不小于1 m的概率是________.三、解答题9.一海豚在水池中自由游弋,水池为长30 m、宽20 m的长方形,求此刻海豚嘴尖离岸边不超过2 m的概率.10.一个路口的红灯亮的时间为30秒,黄灯亮的时间为5秒,绿灯亮的时间为40秒,当你到达路口时,看见下列三种情况的概率各是多少?(1)红灯亮;(2)黄灯亮;(3)不是红灯亮.B级能力提升1.(2016·全国Ⅱ卷)从区间[0,1]随机抽取2n个数x1,x2,…,x n,y1,y2,…,y n,构成n个数对(x1,y1),(x2,y2),…,(x n,y n),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为( )A.4nmB.2nmC.4mnD.2mn2.小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若此点到圆心的距离大于12,则周末去看电影;若此点到圆心的距离小于14,则去打篮球;否则,在家看书.则小波周末不在家看书的概率为________.3.如图所示,已知AB是半圆O的直径,AB=8,M,N,P是将半圆圆周四等分的三个分点.(1)从A,B,M,N,P这5个点中任取3个点,求这3个点组成直角三角形的概率;(2)在半圆内任取一点S,求△SAB的面积大于82的概率.第三章3.3 几何概型 3.3.1 几何概型 3.3.2 均匀随机数的产生A 级 基础巩固一、选择题1.下列关于几何概型的说法中,错误的是( ) A .几何概型是古典概型的一种,基本事件都具有等可能性 B .几何概型中事件发生的概率与它的位置或形状无关 C .几何概型在一次试验中可能出现的结果有无限多个 D .几何概型中每个结果的发生都具有等可能性 解析:几何概型和古典概型是两种不同的概率模型. 答案:A2.有下列四个游戏盘,将它们水平放稳后,向上面扔一颗小玻璃球,若小球落在阴影部分,则可中奖,小明要想增加中奖机会,应选择的游戏盘是( )解析:A 中奖概率为38,B 中奖概率为14,C 中奖概率为13,D 中奖概率为13.答案:A3.在400毫升自来水中有一个大肠杆菌,今从中随机取出2毫升水样放到显微镜下观察,则发现大肠杆菌的概率为( )A .0.008B .0.004C .0.002D .0.005答案:D4.在2016年春节期间,3路公交车由原来的每15分钟一班改为现在的每10分钟一班,在车站停1分钟,则乘客到达站台立即乘上车的概率是( )A.110 B.19 C.111 D.910解析:记“乘客到达站台立即乘上车”为事件A ,则A 所占时间区域长度为1分钟,而整个区域的时间长度为10分钟,故由几何概型的概率公式,得P (A )=110. 答案:A5.在腰长为2的等腰直角三角形内任取一点,则该点到此三角形的直角顶点的距离小于1的概率为( )A.π16 B.π8 C.π4 D. π2解析:该点到此三角形的直角顶点的距离小于1,则此点落在以直角顶点为圆心、1为半径的14圆内.所以所求的概率为14π12×2×2=π8.答案:B 二、填空题6.在正方体ABCD -A 1B 1C 1D 1内随机抽取一点,则该点在三棱锥A 1-ABC 内的概率是________. 解析:P =VA 1-ABC VABCD -A 1B 1C 1D 1=16.答案:167.某人对某台的电视节目进行了长期的统计后得出结论,他任意时间打开电视机看该台节目时,看不到广告的概率为910,那么该台每小时约有________分钟的广告. 解析:60×⎝⎛⎭⎪⎫1-910=6(分钟). 答案:68.有一根长度为3 m 的绳子,拉直后在任意位置剪断,那么剪得的两段的长度都不小于1 m 的概率是________.解析:从每一个位置剪断都是一个基本事件,剪断位置可以是长度为3 m 的绳子上的任意一点.如上图,记“剪得两段的长都不小于1 m ”为事件A .把绳子三等分,于是当剪断位置处在中间一段上时,事件A 发生.由于中间一段的长度等于绳长的13,于是事件A 发生的概率P (A )=13. 答案:13三、解答题9.一海豚在水池中自由游弋,水池为长30 m 、宽20 m 的长方形,求此刻海豚嘴尖离岸边不超过2 m 的概率.解:如下图所示,四边形ABCD 是长30 m 、宽20 m 的长方形.图中的阴影部分表示事件A “海豚嘴尖离岸边不超过2 m ”.问题可化为求海豚嘴尖出现在阴影部分的概率. 因为S 长方形ABCD =30×20=600(m 2),S 长方形A ′B ′C ′D ′=(30-4)×(20-4)=416(m 2),所以S 阴影部分=S 长方形ABCD -S 长方形A ′B ′C ′D ′=600-416=184(m 2), 根据几何概型的概率公式,得P (A )=184600=2375≈0.31. 10.一个路口的红灯亮的时间为30秒,黄灯亮的时间为5秒,绿灯亮的时间为40秒,当你到达路口时,看见下列三种情况的概率各是多少?(1)红灯亮; (2)黄灯亮; (3)不是红灯亮.解:在75秒内,每一时刻到达路口亮灯的时间是等可能的,属于几何概型. (1)P =红灯亮的时间全部时间=3030+40+5=25.(2)P =黄灯亮的时间全部时间=575=115.(3)P =不是红灯亮的时间全部时间=黄灯亮或绿灯亮的时间全部时间=4575=35,或P =1-P (红灯亮)=1-25=35.B 级 能力提升1.(2016·全国Ⅱ卷)从区间[0,1]随机抽取2n 个数x 1,x 2,…,x n ,y 1,y 2,…,y n ,构成n 个数对(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为( )A.4nmB.2nmC.4m n D.2m n答案:C2.小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若此点到圆心的距离大于12,则周末去看电影;若此点到圆心的距离小于14,则去打篮球;否则,在家看书.则小波周末不在家看书的概率为________.解析:记“小波周末去看电影”为事件A ,则P (A )=1-π·⎝ ⎛⎭⎪⎫122π=34,记“小波周末去打篮球”为事件B ,则P (B )=π·⎝ ⎛⎭⎪⎫142π=116,点到圆心的距离大于12与点到圆心的距离小于14不可能同时发生,所以事件A 与事件B 互斥,则小波周末不在家看书为事件A +B .P (A +B )=P (A )+P (B )=34+116=1316.答案:13163.如图所示,已知AB 是半圆O 的直径,AB =8,M ,N ,P 是将半圆圆周四等分的三个分点.(1)从A ,B ,M ,N ,P 这5个点中任取3个点,求这3个点组成直角三角形的概率; (2)在半圆内任取一点S ,求△SAB 的面积大于82的概率.解:(1)从A ,B ,M ,N ,P 这5个点中任取3个点,一共可以组成10个三角形:△ABM ,△ABN ,△ABP ,△AMN ,△AMP ,△ANP ,△BMN ,△BMP ,△BNP ,△MNP ,其中是直角三角形的只有△ABM ,△ABN ,△ABP 3个,所以组成直角三角形的概率为310.(2)如下图所示,连接MP ,取线段MP 的中点D ,则OD ⊥MP .易求得OD =2 2.当点S 在线段MP 上时,S △ABS =12×22×8=82,所以只有当点S 落在阴影部分时,△SAB 的面积才能大于82,而S 阴影=S 扇形MOP -S △OMP =12·π2·42-12×42=4π-8,所以由几何概型的概率公式得△SAB 的面积大于82的概率为4π-88π=π-22π.。
