经纬度坐标转平面笛卡尔坐标
经纬度转平面坐标

经纬度转平面坐标
1、找到数据为txt格式的经纬度坐标文件,然后打开QGIS主界面;
2、创建矢量图层:打开QGIS,选择Layer-->AddLayer-->AddDelimitedTextLayer菜单;
3、导入文本坐标:弹出创建图层对话框,选择带有坐标的文本文件,选择自定自定义分割符(Customdelimiters),选择空格(Space),在Xfield和Yfield下拉框中选择对应的x、y坐标,然后点击确定;
4、选择坐标系:点击确定之后需要选择坐标系,这里选择WGS84地理坐标系,在Filter搜索框中输入:WGS84选择EPSG:4326的坐标系;
5、另存矢量图层到本地计算机:这时数据就被导入进来了,然后另存数据,选中导入的图层,右键,选择SaveAs;
6、设置导出图层参数:打开另存为对话框,这里导出的格式为ShapeFile。
填写好文件路径和坐标系之后,点击确定就可以导出了,导出后文件会自动加载到QGIS中;
7、打开属性表:右键打开shp图层的属性表;
8、打开字段计算器:打开属性表后开始计算X、Y坐标,点击属性表上面的:字段计算器Calculator;。
经纬度高度 转坐标系-概述说明以及解释

经纬度高度转坐标系-概述说明以及解释1.引言概述部分主要介绍本文讨论的主题以及经纬度和高度转坐标系的背景和重要性。
下面是概述部分的内容:1.1 概述随着社会的发展和科技的进步,人们对于位置信息的需求越来越高,经纬度以及高度等位置参数逐渐成为了重要的数据。
经纬度是地理系统中的两个重要坐标参数,它能够唯一确定地球上的一个位置点。
而高度则表示了该位置点在地球表面上的相对高度。
然而,经纬度和高度在不同的应用场景中可能需要转换到不同的坐标系统。
比如,地图软件中常用的是平面坐标系,大地测量等领域则使用地理坐标系统。
因此,研究和掌握经纬度和高度转换为其他坐标系的方法和应用显得尤为重要。
本文将围绕经度、纬度和高度的定义和意义,以及不同坐标系的概念和作用展开讨论。
我们还将介绍经纬度高度转换为不同坐标系的方法和应用,并总结其在实际中的重要性和应用。
最后,我们会展望未来相关研究的发展方向,并给出结论。
通过本文的阅读,相信读者们将能更好地理解经纬度和高度转换为不同坐标系的重要性,以及其在各个领域中的广泛应用。
1.2 文章结构文章结构是指在撰写一篇长文时,为了使内容有条理和逻辑,按照一定的顺序和组织方式进行组织和安排。
本文的结构主要分为引言、正文和结论三个部分。
引言部分主要包括概述、文章结构和目的三个部分。
在概述中,可以简要介绍经纬度高度转坐标系的背景和重要性,引发读者的兴趣。
之后,可以在文章结构中列出各个部分的标题和编号,以给读者一个清晰的整体架构。
最后,在目的部分,可以明确说明本文的写作目的和意义,以便读者在阅读时能够更好地理解和理解文章的内容。
文章正文是重点部分,主要围绕经度、纬度和高度的定义和意义、坐标系的概念和作用,以及经纬度高度转换为不同坐标系的方法和应用这三个方面展开。
在2.1节中,可以详细解释经度、纬度和高度的概念和意义,包括其物理定义、测量方法和相关应用。
在2.2节中,可以介绍坐标系的概念和作用,包括地球坐标系、投影坐标系等,并阐述其在地理信息系统等领域的应用。
经纬度笛卡尔坐标系转换

经纬度笛卡尔坐标系转换经纬度是地球表面位置的坐标系统,利用经度(表示东西方向)和纬度(表示南北方向)来确定一个地点。
而笛卡尔坐标系是数学中常用的二维或三维坐标系统,它使用直角坐标系,通过指定与坐标轴的距离来确定一个点的位置。
这两种坐标系在地理信息系统、导航系统和地图绘制中都有广泛的应用。
因此,经纬度到笛卡尔坐标系的转换是非常有实际意义的。
首先,我们需要了解经纬度和笛卡尔坐标系之间的转换公式及原理。
经纬度的取值范围为经度-180到+180,纬度-90到+90。
而笛卡尔坐标系是基于直角坐标系的,其原点可以放置在地球的中心,并以一个球心和一组正交轴来表示。
转换的关键是首先将经纬度转换为球面坐标,再将球面坐标转换为笛卡尔坐标。
下面我们来一步一步回答如何进行经纬度到笛卡尔坐标系的转换。
第一步:将经纬度转换为球面坐标在进行经纬度到笛卡尔坐标系的转换之前,首先需要将经纬度坐标转换为球面坐标。
这是因为地球是近似于一个椭球体,而不是一个完美的球体。
球面坐标可以通过经度和纬度来表示,其取值范围为经度0到360,纬度-90到+90。
经度转换为球面坐标的公式为:x = R * cos(lat) * cos(lon)y = R * cos(lat) * sin(lon)z = R * sin(lat)其中,x、y、z为球面坐标系中的坐标,R为地球的平均半径,lat为点的纬度,lon为点的经度。
第二步:将球面坐标转换为笛卡尔坐标一旦得到了地球表面上的点的球面坐标,我们可以通过将其转换为笛卡尔坐标来确定该点在笛卡尔坐标系中的位置。
这个转换需要考虑到球面坐标系的原点在地球的中心,因此需要加上地球的半径。
笛卡尔坐标可以用三维向量来表示,即(x, y, z),其中x、y、z代表点在坐标系中的位置。
这可以通过以下公式实现:X = (R + Altitude) * cos(lat) * cos(lon)Y = (R + Altitude) * cos(lat) * sin(lon)Z = (R + Altitude) * sin(lat)其中,R为地球的平均半径,Altitude为点相对于地球表面的海拔高度。
经纬度转笛卡尔坐标系工具

经纬度转笛卡尔坐标系工具经纬度转笛卡尔坐标系工具是一种用于将地球表面上的经纬度坐标转换为笛卡尔坐标系下的坐标的工具。
这种工具在地理信息系统、地球物理学、地球科学等领域中得到了广泛的应用。
在地球表面上,经度和纬度是用来表示一个点的位置的两个坐标。
经度是指一个点与本初子午线之间的角度,可以用东经或西经来表示。
纬度是指一个点与赤道之间的角度,可以用北纬或南纬来表示。
而在笛卡尔坐标系下,一个点的位置是由三个坐标来表示的,分别是x、y 和z坐标。
因此,需要将经纬度坐标转换为笛卡尔坐标系下的坐标,才能在地球上进行精确的定位和测量。
经纬度转笛卡尔坐标系工具的原理是利用地球的形状和大小来进行计算。
地球的形状可以近似看作一个椭球体,因此可以通过椭球体的参数来计算出一个点在笛卡尔坐标系下的坐标。
具体的计算方法包括椭球体参数的选择、经纬度坐标的转换、坐标系的转换等步骤。
在实际应用中,经纬度转笛卡尔坐标系工具可以用于地图制作、导航系统、地震勘探、卫星定位等领域。
例如,在地图制作中,可以将地图上的经纬度坐标转换为笛卡尔坐标系下的坐标,以便进行地图的绘制和测量。
在导航系统中,可以将目的地的经纬度坐标转换为笛卡尔坐标系下的坐标,以便进行导航和路径规划。
在地震勘探中,可以将地震波的传播路径转换为笛卡尔坐标系下的坐标,以便进行地下结构的探测和分析。
在卫星定位中,可以将卫星接收到的信号的时间和位置信息转换为笛卡尔坐标系下的坐标,以便进行卫星定位和导航。
总之,经纬度转笛卡尔坐标系工具是一种非常重要的工具,它可以将地球表面上的经纬度坐标转换为笛卡尔坐标系下的坐标,从而实现地图制作、导航系统、地震勘探、卫星定位等领域的应用。
随着科技的不断发展,这种工具的应用范围也将越来越广泛。
经纬度转换成平面坐标如何实现经度纬度到平面坐标的相互转换

经纬度转换成平面坐标如何实现经度纬度到平面坐标的相互转换如何实现经度纬度到平面坐标的相互转换现在好多人在使用ArcObject的时候都可能需要作经纬度和平面坐标的相互转换。
由于经纬度是球面坐标,平面坐标是X-Y的笛卡尔坐标系统,所以这是一个看起来比较难的问题。
好多人一上来就搬出地图学、地图投影学或者测绘学中的投影公式(如高斯投影或墨卡托投影),又是基准坐标又是角度的搞的人头都大了。
实际上要想实现这个功能非常easy。
ARC Engine中的IPoint就可以进行投影和反投影运算了。
投影过程(C#):/// flatref 投影的坐标系统,这里的54013是世界投影,世界投影所有经纬度都可以转换为平面坐标,但是由于投影面积大失真也会比较大(相当于把整个地球劈成一片片的,然后拉伸最后贴到平面上,失真当然大了)。
当然也可以选择精度更高的平面如:esriSRProjCS_Beijing1954GK_23N 对应数值21483 仅仅把北京附近的地球平面拉伸铺在平面上,由于投影面积变小,所以投影经度提高。
但是由于面积变小,所以有些经度纬度不能转换,比如所美国的精度纬度用北京投影就投不了。
flatref = pfactory.CreateProjectedCoordinateSystem(54013);//没什么说的,标准大地经纬度,可以将X-Y逆投影为经度和纬度earthref = pfactory.CreateGeographicCoordinateSystem((int)esriSRGe oCST ype.esriSRGeoCS_NAD1983);/// 将经纬度点转换为平面坐标。
private IPoint GetProject(double x, double y) {IPoint pt = new PointClass();pt.PutCoords(x, y);IGeometry geo = (IGeometry)pt;geo.SpatialReference = earthref;geo.Project(flatref);return pt;}/// 将平面坐标转换为经纬度。
python经纬度转换为平面坐标的方法

python经纬度转换为平面坐标的方法经纬度是地理坐标系统中常用的表示地点位置的方法,但在某些应用中,需要将经纬度转换为平面坐标,以便进行计算和分析。
Python提供了多种方法来实现这种转换,本文将介绍其中几种常用的方法。
一、通过Proj库进行经纬度与平面坐标的转换Proj库是一个用于地图投影和坐标转换的Python库,它可以将经纬度坐标转换为平面坐标。
以下是使用Proj库进行经纬度与平面坐标转换的步骤:1. 安装Proj库在Python中安装Proj库的常用方法是使用pip工具进行安装。
打开命令行窗口,并输入以下命令:```pip install pyproj```2. 导入Proj库在Python脚本中导入Proj库,示例如下:```pythonimport pyproj```3. 定义投影坐标系统使用Proj库需要定义使用的投影坐标系统。
常用的投影坐标系统有很多种,可以根据实际需要选择合适的投影坐标系统。
以下是使用WGS84和Web Mercator 坐标系的示例代码:```python# 定义WGS84坐标系wgs84 = pyproj.CRS('EPSG:4326')# 定义Web Mercator坐标系web_mercator = pyproj.CRS('EPSG:3857')```4. 创建Proj转换对象创建Proj转换对象时,需要指定源坐标系和目标坐标系。
以下是将WGS84坐标系转换为Web Mercator坐标系的示例代码:```pythontransform = pyproj.Transformer.from_crs(wgs84, web_mercator, always_xy=True) ```5. 转换坐标使用Proj转换对象将经纬度坐标转换为平面坐标。
以下是将经纬度(39.9042, 116.4074)转换为平面坐标的示例代码:```pythonx, y = transform.transform(116.4074, 39.9042)print(x, y)```二、通过geopy库进行经纬度与平面坐标的转换geopy库是一个用于地理编码和逆地理编码的Python库,它也可以将经纬度坐标转换为平面坐标。
经纬度和平面坐标的相互转换知识分享

经纬度和平面坐标的相互转换经纬度和平面坐标的相互转换首先,RTK中测量的坐标,想要再转换成经纬度,很简单,其实不用转。
直接打开所测量的工程,在坐标管理库中有数据导出的功能,可以直接导出来你所测的每一个点的经纬度或者是把工程文件中的.RTK文件复制出来,用EXCEL表格打开,直接提取经纬度即可。
如果是别人提供的平面坐标,或者以前测量的原始文件删除了,那就需要通过软件进行转换来获得大地坐标GPStool GPS工具箱是常用的坐标转换软件,已上传到百度网盘。
第一步,打开软件新建作业一一起名,保存:,,""ra#s阿mm 寸人1 I.須渥出第二步,设置转换参数■ GPSIB®5.a.20150116|坤烷畳]卖用工翼「挎頼前坐源霉球至r空囘坐昌标*(球乘投些参数塔r投第坐拟含套甑单点捋陨七春魏绘•坐様轄換一四参数r據合誉数厂校正螯数r七卷数-平面塞数犬地纬JIE 貴地经度q正更咬正" 言程模式选揑源椭球,肯定选择WGS84。
投影参数设置,中心经度,也就是中央子午线,输入进去,在这里中央子午线的输入格式是“度•分秒”格式,(举例126度02分03.55秒就输126.020355注意千万不要输成126.2355中间的0不能少),其他一般不用。
四参数,校正参数,拟合参数,七参数这四个参数,有哪些,输哪些。
一般都是四参数+高程拟合参数+校正参数或者七参数+校正参数。
視商球栗目至揑至援曲阳須设豈七绘设置歸粗~ 箜面应萎数高程校n童戲这里以校正参数为例,记得使用校正参数一定打勾!目标椭球,以西安80为例投尉方式选择:1高斯接影*心126卩设置取消Y坐标加常数:500000投影比刑尺:p投駁高:|ol平行圈1: 『平行圈打[0转换前坐标设置为大地坐标,格式有多种选择,一般选度或者无格式。
度就是度的格式,举个例子,125度30分,度的格式下,就应该输125.5。
无格式的情况下,就输入125.30或者125.3 (末位的0可以不用输)说到这,告诉大家怎么区分“度”和“£分秒”的区别,当你拿到一些经纬度时,出现43.6579 125.7484这种情况,肯定就是“度”的格式了,因为度分秒中,分秒不会大于60的。
笛卡尔坐标系的应用解析

笛卡尔坐标系的应用解析笛卡尔坐标系是一种广泛应用于数学、科技和工程等领域的坐标系。
它的引入极大地便利了对于空间中对象的描述和分析。
本文将重点介绍笛卡尔坐标系的应用解析。
一、笛卡尔坐标系的介绍笛卡尔坐标系是由法国数学家笛卡尔在17世纪发明的。
它为每一个点在平面或者空间中指定了一个唯一的坐标,通常用一个有序元组 $(x, y)$ 或者 $(x, y, z)$ 来表示。
其中 $x, y$ 为在平面中的坐标,$z$ 则为在空间中的坐标。
在笛卡尔坐标系中,一个点的坐标可以用几何上的位置和坐标轴之间的关系来确定。
在平面直角坐标系中,横轴和纵轴上的两个点分别称为坐标原点,$x$ 轴和 $y$ 轴,两条轴夹角为$90^\circ$,形成一个直角。
二、普适性笛卡尔坐标系是一种十分普适的坐标系,几乎应用于所有的科技和工程领域。
比如,在机械加工中,笛卡尔坐标系可以精确定位加工目标,在水准测量中可以通过笛卡尔坐标系来定位测量仪器的位置。
在电路布局设计中,笛卡尔坐标系也发挥着十分显著的作用。
它可以方便地处理电子元器件的位置,确定电路的尺寸和形状,同时电路中的各个元器件的布局也会遵循笛卡尔坐标系的规律。
而在计算机图形学中,从二维平面绘图开始,到三维建模,笛卡尔坐标系都扮演了一个十分重要的角色。
三、实际应用1. 导航在导航领域中,笛卡尔坐标系被广泛用于提供地图和路线规划服务。
导航系统会利用 GPS 技术获取当前的经纬度信息,并通过地图服务提供商来提供地图和路线规划。
在实际应用中,导航系统会将经纬度转化为笛卡尔坐标系的值,进而根据目标位置和当前位置之间的直接距离和角度计算得到行进路线。
2. 机器人和自动化生产线在自动化生产线上,笛卡尔坐标系可以方便地控制机器人的运动和操作。
常常通过计算不同位置的笛卡尔坐标系的值,并通过机器人的运动轴控制来实现不同位置的自动化加工或者操作。
3. 航空航天笛卡尔坐标系在航空航天领域有着非常重要的应用。
不同经纬度转换坐标方法

不同经纬度转换坐标方法一、经纬度转换为直角坐标系坐标经纬度是地球表面上一个点的位置坐标,而直角坐标系是平面上的坐标系。
为了将经纬度转换为直角坐标系的坐标,可以使用投影算法来实现。
1. 地心经纬度坐标系转换为地心直角坐标系地心经纬度坐标系是以地球中心为原点建立的坐标系,将地球表面上的点投影到地球球面上。
将地心经纬度坐标系转换为地心直角坐标系,可以使用球面转直角坐标变换公式来实现。
2. 大地坐标系转换为地心直角坐标系大地坐标系是以地球表面上某一点为原点建立的坐标系,将地球表面上的点投影到地球球面上。
将大地坐标系转换为地心直角坐标系,可以使用大地坐标系转换为地心经纬度坐标系的公式,再将地心经纬度坐标系转换为地心直角坐标系。
二、直角坐标系转换为经纬度将直角坐标系的坐标转换为经纬度,可以使用反投影算法来实现。
1. 地心直角坐标系转换为地心经纬度坐标系地心直角坐标系是以地球中心为原点建立的坐标系,将地球表面上的点投影到地球球面上。
将地心直角坐标系转换为地心经纬度坐标系,可以使用直角坐标转球面坐标变换公式来实现。
2. 地心直角坐标系转换为大地坐标系地心直角坐标系转换为大地坐标系的方法与地心经纬度坐标系转换为大地坐标系类似,只是在转换过程中需要考虑椭球参数。
三、经纬度转换为平面坐标系坐标在地图制图和测量等应用中,经常需要将经纬度坐标转换为平面坐标系的坐标。
常用的转换方法有以下几种:1. 经纬度转换为UTM坐标UTM坐标是一种平面坐标系,适用于大范围的地图测绘。
将经纬度转换为UTM坐标,可以使用UTM投影算法来实现。
2. 经纬度转换为高斯-克吕格坐标高斯-克吕格坐标是一种平面坐标系,适用于小范围的地图测绘。
将经纬度转换为高斯-克吕格坐标,可以使用高斯投影算法来实现。
四、平面坐标系坐标转换为经纬度将平面坐标系的坐标转换为经纬度,可以使用反投影算法来实现。
1. UTM坐标转换为经纬度将UTM坐标转换为经纬度,可以使用UTM反投影算法来实现。
ecef转为平面直角坐标系

ecef转为平面直角坐标系
在平面直角坐标系中,一个点的坐标表示为(x, y),其中x表示点在x轴上的位置,y表示点在y轴上的位置。
而ecef坐标系是一个地球坐标系,它使用地球的中心点作为原点,x轴指向经度为0度的点,y轴指向经度为90度的点,z轴指向地球的北极点。
要将一个点的ecef坐标转换为平面直角坐标系,可以按照以下步骤进行计算:
1. 计算球面坐标系中点的经度(λ)和纬度(φ)。
可以使用以下公式来计算:
λ = atan2(y, x)
φ = atan2(z, sqrt(x^2 + y^2))
2. 将球面坐标系中的经度和纬度转换为弧度。
3. 使用球面坐标系中的经度和纬度以及地球半径(R)来计算点在地球上的位置坐标:
X = R * cos(φ) * cos(λ)
Y = R * cos(φ) * sin(λ)
Z = R * sin(φ)
4. 将点在地球上的位置坐标投影到平面直角坐标系中。
这可以通过将点的纬度和经度视为x和y坐标来实现。
综上所述,可以按照上述步骤将ecef坐标转换为平面直角坐标系。
经纬坐标投影为平面直角坐标的matlab代码-概述说明以及解释

经纬坐标投影为平面直角坐标的matlab代码-概述说明以及解释1.引言1.1 概述概述经纬坐标投影为平面直角坐标是一种常用的地图坐标转换方法,它通过将地球上的经纬度坐标投影到平面直角坐标系上,实现地理信息的可视化和分析。
在地理信息系统(GIS)和地图制图中,经纬度坐标是最常见的地理坐标表示方式,但在某些应用场景中,需要将经纬度坐标转换为平面直角坐标,以满足特定的需求和分析要求。
通过经纬坐标投影为平面直角坐标,我们可以更加直观地展现地理信息,并进行各种地理空间分析。
这种转换方法广泛应用于海图制图、城市规划、导航系统、地震研究等领域。
由于地球是一个近乎球体的椭球体,经纬度坐标的转换涉及到复杂的数学计算和映射方法,因此需要借助计算机软件进行具体的实现。
本文的目的是介绍如何使用MATLAB编写经纬坐标投影为平面直角坐标的代码。
我们将讨论不同的投影方法和相应的数学模型,以及如何在MATLAB环境下实现这些模型。
通过本文的学习,读者将能够理解经纬坐标投影的原理和实现方法,并且具备编写该转换代码的能力。
文章结构本文包含三个主要部分:引言、正文和结论。
在引言部分,我们将对经纬坐标投影为平面直角坐标进行概述,介绍其背景和应用价值,以及本文的目的和结构。
在正文部分,我们将详细讨论经纬坐标投影的概念和平面直角坐标的概念。
我们将介绍不同的投影方法,包括等积投影、等角投影和等距投影,并深入探讨它们的数学原理和转换公式。
同时,我们将介绍平面直角坐标的定义和转换方式,为后续的MATLAB代码实现做好准备。
在结论部分,我们将强调经纬坐标投影为平面直角坐标的重要性,并总结本文的主要内容。
我们还将展示如何使用MATLAB编写相应的代码,以实现经纬坐标投影为平面直角坐标的转换功能。
通过结论部分,读者将能够全面了解经纬坐标投影的实际应用和实现方法,并且具备在MATLAB 环境下进行相关编程的能力。
通过本文的阅读,读者将能够掌握经纬坐标投影为平面直角坐标的基本原理和实现方法,以及在MATLAB环境下编写相应代码的技巧和步骤。
经纬度与坐标系转换的公式与工具推荐

经纬度与坐标系转换的公式与工具推荐导语:在如今快速发展的科技时代,地理信息系统(Geographic Information System, GIS)的应用越来越广泛。
在GIS中,经纬度与坐标系之间的转换是非常重要的环节。
本文将介绍经纬度与坐标系之间的转换公式,并推荐一些实用的工具,帮助读者更好地处理地理数据。
一、经纬度与平面坐标系的转换公式1. 经纬度转换为平面坐标系:将经纬度转换为平面坐标系的最常用公式是墨卡托投影(Mercator Projection)。
墨卡托投影将地球表面的经纬度转换为平面坐标系。
其转换公式为: X = lon * RY = ln(tan(π/4 + lat/2)) * R其中,X和Y分别表示平面坐标系中的横坐标和纵坐标,lon和lat分别表示经度和纬度,R表示地球的半径。
2. 平面坐标系转换为经纬度:平面坐标系转换为经纬度需要使用反算公式。
其中,UTM投影是最常用的平面坐标系之一。
UTM投影将地球划分为60个分带,每个分带的投影方式都有所不同。
以UTM投影为例,其反算公式为:X = K0 * (B + V1*sin(2B) + V2*sin(4B) + V3*sin(6B))Y = K0 * (M + N*tan(B)*(V11 + V12*cos(2B) + V13*cos(4B) + V14*cos(6B)))其中,X和Y分别表示平面坐标系中的横坐标和纵坐标,B表示纬度,K0为比例因子。
二、实用的转换工具推荐1. GPS坐标转换网站:GPS坐标转换网站是一种方便实用的在线工具,可以将经纬度转换为各种平面坐标系,如UTM、Mercator等,同时还支持平面坐标系转换为经纬度。
用户只需输入对应的经纬度或平面坐标系值,即可获得转换结果。
常用的GPS坐标转换网站有“GPS坐标转换”、“百度地图坐标拾取器”等。
2. GIS软件:GIS软件是一种功能强大的地理信息处理工具,可以进行经纬度与坐标系的转换,同时还能进行空间分析、地图制图等操作。
经纬度笛卡尔坐标系转换

经纬度笛卡尔坐标系转换经纬度和笛卡尔坐标系是地理信息系统中常用的两种坐标表示方法,经纬度用来表示地球表面上的位置,而笛卡尔坐标系则是平面坐标系,用来表示二维平面上的位置。
在地图制作、导航系统等领域,经常需要将经纬度坐标转换为笛卡尔坐标系,或者将笛卡尔坐标系转换为经纬度坐标。
经纬度坐标是地球表面上某一点的经度和纬度的组合,经度表示东西方向,纬度表示南北方向。
经度的取值范围是-180到180度,纬度的取值范围是-90到90度。
经纬度坐标以度为单位,通常表示为度分秒的形式。
例如,北京的经度为116°23′30″E,纬度为39°54′22″N。
笛卡尔坐标系是平面坐标系,由两个坐标轴组成,通常用x和y表示。
坐标系的原点是(0,0),x轴代表水平方向,y轴代表垂直方向。
在笛卡尔坐标系中,坐标点的位置由其在x轴和y轴上的坐标值确定。
将经纬度坐标转换为笛卡尔坐标系的方法是通过地球的几何模型,将地球上的点投影到平面上。
常用的投影方法有墨卡托投影、兰伯特投影等。
不同的投影方法会导致坐标的精度和形状的变化,需要根据具体的应用场景选择合适的投影方法。
另一种常用的方法是利用数学公式进行坐标转换。
以球面坐标系为例,可以使用以下公式将经纬度坐标转换为笛卡尔坐标系:x = r * cos(纬度) * cos(经度)y = r * cos(纬度) * sin(经度)z = r * sin(纬度)其中,r是地球的半径,经纬度坐标为弧度制。
需要注意的是,在坐标转换过程中,要考虑地球的椭球形状和椭球参数,以及坐标系的标准化和转换。
不同的坐标系和投影方法会影响坐标的精度和准确性,需要根据具体的应用需求进行选择。
总的来说,经纬度坐标和笛卡尔坐标系是地理信息系统中常用的坐标表示方法,坐标转换是地图制作和导航系统等应用的重要环节。
通过合理的坐标转换方法,可以实现不同坐标系之间的无缝连接,为地理空间数据的处理和分析提供便利。
java经纬度转笛卡尔坐标系

java经纬度转笛卡尔坐标系摘要:I.引言A.介绍Java 编程语言B.介绍经纬度转笛卡尔坐标系的概念C.介绍本文的目的和结构II.Java 中经纬度转笛卡尔坐标系的实现A.导入相关库B.创建经纬度转笛卡尔坐标的函数1.创建坐标参考系统(crs)2.创建坐标转换工厂(ctFactory)3.创建从经纬度到笛卡尔坐标的转换(transform)4.执行转换III.总结与展望A.总结本文的主要内容B.展望Java 在地理信息系统领域的应用前景正文:I.引言A.Java 是一种广泛应用于各种领域的编程语言,具有跨平台、面向对象、易于学习等特点B.经纬度转笛卡尔坐标系是地理信息系统中常见的一种数据转换操作,有助于将地理信息数据与二维平面坐标系相结合C.本文旨在介绍如何在Java 中实现经纬度转笛卡尔坐标系的功能,为地理信息系统开发提供参考II.Java 中经纬度转笛卡尔坐标系的实现A.在Java 中,可以通过使用开源库(如GDAL、PROJ4J 等)或自行编写代码来实现经纬度转笛卡尔坐标系的功能B.以下是一个简单的Java 代码示例,演示了如何将经纬度坐标转换为笛卡尔坐标系1.首先,需要导入相关的库,如:`import org.osgeo.proj4j.*;`2.接着,创建一个经纬度转笛卡尔坐标的函数,如:`public static void convertLatLonToXY(double lat, double lon, double[] xy) {...}`3.在这个函数中,首先使用CRSFactory 类创建一个坐标参考系统(crs),然后创建一个坐标转换工厂(ctFactory)4.接下来,创建一个从经纬度到笛卡尔坐标的转换(transform),使用createTransform() 方法5.最后,调用transform.transform() 方法执行转换,将经纬度坐标转换为笛卡尔坐标系III.。
c++ wgs84转笛卡尔坐标系的测试用例

一、简介在地理信息系统(GIS)和全球定位系统(GPS)等领域,常常需要将地理坐标(经纬度)转换为笛卡尔坐标系的坐标。
WGS84是一种地球坐标系,而笛卡尔坐标系则是直角坐标系,在实际应用中需要进行坐标系转换,这对于开发地理信息系统和GPS导航系统具有重要意义。
C++作为一种高效的编程语言,其数学计算和坐标转换的性能得到了广泛的应用。
本文将介绍使用C++编写WGS84转换为笛卡尔坐标系的测试用例。
二、WGS84转笛卡尔坐标系的原理1. WGS84坐标系WGS84是一种地球椭球体的坐标系,它由地球椭球体的参数来定义地理坐标系。
WGS84坐标系通常用经度(longitude)和纬度(latitude)来表示地理位置。
2. 笛卡尔坐标系笛卡尔坐标系是直角坐标系,用X、Y和Z坐标表示一个点的位置。
在地理信息系统和导航系统中,常常需要将地理坐标转换为笛卡尔坐标系的坐标。
3. 坐标转换原理WGS84坐标转换为笛卡尔坐标系的过程包括坐标系转换和大地坐标系的转换。
坐标系转换主要是将经度和纬度转换为弧度表示,然后利用大地坐标系的转换公式将地理坐标转换为笛卡尔坐标。
三、C++编写WGS84转笛卡尔坐标系的测试用例1. 环境准备在使用C++编写WGS84转笛卡尔坐标系的测试用例之前,首先需要配置C++开发环境。
可以选择Visual Studio、Eclipse等集成开发环境,也可以选择gcc、g++等编译器。
2. 编写转换函数在C++中可以定义一个函数,接受经度和纬度作为输入参数,然后计算并返回笛卡尔坐标系的坐标值。
函数的定义需要考虑精度和计算误差,通常使用双精度浮点数来表示坐标值。
3. 编写测试用例编写测试用例是C++编程的一个重要环节,它可以验证转换函数的正确性和稳定性。
测试用例需要覆盖不同的地理位置和边界情况,例如赤道附近、极地附近等。
4. 执行测试用例在编写完测试用例后,可以编译并执行代码,观察测试结果。
如果测试用例通过,说明转换函数的实现是正确的,可以在实际项目中使用。
经纬度和平面坐标的相互转换
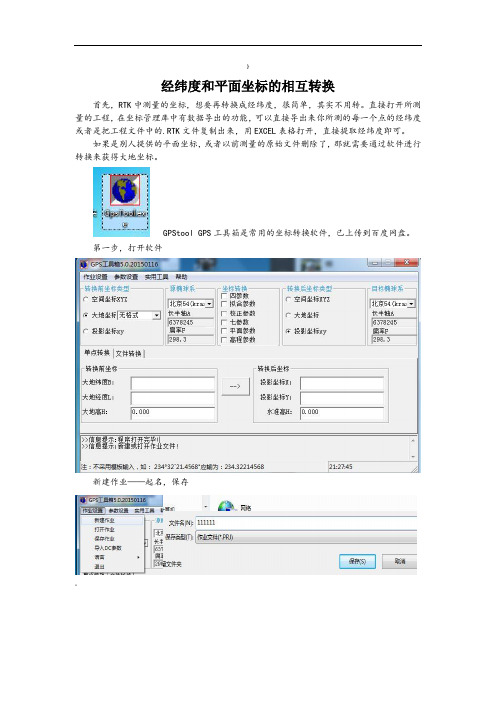
}经纬度和平面坐标的相互转换首先,RTK中测量的坐标,想要再转换成经纬度,很简单,其实不用转。
直接打开所测量的工程,在坐标管理库中有数据导出的功能,可以直接导出来你所测的每一个点的经纬度或者是把工程文件中的.RTK文件复制出来,用EXCEL表格打开,直接提取经纬度即可。
如果是别人提供的平面坐标,或者以前测量的原始文件删除了,那就需要通过软件进行转换来获得大地坐标。
GPStool GPS工具箱是常用的坐标转换软件,已上传到百度网盘。
第一步,打开软件新建作业——起名,保存"第二步,设置转换参数源椭球,肯定选择WGS84。
目标椭球,以西安80为例投影参数设置,中心经度,也就是中央子午线,输入进去,在这里中央子午线的输入格式是“度.分秒”格式,(举例126度02分秒就输注意千万不要输成中间的0不能少),其他一般不用。
]四参数,校正参数,拟合参数,七参数这四个参数,有哪些,输哪些。
一般都是四参数+高程拟合参数+校正参数或者七参数+校正参数。
这里以校正参数为例,记得使用校正参数一定打勾!转换前坐标设置为大地坐标,格式有多种选择,一般选度或者无格式。
度就是度的格式,举个例子,125度30分,度的格式下,就应该输。
无格式的情况下,就输入或者(末位的0可以不用输)说到这,告诉大家怎么区分“度”和“度.分秒”的区别,当你拿到一些经纬度时,出现这种情况,肯定就是“度”的格式了,因为度分秒中,分秒不会大于60的。
如果所有的经纬度中,小数点后第一位和第三位都小于6,那么基本就可以判断,这是“度.分秒”的格式。
¥转换后类型,根据需要,自己选择。
经纬度转平面,转换前椭球选择WGS84,类型选择大地坐标,转换后椭球选择80,类型选择平面坐标。
平面转经纬度,转换前椭球选择80,类型选择平面坐标,转换后椭球选择WGS84,类型选择大地坐标。
这是单点转换的例子,很简单,输入经纬度点箭头,就出平面。
这是平面转经纬度|很多时候,我们手中需要转换的不止一个点,或许有成百上千个,那就需要批量转换了。
经纬度和平面坐标相互转换

经纬度和平面坐标相互转换经纬度和平面坐标的相互转换首先,RTK中测量的坐标,想要再转换成经纬度,很简单,其实不用转。
直接打开所测量的工程,在坐标管理库中有数据导出的功能,可以直接导出来你所测的每一个点的经纬度或者是把工程文件中的.RTK文件复制出来,用EXCEL表格打开,直接提取经纬度即可。
如果是别人提供的平面坐标,或者以前测量的原始文件删除了,那就需要通过软件进行转换来获得大地坐标。
GPStool GPS工具箱是常用的坐标转换软件,已上传到百度网盘。
第一步,打开软件新建作业——起名,保存第二步,设置转换参数源椭球,肯定选择WGS84。
目标椭球,以西安80为例投影参数设置,中心经度,也就是中央子午线,输入进去,在这里中央子午线的输入格式是“度.分秒”格式,(举例126度02分03.55秒就输126.020355 注意千万不要输成126.2355 中间的0不能少),其他一般不用。
四参数,校正参数,拟合参数,七参数这四个参数,有哪些,输哪些。
一般都是四参数+高程拟合参数+校正参数或者七参数+校正参数。
这里以校正参数为例,记得使用校正参数一定打勾!转换前坐标设置为大地坐标,格式有多种选择,一般选度或者无格式。
度就是度的格式,举个例子,125度30分,度的格式下,就应该输125.5。
无格式的情况下,就输入125.30或者125.3(末位的0可以不用输)说到这,告诉大家怎么区分“度”和“度.分秒”的区别,当你拿到一些经纬度时,出现43.6579 125.7484这种情况,肯定就是“度”的格式了,因为度分秒中,分秒不会大于60的。
如果所有的经纬度中,小数点后第一位和第三位都小于6,那么基本就可以判断,这是“度.分秒”的格式。
转换后类型,根据需要,自己选择。
经纬度转平面,转换前椭球选择WGS84,类型选择大地坐标,转换后椭球选择80,类型选择平面坐标。
平面转经纬度,转换前椭球选择80,类型选择平面坐标,转换后椭球选择WGS84,类型选择大地坐标。
墨卡托坐标表示法象限

墨卡托坐标表示法象限墨卡托坐标表示法是一种常用的地理坐标表示法,它将地球表面的经纬度坐标转换为二维平面上的笛卡尔坐标。
在墨卡托坐标系中,地球被划分为四个象限,分别是第一象限、第二象限、第三象限和第四象限。
每个象限都有其特定的经纬度范围和特点。
第一象限位于东半球的北半部分,其经度范围从0度到180度,纬度范围从0度到90度。
在第一象限中,经度和纬度都是正值。
这个象限包含了大部分的欧洲、亚洲和北美洲。
第二象限位于西半球的北半部分,其经度范围从-180度到0度,纬度范围从0度到90度。
在第二象限中,经度是负值,纬度是正值。
这个象限包含了大部分的北美洲和南美洲。
第三象限位于西半球的南半部分,其经度范围从-180度到0度,纬度范围从-90度到0度。
在第三象限中,经度和纬度都是负值。
这个象限包含了大部分的南美洲、非洲和大洋洲。
第四象限位于东半球的南半部分,其经度范围从0度到180度,纬度范围从-90度到0度。
在第四象限中,经度是正值,纬度是负值。
这个象限包含了大部分的非洲、亚洲和大洋洲。
墨卡托坐标表示法的象限划分对于地理数据的分析和处理非常重要。
不同象限中的数据具有不同的特点和规律。
例如,在第一象限中,地理数据通常是正值,代表东半球的位置;而在第三象限中,地理数据通常是负值,代表南半球的位置。
通过对不同象限中的数据进行分析,可以更好地理解和解释地球上的地理现象。
墨卡托坐标表示法以象限为基础,将地球表面的经纬度坐标转换为二维平面上的笛卡尔坐标。
不同象限中的数据具有不同的特点和规律,通过对不同象限中的数据进行分析,可以更好地理解和解释地球上的地理现象。
墨卡托坐标表示法的象限划分对于地理数据的分析和处理非常重要。
matlab经纬度转换函数

matlab经纬度转换函数摘要:一、引言二、经纬度转换的重要性三、MATLAB 中的经纬度转换函数1.GDX22.GDX2_STD3.PIX2LATLON四、经纬度转换实例1.读取图像2.坐标转换五、结论正文:一、引言在许多应用中,经纬度坐标系被广泛使用,特别是在地理信息系统(GIS) 和遥感领域。
然而,在某些情况下,需要将经纬度坐标转换为其他坐标系,如平面直角坐标系。
在MATLAB 中,有一些函数可以用来进行这种转换。
本文将介绍这些函数以及如何使用它们进行经纬度转换。
二、经纬度转换的重要性经纬度坐标系是地球表面上点的唯一标识,但在某些应用中,需要将其转换为平面直角坐标系。
例如,在遥感图像处理中,图像上的像素需要转换为实际的地理坐标。
此外,在进行地图可视化时,也需要将经纬度坐标转换为平面直角坐标。
因此,经纬度转换在地理信息处理和遥感领域具有重要意义。
三、MATLAB 中的经纬度转换函数在MATLAB 中,可以使用以下函数进行经纬度转换:1.GDX2:该函数可以将地球上的经纬度坐标转换为笛卡尔坐标。
函数语法如下:`x = gdx2(lat,lon)`其中,`lat`和`lon`分别是经度和纬度。
2.GDX2_STD:该函数与GDX2 类似,但它使用标准地球模型进行转换。
函数语法如下:`x = gdx2_std(lat,lon)`3.PIX2LATLON:该函数可以将图像上的像素坐标转换为经纬度坐标。
函数语法如下:`[lat,lon] = pix2latlon(image,row,col)`其中,`image`是图像,`row`和`col`是像素坐标。
四、经纬度转换实例假设我们有一个遥感图像,需要将图像上的像素坐标转换为实际的地理坐标。
以下是一个简单的示例:1.读取图像:```matlabimage = imread("path/to/image.tif");```2.坐标转换:```matlabrow = 100;col = 200;lat = pix2latlon(image, row, col);```这将返回经纬度坐标,例如:`lat = [39.9041, 116.4072]`。
