钢板剪切力计算
剪切计算及常用材料强度

2.剪切强度计算1 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力;[]sF A ττ=≤5-6这里τ为许用剪应力,单价为Pa 或MPa;由于剪应力并非均匀分布,式5-2、5-6算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n,得许用剪应力τ;[]n ττ= 5-7 各种材料的剪切许用应力应尽量从相关规范中查取;一般来说,材料的剪切许用应力τ与材料的许用拉应力σ之间,存在如下关系:对塑性材料: 对脆性材料: 2 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了;但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切;下面通过几个简单的例题来说明;例5-1 图5-12a 所示电瓶车挂钩中的销钉材料为20号钢,τ=30MPa,直径d=20mm;挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm;牵引力F=15kN;试校核销钉的剪切强度;图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12b 所示;根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动;所以有两个剪切面,是一个双剪切问题;由平衡方程容易求出:销钉横截面上的剪应力为:故销钉满足剪切强度要求;例5-2 如图5-13所示冲床,F max =400KN,冲头σ=400MPa ,冲剪钢板的极限剪应力τb =360 MPa;试设计冲头的最小直径及钢板最大厚度;图5-13 冲床冲剪钢板及冲剪部分受力示意图解:1 按冲头压缩强度计算d所以2 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面; 所以例5-3 如图5-14所示螺钉受轴向拉力F 作用,已知τ=σ,求其d :h 的合理比值;图5-14 螺钉受轴向拉力示意图解:螺杆承受的拉应力小于等于许用应力值:螺帽承受的剪应力小于等于许用剪应力值:当σ、τ同时分别达到σ、τ时.材料的利用最合理,既所以可得------=extPart_01C9B6CD.第二节冲压常用材料的化学成分和力学性能一、黑色金属1.深拉深用冷轧钢板发化学成分和力学性能1深拉深钢板的化学成分深拉深用冷轧钢板主要有08Al、08F、08、及10、15、20钢;其化学成分如表8—44所示;表8—44 深拉深冷轧薄钢板的化学成分GB/T5213—1985和GB/T710—1991钢板化学成分质量分数 %C Si Mn P S Ni Cr Cu Al08Al ≤≤~≤≤≤≤≤~08F ~≤~≤≤≤≤≤—08 ~~~≤≤≤≤≤—10 ~~~≤≤≤≤≤—15 ~~~≤≤≤≤≤—20 ~~~≤≤≤≤≤—2影响钢板冲压性能的主要因素化学成分、金属组织、力学性能和表面质量等均影响冲压性能在上述钢号中用量最大的是08钢,并有沸腾钢与镇静钢之分,沸腾钢08F 价廉,表面质量好,但偏析比较严重,且有“应变时效”倾向,对于冲压性能要求高,外观要求严格的零件不适合;08Al镇静钢板价格较高,但性能均匀,“应变时效”倾向小,适用于汽车、拖拉机覆盖件的拉深;108钢中主要元素对冲压性能的影响表8—45表8—45 主要元素对08钢冲压性能的影响2深拉深冷轧薄板铁素体晶粒度的标准表8—46表8—46 深拉深冷轧薄钢板铁素体晶粒级别1铝镇静钢08Al按其拉深质量分为三级:ZF—拉深最复杂零件;HF—拉深很复杂零件;F—拉深复杂零件2其他深冲薄钢板包括热轧板按冲压性能分级为:Z—最伸拉深件;S —深拉深件;P—普通拉深件3深拉深冷轧薄钢板的力学性能表8—47表8—47 深拉深冷轧薄钢板的力学性能GB/T5213—1985和GB/T710—19914深拉深冷轧薄钢板的杯突试验冲压深度表8—48表8—48 深拉深冷轧薄钢板的杯突试验冲压深度GB/T5213—1985和GB/T710—19912.常用材料的力学性能1黑色金属材料的力学性能表8—49 表8—49 黑色金属材料的力学性能2钢在加热时的抗剪强度表8—50表8—50 钢在加热状态的抗剪强度单位:MPa3 普通碳素钢冷弯实验指标8-51表8—51 普通碳素钢冷弯试验指标 GB700—1988牌号试样方向冷弯试验B=2a180°备注钢材厚度或直径/mm≤60 >60~100 >100~200弯心直径dQ195 纵0——各牌号A级钢的冷弯试验,在需方有要求时才进行冷弯试验合格时,抗拉强度上限可以不作交货条件横Q215 纵2a 横 a 2aQ235 纵 a 2a横3aQ255 2a 3aQ275 3a 4a注:B—试样宽度二、有色金属有色金属的力学性能表8—52表8—52 有色金属的力学性能材料名称牌号材料状态抗剪强度τ/MPa抗拉强度/MPa伸长率/%屈服点/MPa弹性模量E/MPa铝1070A,1050A1200已退火80 75~110 25 50~8072000 冷作硬化100 120~150 4 120~240铝锰合金3A21 已退火70~100 110~145 19 50 71000硬480~520 600~650 3~5 540 —特硬560~600 700~750 1~2 ——铍青铜QBe2软240~480 300~600 30 250~350 117000硬520 660 2 1280 132000~141000白铜B19 软240 300 25——硬360 450 3锌白铜BZn15-20软280 350 35 207 —硬400 5501486 126000~140000 特硬520 650 —镍Ni-3~Ni-5软350 400 35 70 —硬470 550 2 210 210000~230000德银BZn15-20软300 350 35——硬480 550 1特硬560 650 1锌Zn-3~Zn-6 —120~200 140~230 40 75 80000~130000 铅Pb-3~Pb-6 —20~30 25~40 40~50 5~10 15000~17000 锡Sn1~Sn4 —30~40 40~50 —12 41500~55000钛合金TA2退火360~480 450~600 25~30——TA3 440~600 550~750 20~25TA5 640~680 800~850 15 800~900 104000镁合金MB1冷态120~140 170~190 3~5 120 40000 MB8 150~180 230~240 14~15 220 41000 MB1 预热300℃30~50 30~50 50~52 —40000 MB8 50~70 50~70 58~62 —41000银———180 50 30 81000 可伐合金Ni29Co18 —400~500 500~600 ———康铜软—400~600 ———硬—650 ———钨—已退火—720 0 700 312000未退火—1491 1~4 800 380000 钼—已退火20~30 1400 20~25 385 280000未退火32~34 1600 2~5 595 300000三、非金属1非金属材料的极限抗剪强度表8—53表8—53 非金属材料的极限抗剪强度单位:MPa2非金属材料加热时的抗剪强度表8—54表8—54 非金属材料加热时的抗剪强度注:表列抗剪强度用于普通凸模冲裁时的计算值;=600000/2605 <235=600000/4082 <141MPa=146MPa 大于了许用剪切力,不合理。
剪切计算及常用材料强度
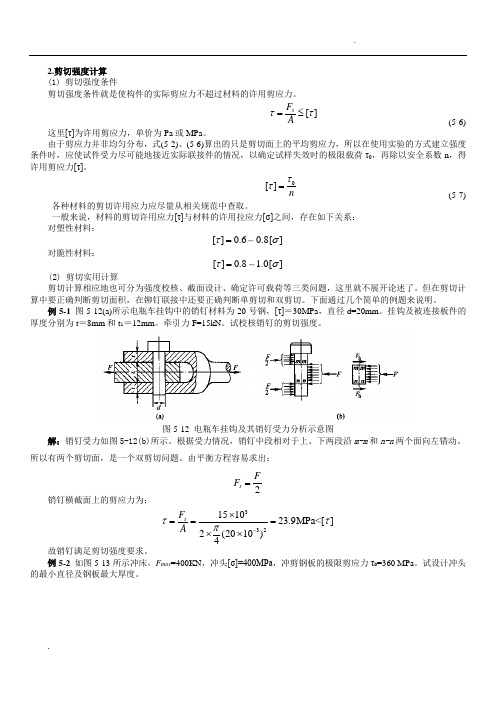
2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料:[]0.60.8[]τσ= 对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s F F =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F FdAσσπ=≤所以3max644400100.034 3.4[]40010Fd m cmπσπ⨯⨯≥===⨯⨯(2) 按钢板剪切强度计算t钢板的剪切面是直径为d高为t的柱表面。
剪切力的计算方法

第3章剪切和挤压的实用计算3.1剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-1a),构件的变形主要表现为沿着与外力作用线平行的剪切面(m - n面)发生相对错动(图3-1b)。
图3-1工程中的一些联接件,如键、销钉、螺栓及铆钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截面法求得。
将构件沿剪切面m-n假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切面上必有与外力平行且与横截面相切的内力F Q (图3-1C)的作用。
F Q称为剪力,根据平衡方程',=0,可求得F Q二F。
剪切破坏时,构件将沿剪切面(如图3-la所示的m-n面)被剪断。
只有一个剪切面的情况,称为单剪切。
图3-1a所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲和拉伸等作用。
在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的计算方法,称为剪切的实用计算或工程计算。
3.2剪切和挤压的强度计算3.2.1剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图试验装置的简图,试件的受力情况如图 3-2b 所示,这是模拟某种销钉联接的工作情形。
当载荷F 增大至破坏载荷 F b 时,试件在剪切面 m - m 及n - n 处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图 3-2c 可求得剪切面上的剪力为F Q图3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法确定,因而工程上一般采用实用计算方法来计算受剪构件的应力。
在这种计算方法中,假设应力在剪切面内是均匀分布的。
抗剪切强度计算公式

抗剪切强度计算公式抗剪切强度是材料力学中一个重要的概念,在工程和科学领域有着广泛的应用。
那咱们就来好好聊聊抗剪切强度计算公式。
咱们先从一个简单的例子说起哈。
就说有一次我去工地,看到工人们正在搭建一座钢结构的桥梁。
这时候我就好奇啦,这桥梁能承受得住那么大的重量和各种力的作用,到底是为啥呢?其中一个关键因素就是材料的抗剪切强度。
抗剪切强度的计算公式通常与材料的性质、受力情况等有关。
一般来说,对于常见的材料,比如钢材,其抗剪切强度可以用τ = F / (A ×sinθ) 这个公式来计算。
这里的τ就是抗剪切强度,F 是施加的剪切力,A 是剪切面的面积,θ 是剪切面与力的夹角。
咱们拿一块钢板来举例。
假设这块钢板的厚度是 5 毫米,宽度是100 毫米,长度是 200 毫米。
然后有一个沿着钢板宽度方向施加的剪切力,大小是 10000 牛顿。
这时候,剪切面的面积 A 就是钢板的厚度乘以宽度,也就是 5 毫米乘以 100 毫米,换算成平方米就是 0.005 平方米乘以 0.1 平方米,等于 0.0005 平方米。
如果剪切力与钢板宽度方向的夹角是45 度,sin45 度约等于0.707。
那么通过公式τ = 10000 / (0.0005 × 0.707) ,就能算出这块钢板的抗剪切强度啦。
在实际应用中,情况可复杂得多。
比如说,不同的材料,像铝合金、铸铁、塑料等等,它们的抗剪切强度特性都不一样。
而且,受力的情况也可能不是这么简单直接,可能是多个方向的力同时作用,还可能存在应力集中的情况。
我还记得有一次在实验室里,我们做材料的抗剪切强度测试。
那是一根圆柱形的试件,要放在专门的试验机上进行加载。
大家都紧张地盯着仪器上的数据变化,心里都盼着能得到准确可靠的结果。
当加载到一定程度,试件终于发生了剪切破坏,那一刻,我们都知道,这一组实验数据对于后续的研究和工程应用有着重要的意义。
再比如说,在汽车制造中,零部件的抗剪切强度可关乎着车辆的安全性能。
剪切计算及常用材料强度

2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料:[]0.60.8[]τσ=对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s F F =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F F d Aσσπ=≤所以3max 644400100.034 3.4[]40010F d m cmπσπ⨯⨯≥===⨯⨯(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
剪切计算及常用材料强度

剪切计算及常用材料强度Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT2.剪切强度计算(1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sFAττ=≤(5-6) 这里[τ]为许用剪应力,单价为Pa或MPa。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n,得许用剪应力[τ]。
[]nττ=(5-7) 各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系:对塑性材料:[]0.60.8[]τσ=对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa,直径d=20mm。
挂钩及被连接板件的厚度分别为t=8mm和t1=12mm。
牵引力F=15kN。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m和n-n两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2sFF=销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4sFAττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2如图5-13所示冲床,F max=400KN,冲头[σ]=400MPa,冲剪钢板的极限剪应力τb=360 MPa。
试设计冲头的最小直径及钢板最大厚度。
剪切计算及常用材料强度

2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料:[]0.60.8[]τσ= 对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s F F =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4FF d Aσσπ=≤所以3max 644400100.034 3.4[]40010F d m cmπσπ⨯⨯≥===⨯⨯(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
剪切计算及常用材料强度

剪切计算及常用材料强度文档编制序号:[KKIDT-LLE0828-LLETD298-POI08]2.剪切强度计算(1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]s FA ττ=≤ (5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ= (5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料: 对脆性材料: (2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:销钉横截面上的剪应力为: 故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算d所以(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
剪切力的计算方法-剪力强度公式

第 3 章剪切和挤压的实用计算3.1 剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图 3-1a),构件的变形主要表现为沿着与外力作用线平行的剪切面(m-n面)发生相对错动(图 3-1b)。
工程中的一些联接件,如键、销钉、螺栓及铆钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截面法求得。
将构件沿剪切面m-n假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切面上必有与外力平行且与横截面相切的内力F Q (图3-1c)的作用。
F Q称为剪力,根据平衡方程Y =0,可求得F Q =F。
剪切破坏时,构件将沿剪切面(如图 3-la 所示的m-n面)被剪断。
只有一个剪切面的情况,称为单剪切。
图 3-1a 所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲和拉伸等作用。
在图 3-1 中没有完全给出构件所受的外力和剪切面上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的计算方法,称为剪切的实用计算或工程计算。
3.2 剪切和挤压的强度计算3.2.1 剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图 3-2a 为一种剪切试验装置的简图,试件的受力情况如图 3-2b 所示,这是模拟某种销钉联接的工作情形。
当载荷F增大至破坏载荷F b时,试件在剪切面m - m及n - n处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图 3-2c 可求得剪切面上的剪力为图 3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法确定,因而工程上一般采用实用计算方法来计算受剪构件的应力。
在这种计算方法中,假设应力在剪切面内是均匀分布的。
钢板剪切力计算范文

钢板剪切力计算范文钢板剪切力是指在剪切过程中作用在钢板上的力量。
钢板剪切力的大小直接影响到钢板的剪切强度和剪切性能。
因此,准确计算钢板剪切力对于设计和选择材料具有重要意义。
本文将结合相关理论和实例,探讨钢板剪切力的计算方法。
1.钢板剪切力的产生原因钢板剪切力的产生主要是由于外力对钢板的作用,例如剪切力、挤压力、冲击力等。
在实际工程中,常见的钢板剪切力包括切割力、折弯力、铣削力等。
这些力量会导致钢板发生塑性变形,在一定程度上影响钢板的强度和形状。
2.钢板剪切力的计算方法F=τ*A其中,F为剪切力,τ为剪切应力,A为钢板的剪切面积。
剪切应力的计算方法为:τ=τ₀+τ₁+τ₂其中,τ₀为弯曲应力,τ₁为应力集中系数造成的应力,τ₂为剪切失效面积系数造成的应力。
弯曲应力的计算方法为:τ₀=(M*y)/I其中,M为弯矩,y为距离中性轴的垂直距离,I为惯性矩。
应力集中系数的计算涉及到钢板的形状和载荷情况,一般可以通过查阅相关手册或进行有限元分析来获取。
剪切失效面积系数的计算方法为:τ₂=k*τ₀其中,k为钢材的剪切失效面积系数,可以通过查阅相关标准或进行实验测试获得。
钢板剪切面积的计算方法与钢板形状有关,常见的钢板形状包括矩形、圆形、槽形等。
对于矩形钢板来说,剪切面积的计算方法为:A=t*b其中,t为钢板的厚度,b为钢板的宽度。
3.钢板剪切力计算的案例分析以钢板剪切刀具的设计为例,对钢板剪切力的计算进行案例分析。
假设钢板的厚度为50mm,宽度为200mm,切割刀具的材料为高速钢。
切割过程中产生的剪切应力为300MPa,弯矩为500Nm,距离中性轴的垂直距离为100mm。
根据上述公式,可以计算出剪切力的大小。
首先计算弯曲应力:τ₀ = (M * y) / I = (500Nm * 100mm) / I然后计算剪切面积:A = t * b = 50mm * 200mm最后计算剪切力:F=τ*A=(τ₀+τ₁+τ₂)*A通过上述计算,可以得出该案例中的钢板剪切力大小。
剪切力的计算方法-剪力强度公式

第3章剪切和挤压的实用计算3. 1剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与英轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-la),构件的变形主要表现为沿着与外力作用线平行的剪切而(加-〃而)发生相对错动(图3-lb)o工程中的一些联接件.如键.销钉、螺栓及钾钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截而法求得。
将构件沿剪切面加-"假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切而上必有与外力平行且与横截而相切的内力匚(图3-lc)的作用° F Q称为剪力,根据平衡方程工Y = 0 ,可求得F Q=F°剪切破坏时,构件将沿剪切而(如图3-la所示的加-"而)被剪断。
只有一个剪切而的情况,称为单剪切。
图3-la 所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压.弯曲和拉伸等作用。
在图3-1 中没有完全给出构件所受的外力和剪切而上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的讣算方法,称为剪切的实用计算或工程讣算匚3.2剪切和挤压的强度计算3.2.1剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图3-2a为一种剪切试验装置的简图,试件的受力情况如图3-2b所示,这是模拟某种销钉联接的工作情形。
当载荷F增大至破坏载荷心时,试件在剪切面加-加及H处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图3-2c可求得剪切面上的剪力为图3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法确泄,因而工程上一般采用实用计算方法来讣算受剪构件的应力。
在这种计算方法中, 假设应力在剪切而内是均匀分布的。
最新剪切计算及常用材料强度

剪切计算及常用材料强度2.剪切强度计算(1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sFAττ=≤(5-6) 这里[τ]为许用剪应力,单价为Pa或MPa。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n,得许用剪应力[τ]。
[]nττ=(5-7) 各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系:对塑性材料:[]0.60.8[]τσ=对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa,直径d=20mm。
挂钩及被连接板件的厚度分别为t=8mm和t1=12mm。
牵引力F=15kN。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m和n-n两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2sFF=销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4sFAττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2如图5-13所示冲床,F max=400KN,冲头[σ]=400MPa,冲剪钢板的极限剪应力τb=360 MPa。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F FdAσσπ=≤所以3max644400100.034 3.4[]40010Fd m cmπσπ⨯⨯≥===⨯⨯(2) 按钢板剪切强度计算t钢板的剪切面是直径为d高为t的柱表面。
剪切力的计算方法

第3章 剪切和挤压的实用计算3.1 剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-1a),构件的变形主要表现为沿着与外力作用线平行的剪切面(n m -面)发生相对错动(图3-1b)。
图3-1工程中的一些联接件,如键、销钉、螺栓及铆钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截面法求得。
将构件沿剪切面n m -假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切面上必有与外力平行且与横截面相切的内力Q F (图3-1c)的作用。
Q F 称为剪力,根据平衡方程∑=0Y ,可求得F F Q =。
剪切破坏时,构件将沿剪切面(如图3-la 所示的n m -面)被剪断。
只有一个剪切面的情况,称为单剪切。
图3-1a 所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲和拉伸等作用。
在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的计算方法,称为剪切的实用计算或工程计算。
3.2 剪切和挤压的强度计算3.2.1 剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图3-2a 为一种剪切试验装置的简图,试件的受力情况如图3-2b 所示,这是模拟某种销钉联接的工作情形。
当载荷F 增大至破坏载荷b F 时,试件在剪切面m m -及n n -处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图3-2c 可求得剪切面上的剪力为2F F Q =图3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法确定,因而工程上一般采用实用计算方法来计算受剪构件的应力。
在这种计算方法中,假设应力在剪切面内是均匀分布的。
剪切计算及常用材料强度..

2.剪切强度计算(1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sF A ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料: 对脆性材料: (2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:销钉横截面上的剪应力为: 故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算d所以(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
所以例5-3 如图5-14所示螺钉受轴向拉力F 作用,已知[τ]=0.6[σ],求其d :h 的合理比值。
剪切力的计算方法

第3章 剪切和挤压的实用计算3.1 剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-1a),构件的变形主要表现为沿着与外力作用线平行的剪切面(n m -面)发生相对错动(图3-1b)。
图3-1工程中的一些联接件,如键、销钉、螺栓及铆钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截面法求得。
将构件沿剪切面n m -假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切面上必有与外力平行且与横截面相切的内力Q F (图3-1c)的作用。
Q F 称为剪力,根据平衡方程∑=0Y ,可求得F F Q =。
剪切破坏时,构件将沿剪切面(如图3-la 所示的n m -面)被剪断。
只有一个剪切面的情况,称为单剪切。
图3-1a 所示情况即为单剪切。
受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲和拉伸等作用。
在图3-1中没有完全给出构件所受的外力和剪切面上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的计算方法,称为剪切的实用计算或工程计算。
3.2 剪切和挤压的强度计算3.2.1 剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图3-2a 为一种剪切试验装置的简图,试件的受力情况如图3-2b 所示,这是模拟某种销钉联接的工作情形。
当载荷F 增大至破坏载荷b F 时,试件在剪切面m m -及n n -处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图3-2c 可求得剪切面上的剪力为2F F Q =图3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法确定,因而工程上一般采用实用计算方法来计算受剪构件的应力。
在这种计算方法中,假设应力在剪切面内是均匀分布的。
剪切计算公式

2.剪切强度计算 (1) 剪切强度条件剪切强度条件就是使构件的实际剪应力不超过材料的许用剪应力。
[]sFA ττ=≤(5-6)这里[τ]为许用剪应力,单价为Pa 或MPa 。
由于剪应力并非均匀分布,式(5-2)、(5-6)算出的只是剪切面上的平均剪应力,所以在使用实验的方式建立强度条件时,应使试件受力尽可能地接近实际联接件的情况,以确定试样失效时的极限载荷τ0,再除以安全系数n ,得许用剪应力[τ]。
[]n ττ=(5-7)各种材料的剪切许用应力应尽量从相关规范中查取。
一般来说,材料的剪切许用应力[τ]与材料的许用拉应力[σ]之间,存在如下关系: 对塑性材料:[]0.60.8[]τσ= 对脆性材料:[]0.8 1.0[]τσ=(2) 剪切实用计算剪切计算相应地也可分为强度校核、截面设计、确定许可载荷等三类问题,这里就不展开论述了。
但在剪切计算中要正确判断剪切面积,在铆钉联接中还要正确判断单剪切和双剪切。
下面通过几个简单的例题来说明。
例5-1 图5-12(a)所示电瓶车挂钩中的销钉材料为20号钢,[τ]=30MPa ,直径d=20mm 。
挂钩及被连接板件的厚度分别为t =8mm 和t 1=12mm 。
牵引力F=15kN 。
试校核销钉的剪切强度。
图5-12 电瓶车挂钩及其销钉受力分析示意图解:销钉受力如图5-12(b)所示。
根据受力情况,销钉中段相对于上、下两段沿m-m 和n-n 两个面向左错动。
所以有两个剪切面,是一个双剪切问题。
由平衡方程容易求出:2s F F =销钉横截面上的剪应力为:332151023.9MPa<[]2(2010)4s F A ττπ-⨯===⨯⨯故销钉满足剪切强度要求。
例5-2 如图5-13所示冲床,F max =400KN ,冲头[σ]=400MPa ,冲剪钢板的极限剪应力τb =360 MPa 。
试设计冲头的最小直径及钢板最大厚度。
图5-13 冲床冲剪钢板及冲剪部分受力示意图解:(1) 按冲头压缩强度计算dmax max2=[]4F F d Aσσπ=≤所以3max 644400100.034 3.4[]40010F d m cm πσπ⨯⨯≥===⨯⨯(2) 按钢板剪切强度计算t钢板的剪切面是直径为d 高为t 的柱表面。
剪切力的计算方法

剪切和挤压的实用计算3.1剪切的概念在工程实际中,经常遇到剪切问题。
剪切变形的主要受力特点是构件受到与其轴线相垂直的大小相等、方向相反、作用线相距很近的一对外力的作用(图3-1a),构件的变形主要表现为沿着与外力作用线平行的剪切面(m n面)发生相对错动(图3-1b)。
4Hlb>图3-1工程中的一些联接件,如键、销钉、螺栓及铆钉等,都是主要承受剪切作用的构件。
构件剪切面上的内力可用截面法求得。
将构件沿剪切面m n假想地截开,保留一部分考虑其平衡。
例如,由左部分的平衡,可知剪切面上必有与外力平行且与横截面相切的内力F Q (图3-1C)的作用。
F Q称为剪力,根据平衡方程丫0,可求得F Q F。
剪切破坏时,构件将沿剪切面(如图3-la所示的m n面)被剪断。
只有一个剪切面的情况,称为单剪切。
图3-1a所示情况即为单剪切。
3-1 受剪构件除了承受剪切外,往往同时伴随着挤压、弯曲和拉伸等作用。
在图中没有完全给出构件所受的外力和剪切面上的全部内力,而只是给出了主要的受力和内力。
实际受力和变形比较复杂,因而对这类构件的工作应力进行理论上的精确分析是困难的。
工程中对这类构件的强度计算,一般采用在试验和经验基础上建立起来的比较简便的计算方法,称为剪切的实用计算或工程计算。
3.2剪切和挤压的强度计算3.2.1剪切强度计算剪切试验试件的受力情况应模拟零件的实际工作情况进行。
图3-2a为一种剪切试验装置的简图,试件的受力情况如图3-2b所示,这是模拟某种销钉联接的工作情形。
当载荷F增大至破坏载荷F b时,试件在剪切面m m及n n处被剪断。
这种具有两个剪切面的情况,称为双剪切。
由图3-2c可求得剪切面上的剪力为F Q i图3-2由于受剪构件的变形及受力比较复杂,剪切面上的应力分布规律很难用理论方法 确定,因而工程上一般采用实用计算方法来计算受剪构件的应力。
在这种计算方法中,假设应力在剪切面内是均匀分布的。
若以A 表示销钉横截面面积,则应力为F Q~A与剪切面相切故为切应力。
