大整数乘法的数据结构及算法选择探究
大整数精确运算的数据结构与基选择

(. E C,o t hn nvri fTo i l giutr , a zo , ia 7 0 C ia 1 T S uh C ia U iesy o rpc r l e D nh u Ha n 5 0 , hn ; N t aA c u n 1 7
究更 多 的 是 集 中在 一 些 国 家级 计 算 中心 、 关 研 究 机 构 , 们 相 他 研究 与开 发 的 大 整 数 系 统 与他 们 具 备 的 软 硬 件 系 统 直 接 相 关 , 因而 缺 乏 普 适 性 。 随 着 大 整 数应 用 领 域 逐 渐 扩 大 及个 人计 算 但 机处 理 能 力 的 快 速 增 强 , 项 工 作 已 经 受 到越 来 越 多 的 科 技 工 这 作 者 的关 注 。 很 多 领 域 的 科 技 工 作 者 , 于 自身 工 作 的 需 要 , 提 出 了 由 也
2 大整 数运 算 的数 据 结构 与“ 选 择 基”
21 大 整 数 处 理 的 数 据 结 构 选 择 .
由于 大 整 数 系统 中 的 大整 数 必 须进 行 数值 运算 , 以 选 择 所 大 整 数 的数 据 结 构 必 须有 利 于 大整 数 的表 达 、 贮 和 运 算 处 理 存
组 基 数 数
文 章 编号 :0 2 83 (0 6 3 —0 4 0 文 献标 识 码 : 中 图 分 类 号 :’ l 10 — 3 120 )2 0 2 — 3 A ,31 I P
Da a S r c u e a d Ra i S S lc t g o g t t u t r n d x’ ee ti f Bi n I t g a ’ l u a i g Ac u a ey n e r l S Cac l t c r t l n
整数相乘算法

整数相乘算法整数相乘算法是计算机科学中的一个重要问题,它涉及到了很多领域,比如高精度计算、密码学、图像处理等。
在本文中,我们将介绍几种常见的整数相乘算法,并对它们的时间复杂度和空间复杂度进行分析。
一、暴力枚举法暴力枚举法是最简单直接的一种整数相乘算法。
它的思路很简单:将两个整数的每一位都相乘,再将结果累加起来。
具体实现时,可以使用两个嵌套循环分别遍历两个整数的每一位,然后将它们相乘并累加到结果中。
这种算法的时间复杂度为O(n^2),其中n为两个整数的位数之和。
二、分治法分治法是一种高效的整数相乘算法。
它的思路是将大问题划分成小问题,并递归地解决小问题。
具体实现时,可以将两个整数分别拆成高位和低位两部分,然后用公式(a1 * 10^n + a2) * (b1 * 10^n + b2)= (a1 * b1) * 10^(2n) + ((a1 + a2) * (b1 + b2) - a1 * b1 - a2 * b2) * 10^n + a2 * b2来计算它们的乘积。
这种算法的时间复杂度为O(n^log3),其中n为两个整数的位数之和。
三、Karatsuba算法Karatsuba算法是一种优化版的分治法。
它的思路是将两个整数分别拆成三部分,然后用公式(a1 * 10^n + a2) * (b1 * 10^n + b2) = (a1 * b1) * 10^(2n) + ((a1 + a2) * (b1 + b2) - a1 * b1 - a2 * b2) *10^n + a2 * b2来计算它们的乘积。
具体实现时,可以将(a1+a2)*(b1+b2)-a1*b1-a2*b2递归地计算出来,然后再用这个结果计算乘积。
这种算法的时间复杂度为O(n^log23),其中n为两个整数的位数之和。
四、FFT算法FFT(快速傅里叶变换)算法是一种高效的整数相乘算法。
它利用了傅里叶变换中的性质,将乘积转化成卷积,然后使用快速傅里叶变换来计算卷积。
算法之大整数乘法

大整数乘法通常,在分析一个算法的计算复杂性时,都将加法和乘法运算当作是基本运算来处理,即将执行一次加法或乘法运算所需的计算时间当作一个仅取决于计算机硬件处理速度的常数。
这个假定仅在计算机硬件能对参加运算的整数直接表示和处理时才是合理的。
然而大整数的算术运算。
请设计一个有效的算法,可以进行两个n位大整数的乘法运算。
大整数的乘法问题描述参考解答设X和Y都是n位的二进制整数,现在要计算它们的乘积XY。
我们可以用小学所学的方法来设计一个计算乘积XY的算法,但是这样做计算步骤太多,显得效率较低。
如果将每2个1位数的乘法或加法看作一步运算,那么这种方法要作O(n2)步运算才能求出乘积XY。
下面我们用分治法来设计一个更有效的大整数乘积算法。
图6-3 大整数X和Y的分段我们将n位的二进制整数X和Y各分为2段,每段的长为n/2位(为简单起见,假设n 是2的幂),如图6-3所示。
由此,X=A2n/2+B ,Y=C2n/2+D。
这样,X和Y的乘积为:XY=(A2n/2+B)(C2n/2+D)=AC2n+(AD+CB)2n/2+BD (1)如果按式(1)计算XY,则我们必须进行4次n/2位整数的乘法(AC,AD,BC和BD),以及3次不超过n位的整数加法(分别对应于式(1)中的加号),此外还要做2次移位(分别对应于式(1)中乘2n和乘2n/2)。
所有这些加法和移位共用O(n)步运算。
设T(n)是2个n位整数相乘所需的运算总数,则由式(1),我们有:(2)由此可得T(n)=O(n2)。
因此,用(1)式来计算X和Y的乘积并不比小学生的方法更有效。
要想改进算法的计算复杂性,必须减少乘法次数。
为此我们把XY写成另一种形式:XY=AC2n+[(A-B)(D-C)+AC+BD]2n/2+BD (3)虽然,式(3)看起来比式(1)复杂些,但它仅需做3次n/2位整数的乘法(AC,BD和(A-B)(D-C)),6次加、减法和2次移位。
由此可得:(4)用解递归方程的套用公式法马上可得其解为T(n)=O(n log3)=O(n1.59)。
两个n位大整数相乘算法

求最大元和次大元1.问题描述从多个数中一次性查找出元素最大的值和最小值,查找元素规模即元素的个数n,用分治的思想编制程序,实现分治的最大元和最小元求法。
进一步改进算法,使之能一次性求出最大和和次大元(即第二大元素)。
2.算法设计思想及描述分治发的基本思想是将一个规模为n 的问题分解为k 个规模较小的子问题,这些子问题相互独立与原问题相同。
递归地解决这些问题,然后将各个子问题的解合并得到原问题的解。
基于课堂的分析知道,对于本问题k 的值取为2,这样可以使子问题的规模是相同的,有利于算法实现。
为平衡分治时子问题的规模,这里约定需要查找元素的规模n 是2的幂次方。
用数组存储需要查找的元素,用结构体存储返回的最大元和最小元。
每次得到局部的最大元和局部次大元,然后局部最大元和最大元比较得到新的局部最大元,次大元和次大元比较得到新的局部次大元。
深入分析,这种方式局部次大元是错误的。
如两组元素中,a1>b1,a2>b2,当然a1和a 2中较大的是新的局部最大元,但是b1和b2中较大的元素不是这四个元素中第二大的。
这样的方法漏掉了b1可能是次大元的情况,也就是说所有的元素中的次大元可能在与最大元比较的时候被漏掉了。
弥补的方法就是每次将每个元素比自身小的元素都用一个淘汰数组保存起来,最后次大元就是最大元的淘汰数组中第二大的那个元素。
3.算法分析运用分治算法解决此问题,是因为这种方法的优越行,下面通过时间复杂度的比较来说明。
通常算法,设置一个变量,等于需要比较的数组的第一个元素,然后依次与后面的n-1经行比较,需要比较n-1次得到最大元。
同理,求得最小元的比较次数仍然是n -1次。
设()n T 表示比较的次数则对于这种算法得到()n T 的值为 ()22n T n =-分治算法求最大元比较1()2()22T n n T ⎧⎪=⎨+⎪⎩解方程结果为() 1.52T n n =-,虽然二者都是线性增长的,可是增长率要小一些。
大数的乘法与除法

大数的乘法与除法大数的乘法和除法是在数学运算中经常遇到的问题,尤其是在计算机科学和数据处理领域。
本文将探讨大数乘法和除法的基本原理,并介绍一些常用的算法和技巧。
一、大数乘法大数乘法是指对超过计算机字长的整数进行乘法运算。
当乘数或被乘数超过计算机的位数限制时,传统的乘法算法将无法执行。
这就需要采用特殊的算法来解决这个问题。
1.1 基本的大数乘法算法最简单直观的大数乘法算法是模拟手工乘法的过程,将乘法转化为逐位相乘和进位相加的问题。
具体步骤如下:1)将被乘数和乘数逐位相乘,得到一系列的乘积;2)逐位对乘积进行进位相加,得到最终的结果。
1.2 Karatsuba乘法Karatsuba乘法是一种改进的大数乘法算法,它可以将乘法问题分解成更小的子问题,并利用递归来解决。
其核心思想是通过减少乘法的次数来提高计算效率。
具体步骤如下:1)将被乘数和乘数分别拆分成高位和低位两部分;2)对高位和低位进行乘法运算,得到四个乘积;3)根据乘积的特点,组合四个乘积并进行加减运算,得到最终的结果。
Karatsuba乘法算法在大数乘法中可以实现更高的运算效率,尤其是在乘数和被乘数位数相同时。
二、大数除法大数除法是指对超过计算机字长的整数进行除法运算。
当被除数或除数超过计算机位数限制时,常规的除法算法无法进行。
以下介绍两种常用的大数除法算法。
2.1 短除法短除法是最基本的除法算法,通过逐位的除法和取模运算来得到商和余数。
具体步骤如下:1)将被除数的最高位与除数进行除法运算,得到商的最高位;2)用被除数减去商的最高位与除数的乘积,得到一个新的被除数;3)重复第一步和第二步,直到被除数不足以进行下一次运算;4)最后得到的各位商组合在一起即为最终的商,最后一次减法所得的值即为余数。
2.2 Newton-Raphson除法Newton-Raphson除法是一种迭代的除法算法,通过不断逼近真实的商的值来得到精确的商和余数。
其核心思想是使用牛顿迭代法来解方程。
一种新的大整数乘法算法

1引言
大 整数 在 密 码 学 、生 物 信 息 、基 因工程 等 多个 领域 都 有重 要 的应用 价值 ,其 中,最重 要 的就 是确
2 大 整 数 的数 据结 构
在 日常 生活 中 ,我 们通 常 采 取十 进 制来 表 示整 数 ,是 一种 很容 易 能够被 我 们 的大脑 所接 受和 处理 的计 数 方 法 。然 而我 们 是 用计 算机 来 处理 数 据 的 , 由于计 算机 处理 数 据是 用零 或者 一 来表示数 据 ,也
用 密钥 长 度 为 l 2 0 4位 的话 ,也就 是 需要 l Kbis t
其 中 ,O <C<m( ,. k ) C≠ 0 m 称 j 1一, -I 且 =0 ,
wt te i lr y f o i d ih h s a i o c mbn wih a g bnr itg r mi t e t lr e iay ne e mu ii t n n mo uu caa t r t s lpc i ad t la o dls h rce i i sc
,
gv s lr e ne e mutpcto o p ln mil ie a a g i g r t l lain n oy o a ii
根 据 大 整 数 的 表 示 形 式 与 多项 式表 示 形 式上 的相 似 性 ,结 合 大整 数 乘 法进 位 与取 模 的 特 点 ,给 出 了一 种 关于 大整 数 乘 法的 多
项 式算 法 。其 方 法 与别 的方 法最 大的 不 同是 , 虽 然是 求 两个 大 整 数 乘 法 ,但 整 个 算 法 没 有 使 用 乘 法 ,只 是 用 加 法运 算 而 已。 关 键 词 :大整 数 乘 法 ; 乘 法 ;多项 式 ; 法 ; 位 算 复杂 度
java大数乘法

java大数乘法Java大数乘法Java是一种高级编程语言,它的强大之处在于它可以处理各种类型的数据,包括大数。
在Java中,大数是指超过了基本数据类型的范围的数字,例如1000位的整数。
在计算机科学中,大数乘法是一种重要的算法,它可以用来计算大数的乘积。
本文将介绍Java中的大数乘法算法。
一、大数乘法的基本原理大数乘法的基本原理是将两个大数分别拆分成若干个小数,然后将小数相乘,最后将结果相加得到最终的乘积。
例如,要计算123456789012345678901234567890的平方,可以将它拆分成123456789012345678901234567和890,然后将这两个数相乘,最后将结果相加得到最终的乘积。
二、Java中的大数乘法实现在Java中,可以使用BigInteger类来实现大数乘法。
BigInteger类是Java中的一个内置类,它可以处理任意长度的整数。
下面是一个使用BigInteger类实现大数乘法的示例代码:```import java.math.BigInteger;public class BigMultiplication {public static void main(String[] args) {BigInteger a = new BigInteger("123456789012345678901234567");BigInteger b = new BigInteger("890");BigInteger c = a.multiply(b);System.out.println(c);}}```在上面的代码中,我们首先创建了两个BigInteger对象a和b,分别表示要相乘的两个大数。
然后,我们使用multiply()方法将它们相乘,得到一个新的BigInteger对象c,表示它们的乘积。
最后,我们使用println()方法将结果输出到控制台。
分治法大整数乘法 计算过程 例子

分治法大整数乘法一、简介分治法是一种常见的解决大规模问题的算法思想。
它将一个大问题分解成小问题,分别解决后再合并结果。
在计算机科学领域中,分治法经常被用来解决大整数乘法的问题。
本文将深入探讨分治法在大整数乘法中的应用,包括计算过程和具体例子。
二、分治法大整数乘法的计算过程1. 分解问题在大整数乘法中,将两个大整数分别为两部分,分别为A和B,分别表示成:A = 10^n/2 * X + YB = 10^n/2 * Z + W其中X、Y、Z、W为长度为n/2的整数。
2. 递归计算首先计算X*Z的乘积P1,然后计算Y*W的乘积P2,最后计算(X+Y)*(Z+W)的乘积P3。
3. 合并结果利用P3 - P1 - P2的差值得到中间结果U = P3 - P1 - P2。
最终的乘积AB为:AB = P1 * 10^n + U * 10^(n/2) + P2三、具体例子举个例子,假设我们需要计算1234和5678的乘积。
按照分治法的计算过程,可以分解成:1234 = 12 * 10^2 + 345678 = 56 * 10^2 + 78接着进行递归计算,得到P1 = 12*56,P2 = 34*78,P3 =(12+34)*(56+78),再合并结果得到最终的乘积。
四、总结和回顾通过分治法,我们可以高效地计算大整数的乘法,将复杂的问题分解成简单的子问题,加快计算速度。
分治法也可以应用到其他大规模问题的解决中,具有广泛的应用前景。
五、个人观点和理解在我看来,分治法是一种非常有趣且高效的解决大规模问题的算法思想。
它不仅可以帮助我们解决大整数乘法的问题,还可以应用到其他领域,如排序、搜索等。
掌握分治法对于一个计算机科学的学生来说是非常重要的,它可以拓展我们的思维,让我们更加深入地理解问题的本质。
在知识全球信息站的文章格式规范下,以上就是一个简单的分治法大整数乘法的例子。
希望对你的学习有帮助!分治法是一种非常重要的算法思想,它在计算机科学领域有着广泛的应用。
大整数加减乘除

大整数加减乘除在数学中,我们经常需要对整数进行加减乘除运算。
通常情况下,我们可以直接使用计算器或者编程语言提供的函数来完成这些运算。
但是,当涉及到大整数时,这些方法可能会遇到一些限制。
本文将介绍大整数加减乘除的算法,并给出相应的实现示例。
一、大整数加法大整数加法是指对两个或多个大整数进行相加的运算。
由于整数的位数很大,不能直接使用普通的加法运算。
下面是一种常用的大整数加法算法:1. 将两个大整数对齐,即使它们的位数不相等。
2. 从个位开始,逐位相加,并将结果保存在一个新的整数中。
3. 如果相加的结果大于等于 10,需要进位,将进位的值加到下一位的相加结果中。
4. 重复上述步骤,直到所有位都相加完毕。
下面是一个示例,演示了如何使用上述算法来实现大整数加法:```pythondef big_int_addition(num1, num2):result = []carry = 0i = len(num1) - 1j = len(num2) - 1while i >= 0 or j >= 0:digit1 = int(num1[i]) if i >= 0 else 0digit2 = int(num2[j]) if j >= 0 else 0carry, digit_sum = divmod(digit1 + digit2 + carry, 10)result.append(str(digit_sum))i -= 1j -= 1if carry:result.append(str(carry))result.reverse()return ''.join(result)```二、大整数减法对于大整数减法,我们可以利用大整数加法的算法,结合负数的概念,将减法转化为加法运算。
具体步骤如下:1. 如果被减数大于减数,则直接进行大整数加法运算;2. 如果被减数小于减数,则将被减数和减数互换位置,并标记结果为负数;3. 利用大整数加法算法,对互换位置后的两个整数进行相加运算,并将结果标记为负数。
五个方法帮你迅速计算大数乘法

五个方法帮你迅速计算大数乘法在计算中,大数乘法是一种常见的操作,它能够帮助我们高效地进行数字相乘的计算。
然而,由于大数乘法涉及到的数字较多,有时候会让人感到困惑和繁琐。
在本文中,我将为你介绍五个方法,帮助你迅速计算大数乘法,让这个过程变得更加简单和高效。
方法一:竖式计算法竖式计算法是大数乘法中最常见的一种方法。
它通过将乘数和被乘数均垂直地写在横线上,然后逐位相乘,再将结果累加得出最终答案。
这种方法的优势在于思路清晰,简单易懂,适用于任何大小的数字。
下面是一个示例:示例:计算12345 × 67891 2 3 4 5× 6 7 8 9------------------8 7 4 6 5 (12345 × 9)7 4 1 6 0 (12345 × 8,向左移动一位)+6 1 7 2 5 (12345 × 7,向左移动两位)+4 9 3 5 (12345 × 6,向左移动三位)------------------8 4 0 2 3 0 0 5通过竖式计算法,我们得出了12345 × 6789 = 84023005 的结果。
你可以尝试使用这种方法来解决其他大数乘法的问题。
方法二:分组计算法分组计算法是一种适用于大数乘法的高效计算方法。
它通过将乘数和被乘数分别分解成多个子序列,然后逐个相乘并将结果相加,最终得到乘法的结果。
下面是一个示例:示例:计算12345 × 6789将乘数和被乘数分别拆分成两个两位数和两个三位数:12345 = 12 × 1000 + 34 × 100 + 56789 = 67 × 100 + 89计算各个子序列的乘积并相加:12 × 67 × 10000 + 12 × 89 × 1000 + 34 × 67 × 100 + 34 × 89 × 10 + 5 ×67 + 5 × 89再将各个子序列的乘积相加并得出最终结果:80640000 + 1068000 + 227800 + 3036 + 335 + 445 = 84023005通过分组计算法,我们得出了12345 × 6789 = 84023005 的结果。
C语言中超大整数乘法运算

C语言中超大整数乘法运算在计算机中,长整型(long int)变量的范围是 -48 至 47,因此若用长整型变量做乘法运算,乘积最多不能超过 10位数。
即便用双精度型(double)变量,也仅能保证 16 位有效数字的精度。
在某些需要更高精度的乘法运算的场合,需要用别的办法来实现乘法运算。
比较容易想到的是做多位数乘法时列竖式进行计算的方法,只要写出模拟这一过程的程序,就能实现任意大整数的乘法运算。
经过查阅资料,找到一种更易于编程的方法,即“列表法”。
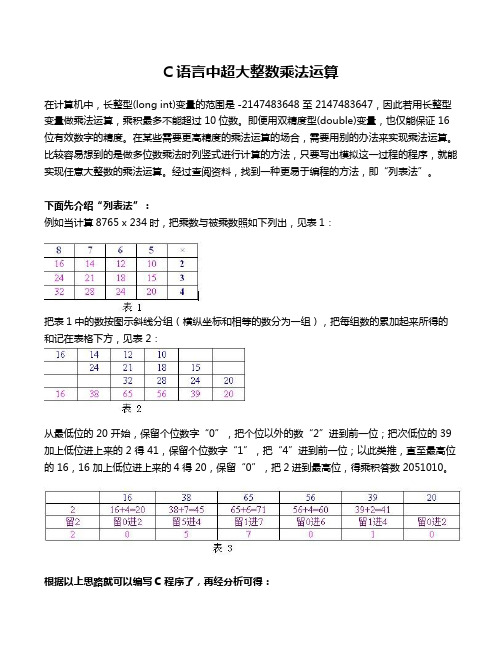
下面先介绍“列表法”:例如当计算8765 x 234时,把乘数与被乘数照如下列出,见表1:把表1中的数按图示斜线分组(横纵坐标和相等的数分为一组),把每组数的累加起来所得的和记在表格下方,见表 2:从最低位的 20 开始,保留个位数字“0”,把个位以外的数“2”进到前一位;把次低位的39 加上低位进上来的 2 得 41,保留个位数字“1”,把“4”进到前一位;以此类推,直至最高位的 16,16 加上低位进上来的4得 20,保留“0”,把2进到最高位,得乘积答数2051010。
根据以上思路就可以编写C 程序了,再经分析可得:1、一个m 位的整数与一个 n 位的整数相乘,乘积为m+n-1 位或m+n 位。
2、程序中,用三个字符数组分别存储乘数、被乘数与乘积。
由第 1 点分析知,存放乘积的字符数组的长度应不小于存放乘数与被乘数的两个数组的长度之和。
3、可以把第二步“计算填表”与第三四步“累加进位”放在一起完成,可以节省存储表格2所需的空间。
4、程序关键部分是两层循环,内层循环累计一组数的和,外层循环处理保留的数字与进位。
编写的程序如下:#define MAXLENGTH 1000#include <>#include <>void compute(char *a, char *b, char *c);void main(void){char a[MAXLENGTH], b[MAXLENGTH], c[MAXLENGTH * 2];puts("Input multiplier :");gets(a);puts("Input multiplicand :");compute(a, b, c);puts("Answer :");puts(c);getchar();}void compute(char *a, char *b, char *c) {int i, j, m, n;long sum, carry;m = strlen(a) - 1;n = strlen(b) - 1;for (i = m; i >= 0; i--)a[i] -= '0';for (i = n; i >= 0; i--)b[i] -= '0';c[m + n + 2] = '\0';for (i = m + n; i >= 0; i--) /* i 为坐标和 */{sum = carry;if ((j = i - m) < 0)j = 0;for ( ; j<=i && j<=n; j++) /* j 为纵坐标 */sum += a[i-j] * b[j]; /* 累计一组数的和 */c[i + 1] = sum % 10 + '0'; /* 算出保留的数字 */carry = sum / 10; /* 算出进位 */}if ((c[0] = carry+'0') == '0') /* if no carry, */c[0] = '\040'; /* c[0] equals to space */}效率分析:用以上算法计算 m位整数乘以n 位整数,需要先进行 m x n次乘法运算,再进行约 m + n次加法运算和 m + n次取模运算(实为整数除法)。
分治法的经典问题——大整数相乘c语言

一、引言在计算机科学领域,分治法是一种常见的问题求解策略。
它通过将问题划分为更小的子问题,并通过递归的方式解决这些子问题,最终将它们的解合并起来得到原始问题的解。
在本文中,我们将探讨分治法在一个经典问题——大整数相乘中的应用,以及如何使用C语言来实现这一算法。
二、大整数相乘问题概述在计算机中,通常情况下我们可以使用基本的数据类型(如int、float 等)来表示和操作数字。
但是,当涉及到非常大的整数时,这些基本的数据类型就显得力不从心了。
两个100位的整数相乘,如果直接使用基本的数据类型进行计算,会导致溢出和精度丢失的问题。
我们需要一种特殊的方法来处理大整数之间的乘法运算。
三、分治法解决大整数相乘问题分治法是一种将问题分解为更小的子问题,并通过递归的方式解决这些子问题,再将它们的解合并起来得到原始问题的解的策略。
在大整数相乘的问题中,可以使用分治法来将两个大整数分别划分为更小的子整数,然后通过递归的方式计算这些子整数的乘积,最终将它们的乘积合并起来得到原始问题的解。
四、C语言实现大整数相乘算法在C语言中,我们可以使用数组来表示大整数,并通过一定的算法来实现大整数相乘的功能。
我们需要将两个大整数表示为数组,然后通过分治法的思想,将这两个数组划分为更小的子数组,通过递归的方式计算这些子数组的乘积。
将这些子数组的乘积合并起来得到原始问题的解。
五、个人观点和理解从简单的分治法到复杂问题的解决,这个经典问题让我深刻理解了分治法的精髓。
在解决大整数相乘的问题时,分治法不仅解决了基本问题,还能很好地处理大整数的溢出和精度问题。
在C语言中实现大整数相乘算法也为我提供了一个很好的实践机会,让我更深入地理解了分治法的应用。
六、总结通过本文的探讨,我们对分治法在大整数相乘问题中的应用有了更深入的理解。
通过C语言实现大整数相乘算法的实例,我们也对分治法的具体实现有了更清晰的认识。
希望本文能够帮助读者更好地理解分治法的应用,并且对大整数相乘问题有进一步的了解和认识。
mbedtls 大整数乘法

mbedtls 大整数乘法mbedtls是一个轻量级的加密库,提供了一系列的加密算法和协议实现,包括大整数乘法。
大整数乘法是一种常见的数学运算,用于处理大数乘法问题。
本文将介绍mbedtls库中的大整数乘法实现原理及其应用。
大整数乘法是指对两个大整数进行乘法运算,其中大整数通常指超过计算机所能表示的标准整数范围的数。
在密码学和安全领域,大整数乘法被广泛应用于RSA、Diffie-Hellman等公钥加密算法中。
mbedtls库提供了高效的大整数乘法函数,用于处理大数的乘法运算。
其实现基于数学上的乘法算法,通过优化算法和数据结构,提高了运算效率和性能。
mbedtls库中的大整数乘法函数采用了经典的竖式乘法算法。
该算法将乘法问题转化为多次的单位数乘法和累加操作。
具体步骤如下:1. 将两个大整数分别表示为十进制或十六进制的字符串形式;2. 将字符串形式的大整数转化为内部表示结构,例如使用数组或链表等数据结构;3. 从低位到高位,依次取出第一个大整数的每一位数字;4. 将每一位数字与第二个大整数的每一位数字相乘,并将结果累加到对应位置;5. 处理进位和对齐问题,确保结果的正确性和完整性;6. 将计算结果转化为字符串形式,作为最终的乘法结果。
mbedtls库中的大整数乘法函数在实现时考虑了性能和安全性的平衡。
为了提高计算速度,mbedtls使用了一些优化技术,如乘法运算的位操作和并行计算等。
此外,mbedtls还提供了多种数据结构和算法选项,以满足不同应用场景的需求。
大整数乘法在密码学和安全领域具有重要的应用价值。
RSA算法中,大整数乘法用于生成和验证数字签名,保证消息的机密性和完整性。
Diffie-Hellman密钥交换算法中,大整数乘法用于计算共享密钥,实现安全通信。
此外,大整数乘法还被应用于数字证书和SSL/TLS 协议等安全机制中。
总结来说,mbedtls库提供了高效的大整数乘法实现,用于处理大数乘法运算。
大整数的运算 数据结构课程设计

目录一、题目概述(内容及要求) (2)二、功能分析 (2)三、设计 (3)四、运行与测试 (4)五、总结 (21)六、参考文献 (21)一、题目概述(内容及要求)内容:请设计一个有效的算法,可以进行两个n位大整数的四则运算。
①长整数长度在二十位以上。
②实现两长整数的加、减、乘、除操作。
要求:1.设计数据结构,存储结构;2.在c兼容环境完成上述题目的代码编写与调试;3.程序运行界面交互性好;4.软件运行,给出测试数据。
二、功能分析1.设计一个实现长整数进行四则运算的程序,长整数长度在二十位以上,有正负数的区别。
2.输入每四位一组,组间用逗号隔开,长整数位数没有上限,以分号结束长整型数据的输入。
用lnode结点数据结构存储数据。
每一个数据有一个头结点,它的data域用来放数据的正负数。
其余结点的数都为正整数。
3.程序包含数据的输入,判断,运算,输出和主函数。
4.具体程序执行的命令包括:a)输入函数:inputa();inputb();//的输入并建立双向循环链表b)判断函数:compare();//比较数据的大小c)运算函数:unsigndeadd();//无符号的加法a)unsigndesub();//无符号的减法b)add();sub();mul();div();//加减乘除四则运算d)输出函数:divput();//除法结果的输出函数a)putoutc();//其余结果的输出函数e)主函数:main();5.系统功能结构框图图2.1 系统功能结构框图三、设计首先要考虑的是如何表示长整型数。
可以4位数形成1组,而一个长整型数可能会有很多组这种4位数,而每节之间是有先后顺序的,因此我们可以考虑用数组和链表来存储数据。
(1)再考虑到每个长整型数的长度在输入之间是无法预知的,因此使用链表在存储空间的分配上更方便一些。
(2)在输入数据时总是从高位到低位地存储,而计算时总是从低位向高位运算,因此采用双向链表更方便,而为了从头结点方便地转到尾结点可以采用循环链表。
大数乘法算法

大数乘法算法
大数乘法算法是指针对超过计算机位数限制的大整数进行乘法运算的算法。
常见的大数乘法算法包括以下几种:
1. 传统竖式乘法算法:将两个大数相乘时,按照传统的竖式乘法算法进行计算。
这种方法的缺点是计算量大,时间复杂度高。
2. 分治算法:将大数拆分成较小的数进行乘法运算,然后将结果组合起来得到最终结果。
这种方法的优点是可以减少计算量,降低时间复杂度。
3. 快速傅里叶变换(FFT)算法:将大数转换为多项式,然后利用FFT算法进行乘法运算。
这种方法的优点是计算速度快,时间复杂度低,但实现较为复杂。
4. Karatsuba算法:将大数拆分成两个较小的数进行乘法运算,然后将结果组合起来得到最终结果。
这种方法的优点是计算速度快,时间复杂度低,实现较为简单。
总的来说,大数乘法算法可以根据具体的需求和应用场景选择不同的算法。
在实际应用中,需要根据计算量、精度要求、时间复杂度等因素进行综合考虑,选择最适合的算法。
C语言中超大整数乘法运算
C语言中超大整数乘法运算在计算机中,长整型(long int)变量的范围是 -2147483648 至 2147483647,因此若用长整型变量做乘法运算,乘积最多不能超过 10位数。
即便用双精度型(double)变量,也仅能保证 16 位有效数字的精度。
在某些需要更高精度的乘法运算的场合,需要用别的办法来实现乘法运算。
比较容易想到的是做多位数乘法时列竖式进行计算的方法,只要写出模拟这一过程的程序,就能实现任意大整数的乘法运算。
经过查阅资料,找到一种更易于编程的方法,即“列表法”。
下面先介绍“列表法”:例如当计算8765 x 234时,把乘数与被乘数照如下列出,见表1:把表1中的数按图示斜线分组(横纵坐标和相等的数分为一组),把每组数的累加起来所得的和记在表格下方,见表 2:从最低位的 20 开始,保留个位数字“0”,把个位以外的数“2”进到前一位;把次低位的 39 加上低位进上来的 2 得 41,保留个位数字“1”,把“4”进到前一位;以此类推,直至最高位的 16,16 加上低位进上来的4得 20,保留“0”,把2进到最高位,得乘积答数 2051010。
根据以上思路就可以编写C 程序了,再经分析可得:1、一个m 位的整数与一个 n 位的整数相乘,乘积为m+n-1 位或m+n位。
2、程序中,用三个字符数组分别存储乘数、被乘数与乘积。
由第 1 点分析知,存放乘积的字符数组的长度应不小于存放乘数与被乘数的两个数组的长度之和。
3、可以把第二步“计算填表”与第三四步“累加进位”放在一起完成,可以节省存储表格 2所需的空间。
4、程序关键部分是两层循环,内层循环累计一组数的和,外层循环处理保留的数字与进位。
编写的程序如下:#define MAXLENGTH 1000#include <stdio.h>#include <string.h>void compute(char *a, char *b, char *c);void main(void){char a[MAXLENGTH], b[MAXLENGTH], c[MAXLENGTH * 2];puts("Input multiplier :");gets(a);puts("Input multiplicand :");gets(b);compute(a, b, c);puts("Answer :");puts(c);getchar();}void compute(char *a, char *b, char *c){inti, j, m, n;long sum, carry;m = strlen(a) - 1;n = strlen(b) - 1;for (i = m; i>= 0; i--)a[i] -= '0';for (i = n; i>= 0; i--)b[i] -= '0';c[m + n + 2] = '\0';carry = 0;for (i = m + n; i>= 0; i--) /* i为坐标和 */{sum = carry;if ((j = i - m) < 0)j = 0;for ( ; j<=i&& j<=n; j++) /* j 为纵坐标 */ sum += a[i-j] * b[j]; /* 累计一组数的和 */c[i + 1] = sum % 10 + '0'; /* 算出保留的数字 */ carry = sum / 10; /* 算出进位 */}if ((c[0] = carry+'0') == '0') /* if no carry, */ c[0] = '\040'; /* c[0] equals to space */}效率分析:用以上算法计算 m位整数乘以n 位整数,需要先进行 m x n次乘法运算,再进行约m + n次加法运算和 m + n次取模运算(实为整数除法)。
俞正强数与运算主题中的整数乘法运算

在撰写这篇文章之前,我首先对俞正强数与运算主题中的整数乘法运算进行全面评估。
整数乘法是数学中非常基础和重要的一部分,它不仅在数学领域有着广泛的应用,还在生活中有着实际的意义。
在本文中,我将从简到繁地探讨整数乘法的概念、性质和运算规律,旨在帮助读者更深入地理解这一主题。
1. 整数乘法的概念整数乘法是指两个整数相乘的操作。
在代数中,我们将整数乘法规定为两个整数相乘的操作,且积仍然为整数。
2乘以3等于6,-4乘以3等于-12。
整数乘法满足交换律、结合律和分配律等运算法则,这些法则是整数乘法运算中非常重要的性质。
2. 整数乘法的性质整数乘法具有多种性质,包括交换律、结合律、分配律、乘法对加法的分配律和乘法对减法的分配律等。
这些性质在进行整数乘法运算时起着重要的作用,可以帮助我们简化乘法运算并准确地求得结果。
在实际运用中,我们常常根据这些性质来进行整数乘法的简化运算,提高运算效率。
3. 整数乘法的运算规律在进行整数乘法运算时,我们需要了解一些基本的运算规律,例如正数乘以正数、正数乘以负数、负数乘以正数、负数乘以负数等情况下的乘法规律。
对于这些规律,我们可以通过具体的例子进行说明,帮助读者更好地理解整数乘法的运算规律。
总结回顾:通过对整数乘法的概念、性质和运算规律进行全面的探讨,我们可以更深入地理解整数乘法在数学中的重要性和应用价值。
整数乘法不仅可以帮助我们简化计算过程,还可以在解决实际问题中发挥重要作用。
在日常生活中,我们常常会遇到整数乘法的应用,因此掌握好整数乘法的相关知识是非常重要的。
个人观点和理解:在我看来,整数乘法是数学中非常基础和重要的一部分,它不仅是数学学习的基础,还在生活中有着广泛的应用。
通过学习整数乘法,我们可以提高自己的计算能力和解决实际问题的能力。
我认为掌握好整数乘法的相关知识对于每个人来说都是非常重要的。
总结而言,整数乘法作为数学中的基础知识,具有非常重要的意义。
通过深入地了解整数乘法的概念、性质和运算规律,我们可以更全面、深刻和灵活地掌握这一知识,从而在数学学习和实际生活中获益良多。
数字整型算法实验报告(3篇)

第1篇一、实验目的1. 理解数字整型算法的基本原理和方法。
2. 掌握常用的数字整型算法,如整数乘法、除法、取余、排序等。
3. 培养算法设计与分析能力,提高编程实践能力。
二、实验内容1. 整数乘法算法2. 整数除法算法3. 整数取余算法4. 快速排序算法5. 堆排序算法三、实验原理1. 整数乘法算法:利用位运算,将两个整数进行逐位相乘,然后求和得到最终结果。
2. 整数除法算法:利用长除法原理,将除数逐步减去被除数的倍数,直到余数小于除数,此时商即为最终结果。
3. 整数取余算法:与整数除法类似,只需取除法的余数即可。
4. 快速排序算法:采用分治策略,将待排序的序列分为两部分,一部分大于等于基准值,另一部分小于基准值,然后递归地对这两部分进行排序。
5. 堆排序算法:利用堆这种数据结构,通过调整堆的性质来实现排序。
四、实验步骤1. 整数乘法算法实现```cint multiply(int a, int b) {int result = 0;while (b != 0) {if (b & 1) {result += a;}a <<= 1;b >>= 1;}return result;}```2. 整数除法算法实现```cint divide(int a, int b) {if (a == 0) return 0;int sign = (a > 0) ^ (b > 0) ? -1 : 1;long long dividend = abs((long long)a), divisor = abs((long long)b); long long quotient = 0;while (dividend >= divisor) {dividend -= divisor;quotient++;}return sign (int)quotient;}```3. 整数取余算法实现```cint remainder(int a, int b) {return a % b;}```4. 快速排序算法实现```cvoid quickSort(int arr[], int low, int high) { if (low < high) {int pivot = partition(arr, low, high); quickSort(arr, low, pivot - 1);quickSort(arr, pivot + 1, high);}}int partition(int arr[], int low, int high) { int pivot = arr[high];int i = low - 1;for (int j = low; j < high; j++) {if (arr[j] <= pivot) {i++;swap(&arr[i], &arr[j]);}}swap(&arr[i + 1], &arr[high]);return i + 1;}```5. 堆排序算法实现```cvoid heapify(int arr[], int n, int i) {int largest = i;int left = 2 i + 1;int right = 2 i + 2;if (left < n && arr[left] > arr[largest]) { largest = left;}if (right < n && arr[right] > arr[largest]) { largest = right;}if (largest != i) {swap(&arr[i], &arr[largest]);heapify(arr, n, largest);}}void heapSort(int arr[], int n) {for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}for (int i = n - 1; i > 0; i--) {swap(&arr[0], &arr[i]);heapify(arr, i, 0);}}```五、实验结果与分析1. 整数乘法算法:通过位运算实现,效率较高,适用于大整数乘法运算。
整数乘法运算整体性教学的思考与实践--以“三位数乘两位数”教学为例

整数乘法运算整体性教学的思考与实践■■以"三位数乘两位数"教学为例”2022版课标〃将〃2011版课标”中”数与代数"领域”数的认识和数的运算”两个主题合并为一个大主题”数与运算数与运算关系密切,数的认识是数的运算的基础,通过数的运算有助于学生更好地认识数。
在数的运算教学中,通过数的意义理解数的运算,关注的是"数”与”运算”的一致性;通过化未知为已知理解掌握”新计算”,关注的是思想方法的一致性。
如何在整数乘法运算教学中渗透并实现这两个一致性呢?以苏教版小学数学四年级下册”三位数乘两位数”单元第一课时教学为例作些研讨。
一、教材内容简析(一)整数乘法运算整数乘法运算,在苏教版小学数学教材中编排了”表内乘法"”两、三位数乘一位数””两位数乘两位数””三位数乘两位数”等单元分步学习。
在”表内乘法”的学习中,学生理解了乘法的含义,掌握了乘法口诀表,是接下来乘法运算的基础。
”两、三位数乘一位数””两位数乘两位数””三位数乘两位数”单元的内容安排如下表:两、三位数乘一位数两位数乘两位数三位数乘两位数口算整十、整百数口算两位数乘整笔算三位数乘两乘一位数十数位数估算两、三位数乘估算两位数乘两常见数量关系:总一位数位数价=单价X数量倍的认识笔算两位数乘两常见数量关系:路求一个数的几倍位数(不进位)程=速度X时间是多少笔算两位数乘两积的变化规律笔算两、三位数乘位数(进位)计算乘数末尾有一位数(不进位)笔算两位数乘整0的乘法笔算两、三位数乘十数一位数(一次进位)用连乘解决实际笔算两、三位数乘问题一位数(连续进位)0乘任何都得0笔算几百零几乘一位数笔算几百几十乘一位数整体分析整数乘法运算内容编排,发现"口算整十乘一位数”的学习,学生从计算”几个一”发展到计算”几个十”,”计数单位”帮助学生经历整数乘法运算的第一次”突围”。
从"位值”的角度理解整数乘法,学生生长出"整十、整百、整干数”乘一位数的"翅膀",感悟乘法运算算理的一致,都是计算有多少个计数单位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
You enjoy it . " ;
在执行这段代码时 ,首先 ,创建一个 System. St ring 类型的对象 ,并将之初始化为文本“Hello World !”。此时. N E T 运行库会为该字符串分配 足够的内存来保存这个文本 ,再设置变量 greet2 ing Text ,表示这个字符串对象 。从语法上看 ,下 一行代码是把更多的文本添加到字符串中 。实际 上并非如此 ,系统创建一个新字符串对象 ,给它分 配足够的内存 ,以保存合并之后的文本 。将最初 的文本“Hello World !”先复制到这个新字符串 中 ,再将第二行中的文本“Yo u enjoy it . ”添加到 其末尾 ,然后更新存储在变量 greeting Text 中的 地址 ,使变量正确地指向新的字符串对象 。旧的 字符串对象被撤销了 ,不再有变量引用它 ,下一次 垃圾收集器清理应用程序中所有未使用的对象 时 ,就会将其删除 。不使用的变量所占用的存储 空间直到垃圾收集器执行清理时才释放 ,. Net 垃 圾收集器何时进行清理 ,由. Net CL R 根据需要决 定 ,而不是由程序开发人员决定 。若程序中有大 量的字符串运算 ,则空间浪费现象会十分严重 。 而 在 C # 中 提 供 另 外 一 种 处 理 字 符 的 类 St ringBuilder ,它的工作方式非常高效 。在使用 St ring 类构造一个字符串时 ,要给它分配足够的 内存来保存字符串 ,但 St ringBuilder 通常分配的
midOne < = len ( PartOne) / 2 ; mid Two < = len ( Part Two) / 2 ;
第 29 卷第 2 期 长 春 工 业 大 学 学 报 (自然科学版) Vol1 29 ,No . 2 2008 年 4 月 Jo urnal of Changchun U niversity of Technology (Nat ural Science Edition) Ap r1 2008
需要重新分配内存 。对字符串的修改就在赋予
St ringBuilder 对象的存储单元中进行 ,这就大大
提高了添加子字符串和替换单个字符的效率 。该
类提供了处理字符数组的大部分功能 ,而且对
St ringBuilder 类型的变量来说 ,它的理论上限是
Int32. MaxValue 个字符 (即 232 - 1 个) ,对于一
void MultiBigInteger (St ringBuilder PartOne , St ringBuild2 er Part Two ,St ringBuilder Result)
{ / / 求出两个串的中间位置 ,并求出 A ,B ,C ,D 的长度 。这 里我们要求串左到右 ,从低向高排列/ / AB 3 CD = > BA 3 DC。
内存会比需要的更多 。开发人员可以选择显示指
定 St ringBuilder 要分配多少内存 ,但如果没有显
示指定 ,存储单元量在默认情况下就根据 St ring2
Builder 初 始 化 时 的 字 符 串 长 度 来 确 定 。为
St ringBuilder 设置初始容量时 ,最好把容量设置
为字符串可能的最大长度 ,确保 St ringBuilder 不
kj f
j =0
n mj
在分解到原子规模时 , 就采取类似原码移位
乘的方法 , 即将各数位相乘 , 然后移位相加 , 并在
此过程中处理进位问题 。
2 实现与效率
2. 1 实现过程 在实现过程中 , 采用 10 为基[7] 。首先 , 将两 个待乘的大整数中位数较大的一个用 X 表示 , 另 一个用 Y 表示 ,然后 , 将 X 分解为 A , B (其中 , A 为 X 中数位的左半部分 , B 为右半部分 , 左半部 分的位数大于等于右半部分位数 , 下面对于 Y 的
X 为 m 位 , Y 为 n 位 , 则计算 X 3 Y 的时间复杂
度就为 O ( m 3 n) 。所以 , 采用分治法[6] 来提高效
率 。分治法的基本思想是将一个规模为 n 的问题
分解为 k 个规模较小的子问题 , 这些子问题相互
独立且与原问题相同 。递归求解各个子问题 , 然
后合并各个子问题的解 , 从而得到原问题的解。
206
长 春 工 业 大 学 学 报 (自然科学版) 第 29 卷
处理也相同) ;将 Y 分解为 C , D 。 则 X 3 Y = (A 3 10^ceiling ( m/ 2) + B) 3 ( C 3 10^ceiling ( n/ 2) + D) = A 3 C 3 10^ceiling ( m/ 2) 3 10^ceiling ( n/ 2) + A 3 D 3 10^ceiling ( m/ 2) + B 3 C 3 10^ceiling (n/ 2) + B 3 D 。 对于 A 3 C ,A 3 D ,B 3 C ,B 3 D ,也用递归方 式进行分解 ,直至 4 个子式的分解子式中的两部 分中的 1 个位数为 1 时 ,就可以对该子式进行运 算 ,否则继续分解 。然后 ,将所有子式分解后相乘 的结果进行累加 ,得到 4 个子式的值 ,最终累加得 到 X 3 Y 的结果 。 接下来创建 1 个专门用于对上面分解完成的 St ringBuilder 对象进行处理的 St ringProcess. cs 。 该类的主要功能就是完成对 2 个大整数的分解 , 相乘和 累 加 。在 类 中 首 先 完 成 对 2 个 给 定 的 St ringBuilder 串的数位对准并相加 ,因为要从最 低的数位开始相加 ,而且在相加的过程中可能产 生进位 ,所以 ,在生成 St ringBuilder 串时 ,采用倒 序方法生成 ,第 0 位保存的是最低数位 ,即所有新 添加的数位都存放在当前 St ringBuilder 对象的 末尾 。然后 ,实现两个 St ringBuilder 串所代表的 大整数相乘 ,再实现大整数的分治法分解 。关键 代码如下 :
Abstract : Wit h C language , t he big integer multiplicatio n is realized based o n divisio n met hod. The algorit hm is efficient , simple and feasible. Key words : big integer ; divisio n ; data st ruct ure.
收稿日期 : 2008203206 作者简介 : 英昌盛 (1979 - ) ,男 ,汉族 ,山东费县人 ,吉林师范大学助教 ,长春理工大学硕士研究生 ,主要从事图像处理方向研究 , E2
mail :laoying79 @163. com.
第 2 期 英昌盛 , 等 : 大整数乘法的数据结构及算法选择探究
205
4 个字节共 32 位 , 保存数值的范围最大可达到 232 - 1 ,但是在运算时 , 涉及到乘法 、进位 、移位等 操作 ,算法复杂 ,效率低下 。而且 C # [5] 语言是托 管的安全语言 ,不能进行相对低级的位操作 。所 以采用整型数组不适合 。这里选取用字符数组来 存储结果的各个数位 ,每个数组元素占用一个字 节 ,存储结果的一个数位 ,这样既可以节省存储空 间 ,又便于程序对各个数位进行处理 (数字和其对 应字符的 A SCII 码只相差 32) 。在 C # 中 ,St ring 类是一个功能非常强大的类 ,它拥有许多有效的 属性和方法 。但是 St ring 类实际上是一个不可 变的数据类型 ,一旦对字符串对象进行了初始化 , 该字符串对象就不能改变了 。修改字符串内容的 方法和运算符 ,实际上是创建一个新的字符串 ,如 果必要 ,可以把旧字符串的内容复制到新字符串 中 。对于字符数组的处理是按只读来进行的 ,如 果对数组内容进行频繁的修改 、删除 ,效率会很 低 ,造成大量空间的浪费 ,甚至系统崩溃 。例如 , 下面的代码 :
为了使处理方法更加行之有效 , 经过大量实践发
现 , 最好使 k 个子问题的规模大致相同 。分治法
通常由递归程序实现 ,所以 ,将一个规模为 n 的问
题分解为 k 个规模为 ( n/ m) 的子问题 , 然后求解
各个子问题 , 再将各个子问题的解合并 , 经求解
得:
logm n - 1
∑ T ( n) = N logm K +
般情况保存相乘的结果已经足够 。
1. 2 大整数乘法的算法选择与分析
大整数乘法中由于要使用字符数组来存储各
个数位 ,进行乘法过程中的转换 、移位 、相乘是提高效率的
关键 。通常的算法都是采用和日常计算乘法相同
的算法 ,即相乘移位相加的方法 。这样 ,如上所设
0 引 言
大整数在密码学 、生物信息 、基因工程等多个 领域都有重要的应用价值 。大整数无法在程序设 计语言能直接表示的整数范围内进行表示和处 理 ,用浮点数只能近似表示其大小 ,而且有效数字 位数也受到影响 。为了能精确表示大整数 ,得到 计算结果中所有数位上的精确数值 ,并提高计算 的效率 ,必须选择合适的数据结构和有效的算法 。
Data structure and algorithm selection of big integer multiplication
YIN G Chang2sheng1 , ZHOU Xi2lo ng2
(1. College of Comp uter , Jilin Normal Universit y , Siping 136000 , China ; 2. School of Co mp uter Science & Engineering , Changchun Universit y of Technology , Changchun 130012 , China)
