二元一次方程经典试题一
《二元一次方程组》试题及答案

《二元一次方程组》试题一、填空题1、二元一次方程4x-3y=12,当x=0,1,2,3时,y=____2、在x+3y=3中,若用x 表示y ,则y= ,用y 表示x ,则x=3、已知方程(k 2-1)x 2+(k+1)x+(k-7)y=k+2,当k=______时,方程为一元一次方程;当k=______时,方程为二元一次方程。
4、对二元一次方程2(5-x)-3(y-2)=10,当x=0时,则y=____;当y=0时,则x=____。
5、方程2x+y=5的正整数解是______。
6、若(4x-3)2+|2y+1|=0,则x+2= 。
7、方程组⎩⎨⎧==+bxy ay x 的一个解为⎩⎨⎧==32y x ,那么这个方程组的另一个解是 。
8、若21=x 时,关于y x 、的二元一次方程组⎩⎨⎧=-=-212by x y ax 的解互为倒数,则=-b a 2 。
二、选择题1、方程2x-3y=5,xy=3,33=+yx ,3x-y+2z=0,62=+y x 中是二元一次方程的有( )个。
A、1 B、2 C、3 D、4 2、方程2x+y=9在正整数范围内的解有( )A 、1个B 、2个C 、3个D 、4个3、与已知二元一次方程5x-y=2组成的方程组有无数多个解的方程是( )A 、10x+2y=4B 、4x-y=7C 、20x-4y=3D 、15x-3y=6 4、若是m y x 25与2214-++n m n y x 同类项,则n m -2的值为 ( )A 、1B 、-1C 、-3D 、以上答案都不对 5、在方程(k 2-4)x 2+(2-3k)x+(k+1)y+3k=0中,若此方程为二元一次方程,则k 值为( ) A 、2 B 、-2 C 、2或-2 D 、以上答案都不对. 6、若⎩⎨⎧-==12y x 是二元一次方程组的解,则这个方程组是( )A 、⎩⎨⎧=+=-5253y x y x B 、⎩⎨⎧=--=523x y x y C 、⎩⎨⎧=+=-152y x y x D 、⎩⎨⎧+==132y x yx7、在方程3)(3)(2=--+x y y x 中,用含x 的代数式表示y ,则 ( )A 、35-=x yB 、3--=x yC 、35+=x yD 、35--=x y 8、已知x=3-k,y=k+2,则y与x的关系是( )A、x+y=5 B、x+y=1 C、x-y=1 D、y=x-1 9、下列说法正确的是( )A、二元一次方程只有一个解 B、二元一次方程组有无数个解C、二元一次方程组的解必是它所含的二元一次方程的解 D、三元一次方程组一定由三个三元一次方程组成10、若方程组⎩⎨⎧=+=+16156653y x y x 的解也是方程3x+ky=10的解,则k的值是( )A、k=6 = B、k=10 C、k=9 D、k=101 三、解答题1、解关于x 的方程)1(2)4)(1(+-=--x a x a a1、代数式by ax +,当2,5==y x 时,它的值是7;当5,8==y x 时,它的值是4,试求5,7-==y x 时代数式by ax -的值。
二元一次方程简单题

二元一次方程简单题
一、知识点回顾
1. 二元一次方程的定义
含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。
一般形式为ax + by=c(a、b、c是常数,a≠0,b≠0)。
2. 二元一次方程的解
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
一般来说,二元一次方程有无数个解。
二、简单例题及解析
1. 例1:判断方程2x + 3y = 7是否为二元一次方程?
- 解析:
- 方程2x+3y = 7中含有两个未知数x和y。
- 且x的次数是1,y的次数也是1。
- 等号两边都是整式。
- 所以方程2x + 3y = 7是二元一次方程。
2. 例2:已知方程3x - 2y=5,判断x = 1 y=-1是否为该方程的解?
- 解析:
- 把x = 1,y=-1代入方程3x-2y的左边得:
- 3×1-2×(-1)=3 + 2=5。
- 方程的右边是5。
- 因为左边=右边。
- 所以x = 1 y=-1是方程3x - 2y = 5的解。
3. 例3:求方程x + y = 3的正整数解。
- 解析:
- 由x + y=3可得y = 3 - x。
- 因为要求正整数解,所以x>0,y>0。
- 即3 - x>0,解得x<3。
- 当x = 1时,y=3 - 1 = 2。
- 当x = 2时,y=3 - 2 = 1。
- 所以方程x + y = 3的正整数解为x = 1 y = 2和x = 2 y = 1。
二元一次方程经典试题一

二元一次方程经典试题一(围:代数: 二元一次方程组)一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………( ) 2、方程组⎩⎨⎧=+-=5231y x xy 的解是方程3x -2y =13的一个解( )3、由两个二元一次方程组成方程组一定是二元一次方程组( )4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ,可以转化为⎩⎨⎧-=--=+27651223y x y x ( )5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程,则a 的值为±1( )6、若x +y =0,且|x |=2,则y 的值为2 …………( )7、方程组⎩⎨⎧=+-=+81043y x xm my mx 有唯一的解,那么m 的值为m ≠-5 …………( )8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有无数多个解 …………( ) 9、x +y =5且x ,y 的绝对值都小于5的整数解共有5组 …………( ) 10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解,反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………( )11、若|a +5|=5,a +b =1则32-的值为b a………()12、在方程4x -3y =7里,如果用x 的代数式表示y ,则437yx +=( ) 二、选择:13、任何一个二元一次方程都有( ) (A )一个解; (B )两个解; (C )三个解;(D )无数多个解;14、一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( ) (A )5个 (B )6个(C )7个(D )8个15、如果⎩⎨⎧=+=-423y x ay x 的解都是正数,那么a 的取值围是( )(A )a <2; (B )34->a ; (C )342<<-a ; (D )34-<a ; 16、关于x 、y 的方程组⎩⎨⎧=-=+my x my x 932的解是方程3x +2y =34的一组解,那么m 的值是( ) (A )2;(B )-1; (C )1; (D )-2;17、在下列方程中,只有一个解的是( ) (A )⎩⎨⎧=+=+0331y x y x(B )⎩⎨⎧-=+=+2330y x y x(C )⎩⎨⎧=-=+4331y x y x(D )⎩⎨⎧=+=+3331y x y x18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( ) (A )15x -3y =6 (B )4x -y =7(C )10x +2y =4(D )20x -4y =319、下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114y x y x(B )⎩⎨⎧=+=+75z y y x(C )⎩⎨⎧=-=6231y x x(D )⎩⎨⎧=-=-1y x xyy x20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解,则a 、b 的值等于( )(A )a =-3,b =-14 (B )a =3,b =-7(C )a =-1,b =9(D )a =-3,b =1421、若5x -6y =0,且xy ≠0,则yx yx 3545--的值等于( )(A )32 (B )23 (C )1 (D )-122、若x 、y 均为非负数,则方程6x =-7y 的解的情况是( ) (A )无解(B )有唯一一个解 (C )有无数多个解(D )不能确定23、若|3x +y +5|+|2x -2y -2|=0,则2x 2-3xy 的值是( ) (A )14(B )-4(C )-12(D )1224、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为( ) (A )21=k ,b =-4 (B )21-=k ,b =4 (C )21=k ,b =4 (D )21-=k ,b =-4 三、填空:25、在方程3x +4y =16中,当x =3时,y =________,当y =-2时,x =_______若x 、y 都是正整数,那么这个方程的解为___________; 26、方程2x +3y =10中,当3x -6=0时,y =_________;27、如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________; 28、若⎩⎨⎧-==11y x 是方程组⎩⎨⎧-=-=+1242a y x b y ax 的解,则⎩⎨⎧==______________b a ; 29、方程|a |+|b |=2的自然数解是_____________; 30、如果x =1,y =2满足方程141=+y ax ,那么a =____________; 31、已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解,则a =______,m =______;32、若方程x -2y +3z =0,且当x =1时,y =2,则z =______; 33、若4x +3y +5=0,则3(8y -x )-5(x +6y -2)的值等于_________;34、若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________; 35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________;36、已知a -3b =2a +b -15=1,则代数式a 2-4ab +b 2+3的值为__________; 四、解方程组37、⎪⎪⎩⎪⎪⎨⎧=-=-1332343n m nm ; 38、)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+; 39、⎪⎪⎩⎪⎪⎨⎧=++=+125432y x yx y x ; 40、⎪⎩⎪⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x ;41、⎪⎪⎩⎪⎪⎨⎧++=++=+=+6253)23(22)32(32523233y x y x yx y x ; 42、⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x ;43、⎪⎩⎪⎨⎧=-+-=-+=-+3113y x z x z y z y x ; 44、⎪⎩⎪⎨⎧=+=+=+101216x z z y y x ;45、⎪⎩⎪⎨⎧=-+=+-=-+35351343z y x z y x z y x ; 46、⎪⎩⎪⎨⎧=+-==30325:3:7:4:z y x z x y x ;五、解答题:47时,甲看错了①式中的x 的系数,解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ;乙看错了方程②中的y 的系数,解得⎪⎪⎩⎪⎪⎨⎧==19177681y x ,若两人的计算都准确无误,请写出这个方程组,并求出此方程组的解;48、使x +4y =|a |成立的x 、y 的值,满足(2x +y -1)2+|3y -x |=0,又|a |+a =0,求a 的值;49、代数式ax 2+bx +c 中,当x =1时的值是0,在x =2时的值是3,在x =3时的值是28,试求出这个代数式;50、要使下列三个方程组成的方程组有解,求常数a 的值。
《二元一次方程组》基础测试题及参考答案

《二元一次方程》基础测试题一、选择题1.方程2x+y =0,3x-xy =1,2x+y ﹣x =7,x −1y =0二元一次方程的个数是( ) A .1个 B .2个 C .3个 D .4个2.把方程2x-y=3改写成用含x 的式子表示y 的形式( )A .y=2x-3B .y=2x+3C .1322x y =+D .132x y =+ 3.若{x =5y =2是关于x 和y 的二元一次方程2x ﹣by =6的解,则b 的值是( ) A . 2 B .﹣2 C . 4 D .﹣44.关于二元一次方程组{y =x +1x −2y =7,消去y 可得( ) A .x-x ﹣1=7 B .x-2x ﹣1=7 C .x-2x ﹣2=7 D .x+2x-2=75.已知二元一次方程组{2x −y =7x −2y =−3,则x+y 的值为( ) A .﹣4 B .4 C .﹣5 D .56.若方程x+y =2,x ﹣2y =8和kx-y =6有公共解,则k 的值是( )A .1B .﹣1C .2D .﹣27.现在小强的年龄是小玲的2倍,2年前小强的年龄是小玲的3倍,今年小强和小玲的年龄是多少岁?设小强今年x 岁,小玲今年y 岁,可列方程组( )A .{x +2=3(y +2)x =2yB .{x −2=3(y −2)x =2yC .{x +2=2(y +2)x =3yD .{x −2=3(y −2)x =3y8.若|x+2y ﹣2|+√x −y +1=0,则x+y 的值为( )A .4B .2C .1D .09.一个两位数数位上的数字之和是8,将它的十位数字和个位数字交换后,得到新的两位数,若新两位数比原两位数小18,则原两位数为( )A .26B .53C .35D .6210.已知关于x 、y 的二元一次方程组的解3+2=+22+3=x y k x y k ⎧⎨⎩满足x+y=2,则k 的值为( ) A .0 B .1 C .2 D .411.已知方程组213616x y z x y z -+=-⎧⎨+-=⎩,则x+y 的值为( ) A .3 B .4 C .5 D .612.今有牛五、羊二,值金十两;牛二、羊五,值金八两,牛、羊各值金几何?题目大意是:5头牛、2只羊共值金10两,2头牛、5只羊共值金8两,每头牛、每只羊各值金多少两?解:设一头牛值金x 两,一只羊值金y 两,则列方程组( )A .{5y −2x =102y −5x =8B .{5y −2x =82y −5x =10C .{5y +2x =102y +5x =8D .{5y +2x =82y +5x =10二、填空题13.方程ax+(a +1)y =3a -1是关于x 、y 的二元一次方程,则a 的范围是_______。
二元一次方程经典40题

二元一次方程经典40题1.甲、乙两人相距30千米,甲的速度是x千米/小时,乙的速度是y千米/小时,若两人同时相向而行,2小时后相遇,求x和y满足的方程。
2.A、B两城相距200千米,一辆汽车从A城开往B城的速度为x千米/小时,从B城返回A城速度为y千米/小时,已知往返共用5小时,写出关于x和y的方程。
3.甲、乙两人在周长为400米的环形跑道上跑步,甲的速度是x米/秒,乙的速度是y米/秒,若两人同时同地反向出发,20秒后相遇,求方程。
4.某人从甲地到乙地,如果步行速度是x米/分钟,骑车速度是y米/分钟,步行先走10分钟后,再骑车20分钟到达乙地,求关于x和y的方程。
5.一艘轮船顺流速度为x千米/小时,逆流速度为y千米/小时,已知水流速度为2千米/小时,求x和y满足的方程。
6.甲、乙两车分别从相距s千米的两地同时出发,甲车速度为x千米/小时,乙车速度为y千米/小时,经过3小时两车相遇,写出方程。
7.汽车从A地到B地,如果以x千米/小时的速度行驶,会迟到2小时,如果以y千米/小时的速度行驶,会早到1小时,A、B两地距离固定,求方程。
8.甲、乙两人分别从A、B两地同时出发相向而行,甲的速度为x千米/天,乙的速度为y千米/天,经过5天相遇,且A、B两地距离为120千米,求方程。
9.一项工程,甲队单独做x天完成,乙队单独做y天完成,两队合作10天完成,求x和y满足的方程。
10.甲、乙两个工程队修建一条公路,甲队每天修x米,乙队每天修y米,两队合作15天修完长为600米的公路,求方程。
11.一件工作,甲单独做x小时完成,乙单独做y小时完成,甲先做2小时后乙再做3小时完成这件工作的一半,求方程。
12.一项工程,甲、乙合作x天完成,乙、丙合作y天完成,甲、丙合作z天完成,设甲、乙、丙单独完成分别需要a、b、c天,求关于a和b的二元一次方程。
13.某工程甲单独做需x天,乙单独做需y天,甲先做3天,然后甲乙合作2天完成工程,求方程。
二元一次方程组练习题(含问题详解)
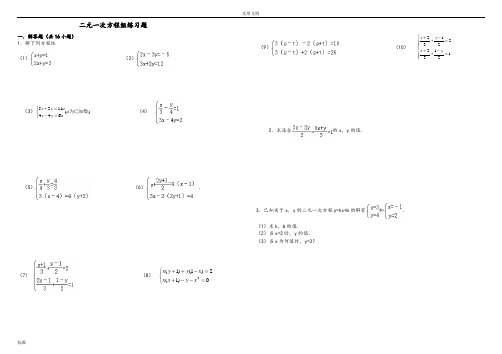
实用文档标准二元一次方程组练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x ay x ⎩⎨⎧=-=+ (4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.word版本二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.考点:解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出y的值,继而求出x的值.解答:解:由题意得:,由(1)×2得:3x ﹣2y=2(3),由(2)×3得:6x+y=3(4),(3)×2得:6x﹣4y=4(5),(5)﹣(4)得:y=﹣,把y的值代入(3)得:x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点:解二元一次方程组.分析:(1)(2)用代入消元法或加减消元法均可;(3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)①﹣②得,﹣x=﹣2,解得x=2,把x=2代入①得,2+y=1,解得y=﹣1.故原方程组的解为.(2)①×3﹣②×2得,﹣13y=﹣39,解得,y=3,把y=3代入①得,2x﹣3×3=﹣5,解得x=2.故原方程组的解为.(3)原方程组可化为,①+②得,6x=36,x=6,①﹣②得,8y=﹣4,y=﹣.所以原方程组的解为.(4)原方程组可化为:,①×2+②得,x=,把x=代入②得,3×﹣4y=6,y=﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:①相同未知数的系数相同或互为相反数时,宜用加减法;②其中一个未知数的系数为1时,宜用代入法.3.解方程组:考点:解二元一次方程组.word版本专题:计算题.分析:先化简方程组,再进一步根据方程组的特点选用相应的方法:用加减法.解答:解:原方程组可化为,①×4﹣②×3,得7x=42,解得x=6.把x=6代入①,得y=4.所以方程组的解为.点评:;二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的方法有代入法和加减法.4.解方程组:考点:解二元一次方程组.专题:计算题.分析:把原方程组化简后,观察形式,选用合适的解法,此题用加减法求解比较简单.解答:解:(1)原方程组化为,①+②得:6x=18,∴x=3.代入①得:y=.所以原方程组的解为.点评:要注意:两个二元一次方程中同一未知数的系数相反或相等时,把这两个方程的两边相加或相减,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减消元法.本题适合用此法.5.解方程组:考点:解二元一次方程组.专题:计算题;换元法.分析:本题用加减消元法即可或运用换元法求解.解答:解:,①﹣②,得s+t=4,①+②,得s﹣t=6,即,解得.所以方程组的解为.点评:此题较简单,要熟练解方程组的基本方法:代入消元法和加减消元法.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?考点:解二元一次方程组.专题:计算题.分析:(1)将两组x ,y 的值代入方程得出关于k、b的二元一次方程组,再运用加减消元法求出k、b的值.(2)将(1)中的k、b代入,再把x=2代入化简即可得出y的值.(3)将(1)中的k、b和y=3代入方程化简即可得出x的值.解答:解:(1)依题意得:①﹣②得:2=4k,所以k=,所以b=.(2)由y=x+,把x=2代入,得y=.word 版本(3)由y=x+把y=3代入,得x=1.点评:本题考查的是二元一次方程的代入消元法和加减消元法,通过已知条件的代入,可得出要求的数.7.解方程组:(1);(2).考点:解二元一次方程组.分析:根据各方程组的特点选用相应的方法:(1)先去分母再用加减法,(2)先去括号,再转化为整式方程解答.解答:解:(1)原方程组可化为,①×2﹣②得:y=﹣1,将y=﹣1代入①得:x=1.∴方程组的解为;(2)原方程可化为,即,①×2+②得:17x=51,x=3,将x=3代入x﹣4y=3中得:y=0.∴方程组的解为.点评:这类题目的解题关键是理解解方程组的基本思想是消元,掌握消元的方法有:加减消元法和代入消元法.根据未知数系数的特点,选择合适的方法.8.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题应把方程组化简后,观察方程的形式,选用合适的方法求解.解答:解:原方程组可化为,①+②,得10x=30,x=3,代入①,得15+3y=15,y=0.则原方程组的解为.点评:解答此题应根据各方程组的特点,有括号的去括号,有分母的去分母,然后再用代入法或加减消元法解方程组.9.解方程组:考点:解二元一次方程组.专题:计算题.分析:本题为了计算方便,可先把(2)去分母,然后运用加减消元法解本题.解答:解:原方程变形为:,两个方程相加,得4x=12,x=3.把x=3代入第一个方程,得4y=11,y=.解之得.点评:本题考查的是二元一次方程组的解法,方程中含有分母的要先化去分母,再对方程进行化简、消元,即可解出此类题目.word版本10.解下列方程组:(1)(2)考点:解二元一次方程组.专题:计算题.分析:此题根据观察可知:(1)运用代入法,把①代入②,可得出x,y的值;(2)先将方程组化为整系数方程组,再利用加减消元法求解.解答:解:(1),由①,得x=4+y③,代入②,得4(4+y )+2y=﹣1,所以y=﹣,把y=﹣代入③,得x=4﹣=.所以原方程组的解为.(2)原方程组整理为,③×2﹣④×3,得y=﹣24,把y=﹣24代入④,得x=60,所以原方程组的解为.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.11.解方程组:(1)(2)考点:解二元一次方程组.专题:计算题;换元法.分析:方程组(1)需要先化简,再根据方程组的特点选择解法;方程组(2)采用换元法较简单,设x+y=a,x﹣y=b,然后解新方程组即可求解.解答:解:(1)原方程组可化简为,解得.(2)设x+y=a,x﹣y=b,∴原方程组可化为,解得,∴∴原方程组的解为.点评:此题考查了学生的计算能力,解题时要细心.12.解二元一次方程组:(1);(2).考点:解二元一次方程组.word版本专题:计算题.分析:(1)运用加减消元的方法,可求出x、y的值;(2)先将方程组化简,然后运用加减消元的方法可求出x、y的值.解答:解:(1)将①×2﹣②,得15x=30,x=2,把x=2代入第一个方程,得y=1.则方程组的解是;(2)此方程组通过化简可得:,①﹣②得:y=7,把y=7代入第一个方程,得x=5.则方程组的解是.点评:此题考查的是对二元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.13.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.考点:解二元一次方程组.专题:计算题.分析:(1)把甲乙求得方程组的解分别代入原方程组即可;(2)把甲乙所求的解分别代入方程②和①,求出正确的a、b,然后用适当的方法解方程组.解答:解:(1)把代入方程组,得,解得:.把代入方程组,得,解得:.∴甲把a看成﹣5;乙把b看成6;(2)∵正确的a是﹣2,b是8,∴方程组为,解得:x=15,y=8.则原方程组的解是.点评:此题难度较大,需同学们仔细阅读,弄清题意再解答.14.考点:解二元一次方程组.分析:先将原方程组中的两个方程分别去掉分母,然后用加减消元法求解即可.解答:解:由原方程组,得,由(1)+(2),并解得x=(3),把(3)代入(1),解得y=∴原方程组的解为.点评:用加减法解二元一次方程组的一般步骤:1.方程组的两个方程中,如果同一个未知数的系数既不互为相反数又不相等,就用适当的数去乘方程的两边,使一个未知数的系数互为相反数或相等;word版本2.把两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;3.解这个一元一次方程;4.将求出的未知数的值代入原方程组的任意一个方程中,求出另一个未知数,从而得到方程组的解.15.解下列方程组:(1);(2).考点:解二元一次方程组.分析:将两个方程先化简,再选择正确的方法进行消元.解答:解:(1)化简整理为,①×3,得3x+3y=1500③,②﹣③,得x=350.把x=350代入①,得350+y=500,∴y=150.故原方程组的解为.(2)化简整理为,①×5,得10x+15y=75③,②×2,得10x﹣14y=46④,③﹣④,得29y=29,∴y=1.把y=1代入①,得2x+3×1=15,∴x=6.故原方程组的解为.点评:方程组中的方程不是最简方程的,最好先化成最简方程,再选择合适的方法解方程.16.解下列方程组:(1)(2)考点:解二元一次方程组.分析:观察方程组中各方程的特点,用相应的方法求解.解答:解:(1)①×2﹣②得:x=1,将x=1代入①得:2+y=4,y=2.∴原方程组的解为;(2)原方程组可化为,①×2﹣②得:﹣y=﹣3,y=3.将y=3代入①得:x=﹣2.∴原方程组的解为.点评:解此类题目要注意观察方程组中各方程的特点,采用加减法或代入法求解.word版本。
二元一次方程组试题及答案-(1)

班级: 姓名:一、填空题:(本大题共10小题,每小题3分,共30分)1. 在方程25x y +=中,用x 的代数式表示y ,得_______y =.2. 若一个二元一次方程的一个解为21x y =⎧⎨=-⎩,则这个方程可以是: (只要求写出一个)3. 下列方程: ①213y x -=; ②332x y +=; ③224x y -=; ④5()7()x y x y +=+;⑤223x =;⑥14x y+=.其中是二元一次方程的是 . 4. 若方程456m n m n x y -+-=是二元一次方程,则____m =,____n =.5. 方程4320x y +=的所有非负整数解为:6. 若23x y -=-,则52____x y -+=.7. 若2(5212)3260x y x y +-++-=,则24____x y +=.8. 有人问某男孩,有几个兄弟,几个姐妹,他回答说:“有几个兄弟就有几个姐妹.”再问他妹妹有几个兄弟,几个姐妹,她回答说:“我的兄弟是姐妹的2倍.”若设兄弟x 人,姐妹y 人,则可列出方程组: .9. 某次足球比赛的记分规则如下:胜一场得3分,平一场得1分,负一场是0分.某队踢了14场,其中负5场,共得19分。
若设胜了x 场,平了y 场,则可列出方程组: .10. 分析下列方程组解的情况.①方程组12x y x y +=⎧⎨+=⎩的解 ;②方程组1222x y x y +=⎧⎨+=⎩的解 .二、选择题:(本大题共6小题,每小题3分,共18分)11. 用代入法解方程组124y x x y =-⎧⎨-=⎩时,代入正确的是( ) A.24x x --=B .224x x --= C.224x x -+=D.24x x -+= 12. 已知10x y =-⎧⎨=⎩和23x y =⎧⎨=⎩都是方程y ax b =+的解,则a 和b 的值是 ( ) A.11a b =-⎧⎨=-⎩ B.11a b =⎧⎨=⎩ C.11a b =-⎧⎨=⎩ D. 11a b =⎧⎨=-⎩13. 若方程组4314(1)6x y kx k y +=⎧⎨+-=⎩的解中x 、y 的值相等,k 为( ) A.4 B.3 C.2 D.114. 已知方程组5354x y ax y +=⎧⎨+=⎩和2551x y x by -=⎧⎨+=⎩有相同的解,则a ,b 的值为 ( )A.12a b =⎧⎨=⎩ B.46a b =-⎧⎨=-⎩ C.62a b =-⎧⎨=⎩ D.142a b =⎧⎨=⎩15. 已知二元一次方程30x y +=的一个解是x a y b =⎧⎨=⎩,其中0a ≠,那么( )A.0b a > B.0b a = C.0b a< D.以上都不对 16. 如图1,宽为50 cm 的矩形图案由10个全等的小长方形拼成,其中一个小长方形的面积为( )A. 400 cm 2B. 500 cm 2C. 600 cm 2D. 4000 cm 2三、解答题:(本大题共8小题,共52分)17.(6分)解方程组356415x z x z -=⎧⎨+=-⎩ ①②18. (6分)解方程组22314m n m n -=⎧⎨+=⎩ ① ②19. (6分)解方程组4(1)3(1)2223x y y x y --=--⎧⎪⎨+=⎪⎩20. (8分)已知方程组45321x y x y +=⎧⎨-=⎩和31ax by ax by +=⎧⎨-=⎩有相同的解,求222a ab b -+的值. 图121. (8分)上杭县某中学七年级学生外出进行社会实践活动,如果每辆车坐45人,那么有15个学生没车坐;如果每辆车坐60人,那么可以空出一辆车。
二元一次方程专题(内含答案详解)

二元一次方程专题一.选择题(共12小题)1.已知是关于x、y的方程4kx﹣3y=﹣1的一个解,则k的值为()A.1 B.﹣1 C.2 D.﹣22.已知与是二元一次方程mx+ny=5的两组解,则m+n的值为()A.1 B.2 C.3 D.43.下列方程中,是二元一次方程的是()A.8x2+1=y B.y=8x+1 C.y= D.xy=14.在方程﹣=5中,用关于x的代数式表示y,正确的是()A.x=y﹣10 B.x=y+10 C.y=x﹣15 D.y=y+155.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为()A.50元、150元B.50元、100元C.100元、50元D.150元、50元6.若关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,则m+n的值为()A.1 B.﹣1 C.3 D.﹣37.将方程x+y=1中的x的系数化为整数,则下列结果正确的是()A.﹣x+y=1 B.x﹣2y=﹣2 C.﹣x+y=2 D.x﹣y=28.已知x和y满足2x+3y=5,则当x=4时,代数式3x2+12xy+y2的值是()A.4 B.3 C.2 D.19.若x、y满足方程组,则x﹣y的值等于()A.﹣1 B.1 C.﹣2 D.210.若方程组的解满足x+y=0,则k的值为()A.﹣1 B.1 C.0 D.不能确定11.一个长方形的长的2倍比宽的5倍还多1cm,宽的3倍又比长多1cm,求这个长方形的长与宽.设长为xcm,宽为ycm,则下列方程组中正确的是()A.B.C.D.12.小明的储钱罐有5角和1元的硬币共100枚,币值共有68元.求5角、1元硬币各有多少枚?设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为()A. B.C. D.二.填空题(共6小题)13.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是.14.有一些苹果及苹果箱,若每箱装25千克,则剩余40千克无处装,如每箱装30千克则余20只空箱,则共有千克苹果,个苹果箱.15.一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了道题.16.把面值20元的纸币换成1元和5元的两种纸币,则共有种换法.17.某同学家离学校12千米,每天骑自行车上学和放学,有一天上学时顺风,从家到学校共用30分钟,放学时逆风,从学校回家共用时40分钟,已知该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则根据题意可列方程组.18.某校在春节运动会比赛中,七年级一班和二班的实力相当,关于比赛结果,甲同学说:一班与二班的得分比为4:3,乙同学说:一班得分比五班得分的2倍少40分.若设一班得x分,二班得y分,则根据题意可列方程组.三.解答题(共6小题)19.解下列方程或方程组:(1)3(2x﹣1)=2(1﹣x)﹣1(2)20.“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?21.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?22.甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?23.某市一种出租车的起步价为10元,两位乘客分别乘这种出租车走了10km 和14km,车费分别为21.2元和27.6元,假设一路顺利,没有停车等候,且不考虑计程器计费的某些特殊规定.请你算出这种出租车起步价所允许行驶的最远路程;并算出超过起步路程但行驶不到15km时,超过部分每千米车费为多少元?24.一个被滴上墨水的方程组如下,小明回忆到:这个方程组的解为,而我求出的解是,经检查后发现,我的错误是由于看错了第二个方程中的x的系数所致,请你根据小明的回忆,把原方程还原出来.二元一次方程专题参考答案与试题解析一.选择题(共12小题)1.已知是关于x、y的方程4kx﹣3y=﹣1的一个解,则k的值为()A.1 B.﹣1 C.2 D.﹣2【分析】把代入方程4kx﹣3y=﹣1,即可得出一个关于k的方程,求出方程的解即可.【解答】解:∵是关于x、y的方程4kx﹣3y=﹣1的一个解,∴代入得:8k﹣9=﹣1,解得:k=1,故选:A.【点评】本题考查了二元一次方程的解和解一元一次方程,能根据题意得出关于k的方程是解此题的关键.2.已知与是二元一次方程mx+ny=5的两组解,则m+n的值为()A.1 B.2 C.3 D.4【分析】代入后得出关于m、n的方程组,两方程相加即可求出答案.【解答】解:∵与是二元一次方程mx+ny=5的两组解,∴代入得:①+②得:5m+5n=10,m+n=2,故选:B.【点评】本题考查了解二元一次方程组和二元一次方程组的解,能根据题意得出关于m、n的方程组是解此题的关键.3.下列方程中,是二元一次方程的是()A.8x2+1=y B.y=8x+1 C.y= D.xy=1【分析】根据二元一次方程的定义求解即可.【解答】解:A、是一元二次方程,故A不符合题意;B、是二元一次方程,故B符合题意;C、是分式方程,故C不符合题意;D、是二元二次方程,故D不符合题意;故选:B.【点评】本题考查了二元一次方程,二元一次方程必须符合以下三个条件:方程中只含有2个未知数;含未知数项的最高次数为一次;方程是整式方程.4.在方程﹣=5中,用关于x的代数式表示y,正确的是()A.x=y﹣10 B.x=y+10 C.y=x﹣15 D.y=y+15【分析】把x看做已知数表示出y即可.【解答】解:方程﹣=5,整理得:y==x﹣15,故选:C.【点评】此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.5.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为()A.50元、150元B.50元、100元C.100元、50元D.150元、50元【分析】设甲种商品的定价分别为x元,则乙种商品的定价分别为y元,根据“若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元”可得出关于x、y的二元一次方程组,解方程组即可得出结论.【解答】解:设甲种商品的定价分别为x元,则乙种商品的定价分别为y元,根据题意得:,解得:.故选:D.【点评】本题考查了解二元一次方程组,根据数量关系列出二元一次方程组是解题的关键.6.若关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,则m+n的值为()A.1 B.﹣1 C.3 D.﹣3【分析】(方法一)根据二元一次方程的定义,即可得出关于m、n的二元一次方程组,解之即可得出m、n的值,将其相加即可得出结论;(方法二)根据二元一次方程的定义,即可得出m+2=1、n﹣1=1,将其相加即可得出m+n的值.【解答】解:(方法一)∵关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,∴,解得:,∴m+n=1.故选A.(方法二)∵关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,∴m+2=1,n﹣1=1,∴m+2+n﹣1=2,∴m+n=1.故选:A.【点评】本题考查了二元一次方程的定义以及解二元一次方程组,熟练掌握二元一次方程的定义是解题的关键.7.将方程x+y=1中的x的系数化为整数,则下列结果正确的是()A.﹣x+y=1 B.x﹣2y=﹣2 C.﹣x+y=2 D.x﹣y=2【分析】方程两边乘以2变形即可得到结果.【解答】解:方程左右两边乘以2得:﹣x+2y=2,即x﹣2y=﹣2.故选:B.【点评】此题考查了解二元一次方程,熟练掌握等式的性质是解本题的关键.8.已知x和y满足2x+3y=5,则当x=4时,代数式3x2+12xy+y2的值是()A.4 B.3 C.2 D.1【分析】根据题意先把x=4代入2x+3y=5求出y的值,然后把x、y的值代入代数式3x2+12xy+y2即可求得.【解答】解:把x=4代入2x+3y=5得:y=﹣1,把x=4,y=1代入3x2+12xy+y2得:3×16+12×4×(﹣1)+1=1,故选:D.【点评】本题考查了二元一次方程的解法,主要运用了代入法,难度适中.9.若x、y满足方程组,则x﹣y的值等于()A.﹣1 B.1 C.﹣2 D.2【分析】方程组的两个方程相减,即可求出答案.【解答】解:,②﹣①得:x﹣y=﹣2,故选:C.【点评】本题考查了解二元一次方程组,能选择适当的方法求解是解此题的关键.10.若方程组的解满足x+y=0,则k的值为()A.﹣1 B.1 C.0 D.不能确定【分析】根据等式的性质,可得答案.【解答】解:①+②,得3(x+y)=3﹣3k,由x+y=0,得3﹣3k=0,解得k=1,故选:B.【点评】本题考查了二元一次方程组的解,利用等式的性质是解题关键.11.一个长方形的长的2倍比宽的5倍还多1cm,宽的3倍又比长多1cm,求这个长方形的长与宽.设长为xcm,宽为ycm,则下列方程组中正确的是()A.B.C.D.【分析】由题意,得长的2倍比宽的5倍还多1cm可得方程2x﹣5y=1;宽的3倍又比长多1cm可得方程3y﹣x=1,即可得方程组.【解答】解:根据题意,得方程组.故选:C.【点评】根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.12.小明的储钱罐有5角和1元的硬币共100枚,币值共有68元.求5角、1元硬币各有多少枚?设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为()A. B.C. D.【分析】根据:①5角钱的枚数+1元钱的枚数=100、②5角的总钱数+1元的总钱数=68元,据此可得方程组.【解答】解:设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为,故选:C.【点评】本题主要考查由实际问题抽象出二元一次方程组,解题的关键是理解题意找到题目蕴含的相等关系.二.填空题(共6小题)13.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是95.【分析】设原来十位上数字为x,个位上的数字为y,分别表示出调换前后的两位数,根据题意列方程组求解.【解答】解:设原来十位上数字为x,个位上的数字为y,由题意得,,解得:,故这个两位数为95.故答案为;95.【点评】本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.14.有一些苹果及苹果箱,若每箱装25千克,则剩余40千克无处装,如每箱装30千克则余20只空箱,则共有3240千克苹果,128个苹果箱.【分析】设共有x千克苹果,y个苹果箱.等量关系:①每箱装25千克,则剩余40千克无处装;②每箱装30千克则余20只空箱.【解答】解:设共有x千克苹果,y个苹果箱.根据题意,得,解,得.则共有3240千克苹果,128个苹果箱.【点评】正确找到等量关系是列方程(组)解应用题的关键.15.一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了5道题.【分析】设答对x道题,答错了y道题,根据对1题给5分,错1题扣2分,不答题不给分也不扣分,总分为65分和有20题选择题可分别列等式求解.【解答】解:设答对x道题,答错了y道题,根据题意可得:,解得:,故他答错了5道题.故答案为:5.【点评】此题主要考查了二元一次方程组的应用,根据题意利用所得分数以及有20题选择题分别得出等式是解题关键.16.把面值20元的纸币换成1元和5元的两种纸币,则共有3种换法.【分析】设1元和5元的纸币各x张、y张,根据题意列出方程,求出方程的正整数解即可.【解答】解:设1元和5元的纸币各x张、y张,根据题意得:x+5y=20,整理得:x=20﹣5y,当x=1,y=15;x=2,y=10;x=3,y=5,则共有3种换法,故答案为:3【点评】此题考查了二元一次方程的应用,弄清题意是解本题的关键.17.某同学家离学校12千米,每天骑自行车上学和放学,有一天上学时顺风,从家到学校共用30分钟,放学时逆风,从学校回家共用时40分钟,已知该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则根据题意可列方程组.【分析】由题意可知:顺风速度=无风时速度+风速,逆风速度=无风时速度﹣风速,根据家与学校之间的距离=顺风速度×顺风时间=逆风速度×逆风时间,列出方程组解答即可.【解答】解:30分钟=小时40分钟=小时设该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则该同学在顺风时骑自行车的速度为(x+y)千米/小时,逆风时骑自行车的速度为(x﹣y)千米/小时,由题意得.故答案为:.【点评】此题考查由实际问题抽象出二元一次方程组,掌握顺风速度、逆风速度、无风时速度、风速之间的关系是解决问题的关键.18.某校在春节运动会比赛中,七年级一班和二班的实力相当,关于比赛结果,甲同学说:一班与二班的得分比为4:3,乙同学说:一班得分比五班得分的2倍少40分.若设一班得x分,二班得y分,则根据题意可列方程组.【分析】根据题意可得等量关系:①一班得分×3=二班的得分×4;②一班得分=五班得分×2﹣40,根据等量关系列出方程组即可.【解答】解:设一班得x分,二班得y分,由题意得:,故答案为:.【点评】此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系.三.解答题(共6小题)19.解下列方程或方程组:(1)3(2x﹣1)=2(1﹣x)﹣1(2)【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1)3(2x﹣1)=2(1﹣x)﹣1,6x﹣3=2﹣2x﹣1,x=,(2),整理得:,②﹣①得:﹣x=1,x=﹣1,把x=﹣1代入①中得:y=5,∴方程组的解为:.【点评】此题考查了解二元一次方程组和一元一次方程,熟练掌握运算法则是解本题的关键.20.“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?【分析】设A型号的空调购买价为x元,B型号的空调购买价为y元,根据“购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元”,即可得出关于x、y的二元一次方程组,解之即可得出结论.【解答】解:设A型号的空调购买价为x元,B型号的空调购买价为y元,依题意得:,解得:.答:A型号的空调购买价为2120元,B型号的空调购买价为2320元.【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.21.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?【分析】设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,根据平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,可列成方程组求解.【解答】解:设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,,解得:.答:需安排25名工人加工大齿轮,安排60名工人加工小齿轮.【点评】本题考查理解题意能力,关键是能准确2个大齿轮和3个小齿轮配成一套,根据此正确列出方程.22.甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?【分析】根据题目中的关键句子:“同向而行,乙10小时可追上甲;若相向而行,2小时两人相遇”找到两个等量关系后列出方程组即可.【解答】解:设甲每小时行x千米,乙每小时行y千米,则可列方程组为,解得,答:甲每小时行10千米,乙每小时行15千米.【点评】本题考查了二元一次方程组的应用的知识,解题的关键是根据题意找到两个等量关系,难度不大.23.某市一种出租车的起步价为10元,两位乘客分别乘这种出租车走了10km 和14km,车费分别为21.2元和27.6元,假设一路顺利,没有停车等候,且不考虑计程器计费的某些特殊规定.请你算出这种出租车起步价所允许行驶的最远路程;并算出超过起步路程但行驶不到15km时,超过部分每千米车费为多少元?【分析】设起步价允许行驶的最远路程是xkm,超过部分每千米车费是y元,关键描述语:出租车的起步价为10元,两位乘客分别乘这种出租车走了10km和14km,车费分别为21.2元和27.6元.【解答】解:设起步价允许行驶的最远路程是xkm,超过部分每千米车费是y元,则,解得:,答:起步价允许行驶的最远路程是3km,超过部分每千米车费是1.6元.【点评】本题考查了二元一次方程组的应用.解题关键是弄清题意,合适的等量关系,列出方程组.24.一个被滴上墨水的方程组如下,小明回忆到:这个方程组的解为,而我求出的解是,经检查后发现,我的错误是由于看错了第二个方程中的x的系数所致,请你根据小明的回忆,把原方程还原出来.【分析】由题意可知是方程组的解,是方程△x+口y=2的解,然后代入求解即可.【解答】解:∵是方程组的解,∴3○+14=8,3△﹣2□=2①,∴○=﹣2.∵是方程△x+口y=2的解,∴﹣2△+2口=2②.将①和②联立得:,解得:△=4,□=5(3分),∴原方程组为.【点评】本题主要考查的是二元一次方程组的解,依据方程组的解得概念列出方程或方程组是解题的关键.。
二元一次方程专题(内含答案详解)

二元一次方程专题一.选择题(共12小题)1.已知是关于x、y的方程4kx﹣3y=﹣1的一个解,则k的值为() A.1 B.﹣1 C.2 D.﹣22.已知与是二元一次方程mx+ny=5的两组解,则m+n的值为()A.1 B.2 C.3 D.43.下列方程中,是二元一次方程的是()A.8x2+1=y B.y=8x+1 C.y= D.xy=14.在方程﹣=5中,用关于x的代数式表示y,正确的是()A.x=y﹣10 B.x=y+10 C.y=x﹣15 D.y=y+155.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为()A.50元、150元B.50元、100元C.100元、50元D.150元、50元6.若关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,则m+n的值为()A.1 B.﹣1 C.3 D.﹣37.将方程x+y=1中的x的系数化为整数,则下列结果正确的是()A.﹣x+y=1 B.x﹣2y=﹣2 C.﹣x+y=2 D.x﹣y=28.已知x和y满足2x+3y=5,则当x=4时,代数式3x2+12xy+y2的值是()A.4 B.3 C.2 D.19.若x、y满足方程组,则x﹣y的值等于()A.﹣1 B.1 C.﹣2 D.210.若方程组的解满足x+y=0,则k的值为()A.﹣1 B.1 C.0 D.不能确定11.一个长方形的长的2倍比宽的5倍还多1cm,宽的3倍又比长多1cm,求这个长方形的长与宽.设长为xcm,宽为ycm,则下列方程组中正确的是()A.B.C.D.12.小明的储钱罐有5角和1元的硬币共100枚,币值共有68元.求5角、1元硬币各有多少枚?设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为()A. B.C. D.二.填空题(共6小题)13.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是.14.有一些苹果及苹果箱,若每箱装25千克,则剩余40千克无处装,如每箱装30千克则余20只空箱,则共有千克苹果,个苹果箱.15.一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了道题.16.把面值20元的纸币换成1元和5元的两种纸币,则共有种换法.17.某同学家离学校12千米,每天骑自行车上学和放学,有一天上学时顺风,从家到学校共用30分钟,放学时逆风,从学校回家共用时40分钟,已知该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则根据题意可列方程组.18.某校在春节运动会比赛中,七年级一班和二班的实力相当,关于比赛结果,甲同学说:一班与二班的得分比为4:3,乙同学说:一班得分比五班得分的2倍少40分.若设一班得x分,二班得y分,则根据题意可列方程组.三.解答题(共6小题)19.解下列方程或方程组:(1)3(2x﹣1)=2(1﹣x)﹣1(2)20.“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?21.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?22.甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?23.某市一种出租车的起步价为10元,两位乘客分别乘这种出租车走了10km 和14km,车费分别为21.2元和27.6元,假设一路顺利,没有停车等候,且不考虑计程器计费的某些特殊规定.请你算出这种出租车起步价所允许行驶的最远路程;并算出超过起步路程但行驶不到15km时,超过部分每千米车费为多少元?24.一个被滴上墨水的方程组如下,小明回忆到:这个方程组的解为,而我求出的解是,经检查后发现,我的错误是由于看错了第二个方程中的x的系数所致,请你根据小明的回忆,把原方程还原出来.二元一次方程专题参考答案与试题解析一.选择题(共12小题)1.已知是关于x、y的方程4kx﹣3y=﹣1的一个解,则k的值为() A.1 B.﹣1 C.2 D.﹣2【分析】把代入方程4kx﹣3y=﹣1,即可得出一个关于k的方程,求出方程的解即可.【解答】解:∵是关于x、y的方程4kx﹣3y=﹣1的一个解,∴代入得:8k﹣9=﹣1,解得:k=1,故选:A.【点评】本题考查了二元一次方程的解和解一元一次方程,能根据题意得出关于k的方程是解此题的关键.2.已知与是二元一次方程mx+ny=5的两组解,则m+n的值为()A.1 B.2 C.3 D.4【分析】代入后得出关于m、n的方程组,两方程相加即可求出答案.【解答】解:∵与是二元一次方程mx+ny=5的两组解,∴代入得:①+②得:5m+5n=10,m+n=2,故选:B.【点评】本题考查了解二元一次方程组和二元一次方程组的解,能根据题意得出关于m、n的方程组是解此题的关键.3.下列方程中,是二元一次方程的是()A.8x2+1=y B.y=8x+1 C.y= D.xy=1【分析】根据二元一次方程的定义求解即可.【解答】解:A、是一元二次方程,故A不符合题意;B、是二元一次方程,故B符合题意;C、是分式方程,故C不符合题意;D、是二元二次方程,故D不符合题意;故选:B.【点评】本题考查了二元一次方程,二元一次方程必须符合以下三个条件:方程中只含有2个未知数;含未知数项的最高次数为一次;方程是整式方程.4.在方程﹣=5中,用关于x的代数式表示y,正确的是()A.x=y﹣10 B.x=y+10 C.y=x﹣15 D.y=y+15【分析】把x看做已知数表示出y即可.【解答】解:方程﹣=5,整理得:y==x﹣15,故选:C.【点评】此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.5.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为()A.50元、150元B.50元、100元C.100元、50元D.150元、50元【分析】设甲种商品的定价分别为x元,则乙种商品的定价分别为y元,根据“若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元”可得出关于x、y的二元一次方程组,解方程组即可得出结论.【解答】解:设甲种商品的定价分别为x元,则乙种商品的定价分别为y元,根据题意得:,解得:.故选:D.【点评】本题考查了解二元一次方程组,根据数量关系列出二元一次方程组是解题的关键.6.若关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,则m+n的值为()A.1 B.﹣1 C.3 D.﹣3【分析】(方法一)根据二元一次方程的定义,即可得出关于m、n的二元一次方程组,解之即可得出m、n的值,将其相加即可得出结论;(方法二)根据二元一次方程的定义,即可得出m+2=1、n﹣1=1,将其相加即可得出m+n的值.【解答】解:(方法一)∵关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,∴,解得:,∴m+n=1.故选A.(方法二)∵关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,∴m+2=1,n﹣1=1,∴m+2+n﹣1=2,∴m+n=1.故选:A.【点评】本题考查了二元一次方程的定义以及解二元一次方程组,熟练掌握二元一次方程的定义是解题的关键.7.将方程x+y=1中的x的系数化为整数,则下列结果正确的是() A.﹣x+y=1 B.x﹣2y=﹣2 C.﹣x+y=2 D.x﹣y=2【分析】方程两边乘以2变形即可得到结果.【解答】解:方程左右两边乘以2得:﹣x+2y=2,即x﹣2y=﹣2.【点评】此题考查了解二元一次方程,熟练掌握等式的性质是解本题的关键.8.已知x和y满足2x+3y=5,则当x=4时,代数式3x2+12xy+y2的值是()A.4 B.3 C.2 D.1【分析】根据题意先把x=4代入2x+3y=5求出y的值,然后把x、y的值代入代数式3x2+12xy+y2即可求得.【解答】解:把x=4代入2x+3y=5得:y=﹣1,把x=4,y=1代入3x2+12xy+y2得:3×16+12×4×(﹣1)+1=1,故选:D.【点评】本题考查了二元一次方程的解法,主要运用了代入法,难度适中.9.若x、y满足方程组,则x﹣y的值等于()A.﹣1 B.1 C.﹣2 D.2【分析】方程组的两个方程相减,即可求出答案.【解答】解:,②﹣①得:x﹣y=﹣2,故选:C.【点评】本题考查了解二元一次方程组,能选择适当的方法求解是解此题的关键.10.若方程组的解满足x+y=0,则k的值为()A.﹣1 B.1 C.0 D.不能确定【分析】根据等式的性质,可得答案.【解答】解:①+②,得3(x+y)=3﹣3k,由x+y=0,得3﹣3k=0,故选:B.【点评】本题考查了二元一次方程组的解,利用等式的性质是解题关键.11.一个长方形的长的2倍比宽的5倍还多1cm,宽的3倍又比长多1cm,求这个长方形的长与宽.设长为xcm,宽为ycm,则下列方程组中正确的是() A.B.C.D.【分析】由题意,得长的2倍比宽的5倍还多1cm可得方程2x﹣5y=1;宽的3倍又比长多1cm可得方程3y﹣x=1,即可得方程组.【解答】解:根据题意,得方程组.故选:C.【点评】根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.12.小明的储钱罐有5角和1元的硬币共100枚,币值共有68元.求5角、1元硬币各有多少枚?设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为()A. B.C. D.【分析】根据:①5角钱的枚数+1元钱的枚数=100、②5角的总钱数+1元的总钱数=68元,据此可得方程组.【解答】解:设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为,故选:C.【点评】本题主要考查由实际问题抽象出二元一次方程组,解题的关键是理解题意找到题目蕴含的相等关系.二.填空题(共6小题)13.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是95.【分析】设原来十位上数字为x,个位上的数字为y,分别表示出调换前后的两位数,根据题意列方程组求解.【解答】解:设原来十位上数字为x,个位上的数字为y,由题意得,,解得:,故这个两位数为95.故答案为;95.【点评】本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.14.有一些苹果及苹果箱,若每箱装25千克,则剩余40千克无处装,如每箱装30千克则余20只空箱,则共有3240千克苹果,128个苹果箱.【分析】设共有x千克苹果,y个苹果箱.等量关系:①每箱装25千克,则剩余40千克无处装;②每箱装30千克则余20只空箱.【解答】解:设共有x千克苹果,y个苹果箱.根据题意,得,解,得.则共有3240千克苹果,128个苹果箱.【点评】正确找到等量关系是列方程(组)解应用题的关键.15.一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了5道题.【分析】设答对x道题,答错了y道题,根据对1题给5分,错1题扣2分,不答题不给分也不扣分,总分为65分和有20题选择题可分别列等式求解.【解答】解:设答对x道题,答错了y道题,根据题意可得:,解得:,故他答错了5道题.故答案为:5.【点评】此题主要考查了二元一次方程组的应用,根据题意利用所得分数以及有20题选择题分别得出等式是解题关键.16.把面值20元的纸币换成1元和5元的两种纸币,则共有3种换法.【分析】设1元和5元的纸币各x张、y张,根据题意列出方程,求出方程的正整数解即可.【解答】解:设1元和5元的纸币各x张、y张,根据题意得:x+5y=20,整理得:x=20﹣5y,当x=1,y=15;x=2,y=10;x=3,y=5,则共有3种换法,故答案为:3【点评】此题考查了二元一次方程的应用,弄清题意是解本题的关键.17.某同学家离学校12千米,每天骑自行车上学和放学,有一天上学时顺风,从家到学校共用30分钟,放学时逆风,从学校回家共用时40分钟,已知该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则根据题意可列方程组.【分析】由题意可知:顺风速度=无风时速度+风速,逆风速度=无风时速度﹣风速,根据家与学校之间的距离=顺风速度×顺风时间=逆风速度×逆风时间,列出方程组解答即可.【解答】解:30分钟=小时40分钟=小时设该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则该同学在顺风时骑自行车的速度为(x+y)千米/小时,逆风时骑自行车的速度为(x﹣y)千米/小时,由题意得.故答案为:.【点评】此题考查由实际问题抽象出二元一次方程组,掌握顺风速度、逆风速度、无风时速度、风速之间的关系是解决问题的关键.18.某校在春节运动会比赛中,七年级一班和二班的实力相当,关于比赛结果,甲同学说:一班与二班的得分比为4:3,乙同学说:一班得分比五班得分的2倍少40分.若设一班得x分,二班得y分,则根据题意可列方程组.【分析】根据题意可得等量关系:①一班得分×3=二班的得分×4;②一班得分=五班得分×2﹣40,根据等量关系列出方程组即可.【解答】解:设一班得x分,二班得y分,由题意得:,故答案为:.【点评】此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系.三.解答题(共6小题)19.解下列方程或方程组:(1)3(2x﹣1)=2(1﹣x)﹣1(2)【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1)3(2x﹣1)=2(1﹣x)﹣1,6x﹣3=2﹣2x﹣1,x=,(2),整理得:,②﹣①得:﹣x=1,x=﹣1,把x=﹣1代入①中得:y=5,∴方程组的解为:.【点评】此题考查了解二元一次方程组和一元一次方程,熟练掌握运算法则是解本题的关键.20.“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?【分析】设A型号的空调购买价为x元,B型号的空调购买价为y元,根据“购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元”,即可得出关于x、y的二元一次方程组,解之即可得出结论.【解答】解:设A型号的空调购买价为x元,B型号的空调购买价为y元,依题意得:,解得:.答:A型号的空调购买价为2120元,B型号的空调购买价为2320元.【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.21.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?【分析】设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,根据平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,可列成方程组求解.【解答】解:设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,,解得:.答:需安排25名工人加工大齿轮,安排60名工人加工小齿轮.【点评】本题考查理解题意能力,关键是能准确2个大齿轮和3个小齿轮配成一套,根据此正确列出方程.22.甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?【分析】根据题目中的关键句子:“同向而行,乙10小时可追上甲;若相向而行,2小时两人相遇”找到两个等量关系后列出方程组即可.【解答】解:设甲每小时行x千米,乙每小时行y千米,则可列方程组为,解得,答:甲每小时行10千米,乙每小时行15千米.【点评】本题考查了二元一次方程组的应用的知识,解题的关键是根据题意找到两个等量关系,难度不大.23.某市一种出租车的起步价为10元,两位乘客分别乘这种出租车走了10km 和14km,车费分别为21.2元和27.6元,假设一路顺利,没有停车等候,且不考虑计程器计费的某些特殊规定.请你算出这种出租车起步价所允许行驶的最远路程;并算出超过起步路程但行驶不到15km时,超过部分每千米车费为多少元?【分析】设起步价允许行驶的最远路程是xkm,超过部分每千米车费是y元,关键描述语:出租车的起步价为10元,两位乘客分别乘这种出租车走了10km和14km,车费分别为21.2元和27。
二元一次方程20道题

二元一次方程20道题一、基础型题目(1 - 10题)1. 已知方程2x + 3y=12,当x = 3时,求y的值。
- 解析:将x = 3代入方程2x+3y = 12中,得到2×3+3y=12,即6 + 3y=12。
方程两边同时减去6,得到3y=12 - 6=6,解得y = 2。
2. 解方程组x + y=5 x - y = 1- 解析:将两个方程相加,(x + y)+(x - y)=5 + 1,即2x=6,解得x = 3。
把x = 3代入x + y=5中,得到3+y = 5,解得y=2。
3. 若3x - 2y=11,且y = 2x - 4,求x和y的值。
- 解析:把y = 2x-4代入3x - 2y=11中,得到3x-2(2x - 4)=11,展开括号得3x-4x + 8 = 11,移项得3x-4x=11 - 8,即-x = 3,解得x=-3。
把x = - 3代入y = 2x-4,得y=2×(-3)-4=-6 - 4=-10。
4. 解方程组2x+3y = 8 3x - 2y=-1- 解析:给第一个方程2x + 3y=8两边同时乘以2,得到4x + 6y = 16;给第二个方程3x-2y=-1两边同时乘以3,得到9x-6y=-3。
将这两个新方程相加,(4x +6y)+(9x-6y)=16+(-3),即13x = 13,解得x = 1。
把x = 1代入2x + 3y=8中,2×1+3y = 8,3y=8 - 2 = 6,解得y = 2。
5. 已知x、y满足方程4x - 3y=1,且x = 2y - 2,求x和y的值。
- 解析:将x = 2y-2代入4x-3y = 1中,得到4(2y-2)-3y = 1,展开括号得8y-8 - 3y=1,移项得8y-3y=1 + 8,5y=9,解得y=(9)/(5)。
把y=(9)/(5)代入x = 2y-2,得x=2×(9)/(5)-2=(18)/(5)-(10)/(5)=(8)/(5)。
(完整版)二元一次方程计算题含答案(最新整理)

∴原方程组可化为
,
解得 ,
∴
∴原方程组的解为 .
点评:此题考查了学生的计算能力,解题时要细心. 12.解二元一次方程组:
(1)
;
(2)
.
考点:解二元一次方程组. 809625
专题:计算题. 分析:(1)运用加减消元的方法,可求出 x、y 的值;
(2)先将方程组化简,然后运用加减消元的方法可求出 x、y 的值. 解答:
11.解方程组:
(1)
(2)
考点:解二元一次方程组. 809625
专题:计算题;换元法. 分析:方程组(1)需要先化简,再根据方程组的特点选择解法;
方程组(2)采用换元法较简单,设 x+y=a,x﹣y=b,然后解新方程组即可求解.
解答:
解:(1)原方程组可化简为
,
解得
.
(2)设 x+y=a,x﹣y=b,
(2)
考点:解二元一次方程组. 809625
分析:观察方程组中各方程的特点,用相应的方法求解. 解答:
解:(1)①×2﹣②得:x=1,
将 x=1 代入①得: 2+y=4, y=2.
∴原方程组的解为 ;
(2)原方程组可化为
,
①×2﹣②得:
﹣y=﹣3, y=3. 将 y=3 代入①得: x=﹣2.
∴原方程组的解为
解答:
解:原方程组可化为
,
①×4﹣②×3,得
7x=42, 解得 x=6. 把 x=6 代入①,得 y=4. 所以方程组的解为 .
点评:注意:二元一次方程组无论多复杂,解二元一次方程组的基本思想都是消元.消元的 方法有代入法和加减法.
4.解方程组:
考点:解二元一次方程组. 809625
二元一次方程专项练习60题+解析答案

一元二次方程专练60题一.解答题(共60小题)1.解二元一次方程组.(1);(2).2.解下列方程组:(1);(2).3.解方程组:(1);(2).4.解方程组.(1);(2).5.解方程组:(1);(2).6.解下列方程组:(1);(2).7.解方程组:(1);(2).8.解二元一次方程组:(1);(2).9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).10.解方程组:(1);(2).11.解下列方程组:(1)(代入消元法);(2)(加减消元法).12.解下列方程组:(1);(2).13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).14.解下列方程组.(1);(2).15.解方程组:(1);(2).16.解下列方程组:(1);(2).17.解二元一次方程组:(1).(2).18.解方程组:(1);(2).19.解方程组:(1);(2).20.用适当的方法解下列方程组:(1)(2).21.解方程组:(1);(2).22.解二元一次方程组:(1);(2).23.解二元一次方程组:(1);(2).24.解方程组:(1);(2).25.解方程组:(1);(2).26.解方程组:(1);(2).27.解方程组:(1);(2).28.解方程组:(1);(2).29.解方程组:(1);(2).30.解方程组:(1);(2).31.解方程组:(1);(2).32.解方程组:(1);(2).33.用适当的方法解方程组:(1);(2).34.解下列方程组:(1);(2).35.解方程组:(1);(2).36.解方程组:(1);(2).37.解方程组:(1);38.解方程组:(1);(2).39.解方程组:(1);(2).40.解下列方程组:(1);41.解下列方程组:(1);(2).42.用加减消元法解方程:(1);(2).43.解二元一次方程组:(1);44.解方程组:(1);(2).45.解方程:(1);(2).46.用适当的方法解下列方程组:(1);47.解方程组:(1);(2).48.解方程组:(1);(2).49.解方程组:(1);(2).50.解方程组:(1);(2).51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.54.已知方程组和方程组的解相同求a、b的值.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b 的值.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.60.已知方程组和有相同的解,求a﹣2b的值.一元二次方程专练60题参考答案与试题解析一.解答题(共60小题)1.解二元一次方程组.(1);(2).【解答】解:(1)①+②,得4x=12,∴x=3.把x=3代入②,得3+2y=3,解得y=0所以原方程组的解为;(2),②化简得:2(x﹣2)﹣3(y﹣2)=6,即2x﹣3y=4③,①+③得:3x=18,解得:x=6,将x=6代入①得:6+3y=14,解得:y=,∴原方程组的解为:.2.解下列方程组:(1);(2).【解答】解:(1),由①得,3x+2y=12③,②×③﹣③×2,得5y=60,解得y=12,将y=12代入③,得3x+24=12,解得x=﹣4,∴原方程组的解为;(2),由①得x+1=5y+10,∴x=5y+9③,由②得6x﹣15﹣12y﹣16=5,整理,得6x﹣12y=36,∴x﹣2y=6④,将③代入④,得5y+9﹣2y=6,解得y=﹣1,将y=﹣1代入③,得x=﹣5+9=4,∴原方程组的解为.3.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x+4x=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②,得6x=24,解得x=4,把x=4代入②,得y=5,故原方程组的解为.4.解方程组.(1);(2).【解答】解:(1),①﹣②得:9y=18,解得:y=2,把y=2代入①中得:3x+10=5,解得:x=﹣,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:24u+27v=36③,③﹣②得:2v=22,解得:v=11,把v=11代入①中得:8u+99=12,解得:u=﹣,∴原方程组的解为:.5.解方程组:(1);(2).【解答】解:(1),①×2﹣②得:5x=﹣5,解得:x=﹣1,将x=﹣1代入①得:﹣3﹣y=﹣4,解得:y=1,故原方程组的解为;(2),①×5+②×3得:19x=19,解得:x=1,将x=1代入①得:2+3y=8,解得:y=2,故原方程组的解为.6.解下列方程组:(1);(2).【解答】解:(1),把②代入①得,6y﹣7﹣y=13,解得y=4;把y=4代入②得,x=6×4﹣7=17,故方程组的解为;(2),①×3﹣②×2得,6x+15y﹣6x﹣4y=24﹣10,解得y=,把y=代入②得,3x+2×=5,解得x=,故方程组的解为.7.解方程组:(1);(2).【解答】解:(1),①+②×2,得11x=33,解得:x=3,把x=3代入①,得9+2y=7,解得:y=﹣1,所以方程组的解是;(2)整理得:,①×2+②,得5x=15,解得:x=3,把x=3代入①,得3+2y=7,解得:y=2,所以方程组的解是.8.解二元一次方程组:(1);(2).【解答】解:(1),①﹣②×2,得7y=﹣14,解得y=﹣2,将y=﹣2代入①,得2x﹣2=2,解得x=2,∴原方程组的解为;(2),由①得,3x+4y=36③,由②得3x﹣2y=9④,③﹣④,得6y=27,解得y=,将y=代入④,得3x﹣9=9,解得x=6,∴原方程组的解为.9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).【解答】解:(1),由②,得y=5﹣3x③,把③代入①,得3x+2(5﹣3x)=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②×2,得7x=21,解得x=3,把x=3代入②,得y=5,故原方程组的解为.10.解方程组:(1);(2).【解答】解:(1),①×4得:8x﹣4y=20③,②+③得:11x=22,解得:x=2,把x=2代入①得:4﹣y=5,解得:y=﹣1,故原方程组的解是:;(2),整理得:,①+②得:8y=24,解得:y=3,把y=3代入②得:x+15=10,解得:x=﹣5,故原方程组的解是:.11.解下列方程组:(1)(代入消元法);(2)(加减消元法).【解答】解:(1),由①得:x=1+2y③,把③代入②,得4(1+2 y)+3y=26,解得:y=2,把y=2代入③,得x=1+2×2=5,所以;(2),由①+②,得7x=21,解得:x=3,把x=3代入①,得2×3+3y=3,解得:y=﹣1,所以.12.解下列方程组:(1);(2).【解答】解:(1)将原方程组化简整理得:,②×4得:8x+20y=28③,③﹣①得:27y=27,解得:y=1,把y=1代入②中得:2x+5=7,解得:x=1,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:9x﹣12y=﹣21③,②×4得:8x+12y=4④,③+④得:17x=﹣17,解得:x=﹣1,把x=﹣1代入②中得:﹣2+3y=1,解得:y=1,∴原方程组的解为:.13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).【解答】解:(1),把①代入②得:4x+3(2x﹣2)=5,解得x=,把x=代入①得:y=2×﹣2=,∴方程组的解为;(2),①×3得:3x+9y=﹣3③,③﹣②得:11y=﹣11,解得:y=﹣1,把y=﹣1代入①得:x﹣3=﹣1,解得:x=2,∴方程组的解为.14.解下列方程组.(1);(2).【解答】解:(1),由①+②得,5x=﹣5,解得x=﹣1,将x=﹣1代入①,得﹣2+5y=8,解得y=2,∴方程组的解为;(2),由①×3,②×2得:,由③+④得,13x=26,解得:x=2,把x=2代入①,得y=4,所以方程组的解为:.15.解方程组:(1);(2).【解答】解:(1),由①得,x=1+2y③,把③代入②,得3(1+2y)﹣y=3,解得y=0,把y=0代入③,得x=1,所以原方程组的解为:;(2)原方程组可化为,①+②得,4x=24,解得x=6,①﹣②得,6y=﹣6,解得y=﹣1,所以原方程组的解为:.16.解下列方程组:(1);(2).【解答】解:(1),①+②,得2x=12,解得x=6,将x=6代入①,得6﹣y=5,解得y=1,∴原方程组的解为;(2)原方程组化为,①﹣②,得25y=10,解得y=,将y=代入①,得5x+6=6,解得x=0,∴原方程组的解为.17.解二元一次方程组:(1).(2).【解答】解:(1),②﹣①×2得:x=6,把x=6代入①得:6+2y=0,解得y=﹣3.∴方程组的解是.(2),①×2+②×3得:13x=65,解得x=5.把x=5代入①得:10+3y=16,解得y=2.∴方程组的解是.18.解方程组:(1);(2).【解答】解:(1)对于方程组,①×2得:4x﹣10y=24③,②﹣③得:﹣13y=26,∴y=﹣2,将y=﹣2代入①得:x=1,∴原方程组的解为:.(2)对于方程组,将①代入②得:2×2y+y=5,∴y=1,将y=1代入①得:x=2,∴原方程组的解为:.19.解方程组:(1);(2).【解答】解:(1),①+②得4x=8,∴x=2,把x=2代入①得2+2y=3,,∴原方程组的解是.(2),整理得:,由①得:s=﹣2t③,把③代入②得:t=﹣2;把t=﹣2 代入③得:s=4,∴原方程组的解是.20.用适当的方法解下列方程组:(1)(2).【解答】解:(1),①+②得:6x=18,解得:x=3,把x=3代入①得:y=﹣4,则方程组的解为;(2),把①代入②得:4x﹣14=2,解得:x=4,把x=4代入①得:y=3,则方程组的解为.21.解方程组:(1);(2).【解答】解:(1),原方程可化为:,①+②×5得:46y=46,∴y=1,将y=1代入①得:x=7,∴原方程组得解为:;(2),原方程可化为:,①×4+②得:19x=57,∴x=3,将x=3代入①得:y=0,∴原方程组得解为:.22.解二元一次方程组:(1);(2).【解答】解:(1),②﹣①,得y=1,把y=1代入①,得x=2,故原方程组的解为;(2)原方程组整理,得,②﹣①×2,得7y=7,解得y=1,把y=1代入①,得x=5.故原方程组的解为.23.解二元一次方程组:(1);(2).【解答】解:(1),由②得y=13﹣2x③,把③代入①,得4x﹣3(13﹣2x)=11,解得x=5,把x=5代入③,得y=3,∴这个方程组的解是;(2),①×2﹣②×3,得﹣19y=19,解得y=﹣1.把y=﹣1代入①,得3x+2=5,解得x=1,∴这个方程组的解为.24.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x﹣8(x﹣3)=14,解得x=2,把x=2代入①,得y=﹣1,故原方程组的解为;(2),①×2﹣②,得7x=35,解得x=5,把x=5代入①,得y=0,故原方程组的解为.25.解方程组:(1);(2).【解答】解:(1),由①+②得:4x=8,解得:x=2,将x=2代入①得:2﹣2y=1,解得:y=,∴方程组的解为:;(2),由①可得:x=3﹣2y③,将③代入②得:3(3﹣2y)﹣4y=4,解得:y=,将y=代入③得:x=3﹣2×,解得:x=2,∴原方程组的解为:.26.解方程组:(1);(2).【解答】解:(1),①×2得:4x﹣2y=0③,②+③得:5x=5,解得:x=1,把x=1代入①中得:y=2,∴原方程组的解为:.(2),②×2,8x﹣2y=6③,①+③得:11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,∴原方程组的解为:.27.解方程组:(1);(2).【解答】解:(1),①+②,得7x=35,解得:x=5,把x=5代入①,得10﹣3y=﹣2,解得:y=4,所以方程组的解是;(2),①+②×2,得11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,所以方程组的解是.28.解方程组:(1);(2).【解答】解:(1),把②代入①得y﹣9+3y=7,解得y=4,把y=4代入②得x=4﹣9=﹣5,所以方程组的解为;(2),①×2+②得10x+3x=34+5,解得x=3,把x=3代入②得9+4y=5,解得y=﹣1,所以方程组的解为.29.解方程组:(1);(2).【解答】解:(1),①+②得:4x=8,解得:x=2,把x=2代入①得:2+2y=﹣1,解得:,∴方程组的解为;(2),由②得:y=2x﹣2,把y=2x﹣2代入①得:4x﹣3(2x﹣2)=5,解得:,把代入y=2x﹣2得:,∴方程组的解为.30.解方程组:(1);(2).【解答】解:(1),将①代入②,可得:3x+2x+3=18,解得x=3,把x=3代入①,可得:y=9,∴原方程组的解是.(2),①×2﹣②,可得7y=35,解得y=5,把y=5代入①,可得:x=0,∴原方程组的解是.31.解方程组:(1);(2).【解答】解:(1),把①代入②得:3x+2(2x﹣1)=5,解得:x=1,把x=1代入①得:y=2﹣1=1,故原方程组的解是:;(2),①+②得:3m=6,解得:m=2,把m=2代入①得:2+3n=5,解得:n=1,故原方程组的解是:.32.解方程组:(1);(2).【解答】解:(1)把②代入①中,得3x+2(2x﹣8)=5.解得x=3.把x=3代入②中,得y=2×3﹣8解得y=﹣2.∴这个方程组的解为;(2)①﹣②,得﹣4y=8.解得y=﹣2.把y=﹣2代入①中,得2x+2=10.解得x=4.∴这个方程组的解为.33.用适当的方法解方程组:(1);(2).【解答】解:(1),②﹣①×3得:x=1,把x=1代入①中,解得:y=1,∴这个方程组的解为;(2)方程组整理为:,②×2+①得:5x=30,解得:x=6,把x=6代入②中,解得:y=9,∴这个方程组的解为.34.解下列方程组:(1);(2).【解答】解:(1),将①代入②,得:3x﹣2(2x+1)=2,解得:x=﹣4,把x=﹣4代入①得:y=﹣7,∴方程组的解为:;(2)①×2+②,得:5x=10,解得:x=2,把x=2代入①,得:4+y=1,解得:y=﹣3,∴方程组的解为:.35.解方程组:(1);(2).【解答】解:(1),①+②得,7x=14,解得x=2,把x=2代入①得,3×2+7y=9,解得y=,∴方程组的解是;(2),①×3得,15x+6y=12③,②×2得,16x+6y=14④,④﹣③得,x=2,把x=2代入①得,y=﹣3,∴方程组的解是.36.解方程组:(1);(2).【解答】解:(1),②﹣①得:y=2,把y=2代入①得:,∴方程组的解为:;(2),由③得:y=3﹣2x,把y=3﹣2x代入④得:3x﹣5(3﹣2x)=11,3x﹣15+10x=11,13x=26,x=2,把x=2代入y=3﹣2x得:y=﹣1,∴方程组的解为:.37.解方程组:(1);(2).【解答】解:(1),①×3得:3x﹣15y=0③,②﹣③得:17y=17,解得:y=1,把y=1代入①得:x﹣5=0,解得:x=5,∴原方程组的解为:;(2),把①代入②得:y﹣13﹣6y=7,解得:y=﹣4,把y=﹣4代入①得:x=﹣4﹣13=﹣17,∴原方程组的解为:.38.解方程组:(1);(2).【解答】解:(1),①+②得:5x=25,解得:x=5,把x=5代入①得:5﹣3y=10,解得:y=﹣,故原方程组的解是:;(2),由①得:3x﹣2y=8③,②+③得:6x=12,解得:x=2,把x=2代入②得:6+2y=4,解得:y=﹣1,故原方程组的解是:.39.解方程组:(1);(2).【解答】解:(1),①+②得:3x=12,解得:x=4,把x=4代入①得:4﹣y=2,解得:y=2,则方程组的解为;(2)方程组整理得:,①×4﹣②×3得:﹣7x=﹣14,解得:x=2,把x=2代入①得:4﹣3y=1,解得:y=1,则方程组的解为.40.解下列方程组:(1);(2).【解答】解:(1),由①,得x=y+3③,把③代入②,得3y+9﹣8y=14,解得y=﹣1,把y=﹣1代入①,得x=2,故原方程组的解为;(2),①×2+②,得11x=11,解得x=1,把x=1代入①,得x=﹣2,故原方程组的解为.41.解下列方程组:(1);(2).【解答】解:(1),②代入①,可得x+2x﹣1=2,解得,x=1,将x=1代入②,可得y=1,故方程组的解为.(2),②﹣①,可得,解得,x=3,将x=3代入①,可得y=2,故方程组的解为.42.用加减消元法解方程:(1);(2).【解答】解:(1),①﹣②得:12y=﹣36,即y=﹣3,把y=﹣3代入①得:x=,则方程组的解为;(2)方程组整理得:,①﹣②得:4y=28,即y=7,把y=7代入①得:x=5,则方程组的解为.43.解二元一次方程组:(1);(2).【解答】解:(1)方程整理得,由①+②得:5a+5b=﹣5,即a+b=﹣1③,由①﹣③×2得:b=1,把b=1代入③得:a+1=﹣1,解得a=﹣2,∴方程组的解是.(2),由②得:x=3y﹣2③,把③代入①得:9(3y﹣2)﹣7y﹣12=0,解得y=,把y=代入③得x=﹣2=,∴方程组的解是.44.解方程组:(1);(2).【解答】解:(1),解:①+②得3x=33,解得x=11,把x=11代入①得y=14,∴方程组的解是;(2),解:原方程组可化为,①﹣②得6x=6,解得x=1,把x=1代入①得,∴方程组的解是.45.解方程:(1);(2).【解答】解:(1),①代入②得,2x+(3x+1)=﹣9,解得:x=﹣2,将x=﹣2代入①得,y=﹣5,∴方程组的解为:;(2),①×2+②得,6x+x=14,解得:x=2,将x=2代入①得6﹣2y=5,解得:,∴方程组的解为:.46.用适当的方法解下列方程组:(1);(2).【解答】解:(1),由①﹣②×2得:3y﹣(﹣2y)=1﹣5×2,解得:,将代入②得:,解得:,∴原方程组的解为;(2),由①×2+②得:7x=14,解得:x=2,把x=2代入①得:2×2+y=2,解得:y=﹣2,∴原方程组的解为.47.解方程组:(1);(2).【解答】解:(1),①×3+②得:7y=28,解得:y=4,将y=4代入①得:x=1,∴方程组的解为:;(2)整理得:,①+②×5得:23y=23,解得y=1,把y=1代入①得:5x﹣2=﹣12,解得x=﹣2,∴方程组的解为.48.解方程组:(1);(2).【解答】解:(1),①+②得,2x=6,解得:x=3,把x=3代入①得y=﹣1,∴方程组的解为;(2),①×2,得10x+4y=50③,③﹣②,得7x=35,解得:x=5,把x=5代入①得,25+2y=25,解得:y=0,所以方程组的解为.49.解方程组:(1);(2).【解答】解:(1),整理得:,由①﹣②得:4y=28,解得:y=7,把y=7代入①得:3x﹣7=8,解得:x=5,∴原方程组的解为:;(2),由②﹣①得:5x=15,解得:x=3,把x=3代入①得:y﹣2×3=0,解得:y=6,∴原方程组的解为.50.解方程组:(1);(2).【解答】解:(1),②×3得:15x+3y=21③,①+③得:19x=38,解得:x=2,把x=2代入②得:10+y=7,解得:y=﹣3,故原方程组的解是:;(2),①×2得:2x﹣4y=16③,②+③得:5x=10,解得:x=2,把x=2代入①得:2﹣2y=8,解得:y=﹣3,故原方程组的解是:.51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.【解答】解:(1)由①得x﹣y=1③,将③代入②得:4×1﹣y=0,解得y=4,把y=4代入①得:x﹣4﹣1=0,解得x=5,故原方程组的解是:;(2),整理得:,把③代入④得:2×2+1+15y=50,解得y=3,把y=3代入①得:3x﹣3﹣2=0,解得x=,故原方程组的解是:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.【解答】解:,①×2﹣②×3得:y=4﹣m,把y=4﹣m代入②得:x=2m﹣6,代入x+y=﹣10得:4﹣m+2m﹣6=﹣10,解得:m=﹣8,则原式=(m﹣1)2=81.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.【解答】解:(1)将x=,y=﹣2代入方程组得:,解得:,将x=3,y=﹣7代入方程组得:,解得:,则甲把a错看成了1;乙把b错看成了1;(2)根据(1)得正确的a=2,b=3,则方程组为,解得:.54.已知方程组和方程组的解相同求a、b的值.【解答】解:方程组的解为,由于方程组和方程组的解相同,所以,解得.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b的值.【解答】解:由题意,是bx+y=12的解得5b+2=12,解得b=2.又是x+ay=5的解得3+2a=5,解得a=1,∴5a﹣2b=5×1﹣2×2=1.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.【解答】解:(1)根据题中的新定义化简得:,解得:;(2)根据题中的新定义得:原式=2×(﹣1)+(﹣4)×1=﹣2﹣4=﹣6.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.【解答】解:(1)由题意,将代入bx﹣4y=4,得4b﹣4=4,∴b=2,将代入ax+3y=9,得3a+6=9,∴a=1;(2),①×2﹣②,得y=1.4,将y=1.4代入①得,x=4.8,∴方程组的解为.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.【解答】解:∵6※15=270,8※10=360,∴,解得:,∴﹣2※1=﹣100+4﹣(﹣2)×1=﹣94.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.【解答】解:(1)两方程组化简可得,,∵两方程组同解,∴①×2+②得:7x=21,解得:x=3,把x=3代入①式得:y=1,∴两个方程组的相同解为;(2)把代入方程组可得:①﹣②式得:2a=﹣4,解得:a=﹣2,把a=﹣2代入②式得:b=﹣5,∴(3a﹣b)2023=(﹣6+5)2023=﹣1.60.已知方程组和有相同的解,求a﹣2b的值.【解答】解:联立得:,①×2+②得:11x=11,解得:x=1,把x=1代入②得:y=﹣2,把代入,得,解得:,则a﹣2b=14﹣4=10.。
二元一次方程组专题训练(一)解析版(苏教版)

二元一次方程组专题训练(一)一.选择题(共11小题)1.已知二元一次方程组无解,则a的值是()A.a=2 B.a=6 C.a=﹣2 D.a=﹣62.已知二元一次方程组,则m﹣n的值是()A.2 B.0 C.3 D.﹣13.若x、y是两个实数,且,则x y y x等于()A.B.C.D.4.若关于x,y的方程组没有实数解,则()A.ab=﹣2 B.ab=﹣2且a≠1 C.ab≠﹣2 D.ab=﹣2且a≠25.如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是()A.∠B=∠D B.∠C=∠AED C.=D.=6.方程组的解的个数为()A.1 B.2 C.3 D.47.某气象台发现:在某段时间里,如果早晨下雨,那么晚上是晴天;如果晚上下雨,那么早晨是晴天,已知这段时间有9天下了雨,并且有6天晚上是晴天,7天早晨是晴天,则这一段时间有()A.9天 B.11天C.13天D.22天8.已知甲校原有1016人,乙校原有1028人,寒假期间甲、乙两校人数变动的原因只有转出与转入两种,且转出的人数比为1:3,转入的人数比也为1:3.若寒假结束开学时甲、乙两校人数相同,则乙校开学时的人数与原有的人数相差多少?()A.6 B.9 C.12 D.189.如图为甲、乙、丙三根笔直的木棍平行摆放在地面上的情形.已知乙有一部分只与甲重迭,其余部分只与丙重迭,甲没有与乙重迭的部分的长度为1公尺,丙没有与乙重迭的部分的长度为2公尺.若乙的长度最长且甲、乙的长度相差x 公尺,乙、丙的长度相差y公尺,则乙的长度为多少公尺?()A.x+y+3 B.x+y+1 C.x+y﹣1 D.x+y﹣310.有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3。
15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需()A.1.2元B.1.05元C.0.95元D.0.9元11.秋天的一个周末,王明的大学同学去帮王明家收梨子,上午大家全部摘梨,下午一半同学(包括王明)继续摘梨,一半同学把梨搬运到果园外的车上以备运走,结果梨都摘完了,而需搬运的梨还留下一个人一天的工作量.如果每个人每搬运两筐梨的时间就能摘一筐梨,那么王明和他的同学共()A.4人 B.6人 C.8人 D.10人二.填空题(共10小题)12.若|x﹣2y+1|+|x+y﹣5|=0,则2x+3y=.13.方程组,则|x﹣3|+xy2007= .14.已知二元一次方程组,则x﹣y=,x+y=.15.用“代入消元法”解方程组时,可先将第方程(填序号即可)变形为,然后再代入.16.若|3a+4b﹣c|+(c﹣2b)2=0,则a:b:c=.17.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面长为8,宽为7的长方形盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是.18.用6块相同的长方形地砖拼成一个矩形,如图所示,那么每个长方形地砖的面积是cm2.19.甲、乙两班共104名学生去西湖划船,大船每只可乘坐12人,小船每只可乘坐5人,如果这些学生把租来的船都坐满,那么应租大船只.20.(中国古代问题)唐太宗传令点兵,若一千零一卒为一营,则剩余一人,若一千零二卒为一营,则剩四人,此次点兵至少有.21.一个工厂得到任务,需要加工A零件6000个和B零件2000个,该厂共有工人214名,每个人加工A零件5个的时间可以加工B零件3个.现将工人分成两组,分别加工一种零件,同时开始,应怎样分组才能使任务最快完成.三.解答题(共19小题)22.解方程(组)(1)=﹣1 (2).23.已知x、y满足方程组,求代数式(﹣x)y的值.24.用指定的方法解下列方程组:(1)(代入法) (2)(加减法) 25.解方程:(1)(2).26.解方程组(1);(2).27.解方程(组):(1);(2).28.解方程组.29.如图,在△ABC中,D、E分别是边AB、AC的中点,F为CA延长线上一点,∠F=∠C.(1)若BC=8,求FD的长;(2)若AB=AC,求证:△ADE∽△DFE.30.如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.31.已知,如图,==,那么△ABD与△BCE相似吗?为什么?32.解方程组.33.解方程组:(1)(2).34.如图,CD、BE分别是锐角△ABC中AB、AC边上的高线,垂足为D、E.(1)证明:△ADC∽△AEB;(2)连接DE,则△AED与△ABC能相似吗?说说你的理由.35.解三元一次方程组.36.为了鼓励市民节约用水,盐城市居民生活用水按阶梯式水价计费.下表是盐城市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:用户每月用水量自来水单价(元/吨)污水处理费用(元/吨)17吨及以下a0.80b0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二元一次方程经典试题一(范围:代数: 二元一次方程组)一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………( ) 2、方程组⎩⎨⎧=+-=5231y x xy 的解是方程3x -2y =13的一个解( )3、由两个二元一次方程组成方程组一定是二元一次方程组( )4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ,可以转化为⎩⎨⎧-=--=+27651223y x y x ( )5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程,则a 的值为±1( )6、若x +y =0,且|x |=2,则y 的值为2 …………( )7、方程组⎩⎨⎧=+-=+81043y x xm my mx 有唯一的解,那么m 的值为m ≠-5 …………( )8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有 …………( )9、x +y =5且x ,y 的绝对值都小于5的整数解共有5组 …………( ) 10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解,反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………( )11、若|a +5|=5,a +b =1则32-的值为ba ………()12、在方程4x -3y =7里,如果用x 的代数式表示y ,则437yx +=( ) 二、选择:13、任何一个二元一次方程都有( ) (A )一个解; (B )两个解; (C )三个解;(D )无数多个解;14、一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( ) (A )5个 (B )6个(C )7个(D )8个15、如果⎩⎨⎧=+=-423y x ay x 的解都是正数,那么a 的取值范围是( )(A )a <2; (B )34->a ; (C )342<<-a ; (D )34-<a ; 16、关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解,那么m 的值是( ) (A )2;(B )-1; (C )1; (D )-2;17、在下列方程中,只有一个解的是( ) (A )⎩⎨⎧=+=+0331y x y x(B )⎩⎨⎧-=+=+2330y x y x(C )⎩⎨⎧=-=+4331y x y x(D )⎩⎨⎧=+=+3331y x y x18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( )(A )15x -3y =6 (B )4x -y =7(C )10x +2y =4(D )20x -4y =319、下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114y x y x(B )⎩⎨⎧=+=+75z y y x(C )⎩⎨⎧=-=6231y x x(D )⎩⎨⎧=-=-1y x xyy x20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解,则a 、b 的值等于( )(A )a =-3,b =-14 (B )a =3,b =-7(C )a =-1,b =9(D )a =-3,b =1421、若5x -6y =0,且xy ≠0,则yx yx 3545--的值等于( )(A )32 (B )23 (C )1 (D )-122、若x 、y 均为非负数,则方程6x =-7y 的解的情况是( ) (A )无解(B )有唯一一个解 (C )有无数多个解(D )不能确定23、若|3x +y +5|+|2x -2y -2|=0,则2x 2-3xy 的值是( ) (A )14(B )-4(C )-12(D )1224、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为( ) (A )21=k ,b =-4 (B )21-=k ,b =4(C )21=k ,b =4 (D )21-=k ,b =-4三、填空:25、在方程3x +4y =16中,当x =3时,y =________,当y =-2时,x =_______ 若x 、y 都是正整数,那么这个方程的解为___________; 26、方程2x +3y =10中,当3x -6=0时,y =_________;27、如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________; 28、若⎩⎨⎧-==11y x 是方程组⎩⎨⎧-=-=+1242a y x b y ax 的解,则⎩⎨⎧==______________b a ; 29、方程|a |+|b |=2的自然数解是_____________; 30、如果x =1,y =2满足方程141=+y ax ,那么a =____________; 31、已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解,则a =______,m =______;32、若方程x -2y +3z =0,且当x =1时,y =2,则z =______; 33、若4x +3y +5=0,则3(8y -x )-5(x +6y -2)的值等于_________;34、若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________; 35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________;36、已知a -3b =2a +b -15=1,则代数式a 2-4ab +b 2+3的值为__________; 四、解方程组□x +5y =13 ①37、⎪⎪⎩⎪⎪⎨⎧=-=-1332343n m nm ; 38、)(6441125为已知数a a y x a y x ⎩⎨⎧=-=+;39、⎪⎪⎩⎪⎪⎨⎧=++=+125432y x yx y x ; 40、⎪⎩⎪⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x ; 41、⎪⎪⎩⎪⎪⎨⎧++=++=+=+6253)23(22)32(32523233y x y x yx y x ; 42、⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x ;43、⎪⎩⎪⎨⎧=-+-=-+=-+3113y x z x z y z y x ; 44、⎪⎩⎪⎨⎧=+=+=+101216x z z y y x ;45、⎪⎩⎪⎨⎧=-+=+-=-+35351343z y x z y x z y x ; 46、⎪⎩⎪⎨⎧=+-==30325:3:7:4:z y x z x y x ;五、解答题:47、甲、乙两人在解方程组 时,甲看错了①式中的x 的系数,解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ;乙看错了方程②中的y 的系数,解得⎪⎪⎩⎪⎪⎨⎧==19177681y x ,若两人的计算都准确无误,请写出这个方程组,并求出此方程组的解;48、使x +4y =|a |成立的x 、y 的值,满足(2x +y -1)2+|3y -x |=0,又|a |+a =0,求a 的值;49、代数式ax 2+bx +c 中,当x =1时的值是0,在x =2时的值是3,在x =3时的值是28,试求出这个代数式;50、要使下列三个方程组成的方程组有解,求常数a 的值。
2x +3y =6-6a ,3x +7y =6-15a ,4x +4y =9a +951、当a 、b 满足什么条件时,方程(2b 2-18)x =3与方程组⎩⎨⎧-=-=-5231b y x y ax 都无解;52、a 、b 、c 取什么数值时,x 3-ax 2+bx +c 程(x -1)(x -2)(x -3)恒等? 53、m 取什么整数值时,方程组⎩⎨⎧=-=+0242y x my x 的解:(1)是正数;(2)是正整数?并求它的所有正整数解。
54、试求方程组⎩⎨⎧-=---=-6|2||5|7|2|y x y x 的解。
六、列方程(组)解应用题55、汽车从甲地到乙地,若每小时行驶45千米,就要延误30分钟到达;若每小时行驶50千米,那就可以提前30分钟到达,求甲、乙两地之间的距离及原计划行驶的时间?56、某班学生到农村劳动,一名男生因病不能参加,另有三名男生体质较弱,教师安排他们与女生一起抬土,两人抬一筐土,其余男生全部挑土(一根扁担,两只筐),这样安排劳动时恰需筐68个,扁担40根,问这个班的男女生各有多少人?57、甲、乙两人练习赛跑,如果甲让乙先跑10米,那么甲跑5秒钟就可以追上乙;如果甲让乙先跑2秒钟,那么甲跑4秒钟就能追上乙,求两人每秒钟各跑多少米?58、甲桶装水49升,乙桶装水56升,如果把乙桶的水倒入甲桶,甲桶装满后,乙桶剩下的水,恰好是乙桶容量的一半,若把甲桶的水倒入乙桶,待乙桶装满后则甲1,求这两个水桶的容量。
桶剩下的水恰好是甲桶容量的359、甲、乙两人在A地,丙在B地,他们三人同时出发,甲与乙同向而行,丙与甲、乙相向而行,甲每分钟走100米,乙每分钟走110米,丙每分钟走125米,若丙遇到乙后10分钟又遇到甲,求A、B两地之间的距离。
60、有两个比50大的两位数,它们的差是10,大数的10倍与小数的5倍的和的201是11的倍数,且也是一个两位数,求原来的这两个两位数。
【参考答案】一、1、√; 2、√; 3、×; 4、×; 5、×; 6、×; 7、√; 8、√; 9、×;10、×; 11、×;12、×;二、13、D ;14、B ; 15、C ; 16、A ; 17、C ; 18、A ;19、C ; 20、A ;21、A ; 22、B ; 23、B ; 24、A ; 三、25、47,8,⎩⎨⎧==14y x ;26、2; 27、4125+=y x ; 28、a =3,b =1;29、⎩⎨⎧==2b a ⎩⎨⎧==11b a ⎩⎨⎧==02b a 30、21; 31、3,-4 32、1; 33、20; 34、a 为大于或等于3的奇数;35、4:3,7:936、0;四、37、⎩⎨⎧==204162n m ; 38、⎪⎩⎪⎨⎧==22a y ax ; 39、⎩⎨⎧-==13y x ; 40、⎩⎨⎧==11y x ; 41、⎩⎨⎧==11y x ; 42、⎪⎩⎪⎨⎧==225y x ; 43、⎪⎩⎪⎨⎧===168z y x ; 44、⎪⎩⎪⎨⎧===397z y x ;45、⎪⎩⎪⎨⎧-=-==212z y x ; 46、⎪⎩⎪⎨⎧===202112z y x ;五、47、⎩⎨⎧-=-=+2941358y x y x ,⎪⎪⎩⎪⎪⎨⎧==231792107y x ;48、a =-1 49、11x 2-30x +19;50、31=a ;51、23=a ,b =±3 52、a =6, b =11,c =-6;53、(1)m 是大于-4的整数,(2)m =-3,-2,0,⎩⎨⎧==48y x ,⎩⎨⎧==24y x ,⎩⎨⎧==12y x ; 54、⎩⎨⎧=-=91y x 或⎩⎨⎧==95y x ; 六、55、A 、B 距离为450千米,原计划行驶9.5小时;56、设女生x 人,男生y 人,⎪⎪⎩⎪⎪⎨⎧=⨯-++=-++682)4(2340423y x y x ⎩⎨⎧==)(32)(21人人y x57、设甲速x 米/秒,乙速y 米/秒 ⎩⎨⎧==-y x y x 641055 ⎩⎨⎧==)/(4)/(6秒米秒米y x58、甲的容量为63升,乙水桶的容量为84升; 59、A 、B 两地之间的距离为52875米; 60、所求的两位数为52和62。
