2018年攻读工商管理硕士学位全国联考数学真题
2018年MBA和MPAcc数学真题解析改最终版本

2018年攻读工商管理硕士学位全国联考数学真题一、问题求解:本大题共15小题,每小题3分,共45分。
下列每题给出的五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选的字母涂黑。
1.学科竞赛设一、二、三等奖,比例1:3:8,获奖率30%,已知10人已获一等奖,则参赛人数为()A.300 B.400 C.500D.550 E.600【答案】(B )【解题过程】由总量=分量÷分量百分比,可得参赛总人数为:10÷(30%÷12)=400。
【考点】比例问题应用题。
2.为了解某公司员工年龄结构,按男女人数比例进行随机抽样,结果如下:男员工年龄(岁)232628303234363841女员工年龄(岁)232527272931据表中数据统计,该公司男员工的平均年龄与全体员工平均年龄分别是()A.32,30 B.32,29.5 C.32,27 D.30,27 E.29.5,27【答案】(A )【解题过程】由表可知,男员工的平均年龄=32,女员工的平均年龄=27,男女员工人数之比=9:6=3:2,总平均年龄为305227332=⨯+⨯。
【考点】平均值问题。
3.某单位分段收费收网站流量(单位:GB )费:每日20(含)GB 以内免,20到30(含)每GB 收1元,30到40(含)每GB 3元,40以上每GB 5元,小王本月用45GB 该交费()元A.45B.65C.75D.85E.135【答案】(B )【解题过程】应该缴费:10+10×3+5×5=65(元)。
【考点】分段计费。
4.圆O 是△ABC 内切圆△ABC 面积与周长比1:2,则图O 面积().A.πB.2πC.3πD.4πE.5π【答案】(A )【解题过程】设内切圆的半径为r ,△的三边为c b a ,,,则2:1)(:2)(=++⨯++c b a rc b a ,化简可得1r =,圆的面积为π。
【考点】平面几何求面积问题。
2018管理类联考数学真题-张全军

2018届(2017年12月)管理类联考数学真题张全军整理一、问题求解:1.学科竞赛设一等奖、二等奖和三等奖. 比例为1:3:8,获奖率为30%,已知10人获一等奖,则参加竞赛的人数为( ).(A)300 (B)400 (C)500 (D)550 (E)6002.为了解某公司员工的年龄结构,按男女的比例进行随机检查,结果如下:)岁.(A)32, 30 (B)32, 29.5 (C)32, 27 (D)30, 27 (E)29.5, 273.某单位采取分段收费的方式收取网络流量(单位:GB)费用;每月流量20(含)以内免费;流量20-30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB 收费5元. 小王这个月用了45GB的流量,则他应该交费( )元.(A)45 (B)65 (C)75 (D)85 (E)1354.如图,圆O是三角形ABC的内切圆,若三角形ABC的面积与周长的大小之比为1:2,则圆O的面积为( ).(A)π(B)2π(C)3π(D)4π(E)5π5.设实数,a b 满足||2a b −=,33||26a b −=,则22a b +=( ).(A)30(B)22(C)15(D)13(E)106.有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买甲、乙两种商品的有8位,同时购买甲、丙两种商品的有12位,同时购买乙、丙两种商品的有6位,三种同时购买有2位,则仅购买一种商品的顾客有( )位.(A)70(B)72(C)74(D)76(E)827.如图,四边形1A 1B 1C 1D 是平行四边形,2A ,2B ,2C ,2D 分别是1A 1B 1C 1D 四边的中点,3A ,3B ,3C ,3D 分别是2A 2B 2C 2D 四边的中点,依次下去,得到四边形序列m A m B m C mD (m =1,2,3…),设m A m B m C m D 的面积为m S 且1S =12,则1S +2S +3S +…= ( ).(A)16(B)20(C)24(D)28(E)308.将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中,若指定的两张卡片要在同一组,则不同的袋法有( )种.(A)12(B)18(C)24(D)30(E)369.甲、乙两人进行围棋比赛,约定先胜2盘者赢得比赛;已知每盘棋甲获胜的概率是0.6,乙获胜的概率是0.4,若乙在第一盘获胜,则甲赢得比赛的概率为( ).(A)0.144(B)0.288(C)0.36(D)0.4(E)0.610.已知圆C:2x +2()y a −=b ,若圆C 在点(1,2)处的切线与y 轴的交点为(0,3),则ab =( ).(A)-2(B)-1(C)0(D)1(E)211.羽毛球队有4名男运动和3名女运动员,从中选出两对参加混双比赛,则不同的选派方式有( )种.(A)9(B)18(C)24(D)36(E)7212.从标号为1到10的10张卡片中随机抽取2张,它们的标号之和能被5整除的概率为( ).(A)15(B)19(C)29(D)215(E)74513.某单位为检查3个部门的工作,由这3个都门的主任和外聘的3名人员组成检查组,2人一组检查工作,每组有1名外聘成员. 规定本部门主任不能检查本部门,则不同的安排方式有 ( )种.(A)6 (B)8(C)12(D)18(E)3614.如图,圆柱体的底面半径为2,高为3,垂直于底面的平面截圆柱体所得截面为矩形ABCD ,若弦AB 所对的圆心角是π3,则截掉部分(较小部分)的体积为( ).(A)3π−(B)26π−(C)2π−(D)2π− (E)π15.函数{}8,max )(22+−=x x x f 的最小值为( ).(A)8 (B)7(C)6(D)5(E)4二、条件充分性判断:16.设为x ,y 实数,则2x y +≤.(1)222x y +≤. (2)1xy ≤.17.设{}n a 为等差数列,则能确定129a a a +++的值.(1)已知1a 的值. (2)已知5a 的值.18.设m ,n 是正整数,则能确定m n +的值.(1)131m n +=. (2)121m n +=.19.甲、乙、丙三人的年收入成等比数列,则能确定乙的年收入的最大值.(1)已知甲、丙两人的年收入之和.(2)已知甲、丙两人的年收入之积.20.如图,在矩形ABCD 中,AE FC =,则三角形AED 与四边形BCFE 能拼接成一个直角三角形.(1)2EB FC =.(2)ED EF =.21.甲购买了若干件A 玩具,乙购买了若干件B 玩具送给幼儿园,甲比乙少花了100元,则能确定甲购买的玩具件数.(1)甲与乙共购买了50件玩具.(2)A 玩具的价格是B 玩具的2倍.22.已知点(,0)1,3(2,1)P m A B ,(),,点(,)x y 在三角形PAB 上,则x y -的最小值与最大值分别为-2和1.(1) 1.m ≤(2) 2.m ≥−23.如果甲公司的年终奖总额增加25%,乙公司的年终奖总额减少10%,两者相等,则能确定两公司的员工人数之比.(1)甲公司的人均年终奖与乙公司的相同.(2)两公司的员工人数之比与两公司的年终奖总额之比相等.24.,a b 为实数,则222x y y +=圆与直线x ay b +=不相交.(1)||a b −>(2)||a b +>25.设函数2()f x x ax =+,则()f x 的最小值与(())f f x 的最小值相等.(1)2a ≥.(2)0a ≤.。
MBA数学历年真题

1997年全国在职攻读工商管理硕士学位入学考试数学试题(本试卷满分为100分,考试时间为180分钟)一、选择题:本大题共20个小题,每小题2.5分,共50分。
1.若某人以1000元购买A 、B 、C 三种商品,且所有金额之比是1∶1.5∶2.5,则他购买A 、B 、C 三种商品的金额(单位:元)依次是A. 100, 300, 600B. 150, 225, 400C. 150, 300, 550D.200, 300, 500E. 200, 250, 5502. 某地连续举办三场国际商业足球比赛, 第二场观众比第一场少了80%, 第三场观众比第二场减少了50%,若第三场观众仅有2500人, 则第一场观众有A. 15000人B. 20000人C. 22500人D. 25000人E. 27500人3. 用一条绳子量井深, 若将绳子折成三折来量, 井外余绳4尺, 折成4折来量, 井外余绳1尺, 则井深是A. 6 尺B. 7尺C. 8尺D. 9尺E. 12尺4. 银行的一年期定期存款利率为10%, 某人于1991年1月1日存入1000元, 1994年1月1日取出, 若按复利计算, 他取出时所得的本金和利息共计是A. 10300元B.10303元C. 13000元D. 13310元E. 14641元 5. 某商品打九折会使销售增加20%, 则这一折扣会使销售额增加的百分比是 A. 18% B. 10% C. 8% D. 5% E. 2%的值是则的几何平均值是的两个实根,若是方程a x x a x x x x ,311076,.621221+=+-A. 2B. 3C. 4D. –2E. –35)23.(7x -的二项展开式中, 3x 的系数是A. –540B. –720C. –160D. 540E. 720 15. 函数xy 4=的一阶导数是A. x4 B. 14-x x C. x xln 4 D. 4ln 4x E. 4ln 4x16. 由方程xy e y=所确定的函数)(x y y =的导数'y 是A. x e y y -B. xe yy + C. y e x y - D. y e x y + E. y x e y -17.=⎰dx xf )3(63' A. )1()2(f f - B. [])1()2(3f f - C. [])1()2(31f f - D.[])1()2(31""f f - E. [])1()2(3""f f - 19. 若A 是3阶矩阵, 且TT A A A +=则,3=A. 6B. 2/3C. 24D. 12E. 9二、计算题:本大题共12小题,前10题每小题4分,后2题每小题5分,共计50分 。
2018年全国硕士研究生入学统一考试数学一试题及答案解析

2018年全国硕士研究生入学统一考试数学一试题及答案解析一、选择题(4分×8)1.下列函数在x = 0处不可导的是 ( )A 、 ()sin f x x x = B、()f x x = C 、()cos f x x = D、()f x = 解 选D 。
由导数定义或左右导数与导数的关系可知:00sin lim lim 0,x x x x x x x x→→==故A 选项不正确;000x x →→==,故B 选项不正确;2002sin cos 12lim lim 0x x x x x x →→-==,故C 选项不正确;20002sin 12lim lim 2x x x x x x→→→-==-,极限不存在,故D 选项正确。
2. 过点(1,0,0),(0,1,0),且与曲面22z x y =+相切的平面为 ( )A 、 01z x y z =+-=与B 、022z x y z =+-=与2C 、1x y x y z =+-=与D 、22x y x y z =+-=与2解 选B 。
由已知,点(1,0,0),(0,1,0)在切平面上,而选项C ,D 显然不满足,故排除C ,D 。
又曲面22z x y =+上任一点(,,)x y z 处的法向量为(2,2,1)x y -,如选项A 正确,1x y z +-=的法向量为(1,1,1)-,可得切点的11,22x y ==,代入曲面方程得12z =,而代入1x y z +-=得0z =,矛盾,故排除A 选项。
3. 023(1)(21)!nn n n +∞=+-=+∑( ) A 、 sin1cos1+ B 、2sin1cos1+C 、2sin12cos1+D 、2sin13cos1+解 选B 。
因00023212(1)(1)(1)(21)!(21)!(21)!nn n n n n n n n n n +∞+∞+∞===++-=-+-+++∑∑∑ 0011(1)2(1)cos12sin1(2)!(21)!n n n n n n +∞+∞===-+-=++∑∑。
2018联考数学真题答案及详细解析
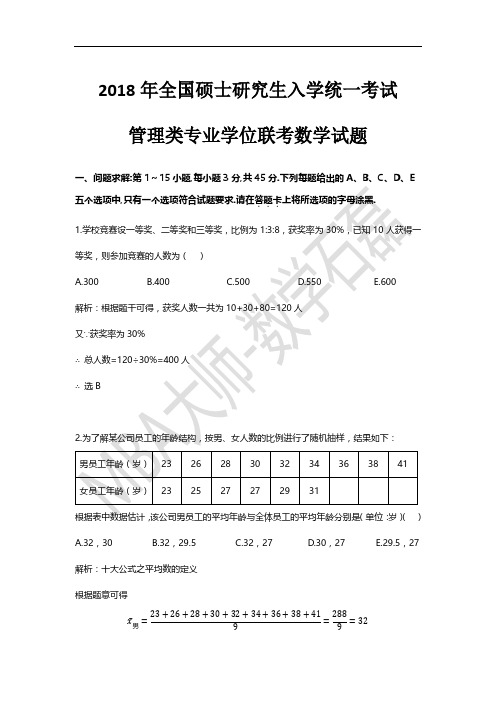
A.30
B.22
C.15
D.13
解析:由题干可得
������ = 3,������ = 1 ∴ ������2 + ������2 = 10 ∴ 选E
E.10
6.有 96 位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买了甲、乙两种
商品的有 8 位,同时购买了甲、丙两种商品的有 12 位,同时购买了乙、丙两种商品的有 6
������ ������
解析:对于(1),������ = 2, ������ = 6、������ = 4, ������ = 4
对于(2),������ = 2, ������ = 4、������ = 3, ������ = 3
∴ 选D
������ + ������ = 8 ������ + ������ = 6
女员工年龄(岁) 23 25 27 27 29 31
根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁)( )
A.32,30
B.32,29.5
C.32,27
D.30,27
E.29.5,27
解析:十大公式之平均数的定义
根据题意可得
23 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 41 288
∴ 选D
12.从标号为 1 到 10 的 10 张卡片中随机抽取 2 张,它们的标号之和能被 5 整除的概率为
()
A.1
B.1
5
9
解析:“M-W”模型
C.2
D. 2
E. 7
9
15
2018 年全国硕士研究生招生考试管理类联考综合真题及答案详解

第126页共344页2018年全国硕士研究生招生考试管理类专业学位联考综合能力试题一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A、B、C、D、E 五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
1.学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%,已知10人获得一等奖,则参加竞赛的人数为().A.300B.400C.500D.550E.6002.为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:男员工年龄(岁)232628303234363841女员工年龄(岁)232527272931根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁)().A.32,30B.32,29.5C.32,27D.30,27E.29.5,273.某单位采取分段收费的方式收取网络流量(单位:GB)费用:每月流量20(含)以内免费,流量20到30(含)的每GB 收费1元,流量30到40(含)的每GB 收费3元,流量40以上的每GB 收费5元.小王这个月用了45GB 的流量,则他应该交费().A.45元B.65元C.75元D.85元E.135元4.如图1,圆O 是三角形ABC 的内切圆,若三角形ABC 的面积与周长的大小之比为1:2,则圆O 的面积为().A.πB.π2 C.π3 D.π4 E.π55.设实数b a ,满足26,233=-=-b a b a ,则=+22b a ().A.30B.22C.15D.13E.106.将6张不同的卡片2张一组分别装入甲、乙、丙3个袋中,若指定2张卡片要在同一组,则不同的装法有().A.12种B.18种C.24种D.30种E.36种7.如图2,四边形1111D C B A 是平行四边形,2222,,,D C B A 分别是1111,,,D C B A 四边的中点,3333,,,D C B A 分别是四边形2222,,,D C B A 的中点,依次下去,得到四边形序列)3,2,1( ,=n D C B A n n n n .设n n n n D C B A 的面积为n S ,且121=S ,则=+++ 321S S S ().A.16B.20C.24D.28E.308.甲、乙两人进行围棋比赛,约定先胜两局者赢得比赛.已知每盘棋甲获胜的概率为0.6,乙获胜的概率为0.4.若乙在第一局获胜,则甲赢得比赛的概率为().A.0.144B.0.288C.0.36D.0.4E.0.69.有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买了甲、乙两种商品的有8位,同时购买了甲、丙两种商品的有12位,同时购买乙、丙两种商品的有6位,同时购买三种商品的有2位.则仅购买一种商品的顾客有().A.70位B.72位C.74位D.76位E.82位10.已知圆C :b a y x =-+22)(.若圆C 在点(1,2)处的切线与y 轴的交点为(0,3),则=ab ().A.-2B.-1C.0D.1E.211.羽毛球队有4名男运动员和3名女运动员,从中选出两对参加混双比赛,则不同的选派方式有().A.9种B.18种C.24种D.36种E.72种12.从标号为1到10的10张卡片中随机抽取2张,它们的标号之和能被5整除的概率为().A.51 B.91 C.92 D.152 E.45713.如图3,圆柱体的底面半径为2,高为3,垂直于底部的平面截圆柱体所得截面为矩形ABCD .若弦AB 所对的圆心角是3π,则截掉部分(较小部分)的体积为().A.3-π B.62-π C.233-π D.332-π E.3-π14.某单位为检查3个部门的工作,由3个部门的主任和外聘的3名人员组成检查组,分2人一组检查工作,每组有1名外聘成员.规定本部门主任不能检查本部门,则不同的安排方式有().A.6种B.8种C.12种D.18种E.36种15.函数{}8,max )(22+-=x x x f 的最小值为().A.8B.7C.6D.5E.4二.条件充分性判断:第16~25小题,每小题3分,共30分。
2018年全国硕士研究生入学统一考试《数学》真题及详解

2018年全国硕士研究生入学统一考试《数学》真题
(总分150, 考试时间180分钟)
一、单项选择题:1-8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题卡指定位置上
1. f(x)=sinx/x()
A 有界,奇
B 有界,偶
C 无界,奇
D 无界,偶
该问题分值: 4
答案:B
2.
A 单减少,凹
B 单减少,凸
C 单增加,凹
D 单增加,凸
该问题分值: 4
答案:D
3.
A 1/e
B 2/e
C 1+e/e2
D 2/e2
该问题分值: 4
答案:B
4. 已知Z=(x-y2)e1+xy,则|dz|(1,-1)=()
A dx+2dy
B -dx+2dy
C dx-2dy
D -dx-2dy
该问题分值: 4
答案:A
5. 设向量组α1,α2,α3与向量α1,α2等价,则()
A α1与α2线性相关
B α1与α2线性无关
C α1,α2,α3线性相关
D α1,α2,α3线性无关
该问题分值: 4
答案:C
6.
该问题分值: 4
由于矩阵形式比较简申只需要求解几个代数余子式带入验证即可,由于
7. 设随机变x,y相互独立,且x,y分别服从参数为1,2的泊松分布,则p{2x+y=2} = ()
该问题分值: 4
答案:C
8.
A Q统计量;服从分布t(10)
B Q统计量;服从分布t(9)
C Q不是统计量;服从分布t(10)
D Q统计量;服从分布t(9)
该问题分值: 4
答案:D。
(完整版)MBA历年试题解析

2009年10月在职攻读工商管理硕士学位全国联考综合能力数学试题一.问题求解(第15~1小题,每小题3分,共45分,下例每题给 出A 、B 、C 、D 、E 五个选项中,只有一项是符合试题要求的,请在答题卡上将所选项的字母涂黑)1. 已知某车间的男工人数比女工人数多80%,若在该车间的一次技术考核中全体工人的平均成绩为75分,而女工平均成绩比男工平均成绩高20%,则女工平均成绩为()分。
(A )88 (B )86 (C )84 (D )82 (E )80[点拨]未知量设少的一方容易计算。
解:设女工人数为x ,男工平均成绩为y ,则842.170758.18.12.1=⇒=⇒=+⨯+⨯y y xx x y x y ,选(C )。
2.某人在市场上买猪肉,小贩称得肉重为4斤,但此人不放心,拿出一个自备的100克重的砝码,将肉与砝码一起让小贩用原秤复称,结果重量为25.4斤,由此可知顾客应要求小贩补猪肉()两(A )3 (B )6 (C )4 (D )7 (E )8[点拨]比例问题,但应先化为同一计量单位。
解:32405.22=⇒=x x ,应要求小贩补猪肉83240=-两。
选(E )。
3. 甲、乙两商店某种商品的进价都是200元,甲店以高于进价20%的价格出售,乙店以高于进价15%的价格出售,结果乙店的售出件数是甲店的两倍,扣除营业税后乙店的利润比甲店多5400元。
若营业税率是营业额的5%,那么甲、乙两店售出该商品各为()件(A )450,900 (B )500,1000 (C )550,1100(D )600,1200 (E )650,1300[点拨]直接设甲店售出件数,在利用利润差。
解:设甲店售出x 件,则甲店的利润为 x x x 28%52.12002.0200=⨯⨯-⨯, 乙店的利润为 x x x 37%5215.1200215.0200=⨯⨯⨯-⨯⨯,60054002837=⇒=-x x x 。
2018管理类联考真题及答案

2018届管理类专业硕士研究生全国联考真题一、问题求解:第1—15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1、学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%、已知10人获得一等奖,则参加竞赛的人数为(A)300 (B)400(C)500 (D)550(E)600【答案】B2、为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁)(A)32,30 (B)32, 29.5(C)32, 27 (D)30, 27(E)29.5, 27【答案】A3、某单位采取分段收费的方式收取网络流量(单位:GB)费用:每月流量20(含)以内免费,流量20到30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB收费5元,小王这个月用了45GB的流量,则他应该交费(A)45元(B)65元(C)75元(D)85元(E)135元【答案】B4、如图,圆O是三角形ABC的内切圆,若三角形ABC的面积与周长的大小之比为1:2,则圆O的面积为【答案】A(A)π(B)2π(C)3π(D)4π(E)5π5、设实数,满足|-|=2,|-|=26, 则+=(A)30 (B)22(C)15 (D)13(E)10【答案】E6、甲、乙两人进行围棋比赛,约定先胜2盘者赢得比赛。
已知每盘棋甲获胜的概率是0.6,乙获胜的概率是0.4,若乙在第一盘获胜,则甲赢得比赛的概率为(A)0.144 (B)0.288(C)0.36 (D)0.4(E)0.6【答案】C7、如图,四边形平行四边形,, , ,分别是四边的中点,,,,分别是四边的中点,依次下去。
得到四边形序列(m=1,2,3…),设的面积为且=12,则+++…=(A)16 (B)20 (C)24 (D)28 (E)30 【答案】C8、已知圆+=b,若圆C在点(1.2)处的切线与y轴的交点为(0.3),则ab=(A)1-2 (B)-1 (C)0 (D)1 (E)2【答案】E9、有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买甲、乙两种商品的有8位,同时购买甲、丙两种商品的有12位,同时购买乙、丙两种商品的有6位,三种同时购买有2位,则仅购买一种商品的顾客有(A)70位(B)72位(C)74位(D)76位(E)82位【答案】C10、将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中,若指定的两张卡片要在同一组,则不同的袋法有(A)12种(B)18种(C)24种(D)30种(E)36种【答案】B11、某单位为检查3个部门的工作。
2018年12月管理类联考数学真题-张全军

2019届(2018年12月)管理类联考数学真题-张全军张全军 整理一、问题求解1.某车间计划10天完成一项任务,工作3天后因故停工2天,但仍需要按计划完成任务,则工作效率需要提高( ).(A)20%(B)30%(C)40%(D)50%(E)60%2.设函数2()2(0)af x x a x=+> 在(0,)+∞的最小值为0()12f x =,则0x =( ). (A)5(B)4(C)3(D)2(E)13.某影城统计了一季度的观众人数,如图1,则一季度的男女观众人数之比为( ).(A)3:4(B) 5:6(C) 12:13(D)13:12(E) 4:34.设实数,a b 满足6,||||6ab a b a b =++−=,则22a b +=( ). (A)10(B)11(C)12(D)13(E)145.设圆C 与圆22(5)2x y −+=关于2y x =对称,则圆C 的方程为( ).(A)22(3)(4)2x y −+−= (B)22(4)(3)2x y ++−= (C)22(3)(4)2x y −++= (D)22(3)(4)2x y +++= (E)22(3)(4)2x y ++−=6.将一批树苗种在一个正方形花园边上,四角都种,如果每隔3m 种一棵树,那么剩下10棵树苗,如果每隔2m 种一棵,那么恰好种满正方形3条边,则这批树苗有( )棵.(A)54(B)60(C)70(D)82(E)947.在分别标记1、2、3、4、5、6的6张卡片里,甲抽取1张,乙从余下的卡片中再抽取2张,乙的卡片的数字之和大于甲的卡片数字的概率为( ).(A)1160(B)1360(C)4360(D)4760(E)49608.十名同学的语文和数学成绩如下:1212(A)E1>E2, δ1>δ2(B)E1>E2, δ1<δ2(C)E1>E2, δ1=δ2(D)E1<E2, δ1>δ2(E)E1<E2,δ1<δ29.如图,正方体于半径为3m球内,且一面位于球的大圆上,则正方体的表面积最大为( ).(A)12(B)18(C)24(D)30(E)3610.在三角形ABC中,AB=4,AC=6,BC=8,D为BC的中点,则AD=( ).(C)3(D)11.某单位要铺设草坪,若甲乙两公司合作需6天完成,工时费共2.4万元;若甲公司单独做4天后由乙公司接着做9天完成,工时费共计2.35万元;若由甲公司单独完成该项目,则工时费共计( )万元.(A)2.25(B)2.35(C)2.4(D)2.45(E)2.512.如下图,六边形ABCDEF 是平面与棱长为2的正方体所截得到的,若A 、B 、D 、E 分别为相应棱的中点,则六边形ABCDEF 的面积为( ).(A)2(C)(D)(E)13.火车行驶72千米用时1小时,其速度v 与行驶时间t 的关系如图所示,则v 0= ( ).(A)72(B)80(C)90(D)95(E)9614.某中学的5个学科各推荐2名教师作为支教候选人,若从中选派来自不同学科的2人参加支教工作,则不同的选派方式有( ).(A)20(B)24(C)30(D)40(E)4515.设数列{}n a 满足110,21n n a a a +=−=,则100a =( ).(A)9921−(B)992(C)9921+(D)10021−(E)10021+二、条件充分性判断:16.甲、乙、丙三人各自拥有不超过10本图书,甲丙购入2本图书后,他们拥有的图书数量构成等比数列,则能确定甲拥有图书的数量.(1)已知乙拥有的图书数量.(2)已知丙拥有的图书数量.17.有甲、乙两袋奖券,获奖率分别为p 和q ,某人从两袋中各随机抽取1张奖券,则此人获奖的概率不小于34. (1)已知p +q =1.(2)已知14pq =.18.直线y kx =与圆22430x y x +−+=有两个交点.(1)0k <<.(2)02k <<.19.能确定小明年龄.(1)小明年龄是完全平方数.(2)20年后小明年龄是完全平方数.20.关于x 的方程210x ax b ++−=有实根.(1)0a b +=.(2)0a b −=.21.如图,已知正方形ABCD 面积,O 为BC 上一点,P 为AO 的中点,Q 为DO 上一点,则能确定三角形PQD 面积.(1)O 为BC 的三等分点.(2)Q 为DO 的三等分点.22.设n 为正整数,则能确定n 除以5的余数.(1)已知n 除以2的余数. (2)已知n 除以3的余数.23.某校理学院五个系每年的录取人数如下表:(1)数学系录取平均分提高了3分,生物系录取平均分降低了2分. (2)化学系录取平均分提高了1分,地学系录取平均分降低了4分.24.设{}n a 的前n 项和为n S ,则数列{}n a 为等差数列.(1)2=2,1,2,3,n S n n n +=.(2)2=21,1,2,3,n S n n n ++=.25.设三角形区域D 由直线8560x y +−=,6420x y −+=与860kx y k −+−=(0)k <组成,则对于任意的(,)x y D ∈,22lg()2x y +≤.(1)(,1]k ∈−∞−.(2)1[1,)8k ∈−−.。
2018考研数学真题及答案

2018考研数学真题及答案考研对于许多学子来说,是一场知识与毅力的较量。
而数学作为其中的重要科目,更是备受关注。
下面就让我们一起来回顾一下 2018 年考研数学的真题,并探讨一下相应的答案。
2018 年考研数学一真题涵盖了高等数学、线性代数、概率论与数理统计等多个方面的知识点。
在高等数学部分,函数、极限、连续的相关题目要求考生对基本概念和定理有深入的理解。
比如,有一道关于函数极限存在性的证明题,需要考生熟练运用极限的定义和性质进行推理。
导数与微分的题目则注重考查考生对导数定义和计算方法的掌握,以及运用导数解决函数单调性、极值和凹凸性等问题的能力。
例如,通过求导判断函数在某个区间内的单调性,并求出极值点。
积分的题目类型多样,包括定积分的计算、不定积分的求解以及利用积分解决几何和物理问题等。
线性代数部分,矩阵、向量和线性方程组是重点。
有题目涉及矩阵的运算、矩阵的秩以及向量组的线性相关性。
要求考生能够灵活运用矩阵的初等变换和线性方程组的解法来解决问题。
概率论与数理统计部分,随机变量及其分布、数字特征以及参数估计等内容均有考查。
像计算随机变量的概率密度、期望和方差,以及利用样本数据进行参数估计等。
接下来,我们看一下对应的答案和解题思路。
对于高等数学中函数极限存在性的证明题,首先要明确极限的定义,然后通过适当的放缩和不等式的运用来逐步推导。
在导数与微分的题目中,要准确计算导数,注意复合函数求导法则的应用。
对于积分的题目,熟练掌握积分公式和换元积分法、分部积分法等技巧是关键。
在线性代数中,处理矩阵的运算要细心,注意矩阵乘法的规则。
判断向量组的线性相关性时,可以通过构造矩阵并求秩来得出结论。
在概率论与数理统计部分,计算概率密度要确定分布类型和参数,运用相应的公式进行计算。
参数估计的题目则要根据给定的样本数据,选择合适的估计方法。
总的来说,2018 年考研数学真题难度适中,既考查了基础知识的掌握,又注重对考生综合运用能力和解题技巧的检验。
2018考研数一真题答案及详细解析

0
0
) ,B= (
0
1
0
) ,则 r (A
0
B)=2 #- r (AT
矿),排除 D.
(7) A
解 由 J(l+x) = J(l-x)可知,J(x)关千x = l对称,所以f�J(x)dx =厂J(x)dx = 0. 5.
r。 r 又已知,J:!<x)dx = O. 6,则 J (x)dx = (x)dx = O. 3.
罕
dr
了
(1 +3r 2)rdx
气f rCl+3尸)了37dr.
✓ 设 1 -3r2 =t,则
气。 亨
21rf r0+3尸)二37dr =
3
(2- t2汒dt
14冗
45
JI又
xdy dz
+
(y 3
+2)dzdx+z3 dxdy = 0,所以
I
14 穴 =百·
:El
08) 解 C I)当 f(x)=x 时,方程化为 y '+y =x,其通解为
假设 O<x,.+1 <立,则
e石t-2
工
e
n+I
=
-1
=e�(0
<
r;
<
X n+l),
X n +l
所以 0 < Xn+2 < Xn+l•
故 {xn} 是单调减少的数列,且有下界,从而 {x九 }收敛.
设
limx n-=
n
=a,得
aea =ea
— 1.
易知
a =O为其解
2018年管理类MBA综合考试数学真题及详细答案解析(word版)

2018年管理类MBA综合考试数学真题及详细答案解析一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
1. 学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%,已知10人获得一等奖,则参加竞赛的人数为()A.300 B. 400 C. 500 D. 550 E. 600解析:(B)解法1:由一等奖:二等奖:三等奖=1:3:8,且一等奖10人,可推出二等奖、三等奖分别为30人和80人,所以获奖人数为10+30+80=120人,所以参加竞赛的人数为12030%=400÷人。
解法2:设参加竞赛的人数为x,根据题意有130%10400138x x=⇒=++。
2. 为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁) A. 32, 30 B. 32, 29.5 C. 32, 27 D. 30, 27 E. 29.5, 27解析:(A)23+26+28+30+32+34+36+38+41==329x男23+25+27+27+29+31==276x 女329+276==3015x⨯⨯总3. 某单位采取分段收费的方式收取网络流量(单位: GB)费用,每月流量20(含)以内免费,流量20到30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB收费5元,小王这个月用了45GB的流量,则他应该交费()A. 45元B. 65元C. 75元D. 85元E. 135元解析:(B)各个流量段所需缴费数额见下表:所以小王应该缴费0+10+30+25=65元。
4. 如图,圆O 是三角形ABC 的内切圆,若三角形ABC 的面积与周长的大小之比为1:2,则圆O 的面积为( ) A. π B.2π C. 3π D. 4π E. 5π解析:(A )解法1:设三角形边长分别为,,a b c ,内切圆O 的半径为r ,则三角形周长L a b c =++,三角形面积12S Lr =(最好记住该结论)。
2018年MBA联考数学真题与答案

【经典资料,WORD文档,可编辑修改】【经典考试资料,答案附后,看后必过,WORD文档,可修改】一、问题求解:第1~15小题,每小题3分,共45分,下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的,请在答题卡上将所选项的字母涂黑。
1.电影开演时观众中女士与男士人数之比为5:4,开演后无观众入场,放映一小时后,女士的20%,男士的15%离场,则此时在场的女士与男士人数之比为(A)4:5 (B)1:1 (C)5:4 (D)20:17 (E)85:642.某商品的成本为240元,若按该商品标价的8折出售,利润率是15%,则该商品的标价为(A)276元 (B)331元 (C)345元 (D)360元 (E)400元3.三名小孩中有一名学龄前儿童(年龄不足6岁),他们的年龄都是质数(素数),且依次相差6岁,他们的年龄之和为(A)21 (B)27 (C)33 (D)39 (E)514.在右边的表格中,每行为等差数列,每列为等比数列,x+y+z=(A)2 (B) 5/2 (C)3 (D) 7/2 (E)42 5/2 3X 5/43/2A Y3/4B C z5.如图1,在直角三角形ABC区域内部有座山,现计划从BC边上的某点D开凿一条隧道到点A,要求隧道长度最短,已知AB长为5km,则所开凿的隧道AD的长度约为(A) (B) (C) (D) (E)6.某商店举行店庆活动,顾客消费达到一定数量后,可以在4种赠品中随机选取2件不同的赠品,任意两位顾客所选的赠品中,恰有1件品种相同的概率是(A) 1/6 (B) 1/4 (C)1/3 (D)1/2 (E)2/37.多项式x3+ax2+bx-6的两个因式是x-1和x-2,则其第三个一次因式为(A)x-6 (B)x-3 (C)x+1 (D)x+2 (E)x+38.某公司的员工中,拥有本科毕业证、计算机登记证、汽车驾驶证得人数分别为130,110,90.又知只有一种证的人数为140,三证齐全的人数为30,则恰有双证得人数为(A)45 (B)50 (C)52 (D)65 (E)1009.甲商店销售某种商品,该商品的进价为每价90元,若每件定价为100元,则一天内能售出500件,在此基础上,定价每增加1元,一天便能少售出10出,甲商店欲获得最大利润,则该商品的定价应为(A)115元(B)120元(C)125元(D)130元(E)135元10.已知直线ax-by+3=0(a>0,b>0)过圆x2+4x+y2-2y+1=0的圆心,则a-b的最大值为(A)9/16 (B)11/16 (C) 3/4 (D) 9/8 (E)9/411.某大学派出5名志愿者到西部4所中学支教,若每所中学至少有一名志愿者,则不同的分配方案共有(A)240种(B)144种(C)120种(D)60种(E)24种(A)1/120 (B)1/168 (C)1/240 (D)1/720 (E)3/100013.某居民小区决定投资15万元修建停车位,据测算,修建一个室内车位的费用为5000元,修建一个室外车位的费用为1000元,考虑到实际因素,计划室外车位的数量不少于室内车位的2倍,也不多于室内车位的3倍,这笔投资最多可建车位的数量为(A)78 (B)74 (C)72 (D)70 (E)6614.如图2,长方形ABCD的两条边长分别为8m和6m,四边形OEFG的面积是4m2,则阴影部分的面积为(A)32m2 (B)28 m2 (C)24 m2 (D)20 m2 (E)16 m215.在一次竞猜活动中,设有5关,如果连续通过2关就算成功,小王通过每关的概率都是1/2,他闯关成功的概率为(A)1/8 (B) 1/4 (C) 3/8 (D)4/8 (E)19/32二、条件充分性判断;第16~25小题,每小题3分,共30分,要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论。
2018年考研管理类联考试题及参考答案

2018年考研管理类联考试题及参考答案一、冋题求解:第L1列極费允 共輻分悔题给出的•臥c.叭E 五个 型页中.只有一顶是符合试鯉求內请在答軀卡上将ffift 顶的审母涂聽K 学科竟寒设一等奖、二等奖和三尊奖,比例为1:3: S,茯奖率为30%、已知10人获得 —等奖,则金力喳寒的人数为(A> 300 (B) 400 (C) 500 (D) 550(E) 6002、为了解某公司员工的年龄结村 按钛 女人数的比例进f 亍了随机抽样,结果如F ;男貝工年龄(岁)23 2620 30 3224362841女員工年龄(岁〉 23 2527272931根將表中数1B 估计,诙公司男员工的平均年龄与全体员工的平均年龄分別杲(单位:岁)(A) 32, 30 (B) 32. 29.5 (C) 32, 27 (D) 30, 27(E) 29_5, 273>某单位采馭分段吹務的方式收取朗络流量(单■位;GB)费用;每月流量其(创 以内 免魏,溢量加到30 {含)的埒GB 收我1元,浚量如到40 (含)的毎GBlft 费弐元,流 量40以上的每GB 收费' 元 小王这个月用了巧GB 的茨邑贝」他应该交費4$元 (B) 65元 (C) 75元 (D)阴元(E) 135 元斗.如凰圆O 是三角形ABC 的内切圆,若三角形ABC 的面积与周长的犬小之比为1: 23(B) 2JT (D) 47TCE) 57T5、设实数a 丄満足阳上|乜3-聞=迪则CAi 30 22 (C) 15 (D) 13CE) 100甲、乙两人曲亍围棋比第约定先胜2盘者蛊得比第已知毎盘楫甲茯胜的槪率是0®乙狂胜的探卒呈丄4,—盘狂匕 川甲嬴唱比暮葩播举力3 K(C) 3HO) 0.144 (B) 0.2SS(C)0.36 (D) 0.4<E) 0.67、如團,四边形4耳G D、平行四边形,4 ,C「D】分别是£ § C】。
2018考研数学一真题及答案及解析,推荐文档

WORD 资料.可编辑
2018 年考研数学一真题及答案解析
专业技术.整理分享
WORD 资料.可编辑 专业技术.整理分享
WORD 资料.可编辑 专业技术.整理分享
WORD 资料.可编辑 专业技术.整理分享
WORD 资料.可编辑 专业技术.整理分享
WORD 资料.可编辑 专业技术.整理分享
WORD 资料.可编辑 专业技术.整理分享
WORD 资料.可编辑 专业技术.整理分享
“
”
“”ຫໍສະໝຸດ At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!
2018年考研管理类联考数学试题解析
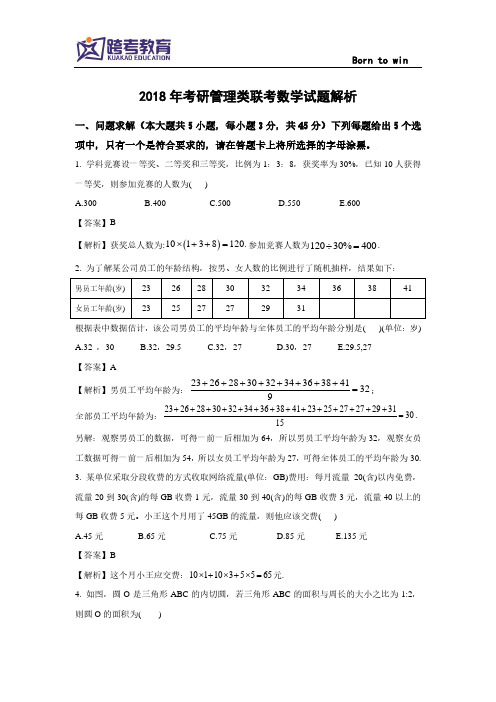
一等奖,则参加竞赛的人数为( )
A.300
B.400
C.500
D.550
E.600
【答案】B
【解析】获奖总人数为:10 1 3 8 120. 参加竞赛人数为120 30% 400 .
2. 为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:
男员工年龄(岁) 23
26 28
全部员工平均年龄为: 23 26 28 30 32 34 36 38 41 23 25 27 27 29 31 30 . 15
另解:观察男员工的数据,可得一前一后相加为 64,所以男员工平均年龄为 32,观察女员
工数据可得一前一后相加为 54,所以女员工平均年龄为 27,可得全体员工的平均年龄为 30.
B.65 元
C.75 元
D.85 元
E.135 元
【答案】B
【解析】这个月小王应交费:101103 55 65 元.
4. 如图,圆 O 是三角形 ABC 的内切圆,若三角形 ABC 的面积与周长的大小之比为 1:2,
则圆 O 的面积为( )
Born to win
A
O
B
C
图.1
A.
【答案】A 【解析】
B. 2
C. 3
D. 4
A
a1
b1
E. 5
a2
rO
b2
B
c1
c2
C
S
1 2
a1r
1 2
b1r
1 2
a2r
1 2
b2r
1 2
c1r
1 2
c2r
1 2
r
a1
b1
a2
b2
全国硕士研究生考试-管理类联考2018年数学真题

2018年全国硕士研究生招生考试管理类专业学位联考——数学一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
(2018-1)学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%,已知10人获得一等奖,则参加竞赛的人数是()(A)300 (B)400 (C)500 (D)550 (E)600 (2018-2)为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁)(A)32,30 (B)32,29.5 (C)32,27 (D)30,27 (E)29.5,27 (2018-3)某单位采取分段收费的方式收取网络流量(单位:GB)费用:每月流量20(含)以内免费,流量20到30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB收费5元。
小王这个月用了45GB的流量,则他应缴费()(A)45元(B)65元(C)75元(D)85元(E)135元(2018-4)如图,圆O是三角形ABC的内切圆,若三角形ABC的面积与周长的大小之比为1:2,则圆O的面积为()(A)(B)(C)(D)(E)(2018-5)设实数a,b满足︱a-b︱=2,︱a3-b3︱=26,则a2+b2=()(A)30 (B)22 (C)15 (D)13 (E)10 (2018-6)有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买了甲、乙两种商品的有8位,同时购买了甲、丙两种商品的有12位,同时购买了乙、丙两种商品的有6位,同时购买了三种商品的有2位,则仅购买了一种商品的顾客有()B C(A )70位 (B )72位 (C )74位 (D )76位 (E )82位 (2018-7)如图,四边形A 1B 1C 1D 1是平行四边形,A 2,B 2,C 2,D 2分别是A 1B 1C 1D 1四边的中点,A 3B 3C 3D 3分别是A 2B 2C 2D 2四边的中点,依次下去,得到四边形序列A n B n C n D n (n=1,2,3,…),设A n B n C n D n 的面积为S n ,且S 1=12,则S 1+S 2+S 3+…=()(A )16 (B )20(C )24 (D )28 (E )30 (2018-8)将6张不同的卡片2张一组分别装入甲、乙、丙3个袋中,若指定的两张卡片要放在同一组,则不同的装法有()(A )12种 (B )18种 (C )24种 (D )30种 (E )36种 (2018-9)甲、乙两人进行围棋比赛,约定先胜两盘者赢得比赛,已知每盘棋甲获胜的概率是0.6,乙获胜的概率是0.4.若乙在第一盘获胜,则甲赢得比赛的概率为()(A )0.14 (B )0.288 (C )0.36 (D )0.4 (E )0.6 (2018-10)已知圆C :x 2+(y-a )2=b ,若圆C 在点(1,2)处的切线与y 轴的交点为(0,3),则ab=()(A )-2 (B )-1 (C )0 (D )1 (E )2 (2018-11)羽毛球队有4名男运动员和3名女运动员,从中选出2对参加混双比赛,则不同的选派方式有()(A )9种 (B )18种 (C )24种 (D )36种 (E )72种 (2018-12)从标号为1到10的10张卡片中随机抽取2张,它们的标号之和能被5整除的概率为()(A )1/5 (B )1/9 (C )2/9 (D )1/15 (E )7/45 (2018-13)某单位为检查3个部门的工作,由这3个部门的主任和外聘的3名人员组成检查组,分2人一组检查工作,每组有1名外聘成员,规定本部门主任不能检查本部门,则不同的安排方式有()(A )6种 (B )8种 (C )12种 (D )18种 (E )36种1 2 1(2018-14)如图,圆柱体的底面半径为2,高为3,垂直于底面的平面截圆柱体所得截面为矩形ABCD,若弦AB所对的圆心角是,则截掉部分(较小部分)的体积为()(C)(D)(E)(2018-15)函数f(x)=max{x2,-x2+8}的最小值为()(A)8 (B)7 (C)6 (D)5 (E)4二、条件充分性判断:第16~25小题,每小题3分,共30分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可知有无穷多解,所以选 E。
【考点】应用题。
25.设函数 f (x) x2 ax ,则 f (x) 最小值与 f ( f (x)) 的最小值相等 (1) a 2 (2) a 0
【答案】(D)
【解题过程】 f (x) x2 ax 与 f [ f (x)] x2 ax 2 a x2 ax 最小值相等,又知当 x a 时, 2
(1) | a b | 1 a2
(2) | a b | 1 a2
【答案】(A) 【解题过程】要使圆与直线不相交,两者的关系是相离的,即圆心到直线的距离大于圆的半径。圆
心为(0,1),半径为 1,直线方程的一般形式为 x ay b 0 ,则 d
a b 1。 1 a2
【考点】解析几何问题。 22.如甲公司年终奖总额增加 25%,乙公司年终奖减少 10%,两者相等,则能确定两公司的员工人数
6.6 张不同卡片两张一组分别装入甲、乙、丙 3 个袋中,指定两张要在同一组,不同装法有( )
种
A.12
B.18
C.24
D.30
E.36
【答案】(B) 【解题过程】 C24C22 3 2 1 18 。
2
【考点】分步计数原理和分组分排问题。
7.四边形 A、B、C、D 是平行四边形,A2B2C2D2 是 A1B1C1D1 四边的中点,A3B3C3D3 是 A2B2C2D2 四 边的中点,依次下去,得到四边形序列 AnBnCnDn(n=1,2,3,…)。设 AnBnCnDn 面积为 Sn,且 S1=12, 则 S1+S2+S3+…=( ) A.16 B.20 C.24 D.28 E.30
(A)条件(1)充分,但条件(2)不充分 (B)条件(2)充分,但条件(1)不充分 (C)条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分 (D)条件(1)充分,条件(2)也充分 (E)条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
16.
{an
}
为等差数列,则能确定a 1
【答案】(A)
【解题过程】设甲、乙、丙三人的年收入分别为 a, b, c ,则 b2 ac 。对于条件(1),由 b ac a c 2
可得,当 a c 的值确定时,即可确定 b 的最大值,充分;对于条件(2),已知 a c 的值,则 b 的
值是确定的,不充分。 【考点】均值不等式问题。
f (x) 取 得 最 小 值 为 a 2 a a , 由 整 体 性 可 知 当 x2 ax a 时 ,
2 2
2
f [ f (x)] a 2 a a 等于 f (x) 。即 x2 ax a 有根,由根的判别式 a2 2a 0 可
A. π 3 B. π 6 C. π 3 3 2
D. 2π 3 3
E. π 3
【答案】(D)
【解题过程】截掉部分的底面积为 1 π 22 3 22 2 π 3 ,体积等于底面积乘以高(高为 3),
6
4
3
可得体积为 2π 3 3 。
【考点】立体几何问题。
15.羽毛球队 4 名男运动员 3 女足动员,从中选出 2 对参加混双比赛,不同选派方式有(
总平均年龄为 32 3 27 2 30 。 5
【考点】平均值问题。
3.某单位分段收费收网站流量(单位:GB)费:每日 20(含)GB 以内免,20 到 30(含)每 GB 收 1
元,30 到 40(含)每 GB 3 元,40 以上每 GB 5 元,小王本月用 45GB 该交费( )元
A.45
的 3 名人员再进行分配共有 3×2×1=6 种方法,由分步原理知共有 12 种方法。
【考点】全错位排列,分步计数原理。 13.从标号 1 到 10 中的 10 张卡片中随机抽 2 张,而它们的标号之和能被 5 整除的概率为( )
1
1
2
2
7
A.
B.
C.
D.
E.
5
9
9
15
45
【答案】(A)
【解题过程】从 10 张卡片中选 2 张,共有 C120 45 ,分母为 45;分子为两张卡片上的数字之和被 5
之比 (1)甲公司的人均年终奖与乙公司相同 (2)两公司的员工数之比与两公司年终奖总额之比相等
【答案】(D)
【解题过程】设去年甲乙两公司的年终奖总额分别为 a, b ,由题意知 25%a 10%b a : b 2 : 5 , 而今年的年终奖总额之比为125%a : 90%b 125 2 : 90 5 ,比值确定。对于条件(1),人均年
a 2
a 的值 9
(1)已知 a1 的值
(2)已知 a5 的值
【答案】(B)
【解题过程】对于条件(1),显然不充分;对于条件(2), S9 9a5 ,故充分。
【考点】等差数列问题。
17.设 m, n 为正整数,则能确定 m n 的值 (1) 1 3 1 mn
(2) 1 2 1 mn
【答案】(D)
E.0.6
【答案】(C)
【解题过程】通过分析,甲要赢得比赛,必须在第二和第三局全胜,概率为 0.6×0.6=0.36。 【考点】概率的独立性。
9.圆 C : x2 ( y a)2 b ,若圆 C 在点(1, 2)处的切线与 y 轴交点为(0, 3),则 ab =( )
A.-2
B.-1
C.0
【答案】(E)
1y 1
【答案】(A)
x y 2 x2 2xy y2 2 x2 y2 4
【解题过程】对于(1),
,条件(1)充分;对于条件(2),
x y 2.
取 x 为 10, y 为 1/10,而 x y 10 ,条件(2)不充分。
A.19
B.18
C.24
D.36
E.72
【答案】(D)
)种
【解题过程】从 4 名男运动员和 3 名女运动员各选取 2 名共有 C24 C32 中方法,再配成两对,共有 2
种选择,故有 C24 C32 2 36 种方式。
【考点】分步计数原理。
二、条件充分性判断:第 16~25 小题,每小题 3 分,共 30 分。要求判断每题给出的条件(1)和条 件(2)能否充分支持题干所陈述的结论。A、B、C、D、E 五个选项为判断结果,请选择一项符合 试题要求的判断,在答题卡上将所选的字母涂黑。
整除,通过穷举法共有{1,4},{1,9},{2,3},{2,8},{3,7},{4,6},{5,10},{7,8},{6,9}共 9 组数据
能被 5 整除。
【考点】古典概率问题。
14.圆柱体底面半径为 2,高为 3,垂直于底面的平面截圆柱体所得截面为矩形 ABCD,若弦 AB 所对
圆心角是 π ,则截去部分(较小那部分)体积为( ) 3
可得 r 1,圆的面积为 π 。
【考点】平面几何求面积问题。
5.实数 a, b 满足
,
,则 a2 b2 ( )
a3 b3 26 a b 2
A.30B.22 C.15
D.13
E.10
【答案】(E)
【解题过程】由已知条件可知 a 3, b 1,则 a2 b2 10 。
【考点】整式分式问题。
2018 年攻读工商管理硕士学位全国联考数学真题
一、问题求解:本大题共 15 小题,每小题 3 分,共 45 分。下列每题给出的五个选项中,只有一项
是符合试题要求的。请在答题卡上将所选的字母涂黑。
1.学科竞赛设一、二、三等奖,比例 1:3:8,获奖率 30%,已知 10 人已获一等奖,则参赛人数为( )
【解题过程】对于条件(1),只有 m 2, n 6和m 4, n 4 两个解,故 m n 8 ,充分;对于
条件(2),只有 m 2, n 4和m 3, n 3 两个解,故 m n 6 ,充分。
【考点】整除问题。 18.甲、乙、丙 3 人年收入成等比,则能确定乙的年收入最大值
(1)已知甲、丙两人年收入之和 (2)已知甲、丙两人年收入之积
【考点】函数问题。
12.某单位为检查 3 个印前工作,由这 3 个部门主任和外聘 3 名人员组成检查组,每组 1 名外聘,规 定本部门主任不能检查本部门,则不同的安排方式有( )
A.6 种
B.8 种
C.12 种 D.18 种
E.36 种
【答案】(C)
【解题过程】3 个部门的主任均不能够担任本部门的检查工作,全错位排列,共有 2 种方法,外聘
终奖相同,那么人数之比就等于年终奖总额之比,充分;对于(2),员工人数之比等于年终奖总额 之比,充分。 【考点】比例问题 23.已知点 P(m,o),A(1,3),B(2,1),点(x,y)在△PAB 上,则 x-y 的最小值与最大值分别为-2 和 1
(1)m≤1 (2)m≥-2 【答案】(C)
【解题过程】通过画图可以得出,当 2 m 1 时,结论成立。
【考点】线性规划问题。 24.甲购买了若干 A 玩具,乙购买了若干 B 玩具送给幼儿园,甲比乙少花了 100 元,则能确定甲购买 的玩具件数
(1)甲与乙共购买了 50 件玩具 (2)A 玩具的价格是 B 玩具的 2 倍 【答案】(E)
【解题过程】显然单独均不成立,联合考察。设 A、B 玩具数量分别为 x,y,A 玩具的价格 为 a,则
女员工年龄(岁) 23 25 27 27 29 31
据表中数据统计,该公司男员工的平均年龄与全体员工平均年龄分别是( )
A.32,30 B.32,29.5 C.32,27
D.30,27
E.29.5,27
【答案】(A)
【解题过程】由表可知,男员工的平均年龄=32,女员工的平均年龄=27,男女员工人数之比=9:6=3:2,
A.70
