2-冷却、形核与凝固
液固相变的热力学基础

液固相变的热力学基础- -金属有液态转变为固态的过程称为凝固。
由于凝固后的固态金属通常是晶体,所以讲这一转变过程称之为结晶。
一般的金属制品都要经过熔炼和铸造,也就是说都要经历由液态转变为固态的相变过程。
1.1 凝固过程的宏观现象1.1.1 过冷现象金属在凝固之前,温度连续下降,当液态金属冷却到理论凝固温度Tm时,并未开始凝固,而是需要继续冷却到Tm之下的某一温度Tn,液态金属才开始凝固。
金属的实际温度Tn与理论凝固温度Tm之差,称为过冷度,以ΔT表示,ΔT=Tm-Tn。
过冷度越大,则实际凝固温度越低。
过冷度随金属的本性和纯度的不同,以及冷却速度的差异可以在很大的范围内变化。
今属不同,过冷度的大小也不同;金属的纯度越高,则过冷度越大。
当以上两因素确定之后,过冷度的大小主要取决于冷却速度,冷却速度越大,则过冷度越大,即实际凝固温度越低。
反之,冷却速度越慢则过冷度越小,实际凝固温度越接近理论凝固温度。
但是,不管冷却速度多么缓慢,也不可能在理论凝固温度进行凝固。
对于一定的金属来说,过冷度有一最小值,若过冷度小于此值,凝固过程就不能进行。
1.1.2 凝固潜热一摩尔物质从一个相转变为另一个相时,伴随着放出或吸收的热量称为相变潜热。
金属熔化时从固相转变为液相是要吸收热量,而凝固时从液相转变为固相则放出热量,前者称为熔化潜热,后者称为凝固潜热。
当液态金属的温度到达凝固温度Tn时,由于凝固潜热的释放,补偿了散失到周围环境的热量,所以冷却过程中出现了温度恒定的现象,温度恒定的这段时间就是凝固过程所需要的时间,凝固过程结束,凝固潜热释放完毕,温度才开始继续下降。
另外,在凝固过程中,如果释放的凝固潜热大于向周围环境散失的热量,温度将会上升,甚至发生已凝固的局部区域的重熔现象。
因此,凝固潜热的石方和散失,是影响凝固过程的一个重要因素。
1.2 金属凝固的微观过程凝固过程是如何进行的?它的微观过程怎样?多年来,人们致力于研究解决这些疑问,关于凝固过程的研究人们做了大量的工作,取得了很多卓有成效的研究结果。
第一章至第七章阶段测验A卷参考答案(李泽亮等同学整理)
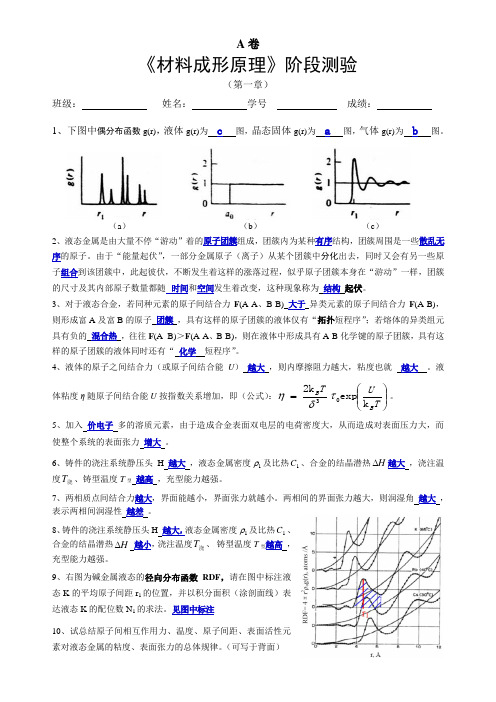
《材料成形原理》阶段测验(第一章)班级:姓名:学号成绩:1、下图中偶分布函数g(r),液体g(r)为c图,晶态固体g(r)为a图,气体g(r)为b图。
(a)(b)(c)2、液态金属是由大量不停“游动”着的原子团簇组成,团簇内为某种有序结构,团簇周围是一些散乱无序的原子。
由于“能量起伏”,一部分金属原子(离子)从某个团簇中分化出去,同时又会有另一些原子组合到该团簇中,此起彼伏,不断发生着这样的涨落过程,似乎原子团簇本身在“游动”一样,团簇的尺寸及其内部原子数量都随时间和空间发生着改变,这种现象称为结构起伏。
3、对于液态合金,若同种元素的原子间结合力F(A-A、B-B) 大于异类元素的原子间结合力F(A-B),则形成富A及富B的原子团簇,具有这样的原子团簇的液体仅有“拓扑短程序”;若熔体的异类组元具有负的混合热,往往F(A -B)>F(A-A、B-B),则在液体中形成具有A-B化学键的原子团簇,具有这样的原子团簇的液体同时还有“化学短程序”。
4、液体的原子之间结合力(或原子间结合能U)越大,则内摩擦阻力越大,粘度也就越大。
液体粘度η随原子间结合能U按指数关系增加,即(公式):⎪⎪⎭⎫⎝⎛=TUTBBkexpk23τδη。
5、加入价电子多的溶质元素,由于造成合金表面双电层的电荷密度大,从而造成对表面压力大,而使整个系统的表面张力增大。
6、铸件的浇注系统静压头H越大,液态金属密度1ρ及比热1C、合金的结晶潜热H∆越大,浇注温度浇T、铸型温度T型越高,充型能力越强。
7、两相质点间结合力越大,界面能越小,界面张力就越小。
两相间的界面张力越大,则润湿角越大,表示两相间润湿性越差。
8、铸件的浇注系统静压头H越大,液态金属密度1ρ及比热1C、合金的结晶潜热H∆越小,浇注温度浇T、铸型温度T型越高,充型能力越强。
9、右图为碱金属液态的径向分布函数RDF,请在图中标注液态K的平均原子间距r1的位置,并以积分面积(涂剖面线)表达液态K的配位数N1的求法。
金属凝固原理复习大纲

金属凝固原理复习大纲绪论1、凝固定义宏观上:物质从液态转变成固态的过程.微观上:激烈运动的液体原子回复到规则排列的过程。
2、液态金属凝固的实质:原子由近程有序状态过渡为长程有序状态的过程液态金属的结构特征:“近程有序”、“远程无序”组成:液态金属是由游动的原子团、空穴或裂纹构成3、液态金属的性质:粘度和表面张力粘度的物理意义:单位接触面积,单位速度梯度下两层液体间的内摩擦力粘度的本质上是原子间的结合力影响液体金属粘度的主要因素是:化学成分、温度和夹杂物表面张力的物理意义:作用于表面单位长度上与表面相切的力,单位N/m影响液体金属表面张力的主要因素是:熔点、温度和溶质元素。
取决于质点间的作用力4、液体结构的特性:近程有序和远程无序晶体:凡是原子在空间呈规则的周期性重复排列的物质称为晶体。
单晶体:在晶体中所有原子排列位向相同者称为单晶体多晶体:大多数金属通常是由位向不同的小单晶(晶粒)组成,属于多晶体。
吸附是液体或气体中某种物质在相界面上产生浓度增高或降低的现象。
金属从液态过渡为固体晶态的转变称为一次结晶金属从一种固态过渡为另一种固体晶态的转变称为二次结晶当向溶液中加入某种溶质后,使溶液表面自由能降低,并且表面层溶质的浓度大于溶液内部深度,则称该溶质为表面活性物质(或表面活性剂),这样的吸附称为正吸附.反之,如果加入溶质后,使溶液的表面自由能升高,并且表面层的溶质浓度小于液体内部的浓度,则称该溶质为非表面活性物质(或非表面活性剂),这样的吸附为负吸附第一章凝固过程的传热1、凝固过程的传热特点:“一热、二迁、三传”“一热”指热量的传输是第一重要;“二迁”指存在两个界面,即固-液相间界面和金属-铸型间界面。
“三传”指动量传输、质量传输和热量传输的三传耦合的三维热物理过程。
2、金属型特点:具有很高的导热性能;非金属型铸造特点:与金属相比具有非常小热导率,故凝固速度主要取决于铸型的传热性能。
铸型外表面温度变化不大,故可把铸型看成是半无限厚的。
材料凝固理论

式中:ΔGm —单位体积固、液自由能差;V —晶核体积;σLS—固、液界 面张力;A —晶核表面积。
8
若假定晶核为球形,则上式
为:
4 3 G自 r Gm 4r 2 LS 3
式中:r - 晶核球半径; ΔGm = ΔSmΔT
若将一定的物理化学参数代
入上式,可得到ΔG-r 关系曲 线。
子碰撞而弹回液相中的几率很小,生长过程不需要很大的过冷度。另外, 对于粗糙界面来说固相和液相之间在结构与键合能力方面的差别很小,
容易在界面过渡层内得到调节,因此动力学能量障碍较小,它不需要很
大的动力学过冷度来驱动新原子进入晶体,并能得到较大的生长速率。
27
2、侧面长大机制(依靠台阶生长)
当晶体在由小平面组成的光滑平面上生长时,不象在粗糙界面上 生长那么容易。因为光滑界面几乎没有显露给液相原子的键合位置, 所以晶体的生长要靠台阶来实现。 根据台阶来源不同,侧面长大又分为二维晶核台阶和缺陷形成台 阶长大两种。对于二维晶核台阶长大,首先要求在光滑界面上产生二
2 LS r S m T
* 3 LS 16 * G自 f ( ) 2 3 (S m T )
式中:
12
影响非自发形核能力的因素: 衬底对金属液的润湿性:润湿 性越好,形核能力越强(参考前 图)。 形核率:即单位时间单位体积金 属液形成的晶核数。形核率越高, 形核能力越强。衬底越凹,形成临 界晶核所包容的原子数越少,形核 能力越强。 右图显示了不同曲率衬 底上形核的情况,由图可知,凸面 上形成的晶核原子数最多,平面次 之,凹面上最少。 衬底粗糙度:粗糙度越大,形 核能力越强。衬底粗糙度实际是通 过其曲率及凹向起作用的。
S S
kT ( ) k ( ) kT H 0 ( ) S m ( ) k kTm 即与熔融熵值SkS 成正比 与熔融熵值 成正比 即
大学材料科学基础第六章材料的凝固

液- 固界面的微观结构
(a) 粗糙界面
(b) 光滑界面
宏观上看,两者却反过来: 光滑界面是由多个小平面组成(又称小平面界面、结晶学 界面),是不平整的; 粗糙界面却是平整光滑的。
常见金属的液固界面为粗糙界面,一些非金属、亚 金属、金属化合物的液固界面多为光滑界面。
动态过冷度比形核过冷度小。不同类型界面, 其长大机制不同。具有粗糙界面的物质,△Tk 仅为 0.01~0.05℃,具有光滑界面的物质,△Tk约为1~ 2℃。 晶体生长时液- 固界面的微观结构 (Microstructure of the solid-liquid interface)
1.粗糙界面 从微观尺度观察时,这种界面上并存在着厚度为几个原 子间距的过渡层。从原子尺度观察,这种界面粗糙的, 高低不平的(又称非小平面界面、非结晶学界面)。 2.光滑界面 从微观尺度观察时,界面两侧的固液两相是截然分开的; 从原子尺度观察,这种界面是光滑平整的。
同样,把临界晶核半径代入总自由能变化 的表达式,可求出形核功:
ΔGk 非 =
16 πσ
3 2
3( ΔGV )
(
2-3 cos θ + cos3 θ 4
)
ΔGk 非 / ΔGk均 = (
2-3 cos θ + cos3 θ 4
)
θ只能在0 ~π间变化,cosθ相应在0 ~ 1之间变化。
ΔGk 非 / ΔGk均 ≤ 1
过冷现象 冷却曲线上出现平台时,液态金属正在结 晶,这时对应的温度就是纯金属的实际结晶温度。 实验表明,纯金属的实际结晶温度总是低于其平 衡结晶温度(熔点),这种现象称为过冷。两者之 间的差值叫过冷度,过冷是金属结晶的必要
条件。
△T = Tm - Ts
第三章金属凝固热力学与动力学

GV 4 3 GV G V A LC r 4 r 2 LC VS 3 VS GV H T / Tm
临界形核半径
2 LC 2 LCTm r GV H T
SL Sc Lc cos
球冠状晶核的体积V冠为
V冠 (r sin ) d (r r cos )
0
2
r3
3
(2 3cos cos 3 )
晶核与液相的接触面积SLc为
SLC 2 r sin (rd ) 2 r 2 (1 cos )
。
二、形核率
形核率是单位体积中、单位时间内形成的晶核数 目。 形核率I:
GA G I C exp( ) exp( ) KT KT 3 16 LC Tm 2 GA I C exp( ) exp( ( ) ) KT 3KT H T
*
形核率
是指单位时间内单位体积液体中形成晶 核的数量。用N=N1*N2表示。
粗糙界面与光滑
界面是在原子尺
度上的界面差别,
注意要与凝固过
程中固-液界面 形态差别相区别, 后者尺度在μ m 数量级。
2.影响因素
如何判断凝固界面的微观结构?
—— 这取决于晶体长大时的热力学条件。
设晶体内部原子配位数为ν,界面上(某一 晶面)的配位数为η,晶体表面上N个原子 位置有NA个原子(
x→0或1处(晶体表面位置
已被占满)。有机物及无 机物属此类; =2~5的物质,常为多种 方式的混合,Bi、Si、Sb
凝固过程的基本原理

第七页,共57页
1. 相变驱动力
系统的自由能随温度的变化关系:
系统的自由焓(G)可表示为:
G=H-TS
H----热焓,S----熵,T----绝对温度
自由焓 G也称等压位,而对应的为自由能F,也称等容位,
F = u- TS,又:G = H-TS = u + PV- TS,
当pV很小时,G =u –TS=F,故有时粗略地将自由焓称为自由能 由G= u+PV-TS 可得:dG = du-TdS -SdT+ PdV + VdP du =δq -δA
型。 Aziz模型:假设凝固界面在推进过程中液相一侧的溶质和溶 剂原子首先在瞬间内全部发生凝固,形成过饱和层,然后,
在非平衡驱动力的作用下,溶质原子向液相反向扩散,直到 下一层原子发生凝固,过量的溶质被保留下来,形成非平衡
溶质分配。 故: ka可通过对凝固界面层中扩散方程的求解确定。
21
第二十一页,共57页
wS=wL*
a)平衡凝固
b)近平衡凝固
c)快速凝固
wL*,wS*:平衡凝固条件下界面上液、固侧溶质分配系数; wLa*,wSa*:非平衡条件下界面上液、固侧溶质分配系数;
16
第十六页,共57页
(2)平衡溶质分配系数k0
极其缓慢条件下, 界面附近溶质迁移、扩散充分,平衡条件下,固相溶
质分数与液相溶质分数之比定义为平衡溶质分配系数k0
平衡溶质分配系数k0、
有效溶质分配系数ke、
非平衡溶质分配因数ka 。
凝固过程溶质分配的平衡条件指:凝固界面上溶质迁移的平衡及固相和液相内部 扩散的平衡。
15
第十五页,共57页
随凝固速率的变化,凝固界面附近溶质分配呈现3种
第一章凝固热力学 - 材料科学和工程

材料成形技术基础
第二章 材料凝固理论 主要内容: • 材料凝固概述 •凝固的热力学基础 •形核 •生长 •溶质再分配 •共晶合金的凝固 •金属及合金的凝固方式 •凝固成形的应用
第一节 材料凝固概述
一、凝固成形的基本问题和发展概况 1、基本问题: 凝固组织的形成与控制 铸造缺陷的防止与控制 铸件尺寸精度与表面粗糙度控制
( S H
)p
1 T
( S T
)p
1 T
( H T
)p
Cp T
dG dH TdS
C
p
(H T
)p
( T 2G 2)p( T S)pC Tp0
等压条件下,体系自由能随温度升高而 降低,且液态金属自由能随温度降低的趋势 大于固态金属。
三、自发过程 判据一、Helmholtz自由能最低原理:
等温等容条件下体系的自由能永不 增大;自发过程的方向力图减低体系的 自由能,平衡的标志是体系的自由能为 极小。 判据二、Gibbs自由能判据:
等温等压条件下,一个只做体积功 的体系,其自由能永不增大;自发过程 的方向是使体系自由能降低,当自由能 降到极小值时,体系达到平衡。
根据力的平衡原理:
SG LS LG cos cos SG LS
LG
,cos0,900,表现为润湿情况
SG
LS
,cos0,900,表现为不润湿
SG
LS
接触角 又称润湿角。
第三节 形核
一、凝固的热力学条件
等压条件下有:
dG Vdp SdT dH TdS Vdp
(G T)p S0
又:
控制铸件的凝固组织是凝固成 形中的一个基本问题。目前已建立 了许多控制组织的方法,如孕育、 动态结晶、定向凝固等。
第04章 凝固与结晶

温度降低,粘度不断增加,在到达结晶转变温度前,粘度增加 到能阻止在重力作用物质发生流动时,即可以保持固定的形状, 这时物质已经凝固,不能发生结晶。例如玻璃、高分子材料。
3. 熔融液体的冷却速度:冷却速度快,到达结晶温度原子来不
及重新排列就降到更低温度,最终到室温时难以重组合成晶体, 可以将无规则排列固定下来。金属材料需要达到106℃/s才能获 得非晶态。
第一节 晶体形成的一般过程
第二节 形核
一、自发形核
存在过冷的液体,依靠自身的原子运动可 能形成晶核,这种方式称为自发形核。
1. 能量变化
在一定的过冷度下,液体中若出现一固 态的晶体,该区域的能量将发生变化,一方 面一定体积的液体转变为固体,体积自由能 会下降,另一方面增加了液-固相界面,增 加了表面自由能,因此总的吉布斯自由能变
在一般生产过程的冷却条件下,金属材料凝固为晶体,这时的凝固过 程也是结晶过程。
第一节 晶体形成的一般过程
二、结晶的热力学条件
结晶过程不是在任何情况下都 能自动发生。自然界的一切自发转 变过程总是向着自由能降低的方向 进行。在单一的组元情况下:
G H-TS dG Vdp-SdT
在恒压下,dp = 0,因此
第三节 晶核的长大
四、负温度梯度下晶体的长大
关于树枝晶:按 树枝方式生长的 晶体称为树枝晶, 先凝固的称为主 干,随后是分支, 再分支。值得指 出的是:
①纯净的材料结晶完毕见不到树枝晶,但凝固过程中一 般体积收缩,树枝之间若得不到充分的液体补充,树枝 晶可保留下来; ②生长中晶体分支受液体流动、温差、 重力等影响,同方向的分支可能出现小的角度差,互相 结合时会留下位错; ③或材料中含有杂质,在结晶时固 体中的杂质比液体少,最后不同层次的分枝杂质含量不 相同,其组织中可见树枝晶。
材料科学基础第三章

• 3.1.2 金属结晶的宏观现象
• 金属结晶伴随着一系列宏观特征的改变, 如结晶潜热的释放,融化熵的变化等。研 究这些宏观特征的变化是研究金属结晶过 程的重要手段。
• 3.1.2.1 冷却曲线与金属结晶温度:用热分 析装置将金属融化后缓慢降温,每隔一定 时间记录一次温度,绘制成温度-时间关系 曲线,称为冷却曲线。这种测定冷却曲线 的方法叫热分析法。
• 液态金属在达到某一过冷度之前基本不形 核,而在有效过冷度ΔΤP时形核率骤增。
• 金属的晶体结构简单,容易结晶。在达到 很大过冷度前已结晶完毕,无曲线后半部。
• 通常液态金属是不纯的。凝固总是从杂质 表面开始,所需要的过冷度很低,称非均 匀形核。将液态金属碎裂成直径10至50μm 的小液滴,则凝固按均匀成核方式进行。 纯金属均匀形核的有效过冷度为 ΔΤp0.2Tm(绝对温度)。
• 2) 拓扑无序模型:一些近程有序的基本几 何单元密集无序堆垛或随机密堆垛。
• 原子处于永恒的热运动。液态中的近程有 序结构只能维持极短时间(~10-11s)即消散, 同时又有新结构出现。形成结构起伏或叫 相起伏。
• 相起伏现象是液态结构的重要特征之一, 是产生晶核的基础。
• 规则排列结构比无规排列结构稳定。在过 冷液体中,短程有序结构越大越稳定,而 稳定结构才可能成为晶核。因此称过冷液 体中尺寸较大的近程规则排列结构为晶胚。
• 3.3.1.1 晶胚形成时的能量变化:
• 体积自由能:晶胚内部原子因规则排列而 低于液相原子自由能的差值称为体积自由 能。其值的降低为结晶动力。
• 表面自由能:晶胚表面原子因受力不均匀而偏离 平恒位置,其自由能反而高于液态原子,其差值 称为表面自由能。其值的增高为结晶阻力。
第三章 凝固过程的基本原理

➢ 当T<Tm时,GL>GS,固相稳定;
➢ 当T>Tm时,GL<GS,液相稳定; 当温度高于熔点或低于熔点时,
△T
△G即为相变的驱动力,
❖ 过冷度
在Tm以下温度时:一克分子物质由液相转变为固相自由能(焓)的变化为:
△GV = GS-GL=(HS-TSS)-(HL-TSL) = ( HS - HL)-T(SS-SL) = △H-T△S △H、△S均为固、液两相的克分子焓和克分子熵的差额,温度的函数,
➢ 凝固过程重要的伴生现象,影响凝固组织
➢ 描述溶质再分配的关键参数:
k ws
溶质分配系数 :
wL
平衡条件下,ws 、 wL由固相线和液相线确定。然而,实 际条件下,平衡是很难的,故引入近平衡凝固、非平衡
凝固分配系数。因此,溶质分配系数有三个层次:
➢ 平衡溶质分配系数k0、 ➢ 有效溶质分配系数ke、 ➢ 非平衡溶质分配因数ka 。 ❖ 凝固过程溶质分配的平衡条件指:凝固界面上溶质迁移的平衡及固相
多元系的凝固(可 用二元系的凝固特 征分析)
因此,对凝固过程基本原理的研究通常以二元系为对象。 在实验和计算的基础上建立了大量的二元相图,为凝固 分析奠定了基础
2
所有二元相图都是由共晶、偏晶、包晶及固溶体四种基本相 图所构成的
单相合金凝固是最典型的, 除共晶点和偏晶点外,其它成分 合金在开始凝固时仅有一个相析 出。
GL VLP SLTp GS VS P SS Tp
△Tp-----因压力改变引起的平衡熔点的变化。
Tp TmV
p
H m
通常金属(VS-VL)=△V<0,则压力升高,平衡熔点上升.而△V>0,的金属 Sb,Bi压力升高,平衡熔点降低.通常压力改变时,熔点的变化很小, 10-2℃/大气压,故生产中靠改变压力来提高过冷度细化晶粒是很困难的。 熔体中导入超声波,产生空化作用,空穴破灭时,产生很大压力,使熔点上升 几十度.
2纯金属凝固-形核

2017/5/4
9
形核功的来源
类似结构起伏,液体金属的微观区域具有能量起 伏的动态平衡特点。 高能原子附上低能量的晶胚或相邻晶胚互相拼接 长大时,可以释放一部分能量,为形核时所需要 的形核功提供能量,形核功依靠液体本身存在的 能量起伏供给。
*
θ=0时,
ΔGS* =0 ,
固体杂质相当于 现成的晶核,不 需要额外形核功。
0<θ<π时, ΔGS*<ΔG*, 形核功减小。
θ=π时,
ΔGS*=ΔG*,
固体杂质表面不 起促进晶胚形核 的作用
22
2017/5/4
非均匀形核的形核率影响因素
过冷度ΔT的影响
1 非均匀形核时在较小的ΔT下可获得较高的形核率; 2 随ΔT增大,形核速率将增大,极值,下降,停止
2017/5/4 16
2.2 非均匀形核
纯金属中含有许多杂质原子,凝固时一般与模 壁有接触,金属实际凝固时都是非均匀形核, 所需要的过冷度一般不超过20℃,远低于均匀 形核时的过冷度
Zr
纯镁结晶时的晶核及晶粒
2017/5/4
17
非均匀形核示意图
•在S相的基底上形成球冠状的α晶核,曲率半径为r,晶核表面 与基底面的接触角为θ(称为润湿角) •σlS,σlα和σαs分别表示液相L与基底S、液相L与晶核α、晶核α 和基底S之间的界面能,在纯金属中用表面张力表示
(12)
2017/5/4
19
晶核α 的体积
晶核α 的表面积(球冠)
3 2 3 cos cos V r 3 3
金属凝固原理--第八章快速凝固

13
§6.1 引言 快速凝固:在极快的冷却速率下完成由液相到固相的相变过 程,从而获得常规凝固方法所无法得到的合金成分、相组成 和显微结构。
获得独特的微观组织、结构特征
所制备材料具有优异的使用性能 (如:力学、物理、化学性能等)
14
§6.1 引言 三. 本章学习内容
(1)
(2)
(3)
(4)
快
速
快速凝固 快速凝固 快速凝固
快速凝固
凝
原理、技术 热力学与 显微结构 晶态(微/纳米晶)
固
及 传热特点
动力学
特征
准晶/非晶 材料及应用
15
§6.2 快速凝固原理、技术及其传热特点—快速凝固原理
快速凝固的内涵
定义1:从液态到固态的冷却速度大于某一临界冷却速率的 凝固过程(103 K/s)。
定义2:由液相到固相的相变过程进行得非常快,从而获得 普通铸件和铸锭无法获得的成分、相结构和显微结构的凝固 过程。
27
§6.2 快速凝固原理、技术及其传热特点—快速凝固技术
02
急冷凝固技术—雾化技术—雾化法
基本原理:以水、气作为冷却介质(水雾化 /气雾化),冲击金属流,冷却速率可达104~ 107 K/s 。
特点:(1)可以大批量生产预合金粉末; (2)粉体可以通过各种不同的固结方法(粉 末冶金方法)加工成块体坯料或成形零件。
§6.6 非晶态合金
3
§6.1 引言
普通凝固过程存在的问题:
冷却速度慢 凝固速度小
常规工艺下金属的冷却速度一般不会超过102 ℃/S
大型砂型铸件及铸锭凝固时的冷却速度约为:10-6 ~10-3 ℃/S;中等铸件及铸锭约为10-3~100 ℃/S; 薄壁铸件、压铸件、普通雾化约为100~102 ℃/S
共晶合金的凝固过程涉及到两个固相的竞争形核及协同生长

快速凝固Co-Sn 合金的组织形态与电学特性共晶合金的凝固过程涉及到两个固相的竞争形核及协同生长, 受冷却速率、过冷度、形核条件和重力水平等因素的制约. 在平衡凝固条件下, Co-Sn共晶合金的凝固组织通常为层片状共晶, 而在非常规凝固条件下, 两相协同生长模式被打破, 呈现出竞争生长的态势, 从而导致组织形貌的显著变化[1~6],譬如, 随着过冷度的增大, 凝固组织由规则层片共晶向不规则共晶转变[4]。
急冷技术可使液态金属获得较大的冷却速率, 实现瞬间形核、生长, 从而获得组织精细、偏析程度小的复相微晶材料及亚稳相结构. 显著细化的组织和特异的相结构必然引起合金物理化学性能的变化. 晶体取向、缺陷、晶界及表面状态对合金的电阻率有着显著的影响[7~12]. 因此, 快速凝固组织形成规律和合金电学特性的研究是材料科学和凝聚态物理共同关注的重要研究课题之一. 本文采用单辊实验技术研究了亚共晶和共晶Co-Sn合金的急冷快速凝固行为和组织特征, 实验测试了合金条带的电阻率, 并对合金偏析行为、组织形态及电阻率与冷却速率之间的相关规律进行了理论探索.1 实验方法Co-20%Sn(质量分数)和Co-34.2%Sn合金均用高纯Co(99.999%)和Sn(99.999%)在超高真空电弧炉中熔配而成. 样品质量约为 1.2 克. 实验之前, 把表面洁净的样品放入底部开有Ø0.8 mm×10 mm 喷嘴的Ø16 mm×150 mm 石英试管中, 再将试管置入配有真空罩的辊轮顶部, 抽真空至1.2×10−2 Pa 后反充高纯He(99.995%)气至1 个大气压. 反复“抽真空-充He 气”3~5 次之后, 使用高频感应熔炼设备加热样品, 使其熔化并过热100 K 以上, 保温3~5 min 后, 向石英试管中吹入高压Ar 气. 液态合金在高压下呈连续液流喷射到高速旋转的Cu 辊表面, 急冷凝固成合金条带. 实验过程中辊面线速度控制在20~52m/s 之间.合金条带经镶嵌、抛光和浸蚀处理后, 用ARMRAY-1000B 型扫描电镜(SEM)分析合金的组织形态, 使用能谱仪(EDS)分析合金相微区化学成分. 所用浸蚀剂为“30 mL 王水+ 5 g CuCl2 + 30 mL H2O”溶液. 采用经典的SZ-82型数字式四探针测试仪测定合金条带的电阻率.2 实验结果与分析讨论合金成分在Co-Sn二元合金相图[4]中的位置如图 1 中的箭头所示. 在平衡凝固条件下,当熔体温度下降到1588 K时, Co-20%Sn合金首先析出初生相αCo枝晶, 在到达共晶温度时αCo枝晶析出量为51.3%. 处于枝晶间隙的剩余液体在1385K下发生共晶转变, 形成由αCo 和γCo3Sn相构成的含量为48.7%的规则层片共晶组织.Co-34.2%Sn 合金则全部形成层片状两相共晶组织.在共晶转变过程中, αCo 相和γCo3Sn相按比例协同生长, 两相质量分数分别为40.2%和59.8%.然而, 在急冷快速凝固条件下, 两相形核与生长条件发生了变化, 因而形成与平衡凝固组织形态迥异的快速凝固组织.图 1 两种合金成分在相图中的位置2.1 快速凝固组织特征2.1.1 Co-20%Sn 亚共晶合金的组织形态Co-20%Sn 亚共晶合金在不同辊速下的快速凝固组织如图2 所示. 图中黑色相为αCo, 灰白色相为γCo3Sn. 初生αCo相按枝晶方式生长, γCo3Sn相分布其间. 图2(a)是辊速为20 m/s的快速凝固组织. 图中, 条带组织沿厚度方向明显分为三个晶区: 近辊面激冷等轴晶区(Ⅰ区)、中部柱状晶区(Ⅱ区)和自由面粗大等轴晶区(Ⅲ区). Ⅰ区金属熔体因受铜辊的激冷作用最强, 形核率大, 凝固组织以均匀细小的等轴晶为特征. Ⅱ区因受辊轮的单向吸热, 在离开辊面的方向上形成较大的温度梯度, αCo 的生长形态以定向生长的细长柱状晶为特征.由于Ⅰ区和Ⅱ区凝固层热阻的影响, Ⅲ区的传热作用减弱, 温度梯度较中部有所减小, 该区中初生αCo 枝晶的生长方向具有明显的随机性, 凝固组织以粗大的等轴晶为特征. 图2(b)为辊速Vr=36m/s的凝固组织. 从图中可以看出, 等轴晶区扩大, 而柱状晶区明显缩小. 当Vr=52 m/s 时柱状晶区完全消失, αCo 相全部转变为细小的等轴晶组织如图2(c)示. 三个晶区的厚度D随辊速的变化趋势如图3 所示.2.1.2 Co-34.2%Sn 共晶合金的组织形态图 4 为Co-34.2%Sn 共晶合金在不同辊速下的快速凝固组织形态.从中可知, 在Vr=20~52 m/s 的范围内, 合金均获得了全部的不规则共晶组织. 同样, 由于受Cu 辊较大的急冷作用, 近辊面晶区组织细化程度非常显著. 另外, 随着冷速的增大, 不规则共晶组织得到了显著地细化, 并且在条带厚度方向上的组织均匀性也获得了明显地改善.2.1.3 冷却速率的理论计算合金条带组织的形成规律与液态合金的冷却速率密切相关. 为了建立冷却速率与辊速之间的内在联系, 将Navier-Stokes方程、连续方程和热传导方程相耦合, 对温度场和冷却速率进行了理论计算. 在模型的建立过程中, 考虑了结晶潜热、熔体粘度和密度随温度的变化以及辊轮的二维动态传热等. 动量传输和热量传输主控方程表达如下[13]具体计算方法和过程及方程说明详见文献[13]. 理论计算用物性参数见表1. 计算获得的冷却速率( T =-dT/dt)随辊速的变化关系如图 5 所示. 可见, 随着辊速的增大, 冷却速率增大. 实验过程中熔体的冷却速率在(3.0~5.0)¯106K/s 范围. 这说明冷却速率是影响合金组织形态演变的重要物理条件.2.1.4 T0 线和αCo 枝晶生长速度的理论计算在快速凝固条件下, 晶体生长速度很快, 溶质截留效应显著, 从而可大幅度地扩展合金相的固溶度, 甚至发生无偏析凝固. 非平衡凝固条件下的溶质分配系数k、液相线斜率m 和生长速度V 之间的关系为[14]式中, me 为平衡液相线斜率, m 为非平衡液相线斜率,ke 为平衡溶质分配系数, k 为非平衡溶质分配系数, V为生长速度, Vd =D0/a0 为扩散速度, a0 为原子间距, 取0.3 nm, D0 为扩散系数, 取5×10−9 m2/s, CS和CL分别为固相和液相的成分. 根据相变热力学理论, 当一定成分的合金熔体过冷至固液两相自由能相等所对应的温度T0 时, 就有可能实现无偏析凝固. 此时, 液、固两相的成分相同, 溶质分配系数k = 1. T0 线的表达式为[14]式中, Tm 为纯组元的熔点; 为界面浓度. *L C将(6)式代入(9) 式, 并令k=1, 可得Co-Sn 合金的T0 线如图1 中虚线所示. 图中, Co-20%Sn 合金对应的无偏析凝固过冷度为397 K. 理论计算表明, 本文实验过程中达到的最大过冷度仅209K, 亦即熔体的冷却速率尚未达到实现无偏析凝固所需的水平. 由于液固界面前沿溶质再分配的结果, 富Sn 的残余液体被快速生长的固液界面推移到枝晶间, 最后凝固形成晶间γCo3Sn 相.基于平衡相图, 分别将平衡条件下Co-20%Sn 合金的液/固相成分和代入(8)式, 可得ke=0.161. 并结合(7)式可求得固相成分CS 与枝晶生长速度之间的关系, 如图 6 所示. 根据EDS分析结果, Sn 在αCo中的固溶度达16.8%Sn, 相应地, αCo 枝晶的生长速度为71 m/s.2.2 合金的电阻率图7 为合金电阻率ρ随辊速的变化关系. 随着辊速的增大, 合金电阻率急剧增大. Co-20%Sn 和Co-34.2%Sn 合金的电阻率变化范围分别为34.6~93.5µΩ·cm和46.7~83.7µΩ·cm. 电阻率随辊速的变化本质上反映了组织形态对电阻率的影响. 冷速增大使凝固组织显著细化, 晶界明显增多. 根据金属薄膜F-S理论[15]和二流体模型[7], 运动的电子在薄膜表面和晶界上都会受到散射, 这将导致参与导电的有效电荷密度的降低, 从而使合金电阻率显著增大, 这便是金属薄膜电阻率尺寸效应. 然而, 由于快速凝固条带的厚度通常在几到几十微米, 远大于电子平均自由程, 即急冷合金条带实际上并不存在明显的电阻率尺寸效应. 因此, 对快速凝固合金而言, 晶界散射便成为影响合金电阻率的主导性因素. 包含体散射(声子和空位引起的散射)和晶界散射的多晶薄膜的电阻率可用Mayadas和Shatzkes[15]提出的晶界电阻率模型(M-S模型)来描述:式中, ρ0 为合金固有电阻率, l0 为电子平均自由程, r为晶界散射系数, d为晶粒尺寸(可观测量). 实验测定的亚共晶和过共晶合金的ρ0 值分别为10.22 和15.05 µΩ·cm, 晶粒尺寸随辊速的变化关系为合金的电子平均自由程取经验值l0=36.5 nm, 将其代入(11)式, 并结合(10)、(12)式对合金电阻率进行理论估算. 计算得到的不同r 值下的电阻率如图7 所示. 从图中可以看出, 电阻率对晶界散射系数十分敏感, 当r=0.992 时理论计算值与实测值吻合良好. 这说明在急冷快速凝固合金中, 晶界散射对合金的电阻率影响十分显著,并且晶界散射系数r→1.据ρg/ρ0—α曲线可对重要的物理量l0 值进行验算, 发现当r→1(取0.992)时, l0值在33.6~42.0 nm范围, 即理论计算用l0 取值合理.实际上, 液态合金在快速凝固过程中, 大的冷却速率不仅使晶粒细化, 晶界数量增多, 而且使合金相的固溶度和空位数也显著增大. 另外, 在辊轮驱动的剪应力强烈冲击下, 凝固组织中不可避免地产生各种晶体缺陷如位错、层错和孪晶等. 因此, 快速凝固合金的电阻率实际上是块体材料的电阻率与各种晶体缺陷引起的电阻率增值之和. 理论计算中r 的取值实际上综合地反映了晶界及晶体缺陷对合金电阻率的影响. 有鉴于目前尚缺乏各种晶体缺陷对合金电阻率影响的定量分析模型, 可通过合理的选取r 值, 应用M-S 模型对快速凝固合金的电阻率进行理论计算. 随着冷速的增大, 晶界、位错等晶体缺陷数量增多, 对自由电子的散射作用增强, 从而导致电阻率的显著增大.3 结论(1) 在急冷快速凝固条件下, Co-20%Sn 亚共晶合金初生αCo 相的生长形态对冷速变化十分敏感. 低冷速下, 合金条带中部会形成一定量的柱状αCo枝晶. 随着冷速的增大, 柱状晶区逐渐缩小并趋于消失, 条带组织也变得明显细化并均匀化, 以致在高冷速下形成以均匀细小的αCo 等轴晶和其间分布的γCo3Sn 相为特征的凝固组织.(2) Co-34.2%Sn 共晶合金获得了全部的不规则共晶组织. 随着冷速的增大, 共晶组织明显细化, 沿条带厚度方向的均匀性显著提高.(3) 随着冷速的增大, 晶界、位错等晶体缺陷数量增多, 对自由电子的散射作用增强, 从而导致电阻率的显著增大. 晶界散射系数r→1, 使用M-S模型可综合分析快速凝固Co-Sn 合金的电导特性.参考文献1 Xie W J, Cao C D, LüY J, et al. Levitation of iridium and liquid mercury by ultrasound. Physical Review Letters, 2002, 89(10): 104304[DOI]2 Han X J, Wang N, Wei B. Rapid eutectic growth under container-less condition. Applied Physics Letters, 2002, 81(4): 778~ 780[DOI]3 Kassner K, Misbah C. Spontaneous parity-breaking transition in directional growth of lamellar eutectic structure. Phys Rev A, 1991, 44: 6533~6543[DOI]4 Yao W J, Han X J, Wei B B. Rapid eutectic growth during free fall. Chinese Science Bulletin, 2002, 47(15): 1316~13205 Kassner K, Misbath C. Similarity laws in eutectic growth. Physi-cal Review Letters, 1991, 66: 445~448[DOI]6 Ghosh G. Coarsening kinetics of Ni3Sn4 scallops during interfacial reaction between liquid eutectic solders and Cu/Ni/Pd metalliza-tion. Journal of Applied Physics, 2000, 88(11): 6887~6896[DOI]7 Reiss G, Vancea J, Hoffmann H. Grain-boundary resistance in polycrystalline metals. Physical Review Letters, 1986, 56(19): 2100~2103 [DOI]8 Gurp G J. Resistivity, grain size, and structure of vaccum- depos-ited Co films. Journal of Applied Physics, 1975, 46(5): 1922~ 19279 Zhou Y Q, Matsubara I, Shin W, et al. Effect of grain size on electric resistivity andthermopower of (Ca2.6 Bi0.4)Co4O9 thin films. Journal of Applied Physics, 2004, 95(2): 625~628[DOI]10 Jen S U, Chen T P, Chang S. Electrical resistivity of Co-Ni-Pd al-loys. Journal of Applied Physics. 1991, 70(10): 5831~5833[DOI]11 Jacob U, Vancea J, Hoffmann H. Surface-roughness contributions to the electrical resistivity of polycrystalline metal films. Physical Review B, 1990, 41(17): 11852~11857[DOI]12 Sheng L, Xing D Y, Wang Z D. Transport theory in metallic films: Crossover from the classical to the quantum regime. Physical Re-view B, 1995, 51(11): 7325~7328[DOI]13 徐锦锋, 魏炳波. 急冷快速凝固过程中液相流动与组织形成的相关规律. 物理学报, 2004, 53(6): 1909~191514 Kurz W, Fisher D J. Fundamentals of solidification. 4th ed. Neth-erlands: Trans Tech Publications, 1998, 28~3315 Mayadas A F, Shatzkes M. Electrical-resistivity model for poly-crystalline films: the case of arbitrary reflection at external sur-faces. Physical Review, 1970, 1(4): 1382~1389与正常凝固相比:一般情况下自然冷却(冷却速度小)所得到的组织晶粒粗大,析出相较多较为复杂。
机械工程材料 第三章 材料的凝固.答案

具有共晶成分的合金称共晶合金。在共晶线上,凡
成分位于共晶点以左的合金称亚共晶合金,位于共
晶点以右的合
金称过共晶合
A
金。 凡具有共晶线
成分的合金液
L+
B
C
D
体冷却到共晶
温度时都将发
生共晶反应。
⑵ 合金的结晶过程 ① 含Sn量小于C点合金(Ⅰ合金)的结晶过程
在3点以前为匀晶转变,结晶出单相 固溶体,这种
根据组元数, 分为二元相图、三元相图和多元相图。
Fe-C二元相图
三元相图
一、二元相图的建立
几乎所有的相图都是通过实验得到的,最常用的是 热分析法。
二元相图的建立步骤为:[以Cu-Ni合金(白铜)为例] 1. 配制不同成分的合金,测出各合金的冷却曲线,
找出曲线上的临界点(停歇点或转折点)。 2. 将临界点标在温度-成分坐标中的成分垂线上。 3. 将垂线上相同意义的点连接起来,并标上相应
1、铁的同素异构转变
铁在固态冷却过程中有两次 晶体结构变化,其变化为:
1394℃
912℃
-Fe ⇄ -Fe ⇄ -Fe
-Fe、 -Fe为体心立方结构(BCC),-Fe为面心立方 结构(FCC)。都是铁的同素异构体。
-Fe
-Fe
2、固态转变的特点 ⑴形核一般在某些特定部
相图被两条线分为三 个相区,液相线以上 为液相区L ,固相线以 下为 固溶体区,两 条线之间为两相共存 的两相区(L+ )。
L
液相线 L
+
固相线
Cu
成分(wt%Ni)
Ni
A portion of the copper-nickel phase diagram for which compositions and phase amounts are determined at point B
有效形核过冷度,临界过冷度,形核过冷度之间的关系

有效形核过冷度,临界过冷度,形核过冷度之间的关系有效形核过冷度、临界过冷度和形核过冷度之间的关系1. 什么是有效形核过冷度?•有效形核过冷度,也称为“深度分析冷度”或“足元冷度”,是指液体变为固体时的温度。
在这个温度下,形成的晶体数量足够多,可以确定液体已经转变为固体。
2. 什么是临界过冷度?•临界过冷度是指超过液体的冷却温度,使液体趋于过饱和状态,此时发生形核的可能性很高。
临界过冷度可以看作是触发形核过程的温度。
3. 什么是形核过冷度?•形核过冷度是指液体的温度低于液体的饱和温度时,形成晶核所需要的过冷度。
晶核是指促使液体变成固体的微小固体颗粒。
4. 三者之间的关系及解释•有效形核过冷度与临界过冷度:–有效形核过冷度和临界过冷度之间存在关联,当液体温度降至临界过冷度以下时,会产生引起结晶的形核。
–有效形核过冷度是液体完全转变为固体的阶段,而临界过冷度是触发形核过程的温度。
–当温度低于临界过冷度时,形核过程开始发生,进一步降低温度可达到有效形核过冷度。
•有效形核过冷度与形核过冷度:–有效形核过冷度和形核过冷度之间的关系是温度的递减。
–当温度低于形核过冷度时,晶核开始形成,进一步降低温度可达到足够多的晶核形成,形成固体。
•形核过冷度与临界过冷度:–形核过冷度和临界过冷度之间的关系是温度的关联。
–当温度低于临界过冷度时,形核过程开始发生,形核过冷度则是形成晶体所需的过冷度。
综上所述,有效形核过冷度、临界过冷度和形核过冷度三者之间存在着密切的关系。
在液体冷却过程中,当温度降至临界过冷度以下时,形核过程开始发生,进一步降温可达到足够的晶核数量,即有效形核过冷度。
形核过冷度是实现液体变成固体的过渡阶段所需的温度。
5. 关于形核过冷度的重要性•形核过冷度对于许多领域都有重要的意义,特别是在晶体生长和凝固等过程中。
•在材料科学中,形核过冷度的控制能够影响材料的晶体质量和性能。
•在医药行业中,形核过冷度的研究可以用于制备高纯度药物晶体。
典型铁碳合金的结晶过程

典型铁碳合金的结晶过程
典型的铁碳合金的结晶过程包括以下几个步骤:
1. 熔化:将合适比例的铁和碳原料进行熔化,通常在高温高压的条件下进行。
熔化后的合金为液态状态。
2. 过冷:将熔融的铁碳合金缓慢冷却,使其温度降至接近其冰点以下。
在过冷过程中,合金会逐渐失去热量,形成过冷液体。
3. 形核:过冷液体中的某些原子开始聚集形成细小的结晶核。
这个过程叫做形核,形成的结晶核通常呈固态。
4. 长大:在形核的基础上,其它的原子会逐渐沉积到结晶核上,导致结晶核与周围液体逐渐分离。
随着时间的推移,结晶核也会逐渐生长。
5. 赋形:当结晶核生长到一定程度时,会与周围的结晶核相互连结,形成完整的晶粒。
晶粒的形状和尺寸取决于铁碳合金的成分和冷却条件。
以上过程中,形核和长大是结晶过程的关键步骤。
形核速率和长大速率受到多种因素的影响,如温度、合金成分、冷却速率等。
通过控制这些因素,可以调控铁碳合金的晶粒尺寸和分布,从而改变合金的力学性能和微观组织特征。
材料科学与工程基础习题答案 (1)

第一章 原子排列与晶体结构1.[110], (111), ABCABC…, 0.74 , 12 , 4 , a r 42=; [111], (110) , 0.68 , 8 , 2 , a r 43= ;]0211[, (0001) , ABAB , 0.74 , 12 , 6 , 2a r =。
2. 0.01659nm 3 , 4 , 8 。
3. FCC , BCC ,减少 ,降低 ,膨胀 ,收缩 。
4. 解答:见图1-15.解答:设所决定的晶面为(hkl ),晶面指数与面上的直线[uvw]之间有hu+kv+lw=0,故有: h+k-l=0,2h-l=0。
可以求得(hkl )=(112)。
6 解答:Pb 为fcc 结构,原子半径R 与点阵常数a 的关系为ar 42=,故可求得a =0.4949×10-6mm 。
则(100)平面的面积S =a 2=0.244926011×0-12mm 2,每个(100)面上的原子个数为2。
所以1 mm 2上的原子个数s n 1==4.08×1012。
第二章合金相结构一、 填空1) 提高,降低,变差,变大。
2) (1)晶体结构;(2)元素之间电负性差;(3)电子浓度 ;(4)元素之间尺寸差别 3) 存在溶质原子偏聚 和短程有序 。
4) 置换固溶体 和间隙固溶体 。
5) 提高 ,降低 ,降低 。
6) 溶质原子溶入点阵原子溶入溶剂点阵间隙中形成的固溶体,非金属原子与金属原子半径的比值大于0.59时形成的复杂结构的化合物。
二、 问答1、 解答: α-Fe 为bcc 结构,致密度虽然较小,但是它的间隙数目多且分散,间隙半径很小,四面体间隙半径为0.291Ra ,即R =0.0361nm ,八面体间隙半径为0.154Ra ,即R =0.0191nm 。
氢,氮,碳,硼由于与α-Fe 的尺寸差别较大,在α-Fe 中形成间隙固溶体,固溶度很小。
金属凝固原理——形核

二、异质形核机理
三、异质形核动力学
精选版课件ppt
16
一、异质形核的热力学条件
如果液相中存在固相质点,且液相又能润湿质 表面,则液体能在固相质点表面形成新相晶核。
设生核衬底的质点表 面为一平面,在其上生 成一球冠的新相(见右 图)。则系统自由能的 变化为:
GV Gv (A)
a 4.8%
c 0.3%
精选版课件ppt
28
小结:界面共格对应原则的实质:增大固、 液两相界面附着力,减小异质形核的 形核功,使固相质点成为异质形核的 有效衬底。
精选版课件ppt
29
2.固相杂质表面的粗糙度
• 杂质表面的粗糙度对非均质形核的影响 凹面杂质形核效率最高,平面次之,凸面最差 。
率半径即球径越大,换句话说,同一半径的临界晶核(球冠) 的体积越小,所含原子数越少,因而在更小的过冷度下就能 形核。
精选版课件ppt
19
同理可推导得异质形核的形核功:
G** f ()G*
f()(2cos)(1cos)2
4
当180完全不润湿f()1 ,则 G**G*
当 90 部分润湿
f ( ) 1 ,则 G** 1G*
Tm
= ΔHm )
Tm及ΔHm对一特定金属或合金为定值,所以过冷度 ΔT是影响相变驱动力的决定因素。过冷度ΔT 越大,
凝固相变驱动力ΔGV 越大。
精选版课件ppt
6
二、大量形核的过冷度( T*)
液态金属只要存 在过冷度T 时就能 形核但不一定能完成 形核过程,只有当 :
TT* (大量形核过冷度) 时,形核过程才能完 成。形成的晶核才能 在 TTk(动力 学过冷度)的过冷度 条件下进行长大,直 至凝固完成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N e
Gc KT
e
G A KT
33
2.3 过冷与形核
• 均质形核速率:
a 13 NkT G A I exp exp kT G 2 h RT V
式中: N— 单位体积液相中的原子总数; k— 玻耳兹曼常数; h— 普朗特常数; GA— 原子跃迁穿透液固界面的激活能; 16 a— 晶核形状因子, 对于球形晶核 a 3 GV— 体积变化自由焓; I— 形核速率, 为单位时间、单位体积液相中形成的晶 核数目。
22
2.3 过冷与形核
• 假设析出晶核为球形,有下式:
G GV Gi
4 3 V r , A 4r 2 3
• 则上述代数和为:
4 3 G总 r Gv 4r 2 3
23
2.3 过冷与形核
• 如图,G总随变化曲线有一最高值。相当于曲线最高 值对应的r就是晶核的临界尺寸,以rc来表示 • 当能量涨落,晶坯可能达到临界尺寸时,晶核才可能 出现,结晶才会开始。否则,即使液体有了过冷度, 24 也不会进行结晶,
8
2.2 冷却曲线与凝固温度
2.2.1纯金属的平衡凝固冷却曲线
9
完全熔化后的金属在几近绝热的情况下冷却, 得到冷却曲线 液态金属变成固态金属过程中,固液并存, 此时,液态金属变成固态金属时放出 热量, 抵消了自然温度的下降 液态金属完全凝固时,温度继续下降 温度不变化的数值,即凝固温度-平衡凝固 温度
L f T Tf
式中:T=T f -T称为过冷度; — 实际体系温度。 T
16
2.3 过冷与形核
由上式可知:
• 过冷度△T是钢水结晶的必要条件; • 过冷度△T越大,△G越负,结晶越容易; • 要得到过冷度,系统自由能必须减少,而自由能减少 就是内能的减少,内能是以潜热形式放出的,结晶是 个放热过程
7
金属在凝固过程存在两个界面,固液界面、 金属铸型界面,在两个界面存在复杂的传热。 凝固过程的液体由于温差将引起对流,由于 温度不同造成热膨胀的差异,从而引起密度 的不同,在重力场中密度较小的流体受到浮 力的作用,同样,液体成份不均匀时也会因 为密度的不同引起浮力,密度不同而产生的 浮力是对流的驱动力。当浮力大于粘滞力时, 即会产生对流(自然对流)。
气体
原子或分子在空间上的排列是无序的。 PV=RT
2
2.1 液体与固体
液体:只能抵抗很小的剪切力,其外形取决于容器形 状,可以流动 凝固:液态—固态的过程,因此液态金属的结构对凝 固后的组织会有影响 液态金属的结构?
金属原子由固态转变为液 态时熵的变化相对于熔点 前熵的增值不算大。实践 证明它更象固体。熔化潜
34
2.3 过冷与形核
Hale Waihona Puke 352.3 过冷与形核
• 对非均质形核而言: • 正常情况下,均质形核很少见,在许多情况下, 形核依赖于液相中的固相质点表面和各种界面 进行, 发生异相形核。 • 并非所有固相质点表面都能使新相形核, 必须 以金属新相能够浸润质点表面为前提。
36
2.3 过冷与形核
为便于分析, 假设作为生核衬底的质点表面为平面, 在其 表面形成球面的固相。
A:液固界面面积, LS 界面能。 • 这部分是结晶的阻力 • 这样,均质形核的自由能变化实际是两个自由能的代 数和。即:
G GV Gi
21
2.3 过冷与形核
界面张力:作用在液 体表面单位长度上的 力,它正好抵消相反 方向使面积增加的外 拉力,叫做界面张力 (0.4Lf) 界面能
• 此后, T 越大,晶核形成速率越大,但形核也需要原 子的跳动。 T 太大时,原子的活动能力太弱,反而不 利于形核。 • 所以,晶核的形成速率和 T 具有比较复杂的关系。
30
2.3 过冷与形核
• 将
2 rc Gv
, G
v
L f T / Tf
代入:
4 3 G总 r Gv 4r 2 3
90%C 6.2% Si 1.7% Mn 28% P 40% S TL 1536 2.6%Cu 2.9% Ni 1.8%Cr 5.1% Al 415.3%C 12.3% Si 6.8% Mn 124.5% P TS 1536 183.9% S 4.3% Ni 1.4%Cr 4.1% Al
13
2.3 过冷与形核
形核过程
结晶过程示意图
14
2.3 过冷与形核
固液相变的驱动力
在熔化温度( Tf)下,金属固、液相处于平衡状态。 即: T=Tf时,固液 系统自由能:G=H-TS,H为克分子焓,S为克分子熵
当金属由液相向固相转变时,单位体积自由能变化:
Gv GS GL ( H S H L ) T (SS SL )
在T与熔化温度Tf相差不大时,
H L f (熔化潜热 )
15
2.3 过冷与形核
Gv L f T (SS SL )
T Tf 时G 0
SS SL
Lf Tf
TL f Tf L f (T f T ) Tf
自由能随温度变化的示意图
Gv L f Gv
• 可以看出,过冷度越大,rc越小 T
rc
27
2.3 过冷与形核
• 另一方面,T越大,最大尺寸的晶坯尺寸r’也越越大 T
r’
28
2.3 过冷与形核
• 二者结合,得到两曲线的交叉点N, T
T*
N
r’
29
2.3 过冷与形核
• • • • T*即为亚稳极限过冷度。 当T <T*时,r’<rc,难于成核 当T =T*时,r’=rc,正好达到成核要求,结晶开始 当T >T*时,r’>rc,即使最小的晶坯尺寸也可以超过 rc,结晶稳定进行
19
2.3 过冷与形核
• 对均质形核而言: • 该过程的系统自由能变化为:
GV VGv
VL f T Tf
式中:T=T f -T称为过冷度; : 晶体体积。 V
• 该部分是结晶的驱动力
20
2.3 过冷与形核
• 但是,当晶核形成以后,产生了液-固界面,出现界 面自由能。
Gi A LS
熔化时的体积变化,% 6.0 5.1 4.2 5.15 4.1 3.0 2.3 -3.2 -5.0
4
2.1 液体与固体
表2:常见金属的熔化潜热和汽化潜热
金属 名称 熔点, ℃ 熔化潜热 沸点, (Lm,kcal/ ℃ mol) 汽化潜热, Lb/Lm (Lb,Kcal/m ol)
铝 铜 铁 锌 镁
660 1083 1537 420 650
2.5 3.06 3.63 1.72 2.08
2480 2950 3070 907 1103
69.6 81.8 81.3 27.5 32.0
27.8 26.7 22.4 16.0 15.4
5
2.1 液体与固体
潜热主要是原子之间的键破坏需要的能量, 可见原子之间的键的破坏主要发生在液-汽 转变。 液态更接近与固态的结构。 关于液态金属结构的研究表明:液态金属是 近程有序的。
6
凝固过程发生放热,液态金属转变为固体金 属的过程,从而改变各相自由能,从而改变 各相相对稳定性,凝固象化学反应一样,也 需要热起伏来驱动,即原子从母相迁移到新 相的概率大于相反方向迁移的概率时,相变 才能发生。从微观来看,凝固是金属原子从 无序状态到有序状态的转变,也就是液体中 无规则的原子集团转变为按一定规则排列的 固态结晶体。换换句话凝固过程主要是晶体 或晶粒的生成和长大过程,所以也称结晶。
热也表明。其中熔化潜热 和汽化潜热之比很大。
3
2.1 液体与固体
表 1 常用金属熔化时的体积变化
金属名称 铝 金 锌 铜 镁 铁 锡 镓 锗
晶体结构 面心立方 面心立方 密排六方 面心立方 密排六方 体心立方/面心立方 四方 面心斜方 金刚石型
熔点,℃ 660 1063 420 1083 650 1537 232 30 937
2
表示晶体在夹杂物表面的润湿倾向。
2
晶核与固体(夹杂物)接触面积:
r (1 cos )
1 3 r (2 3 cos cos 3 ) 3
LC
LS SC LC cos
CS
38
LS
2.3 过冷与形核
上图为一个平面的夹杂物上形成一个半球缺的固体晶核,晶核与液体、 固体有三个界面。处于平衡时:
cos
式中:
ls cs lc
(lc:液体与晶核;ls:液体与固体;cs:晶核与固体)
为界面张力;
均质形核速率:单位时间单位体积液相形成 的晶核数目。
32
2.3 过冷与形核
• 系统能量的涨落达到Gc的几率和几率因子exp(Gc/KT)成比例,所以,单位体积内出现临界晶坯的数 目也应与exp(-Gc/KT)成比例,其中大约1/2的可能 成为晶核。 • 另外,临界尺寸的晶坯要变成晶核,必然要求其周围液 相至少一个原子补充进来,即由液相跨越界面跳到晶核 上,并稳定在那里。这样又存在一个几率问题 • 同样,小晶坯变成大晶坯也是如此 • 即形核速率N可表示如下:
10
2.2 冷却曲线与凝固温度
2.2.2金属凝固时的过冷
过冷:在平衡温度以下,仍存在液体状态的现象
11
原因:温度冷却过快,液态变成固态比较慢, 液态金属变成固态金属释放的能量来不及弥 补温度下降速度 冷却条件不同,得出的冷却曲线也不同
12
2.2 冷却曲线与凝固温度
