Multisim7教程学习8

合集下载

Multisim7基本操作

34
元器件栏各图标名称及其功能如表所示：
35
1.3.4 Multisim 7仪器仪表栏仪器仪表栏 Multisim 7在仪器仪表栏下提供了17个常用仪器仪表，依次为数字万用表、函数发生器、瓦特表、双通道示波器、四通道示波器、波特图仪、频率计、字信号发生器、逻辑分析仪、逻辑转换器、IV分析仪、失真度仪、频谱分析仪、网络分析仪、Agilent 信号发生器、Agilent万用表、Agilent示波器。
原始图像
顺时针旋转90°
逆时针旋转90°
水平翻转
垂直翻转
7
1.1.4 文本基本编辑对文字注释方式有两种：直接在电路工作区输入文字或者在文本描述框输入文字，两种操作方式有所不同。 1. 电路工作区输入文字单击Place / Text命令或使用Ctrl+T快捷操作，然后用鼠标单击需要输入文字的位置，输入需要的文字。用鼠标指向文字块，单击鼠标右键，在弹出的菜单中选择Color命令，选择需要的颜色。双击文字块，可以随时修改输入的文字。
18
2. Workspace选项选项 Workspace选项有三个栏目。Show栏目实现电路工作区显示方式的控制；Sheet size栏目实现图纸大小和方向的设置； Zoom level栏目实现电路工作区显示比例的控制。 3. Wiring选项选项 Wiring选项有两个栏目。Wire width栏目设置连接线的线宽； Autowire栏目控制自动连线的方式。
1. File（文件）菜单（文件）
25
2. Edit（编辑）菜单（编辑）
26
3. View（窗口）菜单（窗口）
27
4. Place（放置）菜单（放置）
28
5. Simulate（仿真）菜单（仿真）

Multisim7课程设计仿真

选择元件
用户可以通过元件库面板选择需要的元件，并将其拖拽到电路图编辑区。
调整元件属性
双击元件，可以在属性对话框中修改元件的参数和属性。
电路图的绘制
01
02
03
电路图编辑区
用于绘制电路图的区域，用户可以在此区域内自由绘制电路图。
连线工具
提供了多种连线工具，包括直线、曲线等，方便用户绘制电路图中的连线。
技巧3
05 利用 Multisim 的自动化功能
。
建议
06 利用软件的自动化布局和布线
功能，提高设计效率。
Multisim 7 的未来发展与展望
发展方向1
增加更多先进的仿真功能。
01
02
展望
随着电子技术的不断发展，Multisim 7 有望增加更多高级的仿真功能，以满足更复杂的设计需求。
发展方向2
1 2
模拟仪器
Multisim 7提供了多种模拟仪器，如示波器、信号发生器、功率表等，可用于测量和调试电路的各种参数。
数字仪器
数字仪器包括逻辑分析仪、逻辑转换仪等，可用于分析数字电路的逻辑关系和转换。
3
仪器设置与调整
用户可以根据需要设置仪器的参数，如输入信号的幅度、频率等，以满足不同的仿真需求。
问题2
仿真结果不准确。
仿真速度过慢。
问题3
解决方法
优化电路设计，减少元件数量和复杂度，或尝试升级计算机硬件。
提高仿真效率的技巧和建议
技巧1
合理使用虚拟仪器。
01
建议
02 在仿真过程中，根据需要选择
合适的虚拟仪器，避免不必要的复杂度。技巧2Fra bibliotek优化电路设计。

multisim教程

multisim教程以下是Multisim的简单教程：Multisim是一款用于电子电路仿真和设计的软件工具。

下面我将介绍一些基本的操作步骤，帮助你开始使用Multisim。

1. 打开Multisim软件并创建新项目。

选择“File”菜单中的“New”选项，然后选择“New Design”来创建一个新的电路设计。

2. 选择器件进行电路设计。

在“Place”菜单中选择合适的器件，如电阻、电容、二极管等，并将它们拖放到电路图板上。

3. 连接器件。

使用连线工具将器件彼此连接起来，这样就可以形成一个完整的电路。

确保连接正确，以保证电路的功能。

4. 设定器件参数。

双击选择的器件，在弹出的属性框中设置相应的参数，如电阻值、电容大小等。

5. 运行仿真。

选择“Simulate”菜单中的“Run”选项，或使用工具栏上的仿真按钮来运行仿真。

Multisim将模拟电路的行为，并显示电路的响应结果。

6. 分析仿真结果。

查看仿真结果，包括电流、电压、功率等参数。

这些结果将帮助你评估电路的性能和功能。

7. 调整和改进电路设计。

根据仿真结果，你可以对电路进行优化和改进。

调整参数、更换器件或重新设计电路布局，以达到设计要求。

8. 保存和导出设计。

将设计保存为Multisim项目文件，以便后续修改和使用。

如果需要，你还可以导出电路图、仿真结果等。

请注意，以上步骤仅为基础操作示例。

Multisim是一款功能强大的软件工具，还提供许多高级功能和特性，如多工程协作、电路板布局等。

你可以进一步学习和探索这些功能，以扩展你的电子电路设计能力。

Multisim_7_课程设计仿真

（1）放置开关点击Multisim 7用户界面的元件工具栏的 Basic元件库按钮，弹出Select a Component 对话框，再点击该对话框左侧Family滚动窗口中的SWITCH，Select a Component对话框变成如图

放置开关
连接电路

在Multisim 7的电路窗口中连接元件非常简捷方便，通常有以下两种类型：（1）元件与元件的连接。将鼠标指针移动到所要连接元件的引脚上，鼠标指针就会变成中间有黑点的十字架，如图。
鼠标放在选中导线中间

（ 3 ）修改元件的参考序号（Reference ID）
元件的参考序号是在从元件库中提取时自动产生的，但有时与我们的工程习惯不相符。可以通过双击该元件，在弹出的属性对话框中修改元件的参考序号。例如双击 R2，弹出如图所示的窗口，将Label标签上的Reference ID栏内的R2改为其他序号。

2、面板设置实际电压表的内阻并不是无穷大，电流表的内阻也不是0。在Multisim7 中，可以通过设置虚拟数字万用表的内阻来真实地模拟实际仪表的测量结果。面板设置如图（2-3）所示。
数字万用表应用举例
万用表测量直流电压和电流值
Function Generator——信号发生器
电路仿真实例

直流动态电路－－电容充放电电路
创建电路图步骤

1 .启动软件Multisim 7软件
点击Windows“开始”菜单中的Multisim 7，就会打开Multisim 7的用户界面，并在电路窗口中自动建立一个文件名为“Circuit1”的电路文件。

Multisim 7电路设计仿真教程

In J.G. Webster (ed.), Wiley Encyclopedia of Electrical and Electronics Engineering,Wiley & Sons, vol. 18, pp. 396-405, 1999Relaxation Oscillators and NetworksDeLiang WangDepartment of Computer and Information Science and Center for Cognitive ScienceThe Ohio State UniversityColumbus, OH 43210-1277Relaxation oscillations comprise a large class of nonlinear dynamical systems, and arise naturally from many physical systems such as mechanics, biology, chemistry, and engineering. Such periodic phenomena are characterized by intervals of time during which little happens, interleaved with intervals of time during which considerable changes take place. In other words, relaxation oscillations exhibit more than one time scale. The dynamics of a relaxation oscillator is illustrated by the mechanical system of a seesaw in Figure 1. At one side of the seesaw is there a water container which is empty at the beginning; in this situation the other side of the seesaw touches the ground. As the weight of water dripping from a tap into the container exceeds that of the other side, the seesaw flips and the container side touches the ground. At this moment, the container empties itself, and the seesaw returns quictly to its original position and the process repeats.Figure 1. An example of a relaxation oscillator: a seesaw with a water container at one end (adapted from(4)).Relaxation oscillations were first observed by van der Pol (1) in 1926 when studying properties of a triode circuit. Such a circuit exhibits self-sustained oscillations. van der Pol discovered that for a certain range of the system parameters the oscillation is almost sinusoidal, but for a different range the oscillation exhibits abrupt changes. In the latter case, the period of the oscillation is proportional to the relaxation time (time constant) of the system, hence the term relaxation oscillation. van der Pol (2) later gave the following defining properties of relaxation oscillations:1. The period of oscillations is determined by some form of relaxation time.2. They represent a periodic autonomous repetition of a typical aperiodic phenomenon.3. Drastically different from sinusoidal or harmonic oscillations, relaxation oscillatorsexhibit discontinuous jumps.4. A nonlinear system with implicit threshold values, characteristic of the all-or-none law.A variety of biological phenomena can be characterized as relaxation oscillations, ranging from heartbeat, neuronal activity, to population cycles; the English physiologist A.V. Hill (3) even stated that relaxation oscillations are the type of oscillations that governs all periodic phenomena in physiology.Givenrelaxation oscillations. TheimportantRELAXATION OSCILLATORSoscillators.arewith electrical circuits.van der Pol oscillator˙˙x+x=c(1−x2)˙x Figure 2. Phase portrait and trajectory of a van der Pol oscillator. A Phase portrait. The x nullcline is the cubic curve, and the y nullcline is the y axis. Arrows indicate phase flows. B limit cycle orbit. The limit cycle is labeled as pqrs, and the arrowheadswhere c > 0 is a parameter. This second-order differential equation can be transformed to a two variable first-order differential equation,˙x=c(y−f(x))(2a)˙y=−x/c(2b)Here f(x) = -x + x3/3. The x nullcline, ˙x = 0, is a cubic curve, while the y nullcline, ˙y = 0, is the y axis. As shown in Fig. 2A, the two nullclines intersect along the middle branch of the cubic, and the resulting fixed point is unstable as indicated by the flow field in the phase plane of Fig. 2A. This equation yields a periodic solution.As c » 1, Eq. (2) yields two time scales: a slow time scale for the y variable and a fast time scale for the x variable. As a result, Eq. (2) becomes the van der Pol oscillator that produces a relaxation oscillation. The limit cycle for the van der Pol oscillator is given in Fig. 2B, and it is composed of four pieces, two slow ones indicated by pq and rs, and two fast ones indicated by qr and sp. In other words, motion along the two branches of the cubic is slow compared to fast alternations, or jumps, between the two branches. Fig. 2C shows x activity of the oscillator with respect to time, where two time scales are clearly indicated by relatively slow changes in x activity interleaving with fast changes.FitzHugh-Nagumo oscillatorBy simplifying the classical Hodgkin-Huxley equations (7) for modeling nerve membranes and action potential generation, FitzHugh (8) and Nagumo et al. (5) gave the following two-variable equation, widely known as the FitzHugh-Nagumo model,˙x=c(y−f(x)+I)(3a)˙y=−(x+by−a)/c(3b) where f(x) is as defined in Eq. (2), I is the injected current, and a, b, and c are system parameters satisfying the conditions: 1 > b > 0, c2 > b, and 1 > a > 1 – 2b/3. In neurophysiological terms, x corresponds to the neuronal membrane potential, and y plays the aggregate role of three variables in the Hodgkin-Huxley equations. Given that the x nullcline is a cubic and the y nullcline is linear, the FitzHugh-Nagumo equation is mathematically similar to the van der Pol equation. Typical relaxation oscillation with two time scales occurs when c » 1. Because of the three parameters and the external input I, the FitzHugh-Nagumo oscillator has additional flexibility. Depending on parameter values, the oscillator can exhibit a stable steady state or a stable periodic orbit. With a perturbation by external stimulation, the steady state can become unstable and be replaced by an oscillation; the steady state is thus referred to as the excitable state.Morris-Lecar oscillatorIn modeling voltage oscillations in barnacle muscle fibers, Morris and Lecar (9) proposed the following equation,˙x=−g Ca m∞(x)(x−1)−g K y(x−x K)−g L(x−x L)+I(4a)˙y=−ε(y∞(x)−y)/τy(x)(4b) wherem ∞(x )=[1+tanh((x −x 1)/x 2)]/2y ∞(x )=[1+tanh((x −x 3)/x 4)]/2τy (x )=1/cosh[(x −x 3)/(2x 4)]and x 1, x 2, x 3, x 4, g Ca , g K , g L , x K , and x L are parameters. Ca stands for calcium, K for potassium, L for leak, and I is the injected current. The parameter ε controls relative time scales of x and y . Like Eq. (4), the Morris-Lecar oscillator is closely related to the Hodgkin-Huxley equations, and it is used as a two-variable description of neuronal membrane properties or the envelope of an oscillating burst (10). The x variable corresponds to the membrane potential, and y corresponds to the state of activation of ionic channels.The x nullcline of Eq. (4) resembles a cubic and the y nullcline is a sigmoid curve. When ε isTerman-Wang oscillatorconsiderations, the following equation,˙x=f (x )−y +I ˙y=ε(g (x )−y )where f(x) = 3x – x 3 + 2, g(x) = α/β)), and I represents oscillator. Thus x nullcline is a sigmoid, where αparameters. When εrelaxation oscillator. When I βperiodic solution alternates between and active (high x behavior. As shown in Fig. respectively. If I spends in these two phases. A largervan der Pol and FitzHugh-Nagumo equations. In neuronal terms, the x variable in Eq. (5) corresponds to the membrane potential, and y the state for channel activation or inactivation.NETWORKS OF RELAXATION OSCILLATORSIn late eighties, neural oscillations about 40 Hz were discovered to in the visual cortex (12-13). The experimental findings can be summarized as the following: (1) neural oscillations are triggered by appropriate sensory stimulation, and thus the oscillations are stimulus-dependent; (2) long-range synchrony with zero phase-lag occurs if the stimuli appear to form a coherent object; (3) no synchronization occurs if the stimuli appear to be unrelated. These intriguing observations are consistent with the temporal correlation theory (14), which states that in perceiving a coherent object the brain links various feature detecting neurons via temporal correlation among the firing activities of these neurons.Since the discovery of coherent oscillations in the visual cortex and other brain areas, neural oscillations and synchronization of oscillator networks have been extensively studied. Most of these models are based on sinusoidal or harmonic oscillators and rely on all-to-all connectivity to reach synchronization across the network. In fact, according to the Mermin and Wagner theorem (15) in statistical physics, no synchrony exists in one- or two-dimensional locally coupled isotropic Heisenberg oscillators, which are similar to harmonic oscillators. However, all-to-all connectivity(16)modulationrelaxationand in this case the effect of the excitatory coupling is to raise the cubic of the other oscillator by a fixed amount.Let us explain the mechanism of fast threshold modulation using the Terman-Wang oscillator as an example. The two oscillators are denoted by o1 = (x1, y1) and o2 = (x2, y2), which are initially in the silent phase and close to each other with o1 leading the way as illustrated in Fig. 4. Figure 4 shows the solution of the oscillator system in the singular limit ε→ 0. The singular solution consists of several pieces. The first piece is when both oscillators move along LB of the uncoupled cubic, denoted as C. This piece lasts until o1 reaches the left knee of C, LK, at t = t1. The second piece begins when o1 jumps up to RB, and the excitatory coupling from o1 to o2 raises the cubic for o2 from C to C E as shown in the figure. Let LK E and RK E denote the left and right knees of C E. If |y1 - y2| is relatively small, then o2 lies below LK E and jumps up. Since these interactions take place in fast time, the oscillators are effectively synchronized in jumping up. As a result the cubic for o1 is raised to C E as well. The third piece is when both oscillators lie on RB and evolve in slow time. Note that the ordering in which the two oscillators track along RB is reversed and now o2 leads the way. The third piece lasts until o2 reaches RK E at t = t2. The fourth piece starts when o2 jumps down to LB. With o2 jumping down, the cubic for o1 is lowered to C. At this time, if o1 lies above RK, as shown in Fig. 4, o1 jumps down as well and both oscillators are now in the silent phase. Once both oscillators are on LB, the above analysis repeats.Based on the fast threshold modulation mechanism, Somers and Kopell further proved a theorem that the synchronous solution in the oscillator pair has a domain of attraction in which the approach to synchrony has a geometric (or exponential) rate (16). The Somers-Kopell theorem is based on comparing the evolution rates of the slow variable right before and after a jump, which are determined by the vertical distances of an oscillator to the y nullcline (see Fig. 4).A network of locally coupled oscillatorsIn the same paper Somers and Kopell suspected that their analysis extends to a network of relaxation oscillators, and performed numerical simulations with one-dimensional rings to support their suggestion. In a subsequent study, by extending Somers and Kopell analysis, Terman and Wang proved a theorem that for an arbitrary network of locally coupled relaxation oscillators there is a domain of attraction in which the entire network synchronizes at an exponential rate (11).In their analysis, Terman and Wang employed the time metric to describe the distance between oscillators. When oscillators evolve either in the silent phase or the active phase, their distances in y in the Euclidean metric change; however, their distances in the time metric remain constant. On the other hand, when oscillators jump at the same time (in slow time), their y distances remain unchanged while their time distances change. Terman and Wang also introduced the condition that the sigmoid for the y nullcline (again consider the Terman-Wang oscillator) is very close to a step function (11), which is the case when β in Eq. (5) is chosen to be very small. This condition implies that in the situation with multiple cubics the rate of evolution of a slow variable does not depend on which cubic it tracks along.LEGION networks: Selective gatingA natural and special form of the temporal correlation theory is oscillatory correlation (19), whereby each object is represented by synchronization of the oscillator group corresponding to the object and different objects in a scene are represented by different oscillator groups which are desynchronized from each other. There are two fundamental aspects in the oscillatory correlationtheory: synchronization and desynchronization. Extending their results on synchronizing locally coupled relaxation oscillators, Terman and Wang used a global inhibitory mechanism to achieve desynchronization (11). The resulting network is called LEGION, to stand for Locally Excitatory Globally Inhibitory Oscillator Networks (19).The original description of LEGION is based on Terman-Wang oscillators, and basic mechanisms extend to other relaxation oscillator models. Each oscillator i is defined as˙xi = f (x i )−y i +I i +S i +ρ(6a)˙yi =ε(g (x i )−y i )(6b)Here f(x) and g(x) are as given in Eq. (5). The parameter ρ denotes the amplitude of Gaussiannoise; to reduce the chance of self-generating oscillations the mean of noise is set to -ρ. In addition to test robustness, noise plays the role of assisting desynchronization. The term S i denotes the overall input from other oscillators in the network:S i = ∑k ∈N (i )W ik H (x k – θx ) – W z H (z – θz )(7)where W ik is the dynamic connection weight from k to i , and N(i) is the set of the adjacent oscillators that connect to i . In a two-dimensional (2-D) LEGION network, N(i) in the simplest case contains four immediate neighbors except on boundaries where no wrap-around is used,thus forming a 2-D grid. This architecture is shown in Fig. 5. H stands for the Heaviside function, defined as H (v ) = 1 if v ≥ 0 and H (v ) = 0 if v < 0. θx is a threshold above which an oscillator can affect its neighbors. W z is the weight of inhibition from the global inhibitor z , whose activity is defined as˙z= φ (σ∞ – z ) (8)where φ is a parameter. The quantity σ∞ = 1 if x i ≥ θz for at least one oscillator i , and σ∞ = 0otherwise. Hence θz (see also Eq. (7))represents a threshold.The dynamic weights W ik 's are formed on the basis of permanent weights T ik 's according to the mechanism of dynamic normalization (20-21), which ensures that each oscillator has equal overall weights of dynamic connections, W T , from its neighborhood. According to reference (11), weight normalization is not a necessary condition for LEGION to work, but it improves the quality of synchronization. Moreover, based on external input W ik can be determined at the start of simulation.To illustrate how desynchronization between blocks of oscillators is achieved in a LEGION network, let us consider an example with two oscillators that are coupled only through the global< y2thefirst one lasts until o1both oscillators are on LB, zpiece starts when o1crosses θz, σ∞on the fast time scale. When zcubic corresponding to both o1from C to C Zis when o1P Zthat o2→P Z, and o2o1 is on RB, which lasts until o1knee of C Z at t = t2o1 jumps down to LB. When o10 in fast time. When zcorresponding to both o1 and oimmediately. Otherwise both o1terminates when o21 and o2 are never in the active phase simultaneously. In general, LEGION exhibits a mechanism of selective gating, whereby an oscillator, say o i, jumping to its active phase quickly activates the global inhibitor, which selectively prevents the oscillators representing different blocks from jumping up, without affecting o i's ability in recruiting the oscillators of the same block because of local excitation. With the selective gating mechanism, Terman and Wang proved the following theorem. For a LEGION network there is a domain of parameters and initial conditions in which the network achieves both synchronization within blocks of oscillators and desynchronization between different blocks in no greater than N cycles of oscillations, where N is the number of patterns in an input scene. In other words, both synchronization and desynchronization are achieved rapidly.The following simulation illustrates the process of synchronization and desynchronization in LEGION (19). Four patterns - two O's, one H, and one I, forming the word OHIO - are simultaneously presented to a 20x20 LEGION network as shown in Figure 7A. Each pattern is a connected region, but no two patterns are connected to each other. The oscillators under stimulation become oscillatory, while those without stimulation remain excitable. The parameter ρis set to represent 10% noise compared to the external input. The phases of all the oscillators on the grid are randomly initialized. Fig. 7B-7F shows the instantaneous activity (snapshot) of the network at various stages of dynamic evolution. Fig. 7B shows a snapshot of the network at thebeginning of the simulation, displaying the random initial conditions. Fig. 7C shows a snapshotshortly afterwards. One can clearly see the effect of synchronization and desynchronization: all the oscillators corresponding to the left O are entrained and have large activity; at the same time, the oscillators stimulated by the other three patterns have very small activity. Thus the left O is segmented from the rest of the input. Figure 7D-F shows subsequent snapshots of the network, where different patterns reach the active phase and segment from the rest. This successive "popout" of the objects continues in an approximately periodic fashion as long as the input stays on. To provide a complete picture of dynamic evolution, Fig. 7G shows the temporal evolution of every oscillator. Synchronization within each object and desynchronization between them are clearly shown in just three oscillation periods, which is consistent with the theorem proven in (11).GLeft OPattern HPattern IRight OInhibitorTimeFigure 7.A A scene composed of four patterns which were presented (mapped) to a 20x20 LEGION network. B A snapshot of the activities of the oscillator grid at the beginning of dynamic evolution. The diameter of each black circle represents the x activity of the corresponding oscillator. C A snapshot taken shortly after the beginning. D Another snapshot taken shortly after C. E Another snapshot taken shortly after D. F Another snapshot taken shortly after E. G The upper four traces show the combined temporal activities of the oscillator blocks representing the four patterns, respectively, and the bottom trace shows the temporal activity of the global inhibitor. The ordinate indicates the normalized x activity of an oscillator. Since the oscillators receiving no external input are excitable during the entire simulation process, they are excluded from the display. The activity of the oscillators stimulated by each object is combined into a single trace in the figure. The differential equations were solved using a fourth-order Runge-Kutta method. (from (19))Time delay networksTime delays in signal transmission are inevitable in both the brain and physical systems. In local cortical circuits, for instance, the speed of nerve conduction is less than 1mm/ms such that connected neurons 1 mm apart have a time delay of more than 4% of the period of oscillation assuming 40 Hz oscillations. Since small delays may completely alter the dynamics of differential equations, it is an important to understand how time delays change the behavior, particularly synchronization, of relaxation oscillator networks.Recently, Campbell and Wang (22) studied locally coupled relaxation oscillators with time delays. They revealed the phenomenon of loose synchrony in such networks. Loose synchrony indemonstrates loosely synchronous behavior in a chain of 50 oscillators with a time delay that is 3%of the oscillation period between adjacent oscillators. The phase relations between the oscillators in the chain become stabilized by the third cycle.Two other results regarding relaxation oscillator networks with time delays are worth mentioning.First, Campbell and Wang (22) identified a range of initial conditions in which the maximum time delays between any two oscillators in a locally coupled network can be contained. Second, they found that in LEGION networks with time delay coupling between oscillators, desynchronous solutions for different oscillator blocks are maintained. Thus, the introduction of time delays does not appear to impact the behavior of LEGION in terms of synchrony and desynchrony.APPLICATIONS TO SCENE ANALYSISA natural scene generally contains multiple objects, each of which can be viewed as a group of similar sensory features. A major motivation behind studies on oscillatory correlation is scene analysis, or the segmentation of a scene into a set of coherent objects. Scene segmentation, or perceptual organization, plays a critical role in the understanding of natural scenes. Although humans perform it with apparent ease, the general problem of scene segmentation remains unsolved in sensory and perceptual information processing.Oscillatory correlation provides an elegant and unique way to represent results of segmentation. As illustrated in Fig. 7, segmentation is performed in time ; after segmentation, each segment pops out at a distinct time from the network and different segments alternate in time. On the basis of new insights into synchronization and desynchronization properties in relaxation oscillator networks,several recent studies have directly addressed the scene segmentation problem.Image segmentationWang and Terman (21) have studied LEGION for segmenting real images. In order to perform effective segmentation, LEGION needs to be extended to handle images with noisy regions.Without such extension, LEGION would treat each region, no matter how small it is, as a separate segment, and result in many fragments. A large number of fragments degrade segmentation results, and a more serious problem is that it is difficult for LEGION to produce more than severalpatterns (11). This number depends on the ratio of the times that a single oscillator spends in the silent and active phases; see, for example, Figs.3 and 7. This limit is called the segmentation capacity of LEGION (21). Noisy fragments therefore compete with major image regions for becoming segments, and the major segments may not be extracted as athat a major block must contain at least one oscillator, denoted as a leader, which lies in the center area of a large homogeneous image region. Such an oscillator receives large lateral excitation from its neighborhood, and thus its lateral potential is charged high. A noisy fragment does not contain such an oscillator.More specifically, a new variable p i, denoting the lateral potential for each oscillator i is introduced into the definition of the oscillator (cf. (6)). p i→ 1 if i frequently receives a high weighted sum from its neighborhood, signifying that i is a leader, and the value of p i determines whether or not the oscillator i is a leader. After an initial time period, the only oscillators which can jump up without lateral excitation from other oscillators are the leaders. When a leader jumps up, it spreads its activity to other oscillators within its own block, so they can also jump up. Oscillators not in this block are prevented from jumping up because of the global inhibitor. Without a leader, the oscillators corresponding to noisy fragments cannot jump up beyond the initial period. The collection of all noisy regions is called the background, which is generally discontiguous.Wang and Terman have achieved a number of rigorous results concerning the extended version of LEGION (21). The main analytical result states that the oscillators with low lateral potentials will become excitable after a beginning period, and the asymptotic behavior of each oscillator belonging to a major region is precisely the same as the network obtained by simply removing all noisy regions. Given the Terman-Wang theorem on original LEGION, this implies that after a number of cycles a block of oscillators corresponding to a major region synchronizes, while any two blocks corresponding to different major regions desynchronize. Also, the number of periods required for segmentation is no greater than the number of major regions plus one.For gray-level images, each oscillator corresponds to a pixel. In a simple scheme for setting up lateral connections, two neighboring oscillators are connected with a weight proportional to corresponding pixel similarity. To illustrate typical segmentation results, Fig. 9A displays a gray-level aerial image to be segmented. To speed up simulation with large number of oscillators needed for processing real images, Wang and Terman also abstracted an algorithm that follows LEGION dynamics (21). Fig. 9B shows the result of segmentation by the algorithm. The entire image is segmented into 23 regions, each of which corresponds to a different intensity level in the figure, which indicates the phases of oscillators. In the simulation, different segments rapidly popped out from the image, as similarly shown in Fig. 7. As can be seen from Fig. 9B, most of the major regions were segmented, including the central lake, major parkways, and various fields. The black scattered regions in the figure represent the background that remains inactive. Due to the use of lateral potentials, all these tiny regions stay in the background.Auditory segregationA listener in a real auditory environment is generally exposed to acoustic energy from different sources. In order to understand the auditory environment, the listener must first disentangle the acoustic wave reaching the ears. This process is referred to as auditory scene analysis, or auditory segregation. According to Bregman (23), auditory scene analysis takes place in two stages. In the first stage, the acoustic mixture reaching the ears is decomposed into a collection of sensory elements. Secondly, elements that are likely to have arisen from the same source are grouped to form a stream that is a perceptual representation of an auditory event.Auditory segregation was first studied from the oscillatory correlation perspective by von der Malsburg and Schneider (14). They constructed a fully connected oscillator network with an ad hoc oscillator model, each representing a specific auditory feature. Additionally, there is a global inhibitory oscillator introduced to segregate oscillator groups. With a mechanism of rapidoscillators. As indicated in the figure, the array quickly segregates to two synchronized groups, within each of which the active phases of the oscillators overlap significantly. Each synchronized group corresponds to a set of correlogram channels that define the formant of a vowel; see Figs. 10B and 10C.Brown and Wang have performed systematic simulations on a vowel set used in psychophysical studies, and confirmed that the results produced by their oscillator array qualitatively match the performance of human listeners; in particular vowel identification performance increases with increasing difference in F0. As illustrated in Fig. 10, a concept emerging from their study is the use of relaxation oscillators as "gates" on their corresponding auditory channels. Specifically, the activity in a channel contributes to the percept of a sound source only when the corresponding oscillator is in its active phase.CONCLUDING REMARKSRelaxation oscillations are characterized by more than one time scale, and exhibit qualitatively different behavior than sinusoidal or harmonic oscillations. Such distinction is particularly prominent in synchronization and desynchronization in networks of relaxation oscillators. These unique properties in relaxation oscillators have led to new and promising applications to neural computation, especially scene analysis. It should be noted that networks of relaxation oscillations often lead to very complex behaviors other than synchronous and antiphase solutions. Even with identical oscillators and nearest neighbor coupling, traveling waves and other complex spatiotemporal patterns can occur (26).Relaxation oscillations with a singular parameter lend themselves to analysis by singular perturbation theory (27). Singular perturbation theory in turn yields a geometric approach to analyzing relaxation oscillation systems, as illustrated in Figs. 4 and 6. Also based on singular solutions, Linsay and Wang (28) recently proposed a fast method to numerically integrate relaxation oscillator networks. Their technique, called the singular limit method, is derived in the singular limit ε→ 0. A numerical algorithm is given for LEGION network, and it produces remarkable speedup compared to commonly used integration methods such as the Runge-Kutta method. The singular limit method makes it possible to simulate large-scale networks of relaxation oscillators.Computation using relaxation oscillator networks is inherently parallel, where each single oscillator behaves fully in parallel with all the other oscillators. This feature is particularly attractive in the context that an image generally consists of many pixels (e.g. 512x512), and current computer technology can support massive parallel computations. The network architecture such as the one shown in Fig. 5 performs computations based on only connections and oscillatory dynamics. The organizational simplicity plus continuous-time dynamics renders oscillator networks particularly feasible for VLSI chip implementation. With its computational properties plus biological plausibility, oscillatory correlation promises to offer a general computational framework. Acknowledgments. I thank X. Liu and M. Wu for their help in figure preparation. The preparation for this article was supported in part by an NSF grant (IRI-9423312) and an ONR Young Investigator Award (N00014-96-1-0676).BIBIOGRAPHY1. B. van der Pol, On 'relaxation oscillations'. Phil. Mag., 2: 978-992, 1926.2. B. van der Pol, Biological rhythms considered as relaxation oscillations. Acta Med. Scand. Suppl., 108: 76-87, 1940.3. A.V. Hill, Wave transmission as the basis of nerve activity. Cold Spring Harbour Symp. Quant. Biol., 1:146-151, 1933.。

Multisim7基本功能与操作

项目9 Multisim7基本功能与操作Multisim7是一个优秀的电工电子技术仿真软件，既可以完成电路设计和版图绘制，也可以创建工作平台进行仿真实验。

Multisim7软件功能完善，操作界面友好，分析数据准确，易学易用，灵活简便，因此，在教学、科研和工程设计等领域得到广泛地应用。

9.1 Multisim7概述随着时代的发展，仿真技术在电路分析和电子设计中发挥着越来越大的作用。

EDA技术（Electronic Design Automation 电子设计自动化)是电工、电子和信息技术发展的卓越成果。

EDA的发展与应用引发了一场电路研究和电子设计的技术革命。

Multisim是加拿大Electronics Workbench公司研发的EDA系列产品，广泛地应用于电路分析和电子技术的教学和科研中。

Multisim7是2003年开发的版本，仿真功能十分强大，几乎可以100%地仿出真实电路的结果。

Multisim7（以下简称Multisim）以SPICE(Simulation Program with Integrated Circuit Emphasis)为核心，为用户提供了良好的操作平台、强大的元器件库、精度很高的仪表库、电路图编辑器和波形产生与分析器，并提供了较为全面的分析功能，如交流分析、直流扫描分析、瞬态分析等19种功能，此外还提供了原理图输入接口、数字电路和模拟电路的仿真、VHDL/Verilog设计接口与仿真、FPGA/CPLG综合与设计、RF设计和后处理等功能。

Multisim系统结构框图，如图12-1所示。

图12-1 Multisim系统结构框图从系统结构图中可以看出，Multisim把电路图创建、测试分析和仿真结果等项目都集成到一个电路窗口中，整个操作界面就像一个实验平台。

创建电路所需的元器件和测试仪器均可直接从窗口中选取，灵活地搭建各种电路，并可随时进行设置和修改。

9.2 Multisim7的基本功能Multisim7提供了全集成化的工作环境以及电路设计、仿真实验、参数测试和电路分析等强大功能，虚拟的工作平台非常接近真实的实验环境。

Multisim7快速入门

第1章Multisim7快速入门1.1电子仿真软件Multisim7简介电子仿真软件Multisim7是加拿大交互图像技术有限公司（Interactive Image Technologies Ltd. CO.）于2003年推出的最新版本。

它将以前推出的EWB5.0和Multisim2001版本功能大大提高，比如EWB5.0版本，在做电路仿真实验调用虚拟仪器时，一个品种每次只能调用一台，这是一个很大的缺陷。

又如Multisim2001版本，它的与实际元件相对应的现实性仿真元件模型只有6种，而Multisim7版本增加到10种；Multisim2001版本的虚拟仪器只有11种，而Multisim7版本增加到17种；特别像示波器这种最常用的电子仪器，Multisim2001版本只能提供双通道示波器，而Multisim7版本却能提供4踪示波器，这给诸如做数字电路仿真实验等需要同时观察多路波形提供了极大的方便。

又比如Multisim2001版本只能提供“亮”与“灭”两种状态黑白指示灯，而Multisim7版本却能提供蓝、绿、红、黄、白5种颜色的指示灯，使用起来更加方便和直观。

总之，Multisim7版本电子仿真软件是目前世界上最先进、功能最强大的仿真软件，是仿真软件的佼佼者。

Multisim7是一个完整的设计工具系统，提供了一个非常大的元件数据库，并提供原理图输入接口、全部的数模Spice仿真功能、VHDL|Verilog设计接口与仿真功能、FPGA|CPLD综合、RF设计能力和后处理功能，还可以进行从原理图到PCB布线工具包（如：Ultiboard2001）的无缝隙数据传输。

它提供的单一易用的图形输入接口可以满足设计需求。

1.2 Multisim7基本界面基本界面如图1-1所示。

基本界面最上方是菜单栏（Menus），共11项；菜单栏下方左面为系统工具栏（System Toolbar），共11项；中间为设计工具栏（Multisim Design Bar），共8项；再往右是使用中元件列表（In Use List）和帮助按钮；右上角为仿真开关（Simulate Switch）。

multisim教程实验指导书第一章

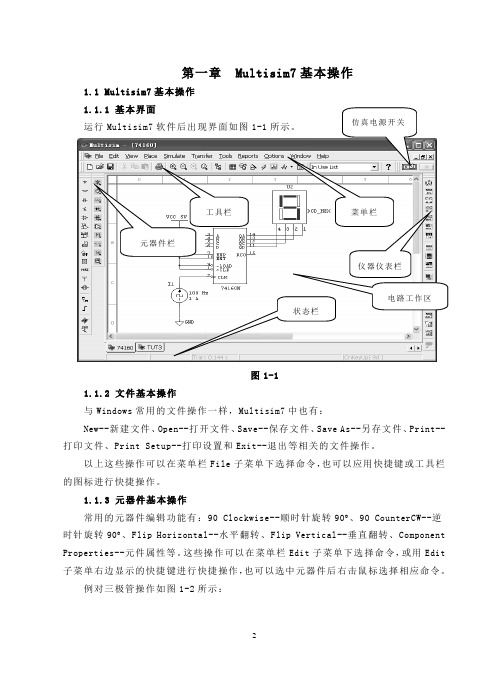
第一章 Multisim7基本操作1.1 Multisim7基本操作图1-11.1.2 文件基本操作与Windows 常用的文件操作一样，Multisim7中也有：New--新建文件、Open--打开文件、Save--保存文件、Save As--另存文件、Print--打印文件、Print Setup--打印设置和Exit--退出等相关的文件操作。

以上这些操作可以在菜单栏File 子菜单下选择命令，也可以应用快捷键或工具栏的图标进行快捷操作。

1.1.3 元器件基本操作常用的元器件编辑功能有：90 Clockwise--顺时针旋转90︒、90 CounterCW--逆时针旋转90︒、Flip Horizontal--水平翻转、Flip Vertical--垂直翻转、Component Properties--元件属性等。

这些操作可以在菜单栏Edit 子菜单下选择命令，或用Edit 子菜单右边显示的快捷键进行快捷操作，也可以选中元器件后右击鼠标选择相应命令。

例对三极管操作如图1-2所示：图1-21.1.4 文本基本编辑对文字注释方式有两种：直接在电路工作区输入文字或者在文本描述框输入文字，两种操作方式有所不同。

1. 电路工作区输入文字单击Place / Text 命令或使用Ctrl+T 快捷操作，然后用鼠标单击需要输入文字的位置，输入需要的文字。

用鼠标指向文字块，单击鼠标右键，在弹出的菜单中选择Color 命令，选择需要的颜色。

双击文字块，可以随时修改输入的文字。

2. 文本描述框输入文字利用文本描述框输入文字不占用电路窗口，可以对电路的功能、实用说明等进行详细的说明，可以根据需要修改文字的大小和字体。

单击View/ Circuit Description Box 命令或使用快捷操作Ctrl+D ，打开电路文本描述框，如图1-3所示，在其中输入需要说明的文字，可以保存和打印输入的文本。

再次单击View/ Circuit Description Box 命令或使用快捷操作Ctrl+D ，可以关闭电路文本描述框。

Multisim7基本操作

#include<reg51.h>#define uchar unsigned char#define uint unsigned intsbit P0_0=P1^1;//sbit P1_0=P1^0;//sbit P1_6=P1^6;//sbit P1_7=P1^7;sbit P2_0=P2^0;void Delay_us(uint);/***********定时器中断****************interrupt1:说明使用了中断1，定时器0中断。

using1:说明使用第一组寄存器timer0：定时器0中断名称，可以按取名规则进行****************/**************************/void timer26(void) interrupt 1{P0_0=~P0_0; //定时器时间到后P0.0取反TH0=250; //定时器高4位恢复初始值TL0=250; //定时器低4位恢复初始值}/***延时子函数**/void Delay_us(uint i){uint j,p;p=i;for(;p!=0;p--)for(j=50;p!=0;j--);}/*******检测子函数********/void Found_out(){if(P2_0==0){Delay_us(10);if(P2_0==0){Delay_us(5);if(P2_0==0){P1_7=0;P1_0=0;while (1){P1_6=1;Delay_us(200);P1_6=0;Delay_us(200);}}}}}/***************主函数*****************/void main(void){TMOD=0X02; //设置定时器0，定时器工作方式1，16位方式TH0=0X250; //定时器的高8位赋初始值TL0=0X250; // 定时器的低8位赋初始值ET0=1; //开定视器0的中断开关，允许中断EA=1; //开CPU的中断开关，允许中断TR0=1; //启动定时器0的中断开关，允许中断while(1) //无限子循环{P1_7=1;Delay_us(200);Found_out();P1_7=0;Delay_us(200);}}。

Multisim 7

第1章Multisim 7概述随着时代的发展，计算机技术在电子电路设计中发挥着越来越大的作用。

20世纪80年代后期，出现了一批优秀的电子设计自动化（Electronic Design Automation，EDA）软件，如PSPICE、EWB等。

EDA软件工具代表着电子系统设计的技术潮流。

本章介绍加拿大IIT公司（Interactive Image Technologies）具有代表性的EDA软件Multisim 7的特点、安装步骤和用户界面。

1.1 EWB与Multisim 7Electronics Workbench（简称EWB）是加拿大IIT公司于20世纪80年代末推出的电子线路仿真软件。

它可以对模拟、数字和模拟/数字混合电路进行仿真，克服了传统电子产品的设计受实验室客观条件限制的局限性，用虚拟的元件搭建各种电路，用虚拟的仪表进行各种参数和性能指标的测试。

因此，在电子工程设计和高校电子类教学领域中得到广泛应用。

与其他电路仿真软件相比，EWB具有以下特点：1．系统集成度高，界面直观，操作方便EWB软件把电路图的创建、电路的测试分析和仿真结果等内容都集成到一个电路窗口中。

整个操作界面就像一个实验平台。

创建电路所需的元器件、仿真电路所需的测试仪器均可以直接从电路窗口中选取，并且虚拟的元器件、仪器与实物外形非常相似，仪器的操作开关、按键同实际仪器也极为相似。

因此，该软件易学易用。

2．具备模拟、数字及模拟/数字混合电路的仿真在电路窗口中既可以对模拟或数字电路进行仿真，还可以对模拟/数字混合电路进行仿真。

3．提供较为丰富的元器件库EWB的元器件库提供了数千种类型的元器件及各类元器件的理想参数。

用户还可以根据需要修改元件参数或创建新元件。

4．电路分析手段完备EWB除了用7种常用的测试仪表来对仿真电路进行测试之外，还提供了电路的直流工作点分析、瞬态分析、傅里叶分析、噪声分析和失真分析等14种常用的分析方法。

Multisim V7教学版使用说明书

Multi sim V7教学版使用说明书目录目录 (1)第一章前言 (3)1.1 关于本手册 (3)1.2 Multisim V7简介 (3)第二章安装 (6)第三章界面 (8)3.1 MultisimV7界面 (8)3.2 定制MultisimV7界面 (10)第四章元件 (15)4.1 关于本章 (15)4.2 元件工具栏 (15)4.3 操作元件 (16)第五章仪表 (24)5.1 数字万用表 (25)5.2 信号发生器 (26)5.3 示波器 (27)5.4 波特图仪 (29)5.5 IV分析仪 (32)第六章分析方法 06.1 分析方法简介 06.2 静态工作点分析 (3)6.3 交流分析 (5)6.4 瞬态分析 (8)6.5 直流扫瞄分析 (10)6.6 参数扫瞄分析 (12)6.7 传递函数分析 (15)第七章模拟电路仿真步骤 (18)7.1 关于本章 (18)7.2 建立电路 (18)7.3 仿真测量电路 (24)7.4 分析电路 (33)第一章前言1.1 关于本手册本手册针对进行一般模拟电路仿真的MultisimV7用户，概括了MultisimV7单机教学版的安装和主要功能，指导读者逐步地建立一个基本电路，并进行仿真、分析。

本手册所描述的大多数功能，各种版本的MultisimV7都具备。

本手册假定读者已经熟悉了Windows应用，例如，选择菜单命令、用鼠标选择条目以及选中或去选一个选项等。

两个常用名词定义：点击：单击鼠标左键；右击：单击鼠标右键。

1.2 Multisim V7简介随着电子技术和计算机技术的发展，以电子电路计算机辅助设计（Computer Aided Design, 简称CAD）为基础的电子设计自动化（Electronic Design Automation, 简称EDA）技术已成为电子学领域的重要学科。

Multisim 是基于PC平台的电子设计软件，是Electronics Workbench（简称EWB）电路设计软件的升级版本。

nejisim7教程

nejisim7教程
软件安装，在解压后先配置文件，之后双击multisim.exe就可打开，有一个注册表的报错，但是亲测不影响实验的使用和测量结果，关闭就可以了。

进软件先保存一个文件（点保存，保存到任意路径，起名），免得电脑突然蓝屏死机然后白干（ctrl s要常按）。

常用的ctrl z撤销可以在不小心撤销了很多的时候复原，刚打开这个软件，只要会ctrl w 会放元件就可以了。

先用ctrl w放好所有的元件，ctrl r顺时针旋转（用shift可以逆时针旋转，但是没必要），右键有很多可选的，但是一开始会这一个就能解决绝大部分问题了。

现在已经放了很多的元件了，放在试验台以后，建议先大概摆放一下位置（注意不要点到那些字，要点框框的空白位置），然后连线：先用鼠标在一个端口，当鼠标变成十字时点一下。

然后拖到另一个端口再点一下就可以了。

注意，T型一般是连接的，十字时不连接的，如果想十字连接，需要先点一下交界处，再拖就可以了。

在实验元件和连线都连接好后，就可以吧电表，电源都拿出来了。

电源，电表都在右侧（归仪器管），拿出来摆放好，连线，确认一下（不确认也不会烧hhh），F5运行，基本上就可以了。

需要测量的，双击仪表就可以，有一些可以改的元件也是双击就可以了。

注意：三极管18级用的是2N222A型号，别的可能有报错，滑动变阻器可以从右侧的基本元件里选一个，那里选的可以调阻值，ctrl
w调不了阻值只能选匝数。

Multisim7教程及应用

第一章电子电路的设计 (1)1.1模拟电子电路的设计方法 (1)1.2模拟电子电路的安装 (6)1.3模拟电子电路的调试 (8)1.4电子电路的故障分析与处理 (12)第二章MULTISIM 7.0 介绍 (14)一、简述 (14)二、M ULTISIM的组成及特点 (14)三、M ULTISIM的基本功能介绍 (15)四、M ULTISIM的常用操作 (34)五、M ULTISIM的分析功能 (42)第三章基础实验 (44)实验一有源滤波器 (44)实验二电压／频率转换电路 (47)实验三集成定时器应用 (49)实验四三相电相序检测与指示 (56)实验五水位控制及报警电路 (58)实验六音频放大器 (60)实验七交流电源过压、欠压保护电路 (62)实验八简易数字电压表的设计 (64)实验九数控音量高效功率放大器 (67)实验十省电防骚扰门铃 (70)实验十一数显电子秤的设计 (72)实验十二心率测试电路 (74)实验十三可调双限温度报警电路 (76)实验十四电冰箱开门报警电路 (80)实验十五LED水位计及报警电路 (85)实验十六交通灯控制电路的设计 (88)实验十七智力竞赛抢答器 (93)实验十八简易数显频率计的设计 (99)第四章设计实验 (102)实验一酒精传感器制作的检测报警器 (102)实验二热释电人体红外传感器制作的高速公路车辆计数器 (104)实验三光电指套式传感器制作的光电数字式脉搏计 (106)实验四温度传感器——电子温度计 (111)实验五气敏传感器—禁止吸烟警告器电路 (112)实验六力敏传感器—电子称重计电路 (113)实验七力敏传感器——便携式电子血压计 (114)实验八超声波倒车防撞报警电路 (117)实验九体温监测报警器 (118)第四章综合实验 (120)实验一可编程函数发生器 (120)实验二电话线路防盗器 (122)实验三简易声控电路 (124)实验四物品遗留提醒报警器 (125)实验五简易玩具电子琴 (127)实验六多功能音乐门铃 (128)第一章电子电路的设计电子电路设计是综合运用电子技术理论知识的过程，必须从实际出发，通过调查研究、查阅有关资料、方案比较及确定，以及设计计算选取元器件等环节，设计出一个符合实际需要、性能和经济指标良好的电路。

Multisim7_第一讲

1.3.2 元器件基本操作常用的元器件编辑功能有：90 Clockwise--顺时针旋转90、 90 CounterCW--逆时针旋转90、Flip Horizontal--水平翻转、Flip Vertical--垂直翻转、Component Properties--元件属性等。这些操作可以在菜单栏Edit子菜单下选择命令，也可以应用快捷键进
完整的电路系统设计、仿真工具；设计功能：
Schematic & HDL
仿真功能：
SPICE VHDL/Verilog RF Co-simulation (原理图—版图联合仿真)
虚拟仪表及分析功能以及3D效果。
Multisim 7 特色
所见即所得的设计环境；互动式的仿真界面；动态显示元件（如LED，七段显示器等）；具有3D效果的仿真电路；虚拟仪表(包括Agilent仿真仪表）；分析功能与图形显示窗口。对电路进行全面的仿真分析和设计。可直接打印输出实验数据、曲线、原理图和元件清单等。
2. Workspace选项 Workspace选项有三个栏目。Show栏目实现电路工作区显示方式的控制；Sheet size栏目实现图纸大小和方向的设置；
Zoom level栏目实现电路工作区显示比例的控制。
3. Wiring选项 Wiring选项有两个栏目。Wire width栏目设置连接线的线宽； Autowire栏目控制自动连线的方式。
Multisim的发展
EWB（Electrionics Workbench）称为电子工作平台，是加拿大IIT公司最早推出的电子设计仿真软件，被誉为 “计算机里的电子实验室”。 EWB发展到5.x版本后进行了较大的变动，增加了更多功能和内容，改进了软件虚拟仪器调用有数量限制的缺陷，更名为Multisim，即为Multisim2001版本。 2003年升级为Multisim7版本，增加了3D元器件和安捷伦仿实物虚拟仪表，使这一电子仿真软件逐步成熟和稳定。 2007年推出NI Multisim10版本。目前最新版本是 Multisim11.0

第1章Multisim 7电子电路仿真软件简介

第1章Multisim 7电子电路仿真软件简介1.1Multisim 7概述随着时代发展，计算机技术在电子电路设计中发挥着越来越大的作用。

传统的电子电路设计手段逐步被EDA（Electronic Design Automation）所取代，EDA覆盖以下三个方面内容：电路设计、电路仿真和系统分析，它代表着现代电子系统设计的潮流。

目前常用的EDA软件有：Protel、Pspice、Orcad和EWB系列软件。

本章介绍EWB系列软件中优秀的Multisim 7仿软件的基本操作方法和仿真功能。

1.1.1 Multisim 7仿真软件的特点Multisim 7仿真软件的前身是EWB（Electronics Workbench）, 该软件是加拿大IIT （Interactive Image Technologies）公司在20世纪80年代后期推出的用于电子电路设计与仿真的EDA软件，它由EWB 4.0逐步升级到EWB 5.0、Multisim V6 ，随后IIT公司对EWB软件进行较大变动，于2001年推出系列化EDA软件Multisim 2001、Ultiboard 2001和Commsim2001。

其中，Multisim2001保留了EWB软件的界面直观、操作方便、易学易懂的特点，增强了软件的仿真测试和分析功能。

IIT公司开设了网站，为用户提供元器件模型的扩充和技术支持。

2003年8月，IIT公司又对Multisim 2001进行了较大的改进，升级为Multisim 7。

Multisim 7软件的主要特点是：●用户界面直观，原理图的设计输入快捷。

Multisim 7 沿袭了EWB界面的特点，提供了一个灵活直观的工作界面来创建和定位电路。

Multisim 7可以使学生几乎不需要知道就可以轻易的完成元件的放置、元件的连接和引线的任意拖动和微调。

●元件丰富，有数千个器件模型。

Multisim 7元件库拥有13000个元件，包括交互元件、3D元件、指示元件和虚拟元件。

Multisim7基本操作

黑白电视机- 简介黑白电视机，是一种只能显示黑白两色的电视机。

在电视发展的早期，包括电视节目的录制和电视机的接收显示，都只能体现黑白两种颜色。

随着科技的发展，在20世纪60年代，逐渐出现了彩色电视。

电视能通过银屏图像和伴声，及时准确形象地展现出社会生活方方面面的信息，极具娱乐性，是大众传媒、朝阳产业。

要对电视机进行安装、焊接、调试等操作，首先应掌握用电安全常识、常用电子元器件和电子仪器的使用，还应该了解黑白电视机基本的工作原理，以及各部分电路所能实现的功能等。

黑白电视机- 工作原理黑白电视机与电视接收机（简称电视机）的工作原理是一样的。

是广播电视系统的中端设备，它的主要作用是把电视台发出的高频信号进行放大、解调，并将放大的图像信号加至显像管栅机极或阴极间，使图像在屏幕上重现，将伴音信号放大，推动扬声器放出声音。

另外，在同步信号作用下产生与发送端同步的行、场扫描电流，供给显像管偏转线圈，使屏幕重现图像。

目前电视机大都采用超外差内载波方式。

黑白电视机- 接收方式与信号分离(1) 电视的接收方式电视信号的接收，主要分为地面广播电视接收、电缆电视技术接收、卫星直播电视接收三种方式。

普通电视机能直接接收地面广播电视和电缆电视，附加一定设备就可接收卫星直播电视。

电视接收机的任务就是将接收到的电视信号转变成黑白或者彩色图像。

它对电视信号可采用模拟或者数字处理方式。

目前电视机正处在从模拟信号处理向数字信号处理过渡的阶段，电视信号的接收正朝着数字处理和多种视听信息综合接收的方向发展。

当代科学技术之飞跃，引起了电视接收技术的变革。

其主要表现是：①利用数字集成电路，对电视信号进行数字化处理，以便压缩频带，获得高质量的图像。

②利用超声波、红外线和微处理技术实现遥控。

完成选台、音量调节、对比度、亮度、色饱和度、静噪控制、电源开关、复位控制等遥控动作。

③利用微处理技术进行自动搜索，自动记忆，预编节目程序。

利用频率合成技术和存贮技术，在屏幕上显示时间、频道数和作电视游戏等。

Multisim V7入门指导

第一部分Multi sim V7原理图编辑，仿真与可编程逻辑入门指导前言祝贺您选择了MultisimV7。

我们有信心将数年来增加的超级设计功能交付给您。

Electronics Workbench是世界领先的电路设计工具供应商，我们的用户比其它任何的EDA开发商的用户都多。

所以我们相信，您将对MultisimV7以及您可能选择的任何其它的Electronics Workbench产品所带来的价值感到满意。

文件惯例当涉及到工具按钮时，相应的工具按钮出现在文字的左边。

虽然multisimV7的电路显示模式是彩色的，但本手册中以黑白模式显示电路。

（您可以将此定制成您喜好的设置）当您看到这样的图标时，所描述的功能只有特定的版本才有。

用户可以购买相应的附加模块。

MultisimV7 用Menu/Item表示菜单命令。

例如，File/|Open表示在File菜单中选择Open命令。

本手册用箭头（）表示程序信息。

MultisimV7文件系列MultisimV7文件包括“MultisimV7入门指导”、“User Guide”和在线帮助。

所有的用户都会收到这两本手册的PDF版本。

用户还会收到所购买MultisimV7版本的印刷版手册。

入门指导“入门指导”向您介绍MultisimV7的界面，并指导您学习电路设计（circuit）、仿真（simulate）、分析（analysis）和报告（report）。

User Guide“User Guide”详细介绍了MultisimV7的各项功能，它是基于电路设计层次进行组织的，详细地描述了MultisimV7的各个方面。

在线帮助MultisimV7提供在线帮助文件系统以支持您使用，选择Help|Multisim Help显示包含参考资料（来自于印刷版的附录）的帮助文件，比如对MultisimV7所提供元器件的详细介绍。

所有的帮助文件窗口都是标准窗口，并提供内容列表与索引。

Multisim7的基本功能与操作

•项项目9 Multisim7基本功能与操作
5、仪器仪表齐全，精度高。 Multisim提供了数字万用表、示波器、逻辑分析仪、波特图仪、函数信号发生器和瓦特表等18种虚拟仪器。仪表外观、面板布置、按键功能和操作方法等与实际仪表基本相同，可以毫无风险地进行使用。
6、强大的分析功能。 Multisim还提供了直流工作点分析、交流分析、直流扫描分析和傅里叶分析等多种分析功能，为电路实验带来了极大的便利。
图9-4 图形注释工具栏
•项项目9 Multisim7基本功能与操作
6、元件工具栏如图9-5所示。元件工具栏通常在基本界面的左边。也可以用鼠标将工具栏拖至界面的上方，呈水平状。从左至右依次是: 电源库(Source)、基本元件库(Basic)、二极管库(Diode)、晶体管库(Transistor)、模拟元件库(Analog)、TTL元件库(TTL)、 CMOS元件库(CMOS)、数字元件库(Miscellaneous Digital)、混合元件库(Mixed)、指示元件库(1ndicator)、其他元件库 (Miscellaneous)、射频元件库(RF)、机电类元件库 (Electromechanical)、放置分层模块、放置总线、登录 WWW．Electronics 和www．网站等。
图9-2 标准工具栏
•项项目9 isim7基本功能与操作
4、仿真开关
如图9-3所示。主要用于仿真控制。
图9.3 仿真开关
•项项目9 Multisim7基本功能与操作
5、图形注释工具栏
如图9-4所示。该工具栏主要用于在基本界面中放置各种图形，从左至右依次是：文本、直线、折线、矩形、椭圆、圆弧、多边形和图片。
•项项目9 Multisim7基本功能与操作

Multisim7教程学习8

Multisim7基本操作

Multisim7课程设计仿真

multisim教程

Multisim_7_课程设计仿真

Multisim 7电路设计仿真教程

Multisim7基本功能与操作

Multisim7快速入门

multisim教程 实验指导书 第一章

Multisim7基本操作

Multisim 7

Multisim V7教学版使用说明书

nejisim7教程

Multisim7教程及应用

Multisim7_第一讲

第1章Multisim 7电子电路仿真软件简介

Multisim7基本操作

Multisim V7入门指导

Multisim7的基本功能与操作

multisim教程实验指导书第一章