超级全能生2019高考全国卷26省12月联考乙卷理科数学

合集下载

超级全能生2019高考全国卷26省12月联考乙卷(理科)数学试题及答案

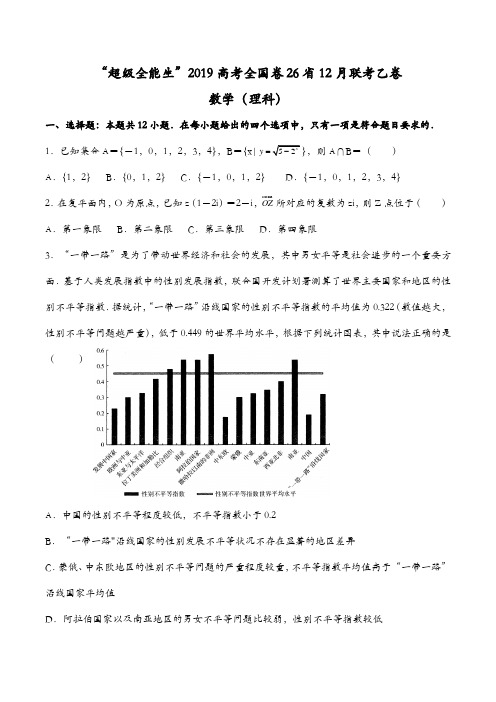
“超级全能生”2019高考全国卷26省12月联考乙卷数学（理科）一、选择题：本题共12小题．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A＝{－1，0，1，2，3，4}，B＝{x|y=，则A∩B＝（）A．{1，2} B．{0，1，2} C．{－1，0，1，2} D．{－1，0，1，2，3，4}2．在复平面内，O为原点，已知z（1－2i）＝2－i，OZ 所对应的复数为zi，则Z点位于（）A．第一象限B．第二象限C．第三象限D．第四象限3．“一带一路”是为了带动世界经济和社会的发展，其中男女平等是社会进步的一个重要方面．基于人类发展指数中的性别发展指数，联合国开发计划署测算了世界主要国家和地区的性别不平等指数．据统计，“一带一路”沿线国家的性别不平等指数的平均值为0.322（数值越大，性别不平等问题越严重），低于0.449的世界平均水平，根据下列统计图表，其中说法正确的是（）A．中国的性别不平等程度较低，不平等指数小于0.2B．“一带一路"沿线国家的性别发展不平等状况不存在显著的地区差异C．蒙俄、中东欧地区的性别不平等问题的严重程度较重，不平等指数平均值高于“一带一路”沿线国家平均值D．阿拉伯国家以及南亚地区的男女不平等问题比较弱，性别不平等指数较低4．已知2sin()63απ+=，则cos(2)3α2π-=（）A ．19-B ．19C ．23 D5．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，E 为△ABC 的中线BD 的中点，0AB BC ⋅= 且1AE =，则ac 的最大值为（） A ．23 B ．43 C ．163 D ．836．已知某几何体的三视图如图所示，则该几何体的内切球半径为（）ABC．12 D．127．已知（x ＋1）n 的展开式中，奇数项的二项式系数和为32，则22()nx x -的展开式的常数项为（）A ．32B ．64C ．120D ．608．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若角A ，32B，C成等差数列，2a c +==，则△ABC 的面积为（） A．12 B．12C1 D1 9．已知实数x ，y 满足230,240,210,x y a x y x y --⎧⎪+-⎨⎪++⎩≤≥≥且z ＝x －2y ＋2的最大值为4，则实数a 的值为（）A ．2B ．92C ．52D ．3210．过抛物线x 2＝8y 焦点的直线交抛物线于M ，N 两点，则OM NO ⋅=（）A ．－20B ．12C ．－12D ．2011．函数f （x ）＝sin （ωx＋φ）（ω＞0，02ϕπ<<）的部分图象如图所示，则下列选项中是函数1()3f x +的单调递增区间的是（）A ．[19，29]和[49，79]B ．[59-，29-]∪[19，49]C ．[59-，29-]和[19，49]D ．[－1，59-]∪[19，29]12．已知f （x ），g （x ）都是定义在R 上的函数，对任意x 均满足f （－x ）＝－f （x ），g （－x ）＝g （x ）≠0，当x ＞0时，总有f′（x ）·g （x ）＞f （x ）·g′（x ），f （2）＝0，则()()303f x g x --≥的解集为（）A ．[1，3]∪[5，＋≦）B ．[－2，0]∪[2，＋≦）C ．（－3，－2）∪（－1，＋≦）D ．[－5，－2]∪[3，＋≦）二、填空题：本题共4小题．13．命题“x ∃∈R ，sinx ＋cosx ＜1”的否定是________．14．已知非零向量a ，b ，满足|a |＝|b |．若|a ＋b |＝|2b －a |，则向量a ，b 的夹角为________．15．双曲线x 2－y 2＝4的渐近线与圆C ：（x －3）2＋（y －2）2＝4交于A ，B 两点，则|AB|＝________．16．如图，点P 在长方体ABCD —A 1B 1C 1D 1的体对角线A 1C 上（不包含线段端点），若AB ＝2AD ＝2AA 1＝2，则下列结论正确的有________．①存在P 点，使直线A 1C 与平面D 1AP 所成角为直角； ②无论P 点在何位置，都有∠APD 1＜90°； ③当112A P PC =时，D 1P ∥平面BDC 1．三、解答题：解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．（一）必考题：17．设S n 为数列{a n }的前n 项和，且a 1＝3，S n ＝An 2＋Bn （A ，B 为常数）．（Ⅰ）证明：数列n S n ⎧⎫⎨⎬⎩⎭为等差数列；（Ⅱ）若a 8＝17，求数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和T n ．18．某羽毛球俱乐部规定，每天一人打球1小时收费30元（不足1小时部分按1小时收费，以此类推），注册成为会员，对会员一天连续打球2小时、3小时的优惠标准如下表：该俱乐部从注册的会员中，随机抽取了40人进行统计，得到统计数据如下表：假设该俱乐部一人一小时活动的成本为5元，根据所给数据，解答下列问题：（Ⅰ）估计该俱乐部一位会员至少打球2小时的概率；（Ⅱ）假设每个会员每天最多打球3小时，以事件发生的频率作为相应事件发生的概率，从该俱乐部的会员中随机抽取2人，记俱乐部从这2位会员的消费中每小时获得的平均利润之和为X，求X的分布列和数学期望E（X）．19．如图，在四棱锥P —ABCD 中，底面ABCD 的对角线互相垂直，且BC ＝CD ，PA ⊥平面ABCD ．（Ⅰ）证明：平面PAC ⊥平面PBD ；（Ⅱ）若1cos 2BAD ∠=-，12AB PA AC ==，M 在PC 上，且2PM MC = ，试求直线BM 与平面PBD 所成角的正弦值．20．已知F 1，F 2分别为椭圆C ：2221x y a+=（a ＞1）的左、右焦点，过F 1且斜率不为零的直线l 与C 交于A ，B 两点．若△AF 1F 2的周长为2+ （Ⅰ）求C 的方程；（Ⅱ）设l 的倾斜角为θ，若2cos 3θ=，直线F 2A ，AB ，F 2B 与直线21x a=-分别交于P ，Q ，R 三个不同的点，记P ，Q ，R 三点的纵坐标分别为y P ，y Q ，y R ，求证：|y P |·|y R |＝|y Q |2．21．已知函数f （x ）＝（e x －1）mx －e x ＋x ＋1，m ∈R ．（Ⅰ）若m ＝0时，求函数f （x ）的极值；（Ⅱ）若关于x 的不等式（m －1）e x ＋x ＋1＞m 在x ∈[12，3）上恒成立，求m 的取值范围．（二）选考题：请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题记分，作答时，请用2B 铅笔在答题卡上将所选题号后的方框涂黑． 22．[选修4—4：坐标系与参数方程]已知曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩（θ为参数）．（Ⅰ）求曲线C 1的普通方程；（Ⅱ）设P 是曲线C 1上的动点，M （－2，5），N （6，1），求|PM|2＋|PN|2的最大值．23．[选修4—5：不等式选讲]已知函数f （x ）＝|2x －1|－|2x －a|（a ＞2且a ∈R ）．（Ⅰ）当a ＝4时，求不等式f （x ）≥x 的解集；（Ⅱ）若f （x ）的最大值为M ，且正实数m ，n 满足12m a m n ++=，求2112m n +--的最小值．“超级全能生”2019高考全国卷26省12月联考乙卷数学（理科）答案详解1 2 3 4 5 6 7 8 9 10 11 12 CBAADBDBBBCA13．x ∀∈R ，sinx ＋cosx≥1 14．3π 15．16．①③17．解：（Ⅰ）证明：依题意，S n ＝An 2＋Bn ，所以nS An B n =+，所以11n n S SA n n+-=+，所以数列n S n ⎧⎫⎨⎬⎩⎭为等差数列．（Ⅱ）依题意可得{a n }为等差数列，183,17,a a =⎧⎨=⎩所以183,30,S S =⎧⎨=⎩所以1,2,A B =⎧⎨=⎩所以S n ＝n 2＋2n ，所以11(2)n S n n =+，所以数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和11111111[(1)()()(2324112n n T n n n n n n+=-+-++-+--++++ ． 18．解：（Ⅰ）在40名会员中，至少打球2小时的会员有12＋8＝20（人），故估计至少打球2小时的概率为201402P ==．（Ⅱ）某会员打球1小时，该俱乐部每小时的平均利润为30－5＝25（元），概率为1201 402P==；某会员打球2小时，该俱乐部每小时的平均利润为1(2300.910)222⨯⨯-=（元），概率为2123 4010P==；某会员打球3小时，该俱乐部每小时的平均利润为1(3300.815)193⨯⨯-=（元），概率为381 405P==；由题意可知，X的所有可能取值为50，47，44，41，38．111(50)224P X==⨯=，133(47)221010P X==⨯⨯=，331129(44)2101025100P X==⨯+⨯⨯=，313(41)210525P X==⨯⨯=，111(38)5525P X==⨯=．所以X的分布列为所以数学期望()504744413845.84101002525100E X=⨯+⨯+⨯+⨯+⨯==．19．解：（Ⅰ）证明：因为底面ABCD的对角线瓦相垂直，所以BD⊥AC，又因为PA⊥平面ABCD，所以BD⊥PA，因为PA∩AC＝A，所以BD⊥平面PAC，又因为BD⊂平面PBD，所以平面PAC⊥平面PBD．（Ⅱ）因为1cos 2BAD ∠=-，所以∠BAC ＝∠DAC ＝60°，又因为12AB AC =，所以∠ABC ＝90°，如图，以BC ，BA ，Bz （Bz ∥AP ）所在直线分别为x ，y ，z 轴建立空间直角坐标系．设PA ＝AB ＝1，所以B （0，0，0），C0，0），A （0，1，0），P （0，1，1），D，32，0），又因为2PM MC =，所以M（3，23，23），所以22(,)333BM = ，设平面PBD 的法向量为m ＝（x ，y ，z ），3(,0)22BD = ，(0,1,1)BP = ，所以0,0,BD BP ⎧⋅=⎪⎨⋅=⎪⎩m m 令y ＝1，有1,1,x y z ⎧=⎪=⎨⎪=-⎩所以(,1)=-m ，所以cos ,55||||BM BM BM ⋅==- m m m 故直线BM 与平面PBD． 20．解：（Ⅰ）由椭圆的定义得|AF 1|＋|AF 2|＝2a ，所以△AF 1F 2的周长为1212||||||2AF AF FF ++=，所以22a +=+a =所以C 的方程为2212x y +=．（Ⅱ）证明：由题意得直线l的方程为(1)2y x =+，联立方程221),1,2y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩ 可得7x 2＋10x ＋1＝0，设A （x 1，y 1），B （x 2，y 2），显然x 1≠1，x 2≠1，所以12107x x +=-，1217x x =．因为l 与直线12x =-交点Q的纵坐标为Q y = 所以25||16Q y =．因为直线F 2A 的方程为11(1)1y y x x =--，故直线F 2A 与直线12x =-交点P 的纵坐标为1132(1)P y y x -=-，同理，点R 的纵坐标为2232(1)R y y x -=-，所以121233||||2(1)2(1)P R y y y y x x --⋅=⋅-- 121294(1)(1)y y x x =-- 1212121259(1)44[()1]x x x x x x x x ⋅+++=-++ 516=，所以|y P |·|y R |＝|y Q |2．21．解：（Ⅰ）若m ＝0时，f （x ）＝－e x ＋x ＋1，所以f′（x ）＝－e x ＋1，令f′（x ）＝0，得x ＝0．故x ∈（－≦，0）时，f′（x ）＞0，f （x ）单调递增；x ∈（0，＋≦）时，f′（x ）＜0，f （x ）单调递减，所以函数f （x ）的极大值为f （0）＝0，无极小值．（Ⅱ）由（m －1）e x ＋x ＋1＞m ，得m （e x －1）＞e x －x －1，由x ∈[12，3）知，e x －1＞0，所以e 11e 1e 1x x x x x m -->=---，令()1e 1x x h x =--，x ∈[12，3），所以2e (1)1()(e 1)x x x h x -+'=-，令g （x ）＝e x （x －1）＋1，g′（x ）＝e x （x －1）＋e x ＝xe x ，因为x ∈[12，3），所以g′（x ）＞0，即g （x ）＝e x （x －1）＋1在[12，3）上单调递增，又1102g ⎛⎫=> ⎪⎝⎭，所以g （x ）＞0恒成立，即2e (1)1()0(e 1)x x x h x -+'=>-，所以h′（x ）＞0在[12，3）上恒成立，所以()1e 1x x h x =--在[12，3）上单调递增，所以33()(3)1e 1h x h <=--，所以331e 1m --≥． 22．解：（Ⅰ）因为曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩（θ为参数），则曲线C 1的普通方程为x 2＋y 2＝16．（Ⅱ）设P （4cosθ，4sinθ）（θ为参数），又因为M （－2，5），N （6，1），所以|PM|2＋|PN|2＝（4cosθ＋2）2＋（4sinθ－5）2＋（4cosθ－6）2＋（4sinθ－1）2＝98－16（3sinθ＋2cosθ）98)θϕ=-+（其中cosϕ=）．因为－1≤sin（θ＋φ）≤1，所以|PM|2＋|PN|2的最大值为98+． 23．解：（Ⅰ）将函数f （x ）＝|2x －1|－|2x －4|去绝对值，当12x ≤时，f （x ）＝－3≥x ⇒x≤－3；当122x <<时，5()4523f x x x x =-⇒<≥≤；当x≥2时，f （x ）＝3≥x ⇒2≤x≤3，综上所述，不等式的解集为（－≦，－3]∪[53，3]．（Ⅱ）由绝对值三角不等式可得||2x －1|－|2x －a||≤|（2x －1）－（2x －a ）|＝|a －1|＝a －1，所以f （x ）的最大值为a －1，因为正实数m ，n 满足12M a m n +==，所以121m n +=，所以2nm n =-，所以2121122122212n n m n n n n +=+=-+=------≥（当且仅当1232n n n -=⇒=-时，取等号），所以2112m n +--的最小值为2。

超级全能生届高考全国卷26省联考乙卷数学理试题Word版含答案

“超级全能生”2018高考全国卷26省9月联考乙卷理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每题5分,共60分.在每题给出的四个选项中，只有一项为哪一项切合题目要求的.1.已知会合A{x|ylog2(4x)},B{x|x22x30}，则AB（）A．(3,4)B．(,1)C．(,4)D．(3,4)(,1)2.已知i是虚数单位，复数z i，则z的虚部为（）22i．2i i2D．2A．B C．5555 3.以下说法正确的选项是（）A．命题“若x23x40，则x 4.”的否命题是“若x23x40，则x4.”B．a0是函数y x a在定义域上单一递加的充足不用要条件C．x0(,0),3x04x0D．若命题P:nn500，则p:n0N,3n0500 N,34.《九章算术》是中国古代的数学专著，此中的一段话“可半者半之，不行半者，副置分母、子之数，以少减多，更相减损，求其等也，以等数约之.”用程序框图表示如图，那么这个程序的作用是（）A．求两个正数a,b的最小公倍数B．求两个正数a,b的最大条约数 C.判断此中一个正数能否能被另一个正数整除D．判断两个正数a,b能否相等5.在ABC中，a,b,c分别是角A,B,C的对应边，若sinC3cosC，则以下式子正确的是（）A．ab2c B．ab2c C.ab2c D．ab2c6.在ABC中，AB4,BC6,ABC2,D是AC的中点，E在BC上，且AE BD，则AEBC（）A．16B．12 C.8D．4学习为了奖赏数学比赛中获奖的优异学生，将梅、兰、竹、菊四幅名画送给获奖的甲、乙、丙三位学生，每个学生起码获取一幅，则在全部送法中甲获取名画“竹”的概率是（）A．2B．1C.1D．1 32368.一个几何的三视图以下图，则表面积为（）A．1823D．943B．18 2 3或12 4 3 C.18 2 3或12 239.已知F是双曲线C:x2y21(a0,b0)的右焦点，P是y轴正半轴上一点，以a2b2OP为直径的圆在第一象限与双曲线的渐近线交于点M（O为坐标原点）.若点P,M,F三点共线，且MFO的面积是PMO的面积的3倍，则双曲线C的离心率为（）A．6B．5 C.3D．210.若正四棱锥P ABCD内接于球O，且底面ABCD过球心O，设正四棱锥PABCD1）的高为，则球O的体积为（A．4B．2 C.4D．2 33211.已知正ABC的边长为23，在平面ABC中，动点P,M知足AP1,M是PC的中点，则线段BM的最小值为（）A ．5B．2C.31D．32112.已知向量a(sinx,cosx),b(1, 1)，函数f(x)ab ，且,xR ，若f(x)2的任何一条对称轴与 x 轴交点的横坐标都不属于区间(3 ,4)，则的取值范围是（）A ．[7,15] [13,19] 12 16 12 16D ．(1,11][11,15] 216 12 16B．[7,11][11,15]C.(1,7][11,19]12 16 12 162 1212 16第Ⅱ卷（共90分）二、填空题（每题 5分，满分20分，将答案填在答题纸上）13. 若(xa2)9的二项睁开式中的x 6的系数为 9，则a．xx y 3, y的取值范围为14. 若实数x,y 知足x y, 则z ．2x y 3,x15. 已知椭圆C:x 2y 2 1与圆M:x 2 y 2222r 20(0 r2)，过椭圆C82的上极点P 作圆M 的两条切线分别与椭圆 C 订交于A,B 两点（不一样于P 点），则直线PA 与直线PB 的斜率之积等于．16. 若对于x 的不等式x|x a| b(a R)在[1,2]上恒成立，则实数b 的取值范围是．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知正项数列{a n }知足a 1a 2a 3...a n1 (a n 1)2(nN *).4（1）求数列{a n }的通项公式；（2）设b n 2n a n ，求数列{b n }的前n 项和T n .18. 如图1，四边形ABCD 为等腰梯形，AB 2,AD DCCB1，将 ADC 沿AC 折起，使得平面ADC 平面ABC ，E 为AB 的中点，连结DE,DB .（1）求证：BC AD ；（2）求直线DE 与平面BCD 所成的角的正弦值 .19. 某研究小组为了研究某品牌智好手机在正常使用状况下的电池供电时间，分别从该品牌手机的甲、乙两种型号中各选用 6部进行测试，其结果以下：甲种手机供电时间（小时）乙种手机供电时间（小时）19 18 21 22 23 2018 17.5 20 23 221）求甲、乙两种手机供电时间的均匀值与方差，并判断哪一种手机电池质量好；2）为了进一步研究乙种手机的电池性能，从上述6部乙种手机中随机抽取4部，记所抽4部手机供电时间不小于20小时的个数为X ，求X 的散布列和数学希望.x 2 y 2 1(ab 0)过点(2,1)，其离心率为220.已知椭圆E:b 2.a 22（1）求椭圆E 的方程；（2）直线l:yxm 与E 订交于A,B 两点，在y 轴上能否存在点C ，使 ABC 为正三角形，若存在，求直线l 的方程；若不存在，请说明原因.21.已知函数f(x)x.x(alnx),g(x)e x（1）若函数f(x)的最小值为1a 的值；，务实数e（2）当a0,x0 时，求证： g(x)f(x)2.e请考生在22、23两题中任选一题作答，假如多做，则按所做的第一题记分 .选修4-4：坐标系与参数方程x2 2cos, 为参数），以坐标原点O 为极点，以x 轴正半轴为极轴建已知圆C:2（ x2sin立极坐标系，点 A,B 的极坐标分别为 (1, ),(1,0).（1）求圆C的极坐标方程；（2）若P为圆C上的一动点，求|PA|2|PB|2的取值范围.选修4-5：不等式选讲已知函数f(x)|2x1||x2|.（1）求不等式f(x)3的解集；（2）若f(x)11(,0)对随意x R恒成立，求m n的最小值. m n mn试卷答案一、选择题1-5:DCDBC6-10:ACBDA11、12：AB二、填空题13.114.[1,)15.116.(2,)3三、解答题解：（1）设数列{a n}的前n项和为S n.当n1时，a11(a11)2,a11，4当n2时，4S n(a n1)2,4S n1(a n11)2，两式相减得4a n a n 2a n22a n12a n1，即(a n a n1)(a n an12)0，又a n0,a n a n12，数列{a n}的首项为12的等差数列，即a n2n1.，公差为（2）b n(2n1)2n,T n121322523...(2n1)2n，①2T n122323524...(2n3)2n(2n1)2n1，②①-②得T n22(2223...2n)(2n1)2n1282n2(2n1)2n162n1(22n1)62n1(32n)，T n 62n1(2n3)18.解：（1）证明：在图1中，作CHAB 于H ，则BH1 3 ,AH，又22BC1, CH3, CA 3,2AC BC ，平面ADC平面ABC ，且平面ADC平面ABCAC ，BC平面ADC ，又AD 平面ADC ，BC AD .（2）取AC 中点F ，连结DF,FE ，易得FA,FE,FD 两两垂直，以 FA,FE,FD 所在直线分别为x 轴、y 轴、z 轴成立空间直角坐标系，以下图，E(0,1,0),D(0,0,1),B(3,1,0),C(3,0,0)22 22DE(0,1,1),BC(0, 1,0),CD(3,0,1)，2 222设m(x,y,z)为平面BCD 的法向量，则mBC 0，即y 0 ，mCD3x z 0取x1，则m(1,0, 3) .设直线DE 与平面BCD 所成的角为，则sin|cos m,DE |6，46 直线DE 与平面BCD 所成的角的正弦值为.419.解：（1）甲的均匀值X 甲 1( 1 2 12 3 0) 20，1(6乙的均匀值X乙20 3 2 2. 5) 20，6甲的方差2 1 19) 218)2( 21)222) 223)220) 2 ]S 甲[( 635 12乙的方差S 乙21[(18)2(17.5)220)2 23)2 22)2(22.5)2]6 14 3由于甲、乙两种手机的均匀数同样，甲的方差比乙的方差小，因此以为甲种手机电池质量更好.（2）6部乙种手机供电时间不小于 20 小时的有4部，小于20 小时的有2部，因此X 得可能取值为2,3,4，则P(X2) C 42C 222,P(X3) C 43C 218,P(X 4) C 44 1 ，C 62 5 C 64 15 C 64 15故X 得散布列为X234P28 151515238 41 8因此EX215 15 .53111a 2b 220.解：（1）由已知得c 2，解得a2,b2.a 2c 2a 2b 2x 2y 2椭圆E 的方程为1.4 2（2）把yxm 代入E 的方程得3x 2 4mx2m 24 0，设(,),(,)，则4m2m 2 4，Ax 1 y 1Bx 2y 2x 1 x 23 ,x 1x 238(6 m 2) 0,6 m6，|AB|1k2(x 1 x 2) 24x 1x 2216m 24 2m 24 42936m3设AB 的中点为P ，则x Px 1 x 22m,y Pm x Pm ,P(2m ,m)2333 3PC:yxm，令x0，则C(0,m)，33由题意可知，|PC|3|AB|24m 2 4m 234 6 m 2 ，解得m 310 .切合0，9 9235直线l 的方程为yx3 105.21.解：（1）f(x)a 1 lnx(x 0) ，由f(x)0，得x e a1，由f(x)0，得0xe a1，f(x)在(0,e a 1)上单一递减，在(ea1,)上单一递加.f(x)minf(e a1)e a 1(a lne a1)e a11 .ea0.（2）证明：当a0,x 0时，由（1）知f(x)x(alnx) ax xlnxxlnx1，1e即f(x).eg(x)x，则g(x)1 x (x 0) ，e xe x由g(x)0，得0x 1，由g(x) 0，得x1，g(x)在(0,1)上单一递加，在 (1,)上单一递减.g(x)g(1)1，e1 1 22 g(x)f(x)g(x)[f(x)]e e，即g(x)f(x).ee22.解：（1）把圆C 的参数方程化为一般方程为(x2)2 (y2)2 2，即x 2 y 24x4y60，由x 2y 22,x cos ,ysin ，得圆C 的极坐标方程为 24 cos 4sin60.（2）设P(2 2cos ,2 2sin ),A,B 的直角坐标分别为(1,0),(1,0)，则|PA|2|PB|2 (3 2cos )2 (22sin )2(12cos )2 (22sin)222 16sin() [6,38]4因此|PA|2|PB|2的取值范围为[6,38].3x 3(x 1)x1(1 223.解：（1）f(x)x 2)，23x 3(x 2)其图象以下图，由图可知 f(x) 3的解集为{x|x0或x2}.（2）由图知f(x)min3, 1 1 3 . m n 3，2m n2mn 2 即m n3mn3 (mn )2，当且仅当mn 时等号成立，2228m,n0 ，解得m nn 时等号成立，当且仅当m3故m n 的最小值为8.3精选文档11。

超级全能生2019高考全国卷26省2月联考乙卷理科综合

“超级全能生”2019高考全国卷26省2月联考乙卷理科综合考生须知：1．答题前，在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号；2．所有答案必须写在答题卷上，写在试卷上无效；3．考试结束后，只需上交答题卷。

可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Cl-35.5 Cu-64一、选择题（本题共13小题，在每小题给出的四个选项中，只有一项是符合题目要求的）1．细胞内某些化合物的元素组成为C、H、O、N、P，下列一定不属于这些化合物的功能的是（）A．可作为细胞中的直接能源物质B．可作为储存遗传信息的物质C．参与构成生物膜的重要成分D．可作为细胞内良好的储能物质2．如图为胰岛B细胞正在进行的某项生理过程，①～⑥为细胞的结构，下列叙述错误的是（）A．胰岛素在①上合成，但合成和分泌过程离不开④的作用B．①和④中均可发生碱基互补配对现象，且配对原则相同C．胰岛A细胞中也有胰岛素基因，只是在该细胞中并未表达D．胰岛素以胞吐的方式排到⑥外，体现了生物膜的流动性3．如图为人在紧急情况下的生命活动调节示意图，下列叙述错误的是（）A．该过程是通过反射弧和体液运输两个途径来进行的B ．紧急信号传到肾上腺髓质的过程中会出现电位变化C ．肾上腺素弥散到体液中，只运输给相应的靶器官、靶细胞D ．该过程中接受信号的细胞有神经细胞、心肌细胞、肝细胞等4．下列关于生态系统的稳定性的叙述，正确的是（）A ．封山育林、合理间伐、科学灌溉等均能提高生态系统的稳定性B ．同等干扰强度下，草原生态系统比沙漠生态系统恢复的速率慢C ．同一个生态系统，不会既有抵抗力稳定性，又有恢复力稳定性D ．复杂度越低的生态系统，抵抗力稳定性越低，恢复力稳定性越高5．下面关于探究淀粉酶的最适温度的实验中叙述正确的是（）A ．可用斐林试剂检测还原糖的含量来反映酶的活性B ．先将淀粉与淀粉酶混合，然后在相应的温度下处理C ．实验需设置一系列温度梯度，不需要单独设置空白对照D ．所有关于探究酶的最适温度的实验，pH 要都为76．下列关于生物育种的叙述，正确的是（）A ．单倍体植株经过人工诱导使染色体数目加倍后都是纯合子B ．低温处理单倍体幼苗的芽尖细胞，能够抑制纺锤体的形成C ．三倍体西瓜没有种子，只能每年制种才能得到三倍体植株D ．在选择育种过程中，因基因型频率改变而使生物不断进化7．化学与生活、环境密切相关，下列有关说法正确的是（）A ．我国在南海成功开采的可燃冰（42CH H O n ）可能会带来酸雨等环境污染B ．我国研制的超高强耐腐蚀性实验室用钢板的熔点高于纯铁的熔点C ．我国研究的氢气低温制备和存储的方法实质上是物理变化D ．我国全面启动的北斗导航系统的信号传输与二氧化硅有关8．柠檬醛是一种香料，既可以被氧化，也可以被还原。

2019年全国乙卷统一高考数学试卷(理科)(新课标II)逐题解析

y2 b2
1（a>0，b>0）的右焦点，O 为坐标原点，以 OF 为直径的
圆与圆 x2+y2=a2 交于 P、Q 两点．若|PQ|=|OF|，则 C 的离心率为
A. 2
B. 3
C. 2
D. 5
解析如下：A
准确画图，由图形对称性得出 P 点坐标，代入圆的方程得到 c 与 a 关系，可求双曲线的离心率．
的方法，如 p 2 时，抛物线焦点为（1，0），椭圆焦点为（±2，0），排除 A，同样可排除
B，C，故选 D．
因为抛物线 y2 2 px( p 0) 的焦点 ( p , 0) 是椭圆 x2 y2 1 的一个焦点，所以
2
3p p
3 p p ( p )2 ，解得 p 8 ，故选 D． 2
本题主要考查抛物线与椭圆的几何性质，渗透逻辑推理、运算能力素养．

9.下列函数中，以为周期且在区间( ， )单调递增的是
2
42
A. f(x)=│cos 2x│
B. f(x)=│sin 2x│
C. f(x)=cos│x│
D. f(x)= sin│x│
解析如下：A 本题主要考查三角函数图象与性质，渗透直观想象、逻辑推理等数学素养．画出各函数图象，即可做出选择．
中位数仍为 x5 ，A 正确．
②原始平均数
x

1 9
( x1

x2

x3

x4

x8

x9 )
，后来平均数
x 17（x2 x3 x4 x8）
平均数受极端值影响较大， x 与 x 不一定相同，B 不正确

超级全能生2019高考全国卷26省12月联考乙卷理科数学

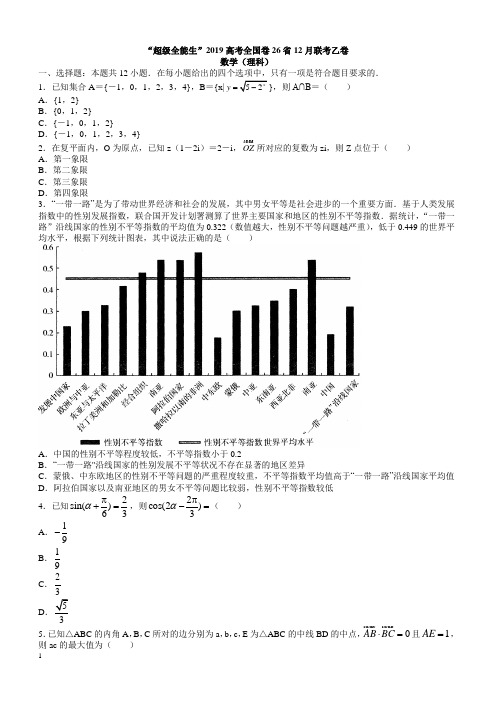
“超级全能生”2019高考全国卷26省12月联考乙卷数学（理科）一、选择题：本题共12小题．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A ＝{－1，0，1，2，3，4}，B ＝{x|y =，则A∩B ＝（） A ．{1，2} B ．{0，1，2}C ．{－1，0，1，2}D ．{－1，0，1，2，3，4}2．在复平面内，O 为原点，已知z （1－2i ）＝2－i ，OZ所对应的复数为zi ，则Z 点位于（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3．“一带一路”是为了带动世界经济和社会的发展，其中男女平等是社会进步的一个重要方面．基于人类发展指数中的性别发展指数，联合国开发计划署测算了世界主要国家和地区的性别不平等指数．据统计，“一带一路”沿线国家的性别不平等指数的平均值为0.322（数值越大，性别不平等问题越严重），低于0.449的世界平均水平，根据下列统计图表，其中说法正确的是（）A ．中国的性别不平等程度较低，不平等指数小于0.2B ．“一带一路"沿线国家的性别发展不平等状况不存在显著的地区差异C ．蒙俄、中东欧地区的性别不平等问题的严重程度较重，不平等指数平均值高于“一带一路”沿线国家平均值D ．阿拉伯国家以及南亚地区的男女不平等问题比较弱，性别不平等指数较低 4．已知2sin()63απ+=，则cos(2)3α2π-=（） A ．19- B ．19 C ．23D 5．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，E 为△ABC 的中线BD 的中点，0AB BC ⋅=且1AE =，则ac 的最大值为（）A ．23 B ．43C ．163D ．836．已知某几何体的三视图如图所示，则该几何体的内切球半径为（）ABC ．12D ．127．已知（x ＋1）n 的展开式中，奇数项的二项式系数和为32，则22()nx x-的展开式的常数项为（） A ．32 B ．64 C ．120 D ．608．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若角A ，32B，C 成等差数列，2a c +==，则△ABC 的面积为（）A ．12B ．12C 1D 19．已知实数x ，y 满足230,240,210,x y a x y x y --⎧⎪+-⎨⎪++⎩≤≥≥且z ＝x －2y ＋2的最大值为4，则实数a 的值为（）A ．2B ．92 C．52D ．3210．过抛物线x 2＝8y 焦点的直线交抛物线于M ，N 两点，则OM NO ⋅=（）A ．－20B ．12C ．－12D ．2011．函数f （x ）＝sin （ωx ＋φ）（ω＞0，02ϕπ<<）的部分图象如图所示，则下列选项中是函数1()3f x +的单调递增区间的是（）A ．[19，29]和[49，79] B ．[59-，29-]∪[19，49]C ．[59-，29-]和[19，49]D ．[－1，59-]∪[19，29]12．已知f （x ），g （x ）都是定义在R 上的函数，对任意x 均满足f （－x ）＝－f （x ），g （－x ）＝g （x ）≠0，当x ＞0时，总有f′（x ）·g （x ）＞f （x ）·g′（x ），f （2）＝0，则()()303f x g x --≥的解集为（）A ．[1，3]∪[5，＋∞）B ．[－2，0]∪[2，＋∞）C ．（－3，－2）∪（－1，＋∞）D ．[－5，－2]∪[3，＋∞）二、填空题：本题共4小题．13．命题“x ∃∈R ，sinx ＋cosx ＜1”的否定是________．14．已知非零向量a ，b ，满足|a |＝|b |．若|a ＋b |＝|2b －a |，则向量a ，b 的夹角为________． 15．双曲线x 2－y 2＝4的渐近线与圆C ：（x －3）2＋（y －2）2＝4交于A ，B 两点，则|AB|＝________． 16．如图，点P 在长方体ABCD —A 1B 1C 1D 1的体对角线A 1C 上（不包含线段端点），若AB ＝2AD ＝2AA 1＝2，则下列结论正确的有________．①存在P 点，使直线A 1C 与平面D 1AP 所成角为直角； ②无论P 点在何位置，都有∠APD 1＜90°； ③当112A P PC =时，D 1P ∥平面BDC 1．三、解答题：解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．（一）必考题：17．设S n 为数列{a n }的前n 项和，且a 1＝3，S n ＝An 2＋Bn （A ，B 为常数）．（Ⅰ）证明：数列n S n ⎧⎫⎨⎬⎩⎭为等差数列；（Ⅱ）若a 8＝17，求数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和T n ．18．某羽毛球俱乐部规定，每天一人打球1小时收费30元（不足1小时部分按1小时收费，以此类推），注册消费时间 1小时 2小时 3小时收费比例 1 0.9 0.8 消费时间 1小时 2小时 3小时人数20128（Ⅰ）估计该俱乐部一位会员至少打球2小时的概率；（Ⅱ）假设每个会员每天最多打球3小时，以事件发生的频率作为相应事件发生的概率，从该俱乐部的会员中随机抽取2人，记俱乐部从这2位会员的消费中每小时获得的平均利润之和为X ，求X 的分布列和数学期望E （X ）．19．如图，在四棱锥P —ABCD 中，底面ABCD 的对角线互相垂直，且BC ＝CD ，PA ⊥平面ABCD ．（Ⅰ）证明：平面PAC ⊥平面PBD ；（Ⅱ）若1cos 2BAD ∠=-，12AB PA AC ==，M 在PC 上，且2PM MC = ，试求直线BM 与平面PBD 所成角的正弦值．20．已知F1，F2分别为椭圆C：2221xy+=（a＞1）的左、右焦点，过F1且斜率不为零的直线l与C交于A，B两点．若△AF1F2的周长为222+（Ⅰ）求C的方程；（Ⅱ）设l的倾斜角为θ，若2cos3θ=，直线F2A，AB，F2B与直线21xa=-分别交于P，Q，R三个不同的点，记P，Q，R三点的纵坐标分别为y P，y Q，y R，求证：|y P|·|y R|＝|y Q|2．21．已知函数f（x）＝（e x－1）mx－e x＋x＋1，m∈R．（Ⅰ）若m＝0时，求函数f（x）的极值；（Ⅱ）若关于x的不等式（m－1）e x＋x＋1＞m在x∈[12，3）上恒成立，求m的取值范围．（二）选考题：请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题记分，作答时，请用2B 铅笔在答题卡上将所选题号后的方框涂黑．22．[选修4—4：坐标系与参数方程]已知曲线C1的参数方程为4cos,4sinxyθθ=⎧⎨=⎩（θ为参数）．（Ⅰ）求曲线C1的普通方程；（Ⅱ）设P是曲线C1上的动点，M（－2，5），N（6，1），求|PM|2＋|PN|2的最大值．23．[选修4—5：不等式选讲]已知函数f（x）＝|2x－1|－|2x－a|（a＞2且a∈R）．（Ⅰ）当a＝4时，求不等式f（x）≥x的解集；（Ⅱ）若f （x ）的最大值为M ，且正实数m ，n 满足12m a m n ++=，求2112m n +--的最小值．“超级全能生”2019高考全国卷26省12月联考乙卷数学（理科）答案详解1 2 3 4 5 6 7 8 9 10 11 12 C B A A D B D B B BC A13．x ∀∈R ，sinx ＋cosx≥114．3π 1516．①③ 17．解：（Ⅰ）证明：依题意，S n ＝An 2＋Bn ，所以nS An B n =+，所以11n n S SA n n+-=+，所以数列n S n ⎧⎫⎨⎬⎩⎭为等差数列．（Ⅱ）依题意可得{a n }为等差数列，183,17,a a =⎧⎨=⎩所以183,30,S S =⎧⎨=⎩所以1,2,A B =⎧⎨=⎩所以S n ＝n 2＋2n ，所以11(2)n S n n =+，所以数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和11111111323[(1)()()()]232411242(1)(2)nn T n n n n n n +=-+-++-+-=--++++ ． 18．解：（Ⅰ）在40名会员中，至少打球2小时的会员有12＋8＝20（人），故估计至少打球2小时的概率为201402P ==．（Ⅱ）某会员打球1小时，该俱乐部每小时的平均利润为30－5＝25（元），概率为1201402P ==；某会员打球2小时，该俱乐部每小时的平均利润为1(2300.910)222⨯⨯-=（元），概率为21234010P ==；某会员打球3小时，该俱乐部每小时的平均利润为1(3300.815)193⨯⨯-=（元），概率为381405P ==；由题意可知，X 的所有可能取值为50，47，44，41，38．111(50)224P X ==⨯=，133(47)221010P X ==⨯⨯=，331129(44)2101025100P X ==⨯+⨯⨯=，313(41)210525P X ==⨯⨯=，111(38)5525P X ==⨯=．所以X所以数学期望()504744413845.84101002525100E X =⨯+⨯+⨯+⨯+⨯==． 19．解：（Ⅰ）证明：因为底面ABCD 的对角线瓦相垂直，所以BD ⊥AC ，又因为PA ⊥平面ABCD ，所以BD ⊥PA ，因为PA∩AC ＝A ，所以BD ⊥平面PAC ，又因为BD ⊂平面PBD ，所以平面PAC ⊥平面PBD ．（Ⅱ）因为1cos 2BAD ∠=-，所以∠BAC ＝∠DAC ＝60°，又因为12AB AC =，所以∠ABC ＝90°，如图，以BC ，BA ，Bz （Bz ∥AP ）所在直线分别为x ，y ，z 轴建立空间直角坐标系．设PA ＝AB ＝1，所以B （0，0，0），C 30，0），A （0，1，0），P （0，1，1），D （32，32，0），又因为2PM MC = ，所以M 3，23，23），所以322(,)33BM = ，设平面PBD 的法向量为m ＝（x ，y ，z ），3,0)2BD = ，(0,1,1)BP = ，所以0,0,BD BP ⎧⋅=⎪⎨⋅=⎪⎩m m 令y ＝1，有1,1,x y z ⎧=⎪=⎨⎪=-⎩所以(,1)=-m ，所以355cos ,55||||BM BM BM ⋅==-m m m ．故直线BM 与平面PBD 355． 20．解：（Ⅰ）由椭圆的定义得|AF 1|＋|AF 2|＝2a ，所以△AF 1F 2的周长为1212||||||222AF AF FF ++=，所以2221222a a +-=+2a =所以C 的方程为2212x y +=．（Ⅱ）证明：由题意得直线l 的方程为51)y x =+，联立方程225(1),21,2y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩ 可得7x 2＋10x ＋1＝0，设A （x 1，y 1），B （x 2，y 2），显然x 1≠1，x 2≠1，所以12107x x +=-，1217x x =．因为l 与直线12x =-交点Q 的纵坐标为5Q y =所以25||16Q y =．因为直线F 2A 的方程为11(1)1y y x x =--，故直线F 2A 与直线12x =-交点P 的纵坐标为1132(1)P y y x -=-，同理，点R 的纵坐标为2232(1)R y y x -=-，所以121233||||2(1)2(1)P R y y y y x x --⋅=⋅-- 121294(1)(1)y y x x =--1212121259(1)44[()1]x x x x x x x x ⋅+++=-++516=，所以|y P |·|y R |＝|y Q |2． 21．解：（Ⅰ）若m ＝0时，f （x ）＝－e x ＋x ＋1，所以f′（x ）＝－e x ＋1，令f′（x ）＝0，得x ＝0．故x ∈（－∞，0）时，f′（x ）＞0，f （x ）单调递增； x ∈（0，＋∞）时，f′（x ）＜0，f （x ）单调递减，所以函数f （x ）的极大值为f （0）＝0，无极小值．（Ⅱ）由（m －1）e x ＋x ＋1＞m ，得m （e x －1）＞e x －x －1，由x ∈[12，3）知，e x －1＞0，所以e 11e 1e 1x x x x xm -->=---，令()1e 1x x h x =--，x ∈[12，3），所以2e (1)1()(e 1)x x x h x -+'=-，令g （x ）＝e x （x －1）＋1， g′（x ）＝e x （x －1）＋e x ＝xe x ，因为x ∈[12，3），所以g′（x ）＞0，即g （x ）＝e x （x －1）＋1在[12，3）上单调递增，又1e 102g ⎛⎫=> ⎪⎝⎭，所以g （x ）＞0恒成立，即2e (1)1()0(e 1)x x x h x -+'=>-，所以h′（x ）＞0在[12，3）上恒成立，所以()1e 1x x h x =--在[12，3）上单调递增，所以33()(3)1e 1h x h <=--，所以331e 1m --≥．22．解：（Ⅰ）因为曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩（θ为参数），则曲线C 1的普通方程为x 2＋y 2＝16．（Ⅱ）设P （4cosθ，4sinθ）（θ为参数），又因为M （－2，5），N （6，1），所以|PM|2＋|PN|2＝（4cos θ＋2）2＋（4sinθ－5）2＋（4cosθ－6）2＋（4sinθ－1）2＝98－16（3sinθ＋2cosθ）98)θϕ=-+（其中cosϕ=）．因为－1≤sin （θ＋φ）≤1，所以|PM|2＋|PN|2的最大值为98+ 23．解：（Ⅰ）将函数f （x ）＝|2x －1|－|2x －4|去绝对值，当12x ≤时，f （x ）＝－3≥x ⇒x≤－3；当122x <<时，5()4523f x x x x =-⇒<≥≤；当x≥2时，f （x ）＝3≥x ⇒2≤x≤3，综上所述，不等式的解集为（－∞，－3]∪[53，3]．（Ⅱ）由绝对值三角不等式可得||2x －1|－|2x －a||≤|（2x －1）－（2x －a ）|＝|a －1|＝a －1，所以f （x ）的最大值为a －1，因为正实数m ，n 满足12M a m n+==，所以121m n +=，所以2n m n =-，所以21211122(2)21222212n n n m n n n n n +=+=-+-⨯=-------≥（当且仅当1232n n n -=⇒=-时，取等号），所以2112m n +--的最小值为2．。

“超级全能生”2019高考全国卷26省12月联考乙卷-数学理科答案

[
)
（分）５由绝对值三角不等式可得｜（２ｘ－１｜－｜２ｘ－ Ⅱ）（）（），ａ｜≤ ｜２ｘ－１－２ｘ－ａ｜＝｜ａ－１｜＝ａ－１所以ｆ（）的最大值为ａ，ｘ－１１２因为正实数ｍ，满足＋＋Ｍ＝ａ，ｎｍｎｎ１２，（分），所以ｍ＝所以＋＝７１ｍｎ－２ｎ１２１２１所以＋＋＝＝ｎ－２＋ ≥ １ｎ－２ｎ－２－２ｎｍ－ｎ－１－２ｎ１１）２（＝２当且仅当ｎ－２＝ｎ＝ｎ－２ ˑ ｎ－２－２ｎ
(
)
(
)
(
)
( {
)
{
３５５故直线ＢＭ与平面ＰＢＤ所成角的正弦值为槡．５５分）（１２
— 数学（理科） ·答１—
解：（由椭圆的定义得｜，２０．ＡＦ＋｜ＡＦ＝２ａ Ⅰ）１｜２｜的周长为所以△ Ａ｜ＡＦＦ｜＋｜ＡＦ｜＋｜Ｆ＝Ｆ１２１２１Ｆ２｜，２２＋２槡
[
) [
)
{
(
)
２２所以｜的最大值为９ＰＭ｜＋｜ＰＮ｜８＋１６３．槡１（分）１０解：（）将函数（）去绝对值，２３． Ⅰ ｆｘ＝｜２ｘ－１｜－｜２ｘ－４｜１ｘ（）；当ｘｆｘ＝－３３ ≥ｘ ≤－ ≤ ２时，１５≤ ｘ；当＜ｘ时，（）＜２＜２ｆｘ＝４ｘ－５ ≥ｘ２３

超级全能生2019高考全国卷26省12月联考乙卷理科综合

“超级全能生”2019高考全国卷26省12月联考乙卷理科综合可能用到的相对原子质量：H－1 C－12 O－16 Ti－48 Sr －88一、选择题Ⅰ：在每小题给出的四个选项中，只有一项是符合题目要求的。

1．关于蛋白质的叙述不正确的是（）A．功能相似的蛋白质，结构可能差别很大B．线粒体内膜上蛋白质的种类和数量比外膜的多C．神经元间的信息交流依赖于神经递质和膜蛋白D．淋巴因子是由浆细胞产生的一种免疫活性物质2．有关细胞周期和细胞分裂方式的叙述正确的是（）A．从一次分裂间期完成时开始到下一次间期完成时为止，为一个细胞周期B．细胞存在染色单体时，其染色体数目一定是其DNA分子数目的一半C．骨髓干细胞中心体的复制和染色体的复制都发生在有丝分裂的间期D．已分化的组织细胞形成像早期胚胎一样的细胞团块后，细胞周期会延长3．下列有关吞噬细胞的说法中，正确的是（）A．吞噬细胞发挥作用能体现细胞膜的物质运输和信息传递等功能B．吞噬细胞和B细胞、T细胞都属于免疫系统组成中的淋巴细胞C．吞噬细胞主要参与人体第二道防线，在第三道防线中几乎不起作用D．吞噬细胞吞噬癌细胞属于免疫系统的功能，吞噬体内衰老的细胞则不是4．将燕麦胚芽鞘和大豆下胚轴切段放在含2％蔗糖的培养液中进行实验，一段时间后向培养液中加入10μmol／L生长素，并定期测定切段的延伸速率，结果如图所示，下列有关该实验的分析，不正确的是（）A．实验前应将燕麦胚芽鞘和大豆下胚轴切段在蒸馏水中浸泡一段时间，以排除内源生长素对实验的干扰B．培养液中蔗糖的作用是为燕麦胚芽鞘和大豆下胚轴切段提供生长所需的营养物质，蔗糖含量为2％是为了防止燕麦胚芽鞘和大豆下胚轴切段失水C．由图可知，10μmol／L生长素对燕麦胚芽鞘和大豆下胚轴切段均起促进作用，且对大豆下胚轴切段促进作用更大D．由图可知，大豆下胚轴切段的延伸速率比燕麦胚芽鞘快且会发生波动，大豆下胚轴切段对生长素的敏感性高于燕麦胚芽鞘5．如图是一个湿地生态公园食物网的一部分，下列有关说法中正确的是（）A．猛禽占据多个营养级，最低属于三级消费者B．蛙类通过叫声求偶，体现了生态系统的功能C．建立湿地生态公园是为了利用生物多样性的直接价值型增长D．因为缺少天敌，蛙类数量会呈现“J”6．某研究小组做人类遗传病的调查时发现，被调查家系中同时存在着红绿色盲和并指两种遗传病，家系图如下所示，两病分别用甲、乙表示，下列说法正确的是（）。

超级全能生2019高考全国卷26省12月联考乙卷(文科)数学试题及答案

“超级全能生”2019高考全国卷26省12月联考乙卷数学（文科）一、选择题：1．已知集合M ＝{x|－1＜x ＜1），N ＝{x|2x 2－x －3≤0），则M∩N＝（）A ．（－1，1）B ．13[,)22-C ．3[1,]2- D ．[－1，1）2．复数4421i z i -=-，则复数z 在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知椭圆22214x y b+=（b ＞0）的上、下顶点分别为A ，B ，左、右焦点分别为F 1，F 2，且四边形AF 1BF 2的面积为4，则该椭圆的离心率为（）A ．14 B ．2 C ．2D ．12 4．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（） A ．24 B ．48 C ．88 D ．1045．已知函数lg ,0,()8,0,x x f x x x >⎧=⎨+≤⎩若f （－5）＝3f （a ），则实数a 的值为（）A ．1B ．3C ．－7或－1D ．10或－76．图中大正方形是由四个全等的直角三角形的斜边组成，每个直角三角形的两条直角边的长分别为a ，b 且a ＝2b ，阴影部分是小正方形的内切圆，则在大正方形内任取一点，此点恰好取自阴影部分的概率为（）A ．13B ．20πC ．5πD ．167．在递增的等差数列{a n }中，a 2，a 8是函数f （x ）＝x 2－4x －5的两个零点，则{a n }的前50项和等于（）A ．2450B ．1125C ．1225D ．－24508．某校高三第一次模拟考试，从全校文科学生中随机抽取10名学生的数学成绩如茎叶图所示，现将每人的分数依次输入到如下程序框图中，则输出的S ＝（）A ．110.5B ．111C ．111.5D ．1129．已知角α的顶点与直角坐标系的原点重合，始边与x 轴的非负半轴重合，终边经过点77,9sin )66P ππ-，则22sin 12cos sin cos αααα=+-（）A ．35B ．12C ．3D ．610．某圆柱的体积、侧面积都为16π，则该圆柱的外接球的体积为（）A ．32π B． C．3D． 11．对函数()3cos 33x xf x =+给出下列命题： ①f （x ）的图象向右平移2π个单位长度后所得的函数是非奇非偶函数；②f （x ）的图象关于点（π，0）中心对称； ③f （x ）的图象关于直线x ＝－2019π对称；④f （x ）在[,]2π-π上单调递增．其中真命题的个数是（）A ．4B ．3C ．2D ．112．已知函数21,1,()62,1,2a x x f x a x x x +⎧≥⎪=⎨--<⎪-⎩当x 1≠x 2时，1221()()0f x f x x x -<-，则函数g （a ）＝2a 2＋16a＋3的值域是A ．[－27，＋≦）B ．（－≦，35]C ．（2，5]D ．（27，35] 二、填空题：13．已知点A （2，－1），(1,3)AC = ，32AB AC =，则点B 的坐标为________．14．已知x ，y 满足约束条件2360,3260,220,x y x y x y -+≥⎧⎪+-≤⎨⎪+-≥⎩则z ＝x －3y 的最小值为________．15．双曲线x 2－y 2＝4的渐近线与圆C ：（x －3）2＋（y －2）2＝4交于A ，B 两点，则|AB|＝________．16．已知正项数列{a n }的前n 项和为S n ，（a n ＋1－2S n ）2＝4S n ＋1S n ，且a 1＝1，设13log n n b S =，则b 1＋b 2＋…＋b 20＝________．三、解答题：（一）必考题：17．△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若cos2A ＋sinBsinA ＝1，3C π=，且△ABC （Ⅰ）求ab的值；（Ⅱ）求△ABC 的面积．18．如图，四棱锥P —ABCD 的底面ABCD 的对角线互相垂直，且BC ＝CD ，PA ⊥平面ABCD ．（Ⅰ）求证：平面PAC ⊥平面PBD ；（Ⅱ）若BD ＝CD ＝4，PA ＝6，M 为PC 上一点，且2PM ＝MC ，试求三棱锥C —BDM 的体积．19．某羽毛球俱乐部规定，每天一人打球1小时收费30元（不足1小时部分按1小时收费，依此类推），注册成为会员，对会员一天连续打球2小时、3小时的优惠标准说明如下表：该俱乐部从注册的会员中，随机抽取了40位进行统计，得到统计数据如下表：假设该俱乐部一人1小时活动的成本为5元，根据所给数据，解答下列问题：（Ⅰ）估计该俱乐部一位会员消费时间至少为2小时的概率；（Ⅱ）若某会员消费时间不超过3小时，以频率作为概率，估计该俱乐部每小时对该会员获取的平均利润；（Ⅲ）小明、小王、小张、小军四名会员周六一起去俱乐部打球，小王打了1小时有事离开了，小军打了2小时，小明、小张打了3小时，他们今天共应付给俱乐部多少费用？20．已知抛物线C ：y 2＝2px （p ＞0）的焦点为F ，准线与x 轴交于A 点，过点F直线l 交C 的准线于B 点，ABF S △ （Ⅰ）求C 的方程；（Ⅱ）已知C 上一点P （t ，4），过点P 作C 的两条弦PD 和PE ，且PD ⊥PE ，求直线DE 恒过的定点的坐标．21．已知函数f （x ）＝3a 2lnx －x 2－5ax （a ∈R ）．（Ⅰ）若x ＝1是f （x ）的极值点，求f （x ）在（1，f （1））处的切线方程；（Ⅱ）讨论f （x ）的单调性．（二）选考题：22．已知曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩（θ为参数）．（Ⅰ）求曲线C 1的普通方程；（Ⅱ）设P 是曲线C 1上的动点，M （－2，5），N （6，1），求|PM|2＋|PN|2的最大值．23．设函数f （x ）＝|2x ＋4|＋|x －a|（a ∈R ）．（Ⅰ）当12a =时，求不等式9()2f x <的解集；（Ⅱ）若1()|2|32f x x a >++-恒成立，求实数a 的取值范围．“超级全能生”2019高考全国卷26省12月联考乙卷数学（文科）答案13．8(,1)314．8413-15．16．－38017．解：（Ⅰ）因为cos2A ＋sinBsinA＝1，所以2sin 2A ＝sinBsinA ，因为sinA≠0，所以sinB ＝2sinA ，由正弦定理得b ＝2a ，所以12a b =．（Ⅱ）由（Ⅰ）知b ＝2a ，因为3C π=，三角形ABC 所以由正弦定理得sin 3c =π，所以c ＝2，由余弦定理得22222422cos 33a a a a a π=+-= ，解得243a =，所以△ABC 的面积为214sin 232323ABC S ab a π====△． 18．解：（Ⅰ）证明：因为底面ABCD 的对角线互相垂直，所以BD ⊥AC ，又PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥PA ，因为PA∩AC＝A ，所以BD ⊥平面PAC ，因为BD ⊂平面PBD ，所以平面PAC ⊥平面PBD ．（Ⅱ）因为PA ⊥平面ABCD ，PA ⊂平面PAC ，所以平面PAC ⊥平面BCD ，过点M 在平面PAC 上作MN ⊥AC 于N 点，所以MN ⊥平面BCD ，因为2PM ＝MC ，所以2PC ＝3CM ，由Rt △PAC ∽Rt △MNC ，所以2PA ＝3MN ，因为PA ＝6，所以MN ＝4，因为BC ＝BD ＝CD ＝4，所以144sin 602BCD S =⨯⨯⨯︒=△，所以三棱锥C —BDM 的体积143C BDM M BCD V V --==⨯=．19．解：（Ⅰ）在40名会员中，消费时间至少为2小时的会员有12＋8＝20（人），故概率201402P ==．（Ⅱ）该会员消费时间为1小时、2小时、3小时的概率分别为12，310，15，所以估计该俱乐部每小时对该会员获取的平均利润为131(305)(300.95)(300.85)22.9()2105⨯-+⨯⨯-+⨯⨯-=元．（Ⅲ）依题意，小王打了1小时应付30元；小军打了2小时，应付2×30×0.9＝54（元）；小明、小张打了3小时，应付3×30×0.8×2＝144（元）；所以他们今天共应付给俱乐部费用为30＋54＋144＝228（元）．20．解：（Ⅰ）由题意知抛物线的焦点(,0)2pF ，所以直线l 的方程为)2py x =-．则可得点B 的坐标为(,)2p-，因为ABF S =△，所以12p =p ＝2．所以抛物线C 的方程为y 2＝4x ．（Ⅱ）由（Ⅰ）可得点P （4，4），且直线DE 的斜率不为0，设直线DE 的方程为x ＝my ＋n ，联立24,,y x x my n ⎧=⎨=+⎩得y 2－4my －4n ＝0，则Δ＝16m 2＋16n ＞0． ① 设D （x 1，y 1），E （x 2，y 2），则由韦达定理知y 1＋y 2＝4m ，y 1y 2＝－4n ．因为PD ⊥PE ，所以1122(4,4)(4,4)PD PE x y x y =----=121212124()164()16x x x x y y y y -+++-++=2222121212124()164()164444y y y y y y y y -+++--+= 2212121212()()34()3216y y y y y y y y -++-++= 22161232160n m n m --+-=，即n 2－12n ＋32＝16m 2＋16m ，整理得（n －6）2＝4（2m ＋1）2，所以n －6＝±2（2m ＋1），即n ＝－4m ＋8或n ＝－4m ＋4（不合题意，舍去），所以直线DE 的方程为x ＝my ＋4m ＋8＝m （y ＋4）＋8．所以直线DE 恒过定点（8，－4）．21．解：（Ⅰ）因为f （x ）＝3a 2lnx －x 2－5ax ，所以2223253()25(0)a x ax a f x x a x x x--+'=--=>，因为x ＝1是f （x ）的极值点，所以3a 2－5a －2＝0，解得a ＝2或13a =-．当a ＝2时，f （1）＝－11，f′（1）＝0，所以f （x ）在（1，f （1））处的切线方程为y ＋11＝0．当13a =-时，2(1)3f =，f′（1）＝0，所以f （x ）在（1，f （1））处的切线方程为203y -=，即3y －2＝0．故f （x ）在（1，f （1））处的切线方程为y ＋11＝0或3y －2＝0．（Ⅱ）由（Ⅰ）知22253(3)(2)()(0)x ax a x a x a f x x x x--+-+-'==>，令f′（x ）＝0得x ＝－3a 或2a x =， ①当a ＝0时，f′（x ）＜0，所以f （x ）的单调递减区间为（0，＋≦）； ②当a ＞0时，32aa -<，由()0,0f x x '>⎧⎨>⎩得02a x <<；由()0,0f x x '<⎧⎨>⎩得2ax >．所以f （x ）在(0,)2a 上单调递增，在(,)2a +∞上单调递减； ③当a ＜0时，33a a ->，由()0,0f x x '>⎧⎨>⎩得0＜x ＜－3a ；由()0,0f x x '<⎧⎨>⎩得x ＞－3a ．所以f （x ）在（0，－3a ）上单调递增，在（－3a ，＋≦）上单调递减．综上，当a ＝0时，f （x ）在（0，＋≦）上单调递减；当a ＞0时，f （x ）在(0,)2a 上单调递增，在(,)2a +∞上单调递减；当a ＜0时，f （x ）在（0，－3a ）上单调递增，在（－3a ，＋≦）上单调递减．22．解：（Ⅰ）因为曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩（θ为参数），则曲线C 1的普通方程为x 2＋y 2＝16．（Ⅱ）设P （4cosθ，4sinθ）（θ为参数），又因为M （－2，5），N （6，1），所以222222||||(4cos 2)(4sin 5)(4cos 6)(4sin 1)PM PN θθθθ+=++-+-+-9816(3sin 2cos )98)θθθϕ=-+=-+（其中cos ϕ=）．因为－1≤sin（θ＋φ）≤1，所以|PM|2＋|PN|2的最大值为98+．23．解：（Ⅰ）当12a =时，1()|24|||2f x x x =++-，所以73,2,291(),2,22713,.22x x f x x x x x ⎧--<-⎪⎪⎪=+-≤≤⎨⎪⎪+>⎪⎩由2,793,22x x <-⎧⎪⎨--<⎪⎩解得823x -<<-；由12,299,22x x ⎧-≤≤⎪⎪⎨⎪+<⎪⎩解得－2≤x＜0；由1,2793,22x x ⎧>⎪⎪⎨⎪+<⎪⎩无解．综上所述，不等式9()2f x <的解集为8(,0)3-．（Ⅱ）因为f （x ）＝|2x ＋4|＋|x －a|，所以1()|2|32f x x a >++-恒成立等价于 1|2|||32x x a a ++->-恒成立，因为|x ＋2|＋|x －a|≥|x＋2＋a －x|＝|2＋a|，所以1|2|32a a +>-，解得a ＜－10或23a >，故实数a 的取值范围为2(,10)(,)3-∞-+∞。

超级全能生2019高考全国卷26省2月联考乙卷理科综合

“超级全能生”2019高考全国卷26省2月联考乙卷理科综合可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Cl-35.5 Cu-64一、选择题（本题共13小题，在每小题给出的四个选项中，只有一项是符合题目要求的）1．细胞内某些化合物的元素组成为C、H、O、N、P，下列一定不属于这些化合物的功能的是（）A．可作为细胞中的直接能源物质B．可作为储存遗传信息的物质C．参与构成生物膜的重要成分D．可作为细胞内良好的储能物质2．如图为胰岛B细胞正在进行的某项生理过程，①～⑥为细胞的结构，下列叙述错误的是（）A．胰岛素在①上合成，但合成和分泌过程离不开④的作用B．①和④中均可发生碱基互补配对现象，且配对原则相同C．胰岛A细胞中也有胰岛素基因，只是在该细胞中并未表达D．胰岛素以胞吐的方式排到⑥外，体现了生物膜的流动性3．如图为人在紧急情况下的生命活动调节示意图，下列叙述错误的是（）A．该过程是通过反射弧和体液运输两个途径来进行的B．紧急信号传到肾上腺髓质的过程中会出现电位变化C．肾上腺素弥散到体液中，只运输给相应的靶器官、靶细胞D．该过程中接受信号的细胞有神经细胞、心肌细胞、肝细胞等4．下列关于生态系统的稳定性的叙述，正确的是（）A．封山育林、合理间伐、科学灌溉等均能提高生态系统的稳定性B．同等干扰强度下，草原生态系统比沙漠生态系统恢复的速率慢C ．同一个生态系统，不会既有抵抗力稳定性，又有恢复力稳定性D ．复杂度越低的生态系统，抵抗力稳定性越低，恢复力稳定性越高5．下面关于探究淀粉酶的最适温度的实验中叙述正确的是（）A ．可用斐林试剂检测还原糖的含量来反映酶的活性B ．先将淀粉与淀粉酶混合，然后在相应的温度下处理C ．实验需设置一系列温度梯度，不需要单独设置空白对照D ．所有关于探究酶的最适温度的实验，pH 要都为76．下列关于生物育种的叙述，正确的是（）A ．单倍体植株经过人工诱导使染色体数目加倍后都是纯合子B ．低温处理单倍体幼苗的芽尖细胞，能够抑制纺锤体的形成C ．三倍体西瓜没有种子，只能每年制种才能得到三倍体植株D ．在选择育种过程中，因基因型频率改变而使生物不断进化7．化学与生活、环境密切相关，下列有关说法正确的是（）A ．我国在南海成功开采的可燃冰（42CH H O n ⋅）可能会带来酸雨等环境污染B ．我国研制的超高强耐腐蚀性实验室用钢板的熔点高于纯铁的熔点C ．我国研究的氢气低温制备和存储的方法实质上是物理变化D ．我国全面启动的北斗导航系统的信号传输与二氧化硅有关8．柠檬醛是一种香料，既可以被氧化，也可以被还原。

超级全能生2019高考全国卷26省2月联考乙卷理科数学

(II )若 (1，2)时,不等式f(x)>3x成立，求实数a的取值范围.
参考答案
“超级全能生”2019高考全国卷26省2月联考乙卷
数学（理科）
1.D
2.C
3.A
4.B
5.C
6.A
7.B
8.D
9.C
10.D
11.C
12.B
13.
14.60
15.18
16.6
17.解法一(I )如图，过点D作DE⊥AB,
15.若ln(2a + 8b) =lna+lnb,则a+b的最小值为________.
16.我国南北朝时期的数学家祖暅提出体积的计算原理(祖暅原理）“幂势既同则积不容异”，“势”即是高，“幂”是面积.意思是:如果两等高的几何体在同等高处的截面积相等，那么这两个几何体的体积相等.已知双曲线，直线y = 0与y=6在第一象限内与双曲线及其渐近线围成如图中阴影部分所示的图形，则该图形绕y轴旋转一周所得几何体的体积为________.
手机依赖症
非手机依赖症
合计
男生
100
女生
100
合计
200
试运用独立性检验的思想方法分析:是否有90%的把握认为“手机依赖症”与“性别”有关?附:参考公式与临界值表: ，其中
0.100
0.050
0.025
0.010
0.001
k
2.706
3.841
5.024
6.635
10.828
19.(12分）
如图，已知AB丄平面ACD，AB//DE，△ACD为等边三角形，AD = DE = 2AB, F为CE的中点.
A. 36
B. 48

超级全能生2019高考全国卷26省12月联考乙卷理科综合

1．关于蛋白质的叙述不正确的是（）A．功能相似的蛋白质，结构可能差别很大B．线粒体内膜上蛋白质的种类和数量比外膜的多C．神经元间的信息交流依赖于神经递质和膜蛋白D．淋巴因子是由浆细胞产生的一种免疫活性物质2．有关细胞周期和细胞分裂方式的叙述正确的是（）A．从一次分裂间期完成时开始到下一次间期完成时为止，为一个细胞周期B．细胞存在染色单体时，其染色体数目一定是其DNA分子数目的一半C．骨髓干细胞中心体的复制和染色体的复制都发生在有丝分裂的间期D．已分化的组织细胞形成像早期胚胎一样的细胞团块后，细胞周期会延长3．下列有关吞噬细胞的说法中，正确的是（）A．吞噬细胞发挥作用能体现细胞膜的物质运输和信息传递等功能B．吞噬细胞和B细胞、T细胞都属于免疫系统组成中的淋巴细胞C．吞噬细胞主要参与人体第二道防线，在第三道防线中几乎不起作用D．吞噬细胞吞噬癌细胞属于免疫系统的功能，吞噬体内衰老的细胞则不是4．将燕麦胚芽鞘和大豆下胚轴切段放在含2％蔗糖的培养液中进行实验，一段时间后向培养液中加入10μmol／L生长素，并定期测定切段的延伸速率，结果如图所示，下列有关该实验的分析，不正确的是（）A．实验前应将燕麦胚芽鞘和大豆下胚轴切段在蒸馏水中浸泡一段时间，以排除内源生长素对实验的干扰B．培养液中蔗糖的作用是为燕麦胚芽鞘和大豆下胚轴切段提供生长所需的营养物质，蔗糖含量为2％是为了防止燕麦胚芽鞘和大豆下胚轴切段失水C．由图可知，10μmol／L生长素对燕麦胚芽鞘和大豆下胚轴切段均起促进作用，且对大豆下胚轴切段促进作用更大D．由图可知，大豆下胚轴切段的延伸速率比燕麦胚芽鞘快且会发生波动，大豆下胚轴切段对生长素的敏感性高于燕麦胚芽鞘5．如图是一个湿地生态公园食物网的一部分，下列有关说法中正确的是（）A．猛禽占据多个营养级，最低属于三级消费者B．蛙类通过叫声求偶，体现了生态系统的功能C．建立湿地生态公园是为了利用生物多样性的直接价值D．因为缺少天敌，蛙类数量会呈现“J”型增长6．某研究小组做人类遗传病的调查时发现，被调查家系中同时存在着红绿色盲和并指两种遗传病，家系图如下所示，两病分别用甲、乙表示，下列说法正确的是（）A．家系中甲病患者男多女少，可判定甲病为伴X染色体隐性遗传病B．家系中乙病患者Ⅲ3的父亲一定不携带乙病的致病基因C．Ⅲ1和Ⅲ2生一个女儿患病的概率比生儿子患病的概率高D．通过在此家系中的调查，可确定遗传病甲和乙的发病率7．化学与生产生活密切相关。

“超级全能生”2019届高考全国卷26省高三联考乙卷

.. .. ..“超级全能生”2019 届高考全国卷26 省 9 月高三联考乙卷地理试题第 I 卷（选择题）一、选择题以下图是 11 月 24 日至 26 日中国局地降雪量散布图。

据此达成下边小题。

1．影响甲、乙两地降雪量差别的主导要素是A．纬度B．地形C．大气环流 D ．海陆地点2．该期间A．甲地土壤温度日变化较小B．乙地春小麦干旱缺水C．丙地作物受冻害最严重D．丁河段今年初次发生凌汛3．次年春天洪涝灾祸最严重的可能是A．甲B．乙C．丙 D ．丁雪莲是新疆的有名特产，生于高峰雪线邻近的岩缝、石壁和冰碛砾石滩中．种子在 0℃抽芽．3-5 ℃生长．幼苗能够抵抗 -21 ℃的低温． 15- 25℃生长旺盛，以天山所产最多，质亦最正确。

可作药用．也有必定的赏析价值。

1906年中国已将天山雪莲列为二级保护植物。

以下图是天山自然带谱垂直散布图，据此达成下边小题。

4．影响天山南北坡自然带谱种类差别的主导要素是()A．光照B．风向C．海拔D．坡度5．天山雪莲最可能的散布区在(）A．高峰冰雪带B．高峰草甸带C．山地草甸草原带D．云杉林带6．天山雪莲人工已种植成功，人工创建的生长环境天气和土壤的突出特点应当是()A．冷湿B．冷干C．暖湿D．暖干橡胶坝，又称橡胶水闸，是用高强度合成纤维织物做受力骨架，内外涂敷橡胶作保护层，经过充水（气）将其充胀形成的袋式挡水坝。

坝硕能够溢流，并可依据需要调理坝高，在上游蓄水并控制上游水位，某县县城建成的橡胶坝剖面图以以下图所示，此中 7-9 月橡胶坝水体自然外溢，据此达成下边小题。

7．依据资料，判断该县属于以下那个省区A．广东B．台湾C．山西D．云南8．在水下泥土中种荷花、水草，水中放养鱼类，主要作用是A．美化环境B．形成良性生态系统C．生产莲藕D．增添蒸腾作用9．橡胶坝水体不可以起到的作用是()A．改良局地天气B．降低热岛效应C．扩大湿地面积D．增添县城降水量建筑容积率是指项目规划建设用地范围内所有建筑面积与规划建设用地面积之比。

苏教版2019届高三12月联考数学(理科)试题(精品Word版,含答案解析)

数学（理科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集U R =，集合(){}30A x x x =-?，{B x y ==，则()U A B Çð等于（） A. ()0,2 B. ()0,3 C. Æ D. (]0,2 【答案】D 【解析】【分析】解不等式得集合A ，进而可得U A ð，求解函数定义域可得集合B ，利用交集求解即可. 【详解】因为集合(){}()300,3U A x x x =-<=ð，(],2B =-?，所以()(]0,2U A B ?ð，故选D.【点睛】本题主要考查了集合的补集及交集的运算，属于基础题.2.复数z 满足(32)43i z i -=+（i 为虚数单位），则复数z 在复平面内对应的点位于（） A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限【答案】A 【解析】由题意得，43(43)(32)11732(32)(32)1313i i i iz i i i +++===+--+，则复数z 在复平面内对应的点位于第一象限，故选A. 3.已知向量()1,3a =，(),1b m =，若//a b ，则m = （） A. 13-B. 13C. 3-D. 3 【答案】B 【解析】【分析】利用两个向量平行的坐标表示列出方程求解即可.【详解】向量()()1,3,,1a b m ==，若//a b ，则113m ?，解得13m =.故选B.【点睛】本题主要考查了向量平行的坐标表示，属于基础题. 4.已知函数()1112xf x e =-+，则()f x 是（） A. 奇函数，且在R 上是增函数 B. 偶函数，且在()0,+?上是增函数C. 奇函数，且在R 上是减函数D. 偶函数，且在()0,+?上是减函数【答案】C 【解析】【分析】先判断定义域是否关于原点对称，进而利用()()0f x f x -+=可得函数为奇函数，再由指数函数的单调性可判断函数的单调性.【详解】定义域为R ，关于原点对称，()1112x f x e --=-+ 112x x e e =-+，有()()0f x f x -+=，所以()f x 是奇函数，函数()1112xf x e =-+，显然是减函数. 故选C.【点睛】本题主要考查了函数的奇偶性和单调性的判断，属于基础题.5.已知一个四棱锥的三视图如图所示，则该四棱锥侧面的4个三角形面积的最大值为（）A. 2B.C.D. 【答案】A 【解析】【分析】还原几何体得四棱锥P ABCD -，其中PA ^面ABCD ，分别计算各侧面的面积即可得解.【详解】还原三视图可得几何体如图所示，四棱锥P ABCD -，其中PA ^面ABCD ，11151,?2,222PADPABPCDSPA ADS PA AB S PDCD ======. PCB 中有PC BC PB =222BC PC PB +=，所以90PCB ??.所以132PCBSPC BC ==. 所以面积最大值是PAB D 的面积，等于2.【点睛】本题主要考查了由三视图还原几何体，并计算几何体的侧面积，需要一定的空间想象力，属于中档题.6.已知等比数列{}n a 的前n 项和为n S ，1352a a +=且2454a a +=，则55S a （）A. 256B. 255C. 16D. 31 【答案】D 【解析】【分析】由等比数列的通项公式，利用基本量运算可得通项公式，进而可得前n 项和，从而可得nnS a ，令5n =求解即可.【详解】由1352a a +=，可得21152a a q +=；由31154a q a q +=. 两式作比可得：可得12q =，12a =，所以212n n a -骣琪=琪桫，2142n n S -骣琪=-琪桫，21n n n S a =-，所以5552131Sa =-=.【点睛】本题主要考查了等比数列的通项公式及前n 项公式，属于公式运用的题目，属于基础题. 7.把函数()sin cos f x x x =-的图象上每个点的横坐标扩大到原来的2倍，再向左平移3p，得到函数()g x 的图象，则函数()g x 的一个单调递增区间为（） A. 175,66p p轾--犏犏臌 B. 57,66p p轾-犏犏臌 C. 24,33p p轾-犏犏臌 D. 719,66p p轾犏犏臌【答案】B 【解析】【分析】利用三角函数的图象变换可得函数()212x g x x p 骣琪-琪桫，再由22212x k p pp -?22k pp ?，k Z Î，可解得单调增区间，即可得解. 【详解】函数()sin cos f x x x =-=4x x p骣琪-琪桫的图象上每个点的横坐标扩大到原来的2倍，可得24x y x p 骣琪-琪桫的图象，再向左平移3p，得到函数()1234g x x p p 轾骣犏琪+-琪犏桫臌212x x p骣琪-琪桫的图象. 由22212x k p pp -?22k p p ?，k Z Î，得574466k xk p pp p -＃+，k Z Î. 当0k =时，函数()g x 的一个单调递增区间57,66p p轾-犏犏臌，故选B.【点睛】本题主要考查了三角函数的图象变换及三角函数的单调性，注意三角函数的平移变换，平移是针对自变量“x”而言的，所以需要将x 的系数提出，属于中档题.8.若实数x ，y 满足约束条件2027030x y x y y ì--?ïï+-?íï-?ïî，则1x z y +=的最小值为（）A.23 B. 1 C. 2 D. 145【解析】【分析】作出不等式的可行域，1x z y+=的几何意义是可行域内的点与点()1,0-连线的斜率的倒数，由斜率的最大值即可得解.【详解】作出不等式组构成的区域，1x z y+=的几何意义是可行域内的点与点()1,0D -连线的斜率的倒数，由图象知AD 的斜率最大，由2703x y y ì+-=ïí=ïî得13x y ì=ïí=ïî，所以()1,3A ，此时11233z +==. 故选A.【点睛】常见的非线性目标函数问题，利用其几何意义求解：z Ax By C =++的几何意义为可行域内的点到直线A 0x By C ++=()()22b z x a y =-+-的几何意义为可行域内的点到点()a,b 的距离的平方。

超级全能生2019高考全国卷26省12月联考乙卷文科数学

“超级全能生”2019高考全国卷26省12月联考乙卷数学（文科）一、选择题：1．已知集合M ＝{x|－1＜x ＜1），N ＝{x|2x 2－x －3≤0），则M∩N ＝（） A ．（－1，1）B ．13[,)22-C ．3[1,]2-D ．[－1，1）2．复数4421i z i -=-，则复数z 在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知椭圆22214x y b+=（b ＞0）的上、下顶点分别为A ，B ，左、右焦点分别为F 1，F 2，且四边形AF 1BF 2的面积为4，则该椭圆的离心率为（） A ．14BCD ．124．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的表面积为（）A ．24B ．48C ．88D ．1045．已知函数lg ,0,()8,0,x x f x x x >⎧=⎨+≤⎩若f （－5）＝3f （a ），则实数a 的值为（）A ．1B ．3C ．－7或－1D ．10或－76．图中大正方形是由四个全等的直角三角形的斜边组成，每个直角三角形的两条直角边的长分别为a ，b 且a ＝2b ，阴影部分是小正方形的内切圆，则在大正方形内任取一点，此点恰好取自阴影部分的概率为（）A ．13B ．20πD ．167．在递增的等差数列{a n }中，a 2，a 8是函数f （x ）＝x 2－4x －5的两个零点，则{a n }的前50项和等于（） A ．2450 B ．1125 C ．1225 D ．－24508．某校高三第一次模拟考试，从全校文科学生中随机抽取10名学生的数学成绩如茎叶图所示，现将每人的分数依次输入到如下程序框图中，则输出的S ＝（）A ．110.5B ．111C ．111.5D ．1129．已知角α的顶点与直角坐标系的原点重合，始边与x 轴的非负半轴重合，终边经过点77,9sin )66P ππ-，则22sin 12cos sin cos αααα=+-（）B ．12C ．3D ．610．某圆柱的体积、侧面积都为16π，则该圆柱的外接球的体积为（） A ．32π B． C．3D ．1282π11．对函数()333cos 33x xf x =+给出下列命题： ①f （x ）的图象向右平移2π个单位长度后所得的函数是非奇非偶函数；②f （x ）的图象关于点（π，0）中心对称； ③f （x ）的图象关于直线x ＝－2019π对称； ④f （x ）在[,]2π-π上单调递增．其中真命题的个数是（） A ．4 B ．3 C ．2 D ．1 12．已知函数21,1,()62,1,2a x x f x a xx x +⎧≥⎪=⎨--<⎪-⎩当x 1≠x 2时，1221()()0f x f x x x -<-，则函数g （a ）＝2a 2＋16a ＋3的值域是 A ．[－27，＋∞）B ．（－∞，35]C ．（2，5]D ．（27，35] 二、填空题：13．已知点A （2，－1），(1,3)AC =，32AB AC =，则点B 的坐标为________．14．已知x ，y满足约束条件2360,3260,220,x y x y x y -+≥⎧⎪+-≤⎨⎪+-≥⎩则z ＝x －3y 的最小值为________．15．双曲线x 2－y 2＝4的渐近线与圆C ：（x －3）2＋（y －2）2＝4交于A ，B 两点，则|AB|＝________．16．已知正项数列{a n }的前n 项和为S n ，（a n ＋1－2S n ）2＝4S n ＋1S n ，且a 1＝1，设13log n n b S =，则b 1＋b 2＋…＋b 20＝________．三、解答题：（一）必考题：17．△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若cos2A ＋sinBsinA ＝1，3C π=，且△ABC 的外接圆直径为33．（Ⅰ）求ab 的值；（Ⅱ）求△ABC 的面积．18．如图，四棱锥P —ABCD 的底面ABCD 的对角线互相垂直，且BC ＝CD ，PA ⊥平面ABCD ．（Ⅰ）求证：平面PAC⊥平面PBD；（Ⅱ）若BD＝CD＝4，PA＝6，M为PC上一点，且2PM＝MC，试求三棱锥C—BDM的体积．19．某羽毛球俱乐部规定，每天一人打球1小时收费30元（不足1小时部分按1小时收费，依此类推），注册成为会员，对会员一天连续打球2小时、3小时的优惠标准说明如下表：消费时间1小时2小时3小时收费比例 1 0.9 0.8该俱乐部从注册的会员中，随机抽取了40位进行统计，得到统计数据如下表：消费时间1小时2小时3小时频数20 12 8假设该俱乐部一人1小时活动的成本为5元，根据所给数据，解答下列问题：（Ⅰ）估计该俱乐部一位会员消费时间至少为2小时的概率；（Ⅱ）若某会员消费时间不超过3小时，以频率作为概率，估计该俱乐部每小时对该会员获取的平均利润；（Ⅲ）小明、小王、小张、小军四名会员周六一起去俱乐部打球，小王打了1小时有事离开了，小军打了2小时，小明、小张打了3小时，他们今天共应付给俱乐部多少费用？20．已知抛物线C：y2＝2px（p＞0）的焦点为F，准线与x轴交于A点，过点Fl 交C 的准线于B 点，ABF S =△ （Ⅰ）求C 的方程；（Ⅱ）已知C 上一点P （t ，4），过点P 作C 的两条弦PD 和PE ，且PD ⊥PE ，求直线DE 恒过的定点的坐标．21．已知函数f （x ）＝3a 2lnx －x 2－5ax （a ∈R ）．（Ⅰ）若x ＝1是f （x ）的极值点，求f （x ）在（1，f （1））处的切线方程；（Ⅱ）讨论f （x ）的单调性．（二）选考题：22．已知曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩（θ为参数）．（Ⅰ）求曲线C 1的普通方程；（Ⅱ）设P 是曲线C 1上的动点，M （－2，5），N （6，1），求|PM|2＋|PN|2的最大值．23．设函数f （x ）＝|2x ＋4|＋|x －a|（a ∈R ）．（Ⅰ）当12a =时，求不等式9()2f x <的解集；（Ⅱ）若1()|2|32f x x a >++-恒成立，求实数a 的取值范围．“超级全能生”2019高考全国卷26省12月联考乙卷数学（文科）答案123 4 5 6 7 8 9 10 11 12 A BCCDBBCAC D D13．8(,1)3 14．8413-1516．－38017．解：（Ⅰ）因为cos2A ＋sinBsinA ＝1，所以2sin 2A ＝sinBsinA ，因为sinA≠0，所以sinB ＝2sinA ，由正弦定理得b ＝2a ，所以12a b =．（Ⅱ）由（Ⅰ）知b ＝2a ，因为3C π=，三角形ABC 43所以由正弦定理得433sin 3c =π，所以c ＝2，由余弦定理得22222422cos 33a a a a a π=+-=，解得243a =，所以△ABC 的面积为2134323sin 233ABC S ab π====△． 18．解：（Ⅰ）证明：因为底面ABCD 的对角线互相垂直，所以BD ⊥AC ，又PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥PA ，因为PA∩AC ＝A ，所以BD ⊥平面PAC ，因为BD ⊂平面PBD ，所以平面PAC ⊥平面PBD ．（Ⅱ）因为PA ⊥平面ABCD ，PA ⊂平面PAC ，所以平面PAC ⊥平面BCD ，过点M 在平面PAC 上作MN ⊥AC 于N 点，所以MN ⊥平面BCD ，因为2PM ＝MC ，所以2PC ＝3CM ，由Rt △PAC ∽Rt △MNC ，所以2PA ＝3MN ，因为PA ＝6，所以MN ＝4，因为BC ＝BD ＝CD ＝4，所以144sin 60432BCD S =⨯⨯⨯︒=△，所以三棱锥C —BDM 的体积11634343C BDMM BCD V V --==⨯=． 19．解：（Ⅰ）在40名会员中，消费时间至少为2小时的会员有12＋8＝20（人），故概率201402P ==．（Ⅱ）该会员消费时间为1小时、2小时、3小时的概率分别为12，310，15，所以估计该俱乐部每小时对该会员获取的平均利润为131(305)(300.95)(300.85)22.9()2105⨯-+⨯⨯-+⨯⨯-=元．（Ⅲ）依题意，小王打了1小时应付30元；小军打了2小时，应付2×30×0.9＝54（元）；小明、小张打了3小时，应付3×30×0.8×2＝144（元）；所以他们今天共应付给俱乐部费用为30＋54＋144＝228（元）． 20．解：（Ⅰ）由题意知抛物线的焦点(,0)2pF ，所以直线l 的方程为2()2py x =-．则可得点B 的坐标为(,2)2p-，因为22ABF S =△ 所以12222p =p ＝2．所以抛物线C 的方程为y 2＝4x ．（Ⅱ）由（Ⅰ）可得点P （4，4），且直线DE 的斜率不为0，设直线DE 的方程为x ＝my ＋n ，联立24,,y x x my n ⎧=⎨=+⎩得y 2－4my －4n ＝0，则Δ＝16m 2＋16n ＞0． ① 设D （x 1，y 1），E （x 2，y 2），则由韦达定理知y 1＋y 2＝4m ，y 1y 2＝－4n ．因为PD ⊥PE ，所以1122(4,4)(4,4)PD PE x y x y =----=121212124()164()16x x x x y y y y -+++-++=2222121212124()164()164444y y y y y y y y -+++--+= 2212121212()()34()3216y y y y y y y y -++-++= 22161232160n m n m --+-=，即n 2－12n ＋32＝16m 2＋16m ，整理得（n －6）2＝4（2m ＋1）2，所以n －6＝±2（2m ＋1），即n ＝－4m ＋8或n ＝－4m ＋4（不合题意，舍去），所以直线DE 的方程为x ＝my ＋4m ＋8＝m （y ＋4）＋8．所以直线DE 恒过定点（8，－4）．21．解：（Ⅰ）因为f （x ）＝3a 2lnx －x 2－5ax ，所以2223253()25(0)a x ax a f x x a x x x--+'=--=>，因为x ＝1是f （x ）的极值点，所以3a 2－5a －2＝0，解得a ＝2或13a =-．当a ＝2时，f （1）＝－11，f′（1）＝0，所以f （x ）在（1，f （1））处的切线方程为y ＋11＝0．当13a =-时，2(1)3f =，f′（1）＝0，所以f （x ）在（1，f （1））处的切线方程为203y -=，即3y －2＝0．故f （x ）在（1，f （1））处的切线方程为y ＋11＝0或3y －2＝0．（Ⅱ）由（Ⅰ）知22253(3)(2)()(0)x ax a x a x a f x x x x--+-+-'==>，令f′（x ）＝0得x ＝－3a 或2ax =，①当a ＝0时，f′（x ）＜0，所以f （x ）的单调递减区间为（0，＋∞）； ②当a ＞0时，32a a -<，由()0,0f x x '>⎧⎨>⎩得02a x <<；由()0,0f x x '<⎧⎨>⎩得2a x >．所以f （x ）在(0,)2a 上单调递增，在(,)2a +∞上单调递减； ③当a ＜0时，33a a ->，由()0,0f x x '>⎧⎨>⎩得0＜x ＜－3a ；由()0,0f x x '<⎧⎨>⎩得x ＞－3a ．所以f （x ）在（0，－3a ）上单调递增，在（－3a ，＋∞）上单调递减．综上，当a ＝0时，f （x ）在（0，＋∞）上单调递减；当a ＞0时，f （x ）在(0,)2a 上单调递增，在(,)2a +∞上单调递减；当a ＜0时，f （x ）在（0，－3a ）上单调递增，在（－3a ，＋∞）上单调递减．22．解：（Ⅰ）因为曲线C 1的参数方程为4cos ,4sin x y θθ=⎧⎨=⎩（θ为参数），则曲线C 1的普通方程为x 2＋y 2＝16．（Ⅱ）设P （4cosθ，4sinθ）（θ为参数），又因为M （－2，5），N （6，1），所以222222||||(4cos 2)(4sin 5)(4cos 6)(4sin 1)PM PN θθθθ+=++-+-+- 9816(3sin 2cos )981613sin()θθθϕ=-+=-+（其中cos 13ϕ=）．因为－1≤sin （θ＋φ）≤1，所以|PM|2＋|PN|2的最大值为981613+．23．解：（Ⅰ）当12a =时，1()|24|||2f x x x =++-，所以73,2,291(),2,22713,.22x x f x x x x x ⎧--<-⎪⎪⎪=+-≤≤⎨⎪⎪+>⎪⎩ 由2,793,22x x <-⎧⎪⎨--<⎪⎩解得823x -<<-；由12,299,22x x ⎧-≤≤⎪⎪⎨⎪+<⎪⎩解得－2≤x ＜0；由1,2793,22x x ⎧>⎪⎪⎨⎪+<⎪⎩无解．综上所述，不等式9()2f x <的解集为8(,0)3-．（Ⅱ）因为f （x ）＝|2x ＋4|＋|x －a|，所以1()|2|32f x x a >++-恒成立等价于1|2|||32x x a a ++->-恒成立，因为|x ＋2|＋|x －a|≥|x ＋2＋a －x|＝|2＋a|，所以1|2|32a a +>-，解得a ＜－10或23a >，故实数a 的取值范围为2(,10)(,)3-∞-+∞．。

超级全能生2019高考全国卷26省2月联考乙卷理科综合

“超级全能生” 2019 高考全国卷26 省 2 月联考乙卷理科综合可能用到的相对原子质量：H-1 C-12 N-14 O-16 Na-23 Cu-64一、选择题（此题共13 小题，在每题给出的四个选项中，只有一项为哪一项切合题目要求的）1．细胞内某些化合物的元素构成为C、 H、 O、 N 、P，以下必定不属于这些化合物的功能的是（）A．可作为细胞中的直接能源物质B．可作为储藏遗传信息的物质C．参加构成生物膜的重要成分D．可作为细胞内优秀的储能物质2．如图为胰岛 B 细胞正在进行的某项生理过程，①～⑥为细胞的构造，以下表达错误的选项是（）A．胰岛素在①上合成，但合成和分泌过程离不开④的作用B．①和④中均可发生碱基互补配对现象，且配对原则同样C．胰岛 A 细胞中也有胰岛素基因，不过在该细胞中并未表达D．胰岛素以胞吐的方式排到⑥外，表现了生物膜的流动性3．如图为人在紧迫状况下的生命活动调理表示图，以下表达错误的选项是（）A．该过程是经过反射弧和体液运输两个门路来进行的4．以下对于生态系统的稳固性的表达，正确的选项是（）A．封山育林、合理间伐、科学浇灌等均能提升生态系统的稳固性B．同样扰乱强度下，草原生态系统比荒漠生态系统恢复的速率慢C．同一个生态系统，不会既有抵挡力稳固性，又有恢复力稳固性D．复杂度越低的生态系统，抵挡力稳固性越低，恢复力稳固性越高5．下边对于研究淀粉酶的最适温度的实验中表达正确的选项是（）A．可用斐林试剂检测复原糖的含量来反应酶的活性D．所有对于研究酶的最适温度的实验，pH 要都为 76．以下对于生物育种的表达，正确的选项是（）A．单倍体植株经过人工引诱使染色体数量加倍后都是纯合子B．低温办理单倍体幼苗的芽尖细胞，能够克制纺锤体的形成C．三倍体西瓜没有种子，只好每年制种才能获取三倍体植株D．在选择育种过程中，因基因型频次改变而使生物不停进化7．化学与生活、环境亲密有关，以下有关说法正确的选项是（）A ．我国在南海成功开采的可燃冰（CH 4 nH 2 O ）可能会带来酸雨等环境污染B．我国研制的超高强耐腐化性实验室用钢板的熔点高于纯铁的熔点C．我国研究的氢气低温制备和储存的方法本质上是物理变化D．我国全面启动的北斗导航系统的信号传输与二氧化硅有关8．柠檬醛是一种香料，既能够被氧化，也能够被复原。

2019年全国乙卷数学理科

2019年全国乙卷数学理科全文共四篇示例，供读者参考第一篇示例：2019年全国乙卷数学理科考试于6月7日举行，考试时间为120分钟，共150分。

本次数学理科试题涵盖了代数、几何、概率统计等多个知识点，考查了考生对数学知识的掌握和运用能力。

在代数部分，本次考试主要考查了一元二次方程、不等式、函数、数列等知识点。

一元二次方程是高中数学的基础内容，也是考生们比较熟悉的内容之一。

在考试中，考生需要掌握一元二次方程的求解方法，包括用公式法、配方法、因式分解等不同的解题方法。

还需要注意不等式的求解方法，掌握函数的性质和图像等内容。

几何部分是数学理科考试中的一个重点，涉及了平面几何和立体几何两个方面。

在平面几何部分，本次考试主要考查了相似三角形、射影关系、面积比等内容。

考生需要掌握相似三角形的性质，了解射影关系的基本概念，并能够运用这些知识解决相关问题。

在立体几何部分，本次考试主要涉及了空间几何体的体积、表面积等内容。

考生需要了解各种几何体的性质，掌握计算体积和表面积的方法，能够灵活运用几何知识解决实际问题。

除代数和几何外，本次数学理科考试还涉及了概率统计等内容。

在概率统计部分，考生需要了解基本概率、事件的独立性、随机变量等知识点。

在统计学部分，考生需要掌握频率分布、样本方差、相关系数等内容。

通过这些知识点的考查，可以考察考生在数据分析和推理能力方面的水平。

2019年全国乙卷数学理科考试难度适中，题型多样，考查面广。

考生需要在考前复习中重点关注代数和几何等基础知识，加强练习，提高解题能力。

要注意题目中的细节和条件，做题时要认真审题，仔细推理，避免粗心错误。

希望考生们能够在考试中取得理想的成绩，实现自己的考试目标。

祝愿所有参加考试的同学们成功！第二篇示例：2019年全国乙卷数学理科试卷是备受关注的考试，涵盖了高中数学知识的各个方面，考查了考生的数学综合运用能力。

本次考试难度适中，题型新颖，让考生在考场上展现自己的数学才能和解题能力。